1 r в физике: Электрическое сопротивление. Закон Ома для участка электрической цепи — урок. Физика, 8 класс.

Электрические схемы. Соединение проводников – Умскул Учебник

На этой странице вы узнаете

• Нужен ли блендер, чтобы попить чай?
• Куда идет ток?
• Когда “сопротивление бесполезно”?

Всем приготовиться к погружению в мир электрических соединений и схем. Сопротивление бесполезно! 

Условное обозначение элементов электрической цепи

Есть история о том, как одного физика-теоретика током ударило. Конечно, в теории он был силен, но знать — одно, а применять знания в жизни — совсем другое дело. Вот и получилось у него всякое, странное. Не советуем повторять: опасно для жизни!

А с чего вся история началась?

Когда мы говорим об электрических приборах, мы понимаем, что сам по себе прибор работать не будет. Его нужно подключить, к источнику тока. А если схема сложная, в которой несколько приборов? И как изобразить цепь на рисунке? Всеми этими вопросами задался наш герой.

Для решения умные люди придумали условные обозначения, которые уже много лет используются в электромире:

Итак, наш физик-теоретик решил по схеме собрать гирлянду. Всё как положено. Лампочки подобрал все одинаковые. И даже соединения между ними учел.

Соединения проводников

Проводники в электрических цепях могут соединяться последовательно и параллельно. Давайте разберем, чем отличаются эти два вида соединений и чем они полезны.

Последовательное соединение	Параллельное соединение
Соединение проводников без разветвлений, когда конец одного проводника соединен с началом другого.	Соединение, в котором начала и концы проводников соединены вместе.
R1 и R2 — сопротивления проводников, R— общее сопротивление,  I1 и I2— сила тока на каждом проводнике, I — общая сила тока,  U1 и U2 — напряжение на каждом проводнике,  U — общее напряжение цепи.	R1 и R2 — сопротивления проводников, R— общее сопротивление,  I1 и  I2— сила тока на каждом проводнике,  I — общая сила тока,  U1 и  U2 — напряжение на каждом проводнике,  U — общее напряжение цепи.
Схема последовательного соединения проводников.	Схема параллельного соединения проводников.
I1 = I2 = I Сила тока, протекающего через каждый проводник, одна и та же (I = const).	I = I1 + I2 Сила тока, протекающего в  неразветвлённой части цепи, равна сумме сил токов, протекающих по каждому из проводников.
U1 = IR1, U2 = IR2; U = U1 + U2 Общее напряжение равно сумме напряжений на отдельных участках цепи.	U1 = I1R1, U2 = I2R2; U = U1 = U2 Напряжение на каждом из проводников одинаково (U = const).
R = R1 + R2 Общее сопротивление цепи равно сумме сопротивлений отдельных участков.	\(\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}\) Проводимость равна сумме проводимостей каждого из проводников.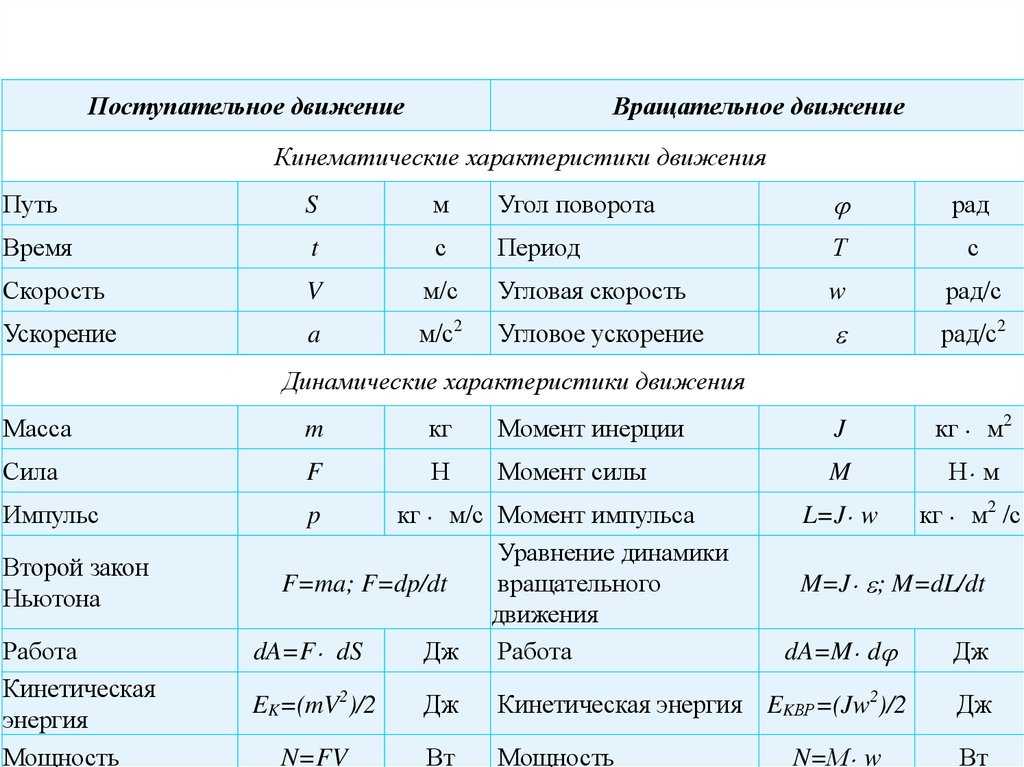
\(\frac{U_1}{U_2} = \frac{R_1}{R_2}\)	\(\frac{I_1}{I_2} = \frac{R_2}{R_1}\)
Если все сопротивления одинаковы, то: R = nr и U = nu, где r и u — соответственно сопротивление одного элемента и  напряжение на нём, n — количество одинаковых проводников в соединении.	Если все сопротивления одинаковы, то: \(R = \frac{r}{n}\) и U = u, где r и u — соответственно сопротивление одного элемента и  напряжение на нём, n — количество одинаковых проводников в соединении.
Общее сопротивление цепи больше наибольшего сопротивления, входящего в  эту цепь.	Общее сопротивление цепи меньше наименьшего сопротивления, входящего в  эту цепь.
Количество теплоты, выделяемое на каждом проводнике, пропорционально их сопротивлениям \(\frac{Q_1}{Q_2} = \frac{R_1}{R_2}\)	Количество теплоты, выделяемое на каждом проводнике, обратно пропорционально их сопротивлениям \(\frac{Q_1}{Q_2} = \frac{R_2}{R_1}\)
Мощность, выделяемая в проводниках, пропорциональна их сопротивлению \(\frac{P_1}{P_2} = \frac{R_1}{R_2}\)	Мощность, выделяемая в проводниках, обратно пропорциональна их сопротивлению \(\frac{P_1}{P_2} = \frac{R_2}{R_1}\)

При последовательном соединении проводников общее сопротивление участка цепи увеличивается, при параллельном соединении — уменьшается.

Важно учитывать, какие приборы, как подключать. Например, елочная гирлянда является примером последовательного соединения. Если одна лампочка перегорит, то вся гирлянда работать перестанет. Это, кстати, относится к недостаткам такого вида соединения. Наш физик-теоритк был в курсе этой особенности.

Тогда зачем такое соединение нужно?

Когда необходимо целенаправленно подключить какой-то один прибор. Например, карманный фонарик. Он будет работать только тогда, когда включена кнопка.

А вот в люстре лучше использовать параллельное соединение. И когда одна лампочка перегорит, все остальные по-прежнему будут светить.

Нужен ли блендер, чтобы попить чай? Бытовые приборы на кухне соединены параллельно. Это значит, что чайник может спокойно работать без микроволновки. И чтобы поджарить тосты, блендер включать необязательно. Но если все эти приборы соединить последовательно, защитный выключатель может не выдержать, и произойдет перегрузка. Что может привести к возгоранию. И не будет нам ни чая, ни взбитого теста для блинчиков, ни тостов.

Задачи на комбинированное соединение проводников удобно решать, используя эквивалентные схемы.

Смешанное (комбинированное) соединение проводников

Комбинированным называется соединение, при котором некоторые проводники соединены последовательно, а некоторые — параллельно.

Куда идет ток? Ток не любит напрягаться. Поэтому ток течёт по пути наименьшего сопротивления.

Рассмотрим пример задачи.

Вопрос: Каким будет сопротивление участка цепи (см. рисунок), если ключ К замкнуть? Каждый из резисторов имеет сопротивление 2R.

Ответ: если ключ К замкнуть, то сопротивление станет равным нулю.

Когда “Сопротивление бесполезно”? После замыкания ключа участок схемы окажется закороченным; ток пойдёт через ключ, минуя резисторы. Сопротивление участка станет равным нулю, как показано на рисунке:

Виды соединения источников тока

Что же произошло к нашим физиком-теоретиком? Он даже соединения источников учел. Только забыл он самое главное правило: сначала собери схему, а только потом подключи ее к источнику. 

Вот он подключил один конец провода с лампочками к источнику, другой конец взял в руку… И навсегда запомнил технику безопасности при работе c электричеством: не стоит человеку становиться звеном цепи, подключенной к источнику.

Источники тока соединяют между собой для совместного питания всей цепи. 

	Последовательное соединение	Параллельное соединение
Схема
Эквивалентное внутреннее сопротивление	rэ = r1 + r2	\(\frac{1}{r_э} = \frac{1}{r_1} + \frac{1}{r_2}\)
Эквивалентное ЭДС	\(\varepsilon_э = \pm \varepsilon_1 \pm \varepsilon_2\) знаки зависят от направления подключения источников	\(\frac{\varepsilon_э}{r_э} = \pm \frac{\varepsilon_1}{r_1} \pm \frac{\varepsilon_2}{r_2}\) знаки зависят от направления подключения источников
Закон Ома для полной цепи	\(I = \frac{\varepsilon_э}{r_э + R}\)	\(I = \frac{\varepsilon_э}{r_э + R}\)
Закон Ома для n одинаковых источников	\(I = \frac{n \varepsilon}{R + nr}\)	\(I = \frac{\varepsilon}{R + rn}\)

Чем отличаются понятия “соединения резисторов” и “соединения источников тока”? Пример резистора — чайник, простой проводник электрического тока. Если чайник подключить параллельно, это никак не повлияет на работу всей цепи. А источник тока — это розетка. Она дает “питание” всей цепи. Без источника тока не будет работать ни один прибор.

Правила подключения амперметра и вольтметра

Важно запомнить правила подключения амперметра и вольтметра. Это необходимо для того, что приборы не перегорели и показывали корректные значения при измерении.

Амперметр	Вольтметр
Амперметр подключается последовательно участку цепи. Соблюдаем полярность: “+” амперметра подключают к “+” источника тока, а “−” подключают к “−” источника тока.	Вольтметр подключается параллельно участку цепи. Соблюдаем полярность: “+” вольтметра подключают к “+” источника тока, а “−” подключают к “−” источника тока.
Шунт  — проводник, присоединяемый параллельно амперметру для увеличения предела его измерений.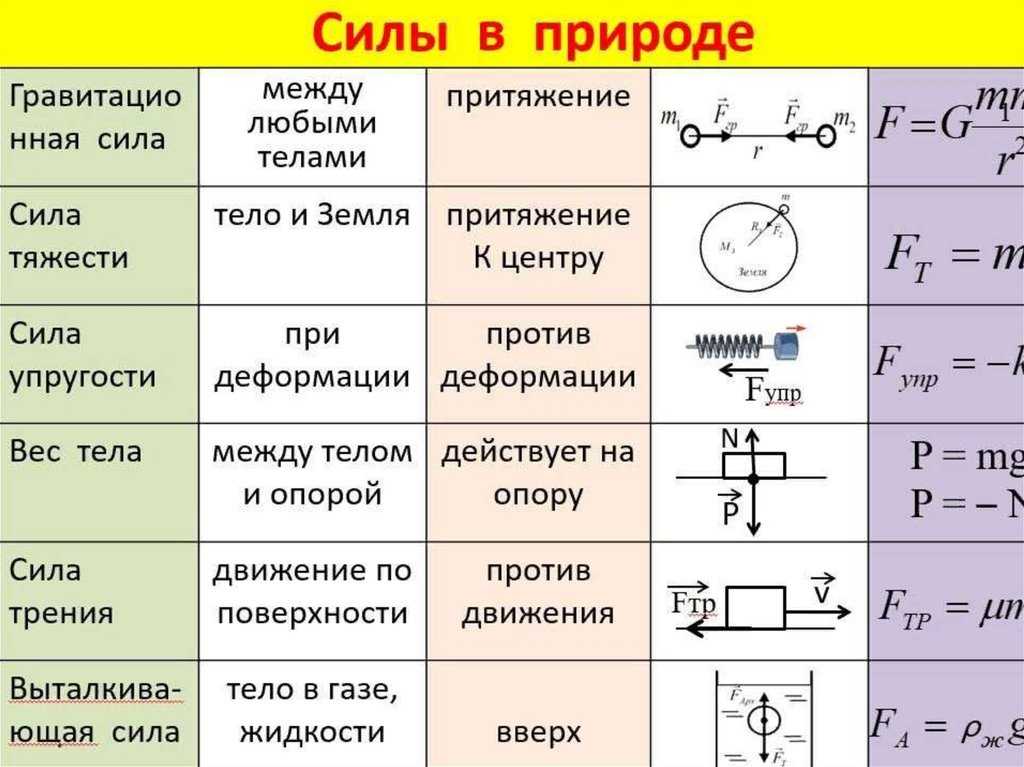 \(R_ш = \frac{R_A}{n — 1}\), где Rш  — сопротивление шунта, RA  — сопротивление амперметра,  n  — число, показывающее, во сколько раз увеличивается предел измерений прибора.	Добавочное сопротивление  — проводник, присоединяемый последовательно с  вольтметром для увеличения предела его измерений. Rд = RV(n-1), где Rд  — добавочное сопротивление, RV  — сопротивление вольтметра,  n  — число, показывающее, во сколько раз увеличивается предел измерений прибора.

Научиться читать электрические схемы важно для любителей электроники. Ведь если правильно ее прочитать, можно спаять что-то интересное, например, карманный фонарик.

Фактчек

• Проводники в электрических цепях могут соединяться последовательно и параллельно.
• При последовательном соединении проводников общее сопротивление участка цепи увеличивается, при параллельном соединении — уменьшается.
• Комбинированным называется соединение, при котором некоторые проводники соединены последовательно, а некоторые — параллельно.
• При подключении приборов обязательно нужно учитывать их полярность.

Проверь себя

Задание 1.
Какие существуют соединения проводников?

1. Последовательное
2. Параллельное
3. Смешанное
4. Все варианты верны

Задание 2.
При последовательном соединении проводников общее сопротивление участка цепи:

1. Увеличивается
2. Уменьшается
3. Не изменяется

Задание 3.
При параллельном соединении проводников общее сопротивление участка цепи:

1. Увеличивается
2. Уменьшается
3. Не изменяется

Задание 4.
Как подключается амперметр в цепи?

1. Последовательно
2. Параллельно
3. Не имеет значения

Задание 5.
Как подключается вольтметр в цепи?

1. Последовательно
2. Параллельно
3. Не имеет значения

Ответы: 1. — 4; 2. — 1; 3. — 2; 4. — 1; 5. — 2

Открытая Физика. Работа и мощность тока

Работа и мощность тока

При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном учестке совершает работу ΔA = (φ₁ – φ₂) Δq = Δφ₁₂ I Δt = U I Δt, где U = Δφ₁₂ – напряжение. Эту работу называют работой электрического тока.

Если обе части формулы RI = U, выражающей закон Ома для однородного участка цепи с сопротивлением R, умножить на IΔt, то получится соотношение R I² Δt = U I Δt = ΔA.

Это соотношение выражает закон сохранения энергии для однородного участка цепи.

Работа ΔA

электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике. ΔQ = ΔA = R I² Δt.

Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца.

Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена: P=ΔAΔt=UI=I2R=U2R.

Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).

Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой ℰ и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. Закон Ома для полной цепи записывается в виде (R + r) I = ℰ.

Умножив обе части этой формулы на Δq = IΔt, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока: R I²Δt + r I²Δt = ℰ IΔt = ΔA_ст.

Первый член в левой части ΔQ = R I²Δt – тепло, выделяющееся на внешнем участке цепи за время Δt, второй член ΔQ_ист = r I²Δt – тепло, выделяющееся внутри источника за то же время.

Выражение ℰ IΔt равно работе сторонних сил ΔA_ст, действующих внутри источника.

При протекании электрического тока по замкнутой цепи работа сторонних сил ΔA_ст преобразуется в тепло, выделяющееся во внешней цепи (ΔQ) и внутри источника (ΔQ_ист). ΔQ

 + ΔQ_ист = ΔA_ст = ℰ IΔt .

Следует обратить внимание, что в это соотношение не входит работа электрического поля. При протекании тока по замкнутой цепи электрическое поле работы не совершает; поэтому тепло производится одними только сторонними силами, действующими внутри источника. Роль электрического поля сводится к перераспределению тепла между различными участками цепи.

Внешняя цепь может представлять собой не только проводник с сопротивлением R, но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под R нужно понимать эквивалентное сопротивление нагрузки. Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, но и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем. Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение.

Полная мощность источника, то есть работа, совершаемая сторонними силами за единицу времени, равна Pист=ℰI=ℰ2R+r. Во внешней цепи выделяется мощность P=RI2=ℰI-rI2=ℰ2R(R+r)2. Отношение η=PPист, равное η=PPист=1-rℰI=RR+r, называется коэффициентом полезного действия источника.

На рис. 1.11.1 графически представлены зависимости мощности источника P_ист, полезной мощности P, выделяемой во внешней цепи, и коэффициента полезного действия η от тока в цепи I для источника с ЭДС, равной ℰ, и внутренним сопротивлением r. Ток в цепи может изменяться в пределах от I = 0 (при R=∞) до I=Iкз=ℰr (при R = 0).

Зависимость мощности источника P_ист , мощности во внешней цепи P и КПД источника η от силы тока

Из приведенных графиков видно, что максимальная мощность во внешней цепи P_max, равная Pmax=ℰ24r, достигается при R = r. При этом ток в цепи Imax=12Iкз=ℰ2r, а КПД источника равен 50 %. Максимальное значение КПД источника достигается при I → 0, т.  е. при R → ∞. В случае короткого замыкания полезная мощность P = 0 и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. КПД источника при этом обращается в нуль.





седло на тягач на сайте

sedlo-tyagacha.ru

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.

А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ “Облако знаний”.

Закон Ома: сопротивление и простые цепи

Цели обучения

К концу этого раздела вы сможете:

• Объяснить происхождение закона Ома.
• Расчет напряжения, тока или сопротивления по закону Ома.
• Объясните, что такое омический материал.
• Опишите простую схему.

Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, он создает разность потенциалов V , создающий электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.

Закон Ома

Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В . Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :

[латекс]I\propto{V}\\[/latex ].

Это важное соотношение известно как закон Ома . Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием.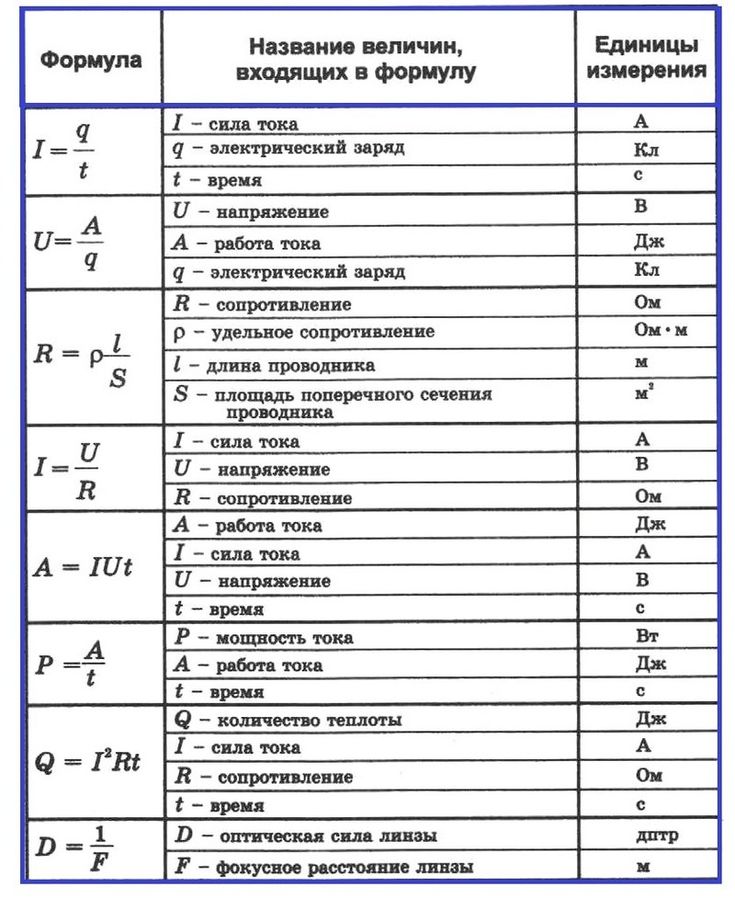 Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место.

Сопротивление и простые схемы

Если напряжение управляет током, что этому препятствует? Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется 9.0017 сопротивление R . Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или

[латекс]I\propto \frac{1}{R}\\[/латекс].

Так, например, ток уменьшается вдвое, если сопротивление удваивается. Сочетание отношений тока к напряжению и тока к сопротивлению дает

[латекс]I=\frac{V}{R}\\[/латекс].

Это соотношение также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омический . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление Ом , которое не зависит от напряжения В и тока I . Объект, имеющий простое сопротивление, называется резистором , даже если его сопротивление невелико. Единицей измерения сопротивления является Ом и обозначается символом Ω (греческая омега в верхнем регистре). Перестановка I = V/R дает R = V/I , поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:

[латекс]1 \Omega=1\frac{V}{A}\\[ /латекс].

На рис. 1 показана схема простой цепи. Простая схема имеет один источник напряжения и один резистор. Провода, соединяющие источник напряжения с резистором, можно считать имеющими пренебрежимо малое сопротивление, или их сопротивление можно включить в R .

Рисунок 1. Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.

Пример 1. Расчет сопротивления: автомобильная фара

Каково сопротивление автомобильной фары, через которую протекает ток 2,50 А при подаче на нее напряжения 12,0 В?

Стратегия

Мы можем преобразовать закон Ома в соответствии с формулой I = V/R и использовать его для нахождения сопротивления.

Решение

Перестановка I = V/R и подстановка известных значений дает

[латекс]R=\frac{V}{I}=\frac{\text{12}\text{.}\ text{0 V}}{2\text{.}\text{50 A}}=\text{4}\text{.}\text{80 \Omega }\\[/latex].

Обсуждение

Это относительно небольшое сопротивление, но оно больше морозостойкости фары. Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампочка имеет более низкое сопротивление при первом включении и будет потреблять значительно больший ток в течение короткого периода прогрева.

Диапазон сопротивлений превышает многие порядки. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 ¹²  Ом или больше. У сухого человека сопротивление руки к ноге может составлять 10 ⁵ Ом, тогда как сопротивление человеческого сердца составляет около 10 ³ Ом. Метровый отрезок медного провода большого диаметра может иметь сопротивление 10 ⁻⁵ Ом, а сверхпроводники вообще не имеют сопротивления (они неомические). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделе «Сопротивление и удельное сопротивление». Дополнительную информацию можно получить, решив  I = V/R  для В , что дает

В = IR

Это выражение для В можно интерпретировать как падение напряжения на резисторе, создаваемое протеканием тока I . Для этого напряжения часто используется фраза IR drop . Например, фара в Примере 1 выше имеет падение IR  12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой цепи (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку PE = q Δ V , и через каждый протекает тот же самый q . Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. рис. 2.)

Рис. 2. Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.

Соединения: сохранение энергии

В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.

Исследования PhET: Закон Ома

Посмотрите, как формула закона Ома соотносится с простой цепью. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.

Нажмите, чтобы запустить симуляцию.

Резюме раздела

• Простая цепь — это цепь, в которой есть один источник напряжения и одно сопротивление.
• Одно из утверждений закона Ома дает отношение между током I , напряжением В и сопротивлением R  в простой цепи [латекс]I=\frac{V}{R}\\[/latex] .
• Сопротивление выражается в омах (Ом) и относится к вольтам и амперам как 1 Ом = 1 В/А.
• Падение напряжения или IR  на резисторе, вызванное протеканием через него тока, определяется как В = IR .

Концептуальные вопросы

1. Падение IR на резисторе означает, что на резисторе произошло изменение потенциала или напряжения. Изменяется ли ток при прохождении через резистор? Объяснять.
2. Чем падение IR на резисторе похоже на падение давления в жидкости, протекающей по трубе?

Задачи и упражнения

1. Какой ток протекает через лампу фонарика на 3,00 В, если ее сопротивление в горячем состоянии равно 3,60 Ом?

2. Рассчитайте эффективное сопротивление карманного калькулятора с батареей на 1,35 В, через который протекает ток 0,200 мА.

3. Каково эффективное сопротивление стартера автомобиля, когда через него протекает ток 150 А, когда автомобильный аккумулятор подает на двигатель напряжение 11,0 В?

4. Какое напряжение подается на световой индикатор DVD-плеера с сопротивлением 140 Ом, если через него проходит ток 25,0 мА?

5. а) Найдите падение напряжения в удлинителе с сопротивлением 0,0600 Ом, по которому протекает ток 5,00 А. (b) Более дешевый шнур использует более тонкую проволоку и имеет сопротивление 0,300 Ом. Каково падение напряжения в нем при протекании 5,00 А? в) Почему напряжение любого используемого электроприбора уменьшается на эту величину? Каково влияние на прибор?

6. Линия электропередачи подвешена к металлическим опорам со стеклянными изоляторами сопротивлением 1,00×10

9 Ом. Какой ток протекает через изолятор, если напряжение равно 200 кВ? (Некоторые высоковольтные линии постоянного тока.)

Глоссарий

Закон Ома:

эмпирическое соотношение, утверждающее, что ток I пропорционален разности потенциалов В , ∝ В ; его часто записывают как I = V/R , где R это сопротивление

сопротивление:

электрическое свойство, препятствующее току; для омических материалов это отношение напряжения к току, R = V/I

Ом:

единица сопротивления, определяемая как 1 Ом = 1 В/А

омический:

тип материала, для которого действует закон Ома

простая схема:

схема с одним источником напряжения и одним резистором

Избранные решения задач и упражнений

1. 0,833 А

3. 7,33 × 10 ⁻² Ом

5. (а) 0,300 В

5

4

(б) (c) Подаваемое напряжение независимо от того, какой прибор используется, уменьшается, потому что общее падение напряжения от стены до конечного выхода устройства является фиксированным. Таким образом, если падение напряжения на удлинителе велико, падение напряжения на устройстве значительно уменьшается, поэтому выходная мощность устройства может быть значительно снижена, что снижает способность устройства работать должным образом.

Схема – Схемы – Физика 106

Схема — схемы Электрические цепи. Определение терминов Электрический ток I равен скорости протекания тока. Для постоянного тока I = q/t. Для переменного тока I = dq/dt. На рис. 1 выше электрон движется в проводнике с эквивалент постоянной скорости дрейфа v d в постоянное электрическое поле E. В действительности электрон испытывает серия ускорений в электрическом поле после столкновений с ядрами и внутренними электронами атомов, составляющих материал. Пусть n = число электронов/объем, e заряд электрона, A площадь поперечного сечения проводника, а L его длина = v д т, где t — время, за которое электрон проходит длину проводника. Тогда суммарный заряд в движении равен q = neAv d t а ток I = q/t = neAv d . Пример проблемы в 106 Набор задач для цепей : 1. Сопротивления Сопротивление R проводника прямо пропорционально к его длине L, обратно пропорционально его поперечному сечению области A и зависит от сопротивления материала r. R = rL/А. Закон Ома. Разность потенциалов V ab через сопротивление R от a до b с током I от a до b определяется законом Ома, эмпирическим законом, В аб = ИК. Комбинации резисторов Резисторы в серии Ток I одинаков в каждом резисторе Разность потенциалов на всех резисторах равна сумме индивидуальных разностей потенциалов: В аб = В ac + В кд + В дб R eq = V ab / I = V ac / I + V cd /I + V db /I = R 1 + R 2 + R 3 (рис. 2а ниже) Резисторы параллельно Разность потенциалов В аб параллельно все резисторы одинаковые. Общий ток I равен сумме токов в каждом из резисторов:   I = I 1 + Я 2 + Я 3 I/V ab = I 1 /V ab + I 2 /V аб + I 3 /V аб 1/R экв. = 1/R 1 + 1/R 2 + 1/R 3  (рис. 2b ниже) Примеры проблем в 106 Набор задач для цепей : 2, 3, 7. Мощность Мощность = P = (U a – U b )/t = q(V a – V b )/t = (q/t)(V a – V b ) = IV ab Приведенное выше утверждение всегда верно. Если элемент цепи между a и b является омическим резистор, для которого В аб = IR, тогда P = I(V аб ) может можно записать как P = I(IR) = I 2 R   или P = (I)V ab  можно записать как P = (V ab /R)V ab = (V аб ) 2 /R. Пример проблемы в 106 Набор задач для схем : 4. Электродвижущая сила e Электродвижущая сила e = энергия/заряд = U/q   или qe = U и мощность = P = U/t = (q/t)e = Ie. Для схемы, показанной на рис. 3 выше, r — внутреннее сопротивление. аккумулятора. Для этой цепи: Входная мощность = Выходная мощность Химическая энергия в электрическую = электрическая мощность в тепло Тэ = Я 2 Р + I 2 r         (уравнение 1) Из уравнения. 1, I = e/(R + r) е – Ир = ИК = В аб Напряжение на клеммах батареи В ab = е-Ир Примеры проблем в 106 Проблема Набор для цепей : 5, 8. Правила Кирхгофа Правило соединения. Сумма токов, входящих в любой переход равна сумме токов, выходящих из этого соединения. Этот это просто утверждение о сохранении заряда. Правило цикла. Сумма разностей потенциалов по каждому элемент вокруг любой замкнутой цепи равен нулю. Это просто заявление о сохранении энергии. Если перейти от минуса к плюсу аккумулятора, химическая энергия превращается в электрическую и вы собираете энергию, поэтому знак плюс. Если перейти от плюса батареи к минусу знак, знак отрицательный. Если обойти петлю в том же направлении, что и ток, электрическая энергия превращается в тепло, и вы теряете энергию поэтому этот IR отрицателен. Если пройти по петле напротив к направлению течения, вы идете от более низкий потенциал к более высокому потенциалу, поэтому этот IR положительный. Общий комментарий. Как только вы выбираете направления токов, и обходя петлю по часовой стрелке или против часовой стрелки, оставайтесь с ним. Вы можете изменить направление движения вокруг петли для второй петли, но не меняйте направления течений. Пример проблемы в 106 Набор задач для схем: 9. RC-цепи Разность потенциалов на омическом резисторе = IR и на конденсаторе = q/C Когда переключатель S переведен в положение зарядки Используя правило цикла, находим е = ИК + к/с. Поскольку I = dq/dt, мы можем записать это как е = dq/dt R + q/C             (Уравнение 2) Арифметика дает нам (dq/dt)RC = -(q – eC)          (Уравнение 3) Разделение переменных: dq/(q – EC) = -1/RC dt              (уравнение 4) Интеграция с обеих сторон: или ln [(q-eC)/-eC} = -t/RC              (Уравнение 5) Взяв антилогарифм обеих частей уравнения. 5: (q-eC)/-eC = e -t/RC q – eC = -eC(e -т/RC ) или наконец, q(t) = eC(1 – e -t/RC ) (Уравнение 6) Разность потенциалов на конденсаторе для зарядки конденсатор V cb иногда называют В С = q/C = e(1 – e -t/RC  ). (Уравнение 7) Текущий I = dq/dt = e/R( е -т/RC  ) (Уравнение 8) Разность потенциалов на резисторе для зарядки конденсатор В ac  иногда называется В Р = ИК = е( e -t/RC  )               (Уравнение 9) Для рисунков 4 (вверху) и 5 ​​(внизу) я выбрал e = 1,0 В, R = 10 6 Вт = 10 6 В/А, и C = 5 x 10 -6 F = 5 х 10 -6 К/В. Постоянная времени = RC =10 6 В/А x 5 x 10 -6 C/В = 5 C/А = 5 Кл/(Кл/с) = 5 с. Для накопления заряда,  В C (t) = e(1 – e -t/RC ). Когда t = RC = 5 с, В C (RC) = 1,0 В (1 – e -RC/RC ) = 1,0 V(1 – e -1 ) = 1,0 В(0,632) = 0,632 В, как показано ниже. Для накопления заряда  V R (t) = ee -t/RC . Когда t = RC = 5 с, В C (RC) = 1,0 В (e -RC/RC ) = 1,0 V(e -1 ) = 1,0 В (0,368) = 0,368 В, как показано выше. Когда переключатель опущен, батарея больше не в цепи и конденсатор разряжается. В аб = 0 = IR + q/C = dq/dt R + q/C              (Уравнение 10) Преобразование уравнения: dq/q = -dt/RC Пределы теперь от максимального заряда Q = eC к q, когда t изменяется от 0 до t. Конденсатор разряжается а я в противоположном направлении. ln q/eC = – t/RC или q(t) = Qe -t/RC = eCe -t/RC                   (Уравнение 11) I(t) = dq/dt = -(eC/RC)e -t/RC = – (e/R)e -t/RC V cb = V C = q/C = ee -t/RC и    V ac = ИК = -ee -т/RC Ссылаясь на рис. 5b ниже, Для распада заряда, В C (t) = e е -т/RC . Когда t = RC = 5 с, В C (RC) = 1,0 В (e -RC/RC ) = 1,0 В ( e -1 ) = 1,0 В (0,368) = 0,368 В. Больше новостей Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт