Урок 8.3 – Логические элементы
8.3. Логические элементы
Все, абсолютно все электронные компоненты, обрабатывающие цифровые сигналы, состоят из небольшого набора одинаковых «кирпичиков». В микросхемах малой степени интеграции могут быть единицы и десятки таких элементов, а в современных процессорах их может быть очень и очень много. Они называются логические элементы. Логическим элементом называется электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными. Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления.
Тем не менее, принцип работы цифровой логики остается неизменным – на входе логического элемента (входов может быть несколько) должен быть цифровой сигнал (сигналы, если входов несколько), который однозначно определяет сигнал на выходе логического элемента.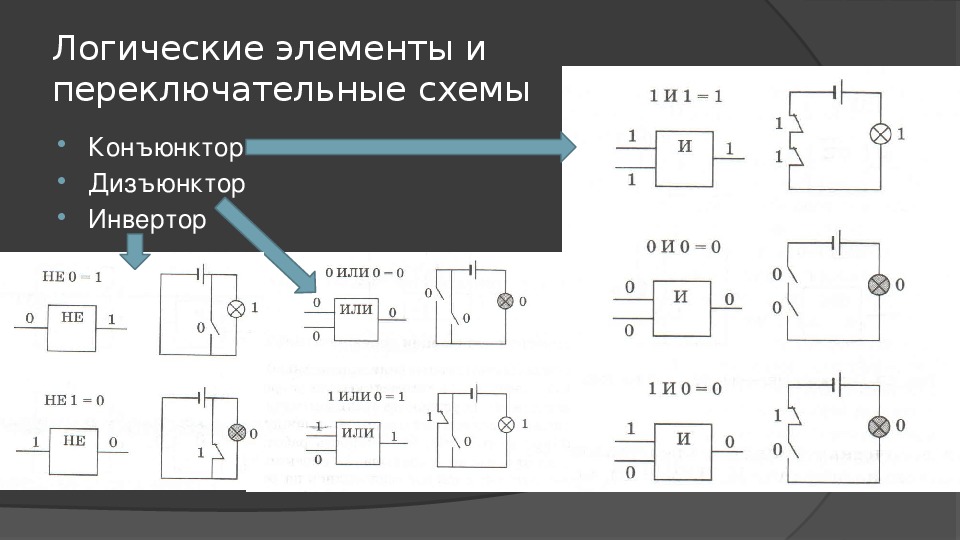
Конечно, логические элементы строятся, в свою очередь, из уже рассмотренных в предыдущих уроках резисторов, транзисторов и других электронных компонентов, но с точки зрения разработки цифровых схем именно логический элемент является их «элементарной» частицей.
При анализе работы логических элементов используется так называемая булева алгебра . Начала этого раздела математики было изложено в работах Джорджа Буля – английского математика и логика 19-го века, одного из основателей математической логики. Основами булевой алгебры являются высказывания, логические операции, а также функции и законы. Для понимания принципов работы логических элементов нет необходимости изучать все тонкости булевой алгебры, мы освоим ее основы в процессе обучения с помощью таблиц истинности.
Еще несколько замечаний. Логические элементы (как, впрочем, и другие элементы электронных схем) принято обозначать так, чтобы входы были слева, а выходы справа. Число входов может быть, вообще говоря, любым, отличным от нуля.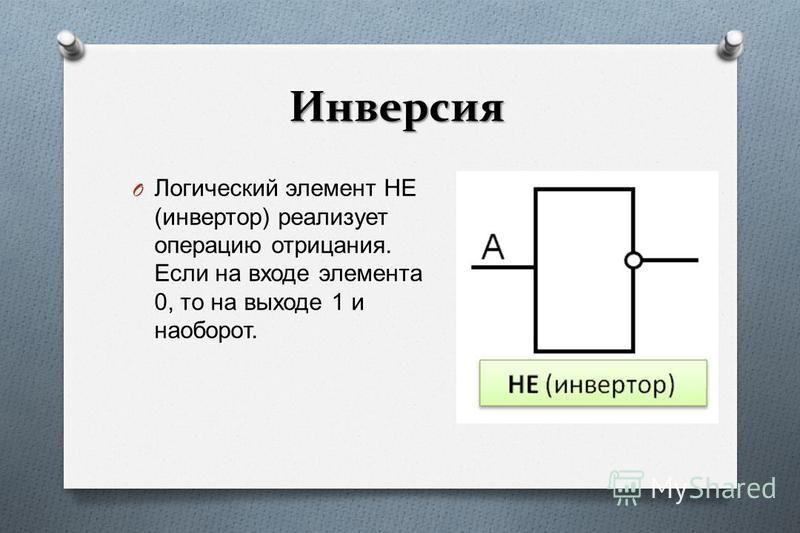
Реальные цифровые микросхемы могут иметь до 8 входов, но мы ограничимся двумя – этого достаточно для понимания. Условные обозначения соответствуют отечественному ГОСТу, в других стандартах они могут быть иными.
Какие же бывают логические элементы?
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
Элемент «И» (AND), он же конъюнктор, выполняет операцию логического умножения:
Условное обозначение – Таблица истинности
Здесь изображен логический элемент «2И» (цифра перед буквой «И» означает число входов). Знак & (амперсант) в левом верхнем углу прямоугольника указывает, что это логический элемент «И».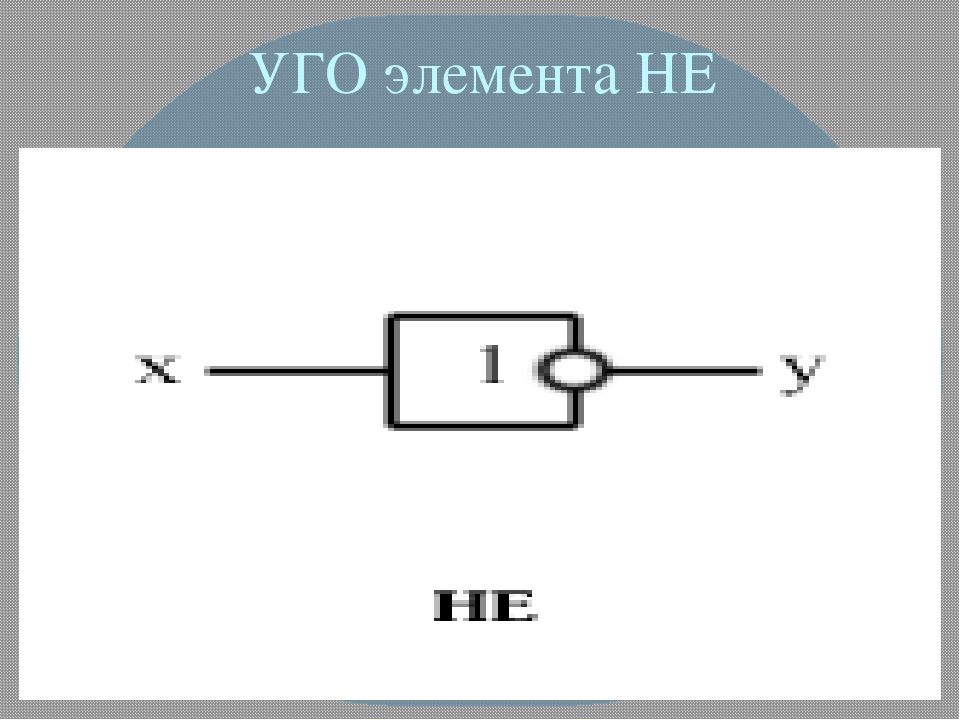
Первые две буквы обозначения DD1.2 указывают на то, что это цифровая микросхема (Digital), цифра слева от точки указывает номер микросхемы на принципиальной схеме, а цифра справа от точки – номер логического элемента в составе данной микросхемы. Одна микросхема может содержать несколько логических элементов.
Состояние входов в таблице обозначаются «0» и «1» («ложь» и «истина»). Из таблицы видно, что выход «Y» будет иметь состояние «1» только в том случае, когда на обоих входах «Х1» и «Х2» будут «1». Это легко запомнить: умножение на «0» всегда дает «0».
Элемент «ИЛИ» (OR), он же дизъюнктор, выполняет операцию логического сложения:
Условное обозначение – Таблица истинности
Состояние «1» на выходе будет всегда, пока есть хотя бы одна «1» на входах.
Элемент «НЕ» (NOT), он же инвертор, выполняет операцию логического отрицания:
Условное обозначение – Таблица истинности
Состояние на входе обратно состоянию на входе.
Вот из этих трех элементов строятся все цифровые устройства!
Рассмотрим еще три логических элемента, которые можно получить, комбинируя уже рассмотренные. В силу исторически сложившихся схемотехнических решений эти скомбинированные схемы тоже считаются логическими элементами.
Элемент «И-НЕ» (NAND), конъюнктор с отрицанием:
Условное обозначение – Таблица истинности
Элемент И-НЕ работает точно так же как «И», только выходной сигнал противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» будет единица. И наоборот.
Элемент «ИЛИ-НЕ» (NOR), дизъюнктор с отрицанием:
Условное обозначение – Таблица истинности
Элемент работает так же как и «ИЛИ», но с инверсией выхода.
Элемент «Исключающее ИЛИ» (XOR), сумматор по модулю 2:
Условное обозначение – Таблица истинности
В этом элемента «1» на выходе будет только тогда, когда на входах разные состояния.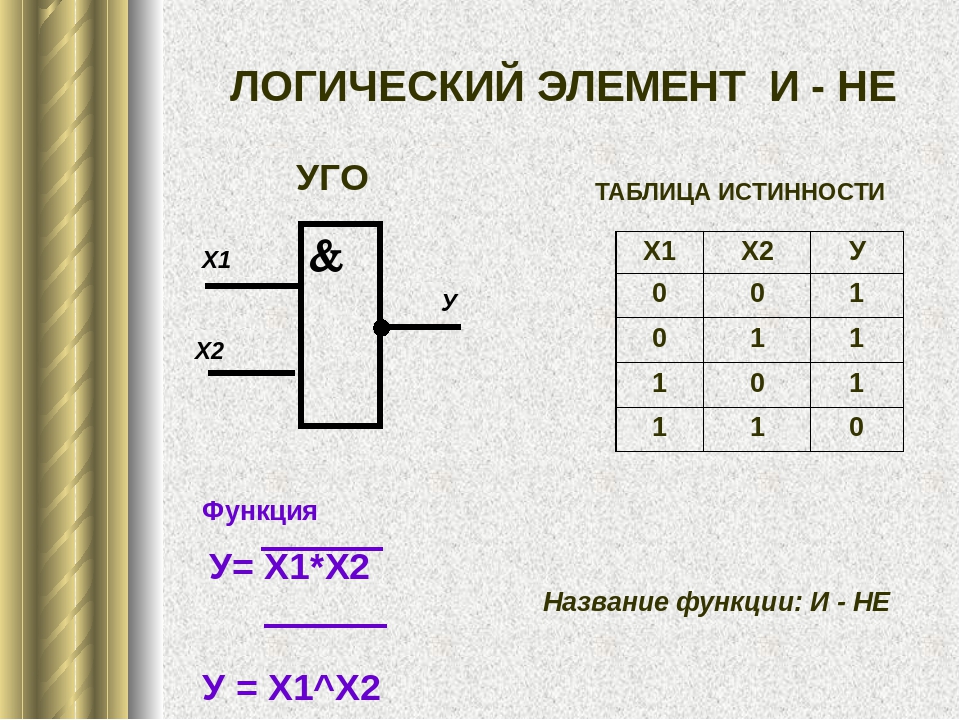
На таких элементах строят сумматоры двоичных многоразрядных чисел. Для этого используется еще один дополнительный выход, на котором при появлении на входах двух «1» появляется сигнал переноса разряда.
Мы рассмотрели логические элементы, которые применяются в цифровой технике для построения логических схем любого уровня сложности, но рассмотренные нами элементы не могут делать одну крайне важную работу – они не умеют хранить информацию. Для хранения используется более сложный класс устройств, называемый элементами с памятью или конечными автоматами. В этот класс входят триггеры, регистры, счетчики, шифраторы (дешифраторы), мультиплексоры (демультиплексоры) и сумматоры. Некоторый из этих устройств мы рассмотрим в следующем уроке.
Логические элементы
Мы с вами знаем следующие
логические операции: конъюнкция (логическое умножение), дизъюнкция (логическое
сложение) и инверсия (отрицание). Все эти операции используются в алгебре
логики.
Сегодня на уроке мы с вами узнаем, что такое логический элемент, познакомимся с такими логическими элементами, как конъюнктор, дизъюнктор и инвертор. А также научимся находить выходные данные исходя из предоставленной электронной схемы.
Алгебра логики является незаменимым элементом в конструировании автоматических устройств, разработке аппаратных и программных средств информационных и коммуникационных технологий.
Мы с вами уже знаем, что любую информацию можно представить в дискретной форме. Дискретная форма – это форма представления, при которой информация преподнесена в виде фиксированного набора отдельных значений. То есть, например, последовательностью нулей и единиц. В свою очередь,
В свою очередь, логический
элемент – это дискретный преобразователь, который выдаёт после обработки
двоичных сигналов значение одной из логических операций.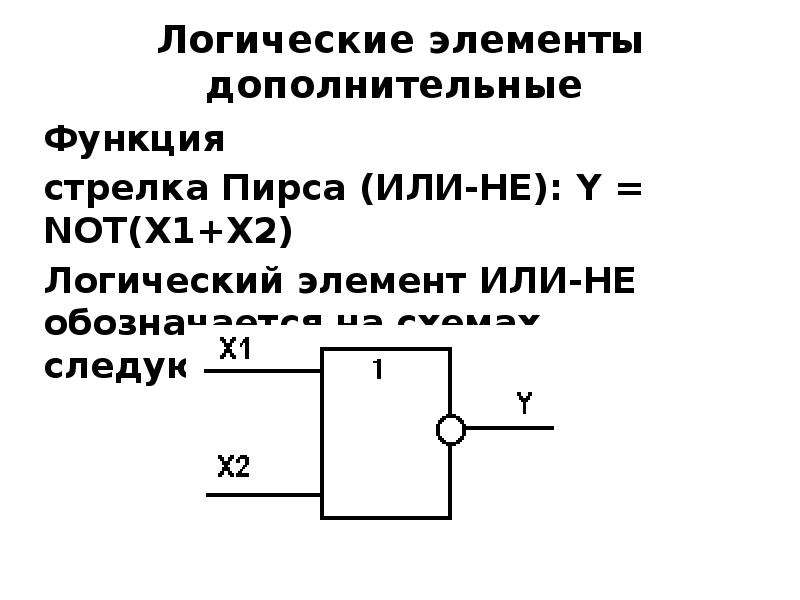
Перед вами представлены условные обозначения (схемы) логических элементов, с помощью которых реализуется логическое умножение, логическое сложение и отрицание. Давайте разберёмся с каждой схемой отдельно.
Итак, первый логический элемент И (конъюнктор). С его помощью реализуется операция логического умножения. Рассмотрим его.
А – это входные данные первого элемента, B – второго, F – выходные данные. Вспомним таблицу истинности для конъюнкции.
Всевозможные входные данные А и B нам даны в первых двух столбцах. В третьем нам дан результат при выполнении конъюнкции – выходные данные. То есть значение F. Таким образом, можно сказать, что единица на выходе получится тогда и только тогда, когда на всех входах будут единицы. Или же, другими словами, в результате мы можем получить для F единицу тогда и только тогда, когда А и B равны единице.
Следующий логический
элемент – ИЛИ (дизъюнктор).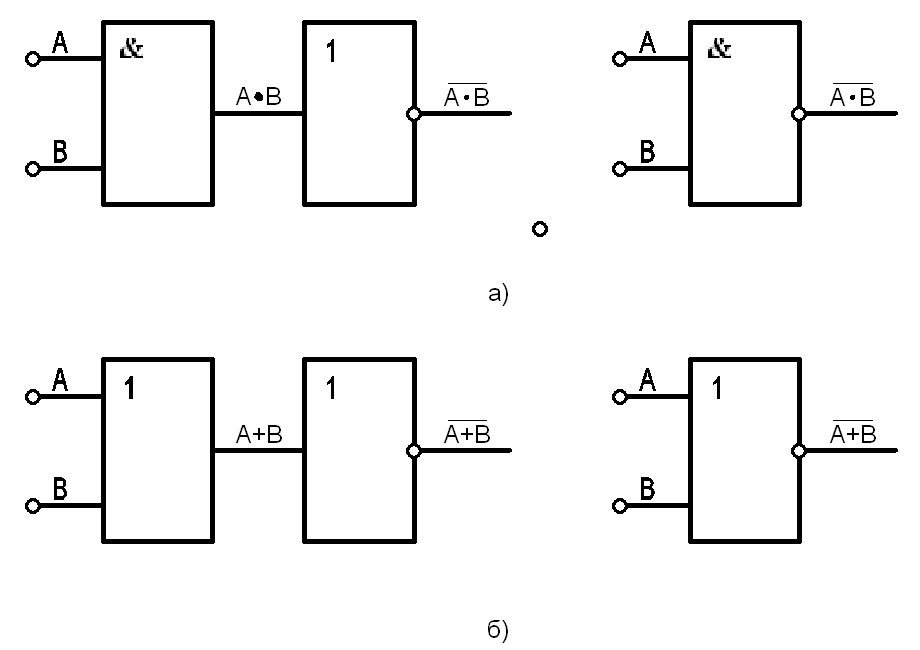
Как вы уже, наверное, догадались, с его помощью реализуется операция логического сложения. И снова обратимся к таблице истинности для дизъюнкции.
В первых двух столбцах даны всевозможные входные данные для А и B. В третьем выходные данные, которые будут равны F. Исходя из этой таблицы можно сказать, что на выходе мы получим единицу тогда, когда хотя бы на одном входе будет единица. То есть, если А или B будет равно единице, то F также будет равно единице.
И последний логический элемент – НЕ (инвертор).
С его помощью реализуется операция отрицания.
Здесь всё просто. Снова нам понадобится таблица истинности для инверсии. Если на входе у нас элемент ноль, то на выходе будет единица, и наоборот. То есть, если А = 0, то F будет равно 1. И, если А = 1, то F = 0.
Также необходимо знать,
что все компьютерные устройства, которые производят операции над двоичными
числами, и ячейки, в которых хранятся данные, представляют собой электронные
схемы.
Они же в свою очередь состоят из отдельных логических операций.
А сейчас давайте попробуем проанализировать несколько электронных схем и узнать, какой сигнал получится на выходе.
Смотрим на первую схему.
В ней используется только один элемент А. Снова будем использовать таблицу истинности. В первый столбец внесём входные данные ноль и один. Во второй столбец будем вносить данные, которые получаются при конъюнкции, в третьей – при инверсии. Он же будет являться столбцом, который будет обозначать выходные данные.
Мы видим, что от А идут две прямые. Это говорит о том, что одни и те же данные будут идти в двух направлениях. Первая операция – конъюнкция. При конъюнкции получим те же данные, что и в самом начале.
Далее идёт операция отрицания. При исходных данных, равных нулю получаем единицу, и наоборот, при исходных данных, равных единице получаем ноль.
Таким образом в итоге мы
получили Ā.
Рассмотрим ещё одну схему.
Она немного сложнее первой. Снова будем использовать таблицу истинности. Она будет состоять из 8 столбцов. В первых двух будут находится входные данные А и B. В третьем конъюнкция А, в четвёртом – конъюнкция B. В пятые и шестые столбцы запишем отрицания конъюнкций А и B соответственно. Для упрощения отрицания конъюнкций А и B запишем как Ā и . В седьмом будет находится конъюнкция Ā и . И в последнем отрицание конъюнкции Ā и .
Таким образом мы с вами переписали все операции со схемы в таблицу истинности. Нам осталось только заполнить таблицу соответствующими данными. Итак, при конъюнкции двух А мы получим такие же данные как и в первом столбце. Перепишем их.
Аналогично поступим и с конъюнкцией двух B. Только данные будем брать со второго столбца.
Пятый столбец – Ā. Преобразуем
данные, находящиеся в третьем столбце.
Необходимо помнить, что при исходных
данных, равных нулю, мы получим единицу. А при исходных данных, равных единице,
получим ноль.
Аналогично и с шестым столбцом, а данные будем брать с четвёртого.
Седьмой столбец – это конъюнкция Ā и . Данные будем брать из пятого и шестого столбцов. Мы с вами помним, что на выходе получим единицу тогда и только тогда, когда на всех входах будут единицы. Заполним таблицу.
И последняя операция – отрицание конъюнкции Ā и . Исходные данные будем брать из седьмого столбца. И снова нужно знать, что если исходные данные равны нулю, то на выходе мы получим один, и наоборот, если исходные данные равны единице, то на выходе получим ноль.
Таким образом мы с вами узнали, какие получатся выходные данные в нашей схеме. То есть данные из восьмого и есть наша F.
Если мы построим выражение исходя из таблицы истинности, то получим следующее:
И снова рассмотрим схему,
но более простую.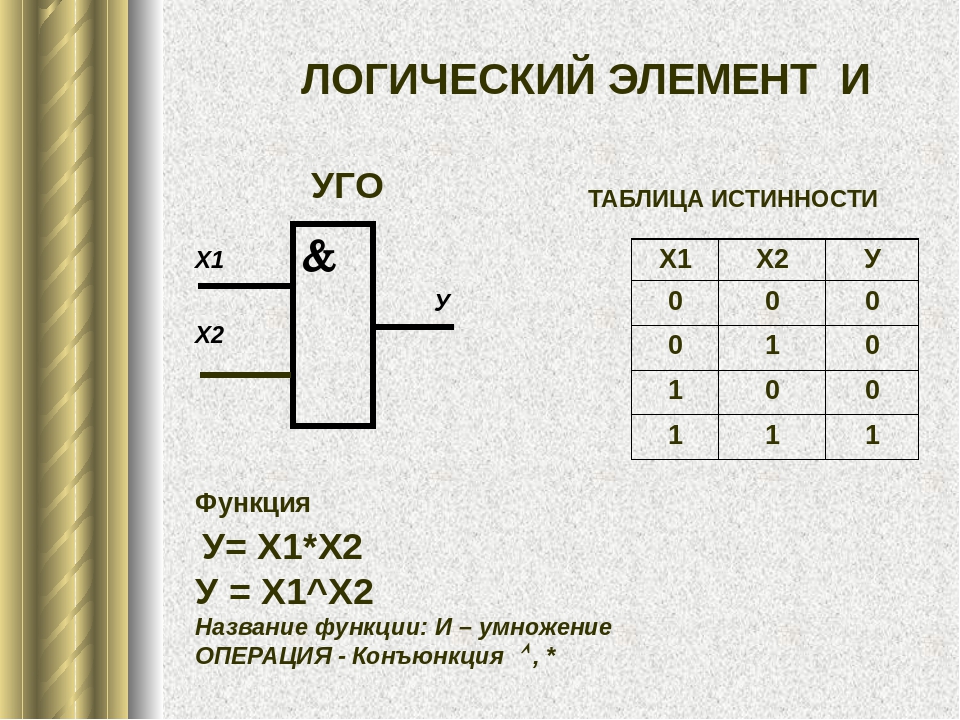
Для начала составим логическое выражение. Будем идти справа налево. Последний логических элемент, который к нас изображён – это инвертор. В него поступают сигналы от дизъюнктора. В свою очередь в дизъюнктор поступают данные от входа А и входа Бэ. В результате мы получим следующее:
А сейчас давайте на основании этого логического выражения составим таблицу истинности и узнаем, какие данные получатся на выходе.
Таблица будет состоять из 4 столбцов. В первые два вносим исходные данные А и B соответственно. Далее мы будем выполнять дизъюнкцию, а затем инверсию. Это и будет являться заголовками наших столбцов.
Итак, первая операция – дизъюнкция. Мы с вами знаем, что на выходе мы получим единицу тогда, когда хотя бы на одном входе будет единица. Данные будем брать из первого и второго столбцов. Заполним третий столбец.
Для того, чтобы внести
данные в четвёртый столбец, нам нужно брать входные данные из третьего.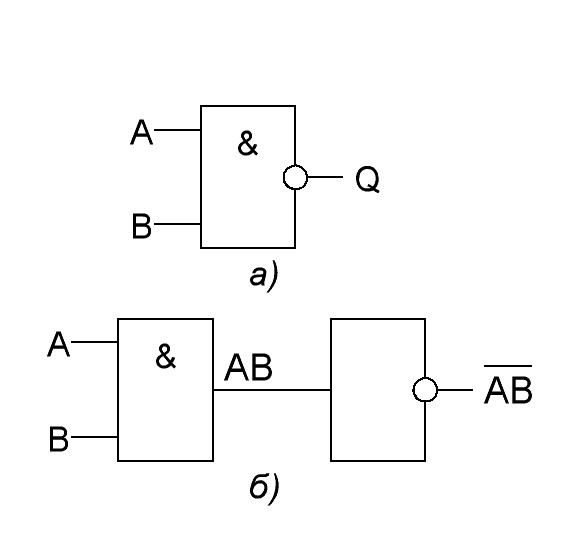
Если у
нас входные данные равны нулю, то на выходе мы получим единицу, а если входные
данные равны единицы, то на выходе будет ноль. Снова заполним таблицу.
В четвёртом столбце находятся выходные данные для нашего выражения F.
А сейчас давайте рассмотрим пример, в котором мы сами научимся строить электронную схему исходя из логического выражения. А также найдём выходные данные с помощью таблицы истинности.
Итак, наше выражение выглядит следующим образом:
Сначала будет выполняться конъюнкция А и B. Изобразим А и B.
От них проведём две прямых и нарисуем прямоугольник, который будет обозначать конъюнктор. Поставим внутри соответствующий знак.
Далее у нас идёт дизъюнкция конъюнкции А и B с C. Изобразим C.
Затем проведём от неё ломанную.
От конъюнктора также проведём прямую. И снова нарисуем прямоугольник, который
будет изображать дизъюнктор.
Снова поставим внутри соответствующий знак.
Нам осталось изобразить инвертор. Проведём от правой стороны дизъюнктора прямую и на пересечении дизъюнктора и прямой нарисуем незакрашенный кружок. Над выходной прямой напишем букву F.
Мы построили электронную схему. Теперь осталось построить таблицу истинности и найти выходные данные.
Таблица будет состоять из 6 столбцов. В первых трёх запишем всевозможные входные данные для А, B и C.
Четвёртый столбец – конъюнкция А и B, пятый дизъюнкция конъюнкции А и B и переменной C. Шестой инверсия всего выражения.
Теперь осталось заполнить таблицу данными.
При конъюнкции на выходе единица будет тогда и только тогда, когда на всех входах будут единицы. Для заполнения четвёртого столбца будем брать данные из первого и второго. Внесём данные в соответствии с данными.
Пятый столбец –
дизъюнкция. Данные будем брать из третьего и четвёртого столбцов.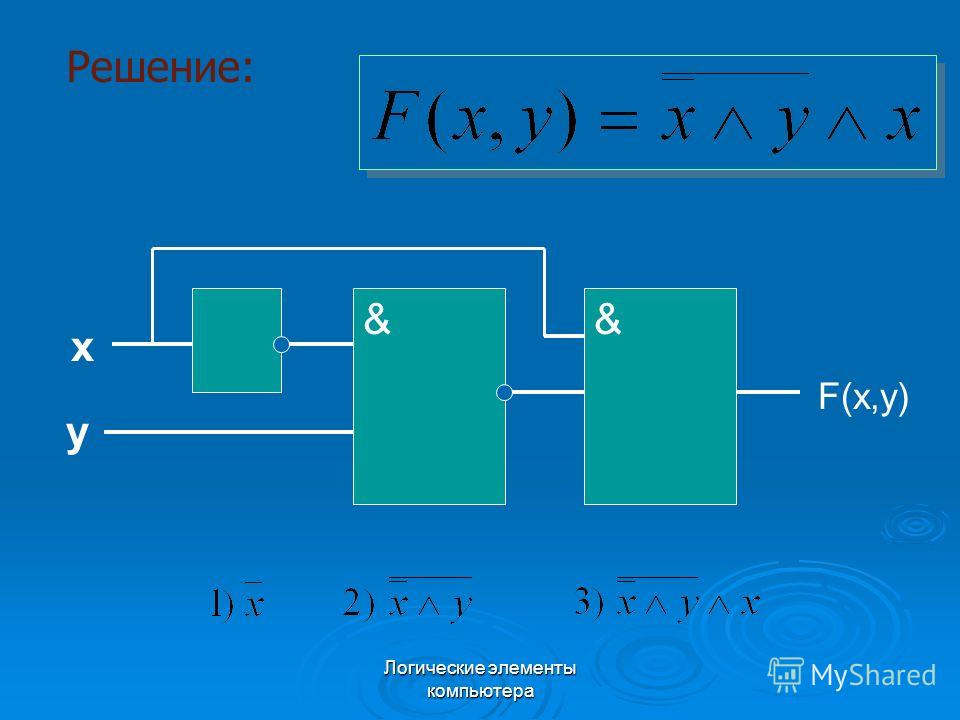
Заполним
столбец в соответствии с правилом: на выходе будет единица тогда, когда хотя бы
на одном входе будет единица.
И последний, шестой столбец – инверсия. Данные будем брать из пятого столбца. Если на входе у нас элемент ноль, то на выходе будет единица, и наоборот. Заполним столбец.
Данные этого столбца являются выходными данными построенной нами электронной схемы.
А теперь давайте исходя из таблицы истинности составим выражение, а исходя из выражения – построим электронную схему.
Нам дана таблица истинности, в которой записаны входные данные и операции, которые необходимо выполнить. Все операции указаны в порядке выполнения их в выражении. Для начала давайте заполним таблицу и найдём выходные данные.
Первая операция –
дизъюнкция А и B. На выходе будет единица
тогда, когда хотя бы на одном входе будет единица. Заполним четвёртый столбец
исходя из данных первого и второго столбцов.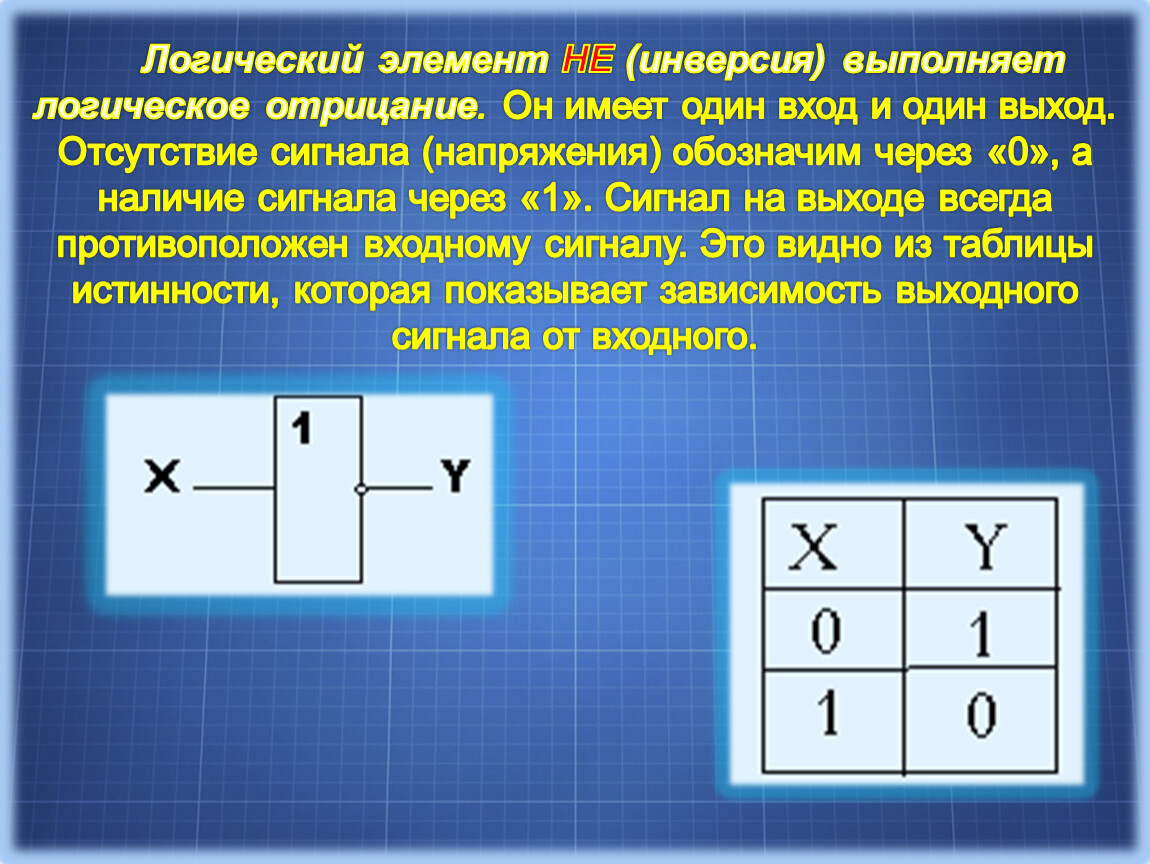
Вторая операция – инверсия C. Заполним пятый столбец исходя из данных третьего столбца. Необходимо помнить, что если входные данные равны нулю, то на выходе мы получим единицу. А если входные данные равны единице, то на выходе мы получим ноль. Внесём данные.
И последний столбец – конъюнкция дизъюнкции А или B и инверсии C. При выполнении конъюнкции мы с вами знаем, что на выходе единица будет тогда и только тогда, когда все входные данные равны единице. Заполним шестой столбец исходя из данных третьего и четвёртого столбцов.
Можно заметить, что всё наше выражение записано в шапке последнего шестого столбца. То есть, мы получим следующее:
Нам осталось построить электронную схему.
Запишем А и B и проведём от них прямые к прямоугольнику, который будет обозначать дизъюнктор. Обозначим это соответствующим символом.
Теперь нам нужно
изобразить инвертор.
Для этого от C
идут ломанные к конъюнктору. А на пересечение прямой, которая выходит из
конъюнктора изобразим кружок, который и будет изображать отрицание.
Теперь проводим кривые от дизъюнктора и конъюнктора к новому прямоугольнику. Он будет изображать конъюнктор. Обозначим его соответствующим знаком.
Проводим прямую из правой стороны крайнего конъюнктора, которая будет обозначать выходные данные. Обозначим её буквой F.
Мы выполнили с вами задание, в котором записали выражение исходя из таблицы истинности и построили электронную схему.
А сейчас пришла пора подвести итоги урока.
Сегодня мы с вами познакомились с такими логическими элементами, как конъюнктор, дизъюнктор и инвертор.
Научились исходя из схемы
при помощи таблицы истинности определять, какие данные должны получиться на
выходе, а также научились строить электронные схемы по данному выражению и
таблице истинности.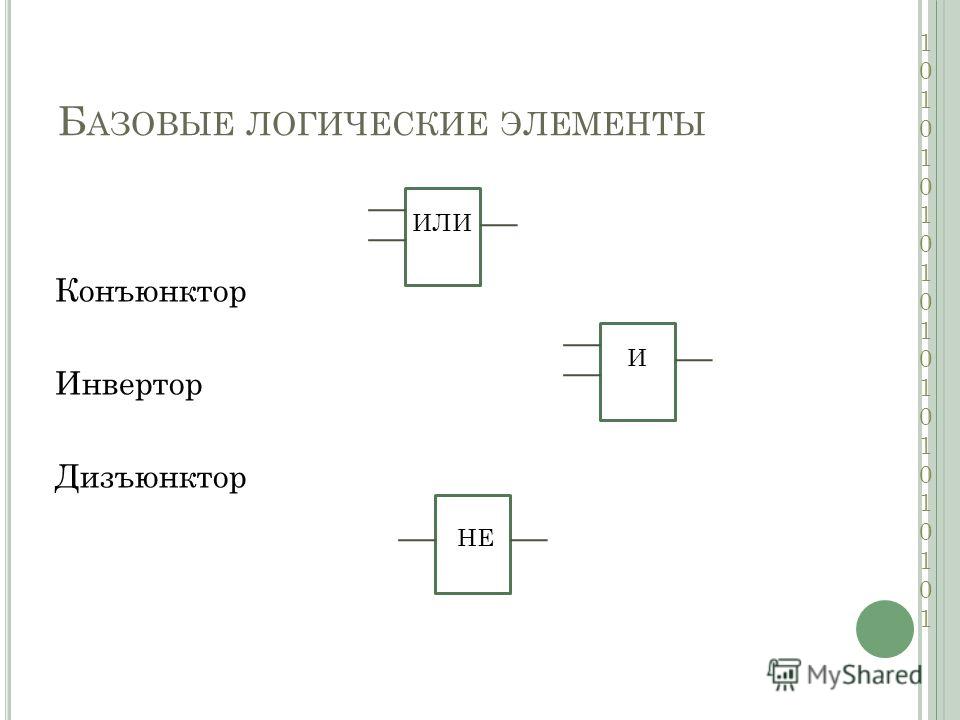
Базовые логические элементы
Базовые логические элементы “И”, “ИЛИ”, “НЕ”.
Алгебра логики – это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.
Создателем алгебры логики является английский математик Джордж Буль (19 век), в честь которого она названа булевой алгеброй высказываний.
| Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно. |
Например,
предложение «6 – четное число» – высказывание, так как оно истинное.
Математический аппарат алгебры
логики очень удобен для описания того, как функционируют аппаратные средства
компьютера, поскольку основной системой счисления в компьютере является
двоичная, в которой используются цифры 1 и 0, а значений логических переменных
тоже два: 1 и 0.
| Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию. |
Логическими элементами
компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и др.
(называемые также вентилями), а также триггер.
С помощью этих схем можно реализовать
любую логическую функцию, описывающую работу устройств компьютера.
Работу логических элементов описывают
с помощью таблиц истинности.
Базовые логические элементы И, ИЛИ, НЕ
Схема И реализует конъюнкцию (логическое умножение) двух или более
логических значений.
Эл. | |
схемаТаблица истинности | ||
х | y | х и у |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Единица на выходе
схемы И будет тогда и только тогда, когда на всех входах будут единицы.
у (читается
как «х и у»).
Операция конъюнкции на
функциональных схемах обозначается знаком & (читается как «амперсэнд»),
являющимся сокращенной записью английского слова and.
Схема ИЛИ реализует дизъюнкцию (логическое сложение) двух или более логических значений.
Эл. схема | |
Таблица истинности | ||
х | y | х или у |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 10 |
1 | 1 | 1 |
Когда хотя бы на
одном входе схемы ИЛИ будет единица, на ее выходе также будет единица.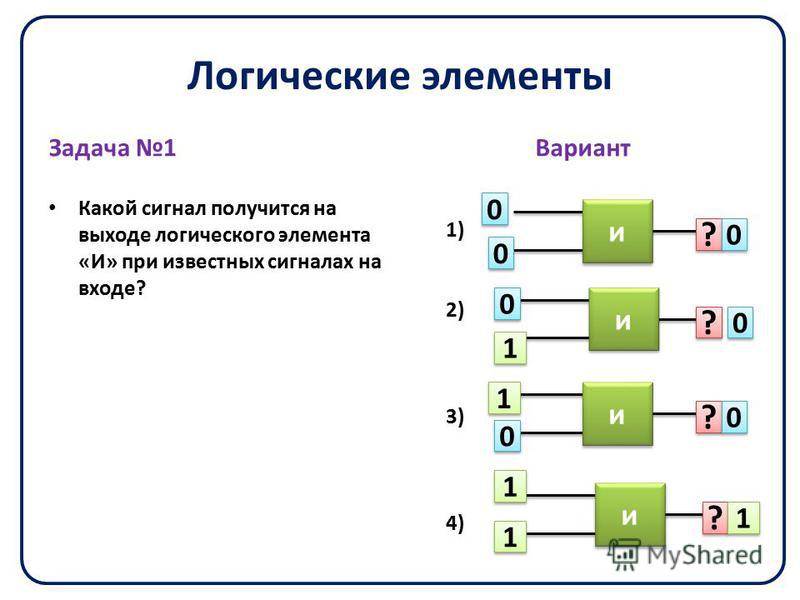
Знак «1» на схеме — от устаревшего
обозначения дизъюнкции как «>=!» (т.е. значение дизъюнкции равно единице,
если сумма значений операндов больше или равна 1). Связь между выходом
z этой схемы и входами х и у описывается соотношением z = х или у.
Схема НЕ (инвертор) реализует операцию отрицания.
| |||||||||
Связь между входом х этой схемы и выходом z можно записать соотношением Z = ,
где х читается как «не х» или «инверсия.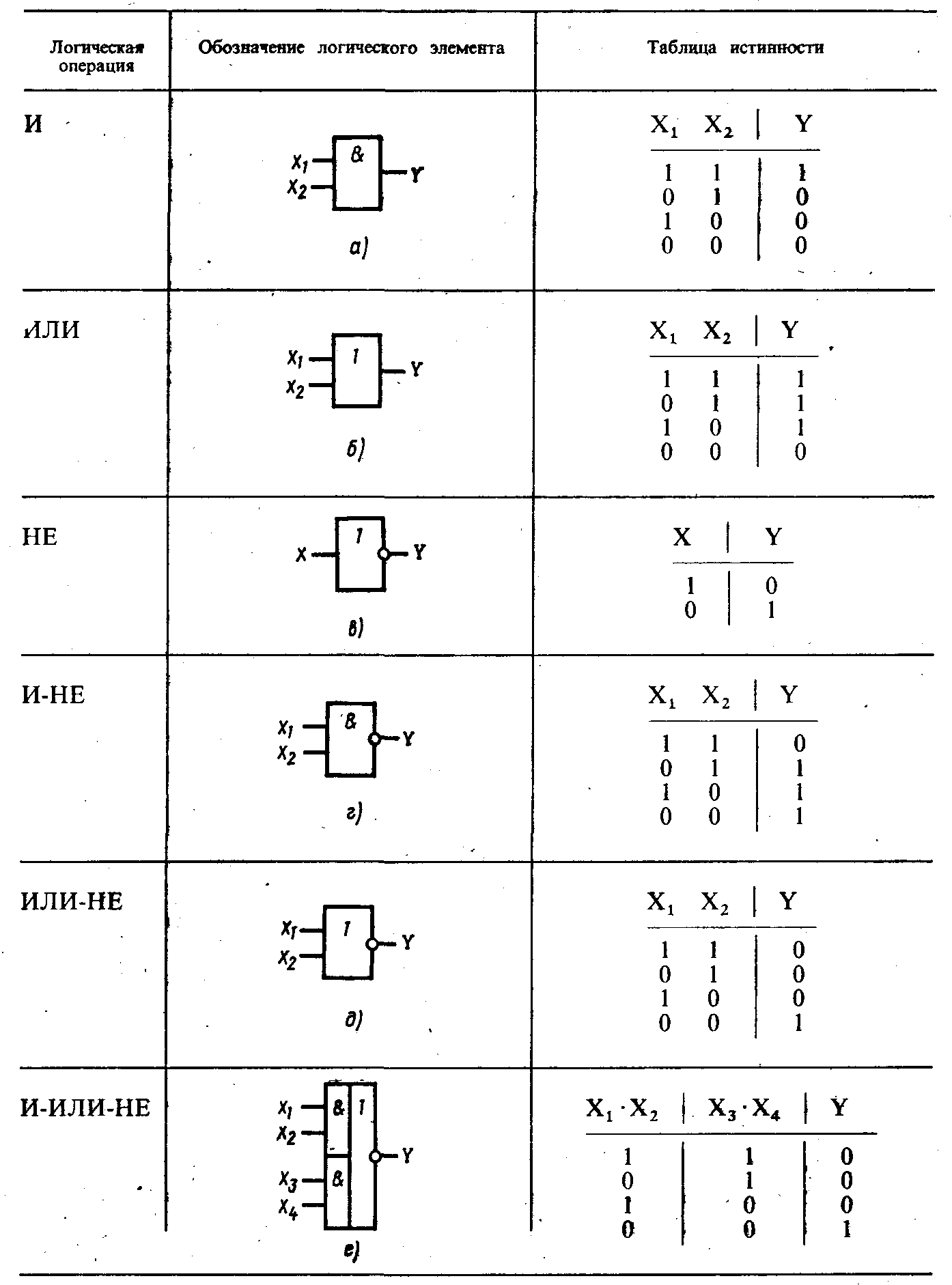
Если на входе схемы 0, то на выходе 1. Когда на входе 1 на выходе
0.
Логические элементы
Логические элементыЛогические элементы
Логическим элементом
называется электрическая схема,
выполняющая какую-либо логическую
операцию (операции) над входными
данными, заданными в виде уровней
напряжения, и возвращающая
результат операции в виде
выходного уровня напряжения. Так
как операнды логических операций
задаются в двоичной системе
счисления, то логический элемент
воспринимает входные данные в виде
высокого и низкого уровней
напряжения на своих входах.
Соответственно, высокий уровень
напряжения (напряжение логической
1) символизирует истинное значение
операнда, а низкий (напряжение
логического 0) – ложное. Значения
высокого и низкого уровней
напряжения определяются
электрическими параметрами схемы
логического элемента и одинаковы
как для входных, так и для выходных
сигналов.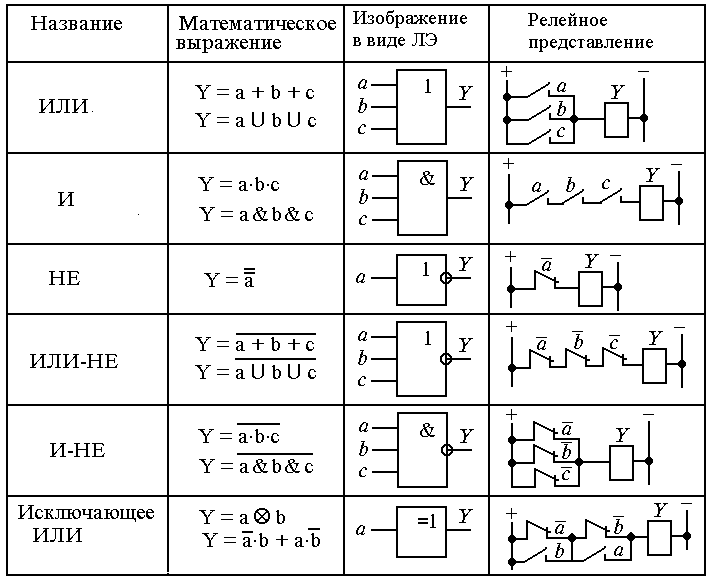
Обычно, логические
элементы собираются как отдельная
интегральная микросхема. К числу
логических операций, выполняемых
логическими элементами относятся
конъюнкция (логическое умножение,
И), дизъюнкция (логическое сложение,
ИЛИ), отрицание (НЕ) и сложение по
модулю 2 (исключающее ИЛИ).
Рассмотрим основные типы
логических элементов.
Элемент И
Логический элемент И выполняет операцию логического умножения (конъюнкция) над своими входными данными и имеет от 2 до 8 входов и один выход (как правило, выпускаются элементы с двумя, тремя, четырьмя и восемью входами). На рис. 1. изображены условные графические обозначения (УГО) логических элементов И с двумя, тремя и четырьмя входами соответственно. Элементы И обозначаются как NИ, где N – количество входов логического элемента (например, 2И, 3И, 8И и т.д.).
| Рис. 1 |
Элемент ИЛИ
Логический элемент ИЛИ
выполняет операцию логического
сложения (дизъюнкция) над своими
входными данными и, также как и
логический элемент И, имеет от 2 до 8
входов и один выход.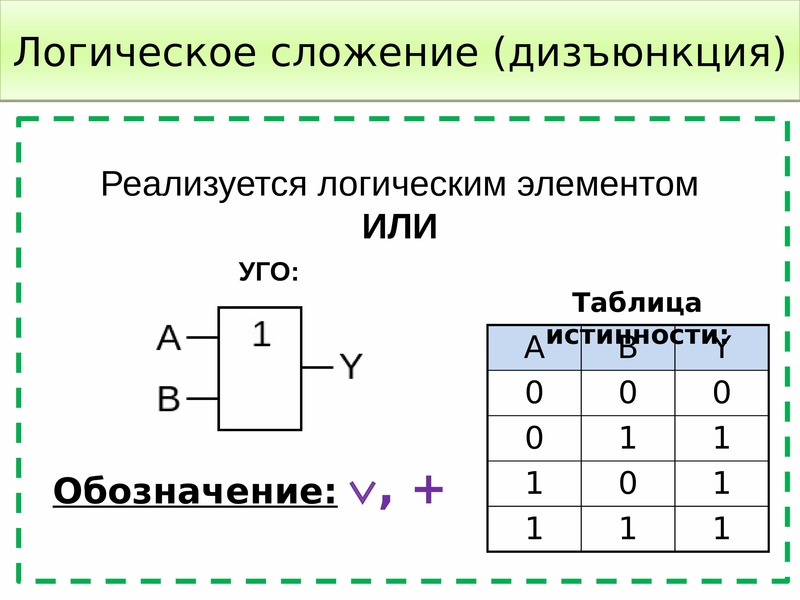
На рис. 2.
изображены УГО логических
элементов ИЛИ с двумя, тремя и
четырьмя входами соответственно.
Элементы ИЛИ обозначаются также,
как и элементы И (2ИЛИ, 4ИЛИ и т.д.).
| Рис. 2 |
Элемент НЕ (инвертор)
Логический элемент НЕ выполняет операцию логического отрицания над своими входными данными и имеет один вход и один выход. Иногда его называют инвертор, так как он инвертирует входной сигнал. На рис. 3 изображено УГО элемента НЕ.
| Рис. 3 |
Элемент И-НЕ
Логический элемент И-НЕ
выполняет операцию логического
умножения над своими входными
данными, а затем инвертирует
(отрицает) полученный результат и
выдаёт его на выход.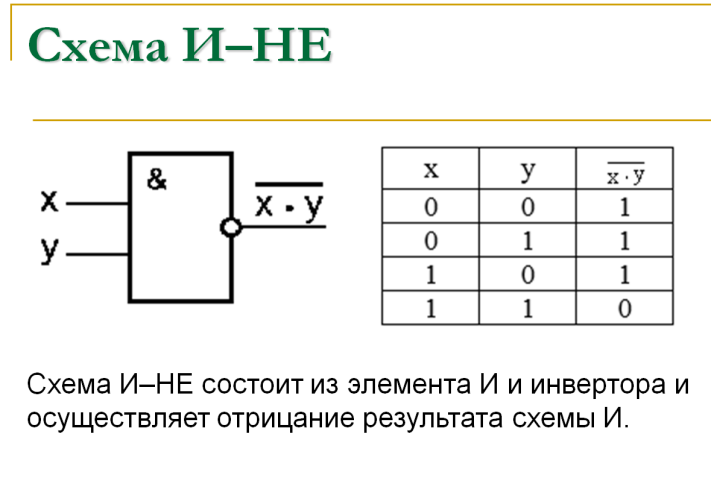
Таким образом,
можно сказать, что логический
элемент И-НЕ – это элемент И с
инвертором на выходе. УГО элемента 3И-НЕ
приведено на рис. 4.
| Рис. 4 |
Элемент ИЛИ-НЕ
Логический элемент ИЛИ-НЕ выполняет операцию логического сложения над своими входными данными, а затем инвертирует (отрицает) полученный результат и выдаёт его на выход. Таким образом, можно сказать, что логический элемент ИЛИ-НЕ – это элемент ИЛИ с инвертором на выходе. УГО элемента 3ИЛИ-НЕ приведено на рис. 5.
| Рис. 5 |
Элемент сложения по модулю 2
Этот логический элемент
выполняет логическую операцию
сложения по модулю 2 и, как правило,
имеет 2 входа и один выход.
Такой
элемент, в основном, используется в
схемах аппаратного контроля. УГО
элемента приведено на рис. 6.
| Рис. 6 |
Комбинационные логические элементы
Существуют и более сложные логические элементы, выполняющие несколько логических операций над своими входными данными. Например, элемент 2И-ИЛИ, УГО и схема которого приведено на рис. 7, сначала выполняет операцию логического умножения над парами операндов x1, x2 и x3, x4, а затем выполняет операцию логического сложения над полученными результатами, т.е. y = x1x2 + x3x4. Можно придумать и более сложные комбинационные логические элементы, например 3-2И-ИЛИ-НЕ (рис. 8).
| Рис. 7 |
Рис. 8 |
Универсальные логические элементы
Универсальные логические элементы могут использоваться для выполнения разнообразных операций над своими входными данными. Конкретная операция зависит от того, какие сигналы поданы на управляющие входы. Чтобы синтезировать такой универсальный логический элемент, обычно пользуются СКНФ или СДНФ, как и в синтезе комбинационных логических схем.
Электрические принципиальные схемы логических элементов
При рассмотрении
электрических принципиальных схем
логических элементов пользуются
термином тип логики. Тип логики
определяет элементную базу, на
которой собран логический элемент,
а также отражает некоторые
особенности отдельных элементов
этой элементной базы и
характеристики самого логического
элемента. Наиболее распространены
следующие типы логик: ТТЛ, ДТЛ, МОП,
КМОП, также существуют типы логик
ЭСЛ, РЕТЛ и некоторые другие.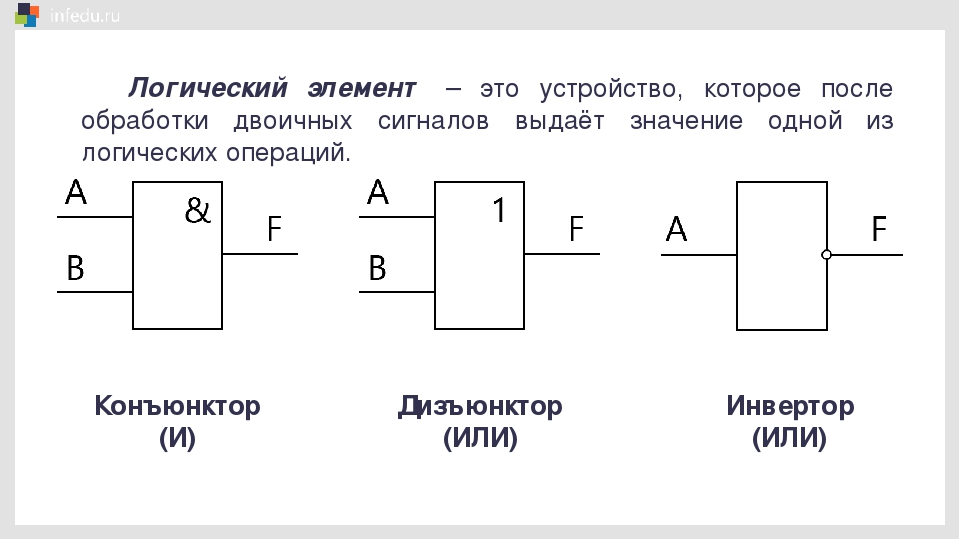
Тип
логики ТТЛ
(транзисторно-транзисторная
логика) определяет элементную базу,
на которой собран логический
элемент, как состоящую
преимущественно из транзисторов,
причём транзисторы используются и
на входе, и на выходе логического
элемента (отсюда и название –
транзисторно-транзисторная). Тип
логики ДТЛ (диодно-транзисторная
логика) определяет элементную базу
как состоящую преимущественно из
транзисторов и диодов (диоды на
входе, транзисторы – на выходе). Типы
логик МОП
(металл-оксид-полупроводник) и КМОП
определяет элементную базу как
состоящую из транзисторов МДП
(металл-диэлектрик-полупроводник),
причём микросхемы этого типа имеют
очень низкую потребляемую
мощность, засчёт особенностей МДП
транзисторов оперировать малыми
токами и имеющими очень малый ток
утечки.
Рассмотрим электрические принципиальные схемы логического элемента И-НЕ с n входами – ДТЛ (рис. 9) и логического элемента И-НЕ с n входами – ТТЛ (рис. 10).
Рис. 9 |
| Рис. 10 |
На рисунках +U обозначает положительный потенциал источника питания, а -U – отрицательный.
Рассмотрим сначала работу
схемы на рис. 9. Если к одному из
входных диодов приложено
напряжение логического 0, то этот
диод открыт и на базу транзистора
подаётся напряжение логического 0.
Транзистор закрывается и на выходе y устанавливается напряжение
логической 1. Только когда ко всем
входным диодам будет приложено
напряжение логической 1 транзистор
откроется и на выходе установится
напряжение логического 0.
Оставшиеся каскады на транзисторах
выполняют функцию усиления сигнала
и инвертирования. При подаче на
вход второго транзистора
напряжения логического 0, он
закроется, подключив базы
транзисторов оконечного каскада
через резисторы к плюсу и к минусу
источника питания. Один из
транзисторов оконечного каскада
откроется, а другой – закроется и на
выходе установится напряжение
логической 1.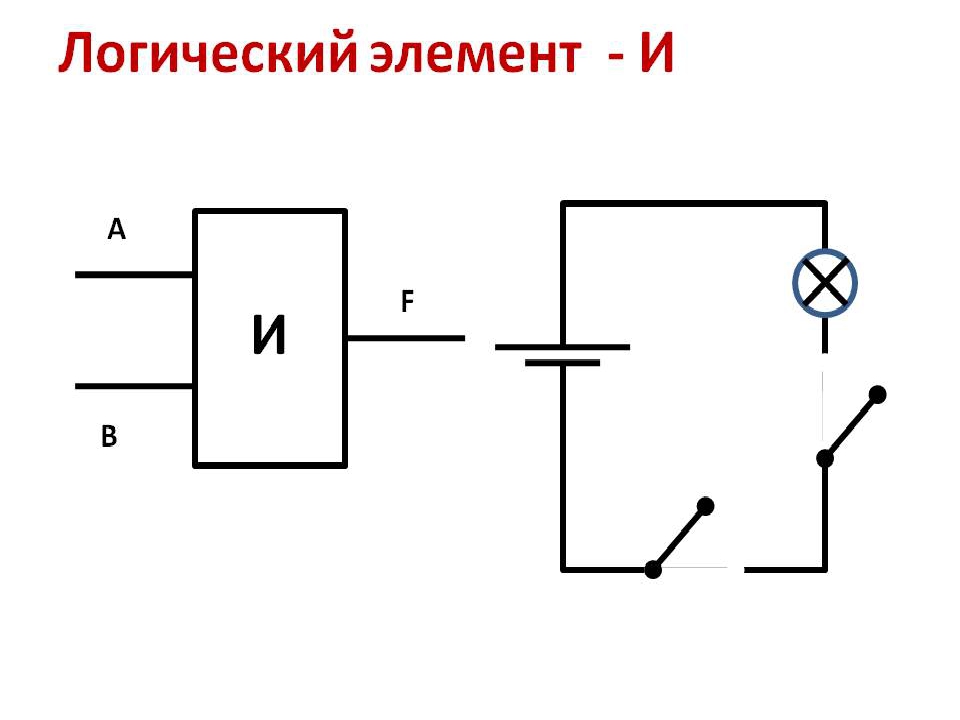
При подаче на второй
транзистор напряжения логической 1,
он откроется. Теперь открытый и
закрытый транзисторы оконечного
каскада поменяются местами и на
выходе установится напряжение
логического 0.
Теперь рассмотрим работу схемы на рис. 10. Вызывает некоторый интерес необычный транзистор на входе и схема его включения. Такие многоэмиттерные транзисторы всегда используются на входах логических элементов ТТЛ. Сам транзистор выполняет логическую операцию И. При подаче на один из входов напряжения логического нуля, транзистор открывается и, таким образом, на коллекторе устанавливается напряжение логического 0. Напряжение логической 1 будет на коллекторе только тогда, когда на всех входах будет напряжение логической 1. Подобный транзистор можно рассматривать как много n-p переходов, а соответственно, как много диодов. Таким образом такое включение транзистора в цепь эквивалентно диодной сборке на входе логического элемента И на рис. 9.
Применение логических элементов
Логические элементы могут
использоваться как
самостоятельные части схемы, так и
входить в состав более сложной
цифровой комбинационной схемы или
схемы с памятью.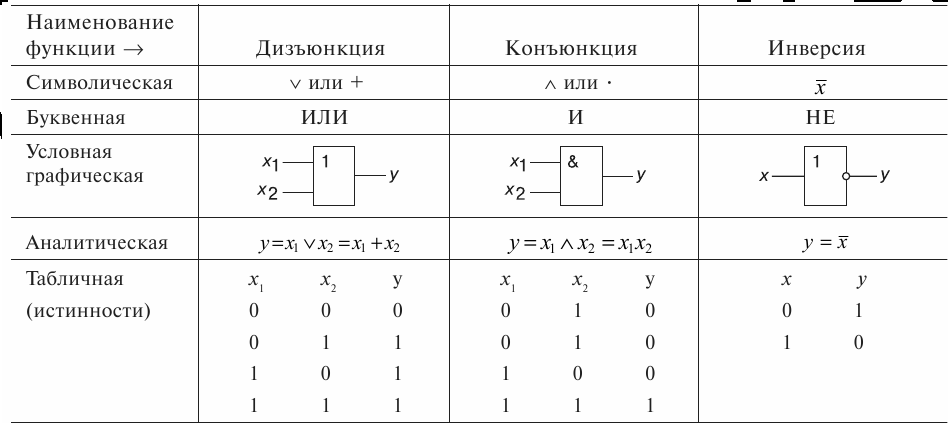
Как
самостоятельные части схемы,
логические элементы могут
применяться в качестве управляющей
логики какого-либо устройства, а
также в качестве генератора
прямоугольных импульсов с
подключённой ёмкостью или
кварцевым резонатором. В качестве
комбинационных схем логические
элементы используются в составе
микросхем БИС и СБИС, а также в
дешифраторах и шифраторах,
выполненных в виде отдельных
микросхем. Также, логические
элементы могут входить в состав
схем с памятью (триггеры, регистры,
счётчики и т.д.), выполненных в виде
отдельной микросхемы или в составе
других микросхем.
Элементы Исключающее ИЛИ/Исключающее ИЛИ-НЕ/Нечётность/Чётность
| Библиотека: | Базовые |
| Введён в: | 2.0 Beta 1 для Исключающее ИЛИ/Нечётность/Чётность; 2.0 Beta 6 для Исключающее ИЛИ-НЕ |
| Внешний вид: |
Поведение
Элементы Исключающее ИЛИ, Исключающее ИЛИ-НЕ, Нечётность и Чётность вычисляют соответствующую функцию от значений на входах и выдают результат на выход.
По умолчанию, неподключенные входы игнорируются – то есть, если входы действительно не имеют ничего подключенного к ним – даже провода. Таким образом, вы можете добавить 5-входовый элемент, но подключить только два входа, и он будет работать как 2-входовый элемент; это избавляет вас от необходимости беспокоиться о настройке количества входов каждый раз при создании элемента. (Если все входы не подключены, то на выходе значение ошибки X.) Некоторые пользователи, однако, предпочитают, чтобы Logisim настаивал, чтобы все входы были подключены, поскольку это соответствует реальным элементам. Вы можете включить это поведение, выбрав меню Проект > Параметры…, перейдя на вкладку Моделирование, и выбрав вариант Ошибка для неопределённых входов
для Выход элемента при неопределённости
.
Двухвходовая таблица истинности для элементов следующая.
| x | y | Исключающее ИЛИ | Исключающее ИЛИ-НЕ | Нечётность | Чётность |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
Как вы можете видеть, элементы Нечётность и Исключающее ИЛИ ведут себя одинаково в случае двух входов; аналогично, элементы Чётность и Исключающее ИЛИ-НЕ ведут себя одинаково. Но если входов с определённым значением больше двух, то элемент Исключающее ИЛИ будет давать на выходе 1, когда единица строго на одном входе, тогда как элемент Нечётность даст на выходе 1, когда единица на нечётном количестве входов. Элемент Исключающее ИЛИ-НЕ будет давать на выходе 1, когда входов с единицей строго не один, тогда как элемент Чётность даст 1, когда входов с единицей чётное количество. Элементы Исключающее ИЛИ и Исключающее ИЛИ-НЕ имеют атрибут, названный Многовходовое поведение, который позволяет настроить их на использование поведения элементов Нечётность и Чётность.
Если на каких-либо входах значение ошибки (например, если противоречивые значения поступают на один и тот же провод) или плавающее значение, то на выходе будет значение ошибки.
Многобитные версии каждого элемента будут выполнять свои однобитные преобразования над входами поразрядно.
Примечание: многие специалисты утверждают, что поведение фигурного элемента Исключающее ИЛИ должно соответствовать поведению элемента Нечётность, но по этому вопросу нет согласия. Поведение Logisim по умолчанию для элемента Исключающее ИЛИ основано на стандарте IEEE 91. Это также согласуется с интуитивным пониманием термина Исключающее ИЛИ: официант, спрашивающий, хотите вы гарнир из картофельного пюре, моркови, зеленого горошка, или шинкованной капусты, примет только один выбор, а не три, независимо от того, что вам могут сказать некоторые специалисты. (Должен признать, однако, что я не подвергал это заявление серьезным испытаниям.) Вы можете настроить элементы Исключающее ИЛИ и Исключающее ИЛИ-НЕ на использование одного из вариантов, меняя его атрибут Многовходовое поведение
.
Контакты (предполагается, что компонент направлен на восток)
- Западный край (входы, разрядность соответствует атрибуту Биты данных)
Входы компонента. Их будет столько, сколько указано в атрибуте Количество входов.
Заметьте, что если вы используете фигурные элементы, то западный край элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет искривлён. Тем не менее, входные контакты расположены вряд. Logisim отрисовывает короткие отрезки чтобы показать это; если вы перекроете отрезок, программа будет без предупреждений предполагать, что вы не хотели перекрыть его. При использовании “Вида для печати”, эти отрезки не будут отрисованы, если не подключены к проводам.
- Восточный край (выход, разрядность соответствует атрибуту Биты данных)
Выход элемента, значение на котором вычисляется на основании текущих значений на входах, как описано выше.
Атрибуты
Когда компонент выбран, или уже добавлен, клавиши от 0 до 9 меняют его атрибут Количество входов
, комбинации от Alt-0 до Alt-9 меняют его атрибут Биты данных
, а клавиши со стрелками меняют его атрибут Направление
.
- Направление
- Направление компонента (его выхода относительно его входов).
- Биты данных
- Разрядность входов и выходов компонента.
- Размер элемента
- Определяет, следует отрисовывать широкую или узкую версию компонента. Это не влияет на количество входов, которое определяется атрибутом Количество входов; правда, если количество входов превышает 3 (для узкого компонента) или 5 (для широкого), то элемент будет отрисовываться с “крыльями”, чтобы вместить запрошенное количество входов.
- Количество входов
- Определяет, сколько контактов на западном крае будет иметь компонент.
- Многовходовое поведение (только для Исключающее ИЛИ и Исключающее ИЛИ-НЕ)
- Когда входов три или более, то значение на выходе элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет основано или на том, что 1 строго на одном входе (по умолчанию), или на нечётном количестве входов.
Поведение Инструмента Нажатие
Нет.
Поведение Инструмента Текст
Нет.
Назад к Справке по библиотеке
8. Понятие о логических элементах и микропроцессорах
8.1. Логические элементы
Логические элементы (узлы) предназначены для выполнения различных логических (функциональных) операций над дискретными сигналами при двоичном способе их представления (1; 0).
Преимущественное распространение получили логические элементы потенциального типа. В них используются дискретные сигналы, нулевому значению «0» которых соответствует уровень низкого потенциала, а единичному значению «1» – уровень высокого потенциала (отрицательного или положительного).
Потенциальные логические элементы нашли исключительное применение в интегральном исполнении в виде микросхем.
Микросхема – это электронный узел, блок или устройство, изготовленное с высокой степенью миниатюризации, в которой каждый электронный компонент представляет собой не отдельно взятый транзистор, диод, резистор, конденсатор и т. д., а их неразъемное схемное соединение. Количество элементов, входящих в микросхему, может достигать тысяч и более элементов.
Применение микросхем легло в основу современного направления электроники – микроэлектроники, которая решает проблемы повышения надёжности, уменьшения массогабаритных показателей и стоимости электронной аппаратуры.
Логические биполярные микросхемы чаще всего выполняются на транзисторах типа n-p-n c напряжением питания Eк > 0, причём «1» – соответствует закрытое состояние транзистора, а «0» – открытое. Процесс перехода транзистора из одного состояния в другое достаточно быстрый.
Все схемы цифровой техники выполняются на логических интегральных микросхемах.
Работу логического элемента можно описать зависимостью логического значения выходного сигнала F от совокупности логических значений входных сигналов x. Такую зависимость принято представлять таблицей истинности.
Для любых логических преобразований достаточно иметь три элементарных логических элемента, выполняющих следующие операции: логическое сложение (логическое ИЛИ), логическое умножение (логическое И) и логическое отрицание (логическое НЕ).
Логический элемент ИЛИ – имеет несколько входов и один общий выход. Элемент ИЛИ осуществляет логическое сложение (дизъюнкцию).
F = x1 x2, или F = x1 + x2
где F – функция; x1……xn – аргументы (переменные двоичные сигналы на входе).
Его условное обозначение показано на рис. 67, а, а электрическая схема на полупроводниковых диодах – на рис. 67, б.
Функция F = 0, когда все ее аргументы равны нулю, и F = 1 при одном, нескольких или всех аргументах, равных единице. Значение F = 1 на выходе создается передачей входного сигнала вследствие отпирания соответствующего диода. К диодам, для которых входной сигнал равен нулю, прикладывается обратное напряжение, и они находятся в закрытом состоянии.
F = x1 x2 … xn или F = x1 + x2 +…+ xn.
Логический элемент И – имеет несколько входов и один выход. Элемент И осуществляет логическое умножение (конъюнкцию).
F = x1 x2 или F = x1x2
Его условное обозначение показано на рис. 68, а, а электрическая схема на полупроводниковых диодах – на рис. 68, б.
F = x1 x2… xn или F = x1x2… xn.
Функция F = 0, когда хотя бы один из ее аргументов равен нулю и F = 1 при всех аргументах, равных единице.
Логический элемент И является схемой совпадения: сигнал «1» на выходе появляется при совпадении сигналов «1» на всех входах. Отличие схемы И (рис. 68, б) от схемы ИЛИ (рис. 67, б) заключается в изменении полярности включения диодов и наличии резистора R1, подключенного к шине «+» источника питания. При всех входных сигналах, равных единице, на катодах диодов имеется положительный потенциал относительно общей точки и все диоды закрыты. На выходе схемы создается напряжение ER2 / (R1+R2), определяющее F = 1. При нулевом значении сигнала хотя бы на одном из входов соответствующий диод будет проводить ток и шунтировать резистор R2, выполняющий роль нагрузки. Напряжение на выходе при этом определяется падением напряжения на открытом диоде и близко к нулю (F = 0). На рис. 68, б показан вариант, когда x1 = 0 и ток проводит диод VD1. Увеличение числа входов с нулевым значением сигнала приводит только к увеличению числа проводящих диодов, а функция F остается равной нулю.
Логический элемент НЕ – имеет один вход и один выход. Элемент НЕ выполняет операцию отрицания (инверсии), в связи с чем его часто называют логическим инвертором. Им реализуется функция
.
Сигнал x = 0 на входе соответствует F = 1 и, наоборот, при x = 1 F = 0. Логический элемент НЕ представляет собой ключевую схему на транзисторе (рис 69, б), его условное обозначение показано на рис. 69, а.
При x = 0 (UВХ = 0) транзистор закрыт, напряжение Uкэ Eк, т. е. F = 1. При x = 1 (Uвх = Uвх.отп) транзистор открыт, напряжение Uкэ = = Uкэ.откр 0, т. е. F = 0. Открытое состояние транзистора обеспечивается заданием тока базы, вводящего транзистор в режим насыщения.
На практике часто используется расширенный набор логических элементов.
К ним относятся логические элементы:
ИЛИ-НЕ (стрелка Пирса), реализующий функцию
;
И-НЕ (штрих Шеффера), реализующий функцию:
.
Рабочие свойства логических элементов определяет ряд параметров:
– быстродействие – время задержки между сменой состояний входного и выходного сигналов;
– нагрузочная способность или коэффициент разветвления – число входов, которые можно подключить к одному выходу;
– помехоустойчивость – максимально допустимый уровень напряжения помехи, не вызывающий ложного переключения;
– степень генерирования помех – интенсивность колебаний тока при переключении элементов;
– мощность рассеяния – мощность потерь энергии в элементах.
Логические элементы
Глава 1. КОМБИНАЦИОННЫЕ СХЕМЫ И ЦИФРОВЫЕ АВТОМАТЫ
1.1. Логические элементы
Различают комбинационные схемы и цифровые автоматы. В комбинационных схемах состояние на выходе в данный момент времени однозначно определяется состояниями на входах в тот же момент времени. Комбинационными схемами, например, являются логические элементы И, ИЛИ, НЕ и их комбинации. В цифровом автомате состояние на выходе определяется не только состояниями на входах в данный момент времени, но и предыдущим состоянием системы. К цифровым автоматам относятся триггеры.
Логическими элементами называются элементы, выполняющие логические операции И, ИЛИ, НЕ и комбинации этих операций. Указанные логические операции можно реализовать с помощью контактно-релейных схем и с помощью электронных схем. В настоящее время в подавляющем большинстве применяется электронные логические элементы, причем электронные логические элементы входят в состав микросхем. Имея в распоряжении логические элементы И, ИЛИ, НЕ, можно сконструировать цифровое электронное устройство любой сложности. Электронная часть любого компьютера состоит из логических элементов.
Система простых логических функций, на основе которой можно получить любую логическую функцию, называется функционально полной.
Отсюда следует, что для построения логического устройства любой сложности достаточно иметь однотипные логические элементы, например, И-НЕ или ИЛИ-НЕ.
Логические элементы могут работать в режимах положительной и отрицательной логики. Для электронных логических элементов в режиме положительной логики логической единице соответствует высокий уровень напряжения, а логическому нулю – низкий уровень напряжения. В режиме отрицательной логики логической единице соответствует низкий уровень напряжения, а логическому нулю – высокий.
Для контактно-релейных схем в режиме положительной логики логической единице соответствует замкнутый контакт ключа или реле, а логическому нулю – разомкнутый. Светящийся индикатор (лампочка, светодиод) соответствует логической единице, а несветящийся – логическому нулю.
Логические элементы, реализующие для режима положительной логики операцию И, для режима отрицательной логики выполняют операцию ИЛИ, и наоборот. Так, например, микросхема, реализующая для положительной логики функции элемента 2И-НЕ, будет выполнять для отрицательной логики функции элемента 2ИЛИ-НЕ.
Как правило, паспортное обозначение логического элемента соответствует функции, реализуемой “положительной логикой”. Логические элементы И, ИЛИ, НЕ имеют один выход, число входов логических элементов И, ИЛИ может быть любым начиная с двух. Логические элементы И и ИЛИ, выпускаемые в составе микросхем, обычно имеют 2, 3, 4, 8 входов. В названии элемента первая цифра указывает число входов.
Прежде всего, рассмотрим реализацию логических элементов с помощью контактно-релейных схем. Рассмотрим логический элемент 2И. Он выполняет операцию логического умножения. На рисунке 1.1,а приведена контактно-релейная схема логического элемента 2И для режима положительной логики.
Обозначение логического элемента 2И на принципиальных схемах показано на рисунке 1.1,б. Знак & (амперсант) в левом верхнем углу прямоугольника указывает, что это логический элемент И. Первые две буквы обозначения DD1.2 указывают на то, что это цифровая микросхема, цифра слева от точки указывает номер микросхемы на принципиальной схеме, а цифра справа от точки – номер логического элемента в составе данной микросхемы.
Функционирование логического элемента обычно задают таблицей истинности. Контактно-релейная схема логического элемента 2И (режим положительной логики) позволяет легко составить таблицу истинности этого элемента. Так как микросхема имеет для подачи входных сигналов два входа, то возможны 22=4 различных комбинации входных сигналов. Необходимо проанализировать состояние лампочки при различных положениях тумблеров Sa1, Sa2, т.е. рассмотреть 4 различных комбинации состояний тумблеров (рис. 1.1,в).
Введение понятия активного логического уровня существенно облегчает анализ функционирования сложных цифровых устройств. Активным логическим уровнем на входе элемента (логический нуль, логическая единица) называется такой уровень, который однозначно задает состояние на выходе элемента независимо от логических уровней на остальных входах элемента. Активный логический уровень на одном из входов элемента определяет уровень на его выходе. Уровни, обратные активным, называются пассивными логическими уровнями.
Активным логическим уровнем для элементов И является логический нуль. Пусть, например, имеем логический элемент 8И. Необходимо проанализировать 28=256 различных состояний для составления таблицы истинности этого элемента. Воспользуемся понятием активного логического уровня. Если хотя бы на одном из входов этого элемента будет активный логический уровень, то состояние на выходе элемента определено однозначно и нет необходимости анализировать состояния на остальных входах элемента.
Таким образом, таблицу истинности логического элемента 8И можно свести к двум строчкам: на выходе этого элемента будет логическая единица, если на всех входах будут сигналы логической единицы и на выходе будет логический нуль, если хотя бы на одном из входов элемента будет сигнал логического нуля.
Логический элемент 2ИЛИ выполняет логическую операцию логического сложения у=х1+х2. Контактно-релейная схема элемента приведена на рисунке 1.2,а, а его условное обозначение – на рисунке 1.2,б. Знание контактно-релейной схемы элемента позволяет составить таблицу истинности (рис.1.2,в). Лампочка будет гореть, если замкнуты контакты хотя бы одного тумблера, т.е. активным логическим уровнем для элементов ИЛИ является уровень логической единицы.
Логический элемент НЕ выполняет операцию отрицания, и для этого элемента проще составить сразу таблицу истинности, а не вычерчивать сначала контактно-релейную схему, а затем по ней составлять таблицу истинности. Для логических элементов И и ИЛИ проще сначала вычертить контактно-релейную схему, а уже потом составлять таблицу истинности.
Напомним алгоритм работы электромагнитного реле с нормально замкнутыми контактами: при отсутствии электрического тока через обмотку реле контакты реле замкнуты, а при протекании достаточного тока через обмотку реле контакты реле разомкнуты. Контактно релейная схема элемента НЕ приведена на рисунке 1.3а, а его условное обозначение – на рисунке 1.3б.
Проанализируем работу контактно-релейной схемы логического элемента НЕ (рис. 1.3а). Если контакты ключа Sa1 разомкнуты, то через обмотку К электромагнитного реле ток протекать не будет. Контакты К1.1 (цифра слева от точки указывает номер реле на принципиальной схеме, а цифра справа – номер контактной группы данного реле) будут замкнуты (электромагнитное реле с нормально замкнутыми контактами). Электрическая лампочка HL1 в этом случае будет гореть, что для режима положительной логики будет означать логическую единицу. При замкнутых контактах ключа Sa1 (на входе элемента логическая единица) через обмотку реле протекает ток, достаточный для размыкания контактов К1.1, поэтому лампочка перестает гореть (логический нуль). В результате анализа мы получили, что сигнал на выходе элемента противоположен сигналу на входе, т.е. если на входе элемента сигнал логической единицы, то на выходе элемента сигнал логического нуля и наоборот (рис. 1.3,в).
При анализе работы логических элементов следует помнить о режиме их работы (режим положительной или отрицательной логики). Логические элементы, реализующие для режима положительной логики операцию И, для
режима отрицательной логики выполняют операцию ИЛИ и наоборот. Решим следующую задачу.
Задача. Какую логическую операцию выполняет контактно-релейная схема, приведенная на рисунке 1.4.
Правильным ответом в этой задаче будет следующий. Указанная контактно-релейная схема выполняет операцию 3И для режима положительной логики и 3ИЛИ для режима отрицательной логики (решение обосновать самостоятельно).
В практической работе широко используются комбинации логических элементов и особенно элементы И-НЕ и ИЛИ-НЕ. Рассмотрим подробнее контактно-релейную схему элемента 2ИЛИ-НЕ, приведенную на рисунке 1.5,а. Условное обозначение элемента на принципиальных схемах показано на рисунке 1.5,б. Заполним таблицу истинности, приведенную на рисунке 1.5в. Если оба ключа разомкнуты (Х1=0, Х2=0), то лампочка HL1 горит, что соответствует логической единице на выходе элемента (Y=1). Замкнем контакты ключа Sa1 (Х1=1), оставляя ключ Sa2 разомкнутым (Х2=0). Лампочка HL1 в этом случае не горит (Y=0). Если замкнут хотя бы один ключ, то лампочка не горит. Следовательно, активным логическим уровнем на входе элемента ИЛИ-НЕ является уровень логической единицы.
Для двух аргументов логического элемента возможны 16 логических функций. В данном пособии рассматриваются логические функции: логическое И, логическое ИЛИ, логическое НЕ, логическое И-НЕ, логическое ИЛИ-НЕ, сумма по модулю 2.
В таблице 1.1 приведены условные обозначения элементов 2И, 2ИЛИ, НЕ, 2И-НЕ, 2ИЛИ-НЕ, исключающее ИЛИ (сумма по модулю 2), условные обозначения выполняемых этими элементами логических операций, таблицы их истинности и контактно-релейные схемы. При анализе контактно-релейной схемы элемента исключающее ИЛИ необходимо учитывать, что положения переключателей SA1 и SA2 в таблице 1.1 соответствуют логическим единицам (верхнее положение подвижного контакта переключателя соответствует логической единице), т.е. Х1=1 и Х2=1. Лампочка HL1 горит лишь в том случае, когда подвижный контакт одного из переключателей находится в верхнем положении, а подвижный контакт второго переключателя в нижнем положении. Из анализа работы данной контактно-релейной схемы получаем таблицу истинности элемента исключающее ИЛИ.
Рассмотрим решение следующей задачи: имея в распоряжении логические элементы 2И-НЕ, сконструировать устройство, реализующее операцию 3ИЛИ-НЕ для режима положительной логики. Эту задачу решим в два этапа. Сначала сконструируем устройство, выполняющее операцию 3И-НЕ для режима положительной логики (рис. 1.6,а), а потом на входах и выходе элемента 3И-НЕ установим логические элементы НЕ (рис. 1.6,б).
По мере развития вычислительной техники электронные логические элементы совершенствовались. Рассмотрим принципиальную схему логического элемента 2И (рис. 1.7,а), построенного на диодах и резисторах. Для простоты рассмотрения будем считать, что напряжение логического «0» на входе элемента равно 0 В, а напряжение логической «1» – 5 В. Внутреннее сопротивление вольтметра значительно больше сопротивления резистора R1.
Вспомним особенности вольтамперной характеристики полупроводникового кремниевого диода небольшой мощности. При обратном напряжении ток, протекающий через диод, составляет десятые доли микроампера. Напряжение на диоде при протекании через него в прямом направлении тока в десятки миллиампер, равно приблизительно 0,7-0,8 В. Определим примерно параметры логических уровней на выходах данного элемента, если на входе действуют логические уровни с указанными ранее параметрами. Если на оба входа поданы напряжения логических «1», то токи через диоды VD1 и VD2 не протекают, и напряжение на выходе элемента при условии, что сопротивление нагрузки значительно больше сопротивления резистора R1, будет примерно равно напряжению питания. Если хотя бы один из входов элемента соединить с минусовым проводом источника питания, то на выходе элемента в случае кремниевых диодов будет напряжение 0,7 – 0,8 В (зависит от сопротивления резистора R1 и напряжения источника питания).
Примечание: для рассмотренного логического элемента логическая «1» на входе будет, если вход никуда не подключен или подключен к плюсовому выводу источника питания.
На рисунке 1.7,б приведена схема простого и удобного в работе стенда для исследования диодно-резистивного логического элемента 2И. Светодиоды VD3 – VD5 являются индикаторами логических сигналов на входах и выходе логического элемента. Вольтметр V позволяет определить напряжения логической единицы и логического нуля. Для диодно-резистивного логического элемента 2И напряжение логического нуля на выходе примерно 0,7-0,8 В, а напряжение логической единицы чуть меньше напряжения на зажимах источника питания (определяется соотношением сопротивлений резистора R1 и нагрузки).
На рисунках 1.8,а и 1.8,б приведены схемы для исследования диодно-резистивного логического элемента 2ИЛИ. Для этого элемента напряжение логического нуля на выходе равно 0 В, а напряжение логической единицы равно напряжению питания минус 0,7-0,8 В.
Следующим этапом совершенствования элементной базы цифровой техники было создание логических элементов диодно-транзисторной логики.
Рассмотрим принципиальную схему логического элемента 2И-НЕ диодно-транзисторной логики (рис. 1.9,а).
Для понимания принципа работы логического элемента 2И-НЕ диодно-транзисторной логики необходимо знать, какой вид имеет зависимость тока коллектора транзистора от напряжения база-эмиттер при постоянном напряжении эмиттер- коллектор. Эта характеристика имеет примерно такой же вид, как и прямая ветвь вольтамперной характеристики полупроводникового диода. Для кремниевых транзисторов при напряжении база-эмиттер (в прямом направлении) менее 0,5 В ток в цепи коллектор-эмиттер практически равен нулю при любых допустимых напряжениях коллектор-эмиттер (транзистор закрыт, сопротивление между коллектором и эмиттером закрытого транзистора VТ1 может достигать единиц МОм). При незначительном увеличении напряжения база-эмиттер (в прямом направлении) более 0,5 В ток коллектора значительно увеличивается, говорят, что транзистор открывается.
Диоды VD1, VD2 и резистор R1 (рис. 1.9,а) образуют логический элемент 2И. Роль инвертора выполняет транзистор VT1. Если транзистор закрыт, то ток в цепи: плюс источника питания, резистор R2, коллектор-эмиттер транзистора VT1, минус источника питания не протекает и напряжение между эмиттером и коллектором транзистора будет равно напряжению на зажимах источника питания. Диоды VД3, VД4 необходимы для надежного закрытия транзистора VТ1, когда хотя бы на одном из входов элемента было напряжение логического нуля.
Если на обоих входах Х1, Х2 присутствуют сигналы логических единиц, транзистор VT1 открывается током базы, протекающим по цепи: плюс источника питания, резистор R1, диоды VD3, VD4, переход база-эмиттер транзистора VT1, минус источника. На выходе элемента будет напряжение 0,1-0,2 В, что соответствует логическому нулю.
На рисунке 1.9,б приведен вариант логического элемента 2И-НЕ на транзисторах. Инвертор на транзисторе VT1 не обеспечивает большую нагрузочную способность, поэтому в качестве инверторов применяют более сложные схемы. Сложный инвертор в микросхемах транзисторно-транзисторной логики будет рассмотрен чуть позже. Сейчас остановимся на принципе работы инверторов, схемы которых приведены на рисунке 1.10.
Рассмотрим делитель напряжения (делитель напряжения источника питания) образованного резистором R3 и цепью коллектор-эмиттер транзистора VТ1 (рис.1.10,а). Если на входе элемента логическая единица (подвижный контакт переключателя SA1 в верхнем положении), то транзистор VT1 открыт и в его коллекторной цепи протекает ток. Напряжение между коллектором и эмиттером транзистора составляет десятые доли вольта (не более 0,4 В). При логическом нуле на входе элемента транзистор закрыт и напряжение на выходе элемента равно напряжению питания, что соответствует логической единице.
На рисунках 1.10,б и 1.10,в приведены схемы инверторов с использованием полевых транзисторов. Напомним устройство и принцип действия полевых транзисторов. Существуют следующие виды полевых транзисторов: полевые транзисторы с управляющим p-n переходом, полевые транзисторы с изолированным затвором со встроенным каналом, полевые транзисторы с изолированным затвором с индуцированным каналом.
Полевые транзисторы называются также униполярными, одноканальными. Полевой транзистор в отличие от биполярного имеет большое входное сопротивление по цепи управления. Ток в выходной цепи полевого транзистора управляется напряжением, в то время как в биполярном транзисторе ток в выходной цепи транзистора управляется током во входной цепи транзистора. Таким образом, мощность управления в полевом транзисторе значительно меньше, чем в биполярном.
Полевой транзистор имеет 3 вывода: исток, сток, затвор. Исток – это вывод полевого транзистора, от которого основные носители заряда идут в канал. Сток – это вывод полевого транзистора, к которому идут основные носители заряда из канала. Затвор – это вывод полевого транзистора, на который подается управляющее напряжение относительно истока или относительно стока.
Наибольшее распространение имеют схемы включения транзистора с общим истоком, когда управляющее напряжение подается на затвор относительно истока.
В вычислительной технике в качестве электронных ключей широко используются полевые транзисторы с изолированным затвором с индуцированным каналом. Рассмотрим устройство и принцип действия полевого транзистора с изолированным затвором с индуцированным каналом n-типа (рис. 1.11). В полупроводнике p-типа сделаны два кармана с проводимостью n-типа. Знак n+ указывает на большую концентрацию электронов, что делается для уменьшения сопротивлений выводов стока и истока. Металлический затвор изолирован от кристалла полупроводника.
При напряжении затвор-исток, равном нулю, в цепи сток-исток ток не протекает при любых допустимых напряжениях сток-исток, так как образуются два p-n перехода, причем верхний подключен в обратном направлении.
Подадим на затвор относительно истока положительный потенциал. В полупроводниках p-типа имеются неосновные носители заряда (электроны). Рассмотрим движение электронов и дырок в слое полупроводника p-типа, прилежащем к затвору. Для упрощения рассмотрения соединим область p-типа с выводом истока. Под действием электрического поля, обусловленного наличием напряжения затвор – исток, дырки будут двигаться вправо, а электроны влево, т.е. в полупроводнике в приграничной к затвору области концентрация дырок уменьшается, а концентрация электронов увеличивается. При определенном напряжении затвор-исток в указанной области концентрация электронов станет больше концентрации дырок, наступит инверсия проводимости, т.е. в приграничной к затвору области появится слой полупроводника n-типа. В этом случае в цепи сток-исток протекает ток, т.к. между выводами стока и истока появился канал n-типа. Этот канал называется индуцированным (наведенным).
Для понимания принципа работы логических элементов на полевых транзисторах необходимо знать, что собой представляет стоко-затворная характеристика полевого транзистора. Стоко-затворная характеристика полевого транзистора в схеме включения с общим истоком (исток является общим для входной и выходной цепи) – это зависимость тока стока от напряжения затвор-исток при постоянном напряжении сток-исток. Эта характеристика полевого транзистора с изолированным затвором с индуцированным каналом n-типа приведена на рисунке 1.12. Особенности стоко-затворных характеристик полевых транзисторов с изолированным затвором с индуцированным каналом позволяют использовать эти транзисторы в качестве электронных ключей. Сравним основные характеристики электронного ключа на полевом транзисторе с характеристиками механического ключа. Сопротивление разомкнутого механического ключа можно считать бесконечно большим (пока не наступит электрический пробой), сопротивление ключа на полевом транзисторе порядка 10 МОм. Когда контакты механического ключа замкнуты сопротивление между контактами составляет сотые доли ома, для такого же состояния полевого транзистора сопротивление между стоком и истоком сотни Ом.
Если на входе инвертора, схема которого приведена на рисунке 1.10,б, напряжение логической единицы, то сопротивление между выводами сток и исток транзистора мало. Сопротивление резистора R1 выбирают значительно больше сопротивления между стоком и истоком открытого полевого транзистора и, следовательно, напряжение на выходе элемента будет близко к нулю вольт. При логическом нуле на входе логического элемента НЕ полевой транзистор будет закрыт, и на выходе элемента будет напряжение, примерно равное напряжению источника питания. Это обусловлено тем, что сопротивление резистора R1 выбирают во много раз меньше сопротивления между стоком и истоком закрытого транзистора.
Рассмотрим принцип работы инвертора (логического элемента НЕ) КМОП (комплиментарный, металл, окисел, полупроводник) структуры (рис. 1.10,в). Комплиментарный означает дополняющий друг друга по типу проводимости. Микросхемы КМОП имеют транзисторы как с каналом p-типа, так и с каналом n-типа. Учтем, что сопротивление между выводами сток-исток открытого транзистора – 200-300 Ом, а сопротивление между выводами сток-исток закрытого транзистора более 10 МОм.
Выберем напряжение питания 9 В. Пусть на вход Х подано напряжение логического «0», тогда транзистор VТ2 будет закрыт, а транзистор VТ1 открыт, так как потенциал затвора транзистора VТ1 относительно истока этого же транзистора равен минус 9В. На выходе элемента логическая единица.
Подадим на вход Х напряжение, соответствующее логической единице. Для рассмотренного случая это + 9 В относительно общего провода. В этом случае транзистор VТ2 будет открыт, а транзистор VТ1 – закрыт и на выходе элемента будет напряжение логического нуля.
Рассмотрим основные параметры, которыми характеризуются цифровые микросхемы.
Помехоустойчивость Uп, макс – наибольшее значение напряжения помехи на входе микросхемы, при котором еще не происходит изменения уровней ее выходного напряжения.
Напряжение логической единицы U1 – значение высокого уровня напряжения для “положительной” логики и значение низкого уровня напряжения для “отрицательной” логики.
Напряжение логического нуля U0 – значение низкого уровня напряжения для “положительной” логики и значение высокого уровня напряжения для “отрицательной” логики.
Пороговое напряжение логической единицы U1пор – наименьшее значение высокого уровня напряжения для “положительной” логики или наибольшее значение низкого уровня напряжения для “отрицательной” логики на входе микросхемы, при котором она переходит из одного устойчивого состояния в другое.
Пороговое напряжение логического нуля U0пор – наибольшее значение низкого уровня напряжения для “положительной” логики или наименьшее значение высокого уровня напряжения для “отрицательной” логики на входе микросхемы, при котором она переходит из одного устойчивого состояния в другое.
Входной ток логической единицы I1вх – измеряется при заданном значении напряжения логической единицы.
Входной ток логического нуля I0вх – измеряется при заданном значении напряжения логического нуля.
Выходной ток логической единицы I1вых – измеряется при заданном значении напряжения логической единицы.
Выходной ток логического нуля I0вых– измеряется при заданном значении напряжения логического нуля.
Ток потребления в состоянии логической единицы I1пот – значение тока, потребляемого микросхемой от источников питания при логических единицах на выходах всех элементов.
Ток потребления в состоянии логического нуля I0пот – значение тока, потребляемого микросхемой от источников питания при логических нулях на выходах всех элементов.
Средний ток потребления Iпот. ср. – значение тока, равное полусумме токов, потребляемых цифровой микросхемой от источников питания в двух устойчивых различных состояниях.
Потребляемая мощность в состоянии логической единицы Р1пот – значение мощности, потребляемой микросхемой от источника питания при логических единицах на выходах всех элементов.
Потребляемая мощность в состоянии логического нуля Р0пот – значение мощности, потребляемой микросхемой от источника питания при логических нулях на выходах всех элементов.
Средняя потребляемая мощность Рпот. ср.– полусумма мощностей, потребляемых микросхемой от источников питания в двух устойчивых различных состояниях.
Время перехода интегральной микросхемы из состояния логической единицы в состояние логического нуля t1,0 – интервал времени, в течение которого напряжение на выходе микросхемы переходит от напряжения логической единицы к напряжению логического нуля, измеренный на уровнях напряжения 0,1 и 0,9 от амплитуды импульса.
Время перехода интегральной микросхемы из состояния логического нуля в состояние логической единицы t0,1 – интервал времени, в течение которого напряжение на выходе микросхемы переходит от напряжения логического нуля к напряжению логической единицы, измеренный на уровнях напряжения 0,1 и 0,9 от амплитуды импульса.
Время задержки распространения сигнала при включении t1,0зд, р – интервал времени между входным и выходным импульсами при переходе напряжения на выходе микросхемы от напряжения логической единицы к напряжению логического нуля, измеренный на уровне 0,5 амплитуды.
Время задержки распространения сигнала при выключении t0,1зд, р – интервал времени между входным и выходным импульсами при переходе напряжения на выходе микросхемы от логического нуля к логической единицы, измеренный на уровне 0,5 амплитуды.
Среднее время задержки распространения сигнала tзд, р.с.– интервал времени, равный полусумме времени задержки распространения сигнала при включении и выключении цифровой микросхемы.
Коэффициент объединения по входу Коб – число входов микросхемы, по которым реализуется логическая функция.
Коэффициент разветвления по выходу Краз – число единичных нагрузок, которые можно одновременно подключить к выходу микросхемы (единичной нагрузкой является один вход основного логического элемента данной серии интегральных микросхем).
Коэффициент объединения по выходу Коб.вых – число соединяемых между собой выходов интегральной микросхемы, при котором обеспечивается реализация соответствующей логической операции.
Сопротивление нагрузки Rн – значение активного сопротивления нагрузки, подключаемой к выходу интегральной микросхемы, при котором обеспечивается заданное значение выходного напряжения (выходного тока) или заданное усиление.
Емкость нагрузки Сн – максимальное значение емкости, подключенной к выходу интегральной микросхемы, при котором обеспечиваются заданные частотные и иные параметры.
Синхронизация работы отдельных узлов ЭВМ и других устройств цифровой техники осуществляется периодическими последовательностями прямоугольных импульсов напряжения. Импульсом напряжения называют отклонение напряжения от первоначального значения в течение короткого промежутка времени. Последовательность импульсов, мгновенные значения которых повторяются через равные промежутки времени, называют периодической последовательностью импульсов. Участок импульса, на котором происходит изменение напряжения от начального уровня до конечного, называют фронтом импульса, а участок, на котором напряжение возвращается к исходному уровню, называется срезом импульса. Длительностью фронта импульса считают время нарастания напряжения от 0,1 Uм до 0,9 Uм, а длительностью среза – время изменения напряжения от 0,9 Uм до 0,1 Uм, где Uм – амплитуда импульса. Когда говорят о длительности импульса, то необходимо указывать, на каком уровне от амплитуды импульса проводились измерения: на уровне 0,1 Uм или 0,5 Uм. Частота следования импульсов – это число импульсов в одну секунду. Период следования импульсов – это минимальное время, через которое повторяются мгновенные значения напряжения. Интервал времени между окончанием одного импульса и началом следующего называется паузой. Величину, равную отношению периода следования импульсов к длительности импульса, называют скважностью импульсов. Периодическая последовательность прямоугольных импульсов при скважности 2 называется меандром. Прямоугольный импульс напряжения иногда рассматривают как совокупность двух перепадов напряжения. Перепады напряжения – это быстрые изменения напряжения между двумя уровнями. Перепад называют положительным, если напряжение изменяется от низкого уровня к высокому, и отрицательным, если напряжение изменяется от высокого уровня к низкому. Перепад напряжения, у которого длительность равна нулю, называется скачком напряжения.
На рисунке 1.13 показано, как определяется длительность фронта входного импульса tф, время перехода интегральной микросхемы из состояния логической единицы в состояние логического нуля t1,0, время перехода интегральной микросхемы из состояния логического нуля в состояние логической единицы t0,1, время задержки распространения при включении t1,0зд, р, время задержки распространения при выключении t0,1зд, р .
Что такое логический вентиль (AND, OR, XOR, NOT, NAND, NOR и XNOR)? Определение с сайта WhatIs.com
Логический вентиль – это устройство, которое действует как строительный блок для цифровых схем. Они выполняют основные логические функции, которые являются фундаментальными для цифровых схем. В большинстве электронных устройств, которые мы используем сегодня, есть логические вентили. Например, логические вентили могут использоваться в таких технологиях, как смартфоны, планшеты или устройства памяти.
В схеме логические вентили будут принимать решения на основе комбинации цифровых сигналов, поступающих с их входов.Большинство логических вентилей имеют два входа и один выход. Логические вентили основаны на булевой алгебре. В любой момент каждый терминал находится в одном из двух двоичных состояний: ложно или истинно . Ложь представляет 0, а истина представляет 1. В зависимости от типа используемого логического элемента и комбинации входов двоичный выход будет отличаться. Логический вентиль можно представить себе как выключатель света, в котором в одном положении выход выключен – 0, а в другом – включен – 1. Логические вентили обычно используются в интегральных схемах (IC).
Базовые логические вентилиСуществует семь основных логических вентилей: И, ИЛИ, ИСКЛЮЧАЮЩЕЕ ИЛИ, НЕ, И-НЕ, ИЛИ-ИЛИ и ИСКЛЮЧАЮЩЕЕ ИЛИ.
И | ИЛИ | XOR | НЕ | NAND | NOR | XNOR
Логический элемент И назван так потому, что, если 0 называется «ложным», а 1 называется «истинным», элемент действует так же, как логический оператор «И». На следующем рисунке и в таблице показаны символы схемы и логические комбинации для логического элемента И. (В символе входные клеммы слева, а выходные клеммы справа.) Выход «истина», когда оба входа «истина». В противном случае вывод будет «ложным». Другими словами, выход равен 1 только тогда, когда оба входа один И два равны 1.
И ворота
| Вход 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Логический элемент ИЛИ получил свое название от того факта, что он ведет себя по образцу логического включающего “или”.«Выход -« истина », если один или оба входа равны« истина ». Если оба входа« ложь », то выход« ложь ». Другими словами, для выхода будет 1, по крайней мере, вход один ИЛИ два должны быть 1.
OR ворота
| Вход 1 | Ввод 2 | Выход |
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 | 1 |
Логический элемент XOR ( исключающее ИЛИ ) вентиль действует так же, как логическое «или / или».«Выходной сигнал« истина », если один из входов, но не оба, являются« истиной ». Выходной сигнал« ложь », если оба входа« ложь »или если оба входа« истина ». Другой способ взглянуть на это Схема должна следить за тем, чтобы на выходе было 1, если входы разные, и 0, если входы одинаковые.
Вентиль XOR
| Вход 1 | Ввод 2 | Выход |
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Логический преобразователь , иногда называемый вентилем НЕ , чтобы отличать его от других типов электронных инверторных устройств, имеет только один вход.Он меняет логическое состояние на обратное. Если на входе 1, то на выходе 0. Если на входе 0, то на выходе 1.
Инвертор или НЕ вентильЛогический элемент И-НЕ работает как логический элемент И, за которым следует логический элемент НЕ. Он действует как логическая операция «и» с последующим отрицанием. На выходе будет «ложь», если оба входа «истина». В противном случае на выходе будет «истина».
вентиль NAND
| Вход 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Логический элемент ИЛИ представляет собой комбинацию логического элемента ИЛИ, за которым следует инвертор.Его выход будет «истина», если оба входа «ложь». В противном случае вывод будет «ложным».
NOR ворота
| Вход 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 |
Логический элемент XNOR (исключающее ИЛИ) – это комбинированный вентиль XOR, за которым следует инвертор.Его вывод – «истина», если входы одинаковые, и «ложь», если входы разные.
Ворота XNOR
| Вход 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Сложные операции могут выполняться с использованием комбинаций этих логических вентилей.Теоретически нет ограничений на количество ворот, которые могут быть объединены в одно устройство. Но на практике существует ограничение на количество ворот, которые могут быть упакованы в данное физическое пространство. Массивы логических вентилей находятся в цифровых ИС. По мере развития технологии ИС требуемый физический объем для каждого отдельного логического элемента уменьшается, и цифровые устройства того же или меньшего размера становятся способными выполнять все более сложные операции с постоянно увеличивающейся скоростью.
Состав логических вентилей
Высокий или низкий двоичные состояния представлены разными уровнями напряжения.Логическое состояние терминала может и обычно часто изменяется по мере того, как схема обрабатывает данные. В большинстве логических вентилей низкое состояние составляет приблизительно ноль вольт (0 В), а высокое состояние – приблизительно пять вольт положительного напряжения (+5 В).
Логические вентили могут быть выполнены из резисторов и транзисторов или диодов. Резистор обычно можно использовать как подтягивающий или понижающий резистор. Подтягивающие и понижающие резисторы используются, когда есть какие-либо неиспользуемые входы логического элемента для подключения к логическому уровню 1 или 0.Это предотвращает ложное переключение ворот. Подтягивающие резисторы подключены к Vcc (+ 5 В), а подтягивающие резисторы подключены к земле (0 В).
Обычно используются логические вентили TTL и CMOS. ИС TTL или транзисторно-транзисторной логики будут использовать биполярные переходные транзисторы типа NPN и PNP. КМОП, или дополнительные металл-оксидно-кремниевые ИС, построены из полевых транзисторов типа MOSFET или JFET. ИС TTL обычно обозначают как микросхемы серии 7400, в то время как ИС КМОП часто обозначают как микросхемы серии 4000.
Основные логические ворота с таблицами истинности
В наши дни компьютеры стали неотъемлемой частью жизни, поскольку они выполняют множество задач и операций за довольно короткий промежуток времени. Одной из наиболее важных функций ЦП в компьютере является выполнение логических операций с использованием оборудования, такого как программные технологии и электронные схемы интегральных схем. Но как это оборудование и программное обеспечение выполняют такие операции – загадочная загадка. Чтобы лучше понять такую сложную проблему, мы должны познакомиться с термином «логическая логика», разработанным Джорджем Булем.Для простой операции компьютеры используют двоичные цифры, а не цифровые. Все операции выполняются воротами базовой логики. В этой статье обсуждается обзор того, что такое базовые логические вентили в цифровой электронике и их работа.
Что такое основные логические вентили?
Логический вентиль – это базовый строительный блок цифровой схемы, имеющей два входа и один выход. Отношения между i / p и o / p основаны на определенной логике. Эти затворы реализованы с помощью электронных ключей типа транзисторов, диодов.Но на практике базовые логические вентили строятся с использованием технологии CMOS, полевых транзисторов и полевых транзисторов MOSFET (Metal Oxide Semiconductor FET). Логические вентили используются в микропроцессорах, микроконтроллерах, встроенных системных приложениях, а также в электронных и электрических схемах проектов. Основные логические элементы делятся на семь категорий: AND, OR, XOR, NAND, NOR, XNOR и NOT. Эти логические вентили с их символами логических вентилей и таблицами истинности объясняются ниже.
Работа с основными логическими вентилямиЧто такое 7 основных логических вентилей?
Основные логические вентили подразделяются на семь типов: вентиль И, вентиль ИЛИ, вентиль ИЛИ, вентиль И-НЕ, вентиль ИЛИ, вентиль ИЛИ-ИЛИ и вентиль НЕ.Таблица истинности используется для демонстрации функции логического элемента. Все логические элементы имеют два входа, кроме элемента НЕ, который имеет только один вход.
При построении таблицы истинности используются двоичные значения 0 и 1. Каждая возможная комбинация зависит от количества входов. Если вы не знаете о логических вентилях и их таблицах истинности и нуждаетесь в руководстве по ним, просмотрите следующую инфографику, которая дает обзор логических вентилей с их символами и таблицами истинности.
Почему мы используем базовые логические вентили?
Базовые логические элементы используются для выполнения основных логических функций.Это основные строительные блоки цифровых ИС (интегральных схем). Большинство логических вентилей используют два двоичных входа и генерируют один выход, например 1 или 0. В некоторых электронных схемах используется несколько логических вентилей, тогда как в некоторых других схемах микропроцессоры включают в себя миллионы логических вентилей.
Реализация логических вентилей может осуществляться с помощью диодов, транзисторов, реле, молекул и оптики, иначе говоря, различных механических элементов. По этой причине основные логические вентили используются как электронные схемы.
Двоичные и десятичные числа
Прежде чем говорить о таблицах истинности логических вентилей, важно знать предысторию двоичных и десятичных чисел. Все мы знаем десятичные числа, которые мы используем в повседневных вычислениях, например от 0 до 9. Такая система счисления включает в себя десятичную систему счисления. Таким же образом двоичные числа, такие как 0 и 1, могут использоваться для обозначения десятичных чисел, если основание двоичных чисел равно 2.
Значение использования двоичных чисел здесь состоит в том, чтобы обозначать положение переключения, в противном случае положение напряжения цифрового компонента .Здесь 1 представляет высокий сигнал или высокое напряжение, тогда как «0» указывает низкое напряжение или низкий сигнал. Таким образом, была начата булева алгебра. После этого каждый логический вентиль обсуждается отдельно, он содержит логику логического элемента, таблицу истинности и ее типичный символ.
Типы логических вентилей
Различные типы логических вентилей и символов с таблицами истинности обсуждаются ниже.
Базовые логические вентилиИ вентиль
Логический вентиль И представляет собой цифровой логический вентиль с “n” i / ps и одним o / p, который выполняет логическое соединение на основе комбинаций своих входов.Выход этого вентиля истинен только тогда, когда все входы истинны. Когда один или несколько входов i / ps логического элемента И являются ложными, тогда только выход логического элемента И является ложным. Таблица символов и истинности логического элемента И с двумя входами показана ниже.
Логический элемент И и его таблица истинностиЛогический элемент ИЛИ
Логический элемент ИЛИ – это цифровой логический вентиль с n i / ps и одним o / p, который выполняет логическое соединение на основе комбинаций своих входов. Выход логического элемента ИЛИ истинен только тогда, когда один или несколько входов истинны.Если все i / ps логического элемента ложны, то ложным является только выход логического элемента ИЛИ. Таблица символов и истинности логического элемента ИЛИ с двумя входами показана ниже.
Логический элемент ИЛИ и его таблица истинностиЭлемент НЕ
Элемент НЕ представляет собой цифровой логический элемент с одним входом и одним выходом, который управляет инверторной операцией входа. Выход логического элемента НЕ является обратным входу. Когда вход логического элемента НЕ истинен, тогда выход будет ложным, и наоборот. Таблица символов и истинности логического элемента НЕ с одним входом показана ниже.Используя этот вентиль, мы можем реализовать вентили ИЛИ и И-НЕ.
Шлюз НЕ и его таблица истинностиШлюз И-НЕ
Логический вентиль И-НЕ – это цифровой логический вентиль с ‘n’ i / ps и одним o / p, который выполняет операцию вентиль И, за которым следует вентиль НЕ. Элемент НЕ разработан путем объединения вентилей И и НЕ. Если вход логического элемента И-НЕ высокий, то выход элемента будет низким. Ниже показаны символы и таблица истинности логического элемента И-НЕ с двумя входами.
Шлюз И-НЕ и его таблица истинностиШлюз ИЛИ
Шлюз ИЛИ-НЕ – это цифровой логический вентиль с n входами и одним выходом, который выполняет операцию логического элемента ИЛИ, за которым следует вентиль НЕ.Ворота NOR спроектированы путем объединения ворот OR и NOT. Когда любой из i / ps логического элемента ИЛИ-НЕ истинен, тогда выход логического элемента ИЛИ-НЕ будет ложным. Таблица символов и истинности ворот ИЛИ-НЕ с таблицей истинности показана ниже. Элемент
ИЛИ-ИЛИ и его таблица истинностиЭлемент исключающего ИЛИ
Элемент исключающего ИЛИ – это цифровой логический вентиль с двумя входами и одним выходом. Краткая форма этих ворот – Ex-OR. Он работает на основе операции логического элемента ИЛИ. . Если на каком-либо из входов этого логического элемента высокий уровень, то выход логического элемента EX-OR будет высоким.Символы и таблица истинности EX-OR показаны ниже. Элемент
EX-OR и его таблица истинностиЭлемент Exclusive-NOR
Элемент Exclusive-NOR – это цифровой логический элемент с двумя входами и одним выходом. Краткая форма этих ворот – Ex-NOR. Он работает на основе работы логического элемента ИЛИ-НЕ. Когда оба входа этого логического элемента имеют высокий уровень, тогда выход элемента ИСКЛЮЧАЮЩЕЕ НЕ будет высоким. Но если один из входов высокий (но не оба), то выход будет низким. Символы и таблица истинности EX-NOR показаны ниже.
Шлюз EX-NOR и его таблица истинностиПрименение логических вентилей в основном определяется на основе их таблицы истинности, то есть режима их работы. Базовые логические вентили используются во многих схемах, таких как кнопочный замок, охранная сигнализация с включением света, предохранительный термостат, автоматическая система полива и т.д. общий метод известен как таблица истинности. Эта таблица включает все комбинации входных логических состояний: высокий (1) или низкий (0) для каждой входной клеммы логического элемента через эквивалентный выходной логический уровень, такой как высокий или низкий.Схема логического элемента НЕ показана выше, и ее таблица истинности действительно чрезвычайно проста.
Таблицы истинности логических элементов очень сложны, но больше, чем вентиль НЕ. Таблица истинности каждого гейта должна включать много строк, как будто есть возможности для эксклюзивных комбинаций для входных данных. Например, для логического элемента НЕ есть две возможности ввода: 0 или 1, тогда как для логического элемента с двумя входами есть четыре возможности, такие как 00, 01, 10 и 11. Таким образом, он включает четыре строки для эквивалентная таблица истинности.
Для логического элемента с 3 входами существует 8 возможных входов, таких как 000, 001, 010, 011, 100, 101, 110 и 111. Следовательно, требуется таблица истинности, включающая 8 строк. Математически необходимое количество строк в таблице истинности эквивалентно двум, увеличенным в степени «нет». i / p терминалов.
Анализ
Сигналы напряжения в цифровых схемах представлены двоичными значениями, такими как 0 и 1, вычисленными относительно земли. Недостаток напряжения в основном означает «0», тогда как наличие полного напряжения питания постоянного тока означает «1».
Логический вентиль – это особый тип схемы усилителя, который в основном предназначен для входных и выходных логических напряжений. Схемы логического затвора чаще всего обозначаются схематической диаграммой с помощью их собственных эксклюзивных символов вместо основных резисторов и транзисторов.
Как и в случае с операционными усилителями, соединения источника питания с логическими вентилями часто неуместны на схематических диаграммах в целях упрощения. Он включает возможные комбинации входных логических уровней через их конкретные выходные логические уровни.
Какой самый простой способ выучить логические ворота?
Ниже объясняется самый простой способ изучить функции основных логических вентилей.
- Для логического элемента И – Если оба входа имеют высокий уровень, то и выход также высокий
- Для ворот ИЛИ – Если минимум одного входа высокий, то выход высокий высокий, тогда высокий только выход
- Шлюз И-НЕ – Если минимальный один вход низкий, то выход высокий
- ИЛИ вентиль – Если оба входа низкие, то выход высокий.
Теорема Де Моргана
Первая теорема ДеМоргана утверждает, что логический элемент, такой как И-НЕ, равен элементу ИЛИ с пузырьком. Логическая функция логического элемента И-НЕ:
A’B = A ’+ B’
Вторая теорема ДеМоргана утверждает, что логический элемент ИЛИ-НЕ равен логическому элементу И с пузырьком. Логическая функция логического элемента ИЛИ-НЕ:
(A + B) ’= A’. B ’
Преобразование логического элемента И-НЕ
Логический элемент И-НЕ может быть сформирован с использованием логического элемента И и НЕ.Булево выражение и таблица истинности показаны ниже.
Формирование логических ворот NANDY = (A⋅B) ‘
A | B | Y ′ = A ⋅B | Y | ||
0 | 0 | 0 | 1 | ||
0 | 1 | 0 | |||
| 1 | 0 | 0 | 1 | ||
| 1 | 1 | 1 |
A | B | Y ′ = A + B | Y | ||
0 | 0 | 0 | 1 | ||
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
Вентиль Ex-OR может быть сформирован с помощью элемента НЕ, И и ИЛИ.Булево выражение и таблица истинности показаны ниже. Этот логический вентиль может быть определен как вентиль, который дает высокий выход, когда на любом его входе высокий уровень. Если на обоих входах этого затвора высокий уровень, то выход будет низким.
Формирование логических вентилей Ex-ORY = A⊕B или A’B + AB ‘
| A | B | Y |
0 | 0 | 0 |
0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | Преобразование ворот Ex-NORВентиль Ex-NOR может быть сформирован с использованием ворот EX-OR & NOT.Булево выражение и таблица истинности показаны ниже. В этом логическом элементе, когда на выходе высокий уровень «1», оба входа будут либо «0», либо «1». Формирование ворот Ex-NORY = (A’B + AB ‘)’ Базовые логические элементы с использованием универсальных воротУниверсальные элементы, такие как элемент И-НЕ и элемент ИЛИ-НЕ, могут быть реализованы с помощью любого логического выражения без использования какого-либо другого типа логического элемента. И их также можно использовать для проектирования любых базовых логических вентилей. Кроме того, они широко используются в интегральных схемах, поскольку они просты и экономичны в изготовлении.Базовая конструкция логических вентилей с использованием универсальных вентилей обсуждается ниже. Базовые логические вентили могут быть спроектированы с помощью универсальных вентилей. Он использует ошибку, небольшой тест, иначе вы можете использовать логическую логику для их достижения через уравнения логических вентилей для логического элемента И-НЕ, а также для элемента ИЛИ-НЕ. Здесь логическая логика используется для решения требуемых выходных данных. Это займет некоторое время, но необходимо выполнить это, чтобы получить представление о логической логике, а также основных логических вентилях. Базовые логические вентили, использующие вентиль И-НЕ Проектирование базовых логических вентилей с использованием логического элемента И-НЕ обсуждается ниже. Проектирование логического элемента НЕ с использованием NAND Проектирование логического элемента НЕ выполняется очень просто, просто соединяя оба входа как один. Проектирование логического элемента И с использованием NAND Проектирование логического элемента И с использованием логического элемента И-НЕ может быть выполнено на выходе логического элемента И-НЕ, чтобы изменить его и получить логическое И. Проектирование логического элемента ИЛИ с использованием NAND Проектирование логического элемента ИЛИ с использованием логического элемента И-НЕ может быть выполнено путем соединения двух вентилей НЕ с использованием логических элементов НЕ на входах ИЛИ для получения логики ИЛИ. Проектирование ворот NOR с использованием NAND Проектирование ворот NOR с использованием логического элемента NAND может быть выполнено простым подключением другого шлюза NOT через логический элемент NAND к выходу логического элемента OR через NAND. Проектирование ворот EXOR с использованием NAND Это немного сложно. Вы разделяете два входа с тремя воротами. Выход первой И-НЕ является вторым входом для двух других. Наконец, другая И-НЕ принимает выходные данные этих двух вентилей И-НЕ, чтобы дать окончательный результат. Базовые логические вентили, использующие вентиль ИЛИ-НЕ Проектирование базовых логических вентилей с использованием логического элемента ИЛИ-НЕ обсуждается ниже. Шлюз НЕ с использованием NOR Проектирование шлюза НЕ с вентилем ИЛИ выполняется просто, соединяя оба входа как один. Шлюз ИЛИ с использованием NOR Проектирование шлюза ИЛИ с вентилем ИЛИ выполняется просто путем подключения к выходу логического элемента ИЛИ-НЕ, чтобы изменить его и получить логику ИЛИ. Логический элемент И с использованием NOR Проектирование логического элемента И с использованием логического элемента ИЛИ-НЕ может быть выполнено путем соединения двух вентилей НЕ с ИЛИ-НЕ на входах ИЛИ-НЕ для получения логического ИЛИ. Шлюз NAND с использованием NOR Проектирование шлюза NAND с использованием элемента NOR может быть выполнено простым подключением другого шлюза NOT через элемент NOR к выходу элемента AND с NOR. EX-NOR Gate с использованием NOR Этот тип подключения немного сложен, потому что два входа могут использоваться совместно с тремя логическими вентилями. Первый выход логического элемента ИЛИ-НЕ является следующим входом для оставшихся двух вентилей. Наконец, другой вентиль ИЛИ-НЕ использует два выхода логического элемента ИЛИ-НЕ для обеспечения последнего выхода. ПриложенияПриложений базовых логических вентилей очень много, однако они в основном зависят от своих таблиц истинности, иначе форма операций. Базовые логические элементы часто используются в схемах, таких как замок с кнопкой, автоматическая система полива, сигнализация о взломе, активируемая светом, предохранительный термостат и другие типы электронных устройств. Основное преимущество базовых логических вентилей состоит в том, что они могут использоваться в другой комбинированной схеме.Кроме того, количество логических вентилей, которые можно использовать в одном электронном устройстве, не ограничено. Но его можно ограничить из-за указанного физического зазора внутри устройства. В цифровых ИС (интегральных схемах) мы обнаружим коллекцию блока области логического элемента. При использовании комбинации базовых логических вентилей часто выполняются сложные операции. Теоретически не существует ограничений на количество ворот, которые могут быть одеты во время одного устройства. Однако в приложении есть ограничение на количество ворот, которые могут быть упакованы в определенную физическую область.Массивы блока логических вентилей находятся в цифровых интегральных схемах (ИС). По мере развития технологии ИС желаемый физический объем для каждого отдельного затвора уменьшается, и цифровые устройства эквивалентного или меньшего размера становятся способными выполнять более сложные операции с постоянно увеличивающейся скоростью. Инфографика логических вентилейЭто все об обзоре того, что является основным логическим вентилем, такими типами, как вентиль И, вентиль ИЛИ, вентиль И-НЕ, вентиль ИЛИ-НЕ, вентиль ИСКЛЮЧАЮЩЕЕ ИЛИ и вентиль ИСКЛЮЧАЮЩЕЕ ИЛИ.В этом случае вентили И, НЕ и ИЛИ являются основными логическими вентилями. Используя эти вентили, мы можем создать любой логический вентиль, комбинируя их. Где ворота NAND и NOR называются универсальными воротами. У этих ворот есть особое свойство, с помощью которого они могут создавать любое логическое логическое выражение, если они спроектированы надлежащим образом. Кроме того, по любым вопросам, касающимся этой статьи или проектов в области электроники, просьба оставлять отзывы, комментируя их в разделе комментариев ниже. Логические ворота | RS ComponentsЛогические вентили – это физические компоненты в схеме, которые управляют потоком сигнала, реализуя логическую функцию, преобразуя сигнал в двоичную информацию.Логические вентили лежат в основе логических схем или любого процесса электронных схем, который включает в себя цифро-аналоговое преобразование сигнала или поток цифровой информации. Логические вентили в основном реализуются с использованием диодов или транзисторов в качестве электрических переключателей, но также могут быть сконструированы с использованием электромагнитных реле (релейная логика), вакуумных ламп, оптики, молекул, жидкостной логики, пневматической логики или даже механических элементов. Типы логических вентилейЛогические вентили имеют различные логические функции.Наиболее распространенные из них известны как основные ворота. К ним относятся:
Есть также комбинированные логические элементы функций, которые изменяют типичные функции с инверсией.
ПриложенияПоскольку процессоры используют двоичную логику, логические вентили, по сути, являются строительными блоками компьютеров. Как таковые, их можно найти во многих типах цифровых схем, таких как:
От логических вентилей к регистрам: изучение 74HC173В связи с ситуацией с Covid-19 и влиянием брексита, поставки в настоящее время ограничены только клиентами из Великобритании и США. От логических вентилей к регистрам: изучение 74HC173Логические вентили – это строительные блоки цифровой электроники. В этой заметке исследуется, что это такое и как они используются для построения 4-битного регистра. Введение в логические вентили Логические вентили – это фундаментальные строительные блоки цифровой электроники. Концептуально вы можете думать о них как о компоненте, который реализует логическую функцию (т. Е. Вывод равен 0 или 1).Их цель – выполнить логическую операцию над двумя или более двоичными входами, чтобы создать один двоичный выход. Они бывают разных видов и выполняют такие логические операции, как AND, OR, XOR, NOT, NOR, XNOR и NAND. Пожалуй, два наиболее наглядных примера этого – логические элементы И и ИЛИ. С вентилем И выход его функции равен 1, когда оба входа равны 1 (или, другими словами, когда A AND B равны 1). С вентилем ИЛИ выход его функции равен 1, когда любой из входов равен 1 (или, другими словами, когда A OR B равно 1). На рисунке 1 показана простая диаграмма логических вентилей И и ИЛИ вместе с соответствующими таблицами истинности, которые показывают, каков будет выход логического элемента для каждого возможного входа: Рисунок 1. Диаграмма и таблица истинности для логических вентилей И / ИЛИКонечно, И и ИЛИ – это всего лишь два примера основных логических вентилей. Но любопытным логическим вентилем для дальнейшего изучения является вентиль И-НЕ (НЕ И), потому что он обладает довольно особым свойством: «функциональной полнотой». Универсальный логический элемент NAND Логический элемент И-НЕ (НЕ И) является особенным, поскольку любая логическая функция может быть реализована с помощью комбинации элементов И-НЕ (это бит «функциональной полноты»).Или, другими словами, вы можете использовать комбинацию вентилей И-НЕ для представления любых других логических вентилей. Он похож на логический элемент И, за исключением того, что его выход инвертирован (это НЕ часть!). На рисунке 2 показаны символы и таблица истинности ворот. Рисунок 2. Схема и таблица истинности для логического элемента И-НЕПоскольку вентиль И-НЕ может использоваться для представления любого другого логического элемента, его можно рассматривать как «универсальный» логический элемент. Вы можете построить любой компонент на основе цифровой логики из логического элемента NAND – если вы так хотите, вы можете даже построить свой собственный компьютер полностью из них! На самом деле, у некоторых есть! Для любопытных, логические элементы NAND могут быть использованы или реализованы в практическом смысле с использованием классической интегральной схемы 74HC00.Этот чип представляет собой четырехканальный логический элемент NAND с двумя входами и основан на технологии CMOS. Вы можете просмотреть технические данные здесь. Рис. 3. Функциональная схема TI CD74HC00EНо прежде чем вы приступите к созданию собственного компьютера с логическим элементом NAND, давайте посмотрим, как с помощью шлюза NAND можно создать очень важный компонент в мире вычислительного оборудования: переворот D-типа. -Флоп. Вспоминая вещи: шлепанцы D-типа Логические вентили – мощные компоненты, но их назначение не ограничивается тривиальными логическими функциями.Логические вентили также могут использоваться для выполнения «последовательной логики» – это означает, что они также могут использоваться для запоминания информации (что довольно удобно). Чтобы сделать это возможным, необходимо организовать логические вентили для создания «защелкивающегося» механизма для хранения определенного фрагмента данных. Часто этот механизм представляет собой “ тактовый ” сигнал, который может запускаться по фронту или по уровню (события с запуском по фронту происходят, когда тактовый сигнал переходит с низкого на высокий, события, запускаемые по уровню, происходят, когда тактовый сигнал высокий) . Хорошим примером этого конкретного механизма или схемы является триггер D-типа (да, странное название) – изображенный на рисунке 4. Эта схема состоит из пяти вентилей И-НЕ (да, всеобщий любимый новый вентиль), с двумя входами и двумя выходами: вход данных (Data), тактовый сигнал (Clk), фиксированные данные (Q) и их инверсия (Q ‘ ), соответственно. Те, кто уже знаком с последовательной логикой, также заметят расположение триггеров SR справа от рисунка. Триггер D-типа работает очень просто: когда Clk высокий (1), выход Q устанавливается в значение Data (0 или 1) в этот момент времени.Когда Clk низкий (0), Q сохраняет свое значение / состояние независимо от значения данных. Q ‘всегда является обратным Q. Рис. 4. Тактовый триггер D-типаКонечно, это может показаться несколько тривиальным примером, но давайте посмотрим на 74HC173 – интегральную схему, которая объединяет несколько триггеров D-типа в одном корпусе. 4-битный регистр из триггеров D-типа 74HC173 – это четырехканальная флип-флип микросхема D-типа. Однако эта ИС не просто содержит четыре изолированных триггера D-типа – она использует общие часы между ними, позволяя синхронно хранить 4 бита информации в одном тактовом импульсе! И это, по сути, позволяет вам использовать IC как 4-битный регистр. Рисунок 5. Логическая схема 74HC173 IC74HC173 содержит более сложный массив триггеров D-типа, чем базовая конфигурация, показанная на рисунке 4, поскольку схемы включают некоторые дополнительные функции:
Чтобы понять это на практическом уровне, на рисунке 6 показана распиновка 74HC173, где D x – выводы данных, а Q x – выводы вывода. Также показаны общие контакты (CP, E1 и E2, OE1 и OE2 и MR). Рисунок 6. Распиновка микросхемы 74HC173.74HC173 – отличный чип для изучения и используется в широком спектре приложений. Его работа и особенности делают его идеальным для использования в качестве 4-битного регистра.Дальнейшее изучение может быть выполнено с помощью таблицы данных 74HC173. Или, чтобы попробовать, почему бы не проверить наш склад 74HC173s и запасных частей для исследования IC. Для любопытных, наша следующая заметка: ROM & RAM: An Introduction to Computer Memory исследует, как концепция регистров может быть использована для создания компьютерной памяти. Вам также могут понравиться: Заметка № 4 Заметка № 6 Заметка № 5 Ознакомьтесь с нашими электронными наборами DIY: Синтезирующая генетическая последовательная логическая схема с генератором тактовых импульсов | BMC Systems BiologyДинамическая модель синтетических генетических логических схемПрименяя математические модели для описания биохимических реакций генетических систем, синтетическая генетическая схема с определенной функцией может быть синтезирована с точки зрения системы. Рассмотрим динамическую модель синтетической генетической логической схемы с L генами, описываемую классом нелинейных дифференциальных уравнений Хилла [7] m˙i = αifiu-λimi + αi, 0, p˙i = βimi-γipi , i = 1,…, L (1) где м и и p и обозначают, соответственно, концентрации мРНК и белка для гена i , λ и и γ и – это, соответственно, скорости деградации мРНК и белка, α и – скорость транскрипции мРНК, β и – скорость синтеза белка, α i , 0 – базальный дебит, f и (⋅) – это функция активности промотора, которая описывает нелинейное поведение транскрипции и отражает силу взаимодействия между регулируемым белком и РНК-полимеразой (РНКп), а u – это концентрация фактора транскрипции (ТФ), который продуцируется другими ген (ы) или индуктор (ы) для контроля скорости транскрипции генов-мишеней. Для гена с участком оператора, который может связывать репрессор или активатор TF, функции активности промотора описаны как и где f НЕ и f Буфер – это функции активности промотора для логического НЕ и буфера [26, 30], соответственно, n – коэффициент Хилла, который обозначает кооперативность связывания между TF и соответствующим оператором, а K – константа Хилла, которые пропорциональны длины или сродства сайтов связывания TF, вставленных в промоторную область генов-мишеней.Для логического элемента НЕ входом является репрессор, а ген продуцирует белок только в отсутствие репрессора; в противном случае присутствие репрессора препятствует связыванию РНКп и промотора. Для генетического буфера вводом является активатор, который увеличивает связывание РНКп и промотора с образованием белка. Структуры двух логических вентилей показаны на рисунках 1 (a) и (b) соответственно. Рисунок 1Выражения класса генетических логических вентилей. (a) ворота НЕ; (b) Буфер; (c) И ворота; (d) OR ворота; (e) вентиль XOR; (f) вентиль NAND; и (g) NOR gate. Для генов с двумя операторскими сайтами, которые могут связывать два репрессорных ТФ или активаторных ТФ, функции промоторной активности описываются в соответствии с их логическими функциями как fANDu1, u2 = u1K1n1u2K2n21 + u1K1n1 + u2K2n2 + u1K1n10003K2K2 9000n2 (4)для ORu1, u2 = u1K1n1 + u2K2n2 + u1K1n1u2K2n21 + u1K1n1 + u2K2n2 + u1K1n1u2K2n2 (5) fXORu1, u2 = u1K1n1 + u2K2n21 + u1K1n1 + u2K2n2 + u1K1n1u2K2n2 (6) fNANDu1, u2 = 1 + u1K1n1 + u2K2n21 + u1K1n1 + u2K2n2 + u1K1n1u2K2n2 (7) и fNORu1, u2 = 11 + u1K1n1 + u2K2n2 + u1K1n1u2K2n2 (8) где f И , f ИЛИ , f XOR , f NAND и f NOR являются, соответственно, функциями промоторной активности логических вентилей AND, OR, XOR, NAND и NOR, и 1 и u 2 – концентрации ТФ репрессора или активатора, K 1 и К 2 – константы Хилла для и 1 и u 2 соответственно и n 1 и n 2 – соответствующие коэффициенты Хилла.Для логических вентилей AND, OR и XOR транскрипционное поведение регулируется двумя активаторными TF с разными сайтами связывания. Два репрессорных TF контролируют генетические выражения логических вентилей NAND и NOR. Их строительные конструкции показаны на рис. 1 (c) – (g). В [38, 39] промотор и RBS рассматриваются как часть промотора-RBS для регулирования генетической экспрессии, поскольку период полужизни мРНК короче, чем у соответствующего белка. (1) можно переписать как p˙i = ρifiu-γipi + ρ0, i, i = 1,…, L (9) , где ρi = αiβiλi, ρ0, i = α0, iβiλi Здесь ρ и и ρ 0, и – это новые скорости синтеза и базальной продукции белка.Динамическая модель дифференциального уравнения 2 L (1) сводится к динамической системе с дифференциальным уравнением L (9). Для реальной реализации, извлекая соответствующие части промотор-RBS из библиотеки промотор-RBS, синтетическая генетическая цепь может быть реализована в генетических системах. Синтетические генетические последовательные логические схемыВ цифровых логических схемах выход последовательной логической схемы зависит не только от текущих входов, но и от прошлых входов.Для синхронных последовательных схем тактовый сигнал используется в качестве метронома для координации действий схем, которые колеблются между состояниями высокого и низкого уровня. Цепи с запущенными тактовыми сигналами становятся активными либо по переднему фронту, либо по спаду, либо по обоим фронтам нарастания и спада. Для последовательной логической схемы, запускаемой по нарастающему фронту тактового сигнала, она становится активной, когда ее тактовый импульс переходит от низкого уровня к высокому (от 0 до 1), и игнорирует переход от высокого уровня к низкому (от 1 до 0). В генетических логических схемах колебательный сигнал, создаваемый репрессилятором, не идеален в качестве тактового генератора для использования в схемах, полагающихся на изменение нарастающего или спадающего фронта тактового сигнала для перехода между состояниями. Предлагаемый нами подход состоит в том, чтобы внедрить идею схемы формирования формы волны в электронике в генетические логические схемы и преобразовать синтезированный сигнал генетических колебаний в четкий тактовый сигнал или сигнал ШИМ с различными рабочими циклами. Регулируя продолжительность рабочего цикла, тактовый импульс может генерироваться с передним или задним фронтом, частота которого согласована с частотой колебаний.Чтобы использовать тактовый импульс, сконструированный генетический счетчик, основанный на топологии электронной последовательной логической схемы, запускается для генерации тактового сигнала, частота которого обратно целочисленно кратна генетическому колебанию. Синтетический генетический осцилляторЯвление колебаний в биологических системах было обнаружено на различных уровнях биологической организации. Его практическая функция заключается в контроле дозировки лекарств или в качестве синхронного механизма межклеточной коммуникации.Способность к колебаниям зависит не только от топологии сети, но и от параметров системы. В настоящее время простейший синтетический генетический осциллятор может быть синтезирован из одного гена, репрессирующего себя с помощью отложенной петли отрицательной обратной связи. Расширение простейшего осциллятора, называемого репрессилятором, состоит из трех генов ( lacI , tetR , cI ), которые репрессируют друг друга в цепочке цикла. Продукт первого гена-репрессора, lacI из E.coli , ингибирует транскрипцию второго гена-репрессора, tetR , из транспозона Tn10 устойчивости к тетрациклину, белковый продукт которого, в свою очередь, ингибирует экспрессию третьего гена-репрессора, cI из фага λ . Наконец, cI ингибирует экспрессию lacI , завершая цикл отрицательной обратной связи [10]. Динамическая модель репрессилятора может быть описана как p˙i = ρifNOT, ipj-γipi (10) где п и и p j – концентрации белков для ( i , j ) ≡ ( lacI , cI ), ( tetR , lacI ) или ( cI , tetR ).Для другой конструкции колебательное поведение может быть вызвано рядом репрессорных и активаторных генов, в которых количество репрессорных генов должно быть нечетным. Чтобы спроектировать генетический осциллятор с желаемыми колебаниями, можно реализовать регуляторную сеть генов для отслеживания эталонного синусоидального сигнала, подаваемого .где y д – сигнал колебаний с заданной амплитудой A , базовая частота ω 0 , фаза φ и y d , 0 – базовый уровень, обеспечивающий неотрицательную концентрацию белка.Более подробно о создании синтетических генетических осцилляторов с помощью алгоритмов оптимизации можно найти в [35]. Схема формирования сигналаВ электронике схема формирования сигнала предназначена для придания входному сигналу желаемой формы в соответствии с характеристической кривой ввода и вывода (I / O). Для колебательного входа и тактового выхода характеристическая кривая ввода-вывода желаемой схемы формирования сигнала показана на рисунке 2. Ступенчатая функция (пунктирная линия) с пороговым уровнем – т используется в электронике.Для входного сигнала, значение которого превышает пороговый уровень, он рассматривается как «высокий логический уровень». В противном случае это называется «низкий логический уровень». Однако в биологических системах не существует идеальной ступенчатой функции. Вместо этого можно использовать сигмовидную функцию (сплошная линия на рисунке 2). На характеристической кривой ввода-вывода сигмовидной функции можно выделить две рабочие области: насыщение и переход. Входной сигнал в области насыщения может быть отключен и удерживаться на высоком уровне или на низком уровне для приближения.В переходной области выигрыш в рабочей точке y т должен быть больше, чем (нормализованный) 1, потому что он гарантирует, что входной сигнал, который больше или меньше порогового уровня, будет усилен или уменьшен. Посредством каскадирования следующей сигмоидной функции входной сигнал колебания будет постепенно достигать области насыщения и оставаться на высоком или низком уровне. Рисунок 2Идея схемы формирования генетической формы волны. В соответствии с этой идеей, схема формирования сигнала может использоваться для регулирования периода логических высоких / низких уровней колебательного сигнала в синусоидальном цикле и генерирования сигнала ШИМ с другим рабочим циклом, определенным в ., где D – рабочий цикл, T 0 – базисный период колебательного сигнала (11) с 2 π / ω 0 и T – – период «логического максимума» в базальном периоде.Для сигналов ШИМ с разными рабочими циклами порог получается путем рассмотрения yT = Asinω0t + φ + yd, 0, t = th ± Ton2 (13) с th = 1ω0sin-11-φω0, th∈0T0 (14) Выбрать пороговый уровень приближающийся к y d , 0 + A , тактовый импульс, служащий нарастающим запускаемым фронтом, генерируется и показан на рисунке 3 (a).Для тактового импульса, рассматриваемого как спадающий запускаемый фронт, показанный на рисунке 3 (b), можно выбрать пороговый уровень, близкий к –. д , 0 – А . Точно так же сигнал ШИМ с коэффициентом заполнения 50%, то есть тактовый сигнал с его частотой, согласованной с генетическим генератором, синтезируется и показан на рисунке 3 (c) при выборе базового уровня сигнала y д , 0 . Другими словами, сигналы ШИМ с разными рабочими циклами могут быть синтезированы из колебательного сигнала через схему формирования формы волны на разных пороговых уровнях. Рисунок 3Идеальные сигналы ШИМ. а) – нарастающий срабатывающий фронт; (b) спадающий срабатывающий фронт; и (c) 50% рабочий цикл. Реализация схемы формирования генетической формы волныВ инженерных схемах генетической логики предлагается использовать генетический буфер [30] в качестве буфера между двумя каскадными генетическими схемами для улучшения передачи логических сигналов. Он используется здесь, чтобы помочь при разработке схемы формирования формы сигнала: p˙k = ρkfBuffer, kuk, Kk, nk-γkpk + ρ0, k, k = 1,…, M (15) Его стационарное решение легко получить как pk, ss = ρkγkfBuffer, kuk, Kk, nk + ρ0, kγk, k = 1,…, M (16) где п к – выходная концентрация буфера k th, p к , СС обозначает его стационарную концентрацию, u к , К к и n к – это, соответственно, входная концентрация, постоянная Хилла и коэффициент Хилла для k -го буфера и ρ к , γ к и ρ 0, к – скорость синтеза, распада и базальная скорость соответственно.Второй член правой части (16) является минимальным уровнем и ρ к / γ к – разница между минимальным и максимальным уровнями. Выходная концентрация генетического буфера – это половина максимальной выходной концентрации, когда входная концентрация равна K к и, следовательно, K к относится к пороговому уровню y т . На каждом этапе соответствующие входы и пороговые уровни задаются как uk = yd, k = 1pk-1,1 (17) и Kk = yT, k = 1ρk-1 + ρ0, k-12γk-1,1 (18) На первом этапе входным сигналом является сигнал колебаний в (11), а пороговый уровень выбирается в соответствии с желаемым рабочим циклом в (13). Для следующего этапа входной сигнал – это выходная концентрация предыдущего буфера, а пороговый уровень – это половина максимального выходного уровня в предыдущем.Топология предлагаемой нами генетической схемы формирования формы волны показана на рисунке 4. Сигнал осцилляции от производства белка любым геном репрессилятора активирует первый ген в генетической схеме формирования формы волны, выработка которого активирует следующий ген. Постепенно колебания можно преобразовать в четкий тактовый сигнал или сигнал ШИМ. Однако проблема медленной сходимости к максимальному уровню возникает для большего порогового уровня K к .Чтобы решить эту проблему, можно снова каскадировать буфер с проектными параметрами (16) на последнем этапе генетической схемы формирования формы волны для компенсации выходного уровня. Топология разработанной схемы генетического формирования сигнала. Прирост в рабочей точке К к получается по Ak = ∂pk, ss∂ukuk = Kk = ρknk4γkKk (19) где A к – это усиление буфера k th.Прирост пропорционален коэффициенту Хилла n к и скорость синтеза ρ к и обратно пропорционально постоянной Хилла K к и скорость распада γ к в рабочей точке u к = К к .Чтобы обеспечить необходимое условие усиления в рабочей точке, К к должно быть больше 1. Сначала выбирается подходящая константа Хилла для желаемого синтезированного ШИМ-сигнала, а затем выбирается подходящий коэффициент Хилла n к , скорость синтеза ρ к и скорость распада γ к удовлетворительное (19).Из параметров системы на предыдущем этапе переходят к выбору соответствующих параметров системы на следующем этапе, удовлетворяющих (18) и (19). Из [38, 39], чтобы реализовать предложенную генетическую логическую схему в реальности, можно найти применимые компоненты промотор-RBS из сконструированной библиотеки промотор-RBS, характеристические кривые ввода-вывода которых способны удовлетворять (18) и (19) . Делитель частоты в электронике – это устройство, которое генерирует выходной сигнал, частота которого обратно кратна частоте входного сигнала.Для достижения этой функции используется последовательная логическая схема счетчика, которая состоит из серии триггеров и запускается тактовым импульсом для генерации тактовых сигналов с кратным базальным периодом. На рисунке 5 показан идеальный синхросигнал при запуске по нарастающему фронту синхросигнала с желаемым базальным периодом. Идеальные тактовые сигналы с (а) базовым периодом; (б) двойной базальный период; и (c) четырехкратный базальный период. Genetic JK flip-flop, основанный на топологии цифровых логических схем в электронике, делится на триггер, запускаемый по переднему фронту, и триггер, запускаемый по заднему фронту, как показано на рисунке 6. Для запуска по переднему фронту генетический триггер JK, его модель описана номером Класс синхронизированных генетических триггеров JK. а) – срабатывающий по нарастающему фронту; и (b) , срабатывающий по заднему фронту. p˙W = ρWfANDpK, pCLK, KW, nW-γWpW, p˙V = ρVfANDpJ, pCLK, KV, nV-γVpV, p˙R = ρRfANDpW, pQ, KR, nR-γRpR, p˙S = ρSfANDpV, pQ ¯, KS, nS-γSpS, p˙Q = ρQfNORpR, pQ¯, KQ, nQ-γQpQ, p˙Q¯ = ρQ¯fNORpS, pQ, KQ¯, nQ¯-γQ¯pQ¯ (20) где п CLK – концентрация тактового импульса от низкого к высокому, p Вт , п. В , п. р , п. S , п. Q и pQ ¯ обозначают, соответственно, концентрации белков генов W , V , R , S , Q и Q¯.Генетический триггер JK, запускаемый по нарастающему фронту, становится активным только тогда, когда тактовый импульс переходит от низкого уровня к высокому. Имеется четыре генетических логических элемента И и два логических элемента ИЛИ, топология показана на рисунке 7. Белки p К и p CLK активирует транскрипцию гена W . Белки р Дж и p CLK активирует транскрипцию гена V .Продукция генов W и Q активирует транскрипцию гена R , а продукция генов V и Q¯ активирует транскрипцию гена S . Белки р р и pQ ¯ ингибируют транскрипцию гена Q и белков p S и p Q подавляют транскрипцию гена Q¯. Топология генетического JK-триггера, запускаемого нарастающим фронтом. Для генетического триггера JK, запускаемого по заднему фронту, модель описывается формулой p˙W = ρWfNANDpK, pCLK, KW, nW-γWpW, p˙V = ρVfNANDpJ, pCLK, KV, nV-γVpV, p˙ R = ρRfNANDpW, pQ, KR, nR-γRpR, p˙S = ρSfNANDpV, pQ¯, KS, nS-γSpS, p˙Q = ρQfNANDpS, pQ¯, KQ, nQ-γQpQ, p˙Q¯ = ρQ¯fNANDpR , pQ, KQ¯, nQ¯-γQ¯pQ¯ (21) где п CLK – концентрация тактового импульса от высокого к низкому.Эта схема состоит из шести генетических логических элементов NAND с топологической структурой, показанной на рисунке 8. Топология генетического JK-триггера, запускаемого падающим фронтом. Для синтеза тактового сигнала с частотой, обратно кратной частоте генетического генератора, можно использовать схему синхронного генетического счетчика. Схема счетчика в электронике работает по нарастающему или спадающему фронту тактового сигнала и подсчитывает количество тактовых импульсов.Основываясь на этой функции, сначала генерируется серия тактовых импульсов, используя предложенную нами схему формирования генетической формы волны, а затем используется сигнал тактовых импульсов для запуска генетического счетчика. Согласно карте Карно в теории цифровой логики, можно определить входные сигналы каждого генетического триггера JK и топологию схемы генетического счетчика. Чтобы синтезировать тактовые сигналы с 2 δ -кратным базальным периодом, в котором δ является положительным целым числом, p˙W1 = ρW1fANDpK1, pCLK1, KW1, nW1-γW1pW1, p˙V1 = ρV1fANDpJ1, pCLK1, KV1, nV1-γV1pV1, p˙R1 = ρR1fANDpW1, pQ1, KR1, npR1, pQ1, KR1, npR1, pQ1, KR1, npR1, pQ1, KR1, npR1 ¯1, KS1, nS1-γS1pS1, p˙Q1 = ρQ1fNORpR1, pQ¯1, KQ1, nQ1-γQ1pQ1, p˙Q¯1 = ρQ¯1fNORpS1, pQ1, KQ¯1, nQ¯1-γQ¯1pQ¯1 , P˙Wδ = ρWδfANDpKδ, pCLK1, KWδ, nWδ-γWδpWδ, p˙Vδ = ρVδfANDpJδ, pCLK1, KVδ, nVδ-γVδpVδ, p˙Rδ = ρRδfANDpWδ, pQδ, KRδSδ, nRδfANDpWδ, pQδ, KRδδ, nRδpδSpδ, nRδpδ-Vδ, nRδSpδ = γδSpδ, nRδSpδ pQ¯δ, KSδ, nSδ-γSδpSδ, p˙Qδ = ρQδfNORpRδ, pQ¯δ, KQδ, nQδ-γQδpQδ, p˙Q¯δ = ρQ¯δfNORpSδ, pQδ, KQ¯δ, nQ¯δ-γQ¯δpQ¯ δ, p˙G1 = ρG1fANDpK2, pQ2, KG1, nG1-γG1pG1, ⋮ p˙Gδ-2 = ρGδ-2fANDpKδ-1, pQδ-1, KGδ-2, nGδ-2-γGδ-2pGδ-2, (22) с входом каждого генетического триггера JK, заданным как pJ1 = pK1 = 1, pJ2 = pK2 = pQ1, pJ3 = pK3 = pG1, ⋮ pJδ = pKδ = pGδ-2 (23) , где pCLK1 – сигнал тактового импульса от низкого к высокому, pQ1, pQ2, pQδ – соответственно тактовые сигналы с двойным, учетверенным и 2 δ -кратным базальным периодом.На рисунке 9 показана топология синхронного генетического счетчика для тактовых сигналов с 2 δ -кратным базальным периодом. Топология синхронного генетического счетчика тактовых сигналов с 2 δ -кратный базальный период. Чтобы синтезировать тактовый сигнал с тройным базальным периодом, синхронный генетический счетчик с двумя генетическими триггерами JK, запускаемыми по фронту, и генетическим триггером JK, запускаемым по фронту, конструируется с помощью p˙W1 = ρW1fANDpK1, pCLK1, KW1, nW1-γW1pW1, p˙V1 = ρV1fANDpJ1, pCLK1, KV1, nV1-γV1pV1, p˙R1 = ρR1fANDpW1, pQ1, KR1, nR1-γR1pR1, p˙S1 = ρS1fANDpV1, p˙S1 = ρS1fANDpV1, KV1 p˙Q1 = ρQ1fNORpR1, pQ¯1, KQ1, nQ1-γQ1pQ1, p˙Q¯1 = ρQ¯1fNORpS1, pQ1, KQ¯1, nQ¯1-γQ¯1pQ¯1, p˙W2 = ρW2fANDpK2, pCLK1, KW2, nW2-γW2pW2, p˙V2 = ρV2fANDpJ2, pCLK1, KV2, nV2-γV2pV2, p˙R2 = ρR2fANDpW2, pQ2, KR2, nR2-γR2pR2, p˙S2 = ρS2fAND2pV2, p˙S2 = ρS2fANDpV2, KV2 p˙Q2 = ρQ2fNORpR2, pQ¯2, KQ2, nQ2-γQ2pQ2, p˙Q¯2 = ρQ¯2fNORpS2, pQ2, KQ¯2, nQ¯2-γQ¯2pQ¯2p˙W3 = ρW3fNANDpK3, pCLK2, KW3 nW3-γW3pW3, p˙V3 = ρV3fNANDpJ3, pCLK2, KV3, nV3-γV3pV3, p˙R3 = ρR3fNANDpW3, pQ3, KR3, nR3-γR3pR3, p˙S3 = ρS3fNANDpV3, pS3 = ρS3fNANDpV3, pS3fNANDpV3, pS3fNANDpV3, pS3fNANDpV3, pS3 Q3 = ρQ3fNANDpS3, pQ¯3, KQ3, nQ3-γQ3pQ3, p˙Q¯3 = ρQ¯3fNANDpR3, pQ3, KQ¯3, nQ¯3-γQ¯3pQ¯3p˙G1 = ρG1fORpQ2, pQ3, KG1, nG1 γG1pG1, (24) с входом каждого генетического триггера JK, заданным как pK1 = pK2 = 1, pJ1 = pQ¯2, pJ2 = pQ1, pJ3 = pQ2, pK3 = pQ¯2 (25) , где pCLK1 – это сигнал тактового импульса от низкого до высокого, pCLK2 – это тактовый импульсный сигнал от высокого до низкого, а pG1 – тактовый сигнал с тройным базальным периодом.Топология синхронного генетического счетчика для тактового сигнала с тройным базальным периодом показана на рисунке 10, а соответствующие идеальные сигналы показаны на рисунке 11. Топология синхронного генетического счетчика тактового сигнала с тройным базальным периодом. (a) Сигнал тактового импульса от низкого к высокому; (b) Сигнал тактового импульса от высокого к низкому; (c) Выходной сигнал pQ1 первого генетического триггера JK; (d) Выходной сигнал pQ2 второго генетического триггера JK; (e) Выходной сигнал pQ3 третьего генетического триггера JK; и (f) Выходной сигнал логического ИЛИ (d) и (e) . Идеальные сигналы для синтеза тактового сигнала с тройным базальным периодом. (a) Сигнал тактового импульса от низкого к высокому; (b) Сигнал тактового импульса от высокого к низкому; (c) Выходной сигнал pQ1 первого генетического триггера JK; (d) Выходной сигнал pQ2 второго генетического триггера JK; (e) Выходной сигнал pQ3 третьего генетического триггера JK; и (f) Выходной сигнал логического ИЛИ (d) и (e) . Вышеупомянутый подход является общим, аналогичным образом можно определить соответствующие входы каждого генетического триггера JK на основе инженерной теории цифровой логики [40] и каскадировать эти базовые триггеры, чтобы напоминать другие типы генетических триггеров. счетчики с желаемой рабочей частотой. Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт. Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины: Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня. Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется. Как правило, в cookie-файлах может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать. Логические вентили – это фундаментальные строительные блоки цифровых электронных схем.Они следуют правилам булевой алгебры, которые очень легко понять и реализовать для всех, в том числе для начинающих дизайнеров. Они помогают схемам принимать решения, поэтому составляют значительную часть схемы микропроцессора и микроконтроллера. По сути, существует семь типов логических вентилей, из которых мы обсудили три (И, ИЛИ, ИЛИ) в предыдущем сообщении в блоге. В этом сообщении блога мы рассмотрим следующие шлюзы и посмотрим, как они работают при включении в цифровые схемы: К концу этого поста вы сможете выполнять различные математические операции с использованием логических вентилей и строить полезные схемы, использующие функции нескольких логических вентилей. , безусловно, является самым простым логическим элементом, поскольку он выполняет основную функцию инвертирования, поэтому элемент НЕ также называется инвертором. Что делает логический инвертор? Логический инвертор или вентиль НЕ инвертирует логический уровень, присутствующий на его входной клемме. Например, если есть «1» на входе логического элемента НЕ, он будет генерировать «0» на выходе и наоборот. Ворота НЕ являются единственными воротами с одной входной клеммой, в то время как все остальные ворота имеют две или более входных клеммы.Булево уравнение для логического элемента НЕ может быть записано следующим образом: Ф = А Что дает следующую таблицу истинности: Мы можем использовать резисторы и транзисторы, чтобы представить внутреннюю работу логического элемента НЕ. База транзистора действует как входная клемма, а выход измеряется от клеммы коллектора. Схема спроектирована, как показано на схеме ниже. Пробники напряжения используются для измерения логического уровня на входных и выходных клеммах. V (A) представляет собой точку, в которой измеряется входной сигнал, а V (F) представляет собой выходной терминал. Как видите, на входе присутствует сигнал 0 В, что означает, что вентиль НЕ должен инвертировать этот сигнал. Изучим результаты моделирования. Синяя линия представляет входной сигнал, который присутствует на логическом уровне 0 (0 Вольт), а красная линия представляет выходной сигнал, который находится на логическом уровне 1; Именно так работает вентиль НЕ.Если на входе присутствует логический уровень «1», на выходе будет «0». Простая схема шлюза НЕ Давайте посмотрим, как мы можем использовать этот вентиль для реализации практической схемы, используемой в реальных приложениях. Рассмотрим шкаф, в котором вы хотите установить лампочку, которая загорается при открытии дверцы шкафа и гаснет, когда дверца закрывается. Для этого вам понадобится кнопочный переключатель, установленный внутри шкафа, так что, когда дверь закрывается, кнопка остается нажатой, а когда дверь открывается, кнопка возвращается в исходное состояние; где не нажимается. Мы можем смоделировать этот сценарий, используя цифровой импульсный сигнал, представляющий открытие и закрытие двери. Когда дверь открыта, кнопка не нажимается; следовательно, он характеризуется логическим уровнем 0. Элемент НЕ инвертирует этот сигнал в высокий логический уровень, который, в свою очередь, включает свет. Схема и ее моделирование показаны ниже: В результатах моделирования, показанных выше, синяя линия представляет вход кнопки, что означает, что, когда дверь шкафа закрыта, вход находится на логическом уровне 1.Выходной сигнал (обозначен зеленым и красным) низкий, что означает, что лампочка выключена. Точно так же при открытии дверцы шкафа загорается лампочка. NAND – один из наиболее часто используемых логических вентилей. Это комбинация ворот И и НЕ. Если вы посмотрите на символ, то это просто логический элемент И с крошечным «пузырем», соединенным последовательно с ним; этот пузырек представляет инвертор, то есть НЕ вентиль. Работа логического элемента И-НЕ аналогична И, за исключением того, что выход инвертируется.Например, если у вас есть два «высоких» сигнала и вы выполняете над ними операцию И, вы получите высокий выходной сигнал. Но с NAND вы получите низкий выход для двух единиц на входных клеммах. Таким образом, мы можем представить логический элемент И-НЕ следующим логическим уравнением: F = A.B , который генерирует следующую таблицу истинности, показывающую результат F для всех возможных комбинаций входов: Как и ранее обсуждавшиеся вентили, мы можем представить внутреннюю работу логического элемента И-НЕ с помощью транзисторов и резисторов, как показано на принципиальной схеме ниже.Два транзистора соединены последовательно, эмиттер первого подключен к коллектору второго транзистора. Базы двух транзисторов действуют как входные клеммы затвора И-НЕ, в то время как выход измеряется с коллектора первого транзистора. Чтобы выходной сигнал был высоким, необходимо отключить один из транзисторов. Мы можем проверить результаты с помощью графика моделирования, показанного ниже. Выход логического элемента И-НЕ имеет низкий уровень только тогда, когда оба входа имеют высокий уровень.Это можно увидеть из результатов моделирования выше, где красная линия указывает выходной импульс, а синий и зеленый импульсы представляют входные сигналы. Теперь, когда вы знаете, как работает вентиль NAND, давайте спроектируем простую схему, в которой вентиль NAND выполняет реальную задачу. Вы можете использовать ворота NAND, чтобы создать простую охранную сигнализацию, которая срабатывает, когда либо обнаруживается тень грабителя, либо грабитель стоит на датчике давления, установленном на входе в дом, или если оба условия выполняются одновременно. LDR используется для обнаружения тени грабителя, а датчик давления используется для определения присутствия вора по давлению, которое его тело оказывает на землю. Для моделирования этого сценария используются источники напряжения, представляющие LDR и датчик давления. LDR и датчик давления выдают низкий выходной сигнал при наличии грабителя. Результаты моделирования следующие: Синий импульс представляет уровни напряжения сигнализации, показывая, что сигнализация отключена только тогда, когда на входе нет тени и не ощущается какое-либо давление.Это тот случай, когда в дверях дома никого нет. Использовать один вентиль NAND для построения схемы было довольно просто, поэтому давайте перейдем к разработке схемы с несколькими вентилями NAND. Мы можем использовать различные вентили И-НЕ с 2 входами, чтобы разработать вентиль И-НЕ с 4 входами. Когда все четыре входа имеют высокий уровень, выход будет низким, а когда один из входов равен 0, результат будет высоким. Два логических элемента NAND используются в качестве входных вентилей. Затем присутствуют два промежуточных логических элемента И-НЕ, которые отправляют сигнал на выходной вентиль.В общей сложности пять вентилей И-НЕ используются для разработки 4-входного логического элемента И-НЕ, как показано на схеме ниже. Красный импульс показывает выход (F) схемы затвора И-НЕ с 4 входами, который имеет низкий уровень только тогда, когда все четыре входа (A, B, C, D) имеют высокий уровень. В противном случае выход останется высоким. XOR, также известный как элемент Exclusive OR, широко используется во многих логических и комбинационных схемах.Выход этого элемента является высоким только тогда, когда оба его входа отличаются друг от друга. то есть, если входной сигнал – «01» или «10», только тогда выход будет «1». В противном случае на выходе будет низкий уровень, т.е. логический уровень 0. В качестве альтернативы мы можем понять принцип работы логического элемента XOR по-другому. Его выход высокий, когда на входных клеммах присутствует нечетное количество единиц. Например, если у нас есть входы как A = 1 и B = 0, то у нас есть только один 1, i.е., на входе присутствует нечетное количество единиц, поэтому на выходе будет высокий уровень, то есть F = 1. Логическое выражение для логического элемента XOR с 2 входами записывается как: F = AB + AB Что дает следующую таблицу истинности: Мы можем понять внутреннюю работу логического элемента XOR, используя комбинацию других логических элементов, таких как OR, AND и NAND. Помните, что вентиль XOR – это не оригинальный вентиль, это комбинация базовых вентилей, которые мы изучили ранее. Прежде чем перейти к схеме, важно понять, что есть разные способы написания булевых уравнений. Вы можете упростить уравнение и преобразовать его в другую форму, применив простые правила булевой алгебры. Мы не будем вдаваться в подробности рассматриваемой здесь математики, но все, что вам нужно знать на этом этапе, – это то, что мы также можем написать логическое уравнение для двухвходового логического элемента XOR следующим образом: F = A + B. (A.B) Теперь перейдем к эквивалентной схеме XOR. Как видите, входы A и B применяются к логическим элементам OR и NAND, а затем их выходы подключаются к входам логического элемента AND. Результат точно такой же, как и при использовании логического элемента XOR. Если вы составите уравнение для выхода F, уравнения вентилей будут соответствовать уравнению логического элемента ИЛИ. Уравнение для выхода логического элемента ИЛИ – A + B, а для И-НЕ – (A.B), и если мы поместим эти уравнения в уравнение логического элемента И, мы получим F = A + B.(А. Б.). По результатам моделирования можно определить, что выход высокий, если входы не идентичны, то есть когда вход либо A = 0 и B = 1, либо A = 1 и B = 0. Мы можем построить полусумматор, используя вентиль XOR и вентиль AND. Эта схема добавляет два бита за раз и генерирует два выходных бита; один называется «суммой», а другой – «переносом». Это аналогично сложению вручную больших чисел в десятичном формате, когда мы переносим числа больше 9 на число слева, а затем добавляем его.Вот как выглядит полусумматор: Выход этой схемы моделируется следующим образом: Чтобы лучше понять это, давайте изучим таблицу истинности для полусумматора. Когда мы складываем 1 и 0, сумма равна 1, а бит переноса равен 0. Однако, когда две единицы складываются вместе, сумма равна 0, а бит переноса равен 1.Именно это и происходит в схеме полусумматора, и вы можете подтвердить это, изучив график моделирования, где красный импульс представляет собой сумму, а зеленый импульс представляет собой бит переноса. Как насчет использования нескольких вентилей XOR в одной схеме? Генератор битов четности для 3-битного сообщения может быть создан с помощью различных вентилей XOR в одной и той же схеме. Генератор четности – это инструмент исправления ошибок, используемый в цифровых схемах.Генератор четности сначала просканирует сообщение на количество единиц. Если они четные, нет необходимости добавлять 1; следовательно, он добавит 0 как бит четности. В противном случае, если количество единиц нечетное, генератор четности добавит «1» в качестве бита четности, чтобы сделать количество единиц четным. Вот как выглядит схема. В результатах моделирования очевидно, что бит четности равен 1, когда на входе нечетное (1 или 3) количество единиц, и 0, когда количество единиц во входном сигнале четное (2). XNOR, также известный как шлюз Exclusive NOR, является частью многих цифровых электронных схем. Его символ аналогичен объявлению XOR, за исключением того, что на выходе присутствует «пузырь» инвертора, что означает, что выход XNOR противоположен выходу логического элемента XOR. Мы также можем представить логический элемент XNOR как логический элемент XOR, соединенный последовательно с инвертором, как показано ниже. Выход логического элемента XNOR становится 1, когда оба его входа одинаковы друг для друга, т.е.е. для логического элемента XNOR с 2 входами выход будет высоким для комбинаций входов «00» и «11». В противном случае, когда входы отличаются друг от друга, выход будет низким. Поскольку этот вентиль дает высокий выходной сигнал, когда его входы совпадают, его также называют «вентилем эквивалентности», потому что вы можете определить, равны ли два входа логически или нет. Другой способ понять работу логического элемента XNOR – обеспечить высокий выходной сигнал, когда количество единиц на входных клеммах четное.Например, если комбинация входов для логического элемента XNOR с 3 входами равна «101», тогда выход будет высоким (1), потому что на входных клеммах присутствуют две единицы, что является четным счетом. Логическое уравнение для логического элемента XNOR записывается как: F = A.B + A.B , который генерирует следующую таблицу истинности для двухвходового логического элемента XNOR: Мы можем понять внутреннюю работу шлюза XNOR, разбив его на комбинацию основных ворот, таких как ворота И, ИЛИ и НЕ.Используя логическое уравнение, мы можем спроектировать простую схему логических вентилей следующим образом: Результаты моделирования показывают выходной импульс синего цвета, который имеет высокий уровень только тогда, когда оба входа логически равны. В противном случае выход находится на логическом уровне 0. Вентили XNOR широко используются в цифровых электронных схемах, включая полные сумматоры, вычитатели, устройства проверки четности и генераторы. Теперь, когда вы изучили различные типы логических вентилей, их уравнения, таблицы истинности, внутреннюю работу, схемы и приложения, давайте посмотрим, как мы можем объединить все или некоторые из семи типов логических вентилей в одной схеме. 4-битный компаратор, как следует из названия, сравнивает два 4-битных сигнала и генерирует результат, равный (A = B), меньшему (A Рассмотрим первое 4-битное слово A = A3A2A1A0 и второе слово B = B3B2B1B0, где A3 и B3 – самые старшие биты, а A0 и B0 – младшие значащие биты.Схема 4-битного компаратора для сравнения слов A и B показана ниже. Входные сигналы для 8 битов имеют форму цифровых импульсов, которые периодически колеблются между логическими уровнями 0 и 1. Выходные данные генерируются на основе сравнения двух 4-битных слов, сформированных как комбинация 8 бит. Результаты смоделированы ниже: Здесь жирная красная линия представляет выходную клемму A = B.В показанной точке слова A и B равны; следовательно, импульс v (равный) высокий. Если вы внимательно посмотрите на значения битов, вы увидите, что A0 = B0, A1 = B1, A2 = B2 и A3 = B3. Другой пример сложной схемы, в которой используются несколько логических вентилей в одной схеме, – это декодер 3 × 8. Он имеет три входных линии (A, B, C) и восемь выходных линий (Y0, Y1…, Y7). Контакт включения (EN) активирует выход в зависимости от комбинации входов. Каждый выход активируется с помощью 3-битного входного кода, уникального для каждого выхода. Используя комбинацию логических элементов И и НЕ, мы можем построить схему следующим образом: Восемь вентилей И создают выходы Y0, Y1, Y2, Y3, Y4, Y5, Y6 и Y7, а вентили НЕ снабжены входами A, B и C. Выходы меняются в соответствии с таблицей ниже: Это можно проверить с помощью результатов моделирования, показанных ниже: Формы выходных сигналов зависят от приведенной выше таблицы истинности.Например, когда все три входных сигнала v (a), v (b) и v (c) имеют высокий уровень, выход Y7 активируется, как показано в результатах моделирования. – полезные электронные компоненты, поскольку они могут выполнять множество задач, включая математические операции и условное программирование. Они широко используются в микроконтроллерах, микропроцессорах и некоторых других электронных устройствах, имеющихся вокруг вас. Все, что вам нужно знать, это то, как они работают, и вы можете самостоятельно создавать цифровые логические схемы и проверять их результаты с помощью моделирования EAGLE. |
