Значения действующего напряжения и силы тока. Определение. Соотношение с амплитудой для разной формы. (10+) Понятие эффективных (действующих) значений напряжения и силы тока Когда мы говорим о переменных напряжении или силе тока, особенно сложной формы, то встает вопрос о том, как их измерять. Ведь напряжение постоянно меняется. Можно измерять амплитуду сигнала, то есть максимум модуля значения напряжения. Такой метод измерения нормально подходит для сигналов относительно гладкой формы, но наличие коротких всплесков портит картину. Еще одним критерием выбора способа измерения является то, для каких целей делается измерение. Так как в большинстве случаев интерес представляет мощность, которую может отдать тот или иной сигнал, то применяется действующее (эффективное) значение.
|
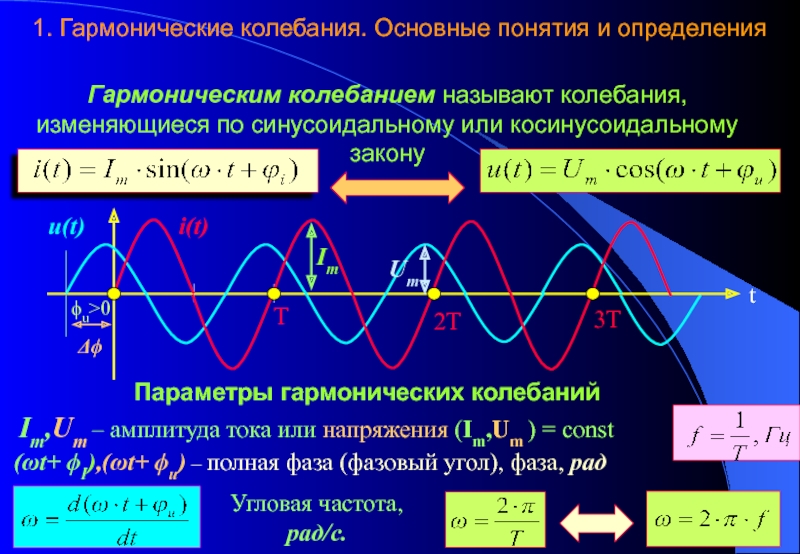
Действующее, амплитудное, среднее значение величины на синусоиде
- Главная
- Электротехника и электроника
- Формы сигналов в электронике
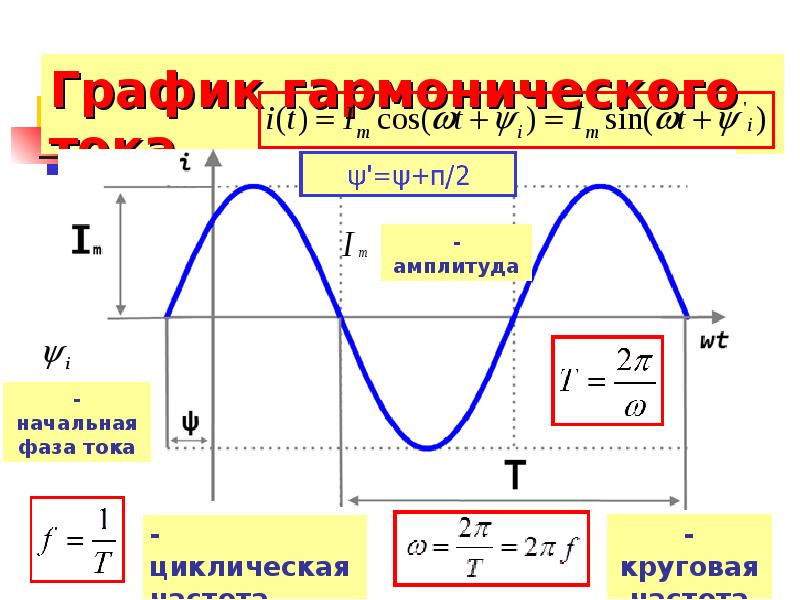
Синусоида (синус) – самый наш идеальный и необходимый вариант. Используется на выходе из генераторов для передачи на расстояния и затем используется вами из розетки (какой ток в розетке?). Самый распространенный сигнал, вероятно, если я чего-то не знаю. Рассмотрим основные элементы графика переменного тока:
Период – это время, через которое функция начинает повторяться, величина обратная частоте. Обозначается буквой Т. Т=2тт/w.
тт – так почему-то в интернетах принято обозначать число “пи”, против толпы не попрешь, так сказать, хотя можно просто 3,14 написать или “пи”. Дело вкуса.
Амплитудное значение (амплитуда) – значения, в которых график синусоиды достигает максимумов. То есть для синусоиды таких значения два на период – положительное и отрицательное.
Действующее значение – это 0,707 от амплитудного значения. Есть у нас цепь – в этой цепи за время Т1 постоянный ток определенной величины I1 выделит определенное количество тепла Q1, если в той же цепи пустить переменный ток, то за тоже время Т1 он выделит такое же количества тепла Q1 при действующем значении равном I1. И это значение I1 для синусоиды будет равно 0,707 от амплитудного – что означает единица делить на корень из двух. Если вам интересно, откуда это такое взялось, то плиз велком:
Мгновенное значение – значение величины в определенный момент времени. Если посмотреть на синусоиду, то видно, что мгновенное значение постоянно передвигается и на протяжении одного периода постоянно меняет свои значения. В следующем периоде опять идет тем же путем. Остановись мгновение =) Значение мгновенного значения определяется как Im*sin(wt) – амплитудное значение умноженное на “синус омега тэ” – где “омега тэ” – произведение угловой скорости на момент времени. Омега равно два пи делить на период Т.
Среднее значение – сумма всех мгновенных значений за полпериода. Для синусоиды равно 0,6366197730950255438113531364418 ~ 0,637 от амплитудного значения. Если вновь стало интересно, откуда число, то ответ ниже на примере переменного тока:
Если амплитудное значение разделить на действующее значение, то мы получим, правильно корень из двух для синусоиды – его еще называют коэффициентом амплитуды. Если же мы разделим действующее значение на среднее – то получим для синусоиды 1,11 – это отношение называется коэффициентом формы кривой.
Сколько инженеров, столько и форм кривых в электронике, а если серьезно, то существуют например такие: Форма сигнала меандр – сигнал, в котором отсутствуют четные гармоники, имеет прямоугольную форму. В отличие от прямоугольного импульса, у которого длительность сигнала и длительность паузы могут отличаться, у меандра они равны. Сигнал такой формы может встречаться в импульсных источниках бесперебойного питания и прочих электронных схемах, ШИМ.
Пилообразный сигнал – сигнал пилообразной формы может идти и в одну сторону и в другую (знак минус в формуле функции). Для создания этой и других форм сигналов применяются генераторы сигналов. Применяются в старых осциллографах, мониторах, как и треугольные.
Треугольный сигнал – у треугольного сигнала длина роста и длина падения равны.
Каждая из этих форм может быть представлена через преобразование фурье, смысл которого в разбиении функции на гармонические составляющие от единицы до бесконечности с набором определенных гармоник – нечетных например, как для меандра. В функциях выше, которые были построены в маткаде, смысл построения в следующем, чем больше составляющих вы берете для построения (ближе к бесконечности), тем красивее получается график.
Что называют действующими значениями силы тока и напряжения. Эффективное, действующее напряжение, сила тока
Переменный синусоидальный ток в течение периода имеет разные секундные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?
При расчетах цепей переменного тока, также при электронных измерениях неловко воспользоваться моментальными либо амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Не считая того, об электронном эффекте временами изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.
Более комфортным оказалось введение понятий так именуемых действующих значений тока и напряжения . В базу этих понятий положено термическое (либо механическое) действие тока, не зависящее от его направления.
— это значение неизменного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.
Для оценки деяния, производимого переменным током, мы сравним его деяния с термическим эффектом неизменного тока.
Мощность Р неизменного тока I , проходящего через сопротивление r , будет Р = Р 2 r .
Мощность переменного тока выразится как средний эффект моментальной мощности I 2 r за целый период либо среднее значение от (Im х sinωt ) 2 х r за то же время.
Пусть среднее значение t2 за период будет М. Приравнивая мощность неизменного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √ M ,
Величина I именуется действующим значением переменного тока.
Среднее значение i2 при переменном токе определим последующим образом.
Построим синусоидальную кривую конфигурации тока. Возведя в квадрат каждое секундное значение тока, получим кривую зависимости Р от времени.
Обе половины этой кривой лежат выше горизонтальной оси, потому что отрицательные значения тока (-i ) во 2-ой половине периода, будучи построены в квадрат, дают положительные величины.
Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное с помощью высшей арифметики, будет равно 1/2I 2 m . Как следует, М = 1/2I 2 m
Потому что действующее значение I переменного тока равно I = √ M , то совсем I = Im / √ 2
Аналогично зависимость меж действующим и амплитудным значениями для напряжения U и Е имеет вид:
U = Um / √ 2 , E= Em / √ 2
Действующие значения переменных величин обозначаются строчными знаками без индексов (I , U, Е).
На основании произнесенного выше можно сказать, что действующее значение переменного тока равно такому неизменному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.
Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, демонстрируют действующие значения тока либо напряжения.
При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √ 2 раз. От этого размещение векторов на диаграмме не меняется.
Школа для электрика
Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.
В современной литературе чаще используется математическое определение этой величины – среднеквадратичное значение переменного тока.{2}dt}}.}
Для синусоидального тока:
I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , {\displaystyle I={\frac {1}{\sqrt {2}}}\cdot I_{m}\approx 0{,}707\cdot I_{m},}
I m {\displaystyle I_{m}} – амплитудное значение тока.
Для тока треугольной и пилообразной формы:
I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . {\displaystyle I={\frac {1}{\sqrt {3}}}\cdot I_{m}\approx 0{,}577\cdot I_{m}.}
Аналогичным образом определяются действующие значения ЭДС и напряжения.
Дополнительные сведения
В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value – эффективное значение. Также применяется аббревиатура RMS (rms) – root mean square – среднеквадратичное (значение).
В электротехнике приборы электромагнитной, электродинамической и тепловой систем калибруются на действующее значение.
Источники
- «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
- Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
- «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 – § 7.10
Ссылки
- Действующие значения тока и напряжения
- Среднеквадратичное значение
Мгновенные, максимальные, действующие и средние значения электрических величин переменного тока
Мгновенное и максимальное значения. Величину переменной электродвижущей силы, силы тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин и обозначают соответственно строчными буквами (e, i, u, p ).
Максимальным значением (амплитудой) переменной э. д. с. (или напряжения или тока) называется та наибольшая величина, которой она достигает за один период. Максимальное значение электродвижущей силы обозначается Е m , напряжения – U m , тока – I m .
Действующим (или эффективным) значением переменного тока называется такая сила постоянного тока, которая, протекая через равное сопротивление и за одно и то же время, что и переменный ток, выделяет одинаковое количество тепла.
Для синусоидального переменного тока действующее значение меньше максимального в 1,41 раз, т. е. в раз.
Аналогично действующие значения переменной электродвижущей силы и напряжения меньше их максимальных значений тоже в 1,41 раза.
По величине измеренных действующих значений силы переменного тока, напряжения или электродвижущей силы можно вычислить их максимальные значения:
E m = E · 1,41; U m = U · 1,41; I m = I · 1,41;
Среднее значение = отношению количества эл энергии прошедшего через сечение проводника за половину периода к величине этого полупериода.
Под средним значением понимают среднеарифметическое ее значение за половину периода.
/ Среднее и действующие значения синусоидальных токов и напряжений
Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока
т. е. среднее значение синусоидального тока составляет от амплитудного. Аналогично,
Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока
Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично,
Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.
Количество теплоты, выделенное за один период синусоидальным током,
Выделенная за то же время постоянным током теплота равна Приравняем их:
Таким образом, действующее значение синусоидального тока численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.
Для установления эквивалентности переменного тока в отношении энергии и мощности, общности методов расчета, а также сокращения вычислительной работы изменяющиеся непрерывно во времени токи. ЭДС и напряжения заменяют эквивалентными неизменными во времени величинами. Действующим или эквивалентным значением называется такой неизменный во времени ток, при котором выделяется в резистивном элементе с активным сопротивлением r за период то же количество энергии, что и при действительном изменяющемся синусоидально токе.
Энергия за период, выделяющаяся в резистивном элементе при синусоидальном токе,
i 2r dt = | I m 2 sin2 ωt r dt. . | |||
При неизменном во времени токе энергия
W = I 2rT
Приравняв правые части
I m
0,707I m .
Таким образом, действующее значение тока меньше амплитудного в √2 раз.
Аналогично определяют действующие значения ЭДС и напряжения:
Е = E m / √2, U = U m / √2.
Действующему значению тока пропорциональна сила, действующая на ротор двигателя переменного тока, подвижную часть измерительного прибора и т. д. Когда говорят о значениях напряжения, ЭДС и тока в цепях переменного тока, имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока отградуированы соответственно в действующих значениях тока и напряжения. Например, если прибор показывает 10 А, то это значит, что амплитуда тока
I m = √2I = 1,41 10 = 14,1 A,
и мгновенное значение тока
i = I m sin (ωt + ψ) = 14,1 sin (ωt + ψ).
При анализе и расчет выпрямительных устройств пользуются средними значениями тока, ЭДС и напряжения, под которыми понимают среднее арифметическое значение соответствующей величины за полпериода (среднее значение за период, как известно, равно нулю):
T 2 | ||||||||||
Е ср = | Е т sin ωt dt = | sin ωt d ωt = | |cos ωt | π 0 = | 0,637Е т . | ||||||
Аналогично можно найти средние значения тока и напряжения:
I ср = 2I т /π; U ср = 2U т /π.
Отношение действующего значения к среднему значению какой-либо периодически изменяющейся величины называется коэффициентом формы кривой. Для синусоидального тока
Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока. Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления. Действующее значение переменного тока – это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока. Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р2r. Мощность переменного тока выразится как средний эффект мгновенной мощности I2r за целый период или среднее значение от (Im х sinωt)2 х rза то же время. Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I2r = Mr, откуда I = √M, Величина I называется действующим значением переменного тока. Среднее значение i2 при переменном токе определим следующим образом. Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени. Действующее значение переменного тока Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно1/2I2m. Следовательно, М = 1/2I2m Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2 Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид: U = Um / √2,E= Em / √2 Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е). На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии. Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения. При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √2 раз. От этого расположение векторов на диаграмме не изменяется. |
Список параметров напряжения и силы электрического тока
В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока
Значения переменного напряжения (тока)
Мгновенное значение
Мгновенное значение – это значение сигнала в определённый момент времени, функцией которого является (u (t) , i (t) {\displaystyle u(t)~,\quad i(t)}).{2}(t)dt}}}
Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I {\displaystyle I} и U {\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.
Когда не оговаривают особо, то обычно имеют ввиду именно среднеквадратичные значения величины напряжения или силы тока.
В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.
Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.
Среднее значение
Среднее значение (смещение) – постоянная составляющая напряжения или силы тока
U = 1 T ∫ 0 T u (t) d t , I = 1 T ∫ 0 T i (t) d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}
В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения).{T}\mid i(t)\mid dt}
На практике используется редко, однако большинство измерительных приборов переменного тока – магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.
Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.
Коэффициенты пересчёта значений
- Коэффициент формы кривой переменного напряжения (тока) – величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} .
- Коэффициент амплитуды кривой переменного напряжения (тока) – величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2 {\displaystyle {\sqrt {2}}} .
Параметры постоянного тока
- Размах пульсации напряжения (тока) – величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени
- Коэффициент пульсации напряжения (тока) – величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по действующему значению – величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсации напряжения (тока) пo среднему значению – величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)
Литература и документация
Литература
- Справочник по радиоэлектронным устройствам : В 2-х т.; Под ред. Д. П. Линде – М.: Энергия, 1978
- Шульц Ю. Электроизмерительная техника: 1000 понятий для практиков: Справочник: Пер. с нем. М.:Энергоатомиздат, 1989
Нормативно-техническая документация
- ГОСТ 16465-70 Сигналы радиотехнические измерительные. Термины и определения
- ГОСТ 23875-88 Качество электрической энергии. Термины и определения
- ГОСТ 13109-97 Электрическая энергия. Совместимость технических средств. Нормы качества электрической энергии в системах электроснабжения общего назначения
Ссылки
- Электрические цепи постоянного тока
- Переменный ток. Изображение синусоидальных переменных
- Амплитудное, среднее, эффективное
- Периодические несинусоидальные ЭДС, токи и напряжения в электрических цепях
- Системы тока и номинальные напряжения электроустановок
- Электричество
- Проблемы высших гармоник в современных системах электропитания
Какой физический смысл имеет действующее значение напряжения и тока
Александр титов
Действующее значение силы ПЕРЕМЕННОГО тока – это такое значение величины ПОСТОЯННОГО тока, действие которого произведёт ту же самую работу (или тепловой эффект) , что и действие переменного тока за время одного периода его действия.2 = Im/2, откуда I = Im / корень из 2. Это и есть действующее значение тока.
То же самое с действующим значением напряжения и ЭДС.
Vitas latish
можно грубо сказать
– напряжение – потенциальная энергия…. расческа- волосы…. напряжение = свечение, искорки, подъем волос… .
– ток это работа, действие, сила.. . тепло, горение, движение выплеск кенетической энергии
Определение 1
Эффективным (действующим) называют значение переменного тока равное величине эквивалентного постоянного тока, который при прохождении через такое же сопротивление, что и переменный ток выделяет на нем то же количество тепла за одинаковые промежутки времени.
Количественная связь амплитуд силы и напряжения переменного тока и эффективных значений
Количество тепла, которое выделяется переменным током на сопротивлении $R$ за малый промежуток времени $dt$, равно:
Тогда за один период переменный ток выделяет тепла ($W$):
Обозначим через $I_{ef}$ силу постоянного тока, который на сопротивлении $R$ выделяет такое же количество тепла ($W$), как и переменный ток $I$ за время равное периоду колебаний переменного тока ($T$). Тогда выразим $W$ через постоянный ток и приравняем выражение к правой части уравнения (2), имеем:
Выразим из уравнения (3) силу эквивалентного постоянного тока, получим:
Если сила тока изменяется по синусоидальному закону:
подставим выражение (5) для переменного тока в формулу (4), тогда величина постоянного тока выразится как:
Следовательно, выражение (6) может быть преобразовано к виду:
где $I_{ef}$ называют эффективным значением силы тока. Аналогично записывают выражения для эффективных (действующих) значений напряжений:
Применение действующих значений тока и напряжения
Когда в электротехнике говорят о силе переменного тока и напряжении, то имеют в виду их эффективные значения. В частности, вольтметры и амперметры градуируют обычно на эффективные значения. Следовательно, максимальное значение напряжения в цепи переменного тока примерно в 1,5 раза больше того, что показывает вольтметр. Этот факт следует учесть при расчете изоляторов, исследовании проблем безопасности.
Эффективные значения используют для характеристики формы сигнала переменного тока (напряжения). Так, вводят коэффициент амплитуды ($k_a$). равный:
и коэффициент формы ($k_f$):
где $I_{sr\ v}=\frac{2}{\pi }\cdot I_m$ –средневыпрямленное значение силы тока.
Для синусоидального тока $k_a=\sqrt{2},\ k_f=\frac{\pi }{2\sqrt{2}}=1,11.$
Пример 1
Задание: Напряжение, которое показал вольтметр равно $U=220 В$. Какова амплитуда напряжения?
Решение:
Как было сказано, вольтметры и амперметры обычно градуируют на действующие значения напряжения (силу тока), следовательно, прибор показывает в наших обозначениях $U_{ef}=220\ В.$ В соответствии с известным соотношением:
найдем амплитудное значение напряжения, как:
Вычислим:
Ответ: $U_m\approx 310,2\ В.$
Пример 2
Задание: Как связана мощность переменного тока на сопротивлении $R$ и эффективные значения тока и напряжения?
Решение:
Среднее значение мощности переменного тока в цепи равно
\[\left\langle P\right\rangle =\frac{A_T}{T}=\frac{U_mI_mcos\varphi }{2}\left(2.2}_mR=\frac{U_mI_mcos \varphi}{2}\left(2.3\right),\]
где $I_m\ $- амплитуда силы тока, $U_m$ — амплитуда внешнего напряжения, $\varphi$ — разность фаз между силой тока и напряжением.
У постоянного тока мгновенная мощность совпадает со средней. Для $I_{ef}$=const можно положить $cos\varphi =1,\ $значит формулу (2.3) можно записать как:
если вместо амплитудных значений ($U_m\ и\ I_m$) использовать их эффективные (действующие) значения:
Следовательно, мощность тока можно записать как:
где $cos \varphi$ — коэффициент мощности. В технике этот коэффициент делают как можно большим. При малом $cos\varphi $ для того, чтобы в цепи выделялась необходимая мощность нужно пропускать большой ток, что ведет к росту потерь в подводящих проводах.
Такую же мощность (как в выражении (2.3)) развивает постоянный ток, сила которого представлена в формуле (2.5).
Ответ: $P_{tR}=U_{ef}I_{ef}cos\varphi .$
При расчете цепей переменного тока обычно пользуются понятием действующих (эффективных) значений переменного тока, напряжения и э. д. с.
Действующие значения тока, напряжения и э. д. с. обозначаются прописными буквами .
На шкалах измерительных приборов и технической документации также указываются действующие значения величин.
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.
Количество тепла, выделенное переменным током в со противлении за бесконечно малый промежуток времени
а за период переменного тока Т
Приравняв Полученное выражение количеству тепла выделенному в том же сопротивлении постоянным током за то же время Т, получим:
Сократив общий множитель , получим действующее значение тока
Рис. 5-8. График переменного тока и квадрата тока.
На рис. 5-8 построена кривая мгновенных значений тока i и кривая квадратов мгновенных значений Площадь, ограниченная последней кривой и осью абсцисс, представляет собой в некотором масштабе величину, определяемую выражением Высота прямоугольника равновеликого площади, ограниченной кривой и осью абсцисс, равная среднему значению ординат кривой представляет собой квадрат действующего значения тока
Если ток изменяется по закону синуса, т. е.
Аналогично для действующих значений синусоидальных напряжений и э. д. с. можно написать:
Кроме действующего значения тока и напряжения, иногда пользуются еще понятием среднего значения тбка и напряжения.
Среднее значение синусоидального тока за период равно нулю, так как в течение первой половины периода определенное количество электричества Q проходит через поперечное сечение проводника в прямом направлении. В течение второй половины периода то же количество электричества проходит через сечение проводника в обратном направлении. Следовательно, количество электричества, прошедшее через сечение проводника за период, равно нулю, равно нулю и среднее за период значение синусоидального тока.
Поэтому среднее значение синусоидального тока вычисляют за полупериод, в течение которого ток остается положительным. Среднее значение тока равно отношению количества электричества, прошедшего через сечение проводника за половину периода, к продолжительности этого полупериода.
В механической системе вынужденные колебания возникают при действии на нее внешней периодической силы. Аналогично этому вынужденные электромагнитные колебания в электрической цепи происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.
Вынужденные электромагнитные колебания в электрической цепи представляют собой переменный электрический ток .
- Переменный электрический ток – это ток, сила и направление которого периодически меняются.
Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:
\(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,
где u – мгновенное значение напряжения, U m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае
\(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,
где φ c – разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Исходя из этого можно дать еще такое определение:
- Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.
Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.
Генератор переменного тока
Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими гармонические колебания.
- Генератором переменного тока называется электротехническое устройство, предназначенное для преобразования механической энергии в энергию переменного тока.
ЭДС индукции генератора изменяется по синусоидальному закону
\(e={\rm E}_{m} \cdot \sin \omega \cdot t,\)
где \({\rm E}_{m} =B\cdot S\cdot \omega\) – амплитудное (максимальное) значение ЭДС. При подключении к выводам рамки нагрузки сопротивлением R , через нее будет проходить переменный ток. По закону Ома для участка цепи сила тока в нагрузке
\(i=\dfrac{e}{R} =\dfrac{B \cdot S \cdot \omega }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\)
где \(I_{m} = \dfrac{B\cdot S\cdot \omega }{R}\) – амплитудное значение силы тока.
Основными частями генератора являются (рис. 1):
- индуктор – электромагнит или постоянный магнит, который создает магнитное поле;
- якорь – обмотка, в которой индуцируется переменная ЭДС;
- коллектор со щетками – устройство, посредством которого снимается с вращающихся частей или подается по ним ток.
Неподвижная часть генератора называется статором , а подвижная – ротором . В зависимости от конструкции генератора его якорь может быть как ротором, так и статором. При получении переменных токов большой мощности якорь обычно делают неподвижным, чтобы упростить схему передачи тока в промышленную сеть.
На современных гидроэлектростанциях вода вращает вал электрогенератора с частотой 1-2 оборота в секунду. Таким образом, если бы якорь генератора имел только одну рамку (обмотку), то получался бы переменный ток частотой 1-2 Гц. Поэтому, для получения переменного тока промышленной частоты 50 Гц якорь должен содержать несколько обмоток, позволяющих увеличить частоту вырабатываемого тока. Для паровых турбин, ротор которых вращается очень быстро, используют якорь с одной обмоткой. В этом случае частота вращения ротора совпадает с частотой переменного тока, т.е. ротор должен делать 50 об/с.
Мощные генераторы вырабатывают напряжение 15-20 кВ и обладают КПД 97-98 %.
Из истории . Первоначально Фарадей обнаружил лишь едва заметный ток в катушке при движении вблизи нее магнита. «Какая от этого польза?» – спросили его. Фарадей ответил: «Какая может быть польза от новорожденного?» Прошло немногим более половины столетия и, как сказал американский физик Р. Фейнман, «бесполезный новорожденный превратился в чудо-богатыря и изменил облик Земли так, как его гордый отец не мог себе и представить».
*Принцип действия
Принцип действия генератора переменного тока основан на явлении электромагнитной индукции.
Пусть проводящая рамка площадью S вращается с угловой скоростью ω вокруг оси, расположенной в ее плоскости перпендикулярно однородному магнитному полю индукцией \(\vec{B}\) (см. рис. 1).
При равномерном вращении рамки угол α между направлениями вектора индукции магнитного поля \(\vec{B}\) и нормали к плоскости рамки \(\vec{n}\) меняется со временем по линейному закону. Если в момент времени t = 0 угол α 0 = 0 (см. рис. 1), то
\(\alpha = \omega \cdot t = 2\pi \cdot \nu \cdot t,\)
где ω – угловая скорость вращения рамки, ν – частота ее вращения.
В этом случае магнитный поток, пронизывающий рамку будет изменяться следующим образом
\(\Phi \left(t\right)=B\cdot S\cdot \cos \alpha =B\cdot S\cdot \cos \omega \cdot t.\)
Тогда согласно закону Фарадея индуцируется ЭДС индукции
\(e=-\Phi “(t)=B\cdot S\cdot \omega \cdot \sin \omega \cdot t = {\rm E}_{m} \cdot \sin \omega \cdot t.\)
Подчеркнем, что ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное, которое также остается неизменным в течение следующего полуоборота.
Действующие значения силы тока и напряжения
Пусть источник тока создает переменное гармоническое напряжение
\(u=U_{m} \cdot \sin \omega \cdot t.\;\;\;(1)\)
Согласно закону Ома, сила тока в участке цепи, содержащей только резистор сопротивлением R , подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
\(i = \dfrac{u}{R} =\dfrac{U_{m} }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\;\;\; (2)\)
где \(I_m = \dfrac{U_{m}}{R}.\) Как видим, сила тока в такой цепи также меняется с течением времени по синусоидальному закону. Величины U m , I m называются амплитудными значениями напряжения и силы тока . Зависящие от времени значения напряжения u и силы тока i называют мгновенными .
Кроме этих величин используются еще одна характеристика переменного тока: действующие (эффективные) значения силы тока и напряжения .
- Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Обозначается буквой I .
- Действующим (эффективным) значением напряжения переменного тока называется напряжение такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Обозначается буквой U .{2}}{R}.\)
Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R , выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе.
Действующие значения гармонических токов и напряжений. Действующие значения силы тока и напряжения
Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?
При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.
Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.
Действующее значение переменного тока – это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.
Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.
Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р 2 r.
Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от (Im х sinωt) 2 х rза то же время.
Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √M,
Величина I называется действующим значением переменного тока.
Среднее значение i2 при переменном токе определим следующим образом.
Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.
Действующее значение переменного тока
Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины.
Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно1/2I 2 m. Следовательно, М = 1/2I 2 m
Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2
Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:
U = Um / √2,E= Em / √2
Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е).
На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.
Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.
При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √2 раз. От этого расположение векторов на диаграмме не изменяется.
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, – периодом Т. Для периодического тока имеем
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i – мгновенное значение тока ;
u – мгновенное значение напряжения ;
е – мгновенное значение ЭДС ;
р – мгновенное значение мощности .
Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ).
Амплитуда тока;
Амплитуда напряжения;
Амплитуда ЭДС.
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:
Значения
аргументов синусоидальных функций
иназываютсяфазами синусоид,
а значение фазы в начальный момент
времени (t =0): и
–начальной
фазой ( ).
Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .
Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:
Векторное изображение синусоидально изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное ) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:
Каждый из этих токов синусоидален и может быть представлен уравнением
Результирующий ток также будет синусоидален:
Определение амплитудыи начальной фазыэтого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
.
Построение векторной диаграммы в масштабе позволяет определить значения ииз диаграммы, после чего может быть записано решение для мгновенного значенияпутем формального учета угловой частоты:.
Физический смысл данных понятий примерно таков же, как физический смысл средней скорости или других величин, усредненных по времени. В различные моменты времени сила переменного тока и его напряжение принимают разные значения, поэтому говорить о силе переменного тока вообще можно лишь условно.
Вместе с тем совершенно очевидно, что различные токи имеют различные энергетические характеристики – они производят разную работу за один и тот же промежуток времени. Произведенная током работа принята за основу при определении действующего значения силы тока. Задаются определенным промежутком времени и рассчитывают работу, совершенную переменным током за этот промежуток времени. Затем, зная эту работу, производят обратное вычисление: узнают силу постоянного тока, который произвел бы аналогичную работу за тот же промежуток времени. То есть производят усреднение по мощности. Вычисленная сила гипотетически протекающего через тот же проводник постоянного тока, производящего ту же самую работу и есть – действующее значение исходного переменного тока. Аналогично поступают и с напряжением. Данный расчет сводится к определению величины такого интеграла:
Откуда берется данная формула? Из хорошо известной формулы для мощности тока, выражаемой через квадрат его силы.
Действующие значения периодических и синусоидальных токов
Вычислять действующее значение для произвольных токов – занятие малопродуктивное. Зато для периодического сигнала данный параметр может оказаться весьма полезным. Известно, что любой периодический сигнал может быть разложен в спектр. То есть, представлен как конечная или бесконечная сумма синусоидальных сигналов. Поэтому для определения величины действующего значения такого периодического тока нам нужно знать, как вычислять действующее значение простого синусоидального тока. В итоге, сложив действующие значения нескольких первых гармоник с максимальной амплитудой, мы получим приближенное значение действующего значения тока для произвольного периодического сигнала. Подставляя в вышеприведенную формулу выражение для гармонического колебания, получим такую приближенную формулу.
Переменный синусоидальный ток
Переменный ток – это ток, который периодически изменяется как по модулю, так и по направлению. Появляется переменный ток благодаря электромагнитной индукции. Электромагнитная индукция это явление возникновения тока в замкнутом контуре при изменении магнитного потока проходящего через него. Чтобы понять, как именно возникает ток, представим себе рамку (кусочек проволоки прямоугольной формы), которая находится под воздействием магнитного поля B.
Пока рамка находится в покое, тока в ней нет. Но как только мы начнём её поворачивать, электроны, которые находятся в рамке, начнут перемещаться вместе с ней, то есть двигаться в магнитном поле. Вследствие этого магнитное поле начинает действовать на электроны, заставляя их двигаться по рамке. Чем больше линий магнитного поля пронизывает рамку, тем сила действующая на электроны больше, следовательно, и электрический ток тоже. Получается, что ток достигает максимума в момент, когда рамка перпендикулярна магнитному полю (наибольшее количество линии пронизывает рамку) и равен нулю, когда параллельна (наименьшее количество линии пронизывает рамку). Соответственно и сила, которая действует на электроны, тоже изменяется. После прохождения момента, когда рамка параллельна вектору магнитной индукции B, ток в ней начинает течь в обратную сторону.
Ток, который получается при вращении рамки, изменяясь во времени, описывает синусоиду, то есть является синусоидальным. Переменный синусоидальный ток является частным случаем периодического переменного тока. Закон, описывающий изменение тока, имеет вид:
Амплитуда Im – это наибольшая абсолютная величина, которую принимает периодически изменяющийся ток.
Начальная фаза ψ – аргумент синусоидального тока (угол), отсчитываемый от точки перехода тока через нуль к положительному значению.
Время, за которое ток в проводнике дважды изменяет своё направление, называют периодом T. Период измеряется в секундах.
Циклической частотой f называется величина обратная периоду . Измеряется в Герцах, в домашней розетке циклическая частота тока равна 50 Гц, её также называют промышленной частотой. При такой частоте период тока равен , это значит, что за две сотых секунды ток в нашей розетке меняет свое направление два раза.
Угловая частота ω показывает с какой скоростью изменяется фаза тока и определяется как
Среднее значение Iср синусоидального тока за период Т определяют из геометрических представлений: площадь прямоугольника с основанием T/2 и высотой Iср приравнивают площади ограниченной кривой тока:
После упрощения получаем формулу:
Действующее значение синусоидального тока определяется из энергетических представлений: действующий ток равен по величине такому постоянному току I, который в активном сопротивлении R за период Т выделяет такое количество энергии, как и данный ток i. То есть действующее значение, это своеобразная аналогия между переменным и постоянным током.
Для синусоидального тока действующее значение определяется по формуле:
или
Это основное что нужно знать о переменном синусоидальном токе.
Читайте также – Мгновенная мощность
Действующее значение переменного напряжения имеет. Действующее значение переменного тока и напряжения
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, – периодом Т. Для периодического тока имеем
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i – мгновенное значение тока ;
u – мгновенное значение напряжения ;
е – мгновенное значение ЭДС ;
р – мгновенное значение мощности .
Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ).
Амплитуда тока;
Амплитуда напряжения;
Амплитуда ЭДС.
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:
Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t =0): и –начальной фазой ( ).
Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .
Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:
Векторное изображение синусоидально изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное ) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:
Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока.
Действующим илиэффективным значением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе.
Свяжем
эффективное значение тока с его
амплитудным значением. Для этого
рассчитаем количество теплоты, выделяемое
на активном сопротивлении переменным
током за время, равное периоду колебаний.
Напомним, что по закону Джоуля-Ленца
количество теплоты, выделяющееся на
участке цепи cсопротивлениемприпостоянном токеза время,
определяется по формуле
.
Переменный ток можно считать постоянным
только в течение очень малых промежутков
времени
.
Поделим период колебанийна очень большое число малых промежутков
времени
.
Количество теплоты
,
выделяемое на сопротивленииза время
:
.
Общее количество теплоты, выделяемое
за период, найдется суммированием
теплот, выделяемых за отдельные малые
промежутки времени, или, другими словами,
интегрированием:
.
Сила тока в цепи изменяется по синусоидальному закону
,
.
Опуская вычисления, связанные с интегрированием, запишем окончательный результат
.
Если бы по
цепи шёл некоторый постоянный ток
,
то за время, равное,
выделилось бы тепло
.
По определению постоянный ток,
оказывающий такое же тепловое действие,
что и переменный, будет равен эффективному
значению переменного тока
.
Находим эффективное значение силы
тока, приравнивая теплоты, выделяемые
за период, в случаях постоянного и
переменного токов
(4.28)
Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током:
(4.29)
Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В.
4.4.5. Мощность в цепи переменного тока
Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам:
,
.
Тогда мгновенное значение мощности, выделяемой на участке цепи,
Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний):
С использованием известной тригонометрической формулы
.
Величину
усреднять не нужно, так как она не зависит
от времени, следовательно:
.
За длительное время значение косинуса много раз успевает измениться, принимая как отрицательные, так и положительные значения в пределах от (1) до 1. Понятно, что среднее во времени значение косинуса равно нулю
,
поэтому
(4.30)
Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим
. (4.31)
Мощность, выделяемая на участке цепи с
переменным током, зависит от эффективных
значений тока и напряжения и сдвига
фаз между током и напряжением . Например,
если участок цепи состоит из одного
только активного сопротивления, то
и
.
Если участок цепи содержит только
индуктивность или только ёмкость, то
и
.
Объяснить среднее нулевое значение мощности, выделяемой на индуктивности и ёмкости можно следующим образом. Индуктивность и ёмкость лишь заимствуют энергию у генератора, а затем возвращают её обратно. Конденсатор заряжается, а затем разряжается. Сила тока в катушке увеличивается, затем снова спадает до нуля и т. д. Именно по той причине, что на индуктивном и ёмкостном сопротивлениях средняя расходуемая генератором энергия равна нулю, их назвали реактивными. На активном же сопротивлении средняя мощность отлична от нуля. Другими словами провод с сопротивлением при протекании по нему тока нагревается. И энергия, выделяемая в виде тепла, назад в генератор уже не возвращается.
Если участок цепи содержит несколько элементов, то сдвига фаз может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27).
Пример 4.7. К генератору переменного
синусоидального тока подключён резистор
с сопротивлением.
Во сколько раз изменится средняя
мощность, расходуемая генератором, если
к резистору подключить катушку с
индуктивным сопротивлением
а) последовательно, б) параллельно (рис.
4.10)? Активным сопротивлением катушки
пренебречь.
Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность
(см. формулу (4.30)).
Рассмотрим цепь на рис. 4.10, а. В примере
4.6 было определено амплитудное значение
силы тока генератора:
.
Из векторной диаграммы на рис. 4.11,а
определяем сдвиг фаз между током и
напряжением генератора
.
В результате средняя расходуемая генератором мощность
.
Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза.
Рассмотрим цепь на рис. 4.10,б. В примере
4.6 было определено амплитудное значение
силы тока генератора
.
Из векторной диаграммы на рис. 4.11,б
определяем сдвиг фаз между током и
напряжением генератора
.
Тогда средняя мощность, расходуемая генератором
Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.
Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.
В современной литературе чаще используется математическое определение этой величины – среднеквадратичное значение переменного тока.{2}dt}}.}
Для синусоидального тока:
I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , {\displaystyle I={\frac {1}{\sqrt {2}}}\cdot I_{m}\approx 0{,}707\cdot I_{m},}
I m {\displaystyle I_{m}} – амплитудное значение тока.
Для тока треугольной и пилообразной формы:
I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . {\displaystyle I={\frac {1}{\sqrt {3}}}\cdot I_{m}\approx 0{,}577\cdot I_{m}.}
Аналогичным образом определяются действующие значения ЭДС и напряжения.
Дополнительные сведения
В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value – эффективное значение. Также применяется аббревиатура RMS (rms) – root mean square – среднеквадратичное (значение).
В электротехнике приборы электромагнитной, электродинамической и тепловой систем калибруются на действующее значение.
Источники
- «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
- Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
- «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 – § 7.10
Ссылки
- Действующие значения тока и напряжения
- Среднеквадратичное значение
Мгновенные, максимальные, действующие и средние значения электрических величин переменного тока
Мгновенное и максимальное значения. Величину переменной электродвижущей силы, силы тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин и обозначают соответственно строчными буквами (e, i, u, p ).
Максимальным значением (амплитудой) переменной э. д. с. (или напряжения или тока) называется та наибольшая величина, которой она достигает за один период. Максимальное значение электродвижущей силы обозначается Е m , напряжения – U m , тока – I m .
Действующим (или эффективным) значением переменного тока называется такая сила постоянного тока, которая, протекая через равное сопротивление и за одно и то же время, что и переменный ток, выделяет одинаковое количество тепла.
Для синусоидального переменного тока действующее значение меньше максимального в 1,41 раз, т. е. в раз.
Аналогично действующие значения переменной электродвижущей силы и напряжения меньше их максимальных значений тоже в 1,41 раза.
По величине измеренных действующих значений силы переменного тока, напряжения или электродвижущей силы можно вычислить их максимальные значения:
E m = E · 1,41; U m = U · 1,41; I m = I · 1,41;
Среднее значение = отношению количества эл энергии прошедшего через сечение проводника за половину периода к величине этого полупериода.
Под средним значением понимают среднеарифметическое ее значение за половину периода.
/ Среднее и действующие значения синусоидальных токов и напряжений
Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока
т. е. среднее значение синусоидального тока составляет от амплитудного. Аналогично,
Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока
Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично,
Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.
Количество теплоты, выделенное за один период синусоидальным током,
Выделенная за то же время постоянным током теплота равна Приравняем их:
Таким образом, действующее значение синусоидального тока численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.
Для установления эквивалентности переменного тока в отношении энергии и мощности, общности методов расчета, а также сокращения вычислительной работы изменяющиеся непрерывно во времени токи. ЭДС и напряжения заменяют эквивалентными неизменными во времени величинами. Действующим или эквивалентным значением называется такой неизменный во времени ток, при котором выделяется в резистивном элементе с активным сопротивлением r за период то же количество энергии, что и при действительном изменяющемся синусоидально токе.
Энергия за период, выделяющаяся в резистивном элементе при синусоидальном токе,
i 2r dt = | I m 2 sin2 ωt r dt. . | |||
При неизменном во времени токе энергия
W = I 2rT
Приравняв правые части
I m
0,707I m .
Таким образом, действующее значение тока меньше амплитудного в √2 раз.
Аналогично определяют действующие значения ЭДС и напряжения:
Е = E m / √2, U = U m / √2.
Действующему значению тока пропорциональна сила, действующая на ротор двигателя переменного тока, подвижную часть измерительного прибора и т. д. Когда говорят о значениях напряжения, ЭДС и тока в цепях переменного тока, имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока отградуированы соответственно в действующих значениях тока и напряжения. Например, если прибор показывает 10 А, то это значит, что амплитуда тока
I m = √2I = 1,41 10 = 14,1 A,
и мгновенное значение тока
i = I m sin (ωt + ψ) = 14,1 sin (ωt + ψ).
При анализе и расчет выпрямительных устройств пользуются средними значениями тока, ЭДС и напряжения, под которыми понимают среднее арифметическое значение соответствующей величины за полпериода (среднее значение за период, как известно, равно нулю):
T 2 | ||||||||||
Е ср = | Е т sin ωt dt = | sin ωt d ωt = | |cos ωt | π 0 = | 0,637Е т . | ||||||
Аналогично можно найти средние значения тока и напряжения:
I ср = 2I т /π; U ср = 2U т /π.
Отношение действующего значения к среднему значению какой-либо периодически изменяющейся величины называется коэффициентом формы кривой. Для синусоидального тока
Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока. Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления. Действующее значение переменного тока – это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока. Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р2r. Мощность переменного тока выразится как средний эффект мгновенной мощности I2r за целый период или среднее значение от (Im х sinωt)2 х rза то же время. Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I2r = Mr, откуда I = √M, Величина I называется действующим значением переменного тока. Среднее значение i2 при переменном токе определим следующим образом. Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени. Действующее значение переменного тока Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно1/2I2m. Следовательно, М = 1/2I2m Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2 Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид: U = Um / √2,E= Em / √2 Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е). На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии. Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения. При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √2 раз. От этого расположение векторов на диаграмме не изменяется. |
Список параметров напряжения и силы электрического тока
В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока
Значения переменного напряжения (тока)
Мгновенное значение
Мгновенное значение – это значение сигнала в определённый момент времени, функцией которого является (u (t) , i (t) {\displaystyle u(t)~,\quad i(t)}).{2}(t)dt}}}
Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I {\displaystyle I} и U {\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.
Когда не оговаривают особо, то обычно имеют ввиду именно среднеквадратичные значения величины напряжения или силы тока.
В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.
Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.
Среднее значение
Среднее значение (смещение) – постоянная составляющая напряжения или силы тока
U = 1 T ∫ 0 T u (t) d t , I = 1 T ∫ 0 T i (t) d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}
В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения).{T}\mid i(t)\mid dt}
На практике используется редко, однако большинство измерительных приборов переменного тока – магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.
Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.
Коэффициенты пересчёта значений
- Коэффициент формы кривой переменного напряжения (тока) – величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} .
- Коэффициент амплитуды кривой переменного напряжения (тока) – величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2 {\displaystyle {\sqrt {2}}} .
Параметры постоянного тока
- Размах пульсации напряжения (тока) – величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени
- Коэффициент пульсации напряжения (тока) – величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по действующему значению – величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсации напряжения (тока) пo среднему значению – величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)
Литература и документация
Литература
- Справочник по радиоэлектронным устройствам : В 2-х т.; Под ред. Д. П. Линде – М.: Энергия, 1978
- Шульц Ю. Электроизмерительная техника: 1000 понятий для практиков: Справочник: Пер. с нем. М.:Энергоатомиздат, 1989
Нормативно-техническая документация
- ГОСТ 16465-70 Сигналы радиотехнические измерительные. Термины и определения
- ГОСТ 23875-88 Качество электрической энергии. Термины и определения
- ГОСТ 13109-97 Электрическая энергия. Совместимость технических средств. Нормы качества электрической энергии в системах электроснабжения общего назначения
Ссылки
- Электрические цепи постоянного тока
- Переменный ток. Изображение синусоидальных переменных
- Амплитудное, среднее, эффективное
- Периодические несинусоидальные ЭДС, токи и напряжения в электрических цепях
- Системы тока и номинальные напряжения электроустановок
- Электричество
- Проблемы высших гармоник в современных системах электропитания
Какой физический смысл имеет действующее значение напряжения и тока
Александр титов
Действующее значение силы ПЕРЕМЕННОГО тока – это такое значение величины ПОСТОЯННОГО тока, действие которого произведёт ту же самую работу (или тепловой эффект) , что и действие переменного тока за время одного периода его действия.2 = Im/2, откуда I = Im / корень из 2. Это и есть действующее значение тока.
То же самое с действующим значением напряжения и ЭДС.
Vitas latish
можно грубо сказать
– напряжение – потенциальная энергия…. расческа- волосы…. напряжение = свечение, искорки, подъем волос… .
– ток это работа, действие, сила.. . тепло, горение, движение выплеск кенетической энергии
Физический смысл данных понятий примерно таков же, как физический смысл средней скорости или других величин, усредненных по времени. В различные моменты времени сила переменного тока и его напряжение принимают разные значения, поэтому говорить о силе переменного тока вообще можно лишь условно.
Вместе с тем совершенно очевидно, что различные токи имеют различные энергетические характеристики – они производят разную работу за один и тот же промежуток времени. Произведенная током работа принята за основу при определении действующего значения силы тока. Задаются определенным промежутком времени и рассчитывают работу, совершенную переменным током за этот промежуток времени. Затем, зная эту работу, производят обратное вычисление: узнают силу постоянного тока, который произвел бы аналогичную работу за тот же промежуток времени. То есть производят усреднение по мощности. Вычисленная сила гипотетически протекающего через тот же проводник постоянного тока, производящего ту же самую работу и есть – действующее значение исходного переменного тока. Аналогично поступают и с напряжением. Данный расчет сводится к определению величины такого интеграла:
Откуда берется данная формула? Из хорошо известной формулы для мощности тока, выражаемой через квадрат его силы.
Действующие значения периодических и синусоидальных токов
Вычислять действующее значение для произвольных токов – занятие малопродуктивное. Зато для периодического сигнала данный параметр может оказаться весьма полезным. Известно, что любой периодический сигнал может быть разложен в спектр. То есть, представлен как конечная или бесконечная сумма синусоидальных сигналов. Поэтому для определения величины действующего значения такого периодического тока нам нужно знать, как вычислять действующее значение простого синусоидального тока. В итоге, сложив действующие значения нескольких первых гармоник с максимальной амплитудой, мы получим приближенное значение действующего значения тока для произвольного периодического сигнала. Подставляя в вышеприведенную формулу выражение для гармонического колебания, получим такую приближенную формулу.
Значения действующего напряжения и силы тока. Определение. Соотношение с амплитудой для разной формы. (10+)
Понятие эффективных (действующих) значений напряжения и силы тока
Когда мы говорим о переменных напряжении или силе тока, особенно сложной формы, то встает вопрос о том, как их измерять. Ведь напряжение постоянно меняется. Можно измерять амплитуду сигнала, то есть максимум модуля значения напряжения. Такой метод измерения нормально подходит для сигналов относительно гладкой формы, но наличие коротких всплесков портит картину. Еще одним критерием выбора способа измерения является то, для каких целей делается измерение. Так как в большинстве случаев интерес представляет мощность, которую может отдать тот или иной сигнал, то применяется действующее (эффективное) значение.
Вашему вниманию подборка материалов: Действующее (эффективное) значение для сигналов стандартной формыСинусоидальный сигнал (синус, синусоида) [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 2 ] Прямоугольный сигнал (меандр) [Действующее значение ] = [Амплитудное значение ] Треугольный сигнал [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 3 ] Закон Ома и мощность для действующих значений напряжения и силы токаЭффективное значение напряжения измеряется в Вольтах, а силы тока в Амперах. Для эффективных значений верен закон Ома: = / [Сопротивление нагрузки, Ом ] [Рассеиваемая на омической нагрузке мощность, Вт ] = [Действующее значение силы тока, А ] * [Действующее значение напряжения, В ] К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости , чтобы быть в курсе. Если что-то непонятно, обязательно спросите! Еще статьи Микроконтроллеры – пример простейшей схемы, образец применения. Фузы (… Практика проектирования электронных схем. Самоучитель электроники…. Силовой мощный импульсный трансформатор, дроссель. Намотка. Изготовить… Силовой резонансный фильтр для получения синусоиды от инвертора… Бесперебойник своими руками. ИБП, UPS сделать самому. Синус, синусоида… Преобразователь однофазного напряжения в трехфазное. Принцип действия,… Электрическое напряжение. Амплитуда сигнала. Амплитудное. Вольт. Volt…. |
Что называют действующим значением силы переменного тока. Действующее значение переменного тока и напряжения
,
После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:
Аналогичные соотношения могут быть получены также для напряжения и ЭДС:
Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.
Учитывая, например, что действующее значение напряжения в нашей сети составляет 220В, можно определить амплитудное значение напряжения в сети: U m =U Ö2=311В. Соотношение между действующим и амплитудным значениями напряжений и токов важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.
Действующее значение переменного тока
Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел.
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, – периодом Т. Для периодического тока имеем
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i – мгновенное значение тока ;
u – мгновенное значение напряжения ;
е – мгновенное значение ЭДС ;
р – мгновенное значение мощности .
Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ).
Амплитуда тока;
Амплитуда напряжения;
Амплитуда ЭДС.
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
, |
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:
Значения аргументов синусоидальных функций и называются фазами синусоид, а значение фазы в начальный момент времени (t =0): и – начальной фазой ( ).
Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .
Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:
Векторное изображение синусоидально изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное ) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:
Каждый из этих токов синусоидален и может быть представлен уравнением
Результирующий ток также будет синусоидален:
Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
.
Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .
Действующее и среднее значения переменного тока и напряжения.
Среднее или среднеарифметическое значение Fcp произвольной функции времени f (t )за интервал времени Т определяется по формуле:
Численно среднее значение Fср равно высоте прямоугольника, равновеликого по площади фигуре, ограниченной кривой f (t ), осью t и пределами интегрирования 0 – Т (рис. 35).
Для синусоидальной функции среднее значение за полный период Т (или за целое число полных периодов) равно нулю, так как площади положительной и отрицательной полуволн этой функции равны. Для переменного синусоидального напряжения определяют среднее по модулю значение за полный период Т или среднее значение за половину периода (Т /2) между двумя нулевыми значениями (рис. 36) :
Ucp = Um∙ sinwt dt = 2R . Таким образом, количественные параметры электрической энергии на переменном токе (количество энергии, мощность) определяются действующими значениями напряжения U и тока I . По этой причине в электроэнергетике все теоретические расчеты и экспериментальные измерения принято выполнять для действующих значений токов и напряжений. В радиотехнике и в технике связи, наоборот, оперируют максимальными значениями этих функций.
Приведенные выше формулы для энергии и мощности переменного тока полностью совпадают с аналогичными формулами для постоянного тока. На этом основании можно утверждать, что энергетически постоянному току эквивалентно действующее значение переменного тока.
Что берется за действующее значение силы переменного тока и переменного напряжения
что берется за действующее значение силы переменного тока и переменного напряжения?
Боевое яйцо
Переменный ток, в широком смысле электрический ток, изменяющийся во времени. Обычно в технике под П. т. понимают периодический ток, в котором среднее значение за период силы тока и напряжения равно нулю.
Переменные токи и переменные напряжения постоянно изменяются по величине. В каждое другое мгновение у них другая величина. Возникает вопрос, как же их измерять? Для их измерения введено понятие действующее значение.
Действующим или эффективным значением переменного тока называют величину такого постоянного тока, который по своему тепловому действию равноценен данному переменному току.
Действующим или эффективным значением переменного напряжения называют величину такого постоянного напряжения, которое по своему тепловому действию равноценно данному переменному напряжению.
Все переменные токи и напряжения в технике измеряются в действующих значениях. Приборы измеряющие переменные величины показывают их действующее значение.
Вопрос: напряжение в электросети 220 В, что это значит?
Это значит, что источник постоянного напряжения с напряжением 220 В оказывает такое же тепловое действие как и электросеть.
Действующее значение тока или напряжения синусоидальной формы в 1,41 раз меньше амплитуды этого тока или напряжения.
Пример: Определить амплитуду напряжения электросети с напряжением 220 В.
Амплитуда равна 220 * 1,41=310,2 В.
Физический смысл данных понятий примерно таков же, как физический смысл средней скорости или других величин, усредненных по времени. В различные моменты времени сила переменного тока и его напряжение принимают разные значения, поэтому говорить о силе переменного тока вообще можно лишь условно.
Вместе с тем совершенно очевидно, что различные токи имеют различные энергетические характеристики – они производят разную работу за один и тот же промежуток времени. Произведенная током работа принята за основу при определении действующего значения силы тока. Задаются определенным промежутком времени и рассчитывают работу, совершенную переменным током за этот промежуток времени. Затем, зная эту работу, производят обратное вычисление: узнают силу постоянного тока, который произвел бы аналогичную работу за тот же промежуток времени. То есть производят усреднение по мощности. Вычисленная сила гипотетически протекающего через тот же проводник постоянного тока, производящего ту же самую работу и есть – действующее значение исходного переменного тока. Аналогично поступают и с напряжением. Данный расчет сводится к определению величины такого интеграла:
Откуда берется данная формула? Из хорошо известной формулы для мощности тока, выражаемой через квадрат его силы.
Действующие значения периодических и синусоидальных токов
Вычислять действующее значение для произвольных токов – занятие малопродуктивное. Зато для периодического сигнала данный параметр может оказаться весьма полезным. Известно, что любой периодический сигнал может быть разложен в спектр. То есть, представлен как конечная или бесконечная сумма синусоидальных сигналов. Поэтому для определения величины действующего значения такого периодического тока нам нужно знать, как вычислять действующее значение простого синусоидального тока. В итоге, сложив действующие значения нескольких первых гармоник с максимальной амплитудой, мы получим приближенное значение действующего значения тока для произвольного периодического сигнала. Подставляя в вышеприведенную формулу выражение для гармонического колебания, получим такую приближенную формулу.
>> Активное сопротивление. Действующие значения силы тока и напряжения
§ 32 АКТИВНОЕ СОПРОТИВЛЕНИЕ. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ
Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.
Сила тока в цени с резистором. Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.
В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряже ния (рис. 4.11), а амплитуда силы тока определяется равенством
Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.
Как правило, нам нужно бывает знать среднюю мощ ностъ тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найчи среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.
Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой
P = I 2 R. (4.18)
На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.
Поэтому мгновенная моoность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой
P = i 2 R. (4.19)
Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение
График зависимости мгновенной мощности от времени изображен на рисунке 4.12, а. Согласно графику (рис. 4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем . Зато на протяжении следующей восьмой части периода, когда cos 2t
Средняя мощность равна, таким образом, первому члену в формуле (4.20):
Действующие значения силы тока и напряжения . Из формулы (4.21) видно, что величина есть среднее за период значение квадрата силы тока:
Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы неременного тока. Действующее зртачепие силы неременного тока обозначается через I:
Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты , что и при переменном токе за то же время.
Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:
Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем
Это закон Ома для участка цепи переменного тока с резистором.
Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока:
P = I 2 R = UI.
Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.
1. Чему равна амплитуда напряжения в осветительных сетях переменного тока, рассчитанных на напряжение 220 В!
2. Что называют действующими значениями силы тока и напряжения!
Мякишев Г. Я., Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. – 17-е изд., перераб. и доп. – М. : Просвещение, 2008. – 399 с: ил.
Библиотека с учебниками и книгами на скачку бесплатно онлайн , Физика и астрономия для 11 класса скачать , школьная программа по физике, планы конспектов уроков
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиРассмотрим следующую цепь.
Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.
Активное сопротивление
Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:
U = Um*cos(ω*t).
Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения.
I = u/R = Um*cos(ω*t)/R = Im*cos(ω*t).
Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует.
Действующее значение силы тока
Амплитуда силы тока определяется по следующей формуле:
Среднее значение квадрата силы тока за период вычисляется по следующей формуле:
Здесь Im есть амплитуда колебания силы тока.2) = Um/√2.
Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим:
Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний – такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.
Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.
Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.
Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.{2}dt}}.}
Для синусоидального тока:
I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , {\displaystyle I={\frac {1}{\sqrt {2}}}\cdot I_{m}\approx 0{,}707\cdot I_{m},}
I m {\displaystyle I_{m}} – амплитудное значение тока.
Для тока треугольной и пилообразной формы:
I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . {\displaystyle I={\frac {1}{\sqrt {3}}}\cdot I_{m}\approx 0{,}577\cdot I_{m}.}
Аналогичным образом определяются действующие значения ЭДС и напряжения.
Дополнительные сведения
В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value – эффективное значение. Также применяется аббревиатура RMS (rms) – root mean square – среднеквадратичное (значение).
В электротехнике приборы электромагнитной, электродинамической и тепловой систем калибруются на действующее значение.
Источники
- «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
- Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
- «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 – § 7.10
Ссылки
- Действующие значения тока и напряжения
- Среднеквадратичное значение
Мгновенные, максимальные, действующие и средние значения электрических величин переменного тока
Мгновенное и максимальное значения. Величину переменной электродвижущей силы, силы тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин и обозначают соответственно строчными буквами (e, i, u, p ).
Максимальным значением (амплитудой) переменной э. д. с. (или напряжения или тока) называется та наибольшая величина, которой она достигает за один период. Максимальное значение электродвижущей силы обозначается Е m , напряжения – U m , тока – I m .
Действующим (или эффективным) значением переменного тока называется такая сила постоянного тока, которая, протекая через равное сопротивление и за одно и то же время, что и переменный ток, выделяет одинаковое количество тепла.
Для синусоидального переменного тока действующее значение меньше максимального в 1,41 раз, т. е. в раз.
Аналогично действующие значения переменной электродвижущей силы и напряжения меньше их максимальных значений тоже в 1,41 раза.
По величине измеренных действующих значений силы переменного тока, напряжения или электродвижущей силы можно вычислить их максимальные значения:
E m = E · 1,41; U m = U · 1,41; I m = I · 1,41;
Среднее значение = отношению количества эл энергии прошедшего через сечение проводника за половину периода к величине этого полупериода.
Под средним значением понимают среднеарифметическое ее значение за половину периода.
/ Среднее и действующие значения синусоидальных токов и напряжений
Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока
т. е. среднее значение синусоидального тока составляет от амплитудного. Аналогично,
Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока
Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично,
Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.
Количество теплоты, выделенное за один период синусоидальным током,
Выделенная за то же время постоянным током теплота равна Приравняем их:
Таким образом, действующее значение синусоидального тока численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.
Для установления эквивалентности переменного тока в отношении энергии и мощности, общности методов расчета, а также сокращения вычислительной работы изменяющиеся непрерывно во времени токи. ЭДС и напряжения заменяют эквивалентными неизменными во времени величинами. Действующим или эквивалентным значением называется такой неизменный во времени ток, при котором выделяется в резистивном элементе с активным сопротивлением r за период то же количество энергии, что и при действительном изменяющемся синусоидально токе.
Энергия за период, выделяющаяся в резистивном элементе при синусоидальном токе,
i 2r dt = | I m 2 sin2 ωt r dt. . | |||
При неизменном во времени токе энергия
W = I 2rT
Приравняв правые части
I m
0,707I m .
Таким образом, действующее значение тока меньше амплитудного в √2 раз.
Аналогично определяют действующие значения ЭДС и напряжения:
Е = E m / √2, U = U m / √2.
Действующему значению тока пропорциональна сила, действующая на ротор двигателя переменного тока, подвижную часть измерительного прибора и т. д. Когда говорят о значениях напряжения, ЭДС и тока в цепях переменного тока, имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока отградуированы соответственно в действующих значениях тока и напряжения. Например, если прибор показывает 10 А, то это значит, что амплитуда тока
I m = √2I = 1,41 10 = 14,1 A,
и мгновенное значение тока
i = I m sin (ωt + ψ) = 14,1 sin (ωt + ψ).
При анализе и расчет выпрямительных устройств пользуются средними значениями тока, ЭДС и напряжения, под которыми понимают среднее арифметическое значение соответствующей величины за полпериода (среднее значение за период, как известно, равно нулю):
T 2 | ||||||||||
Е ср = | Е т sin ωt dt = | sin ωt d ωt = | |cos ωt | π 0 = | 0,637Е т . | ||||||
Аналогично можно найти средние значения тока и напряжения:
I ср = 2I т /π; U ср = 2U т /π.
Отношение действующего значения к среднему значению какой-либо периодически изменяющейся величины называется коэффициентом формы кривой. Для синусоидального тока
Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока. Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления. Действующее значение переменного тока – это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока. Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р2r. Мощность переменного тока выразится как средний эффект мгновенной мощности I2r за целый период или среднее значение от (Im х sinωt)2 х rза то же время. Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I2r = Mr, откуда I = √M, Величина I называется действующим значением переменного тока. Среднее значение i2 при переменном токе определим следующим образом. Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени. Действующее значение переменного тока Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно1/2I2m. Следовательно, М = 1/2I2m Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2 Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид: U = Um / √2,E= Em / √2 Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е). На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии. Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения. При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √2 раз. От этого расположение векторов на диаграмме не изменяется. |
Список параметров напряжения и силы электрического тока
В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока
Значения переменного напряжения (тока)
Мгновенное значение
Мгновенное значение – это значение сигнала в определённый момент времени, функцией которого является (u (t) , i (t) {\displaystyle u(t)~,\quad i(t)}).{2}(t)dt}}}
Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I {\displaystyle I} и U {\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.
Когда не оговаривают особо, то обычно имеют ввиду именно среднеквадратичные значения величины напряжения или силы тока.
В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.
Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.
Среднее значение
Среднее значение (смещение) – постоянная составляющая напряжения или силы тока
U = 1 T ∫ 0 T u (t) d t , I = 1 T ∫ 0 T i (t) d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}
В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения).{T}\mid i(t)\mid dt}
На практике используется редко, однако большинство измерительных приборов переменного тока – магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.
Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.
Коэффициенты пересчёта значений
- Коэффициент формы кривой переменного напряжения (тока) – величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} .
- Коэффициент амплитуды кривой переменного напряжения (тока) – величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2 {\displaystyle {\sqrt {2}}} .
Параметры постоянного тока
- Размах пульсации напряжения (тока) – величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени
- Коэффициент пульсации напряжения (тока) – величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по действующему значению – величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсации напряжения (тока) пo среднему значению – величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)
Литература и документация
Литература
- Справочник по радиоэлектронным устройствам : В 2-х т.; Под ред. Д. П. Линде – М.: Энергия, 1978
- Шульц Ю. Электроизмерительная техника: 1000 понятий для практиков: Справочник: Пер. с нем. М.:Энергоатомиздат, 1989
Нормативно-техническая документация
- ГОСТ 16465-70 Сигналы радиотехнические измерительные. Термины и определения
- ГОСТ 23875-88 Качество электрической энергии. Термины и определения
- ГОСТ 13109-97 Электрическая энергия. Совместимость технических средств. Нормы качества электрической энергии в системах электроснабжения общего назначения
Ссылки
- Электрические цепи постоянного тока
- Переменный ток. Изображение синусоидальных переменных
- Амплитудное, среднее, эффективное
- Периодические несинусоидальные ЭДС, токи и напряжения в электрических цепях
- Системы тока и номинальные напряжения электроустановок
- Электричество
- Проблемы высших гармоник в современных системах электропитания
Какой физический смысл имеет действующее значение напряжения и тока
Александр титов
Действующее значение силы ПЕРЕМЕННОГО тока – это такое значение величины ПОСТОЯННОГО тока, действие которого произведёт ту же самую работу (или тепловой эффект) , что и действие переменного тока за время одного периода его действия.2 = Im/2, откуда I = Im / корень из 2. Это и есть действующее значение тока.
То же самое с действующим значением напряжения и ЭДС.
Vitas latish
можно грубо сказать
– напряжение – потенциальная энергия…. расческа- волосы…. напряжение = свечение, искорки, подъем волос… .
– ток это работа, действие, сила.. . тепло, горение, движение выплеск кенетической энергии
Калькулятор полного гармонического искажения тока
Следующий калькулятор вычисляет полное гармоническое искажение тока (THDc), пиковый ток, среднеквадратичный ток и пик-фактор на основе индивидуальных значений гармонических искажений тока между 1-й и 50-й гармониками. Введите основной ток и токи отдельных гармоник для вычисления THDc, а также для просмотра графика формы волны на основе входных значений. График формы волны предполагает, что все фазовые углы для отдельных значений искажения тока равны нулю градусов (в фазе с основным током).
При вводе данных обязательно используйте согласованные единицы ампер или единицу ампера.
Интересно …
Общее гармоническое искажение тока (THDC) токового сигнала – это измерение присутствующего гармонического искажения, которое определяется как отношение суммы мощности всех гармонических составляющих тока к мощности. тока основной частоты. THDc используется для характеристики качества мощности электрической нагрузки и тока, протекающего в проводниках вашей системы.Коэффициент искажения – это тесно связанный термин, который иногда используется как заменяющий термин.
IEEE 519, «Рекомендуемая практика и требования для контроля гармоник в электроэнергетических системах» предоставляет предлагаемые пределы гармонических искажений тока, как показано в таблицах 10.1, 10.2 и 10.3 ниже. Таблицы зависят от нескольких переменных и концепций, определенных следующим образом:
- PCC: точка общего соединения. Эта точка определяется как точка в коммунальном обслуживании конкретного потребителя, к которой может быть подключен другой потребитель.Его часто выбирают в качестве точки учета коммунальных услуг.
- I SC : Доступный ток короткого замыкания.
- I L : максимальный ток потребления 15 или 30 минут (в среднем).
- TDD: Общее искажение спроса. TDD идентичен THD, за исключением того, что IL (как определено ранее) используется вместо основной составляющей тока.
- I SC / I L : отношение тока короткого замыкания к потребляемому току.
Мыслительные процессы, лежащие в основе разработки этих таблиц, заключаются в следующем: 1) заказчик должен нести ответственность за ограничение гармонических токов в соответствии с таблицами 10.1, 10.2 и 10.3 и 2) электросеть должна нести ответственность за ограничение гармонического напряжения в соответствии с таблицей 10.4, представленной на нашей странице калькулятора для гармонических искажений напряжения.
Коэффициент гребней – это мера формы волны, показывающая отношение пикового значения к среднеквадратичному значению. Пик-фактор 1,0 указывает на отсутствие пиков, как в случае с напряжением постоянного тока. Форма волны напряжения с 0% THD будет иметь пик-фактор, равный 1,414. Пик-фактор, превышающий 1,414, обычно указывает на наличие гармонических искажений.
Калькулятор
Известные переменные: Усилители основной частоты, Усилители гармоник
Браузер не поддерживает JavaScript. Расчеты, созданные с помощью SpreadsheetConverter, работать не будут. Пожалуйста, войдите на веб-страницу в другом браузере.информационных чтений
Гармоники вырабатываются диодом-конденсатором входная секция источников питания. Секция диодно-конденсаторная выпрямляет входную мощность переменного тока. в напряжение постоянного тока, используемое внутренними цепями.Персональный компьютер использует напряжение постоянного тока внутренне для питания различных схем и плат, составляющих компьютер. Схема блока питания потребляет ток от сети переменного тока только во время пиков напряжения. форма волны, тем самым заряжая конденсатор до пика линейного напряжения. Оборудование постоянного тока требования поступают от этого конденсатора, и, в результате, форма волны тока становится искаженный.
Гармоники в распределении электроэнергии Система объединяется с основной (60 Гц) для создания искажений.Уровень искажения напрямую связано с частотами и амплитудами гармонического тока. Все токи гармонической частоты в сочетании с током основной гармоники образуют общую гармонические искажения. (THD) Значение THD выражается в процентах от основной гармоники. ток и любые значения THD, превышающие 10%, достаточно серьезны для беспокойства.
Современные приборы качества электроэнергии читают гармоники и выполните расчет по приведенной выше формуле. Их предпочтительно используют обученные операторы.Если вы подозреваете, что у вас проблемы, или хотите убедиться, что у вас их нет гармоник, присутствующих в вашей системе распределения электроэнергии, обратитесь к специалисту по область качества электроэнергии.
Везде, где имеется большое количество нелинейных нагрузок, в системе распределения есть гармоники. Это не редкость для уровней THD в промышленных предприятий до 25%. Обычно уровни THD в офисных настройках ниже, чем на промышленных предприятиях, но офисное оборудование гораздо более восприимчиво к колебаниям мощности качественный.
Нечетные гармоники (3-я, 5-я, 7-я и т. Д.) наибольшее беспокойство в системе распределения электроэнергии. Четные числовые гармоники обычно смягчается, потому что гармоники колеблются одинаково как в положительном, так и в отрицательном направлении. направление.
Эффект нагрева вызывает наибольшие проблемы в электрические распределительные системы и оборудование. Электрооборудование часто перегревается и выходит из строя даже при работе ниже номинальных значений. Повышение температуры составляет напрямую связано с увеличением среднеквадратичного тока.
Частоты гармоник всегда выше 60 Основная частота Гц, поэтому “скин-эффект” также становится фактором. Скин-эффект есть явление, когда более высокая частота заставляет электроны течь к внешнему стороны проводника. Это снижает способность проводника проводить ток на уменьшение диаметра поперечного сечения проводника и тем самым уменьшение силы тока номинальная грузоподъемность проводника. Скин-эффект увеличивается как по частоте, так и по амплитуде. увеличиваются, и это причина того, что более высокие частоты гармоник вызывают большую степень нагрев в проводниках.
Промышленная среда может состоять из трех фаз, нелинейные нагрузки, потребляющие высокие уровни тока нагрузки. Влияние на работу трансформатора при подключении нескольких нагрузок каждая нагрузка генерирует тройные гармонические токи на нейтральный провод. Они отправляются во вторичную обмотку трансформатора и отражаются в дельта-первичная обмотка, и эти токи циркулируют внутри дельта-первичной обмотки, вызывая перегрев, сокращение срока службы, катастрофический отказ или что-то еще хуже.
В сбалансированных трехфазных системах без гармоник содержание, линейные токи не совпадают по фазе на 120, компенсируют друг друга и приводят к очень слабый нейтральный ток. Однако, когда есть искажения в любой из фаз токи, гармонические токи увеличиваются, и эффект компенсации уменьшается. В Обычный результат – THD нейтрального тока значительно выше запланированного. Тройка гармоники (нечетные кратные трем) складываются в нейтрали и могут быстро вызвать опасный перегрев.
Теоретически максимальный ток нейтрали будет перенос тока в 1,73 раза превышает фазный ток, и при неправильном размере может возникнуть перегрев. Ток нейтрали выше нормального приведет к падению напряжения между нейтралью и землей. которые намного выше нормы. Показания выше 4 вольт указывают на высокий ток нейтрали.
Параллельный резонанс между батареей конденсаторов и Импеданс источника может вызвать резонанс системы, в результате чего токи будут выше нормальных. и напряжения.Результирующий отказ конденсатора коррекции коэффициента мощности может быть непосредственно отнесены к гармоникам. Индуктивное реактивное сопротивление напрямую зависит от частоты (XL = 2×3,14 эт).
Большинство проблем возникает при резонансном частота близка к 5-й или 7-й гармонике. Это самая большая гармоника числа амплитуды, которые создают большинство приводов с регулируемой скоростью. Когда возникает такая ситуация, Конденсаторные батареи должны быть изменены, чтобы сместить резонансную точку на другую частоту.
Распределительные панели для современной электроники имеют наконечники для нейтрали, в 2 раза превышающие сечение фазных проводов в расчете на токи нейтрали. Рейтинг K трансформаторы также рассчитаны на высокие токи нейтрали.
Еще один полезный параметр – коэффициент искажения, или% DF. % DF – это полное гармоническое искажение, относящееся к общему среднеквадратичному сигналу. % DF выражается в процентах и не может быть больше 100%. Международный стандарт IEC-555 предъявляет требования к оборудованию, которому необходимо соответствовать.
Ниже приведены шаги, которые необходимо предпринять для облегчения при наличии гармоник в системе распределения электроэнергии возникает множество проблем. Шаг № 1 может быть начат неспециалистом, после чего должен быть вызван профессионал.
1. Инвентаризация всего оборудования, которое может генерировать гармонические токи.
2. Перечислите нелинейные нагрузки на каждую ветку. схема.
3. Запишите истинное среднеквадратичное значение тока в каждой фазе на служебный вход.
4. Запишите ток нейтрали трансформатора. вторичный.
5. Сравните измеренные нейтральный ток относительно ожидаемого тока из-за дисбаланса фаз. Если фазные токи равны, сумма векторов нейтральных токов будет равна нулю. Если чрезмерно количество тройных гармоник присутствует в нейтрали, ток нейтрали может превышать фазный Текущий. Проконсультируйтесь с NEC по поводу максимальной пропускной способности для каждого из проводников, у которых есть был измерен.
6. Измерьте содержание гармоник в каждом фидере. Высота градуса в этом месте часто слышен как жужжащий звук. Показание THD напряжения также полезно в этом месте.
Стандарт IEEE 519-1992 – это руководящий документ для коммунальных предприятий и потребителей электроэнергии, в котором указаны как максимальные уровни искажений, так и рекомендует уровни коррекции. Предел гармонических искажений в 5% оказался оптимальным. точка, в которой гармоники начинают оказывать пагубное влияние на электрическое распределение система.
Измерения гармонического тока определяют гармонический характеристики генерации нагрузки, поэтому измерения следует проводить там, когда возможный. Измерения напряжения определяют реакцию системы и обычно выполняются на индивидуальные автобусы.
Распределительные системы усугубляют проблемы, которые гармонические токи присутствуют в системе. Нелинейные гармонические токи нагрузки также имеют Отношение закона Ома к сопротивлению источника системы для создания напряжения гармоники.Рассмотрим сильно нагруженный трансформатор, на который воздействует одна параллельная цепь. подача нелинейной нагрузки; результирующие гармоники напряжения затем могут быть переданы на все остальные цепи питаются от этого трансформатора.
Гармоники напряжения
Гармоники напряжения могут вызвать разрушение внутри система распределения электроэнергии. Двигатели обычно считаются линейными; однако, когда напряжение источника питания богато гармониками, двигатель будет потреблять гармоники. Текущий.Результатом обычно является более высокая рабочая температура и сокращение срок службы.
Гармонические токи различной частоты могут вызывать дополнительные вращающиеся поля в двигателе. В зависимости от частоты двигатель будет вращаться. в обратном направлении (противодействие). Пятая гармоника, которая очень распространена, – гармоника обратной последовательности, вызывающая вращение двигателя в обратном направлении, что сокращает срок службы.
Шум может улавливаться в компьютерных сетях, оборудование связи и телефонные системы, когда гармоники присутствуют в аудио или радио частоты.С увеличением скорости компьютерных сетей будущее принесет эти системы в частоты, где они будут больше подвержены влиянию гармонического шума. Шум индуктивно или емкостно связан с линиями связи и данных.
При мониторинге индукционно-дисковых ваттметров нелинейные нагрузки, в зависимости от содержания гармоник, диск может работать медленнее или быстрее, что приведет к ошибочным показаниям.
Большинство генераторов и трансформаторов база их рабочие характеристики при отсутствии возмущений сигналов с частотой 60 Гц.Когда формы волны богатые гармониками, сокращение срока службы или полный отказ обязательно будут результатом.
Один вариант в системе распределения, если гармоники присутствует для снижения мощности трансформатора, питающего систему. Коэффициенты снижения рейтинга K могут быть применяется специально к трансформаторам, чтобы избежать опасного нагрева при питающие токи нагрузки с высоким содержанием гармоник.
Коэффициент K определяется путем измерения истинного среднеквадратичного значения. ток каждой гармоники, умноженный на порядок гармоник и возведенный в квадрат.Общая сумма составляет затем умножается на потери на вихревые токи. Коэффициент K трансформатора должен быть считается показателем способности трансформатора выдерживать нелинейную нагрузку. токи без аномального нагрева.
Альтернативный метод снижения номинальных характеристик трансформаторов: для зданий, питающих однофазные розетки на 120 В переменного тока. Этот метод установлен Ассоциацией производителей компьютеров и оборудования для бизнеса (CBEMA).
Коэффициент снижения рейтинга CBEMA = 1.414 разделено на Крест-фактор
Пик-фактор (CF) = пиковое значение, деленное на среднеквадратичное значение
Снижение номинальных значений некоторых типов электрических оборудование – это самый простой способ ограничить воздействие повышенного нагрева на оборудование. А Снижение номинальных значений трансформаторов и генераторов на 25% обычно применяется в промышленности.
В настоящее время наиболее часто используемым методом является фильтрация. для ограничения воздействия гармоник на остальную систему. Фильтры обычно состоят из настроенных последовательных цепей L-C.Импеданс фильтра незначителен по сравнению с остальная часть системы распределения. Эти фильтрующие продукты доступны в продаже под разные торговые наименования. Эффективность большинства фильтрующих продуктов составляет не более 50%. Самый лучший решением является установка трансформаторов с соответствующим рейтингом K и проводкой, которая размер, соответствующий потребностям оборудования и систем.
фунтов / кв. Дюйм 1995
Доступна эта информация в формате Microsoft Word 97 для скачивания (59.5кб)
Основы измерения мощности переменного тока
Количественная оценка производительности импульсных преобразователей мощности становится все более важным аспектом проектирования системы.Часто требуется, чтобы системы соответствовали стандартам эффективности, мощности в режиме ожидания, коэффициента мощности, гармонических искажений и т. Д. В импульсных преобразователях мощности ко входу переменного тока подключены конденсаторы большой емкости, что приводит к сложной форме входных сигналов. Их характеристики нельзя правильно проанализировать на основе упрощенных предположений о входных значениях синусоидального напряжения и тока. В этом разделе часто задаваемых вопросов будут рассмотрены основы измерения мощности переменного тока, которые послужат основой для обсуждения того, как проверить определенные аспекты производительности преобразователя мощности в следующем разделе часто задаваемых вопросов.
Среднеквадратичные измерения переменного тока
Среднеквадратичное значение (RMS) – это наиболее часто используемая величина для измерения переменного тока и напряжения. Среднеквадратичное значение эквивалентно количеству мощности постоянного тока, которое привело бы к такому же рассеиванию мощности в чисто резистивной нагрузке. Вычисление среднеквадратичного значения с использованием формата «амплитуда» может быть полезным. Амплитуда «A» на рисунке ниже может представлять напряжение, ток или другие параметры.
Среднеквадратичное значение – это эквивалентное установившееся значение колебательного сигнала.Красный – это фактический сигнал. Синий – это сигнал, используемый для анализа амплитуды. Хотя это изображение представляет собой синусоидальную волну, концепция значений RMS может быть применена к любой произвольной форме волны. (Изображение: Siemens)Форма волны переменного напряжения колеблется выше и ниже нуля со средним значением, равным нулю. Это не лучший показатель эффективного напряжения. Среднеквадратичное значение используется для получения эквивалентного установившегося значения. Используя формат амплитуды (или пикового значения), среднеквадратичное значение вычисляется путем возведения в квадрат максимальной амплитуды «A» волны, деления ее на два, чтобы найти среднее значение, а затем извлечения квадратного корня из полученного значения.Для простой синусоиды значение RMS может быть представлено как 0,707 * A.
Для более сложных сигналов значение RMS определяется как квадратный корень из среднего арифметического квадратов значений (рассмотрите эквивалент вертикальных «срезов» на изображении выше) или квадрата функции, определяющей непрерывная форма волны. Среднеквадратичные значения особенно полезны при расчетах мощности, а перечисленные напряжения для розеток обычно указываются как среднеквадратичные, а не пиковые значения.Пиковое значение равно среднеквадратичному значению, умноженному на √2. Например, в случае 120 В переменного тока пиковое напряжение составляет около 170 В переменного тока. При европейском сетевом напряжении пиковое значение составляет около 325, а размах напряжения составляет около 650 В
.Пик-фактор
Отношение между среднеквадратичным значением и пиковым значением называется пик-фактором сигнала и определяется как: пик-фактор = пиковое значение / среднеквадратичное значение. Для синусоидальной волны: пиковое значение = RMS x √2; а пик-фактор равен √2, или около 1.41.
Большинство электронных преобразователей мощности, таких как источники питания переменного тока в постоянный, приводы двигателей и источники питания освещения, имеют на входе большие конденсаторы, которые приводят к возникновению несинусоидальных токов с пик-фактором, намного большим, чем 1,41. Типичный импульсный преобразователь мощности имеет импульсную форму входного сигнала переменного тока. Коэффициент амплитуды для этих преобразователей мощности часто превышает 3. Это означает, что распределительная сеть переменного тока должна поддерживать высокий коэффициент амплитуды, а не только средний уровень мощности. Как обсуждается ниже, это один из факторов, влияющих на требования к коррекции коэффициента мощности, когда пик-фактор снижается до значения, близкого к 1.41, как в типичной синусоиде.
Мощность: действительная, реактивная, полная и треугольник мощности
Если нагрузка является чисто резистивной, формы сигналов тока и напряжения синусоидальны, и две величины меняют полярность в один и тот же момент. Власть течет только в одном направлении и называется истинной силой или реальной властью.
В случае чисто реактивной нагрузки напряжение и ток сдвинуты по фазе на 90 градусов. И реактивная мощность «течет». Мощность (произведение напряжения и тока) положительна в течение двух четвертей каждого цикла и отрицательна в течение двух кварталов.Поскольку в нагрузку поступает много энергии, полезная передача энергии из нагрузки отсутствует. Но ток течет в обоих направлениях, и провода должны иметь такой размер, чтобы пропускать этот ток, даже если сама нагрузка потребляет нулевую энергию.
Реальные нагрузки состоят из комбинации сопротивления, емкости и индуктивности. Присутствуют как активная, так и реактивная мощности, что приводит к полной мощности, которая является произведением среднеквадратичных значений напряжения и тока. Полная мощность должна учитываться при проектировании распределительных сетей.Электропроводка и другие токоведущие компоненты должны пропускать полный ток, а не только ток, обеспечивающий полезную работу.
Реальная или «истинная» мощность измеряется в ваттах. Кажущаяся или «общая» мощность измеряется в вольт-амперах (ВА) и является произведением среднеквадратичного напряжения и среднеквадратичного тока. Наконец, реактивная мощность выражается в VAr, что означает реактивная мощность вольт-ампер. Реактивная мощность также называется «мощностью без мощности», поскольку она не передает полезную энергию нагрузке. Как показано ниже, коэффициент мощности измеряет соотношение между полной и реальной мощностью (или соотношение между полной и реальной мощностью).Нагрузка с низким коэффициентом мощности потребляет больше тока, чем нагрузка с высоким коэффициентом мощности, при том же количестве передаваемой полезной мощности. По мере уменьшения реактивной мощности (нагрузка становится более резистивной) общая мощность и истинная мощность выравниваются, а коэффициент мощности приближается к единице.
Коэффициент мощности измеряет отношение реальной или истинной мощности к полной или полной мощности. Он определяется как косинус θ. Когда нагрузка становится более резистивной, реактивная мощность приближается к нулю; полная (полная) мощность и реальная (истинная) мощность выравниваются, а коэффициент мощности становится равным 1.0. (Изображение: Tektronix)В источниках питания переменного / постоянного тока активная коррекция коэффициента мощности (PFC) регулирует ток, протекающий в блоке питания, для улучшения коэффициента мощности. Повышающий преобразователь вставляется между мостовым выпрямителем и основными входными конденсаторами в однофазных источниках питания. Повышающий преобразователь (каскад PFC) управляется для поддержания постоянного напряжения на его выходе при одновременном потреблении тока, синфазного и той же частоты, что и линейный вход переменного тока.
Коэффициент мощности: положительный и отрицательный, смещение и искажение
Знак (положительный или отрицательный) коэффициента мощности зависит от используемого стандарта и отличается для IEC и IEEE.Используя стандарт IEC, направление потока реальной мощности определяет знак коэффициента мощности. коэффициент мощности положителен для «нормального» (положительного) потока реальной мощности, когда нагрузка потребляет энергию. Коэффициент мощности отрицательный для «обратного» (отрицательного) потока реальной мощности, когда нагрузка вырабатывает энергию.
Согласно IEEE, знак коэффициента мощности зависит только от характера нагрузки, а не от направления потока реальной мощности. Для емкостной нагрузки коэффициент мощности положительный, а для индуктивной нагрузки – отрицательный. Обратите внимание, что при использовании соглашения о знаках IEC или IEEE абсолютное значение PF не изменяется; меняется только знак.
Сравнение условных обозначений коэффициента мощности IEC и IEEE. (Изображение: Schneider Electric)«Коэффициент мощности смещения» может возникать в цепях с синусоидальными токами и напряжениями. Коэффициент мощности определяется разницей (смещением) фаз между током и напряжением. «Коэффициент мощности искажения» – это элемент искажения, связанный с различными гармоническими токами и напряжениями, связанными с нелинейными нагрузками. Нелинейные нагрузки изменяют форму волны тока с синусоидальной на другую, например пульсирующую.В результате нелинейные нагрузки имеют тенденцию создавать гармонические токи, способствующие коэффициенту мощности искажения. Для нелинейных нагрузок знание коэффициента амплитуды полезно при количественной оценке уровня искажения .
Синусоидальное напряжение и несинусоидальный ток приводят к пик-фактору, значительно превышающему 1,41, и коэффициенту мощности искажения 0,75 для этой нагрузки блока питания компьютера. (Изображение: Википедия)Гармонические искажения
Гармоники в системе электроснабжения переменного тока – это напряжения или токи, кратные основной частоте системы.Гармоники вызываются нелинейными нагрузками, такими как телекоммуникационные выпрямители, приводы с регулируемой скоростью, осветительные балласты и источники питания переменного / постоянного тока. Полупроводниковые устройства, такие как диоды, транзисторы, MOSFET и IGBT, также являются примерами нелинейных нагрузок. Гармоники в электросети могут вызвать проблемы с качеством электроэнергии, что приведет к повышенному нагреву проводников и других компонентов в сети. При нормальной работе электродвигатели не вносят существенного вклада в гармоники. Но и двигатели, и трансформаторы могут создавать гармоники, если они перенапряжены или насыщены.
Полный коэффициент гармонических искажений (THD) – это мера общего присутствующего искажения. Он определяется как отношение суммы мощностей всех гармонических составляющих к мощности основной частоты. Коэффициент искажения является тесно связанным понятием и иногда используется как синоним THD. Нормы, ограничивающие допустимые уровни THD, широко распространены и часто основываются на EN61000-3.
В следующем разделе часто задаваемых вопросов будет рассмотрено, как различные измерения мощности переменного тока, описанные выше, могут проверить характеристики источника питания переменного / постоянного тока.В третьем и последнем часто задаваемых вопросах будут рассмотрены важные соображения при проверке целостности электропитания в сетях распределения электропитания встроенных систем.
Список литературы
Основы измерения мощности переменного тока, Коэффициент мощности Tektronix
, Википедия
В чем разница между стандартами IEEE и IEC PF, Schneider Electric
для гармоник и истинного среднеквадратичного значения
Решение
для«Гармоники и истинное среднеквадратичное значение»
Решение вопроса № 1:
Суммарное действующее значение тока нагрузки равно 11.18 ампер RMS. Измеритель True RMS будет
прочтите это значение 11.18A
Решение вопроса № 2:
THD тока нагрузки составляет 50%
Решение вопроса № 3:
Суммарное среднеквадратичное значение нового тока нагрузки по-прежнему составляет 11,18 А. Не важно
какова частота гармоники. Если у вас 10А основного тока и 5А
гармоника, измеритель истинного среднеквадратичного значения по-прежнему показывает 11,18 А. Помните, что среднеквадратичное значение не зависит от
частота.
Решение вопроса № 4:
THD нового тока нагрузки остается прежним. THD – это просто измерение
сколько присутствует среднеквадратичный гармонический ток по сравнению с величиной основной гармоники
Текущий. THD НЕ учитывает частоту.
ПОЯСНЕНИЕ
Среднеквадратичное значение синусоидальной волны независимо от частоты – это просто пиковое значение
синусоида, деленная на квадратный корень из 2.(В означает напряжение)
Линейные нагрузки в энергосистеме потребляют ток нагрузки, который представляет собой чистую синусоидальную волну на частота сети 60 Гц. Почти каждый видел типичную синусоидальную волну напряжения 60 Гц, которая может отображаться на осциллографе. Линейная нагрузка рисует форму волны тока такой же форма.
Когда нелинейная нагрузка потребляет ток от энергосистемы (т.е. трансформатор), форма волны тока искажается от математически совершенной формы синусоидальная волна.Прямоугольная или пилообразная форма волны является примером искаженной формы волны.
Искаженная форма волны на самом деле представляет собой сумму синуса основной частоты. волна и множество гармоник. На самом деле гармоники сами по себе являются чистыми синусоидальными волнами, но каждая имеет частоту, кратную 60 Гц (т. е. 3-я гармоника = 3 x 60 = 180 Гц, 5-я гармоника = 5 x 60 = 300 Гц).
Чтобы найти полное среднеквадратичное значение любой искаженной волны, вы должны взять ” квадратный корень из суммы квадратов “среднеквадратичного значения фундаментальной и серия гармоник.(правда, это легче увидеть, чем объяснить это !!)
Вот уравнение (буква «I» означает ток):
Обратите внимание, что среднеквадратичное значение каждой синусоидальной волны тока от I1 до I4 и далее равно в квадрате. Затем эти квадраты значений складываются и получается квадратный корень из общей суммы. добавление берется.
I1 представляет собой среднеквадратичное значение фундаментальный компонент.Остальные I – это просто среднеквадратичные значения любых гармоник, которые присутствует в искаженной форме волны.
Irms – это общее среднеквадратичное значение, которое будет читать на измерителе истинного среднеквадратичного значения.
Для нашей нелинейной нагрузки основная частота тока 60 Гц составляет 10 А RMS. Для гармонического (и частота не имеет значения) у нас есть среднеквадратичное значение 5А. Таким образом, общая RMS составляет
.(10 х 10 + 5 х 5) = (100 + 25) = 125
Квадратный корень из 125 равен 11.18A, как показывает прибор.
Total Harmonic Distortion – это измерение среднеквадратичного значения ТОЛЬКО гармоник. делится на среднеквадратичное значение фундаментального значения и выражается в процентах.
В этом примере основной ток составляет 10 ампер. Среднеквадратичное значение гармоник составляет 5. усилители.
5/10 x 100% = 0,5 x 100% = 50%
Следовательно, THD составляет 50% независимо от частоты гармоник.
По правде говоря, THD ограничен в своем применении.Это действительно хорошо только для выражения гармонические ограничения на фидере или которые производятся нагрузкой в общем случае. Это не сообщить вам, какие гармоники присутствуют и сколько в каждой гармонике (т.е. их среднеквадратичные значения) настоящее.
Для этого вам необходимо выполнить анализ гармонического спектра, который легко сделать. с зажимом на счетчиках, которые легко доступны. (У Fluke есть несколько портативных моделей, которые стоимость около 1500 долларов) .Эти измерители покажут, какие гармоники присутствуют, их соответствующие среднеквадратичные значения и даже фазовый угол между гармоникой и основной гармоникой.(Фазовый угол редко используется в расчетах или изучении гармоник.)
У вас должен быть спектральный анализ, выполненный в разных точках вашей мощности. системы (например, при нелинейной нагрузке, в трансформаторе, в конденсаторных батареях, щит и т. д.) до того, как будет предпринято какое-либо решение любой гармонической проблемы.
После завершения анализа и если гармоники вызывают у вас проблемы (например, как перегрев трансформаторов, сгорание предохранителей блока крышек, срабатывание автоматических выключателей, помехи и т. д.), информацию можно использовать для применения фильтров гармоник до размера K номинальные трансформаторы, или для установки оборудования для подавления гармоник.
Теория гармоник изучается в “Электроэнергетическом форуме”. семинары. Объясняются возможные проблемы и практические решения. После пройдя курс, вы не будете в них знатоком, но будете хорошо разбираться в том, что они такие, почему они существуют, какие проблемы вызывают и как их смягчать.
Вы также точно узнаете, что означает вся эта модная терминология, например K Коэффициент, THD, дельта-обмотка, улавливающая гармоники третьего порядка и т. Д. Если вы когда-нибудь слышали фраза «гармоники третьего порядка добавить в нейтраль» и поинтересовалась, что это значит, и почему это происходит – мы вам покажем (мы очень гордимся именно этой демонстрацией!) люди считают эту часть курса самой стоящей … и это (если мы так говорим мы сами)!
Выберите новую викторину
Вернуться на главную страницу Lehman Engineering
Суммарные гармонические искажения напряжения – обзор
24.5 Методы управления
Основная задача системы управления в ИБП – минимизировать общие гармонические искажения выходного напряжения при различных профилях нагрузки. Кроме того, он должен обеспечивать надлежащий механизм для перезарядки комплекта батарей и поддерживать высокий коэффициент входной мощности и низкие гармонические искажения общего входного тока. Другими факторами, которые учитываются для хорошей техники управления, являются почти нулевая ошибка выходного напряжения инвертора в установившемся режиме, хорошее регулирование напряжения, надежность, быстрая переходная характеристика и защита инвертора от перегрузки при линейных / нелинейных нагрузках.
Наиболее распространенным методом переключения является синусоидальная ШИМ. Этот метод можно использовать как для однофазных, так и для трехфазных систем. Преимущество этого метода – низкие гармоники выходного напряжения и надежность. Эта стратегия использует один контур обратной связи для обеспечения хорошо стабилизированного выходного напряжения с низким THD. Управление с обратной связью может быть непрерывным или прерывистым. Аналоговые методы используются в непрерывном подходе. Синусоидальная ШИМ (SPWM) может быть естественного типа выборки, среднего типа или мгновенного типа [17, 18].
При естественном типе дискретизации пиковое значение выходного напряжения обнаруживается и сравнивается с опорным напряжением, чтобы получить ошибку, которая используется для управления опорным сигналом модулятора. Средний подход в основном такой же; но измеренное напряжение преобразуется в среднее значение и после этого сравнивается с опорным сигналом. Эти подходы управляют только амплитудой выходного напряжения и хороши только на высоких частотах. При управлении SPWM с мгновенной обратной связью по напряжению выходное напряжение непрерывно сравнивается с опорным сигналом, улучшая динамические характеристики инвертора ИБП.
Типичная блок-схема трехфазного инвертора постоянного / переменного тока для систем ИБП и метод управления переключением SPWM показана на рис. 24.13. Недостатком этого метода является отсутствие гибкости при нелинейных нагрузках. Для инвертора могут использоваться другие методы запрограммированной ШИМ, такие как избирательное подавление гармоник, минимальные THD, минимальные потери, минимальные пульсации тока и уменьшенный акустический шум.
РИСУНОК 24.13. (а) Конфигурация трехфазного инвертора постоянного / переменного тока для систем ИБП и (б) простой контроллер напряжения с использованием метода ШИМ.
Лучшая производительность даже при нелинейных и скачкообразных нагрузках может быть достигнута с помощью нескольких стратегий контура управления [19]. Как показано на рис. 24.14, существует два контура управления: внешний и внутренний. Внешний контур управления использует выходное напряжение в качестве сигнала обратной связи, который сравнивается с опорным сигналом. Погрешность компенсируется Pi-интегратором для достижения стабильного выходного напряжения в установившемся режиме работы. Эта ошибка также используется в качестве опорного сигнала для внутреннего контура регулятора тока, который использует индуктивность или ток выходного фильтра конденсатора в качестве сигнала обратной связи.Контур второстепенного тока обеспечивает быстрые динамические характеристики, обеспечивая хорошую производительность при нелинейных или скачкообразных нагрузках. Основными регуляторами тока, используемыми в качестве вспомогательной токовой петли, являются: регуляторы гистерезиса, регулятор синусоидальной ШИМ и прогнозирующие регуляторы. В типичном регуляторе гистерезиса опорный сигнал сравнивается с сигналом обратной связи. Знак и заданная амплитуда ошибки определяют выходной сигнал модулятора. Продолжительность между двумя последовательными уровнями определяется крутизной опорного сигнала.Выходное напряжение отслеживает опорный сигнал в пределах верхнего и нижнего граничных уровней. Этот гистерезисный контроль имеет быструю переходную реакцию; но частота переключения широко варьируется [20].
РИСУНОК 24.14. Типовые контуры регулирования тока и напряжения для инвертора ИБП.
В методе управления SPWM обратная связь по выходному напряжению сравнивается с синусоидальным опорным сигналом, а напряжение ошибки компенсируется ПИ-регулятором для создания опорного тока. Ток через катушку индуктивности или конденсатор измеряется и сравнивается с опорным сигналом.После компенсации с помощью ПИ-регулятора сигнал ошибки сравнивается с треугольной формой волны для генерации сигнала SPWM для управления переключением. Регулятор тока SPWM имеет постоянную частоту переключения, а также обеспечивает быстрые динамические характеристики. В методе прогнозируемого управления током моменты переключения определяются подходящими границами ошибок. Когда текущий вектор касается граничной линии, следующий вектор состояния переключения определяется прогнозированием и оптимизацией, чтобы минимизировать ошибку.Прогнозирующее управление током требует хорошего знания параметров нагрузки. Все эти регуляторы тока обычно используются в качестве внутреннего контура для регулирования тока в катушке индуктивности фильтра. Опорный ток для регулятора тока получается путем суммирования ошибки во внешнем контуре напряжения с фактическим током нагрузки, чтобы получить номинальное выходное напряжение.
С увеличением скорости и надежности цифровых процессоров и снижением их стоимости за последние несколько лет цифровые процессоры столкнулись с огромным ростом популярности в приложениях управления.Многие цифровые и дискретные методы управления, такие как мертвое биение [21], управление на основе диссипативности [22], управление в скользящем режиме [23], пространственное векторное управление [24] и контур с множественной обратной связью [25], имеют были разработаны с использованием цифровых сигнальных процессоров (DSP).
В этом разделе объясняется фундаментальный анализ метода управления мертвыми импульсами для трехфазной конфигурации ИБП, показанной на рис. 24.13a. Уравнения пространства состояний одной фазы этой системы в непрерывной временной области следующие.
(24,1) GFdVadt = iLF- iLa
(24,2) LFdiLFdt = VA- Va
Рассматривая V a и i LF как переменные состояния, уравнение пространства состояний системы выглядит следующим образом :
(24.3) [VaiLF] • = [0-1 / LF 1 / CF0] [VaiLF] + [01 / LF] VA + [-1 / CF0] iLa
Эти уравнения непрерывного пространства состояний во временной области являются преобразованы в прерывистую временную область с периодом дискретизации T с [26].
(24.4) [Va (k + 1) iLF (k + 1)] = [cos ω0 Ts sinω0Tsw0CF-sinω0Tsω0LF cos ω0 Ts] [Va (k) iLF (k)] + [1- cos ω0 Ts1ω02 LFsin ω0 Fs] VA (k) + [-1w0CFsin ω0Ts1- cos ω0 Ts] iLa (k)
, где ω 0 – частота углового резонанса L F и C F . Частота дискретизации системы всегда считается намного выше, чем резонансная частота L F и C F . С этим предположением, уравнение.(24.4) упрощается до уравнения. (24,5). Это преобразование действительно для почти f s ≥ 20 f 0 .
(24,5) [Va (k + 1) iLF (k + 1)] = [1- Ts / LF Ts / CF1] [Va (k) iLF (k)] + [0Ts / LF] VA (k) + [-Ts / CF0] iLa (k)
Текущее уравнение согласно формуле. (24,5) определяется по формуле:
(24,6) iLF (k + 1) = iLF (k) + TsLF [VA (k) – Va (k)]
В качестве альтернативы это уравнение может быть получено путем преобразования уравнения. (24.2) от дифференциального уравнения к разностному.То же самое предложение f s ≥ 20 f 0 должно быть сделано и для этого преобразования. Если V a и i * LF считаются постоянными в течение следующего периода переключения, выходное напряжение инвертора, которое исправляет ошибку i LF после двух периодов выборки, описывается следующим образом: :
(24,7) VA (k + 1) = Va (k + 1) + LFTS [i * LF (k +1) – iLF (k +1)]
Линейная оценка В a ( k + 1) можно получить из предыдущих значений:
(24.8) Va (k + 1) = Va (k) + [Va (k -1)] = 2 Va (k) – Va (k – 1)
Подставляя уравнения. (24.8) и (24.10) в уравнении. (24.9) и обновления эталонного тока для i LF через каждые два периода выборки, цифровое управление мертвыми импульсами для последовательного преобразователя описывается следующим образом:
(24,9) ВА (k + 1) = LFTS [i * LF (k) – VA (k) + 3Va (k) -Va (k – 1)
Уравнение (24.9) гарантирует, что текущая ошибка между i LF и i * LF в момент времени k + 2 переходит в ноль с задержкой в два периода выборки.Во избежание взаимодействия между контурами управления напряжением и током, напряжение нагрузки, В, a , дискретизируется на половине частоты дискретизации тока. Уравнение напряжения согласно формуле. (24.5) выглядит следующим образом.
(24,10) Va (k + 1) = Va (k) + TsCFiCF (k)
(24,11) Va (k + 2) = Va (k + 1) + TsCFiCF (k +1) = Va (k ) + TsCFiCF (k) + TsCFiCF (k +1)
Поскольку управление по току предлагается в мертвом режиме с задержкой в два периода выборки, задается ток конденсатора во время кОм и ( к + 1) по:
(24.12) iCE (k) = i * CF (k -2), iCF (k + 1) = i * CF (k-1)
Подставляя уравнение. (24.12) в уравнении. (24.11) и обновляя эталонный ток в каждом из двух периодов выборки, V a (k + 2) определяется по формуле:
(24,13) Va (k + 2) = Va (k) + 2TsCFi * CF (k +2)
Ток i * CF во время k , который исправляет ошибку напряжения V a во время k + 4, выглядит следующим образом.
(24,14) i * CF (k) = CF2Ts [V * a (k) -Va (k)] – i * CF (k-2)
Блок-схема реализации управления напряжением и током инвертор показан на рис.24.15. Блок-схема регулятора тока и напряжения для инвертора также представлена на рис. 24.16. Стабилизатор напряжения представляет собой чисто мертвый контроллер с задержкой в два периода выборки, включая время, затраченное на расчет. G 1 – время задержки, необходимое для вычислений и аналого-цифрового преобразования. G 2 – это временная задержка, вызванная инвертором PWM, а G 3 – передаточная функция фильтра нижних частот.Регулятор тока также рассматривается как чистая задержка. Выходное напряжение инвертора следует за эталоном с четырьмя периодами задержки выборки. На практике динамика регулятора тока не является чистой задержкой и показывает некоторое отклонение от мертвого регулятора.
РИСУНОК 24.15. Реализация управления током и напряжением для инвертора показана на рисунке 24.13a.
РИСУНОК 24.16. Блок-схема регулятора тока и напряжения для инвертора представлена на рисунке 24.13а.
Трехфазные трансформаторы – часть 4: Гармоники
Гармоники
Гармоники – это напряжения или токи, которые действуют на частоте, которая кратное основной частоте сети. Если фундаментальная сила частота 60 герц, например, вторая гармоника будет 120 герц, третья гармоника – 180 герц и так далее. Гармоники производятся нелинейными нагрузками, потребляющими ток в импульсах, а не в непрерывном манера.Гармоники в однофазных линиях электропередачи обычно вызваны устройствами. такие как компьютерные блоки питания, электронные балласты в люминесцентных лампах и симисторы диммеры и тд. Обычно возникают трехфазные гармоники. частотно-регулируемыми приводами для двигателей переменного тока и электронными приводами для Двигатели постоянного тока. Хорошим примером пульсирующей нагрузки является нагрузка, преобразующая переменный ток в DC, а затем регулирует напряжение постоянного тока с помощью широтно-импульсной модуляции.
Таким образом работают многие регулируемые источники питания.Мостовой выпрямитель преобразует переменный ток в пульсирующий постоянный ток. Конденсатор фильтра используется для сглаживания пульсации. Транзистор включается и выключается для подачи питания на нагрузка. Время, на которое транзистор включен по сравнению с время выключения определяет выходное напряжение постоянного тока. Каждый раз транзистор включается, это вызывает разряд конденсатора. Когда транзистор выключится, конденсатор снова начнет заряжаться. Ток берется из линии переменного тока каждый раз, когда конденсатор заряжается.Эти пульсации тока производимый зарядным конденсатором, может привести к тому, что синусоидальная волна переменного тока станет искаженный. Эти искаженные формы сигналов тока и напряжения текут обратно в другие части энергосистемы.
+++++ 30 Широтно-импульсная модуляция регулирует выходное напряжение путем изменения время, в течение которого транзистор проводит, по сравнению со временем, когда он выключен. Фильтр конденсатор Мостовой выпрямитель переменного тока Транзистор Регулятор напряжения Нагрузка Ширина между импульсами определяет выходное напряжение
+++++ 31 Гармоники вызывают искажение синусоидальной волны переменного тока.Типичный синусоида Типичная волна искаженного тока из-за гармоник; Типичный искаженный волна напряжения из-за гармоник
Гармонические эффекты
Гармоники могут оказывать очень вредное воздействие на электрооборудование. Некоторые общие симптомы гармоник – перегретые проводники, трансформаторы и цепь выключатели, которые, кажется, срабатывают, когда этого не следует. Гармоники классифицируются по имени, частоте и последовательности. Название указывает на то, насколько гармоничен это вторая, третья, четвертая или так далее основной частоты.В частота относится к рабочей частоте гармоники. Секунда гармоника работает на 120 Гц, третья на 180 Гц, четвертая на 240 герц и так далее. Последовательность относится к вращению вектора относительно к основной форме волны.
В асинхронном двигателе гармоника прямой последовательности будет вращаться в в том же направлении, что и основная частота. Гармоника обратной последовательности будет вращаться в направлении, противоположном основной частоте.А конкретный набор гармоник, называемых «тройками», имеет нулевую последовательность. Триплены – это нечетные кратные третьей гармоники (третьей, девятой, пятнадцатой, двадцать первое и т. д.). Диаграмма, показывающая последовательность первых девяти гармоник показан в ==== 1.
==== 1 Название, частота и последовательность первых девяти гармоник
+++++ 32 В трехфазной четырехпроводной системе, соединенной звездой, центр вторичная обмотка, соединенная звездой, имеет ответвления для образования нейтрального проводника.Фаза дирижер; Фазовый проводник; Нейтральный проводник; Фазовый проводник:
Гармоники прямой последовательности обычно вызывают перегрев проводов, трансформаторы и автоматические выключатели. Гармоники обратной последовательности могут вызвать те же проблемы с нагревом, что и положительные гармоники, плюс дополнительные проблемы с моторами. Поскольку вращение вектора отрицательной гармоники противоположно основной частоты, это будет иметь тенденцию к ослаблению вращающегося магнитное поле асинхронного двигателя, вызывающее меньший крутящий момент.Уменьшение крутящего момента заставляет двигатель работать со скоростью ниже нормальной. Снижение скорости приводит к чрезмерному току двигателя и перегреву.
Хотя у триплетов нет вращения вектора, они могут проблема в трехфазной четырехпроводной системе, такой как 208/120 вольт или система на 480/277 вольт. В обычной системе с соединением звездой на 208/120 В первичная обмотка обычно подключается по схеме треугольник, а вторичная подключается в Уай.
Однофазные нагрузки, работающие от 120 В, подключаются между любыми фазный провод и нейтральный провод. Нейтральный ток – это векторная сумма фазных токов. В симметричной трехфазной цепи (все фазы, имеющие равный ток), ток нейтрали равен нулю. Хотя однофазный нагрузки имеют тенденцию вызывать несбалансированное состояние, векторная сумма токов обычно приводит к тому, что нейтральный проводник пропускает меньше тока, чем любой из фазные проводники.Это верно для линейных нагрузок и непрерывный синусоидальный ток. Когда пульсирующие (нелинейные) токи подключен к трехфазной четырехпроводной системе, тройные гармонические частоты нарушает нормальное соотношение фазовых токов и может заставляют фазные токи суммироваться в нейтральном проводе, а не отменять. Поскольку нейтральный проводник не защищен предохранителем или автоматическим выключателем, существует реальная опасность чрезмерного нагрева нейтрального проводника.
Гармонические токи также отражаются в первичной обмотке треугольником, где они циркулируют и вызывают перегрев. Возникли другие проблемы с нагревом. по вихревым токам и гистерезисным потерям. Трансформаторы обычно проектируются для работы 60 герц. Более высокие частоты гармоник производят большую сердцевину потерь, на которые рассчитан трансформатор. Трансформеры, которые подключенных к цепям, которые производят гармоники, иногда необходимо снизить или заменены трансформаторами, специально разработанными для работы с гармонические частоты.
Трансформаторы – не единственный электрический компонент, на который влияют гармоники. токи. Аварийные и резервные генераторы также могут быть повреждены в так же, как трансформаторы. Особенно это актуально для резервных генераторов. используется для питания оборудования обработки данных в случае сбоя питания.
Некоторые гармонические частоты могут даже исказить переход сигнала через нуль. производится генератором.
В термомагнитных выключателях используется биметаллический отключающий механизм, который чувствителен к теплу, выделяемому током цепи.Эти схемы выключатели спроектированы так, чтобы реагировать на тепловое воздействие истинного среднеквадратичного значения. текущая стоимость.
Если ток становится слишком большим, биметаллический механизм отключает выключатель. открытым. Гармонические токи вызывают искажение среднеквадратичного значения, которое может приводить к срабатыванию автоматического выключателя, когда он не должен срабатывать, или не срабатывать, когда он должен. Тем не менее, термомагнитные выключатели обычно обеспечивают лучшую защиту. против гармонических токов, чем электронные автоматические выключатели.Электронный выключатели определяют пиковое значение тока. Пики гармонических токов обычно выше, чем основная синусоида. Хотя вершины гармонических токов обычно выше основной частоты, они могут быть ниже. В некоторых случаях электронные прерыватели могут срабатывать при малых токах, а в других случаях они могут вообще не споткнуться.
+++++ 33 Гармонические сигналы обычно имеют более высокие пиковые значения, чем основная форма волны.
Форма гармонического сигнала Основная синусоида:
Токи тройной гармоники могут также вызвать проблемы с проводами нейтральной шины и подключением. ушки. Нейтральная шина рассчитана на пропускание номинального фазного тока.
Поскольку тройные гармоники могут привести к тому, что ток нейтрали будет выше, чем фазный ток может привести к перегрузке нейтральной шины.
Электрические панели и шинопроводы рассчитаны на токи, которые работают на 60 герц.Гармонические токи создают магнитные поля, которые действуют при более высокие частоты. Если эти поля станут механически резонансными с кожухами панелей или шинопроводов панели и кабельные каналы могут вибрировать и издавать жужжащие звуки с гармонической частотой.
Телекоммуникационное оборудование часто подвержено воздействию гармонических токов.
Телекоммуникационный кабель часто проходит рядом с линиями электропередач. Чтобы свести к минимуму помех, коммуникационные кабели проложены как можно дальше от фазных проводов как можно ближе к нейтральному проводнику.Гармонический токи в нейтральном проводе индуцируют высокочастотные токи в кабель связи. Эти высокочастотные токи можно услышать как высокие частоты. жужжащий звук в телефонных линиях.
+++++ 34 Сравнение амперметров со средним и истинным среднеквадратичным значением. Отклик синусоидальной волны Тип амперметра Отклик прямоугольной волны Искаженная волновая характеристика Правильно Среднее количество ответов Прибл. 10% высокий До 50% низкий; Верный; True-RMS ответ; Верный; Правильный
+++++ 35 Средние текущие значения обычно меньше истинного среднеквадратичного значения в искаженной форме волны.Действующее значение RMS; Среднее текущее значение
Определение гармонических проблем в однофазных системах
Чтобы определить, есть ли проблема с гармоники.
Один из шагов – сделать обзор оборудования. Это особенно важно в определении наличия проблем с гармониками в однофазной системе.
1. Проведите проверку оборудования. Такое оборудование, как персональные компьютеры, принтеры и люминесцентные лампы. фары с электронным балластом, как известно, излучают гармоники.Любой кусок оборудования, которое потребляет ток в импульсах, может генерировать гармоники.
2. Просмотрите записи о техническом обслуживании, чтобы узнать, не было ли проблем. с отключением автоматических выключателей без видимой причины.
3. Проверить трансформаторы на перегрев. Если вентиляционные отверстия не закрыты и трансформатор работает слишком горячо, проблема может заключаться в гармониках. Проверьте токи трансформатора с помощью амперметра, способного показать истинное среднеквадратичное значение. текущая стоимость.Убедитесь, что номинальные значения напряжения и тока трансформатор не был превышен.
Необходимо использовать амперметр, который реагирует на истинный среднеквадратичный ток, когда делая эту проверку. Некоторые амперметры реагируют на среднее значение, а не на Среднеквадратичное значение. Измерители, которые реагируют на истинное среднеквадратичное значение, обычно указывают на это. на счетчике. Счетчики, которые реагируют на среднее значение, обычно меньше дорогие, и не указывайте, что это измерители RMS.
Измерители, которые реагируют на среднее значение, используют выпрямитель для преобразования Переменный ток в постоянный.Это значение должно быть увеличено в 1,111 раза, чтобы изменить среднее значение RMS для синусоидального тока. True-RMS отвечающие счетчики рассчитывают эффект нагрева от тока. График на показывает некоторые различия между показывающими среднее значение метрами и истинными Измерители RMS. В искаженной форме волны истинное среднеквадратичное значение тока будет больше не будет Среднее x 1,111. Искаженная форма волны обычно вызывает среднее значение должно быть на 50% меньше среднеквадратичного значения.
Другой метод определения наличия гармонической проблемы в однофазной система должна сделать две отдельные текущие проверки. Одна проверка выполняется с использованием амперметр, который показывает истинное среднеквадратичное значение, а другой – с использованием измеритель, показывающий среднее значение. В этом примере предполагается что амперметр с истинным среднеквадратичным значением показывает значение 36,8 ампер, а среднее значение Амперметр показывает значение 24,8 ампера. Определите соотношение двух измерения путем деления среднего значения на истинное среднеквадратичное значение:
Коэффициент= Среднее значение
________ RMS
Коэффициент= 24.8 А
______ 36,8 А
Коэффициент= 0,674
Коэффициент 1 означает отсутствие гармонических искажений. Коэффициент 0,5 будет указывают на крайние гармонические искажения. Этот метод не раскрывает название или последовательность гармонических искажений, но это дает указание что есть проблема с гармониками. Определить название, последовательность и количество присутствующих гармонических искажений следует использовать анализатор гармоник.
+++++ 36 Определение гармонических проблем с помощью двух амперметров.
Измеритель истинного среднеквадратичного значения показывает значение 36,8 ампер. значение 24,8 ампер
==== 2 Трехфазная четырехпроводная система с соединением звездой
Дирижер | Амперметр с истинным среднеквадратичным значением | Амперметр среднечастотный
Фаза 1365 A 292 A Фаза 2396 A 308 A Фаза x 387 A 316 A Нейтраль 488 А 478 А
Определение гармонических задач в трехфазных системах
Определение наличия проблемы с гармониками в трехфазной системе аналогично определению проблемы в однофазной системе.Потому что гармонические проблемы в трехфазной системе обычно возникают при соединении звездой четырехпроводная система, в этом примере предполагается подключение первичной обмотки треугольником и соединение звездой вторичный с нейтральным отводом. Для проверки гармонических искажений в трехфазной четырехпроводной системе измерьте все фазные токи и нейтральный ток с показанием амперметра с истинным среднеквадратичным значением и показанием среднего значения амперметр. Предполагается, что испытуемая трехфазная система запитана трансформатором на 200 кВ, а указанные значения тока были записано.Текущие значения указывают на то, что проблема с гармониками существуют в системе. Обратите внимание на более высокие измерения тока, сделанные с помощью показывающий амперметр истинного среднеквадратичного значения, а также тот факт, что ток нейтрали выше любого фазного тока.
Работа с гармоническими проблемами
После того, как было определено, что существуют проблемы с гармониками, что-то должно сделать, чтобы справиться с проблемой. Как правило, удалять оборудование, вызывающее гармонические искажения, поэтому необходимо использовать другие методы. заняты.Рекомендуется проконсультироваться со специалистом по качеству электроэнергии, чтобы определить точный характер и количество присутствующих гармонических искажений. Некоторые общие ниже приведены процедуры работы с гармониками.
1. В трехфазной четырехпроводной системе 60-герцовая часть нейтрали ток можно уменьшить, уравновешивая ток в фазных проводниках. Если все фазы имеют равный ток, ток нейтрали будет равен нулю.
2. Если в нейтральном проводе присутствуют тройные гармоники, гармоника фильтры могут быть добавлены при загрузке.Эти фильтры могут помочь уменьшить количество гармоник на линии.
3. Вытяните лишние нейтральные проводники. Идеальной ситуацией было бы использование отдельная нейтраль для каждой фазы вместо использования общей нейтрали.
4. Установите нейтральный провод большего диаметра. Если нецелесообразно поставлять отдельный нейтральный провод для каждой фазы, увеличьте размер общего нейтральный.
5. Уменьшите или уменьшите нагрузку на трансформатор.Гармонические проблемы обычно связаны с перегревом трансформатора. Во многих случаях это необходимо снизить номинальные параметры трансформатора до такой степени, чтобы он мог справиться с дополнительный ток, вызванный гармоническими искажениями. Когда это будет сделано, обычно необходимо добавить второй трансформатор и разделить нагрузку между двумя.
==== 3 пиковых тока добавлены в диаграмму проводника True-RMS, ответ амперметр Амперметр среднего срабатывания Фаза 1365 A 292 A Фаза 2396 A 308 A Фаза x 387 A 316 A Нейтраль 488 A Мгновенный пиковый ток 716A 794 А 737 А 957 А 478 А
Определение коэффициента снижения гармоник трансформатора
Вероятно, самый практичный и простой метод определения коэффициент снижения мощности трансформатора рекомендован Computer and Business Ассоциация производителей оборудования.Чтобы использовать этот метод, два измерения ампер должны быть сделаны. Один – это истинный среднеквадратичный ток фаз, а второй – – мгновенный пиковый фазный ток. Мгновенный пиковый ток можно определить с помощью осциллографа, подключенного к токовому пробнику или с амперметром, способным показывать пиковое значение тока. Многие из цифровые токоизмерительные клещи могут отображать среднее значение, истинное среднеквадратичное значение и пик значения тока. В этом примере предполагается, что пиковые значения тока измерены для трансформатора на 200 кВ, о котором говорилось ранее.Эти значения добавляются к предыдущим данным, полученным с помощью истинного среднеквадратичного значения и среднего значения. амперметры.
Формула для определения коэффициента снижения гармонических характеристик трансформатора:
THDF = (1,414) (среднеквадратичный фазный ток)
_______
мгновенный пиковый ток
Эта формула дает коэффициент снижения мощности где-то между 0 и 1,0. Поскольку мгновенное пиковое значение тока равно среднеквадратичному значению x 1.414, если форма волны тока синусоидальная (без гармонических искажений), формула дает коэффициент снижения мощности 1,0. Как только фактор снижения номинальных характеристик определяется, умножьте коэффициент снижения мощности на киловольт-амперную емкость. трансформатора. Товар представляет собой максимальную нагрузку, которую следует разместить на трансформаторе.
Если фазные токи не равны, найдите среднее значение, добавив токи вместе и разделенные на три:
Трансформатор на 200 киловольт-ампер в этом примере должен быть снижен. к 144.4 киловольта-ампера (200 кВА x 0,722).
Устранение неполадок, связанных с гармониками мощности: базовое устранение неполадок с помощью мультиметров и токовых клещей
В этом примечании к применению подробно описаны процедуры использования анализаторов качества электроэнергии Fluke для измерения средних ватт и их преобразования в ватт-часы.
Новые технологии, новые вызовы
Гармоники – это побочные продукты современной электроники. Они особенно распространены там, где имеется большое количество персональных компьютеров, приводов с регулируемой скоростью и другого оборудования, потребляющего ток короткими импульсами.Как добраться до корня проблемы
Найти проблему относительно легко, если вы знаете, что искать и где искать. Симптомы гармоник обычно неуловимы. В этом примечании к применению приведены некоторые основные указания по поиску гармоник и несколько предложений о способах решения проблем, которые они создают.Источники гармоник
Определение проблемы
Гармоники – это токи или напряжения с частотами, кратными основной частоте сети.Например, если основная частота равна 60 Гц, то вторая гармоника – 120 Гц, третья – 180 Гц и т. Д.Гармоники создаются нелинейными нагрузками, которые потребляют ток резкими импульсами, а не плавно синусоидальным образом. Эти импульсы вызывают искаженную форму волны тока, которая, в свою очередь, заставляет гармонические токи течь обратно в другие части энергосистемы.
История изнутри
Это явление особенно распространено в оборудовании, имеющем входные источники питания диодно-конденсаторные; я.е., персональные компьютеры, принтеры и медицинское испытательное оборудование.Электрически происходит то, что входящее переменное напряжение выпрямляется диодом и затем используется для зарядки большого конденсатора. После нескольких циклов конденсатор заряжается до пикового напряжения синусоидальной волны (например, 170 В для линии 120 В переменного тока). Затем электронное оборудование потребляет ток от этого высокого постоянного напряжения для питания остальной схемы.
Влияние токов гармоник
Симптомы гармоник обычно проявляются в оборудовании распределения питания, которое поддерживает нелинейные нагрузки.Существует два основных типа нелинейных нагрузок: однофазные и трехфазные. Однофазные нелинейные нагрузки распространены в офисах, а трехфазные нагрузки широко распространены на промышленных предприятиях.Каждый компонент системы распределения мощности проявляет влияние гармоник немного по-своему, но все они могут быть повреждены и работать неэффективно, если не предназначены для работы с электронными нагрузками.
Нейтральные проводники
В трехфазной четырехпроводной системе нейтральные проводники могут сильно пострадать от нелинейных нагрузок, подключенных к параллельным цепям 120 В.В нормальных условиях для сбалансированной линейной нагрузки основная часть фазных токов 60 Гц будет компенсироваться в нейтральном проводе.В четырехпроводной системе с однофазными нелинейными нагрузками некоторые нечетные гармоники, называемые тройными – нечетные кратные третьей гармоники: 3-я, 9-я, 15-я и т. Д. – не отменяются, а складываются в нейтральный проводник.
Избыточный ток в нейтральном проводе также может вызвать падение напряжения между нейтральным проводом и землей в розетке с напряжением 120 В. выше нормального.
Автоматические выключатели
В обычных термомагнитных автоматических выключателях используется биметаллический отключающий механизм, который реагирует на нагревательное воздействие тока цепи. Они предназначены для реагирования на истинное среднеквадратичное значение формы волны тока и срабатывают, когда механизм отключения становится слишком горячим. Этот тип выключателя имеет хорошие шансы защитить от перегрузок по гармоническому току.Электронный автоматический выключатель с измерением пикового уровня реагирует на пиковую форму волны тока. В результате он не всегда правильно реагирует на гармонические токи.
Поскольку пик гармонического тока обычно выше, чем обычно, этот тип автоматического выключателя может преждевременно отключиться при низком токе. Если пиковое значение ниже нормы, прерыватель может не сработать, когда это необходимо.
Шины и соединительные наконечники
Нейтральные шины и соединительные наконечники рассчитаны на пропускание полного значения номинального фазного тока. Они могут получить перегрузку при перегрузке нейтральных проводников дополнительной суммой тройных гармоник.Электрические панели
Панели, рассчитанные на ток 60 Гц, могут стать механически резонансными магнитным полям, создаваемым гармоническими токами более высокой частоты.Когда это происходит, панель вибрирует и издает жужжащий звук на гармонических частотах.Телекоммуникации
Телекоммуникационные системы часто дают первый ключ к проблеме гармоник, потому что кабель можно проложить рядом с силовыми кабелями. Чтобы свести к минимуму индуктивные помехи от фазных токов, телекоммуникационные кабели прокладывают ближе к нейтральному проводу.Трижды в нейтральном проводе обычно вызывают индуктивные помехи, которые можно услышать в телефонной линии. Это часто является первым признаком проблемы с гармониками и дает вам фору в обнаружении проблемы до того, как она нанесет серьезный ущерб.
Поиск гармоник
Обзор гармоник даст вам хорошее представление о том, есть ли у вас проблема и где она находится. Вот несколько рекомендаций, которым нужно следовать.- Загрузить инвентарь.
- Тепловая проверка трансформатора.
- Вторичный ток трансформатора
- Проверка тока нейтрали подпанели
- Проверка напряжения нейтрали розетки относительно земли
Инструменты для поиска и устранения неисправностей
Чтобы определить, есть ли у вас проблема с гармониками, вам необходимо измерить истинное среднеквадратичное значение и мгновенный пик значение формы волны.Для отдельных приложений вам понадобятся либо токоизмерительные клещи, такие как Fluke 335, 336 или 337, либо мультиметры, подобные тем, что используются в сериях Fluke 80, 170 и 180, которые производят измерения истинных среднеквадратичных значений. Для трехфазных приложений вам понадобится анализатор качества электроэнергии, такой как Fluke 430 Series.«Истинное среднеквадратичное значение» относится к среднеквадратическому или эквивалентному значению нагрева формы волны тока или напряжения. «Истина» отличает измерения от измерений, выполненных измерителями со «средним откликом». Подавляющее большинство недорогих портативных счетчиков имеют средний отклик.Эти инструменты дают правильные показания только для чистых синусоидальных волн и обычно показывают низкие значения на целых 50 процентов, когда сталкиваются с искаженной формой волны тока. Измерители истинных среднеквадратичных значений дают правильные показания для любой формы волны в пределах пик-фактора прибора и характеристик полосы пропускания.



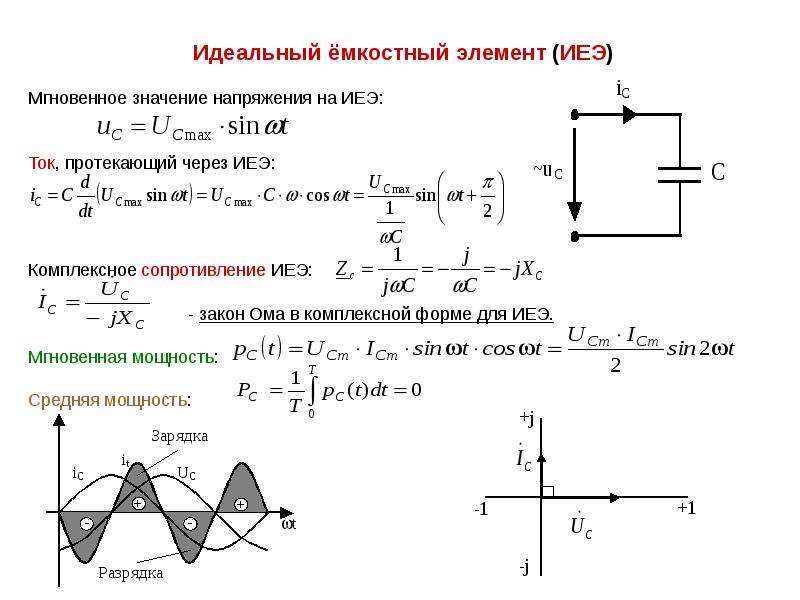 …
…
 Примечание — Аналогично определяют действующие значения периодических электрического напряжения, электродвижущей силы, магнитного потока и т. д. [ГОСТ Р 52002 2003]… …
Примечание — Аналогично определяют действующие значения периодических электрического напряжения, электродвижущей силы, магнитного потока и т. д. [ГОСТ Р 52002 2003]… … Часть 2. Пусковые конденсаторы – Терминология ГОСТ Р МЭК 60252 2 2008: Конденсаторы для двигателей переменного тока. Часть 2. Пусковые конденсаторы оригинал документа: 1.3.11 длительность рабочего цикла (duty cycle duration): Общее время одного нагружения (подачи напряжения) и… … Словарь-справочник терминов нормативно-технической документации
Часть 2. Пусковые конденсаторы – Терминология ГОСТ Р МЭК 60252 2 2008: Конденсаторы для двигателей переменного тока. Часть 2. Пусковые конденсаторы оригинал документа: 1.3.11 длительность рабочего цикла (duty cycle duration): Общее время одного нагружения (подачи напряжения) и… … Словарь-справочник терминов нормативно-технической документации


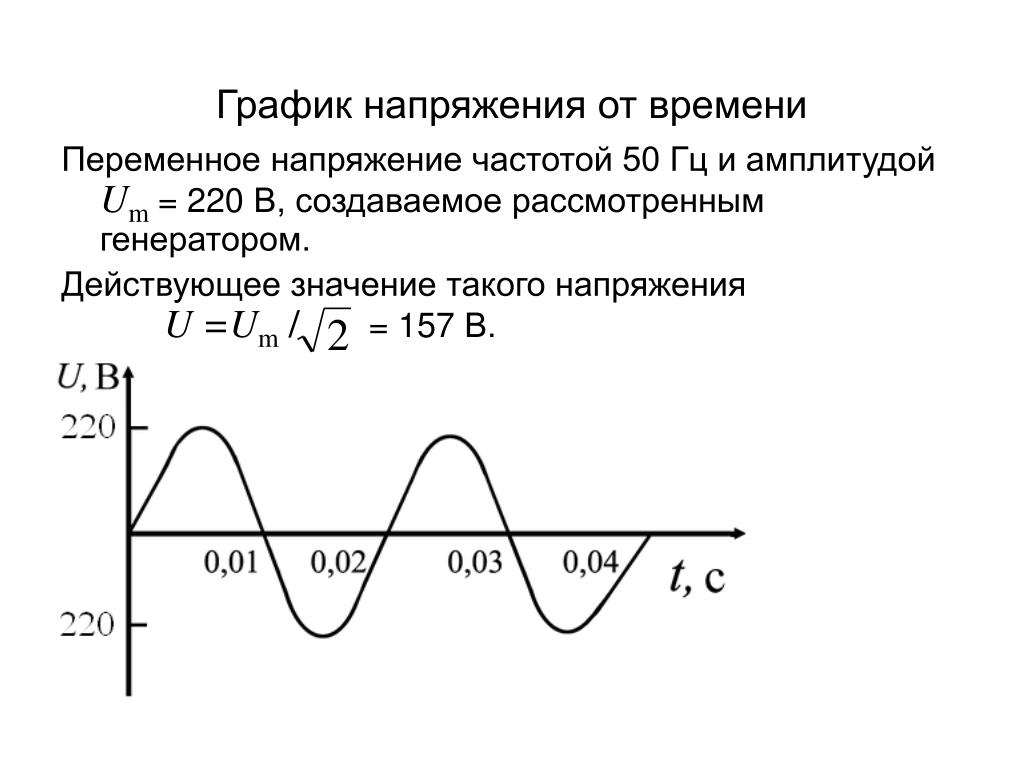 Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.
Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.