Ступенчатая аппроксимация синусоиды при работе от аккумуляторов, ИБП синус
ИБП с чистым синусом
Когда ИБП с аппроксимированной синусоидой применять нельзя?
Для устройств со значительной реактивной составляющей расходуемой мощности, индуктивной нагрузкой и для помеховосприимчивых приборов подойдёт только чистый сигнал. К таким устройствам относятся асинхронные двигатели и оборудование, содержащее их – насосы, отопительные котлы, трансформаторы и старая электроника с трансформаторными блоками питания. ИБП с модифицированной синусоидой генерируют помехи, дают низкий эффективный ток (среднее напряжение), превышение силы потребляемого тока.
На практике это означает, в лучшем случае, невозможность включения оборудования, в худших вариантах – нехватку мощности при возрастающей силе тока, перегрев, быстрый выход приборов из строя или значительное уменьшение жизненного цикла. У лучших линейно-интерактивных ИБП коэффициент искажений не превышает 3–5%, у источников с двойным преобразованием синусоида чистая – сигнал формируется инвертором заново.
В каталоге интернет-магазина 220 Volt имеются сотни моделей ИБП оффлайн, интерактивного и онлайн типов в широчайшем ценовом разнообразии. Если вы сомневаетесь в том, какой ИБП купить, – специалисты магазина ответят на все вопросы и помогут в выборе бесперебойника и другой электротехники.
Читайте также: Новости Харькова.
Источник: https://MyKharkov.info/news/kogda-mozhno-ispolzovat-ibp-s-approksimirovannoj-sinusoidoj-24538.html
impulsnik ›
Блог ›
Самодельный инвертор 12-220 вольт с чистым синусом
Напрягает ситуация когда отключают свет, я живу в частном доме и воду добываю с помощью погружного вибрационного насоса, не то чтобы часто отключают, но пару раз без воды оставался, неприятно. Так вот, что бы исключить повторения такой ситуации в будущем, решил собирать инвертор, решался честно долго, не мог подобрать оптимальный вариант получения синуса, мучить насос модифицированной синусоидой не стал, и вот как то наткнулся на специальный модуль под названием EGS002./dotdash_Final_Sine_Wave_Feb_2020-01-b1a62c4514c34f578c5875f4d65c15af.jpg)
Для получения синуса одной платки конечно мало, самое главное нам потребуется преобразователь напряжения с 12 до 350 вольт ватт на 300, четыре полевых транзистора для коммутации постоянного напряжения (350в) и выходной фильтр, для превращения прямоугольных импульсов разной длительность в синусоиду.
На схеме все что выделено слева, это сам модуль, а то что с права это то что нам нужно прикрутить.
Первая версия печатной платы была испытана Николаем Шумиловым на радиоскоте.
Все заработало практически с первого раза, форму сигнала на выходе было нечем посмотреть, работало все исправно, но только на лампочках, стоило подключить индукционную нагрузку и через некоторое время броском напряжения вышибло выходные ключи, так как я допустил фатальную ошибку, не предусмотрел места на печатке для снабберов.
Прилагаю пока только скрины печатки, те кто ждал готовое устройство, уж простите) работаю сейчас над плазморезом) за инвертор возьмусь после.
Источник: https://www.drive2.ru/b/492980882794086771/
Как получить чистую синусоиду из модифицированной. Часть 1
Журнал РАДИОЛОЦМАН, ноябрь 2013
Валентин Володин
Вступление
Еще не стерлись из памяти события «лихих» 90-х. Помнится МММ, разгул криминала, веерные отключения электроэнергии. На Украине, например, во второй половине 90-х дело доходило до того, что свет в жилых районах выключали на 2 часа через каждые 2 часа. Помнится, наиболее коварным был зимний период темноты между пятью и семью часами вечера. Как раз, когда народ возвращался с работы. Выгружаешься на остановке, автобус уезжает, и ты остаешься в полной темноте. Пытаешься привыкнуть, трешь глаза, давишь на глазные яблоки. Все безрезультатно, вокруг полная темнота. Делать нечего, осторожно ступаешь во мраке, пытаясь нащупать заветный забор, который должен вывести к родной калитке и потихоньку, на ощупь, домой.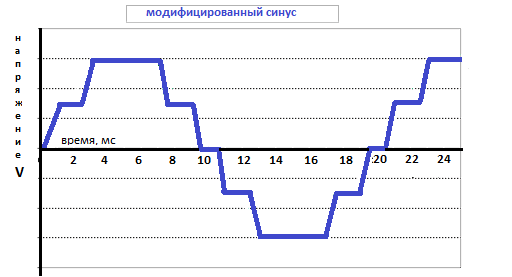
Однако в этих мытарствах были и положительные элементы. Например, резко возрос спрос на разные бензо- и дизель-генераторы, а также на электронные преобразователи и бесперебойные источники тока. Последнее обстоятельство позволило людям творческим применить свои профессиональные навыки и даже немного улучшить на этом поприще свое финансовое положение. А там, глядишь, появились различные фирмочки, выпускающие эти самые преобразователи и бесперебойники. Какой-никакой подъем в экономике образовался, дополнительные рабочие места и т. п. Собственно, и Ваш покорный слуга, примерно в те времена, из электроники слабосильной подался в электронику силовую.
Нельзя сказать, что тогда с этой самой электроникой сильно мудрили. Делали, чтобы было просто, надежно и дешево. В принципе, для того чтобы питать одну-две лампочки, больше ничего и не требовалось. Однако по мере развития процесса конкуренция ужесточалась. Народу уже стало из чего выбирать. Особо привередливые начали интересоваться формой напряжения на выходе преобразователей и бесперебойников. На что им очень обтекаемо отвечали, что форма там практически синусоидальная, но лишь слегка модифицированная. Более честные говорили, что там присутствует синусоида, но только квадратная. А уж совсем честные говорили напрямую, что их преобразователи и бесперебойники формируют на выходе прямоугольное напряжение с паузой. Но параметры этого напряжения (амплитудное и действующее значение, а также частота) практически соответствуют аналогичным параметрам однофазного переменного напряжения бытовой электросети. В принципе, такое напряжение вполне подходило для основных бытовых электропотребителей, таких телевизоры, компьютеры, а также накальные и люминесцентные лампы. Те же электропотребители, которые требовали чисто синусоидального напряжения (асинхронные двигатели, например), были в меньшинстве и погоды особой не делали.
Однако такое положение не могло длиться вечно. Количество отключений сокращалось и в какой-то момент они практически вообще прекратились. Однако параллельно на рынке бытовых товаров стали появляться отопительные котлы, оборудованные циркуляционными насосами, приводными задвижками и электронным управлением. Такие котлы требовали высококачественного бесперебойного электропитания. В противном случае, при отключении электричества работа системы отопления полностью нарушалась.
Однако параллельно на рынке бытовых товаров стали появляться отопительные котлы, оборудованные циркуляционными насосами, приводными задвижками и электронным управлением. Такие котлы требовали высококачественного бесперебойного электропитания. В противном случае, при отключении электричества работа системы отопления полностью нарушалась.
И вот тут возникала некая дилемма. Многие владельцы отопительного чуда уже обладали бесперебойными источниками, мощности которых с лихвой хватало для питания котла. Однако, вот беда, циркуляционные насосы ни в какую не хотели крутиться от «прямоугольной синусоиды». Для чудо-котла надо было приобретать новый чудо-бесперебойный источник, формирующий на выходе чистейшую синусоиду. А куда же теперь девать старый, к которому уже душой прикипели. Нехорошо как-то все это!
Но положение не безвыходное и старый друг нам еще послужит! Для питания асинхронного двигателя от прямоугольного напряжения можно использовать фильтр Отто. Есть множество положительных примеров практического воплощения такого подхода. Однако такой вариант не самый простой и, уж точно, не универсальный. После продолжительной и утомительной настройки фильтр можно будет использовать только с конкретным двигателем. Хотелось бы чего-то более универсального. Таким более универсальным решением будет использование в качестве фильтра феррорезонансного или подобного ему стабилизатора. При этом феррорезонансный стабилизатор, включенный после бесперебойного источника, будет не только исправлять форму его выходного напряжения в периоды отсутствия сети (работа от аккумулятора), но и будет стабилизировать напряжение сети в моменты его присутствия.
Ниже приводится описание и принципиальная электрическая схема феррорезонансного стабилизатора мощностью 1000 Вт. В статье приведены формулы и методика расчета, которая позволит вам пересчитать стабилизатор на другую мощность, если это потребуется.
Феррорезонансный стабилизатор
Феррорезонансные стабилизаторы имеют ряд достоинств, таких как высокая надежность и быстродействие, широкий диапазон входных напряжений, хорошая стабильность выходного напряжения, способность к исправлению формы сильно искаженного входного напряжения. Однако, не смотря на все свои достоинства, эти стабилизаторы имеют и некоторые недостатки, к которым можно отнести относительно низкую удельную мощность и высокий уровень шумов, создаваемых при работе.
Однако, не смотря на все свои достоинства, эти стабилизаторы имеют и некоторые недостатки, к которым можно отнести относительно низкую удельную мощность и высокий уровень шумов, создаваемых при работе.
Не так давно, в 60-80-х годах прошлого века, феррорезонансные стабилизаторы широко использовались в быту для питания ламповых телевизоров. И старшее поколение читателей, скорей всего, до сих пор помнит тот надрывный гул, которым сопровождалась работа этих аппаратов, которые различались формой и расцветкой, но имели вес 10-15 кг при мощности 250-350 Вт.
Основным источником шумов в феррорезонансном стабилизаторе является насыщающийся дроссель. В работе сердечник этого дросселя постоянно насыщается, что приводит к изменению его линейных размеров. Это явление называется магнитострикционным эффектом. О «шумности» этого эффекта говорит хотя бы тот факт, что он широко используется в гидроакустике для генерации мощных акустических волн. Следовательно, если мы хотим построить тихий стабилизатор, то в первую очередь должны избавиться от насыщающегося дросселя. Однако нельзя просто так выбрасывать неугодные комплектующие из стабилизатора. В этом случае мы рискуем потерять его функциональность. Чтобы этого не произошло, сначала нужно найти достойную замену. И на нашу удачу такая достоянная замена имеется. Еще в 70-х годах прошлого столетия была доказана возможность замены насыщающегося дросселя последовательной цепочкой, состоящей из линейного дросселя и двух встречно-параллельных тиристоров . Такая цепь ведет себя аналогично насыщающемуся дросселю, но в отличие от него имеет меньшие размеры и массу, может оперативно регулироваться за счет управления тиристорами, обеспечивает меньшие потери и, самое главное, гораздо меньше шумит. В технической литературе такая цепочка зачастую называется резонансным тиристорным регулятором (РТР) . При необходимости, два встречно-параллельных тиристора РТР можно с успехом заменить одним симистором.
Работа стабилизатора
Функциональная схема стабилизатора с РТР изображена на Рисунке 1.
| Рисунок 1. | Функциональная схема стабилизатора с РТР. |
Стабилизатор с РТР имеет практически тот же принцип действия, что и феррорезонансный стабилизатор. Выходное напряжение UН поддерживается на требуемом уровне (220 В). Когда напряжение питающей сети UС имеет минимальное значение, симистор VS1 заперт. При этом напряжение UН поднимается до требуемого уровня за счет резонанса в колебательном контуре L1C1. Если же напряжение питающей сети UС имеет максимально допустимое значение, то симистор VS1 постоянно открыт. При этом дроссели L1 и L2 образуют делитель переменного напряжения, уменьшающий сетевое напряжение до требуемого уровня. В феррорезонансном стабилизаторе насыщающийся дроссель также максимально используется при максимальном входном напряжении, и минимально при минимальном. Дроссель L3 совместно с конденсатором С1 образует фильтр третьей гармоники, улучшающий форму выходного напряжения стабилизатора.
| Рисунок 2. | Осциллограммы основных напряжений и токов стабилизатора с РТР. |
Рассмотрим подробнее работу стабилизатора с РТР. На Рисунке 2 изображены осциллограммы основных напряжений и токов стабилизатора с РТР. Выходное напряжение стабилизатора UН выпрямляется при помощи выпрямителя В2. Выпрямленное напряжение UВ2 поступает на фильтр Ф, который выделяет из него среднее, действующее или амплитудное значение, в зависимости от того, какое значение выходного напряжения UН требуется стабилизировать. Далее напряжение с выхода фильтра поступает на сумматор, где сравнивается с опорным напряжением UОП. С выхода сумматора напряжение ошибки поступает на регулятор Рег, который формирует управляющий сигнал, призванный компенсировать отклонение выходного напряжения стабилизатора. Выходное напряжение регулятора UПОР поступает на вход порогового устройства ПУ и определяет его порог срабатывания. На другой вход порогового устройства подается синхронизирующее напряжение UВ1, привязанное к моментам перехода через ноль выходного напряжения UН стабилизатора. На выходе порогового устройства ПУ формируются импульсы управления UУПР, которые усиливаются усилителем мощности УМ и в требуемой полярности поступают на управляющий электрод симистора VS1. Синхронизирующее напряжение создается при помощи интегратора Инт и выпрямителя В1. Благодаря интегратору, импульсы выпрямленного напряжения UВ1 отстают от импульсов UВ2 на 5 мс (фазовый сдвиг –90°).
На выходе порогового устройства ПУ формируются импульсы управления UУПР, которые усиливаются усилителем мощности УМ и в требуемой полярности поступают на управляющий электрод симистора VS1. Синхронизирующее напряжение создается при помощи интегратора Инт и выпрямителя В1. Благодаря интегратору, импульсы выпрямленного напряжения UВ1 отстают от импульсов UВ2 на 5 мс (фазовый сдвиг –90°).
Импульсы управления UУПР формируются на нарастающем фронте UВ1 между нулевым и амплитудным значением этого напряжения. При увеличении порогового напряжения UПОР импульсы управления максимально сдвигаются к амплитудному значению UВ1 и, соответственно, к нулевому значению UВ2. В этом случае симистор открывается в районе нулевого значения UН и через линейный дроссель L2 протекает незначительный ток IL2, который не оказывает существенного влияния на выходное напряжение стабилизатора. При уменьшении порогового напряжения Uпор импульс управления сдвигается в сторону амплитудного значения UН и через линейный дроссель L2 начинает протекать существенный ток, который шунтирует выход стабилизатора и уменьшает величину его выходного напряжения.
Если выходное напряжение стабилизатора меньше требуемого, то регулятор Рег увеличивает пороговое напряжение UПОР. В результате ток, протекающий через дроссель L2, уменьшается, и выходное напряжение стабилизатора возрастает за счет резонанса в колебательном контуре L1C1. Если выходное напряжение больше требуемого, то регулятор Рег уменьшает пороговое напряжение UПОР. В результате ток, протекающий через дроссель L2, увеличивается и выходное напряжение стабилизатора уменьшается.
Расчет силовой схемы стабилизатора
Рассмотрим практическую методику расчета стабилизатора мощностью 1000 ВА. Такой стабилизатор может использоваться как независимое устройство или совместно с устаревшими источниками бесперебойного питания для получения синусоидальной формы напряжения.
Принципиальная электрическая схема силовых цепей стабилизатора с РТР мощностью SН = 1000 ВА изображена на Рисунке 3. Стабилизатор рассчитан на работу от сети переменного тока 220 В 50 Гц c нагрузкой, имеющей коэффициент мощности cos φН ≥ 0.7, и формирует выходное напряжение UН = 220 В ±1% во всем диапазоне нагрузок при изменении входного напряжения от 150 до 260 В.
Стабилизатор рассчитан на работу от сети переменного тока 220 В 50 Гц c нагрузкой, имеющей коэффициент мощности cos φН ≥ 0.7, и формирует выходное напряжение UН = 220 В ±1% во всем диапазоне нагрузок при изменении входного напряжения от 150 до 260 В.
| Рисунок 3. | Принципиальная электрическая схема силовых цепей стабилизатора с РТР мощностью 1000 ВА. |
Первым делом необходимо определить емкость резонансного конденсатора. Реактивную мощность резонансного конденсатора для стабилизатора без фильтра третьей гармоники можно найти по формуле:
где:
– угловая частота сетевого напряжения, рад/с.
Зная реактивную мощность резонансного конденсатора, найдем его емкость:
Найдем индуктивность линейного дросселя L1:
Найдем индуктивность линейного дросселя L2:
Найдем индуктивность линейного дросселя L3:
Так как в стабилизаторе для улучшения формы выходного напряжения установлен фильтр третьей гармоники, емкость резонансного конденсатора можно уменьшить:
В качестве C1 можно использовать компенсирующие конденсаторы типа К78-99 или аналогичные, предназначенные для коррекции коэффициента мощности электромагнитных дросселей газоразрядных ламп. Например, можно использовать два включенных параллельно конденсатора К78-99 емкостью 50 мкФ, рассчитанных на напряжение 250 В переменного тока. Для этой же цели можно использовать конденсатор типа МБГВ 100 мкФ на напряжение 1000 В.
Окончание
Источник: https://www.rlocman.ru/shem/schematics.html?di=152071
Источники бесперебойного питания. Решения компании APC
При деловом применении компьютерной техники (ПК, серверов, дисковых массивов) возможный размер убытков от потери данных или простоя при проблемах с электроэнергией может многократно превысить стоимость ИБП. Поэтому все больше компаний и частных пользователей приходят к обязательному использованию источников бесперебойного питания.
Рассмотрим возможные проблемы сети электропитания:
- Пониженное/повышенное напряжение
- Отсутствие напряжения
- Отклонение частоты питающего напряжения
- Импульсные помехи
По данным компании Bell Labs соотношение по числу инцидентов примерно следующее:
Это данные для электросетей США однако для нашей страны соотношение по мнению экспертов компании APC примерно такое же.
Все источники бесперебойного питания (ИБП) делятся на две основные группы, характеризующие их архитектуру и методы работы:
ИБП типа Off-line имеют более простую конструкцию, доступную цену и широкую сферу применения. По оценкам компании ITResearch они составляют до 70% российского парка источников бесперебойного питания.
Независимо от архитектуры в любом ИБП присутствуют 3 обязательных компонента: Выпрямитель переменного тока, аккумуляторная батарея и инвертор.
В ИБП архитектуры Off-line инвертор активен только при работе от батареи (инвертор преобразует постоянный ток аккумуляторной батареи в переменный выходной ток). В ИБП архитектуры On-line инвертор работает постоянно. Зачем, мы рассмотрим ниже.
В архитектуре Off-line существует 2 топологии построения ИБП: Stand-By и Line-Interactive:
- Топология Stand-By (модели APC Back-UPS CS/ES/HS)
ИБП топологии stand-by (резервные ИБП) в нормальном режиме подает электроэнергию на выход источника прямо с входа (через сетевой фильтр) и только в случае сбоя сетевого электропитания задействует инвертор и батарею.
Основное достоинство ИБП топологии stand-by самая низкая стоимость и высокий КПД, однако время переключения на батарею при пропадании напряжения в сети самое большое из всех типов ИБП. Впрочем, этого обычно достаточно для обычных рабочих ПК. Также к числу недостатков относится ступенчатая форма выходного сигнала при работе от батареи (ступенчатая аппроксимация синусоиды).

- Топология Line-Interactive (модели APC Back-UPS RS, Smart-UPS, Smart-UPS XL)
ИБП технологии Stand-by не осуществляет коррекции входного напряжения (за исключением погашения импульсных помех), а лишь переключается на работу от батареи если напряжение “выходит” из рабочего диапазона. Этого недостатка лишены ИБП топологии Line-Interactive, т.к. там добавлен еще один важный компонент – стабилизатор напряжения. Форма выходного сигнала у Line-Interactive почти чистая синусоида при работе от батареи.
- Архитектура On-Line, топология Double Conversion (двойное преобразование, модели Smart-UPS RT/VT)
При данной архитектуре инвертор работает постоянно. Это и обеспечивает главные преимущества архитектуры On-Line: нулевое время переключения на питание от батареи и отличная стабилизация выходного напряжения и формы сигнала (чистая синусоида на выходе).
Однако данная конструкция обуславливает гораздо более высокую стоимость ИБП, чем в ИБП класса Off-Line. Постоянно работающие инвертор и батарея выделяют тепло, что приводит к необходимости принудительного охлаждения узлов ИБП и несколько более низкому КПД по сравнению с off-line моделями.
Невелика была бы полезность источников бесперебойного питания, если бы они не имели обратной связи с оборудованием, которое защищают. Для взаимодействия между ПК, серверами и ИБП APC служит программное обеспечение APC PowerChute. Подключение осуществляется по интерфейсам RS-232, USB и LAN. В зависимости от модели ИБП программное обеспечение бывает одной из 3-х версий:
| PowerChute Personal Edition | PowerChute Business Edition | PowerChute Network Shutdown |
| Корректное завершение работы системы | Корректное завершение работы системы | Надежная схема организации корректного завершения работы множественных систем, функционирующая на базе компьютерной сети |
| Автоматическое оповещение пользователя | Автоматическое оповещение системного администратора | |
| Управление системой | Управление ИБП и корректное завершение работы серверов и рабочих станций | |
Связь через USB (работает только с Back-UPS CS, RS, ES)
Поддержка ОС: Mac OS X, Windows 2000, Windows 2003, Windows XP.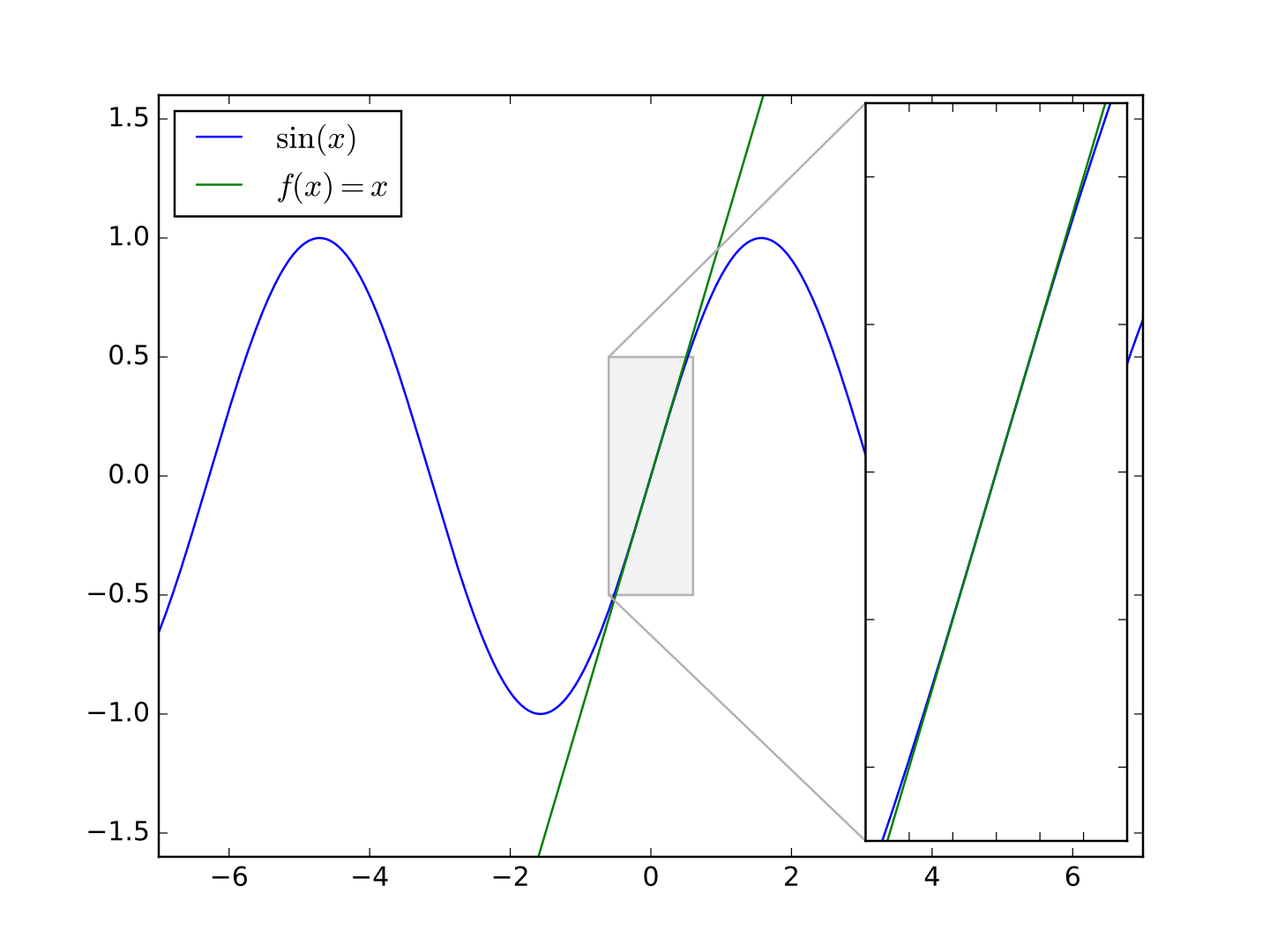 |
Связь через Сom Port, USB (Smart-UPS, XL, RT, Matrix) Работает с Back-UPS CS, RS, ES только через Соm Поддержка ОС: Linux, Novell, Solaris, WinNT, Windows 2000, Windows 2003, Windows XP. | Связь через LAN (Smart-UPS c 750 Ва, XL, RT, VT, Symmetra, Silcon) Поддержка ОС: AIX, HP/UX, Linux, Mac OS X, Novell, Solaris, WinNT, Windows 2000, Windows 2003, Windows XP. |
Приведем небольшой глоссарий по технологиям используемым в ИБП производства APC – мирового лидера этих устройств:
Горячая замена батареи – возможность заменить аккумуляторную батарею в ИБП без отключения его от нагрузки
“Холодный старт” – возможность включения оборудования (ПК, сервера) на работу от батареи при отсутствии напряжения в сети
SmartSlot – внутренний разъем в ИБП APC для установки дополнительных аксессуаров, расширяющих функционал устройства
Режимы SmartBoost и SmartTrim – коррекция входного напряжения до оптимального диапазона
WEB-карта – аксессуар наделяющий ИБП APC собственным сетевым интерфейсом (MAC-адресом и IP), что позволяет удаленно управлять ИБП
Позиционирование ИБП APC:
Back-UPS
- Защита питания для ПК и рабочих станций
Smart-UPS
- Защита питания для рабочих станций, серверов, сетей голосовой связи и передачи данных. 5 мин – 100% нагрузка
Smart-UPS XL
- Защита питания с масштабированием по времени работы от аккумуляторов для серверов, сетей голосовой связи и передачи данных. > 5 мин – 100% нагрузка
Smart-UPS RT
- Высококачественная защита питания с возможностью масштабирования по времени работы от аккумуляторов для компьютерных залов, испытывающих дефицит пространства, сетей голосовой связи и передачи данных
- Защита оборудования в регионах с плохим качеством электропитания
- Работа с дизель-генератором
- Защита оборудования, требующего точные параметры электропитания
- Специальные требования в тендерах
Smart-UPS VT
- Качественная Защита трехфазного электропитания с наращиваемым временем работы от батарей для небольших центров обработки данных (ЦОД), производственных линий, систем АСУ ТП
- Медицинское оборудование
Таким образом при выборе ИБП необходимо учитывать предстоящий объем нагрузки (Вт), возможность наращивания мощности (масштабирование), характер подключамого оборудования (требования по качеству питания).
Для того чтобы выбрать конкретную модель ИБП наиболее точно отвечающую задачам можно воспользовавшись удобным пошаговым мастером на сайте компании APC, a также обратиться к менеджерам нашей компании по многоканальному телефону (495) 258-0071.
При подготовке раздела использовались маркетинговые материалы компании APC
Модулированная синусоида или ступенчатая аппроксимация синусоиды
Форма выходного сигнала
Форма выходного напряжения ИБП.
Возможные формы выходного напряжения: синусоида, ступенчатая аппроксимация синусоиды.
Ступенчатая аппроксимация синусоиды используется в основном в простых и недорогих моделях ИБП. При использовании в качестве нагрузки компьютерных систем и другой электроники с импульсными блоками питания вполне допустима такая форма питающего напряжения.
Чистая синусоида используется во многих моделях линейно-интерактивных ИБП и в ИБП с двойным преобразованием. Для создания “правильной” формы выходного сигнала используется более сложная схема инвертора.
Основные преимущества синусоидальной формы выходного напряжения: при переключении нагрузки с питания от сети на питание от батарей переходные процессы значительно меньше, чем в случае с прямоугольными импульсами, соответственно, повышается надежность работы ИБП.
Использование питающего напряжения грубой формы приводит к появлению высокочастотной составляющей в линиях питания, которая может вызвать наводки на сигнальные линии в электронных устройствах.
Для нагрузки, в которой используются линейные (трансформаторные) блоки питания, например, для аудиотехники, можно использовать только ИБП с чистой синусоидой на выходе.
Очень рекомендую прочитать ветку , я из-за этого не могу подобрать себе ИБП
Q: Существуют ли проблемы совместной работы UPS и блоков питания с APFC? Оказывает ли влияние форма выходного сигнала UPS (синусоида или ее аппроксимация) на такую работу?
Форма выходного сигнала
Форма выходного напряжения ИБП.
Возможные формы выходного напряжения: синусоида, ступенчатая аппроксимация синусоиды.
Ступенчатая аппроксимация синусоиды используется в основном в простых и недорогих моделях ИБП. При использовании в качестве нагрузки компьютерных систем и другой электроники с импульсными блоками питания вполне допустима такая форма питающего напряжения.
Чистая синусоида используется во многих моделях линейно-интерактивных ИБП и в ИБП с двойным преобразованием. Для создания “правильной” формы выходного сигнала используется более сложная схема инвертора.
Основные преимущества синусоидальной формы выходного напряжения: при переключении нагрузки с питания от сети на питание от батарей переходные процессы значительно меньше, чем в случае с прямоугольными импульсами, соответственно, повышается надежность работы ИБП.
Использование питающего напряжения грубой формы приводит к появлению высокочастотной составляющей в линиях питания, которая может вызвать наводки на сигнальные линии в электронных устройствах.
Для нагрузки, в которой используются линейные (трансформаторные) блоки питания, например, для аудиотехники, можно использовать только ИБП с чистой синусоидой на выходе.
Очень рекомендую прочитать ветку , я из-за этого не могу подобрать себе ИБП
Q: Существуют ли проблемы совместной работы UPS и блоков питания с APFC? Оказывает ли влияние форма выходного сигнала UPS (синусоида или ее аппроксимация) на такую работу?
Источники бесперебойного питания (ИБП, UPS) — востребованная продукция, особенно этой зимой. Но больше всего заказов поступает на ИБП с правильной синусоидой — их покупают для котлов отопления, серверов, насосов. Что это, почему именно они, чем такие бесперебойники отличаются от других видов? Мы постараемся ответить в этой статье на наиболее частые вопросы наших покупателей.
В представлении многих ИБП — это устройство, которое при отключении питания некоторое время поддерживает работу подключенной к нему техники. Все верно, но не все так просто. От того, КАК ИМЕННО происходит эта поддержка и какие дополнительные “плюшки” для вашего электрооборудования может обеспечить бесперебойник, зависит:
Все верно, но не все так просто. От того, КАК ИМЕННО происходит эта поддержка и какие дополнительные “плюшки” для вашего электрооборудования может обеспечить бесперебойник, зависит:
- срок службы оборудования;
- вероятность его (оборудования) скорого выхода из строя;
- цена ИБП и другое.
К примеру, обычный UPS, к которому подключают домашние/офисные компьютеры не подойдет в качестве источника бесперебойного питания для газового котла отопления, или чувствительного серверного или телекоммуникационного оборудования. А все потому, что есть такой значимый параметр, как форма выходного сигнала.
404
Дополнительная скидка
Вы хотите приобрести данный товар с дополнительной скидкой? Оставьте Ваши контактные данные и мы рассмотрим возможность предоставления скидки.Когда возможна дополнительная скидка
- Вы наш постоянный клиент
- Вы нашли товар дешевле в другом магазине
- Вы планируете купить товар оптом
- Некоторые другие случаи
ОК
×
Консультация
Укажите Ваши имя и номер телефона, наш специалист свяжется с Вами в самое ближайшее время для консультации.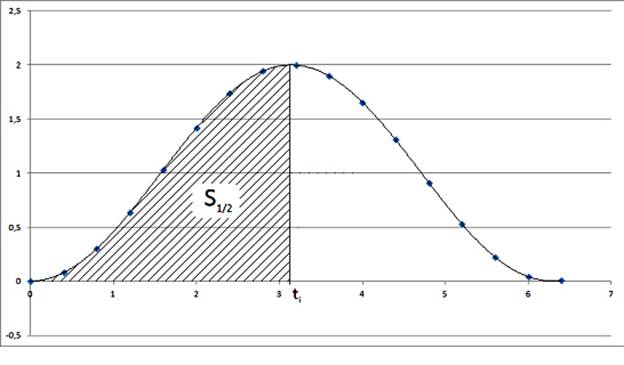
ОК
×404
“Извините, запрашиваемая вами страница не найдена”
Правильная или модифицированная синусоида. Особенности выбора автомобильного инвертора (Power Invertor)
- Подробности
- Категория: Магазин
Запитать любой электроприбор напряжением 220В даже в лесу или в поле — на сегодняшний день это уже не проблема! Достаточно купить автомобильный инвертор (автомобильный преобразователь напряжения). При выборе такого прибора нужно знать о некоторых его особенностях и принципах работы.
Автомобильные инверторы бывают двух видов: с синусоидальным выходным сигналом (правильный синус) и модифицированной синусоидой. В чем состоит отличие сигналов?
Модифицированная синусоида
Модифицированная синусоида — это приближение к правильному синусоидальному сигналу с помощью сигналов «прямоугольной» формы. Самое элементарное приближение, сигнал прямоугольной формы переменной полярности — меандр. В большинстве случаев, такой сигнал не используют, «набирая» форму сигнала с использованием прямоугольных ступенек. Чем дороже инвертор, тем из большего количества ступенек состоит сигнал на выходе.
Чем правильный синус лучше модифицированного синуса?
Для некоторой аппаратуры форма сигнала есть очень немаловажной.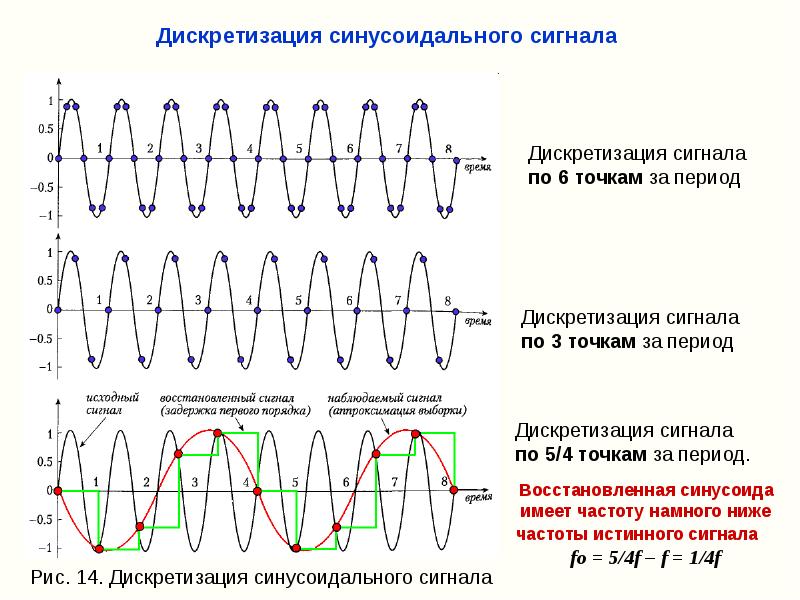 Сюда относится аппаратура, которая, чувствительна к разного рода помехам, либо аппаратура с трансформаторными источниками питания, компрессоры, электродвигатели, насосы и пр. Приборы, которые совсем не чувствительны к форме сигнала — это нагревательные приборы, лампы накаливания,, приборы, которые имеют импульсные источники питания (компьютеры, ноутбуки, цифровые телевизоры). Когда работает преобразователь с модифицированной синусоидой, в электросеть попадает больше количество помех, поэтому медицинская техника и системы связи могут работать нестабильно. Появляется неблагоприятное явление, влияющее на трансформаторы и электродвигатели: устройство начинает греться, снижается КПД.
Сюда относится аппаратура, которая, чувствительна к разного рода помехам, либо аппаратура с трансформаторными источниками питания, компрессоры, электродвигатели, насосы и пр. Приборы, которые совсем не чувствительны к форме сигнала — это нагревательные приборы, лампы накаливания,, приборы, которые имеют импульсные источники питания (компьютеры, ноутбуки, цифровые телевизоры). Когда работает преобразователь с модифицированной синусоидой, в электросеть попадает больше количество помех, поэтому медицинская техника и системы связи могут работать нестабильно. Появляется неблагоприятное явление, влияющее на трансформаторы и электродвигатели: устройство начинает греться, снижается КПД.
Какой выбрать инвертор?
В случае ориентирования на телекоммуникационную и медицинскую аппаратуру — только синус. Нагреватели, лампы освещения, цифровая техника — вполне безопасно и смело можно использовать модифицированный синус. В других случаях есть немаловажные особенности, которые нужно знать при покупке инвертора, а именно:
- Техника с импульсным блоком питания. Нужно иметь ввиду, что проблема кроется в стартовых токах, которые могут в десятки раз превышать потребление источника питания в стандартном режиме работы после запуска. В этом случае инвертор запускается, но тут же срабатывает защита от перегрузки. Выход из ситуации простой: покупать преобразователь напряжения в 2 раза мощнее, чем мощность блока питания подключаемого прибора.
- Техника с трансформаторным блоком питания. В случае, когда блок питания оптимизирован, а нагрузка имеет постоянность — покупайте инвертор с правильной синусоидой. Если же трансформатор имеет запас по мощности и рассчитан на максимальную нагрузку, которая может появиться лишь иногда и носит кратковременный характер – можно купить инвертор с модифицированной синусоидой. Может иметь место повышение температуры трансформатора, но она не критично возрастает, прибор нормально функционирует.

- Электроприборы с моторами. Для компрессоров, дрелей, болгарок и других им подобных можно покупать инверторы с модифицированным синусом, но обязательным условием есть запас по мощности, который в 1.5-2 раза должен быть больше. Нужно также не забывать, что механическая мощность электроприбора немного уменьшается, мотор греется немного больше, чем обычно.
В нашем магазине представлены надежные бытовые и автомобильные инверторы с правильной и модифицированной синусоидой.
Добавить комментарий
Источник бесперебойного питания CyberPower UT650EG
Источник бесперебойного питания начального уровня. Высокое качество выходного электропитания.
Линейка
UT
Тип
Источник бесперебойного питания
Типология ИБП
Линейно-интерактивный
Полная выходная мощность
650 ВА
Активная выходная мощность
360 Вт
Количество фаз
1
Номинальное входное напряжение
220 В
Входная частота
45 – 65 Гц
Диапазон входного напряжения при работе от сети
165 – 290 В
Количество фаз
1
Номинальное выходное напряжение
230 В
Выходная частота (синхронизированная с электросетью)
45 – 65 Гц
Выходная частота (не синхронизированная с электросетью)
50 Гц +/- 1 Гц
Тип формы напряжения
Ступенчатая аппроксимация синусоиды
Пик-фактор
3: 1
Время переключения на работу от аккумулятора типичное
4 мс
Время переключения на работу от аккумулятора максимальное
8 мс
Коэффициент выходной мощности
0. 55
55
Максимальный ток нагрузки, не более
2.83 А
Автоматический регулятор напряжения (AVR)
Есть
Тип входного разъема
Фиксированное кабельное подключение
Неразъемный кабель с евровилкой СEE7
1 шт
Длина входного кабеля
1.2 м
Выходные разъемы
Schuko CEE 7
Бытовые (Schuko CEE 7)
3 шт
Наличие в поставке
Есть
Тип
Необслуживаемая
Ёмкость
5 Ач
Напряжение
12 В
Количество батарей (картриджей) в комплекте
1 шт
Линейное напряжение сборки
12 В
Энергия батареи при токе 10-часового разряда
60 Вт*ч
Типовое время заряда
10 ч
Максимальный ток заряда АБ, не более
1. 5 А
5 А
Размеры сменного аккумулятора
90 x 107 x 70 мм
Возможность самостоятельной замены батарей
Есть
Возможность горячей замены (Hot Swap) батареи
Нет
Возможность подключения внешних батарей
Нет
ЖК дисплей
Нет
Индикация
Питания, Режима работы, Сети, Состояния батареи
Звуковые сигналы
Низкий уровень заряда, Ошибка ИБП, Перегрузка, Работа от аккумулятора
Кнопка включения
Есть
Самотестирование
Есть
Автозарядка
Есть
Холодный старт
Есть
Степень защиты
IP20
Защита от короткого замыкания
Есть
Защита от высоковольтных импульсов
Есть
Фильтрация помех
Есть
Защита от перегрузки
Есть
Защита от понижения напряжения
Есть
Защита от повышения напряжения
Есть
Защита цепи нагрузки
Есть
Защита входной цепи
Есть
Защита от переразряда батареи
Есть
Защита телефонной линии/коммуникационной сети
Есть
Рабочий диапазон температуры
от 0 до +40°С
Температура хранения
от -15 до +45°C
Рабочий диапазон относительной влажности
от 0 до 95%
Относительная влажность хранения
от 0 до 95%
Форм-фактор
Напольный, Настольный
Материал корпуса
Сталь, пластик
Охлаждение
Воздушное
Цвет
Черный
Габариты
84 x 174 x 280 мм
Вес нетто
4 кг
RPT-1000AP USB, Источник бесперебойного питания (ИБП/UPS), 1000ВА/600Вт, IEC, line-interactive, черный
Тип ИБП: Линейно-интерактивныйИсполнение: Напольный
Мощность: 1000 ВА/ 600 Вт
Входное напряжение: 160~275 В, 50 Гц или 60 Гц ± 10% (автоопределение)
Выходное напряжение: 220/230/240 В ± 5%, 50 Гц или 60 Гц ± 1%
Форма выходного напряжения: Ступенчатая аппроксимация синусоиды
Автоматическая регулировка напряжения (AVR): Автоматический стабилизатор напряжения с 1 ступенью понижения и 1 ступенью повышения
Время переключения: От 2 до 4 мс включая время определения (типовое)
Аккумуляторная батарея: Герметичная необслуживаемая свинцово-кислотная, срок службы 3~5 лет.
Напряжение и емкость батареи: 12В 9Ач
Типовое время перезарядки: 3~4 часа
Время батарейной поддержки (работа ПК с 17″ монитором, нагрузка 100Вт): ~ 20 минут
Холодный старт: есть
USB-порт: Определение и отображение уровня заряда аккумулятора, входного и выходного напряжения, установка расписания включения/выключения, корректное завершение работы компьютера и т.п.
Выходные разъемы: 3 розетки IEC320 C13 с резервным питанием
Размеры (Ш*Г*В), мм: 100 х 278 х 140
Вес нетто, кг: 4.5
Индикация: Светодиодная
Звуковая сигнализация: В режиме работы от батареи – повторяющийся звуковой сигнал каждые 2 секунды в течение первых 15 секунд, далее два раза в минуту; Низкий заряд батареи – повторяющийся звуковой сигнал два раза в секунду; Перегрузка – продолжительный звуковой сигнал.
Линейно-интерактивные ИБП серии RAPTOR предназначены для защиты персональных компьютеров и сетевого оборудования от основных неполадок с электропитанием: перегрузки или короткого замыкания; понижений, повышений и полного исчезновения напряжения в электросети. Благодаря наличию встроенного стабилизатора напряжения все модели серии RAPTOR поддерживают выходное напряжение в пределах нормы при постоянно пониженном напряжении электросети, не используя ресурс аккумулятора. Для удобства подключения оборудования в ИБП предусмотрено три выходных разъема с батарейной поддержкой. Коммуникационный порт для связи с компьютером позволит своевременно завершить работу системы с сохранением данных. ИБП серии RAPTOR, отличаясь невысокой ценой, обеспечат защиту Вашей техники от основных проблем электросети, занимая минимум рабочего пространства.
4 $$и замена $ x $ 1 $ дает второе ограничение:
$$ a_0 + 3 a_1 + 5 a_2 = 0 \ tag2 $$
Теперь мы можем использовать наши два ограничения, чтобы найти $ a_1 $ и $ a_2 $ в терминах $ a_0 $.
$$ a_1 = \ frac {5} {2} -2a_0 \\ a_2 = a_0- \ frac {3} {2} \ tag {3}
$ Все, что осталось, – это подправить $ a_0 $, чтобы он лучше подошел.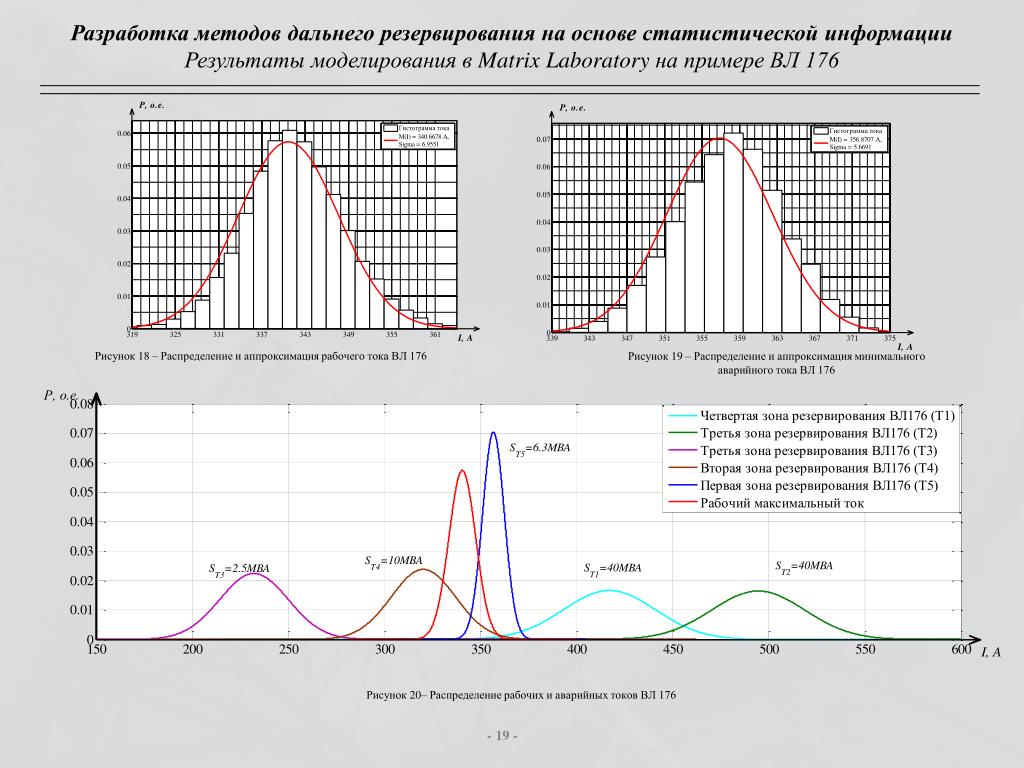 5 \\
a_0 = 1 – a_1 – a_2 \ примерно 1.6}. $
5 \\
a_0 = 1 – a_1 – a_2 \ примерно 1.6}. $
Это приближение имеет небольшой угол на границах полупериода, потому что полином имеет нулевую производную не при $ x = \ pm 1 $, а при $ x \ приблизительно \ pm 1.002039940. $ При $ x = 1 $ значение производная составляет около $ 0,0049828 $. Это приводит к более медленному асимптотическому убыванию амплитуд гармоник при больших $ k, $ по сравнению с приближением 5-го порядка, которое имеет непрерывную производную.
7-й порядок
Аналогично можно найти приближение 7-го порядка без непрерывной производной.8}. $
Исходный код Python
из символов импорта sympy, пи, решить, множитель, бином
numEq = 3 # Количество уравнений
numHarmonics = 6 # Количество гармоник для оценки
a1, a2, a3, k = символы ("a1, a2, a3, k")
коэффициенты = [a1, a2, a3]
HarmonyRelativeAmplitude = (2 * pi ** 4 * a1 * k ** 4 * (pi ** 2 * k ** 2-12) + 4 * pi ** 2 * a2 * k ** 2 * (pi ** 4 * к ** 4-60 * пи ** 2 * к ** 2 + 480) + 6 * а3 * (пи ** 6 * к ** 6-140 * пи ** 4 * к ** 4 + 6720 * pi ** 2 * k ** 2-53760) + pi ** 6 * k ** 6) * (1 - (- 1) ** k) / (2 * k ** 8 * (2 * pi ** 4 * a1 * (пи ** 2-12) + 4 * пи ** 2 * a2 * (пи ** 4-60 * пи ** 2 + 480) + 6 * a3 * (пи ** 6-140 * пи ** 4 + 6720 * пи ** 2-53760) + пи ** 6))
HarmonicRelativeAmplitude = []
для i в диапазоне (0, numHarmonics):
гармоническая относительная амплитуда.append (HarmonicRelativeAmplitude.subs (k, 3 + 2 * i))
numCandidateEqs = 2 ** numHarmonics
numSignCombinations = 2 ** numEq
useHarmonics = диапазон (numEq + 1)
bestSolution = []
bestRelativeAmplitude = 1
bestUnevaluatedRelativeAmplitude = 1
numSolutions = binomial (numHarmonics, numEq + 1) * 2 ** numEq
solutionIndex = 0
для i в диапазоне (0, numCandidateEqs):
temp = я
кандидатNumHarmonics = 0
j = 0
в то время как (темп):
если (темп & 1):
если кандидатNumHarmonics > = 1
j + = 1
если (кандидатаNumHarmonics == numEq + 1):
для j в диапазоне (0, numSignCombinations):
eqs = []
temp = j
для n в диапазоне (0, numEq):
если темп & 1:
экв. append (гармонические относительные амплитуды [useHarmonics [0]] - гармонические относительные амплитуды [useHarmonics [1 + n]])
еще :
eqs.append (гармонические относительные амплитуды [useHarmonics [0]] + гармонические относительные амплитуды [useHarmonics [1 + n]])
темп >> = 1
решение = решить (уравнения, коэффициенты, руководство = True)
solutionIndex + = 1
print "Решение-кандидат% d из% d"% (solutionIndex, numSolutions)
решение для печати
solutionRelativeAmplitude = гармоническийRelativeAmplitude
для n в диапазоне (0, numEq):
solutionRelativeAmplitude = solutionRelativeAmplitude.subs (коэффициенты [n], решение [0] [n])
solutionRelativeAmplitude = фактор (solutionRelativeAmplitude)
решение для печати
solutionWorstRelativeAmplitude = 0
для n в диапазоне (0, numHarmonics):
solutionEvaluatedRelativeAmplitude = abs (factor (solutionRelativeAmplitude.subs (k, 3 + 2 * n)))
if (solutionEvaluatedRelativeAmplitude> solutionWorstRelativeAmplitude):
solutionWorstRelativeAmplitude = solutionEvaluatedRelativeAmplitude
решение для печатиWorstRelativeAmplitude
if (solutionWorstRelativeAmplitude
append (гармонические относительные амплитуды [useHarmonics [0]] - гармонические относительные амплитуды [useHarmonics [1 + n]])
еще :
eqs.append (гармонические относительные амплитуды [useHarmonics [0]] + гармонические относительные амплитуды [useHarmonics [1 + n]])
темп >> = 1
решение = решить (уравнения, коэффициенты, руководство = True)
solutionIndex + = 1
print "Решение-кандидат% d из% d"% (solutionIndex, numSolutions)
решение для печати
solutionRelativeAmplitude = гармоническийRelativeAmplitude
для n в диапазоне (0, numEq):
solutionRelativeAmplitude = solutionRelativeAmplitude.subs (коэффициенты [n], решение [0] [n])
solutionRelativeAmplitude = фактор (solutionRelativeAmplitude)
решение для печати
solutionWorstRelativeAmplitude = 0
для n в диапазоне (0, numHarmonics):
solutionEvaluatedRelativeAmplitude = abs (factor (solutionRelativeAmplitude.subs (k, 3 + 2 * n)))
if (solutionEvaluatedRelativeAmplitude> solutionWorstRelativeAmplitude):
solutionWorstRelativeAmplitude = solutionEvaluatedRelativeAmplitude
решение для печатиWorstRelativeAmplitude
if (solutionWorstRelativeAmplitude непрерывных сигналов - Минимальное количество точек для задания синусоидальной волны с заданной точностью
непрерывных сигналов - Минимальное количество точек для задания синусоидальной волны с заданной точностью - Обмен стеком обработки сигналовСеть обмена стеком
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
- 0
- +0
- Авторизоваться Зарегистрироваться
Signal Processing Stack Exchange - это сайт вопросов и ответов для практиков в области обработки сигналов, изображений и видео.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 3к раз
$ \ begingroup $ Я генерирую синусоидальную волну от ЦАП с постоянной частотой. Если каждый полный цикл определяется N точками данных, какова взаимосвязь между точностью визуализированной синусоидальной волны и N?
Если каждый полный цикл определяется N точками данных, какова взаимосвязь между точностью визуализированной синусоидальной волны и N?
N = 1, очевидно, будут импульсами. N = 4 (пики и пересечения нуля) даст своего рода треугольную волну. Есть ли какое-нибудь уравнение, которое показывает, насколько хорошо создается приближение синусоидальной волны? [Очевидно, я могу пропустить это через фильтр пост-ЦАП, чтобы сгладить его и т. Д.]
Я ищу такой ответ: «Задание синусоидальной волны с N точками дает точность 1: X»
Создан 11 дек.
Дирк БруэрDirk Bruere17722 серебряных знака88 бронзовых знаков
$ \ endgroup $ 1 $ \ begingroup $Я думаю, что вы спрашиваете, «какова частота дискретизации, необходимая для дискретизации синусоидальной волны с заданной точностью».В основном это и есть теорема выборки (см., Например, http://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem). Удивительный ответ (более или менее): «больше двух». Как только вы соответствуете критериям выборки, все в порядке и точность НЕ увеличивается при более частой выборке.
В вашем случае 3 точки за период будут работать нормально (при условии, что ваш ЦАП имеет правильный фильтр сглаживания).
Создан 11 дек.
Хильмар19.8k11 золотой знак1616 серебряных знаков3030 бронзовых знаков
$ \ endgroup $ $ \ begingroup $Я не знаю формулы, но я знаю из экспериментов, что N = 256 дает синусоидальную волну с разумным SNR для общего использования звука, хотя, если вам нужна полная 16-битная точность (то есть> 90 дБ SNR), вы Возможно, мне нужно будет подняться выше этого.
Если вы проходите через LUT синусоидальной волны с нецелочисленной скоростью (для генерации произвольной частоты), то использование интерполяции между значениями LUT снижает SNR, так что вы можете использовать LUT меньшего размера, чем если бы вы не интерполировали (например.грамм. если вы просто усечете индекс образца).
Создан 11 дек.
Пол РПаул Р3,2221616 серебряных знаков3232 бронзовых знака
$ \ endgroup $ Обмен стеком обработки сигналов лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Блог Эдди по математике и калькулятору: Длина дуги sin (x)
Запись в блоге № 102
Длина дуги синусоиды
Синусоида - одна из самых интересных кривых в математике.Икс). Следовательно, необходимо использовать численные методы.
Поиск приближенной кривой
Используя TI nSpire CX CAS, я использовал функции электронной таблицы, подбора кривой и построения графиков для определения приблизительного полинома. Длина дуги - от начала координат (0,0) до (π, 0).
Примечание: x1 = 0, x2 = π
Вот краткое изложение того, что я сделал:
1. Создал электронную таблицу со следующими столбцами:
Столбец A: последовательность чисел от 0.От 25 до 5 с шагом 0,25. Результирующий список называется , усилитель .
Столбец B: Используйте функцию arcLen nSpire, чтобы получить длину дуги синусоидальной кривой, используя амплиста в качестве значений для и . Этот список называется arc1 .
2. Нажатие клавиши меню позволило мне получить доступ к меню Статистика . Используя опцию Stat Calculations , я использовал различные типы регрессии, включая степенную и четвертную регрессию.2 + .2071162669684 x + 3.0881429428239
Этот многочлен был сохранен в функции f1 (x).
3. Я создал страницу графиков и сделал два графика:
* График рассеяния, где x = амплитуда, y = arc1. (Точки красного цвета)
* Функция f1 (x) (см. Шаг 2). (Кривая синего цвета)
Если установить масштаб для соответствия данным, кривая будет выглядеть хорошо.
Вы можете создать аналогичный график с помощью модуля «Данные и статистика», но я подумал, что на этот раз все будет по-другому.
Насколько хорошо подходит многочлен?
4. Я вернулся к таблице и добавил еще два столбца.
Столбец C: est1 = f1 (усилитель). (оценка длины дуги)
Столбец D: err1 = abs (arc1 - est1)
Прокручивая вниз столбец D, полином четвертой степени точно оценивал длину дуги синусоидальной кривой от 0 до π как минимум с двумя десятичными знаками.
Заключение
Мы пытались найти длину дуги кривой y = a sin x от x = 0 до x = π.2 + .2071162669684 x + 3.0881429428239
Как всегда, спасибо и скоро с вами свяжемся!
Эдди
Этот блог является собственностью Эдварда Шора. © 2012
Задача моделирования - построение приближенного синусоидального сигнала
* Это одна из серии задач моделирования , которые вы можете использовать для проверки своих навыков в SOLIDWORKS. Сначала прочтите задание и попытайтесь найти решение самостоятельно. Затем сравните свое решение с моими хорошими, лучшими и лучшими рекомендациями.Как всегда, не стесняйтесь делиться еще большим количеством советов и уловок в комментариях ниже.
Позвольте мне начать с заявления об отказе от ответственности, поскольку я знаю, что иду на цыпочках по шатким основаниям, учитывая техническую аудиторию, которая часто посещает этот блог. Фактически, наша команда по разработке продуктов была бы первой, кто закричал бы: «Математически невозможно представить синусоидальную волну (любую ее часть) кривой Безье!» (как я и собираюсь сделать). Я знаю, потому что они мне сказали именно это. Пожалуйста, обратите внимание на слово «приблизительно» в заголовке этого сообщения в блоге.Моя цель - показать вам самый быстрый и простой способ набросать аппроксимацию синусоидальной кривой. Если вы ищете эмпирическую синусоидальную кривую для разработки сверхточных кулачков, я бы посоветовал проверить некоторые из наших партнерских продуктов, например CamTrax для SOLIDWORKS. Если вам нравится фраза «чертовски близко», продолжайте.
Одним из первых инструментов, к которым я обратился, были наши кривые, управляемые уравнениями, которые были представлены в 2009 году. Как явные, так и параметрические уравнения могут использоваться для управления геометрией на двухмерной плоскости или в трехмерном эскизе.В нашем случае я просто хотел бы набросать половину периода синусоидальной волны, начиная с максимальной отрицательной амплитуды и заканчивая пиком максимальной положительной амплитуды (см. Ниже). Объединение последовательности этих синусоидальных кривых является популярной практикой для проектирования первоначальной 2D-схемы цилиндрического кулачка.
Чтобы это произошло, нам придется отбросить пыль в наших учебниках по математике и вспомнить, что функция синусоидальной волны выглядит примерно так: Y (x) = A * sin (Bx + C), где A - амплитуда, B - угловая частота, а C - фаза… yada, yada, yada.Обычно это слишком много, чтобы запомнить мой простой ум. Все, что меня волнует, - это общая высота (она же амплитуда) и длина (она же период). Каждый раз, когда вы хотите упростить и централизовать входные данные, которые управляют вашей моделью САПР, рассмотрите возможность использования глобальных переменных (и в данном случае также уравнений). Таким образом, я могу сохранить это как шаблон и использовать его снова и снова, настраивая пару глобальных переменных, вместо того, чтобы воссоздавать его с нуля.
- Откройте диалоговое окно «Уравнения».
Я часто использую уравнения, поэтому рекомендую добавить эту кнопку на верхнюю панель инструментов (где расположены кнопки «Новый документ», «Сохранить» и «Печать»), чтобы она всегда была легко доступна. - Создайте две глобальные переменные для наших основных входов - «ДЛИНА» и «ВЫСОТА».
Введите любое имя, которое вы предпочитаете, и текущее значение. - Создайте глобальную переменную для каждой переменной синусоидальной волновой функции - «A», «B» и «C».
Математические уравнения могут быть созданы путем ссылки на другие глобальные переменные, пользовательские свойства или размеры. Чтобы вам было легче вспомнить этот метод до безумия, всегда добавляйте полезные комментарии к своим уравнениям.
- Начать 2D-эскиз
- Создайте кривую, управляемую уравнением, введя следующие значения в поля ввода PropertyManager.
Вы можете ссылаться на глобальные переменные, вводя их имена в кавычках.
- Вам нужно будет определить местоположение и положение кривой, управляемой уравнением, используя взаимосвязи и размеры эскиза, чтобы полностью определить эскиз.
Это именно то, что я искал с точки зрения формы, но для этого потребовалось гораздо больше размышлений, чем мой мозг предпочел бы потратить на один эскизный объект всей модели.Тем не менее, не стоит недооценивать силу кривых, управляемых уравнениями. Как только вы начнете экспериментировать с 3D-кривыми, геометрия, которую вы можете создать с помощью креативной математики, станет довольно приятной. Это позволяет очень легко разрабатывать такие изделия, как волнистые пружины / шайбы.
По общему признанию, этот пример - довольно хитрое решение, но потерпите меня. Когда ты в отчаянии, ты попробуешь что угодно. Кроме того, есть несколько советов, которые можно извлечь из этого подхода, и он очень удобно настроит мое лучшее решение.
С помощью шлицев можно рисовать практически все, что угодно. Допустим, у вас есть изображение профиля синусоидальной волны, на которое можно ссылаться при рисовании сплайна. Все, что вам нужно сделать, это вставить изображение эскиза, соответствующим образом масштабировать его, а затем запустить другой эскиз поверх него ( Я предпочитаю держать изображение эскиза изолированным в собственном эскизе, чтобы вы могли легко переключать его видимость из дерева FeatureManager при редактировании отдельного эскиза ), чтобы создать вашу сплайн-волну ... я имею в виду синусоидальную волну.В моем случае у нас уже есть кривая, управляемая уравнениями, которую я создал в предыдущей попытке, поэтому мы будем использовать ее как ссылку.
- Эскиз 2-точка сплайна, помещая две конечные точки на обоих концах опорного синусоидального сигнала
- Выберите сплайн, чтобы появились маркеры сплайна
- Перетащите ромбовидную фигуру на ручку сплайна, чтобы изменить положение начальной траектории сплайна, и, пока она все еще выделена, добавьте к ней горизонтальную связь. модификация, которую вы сделаете (направление, величина).Или вы можете перетащить точку на конце стрелки, чтобы изменить направление и величину одновременно.
- Повторите шаг 3 для противоположной шлицевой ручки
- Перетащите стрелки каждого маркера сплайна, пока он не будет точно соответствовать базовой ссылке
- Активируйте инструмент «Умный размер» и примените размер к стрелке одного из маркеров сплайна.
Не беспокойтесь о конкретном значении. Это всего лишь величина и не соответствует действительному линейному расстоянию.Несмотря на то, что значение немного загадочно, довольно круто, что вы можете использовать эти размеры для полного определения сплайна. - Повторите шаг № 7 для противоположной стрелки, но вместо того, чтобы вводить числовое значение, введите «=» и затем щелкните размер, созданный на шаге № 7, чтобы второй размер всегда был равен первому.
Ввод «=» означает быстрый способ создавать уравнения на лету. Это можно сделать даже в полях ввода PropertyManager. Кроме того, вы можете добавлять комментарии на лету, набрав «‘ »(апостроф) в конце уравнения, а затем комментарий. - Измените первый размер для автоматического обновления сразу обоих размеров для точной настройки формы сплайна
Этот метод слишком неточен из-за ручного характера техники. Я не соврал, когда сказал, что это чушь, но, не испытав боли, связанной с этим подходом, вы не сможете полностью оценить удобство моего следующего (и лучшего) решения.
Иногда слишком много настроек и гибкости - это плохо.Иногда это может происходить с традиционными сплайнами. Слишком большой ручной контроль над маркерами сплайна (особенно на сплайне с множеством управляющих вершин) может затруднить управление окончательной формой и затруднить полное определение. В 2014 году были представлены сплайны стиля, чтобы упростить создание сплайнов, когда не требуется высокий уровень настройки. Отказавшись от небольшого контроля, SOLIDWORKS может автоматически управлять скоростью кривизны по всей длине сплайна стиля, что гарантирует получение кривой высочайшего качества каждый раз практически без проблем.Лучше всего то, что сплайны стиля чрезвычайно легко полностью определить, что делает их идеальным решением для таких точных приложений, как моделирование синусоидальной волны.
- Создание 4-точечного сплайна стиля по наклонному ступенчатому шаблону (см. Ниже)
Вместо управляющих маркеров, сплайны стиля управляются многоугольником вспомогательных линий, что значительно упрощает их полное определение с помощью традиционных схем размеров. - Добавить отношения "Горизонталь" и "Равенство" к первой и последней линиям построения
- Добавьте габаритную длину и высоту
- Добавьте размер к одной из горизонтальных вспомогательных линий и сделайте его равным общей длине, умноженной на магическое отношение 0.3642.
Не просите меня объяснять это значение, но я протестировал его на многих сплайновых кривых, и оказалось, что он дает неизменно точные результаты.
Вот и все! Независимо от общей длины и высоты кривой, это соотношение дает отличные результаты. Вы мне не верите? Создайте твердое тело, используя традиционную технику, и воссоздайте отдельное тело в том же месте, используя мою технику. Затем с помощью инструмента «Объединить» вычтите одно тело из другого и посмотрите, что получится.Если вы получаете сообщение об ошибке, это, скорее всего, связано с тем, что разница между телами слишком мала для расчета. Если у вас есть лицензия на SOLIDWORKS Professional или Premium, вы можете использовать служебную программу «Сравнить», чтобы сравнить геометрию двух тел с лучшей визуальной обратной связью.
Одна из лучших частей этого решения заключается в том, что как только вы создаете этот эскиз в первый раз, вы можете перетащить его в свою Библиотеку дизайна, где он будет сохранен как блок эскиза. В любое время в будущем вы ( или кто-либо в вашей компании, если вы храните свою библиотеку дизайна на общем диске сервера) можете перетащить этот блок эскиза из библиотеки дизайна в активный эскиз, привязать его к месту с помощью взаимосвязей эскиза , отредактируйте блок, измените значения длины и высоты, и все готово! Фактически, вы можете скачать мой предварительно созданный блок эскиза синусоидальной волны 2018 года здесь.
Впечатлены простотой использования и качеством Style Splines? Попробуй это. Вернитесь к одному из своих старых проектов, который содержит сплайн, выберите сплайн в эскизе, в котором он был изначально создан, а затем выберите «Преобразовать в сплайн стиля» на контекстной панели инструментов. Благодаря этой полезной кнопке вы можете переключаться между традиционными сплайнами и стилями сплайнов (и наоборот) в любое время. Для сложных форм иногда проще нарисовать начальную форму с помощью традиционного сплайна, преобразовать его в сплайн стиля, а затем полностью ограничить его связями и размерами.Пожалуйста, изучите эту технику и дайте мне знать, как она вам нравится, в комментариях ниже.
прямоугольных сигналов | Сигналы переменного тока смешанной частоты
Было обнаружено, что любая повторяющаяся несинусоидальная форма волны может быть приравнена к комбинации постоянного напряжения, синусоидальных волн и / или косинусоидальных волн (синусоидальных волн с фазовым сдвигом 90 градусов) с различными амплитудами и частотами.
Это верно независимо от того, насколько странной или запутанной может быть рассматриваемая форма волны. Если он регулярно повторяется с течением времени, его можно свести к этой серии синусоидальных волн.
В частности, было обнаружено, что прямоугольные волны математически эквивалентны сумме синусоидальной волны на той же частоте плюс бесконечная серия синусоид с нечетно-кратной частотой с уменьшающейся амплитудой:
Поначалу эта истина о формах волны может показаться слишком странной, чтобы в нее поверить. Однако, если прямоугольная волна на самом деле представляет собой бесконечную серию сложенных вместе синусоидальных гармоник, очевидно, что мы должны иметь возможность доказать это, сложив вместе несколько гармоник синусоидальной волны, чтобы получить близкое приближение к прямоугольной волне.
Это рассуждение не только здраво, но и легко демонстрируется с помощью SPICE.
Схема, которую мы будем моделировать, представляет собой не что иное, как несколько источников синусоидального переменного напряжения соответствующей амплитуды и частоты, соединенных последовательно. Мы будем использовать SPICE, чтобы построить кривые напряжения при последовательном добавлении источников напряжения, например:
Прямоугольная волна аппроксимируется суммой гармоник.
В этом конкретном моделировании SPICE я суммировал последовательно последовательно подключенные источники напряжения 1-й, 3-й, 5-й, 7-й и 9-й гармоник, всего пять источников переменного напряжения.Основная частота составляет 50 Гц, и каждая гармоника, конечно, кратна этой частоте.
Значения амплитуды (напряжения) не являются случайными числами; скорее, они были получены с помощью уравнений, показанных в частотном ряду (дробь 4 / π, умноженная на 1, 1/3, 1/5, 1/7 и т. д. для каждой возрастающей нечетной гармоники).
строить квадратную волну v1 1 0 sin (0 1,27324 50 0 0) 1-я гармоника (50 Гц) v3 2 1 sin (0 424.413m 150 0 0) 3-я гармоника v5 3 2 sin (0 254.648м 250 0 0) 5-я гармоника v7 4 3 sin (0 181,891m 350 0 0) 7-я гармоника v9 5 4 sin (0 141.471m 450 0 0) 9-я гармоника r1 5 0 10к .tran 1м 20м .plot tran v (1,0) График 1-й гармоники .plot tran v (2,0) График 1-й + 3-й гармоник .plot tran v (3,0) График 1-й + 3-й + 5-й гармоник .plot tran v (4,0) График 1-й + 3-й + 5-й + 7-й гармоник . участок tran v (5,0) Участок 1-й +. . . + 9-я гармоника .конец
Я расскажу об анализе шаг за шагом, объясняя, на что мы смотрим.На этом первом графике мы видим синусоиду основной частоты 50 Гц. Это не что иное, как чистая синусоида без дополнительных гармоник. Это форма волны, генерируемая идеальным источником питания переменного тока:
Чистая синусоида 50 Гц.
Затем мы посмотрим, что происходит, когда этот чистый и простой сигнал объединяется с третьей гармоникой (трижды по 50 Гц или 150 Гц). Внезапно он больше не выглядит как чистая синусоида:
Сумма 1-й (50 Гц) и 3-й (150 Гц) гармоник приближается к прямоугольной волне 50 Гц.
Время нарастания и спада между положительными и отрицательными циклами теперь намного круче, а гребни волны ближе к тому, чтобы стать плоскими, как прямоугольная волна. Посмотрите, что происходит, когда мы добавляем следующую нечетную частоту гармоники:
.Сумма 1-й, 3-й и 5-й гармоник аппроксимирует прямоугольную волну.
Наиболее заметным изменением здесь является то, что гребни волны стали еще более плоскими. На каждом конце волны есть несколько провалов и гребней, но эти провалы и гребни меньше по амплитуде, чем были раньше.Посмотрите еще раз, как мы добавляем в микс следующую форму волны нечетной гармоники:
Сумма 1-й, 3-й, 5-й и 7-й гармоник приближается к прямоугольной волне.
Здесь мы видим, что волна становится более плоской на каждом пике. Наконец, добавив 9-ю гармонику, пятый источник синусоидального напряжения в нашу схему, мы получим следующий результат:
Сумма 1-й, 3-й, 5-й, 7-й и 9-й гармоник приближается к прямоугольной волне.
Конечный результат сложения первых пяти нечетных гармонических сигналов вместе (конечно, все с правильными амплитудами) является близким приближением прямоугольной волны. Смысл в том, чтобы проиллюстрировать, как мы можем построить прямоугольную волну из нескольких синусоид на разных частотах, чтобы доказать, что чистая прямоугольная волна на самом деле эквивалентна серии синусоидальных волн.
Когда прямоугольное переменное напряжение подается в цепь с реактивными компонентами (конденсаторами и катушками индуктивности), эти компоненты реагируют так, как если бы они подвергались воздействию нескольких синусоидальных напряжений с разными частотами, что на самом деле так и есть.
Тот факт, что повторяющиеся несинусоидальные волны эквивалентны определенной серии аддитивного постоянного напряжения, синусоидальных и / или косинусоидальных волн, является следствием того, как работают волны: фундаментальное свойство всех связанных с волнами явлений, электрических или иных. .
Математический процесс сведения несинусоидальной волны к этим составляющим частотам называется анализ Фурье , детали которого выходят далеко за рамки этого текста. Однако были созданы компьютерные алгоритмы для выполнения этого анализа на высоких скоростях реальных сигналов, и их применение для анализа качества электроэнергии и сигналов переменного тока широко распространено.
SPICE может выполнять выборку формы волны и преобразовывать ее в составляющие ее гармоники синусоидальной волны с помощью алгоритма преобразования Фурье , выводя частотный анализ в виде таблицы чисел. Давайте попробуем это на прямоугольной волне, которая, как мы уже знаем, состоит из нечетных гармонических синусоид:
список соединений для анализа прямоугольных волн v1 1 0 импульс (-1 1 0. 1 м. 1 м 10 м 20 м) r1 1 0 10к .tran 1м 40м .plot tran v (1,0) . четыре 50 в (1,0) .конец
Параметр pulse в строке списка соединений, описывающей источник напряжения v1, инструктирует SPICE моделировать прямоугольную «импульсную» форму волны, в данном случае симметричную (равное время для каждого полупериода) и пиковую амплитуду 1 вольт.Сначала построим прямоугольную волну для анализа:
.Прямоугольная волна для анализа Фурье SPICE
Затем мы распечатаем анализ Фурье, сгенерированный SPICE для этой прямоугольной волны:
компоненты Фурье переходной характеристики v (1) компонент постоянного тока = -2,439E-02 гармоническая частота, нормализованная по Фурье, фаза, нормализованная нет (hz) компонент компонент (град) фаза (град) 1 5.000E + 01 1.274E + 00 1.000000 -2.195 0.000 2 1.000E + 02 4.892E-02 0.038415 -94.390 -92.195 3 1.500E + 02 4.253E-01 0.333987 -6.585 -4.390 4 2.000E + 02 4.936E-02 0,038757 -98,780 -96,585 5 2.500E + 02 2.562E-01 0.201179 -10.976 -8.780 6 3.000E + 02 5.010E-02 0.039337 -103.171 -100.976 7 3.500E + 02 1.841E-01 0.144549 -15.366 -13.171 8 4.000E + 02 5.116E-02 0,040175 -107.561 -105,366 9 4.500E + 02 1.443E-01 0.113316 -19.756 -17.561 общее гармоническое искажение = 43,805747 процентов
График результатов анализа Фурье.
Здесь (рисунок выше) SPICE разбил форму волны на спектр синусоидальных частот вплоть до девятой гармоники плюс небольшое постоянное напряжение, обозначенное как постоянная составляющая.
Мне пришлось сообщить SPICE основную частоту (для прямоугольной волны с периодом 20 миллисекунд эта частота составляет 50 Гц), поэтому он знал, как классифицировать гармоники.Обратите внимание, насколько малы цифры для всех четных гармоник (2-я, 4-я, 6-я, 8-я) и как уменьшаются амплитуды нечетных гармоник (1-я наибольшая, 9-я наименьшая).
Тот же самый метод «преобразования Фурье» часто используется в компьютеризированных силовых приборах, дискретизируя форму (сигналы) переменного тока и определяя их гармоническое содержание. Распространенным компьютерным алгоритмом (последовательностью программных шагов для выполнения задачи) для этого является функция Fast Fourier Transform или FFT .
Вам не нужно беспокоиться о том, как именно работают эти компьютерные подпрограммы, но нужно знать об их существовании и применении.
Тот же математический метод, который используется в SPICE для анализа гармонического содержания волн, может быть применен к техническому анализу музыки: разбиение любого конкретного звука на составляющие его частоты синусоидальной волны.
На самом деле, вы, возможно, уже видели устройство, предназначенное именно для этого, не осознавая, что это было! Графический эквалайзер - это высококачественное стереооборудование, которое контролирует (а иногда и отображает) характер гармонического содержания музыки.
Оснащенный несколькими ручками или ползунками, эквалайзер может выборочно ослаблять (уменьшать) амплитуду определенных частот, присутствующих в музыке, для «настройки» звука в интересах слушателя. Обычно рядом с каждым рычагом управления отображается «гистограмма», отображающая амплитуду каждой конкретной частоты.
Hi-Fi аудио графический эквалайзер.
Устройство, предназначенное исключительно для отображения, а не контроля, амплитуд каждого частотного диапазона для сигнала со смешанной частотой, обычно называется анализатором спектра .
Конструкция анализаторов спектра может быть такой же простой, как набор схем «фильтров» (подробности см. В следующей главе), предназначенных для разделения различных частот друг от друга, или сложной, как специальный цифровой компьютер, на котором работает алгоритм БПФ. чтобы математически разделить сигнал на его гармонические составляющие.
Анализаторы спектрачасто предназначены для анализа чрезвычайно высокочастотных сигналов, таких как сигналы, создаваемые радиопередатчиками и компьютерным сетевым оборудованием.В таком виде они часто выглядят как осциллограф:
Анализатор спектра показывает зависимость амплитуды от частоты.
Подобно осциллографу, анализатор спектра использует ЭЛТ (или компьютерный дисплей, имитирующий ЭЛТ) для отображения графика сигнала.
В отличие от осциллографа, этот график представляет собой амплитуду на частоте , а не амплитуду на времени . По сути, частотный анализатор дает оператору график сигнала Боде: то, что инженер может назвать частотной областью , а не анализом временной области .
Термин «область» является математическим: сложное слово для описания горизонтальной оси графика. Таким образом, график зависимости амплитуды (по вертикали) от времени (по горизонтали) на осциллографе представляет собой анализ «во временной области», тогда как график зависимости амплитуды (по вертикали) от частоты (по горизонтали) анализатора спектра представляет собой анализ «в частотной области».
Когда мы используем SPICE для построения графика амплитуды сигнала (напряжения или тока) в диапазоне частот, мы выполняем анализ в частотной области .
Обратите внимание на то, что анализ Фурье из последнего моделирования SPICE не «идеален». В идеале амплитуды всех четных гармоник должны быть абсолютно нулевыми, как и составляющая постоянного тока. Опять же, это не столько причуда SPICE, сколько свойство сигналов в целом.
Сигнал бесконечной продолжительности (бесконечное количество циклов) может быть проанализирован с абсолютной точностью, но чем меньше циклов доступно компьютеру для анализа, тем менее точным будет анализ.Только когда у нас есть уравнение, полностью описывающее форму волны, анализ Фурье может свести ее к определенной серии синусоидальных форм волны.
Чем меньше циклов волна повторяет, тем менее определена ее частота. Если довести эту концепцию до логического предела, короткий импульс - форма волны, которая даже не завершает цикл - на самом деле не имеет частоты , а действует как бесконечный диапазон частот. Этот принцип является общим для всех волновых явлений , а не только для переменного напряжения и тока.
Достаточно сказать, что количество циклов и достоверность частотной составляющей сигнала напрямую связаны.
Мы могли бы улучшить точность нашего анализа, позволив волне колебаться в течение многих циклов, и в результате получился бы спектральный анализ, более соответствующий идеалу. В следующем анализе для краткости я опустил график формы волны - это просто действительно длинная прямоугольная волна:
прямоугольная волна v1 1 0 импульс (-1 1 0.1м. 1м 10м 20м) r1 1 0 10к .option limpts = 1001 .tran 1м 1 .plot tran v (1,0) . четыре 50 в (1,0) .конец компоненты Фурье переходной характеристики v (1) компонент постоянного тока = 9.999E-03 гармоническая частота, нормализованная по Фурье, фаза, нормализованная нет (hz) компонент компонент (град) фаза (град) 1 5.000E + 01 1.273E + 00 1.000000 -1.800 0.000 2 1.000E + 02 1.999E-02 0.015704 86.382 88.182 3 1.500E + 02 4.238E-01 0.332897 -5,400 -3,600 4 2.000E + 02 1.997E-02 0,015688 82,764 84,564 5 2.500E + 02 2.536E-01 0.199215 -9.000 -7.200 6 3.000E + 02 1.994E-02 0,015663 79,146 80,946 7 3.500E + 02 1.804E-01 0.141737 -12.600 -10.800 8 4.000E + 02 1.989E-02 0,015627 75,529 77,329 9 4.500E + 02 1.396E-01 0.109662 -16.199 -14.399
Улучшенный анализ Фурье.
Обратите внимание, как этот анализ (рисунок выше) показывает меньшее напряжение составляющей постоянного тока и меньшие амплитуды для каждой из синусоидальных волн четной гармонической частоты, все потому, что мы позволяем компьютеру измерять больше периодов волны. Опять же, неточность первого анализа - это не столько недостаток SPICE, сколько фундаментальное свойство волн и анализа сигналов.
ОБЗОР:
- Прямоугольные волны эквивалентны синусоидальной волне на той же (основной) частоте, добавленной к бесконечной серии нечетно-кратных синусоидальных гармоник с уменьшающимися амплитудами.
- Существуют компьютерные алгоритмы, которые могут выбирать формы волн и определять составляющие их синусоидальные компоненты. Алгоритм преобразования Фурье (в частности, быстрое преобразование Фурье или FFT ) обычно используется в программах моделирования компьютерных схем, таких как SPICE, и в электронном измерительном оборудовании для определения качества электроэнергии.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Решение | Можем ли мы приблизительно определить площадь под этой синусоидальной кривой? | Представляем Calculus
Нарисуйте график \ (y = \ sin x \) для \ (0 \ leq x \ leq \ pi \), нанося точки с \ (x \) - координатами с интервалами \ (\ dfrac {\ pi} { 6} \) и пометив их последовательно \ (O, A, B, C, D, E, F \).
Начнем с составления таблицы значений.
Значения \ (\ sin x \), которые мы ищем, даются при рассмотрении этих треугольников;
| \(Икс\) | \ (0 \) | \ (\ пи / 6 \) | \ (2 \ пи / 6 \) | \ (3 \ пи / 6 \) | \ (4 \ пи / 6 \) | \ (5 \ пи / 6 \) | \ (6 \ пи / 6 \) |
|---|---|---|---|---|---|---|---|
| \ (\ грех х \) | \ (0 \) | \ (1/2 \) | \ (\ sqrt {3} / 2 \) | \ (1 \) | \ (\ sqrt {3} / 2 \) | \ (1/2 \) | \ (0 \) |
Теперь мы можем построить эти семь точек, чтобы дать нам приближение к требуемому графику.
Вычислите площадь многоугольника \ (OABCDEF \), разделив его на полосы, параллельные оси \ (y \) - или иным образом.
Если мы разделим многоугольник, как предложено, мы получим два треугольника и четыре трапеции. Обратите внимание, что форма симметрична, поэтому мы можем просто вычислить площади одного треугольника и двух трапеций и удвоить результат.
\ [\ begin {align *} \ text {Area} _1 & = \ frac {1} {2} \ times \ frac {\ pi} {6} \ times \ frac {1} {2} = \ frac {\ pi} {24} \\ \ text {Area} _2 & = \ frac {1} {2} \ times \ frac {\ pi} {6} \ times \ left (\ frac {1} {2} + \ frac {\ sqrt {3}} {2} \ right) = \ frac {\ pi} {24} (1+ \ sqrt {3}) \\ \ text {Area} _3 & = \ frac {1} {2} \ times \ frac {\ pi} {6} \ times \ left (\ frac {\ sqrt {3}} {2} +1 \ right) = \ frac {\ pi} {24} (\ sqrt {3} +2) \\ \ implies \ quad \ text {Area} _ {\ text {half}} & = \ frac {\ pi} {24} (4 + 2 \ sqrt {3}) \ конец {выравнивание *} \]Таким образом, площадь всего многоугольника равна \ (\ dfrac {\ pi} {6} (2+ \ sqrt {3}) = 1.{\ pi / 2} \ sin x \: dx. \]
Значение интеграла, которое мы должны аппроксимировать, - это площадь под кривой до ее максимальной точки. Это примерно равно половине площади многоугольника \ (0.977 \) (\ (3 \) s.f.). Из диаграммы видно, что это немного занижено.
Используя исчисление, можно точно вычислить требуемый интеграл, как \ (- \ cos (\ pi / 2) - (- \ cos 0) = 1 \).
Семь распространенных способов генерации синусоидальной волны
Синусоидальная волна - это естественная форма сигнала в коммуникациях и других электронных приложениях.
Во многих электронных продуктах используются сигналы синусоидальной формы. Аудио, радио и силовое оборудование обычно генерирует или обрабатывает синусоидальные волны. Как оказалось, есть буквально десятки способов сгенерировать синусоидальную волну. В этой статье представлены некоторые популярные методы, с которыми вам следует ознакомиться.
Осциллятор Wien Bridge
Популярным синусоидальным генератором низкой частоты (аудио и примерно до 100 кГц или около того) является мост Вина, показанный на рис. 1 .
РИСУНОК 1. Популярный мостовой генератор Вина. Старый, но хороший. Частоту можно изменять, используя потенциометры для R и используя разные значения включенного C.
В нем используется RC-цепь, которая производит сдвиг фазы нулевого градуса от выхода обратно к входу, создавая положительную обратную связь, которая, в свою очередь, вызывает колебания. Операционный усилитель используется для получения трехкратного усиления, которое компенсирует затухание RC-цепи. При чистом усилении замкнутого контура, равном единице, схема колеблется с частотой, определяемой значениями RC-цепи:
f = 1 / 2πRC
Эта схема отлично работает и дает очень чистую синусоидальную волну с низким уровнем искажений.Проблема заключается в том, что нестабильность усиления и фазы может привести к тому, что схема полностью прекратит колебания или войдет в состояние насыщения, что приведет к ограничению синусоидальной или прямоугольной волны. Некоторые компоненты компенсации обычно добавляются для устранения этой проблемы.
Простое решение - заменить R1 маленькой лампочкой накаливания, сопротивление которой изменяется в зависимости от тока. По мере увеличения выходного сигнала ток и сопротивление лампы увеличиваются, а коэффициент усиления уменьшается для компенсации. Если выходная мощность падает, ток уменьшается, уменьшая сопротивление и увеличивая коэффициент усиления, чтобы выходная мощность оставалась постоянной.Один рабочий пример - сделать R2 390 Ом, а R1 лампочкой типа 327. В других более сложных схемах полевой транзистор используется в качестве переменного резистора для изменения коэффициента усиления.
Эта схема работает и имеет частоту около 1592 Гц. Амплитуда выходного сигнала зависит от напряжения источника питания.
Генератор с фазовым сдвигом
Популярным способом создания синусоидального генератора является использование RC-цепи для создания фазового сдвига на 180 градусов для использования в тракте обратной связи инвертирующего усилителя. Установка усиления усилителя для компенсации затухания RC-цепи приведет к возникновению колебаний.Существует несколько вариантов фазовращателей, включая схему Twin-T RC и каскадные RC-секции верхних частот, которые производят сдвиг на 45 или 60 градусов на каждой ступени. Усилитель может быть одним транзистором, одним операционным усилителем или несколькими операционными усилителями. На рисунке 2 показан один популярный вариант.
РИСУНОК 2. Фиксированная частота - это недостаток, но для одной частоты - хорошо. Чистый выход необходимо буферизовать с помощью повторителя операционного усилителя, если вы собираетесь управлять нагрузкой.
Эти генераторы генерируют очень чистую синусоидальную волну с низким уровнем искажений. Однако частота фиксируется в точке, где каждая RC-секция производит фазовый сдвиг на 60 градусов. Примерная частота:
.f = 1 / 2.6RC
В схеме Рисунок 2 частота должна быть около 3,85 кГц.
Кристаллический осциллятор Колпитса
Кристаллы кварца часто используются для установки частоты генератора из-за их точной частоты колебаний и стабильности.Эквивалентная схема кристалла представляет собой последовательную или параллельную LC-цепь. Рис. 3 - очень популярный генератор синусоидальной волны типа Колпитца, что определяется схемой обратной связи с двумя конденсаторами.
РИСУНОК 3. Популярный кварцевый генератор, работающий каждый раз.
Это еще одна широко используемая схема, потому что ее легко реализовать и она очень стабильна. Его полезный частотный диапазон составляет приблизительно от 100 кГц до 40 МГц. На выходе получается синусоида с небольшими искажениями.
Кстати, если вам нужен кварцевый генератор с синусоидальным выходом, обычно можно купить коммерческую схему. Они широко доступны практически для любой желаемой частоты. Они упакованы в металлические банки и имеют размер типичной микросхемы. Источник постоянного тока обычно составляет пять вольт.
Прямоугольная волна и фильтр
Интересный способ создать синусоидальную волну - выбрать ее с помощью фильтра. Идея состоит в том, чтобы сначала сгенерировать прямоугольную волну. Оказывается, зачастую проще сгенерировать прямоугольную или прямоугольную волну, чем синусоидальную волну.Согласно теории Фурье, прямоугольная волна состоит из основной синусоидальной волны и бесконечного числа нечетных гармоник.
Например, прямоугольная волна 10 кГц содержит синусоидальную волну 10 кГц и синусоидальные волны на 3-й, 5-й, 7-й и т. Д., Гармоники 30 кГц, 50 кГц, 70 кГц и так далее. Идея состоит в том, чтобы подключить прямоугольный сигнал к фильтру, который выбирает желаемую частоту.
На рисунке 4 показан один пример.
РИСУНОК 4. КМОП-версия модели 555 рекомендуется, но вы можете заставить ее работать со стандартным 555, исключив резистор 100 кОм.
Микросхема таймера CMOS 555 создает прямоугольную волну с коэффициентом заполнения 50%. Его выходной сигнал направляется на RC-фильтр нижних частот, который отфильтровывает гармоники, оставляя только основную синусоиду. Некоторое искажение является обычным явлением, поскольку полностью устранить гармоники сложно. Для улучшения качества синусоидальной волны можно использовать более селективный LC-фильтр. Имейте в виду, что вы также можете использовать селективный полосовой фильтр, чтобы выделить одну из гармонических синусоидальных волн.
Эта схема рассчитана на частоту 1600 Гц.
Прямой цифровой синтез
Интересный способ создать синусоидальную волну - это сделать это в цифровом виде. См. Рисунок 5 .
РИСУНОК 5. Прямой цифровой синтез.
Он начинается с постоянной памяти (ПЗУ), в которой хранится ряд двоичных значений, представляющих значения, соответствующие уравнению тригонометрии для синусоидальной волны. Эти значения затем считываются из ПЗУ по одному и применяются к цифро-аналоговому преобразователю (ЦАП).Тактовый сигнал воздействует на счетчик адреса, который затем последовательно обращается к значениям синуса в ПЗУ и отправляет их в ЦАП. ЦАП генерирует аналоговый выходной сигнал, пропорциональный двоичному значению из ПЗУ. Вы получаете ступенчатую аппроксимацию синусоидальной волны.
Рисунок 6 является грубым примером.
РИСУНОК 6. Ступенчатая аппроксимация синусоидальной волны. Прохождение сигнала через фильтр нижних частот сгладит ступеньки.
Если вы используете достаточно отсчетов и используете больше битов для двоичного значения, шаги будут меньше, и возникнет более мелкозернистая синусоида.Частота синусоидальной волны зависит от количества выборок или значений, которые вы используете для синусоидальной волны, и частоты тактового сигнала, который считывает значения из ПЗУ. Если шаги слишком велики, вы можете пропустить ступенчатый сигнал через фильтр нижних частот, чтобы сгладить его. Доступны специальные микросхемы прямого цифрового синтеза (DDS), подобные микросхемам Analog Devices, для генерации синусоидальных волн от 1 Гц до многих МГц.
Генератор функций
Функциональный генератор - это имя устройства, которое генерирует синусоидальные, квадратные и треугольные волны.Он может описывать часть оборудования для стендовых испытаний или ИС. Одна старая, но все еще хорошая ИС функционального генератора - XR-2206. Впервые он был изготовлен Exar в 1970-х годах, но до сих пор существует.
Если вам нужен генератор синусоидальной волны, который можно настроить на любую частоту в диапазоне от 0,01 Гц до 1 МГц или более, обратите внимание на XR-2206. На рисунке 7 показан XR-2206, подключенный как генератор синусоидальной волны.
РИСУНОК 7. XR-2206 - это более старая ИС, которая все еще доступна и является отличным способом генерации синусоидальных, прямоугольных и треугольных волн в широком диапазоне частот.
Частота задается R и C и вычисляется по выражению:
f = 1 / RC
Внутренний генератор генерирует прямоугольную и треугольную волну. Схема формирователя синусоиды принимает треугольную волну и преобразует ее в синусоидальную волну.
Это по-прежнему отличная фишка. Помимо трех обычных сигналов, которые он генерирует, он также может их модулировать по амплитуде или частоте.
Импульсные генераторы синусоидальной волны
Есть несколько других умных способов получить приблизительную синусоидальную волну из импульсов и фильтров.Один из способов - просто сложить две прямоугольные волны одинаковой амплитуды, одна из которых смещена на 90 градусов относительно другой (, рис. 8, ). Пара JK-триггеров, управляемых синхронизирующими импульсами в противофазе, может генерировать две прямоугольные волны, которые нужно добавить.
РИСУНОК 8. Грубый способ сделать приближение синусоиды, которая может работать для некоторых приложений питания переменного тока.
В результате получается сигнал, который можно использовать в некоторых приложениях для замены синусоидальной волны.Некоторые грубые преобразователи постоянного тока в переменный используют этот метод. Эффект представляет собой среднюю мощность, аналогичную той, которую синусоидальная волна передает нагрузке. Некоторая RC- или LC-фильтрация может сгладить волну до более непрерывной синусоидальной формы. Этот метод используется в некоторых источниках бесперебойного питания (ИБП) или инверторах солнечной энергии, где идеальная синусоида не требуется.
Интересный метод использует последовательность импульсов переменной ширины, которые фильтруются в синусоидальную волну. Если вы примените прямоугольный сигнал с равным временем включения и выключения к фильтру нижних частот, на выходе будет среднее значение импульсного напряжения за период включения-выключения.При импульсе в пять вольт средний выходной сигнал за полный цикл волны будет 2,5 вольта. Изменяя длительность или ширину импульса, можно получить разные средние напряжения.
Пример приведен на рис. 9 .
РИСУНОК 9. Схема ШИМ для генерации синусоидальной волны, эквивалентной импульсу. Использование нескольких импульсов снижает гармонические искажения и превращает их в более гладкую синусоидальную волну.
Амплитуды импульсов постоянны, но ширина или длительность импульса варьируются.По мере увеличения длительности импульса фильтр нижних частот производит более высокое среднее выходное напряжение. По мере сужения импульсов среднее выходное напряжение уменьшается. Нагрузка усредняет импульсы до синуса, близкого к синусу. Использование большего количества импульсов приводит к более гладкой выходной синусоиде. Импульсы постепенно увеличиваются, а затем постепенно уменьшаются, и их среднее значение представляет собой синусоидальную волну. При необходимости можно добавить дополнительную фильтрацию.
Этот метод используется в некоторых системах приводов с регулируемым двигателем для изменения частоты синусоидальной волны, подаваемой на асинхронный двигатель переменного тока, для изменения его скорости (как в инверторах солнечной энергии и источниках бесперебойного питания).
Последовательность импульсов переменной ширины обычно генерируется микроконтроллером. Большинство этих процессоров имеют инструкции широтно-импульсной модуляции (ШИМ) и один или несколько выходов ШИМ. Ключом к созданию синусоидальной волны с низким уровнем искажений является выбор количества, последовательности и формы импульсов. Известный инженер и писатель Дон Ланкастер разработал математический метод определения количества импульсов и их длительности для создания синусоидальной волны с минимальными гармоническими искажениями. Это называется волшебными синусоидальными волнами.Взгляните на www.tinaja.com .
Схемы, описанные здесь, работают, если вы хотите поиграть с ними.


