ГАЗОВАЯ ПОСТОЯННАЯ — Физический энциклопедический словарь
(R), универсальная фнз. постоянная, входящая в ур-ние состояния 1 моля идеального газа: pv=RT (см. КЛАПЕЙРОНА УРАВНЕНИЕ), где р — давление, v — объём моля, Т — абс. темп-pa. Г. п. по своему физ. смыслу — работа расширения 1 моля идеального газа под пост. давлением при нагревании на 1 К. С другой стороны, Г. п.— разность молярных теплоёмкостей при пост. давлении и при пост. объёме cр-cv=R (для всех сильно разреженных газов). Численное значение Г. п. в единицах СИ (на 1980) 8,31441(26) Дж/(моль•К). В других ед. R = 8,314•107 эрг/(моль•К)=1,9872 кал/(моль•К) = 82,057 см3•атм/(моль•К).
Источник: Физический энциклопедический словарь на Gufo.me
Значения в других словарях
- газовая постоянная — ГАЗОВАЯ ПОСТОЯННАЯ универсальная фундаментальная физ. константа R, равная произведению постоянной Больцмана k на постоянную Авогадро NA: R = kNA = 8,31441(26) Дж/(моль∙К). Химическая энциклопедия
- Газовая постоянная — Универсальная физическая постоянная R, входящая в уравнение состояния 1 моля идеального газа: pv = RT (см. Клапейрона уравнение), где р — давление, v — объём, Т — абсолютная температура. Г. Большая советская энциклопедия
- ГАЗОВАЯ ПОСТОЯННАЯ — ГАЗОВАЯ ПОСТОЯННАЯ (обозначение R), универсальная постоянная в газовом уравнении (см. ЗАКОН ИДЕАЛЬНОГО ГАЗА), также называемая универсальной молярной газовой постоянной, равна 8,314510 ДжК-1 моль-1. Научно-технический словарь
- ГАЗОВАЯ ПОСТОЯННАЯ — ГАЗОВАЯ ПОСТОЯННАЯ — физическая постоянная, входящая в уравнение состояния 1 моля идеального газа; обозначается R, равна 8,314 Дж/(К·моль) = 1,987 кал/(К·моль). Большой энциклопедический словарь

gufo.me
Уравнение Клапейрона-Менделеева. Единицы измерения универсальной газовой постоянной. Пример задачи
Содержание статьи:Термодинамика – это самостоятельный раздел физики, который изучает процессы перехода между состояниями системы, оперируя при этом макроскопическими характеристиками. Одним из важных объектов изучения термодинамики является идеальный газ. Данная статья посвящена рассмотрению концепции идеального газа и единицам измерения универсальной газовой постоянной.
Идеальный газ
Газовое агрегатное состояние материи характеризуется хаотичным расположением частиц, расстояние между которыми значительно больше их размеров. Эти частицы находятся в постоянном движении, поэтому газ не сохраняет свою форму и свой объем.
Вам будет интересно:Ретироваться — это значит уходить: толкование слова
Идеальным газом называется любое вещество, размерами частиц которого и взаимодействиями между которыми можно пренебречь. В рамках концепции идеального газа считают, что любые столкновения частиц со стенками сосуда носят абсолютно упругий характер. Средняя кинетическая энергия частиц однозначно определяет температуру идеального газа.
Большинство реальных газов, которые находятся при не слишком высоких давлениях и не слишком низких температурах, можно считать с высокой точностью идеальными.
Универсальное уравнение состояния
Так называют уравнение, которое объединяет в рамках одного выражения все важные термодинамические параметры идеальной газовой системы. Запишем его:
P*V = n*R*T.
Здесь P и V – давление в паскалях и объем в метрах кубических, n и T – количество вещества в молях и температура системы в Кельвинах. Это равенство также называется уравнением или законом Клапейрона-Менделеева в честь французского физика и инженера и русского химика XIX века, которые вывели это уравнение из накопленного предыдущими поколениями ученых экспериментального опыта.
Универсальное уравнение состояния системы позволяет получить любой газовый закон. Например, закон Гей-Люссака следует из него непосредственно, если положить постоянным объем во время термодинамического процесса.
Мы выше расшифровали 4 из 5 обозначений, присутствующих в формуле. Пятым является коэффициент R. Он называется универсальной газовой постоянной. Единицей измерения в СИ для него является джоуль на моль-кельвин (Дж/(моль*К)). Что это за величина, рассмотрим подробнее дальше в статье.
Постоянная R в физике
Выше мы увидели, что это некоторый коэффициент пропорциональности между давлением, объемом, температурой и количеством вещества. Единицей измерения универсальной газовой постоянной в системе СИ является Дж/(моль*К). Ее значение с точностью до трех знаков после запятой равно 8,314. Это число означает, что один моль идеального газа, будучи нагретым на 1 кельвин, в процессе своего расширения совершит работу 8,314 джоуля.
Постоянную R можно также интерпретировать несколько иначе: если затратить на нагрев одного моль газа энергию в 8,314 джоуля, то его температура возрастет на 1 кельвин. Иными словами, R характеризует связь между энергией и температурой для фиксированного количества вещества.
Заметим, что величина R в физике не является базовой (фундаментальной) константой такой, как скорость света или постоянная Планка. Поэтому с помощью выбора соответствующей температурной шкалы и количества частиц в системе можно добиться того, что R будет равно 1.
Впервые постоянную R в физику ввел Д. И. Менделеев, заменив ею в универсальном уравнении состояния Клапейрона ряд других констант. Отметим, что хотя величина R введена для газов, в современной физике она используется также в уравнениях Дюлонга и Пти, Клаузиуса-Моссотти, Нернста и в некоторых других.
Постоянные kB и R
Люди, которые знакомы с физикой, могли заметить, что существует еще одна постоянная величина, которая во всех физических уравнениях выступает в качестве переводного коэффициента между энергией и температурой. Эта величина называется постоянной Больцмана (kB). Она равна 1,38*10-23 Дж/К. Очевидно, что должна существовать математическая связь между kB и R. Такая связь действительно существует, она имеет следующий вид:
R = kB*NA.
Здесь NA – это огромное число, которое называется числом Авогадро. Равно оно 6,02*1023. Если количество частиц системы равно NA, то говорят, что система содержит 1 моль вещества.
Таким образом, постоянная Больцмана и универсальная газовая постоянная, по сути, это один и тот же переводной коэффициент между температурой и энергией с той лишь разницей, что kB используется для микроскопических процессов, а R – для макроскопических.
Решение задачи
После знакомства с единицами измерения универсальной газовой постоянной предлагается получить их из универсального уравнения для идеального газа, которое было приведено в статье. Ниже на рисунке изображено это уравнение.
Выразим из него величину R, получаем:
R = P*V/(n*T).
Теперь подставим для каждой физической величины соответствующую единицу измерения и упростим полученное выражение:
[R] = [Па*м3/(моль*К)] = [Н/м2*м3/(моль*К)] = [Н*м/(моль*К)] = [Дж/(моль*К)].
Как видно, при получении единиц измерения для R мы упрощали только единицы измерения числителя. Сначала была использована формула для давления, а затем произведение единиц силы на единицы расстояния были преобразованы в единицы работы.
Источник
1ku.ru
| Азот газовая постоянная азота | 297 (Джоуль / (Килограмм · Кельвин)) |
| Аммиак газовая постоянная аммиака | 488 (Джоуль / (Килограмм · Кельвин)) |
| Аргон газовая постоянная аргона | 208 (Джоуль / (Килограмм · Кельвин)) |
| Ацетилен газовая постоянная ацетилена | 320 (Джоуль / (Килограмм · Кельвин)) |
| Бутан газовая постоянная бутана | 143 (Джоуль / (Килограмм · Кельвин)) |
| Водород газовая постоянная водорода | 4125 (Джоуль / (Килограмм · Кельвин)) |
| Водяной пар (100°C) газовая постоянная водяного пара | 461 (Джоуль / (Килограмм · Кельвин)) |
| Воздух газовая постоянная воздуха | 287 (Джоуль / (Килограмм · Кельвин)) |
| Гелий газовая постоянная гелия | 2078 (Джоуль / (Килограмм · Кельвин)) |
| Двуокись углерода газовая постоянная углекислого газа | 189 (Джоуль / (Килограмм · Кельвин)) |
| Кислород газовая постоянная кислорода | 260 (Джоуль / (Килограмм · Кельвин)) |
| Метан газовая постоянная метана | 519 (Джоуль / (Килограмм · Кельвин)) |
| Неон газовая постоянная неона | 412 (Джоуль / (Килограмм · Кельвин)) |
| Окись углерода газовая постоянная угарного газа | 297 (Джоуль / (Килограмм · Кельвин)) |
| Пропан газовая постоянная пропана | 189 (Джоуль / (Килограмм · Кельвин)) |
| Пропилен газовая постоянная пропилена | 198 (Джоуль / (Килограмм · Кельвин)) |
| Фреон газовая постоянная фреона | 68.7 (Джоуль / (Килограмм · Кельвин)) |
| Этан газовая постоянная этана | 277 (Джоуль / (Килограмм · Кельвин)) |
| Этилен газовая постоянная этилена | 297 (Джоуль / (Килограмм · Кельвин)) |
www.fxyz.ru
Универсальная газовая постоянная, формула и примеры
Уравнение состояния идеального газа
Для неизменной массы идеального газа отношение произведения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная:
Выясним, чему равна эта постоянная величина. Рассмотрим 1 моль идеального газа. При нормальных условиях газ имеет температуру =273 K и давление =101325 Па. При таких условиях 1 моль этого газа занимает объем .
Подставив эти значения в уравнение состояния, получим:
Универсальная газовая постоянная
Таким образом, для 1 моля идеального газа произведение давления на объем, отнесенное к абсолютной температуре есть величина постоянная для всех газов. Эта величина называется
Уравнение состояния идеального газа было получено французским физиком Б. Клапейроном в 1834 г. Это уравнение полностью определяет параметры состояния термодинамической системы при переходе из одного состояния в другое.
При переходе системы из состояния 1 в состояние 2 уравнение состояния записывают в виде:
Знание уравнения состояния очень важно при исследовании тепловых процессов. Это уравнение позволяет полностью или частично ответить на ряд вопросов:
- уравнение состояния позволяет определить одну из величин, характеризующих состояние, например температуру, если известны две другие величины.
- уравнение состояния позволяет определить, как протекают в системе различные процессы при определенных внешних условиях: например, как будет меняться давление газа, если увеличивать его объем при неизменной температуре, и т. д.
- зная уравнение состояния, можно определить, как меняется состояние системы, если она совершает работу или получает теплоту от окружающих тел.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Постоянная Больцмана

Больцман Людвиг (1844—1906) — великий австрийский физик, один из основоположников молекулярно-кинетической теории. В трудах Больцмана молекулярно-кинетическая теория впервые предстала как логически стройная, последовательная физическая теория. Больцман дал статистическое истолкование второго закона термодинамики. Им много сделано для развития и популяризации теории электромагнитного поля Максвелла. Борец по натуре, Больцман страстно отстаивал необходимость молекулярного истолкования тепловых явлений и принял на себя основную тяжесть борьбы с учеными, отрицавшими существование молекул.
В уравнение (4.5.3) входит отношение универсальной газовой постоянной R к постоянной Авогадро NA. Это отношение одинаково для всех веществ. Оно называется постоянной Больцмана, в честь Л. Больцмана, одного из основателей молекулярно-кинетической теории.
Постоянная Больцмана равна:
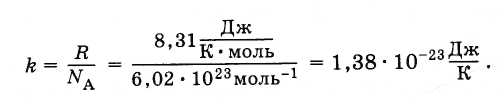 (4.5.4)
(4.5.4)
Уравнение (4.5.3) с учетом постоянной Больцмана записывается так:
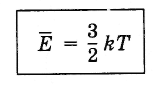 (4.5.5)
(4.5.5)
Физический смысл постоянной Больцмана
Исторически
температура была впервые введена как
термодинамическая величина, и для нее
была установлена единица измерения —
градус (см. § 3.2). После установления
связи температуры со средней кинетической
энергией молекул стало очевидным, что
температуру можно определять как среднюю
кинетическую энергию молекул и выражать
ее в джоулях или эргах, т. е. вместо
величины Т ввести
величину Т* так,
чтобы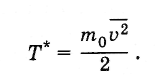
Определенная таким образом температура связана с температурой, выражаемой в градусах, следующим образом:

Поэтому постоянную Больцмана можно рассматривать как величину, связывающую температуру, выражаемую в энергетических единицах, с температурой, выраженной в градусах.
Зависимость давления газа от концентрации его молекул и температуры
Выразив Е из соотношения (4.5.5) и подставив в формулу (4.4.10), получим выражение, показывающее зависимость давления газа от концентрации молекул и температуры:
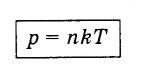 (4.5.6)
(4.5.6)
Из формулы (4.5.6) вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же.
Отсюда следует закон Авогадро: в равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Средняя кинетическая энергия поступательного движения молекул прямо пропорциональна абсолютной температуре. Коэффициент пропорциональности — постоянную Больцмана k = 10-23Дж/К — надо запомнить.
§ 4.6. Распределение максвелла
В большом числе случаев знание одних средних значений физических величин недостаточно. Например, знание среднего роста людей не позволяет планировать выпуск одежды различных размеров. Надо знать приблизительное число людей, рост которых лежит в определенном интервале. Точно так же важно знать числа молекул, имеющих скорости, отличные от среднего значения. Максвелл первым нашел, как эти числа можно определять.
Вероятность случайного события
В §4.1 мы уже упоминали, что для описания поведения большой совокупности молекул Дж. Максвелл ввел понятие вероятности.
Как неоднократно подчеркивалось, в принципе невозможно проследить за изменением скорости (или импульса) одной молекулы на протяжении большого интервала времени. Нельзя также точно определить скорости всех молекул газа в данный момент времени. Из макроскопических условий, в которых находится газ (определенный объем и температура), не вытекают с необходимостью определенные значения скоростей молекул. Скорость молекулы можно рассматривать как случайную величину, которая в данных макроскопических условиях может принимать различные значения, подобно тому как при бросании игральной кости может выпасть любое число очков от 1 до 6 (число граней кости равно шести). Предсказать, какое число очков выпадет при данном бросании кости, нельзя. Но вероятность того, что выпадет, скажем, пять очков, поддается определению.
Что же такое вероятность наступления случайного события? Пусть произведено очень большое число N испытаний (N — число бросаний кости). При этом в N‘ случаях имел место благоприятный исход испытаний (т. е. выпадение пятерки). Тогда вероятность данного события равна отношению числа случаев с благоприятным исходом к полному числу испытаний при условии, что это число сколько угодно велико:
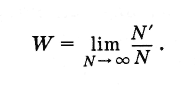 (4.6.1)
(4.6.1)
Для
симметричной кости вероятность любого
выбранного числа очков от 1 до 6 равна 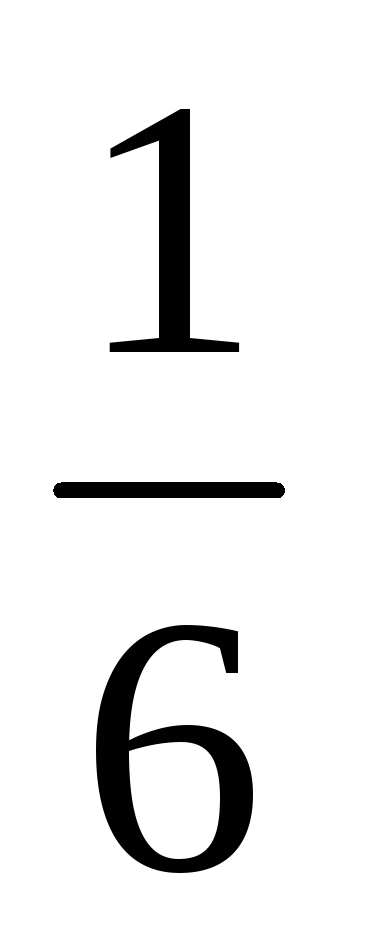 .
.
Мы
видим, что на фоне множества случайных
событий обнаруживается определенная
количественная закономерность, появляется
число. Это число — вероятность —
позволяет вычислять средние значения.
Так, если произвести 300 бросаний кости,
то среднее число выпаданий пятерки, как
это следует из формулы (4.6.1), будет равно:
300 ·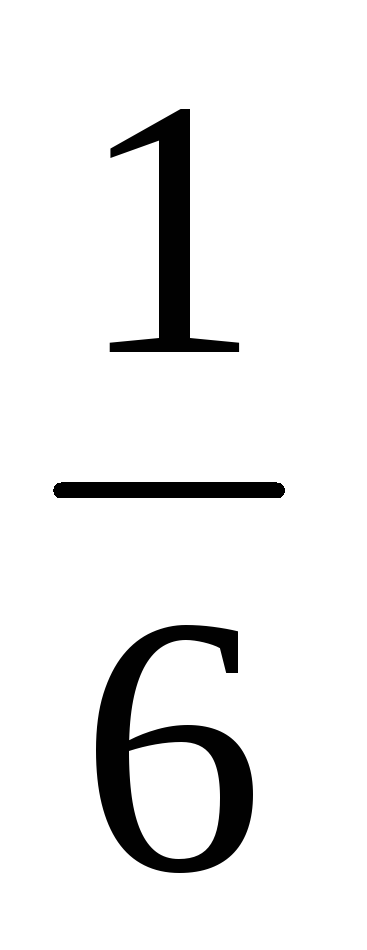 = 50, причем совершенно безразлично,
бросать 300 раз одну и ту же кость или
одновременно 300 одинаковых костей.
= 50, причем совершенно безразлично,
бросать 300 раз одну и ту же кость или
одновременно 300 одинаковых костей.
Несомненно, что поведение молекул газа в сосуде гораздо сложнее движения брошенной игральной кости. Но и здесь можно надеяться обнаружить определенные количественные закономерности, позволяющие вычислять статистические средние, если только ставить задачу так же, как в теории игр, а не как в классической механике. Нужно отказаться от неразрешимой задачи определения точного значения скорости молекулы в данный момент и попытаться найти вероятность того, что скорость имеет определенное значение.
studfile.net
по какой формуле определяется R? Физика
Если R-это сопротивление, то U/I.
R=U/I, напряжение делим на силу тока.
Основной формулой, используемой для решения задач, является: I = U / R – то есть сила тока равняется отношению напряжения к сопротивлению. следовательно R равно U / I
из закона Ома I=U/R, следовательно R=U/I( напряжение делить на силу тока)
А че все одно и то же пишут? )))))))))) А если не из закона Ома?
3,14здец они валенки. R = U/I где R — сопротивление, Ом; U — разность электрических потенциалов (напряжение) на концах проводника, В; I — сила тока, протекающего между концами проводника под действием разности потенциалов, А. ИЛИ R=(P(ро) *L)/S где ρ — удельное сопротивление вещества проводника, l — длина проводника, а S — площадь сечения
Основная формула R=rL/S где r удельное сопротивление материала L длина проводника S площадь поперечного сечения. также сопротивление можно найти по формуле R=U/I
touch.otvet.mail.ru


