Число оборотов в минуту – Revolutions per minute
“rpm” перенаправляется сюда. Для использования в других целях, см rpm (значения) .| Число оборотов в минуту | |
|---|---|
| Единица | Скорость вращения |
| Символ | об / мин или об / мин |
| Конверсии | |
| 1 об / мин в … | … равно … |
| SI угловая скорость | 2π / 60 рад / с ≈ 0,1047198 рад / с |
| Частота SI | 1 / 60 Гц ≈ 0,01666667 Гц |
| Производная частота вращения SI | 1 / 60 с −1 , 1 / 60 / с |
| Производная скорость вращения SI | 1 мин −1 , 1 / мин |
Число оборотов в минуту (сокращенно оборотов в минуту
 Это единица скорости вращения или частоты от вращения вокруг неподвижной оси .
Это единица скорости вращения или частоты от вращения вокруг неподвижной оси .Международная система единиц
Согласно Международной системе единиц (СИ), об / мин не является единицей. Это потому, что слово « революция» – это скорее семантическая аннотация , чем единица. Вместо этого примечание делается в виде нижнего индекса знака формулы, если это необходимо. Из измеренной физической величины , формула знак должен быть е для (вращательной) частоты и со или Q , для угловой скорости . Соответствующая базовая производная единица СИ – с -1 или Гц . При измерении угловой скорости используется единица радиан в секунду .
|
Хотя они имеют одинаковые размеры (с -1 ), герц (Гц) и радиан в секунду (рад / с) – это две разные единицы, представляющие две разные, но пропорциональные величины ISQ : частота и угловая частота (угловая скорость, величина угловой скорости).
- ω знак равно 2 π ж , ж знак равно ω 2 π . {\ displaystyle \ omega = 2 \ pi f \ ,, \ qquad f = {\ frac {\ omega} {2 \ pi}} \ ,.}
Таким образом, диск, вращающийся со скоростью 60 об / мин, считается вращающимся со скоростью 2 π рад / с или 1 Гц, где первый измеряет угловую скорость, а второй отражает количество оборотов в секунду.
Если не-СИ единица об / мин считается единицей частоты, то 1 об / мин = 1 / 60 Гц . Если вместо этого считается, что это единица измерения угловой скорости, а слово «вращение» означает 2 π радиан , то 1 об / мин = 2 π / 60 рад / с .
Примеры
- На многих типах носителей для записи дисков скорость вращения носителя под считывающей головкой является стандартной и выражается в об / мин. Фонограф (граммофонные) записи , например, как правило , вращаются непрерывно в 16 2 / 3 , 33 1 ⁄ 3 , 45 или 78 об / мин (0,28, 0,55, 0,75 или 1,3 Гц соответственно).

- Современные стоматологические буры с воздушной турбиной могут вращаться со скоростью до 800 000 об / мин (13,3 кГц).
- Вторая рука обычных аналоговых вращается на 1 тактовых оборотов в минуту.
- Проигрыватели аудио CD читают свои диски с точной постоянной скоростью (4,3218 Мбит / с необработанных физических данных для 1,4112 Мбит / с (176,4 кБ / с) пригодных для использования аудиоданных) и, следовательно, должны изменять скорость вращения диска от 8 Гц (480 об / мин) при считывании по самому внутреннему краю до 3,5 Гц (210 об / мин) по внешнему краю.
- DVD- плееры также обычно читают диски с постоянной линейной скоростью. Скорость вращения диска варьируется от 25,5 Гц (1530 об / мин) при чтении по внутреннему краю до 10,5 Гц (630 об / мин) по внешнему краю.
- А стиральной машины барабанного «сек может вращаться со скоростью от 500 до 2000 оборотов в минуту (8-33 Гц) во время отжиме.
- Турбина для выработки электроэнергии ( с двухполюсным генератором переменного тока ) вращается со скоростью 3000 об / мин (50 Гц) или 3600 об / мин (60 Гц), в зависимости от страны – см.
 Вилки и розетки переменного тока .
Вилки и розетки переменного тока . - Современные автомобильные двигатели обычно работают со скоростью около 2 000–3 000 об / мин (33–50 Гц) в крейсерском режиме с минимальной скоростью (холостой ход) около 750–900 об / мин (12,5–15 Гц) и верхним пределом от 4500 до 10 000 об / мин ( 75–166 Гц) для дорожного автомобиля или почти (иногда выше) 20 000 об / мин для гоночных двигателей, например, в автомобилях Формулы 1 (в течение сезона 2006 года с двигателем 2.4 LN / A V8 ; в настоящее время ограничено 15 000 об / мин, с 1,6 л V6 турбо – гибридные конфигурации двигателя). Выхлопа из V8 автомобилей F1 имеют гораздо более высокую высоту , чем I4 двигатель , потому что каждый из цилиндров в течение четырехтактный двигатель срабатывает один раз на каждые два оборота коленчатого вала . Таким образом, восьмицилиндровый двигатель, вращающийся 300 раз в секунду, будет иметь частоту выхлопа 1200 Гц.
- Поршневой авиационный двигатель обычно вращается со скоростью от 2000 до 3000 об / мин (30–50 Гц).

- Компьютерные жесткие диски обычно вращаются со скоростью 5400 или 7200 об / мин (90 или 120 Гц), что является наиболее распространенной скоростью для дисков ATA или SATA в потребительских моделях. Высокопроизводительные диски (используемые в файловых серверах и игровых ПК для энтузиастов) вращаются со скоростью 10 000 или 15 000 об / мин (160 или 250 Гц), обычно с интерфейсами SATA, SCSI или Fibre Channel более высокого уровня и меньшими пластинами, чтобы обеспечить эти более высокие скорости, сокращение емкостью памяти и максимальной скоростью вращения по внешнему краю окупаются гораздо меньшим временем доступа и средней скоростью передачи благодаря высокой скорости отжима. До недавнего времени можно было найти недорогие и энергоэффективные накопители для ноутбуков со скоростью вращения шпинделя 4200 или даже 3600 об / мин (70 и 60 Гц), но они потеряли популярность из-за их более низкой производительности, повышения энергоэффективности в более быстрых моделях.

- Приводы гибких дисков обычно работали с постоянной скоростью 300 или иногда 360 об / мин (относительно медленные 5 или 6 Гц) с постоянной плотностью данных на оборот, что было просто и недорого реализовать, хотя и неэффективно. Некоторые конструкции, такие как те, которые использовались на старых компьютерах Apple (Lisa, ранний Macintosh, позже II), были более сложными и использовали переменные скорости вращения и плотность хранения на дорожку (при постоянной скорости чтения / записи) для хранения большего количества данных на диске; например, между 394 об / мин (с 12 секторами на дорожку) и 590 об / мин (8 секторов) с диском Mac с двойной плотностью 800 КБ при постоянной 39,4 КБ / с (макс.

- Циппе типа центрифуги для обогащения урана вращается со скоростью 90000 оборотов в минуту (1500 Гц) или быстрее.
- Газотурбинные двигатели вращаются со скоростью десятки тысяч оборотов в минуту. Турбины авиамоделей JetCat способны развивать скорость более 100 000 об / мин (1700 Гц), а самая быстрая – 165 000 об / мин (2750 Гц).
- Система накопления энергии с маховиком работает в диапазоне 60 000–200 000 об / мин (1–3 кГц) с использованием пассивно магнитного маховика, левитирующего в вакууме. Материал маховика выбирается не из самого плотного, но из такого, который измельчается наиболее безопасно, при поверхностных скоростях, примерно в 7 раз превышающих скорость звука.
- Типичный компьютерный вентилятор диаметром 80 мм и 30 куб. Футов в минуту будет вращаться со скоростью 2600–3000 об / мин (43–50 Гц) при питании от источника постоянного тока 12 В.

- Миллисекундный пульсар может иметь вблизи 50000 оборотов в минуту (833 Гц).
- Турбокомпрессора может достигать 290000 оборотов в минуту (4,8 кГц), в то время как 80,000-200,000 оборотов в минуту (1-3 кГц) является общим.
- Нагнетателя может вращаться со скоростью от или на уровне 50,000-65,000 оборотов в минуту (833-1083 Гц)
- Молекулярная микробиология – молекулярные двигатели. Было измерено, что скорость вращения бактериальных жгутиков составляет 10 200 об / мин (170 Гц) для Salmonella typhimurium
Смотрите также
Рекомендации
<img src=”https://en.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=”” title=””>Основные определения и формулы
Скорость резания V (м/мин) – это окружная скорость перемещения режущих кромок фрезы. Эта величина определяет эффективность обработки и лежит в рекомендованных для каждого инструментального материала пределах. За один оборот фрезы точка режущей кромки, находящаяся на окружности фрезы диаметра D (мм), сможет пройти путь, равный длине окружности, то есть πD. Для того чтобы определить длину пути, пройденного точкой за одну минуту, нужно умножить длину пути за один оборот на частоту вращения фрезы, то есть πDN (мм/мин). Таким образом, формула для определения скорости резания будет следующей:
V = πDN/1000 (мм/мин).
Частота вращения шпинделя N (об/мин) равняется числу оборотов фрезы в минуту. Вычисляется в соответствии с рекомендованной для данного типа обработки скоростью резания:
N = 1000V/nD (об/мин).
При фрезеровании различают минутную подачу, подачу на зуб и подачу наоборот фрезы.
Подача на зуб Fz (мм/зуб) – величина перемещения фрезы или рабочего стола с заготовкой за время поворота фрезы на один зуб.
Подача на оборот Fo (мм/об) – величина перемещения фрезы или рабочего стола с заготовкой за один оборот фрезы. Подача на оборот равняется произведению подачи на зуб на число зубьев фрезы Z:
Fo = FzZ (мм/об).
Минутной подачей Fm (мм/мин) называется величина относительного перемещения фрезы или рабочего стола с заготовкой за одну минуту. Минутная подача равняется произведению подачи на оборот на частоту вращения фрезы:
Fm = FoN = FzZN (мм/мин).
Глубиной фрезерования h (мм) называется расстояние между обработанной и необработанной поверхностями, измеряемое вдоль оси фрезы.
Шириной фрезерования b (мм) называется величина срезаемого припуска, измеренная в радиальном направлении, или ширина контакта заготовки и инструмента.
Производительность снятия материала Q (см3) – это объем удаляемого материала в единицу времени, определяемый глубиной, шириной обработки и величиной подачи.
Q = (h × b × Fm)/1000.
Движение по окружности, угловая скорость, частота, период, центростремительное ускорение. Формулы, определения, пояснения
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Формула угловой скорости в физике
Содержание:
Определение и формула угловой скорости
Определение
Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота
$(\varphi)$ . Часто используют вектор элементарного поворота
$\bar{d\varphi}$ , который равен по величине элементарному углу поворота тела
$(d \varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.
Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.
Определение
Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой $\omega$ . Математически определение угловой скорости записывают так:
$$\bar{\omega}=\frac{d \bar{\varphi}}{d t}=\dot{\bar{\varphi}}(1)$$Угловая скорость – векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ($\bar{\omega}$ при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол,
то такое вращение называют равномерным.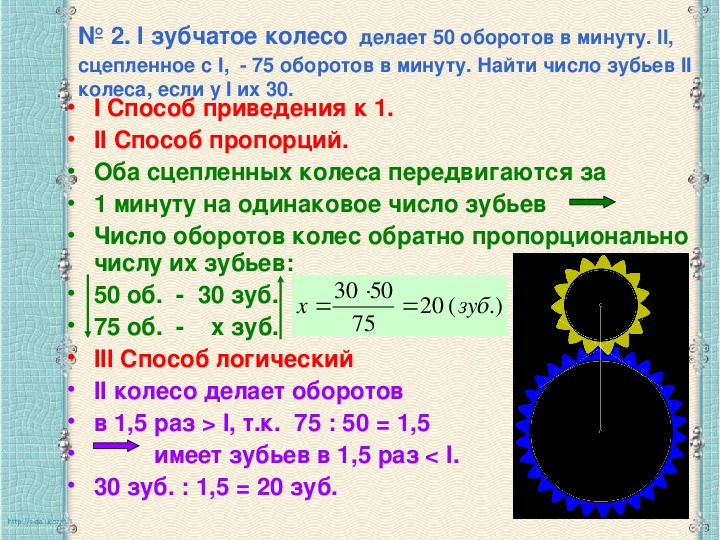 При этом модуль угловой скорости находят как:
При этом модуль угловой скорости находят как:
где $(\varphi)$ – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ($\Delta \varphi=2 \pi$). Угловая скорость связана с периодом обращения как:
$$\omega=\frac{2 \pi}{T}(3)$$С числом оборотов в единицу времени ($\nu) угловая скорость связана формулой:
$$\omega=2 \pi \nu(4)$$Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости.
Формула, связывающая линейную и угловую скорости
Линейная скорость $\bar{v}$ точки А (рис.1), которая расположена на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:
$$\bar{v}=[\bar{\omega} \bar{R}](5)$$где $\bar{R}$ – перпендикулярная к оси вращения компонента радиус-вектора точки
$A (\bar{r})$ (рис.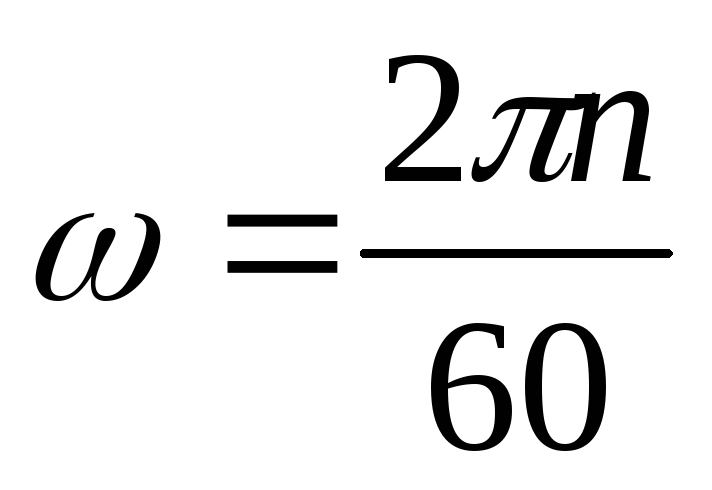 {3} \approx 20(\mathrm{rad})$$
{3} \approx 20(\mathrm{rad})$$
Ответ. $\varphi = 20$ рад.
Читать дальше: Формула удельного веса.
Урок 5. поступательное движение. вращательное движение твердого тела – Физика – 10 класс
Физика, 10 класс
Урок 05. Поступательное движение. Вращательное движение твёрдого тела
Перечень вопросов, рассматриваемых на уроке:
- Поступательное и вращательное движение абсолютно твердого тела.
- Характеристики вращательного движения абсолютно твердого тела.
Глоссарий по теме
1. Абсолютно твердое тело – это тело, расстояние между любыми двумя точками которого остается постоянным при его движении.
2. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе. Одинаковыми остаются при поступательном движении перемещение, траектория, путь, скорость, ускорение.
3. Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой перпендикулярной плоскостям этих окружностей. Сама эта прямая есть ось вращения.
4. Угол поворота – угол, на который поворачивается радиус-вектор, соединяющий центр окружности с точкой вращающегося тела.
5. Угловая скорость – отношение угла поворота φ к промежутку времени, в течение которого совершен этот поворот при равномерном движении.
6. Линейная скорость – отношение длины дуги окружности пройденной точкой тела к промежутку времени, в течение которого этот поворот совершен.
7. Период – промежуток времени, за который тело делает один полный оборот.
8. Частота обращения тела – число оборотов за единицу времени
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.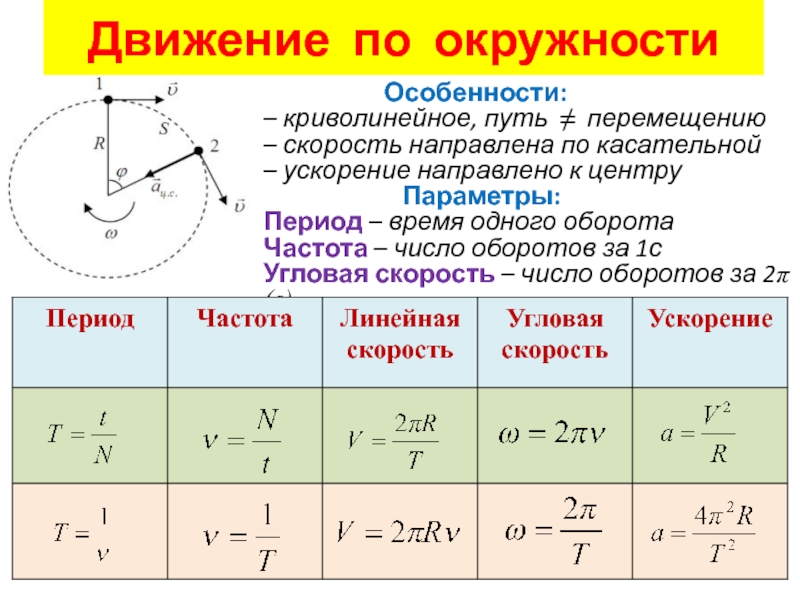 : Просвещение, 2016. – С. 57-61
: Просвещение, 2016. – С. 57-61
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22
Открытые электронные ресурсы:
http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm
Теоретический материал для самостоятельного изучения
1. Вы знаете, что в физике для упрощения исследования реальных ситуаций часто используются модели. Одной из механических моделей, используемых при описании движения и взаимодействия тел, является абсолютно твёрдое тело- тело, расстояние между любыми двумя точками которого остаётся постоянным при его движении.
2. Поступательным называется такое движение абсолютно твёрдого тела, при котором любой отрезок, соединяющий любые две точки тела, остаётся параллельным самому себе. Примером поступательного движения может служить свободное падение тел, движение лифта, поезда на прямолинейном участке дороги. При поступательном движении все точки тела описывают одинаковые траектории, совершают одинаковые перемещения, проходят одинаковые пути, в каждый момент времени имеют равные скорости и ускорения.
Для описания поступательного движения абсолютно твёрдого тела достаточно написать уравнение движения одной из его точек.
3. Вращательным движением абсолютно твёрдого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения. При этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения.
Вращательное движение позволяет осуществить непрерывный процесс работы с использованием больших скоростей. Вращающиеся механизмы более компактны и более экономичны, так как потери энергии на преодоление сил трения качения меньше, чем на преодоление сил трения скольжения. Поэтому в современной технике вращательное движение рабочих частей машин всё более вытесняет возвратно-поступательное. Например, вместо ножовочной пилы в технике используют вращающуюся дисковую пилу, поршневые насосы в большинстве случаев вытесняются центробежными.
4. Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела ∆φ к промежутку времени ∆t, за которое этот поворот произошёл.
Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению запишем формулу угловой скорости;
При равномерном вращательном движении угловая скорость у всех точек вращающегося тела одинаковая. Поэтому угловая скорость, так же как и угол поворота, является характеристикой движения всего вращающегося тела, а не только отдельных его частей.
Примером вращательного движения, близкого к равномерному, может служить вращение Земли вокруг своей оси.
Угловая скорость в СИ выражается в радианах в секунду (рад/с).
Один радиан – это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.
Угловая скорость положительна, если угол между радиусом вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательным, когда он уменьшается
5.
Частоту обозначают греческой буквой «ню». Единица измерения частоты является секунда в минус первой степени
Время, за которое тело совершает один полный оборот, называют периодом обращения и обозначают буквой Т.
7. Связь между линейной и угловой скоростями:
8. Связь между ускорением и угловой скоростью:
Итак, мы рассмотрели два простейших движения абсолютно твердого тела – поступательное и вращательное. В жизни мы чаще встречаем сложное движение абсолютно твердого тела, однако, в этом случае любое сложное движение можно представить как сумму двух независимых движений: поступательного и вращательного.
Примеры и разбор типового тренировочного задания
- Ротор мощной паровой турбины делает 100 оборотов за 2 с. Определите угловую скорость.
Дано:
N=100 об.
t = 2 c
Найти: ω.
Решение:
2. Два шкива, соединенные друг с другом ремнем, вращаются вокруг неподвижных осей (см.рис). Больший шкив радиусом 20см делает 50 оборотов за 10 секунд, а частота вращения меньшего шкива 2400 оборотов в минуту. Чему равен радиус меньшего шкива? Шкивы вращаются без проскальзывания.
Дано:
Найти –
Решение:
Из условия задачи ученик видит что, шкивы соединены ремнем, следовательно, линейные скорости их равны:
но частота вращения разная.
Сокращает на 2π обе части.
Отсюда имеем:
и так, как в условии известно , то можем записать:
Отсюда находим радиус второго шкива:
Вторая неизвестная величина
Запишем формулу периода обращения для большего шкива:
так как по условию задачи нам известно число оборотов за 10 секунд.
Подставим в формулу (1) и получим конечную формулу:
Центрифуги
Центрифугирование используется почти во всех ежедневных задачах в области химии, биологии и фармацевтики. Большой выбор центрифуг производства Hettich и IKA, в том числе с московского склада, доступен в компании ГалаХим.
Большой выбор центрифуг производства Hettich и IKA, в том числе с московского склада, доступен в компании ГалаХим.Для решения различных задач предназначены разные роторы. В лабораторных центрифугах, как правило, используются: угловые и горизонтальные роторы. Оба типа роторов имеют свои преимущества.
Угловой ротор
Прочные угловые роторы используются преимущественно при центрифугировании на высоких скоростях, которые могут быть достигнуты благодаря малому сопротивлению воздуха. Наклонное положение пробирок обеспечивает сокращение пути, который должны пройти осаждаемые частицы, что дополнительно сокращает время разделения.Горизонтальный ротор
Во время центрифугирования сосуды совершают движение из исходного в горизонтальное положение. При этом осадок оседает в центре дна сосуда, границы фаз располагаются горизонтально. Горизонтальные роторы применяются в тех случаях, когда требуется получить высокую производительность в диапазоне средних скоростей. Отличительной чертой данного типа роторов является наличие большого разнообразия принадлежностей к ним.
Относительное центробежное ускорение
Производительность центрифуги часто описывается скоростью вращения ротора. Но силу, реально действующую на центрифугируемый образец обозначают как относительное центробежное ускорение (RCF). Для расчета значения RCF служит следующая формула :RCF = (n/1000)² x r x 11,18
n = количество оборотов в минуту (мин-1)
r = радиус, см
Из формулы следует, что удвоение радиуса ведет к увеличению RCF в два раза, а удвоение скорости вращения – к увеличению RCF в четыре раза. Поэтому производительность центрифуг необходимо сравнивать только по значению RCF.
Иногда в характеристиках центрифуг встречается числовое значение без единиц измерения. Оно обозначает кратность, с которой центробежное ускорение превышает ускорение свободного падения g.
Скорость резания от диаметра Таблица / Surface speed to RPM conversion
Перевод оборотов в минуту в линейную скорость Справочная таблица Скорости резания в зависимости от диаметра режущего инструмента
Перевод оборотов в минуту в линейную скорость Справочная таблица Скорости резания в зависимости от диаметра режущего инструмента _ Расчет частоты вращения vc Скорость резания (Vc, м/ ин) Диаметр 20 30 40 50 60 70 80 90 100 120 140 150 180 200 250 300 0. 2 31,831 47,746 63,662 79,577 95,493 111,408 127,324 143,239 159,155 190,986 222,817 23,872 286,479 318,310 397,887 477,465 0.3 21,221 31,831 42,441 53,052 63,662 74,272 84,883 95,493 106,103 127,324 148,545 159,155 190,986 212,207 265,258 318,310 0.4 15,915 23,873 31,831 39,789 47,746 55,704 63,662 71,620 79,577 95,493 111,408 119,366 143,239 159,155 198,944 238,732 0.5 12,732 19,099 25,465 31,831 38,197 44,563 50,930 57,296 63,662 76,394 89,127 95,493 114,592 127,324 159,155 190,986 0.6 10,610 15,915 21,221 26,526 31,831 37,136 42,441 47,746 53,052 63,662 74,272 79,577 95,493 106,103 132,629 159,155 0.7 9,095 13,642 18,189 22,736 27,284 31,831 36,378 40,926 45,473 54,567 63,662 68,209 81,851 90,946 113,682 136,419 0.8 7,958 11,937 15,915 19,894 23,873 27,852 31,831 35,810 39,789 47,746 55,704 59,683 71,620 79,577 99,472 119,366 0.9 7,074 10,610 14,147 17,684 21,221 24,757 28,294 31,831 35,368 42,441 49,515 53,052 63,662 70,736 88,419 106,103 6,366 9,549 12,732 15,915 19,009 22,282 25,465 28,648 31,831 38,197 44,563 47,746 57,296 63,662 79,577 95,793 1.
2 31,831 47,746 63,662 79,577 95,493 111,408 127,324 143,239 159,155 190,986 222,817 23,872 286,479 318,310 397,887 477,465 0.3 21,221 31,831 42,441 53,052 63,662 74,272 84,883 95,493 106,103 127,324 148,545 159,155 190,986 212,207 265,258 318,310 0.4 15,915 23,873 31,831 39,789 47,746 55,704 63,662 71,620 79,577 95,493 111,408 119,366 143,239 159,155 198,944 238,732 0.5 12,732 19,099 25,465 31,831 38,197 44,563 50,930 57,296 63,662 76,394 89,127 95,493 114,592 127,324 159,155 190,986 0.6 10,610 15,915 21,221 26,526 31,831 37,136 42,441 47,746 53,052 63,662 74,272 79,577 95,493 106,103 132,629 159,155 0.7 9,095 13,642 18,189 22,736 27,284 31,831 36,378 40,926 45,473 54,567 63,662 68,209 81,851 90,946 113,682 136,419 0.8 7,958 11,937 15,915 19,894 23,873 27,852 31,831 35,810 39,789 47,746 55,704 59,683 71,620 79,577 99,472 119,366 0.9 7,074 10,610 14,147 17,684 21,221 24,757 28,294 31,831 35,368 42,441 49,515 53,052 63,662 70,736 88,419 106,103 6,366 9,549 12,732 15,915 19,009 22,282 25,465 28,648 31,831 38,197 44,563 47,746 57,296 63,662 79,577 95,793 1. 5 4,244 6,366 8,488 10,610 12,732 14,854 16,977 19,099 21,221 25,465 29,709 31,831 38,197 42,441 53,052 63,662 2 3,183 4,775 6,366 7,958 9,549 11,141 12,732 14,324 15,915 19,099 22,282 23,873 28,648 31,831 39,789 47,746 2.5 2,546 3,820 5,093 6,366 7,639 8,913 10,186 11,459 12,732 15,279 17,825 19,099 22,918 25,465 31,831 38,197 3 2,122 3,183 4,244 5,305 6,366 7,427 8,488 9,549 10,610 12,732 14,854 15,915 19,099 21,221 26,526 31,831 3.5 1,819 2,728 3,638 4,547 5,457 6,366 7,276 8,185 9,095 10,913 12,732 13,642 16,370 18,189 22,736 27,284 4 1,592 2,387 3,183 3,979 4,775 5,570 6,366 7,162 7,958 9,549 11,141 11,937 14,324 15,915 19,894 23,873 4.5 1,415 2,122 2,829 3,537 4,244 4,951 5,659 6,366 7,074 8,488 9,903 10,610 12,732 14,147 17,684 21,221 5 1,273 1,910 2,546 3,183 3,820 4,456 5,093 5,730 6,366 7,639 8,913 9,549 11,459 12,732 15,915 19,099 5.5 1,157 1,736 2,315 2,894 3,472 4,051 4,630 5,209 5,787 6,945 8,102 8,681 10,417 11,575 14,469 17,362 6 1,061 1,592 2,122 2,653 3,183 3,714 4,244 4,775 5,305 6,366 7,427 7,958 9,549 10,610 13,263 15,915 6.
5 4,244 6,366 8,488 10,610 12,732 14,854 16,977 19,099 21,221 25,465 29,709 31,831 38,197 42,441 53,052 63,662 2 3,183 4,775 6,366 7,958 9,549 11,141 12,732 14,324 15,915 19,099 22,282 23,873 28,648 31,831 39,789 47,746 2.5 2,546 3,820 5,093 6,366 7,639 8,913 10,186 11,459 12,732 15,279 17,825 19,099 22,918 25,465 31,831 38,197 3 2,122 3,183 4,244 5,305 6,366 7,427 8,488 9,549 10,610 12,732 14,854 15,915 19,099 21,221 26,526 31,831 3.5 1,819 2,728 3,638 4,547 5,457 6,366 7,276 8,185 9,095 10,913 12,732 13,642 16,370 18,189 22,736 27,284 4 1,592 2,387 3,183 3,979 4,775 5,570 6,366 7,162 7,958 9,549 11,141 11,937 14,324 15,915 19,894 23,873 4.5 1,415 2,122 2,829 3,537 4,244 4,951 5,659 6,366 7,074 8,488 9,903 10,610 12,732 14,147 17,684 21,221 5 1,273 1,910 2,546 3,183 3,820 4,456 5,093 5,730 6,366 7,639 8,913 9,549 11,459 12,732 15,915 19,099 5.5 1,157 1,736 2,315 2,894 3,472 4,051 4,630 5,209 5,787 6,945 8,102 8,681 10,417 11,575 14,469 17,362 6 1,061 1,592 2,122 2,653 3,183 3,714 4,244 4,775 5,305 6,366 7,427 7,958 9,549 10,610 13,263 15,915 6. 5 979 1,469 1,959 2,449 2,938 3,428 3,918 4,407 4,897 5,876 6,856 7,346 8,815 9,794 12,243 14,691 7 909 1,364 1,819 2,274 2,728 3,183 3,638 4,093 4,547 5,457 6,366 6,821 8,185 9,095 11,368 13,642 7.5 849 1,273 1,698 2,122 2,546 2,971 3,395 3,820 4,244 5,093 5,942 6,366 7,639 8,488 10,610 12,732 8 796 1,194 1,592 1,989 2,387 2,785 3,183 3,581 3,979 4,775 5,570 5,968 7,162 7,958 9,947 11,937 8.5 749 1,123 1,498 1,872 2,247 2,621 2,996 3,370 3,745 4,494 5,243 5,617 6,741 7,490 9,362 11,234 9 707 1,061 1,415 1,768 2,122 2,476 2,829 3,183 3,537 4,244 4,951 5,305 6,366 7,074 8,842 10,610 9.5 670 1,005 1,340 1,675 2,010 2,345 2,681 3,016 3,351 4,021 4,691 5,026 6,031 6,701 9,377 10,052 10 637 955 1,273 1,592 1,910 2,228 2,546 2,865 3,183 3,820 4,456 4,775 5,730 6,366 7,958 9,549 11 579 868 1,157 1,447 1,736 2,026 2,315 2,604 2,894 3,472 4,051 4,341 5,209 5,787 7,234 8,681 12 531 796 1,061 1,326 1,592 1,857 2,122 2,387 2,653 3,183 3,714 3,979 4,775 5,305 6,631 7,958 13 490 735 979 1,224 1,469 1,714 1,959 2,204 2,449 2,938 3,428 3,673 4,407 4,897 6,121 7,346 14 455 682 909 1,137 1,364 1,592 1,819 2,046 2,274 2,728 3,183 3,410 4,093 4,547 5,684 6,821 15 424 637 849 1,061 1,273 1,485 1,698 1,910 2,122 2,546 2,971 3,183 3,820 4,244 5,305 6,366 16 398 597 796 995 1,194 1,393 1,592 1,790 1,989 2,387 2,785 2,984 3,581 3,979 4,974 5,968 17 374 562 749 969 1,123 1,311 1,498 1,685 1,872 2,247 2,621 2,809 3,370 3,745 4,681 5,617 18 354 531 707 884 1,061 1,238 1,415 1,592 1,768 2,122 2,476 2,653 3,183 3,537 4,421 5,305 19 335 503 670 838 1,005 1,173 1,340 1,508 1,675 2,010 2,345 2,513 3,016 3,351 4,188 5,026 20 318 477 637 796 955 1,114 1,273 1,432 1,592 1,910 2,228 2,387 2,865 3,183 3,979 4,775 21 303 455 606 758 909 1,061 1,213 1,364 1,516 1,819 2,122 2,274 2,728 3,032 9,789 4,547 22 289 434 579 723 868 1,013 1,157 1,302 1,447 1,736 2,026 2,170 2,604 2,894 3,617 4,341 23 277 415 554 692 830 969 1,107 1,246 1,384 1,661 1,938 2,076 2,491 2,768 3,460 4,152 24 265 398 531 663 796 928 1,061 1,194 1,326 1,592 1,857 1,989 2,387 2,653 3,316 3,979 25 255 382 509 637 764 891 1,019 1,146 1,273 1,528 1,783 1,910 2,292 2,546 3,183 3,820 гНННЬ 28 Влияние длины рабочей части (вылета фрезы) Концевые фрезы Влияние рабочей части на деформацию изгиба Относительная длина рабочей части фрезы Длину рабочей части фрезы принято измерять в количестве её диаметров I Id При мер) 3D, 15D, 22D Деформация изгиба определяется силой упругости.
5 979 1,469 1,959 2,449 2,938 3,428 3,918 4,407 4,897 5,876 6,856 7,346 8,815 9,794 12,243 14,691 7 909 1,364 1,819 2,274 2,728 3,183 3,638 4,093 4,547 5,457 6,366 6,821 8,185 9,095 11,368 13,642 7.5 849 1,273 1,698 2,122 2,546 2,971 3,395 3,820 4,244 5,093 5,942 6,366 7,639 8,488 10,610 12,732 8 796 1,194 1,592 1,989 2,387 2,785 3,183 3,581 3,979 4,775 5,570 5,968 7,162 7,958 9,947 11,937 8.5 749 1,123 1,498 1,872 2,247 2,621 2,996 3,370 3,745 4,494 5,243 5,617 6,741 7,490 9,362 11,234 9 707 1,061 1,415 1,768 2,122 2,476 2,829 3,183 3,537 4,244 4,951 5,305 6,366 7,074 8,842 10,610 9.5 670 1,005 1,340 1,675 2,010 2,345 2,681 3,016 3,351 4,021 4,691 5,026 6,031 6,701 9,377 10,052 10 637 955 1,273 1,592 1,910 2,228 2,546 2,865 3,183 3,820 4,456 4,775 5,730 6,366 7,958 9,549 11 579 868 1,157 1,447 1,736 2,026 2,315 2,604 2,894 3,472 4,051 4,341 5,209 5,787 7,234 8,681 12 531 796 1,061 1,326 1,592 1,857 2,122 2,387 2,653 3,183 3,714 3,979 4,775 5,305 6,631 7,958 13 490 735 979 1,224 1,469 1,714 1,959 2,204 2,449 2,938 3,428 3,673 4,407 4,897 6,121 7,346 14 455 682 909 1,137 1,364 1,592 1,819 2,046 2,274 2,728 3,183 3,410 4,093 4,547 5,684 6,821 15 424 637 849 1,061 1,273 1,485 1,698 1,910 2,122 2,546 2,971 3,183 3,820 4,244 5,305 6,366 16 398 597 796 995 1,194 1,393 1,592 1,790 1,989 2,387 2,785 2,984 3,581 3,979 4,974 5,968 17 374 562 749 969 1,123 1,311 1,498 1,685 1,872 2,247 2,621 2,809 3,370 3,745 4,681 5,617 18 354 531 707 884 1,061 1,238 1,415 1,592 1,768 2,122 2,476 2,653 3,183 3,537 4,421 5,305 19 335 503 670 838 1,005 1,173 1,340 1,508 1,675 2,010 2,345 2,513 3,016 3,351 4,188 5,026 20 318 477 637 796 955 1,114 1,273 1,432 1,592 1,910 2,228 2,387 2,865 3,183 3,979 4,775 21 303 455 606 758 909 1,061 1,213 1,364 1,516 1,819 2,122 2,274 2,728 3,032 9,789 4,547 22 289 434 579 723 868 1,013 1,157 1,302 1,447 1,736 2,026 2,170 2,604 2,894 3,617 4,341 23 277 415 554 692 830 969 1,107 1,246 1,384 1,661 1,938 2,076 2,491 2,768 3,460 4,152 24 265 398 531 663 796 928 1,061 1,194 1,326 1,592 1,857 1,989 2,387 2,653 3,316 3,979 25 255 382 509 637 764 891 1,019 1,146 1,273 1,528 1,783 1,910 2,292 2,546 3,183 3,820 гНННЬ 28 Влияние длины рабочей части (вылета фрезы) Концевые фрезы Влияние рабочей части на деформацию изгиба Относительная длина рабочей части фрезы Длину рабочей части фрезы принято измерять в количестве её диаметров I Id При мер) 3D, 15D, 22D Деформация изгиба определяется силой упругости. которая пропорциональна прогибу стержня. Вел ичин а деформация изгиба определяется по закону Гука С ув еличением вылета фрезы увеличивается деформация изгиба. С увел ичением количества зубьев жесткость возрастает. Малый размер стружечной канавки обеспечивает более высокую жесткость. 5 = Относительная деформация I = Длина рабочей части P = Сила резания Е = Модуль Юнга I = Момент инерции ( 1 5 = ltd4 14 >218 >51 -> 51 =851 =52 3
которая пропорциональна прогибу стержня. Вел ичин а деформация изгиба определяется по закону Гука С ув еличением вылета фрезы увеличивается деформация изгиба. С увел ичением количества зубьев жесткость возрастает. Малый размер стружечной канавки обеспечивает более высокую жесткость. 5 = Относительная деформация I = Длина рабочей части P = Сила резания Е = Модуль Юнга I = Момент инерции ( 1 5 = ltd4 14 >218 >51 -> 51 =851 =52 3
Как рассчитать частоту вращения двигателя
При эксплуатации, мониторинге, ремонте или замене двигателя важно понимать его характеристики. Одним из важнейших показателей является число оборотов в минуту, или об / мин, которое описывает скорость двигателя. В этом руководстве мы обсудим, как рассчитать частоту вращения двигателя и почему это так важно.
Что такое частота вращения двигателя?
об / мин – это измерение, используемое для описания скорости двигателя. Он обозначает количество оборотов в минуту и описывает скорость, с которой вращается ротор, то есть количество раз, когда вал ротора совершает полный оборот в минуту. Его можно использовать для измерения скорости двигателей, турбин, центрифуг, конвейеров и другого оборудования.
Его можно использовать для измерения скорости двигателей, турбин, центрифуг, конвейеров и другого оборудования.
Почему важно рассчитывать об / мин
Расчет оборотов двигателя, а также другие измерения, такие как крутящий момент, напряжение и мощность, важны при выборе двигателя для конкретного применения. Расчет скорости двигателя может помочь вам выбрать правильный тип двигателя при замене компонентов и помочь вам принять более правильные решения по ремонту. Вам также необходимо понимать число оборотов в минуту, чтобы эффективно контролировать и контролировать работу двигателя.
Скорость асинхронного двигателя переменного тока
Двигатели переменного тока предназначены для работы на определенных скоростях. Эти скорости одинаковы даже для разных моделей и производителей. Скорость данного двигателя зависит от частоты сети источника питания, а не от напряжения, а также от количества полюсов, которые он имеет. Двигатели переменного тока часто имеют два или четыре полюса, но может быть и больше. Взаимосвязь между полюсами и частотой вращения двигателя связана с магнитным полем, создаваемым в полюсах статора.Это поле приводит к созданию магнитных полей в роторе, которые зависят от частоты поля в статоре.
Взаимосвязь между полюсами и частотой вращения двигателя связана с магнитным полем, создаваемым в полюсах статора.Это поле приводит к созданию магнитных полей в роторе, которые зависят от частоты поля в статоре.
Вы также должны учитывать скольжение, которое представляет собой разницу между синхронной скоростью статора и фактической рабочей скоростью. Ротор всегда вращается немного медленнее, чем магнитное поле статора, и всегда пытается его «догнать», что и создает крутящий момент, необходимый для запуска двигателя.
Для регулировки скорости трехфазного двигателя переменного тока вы можете отрегулировать частоту источника питания двигателя переменного тока с помощью элемента управления.Многие элементы управления переменного тока также имеют однофазный вход, что позволяет запускать трехфазные двигатели, даже если трехфазное питание отсутствует. С другой стороны, большинство однофазных двигателей переменного тока не регулируются, поскольку они подключаются непосредственно к стандартной розетке и используют доступную частоту.
Скорость двигателя постоянного тока
Как и асинхронные двигатели переменного тока, двигатели постоянного тока с постоянными магнитами также имеют полюса, но они не влияют на скорость, как в двигателях переменного тока. Несколько других факторов влияют на скорость в двигателях постоянного тока, включая рабочее напряжение двигателя, силу магнитов и количество витков проволоки, которые имеет якорь.Двигатели постоянного тока могут работать только на скоростях, рассчитанных на доступное им напряжение.
Если аккумулятор, на котором работает двигатель, начинает разряжаться и подавать меньшее напряжение, скорость двигателя снижается. Если вы подключите двигатель к источнику питания, скорость увеличится, хотя это может вызвать дополнительный износ вашего двигателя. Вы также можете использовать элементы управления для регулировки скорости двигателя постоянного тока, который работает путем изменения напряжения, доступного для двигателя.
Ремонт двигателей постоянного и переменного тока
Как рассчитать число оборотов двигателя
Для расчета числа оборотов асинхронного двигателя переменного тока необходимо умножить частоту в герцах (Гц) на 60 – количество секунд в минуте – на два для отрицательного и положительного импульсов в цикле. Затем делите на количество полюсов двигателя:
Затем делите на количество полюсов двигателя:
- (Гц x 60 x 2) / количество полюсов = об / мин без нагрузки
Вы также можете рассчитать номинальное скольжение, вычтя номинальную скорость при полной нагрузке из синхронной скорости, разделив полученный ответ на синхронную скорость и умножив полученный ответ на 100:
- ((номинальная синхронная скорость при полной нагрузке) / (синхронная скорость)) x 100 = номинальное скольжение
Затем, чтобы найти число оборотов в минуту при полной нагрузке, вы конвертируете номинальное скольжение в число оборотов в минуту, а затем вычитаете его из числа оборотов холостого хода:
- Чтобы преобразовать номинальное скольжение в об / мин: об / мин x рейтинг скольжения = скольжение
- Для расчета об / мин при полной нагрузке: об / мин – скольжение об / мин = об / мин при полной нагрузке
Число оборотов двигателя постоянного тока зависит от напряжения, подаваемого на двигатель. Обычно производитель двигателя сообщает вам ожидаемую скорость вращения при различных напряжениях. Затем для достижения желаемых оборотов вы можете отрегулировать напряжение в соответствии с инструкциями.
Обычно производитель двигателя сообщает вам ожидаемую скорость вращения при различных напряжениях. Затем для достижения желаемых оборотов вы можете отрегулировать напряжение в соответствии с инструкциями.
Примеры расчета оборотов двигателя
Давайте рассмотрим несколько примеров. Для двигателя переменного тока количество полюсов и частота определяют обороты холостого хода. Для системы 60 Гц с четырьмя полюсами расчеты для определения числа оборотов будут:
- (Гц x 60 x 2) / количество полюсов = об / мин без нагрузки
- (60 х 60 х 2) / 4
- 7200/4 = 1800 об / мин
Величина скольжения незначительно меняется в зависимости от конструкции двигателя.Приемлемая скорость при полной нагрузке для четырехполюсного двигателя 60 Гц составляет 1725 об / мин. Скольжение – это разница между скоростью холостого хода и скоростью полной нагрузки. В данном случае это будет:
- Об / мин при полной нагрузке – об / мин без нагрузки = скольжение об / мин
- 1800-1725 = 75 об / мин
При 60 Гц двухполюсный двигатель работает со скоростью 3600 об / мин без нагрузки и около 3450 об / мин с нагрузкой:
- (Гц x 60 x 2) / количество полюсов = об / мин без нагрузки
- (60 х 60 х 2) / 4
- 7200/2 = 3600 об / мин
При 60 Гц шестиполюсный двигатель будет работать со скоростью 1200 об / мин без нагрузки и со скоростью примерно 1175 об / мин под нагрузкой. Двигатель с восемью полюсами будет работать со скоростью 900 об / мин без нагрузки и около 800 об / мин под нагрузкой. 12-полюсные двигатели, которые встречаются даже реже, чем шестиполюсные и восьмиполюсные модели, работают со скоростью 600 об / мин без нагрузки, а 16-полюсные двигатели работают со скоростью 450 об / мин.
Двигатель с восемью полюсами будет работать со скоростью 900 об / мин без нагрузки и около 800 об / мин под нагрузкой. 12-полюсные двигатели, которые встречаются даже реже, чем шестиполюсные и восьмиполюсные модели, работают со скоростью 600 об / мин без нагрузки, а 16-полюсные двигатели работают со скоростью 450 об / мин.
Ремонт двигателей от Global Electronic Services
Важно понимать технические характеристики вашего оборудования, чтобы вы могли лучше его эксплуатировать и обслуживать. Скорость вашего двигателя является неотъемлемой частью его производительности, а возможность рассчитывать и контролировать число оборотов в минуту поможет вам получить максимальную отдачу от ваших машин.
Профессиональные услуги по ремонту и техническому обслуживанию также могут сыграть важную роль в том, чтобы помочь вам в полной мере использовать возможности вашего оборудования. В Global Electronic Services мы имеем обширный опыт ремонта и обслуживания широкого спектра промышленного оборудования, включая двигатели переменного и постоянного тока, серводвигатели, промышленную электронику, гидравлику и пневматику и многое другое. Чтобы узнать больше о ремонте двигателей переменного или постоянного тока или наших услугах, свяжитесь с нами сегодня.
Чтобы узнать больше о ремонте двигателей переменного или постоянного тока или наших услугах, свяжитесь с нами сегодня.
Запросить цену
Расчет выходной скорости с использованием диаметра шкива и входной скорости
Расчет выходной скорости с использованием диаметра шкива и входной скорости
ONEPROD Hawk | диагностика машин | мониторинг состояния | вибрация машин | Ястреб
Майкл Кеохейн 10 мая 2017 г.
Знание правильной частоты вращения обоих валов на машине с ременным приводом важно при выполнении диагностики оборудования.В идеале вы должны сначала определить скорости ввода и вывода с помощью стробоскопа, фототахометра или лазерного тахометра. Как только вы узнаете точную скорость обоих компонентов, используйте эту формулу для определения коэффициента умножения:
Выход об / мин / вход об / мин = коэффициент умножения
Для вентилятора с ременным приводом требуются две основные скорости – это частота вращения двигателя и частота вращения вентилятора. Например, если вы знаете, что скорость двигателя составляет 1778 об / мин, а скорость вентилятора – 944 об / мин, коэффициент умножения будет:
Например, если вы знаете, что скорость двигателя составляет 1778 об / мин, а скорость вентилятора – 944 об / мин, коэффициент умножения будет:
944/1778 =.5309
Коэффициент умножения вводится в Nest при сборке машины.
Если вы не можете добраться до вала вентилятора, чтобы запустить его, но знаете диаметры шкивов, вот как вы можете определить выходную скорость и коэффициент умножения.
Формула
Об / мин на входе / об / мин на выходе = наружный диаметр / дюйм
Диаметр шкива вентилятора = 11,5 дюймов Диаметр шкива двигателя = 6.5 дюймов
Обороты на выходе =? Входная частота вращения = 1773
Формула
Об / мин на входе / об / мин на выходе = диаметр на выходе / диаметр в дюймах
1773 / об / мин Выход = 11,5 / 6,5
(выход об / мин) (11,5) = (1773) (6,5)
(выход об / мин) (11,5) = 11524,5
оборотов в минуту на выходе = 1 002,13
Это число действительно имеет смысл, поскольку вентилятор будет работать медленнее, поскольку у него шкив большего размера.
Коэффициент умножения = Число оборотов на выходе / Число оборотов на входе = 1002,13 / 1773 = 0,5652
Введите 0,5652 как коэффициент умножения в Nest.
Вот несколько видеороликов, в которых обсуждается важность 1X и то, как ввести коэффициент умножения в Nest при анализе механизмов с ременным приводом.
Важность поиска 1X: https://www.youtube.com/watch?v=ZWxjWiuQpv0
Ввод коэффициентов умножения в гнездо: https://www.youtube.com/watch?v=ugYyfdvwmf4
Об авторе
Майкл Кеохан Майк Кеохейн занимается вопросами надежности оборудования с 1985 года.Он начинал как инженер по обслуживанию в IRD Mechanalysis. До этого он работал регистратором на кабеле в компании Schlumberger Well Services. Он присоединился к VibrAlign в 1992 году и поддерживает клиентов в Джорджии, Южной Каролине, Алабаме и Флориде Панхандл. Помимо точной центровки, он имеет опыт работы в полевых условиях в области анализа вибрации, балансировки в полевых и цеховых условиях, анализа масла и ультразвуковой диагностики. Майк имеет степень бакалавра медицинских наук в Университете штата Мичиган. Майк, его жена и двое детей в настоящее время живут в Пичтри-Сити, штат Джорджия.
Помимо точной центровки, он имеет опыт работы в полевых условиях в области анализа вибрации, балансировки в полевых и цеховых условиях, анализа масла и ультразвуковой диагностики. Майк имеет степень бакалавра медицинских наук в Университете штата Мичиган. Майк, его жена и двое детей в настоящее время живут в Пичтри-Сити, штат Джорджия.
Центростремительная и центробежная сила – ускорение
Центростремительная и центробежная сила – это пара сил действия-противодействия, связанная с круговым движением.
Центростремительное ускорение
Скорость – это вектор, определяющий, насколько быстро (или медленно) пройдено расстояние и направление движения. Поскольку вектор скорости (направление) тела изменяется при движении по окружности – возникает ускорение.
Это ускорение называется центростремительным ускорением и может быть выражено как
a c = v 2 / r
= ω 2 r
90π191 = (2 n об / с ) 2 r
= (2 π n об / мин /60) 2 об
= (π n 30193 об / мин /2 r (1)
где
a c = центростремительное ускорение (м / с 2 , фут / с 2 )
v = тангенциальная скорость (м) / с, фут / с)
r = радиус окружности (м, фут)
ω = угловая скорость (рад / с)
n об / с = оборотов в секунду (об / с, 1 / с)
n об / мин = оборотов в минуту (об / мин, 1 / мин)
Центростремительная сила
по секундам Ньютона По закону центростремительная сила может быть выражена как
F c = ma c
= mv 2 / r
= m ω 2 9 = m (2 π n s ) 2 r
= m (2 π n об / мин /60) 2
= м (π n об / мин /30) 2 об (2)
, где
F c = центростремительная сила (Н, фунт f )
м = масса (кг, пули )
Согласно Третьему закону Ньютона Центростремительная сила, действующая на объект, имеет центробежную силу такой же величины, действующую в противоположном направлении.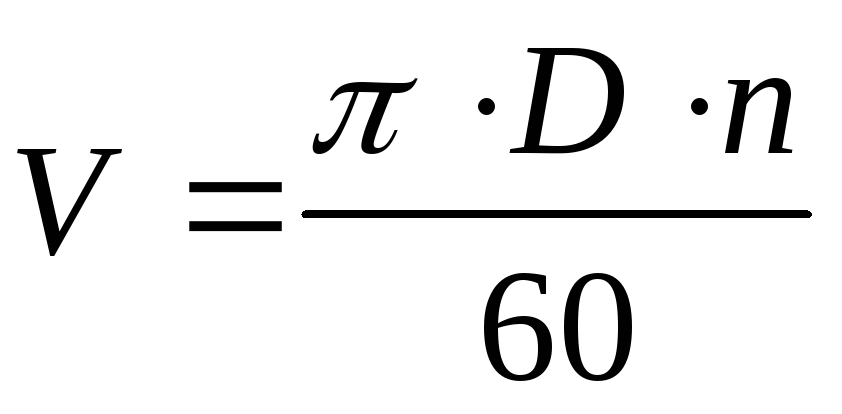
Пример – центростремительное ускорение и сила, действующая на автомобиль по кривой
Метрические единицы
Автомобиль массой 1000 кг проезжает кривую радиусом 200 м со скоростью 50 км / ч . Центростремительное ускорение можно рассчитать как
a c = ((50 км / ч) (1000 м / км) (1/3600 ч / с)) 2 / (200 м)
= 0,965 м / с 2
= 0.1 g
, где
1 g = ускорение свободного падения (9,81 м / с 2 )
Центростремительная сила может быть рассчитана как
F c = (1000 кг) ( 0,965 м / с 2 )
= 965 Н
= 0,97 кН
В зависимости от силы тяжести – вес:
F г = (1000 кг) (1000 кг) ( 9,81 м / с 2 )
= 9810 Н
= 9.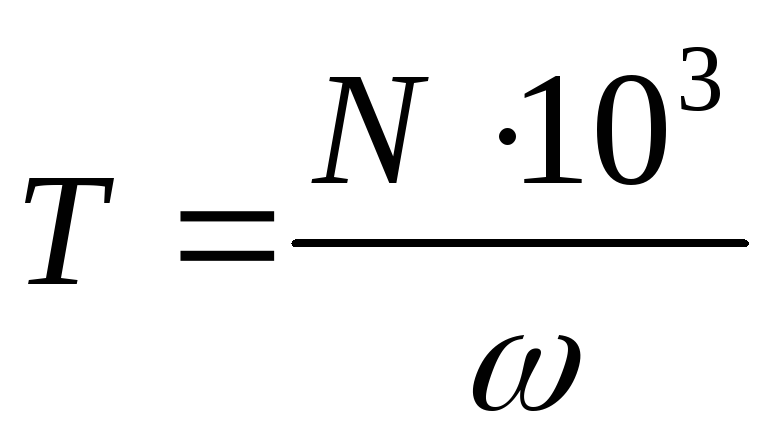 8 кН
8 кН
Имперские единицы
Автомобиль с массой (сила тяжести) 3000 фунтов движется по кривой радиусом 100 футов со скоростью 15 миль / ч .
Массу автомобиля можно рассчитать как
м = (3000 фунтов) / (32 фут / с 2 )
= 94 пули
Центростремительное ускорение можно рассчитать как
a c = ((15 миль / ч) (5280 футов / миля) / (3600 с / ч)) 2 / (100 футов)
= 4.84 фут / с 2
Центростремительная сила может быть рассчитана как
F c = (94 пули) (4,84 фут / с 2 )
= 455 фунтов фунтов
Центростремительный (центробежный) калькулятор – скорость
Этот калькулятор можно использовать, если известна скорость объекта – например, автомобиля на повороте.
Центростремительная (центробежная) сила – об / мин
Уравнение (2) можно изменить, чтобы выразить центростремительную или центробежную силу как функцию числа оборотов в минуту – об / мин – как
F c = 0.
01097 mrn об / мин 2 (3)
где
n об / мин = число оборотов в минуту (об / мин)
Центростремительный (центробежный) Калькулятор
, если используется об / мин. скорость вращения объекта известна – как токарный стакан в токарном станке.
Центробежная сила
Сила – это абстракция, представляющая толкающее и тянущее взаимодействие между объектами.Третий закон Ньютона гласит, что
- для каждой действующей силы существует равная и противоположная сила реакции.
Следовательно, должна быть равная и противоположная центростремительной силе сила реакции – центробежная сила .
Приложение 8. Примечания по центрифугированию
Приложение 8. Примечания по центрифугированиюСедиментация
Частицы взвеси оседают на дне
судно с течением времени.Это происходит из-за гравитации, которая является следствием земного
гравитационное поле. Эта сила выражается как г. Центрифугирование
увеличивает скорость осаждения за счет вращения образцов и создания
центробежная сила, действующая на частицы.
Эта сила выражается как г. Центрифугирование
увеличивает скорость осаждения за счет вращения образцов и создания
центробежная сила, действующая на частицы.
Оборотов в минуту (об / мин)
Скорость вращения центрифуги выражается как число оборотов в минуту.
Радиус вращения ®
Расстояние от центра вращения до положения в центрифужная пробирка вращающегося материала имеет радиус вращения измеряется в сантиметрах.В примерах центрифугирования, используемых в данном руководстве, это это расстояние от центра центрифуги до дна трубка.
Относительное центробежное поле (RCF)
Относительная центробежная сила – сила, действующая на образцы. во время центрифугирования. Он выражается как кратное земному гравитационному поле ( г ).
Например, 500 г = 500 RCF
Связь между RCF, RPM и r
RCF, RPM и r связаны уравнением для расчета
RCF.
RCF = 11,2 × r (об / мин / 1000) 2 или RCF = 1,12 × 10 -5 (об / мин) 2 . Это уравнение может быть изменен для расчета числа оборотов в минуту от заданной RCF.
об / мин = 1000… (RCF / 11,2 × г)
Резюме
В данном руководстве инструкции по центрифугированию представлены в виде вращение с заданной RCF ( г ) в течение определенного периода времени. Это значение может затем можно использовать для расчета правильного числа оборотов в минуту для доступной центрифуги.Стол показывает значения RCF, округленные до ближайшего 10 для типичной настольной центрифуги радиусом 18,6 см.
Таблица 9: Взаимосвязь между RCF ( г ) и числом оборотов в минуту для центрифуга с радиусом ® = 18,6 см
RCF г | об / мин |
500 | 1 500 |
850 | 2 000 |
Понимание уравнений резки | Производство режущего инструмента
Площадь в футах в минуту, нагрузка стружки, толщина недеформированной стружки и утонение стружки – это привычные рабочие термины. Однако за последние несколько недель несколько происшествий в нашем цехе заставили меня понять, что многие профессионалы в области металлообработки не понимают этих терминов и связанных с ними расчетов. Независимо от того, работаете ли вы в небольшом производственном цехе или у крупного контрактного производителя, важно понимать расчеты режущего инструмента и то, как их использовать, чтобы добиться значительного повышения эффективности.
Однако за последние несколько недель несколько происшествий в нашем цехе заставили меня понять, что многие профессионалы в области металлообработки не понимают этих терминов и связанных с ними расчетов. Независимо от того, работаете ли вы в небольшом производственном цехе или у крупного контрактного производителя, важно понимать расчеты режущего инструмента и то, как их использовать, чтобы добиться значительного повышения эффективности.
Расчеты скорости резания могут быть самыми важными. Они просты в использовании и, после небольшого объяснения, их легко понять.Скорость резания инструмента выражается в поверхностных футах в минуту (sfm) или поверхностных метрах в минуту (м / мин). Подобно миль в час для автомобиля, sfm – это линейное расстояние, которое режущий инструмент проходит за минуту. Чтобы лучше понять масштаб, например, 300 SFM преобразуются в 3,4 мили в час.
Инструментальщики рекомендуют скорость резания для различных типов обрабатываемых материалов. Когда производитель инструмента предлагает 100 футов в минуту, это означает, что внешняя поверхность вращающегося инструмента должна двигаться со скоростью, равной 100 погонных футов в минуту. Если инструмент имеет окружность (диаметр × π) 12 дюймов, ему необходимо будет вращаться со скоростью 100 об / мин, чтобы достичь 100 футов в минуту.
Если инструмент имеет окружность (диаметр × π) 12 дюймов, ему необходимо будет вращаться со скоростью 100 об / мин, чтобы достичь 100 футов в минуту.
Все изображения любезно предоставлены C. Tate
Представьте себе режущий инструмент как катящееся кольцо или цилиндр. Расстояние, пройденное за один оборот, умноженное на об / мин, и есть его поверхностная скорость. Если бы круг выше имел диаметр 3,82 дюйма, длина окружности была бы 12 дюймов. В результате каждый оборот будет производить линейное расстояние 1 фут, а скорость шпинделя 100 об / мин будет скоростью резания 100 sfm.
Следующее уравнение используется для вычисления скорости шпинделя: об / мин = sfm ÷ диаметр × 3,82, где диаметр – это диаметр режущего инструмента или диаметр детали на токарном станке в дюймах, а 3,82 – константа, полученная из алгебраической упрощение более сложной формулы: rpm = (sfm × 12) ÷ (диаметр × π).
Поскольку диаметр инструмента измеряется в дюймах, «футы» в sfm необходимо преобразовать в дюймы, а поскольку в футе 12 дюймов, умножьте sfm на 12. Кроме того, длина окружности инструмента определяется по формуле умножая диаметр инструмента на π, или 3.14 для упрощения. Результат: об / мин = (sfm × 12) ÷ (диаметр × π) = (sfm ÷ диаметр) × (12 ÷ π) = (sfm ÷ диаметр) × 3,82.
Кроме того, длина окружности инструмента определяется по формуле умножая диаметр инструмента на π, или 3.14 для упрощения. Результат: об / мин = (sfm × 12) ÷ (диаметр × π) = (sfm ÷ диаметр) × (12 ÷ π) = (sfm ÷ диаметр) × 3,82.
Обратите внимание на вертикальные линии, называемые метками инструмента, на внешней стороне обрабатываемой детали. По мере увеличения скорости подачи расстояние между линиями также увеличивается. Толщина стружки примерно равна подаче.
Скорости резания указаны в SFM, потому что идеальная скорость резания для определенного семейства инструментов теоретически будет одинаковой независимо от размера инструмента.Ожидается, что инженер, программист или машинист рассчитает число оборотов в минуту, необходимое для обеспечения правильной скорости резания для каждого выбранного инструмента.
Так о чем это нам говорит? Допустим, инструмент диаметром 1 дюйм должен работать со скоростью 100 футов в минуту. Согласно уравнению, этот инструмент должен вращаться со скоростью 382 об / мин, чтобы достичь 100 футов в минуту: 100 ÷ 1 × 3,82 = 382.
Другой способ рассмотреть эту концепцию – это подумать о расстоянии, которое пролетел бы 1-дюймовый инструмент, если бы он совершил 382 вращения по цеху. В этом сценарии он прошел бы 100 футов; сделай это за 60 секунд и было бы путешествовать 100 SFM.
Токарные станки, конечно, разные, потому что вместо фрезы вращается заготовка. Поскольку формула для скорости резания зависит от диаметра, по мере уменьшения диаметра заготовки число оборотов в минуту должно увеличиваться, чтобы поддерживать постоянную скорость резания. После каждого кругового резания на токарном станке наружный диаметр детали уменьшается или внутренний диаметр увеличивается, и необходимо увеличивать частоту вращения детали в минуту, чтобы поддерживать желаемую скорость резания. В результате производители ЧПУ разработали функцию постоянной площади поверхности для управления токарным станком.Эта функция позволяет программисту вводить желаемую скорость резания в sfm или м / мин. и система управления вычисляет правильные обороты для изменяющегося диаметра.
Когда инструмент или деталь вращаются, станок должен знать, с какой скоростью двигаться, когда фреза входит в обрабатываемую деталь. Подача – это термин, который описывает скорость перемещения при резании.
Скорость подачи при фрезеровании обычно выражается в дюймах в минуту (ipm) и рассчитывается по формуле: ipm = об / мин × количество. канавок × загрузка стружки.
Что такое загрузка микросхемы? При фрезеровании это количество материала, которое режущая кромка удаляет каждый раз при вращении. При токарной обработке это расстояние, на которое деталь перемещается за один оборот, когда она находится в контакте с инструментом. Иногда это называют толщиной стружки, что в некотором роде верно. Толщина стружки может измениться при изменении других параметров, таких как радиальный DOC или угол подъема инструмента.
Производители инструментов публикуют рекомендации по нагрузке на стружку вместе с рекомендациями по скорости резания и выражают их в тысячных долях дюйма (миллиметры для метрических единиц).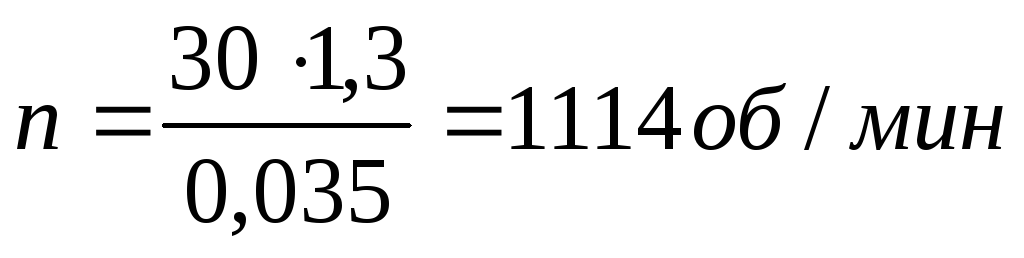 Для фрезерных и сверлильных операций нагрузка стружки выражается в тысячных долях дюйма на канавку. Канавки, зубья и режущие кромки описывают одно и то же, и должен быть по крайней мере один, но теоретически нет ограничений на количество, которое может иметь инструмент.
Для фрезерных и сверлильных операций нагрузка стружки выражается в тысячных долях дюйма на канавку. Канавки, зубья и режущие кромки описывают одно и то же, и должен быть по крайней мере один, но теоретически нет ограничений на количество, которое может иметь инструмент.
Рекомендации по нагрузке на стружку для токарных операций чаще всего даются в тысячных долях дюйма на оборот или подаче на оборот. Это расстояние, на которое инструмент продвигается каждый раз, когда деталь выполняет один оборот.
Какие обороты и скорость подачи следует запрограммировать для концевой фрезы с 4 канавками, 1 дюйм, работающей с рекомендованной скоростью резания 350 sfm и рекомендуемой стружкой 0.005 дюймов на зуб (IPT)? Используя уравнение, об / мин = sfm ÷ диаметр × 3,82 = 350 ÷ 1,0 × 3,82 = 1,337, скорость подачи = об / мин × количество. канавок × нагрузка на стружку = 1337 × 4 × 0,005 = 26,74 дюймов в минуту.
Здесь все становится интересным, потому что при изменении значений в формуле взаимосвязь различных переменных становится очевидной. Попробуйте применить 2-дюймовый инструмент вместо 1-дюймового. Что случилось? Скорость вращения и скорость подачи уменьшаются вдвое.
Попробуйте применить 2-дюймовый инструмент вместо 1-дюймового. Что случилось? Скорость вращения и скорость подачи уменьшаются вдвое.
Понимание этих взаимоотношений и творческое мышление могут обеспечить значительный выигрыш в эффективности.Я расскажу, как использовать эти отношения в своей следующей колонке. CTE
Об авторе: Кристофер Тейт (Christopher Tate) – старший инженер-технолог в компании Milwaukee Electric Tool Corp., Брукфилд, Висконсин. Он работает на производственном предприятии компании в Джексоне, штат Миссисипи. Он имеет 19-летний опыт работы в металлообрабатывающей промышленности и имеет диплом Магистр и бакалавр наук Государственного университета Миссисипи. Электронная почта: [email protected].
Преобразование оборотов в минуту в g Force (RCF) и наоборот
Сила g или относительная центробежная сила (RCF) – это величина ускорения, прикладываемого к образцу.Это зависит от числа оборотов в минуту (об / мин) и радиуса ротора, а также относительно силы тяжести Земли.
Хороший и точный протокол центрифугирования предписывает вам использовать силу перегрузки, а не число оборотов в минуту, потому что размер ротора может отличаться, а сила перегрузки будет другой, а количество оборотов в минуту останется прежним. К сожалению, многие протоколы пишутся в спешке, а инструкции даются в пакетах RPM. Следовательно, вам необходимо преобразовать перегрузочную силу (RCF) в число оборотов в минуту (об / мин) и наоборот.
Современные центрифуги имеют автоматический преобразователь, а старые нет. Для вычисления этого есть простая формула, но для этого требуется некоторое время. Между тем, ваши клетки могут погибнуть или биохимическая реакция продолжится в три раза дольше, чем следовало бы.
Есть несколько способов произвести конвертацию:
Используйте веб-сайт, на котором можно выбрать модель центрифуги и головку ротора.
Воспользуйтесь онлайн-конвертерами.

Используйте номограмму (номограф).
Сделайте расчет самостоятельно.
1. Самый точный способ произвести конверсию – использовать преобразователи для конкретной центрифуги и головки ротора. Компании предоставляют данные. Вот ссылки на ресурсы в Интернете, где вы можете забрать модель и ротор:
Beckman, Sorvall или Thermo Fisher Scientific
Сорвалл, Бекман и Эппендорф
Eppendorf
Thermo Fisher Scientific
Science Gateway может перечислить некоторые центрифуги, которых нет выше.
2. Вот несколько ссылок на онлайн-конвертеры:
Insilico
Сломанная симметрия
ЭнКор Биотехнология
Инсиликас
3. Распечатайте и используйте Номограмму (графический калькулятор). Их можно получить по следующему адресу:
Веб-сайт Мэрилендского университета
DJB Labcare
Планета оптики
4. Формулу всегда полезно иметь на случай, если ваш интернет не работает или указанные выше ссылки перестают существовать.
Формулу всегда полезно иметь на случай, если ваш интернет не работает или указанные выше ссылки перестают существовать.
г Сила (RCF) = (об / мин) 2 × 1.118 × 10 -5 × r
об / мин = √ [RCF / (r × 1,118)] × 1 × 10 5
г = относительная центрифужная сила
r = радиус вращения (см)
N =
оборотов в минуту (об / мин)Надеюсь, что приведенная выше информация упростит вам расчет.
Следующие две вкладки изменяют содержимое ниже. Продукты Promega используются учеными-биологами, которые задают фундаментальные вопросы о биологических процессах, и учеными, которые применяют научные знания для диагностики и лечения заболеваний, открывают новые методы лечения и используют генетику и тестирование ДНК для идентификации человека.Первоначально основанная в 1978 году в Мэдисоне, штат Висконсин, США, Promega имеет филиалы в 16 странах и более 50 глобальных дистрибьюторов, обслуживающих 100 стран.
Нравится:
Нравится Загрузка …
Связанныеоборотов в минуту для преобразования в герцы (об / мин в Гц)
Введите ниже частоту в оборотах в минуту, чтобы преобразовать значение в герцы.
Как преобразовать число оборотов в минуту в герцы
Чтобы преобразовать число оборотов в минуту в измерение в герцах, разделите частоту на коэффициент преобразования.
Поскольку один герц равен 60 оборотам в минуту, вы можете использовать эту простую формулу для преобразования:
герц = оборотов в минуту ÷ 60
Частота в герцах равна делению числа оборотов в минуту на 60.
Например, вот как преобразовать 5 оборотов в минуту в герцы, используя формулу выше.5 об / мин = (5 ÷ 60) = 0.083333 Гц
Обороты в минуту и герцы – это единицы измерения частоты. Продолжайте читать, чтобы узнать больше о каждой единице измерения.
Продолжайте читать, чтобы узнать больше о каждой единице измерения.
Число оборотов в минуту – это количество оборотов, или оборотов в минуту.
Число оборотов в минуту может быть сокращено как об / мин , а также иногда сокращено как об / мин или об / мин .Например, 1 оборот в минуту можно записать как 1 об / мин, 1 об / мин или 1 об / мин.
Число оборотов в минуту можно выразить формулой: Частота вращения = время оборотов м
Герц формально определяется как частота, равная одному циклу в секунду. [1]
Герц – это производная единица СИ для частоты в метрической системе.Герц может быть сокращен как Гц ; например, 1 герц можно записать как 1 Гц.


