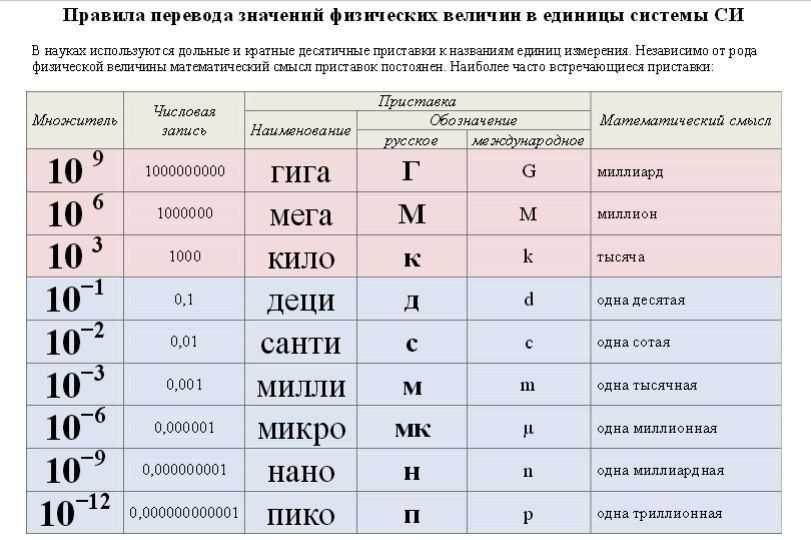
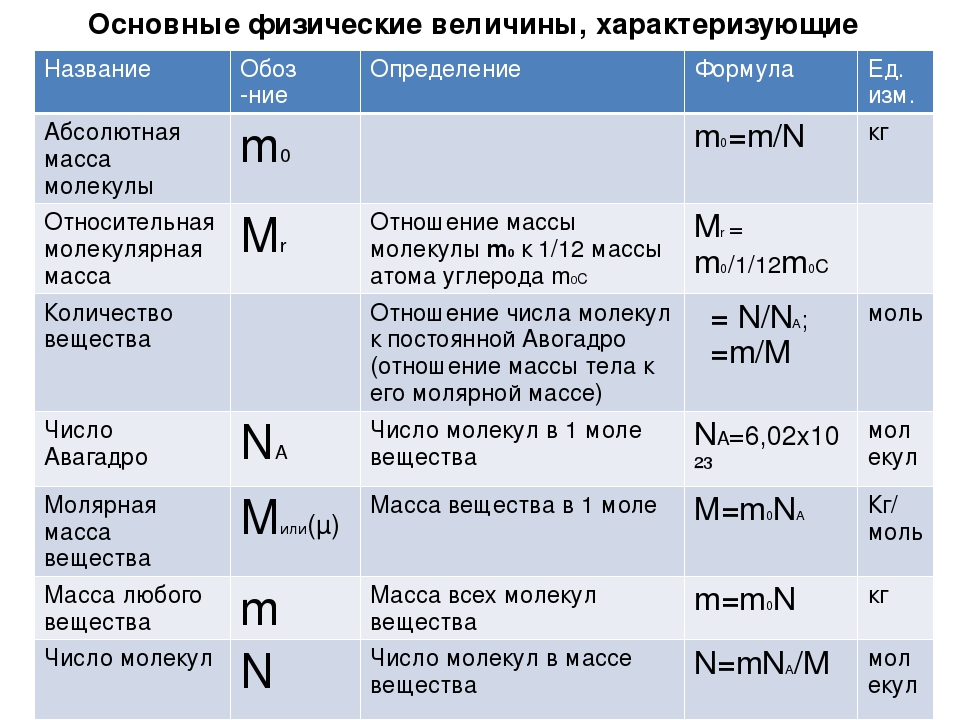
Что означает буква r в физике. Основные физические величины, их буквенные обозначения в физике. Правила образования десятичных кратных и дольных единиц, а также их наименований и обозначений
Каждое измерение – это сравнение измеряемой величины с другой, однородной с ней величиной, которую считают единичной. Теоретически единицы для всех величин в физике можно выбрать независимыми друг от друга. Но это крайне неудобно, так как для каждой величины следовало бы ввести свой эталон. Кроме этого во всех физических уравнениях, которые отображают связь между разными величинами, возникли бы числовые коэффициенты.
Основная особенность используемых в настоящее время систем единиц состоит в том, что между единицами разных величин имеются определенные соотношения. Эти соотношения установлены теми физическими законами (определениями), которыми связываются между собой измеряемые величины. Так, единица скорости выбрана таким образом, что она выражается через единицы расстояния и времени.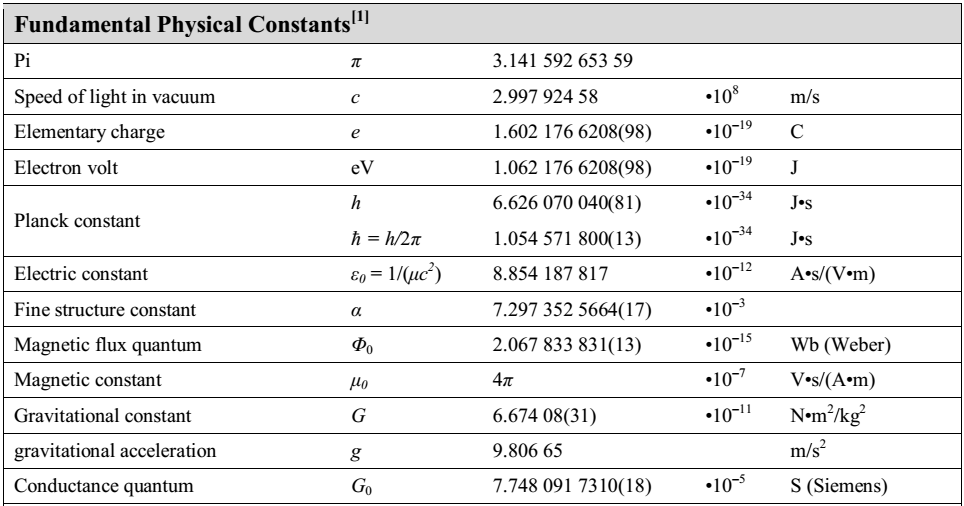
При построении определенной системы единиц, выбирают несколько физических величин, единицы которых устанавливают независимо друг от друга. Единицы таких величин называют основными. Единицы остальных величин выражают через основные, их называют производными.
Таблица единиц измерения “Пространство и время”
Физическая величина | Символ | Ед. изм. физ. вел. | Описание | Примечания | |
l, s, d | Протяжённость объекта в одном измерении. | ||||
S | квадратный метр | Протяженность объекта в двух измерениях. | |||
Объем, вместимость | V | кубический метр | Протяжённость объекта в трёх измерениях. | экстенсивная величина | |
t | Продолжительность события. | ||||
Плоский угол | α , φ | Величина изменения направления. | |||
Телесный угол | α , β , γ | стерадиан | Часть пространства | ||
Линейная скорость | v | метр в секунду | Быстрота изменения координат тела. | ||
Линейное ускорение | a, w | метр в секунду в квадрате | Быстрота изменения скорости объекта. | ||
Угловая скорость | ω | радиан в секунду | рад/с = | Скорость изменения угла. | |
Угловое ускорение | ε | радиан на секунду в квадрате | рад/с 2 = | Быстрота изменения угловой скорости |
Таблица единиц измерения “Механика”
Физическая величина | Символ | Единица измерения физической величины | Ед. изм. физ. вел. | Описание | Примечания |
m | килограмм | Величина, определяющая инерционные и гравитационные свойства тел. | экстенсивная величина | ||
Плотность | ρ | килограмм на кубический метр | кг/м 3 | Масса на единицу объёма. | интенсивная величина |
Поверхностная плотность | Масса на единицу площади. | кг/м 2 | Отношение массы тела к площади его поверхности | ||
Линейная плотность | ρ l | Масса на единицу длины. | Отношение массы тела к его линейному параметру | ||
Удельный объем | v | кубический метр на килограмм | м 3 /кг | Объём, занимаемый единицей массы вещества | |
Массовый расход | Q m | килограмм в секунду | Масса вещества, которая проходит через заданную площадь поперечного сечения потока за единицу времени | ||
Объемный расход | Q v | кубический метр в секунду | м 3 /с | Объёмный расход жидкости или газа | |
P | килограмм-метр в секунду | кг м/с | Произведение массы и скорости тела. | ||
Момент импульса | L | килограмм-метр в квадрате в секунду | кг м 2 /с | Мера вращения объекта. | сохраняющаяся величина |
J | килограмм-метр в квадрате | кг м 2 | Мера инертности объекта при вращении. | тензорная величина | |
Сила, вес | F, Q | Действующая на объект внешняя причина ускорения. | |||
Момент силы | M | ньютон-метр | (кг·м 2 /с 2) | Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы. | |
Импульс силы | I | ньютон-секунда | Произведение силы на время её действия | ||
Давление, механическое напряжение | p , σ | Па = (кг/(м·с 2)) | Сила, приходящаяся на единицу площади. | интенсивная величина | |
A | Дж = (кг·м 2 /с 2) | Скалярное произведение силы и перемещения. | |||
E, U | Дж = (кг·м 2 /с 2) | Способность тела или системы совершать работу. | экстенсивная, сохраняющаяся величина, скаляр | ||
Мощность | N | Вт = (кг·м 2 /с 3) | Скорость изменения энергии. |
Таблица единиц измерения “Периодические явления, колебания и волны”
Физическая величина | Символ | Единица измерения физической величины | Ед. | Описание | Примечания |
T | Промежуток времени, за который система совершает одно полное колебание | ||||
Частота периодического процесса | v, f | Число повторений события за единицу времени. | |||
Циклическая (круговая) частота | ω | радиан в секунду | рад/с | Циклическая частота электромагнитных колебаний в колебательном контуре. | |
Частота вращения | n | секунда в минус первой степени | Периодический процесс, равный числу полных циклов, совершённых за единицу времени. | ||
Длина волны | λ | Расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе. | |||
Волновое число | k | метр в минус первой степени | Пространственная частота волны |
Таблица единиц измерения “
Тепловые явления”Физическая величина | Символ | Единица измерения физической величины | Ед. изм. физ. вел. | Описание | Примечания |
Температура | T | Средняя кинетическая энергия частиц объекта. | Интенсивная величина | ||
Температурный коэффициент | α | кельвин в минус первой степени | Зависимость электрического сопротивления от температуры | ||
Температурный градиент | gradT | кельвин на метр | Изменение температуры на единицу длины в направлении распространения теплоты. | ||
Теплота (количество теплоты) | Q | Дж = (кг·м 2 /с 2) | Энергия, передаваемая от одного тела к другому немеханическим путём | ||
Удельная теплота | q | джоуль на килограмм | Дж/кг | Кол-во теплоты, которое необходимо подвести к веществу, взятому при температуре плавления, чтобы расплавить его. | |
Теплоемкость | C | джоуль на кельвин | Кол-во теплоты, поглощаемой (выделяемой) телом в процессе нагревания. | ||
Удельная теплоемкость | c | джоуль на килограмм-кельвин | Дж/(кг К) | Теплоёмкость единичной массы вещества. | |
Энтропия | S | джоуль на килограмм | Дж/кг | Мера необратимого рассеивания энергии или бесполезности энергии. |
Таблица единиц измерения “
Молекулярная физика”Физическая величина | Символ | Единица измерения физической величины | Ед. | Описание | Примечания |
Количество вещества | v, n | моль | Количество однотипных структурных единиц, из которых состоит вещество. | Экстенсивная величина | |
Молярная масса | M , μ | килограмм на моль | кг/моль | Отношение массы вещества к количеству молей этого вещества. | |
Молярная энергия | H мол | джоуль на моль | Дж/моль | Энергия термодинамической системы. | |
Молярная теплоемкость | с мол | джоуль на моль-кельвин | Дж/(моль К) | Теплоёмкость одного моля вещества. | |
Концентрация молекул | c, n | метр в минус третьей степени | Число молекул, содержащихся в единице объема. | ||
Массовая концентрация | ρ | килограмм на кубический метр | кг/м 3 | Отношение массы компонента, содержащегося в смеси, к объёму смеси. | |
Молярная концентрация | с мол | моль на кубический метр | моль/м 3 | ||
Подвижность ионов | В , μ | квадратный метр на вольт-секунду | м 2 /(В с) | Коэффициент пропорциональности между дрейфовой скоростью носителей и приложенным внешним электрическим полем. |
Таблица единиц измерения “
Электричество и магнетизм”Физическая величина | Символ | Единица измерения физической величины | Ед. | Описание | Примечания |
Сила тока | I | Протекающий в единицу времени заряд. | |||
Плотность тока | j | ампер на квадратный метр | Сила электрического тока, протекающего через элемент поверхности единичной площади. | Векторная величина | |
Электрический заряд | Q , q | Кл = (А·с) | Способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. | экстенсивная, сохраняющаяся величина | |
Электрический дипольный момент | p | кулон-метр | Электрические свойства системы заряженных частиц в смысле создаваемого ею поля и действия на неё внешних полей. | ||
Поляризованность | P | кулон на квадратный метр | Кл/м 2 | Процессы и состояния, связанные с разделением каких-либо объектов, преимущественно в пространстве. | |
Напряжение | U | Изменение потенциальной энергии, приходящееся на единицу заряда. | |||
Потенциал, ЭДС | φ, σ | Работа сторонних сил (некулоновских) по перемещению заряда. | |||
E | вольт на метр | Отношение силы F, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q | |||
Электрическая емкость | C | Мера способности проводника накапливать электрический заряд | |||
Электрическое сопротивление | R, r | Ом = (м 2 ·кг/(с 3 ·А 2)) | сопротивление объекта прохождению электрического тока | ||
Удельное электрическое сопротивление | ρ | Способность материала препятствовать прохождению электрического тока | |||
Электрическая проводимость | G | Способность тела (среды) проводить электрический ток | |||
Магнитная индукция | B | Векторная величина, являющаяся силовой характеристикой магнитного поля | Векторная величина | ||
Магнитный поток | Ф | (кг/(с 2 ·А)) | Величина, учитывающая интенсивность магнитного поля и занимаемую им область. | ||
Напряженность магнитного поля | H | ампер на метр | Разность вектора магнитной индукции B и вектора намагниченности M | Векторная величина | |
Магнитный момент | p m | ампер-квадратный метр | Величина, характеризующая магнитные свойства вещества | ||
Намагниченность | J | ампер на метр | Величина, характеризующая магнитное состояние макроскопического физического тела. | векторная величина | |
Индуктивность | L | Коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и полным магнитным потоком | |||
Электромагнитная энергия | N | Дж = (кг·м 2 /с 2) | Энергия, заключенная в электромагнитном поле | ||
Объемная плотность энергии | w | джоуль на кубический метр | Дж/м 3 | Энергия электрического поля конденсатора | |
Активная мощность | P | Мощность в цепи переменного тока | |||
Реактивная мощность | Q | Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока | |||
Полная мощность | S | ватт-ампер | Суммарная мощность с учетом активной и реактивной ее составляющих, а также отклонения формы тока и напряжения от гармонической |
Таблица единиц измерения “
Оптика, электромагнитное излучение”Физическая величина | Символ | Единица измерения физической величины | Ед. | Описание | Примечания |
Сила света | J, I | Количество световой энергии, излучаемой в заданном направлении в единицу времени. | Световая, экстенсивная величина | ||
Световой поток | Ф | Физическая величина, характеризующая количество «световой» мощности в соответствующем потоке излучения | |||
Световая энергия | Q | люмен-секунда | Физическая величина, характеризует способность энергии, переносимой светом, вызывать у человека зрительные ощущения | ||
Освещенность | E | Отношение светового потока, падающего на малый участок поверхности, к его площади. | |||
Светимость | M | люмен на квадратный метр | лм/м 2 | Световая величина, представляющая собой световой поток | |
L, B | кандела на квадратный метр | кд/м 2 | Сила света, излучаемая единицей площади поверхности в определенном направлении | ||
Энергия излучения | E, W | Дж = (кг·м 2 /с 2) | Энергия, переносимая оптическим излучением |
Таблица единиц измерения “Акустика”
Физическая величина | Символ | Единица измерения физической величины | Ед. изм. | Описание | Примечания |
Звуковое давление | p | Переменное избыточное давление, возникающее в упругой среде при прохождении через неё звуковой волны | |||
Объемная скорость | c, V | кубический метр в секунду | м 3 /с | Отношение объема сырья, подаваемого в реактор в час к объему катализатора | |
Скорость звука | v, u | метр в секунду | Скорость распространения упругих волн в среде | ||
Интенсивность звука | l | ватт на квадратный метр | Вт/м 2 | Величина, характеризующая мощность, переносимую звуковой волной в направлении распространения | скалярная физическая величина |
Акустическое сопротивление | Z a , R a | паскаль-секунда на кубический метр | Па с/м 3 | Отношение амплитуды звукового давления в среде к колебательной скорости её частиц при прохождении через среду звуковой волны | |
Механическое сопротивление | R m | ньютон-секунда на метр | Н с/м | Указывает силу, необходимую для движения тела при каждой частоте |
Таблица единиц измерения “
Атомная и ядерная физика. Радиоактивность”
Радиоактивность” Физическая величина | Символ | Единица измерения физической величины | Ед. изм. физ. вел. | Описание | Примечания |
Масса (масса покоя) | m | килограмм | Масса объекта, находящегося в состоянии покоя. | ||
Дефект массы | Δ | килограмм | Величина, выражающая влияние внутренних взаимодействий на массу составной частицы | ||
Элементарный электрический заряд | e | Минимальная порция (квант) электрического заряда, наблюдающегося в природе у свободных долгоживущих частиц | |||
Энергия связи | E св | Дж = (кг·м 2 /с 2) | Разность между энергией состояния, в котором составляющие части системы бесконечно удалены | ||
Период полураспада, среднее время жизни | T, τ | Время, в течение которого система распадается в примерном отношении 1/2 | |||
Эффективное сечение | σ | квадратный метр | Величина, характеризующая вероятность взаимодействия элементарной частицы с атомным ядром или другой частицей | ||
Активность нуклида | беккерель | Величина, равная отношению общего числа распадов радиоактивных ядер нуклида в источнике ко времени распада | |||
Энергия ионизирующего излучения | E,W | Дж = (кг·м 2 /с 2) | Вид энергии, высвобождаемой атомами в форме электромагнитных волн (гамма- или рентгеновское излучение) или частиц | ||
Поглощенная доза ионизирующего излучения | Д | Доза, при которой массе 1 кг передаётся энергия ионизирующего излучения в 1 джоул | |||
Эквивалентная доза ионизирующего излучения | H , Д эк | Поглощенная доза любого ионизирующего излучения, равная 100 эрг на 1 грамм облученного вещества | |||
Экспозиционная доза рентгеновского и гамма-излучения | Х | кулон на килограмм | Кл/кг | отношение суммарного электрического заряда ионов одного знака от внешнего гамма-излучения |
Обозначения в физике с несколькими буквами
Для обозначения некоторых величин иногда используют несколько букв или и отдельные слова или аббревиатуры. Так, постоянная величина в формуле обозначается часто как
Так, постоянная величина в формуле обозначается часто какДифференциал обозначается малой буквой
Перед названием величины, например .
Специальные символы
Для удобства написания и чтения в среде ученых физиков принято использовать специальные символы, характеризующие те или иные явления и свойства.В физике принято использовать не только формулы, которые применяют в математике, но и специализированные скобки.
Диакритические знаки
Диакритические знаки добавляются к символу физической величины для обозначения определённых различий. Ниже диакритические знаки добавлены для примера к букве x.
А какая Ваша оценка этой статьи?
Построение чертежей – дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.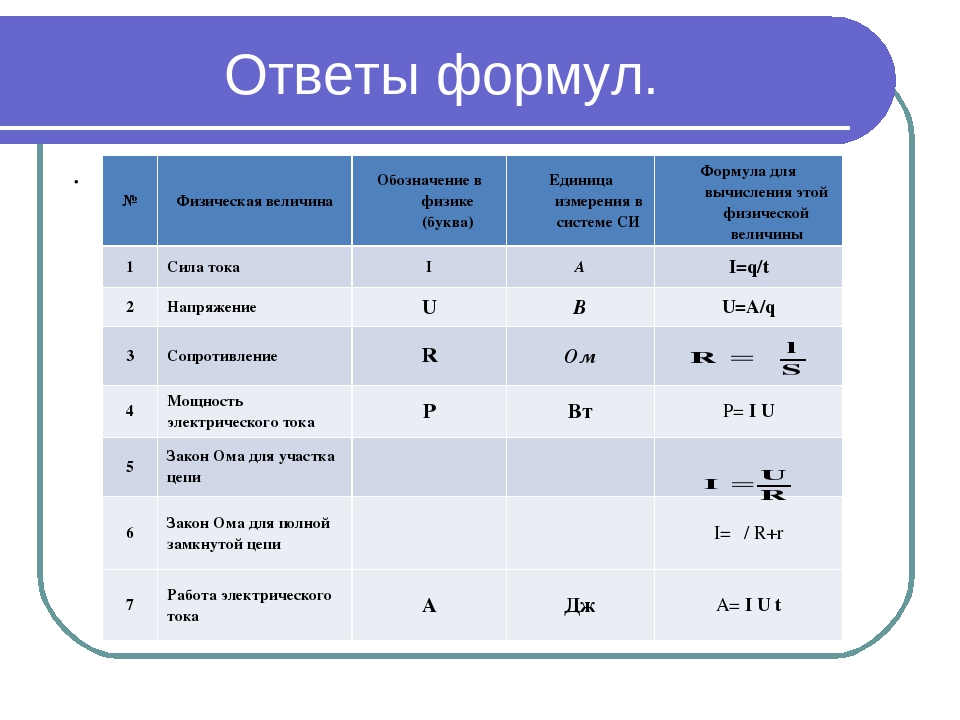
Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.
Величины
Площадь, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.
Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения – это ширина и длина, если их три – добавляется еще и высота.
Если присутствуют два измерения – это ширина и длина, если их три – добавляется еще и высота.
Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.
Ширина
Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой греческого или английского названия величины. При этом ширина на английском будет выглядеть как “width”.
Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Длина
Как уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина – в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.
В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова – «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.
Высота
Наличие этой величины указывает на то, что приходится иметь дело с более сложным – трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.
На английском она пишется как “height”. Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).
Радиус и диаметр
Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.
Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как “radius”. Отсюда и строчная или заглавная «R»/«r».
Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как “radius”. Отсюда и строчная или заглавная «R»/«r».
Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.
Численно диаметр равен двум радиусам. По-английски это слово пишется так: “diameter”. Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø».
Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».
Толщина
Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.
Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.
Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как “thickness”, а в латинском варианте – “crassities”. Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.
Периметр и площадь
В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от “περιμετρέο” («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык (“perimeter”) и закрепилось в системе СИ в виде сокращения буквой «Р».
Площадь – это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.
В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.
Некоторые по незнанию думают, что это связано с английским написанием слова “square”. Однако в нем математическая площадь – это “area”, а “square” – это площадь в архитектурном понимании. Кстати, стоит вспомнить, что “square” – название геометрической фигуры “квадрат”. Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода “area” в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» (“fortis”).
Другие распространенные сокращения
Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей.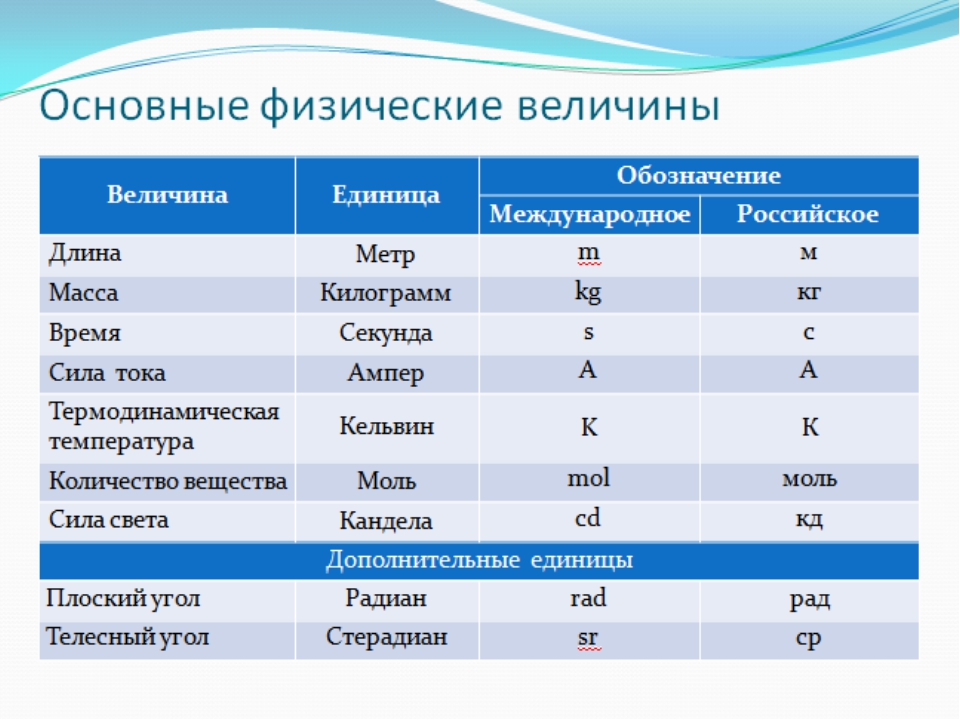 Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера – это шаг (винтовых пружин, и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.
Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера – это шаг (винтовых пружин, и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.
Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые – «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?
Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
Необходимо проверить качество перевода и привести статью в соответствие со стилистическими правилами Википедии. Вы можете помочь … Википедия
Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Физическая … Википедия
Физическая величина это количественная характеристика объекта или явления в физике, либо результат измерения. Размер физической величины количественная определенность физической величины, присущая конкретному материальному объекту, системе,… … Википедия
У этого термина существуют и другие значения, см. Фотон (значения). Фотон Символ: иногда … Википедия
У этого термина существуют и другие значения, см. Борн. Макс Борн Max Born … Википедия
Примеры разнообразных физических явлений Физика (от др. греч. φύσις … Википедия
греч. φύσις … Википедия
Фотон Символ: иногда Излученные фотоны в когерентном луче лазера. Состав: Семья … Википедия
У этого термина существуют и другие значения, см. Масса (значения). Масса Размерность M Единицы измерения СИ кг … Википедия
CROCUS Ядерный реактор это устройство, в котором осуществляется управляемая цепная ядерная реакция, сопровождающаяся выделением энергии. Первый ядерный реактор построен и запущен в декабре 1942 года в … Википедия
Книги
- Гидравлика. Учебник и практикум для академического бакалавриата , Кудинов В.А.. В учебнике изложены основные физико-механические свойства жидкостей, вопросы гидростатики и гидродинамики, даны основы теории гидродинамического подобия и математического моделирования…
- Гидравлика 4-е изд., пер. и доп. Учебник и практикум для академического бакалавриата , Эдуард Михайлович Карташов. В учебнике изложены основные физико-механические свойства жидкостей, вопросы гидростатики и гидродинамики, даны основы теории гидродинамического подобия и математического моделирования…
Шпаргалка с формулами по физике для ЕГЭ
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
Для начала картинка, которую можно распечатать в компактном виде.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 –υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ –υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 – Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 – Т 2)/ Т 1
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeXе, объяснения и примеры использования. Кроме указанных… … Википедия
Кроме указанных… … Википедия
Список используемых в математике специфических символов можно увидеть в статье Таблица математических символов Математические обозначения («язык математики») сложная графическая система обозначений, служащая для изложения абстрактных… … Википедия
Список знаковых систем (систем обозначений и т.п.), используемых человеческой цивилизацией, за исключением письменностей, для которых имеется отдельный список. Содержание 1 Критерии включения в список 2 Математика … Википедия
Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8& … Википедия
Дирак, Поль Адриен Морис Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8 августа 1902(… Википедия
Готфрид Вильгельм Лейбниц Gottfried Wilhelm Leibniz … Википедия
У этого термина существуют и другие значения, см. Мезон (значения). Мезон (от др. греч. μέσος средний) бозон сильного взаимодействия. В Стандартной модели, мезоны это составные (не элементарные) частицы, состоящие из чётного… … Википедия
Ядерная физика … Википедия
Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности (ОТО) или существенно (количественно или принципиально) модифицирующие ее. К альтернативным теориям гравитации… … Википедия
К альтернативным теориям гравитации… … Википедия
Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности или существенно (количественно или принципиально) модифицирующие ее. К альтернативным теориям гравитации часто… … Википедия
Богданов К.Ю. – учебник по физике для 10 класса
§ 24. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ЗАКОН АВОГАДРО
Уравнение состояния идеального газа связывает между собой три его макроскопические характеристики – занимаемый газом объём, его давление и температуру.
В §23 мы вывели формулу, связывающую давление идеального газа, p, концентрацию молекул в нём, n, и его абсолютную температуру, Т:
p = nkT , (24.1)
где k – постоянная
Больцмана. Однако в большинстве случаев пользоваться формулой (24. 1) неудобно,
т.к. величина n, как правило, неизвестна, а мы лишь знаем, какой это газ и
какой объём он занимает. Чтобы в этих случаях формулой
(24.1) было пользоваться проще, преобразуем её следующим образом. Пусть газ,
состоящий из N молекул, находится в сосуде объёмом V. Тогда концентрация, n молекул равна:
1) неудобно,
т.к. величина n, как правило, неизвестна, а мы лишь знаем, какой это газ и
какой объём он занимает. Чтобы в этих случаях формулой
(24.1) было пользоваться проще, преобразуем её следующим образом. Пусть газ,
состоящий из N молекул, находится в сосуде объёмом V. Тогда концентрация, n молекул равна:
где m и n – масса и количество вещества, содержащееся в газе с молярной массой M и объёмом V, а NA – число Авогадро (см. 19.1 и 19.2). Подставляя (24.2) в (24.1), получаем:
Произведение kNA обозначают буквой R и называют универсальной
(молярной) газовой постоянной, которая равна 8,31 Дж/(моль. К). Заменяя kNA на R в формуле (24.3), получаем:
К). Заменяя kNA на R в формуле (24.3), получаем:
Уравнение (24.4) называют уравнением состояния идеального газа или уравнением Менделеева-Клапейрона, названным в честь русского учёного Д.И. Менделеева и французского физика Б. Клапейрона. Формула (24.4) определяет взаимозависимость трёх макроскопических характеристик данной массы газа, определяющих его состояние, – давления, объёма и температуры.
Уравнение
Менделеева-Клапейрона позволяет вычислить одну из пяти переменных (p, V, m, M и T), если значения остальных четырёх
известны. Можно, например, найти молярную массу, М
газа, т.е. определить его относительную молекулярную массу, если измерить его
давление, объём, массу и температуру.
Из уравнения (24.4) следует, что если данная масса газа находится в состоянии 1, в котором её давление, объём и температуры равны p1, V1 и T1, соответственно, а потом переходит в состояние 2 (см. рис. 24а), в котором её давление, объём и температуры становятся равными p2, V2 и T2, то:
Уравнение (24.5), называемое уравнением Клапейрона, позволяет вычислить значение одной из макроскопических характеристик газа в состоянии 2, если остальные две известны.
Возьмём одинаковое число молей n двух
разных газов (А и Б). Пусть эти газы имеют одинаковую температуру
T0 и давление p0. Тогда из уравнения (24. 4) следует, что объёмы этих
газов, VА и VБ, тоже равны:
4) следует, что объёмы этих
газов, VА и VБ, тоже равны:
Таким образом, при одинаковых давлении и температуре равные объёмы различных газов содержат одинаковое количество вещества, т.е. молекул. Этот вывод называют законом Авогадро. Из закона Авогадро и формулы (24.6) следует, что при нормальных условиях, т.е. при температуре 0оС (Т0=273 К) и нормальном атмосферном давлении (p0=101325 Па), газ, взятый в количестве 1 моль, занимает объём 0,0224 м3 или 22,4 литра (см. рис. 24б).
Вопросы для повторения:
· Сформулируйте уравнение Менделеева-Клапейрона. Для каких газов оно справедливо?
· Как связана универсальная газовая постоянная с постоянными Больцмана и Авогадро?
·
Сформулируйте закон Авогадро.
· Какие объёмы занимает один, два и три моля идеального газа при нормальных условиях?
Рис. 24. (а) – связь между параметрами газа в двух его состояниях; (б) – связь между параметрами одного моля газа при нормальных условиях.
Справочный материал для ЕГЭ по физике / Блог / Справочник :: Бингоскул
Физические величины и единицы их измерения
Десятичные приставки
| Наименование | Обозначение | Множитель |
| гига | Г | 109 |
| мега | М | 106 |
| кило | к | 103 |
| гекто | г | 102 |
| деци | д | 10-1 |
| санти | с | 10-2 |
| милли | м | 10-3 |
| микро | мк | 10-6 |
| нано | н | 10-9 |
| пико | п | 10-12 |
Константы
| число π | π = 3,14 |
| ускорение свободного падения на Земле | g = 10 м/с2 |
| гравитационная постоянная | G = 6,7·10–11 Н·м2/кг2 |
| универсальная газовая постоянная | R = 8,31 Дж/(моль·К) |
| постоянная Больцмана | k = 1,38·10–23 Дж/К |
| постоянная Авогадро | NА = 6·1023 моль–1 |
| скорость света в вакууме | с = 3·108 м/с |
| коэффициент пропорциональности в законе Кулона | k = 1/4πε0= 9·109 Н·м2/Кл2 |
| модуль заряда электрона (элементарный электрический заряд) | e = 1,6·10–19 Кл |
| постоянная Планка | h = 6,6·10–34 Дж·с |
Соотношение между различными единицами
| температура | 0 К = –273 °С |
| атомная единица массы | 1 а. е.м. = 1,66⋅10–27 кг е.м. = 1,66⋅10–27 кг |
| 1 атомная единица массы эквивалентна | 931,5 МэВ |
| 1 электронвольт | 1 эВ = 1,6⋅10–19 Дж |
| 1 астрономическая единица | 1 а.е. ≈ 150 000 000 км |
| 1 световой год | 1 св. год ≈ 9,46·1015 м |
| 1 парсек | 1 пк ≈3,26 св. года |
Масса частиц
| электрона | 9,1⋅10–31кг ≈ 5,5⋅10–4 а.е.м. |
| протона | 1,673⋅10–27 кг ≈ 1,007 а.е.м. |
| нейтрона | 1,675⋅10–27 кг ≈ 1,008 а.е.м. |
Астрономические величины
| средний радиус Земли | R⊕ =6370 км |
| радиус Солнца | R = 6,69 ⋅ 108 м |
| температура поверхности Солнца | T = 6000 К |
Плотность
| воды | 1000 кг/м3 |
| древесины (сосна) | 400 кг/м3 |
| керосина | 800 кг/м3 |
| подсолнечного масла | 900 кг/м3 |
| алюминия | 2700 кг/м3 |
| железа | 7800 кг/м3 |
| ртути | 13600 кг/м3 |
Удельная теплоёмкость
| воды | 4,2⋅103 Дж/(кг⋅К) |
| льда | 2,1⋅103 Дж/(кг⋅К) |
| железа | 460 Дж/(кг⋅К) |
| свинца | 130 Дж/(кг⋅К) |
| алюминия | 900 Дж/(кг⋅К) |
| меди | 380 Дж/(кг⋅К) |
| чугуна | 500 Дж/(кг⋅К) |
Удельная теплота
| парообразования воды | 2,3⋅106 Дж/кг |
| плавления свинца | 2,5⋅104 Дж/кг |
| плавления льда | 3,2⋅105 Дж/кг |
Нормальные условия: давление – 105 Па, температура – 0°С
Молярная маcса
| азота | 28⋅10–3 кг/моль |
| аргона | 40⋅10–3 кг/моль |
| водорода | 2⋅10–3 кг/моль |
| воздуха | 29⋅10–3 кг/моль |
| воды | 18⋅10–3 кг/моль |
| гелия | 4⋅10–3 кг/моль |
| кислорода | 32⋅10–3 кг/моль |
| лития | 6⋅10–3 кг/моль |
| неона | 20⋅10–3 кг/моль |
| углекислого газа | 44⋅10–3 кг/моль |
Смотри также:
ЧЕМУ РАВНО ЧИСЛО ПИ? – Ньютонов ⚛ физика
***
Что общего между колесом от Лады Приоры, обручальным кольцом и блюдцем вашего кота? Вы, конечно, скажете красота и стиль! Но я осмелюсь с вами поспорить. Число Пи! Это число, объединяющее все окружности, круги и округлости, к коим в частности можно отнести и мамино кольцо, и колесо от любимой папиной машины и даже блюдце любимого кота Мурзика. Готов поспорить, что в рейтинге самых популярных физических и математических констант число Пи несомненно займет первую строчку. Но что скрывается за ним? Может какие-то страшные ругательства математиков? Давайте попробуем разобраться в этом вопросе.
Число Пи! Это число, объединяющее все окружности, круги и округлости, к коим в частности можно отнести и мамино кольцо, и колесо от любимой папиной машины и даже блюдце любимого кота Мурзика. Готов поспорить, что в рейтинге самых популярных физических и математических констант число Пи несомненно займет первую строчку. Но что скрывается за ним? Может какие-то страшные ругательства математиков? Давайте попробуем разобраться в этом вопросе.
Что же такое число «Пи»
и откуда оно взялось?Современное обозначение числа π (Пи) появилось благодаря английскому математику Джонсу в 1706 году. Это первая буква греческого слова περιφέρεια (периферия, или окружность).
Для тех, кто проходил математику давно, да и к тому же мимо, напомним, что число Пи — это отношение длины окружности к её диаметру. Величина является константой, то есть постоянна для любой окружности, независимо от её радиуса. Люди знали об этом еще в древности.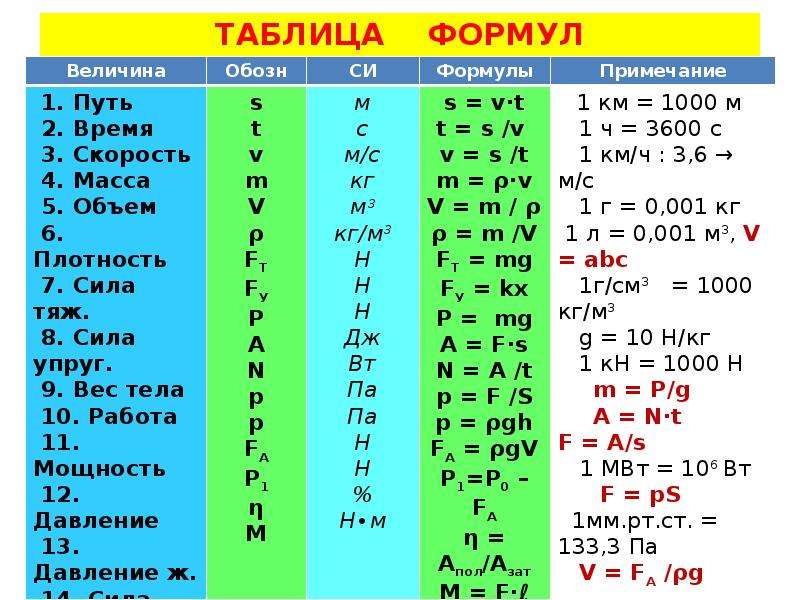 Так в древнем Египте число Пи принимали равным отношению 256/81, а в ведических текстах приводится значение 339/108, Архимед же предлагал соотношение 22/7. Но ни эти, ни многие другие способы выражения числа Пи не давали точный результат.
Так в древнем Египте число Пи принимали равным отношению 256/81, а в ведических текстах приводится значение 339/108, Архимед же предлагал соотношение 22/7. Но ни эти, ни многие другие способы выражения числа Пи не давали точный результат.
Оказалось, что число Пи трансцендентное, соответственно, и иррациональное. А это значит, его нельзя представить в виде простой дроби. Если же его выразить через десятичную, то последовательность цифр после запятой устремятся в бесконечность, к тому же периодически не повторяясь. Что все это значит? Очень просто. Хотите узнать номер телефона понравившейся девушки? Его наверняка можно найти в последовательности цифр после запятой числа Пи.
Телефон можно посмотреть здесь ↓
Число Пи с точностью до 1000 знаков.
π= 3,
1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989.
 .
.Не нашли? Тогда посмотрите здесь.
Все в числе «Пи»
Вообще это может быть не только номер телефона, а любая информация, закодированная с помощью цифр. К примеру, если представить все произведения Александра Сергеевича Пушкина в цифровом виде, то они хранились в числе Пи еще до того, как он их написал, даже до того, как он родился. В принципе, они хранятся там до сих пор. Кстати, ругательства математиков в π тоже присутствуют, да и не только математиков.
Словом, в числе Пи есть всё, даже мысли, которые посетят вашу светлую голову завтра, послезавтра, через год, а может, через два. В это очень трудно поверить, но даже если мы представим, что поверили, еще труднее будет получить оттуда информацию и расшифровать её. Так что вместо того, чтобы копаться в этих цифрах, может проще подойти к понравившейся девушке и спросить у неё номер?.. Но для тех, кто не ищет легких путей, ну или просто интересующихся, чему же равно число Пи, предлагаю несколько способов его вычисления.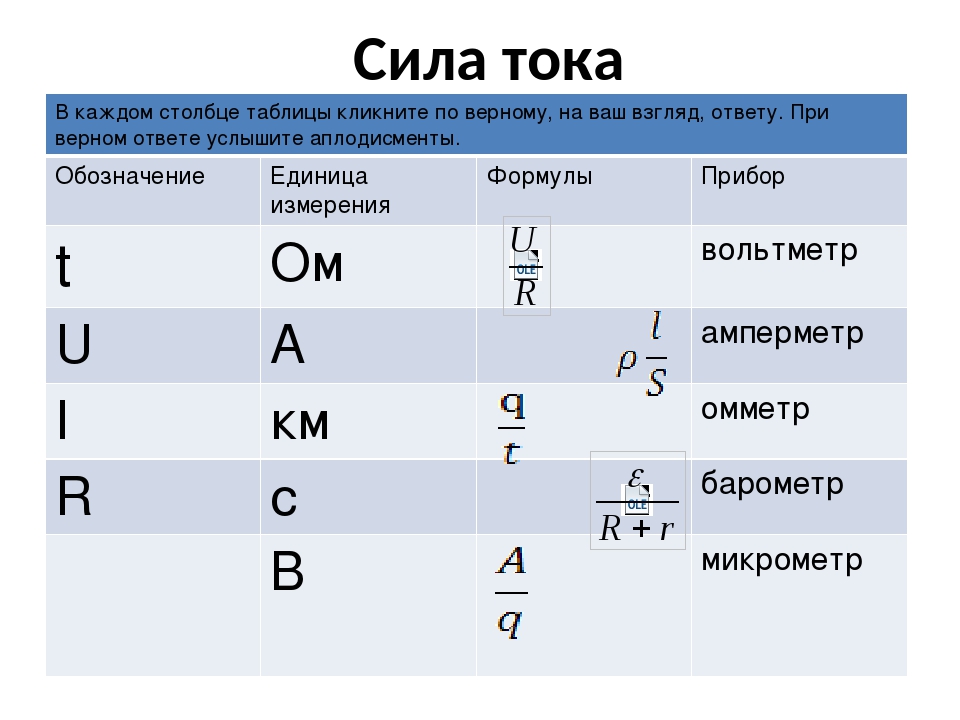 Считайте на здоровье.
Считайте на здоровье.
Чему равно число Пи?
Методы его вычисления:Экспериментальный метод.
Если число Пи это отношение длины окружности к её диаметру, то первый, пожалуй, самый очевидный способ нахождения нашей загадочной константы будет вручную произвести все измерения и вычислить число Пи по формуле π=l/d. Где l — длина окружности, а d — её диаметр. Все очень просто, необходимо лишь вооружится ниткой для определения длины окружности, линейкой для нахождения диаметра, и, собственно, длины самой нитки, ну и калькулятором, если у вас проблемы с делением в столбик. В роли измеряемого образца может выступить кастрюля или банка из под огурцов, неважно, главное? чтоб в основании была окружность.
Рассмотренный способ вычисления самый простой, но, к сожалению, имеет два существенных недостатка, отражающихся на точности полученного числа Пи. Во-первых, погрешность измерительных приборов (в нашем случае это линейка с ниткой), а во-вторых, нет никакой гарантии, что измеряемая нами окружность будет иметь правильную форму. Поэтому не удивительно, что математика подарила нам множество других методов вычисления π, где нет нужды производить точные измерения.
Поэтому не удивительно, что математика подарила нам множество других методов вычисления π, где нет нужды производить точные измерения.
Ряд Лейбница.
Существует несколько бесконечных рядов, позволяющих точно вычислять число Пи до большого количества знаков после запятой. Одним из самых простых рядов является ряд Лейбница. π = (4/1) — (4/3) + (4/5) — (4/7) + (4/9) — (4/11) + (4/13) — (4/15) …
Все просто: берем дроби с 4 в числителе (это то что сверху) и одним числом из последовательности нечетных чисел в знаменателе (это то что снизу), последовательно складываем и вычитаем их друг с другом и получаем число Пи. Чем больше итераций или повторений наших нехитрых действий, тем точнее результат. Просто, но не эффективно, к слову, необходимо 500000 итераций чтоб получить точное значение числа Пи с десятью знаками после запятой. То есть, нам придется несчастную четверку разделить аж 500000 раз, а помимо этого полученные результаты мы должны будем 500000 раз вычитать и складывать. Хотите попробовать?
Хотите попробовать?
Ряд Нилаканта
Нет времени возится с рядом Лейбница? Есть альтернатива. Ряд Нилаканта, хотя он немного сложнее, но позволяет быстрее получить нам искомый результат. π = 3 + 4/(2*3*4) — 4/(4*5*6) + 4/(6*7*8) — 4/(8*9*10) + 4/(10*11*12) — (4/(12*13*14) … Думаю, если внимательно посмотреть на приведенный начальный фрагмент ряда, все становится ясным, и комментарии излишни. По этому идем дальше.
Метод «Монте-Карло»
Довольно интересным методом вычисления числа Пи является метод Монте Карло. Столь экстравагантное название ему досталось в честь одноименного города в королевстве Монако. И причина тому случайность. Нет, его не назвали случайно, просто в основе метода лежат случайные числа, а что может быть случайней чисел, выпадающих на рулетках казино Монте Карло? Вычисление числа Пи не единственное применение этого метода, так в пятидесятых годах его использовали при расчетах водородной бомбы. Но не будем отвлекаться.
Возьмем квадрат со стороной, равной 2r, и впишем в него круг радиусом r. Если наугад ставить точки в квадрате, то вероятность P того, что точка угодит в круг, есть отношение площадей круга и квадрата. P=Sкр/Sкв=πr2/(2r)2=π/4.
Если наугад ставить точки в квадрате, то вероятность P того, что точка угодит в круг, есть отношение площадей круга и квадрата. P=Sкр/Sкв=πr2/(2r)2=π/4.
Теперь отсюда выразим число Пи π=4P. Остается только получить экспериментальные данные и найти вероятность Р как отношение попаданий в круг Nкр к попаданиям в квадрат Nкв. В общем виде расчетная формула будет выглядеть следующим образом: π=4Nкр / Nкв.
Хочется отметить, что для того, чтобы реализовать этот метод, в казино идти необязательно, достаточно воспользоваться любым более или менее приличным языком программирования. Ну а точность полученных результатов будет зависеть от количества поставленных точек, соответственно, чем больше, тем точнее. Желаю удачи 😉
Число Тау
(Вместо заключения).Люди, далекие от математики, скорее всего не знают, но так сложилось, что число Пи имеет брата, который больше его в два раза. Это число Тау(τ) , и, если Пи — это отношение длины окружности к диаметру, то Тау — это отношение этой длины к радиусу. И на сегодняшний день есть предложения некоторых математиков отказаться от числа Пи и заменить его на Тау, так как это во многом более удобно. Но пока это только предложения, и как говорил Лев Давидович Ландау: «Новая теория начинает господствовать тогда, когда вымрут сторонники старой».
Это число Тау(τ) , и, если Пи — это отношение длины окружности к диаметру, то Тау — это отношение этой длины к радиусу. И на сегодняшний день есть предложения некоторых математиков отказаться от числа Пи и заменить его на Тау, так как это во многом более удобно. Но пока это только предложения, и как говорил Лев Давидович Ландау: «Новая теория начинает господствовать тогда, когда вымрут сторонники старой».
Термодинамика – Физика – Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Теплоемкость вещества
К оглавлению…
Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c. Тогда количество теплоты (энергии) необходимое для изменения температуры некоторого тела массой m можно рассчитать по формуле:
При этом в этой формуле абсолютно не важно в каких единицах подставлена температура, так как нам важно не ее абсолютное значение, а изменение.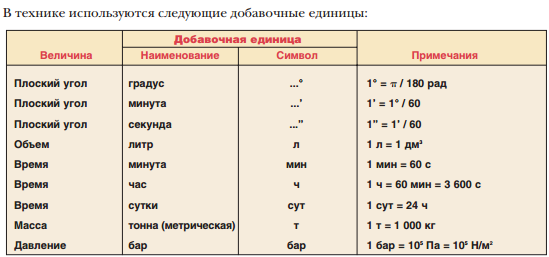 Единица измерения удельной теплоемкости вещества: Дж/(кг∙К).
Единица измерения удельной теплоемкости вещества: Дж/(кг∙К).
- Если t2 > t1, то Q > 0 – тело нагревается (получает тепло).
- Если t2 < t1, то Q < 0 – тело охлаждается (отдает тепло).
Произведение массы тела на удельную теплоемкость вещества, из которого оно изготовлено называется теплоемкостью тела (т.е. просто теплоемкостью без слова «удельная»):
Если в условии задачи сказано про теплоемкость тела, то количество теплоты, отданное или полученное этим телом, можно рассчитать по формуле:
Итак, запомните:
- Удельная теплоемкость обозначается маленькой буквой с, и является характеристикой вещества.
- (Просто) Теплоемкость обозначается большой буквой С, и является характеристикой данного тела.
Напомним, что количество теплоты Q отданное каким–либо источником (нагревателем) рассчитывается по формуле: Q = Pt, где: P – мощность источника, t – время, в течение которого источник отдавал тепло. При решении задач не путайте время работы источника и температуру.
При решении задач не путайте время работы источника и температуру.
Фазовые превращения
К оглавлению…
Фазой вещества называется однородная система, например, твердое тело, физические свойства которой во всех точках одинаковые. Между различными фазами вещества при обычных условиях существует четко выраженная граница (поверхность) раздела. При изменении внешних условий (температуры, давления, электрических и магнитных полей) вещество может переходить из одной фазы в другую. Такие процессы называются фазовыми превращениями (переходами).
Процесс фазового перехода из жидкого состояния в газообразное (парообразование) или из твердого в жидкое (плавление) может происходить только при сообщении веществу некоторого количества теплоты. Обратные фазовые переходы (конденсация и кристаллизация, или отвердевание) сопровождаются выделением такого же количества теплоты.
Количество теплоты, поступающее в систему или выделяющееся из нее, изменяет ее внутреннюю энергию. Это означает, что внутренняя энергия пара при 100°С больше, чем жидкости при той же температуре. Указанные фазовые переходы идут при постоянных температурах, которые называются соответственно температурой кипения и температурой плавления. Количество теплоты, необходимое для превращения жидкости в пар или выделяемое паром при конденсации, называется теплотой парообразования:
где: r – удельная теплота парообразования. Единица измерения [r] = 1 Дж/кг. Физический смысл удельной теплоты парообразования: она равна количеству теплоты, необходимому для превращения в пар 1 кг жидкости, находящейся при температуре кипения. Превращение жидкости в пар не требует доведение жидкости до кипения. Вода может превратиться в пар и при комнатной температуре. Такой процесс называется испарением.
Количество теплоты, необходимое для плавления тела или выделяемое при кристаллизации (отвердевании), называется теплотой плавления:
где: λ – удельная теплота плавления. Единица измерения [λ] = 1 Дж/кг. Физический смысл удельной теплоты плавления: теплота, необходимая для плавления 1 кг вещества, находящегося при температуре плавления. Удельные теплоты парообразования и плавления называются также скрытыми теплотами, поскольку при фазовых переходах температура системы не меняется, несмотря на то, что теплота к ней подводится.
Обратите внимание: что во время фазовых переходов температура системы не изменяется. А также на то, что сами фазовые переходы начинаются только после достижения необходимой температуры.
Наиболее распространенным источником энергии для нужд человека является топливо – вещество, при сгорании которого выделяется некоторое количество теплоты. Количество теплоты, выделяемое при сгорании топлива массой m, называется теплотой сгорания топлива:
где: q – удельная теплота сгорания (теплотворная способность, калорийность) топлива. Единица измерения [q] = 1 Дж/кг. Физический смысл удельной теплоты сгорания топлива: величина, показывающая, какое количество теплоты выделяется при полном сгорании 1 кг топлива.
Физический смысл удельной теплоты сгорания топлива: величина, показывающая, какое количество теплоты выделяется при полном сгорании 1 кг топлива.
Уравнение теплового баланса
К оглавлению…
В соответствии с законом сохранения энергии для замкнутой системы тел, в которой не происходит никаких превращений энергии, кроме теплообмена, количество теплоты, отдаваемое более нагретыми телами, равно количеству теплоты, получаемому более холодными. Теплообмен прекращается в состоянии термодинамического равновесия, т.е. когда температура всех тел системы становится одинаковой. Сформулируем уравнение теплового баланса: в замкнутой системе тел алгебраическая сумма количеств теплоты, отданных и полученных всеми телами, участвующими в теплообмене, равна нулю:
При использовании такой формы записи уравнения теплового баланса, чтобы не сделать ошибку, запомните: когда Вы будете считать теплоту при нагревании или охлаждении тела, нужно из большей температуры вычитать меньшую, чтобы теплота всегда была положительной. Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то уравнение теплового баланса можно записать в виде:
Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то уравнение теплового баланса можно записать в виде:
При использовании такой формы записи, нужно всегда от конечной температуры отнимать начальную. При таком подходе знак их разности сам «покажет» отдаёт тело теплоту или получает.
Запомните, что тело поглощает теплоту если происходит:
- Нагревание,
- Плавление,
- Парообразование.
Тело отдает теплоту если происходит:
- Охлаждение,
- Кристаллизация,
- Конденсация,
- Сгорание топлива.
Именно в этой теме, имеет смысл не решать задачи в общем виде, а сразу подставлять числа.
Взаимные превращения механической и внутренней энергии
При неупругих ударах механическая энергия частично или полностью переходит во внутреннюю энергию тел, то есть тела могут нагреваться и плавится. В общем случае изменение механической энергии равно выделяющемуся количеству теплоты.
В общем случае изменение механической энергии равно выделяющемуся количеству теплоты.
Работа идеального газа
К оглавлению…
Термодинамика – это наука о тепловых явлениях. В противоположность молекулярно–кинетической теории, которая делает выводы на основе представлений о молекулярном строении вещества, термодинамика исходит из наиболее общих закономерностей тепловых процессов и свойств макроскопических систем. Выводы термодинамики опираются на совокупность опытных фактов и не зависят от наших знаний о внутреннем устройстве вещества, хотя в целом ряде случаев термодинамика использует молекулярно–кинетические модели для иллюстрации своих выводов.
Термодинамика рассматривает изолированные системы тел, находящиеся в состоянии термодинамического равновесия. Это означает, что в таких системах прекратились все наблюдаемые макроскопические процессы. Важным свойством термодинамически равновесной системы является выравнивание температуры всех ее частей.
Если термодинамическая система была подвержена внешнему воздействию, то в конечном итоге она перейдет в другое равновесное состояние. Такой переход называется термодинамическим процессом. Если процесс протекает достаточно медленно (в пределе бесконечно медленно), то система в каждый момент времени оказывается близкой к равновесному состоянию. Процессы, состоящие из последовательности равновесных состояний, называются квазистатическими (или квазистационарными, еще одно название таких процессов – равновесные).
В изобарном процессе работу идеального газа можно рассчитывать по формулам:
Подчеркнем еще раз: работу газа по расширению можно считать по этим формулам только если давление постоянно. Согласно данной формуле, при расширении газ совершает положительную работу, а при сжатии – отрицательную (т.е. газ сопротивляется сжатию и над ним нужно совершать работу чтобы оно состоялось).
Если давление нельзя считать постоянным, то работу газа находят, как площадь фигуры под графиком в координатах (p, V). Очевидно, что в изохорном процессе работа газа равна нулю.
Ввиду того, что работа газа численно равна площади под графиком, становится понятно, что величина работы зависит от того, какой именно процесс происходил, ведь у каждого процесса свой график, а под ним своя площадь. Таким образом, работа зависит не только и не столько от начального и конечного состояний газа, сколько от процесса, с помощью которого конечное состояние было достигнуто.
Внутренняя энергия
К оглавлению…
Одним из важнейших понятий термодинамики является внутренняя энергия тела. Все макроскопические тела обладают энергией, заключенной внутри самих тел. С точки зрения молекулярно–кинетической теории внутренняя энергия вещества складывается из кинетической энергии всех атомов и молекул и потенциальной энергии их взаимодействия друг с другом. В частности, внутренняя энергия идеального газа равна сумме кинетических энергий всех частиц газа, находящихся в непрерывном и беспорядочном тепловом движении. Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема. Внутренняя энергия одноатомного идеального газа рассчитывается по формулам:
В частности, внутренняя энергия идеального газа равна сумме кинетических энергий всех частиц газа, находящихся в непрерывном и беспорядочном тепловом движении. Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема. Внутренняя энергия одноатомного идеального газа рассчитывается по формулам:
Таким образом, внутренняя энергия U тела однозначно определяется макроскопическими параметрами, характеризующими состояние тела. Она не зависит от того, каким путем было реализовано данное состояние. Принято говорить, что внутренняя энергия является функцией состояния. Это значит, что изменение внутренней энергии не зависит от того, как система была переведена из одного состояния в другое (а зависит лишь от характеристик первоначального и конечного состояний) и всегда, в любых процессах для одноатомного идеального газа определяется выражением:
Обратите внимание: эта формула верна только для одноатомного газа, зато она применима ко всем процессам (а не только к изобарному, как формула для работы). Как видно из формулы, если температура не изменялась, то внутренняя энергия остаётся постоянной.
Как видно из формулы, если температура не изменялась, то внутренняя энергия остаётся постоянной.
Первый закон термодинамики
К оглавлению…
Если система обменивается теплом с окружающими телами и совершает работу (положительную или отрицательную), то изменяется состояние системы, то есть изменяются ее макроскопические параметры (температура, давление, объем). Так как внутренняя энергия U однозначно определяется макроскопическими параметрами, характеризующими состояние системы, то отсюда следует, что процессы теплообмена и совершения работы сопровождаются изменением ΔU внутренней энергии системы.
Первый закон (начало) термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом: Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.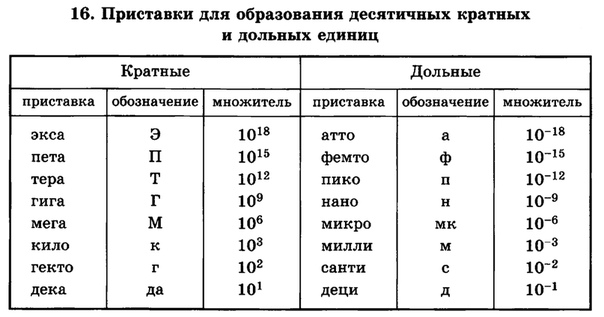 Однако, соотношение, выражающее первый закон термодинамики, чаще записывают в немного другой форме:
Однако, соотношение, выражающее первый закон термодинамики, чаще записывают в немного другой форме:
Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами (такая формулировка более удобна и понятна, в таком виде совсем очевидно, что это просто закон сохранения энергии).
Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких–либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии.
Адиабатным (адиабатическим) называют процесс, в ходе которого система не обменивается теплотой с окружающей средой. При адиабатном процессе Q = 0. Поэтому: ΔU + A = 0, то есть: A = – ΔU. Газ совершает работу за счет уменьшения собственной внутренней энергии.
Первое начало термодинамики и изопроцессы
К оглавлению…
Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const):
Изобарный процесс (p = const):
Изотермический процесс (T = const):
Адиабатный процесс (Q = 0):
Если в задаче явно не сказано, что газ одноатомный (или не назван один из инертных газов, например, гелий), то применять формулы из этого раздела нельзя.
Циклы. Тепловые машины
К оглавлению…
Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами.
Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т.д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние.
Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q1 > 0 и отдает холодильнику количество теплоты Q2 < 0.
КПД тепловой машины может быть рассчитан по формуле:
где: Q1 – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q2 – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл:
Коэффициент полезного действия указывает, какая часть тепловой энергии, полученной рабочим телом от «горячего» теплового резервуара, превратилась в полезную работу. Остальная часть (1 – η) была «бесполезно» передана холодильнику. Коэффициент полезного действия тепловой машины всегда меньше единицы (η < 1).
Наибольший КПД при заданных температурах нагревателя T1 и холодильника T2, достигается если тепловая машина работает по циклу Карно. Цикл Карно состоит из двух изотерм и двух адиабат. КПД цикла Карно равен:
Второе начало (второй закон) термодинамики
К оглавлению…
Первый закон термодинамики не устанавливает направление протекания тепловых процессов. Однако, как показывает опыт, многие тепловые процессы могут протекать только в одном направлении. Такие процессы называются необратимыми. Например, при тепловом контакте двух тел с разными температурами тепловой поток всегда направлен от более теплого тела к более холодному. Никогда не наблюдается самопроизвольный процесс передачи тепла от тела с низкой температурой к телу с более высокой температурой. Следовательно, процесс теплообмена при конечной разности температур является необратимым.
Обратимыми процессами называют процессы перехода системы из одного равновесного состояния в другое, которые можно провести в обратном направлении через ту же последовательность промежуточных равновесных состояний. При этом сама система и окружающие тела возвращаются к исходному состоянию.
Необратимыми являются процессы превращения механической работы во внутреннюю энергию тела из–за наличия трения, процессы диффузии в газах и жидкостях, процессы перемешивания газа при наличии начальной разности давлений и т.д. Все реальные процессы необратимы, но они могут сколь угодно близко приближаться к обратимым процессам. Обратимые процессы являются идеализацией реальных процессов.
Первый закон термодинамики не может отличить обратимые процессы от необратимых. Он просто требует от термодинамического процесса определенного энергетического баланса и ничего не говорит о том, возможен такой процесс или нет. Направление самопроизвольно протекающих процессов устанавливает второй закон термодинамики. Он может быть сформулирован в виде запрета на определенные виды термодинамических процессов.
Английский физик У.Кельвин дал в 1851 году следующую формулировку второго закона: В циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного теплового резервуара.
Гипотетическую тепловую машину, в которой мог бы происходить такой процесс, называют «вечным двигателем второго рода». Как уже должно было стать понятно, второе начало термодинамики запрещает существование такого двигателя.
Немецкий физик Р.Клаузиус дал другую формулировку второго закона термодинамики: Невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от тела с низкой температурой к телу с более высокой температурой. Следует отметить, что обе формулировки второго закона термодинамики эквивалентны.
Сложные задачи по термодинамике
К оглавлению…
При решении различных нестандартных задач по термодинамике необходимо учитывать следующие замечания:
- Для нахождения работы идеального газа надо построить график процесса в координатах p(V) и найти площадь фигуры под графиком. Если дан график процесса в координатах p(T) или V(T), то его сначала перестраивают в координаты p(V). Если же в условии задаётся математическая зависимость между параметрами газа, то сначала находят зависимость между давлением и объёмом, а затем строят график p(V).
- Для нахождения работы смеси газов используют закон Дальтона.
- При объединении теплоизолированных сосудов не должна изменяться внутренняя энергия всей системы, т.е. на сколько джоулей увеличится внутренняя энергия газа в одном сосуде, на столько уменьшится в другом.
- Вообще говоря, давление и температуру газа можно измерять только в состоянии термодинамического равновесия, когда давление и температура во всех точках сосуда одинаковы. Но бывают ситуации, когда давление одинаково во всех точках, а температура нет. Это может быть следствием разной концентрации молекул в разных частях сосуда (проанализируйте формулу: p = nkT).
- Иногда приходится в задачах по термодинамике использовать знания из механики.
Расчет КПД циклов по графику
К оглавлению…
Задачи данной темы по праву считаются одними из самых сложных задач в термодинамике. Итак, для решения Вам придется, во-первых, перевести график процесса в p(V) – координаты. Во-вторых, надо рассчитать работу газа за цикл. Полезная работа равна площади фигуры внутри графика циклического процесса в координатах p(V). В-третьих, необходимо разобраться, где газ получает, а где отдает теплоту. Для этого вспомните первое начало термодинамики. Внутренняя энергия идеального газа зависит только от его температуры, а работа – от объема. Поэтому, газ получает теплоту, если:
- Увеличиваются и его температура, и объем;
- Увеличивается объем, а температура постоянна;
- Увеличивается температура, а объем постоянен.
Газ отдает теплоту, если:
- Уменьшаются и его температура, и объем;
- Уменьшается объем, а температура постоянна;
- Уменьшается температура, а объем постоянен.
Если один из параметров увеличивается, а другой уменьшается, для того, чтобы понять, отдает газ теплоту или получает ее, необходимо «в лоб» по первому началу термодинамики рассчитать теплоту и посмотреть на ее знак. Положительная теплота – газ ее получает. Отрицательная – отдает.
Первый тип задач. В p(V) – координатах график цикла представляет собой фигуру с легко вычисляемой площадью, и газ получает теплоту в изохорных и изобарных процессах. Применяйте формулу:
Обратите внимание, что в знаменателе стоит только теплота, полученная газом за один цикл, то есть теплота только в тех процессах, в которых газ получал ее.
Второй тип задач. В p(V) – координатах график цикла представляет собой фигуру с легко вычисляемой площадью, и газ отдает теплоту в изохорных и изобарных процессах. Применяйте формулу:
Обратите внимание, что в знаменателе стоит только теплота, отданная газом за один цикл, то есть теплота только в тех процессах, в которых газ отдавал ее.
Третий тип задач. Газ получает теплоту не в удобных для расчета изохорных или изобарных процессах, в цикле есть изотермы или адиабаты, или вообще «никакие» процессы. Применяйте формулу:
Свойства паров. Влажность
К оглавлению…
Любое вещество при определенных условиях может находиться в различных агрегатных состояниях – твердом, жидком и газообразном. Переход из одного состояния в другое называется фазовым переходом. Испарение и конденсация являются примерами фазовых переходов.
Испарением называется фазовый переход из жидкого состояния в газообразное. С точки зрения молекулярно–кинетической теории, испарение – это процесс, при котором с поверхности жидкости вылетают наиболее быстрые молекулы, кинетическая энергия которых превышает энергию их связи с остальными молекулами жидкости. Это приводит к уменьшению средней кинетической энергии оставшихся молекул, то есть к охлаждению жидкости (если нет подвода энергии от окружающих тел).
Конденсация – это процесс, обратный процессу испарения. При конденсации молекулы пара возвращаются в жидкость.
В закрытом сосуде жидкость и ее пар могут находиться в состоянии динамического равновесия, т.е. число молекул, вылетающих из жидкости, равно числу молекул, возвращающихся в жидкость из пара, это значит, что скорости процессов испарения и конденсации одинаковы. Такую систему называют двухфазной. Пар, находящийся в равновесии со своей жидкостью, называют насыщенным.
Насыщенный пар имеет максимальные: давление, концентрацию, плотность при данной температуре. Они зависят только от температуры насыщенного пара, но не от его объема.
Это означает, что если бы мы сосуд закрыли не крышкой, а поршнем, и после того, как пар стал насыщенным, стали бы его сжимать, то давление, плотность и концентрация пара не изменились бы. Если быть более точным, то давление, плотность и концентрация на небольшое время увеличились бы, и пар стал бы перенасыщенным. Но сразу же часть пара превратилась бы в воду, и параметры пара стали бы прежними. Если поднять поршень, то пар перестанет быть насыщенным. Однако за счёт испарения через некоторое время снова станет насыщенным. Здесь следует учесть, что если воды на дне сосуда нет или её немного, то это испарение может оказаться недостаточным, чтобы пар снова стал насыщенным.
- Фраза: «В закрытом сосуде с водой…» – означает, что над водой насыщенный пар.
- Выпадение росы означает, что пар становится насыщенным.
Абсолютной влажностью ρ называют количество водяного пара, содержащегося в 1 м3 воздуха (т.е. просто плотность водяных паров; из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):
где: р – парциальное давление водяного пара, М – молярная масса, R – универсальная газовая постоянная, Т – абсолютная температура. Единица измерения абсолютной влажности в СИ [ρ] = 1 кг/м3, хотя обычно используют 1 г/м3.
Относительной влажностью φ называется отношение абсолютной влажности ρ к тому количеству водяного пара ρ0, которое необходимо для насыщения 1 м3 воздуха при данной температуре:
Относительную влажность можно также определить как отношение давления водяного пара р к давлению насыщенного пара р0 при данной температуре:
Испарение может происходить не только с поверхности, но и в объеме жидкости. В жидкости всегда имеются мельчайшие пузырьки газа. Если давление насыщенного пара жидкости равно внешнему давлению (то есть давлению газа в пузырьках) или превышает его, жидкость будет испаряться внутрь пузырьков. Пузырьки, наполненные паром, расширяются и всплывают на поверхность. Этот процесс называется кипением. Таким образом, кипение жидкости начинается при такой температуре, при которой давление ее насыщенных паров становится равным внешнему давлению.
В частности, при нормальном атмосферном давлении вода кипит при температуре 100°С. Это значит, что при такой температуре давление насыщенных паров воды равно 1 атм. Важно знать, что температура кипения жидкости зависит от давления. В герметически закрытом сосуде жидкость кипеть не может, т.к. при каждом значении температуры устанавливается равновесие между жидкостью и ее насыщенным паром.
Поверхностное натяжение
К оглавлению…
Молекулы вещества в жидком состоянии расположены почти вплотную друг к другу. В отличие от твердых кристаллических тел, в которых молекулы образуют упорядоченные структуры во всем объеме кристалла и могут совершать тепловые колебания около фиксированных центров, молекулы жидкости обладают большей свободой. Каждая молекула жидкости, также как и в твердом теле, «зажата» со всех сторон соседними молекулами и совершает тепловые колебания около некоторого положения равновесия. Однако, время от времени любая молекула может скачком переместиться в соседнее вакантное место. Такие перескоки в жидкостях происходят довольно часто; поэтому молекулы не привязаны к определенным центрам, как в кристаллах, и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей.
Вследствие плотной упаковки молекул сжимаемость жидкостей, то есть изменение объема при изменении давления, очень мала; она в десятки и сотни тысяч раз меньше, чем в газах.
Наиболее интересной особенностью жидкостей является наличие свободной поверхности. Жидкость, в отличие от газов, не заполняет весь объем сосуда, в который она налита. Между жидкостью и газом (или паром) образуется граница раздела, которая находится в особых условиях по сравнению с остальной массой жидкости. Молекулы в пограничном слое жидкости, в отличие от молекул в ее глубине, окружены другими молекулами той же жидкости не со всех сторон. Силы межмолекулярного взаимодействия, действующие на одну из молекул внутри жидкости со стороны соседних молекул, в среднем взаимно скомпенсированы. Любая молекула в пограничном слое притягивается молекулами, находящимися внутри жидкости (силами, действующими на данную молекулу жидкости со стороны молекул газа (или пара) можно пренебречь). В результате появляется некоторая равнодействующая сила, направленная вглубь жидкости. Если молекула переместится с поверхности внутрь жидкости, силы межмолекулярного взаимодействия совершат положительную работу. Наоборот, чтобы вытащить некоторое количество молекул из глубины жидкости на поверхность (то есть увеличить площадь поверхности жидкости), надо затратить положительную работу внешних сил ΔAвнеш, пропорциональную изменению ΔS площади поверхности.
Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия Ep поверхности жидкости пропорциональна ее площади:
Коэффициент σ называется коэффициентом поверхностного натяжения (σ > 0). Таким образом, коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости на единицу при постоянной температуре. В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м2) или в ньютонах на метр (1 Н/м = 1 Дж/м2).
Из механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии (любое тело всегда стремится скатиться с горы, а не забраться на нее). Отсюда следует, что свободная поверхность жидкости стремится сократить свою площадь. По этой причине свободная капля жидкости принимает шарообразную форму. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие (стягивающие) эту поверхность. Эти силы называются силами поверхностного натяжения. Наличие сил поверхностного натяжения делает поверхность жидкости похожей на упругую растянутую пленку. Сила поверхностного натяжения, действующая на участок границы жидкости длиной L вычисляется по формуле:
Таким образом, коэффициент поверхностного натяжения σ может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность.
Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются. При этом высота столба жидкости в капилляре:
где: r – радиус капиляра (т.е. тонкой трубки). При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной:
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
СТАТИСТИЧЕСКАЯ ФИЗИКА • Большая российская энциклопедия
СТАТИСТИ́ЧЕСКАЯ ФИ́ЗИКА, раздел физики, в котором на основе статистических (вероятностных) представлений описываются свойства физич. объектов любой природы, находящихся в тепловом контакте с внешним окружением (напр., термостатом с фиксированной температурой $T_0$). В общем случае С. ф. является неравновесной (её полная теория пока отсутствует), однако в случае теплового (термодинамического) равновесия между объектом и термостатом существует детально и окончательно разработанная равновесная статистич. физика.
Статистич. характер описания физич. объекта в рамках С. ф. (в отличие от более полного и информативного динамического) обусловлен неконтролируемым (вероятностным, стохастическим) влиянием окружающей среды (термостата), что предполагает выполнение условия $f_{окр} ≫ f_{об}$; здесь $f_{окр}$ и $f_{об}$ – числа степеней свободы окружающей среды и объекта соответственно. Связь с экспериментально наблюдаемыми физич. величинами в С. ф. реализуется посредством усреднения микро- или макроскопич. характеристик объекта по времени. Связь между динамич. и статистич. описанием определяется эргодической гипотезой, которая позволяет заменить усреднение по времени усреднением по статистическому ансамблю.
Равновесная С. ф. включает в себя два подхода – статистическую механику, созданную Дж. Гиббсом для классич. объектов в 1902 и обобщённую для квантовых объектов Дж. фон Нейманом в 1927, и статистическую термодинамику, построенную А. Эйнштейном в 1903–04 и завершённую Л. Силардом в 1925. Оба подхода С. ф. физически и математически эквивалентны, а конкретный выбор подхода определяется физич. постановкой задачи.
Как правило, описываемые в С. ф. объекты являются макроскопическими и состоят из большого числа (порядка Авогадро числа, 1023) микрочастиц (молекул, атомов, ионов, электронов и т. п.), однако в рамках С. ф. вполне возможно также рассмотрение находящихся в термостате одиночных частиц или выделенных мод электромагнитного излучения. Выбор классич. или квантового описания определяется внешними физич. условиями, напр. значениями темп-ры $T_0$ по сравнению с темп-рой квантового вырождения для данного объекта.
В отличие от соотношений классич. (или феноменологической) термодинамики, имеющих универсальный характер для всех объектов, соотношения С. ф. различны для разл. классов объектов, напр. классич. и квантовых идеальных или неидеальных газов, магнитных (спиновых) систем, теплового излучения и т. п., и требуют информации о внутр. свойствах конкретного объекта, прежде всего о микроскопич. свойствах этих частиц – их массы, заряда, спина и т. п.
Функции распределения
Осн. инструмент описания в С. ф. – статистич. функции распределения $w$, которые в рамках статистич. механики определены в фазовом пространстве обобщённых координат $q$ и импульсов $p$ объекта, а в рамках статистич.2/(2m_0)$ (в нерелятивистском приближении), $ℰ_п(q)=ℰ_{вн}(q;V_0)=0$, распределение (2) было получено Дж. Максвеллом в 1859, а с учётом потенциальной энергии во внешнем поле $ℰ_{вн}(q;V_0)$ – Л. Больцманом в 1871.
Если для объекта в данных физич. условиях необходимо квантовое описание, то принципиальная схема описания остаётся той же, однако вычислит. часть становится существенно сложнее. Функция распределения по квантовым состояниям, определяемым совокупностью квантовых чисел $\{n, α\}$ ($n$ – гл. квантовое число, $α$ – совокупность остальных квантовых чисел), имеет вид (при суммировании для ферми-частиц учитывается Паули принцип): $$w_{n,α}(V_0,T_0)=\exp \{[F(V_0,T_0)-ℰ_{n,α}(V_0)]/kT_0\},\\ \sum_{n,α}w_{n,α}(V_0,T_0)\equiv1. \tag{4}$$ Здесь $ℰ_{n,α}(V_0)$ – энергетич. спектр физич. объекта, определяемый посредством решения стационарного Шрёдингера уравнения (с учётом граничных условий) с операторным аналогом выражения (1) для энергии.
Во многих практически важных случаях спектр $ℰ_{n,α}$ фактически зависит только от гл. квантового числа $n$, т. е. имеет место вырождение по др. квантовым числам α с кратностью $g_n ⩾ 1$. Тогда формула (4) принимает вид$$w_n(V_0,T_0)=\\=g_n \exp \{[F(V_0,T_0)-ℰ_{n,α}(V_0)]/kT_0\},\\ \sum_n w_n(V_0,T_0)\equiv 1, \tag{5}$$ одинаковый как в статистич. механике, так и в статистич. термодинамике квантового объекта. Соответственно, аналог выражения (5) для классич. объекта может быть получен из формул (2) и (3) посредством введения структурной функции, или плотности состояний, $g(ℰ) > 1$, причём $g(ℰ)dℰ$ – число разл. состояний объекта в фазовом пространстве, приходящихся на малый интервал энергий $dℰ$. Существенно, что имеется связь $S_B(ℰ)=k \ln g(ℰ)$, где $S_B(ℰ)$ – энтропия Больцмана. Тогда в рамках статистич. термодинамики имеет место выражение $$w(ℰ;V_0,T_0)=\\= \exp \{[F(V_0,T_0)-S_B(ℰ )T_0-ℰ_{n,α} (V_0)]/kT_0\},\\ \int dpdq(.2 \propto 1/\sqrt{N}$для любых величин $A$ малы для макроскопич. объектов, однако играют важную роль вблизи критич. точек $Т_{кр}$ фазовых переходов, где обобщённые восприимчивости обнаруживают аномальный рост.
Для расчёта ср. величин и корреляционных функций полная функция распределения (2) содержит избыточную информацию и вполне достаточно ограничиться $r$-частичными $(r=1,2,…)$ функциями распределения $w_r$, представляющими собой условные вероятности, или полную функцию распределения $w_N$ (2), проинтегрированную по всем остальным $N-r$ пáрам переменных фазового пространства ($N$ – полное число частиц объекта).
Кинетические уравнения
Для набора $r$-частичных функций распределения существует цепочка кинетич. уравнений, определяемая взаимодействием частиц и позволяющая при определённых приближениях найти явный вид одно- и двухчастичных функций распределения.
В неравновесной С. ф. все функции распределения $w_r$ приобретают явную зависимость от времени $t$, причём, как и в равновесном случае, для величин $𝜕w_r/𝜕t$ имеет место цепочка кинетич. уравнений, решение которых в пределе $t→∞$ (фактически уже при $t ≫ τ$, где $τ$ – время термодинамич. релаксации) воспроизводит набор канонич. $r$-частичных функций распределения. Существенно, что в ходе временнóй эволюции энтропия объекта $S(t)$ растёт в соответствии со вторым началом термодинамики; впервые такой подход сформулировал Л. Больцман в 1871, получивший Максвелла распределение в качестве решения своего уравнения для случая идеального классич. газа. В совр. равновесной и неравновесной С. ф. используются математич. методы, заимствованные из квантовой теории поля, т. к. объекты в этих разделах физики обладают очень большим числом степеней свободы.
Приложения
Приложения С. ф. к конкретным физич. объектам многочисленны и разнообразны – см. Идеальный газ, Квантовый газ, Жидкость, Твёрдое тело, Металлы, Плазма, Тепловое излучение, Бозе – Эйнштейна статистика, Ферми – Дирака статистика, Квазичастицы, Кинетика физическая, Фазовый переход.
Молекулярная физика – Основные формулы
1. Основы молекулярно-кинетической теории. Газовые законы
1.1 Количество вещества
m — масса;
μ — молярная масса вещества;
N — число молекул;
NA = 6,02·1023 моль-1 — число Авогадро
1.2 Основное уравнение молекулярно-кинетической теории идеального газа
p — давление идеального газа;
m — масса одной молекулы;
n = N/V — концентрация молекул;
V — объем газа;
N — число молекул;
— среднее значение квадрата скорости молекул.
1.3 Средняя квадратичная скорость молекул идеального газа
k = 1,38·10-23 Дж/К — постоянная Больцмана;
R = kNA = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T = t+273 — абсолютная температура;
t — температура по шкале Цельсия.
1.4 Средняя кинетическая энергия молекулы одноатомного газа
1.5 Давление идеального газа
n — концентрация молекул;
k — постоянная Больцмана;
T — абсолютная температура.
1.6 Закон Бойля-Мариотта
p — давление;
V — объем газа.
1.7 Закон Шарля
p0 — давление газа при 0 °С;
α = 1/273 °C-1 — температурный коэффициент давления.
1.8 Закон Гей-Люссака
V0 — объем газа при 0 °С.
1.9 Уравнение Менделеева-Клапейрона
1.10 Объединенный закон газового состояния (уравнение Клапейрона)
1.11 Закон Дальтона
pi — парциальное давление i-й компоненты смеси газов.
2. Основы термодинамики
2.1 Внутренняя энергия идеального одноатомного газа
ν — количество вещества;
R = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T — абсолютная температура.
2.2 Элементарная работа, совершаемая газом,
при изменении объема на бесконечно малую величину dV
p — давление газа.
При изменении объема от V1 до V2
2.3 Первый закон термодинамики
ΔQ — количество подведенной теплоты;
ΔA — работа, совершаемая веществом;
ΔU — изменение внутренней энергии вещества.
2.4 Теплоемкость идеального газа
ΔQ — количество переданной системе теплоты на участке процесса;
ΔT — изменение температуры на этом участке процесса.
постоянная Ридберга | Определение, формула, значение и факты
Константа Ридберга , (символ R ∞ или R Η ), фундаментальная константа атомной физики, которая появляется в разработанных формулах (1890 г.) шведским физиком Йоханнесом Ридбергом, описывающим длины волн или частоты света в различных сериях связанных спектральных линий, в первую очередь тех, которые излучаются атомами водорода в серии Бальмера.Значение этой константы основано на предположении, что ядро атома, излучающего свет, чрезвычайно массивно по сравнению с одним вращающимся электроном (отсюда и символ бесконечности ∞). Константа может быть выражена как α 2 m e c /2 h , где α – постоянная тонкой структуры, m e – масса электрона, c – масса электрона. скорость света, а ч – постоянная Планка.
Бальмеровская серия водородных линийБальмеровская серия атомарного водорода.Эти линии излучаются, когда электрон в атоме водорода переходит с орбитали n = 3 или выше на орбиталь n = 2. Длины волн этих линий равны 1 / λ = R H (1/4 – 1/ n 2 ), где λ – длина волны, R H – постоянная Ридберга, n – уровень исходной орбиты.
Фото: Артур Л. Шавлов, Стэнфордский университет, и Теодор В.Ханш, Институт квантовой оптики Макса Планка; Масштаб: Encyclopædia Britannica, Inc. .Британская викторина
Викторина “Все о физике”
Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.
Значение постоянной Ридберга R ∞ составляет 10 973 731,56816 на метр. При использовании в этой форме в математическом описании серий спектральных линий результатом является количество волн на единицу длины или волновые числа. Умножение на скорость света дает частоты спектральных линий.
Химическое определение газовой постоянной (R)
Уравнения химии и физики обычно включают букву “R”, которая является символом газовой постоянной, молярной газовой постоянной или универсальной газовой постоянной.
Газовая постоянная – это физическая постоянная в уравнении закона идеального газа:
P – давление, V – объем, n – количество молей, T – температура.
Это также можно найти в уравнении Нернста, связывающем восстановительный потенциал полуячейки со стандартным электродным потенциалом:
E – потенциал ячейки, E 0 – стандартный потенциал ячейки, R – газовая постоянная, T – температура, n – количество моль обмениваемых электронов, F – постоянная Фарадея, Q – коэффициент реакции.
Газовая постоянная эквивалентна постоянной Больцмана, просто выраженной в единицах энергии на температуру на моль, в то время как постоянная Больцмана дается в единицах энергии на температуру на одну частицу. С физической точки зрения газовая постоянная – это константа пропорциональности, которая связывает шкалу энергии с температурной шкалой для моля частиц при данной температуре.
Единицы измерения газовой постоянной меняются в зависимости от других единиц, используемых в уравнении.
Одно общее значение – 8.3145 Дж / моль · К.
Значение газовой постоянной
Значение газовой постоянной «R» зависит от единиц измерения давления, объема и температуры.
- R = 0,0821 литр · атм / моль · K
- R = 8,3145 Дж / моль · K
- R = 8,2057 м 3 · атм / моль · K
- R = 62,3637 л · торр / моль · K или л · мм рт. Ст. / Моль · K
Почему R используется для газовой постоянной
Некоторые люди предполагают, что символ R используется для обозначения газовой постоянной в честь французского химика Анри Виктора Реньо, который провел эксперименты, которые впервые были использованы для определения постоянной.Однако неясно, является ли его имя истинным источником соглашения, используемого для обозначения константы.
Удельная газовая постоянная
Связанный фактор – это удельная газовая постоянная или индивидуальная газовая постоянная. Это может быть обозначено R или R , газ . Это универсальная газовая постоянная, деленная на молярную массу (M) чистого газа или смеси. Эта постоянная специфична для конкретного газа или смеси (отсюда и ее название), в то время как универсальная газовая постоянная одинакова для идеального газа.
Нижний регистр букв | верхний case Letters | Греческие буквы * и их имена | Сокращенное обозначение уравнения для физической величины | Символ единицы | С.I. Префикс и
его значение NB оно всегда предшествует символу единицы | |||
| а | А | α | Α | альфа | А = площадь A = нуклон число (атомная масса) а = ускорение а = Константа Вейна a = альфа-частица | а = атто | х 10 -18 | |
| б | B | β | Β | бета | В = плотность магнитного потока б = бета-частица | В = звонок (интенсивность звука) Бк = беккерель (активность) | ||
| c | C | χ | Χ | χ | С = емкость c = скорость света c = удельная теплоемкость | o С = градус Цельсия (температура) | с = сенти | х 10 -2 |
| d | D | δ | Δ | δ | д = диаметр d = расстояние D = расстояние от экрана до рисунка бахромы D = поглощенная доза Δ = изменение в δ = небольшое изменение | D = диоптрия (оптическая сила линзы) дБ = децибел (интенсивность звука) | д = деци да = дека (или дека) | х 10 -1 х 10 1 |
| е | E | ε | Ε | ε | e = заряд электрона E = энергия E k = кинетическая энергия E = напряженность электрического поля E = модуль Юнга ε = ЭДС ε = деформация растяжения ε o = диэлектрическая проницаемость свободного пространства | эВ = электрон-вольт (энергия) | E = exa | х 10 18 |
| ж | F | φ | Φ | фи | F = усилие f = частота f = фокусное расстояние f e = фокусное расстояние линзы окуляра f o = фокусное расстояние линзы объектива Φ = поток φ = работа выхода | F = фарад (емкость) | f = femto | х 10 -15 |
| грамм | грамм | γ | Γ | гамма | г = напряженность гравитационного поля g = ускорение свободного падения G = гравитационная постоянная G = проводимость γ = гамма-луч | Гр = серый (поглощенная доза) | G = гига | х 10 9 |
| час | ЧАС | η | Η | эта | h = высота h = постоянная Планка H = эквивалент дозы> H = постоянная Хаббла Η = коэффициент вязкости | H = Генри (индуктивность) Гц = герц (частота) | h = гектар | х 10 2 |
| я | я | ι | Ι | йота | I = текущий I 0 = пиковый ток I = интенсивность звука I = момент инерции | |||
| j | J | θ | Θ | тета | Дж = плотность тока Дж = момент инерции Θ = угол | Дж = джоуль (энергия) | ||
| k | K | κ | Κ | каппа | k = постоянная Больцмана k = жесткость пружины | K = кельвин (абсолютная температура) кг = килограмм (масса) | кг = | кгх 10 3 |
| л | L | λ | Λ | лямбда | л = длина л = удельная скрытая теплоемкость λ = длина волны λ = постоянная затухания L = собственная индуктивность L = угловой момент ln = натуральный логарифм журнал = журнал по основанию 10 | л = литр (= 1000 см 3 ) – измерение объема | ||
| м | M | м | μ | му | m = масса M = увеличение μ = проницаемость μ = коэффициент трения | м = метр (длина) м 2 = квадратный метр (площадь) м 3 = кубический метр (объем) | M = мега м = миллимк = микро | х 10 6 х 10 -3 х 10 -6 |
| п | N | ν | Ν | nu | N = номер N O = исходный номер N A = постоянная Авогадро N = количество витков провода n = количество родинок n = порядок дифракции n = количество носителей заряда на единицу объема n = показатель преломления | N = ньютон (сила или вес) | н. = нано | х 10 -9 |
| о | О | ο | Ο | омикрон | НЕ используется ни для чего – его слишком легко спутать с числом ноль | |||
| п | п | π | Π | пи | P = мощность p = давление p = импульс π = 3.14 | Па = паскаль (давление) | p = pico P = пета | х 10 -12 х 10 15 |
| q | Q | Q = заряд Q = тепло энергия Q = качество фактор | ||||||
| р | р | ρ | Ρ | rho | r = радиус R = сопротивление R = молярная газовая постоянная R = реакционная сила ρ = плотность ρ = удельное сопротивление рад = радиан | |||
| s | S | σ | Σ | сигма | s = смещение (векторная версия расстояния) s = ширина щели σ = проводимость σ = растягивающее напряжение σ = постоянная Стефана Σ = сумма | с = секунда (время) Зв = зиверт (эквивалент дозы) S = сименс (проводимость) | ||
| т | Т | τ | Τ | тау | t = время T = температура T = период формы волны T 1/2 = период полураспада T E = эффективный период полураспада T B = биогенный период полураспада T P = физический период полураспада | T = тесла (плотность магнитного потока) | Т = тера | х 10 12 |
| ты | U | υ | Υ | ипсилон | u = начальная скорость u = расстояние изображения U = U-значение U = внутреннее тепло системы | u = атомная единица массы (масса на атомных уровнях) | ||
| v | V | v = скорость v = конечная скорость (при использовании вместе с ‘u’) v = расстояние изображения V = объем В = разность потенциалов В 0 = пиковое напряжение | В = вольт (электрический потенциал) | |||||
| ш | W | ω | Ω | омега | W = проделанная работа ω = угловая скорость w = ширина бахромы | Ом = Ом (электрическое сопротивление) Вт = ватт (мощность) Wb = weber (магнитный поток) | ||
| Икс | Икс | χ | Χ | чи | x = ширина X = реактивное сопротивление | |||
| y | Y | ξ | Ξ | xi | y = высота | г = йокто Y = yotta | х 10 -24 х 10 24 | |
| z | Z | ζ | Ζ | дзета | z = глубина Z = число протонов (атомный номер) | z = zepto Z = дзета | х 10 -21 х 10 21 | |
| ПРИМЕЧАНИЕ НАСКОЛЬКО ВАЖНА ПЕРЕДАЧА БУКВЫ – УЗНАТЬ ПРИНЯТЫЕ СИМВОЛЫ ОСТОРОЖНО!!! | ||||||||
NB A кандидаты уровня должны: | ||||||||
определение R из The Free Dictionary
R
1 r 1 [ɑːʳ] N (= буква ) → R, r fR для Роберта → R de Ramón
три Rs (= чтения, письма и ) lectura, escritura y aritmética THREE RS
R
2 r 2 A. ABBR1. ( Brit ) = Rex → R
2. ( Brit ) = Regina → R
3. ( Geog 1066445) = река → R
4. = справа → dcha, der, der o
5. = Реомюр (шкала)
6. ( US ) ( Pol ) = Республиканский
Словарь испанского языка Коллинза – полное и несокращенное 8-е издание 2005 г. © William Collins Sons & Co.Ltd. 1971, 1988 © HarperCollins Publishers 1992, 1993, 1996, 1997, 2000, 2003, 2005
R
r [ˈɑː r ] n (= буква ) → R, r mR для Роберта, R для Roger (США) → R по Raoul
R
[ˈɑː r ] abbr(= справа ) → dr
(= Реомюра (шкала) ) → R
(США) (CINEMA) (= ограничено ) interdit aux moins de 17 ans
(British) (= Rex, Regina )
Collins Английский / французский электронный ресурс.© HarperCollins Publishers 2005
R
, r n → R nt , → r nt ; три рупии (= чтение, письмо и арифметика) → Lesen, Schreiben und Rechnen (die drei grundlegenden Fähigkeiten eines gebildeten Menschen)R
r
abbr of right → r.Немецкий словарь Коллинза – полное и несокращенное седьмое издание 2005 г. © William Collins Sons & Co. Ltd. 1980 © HarperCollins Publishers 1991, 1997, 1999, 2004, 2005, 2007
R
r [ɑːʳ] n ( letter ) → R, r f or m invthe three Rs → leggere, scrivere e far di conto
R для Роберта ( Am ) R для Roger → R come Roma
Collins Italian Dictionary 1st Edition © HarperCollins Издатели 1995
| количество | символ | значение |
|---|---|---|
| ускорение свободного падения | г | 9.806 65 м / с 2 |
| Возраст Вселенной | т 0 | 15 (5) Гр |
| единица атомной массы, унифицированная | u | 931,494 32 (28) МэВ / c 2 = 1,660 540 2 (10) x 10 -27 кг |
| астрономическая единица | а.е. | 1,495 978706 6 (2) x 10 11 м |
| Константа Авогадро | N A | 6.022136 7 (36) x 10 23 моль -1 |
| Магнетон Бора | mu B | 5,788 382 63 (52) x 10 -11 МэВ / Тл |
| Радиус Бора | a oo | 0,529 177 249 (24) x 10 -10 м |
| Постоянная Больцмана | к | 1,380 658 (12) x 10 -23 Дж / К = 8,617 385 (73) x 10 -5 эВ / К |
| Плотность энергии космического фона | rho гамма | 4.647 7 x 10 -34 ( T / 2,726 K) 4 г / см 3 = 0,260 71 ( T / 2,726 K) 4 эВ / см 3 |
| космический фон числовая плотность | n гамма | 410,89 ( T / 2,726 K) 3 см -3 |
| температура космического фона | T 0 | 2,726 + – 0,005 K |
| критическая плотность Вселенной | rho c | 2.775366 27 x 10 11 h 0 2 M S Mpc -3 = 1,878 82 (24) x 10 -29 h 0 2 г / см 3 = 1,053 94 (13) x 10 -5 h 0 2 ГэВ / см 3 |
| день, среднее звездное значение | d сидерический | 23 h 56 м 04 с .090 53 |
| дейтрон ( 2 H) масса | м г | 1875.613 39 (57) МэВ / c 2 |
| Масса Земли | M E | 5,973 70 (76) x 10 24 кг |
| Радиус Земли (экваториальный) | R E | 6,378 140 x 10 6 м |
| величина заряда электрона | e | 1.602 177 33 (49) x 10 -19 C = 4.803 206 8 (15) x 10 -10 esu |
| масса электрона | м e | 0.510 999 06 (15) МэВ / c 2 = 9,109 389 7 (54) x 10 -31 кг |
| радиус электрона, классический | r e | 2,817 940 92 (38) x 10 -15 м |
| электрон Комптоновская длина волны | лямбдабар е | 3,861593 23 (35) x 10 -13 м |
| плотность энтропии / постоянная Больцмана | с / к | 2.892 4 ( T / 2,726 K) 3 см -3 |
| постоянная тонкой структуры | альфа | 1 / 137,035 989 5 (61) |
| гравитационная постоянная | G N | 6,672 59 (85) x 10 -11 м 3 / (кг с 2 ) = 6,707 11 (86) x 10 -39 hc / (ГэВ / c 2 ) 2 |
| Постоянная Хаббла | H 0 | 100 h 0 км / (с Мпк) = h 0 /9.778 13 Гр |
| Постоянная Хаббла, нормированная | h 0 | 0,5 < h 0 <0,85 |
| jansky | Ян | 10 -26 Вт / (м 2 Гц) |
| световой год (устарело) | св. Лет | 0,306 6 … pc = 0,946 1 … x 10 16 м |
| Основание наперского (натурального) логарифма | e | 2.718 281 828 459045 235 |
| ядерный магнетон | mu N | 3,152 451 66 (28) x 10 -14 МэВ / Тл |
| парсек (а.е. / угл.сек) | шт. | 3,085 677 580 7 (4) x 10 16 м = 3,262 … ly |
| проницаемость свободного пространства | mu 0 | 4 pi x 10 -7 НЕТ 2 = 12,566 370 614… x 10 -7 НЕТ 2 |
| диэлектрическая проницаемость свободного пространства | эпсилон 0 | 8,854 187817 … x 10 -12 Ф / м |
| пи | пи | 3,141 592 653 589 7 |
| Постоянная Планка | ч | 6,626075 5 (40) x 10 -34 Дж с |
| Постоянная Планка, приведенная | бар | 1.054572 66 (63) x 10 -34 Дж с = 6,582 122 0 (20) x 10 -22 МэВ с |
| Планковская масса | м P | 1,221 047 (79) x 10 19 ГэВ / c 2 = 2,176 71 (14) x 10 -8 кг |
| масса протона ( 1 H) | м p | 938,272 31 (28) МэВ / c 2 = 1,672 623 1 (10) x 10 -27 кг = 1.007276470 (12) u = 1836,152 701 (37) м e |
| энергия Ридберга | h c R oo | 13,605 698 1 (40) эВ |
| Радиус Солнца по Шварцшильду | 2 G N M S / c 2 | 2,953 250 08 км |
| скорость света в вакууме | с | 299 792 458 м / с |
| Константа Стефана-Больцмана | сигма | 5.670 51 (19) x 10 -8 Вт / (м 2 K 4 ) |
| константа сильной связи | альфа с | 0,118 (3) |
| Солнечное расстояние от ядра | R o | 8,0 (5) кпк |
| Светимость Солнца | л ю | 3.846 x 10 26 W |
| Солнечная масса | M S | 1.988 92 (25) x 10 30 кг |
| Радиус Солнца (экваториальный) | R S | 6,96 x 10 8 м |
| Скорость солнца вокруг ядра | Theta o | 220 (20) км / с |
| Скорость Солнца относительно космического фона | 369,5 + – 3,0 км / с | |
| Поперечное сечение Томпсона | сигма T | 0.665 246 16 (18) сарай |
| W + – Масса бозона | м Вт | 80,33 (15) ГэВ / c 2 |
| Константа закона смещения Вина | б | 2,897 756 (24) x 19) x 10 -3 м K |
| год, сидерический (неподвижная звезда в неподвижную звезду, 1994) | y сидерический | 31 558 149,8 s |
| год, тропический (от равноденствия до равноденствия, 1994) | г | 31 556 925.2 с |
| Z 0 Масса бозона | м Z | 91,187 (7) ГэВ / c 2 |
Определение, значения и единицы ~ ChemistryGod
Идеальная газовая постоянная также известна как универсальная газовая постоянная или молярная газовая постоянная или просто газовая постоянная . Это очень важная константа в химии и физике. Обозначается как R . Размерность газовой постоянной выражается в энергии на единицу моля на единицу температуры.Значение газовой постоянной в единицах СИ составляет 8,314 Дж моль −1 K −1 . Газовая постоянная имеет те же единицы, что и энтропия и молярная теплоемкость.
Происхождение символа R для идеальной газовой постоянной до сих пор неясно. Некоторые говорят, что символ газовой постоянной назван в честь французского химика Анри Реньо. Он известен своими работами по измерению тепловых свойств газов.
Содержание
Определение постоянной идеального газа
Постоянная идеального газа – это константа пропорциональности в уравнении идеального газа.Это отношение произведения давления и объема к произведению моля и температуры.
Формула газовой постоянной
Формула газовой постоянной из уравнения закона идеального газа:
, где P – давление идеального газа,
V – объем, который занимает газ,
n – количество молей газа,
и T – температура в кельвинах.
Единица измерения постоянной идеального газа в системе СИ
Единица измерения постоянной идеального газа в системе СИ может быть определена как:
Единица измерения давления в системе СИ – Па или Н · м −2 .
Теперь Н · м эквивалентен джоуля, который является единицей энергии в системе СИ.
Значение постоянной идеального газа в единицах СИ
На STP ( P = 101325 Па, T = 273,15 K) молярный объем или объем на моль составляет 22,414 × 10 −3 м 3 моль -1 . Следовательно, мы можем рассчитать значение R как
Это приблизительное значение постоянной идеального газа.
На 26 -й сессии Генеральной конференции по мерам и весам (CGPM) пересмотренное и точное значение газовой постоянной составляет 8.314 462 618 153 24 Дж моль −1 K −1 .
Значения идеальной константы в разных единицах
Значение R в различных единицах представлено в таблице ниже.
| Значение | Единица |
|---|---|
| 8,314 462618 153 24 | Дж моль −1 K −1 |
| Дж кмоль −1 K −1 | |
| 8.314462618153 24 × 10 7 | эрг моль −1 K −1 |
| 8.314 462618153 24 × 10 3 | а.е.м. 2 с – 2 K −1 |
| 8.205 733 8 (47) × 10 −5 | м 3 атм моль −1 K −1 |
| 0,082 057338 (47) | л атм моль −1 K −1 |
| 1.987203 6 (11) | кал-моль −1 K −1 |
| 62,363 577 (36) | мм рт. Ст. Л моль −1 K −1 |
| 62,363 577 (36 ) | торр л моль −1 K −1 |
| 1 545,348 96 (3) | фут-фунт f фунт-моль −1 K −1 |
| 1.985 88 | Btu фунт-моль -1 R -1|
| 998.970 1 (17) | фут 3 мм рт. |
Удельная газовая постоянная
Удельная газовая постоянная – это версия идеальной газовой постоянной в массовой форме, а не в молярной. Он определяется как отношение постоянной идеального газа к молярному газу газа. Он имеет размерность энергии на единицу массы на единицу абсолютной температуры.Единица СИ – Дж кг −1 K −1 . Обозначается как R sp .
, где M w – молярная масса или молекулярная масса газа.
Молекулярная масса газообразного водорода составляет 2 г · моль -1 . Итак, R sp для водорода рассчитывается как:
Аналогично, для воздуха с молекулярной массой 28,84 г / моль -1 .
Кроме того, удельная газовая постоянная находится в соотношении Майера.
, где c p – удельная газовая постоянная при постоянном давлении, а c v – удельная теплоемкость при постоянном объеме.
Удельная газовая постоянная очень полезна в инженерных приложениях термодинамики.
Постоянная Больцмана и постоянная идеального газа
Постоянная идеального газа и постоянная Больцмана ( k B ) связаны постоянной Авогадро ( N A ).Постоянная Больцмана – это отношение постоянной идеального газа к постоянной Авогадро.
Используя уравнение
,, где м – масса молекулы газа.
Газовая постоянная в других важных уравнениях
Помимо приведенных выше уравнений, газовая постоянная также находится во многих других важных уравнениях химии. Некоторые из этих уравнений обсуждаются ниже.
Уравнение Нернста
Уравнение Нернста – это уравнение в электрохимии, которое связывает потенциал электрохимической реакции с потенциалом стандартного электрода.Уравнение названо в честь немецкого химика Вальтера Нернста. Для электрохимической полуячейки уравнение Нернста:
, где:
E красный – приведенный потенциал полуячейки при температуре T ,
E ⊖
красный – стандартный потенциал полуячейки,
α красный и α ox – активности восстановленных и окисленных частиц,
и z и F – количество перенесенных электронов и постоянная Фарадея.
Уравнение Аррениуса
Уравнение Аррениуса – важное уравнение, используемое в химической кинетике. Используется для определения константы скорости k .
, где A – постоянная Аррениуса, а E a – энергия активации.
Сопутствующие статьи
Закон об идеальном газе | Физика
Цели обучения
К концу этого раздела вы сможете:
- Сформулируйте закон идеального газа, используя молекулы и моль.
- Используйте закон идеального газа для расчета изменения давления, температуры, изменения объема или количества молекул или молей в заданном объеме.
- Используйте число Авогадро для преобразования числа молекул в число молей.
Рис. 1. Воздух внутри воздушного шара, летящего над Путраджайей, Малайзия, горячее окружающего воздуха. В результате воздушный шар испытывает подъемную силу, толкающую его вверх. (Источник: Кевин По, Flickr)
В этом разделе мы продолжаем исследовать термическое поведение газов.В частности, мы исследуем характеристики атомов и молекул, из которых состоят газы. (Большинство газов, например азот, N 2 , и кислород, O 2 , состоят из двух или более атомов. Мы в первую очередь будем использовать термин «молекула» при обсуждении газа, потому что этот термин также может применяться к одноатомные газы, такие как гелий.)
Газы легко сжимаются. Мы можем увидеть доказательства этого в Таблице 1 в Термическом расширении твердых тел и жидкостей, где вы заметите, что газы имеют наибольших коэффициентов объемного расширения.Большие коэффициенты означают, что газы расширяются и сжимаются очень быстро при изменении температуры. Кроме того, вы заметите, что большинство газов расширяются с такой же скоростью или имеют такое же значение β . Это поднимает вопрос о том, почему все газы должны действовать почти одинаково, когда жидкости и твердые тела имеют сильно различающиеся скорости расширения.
Ответ заключается в большом разделении атомов и молекул в газах по сравнению с их размерами, как показано на рисунке 2. Поскольку атомы и молекулы имеют большие расстояния, силы между ними можно игнорировать, за исключением случаев, когда они сталкиваются друг с другом во время столкновений. .Движение атомов и молекул (при температурах, значительно превышающих температуру кипения) происходит быстро, так что газ занимает весь доступный объем, и газы расширяются быстро. Напротив, в жидкостях и твердых телах атомы и молекулы расположены ближе друг к другу и весьма чувствительны к силам между ними.
Рис. 2. Как показано, атомы и молекулы в газе обычно широко разделены. Поскольку силы между ними на этих расстояниях довольно слабы, свойства газа больше зависят от количества атомов в единице объема и температуры, чем от типа атома.
Чтобы получить некоторое представление о том, как давление, температура и объем газа связаны друг с другом, рассмотрим, что происходит, когда вы закачиваете воздух в изначально спущенную шину. Объем шины сначала увеличивается прямо пропорционально количеству впрыскиваемого воздуха без значительного увеличения давления в шине. Когда шина расширилась почти до своего полного размера, стенки ограничивают объемное расширение. Если продолжать закачивать в него воздух, давление возрастает. Давление будет еще больше увеличиваться, когда автомобиль едет, а шины двигаются.Большинство производителей указывают оптимальное давление в шинах для холодных шин. (См. Рисунок 3.)
Рис. 3. (a) Когда воздух закачивается в спущенную шину, его объем сначала увеличивается без значительного увеличения давления. (b) Когда шина заполнена до определенной точки, стенки шины сопротивляются дальнейшему расширению, и давление увеличивается с увеличением количества воздуха. (c) Когда шина накачана, ее давление увеличивается с температурой.
При комнатной температуре столкновениями между атомами и молекулами можно пренебречь.В этом случае газ называется идеальным газом, и в этом случае соотношение между давлением, объемом и температурой задается уравнением состояния, называемым законом идеального газа.
Закон об идеальном газе
Закон идеального газа гласит, что PV = NkT , где P – абсолютное давление газа, V – объем, который он занимает, N – количество атомов и молекул в газе. газа, а Т – его абсолютная температура.Константа k называется постоянной Больцмана в честь австрийского физика Людвига Больцмана (1844–1906) и имеет значение k = 1,38 × 10 −23 Дж / К.
Закон идеального газа может быть выведен из основных принципов, но первоначально он был выведен из экспериментальных измерений закона Чарльза (объем, занимаемый газом, пропорционален температуре при фиксированном давлении) и закона Бойля (для фиксированной температуры, произведение PV является константой).В модели идеального газа объем, занимаемый его атомами и молекулами, составляет ничтожную долю от V . Закон идеального газа описывает поведение реальных газов в большинстве условий. (Обратите внимание, например, что N – это общее количество атомов и молекул, независимо от типа газа.)
Давайте посмотрим, как закон идеального газа согласуется с поведением заполнения шины, когда она накачивается медленно и температура постоянна. Сначала давление P по существу равно атмосферному давлению, а объем V увеличивается прямо пропорционально количеству атомов и молекул N , введенных в шину.Как только объем шины остается постоянным, уравнение PV = NkT предсказывает, что давление должно увеличиваться пропорционально числу N атомов и молекул .
Пример 1. Расчет изменений давления из-за изменений температуры: давление в шинах
Предположим, шина велосипеда полностью накачана, с абсолютным давлением 7,00 × 10 5 Па (манометрическое давление чуть менее 90,0 фунтов / дюйм 2 ) при температуре 18,0 ° C.Какое давление будет после повышения температуры до 35,0ºC? Предположим, что нет заметных утечек или изменений объема.
Стратегия
Давление в шине меняется только из-за изменения температуры. Сначала нам нужно определить, что мы знаем и что мы хотим знать, а затем определить уравнение, которое нужно решить для неизвестного.
Нам известно начальное давление P 0 = 7,00 × 10 5 Па, начальная температура T 0 = 18.0ºC, а конечная температура T f = 35,0ºC. Мы должны найти конечное давление P f . Как мы можем использовать уравнение PV = NkT ? На первый взгляд может показаться, что информации недостаточно, потому что объем V и количество атомов N не указаны. Мы можем использовать уравнение дважды: P 0 V 0 = NkT 0 и P f V f = NkT f .Если разделить P f V f на P 0 V 0 , мы можем получить уравнение, которое позволяет нам решить для P f .
[латекс] \ displaystyle \ frac {P _ {\ text {f}} V _ {\ text {f}}} {P_0V_0} = \ frac {N _ {\ text {f}} kT _ {\ text {f}}} {N_0kT_0} \\ [/ latex]
Поскольку объем постоянный, V f и V 0 одинаковы и взаимно компенсируются. То же самое верно для N f и N 0 и k , что является константой.Следовательно,
[латекс] \ displaystyle \ frac {P _ {\ text {f}}} {P_0} = \ frac {T _ {\ text {f}}} {T_0} \\ [/ latex]
Затем мы можем изменить это, чтобы решить для P f : [latex] P _ {\ text {f}} = P_0 \ frac {T _ {\ text {f}}} {T_0} \\ [/ latex] , Где температура должна быть в единицах кельвина, потому что T 0 и T f являются абсолютными температурами.
Решение
Преобразование температуры из Цельсия в Кельвин:
Т 0 = (18.5 \ text {Pa} \\ [/ latex]
Обсуждение
Конечная температура примерно на 6% выше исходной температуры, поэтому конечное давление также примерно на 6% больше. Обратите внимание, что абсолютное давление и абсолютное давление должны использоваться в законе идеального газа.
Установление соединений: домашний эксперимент – охлаждение воздушного шара
Надуйте баллон при комнатной температуре. Оставьте надутый баллон в холодильнике на ночь.Что происходит с воздушным шаром и почему?
Пример 2. Расчет количества молекул в кубическом метре газа
Сколько молекул содержится в типичном объекте, таком как газ в шине или вода в напитке? Мы можем использовать закон идеального газа, чтобы дать нам представление о типичных размерах N .
Вычислите количество молекул в кубическом метре газа при стандартной температуре и давлении (STP), которые определены равными 0ºC и атмосферному давлению.
Стратегия
Поскольку давление, объем и температура заданы, мы можем использовать закон идеального газа PV = NkT , чтобы найти N .{25} \ text {молекулы} \\ [/ latex]
Обсуждение
Это число, несомненно, велико, учитывая, что газ – это в основном пустое пространство. N огромен даже в небольших объемах. Например, 1 см 3 газа в STP содержит 2,68 × 10 19 молекул. Еще раз отметим, что N одинаков для всех типов или смесей газов.
Родинки и число Авогадро
Иногда при измерении количества вещества удобно работать с единицей, отличной от молекул. моль (сокращенно моль) определяется как количество вещества, которое содержит столько атомов или молекул, сколько атомов содержится ровно в 12 граммах (0,012 кг) углерода-12. Фактическое количество атомов или молекул в одном моле называется числом Авогадро ( N A ) по признанию итальянского ученого Амедео Авогадро (1776–1856). Он разработал концепцию мола, основываясь на гипотезе о том, что равные объемы газа при одинаковом давлении и температуре содержат равное количество молекул.То есть количество не зависит от типа газа. Эта гипотеза подтвердилась, и значение числа Авогадро составляет N A = 6,02 × 10 23 моль -1 .
Число Авогадро
Один моль всегда содержит 6,02 × 10 23 частиц (атомов или молекул), независимо от элемента или вещества. Моль любого вещества имеет массу в граммах, равную его молекулярной массе, которую можно вычислить из атомных масс, указанных в периодической таблице элементов.
N A = 6,02 × 10 23 моль −1
Рис. 4. Насколько велика родинка? На макроскопическом уровне один крот мячей для настольного тенниса покроет Землю на глубину около 40 км.
Проверьте свое понимание
Активным ингредиентом таблетки Тайленола является 325 мг ацетаминофена (C 8 H 9 NO 2 ). Найдите количество активных молекул парацетамола в одной таблетке.
Решение
Сначала нам нужно вычислить молярную массу (массу одного моля) ацетаминофена.{-3} \ text {moles} \\ [/ latex]
Затем используйте число Авогадро, чтобы вычислить количество молекул.
N = (2,15 × 10 −3 моль) (6,02 × 10 23 молекул / моль) = 1,30 × 10 21 молекул
Пример 3. Расчет молей на кубический метр и литров на моль
Рассчитайте следующее:
- Количество молей в 1,00 м 3 газа на СТП
- Количество литров газа на моль.3} = 22,5 \ text {л / моль} \\ [/ latex]
Обсуждение
Это значение очень близко к принятому значению 22,4 л / моль. Небольшая разница связана с ошибками округления, вызванными использованием трехзначного ввода. Опять же, это число одинаково для всех газов. Другими словами, он не зависит от газа.
(Средняя) молярная масса воздуха (примерно 80% N 2 и 20% O 2 составляет M = 28,8 г. Таким образом, масса одного кубического метра воздуха составляет 1,28 кг.Если гостиная имеет размеры 5 м × 5 м × 3 м, масса воздуха внутри комнаты составляет 96 кг, что является типичной массой человека.
Проверьте свое понимание
Плотность воздуха при стандартных условиях ( P = 1 атм и T = 20ºC) составляет 1,28 кг / м 3 . При каком давлении будет плотность 0,64 кг / м 3 , если температура и количество молекул остаются постоянными?
Решение
Лучший способ подойти к этому вопросу – подумать о том, что происходит.Если плотность упадет до половины от первоначального значения и никакие молекулы не потеряны, объем должен удвоиться. Если мы посмотрим на уравнение PV = NkT , мы увидим, что при постоянной температуре давление обратно пропорционально объему. Следовательно, если объем увеличивается вдвое, давление должно упасть до половины от исходного значения, и P f = 0,50 атм.
Закон об идеальном газе, переформулированный с использованием молей
Очень распространенное выражение закона идеального газа использует число молей, n , а не число атомов и молекул, N .Мы начинаем с закона идеального газа, PV = NkT , и умножаем и делим уравнение на число Авогадро N A . Это дает [latex] PV = \ frac {N} {N _ {\ text {A}}} N _ {\ text {A}} kT \\ [/ latex].
Обратите внимание, что [латекс] n = \ frac {N} {N _ {\ text {A}}} \\ [/ latex] – это количество молей. Мы определяем универсальную газовую постоянную R = N A k и получаем закон идеального газа в молях.
Закон идеального газа (в молях)
Закон идеального газа (в молях): PV = nRT .
Числовое значение R в единицах СИ составляет R = N A k = (6,02 × 10 23 моль −1 ) (1,38 × 10 −23 Дж / К ) = 8,31 Дж / моль · К.
В прочих единицах,
R = 1,99 кал / моль · K
R = 0,0821 л · атм / моль · K
Вы можете использовать любое значение R , наиболее подходящее для конкретной задачи.
Пример 4. Расчет количества молей: газ в шине велосипеда
Сколько молей газа в шине велосипеда объемом 2.00 × 10 −3 м 3 (2,00 л), давление 7,00 × 10 5 Па (манометрическое давление чуть менее 90,0 фунт / дюйм 2 ) и при температуре 18,0 ° C?
Стратегия
Определите известные и неизвестные и выберите уравнение для решения неизвестного. В этом случае мы решаем закон идеального газа, PV = nRT , для числа молей n .
Решение
Определите известных:
[латекс] \ begin {array} {lll} P & = & 7.3 \ right)} {\ left (8.31 \ text {J / mol} \ cdot \ text {K} \ right) \ left (291 \ text {K} \ right)} \\\ text {} & = & 0. 579 \ text {mol} \ end {array} \\ [/ latex]
Обсуждение
Наиболее удобный выбор для R в этом случае – 8,31 Дж / моль · К, поскольку известные нам величины выражены в единицах СИ. Давление и температура получены из начальных условий в Примере 1, но мы получили бы тот же ответ, если бы использовали окончательные значения.
Закон идеального газа можно рассматривать как еще одно проявление закона сохранения энергии (см. Сохранение энергии).Работа, выполняемая с газом, приводит к увеличению его энергии, увеличению давления и / или температуры или уменьшению объема. Эту повышенную энергию также можно рассматривать как увеличенную внутреннюю кинетическую энергию с учетом атомов и молекул газа.
Закон идеального газа и энергия
Давайте теперь исследуем роль энергии в поведении газов. Когда вы накачиваете велосипедную шину вручную, вы выполняете работу, многократно прилагая силу на расстоянии. Эта энергия идет на повышение давления воздуха внутри шины и повышение температуры насоса и воздуха.
Закон идеального газа тесно связан с энергией: единицы измерения с обеих сторон – джоули. Правая часть закона идеального газа в PV = NkT составляет NkT . Этот термин примерно соответствует количеству поступательной кинетической энергии N атомов или молекул при абсолютной температуре T , как мы формально увидим в «Кинетической теории: атомное и молекулярное объяснение давления и температуры». Левая часть закона идеального газа – PV , который также имеет единицы измерения в джоулях.Из нашего исследования жидкостей мы знаем, что давление – это один из видов потенциальной энергии на единицу объема, поэтому давление, умноженное на объем, является энергией. Важным моментом является то, что в газе есть энергия, связанная как с его давлением, так и с его объемом. Энергия может быть изменена, когда газ выполняет работу по мере расширения – это мы исследуем в разделе «Методы теплопередачи и теплопередачи» – аналогично тому, что происходит в бензиновых или паровых двигателях и турбинах.
Стратегия решения проблем: Закон об идеальном газе
Шаг 1. Изучите ситуацию, чтобы определить, что речь идет об идеальном газе. Большинство газов почти идеальны.
Шаг 2. Составьте список того, какие количества указаны или могут быть выведены из проблемы, как указано (определить известные количества). Преобразуйте известные значения в соответствующие единицы СИ (K для температуры, Па для давления, m 3 для объема, молекул для N и молей для n ).
Шаг 3. Определите, что именно необходимо определить в проблеме (определите неизвестные количества).Письменный список полезен.
Шаг 4. Определите, известно ли количество молекул или количество молей, чтобы решить, какую форму закона идеального газа использовать. Первая форма – PV = NkT и включает N , количество атомов или молекул. Вторая форма – PV = nRT и включает n , количество молей.
Шаг 5. Решите закон идеального газа для количества, которое необходимо определить (неизвестное количество).Вам может потребоваться взять отношение конечных состояний к начальным состояниям, чтобы исключить неизвестные количества, которые остаются фиксированными.
Шаг 6. Подставьте известные величины вместе с их единицами в соответствующее уравнение и получите численные решения с указанием единиц. Обязательно используйте абсолютную температуру и абсолютное давление.
Шаг 7. Проверьте ответ, чтобы узнать, разумен ли он: имеет ли он смысл?
Проверьте свое понимание
Жидкости и твердые вещества имеют плотность примерно в 1000 раз больше, чем газы.Объясните, как это означает, что расстояния между атомами и молекулами в газах примерно в 10 раз больше, чем размер их атомов и молекул.
Решение
Атомы и молекулы в твердых телах и жидкостях расположены близко друг к другу. В газах они разделены пустым пространством. Таким образом, газы имеют меньшую плотность, чем жидкости и твердые тела. Плотность – это масса на единицу объема, а объем связан с размером тела (например, сферы) в кубе. Таким образом, если расстояние между атомами и молекулами увеличивается в 10 раз, то занимаемый объем увеличивается в 1000 раз, а плотность уменьшается в 1000 раз.
Краткое содержание раздела
- Закон идеального газа связывает давление и объем газа с количеством молекул газа и температурой газа.
- Закон идеального газа можно записать в терминах числа молекул газа: PV = NkT , где P – давление, V – объем, T – температура, N – число. молекул, k – постоянная Больцмана k = 1,38 × 10 –23 Дж / K.
- Моль – это количество атомов в образце углерода-12 массой 12 г.
- Число молекул в моле называется числом Авогадро NA , NA = 6,02 × 10 23 моль -1 .
- Моль любого вещества имеет массу в граммах, равную его молекулярной массе, которая может быть определена из периодической таблицы элементов.
- Закон идеального газа также может быть записан и решен в терминах числа молей газа: PV = nRT , где n – число молей, а R – универсальная газовая постоянная, R = 8 .31 Дж / моль ⋅ К.
- Закон идеального газа обычно действует при температурах, значительно превышающих температуру кипения.
Концептуальные вопросы
Узнайте человеческое население Земли. Есть ли на Земле крот людей? Если средняя масса человека 60 кг, рассчитайте массу родинки людей. Как соотносится масса крота людей с массой Земли?
При каких обстоятельствах вы ожидаете, что газ будет вести себя значительно иначе, чем предсказывает закон идеального газа?
Газовый термометр постоянного объема содержит фиксированное количество газа.Какое свойство газа измеряется, чтобы указать его температуру?
Задачи и упражнения
- Манометрическое давление в шинах вашего автомобиля составляет 2,50 × 10 5 Н / м 2 при температуре 35,0 ° C, когда вы едете на пароме на Аляску. Какое у них манометрическое давление позже, когда их температура упадет до –40,0ºC?
- Преобразуйте абсолютное давление 7,00 × 10 5 Н / м 2 в манометрическое давление в фунтах / дюймах 2 .(Это значение было заявлено чуть меньше 90,0 фунтов / дюйм 2 в Примере 4. Это так?)
- Предположим, что газовая лампа накаливания изготовлена таким образом, что газ внутри колбы находится под атмосферным давлением, когда колба имеет температуру 20,0 ° C. (a) Найдите манометрическое давление внутри такой колбы, когда она горячая, при условии, что ее средняя температура составляет 60,0ºC (приблизительное значение), и пренебрегая любыми изменениями в объеме из-за теплового расширения или утечки газа. (b) Фактическое конечное давление для лампочки будет меньше, чем рассчитано в части (а), потому что стеклянная колба расширится.Каким будет фактическое конечное давление с учетом этого? Это незначительная разница?
- Большие шары, наполненные гелием, используются для подъема научного оборудования на большие высоты. а) Каково давление внутри такого воздушного шара, если он начинается на уровне моря с температурой 10,0ºC и поднимается на высоту, на которой его объем в двадцать раз превышает первоначальный объем, а его температура составляет –50,0ºC? б) Какое манометрическое давление? (Предположим, что атмосферное давление постоянно.)
- Подтвердите, что единицы nRT являются единицами энергии для каждого значения R: (a) 8.31 Дж / моль K, (b) 1,99 кал / моль K, и (c) 0,0821 л ⋅ атм / моль ⋅ K.
- В тексте показано, что N / V = 2,68 × 10 25 м −3 для газа на СТП. (a) Покажите, что это количество эквивалентно N / V = 2,68 × 10 19 см −3 , как указано. (b) Примерно сколько атомов содержится в одном мкм 3 (кубический микрометр) в STP? (c) Что ваш ответ на часть (b) подразумевает разделение атомов и молекул?
- Рассчитайте количество родинок в 2.00-литровый объем воздуха в легких обычного человека. Учтите, что температура воздуха 37,0 ° C (температура тела).
- У пассажира самолета 100 см. 3 воздуха в желудке непосредственно перед вылетом из аэропорта на уровне моря. Какой объем будет в воздухе на крейсерской высоте, если давление в салоне упадет до 7,50 × 10 4 Н / м 2 ?
- (a) Каков объем (в км 3 ) количества песчинок Авогадро, если каждое зерно представляет собой куб и имеет стороны равные 1.0 мм в длину? (b) Сколько километров протяженностью пляжей это покрыло бы, если бы ширина пляжа в среднем составляла 100 м, а глубина – 10,0 м? Пренебрегайте воздушными промежутками между зернами.
- Дорогая вакуумная система может достичь давления всего 1,00 × 10 –7 Н / м 2 при 20 ° C. Сколько атомов в кубическом сантиметре при таком давлении и температуре?
- Плотность атомов газа в определенном месте в пространстве над нашей планетой составляет примерно 1,00 × 10 11 м −3 , а давление равно 2.75 × 10 –10 Н / м 2 в этом пространстве. Какая там температура?
- Велосипедная шина имеет давление 7,00 × 10 5 Н / м 2 при температуре 18,0 ° C и содержит 2,00 л газа. Каким будет его давление, если вы выпустите воздух объемом 100 см3 при атмосферном давлении? Предположим, что температура и объем шины остаются постоянными.
- Газовый баллон высокого давления содержит 50,0 л токсичного газа при давлении 1,40 × 10 7 Н / м 2 и температуре 25 ° C.0ºC. Его клапан протекает после падения баллона. Цилиндр охлаждается до температуры сухого льда (–78,5 ° C), чтобы снизить скорость утечки и давление, чтобы его можно было безопасно отремонтировать. (а) Каково конечное давление в резервуаре, если предположить, что утечка газа при охлаждении незначительна, и что фазового перехода нет? б) Какое будет конечное давление, если одна десятая часть газа улетучится? (c) До какой температуры необходимо охладить резервуар, чтобы снизить давление до 1,00 атм (при условии, что газ не меняет фазу и что во время охлаждения нет утечки)? (d) Является ли охлаждение резервуара практическим решением?
- Найдите количество родинок в 2.00 л газа при 35,0ºC и давлении 7,41 × 10 7 Н / м 2 .
- Вычислите глубину, на которую количество мячей Авогадро для настольного тенниса покроет Землю. Каждый шар имеет диаметр 3,75 см. Предположим, что пространство между шарами добавляет дополнительные 25,0% к их объему, и предположим, что они не раздавлены собственным весом.
- (a) Каково манометрическое давление в автомобильной шине 25,0 ° C, содержащей 3,60 моль газа в объеме 30,0 л? (b) Каким будет его манометрическое давление, если вы добавите 1.00 л газа первоначально при атмосферном давлении и 25,0 ° C? Предположим, что температура возвращается к 25,0 ° C, а объем остается постоянным.
- (a) В глубоком космосе между галактиками плотность атомов всего лишь 10 6 атомов / м 3 , а температура – холодная 2,7 К. Что такое давление? б) Какой объем (в м 3 ) занимает 1 моль газа? (c) Если этот объем является кубом, какова длина его сторон в километрах?
Глоссарий
закон идеального газа: физический закон, который связывает давление и объем газа с числом молекул газа или числом молей газа и температурой газа
Постоянная Больцмана: k , физическая постоянная, которая связывает энергию с температурой; к = 1.38 × 10 –23 Дж / К
Число Авогадро: NA , количество молекул или атомов в одном моль вещества; NA = 6,02 × 10 23 частиц / моль
моль: количество вещества, масса которого (в граммах) равна его молекулярной массе
Избранные решения проблем и упражнения
1.










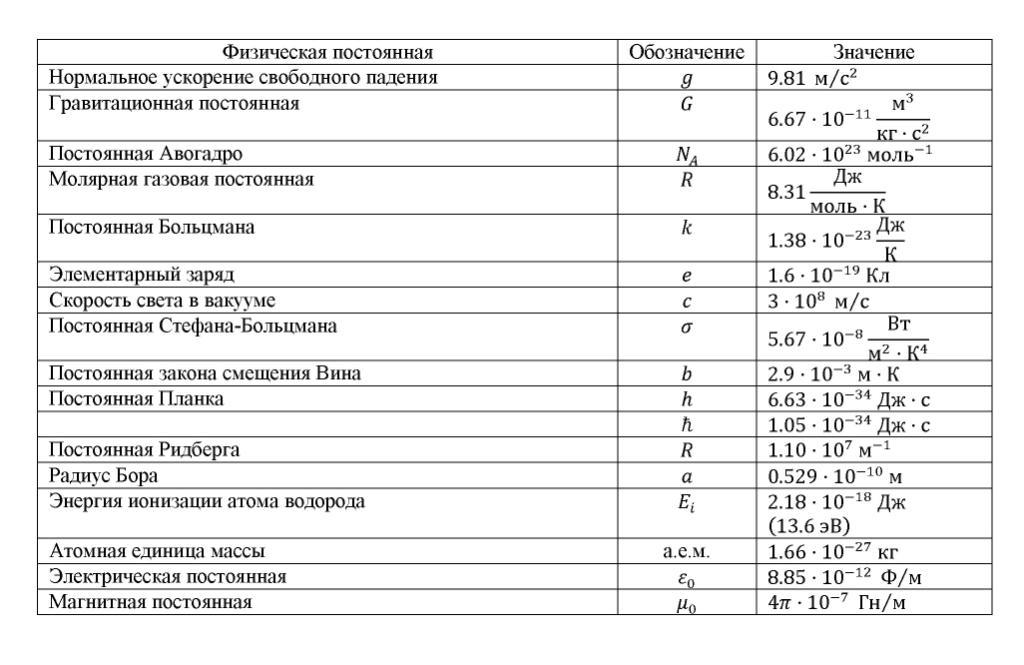
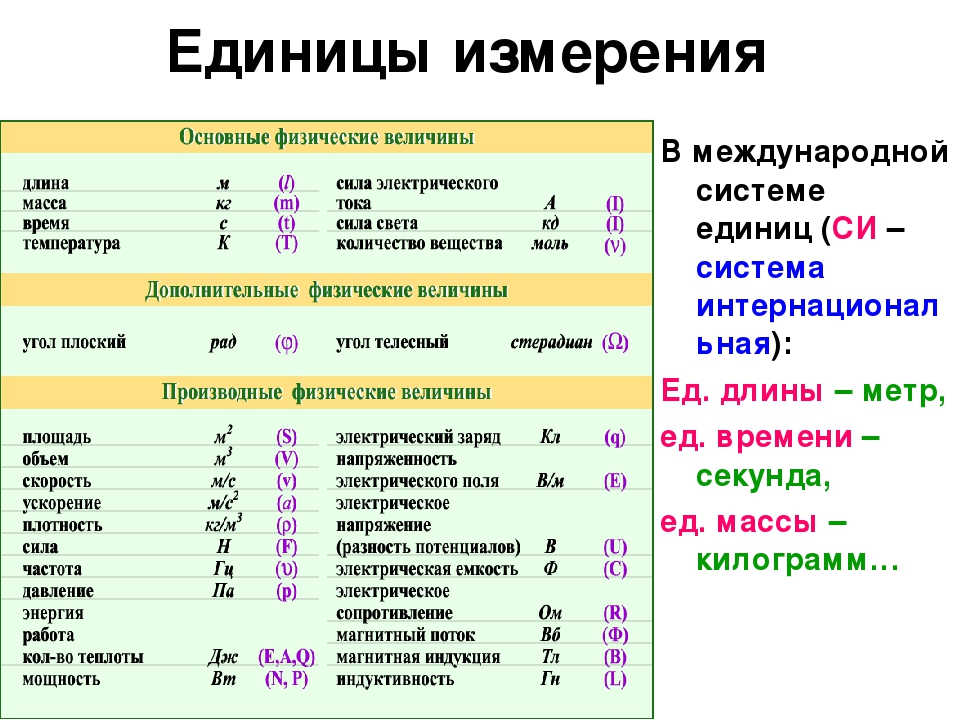 изм. физ. вел.
изм. физ. вел.
 изм. физ. вел.
изм. физ. вел. 

 изм. физ. вел.
изм. физ. вел. 
 физ. вел.
физ. вел. 