Что называется падением напряжения на участке цепи: при нагрузке, порядок расчета и способы определения

Приложенное напряжение и падение напряжения на участке цепи.

Напряжения, действующие в электрических цепях, условно можно разделить на два типа:
– приложенное к цепи напряжение;
– падение напряжения на участках цепи или на всей цепи.
Приложенное напряжение это напряжение, подведенное к цепи (рис. 1.).

Рисунок 1. Приложенное напряжение и падение напряжения на участке цепи.

Источник напряжения подключен к цепи, поток электронов перемещается от минуса к плюсу источника напряжения. Если источник напряжения имеет значение напряжения 12 вольт (например, автомобильная аккумуляторная батарея), то приложенное напряжение будет иметь значение так же 12 вольт.
При движении потока электронов по цепи они встречает, как мы знаем, сопротивление. Таким образом, когда электроны проходят через нагрузку (или другие элементы цепи), то они теряют энергию. Та энергия, которую электроны отдали в нагрузку, называется падением напряжения на участке цепи

. В основном эта энергия выделяется на нагрузке в виде тепла. Энергия, которая отдается в нагрузку, равна энергии сообщаемой электронам источником напряжения.
Если автомобильный аккумулятор напряжением 12 вольт подключить к автомобильной 12 вольтовой лампе, то приложенное к цепи напряжение будет равно 12 вольт, а падение напряжения на лампе так же будет 12 вольт (рис. 2.). Энергия в объеме 100% потребляется в цепи.

Рисунок 2. Пример приложенного напряжения в 12 В и падения напряжения на лампе.

Если к тому же 12-вольтовому автомобильному аккумулятору подключить две соединенные последовательно 6-вольтовые лампочки, то при том же приложенном напряжении в 12 В падение напряжение на лампочках будет по 6 вольт (рис. 3.). В этом случае все равно общее падение напряжение будет 12 вольт.

 

Рисунок 3.

В другом случае если взять две лампочки на разное напряжение, к примеру на 9 и 3 вольта, и включить их последовательно в цепь с источником напряжения 12 вольт, то соответственно на 9-ти вольтовой лампочке будет падать 9 вольт, а на 3-х вольтовой 3 вольта (рис.

4.). Как и всегда общее падение напряжения на лампочках равно 12 вольт.

Рисунок 4.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Падение напряжения – это… Что такое Падение напряжения?

Падение напряжения — Падение напряжение на участке цепи с двумя резисторами. Падение напряжения  постепенное уменьшение напряжения вдоль проводника, по которому течёт электрический ток, обу …   Википедия

ПАДЕНИЕ НАПРЯЖЕНИЯ — разность потенциалов на участке электрической цепи, обтекаемой током. П. Н. равно произведению силы тока на сопротивление участка цепи. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 …   Морской словарь

ПАДЕНИЕ НАПРЯЖЕНИЯ — разность между напряжением у источника тока и напряжением на зажимах приемника, затрачиваемая на преодоление сопротивления проводника при прохождении по нему электр. тока. П. н. измеряется в вольтах. Согласно закону Ома П. н. (в вольтах)… …   Технический железнодорожный словарь

Падение напряжения — 92 Падение напряжения Напряжение на участке электрической цепи или ее элементе Источник: ГОСТ 19880 74: Электротехника. Основные понятия. Термины и определения оригинал документа Смотри также родственные тер …   Словарь-справочник терминов нормативно-технической документации

падение напряжения — 1 падение напряжения [IEV number 151 15 08] EN voltage drop (1) tension drop (1) voltage between the terminals of a resistive element being part of an electric circuit due to the electric current through that element [IEV number 151 15 08] FR… …   Справочник технического переводчика

падение напряжения — įtampos krytis statusas T sritis fizika atitikmenys: angl. voltage drop vok. Spannungsabfall, m; Spannungsfall, m rus. падение напряжения, n pranc. chute de tension, f …   Fizikos terminų žodynas

падение напряжения — Разность между действующими значениями напряжения (как вектора), по концам элемента электрической системы …   Политехнический терминологический толковый словарь

падение напряжения на интегральной микросхеме — падение напряжения Разность между входным и выходным напряжением интегральной микросхемы в заданном режиме.

Обозначение Uпд [ГОСТ 19480 89] Тематики микросхемы Синонимы падение напряжения …   Справочник технического переводчика

падение напряжения (в процентах) (в УЗИП) — ∆U=[(Uвход Uвых)/Uвход]х100, где Uвход, Uвых входное и выходное напряжения соответственно, измеренные одновременно при подключенной полной активной нагрузке. Данный параметр применяют исключительно для двух вводных УЗИП. [ГОСТ Р 51992 2011 (МЭК… …   Справочник технического переводчика

падение напряжения в активном сопротивлении — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN resistance dropresistive drop …   Справочник технического переводчика

Закон Ома

Закон Ома – физический закон, определяющий зависимость между электрическими величинами – напряжением, сопротивлением и током для проводников.

Впервые открыл и описал его в 1826 году немецкий физик Георг Ом, показавший (с помощью гальванометра) количественную связь между электродвижущей силой, электрическим током и свойствами проводника, как пропорциональную зависимость.
Впоследствии свойства проводника, способные противостоять электрическому току на основе этой зависимости, стали называть электрическим сопротивлением (Resistance), обозначать в расчётах и на схемах буквой R и измерять в Омах в честь первооткрывателя.
Сам источник электрической энергии также обладает внутренним сопротивлением, которое принято обозначать буквой r.

Закон Ома для участка цепи

Со школьного курса физики всем хорошо известна классическая трактовка Закона Ома:

Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.

I = U/R

Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер.

Отсюда следуют ещё два полезных соотношения:

Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения).

U = IR

Если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.

R = U/I

Вышеописанные формулы в таком виде могут быть применимы для переменного тока лишь в том случае, если цепь состоит только из активного сопротивления R.
Кроме того, следует помнить, что Закон Ома справедлив только для линейных элементов цепи.

Предлагается простой Онлайн-калькулятор для практических расчётов.

Закон Ома. Расчёт напряжения, сопротивления, тока, мощности.
После сброса ввести два любых известных параметра.

I=U/R;   U=IR;   R=U/I; P=UI   P=U²/R;   P=I²R; R=U²/P;   R=P/I²   U=√(PR)   I= √(P/R)

---

Закон Ома для замкнутой цепи

Если к источнику питания подключить внешнюю цепь сопротивлением R, в цепи пойдёт ток с учётом внутреннего сопротивления источника:

I – Сила тока в цепи.
– Электродвижущая сила (ЭДС) – величина напряжения источника питания не зависящая от внешней цепи (без нагрузки). Характеризуется потенциальной энергией источника.
r – Внутреннее сопротивление источника питания.

Для электродвижущей силы внешнеее сопротивление R и внутреннее

r соединены последовательно, значит величина тока в цепи определится значением ЭДС и суммой сопротивлений: I = /(R+r) .

Напряжение на выводах внешней цепи определится исходя из силы тока и сопротивления R соотношением, которое уже рассматривалось выше: U = IR.
Напряжение U, при подключении нагрузки R, всегда будет меньше чем ЭДС на величину произведения I*r, которую называют падением напряжения на внутреннем сопротивлении источника питания.
С этим явлением мы сталкиваемся достаточно часто, когда видим в работе частично разряженные батарейки или аккумуляторы.
По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника, значит уменьшается внешнее напряжение U = – I*r.
Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах

U.
Если ток в цепи равен нулю, следовательно, = U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах.

В случаях, когда внутренним сопротивлением источника можно пренебречь (r ≈ 0), напряжение на выводах источника будет равно ЭДС ( ≈ U ) независимо от сопротивления внешней цепи R.
Такой источник питания называют источником напряжения.

---

Закон Ома для переменного тока

При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление.
В таком случае запись Закона Ома будет иметь вид:

I = U/Z

Здесь Z – полное (комплексное) сопротивление цепи – импеданс. В него входит активная R и реактивная X составляющие.
Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи.

Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.

С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:

– комплексная амплитуда тока. = I_ampe ^jφ
– комплексная амплитуда напряжения. = U_ampe ^jφ
– комплексное сопротивление. Импеданс.
φ – угол сдвига фаз между током и напряжением.
e – константа, основание натурального логарифма.
j – мнимая единица.
I_amp , U_amp – амплитудные значения синусоидального тока и напряжения.

Нелинейные элементы и цепи

Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников.
Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы.
Такие элементы и цепи, в которых они используются, называют нелинейными.

Похожие статьи: Постоянный ток. Переменный ток.

---

Замечания и предложения принимаются и приветствуются!

Урок 8. Делим ток и роняем напряжение

Сегодня мы поговорим о нескольких видах простейших электрических цепей и узнаем, как же можно уронить напряжение и разделить ток на несколько частей. Урок будет длиииииинный, но содержательный, с разбором задачи в конце. Начнем с давно забытого всеми урока за номером четыре, где велся разговор о законе Ома для полной цепи. Было указано, что сила тока в цепи зависит от суммы сопротивлений: внешнего (нагрузки) и внутреннего сопротивления источника. Однако, а почему это мы так вдруг решили, что от суммы, а не, например, от разности или корня квадратного? Бездоказательно, однако! Рассмотрим схему этой цепи, немного отступив от правил прошлого урока… «Ну вот, учили-учили, а теперь забываем применять?! – скажете вы. » Нет, эти правила действительно нужны и мы их будем применять, но только когда нам нужно нарисовать именно принципиальную схему устройства, а сейчас мы будем рассматривать некую небольшую абстрактную схему и для наглядности и простоты некоторых (только некоторых!) правил не будем придерживаться. Но для начала посмотрим, как изображается и обозначается на принципиальной электрической схеме давно уже известное нам сопротивление.


Как видите, это обычный прямоугольник, размерами 10мм*4мм.
Итак, наша схема будет состоять из двух сопротивлений и идеального источника, нарисуем ее.

Рисунок 8.1 – Источник питания с внутренним сопротивлением

На этой схеме внутреннее сопротивление источника GB1 обозначено как r, а сопротивление внешней цепи (нагрузка) – как R. Причем, считаем, что R>>r. Здесь мы и отступаем от норм ГОСТ, поскольку для простоты понимания опускаем цифровые обозначения сопротивлений и добавляем на схему некоторые точки A, B и C. Такое включение сопротивлений называют последовательным, так как включены они как бы друг за другом – конец сопротивления r подключен к началу сопротивления R (точка B) и между ними нет больше каких-либо элементов или отводов. Закон Ома для полной цепи говорит, что ток, в электрической цепи зависит от сопротивления этой цепи и одинаков для всех элементов, то есть ток, протекающий через r, равен току, протекающему через R. Давайте рассмотрим этот момент с помощью метода доказательства «от противного». Предположим, что токи, протекающие через сопротивления различны. Ток через большее сопротивление R, исходя из закона Ома, должен быть меньше тока через r. В таком случае в точке B начал бы накапливаться заряд, поскольку ток, выходящий из точки B меньше тока, входящего в нее, а ток есть ни что иное, как отношение перенесенного полем заряда на время. Накапливаемый в точке B заряд создает в этой точке потенциал, который в некоторый момент времени сравняется с потенциалом положительной клеммы аккумулятора (точка A). В этом случае ток в цепи прекращается, поскольку при разности потенциалов двух точек равной нулю потенциальные энергии зарядов в этих точках равны, и работа поля равна нулю. Это умозаключение, кстати говоря, приводит нас к одному интересному выводу:

между точками одинакового потенциала протекание электрического тока невозможно.

Однако, электроны, образующие не скомпенсированный заряд в точке B постепенно будут поглощаться ионами материала, что приведет к снижению потенциала и возобновлению тока, который восстановит потенциал и опять прервёт сам себя. Но это бы противоречило закону Ома, который говорит, что ток в цепи всегда постоянен, а здесь имеет место прерывистый ток, значение которого зависит от времени. Соответственно, такой ситуации быть не может, мы пришли к противоречию.

Если же мы представим, что r>>R, тогда ток через большее сопротивление r исходя из закона Ома должен быть меньше тока через R. В этом случае ток, втекающий в точку B будет меньше, чем ток, вытекающий из нее, что приведет к уменьшению числа свободных электронов в материале до нуля и ток опять прекратится. Со временем за счет дрейфа и превращения атомов материала в ионы свободные электроны вновь образуются, и ток возобновиться, но истощение заряда продолжится, и ток опять прекратит сам себя. То есть мы видим такую же ситуацию, как в первом случае.

Остаётся только одно разумное решение:

ток в последовательной цепи одинаков для каждого элемента этой цепи.

В этом случае поддерживается постоянный баланс потенциалов всех точек цепи. Это не говорит о том, что потенциалы одинаковы! Это значит, что потенциал каждой точки строго определён протекающим в ней током.
Теперь давайте разберемся, почему ток в цепи будет зависеть от суммы сопротивлений. Тут всё довольно просто. Последовательное соединение двух проводников приводит к увеличению длины эквивалентного проводника, а это в свою очередь – к росту сопротивления (формула из Урока 3). Отсюда запоминаем еще одно важное правило:

эквивалентное сопротивление участка цепи с последовательно включенными сопротивлениями равно сумме этих сопротивлений.

Наш вывод относительно протекания тока между точками одинакового потенциала приводит к тому, что точки A, B и C обладают различными потенциалами, раз ток в цепи существует. Причем потенциал точки C меньше потенциала точки B, а точки B меньше, чем точки A. Почему? А потому что уменьшение количества свободных электронов (за счет столкновения с узлами кристаллической решётки и прочих потерь в материале) происходит последовательно от «минуса» аккумулятора (он же является их источником!) через сопротивления R и r к «плюсу» аккумулятора (а он уже является источником положительных ионов). К тому же мы ведь считаем, что ток «течет» от «плюса» к «минусу», а электроны наоборот – от «минуса» к «плюсу», поэтому, исходя из формулы Урока 3 для потенциальной энергии заряда, видно, что наибольшим потенциалом обладает точка с наименьшим зарядом, – «плюс» аккумулятора.

А раз две точки имеют разный потенциал, то между ними есть напряжение, которое называют падением напряжения. Нетрудно догадаться, что падение напряжения на элементе пропорционально току, протекающему через него, так как величина тока регулирует количество заряда на концах элемента, т.е. разность потенциалов. По сути величина падения напряжения подчиняется закону Ома для участка цепи:

U_R=I_R∙R, где

I_R – ток, протекающий через сопротивление,
R – величина этого сопротивления.
Для нашей схемы на Рисунке 8.1 справедливы следующие соотношения:

U_AB=I∙r,
U_BC=I∙R,
U_AC=I∙(R+r)=ε_GB1

Из этих соотношений хорошо видно, что падение напряжения – часть эдс источника, доставшаяся участку цепи. Часто на схемах можно встретить такие обозначения падения напряжения:

Рисунок 8.2 – Обозначение падения напряжения

Стрелку направляют в сторону уменьшения потенциала. Разумеется, на принципиальных электрических схемах падение напряжения указывать не допускается.
Раз мы заговорили о последовательных цепях, наверное, существуют и параллельные? Да, действительно, такие соединения есть и выглядят они следующим образом:

Рисунок 8.3 – Параллельное соединение сопротивлений

Параллельным соединением называется такое соединение, при котором выходы элементов соединены в одних точках. На нашей схеме это точки A и B. Поскольку элементы имеют общие точки, разность потенциалов на этих элементах будет одинакова, как и падение напряжения. То есть, напряжение на параллельных ветвях электрической цепи одинаково.

Для удобства дальнейшего рассмотрения процессов в электрических цепях введем такие понятия как: узел, ветвь и контур. Ветвью называют любой двухполюсник, входящий в цепь, например, на Рисунке 8.3 отрезок AB есть ветвь. Узлом называют точку соединения трех и более ветвей (на Рисунке 8.3 обозначены жирными точками. На рисунке 8.1 точки A, B и C не являются узлами).

Контур – замкнутый цикл из ветвей. Термин замкнутый цикл означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам. Например, контуром можно назвать параллельное соединение сопротивлений R₁ и R₂ на Рисунке 8.3
Рассмотрим теперь, что происходит с токами ветвей I, I₁ и I₂:

Эти соотношения получаются из довольно простого логического заключения: если источник включен параллельно сопротивлению, то падение напряжения на сопротивлении не может быть отличным от эдс источника, ведь потенциалы концов сопротивления R₁ соответственно равны потенциалам концов сопротивления R₂. Причем не играет роли, какое количество параллельных ветвей будет подключено – на каждой из них напряжение будет одно и то же. Как же получить выражение для тока I? Начнем рассуждать с того, что мощность, отдаваемая источником должна быть равна мощности, потребляемой нагрузкой, ведь закон сохранения энергии никто не отменял. Запишем выражения для мощностей, пренебрегая внутренним сопротивлением источника:
P_ист=I∙ε
P_нагр=P_R1+P_R2=I₁∙U_R1+I₂∙U_R2=I₁∙ε+I₂∙ε=(I₁+I₂)∙ε
Приравнивая правые части уравнений, получим:

(I₁+I₂ )∙ε=I∙ε

Таким образом, сокращая на ε:

I=I₁+I₂

То есть, в параллельных ветвях происходит деление тока. Если перенести слагаемые I₁ и I₂ в левую часть уравнения, получим, что алгебраическая сумма токов в каждом узле электрической цепи равна нулю.

Учитывается именно алгебраическая сумма (с учетом знака), потому что направление тока мы можем положить любым, ведь в сложной схеме можем заранее не знать, втекает ток в узел или вытекает из него (втекающий ток берётся со знаком «плюс», вытекающий – со знаком «минус»). То есть мы, например, могли бы перенести слагаемое I в правую часть и получили бы уравнение, в котором втекающие токи были бы со знаком «минус», а вытекающие со знаком «плюс», но ничего не мешает нам поделить обе части уравнения на -1. Это утверждение называется I правило Кирхгофа или правило токов Кирхгофа. Иногда его не совсем корректно называют законом Кирхгофа. Всё-таки это правило, потому что оно не является фундаментальным законом природы, а вытекает из других фундаментальных законов.

Кроме I правила Кирхгофа существует еще и II правило Кирхгофа:

алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме эдс ветвей этого контура. Если в контуре нет источников ЭДС, то суммарное падение напряжений равно нулю.

Закон Ома является частным случаем II правила Кирхгофа для цепи из одного контура. Здесь выражение «алгебраическая сумма» значит, ровно то же, что и для I правила, только для напряжений.
Как использовать эти правила для расчета сложных электрических цепей мы рассмотрим на следующем уроке, который полностью будет посвящен практике.

Возвращаясь к схеме на рисунке 8.3 возникает логичный вопрос: как же нам рассчитать эквивалентное сопротивление параллельных ветвей? Ясно, что формула для последовательной цепи сюда не подойдет. Давайте заменим сопротивления R₁ и R₂ одним эквивалентным сопротивлением:

Рисунок 8.4 – Замена параллельных сопротивлений эквивалентным сопротивлением

Теперь ничто не мешает нам применить закон Ома, чтобы рассчитать R_экв:

При подобной замене мы будем пользоваться следующим вариантом записи:

Пришло время запоминать еще одно важное правило: величина, обратная общему сопротивлению параллельных ветвей, равна сумме величин, обратных сопротивлениям каждой ветви

Или, иначе: эквивалентная проводимость параллельных ветвей равна сумме проводимостей этих ветвей.

Немного тавтологии, пожалуй, не помешает…

Схема на рисунке 8.3 называется делитель тока и находит широкое применение. Более подробно применение делителя тока мы рассмотрим позже, а сейчас приведем такой пример, чтобы хоть немного убедить читателя в полезности этого схемного решения. Рассмотрим схему на рисунке 8.4. Допустим, эдс источника ε=5В, а сопротивление нагрузки R_экв=1Ом, тогда мощность, выделяемая в нагрузке равна:

Посмотрим, что произойдёт, если мы заменим эквивалентное сопротивление двумя одинаковыми параллельно включенными сопротивлениями (рисунок 8.3). Чтобы сохранить величину эквивалентного сопротивления равным 1Ом, рассчитаем величины сопротивлений R₁ и R₂:

то есть каждое из сопротивлений должно быть больше эквивалентного в 2 раза.
Рассчитаем мощность, выделяемую на каждом из этих сопротивлений:

Суммарная мощность нагрузки осталась прежней, однако, как нам уже известно, мощность выделяемая на сопротивлении, полностью переходит в тепло, следовательно, при одной и той же рассеиваемой мощности, во втором случае мы получим более комфортный температурный режим для нагрузки (температура каждого сопротивления будет ниже, чем температура эквивалентного сопротивления) за счет увеличения в 2 раза площади рассеивания (ведь мы используем два проводника вместо одного). Соответственно, трата дополнительных денег на приобретение двух проводников позволяет нам сэкономить на охлаждении. Часто бывают такие ситуации, что слишком большой перегрев элемента может приводить к выходу его из строя (даже такой простой вещи как кусок проводника). Кроме того, многие полупроводниковые приборы (диод, транзистор, тиристор) рассчитаны на определенный номинальный ток, и, чтобы увеличить предел номинального тока, такие приборы включают параллельно. Можно, конечно, взять прибор с большим номинальным током, но чаще всего стоимость таких прибор намного больше. Экономия, однако…

Давайте немного изменим эту схему, пренебрегая внутренним сопротивлением и добавив еще одно сопротивление во внешнюю цепь:

Рисунок 8.5 – Последовательное соединение сопротивлений

По сути, это та же схема последовательного соединения двух сопротивлений, только теперь оба эти сопротивления являются частью нагрузки. Из вышеприведенных соотношений видно, что напряжение на каждом сопротивлении определяется протекающим током и значением этого сопротивления. Используя закон Ома, выразим величину тока, протекающего через сопротивления:

тогда, подставляя значение тока в выражение для падения напряжения, получим:

Из полученных соотношений видно, что величина падения напряжения зависит от эдс источника и соотношения сопротивлений.

При R₁=R₂ падение напряжения на каждом сопротивлении составит ровно половину эдс источника. Таким образом мы поделили напряжение пополам и теперь можем использовать отвод в точке А в качестве «плюса» своеобразного источника питания, но с пониженным напряжением. Такая схема называется делителем напряжения. Ее полезно применять, когда имеется источник с большим напряжением, чем требуется. Сопротивление R₁ называется верхним плечом, а сопротивление R₂ – нижним. Однако, резистивный делитель напряжения обладает существенными недостатками: во-первых, потери мощности на плечах делителя снижают кпд устройства, поскольку просто переходят в тепло, а, во-вторых, сопротивление выходного плеча (с которого снимается часть эдс) должно быть согласовано с сопротивлением нагрузки, чтобы сохранять требуемое напряжение. Рассмотрим эти два момента на примере общего случая включения сопротивлений так называемого смешанного соединения.

Рисунок 8.6 – Смешанное соединение сопротивлений

Как мы видим, сопротивления R₂ и R_н включены параллельно, а их эквивалентное сопротивление включено последовательно с R₁. Теперь сформулируем условия задачи: на нагрузке мощностью
P_н=20 Вт необходимо получить напряжение U_н=5 В, если имеется аккумуляторная батарея номинальной эдс ε=12 В.
Для начала обозначим направления протекания токов в каждой ветви.

Рисунок 8.7 – Направления протекания токов

Рассчитаем параметры нагрузки по известной мощности и напряжению:

Однако, нам неизвестны токи I₁ и I₂, так же как и сопротивления R₁ и R₂. В таких случаях при разработке схемы необходимо самому задать необходимые недостающие условия, но так, чтобы задача имела решение. Например, мы могли бы задать R₁=10 Ом, но ведь ток I₁ не может быть менее 4А, а значит:
U_R1>I₁∙R₁=4А∙10Ом=40В,
что заведомо больше, чем напряжение на аккумуляторе. Чтобы не угадывать значения сопротивлений, давайте для уменьшения потерь на сопротивлении R₂ зададим ток I₂ равным 10% от тока нагрузки, ведь ничто не мешает нам так сделать.

I₂=0.1I_н=0.4 А

Напряжение U_н равно напряжению U_R2, так как эти сопротивления включены параллельно, значит, сопротивление R₂ из закона Ома равно:

Ток I₁ можно рассчитать двумя способами:

• Исходя из I правила Кирхгофа для узла А:

  I₁=I₂+I_н

• Используя закон Ома.

Для начала давайте рассчитаем его, используя второй способ, а потом сравним результаты.
Поскольку нижним плечом делителя является эквивалентное сопротивление параллельно включенных сопротивлений R₁ и R_н, рассчитаем его:

Заметьте, что эквивалентное сопротивление всегда меньше меньшего сопротивления!
Ток I₁ соответствует току через последовательное соединение сопротивлений R₁ и R_экв. Его можно найти из закона Ома:

Теперь рассчитаем этот же ток, используя первый способ:

I₁=I₂+I_н=0.4А + 4А = 4.4А

Результаты совпали, значит, расчет выполнен верно.
Рассчитаем величину сопротивления R₁, пользуясь опять же законом Ома:

Итак, при помощи двух сопротивлений мы спроектировали (ого-го!) устройство понижения напряжения с 12 В до 5 В. Давайте оценим кпд этого устройства. Полезной мощностью у нас является мощность нагрузки P_н=20 Вт, а полной мощностью – мощность, отдаваемая аккумуляторной батареей, которая равна произведению потребляемого тока (I₁) на эдс батареи:

P_GB1=ε∙I₁=12В ∙ 4.4А = 52.8Вт

Тогда кпд равен:

Всего-то! Ужасно! Давайте подумаем, как можно увеличить этот показатель…
Но сначала разберемся откуда берутся такие большие потери мощности… А браться им, кроме как на нагрев сопротивлений R₁ и R₂ неоткуда. Давайте рассчитаем мощность потерь для каждого из них:

P_R1=I₁²∙R₁=(4.4 А)²∙1.136 Ом=30.8 Вт
P_R2=I₂²∙R₂=(0.4 А)²∙1.59 Ом=2 Вт

Сразу видно, что наибольшие потери рассеиваются на сопротивлении R_1. Величину тока мы значительно изменить не можем, так как она не может быть меньше величины тока нагрузки. Можно подкорректировать величину заданного нами тока I₂… Стоп. А зачем нам вообще это сопротивление? Ведь делитель может быть собран с помощью самой нагрузки в качестве нижнего плеча! Смело убираем R₂ из схемы.

Рисунок 8.8 – Модернизированная схема

Теперь нам не нужен этот «паразитный» ток I₂. Пересчитаем величину сопротивления R₁:

Потери мощности на нем:

P_R1=I_н²∙R₁=(4 А)²∙1. 75 Ом=28 Вт

И кпд:

Кпд вырос, но потери все равно огромные! Но больше мы сделать, к сожалению ничего не можем: такая схема попросту неэффективна… Мы впустую потратили больше энергии, чем получили полезной работы. Вот такой первый недостаток схемы делителя напряжения.

Теперь посмотрим, что будет, если мы изменим параметры нагрузки, например, вместо 20 Вт подключим 15 Вт. Изменится величина сопротивления нагрузки, ведь она определена номинальными значениями мощности и напряжения:

Посмотрим, что произойдет с напряжением на нижнем плече делителя, то есть на нагрузке:

В сумме напряжения на плечах делителя равны эдс источника, значит:

Тогда нагрузке достанется часть эдс, равная:

U_н=ε-U_R1=12 В-6.15 В=5.85 В

Получается, что мы превысили номинальное напряжение на ≈17%. И нельзя точно сказать, выдержит ли наша нагрузка такого превышения. А может она попросту выйдет из строя… Получается, что без изменения R₁ подключать нагрузку, отличную от расчетной, нельзя. Это и есть второй недостаток схемы делителя. В основном эта схема применяется там, где мощность потерь невелика, например, в цепях с силой тока единицы – десятки миллиампер.

Теперь кратко опишем важные моменты урока, а на этом я с вами прощаюсь, ждем следующего урока, в котором подробно разберем задачу на расчет сложной электрической цепи.

• Между точками одинакового потенциала протекание электрического тока невозможно.
• Ветвью называют любой двухполюсник, входящий в цепь.
• Узлом называют точку соединения трех и более.
• Контуром называют замкнутый цикл из ветвей.
• При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла.
  Ток в последовательной цепи одинаков для каждого элемента.
  Эквивалентное сопротивление цепи равно сумме входящих в нее сопротивлений:
  
• При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.
  Напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. Эквивалентное сопротивление цепи может быть рассчитано по формуле:
  
• I правило Кирхгофа: алгебраическая сумма токов в каждом узле электрической цепи равна нулю.
  
• II правило Кирхгофа: алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме эдс ветвей этого контура. Если в контуре нет источников ЭДС, то суммарное падение напряжений равно нулю.
  

← Урок 7. Основы составления электрических схем | Содержание | →

Напряжение на участке цепи.

Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка.

На рис. 13 изображен участок цепи, на котором есть резистор сопротивлением и нет ЭДС. Крайние точки этого участка обозначены буквами a и b. Пусть ток течет от точки a к точке b.

Рис. 13. Участок электрической цепи

На участке без ЭДС ток течет от более высокого потенциала к более низкому. Следовательно, потенциал точки a выше потенциала точки b на величину, равную произведению тока на сопротивление :

.

В соответствии с определением, напряжение между точками a и b

. (8)

Другими словами, напряжение на резисторе равно произведению тока, протекающего по резистору, на величину сопротивления этого резистора.

В электротехнике разность потенциалов на концах резистора принято называть либо «напряжением на резисторе», либо «падением напряжения». В литературе встречаются оба этих определения.

Рассмотрим теперь вопрос о напряжении на участке цепи, содержащем не только резистор, но и источник ЭДС.

На рис. 14 а и б показаны участки некоторых цепей, по которым протекает ток .. Найдем напряжение между точками a и c для этих участков.

а) б)

Рис. 14. Участки электрической цепи

По определению

. (9)

Выразим потенциал точки a через потенциал точки c. При перемещении от точки c к точке b (рис. 14,а) идем встречно ЭДС , поэтому потенциал точки b оказывается меньше, чем потенциал точки c на величину ЭДС , т.е.

. (10)

На рис. 14,б при перемещении от точки c к точке b идем согласно ЭДС и потому потенциал точки b оказывается больше, чем потенциал точки c на величину ЭДС , т. е.

. (11)

Ранее говорилось, что на участке цепи без ЭДС ток течет от более высокого потенциала к более низкому. Поэтому в обеих схемах рис. 14 потенциал точки a выше, чем потенциал точки b на величину падения напряжения на резисторе сопротивлением :

. (12)

Таким образом, для рис. 14,а имеем

, или

. (13)

И для рис. 14, б имеем

, или

. (14)

Положительное направление напряжения указывают на схемах стрелкой. Стрелка должна быть направлена от первой буквы индекса ко второй. Так, положительное направление напряжения изобразится стрелкой, направленной от a к c.

Из самого определения напряжения следует также, что .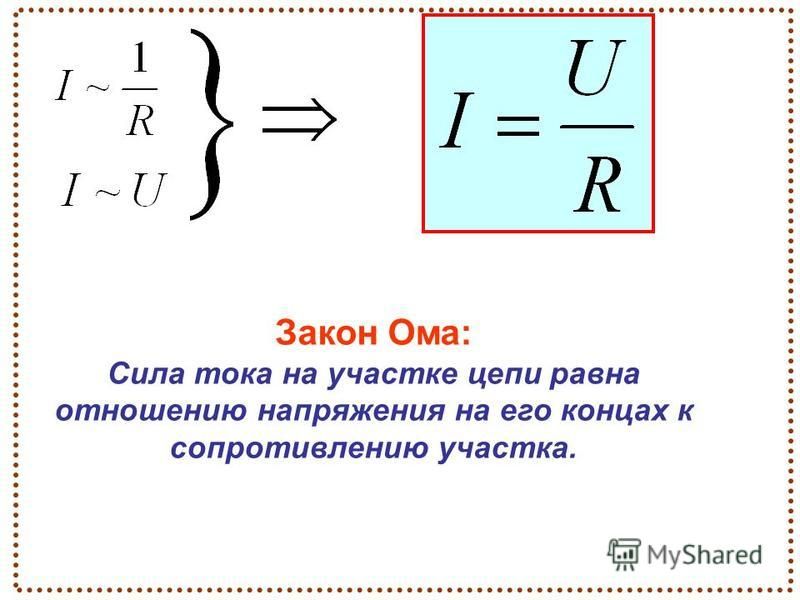 Поэтому . Другими словами, изменение чередования индексов равносильно изменению знака этого напряжения. Из изложенного ясно, что напряжение может быть и положительной, и отрицательной величиной.

6. Закон Ома для участка цепи, не содержащего эдс.

Закон Ома устанавливает связь между током и напряжением на некотором участке цепи. Так, применительно к участку цепи, изображенному на рис. 13 имеем

или

. (15)

7. Закон Ома для участка цепи, содержащего эдс.

Закон Ома для участка цепи, содержащего ЭДС, позволяет найти ток этого участка по известной разности потенциалов на концах этого участка и имеющейся на этом участке ЭДС . Так из уравнения (13) имеем для схемы рис. 14, а

. (16)

Аналогично из уравнения (14) для схемы рис. 14, б следует

. (17)

Уравнения (16) и (17) выражают собой закон Ома для участка цепи, содержащего ЭДС, для разных случаев включения ЭДС .

Как на резисторах, конденсаторах и индуктивностях делить напряжение

Как на резисторах, конденсаторах и индуктивностях делить напряжение

Электри́ческое напряже́ние между точками A и B электрической цепи или электрического поля — физическая величина, значение которой равно работе эффективного электрического поля (включающего сторонние поля), совершаемой при переносе единичного пробного электрического заряда из точки A в точку B.

С целью получения фиксированного значения напряжения, равного доле от исходного значения, в электрических цепях применяют делители напряжения. Делители напряжения могут состоять из двух или более элементов, которыми могут служить резисторы либо реактивные сопротивления (конденсаторы или катушки индуктивности).

В простейшем виде делитель напряжения представляется парой участков электрической цепи, соединенных последовательно друг с другом, которые и называются плечами делителя. Верхним плечом называется тот участок, который расположен между точкой положительного напряжения и выбранной точкой соединения участков, а нижним плечом — участок между точкой соединения (выбранной точкой, нулевой точкой) и общим проводом.

Делители напряжения на резисторах

Конечно, делители напряжения могут применяться как в цепях постоянного тока, так и в цепях тока переменного. Делители на резисторах подходят и для тех, и для других цепей, однако используются они только в цепях низкого напряжения. Для питания устройств делители напряжения на резисторах не применяют.

В простейшем виде резистивный делитель напряжения состоит всего из пары резисторов, соединенных последовательно. Делимое напряжение подается на делитель, в результате на каждом резисторе падает определенная доля этого напряжения, пропорциональная номиналу резистора. Сумма падений напряжений равна здесь напряжению подаваемому на делитель.

Согласно закону Ома для участка электрической цепи, на каждом резисторе падение напряжения будет прямо пропорционально току и величине сопротивления резистора. А согласно первому правилу Кирхгофа, ток через данную цепь будет везде один и тот же. Так, на каждый резистор придутся падения напряжения:

И напряжение на концах участка цепи будет равно:

А ток в цепи делителя составит:

Теперь если подставить выражение для тока в формулы для падений напряжений на резисторах, то получим формулы для нахождения величин напряжений на каждом из резисторов делителя:

Используя делитель напряжения на резисторах для тех или иных целей, важно понимать, что присоединенная к одному из плеч делителя нагрузка, будь то измерительный прибор или что-нибудь другое, должна иметь собственное сопротивление значительно большее, чем общее сопротивление резисторов, образующих делитель. В противном случае сопротивление нагрузки само должно учитываться в расчетах, будучи рассмотрено как параллельный плечу резистор, входящий в состав делителя.

Пример: есть источник постоянного напряжения 5 вольт, необходимо подобрать к нему резисторы для делителя напряжения, чтобы снимать с делителя измерительный сигнал величиной в 2 вольта. Допустимая рассеиваемая на делителе мощность не должна превышать 0,02 Вт.

Решение: Пусть максимальная мощность, рассеиваемая на делителе, равна 0,02 Вт, тогда минимальное общее сопротивление делителя при 5 вольтах найдем из закона Ома, оно получится равно 1250 Ом. Пусть 1,47 кОм — выбранное нами общее сопротивление делителя, тогда 2 вольта упадет на 588 омах. Выберем постоянный резистор на 470 Ом и переменный на 1 кОм. Установим на переменном резисторе значение в 588 Ом.

Делители напряжения на резисторах широко применяются сегодня в электронных схемах. На этих схемах значения величин резисторов для делителей выбираются исходя из параметров активных элементов схем. Как правило, делители стоят в измерительных цепях схем, в цепях обратной связи преобразователей напряжения и т. д. Минус таких решений заключается в том, что резисторы рассеивают на себе мощность в виде тепла, однако целесообразность оправдывает эти малые потери энергии.

Делители напряжения на конденсаторах

В цепях переменного тока, в высоковольтных схемах, применяют делители напряжения на конденсаторах. Здесь используется реактивный характер сопротивления конденсаторов в цепях переменного тока. Величина реактивного сопротивления конденсатора в цепи переменного тока зависит от электроемкости конденсатора и от частоты напряжения. Вот формула для нахождения этого сопротивления:

Формула свидетельствует о том, что чем больше электроемкость конденсатора — тем его реактивное (емкостное) сопротивление меньше и чем выше частота — тем так же меньше реактивное сопротивление. Такие делители используются в измерительных схемах цепей переменного тока, падения напряжений на плечах считается аналогично случаю с постоянными активными сопротивлениями (резисторами, см. выше).

Достоинство конденсаторов, применяемых в делителях, состоит в том, что рассеивание энергии в форме тепла получается минимальным, и зависит только от качества диэлектрика.

Делитель напряжения на индуктивностях

Индуктивный делитель напряжения — еще один вид делителей, применяемых в измерительной электронике переменного тока, особенно в низковольтных схемах, работающих на высоких частотах. Сопротивление катушек для переменного тока высокой частоты носит преимущественно реактивный (индуктивный) характер, оно находится по формуле:

Формула свидетельствует о том, что чем больше индуктивность и чем выше частота — тем выше сопротивление катушки переменному току. Здесь важно понимать, что провод катушки имеет активное сопротивление, поэтому мощность, рассеиваемая в виде тепла, свойственная делителю на индуктивностях, значительно выше, чем у делителей на конденсаторах.

В любительской электронике делители напряжения часто используются при подключении аналоговых датчиков к модулям Ардуино. 

Ранее ЭлектроВести писали, что немецкие инженеры разработали полевой транзистор на основе оксида галлия с пробивным напряжением 1,8 кВ и рекордной добротностью — 155 МВт на квадратный сантиметр. Такие показатели приближают элемент к теоретическому лимиту оксида галлия.

По материалам: electrik.info.

Постоянный электрический ток

 на главную   

 

Официальный сайт АНО ДО Центра “Логос”, г.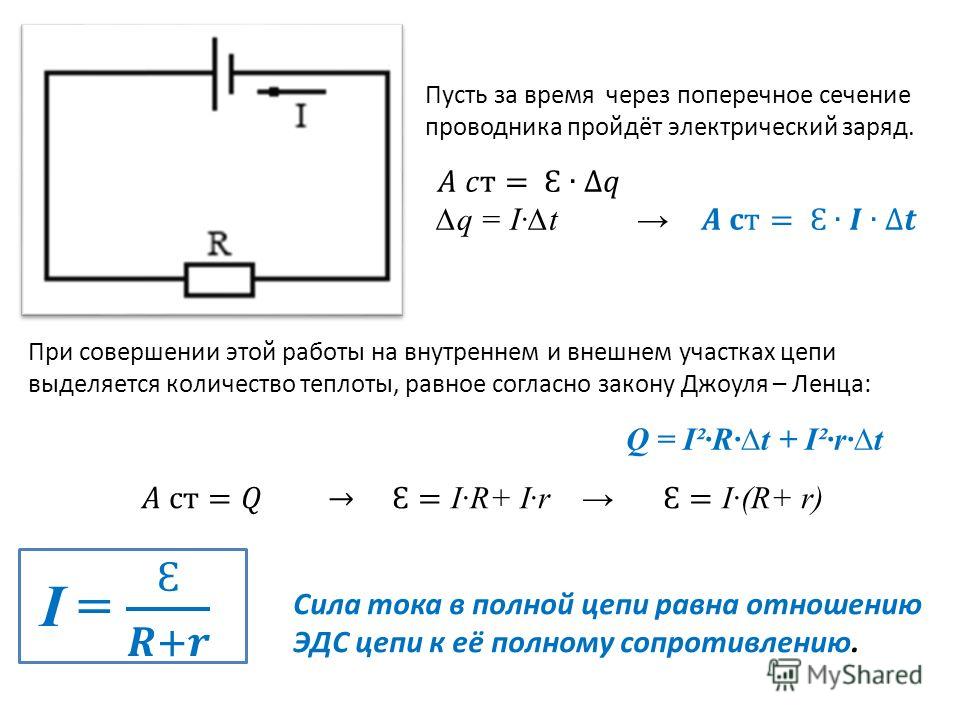 Глазов

http://logos-glz.ucoz.net/

 

ГОТОВИМСЯ К УРОКУ

Кинематика

Динамика

МКТ

Термодинамика 

Электростатика

Электрический ток

Электрический ток в средах

Магнитное поле Электромагнитная индукция

Оптика

Методы познания

постоянный электрический ток                                                      немного о физике:   

 

Что называют электрическим током?

 

Электрический ток – упорядоченное движение заряженных частиц под действием сил электрического поля или сторонних сил.

За направление тока выбрано направление движения положительно заряженных частиц.

Электрический ток называют постоянным, если сила тока и его направление не меняются с течением времени.

 

Условия существования постоянного электрического тока.

 

Для существования постоянного электрического тока необходимо наличие свободных заряженных частиц и наличие источника тока. в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.

Источник тока – устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля. В источнике тока на заряженные частицы в замкнутой цепи действуют сторонние силы. Причины возникновения сторонних сил в различных источниках тока различны. Например в аккумуляторах и гальванических элементах сторонние силы возникают благодаря протеканию химических реакций, в генераторах электростанций они возникают  при движении проводника в магнитном поле, в фотоэлементах – при действия света на электроны в металлах и полупроводниках.

Электродвижущей силой источника тока называют отношение работы сторонних сил к величине положительного заряда, переносимого от отрицательного полюса источника тока к положительному.

 

Основные понятия.

 

Сила тока – скалярная физическая величина, равная отношению заряда, прошедшего через проводник, ко времени, за которое этот заряд прошел.

где I – сила тока, q – величина заряда (количество электричества), t – время прохождения заряда.

Плотность тока – векторная физическая величина, равная отношению силы тока к площади поперечного сечения проводника.

где j –плотность тока,  S – площадь сечения проводника.

Направление вектора плотности тока совпадает с направлением движения положительно заряженных частиц.

Напряжение – скалярная физическая величина, равная отношению полной работе кулоновских и сторонних сил при перемещении положительного заряда на участке к значению этого заряда.

где A – полная работа сторонних и кулоновских сил,  q – электрический заряд.

Электрическое сопротивление – физическая величина, характеризующая  электрические свойства участка цепи.

где ρ – удельное сопротивление проводника, l – длина участка проводника,  S – площадь поперечного сечения проводника.

 

Проводимостью называется величина, обратная сопротивлению

где  G – проводимость.

 

 

Законы Ома.

 

Закон Ома для однородного участка цепи.

Сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении участка  и обратно пропорциональна сопротивлению участка при постоянном напряжении.

где U – напряжение на участке,  R – сопротивление участка.

 

 

Закон Ома для произвольного участка цепи, содержащего источник постоянного тока.

где   φ_{1– φ2 + ε = U} напряжение на заданном участке цепи, R – электрическое сопротивление  заданного участка цепи.

 

 

Закон Ома для полной цепи.

Сила тока в полной цепи равна отношению электродвижущей силы источника к сумме сопротивлений внешнего и внутреннего участка цепи.

где R – электрическое сопротивление внешнего участка цепи,  r – электрическое сопротивление внутреннего участка цепи.

 

Короткое замыкание.

Из закона Ома для полной цепи следует, что сила тока в цепи  с заданным источником тока зависит только от сопротивления внешней цепи R.

Если к полюсам источника тока подсоединить проводник с сопротивлением  R<< r, то тогда только  ЭДС источника тока и его сопротивление будут определять  значение силы тока в цепи. Такое значение силы тока будет являться предельным для данного источника тока и называется током короткого замыкания. 

 

Последовательное и параллельное

соединение проводников.

 

Электрическая цепь включает в себя источника тока и проводники (потребители, резисторы и др), которые могут соединятся  последовательно или параллельно.

 

При последовательном соединении конец предыдущего проводника соединяется с началом следующего.     Во всех  последовательно соединенных проводниках сила тока одинакова: I1= I2=I   Сопротивление всего участка равно сумме сопротивлений всех отдельно взятых проводников: R = R1+ R2       Падение напряжения на всем участке равно сумме паданий напряжений на всех отдельно взятых проводниках: U= U1 +U2   Напряжения на последовательно соединенных проводниках пропорциональны их сопротивлениям.

При параллельном соединении проводники подсоединяются к одним и тем же точкам цепи. Сила тока в неразветвленной части цепи равна сумме токов, текущих в каждом проводнике: I = I1+ I2   Величина, обратная сопротивлению разветвленного участка,  равна сумме обратных величин обратных сопротивлениям каждого отдельно взятого проводника:        Падение напряжения во всех проводниках одинаково: U= U1 = U2     Силы тока в проводниках обратно пропорциональны их сопротивлениям

 

Смешанное соединение – комбинация  параллельного и последовательного  соединений.

 

 

Правила Кирхгофа.

Для расчета разветвленных цепей, содержащих неоднородные участки, используют правила Кирхгофа. Расчет сложных цепей состоит в отыскании токов в различных участках цепей.

Узел – точка разветвленной цепи, в которой сходится более двух проводников.

1 правило Кирхгофа: алгебраическая сумма сил токов, сходящихся в узле, равна нулю;

где n – число проводников, сходящихся в узле, I_{i– сила тока в проводнике.}

токи, входящие в узел считают положительными, токи, отходящие из узла – отрицательными.

2 правило Кирхгофа: в любом произвольно выбранном замкнутом контуре разветвленной цепи алгебраическая сумма произведений сил токов и сопротивлений каждого из участков этого контура равна алгебраической сумме ЭДС в контуре.

 

Чтобы учесть знаки сил токов и ЭДС выбирается определенное направление обхода контура(по часовой стрелке или против нее). Положительными считают токи, направление которых совпадает с направлением обхода контура, отрицательными считают  токи противоположного направления. ЭДС источников  электрической энергии считают положительными если они создают токи, направление которых совпадает с направлением обхода контура, в противном случае – отрицательными.

 

Порядок расчета сложной цепи постоянного тока.

1. Произвольно выбирают направление токов во всех участках цепи.

2. Первое правило Кирхгофа  записывают  для  (m-1)  узла, где m – число узлов в цепи.

3. Выбирают произвольные замкнутые контуры, и после выбора направления обхода записывают второе правило Кирхгофа.

4. Система из составленных уравнений должна быть разрешимой: число уравнений должно соответствовать количеству неизвестных.

Шунты и добавочные сопротивления.

Шунт – сопротивление, подключаемое параллельно к амперметру (гальванометру), для расширения его шкалы при измерении силы тока.

Если  амперметр рассчитан на силу тока I_{0, а с помощью него необходимо измерить силу тока, превышающую в n раз допустимое значение, то сопротивление, подключаемого шунта должно удовлетворять следующему условию:}

 

 

Добавочное сопротивление – сопротивление, подключаемое последовательно с вольтметром (гальванометром),  для расширения его шкалы при измерении напряжения.

Если  вольтметр рассчитан на напряжение U_{0, а с помощью него необходимо измерить напряжение, превышающее в n раз допустимое значение, то добавочное сопротивление должно удовлетворять следующему условию:}

 

 

Что такое падение напряжения в электрической цепи?

В этом частом техническом вопросе мы дадим краткое концептуальное объяснение падений напряжения и обсудим полярность напряжений, падающих на резисторы, конденсаторы и катушки индуктивности.

Напряжение, работа и ток

Батарея преобразует химическую энергию в электрическую, создавая напряжение, т. Е. Разность электрических потенциалов, на двух своих выводах. Резистор – это компонент, который создает определенное сопротивление электрическому току.Когда мы подключаем два вывода резистора к двум выводам батареи, носители заряда перемещаются по цепи, и мы называем это электрическим током.

Voltage передает способность выполнять работу по перемещению заряда из одной точки в другую. Например, батарея на 5 В может выполнять 5 джоулей работы за кулон заряда. Когда через резистор протекает ток, мы можем измерить объем работы (на единицу заряда), необходимый для поддержания тока, протекающего через резистор.

Это суть падения напряжения: батарея (или источник напряжения) поставляет энергию для выполнения работы по перемещению заряда.Когда ток течет, компоненты, такие как резисторы , потребляют энергии, и количество работы на единицу заряда, связанное с током, протекающим через данный компонент, является падением напряжения компонента.

Падение напряжения на компоненте составляет часть напряжения, генерируемого батареей. Другими словами, работа, выполняемая аккумулятором, распределяется между компонентами схемы.

Мы можем интуитивно понять, что пропускание заданного количества тока через большее сопротивление потребует больше усилий.Таким образом, если два резистора включены последовательно (что означает, что они имеют одинаковый ток), резистор с большим сопротивлением будет иметь большее падение напряжения. Это основа работы схемы делителя напряжения.

Полярность падений напряжения

Резистор всегда работает как нагрузка, то есть как компонент, потребляющий энергию. Если мы примем традиционную модель протекания тока, в которой ток течет от более высокого напряжения к более низкому напряжению, падение напряжения на резисторе будет положительным, когда ток входит в резистор, и отрицательным, когда ток выходит из резистора:

Модель протекания тока, показывающая, как падение напряжения является положительным, когда ток входит в резистор, и отрицательным, когда он выходит.

Эта полярность «противостоит» напряжению источника: если мы подключим батарею с такой же ориентацией полярности, она будет направлять ток в противоположном направлении (или будет противодействовать напряжению источника, в зависимости от того, как вы об этом думаете).

Конденсаторы и катушки индуктивности накапливают энергию и, следовательно, могут работать как нагрузка или как источник. Когда они действуют как нагрузки, они имеют ту же полярность падения напряжения, что и резистор.

При работе в качестве нагрузки конденсаторы и катушки индуктивности имеют ту же полярность падения напряжения, что и резистор.

Полярность падения напряжения конденсатора не меняется, когда он начинает разряжаться. Несмотря на то, что он действует как источник, он производит ток, направление которого противоположно направлению зарядного тока.

Однако, когда индуктор разряжается, он пытается поддерживать ток. Таким образом, полярность падения напряжения индуктора изменяется, поскольку он генерирует ток, направление которого совпадает с направлением зарядного тока, производимого источником.

Изображение того, как индуктор пытается поддерживать ток при разрядке.

---

Какие еще вопросы у вас есть по поводу падений напряжения? Делитесь своими вопросами в комментариях ниже.

Потенциал

– Что такое «падение напряжения» на элементе схемы?

Если у вас простая схема с резисторами, напряжение на источнике уменьшается по всей цепи. Например, на положительной клемме аккумулятора может быть напряжение 9 В, а на отрицательной клемме можно принять потенциал земли 0 В.

Напряжение между этими выводами (то есть через цепь) уменьшается от положительного напряжения 9 В до потенциала земли 0 В.

Как уменьшается? Мы предполагаем, что у нас есть идеальные проводники в виде проводов, что означает, что они имеют одинаковый потенциал в каждой точке, то есть в начале и в конце провода, напряжение одинаково. Единственные точки в цепи, где напряжение может снизиться, – это резисторы в этом случае. Перед резистором более высокое напряжение, а за ним более низкое напряжение.Разница в падении напряжения. Он соответствует количеству мощности, рассеиваемой в резисторе, и пропорционален сопротивлению.

Вот схема простой схемы. Как видите, есть три последовательно включенных резистора и источник напряжения 9 В.

Ток величиной 0,5 мА протекает по цепи и проходит через все элементы схемы. Мы можем рассчитать этот ток, найдя эквивалентное сопротивление цепи. Для последовательного соединения трех резисторов мы просто складываем их сопротивления: $$ R = R_1 + R_2 + R_3 = 3 k \ Omega + 10 k \ Omega + 5 k \ Omega = 18 k \ Omega $$

Из $ U = R I $ мы можем найти ток, протекающий через каждый элемент: $$ I = \ frac {U} {R} = \ frac {9 V} {18 k \ Omega} = 0.5 мА $$

Теперь мы можем узнать, сколько напряжения падает на каждом элементе. Это пропорционально его сопротивлению. Поскольку теперь мы знаем ток и сопротивление на каждом элементе, мы можем рассчитать падение напряжения.

Для напряжения, которое падает на $ R_1 $, мы пишем: $$ \ Delta U_1 = R_1 I = 3 k \ Omega \ cdot 0,5 мА = 1,5 В $$

Аналогично для других резисторов мы получаем 5 В $ для $ R_2 $ и $ 2,5 В $ для $ R_3 $.

На схеме выше мы можем видеть, как это изменяет уровни напряжения в каждой части схемы.Исходя из положительной клеммы источника напряжения, напряжение составляет 9 В. Оно сохраняется до тех пор, пока не достигнет первого резистора. На передней панели резисторов (по направлению тока, по часовой стрелке) напряжение 9 В (красная часть), но напряжение за резистором ниже: теперь оно составляет всего 9 В – 1,5 В = 7,5 В $ ( желтая часть). Напряжение на резисторе упало. Если вы измеряете напряжение за резистором, вы должны измерить 7,5 В.

Аналогичным образом это работает для всех последующих резисторов: резистор 10 кОм упадет на 5 В, что означает, что перед ним у нас уровень 7. 5 В (желтый), а за ним 7,5 В – 5 В = 2,5 В $ (зеленый). Наконец, последний резистор падает на 2,5 В, в результате чего напряжение на конце падает до 0 В (синий).

FAQ – Падение напряжения

Что такое напряжение уронить? Падение напряжения в электрической цепи обычно возникает, когда по проводу проходит ток. Чем больше сопротивление цепи, тем выше падение напряжения.

Сколько напряжения падение приемлемо? A сноска (NEC 210-19 FPN No.4) в Национальном электротехническом кодексе говорится, что напряжение падение на 5% в самом дальнем гнезде ответвленной проводки схема приемлема для нормальной эффективности. Через 120 цепь вольт 15 ампер, значит, должно быть падение не более 6 вольт (114 вольт) на самом дальнем расстоянии розетку, когда цепь полностью загружена. Это также означает что цепь имеет сопротивление, не превышающее 0,4 Ом.

Причины «Чрезмерное падение напряжения» в параллельной цепи ? Причина обычно:

1.Высокая стойкость соединения в местах соединения проводов или выходных клемм, обычно вызывается:

• плохие стыки в любом месте цепи
• отдельно или прерывистые соединения в любом месте цепи
• корродированный соединения в любом месте цепи
  • неадекватны посадка провода в разъем на с обратной связью «вставного типа» розетки и выключатели.

2. Провод делает не соответствуют нормам кодов (недостаточно большой калибр для длина пробега).

Какие последствия «избыточного» падения напряжения в схема? Чрезмерное падение напряжения может вызвать следующие условия:

1. Низкое напряжение до оборудование, на которое подается питание, что приводит к неправильной, неустойчивой, или нет работы – и повреждение оборудования.

2. Низкая эффективность и потраченная впустую энергия.

3. Обогрев при соединение / сращивание с высоким сопротивлением может привести к пожару на высокие амперные нагрузки.

На какой% падение напряжения делает цепь опасной? Это сложно сказать, в какой момент будет превышение падения напряжения вызвать пожар, потому что это зависит от силы тока протекает через соединение с высоким сопротивлением, что сопротивление этой связи и потому что многие необходимо учитывать факторы относительно того, в какой момент произойдет возгорание, e.г .:

1. Высокий соединение сопротивления при контакте с горючим материал?

2. Есть ли воздух? поток для рассеивания тепла?

3. Является ли площадь изоляция вокруг соединения, чтобы тепло не побег.

NFPA сообщает [1], что с 1988-1992 гг. было в среднем 446 300 пожаров в год в домах, в результате 3860 смертей и имущества на 4,4 миллиарда долларов повреждать.42 300 (9%) из этих пожаров происходили ежегодно по Электрические распределительные системы . Самый большой часть пожаров, вызванных распределением электроэнергии систем (48%) были вызваны неисправностью фиксированной проводки, розетки и выключатели .

Электрооборудование Пожары распределительного оборудования в домах в США 2

1988–1992 В среднем

Причина пожара	№Огней
Общее распределение электроэнергии Система	42 300 (100%)
Неисправность фиксированной проводки	15400 (36%)
Выключатели, розетки, розетки	4800 (11%)

Результаты тщательное расследование 149 пожаров в жилых домах, вызванных системы распределения электроэнергии были резюмированы в статья Smith & McCoskrie [2]. О пожарах, происходящих как результат:

1. неисправность исправлена проводка – плохие / неплотные соединения, поврежденные разъемы, неправильная установка и замыкания на землю составили 94% этих пожаров.

2. розетки и переключатели – неплотные / плохие соединения составили 59% этих пожаров .

3. Освещение арматура – ослабленные или плохие соединения составили 37% этих пожаров.

Большинство из них неисправные цепи и розетки могли быть ранее идентифицированные как опасности при нагрузке 15 ампер испытание, и многие из этих пожаров могли быть легко предотвратил.

The Philadelphia Корпорация жилищного строительства требует подрядчиков выполнить испытание под нагрузкой 15 ампер перед изоляцией существующие дома с утеплителем на чердаке места в старых домах-рядах. [3] До учреждения испытания, тлеющие пожары были связаны с полдюжиной установки. PHDC обнаружил, что 70% домов провалил испытание на максимальное падение напряжения 5% с оценкой «a кластер около 6% ». PHDC произвольно установлен 10% как недопустимое падение напряжения, за пределами которого подрядчик должен отремонтировать / заменить цепь до приступаем к проекту изоляции. PHDC был успешно используя этот критерий в течение 2 лет (нет пожаров в 2500 установок).

РЕКОМЕНДАЦИИ

Для мощности КПД, стандарт NEC: максимальное падение напряжения 5% Рекомендовано.

Из безопасности перспектива, потому что проводка в некоторых домах со временем ухудшаются (особенно в домах, где алюминиевая проводка для силовых цепей), и своими руками модификации могут быть не профессиональные, лишние падение напряжения вызывает беспокойство из-за потенциального возгорания опасность на соединениях с высоким сопротивлением, особенно на цепи, которые приводят в действие электродвигатели, когда они находятся в жилище спят, e. грамм. Кондиционеры, холодильники, печные вентиляторы, вытяжные вентиляторы и др.

Некоторые агентства произвольно установите критерий максимального падения напряжения от 10% до считаться неприемлемым и опасным. Автор считает, что любая разница падения напряжения> 1% от соседняя емкость должна быть исследована, чтобы разница падения напряжения> 2% от соседнего емкость следует рассматривать как опасность, а использование критерии максимального падения напряжения более 8% (на 3% выше рекомендация «эффективность») ухаживает катастрофа.Падение напряжения 3% (3,6 В при 120 В цепь) при одном подключении при токе 15 ампер развивается 54 Вт тепла – что может вызвать возгорание при определенных условия.

---

Сноски

[1] NFPA Отчет о продуктах для дома в США, 1988–1992 гг. (Приборы и оборудование) Элисон Л. Миллер Август, 1994

[2] Смит, Линда и Деннис МакКоскри, «Что вызывает возгорание электропроводки в жилых домах» Пожар Журнал , январь / февраль 1990: 19-24, 69

[3] Кинни, Ларри «Оценка целостности Электропроводки » Home Energy Сентябрь / Октябрь 1995 год: 5,6

Учебное пособие по физике: Параллельные схемы

Как упоминалось в предыдущем разделе Урока 4, два или более электрических устройства в цепи могут быть соединены последовательным или параллельным соединением. Когда все устройства соединены с использованием параллельных соединений, схема называется параллельной схемой . В параллельной схеме каждое устройство помещается в свою отдельную ветвь . Наличие ответвлений означает, что существует несколько путей, по которым заряд может проходить через внешнюю цепь. Каждый заряд, проходящий через контур внешней цепи, будет проходить через единственный резистор, присутствующий в одной ветви. По прибытии в место разветвления или узел плата делает выбор относительно того, через какую ветвь пройти на обратном пути к терминалу с низким потенциалом.

Краткое сравнение и контраст между последовательными и параллельными цепями было сделано в предыдущем разделе Урока 4. В этом разделе было подчеркнуто, что добавление большего количества резисторов в параллельную цепь приводит к довольно неожиданному результату – уменьшению общего сопротивления. . Поскольку существует несколько путей, по которым может протекать заряд, добавление еще одного резистора в отдельную ветвь обеспечивает еще один путь, по которому заряд может проходить через основную область сопротивления в цепи. Это уменьшенное сопротивление в результате увеличения количества ветвей будет иметь эффект увеличения скорости, с которой течет заряд (также известной как ток). Чтобы сделать этот довольно неожиданный результат более разумным, была введена аналогия с платными дорогами. Плата за проезд – это основное место сопротивления автомобильному потоку на платной дороге. Добавление дополнительных пунктов сбора платы за проезд в пределах их собственного отделения на платной дороге обеспечит больше путей для автомобилей, проезжающих через станцию ​​сбора платы за проезд. Эти дополнительные пункты пропуска снизят общее сопротивление потоку автомобилей и увеличат скорость их движения.

Текущий

Скорость, с которой заряд проходит через цепь, называется током. Заряд НЕ накапливается и не начинает накапливаться в любом конкретном месте, так что ток в одном месте больше, чем в других местах. Заряд НЕ расходуется резисторами таким образом, что в одном месте ток меньше, чем в другом. В параллельной схеме заряд делит на отдельные ветви, так что в одной ветви может быть больше тока, чем в другой.Тем не менее, если брать в целом, общая сумма тока во всех ветвях при сложении равна величине тока в местах за пределами ветвей. Правило, что ток везде одинаковый все еще работает, только с закруткой. Сила тока вне ветвей равна сумме токов в отдельных ветвях. Это все еще та же величина тока, только разделенная на несколько путей.

В форме уравнения этот принцип можно записать как

I _итого = I ₁ + I ₂ + I ₃ +…

, где I _total – это общая величина тока вне ветвей (и в батарее), а I ₁ , I ₂ и I ₃ представляют ток в отдельных ветвях цепи.

В этом блоке широко использовалась аналогия между расходом заряда и расходом воды. Еще раз вернемся к аналогии, чтобы проиллюстрировать, как сумма текущих значений в ветвях равна сумме вне ветвей. Поток заряда в проводах аналогичен потоку воды в трубах. Рассмотрим приведенные ниже схемы, на которых поток воды в трубах делится на отдельные ответвления. В каждом узле (место разветвления) вода проходит двумя или более отдельными путями. Скорость, с которой вода поступает в узел (измеряется в галлонах в минуту), будет равна сумме расходов в отдельных ветвях за пределами узла. Точно так же, когда две или более ветви подаются в узел, скорость, с которой вода вытекает из узла, будет равна сумме расходов в отдельных ветвях, которые подаются в узел.

Тот же принцип разделения потока применяется к электрическим цепям. Скорость, с которой заряд поступает в узел, равна сумме расходов в отдельных ветвях за пределами узла. Это проиллюстрировано в приведенных ниже примерах. В примерах вводится новый символ схемы – буква A, заключенная в круг. Это символ амперметра – устройства, используемого для измерения силы тока в определенной точке. Амперметр может измерять ток, оказывая при этом незначительное сопротивление потоку заряда.

Диаграмма A показывает два резистора, подключенных параллельно узлам в точках A и B. Заряд течет в точку A со скоростью 6 ампер и делится на два пути – один через резистор 1, а другой через резистор 2. Ток в ветви с резистором 1 составляет 2 ампера, а ток в ветви с резистором 2 составляет 4 ампера. После того, как эти две ветви снова встретятся в точке B, чтобы сформировать единую линию, ток снова станет 6 ампер. Таким образом, мы видим, что принцип, согласно которому ток за пределами ветвей равен сумме тока в отдельных ветвях, выполняется.

I _всего = I ₁ + I ₂

6 ампер = 2 ампера + 4 ампера

Схема B выше может быть немного более сложной, если три резистора расположены параллельно. На схеме обозначены четыре узла, обозначенные буквами A, B, C и D. Заряд течет в точку A со скоростью 12 ампер и делится на два пути: один проходит через резистор 1, а другой направляется к точке B (и резисторам 2). и 3). 12 ампер тока делятся на 2-амперную (через резистор 1) и 10-амперную (в направлении точки B).В точке B происходит дальнейшее разделение потока на два пути – один через резистор 2, а другой через резистор 3. Ток в 10 ампер, приближающийся к точке B, делится на 6-амперный канал (через резистор 2) и 4-канальный. -амперный тракт (через резистор 3). Таким образом, видно, что значения тока в трех ветвях составляют 2 ампера, 6 ампер и 4 ампера и что сумма значений тока в отдельных ветвях равна току вне ветвей.

I _всего = I ₁ + I ₂ + I ₃

12 ампер = 2 ампер + 6 ампер + 4 ампер

Анализ потока в точках C и D также может быть проведен, и будет замечено, что сумма расходов потока в этих точках равна скорости потока, находящейся непосредственно за этими точками.

Эквивалентное сопротивление

Фактическая величина тока всегда изменяется обратно пропорционально величине общего сопротивления. Существует четкая взаимосвязь между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Чтобы исследовать эту взаимосвязь, давайте начнем с простейшего случая, когда два резистора помещены в параллельные ветви, каждый из которых имеет одинаковое значение сопротивления 4 Ом.Поскольку схема предлагает два равных путей для потока заряда, только половина заряда выберет для прохождения через данную ветвь. Хотя каждая отдельная ветвь обеспечивает сопротивление 4 Ом любому заряду, который проходит через нее, только половина всего заряда, протекающего по цепи, будет встречать сопротивление 4 Ом этой отдельной ветви. Таким образом, что касается аккумулятора, который накачивает заряд, наличие двух параллельно подключенных резисторов 4 Ом было бы эквивалентно наличию одного резистора 2 Ом в цепи.Таким же образом, наличие двух параллельно подключенных резисторов сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 3 Ом. А наличие двух параллельных резисторов 12 Ом было бы эквивалентно наличию в цепи одного резистора 6 Ом.

Теперь давайте рассмотрим другой простой случай, когда параллельно соединены три резистора, каждый из которых имеет одинаковое сопротивление 6 Ом. При трех равных путях прохождения заряда через внешнюю цепь только одна треть заряда будет проходить через данную ветвь.Каждая отдельная ветвь обеспечивает сопротивление 6 Ом проходящему через нее заряду. Однако тот факт, что только одна треть заряда проходит через определенную ветвь, означает, что общее сопротивление цепи составляет 2 Ом. Что касается батареи, которая накачивает заряд, наличие трех параллельно подключенных резисторов 6 Ом было бы эквивалентно наличию одного резистора 2 Ом в цепи. Таким же образом, наличие трех параллельно подключенных резисторов сопротивлением 9 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 3 Ом.А наличие трех параллельно подключенных резисторов на 12 Ом было бы эквивалентно наличию в цепи одного резистора 4 Ом.

Это концепция эквивалентного сопротивления. Эквивалентное сопротивление схемы – это величина сопротивления, которая потребуется одному резистору, чтобы сравняться с общим эффектом от набора резисторов, присутствующих в схеме. Для параллельных цепей математическая формула для вычисления эквивалентного сопротивления (R _экв ) составляет

. 1 / R _экв. = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ +…

, где R ₁ , R ₂ и R ₃ – значения сопротивления отдельных резисторов, подключенных параллельно. Приведенные выше примеры можно рассматривать как простые случаи, в которых все пути оказывают одинаковое сопротивление отдельному заряду, который проходит через них. Вышеупомянутые простые случаи были выполнены без использования уравнения. Однако это уравнение подходит как для простых случаев, когда резисторы ответвления имеют одинаковые значения сопротивления, так и для более сложных случаев, когда резисторы ответвления имеют разные значения сопротивления. Например, рассмотрим применение уравнения к одному простому и одному сложному случаю ниже.

Корпус 1 : Три резистора 12 Ом включены параллельно	1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 1 / R экв = 1 / (12 Ом) + 1 / (12 Ом) + 1 / (12 Ом) Использование калькулятора … 1 / R экв = 0,25 Ом -1 R экв = 1 / (0,25 Ом -1 ) R экв = 4,0 Ом
Случай 2 : резисторы 5,0 Ом, 7,0 Ом и 12 Ом подключены параллельно	1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 1 / R экв = 1 / (5.0 Ом) + 1 / (7,0 Ом) + 1 / (12 Ом) Использование калькулятора . .. 1 / R экв = 0,42619 Ом-1 R экв = 1 / (0,42619 Ом -1 ) R экв = 2,3 Ом

Ваша очередь попробовать

Нужно больше практики? Используйте два параллельных резистора виджет ниже, чтобы попробовать некоторые дополнительные проблемы.Введите два любых желаемых значения сопротивления. Используйте свой калькулятор, чтобы определить значения R _eq . Затем нажмите кнопку Отправить , чтобы проверить свои ответы. Попробуйте столько раз, сколько хотите, с разными значениями сопротивления.

Падения напряжения для параллельных ветвей

В разделе «Схемы» учебного пособия «Физический класс» подчеркивалось, что любое повышение напряжения, полученное за счет заряда в батарее, теряется из-за заряда, когда он проходит через резисторы внешней цепи. Общее падение напряжения во внешней цепи равно увеличению напряжения при прохождении заряда по внутренней цепи. В параллельной схеме заряд не проходит через каждый резистор; скорее, он проходит через единственный резистор. Таким образом, полное падение напряжения на этом резисторе должно соответствовать напряжению батареи. Не имеет значения, проходит ли заряд через резистор 1, резистор 2 или резистор 3, падение напряжения на резисторе, которое выбирает для прохождения, должно равняться напряжению батареи.В форме уравнения этот принцип может быть выражен как

V _{батарея} = V ₁ = V ₂ = V ₃ = …

Если три резистора размещены в параллельных ветвях и питаются от 12-вольтовой батареи, то падение напряжения на каждом из трех резисторов составляет 12 вольт. Заряд, протекающий по цепи, встретит только один из этих трех резисторов и, таким образом, столкнется с одним падением напряжения на 12 вольт.

Диаграммы электрических потенциалов были представлены в Уроке 1 этого устройства и впоследствии использовались для иллюстрации последовательных падений напряжения, происходящих в последовательных цепях.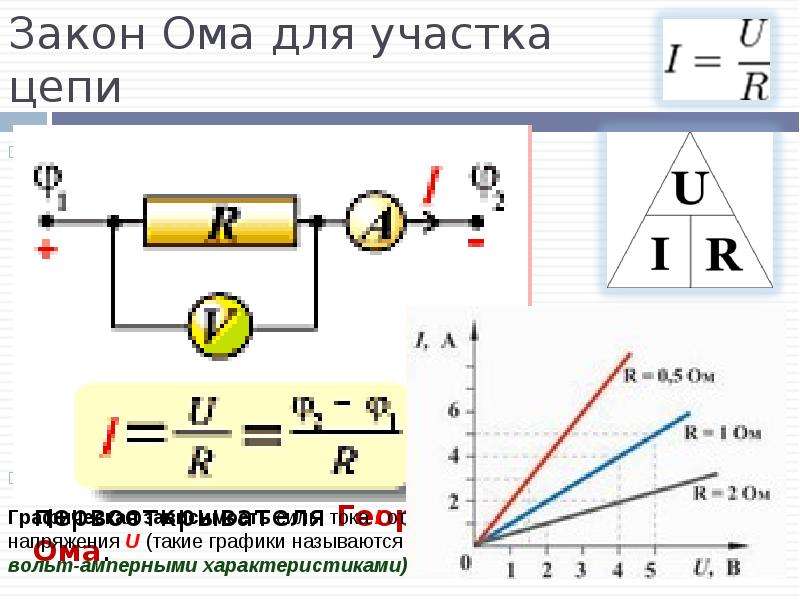 Диаграмма электрических потенциалов – это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками в электрической цепи. Рассмотрим приведенную ниже принципиальную схему и соответствующую диаграмму электрических потенциалов.

Как показано на диаграмме электрических потенциалов, все позиции A, B, C, E и G имеют высокий электрический потенциал. Один заряд выбирает только один из трех возможных путей; таким образом, в позиции B один заряд будет двигаться к точкам C, E или G, а затем проходит через резистор, находящийся в этой ветви.Заряд не теряет свой высокий потенциал до тех пор, пока не пройдет через резистор, либо от C к D, от E к F или от G к H. Как только он проходит через резистор, заряд возвращается почти до 0 В и возвращается к отрицательному значению. клемму аккумуляторной батареи для повышения ее напряжения. В отличие от последовательных цепей, заряд в параллельной цепи встречает единственное падение напряжения на своем пути через внешнюю цепь.

Ток через данную ветвь можно предсказать, используя уравнение закона Ома, падение напряжения на резисторе и сопротивление резистора.Поскольку падение напряжения на каждом резисторе одинаковое, фактором, определяющим наибольший ток резистора, является сопротивление. Резистор с наибольшим сопротивлением испытывает наименьший ток, а резистор с наименьшим сопротивлением – наибольший ток. В этом смысле можно сказать, что заряд (как и люди) выбирает путь наименьшего сопротивления. В форме уравнения это может быть указано как

I 1 = Δ V 1 / R 1

I 2 = Δ V 2 / R 2

I 3 = Δ V 3 / R 3

Этот принцип иллюстрируется схемой, показанной ниже. Произведение I • R одинаково для каждого резистора (и равно напряжению батареи). Тем не менее, ток у каждого резистора разный. Ток наибольший там, где сопротивление наименьшее, и ток наименьший, где сопротивление наибольшее.

Математический анализ параллельных цепей

Приведенные выше принципы и формулы могут использоваться для анализа параллельной цепи и определения значений тока и разности электрических потенциалов на каждом из резисторов в параллельной цепи.Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R _eq ), тока через аккумулятор (I _до ), а также падений напряжения и тока для каждого из трех резисторов.

Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.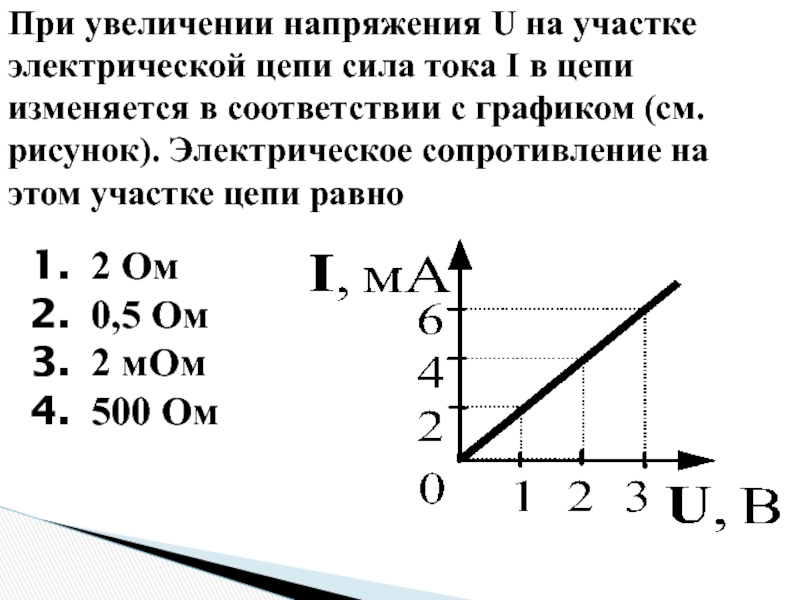

1 / R _экв = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ = (1/17 Ом) + (1/12 Ом) + (1/11 Ом)

1 / R _экв = 0.23306 Ом ^-1

R _экв = 1 / (0,23306 Ом ^-1 )

R _экв = 4,29 Ом

(округлено от 4,29063 Ом)

Теперь, когда известно эквивалентное сопротивление, ток в батарее можно определить с помощью уравнения закона Ома. При использовании уравнения закона Ома (ΔV = I • R) для определения тока в батарее важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R.Расчет показан здесь:

I _tot = ΔV _{аккумулятор} / R _eq = (60 В) / (4,29063 Ом)

I _до = 14,0 А

(округлено от 13,98396 А)

Напряжение батареи 60 В представляет собой усиление электрического потенциала за счет заряда, проходящего через батарею. Заряд теряет такое же количество электрического потенциала при любом прохождении через внешнюю цепь.То есть падение напряжения на каждом из трех резисторов такое же, как и напряжение, полученное в батарее:

ΔV _{аккумулятор} = ΔV ₁ = ΔV ₂ = ΔV ₃ = 60 В

Осталось определить три значения – ток каждого отдельного резистора. Закон Ома снова используется для определения значений тока для каждого резистора – это просто падение напряжения на каждом резисторе (60 В), деленное на сопротивление каждого резистора (указанное в формулировке задачи).Расчеты показаны ниже.

I 1 = ΔV 1 / R 1 I 1 = (60 В) / (17 Ом) I 1 = 3,53 А

I 2 = ΔV 2 / R 2 I 2 = (60 В) / (12 Ом) I 2 = 5,00 А

I 3 = ΔV 3 / R 3 I 3 = (60 В) / (11 Ом) Я 3 = 5.45 А

В качестве проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли вычисленные значения принципу, согласно которому сумма значений тока для каждого отдельного резистора равна общему току в цепи (или в батарее). . Другими словами, I _tot = I ₁ + I ₂ + I ₃ ?

Является ли I _tot = I ₁ + I ₂ + I ₃ ?

Из 14.0 ампер = 3,53 ампер + 5,00 ампер + 5,45 ампер?

14,0 А = 13,98 А?

Да !!

(Разница в 0,02 ампера – это просто результат предыдущего округления значения I _до с 13,98.)

Математический анализ этой параллельной цепи включал смесь концепций и уравнений. Как это часто бывает в физике, отделение концепций от уравнений при принятии решения физической проблемы является опасным актом.Здесь необходимо учитывать концепции, согласно которым падение напряжения на каждом из трех резисторов равно напряжению батареи, а сумма тока в каждом резисторе равна общему току. Эти представления необходимы для завершения математического анализа. В следующей части Урока 4 будут исследованы комбинированные или составные схемы, в которых одни устройства включены параллельно, а другие – последовательно.

Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже.Создайте себе проблему с любым количеством резисторов и любыми номиналами. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.

Мы хотели бы предложить … Зачем просто читать об этом и когда можно с ним взаимодействовать? Взаимодействие – это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключить их так, как хотите. Вольтметры и амперметры позволяют измерять ток и падение напряжения. Нажав на резистор или источник напряжения, вы можете изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванной).

Проверьте свое понимание

1. По мере того, как в цепь добавляется все больше и больше резисторов, эквивалентное сопротивление цепи ____________ (увеличивается, уменьшается), а общий ток цепи ____________ (увеличивается, уменьшается).

2.Три одинаковые лампочки подключены к D-ячейке, как показано ниже. P, Q, X, Y и Z обозначают местоположения вдоль цепи. Какое из следующих утверждений верно?

а. Ток в точке Y больше, чем ток в точке Q.

г. Ток на Y больше, чем на P.

.

г. Ток в точке Y больше, чем ток в точке Z.

г. Ток в точке P больше, чем ток в точке Q.

.

e.Ток на Q больше, чем на P.

.

ф. Сила тока во всех местах одинакова.

3. Три одинаковые лампочки подключены к D-ячейке, как показано ниже. P, Q, X, Y и Z обозначают местоположения вдоль цепи. В каком месте (ах), если таковые имеются, будет ток …

а. … так же, как у X?

г…. такой же, как у Q?

г. … так же, как у Y?

г. … меньше, чем у Q?

e. … меньше, чем у P?

ф. … вдвое больше, чем у Z?

г. … в три раза больше, чем в Y?

4. Какие изменения можно внести в схему ниже, чтобы уменьшить ток в ячейке? Перечислите все подходящие варианты.

а. Увеличьте сопротивление лампы X.

г. Уменьшите сопротивление лампы X.

г. Увеличьте сопротивление лампы Z.

.

г. Уменьшите сопротивление лампы Z.

.

e. Увеличьте напряжение ячейки (как-нибудь).

ф. Уменьшите напряжение ячейки (как-нибудь).

г. Снять лампу Y.

.

5.Аккумулятор на 12 В, резистор на 12 Ом и резистор на 4 Ом подключаются, как показано на рисунке. Ток в резисторе 12 Ом равен ____ току в резисторе 4 Ом.

а. 1/3	г. 1/2	г. 2/3
г. то же, что		e.1,5 раза
ф. дважды		г. трижды
ч. четыре раза

6. Аккумулятор 12 В, резистор на 12 Ом и резистор на 4 Ом подключены, как показано.Падение напряжения на резисторе 12 Ом равно ____ падению напряжения на резисторе 4 Ом.

а. 1/3	г. 1/2	г. 2/3
г. то же, что		e. 1,5 раза
ф.дважды		г. трижды
ч. четыре раза

7. Аккумулятор на 12 В и резистор на 12 Ом подключаются, как показано на схеме. Резистор на 6 Ом добавлен к резистору на 12 Ом, чтобы создать цепь Y, как показано.Падение напряжения на резисторе 6 Ом в цепи Y равно ____ падению напряжения на резисторе X.

а. больше, чем

г. меньше

г. то же, что

8. Используйте свое понимание эквивалентного сопротивления, чтобы заполнить следующие утверждения:

а. Два резистора 6 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.

г. Три резистора 6 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.

г. Три резистора сопротивлением 8 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.

г. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом размещены параллельно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

e. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом размещены параллельно.Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

ф. Три резистора с сопротивлением 12 Ом, 6 Ом и 21 Ом размещены параллельно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

9. На основании ваших ответов на вышеуказанный вопрос заполните следующую формулировку:

Общее или эквивалентное сопротивление трех параллельно включенных резисторов будет _____.

а. больше, чем сопротивление самого большого из трех значений R.

г. меньше, чем сопротивление наименьшего значения R из трех.

г. где-то между наименьшим значением R и наибольшим значением R.

г. … ерунда! Такого обобщения сделать нельзя. Результаты меняются.

10. Три резистора включены параллельно.При размещении в цепи с источником питания 12 В. Определите эквивалентное сопротивление, общий ток цепи, падение напряжения и ток в каждом резисторе.

Как рассчитать падение напряжения на резисторе в параллельной цепи

Обновлено 28 декабря 2020 г.

Автор: S.Hussain Ather

••• Syed Hussain Ather

TL; DR (слишком долго; не читал)

На приведенной выше схеме параллельной цепи падение напряжения можно найти, суммировав сопротивления каждого резистора и определив, какое напряжение вытекает из тока в этой конфигурации. Эти примеры параллельных цепей иллюстрируют концепции тока и напряжения в разных ветвях.

На схеме параллельной цепи падение напряжения на резисторе в параллельной цепи одинаково для всех резисторов в каждой ветви параллельной цепи.Напряжение, выраженное в вольтах, измеряет электродвижущую силу или разность потенциалов в цепи.

Если у вас есть цепь с известной величиной тока , поток электрического заряда, вы можете рассчитать падение напряжения в схемах параллельной цепи по:

1. Определите объединенное сопротивление или сопротивление к потоку заряда параллельных резисторов. Суммируйте их как 1/_{, всего} = 1/ ₁ + 1/ ₂ … для каждого резистора. Для приведенной выше параллельной цепи полное сопротивление можно найти как:
   1. 1 / R _всего = 1/5 Ом + 1/6 Ом + 1/10 Ом
      
   2. 1 / R _всего = 6/30 Ом + 5/30 Ом + 3/30 Ом
      
   3. 1 / R _всего = 14/30 Ом
      
   4. R _всего = 30/14 Ом = 15/7 Ом
2. Умножьте ток на полное сопротивление, чтобы получить падение напряжения в соответствии с законом Ома В = IR .Это равно падению напряжения во всей параллельной цепи и на каждом резисторе в параллельной цепи. В этом примере падение напряжения составляет В = 5 А x 15/7 Ом = 75/7 В.

Этот метод решения уравнений работает, потому что ток, входящий в любую точку параллельной цепи, должен быть равен текущий уход. Это происходит из-за текущего закона Кирхгофа, который гласит: «алгебраическая сумма токов в сети проводников, встречающихся в одной точке, равна нулю.”Калькулятор параллельной цепи мог бы использовать этот закон в ветвях параллельной цепи.

Если мы сравним ток, входящий в три ветви параллельной цепи, он должен равняться общему току, выходящему из ветвей. Поскольку падение напряжения остается постоянная на каждом параллельном резисторе, это падение напряжения, вы можете суммировать сопротивление каждого резистора, чтобы получить общее сопротивление и определить напряжение по этому значению. Примеры параллельных цепей показывают это. Hussain Ather

В последовательной цепи, с другой стороны, вы можете рассчитать падение напряжения на каждом резисторе, зная, что в последовательной цепи ток постоянен на всем протяжении.Это означает, что падение напряжения на каждом резисторе разное и зависит от сопротивления в соответствии с законом Ома V = IR . В приведенном выше примере падение напряжения на каждом резисторе составляет:

V_1 = R_1I = 3 \ times 3 = 9 \ text {V} \\ V_2 = R_2I = 10 \ times 3 = 30 \ text {V} \\ V_3 = R_3I = 5 \ times 3 = 15 \ text {V}

Сумма каждого падения напряжения должна быть равна напряжению батареи в последовательной цепи. Это означает, что наша батарея имеет напряжение 54 В.

Этот метод решения уравнений работает, потому что падение напряжения на всех резисторах, установленных последовательно, должно в сумме составлять общее напряжение последовательной цепи.Это происходит из-за закона напряжения Кирхгофа , который гласит, что «направленная сумма разностей потенциалов (напряжений) вокруг любого замкнутого контура равна нулю». Это означает, что в любой точке замкнутой последовательной цепи падение напряжения на каждом резисторе должно равняться общему напряжению цепи. Поскольку ток в последовательной цепи постоянный, падение напряжения должно быть различным для каждого резистора.

Параллельные и последовательные схемы

В параллельной схеме все компоненты схемы подключаются между одними и теми же точками на схеме.Это дает им их разветвленную структуру, в которой ток разделяется между каждой ветвью, но падение напряжения на каждой ветви остается неизменным. Сумма каждого резистора дает общее сопротивление, обратное каждому сопротивлению ( 1 / R _всего = 1 / R ₁ + 1 / R ₂ … для каждого резистора).

В последовательной цепи, напротив, есть только один путь для прохождения тока. Это означает, что ток остается постоянным на всем протяжении, а падение напряжения на каждом резисторе отличается.Сумма каждого резистора дает общее сопротивление при линейном суммировании ( R _всего = R ₁ + R ₂ … для каждого резистора).

Последовательно-параллельные схемы

Вы можете использовать оба закона Кирхгофа для любой точки или петли в любой цепи и применять их для определения напряжения и тока. Законы Кирхгофа дают вам метод определения тока и напряжения в ситуациях, когда природа цепи как последовательной и параллельной может быть не такой простой.

Как правило, для цепей, которые имеют как последовательные, так и параллельные компоненты, вы можете рассматривать отдельные части схемы как последовательные или параллельные и соответственно комбинировать их.

Эти сложные последовательно-параллельные схемы можно решить несколькими способами. Один из методов – рассматривать их части как параллельные или последовательные. Другой метод – использование законов Кирхгофа для определения обобщенных решений, использующих систему уравнений. Калькулятор последовательно-параллельных цепей учитывает различную природу цепей.

••• Syed Hussain Ather

В приведенном выше примере текущая точка выхода A должна равняться текущей точке выхода A. Это означает, что вы можете написать:

(1). I_1 = I_2 + I_3 \ text {или} I_1-I_2-I_3 = 0

Если рассматривать верхний контур как замкнутую последовательную цепь и рассматривать падение напряжения на каждом резисторе, используя закон Ома с соответствующим сопротивлением, вы можете написать:

(2). V_1-R_1I_1-R_2I_2 = 0

и, проделав то же самое для нижнего контура, вы можете обрабатывать каждое падение напряжения в направлении тока в зависимости от тока и сопротивления, чтобы записать:

(3).V_1 + V_2 + R_3I_3-R_2I_2 = 0

Это дает вам три уравнения, которые можно решить несколькими способами. Вы можете переписать каждое из уравнений (1) – (3) так, чтобы напряжение было с одной стороны, а ток и сопротивление – с другой. Таким образом, вы можете рассматривать три уравнения как зависимые от трех переменных I ₁ , I ₂ и I ₃ с коэффициентами комбинаций R ₁ , R ₂ и R ₃ .

\ begin {align} & (1).I_1-I_2-I_3 = 0 \\ & (2). R_1I_1 + R_2I_2 + 0 \ times I_3 = V_1 \\ & (3). 0 \ times I_1 + R_2I_2-R_3I_3 = V_1 + V_2 \ end {выровнено}

Эти три уравнения демонстрируют, как напряжение в каждой точке цепи каким-то образом зависит от тока и сопротивления. Если вы помните законы Кирхгофа, вы можете создать эти обобщенные решения схемных задач и использовать матричную запись для их решения. Таким образом, вы можете подставить значения для двух величин (среди которых напряжение, ток, сопротивление), чтобы найти третью.

Расчет падения напряжения | Инженеры Edge

Связанные ресурсы: приборы

Расчет падения напряжения

Падение напряжения определяется как уменьшение подводимой энергии источника напряжения по мере прохождения электрического тока через пассивные элементы (элементы, которые не подают напряжение) электрической цепи. Падения напряжения на внутренних сопротивлениях источника, проводниках, контактах и ​​разъемах нежелательны; подаваемая энергия теряется (рассеивается).Желательны падения напряжения на нагрузках и на других активных элементах схемы; подаваемая энергия выполняет полезную работу. Напомним, что напряжение представляет собой энергию на единицу заряда. Например, электрический обогреватель может иметь сопротивление десять Ом, а питающие его провода могут иметь сопротивление 0,2 Ом, что составляет около 2% от общего сопротивления цепи. Это означает, что примерно 2% подаваемого напряжения теряется в самом проводе. Чрезмерное падение напряжения может привести к неудовлетворительной работе и повреждению электрического и электронного оборудования.

Национальные и местные электротехнические нормы и правила могут устанавливать рекомендации по максимально допустимому падению напряжения в электропроводке, чтобы гарантировать эффективность распределения и правильную работу электрического оборудования. Максимально допустимое падение напряжения варьируется от страны к стране. В электронной конструкции и передаче энергии используются различные методы для компенсации эффекта падения напряжения в длинных цепях или там, где необходимо точно поддерживать уровни напряжения. Самый простой способ уменьшить падение напряжения – увеличить диаметр проводника между источником и нагрузкой, что снизит общее сопротивление.Более сложные методы используют активные элементы для компенсации нежелательного падения напряжения.

Падение напряжения в цепях переменного тока: полное сопротивление

В цепях переменного тока сопротивление току действительно возникает из-за сопротивления (как и в цепях постоянного тока). Цепи переменного тока также представляют собой второй вид сопротивления протеканию тока: реактивное сопротивление. Это «полное» противостояние (сопротивление «плюс» реактивное сопротивление) называется импедансом. Импеданс в цепи переменного тока зависит от расстояния и размеров элементов и проводников, частоты переменного тока и магнитной проницаемости элементов, проводников и их окружения.

Падение напряжения в цепи переменного тока является произведением силы тока и полного сопротивления (Z) цепи. Электрический импеданс, как и сопротивление, выражается в омах. Электрический импеданс – это векторная сумма электрического сопротивления, емкостного реактивного сопротивления и индуктивного реактивного сопротивления. Он выражается формулой E = IZ, аналогичной закону Ома для цепей постоянного тока.

Падение напряжения в электропроводке здания

Большинство цепей в доме не имеют достаточного тока или длины для создания высокого падения напряжения.В случае очень длинных цепей, например, при подключении дома к отдельному зданию на том же участке, может потребоваться увеличить размер проводов сверх минимального требования для номинального тока цепи. Для сильно нагруженных цепей может также потребоваться увеличение размера кабеля для соответствия требованиям к падению напряжения, установленным в правилах электромонтажа.

Нормы и правила электропроводки устанавливают верхний предел допустимого падения напряжения в параллельной цепи. В США Национальный электротехнический кодекс (NEC) рекомендует падение напряжения на розетке не более 5%.Канадский электротехнический кодекс требует не более 5% перепада между служебным входом и местом использования. Нормы Великобритании ограничивают падение напряжения до 4% от напряжения питания.

Расчет падения напряжения

В ситуациях, когда проводники цепи проходят на большие расстояния, рассчитывается падение напряжения. Если падение напряжения слишком велико, провод цепи необходимо увеличить для поддержания тока между точками. Расчеты для однофазной схемы и трехфазной схемы немного отличаются.

Расчет однофазного падения напряжения:

VD = [2 x L x R x I] / 1 000
VD% = [VD / Напряжение источника] x 100

Расчет трехфазного падения напряжения:

VD = [(2 x L x R x I) / 1000] x 0,866
VD% = [VD / Напряжение источника] x 100

Где:

VD = Падение напряжения (температура проводника 75 ° C) в вольтах

VD% = процент падения напряжения (VD ÷ напряжение источника x 100). Именно это значение обычно называют «падением напряжения» и указывается в NEC 215.2 (A) (4) и во всем NEC.

L = длина фидера контура в одном направлении (в футах)

R = коэффициент сопротивления согласно NEC, глава 9, таблица 8, Ом / кф

I = ток нагрузки (в амперах)

Напряжение источника = Напряжение параллельной цепи источника питания. Обычно напряжение источника составляет 120, 208, 240, 277 или 480 В.

© Copyright 2000 – 2021, Engineers Edge, LLC www.engineersedge.com
Все права защищены
Отказ от ответственности | Обратная связь | Реклама | Контакты

Дата / Время:

Расчет падения напряжения

| Electrical4U

Падение напряжения означает снижение напряжения или потери напряжения.Из-за наличия импеданса или пассивных элементов будет некоторая потеря напряжения при прохождении тока по цепи.

То есть энергия, подаваемая от источника напряжения, будет уменьшаться по мере протекания тока по цепи. Слишком большое падение напряжения может привести к повреждению и неправильной работе электрического и электронного оборудования. В основном, расчет падения напряжения выполняется по закону Ома.

Падение напряжения в цепях постоянного тока

В цепях постоянного тока причиной падения напряжения является сопротивление.Чтобы понять падение напряжения в цепи постоянного тока, мы можем взять пример. Предположим, что цепь состоит из источника постоянного тока, двух последовательно соединенных резисторов и нагрузки.

Здесь; каждый элемент схемы будет иметь определенное сопротивление, они получают и теряют энергию до некоторой величины. Но решающим фактором ценности энергии являются физические характеристики элементов. Когда мы измеряем напряжение между источником постоянного тока и первым резистором, мы видим, что оно будет меньше, чем напряжение питания.

Мы можем рассчитать энергию, потребляемую каждым сопротивлением, измеряя напряжение на отдельных резисторах. В то время как ток течет по проводу, начиная от источника постоянного тока к первому резистору, некоторая энергия, которую дает источник, рассеивается из-за сопротивления проводника. Для проверки падения напряжения используются , закон Ома и закон Кирхгофа, которые кратко изложены ниже. Закон
Ома представлен как

В → Падение напряжения (В)
R → Электрическое сопротивление (Ом)
I → Электрический ток (A)

Для замкнутых цепей постоянного тока мы также используем закон Кирхгофа для расчета падения напряжения .Он выглядит следующим образом:
Напряжение питания = сумма падений напряжения на каждом компоненте цепи.

Расчет падения напряжения на линии электропередачи постоянного тока

Здесь мы берем пример 100-футовой линии электропередачи. Так; для 2 линий, 2 × 100 футов. Пусть электрическое сопротивление будет 1,02 Ом / 1000 футов, а ток – 10 А.

Падение напряжения в цепях переменного тока

В цепях переменного тока; В дополнение к сопротивлению (R) будет второе противодействие протеканию тока – реактивное сопротивление (X), которое состоит из X _C и X _L .И X, и R будут противодействовать текущему потоку, также сумма двух называется импедансом (Z).
X _C → Емкостное реактивное сопротивление
X _L → Индуктивное реактивное сопротивление

Величина Z зависит от таких факторов, как магнитная проницаемость, электрические изолирующие элементы и частота переменного тока.
Подобно закону Ома в цепях постоянного тока, здесь он задается как

E → Падение напряжения (В)
Z → Электрический импеданс (Ом)
I → Электрический ток (A)

I _B → Ток полной нагрузки ( A)
R → Сопротивление жилы кабеля (Ом / 1000 футов)
L → Длина кабеля (с одной стороны) (Kft)
X → Индуктивное реактивное сопротивление (Ω / 1000f)
В _n → Напряжение между фазой и нейтралью
U _n → Междуфазное напряжение
Φ → Фазовый угол нагрузки

Круговые милы и расчет падения напряжения

Круговые милы – это действительно единица площади.Он используется для обозначения площади круглого поперечного сечения провода или проводника. Падение напряжения с использованием милов определяется как:

L → Длина провода (фут)
K → Удельное сопротивление (Ом-круговые милы / фут).
P → Фазовая постоянная = 2 для одной фазы = 1,732 для трех фаз
I → Площадь провода (круглые милы)

Расчет падения напряжения на медном проводнике по таблице

Падение напряжения на медном проводе (проводнике) можно узнать следующим образом:

f – коэффициент, который мы получаем из стандартной таблицы ниже.

905 905

905 905

РАЗМЕР МЕДНОГО ПРОВОДНИКА		КОЭФФИЦИЕНТ, f
AWG	мм 2	ОДНОФАЗНЫЙ	ТРЕХФАЗНЫЙ
12	3,31	0,313	0,26
10	5,26	0,196	0,17
8	8,37	0. Больше новостей Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт