Что такое реактивная мощность простым языком: Реактивная мощность на ощупь, простым языком, без графиков | Электромозг

Содержание

Реактивная мощность на ощупь, простым языком, без графиков | Электромозг

Сегодня я постараюсь объяснить простым языком, что же такое реактивная мощность электрической энергии.

Активная мощность

Для начала, расскажу про наиболее привычную нам активную мощность, за которую мы, собственно, и платим по счётчику. Эта мощность, потребляемая нагрузкой типа обычного сопротивления. Как правило, это все нагревательные приборы (бойлеры, обычные электроплитки, электро калориферы и т.п.). Потребляемая мощность этих приборов полностью активная. В этих приборах электрическая энергия безвозвратно и полностью преобразуется в другой вид энергии (тепловую и другие).

Активная мощность обозначается буквой P и измеряется в ваттах (Вт).

Величина активной мощности, потребляемой такими приборами считается просто — умножением напряжения в розетке на ток, протекающей в цепи включенного нагревательного прибора:

P = U * I

Тут всё просто. Нагрузка пассивна, постоянна, никаких неожиданностей.

Замечу, что в цепях постоянного тока существует только активная мощность, поскольку значение мгновенной и средней мощности там совпадают.

Реактивная мощность

Если включить в сеть переменного тока не нагревательный прибор, а, например, электромагнит, то помимо активной, в цепи возникает реактивная энергия, которая с частотой переменного тока то потребляется прибором, то возвращается обратно в сеть. Эта энергия переносится от источника к электромагниту и обратно дважды за период, каждую четверть периода меняя направление.

Это происходит из-за того, что при потреблении электроэнергии, например, обмоткой магнита, каждый полупериод в нём происходит временное запасание энергии в магнитном поле катушки, и последующая отдача её назад, из-за чего происходит рассинхронизация синусоид величин напряжения и тока в сети.

Изменения тока в цепи отстаёт от соответствующих синусоидальных изменений напряжения. Такое поведение присуще любой т.н. индуктивной нагрузке (трансформаторы, электродвигатели, дроссели, электромагниты).

Помимо индуктивной нагрузки существует емкостная (различные электронные устройства с конденсаторами, как накопителями энергии, например, в импульсном блоке питания), в которой ток, наоборот, опережает напряжение за счёт временного накопления энергии конденсаторами и последующей отдачи её назад. И в том и в другом случае в цепи помимо активной возникает реактивная энергия.

Вред реактивной энергии в электроэнергетике очевиден — она никак не используется, но шляется туда-сюда по проводам, дополнительно нагружая их. Кроме того, при таком «шлянии» эта энергия ещё и частично теряется, преобразуясь в активную энергию при нагреве проводов. Однако в радиотехнике реактивная мощность может быть и полезной (например, в колебательных контурах).

Реактивная мощность обозначается буквой Q и измеряется в вольт-амперах реактивных (вар).

Для вычисления доли реактивной мощности применяется формула:

Q = U * I * sin φ, где:
sin φ — коэффициент мощности, показывающий, какую долю полной мощности составляет реактивная мощность.

Для вычисления активной мощности в сетях с реактивной составляющей применяется формула:

P = U * I * cos φ, где:
cos φ — коэффициент мощности, показывающий, какую долю полной мощности составляет активная мощность.

Коэффициенты мощностей разных приборов обычно указываются в паспортах на них.

Неактивная мощность

Неактивная мощность (пассивная мощность) — это вся мощность кроме активной, т.е. как реактивная мощность, так и мощность любых нелинейных искажений синусоиды, в том числе и мощность колебаний в колебаниях (высших гармоник).

Неактивная мощность обозначается буквой N и измеряется в вольт-амперах реактивных (вар).

Нелинейные искажения могут быть вызваны такой нелинейной нагрузкой, как, например, импульсные блоки питания без корректора коэффициента мощности.

Полная мощность

Полная мощность — эта вся мощность, и активная и неактивная.

Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА).

Полная мощность равна корню квадратному из суммы квадратов активной и неактивной мощности:

S = √(P² + N²)

В случае линейной (равномерной на протяжении периода) нагрузки полная мощность равна корню квадратному из суммы квадратов активной и реактивной мощности. В этом случае неактивная мощность полностью состоит из реактивной составляющей.

S = √(P² + Q²)

То есть, полная мощность получается не лобовым сложением активной и неактивной частей, а по закону прямоугольного треугольника:

Надеюсь, я немного прояснил данный вопрос.

Если тема всё ещё непонятна, почитайте мою новую статью, где я более тщательно расписал физику процесса.

Ставьте лайки, если статья понравилось. Пишите комментарии.

Делитесь также этой статьёй в социальных сетях (соответствующие кнопочки рядом со статьёй в наличии) и, конечно, подписывайтесь на мой канал! Жду ваших отзывов! Удачи!

Реактивная мощность – jelectro.

Главная цель при передаче электроэнергии – повышение эффективности работы сетей. Следовательно, необходимо уменьшение потерь. Основной причиной потерь является реактивная мощность, компенсация которой значительно повышает качество электроэнергии.

Батареи статических конденсаторов

Реактивная мощность вызывает ненужный нагрев проводов, перегружаются электроподстанции. Трансформаторная мощность и кабельные сечения вынужденно подвергаются завышениям, сетевое напряжение снижается.

Понятие о реактивной мощности

Для выяснения, что же такое реактивная мощность, надо определить другие возможные виды мощности. При существовании в контуре активной нагрузки (резистора) происходит потребление исключительно активной мощности, полностью расходуемой на энергопреобразование. Значит, можно сформулировать, что такое активная мощность, – та, при которой ток совершает эффективную работу.

На постоянном токе происходит потребление исключительно активной мощности, рассчитываемой соответственно формуле:

P = U x I.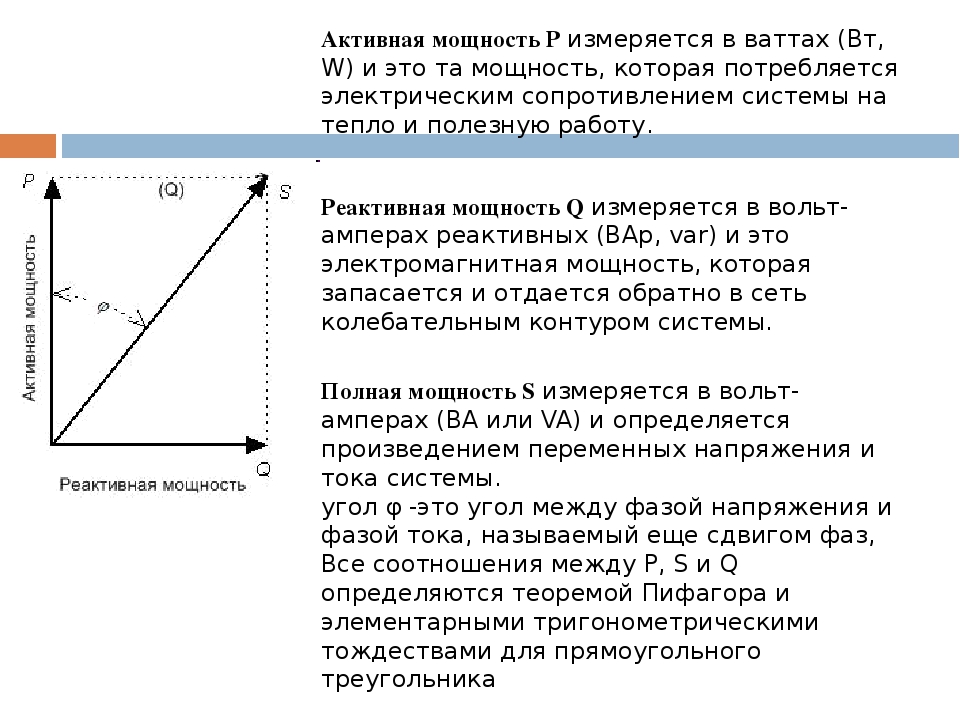

Измеряется в ваттах (Вт).

В электроцепях с переменным током при наличии активной и реактивной нагрузки мощностной показатель суммируется из двух составных частей: активной и реактивной мощности.

Реактивная нагрузка бывает двух видов:

Емкостная (конденсаторы). Характеризуется фазовым опережением тока по сравнению с напряжением;
Индуктивная (катушки). Характеризуется фазовым отставанием тока по отношению к напряжению.

Емкостная и индуктивная нагрузка

Если рассмотреть контур с переменным током и подсоединенной активной нагрузкой (обогреватели, чайники, лампочки с накаливающейся спиралью), ток и напряжение будут синфазными, а полная мощность, взятая в определенную временную отсечку, вычисляется путем перемножения показателей напряжения и тока.

Однако когда схема содержит реактивные компоненты, показатели напряжения и тока не будут синфазными, а будут различаться на определенную величину, определяемую углом сдвига «φ». Пользуясь простым языком, говорится, что реактивная нагрузка возвращает столько энергии в электроцепь, сколько потребляет. В результате получится, что для активной мощности потребления показатель будет нулевой. Одновременно по цепи протекает реактивный ток, не выполняющий никакую эффективную работу. Следовательно, потребляется реактивная мощность.

Реактивная мощность – часть энергии, которая позволяет устанавливать электромагнитные поля, требуемые оборудованием переменного тока.

Расчет реактивной мощности ведется по формуле:

Q = U x I x sin φ.

В качестве единицы измерения реактивной мощности служит ВАр (вольтампер реактивный).

Выражение для активной мощности:

P = U x I x cos φ.

Треугольник мощностей

Взаимосвязь активной, реактивной и полной мощности для синусоидального тока переменных значений представляется геометрически тремя сторонами прямоугольного треугольника, называемого треугольником мощностей.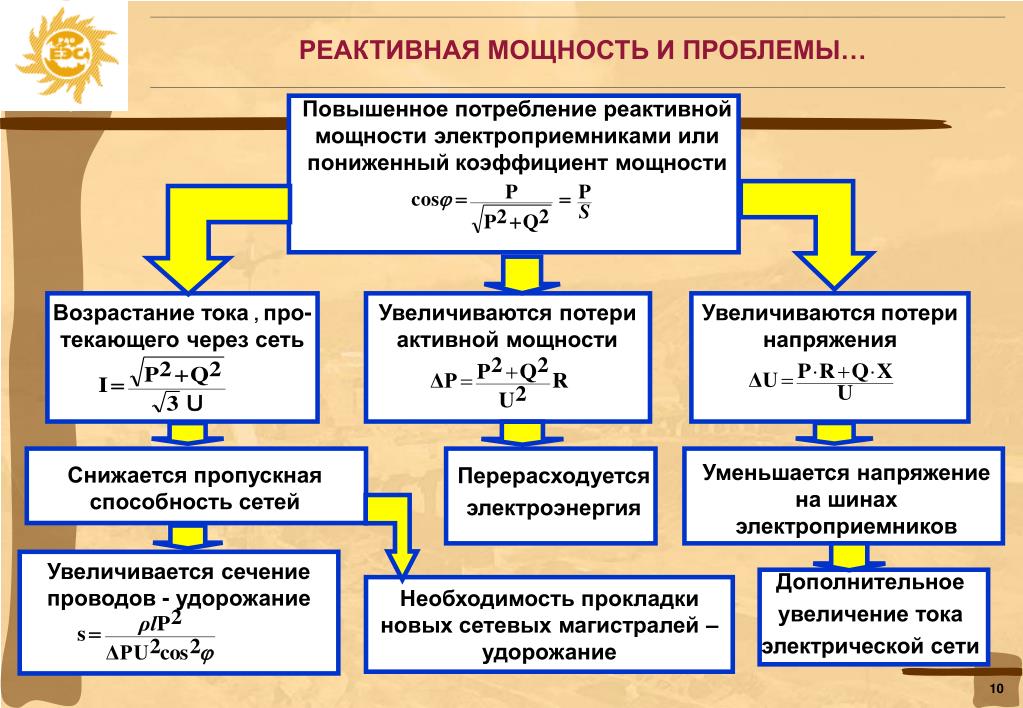 Электроцепи переменного тока потребляют две разновидности энергии: активную мощность и реактивную. Кроме того, значение активной мощности никогда не является отрицательным, тогда как для реактивной энергии возможна либо положительная величина (при индуктивной нагрузке), либо отрицательная (при емкостной нагрузке).

Треугольник мощностей

Важно! Из треугольника мощностей видно, что всегда полезно снизить реактивную составляющую, чтобы повысить эффективность системы.

Полная мощность не находится как алгебраическая сумма активного и реактивного мощностного значения, это векторная сумма P и Q. Ее количественное значение вычисляется извлечением квадратного корня из суммы квадратов мощностных показателей: активного и реактивного. Измеряться полная мощность может в ВА (вольтампер) или производных от него: кВА, мВА.

Чтобы была рассчитана полная мощность, необходимо знать разность фаз между синусоидальными значениям U и I.

Коэффициент мощности

Пользуясь геометрически представленной векторной картиной, можно найти отношение сторон треугольника, соответствующих полезной и полной мощности, что будет равно косинусу фи или мощностному коэффициенту:

cos φ = P/S.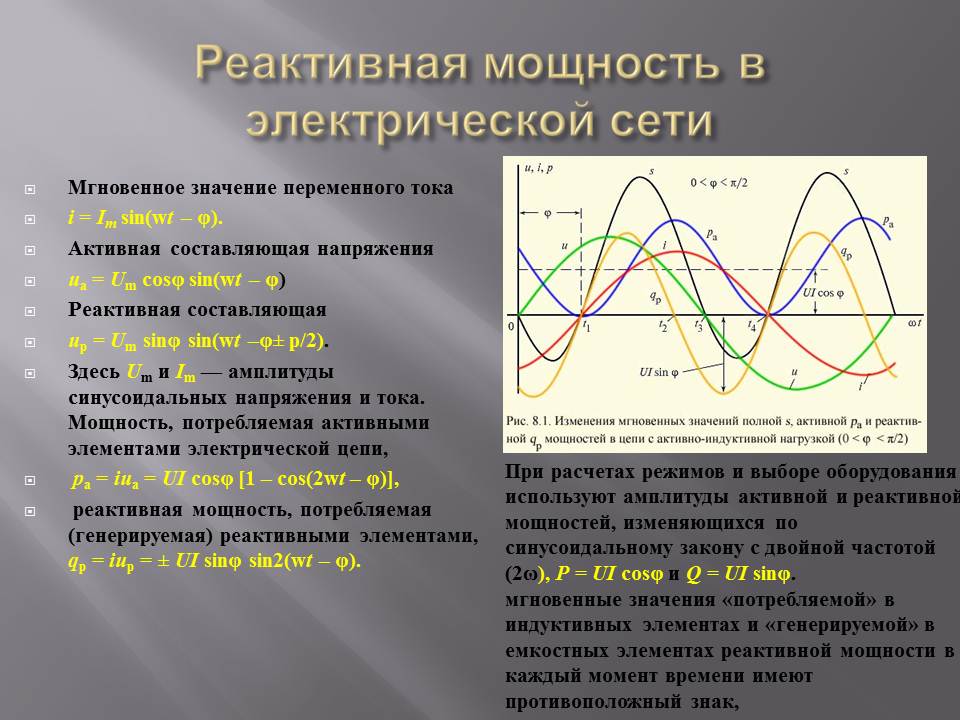

Данный коэффициент находит эффективность работы сети.

Количество потребляемых ватт – то же самое, что и количество потребляемых вольтампер при мощностном коэффициенте, равном 1 или 100%.

Важно! Полная мощность тем ближе к показателю активной, чем больше cos φ, или чем меньше угол сдвига синусоидальных величин тока и напряжения.

Если, к примеру, имеется катушка, для которой:

Р = 80 Вт;
Q = 130 ВАр;
тогда S = 152,6 BA как среднеквадратичный показатель;
cos φ = P/S = 0,52 или 52%

Можно сказать, что катушка требует 130 ВАр полной мощности для выполнения полезной работы 80 Вт.

Коррекция cos φ

Для коррекции cos φ применяется тот факт, что при емкостной и индуктивной нагрузке вектора реактивной энергии располагаются в противофазе. Так как большинство нагрузок является индуктивными, подключив емкость, можно добиться увеличения cos φ.

Принцип компенсации реактивной мощности

Главные потребители реактивной энергии:

Трансформаторы. Представляют собой обмотки, имеющие индуктивную связь и посредством магнитных полей преобразуюшие токи и напряжения. Эти аппараты являются основным элементом электросетей, передающих электроэнергию. Особенно увеличиваются потери при работе на холостом ходу и при низкой нагрузке. Широко используются трансформаторы в производстве и в быту;
Индукционные печи, в которых расплавляются металлы путем создания в них вихревых токов;
Асинхронные двигатели. Крупнейший потребитель реактивной энергии. Вращающий момент в них создается посредством переменного магнитного поля статора;
Преобразователи электроэнергии, такие как силовые выпрямители, используемые для питания контактной сети железнодорожного транспорта и другие.

Конденсаторные батареи подсоединяются на электроподстанциях для того, чтобы контролировать напряжение в пределах установленных уровней. Нагрузка меняется в течение дня с утренними и вечерними пиками, а также на протяжении недели, снижаясь в выходные, что изменяет показатели напряжения. Подключением и отключением конденсаторов варьируется его уровень. Это делается от руки и с помощью автоматики.

Как и где измеряют cos φ

Реактивная мощность проверяется по изменению cos φ специальным прибором – фазометром. Его шкала проградуирована в количественных значениях cos φ от нуля до единицы в индуктивном и емкостном секторе. Полностью скомпенсировать негативное влияние индуктивности не удастся, но возможно приближение к желаемому показателю – 0,95 в индуктивной зоне.

Фазометр

Фазометры применяются при работе с установками, способными повлиять на режим работы электросети через регулирование cos φ.

Так как при финансовых расчетах за потребленную энергию учитывается и ее реактивная составляющая, то на производствах устанавливаются автоматические компенсаторы на конденсаторах, емкость которых может меняться. В сетях, как правило, используются статические конденсаторы;
При регулировании cos φ у синхронных генераторов путем изменения возбуждающего тока необходимо его отслеживать визуально в ручных рабочих режимах;
Синхронные компенсаторы, представляющие собой синхронные двигатели, работающие без нагрузки, в режиме перевозбуждения выдают в сеть энергию, которая компенсирует индуктивную составляющую. Для регулирования возбуждающего тока наблюдают за показаниями cos φ по фазометру.

Синхронный компенсатор

Коррекция коэффициента мощности – одна из эффективнейших инвестиций для сокращения затрат на электроэнергию. Одновременно улучшается качество получаемой энергии.

Видео

Оцените статью:

Электрическая мощность. Мощность электрического тока. « ЭлектроХобби

В этой теме хотелось бы раскрыть понятие электрической мощности в простой и понятной форме. И, пожалуй, прежде чем говорить об электрической мощности, сперва следует определиться с понятием мощности в общем смысле. Обычно, когда люди говорят о мощности, они подразумевают некую «силу», которой обладает тот или иной предмет (мощный электродвигатель) либо действие (мощный взрыв). Но как мы знаем из школьной физики, сила и мощность — это разные понятия, но зависимость у них есть.

Первоначально мощность (N), это характеристика, относящаяся к определённому событию (действию), а если оно привязано к некоторому предмету, то с ним также условно соотносят понятие мощности. Любое физическое действие подразумевает воздействие силы. Сила (F), с помощью которой был пройден определённый путь (S) будет равняться совершенной работе (А). Ну, а работа, проделанная за определённое время (t) и будет приравниваться к мощности.

Мощность — это физическая величина, которая равна отношению совершенной работы, что выполняется за некоторый промежуток времени, к этому же промежутку времени. Поскольку работа является мерой изменения энергии, то ещё можно сказать так: мощность — это скорость преобразования энергии системы.

Разобравшись с понятием механической мощности, перейдём к рассмотрению электрической мощности (мощность электрического тока). Как Вы должны знать U — это работа, выполняемая при перемещении одного кулона, а ток I — количество кулонов, проходящих за 1 сек. Поэтому произведение тока на напряжение показывает полную работу, выполненную за 1 сек, то есть электрическую мощность или мощность электрического тока.

Анализируя приведённую формулу, можно сделать очень простой вывод: поскольку электрическая мощность

«P» в одинаковой степени зависит от тока «I» и от напряжения «U», то, следовательно, одну и ту же электрическую мощность можно получить либо при большом токе и малом напряжении, или же, наоборот, при большом напряжении и малом токе (Это используется при передачи электроэнергии на удалённые расстояния от электростанций к местам потребления, путём трансформаторного преобразования на повышающих и понижающих электроподстанциях).

Активная электрическая мощность (это мощность, которая безвозвратно преобразуется в другие виды энергии — тепловую, световую, механическую и т.д.) имеет свою единицу измерения — Вт (Ватт). Она равна произведению 1 вольта на 1 ампер. В быту и на производстве мощность удобней измерять в кВт (киловаттах, 1 кВт = 1000 Вт).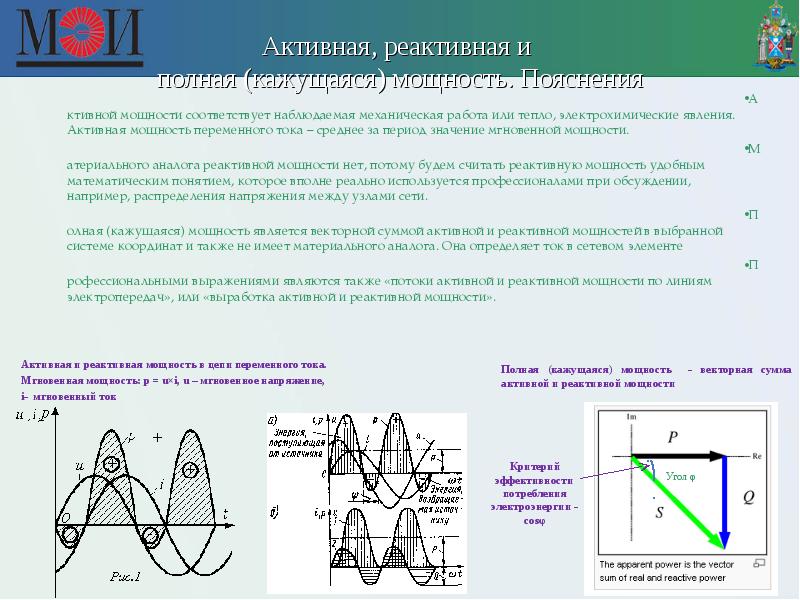 На электростанциях уже используются более крупные единицы — мВт (мегаватты, 1 мВт = 1000 кВт = 1 000 000 Вт).

Реактивная электрическая мощность — это величина, которая характеризует такой вид электрической нагрузки, что создаются в устройствах (электрооборудовании) колебаниями энергии (индуктивного и емкостного характера) электромагнитного поля. Для обычного переменного тока она равна произведению рабочего тока I и падению напряжения U на синус угла сдвига фаз между ними: Q = U*I*sin(угла). Реактивная мощность имеет свою единицу измерения под названием ВАр (вольт-ампер реактивный). Обозначается буквой «Q».

Простым языком активную и реактивную электрическую мощность на примере можно выразить так: у нас имеется электротехническое устройство, которое имеет нагревательные тэны и электродвигатель. Тэны, как правило, сделаны из материала с высоким сопротивлением. При прохождении электрического тока по спирали тэна, электрическая энергия полностью преобразуется в тепло.

Такой пример характерен активной электрической мощности.

Электродвигатель этого устройства внутри имеет медную обмотку. Она представляет собой индуктивность. А как мы знаем, индуктивность обладает эффектом самоиндукции, а это способствует частичному возврату электроэнергии обратно в сеть. Эта энергия имеет некоторое смещение в значениях тока и напряжения, что вызывает негативное влияние на электросеть (дополнительно перегружая её).

Похожими способностями обладает и ёмкость (конденсаторы). Она способна накапливать заряд и отдавать его обратно. Разница ёмкости от индуктивности заключается в противоположном смещении значений тока и напряжения относительно друг друга. Такая энергия ёмкости и индуктивности (смещённая по фазе относительно значения питающей электросети) и будет, по сути, являться реактивной электрической мощностью.

Более подробно о свойствах реактивной мощности мы поговорим в соответствующей статье, а в завершении этой темы хотелось сказать о взаимном влиянии индуктивности и ёмкости.

Поскольку и индуктивность, и ёмкость обладают способностью к сдвигу фазы, но при этом каждая из них делает это с противоположным эффектом, то такое свойство используют для компенсации реактивной мощности (повышение эффективности электроснабжения). На этом и завершу тему, электрическая мощность, мощность электрического тока.

P.S. Говоря об электрической мощности электротехнических устройств мы должны помнить, что она в них ограничивается номинальными и максимальными значениями тока и напряжения, а эти ограничения уже зависят от материала, рабочих частот, технологии изготовления и прочих факторов.

Расчет и компенсация реактивной мощности.

Доброго времени суток. Сегодня, в рубрике «Советы и рекомендации» — Расчет и компенсация реактивной мощности.

Возможно, Вас заинтересует – «Простой выпрямитель».

Прежде чем говорить о реактивной мощности, давайте разберемся, что такое электрическая мощность? Говоря простым языком, мощность — это работа, совершаемая электрическим током в единицу времени. Измеряется она в ваттах (Вт или W).

Расчет и компенсация реактивной мощности.

Расчет реактивной мощности.

Если с постоянным током при определении мощности проблем нет, то с переменным начинают твориться чудеса. По отношению к резистивным нагрузкам (нагревательные элементы, лампы накаливания) переменный электроток ведет себя также как и постоянный. Но когда в цепи появляются индуктивные (трансформаторы, дроссели, электродвигатели) и емкостные (конденсаторы) электронагрузки – возникают паразитные токи, не только не участвующие в полезной работе, но и создающие ей помехи. В индуктивностях ток начинает отставать от напряжения, а в емкостях наоборот – опережает. Это называется сдвигом фаз, угол которых принято обозначать символом ϕ.

В итоге, мощность разделяется на активную и реактивную. Первая участвует в работе, а реактивная или ничего не делает или мешает. Зависимость угла сдвига фаз принято выражать через cos ϕ.

COS φ = Р/S

Где Р – активная мощность, S – реактивная. Это отношение называется коэффициентом мощности (Pf) и может варьироваться от 0 до 1. И чем эта величина ближе к единице, тем меньше реактивная мощность, а значит выше КПД.

Также читайте – «Время-токовые характеристики автоматов».

Опираясь на то, что S находится в зависимости от угла ϕ, мы имеем возможность сделать ее расчет по формуле:

Q = U*I*sinφ.

Где Q– реактивная составляющая, единицей измерения является вар или квар.

А по формуле:

P = U*I*cosφ — производят расчет активной составляющей.

Расчет и компенсация реактивной мощности.

Компенсация реактивной составляющей.

Поскольку реактивная энергия оказывает влияние на работу электрооборудования, имеющего индуктивные и емкостные электропотребители, для них применяются специальные компенсирующие устройства. Схема действия компенсации основана на способностях емкостных и индуктивных нагрузок сдвигать фазы в противоположные направления. Ввиду того, что основную часть реактивной энергии создают индуктивности, для ее компенсации используют конденсаторы большой емкости, присоединяемые параллельно нагрузке. Казалось бы что вопрос решен. Но на практике, на производстве с большим процентом электродвигателей не все так гладко. Электромоторы на конвейерах и другом оборудовании не включаются все сразу, а работают по своему алгоритму. В иные моменты одновременно могут находиться в работе как большое, так и минимальное количество электропотребителей этого типа. А перекомпесация не менее вредна недокомпенсации.

Это интересно – «Защита электрооборудования от перенапряжения».

И поэтому, подключением конденсаторных блоков управляет контроллер на микропроцессоре, измеряющий реактивную энергию в каждый момент времени. И в зависимости от потребности, выбирает и присоединяет к потребителям определенное количество конденсаторов.

Автоматическая установка компенсации реактивной энергии УКРМ.

Компенсация реактивной энергии в быту.

Современные квартиры напичканы всевозможным электрическим оборудованием разной мощности. Основная часть приборов большого энергопотребления, это активные потребители с cosφ = 1. (электрочайник, утюг, нагревательный элемент стиральной машины, электродуховка…). Но есть и домашние помощники с реактивной нагрузкой (СВЧ печь, двигатель стиральной машины, блендеры, кухонные комбайны, холодильник…). Но их электропотребление настолько мало (кроме СВЧ печи, работающей по полчаса – час в сутки), что устраивать компенсацию нет смысла.

Вас может заинтересовать – «Расчет и выбор сечения кабеля».

Однако, если у Вас свой дом, с мастерской, оборудованной станками с асинхронными электродвигателями, стоит задуматься о компенсации реактивной мощности.

Стоит ли покупать рекламируемые устройства компенсации.Рекламируемые бытовые компенсаторы реактивной энергии.

Интернет и телевидение пестрит рекламируемыми устройствами компенсации реактивной мощности. Такими как Saving box, Smart Boy, EkoEnerji, Electricity Energy Electric Power Saver. Стоит ли покупать эти чудо-приборы? Ответ однозначный – НЕТ! Вышеназванные устройства ни в коей мере неспособны компенсировать реактивную мощность даже самых неэнергоемких потребителей. Все эти мини и микро компенсаторы – полный развод на деньги.

Коэффициент мощности

В этой статье мы поговорим о коэффициенте мощности (КМ) – определим, что это такое, где применяется и зачем был введен такой термин. Думаю, что каждый, кто занимается электричеством профессионально, сталкивался в своих расчетах с таким понятием, как коэффициент мощности, или cos φ. Хотя даже если вы непрофессионал, то понятие мощность из курса физики должно быть вам знакомо.

В этой статье мы поговорим простым языком о сложном, разберем на конкретных примерах, что значит сочетание слов “коэффициент мощности” в практическом смысле, обратившись к миру физических величин.

Коэффициент мощности, применяемый в проектировании, нужен для того, чтобы рассчитать сечение кабеля, который требуется, чтобы подключить электродвигатель.

Чтобы разобраться в назначении КМ, нужно затронуть несколько важных понятий: активная и реактивная мощности.

Само понятие мощности в физике определяет как работу, совершаемую электрическим током за отрезок времени (электрический ток во время своего движения тоже совершает работу, так же как, например, вода, когда падает из более высокой точки в более низкую). Единицей измерения мощности в физике принято считать Ватты(Вт).

Активная мощность измеряется в Вольт-амперах (ВА), единицей измерения реактивной мощности принято считать ВАР(Вольт-ампер реактивный).

При работе утюга возникает нагрузка, при которой энергия электричества превращается в тепловую полностью и без остатка. В этом случае говорят, что мощность активная.

Другой пример – электродвигатель. Здесь энергия превращается не полостью, это связано с особенностями его строения, в таком случае будет идти речь уже об реактивной мощности.

В случае с электродвигателем при прохождении тока через него нагрузка будет индуктивной, то есть такой, при которой синусоида тока сдвигается относительно графика напряжения на угол, который, как впоследствии мы покажем, и является коэффициентом мощности, или cos.

Этот сдвиг зависит от частоты, с которой этот переменный ток действует.

Часть энергии в этом случае возвращается обратно в сеть. Реактивная мощность является своего рода “паразитной” мощностью, поскольку не вся энергия используется потребителем.

Для потребителя важно знать долю реактивной мощности в работе электродвигателя, и мы уже показали эта доля зависит от угла, на который ток сдвигается относительно напряжения, или коэффициента мощности.

В случае с активной мощностью косинус равен 1.

Чем ближе cos φ к единице, тем лучше, это значит, что нет ” паразитной” мощности. Однако, как только отклонение тока возникает, мы имеем с ней дело.

При больших мощностях задача проекта электроснабжения – компенсировать уход энергии обратно в сеть, посредством применения соответствующего оборудования.

Это делается с помощью емкостной нагрузки, так достигается компенсация реактивной мощности, и повышается эффективность оборудования и системы электроснабжения в целом.

Данные приборы определяются посредством расчётов.

Мероприятия по компенсации реактивной мощности позволят выполнить задачу по энергосбережению на объекте.

< НАЗАД К СТАТЬЯМ

Активная реактивная полная мощность. Что такое реактивная мощность и как с ней бороться. Перспективы дальнейшего изучения реактивной энергии, как явления

Мощностные характеристики установки или сети являются основными для большинства известных электрических приборов. Активная мощность (проходящая, потребляема) характеризует часть полной мощности, которая передается за определенный период частоты переменного тока.

Определение

Активная и реактивная мощность может быть только у переменного тока, т. к. характеристики сети (силы тока и напряжения) у постоянного всегда равны. Единица измерений активной мощности Ватт, в то время, как реактивной – реактивный вольтампер и килоВАР (кВАР). Стоит отметить, что как полная, так и активная характеристики могут измеряться в кВт и кВА, это зависит от параметров конкретного устройства и сети. В промышленных цепях чаще всего измеряется в килоВаттах.

Электротехника используется активную составляющую в качестве измерения передачи энергии отдельными электрическими приборами. Рассмотрим, сколько мощности потребляют некоторые из них:

Исходя из всего, сказанного выше, активная мощность – это положительная характеристика конкретной электрической цепи, которая является одним из основных параметров для выбора электрических приборов и контроля расхода электричества.

Обозначение реактивной составляющей:

Это номинальная величина, которая характеризует нагрузки в электрических устройствах при помощи колебаний ЭМП и потери при работе прибора. Иными словами, передаваемая энергия переходит на определенный реактивный преобразователь (это конденсатор, диодный мост и т. д.) и проявляется только в том случае, если система включает в себя эту составляющую.

Расчет

Для выяснения показателя активной мощности, необходимо знать полную мощность, для её вычисления используется следующая формула:

S = U \ I, где U – это напряжение сети, а I – это сила тока сети.

Этот же расчет выполняется при вычислении уровня передачи энергии катушки при симметричном подключении. Схема имеет следующий вид:

Расчет активной мощности учитывает угол сдвига фаз или коэффициент (cos φ), тогда:

S = U * I * cos φ.

Очень важным фактором является то, что эта электрическая величина может быть как положительной, так и отрицательной. Это зависит от того, какие характеристики имеет cos φ. Если у синусоидального тока угол сдвига фаз находится в пределах от 0 до 90 градусов, то активная мощность положительная, если от 0 до -90 – то отрицательная. Правило действительно только для синхронного (синусоидального) тока (применяемого для работы асинхронного двигателя, станочного оборудования).

Также одной из характерных особенностей этой характеристики является то, что в трехфазной цепи (к примеру, трансформатора или генератора), на выходе активный показатель полностью вырабатывается.

Максимальная и активная обозначается P, реактивная мощность – Q.

Из-за того, что реактивная обуславливается движением и энергией магнитного поля, её формула (с учетом угла сдвига фаз) имеет следующий вид:

Q L = U L I = I 2 x L

Для несинусоидального тока очень сложно подобрать стандартные параметры сети. Для определения нужных характеристик с целью вычисления активной и реактивной мощности используются различные измерительные устройства. Это вольтметр, амперметр и прочие. Исходя от уровня нагрузки, подбирается нужная формула.

Из-за того, что реактивная и активная характеристики связаны с полной мощностью, их соотношение (баланс) имеет следующий вид:

S = √P 2 + Q 2 , и все это равняется U*I .

Но если ток проходит непосредственно по реактивному сопротивлению. То потерь в сети не возникает. Это обуславливает индуктивная индуктивная составляющая – С и сопротивление – L. Эти показатели рассчитываются по формулам:

Сопротивление индуктивности: x L = ωL = 2πfL,

Сопротивление емкости: хc = 1/(ωC) = 1/(2πfC).

Для определения соотношения активной и реактивной мощности используется специальный коэффициент. Это очень важный параметр, по которому можно определить, какая часть энергии используется не по назначению или «теряется» при работе устройства.

При наличии в сети активной реактивной составляющей обязательно должен рассчитываться коэффициент мощности. Эта величина не имеет единиц измерения, она характеризует конкретного потребителя тока, если электрическая система содержит реактивные элементы. С помощью этого показателя становится понятным, в каком направлении и как сдвигается энергия относительно напряжения сети. Для этого понадобится диаграмма треугольников напряжений:

К примеру, при наличии конденсатора формула коэффициента имеет следующий вид:

cos φ = r/z = P/S

Для получения максимально точных результатов рекомендуется не округлять полученные данные.

Компенсация

Учитывая, что при резонансе токов реактивная мощность равняется 0:

Q = QL – QC = ULI – UCI

Для того чтобы улучшить качество работы определенного устройства применяются специальные приборы, минимизирующие воздействие потерь на сеть. В частности, это ИБП. В данном приборе не нуждаются электрические потребители со встроенным аккумулятором (к примеру, ноутбуки или портативные устройства), но для большинства остальных источник бесперебойного питания является необходимым.

При установке такого источника можно не только установить негативные последствия потерь, но и уменьшить траты на оплату электричества. Специалисты доказали, что в среднем, ИБП поможет экономить от 20 % до 50 %. Почему это происходит :

Провода меньше нагреваются, это не только положительно влияет на их работу, но и повышает безопасность;

У сигнальных и радиоустройств уменьшаются помехи;

На порядок уменьшаются гармоники в электрической сети.

В некоторых случаях специалисты используют не полноценные ИБП, а специальные компенсирующие конденсаторы. Они подходят для бытового использования, доступны и продаются в каждом электротехническом магазине. Для расчета планируемой и полученной экономии можно использовать все вышеперечисленные формулы.

Реактивная мощность

Электри́ческая мо́щность – физическая величина, характеризующая скорость передачи или преобразования электрической энергии.

Если элемент цепи – резистор c электрическим сопротивлением R , то

Мощность переменного тока

Активная мощность

Среднее за период Т значение мгновенной мощности называется активной мощностью: . В цепях однофазного синусоидального тока , где U и I – действующие значения напряжения и тока , φ – угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением . Единица активной мощности – ватт (W , Вт ). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.

Реактивная мощность

Реактивная мощность – величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока, равна произведению действующих значений напряжения U и тока I , умноженному на синус угла сдвига фаз φ между ними: Q = UI sin φ . Единица реактивной мощности – вольт-ампер реактивный (var , вар ). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: . Реактивная мощность в электрических сетях вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения). В некоторых электрических установках реактивная мощность может быть значительно больше активной. Это приводит к появлению больших реактивных токов и вызывает перегрузку источников тока. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности. Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.

Необходимо отметить, что величина sinφ для значений φ от 0 до плюс 90 ° является положительной величиной. Величина sinφ для значений φ от 0 до минус 90 ° является отрицательной величиной. В соответствии с формулой Q = UI sinφ реактивная мощность может быть отрицательной величиной. Но отрицательное значение мощности нагрузки характеризует нагрузку как генератор энергии. Активное, индуктивное, емкостное сопротивление не могут быть источниками постоянной энергии. Модуль величины Q = UI sinφ приблизительно описывает реальные процессы преобразования энергии в магнитных полях индуктивностей и в электрических полях емкостей. Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения. Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sinφ , более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.

Полная мощность

Полная мощность – величина, равная произведению действующих значений периодического электрического тока в цепи I и напряжения U на её зажимах: S = U×I ; связана с активной и реактивной мощностями соотношением: , где Р – активная мощность, Q – реактивная мощность (при индуктивной нагрузке Q > 0 , а при ёмкостной Q ). Единица полной электрической мощности – вольт-ампер (VA , ВА ).

Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:

Измерения

Для измерения электрической мощности применяются ваттметры и варметры , можно также использовать косвенный метод, с помощью вольтметра и амперметра .
Для измерения коэффициента реактивной мощности применяют фазометры

Литература

Ссылки

См. также

Список параметров напряжения и силы электрического тока

Wikimedia Foundation . 2010 .

Смотреть что такое “Реактивная мощность” в других словарях:

реактивная мощность – Величина, равная при синусоидальных электрическом токе и электрическом напряжении произведению действующего значения напряжения на действующее значение тока и на синус сдвига фаз между напряжением и током двухполюсника. [ГОСТ Р 52002 2003]… … Справочник технического переводчика

Электр. мощность в цепи переменного тока, расходуемая на поддержание вызываемых переменным током периодических изменений: 1) магнитного поля при наличии в цепи индуктивности; 2) заряда конденсаторов при наличии конденсаторов и проводов (напр.… … Технический железнодорожный словарь

Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля. Для синусоидального тока равна произведению действующих тока I и напряжения U на синус угла сдвига фаз между ними: Q =… … Большой Энциклопедический словарь

РЕАКТИВНАЯ МОЩНОСТЬ – величина, характеризующая скорость обмена энергией между генератором переменного тока и магнитным (млн. электрическим) полем цепи, создаваемым электротехническими устройствами (индуктивностью и ёмкостью). Р. м. возникает в цепи при наличии сдвига … Большая политехническая энциклопедия

реактивная мощность – 3.1.5 реактивная мощность (вар): Реактивная мощность сигналов синусоидальной формы какой либо отдельной частоты в однофазной цепи, определяемая как произведение среднеквадратических значений тока и напряжения и синуса фазового угла между ними.… … Словарь-справочник терминов нормативно-технической документации

реактивная мощность – reaktyvioji galia statusas T sritis Standartizacija ir metrologija apibrėžtis Menamoji kompleksinės galios dalis, skaičiuojama pagal formulę Q² = S² – P²; čia Q – reaktyvioji galia, S – pilnutinė galia, P – aktyvioji galia. Matavimo vienetas –… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

реактивная мощность – reaktyvioji galia statusas T sritis fizika atitikmenys: angl. reactive power; wattless power vok. Blindleistung, f; wattlose Leistung, f rus. безваттная мощность, f; реактивная мощность, f pranc. puissance déwatée, f; puissance réactive, f … Fizikos terminų žodynas

Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля. Для синусоидального тока равна произведению действующих тока I и напряжения U на синус угла сдвига фаз между ними:… … Энциклопедический словарь

реактивная мощность – reaktyvioji galia statusas T sritis automatika atitikmenys: angl. reactive power vok. Blindleistung, f; wattlose Leistung, f rus. реактивная мощность, f pranc. puissance réactive, f … Automatikos terminų žodynas

Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока (См. Переменный ток). Р. м. Q равна произведению действующих значений напряжения U и тока… … Большая советская энциклопедия

Книги

Электротехника и электроника на судах рыбопромыслового флота , Белов О.А., Парфенкин А.И.. Рассмотрены общие вопросы электротехники и электроники, физические явления, лежащие в основе производства и использования электричества, работы электронных устройств. Приведены примеры…

Содержание:

В электротехнике среди множества определений довольно часто используются такие понятия, как активная, реактивная и полная мощность. Эти параметры напрямую связаны с током и напряжением , когда включены какие-либо потребители. Для проведения вычислений применяются различные формулы, среди которых основной является произведение напряжения и силы тока. Прежде всего это касается постоянного напряжения. Однако в цепях переменного разделяется на несколько составляющих, отмеченных выше. Вычисление каждой из них также осуществляется с помощью формул, благодаря которым можно получить точные результаты.

Формулы активной, реактивной и полной мощности

Основной составляющей считается активная мощность. Она представляет собой величину, характеризующую процесс преобразования электрической энергии в другие виды энергии. То есть по-другому является скоростью, с какой . Именно это значение отображается на электросчетчике и оплачивается потребителями. Вычисление активной мощности выполняется по формуле : P = U x I x cosф.

В отличие от активной, которая относится к той энергии, которая непосредственно потребляется электроприборами и преобразуется в другие виды энергии – тепловую, световую, механическую и т.д., реактивная мощность является своеобразным невидимым помощником. С ее участием создаются электромагнитные поля, потребляемые электродвигателями. Прежде всего она определяет характер нагрузки, и может не только генерироваться, но и потребляться. Расчеты реактивной мощности производятся по формуле : Q = U x I x sinф.

Полной мощностью является величина, состоящая из активной и реактивной составляющих. Именно она обеспечивает потребителям необходимое количество электроэнергии и поддерживает их в рабочем состоянии. Для ее расчетов применяется формула: S = .

Как найти активную, реактивную и полную мощность

Активная мощность относится к энергии, которая необратимо расходуется источником за единицу времени для выполнения потребителем какой-либо полезной работы. В процессе потребления, как уже было отмечено, она преобразуется в другие виды энергии.

В цепи переменного тока значение активной мощности определяется, как средний показатель мгновенной мощности за установленный период времени. Следовательно, среднее значение за этот период будет зависеть от угла сдвига фаз между током и напряжением и не будет равной нулю, при условии присутствия на данном участке цепи активного сопротивления. Последний фактор и определяет название активной мощности. Именно через активное сопротивление электроэнергия необратимо преобразуется в другие виды энергии.

При выполнении расчетов электрических цепей широко используется понятие реактивной мощности. С ее участием происходят такие процессы, как обмен энергией между источниками и реактивными элементами цепи. Данный параметр численно будет равен амплитуде, которой обладает переменная составляющая мгновенной мощности цепи.

Существует определенная зависимость реактивной мощности от знака угла ф, отображенного на рисунке. В связи с этим, она будет иметь положительное или отрицательное значение. В отличие от активной мощности, измеряемой в , реактивная мощность измеряется в вар – вольт-амперах реактивных. Итоговое значение реактивной мощности в разветвленных электрических цепях представляет собой алгебраическую сумму таких же мощностей у каждого элемента цепи с учетом их индивидуальных характеристик.

Основной составляющей полной мощности является максимально возможная активная мощность при заранее известных токе и напряжении. При этом, cosф равен 1, когда отсутствует сдвиг фаз между током и напряжением. В состав полной мощности входит и реактивная составляющая, что хорошо видно из формулы, представленной выше. Единицей измерения данного параметра служит вольт-ампер (ВА).

Понятие о реактивной мощности

Измеряется в ваттах (Вт).

Емкостная (конденсаторы). Характеризуется фазовым опережением тока по сравнению с напряжением;
Индуктивная (катушки). Характеризуется фазовым отставанием тока по отношению к напряжению.

Расчет реактивной мощности ведется по формуле:

Q = U x I x sin φ.

В качестве единицы измерения реактивной мощности служит ВАр (вольтампер реактивный).

Выражение для активной мощности:

P = U x I x cos φ.

Чтобы была рассчитана полная мощность, необходимо знать разность фаз между синусоидальными значениям U и I.

Коэффициент мощности

Данный коэффициент находит эффективность работы сети.

Если, к примеру, имеется катушка, для которой:

Р = 80 Вт;
Q = 130 ВАр;
тогда S = 152,6 BA как среднеквадратичный показатель;
cos φ = P/S = 0,52 или 52%

Можно сказать, что катушка требует 130 ВАр полной мощности для выполнения полезной работы 80 Вт.

Коррекция cos φ

Главные потребители реактивной энергии:

Трансформаторы. Представляют собой обмотки, имеющие индуктивную связь и посредством магнитных полей преобразуюшие токи и напряжения. Эти аппараты являются основным элементом электросетей, передающих электроэнергию. Особенно увеличиваются потери при работе на холостом ходу и при низкой нагрузке. Широко используются трансформаторы в производстве и в быту;
Индукционные печи, в которых расплавляются металлы путем создания в них вихревых токов;
Асинхронные двигатели. Крупнейший потребитель реактивной энергии. Вращающий момент в них создается посредством переменного магнитного поля статора;
Преобразователи электроэнергии, такие как силовые выпрямители, используемые для питания контактной сети железнодорожного транспорта и другие.

Как и где измеряют cos φ

Так как при финансовых расчетах за потребленную энергию учитывается и ее реактивная составляющая, то на производствах устанавливаются автоматические компенсаторы на конденсаторах, емкость которых может меняться. В сетях, как правило, используются статические конденсаторы;
При регулировании cos φ у синхронных генераторов путем изменения возбуждающего тока необходимо его отслеживать визуально в ручных рабочих режимах;
Синхронные компенсаторы, представляющие собой синхронные двигатели, работающие без нагрузки, в режиме перевозбуждения выдают в сеть энергию, которая компенсирует индуктивную составляющую. Для регулирования возбуждающего тока наблюдают за показаниями cos φ по фазометру.

Видео

Наверняка многие из вас слышали о реактивной электроэнергии. Зная, насколько сложен для понимания этот термин, давайте разберём детально отличия реактивной и активной энергии. Важно осознать тот факт, что реактивную электроэнергию мы можем наблюдать только в переменном токе. Там, где течёт постоянный ток, реактивная энергия не присутствует. Обусловлено это природой появления реактивной энергии .

Через несколько понижающих трансформаторов к потребителю поступает переменный ток, конструкция которых разделяет обмотки низкого и высокого напряжения. То есть получается так, что в трансформаторе отсутствует физический контакт между двумя обмотками, при этом ток всё равно течёт. Объяснить это довольно просто. Электроэнергия всегда передаётся через воздух, который является прекрасным диэлектриком, при помощи электромагнитного поля, составляющая которого – переменное магнитное поле. Оно регулярно пересекает обмотку, появляясь в другой, и не имеет с первой электрического контакта, наводя электродвижущую силу. Коэффициент полезного действия у современных трансформаторов достаточно велик, отсюда потеря электроэнергии сводиться к минимуму, и потому вся мощь переменного тока, который протекает в первичной обмотке, оказывается в цепи вторичной обмотки. Тоже самое происходит в конденсаторе, правда, уже за счёт электрического поля. Ёмкость и индуктивность вместе порождают реактивную энергию. Активная энергия (которой мешает возврат реактивной энергии) преобразовывается в тепловую, механическую и другую.

Реактивная составляющая электрического тока возникает только в цепях, содержащих реактивные элементы (индуктивности и ёмкости) и расходуется обычно на бесполезный нагрев проводников, из которых составлена эта цепь. Примером таких реактивных нагрузок являются электродвигатели различного типа, переносные электроинструменты (электродрели, «болгарки», штроборезы и т.п.), а также различная бытовая электронная техника. Полная мощность этих приборов, измеряемая в вольт-амперах, и активная мощность (в ваттах) соотносятся между собой через коэффициент мощности cosφ, который может принимать значение от 0,5 до 0,9. На этих приборах указывается обычно активная мощность в ваттах и значение коэффициента cosφ. Для определения полной потребляемой мощности в ВА, необходимо величину активной мощности (Вт) разделить на коэффициент cosφ.

Пример : если на электродрели указана величина мощности в 800 Вт и cosφ = 0,8, то отсюда следует, что потребляемая инструментом полная мощность составляет 800/0,8=1000 ВА. При отсутствии данных по cosφ можно брать его приблизительное значение, которое для домашнего электроинструмента составляет примерно 0,7.

Реактивный тип нагрузки характеризуется тем, что сначала, неторое время, в нём происходит накопление энергии, поставляемой источником питания. Затем запасённая энергия отдаётся обратно в этот источник. К подобным нагрузкам относятся такие элементы электрических цепей, как конденсаторы и катушки индуктивности, а также устройства, содержащие их. При этом в такой нагрузке между напряжением и током присутствует сдвиг фаз, равный 90 градусам. Поскольку основной целью существующих систем электроснабжения является полезная доставка электроэнергии от производителя непосредственно к потребителю – реактивная составляющая мощности обычно считается вредной характеристикой цепи.

Для того, чтобы компенсировать противодействие реактивной энергии, применяются специальные устанавливаемые конденсаторы. Это заставляет свести к минимуму появляющееся негативное влияние реактивной энергии. Мы уже отмечали, что реактивная мощность существенно влияет на потерю электрической энергии в сети. Потому получается, что величину той самой негативной энергии приходиться постоянно держать под контролем, и лучший для этого способ – организовать её учёт.

Там, где озабочены этой проблемой (различные промышленные предприятия) довольно часто ставят отдельные специальные приборы, которые ведут учёт не только самой реактивной энергии, но и активной её части. Учёт ведётся в трёхфазных сетях по индуктивной и ёмкостной составляющей. Обычно такие счётчики, это не что иное, как аналого-цифровое устройство, которое преобразует мощность в аналоговый сигнал, который превращается в частоту следования электро-импульсов. Сложив их, мы можем судить о количестве потребляемой энергии. Обычно счётчик сделан из пластмассового корпуса, где установлены 3 трансформатора и блок учёта на печатной плате. На внешней стороне располагается ЖК экран или светодиоды.

Предприятия в настоящее время всё чаще ставят универсальные счётчики учёта электроэнергии, которые измеряют количество как активной, так и реактивной энергии. Более того, такие приборы могут совмещать функции от двух, а иногда и более устройств, что позволяет снижать затраты на обслуживание и позволяет сэкономить во время покупки. Такие устройство способны вычислять реактивную и активную мощность, а также измерять мгновенные значения напряжений. Счётчик фиксирует, каков уровень потребления энергии и показывает всю информацию на дисплее 3-мя сменяющимися кадрами (индуктивная составляющая, ёмкостная составляющая, а также объём активной энергии). Современные модели позволяют передавать данные по ИК цифровому каналу, защищены от магнитных полей, хищения энергии. Более того, мы получаем более точные измерения и малое энергопотребление, что выгодно отличает новые модели от предшественников.

Понятия активной, полной и реактивной мощностей. Разбираемся с понятиями активной и реактивной нагрузки

Реактивная мощность – это величина, характеризующая нагрузки создаваемые различными колебаниями электромагнитных полей, которые встречаются цепях с конденсаторами и индуктивностями. А по своей сути это энергия, которая переходит от источника питания к потребителю (нагрузке), а затем возвращается обратно этими реактивными компонентами в течении одного полупериода.

Существуют потребители электрической энергии, которые создают чисто активную нагрузку. К ним можно отнести различные нагревательные элементы, тэны, лампы накаливания и т.п. Эти потребители не способны генерировать значительных электромагнитных полей. А вот другие потребители способны генерировать реактивную нагрузку. Т.е создавать сильные электромагнитные поля. Основными представителями этой группы можно считать устройства имеющие в своих питающих цепях конденсаторы и катушки индуктивность. Как мы уже знаем, и по разному оказывают влияние на величину реактивной мощности появляющейся в электрической цепи.

Так если приложить к катушки индуктивности ток и напряжение с нулевым сдвигом по фазе, то на выходе схемы увидим отставание тока от напряжения. А вот если подать тоже самое на конденсатор, то на выходе получим опережение током напряжения. Для понимания процесса смотри рисунок, где схематически показано опережение током напряжения при емкостном характере нагрузки.

Такие свойства реактивных нагрузок используют для регулировки уровня напряжения в сети методом компенсации большой индуктивности емкостными нагрузками, и наоборот больших емкостей – индуктивностью.

реактивная мощность вычисляется по следующим формулам:

Где, x – , I и U – ток и напряжение протекающие в цепи, sinφ – коэффициент реактивной мощности

Единицей измерения реактивной мощности по СИ, является вольт ампер реактивный – ВАр

Природу потерь в электрических цепях с реактивными компонентами можно увидеть по графикам на рисунках ниже:

При отсутствии активной составляющей в нагрузке, сдвиг фаз между током и напряжением будет 90°. В начальный момент времени, когда уровень напряжение максимален – ток будет стремиться нулю, поэтому, мгновенное значение мощности UI в это время будет нулевым. В течении первой ¼ периода, мощность можно визуализировать на графике, как произведение UI (тока и напряжения), которое станет нулевым при максимуме тока и нулевом значении напряжения.

В следующую ¼ периода, UI будет лежать в отрицательной области координат, поэтому, мощность будет уходить обратно в источник питания. То же самое случится и в отрицательном токовом полупериоде. В результате средняя (активная) потребляемая мощность P avg за период будет нулевой.

В этом случае реактивная мощность, в соответствии с формулой выше стремится к нулю. Потребляемая мощность равна произведению тока и напряжения, Полная мощность будет равна только активной мощности. Коэффициент мощности будет равен единице (P/S = 1 ).

Рассмотрим случай равенства реактивного и активного сопротивлений в нагрузке , т.е сдвиг фаз между током и напряжением на 45°.

В этом случае: Q = U×I×sin45° = 0.71×U×I . Коэффициент мощности = 0.71

Как вы наверное заметили, реактивная мощность оказывает обычно отрицательное воздействие, в связи с чем, необходима ее компенсация.

В отличии от сетей постоянного тока, где мощность имеет выражение и не изменяется во времени, в сетях переменного тока это не так.

Мощность в цепи переменного тока также есть переменной величиной. На любом участке цепи в любой момент времени t она определяется как произведение мгновенных значений напряжения и тока.

Рассмотрим, что представляет активная мощность

В цепи с чисто активным сопротивлением она равна:

Если принять и тогда выйдет:

Исходя из выражений выше — активная энергия состоит из двух частей — постоянной и переменной , которая меняется с двойной частотой. Среднее ее значение

График Р(ωt)

Отличие реактивной мощности от активной

В цепи, где есть реактивное сопротивление (возьмем для примера индуктивное) значение мгновенной мощности равно:

Соответственно и в итоге получим:

Данное выражение показывает, что реактивная энергия содержит только переменную часть, которая изменяется с двойной частотой, а ее среднее значение равно нулю

График q(ωt)

Если ток и напряжение имеют синусоидальную форму и сеть содержит элементы типа R-L или R-C, то в таких сетях кроме преобразования энергии в активном элементе R вдобавок еще и изменяется энергия электрического и магнитного полей в реактивных элементах L и C.

В таком случае полная мощность сети будет равна сумме:

Что такое полная мощность на примере простой R-L цепи

Графики изменения мгновенных значений u,i:

φ — фазовый сдвиг между током и напряжением

Уравнение для S примет следующий вид

Подставим вместо и заменим амплитудные значения на действующие:

Значение S рассматривается как сумма двух величин , где

И — мгновенные активные и реактивные мощности на участках R-L.

Графики p,q,s:

Как видим из графика, наличие индуктивной составляющей повлекло за собой появление отрицательной части в полной мощности (заштрихованная часть графика), что снижает ее среднее значение. Это происходит из-за фазового сдвига, в какой-то момент времени ток и напряжение находятся в противофазе, поэтому появляется отрицательное значение S.

Итоговые выражения для действующих значений:

Активная составляющая сети выражается в ваттах (Вт), а реактивная в вольт-амперах реактивных (вар).

Полная мощность сети S, обусловлена номинальными данными генератора. Для генератора она обусловлена выражением:

Для нормальной работы генератора ток в обмотках и напряжение на зажимах не должны превышать номинальные значения I н, U н . Для генератора значения P и S одинаковы, однако все-таки на практике условились S выражать в вольт-амперах (ВА).

Также энергию сети можно выразить через каждую составляющую отдельно:

Где S, P, Q – соответственно активное, реактивное и полное сопротивление сети. Они образуют треугольник мощностей:

Треугольник мощностей с преобладающей индуктивной нагрузкой

Если вспомнить теорему Пифагора, то из прямоугольного треугольника можно получить такое выражение:

Реактивная составляющая в треугольнике является положительной (Q L), когда ток отстает от напряжения, и отрицательной (Q C), когда опережает:

Треугольник мощностей с преобладающей емкостной нагрузкой

Для реактивной составляющей сети справедливо алгебраическое выражение:

Из чего следует что индуктивная и емкостная энергия взаимозаменяемы. То есть если вы хотите уменьшить влияние индуктивной части цепи, вам необходимо добавить емкость, и наоборот. Ниже пример данной схемы:

Схема компенсации реактивной составляющей

Векторная диаграмма показывает влияние конденсатора на cosφ. Как видно, что при включении конденсатора cosφ 2 > cosφ 1 и I л
Векторная диаграмма

Связь между полной и реактивной энергии выражается:

сosφ – это коэффициент мощности. он показывает какую долю от полной энергии составляет активная энергия. Чем ближе он к 1, тем больше полезной энергии потребляется из сети.

Выводы о трех составляющих цепи переменного тока

В отличии от цепей постоянного тока, цепи переменного напряжения имеют три вида мощности – активная, реактивная, полная. Активная энергия, как и в цепях постоянного тока, выполняет полезную работу. Реактивная – не выполняет ничего полезного, а только снижает КПД сети, греет провода, грузит генератор. Полная – сумма активной и реактивной, она равна мощности сети. Индуктивная составляющая реактивной энергии может быть скомпенсирована емкостной. На практике в промышленности это реализовано в виде .

и является суммой двух величин, одна из которых постоянна во времени, а другая пульсирует с двойной частотой.

Среднее значение p(t) за период Т называется активной мощностью и полностью определяется первым слагаемым уравнения (5.1):

Активная мощность ха-рактеризует энергию, расходуемую необратимо источником в единицу времени на производство полезной работы потребителем. Активная энергия, потребляемая электроприёмниками, преобразуется в другие виды энергии : механическую, тепловую, энергию сжатого воздуха и газа и т. п.

Среднее значение от второго слагаемого мгновенной мощности (1.1) (пульсирует с двойной частотой) за время Т равно нулю, т. е. на ее создание не требуется каких-либо материальных затрат и поэтому она не может совершать полезной ра-боты. Однако ее присутствие указывает, что между источником и приемником происходит обратимый процесс обмена энергией. Это возможно, если имеются элементы, способные накапливать и отдавать электромагнитную энергию – емкость и индуктивность . Эта составляющая характеризует реактивную мощность.

Полную мощность на зажимах приемника в комп-лексной форме можно представить следующим образом:

Единица измерения полной мощности S = UI – ВА.

Реактивная мощность – величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями (обменом) энергии между источником и приемником. Для синусоидального тока она равна произведению действующих значений тока I и напряжения U на синус угла сдвига фаз между ними: Q = UI sinφ. Единица измерения – ВАр.

Реактивная мощность не связана с полезной работой ЭП и расходуется только на создание переменных электромагнитных полей в электродвигателях, трансформаторах, аппаратах, линиях и т. д.

Для реактивной мощности приняты такие понятия, как генерация, потребление, передача, потери, баланс. Считается, что если ток отстает по фазе от напряжения (индуктивный характер нагрузки), то реактивная мощ-ность потребляется и имеет положительный знак, а если ток опережает напряжение (емкостный характер нагрузки), то реактивная мощность ге-нерируется и имеет отрицательное значение.

Основными потребителями реактивной мощности на промышленных предприятиях являются асинхронные двигатели (60-65 % общего потреб-ления), трансформаторы (20-25 %), вентильные преобразователи, реакторы, воздушные электрические сети и прочие приемники (10 %).

Передача реактивной мощности загружает электрические сети и установленное в ней оборудование, уменьшая их пропускную способность. Реактивная мощность генерируется синхронными генераторами электростанций, синхронными компенса-торами, синхронными двигателями (регулирование током возбуждения), батареями конденсаторов (БК) и линиями электропередачи.

Реактивная мощность, вырабатываемая емкостью сетей, имеет следующий порядок величин: воздушная линия 20 кВ генерирует 1 кВАр на 1 км трехфазной линии; подземный кабель 20 кВ – 20 кВАр/км; воздушная линия 220 кВ – 150 кВАр/км; подземный кабель 220 кВ – 3 МВАр/км.

Коэффициент мощности и коэффициент реактивной мощности.

Векторное представление величин, характеризующих состояние сети, приводит к представлению реактивной мощности Q вектором, перпендикулярным вектору активной мощности Р (рис. 5.2). Их векторная сумма дает полную мощность S .

Рис. 5.1. Треугольник мощностей

Согласно рис. 5.1 и (5.2) следует, что S 2 = Р 2 + Q 2 ; tgφ = Q/P; cosφ = P/S.

Основным нормативным показателем, характе-ризующим реактивную мощность, ранее был коэффициент мощности cosφ. На вводах, питающих промышленное предприятие, средневзвешенное значение этого коэффициента должно было находиться в пределах 0,92-0,95. Однако выбор соотношения P/S в качестве нормативного не дает четкого представления о динамике изменения реального значения реактивной мощности. Например, при изменении коэффициента мощности от 0,95 до 0,94 реактивная мощность изменяется на 10 %, а при изменении этого же коэффициента от 0,99 до 0,98 приращение реактивной мощности составляет уже 42 %. При расчетах удобнее оперировать соотношением tgφ = Q/P , которое называют коэффициентом реактивной мощности.

Предприятиям, у которых присоединенная мощность более 150 кВт (за исключением «бытовых» потребителей), определены предельные значения коэффициента реактивной мощности , потребляемой в часы больших суточных нагрузок электрической сети – с 7 до 23 часов (Приказ Министерства промышленности и энергетики РФ от 22.02.2007 г. № 49 «О порядке расчета значений соотношения потребления активной и реактивной мощности для отдельных энергопринимающих устройств потребителей электрической энергии, применяемых для определения обязательств сторон в договорах об оказании услуг по передаче электрической энергии »).

Предельные значения коэффициентов реактивной мощности (tgφ) нормируются в зависимости от положения точки (напряжения) присоединения потребителя к сети. Для напряжения сети 100 кВ tgφ = 0,5; для сетей 35, 20, 6 кВ – tgφ = 0,4 и для сети 0,4 кВ – tgφ = 0,35.

Введение новых директивных документов по компен-сации реактивной мощности было направлено на повышение эффективности работы всей системы электроснабжения от генераторов энергосистемы до приемников электроэнергии.

С введением коэффициента реактивной мощности стало возможным представлять потери активной мощности через активную или реактивную мощности: Р = (P 2 /U 2) R (l + tg 2 φ).

Угол между векторами мощностей Р и S соответствует углу φ между векторами активной составляющей тока I а и полного тока I , который, в свою очередь, представляет собой векторную сумму активного тока I а, находящегося в фазе с напряжением, и реактивного тока I р, находящегося под углом 90° к нему. Это расположение токов является расчетным приемом, связанным с разложением на активную и реактивную мощности, которое можно считать естественным.

Большинство потребителей нуждаются в реактивной мощности, поскольку они функционируют благодаря изменению магнитного поля . Для наиболее употребительных двигателей в нормальном режиме работы можно привести следующие примерные значения tgφ.

В момент пуска двигателей требуется значительное количество реактивной мощности, при этом tgφ = 4-5 (cosφ = 0,2-0,24).

Синхронные машины обладают способностью потреблять или выдавать реактивную мощность в зависимости от степени возбуждения.

В синхронных генераторах и двигателях размеры цепей возбуждения ограничивают возможность поставки реактивной мощности до максимальных значений tgφ = 0,75 (cosφ = 0,8) или до tgφ = 0,5 (cosφ = 0,9) (табл. 5.1).

Синхронные двигатели, выпускаемые отечественной промышленностью, рассчитаны на опережающий коэффициент мощности (cosφ = 0,9) и при номинальной активной нагрузке P ном и напряжении U ном могут вырабатывать номинальную реактивную мощность Q ном ≈ 0,5P ном.

При недогрузке СД по активной мощности β = P/P ном Q /Q ном > 1.

Преимуществом СД, используемым для компенсации реактивной мощности, по сравнению с КБ является возможность плавного регулирования генерируемой реактивной мощности. Недостатком является то, что активные потери на генерирование реактивной мощности для СД больше, чем для КБ.

Дополнительные активные потери в обмотке СД, вызываемые генерируемой реактивной мощностью в пределах изменения cosφ от 1 до 0,9 при номинальной активной мощности СД, равной P ном, кВт:

Р ном = Q 2 ном R /U 2 ном,

где Q ном – номинальная реактивная мощность СД, кВ Ар; R – сопротивление одной фазы обмотки СД в нагретом состоянии, Ом; U ном – номинальное напряжение сети, кВ.

В системах электроснабжения промышленных предприятий КБ компенсируют реактивную мощность базисной (основной) части графиков нагрузок, а СД снижают пики нагрузок графика.

Таблица 5.1

Зависимости коэффициента перегрузки по реактивной мощности синхронных двигателе й

Синхронные компенсаторы.

Разновидностью СД являются синхронные компенсаторы (СК), которые представляют собой СД без нагрузки на валу. В настоящее время выпускается СК мощностью выше 5000 кВ?Ар. Они имеют ограниченное применение в сетях промышленных предприятий. Для улучшения показателей качества напряжения у мощных ЭП с резкопеременной, ударной нагрузкой (дуговые печи, прокатные станы и т. п.) используются СК.

Статические тиристорные компенсирующие устройства.

В сетях с резкопеременной ударной нагрузкой на напряжении 6-10 кВ рекомендуется применение не конденсаторных батарей, а специальных быстродействующих источников реактивной мощности (ИРМ), которые должны устанавливаться вблизи таких ЭП. Схема ИРМ приведена на рис. 5.2. В ней в качестве регулируемой индуктивности используются индуктивности LR и нерегулируемые ёмкости С 1-С 3.

Рис. 5.2. Быстродействующие источники реактивной мощности

Регулирование индуктивности осуществляется тиристорными группами VS , управляющие электроды которых подсоединены к схеме управления. Достоинствами статических ИРМ являются отсутствие вращающихся частей, относительная плавность регулирования реактивной мощности, выдаваемой в сеть, возможность трёх- и четырёхкратной перегрузки по реактивной мощности. К недостаткам относится появление высших гармоник, которые могут возникнуть при глубоком регулировании реактивной мощности.

За счет дополнительных потерь мощности в сети, вызванных потреблением реактивной мощности, увеличивается общее потребление электроэнергии. Поэтому снижение перетоков реактивной мощности является одной из основных задач эксплуатации электрических сетей.

Реактивная мощность – часть электрической энергии, возращенная нагрузкой источнику. Явление возникновения ситуации считается вредным.

Возникновение реактивная мощность

Допустим, цепь содержит источник питания постоянного тока и идеальную индуктивность. Включение цепи порождает переходный процесс. Напряжение стремится достичь номинального значения, росту активно мешает собственное потокосцепление индуктивности. Каждый виток провода согнут круговой траекторией. Образуемое магнитное поле будет пересекать соседствующий сегмент. Если витки расположены один за другим, характер взаимодействия усилится. Рассмотренное называется собственным потокосцеплением.

Характер процесса таков: наводимая ЭДС препятствует изменениям поля. Ток пытается стремительно вырасти, потокосцепление тянет обратно. Вместо ступеньки видим сглаженный выступ. Энергия магнитного поля потрачена, чтобы воспрепятствовать процессу создавшему. Случай возникновения реактивной мощности. Фазой отличается от полезной, вредит. Идеально: направление вектора перпендикулярно активной составляющей. Подразумевается, сопротивление провода нулевое (фантастический расклад).

При выключении цепи процесс повторится обратным порядком. Ток стремится мгновенно упасть до нуля, в магнитном поле запасена энергия. Пропади индуктивность, переход пройдет внезапно, потокосцепление придает процессу иную окраску:

Уменьшение тока вызывает снижение напряженности магнитного поля.
Произведенный эффект наводит противо-ЭДС витков.
В результате после отключения источника питания ток продолжает существовать, понемногу затухая.

Графики напряжения, тока, мощности

Реактивная мощность некое звено инерции, постоянно запаздывающее, мешающее. Первый вопрос: зачем тогда нужны индуктивности? О, у них хватает полезных качеств. Польза заставляет мириться с реактивной мощностью. Распространенным положительным эффектом назовем работу электрических двигателей. Передача энергии идет через магнитный поток. Меж витками одной катушки, как было показано выше. Взаимодействию подвержены постоянный магнит, дроссель, все, способное захватить вектором индукции.

Случаи нельзя назвать в смысле описательном всеобъемлющими. Иногда применяется поток сцепления в виде, показанном для примера. Принцип используют пускорегулирующие аппараты газоразрядных ламп. Дроссель снабжен несметным количеством витков: отключение напряжения вызывает не плавное снижение тока, но выброс большой амплитуды противоположной полярности. Индуктивность велика: отклик поистине потрясающий. Превышает исходные 230 вольт на порядок. Достаточно, чтобы возникла искра, лампочка зажглась.

Реактивная мощность и конденсаторы

Реактивная мощность запасается энергией магнитного поля индуктивностями. А конденсатор? Выступает источником возникновения реактивной составляющей. Дополним обзор теорией сложения векторов. Поймет рядовой читатель. В физике электрических сетей часто используются колебательные процессы. Всем известные 220 вольт (теперь принятые 230) в розетке частотой 50 Гц. Синусоида, амплитуда которой равна 315 вольт. Анализируя цепи, удобно представить вращающимся по часовой стрелке вектором.

Анализ цепей графическим методом

Упрощается расчет, можно пояснить инженерное представление реактивной мощности. Угол фазы тока считают равным нулю, откладывается вправо по оси абсцисс (см. рис.). Реактивная энергия индуктивности совпадает фазой с напряжением UL, опережает на 90 градусов ток. Идеальный случай. Практикам приходится учитывать сопротивление обмотки. Реактивной на индуктивности будет часть мощности (см. рис.). Угол меж проекциями важен. Величина называется коэффициентом мощности. Что означает на практике? Перед ответом на вопрос рассмотрим понятие треугольника сопротивлений.

Треугольник сопротивлений и коэффициент мощности

Чтобы проще вести анализ электрических цепей, физики предлагают использовать треугольник сопротивлений. Активная часть откладывается, как ток, – вправо оси абсцисс. Договорились, индуктивность направлять вверх, емкость – вниз. Вычисляя полное сопротивление цепи, значения вычитаем. Исключено комбинированный случай. Доступно два варианта: реактивное сопротивление положительное, либо отрицательное.

Получая емкостное/индуктивное сопротивление, параметры элементов цепи домножают коэффициентом, обозначаемым греческой буквой «омега». Круговая частота – произведение частоты сети на удвоенное число Пи (3.14). Еще одно замечание по поводу нахождения реактивных сопротивлений укажем. Если индуктивность просто домножается указанным коэффициентом, для емкостей берутся величины обратные произведению. Понятно из рисунка, где приведены указанные соотношения, помогающие вычислять напряжения. После домножения берем алгебраическую сумму индуктивного, емкостного сопротивлений. Первые рассматриваются положительными величинами, вторые – отрицательными.

Формулы реактивных составляющих

Две составляющие сопротивления – активная и мнимая – являются проекциями вектора полного сопротивления на оси абсцисс и ординат. Углы сохраняются при переносе абстракций на мощности. Активная откладывается по оси абсцисс, реактивная — вдоль сои ординат. Емкости и индуктивности являются основополагающей причиной возникновения в сети негативных эффектов. Было показано выше: без реактивных элементов становится невозможным построение электротехнических устройств.

Коэффициентом мощности принято называть косинус угла меж полным вектором сопротивления и горизонтальной осью. Столь важное значение параметру приписывают, поскольку полезная часть энергии источника является долей полных трат. Доля высчитывается умножением полной мощности на коэффициент. Если векторы напряжения и тока совпадают, косинус угла равен единице. Мощность теряется нагрузкой, улетучиваясь теплом.

Сказанному верить! Средняя мощность периода при подключении к источнику чисто реактивного сопротивления равна нулю. Половину времени индуктивность принимает энергию, вторую отдает. Обмотка двигателя обозначается на схемах прибавлением источника ЭДС, описывающего передачу энергии валу.

Практическое истолкование коэффициента мощности

Многие замечают неувязку в случае практического рассмотрения реактивной мощности. Для снижения коэффициента рекомендуют параллельно обмоткам двигателя включать конденсаторы большого размера. Индуктивное сопротивление уравновешивает емкостное, ток вновь совпадает с напряжением фазой. Сложно понять вот по какой причине:

Допустим, к источнику переменного напряжения подключили первичную обмотку трансформатора.
В идеале активное сопротивление равно нулю. Мощность должна быть реактивной. Но это плохо: угол между напряжением и током стремятся сделать нулевым!

Но! Колебательный процесс безучастен работе двигателей, трансформаторов. Теория реактивной мощности предполагает: колебания совершает вся энергия. До последней капли. В трансформаторе, двигателе из поля происходит активная «утечка» энергии на совершение работы, наведение тока вторичной обмотки. Энергия циркулировать между источником и потребителем не может.

Реальная цепь процесс согласования отдельных участков затрудняет. Для перестраховки поставщики требуют установить параллельно обмотке двигателя конденсаторы, чтобы энергия циркулировала в локальном сегменте, не выходила наружу, нагревая соединительные провода. Важно избежать перекомпенсации. Если емкость конденсаторов будет слишком велика, батарея станет причиной увеличения коэффициента мощности.

Что касается сдвига фаз, возникает на вторичной обмотке трансформатора подстанции. Роль играет не это. Двигатель работает, часть энергии не преобразована в полезную работу, отражается назад. В результате возникает коэффициент мощности. Участвующая составляющая индуктивности – технологический, конструкционный дефект. Часть, не приносящая пользы. Скомпенсируем, добавляя конденсаторные блоки.

Проверка правильности согласования ведется по факту отсутствия сдвига фаз между напряжением и током работающего электродвигателя. Лишняя энергия циркулирует меж избыточной индуктивностью обмоток, установленным конденсаторным блоком. Достигнута цель мероприятия – избежать нагрева проводников питающей устройство сети.

Что предлагают под видом экономии электроэнергии

В сети предлагают купить устройства экономии электроэнергии. Компенсаторы реактивной мощности. Важно не перегнуть палку. Допустим, компенсатор будет уместно смотреться рядом с включенным компрессором холодильника, коллекторным двигателем пылесоса, обременять квартиру мерами при работающих лампочках накала – предприятие сомнительное. До установки потрудитесь узнать сдвиг фаз меж напряжением и током, согласно информации, правильно рассчитайте объем блока конденсаторов. Иначе попытки сэкономить таким образом потерпят неудачу, разве случайно удастся навести палец в небо, попасть в точку.

Вторым аспектом компенсации реактивной мощности является учет. Делается для крупных предприятий, где стоят мощные двигатели, создающие большие углы сдвига фаз. Внедряют специальные счетчики учета реактивной мощности, оплачиваемой согласно тарифу. Для расчетов коэффициента оплаты применяется оценка тепловых потерь проводов, ухудшение режима эксплуатации кабельной сети, некоторые другие факторы.

Перспективы дальнейшего изучения реактивной энергии, как явления

Реактивная мощность выступает явлением отражения энергии. Идеальные цепи явления лишены. Реактивная мощность проявляется выделенным теплом на активном сопротивлении кабельных линий, искажает синусоидальную форму сигнала. Отдельная тема разговора. При отклонениях от нормы двигатели работают не столь гладко, трансформаторам – помеха.

Понятие о реактивной мощности

Измеряется в ваттах (Вт).

Емкостная (конденсаторы). Характеризуется фазовым опережением тока по сравнению с напряжением;
Индуктивная (катушки). Характеризуется фазовым отставанием тока по отношению к напряжению.

Расчет реактивной мощности ведется по формуле:

Q = U x I x sin φ.

В качестве единицы измерения реактивной мощности служит ВАр (вольтампер реактивный).

Выражение для активной мощности:

P = U x I x cos φ.

Чтобы была рассчитана полная мощность, необходимо знать разность фаз между синусоидальными значениям U и I.

Коэффициент мощности

Данный коэффициент находит эффективность работы сети.

Если, к примеру, имеется катушка, для которой:

Р = 80 Вт;
Q = 130 ВАр;
тогда S = 152,6 BA как среднеквадратичный показатель;
cos φ = P/S = 0,52 или 52%

Можно сказать, что катушка требует 130 ВАр полной мощности для выполнения полезной работы 80 Вт.

Коррекция cos φ

Главные потребители реактивной энергии:

Трансформаторы. Представляют собой обмотки, имеющие индуктивную связь и посредством магнитных полей преобразуюшие токи и напряжения. Эти аппараты являются основным элементом электросетей, передающих электроэнергию. Особенно увеличиваются потери при работе на холостом ходу и при низкой нагрузке. Широко используются трансформаторы в производстве и в быту;
Индукционные печи, в которых расплавляются металлы путем создания в них вихревых токов;
Асинхронные двигатели. Крупнейший потребитель реактивной энергии. Вращающий момент в них создается посредством переменного магнитного поля статора;
Преобразователи электроэнергии, такие как силовые выпрямители, используемые для питания контактной сети железнодорожного транспорта и другие.

Как и где измеряют cos φ

Так как при финансовых расчетах за потребленную энергию учитывается и ее реактивная составляющая, то на производствах устанавливаются автоматические компенсаторы на конденсаторах, емкость которых может меняться. В сетях, как правило, используются статические конденсаторы;
При регулировании cos φ у синхронных генераторов путем изменения возбуждающего тока необходимо его отслеживать визуально в ручных рабочих режимах;
Синхронные компенсаторы, представляющие собой синхронные двигатели, работающие без нагрузки, в режиме перевозбуждения выдают в сеть энергию, которая компенсирует индуктивную составляющую. Для регулирования возбуждающего тока наблюдают за показаниями cos φ по фазометру.

Видео

Что такое реактивная мощность? – Определение из Техопедии

Что означает реактивная мощность?

В системах электросетей реактивная мощность – это мощность, которая течет обратно от пункта назначения к сети в сценарии переменного тока.

В системе постоянного тока напряжение и нагрузка статичны, и, проще говоря, направление энергии «одностороннее», но в переменном токе есть разные фазы, связанные с элементами системы, такими как конденсаторы. и индукторы.

Реактивная мощность возвращает энергию обратно в сеть во время пассивных фаз.

Реактивная мощность также известна как фантомное питание.

Techopedia объясняет реактивную мощность

Другой способ объяснить это состоит в том, что реактивная мощность – это результирующая мощность в ваттах цепи переменного тока, когда форма волны тока не совпадает по фазе с формой волны напряжения, обычно на 90 градусов, если нагрузка является чисто реактивной, и является результатом емкостных или индуктивных нагрузок.

Фактическая работа выполняется только тогда, когда ток находится в фазе с напряжением, например, в резистивных нагрузках. Примером может служить лампа накаливания; в реактивной нагрузке энергия течет к нагрузке половину времени, тогда как в другой половине мощность течет от нее, что создает иллюзию того, что нагрузка не рассеивает и не потребляет мощность.

Три вида мощности

Реактивная мощность – это один из трех типов мощности, присутствующих в нагруженных цепях.

Истинная мощность

Фактическая мощность в ваттах, рассеиваемая схемой

Реактивная мощность

Рассеиваемая мощность от индуктивных и емкостных нагрузок, измеренная в вольт-амперах, реактивная (VAR)

Полная мощность

Комбинация измерения реактивной и истинной мощности в вольт-амперах (ВА)

Реактивная мощность также называется «фантомной мощностью», потому что неясно, куда она идет.Общеизвестно, что реактивные нагрузки, такие как конденсаторы и катушки индуктивности, на самом деле не рассеивают мощность в том смысле, что она не используется для их питания, но измерение напряжения и тока вокруг них указывает на то, что они падают напряжение и потребляют ток.

Мощность, рассеиваемая при этом падении напряжения и потребляемом токе, находится в форме тепла или ненужной энергии и не выполняется как фактическая работа; поэтому инженеры искали способы уменьшить это. Из-за этого фантомного питания проводники и генераторы должны иметь соответствующие номиналы и размеры, чтобы выдерживать общий ток, включая отходы, а не только ток, который выполняет фактическую работу.

Маятник часов

Некоторые эксперты в области энергетики говорят о реактивной мощности как части движения конденсатора, которое напоминает движение маятника часов от зенита до надира. По этой аналогии, когда маятник качается вверх, переменный ток подает активную мощность на устройство назначения. По мере того, как маятник движется вниз, реактивная мощность возвращается в сеть для поглощения.

В таких определениях эксперты сказали бы, что реактивная энергия – это энергия, циркулирующая взад и вперед между источником и нагрузкой, а именно, что реактивная мощность «исчезает» обратно к источнику.В некотором смысле это связано с задержкой между током и напряжением. Помимо конденсаторов, статические компенсаторы VAr и синхронные конденсаторы могут использоваться для управления реактивной мощностью в системе.

Ключевым моментом является размещение оборудования реактивного тока рядом с силовыми нагрузками. Это уменьшает количество реактивного тока, который система доставки должна переносить на определенное расстояние.

Реактивная мощность в сети

Чтобы справиться с реалиями переменного тока и изменения путей передачи энергии, проектировщики обязательно принимают меры по контролю напряжения.Эксперты в области энергетики отмечают, что даже 5% -ное изменение напряжения в данной системе может вызвать отключение электроэнергии и другие проблемы.

С этой целью многие элементы электрической системы, такие как трансформаторы, могут переключаться с подачи на поглощение реактивной мощности по фазам. Но те, кто близок к отрасли, подчеркивают, что это станет еще более важным, когда мы переведем части американской электросети на возобновляемые источники энергии.

Реактивная мощность и возобновляемые источники

Реактивная мощность также очень важна в контексте меняющихся энергосистем.

По многим важным причинам возобновляемые источники энергии, такие как солнце и ветер, заменяют традиционные источники энергии, такие как уголь и природный газ. Но это может иметь разветвления для электросети в целом.

«Всплеск возобновляемых источников энергии в сети без достаточной вращающейся массы может вызвать серьезные проблемы: отключение электроэнергии в определенных областях, чтобы привести спрос в соответствие с предложением; и отключение крупных электростанций от сети, чтобы предотвратить их перегрузку », – пишет Арчи Робб из Renewable Energy World, описывая принцип« инерции сети »и то, как это применимо к управлению реактивной мощностью в системе, которая переходит на возобновляемые источники энергии. строить.

Поскольку возобновляемые источники энергии поставляют энергию в сеть по-разному, возникнет потребность в микроуправлении активной и реактивной мощностью соответственно.

Что такое реактивная мощность? – Определение из Техопедии

Что означает реактивная мощность?

Реактивная мощность возвращает энергию обратно в сеть во время пассивных фаз.

Реактивная мощность также известна как фантомное питание.

Techopedia объясняет реактивную мощность

Три вида мощности

Реактивная мощность – это один из трех типов мощности, присутствующих в нагруженных цепях.

Истинная мощность

Фактическая мощность в ваттах, рассеиваемая схемой

Реактивная мощность

Рассеиваемая мощность от индуктивных и емкостных нагрузок, измеренная в вольт-амперах, реактивная (VAR)

Полная мощность

Комбинация измерения реактивной и истинной мощности в вольт-амперах (ВА)

Маятник часов

Реактивная мощность в сети

Реактивная мощность и возобновляемые источники

Реактивная мощность также очень важна в контексте меняющихся энергосистем.

Что конкретно такое реактивная мощность?

Поскольку я не знаю, что вы знаете, я объясню несколько связанных понятий, связанных с однофазным синусоидальным электричеством.

Короткий ответ: мнимая часть мощности возникает из-за сдвига фаз между напряжением и током. Если они синфазны, мнимая часть равна нулю.Если они сдвинуты по фазе на 90 градусов, действительная часть равна нулю. Между этими двумя углами будет получен промежуточный результат. Итак, почему?

Первое понятие – коэффициент мощности. Когда источник подает напряжение на нагрузку, ток, потребляемый нагрузкой, будет синусоидальным (при условии, что это линейная нагрузка … например, катушка индуктивности, конденсатор, резистор или их комбинация), но может не совпадать по фазе с напряжением. Если нагрузка представляет собой резистор, то ток находится в фазе с напряжением, что означает, что пик тока и пик напряжения происходят в один и тот же момент, а коэффициент мощности равен 1.0.

Вот как это выглядит. Обратите внимание, что напряжение и ток всегда имеют один и тот же знак. Таким образом, произведение I (t) * V (t) всегда положительно, что означает, что мощность подается на нагрузку в течение всего цикла (за исключением одного момента при пересечении нуля).

Если нагрузка не является резистивной по своей природе, то это идентично утверждению, что нагрузка РЕАКТИВНА, или что коэффициент мощности меньше 1, или что нагрузка содержит конденсаторы и / или катушки индуктивности.Все разные способы сказать одно и то же.

Но, если напряжение и ток не совпадают по фазе, это означает, что существует часть каждого цикла синусоидального напряжения, когда энергия доставляется к источнику от нагрузки (другими словами, в обратном направлении). Это еще один способ сказать, что нагрузка накапливает часть переданной ей энергии и возвращает ее источнику во время других частей цикла. Каждый раз, когда знак формы волны напряжения противоположен знаку формы волны тока, поток энергии идет в отрицательном направлении от нагрузки к источнику.Вот как это выглядит. Заштрихованная область между красными вертикальными линиями показывает противоположные знаки и обратный поток энергии.

Средняя мощность, подаваемая на нагрузку, может быть получена путем интегрирования мгновенной мощности за полный цикл и деления на один период. Но люди уже разработали краткий ответ, что это IRMS * VRMS * PF, где PF – коэффициент мощности, который является косинусом разности фаз между током и напряжением. И это только реальная часть сложной мощности.

Думаю, воображаемую часть можно рассматривать как энергию, которая не потребляется нагрузкой. Когда фазовый угол между напряжением и током составляет 90 градусов, знаки напряжения и тока противоположны в половине случаев, что означает, что энергия течет вперед и назад, но не потребляется. Это тот случай, когда нагрузка является чисто реактивной (катушка индуктивности или конденсатор) или мощность является чисто мнимой, а не реальной. Это выглядит так:

Что такое реактивная мощность и почему она имеет значение?

читать | Доля:

Реактивная мощность имеет решающее значение для поддержания уровней напряжения в системе передачи.

Но что именно?

Используя аналогию с муниципальной системой водоснабжения, подумайте о напряжении как об эквиваленте «давления» водяной системы – без него вода просто сидит в трубах, а при слишком большом количестве трубы взрываются. Поэтому очень важно, чтобы давление воды было постоянным и постоянным.

Напряжение играет аналогичную роль в электрической системе в обеспечении стабильности потоков мощности. Однако последствия несоблюдения напряжения в электрической системе гораздо более ужасны, поскольку падение напряжения может серьезно повредить генерирующее, передающее и распределительное оборудование и привести к широко распространенным каскадным отключениям.

Реактивная мощность генерируется или поглощается электрическими генераторами (или, в некоторых случаях, устройствами, известными как «конденсаторы») для поддержания постоянного уровня напряжения, обычно называемого «поддержкой напряжения». Генераторы, обеспечивающие поддержание напряжения, часто несут потери на нагрев, что приводит к снижению способности вырабатывать «реальную» мощность. Мы все больше знакомы с реальной мощностью: она зажигает лампочки, вращает моторы и заряжает айфоны. Важно то, что реальная мощность – это то, что компенсируется на оптовых рынках электроэнергии RTO.Таким образом, когда системные операторы приказывают генераторам генерировать или поглощать реактивную мощность для поддержания напряжения, они жертвуют своей способностью генерировать реальную мощность и получать рыночные доходы RTO. Рассчитанная маржа на эти упущенные рыночные доходы выплачивается производителям, обеспечивающим поддержку напряжением, посредством внебиржевых платежей.

Основная проблема использования реактивной мощности для управления напряжением заключается в том, что реактивная мощность не распространяется до реальной мощности в электрической системе. Во многих случаях самые дешевые источники реальной мощности расположены удаленно от центров нагрузки, и системные операторы должны контролировать уровни напряжения в центрах нагрузки, чтобы гарантировать поддержание постоянного уровня напряжения.Если уровни напряжения становятся слишком высокими или слишком низкими, генераторы в центре нагрузки работают для стабилизации уровней напряжения, генерируя или потребляя реактивную мощность.

Проблема реактивной мощности вышла на первый план на территории PJM Interconnection. Поскольку зона обслуживания PJM расширилась, а использование более дешевой удаленной генерации для обслуживания центров нагрузки стало более распространенным явлением, PJM расширила свои возможности мониторинга напряжения за счет внедрения интерфейсов передачи. Такие интерфейсы измеряют потоки мощности по выбранным высоковольтным линиям электропередачи в удаленные центры нагрузки, чтобы указать, когда необходима дополнительная локальная генерация (в центре нагрузки) для поддержания уровней напряжения.

Еще несколько лет назад способность генерировать реактивную мощность в PJM в основном воспринималась как должное. Поддержка напряжения обычно обеспечивалась унаследованными станциями, генерирующими базовую нагрузку, которые уже давно оплатили капитальные затраты на оборудование, необходимое для предоставления этой услуги, либо с помощью исторической регулируемой базы тарифов, либо с помощью тарифных положений PJM, которые позволяют возмещать такие затраты.

Две тенденции изменили статус-кво. Во-первых, поскольку цены на природный газ снизились, генерирующие мощности базовой нагрузки, которые исторически обеспечивали поддержание напряжения (т.е. угольные станции) уже не работают так стабильно или экономично. В некоторых случаях они запускались и работали без потерь, чтобы обеспечить реактивную мощность. Во-вторых, из-за экономических факторов и приближающихся экологических норм, многие из тех же генерирующих объектов базовой нагрузки теперь потребовали вывода из эксплуатации. Эти тенденции привели к существенным выплатам вне рынка этих генераторов базовой нагрузки, поскольку они были отправлены исключительно для обеспечения поддержки напряжением. В некоторых случаях контракты по обеспечению надежности использовались для поддержания работоспособности генерирующих мощностей в целях обеспечения реактивной мощности, включая некоторые угольные блоки в Пенсильвании.

Итак, что все это значит для наших клиентов в будущем?

По мере накопления внебиржевых платежей за поддержку напряжения и запросов на вывод из эксплуатации PJM провела модернизацию системы передачи для смягчения основных проблем с напряжением, расходы на которые несут налогоплательщики. Ожидается, что разработка таких обновлений будет продолжена.

PJM сейчас начинает обсуждения по моделированию потребности в реактивной мощности на своих рынках на сутки вперед и в реальном времени, что означает, что рыночные цены могут начать отражать реактивную мощность.Кроме того, с увеличением количества распределенных ресурсов все большее внимание уделяется обеспечению наличия адекватной реактивной способности, особенно учитывая, что высокая степень проникновения солнечной энергии требует большей реактивной мощности. Это может привести к необходимости возмещения капитальных затрат через рынки или тарифные планы PJM. Поскольку FERC фокусируется на ценообразовании – что в некотором смысле является кодом для поиска дополнительных доходов для производителей в эпоху низких цен на природный газ – существует вероятность того, что реактивная мощность станет более явным продуктом, требующим дополнительной компенсации.

Следите за обновлениями в бизнес-блоге Direct Energy, чтобы узнать о дальнейших политических и нормативных изменениях. Прочтите о том, как законопроект № 380 Сената Калифорнии может потенциально повлиять на цены на природный газ в Южной Калифорнии.

Размещено: 23 мая 2016 г.

Ознакомьтесь со своим измерителем мощности – что такое реальная, полная и реактивная мощность

Первое – простой вопрос

Верно или нет? Мощность = Напряжение x Ток. Это утверждение верно для систем постоянного тока, но для систем переменного тока есть две основные сложности.

Значение тока и напряжения постоянно меняется. Какое значение вы используете?
Напряжение и ток могут не совпадать по фазе. Умножение тока и напряжения, когда они не совпадают по фазе, требует регулировки для компенсации фазы. Именно этот фазовый сдвиг заставляет нас определять реальную, полную и реактивную мощность.
Этот фазовый сдвиг происходит, когда источник питания питает индуктивную или емкостную нагрузку ». Большинство нагрузок являются индуктивными (двигатели) или резистивными (нагреватели), поэтому сдвиг фаз обычно в одном направлении.
Двигатель имеет обмотку. Обмотанный проводник по существу определяет индуктор. Таким образом, обмотка представляет собой сопротивление намотанного провода и индуктивность обмотки.

Среднеквадратичное или эффективное значение

Пиковые значения на кривых переменного напряжения или тока сохраняются лишь на короткое время. Они на самом деле не отражают способность напряжения и тока выполнять работу и поэтому не используются в расчетах мощности.Ученые используют статистический метод для определения эффективных значений. Это называется среднеквадратичным или среднеквадратичным значением. Результатом определения является следующее: Veff / rms = 0,707 x V пиковое. То же самое относится и к току. СОВЕТ: вы можете разумно предположить, что все напряжения и токи, сообщаемые измерителем мощности, представлены как среднеквадратичные или эффективные значения, если не указано иное. .

СОВЕТ: Большинство мультиметров сообщают среднеквадратичные значения

Полная мощность

Полная мощность – это мощность, передаваемая источником питания такой нагрузке, как двигатель.Практически во всех реальных ситуациях, когда используется переменный ток, вам необходимо подавать на устройство больше энергии (кажущаяся мощность), чем оно будет работать (реальная мощность). (Векторная) разница между ними представляет работу, проделанную для преодоления индуктивной и Возможности воздействия нагрузки. Полная мощность измеряется в единицах ВА – Вольт-амперы. На самом деле это ватты, но мы используем новое название единицы, чтобы избежать путаницы. Таким образом, когда вы видите VA на листе технических данных, вы можете сделать разумный вывод, что речь идет о кажущейся мощности.Полная мощность рассчитывается: S (общий символ для полной мощности) = Veff / rms x Ieff / rms – однофазный расчет

Коэффициент мощности и фаза

Рассчитан коэффициент мощности: PF = косинус (фазовый угол в радианах) Коэффициент мощности не имеет инженерных единиц. Значение PF находится в диапазоне от -1 до 0 до 1 (запаздывание – без опережения). Коэффициент мощности резистивной нагрузки (без емкости или индуктивности) равен 1. Индуктивные нагрузки

Фаза тока отстает от номинального напряжения – Трансформаторы и двигатели (намотанные проводники)

Емкостная нагрузка

Токовые выводы Типичное напряжение – Скрытые кабели, конденсаторные батареи Нет ничего «плохого» в том, что коэффициент мощности не равен 1,0.

Реальная мощность и реактивная мощность

Думайте о реальной мощности как о полезной мощности – мере того, как много работы выполняется.Единицы измерения реальной мощности – ватты. Реальная мощность рассчитывается: P (реальная) = S (полная мощность) x pf Реактивная мощность – это (векторная) разница между полной и реальной мощностью. Энергия, используемая для производства реактивной мощности, сохраняется в магнитном / электрическом поле индуктивной нагрузки. В случае емкостной нагрузки магнитное / электрическое поле индуктивной нагрузки создает реактивную мощность. Реактивную мощность нельзя использовать для полезной работы. Реактивная мощность обозначается символом: Q

Технические единицы реактивной мощности – VAR – вольт-амперы реактивной мощности.Это также ватты, но мы используем VAR, чтобы знать, что мы говорим о реактивной мощности.

Диаграмма: измерение RMS

Диаграмма: вперед / назад

THD – Общее гармоническое искажение (также называемое искажением)

Проще говоря, THD – это мера искажения, выраженная в%. Если устройству (любому активному устройству, но представьте себе выпрямители, приводы с регулируемой скоростью… как практические примеры) подается синусоида на входе, выход никогда не будет точным 100% воспроизведением входа.Серия гармоник исходной волны искажает исходную форму волны. THD% – это попытка «пронумеровать» степень искажения для сравнения. Число% несколько спорно, потому что некоторые гармоники более важны, чем другие, и нет взвешивания.

THD (%) = 100 * SQRT [(V22 + V32 + V42 +… + Vn2)] / Vt Где V2, V3 – среднеквадратичные значения каждой гармоники напряжения, а Vt – общее среднеквадратичное выходное напряжение.

Провисание / вздутие или провал / скачок

Продолжительность 0.5 цикл и выше. Падения напряжения – это наиболее частые нарушения питания. Падения напряжения могут исходить от электросети. В большинстве случаев провисания возникают внутри здания. Например, в бытовой электропроводке наиболее частой причиной провалов напряжения является пусковой ток, потребляемый двигателями холодильника и кондиционера. Мешки обычно не мешают лампам накаливания или люминесцентному освещению. двигатели или обогреватели. Однако у некоторого электронного оборудования отсутствует достаточный внутренний накопитель энергии, и поэтому оно не может выдерживать провалы напряжения питания.Оборудование может выдерживать очень короткие глубокие провалы или более длинные, но более мелкие провалы.

Пониженное / повышенное напряжение

Перенапряжение – это увеличение действующего напряжения более чем на 110% в течение более одной минуты. Пониженное напряжение – это снижение эффективного напряжения до менее 90% в течение более одной минуты. Будьте осторожны с этим определением, потому что оно имеет тенденцию меняться от поставщика к поставщику.

Переходные напряжения / скачки / скачки

Относится к кратковременным (менее 1 цикла) событиям. Низкочастотные переходные процессы часто называют «переходными процессами при переключении конденсаторов». Высокочастотные переходные процессы часто называют импульсами, пиками или скачками. Они могут быть вызваны включением разряженного конденсатора коррекции коэффициента мощности по линии. Высокочастотные переходные процессы вызваны молнией или отключением индуктивных нагрузок.Типичное время нарастания порядка микросекунды; типичные времена затухания составляют от десятков до сотен микросекунд. Часто затухание представляет собой экспоненциально затухающую форму кольцевого сигнала с частотой приблизительно 100 кГц. Чрезвычайно быстрые переходные процессы, или EFT, имеют время нарастания и спада в наносекундной области. Они вызываются дуговыми замыканиями, такими как неисправные щетки в двигателях, и быстро гасятся даже несколькими метрами распределительной проводки. Стандартные сетевые фильтры, входящие в комплект почти всего электронного оборудования, устраняют EFT.

Определение реактивной мощности

Понять, что такое реактивная мощность, крайне важно для всех инженеров-электриков. Просто перейдите к основам альтернативы. и базовое определение мощности P (ватт) = вольт (т.е. джоули / кулон) XI амперы (т.е. кулон / сек) = V x I (джоуль / сек = ватты) Для частоты системы постоянного тока = 0, следовательно, индуктивное реактивное сопротивление равно нулю, а емкостное реактивное сопротивление бесконечно, следовательно, мощность рассеивается только резистивными нагрузками, в основном в активной видимой форме тепла или используемой для движущей нагрузки / освещения.эту мощность принято называть активной мощностью.

Мощность, необходимая для создания магнитного поля / электрического поля, называется реактивной мощностью. Поскольку магнитное поле / электрическое поле невидимо, эту силу невозможно ощутить. Кроме того, эта мощность колеблется с двойной частотой системы.
на этом фоне, если мы посмотрим на генератор переменного тока, управляемый первичным двигателем, при холостом токе i (t) произведенный равен нулю с напряжением на клеммах, v (t) полезная мощность = v (t) x i (t) = 0
при подключении реактивной нагрузки R i (t) = v (t) / R полезная мощность = v (t) x v (t) / R
поскольку квадрат любого количества (в данном случае v (t)) всегда будет положительной полезной мощностью, подаваемой в резистивной нагрузке, она является однонаправленной, то есть всегда от источника к нагрузке.Никакой реакции от нагрузки к источнику нет.
Теперь давайте посмотрим, что происходит при доставке чисто индуктивной нагрузки Реактивное сопротивление X = 1 Ом (pf = нулевая задержка)
Основной поток, создаваемый обмоткой возбуждения, остается прежним, однако ток, протекающий через статор, создает поле, которое на 90 градусов отстает от основного потока / поля
power = v (t) xi (t) = Vm Sinὠt x Im (Sinὠt- pi / 2) = -Vm X Im (Sinὠt) X (cos ὠt) = (Vm X Im) / 2 X Sin2ὠt) (ὠ равно 2pi x частота)

Эта мощность представляет собой реактивную мощность, колеблющуюся с удвоенной частотой.
Мощность не рассеивается в чисто реактивной нагрузке. Хотя он попеременно поглощается и возвращается к источнику.
Обратите внимание, что мощность одинаково чередуется между положительными и отрицательными циклами. Это означает, что мощность поочередно поглощается и возвращается к источнику. Если бы источником был механический генератор, для вращения вала не потребовалось бы (практически) никакой полезной механической энергии, потому что нагрузка не использовала бы никакой энергии. Вал генератора можно было бы легко вращать, а катушка индуктивности не нагревалась бы, как резистор.
Подобно тому, как нехватка активной мощности в системе влияет на стабильность, нехватка реактивной мощности также приводит к нестабильности напряжения и серьезной работе системы, хотя в системе может быть достаточно активной мощности.

РЕАКТИВНАЯ МОЩНОСТЬ – прикладное промышленное электричество

Рисунок 6.1 Чисто резистивная цепь переменного тока: напряжение и ток резистора совпадают по фазе.

Если бы мы изобразили ток и напряжение для очень простой цепи переменного тока, состоящей из источника и резистора (рисунок выше), это выглядело бы примерно так: (рисунок ниже)

Рисунок 6.2 Напряжение и ток «синфазны» для резистивной цепи.

Поскольку резистор просто и напрямую сопротивляется протеканию тока в любое время, форма волны падения напряжения на резисторе точно совпадает по фазе с формой волны тока через него. Мы можем посмотреть в любой момент времени по горизонтальной оси графика и сравнить эти значения тока и напряжения друг с другом (любой «снимок», показывающий значения волны, называется мгновенными значениями , то есть значениями при этом момент времени ).Когда мгновенное значение тока равно нулю, мгновенное напряжение на резисторе также равно нулю. Аналогичным образом, в момент времени, когда ток через резистор находится на своем положительном пике, напряжение на резисторе также находится на своем положительном пике, и так далее. В любой момент времени на волнах закон Ома справедлив для мгновенных значений напряжения и тока.

Мы также можем рассчитать мощность, рассеиваемую этим резистором, и нанести эти значения на тот же график: (рисунок ниже)

Рисунок 6.3 Мгновенная мощность переменного тока в чисто резистивной цепи всегда положительная.

Резисторы и индукторы

Катушки индуктивности ведут себя иначе, чем резисторы. В то время как резисторы просто противодействуют протеканию тока через них (снижая напряжение, прямо пропорциональное току), индукторы противодействуют изменениям тока через них, снижая напряжение, прямо пропорциональное скорости изменения тока. В соответствии с законом Ленца , это индуцированное напряжение всегда имеет такую полярность, чтобы поддерживать ток на его текущем значении.То есть, если ток увеличивается по величине, индуцированное напряжение будет «противодействовать» протеканию тока; если ток уменьшается, полярность изменится на противоположную и «подтолкнет» ток, чтобы противодействовать уменьшению. Это противодействие текущему изменению называется реактивным сопротивлением , а не сопротивлением . Выражаясь математически, соотношение между падением напряжения на катушке индуктивности и скоростью изменения тока через катушку индуктивности выглядит следующим образом:

[латекс] e = L \ frac {d_i} {d_t} [/ латекс]

Переменный ток в простой индуктивной цепи

Выражение di / dt – это выражение из расчетов, означающее скорость изменения мгновенного тока (i) во времени в амперах в секунду.Индуктивность (L) измеряется в Генри, а мгновенное напряжение (е), конечно, выражается в вольтах. Иногда вы можете встретить скорость мгновенного напряжения, выраженную как «v» вместо «e» (v = L di / dt), но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую цепь индуктивности:

Рисунок 6.4 Чистая индуктивная цепь: ток индуктора отстает от напряжения индуктора на 90 °.

Если бы мы изобразили ток и напряжение для этой очень простой схемы, это выглядело бы примерно так:

Рисунок 6.5 Чистая индуктивная цепь, формы сигналов.

Помните, что падение напряжения на катушке индуктивности является реакцией на изменение тока через нее на . Следовательно, мгновенное напряжение равно нулю всякий раз, когда мгновенный ток достигает пика (нулевое изменение или наклон уровня на синусоидальной волне тока), а мгновенное напряжение находится на пике везде, где мгновенный ток имеет максимальное изменение (точки самый крутой наклон на текущей волне, где она пересекает нулевую линию).Это приводит к появлению волны напряжения, сдвинутой по фазе на 90 ° с волной тока. Глядя на график, кажется, что волна напряжения имеет «фору» по сравнению с волной тока; напряжение «опережает» ток, а ток «отстает» от напряжения.

Ток отстает от напряжения на 90 ° в чисто индуктивной цепи.

Все становится еще интереснее, когда мы строим график мощности для этой схемы:

Рисунок 6.6 В чисто индуктивной цепи мгновенная мощность может быть положительной или отрицательной.

Поскольку мгновенная мощность является произведением мгновенного напряжения и мгновенного тока (p = ie), мощность равна нулю всякий раз, когда мгновенный ток или напряжение равно нулю. Если мгновенный ток и напряжение положительные (над линией), мощность положительная. Как и в примере с резистором, мощность также положительна, когда мгновенные ток и напряжение отрицательны (ниже линии). Однако, поскольку волны тока и напряжения сдвинуты по фазе на 90 °, бывают случаи, когда одна из них положительна, а другая – отрицательна, что приводит к одинаково частым возникновению отрицательной мгновенной мощности .

Что такое отрицательная сила?

Но что означает отрицательная мощность ? Это означает, что катушка индуктивности возвращает мощность в цепь, в то время как положительная мощность означает, что она поглощает мощность из цепи. Поскольку положительные и отрицательные циклы мощности равны по величине и продолжительности с течением времени, индуктор возвращает обратно в цепь столько же мощности, сколько потребляет в течение полного цикла. В практическом смысле это означает, что реактивное сопротивление катушки индуктивности рассеивает нулевую полезную энергию, в отличие от сопротивления резистора, который рассеивает энергию в виде тепла.Имейте в виду, это только для идеальных катушек индуктивности, у которых нет сопротивления провода.

Реактивное сопротивление в зависимости от сопротивления

Противодействие катушки индуктивности изменению тока означает противодействие переменному току в целом, который по определению всегда изменяется по мгновенной величине и направлению. Это противодействие переменному току аналогично сопротивлению, но отличается тем, что всегда приводит к сдвигу фаз между током и напряжением и рассеивает нулевую мощность. Из-за различий он имеет другое название: реактивное сопротивление .Реактивное сопротивление по переменному току выражается в омах, как и сопротивление, за исключением того, что его математический символ – X вместо R. Чтобы быть конкретным, реактивное сопротивление, связанное с индуктором, обычно обозначается заглавной буквой X с буквой L в качестве нижнего индекса, например это: X _L.

Поскольку напряжение на катушках индуктивности падает пропорционально скорости изменения тока, они будут снижать большее напряжение при более быстром изменении тока и меньшее напряжение при более медленном изменении тока. Это означает, что реактивное сопротивление в Ом для любой катушки индуктивности прямо пропорционально частоте переменного тока.Точная формула для определения реактивного сопротивления выглядит следующим образом:

[латекс] X_L = 2πfL [/ латекс]

Если мы подвергнем индуктор 10 мГн воздействию частот 60, 120 и 2500 Гц, он проявит реактивные сопротивления, указанные в таблице ниже.

Реактивное сопротивление индуктора 10 мГн:

Таблица 6.1 Реактивное сопротивление индуктора 10 мГн
Частота (Герцы)	Реактивное сопротивление (Ом)
60	3.7699
120	7,5398
2500	157.0796

В уравнении реактивного сопротивления термин «2πf» (все в правой части, кроме L) имеет особое значение. Это количество радиан в секунду, на которое «вращается» переменный ток, если вы представите себе один цикл переменного тока, представляющий вращение полного круга. радиан – это единица измерения угла: в одном полном круге 2π радиана, так же как в полном круге 360 °.Если генератор переменного тока является двухполюсным, он будет производить один цикл на каждый полный оборот вала, что составляет каждые 2π радиан или 360 °. Если эту константу 2π умножить на частоту в герцах (циклов в секунду), результатом будет число в радианах в секунду, известное как угловая скорость системы переменного тока.

Угловая скорость в системах переменного тока

Угловая скорость может быть представлена выражением 2πf или ее собственным символом, строчной греческой буквой омега, которая похожа на нашу строчную римскую букву «w»: ω.Таким образом, формула реактивного сопротивления X _L = 2πfL также может быть записана как X _L = ωL.

Следует понимать, что эта «угловая скорость» является выражением того, насколько быстро колеблются формы колебаний переменного тока, полный цикл равен 2π радиан. Это не обязательно отражает фактическую скорость вала генератора переменного тока. Если генератор имеет более двух полюсов, угловая скорость будет кратной скорости вала. По этой причине ω иногда выражается в единицах электрических радиан в секунду, а не в (простых) радианах в секунду, чтобы отличить его от механического движения.

Каким бы способом мы ни выразили угловую скорость системы, очевидно, что она прямо пропорциональна реактивному сопротивлению в катушке индуктивности. По мере увеличения частоты (или скорости вала генератора переменного тока) в системе переменного тока катушка индуктивности будет оказывать большее сопротивление прохождению тока, и наоборот. Переменный ток в простой индуктивной цепи равен напряжению (в вольтах), деленному на индуктивное реактивное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на сопротивление (в Ом).Пример схемы показан здесь:

Индуктивное сопротивление
(Индуктивное сопротивление индуктора 10 мГн при 60 Гц)
[латекс] X_L = 3,7600 Ом [/ латекс]
[латекс] I_ {X_ {L}} = \ frac {E} {X} [/ латекс]
[латекс] = \ frac {10 В} {3,7600 Ом} [/ латекс]
[латекс] \ mathbf {= 2.6526A} [/ латекс]
Фазовые углы
Однако нужно иметь в виду, что здесь напряжение и ток не совпадают по фазе. Как было показано ранее, напряжение имеет фазовый сдвиг + 90 ° по отношению к току.Если мы представим эти фазовые углы напряжения и тока математически в виде комплексных чисел, мы обнаружим, что сопротивление катушки индуктивности току также имеет фазовый угол:
[латекс] \ text {Opposition} = \ frac {\ text {Voltage}} {\ text {Current}} [/ latex]
[латекс] \ text {Opposition} = \ frac {10 V \ angle \ text {90 °}} {2.6526A \ angle \ text {90 °}} [/ латекс]
[латекс] \ begin {align} \ text {Opposition} = & 3.7699 \ Omega \ angle \ text {90 °} \\ \ text {or} & 0 + j3.7699 \ Omega \ end {align} [/ latex]
Математически мы говорим, что фазовый угол сопротивления катушки индуктивности току равен 90 °, что означает, что сопротивление катушки индуктивности току является положительной мнимой величиной. Этот фазовый угол реактивного сопротивления току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где реактивное сопротивление и сопротивление взаимодействуют. Будет полезно представить любую оппозицию компонента току в терминах комплексных чисел, а не скалярных величин сопротивления и реактивного сопротивления.
Индуктивное реактивное сопротивление – это противодействие, которое индуктор предлагает переменному току из-за сдвинутого по фазе накопления и высвобождения энергии в его магнитном поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах, как и сопротивление (R).
Индуктивное реактивное сопротивление можно рассчитать по следующей формуле: X _L = 2πfL
Угловая скорость цепи переменного тока – это еще один способ выразить ее частоту в единицах электрических радиан в секунду вместо циклов в секунду.Его символизирует строчная греческая буква «омега» или ω.
Индуктивное реактивное сопротивление увеличивается с увеличением частоты . Другими словами, чем выше частота, тем сильнее он противодействует потоку электронов переменного тока.
Возьмем эту схему в качестве примера для работы:
Цепь индуктивности последовательного резистора: ток отстает от приложенного напряжения от 0 ° до 90 °.
Резистор будет обеспечивать сопротивление 5 Ом переменному току независимо от частоты, а катушка индуктивности – 3 Ом.Реактивное сопротивление 7699 Ом на переменный ток при 60 Гц.
Поскольку сопротивление резистора является действительным числом (5 Ом 0 ° или 5 + j0 Ом), а реактивное сопротивление катушки индуктивности – мнимым числом (3,7699 Ом ∠ 90 ° или 0 + j3,7699 Ом), совокупный эффект двух компонентов будет противодействовать току, равному комплексной сумме двух чисел.
Это комбинированное противодействие будет векторной комбинацией сопротивления и реактивного сопротивления. Чтобы выразить это противопоставление лаконично, нам нужен более полный термин для обозначения сопротивления току, чем просто сопротивление или реактивное сопротивление.
Этот термин называется импедансом , его символ – Z, и он также выражается в единицах Ом, точно так же, как сопротивление и реактивное сопротивление. В приведенном выше примере полное сопротивление цепи составляет:
Сопротивление по закону Ома
Импеданс связан с напряжением и током, как и следовало ожидать, аналогично сопротивлению в законе Ома:
.
На самом деле, это гораздо более полная форма закона Ома, чем то, чему учили в электронике постоянного тока (E = IR), точно так же, как импеданс является гораздо более полным выражением сопротивления потоку тока, чем сопротивление. Любое сопротивление и любое реактивное сопротивление, по отдельности или в комбинации (последовательно / параллельно), могут и должны быть представлены как единый импеданс в цепи переменного тока.
Чтобы рассчитать ток в приведенной выше схеме, нам сначала нужно указать опорный угол сдвига фаз для источника напряжения, который обычно принимается равным нулю. (Фазовые углы резистивного и индуктивного импеданса равны , всегда 0 ° и + 90 °, соответственно, независимо от заданных фазовых углов для напряжения или тока).
Как и в случае чисто индуктивной цепи, волна тока отстает от волны напряжения (источника), хотя на этот раз отставание не так велико: всего 37,016 ° по сравнению с полными 90 °, как в случае чисто индуктивного схема.
Ток отстает от напряжения в последовательной цепи L-R.
Для резистора и катушки индуктивности соотношение фаз между напряжением и током не изменилось.Напряжение на резисторе синфазно (сдвиг 0 °) с током через него, а напряжение на катушке индуктивности на + 90 ° не совпадает по фазе с током, проходящим через него. Мы можем проверить это математически:
Напряжение на резисторе имеет тот же фазовый угол, что и ток через него, что говорит нам о том, что E и I находятся в фазе (только для резистора).
Напряжение на катушке индуктивности имеет фазовый угол 52.984 °, в то время как ток через катушку индуктивности имеет фазовый угол -37,016 °, разница между ними составляет ровно 90 °. Это говорит нам о том, что E и I все еще не совпадают по фазе на 90 ° (только для катушки индуктивности).
Используйте закон Кирхгофа о напряжении
Мы также можем математически доказать, что эти комплексные значения в сумме составляют общее напряжение, как и предсказывает закон напряжения Кирхгофа:
Давайте возьмем те же компоненты для нашей схемы последовательного примера и подключим их параллельно:
Рисунок 6.7 Параллельная цепь R-L.
Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и катушка индуктивности имеют одинаковые значения сопротивления и индуктивности, соответственно, они также должны иметь одинаковые значения импеданса. Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:
Таблица 6.2 Таблица анализа импеданса 1
Единственная разница в нашей методике анализа на этот раз состоит в том, что мы будем применять правила для параллельных цепей вместо правил для последовательных цепей.Принцип такой же, как и для DC. Мы знаем, что напряжение распределяется равномерно между всеми компонентами в параллельной цепи, поэтому мы можем передать значение общего напряжения (10 вольт ∠ 0 °) на все столбцы компонентов:
Таблица 6.3. Таблица анализа импеданса 2
Теперь мы можем применить закон Ома (I = E / Z) по вертикали к двум столбцам таблицы, рассчитав ток через резистор и ток через катушку индуктивности:
Таблица 6.4 Таблица анализа импеданса 3
Так же, как и в случае цепей постоянного тока, токи ответвления в параллельной цепи переменного тока складываются в общий ток (Закон Кирхгофа по току все еще сохраняется для переменного тока, как и для постоянного тока):
Таблица 6.5 Таблица анализа импеданса 4
Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z = E / I) по вертикали в столбце «Всего». Между прочим, параллельный импеданс также можно рассчитать, используя обратную формулу, идентичную той, которая используется при вычислении параллельных сопротивлений.
[латекс] \ tag {6.1} Z_ {parallel} = \ frac {1} {\ frac {1} {Z_1} + \ frac {1} {Z_2} + \ dots \ frac {1} {Z_n}} [ / латекс]
Единственная проблема с использованием этой формулы заключается в том, что она обычно требует большого количества нажатий клавиш калькулятора.И если вы полны решимости использовать формулу, подобную этой «от руки», будьте готовы к очень большому объему работы! Но, как и в случае с цепями постоянного тока, у нас часто есть несколько вариантов расчета величин в наших таблицах анализа, и этот пример ничем не отличается. Независимо от того, каким способом вы рассчитываете полное сопротивление (закон Ома или обратная формула), вы получите одно и то же значение:
Таблица 6.6 Таблица анализа импеданса 5
Импедансами (Z) управляют так же, как сопротивлениями (R) при анализе параллельной цепи: параллельные импедансы уменьшаются, образуя общий импеданс, с использованием обратной формулы.Только обязательно выполняйте все вычисления в сложной (не скалярной) форме!
[латекс] Z_ {parallel} = \ frac {1} {(\ frac {1} {Z1} + \ frac {1} {Z2} +… \ Frac {1} {Zn})} [/ латекс]
Закон Ома для цепей переменного тока:
[латекс] E = {I} {Z} [/ латекс]; [латекс] I = \ frac {E} {Z} [/ latex]; [латекс] Z = \ frac {E} {I} [/ latex]
Когда резисторы и катушки индуктивности смешаны вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и + 90 °.Ток в цепи будет иметь фазовый угол от 0 ° до -90 °.
Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока: напряжение равномерно по всей цепи, токи ответвления складываются, чтобы сформировать общий ток, а импедансы уменьшаются (по обратной формуле), чтобы сформировать общий импеданс.
В идеальном случае индуктор действует как чисто реактивное устройство. То есть его противодействие переменному току строго основано на индуктивной реакции на изменения тока, а не на трении электронов, как в случае с резистивными компонентами.Однако индукторы не так чисты в своем реактивном поведении. Начнем с того, что они сделаны из проволоки, и мы знаем, что все проволоки обладают некоторой измеримой величиной сопротивления (кроме сверхпроводящей проволоки). Это встроенное сопротивление действует так, как если бы оно было подключено последовательно с идеальной индуктивностью катушки, например:
Рисунок 6.8 Катушка индуктивности Эквивалентная схема реальной катушки индуктивности.
Следовательно, полное сопротивление любой реальной катушки индуктивности всегда будет представлять собой сложную комбинацию сопротивления и индуктивного реактивного сопротивления.
Эту проблему усугубляет то, что называется скин-эффектом , который представляет собой тенденцию переменного тока проходить через внешние области поперечного сечения проводника, а не через середину. Когда электроны движутся в одном направлении (постоянный ток), они используют для движения всю площадь поперечного сечения проводника. С другой стороны, электроны, меняющие направление потока, стремятся избежать прохождения через самую середину проводника, ограничивая доступную эффективную площадь поперечного сечения. Скин-эффект становится более выраженным с увеличением частоты.
Кроме того, переменное магнитное поле индуктора, питаемого переменным током, может излучаться в космос как часть электромагнитной волны, особенно если переменный ток имеет высокую частоту. Эта излучаемая энергия не возвращается к катушке индуктивности и поэтому проявляется в виде сопротивления (рассеяния мощности) в цепи.
Помимо резистивных потерь в проводе и излучения, в индукторах с железным сердечником действуют и другие эффекты, которые проявляются как дополнительное сопротивление между выводами.Когда на индуктор подается переменный ток, создаваемые переменные магнитные поля имеют тенденцию индуцировать циркулирующие токи в железном сердечнике, известные как вихревые токи , . Эти электрические токи в железном сердечнике должны преодолевать электрическое сопротивление, обеспечиваемое железом, который не так хорош в качестве проводника, как медь. Вихретоковым потерям в первую очередь противодействуют, разделив железный сердечник на множество тонких листов (пластин), каждый из которых отделен от другого тонким слоем электроизоляционного лака.Поскольку поперечное сечение сердечника разделено на множество электрически изолированных участков, ток не может циркулировать в пределах этой площади поперечного сечения, и из-за этого не будет (или будет очень мало) резистивных потерь.
Как и следовало ожидать, потери на вихревые токи в металлических сердечниках индуктора проявляются в виде тепла. Эффект более выражен на высоких частотах и может быть настолько сильным, что иногда его используют в производственных процессах для нагрева металлических предметов! Фактически, этот процесс «индукционного нагрева» часто используется при литье металлов высокой чистоты, где металлические элементы и сплавы должны нагреваться в вакууме, чтобы избежать загрязнения воздухом, и, следовательно, там, где стандартная технология нагрева сжиганием была бы бесполезной.Это «бесконтактная» технология, когда нагретое вещество не должно касаться катушки (катушек), создающей магнитное поле.
В высокочастотной среде вихревые токи могут возникать даже в поперечном сечении самого провода, что способствует дополнительным резистивным эффектам. Чтобы противодействовать этой тенденции, можно использовать специальный провод, сделанный из очень тонких, индивидуально изолированных жил, который называется Litz wire (сокращенно от Litzendraht ). Изоляция, отделяющая жилы друг от друга, предотвращает циркуляцию вихревых токов по всей площади поперечного сечения провода.
Кроме того, любой магнитный гистерезис, который необходимо преодолевать при каждом изменении направления магнитного поля индуктора, представляет собой расход энергии, который проявляется как сопротивление в цепи. Некоторые материалы сердечника (например, феррит) особенно известны своим гистерезисным эффектом. Противодействовать этому эффекту лучше всего за счет правильного выбора материала сердечника и ограничения пиковой напряженности магнитного поля, генерируемой в каждом цикле.
В целом паразитные резистивные свойства реального индуктора (сопротивление провода, радиационные потери, вихревые токи и гистерезисные потери) выражаются одним термином «эффективное сопротивление»:
Рисунок 6.9 Эквивалентная схема реального индуктора с потерями на скин-эффект, излучение, вихревые токи и гистерезис.
Стоит отметить, что скин-эффект и потери на излучение применимы к прямым отрезкам провода в цепи переменного тока так же хорошо, как и к спиральному проводу. Обычно их совокупный эффект слишком мал, чтобы его можно было заметить, но на радиочастотах они могут быть довольно большими. Например, антенна радиопередатчика спроектирована специально для рассеивания наибольшего количества энергии в виде электромагнитного излучения.
Конденсаторы Vs. Резисторы
Конденсаторы ведут себя не так, как резисторы. В то время как резисторы пропускают через себя поток электронов, прямо пропорциональный падению напряжения, конденсаторы противодействуют изменениям напряжения, потребляя или подавая ток, когда они заряжаются или разряжаются до нового уровня напряжения. Поток электронов «через» конденсатор прямо пропорционален скорости изменения напряжения на конденсаторе. Это противодействие изменению напряжения является другой формой реактивного сопротивления , но оно прямо противоположно тому, которое демонстрируют индукторы.
Характеристики цепи конденсатора
Выражаясь математически, соотношение между током, протекающим через конденсатор, и скоростью изменения напряжения на конденсаторе выглядит следующим образом:
[латекс] i = C \ frac {d_e} {d_t} [/ латекс]
Выражение de / dt – это выражение из расчета, означающее скорость изменения мгновенного напряжения (e) во времени в вольтах в секунду. Емкость (C) выражается в фарадах, а мгновенный ток (i), конечно, выражается в амперах.Иногда скорость мгновенного изменения напряжения с течением времени выражается как dv / dt вместо de / dt: вместо напряжения используется строчная буква «v» или «e», но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую схему конденсатора:
Рисунок 6.10 Чистая емкостная цепь: напряжение конденсатора отстает от тока конденсатора на 90 °
Если бы мы изобразили ток и напряжение для этой очень простой схемы, это выглядело бы примерно так:
Рисунок 6.11 Формы сигналов чисто емкостной цепи.
Помните, что ток через конденсатор – это реакция на изменение напряжения на нем на . Следовательно, мгновенный ток равен нулю всякий раз, когда мгновенное напряжение находится на пике (нулевое изменение или наклон уровня на синусоидальной волне напряжения), а мгновенный ток находится на пике везде, где мгновенное напряжение имеет максимальное изменение (точки самый крутой наклон на волне напряжения, где она пересекает нулевую линию).Это приводит к появлению волны напряжения, которая на -90 ° не совпадает по фазе с волной тока. Глядя на график, кажется, что волна тока имеет «фору» по сравнению с волной напряжения; ток «опережает» напряжение, а напряжение «отстает» от тока.
Рисунок 6.12 Напряжение отстает от тока на 90 ° в чисто емкостной цепи.
Как вы могли догадаться, та же необычная волна мощности, которую мы видели в простой цепи индуктивности, присутствует и в простой цепи конденсатора:
Рисунок 6.13 В чисто емкостной цепи мгновенная мощность может быть положительной или отрицательной.
Как и в случае с простой схемой индуктивности, сдвиг фазы на 90 градусов между напряжением и током приводит к появлению волны мощности, которая в равной степени чередуется между положительной и отрицательной полярностью. Это означает, что конденсатор не рассеивает мощность, поскольку он реагирует на изменения напряжения; он просто поочередно поглощает и высвобождает энергию.
Реактивное сопротивление конденсатора
Противодействие конденсатора изменению напряжения означает сопротивление переменному напряжению в целом, которое по определению всегда изменяется по мгновенной величине и направлению.Для любой данной величины переменного напряжения на данной частоте конденсатор данного размера будет «проводить» определенную величину переменного тока. Точно так же, как ток через резистор является функцией напряжения на резисторе и сопротивления, предлагаемого резистором, переменный ток через конденсатор является функцией переменного напряжения на нем и реактивного сопротивления , обеспечиваемого конденсатором. Как и в случае катушек индуктивности, реактивное сопротивление конденсатора выражается в омах и обозначается буквой X (или, если точнее, X _C).
Поскольку конденсаторы «проводят» ток пропорционально скорости изменения напряжения, они будут пропускать больше тока при более быстром изменении напряжения (поскольку они заряжаются и разряжаются до тех же пиков напряжения за меньшее время) и меньший ток при более медленном изменении напряжения. . Это означает, что реактивное сопротивление в Ом для любого конденсатора равно обратно пропорционально частоте переменного тока .
[латекс] X_C = \ frac {1} {2πfC} [/ латекс]
Реактивное сопротивление конденсатора 100 мкФ:
Частота (Герцы) Реактивное сопротивление (Ом)
60 26.5258
120 13,2629
2500 0,6366
Обратите внимание, что отношение емкостного реактивного сопротивления к частоте прямо противоположно отношению индуктивного реактивного сопротивления. Емкостное реактивное сопротивление (в омах) уменьшается с увеличением частоты переменного тока. И наоборот, индуктивное реактивное сопротивление (в омах) увеличивается с увеличением частоты переменного тока. Индукторы противодействуют более быстрому изменению токов, создавая большие падения напряжения; Конденсаторы противодействуют более быстрому изменению падений напряжения, допуская большие токи.
Как и в случае с индукторами, член 2πf в уравнении реактивного сопротивления может быть заменен строчной греческой буквой Омега (ω), которая обозначается как угловая скорость цепи переменного тока. Таким образом, уравнение X _C = 1 / (2πfC) также может быть записано как X _C = 1 / (ωC), с приведением ω в единицах радиан в секунду .
Переменный ток в простой емкостной цепи равен напряжению (в вольтах), деленному на емкостное реактивное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на сопротивление (в Ом).Следующая схема иллюстрирует это математическое соотношение на примере:
Емкостное реактивное сопротивление.
[латекс] X_C = 26,5258 Ом [/ латекс]
[латекс] I = \ frac {E} {X} [/ латекс]
[латекс] I = \ frac {10} {26,5258 Ом} [/ латекс]
[латекс] I = 0,3770A [/ латекс]
Однако нужно иметь в виду, что здесь напряжение и ток не совпадают по фазе. Как было показано ранее, ток имеет фазовый сдвиг + 90 ° по отношению к напряжению.Если мы математически представим эти фазовые углы напряжения и тока, мы сможем вычислить фазовый угол реактивного сопротивления конденсатора току.
Напряжение в конденсаторе отстает от тока на 90 °.
Математически мы говорим, что фазовый угол сопротивления конденсатора току составляет -90 °, что означает, что сопротивление конденсатора току является отрицательной мнимой величиной. (См. Рисунок выше.) Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где реактивное сопротивление и сопротивление взаимодействуют.Будет полезно представить любую оппозицию компонента току в виде комплексных чисел, а не только скалярных величин сопротивления и реактивного сопротивления.
Емкостное реактивное сопротивление – это противодействие, которое конденсатор предлагает переменному току из-за его сдвинутого по фазе накопления и выделения энергии в его электрическом поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах, как и сопротивление (R).
Емкостное реактивное сопротивление можно рассчитать по следующей формуле: XC = 1 / (2πfC)
Емкостное реактивное сопротивление уменьшается с увеличением частоты .Другими словами, чем выше частота, тем меньше он противодействует (тем больше «проводит») переменному току.
Используя компоненты с одинаковыми значениями в нашей схеме последовательного примера, мы подключим их параллельно и посмотрим, что произойдет:
Рисунок 6.14 Параллельная цепь RC.
Параллельный резистор и конденсатор
Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и конденсатор имеют одинаковые значения сопротивления и емкости, соответственно, они также должны иметь одинаковые значения импеданса.Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:
Таблица 6.7
Сейчас это параллельная схема, мы знаем, что напряжение распределяется поровну между всеми компонентами, поэтому мы можем поместить цифру для общего напряжения (10 вольт ∠ 0 °) во все столбцы:
Таблица 6.8 Расчет
по закону Ома
Теперь мы можем применить закон Ома (I = E / Z) по вертикали к двум столбцам таблицы, вычислив ток через резистор и ток через конденсатор:
Таблица 6.9
Так же, как и в цепях постоянного тока, токи ответвления в параллельной цепи переменного тока складываются в общий ток (снова Закон Кирхгофа):
Таблица 6.10.
Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z = E / I) по вертикали в столбце «Всего». Как мы видели в главе об индуктивности переменного тока, параллельный импеданс также можно рассчитать, используя обратную формулу, идентичную той, которая используется при вычислении параллельных сопротивлений. Следует отметить, что это правило параллельного импеданса остается в силе независимо от типа импедансов, подключенных параллельно.Другими словами, не имеет значения, рассчитываем ли мы схему, состоящую из параллельных резисторов, параллельных катушек индуктивности, параллельных конденсаторов или какой-либо их комбинации: в форме импедансов (Z) все термины являются общими и могут применяться равномерно по той же формуле. И снова формула параллельного импеданса выглядит так:
[латекс] Z_ {parallel} = \ frac {1} {\ frac {1} {Z_1} + \ frac {1} {Z_2} + \ dots \ frac {1} {Z_n}} [/ латекс]
Единственным недостатком использования этого уравнения является значительный объем работы, необходимой для его вычисления, особенно без помощи калькулятора, способного манипулировать сложными величинами.Независимо от того, как мы рассчитываем полное сопротивление для нашей параллельной цепи (закон Ома или обратная формула), мы получим ту же цифру:
Импедансами (Z) управляют так же, как сопротивлениями (R) при анализе параллельной цепи: параллельные импедансы уменьшаются, образуя общий импеданс, с использованием обратной формулы. Только не забудьте
выполнять все вычисления в комплексной (не скалярной) форме! ZTotal = 1 / (1 / Z1 + 1 / Z2 +.. 1 / Zn)
Закон Ома для цепей переменного тока: E = IZ; I = E / Z; Z = E / I
Когда резисторы и конденсаторы смешиваются вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и -90 °.Ток в цепи будет иметь фазовый угол от 0 ° до + 90 °.
Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока: напряжение равномерно по всей цепи, токи ответвления складываются, чтобы сформировать общий ток, а импедансы уменьшаются (по обратной формуле), чтобы сформировать общий импеданс.
(Следующий раздел был адаптирован из: Уроки электрических цепей, Том II, Глава 5 – Реактивное сопротивление и импеданс – R, L и C)
Прежде чем мы начнем исследовать влияние резисторов, катушек индуктивности и конденсаторов, соединенных вместе в одних и тех же цепях переменного тока, давайте кратко рассмотрим некоторые основные термины и факты.
Сопротивление
Это по сути трение против тока. В той или иной степени он присутствует во всех проводниках (кроме проводов super !), Особенно в резисторах. Когда переменный ток проходит через сопротивление, возникает падение напряжения, синфазное с током. Сопротивление математически обозначается буквой «R» и измеряется в омах (Ом).
Реактивное сопротивление
Это, по сути, инерция , против потока тока.Он присутствует везде, где электрические или магнитные поля развиваются пропорционально приложенному напряжению или току, соответственно; но особенно в конденсаторах и катушках индуктивности. Когда переменный ток проходит через чистое реактивное сопротивление, возникает падение напряжения, которое на 90 ° не совпадает по фазе с током. Реактивное сопротивление математически обозначается буквой «X» и измеряется в омах (Ом).
Импеданс
Это исчерпывающее выражение любых форм противодействия протеканию тока, включая как сопротивление, так и реактивное сопротивление.Он присутствует во всех схемах и во всех компонентах. Когда переменный ток проходит через полное сопротивление, возникает падение напряжения, которое находится где-то между 0 ° и 90 ° не в фазе с током. Импеданс математически обозначается буквой «Z» и измеряется в единицах Ом (Ом) в сложной форме.
Идеальные резисторы обладают сопротивлением, но не реактивным сопротивлением. Идеальные катушки индуктивности и идеальные конденсаторы обладают реактивным сопротивлением, но не имеют сопротивления. Все компоненты обладают импедансом, и из-за этого универсального качества имеет смысл перевести все значения компонентов (сопротивление, индуктивность, емкость) в общие термины импеданса в качестве первого шага при анализе цепи переменного тока.
Рис. 6.15. Идеальный резистор, катушка индуктивности и конденсатор.
Фазовый угол импеданса для любого компонента – это фазовый сдвиг между напряжением на этом компоненте и током через этот компонент. Для идеального резистора падение напряжения и ток всегда синфазны друг с другом, поэтому угол импеданса резистора считается равным 0 °. Для идеального индуктора падение напряжения всегда опережает ток на 90 °, поэтому фазовый угол импеданса индуктора равен + 90 °.Для идеального конденсатора падение напряжения всегда отстает от тока на 90 °, поэтому считается, что фазовый угол импеданса конденсатора составляет -90 °.
Импедансы в переменном токе ведут себя аналогично сопротивлениям в цепях постоянного тока: они добавляются последовательно и уменьшаются параллельно. Пересмотренная версия закона Ома, основанная на импедансе, а не на сопротивлении, выглядит так:
Закон Ома для цепи переменного тока
[латекс] \ begin {align} \ tag {6.2} \ text {E} & = {I} {Z} \\ \ text {I} & = \ frac {E} {Z} \\ \ text {Z } & = \ frac {E} {I} \ end {align} [/ latex]
Мы можем взять те же компоненты из последовательной схемы и переставить их в параллельную конфигурацию для простого примера схемы:
Рисунок 6.16 Пример параллельной схемы R, L и C.
Импеданс в параллельных компонентах
Тот факт, что эти компоненты подключены параллельно, а не последовательно, теперь абсолютно не влияет на их индивидуальные импедансы. Пока источник питания имеет ту же частоту, что и раньше, индуктивное и емкостное сопротивление вообще не изменится.
Рисунок 6.17 Пример параллельной цепи R, L и C с импедансами, заменяющими значения компонентов.
Со всеми значениями компонентов, выраженными как импедансы (Z), мы можем настроить таблицу анализа и действовать, как в предыдущем примере задачи, за исключением того, что на этот раз следуя правилам параллельных цепей вместо последовательного.
Зная, что напряжение распределяется поровну между всеми компонентами в параллельной цепи, мы можем перенести цифру для общего напряжения во все столбцы компонентов в таблице:
Значения компонентов в таблице 6.11 выражаются в виде импеданса изображения 2
Теперь мы можем применить закон Ома (I = E / Z) по вертикали в каждом столбце, чтобы определить ток через каждый компонент:
Таблица 6.12. Значения компонентов выражаются как изображение импеданса 3
Расчет полного тока и полного импеданса
Есть две стратегии для расчета общего тока и полного импеданса.Во-первых, мы могли рассчитать общий импеданс из всех отдельных параллельных сопротивлений (Z _Total = 1 / (1 / Z _R + 1 / Z _L + 1 / Z _C), а затем вычислить общий ток путем деления напряжения источника на полное сопротивление (I = E / Z).
Тем не менее, работа с уравнением параллельного импеданса с комплексными числами – непростая задача, учитывая все взаимные колебания (1 / Z). Это особенно верно, если вам не повезло, что у вас нет калькулятора, который обрабатывает комплексные числа, и вы вынуждены делать все это вручную (преобразовать индивидуальные импедансы в полярную форму, затем преобразовать их все в прямоугольную форму для сложения, а затем преобразовать обратно в полярную форму для окончательной инверсии, затем инвертировать).Второй способ рассчитать общий ток и полное сопротивление – сложить все токи ответвления, чтобы получить общий ток (полный ток в параллельной цепи – переменного или постоянного тока – равен сумме токов ответвления), а затем использовать закон Ома. для определения полного сопротивления по общему напряжению и общему току (Z = E / I).
Таблица 6.13 Расчет полного тока и полного импеданса
Любой из методов, выполненный должным образом, даст правильные ответы.
За заметным исключением расчетов мощности (P), все расчеты цепей переменного тока основаны на тех же общих принципах, что и расчеты для цепей постоянного тока.Единственное существенное отличие состоит в том, что в расчетах переменного тока используются комплексные величины, в то время как в расчетах постоянного тока используются скалярные величины. Закон Ома, законы Кирхгофа и даже сетевые теоремы, изученные на постоянном токе, остаются верными для переменного тока, когда напряжение, ток и импеданс выражаются комплексными числами. Те же стратегии поиска и устранения неисправностей, которые применяются в цепях постоянного тока, справедливы и для переменного тока, хотя с переменным током, безусловно, может быть труднее работать из-за фазовых углов, которые не регистрируются портативным мультиметром.
Power – это отдельная тема, которая будет рассмотрена в отдельной главе этой книги. Поскольку мощность в реактивной цепи одновременно поглощается и высвобождается, а не просто рассеивается, как в случае с резисторами, ее математическая обработка требует более прямого применения тригонометрии для решения.
При анализе цепи переменного тока первым шагом в анализе является преобразование всех значений компонентов резистора, катушки индуктивности и конденсатора в импедансы (Z) в зависимости от частоты источника питания.После этого выполните те же шаги и стратегии, которые были изучены для анализа цепей постоянного тока, используя новую форму закона Ома: E = IZ; I = E / Z; и Z = E / I
Помните, что только рассчитанные значения, выраженные в полярной форме , применимы непосредственно к эмпирическим измерениям напряжения и тока. Прямоугольные обозначения – это просто полезный инструмент для сложения и вычитания сложных величин. Полярная запись, где величина (длина вектора) напрямую связана с величиной измеряемого напряжения или тока, а угол напрямую связан с фазовым сдвигом в градусах, является наиболее практичным способом выражения сложных величин для анализа схем.

Частота (Герцы)	Реактивное сопротивление (Ом)
60	26.5258
120	13,2629
2500	0,6366