Господа, в прошлой статье мы говорили про мощность и работу переменного тока. Напомню, что тогда мы считали ее через некоторый интеграл, а в самом конце статьи я вскользь сказал, что существуют способы облечения и без того нелегкой жизни и часто можно обойтись вообще без взятия интеграла, если знать про действующее значение тока. Сегодня про него и поговорим!
Господа, вероятно, для вас не станет секретом, что в природе существует большое число видов переменного тока: синусоидальный, прямоугольный, треугольный и так далее. И как их вообще можно сравнивать между собой? По форме? Хмм…Пожалуй, да. Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие
Итак, действующее (или среднеквадратичное) значение переменного тока – это такая величина некоторого постоянного тока, который за время, равное периоду переменного тока выделит столько же тепла на резисторе, что и наш переменный ток. Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.
Итак, у нас есть переменный ток. Допустим, синусоидальный. У него своя амплитуда Аm и период Tпериод (ну или частота f). На фазу в данном случае пофиг, считаем ее равной нулю. Этот переменный ток течет через некоторый резистор R и на этом резисторе выделяется энергия. За один период Tпериод нашего синусоидального тока выделится вполне определенное количество джоулей энергии. Это число джоулей мы можем точно посчитать по формулам с интегралом, которые я приводил в прошлый раз. Допустим, мы насчитали, что за один период Tпериод синусоидального тока выделится Q джоулей тепла. А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе
Итак, суть вопроса, надеюсь, стала понятной, поэтому давайте все сказанное выше переведем на язык математики. Как мы уже писали в прошлой статье, закон изменения мощности переменного тока равен
Количество выделившейся энергии при работе тока за время Tпериод – соответственно, равно интегралу за время периода Tпериод:
Господа, теперь нам надо взять этот интеграл. Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками .Итак, как его нам брать? Ну, величины Im2 и R являются константами и их можно сразу вынести за знак интеграла. А для квадрата синуса нам надо применить формулу понижения степени из курса тригонометрии. Надеюсь, вы ее помните . А если нет, то напомню еще раз:
Погнали считать!
Теперь давайте разобьем интеграл на два интеграла. Можно воспользоваться тем, что интеграл от суммы или разности равен сумме или разности интегралов. В принципе, это очень даже логично, если вспомнить про то, что интеграл – это площадь.
Итак, имеем
Господа, у меня есть для вас просто отличнейшая новость. Второй интеграл равен нулю!
Почему это так? Да просто потому, что интеграл любого синуса/косинуса на величине, кратной его периоду, равен нулю. Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.
Итак, отбрасывая интеграл с косинусом, получаем
Ну и не надо быть большим гуру математики, чтобы сказать, что этот интеграл равен
И, таким образом, получаем ответ
Это мы получили количество джоулей, которое выделится на резисторе R при протекании через него синусоидального тока амплитудой Im в течении периода T период. Теперь, чтобы найти чему в данном случае равен действующий ток нам надо исходить из того, что на том же самом резисторе R за то же самое время Tпериод выделится то же самое количество энергии Q. Поэтому мы можем записать
Если не совсем понятно, откуда здесь взялась левая часть, рекомендую вам повторить статью про закон Джоуля-Ленца. А мы тем временем выразим действующее значение тока Iдейств. из этого выражения, предварительно сократив все, что можно
Вот такой вот результат, господа. Действующее значение переменного синусоидального тока в корень из двух раз меньше его амплитудного значения. Хорошо запомните этот результат, это важный вывод.
Вообще говоря никто не мешает по аналогии с током ввести действующее значение напряжения. При этом у нас зависимость мощности от времени примет вот такой вид
Именно его мы будем подставлять под интеграл и выполнять все преобразования. Господа, каждый из вас может на досуге при желании это проделать, я же просто приведу конечный результат, поскольку он полностью аналогичен случаю с током. Итак, действующее значение напряжения синусоидального тока равно
Как видим, аналогия полнейшая. Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.
Подобным образом можно рассчитать действующее значение тока и напряжения для сигнала абсолютно любой формы: надо только лишь записать закон изменения мощности для этого сигнала и выполнить пошагово все вышеописанные преобразования.
Все вы, наверняка, слышали, что у нас в розетках напряжение 220 В. А каких вольт? У нас ведь теперь есть два термина – амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках – это действующее значение! Вольтметры и амперметры, включаемые в цепи переменного тока показывают именно действующие значения. А форму сигнала вообще и его амплитуду в частности можно посмотреть с помощью осциллографа. Ну, мы же уже говорили, что всем интересны деньги, то бишь работа тока, а не какая-то там непонятная амплитуда. Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать
Отсюда получаем
Вот так вот, господа. В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.
Рисунок 1 – Закон изменения напряжения в розетках
И специально для вас, господа, я посмотрел
ВНИМАНИЕ! Если у вас нет достаточного опыта работы с высоким напряжением, если вы абсолютно четко не представляете себе как могут течь токи при измерениях в гальванически не отвязанных от сети цепях, настоятельно не рекомендую проводить подобный эксперимент самостоятельно, это опасно! Дело в том, что при подобных измерениях с помощью осциллографа, подключенного к розетке с заземлением есть очень большой шанс что произойдет короткое замыкание через внутренние земли осциллографа и прибор сгорит без возможности восстановления! А если делать эти измерения с помощью осциллографа, подключенного к розетке без заземления
, на его корпусе, кабелях и разъемах может присутствовать смертельно опасный потенциал! Это не шутки, господа, если нет понимания, почему это так, лучше этого не делать, тем более, что осциллограммы уже сняты и вы можете их наблюдать на рисунке 2.Рисунок 2 – Осциллограмма напряжения в розетке (делитель 1:5)
На рисунке 2 мы видим, что амплитуда синуса составляет около 62 вольт, а частота – ровно 50 Гц. Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна
Как мы видим, результат измерения очень близок к теоретическому, не смотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это свидетельствует о том, что все наши расчеты верны.
На этом на сегодня все, господа. Сегодня мы узнали, что такое действующий ток и действующее напряжение, научились их рассчитывать и проверили результаты расчетов на практике. Спасибо что прочитали это и до новых статей!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Действующие значения тока — Знаешь как
 Расчет цепей переменного тока упрощается, если пользоваться понятием действующего (эффективного) значения переменного тока.
Расчет цепей переменного тока упрощается, если пользоваться понятием действующего (эффективного) значения переменного тока.
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период переменного тока то же количество тепла.
Согласно ГОСТ действующие значения обозначаются прописными буквами, т. е ток I, напряжение U.
На шкалах измерительных приборов всегда наносятся действующие значения тока или напряжения.
Если ток изменяется по синусоидальному закону, то действующее значение его составляет 0,707 амплитудного значения тока, т. е.
I = (Iм : √2) = Iм: 1,41 = 0,707Iм
То же соотношение имеет место и для синусоидального напряжения, т. е.
U = (Uм : √2) = 0,707Uм
Докажем правильность приведенных соотношений. Количество тепла, выделенного постоянным током I в сопротивлении r за период переменного тока Т:
Q’ = I2rT
Количество тепла, выделенного переменным током в том же сопротивлении за период Т, может быть выражено через среднее значение мощности Р переменного тока
Q» = PT
Если Q’= Q», то
I2rT=РТ.
В последнем выражении согласно данному выше определению значение эквивалентного постоянного тока I равно действующему значению переменного тока. Таким образом, действующее значение тока
I = √ (P : r)
Мгновенная мощность при синусоидальном токе p = i2r = I2мr sin2ωt
или, приняв во внимание, что sin2 α = (11 : 2) — (1 : 2) cos 2α, получим:
p = (I2мr : 2) — (I2мr : 2) cos 2ωt
Мгновенная мощность при синусоидальном токе может быть представлена суммой двух слагаемых постоянной ½ I2мr и переменной, изменяющейся по периодическому синусоидальному закону.
Среднее значение мощности синусоидального тока будет равно постоянной слагаемой
P = ½I2мr
так как среднее значение за пер и синусоидальной слагаемой ½I2мr cos 2ωt равно нулю.
Действующее значение переменного синусоидального тока
I = √(P : r) = √ (½I2мr : r) = Iм : √2 = 0,707Iм
Так как действующие значения синусоидальных токов и
напряжений в √2 раз меньше амплитудных значений, то вектор, выражающий в одном масштабе амплитудное значение, в другом масштабе представляет действующее значение той же величины. В дальнейшем выбор масштабов векторов будет производиться, исходя из действующих значений.
Пример 5-4. Вольтметр,, включенный в сеть, показал напряжение 380 в.
Определить амплитуду напряжения сети:
UM = √2 U = 1,41 • 380=536 в.
ОБЩИЕ ЗАМЕЧАНИЯ О ЦЕПЯХ ПЕРЕМЕННОГО ТОКА
Любая электрическая цепь обладает параметрами: .сопротивлением r, индуктивностью L и емкостью С,
В цепи постоянного тока при неизменном напряжении будут неизмененными: ток, мощность и запас энергии в электрическом и магнитном полях.
При переменном напряжении на зажимах цепи в ней будет проходить переменный ток, будет изменяться и энергия электрического и магнитного полей. В технике встречаются цели, физические явления в которых определяются наличием одного из параметров r, L или С, тогда как другие параметры выявлены слабо и влиянием их можно пренебречь.
Например, лампу накаливания, нагревательный прибор, реостат можно рассматривать как цепь с сопротивлением r, влиянием емкости и индуктивности которой можно пренебречь.
Цепь ненагруженного трансформатора можно рассматривать как индуктивность, пренебрегая влиянием сопротивления и емкости этой цепи.
Наконец, кабель, работающий вхолостую, можно рассматривать как емкость, так как влияние индуктивности и сопротивления этой цепи незначительны.
Статья на тему Действующие значения тока
Также, рассматриваемый метод позволяет измерять частоту сетевого напряжения без использования внешних дополнительных средств, таких как компараторы. Но, при этом приходится жертвовать либо временными ресурсами МК, либо точностью измерения частоты.
Почему важно измерять действующее значение, а не какое либо другое, например, средневыпрямленное? Большинство “китайских” электронных вольтметров измеряют сетевое напряжение по средневыпрямленному значению. Методика измерения следующая: за период сетевого напряжения делается выборка из N значений амплитуды напряжения, результаты суммируются (без знака), делятся на N (усредняются), после чего полученный результат умножается на коэффициент
Указанный коэффициент определяет зависимость действующего значения синусоидального (!) сигнала от средневыпрямленного.
Такая методика измерения проста, не требует много ресурсов микроконтроллера (как временных, так и ресурсов памяти). Основным недостатком такой методики измерения является большая ошибка измерения на несинусоидальных сигналах.
Как все знают, изменение сигнала сетевого напряжения подчиняется синусоидальному закону (вследствие применения синхронных генераторов на электростанции), с частотой изменения сигнала 50 Гц (60 Гц). Однако, на практике вследствие влияния сторонних факторов (в основном подключение к сети мощных нелинейных нагрузок), а также применения инверторов с квазисинусоидальным выходным напряжением (см. рисунок), синусоида напряжения либо значительно искажается, либо заменятся прямоугольными импульсами. В таких случаях указанный выше метод измерения даст очень большую погрешность (например, в квазисинусоидальных инверторах выходное напряжение, измеренное “китайским» вольтметром может быть равно 180-200В, в то время как действующее напряжение будет равно 220В ).
Например, напряжение у меня дома
Почему важно измерять именно действующее значение напряжения (тока)? Потому что именно действующие (еще называют его эффективными) значения напряжения и тока определяют работу электрической системы (грубо говоря, электронагреватель выделяет тепло в прямой зависимости от действующих значений напряжения и тока сети).
Действующее значение измеряемой периодической величины рассчитывается по формуле
Или после дискретизации получим
Т.е. нам нужно делать выборку ряда значений за период сетевого напряжения, просуммировать значения квадратов точек выборки, поделить на количество точек за период (при определении количества точек выборки не забываем про теорему Котельникова-Шеннона), и взять квадратный корень из полученного результата.
Вроде бы ничего сложного, если бы не но:
1) Каждый период точки выборки набираются заново, что увеличивает погрешность измерения;
2) В реальной сети, около нуля напряжения, могут встречаться как “нулевые полки”, так и повторные переходы через ноль напряжения, что значительно внесет погрешность в измерение.
С первым пунктом будем бороться измерением измерением суммы квадратов точек выборки за каждый полупериод, после чего суммируя n-ую сумму квадратов с (n+1)-й и откидывая (n-1)-ую.
Со вторым пунктом будем бороться введением зон нечувствительности по напряжению (введем границы напряжения перехода через ноль с положительной и отрицательной сторон) обычно 5-10 В в обе стороны, а также зон нечувствительности по частоте (ограничим допустимую частоту сигнала напряжения).
Таким образом, мы получим рассчитанное значение действующего значения сетевого напряжения за период на каждом полупериоде сетевого напряжения.
Частота напряжения вычисляется по формуле:
где Fд — частота дискретизации (для удобства и увеличения точности измерения частоты выбрана равной 10 кГц (период выборки — 100 мкс)).
Теперь рассмотрим структурную схему измерительной части (в реальной схеме следует добавить фильтрующие и защитные элементы).
Внимание! В данном методе измерения не реализована гальваническая развязка микроконтроллера от сети. Гальваноразвязка реализуется на стороне цифрового интерфейса передачи данных от микроконтроллера.
На входе установлен дифференциальный операционный усилитель с делителем напряжения, опертым на половину опорного напряжения (2,048 В). Поскольку, для уменьшения размеров лучше применять маломощные резисторы, устанавливаем их минимум 3 шт. равными по сопротивлению — чтобы увеличить суммарное пробивное напряжения резисторов. При этом нужно подсчитать мощность потерь при максимальном входном напряжении (P=U^2/R) — чтобы не превышала допустимой мощности резисторов. Плечи дифференциального усилителя тоже делаем равными. Тогда, напряжение в точке 1 рассчитывается по формуле:
А напряжение в точке 1 будет иметь вид:
Также, половина опорного напряжения подается на один из каналов АЦП. Это позволяет в постоянном режиме (например, один раз за период) определять положение уровня нуля измеряемого напряжения.
Т.е. мы обошлись операционным усилителем с однополярным питанием, и наш входной сигнал в точке 1 изменяется от 0 до Uоп. Такой способ дает достаточно точные результаты, по сравнению, например, с выпрямлением напряжения с помощью диодов.
Расчет делителя и коэффициента АЦП сводится к следующему:
где A и В — замеры АЦП (за вычетом измеренного значения нуля сигнала — AN1) для текущего и предыдущего полупериодов; N1, N2 — число замеров для текущего и предыдущего полупериодов; Nadс — разрядность АЦП; U’оп — опорное напряжение за вычетом зон нелинейности (нечувствительности) операционного усилителя (обычно 0,6 В).
Расчет делителя удобно проводить считая сигнал постоянным, приведенным к амплитуде синусоидального, а не синусоидальным. Тогда действующее значение сигнала равно амплитудному и равно значению каждого замера.
Например, нужно рассчитать делитель для измерения максимального значения 420В переменного тока:
Сопротивление Ra выбирается в диапазоне от 500 кОм до 1500 кОм. По выбранному сопротивлению Ra рассчитывается Rb.
В итоге, алгоритм расчета действующего значения напряжения и частоты примет вид:
При этом часть затратных расчетов (деление, извлечение корня) можно перенести из прерывания в основную программу.
При расчете действующих значений на 8-ми битном МК целесообразно пользоваться целочисленными методами (с использованием масштабных коэффициентов) не прибегая к расчетам с плавающей запятой, а также упрощать по возможности арифметические операции (деление, изъятие квадратного корня и проч.). Это значительно экономит ресурсы МК.
Переменное напряжение и его параметры
Всем доброго времени суток! В прошлой статье я рассказал, как рассчитать индуктивность катушки выполненной на разомкнутом сердечнике (например, ферритовой антенны, контурных катушек радиоприёмников, катушек с построечными сердечниками и т. д.). Сегодняшняя статья посвящена переменному напряжению и параметрам, которые его характеризуют.
Что такое переменное напряжение?
Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.
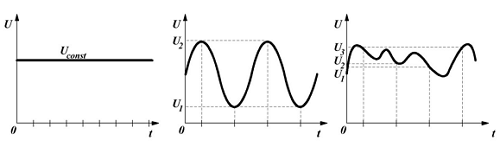

Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.
Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид
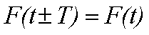
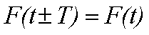
где Т – период.
Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда
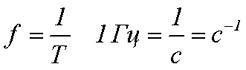
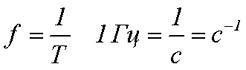
Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже
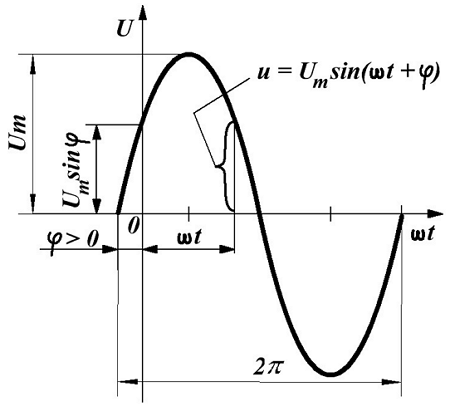
 Синусоидальное переменное напряжение.
Синусоидальное переменное напряжение.
Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.
Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением
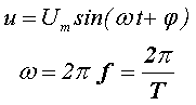
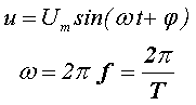
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла),
φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.
Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.
Таким образом, амплитуда Um, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.
Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда
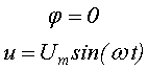
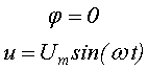
В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.
Что такое действующее напряжение переменного тока?
Как я писал выше, одним из основных параметров переменного напряжения является амплитуда Um, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному Um ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?
Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения
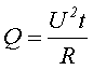
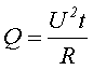
Для переменного напряжения мгновенное значение выделяемой энергии составит
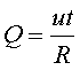
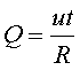
где u – мгновенное значение напряжения
Тогда количество энергии за полный период от t0 = 0 до t1 = T составит
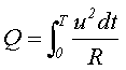
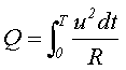
Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения
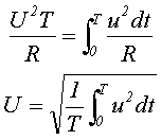
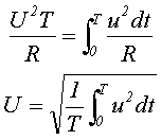
Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.
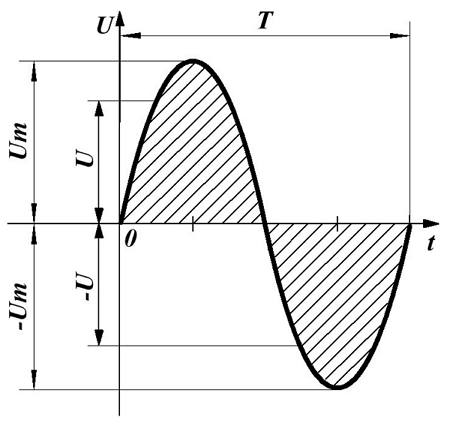

Действующее значение синусоидального напряжения.
Вычислим действующее значение синусоидального напряжения
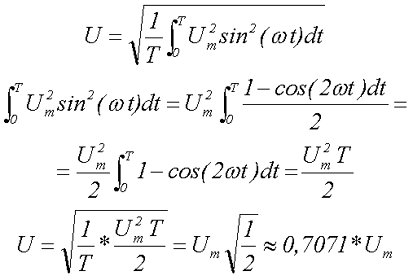
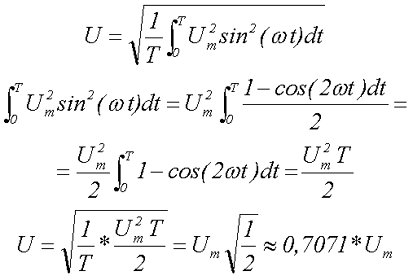
Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.
Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение
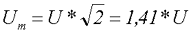
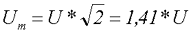
Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения
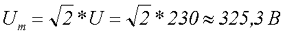
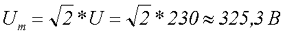
Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.
С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.
Что такое среднее значение переменного напряжения?
Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением
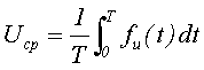
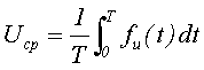
где Т – период переменного напряжения,
fu(t) – функциональная зависимость напряжения от времени.
Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией fu(t) и осью Ox за период Т.
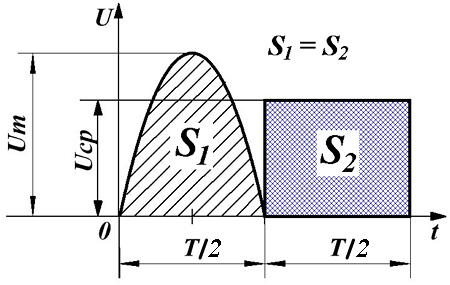

Среднее значение переменного напряжения.
В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.
Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно
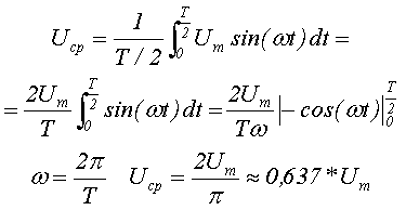
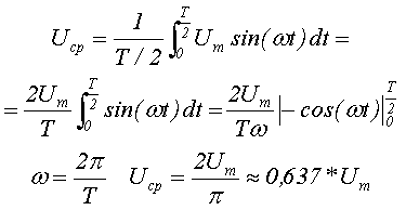
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла).
Какие коэффициенты, характеризуют переменное напряжение?
Иногда возникает необходимость охарактеризовать форму переменного напряжения. Для этой цели существует ряд параметров данного переменного напряжения:
1. Коэффициент формы переменного напряжения kф – показывает как относится действующее значение переменного напряжения U к его среднему значению Ucp.
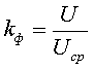
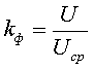
Так для синусоидального напряжения коэффициент формы составит
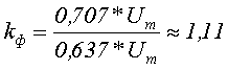
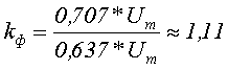
2. Коэффициент амплитуды переменного напряжения kа – показывает как относится амплитудное значение переменного напряжения Um к его действующему значению U
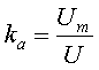
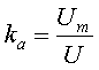
Так для синусоидального напряжения коэффициент амплитуды составит
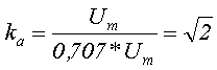
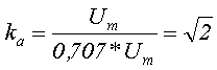
На сегодня всё, в следующей статье я рассмотрю прохождение переменного напряжения через сопротивление, индуктивность и емкость.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Действующее значение синусоидального
переменного напряжения – тока.
data-ad-client=”ca-pub-5076466341839286″
data-ad-slot=”1404500382″>
♦Переменный электрический ток в нашей бытовой электросети представляет собой синусоиду, как на рисунке 1.
Напряжение меняет свою величину от 0 до + Umax и от 0 до — Umax . Полный цикл этих изменений называется периодом.
Период измеряется в секундах и обозначается буквой Т.
Количество периодов переменного тока за 1 секунду, есть частота f.
Частота переменного тока f измеряется в герцах .
f = 1 / T.
Например.
Частота в нашей электрической сети 50 Гц. Период этих колебаний будет равен:
T = 1 / f = 1 / 50 = 0,02 сек.
Наибольшее значение изменяющегося переменного напряжения – тока называется амплитудным значением или амплитудой.
Umax = Ua и Imax = Ia
За один период напряжение принимает эти значения два раза: + Ua и — Ua .
♦ Если подключить в цепь переменного напряжения какую-нибудь активную нагрузку, например паяльник, в цепи потечет переменный электрический ток, так же принимающий значения +Ia и — Ia, и повторяющий форму синусоиды.
На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный. Выделение тепла не зависит от направления тока в цепи.
Выделенное тепло будет равно той энергии, которую затрачивает электрический ток при прохождении по сопротивлению нагрузки.
Введено понятие действующего значения переменного напряжения Uд и тока Iд.
Действующее значение переменного тока — это такое значение величины постоянного тока, который проходя по сопротивлению нагрузки за тот же промежуток времени, выделит такое же количество тепла, что и переменный ток.
♦ Переменный ток оказывает такое же тепловое действие, как и постоянный ток, если амплитуда синусоидального переменного тока превышает величину постоянного тока в 1,41 раз.
Следовательно действующее (или эффективное) значение переменного тока будет равно:
Iд = Ia / 1,41 = 0,707 Ia. – действующее значение переменного тока
Uд = Ua / 1,41 = 0,707 Ua — действующее значение переменного напряжения
На все эти теоретические размышления можно посмотреть иначе!
♦Имеем синусоиду переменного напряжения длительностью в 1 период как на рисунке 1.
После выпрямительных диодов оно принимает вид как на рисунке 2.
Нижняя половинка синусоиды перевернута вверх, чтобы удобнее было представить процесс преобразования.
♦На рисунке приняты обозначения:
Um = Ua = 1 — амплитудное значение величины переменного напряжения. Значение Ua примем за единицу.
Из формулы приведенной выше Uд = 1 / 1,41 = 0,707 — действующее напряжение равно 0,707 от амплитудного значения Ua = 1.
Заштрихованная часть синусоиды обозначает затраченную на нагревание паяльника электрическую энергию. В промежутках между половинками синусоид ток по цепи не протекает, а следовательно и не выделяется электрическая мощность.
♦Проведем линию, обозначающую Uд = 0,707.
Она отсекает верхнюю часть половинок синусоид.
Если эти отсеченные вершинки синусоиды уложить в провалы между полупериодами, получится полностью заполненная площадь соответствующая значениям постоянного напряжения U и тока I.
Получается, что мощность синусоидального переменного тока с амплитудными значениями Ua и Ia равна мощности действующего значения Uд и Iд переменного тока и равна мощности постоянного тока со значениями U и I.
Одна и та же электрическая мощность, выраженная в трех видах.
P = Ua х Ia = Uд х Iд = U х I
♦ Электрические приборы для измерения переменного напряжения и тока отградуированы на отображение действующих значений Uд и Iд.
В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно 220 вольт.
Максимальное, амплитудное значение напряжения в сети равно:
Um = Ua = Uд х 1,41 = 220 х 1,41 = 310,2 вольт.
Процесс поэтапного преобразования переменного напряжения в пульсирующее напряжение, а затем в постоянное напряжение, наблюдается в схемах выпрямителей.
data-ad-client=”ca-pub-5076466341839286″
data-ad-slot=”1404500382″>
Действующее напряжение Википедия
В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока
Значения переменного напряжения (тока)
Далее для определенности будем говорить большей частью о параметрах напряжения, хотя они справедливы и для токов.
Мгновенное значение
Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является ( u ( t ) , i ( t ) {\displaystyle u(t)~,\quad i(t)} ). Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой или цифровой осциллограф.
Амплитудное значение
- Амплитудное (пиковое) значение, иногда называемое просто «амплитуда» — наибольшее мгновенное значение напряжения или силы тока за период (без учёта знака):
- U M = max ( | u ( t ) | ) , I M = max ( | i ( t ) | ) {\displaystyle U_{M}=\max(|u(t)|)~,\qquad I_{M}=\max(|i(t)|)}
Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.
Среднеквадратичное значение
Среднеквадратичное значение (устар. действующее, эффективное) — корень квадратный из среднего значения квадрата напряжения или тока.
- U = 1 T ∫ 0 T u 2 ( t ) d t , I = 1 T ∫ 0 T i 2 ( t ) d t {\displaystyle U={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}~,\qquad I={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}i^{2}(t)dt}}}
Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I {\displaystyle I} и U {\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.
Когда не оговаривают особо, то обычно имеют в виду именно среднеквадратичные значения величины напряжения или силы тока.
В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.
Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.
Среднее значение
Среднее значение (смещение) — постоянная составляющая напряжения или силы тока
- U = 1 T ∫ 0 T u ( t ) d t , I = 1 T ∫ 0 T i ( t ) d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}
В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения). Геометрически это разность площадей под и над осью времени, делённая на период. Для синусоидального сигнала смещение равно нулю.
Средневыпрямленное значение
Средневыпрямленное значение — среднее значение модуля сигнала
- U = 1 T ∫ 0 T ∣ u ( t ) ∣ d t , I = 1 T ∫ 0 T ∣ i ( t ) ∣ d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}\mid u(t)\mid dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}\mid i(t)\mid dt}
На практике используется редко, однако большинство измерительных приборов переменного тока – магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.
Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.
Коэффициенты пересчёта значений
- Коэффициент формы кривой переменного напряжения (тока) — величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} .
- Коэффициент амплитуды кривой переменного напряжения (тока) — величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2 {\displaystyle {\sqrt {2}}} .
Параметры постоянного тока
- Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени
- Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)
Литература и документация
Литература
Нормативно-техническая документация
Ссылки
См. также
Переменное напряжение и его значения – Help for engineer
Переменное напряжение и его значения
Все мы знаем, что дома в розетках у нас напряжение 220В. Но не каждый знает, какое именно это напряжение. Давайте же разберемся с этой ситуацией.
Для упрощения рассматриваемого примера будем считать, что вид напряжения – синусоида, то есть переменное напряжение (с определенной периодичностью меняет значение с положительного на отрицательное).

Рисунок 1 – Вид переменного напряжения
На рисунке 1 изображен вид идеального синусоидального напряжения одного периода Т. Есть несколько значений напряжения, о которых обычно говорят и используют, рассмотрим:
| Амплитудное значение напряжения (Um) – это максимальное, мгновенное значение напряжения, то есть амплитуда синусоиды. |
Теперь правильнее будет говорить о токе.
| Действующее значение переменного тока – это величина постоянного тока, который может выполнить ту же самую работу (нагрев). |
Действующее значение напряжения (U) обозначают латинской буквой без индекса, в литературе может еще использоваться термин – эффективное значение напряжения.
Для периодически изменяющегося сигнала за период Т, величина действующего напряжения находится:
 |
Приведем формулу к простому виду, приняв за изменяющийся сигнал синусоиду. Между рассмотренными выше двумя параметрами существует зависимость, которая выражается формулой:

То есть амплитудное значение в 1,414 раза больше действующего.
Вернемся к домашним розеткам с напряжением 220В. Это действующее значение напряжения, которое можно измерить тестером. Определим его амплитудное значение напряжения:

Среднее значение синусоидального тока, напряжения будет равно нулю. Поэтому если говорят о среднем значении переменного тока, то подразумевают рассматривание его в пол периода.
Недостаточно прав для комментирования
90000 Voltage and Current Data Loggers and Recorders 90001 90002 Find a wide selection of highly accurate and reliable voltage and current data loggers from one of the leaders in data logger industry. MicroDAQ.com has been an authorized distributor of data loggers for over 18 years, carrying over 30 well-respected brands. Whether you’re looking for a current data logger or a power meter that can measure, store and analyze up to 144 different power and energy parameters, we have models for every application and budget.90003 90004 90005 Voltage and Current Data Loggers 90006 90002 Current and voltage data loggers are used when you want to monitor and record voltage and amperage levels. They are available in AC and DC versions as well as for single and multiphase applications. They range from low voltage or current models used to monitor sensor outputs all the way up to large multi-circuit meters used to identify usage trends. 90003 90002 90005 Energy and Power Meters 90006 90003 90002 An energy meter is used to measure and record power consumption, and they can be used in both residential and commercial applications.These devices monitor and record different electrical parameters that can include volts, amps, watts, volt-amps (VA), volt-amps reactive (VAR), kilowatts (kW), kilowatt hours (kWH), power factor and harmonics. 90003 90002 90005 Multi-Circuit Power Submeters 90006 90003 90002 Our multi-circuit power submeters let you monitor multiple independent loads without having to purchase individual energy meters. These devices can be integrated into building management systems and used to record and track tenant power consumption or monitor power consumption across multiple devices.90003 90002 90003 90023 90024 90025 90026 90027 90028 90029 LCV 90030 90002 $ 179.00 90003 90033 90027 90004 90036 90024 Measure and Record Single Phase AC Current and AC Voltage with External Sensors 90038 90024 Measurement Range of 0 to 300 Amp AC (Current) and 0 to 500 Volts AC (Voltage) 90038 90024 Records onto Internal Memory up to a Total of 21,500 Readings (10,750 / Sensor) 90038 90024 1 Second to 18 Hour User-Selectable Sampling Rate 90038 90024 User-Replaceable Battery with 20 to 40 Month Life 90038 90024 Includes AC Current Clamp and 4.5 ft Voltage Leads 90038 90049 90002 90005 Requires 9 Volt Battery and LOGiT PC Software Kit 90006 90003 Learn More | Add to Compare 90033 90055 90056 90038 90024 90025 90026 90027 90062 90033 90055 90056 90038 90067.90000 Finally, High Voltage Current Sensing Made Easy 90001 90002 The LT6100 and LTC6101 are high voltage precision high-side current sense amplifiers. Their simple architectures make them flexible and easy to use, while careful design has made them reliable and robust. 90003 90002 Key features include high supply range, user-configurable gains, low input current, high PSRR and low offset voltage. These features make the LT6100 and LTC6101 perfect for precision industrial and automotive sensing applications as well as current-overload protection circuits.90003 90002 The LT6100 operates to 48V, is the simpler of the two to use, requiring almost no external components, draws little power, and is tolerant of several abnormal conditions such as split inputs, power off, and reverse battery. 90003 90002 The LTC6101 is the higher speed of the two, operates to 70V, and is more flexible, having external resistors set the gain. Both parts are available in a variety of small packages. 90003 90002 Current sensing is commonly accomplished in one of two ways.One method is magnetic, where a structure is created using permeable materials to couple an m-field to a coil or Hall effect sensor. While non-intrusive to the measured circuit, a coil type pickup is intrinsically unable to provide any DC information (though exotic “Flux-gate” techniques are possible), and Hall sensors generally lack the accuracy and sensitivity for most DC measurements. 90003 90002 The alternative is the introduction of a known “sense” resistance in the load path, thereby creating a small voltage drop that is directly proportional to the load current.Generally, the preferred connection for a sense resistor is in the supply side of the circuit, so that common grounding practices can be retained and load faults can be detected. In the case of positive supply potentials, this connection is commonly referred to as a “high-side” sense configuration, as shown schematically in Figure 1. This means that the sense voltage is a small difference on a large common-mode signal from the perspective of the sense amplifier, which poses unusual demands on the implementation to preserve accuracy and dynamic range.90003 90002 Figure 1. Typical high-side current-sense circuit. 90003 90002 T raditional grow-your -own solutions use operational or instrumentation amplifiers, but these are commonly limited in the voltage range of operation and / or require a number of additional components to perform the voltage translation function to create a ground-referenced readout signal. Far better and simpler solutions are attainable by using the LT6100 and LTC6101, which solve most high side current sensing requirements.90003 90002 For an index of these and other current sense solutions, see Table 1. For specific applications where the current sensing is performed within dedicated chips or chip sets, see Table 2. 90003 90020 90021 Table 1. Use this index of publications to find detailed applications information for current sensing solutions. 90022 90023 90024 90025 Publication 90026 90025 Hi Side / Low Side 90026 90025 Uni / Bi Directional 90026 90025 V 90032 OS 90033 (CMRR) 90026 90025 Input Voltage / Feature 90026 90037 90024 90025 LT6100 Data Sheet 90026 90025 Hi Side 90026 90025 Uni 90026 90025 300 90026 90025 48V 90026 90037 90024 90025 LT6101 Data Sheet 90026 90025 Hi Side 90026 90025 Uni 90026 90025 300 90026 90025 60V 90026 90037 90024 90025 LT1787 Data Sheet 90026 90025 Hi Side 90026 90025 Bi 90026 90025 75μV 90026 90025 60V, 70μA 90026 90037 90024 90025 LT1990 Data Sheet, pp.1, 16 90026 90025 Both 90026 90025 Bi 90026 90025 (80dB) 90026 90025 ± 250V 90026 90037 90024 90025 LT1991 Data Sheet, pp. 1, 19-22 90026 90025 Both 90026 90025 Bi 90026 90025 (80dB) 90026 90025 ± 60V 90026 90037 90024 90025 LT1995 Data Sheet, p. 20 90026 90025 Both 90026 90025 Bi 90026 90105 90025 Hi Speed 90026 90037 90024 90025 LTC2054 Data Sheet, p.12 90026 90025 Hi Side 90026 90025 Bi 90026 90025 3μV 90026 90025 60V 90026 90037 90024 90025 3μV 90026 90025 Low Side 90026 90025 Uni 90026 90025 3μV 90026 90025 -48V 90026 90037 90024 90025 LT1494 Data Sheet, p. 1, 16 90026 90025 Hi Side 90026 90025 Uni, B 90026 90025 ~ 1mV 90026 90025 36V 90026 90037 90024 90025 LTC2053 Data Sheet, p.13 90026 90025 Hi Side (Both possible) 90026 90025 Uni 90026 90025 10μV 90026 90025 5V 90026 90037 90024 90025 LTC6800 Data Sheet, p. 1 90026 90025 Hi Side (Both possible) 90026 90025 Uni 90026 90025 100μV 90026 90025 5V 90026 90037 90024 90025 LTC6943 Data Sheet p. 1 90026 90025 Both 90026 90025 Uni 90026 90025 (120dB) 90026 90025 18V 90026 90037 90024 90025 LT1620 Data Sheet 90026 90025 Both 90026 90025 Uni 90026 90025 5mV 90026 90025 36V, power 90026 90037 90024 90025 LT1366 Data Sheet, p.1 90026 90025 Hi Side 90026 90025 Uni 90026 90025 200μV 90026 90025 36V 90026 90037 90024 90025 LT1797 Data Sheet, p. 1 90026 90025 Low Side 90026 90025 Uni 90026 90025 1mV 90026 90025 -48V, fast 90026 90037 90024 90025 InfoCard 27 90026 90105 90105 90105 90025 Various circuits 90026 90037 90024 90025 LT1637 Data Sheet, p.13 90026 90025 LT1637 Data Sheet, p. 13 90026 90025 Uni 90026 90025 ~ 1mV 90026 90025 44V, Over-The-Top 90026 90037 90024 90025 LT1490A Data Sheet, p. 1 90026 90025 Hi Side 90026 90025 Bi 90026 90025 ~ 1mV 90026 90025 12V, Over-The-Top 90026 90037 90024 90025 Design Note 341 90026 90025 Low Side 90026 90025 Uni 90026 90025 ~ 1μV 90026 90025 -48V, Direct ADC 90026 90037 90024 90025 Linear Technology Magazine Aug.2004, p. 33 90026 90025 Low Side 90026 90025 Bi 90026 90025 2.5μV 90026 90025 Direct ADC 90026 90037 90024 90025 Design Note 297 90026 90025 Hi Side 90026 90025 Uni 90026 90025 2.5μV 90026 90025 Direct ADC 90026 90037 90024 90025 LTC1966 Data Sheet, pp. 29, 32 90026 90025 Both (AC) 90026 90105 90105 90025 RMS Current 90026 90037 90024 90025 Application Note 92 90026 90025 Hi Side 90026 90025 Uni 90026 90025 various 90026 90025 Avalanche PDs 90026 90037 90308 90309 90020 90021 Table 2.Linear Technology offers ICs for application-specific current-sensing solutions. Use this table to find publications that cover specific applications. 90022 90023 90024 90025 Publication 90026 90025 Application 90026 90037 90024 90025 LTC4060 Data Sheet 90026 90025 NiMH / NiCd charger 90026 90037 90024 90025 Linear Technology Magazine Mar. 2003 p. 24 90026 90025 Battery chargers 90026 90037 90024 90025 Linear Technology Magazine May 2004, p.24 90026 90025 Battery gas gauge 90026 90037 90024 90025 Application Note 89 90026 90025 5V, TEC Controller 90026 90037 90024 90025 Application Note 66, Application Note 84 90026 90025 Switch Mode Power 90026 90037 90024 90025 LT Chronicle Jan. 2003 p. 7 90026 90025 Automotive Temp 90026 90037 90024 90025 Design Note 1009 90026 90025 Photo Flash 90026 90037 90024 90025 Design Note 312 90026 90025 VRM9.x 90026 90037 90024 90025 Design Note 347 90026 90025 Bricks 90026 90037 90024 90025 LTC4259, LTC4267 Data Sheet 90026 90025 Power over Ethernet 90026 90037 90024 90025 Design Solution 43 90026 90025 Altera FPGAs 90026 90037 90308 90309 90002 As with any sensor design, there are several potential sources of error to consider. The accuracy of the circuit depends largely on how well the value of the sense resistor is known.The sense resistor itself has defined tolerances and temperature dependencies that introduce errors. Stray resistance in the measurement path or large dI / dt loops can also add errors. It is important to properly implement Kelvin connections to the sense resistor to minimize these effects. 90389 1 90390 90003 90002 After sense resistance, the most significant source of error is the voltage offset of the sense amplifier, since it generates a level-independent uncertainty in the measurement. This is particularly important for preserving accuracy at current levels that are substantially below the maximum design value.In some applications it is desirable to calibrate out the static component of this term (in software, for example), but this may not always be practical. 90003 90002 An additional error source to consider is the tolerance of any resistors that may be required for setting scale factors. This can contribute to full-scale uncertainty along with the sense resistor and Kelvin connection tolerances. For the LT6100, scaling resistors are all provided on-chip, so the tolerances are well defined and accounted for in the data sheet specifications.In the case of the LTC6101, the scaling accuracy is set strictly by the user’s choice of resistors, thereby allowing optimization for particular requirements. 90003 90002 Figure 2 shows a simplified schematic of the LT6100 sensing across a 100mΩ sense resistor. The differential voltage across the sense resistor is imposed upon internal resistor R 90032 G2 90033 by the action of the op amp A1 through Q1’s collector. The resulting current through R 90032 G2 90033 is thus I = V 90032 SENSE 90033 / R 90032 G2 90033, and this current flows through Q1 and R 90032 O 90033.The voltage which appears across R 90032 O 90033 is R 90032 O 90033 • V 90032 SENSE 90033 / R 90032 G2 90033. But R 90032 O 90033 is ten times the value of R 90032 G2 90033, so the voltage is simply 10 • V 90032 SENSE 90033. This gives rise to the LT6100’s inherent gain of 10 up to this point. The next stage involving op amp A2 gives the designer the flexibility of selecting further gain by grounding or floating pins A2 and A4 or connecting them to the output. Gains of 1, 1.25, 2, 2.5, 4, and 5 can be set here, for overall gains of 10, 12.5, 20, 25, 40, and 50. Series resistor R 90032 E 90033 is provided between the two stages to allow simple low pass filtering by adding a capacitor at the FIL pin. 90003 90002 Figure 2. LT6100 simplified schematic. 90003 90002 Figure 3 shows a simplified schematic of the LTC6101 in a basic currentsense circuit. As before, a sense resistor, R 90032 SENSE 90033, is added in series with the system supply at the positive (High side) of the supply. The internal amplifier of the LTC6101 acts as a voltage follower, driving its inverting input (IN 90389 – 90390) to the same voltage as its non-inverting input (IN 90389 + 90390).This sets a voltage across R 90032 IN 90033 that is equal to the voltage across R 90032 SENSE 90033: 90003 90002 The current in R 90032 IN 90033 is therefore: 90003 90002 Figure 3. LTC6101 simplified schematic. 90003 90002 The amplifier inputs are high impedance, so this current does not flow into the amplifier. It is instead conducted through an internal MOSFET to the OUT pin, where it flows through R 90032 OUT 90033 to ground. The output voltage is then: 90003 90002 and the gain is: 90003 90002 Substitute: 90003 90002 to yield the desired ratio of output voltage to sense current: 90003 90002 As with most current-sense solutions, the input and output voltages, as well as output current, are dictated by the application.In order to allow compatibility with most circuits, the LTC6101 supports input voltages between 0V and 500mV. This makes it suitable for most applications that use a small series sense resistor (or shunt). The LTC6101’s output may be required to drive a comparator, ADC, or other circuitry. The output voltage can swing from 0V, since it is open-drain, to 8V. The output current may be set as high as 1mA, allowing useful speed and drive capability. The external gain resistors, R 90032 IN 90033 and R 90032 OUT 90033, allow a wide range of gains to work in concert with these circuit constraints.90003 90002 Both the LT6100 and LTC6101 are very precise. They boast 300μV maximum input offset (500μV and 535μV, respectively, over temperature). Neither part draws supply current from the input sense pins. The LT6100 draws 5μA from its Over-The-Top 90389 ® 90390 inputs, while the LTC6101 provides a separate supply pin (V +) to be connected to the sensed supply directly and draws only 100nA bias current at its inputs. This makes the LTC6101 ideal for very low current monitoring. In addition, the LTC6101 sense input currents are well matched so a second input resistor, R 90032 IN + 90033 (Figure 4), may be added to cancel the effect of input bias.In this way the LTC6101 effective input bias error can be reduced to less than 15nA. The LT6100 provides these matched resistors internally, reducing its effective input bias current error to below 1μA. 90003 90002 Figure 4. Second input resistor minimizes error due to input bias current. 90003 90002 90469 The LT6100: Robust and Easy to Use 90470 90003 90002 The LT6100 tolerates a reverse battery on its inputs up to -50V, while guaranteeing less than 100μA of resultant fault current.In addition, it can also be used to sense across fuses and MOSFETs as shown in Figure 5. The LT6100 has no problem when the fuse or MOSFET opens because it has high voltage pnp’s and a unique input topology that features full high impedance differential input swing capability to ± 48V. This allows direct sensing of fuse or MOSFET voltage drops, without concern for the fuse or MOSFET open circuit condition. 90003 90002 Figure 5. Sense across a MOSFET or fuse without worry. LT6100 inputs can split while remaining high Z.90003 90002 Another unique benefit of the LT6100 is that you can leave it connected to a battery even when it is unpowered. When the LT6100 loses power, or is intentionally powered down, both sense inputs remain high impedance (see Figure 6). This is due to the implementation of Linear Technology’s Over-The-Top input topology at the front end. In fact, when powered down, the LT6100 inputs actually draw less current than when powered up. Powered up or down, it represents a benign load. 90003 90002 Figure 6.Remove power from the LT6100 with no need to disconnect the battery. The LT6100 inputs remain high Z. 90003 90002 90469 The LTC6101: Delivers Accuracy and Speed in High Voltage Applications 90470 90003 90002 The LTC6101 boasts a fully specified operating supply range of 4V to 60V, with a maximum supply voltage of 70V. Applications that require high operating voltages, such as motor control and telecom supply monitoring, or temporary high-voltage survival, such as with automotive load dump conditions, benefit from this wide supply range.The accuracy is preserved across this supply range by a high typical PSRR of 140dB. 90003 90002 The fast response time of the LTC6101 makes it suitable for overcurrent-protection circuits. The typical response time is less than 1μs for the output to rise 2.5V on a 5V output transition. The LTC6101 can detect a load fault and signal a comparator or microprocessor in time to open a switch in series with the load before supply, load or switch damage occurs. 90003 90002 The architecture of the LTC6101 is the key to its flexibility.The gain is completely controlled by external resistors (R 90032 IN 90033 and R 90032 OUT 90033, Figure 3). This is convenient because most applications specify a small maximum shunt voltage (to minimize power loss), which must be matched to either a specific comparator threshold or a desired ADC resolution. This requires that gain be carefully set to maintain performance. In solutions where the gain resistors are not user-selectable (Figure 7a), the gain will be fixed, and may not be set to an appropriate value.Another approach is to include internal input resistors (Figure 7b), which allows user-configured gain, but may force the use of a very large output resistor in order to get high gain (10-100 or more). A large output resistor will cause the output to be slower and more susceptible to system noise, and may be too high an impedance to drive a desired ADC. The LTC6101 avoids these problems by allowing the application designer to choose both R 90032 IN 90033 and R 90032 OUT 90033. R 90032 IN 90033 can be quite small, its value limited only by the gain error due to stray board resistance and the 1mA maximum output current specification.Therefore high gain and high speed can be achieved even with small V 90032 SENSE 90033 and R 90032 OUT 90033 requirements. Gain accuracy is determined only by the accuracy of the external resistors. 90003 90002 Figure 7. The LT6101 achieves unparalled versatility in high side current sensing applications by allowing the user to select the gain via external R 90032 IN 90033 and R 90032 OUT 90033 resistors. In most architectures, some or all of these resistors are internal to the device, as shown here.Fixed gain devices, such as in (a), limit flexibility. Those with fixed input resistors, as in (b), limit gain and speed. 90003 90002 In addition, the open-drain output architecture provides an advantage for remote-sensing applications. If the LTC6101 output must drive a circuit that is located remotely, such as an ADC, then the output resistor can be placed near the ADC. Since the open-drain output is a high-impedance current source, the resistive drop in the output wire will not affect the result at the converter.System noise that is coupled onto the long wire can be easily reduced with a series filter placed before R 90032 OUT 90033, or with a simple capacitor in parallel with R 90032 OUT 90033, with no loss of DC accuracy (Figure 8). The output may also be level shifted above V- by terminating R 90032 OUT 90033 at a voltage that is held higher than V- (figure 9), provided that the maximum difference between V 90032 OUT 90033 and V- does not exceed the maximum specified output of the LTC6101. 90003 90002 Figure 8.Open drain output enhances remote sensing accuracy. 90003 90002 Figure 9. Output reference level shifted above V-. 90003 90002 90469 Micro-Hotplate Current Monitor 90470 90003 90002 Materials science research examines the properties and interactions of materials at various temperatures. Some of the more interesting properties can be excited with localized nano-technology heaters and detected using the presence of interactive thin films. 90003 90002 While the exact methods of detection are highly complex and relatively proprietary, the method of creating localized heat is as old as the light bulb.Figure 10 shows the schematic of the heater elements of a Micro-hotplate from Boston Microsystems (www.bostonmicrosystems.com). The physical dimensions of the elements are tens of microns. They are micromachined out of SiC and heated with simple DC electrical power, being able to reach 1000 ° C without damage. 90003 90002 Figure 10. LT6100 and LT1991 monitor the current and voltage through a wide range of drive levels applied to a Microhotplate. 90003 90002 The power introduced to the elements, and thereby their temperature, is ascertained from the voltage-current product with the LT6100 measuring the current and the LT1991 measuring the voltage.The LT6100 senses the current by measuring the voltage across the 10Ω resistor, applies a gain of 50, and provides a ground referenced output. The I to V gain is therefore 500mV / mA, which makes sense given the 10mA full scale heater current and the 5V output swing of the LT6100. The LT1991’s task is the opposite, applying precision attenuation instead of gain. The full scale voltage of the heater is a total of 40V (± 20), beyond which the life of the heater may be reduced in some atmospheres. The LT1991 is set up for an attenuation factor of 10, so that the 40V full scale differential drive becomes 4V ground referenced at the LT1991 output.In both cases, the voltages are easily read by 0V-5V PC I / O cards and the system readily software controlled. 90003 90002 90469 White LED Current Controller 90470 90003 90002 Figure 11 shows the LT6100 used in conjunction with the LT3436 switch mode power converter to efficiently drive a white LED with a constant current. By closing the switch on pin A2 of the LT6100, its gain is adjusted between 40 (open) and 50 (closed). 90003 90002 Figure 11. 1Amp / 800mA white LED current controller.90003 90002 The FB pin of the LT3436 is a control pin referenced to a 1.2V set point. When the FB pin is above 1.2V, the LT3436 stops operation; when below 1.2V, the LT3436 continues operation. The output voltage (> 1.2V) is usually regulated by applying a resistive divider from the output voltage back to the FB pin to close the feedback loop. To achieve a constant output current, rather than a constant output voltage, the feedback loop must convert the load current to a voltage. Enter the LT6100.90003 90002 It senses the LED current by measuring the voltage across a 30mΩ resistor, applies a gain, and feeds the resulting voltage back to the FB pin. 90003 90002 The 1.2V set point at the LT3436 can be referred back across the sense resistor by dividing by the LT6100 gains of 40 and 50. This gives 30mV and 24mV respectively. Dividing by the sense resistor of 30mΩ gives set point currents of 1A and 800mA. 90003 90002 90469 Monitor the Current of Automotive Load Switches 90470 90003 90002 With its 60V input rating, the LTC6101 is ideally suited for directly monitoring currents on vehicular power systems, without need for additional supply conditioning or surge protection components.90003 90002 Figure 12 shows an LT1910-based intelligent automotive high-side switch with an LTC6101 providing an analog current indication. The LT1910 high-side switch controls an N-channel MOSFET that drives a controlled load, and uses a sense resistance to provide overload detection (note the surge-current of lamp filaments may cause a protection trip, thus are not recommended loads with the LT1910). The sense resistor is shared by the LT6101 to provide the current measurement. 90003 90002 Figure 12.Automotive smart-switch with current readout. 90003 90002 The LTC6101 supplies a current output, rather than a voltage output, in proportion to the sense resistor voltage drop. The load resistor for the LTC6101 may be located at the far end of an arbitrary length connection, thereby preserving accuracy even in the presence of ground-loop voltages. 90003 90002 The LT6100 and LTC6101 are precise high side current sensing solutions. Although very similar in obvious respects, each has its unique advantages.The LT6100 draws much less power, can be powered down while maintaining high Z characteristics, and has nearly indestructible inputs. The LTC6101 can withstand up to 70V, is infinitely gain configurable, and provides an open drain output. 90003 .

