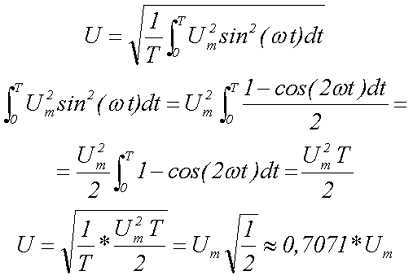Действующее напряжение – действующее значение напряжения | Электрознайка. Домашний Электромастер.

Содержание

действующее значение напряжения | Электрознайка. Домашний Электромастер.

Действующее значение синусоидального
переменного напряжения – тока.

data-ad-client=”ca-pub-5076466341839286″
data-ad-slot=”1404500382″>
♦Переменный электрический ток в нашей бытовой электросети представляет собой синусоиду, как на рисунке 1.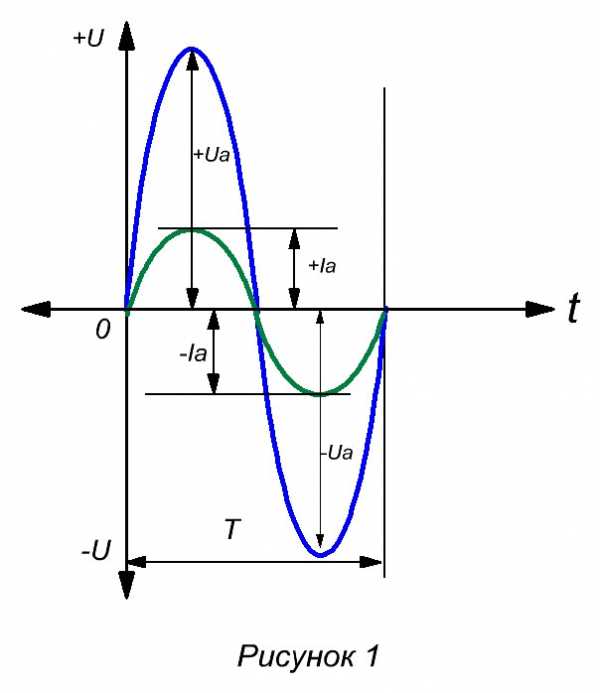

Напряжение меняет свою величину от 0 до + Umax и от 0 до — Umax . Полный цикл этих изменений называется периодом.
Период измеряется в секундах и обозначается буквой Т.
Количество периодов переменного тока за 1 секунду, есть частота f.
Частота переменного тока f измеряется в герцах .

f = 1 / T.

Например.
Частота в нашей электрической сети 50 Гц. Период этих колебаний будет равен:

T = 1 / f = 1 / 50 = 0,02 сек.

Наибольшее значение изменяющегося переменного напряжения – тока называется амплитудным значением или амплитудой.

Umax = Ua и Imax = Ia

За один период напряжение принимает эти значения два раза: + Ua и — Ua .

♦ Если подключить в цепь переменного напряжения какую-нибудь активную нагрузку, например паяльник, в цепи потечет переменный электрический ток, так же принимающий значения +Ia и — Ia, и повторяющий форму синусоиды.
На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный. Выделение тепла не зависит от направления тока в цепи.
Выделенное тепло будет равно той энергии, которую затрачивает электрический ток при прохождении по сопротивлению нагрузки.
Введено понятие действующего значения переменного напряжения Uд и тока Iд.

Действующее значение переменного тока — это такое значение величины постоянного тока, который проходя по сопротивлению нагрузки за тот же промежуток времени, выделит такое же количество тепла, что и переменный ток.

♦ Переменный ток оказывает такое же тепловое действие, как и постоянный ток, если амплитуда синусоидального переменного тока превышает величину постоянного тока в 1,41 раз.
Следовательно действующее (или эффективное) значение переменного тока будет равно:

Iд = Ia / 1,41 = 0,707 Ia. – действующее значение переменного тока

Uд = Ua / 1,41 = 0,707 Ua — действующее значение переменного напряжения

На все эти теоретические размышления можно посмотреть иначе!

♦Имеем синусоиду переменного напряжения длительностью в 1 период как на рисунке 1.
После выпрямительных диодов оно принимает вид как на рисунке 2.

Нижняя половинка синусоиды перевернута вверх, чтобы удобнее было представить процесс преобразования.

♦На рисунке приняты обозначения:

Um = Ua = 1 — амплитудное значение величины переменного напряжения. Значение Ua примем за единицу.

Из формулы приведенной выше Uд = 1 / 1,41 = 0,707 — действующее напряжение равно 0,707 от амплитудного значения Ua = 1.
Заштрихованная часть синусоиды обозначает затраченную на нагревание паяльника электрическую энергию. В промежутках между половинками синусоид ток по цепи не протекает, а следовательно и не выделяется электрическая мощность.
♦Проведем линию, обозначающую Uд = 0,707.
Она отсекает верхнюю часть половинок синусоид.
Если эти отсеченные вершинки синусоиды уложить в провалы между полупериодами, получится полностью заполненная площадь соответствующая значениям постоянного напряжения U и тока I.
Получается, что мощность синусоидального переменного тока с амплитудными значениями

Ua и Ia равна мощности действующего значения Uд и Iд переменного тока и равна мощности постоянного тока со значениями U и I.
Одна и та же электрическая мощность, выраженная в трех видах.

P = Ua х Ia = Uд х Iд = U х I

♦ Электрические приборы для измерения переменного напряжения и тока отградуированы на отображение действующих значений Uд и Iд.
В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно 220 вольт.
Максимальное, амплитудное значение напряжения в сети равно:
Um = Ua = Uд х 1,41 = 220 х 1,41 = 310,2 вольт.

Процесс поэтапного преобразования переменного напряжения в пульсирующее напряжение, а затем в постоянное напряжение, наблюдается в схемах выпрямителей.

data-ad-client=”ca-pub-5076466341839286″
data-ad-slot=”1404500382″>

domasniyelektromaster.ru

Действующее значение тока. Действующее значение напряжения

Господа, в прошлой статье мы говорили про мощность и работу переменного тока. Напомню, что тогда мы считали ее через некоторый интеграл, а в самом конце статьи я вскользь сказал, что существуют способы облечения и без того нелегкой жизни и часто можно обойтись вообще без взятия интеграла, если знать про действующее значение тока. Сегодня про него и поговорим!

Господа, вероятно, для вас не станет секретом, что в природе существует большое число видов переменного тока: синусоидальный, прямоугольный, треугольный и так далее. И как их вообще можно сравнивать между собой? По форме? Хмм…Пожалуй, да. Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие

действующего тока.

Итак, действующее (или среднеквадратичное) значение переменного тока – это такая величина некоторого постоянного тока, который за время, равное периоду переменного тока выделит столько же тепла на резисторе, что и наш переменный ток. Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.

Итак, у нас есть переменный ток. Допустим, синусоидальный. У него своя амплитуда А_m и период T_период (ну или частота f). На фазу в данном случае пофиг, считаем ее равной нулю. Этот переменный ток течет через некоторый резистор R и на этом резисторе выделяется энергия. За один период T_период нашего синусоидального тока выделится вполне определенное количество джоулей энергии. Это число джоулей мы можем точно посчитать по формулам с интегралом, которые я приводил в прошлый раз. Допустим, мы насчитали, что за один период T_период синусоидального тока выделится Q

джоулей тепла. А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе R за то же самое время T_период выделилось ровно такое же количество джоулей Q. Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока. А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли?

Итак, суть вопроса, надеюсь, стала понятной, поэтому давайте все сказанное выше переведем на язык математики. Как мы уже писали в прошлой статье, закон изменения мощности переменного тока равен

Количество выделившейся энергии при работе тока за время

T_период – соответственно, равно интегралу за время периода T_период:

Господа, теперь нам надо взять этот интеграл. Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками .

Итак, как его нам брать? Ну, величины I_m² и R являются константами и их можно сразу вынести за знак интеграла. А для квадрата синуса нам надо применить формулу понижения степени из курса тригонометрии. Надеюсь, вы ее помните . А если нет, то напомню еще раз:

Погнали считать!

Теперь давайте разобьем интеграл на два интеграла. Можно воспользоваться тем, что интеграл от суммы или разности равен сумме или разности интегралов. В принципе, это очень даже логично, если вспомнить про то, что интеграл – это площадь.

Итак, имеем

Господа, у меня есть для вас просто отличнейшая новость. Второй интеграл равен нулю!

Почему это так? Да просто потому, что интеграл любого синуса/косинуса на величине, кратной его периоду, равен нулю. Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.

Итак, отбрасывая интеграл с косинусом, получаем

Ну и не надо быть большим гуру математики, чтобы сказать, что этот интеграл равен

И, таким образом, получаем ответ

Это мы получили количество джоулей, которое выделится на резисторе

R при протекании через него синусоидального тока амплитудой I_m в течении периода T_период. Теперь, чтобы найти чему в данном случае равен действующий ток нам надо исходить из того, что на том же самом резисторе R за то же самое время T_период выделится то же самое количество энергии Q. Поэтому мы можем записать

Если не совсем понятно, откуда здесь взялась левая часть, рекомендую вам повторить статью про закон Джоуля-Ленца. А мы тем временем выразим действующее значение тока I_{действ.} из этого выражения, предварительно сократив все, что можно

Вот такой вот результат, господа. Действующее значение переменного синусоидального тока в корень из двух раз меньше его амплитудного значения. Хорошо запомните этот результат, это важный вывод.

Вообще говоря никто не мешает по аналогии с током ввести действующее значение напряжения. При этом у нас зависимость мощности от времени примет вот такой вид

Именно его мы будем подставлять под интеграл и выполнять все преобразования. Господа, каждый из вас может на досуге при желании это проделать, я же просто приведу конечный результат, поскольку он полностью аналогичен случаю с током. Итак, действующее значение напряжения синусоидального тока равно

Как видим, аналогия полнейшая. Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.

Подобным образом можно рассчитать действующее значение тока и напряжения для сигнала абсолютно любой формы: надо только лишь записать закон изменения мощности для этого сигнала и выполнить пошагово все вышеописанные преобразования.

Все вы, наверняка, слышали, что у нас в розетках напряжение 220 В. А каких вольт? У нас ведь теперь есть два термина – амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках – это действующее значение! Вольтметры и амперметры, включаемые в цепи переменного тока показывают именно действующие значения. А форму сигнала вообще и его амплитуду в частности можно посмотреть с помощью осциллографа. Ну, мы же уже говорили, что всем интересны деньги, то бишь работа тока, а не какая-то там непонятная амплитуда. Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать

Отсюда получаем

Вот так вот, господа. В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.

Рисунок 1 – Закон изменения напряжения в розетках

И специально для вас, господа, я посмотрел напряжение в розетке с помощью осциллографа. Смотрел я его через делитель напряжения 1:5. То есть форма сигнала полностью сохранится, а амплитуда сигнала на экране осциллографа будет в пять раз меньше, чем на самом деле в розетке. Зачем я так сделал? Да просто потому, что из-за большого размаха входного напряжения картинка целиком не влезает на экран осциллографа.

ВНИМАНИЕ! Если у вас нет достаточного опыта работы с высоким напряжением, если вы абсолютно четко не представляете себе как могут течь токи при измерениях в гальванически не отвязанных от сети цепях, настоятельно не рекомендую проводить подобный эксперимент самостоятельно, это опасно! Дело в том, что при подобных измерениях с помощью осциллографа, подключенного к розетке с заземлением есть очень большой шанс что произойдет короткое замыкание через внутренние земли осциллографа и прибор сгорит без возможности восстановления! А если делать эти измерения с помощью осциллографа, подключенного к розетке без заземления, на его корпусе, кабелях и разъемах может присутствовать смертельно опасный потенциал! Это не шутки, господа, если нет понимания, почему это так, лучше этого не делать, тем более, что осциллограммы уже сняты и вы можете их наблюдать на рисунке 2.

Рисунок 2 – Осциллограмма напряжения в розетке (делитель 1:5)

На рисунке 2 мы видим, что амплитуда синуса составляет около 62 вольт, а частота – ровно 50 Гц. Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна

Как мы видим, результат измерения очень близок к теоретическому, не смотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это свидетельствует о том, что все наши расчеты верны.

На этом на сегодня все, господа. Сегодня мы узнали, что такое действующий ток и действующее напряжение, научились их рассчитывать и проверили результаты расчетов на практике. Спасибо что прочитали это и до новых статей!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

myelectronix.ru

Переменное напряжение и его значения – Help for engineer

Переменное напряжение и его значения

Все мы знаем, что дома в розетках у нас напряжение 220В. Но не каждый знает, какое именно это напряжение. Давайте же разберемся с этой ситуацией.

Для упрощения рассматриваемого примера будем считать, что вид напряжения – синусоида, то есть переменное напряжение (с определенной периодичностью меняет значение с положительного на отрицательное).

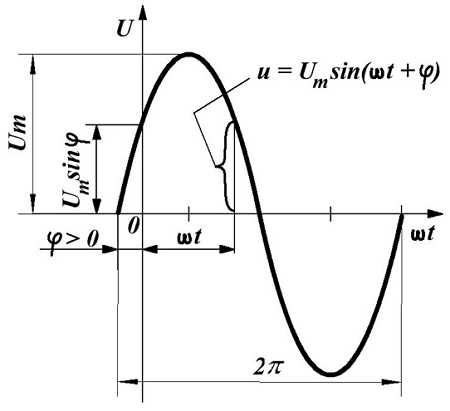
Рисунок 1 – Вид переменного напряжения

На рисунке 1 изображен вид идеального синусоидального напряжения одного периода Т. Есть несколько значений напряжения, о которых обычно говорят и используют, рассмотрим:

Амплитудное значение напряжения (U_m) – это максимальное, мгновенное значение напряжения, то есть амплитуда синусоиды.

Теперь правильнее будет говорить о токе.

Действующее значение переменного тока – это величина постоянного тока, который может выполнить ту же самую работу (нагрев).

Действующее значение напряжения (U) обозначают латинской буквой без индекса, в литературе может еще использоваться термин – эффективное значение напряжения.

Для периодически изменяющегося сигнала за период Т, величина действующего напряжения находится:

Приведем формулу к простому виду, приняв за изменяющийся сигнал синусоиду. Между рассмотренными выше двумя параметрами существует зависимость, которая выражается формулой:

То есть амплитудное значение в 1,414 раза больше действующего.

Вернемся к домашним розеткам с напряжением 220В. Это действующее значение напряжения, которое можно измерить тестером. Определим его амплитудное значение напряжения:

Среднее значение синусоидального тока, напряжения будет равно нулю. Поэтому если говорят о среднем значении переменного тока, то подразумевают рассматривание его в пол периода.

Добавить комментарий

h4e.ru

Действующее напряжение Википедия

В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока

Значения переменного напряжения (тока)

Далее для определенности будем говорить большей частью о параметрах напряжения, хотя они справедливы и для токов.

Мгновенное значение

Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является ( u(t) ,i(t){\displaystyle u(t)~,\quad i(t)} ). Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой или цифровой осциллограф.

Амплитудное значение

Амплитудное (пиковое) значение, иногда называемое просто «амплитуда» — наибольшее мгновенное значение напряжения или силы тока за период (без учёта знака):

UM=max(|u(t)|) ,IM=max(|i(t)|){\displaystyle U_{M}=\max(|u(t)|)~,\qquad I_{M}=\max(|i(t)|)}

Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.

Среднеквадратичное значение

Среднеквадратичное значение (устар. действующее, эффективное) — корень квадратный из среднего значения квадрата напряжения или тока.

U=1T∫0Tu2(t)dt ,I=1T∫0Ti2(t)dt{\displaystyle U={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}~,\qquad I={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}i^{2}(t)dt}}}

Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I{\displaystyle I} и U{\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.

Когда не оговаривают особо, то обычно имеют в виду именно среднеквадратичные значения величины напряжения или силы тока.

В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.

Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.

Среднее значение

Среднее значение (смещение) — постоянная составляющая напряжения или силы тока

U=1T∫0Tu(t)dt ,I=1T∫0Ti(t)dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}

В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения). Геометрически это разность площадей под и над осью времени, делённая на период. Для синусоидального сигнала смещение равно нулю.

Средневыпрямленное значение

Средневыпрямленное значение — среднее значение модуля сигнала

U=1T∫0T∣u(t)∣dt ,I=1T∫0T∣i(t)∣dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}\mid u(t)\mid dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}\mid i(t)\mid dt}

На практике используется редко, однако большинство измерительных приборов переменного тока – магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.

Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.

Коэффициенты пересчёта значений

Коэффициент формы кривой переменного напряжения (тока) — величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π/22≈1.11{\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11}.

Коэффициент амплитуды кривой переменного напряжения (тока) — величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2{\displaystyle {\sqrt {2}}}.

Параметры постоянного тока

Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени

Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей

Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)

Литература и документация

Литература

Нормативно-техническая документация

Ссылки

См. также

wikiredia.ru

Действующее значение тока и напряжения

Переменный ток, протекая по проводнику, нагревает его так же, как и постоянный ток. Силу переменного тока удобно оценивать по его тепловому действию (эффекту) или, как говорят, по действующей, эффективной его величине.

Действующее или эффективное значение переменного тока равно силе такого постоянного тока, который, протекая по данному проводнику, выделяет в нем ежесекундно то же количество энергии в виде тепла, что и переменный ток.

Тепловой эффект тока, а значит, и действующие (эффективные) значения переменного тока зависят не только от наибольших значений, которых достигает переменный ток, но и от формы тока.

Вообще говоря, в электротехнике, и особенно в радиотехнике, приходится иметь дело с токами довольно сложной формы. Но все эти токи могут быть представлены в виде суммы нескольких синусоидальных токов с различными частотами, амплитудами и начальными фазами. Поэтому очень важную роль играет связь между амплитудным и действующем значениями для синусоидального тока.

Если известна амплитуда переменного синусоидального тока, то действующее или эффективное его значение определяется по формуле:

то есть эффективное значение синусоидального тока в раз меньше его амплитудного значения.

Аналогичная формула применяется и для вычисления эффективного значения синусоидального напряжения:

Протекая по проводнику, переменный ток создает в нем эффективное падение напряжения, равное произведению эффективного значения силы тока на сопротивление проводника, что эквивалентно закону Ома для постоянного тока, то есть:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Действующее значение переменного тока

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, – периодом Т. Для периодического тока имеем

(1)

Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):

(2)

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц.

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i – мгновенное значение тока ;

u – мгновенное значение напряжения ;

е – мгновенное значение ЭДС ;

р– мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m).

– амплитуда тока;

– амплитуда напряжения;

– амплитуда ЭДС.

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

(3)

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е₁ и е₂соответствуют уравнения:

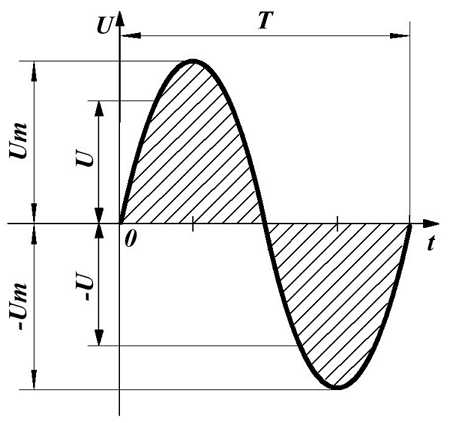Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t=0): и –начальной фазой ().

Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.

Для синусоидальных ЭДС е₁ и е₂угол сдвига фаз:

Векторное изображение синусоидально изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е₁ и е₂(рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:

Каждый из этих токов синусоидален и может быть представлен уравнением

и.

Результирующий ток также будет синусоидален:

Определение амплитудыи начальной фазыэтого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt=0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

Построение векторной диаграммы в масштабе позволяет определить значения ииз диаграммы, после чего может быть записано решение для мгновенного значенияпутем формального учета угловой частоты:.

studfiles.net

Действующее значение синусоидального переменного напряжения – тока.

Действующее значение синусоидального
переменного напряжения – тока.

f = 1 / T.

Например.
Частота в нашей электрической сети 50 Гц. Период этих колебаний будет равен:

T = 1 / f = 1 / 50 = 0,02 сек.

Umax = Ua и Imax = Ia

За один период напряжение принимает эти значения два раза: + Ua и — Ua .

Iд = Ia / 1,41 = 0,707 Ia. – действующее значение переменного тока

Uд = Ua / 1,41 = 0,707 Ua — действующее значение переменного напряжения

На все эти теоретические размышления можно посмотреть иначе!

Нижняя половинка синусоиды перевернута вверх, чтобы удобнее было представить процесс преобразования.

♦На рисунке приняты обозначения:

Um = Ua = 1 — амплитудное значение величины переменного напряжения. Значение Ua примем за единицу.

P = Ua х Ia = Uд х Iд = U х I

data-ad-client=”ca-pub-5076466341839286″
data-ad-slot=”1404500382″>

domasniyelektromaster.ru

действующее значение напряжения | Электрознайка. Домашний Электромастер.

Действующее значение синусоидального
переменного напряжения – тока.

Действующее значение тока. Действующее значение напряжения