Действующее значение это: ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ – это… Что такое ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ?

Содержание

ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ – это… Что такое ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ?

ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ: электрической величины (ранее наз. эффективным значением) – среднеквадратическое за период значение периодич. величины (силы тока, электрич. напряжения, эдс и т. д.). Для синусоидально изменяющихся величин Д. з. в корень из 2 раз меньше амплитудного (максимального). Когда без всяких оговорок указывают значение силы перем. тока, напряжения, эдс, то имеют в виду именно Д. з.; напр., напряжение 220 В – Д. з., а Макс. значение этого напряжения (дважды в течение периода) 220 корень из 2 В.

ДЕЙСТВУЮЩАЯ ДЛИНА
ДЕЙСТВУЮЩИХ МАСС ЗАКОН

Смотреть что такое “ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ” в других словарях:

ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ — в электротехнике среднее квадратичное за период значение переменного тока, напряжения, электродвижущей силы, магнитодвижущей силы, магнитного потока и т.
п. Действующее значение синусоидального тока и напряжения в раз меньше их амплитудных… … Большой Энциклопедический словарь
действующее значение — [Интент] Недопустимые, нерекомендуемые среднеквадратическая величинасреднеквадратичная величинаэффективная величинаэффективное значение Тематики электротехника, основные понятия EN effective valuermsrms valueroot mean square valuevirtual value … Справочник технического переводчика
действующее значение — (электротехн.), среднее квадратичное за период значение переменного тока, напряжения, эдс, магнитодвижущей силы, магнитного потока и т. п. Действующие значения синусоидального тока и напряжения в √2 раз меньше их амплитудных значений. * * *… … Энциклопедический словарь
действующее значение — efektinė vertė statusas T sritis Standartizacija ir metrologija apibrėžtis Kintamojo dydžio vertė, lygi jo amplitudinei vertei, padalytai iš 1,41. atitikmenys: angl. effective value vok. Effektivwert, m rus. действующее значение, n; эффективное… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
действующее значение — efektinė vertė statusas T sritis fizika atitikmenys: angl. effective value vok. Effektivwert, m rus. действующее значение, n; эффективное значение, n pranc. valeur effective, f; valeur réelle, f … Fizikos terminų žodynas
ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ — ср. квадратичное за период значение переменного тока, напряжения, эдс, магнитодвижущей силы, магн. потока и т. п. Д. з. синусоидального тока и напряжения в кв. корень из 2 раз меньше их амплитудных значений … Естествознание. Энциклопедический словарь
действующее значение тока — Среднеквадратичное значение периодического электрического тока за период. Примечание — Аналогично определяют действующие значения периодических электрического напряжения, электродвижущей силы, магнитного потока и т. д. [ГОСТ Р 52002 2003]… … Справочник технического переводчика
действующее значение периодической составляющей тока отключения выключателя — Iо.п Действующее значение периодической составляющей тока отключения в момент размыкания контактов [ГОСТ Р 52565 2006] Тематики выключатель, переключательвысоковольтный аппарат, оборудование … Справочник технического переводчика
действующее значение нагрузки — эффективное значение нагрузки — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы эффективное значение нагрузки… … Справочник технического переводчика
действующее значение периодической составляющей тока короткого замыкания рабочей частоты в электроустановке — Среднее квадратическое значение периодической составляющей тока короткого замыкания рабочей частоты в электроустановке за период, середина которого есть рассматриваемый момент времени [ГОСТ 26522 85] Тематики электробезопасность … Справочник технического переводчика

Что такое действующее значение силы тока.

Действующие значения силы тока и напряжения

Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока.

Действующим илиэффективным значением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе.

. Переменный ток можно считать постоянным только в течение очень малых промежутков времени

. Поделим период колебанийна очень большое число малых промежутков времени

. Количество теплоты

, выделяемое на сопротивленииза время

. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:

Сила тока в цепи изменяется по синусоидальному закону

Опуская вычисления, связанные с интегрированием, запишем окончательный результат

Если бы по цепи шёл некоторый постоянный ток , то за время, равное, выделилось бы тепло

. По определению постоянный ток, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока

. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов

(4. 28)

Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током:

(4.29)

Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В.

4.4.5. Мощность в цепи переменного тока

Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам:

Тогда мгновенное значение мощности, выделяемой на участке цепи,

Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний):

С использованием известной тригонометрической формулы

Величину

усреднять не нужно, так как она не зависит от времени, следовательно:

За длительное время значение косинуса много раз успевает измениться, принимая как отрицательные, так и положительные значения в пределах от (1) до 1. Понятно, что среднее во времени значение косинуса равно нулю

, поэтому

(4.30)

Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим

. (4.31)

Мощность, выделяемая на участке цепи с переменным током, зависит от эффективных значений тока и напряжения и сдвига фаз между током и напряжением . Например, если участок цепи состоит из одного только активного сопротивления, то

. Если участок цепи содержит только индуктивность или только ёмкость, то

д. Именно по той причине, что на индуктивном и ёмкостном сопротивлениях средняя расходуемая генератором энергия равна нулю, их назвали реактивными. На активном же сопротивлении средняя мощность отлична от нуля. Другими словами провод с сопротивлением при протекании по нему тока нагревается. И энергия, выделяемая в виде тепла, назад в генератор уже не возвращается.

Если участок цепи содержит несколько элементов, то сдвига фаз может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27).

Пример 4.7. К генератору переменного синусоидального тока подключён резистор с сопротивлением. Во сколько раз изменится средняя мощность, расходуемая генератором, если к резистору подключить катушку с индуктивным сопротивлением

а) последовательно, б) параллельно (рис. 4.10)? Активным сопротивлением катушки пренебречь.

Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность

(см. формулу (4.30)).

Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора:

. Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора

В результате средняя расходуемая генератором мощность

Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза.

Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора

. Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора

Тогда средняя мощность, расходуемая генератором

Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.

Как известно, переменная э.д.с. индукции вызывает в цепи переменный ток. При наибольшем значении э.д.с. сила тока будет иметь максимальное значение и наоборот. Это явление называется совпадением по фазе. Несмотря на то что значения силы тока могут колебаться от нуля и до определенного максимального значения, имеются приборы, с помощью которых можно замерить силу переменного тока.

Характеристикой переменного тока могут быть действия, которые не зависят от направления тока и могут быть такими же, как и при постоянном токе. К таким действиям можно отнести тепловое. К примеру, переменный ток протекает через проводник с заданным сопротивлением. Через определенный промежуток времени в этом проводнике выделится какое-то количество тепла. Можно подобрать такое значение силы постоянного тока, чтобы на этом же проводнике за то же время выделялось этим током такое же количество тепла, что и при переменном токе. Такое значение постоянного тока называется действующим значением силы переменного тока.

В данное время в мировой промышленной практике широко распространен трехфазный переменный ток , который имеет множество преимуществ перед однофазным током. Трехфазной называют такую систему, которая имеет три электрические цепи со своими переменными э.д.с. с одинаковыми амплитудами и частотой, но сдвинутые по фазе относительно друг друга на 120° или на 1/3 периода. Каждая такая цепь называется фазой.

Для получения трехфазной системы нужно взять три одинаковых генератора переменного однофазного тока, соединить их роторы между собой, чтобы они не меняли свое положение при вращении. Статорные обмотки этих генераторов должны быть повернуты относительно друг друга на 120° в сторону вращения ротора. Пример такой системы показан на рис. 3.4.б.

Согласно вышеперечисленным условиям, выясняется, что э.д.с., возникающая во втором генераторе, не будет успевать измениться, по сравнению с э.д.с. первого генератора, т. е. она будет опаздывать на 120°. Э.д.с. третьего генератора также будет опаздывать по отношению ко второму на 120°.

Однако такой способ получения переменного трехфазного тока весьма громоздкий и экономически невыгодный. Чтобы упростить задачу, нужно все статорные обмотки генераторов совместить в одном корпусе. Такой генератор получил название генератор трехфазного тока (рис. 3.4.а). Когда ротор начинает вращаться, в каждой обмотке возникает

а) б)

Рис. 3.4. Пример трехфазной системы переменного тока

а) генератор трёхфазного тока; б) с тремя генераторами;

изменяющаяся э.д.с. индукции. Из-за того что происходит сдвиг обмоток в пространстве, фазы колебаний в них также сдвигаются относительно друг друга на 120°.

Для того чтобы подсоединить трехфазный генератор переменного тока к цепи, нужно иметь 6 проводов. Для уменьшения количества проводов обмотки генератора и приемников нужно соединить между собой, образовав трехфазную систему. Данных соединений два: звезда и треугольник. При использовании и того и другого способа можно сэкономить электропроводку.

Соединение звездой

Обычно генератор трехфазного тока изображают в виде 3 статорных обмоток, которые располагаются друг к другу под углом 120°. Начала обмоток принято обозначать буквами А, В, С , а концы – X, Y, Z . В случае, когда концы статорных обмоток соединены в одну общую точку (нулевая точка генератора), способ соединения называется «звезда». В этом случае к началам обмоток присоединяются провода, называемые линейными (рис. 3.5 слева).

Точно так же можно соединять и приемники (рис. 3.5., справа). В этом случае провод, который соединяет нулевую точку генератора и приемников, называется нулевой. Данная система трехфазного тока имеет два разных напряжения: между линейным и нулевым проводами или, что то же самое, между началом и концом любой обмотки статора. Такая величина называется фазным напряжением (Uл ). Поскольку цепь трехфазная, то линейное напряжение будет в v3 раз больше фазного, т. е.: Uл = v3Uф.

Соединение треугольником.

Рисунок 3.6. Пример соединения треугольником

При использовании данного способа соединения конец X первой обмотки генератора подключают к началу В второй его обмотки, конец Y второй обмотки – к началу С третьей обмотки, конец Z третьей обмотки – к началу А первой обмотки. Пример соединения показан на рис. 3.6. При данном способе соединения фазных обмоток и подключении трехфазного генератора к трехпроводной линии линейное напряжение по своему значению сравнивается с фазным: Uф = Uл

Контрольные вопросы

1. Перечислите основные параметры, характеризующие переменный ток.

2. Дайте определение частоты и единицы её измерения.

3. Дайте определение амплитуды и единицы её измерения.

4. Дайте определение периода и единицы его измерения.

5. Отличие простейшего генератора трёхфазного тока от генератора однофазного тока.

6. Что такое фаза?

7. Что представляет собой ротор генератора трёхфазного тока?

8. Почему сдвинуты по фазе обмотки статора генератора трёхфазного тока?

9. Особенность симметричной системы трёх фаз.

10. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «звезда».

11. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «треугольник».

3.2. Виды сопротивлений в цепях переменного тока

В цепях переменного тока сопротивления разделяют на активные и реактивные.

В активных сопротивлениях , включенных в цепь переменного тока, электрическая энергия преобразуется в тепловую. Активным сопротивлением R обладают, например, провода электрических линий, обмотки электрических машин и т.д.

В реактивных сопротивлениях электрическая энергия, вырабатываемая источником, не расходуется. При включении реактивного сопротивления в цепь переменного тока возникает лишь обмен энергией между ним и источником электрической энергии. Реактивное сопротивление создают индуктивности и ёмкости.

Если не учитывать взаимное влияние отдельных элементов электрической цепи, то в общем случае электрическая цепь синусоидального тока может быть представлена тремя пассивными элементами: активным сопротивлением R, индуктивностью L и емкостью C.

Активное сопротивление в цепи переменного тока .

При включении в цепь переменного тока активного сопротивления, ток и напряжение совпадают по фазе (рис. 3.7) и изменяются по одному и тому же cинусоидальному закону: u=U m sinωt . Они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис. 3.7.б).

Для цепи переменного тока, содержащей только активное сопротивление, закон Ома имеет такую же форму, как и для цепи постоянного тока: I=U/R.

Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения u : p=ui .

Рисунок 3.7. Схема включения в цепь переменного тока активного сопротивления R (a), кривые тока i , напряжения u и мощности p (б) и векторная диаграмма.

Из графика видно, что изменение мощности происходит с двойной частотой по отношению к изменению тока и напряжения, т.е. один период изменения мощности соответствует половине периода изменения тока и напряжения. Все значения мощности положительные, это означает, что энергия передается от источника к потребителю.

Средняя мощность Рcp , потребляемая активным сопротивлением, P=UI=I 2 R – это и есть активная мощность.

Под индуктивностью L будем понимать элемент электрической цепи (катушку индуктивности, потерями которой можно пренебречь), способный запасать энергию в своём магнитном поле, который не имеет активного сопротивления и ёмкостиС (рис.3.8).

При включении в цепь переменного тока индуктивности, изменяющийся ток непрерывно индуцирует в ней э.д.с. самоиндукции e L = LΔi/Δt, где Δi/Δt – скорость изменения тока.

Когда угол ωt равен 90° и 270° скорость изменения тока Δi/Δt =0, поэтому э.д.с. e L =0.

Скорость изменения тока будет наибольшей, когда угол ωt равен 0°, 180° и 360°. В эти минуты времени э.д.с. имеет наибольшее значение.

Кривая мощности представляет собой синусоиду, которая изменяется с двойной частотой по сравнению с частотой изменения тока и напряжения. Мощность имеет положительные и отрицательные значения, т.е. возникает непрерывный колебательный процесс обмена энергией между источником и индуктивностью.

Рисунок 3.8. Схема включения в цепь переменного тока индуктивности (а), кривые тока i , напряжения u , э.д.с. e L (б) и векторная диаграмма (в)

Э.д.с. самоиндукции согласно правилу Ленца направлена так, чтобы препятствовать изменению тока. В первую четверть периода, когда ток увеличивается, э.д.с. имеет отрицательное значение (направлена против тока).

Во вторую четверть периода, когда ток уменьшается, э.д.с. имеет положительное значение (совпадает по направлению с током).

В третью четверть периода ток меняет своё направление и увеличивается, поэтому э.д.с. направлена против тока и имеет положительное значение.

В четвёртую четверть периода ток уменьшается и э.д.с. самоиндукции стремится поддержать прежнее положение тока и имеет отрицательное значение. В результате ток отстает от напряжения по фазе на угол 90 О.

Сопротивление катушки или проводника переменному току, вызванное действием э.д.с. самоиндукции, называется индуктивным сопротивлением Х L [Ом]. Индуктивное сопротивление не зависит от материала катушки и от площади поперечного сечения проводника.

В цепях переменного тока катушки индуктивности соединяют последовательно и параллельно.

При последовательном соединении катушек эквивалентная индуктивностьLэ и эквивалентное индуктивное сопротивление X L э будут равны:

Lэ=L 1 +L 2 +… X L э=X L 1 +X L 2 +…

При параллельном соединении катушек:

1/Lэ=1/L 1 +1/L 2 +… 1/X L э=1/X L 1 +1/X L 2 +…

Контрольные вопросы

1. Какие виды сопротивления в цепях переменного тока Вы знаете?

2. Что значит активное сопротивление?

3. Что такое реактивное сопротивление?

4. Какие элементы цепи создают реактивное сопротивление?

5. Что такое активная мощность?

1. Дайте определение индуктивности.

2. Что происходит в первую четверть периода колебательного процесса обмена энергией между источником и индуктивностью?

3. Что происходит во вторую четверть периода колебательного процесса обмена энергией между источником и индуктивностью?

4. Дайте определение индуктивного сопротивления.

3.3. Конденсаторы. Ёмкость в цепи переменного тока

Конденсатор – устройство, способное накапливать электрические заряды.

Простейший конденсатор представляет собой две металлические пластины (электроды), разделенные диэлектриком.

Каждый конденсатор характеризуется номинальной емкостью и допустимым напряжением. Напряжение конденсатора указывают на корпусе, и превышать его нельзя. Конденсаторы различаются формой электродов (плоский), типом диэлектрика и ёмкостью (постоянной и переменной).

Cтраница 2

Действующим значением силы тока I называется сила постоянного тока, выделяющего в проводнике за то же время такое же количество теплоты, что и переменный ток.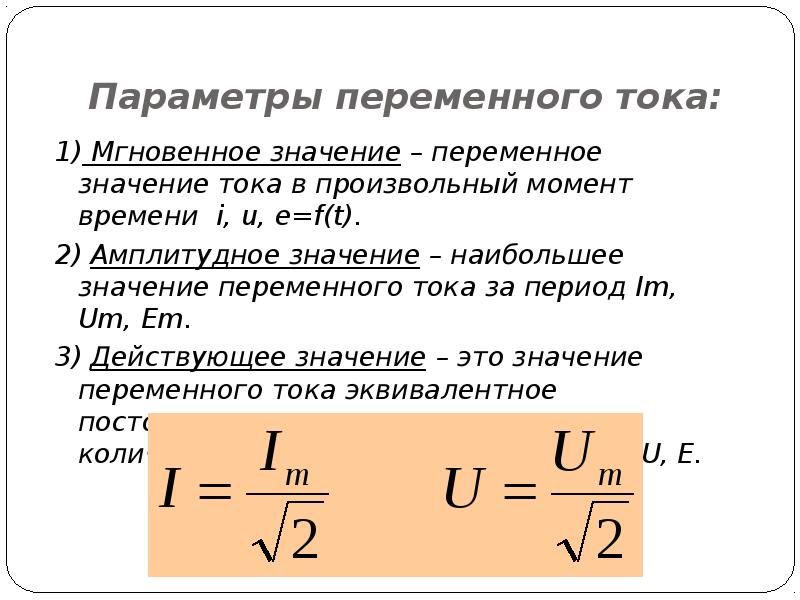

Как видно из рисунка, в каждый момент времени величины напряжения и силы тока принимают различные значения. Поэтому, чтобы судить о величине силы тока и напряжения переменного тока, пользуются действующим значением силы тока и напряжения. Чтобы определить действующее значение силы переменного тока, его приравнивают к силе постоянного тока, которое выделило бы в проводнике такое же количество тепла, как и переменный ток.

Трансформатор, содержащий в первичной обмотке 300 витков, включен в сеть переменного тока с действующим напряжением 220 В. Вторичная цепь трансформатора питает нагрузку с активным сопротивлением 50 Ом. Найти действующее значение силы тока во вторичной цепи, если падение напряжения во вторичной обмотке трансформатора, содержащей 165 витков, равно 50 В.

Таким образом, при замене операции извлечения корня сравнением время, за которое интегрируемый сигнал с ГЛИН станет равен интегралу от квадрата измеренной силы тока, пропорционально действующему значению силы тока. До этого К2 был открыт в течение времени т и пропускал на счетчик СИ импульсы с генератора тактовых импульсов ГТИ. Число импульсов TV / гтит записанное в СЧ, пропорционально действующему значению силы тока. Это число хранится в / 77, а по окончании цикла измерения отображается на ЦИ.

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения и средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Рх o jjFr В слУчае т – н – СУХОЙ лампы применяют способ термометра, подвешиваемого вблизи генераторной лампы, и отмечают его показание. Затем, разрывая цепь колебательного контура генератора, дают на сетку генераторной лампы положительный потенциал до тех пор, пока термометр не по. Беря в последнем случае величины 1а и Еа как исходные, определяем Рх из соотношения Рх1а Еа. Мощность в антенне определяется по ф-ле Рх – / /, где РЯ – мощность eW, ra – активное сопротивление антенны в Q и 1а – действующее значение силы тока в антенне в А. По скольку по современным международным нормам под мощностью передатчика принято понимать мощность в антенне, то упомянутая выше ф-ла определяет одновременно и мощность передатчика.

Тепловые измерители имеют наиболее широкое практич. Действие тепловых измерителей состоит в удлинении тонкой проволоки при нагревании ее проходящим по ней переменным током высокой частоты. Сам по себе эффект ограничивает пределы применимости таких измерителей токами от нескольких тА до 1 – 3 А в зависимости от материала тонкой проволоки, примененной в измерителе. Применяются сплавы серебра с платиной, платины с иридием и др. Если сплав применяется в виде проволоки, то она имеет диаметр сотых долей мм. При ленте толщина составляет 0 01 мм, ширина 3 мм и длина 25 – 30 мм. Удлинение нити нагреваемым током пропорционально квадрату действующего значения силы тока. Перемещение по шкале измерителя стрелки, связанной с той же проволокой с помощью особой подвижной системы, обычно пропорционально квадратному корню из действующей силы тока. Из-за этого шкалы тепловых измерителей имеют неравномерные интервалы между делениями.

В данном случае колебания тока являются гармоническими (график колебаний – синусоида) и вынужденными, поскольку параметры колебаний (частота, амплитуда) определяются внешним источником – генератором. Некоторые электротехнические устройства (например, колебательный контур) способны генерировать свободные гармонические колебания электрического тока. По левой ветви рамки – от нас и, поскольку в этом случае через клемму а течет ток в направлении, обратном показанному на рис. 12.1, ее полярность – минус. Поскольку при данном положении рамки сила тока имеет наибольшее значение, фаза колебаний может быть г / 2 или 3 / 2ir, в зависимости от того, какое направление тока в рамке мы принимаем за положительное. Сравнивая формулу (12.1) и заданную зависимость, нетрудно заметить, что 1т 10 А и ш 4тград / с. Далее, используя формулу (12.2), определяем частоту колебаний (отв. Используя закон Джоуля – Ленца (Q I2Rt), определяем действующее значение силы тока (отв.

Действительное значение тока. Эффективное, действующее напряжение, сила тока. Значение

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, – периодом Т. Для периодического тока имеем

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i – мгновенное значение тока ;

u – мгновенное значение напряжения ;

е – мгновенное значение ЭДС ;

р – мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ).

Амплитуда тока;

Амплитуда напряжения;

Амплитуда ЭДС.

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:

Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t =0): и –начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .

Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:

Векторное изображение синусоидально изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное ) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:

При расчете цепей переменного тока обычно пользуются понятием действующих (эффективных) значений переменного тока, напряжения и э. д. с.

Действующие значения тока, напряжения и э. д. с. обозначаются прописными буквами .

На шкалах измерительных приборов и технической документации также указываются действующие значения величин.

Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.

Количество тепла, выделенное переменным током в со противлении за бесконечно малый промежуток времени

а за период переменного тока Т

Приравняв Полученное выражение количеству тепла выделенному в том же сопротивлении постоянным током за то же время Т, получим:

Сократив общий множитель , получим действующее значение тока

Рис. 5-8. График переменного тока и квадрата тока.

На рис. 5-8 построена кривая мгновенных значений тока i и кривая квадратов мгновенных значений Площадь, ограниченная последней кривой и осью абсцисс, представляет собой в некотором масштабе величину, определяемую выражением Высота прямоугольника равновеликого площади, ограниченной кривой и осью абсцисс, равная среднему значению ординат кривой представляет собой квадрат действующего значения тока

Если ток изменяется по закону синуса, т. е.

Аналогично для действующих значений синусоидальных напряжений и э. д. с. можно написать:

Кроме действующего значения тока и напряжения, иногда пользуются еще понятием среднего значения тбка и напряжения.

Среднее значение синусоидального тока за период равно нулю, так как в течение первой половины периода определенное количество электричества Q проходит через поперечное сечение проводника в прямом направлении. В течение второй половины периода то же количество электричества проходит через сечение проводника в обратном направлении. Следовательно, количество электричества, прошедшее через сечение проводника за период, равно нулю, равно нулю и среднее за период значение синусоидального тока.

Поэтому среднее значение синусоидального тока вычисляют за полупериод, в течение которого ток остается положительным. Среднее значение тока равно отношению количества электричества, прошедшего через сечение проводника за половину периода, к продолжительности этого полупериода.

Лекции по ТОЭ/ №13 Действующее значение переменного тока.

Понятие действующего значения тока вводится в связи с необходимостью производства измерений. Что измерять у переменного тока? Если бы мы имели дело только с синусоидами – кривыми одной формы, то можно было бы измерять амплитуды. Но на практике встречаются самые разные кривые, и может оказаться так, что два различных по форме тока имеют одинаковые амплитуды, хотя очевидно, что на электрическую цепь они будут оказывать разное воздействие.

Поэтому наиболее целесообразно оценивать величину тока по той работе, которую он совершает. При такой оценке действие переменного тока сравнивается с аналогичным действием постоянного тока. Например, если некоторый переменный ток выделяет на участке цепи такое же количество тепла, что и постоянный ток силой 10 ампер, то говорят, что величина этого переменного тока составляет 10 ампер. Это значение тока и называют действующим.

Итак, действующим значением переменного тока называется численное значение такого постоянного тока, который за время, равное одному периоду, выделяет в сопротивлении такое же количество тепла, что и ток переменный..

Таким образом, для оценки величины переменного тока мы должны сделать следующее.

1.Определить количество теплоты, выделяющейся в сопротивлении R за время Т при протекании переменного тока i. Это количество теплоты равно:

2.Подобрать такой постоянный ток I, который за то же время Т в том же сопротивлении R выделяет такое же количество тепла. При постоянном токе оно равно: W=I 2 RT.

3. Приравнять W=W:

Последняя формула и определяет действующее значение переменного тока.

Пример 2.1. На вход некоторой цепи подается импульсное напряжение треугольной формы (рис. 2.4, а). Чему равно его действующее значение?

Пример 2.2. На рис. 2.4, б показана кривая напряжения на выходе схемы однофазного однополупериодного выпрямления. Чему равно действующее значение напряжения, если его амплитудное значение Um составляет 311 В?

Пример 2.3. Определить действующее значение синусоидального тока i=I m sin(ωt):

Рассмотренные примеры показывают, что действующее значение переменного тока зависит от его формы.

Желаем удачного изучения материала и успешной сдачи!

Значения действующего напряжения и силы тока. Определение. Соотношение с амплитудой для разной формы. (10+)

Понятие эффективных (действующих) значений напряжения и силы тока

Когда мы говорим о переменных напряжении или силе тока, особенно сложной формы, то встает вопрос о том, как их измерять. Ведь напряжение постоянно меняется. Можно измерять амплитуду сигнала, то есть максимум модуля значения напряжения. Такой метод измерения нормально подходит для сигналов относительно гладкой формы, но наличие коротких всплесков портит картину. Еще одним критерием выбора способа измерения является то, для каких целей делается измерение. Так как в большинстве случаев интерес представляет мощность, которую может отдать тот или иной сигнал, то применяется действующее (эффективное) значение.

Вашему вниманию подборка материалов:

Действующее (эффективное) значение для сигналов стандартной формы

Синусоидальный сигнал (синус, синусоида) [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 2 ]

Прямоугольный сигнал (меандр) [Действующее значение ] = [Амплитудное значение ]

Треугольный сигнал [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 3 ]

Закон Ома и мощность для действующих значений напряжения и силы тока

Эффективное значение напряжения измеряется в Вольтах, а силы тока в Амперах.

Для эффективных значений верен закон Ома: = / [Сопротивление нагрузки, Ом ]

[Рассеиваемая на омической нагрузке мощность, Вт ] = [Действующее значение силы тока, А ] * [Действующее значение напряжения, В ]

К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости , чтобы быть в курсе.

Если что-то непонятно, обязательно спросите!
Задать вопрос. Обсуждение статьи.

Еще статьи

Микроконтроллеры – пример простейшей схемы, образец применения. Фузы (…
Самая первая Ваша схема на микро-контроллере. Простой пример. Что такой фузы?…

Время переключения полевого транзистора. Емкость затвор – сток, исток….
Переключение полевого транзистора. Входные емкости. Встроенный диод. …

Повышающий импульсный преобразователь напряжения. Силовой ключ – бипол…
Как сконструировать повышающий импульсный источник питания. Как выбрать мощный т…

Удлинитель пульта дистанционного управления, ду, инфракрасного, ик…
Пульт ДУ работает только в условиях прямой видимости с дистанционно управляемым…

Цветомузыка, цветомузыкальное оборудование своими руками. Схема ЦМУ, к…
Как самому сделать цвето-музыку. Оригинальная конструкция цвето-музыкальной сист…

Магнитный усилитель – проектирование, формулы, расчет онлайн (online)….
Расчет магнитного усилителя. Формулы для проектирования….

Как сконструировать обратноходовый импульсный преобразователь. Как выбрать часто…

Пушпульный импульсный преобразователь напряжения. Выбор ключа – биполя…
Как сконструировать пуш-пульный импульсный источник питания. Как выбрать мощные…

Как определить действующее значение силы тока

Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.<2>dt>>.>

Содержание

Действующее значение в типичных случаях [ править | править код ]

Приведены формулы для электрического тока. Аналогичным образом определяются действующие значения ЭДС и напряжения.

Синусоида [ править | править код ]

I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , <displaystyle I=<frac <1><sqrt <2>>>cdot I_approx 0<,>707cdot I_,>

Прямоугольная форма [ править | править код ]

Для тока, имеющего форму однополярного прямоугольного импульса, действующее значение тока зависит от скважности:

I = I m D , <displaystyle I=I_<sqrt >,>

В частности, для тока, имеющего форму однополярного меандра (коэффициент заполнения 0,5):

I = I m 0 , 5 ≈ 0 , 707 ⋅ I m . <displaystyle I=I_<sqrt <0,5>>approx 0,707cdot I_.>

Для тока, имеющего форму двухполярного меандра:

I = I m . <displaystyle I=I_.>

Треугольная форма [ править | править код ]

Для тока треугольной и пилообразной формы (независимо от того, меняется ли направление тока):

I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . <displaystyle I=<frac <1><sqrt <3>>>cdot I_approx 0<,>577cdot I_.>

Трапециевидная форма [ править | править код ]

Для тока трапециевидной формы действующее значение можно определить разбив период на отрезки положительного фронта, действия максимального значения и отрицательного фронта:

I = I m t 1 + 3 t 2 + t 3 3 T , <displaystyle I=I_<sqrt <frac +3t_<2>+t_<3>><3T>>>,> 1>

Дугообразная форма [ править | править код ]

Для тока имеющего форму дуги (половины окружности):

I = I m 2 3 ≈ 0,816 ⋅ I m . <displaystyle I=I_<sqrt <frac <2><3>>>approx 0<,>816cdot I_.>

Дополнительные сведения [ править | править код ]

В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS или rms — root mean square — среднеквадратичное (значение).<2>dt>>.>

Содержание

Действующее значение в типичных случаях [ править | править код ]

Синусоида [ править | править код ]

I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , <displaystyle I=<frac <1><sqrt <2>>>cdot I_approx 0<,>707cdot I_,>

Прямоугольная форма [ править | править код ]

I = I m D , <displaystyle I=I_<sqrt >,>

В частности, для тока, имеющего форму однополярного меандра (коэффициент заполнения 0,5):

I = I m 0 , 5 ≈ 0 , 707 ⋅ I m . <displaystyle I=I_<sqrt <0,5>>approx 0,707cdot I_.>

Для тока, имеющего форму двухполярного меандра:

I = I m . <displaystyle I=I_.>

Треугольная форма [ править | править код ]

Для тока треугольной и пилообразной формы (независимо от того, меняется ли направление тока):

I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . <displaystyle I=<frac <1><sqrt <3>>>cdot I_approx 0<,>577cdot I_.>

Трапециевидная форма [ править | править код ]

I = I m t 1 + 3 t 2 + t 3 3 T , <displaystyle I=I_<sqrt <frac +3t_<2>+t_<3>><3T>>>,> 1>

Дугообразная форма [ править | править код ]

Для тока имеющего форму дуги (половины окружности):

I = I m 2 3 ≈ 0,816 ⋅ I m . <displaystyle I=I_<sqrt <frac <2><3>>>approx 0<,>816cdot I_.>

Дополнительные сведения [ править | править код ]

Электроизмерительные приборы (амперметры, вольтметры) для измерения в цепях переменного тока обычно градуируются так, чтобы их показания соответствовали действующему значению синусоидального тока или напряжения. При измерении несинусоидальных токов и напряжений приборы различных систем могут давать разные показания [1] .

Господа, в прошлой статье мы говорили про мощность и работу переменного тока. Напомню, что тогда мы считали ее через некоторый интеграл, а в самом конце статьи я вскользь сказал, что существуют способы облечения и без того нелегкой жизни и часто можно обойтись вообще без взятия интеграла, если знать про действующее значение тока. Сегодня про него и поговорим!

Господа, вероятно, для вас не станет секретом, что в природе существует большое число видов переменного тока: синусоидальный, прямоугольный, треугольный и так далее. И как их вообще можно сравнивать между собой? По форме? Хмм…Пожалуй, да. Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока.

Итак, действующее (или среднеквадратичное) значение переменного тока – это такая величина некоторого постоянного тока, который за время, равное периоду переменного тока выделит столько же тепла на резисторе, что и наш переменный ток. Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.

Итак, у нас есть переменный ток. Допустим, синусоидальный. У него своя амплитуда А_m и период T_период (ну или частота f). На фазу в данном случае пофиг, считаем ее равной нулю. Этот переменный ток течет через некоторый резистор R и на этом резисторе выделяется энергия. За один период T_период нашего синусоидального тока выделится вполне определенное количество джоулей энергии. Это число джоулей мы можем точно посчитать по формулам с интегралом, которые я приводил в прошлый раз . Допустим, мы насчитали, что за один период T_период синусоидального тока выделится Q джоулей тепла. А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе R за то же самое время T_период выделилось ровно такое же количество джоулей Q. Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока. А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли?

Итак, суть вопроса, надеюсь, стала понятной, поэтому давайте все сказанное выше переведем на язык математики. Как мы уже писали в прошлой статье , закон изменения мощности переменного тока равен

Количество выделившейся энергии при работе тока за время T_период – соответственно, равно интегралу за время периода T_период:

Господа, теперь нам надо взять этот интеграл. Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками .

Итак, как его нам брать? Ну, величины I_m 2 и R являются константами и их можно сразу вынести за знак интеграла. А для квадрата синуса нам надо применить формулу понижения степени из курса тригонометрии. Надеюсь, вы ее помните . А если нет, то напомню еще раз:

Теперь давайте разобьем интеграл на два интеграла. Можно воспользоваться тем, что интеграл от суммы или разности равен сумме или разности интегралов. В принципе, это очень даже логично, если вспомнить про то, что интеграл – это площадь.

Господа, у меня есть для вас просто отличнейшая новость. Второй интеграл равен нулю!

Почему это так? Да просто потому, что интеграл любого синуса/косинуса на величине, кратной его периоду, равен нулю. Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.

Итак, отбрасывая интеграл с косинусом, получаем

Ну и не надо быть большим гуру математики, чтобы сказать, что этот интеграл равен

И, таким образом, получаем ответ

Это мы получили количество джоулей, которое выделится на резисторе R при протекании через него синусоидального тока амплитудой I_m в течении периода T_период. Теперь, чтобы найти чему в данном случае равен действующий ток нам надо исходить из того, что на том же самом резисторе R за то же самое время T_период выделится то же самое количество энергии Q. Поэтому мы можем записать

Если не совсем понятно, откуда здесь взялась левая часть, рекомендую вам повторить статью про закон Джоуля-Ленца . А мы тем временем выразим действующее значение тока I _{действ.} из этого выражения, предварительно сократив все, что можно

Вот такой вот результат, господа. Действующее значение переменного синусоидального тока в корень из двух раз меньше его амплитудного значения. Хорошо запомните этот результат, это важный вывод.

Вообще говоря никто не мешает по аналогии с током ввести действующее значение напряжения. При этом у нас зависимость мощности от времени примет вот такой вид

Именно его мы будем подставлять под интеграл и выполнять все преобразования. Господа, каждый из вас может на досуге при желании это проделать, я же просто приведу конечный результат, поскольку он полностью аналогичен случаю с током. Итак, действующее значение напряжения синусоидального тока равно

Как видим, аналогия полнейшая. Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.

Подобным образом можно рассчитать действующее значение тока и напряжения для сигнала абсолютно любой формы: надо только лишь записать закон изменения мощности для этого сигнала и выполнить пошагово все вышеописанные преобразования.

Все вы, наверняка, слышали, что у нас в розетках напряжение 220 В. А каких вольт? У нас ведь теперь есть два термина – амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках – это действующее значение! Вольтметры и амперметры , включаемые в цепи переменного тока показывают именно действующие значения. А форму сигнала вообще и его амплитуду в частности можно посмотреть с помощью осциллографа. Ну, мы же уже говорили, что всем интересны деньги, то бишь работа тока, а не какая-то там непонятная амплитуда. Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать

Вот так вот, господа. В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.

Рисунок 1 – Закон изменения напряжения в розетках

И специально для вас, господа, я посмотрел напряжение в розетке с помощью осциллографа. Смотрел я его через делитель напряжения 1:5. То есть форма сигнала полностью сохранится, а амплитуда сигнала на экране осциллографа будет в пять раз меньше, чем на самом деле в розетке. Зачем я так сделал? Да просто потому, что из-за большого размаха входного напряжения картинка целиком не влезает на экран осциллографа.

ВНИМАНИЕ! Если у вас нет достаточного опыта работы с высоким напряжением, если вы абсолютно четко не представляете себе как могут течь токи при измерениях в гальванически не отвязанных от сети цепях, настоятельно не рекомендую проводить подобный эксперимент самостоятельно, это опасно! Дело в том, что при подобных измерениях с помощью осциллографа, подключенного к розетке с заземлением есть очень большой шанс что произойдет короткое замыкание через внутренние земли осциллографа и прибор сгорит без возможности восстановления! А если делать эти измерения с помощью осциллографа, подключенного к розетке без заземления, на его корпусе, кабелях и разъемах может присутствовать смертельно опасный потенциал! Это не шутки, господа, если нет понимания, почему это так, лучше этого не делать, тем более, что осциллограммы уже сняты и вы можете их наблюдать на рисунке 2.

Рисунок 2 – Осциллограмма напряжения в розетке (делитель 1:5)

На рисунке 2 мы видим, что амплитуда синуса составляет около 62 вольт, а частота – ровно 50 Гц. Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна

Как мы видим, результат измерения очень близок к теоретическому, не смотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это свидетельствует о том, что все наши расчеты верны.

На этом на сегодня все, господа. Сегодня мы узнали, что такое действующий ток и действующее напряжение, научились их рассчитывать и проверили результаты расчетов на практике. Спасибо что прочитали это и до новых статей!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Среднеквадратичное (действующее, эффективное) значение

Что же из себя представляет среднеквадратичное значение напряжения и как его замерить? Давайте разберем значение этого термина. Поможет нам в этих делах наш осциллограф OWON SDS6062 , Блок питания, а также ЛАТР (Лабораторный автотрансформатор). Для того, чтобы разобраться в этом, мы проведем простейший опыт.

Лампочка и постоянное напряжение

Для опытов нам также понадобится простая автомобильная лампа накаливания на напряжение 12 Вольт

Вот ее характеристики: рабочее напряжение U=12 Вольт, мощность Р = 21 Ватт.

Следовательно, зная мощность и напряжение лампы, можно узнать, какую силу тока будет потреблять лампочка. Из формулы P=IU, где I – сила тока, можно найти I. Значит I=P/U=21/12=1,75 Ампер.

Ладно, с лампочкой разобрались. Давайте ее зажжем. Для этого на нашем блоке питания выставляем рабочее напряжение для нашей лампы

Подаем напряжение с блока питания на лампу и вуаля!

Замеряем напряжение на клеммах-крокодилах блока питания с помощью мультиметра . Ровнехонько 12 Вольт, как и предполагалось.

К этим же клеммах цепляем и наш осциллограф

Смотрим осциллограмму:

Видите прямую линию? Это и есть осциллограмма постоянного напряжения. В течение времени у нас напряжение остается таким, каким и было и не меняется. Если посчитать, то можно вычислить, чему равняется напряжение. Так как одна клеточка у нас 5 Вольт (на фото внизу слева), то значит, наше напряжение 12 Вольт. Я также вывел это значение на дисплей осциллографа в самом нижнем левом углу: 12,03 Вольт. Все верно.

[quads id=1]

Замеряем силу тока. Как правильно замерить силу тока в цепи, можно узнать, прочитав статью как измерить ток и напряжение мультиметром?.

Получили 1,72 Ампер. А как вы помните, наше расчетное значение было 1,75 Ампер. Думаю, вину можно переложить на погрешность прибора или на лампочку 😉

Лампочка и переменное напряжение

Теперь начинается самое интересное. Берем наш ЛАТР

Ставим прибор на измерение переменного напряжения и выставляем с помощью крутилки ЛАТРа напряжение в 12 Вольт. Обратите внимание, что крутилка на мультиметре находится в диапазоне измерения переменного напряжения. Забегая вперед, скажу, что мультиметр измеряет среднеквадратичное напряжение.

Цепляем осциллограф к клеммах ЛАТРа, не забывая на осциллографе выставить замеры переменного напряжения и смотрим получившуюся осциллограмму:

Смотрим, сколько силы тока кушает наша лампочка. Все как положено, 1,71 Ампер.

Среднеквадратичное значение напряжения

Итак, что же у нас получилось? Как и постоянное напряжение, так и переменное напряжение зажигали одну и ту же лампочку, которая кушала одну и ту же мощность. Значит эта осциллограмма

и вот эта осциллограмма

Чем то похожи? Но чем???

Среднеквадратичное значение напряжения – это такое значение переменного напряжения, при котором нагрузка потребляет столько же силы тока, как и при постоянном напряжении. То есть лампочка у нас потребляла 1,71 Ампер и при постоянном токе и при переменном. То есть, в двух этих случаях, мощность, которую потребляла лампочка, была одинакова.

Также среднеквадратичное напряжение еще называют действующим или эффективным значением напряжения. С помощью несложных умозаключений, инженеры-электрики пришли к выводу действующее (оно же среднеквадратичное) напряжение синусоидального сигнала любой частоты равняется максимальной его амплитуде, поделенной на корень из двух

Стоп! Мы ведь не разобрали, что такое максимальная амплитуда! На осциллограмме максимальная амплитуда выглядит примерно вот так:

Если даже посчитать по клеточкам и посмотреть, чему равняется одна клеточка по вертикали (смотрим внизу слева, она равняется 5 Вольт), то U_max = 17 Вольт. Делим это значение на корень из двух. Я беру это значение как 1,41. Получаем, что среднеквадратичное значение равняется 17/1,41=12,06 Вольт. Ну что, все верно 😉

Значит, когда нам говорят, что напряжение в розетке равняется 220 Вольт, то мы то знаем, что на самом деле это среднеквадратичное напряжение. Максимальная амплитуда этих 220 Вольт равняется 220х1,41=310 Вольт.

Где же среднеквадратичное напряжение и максимальная амплитуда сигнала прячутся на табличке измерений? Да вот же они!

Vk – это и есть среднеквадратичное напряжение этого сигнала.

Ma – это и есть Umax.

Конечно, 16,6/1,41=11,8 Вольт, а он пишет 12,08 Вольт.

Урок 8. переменный электрический ток – Физика – 11 класс

Физика, 11 класс

Урок 8. Переменный электрический ток

Перечень вопросов, рассматриваемых на уроке:

1) Свойства переменного тока;

2) Понятия активного сопротивления, индуктивного и ёмкостного сопротивления;

3) Особенности переменного электрического тока на участке цепи с резистором;

4) Определение понятий: переменный электрический ток, активное сопротивление, индуктивное сопротивление, ёмкостное сопротивление.

Глоссарий по теме

Переменный электрический ток — это ток, периодически изменяющийся со временем.

Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю называют активным сопротивлением.

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Величину Х_C,обратную произведению ωC циклической частоты на электрическую ёмкость конденсатора, называют ёмкостным сопротивлением.

Величину Х_L, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. – М.: Дрофа, 2014. – С. 128 – 132.

Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.

Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004

Основное содержание урока

Сейчас невозможно представить себе нашу цивилизацию без электричества. Телевизоры, холодильники, компьютеры – вся бытовая техника работает на нем. Основным источником энергии является переменный ток.

Электрический ток, питающий розетки в наших домах, является переменным А что это такое? Каковы его характеристики? Чем же переменный ток отличается от постоянного? Об этом мы поговорим на данном уроке.

В известном опыте Фарадея при движении полосового магнита относительно катушки появлялся ток, что фиксировалось стрелкой гальванометра, соединенного с катушкой. Если магнит привести колебательное движение относительно катушки, то стрелка гальванометра будет отклоняться то в одну сторону, то в другую – в зависимости от направления движения магнита. Это означает, что возникающий в катушке ток меняет свое направление. Такой ток называют переменным.

Электрический ток, периодически меняющийся со временем по модулю и направлению, называется переменным током.

Переменный электрический ток представляет собой электромагнитные вынужденные колебания. Переменный ток в отличие от постоянного имеет период, амплитуду и частоту.

Сила тока и напряжение меняются со временем по гармоническому закону, такой ток называется синусоидальным. В основном используется синусоидальный ток. Колебания тока можно наблюдать с помощью осциллографа.

Если напряжение на концах цепи будет меняться по гармоническому закону, то и напряженность внутри проводника будет так же меняться гармонически. Эти гармонические изменения напряженности поля, в свою очередь вызывают гармонические колебания упорядоченного движения свободных частиц и, следовательно, гармонические колебания силы тока. При изменении напряжения на концах цепи, в ней с очень большой скоростью распространяется электрическое поле. Сила переменного тока практически во всех сечениях проводника одинакова потому, что время распространения электромагнитного поля превышает период колебаний.

Рассмотрим процессы, происходящие в проводнике, включенном в цепь переменного тока. Сопротивление проводника, в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным. При изменении напряжения на концах цепи по гармоническому закону, точно так же меняется напряженность электрического поля и в цепи появляется переменный ток.

При наличии такого сопротивления колебания силы тока и напряжения совпадают по фазе в любой момент времени.

𝒾 – мгновенное значение силы тока;

ℐ_m– амплитудное значение силы тока.

– колебания напряжения на концах цепи.

Колебания ЭДС индукции определяются формулами:

При совпадении фазы колебаний силы тока и напряжения мгновенная мощность равна произведению мгновенных значений силы тока и напряжения. Среднее значение мощности равно половине произведения квадрата амплитуды силы тока и активного сопротивления.

Часто к параметрам и характеристикам переменного тока относят действующие значения. Напряжение, ток или ЭДС, которая действует в цепи в каждый момент времени – мгновенное значение (помечают строчными буквами – і, u, e). Однако оценивать переменный ток, совершенную им работу, создаваемое тепло сложно рассчитывать по мгновенному значению, так как оно постоянно меняется. Поэтому применяют действующее, которое характеризует силу постоянного тока, выделяющего за время прохождения по проводнику столько же тепла, сколько это делает переменный.

U_m – амплитудное значение напряжения.

Действующие значения силы тока и напряжения:

Электрическая аппаратура в цепях переменного тока показывает именно действующие значения измеряемых величин.

Конденсатор включенный в электрическую цепь оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.

Величину Х_C, обратную произведению циклической частоты на электрическую ёмкость конденсатора, называют ёмкостным сопротивлением.

Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току.

Если включить в электрическую цепь катушку индуктивности, то она будет влиять на прохождение тока в цепи, т.е. оказывать сопротивление току. Это можно объяснить явлением самоиндукции.

X_L=ωL

Если частота равна нулю, то индуктивное сопротивление тоже равно нулю.

При увеличении напряжения в цепи переменного тока сила тока будет увеличиваться так же, как и при постоянном токе. В цепи переменного тока содержащем активное сопротивление, конденсатор и катушка индуктивности будет оказываться сопротивление току. Сопротивление оказывает и катушка индуктивности, и конденсатор, и резистор. При расчёте общего сопротивления всё это надо учитывать. Основываясь на этом закон Ома для переменного тока формулируется следующим образом: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

Если цепь содержит активное сопротивление, катушку и конденсатор соединенные последовательно, то полное сопротивление равно

Закон Ома для электрической цепи переменного тока записывается имеет вид:

Преимущество применения переменного тока заключается в том, что он передаётся потребителю с меньшими потерями.

В электрической цепи постоянного тока зная напряжение на зажимах потребителя и протекающий ток можем легко определить потребляемую мощность, умножив величину тока на напряжение. В цепи переменного тока мощность равна произведению напряжения на силу тока и на коэффициент мощности.

Мощность цепи переменного тока

P=IU cosφ

Величина cosφ – называется коэффициентом мощности

Коэффициент мощности показывает какая часть энергии преобразуется в другие виды. Коэффициент мощности находят с помощью фазометров. Уменьшение коэффициента мощности приводит к увеличению тепловых потерь. Для повышения коэффициента мощности электродвигателей параллельно им подключают конденсаторы. Конденсатор и катушка индуктивности в цепи переменного тока создают противоположные сдвиги фаз. При одновременном включении конденсатора и катушки индуктивности происходит взаимная компенсация сдвига фаз и повышение коэффициента мощности. Повышение коэффициента мощности является важной народнохозяйственной задачей.

Разбор типовых тренировочных заданий

1. Рамка вращается в однородном магнитном поле. ЭДС индукции, возникающая в рамке, изменяется по закону e=80 sin 25πt. Определите время одного оборота рамки.

Дано: e=80 sin 25πt.

Найти: T.

Решение:

Колебания ЭДС индукции в цепи переменного тока происходят по гармоническому закону

Согласно данным нашей задачи:

Время одного оборота, т.е. период связан с циклической частотой формулой:

Подставляем числовые данные:

Ответ: T = 0,08 c.

2. Чему равна амплитуда силы тока в цепи переменного тока частотой 50 Гц, содержащей последовательно соединенные активное сопротивление 1 кОм и конденсатор емкости С = 1 мкФ, если действующее значение напряжения сети, к которой подключен участок цепи, равно 220 В?

Дано:

ν=50 Гц,

R=1 кОм=1000 Ом,

C=1 мкФ=10^-6 Ф,

U=220 В.

Найти: I_m

Решение:

Напишем закон Ома для переменного тока:

I=U/Z

Для амплитудных значений силы тока и напряжения, мы можем записать I_m=U_m/Z?

Полное сопротивление цепи равно:

Подставляя числовые данные находим полное сопротивление Z≈3300 Ом. Так как действующее значение напряжения равно:

то после вычислений получаем I_m ≈0,09 Ом.

Ответ: I_m ≈0,09 Ом.

2. Установите соответствие между физической величиной и прибором для измерения.

Физические величины	Физические приборы
Сила тока	Омметр
Напряжение	Вольтметр
Сопротивление	Амперметр
Мощность	Ваттметр

Правильный ответ:

Физические величины	Физические приборы
Сила тока	Амперметр
Напряжение	Вольтметр
Сопротивление	Омметр
Мощность	Ваттметр

Действующее значение тока и напряжения кратко. Действующее значение напряжения

>> Активное сопротивление. Действующие значения силы тока и напряжения

§ 32 АКТИВНОЕ СОПРОТИВЛЕНИЕ. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ

Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.

Сила тока в цени с резистором. Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряже ния (рис. 4.11), а амплитуда силы тока определяется равенством

Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.

Как правило, нам нужно бывает знать среднюю мощ ностъ тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найчи среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой

P = I 2 R. (4.18)

На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.

Поэтому мгновенная моoность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой

P = i 2 R. (4.19)

Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение

График зависимости мгновенной мощности от времени изображен на рисунке 4.12, а. Согласно графику (рис. 4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем . Зато на протяжении следующей восьмой части периода, когда cos 2t

Средняя мощность равна, таким образом, первому члену в формуле (4.20):

Действующие значения силы тока и напряжения . Из формулы (4.21) видно, что величина есть среднее за период значение квадрата силы тока:

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы неременного тока. Действующее зртачепие силы неременного тока обозначается через I:

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты , что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:

Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем

Это закон Ома для участка цепи переменного тока с резистором.

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока:

P = I 2 R = UI.

Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.

1. Чему равна амплитуда напряжения в осветительных сетях переменного тока, рассчитанных на напряжение 220 В!
2. Что называют действующими значениями силы тока и напряжения!

Мякишев Г. Я., Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. – 17-е изд., перераб. и доп. – М. : Просвещение, 2008. – 399 с: ил.

Библиотека с учебниками и книгами на скачку бесплатно онлайн , Физика и астрономия для 11 класса скачать , школьная программа по физике, планы конспектов уроков

Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки

Свяжем эффективное значение тока с его амплитудным значением. Для этого рассчитаем количество теплоты, выделяемое на активном сопротивлении переменным током за время, равное периоду колебаний. Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи cсопротивлениемприпостоянном токеза время, определяется по формуле
. Переменный ток можно считать постоянным только в течение очень малых промежутков времени
. Поделим период колебанийна очень большое число малых промежутков времени
. Количество теплоты
, выделяемое на сопротивленииза время
:
. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:

Сила тока в цепи изменяется по синусоидальному закону

Опуская вычисления, связанные с интегрированием, запишем окончательный результат

Если бы по цепи шёл некоторый постоянный ток , то за время, равное, выделилось бы тепло
. По определению постоянный ток, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока
. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов

(4.28)

(4.29)

4.4.5. Мощность в цепи переменного тока

,
.

Тогда мгновенное значение мощности, выделяемой на участке цепи,

С использованием известной тригонометрической формулы

Величину
усреднять не нужно, так как она не зависит от времени, следовательно:

, поэтому
(4.30)

Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим

. (4.31)

Объяснить среднее нулевое значение мощности, выделяемой на индуктивности и ёмкости можно следующим образом. Индуктивность и ёмкость лишь заимствуют энергию у генератора, а затем возвращают её обратно. Конденсатор заряжается, а затем разряжается. Сила тока в катушке увеличивается, затем снова спадает до нуля и т. д. Именно по той причине, что на индуктивном и ёмкостном сопротивлениях средняя расходуемая генератором энергия равна нулю, их назвали реактивными. На активном же сопротивлении средняя мощность отлична от нуля. Другими словами провод с сопротивлением при протекании по нему тока нагревается. И энергия, выделяемая в виде тепла, назад в генератор уже не возвращается.

Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность

(см. формулу (4.30)).

Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора:
. Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора

В результате средняя расходуемая генератором мощность

Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора
. Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора

Тогда средняя мощность, расходуемая генератором

Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.

После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:

Аналогичные соотношения могут быть получены также для напряжения и ЭДС:

Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.

Учитывая, например, что действующее значение напряжения в нашей сети составляет 220В, можно определить амплитудное значение напряжения в сети: U m =U Ö2=311В. Соотношение между действующим и амплитудным значениями напряжений и токов важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.

Действующее значение переменного тока

Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел.

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i – мгновенное значение тока ;

u – мгновенное значение напряжения ;

е – мгновенное значение ЭДС ;

р – мгновенное значение мощности .

Амплитуда тока;

Амплитуда напряжения;

Амплитуда ЭДС.

Значения действующего напряжения и силы тока. Определение. Соотношение с амплитудой для разной формы. (10+)

Понятие эффективных (действующих) значений напряжения и силы тока

Вашему вниманию подборка материалов:

Действующее (эффективное) значение для сигналов стандартной формы

Прямоугольный сигнал (меандр) [Действующее значение ] = [Амплитудное значение ]

Треугольный сигнал [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 3 ]

Закон Ома и мощность для действующих значений напряжения и силы тока

Эффективное значение напряжения измеряется в Вольтах, а силы тока в Амперах.

Для эффективных значений верен закон Ома: = / [Сопротивление нагрузки, Ом ]

Если что-то непонятно, обязательно спросите!
Задать вопрос. Обсуждение статьи.

Еще статьи

Практика проектирования электронных схем. Самоучитель электроники….
Искусство разработки устройств. Элементная база радиоэлектроники. Типовые схемы….

Силовой мощный импульсный трансформатор, дроссель. Намотка. Изготовить…
Приемы намотки импульсного дросселя / трансформатора….

Силовой резонансный фильтр для получения синусоиды от инвертора…
Для получения синусоиды от инвертора нами был применен самодельный силовой резон…

Бесперебойник своими руками. ИБП, UPS сделать самому. Синус, синусоида…
Как сделать бесперебойник самому? Чисто синусоидальное напряжение на выходе, при…

Принцип работы, самостоятельное изготовление и наладка импульсного силового прео…

Преобразователь однофазного напряжения в трехфазное. Принцип действия,…
Принцип действия, сборка и наладка преобразователя однофазного напряжения в трех…

Электрическое напряжение. Амплитуда сигнала. Амплитудное. Вольт. Volt….
Понятие напряжения и разности электрических потенциалов. Амплитуда. Единицы изме…

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:

Значения аргументов синусоидальных функций и называются фазами синусоид, а значение фазы в начальный момент времени (t =0): и – начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.

Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:

Векторное изображение синусоидально изменяющихся величин

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:

Каждый из этих токов синусоидален и может быть представлен уравнением

Результирующий ток также будет синусоидален:

Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .

Действующее и среднее значения переменного тока и напряжения.

Среднее или среднеарифметическое значение Fcp произвольной функции времени f (t )за интервал времени Т определяется по формуле:

Численно среднее значение Fср равно высоте прямоугольника, равновеликого по площади фигуре, ограниченной кривой f (t ), осью t и пределами интегрирования 0 – Т (рис. 35).

Для синусоидальной функции среднее значение за полный период Т (или за целое число полных периодов) равно нулю, так как площади положительной и отрицательной полуволн этой функции равны. Для переменного синусоидального напряжения определяют среднее по модулю значение за полный период Т или среднее значение за половину периода (Т /2) между двумя нулевыми значениями (рис. 36) :

Ucp = Um∙ sinwt dt = 2R . Таким образом, количественные параметры электрической энергии на переменном токе (количество энергии, мощность) определяются действующими значениями напряжения U и тока I . По этой причине в электроэнергетике все теоретические расчеты и экспериментальные измерения принято выполнять для действующих значений токов и напряжений. В радиотехнике и в технике связи, наоборот, оперируют максимальными значениями этих функций.

Приведенные выше формулы для энергии и мощности переменного тока полностью совпадают с аналогичными формулами для постоянного тока. На этом основании можно утверждать, что энергетически постоянному току эквивалентно действующее значение переменного тока.

Что берется за действующее значение силы переменного тока и переменного напряжения

что берется за действующее значение силы переменного тока и переменного напряжения?

Боевое яйцо

Переменный ток, в широком смысле электрический ток, изменяющийся во времени. Обычно в технике под П. т. понимают периодический ток, в котором среднее значение за период силы тока и напряжения равно нулю.

Переменные токи и переменные напряжения постоянно изменяются по величине. В каждое другое мгновение у них другая величина. Возникает вопрос, как же их измерять? Для их измерения введено понятие действующее значение.

Действующим или эффективным значением переменного тока называют величину такого постоянного тока, который по своему тепловому действию равноценен данному переменному току.

Действующим или эффективным значением переменного напряжения называют величину такого постоянного напряжения, которое по своему тепловому действию равноценно данному переменному напряжению.

Все переменные токи и напряжения в технике измеряются в действующих значениях. Приборы измеряющие переменные величины показывают их действующее значение.

Вопрос: напряжение в электросети 220 В, что это значит?

Это значит, что источник постоянного напряжения с напряжением 220 В оказывает такое же тепловое действие как и электросеть.

Действующее значение тока или напряжения синусоидальной формы в 1,41 раз меньше амплитуды этого тока или напряжения.

Пример: Определить амплитуду напряжения электросети с напряжением 220 В.

Амплитуда равна 220 * 1,41=310,2 В.

Переменный синусоидальный ток в течение периода имеет разные секундные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?

При расчетах цепей переменного тока, также при электронных измерениях неловко воспользоваться моментальными либо амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Не считая того, об электронном эффекте временами изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.

Более комфортным оказалось введение понятий так именуемых действующих значений тока и напряжения . В базу этих понятий положено термическое (либо механическое) действие тока, не зависящее от его направления.

— это значение неизменного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.

Для оценки деяния, производимого переменным током, мы сравним его деяния с термическим эффектом неизменного тока.

Мощность Р неизменного тока I , проходящего через сопротивление r , будет Р = Р 2 r .

Мощность переменного тока выразится как средний эффект моментальной мощности I 2 r за целый период либо среднее значение от (Im х sinωt ) 2 х r за то же время.

Пусть среднее значение t2 за период будет М. Приравнивая мощность неизменного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √ M ,

Величина I именуется действующим значением переменного тока.

Среднее значение i2 при переменном токе определим последующим образом.

Построим синусоидальную кривую конфигурации тока. Возведя в квадрат каждое секундное значение тока, получим кривую зависимости Р от времени.

Обе половины этой кривой лежат выше горизонтальной оси, потому что отрицательные значения тока (-i ) во 2-ой половине периода, будучи построены в квадрат, дают положительные величины.

Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное с помощью высшей арифметики, будет равно 1/2I 2 m . Как следует, М = 1/2I 2 m

Потому что действующее значение I переменного тока равно I = √ M , то совсем I = Im / √ 2

Аналогично зависимость меж действующим и амплитудным значениями для напряжения U и Е имеет вид:

U = Um / √ 2 , E= Em / √ 2

Действующие значения переменных величин обозначаются строчными знаками без индексов (I , U, Е).

На основании произнесенного выше можно сказать, что действующее значение переменного тока равно такому неизменному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, демонстрируют действующие значения тока либо напряжения.

При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √ 2 раз. От этого размещение векторов на диаграмме не меняется.

Школа для электрика

Integrated Publishing – Ваш источник военных спецификаций и образовательных публикаций

Администрация – Навыки, процедуры, обязанности военнослужащих и т. Д.

Продвижение – Военное продвижение по службе книги и др.

Аэрограф / Метеорология – Метеорология основы, физика атмосферы, атмосферные явления и др.
Руководство по аэрографии и метеорологии ВМФ

Автомобили / Механика – Руководства по техническому обслуживанию автомобилей, механика дизельных и бензиновых двигателей, руководства по автомобильным запчастям, руководства по запчастям дизельных двигателей, руководства по запчастям для бензиновых двигателей и т. Д.
Автомобильные аксессуары | Перевозчик, Персонал | Дизельные генераторы | Механика двигателя | Фильтры | Пожарные машины и оборудование | Топливные насосы и хранилище | Газотурбинные генераторы | Генераторы | Обогреватели | HMMWV (Хаммер / Хаммер) | и т.п…

Авиация – Принципы полета, авиастроение, авиационная техника, авиационные силовые установки, руководства по авиационным деталям, руководства по деталям самолетов и т. д.
Руководства по авиации ВМФ | Авиационные аксессуары | Общее техническое обслуживание авиации | Руководства по эксплуатации вертолетов AH-Apache | Руководства по эксплуатации вертолетов серии CH | Руководства по эксплуатации вертолетов Chinook | и т.д …

Боевой – Служебная винтовка, пистолет меткая стрельба, боевые маневры, органическое вспомогательное оружие и т. д.
Химико-биологические, маски и оборудование | Одежда и индивидуальное снаряжение | Инженерная машина | и т.д …

Дайвинг – Руководства по дайвингу и утилизации разного оборудования.

Чертежник – Основы, приемы, составление проекций, эскизов и др.

Инженерное дело – Основы и приемы черчения, черчение проекций и эскизов, деревянное и легкое каркасное строительство и т. Д.
Военно-морское дело | Программа исследования прибрежных заливных отверстий в армии | так далее…

Еда и кулинария – Руководства по рецептам и оборудованию для приготовления пищи.

Логистика – Логистические данные для миллионов различных деталей.

Математика – Арифметика, элементарная алгебра, предварительное исчисление, введение в вероятность и т. д.

Медицинские книги – Анатомия, физиология, пациент уход, оборудование для оказания первой помощи, аптека, токсикология и др.
Медицинские руководства ВМФ | Агентство регистрации токсичных веществ и заболеваний

MIL-SPEC – Правительственные MIL-Specs и другие сопутствующие материалы

Музыка – мажор и минор масштабные действия, диатонические и недиатонические мелодии, ритм биения, пр.

Ядерные основы – Теории ядерной энергии, химия, физика и др.
Справочники DOE

Фотография и журналистика – Теория света, оптические принципы, светочувствительные материалы, фотографические фильтры, копия редактирование, написание статей и т. д.
Руководства по фотографии и журналистике военно-морского флота | Армейская фотография Полиграфия и пособия по журналистике

Религия – Основные религии мира, функции поддержки поклонения, венчания в часовне и т. д.

Пиковое против среднего vs.Действующее значение напряжения

Термин «среднеквадратичное значение» означает «среднеквадратическое значение», также называемое эквивалентом переменного тока и постоянного напряжения.

Термин «среднеквадратичное значение» означает «среднеквадратическое значение», также называемое эффективным или тепловым значением переменного тока, эквивалентно напряжению постоянного тока, которое будет обеспечивать такое же количество тепловыделения в резисторе, как и напряжение переменного тока. если применяется к тому же резистору.

RMS не является «средним» напряжением, и его математическое отношение к пиковому напряжению зависит от типа формы сигнала.Среднеквадратичное значение – это квадратный корень из среднего (среднего) значения функции квадрата мгновенных значений.

Поскольку напряжение переменного тока повышается и понижается со временем, для получения заданного среднеквадратичного напряжения требуется большее напряжение переменного тока, чем для постоянного тока. Например, для достижения среднеквадратичного значения 120 вольт (0,707 x169) потребуется пиковое значение переменного тока 169 вольт.

В этом примере величина нагрева напряжения 169 переменного тока эквивалентна значению нагрева источника постоянного тока на 120 вольт. Большинство мультиметров, будь то вольтметры или амперметры, измеряют среднеквадратичное значение, принимая чисто синусоидальную форму волны.

Важные термины, которые следует запомнить

Пиковое напряжение (Vp)

Максимальное мгновенное значение функции, измеренное от нулевого напряжения. Для формы волны, показанной выше, пиковая амплитуда и пиковое значение одинаковы, поскольку среднее значение функции равно нулю вольт.

Пиковое напряжение (В пик-пик)

Полное напряжение между положительным и отрицательным пиками формы волны; то есть сумма величин положительного и отрицательного пиков.

RMS Напряжение (Vrms)

Среднеквадратичное или эффективное значение сигнала.

Среднее напряжение (Vavg)

Уровень формы волны, определяемый условием, что площадь, ограниченная кривой выше этого уровня, в точности равна площади, ограниченной кривой ниже этого уровня.

Важные уравнения, которые следует запомнить

Vp x 0,707 = Vrms
Vrms = 1,11 x Vavg
1.414 x Vrms = Vp
Vavg = 0,637 x Vp

Дополнительная литература / Источники

Мгновенное значение напряжения или тока – это индуцированное напряжение или ток, протекающий в любой момент во время цикл.Синусоидальная волна представляет собой серию этих значения. Мгновенное значение напряжения меняется от нуля при 0 ° до максимума при 90 °, обратно до нуля при 180 °, максимум в обратном направлении на 270 °, и снова до нуля на 360 °. Любая точка на синусоиде считается мгновенным значением напряжения.

Пиковое значение

Пиковое значение – это наибольшее мгновенное значение. В наибольшее положительное значение возникает, когда синусоидальная волна напряжения составляет 90 °, а наибольшее отрицательное значение происходит при 270 °.Максимальное значение 1,41 раза эффективное значение. Это так называемые пиковые значения.

Эффективное значение

Действующее значение также известно как среднеквадратичное значение или среднеквадратичное значение, которое относится к математическому процессу по которому выводится значение. Большинство вольтметров переменного тока при использовании будет отображать эффективное или среднеквадратичное значение. Действующее значение меньше максимального значения, так как равняется 0,707 максимальному значению.

Эффективное значение синусоиды на самом деле является мерой теплового эффекта синусоидальной волны.Фигура 10-107 показано, что происходит, когда резистор подключен к источнику переменного напряжения. В иллюстрации A, некоторое количество тепла выделяется мощность в резисторе. На рисунке B показано то же самое. резистор теперь вставлен в источник постоянного напряжения. В значение источника постоянного напряжения теперь можно регулировать так что резистор рассеивает такое же количество тепла, как это было, когда он был в цепи переменного тока. Среднеквадратичное или эффективное значение синусоидальной волны равно постоянное напряжение, выделяющее такое же количество тепла как синусоидальное напряжение.

Пиковое значение синусоиды может быть преобразовано в соответствующее среднеквадратичное значение, используя следующие отношение.

Может применяться как к напряжению, так и к току.

Алгебраическое преобразование формулы и решение для Vp также может определять пиковое напряжение. Результирующий формула:

В (размах) = 1,414 В (среднекв.)

Таким образом, значение 110 вольт дано для переменного тока. в дома поставлено всего 0.707 от максимального напряжения этого предложения. Максимальное напряжение примерно 155 вольт (110 1,41 = максимум 155 вольт).

При исследовании переменного тока используются любые значения. для тока или напряжения считаются действующими значениями если не указано иное, и на практике только используются действующие значения напряжения и тока. Аналогично вольтметры и амперметры переменного тока измерить эффективное значение.

Среднеквадратичное значение – обзор

8.4.4.2.2 Временная область

В главе 5 тома I мы представили подход во временной области к решению проблемы случайного отклика; в главе 7 тома I мы расширили обсуждение до систем с несколькими степенями свободы. Процедура буфета во временной области проста и относительно проста по концепции. Он основан на предположении, что анализ «шведского стола» со стационарными случайными и эргодическими силами и численное решение во временной области, если оно достаточно продолжительное, даст соответствующие статистические результаты.Действительно, Broussinos и Kabe (1990) использовали подход во временной области для проверки соответствующего решения в частотной области, где мощность возбуждения и кросс-мощностные спектральные плотности были получены из временных диаграмм силы удара.

Историю времени возбуждения буфета можно составить двумя способами. Первый из них, как обсуждалось выше, где графики силы во времени генерируются из данных испытаний в аэродинамической трубе. Второй устанавливает хронологию на основе существующих функций спектральной плотности мощности возбуждения.Поскольку площадь под функцией спектральной плотности мощности является среднеквадратичным значением, мы можем вычислить среднеквадратичное значение для каждой спектральной линии, предполагая, что она охватывает площадь на полпути к соседним спектральным линиям. Затем мы можем приравнять каждый из них к синусоидальной функции с соответствующей частотой и амплитудой спектральной линии, что даст такое же среднеквадратичное значение. Мы не можем установить с помощью функции спектральной плотности мощности фазовое соотношение между ее различными спектральными компонентами. Однако, поскольку мы знаем, что история времени является случайной по своей природе, предполагая, что фазовое соотношение между различными гармоническими составляющими является случайным, мы можем разработать случайную историю времени, которая имеет желаемую функцию спектральной плотности мощности.

Среднеквадратичное значение синусоидальной функции амплитуды A равно

(8.4-74) A2¯ = 1T∫0TA2sin2ωtdt = A2 / 2

Следовательно, при данном среднеквадратичном значении спектральной линии эквивалентная синусоидальная амплитуда будет быть квадратным корнем из удвоенного значения. Суммирование синусоидальных функций, по одной для каждой спектральной линии, при назначении каждой фазового угла θj, оттянутого случайным образом между 0 и 2π, дает искомую временную диаграмму,

(8,4-75) f (t) = 2∑j = 1Nfj2¯sin (ωjt + θj)

где fj2¯ – это среднеквадратичное значение, полученное из функции спектральной плотности мощности для j-й спектральной линии.Обратите внимание, что N должно быть достаточно большим, а спектральные линии должны доходить до частоты Найквиста. Это может потребовать добавления дополнительных спектральных линий к спектральной плотности мощности путем интерполяции между существующими частотами.

Учитывая хронологию функции форсирования буфета, полученную непосредственно из испытаний в аэродинамической трубе или выведенную из функций спектральной плотности мощности, теперь мы можем численно интегрировать уравнения движения, используя процедуры из тома I,

(8.4-76) [I] {q¨ (t)} + ([D] + [N˙]) {q˙ (t)} + ([ωn2] – [N]) {q (t)} = [ ϕ] T {f (t)}

Ур. (8.4-76) был получен в разделе 8.4.2 этой главы и включает аэродинамическое демпфирование и жесткость [N˙] и [N], соответственно. Опыт показывает, что эти термины не имеют значения при вычислении ответов о буфете и поэтому могут быть исключены. Однако при желании условия всегда можно сохранить. Кроме того, поскольку функции принуждения имеют нулевое значение , моделирование автопилота не требуется для стабильности, хотя его включение обычно увеличивает эквивалентное демпфирование в нижних режимах .Временные истории, полученные с помощью формул. (8.4-76) теперь можно использовать для вычисления хронологии интересующих физических величин, таких как нагрузки, смещения и ускорения. По ним можно вычислить среднеквадратические значения каждого параметра; для нагрузок, например, вычисление будет:

(8.4-77) {L2¯} = 1T∫0T {L2 (t)} dt

, где {L2¯} содержит среднеквадратичные значения, полученные из историй времени загрузки , {L (t)}, а T – длительность временных историй. Квадратные корни из членов в {L2¯} являются искомыми среднеквадратичными значениями.

Как только истории времени отклика буфета станут доступны, их можно будет использовать либо непосредственно в комбинации Монте-Карло с историями времени других участников, такими как реакции турбулентности / порыва, либо они могут быть использованы для получения среднеквадратичных значений, которые могут быть используется напрямую или в уравнении сочетания нагрузок. В подходе Монте-Карло, например, сегменты историй времени отклика «шведского стола» будут выбираться случайным образом из более длинных временных историй и объединяться со случайно выбранными, но более короткими историями времени отклика турбулентности / порыва; другие участники также могут быть включены.Пиковые значения будут извлечены из каждой комбинации, разработаны гистограммы и определены уровни статистической изоляции. В подходе уравнения комбинации нагрузок среднеквадратичные значения будут использоваться для определения соответствующих средних значений распределения Рэлея и дисперсных частей, которые затем могут быть объединены с соответствующими значениями от других участников. Оба подхода подробно обсуждаются в главе 7.

Продолжительность истории времени, T, требует дальнейшего обсуждения.В подходе «временной области» предполагается, что временные истории вынуждающих функций и, следовательно, истории времени отклика являются стационарными, случайными и эргодическими. Это, следовательно, требует, чтобы продолжительность вынуждающих функций была достаточно большой для получения сходящихся статистических результатов. Требуемая длина может быть установлена путем сравнения среднеквадратичных значений, полученных для увеличения продолжительности временной истории. Например, можно начать с временной истории, скажем, 10 с и вычислить среднеквадратичное значение отклика, затем увеличить продолжительность и пересчитать среднеквадратичное значение.Это можно повторять до тех пор, пока значения не сойдутся в пределах желаемого допуска. Следует отметить, что чем ниже основная частота упругой моды системы, тем длиннее должна быть временная история. Успешно использовались 30–60-секундные хронологические диаграммы, а для систем с очень низкими фундаментальными частотами моды длительности временных хронологий пришлось увеличить до 100 с.

В главе 5 тома I среднеквадратичные значения хронологий бесконечной продолжительности получены аналитически и показаны как эквивалентные значениям, полученным в частотной области.Кроме того, в главе содержится закрытое решение вопроса о продолжительности. Получено соотношение, которое устанавливает длину функции принуждения, которая требуется, так что в среднем средний квадрат находится в пределах указанного допуска решения бесконечной длины. Отношение является функцией собственной частоты, связанной с любой данной модой .

Среднеквадратичные значения, вычисленные, как описано выше, будут очень близки к значениям, полученным путем извлечения квадратного корня из площади под соответствующими кривыми спектральной плотности мощности, полученными в анализе частотной области, который использовал спектральную плотность мощности и спектральную плотность перекрестной мощности. форсирующие функции, полученные из временных историй форсирующих функций.Однако выполнение анализа во временной области дает ряд преимуществ:

(1): Временные истории различных нагрузок могут быть объединены, и синхронизация по времени будет правильной. Затем можно вычислить среднеквадратичные значения с объединенной историей времени. Это может уменьшить ненужный консерватизм за счет использования временной фазировки, чего нельзя добиться с помощью частотной области, если комбинация нагрузок является нелинейной, например, комбинируя две ортогональные компоненты нагрузки.
(2): Размер вычислительной задачи может быть уменьшен, поскольку для вычисления правильных нагрузок в частотной области следует использовать кросс-спектры вынуждающих функций. Они часто игнорируются или используются лишь частично для экономии вычислительных ресурсов. Подход во временной области включает строгое правильное фазирование между всеми функциями форсирования при условии, что они были измерены в одном и том же испытании в аэродинамической трубе.
(3): Историю времени отклика можно использовать в последующих анализах, таких как комбинация нагрузок Монте-Карло.
(4): Доступность хронологии имеет большое значение для понимания физического поведения системы.

Измерение действующих значений напряжения и тока

ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ (ТОКА)

Стандартные классические измерения значений напряжения (тока) основаны на двух основных методах: «средний» или «эффективный».
«Среднее» значение функции времени – это чистая площадь функции, вычисленная за определенный интервал времени, деленная на этот интервал времени.
В частности,
(Уравнение 1)
Если напряжение (ток) является постоянным или периодическим, то измерение его среднего значения не зависит от интервала, в течение которого выполняется измерение. Если, с другой стороны, функция напряжения (тока) неограниченно возрастает со временем, среднее значение зависит от интервала измерения и не обязательно будет постоянным, т. Е. Среднего значения не существует. К счастью, в практическом мире электричества значения напряжения (тока) не растут безмерно и, следовательно, имеют хорошие средние значения.Это результат того факта, что реальные источники напряжения (тока) обычно либо; (1) батареи с постоянными или медленно (экспоненциально) убывающими значениями, (2) ограниченные синусоидальные функции времени или (3) комбинации вышеперечисленного. Синусоидальные функции с постоянной амплитудой имеют чистое нулевое среднее значение по временным интервалам, которые равны целым кратным синусоидальному периоду. Более того, средние значения можно вычислять по бесконечному количеству интервалов, которые не равны синусоидальному периоду.Эти средние значения также равны нулю. Хотя среднее значение ограниченной синусоидальной функции равно нулю, «эффективное» значение не равно нулю. Например, электрические водонагреватели очень хорошо работают на синусоидальных напряжениях с нулевыми средними значениями.
ЭФФЕКТИВНОЕ ЗНАЧЕНИЕ
«Эффективное» значение симметричных периодических функций напряжения (тока) от времени основано на концепции «нагревательной способности». Рассмотрим испытательное приспособление, показанное на рисунке 1.

Рисунок 1: Испытательное приспособление
Этот сосуд изолирован и заполнен некоторой стабильной жидкостью (например, трансформаторным маслом), способной достичь термодинамического равновесия.Если к внутреннему нагревателю сосуда приложить напряжение постоянного тока Vx, температура жидкости повысится. В конце концов, электрическая энергия, приложенная к этому сосуду, установит состояние равновесия, при котором подводимая энергия равна потерянной энергии (теплу), а жидкость в сосуде достигнет равновесной температуры, Tx градусов.
Затем в этом экспериментальном сценарии замените источник постоянного напряжения Vx на изменяющееся во времени напряжение, которое не может неограниченно увеличиваться. В конце концов, через некоторое время Tfinal снова установится тепловое равновесие.Если это условие равновесия устанавливает ту же температуру Tx, которая была достигнута ранее с приложенным напряжением Vx постоянного тока, то можно сказать, что «эффективное» значение этой изменяющейся во времени функции равно Vx.
Отсюда и определение «действующей стоимости». Уравнение 2 иллюстрирует это тепловое равновесие. (Уравнение 2)
Если V (t) является периодической функцией времени с периодом цикла Tp, а T _final представляет собой целое число «n», умноженное на период (n * Tp), то интеграл по T _final равен n умноженный на интеграл по Tp.Результаты этих замен показаны в уравнении 3.
(Уравнение 3)
Уравнение 3 показывает, что эффективная эквивалентная нагревательная способность ограниченной периодической функции напряжения (тока) может быть определена всего за один цикл. Это уравнение признано старой знакомой формой «квадрат R oot из M ean (в среднем) S quared»; отсюда и название « RMS ».
ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ УРАВНЕНИЯ “RMS”
Следующие результаты могут быть получены прямым применением уравнения 3.
Синусоидальная функция, пик Vp
Симметричная периодическая импульсная волна, пик Vp
Несимметричная периодическая импульсная волна, все положительные пики Vp, с рабочим циклом D
Симметричная периодическая треугольная волна, пик Vp
Двухполупериодная выпрямленная синусоида, пиковое Vp
Полуволновая выпрямленная синусоида, пиковое Vp
Примечание: Эти примеры показывают, что форма периодической функции может определять ее среднеквадратичное значение.Пик (пик) функции напряжения (тока) от времени, деленный на √ 2 часто ошибочно используется для расчета среднеквадратичного значения. Этот метод может привести к ошибкам, и его явно следует избегать.
ЭФФЕКТИВНЫЕ (СКЗ) ЗНАЧЕНИЯ КОМПЛЕКСНЫХ ФУНКЦИЙ
Чрезвычайно полезный факт при определении значений RMS состоит в том, что любая ограниченная периодическая функция времени с хорошим поведением может быть выражена, например, как среднее значение плюс сумма синусоид (теорема Фурье);
(Уравнение 4)
Где ωo – радианная частота V (t), а An, Bn, Ao – коэффициенты амплитуды Фурье.
Когда этот ряд подставляется в интегральное выражение Уравнение 2 для RMS, получается следующее;
(Уравнение 5)
Примечание: (A _n) ² и (B _n) ²/2 – квадраты среднеквадратичных значений для каждого n ^-го компонента Sin и косинуса.
Важный вывод:
Ограниченная периодическая функция времени имеет среднеквадратичное значение, равное квадратному корню из суммы квадрата среднеквадратичного значения каждого отдельного компонента.
ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ
На рисунке 2 показаны составные кривые, образованные добавлением двух синусоид, одна с частотой 60 Гц и одна с частотой 180 Гц. Кривая 1 соответствует нулевой разности фаз, а кривая 2 – разности фаз 90 градусов.
Конкретно;
Кривая 1 V (t) = 170 * Sin (377 * t) + 50 * Sin (1131 * t)
Кривая 2 V (t) = 170 * Sin (377 * t) + 50 * Cos (1131 * t)
Примечание: Форма составной кривой определяется гармониками фазы и частоты.

Рисунок 2: Фундаментальный с третьей гармоникой Добавлен
Кривая 2170 * Sin (377 * t) + 50 * Cos (1131 * t)
Кривая 1170 * Sin (377 * t) + 50 * Sin (1131 * t)
Промышленные синусоидальные функции напряжения (тока) часто содержат гармоники, которые влияют на форму волны и пиковые (пиковые) значения. Например, кривая 2 типична для токов намагничивания в трансформаторах и двигателях 60 Гц.В недорогих устройствах для считывания среднеквадратичных значений часто используются схемы выпрямителя, которые фиксируют пиковое значение, которое затем масштабируется на 0,707 и отображается как среднеквадратичное значение. Очевидно, что этот метод может дать неверные показания RMS. В этом примере использование Vpeak ÷ √2 явно дает неверные значения.
Кривая 1: 203 * 0,707 = 144 вольт, не соответствует действительности RMS
Кривая 2: 155 * 0,707 = 110 вольт, не соответствует среднеквадратическому значению
Правильное среднеквадратичное значение для обеих этих составных синусоидальных функций:
[(170) ²/2 + (50) ²/2] ^1/2 = 125.3 вольта RMS
Таблица 1 иллюстрирует два примера вычислений RMS с использованием индивидуальных коэффициентов Фурье и уравнения 5. Примером является двухполупериодная выпрямленная пиковая синусоида 1 В. Обратите внимание, что для функции двухполупериодного выпрямления измерительному устройству, необходимому для получения показаний RMS с погрешностью 0,01%, требуется полоса пропускания, которая включает пятую (5) гармонику, и разрешение для считывания уровней 10 мВ. Другой пример, проиллюстрированный в Таблице 1, представляет собой пиковую функцию 1 В с зубцами.В этом примере измерительному устройству для пилообразной функции, необходимому для получения показаний RMS с погрешностью 0,3%, требуется полоса пропускания, которая включает двадцать пятую (25) гармонику, и разрешение для считывания уровней 10 мВ.
Предположим, в целях иллюстрации, что пульсации переменного тока на выходе постоянного тока выпрямителя могут быть аппроксимированы пилообразной функцией. Таблица 1 показывает, что для измерения с погрешностью 0,3% среднеквадратичных пульсаций переменного тока на выходе постоянного тока выпрямителя 20 кГц измерительное устройство должно иметь полосу пропускания более 500 кГц и разрешение для считывания уровней напряжения на 40 дБ (100 микровольт). для пиковой пульсации 10 мВ).Этот пример ясно показывает, что форма сигнала, а также ширина полосы измерения и разрешение чрезвычайно важны для определения точности измерения истинного среднеквадратичного значения.
Любое устройство измерения «истинного среднеквадратичного значения» должно быть способно точно реализовать уравнение 3. Тонкость этого утверждения состоит в том, что электронная реализация уравнения 3 требует, чтобы устройство имело очень большую полосу пропускания и было способно определять малые величины.
КРЕСТ-ФАКТОР
Еще одним показателем качества, часто используемым для характеристики периодической временной функции напряжения (тока), является пик-фактор (CF).Пик-фактор для конкретной формы волны определяется как пиковое значение, деленное на среднеквадратичное значение. В частности,
ПРИБОРЫ ИЗМЕРЕНИЯ СРЕДНЕКВАДРАТИЧЕСКИХ ДАННЫХ
Для истинных измерений среднеквадратичного значения требуются измерительные приборы, которые точно реализуют уравнение 3, «уравнение среднеквадратичного значения». Эти устройства должны иметь широкую полосу пропускания и хорошее разрешение низкого уровня, чтобы поддерживать высокие коэффициенты амплитуды. Dataforth разработала три продукта, которые удовлетворяют этим требованиям; модули ввода SCM5B33, DSCA33 и 8B33 True RMS.Эти продукты обеспечивают изоляционный барьер 1500 В среднеквадратичного значения между входом и выходом. SCM5B33 Модуль изолированного ввода истинного среднеквадратичного значения
Интерфейсы Среднеквадратичное напряжение (0 – 300 В) или действующий ток (0 – 5 А)
разработан для стандартной работы с частотами от 45 Гц до 1000 Гц (расширенный диапазон до 20 кГц)
Совместим со стандартными трансформаторами тока и напряжения
Промышленный стандартный выход 0-1 мА, 0-20 мА, 4-20 мА, 0-5 В или 0-10 В постоянного тока
± 0.25% заводская калибровка точности (класс точности 0,2)
Изоляция непрерывного трансформатора 1500 В среднекв.
Защита входа от перегрузки до 480 В макс. (Пиковое напряжение переменного и постоянного тока) или 10 А RMS в непрерывном режиме
ANSI / IEEE C37.90.1 Защита от переходных процессов
Сертификат CSA, соответствие CE и ATEX
DSCA33 Изолированный формирователь входного сигнала истинного среднеквадратичного значения
Интерфейсы Среднеквадратичное напряжение (0 – 300 В) или действующий ток (0 – 5 А)
разработан для стандартной работы с частотами от 45 Гц до 1000 Гц (работа в расширенном диапазоне до 20 кГц)
Совместим со стандартными трансформаторами тока и напряжения
Промышленный стандартный выход 0-1 мА, 0-20 мА, 4-20 мА, 0-5 В или 0-10 В постоянного тока
± 0.25% заводская калибровка точности (класс точности 0,2)
± 5% Регулируемые ноль и диапазон
Изоляция трансформатора 1500Vrms
Защита входа от перегрузки до 480 В (пиковое напряжение переменного и постоянного тока) или 10 А среднеквадратичного значения в непрерывном режиме
ANSI / IEEE C37.90.1 Защита от переходных процессов
легко устанавливается на стандартную DIN-рейку
Внесено в список
C-UL-US
Соответствие CE и ATEX
8B33 Миниатюрный модуль ввода истинного среднеквадратичного значения
Интерфейсы для среднеквадратичного напряжения (0-300 В) или действующего тока (0-1 А)
разработан для стандартной работы с частотами от 45 Гц до 1000 Гц (расширенный диапазон до 10 кГц)
Совместим со стандартными трансформаторами тока и напряжения
Промышленный стандартный выход от 0 до 5 В постоянного тока
± 0.25% погрешность, откалиброванная на заводе
Изоляция трансформатора 1500Vrms
Защита входа от перегрузки до 350 В среднеквадратического значения (пиковое значение переменного и постоянного тока) или 2 А постоянного тока
120 дБ CMR
70 дБ ЯМР при 60 Гц
ANSI / IEEE C37.90.1 Защита от переходных процессов
CE соответствует требованиям
Внесено в список
C-UL-US
Ожидается соответствие ATEX
Типы модулей Mix and Match на задней панели
электрических цепей – Почему мы используем среднеквадратические значения (RMS), когда говорим о напряжении переменного тока
Попытки найти среднее значение AC напрямую дадут вам ответ ноль … Следовательно, используются значения RMS. Они помогают найти эффективное значение переменного тока (напряжения или тока).
Это RMS – математическая величина (используется во многих математических полях ), используемая для сравнения как переменного, так и постоянного тока (или напряжения). Другими словами (в качестве примера), среднеквадратичное значение переменного тока (тока) – это постоянный ток, который при пропускании через резистор в течение заданного периода времени будет производить такое же тепло, что и переменный ток при прохождении через такой же резистор за то же время.2/2 $, а затем определение квадратного корня $ I_0 / \ sqrt {2} $ даст среднеквадратичное значение.
Это пример время: (я думаю, вы не просили о выводе RMS)
Учтите, что обе лампы выдают одинаковый уровень яркости. Таким образом, они теряют одинаковое количество тепла (независимо от того, переменный или постоянный ток). Чтобы связать и то и другое, нам нечего использовать лучше, чем значение RMS. Постоянное напряжение лампы 115 В, переменное 170 В.2} $$
Среднеквадратичное значение, среднее значение, пиковое значение, пик-фактор, форм-фактор в AC
Что такое среднеквадратичное значение, пиковое значение, среднее значение, значение экземпляров, форм-фактор, пик-фактор и другие термины, относящиеся к цепям переменного тока и синусоиде?
Токи переменного и постоянного тока
Известно, что полярность постоянного напряжения и направление постоянного тока всегда одинаковы, то есть это однонаправленное значение, которое не меняет полярность, а также направление, как показано на рис.1.
С другой стороны, (AC) переменный ток или напряжение – это ток, который регулярно меняет свое направление, а также свое значение. Другими словами, переменный ток (AC) – это тип тока, который течет сначала в одном направлении, а во-вторых, он течет в противоположном направлении. В каждом цикле он меняет значение от нуля до максимального и снова достигает нулевого значения.
Значение переменного тока или напряжения может быть выражено в переменном токе (синусоидальном). Синусоидальная волна, как показано на рис. (1) ниже.
Рис. 1 Разница между переменным током и постоянным током
В переменном токе невозможно представить величины, поскольку его амплитуда синусоидальной волны переменного тока непрерывно изменяется со временем.
Таким образом, у нас есть несколько вариантов для выражения амплитуды и различных значений, связанных с синусоидальной волной переменного тока, например:
RMS Value
Average Value
Instance Value
Maximum or Peak Value
Peak to Peak Value
Пик-фактор
Форм-фактор
Прочие связанные термины
Мы подробно обсудим их все ниже.
Что такое среднеквадратичное значение?
Значение RMS ( среднеквадратическое значение ) (также известное как эффективное значение или виртуальное значение ) переменного тока (AC) – это значение постоянного тока (DC) при протекании через цепь или резистор в течение определенного периода времени и производит такое же количество тепла, которое вырабатывается переменным током (AC) при протекании через ту же цепь или резистор в течение определенного времени.
Значение переменного тока, которое при прохождении через нагревательный элемент (например, резистор) будет выделять такое же количество тепла, как и постоянный ток через элемент, называется значением R.M.S.
Короче говоря,
Среднеквадратичное значение переменного тока заключается в том, что при сравнении с постоянным током и переменный, и постоянный ток выделяют одинаковое количество тепла при прохождении через одну и ту же цепь в течение определенного периода времени.
Для синусоидальной волны
или
I _RMS = 0.707 x I _M, E _RMS = 0,707 E _M
Фактически, RMS-значение синусоидальной волны является мерой теплового эффекта синусоидальной волны. Например, когда резистор подключен к источнику переменного напряжения, он выделяет определенное количество тепла (рис. 2 – а). Когда тот же резистор подключен к источнику постоянного напряжения, как показано на (рис. 2 – b). Регулируя значение постоянного напряжения, чтобы получить такое же количество тепла, которое ранее выделялось в источнике переменного напряжения на рис.Это означает, что среднеквадратичное значение синусоидальной волны равно источнику постоянного напряжения, производящему такое же количество тепла, выделяемого источником переменного напряжения.
Рис. 2 – Среднеквадратичные значения тока и напряжения
Говоря более ясными словами, уровень внутреннего напряжения в США составляет 110 В, а в Великобритании – 220 В переменного тока. Этот уровень напряжения показывает действующее значение (110 В или 220 В R.M.S) и показывает, что домашняя розетка способна обеспечить такое же количество средней положительной мощности, что и напряжение 110 В или 220 В постоянного тока.
Имейте в виду, что амперметры и вольтметры, подключенные к цепям переменного тока, всегда показывают среднеквадратичные значения (тока и напряжения).
Для синусоидальной волны переменного тока среднеквадратичные значения тока и напряжения:
I _RMS = 0,707 x I _M, В _RMS = 0,707 В _M
Чтобы найти среднеквадратичное значение синусоидальной волны, мы можем использовать следующие два метода.
Метод средней ординаты
Метод интегрирования.
Давайте посмотрим, как найти значения R.M.S синусоидальной волны.
Методы определения среднеквадратичного значения синусоиды.
Аналитический метод
Метод 1
Мы знаем, что значение синусоидального переменного тока (AC) =
I _m Sin ω θ = I _m Sin θ
В то время как Среднее квадратическое значение мгновенных значений тока за половину или полный цикл составляет:
Квадратный корень из этого значения:
Следовательно, среднеквадратичное значение тока равно (если положить I = I _м Sin θ):
Now,
Следовательно, мы можем обнаружить, что для симметричного синусоидального тока:
I _RMS = максимальное значение тока x 0.707
Метод 2.
Пусть i = Sin ω θ = I _м Sin θ
Среднее значение i ₂
Метод 3
Пусть i = Sin ω θ = I _м Sin θ
Графический или среднеординатный метод
Этот метод известен как средний ординатный или графический метод, позволяющий найти значение среднеквадратичного напряжения с использованием средних ординат или нахождения мгновенного значения Форма волны переменного тока.Для ясного понимания ниже пояснения приведен решенный пример.
В синусоидальной волне переменного тока существует множество мгновенных значений напряжения, и это зависит от временного интервала. Как показано на рис. 3 ниже, где число средних ординат равно 12 (чем больше средних ординат, тем точнее будет результат). Он показывает при t = 1, t = 2, t = 3…. tn, уровни мгновенных напряжений равны V ₁, V ₂, V ₃…. V _n соответственно.
Рис. 3 – Среднеординатный или графический метод для RMS
Во-первых, мы найдем мгновенные значения напряжений для каждого периода времени, например t = 1, t = 2… t = n и т. Д.Чтобы найти значение RMS, нам нужно будет найти квадратные значения каждого уровня напряжения в форме волны переменного тока, которая показывает квадратную часть значения RMS.
V ₁ ² + V ₂ ² + V ₃ ² +… .. V _n ²
Теперь квадратные значения напряжений делятся на количество средних ординат, которое показывает среднее значение среднеквадратичного напряжения.
Например,
Число ординат, использованных на рис. 3 выше, = 12
Предположим пиковое значение напряжения (Max Voltage i.е. амплитуда = V _PK или V _Max) составляет 12 В для переменного сигнала. Форма сигнала разделена на 12 средних ординат, как показано ниже:
4V Напряжение 5 :
Таким образом, значение RMS напряжения равно 6.97 В, используя графический метод или метод средней оси ординат, чтобы найти среднеквадратичное значение напряжения.
Уравнения среднеквадратичного напряжения и тока
Действующие значения тока и напряжения, относящиеся к пиковому значению или максимальному значению (оба одинаковы).
V _RMS = 0,707 x V _PK, I _RMS = 0,707 x I _PK
V _RMS = 0,707 x V _M RMS _M = 0.707 x I _M
Действующие значения тока и напряжения, относящиеся к размаху .
V _RMS = 0,3536 x V _P-P, I _RMS = 0,3536 x I _P-P
RMS-значения тока и напряжения, относящиеся к среднему значению.
V _RMS = 1,11 x V _AV, I _RMS = 1,11 x I _AV
Здесь все на одном изображении.
Формулы среднеквадратичного значения напряжения для различных форм волны
В приведенной ниже таблице формулы среднеквадратичного значения напряжения показаны для различных типов синусоидальных форм волны.
Напряжение 2 В 4 В 6 В 8 В 10 В 12 В 10 В 12 В 10 В 2V 0V
Угол 15 ^o 30 ^o 45 ^o 60 ^o 9069 9069 105 ^o 120 ^o 135 ^o 150 ^o 165 ^o 180 ^o
Половинная волна
Тип сигнала Формула для среднеквадратичного значения (В _СКЗ)
Синусоидальная волна В _PK / √2 В
_PK / √2
Двухполупериодная выпрямленная синусоида В _PK / √2
Прямоугольная волна V _PK
Треугольник 9029 √ 3
Пилообразная форма волны В _PK / √3
Калькулятор среднеквадратичного напряжения
В калькуляторе среднеквадратичного значения напряжения вы можете рассчитать значение среднеквадратичного напряжения из различных связанных значений, таких как среднее значение, пиковое значение Значение и максимальное значение.
Что такое среднее значение
Если мы преобразуем синусоидальную волну переменного тока в синусоидальную волну постоянного тока (DC) через выпрямители, то преобразованное значение в постоянный ток будет известно как среднее значение этого синусоидального сигнала переменного тока. волна.
Рис. 4 – Среднее значение напряжения
Если максимальное значение переменного тока равно «I _MAX», то значение преобразованного постоянного тока через выпрямитель будет «0,637 I _M», что известно как среднее значение Синусоидальная волна переменного тока (I _AV).
Среднее значение тока = I _AV = 0,637 I _M
Среднее значение напряжения = E _AV = 0,637 E _M
Среднее значение (также известное как среднее значение) переменного тока (AC) выражается тем постоянным током (DC), который передает по любой цепи такое же количество заряда, какое передается этим переменным током (AC) в течение того же времени.
Имейте в виду, что среднее или среднее значение полной синусоидальной волны равно «нулю», значение тока в первой половине (положительное) равно следующему полупериоду (отрицательное) в противоположном направлении.Другими словами, в положительном и отрицательном полупериоде присутствует одинаковое количество тока, который течет в противоположном направлении, поэтому среднее значение для полной синусоидальной волны будет «0». По этой причине мы не используем среднее значение для покрытия и зарядки аккумулятора. Если волна переменного тока преобразуется в постоянный ток через выпрямитель, ее можно использовать для электрохимических работ.
Рис. 5 – Среднее значение тока
Короче говоря, среднее значение синусоидальной волны, взятой за полный цикл, всегда равно нулю, потому что положительные значения (выше точки пересечения нуля) смещают или нейтрализуют отрицательные значения (ниже точки пересечения нуля.)
Связанный пост: Соединение звездой (Y): трехфазная мощность, значения напряжения и тока
Методы определения среднего значения синусоиды.
Среднеординатный или графический метод
В этом методе полупериод синусоидальной волны делится на равное количество периодов времени, причем продолжительность каждого периода времени равна «t / n».
Предположим, что средние значения мгновенных токов в каждом временном интервале равны I ₂, 1 ₂, I ₃… I _n.Чтобы найти среднее значение для каждого временного интервала, левая и правая вертикальные линии складываются и делятся на два. То же самое применимо ко всем временным интервалам, чтобы найти среднее значение для каждого экземпляра.
Теперь все средние значения складываются и делятся на числовые средние ординаты (то есть периоды времени), которые показывают общее среднее значение полупериода синусоидальной волны. формула для среднего значения показана ниже:
Пример:
Рис. Текущий i.е. амплитуда = I _PK или I _Max) составляет 12 А для переменного сигнала. Форма сигнала разделена на 12 средних ординат, как показано ниже:
Текущее значение
Ток 2A 4A 6A 8A 10A 12A 10A 12A 9A 4A 2A 0A
Угол 15 ^o 30 ^o 45 ^o 60 ^o 9077 9069 60 9069 105 ^o 120 ^o 135 ^o 150 ^o 165 ^o 180 ^o
6A, используя графический метод или метод средней ординаты, чтобы найти среднее значение тока.
Аналитический метод
Мы знаем, что стандартное уравнение переменного тока:
i = Sin ω θ = I _м Sin θ
Максимальное значение тока на синусоиде = I _м
Среднее значение тока на синусоиде = I _AV
Мгновенное значение тока на синусоиде = i
Угол, указанный для « i » после нулевого положения тока = θ
Угол полупериода = Π радиан
Угол полного круга = 2π радиан
(a) Среднее значение полного цикла:
Пусть i = Sin ω θ = I _м Sin θ
Таким образом, среднее значение синусоидальной волны за полный цикл равна нулю.
(b) Среднее значение тока за полупериод
Среднее значение тока (полупериод)
I _AV = 0,637 В _M
Аналогично среднее значение напряжения за полупериод
В _AV = 0,637 В _M
Уравнения среднего напряжения и тока
Его среднее значение среднего напряжения или тока равно умножению максимального или пикового значения напряжения и ток соответственно с постоянной 0.637.
Например, если максимальное значение или пиковое значение синусоидальной волны составляет 360 В _PK или 360 В _Макс, используя приведенное выше уравнение, среднее значение напряжения будет:
0,637 x 360 В _PK = 229,32 Av .
Формулы среднего значения и среднеквадратичного значения для различных форм волны
В приведенной ниже таблице формулы среднего значения и среднеквадратичного значения напряжения показаны для различных типов синусоидальных форм волны.
Тип сигнала Формула для среднеквадратичного напряжения Формула для среднего напряжения
Синусоидальная волна В _RMS = V _PK2 √ _PK2 = 0
Полное выпрямленное напряжение V _RMS = V _PK / √2 V _AV = 0.637 В _PK
Половина выпрямленного сигнала В _СКЗ = В _PK/2 В _AV = 0,318 В _PK
Синусоидальная волна 9069 со смещением постоянного тока 9069 RMS = √ (VDC ² + V _PK ²/2) V _AV = Vdc
Половина синусоиды с длительностью T и частотой f V _RMS = V x √ (fx T / 2) V _AV = 2f x T x V _PK / π
Положительный прямоугольный сигнал с длительностью T и частотой f V _RMS = V _PK x √ (fx T) V _AV = fx T x V _PK
Волна зубьев пилы с длительностью T и частотой f V _RMS = V _PK x √ (fx T / 3) V _AV = fx T x V _PK/2
Трапециевидная волна e с частотой f, верхним сегментом T и базовым сегментом B. V _RMS = V _PK x √ (fx ((BT) + 3xT) / 3) V _AV = fx V _PK x ((T + B) / 2)
Что такое мгновенное значение
Значение, достигаемое переменной величиной в любой момент времени, называется мгновенным значением. Обозначается буквами «i» и e.
другими словами, значение переменного тока или напряжения в любой конкретный момент мы называем мгновенным значением.
На рис. 7 ниже показаны различные мгновенные значения напряжений или токов в определенный момент и период времени.Значения мгновенного тока или напряжения равны «+» в положительном цикле и «-» в отрицательном цикле в синусоидальной волне. Кривые показывают значения различных мгновенных напряжений, в то время как такая же кривая может быть построена и для тока. На рис. 7 значения мгновенных напряжений составляют 2,5 В при 1 мкс, 5,1 В при 2 мкс, 8,9 В при 3 мкс. В то время как это -2,3 В при 4 мкс, -6,1 В при 5 мкс и -9,2 В при 6 мкс.
Рис. 7 – Мгновенное значение напряжения
Что такое пиковое напряжение или максимальное значение напряжения?
Пиковое значение также известно как Максимальное значение , Пиковое значение или Амплитуда .Это максимальное значение переменного тока или напряжения из положения «0» независимо от положительного или отрицательного полупериода в синусоидальной волне, как показано на рис. 8. Оно выражается как I _M и E _M или В _P и I _M.
Уравнения значения пикового напряжения :
В _P = √2 x V _RMS = 1,414 V _RMS
V _P = V _PP/2 = 0.5 В _PP
В _P = π / 2 x V _AV = 1,571 x V _AV
Другими словами, это значение напряжения или тока на положительном или отрицательном полюсе. максимум (пики) относительно нуля. Проще говоря, это мгновенное значение с максимальной интенсивностью.
Рис. 8 – Пиковые или максимальные значения напряжений
Пиковое значение Значение
Сумма положительных и отрицательных пиковых значений называется размахом до пика.Выражается как I _PP или V _PP.
Уравнения и формулы для Пиковое напряжение следующие:
В _PP = 2√2 x В _RMS = 2,828 x V _RMS 9000 V _PP = 2 x V _P
V _PP = π x V _AV = 3,141 x V _AV
Другими словами, от пика до пика значение синусоидальной волны – это напряжение или ток от положительного пика до отрицательного пика, и его значение в два раза больше по сравнению с пиковым значением или максимальным значением, как показано на рис. 8 выше.
Что такое пик-фактор
Пик-фактор также известен как пик-фактор или коэффициент амплитуды.
Это соотношение между максимальным значением и среднеквадратичным значением переменной волны.
Для синусоидального переменного напряжения:
Для синусоидального переменного тока:
Что такое форм-фактор
Отношение между среднеквадратичным значением и средним значением переменной величины (ток или напряжение) равно известный как форм-фактор.
В приведенной ниже таблице формулы и значения форм-фактора показаны для различных типов синусоидальных форм волны.
Форма волны Тип Формула для форм-фактора Значение
Синусоидальная волна π / 2√2 Синусоида 90π / 2 1,5707963
Двухполупериодная выпрямленная синусоида π / 2√2 1.11072073
Прямоугольная волна 1 1
Треугольник 2 / √3 1,15470054
Другие термины, относящиеся к цепям переменного тока
Форма волны
Путь, отслеживаемый величиной (например, напряжением или током), нанесенной на график как функция некоторой переменной (такой как время, градусы, радианы, температура и т. Д.)) называется формой волны.
Цикл
Один полный набор положительных и отрицательных значений переменного качества (таких как напряжение и ток) известен как цикл.
Часть сигнала, содержащаяся в одном периоде времени, называется циклом.
Расстояние между двумя одинаковыми точками, связанное со значением и направлением, называется циклом.
Цикл – это полное чередование.
Период
Время, необходимое переменной величине (например, току или напряжению) для завершения одного цикла, называется ее периодом времени «T».
Она обратно пропорциональна частоте « f » и обозначается буквой «T», где единицей измерения периода времени является секунда.
Математически;
T = 1/ f
Частота
Частота – это число, если количество циклов проходит за секунду. Он обозначается буквой «f» и имеет единицу цикла в секунду, то есть Гц (Герты).
Количество завершенных циклов за 1 секунду называется частотой.
Это количество циклов переменного количества в секунду в герцах.
Частота – это количество циклов, которые синусоида завершается за одну секунду, или количество циклов, которые происходят за одну секунду.
f = 1 / T
Амплитуда
Максимальное положительное или отрицательное значение переменной величины, такой как напряжение или ток, называется ее амплитудой. Обозначается V _P, I _P или E _MAX и I _MAX.
Чередование
Один полупериод синусоидальной волны (отрицательный или положительный) известен как чередование, диапазон которого составляет 180 °.
Больше новостей

Навигация по записям
Загадки электричества: Загадки про электричество
Atmega168 datasheet на русском: Atmega48 описание на русском – Вэб-шпаргалка для интернет предпринимателей!
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Интересн
Интересные факты
Новинки
Новые
Передатчик
Передатчики
Примеры схем
Простые
Разное
Советы
Схем
Схемы
Электрон
Электроника
© 2019 «Tree of life» — Производство и продажа аксессуаров для iPhone
* iPad, iPhone, iPod, iPod classic, iPod nano, iPod shuffle и iPod touch являются торговыми марками компании Apple Inc, зарегистрированными в США и других странах. Apple Store является торговой маркой компании Apple Inc. PhotoFast является зарегистрированной торговой маркой компании PhotoFast Company Limited.
Вступайте в клуб любителей

Тип сигнала	Формула для среднеквадратичного значения (В _СКЗ)
Синусоидальная волна	В _PK / √2	В
_PK / √2
Двухполупериодная выпрямленная синусоида	В _PK / √2
Прямоугольная волна	V _PK
Треугольник 9029 √ 3
Пилообразная форма волны	В _PK / √3

Ток	2A	4A	6A	8A	10A	12A	10A	12A	9A 4A	2A	0A
Угол	15 ^o	30 ^o	45 ^o	60 ^o 9077 9069 60 9069	105 ^o	120 ^o	135 ^o	150 ^o	165 ^o	180 ^o

Тип сигнала	Формула для среднеквадратичного напряжения	Формула для среднего напряжения
Синусоидальная волна	В _RMS = V _PK2 √ _PK2 = 0
Полное выпрямленное напряжение	V _RMS = V _PK / √2	V _AV = 0.637 В _PK
Половина выпрямленного сигнала	В _СКЗ = В _PK/2	В _AV = 0,318 В _PK
Синусоидальная волна 9069 со смещением постоянного тока 9069 RMS = √ (VDC ² + V _PK ²/2)	V _AV = Vdc
Половина синусоиды с длительностью T и частотой f	V _RMS = V x √ (fx T / 2)	V _AV = 2f x T x V _PK / π
Положительный прямоугольный сигнал с длительностью T и частотой f	V _RMS = V _PK x √ (fx T)	V _AV = fx T x V _PK
Волна зубьев пилы с длительностью T и частотой f	V _RMS = V _PK x √ (fx T / 3)	V _AV = fx T x V _PK/2
Трапециевидная волна e с частотой f, верхним сегментом T и базовым сегментом B.	V _RMS = V _PK x √ (fx ((BT) + 3xT) / 3)	V _AV = fx V _PK x ((T + B) / 2)

Форма волны Тип	Формула для форм-фактора	Значение
Синусоидальная волна	π / 2√2	Синусоида 90π / 2	1,5707963
Двухполупериодная выпрямленная синусоида	π / 2√2	1.11072073
Прямоугольная волна	1	1
Треугольник	2 / √3	1,15470054

	Другие термины, относящиеся к цепям переменного тока Форма волны Путь, отслеживаемый величиной (например, напряжением или током), нанесенной на график как функция некоторой переменной (такой как время, градусы, радианы, температура и т. Д.)) называется формой волны. Цикл Один полный набор положительных и отрицательных значений переменного качества (таких как напряжение и ток) известен как цикл. Часть сигнала, содержащаяся в одном периоде времени, называется циклом. Расстояние между двумя одинаковыми точками, связанное со значением и направлением, называется циклом. Цикл – это полное чередование. Период Время, необходимое переменной величине (например, току или напряжению) для завершения одного цикла, называется ее периодом времени «T». Она обратно пропорциональна частоте « f » и обозначается буквой «T», где единицей измерения периода времени является секунда. Математически; T = 1/ f Частота Частота – это число, если количество циклов проходит за секунду. Он обозначается буквой «f» и имеет единицу цикла в секунду, то есть Гц (Герты). Количество завершенных циклов за 1 секунду называется частотой. Это количество циклов переменного количества в секунду в герцах. Частота – это количество циклов, которые синусоида завершается за одну секунду, или количество циклов, которые происходят за одну секунду. f = 1 / T Амплитуда Максимальное положительное или отрицательное значение переменной величины, такой как напряжение или ток, называется ее амплитудой. Обозначается V _P, I _P или E _MAX и I _MAX. Чередование Один полупериод синусоидальной волны (отрицательный или положительный) известен как чередование, диапазон которого составляет 180 °. Больше новостей Навигация по записям Загадки электричества: Загадки про электричество Atmega168 datasheet на русском: Atmega48 описание на русском – Вэб-шпаргалка для интернет предпринимателей! Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Найти: Рубрики Интересн Интересные факты Новинки Новые Передатчик Передатчики Примеры схем Простые Разное Советы Схем Схемы Электрон Электроника © 2019 «Tree of life» — Производство и продажа аксессуаров для iPhone * iPad, iPhone, iPod, iPod classic, iPod nano, iPod shuffle и iPod touch являются торговыми марками компании Apple Inc, зарегистрированными в США и других странах. Apple Store является торговой маркой компании Apple Inc. PhotoFast является зарегистрированной торговой маркой компании PhotoFast Company Limited. Вступайте в клуб любителей

Действующее значение это: ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ – это… Что такое ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ?

ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ – это… Что такое ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ?

Смотреть что такое “ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ” в других словарях:

Что такое действующее значение силы тока.

4.4.5. Мощность в цепи переменного тока

Действительное значение тока. Эффективное, действующее напряжение, сила тока. Значение

Синусоидально изменяющийся ток

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Векторное изображение синусоидально изменяющихся величин

Действующее (эффективное) значение для сигналов стандартной формы

Закон Ома и мощность для действующих значений напряжения и силы тока

Как определить действующее значение силы тока

Содержание

Действующее значение в типичных случаях [ править | править код ]

Синусоида [ править | править код ]

Прямоугольная форма [ править | править код ]

Треугольная форма [ править | править код ]

Трапециевидная форма [ править | править код ]

Дугообразная форма [ править | править код ]

Дополнительные сведения [ править | править код ]

Содержание

Действующее значение в типичных случаях [ править | править код ]

Синусоида [ править | править код ]

Прямоугольная форма [ править | править код ]

Треугольная форма [ править | править код ]

Трапециевидная форма [ править | править код ]

Дугообразная форма [ править | править код ]

Дополнительные сведения [ править | править код ]

Среднеквадратичное (действующее, эффективное) значение

Лампочка и постоянное напряжение

Лампочка и переменное напряжение

Среднеквадратичное значение напряжения

Урок 8. переменный электрический ток – Физика – 11 класс

Действующее значение тока и напряжения кратко. Действующее значение напряжения

Действующее (эффективное) значение для сигналов стандартной формы

Закон Ома и мощность для действующих значений напряжения и силы тока

4.4.5. Мощность в цепи переменного тока

Действующее значение переменного тока

Синусоидально изменяющийся ток

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Векторное изображение синусоидально изменяющихся величин

Действующее и среднее значения переменного тока и напряжения.

Что берется за действующее значение силы переменного тока и переменного напряжения

Integrated Publishing – Ваш источник военных спецификаций и образовательных публикаций

Integrated Publishing – Ваш источник военных спецификаций и образовательных публикаций

Пиковое против среднего vs.Действующее значение напряжения

Термин «среднеквадратичное значение» означает «среднеквадратическое значение», также называемое эквивалентом переменного тока и постоянного напряжения.

Важные термины, которые следует запомнить

Важные уравнения, которые следует запомнить

Дополнительная литература / Источники

Комментарии

Среднеквадратичное значение – обзор

8.4.4.2.2 Временная область

Измерение действующих значений напряжения и тока

ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ (ТОКА)

ЭФФЕКТИВНОЕ ЗНАЧЕНИЕ

ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ УРАВНЕНИЯ “RMS”

ЭФФЕКТИВНЫЕ (СКЗ) ЗНАЧЕНИЯ КОМПЛЕКСНЫХ ФУНКЦИЙ

ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ

КРЕСТ-ФАКТОР

ПРИБОРЫ ИЗМЕРЕНИЯ СРЕДНЕКВАДРАТИЧЕСКИХ ДАННЫХ

электрических цепей – Почему мы используем среднеквадратические значения (RMS), когда говорим о напряжении переменного тока

Среднеквадратичное значение, среднее значение, пиковое значение, пик-фактор, форм-фактор в AC

Формулы среднеквадратичного значения напряжения для различных форм волны

Калькулятор среднеквадратичного напряжения

Формулы среднего значения и среднеквадратичного значения для различных форм волны

Амплитуда

Чередование

Больше новостей

Добавить комментарий Отменить ответ