Действующий ток это: Действующее значение тока и напряжения

Содержание

Действующее напряжение и амплитудное напряжение

Все знают, что действующее напряжение в розетке 220 Вольт (230 по новым нормам, но для данной темы это не имеет особого значения). Это легко проверить при помощи мультиметра, который измерит разность потенциалов между фазой и рабочим нулевым проводником. То есть, при идеальных условиях, потенциал на нулевом проводе 0, а на фазном 220 Вольт. На самом деле все немного не так — переменный ток имеет синусоидальную форму с потенциалом на пиках 310 и -310 Вольт (амплитудное напряжение). Для того чтобы это увидеть, необходимо воспользоваться осциллографом.

Синусоида действующего и амплитудного напряжения

Понятно, что данный материал в большей степени ориентирован на простую аудиторию, у которой не то, что осциллографа нет, даже мультиметр наверняка не у каждого есть. Поэтому все примеры будут браться из среды программы Electronics Workbench, доступной каждому.

И первое, что нам нужно посмотреть — это синусоиду напряжения фазы из розетки. Для этого в программе отрисуем трехфазную сеть и подключим осциллограф к одной из фаз:

Как видно при показании вольтметра 219,4 Вольт между одной из фаз и PEN проводником, осциллограф показал синусоиду с амплитудой 309,1 Вольт. Это значение напряжения называется максимальным (амплитудным). А 219,4 Вольт, которые показывает вольтметр — это действующее напряжение. Его также называют среднеквадратичным или эффективным. И прежде чем перейти к рассмотрению данной особенности, кратко, простыми словами пройдемся по отрисованной схеме трехфазной сети и разберемся в природе синусоиды.

Начнем со схемы:

Слева на право — три источника переменного напряжения с фазовыми углами 0, 120, 240 градусов и соединенными звездой.
Резистор 4 Ом — это заземление нейтрали трансформатора.
Резисторы по 0,8 Ом — условное сопротивление проводов, зависящее от сечения провода и длины линии.
Резисторы 15, 10 и 20 Ом — нагрузка потребителей по трем фазам.
К одной из фаз подключен осциллограф, показывающий амплитуду 309,1 Вольт.

Теперь рассмотрим синусоиду. Переменное напряжение в отличие от постоянного, график которого прямая на осциллографе, непрерывно изменяется как по величине, так и по направлению. Причем изменения эти происходят периодически, то есть точно повторяются через равные промежутки времени.

Переменное напряжение генерируется на электростанциях и посредством повышающих и понижающих распределительных трансформаторов попадает к конечному потребителю. При этом трансформация по пути никак не сказывается на синусоиде напряжения.

Видео — действующее напряжение и амплитудное

С полным и наглядным изложением рассматриваемого вопроса вы можете ознакомиться в следующем видео:

Работа генератора трехфазного переменного тока

Рассмотрим упрощенно работу генератора трехфазного переменного тока. Обмотки статора (фазы А, В и С) генератора расположены под углом 120 градусов относительно друг друга. Ротор с магнитом вращаясь индуцирует в обмотках статора периодически изменяющиеся ЭДС. Выглядит это следующим образом:

Такое вращение происходит с частотой 50 оборотов в секунду, то есть с частотой 50 Герц. Это значит, что электроны движутся в течение 1 секунды 50 раз в одном направлении (положительный полупериод синусоиды), и 50 — в обратном (отрицательный полупериод), 100 раз проходя чрез нулевое значение. Получается, что к примеру обычная лама накаливания, включенная в сеть с такой частотой, будет затухать и вспыхивать примерно 100 раз за секунду, однако мы этого не замечаем в силу особенностей своего зрения.

Определение действующего напряжения

Теперь непосредственно о том, почему произошел переход от максимального, амплитудного значения напряжения 310 Вольт к действующему 220 Вольт. Ответ можно найти в самом определении.

Действующее (эффективное или среднеквадратичное) значение напряжения — это такое напряжение постоянного тока, которое на такой же резистивной нагрузке выделит такую же мощность, как измеряемое переменное напряжение. Соответственно, действующее значение силы тока — такое значение силы постоянного тока, при прохождении которого через резистивную нагрузку выделится такая же мощность, что и при прохождении измеряемого тока.

Можно сформулировать и немного иначе. Действующее значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведет такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.

Общая формула расчета действующего напряжения произвольной формы следующая:

Объяснение действующего напряжения

Определение и формула — это хорошо. Но лучше все понять на наглядном примере. Объяснить все можно через мощность. Причем есть сложный для восприятия способ и более простой, который мы и рассмотрим далее.

Нам нужно взять один период синусоиды переменного напряжения, на этом промежутке построить синусоиду переменного тока и проанализировать мощность. Начнем с периода синусоиды переменного напряжения. Здесь же построим синусоиду переменного тока с учетом условной резистивной нагрузки (например, лампочки). По закону Ома сила тока равна напряжению, деленному на сопротивление.

Точные значения в конкретный момент при данном объяснении не принципиальны, поэтому все построения приблизительные. Естественно нужно понимать, что деля напряжение на сопротивление, мы получим синусоиду переменного тока с амплитудой в R раз меньшей, чем у напряжения. R – это значение сопротивления.

Теперь по двум синусоидам строим график мощности по формуле мощность равна силе тока умноженной на напряжение (P = I × U). Так как напряжение и ток имеют общие нулевые точки, то график мощности не будет заходить в отрицательную область. То есть сила тока со знаком «+» и напряжение со знаком «+» дадут мощность со знаком «+», так же как и сила тока со знаком «-» и напряжение со знаком «-» дадут мощность со знаком «+».

Анализируя полученный график можно отметить, что мощность пульсирующая. Она поднимается до максимального значения и падает до нуля, потом опять поднимается и снова падает. Как на эти колебания мощности реагируют электроприборы? Никак. Поскольку частота переменного тока 50 Герц, то эти колебания происходят очень быстро. Электроприборы откликаются не на максимальные и минимальные значения мощности, а на усредненные. То есть берется максимальное значение мощности и делится на два. Это значение называется действующим и находится по следующей формуле:

Pд = (Imax × Umax) / 2, где Pд — мощность действующая, Imax — сила тока максимальная, Umax — напряжение максимальное.

Двойку можно представить в виде корень из двух умножить на корень из двух. Получаем Действующее значение мощности = сила тока максимальная деленная на корень из двух умноженная на напряжение максимальное деленное на корень из двух (Pд = (Imax/√2) × (Umax/√2)).

Соответственно сила тока максимальная деленная на корень из двух — это действующее значение силы переменного тока, а напряжение максимальное деленное на корень из двух – это действующее значение переменного напряжения.

И действительно, если мы возьмем максимальное напряжение из предыдущего примера 309,1 Вольт и разделим на корень из двух, то получим действующее напряжение (то, которое показывает вольтметр) 219,4 Вольт.

Действующие значения силы тока и напряжения.

Презентация по физике

Переменный электрический ток. Активное сопротивление. Действующие значения силы тока и напряжения.

Выполняли ученицы 11 «А» класса Радукан Яна, Иванова Алина.

Переменный электрический ток

Как известно, ток (электрический) бывает переменным и постоянным.Переме́нный ток (англ. alternating current — переменный ток) — электрический ток, который периодически изменяется по модулю и направлению.В настоящее время очень широко используется переменный электрический ток. Его можно получить с помощью электрогенераторов переменного тока с применением эффекта электромагнитной индукции. На рисунке изображена примитивная установка для выработки переменного тока.

Принцип действия установки прост. Проволочная рамка вращается в однородном магнитном поле с постоянной скоростью. Своими концами рамка закреплена на кольцах, вращающихся вместе с ней. К кольцам плотно прилегают пружины, выполняющие роль контактов. Через поверхность рамки непрерывно будет протекать изменяющийся магнитный поток, но поток, создаваемый электромагнитом, останется постоянным. В связи с этим в рамке возникнет ЭДС индукции.

Под переменным током также подразумевают ток в обычных одно- и трёхфазных сетях. В этом случае мгновенные значения тока и напряжения изменяются по гармоническому закону.

Ф = BScoswt “

Переменный ток в осветительной сети квартиры, применяемый па заводах и фабриках и т. д., представляет собой не что иное, как вынужденные электромагнитные колебания. Данные колебания напряжения легко обнаружить с помощью осциллографа.

(рис. 4.8)

Стандартная частота промышленного переменного тока равна 50 Гц. Это означает, что на протяжении 1 с ток 50 раз идет в одну сторону и 50 раз — в противоположную. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц. Если напряжение на концах цепи меняется по гармоническому закону, то и напряженность электрического поля внутри проводников будет также меняться гармонически.

Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока. Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла а между нормалью к рамке и вектором магнитной индукции (рис. 4.9):

Ф = BScos а

При равномерном вращении рамки угол а увеличивается прямо пропорционально времени: а=2Пnt , где n – частота вращения. Поэтому поток магнитной индукции меняется гармонически :

Ф = BS cos 2Пnt , Здесь 2Пn число колебаний магнитного потока за 2П с. Это ЦИКЛИЧЕСКАЯ ЧАСТОТА колебаний w=2Пn = Ф = BScoswt

Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «-» скорости изменения потока магнитной индукции, т. е. производной потока магнитной индукции по времени:

Если к рамке подключить колебательный контур, то угловая скорость w вращения рамки определит частоту w колебаний значений ЭДС, напряжения на paзличныx участках цепи и силы тока.

Если напряжение меняется с циклической частотой , то и сила тока в цепи будет меняться с той же частотой. Но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока і в любой момент времени (мгновенное значение силы тока) определяется по формуле

Здесь I m – амплитуда силы тока, т. е. максимальное по модулю значение силы тока, а — разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Активное сопротивление .

Действующие значения силы тока и напряжения.

Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.

Сила тока в цени с резистором. Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.

Сопротивление R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются. Будем считать, что напряжение на зажимах цепи меняется по гармоническому закону:

u = U m cos w t

Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома :

Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.

Как правило, нам нужно бывает знать среднюю мощность тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найти среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии, поступающей в цепь за период, к периоду.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой :

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения (рис. 4.17), а амплитуда силы тока определяется равенством

P = I 2 R. (4.18)

На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.

Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение

Поэтому мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой :

P = i 2 R. (4.19)

Средняя мощность

равна первому члену в формуле (4.20)

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока. Действующее значение силы переменного тока обозначается через I:

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:

Заменяя в формуле (4. 17) амплитудные значения силы тока и напряжения на их действующие значения, получаем закон Ома для участка цепи переменного тока с резистором

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока:

P = I 2 R = UI.

Конденсатор в цепи переменного тока

Постоянный ток не может идти по цепи, содержащей конденсатор. Ведь фактически при этом цепь оказывается разомкнутой, так как обкладки конденсатора разделены диэлектриком.

Пусть у нас имеются источники постоянного и переменного напряжений, причем постоянное напряжение на зажимах источника равно действующему значению переменного напряжения. Цепь состоит из конденсатора и лампы накаливания (рис. 4.13), соединенных последовательно. При включении постоянного напряжения (переключатель повернут влево, цепь подключена к точкам АА’) лампа не светится. Но при включении переменного напряжения (переключатель повернут вправо, цепь подключена к точкам ВВ’) лампа загорается, если емкость конденсатора достаточно велика.

Переменный же ток может идти по цепи, содержащей конденсатор. В этом можно убедиться с помощью простого опыта.

Как же переменный ток может идти по цепи, если она фактически разомкнута (между пластинами конденсатора заряды перемещаться не могут)? Все дело в том, что происходит периодическая зарядка и разрядка конденсатора под действием переменного напряжения. Ток, идущий в цепи при перезарядке конденсатора, нагревает нить лампы.

Сила тока, представляющая собой производную заряда по времени , равна:

Установим, как меняется со временем сила тока в цепи, содержащей только конденсатор, если сопротивлением проводов и обкладок конденсатора можно пренебречь (рис. 4.14).

Следовательно, колебания силы тока опережают по фазе колебания напряжения на конденсаторе на

(рис. 4.15).

Напряжение на конденсаторе

Чем больше емкость конденсатора, тем больше ток перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора.

Амплитуда силы тока равна:

I m = U m C

(4.29)

Если ввести обозначение :

В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение X c . С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты

и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим :

Величину X c , обратную произведению

циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением .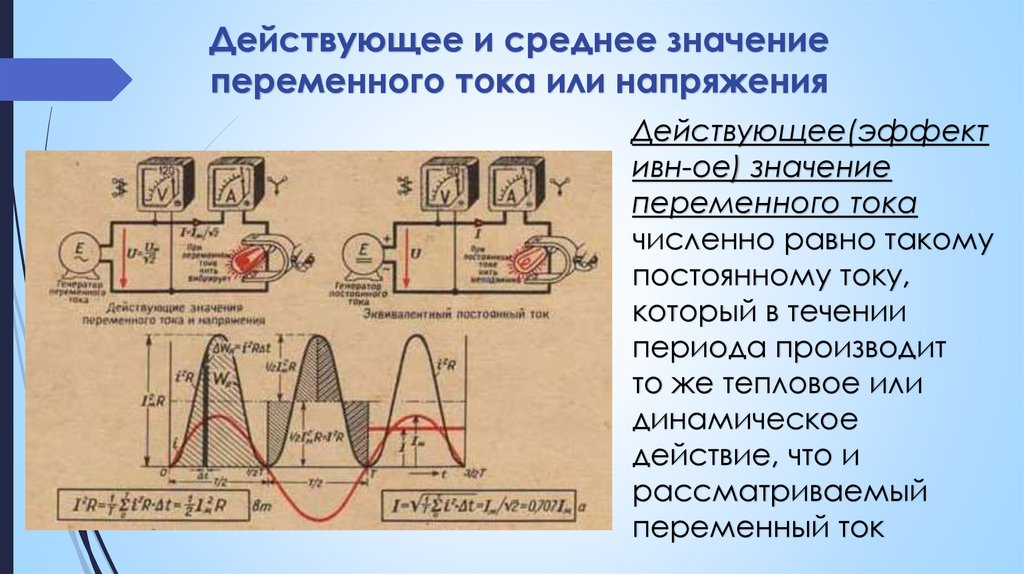

Сопротивление цепи с конденсатором обратно пропорционально произведению циклической частоты на электроемкость. Колебания силы тока опережают по фазе колебания напряжения на

Действующее значение силы тока связано с действующим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока.

КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА

Индуктивность в цепи влияет на силу переменного тока. Это можно доказать с помощью простого опыта.

Опыт показывает, что лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы переменного тока в рассматриваемой цепи меньше силы постоянного тока.

Соберем цепь из катушки с большой индуктивностью и электрической лампы накаливания (рис. 4.16). С помощью переключателя можно подключить эту цепь либо к источнику постоянного напряжения, либо к источнику переменного напряжения. При этом постоянное напряжение и действующее значение переменного напряжения должны быть равны.

Объясняется это различие явлением самоиндукции.

Если напряжение быстро меняется, то сила тока не будет успевать достигнуть тех значений, которые она приобрела бы с течением времени при постоянном напряжении.

Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения.

Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (рис. 4.17). Для этого предварительно найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.

–

Из равенства

следует, что удельная работа вихревого поля (т. е. ЭДС самоиндукции е і ) равна по модулю и противоположна по знаку удельной работе кулоновского поля. Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, можно записать: е і = -u.

Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю. Иначе сила тока, согласно закону Ома, была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля

При изменении силы тока по гармоническому закону :

i = I m sin

ЭДС самоиндукции равна:

порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля

e і = – L i ‘ = – L

l m cos

Так как u = -е і , то напряжение на концах катушки оказывается равным

создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.

Следовательно, колебания напряжения на катушке опережают по фазе колебания силы тока на

Индуктивное сопротивление зависит от частоты

что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на (рис. 4.18)

Постоянный ток вообще «не замечает» индуктивности катушки. При = 0

индуктивное сопротивление равно нулю (X L = 0).

Амплитуда силы тока в катушке равна:

Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока.

Катушка индуктивности оказывает сопротивление переменному току.

и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим:

Это сопротивление, называемое индуктивным, равно произведению циклической частоты на индуктивность.

Колебания силы тока в цепи с индуктивностью отстают по фазе от колебаний напряжения на

Величину X L , равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Согласно формуле (4.35) действующее значение силы тока связано с действующим значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.

Спасибо за внимание!

Источники:https://vk. com/away.php?to=http%3A%2F%2Fselectelement.ru%2Fbasic-concepts%2Felectric-ac.php&cc_key= https://vk.com/away.php?to=https%3A%2F%2Fsites.google.com%2Fsite%2Fopatpofizike%2Fteoria%2Fteoria-11-klass%2Feds-zakon-oma-dla-polnoj-cepi%2Fperemennyj-elektriceskij-tok-aktivnoe-induktivnoe-eemkostnoe-soprotivlenia&cc_

Статья об эффективном+текущем в The Free Dictionary

Эффективном+текущем | Статья об эффективном+текущем от The Free Dictionary

Действующий+текущий | Статья об эффективном+текущем The Free Dictionary

Слово, не найденное в Словаре и Энциклопедии.

Возможно, Вы имели в виду:

Пожалуйста, попробуйте слова отдельно:

эффективный текущий

Некоторые статьи, соответствующие вашему запросу:

Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.

Полный браузер ?

▲
Эффективное время на станции
Эффективная верхняя труба
Эффективный крутящий момент
Эффективное обучение и развитие
Дата вступления в силу передачи
эффективная группа трансформации
Эффективный поступательный подъем
Эффективная скорость передачи
Программа эффективного управления судебными разбирательствами
Эффективная истинная скорость полета
Эффективная истинная скорость полета
Действующий контроль США
эффективных корабля, контролируемых США
эффективных корабля, контролируемых США
Идентификатор действующего пользователя
Действующий идентификатор пользователя
Эффективный пользовательский интерфейс
эффективное значение
Эффективный желудочковый рефрактерный период
Эффективная видимость Исполнение

Эффективные боевые действия в спорной среде
эффективная длина волны
эффективная длина волны
эффективная длина волны
эффективная длина волны
эффективный ветер
Эффективная рабочая длина
Фактический год постройки
Эффективный выход
Эффективная доходность
действующий+текущий
Эффективный, доступный, многоразовый Преобразование речи в текст
Теория эффективной массы
Преобразование эффективных адресов в реальные
Эффективная/эквивалентная температура черного тела
эффективно
эффективно
эффективно
эффективно
эффективно
Эффективная интеграция затенения

Эффективно вычислимый
эффективно вычислимая функция
эффективно связать заработок и прибыль
Эффективно подключенный доход
Эффективно связанный налогооблагаемый доход
эффективно заземленный
Эффективно отделяемый
Эффективно протестированный драм
эффективность
эффективность
эффективность
эффективность
Эффективность и пригодность
Бюллетени эффективности здравоохранения
Индекс эффективности
уровень эффективности
Эффективность антигельминтных средств: общие рекомендации
Эффективность образовательных технологий
Эффективность морских систем радиоэлектронной борьбы
Отчет об эффективности — отчет о производительности
▼

Сайт: Следовать:

Делиться:

Открыть / Закрыть

Если эффективный ток в цепи переменного тока с 50 циклами равен 5 А, каково пиковое значение тока? Чему равен ток через 1//600 с после того, как он стал равным нулю?

Вопрос

Обновлено:26/04/2023

ПУБЛИКАЦИЯ CHETANA-СХЕМЫ ПЕРЕМЕННОГО ТОКА-Упражнение

21 видео на экзаменах.

Ab Padhai каро бина объявления ке

Khareedo DN Про и дехо сари видео бина киси объявление ки rukaavat ке!

সংশ্লিষ্ট ভিডিও

Если действующее значение тока при 50 Гц переменного тока ток в цепи 5,0 А. Что такое (i) пиковое значение или ток (ii) среднее значение тока за половину цикла (iii) значение тока через 1//300 с после того, как оно стало равным нулю?

12012805

Действующее значение тока при 50 циклах переменного тока. ток в цепи 5,0 А. Чему равно значение тока (1//300) с после того, как он станет равным нулю?

12013331

Действующее значение тока в 50 циклах переменного тока. ток в цепи 5 А. Каково значение тока через 1/300 секунды после того, как он стал равным нулю?

17959204

Действующее значение тока в цепи переменного тока составляет 10 А. Каков пиковый ток?

113076036

ं धारा का शिखर मान 5A है। यदि परीपथ में प्रत्यावर्ती धारा अमीटर जोड़ें तो उनके पाठ्यांक क्या होंगे?

223421969

ं धारा का शिखर मान 5A है। यदि परीपथ में दिष्ट धारा अमीटर जोड़ें तो उनके पाठ्यांक क्या होंगे?

223421972

धारा का शिखर मान 10A है यदि परिपथ में
दिष्ट धार ा अमीटर जोड़े तो उनके पाठ्यांक क्या होंगे ?

304863228

В цепи переменного тока с частотой 100 Гц действующее значение тока составляет 6 А. Рассчитайте (i) пиковое значение тока, (ii) среднее значение тока за полупериод и (iii) значение тока 1/ 500 с после того, как он стал нулем.

415578122

Найдите пиковое и среднее значение тока за полупериод, если эффективный ток в цепи переменного тока частотой 40 Гц равен 7 А.

415578201

Если действующее значение тока при 50 Гц перем. цепь составляет 5,0 А. Что такое (i) пиковое значение тока, (ii) среднее значение тока за половину цикла и (iii) значение тока через 1300 с после того, как оно стало равным нулю?

425871454

Эффективный ток в 50 c.p.s. Цепь переменного тока 20А. Каково пиковое значение тока и тока через 1/600 с после того, как оно стало равным нулю?

425871609

यदि 50 चक्र वाले ac परिपथ में प्रभाव ी धारा 50 A है, तो (a) धारा का शिखर मान और (b) शून्य के (1/300)s बाद धारा का मान क्या है?

540824422

(a) Пиковое напряжение сети переменного тока составляет 300 В. Каково среднеквадратичное значение напряжения?
(b) Среднеквадратичное значение тока в цепи переменного тока равно 10 А.