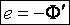В материале разберемся в понятии ЭДС индукции в ситуациях ее возникновения. Также рассмотрим индуктивность в качестве ключевого параметра возникновения магнитного потока при появлении электрического поля в проводнике.
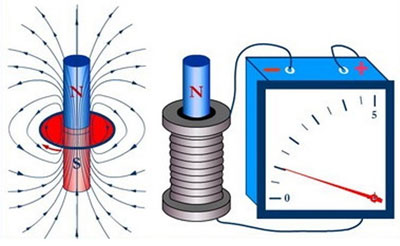

Электромагнитная индукция представляет собой генерирование электрического тока магнитными полями, которые изменяются во времени. Благодаря открытиям Фарадея и Ленца закономерности были сформулированы в законы, что ввело симметрию в понимание электромагнитных потоков. Теория Максвелла собрала воедино знания об электрическом токе и магнитных потоках. Благодаря открытия Герца человечество узнало о телекоммуникациях.
Магнитный поток
Вокруг проводника с электротоком появляется электромагнитное поле, однако параллельно возникает также обратное явление – электромагнитная индукция. Рассмотрим магнитный поток на примере: если рамку из проводника поместить в электрическое поле с индукцией и перемещать ее сверху вниз по магнитным силовым линиям или вправо-влево перпендикулярно им, тогда магнитный поток, проходящий через рамку, будет постоянной величиной.
При вращении рамки вокруг своей оси, тогда через некоторое время магнитный поток изменится на определенную величину. В результате в рамке возникает ЭДС индукции и появится электрический ток, который называется индукционным.
ЭДС индукции
Разберемся детально, что такое понятие ЭДС индукции. При помещении в магнитное поле проводника и его движении с пересечением силовых линий поля, в проводнике появляется электродвижущая сила под названием ЭДС индукции. Также она возникает, если проводник остается в неподвижном состоянии, а магнитное поле перемещается и пересекается с проводником силовыми линиями.
Когда проводник, где происходит возникновение ЭДС, замыкается на вешнюю цепь, благодаря наличию данной ЭДС по цепи начинает протекать индукционный ток. Электромагнитная индукция предполагает явление индуктирования ЭДС в проводнике в момент его пересечения силовыми линиями магнитного поля.
Электромагнитная индукция являет собой обратный процесс трансформации механической энергии в электроток. Данное понятие и его закономерности широко используются в электротехнике, большинство электромашин основывается на данном явлении.
Законы Фарадея и Ленца
Законы Фарадея и Ленца отображают закономерности возникновения электромагнитной индукции.
Фарадей выявил, что магнитные эффекты появляются в результате изменения магнитного потока во времени. В момент пересечения проводника переменным магнитным током, в нем возникает электродвижущая сила, которая приводит к возникновению электрического тока. Генерировать ток может как постоянный магнит, так и электромагнит.
Ученый определил, что интенсивность тока возрастает при быстром изменении количества силовых линий, которые пересекают контур. То есть ЭДС электромагнитной индукции пребывает в прямой зависимости от скорости магнитного потока.
Согласно закону Фарадея, формулы ЭДС индукции определяются следующим образом:
Е = — dФ/dt.
Знак «минус» указывает на взаимосвязь между полярностью индуцированной ЭДС, направлением потока и изменяющейся скоростью.
Согласно закону Ленца, можно охарактеризовать электродвижущую силу в зависимости от ее направленности. Любое изменение магнитного потока в катушке приводит к появлению ЭДС индукции, причем при быстром изменении наблюдается возрастающая ЭДС.
Если катушка, где есть ЭДС индукции, имеет замыкание на внешнюю цепь, тогда по ней течет индукционный ток, вследствие чего вокруг проводника появляется магнитное поле и катушка приобретает свойства соленоида. В результате вокруг катушки формируется свое магнитное поле.
Э.Х. Ленц установил закономерность, согласно которой определяется направление индукционного тока в катушке и ЭДС индукции. Закон гласит, что ЭДС индукции в катушке при изменении магнитного потока формирует в катушке ток направления, при котором данный магнитный поток катушки дает возможность избежать изменения постороннего магнитного потока.
Закон Ленца применяется для всех ситуаций индуктирования электротока в проводниках, вне зависимости от их конфигурации и метода изменения внешнего магнитного поля.
Движение провода в магнитном поле
Значение индуктированной ЭДС определяется в зависимости от длины проводника, пересекаемого силовыми линиями поля. При большем количестве силовых линий возрастает величина индуктируемой ЭДС. При увеличении магнитного поля и индукции, большее значение ЭДС возникает в проводнике. Таким образом, значение ЭДС индукции в движущемся в магнитном поле проводнике находится в прямой зависимости от индукции магнитного поля, длины проводника и скорости его движения.
Данная зависимость отражена в формуле Е = Blv, где Е — ЭДС индукции; В — значение магнитной индукции; I — длина проводника; v —скорость его перемещения.
Отметим, что в проводнике, который движется в магнитном поле, ЭДС индукции появляется, только когда он пересекает силовые линии магнитного поля. Если проводник движется по силовым линиям, тогда ЭДС не индуктируется. По этой причине формула применяется только в случаях, когда движением проводника направлено перпендикулярно силовым линиям.
Направление индуктированной ЭДС и электротока в проводнике определяется направлением движения самого проводника. Для выявления направления разработано правило правой руки. Если держать ладонь правой руки таким образом, чтобы в ее направлении входили силовые линии поля, а большой палец указывает направление движения проводника, тогда остальные четыре пальца показывают направление индуктированной ЭДС и направление электротока в проводнике.
Вращающаяся катушка
Функционирование генератора электротока основывается на вращении катушки в магнитном потоке, где имеется определенное количество витков. ЭДС индуцируется в электрической цепи всегда при пересечении ее магнитным потоком, на основании формулы магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на площадь поверхности, через которую проходит магнитный поток, и косинус угла, сформированный вектором направления и перпендикулярной плоскости линии).
Согласно формуле, на Ф воздействуют изменения в ситуациях:
- при изменении магнитного потока меняется вектор направления;
- изменяется площадь, заключенная в контур;
- меняется угол.
Допускается индуцирование ЭДС при неподвижном магните или неизменном токе, а просто при вращении катушки вокруг своей оси в пределах магнитного поля. В данном случае магнитный поток изменяется при смене значения угла. Катушка в процессе вращения пересекает силовые линии магнитного потока, в итоге появляется ЭДС. При равномерном вращении возникает периодическое изменение магнитного потока. Также число силовых линий, которые пересекаются ежесекундно, становится равным значениям через равные временные промежутки.
На практике в генераторах переменного электротока катушка остается в неподвижном состоянии, а электромагнит выполняет вращения вокруг нее.
ЭДС самоиндукции
При прохождении через катушку переменного электротока генерируется переменное магнитное поле, которое характеризуется меняющимся магнитным потоком, индуцирующим ЭДС. Данное явление называется самоиндукцией.
В силу того, что магнитный поток пропорционален интенсивности электротока, тогда формула ЭДС самоиндукции выглядит таким образом:
Ф = L x I, где L – индуктивность, которая измеряется в Гн. Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.
Взаимоиндукция
При расположении двух катушек рядом в них наблюдается ЭДС взаимоиндукции, которая определяется конфигурацией двух схем и их взаимной ориентацией. При возрастании разделения цепей значение взаимоиндуктивности уменьшается, поскольку наблюдается уменьшение общего для двух катушек магнитного потока.
Рассмотрим детально процесс возникновения взаимоиндукции. Есть две катушки, по проводу одной с N1 витков течет ток I1, которым создается магнитный поток и идет через вторую катушку с N2 числом витков.
Значение взаимоиндуктивности второй катушки в отношении первой:
М21 = (N2 x F21)/I1.
Значение магнитного потока:
Ф21 = (М21/N2) x I1.
Индуцированная ЭДС вычисляется по формуле:
Е2 = — N2 x dФ21/dt = — M21x dI1/dt.
В первой катушке значение индуцируемой ЭДС:
Е1 = — M12 x dI2/dt.
Важно отметить, что электродвижущая сила, спровоцированная взаимоиндукцией в одной из катушек, в любом случае прямо пропорциональна изменению электрического тока в другой катушке.
Тогда взаимоиндуктивность считается равной:
М12 = М21 = М.
Вследствие этого , E1 = — M x dI2/dt и E2 = M x dI1/dt. М = К √ (L1 x L2), где К является коэффициентом связи между двумя значениями инжуктивности.
Взаимоиндукция широко используется в трансформаторах, которые дают возможность менять значения переменного электротока. Прибор представляет собой пару катушек, которые намотаны на общий сердечник. Ток в первой катушке формирует изменяющийся магнитный поток в магнитопроводе и ток во второй катушке. При меньшем числе витков в первой катушке, чем во второй, возрастает напряжение, и соответственно при большем количестве витков в первой обмотке напряжение снижается.
Помимо генерирования и трансформации электрической энергии, явление магнитной индукции используется в прочих приборах. К примеру, в магнитных левитационных поездах, движущихся без непосредственного контакта с током в рельсах, а на пару сантиметров выше по причине электромагнитного отталкивания.
Электромагнитная индукция – FIZI4KA

Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.


Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
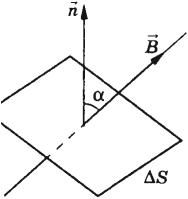
Магнитным потоком через площадь \( S \) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции \( B \), площади поверхности \( S \), пронизываемой данным потоком, и косинуса угла \( \alpha \) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
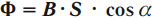
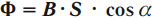

Обозначение – \( \Phi \), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
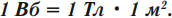
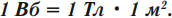
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла \( \alpha \) магнитный поток может быть положительным (\( \alpha \) < 90°) или отрицательным (\( \alpha \) > 90°). Если \( \alpha \) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
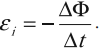
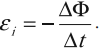
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из \( N \) витков, то ЭДС индукции:
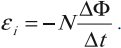
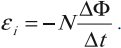
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением \( R \):
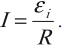
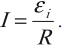
При движении проводника длиной \( l \) со скоростью \( v \) в постоянном однородном магнитном поле с индукцией \( \vec{B} \) ЭДС электромагнитной индукции равна:
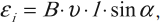
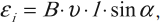
где \( \alpha \) – угол между векторами \( \vec{B} \) и \( \vec{v} \).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
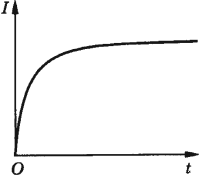

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
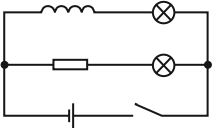

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции \( \varepsilon_{is} \), возникающая в катушке с индуктивностью \( L \), по закону электромагнитной индукции равна:
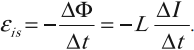
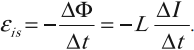
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток \( \Phi \) через контур из этого проводника пропорционален модулю индукции \( \vec{B} \) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
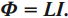
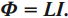
Индуктивность – коэффициент пропорциональности \( L \) между силой тока \( I \) в контуре и магнитным потоком \( \Phi \), создаваемым этим током:
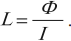
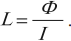
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
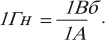
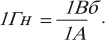
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
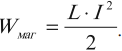
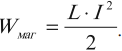
Основные формулы раздела «Электромагнитная индукция»


Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3.7 (73.33%) 3 votesЭлектродвижущая сила индукции
Электрические токи порождают вокруг себя магнитные поля. Данная связь дала толчок к многочисленным попыткам создать электрический ток в контуре при помощи магнитного поля.
Данную задачу решил М. Фарадей в 1831 году. Ученый открыл явление электромагнитной индукции.
Электромагнитная индукция
Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре, если изменяется поток магнитной индукции, который рассматриваемый контур охватывает, появляется электрический ток. Возникающий электрический ток называют током индукции.
Анализируя свои множественные эксперименты, М. Фарадей пришел к выводу о том, что:
- Индукционный ток появляется всегда при изменении магнитного потока, который охватывает проводящий контур. Так, если в однородном магнитном поле проводящий замкнутый контур повернуть, то в момент разворота в нем будет течь ток индукции. В этом случае индукция магнитного поля постоянна около проводящего контура, переменным является только поток магнитной индукции, который изменяется за счет изменения площади контура.
- Величина тока индукции не связана со способом изменения магнитного потока. Она определена только скоростью его изменения. Сила тока индукции тем больше, чем больше скорость перемещения магнита, или быстрота изменения силы тока, или скорость перемещения катушек.
Готовые работы на аналогичную тему
Электромагнитная индукция подтверждает связь между электрическими и магнитными явлениями.
Закон Фарадея
Анализируя данные своих экспериментов, М. Фарадей предложил количественный закон, описывающий электромагнитную индукцию. Ученый доказал, что каждый раз при изменении потока магнитной индукции, который сцеплен с проводящим контуром, в проводнике появляется ток индукции. Наличие индукционного тока означает то, что в цепи присутствует электродвижущая сила (ЭДС), которую в данном случае называют электродвижущей силой электромагнитной индукции ($Ɛ_i$).
Величина тока индукции, а значит, и величина $Ɛ_i$ зависит от скорости изменения магнитного потока:
$\left|Ɛ_{i} \right|=\frac{dФ}{dt}\left( 1 \right)$.
где $Ф$ – поток магнитной индукции.
Определимся со знаком ЭДС индукции. Знак потока магнитной индукции связан с выбором положительной нормали к рассматриваемому проводящему контуру. А направление силы тока и направление нормали связывает правило правого буравчика (винта). Получается, что фиксируя направление нормали, мы устанавливаем знак магнитного потока, направление тока и $Ɛ_i$ в контуре.
Сформулируем закон электромагнитной индукции Фарадея в окончательном виде:
Определение 1
Не зависимо от причины изменения магнитного потока, который охватывает замкнутый проводящий контур, электродвижущая сила индукции, появляющаяся в этом контуре равна:
$Ɛ_{i}=-\frac{dФ}{dt}\left( 2 \right)$.
где под $\frac{dФ}{dt}$ понимают полную скорость изменения потока магнитной индукции, охватываемого проводником.
Минус в формуле (2) указывает на то, что:
- При росте потока магнитной индукции (скорость изменения магнитного потока больше нуля) ($\frac{dФ}{dt}>0)$, ЭДС индукции меньше нуля ($Ɛ_i
- При уменьшении потока магнитной индукции (скорость изменения магнитного потока меньше нуля), ЭДС индукции больше нуля ($Ɛ_i>0$). Что значит, направление потока и направление поля тока индукции совпадают.
Замечание 1
Знак минус в формуле (2) – это математическое отображение правила Ленца, которое используют для того, чтобы найти направление тока индукции.
Закон Фарадея справедлив при:
- произвольных перемещениях замкнутого проводящего контура;
- при любых его деформациях;
- изменениях магнитного поля.
ЭДС индукции измеряется с Международной системе единиц (СИ) в вольтах (В).
$\left[ Ɛ_{i} \right]=\left[ \frac{dФ}{dt} \right]=\frac{Вб}{с}$=В.
Значение закона Фарадея
Закон Фарадея выражает новое физическое явление, в котором переменное магнитное поле порождает электрическое поле. Отсюда делается вывод о том, что электрическое поле может порождаться не только электрическими зарядами, но и изменяющимся магнитным полем.
Электромагнитная индукция – это всеобщий фундаментальный закон природы, реализующий связь между электрическими и магнитными полями.
Природа электродвижущей силы индукции
Если проводник перемещается в магнитном поле, то на свободные электроны его вещества действуют силы Лоренца. Эти электроны под воздействием названной силы приходят в движение относительно проводника, что означает: в проводнике появляется ток.
Рисунок 1. Проводники. Автор24 — интернет-биржа студенческих работ
Рассмотрим прямой участок $DG$ проводника на рис.1. Этот участок перемещается со скоростью $\vec v$ по проводникам $CK$ и $AL$, как по направляющим. При этом контур $AGDCA$ постоянно замкнут. Вектор индукции внешнего магнитного поля нормален плоскости рассматриваемого контура. Магнитное поле будем считать однородным. На заряды, которые перемещаются вместе с проводником, действует сила Лоренца, равная:
$\vec{F}_{L}=q\left( \vec{v}\times \vec{B} \right)\left( 3 \right)$.
где$ \vec{B}$– индукция внешнего магнитного поля. Под воздействием силы Лоренца свободные электроны проводника приходят в движение и образуют электрический ток. Направление этого тока принимают за положительный обход контура, положительная нормаль ($\vec n$) к площади контура указана на рис.1.
Наличие силы Лоренца эквивалентно тому, что в проводнике на заряды действует электрическое поле напряженность которого равна:
$\vec{E}=\frac{\vec{F}_{L}}{q}=\vec{v}\times \vec{B}\left( 4 \right)$.
Поэтому ЭДС индукции между точками 1 и 2 проводника найдем как:
$\left( Ɛ_{i} \right)_{21}=\int\limits_1^2 \vec{E} d\vec{l}=\int\limits_1^2\left( \vec{v}\times \vec{B} \right) d\vec{l}\left( 5 \right)$.
В случае, который мы рассматриваем на рис.1 точки 1 и 2 соответствуют точкам $D$ и $G$:
$\left( Ɛ_{i} \right)_{DG}=\int\limits_G^D {vBdl=vBl\, \left( 6 \right).} $
На не движущихся участках замкнутого контура, который мы рассматриваем, ЭДС не возникает. Следовательно, ЭДС контура равна ЭДС подвижного проводника $DG$, перемещающейся в магнитном поле.
$Ɛ_{i}=\int\limits_{AGDCA} {\vec{E}d\vec{l}=vBl\, \left( 7 \right).} $
Скорость перемещения проводника выразим как:
$v=\frac{dx}{dt}\left( 8 \right)$.
где $x$ – координата контактов проводника в точках $D$ и $G$ направляющими проводниками:
$Ɛ_{i}=Bl\frac{dx}{dt}\left( 9 \right)$.
Учитывая, что:
$Ф=-xlB$ (10),
где $Ф$ – поток магнитной индукции через поверхность, которую ограничивает контур $AGDCA$. Знак минус указывает на то, что направления векторов $\vec B$ и $ d\vec S$ противоположны,
окончательно имеем:
$Ɛ_{i}=-\frac{dФ}{dt}\left( 11 \right)$.
Выражение (11) мы получили, рассматривая движение части проводника. При перемещении нескольких участков проводника, ЭДС индукции находят как алгебраическую сумму ЭДС индукции, появляющихся на каждом участке.
Электродвижущая сила — Википедия
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил, то есть любых сил неэлектрического происхождения, действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура[1][2].
По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил E → e x {\displaystyle {\vec {E}}_{ex}} , под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд к величине этого заряда. Тогда в замкнутом контуре L {\displaystyle L} ЭДС будет равна:
- E = ∮ L E → e x ⋅ d l → , {\displaystyle {\mathcal {E}}=\oint \limits _{L}{\vec {E}}_{ex}\cdot {\vec {dl}},}
где d l → {\displaystyle {\vec {dl}}} — элемент контура.
ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами источника тока вне самого́ источника равна нулю.
ЭДС и закон Ома
Электродвижущая сила источника связана с электрическим током, протекающим в цепи, соотношениями закона Ома. Закон Ома для неоднородного участка цепи имеет вид[1]:
- φ 1 − φ 2 + E = I R , {\displaystyle \varphi _{1}-\varphi _{2}+{\mathcal {E}}=IR,}
где φ 1 − φ 2 {\displaystyle \varphi _{1}-\varphi _{2}} — разность между значениями потенциала в начале и в конце участка цепи, I {\displaystyle I} — сила тока, текущего по участку, а R {\displaystyle R} — сопротивление участка.
Если точки 1 и 2 совпадают (цепь замкнута), то φ 1 − φ 2 = 0 {\displaystyle \varphi _{1}-\varphi _{2}=0} и предыдущая формула переходит в формулу закона Ома для замкнутой цепи[1]:
- E = I R , {\displaystyle {\mathcal {E}}=IR,}
где теперь R {\displaystyle R} — полное сопротивление всей цепи.
В общем случае полное сопротивление цепи складывается из сопротивления внешнего по отношению к источнику тока участка цепи ( R e {\displaystyle R_{e}} ) и внутреннего сопротивления самого́ источника тока ( r {\displaystyle r} ). С учётом этого следует:
- E = I R e + I r . {\displaystyle {\mathcal {E}}=IR_{e}+Ir.}
ЭДС источника тока
Если на участке цепи не действуют сторонние силы (однородный участок цепи) и, значит, источника тока на нём нет, то, как это следует из закона Ома для неоднородного участка цепи, выполняется:
- φ 1 − φ 2 = I R . {\displaystyle \varphi _{1}-\varphi _{2}=IR.}
Значит, если в качестве точки 1 выбрать анод источника, а в качестве точки 2 — его катод, то для разности между потенциалами анода φ a {\displaystyle \varphi _{a}} и катода φ k {\displaystyle \varphi _{k}} можно записать:
- φ a − φ k = I R e , {\displaystyle \varphi _{a}-\varphi _{k}=IR_{e},}
где как и ранее R e {\displaystyle R_{e}} — сопротивление внешнего участка цепи.
Из этого соотношения и закона Ома для замкнутой цепи, записанного в виде E = I R e + I r {\displaystyle {\mathcal {E}}=IR_{e}+Ir} нетрудно получить
- φ a − φ k E = R e R e + r {\displaystyle {\frac {\varphi _{a}-\varphi _{k}}{\mathcal {E}}}={\frac {R_{e}}{R_{e}+r}}} и затем φ a − φ k = R e R e + r E . {\displaystyle \varphi _{a}-\varphi _{k}={\frac {R_{e}}{R_{e}+r}}{\mathcal {E}}.}
Из полученного соотношения следуют два вывода:
- Во всех случаях, когда по цепи течёт ток, разность потенциалов между клеммами источника тока φ a − φ k {\displaystyle \varphi _{a}-\varphi _{k}} меньше, чем ЭДС источника.
- В предельном случае, когда R e {\displaystyle R_{e}} бесконечно (цепь разорвана), выполняется E = φ a − φ k . {\displaystyle {\mathcal {E}}=\varphi _{a}-\varphi _{k}.}
Таким образом, ЭДС источника тока равна разности потенциалов между его клеммами в состоянии, когда источник отключён от цепи[1].
ЭДС индукции
Причиной возникновения электродвижущей силы в замкнутом контуре может стать изменение потока магнитного поля, пронизывающего поверхность, ограниченную данным контуром. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
- E = − d Φ d t , {\displaystyle {\mathcal {E}}=-{\frac {d\Phi }{dt}},}
где Φ {\displaystyle \Phi } — поток магнитного поля через замкнутую поверхность, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца). В свою очередь причиной изменения магнитного потока может быть как изменение магнитного поля, так и движение контура в целом или его отдельных частей.
Неэлектрический характер ЭДС
Внутри источника ЭДС ток течёт в направлении, противоположном нормальному. Это невозможно без дополнительной силы неэлектрической природы, преодолевающей силу электрического отталкиванияКак показано на рисунке, электрический ток, нормальное направление которого — от «плюса» к «минусу», внутри источника ЭДС (например, внутри гальванического элемента) течёт в противоположном направлении. Направление от «плюса» к «минусу» совпадает с направлением электрической силы, действующей на положительные заряды. Поэтому для того, чтобы заставить ток течь в противоположном направлении, необходима дополнительная сила неэлектрической природы (центробежная сила, сила Лоренца, силы химической природы) которая бы преодолевала электрическую силу.
Сторонние силы
Сторонними силами называются силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля. Например, в гальваническом элементе или аккумуляторе сторонние силы возникают в результате электрохимических процессов, происходящих на границе соприкосновения электрода с электролитом; в электрическом генераторе постоянного тока сторонней силой является сила Лоренца[3].
См. также
Примечания
В статье понятным и простым языком объясняется явление ЭДС. Представлена краткая историческая справка, рассмотрены типы ЭДС и её связь с параметрами электрической цепи. Текст подкреплён элементарными формулами.
Что такое ЭДС в физике – физический смысл
Электрический ток будет проходить через проводник только в том случае, если единовременно соблюдаются два простых условия:
- В проводнике присутствуют свободные электроны (например, в металлах электронов, не связанных с атомом, большинство).
- В проводнике присутствует сила, вынуждающая электроны двигаться.
Допустим, на концы электрода подали разные по знаку заряды, которые под действием кулоновской силы начинают притягиваться друг к другу.


Однако без сторонних сил электрическое поле, появившееся в результате такого взаимодействия, исчезнет, как только электроны придут в равновесие, поэтому для поддержания в проводнике электрического тока нужен источник питания, например батарейка.
ВАЖНО: электроны могут перемещаться только силами неэлектрического происхождения (сторонними силами), ярким примером которых являются химические процессы, происходящие в батарее.
При замыкании цепи «проводник – источник тока» электроны вновь начнут движение друг к другу, но как только положительный заряд приблизится к отрицательному, сторонние силы перенесут его обратно.


Так, работа этих сторонних сил по переносу единичного положительного заряда называется ЭДС.
Что такое ЭДС в электротехнике?
В электротехнике ЭДС характеризует источники питания и создаёт и поддерживает в течение длительного периода времени разность потенциалов. Численно ЭДС равна работе, которую должны совершить либо сторонние силы, чтобы переместить положительный заряд внутри источника, либо сам источник, чтобы провести заряд по цепи. Таким образом, формула для вычисления ЭДС имеет вид:
E = A / q,
где E – ЭДС,
А – работа,
q – заряд.
ЭДС необходима для поддержания в цепи постоянного тока, причём в технике применяется несколько видов ЭДС.
| Вид | Область применения |
| Химическая | Батарейки и аккумуляторы |
| Термоэлектрическая | Холодильники и термопары |
| Индукционная | Электродвигатели, генераторы и трансформаторы |
| Фотоэлектрическая | Фотоэлементы |
| Пьезоэлектрическая | Пьезоэлементы, датчики, кварцевые генераторы |
СПРАВКА: в теории существует идеальный источник ЭДС – генератор с нулевым внутренним сопротивлением, мощность которого приравнивается к бесконечности.
Расшифровка ЭДС
Аббревиатура ЭДС общепринятая и расшифровывается как «электродвижущая сила».
СПРАВКА: понятие ЭДС введено Георгом Омом в 1827 году, а её значение определено Густавом Кирхгофом в 1857.
В чём измеряется ЭДС – единица измерения
Уже было отмечено, что ЭДС – отношение работы к заряду, то есть:
Единица измерения E = 1 джоуль (Дж) / 1 кулон (Кл) = 1 вольт (В).
Таким образом, ЭДС, как напряжение, измеряется в вольтах. Причём на практике часто используют более крупные и мелкие единицы:
- киловольт (кВ): 1 кВ = 103 В;
- милливольт (мВ): 1мВ = 10-3 В;
- микровольт (мкВ): 1 мкВ = 10-6 В.
Чем отличается ЭДС от напряжения?
Известно, что напряжение характеризует работу электрического поля по переносу положительного заряда и измеряется в вольтах. Таким образом, на первый взгляд ЭДС и напряжение мало чем отличаются друг от друга, однако различие между этими понятиями есть и весьма существенное.

 Схема с ЭДС
Схема с ЭДСВ реальной электрической цепи присутствует внутреннее сопротивление, на котором происходит падение напряжения. Причём, если разомкнуть цепь и соединить вольтметр с батареей, он покажет значение ЭДС – 1,5 В, но при подключении нагрузки, например лампочки, на клеммах будет меньшее значение. Эти процессы описываются законом Ома для полной цепи.
То есть основная разница между величинами состоит в том, что напряжение зависит от нагрузки и тока в цепи, а ЭДС – от источника питания.
СПРАВКА: в идеальной электрической цепи, где отсутствует внутреннее сопротивление, между напряжением и ЭДС не будет разницы.
ЭДС электромагнитной индукции
29 августа 1831 года Майкл Фарадей открыл электромагнитную индукцию – явление возникновения электрического тока при движении замкнутого проводящего контура в магнитном поле или при изменении в течение времени этого поля.
Фарадей в ходе эксперимента обнаружил, что возникающая ЭДС зависит от скорости изменения магнитного потока через поверхность замкнутого контура, но не зависит от причины этого изменения.
Eинд = — dФ / dt,
где Eинд – ЭДС индукции,
Ф – магнитный поток, измеряемый в веберах (Вб),
t – время.
Знак дифференциала d характеризует изменение величин, а минус перед отношением отражает правило Ленца, согласно которому индукционный ток, вызванный ЭДС индукции, направлен таким образом, чтобы противодействовать изменению магнитного потока.
ЭДС источника тока
Электродвижущая сила источника тока характеризует его способность создавать и поддерживать разность потенциалов на зажимах.
ВНИМАНИЕ: ЭДС может возникнуть в источнике и при разомкнутой цепи, при этом данную ситуацию называют «холостым ходом», а величина силы приравнивается к разнице потенциалов.
ЭДС индукции в движущихся проводниках
Пусть в однородном магнитном поле с постоянной скоростью движется проводник. Тогда на каждый свободный электрон проводника будет действовать сила Лоренца, под действием которой отрицательные частицы начнут движение. В результате один из концов проводника зарядится отрицательно, второй – положительно, то есть возникнет разница потенциалов. Исходя из этого можно сделать вывод, что данный проводник в такой ситуации будет представлять собой источник тока, а разность потенциалов на его концах, по сути, представляет собой ЭДС.
Eинд = B∙l∙v∙sinα,
где B – вектор индукции магнитного поля,
l – длина проводника,
v – скорость его перемещения в магнитном поле,
α – угол направления движения к направлению действия поля, то есть угол между B и v.
ЭДС катушки индуктивности
Особенность катушки – способность создавать магнитное поле, если по её проводу течёт электрический ток, что называется индуктивностью.

 Схема ЭДС с катушкой индуктивности
Схема ЭДС с катушкой индуктивностиДопустим, собрана схема с катушкой с железным сердечником и лампочкой, подключенной параллельно. Если сначала замкнуть цепь, дав току, протекающему в неё, установиться, а потом резко разомкнуть, лампочка резко вспыхнет. Что свидетельствует о том, что при отключении цепи от источника питания ток из катушки перешёл в лампу. То есть ток в катушке был и имел вокруг себя магнитное поле, после исчезновения которого возникла ЭДС.
Такая электродвижущая сила называется ЭДС самоиндукции, так как она появилась от собственного магнитного поля катушки.
ЭДС гальванического элемента
Гальванический элемент – это источник тока, создающий его из химической энергии. Рассмотрим элемент Даниэля-Якоби, представляющий собой цинковую и медную пластины в соответствующих растворах сульфатов, соединённые между собой электролитом. Если соединить пластины металлическим стержнем, начнётся перераспределение зарядов: свободные электроны будут перемещаться к электроду с менее отрицательным зарядом (медной пластине). То есть возникнет электрический ток. Его работа будет максимальной в том случае, когда процессы на электродах (окисление и восстановление вследствие изменения числа электронов) будут протекать бесконечно медленно.
ЭДС гальванического элемента – максимальная разность потенциалов, возможная в такой ситуации.
Мощность через ЭДС
Известно, что мощность тока – это работа, совершаемая в единицу времени, то есть:
P = A / Δt,
где P – мощность.
Кроме этого, существует формула для вычисления мощности на участке цепи, связывающая эту величину с напряжением и током:
P = U∙I,
где U – напряжение,
I – ток.
В случае, если участок цепи содержит источник тока, имеющий ЭДС, формула будет иметь вид:
P = (u1—u2)∙I + E∙I,
где u1—u2 – разность потенциалов.
ЭДС через магнитный поток
Было отмечено, что Фарадей установил соотношение зависимости ЭДС от магнитного потока:
E = — ΔФ / Δt.
Известно, что магнитный поток можно найти, опираясь на выражение:
Ф = B∙S∙cosα,
где S – площадь поверхности, через которую проходит поток,
α – угол между вектором магнитной индукции и нормалью к поверхности.
Для некоторого упрощения допустим, что плоскость контура располагается перпендикулярно к магнитному полю, то есть α = 0. Учитывая, что ΔФ = Ф2 — Ф1 = B∙(S2 — S1), формула ЭДС может иметь вид:
E = — B∙(S2 — S1) / Δt.
Напряжение через ЭДС
Согласно закону Ома для участка цепи:
I = U / R,
где R – сопротивление.
Этот же закон для полной цепи имеет вид:
I = E / (R+r),
где r – сопротивление источника питания.
Пусть количество электронов, произведённых источником тока, равно количеству зарядов, которые «ушли» в цепь. Тогда справедливо равенство:
U / R = E / (R+r).
Путём элементарных математических действий можно получить связь напряжения и ЭДС:
U = E∙R / (R+r).
СПРАВКА: для идеальной цепи: U = E.
Как обозначается ЭДС на схеме?
Источник ЭДС обычно изображается буквой «Е», расположенной рядом со стрелкой, помещённой в круг. Рассмотрим несколько схем, встречающихся на практике.

 Как обозначается ЭДС на схеме
Как обозначается ЭДС на схемеНа рисунке под буквой «а» изображён идеальный источник ЭДС, под «б» – реальный источник, обладающий внутренним сопротивлением, под «в» – элементарная электрическая цепь: реальный источник ЭДС и потребитель.
Как можно повысить точность измерения ЭДС источника тока?
Одним из способов повышения точности является проведение серии измерений, что позволит снизить риск случайных ошибок. Кроме этого, в серию испытания можно включить измерение разности потенциалов, тока, внутреннего сопротивления источника, а после вычислить среднее значение требуемой величины.
Наиболее простой способ повышение точности – использование вольтметра высокого класса точности.
Формула ЭДС индукции, E
Закон Фарадея – Максвелла для электромагнитной индукции
Основной формулой, которая определяет ЭДС индукции, является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). Этот закон утверждает, что ЭДС индукции в контуре, находящемся в переменном магнитном поле, равна по величине и противоположна по знаку скорости изменения магнитного потока () через поверхность, которую ограничивает данный контур:
где – скорость изменения магнитного потока. Полная производная в законе (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) соответствует правилу Ленца. Формула (1) для ЭДС индукции записана для системы СИ.
В случае равномерного изменения магнитного потока формулу ЭДС индукции можно записать как:
Частные случаи формул ЭДС индукции
Если контур содержит N витков, которые соединяются последовательно, то ЭДС индукции вычисляют как:
где – потокосцепление.
При движении прямолинейного проводника в однородном магнитном поле в нем возникает ЭДС индукции, которая равна:
где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; .
При вращении с постоянной скоростью в однородном магнитном поле плоского контура вокруг оси, которая лежит в плоскости контура в нем возникает ЭДС индукции, равная:
где S – площадь, которую ограничивает виток; – поток самоиндукции витка; — угловая скорость; () – угол поворота контура. Следует учесть, что формула (5) справедлива, если ось вращения составляет прямой угол с направлением вектора внешнего поля .
Если во вращающейся рамке имеется N витков и самоиндукцией рассматриваемой системы можно пренебречь, то:
В стационарном проводнике, который находится в переменном магнитном поле, ЭДС индукции находят по формуле:
Примеры решения задач по теме «ЭДС индукции»
| Электромагнитная индукция | |
1831 г. – М. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает так называемый индукционный ток. (Индукция, в данном случае, – появление, возникновение). |
|
Индукционный ток в катушке возникает при перемещении постоянного магнита относительно катушки; при перемещении электромагнита относительно катушки; при перемещении сердечника относительно электромагнита, вставленного в катушку; при регулировании тока в цепи электромагнита; при замыкании и размыкании цепи |
|
Появление тока в замкнутом контуре при изменении магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил (или о возникновении ЭДС индукции). Явление возникновения ЭДС в замкнутом проводящем контуре при изменении магнитного поля (потока), пронизывающего контур, называется электромагнитной индукцией. Или: явление возникновения электрического поля при изменении магнитного поля (потока), называется электромагнитной индукцией. |
|
Закон электромагнитной индукции При всяком изменении магнитного потока через проводящий замкнутый контур в этом контуре возникает электрический ток. I зависит от свойств контура (сопротивление): ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром. |
|
Основные применения электромагнитной индукции: генерирование тока (индукционные генераторы на всех электростанциях, динамомашины), трансформаторы. |
|
Возникновение индукционного тока – следствие закона сохранения энергии! В случае 1: При приближении магнита, увеличении тока, замыкании цепи: В случае 2: при удалении магнита, уменьшении тока, размыкании цепи: |
|
Источником магнитного поля является ток. Поэтому: Возникающий в замкнутом контуре индукционный ток имеет такое направление, что созданный им поток магнитной индукции через площадь, ограниченную контуром, стремится компенсировать то изменение потока магнитной индукции, которое вызывает данный ток (правило Ленца). |
|
Ток в контуре имеет отрицательное направление ( Поэтому с учетом правила Ленца (знака) выражение для закона электромагнитной индукции записывается: Данная формула справедлива для СИ (коэффициент пропорциональности равен 1). В других системах единиц коэффициент другой. |
|
Если контур (например, катушка) состоит из нескольких витков, то где n – количество витков. Все предыдущие формулы справедливы в случае линейного (равномерного) изменения магнитного потока. В произвольном случае закон записывается через производную: |
|
Электромагнитная индукция – это то, где в проводнике создается напряжение или ток в результате изменения магнитного потока. Это может произойти, когда магнит перемещается в соленоиде, что приводит к изменению магнитного потока.
Когда спиральный провод вводится рядом с магнитом, магнитные силовые линии проходят через катушку. Это вызывает изменение магнитного потока. Магнитный поток представлен символом Φ {\ displaystyle {\ Phi}} Поэтому мы можем сказать, что Φ {\ displaystyle {\ Phi}} = BAcos (a) и полученная единица будет T м 2 {\ displaystyle Tm ^ {2}} где Т – единица измерения магнитного поля и м 2 {\ displaystyle m ^ {2}} это единица измерения площади.
Изменяющийся магнитный поток генерирует электродвижущую силу (ЭДС). Эта сила перемещает свободные электроны определенным образом, которые составляют ток.
Майкл Фарадей обнаружил, что электродвижущая сила возникает при изменении магнитного потока в проводнике.
Его законы гласят, что:
Е знак равно – d Φ d T {\ displaystyle {\ mathcal {E}} = {- {d \ Phi} \ over dt}}
где,
Е {\ displaystyle {\ mathcal {E}}} электродвижущая сила, измеренная в вольтах;
d Φ {\ displaystyle {d \ Phi}} изменение магнитного потока, измеряемое по Веберу;
d T {\ displaystyle dt} это изменение во времени, измеренное в секундах.
В случае соленоида:
Е знак равно – N d Φ d T {\ displaystyle {\ mathcal {E}} = {- N {d \ Phi} \ over dt}}
где,
N – количество петель в соленоиде.
Отрицательный знак в обоих уравнениях выше является результатом закона Ленца, названного в честь Генриха Ленца. Его закон гласит, что электродвижущая сила (ЭДС) создает ток, который противодействует движению изменяющегося магнитного потока.
,Что такое ЭДС? – типы индуцированной ЭДС
Электродвижущая сила или ЭДС , как говорят, индуцируется, когда поток, соединяющийся с проводником или катушкой, изменяется. 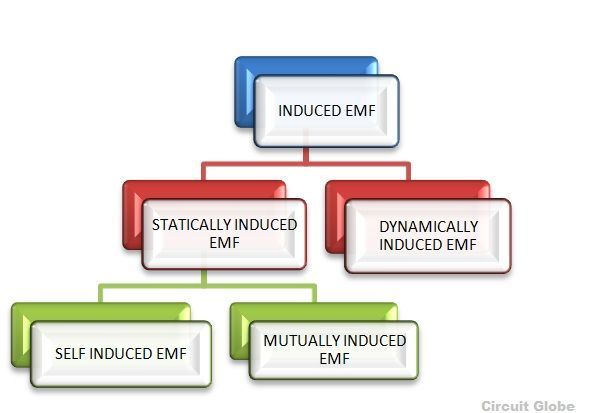
Это изменение потока может быть получено двумя различными способами; то есть статически или динамически индуцированной ЭДС. Они объяснены ниже
Содержание:
1. СТАТИЧЕСКИ ИНДУЦИРОВАННАЯ ЭДС
Этот тип ЭДС генерируется, если держать катушку и систему магнитного поля неподвижными одновременно; это означает, что изменение потока, связывающего с катушкой, происходит без перемещения проводника (катушки) или полевой системы.
Это изменение потока, создаваемого полевой системой, соединяющейся с катушкой, получается путем изменения электрического тока в полевой системе.
Далее делится на два пути
- Самоиндуцированная электродвижущая сила (ЭДС, которая индуцируется в катушке из-за изменения потока, возникающего при ее соединении с собственными витками.)
- Взаимно индуцированная электродвижущая сила (ЭДС, которая индуцируется в катушке из-за изменения потока, создаваемого другой катушкой, связывающейся с ней.)
2. ДИНАМИЧЕСКИ ИНДУЦИРОВАННАЯ ЭДС
В динамически индуцированной электродвижущей силе система магнитного поля остается неподвижной, и проводник движется, или система магнитного поля движется, и проводник неподвижен. Таким образом, следуя любому из двух процессов, проводник пересекает магнитное поле, и в катушке индуцируется ЭДС.
Это явление имеет место в электрических генераторах и противо-ЭДС двигателей, а также в трансформаторах.
,ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯНа рисунке 32.1 показан стержень из проводящего материала, перемещаемый с скорость v в однородном магнитном поле B. Магнитная сила, действующая на свободную электрон в стержне будет направлен вверх и имеет величину, равную
(32.1)
Рисунок 32.1. Движущийся проводник в магнитном поле. В результате действия магнитной силы электроны начнут накапливаться в верхней части стержня. Распределение заряда стержня будет поэтому меняются, и в верхней части стержня будет избыток электронов (отрицательный заряд), а в нижней части стержня будет дефицит электронов (положительный заряд). Это распределение заряда создаст электрическое поле в жезл Напряженность этого электрического поля будет увеличиваться до электростатическая сила, создаваемая этим полем, равна по величине магнитная сила.В этот момент восходящий поток электронов прекратится и(32.2)
или
(32.3)
Индуцированное электрическое поле будет генерировать разность потенциалов, дельта В между концами стержня, равного
(32.4)
где L – длина стержня. Если концы стержня связаны с Схема, обеспечивающая обратный путь для накопленного заряда, стержень будет Источник ЭДС.Поскольку ЭДС связана с движением стержня через Магнитное поле называется , , ЭДС движения, , . Уравнение (32.4) показывает, что величина эдс пропорциональна скорости v. на рисунке 32.1 мы видим, что vL – это площадь, пройденная стержнем за второй. Величина BvL – это магнитный поток, проходящий через стержень за второй. Таким образом
(32,5)
Хотя эта формула была выведена для особого случая, показанного на рисунке 32.1, это действует в общем. Держит стержни и проволоки произвольной формы, движущиеся через произвольные магнитные поля.
Уравнение (32.5) связывает индуцированную ЭДС со скоростью, с которой изменения магнитного потока. В системе, показанной на рисунке 32.1, поток изменения из-за движения стержня. Прилагаемый магнитный поток также может быть изменяется, если изменяется сила приложенного магнитного поля. В обоих случаях Результатом будет индуцированная ЭДС.Связь между индуцированной ЭДС и изменение магнитного потока известно как закон индукции Фарадея:
«Индуцированная ЭДС вдоль движущейся или изменяющейся математической траектории в константе или изменение магнитного поля равно скорости, с которой магнитный поток проникает через тропинка. “
Если мы рассмотрим замкнутый путь, закон Фарадея можно сформулировать следующим образом:
«Индуцированная ЭДС вокруг замкнутого математического пути в магнитном поле равна к скорости изменения магнитного потока, перехваченного областью в пределах дорожка “
или
(32.6)
Знак минус в уравнении (32.6) указывает, насколько полярность наведенной ЭДС связано со знаком потока и скоростью изменения потока. Знак поток устанавливается по правому правилу:
«Согните пальцы правой руки в том направлении, в котором мы находимся расчет ЭДС вокруг пути; магнитный поток будет положительным, если линии магнитного поля указывают в направлении большого пальца, а отрицательные в противном случае. “
Пример: проблема 32.13
Металлический стержень длиной L и массой m свободно скользит без трения, на двух параллельных металлических дорожках. Треки соединены на одном конце так, чтобы они и стержень образуют замкнутый контур (см. рисунок 32.2). Стержень имеет сопротивление R, и треки имеют незначительное сопротивление. Равномерное магнитное поле перпендикулярно плоскости этой цепи. Магнитное поле увеличивается с постоянной скоростью дБ / дт. Первоначально магнитное поле имеет напряженность B 0 , и стержень находится в состоянии покоя на расстоянии х 0 от соединенный конец рельсов.Выразите ускорение стержня в этом мгновенный с точки зрения заданных количеств.
Рисунок 32.2. Задача 32.13.Магнитный поток [Phi], окруженный стержнем и дорожками в момент времени t = 0 с, равен дается
(32,7)
Магнитное поле увеличивается с постоянной скоростью, и, следовательно, магнитный поток в замкнутом пространстве также увеличивается:
(32,8)
Закон индукции Фарадея теперь можно использовать для определения индуцированной ЭДС:
(32.9)
В результате наведенной ЭДС ток будет протекать через стержень с величина равна
(32.10)
Направление тока вдоль провода и, следовательно, перпендикулярно магнитное поле. Сила, приложенная магнитным полем к стержню, равна дается
(32.11)
(см. главу 31). Объединяя уравнения (32.10) и (32.11), получаем для силы на провод
(32.12)
Следовательно, ускорение стержня в момент времени t = 0 с равно
. (32.13)
Пример: проблема 32.12
а) Длинный соленоид имеет 300 витков провода на метр и имеет радиус 3,0 см Если ток в проводе увеличивается со скоростью 50 А / с, при чем скорость увеличивается сила магнитного поля в соленоиде?
б) Соленоид окружен катушкой со 120 витками.Радиус этого Катушка 6,0 см. Какая индуцированная ЭДС будет генерироваться в этой катушке, пока ток в соленоиде увеличивается?
а) Магнитное поле в соленоиде обсуждалось в главе 31. Если соленоид имеет n витков на метр, и если I – ток через каждую катушку, чем поле внутри соленоида равно
(32.14)
Следовательно,
(32.15)
В этой задаче n = 300 витков / метр и dI / dt = 50 А / с.Изменение в магнитное поле при этом равно
(32.16)
Это уравнение показывает, что магнитное поле увеличивается со скоростью 0,019 T / S.
б) Поскольку магнитное поле в соленоиде меняется, магнитный поток окруженный катушкой тоже изменится. Флюс, окруженный одиночная обмотка этой катушки
(32.17)
где r в = 3.0 см – это радиус соленоида. Здесь мы имеем Предполагается, что сила магнитного поля вне соленоида равна нулю. Общий поток, окруженный внешними катушками, равен
(32.18)
Скорость изменения магнитного потока за счет этого изменения магнитного поля составляет дается
(32.19)
В результате изменения тока в соленоиде будет индуцирована ЭДС во внешней катушке, со значением, равным
(32.20)
Если концы катушки соединены, ток будет течь через проводник. Направление тока в катушке можно определить с помощью закон Ленца , который гласит, что
“индуцированные ЭДС всегда имеют такую полярность, чтобы противостоять изменение, которое порождает их “Давайте применим закон Ленца к проблеме 32.12. Направление магнитного поля может быть определен с использованием правила правой руки и направлен вправо.Если ток в соленоиде увеличивает поток, также увеличивается. Электрический ток во внешней катушке будет течь в таком направлении, чтобы противостоять этому изменению. Это означает, что ток в этой катушке будет течь против часовой стрелки ( поле, создаваемое индуцированным током, направлено противоположно полю генерируется большим соленоидом).
Стержень, движущийся в магнитном поле, будет иметь индуцированную ЭДС в результате магнитная сила, действующая на свободные электроны.Индуцированная ЭДС будет пропорциональна линейной скорости v стержня. Если мы посмотрим на стержень с В системе отсчета, в которой стержень находится в состоянии покоя, магнитная сила будет равна нулю. Тем не менее, все еще должна быть индуцированная ЭДС. Так как этой эдс не может быть генерируется магнитным полем, это должно быть из-за электрического поля, которое существует в движущейся системе отсчета. Величина этого электрического поля должно быть таким, чтобы создавалась та же индуцированная эдс, что и в система отсчета, в которой движется стержень.Это требует, чтобы
(32.21)
Электрическое поле E ‘, которое существует в системе отсчета движущегося стержня, называется индуцированного электрического поля . ЭДС генерируется между Концы стержня равны
(32.22)
что эквивалентно уравнению (32.4). Если индуцированное электрическое поле находится в положении зависимый, то мы должны заменить уравнение (32.22) с интегральным выражением
(32.23)
где интеграл распространяется от одного конца стержня к другому концу стержень.
Разница между наведенным электрическим полем и электрическим полем генерируется распределением статического заряда в том, что в первом случае поле не является консервативным и интеграл по пути по замкнутому пути равен
(32.24)
который не равен нулю, если магнитный поток зависит от времени.
Изменяющийся ток в проводнике (например, в катушке) вызывает изменение магнитного поля. поле.Это зависящее от времени магнитное поле может вызвать ток в секунду проводник, если он находится в этом поле. ЭДС, индуцированная в эту секунду проводник, [эпсилон] 2 , будет зависеть от магнитного потока через него проводник:
(32.25)
Поток [Phi] B1 зависит от напряженности магнитного поля генерируется проводником 1 и, следовательно, пропорционально току Я 1 через этот проводник:
(32.26)
Здесь постоянная L 21 зависит от размера двух катушек, от их расстояние разноса и количество витков в каждой катушке. Постоянная L 21 называется взаимной индуктивностью двух катушек. Используя эту константу, уравнение (32.25) можно переписать как
(32.27)
Единицей индуктивности является Генри (H), и из уравнения (32.27) мы заключаем, что
(32.28)
Когда магнитное поле, создаваемое катушкой, изменяется (из-за изменения ток) магнитный поток, окруженный катушкой, также изменится. Это изменение в потоке будет вызывать ЭДС в катушке, а так как ЭДС вызвана изменением ток через катушку он называется самоиндуцированной ЭДС. ЭДС самоиндукции равна
(32.29)
В уравнении (32.29) L называется самоиндуктивности катушки.Самоиндуцированная ЭДС будет действовать в таком направлении, чтобы противостоять изменениям в ток.
Пример: проблема 32.32
Длинный соленоид радиуса R имеет n витков на единицу длины. Циркуляр Катушка провода радиуса R ‘с n’ витками окружает соленоид. Что взаимная индукция? Имеет ли значение катушка провода?
Предполагается, что поле внутри соленоида бесконечно длинное соленоид и имеет прочность, равную
(32.30)
Поток, окруженный внешней катушкой, равен
(32.31)
Индуцированная ЭДС во внешней катушке равна
(32.32)
Таким образом, взаимная индуктивность L 12 равна
. (32,33)
Если постоянный ток протекает через индуктор, не зависящий от времени магнитный поле создано.Если источник тока внезапно отключается, изменение в замкнутом магнитном потоке будет генерировать ЭДС самоиндукции, которая будет пытаться чтобы сохранить ток в первоначальном направлении. Электрическая энергия доставленный самоиндуцированной ЭДС первоначально был сохранен в индуктивности в форма магнитной энергии. Количество магнитной энергии, накопленной в магнитном поле может быть определено путем расчета полной мощности, передаваемой мощностью источник для создания магнитного поля.Предположим, что после батареи подключенный к индуктору ток увеличивается со скоростью dI / dt. ЭДС самоиндукции, созданная этим зависящим от времени током, равна
(32.34)
Ток должен доставлять дополнительную мощность, чтобы преодолеть эту самоиндуцированную ЭДС. требуемая мощность будет зависеть от времени и равна
(32,35)
Работа, проделанная током, сохраняется в индукторе в виде магнитной энергии. Изменение dU магнитной энергии индуктора при этом равно
(32.36)
Общая энергия, запасенная в магнитном поле индуктора при токе достигает своего конечного значения, можно получить интегрированием уравнения (32.36) между I = 0 и я = I f .
(32,37)
Для соленоида длины l самоиндукция равна
(32.38)
Магнитная энергия, накопленная в соленоиде, равна
(32.39)
где V – объем соленоида. Магнитная энергия может быть выражена в условия B и V:
(32.40)
где B = u 0 n I – магнитное поле в соленоиде. Общая Магнитная энергия индуктора теперь может быть выражена через плотность магнитной энергии u, которая определяется как
(32.41)
Магнитная энергия, запасенная в магнитном поле, равна плотности энергии время объем. Хотя мы вывели формулу для магнитной энергии плотность для частного случая очень длинного соленоида, его вывод действителен для любого произвольного магнитного поля.
Пример: проблема 32.46
Тороид квадратного сечения имеет внутренний радиус R 1 и внешний радиус R 2 .Тороид имеет N витков провода, несущего текущий я; предположим, что N очень большое.
а) Найти плотность магнитной энергии как функцию радиуса.
б) Интегрируя плотность энергии, найдите полную магнитную энергию, запасенную в соленоид.
в) Выведите самоиндуктивность из формулы U = L . I 2 /2.
а) Применим закон Ампера, используя сферическую амперовую петлю с радиусом r
(32.42)
Ток, заключенный в амперную петлю, равен
. (32,43)
Используя закон Ампера, мы можем определить магнитное поле B:
(32.44)
Плотность магнитной энергии при этом равна
(32.45)
б) Предположим, что высота тороида равна h. Посмотрите на кусочек тороид, показанный на рисунке 32.3.
Рисунок 32.3. Поперечное сечение тороида задачи 32.46. Объем dV этого среза равен(32.46)
Магнитная энергия, запасенная в этом сегменте, равна
(32.47)
Общая магнитная энергия, запасенная в тороиде, может быть получена путем интегрирования уравнение (32.47) относительно r между r = R 1 и r = R 2 :
(32.48)
в) Магнитная энергия, запасенная в индуктивности индуктивности L, равна 0.5 л Я 2 . Сравнивая это с уравнением (32.48), мы заключаем, что само индуктивность L тороида равна
(32,49)
Цепь RL состоит из резистора и индуктора, расположенных последовательно с батарея (см. рисунок 32.4). Применяя второе правило Кричхоффа к этому Для одноконтурной схемы получаем следующее дифференциальное уравнение
(32.50)
Рисунок 32.4. Схема RL. Это дифференциальное уравнение имеет решение(32,51)
Это решение действительно, если батарея подключена при t = 0. Уравнение (32.51) показывает, что ток при t = 0 с равен 0 и неуклонно растет, чтобы достичь конечное значение e / R при t = [бесконечность]. Постоянная времени цепи RL L / R. Если ток достиг стабильного значения и батарея внезапно отсоединенный, проводник может генерировать ток через резистор, который будет постепенно затухать как функция времени.Если начальный ток равен [эпсилон] / R, ток в момент времени t будет равен
(32,52)
Пример: проблема 32.54
То, что джоулево тепло рассеивается током в уравнении (32,52) в резистор во временном интервале между t = 0 и t = [бесконечность]? Сравнить с начальная магнитная энергия в индукторе.
Ток через резистор дается в уравнении (32.51).Мощность рассеивается по этому ток в резисторе равен
(32,53)
Полная энергия, рассеиваемая этим током в резисторе между t = 0 и t = [бесконечность] равно
(32,54)
Магнитная энергия, запасенная в индукторе, равна
(32,55)
и мы заключаем, что вся магнитная энергия, накопленная в индукторе, рассеивается как джоулева жара в резисторе.
Присылайте комментарии, вопросы и / или предложения по электронной почте [email protected] и / или посетите домашнюю страницу Фрэнка Вольфса. ,
индукция | Infoplease
индукции, в электричестве и магнетизме, общее название для трех различных явлений. Электромагнитная индукция – это создание электродвижущей силы (ЭДС) в проводнике в результате изменения магнитного поля вокруг проводника, и оно является наиболее важным из трех явлений. Он был открыт в 1831 году Майклом Фарадеем и независимо Джозефом Генри. Изменение поля вокруг проводника может быть вызвано относительным движением между проводником и источником магнитного поля, как в электрическом генераторе, или изменением напряженности всего поля, так что поле вокруг проводника также изменяется ,Поскольку вокруг проводника с током создается магнитное поле, такое поле можно изменить, изменив ток. Таким образом, если проводник, в котором должна быть индуцирована ЭДС, является частью электрической цепи, индукция может быть вызвана изменением тока в этой цепи; это называется самоиндукция. Индуцированная ЭДС всегда такова, что в соответствии с законом Ленца она противостоит изменениям, которые ее вызывают. Изменение тока в данной цепи может также вызвать эдс в другой соседней цепи, не связанной с исходной цепью; Этот тип электромагнитной индукции, называемый взаимной индукцией, является основой трансформатора.Электростатическая индукция – это создание несбалансированного электрического заряда на незаряженном металлическом теле в результате того, что заряженное тело подносится к нему, не касаясь его. Если заряженное тело заряжено положительно, электроны в незаряженном теле будут притягиваться к нему; если противоположный конец тела затем заземлен, электроны будут перетекать на него, чтобы заменить те, которые тянутся к другому концу, тело, таким образом, приобретает отрицательный заряд после разрыва заземления. Аналогичная процедура может быть использована для создания положительного заряда на незаряженном теле, когда к нему приближается отрицательно заряженное тело.Смотрите электричество. Магнитная индукция – это создание магнитного поля в куске немагнитного железа или другого ферромагнитного вещества, когда к нему подносится магнит. Магнит заставляет отдельные частицы железа, которые действуют как крошечные магниты, выстраиваться в линию, так что образец в целом становится намагниченным. Большая часть этого индуцированного магнетизма теряется, когда вызывающий его магнит отнимается. Смотрите магнетизм.Колумбийская электронная энциклопедия, 6-е изд. Copyright © 2012, Columbia University Press.Все права защищены.
См. Больше статей энциклопедии: Электротехника
.


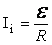 . e не зависит от свойств контура:
. e не зависит от свойств контура: 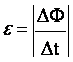 .
.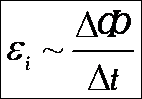
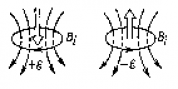
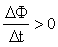 ; Магнитный поток Ф → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю:
; Магнитный поток Ф → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю: 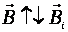 , где
, где 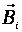 – т.н. индукционное магнитное поле.
– т.н. индукционное магнитное поле.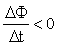 . Магнитный поток Ф → ΔФ<0. Чтобы компенсировать это изменение (уменьшение), необходимо магнитное поле, сонаправленное с внешним полем:
. Магнитный поток Ф → ΔФ<0. Чтобы компенсировать это изменение (уменьшение), необходимо магнитное поле, сонаправленное с внешним полем: 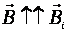 .
.
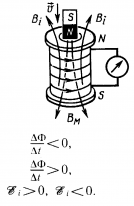
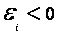 ),если
),если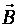 (т.е. ΔΦ>0). Ток в контуре имеет положительное направление (
(т.е. ΔΦ>0). Ток в контуре имеет положительное направление (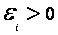 ), если
), если 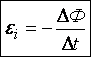 .
.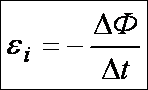
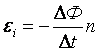 ,
,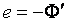 , где e – мгновенное значение ЭДС индукции.
, где e – мгновенное значение ЭДС индукции.