Закон электромагнитной индукции | СПАДИЛО
Магнитный поток наглядно истолковывается как число линий магнитной индукции, пронизывающих поверхность площадью S. Поэтому скорость изменения этого числа есть не что иное, как скорость изменения магнитного потока.
Если за малое время ∆t магнитный поток поменялся на ∆Ф, то скорость изменения магнитного потока равна ΔΦΔt… Поэтому утверждение, которое вытекает непосредственно из опыта, можно сформулировать так:
Сила индукционного тока пропорциональная скорости изменения магнитного потока через поверхность, ограниченную контуром:
Ii~ΔΦΔt.
Известно, что в цепи появляется электрический ток в том случае, когда на свободные заряды проводника действуют сторонние силы. Работу этих сил при перемещении единичного положительного заряда вдоль замкнутого контура называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуров, появляются сторонние силы, действие которых характеризуется ЭДС, называемой  Обозначают ее как εi.
Обозначают ее как εi.
Согласно закону Ома для замкнутой цепи:
Ii=εiR..
Сопротивление проводника не зависит от изменения магнитного потока. Следовательно, сила индукционного тока пропорциональна скорости изменения магнитного потока только потому, что ЭДС индукции тоже пропорциональна этой скорости изменения потока.
Закон электромагнитной индукцииЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.
εi=∣∣∣ΔΦΔt..∣∣∣
Закон электромагнитной индукции формулируется именно для ЭДС, а не для силы тока. При такой формулировке закон выражает сущность явления, не зависящую от свойств проводников, в которых возникает индукционный ток.
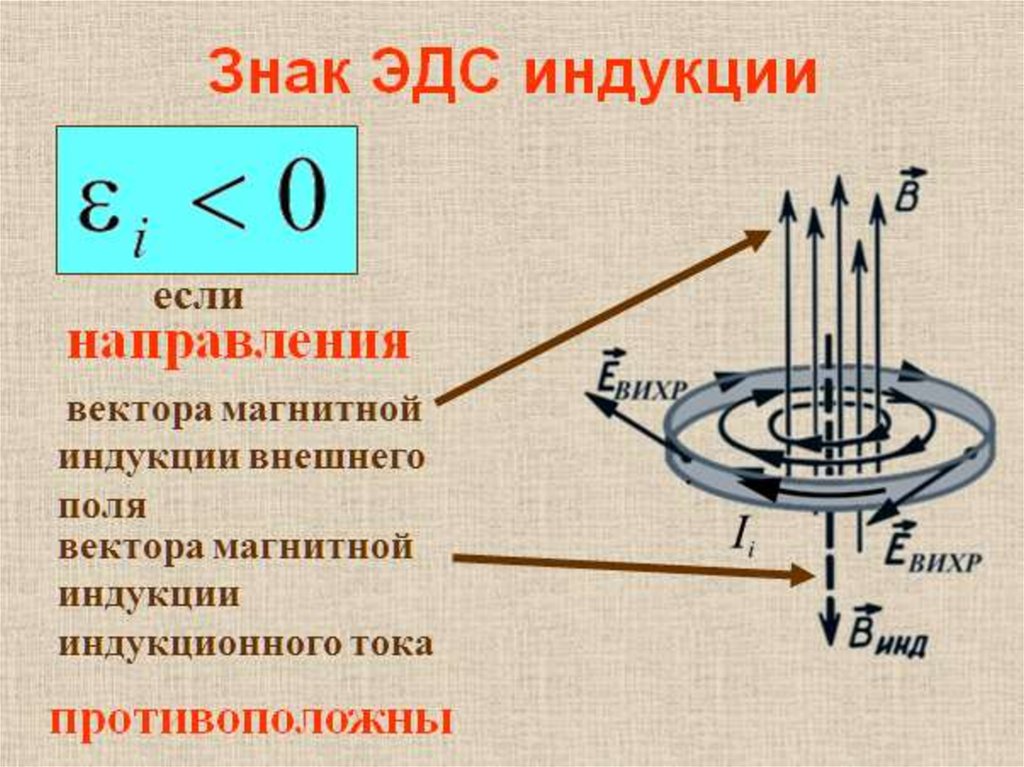
Определение знака ЭДС индукции
На рисунке изображен замкнутый контур. Будем считать положительным направление обхода контура против часовой стрелки. Нормаль →n к контуру образует правый винт с направлением обхода.
Пусть магнитная индукция →B внешнего магнитного поля направлена вдоль нормали к контуру и возрастает со временем.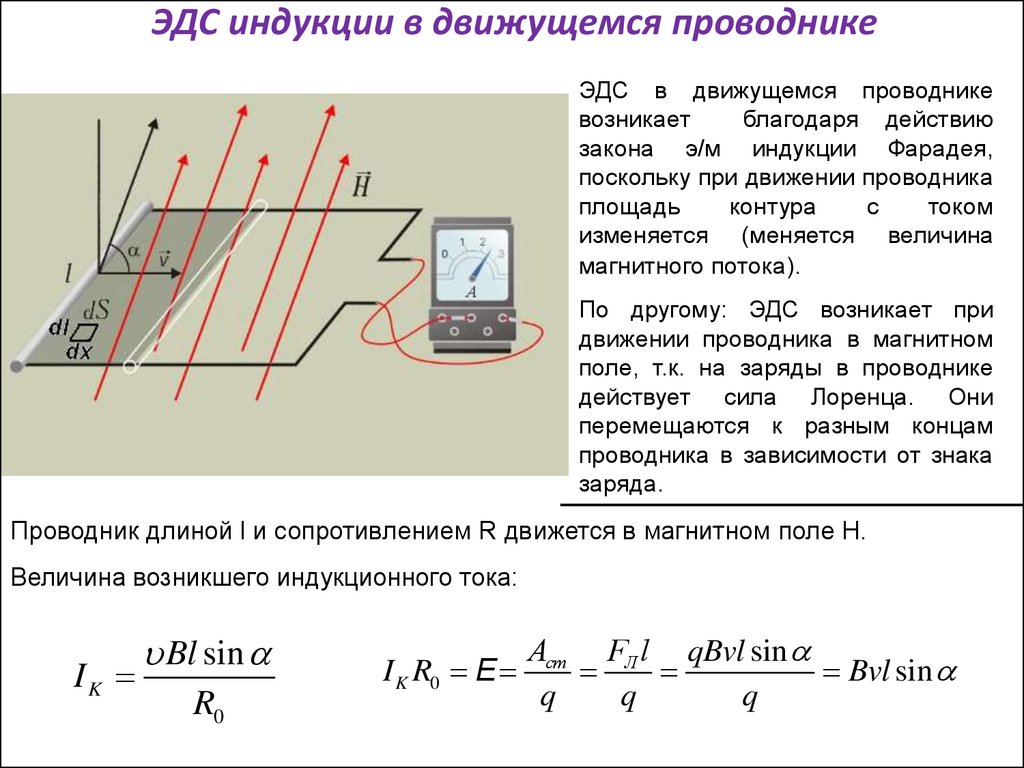 Тогда Φ>0 и ΔΦΔt..>0. Согласно правилу Ленца индукционный ток создает магнитный поток Φ‘<0. Линии магнитной индукции B’ магнитного поля индукционного тока изображены черным цветом. Следовательно, индукционный ток Ii согласно правилу буравчика направлен по часовой стрелке (против направления положительного обхода) и ЭДС индукции отрицательна. Поэтому в законе электромагнитной индукции должен стоять знак «–», указывающий на то, что εi и ΔΦΔt.. имеют разные знаки:
Тогда Φ>0 и ΔΦΔt..>0. Согласно правилу Ленца индукционный ток создает магнитный поток Φ‘<0. Линии магнитной индукции B’ магнитного поля индукционного тока изображены черным цветом. Следовательно, индукционный ток Ii согласно правилу буравчика направлен по часовой стрелке (против направления положительного обхода) и ЭДС индукции отрицательна. Поэтому в законе электромагнитной индукции должен стоять знак «–», указывающий на то, что εi и ΔΦΔt.. имеют разные знаки:
εi=−ΔΦΔt..
Пример №1. Магнитный поток через контур проводника сопротивлением 3∙10–2 Ом за 2 с изменился на 1,2∙10–2 Вб. Найдите силу тока в проводнике, если изменение потока происходило равномерно.
Известно, что:
Ii=εiR..
εi=∣∣∣ΔΦΔt..∣∣∣
Следовательно:
ЭДС индукции в движущихся проводниках
Электроны в неподвижном проводнике приводятся в движение электрическим полем, и это поле порождается переменным магнитным полем.
При движении проводника его свободные заряды движутся вместе с ним. Поэтому на заряды со стороны магнитного поля действует сила Лоренца. Она и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет магнитное происхождение.
Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле (см. рисунок). Пусть сторона контура MN длиной l скользит с постоянной скоростью →v вдоль сторон NC и MD, оставаясь все это время параллельной стороне CD. Вектор магнитной индукции →B однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.
Сила, с которой магнитное поле действует на движущуюся заряженную частицу, равна по модулю:
FL=|q|vBsin.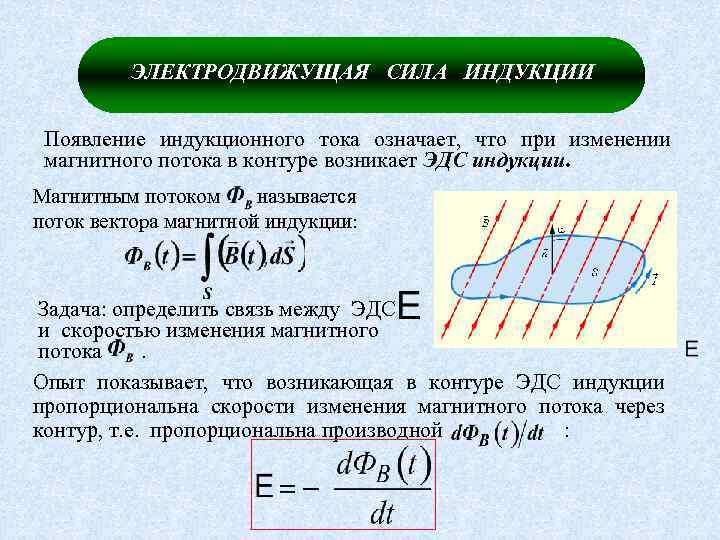 α
α
Направлена эта сила вдоль проводника MN. Работа силы Лоренца на пути l положительна и составляет:
A=FLl=|q|vBlsin.α
Внимание!Формула выше определяет неполную работу силы Лоренца. Кроме силы Лоренца имеется составляющая силы Лоренца, направленная против скорости проводника →v. Такая составляющая тормозит проводник и совершает отрицательную работу. В результате полная работа силы Лоренца оказывается равной нулю.
Электродвижущая сила индукции в проводнике MN равна по определению отношению работы по перемещению заряда q к этому заряду:
εi=A|q|..=vBlsin.α
Эта формула справедлива для любого проводника длиной l, движущегося со скоростью →v в однородном магнитном поле.
В других проводниках контура ЭДС равна нулю, так как проводники неподвижны. Следовательно, ЭДС во всем контуре MNCD равна εi и остается неизменной, если скорость движения →v постоянна. Электрический ток при этом будет увеличиваться, так как при смещении проводника MN вправо уменьшается общее сопротивление контура.
С другой стороны, ЭДС индукции можно вычислить с помощью закона электромагнитной индукции. Магнитный поток через контур MNCD равен:
Φ=BScos.(90°−α)=BSsin.α
угол 90°−α представляет собой угол между векторами →B и нормалью →n к поверхности контура, а S — площадь контура MNCD. Если считать, что в начальный момент времени t=0 проводник MN находится на расстоянии NC
S=l(NC−vt)
За время ∆t площадь контура меняется на ΔS=−lvΔt. Знак «минус» указывает на то, что она уменьшается. Изменение магнитного потока за это время равно:
ΔΦ=−BvlΔtsin.α
Следовательно:
εi=−ΔΦΔt..=Bvlsin.α
Если весь контур MNCD движется в однородном магнитном поле, сохраняя свою ориентацию по отношению к вектору →B, то ЭДС индукции в контуре будет равна нулю, так как поток Φ через поверхность, ограниченную контуром, не меняется. Объяснить это можно так. При движении контура в проводниках MN и CD возникают силы, действующие на электроны в направлениях от N к M и от C к D. Суммарная работа этих сил при обходе контура по часовой стрелке или против нее равна нулю.
Объяснить это можно так. При движении контура в проводниках MN и CD возникают силы, действующие на электроны в направлениях от N к M и от C к D. Суммарная работа этих сил при обходе контура по часовой стрелке или против нее равна нулю.
Пример №2. Проводник длиной 50 см движется в однородном магнитном поле со скоростью 4 м/с перпендикулярно силовым линиям. Найдите разность потенциалов, возникающую на концах проводника, если вектор магнитной индукции 8 мТл.
50 см = 0,5 м
8 мТл = 8∙10–3 Тл
Так как проводник движется перпендикулярно силовым линиям, то угол α равен 90 градусам, а синус прямого угла равен единице. Поэтому:
εi=Bvlsin.α=8·10−3·4·0,5·1=16·10−3 (В)
Задание EF17754В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R=10Ом и стороной l=10см перемещают в плоскости рисунка поступательно со скоростью υ=1м/с. Чему равен индукционный ток в рамке в состоянии 1?
Чему равен индукционный ток в рамке в состоянии 1?
Ответ:
а) 1 мА
б) 5 мА
в) 10 мА
г) 20 мА
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать формулу для определения величины индукционного тока.
3.Записать закон электромагнитной индукции для движущихся проводников.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решения
Запишем исходные данные:
• Модуль вектора магнитной индукции однородного магнитного поля: B = 0,1 Тл.
• Сопротивление внутри квадратной проволочной рамки: R = 10 Ом.
• Сторона рамки: l = 10 см.
• Скорость перемещения рамки: v = 1 м/с.
10 см = 0,1 м
Индукционный ток, возникающий в рамке, определяется по формуле:
Ii=εiR..
Закон электромагнитной индукции для движущихся проводников:
εi=vBlsin.
Отсюда индукционный ток равен:
Ii=vBlsin.αR..
На рисунке вектор магнитной индукции направлен в сторону от наблюдателя. Следовательно, угол между направлением движения рамки и вектором магнитной индукции равен 90 градусам. А синус прямого угла равен единице. Тогда:
Ii=vBlsin.90°R..=1·0,1·0,1·110..=0,001 (А)=1 (мА)
Ответ: аpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17970При вращении в однородном магнитном поле плоскости металлического кольца из тонкой проволоки вокруг оси, перпендикулярной линиям поля, максимальная сила индукционного тока, возникающего в кольце, равна I1. Чему будет равна максимальная сила индукционного тока I2 в этом кольце при уменьшении скорости вращения кольца в 2 раза?
а) I2 = 2I1
б) I2 = I1
в) I2 = 0,5I1
г) I2 = 4I1
Алгоритм решения
1. Записать закон электромагнитной индукции.
Записать закон электромагнитной индукции.
2.Установить зависимость между величиной индукционного тока и скоростью вращения рамки.
3.Определить, как изменится величина индукционного тока в кольце при уменьшении скорости ее вращения.
Решение
Запишем формулу закона электромагнитной индукции:
εi=∣∣∣ΔΦΔt..∣∣∣
Известно, что отношение изменения магнитного потока ко времени его изменения — это величина, характеризующая скорость этого изменения. Если кольцо в однородном магнитном поле вращать медленнее, то и магнитный поток начнет менять медленнее. Так как ЭДС индукции прямо пропорционально зависит от скорости изменения магнитного потока, то при уменьшении скорости вращения кольца в 2 раза она также уменьшится вдвое.
Также известно, что индукционный ток в рамке определяется формулой:
Ii=εiR..
Видно, что индукционный ток и ЭДС индукции — прямо пропорциональные величины. Следовательно, при уменьшении ЭДС индукции вдвое сила индукционного тока тоже уменьшится в 2 раза. Отсюда следует, что I2 = 0,5I1.
Отсюда следует, что I2 = 0,5I1.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18860По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой m = 100 г и сопротивлением R = 0,1 Ом каждый. Расстояние между рельсами l = 10 см, а коэффициент трения между стержнями и рельсами μ = 0,1 Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией B = 1 Тл (см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь. Ответ записать в системе СИ.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать закон электромагнитной индукции для двигающихся стержней.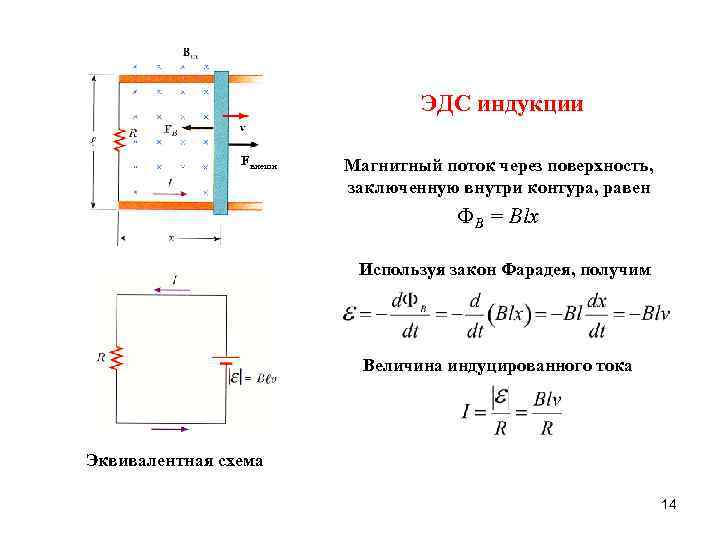
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса стержней: m1=m2=m=100 г.
• Сопротивление стержней: R1=R2=R=0,1 Ом.
• Расстояние между рельсами: l = 10 см.
• Коэффициент трения между стержнями и рельсами: μ = 0,1.
• Модуль вектора магнитной индукции магнитного поля: B = 1 Тл.
• Угол между вектором магнитной индукцией и вектором скорости стержней: α = 90 градусов (синус прямого угла равен «1»).
100 г = 0,1 кг
10 см = 0,1 м
Когда под действием некой силы начинается двигаться первый стержень, магнитный поток, пронизывающий контур, образованные проводящими рельсами и двумя стержнями, меняется. Это приводит к возникновению в этом контуре электродвижущей силы, которую можно определить с помощью закона электромагнитной индукции для двигающихся стержней:
εi=vBlsin.α
Причем v — это разность скоростей стержней (v2 – v1), которая характеризует скорость изменения площади проводящего контура.
Индукционный ток, возникающей в этом контуре, можно выразить, используя закон Ома:
εi=IRк
где Rк — сопротивление контура. Так как стержни соединяются последовательно, и их сопротивления равны R, а сопротивление рельсов ничтожно мало, сопротивление контура равно:
Rк=2R
Отсюда закон Ома принимает вид:
εi=2IR
Тогда ток в контуре равен:
I=εi2R..=vBlsin.α2R..
С одной стороны на стержни действует сила Ампера, с другой — сила трения, возникающего между ними и рельсами. Так как стержни движутся равномерно, равнодействующая сил, приложенных к ним, равна нулю. Следовательно, сила трения и сила Ампера компенсируют друг друга (их модули равны):
Fтр=FА
μmg=BIlsin.α
Подставим сюда выражение, полученное для силы тока в контуре:
μmg=BvBlsin.α2R..lsin.α=vB2l2sin2.α2R..
Отсюда скорость равна:
v=2μmgRB2l2sin2.α..
Так как синус угла равен «1»:
Ответ: 2pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 5. 5k
5k
Электромагнитная индукция. | Объединение учителей Санкт-Петербурга
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Электромагнитная индукция.
| Электромагнитная индукция | |
1831 г. – М. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает так называемый индукционный ток. (Индукция, в данном случае, – появление, возникновение). | |
Индукционный ток в катушке возникает при перемещении постоянного магнита относительно катушки; при перемещении электромагнита относительно катушки; при перемещении сердечника относительно электромагнита, вставленного в катушку; при регулировании тока в цепи электромагнита; при замыкании и размыкании цепи | |
Появление тока в замкнутом контуре при изменении магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил (или о возникновении ЭДС индукции). Явление возникновения ЭДС в замкнутом проводящем контуре при изменении магнитного поля (потока), пронизывающего контур, называется электромагнитной индукцией. Или: явление возникновения электрического поля при изменении магнитного поля (потока), называется электромагнитной индукцией. | |
Закон электромагнитной индукции При всяком изменении магнитного потока через проводящий замкнутый контур в этом контуре возникает электрический ток. I зависит от свойств контура (сопротивление): . e не зависит от свойств контура: . ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром. | |
Основные применения электромагнитной индукции: генерирование тока (индукционные генераторы на всех электростанциях, динамомашины), трансформаторы. |
|
Возникновение индукционного тока – следствие закона сохранения энергии! В случае 1: При приближении магнита, увеличении тока, замыкании цепи: ; Магнитный поток Ф → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю: , где – т.н. индукционное магнитное поле. В случае 2: при удалении магнита, уменьшении тока, размыкании цепи: . Магнитный поток Ф → ΔФ<0. Чтобы компенсировать это изменение (уменьшение), необходимо магнитное поле, сонаправленное с внешним полем: . | |
Источником магнитного поля является ток. Поэтому: Возникающий в замкнутом контуре индукционный ток имеет такое направление, что созданный им поток магнитной индукции через площадь, ограниченную контуром, стремится компенсировать то изменение потока магнитной индукции, которое вызывает данный ток (правило Ленца). |
|
Ток в контуре имеет отрицательное направление (),еслипротивоположно (т.е. ΔΦ>0). Ток в контуре имеет положительное направление (), если совпадает с , (т.е. ΔΦ<0). Поэтому с учетом правила Ленца (знака) выражение для закона электромагнитной индукции записывается: . Данная формула справедлива для СИ (коэффициент пропорциональности равен 1). В других системах единиц коэффициент другой. | |
Если контур (например, катушка) состоит из нескольких витков, то , где n – количество витков. Все предыдущие формулы справедливы в случае линейного (равномерного) изменения магнитного потока. В произвольном случае закон записывается через производную: , где e – мгновенное значение ЭДС индукции. | |
Теги:
конспект
23.
 1 ЭДС индукции и магнитный поток – Колледж физики 2e
1 ЭДС индукции и магнитный поток – Колледж физики 2eЦели обучения
К концу этого раздела вы сможете:
- Рассчитайте поток однородного магнитного поля через петлю произвольной ориентации.
- Описать методы создания электродвижущей силы (ЭДС) с помощью магнитного поля или магнита и проволочной петли.
Аппарат, который Фарадей использовал для демонстрации того, что магнитные поля могут создавать токи, показан на рис. 23.3. Когда переключатель замкнут, в катушке в верхней части железного кольца создается магнитное поле, которое передается на катушку в нижней части кольца. Гальванометр используется для обнаружения любого тока, наведенного в катушке на дне. Было обнаружено, что каждый раз, когда переключатель замыкается, гальванометр регистрирует ток в одном направлении в катушке на дне. (Вы также можете наблюдать это в физической лаборатории.) Каждый раз, когда переключатель размыкается, гальванометр обнаруживает ток в противоположном направлении. Интересно, что если переключатель остается замкнутым или разомкнутым какое-то время, ток через гальванометр отсутствует. Замыкание и размыкание переключателя индуцирует ток. Это изменение магнитного поля создает ток. Более важным, чем текущий ток, является ЭДС , которая его вызывает. Ток является результатом ЭДС , индуцированной изменяющимся магнитным полем , независимо от того, есть ли путь для протекания тока.
Интересно, что если переключатель остается замкнутым или разомкнутым какое-то время, ток через гальванометр отсутствует. Замыкание и размыкание переключателя индуцирует ток. Это изменение магнитного поля создает ток. Более важным, чем текущий ток, является ЭДС , которая его вызывает. Ток является результатом ЭДС , индуцированной изменяющимся магнитным полем , независимо от того, есть ли путь для протекания тока.
Рисунок 23,3 Аппарат Фарадея для демонстрации того, что магнитное поле может производить ток. Изменение поля, создаваемого верхней катушкой, индуцирует ЭДС и, следовательно, ток в нижней катушке. Когда переключатель размыкается и замыкается, гальванометр регистрирует токи в противоположных направлениях. Через гальванометр не протекает ток, когда переключатель остается замкнутым или разомкнутым.
На рис. 23.4 показан простой и часто проводимый в физических лабораториях эксперимент. ЭДС индуцируется в катушке, когда стержневой магнит вдавливается и выталкивается из нее. ЭДС разных знаков создаются движением в противоположных направлениях, а также изменением полярности ЭДС на противоположное. Те же результаты получаются, если перемещать катушку, а не магнит — важно относительное движение. Чем быстрее движение, тем больше ЭДС, а когда магнит неподвижен относительно катушки, ЭДС отсутствует.
ЭДС индуцируется в катушке, когда стержневой магнит вдавливается и выталкивается из нее. ЭДС разных знаков создаются движением в противоположных направлениях, а также изменением полярности ЭДС на противоположное. Те же результаты получаются, если перемещать катушку, а не магнит — важно относительное движение. Чем быстрее движение, тем больше ЭДС, а когда магнит неподвижен относительно катушки, ЭДС отсутствует.
Рисунок 23,4 Движение магнита относительно катушки создает ЭДС, как показано на рисунке. Такие же ЭДС возникают, если катушку перемещать относительно магнита. Чем больше скорость, тем больше величина ЭДС, а ЭДС равна нулю, когда нет движения.
Метод наведения ЭДС, используемый в большинстве электрогенераторов, показан на рис. 23.5. Катушка вращается в магнитном поле, создавая ЭДС переменного тока, которая зависит от скорости вращения и других факторов, которые будут рассмотрены в последующих разделах. Обратите внимание, что генератор очень похож по конструкции на двигатель (еще одна симметрия).
Рисунок 23,5 Вращение катушки в магнитном поле создает ЭДС. Это основная конструкция генератора, в котором работа по вращению катушки преобразуется в электрическую энергию. Обратите внимание, генератор очень похож по конструкции на двигатель.
Итак, мы видим, что изменение величины или направления магнитного поля создает ЭДС. Эксперименты показали, что существует критическая величина, называемая магнитным потоком, ΦΦ, определяемая выражением
Φ=BAcosθ, Φ=BAcosθ,
23,1
, где BB — напряженность магнитного поля на площади AA под углом θθ к перпендикуляру к площади, как показано на рис. 23.6. Любое изменение магнитного потока ΦΦ индуцирует ЭДС. Этот процесс определяется как электромагнитная индукция. Единицами магнитного потока ΦΦ являются T⋅m2T⋅m2. Как видно на рисунке 23.6, Bcosθ=BBcosθ=B ⊥ , который является компонентом BB , перпендикулярным площади AA .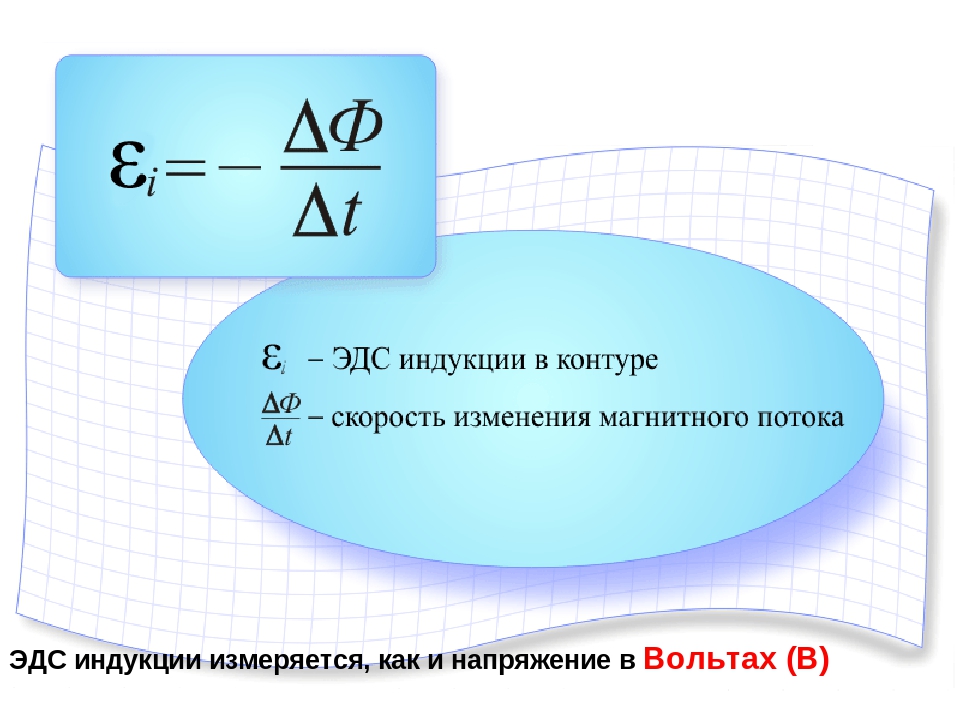 Таким образом, магнитный поток равен Φ=B⊥AΦ=B⊥A, произведению площади и перпендикулярной к ней составляющей магнитного поля.
Таким образом, магнитный поток равен Φ=B⊥AΦ=B⊥A, произведению площади и перпендикулярной к ней составляющей магнитного поля.
Рисунок 23,6 Магнитный поток ΦΦ связан с магнитным полем и площадью, над которой оно существует. Поток Φ=BAcosθΦ=BAcosθ связан с индукцией; любое изменение ΦΦ индуцирует ЭДС.
Вся индукция, включая примеры, приведенные до сих пор, возникает из-за некоторого изменения магнитного потока ΦΦ . Например, Фарадей менял ВВ на и, следовательно, ФФ при размыкании и замыкании переключателя в своем аппарате (показанном на рис. 23.3). Это также верно для стержневого магнита и катушки, показанных на рис. 23.4. При вращении катушки генератора угол θθ и, следовательно, ΦΦ изменен. То, насколько велика ЭДС и какое направление она принимает, зависит от изменения в ΦΦ и от того, как быстро происходит это изменение, как будет рассмотрено в следующем разделе.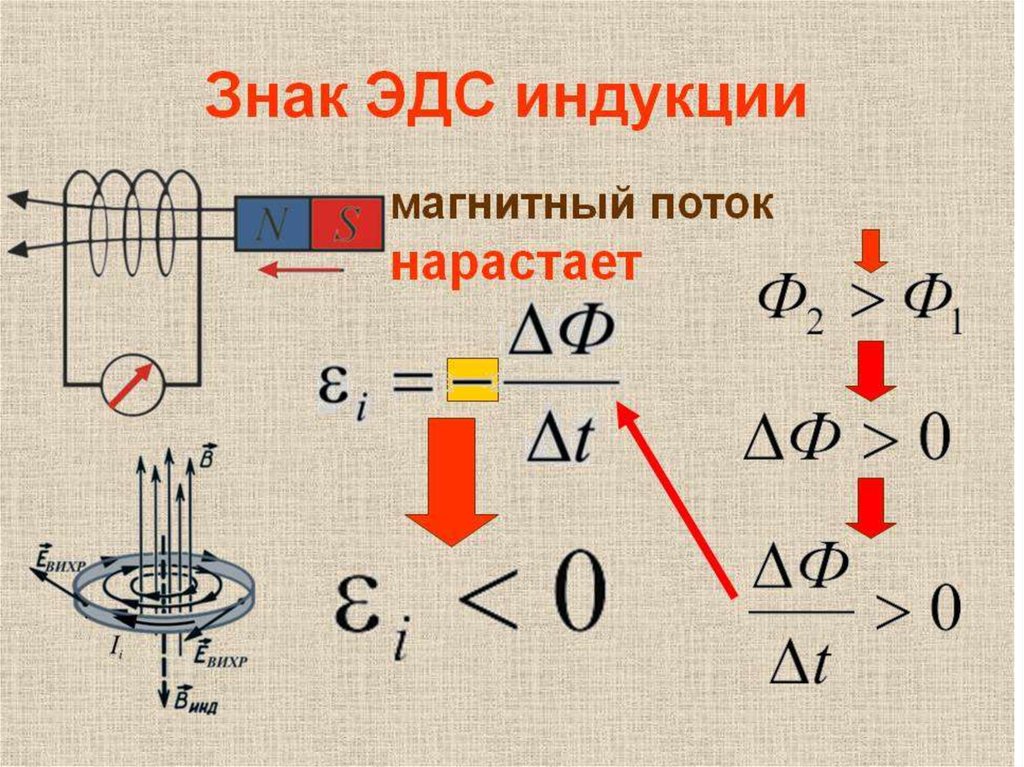
Закон Фарадея
Закон ФарадеяЛюбое изменение магнитной среды катушки с проводом вызовет «индукцию» напряжения (ЭДС) в катушке. Независимо от того, как производится изменение, напряжение будет генерироваться. Это изменение может быть вызвано изменением напряженности магнитного поля, перемещением магнита к катушке или от нее, перемещением катушки в магнитное поле или из него, вращением катушки относительно магнита и т. д.
Закон Фарадея — это фундаментальное соотношение, вытекающее из уравнений Максвелла. Он служит кратким изложением того, как напряжение (или ЭДС) может генерироваться изменяющейся магнитной средой. ЭДС индукции в катушке равна отрицательному значению скорости изменения магнитного потока, умноженной на число витков в катушке.
| Индекс Концепции закона Фарадея | |||||
| 545Вернуться |
Когда ЭДС создается изменением магнитного потока в соответствии с
По закону Фарадея полярность ЭДС индукции такова, что она производит
ток, магнитное поле которого противостоит вызывающему его изменению.
Индуцированное магнитное поле внутри любой петли провода всегда поддерживает постоянный магнитный поток в петле. | Индекс Концепции закона Фарадея | ||
| 545Вернуться |
Когда магнит перемещается в катушку с проводом, изменяя магнитное поле и магнитный поток через катушку, в катушке будет генерироваться напряжение в соответствии с законом Фарадея. В примере, показанном ниже, когда магнит перемещается в катушку, гальванометр отклоняется влево в ответ на возрастающее поле. Когда магнит вытягивают обратно, гальванометр отклоняется вправо в ответ на уменьшение поля.
Полярность ЭДС индукции такова, что она производит
ток, магнитное поле которого противостоит вызывающему его изменению. |





 Это связано с взаимодействием заряда с магнитным полем.
Это связано с взаимодействием заряда с магнитным полем.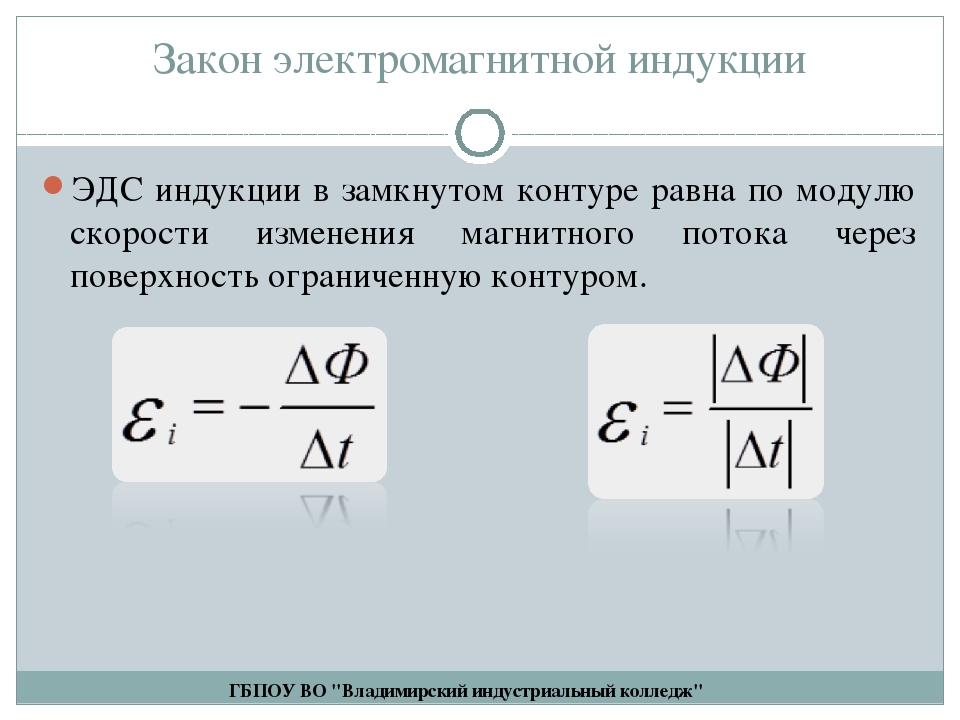 В приведенных ниже примерах, если поле B увеличивается, индуцированное поле действует против него. Если оно уменьшается, индуцированное поле действует в направлении приложенного поля, пытаясь сохранить его постоянным.
В приведенных ниже примерах, если поле B увеличивается, индуцированное поле действует против него. Если оно уменьшается, индуцированное поле действует в направлении приложенного поля, пытаясь сохранить его постоянным.