Эффективное значение напряжения: Эффективное значение тока и напряжения | Формулы и расчеты онлайн

Эффективные значения тока и напряжения – справочник студента

Что же из себя представляет среднеквадратичное значение напряжения и как его замерить? Давайте разберем значение этого термина. Поможет нам в этих делах наш осциллограф OWON SDS6062 , Блок питания, а также ЛАТР (Лабораторный автотрансформатор).

Лампочка и постоянное напряжение

• Для опытов нам также понадобится простая автомобильная лампа накаливания на напряжение 12 Вольт
• Вот ее характеристики:  рабочее напряжение U=12 Вольт, мощность Р = 21 Ватт.

Следовательно, зная мощность и напряжение лампы, можно узнать, какую силу тока будет потреблять лампочка. Из формулы P=IU, где I – сила тока,  можно найти I. Значит  I=P/U=21/12=1,75 Ампер.

Узнай стоимость своей работы

Бесплатная оценка заказа!

Ладно, с лампочкой разобрались. Давайте ее зажжем. Для этого на нашем блоке питания выставляем рабочее напряжение для нашей лампы

2. Подаем напряжение с блока питания на лампу и вуаля!

Замеряем напряжение на  клеммах-крокодилах блока питания с помощью мультиметра . Ровнехонько 12 Вольт, как и предполагалось.

• К этим же клеммах цепляем и наш осциллограф
• Смотрим осциллограмму:

Видите прямую линию? Это и есть осциллограмма постоянного напряжения. В течение времени  у нас напряжение остается  таким, каким и было и не меняется.

Если посчитать, то можно вычислить, чему равняется напряжение. Так как одна клеточка у нас 5 Вольт (на фото внизу слева), то  значит, наше напряжение 12 Вольт.

Я также вывел это значение на дисплей осциллографа в самом нижнем левом углу: 12,03 Вольт. Все верно.

Замеряем  силу тока. Как правильно замерить силу тока в цепи, можно узнать, прочитав статью как измерить ток и напряжение мультиметром?.

Узнай стоимость своей работы

Бесплатная оценка заказа!

Получили 1,72 Ампер. А как вы помните, наше расчетное значение было 1,75 Ампер. Думаю, вину можно переложить  на погрешность прибора  или на лампочку 😉

Лампочка и переменное напряжение

Теперь начинается самое интересное. Берем наш ЛАТР

Ставим прибор на измерение переменного напряжения и выставляем с помощью  крутилки ЛАТРа напряжение в 12 Вольт. Обратите внимание, что крутилка на мультиметре  находится в диапазоне измерения переменного напряжения. Забегая вперед, скажу, что мультиметр измеряет среднеквадратичное напряжение.

2. Цепляем осциллограф к клеммах ЛАТРа, не забывая на осциллографе выставить замеры переменного напряжения и смотрим получившуюся осциллограмму:

Смотрим, сколько  силы тока кушает наша лампочка. Все как положено, 1,71 Ампер.

Среднеквадратичное значение напряжения

Итак, что же у нас получилось? Как и постоянное напряжение, так и переменное напряжение  зажигали одну и ту же лампочку, которая кушала одну и ту же мощность.  Значит эта осциллограмма

• и вот эта осциллограмма

Чем то похожи? Но чем??? 

Среднеквадратичное значение напряжения – это такое  значение переменного напряжения, при котором нагрузка потребляет столько же силы тока, как и при постоянном напряжении.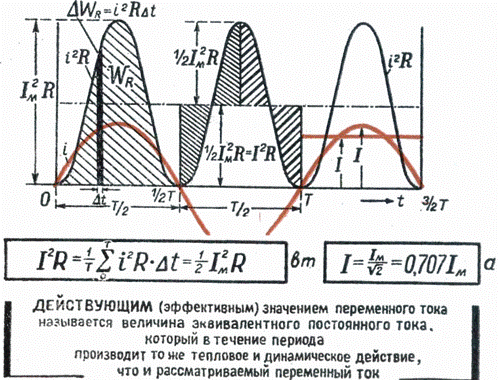   То есть лампочка у нас потребляла 1,71 Ампер и при постоянном токе и при переменном.  То есть, в двух этих случаях, мощность, которую потребляла лампочка, была одинакова.

Также среднеквадратичное напряжение еще называют действующим или эффективным значением напряжения. С помощью несложных умозаключений, инженеры-электрики пришли к выводу действующее (оно же среднеквадратичное) напряжение синусоидального сигнала  любой частоты равняется максимальной его амплитуде, поделенной  на корень из двух

Стоп! Мы ведь не разобрали, что такое максимальная амплитуда! На осциллограмме максимальная амплитуда выглядит примерно вот так:

Если даже посчитать по клеточкам и посмотреть, чему равняется одна клеточка по вертикали (смотрим внизу слева, она равняется 5 Вольт), то Umax = 17 Вольт. Делим это значение на корень из двух. Я беру это значение как 1,41. Получаем, что среднеквадратичное значение равняется 17/1,41=12,06 Вольт. Ну что, все верно 😉

Значит, когда нам говорят, что напряжение в розетке равняется 220 Вольт, то мы то знаем, что на самом деле это среднеквадратичное напряжение.  Максимальная амплитуда этих  220 Вольт равняется 220х1,41=310 Вольт.

Где же  среднеквадратичное напряжение и максимальная амплитуда сигнала прячутся на табличке измерений? Да вот  же они!

1. Vk – это и есть среднеквадратичное напряжение этого сигнала.
2. Ma – это  и есть Umax.

Конечно, 16,6/1,41=11,8  Вольт, а он пишет 12,08 Вольт. Думаю, это связано с тем, что в синусоиде есть небольшие искажения, поэтому измерения немного неточные.

Итак, внимание! Кто первый напишет среднеквадратичное значение  напряжения этого сигнала, получит 100 руб на мобилу 😉

Конкурс уже давненько прошел и первая в х ответила Ирина Молчалина и выиграла 100 руб ;-). Правильный  ответ 1 Вольт. Почему именно так, читаем эту статью.

Источник: https://www.RusElectronic.com/effectivnoe-znachenie-napryazheniya/

Расчет среднего и среднеквадратичного значений тока и напряжения: формулы и калькулятор

Расчет среднего и среднеквадратичного значений тока и напряжения: формулы и калькулятор

03.04.18

Данный текст является расширенным и углубленным вариантом моей старой заметки на сайте we.easyelectronics.ru.

Введение

В рамках данной заметки рассмотрим способы вычисления среднего и среднеквадратичного значений тока и напряжения. При этом для простоты ограничимся формами сигнала, характерными для импульсных источников питания.

Обращаю ваше внимание – все формулы, приводимые в заметке, даются без выводов, дабы не забивать головы читателей мутной и не особо нужной херней.

С другой стороны, если кому-то интересно, откуда данные формулы взялись – можно скачать файл, в котором приведены все необходимые выводы с пояснениями.

Основные определения

Будучи в недавнем прошлом яростным разработчиком всевозможных импульсных источников питания (ИИП), интересовался всяким по данной теме (да и сейчас, бывает, трясу стариной).

В частности, весьма важными мне всегда казались такие характеристики сигнала, как среднее и среднеквадратичное значение токов и напряжений в различных точках схемы, поскольку при расчетах ИИП данные параметры используются сплошь и рядом.

Чтобы понять, где могут быть полезны данные характеристики, сначала определимся с тем, что мы под ними понимаем.

Естественно, существуют строгие «математические» определения как для среднего, так и для среднеквадратичного значений физических величин, периодически изменяющихся во времени по некоторому закону.

Однако, больно уж они мутные и абстрактные, и, на мой взгляд, нужны только при выводе формул.

Разработчику же гораздо важнее понимать физический смысл используемых в расчетах величин, поэтому приводимые ниже определения среднего и среднеквадратичного значений будут носить сугубо прикладной характер.

Среднее значение

переменного тока или напряжения (во вражеских терминах AVG) – это просто их постоянная составляющая. Поэтому вполне очевидно, что среднее значение широко применяется при расчетах схем, выделяющих из переменного сигнала постоянный уровень.

Простейший понижающий преобразователь (Step-Down) с LC-фильтром на выходе, RC-цепочка, призванная выделить постоянное напряжение из поступающего на вход ШИМ-сигнала – всё это примеры того, где без использования среднего значения физической величины ничего толком не посчитаешь.

Среднеквадратичное (действующее, эффективное) значение определяется немного сложнее. Как известно, любой переменный ток (напряжение), проходя через активную линейную нагрузку (например, резистор), выделяет на ней некоторое количество тепла. Но так поступает не только переменный сигнал – постоянный ток тоже будет греть резистор.

Так вот, среднеквадратичное значение переменного тока или напряжения (во вражеских терминах RMS) – это такой постоянный ток (напряжение), который за одинаковый промежуток времени нагреет один и тот же резистор точно так же, как и исходный переменный сигнал.

Поэтому одно из важнейших применений среднеквадратичного значения – расчет потерь и соответствующего нагрева для различных элементов силовых цепей ИИП. Хочешь узнать статические потери на ключе флайбэка – будь добр посчитать среднеквадратичное значение тока первички.

Надо узнать мощность токосчитывающего резистора – туда же.

Даже потери (и приблизительный нагрев) в обмотках трансов и дросселей для хиленьких источников и невысоких частот преобразования в первом приближении можно посчитать при помощи среднеквадратичного значения тока, через эти обмотки протекающего.

В общем, среднее и среднеквадратичное значения используются довольно часто. Поэтому неплохо было бы уметь их рассчитывать для любого сигнала, который может нам встретиться в импульсном источнике питания.

При этом лично я разделяю токи и напряжения в ИИП на две большие группы: сигналы с простой формой (элементарные) и сигналы со сложной формой (т.е. те, которые могут быть представлены в виде суммы нескольких элементарных).

И поскольку принципы расчета среднего и среднеквадратичного значений для этих двух групп немного отличаются, предлагаю рассмотреть их по отдельности.

• Сигналы простой формы
• У сигналов простой формы вычислить среднее и среднеквадратичное значение довольно легко – для этого надо всего лишь взять соответствующую формулу и подставить в нее нужные значения. Чтобы постоянно не шариться по различным справочникам, я завел себе специальную табличку, в которую свел расчетные формулы для наиболее часто встречающихся элементарных сигналов:
• •  прямоугольника:

•  треугольника:

•  трапеции:

•  и пилы:

(данные формулы, кстати, взяты не с потолка – их вывод при желании можно посмотреть в специальной заметке-пояснении).

Здесь хотелось бы заострить внимание на нескольких моментах. Во-первых, на приведенных выше рисунках рассматривается по два варианта каждого из простейших сигналов: «в общем виде» и «без смещения».

При этом с точки зрения разработчика импульсных источников питания наиболее интересным обычно является именно второй вариант, поэтому для него и даны отдельные формулы (чтобы постоянно не подставлять С=0 в «общие» выражения).

Во-вторых, пилообразное напряжение, вообще говоря, является сложным сигналом, поскольку может быть представлено в виде суммы двух простых (либо трапеций, либо треугольников).

Однако, пила настолько часто встречается при расчетах ИИП, а выражения AVG и RMS для нее настолько лаконичны и красивы, что я в результате включил-таки ее в список сигналов, среднее и среднеквадратичное значение которых вычисляется тупо всего по одной формуле.

Ну и в-третьих, вышеприведенная таблица, в принципе, могла бы состоять всего из одной трапеции, ибо из нее легко получить как прямоугольник, так и треугольник, поставляя соответствующие значения «H», «L» и «C». Однако практика показала, что постоянно этим заниматься весьма муторно, ибо мы рассчитываем источник, а не тренируем математические навыки.

Поэтому в итоге я себе выписал готовые формулы AVG и RMS для прямоугольника и треугольника, что оказалось весьма и весьма удобным. Ну а в целом – как ни странно, представленные выше формулы для элементарных сигналов покрывают, наверное, 75-80% всех потребностей разработчика импульсных источников питания, что весьма немало. Однако, всё многообразие токов и напряжений в ИИП отнюдь не ограничивается вышеупомянутыми четырьмя (и даже тремя, если не учитывать пилу) формами. Поэтому рано или поздно любой разработчик импульсников сталкивается с необходимостью вычисления среднего и среднеквадратичного значения сложного сигнала (яркий пример – расчет пуш-пула).

Сигналы сложной формы

Как было сказано выше, сигналы сложной формы – это такие, которые могут быть представлены в виде суммы нескольких элементарных сигналов. Применительно к импульсным источникам питания в качестве последних выступают прямоугольник, треугольник или трапеция, и значительно реже – синус, косинус и прочая «плавная» херня.

Отметим, что в данном случае, в отличие от простейших форм, нахождение аналитических выражений для среднего и среднеквадратичного значений обычно превращается в неблагодарное занятие.

Например, для вывода «среднеквадратичной» формулы нам надо разбить сложный сигнал на несколько простейших, а затем извлечь квадратный корень из суммы квадратов «элементарных» среднеквадратичных значений (думаю, даже понять, о чем говорится в данном предложении, у вас получится далеко не сразу).

Найти среднее значение сложного сигнала немного проще (надо просто просуммировать средние «элементарные» значения), однако поверьте – сделать из этого удобоваримую формулу в подавляющем большинстве случаев не удается:

К счастью, готовая формула для нахождения AVG и RMS сложного сигнала обычно не требуется. Чаще всего нам надо просто узнать среднее или среднеквадратичное значение тока (напряжения) именно для нашего конкретного случая, а не вывести аналитическое выражение на все случаи жизни.

А это существенно упрощает задачу, ибо посчитать числовое значение AVG или RMS для каждого элементарного сигнала на соответствующем временно́м интервале не так уж и сложно.

В качестве примера можно рассмотреть нахождение среднего и среднеквадратичного значения напряжения, характерного для пушпульной, полумостовой и полномостовой схем (данный расчет есть и в специальной заметке-пояснении):

Как следует из предпоследнего рисунка, для начала нам надо разбить исходный сигнал на элементарные. Очевидно, что это будут три трапеции и один прямоугольник:

Дальше нам надо посчитать среднее и среднеквадратичное значение каждого из четырех элементарных сигналов, для чего воспользуемся формулами из вышеприведенной таблицы. Начнем с первого из них — трапеции №1. Как видно из последнего рисунка, это трапеция без смещения с параметрами

h2=11; L1=9; C1=0; tИ1=0,15∙T.

Поэтому в соответствии с формулами для трапеции, приведенными выше, будем иметь:

1. Сигнал №2 – это тоже трапеция без смещения. 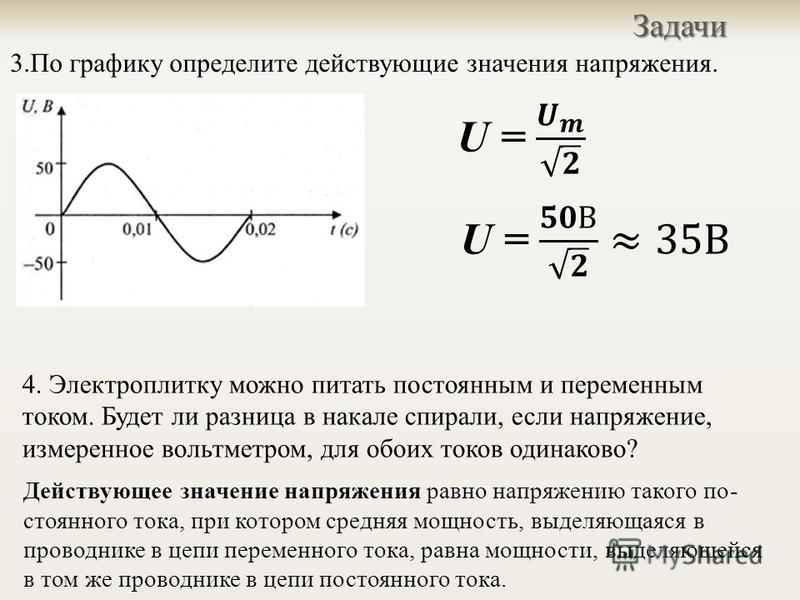Параметры данной трапеции будут таковы:
2. h3=21; L2=19; C2=0; tИ2=0,50∙T – 0,15∙T = 0,35∙T.
3. Поэтому среднее и среднеквадратичное значение второго сигнала составят соответственно

Трапеция №3 полностью совпадает с трапецией №1, просто она сдвинута вправо на полпериода. Поэтому как параметры третьего сигнала, так и его среднее и среднеквадратичное значения будут равны соответствующим значениям первого сигнала:

h4= h2=11; L3= L1=9; C3= C1=0; tИ3= tИ1= 0,65∙T – 0,50∙T = 0,15∙T.

• Ну и остался сигнал №4. Данный сигнал представляет собой прямоугольник с параметрами
• h5=0,5; C4=0; tИ4=1,00∙T – 0,65∙T = 0,35∙T.
• И после использования формул для вычисления среднего и среднеквадратичного значения сигнала №4, получим следующее:

Теперь у нас есть все данные для нахождения AVG и RMS исходного сигнала. Как было сказано выше, среднее значение находится как сумма средних значений элементарных сигналов, на которые был разложен «исходник», а среднеквадратичное – как квадратный корень из суммы квадратов «элементарных» среднеквадратичных значений. То есть в нашем случае будем иметь

Для проверки полученного результата используем широко распространенное бесплатное ПО LTSpice IV от компании Linear Technology Corporation (LTC). Сгенерировав сигнал с требуемыми параметрами, измерим в эмуляторе среднее и среднеквадратичное его значение за 5 периодов:

Как видим, результаты работы эмулятора полностью совпадают с расчетными AVG и RMS, т.е. предложенный способ вычисления среднего и среднеквадратичного значений для сложного сигнала вполне имеет право на жизнь.

Более того, способ этот довольно прост и не требует от разработчика ИИП никаких особых математических навыков. С другой стороны, муторность рассмотренного алгоритма также налицо.

Лично меня дичайше бесит постоянно считать на калькуляторе и выписывать на бумажку средние и среднеквадратичные значения для всех элементарных сигналов, на которые раскладывается исходный, а пото́м складывать их на том же калькуляторе (и это в лучшем случае, ибо если требуется RMS, всё становится еще волшебнее). Поэтому я принял решение сделать себе некий инструмент, упрощающий жизнь разработчика ИИП, которым и хотел бы поделиться с читателями.

Калькулятор

Данный инструмент – это такая специальная «программа» (cko4aTb бесплатно). «Программа» представляет собой обычный экселовский файл (т.к. программист я тот еще), поэтому для работы нам потребуется «Excel» (у меня вот такой: Microsoft® Excel 2002 (10.4302.2625)).

Изначальная и основная задача рассматриваемой «программы» – отрисовка формы трапецеидального сигнала с заданными параметрами (рисуется один период), а также вычисление среднего и среднеквадратичного значений для этого сигнала.

Также «программа» умеет рисовать переменную составляющую заданной трапеции (она получается если из исходного сигнала вычесть постоянную составляющую) и вычислять ее RMS-значение (это уж так, чисто на всякий случай).

Ну и еще предлагаемый софт позволяет быстро посчитать среднее и среднеквадратичное значения для сложного сигнала, состоящего максимум из 16-ти различных элементарных (большее количество в реальной жизни вряд ли потребуется):

Почему в качестве основы взята именно трапеция? Потому что, как было сказано выше, из нее легко получить все основные формы сигналов, встречающихся в импульсных источниках питания, а именно – прямоугольник и треугольник:

Ну а уж на основе этих базовых сигналов можно сляпать и пилу, и напряжение на стоке ключа во флайбэке, и то, что творится на вторичке пушпула и многое другое.

Пользоваться «программой» очень просто. Исходные данные для трапеции вводятся слева в ячейки, выделенные зеленым цветом. После этого чуть ниже можно посмотреть на форму сигнала с введенными параметрами, а еще ниже отобразятся рассчитанные среднее и среднеквадратичное значения этого сигнала.

За переменную составляющую трапеции отвечает правый нижний угол экрана (здесь рисуется ее график и рассчитывается значение RMS). Ну а для работы со сложным сигналом предназначен правый верхний угол.

Здесь в ячейки, выделенные зеленым цветом, вводятся средние и среднеквадратичные значения элементарных сигналов, из которых состоит «исходник», а ниже рассчитываются уже́ его собственные AVG и RMS.

Отмечу, что на всю «программу» наложена магическая защита, позволяющая редактировать только те ячейки, которые можно. При необходимости защита снимается элементарно («Сервис» => «Защита» => «Снять защиту листа»), однако делать это не рекомендую: можно по дури снести какую-нибудь нужную формулу, восстанавливать которую – лишний геморрой.

Вот, в принципе, и всё описание представленной «программы». Несмотря на свою простоту и очевидность, данный софт довольно существенно помогает и экономит время при расчетах ИИП (ну, во всяком случае, у меня происходит именно так).

Например, на расчет среднего и среднеквадратичного значения сложного сигнала, приведенного в предыдущем пункте, понадобится менее минуты. Последовательность действий проста – вводим параметры первой трапеции, затем переписываем рассчитанные для нее значения AVG и RMS в ячейки секции сложного сигнала.

Затем то же самое проделываем для остальных трех элементарных функций, из которых состоит «исходник». Всё, остальное «программа» сделает сама, не надо никаких шаманств с бумажками и калькуляторами:

Ну а у меня на сегодня всё. Желаю удачи при проектировании и изготовлении импульсных (и не только) источников питания!

Обсудить эту заметку можно здесь

1. Ссылки по теме, документация
2. Заметка-пояснение с выводом формул и примером расчета среднего и среднеквадратичного значений сложного сигнала:
3. •  AVG_RMS. pdf;
4. Калькулятор для упрощения вычислений среднего и среднеквадратичного значений простых и сложных сигналов:
5. •  AVG_RMS_Calc.xls;

Источник: http://kmpu.ru/other/raschety_avg-rms/index.html

Среднеквадратичное значение

В зарубежной терминологии применяется аббревиатура RMS (rms) — root mean square.
В математике для набора чисел x1, x2, …, xn количеством n среднеквадратичное значение (rms) определяется выражением:

Например, для чисел 2,3 и 6 среднеквадратичным значением будет квадратный корень из (2²+3²+6²)/3. √(49/3) = 4.04

Среднеквадратичным значением двух или нескольких чисел является квадратный корень из среднеарифметического значения квадратов этих чисел.

Для любой непрерывной функции в интервале T1 — T2 среднеквадратичное значение можно рассчитать по формуле:

Среднеквадратичное значение применяется в расчётах, где существует пропорциональная зависимость не самих переменных значений, а их квадратов.

Действующее значение напряжения и тока

В качестве примера можно рассмотреть квадратичную зависимость мощности или работы электрического тока от значений тока или напряжения.

P = I²R;    A = I²Rt;    P = U²/R;    A = U²t/R

Величина постоянного напряжения или тока является его среднеквадратичным значением.
Среднеквадратичное значение переменного тока равно величине постоянного тока, действие которого произведёт такую же работу в активной (резистивной) нагрузке за время периода.

• Определяющим фактором здесь является среднее (среднеарифметическое) значение мощности Pavg или работы Aavg, пропорциональное квадрату значения тока.
• P = UI = Pavg = UrmsIrms
• Среднеквадратичное значение переменного напряжения или тока часто называют действующим или эффективным.
• Величину переменного напряжения или тока, в большинстве случаев, выражают его среднеквадратичным значением и измеряют приборами электромагнитного типа или специальными среднеквадратичными измерителями — True RMS.

Так же среднеквадратичное значение переменного напряжения за период равносильно по своему воздействию на активную нагрузку такому же значению постоянного напряжения.

Примечание:
Электромагнитные приборы используют для измерения переменного тока и напряжения в промышленных установках. Усилие, создаваемое измерительной катушкой в электромагнитном приборе, пропорционально квадрату тока, поэтому не меняется по направлению.

Угол отклонения стрелки определится некоторым средним усилием F, которое будет пропорционально среднеквадратичному значению тока.

Расчёт действующего значения

В качестве примера рассчитаем среднеквадратичное значение синусоидального напряжения.

Запишем выражение Urms с применением интеграла функции U = Uampsin(t) для одного периода 2π :

Показать расчёт Скрыть расчёт

Вынесем Uamp из под знака радикала.
Воспользуемся табличным интегралом , перепишем и решим последнее выражение с применением формулы Ньютона-Лейбница:

Так как sin(2π), sin(4π) и sin(0) равны нулю, вычисляем RMS синусоиды следующим образом:

В результате решения в итоге получим:

Расчёт RMS для напряжения или тока треугольной и пилообразной формы можно рассмотреть на примере одного периода T для функции , представленной на рисунке:

Выразим Urms искомой функции с помощью определённого интеграла:

Показать расчёт
Скрыть расчёт

Используя табличный интеграл и формулу Ньютона-Лейбница, получаем:

В итоге преобразований получим:

Ток или напряжение любой сложной формы можно рассмотреть, как набор функций в пределах периода. Тогда значением RMS будет квадратный корень из среднеарифметического значения интегралов для квадрата каждой функции, ограниченной её интервалом времени в периоде.

Например, для множества функций F1(t) , F2(t) , … , Fn(t) в соответствующих им интервалах времени (0 — T1), (T1 — T2), …

, (Tn — T), составляющих период T, действующее напряжение (RMS) определится выражением:

Для вариантов однополярного или двуполярного напряжения пилообразной и треугольной формы в периоде 2T или 4T, представленных на рисунке ниже, T и U amp имеют те же расчётные величины, что и в рассмотренном случае c функцией ,
а интегралы, определённые в интервалах, равных T, для квадратов используемых функций , будут иметь одно и то же значение

Следовательно, вышеуказанные варианты однополярного или двуполярного напряжения пилообразной и треугольной формы будут иметь среднеквадратичное значение .

В заключении рассмотрим пример вычисления действующего значения положительных прямоугольных импульсов длительностью Ti .

Выразим Urms одного периода T, как квадратный корень из среднеарифметического значения интегралов, определённых в интервалах 0 — Ti и Ti — T для квадратов всех значений периода.

В результате получаем значение RMS, равное произведению амплитуды импульсов Uamp на квадратный корень из коэффициента заполнения (Ti / T).

В качестве дополнительного материала предлагаем рассмотреть расчёт средеквадратичного значения напряжения накала кинескопа цветного телевизора, исходя из амплитуды и формы напряжения.

Замечания и предложения принимаются и приветствуются!

Источник: https://tel-spb.ru/rms.html

Активное сопротивление. Действующие значения силы тока и напряжения — Класс!ная физика

«Физика — 11 класс»

Активное сопротивление

Сила тока в цепи с резистором

Есть цепь, состоящая из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R.

Сопротивление R называется активным сопротивлением, т.к. при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.

• Напряжение на зажимах цепи меняется по гармоническому закону:
• u = Um cos ωt
• Мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. По закону Ома мгновенное значение силы тока:

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения, а амплитуда силы тока определяется равенством

Мощность в цепи с резистором

В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение меняются. При прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет меняться во времени.

1. Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой
2. Р = I2R
3. Мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой
4. Р = i2R

График зависимости мгновенной мощности от времени (рис.а):

Согласно графику (рис.б) среднее за период значение cos 2ωt равно нулю, а значит равно нулю второе слагаемое в формуле для среднего значения мощности за период.

Действующие значения силы тока и напряжения

Среднее за период значение квадрата силы тока:

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока. Действующее значение силы переменного тока обозначается через I:

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично:

Закон Ома для участка цепи переменного тока с резистором в действующих значениях:

В случае электрических колебаний важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

• Действующие значения непосредственно определяют среднее значение мощности Р переменного тока:
• р = I2R = UI.
• Итак: Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.
• Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Следующая страница «Конденсатор в цепи переменного тока» Назад в раздел «Физика — 11 класс, учебник Мякишев, Буховцев, Чаругин»

Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика

Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях — Аналогия между механическими и электромагнитными колебаниями — Уравнение, описывающее процессы в колебательном контуре.

Период свободных электрических колебаний — Переменный электрический ток — Активное сопротивление.

Действующие значения силы тока и напряжения — Конденсатор в цепи переменного тока — Катушка индуктивности в цепи переменного тока — Резонанс в электрической цепи — Генератор на транзисторе. Автоколебания — Краткие итоги главы

Источник: http://class-fizika.ru/11_27.html

Расчет среднего и среднеквадратичного значений тока/напряжения

. .

Вот здесь есть расширенный и углубленный вариант данной заметки

. . Будучи в очень недавнем прошлом яростным разработчиком всевозможных импульсных источников питания, интересовался всяким по данной теме. В частности – вычислением среднего (AVG, Average) и среднеквадратичного (действующего, эффективного, RMS) значений напряжений и (особенно) токов, живущих в разрабатываемом источнике. Для тех, кто не помнит/не знает – напомню определение среднеквадратичного значения тока/напряжения из Википедии:

Действующим (эффективным) значением силы переменного тока называют величину постоянного тока, действие которого произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток за время одного периода. В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение силы переменного тока

Посему, хочешь узнать статические потери на ключе флайбэка – будь добр посчитать среднеквадратичное значение тока первички. Надо узнать мощность токосчитывающего резистора – туда же. И про выпрямители во вторичной цепи – та же песня. Даже потери (и приблизительный нагрев) в обмотках трансов и дросселей для хиленьких источников и невысоких частот преобразования в первом приближении можно посчитать при помощи среднеквадратичного значения тока, через эти обмотки протекающего. Или, например, делаем могучий источник с высоким КПД. Чтобы оптимально спроектировать обмотку магнитного элемента требуются уже среднее значение тока и среднеквадратичное значение переменной составляющей. В общем – куда ни плюнь, везде фигурируют RMS и AVG (среднее значение, а не антивирус, это важно). Поэтому было принято решение сделать себе некий инструмент, упрощающий жизнь разработчика импульсных источников питания. Вот этим инструментом я и хочу поделиться с общественностью – вдруг кому пригодится.

Как нетрудно заметить, данный инструмент («программа») представляет собой обычный Экселовский файл, поскольку в «компьютерном» программировании я вообще ничего не понимаю.

В задачу рассматриваемой «программы» входит отрисовка формы трапецеидального сигнала с заданными параметрами (рисуется один период) и отрисовка формы переменной составляющей заданного сигнала.

Также «программа» умеет вычислять среднее и среднеквадратичное значения заданного сигнала и RMS-значение его переменной составляющей. Исходные данные вводятся слева в ячейки, выделенные зеленым цветом (на рисунке обведены красным).

Рассчитанные значения AVG и RMS, а также среднеквадратичное значение переменной составляющей заданного сигнала отображаются в правой стороне экрана (обведены синим). Ну а картинки рисуются в нижней части экрана: слева – исходный сигнал, справа – его переменная составляющая.

В нагрузку к «программе» идет короткая заметка, в которой выводятся (а не берутся невесть откуда) расчетные формулы для основных форм сигналов в импульсных источниках питания (трапеции, прямоугольника, треугольника, пилы). Также в этой короткой заметке рассмотрен пример расчета AVG и RMS значений сложного сигнала.

Почему в качестве основы взята именно трапеция? Потому, что из нее легко получить все основные формы сигналов, встречающихся в импульсных источниках питания, а именно – прямоугольник и треугольник А уж на основе этих базовых сигналов можно сляпать и пилу и даже то, что творится на вторичке пушпула: И еще много чего. Пример же расчета среднего и среднеквадратичных значений для сложных (т.е., составленных из простейших) сигналов, повторюсь, есть в короткой заметке-нагрузке. Хотя, если кого-то заинтересует данный аспект, могу впоследствие осветить его и в этом топике. Вот, в принципе, и всё описание представленной «программы». Желаю удачи при проектировании и изготовлении импульсных (и не только) источников питания!

Примечание: все вопросы лучше валить в камменты после заметки, так как не факт, что я смогу на них на все ответить. А вот шансы на то, что в сообществе найдется более прошаренный человек по твоей теме — довольно хорошие. Но уж если зарегистрироваться на сайте совсем никак — можно воспользоваться возможностями электрической почты: [email protected]

Содержание архива (также прилеплен к заметке):

AVG_RMS.zip:

Среднее_и_среднеквадратичное_Трапеция.xls – собственно, «программа» для расчета AVG и RMS в формате Microsoft Excel; Среднее и среднеквадратичное. pdf – короткая заметка-нагрузка с выводом расчетных формул и с примером расчета AVG и RMS значений сложного сигнала.

Источник: http://we.easyelectronics.ru/Theory/raschet-srednego-i-srednekvadratichnogo-znacheniy-toka-napryazheniya.html

Действующие значения тока и напряжения. Эффективные значения тока и напряжения

Рассмотрим следующую цепь.

Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.

Активное сопротивление

• Сопротивление R
  называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:
• U = Um*cos(ω*t).
• Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения. 2) = Um/√2.

  Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим:

  Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток.

  Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени.

  Гораздо важнее будет знать общие характеристики колебаний — такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.

  Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.

  Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.

  Переменный синусоидальный ток в течение периода имеет разные секундные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?

  При расчетах цепей переменного тока, также при электронных измерениях неловко воспользоваться моментальными либо амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Не считая того, об электронном эффекте временами изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.

  Более комфортным оказалось введение понятий так именуемых действующих значений тока и напряжения
  . В базу этих понятий положено термическое (либо механическое) действие тока, не зависящее от его направления.

  — это значение неизменного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.

  Для оценки деяния, производимого переменным током, мы сравним его деяния с термическим эффектом неизменного тока.

  1. Мощность Р неизменного тока I
     , проходящего через сопротивление r
     , будет Р = Р 2 r
     .
  2. Мощность переменного тока выразится как средний эффект моментальной мощности I 2 r за целый период либо среднее значение от (Im х sinωt ) 2 х r за то же время.
  3. Пусть среднее значение t2 за период будет М. Приравнивая мощность неизменного тока и мощность при переменном токе, имеем: I 2 r =
     Mr, откуда I = √
     M
     ,
  4. Величина I именуется действующим значением переменного тока.
  5. Среднее значение i2 при переменном токе определим последующим образом.

  Построим синусоидальную кривую конфигурации тока. Возведя в квадрат каждое секундное значение тока, получим кривую зависимости Р от времени.

  Обе половины этой кривой лежат выше горизонтальной оси, потому что отрицательные значения тока (-i
  ) во 2-ой половине периода, будучи построены в квадрат, дают положительные величины.

  Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное с помощью высшей арифметики, будет равно 1/2I 2 m
  . Как следует, М =
  1/2I 2 m

  • Потому что действующее значение I переменного тока равно I = √
    M
    , то совсем I = Im / √ 2
  • Аналогично зависимость меж действующим и амплитудным значениями для напряжения U и Е имеет вид:
  • U = Um / √ 2
    ,
    E= Em / √ 2
  • Действующие значения переменных величин обозначаются строчными знаками без индексов (I
    , U, Е).
  • На основании произнесенного выше можно сказать, что действующее значение переменного тока равно такому неизменному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.
  • Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, демонстрируют действующие значения тока либо напряжения.

  При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √
  2
  раз. От этого размещение векторов на диаграмме не меняется.

  Школа для электрика

  Значения действующего напряжения и силы тока. Определение. Соотношение с амплитудой для разной формы. (10+)
  

  Понятие эффективных (действующих) значений напряжения и силы тока

  Когда мы говорим о переменных напряжении или силе тока, особенно сложной формы, то встает вопрос о том, как их измерять. Ведь напряжение постоянно меняется. 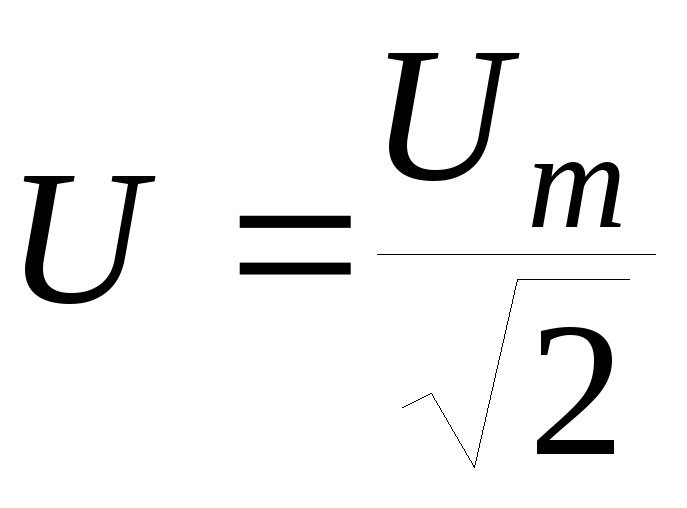Можно измерять амплитуду сигнала, то есть максимум модуля значения напряжения.

  Такой метод измерения нормально подходит для сигналов относительно гладкой формы, но наличие коротких всплесков портит картину. Еще одним критерием выбора способа измерения является то, для каких целей делается измерение.

  Так как в большинстве случаев интерес представляет мощность, которую может отдать тот или иной сигнал, то применяется действующее (эффективное) значение.

  Вашему вниманию подборка материалов: Действующее (эффективное) значение для сигналов стандартной формы Синусоидальный сигнал (синус, синусоида) [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 2 ] Прямоугольный сигнал (меандр) [Действующее значение ] = [Амплитудное значение ] Треугольный сигнал [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 3 ] Закон Ома и мощность для действующих значений напряжения и силы тока Эффективное значение напряжения измеряется в Вольтах, а силы тока в Амперах. Для эффективных значений верен закон Ома: = / [Сопротивление нагрузки, Ом ] [Рассеиваемая на омической нагрузке мощность, Вт ] = [Действующее значение силы тока, А ] * [Действующее значение напряжения, В ] К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости , чтобы быть в курсе.

  Источник: https://lab-music.ru/deistvuyushchie-znacheniya-toka-i-napryazheniya-effektivnye-znacheniya/

  Эффективные значения тока и напряжения

  Для подсчета количества теплоты Q, выделяющейся при прохождении переменного тока по проводнику с активным сопротивлением R, нельзя использовать максимальное значение мощности, так как оно достигается только в отдельные моменты времени.

  Необходимо использовать среднюю за период мощность . Из векторной диаграммы (рис. 7.11) видно, что . Поэтому . Тогда как для постоянного тока . Если ввести действующие значения силы тока и напряжения, положив и , то выражение для средней мощности примет вид , и при , как и для постоянного тока – .

  Таким образом, действующее значение силы переменного тока равно силе такого постоянного тока, который за время, равное периоду колебаний тока, выделяет такое же количество теплоты, что и переменный ток.

  В электротехнике приборы проградуированы по действующим значениям. Поэтому при измерениях нужно учитывать, что в действительности максимальные значения тока и напряжения в 1,5 раза выше тех значений, которые показывают приборы.

  Резонансы в цепи переменного тока

  При протекании токов по электрической цепи, элементы которой соединены последовательно, параллельно или имеют смешанное соединение, могут получаться различные режимы работы этой цепи. Рассмотрим следующие режимы работы электрических цепей: резонанс в цепи с последовательным соединением элементов (резонанс напряжений), резонанс в цепи с параллельным соединением элементов (резонанс токов).

  Резонанс напряжений. Резонанс напряжений наблюдается в цепи, в которой последовательно включены все элементы. Исследуем зависимость амплитуды тока и разности фаз между током и напряжением от частоты изменения электродвижущей силы в цепи, содержащей активное сопротивление, индуктивность и емкость. Для этого воспользуемся полученными ранее формулами:

  , .

  Из приведенных формул видно, что амплитудное значение силы тока и сдвига фаз между током и напряжением зависят от частоты. Графики зависимостей и приведены на рис. 7.14 и 7.15 соответственно.

  Как видно из приведенных рисунков, при возрастании частоты амплитуда тока сначала возрастает, затем проходит через максимум, и, наконец, асимптотически стремится к нулю. Максимальное значение силы тока, равное , достигается при обращении полного реактивного сопротивления в ноль: .

  Этому случаю соответствует частота , называемая резонансной частотой. При этой частоте амплитуда тока определяется только активным сопротивлением .

  Так как для обычных электрических цепей оно невелико, то при резонансе ток может быть очень большим, а напряжения на емкости и индуктивности будут значительно превышать напряжение источника тока. Разность фаз при резонансе .

  Векторная диаграмма принимает вид, изображенный на рис. 7.16. Падения напряжения на емкости и индуктивности полностью взаимно компенсируются, соответствующие векторы равны по величине и противоположны по направлению. Резонанс такого типа называют резонансом напряжений. При резонансе напряжений контур ведет себя как активное сопротивление.

  Резонансный характер изменения тока можно наблюдать и при неизменной частоте, но изменяющейся индуктивности. Максимальное значение тока в этом случае достигается при , то есть при .

  • Заметим, что при резонансе, когда амплитуда силы тока достигает максимума, цепь потребляет извне наибольшее количество энергии, то есть создаются оптимальные условия для передачи энергии от источника в цепь.
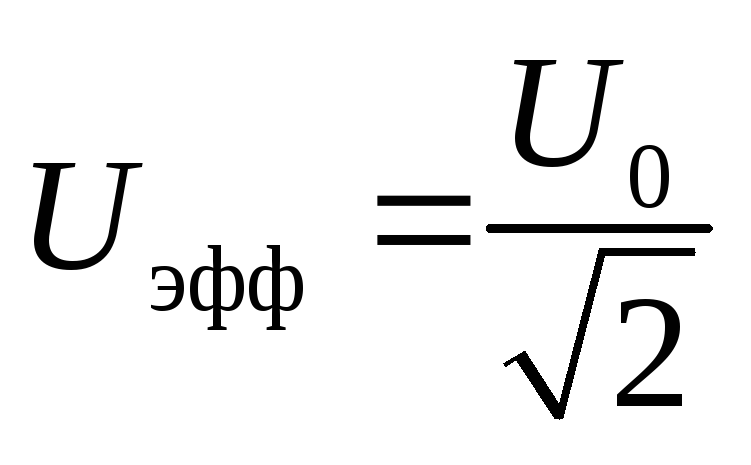
  • Пример
  • Пусть действующее напряжение в цепи равно , частота , активное сопротивление , индуктивность , емкость конденсатора . Тогда индуктивное, емкостное и полное сопротивления цепи будут соответственно равны
  • ,
  • ,

  При резонансе напряжений сдвиг фаз , действующее значение силы тока . Тогда напряжения на емкости и индуктивности будут равны . Таким образом, напряжения на емкости и индуктивности превышают входное напряжение в 5 раз.

  Резонанс токов. Резонанс напряжений наблюдается в цепи, в которой все элементы включены последовательно. При параллельном соединении элементов цепи имеет место резонанс токов. Рассмотрим в качестве примера параллельный RLC-контур, подключенный к внешнему источнику переменного тока (рис. 7.17).

  При построении векторной диаграммы следует учесть, что при параллельном соединении напряжение на всех элементах цепи R, C и L одинаково и равно напряжению внешнего источника.

  Токи, текущие в разных ветвях цепи, отличаются не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Поэтому полное сопротивление цепи нельзя вычислить по законам параллельного соединения цепей постоянного тока. Векторная диаграмма для параллельной RLC-цепи изображена на рис.7.18.

  Через , , обозначены силы токов, текущих через участки цепи, содержащие активное сопротивление, индуктивность и емкость соответственно. Из диаграммы видно, что

  1. .
  2. Поэтому полное сопротивление цепи принимает значение
  3. .

  Максимальное значение полного сопротивления, , достигается при частоте . Фазовый сдвиг между током и напряжением в этом случае равен нулю.

  Полное сопротивление Z принимает максимальное значение, поэтому сила тока в подводящих проводах становится малой. Значения же сил тока и могут быть при этом большими. Имеет место резонанс токов.

  Заряд протекает от емкости к индуктивности и наоборот, происходят колебания тока и заряда на конденсаторе.

  Это интересно!

  Одной из самых ярких, интересных и неоднозначных личностей среди ученых-физиков является Никола Тесла.

  Без его трудов, открытий и изобретений трудно представить себе существование обыденных, казалось бы, вещей, таких как, например, наличие электротока в наших розетках. Подобно Ломоносову, Никола Тесла опередил свое время.

  Резерфорд называл его «вдохновенным пророком электричества». Именно Никола Тесла подарил человечеству генератор переменного тока.

  Будучи студентом Пражского университета, уже на втором курсе молодой Тесла выдвигает идею индукционного генератора переменного тока. Однако университетские профессора сочли эту идею сумасбродством. Но это только подстегнуло изобретателя, и в 1882 г. он строит действующую модель.

  Тесла уезжает в США и прямо с корабля направляется к знаменитому Эдисону – изобретателю угольного микрофона, электрической лампочки, фонографа и динамо-машины. Все изобретения и все научные разработки Эдисона базировались на использовании постоянного тока.

  К идее Тесла Эдисон отнесся довольно прохладно, но все же предложил ему работу в своей лаборатории. Тесла пытался доказать, что пеpеменный ток более эффективен и менее доpог. В октябре 1887 г., не прекращая работать на Эдисона, Никола Тесла получил патент на своё изобретение. Но только в 1888 г.

  , уже работая самостоятельно, Тесла продемонстрировал свое изобретение – генератор переменного тока.

  В1888 г. он открывает явление вращающегося магнитного поля.

  Американский промышленник Джордж Вестингхаус покупает патенты на разработанные Теслой системы передачи электроэнергии посредством многофазного электрического тока, включая генераторы, электродвигатели и трансформаторы, и применяет их в своейгидроэлектростанции на Ниагарском водопаде.

  Изобретения Теслы на десятилетия опередили развитие техники того времени. Площади и улицы Нью-Йорка освещались дуговыми лампами конструкции Теслы. На предприятиях работали его электромоторы, выпрямители, электрогенераторы, трансформаторы, высокочастотное оборудование.

  В конце концов, разработки Теслы и других ученых открыли дорогу строительству электростанций и линий передач переменного тока, который стал широко использоваться в промышленности и для бытового электрического освещения.

  «Я не тружусь более для настоящего, я тружусь для будущего, – сказал Тесла собравшимся в Нью-Йорке журналистам более чем семь десятилетий тому назад. – Будущее принадлежит мне!».

  Сегодня переменный ток – это бесконечная сеть мировой энергосистемы, ставшая доступной человечеству благодаря одному из ее создателей – гениальному Николе Тесле.

  Источник: https://stydopedia.ru/1x18b3.html

  4.4.4. Эффективные напряжение и ток

  Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока.

  Действующим илиэффективнымзначением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе.

  Свяжем эффективное значение тока с его амплитудным значением. Для этого рассчитаем количество теплоты, выделяемое на активном сопротивлении переменным током за время, равное периоду колебаний. Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи cсопротивлениемприпостоянномтокеза время, определяется по формуле. Переменный ток можно считать постоянным только в течение очень малых промежутков времени. Поделим период колебанийна очень большое число малых промежутков времени. Количество теплоты, выделяемое на сопротивленииза время:. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:

  .

  Сила тока в цепи изменяется по синусоидальному закону

  ,

  тогда

  .

  Опуская вычисления, связанные с интегрированием, запишем окончательный результат

  .

  Если бы по цепи шёл некоторый постоянный ток , то за время, равное, выделилось бы тепло. По определению постоянный ток, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов

  (4.28)

  Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током:

  (4. 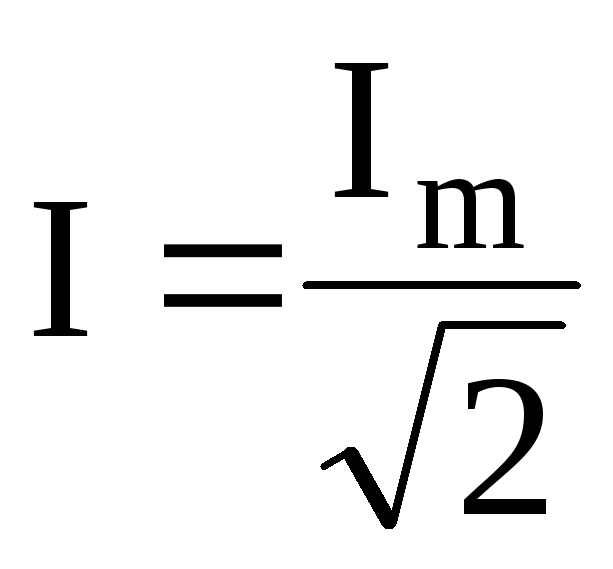29)

  Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В.

  4.4.5. Мощность в цепи переменного тока

  Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам:

  ,.

  Тогда мгновенное значение мощности, выделяемой на участке цепи,

  .

  Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний):

  .

  С использованием известной тригонометрической формулы

  получим

  .

  Величину усреднять не нужно, так как она не зависит от времени, следовательно:

  .

  За длительное время значение косинуса много раз успевает измениться, принимая как отрицательные, так и положительные значения в пределах от (1) до 1. Понятно, что среднее во времени значение косинуса равно нулю

  , поэтому(4.30)

  Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим

  . (4.31)

  Мощность, выделяемая на участке цепи с переменным током, зависит от эффективных значений тока и напряжения и сдвига фаз между током и напряжением. Например, если участок цепи состоит из одного только активного сопротивления, тои. Если участок цепи содержит только индуктивность или только ёмкость, тои.

  Объяснить среднее нулевое значение мощности, выделяемой на индуктивности и ёмкости можно следующим образом. Индуктивность и ёмкость лишь заимствуют энергию у генератора, а затем возвращают её обратно. Конденсатор заряжается, а затем разряжается. Сила тока в катушке увеличивается, затем снова спадает до нуля и т. д. Именно по той причине, что на индуктивном и ёмкостном сопротивлениях средняя расходуемая генератором энергия равна нулю, их назвали реактивными. На активном же сопротивлении средняя мощность отлична от нуля. Другими словами провод с сопротивлением при протекании по нему тока нагревается. И энергия, выделяемая в виде тепла, назад в генератор уже не возвращается.

  Если участок цепи содержит несколько элементов, то сдвига фаз может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27).

  Пример 4.7.К генератору переменного синусоидального тока подключён резистор с сопротивлением. Во сколько раз изменится средняя мощность, расходуемая генератором, если к резистору подключить катушку с индуктивным сопротивлениема) последовательно, б) параллельно (рис. 4.10)? Активным сопротивлением катушки пренебречь.

  Решение.Когда к генератору подключено одно только активное сопротивление, расходуемая мощность

  (см. формулу (4.30)).

  Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора: . Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора

  .

  В результате средняя расходуемая генератором мощность

  .

  Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза.

  Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора . Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора

  .

  Тогда средняя мощность, расходуемая генератором

  . {2}dt}}.}

  Для синусоидального тока:

  I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , {\displaystyle I={\frac {1}{\sqrt {2}}}\cdot I_{m}\approx 0{,}707\cdot I_{m},}

  I m {\displaystyle I_{m}} – амплитудное значение тока.

  Для тока треугольной и пилообразной формы:

  I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . {\displaystyle I={\frac {1}{\sqrt {3}}}\cdot I_{m}\approx 0{,}577\cdot I_{m}.}

  Аналогичным образом определяются действующие значения ЭДС и напряжения.

  Дополнительные сведения

  В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value – эффективное значение. Также применяется аббревиатура RMS (rms) – root mean square – среднеквадратичное (значение).

  В электротехнике приборы электромагнитной, электродинамической и тепловой систем калибруются на действующее значение.

  Источники

  • «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
  • Курс физики. 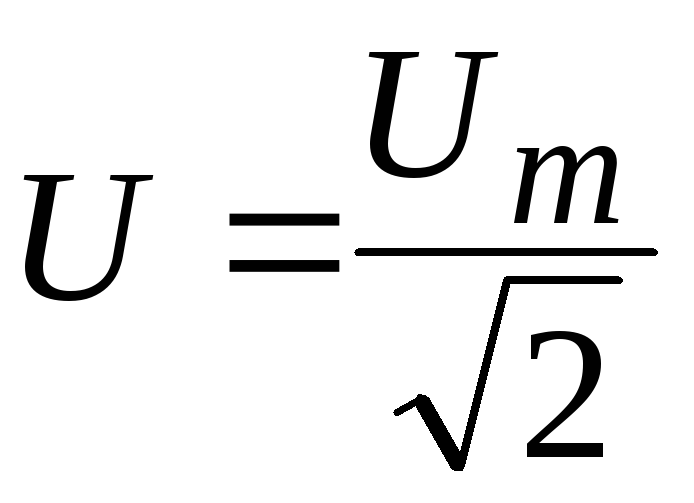А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
  • «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 – § 7.10

  Ссылки

  • Действующие значения тока и напряжения
  • Среднеквадратичное значение

  Мгновенные, максимальные, действующие и средние значения электрических величин переменного тока

  Мгновенное и максимальное значения. Величину переменной электродвижущей силы, силы тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин и обозначают соответственно строчными буквами (e, i, u, p ).
  Максимальным значением (амплитудой) переменной э. д. с. (или напряжения или тока) называется та наибольшая величина, которой она достигает за один период. Максимальное значение электродвижущей силы обозначается Е m , напряжения – U m , тока – I m .

  Действующим (или эффективным) значением переменного тока называется такая сила постоянного тока, которая, протекая через равное сопротивление и за одно и то же время, что и переменный ток, выделяет одинаковое количество тепла.

  Для синусоидального переменного тока действующее значение меньше максимального в 1,41 раз, т. е. в раз.

  Аналогично действующие значения переменной электродвижущей силы и напряжения меньше их максимальных значений тоже в 1,41 раза.

  По величине измеренных действующих значений силы переменного тока, напряжения или электродвижущей силы можно вычислить их максимальные значения:

  E m = E · 1,41; U m = U · 1,41; I m = I · 1,41;

  Среднее значение = отношению количества эл энергии прошедшего через сечение проводника за половину периода к величине этого полупериода.

  Под средним значением понимают среднеарифметическое ее значение за половину периода.

  / Среднее и действующие значения синусоидальных токов и напряжений

  Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока

  т. е. среднее значение синусоидального тока составляет от амплитудного. Аналогично,

  Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока

  Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично,

  Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.

  Количество теплоты, выделенное за один период синусоидальным током,

  Выделенная за то же время постоянным током теплота равна Приравняем их:

  Таким образом, действующее значение синусоидального тока численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.

  Для установления эквивалентности переменного тока в отношении энергии и мощности, общности методов расчета, а также сокращения вычислительной работы изменяющиеся непрерывно во времени токи. ЭДС и напряжения заменяют эквивалентными неизменными во времени величинами. Действующим или эквивалентным значением называется такой неизменный во времени ток, при котором выделяется в резистивном элементе с активным сопротивлением r за период то же количество энергии, что и при действительном изменяющемся синусоидально токе.

  Энергия за период, выделяющаяся в резистивном элементе при синусоидальном токе,

  		i 2r dt =		I m 2 sin2 ωt r dt. .

  При неизменном во времени токе энергия

  W = I 2rT

  Приравняв правые части

  I m

  0,707I m .

  Таким образом, действующее значение тока меньше амплитудного в √2 раз.

  Аналогично определяют действующие значения ЭДС и напряжения:

  Е = E m / √2, U = U m / √2.

  Действующему значению тока пропорциональна сила, действующая на ротор двигателя переменного тока, подвижную часть измерительного прибора и т. д. Когда говорят о значе­ниях напряжения, ЭДС и тока в цепях переменного тока, имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока отградуированы соответственно в действующих значениях тока и напряжения. Например, если прибор показывает 10 А, то это значит, что амплитуда тока

  I m = √2I = 1,41 10 = 14,1 A,

  и мгновенное значение тока

  i = I m sin (ωt + ψ) = 14,1 sin (ωt + ψ).

  При анализе и расчет выпрямительных устройств пользуются средними значениями тока, ЭДС и напряжения, под которыми понимают среднее арифметическое значение соответствующей величины за полпериода (среднее значение за период, как известно, равно нулю):

  		T 2
  Е ср =			Е т sin ωt dt =			sin ωt d ωt =		|cos ωt | π 0 =		0,637Е т .

  Аналогично можно найти средние значения тока и напряжения:

  I ср = 2I т /π; U ср = 2U т /π.

  Отношение действующего значения к среднему значению какой-либо периодически изменяющейся величины называется коэффициентом формы кривой. Для синусоидального тока

  Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока. Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления. Действующее значение переменного тока – это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока. Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р2r. Мощность переменного тока выразится как средний эффект мгновенной мощности I2r за целый период или среднее значение от (Im х sinωt)2 х rза то же время. Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I2r = Mr, откуда I = √M, Величина I называется действующим значением переменного тока. Среднее значение i2 при переменном токе определим следующим образом. Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени. Действующее значение переменного тока Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно1/2I2m. Следовательно, М = 1/2I2m Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2 Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид: U = Um / √2,E= Em / √2 Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е). На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии. Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения. При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √2 раз. От этого расположение векторов на диаграмме не изменяется.

  Список параметров напряжения и силы электрического тока

  В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока

  Значения переменного напряжения (тока)

  Мгновенное значение

  Мгновенное значение – это значение сигнала в определённый момент времени, функцией которого является (u (t) , i (t) {\displaystyle u(t)~,\quad i(t)}). {2}(t)dt}}}

  Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I {\displaystyle I} и U {\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.

  Когда не оговаривают особо, то обычно имеют ввиду именно среднеквадратичные значения величины напряжения или силы тока.

  В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.

  Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.

  Среднее значение

  Среднее значение (смещение) – постоянная составляющая напряжения или силы тока

  U = 1 T ∫ 0 T u (t) d t , I = 1 T ∫ 0 T i (t) d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}

  В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения). {T}\mid i(t)\mid dt}

  На практике используется редко, однако большинство измерительных приборов переменного тока – магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.

  Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.

  Коэффициенты пересчёта значений

  • Коэффициент формы кривой переменного напряжения (тока) – величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} .
  • Коэффициент амплитуды кривой переменного напряжения (тока) – величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2 {\displaystyle {\sqrt {2}}} .

  Параметры постоянного тока

  • Размах пульсации напряжения (тока) – величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени
  • Коэффициент пульсации напряжения (тока) – величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
    • Коэффициент пульсации напряжения (тока) по действующему значению – величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
    • Коэффициент пульсации напряжения (тока) пo среднему значению – величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей

  Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)

  Литература и документация

  Литература

  • Справочник по радиоэлектронным устройствам : В 2-х т. ; Под ред. Д. П. Линде – М.: Энергия, 1978
  • Шульц Ю. Электроизмерительная техника: 1000 понятий для практиков: Справочник: Пер. с нем. М.:Энергоатомиздат, 1989

  Нормативно-техническая документация

  • ГОСТ 16465-70 Сигналы радиотехнические измерительные. Термины и определения
  • ГОСТ 23875-88 Качество электрической энергии. Термины и определения
  • ГОСТ 13109-97 Электрическая энергия. Совместимость технических средств. Нормы качества электрической энергии в системах электроснабжения общего назначения

  Ссылки

  • Электрические цепи постоянного тока
  • Переменный ток. Изображение синусоидальных переменных
  • Амплитудное, среднее, эффективное
  • Периодические несинусоидальные ЭДС, токи и напряжения в электрических цепях
  • Системы тока и номинальные напряжения электроустановок
  • Электричество
  • Проблемы высших гармоник в современных системах электропитания

  Какой физический смысл имеет действующее значение напряжения и тока

  Александр титов

  Действующее значение силы ПЕРЕМЕННОГО тока – это такое значение величины ПОСТОЯННОГО тока, действие которого произведёт ту же самую работу (или тепловой эффект) , что и действие переменного тока за время одного периода его действия. 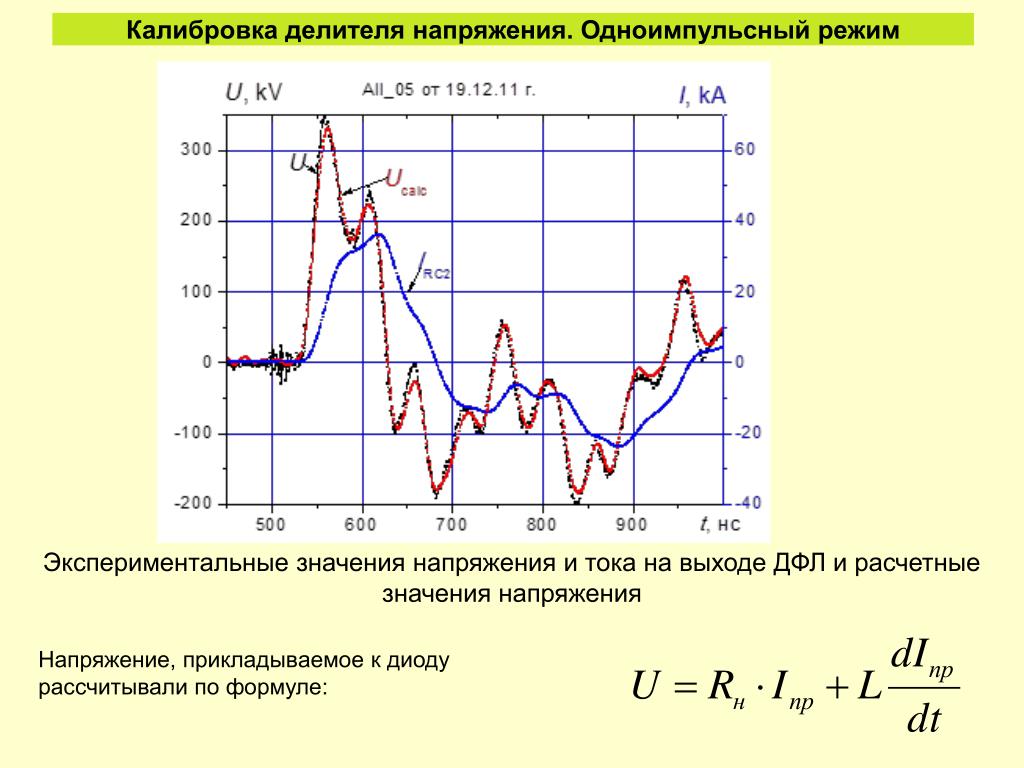2 = Im/2, откуда I = Im / корень из 2. Это и есть действующее значение тока.

  То же самое с действующим значением напряжения и ЭДС.

  Vitas latish

  можно грубо сказать
  – напряжение – потенциальная энергия…. расческа- волосы…. напряжение = свечение, искорки, подъем волос… .
  – ток это работа, действие, сила.. . тепло, горение, движение выплеск кенетической энергии

  Рассмотрим следующую цепь.

  Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.

  Активное сопротивление

  Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:

  U = Um*cos(ω*t). 2) = Um/√2.

  Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим:

  Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний – такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.

  Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.

  Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.

  Значения действующего напряжения и силы тока. Определение. Соотношение с амплитудой для разной формы. (10+)

  Понятие эффективных (действующих) значений напряжения и силы тока

  Когда мы говорим о переменных напряжении или силе тока, особенно сложной формы, то встает вопрос о том, как их измерять. Ведь напряжение постоянно меняется. Можно измерять амплитуду сигнала, то есть максимум модуля значения напряжения. Такой метод измерения нормально подходит для сигналов относительно гладкой формы, но наличие коротких всплесков портит картину. Еще одним критерием выбора способа измерения является то, для каких целей делается измерение. Так как в большинстве случаев интерес представляет мощность, которую может отдать тот или иной сигнал, то применяется действующее (эффективное) значение.

  Вашему вниманию подборка материалов: Действующее (эффективное) значение для сигналов стандартной формы Синусоидальный сигнал (синус, синусоида) [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 2 ] Прямоугольный сигнал (меандр) [Действующее значение ] = [Амплитудное значение ] Треугольный сигнал [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 3 ] Закон Ома и мощность для действующих значений напряжения и силы тока Эффективное значение напряжения измеряется в Вольтах, а силы тока в Амперах. Для эффективных значений верен закон Ома: = / [Сопротивление нагрузки, Ом ] [Рассеиваемая на омической нагрузке мощность, Вт ] = [Действующее значение силы тока, А ] * [Действующее значение напряжения, В ] К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости , чтобы быть в курсе. Если что-то непонятно, обязательно спросите! Задать вопрос. Обсуждение статьи. Еще статьи Микроконтроллеры – пример простейшей схемы, образец применения. Фузы (… Самая первая Ваша схема на микро-контроллере. Простой пример. Что такой фузы?… Практика проектирования электронных схем. Самоучитель электроники…. Искусство разработки устройств. Элементная база радиоэлектроники. Типовые схемы…. Силовой мощный импульсный трансформатор, дроссель. Намотка. Изготовить… Приемы намотки импульсного дросселя / трансформатора. … Силовой резонансный фильтр для получения синусоиды от инвертора… Для получения синусоиды от инвертора нами был применен самодельный силовой резон… Бесперебойник своими руками. ИБП, UPS сделать самому. Синус, синусоида… Как сделать бесперебойник самому? Чисто синусоидальное напряжение на выходе, при… Принцип работы, самостоятельное изготовление и наладка импульсного силового прео… Преобразователь однофазного напряжения в трехфазное. Принцип действия,… Принцип действия, сборка и наладка преобразователя однофазного напряжения в трех… Электрическое напряжение. Амплитуда сигнала. Амплитудное. Вольт. Volt…. Понятие напряжения и разности электрических потенциалов. Амплитуда. Единицы изме…

  Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? Действия тока не определяются ни амплитудным, ни мгновенным значениями. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.

  Мощность P постоянного тока I , проходящего через сопротивление r , будет

  P = I 2 × r .

  Мощность переменного тока выразится как средний эффект мгновенной мощности i 2 × r за целый период или среднее значение от (I m × sin ωt ) 2 × r за то же время.

  Пусть среднее значение i 2 за период будет M . Приравнивая мощность постоянного тока и мощность при переменном токе, имеем:

  I 2 × r = M × r ,

  Величина I называется действующим значением переменного тока.

  Среднее значение i 2 при переменном синусоидальном токе определим следующим образом. Построим синусоидальную кривую изменения тока (рисунок 1).

  
  

  Рисунок 1. Действующее значение синусоидального тока

  Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости i 2 от времени. 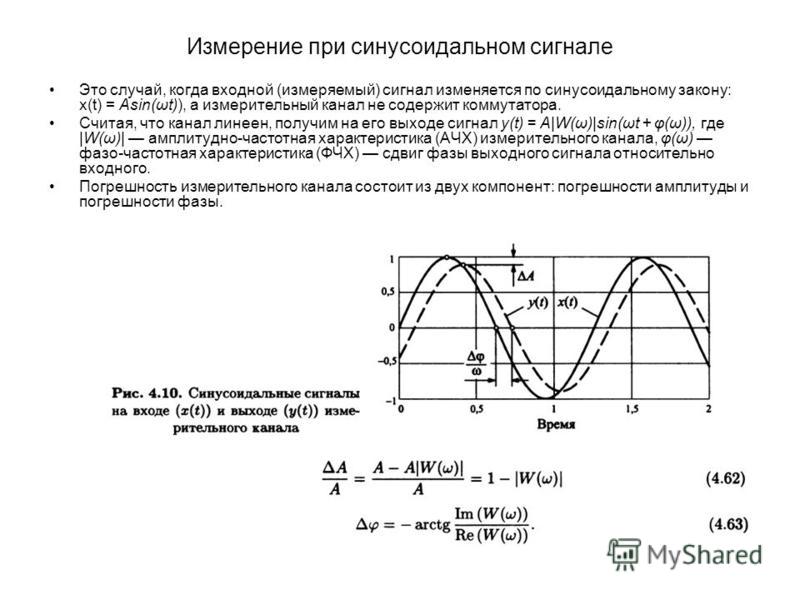Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием T и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника M будет соответствовать среднему значению i 2 за период. Это значение за период, вычисленное при помощи высшей математики, будет равно .

  Следовательно,

  Так как действующее значение переменного тока I равно , то окончательно формула примет вид

  Аналогично зависимость между действующим и амплитудным значениями для напряжения U и E имеет вид:

  Действующие значения переменных величин, то есть действующее значение напряжения, тока и электродвижущей силы, обозначаются прописными буквами без индексов (U , I , E ).

  На основании изложенного выше, можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

  Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующее значение тока и напряжения.

  При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в раз. От этого расположение векторов на диаграмме не изменится.

  ,

  После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:

  Аналогичные соотношения могут быть получены также для напряжения и ЭДС:

  Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.

  Учитывая, например, что действующее значение напряжения в нашей сети составляет 220В, можно определить амплитудное значение напряжения в сети: U m =U Ö2=311В. Соотношение между действующим и амплитудным значениями напряжений и токов важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.

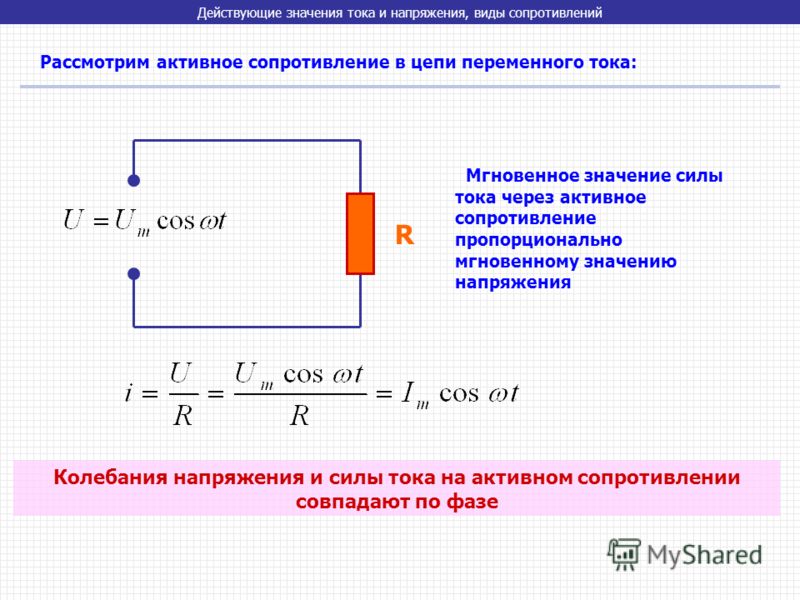
  Действующее значение переменного тока

  Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел.

  Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

  В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

  Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, – периодом Т. Для периодического тока имеем

  Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .

  Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

  i – мгновенное значение тока ;

  u – мгновенное значение напряжения ;

  е – мгновенное значение ЭДС ;

  р – мгновенное значение мощности .

  Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ).

  Амплитуда тока;

  Амплитуда напряжения;

  Амплитуда ЭДС.

  Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

  ,

  Аналогично определяются действующие значения ЭДС и напряжения.

  Синусоидально изменяющийся ток

  Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

  Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

  Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

  Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:

  Значения аргументов синусоидальных функций и называются фазами синусоид, а значение фазы в начальный момент времени (t =0): и – начальной фазой ( ).

  Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.

  При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .

  Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:

  Векторное изображение синусоидально изменяющихся величин

  На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное ) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

  Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:

  Каждый из этих токов синусоидален и может быть представлен уравнением

  Результирующий ток также будет синусоидален:

  Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

  Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

  .

  Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .

  Действующее и среднее значения переменного тока и напряжения.

  Среднее или среднеарифметическое значение Fcp произвольной функции времени f (t )за интервал времени Т оп­ределяется по формуле:

  Численно среднее значение Fср равно высоте прямоугольника, равновели­кого по пло­щади фигуре, ограниченной кривой f (t ), осью t и преде­лами интег­ри­рования 0 – Т (рис. 35).

  Для синусоидальной функции среднее значение за полный период Т (или за целое число полных периодов) равно нулю, так как площади положи­тельной и отрицательной по­луволн этой функции равны. Для переменного си­нусоидаль­ного напряжения определяют среднее по модулю значение за полный период Т или среднее значение за половину периода (Т /2) между двумя нулевыми значе­ниями (рис. 36) :

  Ucp = Um∙ sinwt dt = 2R . Таким образом, количественные параметры электрической энергии на переменном токе (количество энергии, мощность) определяются действующими значениями напряжения U и тока I . По этой при­чине в электроэнергетике все тео­ретические расчеты и экспериментальные из­мерения принято выполнять для действую­щих значений токов и напряжений. В радиотехнике и в технике связи, наобо­рот, оперируют максимальными значе­ниями этих функций.

  Приведенные выше формулы для энергии и мощности переменного тока полностью совпадают с аналогичными формулами для постоянного тока. На этом основании можно ут­верждать, что энергетически постоянному току экви­валентно действующее значение пере­менного тока.

  Что берется за действующее значение силы переменного тока и переменного напряжения

  что берется за действующее значение силы переменного тока и переменного напряжения?

  Боевое яйцо

  Переменный ток, в широком смысле электрический ток, изменяющийся во времени. Обычно в технике под П. т. понимают периодический ток, в котором среднее значение за период силы тока и напряжения равно нулю.

  Переменные токи и переменные напряжения постоянно изменяются по величине. В каждое другое мгновение у них другая величина. Возникает вопрос, как же их измерять? Для их измерения введено понятие действующее значение.

  Действующим или эффективным значением переменного тока называют величину такого постоянного тока, который по своему тепловому действию равноценен данному переменному току.

  Действующим или эффективным значением переменного напряжения называют величину такого постоянного напряжения, которое по своему тепловому действию равноценно данному переменному напряжению.

  Все переменные токи и напряжения в технике измеряются в действующих значениях. Приборы измеряющие переменные величины показывают их действующее значение.

  Вопрос: напряжение в электросети 220 В, что это значит?

  Это значит, что источник постоянного напряжения с напряжением 220 В оказывает такое же тепловое действие как и электросеть.

  Действующее значение тока или напряжения синусоидальной формы в 1,41 раз меньше амплитуды этого тока или напряжения.

  Пример: Определить амплитуду напряжения электросети с напряжением 220 В.

  Амплитуда равна 220 * 1,41=310,2 В.

  Facebook

  Twitter

  Вконтакте

  Одноклассники

  Google+

  Действующие значения э. д. с., напряжения и силы переменного тока

  При синусоидальном переменном токе средние значения напряжения и тока за период равны нулю и не могут служить его характеристиками. Однако среднее значение квадрата силы тока за период отлично от нуля. Следовательно, при включении в цепь переменного тока измерительного прибора, отклонение стрелки которого пропорционально квадрату силы тока, стрелка отклонится и установится на определенном делении шкалы. Каков смысл этого показания?

  Вспомним, что количество выделенного в проводнике тепла изменяется пропорционально квадрату силы тока. Представим себе, что в цепь переменного тока включен тепловой амперметр, действие которого основано на выделении тепла электрическим током. Поскольку шкала такого амперметра градуируется на амперы для постоянного тока, можно заключить, что переменный ток по своему тепловому эффекту эквивалентен постоянному току, силу которого указывает на шкале прибора стрелка. Это позволяет ввести понятие эффективного значения силы переменного тока. Эффективным (или действующим) значением силы переменного тока называют силу такого постоянного тока I, который за один период переменного тока выделяет столько же тепла, сколько последний за то же время.

  Все амперметры, предназначенные для переменного тока, показывают эффективное значение силы тока. В курсе электротехники доказывается, что оно в √2 раз меньше амплитудного значения силы тока Iм, т. е.

  Iм = Iм/√2 ≈ 0,707Iм. (26.5)

  Так как деления на шкале вольтметра соответствуют произведению Iвrв, где при переменном токе Iв — эффективное значение тока, протекающего через вольтметр, а rв — сопротивление вольтметра, то U=Iвrв называют эффективным напряжением переменного тока, которое в √2 раз меньше Uм, т. е.

  U = Uм/√2 ≈ 0,7O7UM.            (26.6)

  Аналогично эффективное значение э. д. с. переменного тока Ɛ в √2 раз меньше его амплитудного значения Ɛм:

  Ɛ  = Ɛм/√2 ≈ 0,707Ɛм.                 (26.7)

  Все вольтметры, предназначенные для переменного тока, показывают эффективные значения э. д. с. и напряжения.

  Связь действующего и амплитудного напряжения. Действующие значения силы тока и напряжения

  Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока.

  Действующим илиэффективным значением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе.

  Свяжем эффективное значение тока с его амплитудным значением. Для этого рассчитаем количество теплоты, выделяемое на активном сопротивлении переменным током за время, равное периоду колебаний. Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи cсопротивлениемприпостоянном токеза время, определяется по формуле

  . Переменный ток можно считать постоянным только в течение очень малых промежутков времени

  . Поделим период колебанийна очень большое число малых промежутков времени

  . Количество теплоты

  , выделяемое на сопротивленииза время

  :

  . Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:

  
  .

  Сила тока в цепи изменяется по синусоидальному закону

  
  ,

  
  .

  Опуская вычисления, связанные с интегрированием, запишем окончательный результат

  
  .

  Если бы по цепи шёл некоторый постоянный ток , то за время, равное, выделилось бы тепло

  . По определению постоянный ток, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока

  . Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов

  
  

  (4.28)

  Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током:

  
  (4.29)

  Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В.

  4.4.5. Мощность в цепи переменного тока

  Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам:

  
  ,

  .

  Тогда мгновенное значение мощности, выделяемой на участке цепи,

  Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний):

  С использованием известной тригонометрической формулы

  
  .

  Величину

  усреднять не нужно, так как она не зависит от времени, следовательно:

  
  .

  За длительное время значение косинуса много раз успевает измениться, принимая как отрицательные, так и положительные значения в пределах от (1) до 1. Понятно, что среднее во времени значение косинуса равно нулю

  
  , поэтому

  (4.30)

  Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим

  
  . (4.31)

  Мощность, выделяемая на участке цепи с переменным током, зависит от эффективных значений тока и напряжения и сдвига фаз между током и напряжением . Например, если участок цепи состоит из одного только активного сопротивления, то

  и

  . Если участок цепи содержит только индуктивность или только ёмкость, то

  и

  .

  Объяснить среднее нулевое значение мощности, выделяемой на индуктивности и ёмкости можно следующим образом. Индуктивность и ёмкость лишь заимствуют энергию у генератора, а затем возвращают её обратно. Конденсатор заряжается, а затем разряжается. Сила тока в катушке увеличивается, затем снова спадает до нуля и т. д. Именно по той причине, что на индуктивном и ёмкостном сопротивлениях средняя расходуемая генератором энергия равна нулю, их назвали реактивными. На активном же сопротивлении средняя мощность отлична от нуля. Другими словами провод с сопротивлением при протекании по нему тока нагревается. И энергия, выделяемая в виде тепла, назад в генератор уже не возвращается.

  Если участок цепи содержит несколько элементов, то сдвига фаз может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27).

  Пример 4.7. К генератору переменного синусоидального тока подключён резистор с сопротивлением. Во сколько раз изменится средняя мощность, расходуемая генератором, если к резистору подключить катушку с индуктивным сопротивлением

  а) последовательно, б) параллельно (рис. 4.10)? Активным сопротивлением катушки пренебречь.

  Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность

  
  (см. формулу (4.30)).

  Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора:

  . Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора

  
  

  .

  В результате средняя расходуемая генератором мощность

  
  .

  Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза.

  Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора

  . Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора

  
  

  .

  Тогда средняя мощность, расходуемая генератором

  Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.

  Как известно, переменная э.д.с. индукции вызывает в цепи переменный ток. При наибольшем значении э.д.с. сила тока будет иметь максимальное значение и наоборот. Это явление называется совпадением по фазе. Несмотря на то что значения силы тока могут колебаться от нуля и до определенного максимального значения, имеются приборы, с помощью которых можно замерить силу переменного тока.

  Характеристикой переменного тока могут быть действия, которые не зависят от направления тока и могут быть такими же, как и при постоянном токе. К таким действиям можно отнести тепловое. К примеру, переменный ток протекает через проводник с заданным сопротивлением. Через определенный промежуток времени в этом проводнике выделится какое-то количество тепла. Можно подобрать такое значение силы постоянного тока, чтобы на этом же проводнике за то же время выделялось этим током такое же количество тепла, что и при переменном токе. Такое значение постоянного тока называется действующим значением силы переменного тока.

  В данное время в мировой промышленной практике широко распространен трехфазный переменный ток , который имеет множество преимуществ перед однофазным током. Трехфазной называют такую систему, которая имеет три электрические цепи со своими переменными э.д.с. с одинаковыми амплитудами и частотой, но сдвинутые по фазе относительно друг друга на 120° или на 1/3 периода. Каждая такая цепь называется фазой.

  Для получения трехфазной системы нужно взять три одинаковых генератора переменного однофазного тока, соединить их роторы между собой, чтобы они не меняли свое положение при вращении. Статорные обмотки этих генераторов должны быть повернуты относительно друг друга на 120° в сторону вращения ротора. Пример такой системы показан на рис. 3.4.б.

  Согласно вышеперечисленным условиям, выясняется, что э.д.с., возникающая во втором генераторе, не будет успевать измениться, по сравнению с э.д.с. первого генератора, т. е. она будет опаздывать на 120°. Э.д.с. третьего генератора также будет опаздывать по отношению ко второму на 120°.

  Однако такой способ получения переменного трехфазного тока весьма громоздкий и экономически невыгодный. Чтобы упростить задачу, нужно все статорные обмотки генераторов совместить в одном корпусе. Такой генератор получил название генератор трехфазного тока (рис. 3.4.а). Когда ротор начинает вращаться, в каждой обмотке возникает

  
  а) б)

  Рис. 3.4. Пример трехфазной системы переменного тока

  а) генератор трёхфазного тока; б) с тремя генераторами;

  изменяющаяся э.д.с. индукции. Из-за того что происходит сдвиг обмоток в пространстве, фазы колебаний в них также сдвигаются относительно друг друга на 120°.

  Для того чтобы подсоединить трехфазный генератор переменного тока к цепи, нужно иметь 6 проводов. Для уменьшения количества проводов обмотки генератора и приемников нужно соединить между собой, образовав трехфазную систему. Данных соединений два: звезда и треугольник. При использовании и того и другого способа можно сэкономить электропроводку.

  Соединение звездой

  Обычно генератор трехфазного тока изображают в виде 3 статорных обмоток, которые располагаются друг к другу под углом 120°. Начала обмоток принято обозначать буквами А, В, С , а концы – X, Y, Z . В случае, когда концы статорных обмоток соединены в одну общую точку (нулевая точка генератора), способ соединения называется «звезда». В этом случае к началам обмоток присоединяются провода, называемые линейными (рис. 3.5 слева).

  Точно так же можно соединять и приемники (рис. 3.5., справа). В этом случае провод, который соединяет нулевую точку генератора и приемников, называется нулевой. Данная система трехфазного тока имеет два разных напряжения: между линейным и нулевым проводами или, что то же самое, между началом и концом любой обмотки статора. Такая величина называется фазным напряжением (Uл ). Поскольку цепь трехфазная, то линейное напряжение будет в v3 раз больше фазного, т. е.: Uл = v3Uф.

  Соединение треугольником.

  Рисунок 3.6. Пример соединения треугольником

  При использовании данного способа соединения конец X первой обмотки генератора подключают к началу В второй его обмотки, конец Y второй обмотки – к началу С третьей обмотки, конец Z третьей обмотки – к началу А первой обмотки. Пример соединения показан на рис. 3.6. При данном способе соединения фазных обмоток и подключении трехфазного генератора к трехпроводной линии линейное напряжение по своему значению сравнивается с фазным: Uф = Uл

  Контрольные вопросы

  1. Перечислите основные параметры, характеризующие переменный ток.

  2. Дайте определение частоты и единицы её измерения.

  3. Дайте определение амплитуды и единицы её измерения.

  4. Дайте определение периода и единицы его измерения.

  5. Отличие простейшего генератора трёхфазного тока от генератора однофазного тока.

  6. Что такое фаза?

  7. Что представляет собой ротор генератора трёхфазного тока?

  8. Почему сдвинуты по фазе обмотки статора генератора трёхфазного тока?

  9. Особенность симметричной системы трёх фаз.

  10. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «звезда».

  11. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «треугольник».

  3.2. Виды сопротивлений в цепях переменного тока

  В цепях переменного тока сопротивления разделяют на активные и реактивные.

  В активных сопротивлениях , включенных в цепь переменного тока, электрическая энергия преобразуется в тепловую. Активным сопротивлением R обладают, например, провода электрических линий, обмотки электрических машин и т.д.

  В реактивных сопротивлениях электрическая энергия, вырабатываемая источником, не расходуется. При включении реактивного сопротивления в цепь переменного тока возникает лишь обмен энергией между ним и источником электрической энергии. Реактивное сопротивление создают индуктивности и ёмкости.

  Если не учитывать взаимное влияние отдельных элементов электрической цепи, то в общем случае электрическая цепь синусоидального тока может быть представлена тремя пассивными элементами: активным сопротивлением R, индуктивностью L и емкостью C.

  Активное сопротивление в цепи переменного тока .

  При включении в цепь переменного тока активного сопротивления, ток и напряжение совпадают по фазе (рис. 3.7) и изменяются по одному и тому же cинусоидальному закону: u=U m sinωt . Они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис. 3.7.б).

  Для цепи переменного тока, содержащей только активное сопротивление, закон Ома имеет такую же форму, как и для цепи постоянного тока: I=U/R.

  Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения u : p=ui .

  Рисунок 3.7. Схема включения в цепь переменного тока активного сопротивления R (a), кривые тока i , напряжения u и мощности p (б) и векторная диаграмма.

  Из графика видно, что изменение мощности происходит с двойной частотой по отношению к изменению тока и напряжения, т.е. один период изменения мощности соответствует половине периода изменения тока и напряжения. Все значения мощности положительные, это означает, что энергия передается от источника к потребителю.

  Средняя мощность Рcp , потребляемая активным сопротивлением, P=UI=I 2 R – это и есть активная мощность.

  Под индуктивностью L будем понимать элемент электрической цепи (катушку индуктивности, потерями которой можно пренебречь), способный запасать энергию в своём магнитном поле, который не имеет активного сопротивления и ёмкостиС (рис.3.8).

  При включении в цепь переменного тока индуктивности, изменяющийся ток непрерывно индуцирует в ней э.д.с. самоиндукции e L = LΔi/Δt, где Δi/Δt – скорость изменения тока.

  Когда угол ωt равен 90° и 270° скорость изменения тока Δi/Δt =0, поэтому э.д.с. e L =0.

  Скорость изменения тока будет наибольшей, когда угол ωt равен 0°, 180° и 360°. В эти минуты времени э.д.с. имеет наибольшее значение.

  Кривая мощности представляет собой синусоиду, которая изменяется с двойной частотой по сравнению с частотой изменения тока и напряжения. Мощность имеет положительные и отрицательные значения, т.е. возникает непрерывный колебательный процесс обмена энергией между источником и индуктивностью.

  Рисунок 3.8. Схема включения в цепь переменного тока индуктивности (а), кривые тока i , напряжения u , э.д.с. e L (б) и векторная диаграмма (в)

  Э.д.с. самоиндукции согласно правилу Ленца направлена так, чтобы препятствовать изменению тока. В первую четверть периода, когда ток увеличивается, э.д.с. имеет отрицательное значение (направлена против тока).

  Во вторую четверть периода, когда ток уменьшается, э.д.с. имеет положительное значение (совпадает по направлению с током).

  В третью четверть периода ток меняет своё направление и увеличивается, поэтому э.д.с. направлена против тока и имеет положительное значение.

  В четвёртую четверть периода ток уменьшается и э.д.с. самоиндукции стремится поддержать прежнее положение тока и имеет отрицательное значение. В результате ток отстает от напряжения по фазе на угол 90 О.

  Сопротивление катушки или проводника переменному току, вызванное действием э.д.с. самоиндукции, называется индуктивным сопротивлением Х L [Ом]. Индуктивное сопротивление не зависит от материала катушки и от площади поперечного сечения проводника.

  В цепях переменного тока катушки индуктивности соединяют последовательно и параллельно.

  При последовательном соединении катушек эквивалентная индуктивностьLэ и эквивалентное индуктивное сопротивление X L э будут равны:

  Lэ=L 1 +L 2 +… X L э=X L 1 +X L 2 +…

  При параллельном соединении катушек:

  1/Lэ=1/L 1 +1/L 2 +… 1/X L э=1/X L 1 +1/X L 2 +…

  Контрольные вопросы

  1. Какие виды сопротивления в цепях переменного тока Вы знаете?

  2. Что значит активное сопротивление?

  3. Что такое реактивное сопротивление?

  4. Какие элементы цепи создают реактивное сопротивление?

  5. Что такое активная мощность?

  1. Дайте определение индуктивности.

  2. Что происходит в первую четверть периода колебательного процесса обмена энергией между источником и индуктивностью?

  3. Что происходит во вторую четверть периода колебательного процесса обмена энергией между источником и индуктивностью?

  4. Дайте определение индуктивного сопротивления.

  3.3. Конденсаторы. Ёмкость в цепи переменного тока

  Конденсатор – устройство, способное накапливать электрические заряды.

  Простейший конденсатор представляет собой две металлические пластины (электроды), разделенные диэлектриком.

  Каждый конденсатор характеризуется номинальной емкостью и допустимым напряжением. Напряжение конденсатора указывают на корпусе, и превышать его нельзя. Конденсаторы различаются формой электродов (плоский), типом диэлектрика и ёмкостью (постоянной и переменной).

  Cтраница 2

  Действующим значением силы тока I называется сила постоянного тока, выделяющего в проводнике за то же время такое же количество теплоты, что и переменный ток.  

  Как видно из рисунка, в каждый момент времени величины напряжения и силы тока принимают различные значения. Поэтому, чтобы судить о величине силы тока и напряжения переменного тока, пользуются действующим значением силы тока и напряжения. Чтобы определить действующее значение силы переменного тока, его приравнивают к силе постоянного тока, которое выделило бы в проводнике такое же количество тепла, как и переменный ток.  

  Трансформатор, содержащий в первичной обмотке 300 витков, включен в сеть переменного тока с действующим напряжением 220 В. Вторичная цепь трансформатора питает нагрузку с активным сопротивлением 50 Ом. Найти действующее значение силы тока во вторичной цепи, если падение напряжения во вторичной обмотке трансформатора, содержащей 165 витков, равно 50 В.  

  Таким образом, при замене операции извлечения корня сравнением время, за которое интегрируемый сигнал с ГЛИН станет равен интегралу от квадрата измеренной силы тока, пропорционально действующему значению силы тока. До этого К2 был открыт в течение времени т и пропускал на счетчик СИ импульсы с генератора тактовых импульсов ГТИ. Число импульсов TV / гтит записанное в СЧ, пропорционально действующему значению силы тока. Это число хранится в / 77, а по окончании цикла измерения отображается на ЦИ.  

  Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения и средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.  

  Рх o jjFr В слУчае т – н – СУХОЙ лампы применяют способ термометра, подвешиваемого вблизи генераторной лампы, и отмечают его показание. Затем, разрывая цепь колебательного контура генератора, дают на сетку генераторной лампы положительный потенциал до тех пор, пока термометр не по. Беря в последнем случае величины 1а и Еа как исходные, определяем Рх из соотношения Рх1а Еа. Мощность в антенне определяется по ф-ле Рх – / /, где РЯ – мощность eW, ra – активное сопротивление антенны в Q и 1а – действующее значение силы тока в антенне в А. По скольку по современным международным нормам под мощностью передатчика принято понимать мощность в антенне, то упомянутая выше ф-ла определяет одновременно и мощность передатчика.  

  Тепловые измерители имеют наиболее широкое практич. Действие тепловых измерителей состоит в удлинении тонкой проволоки при нагревании ее проходящим по ней переменным током высокой частоты. Сам по себе эффект ограничивает пределы применимости таких измерителей токами от нескольких тА до 1 – 3 А в зависимости от материала тонкой проволоки, примененной в измерителе. Применяются сплавы серебра с платиной, платины с иридием и др. Если сплав применяется в виде проволоки, то она имеет диаметр сотых долей мм. При ленте толщина составляет 0 01 мм, ширина 3 мм и длина 25 – 30 мм. Удлинение нити нагреваемым током пропорционально квадрату действующего значения силы тока. Перемещение по шкале измерителя стрелки, связанной с той же проволокой с помощью особой подвижной системы, обычно пропорционально квадратному корню из действующей силы тока. Из-за этого шкалы тепловых измерителей имеют неравномерные интервалы между делениями.  

  В данном случае колебания тока являются гармоническими (график колебаний – синусоида) и вынужденными, поскольку параметры колебаний (частота, амплитуда) определяются внешним источником – генератором. Некоторые электротехнические устройства (например, колебательный контур) способны генерировать свободные гармонические колебания электрического тока. По левой ветви рамки – от нас и, поскольку в этом случае через клемму а течет ток в направлении, обратном показанному на рис. 12.1, ее полярность – минус. Поскольку при данном положении рамки сила тока имеет наибольшее значение, фаза колебаний может быть г / 2 или 3 / 2ir, в зависимости от того, какое направление тока в рамке мы принимаем за положительное. Сравнивая формулу (12.1) и заданную зависимость, нетрудно заметить, что 1т 10 А и ш 4тград / с. Далее, используя формулу (12.2), определяем частоту колебаний (отв. Используя закон Джоуля – Ленца (Q I2Rt), определяем действующее значение силы тока (отв.  

  ТОЭ Лекции – №13 Действующее значение переменного тока

  Понятие действующего значения тока вводится в связи с необходимостью производства измерений. Что измерять у переменного тока? Если бы мы имели дело только с синусоидами – кривыми одной формы, то можно было бы измерять амплитуды. Но на практике встречаются самые разные кривые, и может оказаться так, что два различных по форме тока имеют одинаковые амплитуды, хотя очевидно, что на электрическую цепь они будут оказывать разное воздействие.

  Поэтому наиболее целесообразно оценивать величину тока по той работе, которую он совершает. При такой оценке действие переменного тока сравнивается с аналогичным действием постоянного тока. Например, если некоторый переменный ток выделяет на участке цепи такое же количество тепла, что и постоянный ток силой 10 ампер, то говорят, что величина этого переменного тока составляет 10 ампер. Это значение тока и называют действующим.

  Итак, действующим значением переменного тока называется численное значение такого постоянного тока, который за время, равное одному периоду, выделяет в сопротивлении такое же количество тепла, что и ток переменный..

  Таким образом, для оценки величины переменного тока мы должны сделать следующее.

  1.Определить количество теплоты, выделяющейся в сопротивлении R за время Т при протекании переменного тока i. Это количество теплоты равно:

  2.Подобрать такой постоянный ток I, который за то же время Т в том же сопротивлении R выделяет такое же количество тепла. При постоянном токе оно равно: W=I2RT.

  3. Приравнять W=W:

  откуда

  Последняя формула и определяет действующее значение переменного тока.

  Пример 2.1. На вход некоторой цепи подается импульсное напряжение треугольной формы (рис. 13.1, а). Чему равно его действующее значение?

  Решение

  Пример 2.2. На рис. 13.1, б показана кривая напряжения на выходе схемы однофазного однополупериодного выпрямления. Чему равно действующее значение напряжения, если его амплитудное значение Um составляет 311 В?

  Решение

  Пример 2.3. Определить действующее значение синусоидального тока i=Imsin(ωt):

  Решение

  Рассмотренные примеры показывают, что действующее значение переменного тока зависит от его формы.

  Нормирующие преобразователи действующих значений напряжения и тока

    Статья в журнале “ИСУП” в pdf

  Настоящая статья является продолжением цикла статей в журнале «ИСУП», посвященных нормирующим преобразователям (№3 за 2010 год, №1 за 2012 год). Ранее обсуждались функции нормирующих преобразователей, которые оказываются наиболее ценными в системах с большим числом разнообразных  сигналов и удаленными датчиками.

  Кратко напомним их.

  Во-первых, нормирующие преобразователи реализуют схему и  метод измерения первичных сигналов. Особенно это важно при измерении сигналов термометров сопротивления и термоэлектрических преобразователей (термопар) при измерении температуры. Нормирующие преобразователи обеспечивают трех-, четырехпроводную схему подключения (для термосопротивлений), компенсацию влияния «холодных спаев»  (для термопар), линеаризацию нелинейных статических характеристик, фильтрацию помех и проч. Тем самым нормирующие преобразователи разгружают и упрощают второй уровень измерительной системы.

  Во-вторых, нормирующие преобразователи, как правило, обеспечивают гальваническую развязку сигналов. Это позволяет подключать удаленные датчики, находящиеся под разными потенциалами, и сокращает уровень электромагнитных помех, проникающих в измерительный тракт.

  В-третьих, нормирующие преобразователи унифицируют сигналы в системе, что опять же упрощает построение второго уровня многоканальных систем.

  При этом, обсуждая применение нормирующих преобразователей сигналов, мы до сих пор имели дело с так называемыми постоянными сигналами, значение которых если и изменялось, то очень медленно. Так, если говорить об измерении температуры в технологических процессах, то характерное время изменения  температуры – единицы и десятки секунд. Для того, чтобы нормирующий преобразователь без искажения передавал такие медленно изменяющиеся измеренные сигналы, его полоса пропускания должна составлять всего единицы Герц.

  В данной статье речь пойдет о преобразовании переменных сигналов тока и напряжения в сети частотой  50 Гц. Роль гальванической развязки и унификации сигналов при измерении параметров электрических  сигналов тока и напряжения очевидна и стандартна. Вопросом, достойным обсуждения, является метод измерения действующих значений переменных сигналов, реализованный в нормирующем преобразователе, а также некоторые особенности измерения реальных сигналов.

  Интересно, что на практике само значение переменного сигнала – все время изменяющаяся величина – редко представляет самостоятельный интерес. Более интересным оказывается знание некоторых определенных характеристик переменных сигналов, дающих представление о сигнале в целом.

  Когда говорят о сигнале в сети переменного тока 50 Гц, то обычно имеют в виду гармонический (синусоидальный) сигнал. Как известно, всего три параметра – амплитуда, частота и фаза – полностью характеризуют сигнал, и когда хотят получить информацию о самом сигнале, именно их и измеряют.

  В задачах контроля и управления технологическими процессами, учета электроэнергии, контроля за работоспособностью и функционированием силовой коммутационной техники и прочих важно знать энергетические свойства переменного сигнала, характеризующие  его способность совершать работу. Таким параметром переменного сигнала является  его среднеквадратичное значение. Не менее широко применяются также термины «действующее значение», «эффективное значение». В дальнейшем мы будем использовать термин «действующее значение».

  В соответствии  с ГОСТ 16465-70 «Сигналы радиотехнические измерительные. (Термины и определения)» среднеквадратичное значение (действующие, эффективное значение) есть корень квадратный из среднего значения квадрата сигнала. Усреднение проводится по времени за период переменного сигнала Т, поэтому выражение можно переписать для сигналов напряжения и тока в следующем виде:

                                     (2)

  где U(t), i(t) – мгновенные значения напряжения и тока.

  Физический смысл среднеквадратичного значения напряжения заключается в том, что оно равно такому постоянному напряжению, которое выделяет на активной нагрузке такое же тепло. Отсюда и другие термины «действующее» или «эффективное» значение. Таким образом, действующее значение позволяет сравнивать с энергетической точки зрения переменный сигнал с постоянным.

  Действующие значения напряжения U_ди тока I_ддля гармонического (синусоидального) сигнала определяются его амплитудами U_m и  I_m:

                     .

  Часто рассматривается другая характеристика переменного сигнала – средневыпрямленное значение. Средневыпрямленное значение – это среднее значение модуля сигнала. В интегральной форме средневыпрямленное значение сигнала напряжения и тока записывается в следующей форме:

        

  Средневыпрямленные значения напряжения и тока для гармонического сигнала выражаются через  их амплитуды соотношениями:

                

  Как видим, среднеквадратичные и средневыпрямленные значения линейно связаны между собой:

     

  В связи с  этим для измерения среднеквадратичного значения часто используют результаты измерения средневыпрямленного. Метод измерения действующего значения на основе средневыпрямленного весьма распространен, прежде всего, потому, что его реализация аналоговыми схемотехническими решениями достаточна проста.

  Однако, недостаток этого метода заключается в том, что это соотношение справедливо только для синусоидального  сигнала. На практике сигналы тока и  напряжения могут сильно  отличаться от  правильной синусоидальной формы. Поэтому попытка измерения среднеквадратичного  значения с  помощью выпрямительных приборов приводит к большим погрешностям измерения. Это значит, что, выбирая измерительный прибор для измерения действующих значений напряжения и тока, следует выяснить, является ли сигнал синусоидальным, и какой метод измерения действующего значения  реализует измерительный прибор.

  В реальных условиях вследствие использования нелинейной нагрузки потребителем, в результате процесса передачи и преобразования электроэнергии и ряда других факторов, форма напряжения и тока отличается от синусоидальной формы. Процентное увеличение доли нелинейных, несимметричных, импульсных нагрузок потребителя (персональные компьютеры, приводы с регулируемой скоростью, сварочные инверторы, осветительное оборудование, выпрямительные агрегаты и др.) с каждым годом всё больше растёт. Измерение действующих значений на таком оборудовании с помощью обычных аналоговых измерителей с выпрямленными показаниями может оказаться некорректным.

  Применение цифровых методов измерения  и обработки сигналов, позволяет проводить измерение действующих значений более точно и для сигналов несинусоидальной формы. Дело в том, что цифровые методы измерения позволяют рассчитывать действующее значение сигнала  путем непосредственного вычисления интеграла. Однако, и в этом случае есть некоторые особенности измерения, которые надо учитывать.

  Первая особенность заключается в том, что при цифровом интегрировании непрерывный интеграл заменяется суммой дискретных отсчетов, при этом точность интегрирования напрямую зависит от периода дискретизации Δt. При измерении действующих значений синусоидальных сигналов погрешность вычислений пропорциональна отношению (Δt×f_MAKC)², где f_MAKC – максимальная частота сигнала. Предположим, что частота дискретизации составляет 10 кГц и нас интересует погрешность измерения действующего значения не ниже 0,5 %. Для сетевого напряжения 50 Гц погрешность вычислений составляет всего 0,0025 % и ее можно не принимать в расчет. На частоте 300 Гц эта вычислительная погрешность составляет уже 0,1 %. Поэтому при частоте дискретизации 10 кГц можно измерять действующие значения сигналов с частотой до 300 Гц без появления дополнительной погрешности, а на частоте 1 кГц погрешность составляет 1 %.

  Практический интерес представляет ситуация, когда измеряется действующее значение  напряжения (тока) сети  частотой 50 Гц, но форма сигнала не является чисто гармонической (синусоидальной).  Как известно, периодический негармонический сигнал сети можно представить в виде суперпозиции гармонических составляющих с частотами, кратными 50 Гц. Относительную погрешность вычислений δ в этом случае можно оценить по следующей формуле:

  δ=0,0025 % √(1+∑ K_n n²),

  где К_n=U_n/ U₁ – коэффициент гармоник n-й гармоники. Суммирование ведется по всем учитываемым гармоникам.

  Вторая особенность заключается в том, что усреднение должно производится на периоде сетевого напряжения Т, который, вообще говоря, заранее неизвестен, поскольку частота сети может изменяться. Российскими стандартами установлено, что нормально допустимые и предельно допустимые отклонения частоты сети не должны превышать соответственно ±0,2 Гц и ±0,4 Гц. Отклонение частоты на 0,4 Гц от частоты 50 Гц вызывает погрешность  измерения, связанную с несовпадением периодов усреднения и сигнала, около 0,8 %. Такой уровень погрешности не позволяет достичь требуемый уровень погрешности измерения 0,5 %.

  Существует несколько способов устранения указанной погрешности. Первый способ заключается в том, что увеличивают время усреднения  по сравнению с периодом сигнала. Это простой метод, но его применение приводит к повышению инерционности измерения. Для отклонений частоты на 0,4 Гц требуется около 10 периодов усреднения, чтобы погрешность, вызванную  несовпадением периодов усреднения и сигнала, свести к уровню 0,1 %. Таким образом, при времени инерции измерения 0,2 с мы практически устраняем влияние изменений  частоты сигнала, если частота  лежит в пределах 50 ±0,5 Гц.

  Второй способ предполагает применение алгоритма  измерения частоты в процессе усреднения. Этот метод значительно сложнее первого, при этом он не позволяет отслеживать быстрые изменения частоты, не дает точных результатов в условиях наличия помех в измеряемом сигнале, работает неустойчиво, если сигнал несинусоидальный.

   

  Характеристики преобразователей унифицированных сигналов

  Рассмотрим основные характеристики и особенности, которые необходимо учитывать при выборе нормирующих преобразователей действующих значений переменных сигналов. В качестве примера приведем нормирующие измерительные преобразователи тока и напряжения НПСИ-ДНТВ, выпускаемые Научно-производственной фирмой «КонтрАвт» (см. рис. 1).

   

  Рис. 1. Внешний вид нормирующего преобразователя действующих значений сигналов НПСИ-ДНТВ, выпускаемого НПФ «КонтрАвт»

   

  В силу своего основного функционального предназначения, нормирующие измерительные преобразователи, прежде всего, характеризуются типами и диапазонами входных и выходных сигналов.

  В измерительных преобразователях тока и напряжения НПСИ-ДНТВ  выбор входных и выходных сигналов программируется пользователем. Устанавливаются не только диапазоны преобразования, но и типы сигналов (ток и напряжение). Типы и диапазоны преобразования приведены в табл. 1.

   

  Таблица 1. Типы и диапазоны переменных входных и постоянных выходных сигналов измерительного преобразователя тока и напряжения  НПСИ-ДНТВ

  Типы и диапазоны переменного входного сигнала (программируется пользователем)	Переменный ток	Переменное напряжение
  	(0…1) А (0…2,5) А (0…5) А	(0…150) В (0…300) В (0…400) В
  Типы и диапазоны постоянного выходного сигнала (программируется пользователем)	Постоянный ток	Постоянное напряжение
  	(0…5) мА (0…20) мА (4…20) мА	(0…1) В (0…2,5) В (0…5) В (0…10) В

  Особенность нормирующих измерительных преобразователей тока и напряжения НПСИ-ДНТВ заключается в том, что наряду с переменным напряжением и током они могут измерять и преобразовывать постоянные напряжения и  ток. С учетом физического смысла действующего значения, измеренное действующее значение постоянного сигнала будет равно уровню самого постоянного сигнала.

  Измерительные реобразователи тока и напряжения НПСИ-ДНТВ обеспечивают гальваническую развязку входных и выходных сигналов. Напряжение изоляции составляет 1500 В.

  Основная погрешность измерения действующих значений напряжения и тока в сети частотой 50 Гц и их преобразования в постоянные унифицированные сигналы тока и напряжения составляет 0,5 %. Частота выборки в преобразователе равна 10 кГц, это позволяет измерять с указанной точностью синусоидальные сигналы кратные 50 Гц вплоть до частот 300 Гц (на частоте 1 кГц погрешность составляет 1 %). Преобразователь можно использовать и для измерения  действующих значений напряжения и тока и несинусоидальной формы, например, в цепях с симисторными коммутаторами. В этом случае может появиться дополнительная погрешность, которую следует оценить по приведенным выше формулам.

  С точки зрения надежности и безопасности,  в системе должна присутствовать сигнализация, которая должна срабатывать при достижении сигналами недопустимых уровней. Лучше всего такую сигнализацию реализовать в устройствах, которые максимально приближены к источникам сигнала. Поскольку нормирующие преобразователи находятся на переднем крае на пути прохождения сигналов, то представляется целесообразным возложить выполнение функций сигнализации именно на них. Таким образом, некоторые нормирующие преобразователи наряду с преобразованием и гальваническим разделением сигналов выполняют важнейшую функцию сигнализации.

  Нормирующие измерительные реобразователи тока и напряжения НПСИ-ДНТВ выпускаются как с функцией сигнализации, так и без нее. В модификациях с сигнализацией выполняемая функция выбирается пользователем из четырех возможных вариантов:

  • Функция 1. Сигнализация срабатывает, если сигнал больше заданного уровня;
  • Функция 2. Сигнализация срабатывает, если сигнал меньше заданного уровня;
  • Функция 3. Сигнализация срабатывает, если сигнал больше заданного уровня, и фиксируется в этом состоянии до сброса пользователем;
  • Функция 4. Сигнализация срабатывает, если сигнал меньше заданного уровня, и фиксируется в этом состоянии до сброса пользователем.

   

  Рис.2. Диаграмма работы  сигнализации «превышение»  без защелки

   

   

  Рис.3. Диаграмма работы  сигнализации «превышение»  с  защелкой

   

   

  Действие сигнализации для функций 1 и 3 иллюстрируют рис. 2, 3. Функции 3 и 4 представляют собой сигнализацию с защелкой. Сбросить его может пользователь только с передней панели преобразователя. Даже временное отключение питания не может сбросить защелку – после возобновления питания сигнализация будет включена. Таким образом, сигнализация с защелкой позволяет зафиксировать факт аварийной ситуации, а необходимость выполнения процедуры сброса с панели гарантирует, что обслуживающий персонал обнаружит аварийную ситуацию  и предпримет действия, предусмотренные технологическим регламентом.

  Помимо выполнения функций сигнализации, преобразователи обнаруживают аварийные ситуации, которые могут возникнуть с системе: обрыв линий связи входных и выходных сигналов (только для (4…20) мА), выход сигналов за допустимый диапазон, целостность параметров в энергонезависимой памяти. При обнаружении аварийных ситуаций (не путать с работой сигнализации) на преобразователе зажигается индикатор АВАРИЯ, на дисплее отображается код аварийной ситуации, а выходной ток принимает значение, которое при конфигурировании задает пользователь – низкий или высокий аварийный уровень. Измерительные системы, принимающие сигналы преобразователей,  регистрируют эти аварийные уровни, и следовательно, обнаруживают аварийные ситуации.

  Питание нормирующих измерительных реобразователей напряжения и тока НПСИ-ДНТВ в зависимости от модификации производится либо от сети переменного напряжения 220 В (допустимый диапазон рабочих напряжений (85…265) В), либо от постоянного напряжения 24 В (допустимый диапазон рабочих напряжений (10…42) В).

  Конструктивно измерительные преобразователи напряжения и тока НПСИ-ДНТВ выполнены в корпусе с габаритными размерами (D×H×W) (115×110×22,5) мм, который обеспечивает монтаж на DIN-рельс 35 мм по стандарту EN 50 022.

  Настройка преобразователя тока и напряжения (конфигурирование) осуществляется пользователем с передней панели с помощью кнопок с контролем по цифровому  двухразрядному дисплею (см. рис. 4). На цифровом дисплее отображается уровень сигнала в процентах от диапазона. Уровень сигнала наглядно показывает и линейный бар-граф.

   

  Рис. 4. Органы индикации и управления на передней панели измерительного преобразователя тока и напряжения

  Для удобства монтажа и обслуживания  подключение  внешних соединений производится с помощью разъемных клеммных соединителей (см. рис. 5).

   

  Рис.5. Подключение внешних линий с помощью разъемных клеммных соединителей

  Нормирующие измерительные преобразователи тока и напряжения НПСИ-ДНТВ, выпускаемые НПФ «КонтрАвт», рассчитаны на эксплуатацию при температуре от -40 до +70 °С и относительной влажности 95 %.

  Преобразователи предоставляются в опытную эксплуатацию, поэтому  пользователь имеет возможность опробовать преобразователи в работе,  оценить их характеристики и принять обоснованное решение об их применении.

    Статья в журнале “ИСУП” в pdf

  электрических цепей – Почему мы используем среднеквадратические значения (RMS), когда говорим о напряжении переменного тока

  Попытки найти среднее значение переменного тока непосредственно предоставят вам ответ ноль … Следовательно, используются значения RMS. Они помогают найти эффективное значение переменного тока (напряжения или тока).

  Это RMS – математическая величина (используется во многих математических полях ), используемая для сравнения как переменного, так и постоянного тока (или напряжения). Другими словами (в качестве примера), среднеквадратичное значение переменного тока (тока) – это постоянный ток, который при пропускании через резистор в течение заданного периода времени будет производить такое же тепло, как и тепло, производимое переменным током при прохождении через такой же резистор за то же время.2/2 $, а затем определение квадратного корня $ I_0 / \ sqrt {2} $ даст RMS.

  ---

  Это , пример раз: (я думаю, вы не просили вывести RMS)

  Учтите, что обе лампы выдают одинаковый уровень яркости. Таким образом, они теряют одинаковое количество тепла (независимо от того, переменный или постоянный ток). Чтобы связать и то и другое, нам нечего использовать лучше, чем значение RMS. Постоянное напряжение лампы составляет 115 В, а переменное – 170 В.2} $$

  Измерение синусоидальной волны

  • • Знайте измерения, связанные с синусоидальными волнами
  • • а. Пиковое значение.
  • • б. Амплитуда.
  • • ок. Пиковое значение.
  • • d. Периодическое время.
  • • e. Средняя стоимость.
  • • ф. Среднеквадратичное значение.

  Рис 1.2.1 Характеристики синусоидальной волны

  Форма волны – это график, показывающий изменение, обычно напряжения или тока, во времени.Горизонтальная ось показывает течение времени слева направо. Вертикальная ось показывает измеренную величину (это напряжение на рис. 1.2.1).

  Шесть наиболее важных характеристик синусоидальной волны:

  ПИК ДО ПИК значения.

  МГНОВЕННОЕ значение.

  АМПЛИТУДА.

  Пиковое значение.

  ПЕРИОДИЧЕСКОЕ ВРЕМЯ.

  СРЕДНЕЕ значение.

  RMS значение.

  Эти характеристики показаны на рис. 1.2,1

  Пиковое значение

  Значение PEAK TO PEAK – это расстояние по вертикали между вершиной и основанием волны. Он будет измеряться в вольтах на осциллограмме напряжения и может быть обозначен как V _PP или V _PK-PK . В форме волны тока он будет обозначен как I _PP или I _PK-PK , поскольку I (не C) используется для представления тока.

  Мгновенное значение

  Это значение (напряжение или ток) волны в любой конкретный момент.часто выбирается, чтобы совпасть с каким-то другим событием. Например. Мгновенное значение синусоидальной волны на четвертой части цикла будет равно пиковому значению. См. Точку X на рис. 1.2.1.

  Амплитуда

  АМПЛИТУДА синусоидальной волны – это максимальное расстояние по вертикали, достигнутое в любом направлении от центральной линии волны. Поскольку синусоидальная волна симметрична относительно своей центральной линии, амплитуда волны составляет половину от максимального значения, как показано на рисунке 1.2.2.

  Пиковое значение

  Пиковое значение волны представляет собой наибольшее значение волновые достигает выше опорного значения.Обычно используемое эталонное значение – ноль. В форме волны напряжения пиковое значение может быть обозначено как V _PK или V _MAX (I _PK или I _MAX в форме кривой тока).

  Если измеряемая синусоида симметрична по обе стороны от нуля вольт (или от нуля ампер), это означает, что уровень постоянного или постоянного тока волны равен нулю вольт, тогда пиковое значение должно быть таким же, как амплитуда, то есть половина от максимального до максимального значения.

  Рис. 1.2.2 Определение максимального значения V

  _PK

  Однако это не всегда так, если также присутствует постоянная составляющая, отличная от нуля вольт, синусоида будет симметричной относительно этого уровня, а не нуля.Нижняя осциллограмма на рис. 1.2.2 показывает, что пиковое значение теперь может быть даже больше, чем пиковое значение (однако амплитуда волны остается той же, и это разница между пиковым значением и “центральной линией”). “формы волны).

  Периодическое время и частота

  ПЕРИОДИЧЕСКОЕ ВРЕМЯ (обозначенное символом T) – это время в секундах, миллисекундах и т. Д., Принятое для одного полного цикла волны. Его можно использовать для определения ЧАСТОТЫ волны ƒ по формуле T = 1 / ƒ

  .

  Таким образом, если периодичность волны составляет 20 мс (или 1/50 секунды), то должно быть 50 полных циклов волны за одну секунду.Частота 50 Гц. Обратите внимание, что при использовании этой формулы, если периодическое время указывается в секундах, тогда частота будет в Гц.

  Рис 1.2.3 Среднее значение синусоиды

  Среднее значение

  СРЕДНЕЕ значение. Обычно это означает среднее значение только половины периода волны. Если взять среднее значение полного цикла, оно, конечно, будет равно нулю, так как в синусоидальной волне, симметричной относительно нуля, есть равные отклонения выше и ниже нулевой линии.

  При использовании только половины цикла, как показано на рис. 1.2.3, среднее значение (напряжение или ток) всегда составляет 0,637 пикового значения волны.

  В _AV = В _PK x 0,637

  или

  I _AV = I _PK X 0,637

  Среднее значение – это значение, которое обычно определяет напряжение или ток, показываемые на измерительном приборе. Однако есть некоторые измерители, которые будут считывать значение RMS, они называются «измерителями True RMS».

  Среднеквадратичное значение.

  Среднеквадратичное значение или ROOT MEAN SQUARED – это значение эквивалентного постоянного (неизменяемого) напряжения или тока, которые будут обеспечивать такую ​​же энергию в цепи, как измеренная синусоидальная волна. То есть, если синусоидальная волна переменного тока имеет среднеквадратичное значение 240 вольт, она будет обеспечивать такую ​​же энергию для схемы, что и источник постоянного тока на 240 вольт.

  Можно показать, что среднеквадратичное значение синусоидальной волны составляет 0,707 пикового значения.

  В _RMS = В _PK x 0.707 и I _RMS = I _PK x 0,707

  Кроме того, пиковое значение синусоиды равно 1,414 x среднеквадратичное значение.

  Форм-фактор

  Если V _AV (0,637) умножить на 1,11, получится 0,707, что является среднеквадратичным значением. Это различие называется форм-фактором волны, и соотношение 1,11 справедливо только для идеальной синусоидальной волны. Если волна имеет другую форму, изменится либо среднеквадратичное значение, либо среднее значение (или оба), а также отношения между ними.Это важно при измерении переменного напряжения с помощью измерителя, поскольку это среднее значение, которое фактически измеряет большинство измерителей. Однако они отображают среднеквадратичное значение, просто умножая напряжение на 1,11. Следовательно, если измеряемая волна переменного тока не является идеальной синусоидальной волной, показания будут немного неправильными. Однако, если вы заплатите достаточно денег, вы можете купить истинный измеритель RMS, который фактически вычисляет значение RMS несинусоидальных волн.

  Электроснабжение

  Чтобы продемонстрировать некоторые из этих характеристик при использовании, рассмотрим очень распространенную синусоидальную волну, напряжение сети или форму сигнала линии, которая во многих частях мира составляет номинальное напряжение 230 В.

  Электрооборудование, подключаемое к электросети, всегда имеет этикетку с информацией о том, к какому источнику питания может быть подключено оборудование. Эти метки очень разные по внешнему виду, но часто есть изображение синусоидальной волны, показывающей, что переменный ток. необходимо использовать поставку. Заявленное напряжение будет 230 В (или 120 В в США) или диапазон напряжений, включая эти значения. Эти напряжения фактически относятся к среднеквадратичному значению синусоидальной волны сети. На этикетке также указано, что частота источника питания составляет 50 Гц в Европе или 60 Гц в США.

  Из этого небольшого количества информации можно определить другие значения:

  а. Пиковое напряжение формы волны, как В _PK = В _RMS x 1,414

  г. СРЕДНЕЕ значение сигнала, так как V _AV = V _PK x 0,637

  г. Значение PEAK TO PEAK формы волны. Это вдвое больше АМПЛИТУДЫ, которая (поскольку форма сигнала сети симметрична относительно нуля вольт) совпадает с величиной V _PK .

  Поскольку V _PK уже известен из.следует, что V _PP = V _PK x 2

  г. ПЕРИОДИЧЕСКОЕ ВРЕМЯ, равное T = 1 / ƒ

  Синусоидальные значения, уравнения и методы расчета

  В области электроники мы часто слышим термины «переменный ток» и «постоянный ток». Таким образом, переменная форма волны связана с переменным током. Это означает, что это периодическая форма волны, которая переключается между отрицательными и положительными значениями. И наиболее общий тип сигнала, используемый для представления этого сигнала, – это синусоидальный сигнал.При переходе к форме сигнала постоянного тока значения тока и напряжения в основном находятся в стабильном состоянии. Это настолько упрощено для представления стабильных значений и их значений величин. Но, согласно приведенному выше обсуждению, значения амплитуд сигналов переменного тока не так просты, как потому, что они непрерывно изменяются в соответствии со временем. Чтобы узнать это, существует множество методов, самый популярный из которых – «RMS Voltage». Эта статья четко объясняет всю теорию среднеквадратичного напряжения, ее уравнения, применимые методы и многое другое.

  Что такое действующее напряжение?

  Определение: Во-первых, оно раскрывается как среднеквадратичное значение. Общее определение, данное многими для этого, – это величина рассчитанной мощности переменного тока, которая обеспечивает такое же количество тепловой мощности, что и мощность постоянного тока, но среднеквадратичное напряжение имеет дополнительные функции. Он называется √ среднего значения двойной функции мгновенно генерируемых значений.

  Значение представлено как V _RMS , а текущее значение RMS – I _RMS .Форма сигнала напряжения

  RMS Значения

  RMS вычисляются только для изменяющихся во времени синусоидальных значений напряжения или тока, когда величина волны изменяется в соответствии со временем, но не используются для вычисления значений формы сигнала постоянного тока, поскольку величина остается постоянной. Сравнивая среднеквадратичное значение синусоидальной волны переменного тока, которая обеспечивает такое же количество электроэнергии, с предоставленной нагрузкой, как в аналогичной цепи постоянного тока, это значение известно как эффективное значение.

  Здесь эффективное значение тока представлено как I _eff , а эффективное значение напряжения – V _eff .Или же эффективное значение также указывается как количество ампер или вольт для волны постоянного тока, аналогичное соответствующему способности генерировать аналогичное количество энергии.

  Уравнение

  Более важно знать уравнение среднеквадратичного напряжения , где оно используется для вычисления многих значений, а основное уравнение:

  В _СКЗ = В _{пиковое напряжение} * (1 / (√ 2)) = В _{пиковое напряжение} * 0,7071

  Среднеквадратичное значение напряжения основано на значении амплитуды волны переменного тока и не зависит ни от фазового угла, ни от частоты форм колебаний переменного тока.

  Например: когда пиковое напряжение формы сигнала переменного тока было предоставлено равным 30 вольт, тогда среднеквадратичное напряжение рассчитывается следующим образом:

  В _RMS = В _{пиковое напряжение} * (1 / (√2)) = 30 * 0,7071 = 21,213

  Полученное значение практически идентично как для графических, так и для аналитических методов. Это происходит только в случае синусоидальных волн. В то время как для несинусоидальных волн графический метод – единственный вариант. Вместо использования пикового напряжения мы можем рассчитать, используя напряжение между двумя пиковыми значениями, которое составляет V _P-P .

  Синусоидальные среднеквадратичные значения рассчитываются следующим образом:

  В _СКЗ = В _{пиковое напряжение} * (1 / (√2)) = В _{пиковое напряжение} * 0,7071

  В _RMS = V _{пиковое напряжение} * (1/2 (√2)) = V _{пиковое значение} * 0,3536

  V _RMS = V _{среднее} * ( ∏ / (√2)) = В _{в среднем} * 1.11

  Эквивалент среднеквадратичного напряжения

  Существует два основных подхода к вычислению среднеквадратичного значения напряжения синусоидальной волны или даже другой сложной формы сигнала.Подходы:

  • Графический метод среднеквадратичного напряжения – Он используется для расчета среднеквадратичного напряжения несинусоидальной волны, которое изменяется во времени. Это можно сделать, указав средние ординаты в волне.
  • Аналитический метод среднеквадратичного напряжения – Используется для вычисления напряжения волны посредством математических расчетов.

  Графический подход

  Этот подход показывает ту же процедуру для вычисления RMS-значения для положительной и отрицательной половины волны.Итак, эта статья объясняет процедуру положительного цикла. Значение можно рассчитать, учитывая определенную степень точности для одинакового промежутка времени по всей форме волны.

  Положительный полупериод разделен на «n» равных частей, которые также называются средними ординатами. Чем больше средних ординат, тем точнее результат. Таким образом, ширина каждой средней ординаты будет равна n градусам, а высота – это мгновенное значение волны по оси x волны.

  Графический метод

  Здесь каждое значение средней ординаты в волне удваивается и затем добавляется к следующему значению. Этот подход позволяет получить значение квадрата среднеквадратичного напряжения. Затем полученное значение делится на общее количество средних ординат, где это дает среднее значение среднеквадратичного напряжения. Таким образом, уравнение среднеквадратичного напряжения определяется выражением

  Vrms = [общая сумма средних ординат × (напряжение) 2] / число средних ординат

  В приведенном ниже примере есть 12 средних ординат и среднеквадратичное напряжение. отображается как

  V _RMS = √ (V ₁ ² + V ₂ ² + V ₃ ² + V ₄ ² + V ₅ ² + V ₆ ² + …… + V ₁₂ ² ) / 12

  Предположим, что переменное напряжение имеет пиковое значение напряжения 20 вольт и с учетом 10 средних значений ординат , это дается как

  В _RMS = √ (6.2 ² + 11,8 ² + 16,2 ² + 19 ² + 20 ² + 16,2 ² + 11,8 ² + 6,2 ² + 0 ² ) / 10 = √ ( 2000) / 12

  В _RMS = 14,14 В

  Графический подход показывает отличные результаты в знании RMS-значений волны переменного тока, которая является либо синусоидальной, либо симметричной. Это означает, что графический метод применим даже к сигналам сложной формы.

  Аналитический подход

  Здесь этот метод имеет дело только с синусоидальными волнами, для которых легко найти среднеквадратичные значения напряжения с помощью математического подхода.Периодический вид синусоиды постоянен и задается как

  V _(t) = V _max * cos (ωt).

  Здесь среднеквадратичное значение синусоидального напряжения V _(t) равно

  В _RMS = √ (1 / T ʃ ^T ₀ В _max ² * cos ² (ωt))

  Когда интегральные пределы рассматриваются между 0 ⁰ и 360 ⁰ , тогда

  В _RMS = √ (1 / T ʃ ^T ₀ V _макс. ² * cos ² (ωt))

  В целом, соответствующее напряжениям переменного тока, среднеквадратичное напряжение – лучший способ представления, где оно представляет величину сигнала, значения тока и напряжения.Среднеквадратичное значение не похоже на медианное значение всех мгновенных значений. Пропорция среднеквадратичного напряжения и пикового значения напряжения эквивалентна действующему значению тока и пиковому значению тока.

  Многие мультиметры – амперметры или вольтметры – вычисляют среднеквадратичное значение с учетом точных синусоид. Для измерения среднеквадратичного значения несинусоидальной волны необходим «точный мультиметр». Значение, которое определяется методом RMS для синусоидальной волны, обеспечивает аналогичный эффект нагрева, что и для волны постоянного тока.

  Например, I ² R = I _RMS ² R. В случае напряжений и токов переменного тока они должны рассматриваться как среднеквадратические значения, если не рассматриваются как другие. Таким образом, переменный ток в 10 ампер будет обеспечивать такой же нагревательный эффект, как постоянный ток в 10 ампер и пиковое значение приблизительно 14,12 ампер.

  Таким образом, это все о концепции среднеквадратичного напряжения, его уравнении, синусоидальных формах сигналов, методах, используемых для расчета этих значений напряжения, и подробной теории среднеквадратичного напряжения этого.Кроме того, знаете, как пиковое напряжение, среднее напряжение и размах напряжения преобразуются в среднеквадратичное напряжение с помощью калькулятора RMS?

  Дом

  1. 1. Что такое синусоидальное переменное напряжение (напряжение с синусоидальной формой волны)?
  2. 2. Что такое частота синусоиды?
  3. 3. Что такое коэффициент мощности?
  4. 4. Каков коэффициент мощности для резистивной нагрузки?
  5. 5.Какой коэффициент мощности для реактивного типа нагрузки?
  6. 6. Каковы среднеквадратичные и пиковые значения источника синусоидального переменного напряжения?
  7. 7. Как указывается мощность источника переменного тока?
  8. 8. Что означает указанная номинальная мощность инвертора постоянного и переменного тока?

  1. Что такое синусоидальное переменное напряжение (т.е. напряжение с синусоидальной формой волны)?

  Форма волны напряжения 120 В переменного тока, 60 Гц электросети / электросети похожа на синусоидальную волну.В напряжении с синусоидальной формой мгновенное значение и полярность напряжения меняются во времени, а форма волны подобна синусоиде. За один цикл он медленно повышается в положительном направлении от 0 В до пикового положительного значения + В, пик = 170 В, медленно падает до 0 В, меняет полярность на отрицательную и медленно увеличивается в отрицательном направлении до пикового отрицательного значения. значение – Vpeak = 170 В, а затем медленно падает до 0 В.Таких циклов 60 за 1 сек.

  2. Какая частота синусоиды?

  Количество циклов синусоидальной волны в секунду называется «частотой » и также обозначается « Гц (Гц), ».

  3. Что такое коэффициент мощности?

  Если линейная нагрузка подключена к этому типу напряжения, нагрузка будет потреблять ток, который также будет иметь такую ​​же синусоидальную форму. Однако пиковое значение тока будет зависеть от импеданса нагрузки.Кроме того, фаза синусоидальной формы тока, потребляемого линейной нагрузкой, может быть такой же или опережать / отставать от фазы синусоидальной формы напряжения. Эта разность фаз определяет «коэффициент мощности (математически = косинус разности фаз)» нагрузки.

  4. Каков коэффициент мощности для резистивной нагрузки?

  В резистивном типе нагрузки (например, лампы накаливания, нагреватели и т. Д.) Синусоидальная форма тока, потребляемого нагрузкой, имеет нулевую разность фаз с синусоидальной формой напряжения источника переменного тока.Коэффициент мощности резистивной нагрузки равен единице (1). Номинальная выходная мощность (в ваттах) инверторов обычно указывается для резистивных нагрузок с единичным (1) коэффициентом мощности.

  5. Каков коэффициент мощности для реактивной нагрузки?

  В реактивном типе нагрузки (например, нагрузки с электродвигателем, люминесцентные лампы, компьютеры, аудио / видео оборудование и т. Д.) Фаза синусоидальной формы тока, потребляемого нагрузкой, может опережать или отставать от синусоидальной волны. форма источника переменного напряжения.В этом случае коэффициент мощности реактивных нагрузок ниже единицы (1) – обычно от 0,8 до 0,6. Реактивная нагрузка снижает эффективную мощность, которую может выдать источник переменного тока.

  6. Каковы среднеквадратичные и пиковые значения источника синусоидального переменного напряжения?

  Как объяснялось выше, в синусоиде мгновенные значения переменного напряжения ( Вольт, В) и тока ( Ампер, А) меняются со временем.Обычно используются два значения – среднеквадратическое значение ( RMS ) и пиковое значение. Для простоты значение RMS можно рассматривать как среднее значение. Математически, пиковое значение = 1,414 x среднеквадратичное значение . Например, 120 В переменного тока, 60 Гц. мощность сети / электросети – это среднеквадратичное значение. Соответствующее этому пиковое значение = 1,414 x 120 = 170 В.

  Значения номинального выходного напряжения и тока источника переменного тока являются их действующими значениями

  7. Как указывается мощность источника переменного тока?

  Номинальная мощность источника переменного тока обозначается в вольтах-амперах (ВА) или в ваттах (Вт).

  Мощность в вольтах-амперах (ВА) = среднеквадратичное значение вольта (В) x среднеквадратичное значение в амперах (A)

  Мощность в ваттах = среднеквадратичное значение вольта (В) x среднеквадратичное значение в амперах (A) x коэффициент мощности

  8.Что означает указанная номинальная мощность инвертора постоянного и переменного тока?

  Номинальная мощность инвертора в ваттах (Вт) обычно предназначена для линейного резистивного типа нагрузки, потребляющей линейный ток с коэффициентом мощности, равным единице (1). Если нагрузка является линейной и реактивной, номинальная мощность инвертора в ваттах будет ограничена его нормальной номинальной мощностью в ваттах (Вт) x коэффициент мощности.Например, инвертор мощностью 1000 Вт (при единичном коэффициенте мощности) сможет выдавать всего 600 Вт на нагрузку реактивного типа с коэффициентом мощности 0,6.

  Среднее и среднеквадратичное напряжение – Electronics-Lab.com

  Введение

  В режиме постоянного тока возможно только одно определение значения напряжения, это значение однозначно и определяется разностью между опорным значением 0 В и плоской линией сигнала постоянного тока.

  В режиме переменного тока, однако, может возникнуть путаница, если будет указано только одно значение напряжения. Из простого синусоидального сигнала мы можем по крайней мере перечислить четыре разных определения напряжения:

  рис 1: Иллюстрация пикового, среднего и среднеквадратичного значений

  Пиковое значение соответствует разнице между опорным значением (которое является значением, при котором колеблется сигнал переменного тока) и максимальным значением сигнала. Размах – это пиковое значение, умноженное на коэффициент 2, оно соответствует общей ширине сигнала по вертикали.

  На рис. 1 мы также выделили красным цветом Среднее значение и RMS , на которых мы сосредоточимся в следующем уроке.

  В двух разделах, разработанных в этой статье, будут отдельно представлены значения Average и RMS , мы увидим, как они определены, как их определять, и, наконец, мы увидим, что особенного в значении RMS.

  Среднее напряжение

  Для элементарного симметричного синусоидального, треугольного, квадратного или пилообразного сигнала (см. , рис. 2, и учебное пособие по форме сигнала переменного тока) неясно говорить о среднем значении напряжения, которое мы отметим A в дальнейшем.Действительно, эти типы сигналов в течение половины своего периода являются положительными, а в другой – отрицательными. Другими словами, сигналы 50% времени находятся над горизонтальной осью и 50% под ней.

  Из этого наблюдения легко понять, что если мы рассмотрим среднее значение любого из этих сигналов за полный период, оно будет равно 0 , независимо от пикового значения, и, следовательно, не имеет значения.

  Рис. 2: Элементарные синусоидальные, треугольные, квадратные и пилообразные формы сигналов

  Мы можем продемонстрировать этот результат, объяснив, как вычислить среднее значение.Для конечного набора значений процесс усреднения состоит из суммирования всех значений (V ₁ , V ₂ , V ₃ …) и их деления на кардинальное число N набора (сколько значений имеется в комплекте):

  Для аналогового сигнала, однако, невозможно суммировать все мгновенные значения, также называемые средними ординатами, которые принимает сигнал в течение периода, просто потому, что существует бесконечность. Вместо суммирования используем операцию интегрирования:

  уравнение 1: Среднее значение переменного сигнала V (t) за полный период

  Уравнение 1 – это среднее значение сигнала V (t), взятого между моментами времени 0 и T, то есть за полный период.Член ∫V (t) dt дает значение площади между кривой V (t) и опорным значением 0 В. Поскольку операция интегрирования является линейной, этот член можно разделить на две части:

  Для элементарной формы волны, такой как представленная на рис. 1 , мы видим, что первый и второй члены этой формулы равны, но имеют противоположные знаки, поэтому среднее значение равно 0.

  Для того, чтобы среднее значение таких сигналов имело смысл, мы предпочитаем рассматривать отдельно полуположительные и отрицательные периоды, некоторые из которых соответственно выделены красным и зеленым цветом на следующих Рисунок 3 :

  Рис. 3: Некоторые мгновенные значения для положительного полупериода (красным) и отрицательного полупериода (зеленым) синусоидального сигнала

  Аналогично уравнению , мы можем определить отдельно средние значения для положительного полупериода (A ₊ ) и отрицательного полупериода (A _– ):

  уравнение 3: Средние значения переменного сигнала V (t), взятые для положительного (+) и отрицательного (-) полупериодов

  Значение A ₊ и A _– зависит от сигнала, с которым мы имеем дело, и их соответствующие пиковые значения (V _p ) _. Мы перечисляем ниже абсолютное значение | A | A + и A _– для наиболее распространенных элементарных и симметричных сигналов переменного тока :

  • Форма синусоидального сигнала: | A | = 0,637 × V _p
  • Треугольник: | A | = 0
  • Прямоугольная форма сигнала: | A | = V _p
  • Форма волны пилообразной формы: | A | = 0,5 × В _p

  Мы можем завершить этот раздел, сказав, что когда мы хотим усреднить сигнал, мы должны указать точность, если процесс выполняется на полном периоде или меньшем значении.Для элементарных и симметричных сигналов переменного тока усреднение по полному периоду всегда дает результат 0 В независимо от частоты, пикового значения или периода. По этой причине более целесообразно усреднять эти сигналы в течение их полупериодов.

  RMS напряжение

  RMS обозначает среднеквадратическое значение, это операция, аналогичная приведенной ранее усредненной величине, но вместо этого мгновенные значения возводятся в квадрат, а общая дробь определяется корнем:

  По тем же причинам, что указывалось ранее, мы используем операцию интегрирования для определения V _RMS для аналогового сигнала:

  уравнение 4: Среднеквадратичное значение переменного сигнала V (t) периода T

  В отличие от среднего значения, среднеквадратичное значение всегда определяется для полного периода сигнала, действительно нет никакой путаницы при определении этого значения.

  В качестве примера давайте определим среднеквадратичное значение синусоидального сигнала с пиковым значением В _p и угловой пульсацией ω В (t) = В _p × sin (ωt) . Отметим f частоту, которая удовлетворяет f = ω / 2π и T = 1 / f периоду.

  Прежде всего, мы вычисляем интегральный член, который мы отмечаем I:

  Мы используем тригонометрическое тождество sin ² (x) = (1-cos (2x)) / 2 , чтобы продолжить:

  Оценка члена в скобках между 0 и T дает 2π / ω = T .Следовательно, член интегрирования в конечном итоге равен (πV _p ² ) / ω . Из уравнения видно, что нам все еще нужно умножить на 1 / T, что дает [(πV _p ² ) / ω] × [ω / (2π)] = V _p ² /2 на срок под корень.

  Наконец, после извлечения корня окончательное выражение для среднеквадратичного значения синусоидального сигнала дается следующим образом:

  Мы перечисляем ниже среднеквадратичные значения, которые могут быть вычислены тем же методом, что и в приведенном выше примере синуса для элементарных и симметричных сигналов, указанных в предыдущем разделе:

  • Форма синусоидального сигнала: V _RMS = V _p / √2
  • Треугольник и пилообразный сигнал: V _RMS = V _p / √3
  • Прямоугольная форма сигнала: В _RMS = В _P

  Важно отметить, что V _RMS > | A |, значение RMS всегда больше, чем абсолютное значение среднего.

  Что важно для понимания значения RMS, так это то, что оно создает связь между режимами постоянного и переменного тока в соответствии со следующим Рисунок 4 :

  рис 4: Сходство между режимами переменного и постоянного тока

  Среднеквадратичные значения напряжения и тока – это значения, которые развивают такую ​​же мощность на сопротивлении в режиме постоянного тока.

  Заключение

  Средние и среднеквадратичные значения можно легко измерить с помощью современных вольтметров или осциллографов и предоставить информацию о сигнале переменного тока.

  Численный подход к усреднению состоит из суммирования всех значений сигнала и деления суммы на количество значений. Для реальных сигналов мы предпочитаем использовать операцию интегрирования, которая является расширением суммы для бесконечного набора значений.

  Для среднего значения возможны два определения, в зависимости от того, выполняется ли среднее за полный период или за полупериод. Симметричные сигналы характеризуются средним значением 0 за полный цикл . Среднее значение за полный цикл отличается от 0 только в том случае, если в сигнале присутствует составляющая постоянного тока или если сигнал не является симметричным относительно горизонтального эталона.Усреднение по полупериоду также может быть выполнено для характеристики сигналов с различной симметрией.

  Среднеквадратичное значение определяется аналогично среднему значению, но вместо этого каждое значение суммы возводится в квадрат, а окончательный результат коренится. Среднеквадратичное значение всегда выше, чем абсолютное значение среднего, и устанавливает связь между режимами переменного и постоянного тока, поэтому его особенно используют инженеры.

  Значения переменного тока

  Есть три значения переменного тока, которые мгновенное, пиковое и эффективное (среднеквадратичное, RMS).

  Мгновенное значение

  Мгновенное значение напряжения или тока – это индуцированное напряжение или ток, протекающий в любой момент во время цикл. Синусоидальная волна представляет собой серию этих значения. Мгновенное значение напряжения меняется от нуля при 0 ° до максимума при 90 °, обратно до нуля при 180 °, максимум в обратном направлении на 270 °, и снова до нуля на 360 °. Любая точка на синусоиде считается мгновенным значением напряжения.

  Пиковое значение

  Пиковое значение – это наибольшее мгновенное значение. В наибольшее положительное значение возникает, когда синусоида напряжения составляет 90 °, а наибольшее отрицательное значение происходит при 270 °. Максимальное значение 1,41 раза эффективное значение. Это так называемые пиковые значения.

  Эффективное значение

  Действующее значение также известно как среднеквадратичное значение или среднеквадратичный, который относится к математическому процессу по которому выводится значение.Большинство вольтметров переменного тока при использовании будет отображать эффективное или среднеквадратичное значение. Действующее значение меньше максимального значения, равный 0,707 максимального значения.

  Эффективное значение синусоиды на самом деле является мерой теплового эффекта синусоидальной волны. Фигура 10-107 показано, что происходит, когда резистор подключен к источнику переменного напряжения. В иллюстрации A, некоторое количество тепла выделяется мощность в резисторе.На рисунке B показано то же самое резистор теперь вставлен в источник постоянного напряжения. В значение источника постоянного напряжения теперь можно регулировать так что резистор рассеивает такое же количество тепла, как это было, когда он был в цепи переменного тока. RMS или эффективное значение синусоидальной волны равно постоянное напряжение, выделяющее такое же количество тепла как синусоидальное напряжение.

  Пиковое значение синусоиды можно преобразовать в соответствующее среднеквадратичное значение, используя следующие отношение.

  Может применяться как к напряжению, так и к току.

  Алгебраическое преобразование формулы и решение для Vp также может определять пиковое напряжение. Результирующий формула:

  Vp = 1,414 Vrms

  Таким образом, значение 110 вольт дано для переменного тока. подаваемое в дома составляет всего 0,707 максимального напряжения этого предложения. Максимальное напряжение примерно 155 вольт (110 л.41 = 155 вольт максимум).

  При исследовании переменного тока используются любые значения для тока или напряжения принимаются действующие значения если не указано иное, и на практике только используются действующие значения напряжения и тока. Аналогично вольтметры и амперметры переменного тока измерить эффективное значение.

  Пиковое напряжение переменного тока (AC), напряжение от пика до пика, среднеквадратичное (действующее значение) напряжение

  (DC) – постоянный ток

  Элементы и батареи вырабатывают электрический ток, который всегда протекает по цепи одинаково, это называется постоянным током (DC).

  (AC) – переменный ток

  В Великобритании электросеть поставляется с напряжением около 230 вольт и подается как (переменный) или переменный ток. Это означает, что ток течет в одном направлении, а затем в другом по цепи. Ток постоянно меняет направление (чередуется), поэтому его называют (переменным) переменным током. В Великобритании частота электросети составляет 50 Гц , что означает 50 циклов в секунду.

  Сигналы переменного тока

  Мы можем использовать осциллограф для представления сигнала переменного тока.

  Мы можем использовать осциллограмму в качестве вольтметра, если мы знаем, какое усиление по оси Y установлено на осциллографе. Используя диаграмму выше и зная, что усиление по оси Y было установлено на 10 В / дел, мы можем это решить;

  • размах напряжения = 6 квадратов от самой высокой точки до самой низкой, и каждый квадрат стоит 10В. Таким образом, размах напряжения = 60 В.
  • пик напряжение (В _o ) = половина напряжения от пика до пика = 60/2 = 30 В

  Когда мы знаем пиковое напряжение (V _o ) и сопротивление (R) в цепи, мы можем вычислить пиковый ток (I _o ) , используя уравнение V = IR.

  Среднеквадратичное значение (СКЗ)

  Как п.д. и ток непрерывно изменяются в сигнале переменного тока, нам нужно представить среднее значение для p.d. и ток.

  Среднеквадратичные значения p.d. (V _rms ) и ток (I _rms ) представляют собой действующее значение p.d. и ток в цепи переменного тока.

  • В _{действующее значение} = среднеквадратичная разность потенциалов в вольтах, В
  • В _o = пиковое напряжение в вольтах, В
  • I = среднеквадратичный ток в амперах, А
  • I _o = пиковый ток в амперах, A
  .