Эффективное значение силы тока: Эффективные значения тока и напряжения

Эффективные значения тока и напряжения. Эффективное, действующее напряжение, сила тока

Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока.

Действующим илиэффективным значением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе.

Свяжем эффективное значение тока с его амплитудным значением. Для этого рассчитаем количество теплоты, выделяемое на активном сопротивлении переменным током за время, равное периоду колебаний. Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи cсопротивлениемпри

постоянном токеза время, определяется по формуле
. Переменный ток можно считать постоянным только в течение очень малых промежутков времени
. Поделим период колебанийна очень большое число малых промежутков времени
. Количество теплоты
, выделяемое на сопротивленииза время
:
. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:

.

Сила тока в цепи изменяется по синусоидальному закону

,

.

Опуская вычисления, связанные с интегрированием, запишем окончательный результат

.

Если бы по цепи шёл некоторый постоянный ток , то за время, равное, выделилось бы тепло
. По определению постоянный ток, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока
. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов

(4.28)

Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током:

(4. 29)

Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В.

4.4.5. Мощность в цепи переменного тока

Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам:

,
.

Тогда мгновенное значение мощности, выделяемой на участке цепи,

Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний):

С использованием известной тригонометрической формулы

.

Величину
усреднять не нужно, так как она не зависит от времени, следовательно:

.

За длительное время значение косинуса много раз успевает измениться, принимая как отрицательные, так и положительные значения в пределах от (1) до 1. Понятно, что среднее во времени значение косинуса равно нулю

, поэтому
(4.30)

Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим

. (4.31)

Мощность, выделяемая на участке цепи с переменным током, зависит от эффективных значений тока и напряжения и сдвига фаз между током и напряжением . Например, если участок цепи состоит из одного только активного сопротивления, то
и
. Если участок цепи содержит только индуктивность или только ёмкость, то

и
.

Объяснить среднее нулевое значение мощности, выделяемой на индуктивности и ёмкости можно следующим образом. Индуктивность и ёмкость лишь заимствуют энергию у генератора, а затем возвращают её обратно. Конденсатор заряжается, а затем разряжается. Сила тока в катушке увеличивается, затем снова спадает до нуля и т. д. Именно по той причине, что на индуктивном и ёмкостном сопротивлениях средняя расходуемая генератором энергия равна нулю, их назвали реактивными.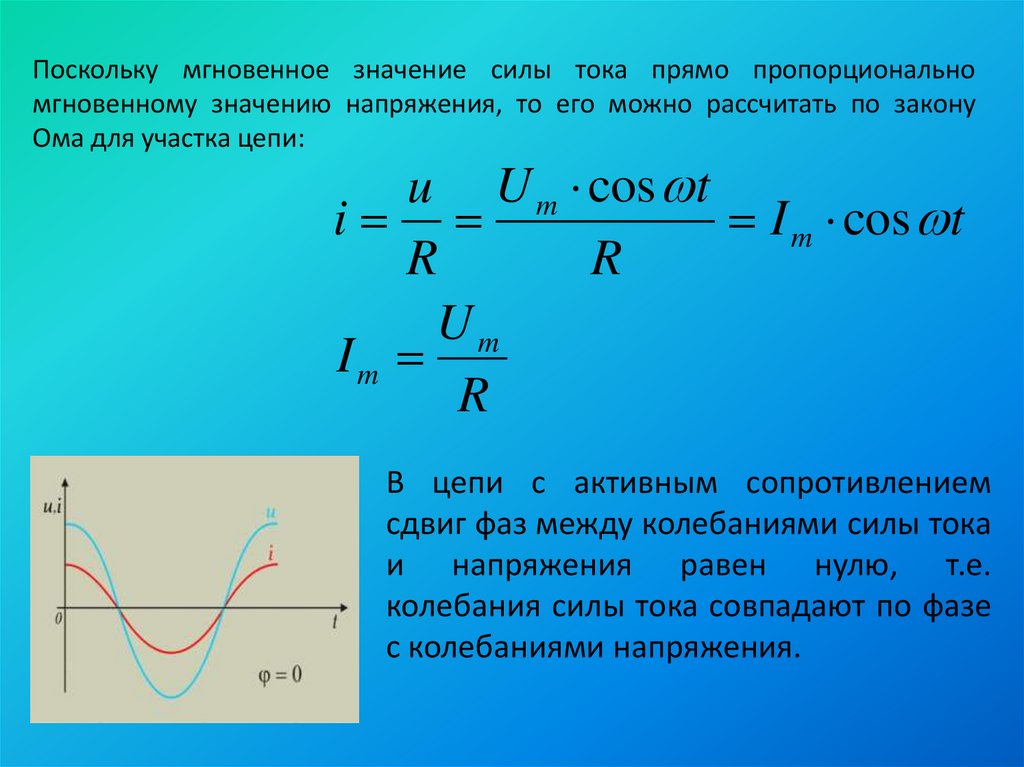 На активном же сопротивлении средняя мощность отлична от нуля. Другими словами провод с сопротивлением при протекании по нему тока нагревается. И энергия, выделяемая в виде тепла, назад в генератор уже не возвращается.

Если участок цепи содержит несколько элементов, то сдвига фаз может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27).

Пример 4.7. К генератору переменного синусоидального тока подключён резистор с сопротивлением. Во сколько раз изменится средняя мощность, расходуемая генератором, если к резистору подключить катушку с индуктивным сопротивлением
а) последовательно, б) параллельно (рис. 4.10)? Активным сопротивлением катушки пренебречь.

Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность

(см. формулу (4.30)).

Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора:
. Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора

.

В результате средняя расходуемая генератором мощность

.

Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза.

Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора
. Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора

.

Тогда средняя мощность, расходуемая генератором

Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.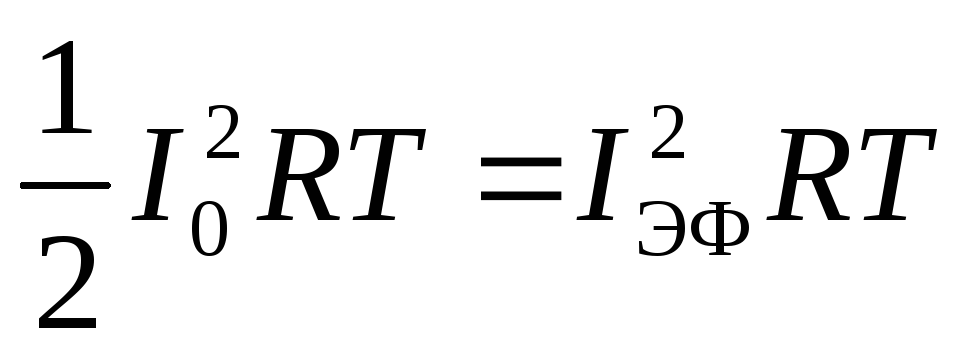

д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, – периодом Т. Для периодического тока имеем

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i – мгновенное значение тока ;

u – мгновенное значение напряжения ;

е – мгновенное значение ЭДС ;

р – мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом

m ).

Амплитуда тока;

Амплитуда напряжения;

Амплитуда ЭДС.

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.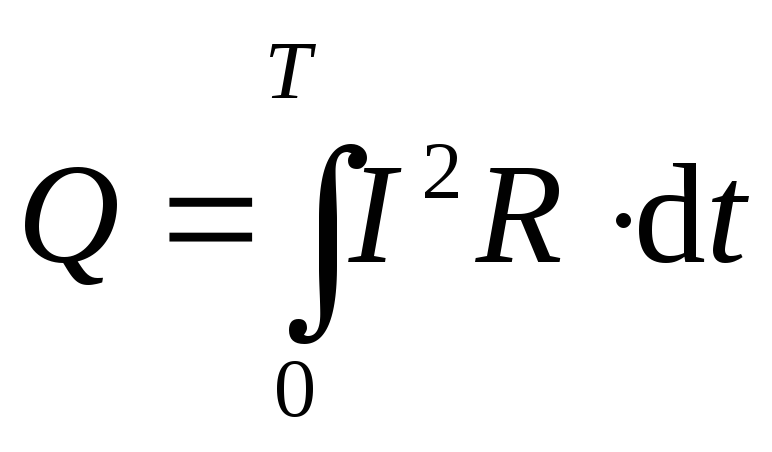

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:

Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t =0): и –начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода

Т изменяется на рад., то угловая частота есть, гдеf– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .

Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:

Векторное изображение синусоидально изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное ) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:

Рассмотрим следующую цепь.

Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.

Активное сопротивление

Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:

U = Um*cos(ω*t).

Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения.

I = u/R = Um*cos(ω*t)/R = Im*cos(ω*t).

Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует.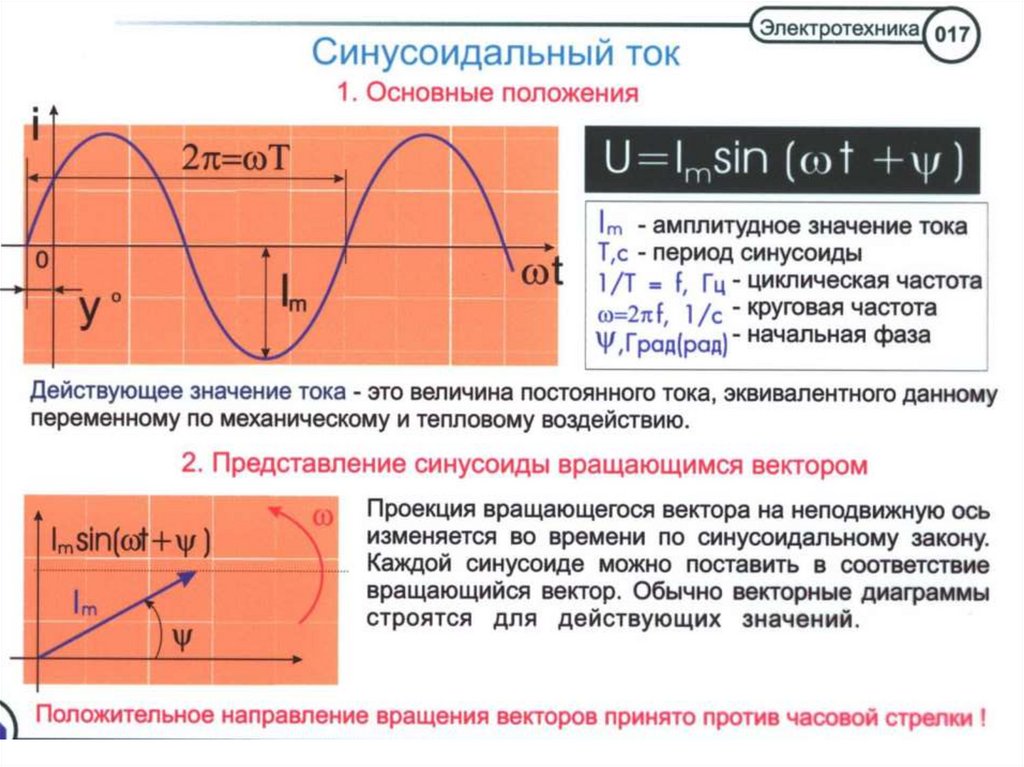 2) = Um/√2.

Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим:

Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний – такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.

Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.

Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? Действия тока не определяются ни амплитудным, ни мгновенным значениями. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.

Мощность P постоянного тока I , проходящего через сопротивление r , будет

P = I 2 × r .

Мощность переменного тока выразится как средний эффект мгновенной мощности i 2 × r за целый период или среднее значение от (I m × sin ωt ) 2 × r за то же время.

Пусть среднее значение i 2 за период будет M . Приравнивая мощность постоянного тока и мощность при переменном токе, имеем:

I 2 × r = M × r ,

Величина I называется действующим значением переменного тока.

Среднее значение i 2 при переменном синусоидальном токе определим следующим образом. Построим синусоидальную кривую изменения тока (рисунок 1).

Рисунок 1. Действующее значение синусоидального тока

Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости i 2 от времени. Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием T и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника M будет соответствовать среднему значению i 2 за период. Это значение за период, вычисленное при помощи высшей математики, будет равно .

Следовательно,

Так как действующее значение переменного тока I равно , то окончательно формула примет вид

Аналогично зависимость между действующим и амплитудным значениями для напряжения U и E имеет вид:

Действующие значения переменных величин, то есть действующее значение напряжения, тока и электродвижущей силы, обозначаются прописными буквами без индексов (U , I , E ).

На основании изложенного выше, можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующее значение тока и напряжения.

При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в раз. От этого расположение векторов на диаграмме не изменится.

В механической системе вынужденные колебания возникают при действии на нее внешней периодической силы. Аналогично этому вынужденные электромагнитные колебания в электрической цепи происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.

Вынужденные электромагнитные колебания в электрической цепи представляют собой переменный электрический ток .

• Переменный электрический ток – это ток, сила и направление которого периодически меняются.

Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:

\(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,

где u – мгновенное значение напряжения, U m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае

\(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,

где φ c – разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Исходя из этого можно дать еще такое определение:

• Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.

Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.

Генератор переменного тока

Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими гармонические колебания.

• Генератором переменного тока называется электротехническое устройство, предназначенное для преобразования механической энергии в энергию переменного тока.

ЭДС индукции генератора изменяется по синусоидальному закону

\(e={\rm E}_{m} \cdot \sin \omega \cdot t,\)

где \({\rm E}_{m} =B\cdot S\cdot \omega\) – амплитудное (максимальное) значение ЭДС. При подключении к выводам рамки нагрузки сопротивлением R , через нее будет проходить переменный ток. По закону Ома для участка цепи сила тока в нагрузке

\(i=\dfrac{e}{R} =\dfrac{B \cdot S \cdot \omega }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\)

где \(I_{m} = \dfrac{B\cdot S\cdot \omega }{R}\) – амплитудное значение силы тока.

Основными частями генератора являются (рис. 1):

• индуктор – электромагнит или постоянный магнит, который создает магнитное поле;
• якорь – обмотка, в которой индуцируется переменная ЭДС;
• коллектор со щетками – устройство, посредством которого снимается с вращающихся частей или подается по ним ток.

Неподвижная часть генератора называется статором , а подвижная – ротором . В зависимости от конструкции генератора его якорь может быть как ротором, так и статором. При получении переменных токов большой мощности якорь обычно делают неподвижным, чтобы упростить схему передачи тока в промышленную сеть.

На современных гидроэлектростанциях вода вращает вал электрогенератора с частотой 1-2 оборота в секунду. Таким образом, если бы якорь генератора имел только одну рамку (обмотку), то получался бы переменный ток частотой 1-2 Гц. Поэтому, для получения переменного тока промышленной частоты 50 Гц якорь должен содержать несколько обмоток, позволяющих увеличить частоту вырабатываемого тока. Для паровых турбин, ротор которых вращается очень быстро, используют якорь с одной обмоткой. В этом случае частота вращения ротора совпадает с частотой переменного тока, т.е. ротор должен делать 50 об/с.

Мощные генераторы вырабатывают напряжение 15-20 кВ и обладают КПД 97-98 %.

Из истории . Первоначально Фарадей обнаружил лишь едва заметный ток в катушке при движении вблизи нее магнита. «Какая от этого польза?» – спросили его. Фарадей ответил: «Какая может быть польза от новорож­денного?» Прошло немногим более половины столетия и, как сказал американский физик Р. Фейнман, «бесполезный новорожденный превратился в чудо-богатыря и изменил облик Земли так, как его гордый отец не мог себе и представить».

*Принцип действия

Принцип действия генератора переменного тока основан на явлении электромагнитной индукции.

Пусть проводящая рамка площадью S вращается с угловой скоростью ω вокруг оси, расположенной в ее плоскости перпендикулярно однородному магнитному полю индукцией \(\vec{B}\) (см. рис. 1).

При равномерном вращении рамки угол α между направлениями вектора индукции магнитного поля \(\vec{B}\) и нормали к плоскости рамки \(\vec{n}\) меняется со временем по линейному закону. Если в момент времени t = 0 угол α 0 = 0 (см. рис. 1), то

\(\alpha = \omega \cdot t = 2\pi \cdot \nu \cdot t,\)

где ω – угловая скорость вращения рамки, ν – частота ее вращения.

В этом случае магнитный поток, пронизывающий рамку будет изменяться следующим образом

\(\Phi \left(t\right)=B\cdot S\cdot \cos \alpha =B\cdot S\cdot \cos \omega \cdot t.\)

Тогда согласно закону Фарадея индуцируется ЭДС индукции

\(e=-\Phi “(t)=B\cdot S\cdot \omega \cdot \sin \omega \cdot t = {\rm E}_{m} \cdot \sin \omega \cdot t.\)

Подчеркнем, что ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное, которое также остается неизменным в течение следующего полуоборота.

Действующие значения силы тока и напряжения

Пусть источник тока создает переменное гармоническое напряжение

\(u=U_{m} \cdot \sin \omega \cdot t. \;\;\;(1)\)

Согласно закону Ома, сила тока в участке цепи, содержащей только резистор сопротивлением R , подключенный к этому источнику, изменяется со временем также по синусоидальному закону:

\(i = \dfrac{u}{R} =\dfrac{U_{m} }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\;\;\; (2)\)

где \(I_m = \dfrac{U_{m}}{R}.\) Как видим, сила тока в такой цепи также меняется с течением времени по синусоидальному закону. Величины U m , I m называются амплитудными значениями напряжения и силы тока . Зависящие от времени значения напряжения u и силы тока i называют мгновенными .

Кроме этих величин используются еще одна характеристика переменного тока: действующие (эффективные) значения силы тока и напряжения .

• Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток. {2}}{R}.\)

  Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R , выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе.

  Резистор в цепи переменного тока. Действующие значения силы тока и напряжения. Школьный курс физики

  
  

  Главная | Физика 11 класс | Резистор в цепи переменного тока

  
  
  
  
  
  
  

  Резистор в цепи переменного тока.

  Пусть электрическая цепь состоит из проводников (резисторов) с малой индуктивностью и большим сопротивлением R. Например, такой цепью может быть нить накаливания электрической лампы и подводящие к ней провода. Величину R, которую мы до сих пор называли сопротивлением, теперь будем называть активным сопротивлением. Итак, в цепи имеется резистор, активное сопротивление которого R, а катушка индуктивности и конденсатор отсутствуют (рис. 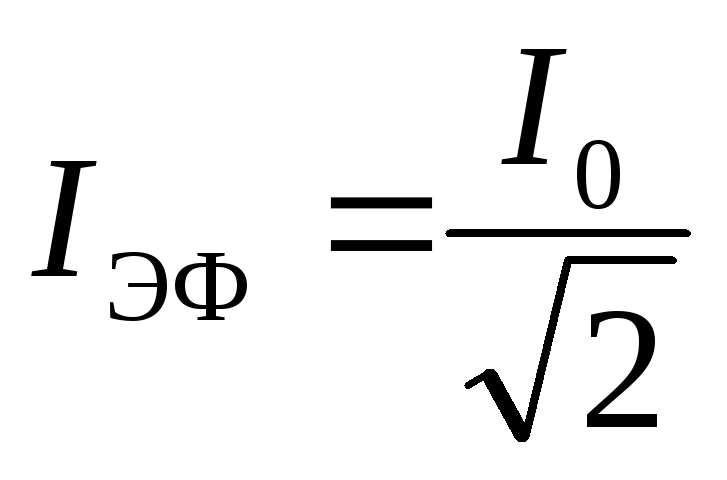6.17).
  

  Рис. 6.17

  Напряжение на концах цени меняется но гармоническому закону:

  Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому можно считать, что мгновенное значение силы тока определяется законом Ома:

  Следовательно, в проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения (рис. 6.18), а амплитуда колебаний силы тока:
  

  Рис. 6.18

  При небольших значениях частоты переменного тока активное сопротивление проводника не зависит от частоты. Можно считать, что оно практически совпадает с сопротивлением в цепи постоянного тока.

  Действующие значения силы тока и напряжения.

  При совпадении фазы колебаний силы тока и напряжения мгновенная мощность переменного тока равна р = i ²R.

  C учётом формулы (1) можно записать:

  Понятно, что мгновенная мощность с течением времени непрерывно изменяется. Определим среднюю мощность переменного тока, выделяемую на резисторе за период:

  Среднее значение функции sin² ωt за период равно 1/2, поэтому

  Данная формула позволяет ввести физические величины, характеризующие переменный ток с точки зрения мощности.

  Действующим значением I силы переменного тока называют квадратный корень из среднего квадрата силы тока:

  Действующее значение переменного напряжения определяется подобным образом:

  В формулах (2) и (3) I_m и U_m — амплитудные значения силы переменного тока и переменного напряжения.

  Средняя мощность переменного тока при совпадении фаз колебаний силы тока и напряжения равна произведению действующих значений силы тока и напряжения:

  Формулы (4), полученные через действующие значения, полностью аналогичны формулам для мощности постоянного тока (см. § 5 “Работа и мощность электрического тока. Закон Джоуля – Ленца”).

  Отметим, что амперметр может измерять силу тока только в цепях постоянного тока. При включении его в цепь переменного тока он покажет нуль. «Это связано с тем, что стрелка обладает инертностью и не успевает отклоняться в такт с изменением силы тока. Поэтому амперметры и вольтметры градуируют таким образом, чтобы они показывали действующее значение силы тока и напряжения. Конечно, можно было бы охарактеризовать силу тока и напряжение амплитудами, а не действующими значениями. Но действующие значения непосредственно определяют мощность переменного тока в цепи.

  Действующее значение силы переменного тока равно силе постоянного тока, выделяющего в цепи такое же количество теплоты, что и переменный ток за то же время.
  

  Вопросы:

  1. Какое сопротивление называют активным?

  2. Как соотносятся между собой фазы колебаний силы переменного тока в резисторе и переменного напряжения между его выводами?

  3. Чем определяется мощность в цепи переменного тока?

  4. Что называют действующим значением:

  а) силы переменного тока;

  б) переменного напряжения?

  5. Почему амперметры и вольтметры градуируют в действующих значениях силы тока и напряжения?
  

  Вопросы для обсуждения:

  1. Что покажет вольтметр при его включении в цепь переменного тока?

  2. В чём состоит отличие амперметров и вольтметров для переменного и постоянного токов?
  

  Пример решения задачи

  Сила переменного тока в электрической цепи изменяется по закону i(t) = 0,564sin 4πt (А). Какое количество теплоты выделится в проводнике с активным сопротивлением 15 Ом за время, равное 10 периодам колебаний тока?

  Таким образом, нас интересует количество теплоты, выделившееся в проводнике за Δt = 10T = 5 с.

  В проводнике выделится такое же количество теплоты, как если бы по нему протекал не переменный, а постоянный ток, такой что

  По закону Джоуля — Ленца:

  Подставляя числовые данные, получим:

  Ответ: Q = 12 Дж.
  

  Упражнения:

  1. В цепь переменного тока стандартной частоты с действующим значением напряжения 220 В включено активное сопротивление, равное 50 Ом. Найдите действующее и амплитудное значения силы тока. Запишите уравнения зависимости напряжения и силы тока от времени.

  2. На участке цепи с активным сопротивлением 4 Ом сила тока изменяется по закону i(t) = 6,4sin10πt (А). Определите действующее значение силы тока и мощность, выделяющуюся на этом участке. Запишите уравнение зависимости u = u(t).

  3. Напряжение в сети изменяется по закону u(t) = 310sin10πt (В). Какое количество теплоты отдаёт за 1 мин электрическая плитка с активным сопротивлением 60 Ом, включённая в эту сеть?

  Предыдущая страницаСледующая страница

  
  
  
  

  Среднее и среднеквадратичное значение — важные понятия и советы для JEE

  Введение в среднее и среднеквадратичное значение

  Дата последнего обновления: 07 апреля 2023 г. 1,51k

  Среднее значение и среднеквадратичное значение являются важными выражениями для синусоидальных волн. Как мы знаем, существует два типа источников и токов: источник переменного тока и источник постоянного тока; переменного и постоянного тока. Переменный ток или переменный ток — это тот, который повторяется через 2π, тогда как источник постоянного тока — это тот, который не меняется. Некоторые важные термины, связанные как с переменным, так и с постоянным током: среднеквадратичное значение, мгновенное значение и среднее значение.

  Среднеквадратичное значение — это количество тепла, выделяемое резистором, когда через него одновременно проходят как переменный, так и постоянный ток. Среднее значение представляет собой площадь одного цикла синусоидальной волны за период времени. Однако мгновенное значение — это значение в конкретный момент времени. Давайте подробнее разберемся в этих концепциях ниже.

  Среднеквадратичное значение тока

  Среднеквадратичное значение тока — это количество тепла, выделяемое резистором или цепью при прохождении через них переменного и постоянного тока. Если мы примем среднеквадратичное значение токов как Irms, а его пиковое значение равно Im, то формула среднеквадратичного значения задается как: 

  $ I_{r m s}=\dfrac{I_{m}}{\sqrt{2}}$ 

  Это также называется среднеквадратичным значением переменного тока, где Im — максимальное значение синусоиды.

  Среднеквадратичное значение синусоиды

  Мы уже видели выражения для среднеквадратичных значений, но теперь мы получим среднеквадратичное значение с помощью аналитического метода. Давайте сначала получим среднеквадратичное значение тока, а затем мы можем обобщить его и для напряжения. Поскольку синусоида симметрична, мы можем рассчитать среднеквадратичное значение, учитывая только полупериод. 9{2}}{2}} \\ &I_{RM S}=\dfrac{I_{m}}{\sqrt{2}} \end{align}$

  Это выражение для среднеквадратичного тока. Весь этот вывод можно повторить и для напряжения, и среднеквадратичное значение напряжения также будет

  $V_{RM S}=\dfrac{V_{m}}{\sqrt{2}}$

  Как обсуждалось выше, среднеквадратичное значение значение синусоиды обозначается как $I_{rm s}=\dfrac{I_{m}}{\sqrt{2}}$ или для синусоидального напряжения $V_{rm s}=\dfrac{V_{m}} {\sqrt{2}}$

  Переменный ток или переменный ток
  

  Im и Vm здесь пиковое значение тока и напряжения соответственно. Vm или Im  можно рассчитать как Vrms $\cdot \sqrt{2}$

  Среднеквадратичное значение прямоугольной волны

  Поскольку мы рассчитали среднеквадратичное значение синусоидальных волн, аналогичным образом мы рассчитаем среднеквадратичное значение квадратной волны. волна. Среднеквадратичное значение — это просто корень из среднеквадратичного значения. Предположим, у нас есть прямоугольная волна, как показано ниже.

   

  Прямоугольная волна
  9{2}} \\ &V_{RM S}=V_{0} \end{align}$

  Это означает, что среднеквадратичное значение прямоугольного сигнала совпадает с его амплитудой. Предположим, что величина прямоугольной волны равна A, тогда ее среднеквадратичное значение также будет равно A. 

  Прямоугольная волна
  

  Среднее значение переменного тока

  Когда переменный ток преобразуется в постоянный с помощью выпрямителя, это преобразованное значение переменного тока называется средним значением переменного тока. Среднее значение синусоидальной волны можно рассчитать графически или с помощью стандартного уравнения синусоидальности. Используя стандартное синусоидальное уравнение, среднее значение переменного тока получается равным $I_{\text {average}}=\dfrac{2 I_{m}}{\pi}$, где Im – пиковое значение синусоидального волна. 9{T} \\ &\bar{i}=\dfrac{I_{m}}{\omega}[-\cos \omega T-(-\cos 0)]\end{align}$

  Теперь мы знаем что период времени связан с угловой частотой как

  $T=\dfrac{2\pi}{\omega}$

  Подставляя это в приведенное выше выражение, получаем

  $\begin{align} &\bar{ i}=\dfrac{I_{m}}{\omega}[-\cos 2 \pi+1] \\ &\bar{i}=0 \end{align}$

  Таким образом, среднее значение AC для полный цикл равен нулю.

  Точно так же для полупериода мы можем найти среднее значение как 9{\dfrac{T}{2}} \end{align}$

  $\begin{align} &\bar{i}=\dfrac{I_{m}}{\omega}\left[-\cos \ влево(\omega \dfrac{T}{2}\right)-(-\cos 0)\right]\\ &\bar{i}=\dfrac{I_{m}}{\omega}\left[- \cos \left(\omega \dfrac{2 \pi}{2 \omega}\right)+1\right] \\&\bar{i}=\dfrac{I_{m}}{\omega}[- \cos (\pi)+1] \\&\bar{i}=\dfrac{I_{m}}{\omega}[-(-1)+1] \\ &\bar{i}=\dfrac {2 I}{\omega} \end{align}$

  Таким образом, среднее значение формулы переменного тока задается как $I_{\text {average}}=\dfrac{2 I_{m}}{\pi} $. Мы подсчитали, что среднее значение для полной синусоиды равно нулю. Поскольку в положительном и отрицательном циклах имеется одинаковое количество тока, и, таким образом, течет в противоположных направлениях, это нейтрализует эффект, и среднее значение полной синусоидальной волны равно нулю. Та же формула справедлива и для переменного напряжения. Таким образом, среднее значение формулы напряжения задается как $V_{\text {average}}=\dfrac{2 V_{m}}{\pi}$.

  Вт

  Верно для полупериода, для полного цикла, однако среднее значение напряжения равно нулю.

  Мгновенное значение

  Мгновенное значение переменного тока, с другой стороны, является его значением в конкретный момент времени. В одном цикле есть несколько экземпляров волны. Посмотрите на рисунок ниже.

  Мгновенное значение синусоиды
  

  Теперь мы знаем, что ток синусоиды можно выразить через ее амплитуду Im как

  $i=I_{m} \sin \omega t$

  Для любого значения t можно найти значение тока. Это означает, что это формула мгновенного тока при конкретном значении t. Если мы хотим найти значение тока для определенного угла $\theta=\omega t$, то мы можем использовать соотношение между периодом времени и угловой частотой, которое задается как

  $T=\dfrac{2\pi }{\омега}$.

  Таким образом мы можем найти мгновенное значение переменного тока.

  Вывод

  Переменный и постоянный ток являются основными источниками питания в электрической цепи, будь то соответствующее напряжение или ток. Переменный ток, как мы знаем, важен, поскольку питание наших домов осуществляется переменным током, а также бытовой техникой. Тем не менее, он не пренебрегает источником постоянного тока, поскольку он также используется для различных приложений. Электронные схемы, такие как часы телевизора, ноутбук, светодиодная лента и т. д., используют источник постоянного тока. Более того, сами солнечные батареи производят постоянный ток. С разными источниками приходят способы их обозначения. Таким образом, средние, среднеквадратичные и мгновенные значения играют важную роль. Каждая из этих величин имеет свое собственное значение, как обсуждалось выше.

  Конкурсные экзамены после 12-го курса естественных наук

  [Решено] Определить средние и эффективные значения заданной волны

  Определить средние и эффективные значения заданной формы волны.

  Этот вопрос ранее задавался в

  SSC JE EE Предыдущий документ 12 (Состоялся: 24 марта 2021 г., вечер)

  Просмотреть все документы SSC JE EE >

  1. В _{В \ 60,6183 = \sqrt {133,3}\) В}
  2. В _{в среднем} = 6,67 В и  \(V = \sqrt {1333,3}\) В
  3. В _сред. = 11,5 В и V = 1,33,3 В
  4. В _сред. = 6,67 В и \(V = \sqrt {133,3}\) В 

  = 2,7 В 6 6 1 9 0 4 : V и \(V = \sqrt {133.3}\) V 

  Бесплатно

  SSC JE: General Intelligence & Reasoning Free Mock Test

  35 тыс. пользователей

  20 вопросов

  20 баллов

  12 минут

  Понятие:

  Среднеквадратичное значение:  Действующее значение или действующее значение переменного тока или напряжения определяется постоянным током или напряжением, которое при протекании или приложении к заданному сопротивлению в течение заданного времени дает то же самое количество тепла, как если бы переменный ток или напряжение текли или прикладывались к одному и тому же сопротивлению в течение того же времени. 9{t = 0,1} 20\;dt\)

  \({V_{Avg}} = \frac{{20}}{{0,3}}\left[ {0,1 – 0} \right]\)

  \ ({V_{Avg}} = \frac{{20}}{3}\)

  В _{Среднее}   =  6,67 В

  Скачать решение PDF

  Поделиться в WhatsApp

  Последние обновления SSC JE EE

  Последнее обновление: 23 февраля 2023 г.