Емкость конденсатора формула через индуктивность и частоту: чему равна емкость конденсатора в колебательном контуре если индуктивность катушки 0.1 гн а резонансная частота…

Измерение частоты, индуктивности и ёмкости в электрических цепях

Измерение частоты, индуктивности и ёмкости в электрических цепях.

Измерение индуктивности и ёмкости.

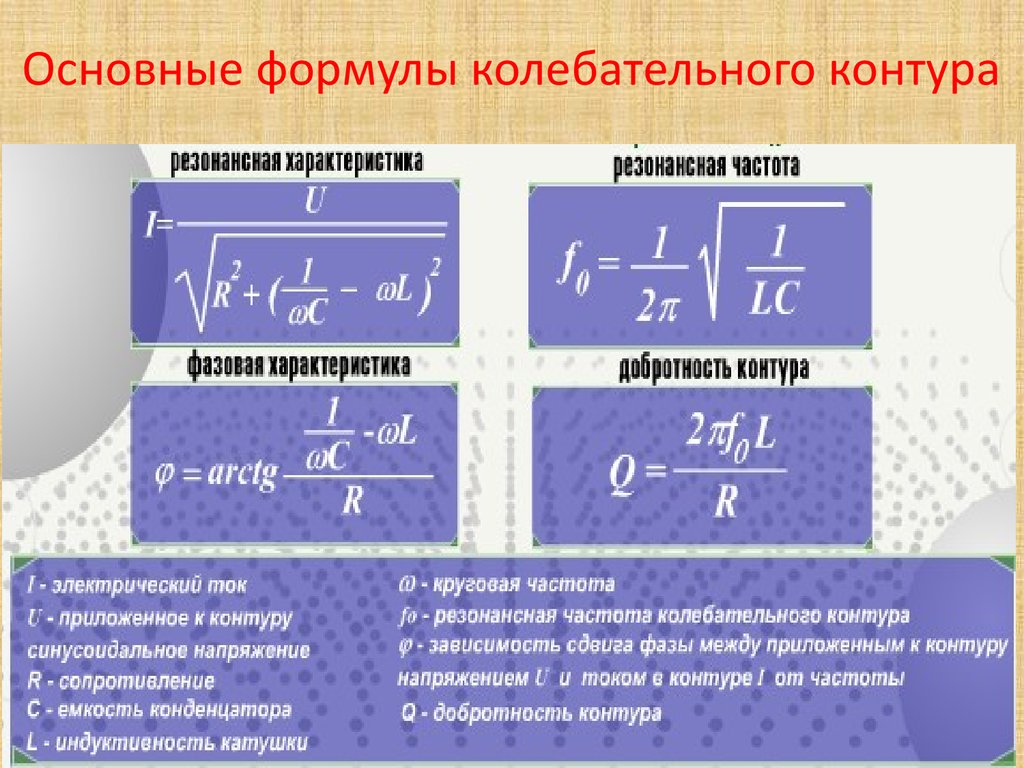
Обычно измерение параметров линейных компонентов (ин­дуктивности и емкости) производят на высокой частоте резо­нансным методом. Он основан на том, что зависимость резо­нансной частоты колебательного контура от его параметров оп­ределяется формулой fo = 1/(2πx LC).

Определив резонансную частоту контура и зная значение эта­лонного компонента (конденсатора или индуктивности), можно определить значение другого.

Рис. 9.10. Измерение фазовых сдвигов:

А — двухканальным осциллографом; б — методом эллипса; в — компенса­ционным методом

Приборы для таких измерений получили название куметров, так как они позволяют определять добротность колебательного контура Q, которая равна отношению напряжения на конденса­торе к напряжению на входе контура.

Куметр включает генера­тор высокой частоты, образ­цовый градуированный в зна­чениях емкости конденсатор и клеммы подключения изме­ряемой катушки индуктивности

или конденсатора. Для измерения индуктивности ка­тушки Lx ее подключают к выводам кат и настройкой генератора высокой частоты добиваются явления последовательного резо­нанса. Его находят по показанию электронного вольтметра, под­ключенного к эталонному конденсатору. Фор­мула LX = 1 / (4π2 · F · C0) где F — частота, C0 — ёмкость образцового конденсатора, позволяет по известным значениям емкости эталонного конденсатора и резонансной частоте определить величину индук­тивности катушки. Напряжение высокочастотного сигнала гене­ратора обычно фиксировано, что позволяет шкалу измерительно­го электронного вольтметра отградуировать непосредственно в значениях добротности Q.

Для измерения емкости конденсатор подключают к выводам схемы конденсатора, а к выводам кат эталонную катушку индуктивности. При вычислении емкости конденсатора необходимо учесть, что параллельно ему подключен эталонный конденсатор, величину емкости которого необходимо вычесть из полученного значения суммарной емкости. Указанные методы измерения значений емкости и индуктивности применимы толь­ко для малых величин, но именно такие методы используются в высокочастотных цепях различной аппаратуры.

Приборы непосредственной оценки и сравнения

К измерительным приборам непосредственной оценки значения измеряемой емкости относятся микрофарадметры, действие которых базируется на зависимости тока или напряжения в цепи переменного тока от значения включенной в нее измеряемой емкости. Значение емкости определяют по шкале стрелочного измерителя.

Более широко для измерения параметров конденсаторов и индуктивностей применяют уравновешенные мосты переменного тока, позволяющие получить малую погрешность измерения (до 1 %). Питание моста осуществляется от генераторов, работающих на фиксированной частоте 400—1000 Гц. В качестве индикаторов применяют выпрямительные или электронные милливольтметры, а также осциллографические индикаторы.

Измерение производят балансированием моста в результате попеременной подстройки двух его плеч. Отсчет показаний берется по лимбам рукояток тех плеч, которыми сбалансирован мост.

В качестве примера рассмотрим измерительные мосты, являющиеся основой измерителя индуктивности ЕЗ-3 (рис. 1) и измерителя емкости Е8-3 (рис. 2).

Рис. 1. Схема моста для измерения индуктивности

Рис. 2. Схема моста для измерения емкости с малыми (а) и большими (б) потерями

При балансе моста (рис. 1) индуктивность катушки и ее добротность определяют по формулам Lx = R1R2C2; Qx = wR1C1.

При балансе мостов (рис. 2) измеряемая емкость и сопротивление потерь определяют по формулам

Измерение емкости и индуктивности методом амперметра-вольметра

Для измерения малых емкостей (не более 0,01 – 0,05 мкФ) и высокочастотных катушек индуктивности в диапазоне их рабочих частот широко используют резонансные методы Резонансная схема обычно включает в себя генератор высокой частоты, индуктивно или через емкость связанный с измерительным LС-контуром. В качестве индикаторов резонанса применяют чувствительные высокочастотные приборы, реагирующие на ток или напряжение.

Методом амперметра-вольтметра измеряют сравнительно большие емкости и индуктивности при питании измерительной схемы от источника низкой частоты 50 – 1000 Гц. Для измерения можно воспользоваться схемами рис. 3.

Рисунок 3. Схемы измерения больших (а) и малых (б) сопротивлений переменному току

По показаниям приборов полное сопротивление

где

из этих выражений можно определить

Когда можно пренебречь активными потерями в конденсаторе или катушке индуктивности, используют схему рис. 4. В этом случае

Рис. 4. Схемы измерения больших (а) и малых (б) сопротивлений методом амперметра — вольтметра

Измерение взаимной индуктивности двух катушек

Измерение взаимной индуктивности двух катушек можно произвести по методу амперметра-вольтметра (рис. 5) и методу последовательно соединенных катушек.

Рис. 5. Измерение взаимной индуктивности по методу амперметра-вольтметра

Значение взаимной индуктивности при измерении по методу амперметра-вольтметра

При измерении по второму методу замеряют индуктивности двух последовательно соединенных катушек при согласном LI и встречном LII включении катушек. Взаимоиндуктивность вычисляется по формуле

 

Измерение индуктивности может быть произведено одним из описанных ранее методов.

Измерение частоты переменного тока

Частоту переменного тока измеряют частотомерами. Обычно применяют резонансные электромагнитные или ферродинамические приборы.

Электромагнитный резонансный частотомер имеет электромагнит 2 (рис. 344, а), в поле которого расположены стальной якорь 1 и соединенный с ним стальной брусок 5. Этот брусок укреплен на упругих пружинах 4 и на нем размещен ряд гибких стальных пластинок 3, площадь поперечного сечения которых подобрана таким образом, что каждая следующая пластинка имеет частоту собственных колебаний на 0,5 Гц больше, чем предыдущая.

Рис. 344. Устройство электромагнитного резонансного частотомера

Рис. 345. Принципиальная схема ферродинамического частотомера .

Свободные концы пластинок введены в прорезь, имеющуюся на шкале прибора. Катушка электромагнита присоединена к сети переменного тока так же, как и катушка вольтметра.

При прохождении по катушке переменного тока электромагнит создает магнитное поле, пульсирующее с частотой изменения тока. Находящийся в этом поле якорь 1 также начнет совершать колебательные движения и вызывать колебания связанных с ним пластинок 3.

Колебания пластинок обычно бывают настолько незначительными, что они не могут быть замечены глазом.

Однако, если частота собственных колебаний какой-либо пластинки совпадает с частотой изменения переменного тока, т. е. с частотой колебаний якоря, то наступит явление механического резонанса, при котором эта пластинка начнет колебаться с большой амплитудой. Белый квадратик на ее конце превращается при этом в белую полоску (рис. 344,б), против которой по шкале можно отсчитывать измеряемую частоту. Значительно слабее колеблются две пластинки, колебания же всех остальных пластинок обычно совершенно незаметны для глаза.

Ферродинамический частотомер (рис. 345) представляет собой логометр ферродинамической системы. Катушки логометра соединяются в две параллельные цепи, которые подключаются к двум точкам а и б, между которыми действует напряжение переменного тока U (так же, как и вольтметры). Последовательно с неподвижной 3 и одной из подвижных 1 катушек включены катушка индуктивности L и конденсатор С, а последовательно с другой подвижной катушкой 2 — резистор с сопротивлением R (могут быть и другие комбинации R, L и С). Поэтому ток I1 в первой параллельной ветви зависит от частоты f, а ток I2 во второй цепи не зависит от f.

В результате при изменении частоты f будут изменяться ток I1 и положение подвижной части логометра до тех пор, пока не наступит равновесие моментов М1 и М2, создаваемых его катушками. Показания такого прибора будут зависеть от частоты f.

Непосредственное измерение частоты производят частотомерами, в основу которых положены различные методы измерения в зависимости от диапазона измеряемых частот и требуемой точности измерения. Наиболее распространенными методами измерения частоты являются:

Метод перезаряда конденсатора за каждый период измеряемой частоты. Среднее значение тока перезаряда пропорционально частоте и измеряется магнитоэлектрическим амперметром, шкала которого проградуирована в единицах частоты. Выпускают конденсаторные частотомеры с пределом измерения 10 Гц – 1 МГц и погрешностью измерения +2%.

Резонансный метод, основанный на явлении электрического резонанса в контуре с подстраиваемыми элементами в резонанс с измеряемой частотой. Измеряемая частота определяется по шкале механизма подстройки. Метод применяется на частотах более 50 кГц. Погрешность измерения можно уменьшить до сотых долей процента.

Метод сравнения измеряемой частоты с эталонной. Электрические колебания неизвестной и образцовой частот смешиваются таким образом, чтобы возникли биения некоторой частоты. При частоте биений, равной нулю, измеряемая частота равна образцовой. Смешение частот осуществляют гетеродинным способом (способ нулевых биений) или осциллографическим.

При последнем способе применяют осциллограф с отключенным генератором внутренней развертки. Напряжение образцовой частоты подают на вход усилителя горизонтальной развертки, а напряжение неизвестной частоты – на вход усилителя вертикального отклонения.

Изменяя образцовую частоту, получают неподвижную или медленно меняющуюся фигуру Лиссажу. Форма фигуры зависит от соотношения частот, амплитуд и фазового сдвига между напряжениями, подаваемыми на отклоняющие пластины осциллографа.

Если мысленно пересечь фигуру по вертикали и горизонтали, то отношение числа пересечений по вертикали m к числу пересечений по горизонтали n равно при неподвижной фигуре отношению измеряемой fх и образцовой fобр частот.

При равенстве частот фигура представляет собой наклонную прямую, эллипс или окружность.

Частота вращения фигуры будет точно соответствовать разности df между частотами fx’ и fx, где fx’ = fобр (m / n) и, следовательно, fx = fобр (m / n) + df. Точность способа определяется в основном погрешностью задания образцовой частоты и определения величины df.

Другой способ измерения частоты методом сравнения – с использованием осциллографа, имеющего калиброванное значение длительности развертки либо встроенный генератор калиброванных меток.

Зная длительность развертки осциллографа, и подсчитав, сколько периодов измеряемой частоты укладывается на выбранной длине центрального участка экрана осциллографа, имеющего наиболее линейную развертку, можно легко определить частоту. Если в осциллографе имеются калибрационные метки, то, зная временной интервал между метками и подсчитав их число на один или несколько периодов измеряемой частоты, определяют длительность периода.

Другим способом является подсчет периодов сигнала измеряемой частоты за фиксированное время, например, за 1 секунду.

Практическая работа № 10
DOC / 30.5 Кб

Калькулятор параллельного колебательного LC-контура

Электрическая цепь, состоящая из соединеных в контур конденсатора емкостью С и катушки индуктивностью L, обладающая сопротивлением R(сопротивление активных потерь в катушке), называется электрическим колебательным контуром. В контуре возникает колебательный процесс ввиду перехода энергии электрического поля в энергию магнитного и наоборот. Реактивные сопротивления индуктивности и емкости зависят от частоты переменного тока. При увеличении частоты реактивное сопротивление индуктивности растет, а емкости падает. При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное – растет. При некоторой частоте ƒ₀, емкостное сопротивление конденсатора и индуктивное сопротивление катушки становятся численно равными: Xc = XL. При этом токи индуктивной и емкостной ветвей также равны, что приводит к возрастанию амплитуды вынужденных колебаний.

Режим, возникающий в цепи, состоящей из генератора и параллельно включенных катушки и конденсатора, при равенстве емкостного и индуктивного сопротивлений, называют режимом резонанса токов. Явление резонанса токов используется в полосовых фильтрах для выделения определенной частоты. Такая схема необходима для работы телевизора, радиоприемника, ёмкостного генератора и т.п.

Расчет частоты резонанса параллельного LC-контура описывается формулами:

X_L =

2πƒL

X_C =

1

 

2πƒC

ƒ₀ =

1

 

2π√LC

X_L — индуктивное реактивное сопротивление, Ом;

X_С — ёмкостное реактивное сопротивление, Ом;

ƒ₀ — резонансная частота, Гц;

Расчет частоты резонанса LC-контура

Введите значения индуктивности и ёмкости конденсатора, чтобы узнать резонансную частоту контура, или введите резонансную частоту генератора, чтобы рассчитать необходимые значения индуктивности и емкости.

IC

IL

Iƒ

мкФнФпФ

ГнмГнмкГн

МГцкГцГц

X_L = X_C = ƒ₀ = φ = °

X_L > X_C Цепь имеет емкостной характер,ее емкостное реактивное сопротивление меньше индуктивного. Угол фазового сдвига между напряжением генератора и током в контуре приближается к 90°

Чем больше частота генератора отличается от собственной (резонансной) частоты контура, тем больше различаются токи IL и Іс, тем больше реактивный ток в общей части цепи и меньше реактивное сопротивление контура.

Внимание! Производители объединяют элементы в серии или ряды: E6, E12, E24…

Для подбора компонентов будет использована серия E12.

Подбор конденсатора на сайте

Подбор катушки индуктивности на сайте

Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.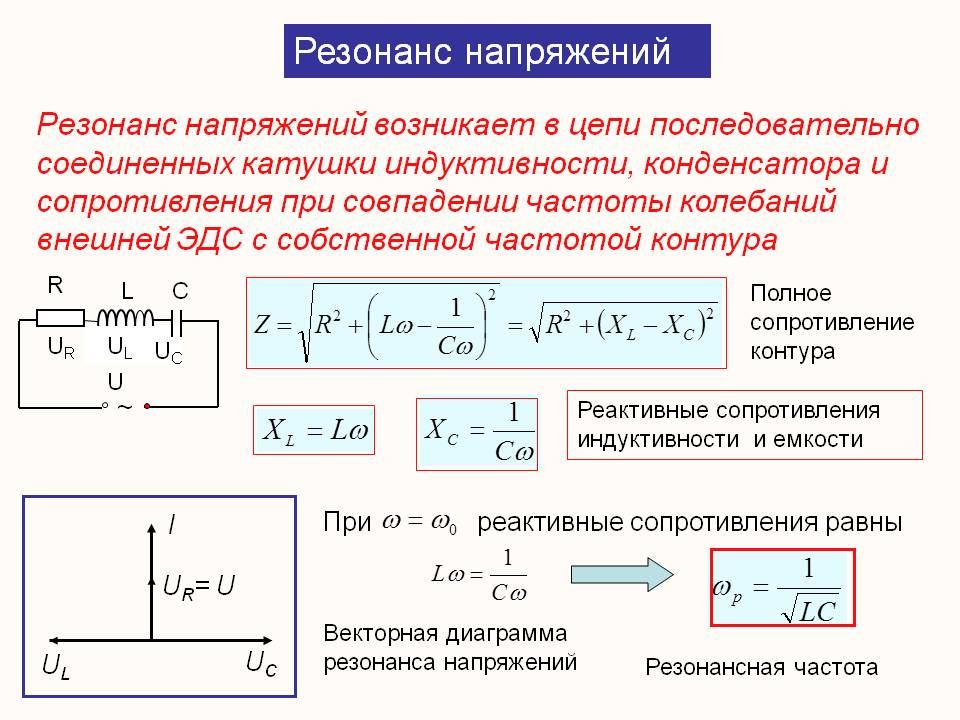
Соблюдайте технику безопасности во время работы с электронными компонентами!

Объяснение урока: Резонанс в цепях переменного тока

В этом объяснении мы узнаем, как рассчитать резонансную частоту простых резистивно-емкостно-индуктивных цепей.

Цепь, содержащая резистор (R), катушку индуктивности (L) и конденсатор (C), подключенная к источнику переменной разности потенциалов показано на следующем рисунке.

Источник переменной разности потенциалов изменяет определенную частоту 𝑓.

Полное сопротивление цепи зависит от частоты переменной разности потенциалов. Увеличение частоты переменной разности потенциалов увеличивает индуктивное сопротивление и уменьшает емкостное сопротивление (но не одинаково). Полное сопротивление цепи зависит от абсолютной разницы между индуктивным и емкостным сопротивлением цепи.

Полное сопротивление последовательной цепи переменного тока с индуктивностью и емкостью определяется по формуле.

Формула: Полное сопротивление

Полное сопротивление цепи 𝑍 определяется выражением 𝑍=𝑅+(𝑋−𝑋), где 𝑅 — сопротивление цепи, 𝑋 — индуктивное сопротивление цепи, 𝑋 — емкостное сопротивление цепи.

Резонансная частота цепи – это частота приложенной переменной разности потенциалов, которая создает наибольшую ток в цепи.

Частоты переменной разности потенциалов вблизи резонансной частоты генерируют токи, близкие по величине к резонансной частотный ток, в то время как частоты дальше от резонансной частоты генерируют токи меньшей величины.

На следующем рисунке показано, как максимальный ток в цепи зависит от частоты.

Из формулы импеданса 𝑍=𝑅+(𝑋−𝑋), мы можем видеть это, когда 𝑋−𝑋=0, должно быть так, что 𝑍=𝑅, что соответствует минимальному импедансу цепи. Ток максимален для этого импеданса.

Значение емкостного сопротивления определяется по формуле.

Формула: емкостное реактивное сопротивление

Емкостное реактивное сопротивление, 𝑋, цепи с емкостью 𝐶, которая несет переменный ток с частотой 𝑓 определяется выражением 𝑋=12𝜋𝑓𝐶.

Значение индуктивного сопротивления находится по формуле.

Формула: индуктивное реактивное сопротивление

Индуктивное реактивное сопротивление 𝑋 цепи с индуктивностью 𝐿, по которой ток с частотой 𝑓 определяется выражением 𝑋=2𝜋𝑓𝐿. 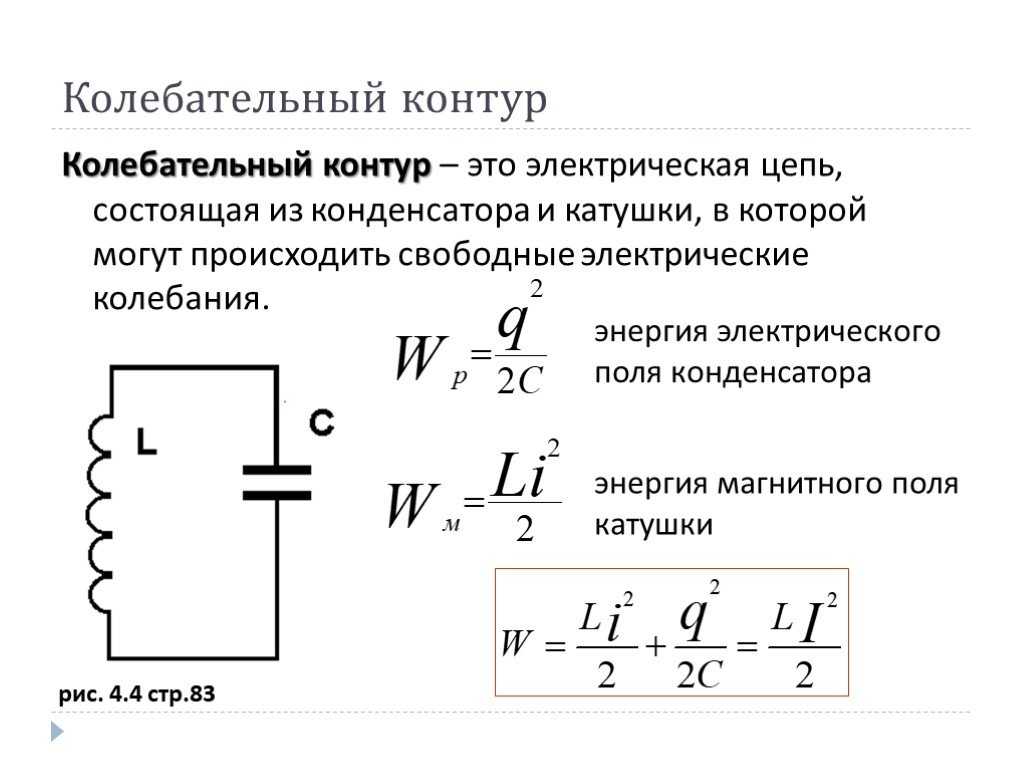

Для минимального импеданса должно быть так, чтобы 2𝜋𝑓𝐿−12𝜋𝑓𝐶=0.

Это уравнение можно преобразовать следующим образом: 2𝜋𝑓𝐿=12𝜋𝑓𝐶2𝜋𝑓=12𝜋𝑓𝐿𝐶(2𝜋𝑓)=1𝐿𝐶2𝜋𝑓=1𝐿𝐶, где 𝑓 — резонансная частота контура.

Отсюда получаем формулу для резонансной частоты.

Формула: Резонансная частота

Резонансная частота 𝑓 контура с индуктивностью 𝐿 и емкость 𝐶 определяется выражением 2𝜋𝑓=1𝐿𝐶.

Давайте теперь рассмотрим несколько примеров.

Пример 1: Определение резонансной частоты контура

Какова резонансная частота контура, показанного на схеме? Дайте ответ с точностью до одного десятичного знака.

Ответ

Резонансная частота 𝑓 определяется выражением 2𝜋𝑓=1𝐿𝐶.

Подставляя значения, указанные в вопросе, получаем 2𝜋𝑓=17,5×3,5×10,HF

С точностью до одного десятичного знака 𝑓 равно 3,1 Гц.

Пример 2. Определение пикового тока в цепи, колеблющейся на резонансной частоте

Цепь, состоящая из последовательно соединенных резистора, конденсатора и катушки индуктивности, имеет резонансную частоту 372 Гц. Резистор имеет сопротивление 440 Ом, а конденсатор имеет емкость 112 мФ. Пиковое напряжение в цепи составляет 28 В. Каков пиковый ток в цепи при переменный ток в цепи имеет частоту 372 Гц? Дайте ответ с точностью до двух знаков после запятой.

Ответ

Резонансная частота контура составляет 372 Гц.

Вопрос требует определения пикового тока.

Максимальная приложенная разность потенциалов составляет 28 В. Для определения пикового тока необходимо определить импеданс цепи.

Полное сопротивление цепи 𝑍 определяется выражением 𝑍=𝑅+(𝑋−𝑋), где 𝑅 — сопротивление цепи, 𝑋 — индуктивное сопротивление цепи, 𝑋 — емкостное сопротивление цепи.

Значения 𝑋 и 𝑋 не указаны. Эти значения мы можем найти по формулам для емкостного и индуктивного сопротивления цепи, 𝑋=12𝜋𝑓𝐶,𝑋=2𝜋𝑓𝐿, и резонансная частота контура, 2𝜋𝑓=1𝐿𝐶.

Однако, поскольку цепь колеблется на своей резонансной частоте, должно быть так, что 𝑋−𝑋=0 и, следовательно, что 𝑍=𝑅.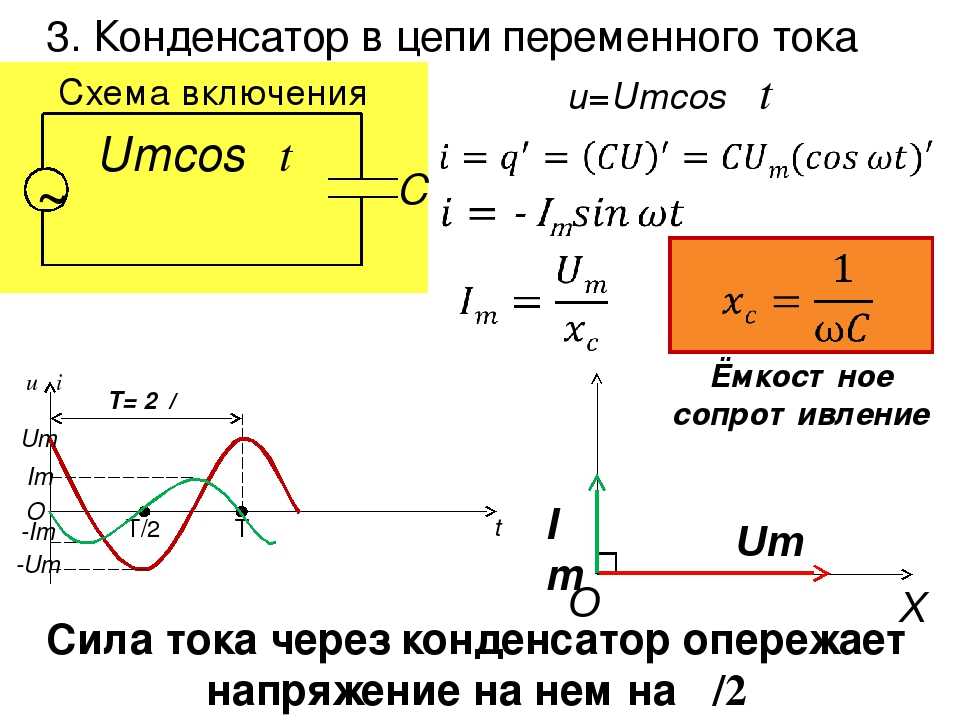

Чтобы найти наибольший ток, нам нужно только разделить наибольшую разность потенциалов на нем на 𝑅: 𝐼=28440.VΩ

С точностью до двух знаков после запятой 𝐼 равно 0,06 А.

Пример 3. Определение емкости цепи, колеблющейся на своей резонансной частоте

Цепь, содержащая последовательно конденсатор и катушку индуктивности, имеет резонансную частоту 575 кГц. Катушка индуктивности в цепи имеет индуктивность 1,25 Гн. Какова емкость конденсатора? Дайте ответ в экспоненциальном представлении с точностью до двух знаков после запятой.

Ответ

Емкость конденсатора связана с резонансной частотой контура, которая определяется выражением 2𝜋𝑓=1𝐿𝐶, где 𝐿 указано как 1,25 H, а 𝑓 указано быть 575 кГц, что составляет 5,75×10 Гц.

Формула должна быть изменена, чтобы 𝐶 стало предметом, следующим образом: (2𝜋𝑓)=1𝐿𝐶𝐶=1(2𝜋𝑓)𝐿.

Подставляя известные значения, получаем 𝐶=1(2𝜋×5,75×10)×1,25.HzH

В экспоненциальном представлении с точностью до двух знаков после запятой 𝐶 6,13×10 F.

Пример 4. Определение индуктивного сопротивления цепи, колеблющейся на резонансной частоте 155 кГц. Конденсатор в цепи имеет емкость 215 мкФ. Чему равно индуктивное сопротивление цепи? Дайте ответ в экспоненциальном представлении с точностью до двух знаков после запятой.

Ответ

Индуктивное сопротивление цепи определяется выражением 𝑋=2𝜋𝑓𝐿, где 𝑓 заявлено как 155 кГц, что составляет 1,55×10 Гц, 𝐿 — индуктивность индуктора.

Значение 𝐿 не указано. Однако его можно найти, используя резонансную частоту контура, который дается 2𝜋𝑓=1𝐿𝐶, где 𝐶 заявлено как 215 мкФ, что составляет 2,15 × 10 F.

Формула резонансной частоты должна быть изменена, чтобы сделать 𝐿 предметом, следующим образом: (2𝜋𝑓)=1𝐿𝐶𝐿=1(2𝜋𝑓)𝐶.

Подставляя известные значения, получаем 𝐿=1(2𝜋×1,55×10)×2,15×10𝐿≈4,9×10.HzFH

Мы можем подставить это значение в 𝑋=2𝜋𝑓𝐿.

В экспоненциальном представлении с точностью до двух знаков после запятой 𝑋 составляет 4,78 × 10 Ом.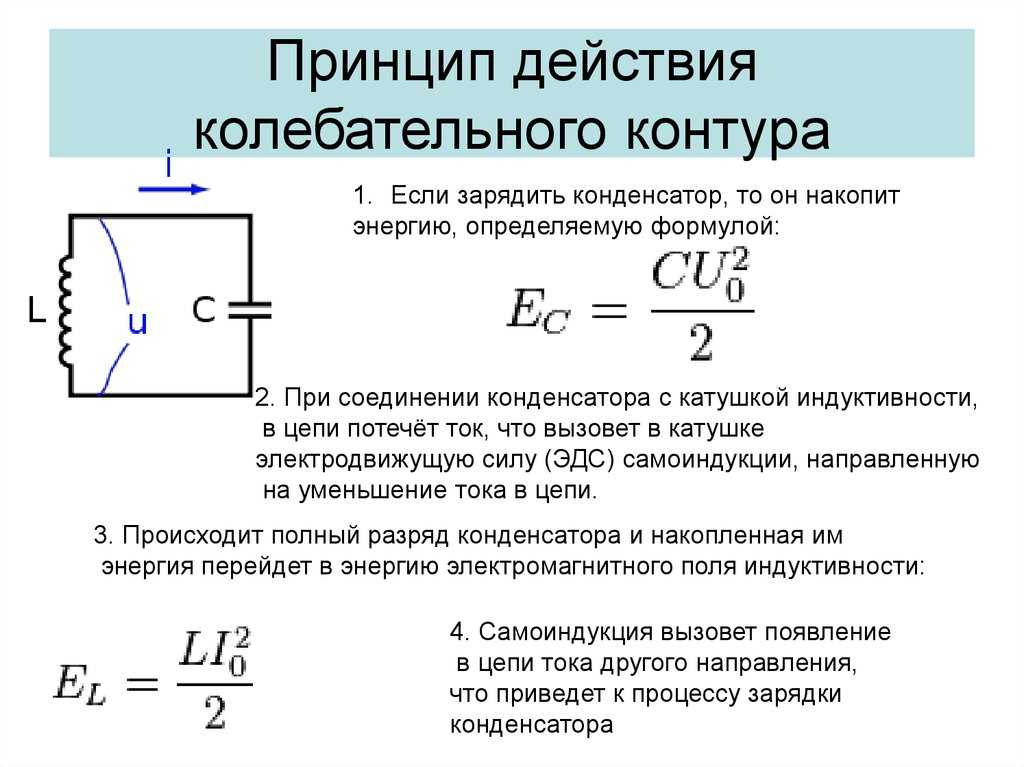

Этот вопрос также можно решить, если вспомнить, что на резонансной частоте цепи емкостная и индуктивная реактивные сопротивления равны, поэтому вместо индуктивного реактивного сопротивления можно было бы рассчитать емкостное реактивное сопротивление. Емкостное сопротивление можно определить просто по частоте и емкости цепи, путем перестановки формулы 𝑋=12𝜋𝑓𝐶, поскольку в вопросе указаны значения 𝑓 и 𝐶.

Давайте теперь обобщим то, что было изучено в этом объяснителе.

Ключевые положения

• Резонансная частота последовательной цепи переменного тока, имеющей индуктивность и емкость, равна частоте при котором приложенная переменная разность потенциалов генерирует наибольший ток.
• При резонансной частоте цепи переменного тока импеданс цепи равен сопротивлению цепи.
• Резонансная частота 𝑓 цепи переменного тока определяется выражением 2𝜋𝑓=1𝐿𝐶, где 𝐿 — индуктивность цепи, а 𝐶 — емкость цепи.

Реактивное, индуктивное и емкостное сопротивление | Физика

Цели обучения

К концу этого раздела вы сможете:

• Зарисовывать зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
• Рассчитать индуктивное и емкостное сопротивление.
• Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.

Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.

Катушки индуктивности и индуктивное реактивное сопротивление

Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рис. 1. Разумно предположить пренебрежимо малое сопротивление, поскольку на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что это оказывает незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.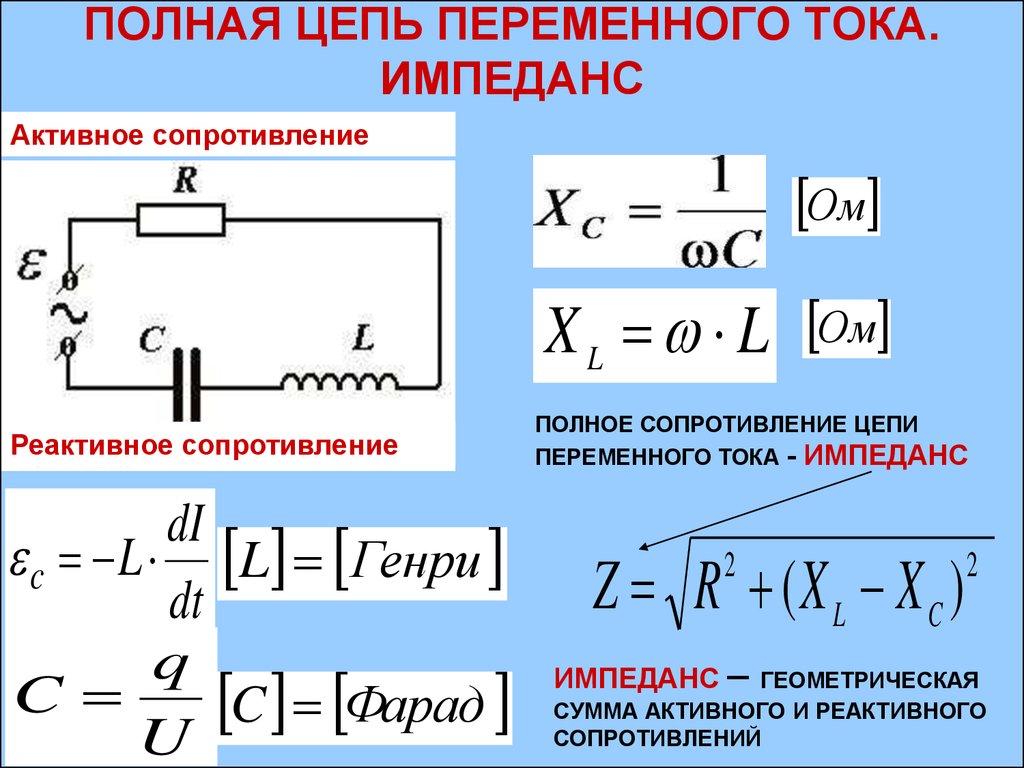

Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.

График на рис. 1(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика 90 153 после 90 154 управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом:

Напряжение переменного тока в катушке индуктивности

Когда к катушке индуктивности приложено синусоидальное напряжение, оно опережает ток на одну четвертую периода или на фазовый угол 90º.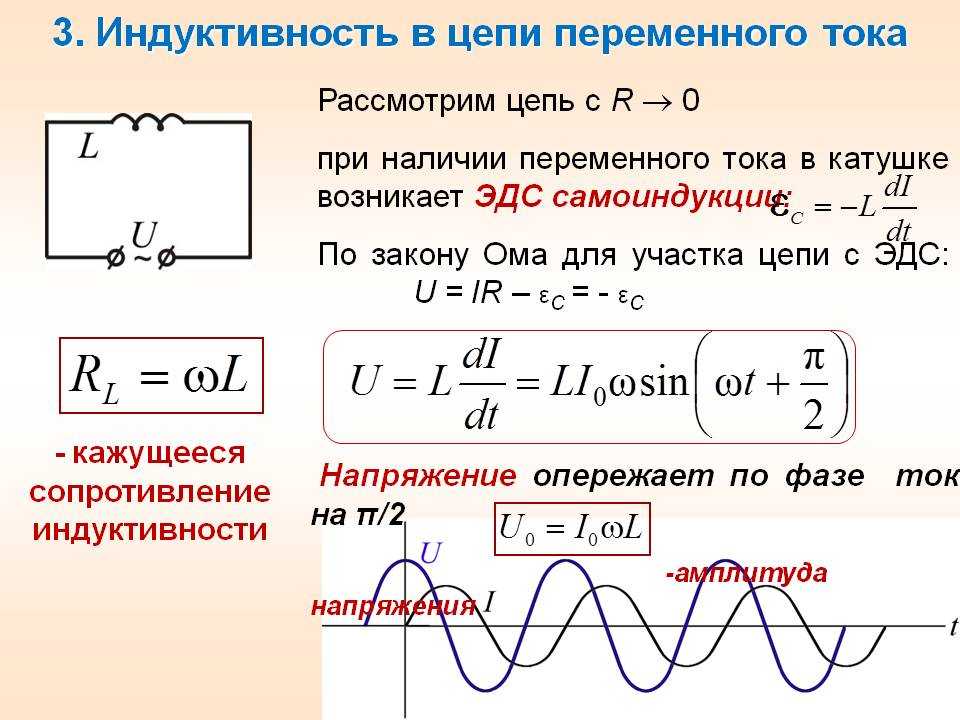

Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует противо-ЭДС В = − L (Δ I / Δ t ). Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока I через дроссель L задается вариантом закона Ома:

[латекс]I=\frac{V}{{X}_{L}}\\[/latex],

, где В — среднеквадратичное значение напряжения. через индуктор и X _L определяется как

[латекс]{X}_{L}=2\pi{fL}\\[/латекс],

с f частотой источника переменного напряжения в герцах (анализ схемы с использованием правила контура Кирхгофа и исчисления фактически дает это выражение). Х _Д называется индуктивным реактивным сопротивлением , потому что индуктор препятствует протеканию тока. X _L измеряется в омах (1 Гн = 1 Ом ⋅ с, так что частота, умноженная на индуктивность, выражается в единицах (циклов/с) (Ом ⋅ с) = Ом)), что согласуется с его ролью в качестве эффективное сопротивление. Имеет смысл, что X _L пропорционально L , поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что X _L пропорционально частоте f , так как большая частота означает большее изменение тока. То есть Δ I / Δ t велико для больших частот (большие f , малые Δ t ). Чем больше изменение, тем больше сопротивление индуктора.

Пример 1. Расчет индуктивного реактивного сопротивления, а затем тока

(a) Рассчитайте индуктивное реактивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?

Стратегия

Индуктивное сопротивление находится непосредственно из выражения X _L   = 2πf L . Как только X _L найдено на каждой частоте, можно использовать закон Ома, как указано в уравнении I = V / X _L , чтобы найти ток на каждой частоте.

Решение для (a)

Ввод частоты и индуктивности в уравнение  x _L = 2πf L Приведен

x _L = 2πf L = (60,0/с.).

Аналогично, на частоте 10 кГц

X _L   = 2πf L = 6,28(1,00 × 10 ^{4 кОм, 1 8,0 мГн) = 10 90 304 мГн при}

Решение для (b)

Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении I  =  В / X _L , при условии, что приложенное среднеквадратичное значение напряжения составляет 120 В. Для первой частоты это дает

[латекс]I=\frac{V}{{X}_{L }}=\frac{120\text{ V}}{1,13\text{ }\Omega}=106\text{ A при } 60\text{ Гц}\\[/latex].

Аналогично, на частоте 10 кГц

[латекс]I=\frac{V}{{X}_{L}}=\frac{120\text{ V}}{188\text{ }\Omega}= 0,637\text { A at } 10\text{ кГц}\\[/latex].

Обсуждение

Катушка индуктивности очень по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.

Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.

Конденсаторы и емкостное реактивное сопротивление

Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис. 2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, и так что можно предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.

Рис. 2. (a) Источник переменного напряжения, включенный последовательно с конденсатором C, имеющим пренебрежимо малое сопротивление. (б) График тока и напряжения на конденсаторе в зависимости от времени.

График на рис. 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен ( 9на нем 0153 Q = 0 ) и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:

Напряжение переменного тока в конденсаторе

Когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на фазовый угол 90º.

Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I в цепи, содержащей только конденсатор C по другой версии закона Ома определяется как

[latex]I=\frac{V}{{X}_{C}}\\[/latex] ,

, где V – это среднеквадратичное напряжение и x _C определяется (как с x _L , эта выражение 3 L , эта выражение 3 3 L , этот выражение 3 3 L . схема с использованием правил и исчисления Кирхгофа) должна быть

[латекс]{X}_{C}=\frac{1}{2\pi fC}\\[/latex],

, где X _C называется емкостным реактивным сопротивлением , поскольку конденсатор препятствует протеканию тока. X _C измеряется в омах (проверка оставлена ​​читателю в качестве упражнения). X _C обратно пропорциональна емкости C ; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте ф ; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.

Пример 2. Расчет емкостного реактивного сопротивления, а затем тока

(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?

Стратегия

Емкостное реактивное сопротивление находится непосредственно из выражения в [latex]{X}_{C}=\frac{1}{2\pi fC}\\[/latex]. Однажды 9На каждой частоте было найдено 0153 X _C . Для определения тока на каждой частоте можно использовать закон Ома, сформулированный как I = В / X _C .

Решение для (a)

Ввод частоты и емкости в [латекс]{X}_{C}=\frac{1}{2\pi fC}\\[/latex], дает

[ латекс]\begin{array}{lll}{X}_{C}& =& \frac{1}{2\pi fC}\\ & =& \frac{1}{6.28\left(60.0/\text {s}\right)\left(5.00\text{ }\mu\text{F}\right)}=531\text{ }\Omega\text{ at }60\text{ Гц}\end{массив}\ \[/латекс]. 9{4}/\text{s}\right)\left(5.00\mu\text{F}\right)}\\ & =& 3.18\text{ }\Omega\text{ при }10 \text{ кГц} \end{массив}\\[/латекс].

Решение для (b)

Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в I  =  В / X _{C действующее значение}

20 9018, при данном приложенном напряжении. Для первой частоты это дает

[латекс]I=\frac{V}{{X}_{C}}=\frac{120 \text{V}}{531\text{ }\Omega}=0,226 \text{ A при }60\text{ Гц}\\[/latex].

Аналогично, на частоте 10 кГц

[латекс]I=\frac{V}{{X}_{C}}=\frac{120 \text{ V}}{3.18\text{ }\Omega}= 3,37 \text{ А при }10 \text{ Гц}\\[/latex].

Обсуждение

Конденсатор очень по-разному реагирует на двух разных частотах, и совершенно противоположным образом реагирует индуктор. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.

Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), X _C стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы действуют на цепи переменного тока противоположно действию катушек индуктивности .

Резисторы в цепи переменного тока

В качестве напоминания рассмотрим рис. 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:

Рис. 3. (a) Источник переменного напряжения, включенный последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.

Переменное напряжение в резисторе

Когда на резистор подается синусоидальное напряжение, оно точно совпадает по фазе с током — фазовый угол равен 0º.

Резюме раздела

• Для катушек индуктивности в цепях переменного тока мы обнаружили, что когда к катушке индуктивности прикладывается синусоидальное напряжение, напряжение опережает ток на одну четвертую периода или на фазовый угол 90º.
• Противодействие катушки индуктивности изменению тока выражается как вид сопротивления переменному току.
• Закон Ома для катушки индуктивности

  [латекс]I=\frac{V}{{X}_{L}}\\[/латекс],

  , где В — среднеквадратичное значение напряжения на катушке индуктивности.

• X _L определяется как индуктивное реактивное сопротивление, определяемое формулой

  [латекс]{X}_{L}=2\pi fL\\[/латекс],

  с f частота источника переменного напряжения в герцах.

• Индуктивное сопротивление  X _L выражается в омах и имеет наибольшее значение на высоких частотах.
• Для конденсаторов мы обнаружили, что когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на фазовый угол 90º.
• Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора

  [латекс]I=\frac{V}{{X}_{C}}\\[/латекс],

  , где В — среднеквадратичное напряжение на конденсаторе.

• Х _С  определяется как емкостное реактивное сопротивление, определяемое выражением

  [латекс]{X}_{C}=\frac{1}{2\pi fC}\\[/latex].

• X _C измеряется в омах и максимальна на низких частотах.

Концептуальные вопросы

1. Пресбиакузис — возрастная потеря слуха, которая постепенно влияет на более высокие частоты. Усилитель слухового аппарата предназначен для одинакового усиления всех частот. Чтобы настроить его выход на пресбиакузис, вы бы включили конденсатор последовательно или параллельно с динамиком слухового аппарата? Объяснять.

2. Будете ли вы использовать большую индуктивность или большую емкость последовательно с системой для фильтрации низких частот, таких как гул частотой 100 Гц в звуковой системе? Объяснять.

3. Высокочастотный шум в сети переменного тока может повредить компьютеры. Использует ли сменный блок, предназначенный для предотвращения этого повреждения, большую индуктивность или большую емкость (последовательно с компьютером) для фильтрации таких высоких частот? Объяснять.

4. Зависит ли индуктивность от тока, частоты или от того и другого? А индуктивное сопротивление?

5. Объясните, почему конденсатор на рис. 4(а) действует как фильтр низких частот между двумя цепями, а конденсатор на рис. 4(б) действует как фильтр высоких частот.

Рис. 4. Конденсаторы и катушки индуктивности. Конденсатор с высокой частотой и низкой частотой.

6. Если конденсаторы на рисунке 4 заменить катушками индуктивности, что будет работать как фильтр низких частот, а что как фильтр высоких частот?

Задачи и упражнения

1. При какой частоте дроссель 30,0 мГн будет иметь реактивное сопротивление 100 Ом?

2. Какое значение индуктивности следует использовать, если требуется реактивное сопротивление 20,0 кОм на частоте 500 Гц?

3. Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при частоте 60,0 Гц?

4. При какой частоте конденсатор емкостью 80,0 мФ будет иметь реактивное сопротивление 0,250 Ом?

5. (a) Найдите ток через катушку индуктивности 0,500 Гн, подключенную к источнику переменного тока с частотой 60,0 Гц и напряжением 480 В. б) Какой будет сила тока на частоте 100 кГц?

6. (a) Какой ток протекает, когда источник переменного тока с частотой 60,0 Гц, 480 В подключен к конденсатору 0,250 мкФ? б) Какой будет сила тока на частоте 25,0 кГц?

7. Источник 20,0 кГц, 16,0 В, подключенный к катушке индуктивности, производит ток силой 2,00 А. Индуктивность какая?

8. Источник 20,0 Гц, 16,0 В производит ток 2,00 мА при подключении к конденсатору. Какова емкость?

9. (a) Катушка индуктивности, предназначенная для фильтрации высокочастотного шума от питания, подаваемого на персональный компьютер, устанавливается последовательно с компьютером. Какая минимальная индуктивность должна быть у него, чтобы создать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? б) Каково его реактивное сопротивление при частоте 60,0 Гц?

10. Конденсатор на рис. 4(а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. (а) Какая емкость необходима для создания реактивного сопротивления 100 кОм на частоте 120 Гц? б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).

11. Конденсатор на рис. 4(b) фильтрует высокочастотные сигналы, замыкая их на землю. (a) Какая емкость необходима для получения реактивного сопротивления [латекс]\текст{10,0 м\Омега}[/латекс] для сигнала частотой 5,00 кГц? б) Каким будет его реактивное сопротивление при частоте 3,00 Гц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).

12. Необоснованные результаты  При записи напряжений, вызванных мозговой активностью (ЭЭГ), на конденсатор подается сигнал 10,0 мВ с частотой 0,500 Гц, производящий ток 100 мА. Сопротивление незначительно. а) Чему равна емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?

13. Создайте свою собственную задачу Рассмотрим использование катушки индуктивности последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, – приемлемое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.