Фильтр Бесселя — Википедия
Материал из Википедии — свободной энциклопедии
Фильтр Бесселя — в электронике и обработке сигналов один из наиболее[источник не указан 2376 дней] распространённых типов линейных фильтров, отличительной особенностью которого является максимально гладкая групповая задержка (линейная фазо-частотная характеристика). Фильтры Бесселя чаще всего используют для аудио-кроссоверов. Их групповая задержка практически не изменяется по частотам полосы пропускания, вследствие чего форма фильтруемого сигнала на выходе такого фильтра в полосе пропускания сохраняется практически неизменной.
Передаточная функция
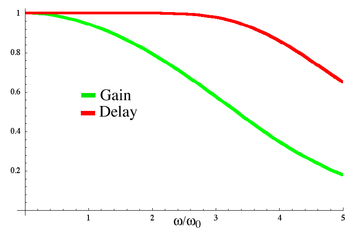График амплитудно-частотной характеристики и групповой задержки для низкочастотного фильтра Бесселя четвёртого порядка. Спад амплитудно-частотной характеристики значительно менее крутой, чем у других линейных фильтров, однако групповая задержка практически не меняется по частотам полосы пропускания.- H ( s ) = θ n ( 0 ) θ n ( s / ω 0 ) {\displaystyle H(s)={\frac {\theta _{n}(0)}{\theta _{n}(s/\omega _{0})}}}
где θ n ( s ) {\displaystyle \theta _{n}(s)} — обратный многочлен Бесселя, из-за чего фильтр и получил своё название; ω 0 {\displaystyle \omega _{0}} — частота среза.
Пример
Дана передаточная функция низкочастотного фильтра Бесселя третьего порядка
- H ( s ) = 15 s 3 + 6 s 2 + 15 s + 15 {\displaystyle H(s)={\frac {15}{s^{3}+6s^{2}+15s+15}}}
с амплитудно-частотной характеристикой
- G ( ω ) = | H ( j ω ) | = 15 ω 6 + 6 ω 4 + 45 ω 2 + 225 {\displaystyle G(\omega )=|H(j\omega )|={\frac {15}{\sqrt {\omega ^{6}+6\omega ^{4}+45\omega ^{2}+225}}}}
и фазо-частотной характеристикой
- ϕ ( ω ) = − a r g ( H ( j ω ) ) = − a r c t g ( 15 ω − ω 3 15 − 6 ω 2 ) {\displaystyle \phi (\omega )=-\mathrm {arg} (H(j\omega ))=-\mathrm {arctg} \left({\frac {15\omega -\omega ^{3}}{15-6\omega ^{2}}}\right)}
Групповая задержка такого фильтра:
- D ( ω ) = − d ϕ d ω = 6 ω 4 + 45 ω 2 + 225 ω 6 + 6 ω 4 + 45 ω 2 + 225 {\displaystyle D(\omega )=-{\frac {d\phi }{d\omega }}={\frac {6\omega ^{4}+45\omega ^{2}+225}{\omega ^{6}+6\omega ^{4}+45\omega ^{2}+225}}}
Разложение групповой задержки в ряд Тейлора по степеням частоты:
- D ( ω ) = 1 − ω 6 225 + ω 8 1125 + ⋯ {\displaystyle D(\omega )=1-{\frac {\omega ^{6}}{225}}+{\frac {\omega ^{8}}{1125}}+\cdots }
Из последнего выражения видно, что коэффициенты перед степенями ω 2 {\displaystyle \omega ^{2}} и ω 4 {\displaystyle \omega ^{4}} равны нулю, а перед более высокими степенями весьма малы, вследствие чего групповая задежка близка к единице на низких частотах.
Сравнение с другими линейными фильтрами
Ниже представлены графики амплитудно-частотных характеристик некоторых наиболее распространённых линейных электронных фильтров с одинаковым количеством коэффициентов:
Как следует из графика, фильтр Бесселя имеет наименьшую крутизну характеристики, в то же время он не имеет пульсаций АЧХ ни в полосе пропускания, ни в полосе подавления.
См. также
Ссылки
Фильтр Бесселя — Википедия Переиздание // WIKI 2
Фильтр Бесселя — в электронике и обработке сигналов один из наиболее[источник не указан 3026 дней] распространённых типов линейных фильтров, отличительной особенностью которого является максимально гладкая групповая задержка (линейная фазо-частотная характеристика). Фильтры Бесселя чаще всего используют для аудио-кроссоверов. Их групповая задержка практически не изменяется по частотам полосы пропускания, вследствие чего форма фильтруемого сигнала на выходе такого фильтра в полосе пропускания сохраняется практически неизменной.
Передаточная функция
График амплитудно-частотной характеристики и групповой задержки для низкочастотного фильтра Бесселя четвёртого порядка. Спад амплитудно-частотной характеристики значительно менее крутой, чем у других линейных фильтров, однако групповая задержка практически не меняется по частотам полосы пропускания.Передаточная функция фильтра Бесселя низких частот определяется следующим выражением:
- H ( s ) = θ n ( 0 ) θ n ( s / ω 0 ) {\displaystyle H(s)={\frac {\theta _{n}(0)}{\theta _{n}(s/\omega _{0})}}}
где θ n ( s ) {\displaystyle \theta _{n}(s)} — обратный многочлен Бесселя, из-за чего фильтр и получил своё название; ω 0 {\displaystyle \omega _{0}} — частота среза.
Пример
Дана передаточная функция низкочастотного фильтра Бесселя третьего порядка
- H ( s ) = 15 s 3 + 6 s 2 + 15 s + 15 {\displaystyle H(s)={\frac {15}{s^{3}+6s^{2}+15s+15}}}
с амплитудно-частотной характеристикой
- G ( ω ) = | H ( j ω ) | = 15 ω 6 + 6 ω 4 + 45 ω 2 + 225 {\displaystyle G(\omega )=|H(j\omega )|={\frac {15}{\sqrt {\omega ^{6}+6\omega ^{4}+45\omega ^{2}+225}}}}
и фазо-частотной характеристикой
- ϕ ( ω ) = − a r g ( H ( j ω ) ) = − a r c t g ( 15 ω − ω 3 15 − 6 ω 2 ) {\displaystyle \phi (\omega )=-\mathrm {arg} (H(j\omega ))=-\mathrm {arctg} \left({\frac {15\omega -\omega ^{3}}{15-6\omega ^{2}}}\right)}
Групповая задержка такого фильтра:
- D ( ω ) = − d ϕ d ω = 6 ω 4 + 45 ω 2 + 225 ω 6 + 6 ω 4 + 45 ω 2 + 225 {\displaystyle D(\omega )=-{\frac {d\phi }{d\omega }}={\frac {6\omega ^{4}+45\omega ^{2}+225}{\omega ^{6}+6\omega ^{4}+45\omega ^{2}+225}}}
Разложение групповой задержки в ряд Тейлора по степеням частоты:
- D ( ω ) = 1 − ω 6 225 + ω 8 1125 + ⋯ {\displaystyle D(\omega )=1-{\frac {\omega ^{6}}{225}}+{\frac {\omega ^{8}}{1125}}+\cdots }
Из последнего выражения видно, что коэффициенты перед степенями ω 2 {\displaystyle \omega ^{2}} и ω 4 {\displaystyle \omega ^{4}} равны нулю, а перед более высокими степенями весьма малы, вследствие чего групповая задежка близка к единице на низких частотах.
Сравнение с другими линейными фильтрами
Ниже представлены графики амплитудно-частотных характеристик некоторых наиболее распространённых линейных электронных фильтров с одинаковым количеством коэффициентов:
Фильтра Бесселя нет на графике, но он имеет наименьшую крутизну характеристики (ещё более пологий, чем фильтр Баттерворта), в то же время он не имеет пульсаций АЧХ ни в полосе пропускания, ни в полосе подавления.
См. также
Ссылки
Эта страница в последний раз была отредактирована 21 января 2020 в 02:25.Фильтр Бесселя — Википедия
Материал из Википедии — свободной энциклопедии
Фильтр Бесселя — в электронике и обработке сигналов один из наиболее[источник не указан 2376 дней] распространённых типов линейных фильтров, отличительной особенностью которого является максимально гладкая групповая задержка (линейная фазо-частотная характеристика). Фильтры Бесселя чаще всего используют для аудио-кроссоверов. Их групповая задержка практически не изменяется по частотам полосы пропускания, вследствие чего форма фильтруемого сигнала на выходе такого фильтра в полосе пропускания сохраняется практически неизменной.
Передаточная функция
График амплитудно-частотной характеристики и групповой задержки для низкочастотного фильтра Бесселя четвёртого порядка. Спад амплитудно-частотной характеристики значительно менее крутой, чем у других линейных фильтров, однако групповая задержка практически не меняется по частотам полосы пропускания.Передаточная функция фильтра Бесселя низких частот определяется следующим выражением:
- H ( s ) = θ n ( 0 ) θ n ( s / ω 0 ) {\displaystyle H(s)={\frac {\theta _{n}(0)}{\theta _{n}(s/\omega _{0})}}}
где θ n ( s ) {\displaystyle \theta _{n}(s)} — обратный многочлен Бесселя, из-за чего фильтр и получил своё название; ω 0 {\displaystyle \omega _{0}} — частота среза.
Пример
Дана передаточная функция низкочастотного фильтра Бесселя третьего порядка
- H ( s ) = 15 s 3 + 6 s 2 + 15 s + 15 {\displaystyle H(s)={\frac {15}{s^{3}+6s^{2}+15s+15}}}
с амплитудно-частотной характеристикой
- G ( ω ) = | H ( j ω ) | = 15 ω 6 + 6 ω 4 + 45 ω 2 + 225 {\displaystyle G(\omega )=|H(j\omega )|={\frac {15}{\sqrt {\omega ^{6}+6\omega ^{4}+45\omega ^{2}+225}}}}
и фазо-частотной характеристикой
- ϕ ( ω ) = − a r g ( H ( j ω ) ) = − a r c t g ( 15 ω − ω 3 15 − 6 ω 2 ) {\displaystyle \phi (\omega )=-\mathrm {arg} (H(j\omega ))=-\mathrm {arctg} \left({\frac {15\omega -\omega ^{3}}{15-6\omega ^{2}}}\right)}
Групповая задержка такого фильтра:
- D ( ω ) = − d ϕ d ω = 6 ω 4 + 45 ω 2 + 225 ω 6 + 6 ω 4 + 45 ω 2 + 225 {\displaystyle D(\omega )=-{\frac {d\phi }{d\omega }}={\frac {6\omega ^{4}+45\omega ^{2}+225}{\omega ^{6}+6\omega ^{4}+45\omega ^{2}+225}}}
Разложение групповой задержки в ряд Тейлора по степеням частоты:
- D ( ω ) = 1 − ω 6 225 + ω 8 1125 + ⋯ {\displaystyle D(\omega )=1-{\frac {\omega ^{6}}{225}}+{\frac {\omega ^{8}}{1125}}+\cdots }
Из последнего выражения видно, что коэффициенты перед степенями ω 2 {\displaystyle \omega ^{2}} и ω 4 {\displaystyle \omega ^{4}} равны нулю, а перед более высокими степенями весьма малы, вследствие чего групповая задежка близка к единице на низких частотах.
Сравнение с другими линейными фильтрами
Ниже представлены графики амплитудно-частотных характеристик некоторых наиболее распространённых линейных электронных фильтров с одинаковым количеством коэффициентов:
Как следует из графика, фильтр Бесселя имеет наименьшую крутизну характеристики, в то же время он не имеет пульсаций АЧХ ни в полосе пропускания, ни в полосе подавления.
См. также
Ссылки
Фильтр Бесселя — Википедия. Что такое Фильтр Бесселя
Материал из Википедии — свободной энциклопедии
Фильтр Бесселя — в электронике и обработке сигналов один из наиболее[источник не указан 2376 дней] распространённых типов линейных фильтров, отличительной особенностью которого является максимально гладкая групповая задержка (линейная фазо-частотная характеристика). Фильтры Бесселя чаще всего используют для аудио-кроссоверов. Их групповая задержка практически не изменяется по частотам полосы пропускания, вследствие чего форма фильтруемого сигнала на выходе такого фильтра в полосе пропускания сохраняется практически неизменной.
Передаточная функция
График амплитудно-частотной характеристики и групповой задержки для низкочастотного фильтра Бесселя четвёртого порядка. Спад амплитудно-частотной характеристики значительно менее крутой, чем у других линейных фильтров, однако групповая задержка практически не меняется по частотам полосы пропускания.Передаточная функция фильтра Бесселя низких частот определяется следующим выражением:
- H ( s ) = θ n ( 0 ) θ n ( s / ω 0 ) {\displaystyle H(s)={\frac {\theta _{n}(0)}{\theta _{n}(s/\omega _{0})}}}
где θ n ( s ) {\displaystyle \theta _{n}(s)} — обратный многочлен Бесселя, из-за чего фильтр и получил своё название; ω 0 {\displaystyle \omega _{0}} — частота среза.
Пример
Дана передаточная функция низкочастотного фильтра Бесселя третьего порядка
- H ( s ) = 15 s 3 + 6 s 2 + 15 s + 15 {\displaystyle H(s)={\frac {15}{s^{3}+6s^{2}+15s+15}}}
с амплитудно-частотной характеристикой
- G ( ω ) = | H ( j ω ) | = 15 ω 6 + 6 ω 4 + 45 ω 2 + 225 {\displaystyle G(\omega )=|H(j\omega )|={\frac {15}{\sqrt {\omega ^{6}+6\omega ^{4}+45\omega ^{2}+225}}}}
и фазо-частотной характеристикой
- ϕ ( ω ) = − a r g ( H ( j ω ) ) = − a r c t g ( 15 ω − ω 3 15 − 6 ω 2 ) {\displaystyle \phi (\omega )=-\mathrm {arg} (H(j\omega ))=-\mathrm {arctg} \left({\frac {15\omega -\omega ^{3}}{15-6\omega ^{2}}}\right)}
Групповая задержка такого фильтра:
- D ( ω ) = − d ϕ d ω = 6 ω 4 + 45 ω 2 + 225 ω 6 + 6 ω 4 + 45 ω 2 + 225 {\displaystyle D(\omega )=-{\frac {d\phi }{d\omega }}={\frac {6\omega ^{4}+45\omega ^{2}+225}{\omega ^{6}+6\omega ^{4}+45\omega ^{2}+225}}}
Разложение групповой задержки в ряд Тейлора по степеням частоты:
- D ( ω ) = 1 − ω 6 225 + ω 8 1125 + ⋯ {\displaystyle D(\omega )=1-{\frac {\omega ^{6}}{225}}+{\frac {\omega ^{8}}{1125}}+\cdots }
Из последнего выражения видно, что коэффициенты перед степенями ω 2 {\displaystyle \omega ^{2}} и ω 4 {\displaystyle \omega ^{4}} равны нулю, а перед более высокими степенями весьма малы, вследствие чего групповая задежка близка к единице на низких частотах.
Сравнение с другими линейными фильтрами
Ниже представлены графики амплитудно-частотных характеристик некоторых наиболее распространённых линейных электронных фильтров с одинаковым количеством коэффициентов:
Как следует из графика, фильтр Бесселя имеет наименьшую крутизну характеристики, в то же время он не имеет пульсаций АЧХ ни в полосе пропускания, ни в полосе подавления.
См. также
Ссылки
Фильтр Бесселя — Википедия. Что такое Фильтр Бесселя
Материал из Википедии — свободной энциклопедии
Фильтр Бесселя — в электронике и обработке сигналов один из наиболее[источник не указан 2376 дней] распространённых типов линейных фильтров, отличительной особенностью которого является максимально гладкая групповая задержка (линейная фазо-частотная характеристика). Фильтры Бесселя чаще всего используют для аудио-кроссоверов. Их групповая задержка практически не изменяется по частотам полосы пропускания, вследствие чего форма фильтруемого сигнала на выходе такого фильтра в полосе пропускания сохраняется практически неизменной.
Передаточная функция
График амплитудно-частотной характеристики и групповой задержки для низкочастотного фильтра Бесселя четвёртого порядка. Спад амплитудно-частотной характеристики значительно менее крутой, чем у других линейных фильтров, однако групповая задержка практически не меняется по частотам полосы пропускания.Передаточная функция фильтра Бесселя низких частот определяется следующим выражением:
- H ( s ) = θ n ( 0 ) θ n ( s / ω 0 ) {\displaystyle H(s)={\frac {\theta _{n}(0)}{\theta _{n}(s/\omega _{0})}}}
где θ n ( s ) {\displaystyle \theta _{n}(s)} — обратный многочлен Бесселя, из-за чего фильтр и получил своё название; ω 0 {\displaystyle \omega _{0}} — частота среза.
Пример
Дана передаточная функция низкочастотного фильтра Бесселя третьего порядка
- H ( s ) = 15 s 3 + 6 s 2 + 15 s + 15 {\displaystyle H(s)={\frac {15}{s^{3}+6s^{2}+15s+15}}}
с амплитудно-частотной характеристикой
- G ( ω ) = | H ( j ω ) | = 15 ω 6 + 6 ω 4 + 45 ω 2 + 225 {\displaystyle G(\omega )=|H(j\omega )|={\frac {15}{\sqrt {\omega ^{6}+6\omega ^{4}+45\omega ^{2}+225}}}}
и фазо-частотной характеристикой
- ϕ ( ω ) = − a r g ( H ( j ω ) ) = − a r c t g ( 15 ω − ω 3 15 − 6 ω 2 ) {\displaystyle \phi (\omega )=-\mathrm {arg} (H(j\omega ))=-\mathrm {arctg} \left({\frac {15\omega -\omega ^{3}}{15-6\omega ^{2}}}\right)}
Групповая задержка такого фильтра:
- D ( ω ) = − d ϕ d ω = 6 ω 4 + 45 ω 2 + 225 ω 6 + 6 ω 4 + 45 ω 2 + 225 {\displaystyle D(\omega )=-{\frac {d\phi }{d\omega }}={\frac {6\omega ^{4}+45\omega ^{2}+225}{\omega ^{6}+6\omega ^{4}+45\omega ^{2}+225}}}
Разложение групповой задержки в ряд Тейлора по степеням частоты:
- D ( ω ) = 1 − ω 6 225 + ω 8 1125 + ⋯ {\displaystyle D(\omega )=1-{\frac {\omega ^{6}}{225}}+{\frac {\omega ^{8}}{1125}}+\cdots }
Из последнего выражения видно, что коэффициенты перед степенями ω 2 {\displaystyle \omega ^{2}} и ω 4 {\displaystyle \omega ^{4}} равны нулю, а перед более высокими степенями весьма малы, вследствие чего групповая задежка близка к единице на низких частотах.
Сравнение с другими линейными фильтрами
Ниже представлены графики амплитудно-частотных характеристик некоторых наиболее распространённых линейных электронных фильтров с одинаковым количеством коэффициентов:
Как следует из графика, фильтр Бесселя имеет наименьшую крутизну характеристики, в то же время он не имеет пульсаций АЧХ ни в полосе пропускания, ни в полосе подавления.
См. также
Ссылки
Операционные усилители (на основе простейших примеров): часть 3 / Хабр
Краткое введение
Продолжаю
Обзор темы
Возможно, Вы уже сталкивались с моделями RC-, LC- и RLC-фильтров. Они вполне подходят для большинства задач. Но для некоторых целей очень важно иметь фильтры с более плоскими характеристиками в полосе пропускания и более крутыми склонами. Вот тут нам и нужны активные фильтры.
Для освежения в памяти, напомню, какие бывают фильтры:
Фильтр Нижних Частот (ФНЧ) — пропускает сигнал, который ниже определенной частоты (ее еще именуют частотой среза). Википедия
Фильтр Высоких Частот (ФВЧ) — пропускает сигнал выше частоты среза. Википедия
Полосовой Фильтр — пропускает только определенный диапазон частот. Википедия
Режекторный Фильтр — задерживает только определенный диапазон частот. Википедия
Ну еще немного лирики. Посмотрите на амплитудно-частотную характеристику (АЧХ) ФВЧ. На этом графике ничего интересного пока не ищите, а просто обратите внимание на участки и их названия:
Самые банальные примеры активных фильтров можно подсмотреть здесь в разделе «Интеграторы и дифференциаторы». Но в данной статье эти схемы трогать не будем, т.к. они не очень эффективны.
Выбираем фильтр
Предположим, что Вы уже определились с частотой, которую хотите фильтровать. Теперь нужно определиться с типом фильтра. Точнее нужно выбрать его характеристику. Иными словами, как фильтр будет себя «вести».
Основными характеристиками являются:
Фильтр Баттерворда — обладает самой плоской характеристикой в полосе пропускания, но имеет плавный спад.
Фильтр Чебышева — обладает самым крутым спадом, но у него самые неравномерные характеристики в полосе пропускания.
Фильтр Бесселя — имеет хорошую фазочастотную характеристику и вполне «приличный» спад. Считается лучшим выбором, если нет специфического задания.
Еще немного информации
Предположим, и с этим заданием вы справились. И теперь можно смело приступить к расчетам.
Есть несколько методов расчета. Не будем усложнять и воспользуемся самым простым. А самый простой — это «табличный» метод. Таблицы можно найти в соответствующей литературе. Чтобы Вы долго не искали, приведу из Хоровица и Хилла «Искусство Схемотехники».
Для ФНЧ:
Скажем так, это все Вы могли бы найти и прочитать и в литературе. Перейдем конкретно к проектированию фильтров.
Расчет
В данном разделе попытаюсь кратко «пробежаться» по всем типам фильтров.
Итак, задание # 1. Построить фильтр низких частот второго порядка с частотой среза 150 Гц по характеристике Баттерворда.
Приступим. Если мы имеем фильтр n-ного четного порядка, это означает, что в нем будет n/2 операционников. В данном задании — один.
Схема ФНЧ:
Для данного типа расчета берется во внимание, что R1 = R2, C1 = C2.
Смотрим в табличку. Видим, что К = 1.586. Это нам пригодится чуть позже.
Для фильтра низких частот справедливо:
, где, разумеется,
— это частота среза.
Сделав подсчет, получаем . Теперь займемся подбором элементов. С ОУ определились — «идеальный» в количестве 1 шт. Из предыдущего равенства можно предположить, что нам не принципиально, какой элемент выбирать «первым». Начнем с резистора. Лучше всего, чтоб его значение сопротивления были в пределах от 2кОм до 500кОм. На глаз, пусть он будет 11 кОм. Соответственно, емкость конденсатора станет равной 0.1 мкФ. Для резисторов обратной связи значение R берем произвольно. Я обычно беру 10 кОм. Тогда, для верхнего значение К возьмем из таблицы. Следовательно, нижний будет иметь значение сопротивления R = 10 кОм, а верхний 5.8 кОм.
Соберем и промоделируем АЧХ.
Задание # 2. Построить фильтр высоких частот четвертого порядка с частотой среза 800 Гц по характеристике Бесселя.
Решаем. Раз фильтр четвертого порядка, то в схеме будет два операционника. Тут все совсем не сложно. Мы просто каскадно включаем 2 схемы ФВЧ.
Сам фильтр выглядит так:
Фильтр же четвертого порядка выглядит:
Теперь расчет. Как видим, для фильтра четвертого порядка у нас аж 2 значения К. Логично, что первое предназначается для первого каскада, второе — для второго. Значения К равны 1.432 и 1.606 соответсвенно. Таблица была для фильтров низких частот (!). Для расчета ФВЧ надо кое-что изменить. Коэффициенты
— нормирующая частота. Она будет равна теперь:
Для фильтров Чебышева и Бесселя как для нижних частот, так и для высоких справедлива одна и та же формула:
Учтите, что для каждого отдельного каскада придется считать отдельно.
Для первого каскада:
Пусть С = 0.01 мкФ, тогда R = 28.5 кОм. Резисторы обратной связи: нижний, как обычно, 10 кОм; верхний — 840 Ом.
Для второго каскада:
Емкость конденсатора оставим неизменной. Раз С = 0.01 мкФ, то R = 32 кОм.
Строим АЧХ.
Для создания полосового или режекторного типа фильтров можно каскадно соединить ФНЧ и ФВЧ. Но такими типами, зачастую, не пользуются из-за плохих характеристик.
Приведу сразу табличку и немного ее объясню. Чтоб сильно не растягивать — значения взяты сразу для полосового фильтра четвертого порядка.
a1 и b1 — расчетные коэффициенты. Q — добротность. Это новый параметр. Чем значение добротности больше — тем более «резким» будет спад. Δf — диапазон пропускаемых частот, причем выборка идет на уровне -3 дБ. Коэффициент α — еще один расчетный коэффициент. Его можно найти используя формулы, которые довольно легко найти в интернете.
Ну ладно, хватит. Теперь рабочее задание.
Задание # 3. Построить полосовой фильтр четвертого порядка по характеристике Баттерворда с центральной частотой 10 кГц, шириной пропускаемых частот 1 кГц и коэффициентом усиления в точке центральной частоты равным 1.
Поехали. Фильтр четвертого порядка. Значит два ОУ. Типовую схему приведу сразу с расчтными элементами.
Для первого фильтра центральная частота определяется как:
Для второго фильтра:
Конкретно в нашем случае, опять же из таблицы, определяем, что добротность Q = 10. Рассчитываем добротность для фильтра. Причем, стоит отметить, что добротность обоих будет равна.
Поправка усиления для области центральной частоты:
Финальная стадия — расчет компонентов.
Пусть конденсатор будет равен 10 нФ. Тогда, для первого фильтра:
В том же порядке, что и (1) находим R22 = R5 = 43.5 кОм, R12 = R4 = 15.4 кОм, R32 = R6 = 54.2 Ом. Только учтите, что для второго фильтра используем
Ну и на последок, АЧХ.
Следующая остановка — полосно-заграждающие фильтры или режекторные.
Тут есть несколько вариаций. Наверное, самый простой — это фильтр Вина-Робинсона (англ. Active Wien-Robinson Filter). Типовая схема — тоже фильтр 4го порядка.
Наше последнее задание.
Задание # 4. Построить режекторный фильтр с центральной частотой 90 Гц, добротностью Q = 2 и коэффициентом усиления в полосе пропускания равным 1.
Прежде всего, произвольно выбираем емкость конденсатора. Допустим, С = 100 нФ.
Определим значение R6 = R7 = R:
Логично, что «играясь» с этими резисторами, мы можем изменять диапазон частот нашего фильтра.
Далее, нам надо определить промежуточные коэффициенты. Находим их через добротность.
Выберем произвольно резистор R2. В данном конкретном случае, лучше всего, чтобы он равнялся 30 кОм.
Теперь можем найти резисторы, которые будут регулировать коэффициент усиления в полосе пропускания.
И на последок, необходимо произвольно выбрать
Собственно, АЧХ:
Практически конец
Кому интересно узнать немного больше, могу посоветовать почитать Хоровица и Хилла «Искусство схемотехники».
Также, D. Johnson «A handbook of active filters».
Википедия
Также, кому не очень нужны расчеты, а нужны именно сами фильтры, могу посоветовать полезный софт
P.S. Добавлю очень полезную ссылку и ее зеркало. За линк спасибо spiritus_sancti
Фильтр Бесселя – это… Что такое Фильтр Бесселя?
Фильтр Бесселя — в электронике и обработке сигналов один из наиболее[источник не указан 241 день] распространённых типов линейных фильтров, отличительной особенностью которого является максимально гладкая групповая задержка (линейная фазо-частотная характеристика). Фильтры Бесселя чаще всего используют для аудио-кроссоверов. Их групповая задержка практически не изменяется по частотам полосы пропускания, вследствие чего форма фильтруемого сигнала на выходе такого фильтра в полосе пропускания сохраняется практически неизменной.
Передаточная функция
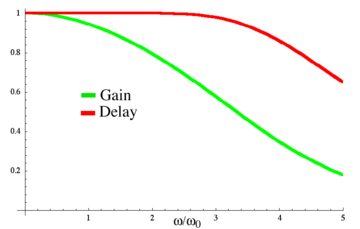График амплитудно-частотной характеристики и групповой задержки для низкочастотного фильтра Бесселя четвёртого порядка. Спад амплитудно-частотной характеристики значительно менее крутой, чем у других линейных фильтров, однако групповая задержка практически не меняется по частотам полосы пропускания.Передаточная функция фильтра Бесселя низких частот определяется следующим выражением:
где — обратный многочлен Бесселя, из-за чего фильтр и получил своё название; — частота среза.
Пример
Дана передаточная функция низкочастотного фильтра Бесселя третьего порядка
с амплитудно-частотной характеристикой
и фазо-частотной характеристикой
Групповая задержка такого фильтра:
Разложение групповой задержки в ряд Тейлора по степеням частоты:
Из последнего выражения видно, что коэффициенты перед степенями и равны нулю, а перед более высокими степенями весьма малы, вследствие чего групповая задежка близка к единице на низких частотах.
Сравнение с другими линейными фильтрами
Ниже представлены графики амплитудно-частотных характеристик некоторых наиболее распространённых линейных электронных фильтров с одинаковым количеством коэффициентов:
Как следует из графика, фильтр Бесселя имеет наименьшую крутизну характеристики, в то же время он не имеет пульсаций АЧХ ни в полосе пропускания, ни в полосе подавления.
См. также
Ссылки
Что такое фильтр Бесселя
Фильтр Бесселя представляет собой разновидность радиочастотного или электронного фильтра, который обеспечивает равномерное распространение или групповую задержку, что делает его идеальным для некоторых приложений.
RF Filters Включает:
RF Filters – основы
Характеристики фильтра
Основы проектирования ВЧ-фильтров
Конструкция фильтра высоких и низких частот
Постоянный k-фильтр
Фильтр Баттерворта
Чебычевский фильтр
Фильтр Бесселя
Эллиптический фильтр
Кристаллический фильтр
Фильтр Бесселя – это тип аналогового линейного фильтра, используемого в ВЧ и других электронных приложениях, который имеет максимально плоскую групповую или фазовую задержку.Это сохраняет форму волны сигналов в полосе пропускания.
Есть некоторые RF и, в частности, аудио приложения, в которых важно сохранение формы волны и фазы компонентов в сигнале. Аудиокроссоверы – лишь один из примеров, хотя существует и множество других. Именно для этих целей фильтр Бесселя является идеальным решением.
Как и следовало ожидать, фильтр Бесселя обеспечивает более медленный переход от полосы пропускания к полосе заграждения, чем для других форм фильтра того же порядка.
Разработка фильтра Бесселя
Фильтр Бесселя получил свое название от немецкого математика и астронома Фридриха Бесселя, жившего между 1784 и 1846 годами. Бессель разработал математическую теорию, на которой основан этот фильтр.
Иногда фильтры также называют фильтрами Бесселя-Томсона. Это связано с тем, что В. Э. Томсон разработал методологию использования функций Бесселя при разработке этого вида фильтра.
Основы фильтра Бесселя
Некоторые из ключевых характеристик фильтра Бесселя можно резюмировать следующим образом:
- Максимально ровная групповая задержка: Максимально ровная групповая задержка фильтра Бесселя означает, что он в равной степени демонстрирует максимально линейную фазовую характеристику.
- Overshoot: Прямой результат максимально плоской групповой задержки фильтра Бесселя. Он дает выходной сигнал для прямоугольной волны без выброса, поскольку все частоты задерживаются на одинаковую величину.
- Медленная отсечка: Переход от полосы пропускания к полосе заграждения для фильтра Бесселя происходит намного медленнее или неглубокий, чем для других фильтров.
Расчет фильтра Бесселя
Фильтр нижних частот Бесселя имеет передаточную функцию вида:
ЧАС ( s ) знак равно θ N ( 0 ) θ N ( s ω 0 )
Передаточная функция фильтра Бесселя – это рациональная функция, знаменатель которой является обратным полиномом Бесселя, например:
| Полином для фильтра Бесселя | |
|---|---|
| Заказать | Полином |
| 1 | с + 1 |
| 2 | с 2 + 3 с + 3 |
| 3 | с 3 + 6 с 2 + 15 с + 15 |
| 4 | с 4 + 10 с 3 + 45 с 2 105 с + 105 |
| 5 | с 5 + 15 с 4 + 105 с 3 + 420 с 2 945 с + 945 |
Другие важные темы по радио:
Радиосигналы
Типы и методы модуляции
Амплитудная модуляция
Модуляция частоты
OFDM
ВЧ микширование
Петли фазовой автоподстройки частоты
Синтезаторы частот
Пассивная интермодуляция
ВЧ аттенюаторы
RF фильтры
Типы радиоприемников
Радио Superhet
Избирательность приемника
Чувствительность приемника
Обработка сильного сигнала приемника
Вернуться в меню тем Радио., ,
Фильтр Бесселя
Фильтр Бесселя – это линейный фильтр, который используется в электронике и обработке сигналов и имеет плоскую групповую задержку (также называемую максимально линейной фазовой характеристикой). Эти фильтры обычно используются в системах кроссовера звука и сохраняют форму волны любых фильтрованных сигналов через групповую задержку в полосе пропускания.
Кто изобрел фильтр Бесселя?
Фильтр Бесселя назван в честь Фридриха Бесселя, немецкого математика, который жил с 1784 по 1846 год и создал математическую теорию, на которой основаны фильтры, используемые сегодня.Эти фильтры также называются фильтрами Томсона или Бесселя-Томсона из-за W.E. Работа Томсона. Он был первым, кто применил функции Бесселя для создания удобного фильтра. 
Что такое аудиокроссовер?
Аудиокроссовер – это электронный фильтр, который используется в аудиоприложениях. Поскольку большинство драйверов динамиков не могут охватить весь звуковой спектр с правильным контролем искажений и диапазоном громкости, они используют для этого комбинацию динамиков и драйверов.Аудиокроссоверы могут разделить аудиосигнал на разные полосы частот, которые затем могут быть направлены на динамики, оптимизированные для использования этих полос во время воспроизведения музыки. Аудио кроссоверы также допускают многополосную обработку и усиление, когда сигнал разделяется на настроенные полосы, прежде чем они будут смешаны вместе, как это делается в шумоподавлении Dolby A.
Для чего нужен фильтр кроссовера аудио?
Аудио кроссоверы могут разделять входящие аудиосигналы на отдельные полосы, которые не могут перекрываться.Это улучшает работу звукового оборудования. В стереосистеме используется один из многих фильтров кроссовера в зависимости от сложности используемого стереооборудования. Как правило, двух- / трехполосный фильтр кроссовера создается с использованием фильтров нижних, верхних частот и полосовых фильтров, где это применимо. 4-полосный кроссоверный фильтр не является распространенным в промышленности из-за его сложности и стоимости, необходимой для достижения минимального прироста производительности. Фильтры Бесселя обычно используются в качестве фильтров второго порядка в кроссовере и являются вторым наиболее часто используемым типом после фильтра Баттерворта.
,Фильтр Бесселя
Фильтр Бесселя Проблема:
Что такое фильтр Бесселя?
Решение:
Термин Бессель относится к типу отклика фильтра, а не к типу фильтра. Он имеет плоскую групповую задержку в полосе пропускания:
Это характеристика фильтров Бесселя, которая делает их ценными для цифровых дизайнеров. Очень немногие фильтры разработаны с учетом прямоугольных волн. Большую часть времени, Отфильтрованные сигналы являются синусоидальными волнами или достаточно близкими, чтобы можно было игнорировать влияние гармоник.Если фильтруется форма волны с высоким содержанием гармоник, например квадрат волны, гармоники могут быть задержаны относительно основной частоты, если используется отклик Баттерворта или Чебышева. Ряд Фурье прямоугольной волны это:
Это означает, что прямоугольная волна представляет собой бесконечную серию нечетных гармоник или синусоид, суммированных вместе, чтобы создать квадратную форму. Очевидно, что если прямоугольная волна передается без искажений, все гармоники – до бесконечности – должны передаваться.Это означает, что прямоугольную волну можно фильтровать верхними частотами без искажение, если точка фильтра на 3 дБ значительно ниже основной гармоники. Однако, если прямоугольная волна фильтруется нижними частотами, ситуация меняется. драматически. Гармоники будут устранены, что приведет к искажению прямоугольной волны. Задача дизайнера – решить, сколько гармоник должно быть прошло и что можно устранить. Предположим, разработчик хочет сохранить пять гармоник. Результирующий сигнал выглядит примерно так:
Это может быть приемлемо для разработчика – это зависит от синхронизации переднего и заднего фронтов сигнала.Исключение гармоник приведет к округлению фронтов и, следовательно, задержка переднего и заднего фронтов цифрового сигнала. Что еще более важно, прошедшие гармоники не будут задерживаться.
Приближение Бесселя имеет плавную полосу пропускания и отклик полосы задерживания, как и приближение Баттерворта. Для того же порядка фильтров затухание в полосе задерживания Бесселя приближение намного ниже, чем приближение Баттерворта.
Следующие рисунки представляют фильтр нижних частот.Характеристики отклика зеркально отображены для фильтров высоких частот.
Разработчик может видеть, что нет пульсаций в полосе пропускания фильтра Бесселя и что у него не так много подавления в полосе заграждения, как у фильтра Баттерворта.
Фазовые характеристики трех типов фильтров показаны ниже. Реакция Бесселя имеет самую низкую скорость изменения фазы.
.Элемент прототипа фильтра нижних частот Бесселя Значения
Фильтры нижних частот
(вверху)
Фильтры Highpass
(вверху)
Полосовые и полосовые фильтры
(см. Выше)
Фильтр Бесселя – это фильтр, импульсная характеристика которого является функцией Бесселя. Фильтры Бесселя предназначены для обеспечения максимально плоской групповой задержки и максимально линейного изменения фазы по полосу и в переходную область.Они очень близки к фильтрам гауссовского типа.
В таблице ниже перечислены значения элементов прототипа для нормализованной функции нижних частот, который предполагает частоту среза 1 рад / сек и импеданс источника и нагрузки 1 Ом. Либо входной конденсатор (верхняя контрольная строка в таблице), либо входная катушка индуктивности (нижняя строка в таблице).
Преобразование значений в другие частоты среза, импедансы и в фильтр верхних частот и полосу пропускания или перекрыть канал с помощью уравнений денормализации.
Вход конденсатора | Вход индуктора |
| 2.000 | |||||||||
| 0.576 | 2,148 | ||||||||
| 0,3374 | 0,9705 | 2.2034 | |||||||
| 0.2334 | 0,6725 | 1.0815 | 2,2404 | ||||||
| 0,1743 | 0,5072 | 0,804 | 1,111 | 2,2582 | |||||
| 0.1365 | 0,4002 | 0,6392 | 0,8538 | 1,1126 | 2,2645 | ||||
| 0,1106 | 0,3259 | 0,5249 | 0,702 | 0,869 | 1,1052 | 2,2659 | |||
| 0.0919 | 0,2719 | 0,4409 | 0,5936 | 0,7303 | 0,8695 | 1.0956 | 2,2656 | ||
| 0,078 | 0,2313 | 0,377 | 0,5108 | 0,6306 | 0,7407 | 0,8639 | 1.0863 | 2,2649 | |
| 0.0672 | 0,1998 | 0,327 | 0,4454 | 0,5528 | 0,6493 | 0,742 | 0,8561 | 1.0781 | 2,2641 |
