порядок, расчет и построение схемы
В данной статье мы поговорим про фильтр Баттерворта, рассмотрим порядки фильтров, декады и октавы, подробно разберем фильтр низких частот Баттерворта третьего порядка с расчетом и схемой.
Введение
В устройствах, которые используют фильтры для формирования частотного спектра сигнала, например, в системах связи или управления, форма или ширина спада, также называемая «полосой перехода», для простого фильтра первого порядка может быть слишком длинной или необходимы широкие и активные фильтры, разработанные с более чем одним «заказом». Эти типы фильтров обычно известны как фильтры «высокого порядка» или «n- го порядка».
Порядок фильтров
Сложность или тип фильтра определяется «порядком» фильтров и зависит от количества реактивных компонентов, таких как конденсаторы или катушки индуктивности в его конструкции. Мы также знаем, что скорость спада и, следовательно, ширина полосы перехода зависит от порядкового номера фильтра и что для простого фильтра первого порядка он имеет стандартную скорость спада 20 дБ / декаду или 6 дБ / октава.
Тогда для фильтра, имеющего n- й порядковый номер, он будет иметь последующую скорость спада 20n дБ / декаду или 6n дБ / октаву. Таким образом:
- фильтр первого порядка имеет скорость спада 20 дБ / декаду (6 дБ / октава)
- фильтр второго порядка имеет скорость спада 40 дБ / декаду (12 дБ / октава)
- фильтр четвертого порядка имеет частоту спада 80 дБ / декада (24 дБ / октава) и т. д.
Фильтры высокого порядка, такие как третий, четвертый и пятый, обычно формируются путем каскадного объединения одиночных фильтров первого и второго порядка.
Например, два фильтра нижних частот второго порядка могут быть соединены каскадно для получения фильтра нижних частот четвертого порядка и так далее. Несмотря на то, что порядок фильтра, который может быть сформирован, не ограничен, при увеличении порядка увеличиваются его размер и стоимость, а также снижается его точность.
Декады и октавы
Последний комментарий о Декадах и Октавах . По шкале частот декада — это десятикратное увеличение (умножение на 10) или десятикратное уменьшение (деление на 10). Например, от 2 до 20 Гц представляют одну декаду, тогда как от 50 до 5000 Гц представляют две декады (от 50 до 500 Гц, а затем от 500 до 5000 Гц).
Октава — это удвоение (умножить на 2) или уменьшение в два раза (деление на 2) по шкале частот. Например, от 10 до 20 Гц представляет одну октаву, а от 2 до 16 Гц — это три октавы (от 2 до 4, от 4 до 8 и, наконец, от 8 до 16 Гц), каждый раз удваивая частоту. В любом случае, логарифмические шкалы широко используются в частотной области для обозначения значения частоты при работе с усилителями и фильтрами, поэтому важно понимать их.
Логарифмическая шкала частот
Поскольку резисторы, определяющие частоту, все равны, как и конденсаторы, определяющие частоту, отсечка или угловая частота ( ƒC ) для первого, второго, третьего или даже для фильтра четвертого порядка также должны быть равны и найдены, используя знакомое уравнение:
Как и в случае фильтров первого и второго порядка, фильтры верхних частот третьего и четвертого порядка формируются простым взаимным обменом положений определяющих частоту компонентов (резисторов и конденсаторов) в эквивалентном фильтре нижних частот. Фильтры высокого порядка можно спроектировать, следуя процедурам, которые мы видели ранее в руководствах по фильтру нижних частот и фильтрам верхних частот. Однако общий коэффициент усиления фильтров высокого порядка является фиксированным, поскольку все компоненты, определяющие частоту, являются одинаковыми.
Аппроксимации фильтра
До сих пор мы рассматривали низкочастотные и высокочастотные схемы фильтра первого порядка, их результирующие частотные и фазовые характеристики. Идеальный фильтр дал бы нам спецификации максимального усиления полосы пропускания и плоскостности, минимального затухания полосы пропускания, а также очень крутой полосы пропускания, чтобы остановить спад полосы (полоса перехода), и поэтому очевидно, что большое количество сетевых откликов будет удовлетворять эти требования.
Неудивительно, что в линейном дизайне аналоговых фильтров есть ряд «аппроксимационных функций», в которых используется математический подход для наилучшего приближения передаточной функции, которая требуется нам для проектирования фильтров.
Такие конструкции известны как Эллиптический, Баттерворт, Чебышев, Бессель, Кауэр и многие другие. Из этих пяти «классических» функций аппроксимации линейного аналогового фильтра только фильтр Баттерворта и особенно конструкция фильтра Баттерворта нижних частот будут рассматриваться здесь как его наиболее часто используемая функция.
Низкочастотный фильтр Баттерворта
Частотная характеристика аппроксимационной функции фильтра Баттерворта также часто называется «максимально плоской» (без пульсаций) характеристикой, поскольку полоса пропускания спроектирована так, чтобы иметь частотную характеристику, которая является настолько плоской, насколько это математически возможно, от 0 Гц (DC) до частоты среза -3 дБ без пульсаций. Более высокие частоты за пределами точки отсечки снижаются до нуля в полосе останова на уровне 20 дБ / декада или 6 дБ / октава. Это потому, что он имеет «фактор качества», «Q» всего 0,707.
Однако одним из основных недостатков фильтра Баттерворта является то, что он достигает этой плоскостности полосы пропускания за счет широкой полосы перехода, когда фильтр изменяется от полосы пропускания к полосе остановки. Он также имеет плохие фазовые характеристики. Идеальная частотная характеристика, называемая фильтром «кирпичной стены», и стандартные аппроксимации Баттерворта для различных порядков фильтра приведены ниже.
Идеальная частотная характеристика для фильтра Баттерворта
Обратите внимание, что чем выше порядок фильтра Баттерворта, тем больше количество каскадных ступеней в конструкции фильтра и тем ближе фильтр подходит к идеальному отклику «кирпичной стены».
Однако на практике идеальная частотная характеристика Баттерворта недостижима, поскольку она вызывает чрезмерную пульсацию в полосе пропускания.
Где обобщенное уравнение, представляющее фильтр Баттерворта «n-го» порядка, частотная характеристика дается как:
Где: n представляет порядок фильтра, ω равно 2πƒ, а ε — максимальное усиление полосы пропускания (A max ).
Если A max определено на частоте, равной угловой точке отсечки -3 дБ (ƒc), тогда ε будет равно единице и, следовательно, ε 2 также будет равно единице. Однако, если вы теперь хотите определить A max при другом значении усиления по напряжению, например, 1 дБ или 1.1220 (1 дБ = 20 * logA max ), тогда новое значение ε находится по формуле :
Подставляя данные в уравнения, получаем:
Частотная характеристика фильтра может быть определена математически его передаточной функции с стандартом передачи напряжения Функция H (jω) и записывается в виде:
Примечание: (jω) также можно записать как (s) для обозначения S-области. и результирующая передаточная функция для фильтра нижних частот второго порядка задается как:
Нормализованные полиномы фильтра Баттерворта низких частот
Чтобы помочь в разработке своих фильтров нижних частот, Баттерворт создал стандартные таблицы нормализованных полиномов нижних частот второго порядка с учетом значений коэффициента, которые соответствуют частоте отсечки угла 1 радиан / с.
| N | Нормализованные полиномы знаменателя в факторизованной форме |
| 1 | (1 + S) |
| 2 | (1 + 1,414 с + с 2 ) |
| 3 | (1 + с) (1 + с + с 2 ) |
| 4 | (1 + 0,765 с + с 2 ) (1 + 1,848 с + с 2 ) |
| 5 | (1 + с) (1 + 0,618 с + с 2 ) (1 + 1,618 с + с 2 ) |
| 6 | (1 + 0,518 с + с 2 ) (1 + 1,414 с + с 2 ) (1 + 1,932 с + с 2 ) |
| 7 | (1 + с) (1 + 0,445 с + с 2 ) (1 + 1,247 с + с 2 ) (1 + 1,802 с + с 2 ) |
| 8 | (1 + 0,390 с + с 2 ) (1 + 1,111 с + с 2 ) (1 + 1,663 с + с 2 ) (1 + 1,962 с + с 2 ) |
| 9 | (1 + с) (1 + 0,347 с + с 2 ) (1 + с + с 2 ) (1 + 1,532 с + с 2 ) (1 + 1,879 с + с 2 ) |
| 10 | (1 + 0,313 с + с 2 ) (1 + 0,908 с + с 2 ) (1 + 1,414 с + с 2 ) (1 + 1,782 с + с 2 ) (1 + 1,975 с + с 2) |
Расчет и схема фильтра Баттерворта низких частот
Найти порядок активного фильтра Баттерворта нижних частот, чьи характеристики приведены в качестве: A макс = 0,5 дБ на частоте полосы пропускания ( ωp ) 200 радиан / сек (31.8 гЦ), и Amin = -20 дБ на частоте полосы остановки ( ωs ) 800 радиан / сек. Также разработайте подходящую схему фильтра Баттерворта, соответствующую этим требованиям.
Во-первых, максимальное усиление полосы пропускания A max = 0,5 дБ, которое равно усилению 1,0593 , помните, что: 0,5 дБ = 20 * log (A) на частоте ( ωp ) 200 рад / с, поэтому значение эпсилона ε находится по:
Во-вторых, минимальное усиление полосы остановки A min = -20 дБ, которое равно усилению 10 (-20 дБ = 20 * log (A)) на частоте полосы остановки ( ωs ) 800 рад / с или 127,3 Гц.
Подстановка значений в общее уравнение для частотной характеристики фильтров Баттерворта дает нам следующее:
Так как n всегда должно быть целым числом, то следующим самым высоким значением 2,42 будет n = 3 , поэтому «требуется фильтр третьего порядка», и для создания фильтра Баттерворта третьего порядка, ступени фильтра второго порядка требуется каскадное соединение со ступенью фильтра первого порядка.
Из приведенной выше таблицы нормализованных полиномов Баттерворта низких частот коэффициент для фильтра третьего порядка дается как (1 + s) (1 + s + s 2 ), и это дает нам усиление 3-A = 1 или A = 2 . В А = 1 + (Rf / R1) , выбирая значение как для резистора обратной связи Rf и резистора R1 дает нам значения 1 кОм и 1 кОм , соответственно, как: ( 1 кОм / 1 кОм) + 1 = 2 .
Мы знаем, что угловая частота отсечки, точка -3 дБ ( ω o ) может быть найдена с помощью формулы 1 / CR , но нам нужно найти ω o по частоте полосы пропускания ω p ,
Таким образом, частота отсечки угла задается как 284 рад / с или 45,2 Гц (284 / 2π), и, используя знакомую формулу 1 / RC, мы можем найти значения резисторов и конденсаторов для нашей схемы третьего порядка.
Обратите внимание, что ближайшее предпочтительное значение до 0,352 мкФ будет 0,36 мкФ или 360 нФ .
И, наконец, наша схема низкочастотного фильтра Баттерворта третьего порядка с угловой частотой среза 284 рад / с или 45,2 Гц, максимальным усилением полосы пропускания 0,5 дБ и минимальным усилением полосы остановки 20 дБ строится следующим образом.
Таким образом, для нашего фильтра низких частот Баттерворта 3-го порядка с угловой частотой 45,2 Гц, C = 360 нФ и R = 10 кОм
meanders.ru
Кроссовер, порядки фильтров – на пальцах.
Сам когда-то искал, кроссы, порядок фильтров???)))Кроссоверы– это устройства в звуковых системах, которые создают нужные рабочие частотные диапазоны для динамиков. Динамики сконструированы таким образом, чтобы работать в определенном частотном диапазоне. Они не приемлют частоты, не входящие в эти рамки. Если на высокочастотный динамик (твитер) подать низкую частоту, то звуковая картина испортится, а если сигнал еще и мощный, то твитер “сгорит”. Высокочастотные динамики должны работать только с высокими частотами, а низкочастотные динамики должны получить от общего звукового сигнала только низкочастотный диапазон. Оставшаяся средняя полоса достается среднечастотным динамикам (мидвуферы). Следовательно, задача кроссоверов заключается в разделении звукового сигнала на нужные (оптимальные) частотные полосы для соответствующих типов динамиков.
Проще говоря, кроссовер – это пара электрических фильтров. Допустим, кроссовер имеет частоту среза равную 1000 Гц. Это означает, что один из его фильтров срезает все частоты ниже 1000 Гц и пропускает только частоты выше 1000 Гц. Такой фильтр называют high-pass фильтром. Другой фильтр, пропускающий частоты ниже 1000 Гц называется low-pass,. Графически работа этого кроссовера представлена на рисунке 3. Точка пересечения двух кривых есть частота среза кроссовера равная 1000 Гц. В трехполосных кроссоверах присутствует еще и среднечастотный фильтр (band-pass), который пропускает только средний диапазон частот (приблизительно от 600 Гц до 5000 Гц.) На рисунке изображена частотная характеристика трехполосного кроссовера.
Порядок чувствительности – это отношение интенсивности выходного сигнала (dB) кроссовера к частоте входного сигнала при условии, что интенсивность входного сигнала постоянна. Обычно чувствительность (крутизну среза) характеризуют как отношение dB/octave. В силу многих математических причин чувствительность кроссоверов всегда кратна 6 децибелам на октаву (6 dB/octave). Кроссовер первого порядка имеет чувствительность 6 dB/octave. Кроссовер второго порядка имеет чувствительность 12 dB/octave, третьего порядка – 18 dB/octave, и чувствительность кроссоверов четвертого порядка равна 24 dB на октаву.
Рассмотрим low-pass фильтр третьего порядка с частотой среза равной 100 Гц. Как уже говорилось выше, этот кроссовер пропустит только частоты ниже 100 Гц, а частоты выше 100 Гц срежет. Срезание частот будет происходить следующим образом: все частоты выше 100 Гц будут терять на выходе из фильтра свою интенсивность кратно 18 dB в зависимости от октавы, в которую они входят. То есть, частота в 200 Гц (первая октава выше частоты среза) потеряет свою интенсивность на 18 Дб, интенсивность частоты в 400 Гц (вторая октава) упадет 36 Гц, а третья октава (800 Гц) ослабеет на 54 Дб. И так далее, все последующие октавы будут ослабевать кратно 18 Дб. Менее чувствительный low-pass фильтр первого порядка с частотой среза в 100 Гц будет делать тоже самое, только ненужные октавы будут ослабевать не на 18 Дб, а на 6 Дб.
Как видим, фильтры, из которых состоят кроссоверы, не могут сразу срезать ненужные частоты, а делают это постепенно, с разной чувствительностью в зависимости от своего порядка.
Кроссоверы первого порядка – это простейший пассивный кроссовер, который состоит из одного конденсатора, и одной катушки индуктивности. Конденсатор работает как high-pass фильтр для защиты твитера от ненужных низких и средних частот. Катушка используется как low-pass фильтр. Чувствительность кроссоверов первого порядка низкая – всего 6 Дб на октаву. Положительная черта этих кроссоверов -отсутствие фазового сдвига между твитером и другим динамиком.
Кроссоверы второго порядка. Их также называют кроссоверами Баттерворта, по имени создателяматематической модели этих кроссоверов. Конструктивно они состоят из одного конденсатора и катушки на твитере и одного конденсатора и катушки на низкочастотном динамике. Они обладают более высокой чувствительностью, равной 12 Дб на октаву, но дают фазовый сдвиг в 180 градусов, что означает несинхронный ход мембран твитера и другого динамика. Для устранения этой проблемы небходимо поменять полярность подключения проводов на твитере.
Кроссоверы третьего порядка. У таких кроссоверов на твитере ставится одна катушка и два конденсатора, тогда как на динамике низкой частоты наоборот. Чувствительность таких кроссоверов равна 18 Дб на октаву, и они имеют хорошие фазовые характеристики при любой полярности. Негативная черта кроссоверов III-го порядка – неприемлемость использования временных задержек для устранения проблем, связанных с динамиками не излучающими на одной и той же вертикальной плоскости.
Кроссоверы четвертого порядка. Кроссоверы Баттерворта четвертого порядка имеют высокую чувствительность равную 24 дБ на октаву, что резко уменьшает взаимовлияние динамиков в области разделения частот. Сдвиг по фазе составляет 360 градусов, что фактически означает его отсутствие. Однако величина фазового сдвига в данном случае непостоянна и может привести к неустойчивой работе кроссовера. Эти кроссоверы практически не применяются на практике.
Оптимизировать конструкцию кроссовера четвертого порядка удалось Линквицу и Рили. Данный кроссовер состоит из двух последовательно соединенных кроссоверов Баттерворта второго порядка для твитера, и тоже самое для басового динамика. Чувствительность их также равна 24 дБ на октаву, однако уровень выходного сигнала на каждом фильтре меньше на 6 дБ, чем уровень выходного сигнала кроссовера. Кроссовер Линквица-Рили не имет фазовых сдвигов и позволяет проводить временную коррекцию для динамиков, не работающих в одной физической плоскости. Эти кроссоверы по сравнению с другими конструкциями дают самые лучшие акустические характеристики.
Конструирование пассивных кроссоверов
Как говорилось выше, пассивный кроссовер состоит из конденсаторов и катушек индуктивности. Для того, чтобы собрать пассивный кроссовер первого порядка необходимо иметь один конденсатор и одну катушку индуктивности. Конденсатор устанавливается последовательно на твитер (high-pass filter), а катушка последовательно на вуфер (low-pass filter). Номинальные значения индуктивности для катушки ((H – микрогенри) и емкости ((F – микрофарады) приводятся в таблице в зависимости от желаемой частоты среза кроссовера и сопротивления динамиков.
Кроссовер I порядка (6 dB/octave)
К примеру, подберем емкость и индуктивность для кроссовера с частотой среза 4000 Гц при сопротивлении динамиков 4 Ом. Из вышеприведенной таблицы находим, что емкость конденсатора первого порядка должна быть равной 10 мФ, а индуктивность катушки 0.2 мГ.
Для определения номинальных значений компонентов для кроссовера второго порядка (12 дБ/октава) необходимо значения из этой же таблицы для конденсатора умножить на коэффициент равный 0.7, а значение для катушки индуктивности умножить на коэффициент 1.414. Надо помнить, что для кроссовера второго порядка необходимо два конденсатора и две катушки индуктивности. Составим кроссовер второго порядка для частоты среза 4000 Гц. Для определения значений для обоих конденсаторов умножаем значение из таблицы 10 мФ на коэффициент 0.7 и получим 7мФ. Далее, значение индуктивности 0.2 мГ умножим на коэффицент 1.414 и получим значение индуктивности для каждой катушки 0.28 мГ. Один из этих конденсаторов устанавливается последовательно на твитер, а второй параллельно на вуфер. Одна катушка параллельно на твитер, а вторая последовательно на вуфер.
Пассивные и активные кроссоверы
Отличие между эти двумя типами кроссоверов очень простое. Активный кроссовер требует подвода питания извне, а пассивный – нет. В силу этого активный кроссовер занимает место в звуковой системе до усилителя, обрабатывая звуковой сигнал с предусилителя головного устройства (допустим, автомагнитолы). Далее, после активного кроссовера устанавливаются два или три усилителя мощности. Один усилитель в этом случае не ставится, так как нет смысла разделенные активным кроссовером сигналы сводить в усилителе в единый сигнал. Разделенные сигналы надо усиливать по отдельности. Как видим, активные кроссоверы применяются в дорогих звуковых системах высокого качества.
Пассивные кроссоверы обрабатывают уже усиленный сигнал и устанавливаются перед динамиками. Возможности пассивных кроссоверов ограничены по сравнению с активными, однако их правильное применение может дать хорошие результаты при минимальных финансовых затратах. Пассивные кроссоверы хорошо себя зарекомендовали при требовании к порядку чувствительности менее 18 дБ на октаву. Выше этого предела хорошо работают только активные кроссоверы.
Пассивные кроссоверы в основном применяются для обработки сигнала твитеров и среднечастотных динамиков. Для низкочастотных динамиков эти кроссоверы применять можно, однако резко возрастает требование в качеству конденсаторов и катушек индуктивности, что приводит к их удорожанию и увеличению в размерах. Пассивные кроссоверы плохо переносят перегрузки. Пиковые интенсивности сигнала, поступающие от усилителя, могут менять частоту среза фильтров. Кроме того, перегруженный фильтр ослабляет звуковой сигнал (damping). Поэтому при выборе пассивных кроссоверов обращайте внимание на их способность выдерживать пиковые нагрузки, создаваемые усилителем.
Активные (или электронные) кроссоверы представляют из себя множество активных фильтров, которыми можно управлять и легко изменять частоту среза любого канала. Порядок чувствительности активных кроссоверов может быть любым, от 6 Дб до 72 Дб на октаву (и выше).В основном активные кроссоверы для автомобильных аудиосистем имеют чувствительность 24 Дб на октаву. При такой чувствительности обмен частотами между динамиками практически исключен. Звуковая картина получается очень качественной. Единственный недостаток активных кроссоверов, – это их дороговизна по сравнению с пассивными.
Фазовый сдвиг
Теперь поговорим о фазовых сдвигах, которые могут возникать в звуковых системах, использующих кроссоверы. Фазовый сдвиг – это неизбежное явление, являющееся следствием конструктивных особенностей high-pass, low-pass и band-pass фильтров.
Фаза – это временная связь двух сигналов. Измеряется фаза в градусах от 0 до 360. Если два одинаковых динамика излучают звуковые волны в противоположной фазе (фазовый сдвиг 180 градусов), то происходит ослабление звука. Проблема устраняется изменением полярности на одном из динамиков .
Когда акустическая система состоит их разных динамиков, работающих в различных частотных диапазонах (твитер и мидвуфер), то устранение фазового сдвига не всегда решается простой сменой “+” на “-“. Длина волны от твитера короче, чем от мидвуфера. Поэтому фронт высокочастотной волны может достигнуть слушателя позже (или раньше) фронта среднечастотной (или низкочастотной) волны. Эта временная задержка является следствием фазового сдвига. Оптимизировать звуковую картину в данном случае можно путем физического выравнивания двух динамиков относительно друг друга в вертикальной плоскости до момента улучшения звуковой картины. К примеру, при частоте волны 1000 Гц временная задержка в одну милисекунду устраняется сдвигом динамиков друг относительно друга на 30 см.
Настройка активного кроссовера
Самое важное в настройке кроссовера – это правильный выбор частоты среза. Если мы имеем трехполосный активный кроссовер, то значит перед нами стоит задача в определении двух точек (частот) среза. Первая точка определяет частоту среза для сабвуфера (low-pass) и начало среднечастотного диапазона для мидвуфера (high-pass). Вторая точка определяет частоту окончания среднего диапазона (low-pass) и отправную частоту высокочастотного диапазона для твитера (high-pass). Самое главное, при установке частот среза кроссовера помнить о частотных характеристиках динамика и не в коем случае не нагружать динамик частотами, которые не входят в его рабочий диапазон.
К примеру, если сабвуфер немного гремит или издает гул (неприятный резонанс корпуса автомобиля) значит он перегружен нежелательными для него средними частотами (выше 100 Гц). Перенесите частоту среза (low-pass) на отметку 75 Гц и/или установите, если возможно, чувствительность на 18 Дб или 24 Дб на октаву. Напомним, что увеличение порядка чувствительности кроссовера (величина dB/octave) более качественно срезает ненужные частоты, не давая им просачиваться через фильтр. Порядок чувствительности high-pass фильтров для мидвуфера можно оставить на 12 Дб/октава (для “мягких” среднечастотных динамиков). Подобная настройка активного кроссовера называется асимметричной.
В этой таблице приведены начальные величины частот среза для различных типов динамиков при настройке активных кроссоверов.
Полезные темы:
magnitola.org
Активный фильтр низких частот первого порядка
Активный фильтр низких частот усиливает низкие частоты. Схема простейшего фильтра низких частот представлена на рис.9.3.
Для этого фильтра коэффициент передачи
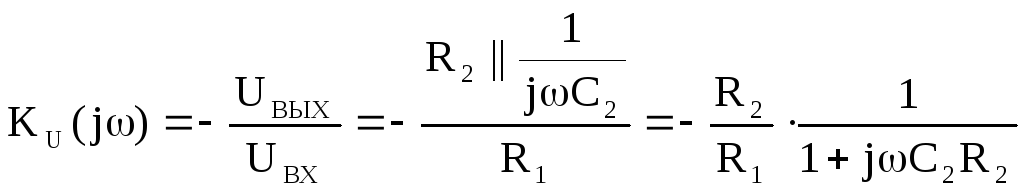. (9.6.)
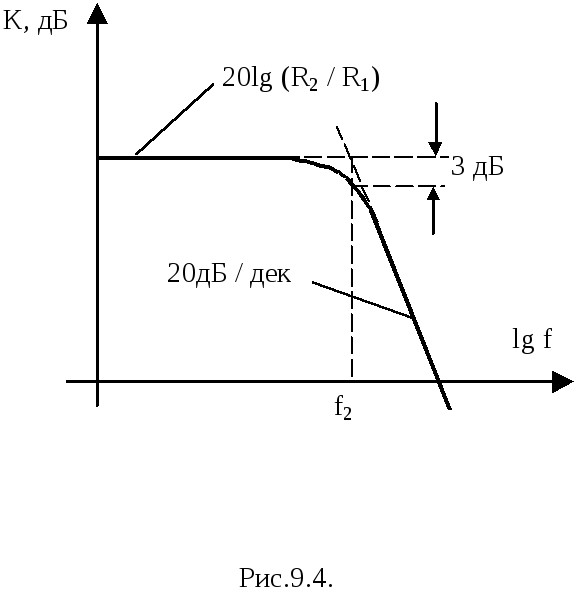
ЛАЧХ данного фильтра приведена на рис.9.4.
Частоту среза находят из условия
2R2C2 = 1,(9.7.)
откуда
. (9.8.)
Частотам f f2 соответствует полоса пропускания
фильтра, а частотамf > f
Полосовой фильтр первого порядка
При объединении фильтров низких и высоких частот получается полосовой фильтр (рис.9.5.), имеющий ЛАЧХ как на рис.9.6. Полосовой фильтр пропускает сигнал в определенной области частот.
Частоты среза
,
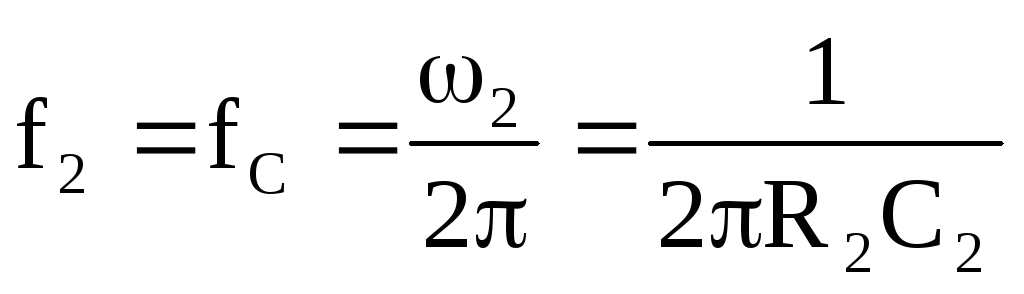. (9.9.)
Полоса пропускания фильтра соответствует диапазону частот f1 f f2.
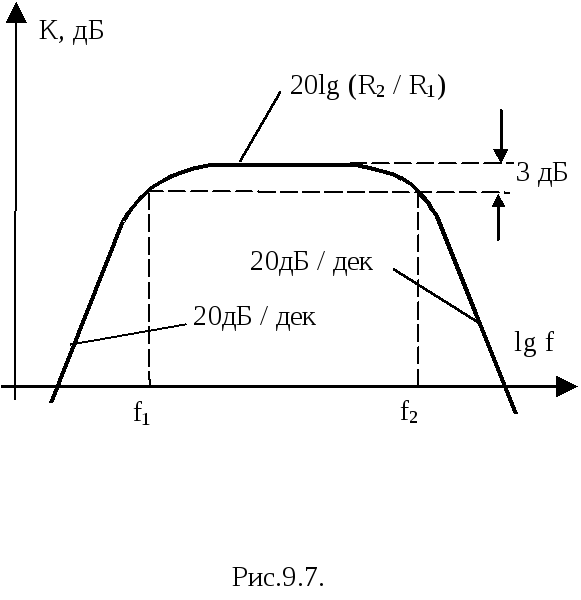
Фильтры второго порядка
Простейшие активные фильтры первого порядка имеют малую крутизну спада ЛАЧХ, что свидетельствует о плохих избирательных свойствах. Чтобы повысить избирательные свойства активного фильтра, нужно увеличить наклон асимптот ЛАЧХ. Для улучшения избирательности нужно повышать порядок передаточных функций за счет введения дополнительных RC-цепочек или последовательного включения идентичных активных фильтров.
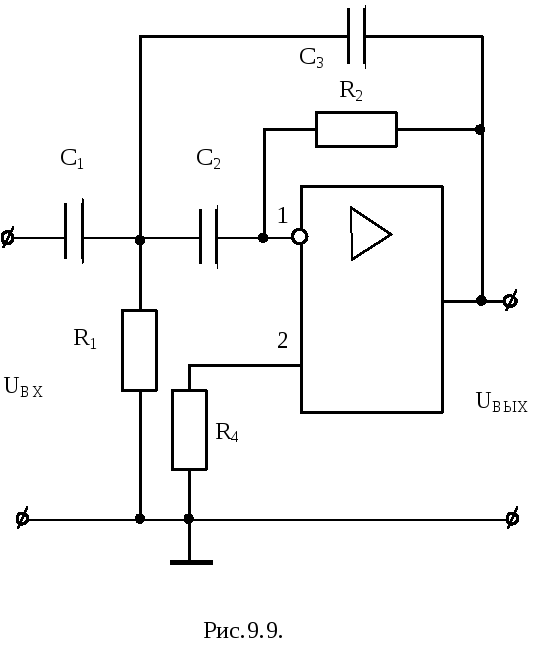
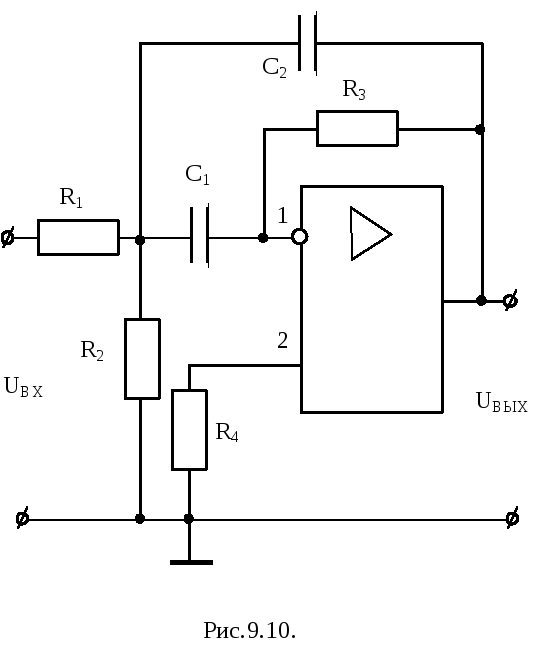
Активные фильтры низких, высоких частот и полосовой фильтр приведены соответственно на рис.9.8, 9.9 и 9.10. При соответствующем подборе резисторов и конденсаторов наклон асимптот у них 40 дБ / дек. Переход от фильтра низких частот к фильтру высоких частот осуществляется заменой резисторов на конденсаторы и наоборот. Полосовой фильтр получают из ФНЧ и ФВЧ.
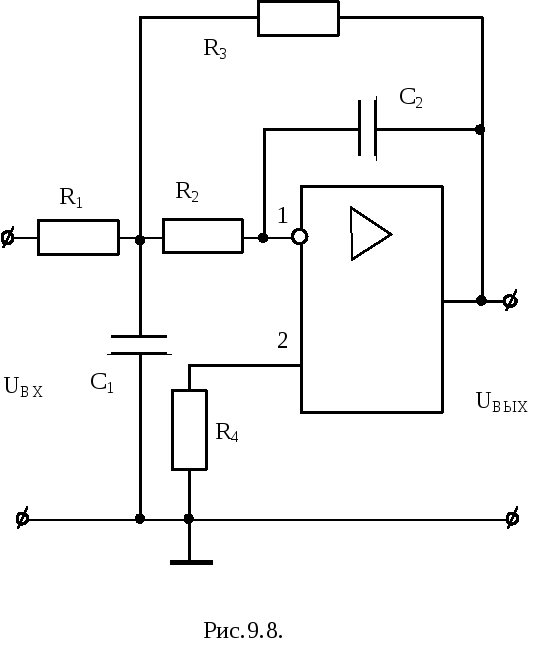
Для фильтра низких частот передаточная функция представляет собой:
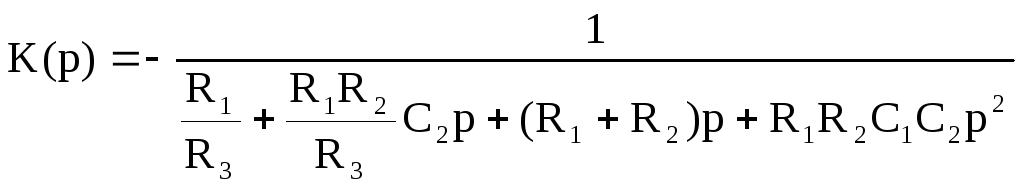
частота сопряжения:
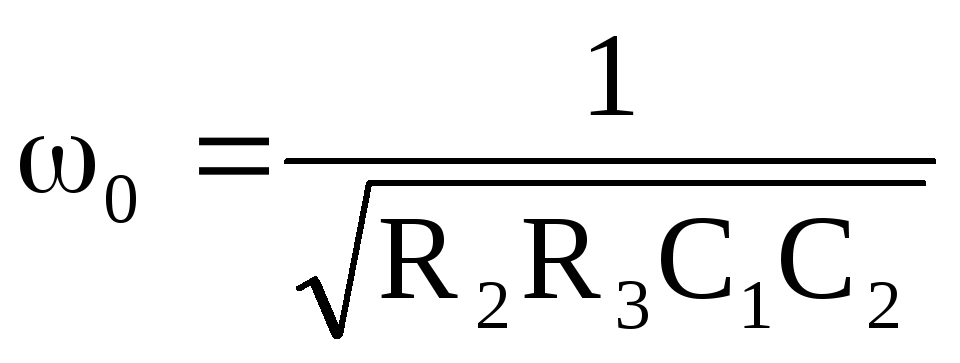. (9.11.)
Для фильтра высоких частот передаточная функция представляет собой:
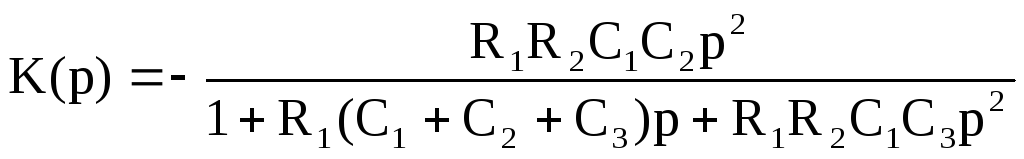, (9.12.)
частота сопряжения:
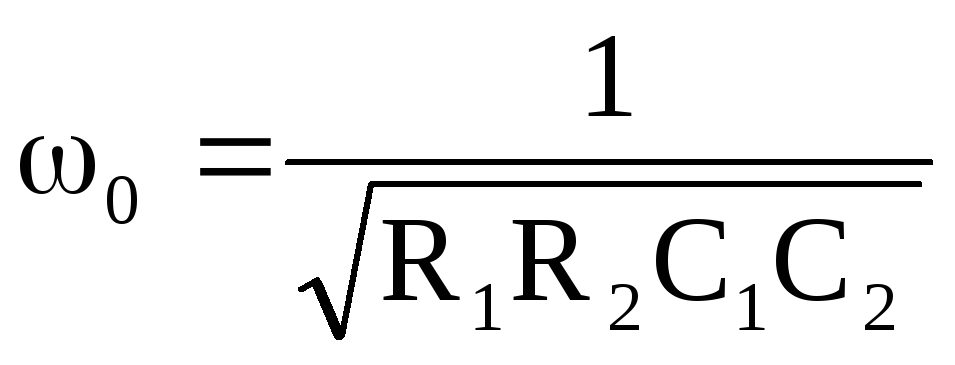. (9.13.)
Для полосового фильтра передаточная функция представляет собой:
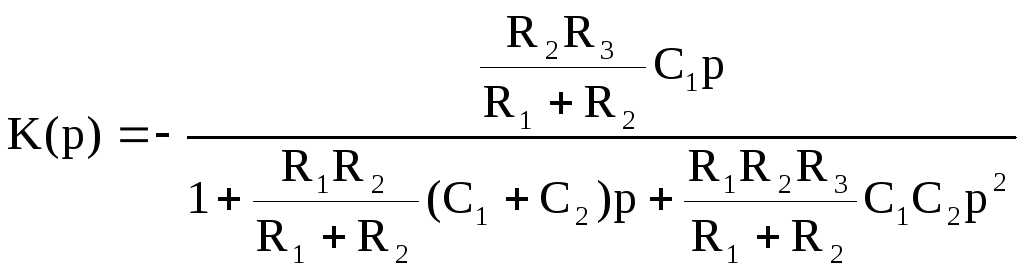, (9.14.)
частота сопряжения:
. (9.15.)
Режекторные фильтры
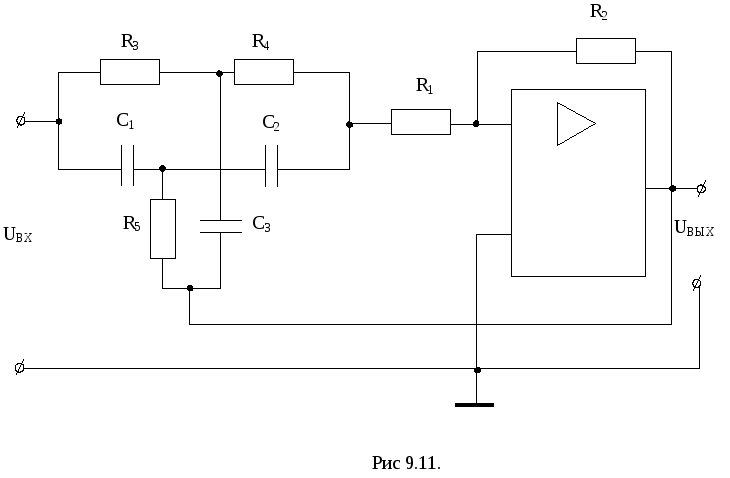
Достаточно часто полосовые фильтры второго порядка реализуют с помощью мостовых цепей. Наиболее распространены двойные Т-образные мосты (которые не пропускают сигнал на резонансной частоте) и мосты Вина (которые на резонансной частоте имеют максимальный коэффициент передачи). Таким образом можно строить режекторные (заграждающие) фильтры, которые не пропускают сигнал в некоторой области частот.
Схема режекторного фильтра с Т-образным мостом представлена на рис.9.11.
35
studfile.net
Фильтр для нч динамика. Пассивный фильтр для низкочастотного динамика своими руками
Трёхполосные акустические системы, состоящие из трёх динамиков, являются самым удачным решением для высококачественного звуковоспроизведения. В них используются три типа звуковых головок. Они отличаются по размеру, конструктивным особенностям и полосе воспроизводимых частот. Для разделения всего частотного диапазона выдаваемого усилителем низкой частоты используются полосовые фильтры-кроссоверы. В них используются конденсаторы дроссели и, реже, резисторы.
Сделать своими руками фильтр для динамика НЧ очень просто.Основным элементом устройства является индуктивность или дроссель. Катушка включается последовательно с низкочастотным динамиком.
Фильтр для низкочастотного динамика
Фильтр нижних частот из дросселя и конденсатора большой ёмкости называется схемой Баттерворта второго порядка. Он обеспечивает спад частот выше частоты среза до 12 dBна октаву. Схема работает следующим образом. Индуктивность в LC контуре выполняет функцию переменного резистора. Его сопротивление прямо пропорционально частоте ивозрастает с увеличением диапазона. Поэтому высокие частоты практически не попадают на НЧ динамик. Такую же функцию выполняет и конденсатор. Его сопротивление обратно пропорционально частоте и он включается параллельно громкоговорителю.
Поскольку схема устройства должна хорошо пропускать низкие частоты и обрезать высокие, то конденсаторы такого устройства имеют большую ёмкость.Пассивный фильтр для динамика может быть выполнен по более сложной схеме. Если соединить две схемы Баттерворта последовательно, то получится устройство четвёртого порядка из двух индуктивностей и двух конденсаторов. Оно обеспечивает спад частотной характеристики низкочастотного громкоговорителя в 24 децибела на октаву.
Для того чтобы выровнять частотную характеристику и более точно согласовать схему Баттерворта и динамик, между катушкой индуктивности и конденсатором, включается резистор с небольшим сопротивлением. Для этой цели лучше использовать проволочные резисторы.
Фильтры для динамиков своими руками
Сделать фильтр для динамика совсем не сложно. Он состоит всего из двух элементов – конденсатора и катушки индуктивности. Рассчитать параметры радиоэлементов для пассивной схемы низкой частоты второго порядка проще всего на онлайн калькуляторе. Там можно задать желаемый уровень среза и сопротивление акустической головки. Программа выдаст требуемую ёмкость конденсатора и индуктивность катушки. Например, выбран уровень среза 150 Гц, а сопротивление динамика равно 4 Ом. Калькулятор выдаст следующие значения:
- Ёмкость конденсатора – 187 мкф
- Индуктивность катушки – 6,003 мГн
Требуемую ёмкость можно получить из параллельно соединённых конденсаторов К78-34, которые специально разработаны для работы в акустических системах. Кроме того есть обновлённая линейка конденсаторов аналогичного типа. Это KZKWhiteLine. В качестве недорогих аналогов, радиолюбители часто используют конденсаторы типа МБГО или МБГП.
Катушка индуктивности на 6 мГн наматывается на оправке диаметром 1 см и длиной 6 см. Поскольку катушка не имеет магнитного сердечника в качестве бобины можно использовать цилиндр из любого материала, на который для удобства намотки, нужно сделать щёчки. Для намотки используется медный провод типа ПЭЛ диаметром 1 мм. Длина проволоки 84 метра. Намотку нужно делать виток к витку.
dinamikservis.ru
ФИЛЬТР ДЛЯ АКУСТИКИ
Тема сведения акустических систем довольно популярна среди радиолюбителей. Этому способствует не только желание созидать, благо динамиков нынче на любой бюджет, но также и неудовлетворительное качестве серийной акустики. Изготовление фильтров требует как правило большого опыта, отчасти эмпирического, так как строгий математический расчет в лице симуляций никак не отражает звучание, и тем более не может дать ответ как сводить. Примерная прикидка не всегда дает ожидаемые результаты.
Виной тому отсутствие внятной теории именно сведения, а не электрических фильтров, с ними все ясно, чего нельзя сказать про сведение, где все базируется на нюансах которые в литературе как правильно не описаны. Цель данной статьи поведать некоторые особенности проектирования фильтров на реальном примере. В этой статье, к величайшему сожалению, не будет полноценного расчета или инструкции как брать и делать, ибо каждый случай уникален и требует персонального рассмотрения, и в лучшем случае можно указать на что обратить внимание и задать вектор размышлений в целом.
Важные характеристики АС
Для начала разберёмся чем характеризуется акустическая система. Тут три характеристики: амплитудная, фазовая и импедансная.
- АЧХ считается наиболее важной, так как больше определяет звучание, впрочем не в ней счастье, ровная АЧХ еще не гарантия хорошего звука.
- ФЧХ сама о себе не слышна, может быть слышен резкий перегиб фазы в точке раздела.
- ИЧХ вовсе на звучание не влияет, зато влияет на усилитель, но не на каждый, а лишь на тот у которого высокое внутреннее сопротивление, в частности ламповые.
Из-за кривого импеданса многие колонки могут не спеться с лампой, вся неровность импеданса вылезет в АЧХ. В каком-то случае это может пойти на пользу, но надеяться на это не стоит, хотя бы потому, что такая акустика будет крайне чувствительна к усилителю, станут слышны лампы, их режимы, а сравнение с каменным усилителем становится вообще не корректным.
Потому, если задаться цель построить акустику мало чувствительную к усилителю, необходимо обеспечить постоянство импеданса во всем диапазоне частот, а это накладывает определенные ограничения. В частности это обязывает применять фильтра настроеные на равную частоту среза и имеющие равную добротность.
Это правило позволяет для настройки фильтра контролировать только линейность импеданса, что исключает необходимость измерения АЧХ фильтров и в случаи отсутствия хорошего микрофона в измерении ачх динамиков, то есть можно обойтись минимальным набором приборов: генератором (возможно программным) и вольтметром.
Практическая работа
Плавно переходим от теории к практике. Достались мне винтажные колонки под названием Kompaktbox B 9251. И первое что было сделано – произведено прослушивание.
С холодным камнем звук был в среднем не плох, а если говорить конкретно, то местами хороший, а местами как попало. С теплой лампой играть вообще отказались. На основе этих наблюдений был сделан вывод о наличии глубоко зарытого потенциала. Вскрытие показало, что немецкие инженеры решили обойтись одним единственным конденсатором последовательно с ВЧ головкой. Измерение АЧХ дало страшную картину. На рисунке АЧХ одной колонки, кривая с глубокой дыркой на 6 кгц из-за плохого контакта разъема, на нее внимание не обращать. АЧХ отдельно ВЧ и НЧ приведены ниже.
Частота раздела
Тут самое время задуматься о частоте раздела. Обычно частота раздела выбирается на ровных горизонтальных участках, вдали от резонансов и завалов, стараясь обойти внезапные неравномерности как потенциальные источники искажений… А если вспомнить что существует фаза, о которой мало известно, а если известно, то векторно ачх на бумажке не сложишь, а из-за кривизны фаз даже на идеально ровной ачх что-то вылезет, что-то провалится в большей или меньшей степени. Также надо помнить что может дать сам динамик, особенно ВЧ, скажем не надо заставлять дюймовый купольник играть от двух, а тем более одного килогерца, даже если он способен их отыграть по АЧХ.
Не забывайте, что большой ход порождает интермодуляционные искажения, поэтому каждому размеру динамика соответствует свой диапазон частот. В свете вышесказанного понятие частоты раздела размазывается на область, куда стоить сводить, а конечную точку подбирать иначе, например на слух. Или вовсе не подбирать, но про это чуть позже.
Итак, смотрим какие уникальные динамики нам достались. Высокочастотник начинает валить с 1,3 кгц, значит ниже его пускать нельзя. С другой стороны низкочастотник пытается играть по самые 10 кгц, с переменным успехом. Однако здравый смысл подсказывает, что выше килогерца его пускать плохая затея. И что спрашивается делать, если рабочие диапазоны динамиков не пересекаются?
Тут есть два варианта: если спады имеют адекватную крутизну, то лучше всего сводить в ямку, особенно если ямка получается широкой. В случае же нашем, когда спады круты как обрывы, надо держатся подальше от самого крутого из них. Чаще всего это может случится с высокочастотником, им всегда тяжко работать у нижней границы диапазона, поэтому им целесообразнее облегчить жизнь возлагая воспроизведение нижней части диапазона на НЧ динамик, который отыграет хоть плохо, но не нагадит. Поэтому ограничиваем диапазон участком от 1,5 кгц до 2,2 кгц.
Порядок фильтра и его добротность
Следующий параметр, с которым надо определиться – это порядок фильтра и его добротность. В данной статье будут рассматриваться два порядка, первый и второй.
- С первым все просто: есть катушка, есть конденсатор, считаем их параметры под требуемую частоту среза и при надобности корректируем значения до получения желаемой АЧХ, ФЧХ, ИЧХ.
- Со вторым порядком по-хитрее, там уже две катушки и два конденсатора. От значений номиналов зависит такой параметр как добротность, он определяет крутизну спада АЧХ и в некоторой степени сдвиг фазы. Поскольку влияние фазового сдвига и крутизны умозрительно не прикинешь, остается просто выбрать в какую сторону думать. А думать тут в сторону низкой добротности, читай больше индуктивности в катушках, меньше емкости в конденсаторах.
Как выбрать порядок. Тут руководствуются уже знакомыми соображениями о том, на что способны излучатели, в особенности высокочастотник. Если большой ход ему противопоказан (как в нашем случае) то предпочтение отдаем второму порядку.
Для полноты картины следует упомянуть, что порядок также определяет степень совместной работы динамиков, но это уже информация для самостоятельного размышления.
Импедансная характеристика динамиков
Когда с примерными параметрами все более или менее ясно, самое время переходить к практике. Снимаем импедансную характеристику динамиков. С целью оценки сопротивления на графике имеется лесенка с шагом в один Ом. Скачек на 110 герцах это переключение с 10 Ом на 20.
Разумеется с такими горбами ни один фильтр нормально, и уж тем более расчетно работать не будет, особенно фильтр НЧ. Фильтру ВЧ этот подъем работать в общем то не мешает, однако как упоминалось ранее такой подъем на конце диапазона приведет к подъему высоких частот, в случае если усилитель имеет высокое сопротивление. Это можно использовать и во благо, оставив подъем небольшим.
Для выравнивания этих подъемов применяют так называемую цепочку Цобеля. Она состоит из последовательно включенных резистора и конденсатора. Проще всего ее подобрать методом научного тыка: берется реостат, горсть конденсаторов, и все это двигается пока не получится ровная линия.
Для примерного представления что от чего зависит привожу набор графиков для различных емкостей и сопротивлений. Ступенька начинается с 10 Ом.
Зная минимальное сопротивление НЧ звена, нужно привести к такому же и ВЧ звено. Тут много вариантов как соединить два резистора и цепочку Цобеля, и каждый кто решился на такой отважный шаг как сведение сам способен определить вид подключения и номиналы резисторов, поэтому описывать данную процедуру здесь излишне. Конкретно в данных колонках по результатам предварительного прослушивания решено было оставить родные резисторы на 2,2 ома и цепочку Цобеля параллельно ВЧ динамику.
Сведение фильтров
Теперь начинается финальный этап – сведение фильтров. Пора намотать катушки… или не намотать? Мотать всегда лень, нет провода, каркасов, конкретных значений индуктивности. В виду этих причин поискав в хламе нашлись пары катушек на 0,8 мкг и 3 мкг – на них и пришлось строить. В крайнем случаи всегда же можно домотать или отмотать лишнее.
По графику видно, что раздел попал в район 1,8 кгц, что вполне вписывается в задуманные границы. Подбором конденсаторов удалось добиться следующего импеданса. На частоте раздела имеется два бугорка, но их высота меньше полу ома – это не критично. Это не конечный его вид, в последствии был несколько увеличен резистор в цепочке Цобеля пищалки.
На приведенных выше картинках АЧХ как самого фильтра, так и АЧХ динамиков с его включением.
Фазировка динамиков
На этом сведение подходит в концу. Остается только определиться с фазировкой динамиков. Тут есть как минимум три способа: на слух, по форме АЧХ и по фазовому сдвигу на частоте раздела. Если у динамиков АЧХ и ФЧХ в меру линейная, и фильтр фазу на разделе сильно не накручивает, то при смене правильной фазы на неправильную на частоте раздела появится глубокий провал, пропустить его сложно. В таком случае стоит подгонять фазу по по ее сдвигу. Сделать это можно осциллографом подавая на горизонтальную развертку сигнал с усилителя, а на вертикальное отклонение с микрофона.
Подают на вход усилителя синус с частотой раздела и не меняя взаимного расположения микрофона и колонки переключают ВЧ и НЧ динамики. По одинаковости фигур Лиссажу делается вывод о равенстве фаз излучателей. Этот метод хорошо подходит для фильтров первого порядка. С кривизной наших динамиков этот метод себя не оправдывает, поэтому сравниваем АЧХ при разной фазировке.
Второй вариант заметно хуже. Однако и первый не предел мечтаний, но так как двигать индуктивности катушек не просто, а ковыряться дальше уже лень, то все было оставлено как есть.
Сборка фильтров
В завершение пару слов про сборку. В фильтре применяются сравнительно большие емкости, 20 мкф, 27 мкф, а места в корпусе и так не много, бумаги или пленки не набрать. Приходится ставить электролиты. И если в фильтре НЧ звучание от их применения пострадает не сильно, а в цобеле их можно и вовсе не услышать, то в фильтре ВЧ звучанием конденсаторов пренебрегать опасно. Именно по этой причини были применены бумажный МБГЧ и пленочный К73-16, а все электролиты зашунтированы бумажными МБГО на 4 мкФ.
Не стоит увлекаться параллеленьем сильно разных конденсаторов. Основной критерий здесь тангенс угла потерь. Если к примеру поставить в шунт к бумажному конденсатору аудиофильский полипропилен, то скорее всего вылезут верха и будут они кислотные. Вероятно тут можно составить аналогию с внутренним сопротивлением, сравнив с ним тангенс угла потерь: чем он меньше, тем больше через конденсатор пройдет сигнала, а поскольку емкость у такого высококачественного конденсатора меньше, то через него пройдет только высокочастотная часть сигнала, отсюда и имеем повышенные уровень верхов. Но это только аналогия, для лучшего понимания влияния шунтов на звук.
Про то как надо разносить катушки и какой толщины применять провода статей написано предостаточно, повторяться здесь не буду. Проще показать картинку (тут неправильно припаян цобель высокочастотника, он должен стоять после резистора).
Звучание системы
И конечно же надо сказать про звук. Стало лучше, сцена получилась очень недурственная. Кривизна АЧХ особо не слышна, даже наоборот, подъем на середине поддает детальности, верхов как ни странно хватает. Был замечен интересный эффект на басу. Как можно заметить по АЧХ на сотне герц большой подъем, а за ним завал, разумеется качающего баса нет, но есть мид бас. К примеру партия гитары кажется немного просаженным, а нижний бас, партия бас гитары, переходит как бы в слышимую область и читается очень четко, создается впечатление наличия того самого низкого баса.
Конечно ящики маловаты, и порой слышно подбубнивание, для устранения этого эффекта в каждую колонку было добавлено по 30 грамм натуральней шерсти. В целом данная акустика играет тепло и мягко даже без лампового усилителя, сохраняя в звуке строгость и точность камня, а вот с теплой лампой получается перебор мягкости. Все же им нужен усилитель по-строже – триод или двухтакт, но это тема для следующих экспериментов. Специально для сайта Радиосхемы – SecreTUseR.
Форум по аудио
Обсудить статью ФИЛЬТР ДЛЯ АКУСТИКИ
radioskot.ru
Фильтры. Вновь. По порядку… | журнал АвтоЗвук
Профессиональный рецепт Огюста Родена наилучшим образом подходит для нашей темы. А тема была давно обещана читателям. Вновь (поскольку «вспомнить всё») разобраться с электрическими фильтрами во всех формах, в которых они применяются в нашей узкой отрасли.
…взять глыбу мрамора и отсечь от нее всё лишнее…
Огюст Роден
Любой фильтр, в сущности, делает со спектром сигнала то же, что Роден с мрамором. Но в отличие от творчества скульптора замысел принадлежит не фильтру, а нам с вами.
Нам с вами по понятным причинам больше всего знакома одна сфера применения фильтров — разделение спектра звуковых сигналов для последующего воспроизведения их динамическими головками (нередко мы говорим «динамиками», но сегодня материал серьёзный, поэтому к терминам будем тоже подходить со всей строгостью). Но эта область использования фильтров, наверное, всё же не основная и совершенно точно, что не первая в историческом плане. Не будем забывать, что электроника когда-то называлась радиоэлектроникой, и первоначальной её задачей было обслуживание нужд радиопередачи и радиоприёма. И даже в те детские годы радио, когда сигналы сплошного спектра не передавались, а радиовещание ещё называлось радиотелеграфией, возникла потребность повышения помехозащищённости канала, и решена эта задача была за счёт использования фильтров в приёмных устройствах. На передающей стороне фильтры применялись для ограничения спектра модулированного сигнала, чем также удалось повысить надёжность передачи. В конце концов, краеугольный камень всей радиотехники тех времён, резонансный контур — не что иное, как частный случай полосового фильтра. Поэтому можно сказать, что вся радиотехника началась с фильтра.
Конечно, первые фильтры были пассивными, состояли они из катушек и конденсаторов, а с помощью резисторов удавалось получить нормированные характеристики. Но все они обладали общим недостатком — их характеристики зависели от импеданса той цепи, которая стоит за ними, то есть цепи нагрузки. В простейших случаях импеданс нагрузки можно было поддерживать достаточно высоким, чтобы этим влиянием можно было пренебречь, в других случаях взаимодействие фильтра и нагрузки приходилось учитывать (между прочим, расчёты зачастую велись даже без логарифмической линейки, просто в столбик). Избавиться от влияния импеданса нагрузки, этого проклятия пассивных фильтров, удалось с появлением активных фильтров.
Изначально предполагалось посвятить этот материал целиком и полностью пассивным фильтрам, их в практике инсталляторов приходится рассчитывать и изготавливать своими силами несравнимо чаще, чем активные. Но логика потребовала, чтобы мы всё же начали с активных. Как ни странно, потому что они проще, что бы ни казалось при первом взгляде на приводимые иллюстрации.
Хочу быть понятым верно: сведения об активных фильтрах не призваны служить исключительно руководством по их изготовлению, такая надобность появляется далеко не всегда. Гораздо чаще возникает нужда понять, как работают уже имеющиеся фильтры (главным образом — в составе усилителей) и почему они не всегда работают так, как нам бы хотелось. И здесь, действительно, может прийти мысль о ручной работе.
Принципиальные схемы активных фильтров
В простейшем случае активный фильтр представляет собой пассивный фильтр, нагруженный на элемент с единичным коэффициентом передачи и высоким входным импедансом — либо на эмиттерный повторитель, либо на операционный усилитель, работающий в режиме повторителя, то есть с единичным усилением. (Можно реализовать и катодный повторитель на лампе, но ламп я, с вашего позволения, касаться не буду, если кому интересно — обратитесь к соответствующей литературе). По идее, не возбраняется таким способом построить активный фильтр любого порядка. Поскольку токи во входных цепях повторителя очень малы, то, казалось бы, элементы фильтра могут быть выбраны очень компактными. Все ли? Представьте себе, что нагрузкой фильтра является резистор 100 Ом, вы хотите сделать фильтр НЧ первого порядка, состоящий из единственной катушки, на частоту 100 Гц. Каков должен быть номинал катушки? Ответ: 159 мГн. Какая уж тут компактность. И главное, что омическое сопротивление такой катушки может оказаться вполне сравнимым с нагрузкой (100 Ом). Поэтому о катушках индуктивности в схемах активных фильтров пришлось забыть, другого выхода просто не было.
Для фильтров первого порядка (рис. 1) я приведу два варианта схемной реализации активных фильтров — с ОУ и с эмиттерным повторителем на транзисторе n-p-n типа, а вы уж сами при случае выберете, с чем вам проще будет работать. Почему n-p-n? Потому, что их больше, и потому, что при прочих равных условиях в производстве они получаются несколько «лучше». Моделирование проводилось для транзистора КТ315Г — единственного, наверное, полупроводникового прибора, цена на который до последнего времени была точно такая же, как и четверть века назад — 40 копеек. Фактически вы можете использовать любой n-p-n транзистор, коэффициент усиления которого (h31э) не намного ниже 100.
Рис. 1. Фильтры ВЧ первого порядка
Резистор в цепи эмиттера (R1 на рис. 1) задаёт ток коллектора, для большинства транзисторов его рекомендуют выбирать примерно равным 1 мА или немного меньше. Частоту среза фильтра определяет ёмкость входного конденсатора C2 и общее сопротивление параллельно включённых резисторов R2 и R3. В нашем случае это сопротивление составляет 105 кОм. Надо только следить, чтобы оно было значительно меньше, нежели сопротивление в цепи эмиттера (R1), умноженное на показатель h31э — в нашем случае это примерно 1200 кОм (в действительности при разбросе значений h31э от 50 до 250 — от 600 кОм до 4 МОм). Выходной конденсатор добавлен, что называется, «для порядка» — если нагрузкой фильтра будет входной каскад усилителя, там, как правило, уже стоит конденсатор для развязки входа по постоянному напряжению.
В схеме фильтра на ОУ здесь (как и в последующем) использована модель TL082C, поскольку этот операционный усилитель очень часто применяется для построения фильтров. Впрочем, можно брать едва ли не любой ОУ из тех, что нормально работают с однополярным питанием, предпочтительнее с входом на полевых транзисторах. Здесь также частота среза определяется соотношением ёмкости входного конденсатора C2 и сопротивлением параллельно включённых резисторов R3, R4. (Почему параллельно включённых? Потому, что с точки зрения переменного тока плюс питания и минус — одно и то же.) Соотношение резисторов R3, R4 определяет среднюю точку, если они будут немного различаться, это не трагедия, это лишь означает, что сигнал максимальной амплитуды начнёт ограничиваться с одной стороны несколько раньше. Фильтр рассчитан на частоту среза 100 Гц. Чтобы её понизить, надо увеличить либо номинал резисторов R3, R4, либо емкость C2. То есть номинал изменяется обратно пропорционально первой степени частоты.
В схемах фильтра НЧ (рис. 2) на пару деталей больше, поскольку входной делитель напряжения не используется как элемент частотно-зависимой цепи и добавляется разделительная ёмкость. Для понижения частоты среза фильтра надо увеличивать входной резистор (R5).
Рис. 2. Фильтры НЧ первого порядка
Разделительная ёмкость имеет нешуточный номинал, так что без электролита обойтись будет трудно (хотя можно ограничиться плёночным конденсатором 4,7 мкФ). Следует учитывать, что разделительная ёмкость совместно с C2 образуют делитель, и чем она меньше, тем выше ослабление сигнала. Как следствие, несколько смещается и частота среза. В некоторых случаях можно обойтись без разделительного конденсатора — если, к примеру, источником является выход другого каскада фильтра. А вообще стремление избавиться от громоздких разделительных конденсаторов и явилось, наверное, основной причиной перехода от однополярного питания к двухполярному.
На рис. 3 и 4 показаны частотные характеристики фильтров ВЧ и НЧ, схемы которых мы только что рассмотрели.
Рис. 3. Характеристики фильтров ВЧ первого порядка
Рис. 4. Характеристики фильтров НЧ первого порядка
Весьма вероятно, что у вас уже возникли два вопроса. Первый: а что это мы так плотно занялись изучением фильтров первого порядка, когда для сабвуферов они не годятся вовсе, да и для разделения полос фронтальной акустики, если верить высказываниям автора, они применимы, мягко говоря, не часто? И второй: а почему автор не упомянул ни Баттерворта, ни его однофамильцев — Линквица, Бесселя, Чебышева, в конце концов? На первый вопрос я пока отвечать не буду, чуть позже вам всё станет ясно. Сразу перехожу ко второму. Баттервортом со товарищи были определены характеристики фильтров от второго порядка и выше, а частотная и фазовая характеристика фильтров первого порядка всегда одна и та же.
Итак, фильтры второго порядка, с номинальной крутизной спада 12 дБ/окт. Такие фильтры повсеместно делаются с использованием ОУ. Можно, конечно, обойтись и транзисторами, но для того, чтобы схема работала точно, приходится учитывать много всего, и в результате простота оказывается чисто мнимой. Известно энное количество вариантов схемной реализации таких фильтров. Я даже не скажу какое, поскольку любое перечисление всегда может оказаться неполным. Да и нам оно мало что даст, поскольку по-настоящему углубляться в теорию активных фильтров нам вряд ли имеет смысл. Тем более что в построении фильтров усилителей участвуют по большей части лишь две схемные реализации, можно даже сказать, что полторы. Начнём с той, которая «целая». Это так называемый фильтр Саллена — Ки (Sallen — Key).
Рис. 5. Фильтр ВЧ второго порядка
Здесь, как и всегда, частота среза определяется номиналами конденсаторов и резисторов, в данном случае — C1, C2, R3, R4, R5. Обратите внимание, для фильтра Баттерворта (ну наконец-то!) номинал резистора в цепи обратной связи (R5) должен быть вдвое меньше номинала резистора, включённого в «землю». Как обычно, в «землю» получаются включенными резисторы R3 и R4 параллельно, и суммарный номинал их 50 кОм.
Теперь несколько слов как бы в сторону. Если у вас фильтр не перестраиваемый, проблем с подбором резисторов не будет. Но если вам надо плавно менять частоту среза фильтра, нужно одновременно изменять два резистора (у нас их три, но в усилителях питание двухполярное, и там один резистор R3, номинала такого же, как наши два R3, R4, включённые параллельно). Специально для таких целей выпускаются сдвоенные переменные резисторы разного номинала, но они и дороже, и не так их много. Кроме того, можно разработать фильтр с очень близкими характеристиками, но у которого оба резистора будут одинаковыми, а ёмкости C1 и C2 — разными. Но это хлопотно. А теперь давайте посмотрим, что будет, если взять фильтр, рассчитанный на среднюю частоту (330 Гц) и начать менять лишь один резистор — тот, который в «землю». (Рис. 6).
Рис. 6. Перестройка фильтра ВЧ
Согласитесь, нечто подобное мы многократно видели на графиках в тестах усилителей.
Схема фильтра НЧ похожа на зеркальное отображение фильтра ВЧ: в обратной связи стоит конденсатор, а в горизонтальной полке буквы «Т» — резисторы. (Рис. 7).
Рис. 7. Фильтр НЧ второго порядка
Как и в случае с фильтром НЧ первого порядка, добавляется разделительный конденсатор (C3). Величина резисторов в цепи создания локальной «земли» (R3, R4) влияет на величину затухания, вносимого фильтром. При указанном на схеме номинале аттенюация около 1,3 дБ, думаю, с этим можно мириться. Как всегда, частота среза обратно пропорциональна номиналу резисторов (R5, R6). Для фильтра Баттерворта номинал конденсатора в обратной связи (C2) должен быть вдвое больше, чем ёмкость C1. Поскольку номинал резисторов R5, R6 один и тот же, для плавной перестройки частоты среза подходит почти любой сдвоенный подстроечный резистор — именно поэтому во многих усилителях характеристики фильтров НЧ более стабильны, нежели характеристики фильтров ВЧ.
На рис. 8 показаны амплитудно-частотные характеристики фильтров второго порядка.
Рис. 8. Характеристики фильтров второго порядка
Вот теперь можно вернуться к тому вопросу, который остался без ответа. Схему фильтра первого порядка мы «проходили» потому, что активные фильтры создаются в основном путём каскадирования базовых звеньев. Так что последовательное соединение фильтров первого и второго порядка даст третий порядок, цепочка из двух фильтров второго порядка даст четвёртый и так далее. Поэтому я приведу лишь два варианта схем: фильтр ВЧ третьего порядка и фильтр НЧ — четвёртого. Тип характеристики — Баттерворт, частота среза — те же 100 Гц. (Рис. 9).
Рис. 9. Фильтр ВЧ третьего порядка
Предвижу вопрос: отчего вдруг изменились номиналы резисторов R3, R4, R5? А отчего бы им не измениться? Если в каждой «половинке» схемы уровню -3 дБ соответствовала частота 100 Гц, значит, совместное действие обеих частей схемы приведёт к тому, что спад на частоте 100 Гц составит уже 6 дБ. А мы так не договаривались. Так что самое привести методику выбора номиналов — пока только для фильтров Баттерворта.
1. По известной частоте среза фильтра задаться одним из характерных номиналов (R или C) и вычислить второй номинал, используя зависимость:
Fc = 1/(2πRC) (1.1)
Поскольку ассортимент номиналов конденсаторов, как правило, более узкий, разумнее всего задаться базовым значением ёмкости C (в фарадах), а по нему определить базовое значение R (Ом). Но если у вас, к примеру, есть пара конденсаторов 22 nF и несколько штук на 47 nF, никто не мешает вам брать и те, и эти — но в разных частях фильтра, если он составной.
2. Для фильтра первого порядка формула (1.1) даёт сразу значение резистора. (В нашем конкретном случае получаем 72,4 кОм, округляем до ближайшего стандартного значения, получаем 75 кОм.) Для базового фильтра второго порядка вы точно так же определяете стартовое значение R, но для того, чтобы получить действительные значения резисторов, надо будет воспользоваться таблицей. Тогда номинал резистора в цепи обратной связи определится как
Rp = KpR (1.2)
а номинал резистора, идущего в «землю», будет равен
Rs = KsR (1.3)
| Порядок фильтра | Kp | Ks |
| 2 | 0,7070 | 1,414 |
| 3 | 0,5000 | 2,000 |
| 4 (1) | 0,3827 | 2,613 |
| 4 (2) | 0,9240 | 1,082 |
Единичкой и двойкой в скобках обозначены строки, относящиеся к первому и второму каскадам фильтра четвёртого порядка. Можете проверить: произведение двух коэффициентов в одной строке равно единице — это, действительно, обратные величины. Впрочем, мы договорились в теорию фильтров не лезть.
Расчёт номиналов определяющих компонентов фильтра НЧ осуществляется сходным образом и по той же таблице. С той только разницей, что в общем случае вам придётся танцевать от удобного номинала резистора, а номиналы конденсаторов подбирать по таблице. Конденсатор в цепи обратной связи определится как
Cp = KsC, (1.4)
а конденсатор, соединяющий вход ОУ с «землёй», как
Cs = KpC (1.5)
Пользуясь вновь приобретёнными знаниями, рисуем фильтр НЧ четвёртого порядка, который уже вполне можно применить для работы с сабвуфером (рис. 10). На схеме я на этот раз привожу расчётные значения емкостей, без округления до стандартного номинала. Это чтобы вы могли себя проверить при желании.
Рис. 10. Фильтр НЧ четвёртого порядка
Я до сих пор ни слова не сказал о фазовых характеристиках, и правильно сделал — вопрос этот отдельный, отдельно им и займёмся. В следующий раз, вы же поняли, мы только начинаем…
Рис. 11. Характеристики фильтров третьего и четвёртого порядка
www.xn--80aeatqv1al.xn--p1ai
Практическое применение операционных усилителей.Часть вторая.
РадиоКот >Статьи >Практическое применение операционных усилителей.Часть вторая.
Итак, в первой части мы рассмотрели схемы включения ОУ в качестве усилителей, в этой части рассмотрим включения ОУ в качестве фильтров.
Фильтр Высоких Частот (ФВЧ, High-Pass – как угодно)
Требуется он для отсекания сигнала, частота которого ниже определенного порога, который называется, кстати, частотой среза.
Простейший ФВЧ выглядит так:
Первая схема с неинвертирующим включением ОУ, вторая – с инвертирующим.
Это фильтр первого порядка с ослаблением ненужного сигнала – крутизной – 6дБ на октаву. Определить частоту среза можно, рассчитывая реактивное сопротивление конденсатора. Когда оно станет равным сопротивлению резистора, включенного последовательно с конденсатором – это будет самое то.
Формула следующая:
Где F – частота в Герцах, C – емкость в Фарадах, Ec – сопротивление в Омах.
Если крутизна фильтра первого порядка кажется недостаточной, можно справить фильтр второго порядка – с крутизной 12 дБ на октаву как показано на рисунке.
Это – так называемый, фильтр Баттерворта. Назван так, в честь товарища Баттерворта, который изобрел много чего математического, в том числе функции полиномиального вида, которыми впоследствии физики описали АЧХ и прочие физические проявления природы. (Спасибо Оля-ля за уточнение личности гражданина Баттерворта.)
Чтобы посчитать его граничную частоту можно воспользоваться следующими соотношениями:
R1=R2; С1=2С2;
При выборе резисторов надо учесть, что их номиналы должны лежать в пределах 10-100 кОм, поскольку выходное сопротивление фильтра растет вместе с частотой и если номиналы резисторов выходят за вышеуказанные рамки это может сказаться на работе фильтра. Отрицательно, разумеется – иначе зачем предупреждать?
Фильтр Низких Частот (ФНЧ, Low-Pass – как угодно)
Работа этого фильтра прямо противоположна предыдущему – он отрезает сигнал, частота которого выше частоты среза.
В принципе, все то же самое, что и в предыдущем случае, только конденсатор включается не последовательно с резистором, а параллельно ему.
Первая схема – неинвертирующее включение, вторая – инвертирующее. Частота среза считается ровно таким же способом, как и в случае ФВЧ.
Ну и схема фильтра второго порядка – того же самого гражданина Баттерворта.
Опять же – считается все точно так же, как было описано выше.
Полосовой Фильтр (Band-Pass)
Полосовой фильтр применяется в тех случаях, когда необходимо выделить некую полосу частот из всего спектра. Например, в спектроанализаторах или вроде того.
Формулы расчета приводить тут не буду – дюже они забористые. Для расчета полосовых фильтром советую воспользоваться замечательной программой – Filter Wiz Pro от Schematica Software. Впрочем, ей так же можно воспользоваться и для расчетов любых других фильтров.
Фильтр-пробка (Notch Filter)
Если вам нужно ослабить (практически до нуля) некую выбранную частоту, то это фильтр как раз для вас.
Формула расчета вот такая:
где R=R3=R4, C=C1=C2;
При построении этого фильтра очень важна точность номиналов компонентов – от этого зависит степень “убивания” выбранной частоты. Так, при применении резисторов и конденсаторов с допуском 1%, можно получить ослабление частоты до 45дБ, хотя, теоретически, можно добиться и 60дБ.
Например, если вы хотите грохнуть ненавистную всем частоту 50Гц, то берем следующие номиналы: R1=R2=10кОм, R3=R4=68кОм, С1=С2=47нФ.
Фильтр-пробка с двойным Т-мостом.
С помощью этого фильтра можно не только ослаблять выбранную частот, но и регулировать степень её ослабления переменным резистором R4. Формула расчета номиналов такая же, как и в предыдущем случае.
С фильтрами все, в следующей части еще кое-что интересное.
Вопросы, как обычно, складываем тут.
Как вам эта статья? | Заработало ли это устройство у вас? |
www.radiokot.ru
