Фильтрация сигналов: Фильтрация сигналов

Фильтрация сигналов ZETLAB, описание, характеристики

Блок-схема

программы фильтрация сигналов

Любой из элементов блок-схемы может быть включен или отключен. Фильтры можно подключать последовательно друг за другом.

Интерфейс

программы фильтрация сигналов

Результат работы фильтров, запущенны при помощи программы Фильтрация сигналов можно увидеть при помощи программы Многоканальный осциллограф. На верхней осциллограмме представлена временная реализация исходного сигнала, на нижней – результат работы функций двойного интегрирования и ФВЧ программы Фильтрация сигналов. В рассмотренном примере обрабатывался сигнал с акселерометра, установленного на неподвижном корпусе балансируемого изделия. Двойное интегрирование применено для получения сигнала перемещения из сигнала ускорения, ФВЧ — для компенсации смещения постоянной составляющей полученного сигнала.

Программа фильтрации создает дополнительные виртуальные каналы, в которых и производится обработка сигналов. Все сигналы – реальные и виртуальные – имеют внутреннюю синхронизацию, что позволяет проводить их совместную обработку, например, при помощи программы Взаимный спектральный анализ. Исходные сигналы для фильтрации остаются неизменными. Все программы ZETLab имеют возможность одновременно обрабатывать исходные реальные сигналы и отфильтрованные виртуальные.

Выбор количества каналов для фильтрации

Программа может одновременно фильтровать несколько каналов. Причем фильтрация может производиться, как одного, так и различных измерительных каналов, включая виртуальные каналы.

Выбор типа фильтра

Дифференцирование и интегрирование сигналов широко используется в вибрации и акустике. Большинство применяемых в вибрации датчиков являются пьезоэлектрическими акселерометрами, т.е. датчики отдают сигнал пропорциональный ускорению. Многие контролируемые вибрационные параметры механизмов задаются в уровнях виброскорости. Для балансировки вращающихся механизмов, необходимо знать виброперемещение в точке крепления вибродатчика. Для получения сигнала виброскорости из сигнала виброускорения необходимо этот сигнал подвергнуть интегрированию первого порядка. Для получения сигнала виброперемещения необходимо провести двойное интегрирование сигнала виброускорения. Аналогично, из сигнала датчика линейного перемещения можно получить сигнал скорости перемещения и сигнал ускорения дифференцированием сигнала.

Применение интегрирующих фильтров позволяет использовать анализатор в качестве виброметра первого класса точности.

Дифференцирование сигнала полезно при виброакустическом мониторинге различных систем. Одним из важнейших параметров мониторинга является тренд процесса, т.е. долговременное изменение уровня контролируемого сигнала по времени (например, интегральный уровень вибрации или уровень шума в полосе). Для контроля изменения этого сигнала можно продифференцировать этот сигнал и следить за уровнем его производной, т. е. уровнем изменения сигнала.

Если входной сигнал является сигналом виброускорения (т.е. единица измерения «g» или «м/с2»), то при интегрировании единица измерения выходного канала становится единица измерения виброскорость – «м/с». При двойном интегрировании сигнала виброускорения единица измерения выходного канала становится единица виброперемещения – «м». Опорные значения для расчета «дБ» также претерпевают изменения. Если у входного канала опорное значения «дБ» были выбраны по системе ISO, то опорные значения выходных каналов для интегрирования и двойного интегрирования также берутся по системе ISO. Если опорные значения дБ выбраны по ГОСТ, то опорные значения выходных каналов задаются также по ГОСТ. В противном случае к единице измерения входного канала при интегрировании добавляется «*с», а при двойном интегрировании – «*с2», при дифференцировании – «/с», при двойном дифференцировании – «/с2». Опорные значения расчета «дБ» при этом не меняются.

Линейный фильтр не производит никаких действий.

Возможности

программы Фильтрация сигналов

• Полосовые фильтры

  Выбор фильтров верхних и нижних частот (ФНЧ, ФВЧ)
  

• Огибающая сигнала

  огибающая сигнала
  

• Частотная коррекция

  выбор частотной коррекции
  

• Долеоктавная фильтрация

  октавные и 1/3-октавные фильтры 1 класса точности по ГОСТ Р 8.714-2010 (МЭК 61260:1995)
  

• Действительный резонатор

  колебательное звено
  

• Коррекция сейсмометра

  для разширения частотного диапазона
  

Встроенный в программу модуль управления и автоматизации из состава ZETLab Studio обеспечивает простоту и удобство при построении собственных программно-измерительных комплексов,

Амплитудно-частотную и фазочастотную характеристику фильтров можно получить с помощью программ «Снятие АЧХ и ФЧХ«.

С помощью программы Арифмометр также можно реализовать режекторные фильтры.

Инженерный вестник Дона | Обработка и фильтрация сигналов. Современное состояние проблемы

Аннотация

В.В. Мисюра, И.В. Мисюра

Дата поступления статьи: 04.12.2013

Приводится обзор исследований связанных с задачами обработки и фильтрации сигналов. Сигнал рассматривается как  случайный процесс, определяемый вероятностными характеристиками. Затрагиваются вопросы истории развития методов фильтрации сигнала. Анализируются недавние научные публикации, в которых представлены результаты и основные направления исследований в области фильтрации и обработки сигналов. Представленный материал расширяет знания о современном состоянии рассматриваемой проблемы.

Ключевые слова: сигнал, фильтрация сигнала, обработка сигнала, случайный процесс

05.13.18 – Математическое моделирование, численные методы и комплексы программ

Как правило, под сигналом понимают информационную функцию, которая несет сообщение о физических свойствах, состоянии или поведении каких-либо объекта, среды, физической системы.

Целью обработки сигналов является извлечение определенной информации и преобразование ее в форму, удобную для восприятия и дальнейшего использования.
Предсказать точно изменения значения информативного параметра невозможно, поскольку источник сигнала выдает информацию с некоторой вероятностью. Таким образом, аналитической моделью сигнала может быть только случайный процесс, который имеет детерминированные или меняющиеся во времени вероятностные характеристики. Но как такового «чистого» сигнала не существует, искажение сигнала происходит за счет присутствия помех и шумов. Шумы, как собственно и сигналы, имеют случайный (стохастический) характер. Принятый сигнал является смесью переданного сигнала и помехи, что является основанием применения аппарата теории вероятностей.
Задачи обработки и фильтрации случайных сигналов, как отображения  случайных явлений, развивающихся во времени решает теория случайных процессов.
Теория случайных процессов – это наука, изучающая закономерности случайных явлений в динамике их развития. Понятие случайного процесса появилось в начале прошлого века и было связано с трудами А.Н.Колмогорова (1903-1987), А.Я.Хинчина (1894-1959), Е.Е.Слуцкого (1880-1948), Н.Винера (1894-1965), Дж. Дуба (1910-2004), П.Леви (1886-1971), В.Феллера (1906-1970) и многих других ученых. В наши дни понятие случайного процесса  является одним из центральных не только в теории вероятностей, но и в теории связи, естествознании, инженерном деле, экономике, производстве.
Одной из основных задач первичной обработки сигналов является выделение полезных составляющих из общей суммы зарегистрированных зашумленных сигналов, а так же максимальное подавление помех и шумов в информационном сигнале при сохранении его полезных составляющих является.
За последнее десятилетие накоплен значительный опыт решения задач обработки и фильтрации сигналов, основные научные результаты хорошо представленные в научной литературе и получили свое подтверждение на практике.
Под сигналом обычно понимается случайный процесс , который  задается уравнение диффузии
, ,     (1)                                              
с детерминированными или со случайными предсказуемыми коэффициентами, удовлетворяющими условию Липшица по переменной t почти всюду. В уравнении – стандартное броуновское движение [1].
При рассмотрении задачи фильтрации предполагается существование пары случайных векторов , которые стохастически связанных между собой. Вектор  – наблюдаемый вектор, вектор  – вектор, подлежащий вычислению. Вектор X при наличии шума представим в виде , где N – шум.
Задача фильтрации сигнала состоит в том, чтобы отделить шум от сигнала, т.е. найти наилучшую оценку Y, основанную на наблюдениях  X. Для решения задач обработки и фильтрации сигнала, разработаны методы, хорошо представленные в научной литературе и получившие свое подтверждение на практике (см. [2 – 7]).
При постановке задачи фильтрации должен быть определен критерий «наилучшей» оценки. Понятно, что критерий оптимальности зависит от практического характера рассматриваемой задачи. Но с точки зрения математической теории преимущественно развиты методы решения поставленной задачи, основанные на минимизации среднеквадратической ошибки.
    (2)                                                                           
Задача состоит в определении функции f такой, что (2) принимает минимальное значение. Как показано в [5] более простой постановкой задачи, приводящей в ряде случаев к аналитически доступным и законченным решениям, является задача отыскания оптимального приближения в классе линейных функций. Наилучшим линейным приближением к случайному вектору  является тот вектор, который находится на кратчайшем расстоянии от него.
Следует отметить работы [8], [9], которые содержат основы теории оптимальной фильтрации случайных процессов.
В теории обработки сигналов очень эффективным оказался метод математического описания случайных сигналов описанных уравнением (1). Например,  фильтр Калмана-Бьюси (фильтр был разработан в 1960 г. – Калманом, а в 1961 г. – Калманом и Бьюси) позволяет оценивать состояние системы, удовлетворяющей «зашумленному» линейному стохастическому дифференциальному уравнению, на основе использованного ряда зашумленных наблюдений.

Заметим, что проблема линейной последовательной фильтрации по критерию минимума дисперсии ошибки к системам с одним входом и одним выходом была решена Винером.
Классический фильтр Винера получается в предположении, что коэффициенты уравнения (1) константы, классический фильтр Калмана получается в предположении, что коэффициенты детерминированы [8]. В связи с диффузионными процессами обобщение  фильтра Калмана на наиболее общий случай сделано в работе [9], в которой он обобщил теорию фильтрации Винера.
Общая теория нелинейной фильтрации описана в работе [10], которая как частный случай включает в себя и теорию линейной фильтрации.
Многие задачи обработки сигналов при действии разнообразных помех и шумов были решены благодаря аппарату нелинейной фильтрации и получили свое развитие в дальнейших исследованиях.
Статистических характеристиках полезного сигнала и помехи  различаются, что широко используется в любой системе обработки сигналов. Если априорная информация об этих характеристиках является неполной или если значения характеристик изменяются с течением времени, широко применяют разнообразные адаптивные методы фильтрации. [11]. С целью увеличения точности оценивания параметров сигнала на основе текущих наблюдений производится их подстройка. При использовании адаптивных методов фильтрации погрешность оценок параметров сигнала  зависит от соотношения между скоростью настройки фильтра и скоростью изменения характеристик сигнала.
На практике различные измерительные системы работают в условиях скачкообразного изменения характеристик сигнала, которые возникают  в случайные моменты времени.  Уравнение   , где независящий от  составной процесс Пуассона используют для описания процесса со скачками. Процессам со скачками (процессам Леви, аддитивным процессам и др.) уделяется в современных исследованиях значительное внимание. Ряд результатов по фильтрации случайных процессов со скачками  представлен в работах [12 – 15]. Задачи оценивания параметров процессов с пуассоновской статистикой потока переключений со случайной скачкообразно изменяющейся структурой  рассматривались в работах [15].
Теория случайных процессов, а вместе с ней и методы и алгоритмы обработки и фильтрации сигналов, продолжает бурно развиваться, в ней появляются новые направления исследований.

Литература:

1. Oksendal B., Sulem A. Applied stochastic control of jump diffusion. [text] / B. Oksendal, A. Sulem – New York: Springer Verlag, 2004 – p.208
2. Вайнштейн Л.А., Зубаков В.Д. Выделение сигналов на фоне случайных помех [Текст] / Л.А.Вайнштейн, В.Д.Зубаков – М.: Советское радио, 1960 – 447 с.
3. Мисюра И.В. Один метод фильтрации случайного сигнала [Текст] // Обозрение прикл. и промышл. матем., 2010 – т. 17, в.6 – С. 911-912.
4. Белицер Э., Еникеева Ф.Н. Адаптивная фильтрация случайного сигнала в гауссовском белом шуме [Текст] // Пробл. передачи информ., 2008 – т.44, в.4, – С. 39-51.
5.  Чернов А.В., Пугачёва О.Ю., Абидова Е.А. Математическое моделирование диагностического сигнала при оценке состояния электроприводной арматуры по сигналу тока двигателя [Электронный ресурс]  // «Инженерный вестник Дона», 2011, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2011/502 (доступ свободный) – Загл. с экрана. – Яз. рус.
6. Тарасова И.А., Леонова А.В., Синютин С.А. Алгоритмы фильтрации сигналов биоэлектрической природы [Электронный ресурс]  // «Инженерный вестник Дона», 2012, №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1481 (доступ свободный) – Загл. с экрана. – Яз. рус.
7. Берестень М.П., Зенов А.Ю. Концепция организации обработки информации в системах диагностики и распознавания[Электронный ресурс]  // «Инженерный вестник Дона», 2013, №1. – Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2013/1568 (доступ свободный) – Загл. с экрана. – Яз. рус.
8. Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов [Текст] / Р.Ш. Липцер, А.Н. Ширяев – М.:Наука,1974. – 696 с.
9. Липцер Р. Ш., Ширяев А. Н. Нелинейная фильтрация диффузионных марковских процессов. [Текст] // Труды МИАН им. В.А. Стеклова АН СССР.. 1968. – Том 104. – С. 135-180..
10. Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов (нелинейная фильтрация и смежные вопросы) [Текст] / Р. Ш. Липцер, А.Н. Ширяев – М.: Наука, 1974. – 696 с.
11. Фомин В.Н. Рекуррентное оценивание и адаптивная фильтрация. [Текст] / В.Н.Фомин – М.: Наука, 1984 – 288 с.
12. Applebaum D. Lévy Processes and Stochastic Calculus. [text] / D. Applebaum – Cambridge: Cambridge University Press, 2004 – p.384
13. Bertoin J. Levy processes. [text] / J. Bertoin – Cambridge: Cambridge University Press, 1996 – p.266
14. Лужецкая П.А., Белявский Г.И. Настройка параметров процессов Леви с использованием быстрого преобразования Фурье [Текст] // Обозрение прикладной и промышленной математики, 2011. – Т.18., в.5. – С. 744-745.
15. Параев Ю.И. Введение в статистическую динамику процессов управления и фильтрации [Текст] / Ю.И. Параев – М.: Сов. радио, 1976. – 184 с.

Фильтрация сигналов: почему и как

Фильтрация — это модификация измеренного или рассчитанного сигнала с использованием алгоритма и/или логики для удаления нежелательных аспектов сигнала перед его использованием в расчетах или в контроллере. Примерами управления являются переменная обратной связи (или управляемая) для ПИД- или АРС-регулятора или вход для контроллера с прямой связью. Примеры расчетов включают расчеты, основанные на установившемся балансе материалов/энергии или отношениях, ориентированных на процесс, а также на показателях процесса и управления.

Основной причиной фильтрации сигнала является уменьшение и сглаживание высокочастотного шума, связанного с такими измерениями, как расход, давление, уровень или температура. Типичным примером является шум, связанный с перепадом давления (DP) на диафрагме, используемый для определения скорости потока. Высокочастотный шум обычно считается случайным и аддитивным к измеряемому сигналу и обычно не коррелирует во времени; т. е. значение шума в любой момент времени τ не зависит от предыдущих значений шума. В идеале мы хотим оценить основной сигнал без шума, внося как можно меньше искажений.

Когда для управления используется зашумленный сигнал, фильтрация важна для эффективного действия производной и для предотвращения чрезмерных движений на выходе контроллера, которые вызывают износ клапана или возмущают другие контуры управления. Усложняющим фактором для случая управления является то, что и фильтрация, и настройка контроллера могут использоваться для уменьшения движения выходного сигнала контроллера.

Проблема запаздывания

Недостатком фильтрации является появление запаздывания, особенно при более интенсивной фильтрации, которое может отрицательно сказаться на своевременном обнаружении изменений в основном сигнале. При использовании для обратной связи отфильтрованное значение может привести к медленному управлению или, в худшем случае, к колебательному или даже нестабильному управлению. По опыту авторов, более типичной проблемой является чрезмерная фильтрация сигнала, а не недостаточная фильтрация.

Источником шума может быть электроника или сам процесс. «Технологический шум» может возникать из-за смешивания, вскипания, конденсации/испарения или из-за неправильной установки измерительного устройства, например, из-за недостаточной длины прямого участка трубы до или после расходомера. К сожалению, во многих случаях фильтрация используется в попытке замаскировать эффект неизмеренного возмущения или проблемы, такой как разрешающая способность клапана или зона нечувствительности в контуре управления. Во многих случаях фильтрация усугубляет проблемы. Фильтр часто устанавливается, а затем забывается до тех пор, пока цикл не будет повторно проверен из-за устранения неполадок цикла из-за плохой производительности или когда будет выполнен проект управления (например, APC).

Рассмотрим влияние фильтрации на производительность ПИД-регулятора. Важной причиной для фильтрации переменной обратной связи (PV) является обеспечение эффективного действия производной. Производное действие важно, когда требуется агрессивное управление, особенно для интегрирующих и почти интегрирующих (с преобладанием запаздывания) систем с дополнительными задержками и мертвым временем. При неправильной фильтрации зашумленные сигналы приведут к неэффективности действия производной из-за неравномерного движения выходного сигнала ПИД-регулятора. К счастью, большинство промышленных ПИД-регуляторов содержат фильтр только для производной, выраженной в виде дроби или делителя заданного производного времени. Дробь обычно находится в диапазоне от 0,10 до 0,20 производной по времени.

Другой причиной для фильтрации PV является смягчение выходного сигнала контроллера (CO), чтобы шум не приводил к чрезмерному движению (и износу) клапана или не вызывал помех в других контурах управления. В прошлом еще одной причиной для фильтрации PV были ограничения разрешения, вызванные аналого-цифровым преобразователем, которые проявлялись в виде заметных скачков в измеренном значении; однако с 16-битными платами ввода-вывода это больше не проблема.

Моделирование системы с замкнутым контуром

Рис. 1. Для оценки фильтров в замкнутом контуре мы моделируем процесс интегрирования с зашумленным измеряемым сигналом и агрессивно настроенным ПИД-регулятором. Формулы лямбда-настройки, модифицированные Макмилланом для обеспечения лучшего подавления помех нагрузки для ПИД-регулятора стандартной формы (показанного в таблице 1), используются для процесса интегрирования, в котором кажущийся незначительным шум усиливается за счет высокого коэффициента усиления ПИД-регулятора.

Таблица 1: Формулы настройки McMillan Lambda

Моделирование приводит к оптимизации

Для оценки фильтров в замкнутом контуре мы моделируем интегрирующую систему с шумным сигналом возмущения и агрессивно настроенным ПИД-регулятором. Детали контура и моделирования показаны на рис. 1. Для процесса интегрирования использовались правила настройки лямбда, модифицированные Макмилланом для обеспечения лучшего подавления возмущений нагрузки для ФИД стандартной формы (показаны в таблице 1). Значение λ = 2 с (удвоенное время простоя контура) использовалось в качестве времени останова (время остановки отклонения) для настройки, поскольку оно приводило к неколебательному отклику как в PV, так и в CO, при условии, что система является линейной. а динамика фиксирована и хорошо известна. Для каждого фильтра оцениваются следующие критерии контура:

Пиковая ошибка: Максимальная ошибка после неизмеренного скачка нагрузки. Пиковая ошибка важна для предотвращения разгрузки, активации сигнализации и SIS, а также нарушения условий окружающей среды.

IAE: Интегрированная абсолютная погрешность с течением времени является общим критерием для измерения производительности контура. Он имеет непосредственное отношение к экономике, поскольку обеспечивает меру количества технологического материала, выходящего за пределы заданного значения.

Превышение уставки:  Максимальное превышение ошибки при изменении уставки. Чрезмерный перерегулирование может иметь экономические последствия или последствия для безопасности.

IAD: Интегрированная абсолютная разность выходного сигнала контроллера. В случае, когда ПИД-регулятор непосредственно управляет клапаном, это общее расстояние перемещения клапана, которое напрямую связано с износом клапана.

Скачковая характеристика без фильтрации

в момент времени = 10 сек. для ПИД-управления без фильтрации хорошо видно влияние шума на μ.

Таблица 2: Результаты ПИД-регулятора в сравнении с ПИ-регулятором при воздействии нагрузки, без фильтрации

Для оценки фильтров с обратной связью мы решили сохранить настройку ПИД-регулятора на том же уровне и не увеличивать фильтрацию до уровня, вызывающего цикличность.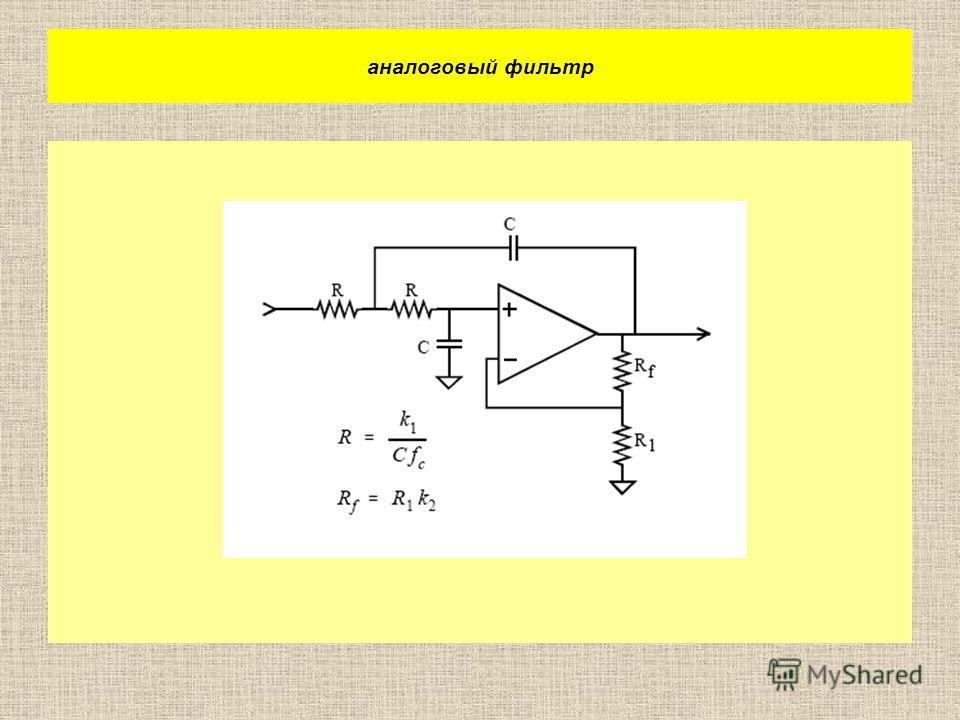 Сильная фильтрация PV способствует задержке и изменяет реакцию процесса, что требует перенастройки. Поскольку нашей целью является агрессивный контроль, мы хотим свести к минимуму влияние фильтрации на контроль, но уменьшить движение CO. На рис. 2 показана реакция γ и μ (CO) на 20-процентный скачок нагрузки ( д ₁ ) в момент времени = 10 сек. для ПИД-регулирования без фильтрации. Хорошо видно влияние шума на μ. В таблице 2 показаны результаты для ПИД-регулирования, а для сравнения также включены результаты для ПИ-регулирования. Хотя PID обеспечивает заметно лучшие результаты PV по сравнению с PI, это достигается за счет значительно большего движения в μ.

Чтобы оценить различные фильтры для ПИД-регулирования, мы настроили параметр фильтра (Τ _F или N ) для достижения того же результата нагрузки IAD (0,5423), что и для ПИ-регулирования. Поскольку параметр скользящего среднего N — это целочисленное значение, невозможно точно сопоставить одно и то же значение IAD, поэтому результаты показаны для значений фильтра N выше и ниже значения PID 0,5423. Результаты показаны в таблице 3 как для отклика нагрузки, так и для заданного значения. Мы видим, что фильтр первого порядка с ПИД-регулированием дает худшие результаты по всем показателям, чем ПИ-регулирование без фильтрации. Примечательно, что фильтры высшего порядка и фильтры скользящего среднего работают лучше, чем ПИ-регулирование. Фильтр 2 ^nd порядка является наиболее эффективным фильтром по всем показателям. По сравнению с 1 9Фильтр порядка 0077 st , фильтр порядка 2 ^nd обеспечивает меньшую пиковую ошибку на 7,3 % и меньший IAE на 19 % для отклика на нагрузку, а также меньшие пиковые ошибки и IAE на 60 % и 5,4 % для отклика уставки. По сравнению с ПИД-регулятором без фильтрации фильтр порядка 2 ^и имеет на 12 % худшую пиковую ошибку и на 3,9 % худшую ошибку IAE для отклика на нагрузку.

Чтобы сравнить все фильтры на одинаковой основе, мы сначала выбираем фильтр скользящего среднего значения, чтобы добиться снижения IAD не менее чем на 90% по сравнению с ПИД-регулированием без фильтра; а затем настроить Τ _F для фильтров более высокого порядка для достижения того же IAD. Эти результаты показаны в таблице 4. Опять же, мы видим, что фильтр второго порядка дает лучшие результаты по всем показателям. По сравнению с фильтром 1 ^st порядка, фильтр 2 ^nd порядка дает на 11 % меньшую пиковую ошибку и на 40 % лучшее IAE для отклика на нагрузку, а также на 71 % и 21 % лучшие результаты для отклика уставки.

На рис. 3 показаны временные характеристики фильтра 1 ^st порядка, а на рис. 4 — временные характеристики фильтра 2 ^nd – фильтр заказа. Отчетливо видно улучшение по сравнению с фильтром порядка 2 ^-й по сравнению с фильтром порядка 1 ^-й . На Рисунке 3 также видно, что отклик с фильтром порядка 1 ^st начинает становиться колебательным. Отметим, что при Τ _F для фильтра первого порядка петля становится неустойчивой. Для остальных фильтров нестабильность контура возникает при Τ _F = 9,73 для фильтра 2 ^-го -го порядка, Τ _F = 0,45 для фильтра 3-го ^-го -го порядка и N = 26 для фильтра скользящего среднего. Таким образом, не требуется много фильтрации, чтобы вызвать нестабильность контура.

Отклики с фильтром 1-го порядка

Рис. 3: Временные отклики ПИД-регулятора для нагрузки (слева) и уставки (справа) начинают становиться колебательными, а контур становится нестабильным при Τ _F = 0,73.

Таблица 3: Результаты ПИД-регулятора с фильтрацией, IAD той же нагрузки, что и PI

На основании приведенных выше результатов моделирование с обратной связью показывает значительное улучшениеФильтр порядка 0077 st возможен при наличии значительного шума и необходимости агрессивного контроля и значительного снижения IAD. Эти результаты также показывают, что фильтр порядка 2 ^и обеспечивает наилучшие показатели, хотя и не всегда с большим отрывом.

Вывод: не переусердствуйте

Чему мы научились, какие уроки? Будьте осторожны, чтобы не слишком фильтровать. То, что хорошо для глаз, обычно слишком много фильтров, особенно для контроля. Уменьшение затухания шума и помех имеет свою цену: чем больше затухание, тем медленнее отфильтрованный сигнал приближается к новому среднему значению, т. е. тем больше временная задержка. Для того же уровня шумоподавления фильтры более высокого порядка (2 ^-й -й и 3-й ^-й -й порядок) и фильтр скользящего среднего приближаются к новому среднему значению быстрее, чем часто используемый экспоненциальный фильтр или фильтр 1 ^-го -го порядка. Фильтр скользящего среднего может обеспечить более высокий уровень ослабления шума, чем фильтры порядков 2 ^nd и 3 ^rd , за счет увеличения количества коэффициентов и хранения предыдущих значений сигнала, но это не должно создавать проблем с сегодняшним управлением. системы. Преимущество фильтра скользящего среднего состоит в том, что он может устранить периодический цикл, если фильтр Δτ и N выбраны соответствующим образом.

Когда для управления используется шумовая переменная, решающим фактором для фильтрации является недопустимое движение управляющей переменной (выход контроллера), вызванное шумом. В этом случае, если требуется агрессивное управление (более высокий коэффициент усиления с действием производной), фильтры более высокого порядка и скользящего среднего значения обеспечивают более точное управление с улучшенными показателями (пиковая ошибка и IAE) по сравнению с экспоненциальным фильтром или фильтром порядка 1 ^st .

Таблица 4: Результаты PID с фильтрацией, 9Снижение нагрузки на 1,5 % IAD

Отклики с фильтром 2-го порядка

Здесь фильтр показывает улучшения как для нагрузки (слева), так и для уставки (справа).

Перед перенастройкой контура обязательно запишите параметры фильтра: постоянную времени или коэффициент фильтра и Δτ. Используйте фильтрацию только для сдерживания движения регулируемой переменной (выход контроллера), вызванного шумом. Если требуется агрессивное управление (более высокий коэффициент усиления и действие производной), фильтры более высокого порядка и скользящего среднего значения обеспечивают более жесткий контроль с улучшенными показателями (пиковая ошибка и IAE) по сравнению с экспоненциальным или 1 ^ст – фильтр заказа. Следует быть осторожным, чтобы не вызвать нестабильность петли при фильтрации. Хотя эти результаты моделирования, а также другие результаты, которые мы выполнили, не являются обширными, в целом показывают, что из рассмотренных фильтров фильтр 2 ^{-го и} -го порядка обеспечивает наилучшие показатели при нацеливании на сниженные уровни ДВР.

Мы использовали простой подход, сохранив настройки без изменений, чтобы показать улучшение, возможное с более сложными фильтрами. В идеале настройку и выбор параметров фильтра следует оптимизировать совместно, например, с помощью оптимизатора настройки контура.

Подождите, есть еще

Мы сосредоточились на линейных фильтрах. Тем не менее, предлагаются следующие дополнительные предложения.

• Если переменная процесса (PV) не может реагировать быстрее, чем на величину X/сек, ограничение скорости PV с этой настройкой может использоваться для фильтрации шума без добавления задержки. В качестве альтернативы, ограничение скорости уставки может быть установлено для блока аналогового вывода или вторичного контура, управляемого ПИД-регулятором, и включена обратная связь с внешним сбросом (например, предел динамического сброса), чтобы предотвратить изменение выходного сигнала ПИД-регулятора быстрее, чем заданное ограничение скорости уставки. Однако при загрузке или во время тестов для проверки и обслуживания ограничение скорости должно быть отключено.
• Для измерений pH использование выбора среднего сигнала трех электродов может уменьшить шум и устранить выбросы, которые обычно возникают из-за несовершенного смешивания и потенциалов земли, без добавления запаздывания, в дополнение к игнорированию более медленно реагирующих электродов из-за старения или загрязнения.
• Для электродов и датчиков температуры увеличение обратного смешивания и фазовых переходов, а также для трубопроводных установок, размещение наконечника посередине трубы на расстоянии не менее 25 диаметров трубы ниже по течению от выпускного отверстия насоса или оборудования может значительно снизить источник технологического шума. для этих критических первичных контуров.

Ссылки

1. Yang, W.Y. (2009). Сигналы и системы с MATLAB . Elsevier, Inc., Оксфорд.
2. Бокс, G.E.P., Дженкинс, G.M., и Reinsel, G. C. (1994). Анализ временных рядов , 3 ^rd Ed. Prentice-Hall., Энглвуд, Нью-Джерси.
3. Макмиллан, Г.К. (2015). Настройка и характеристики контура управления , 4 ^th Ed. Импульс Пресс, Нью-Йорк.

Фильтрация — основы обработки сигналов

Назад к: Основы обработки сигналов

Фильтр — это операция, которая различает компоненты объекта в некоторой области. Например:

• В трехмерном пространстве фильтрация может включать пространственную дискриминацию : удаление грязи и других крупных частиц при пропускании чистой воды.
• В области времени олимпийские квалификационные забеги используют временную дискриминацию : отбрасывание более медленных бегунов и допуск более быстрых.

Фильтрация

В статистике фильтрация применяется статистической дискриминации . Например, фильтр median-5 допускает медианное значение каждого набора из пяти отсчетов и отбрасывает остальные четыре. Эти фильтры применимы для обработки изображений и финансового анализа.

Ввод: 222322122200	Выход: 2222222220

В частотной области при фильтрации применяется частотная дискриминация. Фильтры отклоняют или принимают компоненты данных в зависимости от того, как часто они изменяются.

Вход: Синусоида + постоянный ток	Выход: только синусоида

Фильтры различения по частоте

Примените фильтр, если хотите различать данные по частоте.

Общие примеры включают:

• Отклонение (удаление или фильтрация) частотных составляющих.
• Прием (допуск или пропуск) частотных составляющих.
• Повышение уровня энергии (величины) некоторых компонентов.

Конкретные примеры включают:

• Фильтрация постоянного смещения (постоянное смещение)
• Фильтрация (вырезка) шума 60 Гц
• Отфильтровывание компонентов, не входящих в спецификацию микрофона, акселерометра или других преобразователей
• Отфильтровывание компонентов, не входящих в спецификации громкоговорителя или других шейкеров
• Выравнивание аудиозаписи путем ослабления одних частот и усиления других
• Сглаживание зашумленной последовательности данных путем ослабления быстро меняющихся (высокочастотных) составляющих

Типы операций фильтра

Фильтр выполняет некоторую операцию над последовательностью данных, чтобы получить новую последовательность. Операция может быть чем угодно (или ничем в случае операции идентификации). Однако есть некоторые фильтры, которые инженеры используют так часто, что у них есть название.

Фильтр нижних частот

Фильтр нижних частот ослабляет высокочастотные компоненты выше заданной частоты среза ( f _c ) и пропускает низкочастотные компоненты ниже f _c .

Например, фильтр нижних частот может очищать (или сглаживать) данные, загрязненные шумом, чтобы шаблоны были более очевидными.

Фильтр высоких частот

Фильтр высоких частот ослабляет низкочастотные компоненты ниже заданной частоты среза и пропускает высокочастотные компоненты выше него.

Например, если данные имеют большое смещение по постоянному току, фильтр верхних частот с малой угловой частотой может удалить смещение, чтобы интересующие образцы были более очевидными.

Полосовой фильтр

Полосовой фильтр ослабляет низкие и высокие частоты и пропускает средние частоты.

Режекторный фильтр

Режекторный фильтр является противоположностью полосового фильтра. Режекторный фильтр отклоняет полосу частот и принимает все, что находится за пределами отбрасываемой полосы.

Характеристики фильтра

Частота среза

Как правило, частота среза отклика фильтра H(ω) представляет собой частоту ωc, где спектральная мощность |H(ω)| ² исключено из |H(ω)| ² = 1 в |H(ω)| ² = ½ или |H(ω)|=1/√2.

В децибелах (дБ) спектральная мощность падает с 10log ₁₀ (1) = 0 дБ до:

(1)  

Спад

то есть ни один из них не падает сразу после достижения своей угловой частоты. Вместо этого они скатываются под некоторым уклоном. Реальные фильтры в частотной области похожи не на скалы, а на холмы. Этот холмообразный спад в конце оставляет верхние 5% частот данных недействительными.

Архитектуры фильтров

Математика и инженерия часто синтезируют фильтрацию с помощью полиномов.

Математика : По аппроксимационной теореме Вейерштрасса любая непрерывная функция на замкнутом интервале (0 ≤ время ≤ 10) может быть аппроксимирована с произвольной точностью с помощью полиномов.

Инженерное дело : Многочлен можно реализовать только сложением и умножением. Обе операции легко реализовать с помощью цифровых логических вентилей в процессорах, DSP, FPGA, ASIC и т. д.

Например, y = 5x ²  + 3x + 2 означает:

• Умножьте 5 на x и x, чтобы получить 5x ²
• Умножьте 3 на x, чтобы получить 3x
• Добавьте 5x ² и 3x и 2, чтобы получить y

Фильтры часто проектируются как полиномы от z, где z ^-n представляет задержку на n отсчетов. Следовательно, факторы z ^-n могут быть реализованы аппаратно с помощью простого буфера памяти.

Пример

Если фильтр в области z имеет передаточную функцию:

(2)  

(3)  

(4)  

Тогда в области z:

(5) 3  

временная область:

(6)  

Следовательно, в момент времени n выход фильтра y(n) равен:

(7)  

Сравнение КИХ-БИХ

При ограничении полиномиальной структуры фильтра существует две общие архитектуры фильтров: КИХ-фильтры и БИХ-фильтры.

КИХ-фильтры

Фильтр с конечной импульсной характеристикой (КИХ) представляет собой один полином. Это взвешенная сумма текущих входных данных и конечного числа прошлых входных данных.

Преимущества

• Чрезвычайно стабильный
• Может иметь линейную фазу
• Имеет конечную импульсную характеристику: выходной сигнал будет точно равен нулю в течение фиксированного времени, когда входной сигнал будет равен нулю

Недостатки

• Имеет тенденцию к длительной задержке в цепочке обработки сигналов
• Обычно требуется много математических операций на выборку входных данных (высокий объем вычислений)

БИХ-фильтры

Фильтр с бесконечной импульсной характеристикой (БИХ) представляет собой полином, деленный на полином (рациональное выражение). Это взвешенная сумма текущих входных данных, конечного числа прошлых входных данных и конечного числа прошлых выходных данных.

Преимущества

• Стабильный при правильном проектировании, но возможно неустойчивый при плохом дизайне
• Обычно требуется несколько математических операций на выборку входных данных
• Может иметь линейную фазу

Недостатки

• Обычно имеет нелинейную фазу
• Имеет бесконечную импульсную характеристику: в целом и теоретически выход никогда не достигнет точного нуля после возбуждения входом из-за обратной связи с выхода

Пример

В приведенном ниже примере сравнивается БИХ-фильтр Баттерворта 6-го порядка с КИХ-фильтрами с коэффициентами 17, 33 и 257. Все они имеют целевую угловую частоту 100 Гц. Обратите внимание на следующее:

• FIR с коэффициентом 17 уступает коэффициенту Баттерворта с коэффициентом 13–15.
• FIR с 33 коэффициентами более или менее сопоставим с Butterworth.
• FIR с коэффициентом 257 превосходит Butterworth с точки зрения спада.

КИХ-фильтр с большим количеством коэффициентов вносит значительную задержку в тракт обработки сигнала, как показано ниже на КИХ с 257 коэффициентами.

КИХ-фильтры можно легко спроектировать так, чтобы они имели линейную фазу. Например, все КИХ-фильтры с симметричными коэффициентами имеют линейную фазу (как показано выше).

Это не относится к БИХ-фильтрам, как показано ниже на фазовых характеристиках БИХ. Однако фазовые характеристики фильтра Баттерворта приблизительно линейны.

Как работают фильтры

Фильтрация во времени с помощью свертки

Часто компьютер использует простую арифметику для выполнения фильтрации в частотной области. В частности, каждый выход y(n) часто представляет собой линейную комбинацию входов x(n). Этот тип фильтрации называется свертка.

Например, предположим, что мы хотим отфильтровать постоянный ток (DC). Простой фильтр с входом x(n) и выходом y(n) установит y(n) = x(n) – x(n-1).