Что такое проводник?
Проводник – это вещество или материал, которое отлично проводит электрический ток.
Как вы все знаете, любое вещество состоит из атомов. Атомы в свою очередь состоят из электронов и ядер

Давайте для понимания рассмотрим вот такую картинку. Предположим, что пастух – это ядро, а овцы вокруг него – это электроны.

Те овцы, которые находятся рядом с пастухом, не могут от него просто так взять и убежать, так как он присматривает за ними. Иначе останется без мяса и шерсти к осени. Но вот те овцы, которые находятся поодаль от пастуха, имеют все шансы от него убежать.
То же самое можно сказать и про атомы и электроны. Электроны, которые находятся на самой дальней орбите от ядра менее зависимы, чем те, которые расположены ближе к ядру.

В результате, такие электроны могут “оторваться” от ядра и начать самостоятельное путешествие по веществу. Такие электроны называются свободными электронами.


Чем больше свободных электронов, тем лучше проводимость вещества.
Сопротивление проводника
Удельное сопротивление
И вот мы плавно переходим к другому вопросу, что такое сопротивление проводника? Как я уже говорил выше, чем больше свободных электронов в веществе, тем лучше такое вещество проводит электрический ток. Следовательно, сопротивление проводника зависит от того, сколько свободных электронов содержит такой проводник. Поэтому, в физике есть такое понятие, как удельное сопротивление вещества.
Еще раз. Если в каком-либо веществе полно свободных электронов, то такое вещество будет хорошо проводить электрический ток. Если электронов еще меньше, то такое вещество будет плохо проводить электрический ток. А если свободных электронов почти нет, то такое вещество совсем не будет проводить ток. Поэтому, удельное сопротивление вещества показывает способность этого вещества препятствовать электрическому току, проходящему через него.
Удельное сопротивление выражается в единицах Ом × м.
Формула удельного сопротивления проводника

где
ρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м2
l – длина проводника, м
Площадь поперечного сечения проводника – это что-то типа этого:
 площадь поперечного сечения проводника
площадь поперечного сечения проводника
Формула сопротивления проводника
Итак, мы теперь знаем такую физическую величину, как удельное сопротивление. Теперь мы с легкостью можем найти сопротивление проводника.

где
ρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м2
l – длина проводника, м
Длина проводника
Допустим перед нами стоит задача: у нас есть медный провод с поперечным сечением в 0,1 мм2 . Нам надо получить сопротивление проводника в 1 Ом. Какая длина проводника должна быть?
Оказывается, эта задачка решается очень просто. Достаточно вспомнить формулу выше.

Отсюда получаем, что

Удельное сопротивление меди можно узнать из таблицы. Оно равняется 0,017 Ом × мм2 /м.
Получаем, что

Проводники на печатных платах
Как вы знаете, все схемы состоят из проводов или печатных дорожек, которые соединяют различные радиоэлементы в единое целое. Например, в статье “самый простой усилитель звука“, я с помощью проводов соединял различные радиоэлементы, и у меня получилась схема, которая усиливала звуковые частоты.
Для того, чтобы все было красиво, эстетично и занимало мало пространства, прямо на платах создают “проводки”, которые уже называются “печатными дорожками”.

В домашних условиях все это делается с помощью технологии ЛУТ (Лазерно-Утюжная-Технология).
На другой стороне печатной платы уже располагаются радиоэлементы

Так как радиолюбители стараются делать свои устройства как можно меньше по габаритам, то и плотность монтажа возрастает. Поэтому, в некоторых случаях радиоэлементы и печатные дорожки располагают по обе стороны платы.
Промышленные печатные платы уже делают многослойными. Они состоят из слоев, как торт из коржей:

Бум SMD технологий вызвал в свою очередь нужду в многослойных печатных платах.
Сверхпроводимость
Также в природе существует и такой эффект, как сверхпроводимость. Сверхпроводимость – это когда некоторые материалы и их сплавы вообще не обладают сопротивлением. То есть их сопротивление очень и очень близко к нулю. Но, спешу вас разочаровать, в простых условиях это получить невозможно, так как это достигается только при критических температурах.
Если желаете больше узнать про материалы, которые используются в электронике и электротехнике, скачайте эту книгу.

На первый взгляд может показаться, что эта статья из рублики “Электрику на заметку”.
С одной стороны, а почему бы и нет,
с другой – так ведь и нам, пытливым электронщикам, иногда нужно рассчитать сопротивление обмотки катушки индуктивности, или
самодельного нихромового резистора, да и чего уж там греха таить – акустического кабеля для высококачественной звуковоспроизводящей
аппаратуры.
Формула тут совсем простая R = p*l/S, где l и S соответственно длина и площадь сечения проводника, а p – удельное сопротивление материала, поэтому расчёты эти можно провести самостоятельно, вооружившись калькулятором и Ля-минорной мыслью, что все собранные данные надо привести к системе СИ.
Ну а для нормальных пацанов, решивших сберечь своё время и не нервничать по пустякам, нарисуем незамысловатую таблицу.
ТАБЛИЦА ДЛЯ РАСЧЁТА СОПРОТИВЛЕНИЯ ПРОВОДНИКА
Страница получилась сиротливой, поэтому помещу-ка я сюда таблицу для желающих связать своё время с прокладкой электропроводки, подключить мощный источник энергопотребления, либо просто посмотреть в глаза электрику Василию и, “похлёбывая из котелка” задать справедливый вопрос: “А почему, собственно? Может разорить меня решил? Зачем мне тут четыре квадрата из бескислородной меди для двух лампочек и холодильника? Из-за чего, собственно?”
И расчёты эти мы с вами сделаем не от вольного и, даже не в соответствии с народной мудростью, гласящей, что
“необходимая площадь сечения провода равна максимальному току, делённому на 10”, а в строгом соответствии нормативными
документами Минэнерго России по правилам устройства электроустановок.
Итак.
РАСЧЁТ ПЛОЩАДИ СЕЧЕНИЯ ПРОВОДОВ В ЗАВИСИМОСТИ ОТ МОЩНОСТИ НАГРУЗКИ
Потери в проводниках возникают из-за ненулевого значения их сопротивления, зависящего от длины провода.
Значения мощности этих потерь, выделяемых в виде тепла в окружающее пространство, приведены в таблице.
В итоге к потребителю энергии на другом конце провода напряжение доходит в несколько урезанном виде – меньшим, чем
оно было у источника. Из таблицы видно, что к примеру, при напряжении в сети 220 В и 100 метровой длине провода, сечением 1,5мм2,
напряжение на нагрузке, потребляющей 4 кВт, окажется не 220, а 199 В.
Для каких-то приборов – безразлично, какие-то работать будут, но при пониженной мощности, а какие-то взбрыкнут и пошлют Вас к едрене фене вместе с вашими длинными проводами и умными таблицами.
Поэтому Минэнерго – минэнергой, а собственная голова не повредит ни при каких обстоятельствах. Если ситуация складывается подобным примеру образом – прямая дорога к выбору проводов, большего сечения.
Расчет сечения кабеля | Таблицы, формулы и примеры
Самое уязвимое место в сфере обеспечения квартиры или дома электрической энергией – это электропроводка. Во многих домах продолжают использовать старую проводку, не рассчитанную на современные электроприборы. Нередко подрядчики и вовсе стремятся сэкономить на материалах и укладывают провода, не соответствующие проекту. В любом из этих случаев необходимо сначала сделать

Для чего необходим расчет кабеля
В вопросе выбора сечения проводов нельзя следовать принципу «на глаз». Протекая по проводам, ток нагревает их. Чем выше сила тока, тем сильнее происходит нагрев. Эту взаимосвязь легко доказать парой формул. Первая из них определяет активную силу тока:
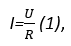
где I – сила тока, U – напряжение, R – сопротивление.
Из формулы видно: чем больше сопротивление, тем больше будет выделяться тепла, т. е. тем сильнее проводник будет нагреваться. Сопротивление определяют по формуле:
R = ρ · L/S (2),
где ρ – удельное сопротивление, L – длина проводника, S – площадь его поперечного сечения.
Чем меньше площадь поперечного сечения проводника, тем выше его сопротивление, а значит выше и активная мощность, которая говорит о более сильном нагреве. Исходя из этого, расчет сечения необходим для обеспечения безопасности и надежности проводки, а также грамотного распределения финансов.
Что будет, если неправильно рассчитать сечение
Без расчета сечения проводника можно столкнуться с одной из двух ситуаций:
- Слишком сильный перегрев проводки. Возникает при недостаточном диаметре проводника. Создает благоприятные условия для самовозгорания и коротких замыканий.
- Неоправданные затраты на проводку. Такое происходит в ситуациях, когда были выбраны проводники избыточного диаметра. Конечно, опасности здесь нет, но кабель большего сечения стоит дороже и не столь удобен в работе.

Что еще влияет на нагрев проводов
Из формулы (2) видно, что сопротивление проводника зависит не только от площади поперечного сечения. В связи с этим на его нагрев будут влиять:
- Материал. Пример – у алюминия удельное сопротивление больше, чем у меди, поэтому при одинаковом сечении проводов медь будет нагреваться меньше.
- Длина. Слишком длинный проводник приводит к большим потерям напряжения, что вызывает дополнительный нагрев. При превышении потерь уровня 5% приходится увеличивать сечение.
Пример расчета сечения кабеля на примере BBГнг 3×1,5 и ABБбШв 4×16
Трехжильный кабель BBГнг 3×1,5 изготавливается из меди и предназначен для передачи и распределения электричества в жилых домах или обычных квартирах. Токопроводящие жилы в нем изолированы ПВХ (В), из него же состоит оболочка. Еще BBГнг 3×1,5 не распространяет горение нг(А), поэтому полностью безопасен при эксплуатации.

Кабель ABБбШв 4×16 четырехжильный, включает токопроводящие жилы из алюминия. Предназначен для прокладки в земле. Защита с помощью оцинкованных стальных лент обеспечивает кабелю срок службы до 30 лет. В компании «Бонком» вы можете приобрести кабельные изделия оптом и в розницу по приемлемой цене. На большом складе всегда есть в наличии вся продукция, что позволяет комплектовать заказы любого ассортимента.

Порядок расчета сечения по мощности
В общем виде расчет сечения кабеля по мощности происходит в 2 этапа. Для этого потребуются следующие данные:
- Суммарная мощность всех приборов.
- Тип напряжения сети: 220 В – однофазная, 380 В – трехфазная.
- ПУЭ 7. Правила устройства электроустановок. Издание 7.
- Материал проводника: медь или алюминий.
- Тип проводки: открытая или закрытая.
Шаг 1. Потребляемую мощность электроприборов можно найти в их инструкции или же взять средние характеристики. Формула для расчета общей мощности:
ΣP = (P₁ + Р₂ + … + Рₙ) · Кс · Кз,
где P1, P2 и т. д. – мощность подключаемых приборов, Кс – коэффициент спроса, который учитывает вероятность включения всех приборов одновременно, Кз – коэффициент запаса на случай добавления новых приборов в доме. Кс определяется так:
- для двух одновременно включенных приборов – 1;
- для 3-4 – 0,8;
- для 5-6 – 0,75;
- для большего количества – 0,7.
Кз в расчете кабеля по нагрузке имеет смысл принять как 1,15-1,2. Для примера можно взять общую мощность в 5 кВт.
Шаг 2. На втором этапе остается по суммарной мощности определить сечение проводника. Для этого используется таблица расчета сечения кабеля из ПУЭ. В ней дана информация и для медных, и для алюминиевых проводников. При мощности 5 кВт и закрытой однофазной электросети подойдет медный кабель сечением 4 мм2.
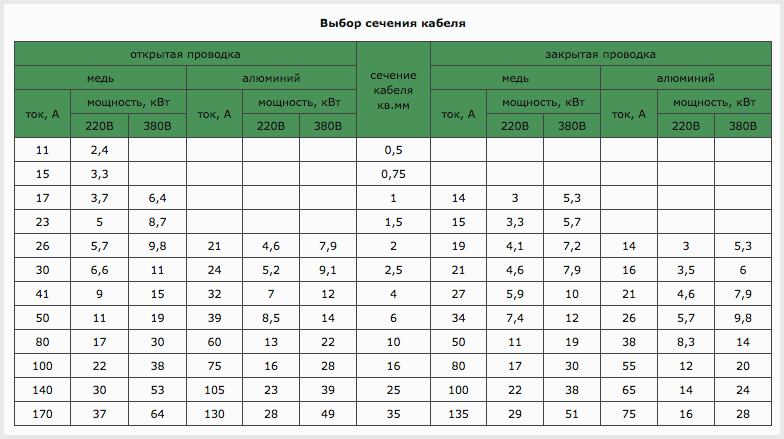
Правила расчета по длине
Расчет сечения кабеля по длине предполагает, что владелец заранее определил, какое количество метров проводника потребуется для электропроводки. Таким методом пользуются, как правило, в бытовых условиях. Для расчета потребуются такие данные:
- L – длина проводника, м. Для примера взято значение 40 м.
- ρ – удельное сопротивление материала (медь или алюминий), Ом/мм2·м: 0,0175 для меди и 0,0281 для алюминия.
- I – номинальная сила тока, А.
Шаг 1. Определить номинальную силу тока по формуле:
I = (P · Кс) / (U · cos ϕ) = 8000/220 = 36 А,
где P – мощность в ваттах (суммарная всех приборов в доме, для примера взято значение 8 кВт), U – 220 В, Кс – коэффициент одновременного включения (0,75), cos φ – 1 для бытовых приборов. В примере получилось значение 36 А.
Шаг 2. Определить сечение проводника. Для этого нужно воспользоваться формулой (2):
R = ρ · L/S.
Потеря напряжения по длине проводника должна быть не более 5%:
dU = 0,05 · 220 В = 11 В.
Потери напряжения dU = I · R, отсюда R = dU/I = 11/36 = 0,31 Ом. Тогда сечение проводника должно быть не меньше:
S = ρ · L/R = 0,0175 · 40/0,31 = 2,25 мм2.
В случае с трехжильным кабелем площадь поперечного сечения одной жилы должна составить 0,75 мм2. Отсюда диаметр одной жилы должен быть не менее (√S/ π) · 2 = 0,98 мм. Кабель BBГнг 3×1,5 удовлетворяет этому условию.
Как рассчитать сечение по току
Расчет сечения кабеля по току осуществляется также на основании ПУЭ, в частности, с использованием таблиц 1.3.6. и 1.3.7. Зная суммарную мощность электроприборов, можно по формуле определить номинальную силу тока:
I = (P · Кс) / (U · cos ϕ).
Для трехфазной сети используется другая формула:
I=P/(U√3cos φ),
где U будет равно уже 380 В.
Если к трехфазному кабелю подключают и однофазных, и трехфазных потребителей, то расчет ведется по наиболее нагруженной жиле. Для примера с общей мощностью приборов, равной 5 кВт, и однофазной закрытой сети получается:
I = (P · Кс) / (U · cos ϕ) = (5000 · 0,75) / (220 · 1) = 17,05 А, при округлении 18 А.
BBГнг 3×1,5 – медный трехжильный кабель. По таблице 1.3.6. для силы тока 18 А ближайшее в значение – 19 А (при прокладке в воздухе). При номинальной силе тока 19 А сечение его токопроводящей жилы должно составлять не менее 1,5 мм2. У кабеля BBГнг 3×1,5 одна жила имеет сечение S = π · r2 = 3,14 · (1,5/2)2 = 1,8 мм2, что полностью соответствует указанному требованию.
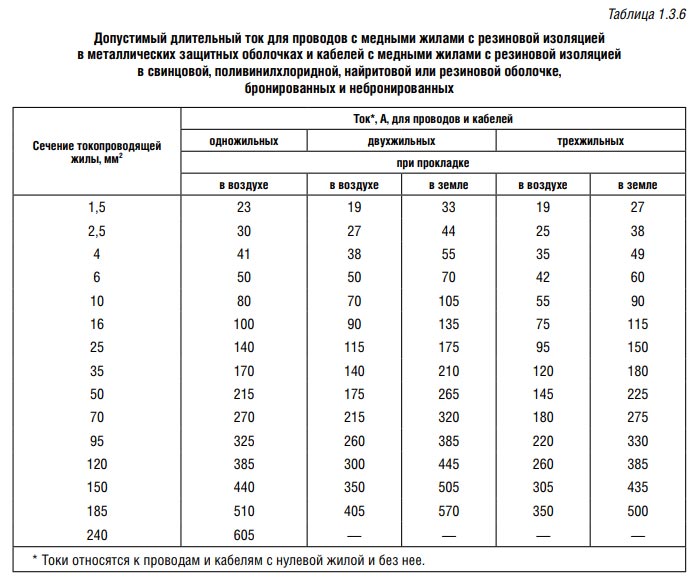
Если рассматривать кабель ABБбШв 4×16, необходимо брать данные из таблицы 1.3.7. ПУЭ, где указаны значения для алюминиевых проводов. Согласно ей, для четырехжильных кабелей значение тока должно определяться с коэффициентом 0,92. В рассматриваемом примере к 18 А ближайшее значение по таблице 1.3.7. составляет 19 А.

С учетом коэффициента 0,92 оно составит 17,48 А, что меньше 18 А. Поэтому необходимо брать следующее значение – 27 А. В таком случае сечение токопроводящей жилы кабеля должно составлять 4 мм2. У кабеля ABБбШв 4×16 сечение одной жилы равно:
S = π · r2 = 3,14 · (4,5/2)2 = 15,89 мм2.
Согласно таблице 1.3.7. этот кабель рациональнее использовать при номинальном токе 60 А (при прокладке по воздуху) и до 90 А (при прокладке в земле).
В данной статье мы подробно разберем что такое удельное сопротивление и электропроводность, ясно опишем все формулы с помощью примеров задач, а так же дадим вам таблицу удельных сопротивлений некоторых проводников.
Описание
Закон Ома гласит, что, когда источник напряжения (V) подается между двумя точками в цепи, между ними будет протекать электрический ток (I), вызванный наличием разности потенциалов между этими двумя точками. Количество протекающего электрического тока ограничено величиной присутствующего сопротивления (R). Другими словами, напряжение стимулирует протекание тока (движение заряда), но это сопротивление препятствует этому.
Мы всегда измеряем электрическое сопротивление в Омах, где Ом обозначается греческой буквой Омега, Ω. Так, например: 50 Ом, 10 кОм или 4,7 МОм и т.д. Проводники (например, провода и кабели) обычно имеют очень низкие значения сопротивления (менее 0,1 Ом), и, таким образом, мы можем пренебречь ими, как мы предполагаем в расчетах анализа цепи, что провода имеют ноль сопротивление. С другой стороны, изоляторы (например, пластиковые или воздушные), как правило, имеют очень высокие значения сопротивления (более 50 МОм), поэтому мы можем их игнорировать и для анализа цепи, поскольку их значение слишком велико.
Но электрическое сопротивление между двумя точками может зависеть от многих факторов, таких как длина проводников, площадь их поперечного сечения, температура, а также фактический материал, из которого он изготовлен. Например, давайте предположим, что у нас есть кусок провода (проводник), который имеет длину L, площадь поперечного сечения A и сопротивление R, как показано ниже.


Электрическое сопротивление R этого простого проводника является функцией его длины, L и площади поперечного сечения A. Закон Ома говорит нам, что для данного сопротивления R ток, протекающий через проводник, пропорционален приложенному напряжению, поскольку I = V / R. Теперь предположим, что мы соединяем два одинаковых проводника вместе в последовательной комбинации, как показано на рисунке.


Здесь, соединив два проводника вместе в последовательной комбинации, то есть, к концу, мы фактически удвоили общую длину проводника (2L), в то время как площадь поперечного сечения A остается точно такой же, как и раньше. Но помимо удвоения длины, мы также удвоили общее сопротивление проводника, дав 2R как: 1R + 1R = 2R.
Таким образом , мы можем видеть , что сопротивление проводника пропорционально его длину, то есть: R ∝ L. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально больше, чем оно длиннее.
Отметим также, что, удваивая длину и, следовательно, сопротивление проводника (2R), чтобы заставить тот же ток I, чтобы течь через проводник, как и раньше, нам нужно удвоить (увеличить) приложенное напряжение I = (2 В) / (2R). Далее предположим, что мы соединяем два идентичных проводника вместе в параллельной комбинации, как показано.


Здесь, соединяя два проводника в параллельную комбинацию, мы фактически удвоили общую площадь, дающую 2А, в то время как длина проводников L остается такой же, как у исходного одиночного проводника. Но помимо удвоения площади, путем параллельного соединения двух проводников мы фактически вдвое сократили общее сопротивление проводника, получив 1 / 2R, поскольку теперь каждая половина тока протекает через каждую ветвь проводника.
Таким образом, сопротивление проводника обратно пропорционально его площади, то есть: R 1 / ∝ A или R ∝ 1 / A. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально меньше, чем больше его площадь поперечного сечения.
Кроме того, удваивая площадь и, следовательно, вдвое увеличивая суммарное сопротивление ветви проводника (1 / 2R), для того же тока, чтобы I протекал через параллельную ветвь провода, как раньше, нам нужно только наполовину уменьшить приложенное напряжение I = (1 / 2V) / (1 / 2R).
Надеемся, мы увидим, что сопротивление проводника прямо пропорционально длине (L) проводника, то есть: R ∝ L, и обратно пропорционально его площади (A), R ∝ 1 / A. Таким образом, мы можем правильно сказать, что сопротивление это:
Пропорциональность сопротивления


Но помимо длины и площади проводника, мы также ожидаем, что электрическое сопротивление проводника будет зависеть от фактического материала, из которого он изготовлен, потому что разные проводящие материалы, медь, серебро, алюминий и т.д., имеют разные физические и электрические свойства. Таким образом, мы можем преобразовать знак пропорциональности (∝) вышеприведенного уравнения в знак равенства, просто добавив «пропорциональную константу» в вышеприведенное уравнение, давая:
Уравнение удельного электрического сопротивления


Где: R — сопротивление в омах (Ω), L — длина в метрах (м), A — площадь в квадратных метрах (м 2 ), и где известна пропорциональная постоянная ρ (греческая буква «rho») — удельное сопротивление .
Удельное электрическое сопротивление
Удельное электрическое сопротивление конкретного материала проводника является мерой того, насколько сильно материал противостоит потоку электрического тока через него. Этот коэффициент удельного сопротивления, иногда называемый его «удельным электрическим сопротивлением», позволяет сравнивать сопротивление различных типов проводников друг с другом при определенной температуре в соответствии с их физическими свойствами без учета их длины или площади поперечного сечения. Таким образом, чем выше значение удельного сопротивления ρ, тем больше сопротивление, и наоборот.
Например, удельное сопротивление хорошего проводника, такого как медь, составляет порядка 1,72 х 10 -8 Ом (или 17,2 нОм), тогда как удельное сопротивление плохого проводника (изолятора), такого как воздух, может быть значительно выше 1,5 х 10 14 или 150 трлн.
Такие материалы, как медь и алюминий, известны низким уровнем удельного сопротивления, благодаря чему электрический ток легко проходит через них, что делает эти материалы идеальными для изготовления электрических проводов и кабелей. Серебро и золото имеют очень низкие значения удельного сопротивления, но по понятным причинам дороже делать из них электрические провода.
Тогда факторы, которые влияют на сопротивление (R) проводника в омах, могут быть перечислены как:
- Удельное сопротивление (ρ) материала, из которого сделан проводник.
- Общая длина (L) проводника.
- Площадь поперечного сечения (А) проводника.
- Температура проводника.
Пример удельного сопротивления № 1
Рассчитайте общее сопротивление постоянному току 100-метрового рулона медного провода 2,5 мм 2, если удельное сопротивление меди при 20 o C составляет 1,72 x 10 -8 Ом метр.
Приведенные данные: удельное сопротивление меди при 20 o C составляет 1,72 x 10 -8 , длина катушки L = 100 м, площадь поперечного сечения проводника составляет 2,5 мм 2, что дает площадь: A = 2,5 x 10 -6 м 2 .


Ответ: 688 МОм или 0,688 Ом.
Удельное электрическое сопротивление материала
Ранее мы говорили, что удельное сопротивление — это электрическое сопротивление на единицу длины и на единицу площади поперечного сечения проводника, таким образом, показывая, что удельное сопротивление ρ имеет размеры в Ом-метрах или Ом · м, как это обычно пишется. Таким образом, для конкретного материала при определенной температуре его удельное электрическое сопротивление определяется как.


Электрическая проводимость
Хотя как электрическое сопротивление (R), так и удельное сопротивление ρ, являются функцией физической природы используемого материала, а также его физической формы и размера, выраженных его длиной (L) и площадью его сечения ( А), Проводимость или удельная проводимость относится к легкости, с которой электрический ток проходит через материал.
Проводимость (G) является обратной величиной сопротивления (1 / R) с единицей проводимости, являющейся сименсом (S), и ей дается перевернутый символ омов mho, ℧. Таким образом, когда проводник имеет проводимость 1 сименс (1S), он имеет сопротивление 1 Ом (1 Ом). Таким образом, если его сопротивление удваивается, проводимость уменьшается вдвое, и наоборот, как: Сименс = 1 / Ом, или Ом = 1 / Ом.
В то время как сопротивление проводников дает степень сопротивления потоку электрического тока, проводимость проводника указывает на легкость, с которой он пропускает электрический ток. Таким образом, металлы, такие как медь, алюминий или серебро, имеют очень большие значения проводимости, что означает, что они являются хорошими проводниками.
Проводимость, σ (греческая буква сигма), является обратной величиной удельного сопротивления. Это 1 / ρ и измеряется в сименах на метр (S / m). Поскольку электропроводность σ = 1 / ρ, предыдущее выражение для электрического сопротивления R можно переписать в виде:
Электрическое сопротивление как функция проводимости


Тогда мы можем сказать, что проводимость — это эффективность, посредством которой проводник пропускает электрический ток или сигнал без потери сопротивления. Поэтому материал или проводник, который имеет высокую проводимость, будет иметь низкое удельное сопротивление, и наоборот, поскольку 1 сименс (S) равен 1 Ом -1 . Таким образом, медь, которая является хорошим проводником электрического тока, имеет проводимость 58,14 x 10 6 Симен на метр.
Пример удельного сопротивления №2
Кабель длиной 20 метров имеет площадь поперечного сечения 1 мм 2 и сопротивление 5 Ом. Рассчитать проводимость кабеля.
Приведенные данные: сопротивление постоянному току, R = 5 Ом, длина кабеля, L = 20 м, а площадь поперечного сечения проводника составляет 1 мм 2, что дает площадь: A = 1 x 10 -6 м 2 .


Ответ: 4 мега-симена на метр длины.
Таблица удельных сопротивлений проводников
| Проводник | Удельное сопротивление ρ | Температурный коэффициент α |
| Алюминий | 0,028 | 4,2 |
| Бронза | 0,095 — 0,1 | — |
| Висмут | 1,2 | — |
| Вольфрам | 0,05 | 5 |
| Железо | 0,1 | 6 |
| Золото | 0,023 | 4 |
| Иридий | 0,0474 | — |
| Константан | 0,5 | 0,05 |
| Латунь | 0,025 — 0,108 | 0,1-0,4 |
| Магний | 0,045 | 3,9 |
| Манганин | 0,43 — 0,51 | 0,01 |
| Медь | 0,0175 | 4,3 |
| Молибден | 0,059 | — |
| Нейзильбер | 0,2 | 0,25 |
| Натрий | 0,047 | — |
| Никелин | 0,42 | 0,1 |
| Никель | 0,087 | 6,5 |
| Нихром | 1,05 — 1,4 | 0,1 |
| Олово | 0,12 | 4,4 |
| Платина | 0.107 | 3,9 |
| Ртуть | 0,94 | 1,0 |
| Свинец | 0,22 | 3,7 |
| Серебро | 0,015 | 4,1 |
| Сталь | 0,103 — 0,137 | 1-4 |
| Титан | 0,6 | — |
| Фехраль | 1,15 — 1,35 | 0,1 |
| Хромаль | 1,3 — 1,5 | — |
| Цинк | 0,054 | 4,2 |
| Чугун | 0,5-1,0 | 1,0 |
Где: удельное сопротивление ρ измеряется в Ом*мм2/м и температурный коэффициент электрического сопротивления металлов α измеряется в 10 -3*C-1(или K -1) .
Краткое описание удельного сопротивления
Мы поговорили в этой статье об удельном сопротивлении, что удельное сопротивление — это свойство материала или проводника, которое указывает, насколько хорошо материал проводит электрический ток. Мы также видели, что электрическое сопротивление (R) проводника зависит не только от материала, из которого сделан проводник, меди, серебра, алюминия и т.д., но также от его физических размеров.
Сопротивление проводника прямо пропорционально его длине (L) как R ∝ L. Таким образом, удвоение его длины удвоит его сопротивление, в то время как последовательное удвоение проводника уменьшит вдвое его сопротивление. Также сопротивление проводника обратно пропорционально его площади поперечного сечения (A) как R ∝ 1 / A. Таким образом, удвоение его площади поперечного сечения уменьшило бы его сопротивление вдвое, тогда как удвоение его площади поперечного сечения удвоило бы его сопротивление.
Мы также узнали, что удельное сопротивление (символ: ρ) проводника (или материала) связано с физическим свойством, из которого он изготовлен, и варьируется от материала к материалу. Например, удельное сопротивление меди обычно дается как: 1,72 х 10 -8 Ом · м. Удельное сопротивление конкретного материала измеряется в единицах Ом-метров (Ом), которое также зависит от температуры.
В зависимости от значения удельного электрического сопротивления конкретного материала его можно классифицировать как «проводник», «изолятор» или «полупроводник». Обратите внимание, что полупроводники — это материалы, в которых их проводимость зависит от примесей, добавляемых в материал.
Удельное сопротивление также важно в системах распределения электроэнергии, так как эффективность системы заземления для системы электропитания и распределения сильно зависит от удельного сопротивления земли и материала почвы в месте расположения системы.
Проводимость — это имя, данное движению свободных электронов в форме электрического тока. Проводимость, σ является обратной величиной удельного сопротивления. Это 1 / ρ и имеет единицу измерения сименс на метр, S / m. Проводимость варьируется от нуля (для идеального изолятора) до бесконечности (для идеального проводника). Таким образом, сверхпроводник имеет бесконечную проводимость и практически нулевое омическое сопротивление.
Использование меди в электротехнических устройствах обусловлено двумя факторами: хорошей проводимостью и относительной дешевизной. При проектировании или ремонте линий электропередач или электронных приборов, необходимо учитывать сопротивление медных проводов. Пренебрежение данным параметром приведет к поломке электрической системы.
Что такое сопротивление медного провода
В металлах ток образуется при появлении электрического поля. Оно «заставляет» двигаться электроны упорядоченно, в одном направлении. Электроны дальних орбит атома, слабо удерживаемые ядром, формируют ток.
 Медные провода
Медные проводаПри прохождении отрицательных частиц сквозь кристаллическую решетку молекул меди, они сталкиваются с атомами и другими электронами. Возникает препятствие или сопротивление направленному движению частиц.
Для оценки противодействия току была введена величина «электрическое сопротивление» или «электрический импеданс». Обозначается она буквой «R» или «r». Вычисляется сопротивление по формуле Георга Ома: R=, где U — разность потенциалов или напряжение, действующее на участке цепи, I — сила тока.
 Понятие сопротивления
Понятие сопротивленияВажно! Чем выше значение импеданса металла, тем меньший ток проходит по нему, и именно медные проводники так широко распространены в электротехнике, благодаря этому свойству.
Исходя из формулы Ома, на величину тока влияет приложенное напряжение при постоянном R. Но резистентность медных проводов меняется, в зависимости от их физических характеристик и условий эксплуатации.
Что влияет на сопротивление медного провода
Электрический импеданс медного кабеля зависит от нескольких факторов:
- Удельного сопротивления;
- Площади сечения проволоки;
- Длины провода;
- Внешней температуры.
Последним пунктом можно пренебречь в условиях бытового использования кабеля. Заметное изменение импеданса происходит при температурах более 100°C.
 Зависимость сопротивления
Зависимость сопротивленияУдельное сопротивление в системе СИ обозначается буквой ρ. Оно определяется, как величина сопротивления проводника, имеющего сечение 1 м2 и длину 1 м, измеряется в Ом ∙ м2. Такая размерность неудобна в электротехнических расчетах, поэтому часто используется единица измерения Ом ∙ мм2.
Важно! Данный параметр является характеристикой вещества — меди. Он не зависит от формы или площади сечения. Чистота меди, наличие примесей, метод изготовления проволоки, температура проводника — факторы, влияющие на удельное сопротивление.
Зависимость параметра от температуры описывается следующей формулой: ρt= ρ20[1+ α(t−20°C)]. Здесь ρ20— удельное сопротивление меди при 20°C, α— эмпирически найденный коэффициент, от 0°Cдо 100°C для меди имеет значение, равное 0,004 °C-1, t — температура проводника.
Ниже приведена таблица значений ρ для разных металлов при температуре 20°C.
 Таблица удельного сопротивления
Таблица удельного сопротивленияСогласно таблице, медь имеет низкое удельное сопротивление, ниже только у серебра. Это обуславливает хорошую проводимость металла.
Чем толще провод, тем меньше его резистентность. Зависимость R проводника от сечения называется «обратно пропорциональной».
Важно! При увеличении поперечной площади кабеля, электронам легче проходить сквозь кристаллическую решетку. Поэтому, при увеличении нагрузки и возрастании плотности тока, следует увеличить площадь сечения.
Увеличение длины медного кабеля влечет рост его резистентности. Импеданс прямо пропорционален протяженности провода. Чем длиннее проводник, тем больше атомов встречаются на пути свободных электронов.
 Выводы
ВыводыПоследним элементом, влияющим на резистентность меди, является температура среды. Чем она выше, тем большую амплитуду движения имеют атомы кристаллической решетки. Тем самым, они создают дополнительное препятствие для электронов, участвующих в направленном движении.
Важно! Если понизить температуру до абсолютного нуля, имеющего значение 0° Kили -273°C, то будет наблюдаться обратный эффект — явление сверхпроводимости. В этом состоянии вещество имеет нулевое сопротивление.
 Температурная корреляция
Температурная корреляцияКак узнать сопротивление 1 метра медного провода
После выяснения всех факторов, влияющих на резистентность медного провода, можно объединить их в формуле зависимости сопротивления от сечения проводника и узнать, как вычислить этот параметр. Математическое выражение выглядит следующим образом: R= pl/s, где:
- ρ — удельное сопротивление;
- l — длина проводника, при нахождении сопротивления медного проводника длиной 1 м, l = 1;
- S— площадь поперечного сечения.
Для вычисления S, в случае провода цилиндрической формы, используется формула: S = π ∙ r2 = π d2/4 ≈ 0.785 ∙ d2, здесь:
- r — радиус сечения провода;
- d — его диаметр.
Если провод состоит из нескольких жил, то суммарная площадь будет равна: S = n d2/1,27, где n — количество жил.
Если проводник имеет прямоугольную форму, то S = a ∙ b, где a — ширина прямоугольника, b — длина.
Важно! Узнать диаметр сечения можно штангенциркулем. Если его нет под рукой, то намотать на любой стержень измеряемую проволоку, посчитать количество витков, желательно, чтобы их было не меньше 10 для большей точности. После этого измерить намотанную часть проводника, и разделить значение на количество витков.
 Вычисление площади сечения
Вычисление площади сеченияКак правильно рассчитать сопротивление провода по сечению
Проектируя электрическую сеть, необходимо правильно подобрать сечение кабеля, чтобы его резистентность не была высокой. Большой импеданс вызовет падение напряжения выше допустимого значения. В результате подключенное к сети электрическое устройство может не заработать. Также, провода начнут перегреваться.
Для правильного расчета минимального сечения необходимо учесть следующие факторы:
- По стандартам ПУЭ падение напряжения не должно быть больше 5%.
- В бытовых условиях ток проходит по двум проводам. Поэтому, при расчете величину сопротивления нужно умножить на 2.
- Учитывать нужно мощность всех подключенных приборов на линии. Для развития предусмотреть запас по нагрузке.
Как вычислить сопротивление проводника по формуле? Для примера можно рассмотреть задачу. Требуется определить: достаточно ли будет медного кабеля сечением 2,5 мм2 и длиной 30 метров для подключения оборудования мощностью 9 кВт.
 Формулы электрической цепи
Формулы электрической цепиЗадача решается следующим образом:
- Резистентность медного кабеля будет равна:
2 ∙ (ρ ∙ L) / S = 2 ∙ (0,0175 ∙ 30) / 2,5 = 0,42 Ом.
- Для нахождения падения напряжения нужно определить силу тока, по формуле: I= P/U.
Здесь P — суммарная мощность оборудования, U — напряжение в цепи. Тогда сила тока будет равна: I = 9000 / 220 = 40,91 А.
- Используя закон Ома, можно найти падение напряжения по кабелю: ΔU = I ∙ R = 40, 91 ∙ 0,42 = 17,18 В.
- От 220 В процент падения составит: U% = (ΔU / U) ∙ 100% = (17,18 / 220) ∙ 100% = 7, 81%>5%.
Падение напряжение выходит за пределы допустимого значения, значит необходимо использовать кабель большего сечения.
Таблица сопротивления медного провода
Узнать резистентность проводника можно по таблицам. В них содержатся готовые результаты вычислений для разных кабелей.
 Таблица меди на метр 1
Таблица меди на метр 1Например, сопротивление меди на метр для различных сечений можно определить без вычислений, из соответствующей таблицы.
 Таблица меди на метр 2
Таблица меди на метр 2Важно! Таблицы не содержат данные о всех сечениях. Если нужно узнать величину импеданса для неуказанного кабеля, то находится среднее значение между двумя ближайшими известными сопротивлениями.
 Таблица сечений, сопротивлений, силы тока
Таблица сечений, сопротивлений, силы токаРасчет сопротивления кабеля является важной задачей при проектировании электрической системы. Воспользовавшись формулами или таблицами, можно успешно ее решить.
Соберём цепь, изображённую на рисунке. Силу тока в цепи измеряют амперметром, напряжение — вольтметром. Зная напряжение на концах проводника и силу тока в нём, по закону Ома можно определить сопротивление каждого из проводников.

В цепь источника тока по очереди будем включать различные проводники, например, никелиновые проволоки одинаковой толщины, но разной длины. Выполнив указанные опыты, мы установим, что из двух никелиновых проволок одинаковой толщины более длинная проволока имеет большее сопротивление.
В следующем эксперименте по очереди будем включать никелиновые проволоки одинаковой длины, но разной толщины (разной площади поперечного сечения). Установим, что из двух никелиновых проволок одинаковой длины большее сопротивление имеет проволока, поперечное сечение которой меньше.
В третьем эксперименте по очереди будем включать никелиновую и нихромовую проволоки одинаковой длины и толщины. Установим, что никелиновая и нихромовая проволоки одинаковых размеров имеют разное сопротивление.
Зависимость сопротивления проводника от его размеров и вещества, из которого изготовлен проводник, впервые на опытах изучил Ом. Он установил:
Сопротивление прямо пропорционально длине проводника, обратно пропорционально площади его поперечного сечения и зависит от вещества проводника.
Обрати внимание!
Сопротивление проводника прямо пропорционально его длине, т.е. чем длиннее проводник, тем больше его электрическое сопротивление.
Сопротивление проводника обратно пропорционально площади его поперечного сечения, т.е. чем толще проводник, тем его сопротивление меньше, и, наоборот, чем тоньше проводник, тем его сопротивление больше.
Причиной наличия сопротивления у проводника является взаимодействие движущихся электронов с ионами кристаллической решётки проводника. Из-за различия в строении кристаллической решётки у проводников, выполненных из различных веществ, сопротивления их отличаются друг от друга. Для характеристики материала вводят величину, которую называют удельным сопротивлением.
Удельное сопротивление — это физическая величина, которая определяет сопротивление проводника из данного вещества длиной \(1\) м и площадью поперечного сечения \(1\) м².
Введём буквенные обозначения: \(ρ\) — удельное сопротивление проводника, \(l\) — длина проводника, \(S\) — площадь его поперечного сечения. Тогда сопротивление проводника \(R\) выразится формулой:
R=ρ⋅lS.
Из этой формулы можно выразить и другие величины:
l=R⋅Sρ, S=ρ⋅lR, ρ=R⋅Sl.
Из последней формулы можно определить единицу удельного сопротивления. Так как единицей сопротивления является \(1\) Ом, единицей площади поперечного сечения — \(1\) м², а единицей длины — \(1\) м, то единицей удельного сопротивления будет:
1 Ом ⋅1м21 м=1 Ом ⋅1 м, т.е. Ом⋅м.
Удобнее выражать площадь поперечного сечения проводника в квадратных миллиметрах, так как она чаще всего бывает небольшой. Тогда единицей удельного сопротивления будет:
1 Ом ⋅1мм21 м, т.е. Ом⋅мм2м.
В таблице приведены значения удельного сопротивления некоторых веществ при \(20\) °С.
Обрати внимание!
Удельное сопротивление с изменением температуры меняется.
Опытным путём было установлено, что у металлов, например, удельное сопротивление с повышением температуры увеличивается.
Обрати внимание!
Из всех металлов наименьшим удельным сопротивлением обладают серебро и медь. Следовательно, серебро и медь — лучшие проводники электричества.
При проводке электрических цепей используют алюминиевые, медные и железные провода.
Во многих случаях нужны приборы, имеющие большое сопротивление. Их изготавливают из специально созданных сплавов — веществ с большим удельным сопротивлением. Например, как видно из таблицы, сплав нихром имеет удельное сопротивление почти в \(40\) раз большее, чем алюминий.
Обрати внимание!
Стекло и дерево имеют такое большое удельное сопротивление, что почти совсем не проводят электрический ток и являются изоляторами.
На практике часто приходится менять силу тока в цепи, делая её то больше, то меньше. Так, изменяя силу тока в динамике радиоприёмника, мы регулируем громкость звука. Изменением силы тока в электродвигателе швейной машины можно регулировать скорость его вращения.
Для регулирования силы тока в цепи применяют специальные приборы — реостаты.
Простейшим реостатом может служить проволока из материала с большим удельным сопротивлением, например, никелиновая или нихромовая. Включив такую проволочку в цепь источника электрического тока через контакты А и С и передвигая подвижный контакт С, можно уменьшать или увеличивать длину включённого в цепь участка АС. При этом будет меняться сопротивление цепи, а следовательно, и сила тока в ней, это покажет амперметр.

Реостатам, применяемым на практике, придают более удобную и компактную форму. Для этой цели используют проволоку с большим удельным сопротивлением. Один из реостатов (ползунковый реостат) изображён на рисунке.

В этом реостате никелиновая проволока намотана на керамический цилиндр. Проволока покрыта тонким слоем не проводящей ток окалины, поэтому витки её изолированы друг от друга. Над обмоткой расположен металлический стержень, по которому может перемещаться ползунок. Своими контактами он прижат к виткам обмотки. От трения ползунка о витки слой окалины под его контактами стирается, и электрический ток в цепи проходит от витков проволоки к ползунку, а через него в стержень, имеющий на конце зажим \(1\). С помощью этого зажима и зажима \(2\), соединённого с одним из концов обмотки и расположенного на корпусе реостата, реостат подсоединяют в цепь. Перемещая ползунок по стержню, можно увеличивать или уменьшать сопротивление реостата, включённого в цепь.
Условное обозначение реостата в схемах показано на рисунке:

Каждый реостат рассчитан на определённое сопротивление и на наибольшую допустимую силу тока, превышать которую не следует, так как обмотка реостата накаляется и может перегореть. Сопротивление реостата и наибольшее допустимое значение силы тока указаны на нём.
Обрати внимание!
Реостат нельзя полностью выводить, так как сопротивление его при этом становится равным нулю, и если в цепи нет других приёмников тока, то сила тока может оказаться очень большой и амперметр испортится.
На рисунке изображён реостат, с помощью которого можно менять сопротивление в цепи не плавно, а ступенями — скачками, т.к. каждая спираль реостата имеет определённое сопротивление.

Источники:
Пёрышкин А.В. Физика. 8 класс// ДРОФА, 2013.
http://class-fizika.narod.ru/8_31.htm
http://electricalschool.info/main/osnovy/394-jelektricheskojj-soprotivlenie.html
http://xn--h2adlho.xn--g1ababalj7azb.xn--p1ai/%D1%83%D0%B4%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5-%D1%81%D0%BE%D0%BF%D1%80%D0%BE%D1%82%D0%B8%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5/
http://xn--h2adlho.xn--g1ababalj7azb.xn--p1ai/%D1%83%D1%80%D0%BE%D0%BA-38-%D1%80%D0%B5%D0%BE%D1%81%D1%82%D0%B0%D1%82%D1%8B/
http://mugo.narod.ru/Fiziks/15.html
DC сопротивление проводников
Это первый из двух постов по сопротивлению проводников. В следующем посте я рассмотрю сопротивление переменного тока, включая скин-эффект, и покажу, как мы можем справиться с этим. Для начала в этом посте будет рассмотрен простой случай сопротивления постоянному току и как его можно рассчитать.
Сопротивление постоянному току по IEC 60287
Международным стандартом для проводников является IEC 60287. Стандарт классифицирует проводники по четырем классам:
– Класс 1: сплошные проводники
– Класс 2: многожильные провода
– Класс 5: гибкие проводники
– класс 6: гибкие проводники (более гибкий, чем класс 5)
Стандарт для каждого класса проводников определяет максимально допустимое сопротивление при 20 o C:
| Минимальное сопротивление проводников в мОм / м | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CSA мм² | Медь (обычная) | Медь (луженая) | Алюминий | |||||||||||||||||
| класс 1 и 2 | класс 5 & 6 | класс 5 & 6 | класс 1 & 2 | |||||||||||||||||
| 0.5 | 36,0 | 39,0 | 40,1 | – | ||||||||||||||||
| 0,75 | 24,5 | 26,0 | 26,7 | – | ||||||||||||||||
| 1 | 18,1 | 19,5 | 20,0 | – | ||||||||||||||||
| 1,5 | 12,1 | 13.3 | 13.7 | – | ||||||||||||||||
| 2.5 | 7.41 | 7.98 | 8.21 | – | ||||||||||||||||
| 4 | 4.61 | 4.95 | 5.09 | – | ||||||||||||||||
| 6 | 3.08 | 3.08 | 3,30 | 3,39 | – | |||||||||||||||
| 10 | 1.83 | 1.91 | 1.95 | 3.08 | ||||||||||||||||
| 16 | 1.15 | 1,21 | 1.24 | 1.91 | ||||||||||||||||
| 25 | 0.272 | 0.78 | 0,795 | 1.20 | 9000 | 0,524 | 0,554 | 0.565 | 0,868 | |||||||||||
| 50 | 0,387 | 0,386 | 0,393 | 0,641 | ||||||||||||||||
| 70 | 0,268 | 0,272 | 0,277 | 0,443 | ||||||||||||||||
| 95 | 0,193 | 0,250 9003 | 0,193 | 0,210 | 0,320 | |||||||||||||||
| 120 | 0.153 | 0.161 | 0.164 | 0.253 | ||||||||||||||||
| 150 | 0.124 | 0.129 | 0.132 | 0.206 | ||||||||||||||||
| 185 | 0,0991 | 0.106 | 0.1050 | 0.1050 | 0.1050 | 0.108 | 0.108 | 0.108 | 0.108 | 0.108 | 0.108 | 0.108 | 0.108 | 0.108 | 0.108 | 0,0754 | 0.0801 | 0,0817 | 0,125 | |
| 300 | 0,0601 | 0,0641 | 0,0654 | 0,100 | ||||||||||||||||
| 400 | 0,0470 | 0,0486 | 0,0495 | 0,0 900 8 | 0,05080,0508 9005 0,0508 0,0508 0,0508 0,0508 0,0508 0801000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 | 0,0384 | 0.0391 | 0,0605 | ||||||||||||
| 630 | 0,0283 | 0,0287 | 0,0292 | 0,0469 | ||||||||||||||||
| 800 | – | – | – | 0,0367 | ||||||||||||||||
| 1000 | – | – | 0,0291 | |||||||||||||||||
| 1200 | – | – | – | 0.0247 | ||||||||||||||||
Сопротивление пост. в м 2 (мм 2 x10 -6 ) и удельное сопротивление ρ в Ом-м, тогда Сопротивление будет в омах. Удельное сопротивление в Ом-м (при 20 o С) для меди составляет 1,72 × 10 -8 и для алюминия 2.82х10 -8 . Приведенные выше формулы не учитывают производственные допуски, компактность многожильных проводников и т. Д. Это приведет к тому, что расчетное сопротивление будет отличаться от любого фактического измеренного сопротивления. Для общего использования, вероятно, лучше использовать цифры из таблицы МЭК 60287, а не вычисления с использованием приведенной выше формулы.
Температурная зависимость
Вышеуказанные значения сопротивления основаны на температуре 20 o С.Удельное сопротивление проводника будет изменяться в зависимости от температуры, причем сопротивление увеличивается с ростом температуры. Это изменение может быть упрощено до линейной функции для приемлемого температурного диапазона следующим образом:
- R = сопротивление проводника при температуре T
- R 20 = сопротивление проводника при 20 o C
- T = рабочая температура проводника
- α = температурный коэффициент удельного сопротивления
Фактические значения α зависят от состава материала в дополнение к температуре.Как для меди, так и для алюминия α, взятый за 0,0039, даст достаточную точность для большинства расчетов проводников.
Переменное сопротивление проводников ->
,Формула сокращения длины В специальной теории относительности говорится, что расстояние между двумя точками может различаться в разных системах отсчета. Расстояние между точками и, следовательно, длина зависит от скорости одной системы отсчета относительно другой. В одной системе отсчета измеряемый объект будет находиться в покое. Это называется правильной длиной и обозначено Δl 0 . В другой системе отсчета наблюдатель увидит движущийся объект. Длина объекта в этой системе отсчета равна наблюдаемой длины и помечена как Δl.Наблюдаемая длина всегда короче правильной длины. Этот эффект называется сокращением длины . Δl 0 и Δl измеряются в метрах (м).
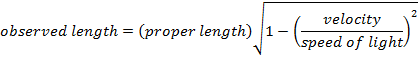
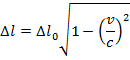
Δl = наблюдаемая длина в системе отсчета, в которой движется объект (м)
Δl 0 = правильная длина в системе отсчета, в которой объект находится в покое (м)
v = скорость (м / с)
c = скорость света (3,0 x 10 8 м / с)
Формула сокращения длины Вопросы:
1) Член экипажа космического корабля измеряет длину судна до 100 метров.Корабль пролетает мимо Земли со скоростью, равной 0,900 скорости света. Если бы наблюдатели на Земле измерили длину корабля, что бы они измерили?
Ответ: Система отсчета члена экипажа корабля является той, в которой судно находится в состоянии покоя. Измеренная длина члена экипажа – это правильная длина, Δl 0 . Наблюдатели на Земле измеряют наблюдаемую длину, Δl. Длину корабля в системе отсчета наземных наблюдателей можно узнать по формуле:
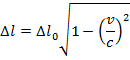
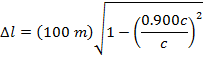
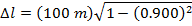
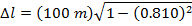

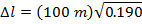

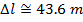
Наблюдатели на Земле измеряют длину корабля до 43.6 м Это меньше, чем длина 100 м, измеренная в системе отсчета члена экипажа судна.
2) Космические лучи, сталкивающиеся с верхней атмосферой Земли, производят высокоэнергетические частицы, называемые мюонами. Наблюдатель обнаруживает, что мюон был создан на 55,0 км над поверхностью Земли. Другой наблюдатель обнаруживает мюон, когда он достигает поверхности. Наблюдатели определяют, что мюон двигался со скоростью 2,97 x 10 8 м / с. В системе отсчета мюона, каково было расстояние между местом его создания и поверхностью Земли?
Ответ: Рассмотрим две позиции: позицию, в которой был создан мюон, и его прибытие на поверхность Земли.Расстояние между этими позициями в системе отсчета наблюдателей составляет Δl. В системе отсчета мюона расстояние между точками правильной длины, Δl 0 . Расстояние в системе отсчета наблюдателей известно, поэтому расстояние в системе отсчета мюона можно найти, переставив формулу сокращения длины:
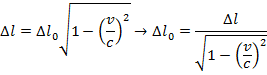
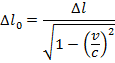
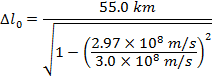
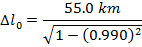
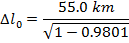
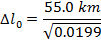

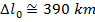
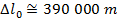
В системе отсчета мюона расстояние между местом его создания и поверхностью Земли составляет приблизительно 390 км, или 390 000 м.Это значительно больше, чем длина контракта, 55,0 км или 55 000 м, измеренная наблюдателями.
Исчисление II – длина дуги
Пол Заметки Онлайн Ноты
Быстрая навигация
Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Применение интегралов Введение
- Площадь поверхности
- глав
- Методы интеграции
- Параметрические уравнения и полярные координаты
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Обзор алгебры и триггеров
- Распространенные математические ошибки
- Комплексное число праймер
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои ученики
- Примечания Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Практика Проблемы Загрузки
- Complete Book – Проблемы только
- Complete Book – Решения
- Текущая глава – только проблемы
- Текущая глава – Решения
- Текущий раздел – только проблемы
- Текущий раздел – Решения
- Проблемы с назначением Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Другие предметы
- Получить URL для загрузки элементов
- Распечатать страницу в текущей форме (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- алгебра
- Предварительные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- полиномов
- Факторинг Полиномы
- Rational Expressions
- Комплексные числа
- Решение уравнений и неравенств
- Решения и комплекты решений
- линейных уравнений
- приложений линейных уравнений
- уравнений с более чем одной переменной
- Квадратичные уравнения – Часть I
- Квадратичные уравнения – Часть II
- Квадратичные уравнения: краткое изложение
- Приложения квадратичных уравнений
Уравнения- , приводимые к квадратичной форме
- Уравнения с радикалами
- линейных неравенств
- Полиномиальное неравенство
- Рациональное неравенство
- Уравнения абсолютной стоимости
- Абсолютное неравенство в значениях
- Графика и функции
- График
- Линии
- Круги
- Определение функции
- Графические функции
- Объединение функций
- Обратные функции
- общих графиков
- Линии, окружности и кусочные функции
- Параболы
- Эллипсы
- Гипербол
- Разные функции
- Преобразования
. Уравнения индуктивности и вычисления индуктивности Уравнения Стили упаковки индуктора
Индукторы – это пассивные устройства, используемые в электронных схемах для накопления энергии в форме
магнитного поля. Они представляют собой комплемент конденсаторов, которые накапливают энергию в форме электрического поля.
идеальный индуктор является эквивалентом короткого замыкания (0 Ом) для постоянного тока (постоянного тока),
и представляет противодействующую силу (реактивное сопротивление) к переменным токам (AC), которая зависит
на частоте тока.Реактивное сопротивление (противодействие току) индуктора
пропорциональна частоте тока, протекающего через него. Индукторы иногда
упоминается как “катушки”, потому что большинство индукторов физически построены из спиральных секций
провода.
Свойство индуктивности, которое противодействует изменению тока, используется для
цель предотвращения прохождения сигналов с более высокой частотой
пропуская сигналы низкочастотных компонентов.Вот почему индукторы иногда
упоминается как “дроссели”, поскольку они эффективно подавляют более высокие частоты. Обычный
применение дросселя в цепи смещения радиоусилителя, где коллектор
транзистор должен быть снабжен постоянным напряжением, не позволяя радиочастотам (радиочастоте)
сигнал от проведения обратно в источник постоянного тока.
При использовании в
серия (левый рисунок) или
параллель (правый чертеж) со своей схемой
комплимент, конденсатор, комбинация индуктор-конденсатор образует цепь, которая резонирует
на определенной частоте, которая зависит от значений каждого компонента.В серии
В цепи, полное сопротивление току на резонансной частоте равно нулю с идеальными компонентами.
В параллельной цепи (справа) полное сопротивление для протекания тока бесконечно с идеальными компонентами.
Реальные индукторы из физических компонентов
проявлять больше, чем просто чистая индуктивность, когда присутствует в цепи переменного тока. Общая схема
модель симулятора показана слева. Он включает в себя актуальный идеальный индуктор с параллельным
резистивный компонент, который реагирует на переменный ток.DC резистивный компонент
последовательно с идеальным индуктором, и конденсатор подключен через весь
сборка и представляет емкость, присутствующую из-за близости обмоток катушки.
Симуляторы типа SPICE используют эту или даже более сложную модель, чтобы облегчить
точные расчеты в широком диапазоне частот.
Связанные страницы по РФ Кафе
– Индукторы и
Расчеты индуктивности
Преобразование индуктивности
Стандартные значения индуктивности
–
Поставщики индукторов
HamWaves.ком
на сайте есть очень сложный калькулятор для индуктивности катушки, который позволяет вам
диаметр проводника.
Уравнения (формулы) для объединения индукторов последовательно и параллельно приведены ниже.
Дополнительные уравнения приведены для индукторов различной конфигурации.
последовательно соединенных индукторов
Общая индуктивность последовательно соединенных индукторов равна сумме отдельных
индуктивностей. Держите единицы постоянными.
Тороидальная рана
Прямоугольное сечение
Индуктивность коаксиального кабеля
Прямая проволока индуктивности
Эти уравнения применяются для когда
длина проволоки намного больше диаметра проволоки (смотрите
диаметр проволоки здесь). Руководство АРРЛ
представляет уравнение для единиц дюймов и мкФ:
Для низких частот – до примерно ОВЧ, используйте эту формулу:
Выше ОВЧ-эффекта скин-эффект приводит к тому, что ¾ в верхнем уравнении приближается к единице (1), поэтому
используйте это уравнение:
Прямой провод параллельно плоскости заземления с заземлением на одном конце
ARRL Handbook представляет это уравнение для прямой проволоки, подвешенной над землей
плоскость, один конец которой заземлен на плоскость:
a = радиус проволоки, l = длина провода параллельно плоскости заземления
h = высота провода над плоскостью заземления
к нижней части провода
Индуктивность параллельной линии
Многослойная воздушная индуктивность сердечника
Уилера
Формула:
параллельно соединенных индукторов
Общая индуктивность параллельно соединенных индукторов равна обратной
сумма обратных величин отдельных индуктивностей.Держите единицы постоянными.
Константы и переменные формулы индуктивности
Следующие физические константы и механические размерные переменные применяются к уравнениям
на этой странице. Единицы для уравнений указаны в квадратных скобках в конце уравнений;
например, означает, что длина
в дюймах и индуктивность в Генри. Если единицы не указаны, то могут быть использованы любые
до тех пор, пока они едины для всех сущностей; все метры, все мкГн и т. д.
C = Емкость
L = Индуктивность
N = Число витков
Вт = Энергия
ε r = Относительная диэлектрическая проницаемость (безразмерная)
ε 0 = 885 x 10 -12 Ф / м (диэлектрическая проницаемость свободного пространства)
µ r = Относительная проницаемость (безразмерная)
µ 0 = 4π
x 10 -7 H / m (проницаемость свободного пространства)
1 метр = 3,2808 фута <-> 1 фут = 0,3048 метра
1 мм =
0,03937 дюймов <-> 1 дюйм = 25,4 мм
Также точки (не путать с десятичными точками)
используются для указания умножения во избежание двусмысленности.
Индуктивное сопротивление
Индуктивное сопротивление (X L , в Ω) пропорционально частоте (ω,
в радианах / с или f в Гц) и индуктивности (L в Генри).Чистая индуктивность имеет фазу
угол 90 ° (напряжение подводит ток с фазовым углом 90 °).
Энергия, Накапливаемая в Индукторе
Энергия (Вт, в Джоулях), накопленная в индукторе, составляет половину произведения индуктивности
(L, у Генри) и ток (у меня, в амперах) через устройство.
Напряжение на Индукторе
Свойство индуктора противодействовать изменению потока тока вызывает встречную ЭДС
(напряжение), чтобы сформировать на своих клеммах, противоположных по полярности к приложенному напряжению.
добротность индуктора
Коэффициент качества – это безразмерное отношение реактивного сопротивления к сопротивлению в индуктивности.
Однослойная индуктивность с круглой катушкой
Уилера
Формула для D >> A:
В целом для a = радиус провода:
Примечание. Если длины проводов значительны, используйте расчет по прямому проводу, чтобы добавить, что
индуктивность.
В поисках эквивалента “R Q ”
С
«Q» индуктора – отношение реактивного компонента к резистивному компоненту,
эквивалентная схема может быть определена резистором параллельно с индуктором. это
Уравнение действует только на одной частоте “f” и должно рассчитываться для каждой частоты
представляет интерес.
,
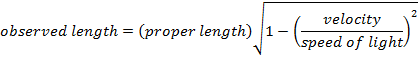
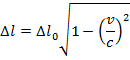
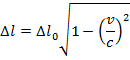
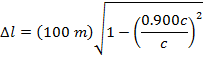
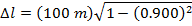
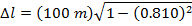

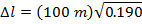

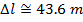
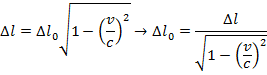
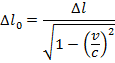
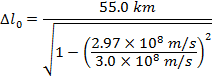
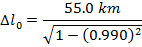
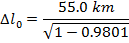
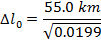

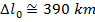
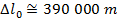
- Предварительные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- полиномов
- Факторинг Полиномы
- Rational Expressions
- Комплексные числа
- Решение уравнений и неравенств
- Решения и комплекты решений
- линейных уравнений
- приложений линейных уравнений
- уравнений с более чем одной переменной
- Квадратичные уравнения – Часть I
- Квадратичные уравнения – Часть II
- Квадратичные уравнения: краткое изложение
- Приложения квадратичных уравнений Уравнения
- , приводимые к квадратичной форме
- Уравнения с радикалами
- линейных неравенств
- Полиномиальное неравенство
- Рациональное неравенство
- Уравнения абсолютной стоимости
- Абсолютное неравенство в значениях
- Графика и функции
- График
- Линии
- Круги
- Определение функции
- Графические функции
- Объединение функций
- Обратные функции
- общих графиков
- Линии, окружности и кусочные функции
- Параболы
- Эллипсы
- Гипербол
- Разные функции
- Преобразования
Стили упаковки индуктора
Индукторы – это пассивные устройства, используемые в электронных схемах для накопления энергии в форме магнитного поля. Они представляют собой комплемент конденсаторов, которые накапливают энергию в форме электрического поля. идеальный индуктор является эквивалентом короткого замыкания (0 Ом) для постоянного тока (постоянного тока), и представляет противодействующую силу (реактивное сопротивление) к переменным токам (AC), которая зависит на частоте тока.Реактивное сопротивление (противодействие току) индуктора пропорциональна частоте тока, протекающего через него. Индукторы иногда упоминается как “катушки”, потому что большинство индукторов физически построены из спиральных секций провода.
Свойство индуктивности, которое противодействует изменению тока, используется для цель предотвращения прохождения сигналов с более высокой частотой пропуская сигналы низкочастотных компонентов.Вот почему индукторы иногда упоминается как “дроссели”, поскольку они эффективно подавляют более высокие частоты. Обычный применение дросселя в цепи смещения радиоусилителя, где коллектор транзистор должен быть снабжен постоянным напряжением, не позволяя радиочастотам (радиочастоте) сигнал от проведения обратно в источник постоянного тока.
При использовании в серия (левый рисунок) или параллель (правый чертеж) со своей схемой комплимент, конденсатор, комбинация индуктор-конденсатор образует цепь, которая резонирует на определенной частоте, которая зависит от значений каждого компонента.В серии В цепи, полное сопротивление току на резонансной частоте равно нулю с идеальными компонентами. В параллельной цепи (справа) полное сопротивление для протекания тока бесконечно с идеальными компонентами.
Реальные индукторы из физических компонентов проявлять больше, чем просто чистая индуктивность, когда присутствует в цепи переменного тока. Общая схема модель симулятора показана слева. Он включает в себя актуальный идеальный индуктор с параллельным резистивный компонент, который реагирует на переменный ток.DC резистивный компонент последовательно с идеальным индуктором, и конденсатор подключен через весь сборка и представляет емкость, присутствующую из-за близости обмоток катушки. Симуляторы типа SPICE используют эту или даже более сложную модель, чтобы облегчить точные расчеты в широком диапазоне частот.
Связанные страницы по РФ Кафе
– Индукторы и
Расчеты индуктивности
Преобразование индуктивности
Стандартные значения индуктивности
–
Поставщики индукторов
HamWaves.ком на сайте есть очень сложный калькулятор для индуктивности катушки, который позволяет вам диаметр проводника.
Уравнения (формулы) для объединения индукторов последовательно и параллельно приведены ниже. Дополнительные уравнения приведены для индукторов различной конфигурации.
последовательно соединенных индукторов
Общая индуктивность последовательно соединенных индукторов равна сумме отдельных индуктивностей. Держите единицы постоянными.
Тороидальная рана
Прямоугольное сечение
Индуктивность коаксиального кабеля
Прямая проволока индуктивности
Эти уравнения применяются для когда длина проволоки намного больше диаметра проволоки (смотрите диаметр проволоки здесь). Руководство АРРЛ представляет уравнение для единиц дюймов и мкФ:
Для низких частот – до примерно ОВЧ, используйте эту формулу:
Выше ОВЧ-эффекта скин-эффект приводит к тому, что ¾ в верхнем уравнении приближается к единице (1), поэтому используйте это уравнение:
Прямой проводпараллельно плоскости заземления с заземлением на одном конце
ARRL Handbook представляет это уравнение для прямой проволоки, подвешенной над землей плоскость, один конец которой заземлен на плоскость:
a = радиус проволоки, l = длина провода параллельно плоскости заземления
h = высота провода над плоскостью заземления
к нижней части провода
Индуктивность параллельной линии
Многослойная воздушная индуктивность сердечника
Уилера Формула:
параллельно соединенных индукторов
Общая индуктивность параллельно соединенных индукторов равна обратной сумма обратных величин отдельных индуктивностей.Держите единицы постоянными.
Константы и переменные формулы индуктивности
Следующие физические константы и механические размерные переменные применяются к уравнениям на этой странице. Единицы для уравнений указаны в квадратных скобках в конце уравнений; например, означает, что длина в дюймах и индуктивность в Генри. Если единицы не указаны, то могут быть использованы любые до тех пор, пока они едины для всех сущностей; все метры, все мкГн и т. д.
C = Емкость
L = Индуктивность
N = Число витков
Вт = Энергия
ε r = Относительная диэлектрическая проницаемость (безразмерная)
ε 0 = 885 x 10 -12 Ф / м (диэлектрическая проницаемость свободного пространства)
µ r = Относительная проницаемость (безразмерная)
µ 0 = 4π
x 10 -7 H / m (проницаемость свободного пространства)
1 метр = 3,2808 фута <-> 1 фут = 0,3048 метра
1 мм =
0,03937 дюймов <-> 1 дюйм = 25,4 мм
Также точки (не путать с десятичными точками) используются для указания умножения во избежание двусмысленности.
Индуктивное сопротивление
Индуктивное сопротивление (X L , в Ω) пропорционально частоте (ω, в радианах / с или f в Гц) и индуктивности (L в Генри).Чистая индуктивность имеет фазу угол 90 ° (напряжение подводит ток с фазовым углом 90 °).
Энергия, Накапливаемая в Индукторе
Энергия (Вт, в Джоулях), накопленная в индукторе, составляет половину произведения индуктивности (L, у Генри) и ток (у меня, в амперах) через устройство.
Напряжение на Индукторе
Свойство индуктора противодействовать изменению потока тока вызывает встречную ЭДС (напряжение), чтобы сформировать на своих клеммах, противоположных по полярности к приложенному напряжению.
добротность индуктора
Коэффициент качества – это безразмерное отношение реактивного сопротивления к сопротивлению в индуктивности.
Однослойная индуктивность с круглой катушкой
Уилера Формула для D >> A:
В целом для a = радиус провода:
Примечание. Если длины проводов значительны, используйте расчет по прямому проводу, чтобы добавить, что индуктивность.
В поисках эквивалента “R Q ”
С «Q» индуктора – отношение реактивного компонента к резистивному компоненту, эквивалентная схема может быть определена резистором параллельно с индуктором. это Уравнение действует только на одной частоте “f” и должно рассчитываться для каждой частоты представляет интерес.
,

