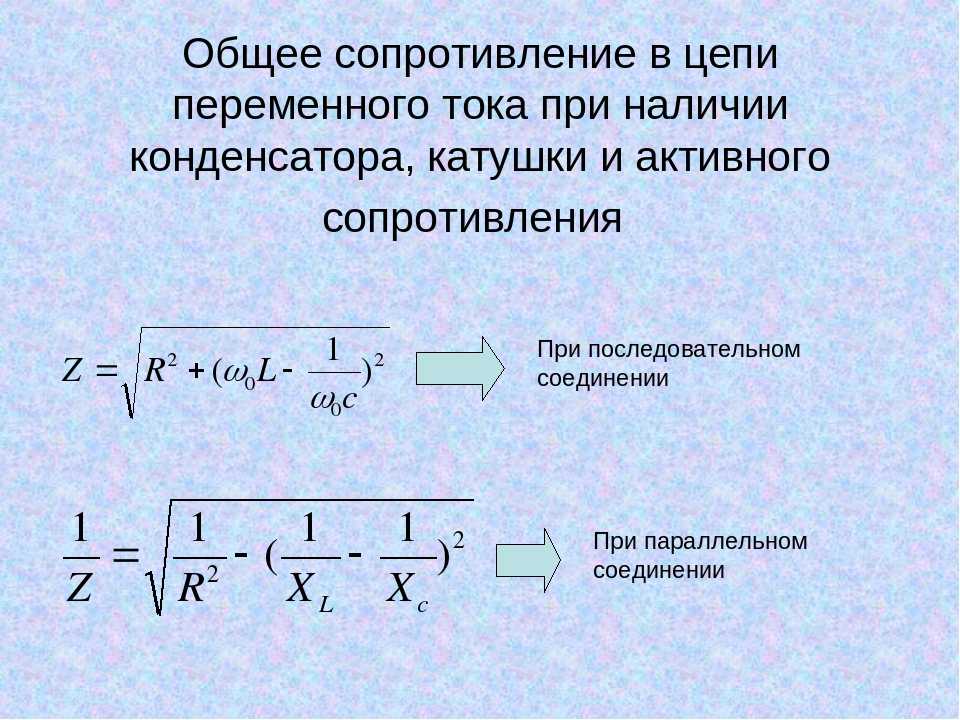
Как найти сопротивление зная мощность и напряжение; какой буквой обозначаться сопротивление, формула сопротивления
Сопротивление – способность материала препятствовать направленному движению заряженных частиц. Определяется величина согласно закону Ома. Точные значения параметра требуются во многих сферах, включая электронику и радиодетали. Определенным уровнем сопротивления обладает каждый материал на планете, вне зависимости от агрегатной формы. Некоторые вещества имеют настолько высокое сопротивление, что проведение через них электрического тока практически невозможно.
Формула удельного сопротивления
Что такое электрическое сопротивление
Что такое сопротивление в физике? Сопротивление – это физическое значение, которым описывается свойство проводящего материала препятствовать прохождению заряженных частиц сквозь него. Согласно закону Ома, данная величина равна значению напряжения на концевых участках проводника, деленному на силу тока в амперах, проходящего по нему. Значение противодействия направленному току заряженных частиц для цепей с переменным током и полей электромагнитного типа характеризуется полями волнового препятствия изменению потенциала и импедансом.
Значение противодействия направленному току заряженных частиц для цепей с переменным током и полей электромагнитного типа характеризуется полями волнового препятствия изменению потенциала и импедансом.
Интересно. На основании данной характеристики также получила название радиодеталь резистор, от английского Resistance – сопротивление. Эта часть требуется для введения в цепи питания активного препятствия электрическому току.
Определение единицы сопротивления – Ом
Что такое электрическое сопротивление
Как обозначается сопротивление? Величина измеряется в Омах (русское обозначение), в то время как в других странах символ для маркировки – омега (Ω). Единица представляет собой значение силы препятствия прохождению электрического тока проводника, по которому течет напряжение в 1В с силой постоянного электрического тока в 1А.
Единица измерения была введена в 1960 году, вместе с принятием международной системы величин в целом. Существующая величина имеет обратное значение в виде проводимости электрического тока, которая измеряется в сименсах.
Средства воспроизведения сопротивления
Сопротивление тока: формула
Для определения меры электрического сопротивления используют:
- Магазин сопротивлений – специальный набор радиоэлементов различного номинала. Данные компоненты специально изготовлены таким образом, чтобы содержать эталонное сопротивление проводников. При подключении электропроводника с постоянным или переменным током к магазину сопротивления можно выбрать подходящий по величине резистор и получить на выходе определенное напряжение, которое затем можно измерить при помощи вольтметра;
- Катушка – устройство, которое работает по сходному с магазином принципу. При подключении на вход прибора можно при помощи имеющихся рычагов и переключателей отрегулировать величину сопротивления агрегата и получить на выходе требуемый вольтаж.
Расчет сопротивления последовательных резисторов
Cила тока: формула
При последовательном сопротивлении нескольких резисторов соответственно увеличивается эквивалентная величина.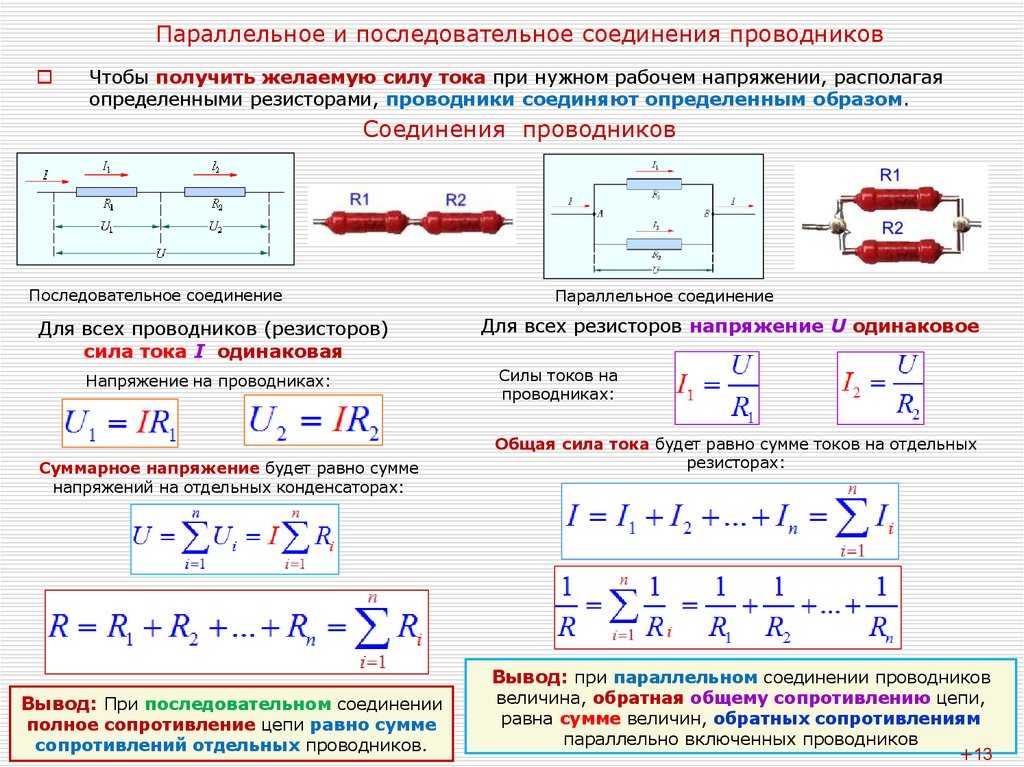 Расчет сопротивления нескольких элементов, соединенных между собой последовательно, проводится за счет суммирования номиналов каждого элемента. Например, при соединении нескольких элементов, которые соединены в одну цепь последовательно, величина электрического сопротивления будет равной сумме уровня противодействия каждого из резисторов. Формула имеет одинаковый вид для любого количества резисторов.
Расчет сопротивления нескольких элементов, соединенных между собой последовательно, проводится за счет суммирования номиналов каждого элемента. Например, при соединении нескольких элементов, которые соединены в одну цепь последовательно, величина электрического сопротивления будет равной сумме уровня противодействия каждого из резисторов. Формула имеет одинаковый вид для любого количества резисторов.
Как найти сопротивление формула для последовательной цепи
Если заменить в последовательной цепи один из элементов, то соответственно изменится уровень противодействия направленному движению частиц в этой цепи. Это также повлечет изменение силы тока.
Резистор
Государственный эталон сопротивления
Удельное сопротивление
Данный государственный стандарт под индексом ГЭТ 14-91 принято описывать в следующем виде.
Величины и характеристики эталонного сопротивления
| Название характеристики | Величина по государственному эталону 14-91 |
| Воспроизводимое значение в Омах | 6453 и 12906 |
| Хранимое значение в Омах | 1 |
| Неточности по первому типу (А) в миллиардных долях | 25 |
| Неточности по второму типу (В) в миллиардных долях | 35 |
| Сумма стандартной неопределенности, ppb | 45 |
| Увеличенная неопределенность при коэффициенте, равном двум, ppb | 90 |
Закон в простой форме
Исследования Ома по изучению вольт-амперных характеристик проводников показали, что сила тока внутри металлического проводника пропорциональна разности потенциалов на его концах (I ~ U) и обратно пропорциональна некоему коэффициенту, то есть I ~ 1/R.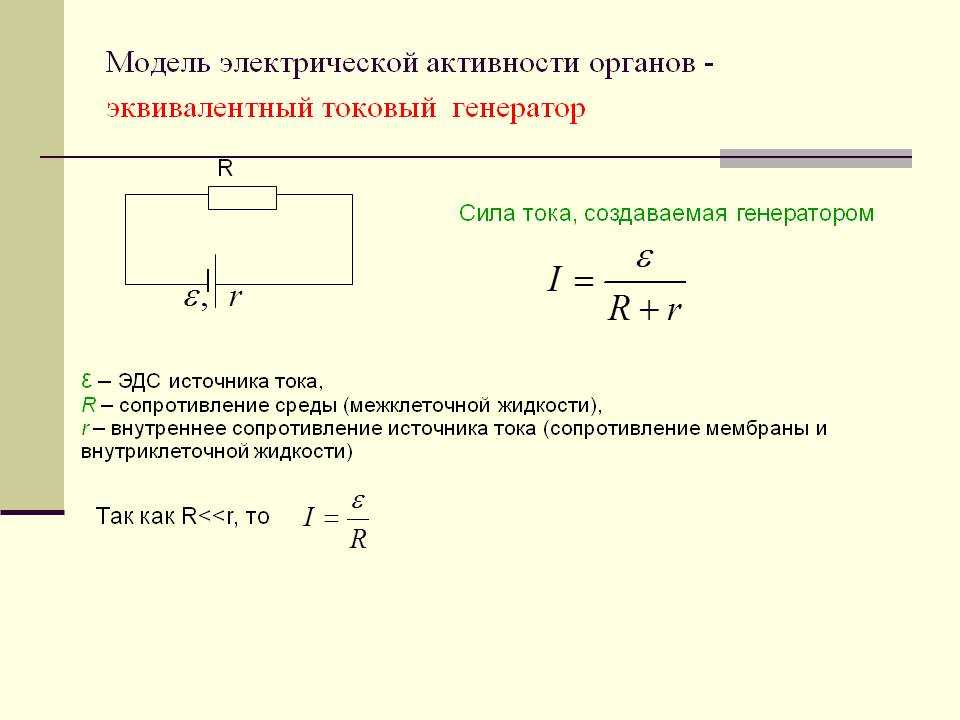 Этот коэффициент стал называться «сопротивление проводника», а единица измерения электрического сопротивления — Ом или В/А.
Этот коэффициент стал называться «сопротивление проводника», а единица измерения электрического сопротивления — Ом или В/А.
Стоит отметить еще вот что. Закон Ома часто используется для расчета сопротивления в цепях.
Зависимость величины от характеристик проводника
В проводнике носителями электрического тока являются свободные отрицательно заряженные частицы. Поведение в веществе подобно газу. Плотность свободных частиц зависят от плотности среды. Исходя из этого, плотность и структура кристаллической решетки определяются типом проводящего материала и его размерами. Из-за этого на проводимость влияют площадь поперечного сечения и температура. Сопротивление через площадь поперечного сечения считается расчетной величиной.
Расчет по площади поперечного сечения
Формула
Общее электросопротивление проводника можно найти по представленной выше формуле. Что касается нахождения показаний для активной, реактивной, отрицательной и удельной разновидности, есть свои специальные формулы. Все они представлены в соответствующей схеме далее с обозначениями.
Все они представлены в соответствующей схеме далее с обозначениями.
Формулы, используемые для расчета значения проводника
Электросопротивление в электродинамике является электротехнической величиной, характеризующей способность металла препятствовать электрическому току. При расчетах используется буква R, вне зависимости от того, какое сопротивление изучается и подсчитывается. Формул для нахождения величины множество. В основном используется R=U/I.
Показатели для твердотельных материалов
Удельное сопротивление сплавов и твердотельных металлов практически не меняется при повышении или снижении температуры. Это происходит из-за плотности кристаллической решетки. Характеристика присуща константану, манганину и другим плотным сплавам. Для такой особенности требуется повышенное удельное значение относительно составляющих компонентов.
Таблица сопротивлений твердотельных материалов
Закон Ома понятным языком
Один из фундаментальных законов, который всегда изучают в курсе физике — это закон Ома
. Он относительно простой, но при этом весьма важен для корректного понимания. Давайте изучим его
Он относительно простой, но при этом весьма важен для корректного понимания. Давайте изучим его
в режиме «для чайников».
С пониманием как такового физического явления
, обуславливающего появление закона Ома, обычно проблем не возникает. Но вот с вариантами формулировки и записи самого закона, а также аспектами, связанными с особенностями его применения в разных случаях, сложности частенько появляются.
В основе закона Ома лежит некая физическая штука, которая называется сопротивление
.
Показатели для жидких проводников
Показатели электросопротивления растворов солей и щелочей являются динамическими. Значения зависят от состава, концентрации вещества. При этом влияние температуры, обратное металлам. Во время нагрева из-за эффекта диффузии значение падает и наоборот. При слишком низких температурах электролит может перейти в твердое агрегатное состояние и не проводить ток. Так, вода, которая кристаллизовалась, не является проводником. Гидравлическое препятствование движению частиц возникает из-за наличия в жидкости производных солей, являющихся проводниками.
Гидравлическое препятствование движению частиц возникает из-за наличия в жидкости производных солей, являющихся проводниками.
Пример из практики
Последовательно с источником освещения включен тестер. Напряжение осветительного прибора = 220 Вольт. Мощность неизвестна. На показателе амперметра указано 276 миллиампер тока. Какая величина у спирали лампы при последовательном включении в схему резисторов?
Формула нахождения сопротивления спирали
Электросопротивление представляет собой физическую величину, которая соответствует степени препятствия движению электрических частиц у каждого материала. Возможно измерить уровень величины мультиметром. В таком случае придется находить значение по формуле. Для предотвращения попадания электрического тока на непредназначенные для этого участки желательно заземлять линии передачи. Данная физическая величина используется во многих радиодеталях, например, светодиодах. В электрической цепи, чтобы узнать величину, требуется подключить к вольтметру фазу и ноль при известной силе тока, затем рассчитать по закону Ома.
Зависимость удельного сопротивления от деформаций
При холодной обработке проводников происходит пластическая деформация сырья с последующим искажением кристаллической решетки, что значительно увеличивает уровень удельного сопротивления.
Электрическое сопротивление – это свойство любого вещества препятствовать движению ионов. Характеристика является динамической и зависит от нескольких факторов. Изоляция и некоторые материалы обладают уровнем сопротивления, при котором электрический ток не способен проходить сквозь вещество. Это может характеризовать некоторые вещества, как плохо проводящие ток из-за малого объема ионов. Что такое сопротивление проводника? Величина, из-за которой происходит потеря мощности при прохождении электричества.
Расчет сопротивления параллельных резисторов
Сопротивление резистора — формула для рассчета
Сопротивление формула для параллельного соединения имеет несколько другой вид.
Формула
Относительно большого количества последовательных элементов при увеличении количества резисторов в цепи соответственно возрастает сложность проведения расчета. Удельное сопротивление буква, которая ему соответствует, – латинская ρ.
Удельное сопротивление буква, которая ему соответствует, – латинская ρ.
Использование параллельного соединения оправдано в цепях, в которых требуется высокая величина параметра. Тогда применяются радиоэлементы с одинаковым параметром мощности и сопротивления. Например, 10 элементов, обладающих уровнем сопротивления 1000 Ом, которые объединены в единую цепь с параллельным соединением, на выходе будут иметь величину препятствия движению заряженных частиц в 100 Ом.
Понятие сопротивление доходчиво
Электрическое сопротивление — это величина, которая определяет способность проводника пропускать электрический ток
. Полезно также освежить знания про электрический ток ( писали в этой статье ).
Представить это проще всего, исходя из строения металлов.
По классической теории металл состоит из кристаллической решетки, а между структурными элементами этой решетки путешествуют свободные электроны.
Внешнее электрическое поле заставляет их перемещаться и образуется электрический ток, т. е. направленное упорядоченное движение частиц
е. направленное упорядоченное движение частиц
.
Решетка металла мешает им двигаться по своему объему
. Электроны трутся об её узлы и не могут протиснуться. Вот это явление и образует сопротивление. Это «сила», которая мешает перемещению.
Ситуация аналогично ситечку на раковине. Вода проходит, но медленнее, чем проходила бы без ситечка.
Аналогичная ситуация присутствует во всех материалах, правда род и тип частичек может меняться. Тип строения тоже разный. Но условно можно принять, что всегда структура мешает им двигаться что в дереве, что в металле.
Закон Ома для полной цепи
Полной цепью
(в отличие от участка цепи, применительно к которому мы излагали всё выше) называется
цепь с учетом источника тока
.
Почему это важно?
Именно потому, что если мы представим себе электрическую цепь условно как систему труб для воды, то участок цепи это будет незамкнутый кусок трубы, а полная цепь — зацикленная система
.
Из примера может показаться, что участок цепи есть незамкнутая в электрическом смысле цепь. Нет, пример приведен не для этого. И там, и там электрическая цепь замкнута.
Просто нам нужно обозначить, что без учета источника тока и его внутреннего сопротивления (r) цепь не полная, а расчёт не всегда способен учитывать все значимые характеристики.
Ну а внутреннее сопротивление
, как вы наверное догадались — это то сопротивление, которым обладает источник тока. Да, току в цепи сложно проходить и через сам источник! Даже сам источник провоцирует энергетические потери. А вот считать его аналогично расчёту для участка цепи нельзя.
Получается, что в закон Ома добавится ещё и внутренне сопротивление. И всё! Ничего страшного.
Формулировка закона Ома для полной цепи немного изменится. Теперь у нас слово напряжение заменится словом ЭДС (электродвижущая сила), а слово сопротивление заменится суммой внешнего сопротивления цепи и внутреннего сопротивления источника тока. Ну и формула будет такая:
Ну и формула будет такая:
Как найти сопротивление, зная мощность и напряжение; какая буква для сопротивления, формула для сопротивления
Очевидно, что ток будет протекать и через него. Это похоже на танец на волнах. Все 5 человек берутся за руки и по очереди производят колебания. Сопротивление уже всем известно. Здесь то же самое.
Содержание
Формула электрического сопротивления для начинающих
Не все хорошо разбираются в физике, особенно в решении задач. Но как говорят все учителя: “Учиться и понимать – это две разные вещи”. Поэтому лучше один раз все понять, чем просто заучить непонятный текст, не зная, как его применить. Итак, давайте ответим на главный вопрос, как рассчитать сопротивление и как найти силу тока.
Итак, с цветовой маркировкой резисторов. С этим мы разобрались, теперь перейдем к следующему вопросу…
Маркировка резисторов на схеме.
Давайте посмотрим на Маркировка резисторов в схемах. Возможны два варианта:
Возможны два варианта:
Кроме того, для обозначения резисторов на схеме используются несколько измененные символы номинальная рассеиваемая мощность. Возникает резонный вопрос – что это за параметр – номинальная рассеиваемая мощность? Когда ток проходит через резистор, в нем выделяется энергия, что приводит к его нагреву. И если мощность превышает номинал, резистор перегревается и просто сгорает. Таким образом, номинальная рассеиваемая мощность – это количество энергии, которое может быть рассеяно резистором без превышения температурного предела. Поэтому, если мощность в цепи меньше или равна номинальной мощности, резистор будет в порядке! Таким образом, мы возвращаемся к обозначениям резисторов:
Вот как маркируются наиболее распространенные резисторы, встречающиеся в схемах, в соответствии с их номинальной мощностью. 2 × [Сопротивление проводника, Ом].
2 × [Сопротивление проводника, Ом].
Ом и корреляция с другими величинами
На заре изучения электричества ученые заметили, что ток, протекающий через различные материалы, отличался, даже если эксперимент проводился в одинаковых условиях и образцы были подключены к одним и тем же источникам. Было сделано предположение, что разные образцы имеют разное сопротивление электрическому току, что определяет силу этого тока.
Закон, связывающий ток и напряжение (закон Ома), был получен экспериментально. Коэффициент в этом законе был назван сопротивлением электрическому току.
Раньше ученые работали только с постоянным током и только со средами, сопротивление которых току не зависит от силы тока, напряжения, времени и условий, т.е. оно постоянно. В настоящее время концепции усложнились, но закон Ома по-прежнему верен для постоянного тока и постоянного сопротивления.
Определение омического сопротивления электрическому току:
[Сила тока, A] = [Напряжение, В] / [Сопротивление, Ом]. 2 / [Сопротивление проводника, Ом].
2 / [Сопротивление проводника, Ом].
[Среднеквадратичный ток, A] = [Среднеквадратичное напряжение, В] / [Сопротивление, Ом].
Если при температуре t0 сопротивление проводника составляет r0и при температуре t равен rtтемпературный коэффициент сопротивления составляет
электропроводность
До сих пор мы считали, что сопротивление проводника – это препятствие, которое проводник ставит перед электрическим током. Но все равно через проводник течет ток. Поэтому, помимо сопротивления (препятствия), проводник также обладает способностью проводить электрический ток, или проводимостью.
Чем больше сопротивление проводника, тем меньше его проводимость, тем хуже он проводит электричество, и наоборот, чем меньше сопротивление проводника, тем больше его проводимость, тем легче по нему течет ток. Поэтому сопротивление и проводимость проводника являются обратными величинами.
Из математики известно, что обратная величина 5 равна 1/5 и, наоборот, обратная величина 1/7 равна 7. Поэтому, если сопротивление проводника обозначить через rтогда проводимость определяется как 1/r. Обычно проводимость обозначается буквой g.
Поэтому, если сопротивление проводника обозначить через rтогда проводимость определяется как 1/r. Обычно проводимость обозначается буквой g.
Электропроводность измеряется в (1/Ом) или сименсах.
Пример 8. Сопротивление проводника составляет 20 Ом. Определите его проводимость.
Если r = 20 Ом, тогда
Пример 9. Проводимость проводника равна 0,1 (1/Ом). Определите его сопротивление,
Если g = 0,1 (1/Ом), то r = 1 / 0,1 = 10 (Ом)
Источник: Смит М. И., “Основы электротехники”. – 9-е издание, переработанное – Москва: Высшая школа, 1964 – 560 с.
Основное назначение резисторов – ограничивать величину тока и напряжения в электрической цепи для обеспечения нормальной работы других электронных компонентов в цепи, таких как транзисторы, диоды, светодиоды, микросхемы и т.д.
Резисторы | Назначение резисторов
Резисторы являются одним из самых простых электронных компонентов для понимания и проектирования. Однако они также наиболее часто используются в электронных схемах. Поэтому очень важно научиться использовать их в практических целях, уметь рассчитывать необходимые параметры и правильно выбирать резистор с нужными характеристиками. В данной статье рассматриваются эти и другие вопросы.
Однако они также наиболее часто используются в электронных схемах. Поэтому очень важно научиться использовать их в практических целях, уметь рассчитывать необходимые параметры и правильно выбирать резистор с нужными характеристиками. В данной статье рассматриваются эти и другие вопросы.
Основное назначение резисторов – ограничивать величину тока и напряжения в электрической цепи для обеспечения нормальной работы других электронных компонентов в электрической цепи, таких как транзисторы, диоды, светодиоды, микросхемы и т.д.
Самым важным параметром любого резистора является его сопротивление. Именно сопротивление затрудняет движение электронов в цепи и, следовательно, уменьшает силу тока. Поэтому сопротивление является не только положительным в том смысле, что оно ограничивает ток, протекающий через другие электронные компоненты, но и паразитным в том смысле, что оно снижает производительность всего устройства. Блуждающее сопротивление включает в себя сопротивление проводов, различных соединений, разъемов и т. д. и целью является его снижение.
д. и целью является его снижение.
Первооткрывателем свойства сопротивления электрической цепи был выдающийся немецкий ученый Георг Симон Ом, поэтому единица измерения электрического сопротивления была принята как ом. Наиболее практичным применением является килограмм Ом, мегомы и gigayoms.
Расширенный список сокращений и префиксов СИ физических величин, используемых в радиоэлектронике. Максимальное значение составляет 1018 – exa, а минимальное – 10-18 – atto. Надеюсь, эта таблица будет вам полезна.
Резисторы условно делятся на два основных подвида: Постоянный и переменный ток.
Фиксированные резисторыФиксированные резисторы могут быть различных конструкций, отличающихся в основном внешним видом и размерами. Характеристикой резисторов постоянного тока является фиксированное значение сопротивления, которое не должно изменяться во время работы электронных устройств.
Регулировочные резисторы используются для тонкой настройки отдельных электронных компонентов на этапе окончательной регулировки перед выпуском их в эксплуатацию. Чаще всего триммеры не имеют специальной ручки регулировки, а сопротивление изменяется с помощью отвертки, что предотвращает непреднамеренное изменение положения узла регулировки и, соответственно, сопротивления.
В некоторых устройствах после окончательной настройки на корпус и поворотный винт регулировочного резистора наносится краска, чтобы предотвратить вращение винта при наличии вибрации. След краски также служит индикатором непреднамеренного поворота регулировочного винта, который может быть визуально обнаружен путем отслаивания краски на вращающихся и неподвижных элементах корпуса.
Многооборотные резисторы широко используются в современной электронике для более точной настройки оборудования. Как правило, они имеют синий прямоугольный пластиковый корпус.
Переменные резисторы используются для изменения электрических параметров в цепи устройства непосредственно во время работы, например, для изменения яркости светодиода или громкости звука в приемнике. Их часто называют вместо “переменного резистора”. потенциометр или реостат ..
К переменным резисторам также относятся радиочастотные компоненты, которые имеют только два вывода и изменяют свое сопротивление в зависимости от света или температуры, например, фоторезисторы или термисторы.
Потенциометры используются для изменения тока или напряжения. Тип тока или напряжения, который можно регулировать, зависит от схемы подключения.
Если переменный резистор или триммер используется в качестве регулятор токаэто называется реостат ..
Ниже приведены две схемы, в которых реостат используется для регулировки тока, протекающего через светодиод VD. Это в конечном итоге изменяет яркость светодиода.
Это в конечном итоге изменяет яркость светодиода.
Обратите внимание, что в первой схеме используются все три контакта реостата, а во второй – только средний (регулировочный) и крайний. Оба контура полностью исправны и выполняют свои предназначенные функции. Однако вторая схема менее выгодна, поскольку свободный конец реостата, как антенна, может “ловить” различные электромагнитные излучения, которые вызовут изменение параметров электрической цепи. Особенно не рекомендуется использовать такую электрическую цепь в усилительных каскадах, где даже небольшая электромагнитная индукция приведет к непредсказуемой работе устройства. Поэтому мы берем за основу первую схему.
Напряжение можно изменять с помощью потенциометра следующим образом: два клеммных вывода подключаются параллельно к питанию; между одним клеммным выводом и средним выводом можно плавно регулировать напряжение от 0 до напряжения питания. В данном случае от нуля до 12 вольт. Потенциометр служит в качестве делителя напряжения, о чем более подробно рассказывается в отдельной статье.
На электрических схемах прямоугольник обозначается независимо от внешнего вида резистора. Прямоугольник подписан латинской буквой R с номером, который указывает на порядковый номер данного элемента на чертеже. Номинальное значение сопротивления приведено ниже.
В некоторых штатах резисторы UGO выглядят следующим образом.
Рассеиваемая мощность через резисторРезистор, как и любой другой элемент с активным сопротивлением, нагревается при протекании через него тока. Природа нагрева заключается в том, что движущиеся электроны встречают на своем пути препятствия и сталкиваются с ними. В результате столкновений кинетическая энергия электрона передается препятствиям, вызывая их нагрев. Точно так же гвоздь нагревается, когда по нему долго бьют молотком.
Рассеиваемая мощность является номинальным параметром для любого резистора, и если этот параметр не соблюдается, произойдет перегрев и возгорание.
Рассеиваемая мощность P линейно зависит от сопротивления R и квадрат тока I
P=I 2 R
Значение допустимого P показывает, какую мощность резистор способен рассеивать без перегрева в течение длительного времени.
В целом, чем выше Pчем больше резистор, тем больше тепла может быть рассеяно.
На электрических схемах этот параметр обозначается специальными знаками.
Если прямоугольник пуст, это означает, что рассеиваемая мощность не соответствует номинальной, поэтому можно использовать самый маленький резистор.
Примерами расчетов являются P можно посмотреть здесь.
Классы допусков и номиналы резисторовНевозможно изготовить любой электронный компонент со 100% соответствием требуемым характеристикам, так как точность связана с рядом параметров и технологических процессов, которым присуща неточность, в основном связанная с точностью производственного оборудования. Поэтому каждая деталь или отдельный компонент будет отличаться от указанных размеров или характеристик. Кроме того, чем меньше отклонение, тем точнее производственное оборудование и тем выше конечная стоимость продукта. Поэтому не всегда оправданно использовать продукты с минимальными различиями в характеристиках. По этой причине были введены классы точности. В радиолюбительской практике чаще всего используются резисторы с тремя классами точности: I, II и III. В последнем случае резисторы с классами точности II и III встречаются довольно редко, но мы рассмотрим их в качестве примера.
Поэтому каждая деталь или отдельный компонент будет отличаться от указанных размеров или характеристик. Кроме того, чем меньше отклонение, тем точнее производственное оборудование и тем выше конечная стоимость продукта. Поэтому не всегда оправданно использовать продукты с минимальными различиями в характеристиках. По этой причине были введены классы точности. В радиолюбительской практике чаще всего используются резисторы с тремя классами точности: I, II и III. В последнем случае резисторы с классами точности II и III встречаются довольно редко, но мы рассмотрим их в качестве примера.
Класс I означает допустимое отклонение сопротивления от номинального значения ±5%, класс II – ±10%, класс III – ±20%. Например, если для резистора класса I значение сопротивления составляет 100 Ом, то допустимое отклонение может составлять 95 … 105 Ом; для класса II – 90 … 110 Ом; для класса III – 80 … 120 Ом.
Резисторы более высокого класса точности с допуском 1% или менее являются прецизионными резисторами. Они более дорогие, поэтому их применение оправдано только в измерительной технике и высокой точности.
Они более дорогие, поэтому их применение оправдано только в измерительной технике и высокой точности.
Все стандартные значения резисторов классов точности I – III приведены в таблице выше, из которой значения можно умножать на 0,1; 1, 10, 100, 1000 и т.д. Например, резисторы класса I выпускаются со значениями 1,3; 13; 130; 1300; 13000; 130000 Ом и т.д.
В зависимости от класса точности номинальные значения промышленно выпускаемых резисторов строго стандартизированы. Например, если вам нужен резистор класса I сопротивлением 17 Ом, вы его не найдете, потому что этот показатель не производится в нужном классе точности. Вместо этого выберите наиболее близкое значение – 16 Ом или 18 Ом.
Маркировка резисторовМаркировка резисторов используется для визуального отображения ряда параметров, характерных для этих электронных компонентов. Среди прочих параметров стоит отметить три основных: номинальное сопротивление, класс точности и рассеиваемая мощность. Именно эти параметры в первую очередь учитываются при выборе рассматриваемых радиочастотных компонентов.
Именно эти параметры в первую очередь учитываются при выборе рассматриваемых радиочастотных компонентов.
На протяжении многих лет существовало множество видов обозначений, но постепенно, с развитием технологических процессов, несколько видов обозначений вытеснили все остальные.
Советские резисторы, которые до сих пор широко используются, маркируются цифрами и буквами. Латинские буквы “E” и “R” рядом с цифрами или сами цифры указывают на сопротивление в омах, например. 21; 21E, 21R – 21 Ом. Буквы “k” и “M” означают килоом и мегом соответственно. Например, если буква стоит перед цифрами или в середине цифр, она также служит десятичной точкой: 68k – 68 кОм; 6k8 – 6,8 кОм; k68 – 0,68 кОм.
Цветовая маркировка резисторовВ настоящее время цветовая маркировка используется для большинства электронных компонентов. Такой подход вполне оправдан, поскольку цветовое кодирование легче воспринимается, чем цифры и буквы, поэтому оно хорошо различимо даже в самых незначительных случаях.
Цветная маркировка резисторов нанесена на корпус в виде четырех или пяти цветных колец или полос. В первом случае (4 полосы) первые две полосы указывают на богомола, а во втором случае (5 полос) три полосы указывают на богомола. Третье или, соответственно, четвертое кольцо указывает на множитель. Четвертый или пятый – допустимое отклонение в процентах от номинального сопротивления.
По моему мнению и личному опыту, гораздо удобнее, проще и практичнее измерять сопротивление с помощью мультиметра. Здесь существует наименьшая вероятность ошибки, поскольку цвета колец не всегда четко различимы. Например, красный цвет может быть принят за оранжевый и наоборот. Однако при проведении измерений избегайте касания пальцами щупа мультиметра и выводов резистора. В противном случае человеческое тело будет шунтировать резистор, и результаты измерения будут занижены.
Маркировка резисторов SMDОсобенностью SMD-резисторов по сравнению с их свинцовыми аналогами является их минимальный размер при сохранении требуемых характеристик.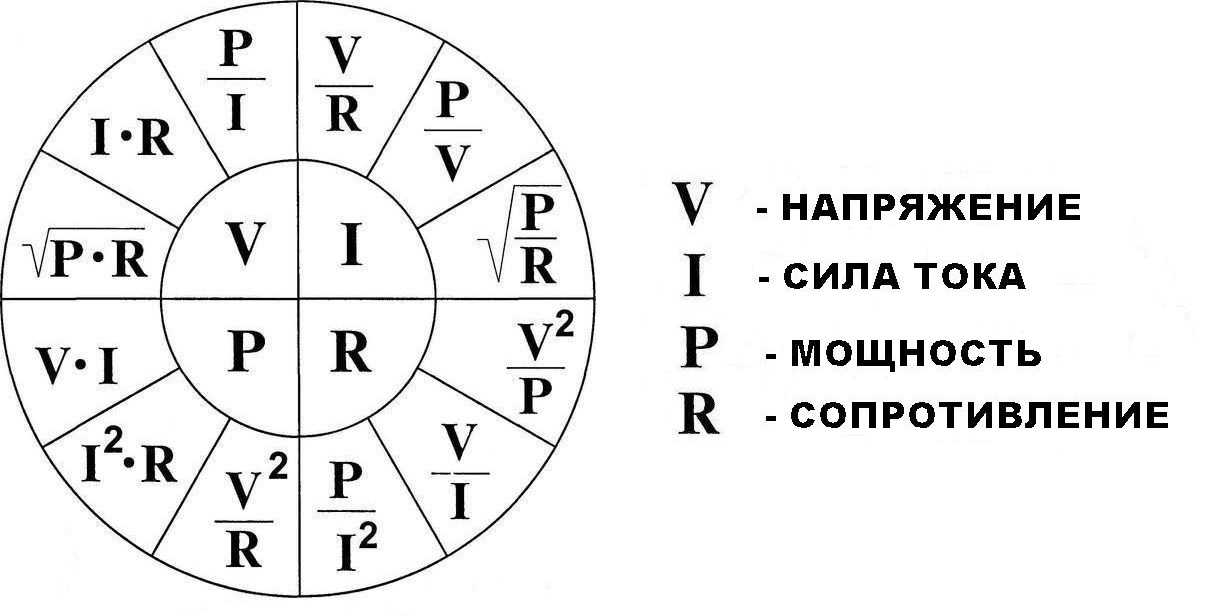
SMD-компоненты не имеют гибких выводов, вместо них имеются контактные площадки, которые используются для припаивания SMD-деталей к аналогичным поверхностям на печатной плате. По этой причине SMD-компоненты называют компонентами поверхностного монтажа.
Переход от традиционного корпуса к SMD упростил автоматизацию производства печатных плат, что значительно сократило время, необходимое для производства электронного изделия, его вес и размер.
Маркировка SMD-резисторов обычно состоит из трех цифр. Первые две обозначают мантиссу, а третья – множитель или количество нулей после двух предыдущих цифр. Например, обозначение 681 означает 68×101 = 680 Ом, что означает, что вы должны добавить один ноль после 68.
Если все три цифры – нули, это перемычка, сопротивление такого SMD-резистора близко к нулю.
Электричество, которое поступает в нашу квартиру по проводам и кабелям от трансформаторной подстанции, побеждено:
Примеры срока службы
Как продлить срок службы электрической лампочки
На пожарной станции в Ливермоле (Калифорния) лампочка удерживает рекорд по самому длительному сроку службы: 117 лет. С 1901 года он работает практически непрерывно и по сей день.
С 1901 года он работает практически непрерывно и по сей день.
Этот срок службы обеспечивается за счет:
- правильный выбор сопротивления для ограничения тока через нить накала и создания экономичного режима освещения;
- Непрерывная работа, исключающая переходные процессы включения/выключения с пусковыми токами;
- Надежная конструкция.
Как регулировать ток от 100 ампер в силовой цепи
Я не повторяю этот случай, а скорее для того, чтобы расширить ваш кругозор и лучше понять процессы электричества.
Ни один обычный резистор не может выдержать ток такой величины в течение какого-либо времени. Он просто перегорит. Однако при установке промышленных генераторов необходимо иметь устройство, способное справиться с такой мощностью.
Это водяной реостат, состоящий из металлического корпуса, прямоугольного ковша, который служит одним из контактов для подключения провода от нагрузки.
Другой контакт представляет собой металлическое лезвие, соединенное изоляторами.
Внутрь ведра наливается вода и засыпается соль: таким образом образуется электролит, который хорошо проводит большие токи.
Перемещение лезвия в электролите изменяет сопротивление среды и позволяет регулировать большие токи. Проводимость может быть изменена концентрацией соли в растворе.
Следовательно, для каждого случая расчета используется своя формула электрического сопротивления, которую следует применять с осторожностью. Специализированный онлайн-калькулятор помогает исключить ошибки в расчетах.
На эту тему рекомендую посмотреть видео Владимира Романова.
Если вы хотите задать вопрос или предоставить дополнительную информацию, пожалуйста, воспользуйтесь разделом комментариев.
Читайте далее:
- Правильное переключение светодиодов; STC ORBITA.
- Измерительный инструмент – это инструмент для измерения. Что такое измерительный инструмент?.
- Переменные резисторы, потенциометры: типы, конструкция, применение, схематические обозначения.
- Важен ли для вас индикатор уведомлений?.
- Основы электроники. Урок 4: Расчет резистора для светодиода.
- Резистор – это резистор. Что такое резистор?.
- Шаговые двигатели: свойства и практические схемы управления. Часть 2.
Электрическая формула для расчета сопротивления – Курсы электротехники eeSasha
Теги: Цепи постоянного тока, Формулы, Сопротивление, Студенческие ошибки
- Сообщение опубликовано: 7 июля 2020 г.
- Категория сообщения: Формулы
- Автор сообщения: Саша Яковлевич
Формула сопротивления
В этой статье мы рассмотрим электрическую формулу расчета сопротивления. Причина, по которой я подчеркиваю «электрическую» формулу, заключается в том, что существует также «физическая» формула для расчета сопротивления. Формула показана слева.
Формула показана слева.
Обычно сопротивление противодействует протеканию тока. Это уравнение на самом деле получается из закона Ома, когда мы решаем его как R.
В этом уравнении сопротивление обозначается буквой R и выражается в Ω (Ом). Буква V используется для обозначения напряжения. Единицей измерения напряжения является: вольт. Буква I используется для тока. Единицей для тока является: Ампер или Ампер для краткости.
Важно отметить, что напряжение V — это напряжение на резисторе, а ток I — это ток, протекающий через резистор.
В этой формуле сопротивление прямо пропорционально напряжению. Это означает, что: чем больше напряжение, тем больше сопротивление. Кроме того, сопротивление обратно пропорционально току. Таким образом: чем больше ток, тем меньше сопротивление.
Сопротивление может быть свойством отрезка провода или проводника, элемента цепи, например резистора, или всей цепи или сети элементов. В теории электрических цепей мы иногда будем использовать выражение «входное сопротивление» или «выходное сопротивление» цепи.
Применение формулы
Вот один из примеров применения формулы для расчета сопротивления.
Постановка задачи
Рассчитайте сопротивление резистора R1, если известно следующее:
- Напряжение источника Vs равно 10 В
- Напряжение V2 на резисторе R2 равно 6 В
- Ток цепи I равен 1 мА 900 14
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2688
- OpenStax
- OpenStax
- Нарисовать цепь с параллельными и последовательными резисторами.

- Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
- Сравните способ расчета общего сопротивления резисторов, включенных последовательно и параллельно.
- Объясните, почему общее сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
- Рассчитайте общее сопротивление цепи, содержащей смесь резисторов, соединенных последовательно и параллельно.
- Сопротивления серии добавить: \(R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}+\dots\)
- Один и тот же ток протекает через каждый резистор последовательно.
- Отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его.
- Параллельное сопротивление находится из \(\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1 }{R_{2}}+\dfrac{1}{R_{3}}+\dots\), и оно меньше любого отдельного сопротивления в комбинации.
- К каждому резистору, подключенному параллельно, приложено одинаковое полное напряжение источника. (Системы распределения электроэнергии чаще всего используют параллельные соединения для питания множества устройств, обслуживаемых одним и тем же напряжением, и позволяют им работать независимо.)
- Параллельные резисторы не получают суммарный ток каждый; они его делят.
- Ответить
Нет, существует множество способов соединения резисторов, не являющихся комбинациями последовательного и параллельного соединения, включая петли и соединения. В таких случаях правила Кирхгофа, которые будут представлены в Правилах Кирхгофа, позволят вам проанализировать схему.

- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает в себя список известных проблем, поскольку они помечены на вашей принципиальной схеме.
- Определите, что именно нужно определить в задаче (идентифицируйте неизвестные). Письменный список полезен.
- Определите, подключены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные. Есть один список для серий и другой для параллельных. Если в вашей задаче сочетаются последовательные и параллельные соединения, уменьшите ее пошагово, рассмотрев отдельные группы последовательных или параллельных соединений, как это делается в этом модуле и в примерах.
 Специальное примечание: при нахождении \(R_p\) необходимо соблюдать осторожность.
Специальное примечание: при нахождении \(R_p\) необходимо соблюдать осторожность. - Проверить разумность и последовательность ответов. Единицы и численные результаты должны быть разумными. Например, общее последовательное сопротивление должно быть больше, тогда как общее параллельное сопротивление должно быть меньше. Мощность должна быть больше для тех же устройств, соединенных параллельно, по сравнению с последовательными и т.д.
- Общее сопротивление электрической цепи с последовательно соединенными резисторами представляет собой сумму отдельных сопротивлений: \(R_s = R_1 + R_2 + R_3 + ….\)
- Через каждый резистор в последовательной цепи протекает одинаковый ток.
- Падение напряжения или рассеиваемая мощность на каждом отдельном резисторе в серии различны, и их общая сумма составляет входную мощность источника питания.
- Общее сопротивление электрической цепи с параллельно соединенными резисторами меньше наименьшего сопротивления любого из компонентов и может быть определено по формуле: \(\dfrac{1}{R_p} = \dfrac{1}{R_1 } +\dfrac{1}{R_2} + \dfrac{1}{R_3} + .
 …\)
…\) - К каждому резистору в параллельной цепи приложено одинаковое полное напряжение источника.
- Ток, протекающий через каждый резистор в параллельной цепи, различен в зависимости от сопротивления.
- Если более сложное соединение резисторов представляет собой комбинацию последовательного и параллельного сопротивления, его можно свести к единому эквивалентному сопротивлению, идентифицируя его различные части как последовательные или параллельные, уменьшая каждую до своего эквивалента и продолжая до тех пор, пока в конечном итоге не будет достигнуто единое сопротивление. .
- Серия
- последовательность резисторов или других компонентов, включенных в цепь один за другим
- резистор
- компонент, обеспечивающий сопротивление току, протекающему по электрической цепи
- сопротивление
- , вызывающий потерю электроэнергии в цепи
- Закон Ома
- соотношение между током, напряжением и сопротивлением в электрической цепи: V=IR
- напряжение
- электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например батареей
- Падение напряжения
- потеря электроэнергии при протекании тока через резистор, провод или другой компонент
- текущий
- поток заряда через электрическую цепь, проходящий через заданную точку измерения
- Закон Джоуля
- Соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое как: \(P_e = IV\)
- параллельный
- соединение резисторов или других компонентов в электрической цепи таким образом, что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы
Решение
Чтобы найти сопротивление, нужно применить формулу: R1=V1/I. Однако значение V1 не задано, поэтому сначала нам нужно рассчитать напряжение на резисторе R1. Если мы применим KVL или закон напряжения Кирхгофа для контура в этой цепи, мы можем написать следующее уравнение напряжения: V1 = Vs-V2. Таким образом, V1 составляет 10–6 В, то есть 4 В.
Теперь у нас есть все необходимое для расчета сопротивления R1. Таким образом, R1 — это V1/I, что составляет 4 В/1 мА, что дает нам 4 кОм. Таким образом, сопротивление резистора R1 равно 4 кОм.
Ошибки учащихся – последовательное соединение
Несмотря на то, что формула расчета сопротивления очень проста, учащиеся иногда допускают ошибки.
Здесь у нас есть пример последовательной цепи. В последовательной цепи все элементы соединены последовательно.
Помните:
Элементы, соединенные последовательно, всегда имеют одинаковый ток!
Таким образом, чтобы рассчитать сопротивление R1, нам нужно разделить напряжение V1 на ток I. Ошибка состоит в том, чтобы разделить напряжение Vs на ток I. Точно так же сопротивление R2 равно V2, деленному на I, а не Vs, деленному на I.
Таким образом, помните, напряжение в формуле должно быть напряжением на резисторе, а не просто любым напряжением в цепи. Тот факт, что ток одинаков для всех элементов, соединенных последовательно, не означает, что их напряжения одинаковы.
Ошибки учащихся – параллельное соединение
Вот похожий, но противоположный пример, когда учащиеся тоже склонны делать ошибки. Эта конкретная схема представляет собой параллельное соединение двух резисторов.
Помните:
Параллельно соединенные элементы всегда имеют одинаковое напряжение!
При параллельном соединении элементы не обязательно имеют одинаковые токи, поэтому нам нужно использовать соответствующий ток при расчете сопротивления. Таким образом, сопротивление R1 равно Vs, деленному на I1, но не Vs, деленному на I. Точно так же сопротивление R2 равно Vs, деленному на I2. Таким образом, мы не можем вычислить R2 как Vs над I.
Таким образом, сопротивление R1 равно Vs, деленному на I1, но не Vs, деленному на I. Точно так же сопротивление R2 равно Vs, деленному на I2. Таким образом, мы не можем вычислить R2 как Vs над I.
Таким образом, ток, который мы используем в этой формуле, должен быть током, протекающим через резистор, а не просто произвольным током в цепи.
Видео и слайды «Формула сопротивления»
Надеюсь, вам понравилась эта статья о Формуле, и сегодня вы узнали что-то новое. Если вы предпочитаете смотреть видео, вот видео для вас.
Я постоянно разрабатываю новые курсы, которые гораздо глубже раскрывают все эти темы. Спасибо, что заглянули и до скорой встречи!
Ниже вы можете найти все слайды, которые я использовал для разработки этого сообщения в блоге и видео:
Предыдущий
Следующий
Наверх
21.1: Резисторы последовательно и параллельно
Цели обучения
К концу этого раздела вы сможете:
Большинство цепей имеют более одного компонента, называемого резистором , который ограничивает поток заряда в цепи. Мера этого предела потока заряда называется сопротивлением . Простейшими комбинациями резисторов являются последовательное и параллельное соединения, показанные на рисунке \(\PageIndex{1}\). Общее сопротивление комбинации резисторов зависит как от их отдельных значений, так и от того, как они соединены.
 (б) Параллельное соединение резисторов.
(б) Параллельное соединение резисторов.Резисторы серии
Когда резисторы серии обозначаются как ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, то \(R_{1}\) на рисунке \(\PageIndex{1}\)(a) может быть сопротивлением стержня отвертки, \ (R_{2}\) сопротивление его ручки, \(R_{3}\) сопротивление тела человека и \(R_{4}\) сопротивление ее обуви.
На рисунке \(\PageIndex {2}\) показаны резисторы, последовательно подключенные к источнику
напряжения . Кажется разумным, что общее сопротивление представляет собой сумму отдельных сопротивлений, учитывая, что ток должен последовательно проходить через каждый резистор. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев высокоомную обувь на резиновой подошве. Это могло бы быть недостатком, если бы одним из сопротивлений был неисправный высокоомный шнур для устройство, которое уменьшило бы рабочий ток.) Рисунок \(\PageIndex{2}\): Три резистора, соединенные последовательно с батареей (слева) и эквивалентное одиночное или последовательное сопротивление (справа).
Это могло бы быть недостатком, если бы одним из сопротивлений был неисправный высокоомный шнур для устройство, которое уменьшило бы рабочий ток.) Рисунок \(\PageIndex{2}\): Три резистора, соединенные последовательно с батареей (слева) и эквивалентное одиночное или последовательное сопротивление (справа). Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потери электроэнергии, называемые
Согласно Закону Ома , падение напряжения \(В\) на резисторе при протекании через него тока рассчитывается по уравнению \(V=IR\), где \(I\) равно току в амперах (А) и \(R\) сопротивление в омах\((\Омега)\). Другой способ думать об этом состоит в том, что \(V\) – это напряжение, необходимое для того, чтобы ток \(I\) протекал через сопротивление \(R\).
Таким образом, падение напряжения на \(R_{1}\) равно \(V_{1}=IR_{1}\), на \(V_{2}=IR_{2}\) и на \ (R_{3}\) равно \(V_{3}=IR_{3}\). Сумма этих напряжений равна выходному напряжению источника; то есть
Сумма этих напряжений равна выходному напряжению источника; то есть
\[V=V_{1}+V_{2}+V_{3}.\]
Это уравнение основано на законах сохранения энергии и заряда. Электрическая потенциальная энергия может быть описана уравнением \(\mathrm{PE}=qV\), где \(q\) – электрический заряд, а \(V\) – напряжение. Таким образом, энергия, подаваемая источником, равна \(qV), а энергия, рассеиваемая резисторами, равна
\[qV_{1}+qV_{2}+qV_{3}.\]
СОЕДИНЕНИЯ: ЗАКОНЫ СОХРАНЕНИЯ
Выводы выражений для последовательного и параллельного сопротивления основаны на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно связаны со всеми электрическими явлениями и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии. Таким образом, \(qV=qV_{1}+qV_{2}+qV_{3}\). Заряд \(q\) отменяется, что дает \(V=V_{1}+V_{2}+V_{3}\), как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для накопления заряда, нет места для утечки заряда, и заряд сохраняется.)
Таким образом, \(qV=qV_{1}+qV_{2}+qV_{3}\). Заряд \(q\) отменяется, что дает \(V=V_{1}+V_{2}+V_{3}\), как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для накопления заряда, нет места для утечки заряда, и заряд сохраняется.)
Теперь подстановка значений отдельных напряжений дает
\[V=IR_{1}+IR_{2}+IR_{3}=I(R_{1}+R_{2}+R_{3}). \]
Обратите внимание, что для эквивалентного последовательного сопротивления \(R_{\mathrm{S}}\) мы имеем
\[V=IR _{\mathrm{S}}.\]
Это означает, что общее или эквивалентное последовательное сопротивление \(R_{\mathrm{S}}\) трех резисторов равно \(R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}\).
Эта логика действительна в целом для любого количества последовательно соединенных резисторов; таким образом, полное сопротивление \(R_{\mathrm{S}}\) последовательного соединения равно
\[R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}+\dots ,\]
как предложено. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, а последовательные сопротивления просто складываются.
Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, а последовательные сопротивления просто складываются.
Пример \(\PageIndex{1}\): расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, выходное напряжение батареи на рисунке \(\PageIndex{2}\) равно \(12,0\mathrm{V}\), а сопротивления равны \(R_{1}=1,00\Омега\), \(R_{2}=6,00\Омега\) и \(R_{3}= 13.0\Омега\). а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (a)
Общее сопротивление представляет собой просто сумму отдельных сопротивлений, определяемую следующим уравнением:
\[R_{\mathrm{S}}=R_{1}+R_ {2}+R_{3}\]
\[=1,00\Омега + 6,00\Омега + 13,0\Омега\]
\[=20,0 \Омега. \]
\]
Стратегия и решение для (b)
Ток определяется по закону Ома \(V=IR\). Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
\[I=\dfrac{V}{R_{\mathrm{S}}}=\dfrac{12,0\Omega}{20,0\Omega}=0,600 \mathrm{A}.\]
Стратегия и решение для (c)
Падение напряжения или \(IR\) на резисторе определяется законом Ома. Ввод тока и значения первого сопротивления дает
\[V_{1}=IR_{1}=(0,600\mathrm{A})(1,0\Omega)=0,600\mathrm{V}.\]
Аналогично,
\[V_{2}=IR_{2}=(0,600\mathrm{A})(6,0\Omega)=3,60\mathrm{V}\]
и
\[V_{3}= IR_{3}=(0,600\mathrm{A})(13,0\Omega)=7,80\mathrm{V}.\]
Обсуждение для (c)
Три капли \(IR\) добавляют к \(12.0\mathrm{V}\), как и предполагалось:
\[V_{1}+V_{2}+V_ {3}=(0,600+3,60+7,80)\mathrm{V}=12,0\mathrm{V}.\]
Стратегия и решение для (d)
Самый простой способ расчета мощности в ваттах (Вт) рассеивается на резисторе в цепи постоянного тока, чтобы использовать закон Джоуля , \(P=IV\), где \(P\) – электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток. Подставив закон Ома \(V=IR\) в закон Джоуля, мы получим мощность, рассеиваемую первым резистором, как 9{2}}{R}\), где \(V\) – падение напряжения на резисторе (не полное напряжение источника). Будут получены одинаковые значения.
В этом случае через каждый резистор протекает одинаковый полный ток. Подставив закон Ома \(V=IR\) в закон Джоуля, мы получим мощность, рассеиваемую первым резистором, как 9{2}}{R}\), где \(V\) – падение напряжения на резисторе (не полное напряжение источника). Будут получены одинаковые значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать \(P=IV\), где \(V\) — напряжение источника. Это дает
\[P=(0,600\mathrm{A})(12,0\mathrm{V})=7,20 \mathrm{W}.\]
Обсуждение для (e)
Обратите внимание, по совпадению, что общая мощность, рассеиваемая резисторами, также составляет 7,20 Вт, как и мощность, выдаваемая источником. то есть
\[P_{1}+P_{2}+P_{3}=(0,360 +2,16+4,68)\mathrm{W}=7,20\mathrm{W}.\]
Мощность – это энергия в единицу времени ( Вт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ В СЕРИИ
Резисторы, включенные параллельно
На рисунке \(\PageIndex{3}\) показаны резисторы, включенные параллельно , подключенные к источнику напряжения. Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен). Например, автомобильные фары, радиоприемник и т. д. соединены параллельно, так что они используют полное напряжение источника и могут работать совершенно независимо. То же самое верно и в вашем доме, или в любом здании. (См. рисунок \(\PageIndex{3}\)(b).)
То же самое верно и в вашем доме, или в любом здании. (См. рисунок \(\PageIndex{3}\)(b).)
Чтобы найти выражение для эквивалентного параллельного сопротивления \(R_{\mathrm{p}}\), давайте рассмотрим протекающие токи и то, как они связаны с сопротивлением. Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны \(I_{1}=\dfrac{V}{R_{1}}\), \(I_{2}=\dfrac{ V}{R_{2}}\) и \(I_{3}=\dfrac{V}{R_{3}}\). Сохранение заряда подразумевает, что полный ток \(I\), производимый источником, представляет собой сумму этих токов:
\[I=I_{1}+I_{2}+I_{3}.\]
Подстановка выражений для отдельных токов дает
\[I=\dfrac{V}{R_{1}} +\dfrac{V}{R_{2}}+\dfrac{V}{R_{3}}=V(\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}} +\dfrac{1}{R_{3}}). \]
\]
Обратите внимание, что закон Ома для эквивалентного единичного сопротивления дает
\[I=\dfrac{V}{R_{\mathrm{p}}}= V(\dfrac{1}{R_{\mathrm{p}}}).\]
Члены в скобках в последних двух уравнениях должны быть равны. Обобщая на любое количество резисторов, общее сопротивление \(R_{\mathrm{p}}\) параллельного соединения связано с отдельными сопротивлениями как
\[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{ R_{3}}+\dots\]
Это соотношение приводит к тому, что общее сопротивление \(R_{\mathrm{p}}\) меньше, чем наименьшее из отдельных сопротивлений. (Это видно в следующем примере.) Когда резисторы соединены параллельно, от источника протекает больший ток, чем для любого из них по отдельности, и поэтому общее сопротивление ниже.
Пример \(\PageIndex{2}\): расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления при параллельном соединении на рисунке \(\PageIndex{3}\) будут такими же, как при рассмотренном ранее последовательном соединении: \(V=12. 0\mathrm{V},\: R_ {1}=1,00\Омега\: R_{2}=6,00\Омега\) и \(R_{3}=13,0\Омега\). а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
0\mathrm{V},\: R_ {1}=1,00\Омега\: R_{2}=6,00\Омега\) и \(R_{3}=13,0\Омега\). а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (a)
Общее сопротивление для параллельной комбинации резисторов определяется с помощью приведенного ниже уравнения. Ввод известных значений дает
\[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac {1}{R_{3}}=\dfrac{1}{1.00\Omega}+\dfrac{1}{6.00\Omega}+\dfrac{1}{13.0\Omega}.\]
Таким образом,
\[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1,00}{\Omega}+\dfrac{0,1667}{\Omega}+\dfrac{0,07692}{\Omega}=\ dfrac{1.2436}{\Omega}.\]
(Обратите внимание, что в этих вычислениях каждый промежуточный ответ показан с дополнительной цифрой. )
)
Мы должны инвертировать это, чтобы найти общее сопротивление \(R_{\mathrm{p}}\). Это дает
\[R_{\mathrm{p}}=\dfrac{1}{1,2436}\Omega=0,8041\Omega.\]
Общее сопротивление с правильным количеством значащих цифр равно \(R_{\ матрм{р}}=0,804\Омега\).
Обсуждение для (a)
\(R_{\mathrm{p}}\), как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, подставив \(R_{\mathrm{p}}\) вместо полного сопротивления. Это дает
\[I=\dfrac{V}{R_{\mathrm{p}}}=\dfrac{12,0\mathrm{V}}{0,8041 \Omega}=14,92 \mathrm{A}.\]
Обсуждение для (б)
Ток \(i\) для каждого устройства намного больше, чем для тех же устройств, соединенных последовательно (см. предыдущий пример). Цепь с параллельными соединениями имеет меньшее общее сопротивление, чем резисторы, соединенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко рассчитать по закону Ома, поскольку на каждый резистор подается полное напряжение. Таким образом,
Таким образом,
\[I_{1}=\dfrac{V}{R_{1}}=\dfrac{12.0\mathrm{V}}{1.00\Omega}=12.0\mathrm{A}.\]
Аналогично,
\[I_{2}=\dfrac{V}{R_{2}}=\dfrac{12.0\mathrm{V}}{6.00\Omega}=2.00\mathrm{A}\]
и
\[I_{3}=\dfrac{V}{R_{3}}=\dfrac{12.0\mathrm{V}}{13.0\Omega}=0,92\mathrm{A}.\]
9{2}}{13.0\Omega}=11.1\mathrm{W}.\]Обсуждение для (d)
Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к одному и тому же напряжению. источник.
Стратегия и решение для (e)
Общая мощность также может быть рассчитана несколькими способами. Выбор \(P=IV\) и ввод общего тока дает
\[P=IV=(14,92\mathrm{A})(12,0\mathrm{V})=179\mathrm{W}.\]
Обсуждение для (д)
Суммарная мощность, рассеиваемая резисторами, также составляет 179 Вт:
\[P_{1}+P_{2}+P_{3}=144\mathrm{W}+24.0\mathrm{W}+11.1\mathrm {W}=179\mathrm{W}. \]
\]
Это согласуется с законом сохранения энергии.
Общее обсуждение
Обратите внимание, что и токи, и мощности при параллельном соединении больше, чем у тех же устройств, соединенных последовательно.
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ, ПОДКЛЮЧЕННЫХ ПАРАЛЛЕЛЬНО
Комбинации последовательного и параллельного соединения
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения. Они часто встречаются, особенно когда учитывается сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Они часто встречаются, особенно когда учитывается сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения могут быть сведены к одному эквивалентному сопротивлению с помощью метода, показанного на рисунке \(\PageIndex{4}\). Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее сокращаются до тех пор, пока не останется единственное сопротивление. Процесс скорее трудоемкий, чем сложный.
Рисунок \(\PageIndex{4}\): Эта комбинация семи резисторов имеет как последовательные, так и параллельные части. Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единое эквивалентное сопротивление. Простейшая комбинация последовательного и параллельного сопротивлений, показанная на рисунке \(\PageIndex{5}\), также является наиболее поучительной, поскольку она встречается во многих приложениях. Например, \(R_{1}\) может быть сопротивлением проводов от автомобильного аккумулятора до его электрических устройств, которые включены параллельно. \(R_{2}\) и \(R_{3}\) могут быть стартером и освещением салона. Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.
Например, \(R_{1}\) может быть сопротивлением проводов от автомобильного аккумулятора до его электрических устройств, которые включены параллельно. \(R_{2}\) и \(R_{3}\) могут быть стартером и освещением салона. Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.
Пример \(\PageIndex{3}\): расчет сопротивления, падения \(IR\), тока и рассеиваемой мощности: объединение последовательных и параллельных цепей
На рисунке \(\PageIndex{5}\) показаны резисторы из предыдущие два примера подключены по-другому – комбинация последовательного и параллельного. Мы можем рассматривать \(R_1\) как сопротивление проводов, ведущих к \(R_2\) и \(R_3\). а) Найдите полное сопротивление. (б) Что такое падение \(IR\) в \(R_1\)? (c) Найдите ток от \(I_2\) до \(R_2\). (d) Какая мощность рассеивается \(R_2\)?
Рисунок \(\PageIndex{5}\). Эти три резистора подключены к источнику напряжения так, что \(R_2\) и \(R_3\) параллельны друг другу, а эта комбинация последовательно с \(R_1\).
Стратегия и решение для (a)
Чтобы найти общее сопротивление, заметим, что \(R_2\) и \(R_3\) параллельны, а их комбинация \(R_p\) последовательно с \(R_1 \). Таким образом, общее (эквивалентное) сопротивление этой комбинации равно \[R_{tot} = R_1 + R_2.\]
Сначала находим \(R_p\), используя уравнение для параллельных резисторов и вводя известные значения: \[\ dfrac{1}{R_p} = \dfrac{1}{R_2} + \dfrac{1}{6,00 \, \Omega} + \dfrac{1}{13,0 \, \Omega} = \dfrac{0,2436}{\ Омега}.\]
Инвертирование дает \[R_p = \dfrac{1}{0,2436}\Omega = 4,11 \, \Omega.\] Таким образом, общее сопротивление равно \[R_{tot} = R_1 + R_p = 1,00 \Omega + 4,11 \Omega. = 5,11 \, \Омега.\]
Обсуждение для (а)
Суммарное сопротивление этой комбинации является промежуточным между чисто последовательными и чисто параллельными значениями (\(20,0 \, \Омега\) и \(0,804 \, \Omega\) соответственно), найденные для тех же резисторов в двух предыдущих примерах.
Стратегия и решение для (b)
Чтобы найти падение \(IR\) в \(R_1\), заметим, что полный ток \(I\) протекает через \(R_1\). Таким образом, его \(IR\) падение равно \[V_1 = IR_1.\]. Мы должны найти \(I\), прежде чем мы сможем вычислить \(V_1\). Полный ток \(I\) находится по закону Ома для цепи. То есть \[I = \dfrac{V}{R_{tot}} = \dfrac{12,0 \, V}{5,11 \, \Omega} = 2,35 \, A.\]. Вводя это в выражение выше, мы получить \[V_1 = IR_1 = (2,35 \, A)(1,00 \, \Omega) = 2,35 \, V.\]
Обсуждение для (б)
Напряжение на \(R_2\) и \(R_3\) меньше общего напряжения на величину \(V_1\). Когда сопротивление проводов велико, это может существенно повлиять на работу устройств, представленных \(R_2\) и \(R_3\).
Стратегия и решение для (c)
Чтобы найти ток через \(R_2\), мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение \(V_p\), потому что оно применяется к параллельной комбинации резисторов. 2(6,00 \, \ омега) = 15,5\, Вт.\]
2(6,00 \, \ омега) = 15,5\, Вт.\]
Обсуждение для (d)
Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.
Практические выводы
Одним из следствий последнего примера является то, что сопротивление в проводах уменьшает ток и мощность, подаваемые на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение \(IR\) в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается двигатель, освещение холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
То, что происходит в таких сильноточных ситуациях, показано на рисунке \(\PageIndex{6}\). Устройство, представленное \(R_3\), имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение \(IR\) в проводах, представленных \(R_1\), уменьшая напряжение на лампочке (которое равно \(R_2\)), которая затем заметно тускнеет.
Этот увеличенный ток вызывает большее падение \(IR\) в проводах, представленных \(R_1\), уменьшая напряжение на лампочке (которое равно \(R_2\)), которая затем заметно тускнеет.
Упражнение \(\PageIndex{1}\)
Можно ли любую произвольную комбинацию резисторов разбить на последовательные и параллельные комбинации? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательных и параллельных соединений.
Стратегии решения проблем для последовательных и параллельных резисторов
Резюме
Глоссарий
Эта страница под названием 21.


