Формула максимального напряжения: Максимальное напряжение на конденсаторе формула. Энергия заряженного конденсатора. применение конденсаторов

Максимальное напряжение на конденсаторе формула. Энергия заряженного конденсатора. применение конденсаторов

Печать

Конденсатор – электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики – емкости . Емкость конденсатора (С) определяется как соотношение количества электрического заряда (Q) к напряжению (U).

Емкость конденсатора измеряется в фарадах (F) – единицах, названых в честь британского ученого физика Майкла Фарадея. Емкость в один фарад (1F) равняется количеству заряда в один кулон (1C), создающему напряжение на конденсаторе в один вольт (1V). Вспомним, что один кулон (1С) равняется величине заряда, прошедшего через проводник за одну секунду (1sec) при силе тока в один ампер (1A).

Однако кулон, это очень большое количество заряда относительно того, сколько способно хранить большинство конденсаторов.

По этой причине, для измерения емкости обычно используют микрофарады (µF или uF), нанофарады (nF) и пикофарады (pF).

• 1µF = 0.000001 = 10 -6 F

• 1nF = 0.000000001 = 10 -9 F

• 1pF = 0.000000000001 = 10 -12 F

Плоский конденсатор

Существует множество типов конденсаторов различной формы и внутреннего устройства. Рассмотрим самый простой и принципиальный — плоский конденсатор. Плоский конденсатор состоит из двух параллельных пластин проводника (обкладок), электрически изолированных друг от друга воздухом, или специальным диэлектрическим материалом (например бумага, стекло или слюда).

Устройство конденсатора

Заряд конденсатора. Ток

По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.

Рассмотрим принцип работы плоского конденсатора. Если подключить к нему источник питания, на одной пластине проводника начнут собираться отрицательно заряженные частицы в виде электронов, на другой – положительно заряженные частицы в виде ионов.

Поскольку между обкладками находиться диэлектрик, заряженные частицы не могут «перескочить» на противоположную сторону конденсатора. Тем не менее, электроны передвигаются от источника питания — до пластины конденсатора. Поэтому в цепи идет электрический ток.

В самом начале включения конденсатора в цепь, на его обкладках больше всего свободного места. Следовательно, начальный ток в этот момент встречает меньше всего сопротивления и является максимальным. По мере заполнения конденсатора заряженными частицами ток постепенно падает, пока не закончится свободное место на обкладках и ток совсем не прекратится.

Время между состояниями «пустого» конденсатора с максимальным значением тока, и «полного» конденсатора с минимальным значением тока (т.е. его отсутствием), называют

переходным периодом заряда конденсатора.

Напряжение

В самом начале переходного периода зарядки, напряжение между обкладками конденсатора равняется нулю. Как только на обкладках начинают появляться заряженные частицы, между разноименными зарядами возникает напряжение. Причиной этому является диэлектрик между пластинами, который «мешает» стремящимся друг к другу зарядам с противоположным знаком перейти на другую сторону конденсатора.

На начальном этапе зарядки, напряжение быстро растет, потому что большой ток очень быстро увеличивает количество заряженных частиц на обкладках. Чем больше заряжается конденсатор, тем меньше ток, и тeм медленнее растет напряжение. В конце переходного периода, напряжение на конденсаторе полностью прекратит рост, и будет равняться напряжению на источнике питания.

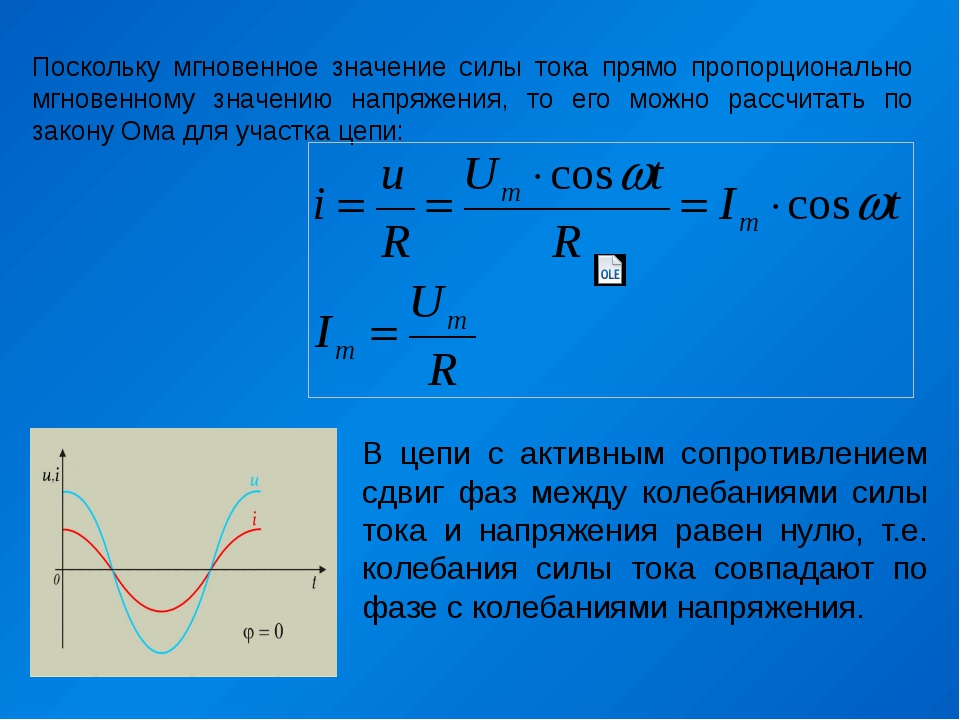
Как видно на графике, сила тока конденсатора напрямую зависит от изменения напряжения.

Формула для нахождения тока конденсатора во время переходного периода:

• Ic — ток конденсатора

• C — Емкость конденсатора

• ?Vc/?t – Изменение напряжения на конденсаторе за отрезок времени

После того как конденсатор зарядился, отключим источник питания и подключим нагрузку R. Так как конденсатор уже заряжен, он сам превратился в источник питания.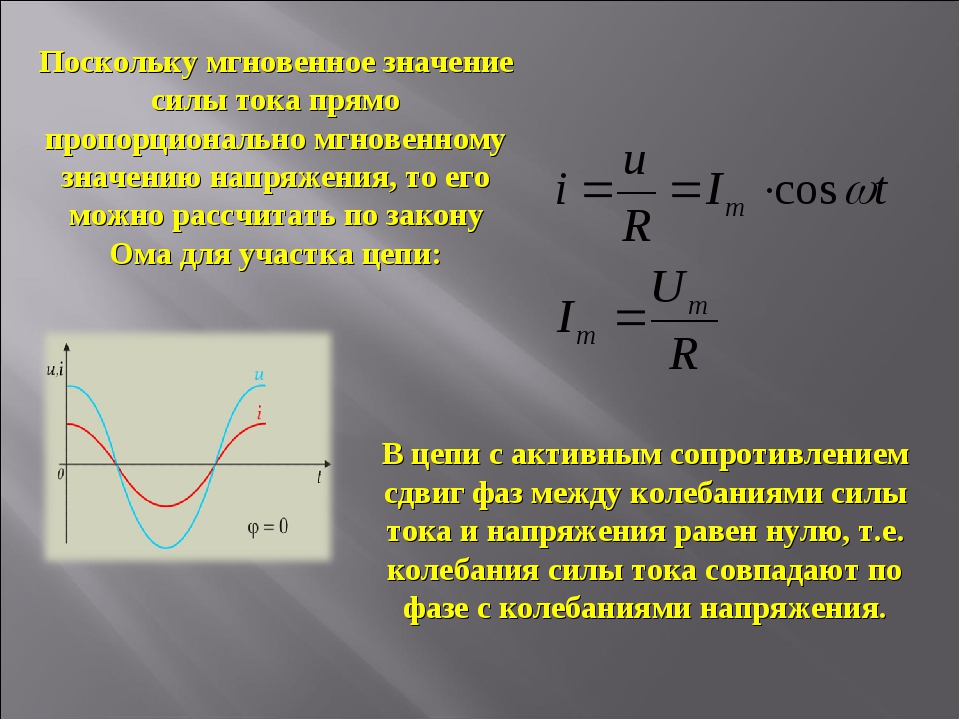 Нагрузка R образовала проход между пластинами. Отрицательно заряженные электроны, накопленные на одной пластине, согласно силе притяжения между разноименными зарядами, двинутся в сторону положительно заряженных ионов на другой пластине.

В момент подключения R, напряжение на конденсаторе то же, что и после окончания переходного периода зарядки. Начальный ток по закону Ома будет равняться напряжению на обкладках, разделенном на сопротивление нагрузки.

Как только в цепи пойдет ток, конденсатор начнет разряжаться. По мере потери заряда, напряжение начнет падать. Следовательно, ток тоже упадет. По мере понижения значений напряжения и тока, будет снижаться их скорость падения.

Время зарядки и разрядки конденсатора зависит от двух параметров – емкости конденсатора C и общего сопротивления в цепи R. Чем больше емкость конденсатора, тем большее количество заряда должно пройти по цепи, и тем больше времени потребует процесс зарядки/разрядки (ток определяется как количество заряда, прошедшего по проводнику за единицу времени). Чем больше сопротивление R, тем меньше ток. Соответственно, больше времени потребуется на зарядку.

Продукт RC (сопротивление, умноженное на емкость) формирует временную константу ? (тау). За один ? конденсатор заряжается или разряжается на 63%. За пять ? конденсатор заряжается или разряжается полностью.

Для наглядности подставим значения: конденсатор емкостью в 20 микрофарад, сопротивление в 1 килоом и источник питания в 10В. Процесс заряда будет выглядеть следующим образом:

Устройство конденсатора. От чего зависит емкость?

Емкость плоского конденсатора зависит от трех основных факторов:

• Площадь пластин — A

• Расстояние между пластинами – d

• Относительная диэлектрическая проницаемость вещества между пластинами — ?

Чем больше площадь пластин конденсатора, тем больше заряженых частиц могут на них разместится, и тем больше емкость.

Расстояние между пластинами

Емкость конденсатора обратно пропорциональна расстоянию между пластинами.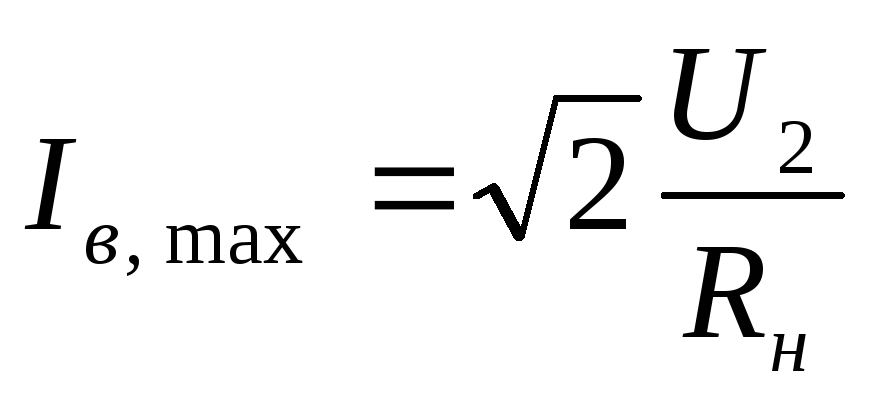

Для того чтобы объяснить природу влияния этого фактора, необходимо вспомнить механику взаимодействия зарядов в пространстве (электростатику).

Если конденсатор не находится в электрической цепи, то на заряженные частицы, расположенные на его пластинах влияют две силы. Первая — это сила отталкивания между одноименными зарядами соседних частиц на одной пластине. Вторая – это сила притяжения разноименных зарядов между частицами, находящимися на противоположных пластинах. Получается, что чем ближе друг к другу находятся пластины, тем больше суммарная сила притяжения зарядов с противоположным знаком, и тем больше заряда может разместится на одной пластине.

Относительная диэлектрическая проницаемость

Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость?

. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.

Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.

Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.

Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.

• Бумага – от 2.5 до 3.5

• Стекло – от 3 до 10

• Слюда – от 5 до 7

• Порошки оксидов металлов – от 6 до 20

Номинальное напряжение

Второй по значимости характеристикой после емкости является максимальное номинальное напряжение конденсатора . Данный параметр обозначает максимальное напряжение, которое может выдержать конденсатор. Превышение этого значения приводит к «пробиванию» изолятора между пластинами и короткому замыканию. Номинальное напряжение зависит от материала изолятора и его толщины (расстояния между обкладками).

Следует отметить, что при работе с переменным напряжением нужно учитывать именно пиковое значение (наибольшее мгновенное значение напряжения за период). Например, если эффективное напряжение источника питания будет 50В, то его пиковое значение будет свыше 70В. Соответственно необходимо использовать конденсатор с номинальным напряжением более 70В. Однако на практике, рекомендуется использовать конденсатор с номинальным напряжением не менее в два раза превышающим максимально возможное напряжение, которое будет к нему приложено.

Ток утечки

Также при работе конденсатора учитывается такой параметр как ток утечки. Поскольку в реальной жизни диэлектрик между пластинами все же пропускает маленький ток, это приводит к потере со временем начального заряда конденсатора.

Если соединить резистор и конденсатор, то получится пожалуй одна из самых полезных и универсальных цепей.

О многочисленных способах применения которой я сегодня и решил рассказать. Но вначале про каждый элемент в отдельности:

Резистор — его задача ограничивать ток. Это статичный элемент, чье сопротивление не меняется, про тепловые погрешности сейчас не говорим — они не слишком велики. Ток через резистор определяется законом ома —

I=U/R , где U напряжение на выводах резистора, R — его сопротивление.

Конденсатор штука поинтересней. У него есть интересное свойство — когда он разряжен то ведет себя почти как короткое замыкание — ток через него течет без ограничений, устремляясь в бесконечность. А напряжение на нем стремится к нулю. Когда же он заряжен, то становится как обрыв и ток через него течь перестает, а напряжение на нем становится равным заряжающему источнику. Получается интересная зависимость — есть ток, нет напряжения, есть напряжение — нет тока.

Чтобы визуализировать себе этот процесс, представь ган… эмм.. воздушный шарик который наполняется водой. Поток воды — это ток. Давление воды на упругие стенки — эквивалент напряжения. Теперь смотри, когда шарик пуст — вода втекает свободно, большой ток, а давления еще почти нет — напряжение мало. Потом, когда шарик наполнится и начнет сопротивляться давлению, за счет упругости стенок, то скорость потока замедлится, а потом и вовсе остановится — силы сравнялись, конденсатор зарядился. Есть напряжение натянутых стенок, но нет тока!

Теперь, если снять или уменьшить внешнее давление, убрать источник питания, то вода под действием упругости хлынет обратно. Также и ток из конденсатора потечет обратно если цепь будет замкнута, а напряжение источника ниже чем напряжение в конденсаторе.

Емкость конденсатора. Что это?
Теоретически, в любой идеальный конденсатор можно закачать заряд бесконечного размера. Просто наш шарик сильней растянется и стенки создадут большее давление, бесконечно большое давление.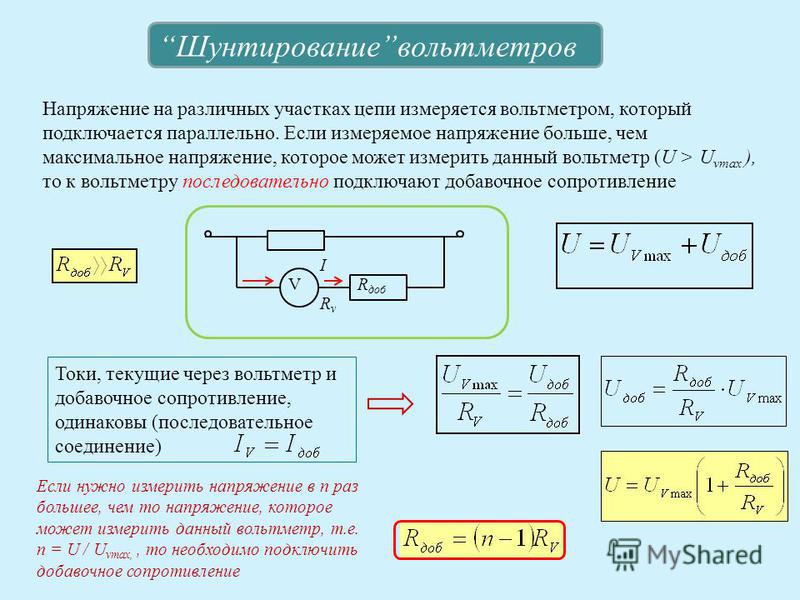
А что же тогда насчет Фарад, что пишут на боку конденсатора в качестве показателя емкости? А это всего лишь зависимость напряжения от заряда (q = CU). У конденсатора малой емкости рост напряжения от заряда будет выше.

Представь два стакана с бесконечно высокими стенками. Один узкий, как пробирка, другой широкий, как тазик. Уровень воды в них — это напряжение. Площадь дна — емкость. И в тот и в другой можно набузолить один и тот же литр воды — равный заряд. Но в пробирке уровень подскочит на несколько метров, А в тазике будет плескаться у самого дна. Также и в конденсаторах с малой и большой емкостью.
Залить то можно сколько угодно, но напряжение будет разным.

Плюс в реале у конденсаторов есть пробивное напряжение, после которого он перестает быть конденсатором, а превращается в годный проводник:)

А как быстро заряжается конденсатор?
В идеальных условиях, когда у нас бесконечно мощный источник напряжения с нулевым внутренним сопротивлением, идеальные сверхпроводящие провода и абсолютно безупречный конденсатор — этот процесс будет происходить мгновенно, с временем равным 0, равно как и разряд.

Но в реальности всегда существуют сопротивления, явные — вроде банального резистора или неявные, такие как сопротивление проводов или внутреннее сопротивление источника напряжения.
В этом случае скорость заряда конденсатора будет зависить от сопротивлений в цепи и емкости кондера, а сам заряд будет идти по экспоненциальному закону .

А у этого закона есть пара характерных величин:

• Т — постоянная времени , это время при котором величина достигнет 63% от своего максимума. 63% тут взялись не случайно, тут прямая завязка на такую формулу VALUE T =max—1/e*max.
• 3T — а при троекратной постоянной значение достигнет 95% своего максимума.

Постоянная времени для RC цепи Т=R*C .

Чем меньше сопротивление и меньше емкость, тем быстрей конденсатор заряжается. Если сопротивление равно нулю, то и время заряда равно нулю.

Рассчитаем за сколько зарядится на 95% конденсатор емкостью 1uF через резистор в 1кОм:
T= C*R = 10 -6 * 10 3 = 0.001c
3T = 0.003c через такое время напряжение на конденсаторе достигнет 95% от напряжения источника.

Разряд пойдет по тому же закону, только вверх ногами. Т.е. через Твремени в на конденсаторе остаенется всего лишь 100% — 63% = 37% от первоначального напряжения, а через 3T и того меньше — жалкие 5%.

Ну с подачей и снятием напряжения все ясно. А если напряжение подали, а потом еще ступенчато подняли, а разряжали также ступеньками? Ситуация тут практически не изменится — поднялось напряжение, конденсатор дозарядился до него по тому же закону, с той же постоянной времени — через время 3Т его напряжение будет на 95% от нового максимума.
Чуть понизилось — подразрядился и через время 3Т напряжение на нем будет на 5% выше нового минимума.
Да что я тебе говорю, лучше показать. Сварганил тут в мультисиме хитровыдрюченный генератор ступечнатого сигнала и подал на интегрирующую RC цепочку:

Видишь как колбасится:) Обрати внимание, что и заряд и разряд, вне зависимости от высоты ступеньки, всегда одной длительности!!!

А до какой величины конденсатор можно зарядить?
В теории до бесконечности, этакий шарик с бесконечно тянущимися стенками. В реале же шарик рано или поздно лопнет, а конденсатор пробьет и закоротит. Вот поэтому у всех конденсаторов есть важный параметр — предельное напряжение . На электролитах его часто пишут сбоку, а на керамических его надо смотреть в справочниках. Но там оно обычно от 50 вольт. В общем, выбирая кондер надо следить, чтобы его предельное напряжение было не ниже того которое в цепи. Добавлю что при расчете конденсатора на переменное напряжение следует выбирать предельное напряжение в 1.4 раза выше. Т.к. на переменном напряжении указывают действующее значение, а мгновенное значение в своем максимуме превышает его в 1.4 раза.

Что следует из вышеперечисленного? А то что если на конденсатор подать постоянное напряжение, то он просто зарядится и все. На этом веселье закончится.

А если подать переменное? То очевидно, что он будет то заряжаться, то разряжаться, а в цепи будет туда и обратно гулять ток. Движуха! Ток есть!

Выходит, несмотря на физический обрыв цепи между обкладками, через конденсатор легко протекает переменный ток, а вот постоянному слабо.

Что нам это дает? А то что конденсатор может служить своего рода сепаратором, для разделения переменного тока и постоянного на соответствующие составляющие.

Любой изменяющийся во времени сигнал можно представить как сумму двух составляющих — переменной и постоянной.

Например, у классической синусоиды есть только переменная часть, а постоянная равна нулю. У постоянного же тока наоборот. А если у нас сдвинутая синусоида? Или постоянная с помехами?

Переменная и постоянная составляющие сигнала легко разделяются!
Чуть выше я тебе показал как конденсатор дозаряжается и подразряжается при изменениях напряжения. Так что переменная составляющая сквозь кондер пройдет на ура, т.к. только она заставляет конденсатор активно менять свой заряд. Постоянная же как была так и останется и застрянет на конденсаторе.

Но чтобы конденсатор эффективно разделял переменную составляющую от постоянной частота переменной составляющей должна быть не ниже чем 1/T

Возможны два вида включения RC цепочки:
Интегрирующая и дифференцирующая . Они же фильтр низких частот и фильтр высоких частот.

Фильтр низких частот без изменений пропускает постоянную составляющую (т.к. ее частота равна нулю, ниже некуда) и подавляет все что выше чем 1/T. Постоянная составляющая проходит напрямую, а переменная составляющая через конденсатор гасится на землю.
Такой фильтр еще называют интегрирующей цепочкой потому, что сигнал на выходе как бы интегрируется. Помнишь что такое интеграл? Площадь под кривой! Вот тут она и получается на выходе.

А дифференцирующей цепью ее называют потому, что на выходе у нас получается дифференциал входной функции, который есть не что иное как скорость изменения этой функции.

• На участке 1 происходит заряд конденсатора, а значит через него идет ток и на резисторе будет падение напряжения.
• На участке 2 происходит резкое увеличение скорости заряда, а значит и ток резко возрастет, а за ним и падение напряжения на резисторе.
• На участке 3 конденсатор просто удерживает уже имеющийся потенциал. Ток через него не идет, а значит на резисторе напряжение тоже равно нулю.
• Ну и на 4м участке конденсатор начал разряжаться, т.к. входной сигнал стал ниже чем его напряжение. Ток пошел в обратную сторону и на резисторе уже отрицательное падение напряжения.

А если подать на вход прямоугольнй импульс, с очень крутыми фронтами и сделать емкость конденсатора помельче, то увидим вот такие иголки:

прямоугольник. Ну, а чо? Правильно — производная от линейной функции есть константа, наклон этой функции определяет знак константы.

Короче, если у тебя сейчас идет курс матана, то можешь забить на богомерзкий Mathcad, отвратный Maple, выбросить из головы матричную ересь Матлаба и, достав из загашников горсть аналоговой рассыпухи, спаять себе истинно ТРУЪ аналоговый компьютер:) Препод будет в шоке:)

Правда на одних только резисторах кондерах интеграторы и диффернциаторы обычно не делают, тут юзают операционные усилители. Можешь пока погуглить на предмет этих штуковин, любопытная вещь:)

А вот тут я подал обычный приямоугольный сигнал на два фильтра высоких и низких частот. А выходы с них на осциллограф:

Вот, чуть покрупней один участок:

При старте кондер разряжен, ток через него вваливат на полную, а напряжение на нем мизерное — на входе RESET сигнал сброса. Но вскоре конденсатор зарядится и через время Т его напряжение будет уже на уровне логической единицы и на RESET перестанет подаваться сигнал сброса — МК стартанет.
А для AT89C51 надо с точностью наоборот RESET организовать — вначале подать единицу, а потом ноль. Тут ситуация обратная — пока кондер не заряжен, то ток через него течет большой, Uc — падение напряжения на нем мизерное Uc=0. А значит на RESET подается напряжение немногим меньше напряжения питания Uпит-Uc=Uпит.
Но когда кондер зарядится и напряжение на нем достигнет напряжения питания (Uпит=Uс), то на выводе RESET уже будет Uпит-Uc=0

Аналоговые измерения
Но фиг сними с цепочками сброса, куда прикольней использовать возможность RC цепи для замера аналоговых величин микроконтроллерами в которых нет АЦП.
Тут используется тот факт, что напряжение на конденсаторе растет строго по одному и тому же закону — экспоненте. В зависимости от кондера, резистора и питающего напряжения. А значит его можно использовать как опорное напряжение с заранее известными параметрами.

Работает просто, мы подаем напряжение с конденсатора на аналоговый компаратор, а на второй вход компаратора заводим измеряемое напряжение. И когда хотим замерить напряжение, то просто вначале дергаем вывод вниз, чтобы разрядить конденсатор. Потом возвращем его в режим Hi-Z, cбрасываем и запускаем таймер. А дальше кондер начинает заряжаться через резистор и как только компаратор доложит, что напряжение с RC догнало измеряемое, то останавливаем таймер.

Зная по какому закону от времени идет возрастание опорного напряжения RC цепи, а также зная сколько натикал таймер, мы можем довольно точно узнать чему было равно измеряемое напряжение на момент сработки компаратора. Причем, тут не обязательно считать экспоненты. На начальном этапе зарядки кондера можно предположить, что зависимость там линейная. Или, если хочется большей точности, аппроксимировать экспоненту кусочно линейными функциями, а по русски — отрисовать ее примерную форму несколькими прямыми или сварганить таблицу зависимости величины от времени, короче, способов вагон просто.

Если надо заиметь аналоговую крутилку, а АЦП нету, то можно даже компаратор не юзать. Дрыгать ножкой на которой висит конденсатор и давать ему заряжаться через перменный резистор.

По изменению Т, которая, напомню T=R*C и зная что у нас С = const, можно вычислить значение R. Причем, опять же необязательно подключать тут математический аппарат, в большинстве случаев достаточно сделать замер в каких-нибудь условных попугаях, вроде тиков таймера. А можно пойти другим путем, не менять резистор, а менять емкость, например, подсоединяя к ней емкость своего тела… что получится? Правильно — сенсорные кнопки!

Если что то непонятно, то не парься скоро напишу статью про то как прикрутить к микроконтроллеру аналоговую фиговину не используя АЦП. Там подробно все разжую.

Как и любая система заряжен-ных тел, конденсатор обладает энер-гией. Вычислить энергию заряжен-ного плоского конденсатора с одно-родным полем внутри него не-сложно.

Энергия заряженного конденса-тора.

Для того чтобы зарядить конденсатор, нужно совершить рабо-ту по разделению положительных и отрицательных зарядов. Согласно закону сохранения энергии эта ра-бота равна энергии конденсатора. В том, что заряженный конденсатор обладает энергией, можно убедиться, если разрядить его через цепь, со-держащую лампу накаливания, рас-считанную на напряжение в не-сколько вольт (рис. 4). При раз-рядке конденсатора лампа вспыхи-вает. Энергия конденсатора пре-вращается в другие формы: тепло-вую, световую.

Выведем формулу для энергии плоского конденсатора .

Напряженность поля, созданного зарядом одной из пластин, равна Е/2, где Е — напряженность поля в конденсаторе. В однородном поле одной пластины находится заряд q, распределенный по поверхности дру-гой пластины (рис. 5). Согласно формуле W p = qEd. для потенциальной энергии заряда в однородном поле энергия конденсатора равна:

Можно доказать, что эти форму-лы справедливы для энергии любого конденсатора, а не только для плос-кого.

Энергия электрического поля.

Согласно теории близкодействия вся энергия взаимодействия заряженных тел сконцентрирована в электриче-ском поле этих тел. Значит, энергия может быть выражена через основную характеристику поля — напря-женность.

Так как напряженность электри-ческого поля прямо пропорциональ-на разности потенциалов

(U = Ed), то согласно формуле

энергия конденсатора прямо пропор-циональна напряженности электри-ческого поля внутри него: W p ~ E 2 . Детальный расчет дает следующее значение для энергии поля, приходя-щейся на единицу объема, т.е. для плотности энергии:

где ε 0 — электрическая постоянная

Применение конденсаторов.

Энер-гия конденсатора обычно не очень велика — не более сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому заряженные конденсаторы не могут заменить, например, акку-муляторы в качестве источников электрической энергии.

Но это совсем не означает, что конденсаторы как накопители энергии не получили практического при-менения. Они имеют одно важное свойство: конденсаторы могут на-капливать энергию более или менее длительное время, а при разрядке через цепь малого сопротивления они отдают энергию почти мгновенно. Именно это свойство используют широко на практике.

Лампа-вспышка, применяемая в фотографии, питается электрическим током разряда конденсатора, заря-жаемого предварительно специаль-ной батареей. Возбуждение кванто-вых источников света — лазеров осу-ществляется с помощью газораз-рядной трубки, вспышка которой происходит при разрядке батареи конденсаторов большой электроем-кости.

Однако основное применение кон-денсаторы находят в радиотехнике. С этим вы познакомитесь в XI классе.

Энергия конденсатора пропор-циональна его электроемкости и квадрату напряжения между плас-тинами.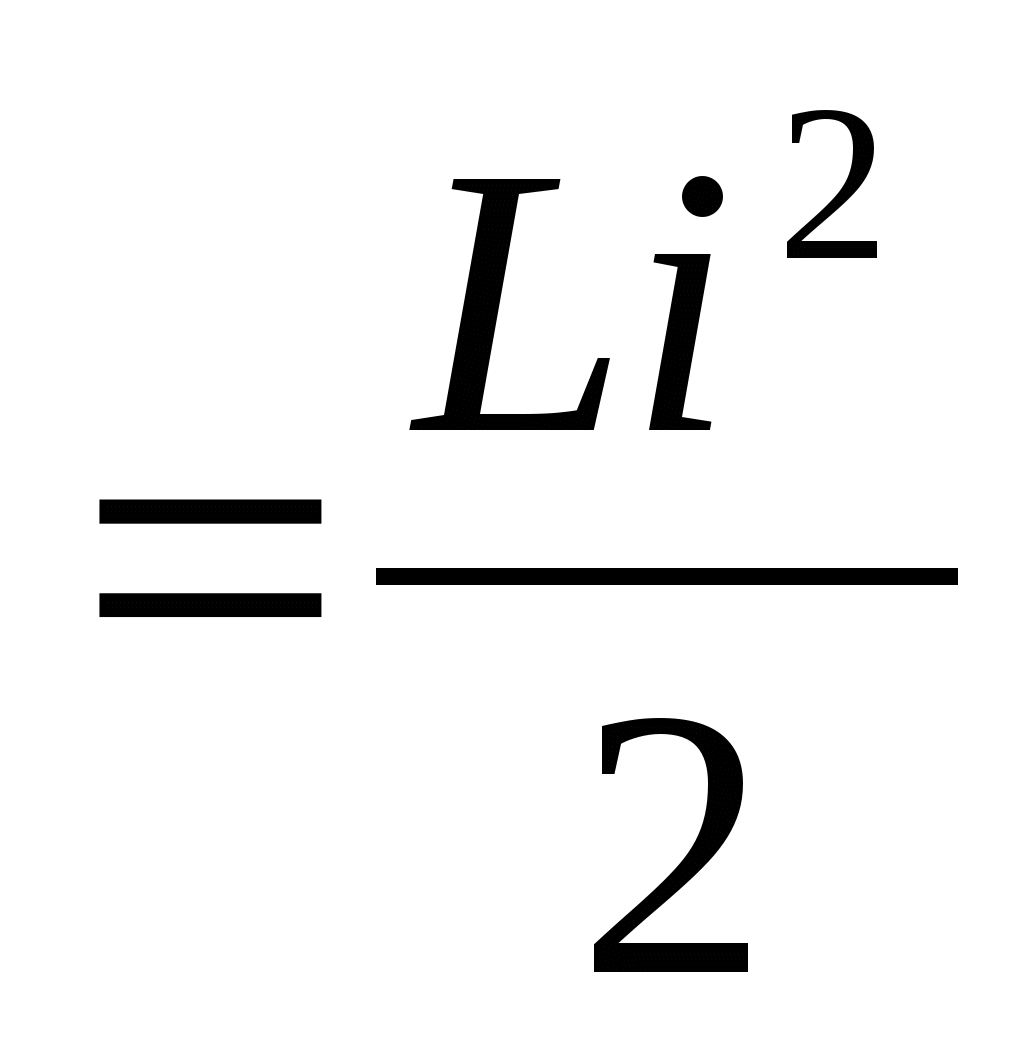 Вся эта энергия сосредото-чена в электрическом поле. Плот-ность энергии поля пропорциональна квадрату напряженности поля.

Рис. 1 Рис. 2

ЗАКОНЫ ПОСТОЯННОГО ТОКА.

Неподвижные электрические заряды редко используются на практике. Для того чтобы заставить электрические заряды слу-жить нам, их нужно привести в движение — создать электрический ток. Электрический ток освещает квартиры, приводит в дви-жение станки, создает радиоволны, циркулирует во всех электрон-но-вычислительных машинах.

Мы начнем с наиболее простого случая движения заряжен-ных частиц — рассмотрим постоянный электрический ток.

ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА

Дадим строгое определение тому, что называют электрическим током.

Напомним, какой величиной ха-рактеризуется ток количественно.

Найдем, как быстро движутся электроны по проводам в вашей квартире.

При движении заряженных час-тиц в проводнике происходит перенос электрического заряда с одного места в другое. Однако если заряженные частицы совершают беспорядочное тепловое движение, как, например, свободные электроны в металле, то переноса заряда не про-исходит (рис.1). Электриче-ский заряд перемещается через по-перечное сечение проводника лишь в том случае, если наряду с беспорядочным движением электроны участвуют в упорядоченном движении (рис. 2). В этом случае говорят, что в проводнике устанавливается электрический ток.

Из курса физики VIII класса вы знаете, что электрическим током называют упорядоченное (направ-ленное) движение заряженных частиц.

Электрический ток возникает при упорядоченном перемещении свобод-ных электронов или ионов.

Если перемещать нейтральное в целом тело, то, несмотря на упо-рядоченное движение огромного чис-ла электронов, и атомных ядер, электрический ток не возникает. Полный заряд, переносимый через любое сечение проводника, будет при этом равным нулю, так как заряды разных знаков с одинаковой средней скоростью.

Электрический ток имеет определенное направление. За направление тока принимают направление движения положительно заряженных частиц. Если ток образован движением отрицательно заряженных частиц, то направление тока считают противоположным направлению дви-жения частиц.

Действия тока. Движение частиц в проводнике мы непосредственно не видим. О наличии электрического тока приходится судить по тем дей-ствиям или явлениям, которые его сопровождают.

Во-первых, проводник, по которо-му течет ток, нагревается.

Во-вторых, электрический ток мо-жет изменять химический состав проводника, например, выделять его химические составные части (медь из раствора медного купороса и т.д.).

В-третьих, ток оказывает силовое воздействие на соседние токи и на-магниченные тела. Это действие то-ка называется магнитным. Так, маг-нитная стрелка вблизи проводника с током поворачивается. Магнитное действие тока в отличие от химиче-ского и теплового является основ-ным, так как проявляется у всех без исключения проводников. Хими-ческое действие тока наблюдается лишь у растворов и расплавов электролитов, а нагревание отсут-ствует у сверхпроводников.

Сила тока.

Если в цепи уста-навливается электрический ток, то это означает, что через поперечное сечение проводника все время пере-носится электрический заряд. Заряд, перенесенный в единицу времени, служит основной количественной ха-рактеристикой тока, называемой си-лой тока.

Таким образом, сила тока равна отношению заряда q, переносимого через поперечное сечение провод-ника за интервал времени t, к этому интервалу времени. Если сила тока со временем не меняется, то ток на-зывают постоянным.

Сила тока, подобно заряду, — ве-личина скалярная. Она может быть как положительной, так и отрица-тельной. Знак силы тока зависит от того, какое из направлений вдоль проводника принять за положитель-ное. Сила тока / > 0, если направ-ление тока совпадает с условно вы-бранным положительным направле-нием вдоль проводника. В против-ном случае /

Сила тока зависит от заряда, переносимого каждой частицей, кон-центрации частиц, скорости их направленного движения и площади поперечного сечения проводника. По-кажем это.

Пусть проводник (рис. 3) имеет поперечное сечение площадью S. За положительное направление в проводнике примем направление сле-ва направо. Заряд каждой частицы равен q 0 . В объеме проводника, ограниченном поперечными сечениям-и 1 и 2, содержится nSl частиц, где п — концентрация частиц. Их общий заряд q = q Q nSl. Если частицы движутся слева направо со средней скоростью υ, то за время

Все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение 2. Поэтому сила тока равна:

формуле (2) где е — модуль заряда электрона.

Пусть, например, сила тока I = 1 А, а площадь по-перечного сечения проводника S = 10 -6 м 2 . Модуль заряда электрона е = 1,6 – 10 -19 Кл. Число электронов в 1 м 3 меди равно числу атомов в этом объеме, так как один из ва-лентных электронов каждого атома меди коллективизирован и является свободным. Это число есть п = 8,5 · 10 28 м -3 Следовательно,

Рис №1. Рис №2 Рис №3

УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА

Что необходимо для создания электрического тока? Подумайте над этим сами и только потом прочтите этот параграф.

Для возникновения и существо-вания постоянного электрического тока в веществе необходимо, во-первых, наличие свободных заряжен-ных частиц. Если положительные и отрицательные заряды связаны друг с другом в атомах или молекулах , то их перемещение не приведет к по-явлению электрического тока.

Наличия свободных зарядов еще недостаточно для возникновения то-ка. Для создания и поддержания упорядоченного движения, заряжен-ных частиц необходима, во-вторых, сила, действующая на них в опре-деленном направлении. Если эта сила перестанет действовать, то упорядоченное движение заряженных частиц прекратится из-за сопротив-ления, оказываемого их движению ионами кристаллической решетки металлов или нейтральными молеку-лами электролитов .

На заряженные частицы, как мы знаем, действует электрическое поле с силой . Обычно именно электрическое поле внутри провод-ника служит причиной, вызываю-щей и поддерживающей упорядочен-ное движение заряженных частиц. Только в статическом случае, когда заряды покоятся, электрическое поле внутри проводника равно нулю.

Если внутри проводника имеется электрическое поле, то между конца-ми проводника в соответствии с фор-мулой существует разность потенциалов. Когда разность потен-циалов не меняется во времени, то в проводнике устанавливается по-стоянный электрический ток. Вдоль проводника потенциал уменьшается от максимального значения на одном конце проводника до минималь-ного — на другом. Это уменьшение потенциала можно обнаружить на простом опыте.

Возьмем в качестве проводника не очень сухую деревянную палку и подвесим ее горизонтально. (Такая палка хотя и плохо, но все же про-водит ток.) Источником напряжения пусть будет электростатическая ма-шина, Для регистрации потенциала различных участков проводника от-носительно земли можно использо-вать листочки металлической фоль-ги, прикрепленные к палке. Один полюс машины соединим с землей, а второй — с одним концом проводни-ка (палки). Цепь окажется незамк-нутой. При вращении рукоятки ма-шины мы обнаружим, что все лис-точки отклоняются на один и тот же угол (рис. 1).

Значит, потен-циал всех точек проводника отно-сительно земли одинаков. Так и должно быть при равновесии заря-дов на проводнике. Если теперь дру-гой конец палки заземлить, то при вращении рукоятки машины карти-на изменится. (Так как земля — проводник, то заземление провод-ника делает цепь замкнутой.) У за-земленного конца листочки вообще не разойдутся: потенциал этого кон-ца проводника практически равен потенциалу земли (падение потен-циала в металлической проволоке мало). Максимальный угол расхож-дения листочков будет у конца про-водника, присоединенного к машине (рис. 2). Уменьшение угла рас-хождения листочков по мере удале-ния от машины свидетельствует о падении потенциала вдоль провод-ника.

Электрический ток может быть получен только в веществе, в котором имеются свободные заряженные частицы. Чтобы они пришли в движение, нужно создать в проводнике электрическое поле.

Рис №1 Рис №2

ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ

В VIII классе изучался закон Ома . Этот закон прост, однако столь важен, что его необходимо повторить.

Вольт – амперная характеристика.

В предыдущем параграфе было уста-новлено, что для существования то-ка в проводнике необходимо создать разность потенциалов на его концах. Сила тока в проводнике определяет-ся этой разностью потенциалов. Чем больше разность потенциалов, тем больше напряженность электриче-ского поля в проводнике и, следо-вательно, тем большую скорость на-правленного движения приобретают заряженные частицы. Согласно фор-муле, это означает увеличение силы тока.

Для каждого проводника — твер-дого, жидкого и газообразного — существует определенная зависи-мость силы тока от приложенной разности потенциалов на концах про-водника. Эту зависимость выражает так называемая вольт – амперная ха-рактеристика проводника. Ее нахо-дят, измеряя силу тока в проводнике при различных значениях напряже-ния. Знание вольт – амперной характе-ристики играет большую роль при изучении электрического тока.

Закон Ома.

Наиболее простой вид имеет вольт – амперная характеристи-ка металлических проводников и растворов электролитов. Впервые (для металлов) ее установил немец-кий ученый Георг Ом, поэтому зависимость силы тока от напря-жения носит название закона Ома. На участке цепи, изображенной на рисунке 109, ток направлен от точки 1 к точке 2. Разность потен-циалов (напряжение) на концах проводника равна: U = φ 1 – φ 2. Так как ток направлен слева направо, то напряженность электрического поля направлена в ту же сторону и φ 1 > φ 2

Согласно закону Ома для участка цепи сила тока прямо пропорцио-нальна приложенному напряжению U и обратно пропорциональна сопро-тивлению проводника R:

Закон Ома имеет очень простую форму, но доказать эксперименталь-но его справедливость довольно трудно. Дело в том, что разность по-тенциалов на участке металлическо-го проводника даже при большой силе тока мала, так как мало сопро-тивление проводника.

Электрометр, о котором шла речь, непригоден для измерения столь малых напряжений: его чув-ствительность слишком мала. Нужен несравненно более чувствительный прибор. Тогда, измеряя силу тока амперметром, а напряжение чув-ствительным электрометром, можно убедиться в том, что сила тока пря-мо пропорциональна напряжению. Применение же обычных приборов для измерения напряжения — вольт-метров — основано на использовании закона Ома.

Принцип устройства, вольтметра такой же, как и ампер-метра. Угол поворота стрелки прибо-ра пропорционален силе тока. Сила тока, проходящего по вольтметру, определяется напряжением между точками цепи, к которой он под-ключен. Поэтому, зная сопротивле-ние вольтметра, можно по силе тока определить напряжение. На практике прибор градуируют так, чтобы он сразу показывал напряжение в воль-тах.

Сопротивление. Основная элек-трическая характеристика проводни-ка — сопротивление. От этой вели-чины зависит сила тока в провод-нике при заданном напряжении. Со-противление проводника представля-ет собой как бы меру противо-действия проводника установлению в нем электрического тока. С помощью закона Ома можно определить сопротивление проводника:

Для этого нужно измерить напря-жение и силу тока.

Сопротивление зависит от мате-риала проводника и его геометри-ческих размеров. Сопротивление про-водника длиной l с постоянной пло-щадью поперечного сечения S равно:

где р — величина, зависящая от рода вещества и его состояния (от тем-пературы в первую очередь). Вели-чину р называют удельным сопро-тивлением проводника. Удельное со-противление численно равно сопро-тивлению проводника, имеющего форму куба с ребром 1 м, если ток направлен вдоль нормали к двум противоположным граням куба.

Единицу сопротивления провод-ника устанавливают на основе зако-на Ома и называют ее ом. Провод-ник имеет сопротивление 1 Ом, если при разности потенциалов 1 В сила тока в нем 1 А.

Единицей удельного сопротивле-ния является 1 Ом?м. Удельное со-противление металлов мало. Диэлектрики обладают очень большим удельным сопротивлением. В табли-це на форзаце приведены примеры значений удельного сопротивления некоторых веществ.

Значение закона Ома.

Закон Ома определяет силу тока в электриче-ской цепи при заданном напря-жении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока. Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротив-ления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

Закон Ома — основа всей элект-ротехники постоянных токов. Формулу — надо хорошо понять и твердо запомнить.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ

От источника тока энергия может быть передана по проводам к устрой-ствам, потребляющим энергию: Элек-трической лампе, радиоприемнику и др. Для этого составляют электри-ческие цепи различной сложности. Электрическая цепь состоит из источника энергии, устройств, по-требляющих электрическую энергию, соединительных проводов и выклю-чателей для замыкания цепи. Часто и электрическую цепь включают приборы, контролирующие силу тока и напряжение на различных участ-ках цепи, – амперметры и вольт-метры.

К наиболее простым и часто встречающимся соединениям провод-ников относятся последовательное и параллельное соединения.

Последовательное соединение проводников.

При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочередно друг за другом. На рисунке 1 показано последовательное соединение двух проводников 1 и 2, имеющих сопротивления R 1 , и R 2 . Это могут быть две лампы, две обмотки элект-родвигателя и др.

Сила тока в обоих проводниках одинакова, т. е. (1)

так как в проводниках электриче-ский заряд в случае постоянного тока не накапливается и через любое поперечное сечение проводника за определенное время проходит один и тот же заряд.

Напряжение на концах рассмат-риваемого участка цепи складывает-ся из напряжений на – первом и вто-ром проводниках:

Надо надеяться, что с доказатель-ством этого простого соотношения вы справитесь сами.

Применяя закон Ома для всего участка в целом и для участков с сопротивлениями R 1 и R 2 , можно до-казать, что полное сопротивление всего участка цепи при последова-тельном соединении равно:

Это правило можно применить для любого числа последовательно соединенных проводников.

Напряжения на проводниках и их сопротивления при последователь-ном соединении связаны соотноше-нием:

Докажите это равенство.

Параллельное соединение про-водников.

На рисунке 2 показано параллельное соединение двух про-водников 1 и 2с сопротивлениями R 1 и R 2 . В этом случае электриче-ский ток 1 разветвляется на две час-ти. Силу тока в первом и втором про-водниках обозначим через I 1 и I 2 . Так как в точке а — разветвлении проводников (такую точку называют узлом) — электрический заряд не на-капливается, то заряд, поступающий в единицу времени в узел, равен заряду, уходящему из узла за это же время. Следовательно, I = I 1 + I 2

Напряжение U на концах про-водников, соединенных параллельно, одно и то же.

В осветительной сети поддержи-вается напряжение 220 или 127 В. На это напряжение рассчитаны при-боры, потребляющие электрическую энергию. Поэтому параллельное сое-динение — самый распространенный способ соединения различных потре-бителей. В этом случае выход из строя одного прибора не отражается на работе остальных, тогда как при последовательном соединении выход из строя одного прибора размы-кает цепь.

Применяя закон Ома для всего участка в целом и для участков с сопротивлениями R 1 и R 2 , можно доказать, что величина, обратная полному сопротивлению участка ab, равна сумме величин, обратных сопротивлениям отдельных провод-ников:

Сила тока в каждом из провод-ников и сопротивления проводников при параллельном соединении свя-заны соотношением

Различные проводники в цепи соединяются друг с другом после-довательно или параллельно. В пер-вом случае сила тока одинакова во всех проводниках, а во втором слу-чае одинаковы напряжения на про-водниках. Чаще всего к осветитель-ной сети различные потребители тока подключаются параллельно.

ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ

Как измерить силу тока ампер-метром, а напряжение вольтметром, должен знать каждый.

Измерение силы тока.

Для изме-рения силы тока в проводнике ам-перметр включают последовательно с этим проводником (рис. 1). Но нужно иметь в виду, что сам ампер-метр обладает некоторым сопротив-лением R a . Поэтому сопротивление участка цепи с включенным ампер-метром увеличивается, и при неиз-менном напряжении сила тока умень-шается в соответствии с законом Ома. Чтобы амперметр оказывал как можно меньшее влияние на силу тока, измеряемую им, его сопротив-ление делают очень малым. Это нужно помнить и никогда не пытать-ся измерять силу тока в освети-тельной сети, подключая амперметр к розетке. Произойдет короткое за-мыкание; сила тока при малом со-противлении прибора достигнет столь большой величины, что обмотка ам-перметра сгорит.

Измерение напряжения.

Для того чтобы измерить напряжение на участке цепи с сопротивлением R, к нему параллельно подключают вольтметр. Напряжение на вольтметре совпа-дает с напряжением на участке цепи (рис. 2).

Если сопротивление вольтметра R B , то после включения его в цепь сопротивление участка будет уже не R, а . Из-за этого измеряемое напряжение на участ-ке цепи уменьшится. Для того чтобы вольтметр не вносил заметных иска-жений в измеряемое напряжение, его сопротивление должно быть большим по сравнению с сопротивлением участка цепи, на котором измеряется напряжение. Вольтметр можно вклю-чать в сеть без риска, что он сгорит, если только он рассчитан на напря-жение, превышающее напряжение сети.

Амперметр включают последова-тельно с проводником, в котором измеряют силу тока. Вольтметр включают параллельно проводнику, на котором измеряют напряжение.

РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА

Электрический ток получил такое широкое применение потому, что он несет с собой энергию. Эта энергия может быть превращена в любую форму.

При упорядоченном движении за-ряженных частиц в проводнике электрическое поле совершает ра-боту; ее принято называть работой тока. Сейчас мы напомним сведения о работе и мощности тока из курса физики VIII класса.

Работа тока.

Рассмотрим произ-вольный участок цепи. Это, может быть однородный проводник, напри-мер нить лампы накаливания, обмот-ка электродвигателя и др. Пусть за время t через поперечное сечение проводника проходит заряд q. Тогда электрическое поле совершит работу A = qU.

Так как сила тока , то эта работа равна:

Работа тока на участке цепи равна произведению силы тока, на-пряжения и времени, в течение ко-торого совершалась работа.

Согласно закону сохранения энергии эта работа должна быть рав-на изменению энергии рассматри-ваемого участка цепи. Поэтому энер-гия, выделяемая на данном участке цепи за время At, равна работе тока (см. формулу (1)).

В случае если на участке цепи не совершается механическая рабо-та и ток не производит химических действий, происходит только нагре-вание проводника. Нагретый про-водник отдает теплоту окружающим телам.

Нагревание проводника происхо-дит следующим образом. Электриче-ское поле ускоряет электроны. После столкновения с ионами кристалличе-ской решетки они передают ионам свою энергию. В результате энергия беспорядочного движения ионов око-ло положений равновесия возраста-ет. Это и означает увеличение внут-ренней энергии. Температура про-водника при этом повышается, и он начинает передавать теплоту окру-жающим телам. Спустя небольшое время после замыкания цепи процесс устанавливается, и температура пе-рестает изменяться со временем. К проводчику за счет работы элект-рического поля непрерывно поступа-ет энергия. Но его внутренняя энер-гия остается неизменной, так как проводник передает окружающим те-лам количество теплоты, равное ра-боте тока. Таким образом, формула (1) для работы тока определяет количество теплоты, передаваемое проводником другим телам.

Если в формуле (1) выразить либо напряжение через силу тока, либо силу тока через напряжение с помощью закона Ома для участка цепи, то получим три эквивалентные формулы:

(2)

Формулой A = I 2 R t удобно пользоваться для последовательного соединения проводников, так как сила тока в этом случае одинакова во всех проводниках. При парал-лельном соединении удобна формула , так как напряжение на всех проводниках одинаково.

Закон Джоуля — Ленца.

Закон, определяющий количество теплоты, которое выделяет проводник с то-ком в окружающую среду, был впервые установлен эксперименталь-но английским ученым Д. Джоу-лем (1818-1889) и русским ученым Э. X. Ленцем (1804-1865). Закон Джоуля — Ленца был сформулиро-ван следующим образом: количество теплоты, выделяемое проводником с током, равно произведению квад-рата силы тока, сопротивления про-водника и времени прохождения то-ка по проводнику:

(3)

Мы получили этот закон с по-мощью рассуждений, основанных на законе сохранения энергии. Формула (3) позволяет вычислить количе-ство теплоты, выделяемое на любом участке цепи, содержащем какие угодно проводники.

Мощность тока.

Любой электри-ческий прибор (лампа, электродвигатель) рассчитан на потребление определенной энергии в единицу вре-мени. Поэтому наряду с работой то-ка очень важное значение имеет по-нятие мощность тока. Мощность то-ка равна отношению работы тока за время t к этому интервалу времени.

Согласно этому определению

(4)

Это выражение для мощности можно переписать в нескольких эквивалентных формах, если исполь-зовать закон Ома для участка цепи:

На большинстве приборов ука-зана потребляемая ими мощность.

Прохождение по проводнику электрического тока сопровождается выделением в нем энергии. Эта энер-гия определяется работой тока: про-изведением перенесенного заряда и напряжения на концах проводника.

ЭЛЕКТРОДВИЖУЩАЯ СИЛА.

Любой источник тока характеризуется электродвижущей силой, или ЭДС. Так, на круглой батарейке для карманного фонарика написано: 1,5 В. Что это значит?

Соедините проводником два ме-таллических шарика, несущих за-ряды противоположных знаков. Под влиянием электрического поля этих зарядов в проводнике возникает электрический ток (рис. 1). Но этот ток будет очень кратковремен-ным. Заряды быстро нейтрализуют-ся, потенциалы шариков станут одинаковыми, и электрическое поле ис-чезнет.

Сторонние силы.

Для того чтобы ток был постоянным, надо поддер-живать постоянное напряжение меж-ду шариками. Для этого необходимо устройство (источник тока), которое перемещало бы заряды от одного шарика к другому в направлении, противоположном направлению сил, действующих на эти заряды со сто-роны электрического поля шариков. В таком устройстве на заряды, кро-ме электрических сил, должны дей-ствовать силы не электростатического происхождения (рис. 2). Одно лишь электрическое поле заряжен-ных частиц (кулоновское поле) не способно поддерживать постоянный ток в цепи.

Любые силы, действующие на электрически заряженные частицы, за исключением сил электростати-ческого происхождения (т. е. кулоновских), называют сторонними си-лами.

Вывод о необходимости сторон-них сил для поддержания посто-янного тока в цепи станет еще оче-виднее, если обратиться к закону сохранения энергии. Электростатиче-ское поле потенциально. Работа это-го поля при перемещении заряжен-ных частиц вдоль замкнутой электри-ческой цепи равна нулю. Прохож-дение же тока по проводникам сопровождается выделением энер-гии — проводник нагревается. Сле-довательно, в любой цепи должен быть какой-то источник энергии, по-ставляющий ее в цепь. В нем, по-мимо кулоновских сил, обязательно должны действовать сторонние не- потенциальные силы. Работа этих сил вдоль замкнутого контура долж-на быть отлична от нуля. Именно в процессе совершения работы этими силами заряженные частицы приобретают внутри источника тока энер-гию и отдают ее затем проводникам электрической цепи.

Сторонние силы приводят в дви-жение заряженные частицы внутри всех источников тока: в генераторах на электростанциях, в гальваниче-ских элементах, аккумуляторах и т.д.

При замыкании цепи создается электрическое поле во всех провод-никах цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны от положительно заряженного электрода к отрица-тельному), а во всей остальной цепи их приводит в движение электриче-ское поле (см. рис. 2).

Аналогия между электрическим током и течением жидкости.

Чтобы лучше понять механизм возникнове-ния тока, обратимся к сходству меж-ду электрическим током в провод-нике и течением жидкости по трубам.

На любом участке горизонталь-ной трубы жидкость течет за счет разности давлений на концах участ-ка. Жидкость перемещается в сторо-ну уменьшения давления. Но сила давления в жидкости — это вид сил упругости, которые являются потен-циальными, подобно кулоновским силам. Поэтому работа этих сил на замкнутом пути равна нулю и одни эти силы не способны вызвать длительную циркуляцию жидкости по трубам. Течение жидкости сопро-вождается потерями энергии вслед-ствие действия сил трения. Для цир-куляции воды необходим насос.

Поршень этого насоса действует на частички жидкости и создает по-стоянную разность давлений на вхо-де и выходе насоса (рис. 3). Благодаря этому жидкость течет по трубе. Насос подобен источнику тока, а роль сторонних сил играет сила, действующая на воду со стороны движущегося поршня. Внутри на-соса жидкость течет от участков с меньшим давлением к участкам с большим давлением. Разность дав-лений аналогична напряжению.

Природа сторонних сил.

Природа сторонних сил может быть разнооб-разной. В генераторах электростанций сторонняя сила — это сила, дей-ствующая со стороны магнитного поля на электроны в движущемся проводнике. Об этом кратко гово-рилось в курсе физики VIII класса.

В гальваническом элементе, на-пример элементе Вольта, действуют химические силы. Элемент Вольта состоит из цинкового и медного электродов, помещенных в раствор серной кислоты. Химические силы вызывают растворение цинка в кис-лоте. В раствор переходят положи-тельно заряженные ионы цинка, а сам цинковый электрод при этом заряжается отрицательно. (Медь очень мало растворяется в серной – кислоте.) Между цинковым и мед-ным электродами появляется раз-ность потенциалов, которая обуслов-ливает ток в замкнутой электриче-ской цепи.

Электродвижущая сила.

Дейст-вие сторонних сил характеризуется важной физической величиной, на-зываемой электродвижущей силой (сокращенно ЭДС).

Электродви-жущая сила в замкнутом контуре представляет собой отношение рабо-ты сторонних сил при перемещении заряда вдоль контура к заряду:

Электродвижущую силу выража-ют в вольтах.

Можно говорить об электродви-жущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единич-ного заряда) не во всем контуре, а только на данном участке. Электро-движущая сила гальванического эле-мента есть работа сторонних сил при перемещении единичного положи-тельного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть вы-ражена через разность потенциалов, так как сторонние силы не потенциальные и их работа зависит от формы траектории. Так, например, работа сторонних сил при переме-щении заряда между клеммами ис-точника тока вне самого источника равна нулю.

Теперь вы знаете, что такое ЭДС. Если на батарейке написано 1,5 В, то это означает, что сторонние силы (химические в данном случае) совер-шают работу 1,5 Дж при переме-щении заряда в 1 Кл от одного полюса батарейки к другому. Постоянный ток не может существовать в замкнутой цепи, если в ней не действуют сторонние силы, т. е. нет ЭДС

Рис №1 Рис №2 Рис №3

ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ

Электродвижущая сила опреде-ляет силу тока в замкнутой электри-ческой цепи с известным сопротив-лением.

Спомощью закона сохранения энергии найдем зависимость силы тока от ЭДС и сопротивления.

Рассмотрим простейшую полную (замкнутую) цепь, состоящую из источника тока (гальванического элемента, аккумулятора или гене-ратора) и резистора сопротивле-нием R (рис. 1). Источник тока имеет ЭДС εи сопротивление r. Сопротивление источника часто на-зывают внутренним сопротивлением в отличие от внешнего сопротивле-ния R цепи. В генераторе r — это сопротивление обмоток, а в гальва-ническом элементе — сопротивление раствора электролита и электродов.

Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление R + r цепи. Эта связь может быть установлена теоретически, если использовать за-кон сохранения энергии и закон Джоуля — Ленца.

Пусть за время t через попе-речное сечение проводника пройдет электрический заряд q. Тогда рабо-ту сторонних сил при перемещении заряда?qможно записать так: А ст = ε · q. Согласно определению силы тока q = It. Поэтому

(1)

При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых r и R, выделяется некоторое количество теплоты. По закону Джоуля — Лен-ца оно равно:

Q = I 2 R · t + I 2 r · t. (2)

Согласно закону сохранения энергии A = Q. Приравнивая (1) и (2), получим:

ε = IR + Ir (3)

Произведение силы тока и сопро-тивления участка цепи часто назы-вают падением напряжения на этом участке. Таким образом, ЭДС равна сумме падений напряжений на внут-реннем и внешнем участках замкну-той цепи.

Обычно закон Ома для замкну-той цепи записывают в форме

(4)

По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.

Формула заряда конденсатора

где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.

Электроемкость конденсатора – это величина, которая зависит то размеров и устройства конденсатора.

Заряд на пластинах плоского конденсатора равен:

где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.

Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.

Заряд на обкладках сферического конденсатора найдем как:

Заряд конденсатора связан с энергией поля (W) внутри него:

Из формулы (6) следует, что заряд можно выразить как:

Рассмотрим последовательное соединение из N конденсаторов (рис. 1).

Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.

При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.

Примеры решения задач по теме «Заряд конденсатора»

ru.solverbook.com

Формула емкости конденсатора, С

Если q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками, то величина C, равная:

называется емкостью конденсатора. Это постоянная величина, которая зависит то размеров и устройства конденсатора.

Рассмотрим два одинаковых конденсатора, разница между которым заключается только в том, что между обкладками одного вакуум (или часто говорят воздух), между обкладками другого находится диэлектрик. В таком случае при равных зарядах на конденсаторах разность потенциалов воздушного конденсатора будет в раз меньше, чем между обкладками второго. Значит емкость конденсатора с диэлектриком (C) в раз больше, чем воздушного ():

где – диэлектрическая проницаемость диэлектрика.

За единицу емкости конденсатора принимают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) служит фарад (Ф).

Формула электрической емкости плоского конденсатора

Поле между обкладками плоского конденсатора обычно считают однородным. Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:

Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:

Формула электрической емкости цилиндрического конденсатора

Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость цилиндрического конденсатора вычисляется как:

Формула электрической емкости сферического конденсатора

Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:

где – радиусы обкладок конденсатора.

Примеры решения задач по теме «Емкость конденсатора»

ru.solverbook.com

Ёмкость конденсатора – Все формулы

Электрическая ёмкость – характеристика проводника (конденсатора), мера его способности накапливать электрический заряд.

Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические.

Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 – φ2) между его обкладками

Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.

Конденсаторы можно классифицировать по следующим признакам и свойствам:

1) по назначению – конденсаторы постоянной и переменной емкости;

2) по форме обкладок различают конденсаторы плоские, сферические, цилиндрические и др.;

3) по типу диэлектрика – воздушные, бумажные, слюдяные, керамические, электролитические и т.д.

Так же есть:

Энергия конденсатора:

Ёмкость цилиндрического конденсатора:

Ёмкость плоского конденсатора:

Емкость сферического конденсатора:

В формуле мы использовали:

Электрическая ёмкость (ёмкость конденсатора)

Потенциал проводника (Напряжение)

Потенциал

Относительная диэлектрическая проницаемость

Электрическая постоянная

Площадь одной обкладки

Расстояние между обкладками

xn--b1agsdjmeuf9e.xn--p1ai

Заряд конденсатора, теория и примеры задач

Определение и заряд конденсатора

Возможность конденсатора накопить электрический заряд зависит от главной характеристики конденсатора – емкости (C).

По своему назначению конденсатор можно уподобить батарейке. Однако существует принципиальное отличие в принципах работы этих элементов. Отличаются, также максимальные емкости и скорости зарядки и разряда конденсатора и батарейки.

Если к конденсатору присоединить источник напряжения (рис.1), то на одной из пластин конденсатора станут накапливаться отрицательные заряды (электроны), на другой положительные частицы (положительные ионы). Между обкладками конденсатора находится диэлектрик, вследствие этого, заряды не могут перебраться на противоположную пластину. Однако заметим, что электроны двигаются от источника тока до пластины конденсатора.

При первоначальном соединении конденсатора и источника тока на обкладках конденсатора много свободного места. Это означает, что сопротивление току этот момент времени минимально, сам ток максимален. В ходе зарядки конденсатора сила тока в цепи постепенно падает, до того момента пока не закончится свободное место на обкладках. При полной зарядке конденсатора ток в цепи прекратится.

Время, которое затрачивается на зарядку конденсатора от нулевого заряда (максимального тока) до полностью заряженного конденсатора (минимальная или нулевая сила тока) называют переходным периодом заряда конденсатора. На практике процесс зарядки конденсатора считают законченным, если сила тока уменьшилась до 1% от начальной величины.

Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:

Примеры решения задач

ru.solverbook.com

Формула электроемкости конденсатора

Обкладки должны иметь такую форму и быть расположены так относительно друг друга, что поле, которое создается данной системой, было максимально сосредоточено в ограниченной области пространства, между обкладками.

Назначение конденсатора в том, чтобы накапливать и отдавать в электрической цепи заряд.

Основной характеристикой конденсатора является электрическая емкость (C). Электрическая емкость конденсатора – это взаимная емкость принадлежащих ему обкладок:

q – величина заряда на обкладке; – разность потенциалов между обкладками.

Электрическая ёмкость конденсатора зависит от диэлектрической проницаемости диэлектрика, который заполняет пространство между его обкладками. Если пространство между обкладками одного конденсатора заполнено диэлектриком с проницаемостью равной , а у второго конденсатора воздух между пластинами, то емкость конденсатора с диэлектриком (C) в раз больше, чем емкость воздушного конденсатора ():

Формула электроемкости основных типов конденсаторов

При расчете электроемкости плоского конденсатора нарушением однородности поля около краёв обкладок обычно пренебрегают. Это становится возможным, если расстояние между пластинами существенно меньше, чем линейные размеры обкладок. В таком случае электрическую емкость плоского конденсатора вычисляют при помощи формулы:

где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.

Если плоский конденсатор между обкладками имеет N слоев диэлектрика, при этом толщина каждого слоя равна , а диэлектрическая проницаемость , то его электрическую емкость рассчитывают при помощи формулы:

Цилиндрический конденсатор составляют две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполнено диэлектриком. При этом емкость цилиндрического конденсатора находят как:

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.

У сферического конденсатора обкладками служат две концентрические сферические проводящие поверхности, пространство обкладками заполняет диэлектрик. Емкость сферического конденсатора вычисляют как:

где – радиусы обкладок конденсатора. Если , то можно считать, что , тогда, мы имеем:

так как – площадь поверхности сферы, и если обозначить , то получим формулу для емкости плоского конденсатора (3). Если расстояние между обкладками сферического и цилиндрического конденсаторов малы (в сравнении с их радиусами), то в приближенных расчетах используют формулу емкости для плоского конденсатора.

Электрическую емкость для линии из двух проводов находят как:

где d – расстояние между осями проводов; R – радиус проводов; l – длина линии.

Формулы для вычисления электрической емкости соединений конденсаторов

Если конденсаторы соединены параллельно, то суммарная емкость батареи (C) находится как сумма емкостей отдельных конденсаторов ():

При последовательном соединении конденсаторов емкость батареи вычисляют как:

Если последовательно соединены N конденсаторов, с емкостями то емкость батареи найдем как:

Сопротивление конденсатора

Если конденсатор включен в цепь с постоянного тока, то сопротивление конденсатора можно считать бесконечно большим.

При включении конденсатора в цепь переменного тока, его сопротивление носит название емкостного, и вычисляют его с помощью формулы:

где – частота переменного тока; – угловая частота тока; C – емкость конденсатора.

Энергия поля конденсатора

Электрическое поле локализованное между пластинами конденсатора обладает энергией, которую можно вычислить при помощи формулы:

где –энергия поля конденсатора; q – заряд конденсатора; C – емкость конденсатора; – разность потенциалов между обкладками конденсатора.

Энергия поля плоского конденсатора:

Примеры решения задач по теме «Электроемкость конденсатора»

ru.solverbook.com

Как найти заряд конденсатора 🚩 как определить величину заряда 🚩 Естественные науки

В обычном (без плагинов и модов) варианте Minecraft такого понятия, как конденсатор, не существует. Вернее, устройство, выполняющее его функции, имеется, но название у него совершенно другое – компаратор. Некоторая путаница в этом плане произошла еще в период разработки такого прибора. Сперва – в ноябре 2012-го – представители Mojang (компании-создателя игры) объявили о скором появлении в геймплее конденсатора. Однако через месяц они высказались уже о том, что как такового этого прибора не будет, а вместо него в игре будет компаратор.

Подобное устройство существует для проверки заполненности расположенных позади него контейнеров. Таковыми могут быть сундуки (в том числе в виде ловушек), варочные стойки, раздатчики, выбрасыватели, печи, загрузочные воронки и т.п.

Помимо этого, его часто используют для сравнения двух сигналов редстоуна между собою – он выдает результат в соответствии с тем, как было запрограммировано в данной цепи, и с тем, какой режим выбран для самого механизма. В частности, компаратор может разрешить зажигание факела, если первый сигнал больше либо равен другому.

Также порой конденсатор-компаратор устанавливают рядом с проигрывателем, подключая его входом к последнему. Когда в звуковоспроизводящем устройстве проигрывается какая-либо пластинка, вышеупомянутый прибор будет выдавать сигнал, равный по силе порядковому номеру диска.

Скрафтить такой компаратор несложно, если имеется достаточно трудно добываемый ресурс – адский кварц. Его надо поставить в центральный слот верстака, над ним и по бокам от него установить три красных факела, а в нижнем ряду – такое же количество каменных блоков.

В большом количестве модов попадаются конденсаторы, имеющие самое разное предназначение. К примеру, в Galacticraft, где у геймеров есть возможность слетать на многие планеты для ознакомления с тамошними реалиями, появляется рецепт крафта кислородного конденсатора. Он служит для создания механизмов вроде коллектора и накопителя газа для дыхания, а также рамки воздушного шлюза. Для его изготовления четыре стальных пластины размещаются по углам верстака, в центре – оловянная канистра, а под нею – воздуховод. Остальные три ячейки занимают пластины из олова.

В JurassiCraft существует конденсатор потока – некий телепорт, позволяющий переместиться в удивительный игровой мир, кишащий динозаврами. Для создания такого прибора нужно поместить в два крайних вертикальных ряда шесть железных слитков, а в средний – два алмаза и между ними единицу пыли редстоуна. Дабы устройство заработало, надо поставить его на свинью либо вагонетку, а затем щелкнуть по нему правой клавишей мыши, быстро запрыгнув туда. При этом требуется поддержание высокой скорости устройства.

С модом Industrial Craft2 у игрока появляется возможность создавать как минимум два вида тепловых конденсаторов – красный и лазуритовый. Они служат исключительно для охлаждения ядерного реактора и для накопления его энергии и хороши для циклических сооружений такого типа. Остужаются они сами, соответственно, красной пылью или лазуритом.

Красный теплоконденсатор делается из семи единиц пыли редстоуна – их надо установить в виде буквы П и расставить под ними теплоотвод и теплообменник. Крафтинг же лазуритового устройства чуть посложнее. Для его создания четыре единицы пыли редстоуна расставляются по углам станка, в центр пойдет блок лазурита, по бокам от него – два красных тепловых конденсатора, сверху – теплоотвод реактора, а снизу – его же теплообменник.

В ThaumCraft, где сделан акцент на настоящем чародействе, конденсаторы тоже используются. Например, один из них – кристаллический – существует для аккумуляции и отдачи магии. Причем, что интересно, создавать его и многие другие вещи разрешено лишь после изучения особого элемента геймплея – исследования, проводимого за специальным столом и с определенными приборами.

Делается такой конденсатор из восьми тусклых осколков, в центр которых на верстаке помещается мистический деревянный блок. К сожалению, подобный прибор – равно как и его составляющие – просуществовал лишь до ThaumCraft 3, а в четвертой версии мода был упразднен.

www.kakprosto.ru

Соединение конденсаторов: формулы

Содержание:

1. Последовательное соединение
2. Онлайн калькулятор
3. Смешанное соединение
4. Параллельное соединение
5. Видео

В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.

Последовательное соединение

При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = ic1 = ic2 = ic3 = ic4.

В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Qобщ= Q1 = Q2 = Q3.

Если рассмотреть три конденсатора С1, С2 и С3, соединенные в последовательную цепь, то выясняется, что средний конденсатор С2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.

Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.

Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/Cобщ = 1/C1 + 1/C2 + 1/C3.

Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.

Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.

Смешанное соединение

Параллельное соединение конденсаторов

Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.

Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что емкость конденсаторов находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, Собщ = С1 + С2 + С3.

Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.

electric-220.ru

Во всех электронных устройствах используются конденсаторы. При их конструировании или изготовлении своими руками параметры устройств рассчитываются по специальным формулам.

Расчёт конденсаторов

Один из главных параметров таких устройств – ёмкость. Рассчитать её можно по следующей формуле:

• C – ёмкость,
• q – заряд одной из обкладок элемента,
• U – разность потенциалов между обкладками.

В электротехнике вместо понятия «разность потенциалов между обкладками» используется «напряжение на конденсаторе».

Ёмкость элемента не зависит от конструкции и размеров устройства, а только от напряжения на нём и заряда обкладок. Но эти параметры могут изменяться в зависимости от расстояния между ними и материала диэлектрика. Это учитывается в формуле:

С=Co*ε, где:

• С – реальная ёмкость,
• Со – идеальная, при условии, что между пластинами вакуум или воздух,
• ε – диэлектрическая проницаемость материала между ними.

Например, если в качестве диэлектрика используется слюда, «ε» которой 6, то ёмкость такого устройства в 6 раз больше, чем воздушного, а при изменении количества диэлектрика меняются параметры конструкции. На этом принципе основана работа ёмкостного датчика положения.

Единицей ёмкости в системе СИ является 1 фарад (F). Это большая величина, поэтому чаще применяются микрофарады (1000000mkF=1F) и пикофарады (1000000pF=1mkF).

Расчет плоской конструкции

• ε – диэлектрическая проницаемость изолирующего материала,
• d – расстояние между пластинами.

Расчет конструкции цилиндрической формы

Цилиндрический конденсатор – это две соосные трубки различного диаметра, вставленные друг в друга. Между ними находится диэлектрик. При радиусе цилиндров, близком друг к другу и намного большем, чем расстояние между ними, цилиндрической формой можно пренебречь и свести расчёт к формуле, аналогичной той, по которой рассчитывается плоский конденсатор.

Вычисляются параметры такого устройства по формуле:

C=(2π*l*R*ε)/d, где:

• l – длина устройства,
• R – радиус цилиндра,
• ε – диэлектрическая проницаемость изолятора,
• d – его толщина.

Расчёт сферической конструкции

Есть устройства, обкладки которых представляют собой два шара, вложенные друг в друга. Формула ёмкости такого прибора:

C=(4π*l*R1*R2*ε)/(R2-R1), где:

• R1 – радиус внутренней сферы,
• R2 – радиус внешней сферы,
• ε – диэлектрическая проницаемость.

Ёмкость одиночного проводника

Кроме конденсаторов, способностью накапливать заряд обладают отдельные проводники. Одиночным проводником считается такой проводник, который бесконечно далёк от других проводников. Параметры заряженного элемента рассчитывается по формуле:

• Q – заряд,
• φ – потенциал проводника.

Объём заряда определяется размером и формой устройства, а также окружающей средой. Материал прибора значения не имеет.

Способы соединения элементов

Не всегда есть в наличии элементы с необходимыми параметрами. Приходится соединять их различными способами.

Параллельное соединение

Это такое соединение деталей, при котором к одной клемме или контакту присоединяются первые обкладки каждого конденсатора. При этом вторые обкладки присоединяются к другой клемме.

При таком соединении напряжение на контактах всех элементов будет одинаковым. Заряд каждого из них происходит независимо от остальных, поэтому общая ёмкость равна сумме всех величин. Её находят по формуле:

где C1-Cn – параметры деталей, участвующих в параллельном соединении.

Важно! Конденсаторы имеют предельное допустимое напряжение, превышение которого приведёт к выходу элемента из строя. При параллельном соединении устройств с различным допустимым напряжением этот параметр получившейся сборки равен элементу с наименьшим значением.

Последовательное соединение

Это такое соединение, при котором к клемме присоединяется только одна пластина первого элемента. Вторая пластина присоединяется к первой пластине второго элемента, вторая пластина второго – к первой пластине третьего и так далее. Ко второй клемме присоединяется только вторая обкладка последнего элемента.

При таком соединении заряд на обкладках конденсатора в каждом приборе будет равен остальным, однако напряжение на них будет разным: для зарядки устройств большей ёмкости тем же зарядом требуется меньшая разность потенциалов. Поэтому вся цепочка представляет собой одну конструкцию, разность потенциалов которой равна сумме напряжений на всех элементах, а заряд конденсатора равен сумме зарядов.

Последовательное соединение увеличивает допустимое напряжение и уменьшает общую ёмкость, которая меньше самого меньшего элемента.

Рассчитываются эти параметры следующим образом:

• Допустимое напряжение:

Uобщ=U1+U2+U3+…Un, где U1-Un – напряжение на конденсаторе;

• Общая ёмкость:

1/Собщ=1/С1+1/С2+1/С3+…1/Сn, где С1-Сn – параметры каждого устройства.

Интересно. Если в цепи только два элемента, то можно воспользоваться упрощённой формулой: Собщ=(С1*С2)/(С1+С2).

Смешанное соединение

Это такое соединение, в котором есть детали, соединённые последовательно, и есть соединённые параллельно. Параметры всей цепи рассчитывается в следующей последовательности:

1. определяются группы элементов, соединённые параллельно;
2. для каждой группы в отдельности рассчитывается эквивалентные значения;
3. рядом с каждой группой параллельно соединённых деталей пишутся получившиеся величины;
4. получившаяся схема эквивалентна последовательной схеме и рассчитывается по соответствующим формулам.

Знание формул, по которым можно найти емкость при изготовлении конденсаторов или их соединении необходимо при конструировании электронных схем.

Видео

Напряжения и расчеты на прочность при изгибе.

Сопротивление материалов

Напряжения при изгибе



Нормальные напряжения при чистом изгибе

Как было установлено ранее, в поперечных сечениях балки при чистом изгибе возникают только нормальные напряжения растяжения и сжатия. Вопрос о распределении этих напряжений по поперечному сечению решается путем рассмотрения деформаций волокон балки.

Рассмотрим участок балки, подверженный деформации чистого изгиба. Двумя поперечными сечениями АВ и СD выделим элемент балки бесконечно малой длины ds (рис 1). Радиус кривизны нейтрального слоя балки обозначим ρ.

Рассмотрим слой волокон mn, находящийся на расстоянии y от нейтрального слоя NN. Это волокно в результате деформации изгиба удлинилось на величину nn₁. Ввиду малости расстояния ds заштрихованные треугольники будем считать прямолинейными; эти треугольники подобны (n₁F || mE):

Δ OEF ~ Δ Fnn₁.

Из подобия треугольников запишем равенство:

nn₁ / ds = y / ρ.

Так как левая часть этого равенства есть относительное удлинение, т. е. nn₁ / ds = ε, то y / ρ = ε.

Применив закон Гука при растяжении и сжатии σ = Еε, получим:

σ = Еy / ρ.

Из этой формулы видно, что нормальные напряжения при изгибе распределены по высоте сечения неравномерно: максимальные напряжения возникают в волокнах, наиболее удаленных от нейтральной оси. По ширине сечения нормальные напряжения не меняются.
Распределение нормальных напряжений изображено на рис. 2.

Полученная формула для определения нормальных напряжений неудобна, так как в нее входит радиус кривизны нейтрального слоя.
Для вывода формулы, связывающей нормальные напряжения с изгибающим моментом, применим метод сечений и рассмотрим равновесие части балки, изображенной на рис. 3.
В плоскости поперечного сечения выделим бесконечно малую площадку dA, в пределах которой будем считать нормальные напряжения σ постоянными; тогда нормальная сила dN, действующая на площадку dA, будет равна:

dN = σdA.

Составим уравнения равновесия:

1.    Σ Z = 0;    ∫dN = 0,     или:     ∫σ dA = ∫Еy / ρ dA = Е / ρ ∫y dA = 0.

(ρ для данного сечения, а также модуль упругости Е – величины постоянные, поэтому вынесены за знак интеграла). Поскольку ρ и Е не равны нулю, значит, ∫y dA = 0. Этот интеграл представляет собой статический момент площади сечения относительно оси x, т. е. нейтральной оси бруса (балки). Равенство нулю статического момента инерции означает, что при изгибе нейтральная ось проходит через центр тяжести площади поперечного сечения;

2.    Σ М_и = 0; – m + ∫y dN = 0.

Так как при чистом изгибе изгибающий момент равен внешнему моменту М_и = m, то

М_и = ∫y dN = ∫y dA = ∫y Еy / ρ dA = Е / ρ ∫y² dA,

откуда:

М_и = Е I / ρ,

где: I = ∫y² dA – момент инерции поперечного сечения относительно нейтральной оси; ЕI – жесткость сечения при изгибе.

Так как при чистом изгибе балки постоянного сечения М_и = const, то:

ρ = EI / М_и = const.

Следовательно, изогнутая ось такой балки представляет собой дугу окружности. Выражение радиуса кривизны подставим в формулу для определения нормальных напряжений; тогда:

σ = Еy / ρ = Ey / EI / М_и = М_и y / I.

Максимальное значение нормальные напряжения будут иметь у волокон, наиболее удаленных от нейтральной оси:

σ_max = М_и y_max / I = М_и / I / y_max = М_и / W,

где W = I / y_max – момент сопротивления изгибу (или осевой момент сопротивления).
Момент сопротивления изгибу есть отношение осевого момента инерции поперечного сечения относительно нейтральной оси к расстоянию от этой оси до наиболее удаленного волокна.
Единица момента сопротивления сечения изгибу [W] = м³.

Итак, наибольшие нормальные напряжения при чистом изгибе вычисляются по формуле

σ_max = М_и / W.

Нетрудно заметить, что эта формула по своей структуре аналогична формулам для определения напряжений при растяжении, сжатии, сдвиге и кручении.

***



Касательные напряжения при изгибе

Очевидно, что при поперечном изгибе, вызванном приложением к балке поперечной силы, в сечениях балки должны возникнуть касательные напряжения.
Определением зависимости между внешними нагрузками, геометрическими и физическими параметрами балок и касательными напряжениями, возникающими в них, занимался русский мостостроитель Д. И. Журавский, который в 1855 году предложил следующую формулу:

τ = QS / (I d).

Эта формула называется формулой Журавского и читается так:
касательные напряжения в поперечном сечении балки равны произведению поперечной силы Q на статический момент S относительно центральной оси части сечения, лежащей выше рассматриваемого слоя волокон, деленному на момент инерции I всего сечения относительно нейтральной оси и на ширину b рассматриваемого слоя волокон.

По формуле Журавского можно вывести зависимости для определения касательных напряжений в балках, имеющих разную форму поперечного сечения (прямоугольную, круглую и т. п.).
Например, для балки круглого сечения формула Журавского в результате преобразований выглядит так:

τ_max = 4Q / (3A) = 4τ_сред / 3,

где Q – поперечная сила, вызывающая изгиб, А – площадь сечения балки.

Большинство балок в конструкциях рассчитывается только по нормальным напряжениям, и только три вида балок проверяют по касательным напряжениям:

– деревянные балки, т. к. древесина плохо работает на скалывание;
– узкие балки (например, двутавровые), поскольку максимальные касательные напряжения обратно пропорциональны ширине нейтрального слоя;
– короткие балки, так как при относительно небольшом изгибающем моменте и нормальных напряжениях у таких балок могут возникать значительные поперечные силы и касательные напряжения.
Максимальное касательное напряжение в двутавровой балке определяется по формуле Журавского, при этом геометрические характеристики таких балок берутся из справочных таблиц .

***

Расчеты на прочность при изгибе

Условие на прочность при изгибе заключается в том, что максимальное нормальное напряжение в опасном сечении не должно превышать допускаемое.
Полагая, что гипотеза о не надавливании волокон справедлива не только при чистом, но и при поперечном изгибе, мы можем нормальные напряжения при поперечном изгибе определять по такой же формуле, что и при чистом изгибе, при этом расчетная формула выглядит так:

σ_max = Ми_max / W ≤ [σ]

и читается так: нормальное напряжение в опасном сечении, определенное по формуле σ_max = Ми_max / W ≤ [σ] не должно превышать допускаемое.
Допускаемое нормальное напряжение при изгибе выбирают таким же, как при растяжении и сжатии.
Максимальный изгибающий момент определяют по эпюре изгибающих моментов или расчетом.
Так как момент сопротивления изгибу W в расчетной формуле стоит в знаменателе, то чем больше W, тем меньшие напряжения возникают в сечении бруса.

Ниже приведены моменты сопротивления изгибу для наиболее часто встречающихся сечений:

1. Прямоугольное сечение размером b x h:    W_пр = bh² / 6.

2. Круглое сечение диаметром d:    W_круг = π d³ / 32 ≈ 0,1d³

3. Кольцо размером D x d:    W_кольца = ≈ 0,1 (D⁴ – d⁴) / D; (момент сопротивления кольцевого сечения нельзя определять, как разность моментов сопротивления большого и малого кругов).

***

Материалы раздела “Изгиб”:

Деформации растяжения и сжатия



Главная страница

Дистанционное образование

Специальности

Учебные дисциплины

Олимпиады и тесты

Переменный электрический ток, действующее напряжение, сила тока. Мощность тока. Курсы по физике

Тестирование онлайн

• Переменный ток. Основные понятия

• Переменный ток

Генератор переменного тока

Устройство, предназначенное для превращения механической энергии в энергию переменного тока, называется генератором переменного тока. В основу работы генератора положено явление электромагнитной индукции.

Рамка вращается в магнитном поле. Поскольку магнитный поток, пронизывающий рамку, изменяется с течением времени, то в ней возникает индуцированная ЭДС:

Ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное.

Основными частями генератора переменного тока являются: индуктор, якорь, коллектор, статор, ротор.

а) устройство ротора; б) работа генератора переменного тока

Переменный ток

Переменный ток изменяется с течением времени по гармоническому закону.

Действующим (эффективным) значением переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделил бы такое же количество теплоты, что и данный переменный ток.

Мощность переменного тока

Мощность в цепи переменного тока изменяется с течением времени. Поэтому введено понятие мгновенной мощности (мощность в некоторый момент времени) и средней мощности (мощность за длительный промежуток времени).

Рассмотрим цепь переменного тока, состоящую из последовательно соединенных резистора, катушки индуктивности и конденсатора, подключенных к источнику переменного напряжения.

Явление резкого увеличения амплитуды переменного тока в такой цепи получило название резонанса напряжений. Частота, при которой наблюдается резонанс, называется резонансной частотой.

Резонансная частота равна частоте свободных колебаний контура.

Максимальные напряжения найдем из формулы (5.24):

МПа.

Пример 5.6.Двутавровое сечение. Определить касательные напряжения в указанных точках сечения и построить эпюру касательных напряжений при величине поперечной силыкН (Рис.5.14).

Рис.5.14

Характерной особенностью этого сечения является резкое изменение ширины сечения при переходе от стенки двутавра к его полке. В основном поперечную силу воспринимает стенка, а на долю полок приходится небольшая ее величина.

Покажем, как определяется статический момент площади для любой произвольной точки сечения двутавра. Для этого рассмотрим произвольную точку К (Рис.5.15). Проведем через эту точку линию, параллельную оси . Статический момент площади верхней отсеченной части (заштрихованой на рис.5.15) может быть найден как сумма статических моментов двух площадейи:

. (а)

Рис.5.15

Наибольшей величины статический момент площади отсеченной части относительно нейтральной линии сечения достигает для половины сечения. Следовательно, максимальные касательные напряжения возникают в волокнах нейтрального слоя.

Вернемся теперь к рис.5.14. Точка №1 сечения принадлежит наиболее отдаленному волокну. Точки №2 и №3 лежат в месте перехода от полки к стенке: точка №2 принадлежит полке, точка №3 – стенке сечения. Точка №4 лежит в центре тяжести сечения и принадлежит нейтральной линии сечения. Сечение симметрично расположено по отношению к оси . Поэтому напряжение в точке №5 будет таким же, как в точке №3, напряжение в точке №6 – таким же, что и в точке №2, напряжение в точке №7 – таким же, что и в точке №1.

Вначале найдем момент инерции сечения относительно оси :

см⁴.

Касательное напряжение в точке №1 поперечного сечения равно нулю, так как отсеченная часть сечения в данном случае представляет собой пространство над сечением, и ввиду отсутствия отсеченной площади, статический момент этой площади равен нулю. С другой стороны, если в качестве отсеченной площади рассматривать все сечение, то статический момент всей площади относительно нейтральной линии сечения , как центральной оси, равен нулю.

Для определения касательного напряжения в точке №2 проводим через точку №2 линию, параллельную оси . Отсеченная площадь лежит выше этой линии и составляетсм². Вычисляем расстояние от центра тяжести отсеченной площади до оси. Оно равно 11см. Находим касательные напряжения в точке №2:

Мпа.

При определении касательного напряжения в точке №3 следует помнить, что статический момент площади отсеченной части в этом случае остается прежним, так как точки №2 и №3 находятся на одинаковом расстоянии от оси . Только точка №2 принадлежит полке, а точка №3 принадлежит стенке двутавра. В связи с этим касательное напряжение в точке №3 будет равно:

Мпа.

Для определения напряжения в точке №4, проведем через эту точку линию, совпадающую с осью . Отсеченная площадь представляет собой тавр. Статический момент площади тавра вычислим, используя выражение (а), приведенное выше. В немпредставляет собой площадь полки,площадь половины стенки;расстояние от центра тяжести полки до оси;расстояние от центра тяжести половины площади стенки до оси. Касательные напряжения в точке №4 будут равны:

Мпа.

Как уже отмечалось выше, в силу симметрии МПа,МПа;.

Откладываем найденные значения касательных напряжений от базисной линии и строим эпюру касательных напряжений (Рис.5.14).

Пример 5.7. Во сколько раз касательное напряжение в точке В больше, чем в точке А? Точка О – центр тяжести сечения (Рис.5.16).

Рис.5.16

Решение:

Проведем через точки А и В линии, параллельные оси . Отсеченные площади на рис.5.16 заштрихованы. Вычислим статические моменты заштрихованных площадей относительно осии отнесем их к ширине сечения в точках А и В соответственно.

При одной и той же поперечной силе и одном и том же моменте инерции сечения относительно оси касательные напряжения в точках В и А относятся как:

.

Таким образом, касательное напряжение в точке В в 7,5 раз больше, чем в точке А.

Пример 5.8. Как изменится максимальное касательное напряжение при изгибе, если поперечное сечение балки перевести из положения I в положение II ? (Рис.5.17).

Рис.5.17

Решение:

При решении данной задачи следует помнить, что при повороте сечения из положения I в положение II меняются не только ширина сечения и статический момент площади сечения (отсеченные площади заштрихованы), но и моменты инерции относительно оси .Поэтому при одной и той же поперечной силе величины максимальных касательных напряжений в положених сечения I и II будут относиться, как:

.

Таким образом, величина максимального касательного напряжения при повороте сечения из положения I в положениеII не изменится.

Пример 5.9.Какая из изображенных эпюр касательных напряжений при изгибе построена правильно? (Рис.5.18).

Рис.5.18

Решение:

При анализе таких эпюр следует помнить:

1. Максимальные касательные напряжения возникают в нейтральном слое. Нейтральная линия сечения проходит через центр тяжести.

2. В месте резкого изменения ширины сечения касательные напряжения меняются скачком. При увеличении ширины сечения напряжения скачкообразно уменьшаются, при уменьшении ширины сечения касательные напряжения скачкообразно увеличиваются. Поэтому из предложенных вариантов эпюр касательных напряжений верным является вариант в).

Урок 8. переменный электрический ток – Физика – 11 класс

Физика, 11 класс

Урок 8. Переменный электрический ток

Перечень вопросов, рассматриваемых на уроке:

1) Свойства переменного тока;

2) Понятия активного сопротивления, индуктивного и ёмкостного сопротивления;

3) Особенности переменного электрического тока на участке цепи с резистором;

4) Определение понятий: переменный электрический ток, активное сопротивление, индуктивное сопротивление, ёмкостное сопротивление.

Глоссарий по теме

Переменный электрический ток — это ток, периодически изменяющийся со временем.

Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю называют активным сопротивлением.

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Величину Х_C, обратную произведению ωC циклической частоты на электрическую ёмкость конденсатора, называют ёмкостным сопротивлением.

Величину Х_L, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. – М.: Дрофа, 2014. – С. 128 – 132.

Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.

Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004

Основное содержание урока

Сейчас невозможно представить себе нашу цивилизацию без электричества. Телевизоры, холодильники, компьютеры – вся бытовая техника работает на нем. Основным источником энергии является переменный ток.

Электрический ток, питающий розетки в наших домах, является переменным А что это такое? Каковы его характеристики? Чем же переменный ток отличается от постоянного? Об этом мы поговорим на данном уроке.

В известном опыте Фарадея при движении полосового магнита относительно катушки появлялся ток, что фиксировалось стрелкой гальванометра, соединенного с катушкой. Если магнит привести колебательное движение относительно катушки, то стрелка гальванометра будет отклоняться то в одну сторону, то в другую – в зависимости от направления движения магнита. Это означает, что возникающий в катушке ток меняет свое направление. Такой ток называют переменным.

Электрический ток, периодически меняющийся со временем по модулю и направлению, называется переменным током.

Переменный электрический ток представляет собой электромагнитные вынужденные колебания. Переменный ток в отличие от постоянного имеет период, амплитуду и частоту.

Сила тока и напряжение меняются со временем по гармоническому закону, такой ток называется синусоидальным. В основном используется синусоидальный ток. Колебания тока можно наблюдать с помощью осциллографа.

Если напряжение на концах цепи будет меняться по гармоническому закону, то и напряженность внутри проводника будет так же меняться гармонически. Эти гармонические изменения напряженности поля, в свою очередь вызывают гармонические колебания упорядоченного движения свободных частиц и, следовательно, гармонические колебания силы тока. При изменении напряжения на концах цепи, в ней с очень большой скоростью распространяется электрическое поле. Сила переменного тока практически во всех сечениях проводника одинакова потому, что время распространения электромагнитного поля превышает период колебаний.

Рассмотрим процессы, происходящие в проводнике, включенном в цепь переменного тока. Сопротивление проводника, в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным. При изменении напряжения на концах цепи по гармоническому закону, точно так же меняется напряженность электрического поля и в цепи появляется переменный ток.

При наличии такого сопротивления колебания силы тока и напряжения совпадают по фазе в любой момент времени.

𝒾 – мгновенное значение силы тока;

ℐ_m– амплитудное значение силы тока.

– колебания напряжения на концах цепи.

Колебания ЭДС индукции определяются формулами:

При совпадении фазы колебаний силы тока и напряжения мгновенная мощность равна произведению мгновенных значений силы тока и напряжения. Среднее значение мощности равно половине произведения квадрата амплитуды силы тока и активного сопротивления.

Часто к параметрам и характеристикам переменного тока относят действующие значения. Напряжение, ток или ЭДС, которая действует в цепи в каждый момент времени – мгновенное значение (помечают строчными буквами – і, u, e). Однако оценивать переменный ток, совершенную им работу, создаваемое тепло сложно рассчитывать по мгновенному значению, так как оно постоянно меняется. Поэтому применяют действующее, которое характеризует силу постоянного тока, выделяющего за время прохождения по проводнику столько же тепла, сколько это делает переменный.

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

U_m – амплитудное значение напряжения.

Действующие значения силы тока и напряжения:

Электрическая аппаратура в цепях переменного тока показывает именно действующие значения измеряемых величин.

Конденсатор включенный в электрическую цепь оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.

Величину Х_C, обратную произведению циклической частоты на электрическую ёмкость конденсатора, называют ёмкостным сопротивлением.

Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току.

Если включить в электрическую цепь катушку индуктивности, то она будет влиять на прохождение тока в цепи, т.е. оказывать сопротивление току. Это можно объяснить явлением самоиндукции.

Величину Х_L, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

X_L= ωL

Если частота равна нулю, то индуктивное сопротивление тоже равно нулю.

При увеличении напряжения в цепи переменного тока сила тока будет увеличиваться так же, как и при постоянном токе. В цепи переменного тока содержащем активное сопротивление, конденсатор и катушка индуктивности будет оказываться сопротивление току. Сопротивление оказывает и катушка индуктивности, и конденсатор, и резистор. При расчёте общего сопротивления всё это надо учитывать. Основываясь на этом закон Ома для переменного тока формулируется следующим образом: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

Если цепь содержит активное сопротивление, катушку и конденсатор соединенные последовательно, то полное сопротивление равно

Закон Ома для электрической цепи переменного тока записывается имеет вид:

Преимущество применения переменного тока заключается в том, что он передаётся потребителю с меньшими потерями.

В электрической цепи постоянного тока зная напряжение на зажимах потребителя и протекающий ток можем легко определить потребляемую мощность, умножив величину тока на напряжение.   В цепи переменного тока мощность равна произведению напряжения на силу тока и на коэффициент мощности.

Мощность цепи переменного тока

P=IU cosφ

Величина cosφ – называется коэффициентом мощности

Коэффициент мощности показывает какая часть энергии преобразуется в другие виды. Коэффициент мощности находят с помощью фазометров. Уменьшение коэффициента мощности приводит к увеличению тепловых потерь. Для повышения коэффициента мощности электродвигателей параллельно им подключают конденсаторы. Конденсатор и катушка индуктивности в цепи переменного тока создают противоположные сдвиги фаз. При одновременном включении конденсатора и катушки индуктивности происходит взаимная компенсация сдвига фаз и повышение коэффициента мощности. Повышение коэффициента мощности является важной народнохозяйственной задачей.

Разбор типовых тренировочных заданий

1. Рамка вращается в однородном магнитном поле. ЭДС индукции, возникающая в рамке, изменяется по закону e=80 sin 25πt. Определите время одного оборота рамки.

Дано: e=80 sin 25πt.

Найти: T.

Решение:

Колебания ЭДС индукции в цепи переменного тока происходят по гармоническому закону

Согласно данным нашей задачи:

Время одного оборота, т.е. период связан с циклической частотой формулой:

Подставляем числовые данные:

Ответ: T = 0,08 c.

2. Чему равна амплитуда силы тока в цепи переменного тока частотой 50 Гц, содержащей последовательно соединенные активное сопротивление 1 кОм и конденсатор емкости С = 1 мкФ, если действующее значение напряжения сети, к которой подключен участок цепи, равно 220 В?

Дано:

ν=50 Гц,

R=1 кОм=1000 Ом,

C=1 мкФ=10^-6 Ф,

U=220 В.

Найти: I_m

Решение:

Напишем закон Ома для переменного тока:

I=U/Z

Для амплитудных значений силы тока и напряжения, мы можем записать I_m=U_m/Z?

Полное сопротивление цепи равно:

Подставляя числовые данные находим полное сопротивление Z≈3300 Ом. Так как действующее значение напряжения равно:

то после вычислений получаем I_m ≈0,09 Ом.

Ответ: I_m ≈0,09 Ом.

2. Установите соответствие между физической величиной и прибором для измерения.

Физические величины	Физические приборы
Сила тока	Омметр
Напряжение	Вольтметр
Сопротивление	Амперметр
Мощность	Ваттметр

Правильный ответ:

Физические величины	Физические приборы
Сила тока	Амперметр
Напряжение	Вольтметр
Сопротивление	Омметр
Мощность	Ваттметр

Электромагнитные колебания в физике: основные формулы

Электромагнитные колебания — это повторяющийся процесс взаимного превращения электрических и магнитных полей.

Электромагнитные колебания возникают в колебательном контуре.

Колебательный контур — это цепь, состоящая из конденсатора и катушки индуктивности (рис. 316).

Если сопротивлением проводов контура можно пренебречь, то такой контур называется идеальным.

При зарядке конденсатора в идеальном колебательном контуре возникают свободные, незатухающие электромагнитные колебания заряда и напряжения на обкладках конденсатора, а также силы тока и ЭДС в катушке индуктивности. Электромагнитные колебания в идеальном колебательном контуре являются высокочастотными и гармоническими.

На рис. 317 изображены графики колебаний заряда, напряжения и силы тока в идеальном колебательном контуре.

Ниже приведены уравнения электромагнитных колебаний и волн.

Уравнения электромагнитных колебаний заряда, силы тока, напряжения и ЭДС:

Здесь q — мгновенный заряд (Кл),

— максимальный заряд (Кл), —циклическая частота колебаний (рад/с), t — время колебаний (с), — начальная фаза (рад), i — мгновенная сила тока (А), — максимальная сила тока (А), u — мгновенное напряжение (В), — максимальное напряжение (В), е — мгновенная ЭДС (В), — максимальная ЭДС (В), S — площадь вращающегося контура , С — емкость конденсатора (Ф).

Период, циклическая частота и частота свободных электромагнитных колебаний в колебательном контуре (формула Томсона)

Здесь Т — период колебаний (с), L — индуктивность катушки (Гн), С— емкость конденсатора (Ф),

—циклическая частота колебаний (рад/с), v — частота колебаний (Гц).

Формула силы переменного тока:

Здесь i — мгновенная сила тока (A),

— первая производная заряда по времени (А), — максимальная сила тока (А), — максимальный заряд (Кл).

Действующие значения переменного тока:

Здесь I — действующее значение силы переменного тока (A),

— максимальное значение силы тока (A), U — действующее значение напряжения (В), — максимальное напряжение (В), — действующая ЭДС (В), — максимальная ЭДС (В).

Индуктивное, емкостное и полное сопротивления в цепи переменного тока

Здесь

— индуктивное сопротивление (Ом), — емкостное сопротивление (Ом), — циклическая частота переменного тока (рад/с), Z — полное сопротивление (Ом), R — активное сопротивление (Ом).

Закон Ома для полной цепи переменного тока:

Здесь I — действующее значение силы переменного тока (A), U — действующее значение напряжения переменного тока (В),

— максимальная сила переменного тока (A), — максимальное напряжение переменного тока (В). Остальные величины названы в предыдущей формуле.

Средняя мощность в цепи переменного тока:

Здесь Р — мощность переменного тока (Вт), U — его действующее напряжение (В), I — действующая сила тока (A),

— коэффициент мощности переменного тока (безразмерный), — сдвиг фаз между током и напряжением (рад).

Коэффициент мощности переменного тока

Здесь все величины названы в предыдущих формулах.

Коэффициент трансформации трансформатора

Здесь k — коэффициент трансформации трансформатора (безразмерный),

— напряжение на первичной обмотке (В), — напряжение на вторичной обмотке (В), — число витков в первичной обмотке (безразмерное), — число витков во вторичной обмотке (безразмерное).

Формулы длины электромагнитной волны в вакууме (воздухе)

Здесь

— длина волны (м), м/с — скорость света в вакууме, Т — период колебаний (с), v — частота колебаний (Гц).

Плотность потока электромагнитного излучения

Здесь I — плотность потока электромагнитного излучения

—электромагнитная энергия, проходящая через некоторую поверхность (Дж), S — площадь этой поверхности — время прохождения энергии (с).

Свободные электромагнитные колебания в идеальном колебательном контуре подчиняются закону сохранения энергии: полная энергия электромагнитных колебаний

равна максимальной энергии электрического поля конденсатора , или равна максимальной энергии магнитного поля катушки индуктивости , или равна сумме мгновенных электрической и магнитной энергий поля конденсатора и катушки в любой промежуточный момент:

Это закон можно записать, развернув значения энергии электрического и магнитного полей через их параметры:

В этом уравнении максимальную энергию электрического поля в зависимости от известных величин можно выразить как

; а его мгновенную энергию — соответственно как . Здесь q, u и i — мгновенные значения заряда, напряжения и силы тока.

Всякий реальный колебательный контур (рис. 318) имеет сопротивление проводов R. Если ему один раз сообщить энергию, например, зарядив конденсатор С, то колебания в нем будут затухающими из-за потерь энергии на джоулево тепло. График затухающих колебаний силы тока изображен на рис. 319.

Чтобы колебания были незатухающими, колебательный контур надо пополнять энергией, например, включив в него источник переменного напряжения (рис. 320).

Если частота пополнения контура энергией будет равна собственной частоте колебаний контура, то в контуре возникнет электрический резонанс — явление резкого возрастания максимальной силы тока в контуре (амплитуды силы тока), когда частота пополнения контура энергией становится равной собственной частоте колебаний в контуре.

При вращении проводящего контура в магнитном поле в нем вследствие явления электромагнитной индукции возникает переменный ток.

Действующим (эффективным) значением переменного тока называют силу такого постоянного тока, который, проходя по контуру, выделяет в единицу времени столько же тепла, что и данный переменный ток. Измерительные приборы, включенные в цепь переменного тока, показывают его действующие значения.

Если в цепь переменного тока включить катушку индуктивности, то в ней возникнет ток самоиндукции, который, согласно правилу Ленца, будет препятствовать изменению переменного тока. Из-за этого колебания силы тока в контуре будут отставать по фазе от колебаний напряжения, поэтому катушка индуктивности, включенная в контур, оказывает индуктивное сопротивление

переменному току.

Если в цепь переменного тока включить конденсатор, то изменение напряжения на его обкладках будет отставать по фазе от изменения силы тока, поэтому конденсатор будет оказывать емкостное сопротивление

переменному току.

Индуктивное и емкостное сопротивления вместе называются реактивным сопротивлением.

Сопротивление R, которое оказывают проводники цепи, называется активным сопротивлением. Джоулево тепло выделяется только на активном сопротивлении — в этом состоит главное отличие активного сопротивления от емкостного и индуктивного сопротивлений.

Устройство для изменения напряжения переменного тока называется трансформатором Т (рис. 321).

Действие трансформатора основано на явлении электромагнитной индукции. Трансформатор состоит из замкнутого ферромагнитного сердечника, на который надеты обмотки. Та обмотка, которую подключают к источнику изменяемого напряжения, называется первичной, а та, с которой измененное напряжение подается на потребитель — вторичной.

Если число витков во вторичной обмотке больше числа витков в первичной, то трансформатор называется повышающим, а если меньше — то понижающим. Величина к, показывающая, во сколько раз трансформатор изменяет напряжение переменного тока, называется коэффициентом трансформации трансформатора.

Напряжение на обмотках прямо пропорционально числу витков в них:

Поскольку КПД трансформатора очень высок, работа тока в его обеих обмотках примерно одинакова. Поэтому силы тока в обмотках

обратно пропорциональны числу витков и в них:

Электромагнитные волны — это распространение в пространстве электромагнитных колебаний.

Микроисточником электромагнитных волн является возбужденный атом, макроисточником — колебательный контур. Электромагнитные волны излучают ускоренно движущиеся заряженные частицы.

Электромагнитные волны являются поперечными волнами, т.к. векторы электрической напряженности

и магнитной индукции в электромагнитной волне колеблются перпендикулярно ее перемещению (рис. 322).

В вакууме электромагнитные волны распространяются с максимальной скоростью

м/с.

Амплитуда электромагнитной волны пропорциональна квадрату ее частоты, а ее энергия пропорциональна частоте в четвертой степени. Электромагнитные волны обладают всеми свойствами волн: интерференцией, дифракцией, дисперсией и поляризацией.

На рис. 323 изображена шкала электромагнитных волн, на которой электромагнитные волны расположены в порядке возрастания их частоты или в порядке убывания длины волны.

Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти страницы:

Напряжение цепи переменного тока | Электрикам

Переменное напряжение — это напряжение, которое изменяется с течением времени. Далее будем рассматривать только гармоническое переменное напряжение (изменяется по синусоиде).

u = U_msin(2πt + Ψ ) = U_msin(ωt + Ψ )

Где u = u(t) — мгновенное значение переменного напряжения [В].

U_m — максимальное значение напряжения (амплитудное значение) [В].

f — частота  равная числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с^-1)

ω — угловая частота (омега) (единица угловой частоты — рад/с или с^-1)

ω = 2πf = 2π/T

Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.

U — Действующее значение напряжения [В]:

Рассмотрим параметры напряжения в бытовой электросети.

Все мы знаем, что у нас дома в розетке поступает переменный ток, с напряжением 220 вольт и частотой 50 герц (в идеальных условиях) на самом деле допускается не большая погрешность как в меньшую, так и в большую сторону так, что не удивляйтесь если ваш вольтметр покажет не 220, а например 210 или даже 230 В.).

Большинство приборов измеряет не амплитудное, а действующее значение переменного напряжения, тока, мощности так, что если мы говорим что у нас напряжение сети 220, 380 В и т. д. то имеется виду именно действующие значения.

• Действующее значение напряжения U = 220 В.
• Амплитудное значение напряжения цепи переменного тока U_m = U*√2 = 220 *√2 = 311 В.
• Угловая частота ω = 2πf = 3,14*2*50 = 314 рад/с.
• Начальная фаза Ψ = 0 град.
• Мгновенное значение u  = 311sin(314t) В.

Как рассчитать максимальное напряжение

Обновлено 28 декабря 2020 г.

Кевин Бек

«Стресс» в повседневном языке может означать любое количество вещей, но в целом подразумевает некоторую срочность, что-то, что проверяет устойчивость некоторая поддающаяся количественному или, возможно, не поддающаяся количественному определению система поддержки. В инженерии и физике напряжение имеет особое значение и относится к количеству силы, которую материал испытывает на единицу площади этого материала.

Расчет максимального напряжения, которое может выдержать данная конструкция или отдельная балка, и согласование его с ожидаемой нагрузкой на конструкцию.это классическая повседневная проблема, с которой инженеры сталкиваются каждый день. Без математических расчетов было бы невозможно построить огромное количество огромных плотин, мостов и небоскребов, которые видели во всем мире.

Силы на Луч

Сумма сил F _net , испытываемых объектами на Земле, включает «нормальную» составляющую, направленную прямо вниз и относящуюся к гравитационному полю Земли, которое вызывает ускорение. г из 9.8 м / с ² в сочетании с массой m объекта, испытывающего это ускорение. (Из второго закона Ньютона F _net = m a. Ускорение – это скорость изменения скорости, которая, в свою очередь, является скоростью изменения смещения.)

Горизонтально ориентированный твердый объект например, балка, имеющая как вертикально, так и горизонтально ориентированные элементы массы, испытывает некоторую степень горизонтальной деформации даже при воздействии вертикальной нагрузки, проявляющейся в изменении длины ΔL.То есть балка заканчивается.

Модуль Юнга Y

Материалы имеют свойство, называемое модулем Юнга или модулем упругости Y , которое является индивидуальным для каждого материала. Более высокие значения означают более высокое сопротивление деформации. Его единицы такие же, как и у давления, в ньютонах на квадратный метр (Н / м ² ), что также является силой на единицу площади.

Эксперименты показывают, что изменение длины ΔL балки с начальной длиной L ₀ , подверженной действию силы F по площади поперечного сечения A, определяется уравнением

\ Delta L = \ bigg (\ frac { 1} {Y} \ bigg) \ bigg (\ frac {F} {A} \ bigg) L_0

Напряжение и деформация

Напряжение в данном контексте представляет собой отношение силы к площади F / A , который появляется справа в приведенном выше уравнении изменения длины.Иногда его обозначают σ (греческая буква сигма).

Напряжение , с другой стороны, представляет собой отношение изменения длины ΔL к исходной длине L, или ΔL / L. Иногда его обозначают буквой ε (греческая буква эпсилон). Деформация – величина безразмерная, то есть не имеет единиц измерения.

Это означает, что напряжение и деформация связаны соотношением

\ frac {Delta L} {L_0} = \ epsilon = \ bigg (\ frac {1} {Y} \ bigg) \ bigg (\ frac {F} {A } \ bigg) = \ frac {\ sigma} {Y}

Пример расчета с учетом напряжения

Сила 1,400 Н действует на 8 метров на 0.2

Калькулятор грузоподъемности двутавровой балки

Вы можете бесплатно найти в Интернете калькулятор стальной балки, аналогичный тому, который представлен в разделе «Ресурсы». На самом деле это вычислитель неопределенных балок, который можно применить к любой линейной опорной конструкции. Это позволяет вам в некотором смысле играть в архитектора (или инженера) и экспериментировать с различными входными усилиями и другими переменными, даже с петлями. Лучше всего то, что этим вы не можете вызвать у строителей какой-либо «стресс» в реальном мире!

Расчет напряжения изгиба секции балки

Как рассчитать напряжение изгиба в балках?

В этом руководстве мы рассмотрим, как рассчитать изгибающее напряжение балки, используя формулу изгибающего напряжения, которая связывает распределение продольных напряжений в балке с внутренним изгибающим моментом, действующим на поперечное сечение балки.Мы предполагаем, что материал балки линейно-упругий (т.е. применим закон Гука). Напряжение изгиба важно, и, поскольку изгиб балки часто является определяющим результатом при проектировании балки, это важно понимать.

1. Расчет напряжения изгиба вручную

Давайте посмотрим на пример. Рассмотрим двутавровую балку, показанную ниже:

На некотором расстоянии по длине балки (ось x) она испытывает внутренний изгибающий момент (M), который обычно можно найти на диаграмме изгибающего момента.Общая формула для изгиба или нормального напряжения в сечении:

Для конкретного сечения балки очевидно, что напряжение изгиба будет максимальным на расстоянии от нейтральной оси (y). Таким образом, максимальное напряжение изгиба будет возникать либо в ВЕРХНЕ, либо в НИЖНЕЙ части секции балки, в зависимости от того, какое расстояние больше:

Давайте рассмотрим реальный пример нашей двутавровой балки, показанной выше. В нашем предыдущем уроке по моменту инерции мы уже обнаружили, что момент инерции относительно нейтральной оси равен I = 4.74 × 10 ⁸ мм ⁴ . Кроме того, в учебнике по центроиду мы обнаружили, что центроид и, следовательно, расположение нейтральной оси находятся на расстоянии 216,29 мм от нижней части секции. Это показано ниже:

Очевидно, что очень часто требуется МАКСИМАЛЬНОЕ напряжение изгиба, которое испытывает секция. Например, предположим, что мы знаем из нашей диаграммы изгибающего момента, что балка испытывает максимальный изгибающий момент 50 кН-м или 50 000 Нм (преобразование единиц изгибающего момента).

Затем нам нужно определить, находится ли верх или низ секции дальше всего от нейтральной оси. Ясно, что нижняя часть секции находится дальше на расстояние c = 216,29 мм. Теперь у нас достаточно информации, чтобы найти максимальное напряжение, используя приведенную выше формулу напряжения изгиба:

Точно так же мы можем найти напряжение изгиба в верхней части секции, так как мы знаем, что оно составляет y = 159,71 мм от нейтральной оси (NA):

Последнее, о чем следует беспокоиться, это то, вызывает ли напряжение сжатие или растяжение волокон секции.Если балка прогибается в форме буквы «U», то верхние волокна испытывают сжатие (отрицательное напряжение), а нижние волокна – растяжение (положительное напряжение). Если балка провисает, как перевернутая буква «U», то все наоборот: нижние волокна сжимаются, а верхние – растягиваются.

2. Расчет напряжения изгиба с использованием балки SkyCiv

Конечно, вам не нужно делать эти расчеты вручную, потому что вы можете использовать SkyCiv Beam – калькулятор напряжения изгиба, чтобы определить напряжение сдвига и изгиба в балке! Просто начните с моделирования балки с опорами и приложите нагрузки.Как только вы нажмете «Решить», программа покажет максимальные напряжения из этого калькулятора напряжения изгиба. На изображении ниже показан пример двутавровой балки, испытывающей напряжение изгиба:

Начните расчет напряжения изгиба с помощью SkyCiv Beam Calculator:

Бесплатный калькулятор луча

Maximum Direct Stress – обзор

P.7.1.

Пластина толщиной 10 мм подвергается изгибающим моментам M _x равным 10 Нм / мм и M _y равным 5 Нм / мм.Рассчитайте максимальные прямые напряжения в пластине.

Ответ: σx, max = ± 600 Н / мм2, σy, max = ± 300 Н / мм2.

П.7.2.

Для пластины и нагрузки задачи P.7.1 найдите максимальный крутящий момент на единицу длины в пластине и направление плоскостей, в которых это происходит.

Ответ: 2,5 Нм / мм под углом 45 ° к осям x и y .

П.7.3.

Пластина из двух предыдущих задач подвергается крутящему моменту 5 Нм / мм по каждой кромке в дополнение к изгибающим моментам M _x = 10 Нм / мм и M _y = 5 Н · м / мм.Определите главные моменты в пластине, плоскости, в которых они действуют, и соответствующие главные напряжения.

Ответ: 13,1 Нм / мм, 1,9 Нм / мм, α = −31,7 °, α = + 58,3 °, ± 786 Н / мм2, ± 114 Н / мм2.

P.7.3 MATLAB Используйте MATLAB для повторения задачи P.7.3 для следующих комбинаций M _x , M _y и M _xy . Не рассчитывайте главные напряжения.

iiiiiiivvMx68101214Mx76543Mx34567

Ответ: (i) MI = 9,5N м / мм, MII = 3,5N м / мм, α = -49,7 ° или 40,3 ° (ii) MI = 11,1N м / мм, MII = 2,9N м / мм, α = -38 ° или 52 ° (iii) MI = 13,1 Н · м / мм, MII = 1,9 Н · м / мм, α = −31,7 ° или 58,3 ° (iv) MI = 15,2 Н · м / мм, MII = 0,8 Н · м / мм, α = −28,2 ° или 61,8 ° (v) MI = 17,4 Н · м / мм, MII = 0,4 Н · м / мм, α = −25,9 ° или 64,1 °

P. 7.4.

Тонкая прямоугольная пластина длиной a и шириной 2 a просто опирается на края x = 0, x = a , y = – a и y = + a .Пластина имеет жесткость на изгиб D , коэффициент Пуассона 0,3 и несет распределение нагрузки, определяемое по формуле q ( x, y ) = q ₀ sin (π x / a ). Если прогиб пластины представлен выражением

w = qa4Dπ41 + Acoshπya + Bπyasinhπyasinπxa

, определите значения констант A и B .

Ответ: A = −0,2213, B = 0,0431.

П.7.5.

Тонкая эластичная квадратная пластина со стороной a просто поддерживается со всех четырех сторон и поддерживает равномерно распределенную нагрузку q . Если начало осей совпадает с центром пластины, покажите, что прогиб пластины можно представить выражением

w = q96 (1 − ν) D [2 (x4 + y4) −3a2 (1 − ν) (x2 + y2) −12νx2y2 + A]

, где D – жесткость при изгибе, v – коэффициент Пуассона и A – постоянная величина. Вычислите значение A и, следовательно, центральный прогиб пластины.

Ответ: A = a4 (5−3ν) /4,Cen.def.=qa4 (5−3ν) / 384D (1 − ν)

P.7.6.

Прогиб квадратной пластины со стороной a , которая поддерживает боковую нагрузку, представленную функцией q (x, y) , определяется как

w (x, y) = w0cosπxacos3πya

, где x и y относятся к осям, начало которых совпадает с центром пластины, а w ₀ – это отклонение в центре.Если жесткость пластины на изгиб составляет D , а коэффициент Пуассона равен ν, определите функцию нагрузки q , условия опоры пластины, реакции на углах пластины и изгибающие моменты в центре пластины.

Ответ: q (x, y) = w0D100π4a4cosπxacos3πya

Пластина просто опирается на все края. Реакции: −6w0Dπa2 (1 − ν)

Mx = w0Dπa2 (1 + 9ν), My = w0Dπa2 (9 + ν)

П.7.7.

Квадратная пластина с простой опорой a × a несет распределенную нагрузку в соответствии с формулой

q (x, y) = q0xa

, где q ₀ – его интенсивность на краю x = .Определите изогнутую форму пластины.

Ответ: w = 8q0a4π6D∑m = 1,2,3∞∑n = 1,3,5∞ (−1) m + 1mn (m2 + n2) 2sinmπxasinnπya

П.7.8.

Эллиптическая пластина с большой и малой осями 2 a и 2 b и небольшой толщины t зажата вдоль ее границы и подвергается равномерному перепаду давления p между двумя поверхностями. Покажите, что обычному дифференциальному уравнению для нормальных перемещений тонкой плоской пластины, подверженной боковой нагрузке, удовлетворяет решение

w = w01 − x2a2 − y2b22

, где w ₀ – это отклонение в центре, которое принимается как происхождение.

Определите w ₀ в терминах p и соответствующих свойств материала пластины и, следовательно, выражений для наибольших напряжений из-за изгиба в центре и на концах малой оси.

Ответ: w0 = 3p (1 − ν2) 2Et33a4 + 2a2b2 + 3b4

Center,

σx, max = ± 3pa2b2 (b2 + νa2) t2 (3b4 + 2a2b2, σ 3b4 + 2a2b2, σ ± 3pa2b2 (a2 + νb2) t2 (3b4 + 2a2b2 + 3a4)

Концы малой оси,

σx, max = ± 6pa4b2t2 (3b4 + 2a2b2 + 3a4), σy, max ± 6pb4a2 + 6pb4a2 3a4)

П.7.9.

Используйте энергетический метод для определения изогнутой формы прямоугольной пластины a × b , просто поддерживаемой вдоль каждого края и несущей сосредоточенную нагрузку W в положении (ξ, η) относительно осей через угол тарелки. Искривленную форму пластины можно представить рядом

w = ∑m = 1∞∑n = 1∞Amnsinmπxasinnπyb

Ответ: Amn = 4Wsinmπξasinnπηbπ4Dab [(m2 / a2) + (n2 / b2)] 2

П.7.10.

Если, в дополнение к точечной нагрузке W , пластина проблемы P.7.9 поддерживает сжимающую нагрузку в плоскости Н _x на единицу длины по краям x = 0 и x = a , рассчитаем результирующую форму отклонения.

Ответ: Amn = 4WsinmπξasinnπηbabDπ4m2a2 + n2b22 − m2Nxπ2a2D

P.7.11.

Квадратная пластина со стороной a просто опирается на все четыре стороны и подвергается поперечной равномерно распределенной нагрузке с интенсивностью q ₀ .Предложено определять отклоненную форму пластины методом Рэлея – Ритца, используя «предполагаемую» форму для прогиба

w = A111−4x2a21−4y2a2

, в котором начало координат берется в центре пластины.

Прокомментируйте степень, в которой выполняются граничные условия, и найдите центральный прогиб, принимая ν = 0,3.

Ответ: 0,0389 q ₀ a ⁴ / Et ³

P.7.11 MATLAB Используйте Symbolic Math Toolbox в MATLAB, чтобы повторить задачу P.7.11. Кроме того, рассчитайте прогиб в следующих точках пластины ( x , y ).

(a / 4, a / 4), (0,0), (a / 3, a / 3)

Ответ: (i) (x, y) = (a / 4, a / 4), w = 0,0218a4q0 / Et3 (ii) (x, y) = (0,0), w = 0,0388a4q0 / Et3 (iii) (x, y) = (a / 3, a / 3), w = 0,012a4q0 / Et3

P.7.12.

Прямоугольная пластина a × b , просто поддерживаемая вдоль каждого края, имеет небольшую начальную кривизну в ненагруженном состоянии, определяемую формулой

w0 = A11sinπxasinπyb

Определите, используя энергетический метод, ее окончательную форму отклонения, когда он подвергается сжимающей нагрузке Н _x на единицу длины по краям x = 0, x = a .

Ответ: w = A111 − Nxa2π2D / 1 + a2b22sinπxasinπyb

Напряжение балки из-за изгибающих моментов – Приложение по прочности материалов для энергетики

Напряжение изгиба

Цели обучения

После завершения этой главы вы сможете:

• Используйте формулу изгиба для расчета максимального напряжения изгиба
• Расчетные балки, безопасно несущие нагрузки
• Определите требуемый модуль упругости сечения балки
• Выберите стандартные конструктивные формы для использования в данной задаче балки

Рассмотрим балку с простой опорой, подверженную внешним нагрузкам, направленным вниз.Балка будет деформироваться (отклоняться) таким образом, что верхняя поверхность поперечного сечения балки будет испытывать сжатие, а нижняя поверхность – растяжение. В некотором месте вдоль вертикальной оси балки напряжение будет нулевым; это место является центром тяжести поперечного сечения, также называемым нейтральной осью.

Формула изгиба

Для определения максимального напряжения из-за изгиба используется формула изгиба :

где:

• σ _max – максимальное напряжение на самой удаленной от нейтральной оси поверхности (может быть верхней или нижней)
• M – изгибающий момент по длине балки, где рассчитывается напряжение
  • если требуется максимальное изгибающее напряжение, то M – максимальный изгибающий момент, действующий на балку
• I _x – момент инерции относительно центральной оси x (горизонтальной)
• c – максимальное расстояние от центральной оси до крайнего волокна (опять же, это может быть верх или низ формы)
• Z _x называется модулем сечения и представляет собой термин, который объединяет момент инерции и расстояние до крайнего волокна ( Z _x = I _x / c )

Формула изгиба действительна при соблюдении следующих критериев:

• балка прямая, относительно длинная и узкая, с равномерным поперечным сечением
• все нагрузки действуют перпендикулярно продольной оси балки
• результирующее напряжение ниже предела пропорциональности материала
• материал балки однороден и имеет равную прочность на растяжение и сжатие.
  • если материал имеет разную прочность на растяжение и сжатие (например, чугун или другие анизотропные материалы), то требуются отдельные расчеты как для поверхностей растяжения, так и для поверхностей сжатия
• нет скручивания, коробления или деформации

Дизайнерские шкафы

Проблемы проектирования могут возникать по разным сценариям:

• рассчитайте размеры поперечного сечения балки (найдите минимальный модуль сечения Z и выберите стандартную форму с большей жесткостью) с учетом геометрии балки, нагрузки и материала.
• выберите материал балки (найдите максимальное рабочее напряжение и выберите материал большей прочности) с учетом размеров балки, нагрузки и размеров / формы.
• определяет, является ли балка безопасной (найдите фактическое рабочее напряжение и сравните с расчетным напряжением), учитывая размеры балки, нагрузку и материал.

Назначенные задачи

Примечание: если не указано иное, используйте конструкцию = 0,6 × σ _YS, , где σ _YS – предел текучести, из учебного приложения B.

Задача 1: Несущая балка длиной 9,9 м нагружается сосредоточенными нагрузками следующим образом:

• 40 кН на расстоянии 1,2 м от левого края
• 10 кН на расстоянии 3,7 м от левого края
• 10 кН на расстоянии 6,2 м от левого края
• 10 кН на расстоянии 8,7 м от левого края

Балка изготовлена ​​из двутаврового профиля W200 × 100 из холоднокатаного материала AISI-1020. AISC рекомендует, чтобы максимальное напряжение изгиба для строительных конструкций при статических нагрузках было ниже 0.66 × S _y . Соответствует ли эта конструкция проектным требованиям?

Задача 2: Трубопровод просто поддерживается над землей на горизонтальных балках длиной 4,5 м. Каждая балка несет вес 20 м трубы Sch 40 DN-600 (см. PanGlobal Academic Extract), заполненной маслом 0,9 SG . Предполагая, что нагрузка действует в центре балки, рассчитайте необходимый модуль упругости балки, чтобы ограничить изгибающее напряжение до 140 МПа; затем выберите самый легкий W-луч SI, который удовлетворяет критериям.

Задача 3: На рисунке показано поперечное сечение балки из алюминия 6061-T6. Балка используется как консоль длиной 45 дюймов. Вычислите максимально допустимую равномерно распределенную нагрузку, которую он может выдержать при ограничении напряжения из-за изгиба до одной пятой от предельной прочности.

Проблема 4: Спроектируйте проход, который будет перекрывать только что проложенный трубопровод на вашем предприятии. Жесткие опоры доступны с каждой стороны трубопровода на расстоянии 14 футов друг от друга.Тротуар должен иметь ширину 3,5 фута и выдерживать равномерно распределенную нагрузку в 60 фунтов / фут ² по всей своей поверхности. Проектируйте только доски настила и боковые балки. Используйте древесину любых размеров и сортов материала из Приложения E к учебникам или других материалов, разработанных вами.

Задача 5: Предложите одну проблему конструкции балки, которую вы сочтете актуальной и полезной для инженеров-энергетиков.

Механика материалов: изгиб – нормальное напряжение »Механика тонких конструкций

---

Моменты области

Чтобы рассчитать напряжение (и, следовательно, деформацию), вызванное изгибом, нам нужно понять, где находится нейтральная ось балки и как рассчитать второй момент площади для данного поперечного сечения.

Начнем с представления произвольного поперечного сечения – чего-то не круглого, не прямоугольного и т. Д.

На изображении выше произвольная форма имеет область, обозначенную A . Мы можем посмотреть на небольшую дифференциальную область dA , которая существует на некотором расстоянии x и y от начала координат. Мы можем посмотреть на первый момент площади в каждом направлении по следующей формуле:

Первый момент площади – это интеграл длины по площади – это означает, что единицы длины будут кубическими [L ³ ].Это важно, потому что помогает нам определить центр тяжести объекта. Центроид определяется как «среднее положение области x (или y )». Математически это утверждение выглядит так:

Крайняя правая часть приведенных выше уравнений будет очень полезна в этом курсе – она ​​позволяет нам разбить сложную форму на простые формы с известными площадями и известными положениями центра тяжести. В большинстве инженерных сооружений есть как минимум одна ось симметрии – и это позволяет нам значительно упростить поиск центроида. Центроид должен располагаться на оси симметрии . Например:

Для поперечного сечения слева мы знаем, что центроид должен лежать на оси симметрии, поэтому нам нужно только найти центроид по оси y . Поперечное сечение справа еще проще – поскольку центр тяжести должен совпадать с осями симметрии, он должен находиться в центре объекта.

Теперь, когда мы знаем, как найти центроид, мы можем обратить внимание на второй момент площади.Как вы могли вспомнить из предыдущего раздела, посвященного кручению, это определяется как:

И, наконец, иногда нам нужно определить второй момент площади относительно произвольной оси x или y – такой, который не соответствует центроиду. В этом случае мы можем использовать теорему о параллельных осях для его вычисления. В этом случае мы используем второй момент площади относительно центроида плюс член, который включает расстояния между двумя осями.

Это уравнение называется теоремой о параллельной оси .Это будет очень полезно на протяжении всего курса. Как описано во вводном видео к этому разделу, вычислить второй момент площади для простой формы может быть несложно. Для более сложных форм нам нужно вычислить I , вычислив отдельные I для каждой простой формы и комбинируя их вместе, используя теорему о параллельных осях.

Диаграммы сдвига и момента

Поперечная нагрузка относится к силам, перпендикулярным длинной оси конструкции.Эти поперечные нагрузки будут вызывать изгибающий момент M , который вызывает нормальное напряжение , и силу сдвига V , которая вызывает напряжение сдвига . Эти силы могут и будут меняться по длине балки, и мы будем использовать диаграммы сдвига и момента (V-M-диаграмма) , чтобы извлечь наиболее подходящие значения. Построение этих диаграмм должно быть вам знакомо по статике , но мы рассмотрим их здесь. При исследовании поперечно нагруженной балки необходимо учитывать два важных момента:

1. Как нагружается балка?

• точечная нагрузка, распределенная нагрузка (равномерная или переменная), сочетание нагрузок…

1. Как поддерживается балка?

• просто поддерживаемые, консольные, нависающие, статически неопределимые…

Знание нагрузок и опор позволит вам нарисовать качественную диаграмму V-M , а затем статический анализ свободного тела поможет вам определить количественное описание кривых.Давайте начнем с того, что вспомним наши условные обозначения .

Эти правила знаков должны быть вам знакомы. Если сдвиг вызывает вращение против часовой стрелки, он положительный. Если момент изгибает балку таким образом, что он изгибается в «улыбку» или U-образную форму, это положительно. Лучший способ вспомнить эти диаграммы – это проработать пример. Начните с этой консольной балки – отсюда вы можете переходить к более сложным нагрузкам.

Нормальное напряжение при изгибе

Во многом изгиб и кручение очень похожи.Изгиб происходит от пары или приложенного изгибающего момента M . Как и при кручении, при чистом изгибе в материале существует ось, на которой напряжение и деформация равны нулю. Это называется нейтральной осью . И, как и при кручении, напряжение перестает быть равномерным по поперечному сечению конструкции – оно меняется. Давайте начнем с рассмотрения того, как ось z изгибает конструкцию. В данном случае мы не будем ограничиваться круговыми сечениями – на рисунке ниже мы будем рассматривать призматическое сечение.

Прежде чем мы углубимся в математику, лежащую в основе изгиба, давайте попробуем разобраться в этом концептуально. Может быть, лучший способ увидеть, что происходит, – это наложить изогнутую балку поверх исходной прямой балки.

Теперь вы можете заметить, что нижняя поверхность балки стала длиннее, а нижняя поверхность балки стала короче. Также по центру балки длина не изменилась – соответствует нейтральной оси. Чтобы повторить это на языке этого класса, мы можем сказать, что нижняя поверхность находится под напряжением, а верхняя поверхность находится под давлением.Что-то более тонкое, но все же можно наблюдать из наложенного выше изображения, это то, что смещение луча изменяется линейно сверху вниз, проходя через ноль на нейтральной оси. Помните, это именно то, что мы видели и с кручением – напряжение линейно изменялось от центра к центру. Мы можем посмотреть на это распределение напряжений в поперечном сечении балки более подробно:

Теперь мы можем найти математическую связь между приложенным моментом и напряжением в балке.Мы уже упоминали, что балка линейно деформируется от одного края к другому – это означает, что деформация в направлении x увеличивается линейно с расстоянием по оси y- (или по толщине балки). Таким образом, деформация будет максимальной при растяжении при y = -c (поскольку y = 0 находится на нейтральной оси, в данном случае в центре балки), и будет максимальной при сжатии при y = c. . Мы можем записать это математически так:

Теперь это говорит нам кое-что о деформации, что мы можем сказать о максимальных значениях напряжения? Что ж, давайте начнем с умножения обеих частей уравнения на E , модуль упругости Юнга.Теперь наше уравнение выглядит так:

Используя закон Гука, мы можем связать эти величины со скобками под ними с напряжением в направлении x и максимальным напряжением. Это дает нам это уравнение для напряжения в направлении x- :

Наш последний шаг в этом процессе – понять, как изгибающий момент соотносится с напряжением. Для этого напомним, что момент – это сила, умноженная на расстояние. Если мы можем представить себе, что смотрим только на очень маленький элемент в балке, дифференциальный элемент, то мы можем математически записать это как:

Поскольку в нашем уравнении есть дифференциалы, мы можем определить момент M , действующий по площади поперечного сечения балки, интегрировав обе части уравнения.И, если мы вспомним наше определение напряжения как силы, приходящейся на площадь, мы можем написать:

Последний член в последнем уравнении – интеграл от y в квадрате – представляет второй момент площади относительно оси z (из-за того, как мы определили наши координаты). В декартовых координатах этот второй момент площади обозначается как I (помните, в цилиндрических координатах он обозначался как J ). Теперь мы можем, наконец, записать наше уравнение для максимального напряжения и, следовательно, напряжения в любой точке оси y , как:

Важно отметить, что индексы в этом уравнении и направление вдоль поперечного сечения (здесь оно измеряется вдоль и ) все будут меняться в зависимости от характера проблемы, т.е.е. направление момента – вокруг какой оси изгибается балка? Мы основали наши обозначения на показе изогнутой балки на первом изображении этого урока.

Помните, в начале раздела я упоминал, что изгиб и кручение на самом деле очень похожи? На самом деле мы очень явно видим это в последнем уравнении. В обоих случаях напряжение (нормальное для изгиба и сдвиг для кручения) равно пара / момент ( M для изгиба и T для кручения), умноженному на местоположения вдоль поперечного сечения. , , потому что напряжение неоднородно вдоль поперечного сечения (с декартовыми координатами для изгиба и цилиндрическими координатами для кручения), все деленное на второй момент площади поперечного сечения.

Сводка

В этом уроке мы узнали о моментов области и диаграммах момента сдвига . Исходя из первого момента площади поперечного сечения, мы можем вычислить центр тяжести . Мы узнали, как вычислить секундный момент площади в декартовых и полярных координатах, и мы узнали, как теорема о параллельной оси позволяет нам вычислить второй момент площади относительно центроида объекта – это полезно для разделения сложного поперечного сечения на несколько простых форм и объединение их вместе.Мы пересмотрели концепцию диаграмм сдвига и момента из статики. Эти диаграммы будут важны для определения максимальной силы сдвига и изгибающего момента вдоль сложно нагруженной балки, которые, в свою очередь, потребуются для расчета напряжений и прогнозирования разрушения. Наконец, мы узнали о нормальном напряжении при изгибе балки. И напряжение, и деформация меняются вдоль поперечного сечения балки, при этом одна поверхность находится в состоянии растяжения, а другая – в состоянии сжатия. Плоскость, проходящая через центроид, образует нейтральную ось – вдоль нейтральной оси нет напряжения или деформации.Напряжение является функцией приложенного момента и второго момента площади относительно оси, вокруг которой находится момент.

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы и выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального научного фонда. Научный фонд.

Калькулятор напряжений

Этот калькулятор напряжений поможет вам решить задачи механики, связанные с напряжением, деформацией и модулем Юнга.За несколько простых шагов вы узнаете зависимость напряжения от деформации для любого материала, который остается эластичным. Мы также научим вас рассчитывать деформацию и применять уравнение напряжения.

Как рассчитать деформацию и напряжение

Деформация определяется как мера деформации – пропорция между изменением длины и исходной длиной объекта. Например, если взять резинку и растянуть ее так, чтобы она была вдвое длиннее, чем изначально, то деформация будет равна 1 (100%).

Формула деформации:

ε = ΔL / L₁ = (L₂ - L₁) / L₁

L₁ обозначает начальную длину, L₂ – конечную длину, а ΔL – изменение длины. Обратите внимание, что деформация безразмерна.

Напряжение, с другой стороны, является мерой давления, которое частицы материала оказывают друг на друга. Он определяется как сила, действующая на объект на единицу площади. Однако это отличается от давления; при расчете напряжения рассматриваемая площадь должна быть настолько маленькой, чтобы анализируемые частицы считались однородными.Если принять во внимание большую площадь, расчетное напряжение обычно является средним значением.

Уравнение напряжения:

σ = F / A

F обозначает силу, действующую на тело, а A обозначает площадь. Единицы измерения напряжения такие же, как и единицы давления – Паскали (символ: Па) или Ньютоны на квадратный метр.

Положительное напряжение означает, что объект находится в напряжении – он «хочет» удлиниться. Отрицательное напряжение означает, что оно находится в состоянии сжатия и «хочет» стать короче.

Модуль Юнга (напряжение относительно деформации)

Если материал линейно упругий , то напряжение и деформация напрямую связаны следующей формулой:

E = σ / ε

E – это модуль упругости или модуль Юнга . Это материальная константа, разная для каждого вещества.

Что такое линейно-упругое поведение материала? Если мы прикладываем напряжение к материалу, деформация увеличивается пропорционально.Это может быть верно только для некоторого диапазона напряжений – после достижения определенного значения материал может сломаться или деформироваться. Под текучестью понимается увеличение деформации при постоянном напряженном состоянии.

Пример расчетов

Предположим, мы хотим найти модуль Юнга стали. Для этого мы подготовили стальной стержень, который тянули с большим усилием.

1. Мы решили, что сила тяги штанги будет равна 30 кН ( 30 * 10³ Н ).
2. Определяем размеры стержня.Предположим, что длина составляет 2 м (2000 мм), а площадь поперечного сечения – 1 см² ( 1 * 10⁻⁴ м² ).
3. Мы заметили, что стержень удлинился на 3 мм.
4. Рассчитываем деформацию стержня по формуле: ε = ΔL / L₁ = 3/2000 = 0,0015 .
5. Рассчитаем напряжение по формуле напряжения: σ = F / A = 30 * 10³ / (1 * 10⁻⁴) = 300 * 10⁶ = 300 МПа .
6. Наконец, разделим напряжение на деформацию, чтобы найти модуль Юнга стали: E = σ / ε = 300 * 10⁶ / 0.0015 = 200 * 10⁹ = 200 ГПа .

Модуль упругости

Единицы модуля Юнга такие же, как единицы давления и напряжения: Паскали или ньютоны на квадратный метр. В единицах СИ

1 Па = 1 Н / 1 м² = 1 кг · м / с² / м² = 1 кг / (м · с²)

Если вас интересует механика, попробуйте калькулятор крутящего момента.

Основы и уравнения прочности материалов | Механика материалов

Сила / Механика материалов Меню

Сопротивление материалов , также называемое механикой материалов , является предметом, который имеет дело с поведением твердых объектов, подверженных напряжениям и деформациям.

В материаловедении прочность материала – это его способность без разрушения выдерживать приложенную нагрузку. Нагрузка, приложенная к механическому элементу, будет вызывать внутренние силы внутри элемента, называемые напряжениями, когда эти силы выражаются в единицах. Напряжения, действующие на материал, по-разному вызывают деформацию материала. Деформация материала называется деформацией, если и эти деформации относятся к единице. Приложенные нагрузки могут быть осевыми (растягивающими или сжимающими) или сдвигающими.Напряжения и деформации, возникающие в механическом элементе, должны быть рассчитаны, чтобы оценить нагрузочную способность этого элемента. Для этого требуется полное описание геометрии элемента, его ограничений, нагрузок, приложенных к элементу, и свойств материала, из которого он состоит. С полным описанием нагрузки и геометрии элемента можно рассчитать состояние напряжения и состояние деформации в любой точке внутри элемента. Как только состояние напряжения и деформации внутри элемента известно, можно рассчитать прочность (несущую способность) этого элемента, его деформации (характеристики жесткости) и его стабильность (способность сохранять свою первоначальную конфигурацию).Рассчитанные напряжения затем можно сравнить с некоторой мерой прочности элемента, такой как текучесть материала или предел прочности. Рассчитанный прогиб элемента можно сравнить с критериями прогиба, основанными на использовании элемента. Расчетную нагрузку на продольный изгиб элемента можно сравнить с приложенной нагрузкой. Расчетная жесткость и распределение массы элемента могут использоваться для расчета динамического отклика элемента, а затем сравниваться с акустической средой, в которой он будет использоваться.

Под прочностью материала понимается точка на инженерной кривой напряжение-деформация (предел текучести), за которой материал испытывает деформации, которые не будут полностью устранены после снятия нагрузки, и в результате элемент будет иметь постоянный прогиб. Предел прочности относится к точке на инженерной кривой «напряжение – деформация», соответствующей напряжению, вызывающему разрушение.

Ниже приведены основные определения и уравнения, используемые для расчета прочности материалов.

---

Напряжение (нормальное)

Напряжение – это отношение приложенной нагрузки к площади поперечного сечения растягиваемого элемента, выраженное в фунтах на квадратный дюйм (psi) или кг / мм ² .

		Нагрузка		л
Напряжение, σ	=		=
		Площадь		А

Деформация (нормальная)

Безразмерная мера деформации материала.

		изменение длины		Δ L
Деформация, ε	=		=
		исходная длина		л

Кривая деформации напряжения

Предел пропорциональности – это точка на кривой зависимости напряжения от деформации, в которой она начинает отклоняться от прямолинейное соотношение между напряжением и деформацией.См. Сопроводительный рисунок в (1 и 2).

Предел упругости – это максимальное напряжение, которому образец может подвергаться и вернитесь к исходной длине после снятия нагрузки. Говорят, что материал подчеркнут в упругая область, когда рабочее напряжение не превышает предела упругости, и подлежащая напряжению в пластической области, когда рабочее напряжение действительно превышает предел упругости. Предел упругости для стали практически такой же, как и предел пропорциональности.См. Сопроводительный рисунок в (1, 2).

Предел текучести – это точка на кривой напряжения-деформации, в которой происходит внезапное увеличение деформации. без соответствующего увеличения стресса. Не все материалы имеют предел текучести. См. Сопроводительный рисунок в (1).

Предел текучести, S _y , это максимальное напряжение, которое может быть приложено без остаточной деформации. образца для испытаний.Это значение напряжения на пределе упругости материалов для который существует предел упругости. Из-за сложности определения предела упругости и поскольку многие материалы не имеют упругой области, предел текучести часто определяется метод смещения, как показано на прилагаемом рисунке в (3). Предел текучести в таком case – значение напряжения на кривой напряжения-деформации, соответствующее определенному количеству постоянных набор или деформация, обычно 0.1 или 0,2% от исходного размера.

---

Модуль упругости

Деформация металла пропорциональна приложенным нагрузкам в диапазоне нагрузок.

Поскольку напряжение пропорционально нагрузке, а деформация пропорциональна деформации, это означает, что напряжение пропорционально деформации. Закон Гука утверждает эту пропорциональность.

Напряжение		σ
	=		=	E
Штамм		ε

Константа, E , представляет собой модуль упругости, модуль Юнга или модуль упругости при растяжении, а также жесткость материала.Модуль Юнга составляет 10 ⁶ psi или 10 ³ кг / мм ² . Если материал подчиняется закону Гука, он эластичен. Модуль не чувствителен к состоянию материала. Нормальная сила напрямую зависит от модуля упругости.

---

Предел пропорциональности

Наибольшее напряжение, при котором материал способен выдерживать приложенную нагрузку без отклонения от пропорциональности напряжения к деформации.Выражается в фунтах на квадратный дюйм (кг / мм ² ).

---

Предел прочности (растяжение)

Максимальное напряжение, которое материал выдерживает при приложении нагрузки. Значение определяется делением нагрузки при разрушении на исходную площадь поперечного сечения.

---

Предел упругости

Точка на кривой “напряжение-деформация”, за которой материал необратимо деформируется после снятия нагрузки.

---

Предел текучести

Точка, в которой материал превышает предел упругости и не возвращается к своей исходной форме или длине, если напряжение снимается. Это значение определяется путем оценки диаграммы напряжение-деформация, полученной во время испытания на растяжение.

---

Коэффициент Пуассона

Отношение поперечной деформации к продольной – это коэффициент Пуассона для данного материала.

		боковая деформация
мкм	=
		продольная деформация

Коэффициент Пуассона – это безразмерная константа, используемая для анализа напряжений и прогибов таких конструкций, как балки, пластины, оболочки и вращающиеся диски.

Алюминий	0,334	Нейзильбер	0,322
Бериллиевая медь	0,285	Фосфорная бронза	0.349
Латунь	0,340	Резина	0,500
Чугун, серый	0,211	Сталь литая	0.265
Медь	0,340	высокоуглеродистый	0,295
Инконель	0,290	легкая	0.303
Свинец	0,431	никель	0,291
Магний	0,350	Кованое железо	0.278
Металлический монель	0,320	цинк	0,331

---

Напряжение изгиба

При сгибании куска металла одна поверхность материала растягивается при растяжении, а противоположная поверхность сжимается.Отсюда следует, что между двумя поверхностями есть линия или область нулевого напряжения, называемая нейтральной осью. Сделайте следующие предположения в простой теории изгиба:

1. Балка изначально прямая, ненапряженная и симметричная.
2. Материал балки линейно эластичный, однородный и изотропный.
3. Пропорциональный предел не превышен.
4. Модуль Юнга материала одинаков при растяжении и сжатии
5. Все прогибы небольшие, поэтому плоские поперечные сечения остаются плоскими до и после изгиба.

Используя классические формулы балки и свойства сечения, можно получить следующую взаимосвязь:

		3 PL
Напряжение изгиба, σ b	=
		2 вес 2

		PL 3
Модуль упругости при изгибе или изгибе, E b	=
		4 вес 3 y

Где:	п.	=	нормальная сила
	л	=	длина балки
	w	=	ширина балки
	т	=	толщина балки
	y	=	прогиб в точке нагрузки

Сообщаемый модуль упругости при изгибе обычно является начальным модулем из кривой зависимости напряжения от деформации при растяжении.

Максимальное напряжение возникает на поверхности балки, наиболее удаленной от нейтральной поверхности (оси), и составляет:

		Mc		М
Максимальное поверхностное напряжение, σ макс	=		=
		I		Z

Где:	М	=	изгибающий момент
	с	=	расстояние от нейтральной оси до внешней поверхности, где возникает максимальное напряжение
	I	=	момент инерции
	Z	=	I / c = модуль упругости сечения

Для прямоугольной консольной балки с сосредоточенной нагрузкой на одном конце максимальное поверхностное напряжение определяется по формуле:

Методы уменьшения максимального напряжения состоят в том, чтобы поддерживать постоянную энергию деформации в балке при изменении профиля балки.Дополнительные профили балки бывают трапециевидные, конические и торсионные.

Где:	д	=	прогиб балки под нагрузкой
	E	=	Модуль упругости
	т	=	толщина балки
	л	=	длина балки

---

Уступая

Податливость возникает, когда расчетное напряжение превышает предел текучести материала. Расчетное напряжение обычно представляет собой максимальное поверхностное напряжение (простое нагружение) или напряжение фон Мизеса (сложные условия нагружения). Критерий текучести фон Мизеса утверждает, что текучесть происходит, когда напряжение фон Мизеса превышает предел текучести при растяжении.Часто в результатах анализа напряжений методом конечных элементов используются напряжения фон Мизеса. Стресс фон Мизеса:

σ v =		(σ 1 – σ 2 ) 2 + (σ 2 – σ 3 ) 2 + (σ 1 – σ 3 ) 2
		2

где σ ₁ , σ ₂ , σ ₃ – главные напряжения.

Коэффициент запаса прочности является функцией расчетного напряжения и предела текучести. Следующее уравнение обозначает коэффициент безопасности f _s .

Где Y _S – предел текучести, а D _S – расчетное напряжение.

Дополнительную информацию см. На странице «Существенные условия и ссылки».

Связанный:

• Прочность материалов Методы измерения момента площади для расчета прогиба в балках, спецификации и характеристики материалов – черные и цветные, опорные колонны и изгиб, момент инерции, модуль упругости сечения, радиусы уравнения вращения, треугольные, шестигранные сечения Момент инерции, Модуль сечения, радиусы круговых уравнений, эксцентрические формы, момент инерции, модуль сечения, радиусы вращения
• Сопротивление материалов Н.М. Беляев Премиум-подписка на 648 страниц, необходимая для просмотра документа / книги
• Прогиб балки и расчет конструкции
• Сечение Момент площади Вычислители инерции
• Допуски, пределы инженерного проектирования и посадки

© Авторские права 2000-2021, Engineers Edge, LLC www.Engineersedge.com
Все права защищены
Заявление об ограничении ответственности | Обратная связь | Реклама | Контакты

Дата / Время:

.