Формула мгновенного напряжения: Мгновенные значения синусоидального тока, напряжения, мощности. Последовательное и параллельное соединение элементов

Формула действующего значения силы тока и напряжения. Действующие значения силы тока и напряжения

Физический смысл данных понятий примерно таков же, как физический смысл средней скорости или других величин, усредненных по времени. В различные моменты времени сила переменного тока и его напряжение принимают разные значения, поэтому говорить о силе переменного тока вообще можно лишь условно.

Вместе с тем совершенно очевидно, что различные токи имеют различные энергетические характеристики – они производят разную работу за один и тот же промежуток времени. Произведенная током работа принята за основу при определении действующего значения силы тока. Задаются определенным промежутком времени и рассчитывают работу, совершенную переменным током за этот промежуток времени. Затем, зная эту работу, производят обратное вычисление: узнают силу постоянного тока, который произвел бы аналогичную работу за тот же промежуток времени. То есть производят усреднение по мощности. Вычисленная сила гипотетически протекающего через тот же проводник постоянного тока, производящего ту же самую работу и есть – действующее значение исходного переменного тока. Аналогично поступают и с напряжением. Данный расчет сводится к определению величины такого интеграла:

Откуда берется данная формула? Из хорошо известной формулы для мощности тока, выражаемой через квадрат его силы.

Действующие значения периодических и синусоидальных токов

Вычислять действующее значение для произвольных токов – занятие малопродуктивное. Зато для периодического сигнала данный параметр может оказаться весьма полезным. Известно, что любой периодический сигнал может быть разложен в спектр. То есть, представлен как конечная или бесконечная сумма синусоидальных сигналов. Поэтому для определения величины действующего значения такого периодического тока нам нужно знать, как вычислять действующее значение простого синусоидального тока. В итоге, сложив действующие значения нескольких первых гармоник с максимальной амплитудой, мы получим приближенное значение действующего значения тока для произвольного периодического сигнала. Подставляя в вышеприведенную формулу выражение для гармонического колебания, получим такую приближенную формулу.

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля.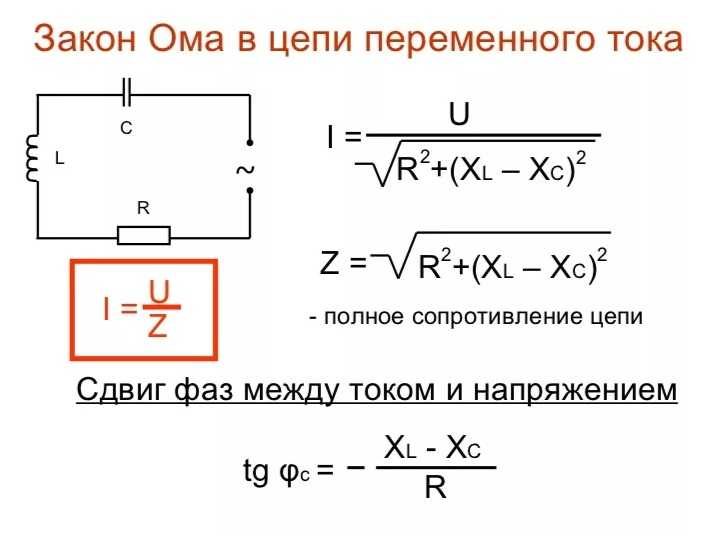

В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, – периодом Т. Для периодического тока имеем

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i – мгновенное значение тока ;

u – мгновенное значение напряжения ;

е – мгновенное значение ЭДС ;

р – мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ).

Амплитуда тока;

Амплитуда напряжения;

Амплитуда ЭДС.

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи.

Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:

Значения аргументов синусоидальных функций иназываются

фазами синусоид, а значение фазы в начальный момент времени (t =0): и –начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .

Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:

Векторное изображение синусоидально изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное

) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w .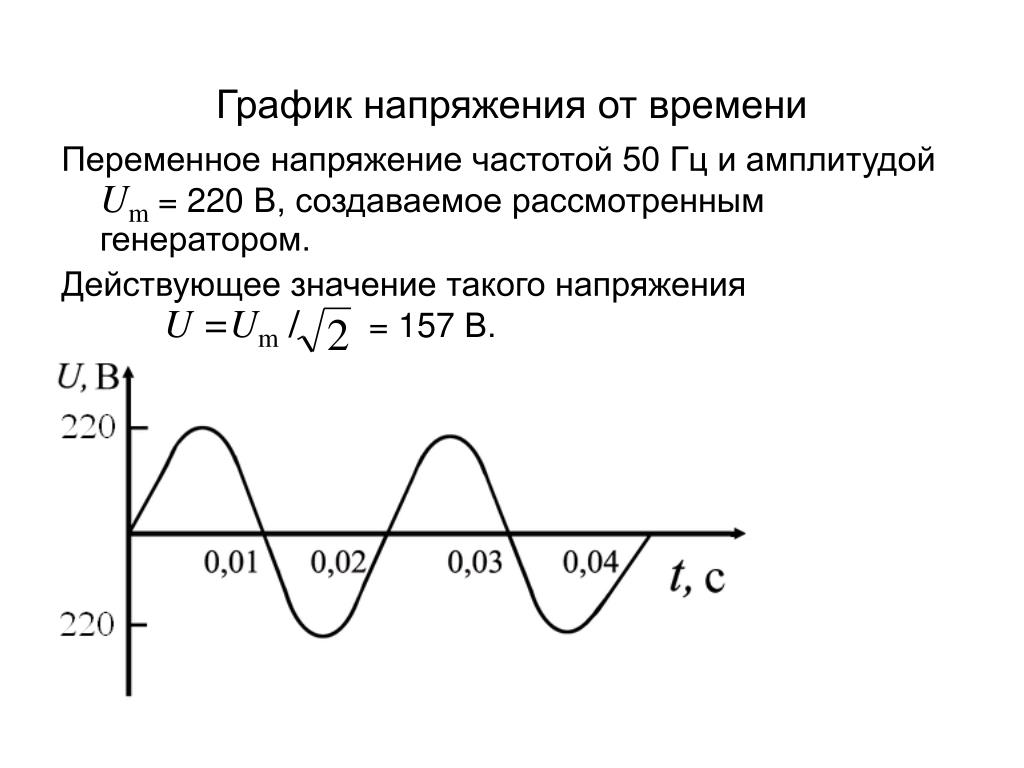 Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:

Каждый из этих токов синусоидален и может быть представлен уравнением

Результирующий ток также будет синусоидален:

Определение амплитудыи начальной фазыэтого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt =0.

При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

.

Построение векторной диаграммы в масштабе позволяет определить значения ииз диаграммы, после чего может быть записано решение для мгновенного значенияпутем формального учета угловой частоты:.

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т.

д.) нельзя судить по амплитуде этого тока.

Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.

Действующее значение переменного тока – это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.

Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.

Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р 2 r.

Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от (Im х sinωt) 2 х rза то же время.

Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √M,

Величина I называется действующим значением переменного тока.

Среднее значение i2 при переменном токе определим следующим образом.

Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.

Действующее значение переменного тока

Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины.

Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно1/2I 2 m. Следовательно, М = 1/2I 2 m

Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2

Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:

U = Um / √2,E= Em / √2

Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е).

На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.

При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √2 раз. От этого расположение векторов на диаграмме не изменяется.

Действующее значение напряжения

В проводниках переменного тока основные электродинамические показатели постоянно изменяются. Вследствие этого возникает вопрос: как можно адекватно оценить напряжение и силу тока в конкретной электроцепи? Так как моментальные и простые усредненные значения недостаточны для полной характеристики электротока, в электродинамике вводят такое понятие, как действующее значение тока.

• Что такое действующее значение напряжения
• Действующее значение тока
• Какие коэффициенты характеризуют переменное напряжение
• Параметры переменного тока
• Формула действующего значение тока

Что такое действующее значение напряжения

Изменение значений переменного тока обычно описывается синусоидальной линией с определенным периодом (Т) и амплитудой напряжения (Um). Кроме напряжения, электрический ток также характеризуется силой (I) и мощностью (P). Для постоянного электротока эти параметры складываются в простую формулу:

P = U × I.

При имеющемся сопротивлении в цепи и с учетом закона Ома (I = U / R) мощность, расходуемую электропотребителем. Можно определить как отношение квадрата напряжения к сопротивлению:

P = U2 / R.

В случае же переменного тока не все так однозначно. С изменением напряжения изменяется и мощность — в каждый момент времени (t) значения отличаются друг от друга. В такой ситуации для оценки электротока удобнее всего использовать его мощностные и тепловые характеристики. Поэтому действующее значение переменного тока приравнивается к работе постоянного тока, производимой за временной промежуток одного периода переменного тока.

При существующей активной нагрузке, независящей от частоты тока и напряжения мгновенная мощность определяется по формуле:

P(t) = U(t) × I(t) = U2 / R

Введя амплитудное значение напряжения, и учитывая период синусоидальной функции, мгновенную мощность можно определить следующим образом:

P(t) = (Um × sin(2π × 1/T))2 / R

Однако этот параметр для переменного тока — не имеет особой важности. Для практических расчетов обычно берут мощность, усредненную за период. Как раз этот показатель указывается на бытовых электроприборах.

Формула усредненной мощности:

Здесь же представлена формула расчета действующего напряжения.

В вышеприведенной формуле интегрирование квадратной величины с последующим извлечением корня дает понять, почему эффективная величина напряжения также носит название «среднеквадратичной». При этом интегральное выражение под корнем является усредненной мощностью, пропорциональной сопротивлению.

Относительно синусоиды напряжение это интегральное выражение упрощается до формулы:

Именно эти цифры показывают вольтметры, настроенные на измерение проводников переменного тока.

Действующее значение тока

Применив метод интегрирования к квадратам амплитудной силы тока и синусу круговой частоты и выведя среднеквадратичные величины, можно получить действующее значение силы тока:

Сравнивая тепловые эффекты постоянного и переменного электротоков, взятые за одинаковый временной отрезок и при одинаковой активной нагрузке, можно обнаружить, что равенство тепловых характеристик проводников того и другого типа достигается в том случае, если сила линейного тока будет меньше максимальных силовых значений в цепи переменного тока в 1,414 раз.

Какие коэффициенты характеризуют переменное напряжение

Помимо базовых параметров переменного тока, в электротехнике принято производить измерения электросигналов, включая выходные напряжения выпрямителей и импульсы различной формы.

Амплитудное значение напряжения

Под амплитудным или пиковым напряжением подразумевают максимальный показатель U за один период синусоиды:

Um = max(|u(t)|)

Для измерения данного параметра обычно используют вольтметр импульсного типа или осциллограф.

Мгновенное значение тока

Параметр обозначает силу тока или напряжение в конкретный временной момент (u(t), i(t)). В зависимости от динамики электрического сигнала, для определения мгновенных значений могут применяться малоинерционные вольтметры, а также шлейфовые или электронно-лучевые осциллографы.

Среднее значение

Показатель является постоянной составляющей переменного тока. Для напряжения оно рассчитывается по следующей интегральной формуле:

Для синусоидного напряжения с симметричной формой среднее значение равно нулю. Это можно определить с помощью обычного вольтметра. В геометрическом виде это может быть выражено как отношение разности площадей с обеих сторон оси t к периоду. Под названием напряжения смещения величина часто применяется в радиоэлектронике и обозначает напряжение, прилагаемое к электроду для выработки конкретных параметров постоянного электротока.

Среднеквадратичное значение

Среднеквадратичные интегральные величины силы тока и напряжения используются достаточно часто, вследствие их удобства для практического определения электродинамических характеристик в реальных проводниках. Они основываются на сравнении работы постоянного и переменного тока с активной нагрузкой и определенными величинами U и I.

К примеру, лампочка или обогреватель будут выполнять одинаковую работу по освещению или обогреву как в сети переменного тока со стандартным напряжением 220 В, так и в цепи постоянного тока, если на нее подать такое же напряжение.

Напряжение в электросети обычно выражают в среднеквадратичном исчислении. Большинство приборов, измеряющих силу тока и напряжение, спроектированы под действующие показатели. Отдельные типы амперметров и вольтметров способны показывать верные эффективные значения только для синусоидального тока. В универсальных устройствах, работающих с любыми формами электросигнала, измерение осуществляется с помощью термопреобразователя. При этом фиксируется температура нагревателя, создающего определенное сопротивление.

Кроме того, в измерительных приборах может быть реализован метод возведения в квадрат мгновенного значения, после чего величина усредняется по временному периоду, а затем выводится квадратный корень.

Средневыпрямленное значение

Величина определяется как взятое по модулю среднеарифметическое всех мгновенных значений напряжения. Для одного периода средневыпрямленная величина равна сумме площадей сверху и снизу оси времени. Хотя параметр не находит практического применения, именно он фиксируется по факту большинством измеряющих устройств магнитоэлектрического принципа действия, несмотря на то, что их шкалы имеют градацию для действительных значений. При этом эффективные и средневыпрямленные значения оказываются близки друг к другу только в случае синусоидального напряжения.

Параметры переменного тока

Синусоидальные гармоники являются типичной характеристикой переменного тока. В этом отношении по синусоиде происходит изменение электродвижущей силы и тока при определенной нагруженности цепи. При этом динамика ЭДС может быть описана следующими параметрами:

• Период — время, за которое электродинамические показатели изменяются по полному циклу. Он напрямую связан с частотой вращения роторного механизма генератора электротока.

• Частота — определяется как число периодов за одну единицу времени. Современные стандарты для электросетей предписывают частоту переменного тока в 50 герц. Это означает, что за 1 секунду ток меняет направление 50 раз, а один период длится 20 миллисекунд.

• Амплитуда — максимальная величина гармоники переменного тока. В строгом смысле параметр применим исключительно к синусоидальному изменению. С некоторыми допущениями амплитуда может быть определена и для других форм электросигнала. За один период электродвижущая сила дважды доходит до пиковых значений и обозначается как Em+ и Em- соответственно положению полупериодов.

• Угловая частота — скорость колебательного движения, измеряемая в радианах в секунду. При этом один период синусоиды приравнивается к значению 2π. Общая формула угловой частоты: ω = 2π / Т.

• Фаза колебаний — стадия синусоидальной волны, принимаемая как аргумент функции тока, которая отсчитывается от среднего нулевого значения. Величина фазы колебаний, используемая для определения синуса или косинуса фазового угла, описывается формулой φ = ωt.

Как в случае со среднеквадратичными значениями тока и напряжения, через основные характеристики определяется и среднее значение ЭДС, которое сводится к следующему выражению:

Формула действующего значение тока

Среднеквадратичные показатели переменного тока определяется как отношение амплитудного значения тока к корню из 2.

Схожим образом обозначаются эффективные значения напряжения и ЭДС.

Действительные значения синусоидального тока помогают производить практическую оценку и описание электроцепей. Несмотря на сложность составляющих понятий, эти величины сводятся к простым выражениям. Номинальное напряжение электрических сетей и приборов представляет собой как раз среднеквадратичное значение. Умножив указанный вольтаж на корень из 2, можно узнать амплитудное значение напряжения электроустройств.

Понравилась статья? Расскажите друзьям:

Оцените статью, для нас это очень важно:

Проголосовавших: 1 чел.
Средний рейтинг: 5 из 5.

Внезапная нагрузка – Сопротивление материалов Вопросы и ответы

Этот набор вопросов и ответов с несколькими вариантами ответов (MCQ) по сопротивлению материалов посвящен «Внезапной нагрузке».

1. Какова связь между максимальным напряжением, вызванным внезапной нагрузкой, и максимальным напряжением при постепенной нагрузке?
а) Максимальное напряжение при внезапной нагрузке равно максимальному напряжению при постепенной нагрузке
б) Максимальное напряжение при внезапной нагрузке составляет половину максимального напряжения при постепенной нагрузке
c) Максимальное напряжение при внезапной нагрузке в два раза больше максимального напряжения при постепенной нагрузке
d) Максимальное напряжение при внезапной нагрузке в четыре раза больше максимального напряжения при постепенной нагрузке
Посмотреть ответ

Ответ: c
Объяснение: Максимальное напряжение при внезапной нагрузка = 2P/A
Максимальное напряжение при постепенной нагрузке = P/A.

2. Какая энергия деформации запасается в теле при внезапном приложении нагрузки?
a) σE/V
b) σE ² /V
c) σV ² /E
d) σV ² /2E
Посмотреть ответ

Ответ: d
Пояснение: Энергия деформации при постепенном нагружении = σ ² V/2E.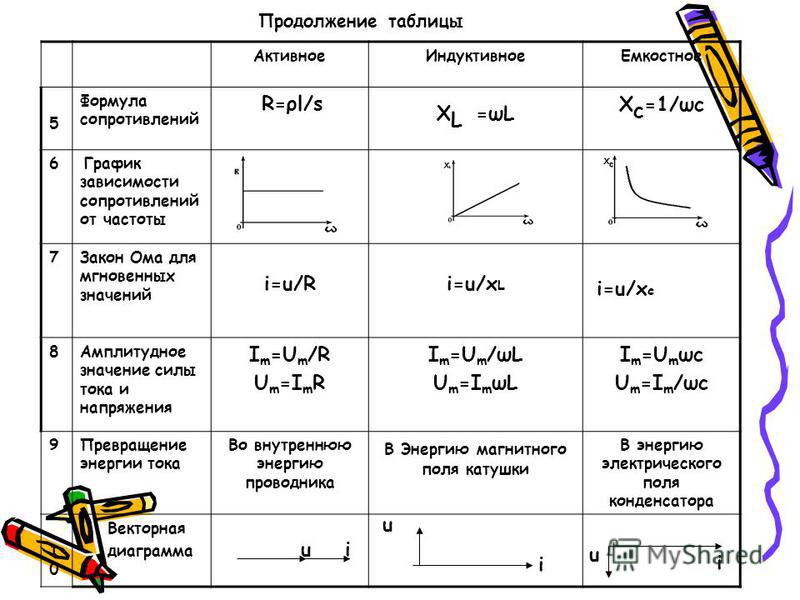

3. К круглому стержню диаметром 4 см внезапно приложена растягивающая нагрузка в 60 кН. Каким будет максимальное мгновенное напряжение?
A) 95,493 Н/мм ²
B) 45,25 Н/мм ²
C) 85,64 Н/мм ²
D) 102,45 Н/мм ²
. Просмотр

: А. : Максимальное мгновенное индуцированное напряжение = 2P/A = 2×60000/400π = 95,49 Н/мм ² .

4. К круглому стержню длиной 4 см и 5 м внезапно прикладывается растягивающая нагрузка 60 кН. Какова будет энергия деформации, поглощенная стержнем, если E=2×105 Н/мм ² ?
a) 140,5 Н-м
b) 100 Н-м
c) 197,45 Н-м
d) 143,2 Н-м
Посмотреть ответ

Ответ: d
Объяснение: Максимальное мгновенное индуцированное напряжение = 2P/A = 2×604π9/5,0000/90. ²
Энергия деформации = σ ² В/2E = 95,492 x 2×106π / (2x2x105) = 143238 Н-мм = 143,23 Н-м.

5. Растягивающую нагрузку в 100 кН внезапно приложили к прямоугольному стержню размером 2 см х 4 см. Каким будет мгновенное напряжение в стержне?
A) 100 Н/мм ²
B) 120 Н/мм ²
C) 150 Н/мм ²
D) 250 Н/мм ²
Посмотреть Ответ

Ответ: D
. : Напряжение = 2x нагрузка / площадь = 2×100 000/(20×40) = 250 Н/мм ² .

Примечание: присоединяйтесь к бесплатным занятиям по санфаянсу в Telegram или на Youtube

реклама

реклама

6. 2 к прямоугольному стержню размером 2 см х 4 см и длиной 5 м внезапно приложена растягивающая нагрузка в 100 кН. Какая энергия деформации будет поглощена стержнем, если E=1×105 Н/мм ² ?
a) 312,5 Н-м
b) 314500 Н-мм
c) 1250 Н-м
d) 634 Н-м
Просмотреть ответ

Ответ: c
Объяснение: Напряжение = 2xнагрузка / площадь = 2×100 000/ (22540 Н/мм ²
Энергия деформации = σ ² В/2E = 250x250x20x40x5000/ (2×100000) = 1250000 Н-мм = 1250 Н-м.

7. Стальной стержень длиной 2 м и диаметром 50 мм. К стержню внезапно прикладывается осевое усилие 100 кН. Каким будет мгновенное напряжение в стержне?
A) 101,89 Н/мм ²
B) 94,25 Н/мм ²
C) 130,45 Н/мм ²
D) 178,63 Н/мм ²
. : Площадь = π/4 d2 = 625π
Нагрузка = 100 кН = 100×1000 Н
Напряжение = 2 x нагрузка / площадь = 2x100x1000 / (625π) = 101,86 Н/мм ² .

реклама

8. Стальной стержень длиной 2 м и диаметром 50 мм. К стержню внезапно прикладывается осевое усилие 100 кН. Какое мгновенное удлинение возникнет в стержне, если Е=22GN/м2?
a) 0,0097 мм
b) 1,0754 мм
c) 1,6354 мм
d) 1,0186 мм
Посмотреть ответ

Ответ: d
Объяснение: Площадь = π/4 d2 = 625π 005 N
Нагрузка = 100k =22GN/м ² = 200 x 109 / 106 = 200 000 Н/мм ²
Напряжение = 2 x нагрузка/площадь = 2x100x1000 / (625 π)
Удлинение = напряжение x длина / E = 101,86 × 2000 / 200000 = 1,0186 мм.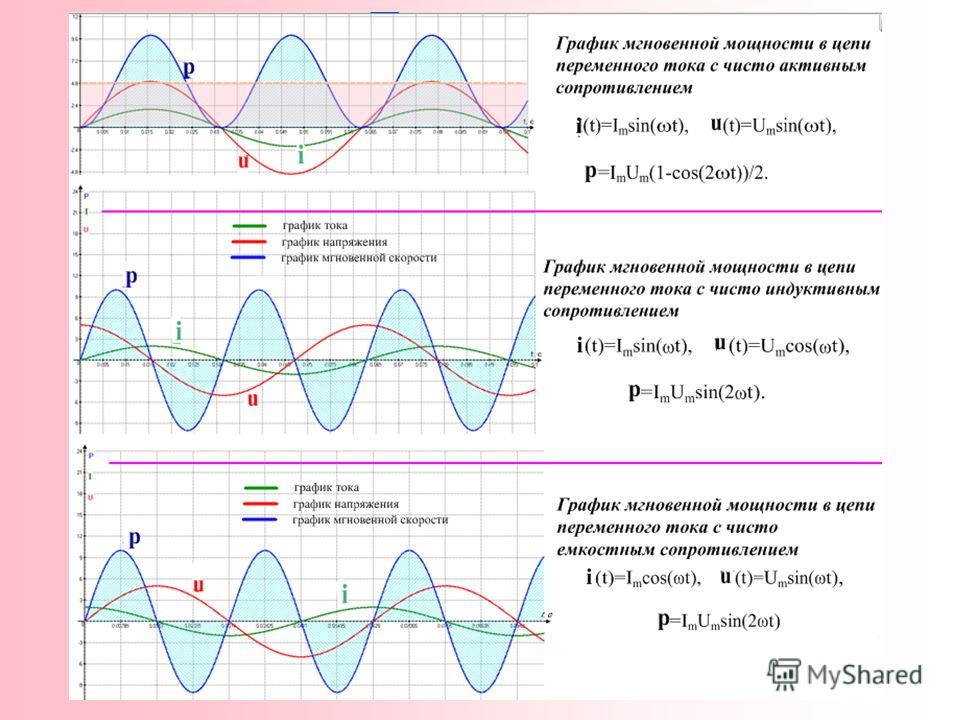

9. Какое осевое усилие будет приложено к стержню диаметром 4 см, чтобы получить мгновенное значение напряжения 143 Н/мм ² ?
a) 50 кН
b) 60 кН
c) 70 кН
d) 80 кН
Посмотреть ответ

Ответ: b
Объяснение: Мгновенное напряжение = 2 x нагрузка / площадь
Нагрузка = мгновенное напряжение x площадь / 2
4 = 0043 3,14/2 = 60кН.

реклама

10. Какое мгновенное напряжение возникнет в стержне 10см ² площадью и длиной 4 м в результате внезапного приложения растягивающей нагрузки неизвестной величины, если удлинение стержня из-за внезапно приложенной нагрузки составляет 1,35 мм, если E = 2×105 Н/мм ² ?
A) 67,5 Н/мм ²
B) 47 Н/мм ²
C) 55,4 Н/мм ²
D) 78,5 Н/мм ²
. : Значение напряжения = нагрузка / площадь, где площадь равна 10 см ² , а нагрузку можно рассчитать по уравнению напряжения-деформации.

Sanfoundry Global Education & Learning Series – Прочность материалов.

Чтобы практиковать все области сопротивления материалов, здесь полный набор из более чем 1000 вопросов и ответов с несколькими вариантами ответов .

Следующие шаги:

• Получите бесплатную грамоту по сопротивлению материалов
• Участие в конкурсе по сертификации прочности материалов
• Станьте лидером в области сопротивления материалов
• Пройти испытания на прочность материалов
• Практические тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
• Пробные тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

Категории Сопротивление материалов MCQ

реклама

реклама

Подпишитесь на наши информационные бюллетени (тематические). Участвуйте в конкурсе сертификации Sanfoundry, чтобы получить бесплатный Сертификат отличия. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!

Ютуб | Телеграмма | Линкедин | Инстаграм | Фейсбук | Твиттер | Пинтерест

Маниш Бходжасиа, ветеран технологий с более чем 20-летним стажем работы в Cisco и Wipro, является основателем и техническим директором компании Sanfoundry . Он живет в Бангалоре и занимается разработкой Linux Kernel, SAN Technologies, Advanced C, Data Structures & Alogrithms. Оставайтесь на связи с ним в LinkedIn.

Подпишитесь на его бесплатные мастер-классы на Youtube и технические обсуждения в Telegram SanfoundryClasses.

Инженерное напряжение/деформация в сравнении с истинным напряжением/деформацией – Yasin ÇAPAR

В инженерии и материаловедении кривая напряжение-деформация для материала дает взаимосвязь между напряжением и деформацией. Это достигается путем постепенного приложения нагрузки к испытательному образцу и измерения деформации при испытаниях на растяжение, при которых можно определить напряжение и деформацию. Эти кривые показывают многие свойства материалов, такие как модуль Юнга, предел текучести, предел прочности при растяжении и так далее.

График напряжения/деформации эксперимента по испытанию на растяжение.

Кривая напряжение-деформация для материала строится путем удлинения образца и регистрации изменения напряжения с деформацией до разрушения образца. Деформация отложена по горизонтальной оси, а напряжение отложена по вертикальной оси. Часто предполагается, что площадь поперечного сечения материала не изменяется в течение всего процесса деформации. Это неверно, так как фактическая площадь будет уменьшаться при деформации из-за упругой и пластической деформации. Кривая, основанная на исходном поперечном сечении и расчетной длине, называется инженерная кривая напряжения-деформации , тогда как кривая, основанная на мгновенной площади поперечного сечения и длине, называется истинной кривой напряжения-деформации .

Для технических напряжений предполагается, что длина и диаметр образца остаются постоянными на протяжении всего эксперимента.

Инженерное напряжение рассчитывается по формуле:

Инженерная деформация рассчитывается по формуле:

Истинное напряжение представляет собой приложенную нагрузку, деленную на фактическую площадь поперечного сечения (изменяющуюся во времени площадь) материала. Инженерное напряжение — это приложенная нагрузка, деленная на исходную площадь поперечного сечения материала. Также известен как номинальное напряжение.

Это показывает, что поперечное сечение образца изменилось в процессе эксперимента.

Сечение не сохраняется постоянно и будет отличаться от заданного значения диаметра. Этот стресс называется истинным стрессом. Приложенная сила делится на площадь сечения в этот момент.

Прежде чем подробно рассмотреть истинное напряжение и деформацию, давайте вспомним об испытаниях на растяжение (испытание на растяжение).

Испытание на растяжение

Испытание на растяжение, также известное как испытание на растяжение, является фундаментальным материаловедением и инженерным испытанием, в ходе которого образец подвергается контролируемому растяжению до разрушения.

Свойства, которые непосредственно измеряются посредством испытания на растяжение, включают предельную прочность на разрыв, прочность на разрыв, максимальное удлинение и уменьшение площади. Из этих измерений также можно определить некоторые свойства: модуль Юнга, коэффициент Пуассона, предел текучести и характеристики деформационного упрочнения. Испытание на одноосное растяжение наиболее часто используется для получения механических характеристик изотропных материалов. Для некоторых материалов используются двухосные испытания на растяжение. Основное различие между этими испытательными машинами заключается в том, как нагрузка прикладывается к материалам.

Поведение при разрушении

Поведение при разрушении рассматривается в рамках двух основных свойств материала, которые называются пластичными и хрупкими материалами.

Пластичный материал:
Перед разрушением проявляется значительная пластическая деформация и поглощение энергии (вязкость). Характерной особенностью пластичного материала является образование шейки перед разрушением материала.

Хрупкий материал :
Перед разрушением обнаруживается небольшая пластическая деформация или поглощение энергии. Характеристика хрупких материалов отличается от пластичных материалов. Хрупкие материалы разрушаются без образования шейки.

Различные материалы проявляют различное поведение/тренды при одинаковых условиях нагрузки.
Более традиционные конструкционные материалы, такие как бетон под напряжением, стекло, металлы и сплавы, демонстрируют адекватную линейную зависимость между напряжением и деформацией до наступления предела текучести.

Испытание на осевое растяжение и испытание на изгиб для двух различных материалов:

A — пластичный материал, а B — хрупкий материал.

Истинное напряжение ( σ _t ) и истинное напряжение ( ε _т ) используются для точного определения пластического поведения пластичных материалов с учетом фактических размеров.

Хрупкие материалы обычно разрушаются вскоре после текучести или даже в пределе текучести, в то время как сплавы и многие стали могут сильно пластически деформироваться перед разрушением. Характеристики каждого материала следует выбирать на основе требований к применению и конструкции.

Истинные напряжения и деформации

Истинные напряжения и деформации отличаются от технических напряжений и деформаций.

При испытании на растяжение истинное напряжение больше инженерного напряжения, а истинное напряжение меньше инженерного напряжения. Разница между истинными и инженерными напряжениями и деформациями будет увеличиваться при пластической деформации. При низких деформациях (в упругой области) различия между ними незначительны.

Истинное напряжение ( σ _t ):

Истинное напряжение – это напряжение, определяемое мгновенной нагрузкой, действующей на мгновенную площадь поперечного сечения.

Истинная деформация ( ε _t ):

Истинная деформация является логарифмической, а инженерная деформация линейной. Однако это оказывается почти таким же для малой деформации из-за малых значений в разложении Тейлора.

Истинное напряжение и деформация могут быть выражены техническими напряжениями и деформациями.

Для истинного напряжения:

Для истинного напряжения:

Проинтегрируйте обе стороны и примените граничное условие,

Напряжение и деформация в месте образования шейки могут быть выражены как:

В заключение

Инженерное напряжение — это приложенная нагрузка, деленная на исходную площадь поперечного сечения материала. Также известен как номинальное напряжение.
Истинное напряжение — это приложенная нагрузка, деленная на фактическую площадь поперечного сечения (изменяющуюся во времени площадь) образца при этой нагрузке
Инженерная деформация — это величина деформации материала на единицу длины при растяжении. тест. Также известна как номинальная деформация.
Истинная деформация равна натуральному логарифму отношения текущей длины к исходной длине.

Во время фазы образования шейки истинное напряжение не снижается. Кроме того, результаты, полученные в результате испытаний на растяжение и сжатие, будут давать по существу один и тот же график при использовании истинного напряжения и истинной деформации. Инженеры создадут допустимое напряжение и допустимую деформацию в данном стержне, и они хотят использовать диаграмму, основанную на инженерном напряжении и инженерной деформации с площадью поперечного сечения A ₀ и длину L ₀ элемента в недеформированном состоянии.

Engineering stress: σ = F/A ₀

The engineering stress is obtained by dividing F by the cross-sectional area A ₀ of the deformed образец. Инженерное напряжение становится очевидным в пластичных материалах после того, как начинается текучесть, прямо пропорциональная силе ( F) уменьшается во время фазы образования шейки.

Истинный стресс: σ _T = F/A

, истинный стресс ( σ _T) , что является σ _T) , от σ _T) , σ _T) , σ _T) , σ _T) , σ _T) , σ _T) . наблюдается постоянное увеличение до тех пор, пока не произойдет разрыв образца.

Инженерная деформация: ε = δ/L ₀
Истинная деформация: ε _t = ln (L/L ₀ )

Разделив каждое приращение Δ L расстояния между контрольными метками на соответствующее значение L , получим элементарную деформацию:

3 Δ

ε = Δ L /L ₀

Adding the values ​​of Δ ε
ε _t = ∑ Δ ε = ∑ Δ L /L
С суммированием по интегралу истинная деформация также может быть выражена как:

σ = F/A 0	Engineering Stress
σ t = F/A	True Stress
ε = δ/L 0	Engineering Strain
ε t = ln (L/L 0 )	True Strain

F	Load
A 0	Cross-sectional area of ​​specimen before deformation has taken place
A	Cross-sectional area of ​​specimen at which the load is Применяется
Δ	Общая удлинение
L 0	. Больше новостей Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт