Формула нахождения длины в физике: Формула нахождения длины а физике

Формула длины волны в физике

Содержание:

Определение и формула длины волны

Определение

Длиной волны называют кратчайшее пространственное расстояние между ее точками, совершающими колебания в одной фазе. Обозначают длину волны, чаще всего буквой $\lambda$ .

Для синусоидальных волн $\lambda$ – это расстояние, на которое волна распространяется за один период (T). Длину волны в этом случае еще называют пространственным периодом. Тогда формулой длины волны можно считать выражение:

$$\lambda=v T=\frac{v}{\nu}=\frac{2 \pi}{k}$$

где v – скорость распространения волны, $\nu=\frac{1}{T}$ – частота колебаний, $k=\frac{\omega}{v}$ – волновое число, $T=\frac{2 \pi}{\omega}$ – период волны, $\omega$ – циклическая частота волны.

Длина стоячей волны

Длиной стоячей волны($\lambda_{st}$) называют расстояние в пространстве между двумя пучностями (или узлами):

$$\lambda_{s t}=\frac{\pi}{k}=\frac{\lambda}{2}(2)$$

где $\lambda$ – длина бегущей волны.

{8}$ м/с), следовательно, длина электромагнитной волны в вакууме, может быть рассчитана при помощи формулы:

$$\lambda=c T=\frac{c}{\nu}(6)$$

Длина электромагнитной волны в веществе равна:

$$\lambda=\frac{c}{n \nu}(7)$$

где $n=\sqrt{\varepsilon \mu}$ – показатель преломления вещества, $\varepsilon$ – диэлектрическая проницаемость вещества, $\mu$ – магнитная проницаемость вещества.

Отметим, что все рассматриваемые формулы относят к случаю T=const.

Единицы измерения длины волны

Основной единицей измерения длины волны в системе СИ является: [$\lambda$]=м

В СГС: [$\lambda$]=см

Примеры решения задач

Пример

Задание. Каково приращение длины электромагнитной волны, имеющей частоту v=1 МГц при ее переходе в немагнитную среду, которая имеет диэлектрическую проницаемость $\varepsilon$=2?

Решение. Так как речь в условии задачи идет о немагнитной среде, в которую переходит волна, то считаем магнитную проницаемость вещества равной единице ($\mu$=1).

{2}(\mathrm{~m})$$

Ответ. Длина волны уменьшится на 150 м

Слишком сложно?

Формула длины волны не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Какова длина плоской синусоидальной волны, которая распространяется по оси X. Две точки, которые находятся на оси X расположенные на расстояниях 2 м и 3 м от источника совершают колебания с разностью фаз равной $\Delta \varphi=\frac{3 \pi}{5}$ . Каким будет период колебаний в волне, если ее скорость в данной среде равна v=2м/с?

Решение. Сделаем рисунок.

Основой для решения задачи будет формула:

$$\Delta \varphi=\frac{2 \pi \Delta x}{\lambda}=\frac{2 \pi\left(x_{2}-x_{1}\right)}{\lambda}(2.1)$$

Выразим из (2.1) искомую длину волны, получим:

$$\lambda=\frac{2 \pi\left(x_{2}-x_{1}\right)}{\Delta \varphi}(2.2)$$

Период колебаний связан с длиной волны формулой:

$$T=\frac{\lambda}{v}(2. 3)$$

C учетом (2.2), имеем:

$$T=\frac{2 \pi\left(x_{2}-x_{1}\right)}{\Delta \varphi v}$$

Проведем вычисления:

$$ \begin{array}{c} \lambda=\frac{2 \pi(3-2)}{3 \pi} \cdot 5=\frac{10}{3}(m) \\ T=\frac{10}{3 \cdot 2}=1,67(c) \end{array} $$

Ответ. $\lambda \approx 3,3 \mathrm{~m} ; T \approx 1,67 \mathrm{c}$

Читать дальше: Формула количества теплоты.

Длина окружности, формула как найти длину окружности

Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так – l

Как найти длину окружности через диаметр

Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:

l=πd, где

π— число пи — математическая константа, равная 3,14

d — диаметр окружности

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

l=2πr , где

π — число пи, равное 3,14

r – радиус окружности

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

где:

π — число пи, равное 3,14

S — площадь круга

 

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник:

l=πd, где

π — число пи, равное 3,14 

d — диагональ прямоугольника

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата: 

l=πa, где

π – математическая константа, равная 3,14

a – сторона квадрата

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

где:

π — математическая константа, она всегда равна 3,14

a — первая сторона треугольника

b — вторая сторона треугольника

c — третья сторона треугольника

S — площадь треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.

Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

где:

π — математическая константа, равная 3,14

S — площадь треугольника

p — полупериметр треугольника

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.

Формула вычисления длины окружности:

где:

π — математическая константа, равная 3,14

a — сторона многоугольника

N — количество сторон многоугольника

Задачи для решения

Давайте тренироваться! Двигаемся от простого к сложному:

Задача 1. Найти длину окружности, диаметр которой равен 5 см.

Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:

l=πd

Подставляем туда известные переменные и получается, что длина окружности равна

l=πd=3,14·5=15,7(см)

Ответ: 15,7 (см)

Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм

Решение. Радиус окружности равен Подставим туда наши переменные и получим

Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.

Так и сделаем:

l=2πr=2·π·4≈2·3,14·4=25,12(дм)

Ответ: l=25,12(дм)
 

Длина волны — формулы, измерение, определение

Волна: продольная и поперечная

Начнем с того, что волна — это распространение колебания в пространстве.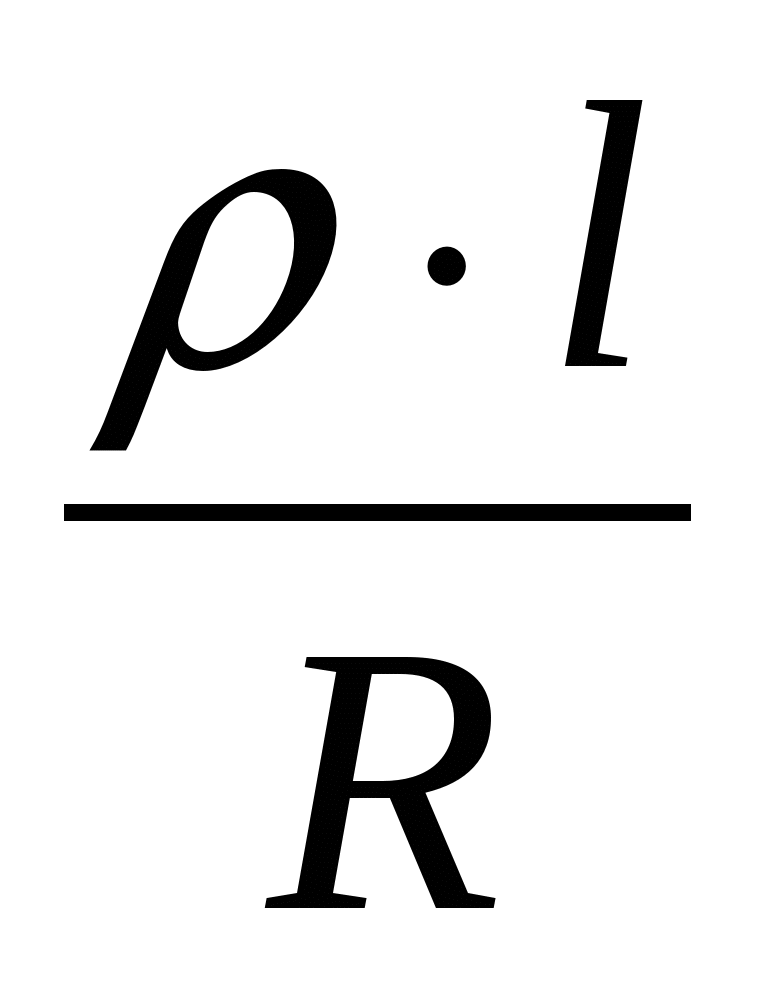

Волны бывают механическими и электромагнитными.

Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.

• Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.

Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.

Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей.

Если приложить ухо к рельсу, то это произойдет значительно быстрее, потому что скорость звука в твердом теле больше, чем в воздухе. Кстати, под водой скорость звука больше, чем в воздухе, но меньше, чем в твердых телах.

Если вы когда-нибудь трогали музыкальную колонку, то знаете, что звук чувствуется и на ощупь. 8 м/с. И источники у них разные.

Волны также принято делить на продольные и поперечные:

Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.

• Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.

Поперечные — волны, у которых колебание происходит поперек направления распространения волны.

• Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
• Видимый свет и дрожание гитарной струны — тоже поперечные волны.

Морская волна — продольная или поперечная?

На самом деле в ней есть и продольная, и поперечная составляющие, поэтому ее нельзя отнести к конкретному типу.

Длина волны: определение и расчет

Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.

• λ — длина волны [м]

Длиной волны называется расстояние между двумя точками этой волны, колеблющихся в одной фазе. Если проще, то это расстояние между двумя «гребнями».

Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.

Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.

Формула периода колебания волны T = t/N T — период [с] t — время [с] N — количество колебаний [-]

Связь со скоростью

Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).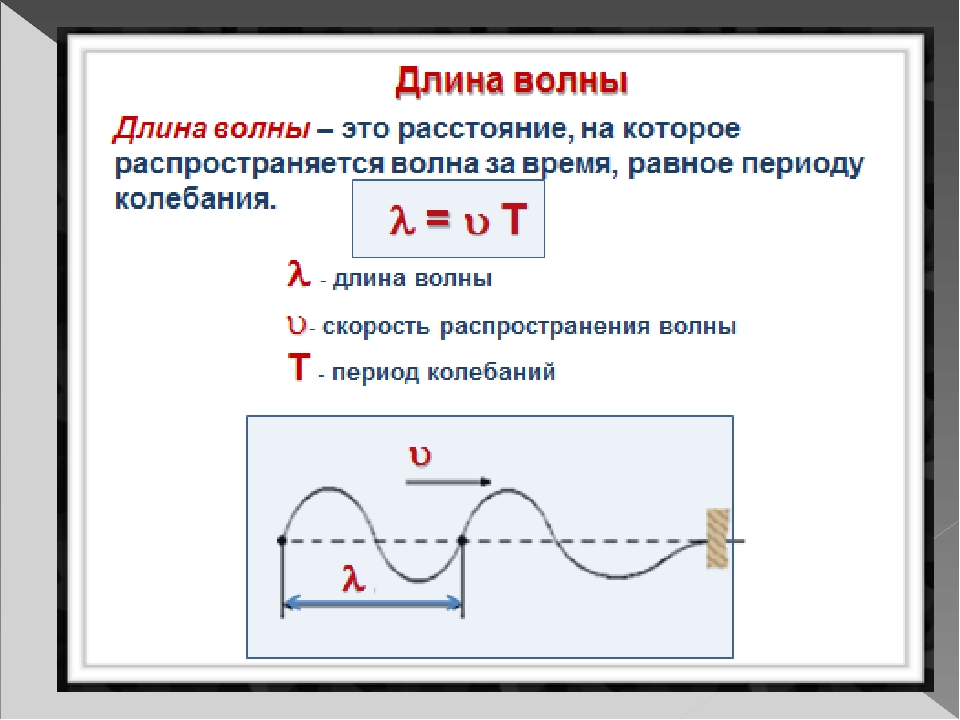

Формула скорости 𝑣 = S/t 𝑣 — скорость [м/с] S — путь [м] t — время [с]

Переходя к волнам, можно провести следующие аналогии:

• путь — длина волны
• время — период

А для скорости даже аналогия не нужна — скорость и Африке скорость.

Формула скорости волны 𝑣 = λ/T 𝑣 — скорость [м/с] λ — длина волны [м] T — период [с]

Задачка

Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?

Решение:

1. Возьмем формулу скорости:

𝑣 = λ/T



2. Нам известна длина волны, но не дан период. Период вычисляется по формуле:

T = t/N

T = 40/10 = 4 с



3. Теперь подставляем величины в формулу

𝑣 = λ/T

𝑣 = ¼ = 0,25 м/с

Ответ: 𝑣 = 0,25 м/с

Резонанс

Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.

На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.

Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.

Формула частоты ν = N/t ν — частота [Гц] t — время [с] N — количество колебаний [-]

В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст🙂

Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.

В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.

Как обозначается длина окружности в физике. Как найти длину окружности: через диаметр и радиус

И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, – это окружность. А вот синее содержимое внутри нее – и есть круг.

Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.

Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.

Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.

Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:

К примеру, радиус – 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.

Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 – это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом

Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:

Ответ: диаметр равен 21,98 метрам.

Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:

D = 2 * (S / Пи) * (1 / 2)

S – в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:

D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414

При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.

Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:

R = S / p (S – площадь заданного треугольника, а p – периметр, разделенный на 2).

Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.

Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.

Возьмем циркуль. Установим ножку циркуля с иглой в точку «O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность .

Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.

• (·)O — называется центром окружности.
• Отрезок, который соединяет центр и любую точку окружности, называется радиусом окружности . Радиус окружности обозначается буквой «R ». На рисунке выше — это отрезок «OA ».
• Отрезок, который соединяет две точки окружности и проходит через её центр, называется диаметром окружности .

  Диаметр окружности обозначается буквой «D ». На рисунке выше — это отрезок «BC ».

  На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение «D = 2R ».

Число π и длина окружности

Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.

В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.

Запомните!

Отношение длины окружности к её диаметру является одинаковым для всех окружностей и обозначается греческой буквой π («Пи»).
π ≈ 3,14…

Число «Пи» относится к числам, точное значение которых записать невозможно ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам для наших вычислений достаточно использовать значение π ,
округленное до разряда сотых π ≈ 3,14…

Теперь, зная, что такое число π , мы можем записать формулу длины окружности.

Запомните!

Длина окружности — это произведение числа π и диаметра окружности. Длина окружности обозначается буквой «С » (читается как «Це»).
C = π D
C = 2π R , так как D = 2R

Как найти длину окружности

Чтобы закрепить полученные знания, решим задачу на окружности.

Виленкин 6 класс. Номер 831

Условие задачи:

Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.

Воспользуемся формулой длины окружности:

C = 2π R ≈ 2 · 3,14 · 24 ≈ 150,72 см

Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.

Виленкин 6 класс. Номер 835

Условие задачи:

Определите диаметр окружности, если её длина равна 56,52 дм. (π ≈ 3,14 ).

Выразим из формулы длины окружности диаметр.

C = π D
D = С / π
D = 56,52 / 3,14 = 18 дм

Хорда и дуга окружности

На рисунке ниже отметим на окружности две точки «A » и «B ». Эти точки делят окружность на две части, каждую из которых называют дугой . Это синяя дуга «AB » и черная дуга «AB ». Точки «A » и «B » называют концами дуг .

Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.

Характеристики фигуры

Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две – А и В – можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.

В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.

Основные термины окружности

Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры – это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр – расстояние между точками , проходящее через центр фигуры.

Основные формулы для вычислений

Параметры используются в формулах вычислений величин окружности:

Диаметр в формулах вычисления

В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С – это искомая величина, D – диаметр.

Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере – длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.

Расчёты по радиусу

Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С – длина, r – радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.

Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?

Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.

Подручные способы вычисления

Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:

• При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
• Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
• Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.

Круглые предметы в истории человеческой жизни

Первое изделие круглой формы, которое изобрёл человек – это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.

Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве – рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.

Нас окружает множество предметов. И многие из них имеют круглую форму. Она задана им для удобного использования. Взять, например, колесо. Если бы оно было изготовлено в форме квадрата, то как бы катилось по дороге?

Для того чтобы изготовить предмет круглой формы, нужно знать, как выглядит формула длины окружности через диаметр. Для этого сначала определим, что же представляет собой это понятие.

Круг и окружность

Окружностью является множество точек, которые размещены на равном расстоянии от основной точки – центра. Это расстояние называется радиусом.

Расстояние между двумя точками на данной линии называется хордой. Помимо того, если хорда проходит через основную точку (центр), тогда она называется диаметром.

А теперь рассмотрим, что такое круг. Совокупность всех точек, которые находятся внутри очертания, называется кругом.

Что такое длина окружности?

После того как мы рассмотрели все определения, мы можем высчитывать диаметр окружности. Формула будет рассмотрена немного позже.

Для начала мы попробуем измерить длину очертания стакана. Для этого мы обмотаем его ниткой, затем ее измерим линейкой и узнаем приблизительную длину воображаемой линии вокруг стакана. Потому что размер зависит от правильного измерения предмета, а данный способ не является надежным. Но тем не менее сделать точные измерения вполне возможно.

Для этого опять вспомним о колесе. Неоднократно мы видели, что если увеличить спицу в колесе (радиус), то увеличится и длина обода колеса (окружности). И так же при уменьшении радиуса окружности уменьшается и длина обода.

Если внимательно проследить за этими изменениями, то увидим, что длина воображаемой круглой линии пропорциональна ее радиусу. И данное число является постоянным. Дальше рассмотрим, как определяется диаметр окружности: формула для этого применится в примере ниже. И рассмотрим ее, следуя шаг за шагом.

Формула окружности через диаметр

Поскольку длина очертания пропорциональна к радиусу, то и соответственно пропорциональна диаметру. Поэтому ее длину мы условно означим буквой C, диаметр – d. Поскольку соотношение длины очертания и диаметра – постоянное число, то его можно определить.

Проделав все подсчеты, мы определим число, которое приблизительно равно 3,1415… По той причине, что при подсчетах конкретное число не получилось, то обозначим его буквой π . Этот значок нам пригодится для того, чтобы была выведена формула длины окружности через диаметр.

Проведем воображаемую линию через центральную точку и измерим расстояние между двумя крайними. Это и будет диаметр. Если будем знать диаметр окружности, формула для определения длины ее самой будет выглядеть так: C = d * π .

Если мы будем определять длину разных очертаний, то если известен их диаметр, формула будет применена одна и та же. Поскольку знак π – это приблизительное исчисление, то и было решено умножать диаметр на 3,14 (число, округленное до сотых).

Как вычислить диаметр: формула

На этот раз попробуем с помощью данной формулы вычислить другие величины, помимо длины очертания. Чтобы вычислить диаметр по длине окружности, формула используется та же. Только для этого ее длину делим на π . Это будет выглядеть так d = C / π .

Рассмотрим, как эта формула действует на практике. К примеру, нам известна длина очертания колодца, следует вычислить его диаметр. Измерить его невозможно, поскольку из-за погодных условий нет доступа к нему. А задача у нас – изготовить крышку. Что будем делать в таком случае?

Нужно воспользоваться формулой. Возьмем длину очертания колодца – к примеру, 600 см. В формулу ставим конкретное число, а именно С = 600 / 3,14. В результате мы получим приблизительно 191 см. Округлим результат до 200 см. Затем с помощью циркуля рисуем круглую линию с радиусом в 100 см.

Поскольку очертание с большим диаметром нужно чертить соответствующим циркулем, то такой инструмент можно изготовить самому. Для этого возьмем рейку нужной длины и на каждом конце вбиваем по гвоздю. Устанавливаем один гвоздь в заготовку и слегка его вбиваем, для того чтобы он не сдвинулся с намеченного места. А с помощью второго чертим линию. Приспособление очень простое и удобное.

Современные технологии позволяют для вычисления длины очертания использовать онлайн-калькулятор. Для этого нужно всего лишь ввести диаметр окружности. Формула будет применена автоматически. Так же можно вычислять длину окружности с помощью радиуса. Кроме того, если вы знаете длину окружности, онлайн-калькулятор вычисляет радиус и диаметр с помощью данной формулы.

Калькулятор круга – это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.

Вычислить радиус

Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.

Рассчитать диаметр

Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.

Узнать длину окружности

Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.

Вычислить площадь круга

Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.

Рассчитать площадь шара

Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.

Вычислить объем шара

Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.

Длина волны. Скорость распространения волн :: Класс!ная физика

ДЛИНА ВОЛНЫ

СКОРОСТЬ РАСПРОСТРАНЕНИЯ ВОЛН

Что ты должен знать и уметь?

1.Определение длины волны.
Длина волны – это расстояние между ближайшими точками, колеблющимися в одинаковых фазах.
2. Величины, характеризующие волну:
длина волны, скорость волны, период колебаний, частота колебаний.
Единицы измерения в системе СИ:
длина волны [лямбда] = 1 м
скорость распространения волны [ v ] = 1м/с
период колебаний [ T ] = 1c
частота колебаний [ ню ] = 1 Гц
3. Расчетные формулы

4. Уметь показать графически длину волны ( для продольных и поперечных волн).

ЕЩЁ ОДНА ИГРУШКА
ДЛЯ УМНЕНЬКИХ И ЛЮБОЗНАТЕЛЬНЫХ

Ощути себя физиком-исследователем – нажми здесь.

ЭТО ИНТЕРЕСНО !

Сейсмические волны.

Сейсмическими волнами называются волны, распространяющиеся в Земле от очагов землетрясений или каких-нибудь мощных взрывов. Так как Земля в основном твердая, в ней одновременно могут возникать 2 вида волн – продольные и поперечные. Скорость этих волн разная: продольные распространяются быстрее поперечных. Например, на глубине 500 км скорость поперечных сейсмических волн 5км/с, а скорость продольных волн – 10км/с.
Регистрацию и запись колебаний земной поверхности, вызанных сейсмическими волнами, осуществляют с помощью приборов – сейсмографов. Распространяясь от очага землетрясения, первыми на сейсмическую станцию приходят продольные волны, а спустя некоторое время – поперечные. Зная скорость распространения сейсмических волн в земной коре и время запаздывания поперечной волны, можно определить расстояние до центра землетрясения. Чтобы узнать точнее , где он находится , используют данные нескольких сейсмических станций.
Ежегодно на земном шаре регистрируют сотни тысяч землетрясений. Подавляющее большинство из них относится к слабым, однако время от времени наблюдаются и такие. которые нарушают целостность грунта, разрушают здания и ведут к человеческим жертвам.

Устали? – Отдыхаем!

Физика обозначение букв и формулы. Обозначение: высота, ширина, длина

Построение чертежей – дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.

Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.

Величины

Площадь, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.

Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.

Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения – это ширина и длина, если их три – добавляется еще и высота.

Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.

Ширина

Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой греческого или английского названия величины. При этом ширина на английском будет выглядеть как “width”.

Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).

Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.

Длина

Как уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина – в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.

В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова – «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.

Высота

Наличие этой величины указывает на то, что приходится иметь дело с более сложным – трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.

На английском она пишется как “height”. Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).

Радиус и диаметр

Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.

Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как “radius”. Отсюда и строчная или заглавная «R»/«r».

Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.

Численно диаметр равен двум радиусам. По-английски это слово пишется так: “diameter”. Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø».

Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».

Толщина

Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.

Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как “thickness”, а в латинском варианте – “crassities”. Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.

Периметр и площадь

В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от “περιμετρέο” («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык (“perimeter”) и закрепилось в системе СИ в виде сокращения буквой «Р».

Площадь – это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.

Некоторые по незнанию думают, что это связано с английским написанием слова “square”. Однако в нем математическая площадь – это “area”, а “square” – это площадь в архитектурном понимании. Кстати, стоит вспомнить, что “square” – название геометрической фигуры “квадрат”. Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода “area” в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» (“fortis”).

Другие распространенные сокращения

Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера – это шаг (винтовых пружин, и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.

Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые – «α», «β», «γ» и «δ». Однако допустимо использовать и другие.

Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?

Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.

Изучение физики в школе длится несколько лет. При этом ученики сталкиваются с проблемой, что одни и те же буквы обозначают совершенно разные величины. Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?

Пугаться такого повтора не стоит. Ученые постарались ввести их в обозначение так, чтобы одинаковые буквы не встретились в одной формуле. Чаще всего ученики сталкиваются с латинской n. Она может быть строчной или прописной. Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.

Что обозначает прописная буква N в физике?

Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях – мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.

Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).

Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).

Что такое N в физике, помимо уже указанных величин? Это может быть:

постоянная Авогадро;

увеличение оптического прибора;

концентрация вещества;

число Дебая;

полная мощность излучения.

Что может обозначать строчная буква n в физике?

Список наименований, которые могут за ней скрываться, достаточно обширен. Обозначение n в физике используется для таких понятий:

показатель преломления, причем он может быть абсолютным или относительным;

нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;

частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).

Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.

Какая физическая величина может быть обозначена n и N?

Ее название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.

Причем «количество» — одна из немногих физических величин, которые не имеют единицы измерения. Это просто число, без наименования. Например, если в задаче идет речь о 10 частицах, то n будет равно просто 10. Но если получается так, что строчная «эн» уже занята, то использовать приходится прописную букву.

Формулы, в которых фигурирует прописная N

Первая из них определяет мощность, которая равна отношению работы ко времени:

В молекулярной физике имеется такое понятие, как химическое количество вещества. Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро :

Кстати, последняя величина тоже обозначается столь популярной буквой N. Только у нее всегда присутствует нижний индекс — А.

Чтобы определить электрический заряд, потребуется формула:

Еще одна формула с N в физике – частота колебаний. Чтобы ее сосчитать, нужно их число разделить на время:

Появляется буква «эн» в формуле для периода обращения:

Формулы, в которых встречается строчная n

В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.

Так, для абсолютного показателя преломления формула записывается следующим образом:

Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.

Формула для относительного показателя преломления несколько сложнее:

n 21 = v 1: v 2 = n 2: n 1 ,

где n 1 и n 2 — абсолютные показатели преломления первой и второй среды, v 1 и v 2 — скорости световой волны в указанных веществах.

Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n 21 = sin α: sin γ.

Чему равно n в физике, если это показатель преломления?

Обычно в таблицах приводятся значения для абсолютных показателей преломления различных веществ. Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.

Итак, стало ясно, что такое n в физике. Чтобы не осталось каких-либо вопросов, стоит рассмотреть некоторые примеры.

Задача на мощность

№1. Во время пахоты трактор тянет плуг равномерно. При этом он прилагает силу 10 кН. При таком движении в течение 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.

Перевод единиц в СИ. Начать можно с силы, 10 Н равны 10000 Н. Потом расстояние: 1,2 × 1000 = 1200 м. Осталось время — 10 × 60 = 600 с.

Выбор формул. Как уже было сказано выше, N = А: t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.

Решение. Вычислим сначала работу, а потом – мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000: 600 = 20 000 Вт.

Ответ. Мощность трактора равна 20 000 Вт.

Задачи на показатель преломления

№2. Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.

В СИ переводить данные не требуется.

При выборе формул остановиться нужно на этой: n = с: v.

Решение. Из указанной формулы видно, что v = с: n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.

Ответ. Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.

№3. Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.

Нужно ли переводить в СИ? Скорости даны во внесистемных единицах. Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.

Выбор формул, необходимых для решения задачи. Потребуется использовать закон преломления света: n 21 = sin α: sin γ. А также: n = с: v.

Решение. В первой формуле n 21 — это отношение двух показателей преломления рассматриваемых веществ, то есть n 2 и n 1 . Если записать вторую указанную формулу для предложенных сред, то получатся такие: n 1 = с: v 1 и n 2 =с: v 2 . Если составить отношение двух последних выражений, получится, что n 21 = v 1: v 2 . Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v 2: v 1).

Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.

Ответ. Значение угла преломления — 26º.

Задачи на период обращения

№4. Лопасти ветряной мельницы вращаются с периодом, равным 5 секундам. Вычислите число оборотов этих лопастей за 1 час.

Переводить в единицы СИ нужно только время 1 час. Оно будет равно 3 600 секундам.

Подбор формул . Период вращения и число оборотов связаны формулой Т = t: N.

Решение. Из указанной формулы число оборотов определяется отношением времени к периоду. Таким образом, N = 3600: 5 = 720.

Ответ. Число оборотов лопастей мельницы равно 720.

№5. Винт самолета вращается с частотой 25 Гц. Какое время потребуется винту, чтобы совершить 3 000 оборотов?

Все данные приведены с СИ, поэтому переводить ничего не нужно.

Необходимая формула : частота ν = N: t. Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.

Решение. В результате деления 3 000 на 25 получается число 120. Оно будет измеряться в секундах.

Ответ. Винт самолета совершает 3000 оборотов за 120 с.

Подведем итоги

Когда ученику в задаче по физике встречается формула, содержащая n или N, ему нужно разобраться с двумя моментами. Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение. Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.

Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.

Физика и основные физические величины

Благодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения – законы Вселенной, конкретнее – то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку.

Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого – первого в России учебника по физике.

Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд – их всего 7:

• длина,
• масса,
• время,
• сила тока,
• температура,
• количество вещества,
• сила света.

Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры – Т. Также у всех величин есть своя единица измерения: у силы света – кандела (кд), а у количества вещества единицей измерения является моль.

Производные физические величины

Производных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным.

Итак, площадь является производной от длины, объем – также от длины, скорость – от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.

Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы – А, а для энергии – Е. Электрический заряд принято обозначать буквой q, а магнитный поток – Ф.

СИ: общие сведения

Международная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов.

Заключение

Итак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных.

Переходя к физическим приложениям производной, мы будем использовать несколько иные обозначения те, которые приняты в физике.

Во-первых, меняется обозначение функций. В самом деле, какие функции мы собираемся дифференцировать? Этими функциями служат физические величины, зависящие от времени. Например, координата тела x(t) и его скорость v(t) могут быть заданы формулами:

(читается ¾икс с точкой¿).

Имеется ещё одно обозначение производной, очень распространённое как в математике, так и в физике:

производная функции x(t) обозначается

(читается ¾дэ икс по дэ тэ¿).

Остановимся подробнее на смысле обозначения (1.16 ). Математик понимает его двояко либо как предел:

либо как дробь, в знаменателе которой стоит приращение времени dt, а в числителе так называемый дифференциал dx функции x(t). Понятие дифференциала не сложно, но мы не будем его сейчас обсуждать; оно ждёт вас на первом курсе.

Физик, не скованный требованиями математической строгости, понимает обозначение (1.16 ) более неформально. Пусть dx есть изменение координаты за время dt. Возьмём интервал dt настолько маленьким, что отношение dx=dt близко к своему пределу (1.17 ) с устраивающей нас точностью.

И тогда, скажет физик, производная координаты по времени есть попросту дробь, в числителе которой стоит достаточно малое изменение координаты dx, а в знаменателе достаточно малый промежуток времени dt, в течение которого это изменение координаты произошло.

Такое нестрогое понимание производной характерно для рассуждений в физике. Далее мы будем придерживаться именно этого физического уровня строгости.

Производная x(t) физической величины x(t) снова является функцией времени, и эту функцию снова можно продифференцировать найти производную производной, или вторую производную функции x(t). Вот одно обозначение второй производной:

вторая производная функции x(t) обозначаетсяx (t)

(читается ¾икс с двумя точками¿), а вот другое:

вторая производная функции x(t) обозначаетсяdt 2

(читается ¾дэ два икс по дэ тэ квадрат¿ или ¾дэ два икс по дэ тэ дважды¿).

Давайте вернёмся к исходному примеру (1.13 ) и посчитаем производную координаты, а заодно посмотрим на совместное использование обозначений (1.15 ) и (1.16 ):

x(t) = 1 + 12t 3t2 )

x(t) = dt d (1 + 12t 3t2 ) = 12 6t:

(Символ дифференцирования dt d перед скобкой это всё равно что штрих сверху за скобкой в прежних обозначениях.)

Обратите внимание, что производная координаты оказалась равна скорости (1.14 ). Это не случайное совпадение. Связь производной координаты со скоростью тела будет выяснена в следующем разделе ¾Механическое движение¿.

1.1.7 Предел векторной величины

Физические величины бывают не только скалярными, но и векторными. Соответственно, часто нас интересует скорость изменения векторной величины то есть, производная вектора. Однако прежде чем говорить о производной, нужно разобраться с понятием предела векторной величины.

Рассмотрим последовательность векторов ~u1 ; ~u2 ; ~u3 ; : : : Сделав, если необходимо, параллельный перенос, сведём их начала в одну точку O (рис.1.5 ):

			Рис. 1.5. lim ~un = ~v
Концы векторов обозначим A1 ; A2 ; A3 ; : : : Таким образом, имеем:

Предположим, что последовательность точек A1 ; A2 ; A3 ; : : : ¾втекает¿2 в точку B:

lim An = B:

Обозначим ~v = OB. Мы скажем тогда, что последовательность синих векторов ~un стремится к красному вектору ~v, или что вектор ~v является пределом последовательности векторов ~un :

~v = lim ~un :

2 Вполне достаточно интуитивного понимания этого ¾втекания¿, но вас, быть может, интересует более строгое объяснение? Тогда вот оно.

Пусть дело происходит на плоскости. ¾Втекание¿ последовательности A1 ; A2 ; A3 ; : : : в точку B означает следующее: сколь бы малый круг с центром в точке B мы ни взяли, все точки последовательности, начиная с некоторой, попадут внутрь этого круга. Иными словами, вне любого круга с центром B имеется лишь конечное число точек нашей последовательности.

А если дело происходит в пространстве? Определение ¾втекания¿ модифицируется незначительно: нужно лишь заменить слово ¾круг¿ на слово ¾шар¿.

Предположим теперь, что концы синих векторов на рис. 1.5 пробегают не дискретный набор значений, а непрерывную кривую (например, указанную пунктирной линией). Таким образом, мы имеем дело не с последовательностью векторов ~un , а с вектором ~u(t), который меняется со временем. Это как раз то, что нам и нужно в физике!

Дальнейшее объяснение почти такое же. Пусть t стремится к некоторому значению t0 . Если

при этом концы векторов ~u(t) ¾втекают¿ в некоторую точку B, то мы говорим, что вектор

~v = OB является пределом векторной величины ~u(t):

t!t0

1.1.8 Дифференцирование векторов

Выяснив, что такое предел векторной величины, мы готовы сделать следующий шаг ввести понятие производной вектора.

Предположим, что имеется некоторый вектор ~u(t), зависящий от времени. Это означает, что длина данного вектора и его направление могут меняться с течением времени.

По аналогии с обычной (скалярной) функцией вводится понятие изменения (или приращения) вектора. Изменение вектора ~u за время t есть векторная величина:

~u = ~u(t + t) ~u(t):

Обратите внимание, что в правой части данного соотношения стоит разность векторов. Изменение вектора ~u показано на рис. 1.6 (напомним, что при вычитании векторов мы сводим их начала в одну точку, соединяем концы и ¾укалываем¿ стрелкой тот вектор, из которого производится вычитание).

~u(t) ~u

Рис. 1.6. Изменение вектора

Если промежуток времени t достаточно мал, то и вектор ~u за это время меняется мало (в физике, по крайней мере, так считается всегда). Соответственно, если при t ! 0 отношение~u= t стремится к некоторому пределу, то этот предел называется производной вектора ~u:

При обозначении производной вектора мы не будем использовать точку сверху (так как символ ~u_ не слишком хорошо смотрится) и ограничиваемся обозначением (1.18 ). Но для производной скаляра мы, разумеется, свободно используем оба обозначения.

Напомним, что d~u=dt это символ производной. Его можно понимать и как дробь, в числителе которой стоит дифференциал вектора ~u, соответствующий промежутку времени dt. Выше мы не стали обсуждать понятие дифференциала, так как в школе его не проходят; не будем обсуждать дифференциал и здесь.

Однако на физическом уровне строгости производную d~u=dt можно считать дробью, в знаменателе которой стоит очень малый интервал времени dt, а в числителе соответствующее малое изменение d~u вектора ~u. При достаточно малом dt величина данной дроби отличается от

предела в правой части (1.18 ) столь мало, что с учётом имеющейся точности измерений этим отличием можно пренебречь.

Этого (не вполне строгого) физического понимания производной нам окажется вполне достаточно.

Правила дифференцирования векторных выражений во многом аналогичны правилам дифференцирования скаляров. Нам понадобятся лишь самые простые правила.

1. Постоянный скалярный множитель выносится за знак производной: если c = const, то

d(c~u) = c d~u: dt dt

Мы используем это правило в разделе ¾Импульс¿, когда второй закон Ньютона

будет переписан в виде:

2. Постоянный векторный множитель выносится за знак производной: если ~c = const, то dt d (x(t)~c) = x(t)~c:

3. Производная суммы векторов равна сумме их производных:

dt d (~u + ~v) =d~u dt +d~v dt :

Последними двумя правилами мы будем пользоваться неоднократно. Посмотрим, как они работают в важнейшей ситуации дифференцирования вектора при наличии в пространстве прямоугольной системы координат OXY Z (рис. 1.7 ).

Рис. 1.7. Разложение вектора по базису

Как известно, любой вектор ~u единственным образом раскладывается по базису единичных

векторов ~ ,~ ,~ : i j k

~u = ux i + uy j + uz k:

Здесь ux , uy , uz проекции вектора ~u на координатные оси. Они же являются координатами вектора ~u в данном базисе.

Вектор ~u в нашем случае зависит от времени, а это значит, что его координаты ux , uy , uz являются функциями времени:

~u(t) = ux (t) i	Uy (t) j	Uz (t)k:

Дифференцируем это равенство. Сначала пользуемся правилом дифференцирования суммы:

ux (t)~ i +

uy (t)~ j

uz (t)~ k:

Затем выносим постоянные векторы за знак производной:

Ux (t)i + uy (t)j + uz (t)k:

Таким образом, если вектор ~u имеет координаты (ux ; uy ; uz ), то координаты производной d~u=dt являются производными координат вектора ~u, а именно (ux ; uy ; uz ).

Ввиду особой важности формулы (1.20 ) дадим более непосредственный её вывод. В момент времени t + t согласно (1.19 ) имеем:

~u(t + t) = ux (t + t) i + uy (t + t) j + uz (t + t)k:

Напишем изменение вектора ~u:

~u = ~u(t + t) ~u(t) =

Ux (t + t) i + uy (t + t) j + uz (t + t)k ux (t) i + uy (t) j + uz (t)k =

= (ux (t + t) ux (t)) i + (uy (t + t) uy (t)) j + (uz (t + t) uz (t)) k =
Ux i + uy j + uz k:
Делим обе части полученного равенства на t:
				T i +			t j +

В пределе при t ! 0 дроби ux = t, uy = t, uz = t переходят соответственно в производные ux , uy , uz , и мы снова получаем соотношение (1.20 ):

Ux i + uy j + uz k.

Поделитесь статьей с друзьями:

Похожие статьи

Формула расчета длины окружности

Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.

Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.

Определение длины окружности

Формула расчёта длинны окружности

 

Произвести расчёт окружности можно по следующей формуле:

 

L = πD = 2πr

 

r – радиус окружности

D – диаметр окружности

L – длина окружности

π – 3.14

Пример нахождения длинны окружности

 

Задача:

Вычислить длину окружности, имеющей радиус 10 сантиметров.

Решение:

Формула для вычисления дины окружности имеет вид:

L = πD = 2πr

где L – длина окружности, π – 3,14, r – радиус окружности, D – диаметр окружности.

Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:

L = 2 × 3,14 × 10 = 31,4 сантиметра

 

Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.

С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.

По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).

Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.

Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.

Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.

Формула сокращения длины

Специальная теория относительности утверждает, что расстояние между двумя точками может отличаться в разных системах отсчета. Расстояние между точками и, следовательно, длина зависит от скорости одной системы отсчета относительно другой. В одной системе отсчета измеряемый объект будет находиться в состоянии покоя. Это называется собственной длины и обозначается Δl ₀ . В другой системе отсчета наблюдатель увидит движущийся объект. Длина объекта в этой системе отсчета равна наблюдаемой длине и обозначена как Δl.Наблюдаемая длина всегда меньше надлежащей. Этот эффект называется сокращением длины . И Δl ₀ , и Δl измеряются в метрах (м).

Δl = наблюдаемая длина в системе отсчета, в которой движется объект (м)

Δl ₀ = надлежащая длина в системе отсчета, в которой объект находится в состоянии покоя (м)

v = скорость (м / с)

c = скорость света (3,0 x 10 ⁸ м / с)

Формула сокращения длины Вопросы:

1) Член экипажа космического корабля измеряет длину корабля 100 м.Корабль пролетает мимо Земли со скоростью, в 0,900 раз превышающей скорость света. Если бы наблюдатели на Земле измерили длину корабля, что бы они измерили?

Ответ: Система отсчета члена экипажа корабля – это система, в которой корабль находится в состоянии покоя. Измеренная длина члена экипажа – надлежащая длина, Δl ₀ . Наблюдатели на Земле измеряют наблюдаемую длину Δl. Длину корабля в системе отсчета наземных наблюдателей можно найти по формуле:

Наблюдатели на Земле измеряют длину корабля в 43.6 мес. Это меньше, чем длина 100 м, измеренная в системе координат члена экипажа корабля.

2) Космические лучи, сталкиваясь с верхними слоями атмосферы Земли, производят частицы высокой энергии, называемые мюонами. Наблюдатель обнаруживает, что мюон был создан на высоте 55 км над поверхностью Земли. Другой наблюдатель обнаруживает мюон, когда он достигает поверхности. Наблюдатели определяют, что мюон двигался со скоростью 2,97 x 10 ⁸ м / с. Какое расстояние в системе отсчета мюона было от места его создания до поверхности Земли?

Ответ: Следует учитывать две позиции: положение, в котором был создан мюон, и его прибытие на поверхность Земли.Расстояние между этими позициями в системе отсчета наблюдателей составляет Δl. В системе отсчета мюона расстояние между точками собственной длины Δl ₀ . Расстояние в системе отсчета наблюдателей известно, поэтому расстояние в системе отсчета мюона можно найти, переписав формулу сокращения длины:

В системе отсчета мюона расстояние между местом его создания и поверхностью Земли составляет приблизительно 390 км, или 390 000 м.Это значительно больше, чем сокращенная длина, 55,0 км или 55 000 м, измеренная наблюдателями.

22.1: Масса, длина и время

1. Последнее обновление

2. Сохранить как PDF

1. Участник

Любую механическую величину можно выразить тремя основными величинами: массой , длиной и временем . Например, скорость – это длина, разделенная на время. Сила – это масса, умноженная на ускорение, и, следовательно, масса, умноженная на расстояние, деленная на квадрат времени.

Поэтому мы говорим, что [Сила] = MLT ⁻² . Квадратные скобки означают: «Размеры количества внутри». Уравнения показывают, как сила зависит от массы, длины и времени. Мы используем символы MLT (не в курсиве ) для обозначения основных измерений массы, длины и времени. В приведенном выше уравнении MLT ^-2 – это , а не , заключенные в квадратные скобки; в этом нет смысла.

Мы различаем измерения физической величины и единицы, в которых она выражается. В случае единиц MKS (которые являются подмножеством единиц СИ), единицами измерения массы, длины и времени являются кг, м и с. Таким образом, можно сказать, что единиц , в которых выражена сила, – это кг · м · с ^-2 , а его размеры равны MLT ^-2 .

Для электромагнитных величин нам нужна четвертая фундаментальная величина. Мы могли бы выбрать, например, количество электричества Q, и в этом случае размерность тока будет QT ^-1 .Мы не касаемся здесь размеров электромагнитных величин. Более подробную информацию можно найти в моих заметках об электричестве и магнетизме, http://orca.phys.uvic.ca/~tatum/elmag.html

.

Чтобы определить размерность физической величины, обычно проще всего взглянуть на определение этой величины. Большинству читателей не составит труда понять, что, поскольку работа – это сила, умноженная на расстояние, размеры работы (и, следовательно, также энергии) равны ML ² T ⁻² .{-1}. \)

Скорость, дистанция, время, калькулятор

Использование калькулятора

Рассчитайте скорость, расстояние или время по формуле d = st, расстояние равно скорости, умноженной на время. Калькулятор скорости, дистанции и времени может решить неизвестные sdt значение с двумя известными значениями.

Время можно ввести или рассчитать в секундах (с), минутах (мин), часах (час) или часах и минутах и ​​секундах (чч: мм: сс).Видеть ярлыки для форматов времени ниже.

Чтобы найти расстояние, используйте формулу для расстояния d = st, или расстояние равно скорости, умноженной на время.

расстояние = скорость x время

Скорость и скорость аналогичны, поскольку они оба представляют собой некоторое расстояние в единицу времени, например мили в час или километры в час. Если ставка r совпадает со скоростью с , r = s = d / t.Вы можете использовать эквивалентную формулу d = rt, что означает, что расстояние равно скорости, умноженной на время.

расстояние = скорость x время

Чтобы найти скорость или коэффициент, используйте формулу для скорости s = d / t, что означает, что скорость равна расстоянию, разделенному на время.

скорость = расстояние / время

Чтобы найти время, используйте формулу для времени, t = d / s, что означает, что время равно расстоянию, разделенному на скорость.

время = расстояние / скорость

Форматы ввода времени чч: мм: сс

В качестве разделителей можно использовать тире (-), точку (.) Или двоеточие (:), при этом всегда необходимо использовать 2 разделителя. Например, 15-06-22, 15.06.22 и 15:06:22 интерпретируются как 15 часов 6 минут 22 секунды или 15:06:22.

Разрешенные ограничения на вход:

• часы 0 до 999
• минут 0 до 59
• секунд от 0 до 59

Ярлыки формата времени

Х..

5 ..

5 часов: 0 минут: 0 секунд

05:00:00

X.Y.

5.22.

5 часов: 22 минут: 0 секунд

05:22:00

X.Y.Z

5.22.10
5.01.15
5.3.6

5 часов: 22 минут: 10 секунд
5 часов: 1 минута: 15 секунд
5 часов: 3 минут: 6 секунд

05:22:10
05:01:15
05:03:06

.Y.

.22.

22 минуты

00:22:00

.Y.Z

. 22,15

22 минуты: 15 секунд

00:22:15

..Z

..5

5 секунд

00:00:05

X..Z

5..05

5 часов: 0 минут: 5 секунд

05:00:05

Связанные калькуляторы

Для физических расчетов со скоростью, смещением и скоростью используйте наш Калькулятор смещения для решения смещения с , средняя скорость v или время t .

5.4 Сокращение длины – Университетская физика, Том 3

Задачи обучения

К концу этого раздела вы сможете:

• Объясните, как связаны одновременность и сокращение длины.
• Опишите связь между сокращением длины и замедлением времени и используйте ее для вывода уравнения сокращения длины.

Длина вагона на рис. 5.8 одинакова для всех пассажиров.Все они договорились бы об одновременном расположении двух концов машины и получили бы одинаковый результат для расстояния между ними. Но одновременные события в одной инерциальной системе отсчета не обязательно должны быть одновременными в другой. Если бы поезд мог двигаться с релятивистскими скоростями, наблюдатель на земле видел бы одновременные местоположения двух конечных точек вагона на разном расстоянии друг от друга, чем наблюдатели внутри вагона. Измеренные расстояния не обязательно должны быть одинаковыми для разных наблюдателей, когда речь идет о релятивистских скоростях.

Фигура 5,8 Люди могут описывать расстояния по-разному, но при релятивистских скоростях расстояния действительно другие. (Источник: «Россия» / Flickr)

Правильная длина

Два проходящих мимо наблюдателя всегда видят одно и то же значение своей относительной скорости. Несмотря на то, что замедление времени подразумевает, что пассажир поезда и наблюдатель, стоящий рядом с путями, измеряют разное время прохождения поезда, они все же согласны с тем, что относительная скорость, которая представляет собой расстояние, разделенное на прошедшее время, одинакова.Если наблюдатель на земле и один в поезде измеряют разное время, за которое поезд проходит мимо наземного наблюдателя, согласование их относительной скорости означает, что они также должны видеть разные пройденные расстояния.

Мюон, обсуждаемый в примере 5.3, иллюстрирует эту концепцию (рисунок 5.9). Для наблюдателя на Земле мюон проходит через 0,950 c за 7,05 мкс с момента образования до распада. Следовательно, он преодолевает расстояние относительно Земли:

L0 = vΔt = (0.950) (3,00 × 108 м / с) (7,05 × 10–6 с) = 2,01 км. L0 = vΔt = (0,950) (3,00 × 108 м / с) (7,05 × 10–6 с) = 2,01 км.

В мюонной системе отсчета время жизни мюона составляет 2,20 мкс. В этой системе координат Земля, воздух и земля имеют достаточно времени только для путешествия:

L = vΔτ = (0,950) (3,00 × 108 м / с) (2,20 × 10–6 с) км = 0,627 км. L = vΔτ = (0,950) (3,00 × 108 м / с) (2,20 × 10–6 с) км = 0,627 км.

Расстояние между одними и теми же двумя событиями (рождением и распадом мюона) зависит от того, кто его измеряет и как они движутся относительно него.

Правильная длина

Правильная длина L0L0 – это расстояние между двумя точками, измеренное наблюдателем, находящимся в состоянии покоя относительно обеих точек.

Земной наблюдатель измеряет правильную длину L0L0, потому что точки, в которых мюон рождается и распадается, стационарны относительно Земли. К мюону движутся Земля, воздух и облака, поэтому расстояние L , которое он видит, не является правильной длиной.

Фигура 5.9 (а) Приближенный к Земле наблюдатель видит, что мюон проходит 2,01 км. (b) Тот же самый путь имеет длину 0,627 км, если смотреть из системы отсчета мюона. Земля, воздух и облака движутся относительно мюона в его системе координат и имеют меньшую длину в направлении движения.

Сокращение длины

Чтобы связать расстояния, измеренные разными наблюдателями, обратите внимание, что скорость относительно земного наблюдателя в нашем примере с мюоном равна

Время относительно земного наблюдателя равно Δt, Δt, потому что измеряемый объект движется относительно этого наблюдателя. Скорость относительно движущегося наблюдателя определяется как

Движущийся наблюдатель движется вместе с мюоном и, следовательно, наблюдает собственное время Δτ.Δτ. Две скорости идентичны; таким образом,

Мы знаем, что Δt = γΔτ.Δt = γΔτ. Подставляя это уравнение в приведенное выше соотношение, получаем

Замена γγ дает уравнение, связывающее расстояния, измеренные разными наблюдателями.

Уменьшение длины

Сокращение длины – это уменьшение измеренной длины объекта от его надлежащей длины при измерении в системе отсчета, которая движется относительно объекта:

L = L01-v2c2L = L01-v2c2

5,4

, где L0L0 – длина объекта в его неподвижной рамке, а L – длина в кадре, движущемся со скоростью v .

Если мы измерим длину всего, что движется относительно нашего кадра, мы обнаружим, что его длина L меньше, чем правильная длина L0L0, которая была бы измерена, если бы объект был неподвижен. Например, в системе отсчета покоя мюона расстояние, на которое Земля движется между местом образования мюона и местом его распада, короче, чем расстояние, пройденное в системе отсчета Земли. Эти точки фиксированы относительно Земли, но движутся относительно мюона. Облака и другие объекты также сжимаются в направлении движения, если смотреть из системы покоя мюона.

Таким образом, два наблюдателя измеряют разные расстояния по направлению их относительного движения, в зависимости от того, какой из них измеряет расстояния между неподвижными объектами.

А как насчет расстояний, измеренных в направлении, перпендикулярном относительному движению? Представьте себе двух наблюдателей, движущихся вдоль своих осей x и проходящих друг мимо друга, удерживая измерительные стержни вертикально в направлении x . На рис. 5.10 показаны две метровые палки M и M′M ′, которые покоятся в системе отсчета двух мальчиков S и S ′, S ′ соответственно.На верхушку (отметка 100 см) палочки M′.M ′ прикреплена маленькая кисточка. Предположим, что S′S ′ движется вправо с очень высокой скоростью v относительно S, и стержни ориентированы так, что они перпендикулярны или поперечны вектору их относительной скорости. Палочки держат так, чтобы при переходе друг в друга их нижние концы (отметки 0 см) совпадали. Предположим, что когда S затем смотрит на свою палку M, он находит нарисованную на ней линию чуть ниже вершины палки. Поскольку щетка прикреплена к верхней части палки M ‘другого мальчика, M’, S может только сделать вывод, что палочка M’M ‘меньше 1.Длина 0 м.

Фигура 5.10 Измерительные стики M и M′M ′ неподвижны в системах отсчета наблюдателей S и S ′, S ′ соответственно. Когда палочки проходят, небольшая кисть, прикрепленная к отметке 100 см M′M ′, рисует линию на M.

Теперь, когда мальчики приближаются друг к другу, S ′, S ′, как и S, видит метровую палку, движущуюся к нему со скоростью v . Поскольку их ситуации симметричны, каждый мальчик должен сделать такое же измерение палки в другом кадре. Итак, если S измеряет стержень M′M ′ меньше 1.Длина 0 м, S′S ′ должен иметь длину палки M, которая также должна быть меньше 1,0 м, и S′S ′ должен видеть, как его кисть проходит через верхнюю часть палочки M, а не рисовать на ней линию. Другими словами, после того же события один мальчик видит нарисованную линию на палке, а другой не видит такой линии на той же палке!

Первый постулат Эйнштейна требует, чтобы законы физики (как, например, применяемые к живописи) предсказывали, что S и S ‘, S’, которые оба находятся в инерциальных системах отсчета, производят одни и те же наблюдения; то есть S и S′S ′ должны либо оба видеть линию, нарисованную на стержне M, либо оба не видеть эту линию.Таким образом, мы вынуждены сделать вывод, что наше первоначальное предположение о том, что S видел линию, нарисованную под вершиной его палки, было неверным! Вместо этого S находит линию, нарисованную прямо на отметке 100 см на M. Тогда оба мальчика согласятся, что линия нарисована на M, и они также согласятся, что обе палки имеют длину ровно 1 м. Мы приходим к выводу, что размеры поперечной длины должны быть одинаковыми в разных инерциальных системах отсчета .

Пример 5.5

Расчет сокращения длины

Предположим, что астронавт, такой как близнец в обсуждении парадокса близнецов, летит так быстро, что γ = 30.00.γ = 30,00. (a) Астронавт путешествует с Земли в ближайшую звездную систему, Альфа Центавра, на расстоянии 4 300 световых лет (лет), как измерено наземным наблюдателем. Как далеко друг от друга находятся Земля и Альфа Центавра по измерениям астронавта? (b) В терминах c , какова скорость космонавта относительно Земли? Вы можете пренебречь движением Земли относительно Солнца (рис. 5.11).

Фигура 5.11 (а) Приближенный к Земле наблюдатель измеряет правильное расстояние между Землей и Альфой Центавра.(b) Астронавт наблюдает сокращение длины, потому что Земля и Альфа Центавра движутся относительно ее корабля. Она может преодолеть это меньшее расстояние за меньшее время (свое собственное время), не превышая скорости света.

Стратегия

Во-первых, обратите внимание, что световой год (световой год) – удобная единица измерения расстояния в астрономическом масштабе – это расстояние, которое свет проходит за год. Для части (а) расстояние в 4,300 св. Лет между Альфой Центавра и Землей является правильным расстоянием L0, L0, потому что оно измеряется наземным наблюдателем, для которого обе звезды (приблизительно) неподвижны.Для астронавта Земля и Альфа Центавра движутся с одинаковой скоростью, поэтому расстояние между ними составляет сокращенную длину L . В части (b) нам даны γ, γ, поэтому мы можем найти v , изменив определение γγ, чтобы выразить v в терминах c .

Решение для (a)

Для части (а):

1. Определите известные: L0 = 4.300ly; γ = 30.00.L0 = 4.300ly; γ = 30.00.
2. Определите неизвестное: L .
3. Выразите ответ в виде уравнения: L = L0γ.L = L0γ.
4. Сделайте расчет: L = L0γ = 4.300ly30.00 = 0.1433ly.L = L0γ = 4.300ly30.00 = 0.1433ly.

Решение для (b)

Для части (b):

1. Определите известное: γ = 30.00.γ = 30.00.
2. Определите неизвестное: v в терминах c .
3. Выразите ответ в виде уравнения. Начнем с: γ = 11 − v2c2.γ = 11 − v2c2. Затем решите для неизвестного v / c , сначала возведя обе стороны в квадрат, а затем переставив: γ2 = 11 − v2c2v2c2 = 1−1γ2vc = 1−1γ2.γ2 = 11 − v2c2v2c2 = 1−1γ2vc = 1−1γ2.
4. Сделайте расчет: vc = 1−1γ2 = 1−1 (30,00) 2 = 0,99944 vc = 1−1γ2 = 1−1 (30,00) 2 = 0,99944 или

Значение

Не забывайте округлять вычисления до окончательного ответа, иначе вы можете получить ошибочные результаты. Это особенно верно для расчетов по специальной теории относительности, где различия могут быть обнаружены только после нескольких десятичных знаков. Релятивистский эффект здесь велик (γ = 30,00), (γ = 30,00), и мы видим, что v приближается (не равняется) скорости света.Поскольку расстояние, измеренное космонавтом, намного меньше, космонавт может преодолеть его за гораздо меньшее время в своем кадре.

Люди, путешествующие с чрезвычайно высокими скоростями, могут преодолевать очень большие расстояния (тысячи или даже миллионы световых лет) и стареть всего за несколько лет в пути. Однако, как и эмигранты прошлых веков, покинувшие свой дом, эти люди навсегда покинут Землю, которую они знают. Даже если бы они вернулись, на Земле прошли бы тысячи или миллионы лет, уничтожив большую часть того, что сейчас существует.Существует также более серьезное практическое препятствие для путешествия с такой скоростью; Для достижения таких высоких скоростей потребовалось бы гораздо больше энергии, чем может быть достигнута классическая физика. Об этом мы поговорим позже в этой главе.

Почему мы не замечаем сокращения длины в повседневной жизни? Расстояние до продуктового магазина, похоже, не зависит от того, переезжаем мы или нет. Изучая уравнение L = L01 − v2c2, L = L01 − v2c2, мы видим, что при малых скоростях (v << c), (v << c) длины почти равны, что является классическим ожиданием.Но сокращение длины вполне реально, если не наблюдается обычно. Например, заряженная частица, такая как электрон, движущийся с релятивистской скоростью, имеет силовые линии электрического поля, сжатые вдоль направления движения, как это видит неподвижный наблюдатель (рис. 5.12). Когда электрон проходит через детектор, такой как катушка с проволокой, его поле взаимодействует гораздо более кратко, эффект, наблюдаемый на ускорителях частиц, таких как Стэнфордский линейный ускоритель (SLAC) длиной 3 км. Фактически, для электрона, движущегося по лучевой трубе в SLAC, ускоритель и Земля все движутся и сокращаются по длине.Релятивистский эффект настолько велик, что длина ускорителя до электрона составляет всего 0,5 м. На самом деле, направить электронный луч по трубе легче, потому что для прохождения по короткой трубе не нужно точно направлять луч, как для прохождения по трубе длиной 3 км. Это снова экспериментальная проверка специальной теории относительности.

Фигура 5,12 Силовые линии электрического поля высокоскоростной заряженной частицы сжимаются вдоль направления движения за счет сокращения длины, производя наблюдаемый другой сигнал, когда частица проходит через катушку.

Проверьте свое понимание 5,4

Частица движется через атмосферу Земли со скоростью 0,750 c . Для наземного наблюдателя расстояние, которое он преодолевает, составляет 2,50 км. Как далеко перемещается частица, если смотреть из системы отсчета частицы?

единиц СИ – длина | NIST

Метр (м) определяется путем принятия фиксированного числового значения скорости света в вакууме c равным 299 792 458 при выражении в единицах m s ^-1 , где секунда определяется как ∆ν _Cs .

Измеритель когда-то определялся физическим артефактом – двумя отметками, начертанными на платино-иридиевом слитке. Длина – эволюция от эталона измерения к фундаментальной постоянной объясняет эволюцию определения счетчика. Следите за этими изменениями с течением времени на временной шкале NIST.

Из счетчика выводятся несколько других единиц измерения, например:

• Единица скорости – метр в секунду (м / с). Скорость света в вакууме составляет 299 792 458 метров в секунду.
• единица ускорения – метр в секунду в секунду (м / с ² ).
• единиц площади – квадратный метр ( ² м).
• Единица объема – кубический метр ( ³ м). Литр (1 кубический дециметр), хотя и не является единицей СИ, принят для использования с СИ и обычно используется при измерении объема жидкости, но также используется при измерении газов и твердых веществ.

FAQ: Когда произошло переопределение дюйма в метрической системе?

В 1958 году конференция англоязычных стран согласилась унифицировать свои стандарты длины и массы и определить их в единицах измерения.В результате американский двор был сокращен, а императорский двор – удлинен. Новые коэффициенты пересчета были объявлены в 1959 г. в уведомлении Федерального реестра 59-5442 (30 июня 1959 г.), в котором говорится об определении стандартного дюйма: значение дюйма, полученное из значения ярда с 1 июля 1959 г. точно соответствует 25,4 мм .

Коэффициент пересчета можно определить:

Единицы длины
10 миллиметров (мм)	=	1 сантиметр (см)
10 см	=	1 дециметр (дм)
10 см	=	100 миллиметров
10 дециметров	=	1 метр (м)
10 дециметров	=	1000 миллиметров
10 метров	=	1 декаметр (плотина)
10 декаметров	=	1 гектометр
10 декаметров	=	100 метров
10 гектометров	=	1 километр (км)
10 гектометров	=	1000 метров

Часто задаваемые вопросы: Как получить метрическую линейку?

Метрические линейки доступны у многих розничных продавцов, которые могут быть идентифицированы с помощью таких поисковых терминов, как «метрическая линейка», «метрическая линейка» или «метрическая линейка».«Линейки для печати, такие как сантиметровые правила цветного квадрата, могут быть распечатаны в цвете на верхних прозрачных листах, чтобы сделать недорогие метрические линейки.

Ресурсы для студентов и преподавателей

• Метр – Будь то бескрайнее расстояние до бабушкиного дома, кусок ткани, количество ярдов до линии ворот или расстояние между невероятно маленькими транзисторами на компьютерном чипе, длина – одна из самых известных единиц измерения. . (NIST)
• Национальный прототип измерителя No.27. (NIST)
.
• Использование метрической линейки. (WeldNotes, видео)
• Использование микрометра. (Университет Торонто)
• Использование штангенциркуля и микрометра. (Кейптаунский университет, факультет физики)
• График шкалы вещей. (Министерство энергетики США)
• Изучите размер и масштаб ячейки с помощью интерактивной графики. (Университет Юты)
• Попрактикуйтесь в измерении длины сантиметрами в упражнении «Квадраты и прямоугольники». (PBS)
• Рассчитайте фокусное расстояние в этом практическом упражнении и изучите эту важную концепцию, которая используется в таких инструментах STEAM, как микроскопы, телескопы и камеры.(Оптическое общество)
• Развивайте понимание того, насколько мал на самом деле нанометр, с помощью активности «Что такое нанометр»? Во время урока ученики будут измерять обычные предметы в классе и переводить результаты в нанометры. (IEEE)
• Ознакомьтесь с измерениями эквивалентной метрической длины в игре «Длина столбца». Проведите линию, чтобы соединить одинаковые измерения. Смотрите внимательно, ведь некоторые предметы не имеют совпадений! (Типичный учебный архив)
• Спроектируйте, спланируйте и начертите план сада в масштабе с помощью метрической линейки.(Калифорнийский университет в Беркли, Ноттингемский университет)
• SI Площадь. Изучите ресурсы, чтобы ознакомиться с единицами измерения площади, включая гектар.
• SI Том. Изучите ресурсы, чтобы познакомиться с единицами измерения объема, включая литр.
• Рассчитайте окружность, площадь и объем. Ознакомьтесь с методами, используемыми для расчета окружности, площади и объема обычных предметов. (NIST)

Кредит: Дж.Ван и Б. Хейс / NIST

Лига супергероев СИ – Человек-метр:

Эта серия анимационных видео в стиле комиксов была разработана, чтобы помочь учащимся средних школ узнать о 7 основных единицах измерения СИ. С его острым взглядом и гибкими руками-линейками человек-метр не может измерить расстояние слишком большое или маленькое. Метр – это расстояние, которое свет проходит за крошечные доли секунды.

Перейдите к дополнительной информации о базовом блоке SI:

60,3.5 Минимальная Tength взлетно-посадочной полосы для этого самолета составляет 514,286 метра

.

Стенограмма видео

Хорошо, это семейство, они говорят, что мы хотели рассчитать перила минимального пробега или самолет с использованием ускорения и скорости взлета самолета. Eso Будет трехступенчатая программа, когда все будет в первую очередь. МКС. Посмотрим от пользователя для ввода. Да, мы воспользуемся услугами «консул – советник», и для расчетов мы проходим непреодолимое преобразование рулевого управления и чисел.А затем мы рассчитаем минимальную длину перил. Мы воспользуемся формулой. Они дали нам длину, равную: Давайте посмотрим, будет скорость взлета. Итак, скорость в квадрате. Затем мы перейдем к вам, разделенному на да, умноженное на ускорение. В этом случае мы собираемся использовать Consul. И помните, что Teoh преобразовал две строки, но в отличие от того, что мы сделали, правильно? Давайте посмотрим, они дают нам пример, когда мы предлагаем пользователю получить гибкую скорость при ускорении.Мы даже увидим, как превратить наш строковый ввод в числа, которые мы можем вычислить, мы собираемся спросить for in print Давайте посмотрим на скорость и ускорение по отдельности, и похоже, что пользователю просто нужно знать, что они должны звонить отдельно.Ладно, на этом этапе мы выполнили это, и я собирался рассчитать это. Я должен сказать, что ссылки будут равны, ну, по формуле, принимающей это. Это было похоже на то, что мощность понижается, чтобы разделить 0,2-кратное ускорение, которое мы получили. Как мы собираемся показать это пользователям? Что ж, с их вывода поздравляем с конфликтом. Принесите нам A. Минимальное расстояние до взлетно-посадочной полосы для этого самолета есть, и они собираются дать номер. Они рассчитали нашу длину, но помните, когда он здесь превратил ее в веревку? Верно.Итак, кто знает, как объединить кучу строк, иначе он не знал бы, как очень легко объединить наше строковое сообщение с номером. Затем давайте посмотрим, как вы дадите это число, и они убедятся, что они сообщили им, что преобразовали его. Вероятно, они даже не спрашивали пользователя и не сообщали ему единицы измерения. Это немного интересно. Вы всегда должны сообщать им об этом. Так что давайте улучшим то, что они нам показали. Допустим, мы хотим скорости и меня. Есть на секунду. Допустим, мы хотим получить ускорение в метрах в секунду в квадрате.Да, насилие отображает их вклад и посмотрим, получим ли мы то же самое. Но когда они его вставили, они поставили для своего теста 60. Гм, я согласен с комментарием на три пункта выше ускорения. Так что это в том, и они заканчивают этим. Видите ли, минимальный разбег для самолета – 5,1, важен для восьми и Аарона шесть. Хорошо.

28.3 Сокращение длины – Колледж Физики, главы 1-17

Уменьшение длины

• Укажите правильную длину.
• Рассчитать сокращение длины.
• Объясните, почему мы не замечаем этих эффектов в повседневной жизни.

Люди могут описывать расстояния по-разному, но при релятивистских скоростях расстояния действительно другие. (Источник: Кори Леопольд, Flickr)

Вы когда-нибудь ездили по дороге, которая кажется бесконечной? Если посмотреть вперед, можно сказать, что у вас осталось около 10 км. Другой путешественник может сказать, что дорога впереди выглядит так, будто ее длина составляет около 15 км. Однако если вы оба измерите дорогу, вы согласитесь.Если вы путешествуете с повседневной скоростью, расстояние, которое вы оба измеряете, будет одинаковым. Однако в этом разделе вы прочитаете, что это неверно для релятивистских скоростей. Близкие к скорости света расстояния, измеренные разными наблюдателями, не совпадают.

Все наблюдатели сходятся во мнении, что относительная скорость. Несмотря на то, что часы измеряют разное прошедшее время для одного и того же процесса, они все же согласны с тем, что относительная скорость, которая равна расстоянию, разделенному на прошедшее время, одинакова.Это означает, что расстояние также зависит от относительного движения наблюдателя. Если два наблюдателя видят разное время, то они также должны видеть разные расстояния, чтобы относительная скорость была одинаковой для каждого из них.

Мюон, обсуждаемый в [ссылка], иллюстрирует эту концепцию. Для наблюдателя на Земле мюон движется со скоростью 0,950 c0,950 c размером 12 {c} {} за 7,05 мкс и 7,05 мкс размером 12 {c} {} с момента образования до распада. Таким образом, он проходит расстояние

L0 = vΔt = (0,950) (3,00 × 108 м / с) (7.05 × 10-6 с) = 2,01 км L0 = vΔt = (0,950) (3,00 × 108 м / с) (7,05 × 10-6 с) = 2,01 км

относительно Земли. В системе отсчета мюона его время жизни составляет всего 2,20 мкс2,20 мкс. Времени на проезд хватает только

L = vΔt0 = (0,950) (3,00 × 108 м / с) (2,20 × 10–6 с) = 0,627 км. L = vΔt0 = (0,950) (3,00 × 108 м / с) (2,20 × 10–6 с) ) = 0,627 км.

Расстояние между одними и теми же двумя событиями (рождением и распадом мюона) зависит от того, кто его измеряет и как они движутся относительно него.

Правильная длина

Правильная длина L0L0 размер 12 {L rSub {размер 8 {0}}} {} – это расстояние между двумя точками, измеренное наблюдателем, находящимся в состоянии покоя относительно обеих точек.

Земной наблюдатель измеряет правильную длину L0L0 размером 12 {L rSub {size 8 {0}}} {}, поскольку точки, в которых мюон образуется и распадается, являются стационарными относительно Земли. По отношению к мюону движутся Земля, воздух и облака, поэтому расстояние LL размером 12 {L} {}, которое он видит, не является надлежащей длиной.

(a) Приближающийся к Земле наблюдатель видит, как мюон проходит 2,01 км между облаками. (b) Мюон видит, что он движется по тому же пути, но только на расстояние 0,627 км. Земля, воздух и облака движутся относительно мюона в его системе координат, и все они, кажется, имеют меньшую длину в направлении движения.

Чтобы разработать уравнение, связывающее расстояния, измеренные разными наблюдателями, отметим, что скорость относительно привязанного к Земле наблюдателя в нашем примере с мюоном равна

v = L0Δt.v = L0Δt. размер 12 {v = {{L rSub {размер 8 {0}}} больше {Δt}}} {}

Время относительно привязанного к Земле наблюдателя составляет ΔtΔt size 12 {Δt} {}, поскольку измеряемый объект движется относительно этого наблюдателя. Скорость относительно движущегося наблюдателя определяется как

v = LΔt0.v = LΔt0.размер 12 {v = {{L rSub {размер 8 {0}}} больше {Δt}}} {}

Движущийся наблюдатель движется вместе с мюоном и, следовательно, наблюдает собственное время Δt0Δt0 size 12 {Δt rSub {size 8 {0}}} {}. Две скорости идентичны; таким образом,

L0Δt = LΔt0.L0Δt = LΔt0. размер 12 {{{L rSub {размер 8 {0}}} больше {Δt}} = {{L} больше {Δt rSub {размер 8 {0}}}}} {}

Мы знаем, что Δt = γΔt0Δt = γΔt0 размер 12 {Δt = γΔt rSub {size 8 {0}}} {}. Подставляя это уравнение в приведенное выше соотношение, получаем

L = L0γ.L = L0γ. размер 12 {L = {{L rSub {размер 8 {0}}} больше {γ}}} {}

Замена γγ на размер 12 {γ} {} дает уравнение, связывающее расстояния, измеренные разными наблюдателями.

Уменьшение длины

Сокращение длины LL, размер 12 {L} {} – это сокращение измеренной длины объекта, движущегося относительно кадра наблюдателя.

L = L01-v2c2.L = L01-v2c2. размер 12 {L – L rSub {размер 8 {0}} sqrt {1 – {{v rSup {размер 8 {2}}} больше {c rSup {размер 8 {2}}}}}} {}

Если мы измерим длину всего, что движется относительно нашей рамы, мы обнаружим, что его длина LL, размер 12 {L} {} меньше, чем правильная длина L0L0, размер 12 {L rSub {размер 8 {0}}} {}, который были бы измерены, если бы объект был неподвижен.Например, в системе отсчета мюона расстояние между точками его образования и распада меньше. Эти точки фиксированы относительно Земли, но движутся относительно мюона. Облака и другие объекты также сжимаются по направлению движения в системе отсчета мюона.

Расчет сокращения длины: расстояние между звездами сокращается, когда вы путешествуете с высокой скоростью

Предположим, что астронавт, такой как близнец, обсуждаемый в книге «Одновременность и замедление времени», летит так быстро, что γ = 30.00γ = 30,00 размер 12 {γ = “30 ″”. ” «00»} {}. (a) Она путешествует с Земли к ближайшей звездной системе, Альфе Центавра, на расстоянии 4 300 световых лет (лет), по данным наблюдателя с Земли. Как далеко друг от друга находятся Земля и Альфа Центавра по измерениям астронавта? (b) Какова ее скорость относительно Земли в кубическом размере 12 {c} {}? Вы можете пренебречь движением Земли относительно Солнца. (См. [Ссылку].)

(a) Присоединившийся к Земле наблюдатель измеряет правильное расстояние между Землей и Альфой Центавра.(b) Астронавт наблюдает сокращение длины, поскольку Земля и Альфа Центавра движутся относительно ее корабля. Она может преодолеть это меньшее расстояние за меньшее время (свое собственное время), не превышая скорости света.

Стратегия

Прежде всего отметим, что световой год (световые годы) – удобная единица измерения расстояния в астрономическом масштабе – это расстояние, которое свет проходит за год. Что касается части (а), обратите внимание, что расстояние в 4,300 св. Лет между Альфа Центавра и Землей является правильным расстоянием L0L0 размером 12 {L rSub {размер 8 {0}}} {}, потому что оно измеряется наземным наблюдателем. которому обе звезды (приблизительно) неподвижны.Для астронавта Земля и Альфа Центавра движутся с одинаковой скоростью, поэтому расстояние между ними составляет сжатую длину LL размером 12 {L} {}. В части (b) нам дан размер γγ 12 {γ} {}, и поэтому мы можем найти vv размера 12 {v} {}, изменив определение размера γγ 12 {γ} {}, чтобы выразить vv размер 12 { v} {} с точки зрения размера копии 12 {c} {}.

Решение для (а)

1. Определите известных. L0−4,300 ллL0−4,300 св. Лет; γ = 30,00 γ = 30,00
2. Опознайте неизвестное.LL, размер 12 {L} {}
3. Выберите соответствующее уравнение. L = L0γL = L0γ размер 12 {L = {{L rSub {размер 8 {0}}} больше {γ}}} {}
4. Переставьте уравнение, чтобы найти неизвестное.

   L = L0γ = 4,300 ly30,00 = 0,1433 lyL = L0γ = 4,300 ly30,00 = 0,1433 lyalignl {стек {
   размер 12 {L = {{L rSub {размер 8 {0}}} больше {γ}}} { } #
   = {{4 “.” «300» лет »} больше {« 30 »«. » «00»}} {} #
   = 0 «.» «1433» «лы» {}
   }} {}

Решение для (b)

1. Определите известное.γ = 30,00 γ = 30,00 размер 12 {γ = “30 ″”. ” «00»} {}
2. Опознайте неизвестное. vv размер 12 {v} {} для размера 12 куб. см {c} {}
3. Выберите соответствующее уравнение. γ = 11 − v2c2γ = 11 − v2c2 размер 12 {γ = {{1} больше {sqrt {1 – {{v rSup {размер 8 {2}}}} больше {c rSup {размер 8 {2}}}}} }}} {}
4. Переставьте уравнение, чтобы найти неизвестное.

   γ = 11 − v2c230.00 = 11 − v2c2γ = 11 − v2c230.00 = 11 − v2c2alignl {stack {
   size 12 {γ = {{1} over {sqrt {1 – {{v rSup {size 8 {2}) }}} больше {c rSup {size 8 {2}}}}}}}} {} #
   «30» «.”« 00 »= {{1} больше {sqrt {1 – {{v rSup {размер 8 {2}}} больше {c rSup {размер 8 {2}}}}}}} {}
   }} {}

   Возведение обеих частей уравнения в квадрат и перестановка членов дает

   900.0 = 11-v2c2900.0 = 11-v2c2 размер 12 {«900» «.» 0 = {{1} больше {1 – {{v rSup {size 8 {2}}} больше {c rSup {size 8 {2}}}}}}} {}

   так что

   1 − v2c2 = 1900.01 − v2c2 = 1900.0 размер 12 {1 – {{v rSup {size 8 {2}}} больше {c rSup {size 8 {2}}}} = {{1} больше {«900») «.» 0}}} {}

   и

   v2c2 = 1−1900.0 = 0,99888… .v2c2 = 1−1900,0 = 0,99888…. размер 12 {{{v rSup {размер 8 {2}}} больше {c rSup {size 8 {2}}}} = 1 – {{1} больше {«900» «.» 0}} = 0 “.” «99888» «.» «.» «.» } {}

   Взяв квадратный корень, находим

   vc = 0,99944, vc = 0,99944, размер 12 {{{v} over {c}} = 0 “.” «99944»} {}

   , который перестраивается для получения значения скорости

   v = 0,9994c.v = 0,9994c. размер 12 {ital «v =» 0 «.» «9994» c} {}

Обсуждение

Во-первых, помните, что вы не должны округлять вычисления до получения окончательного результата, иначе вы можете получить ошибочные результаты.Это особенно верно для расчетов по специальной теории относительности, где различия могут быть обнаружены только после нескольких десятичных знаков. Релятивистский эффект здесь велик (γ = 30,00γ = 30,00 размер 12 {ital «γ =» «30» «.» «00»} {}), и мы видим, что vv размер 12 {v} {} приближается ( не равняется) скорости света. Поскольку расстояние, измеренное космонавтом, намного меньше, космонавт может преодолеть его за гораздо меньшее время в своем кадре.

Люди могут быть отправлены на очень большие расстояния (тысячи или даже миллионы световых лет) и стареют всего на несколько лет в пути, если они путешествуют с чрезвычайно высокими скоростями.Но, как эмигранты прошлых веков, они навсегда покинут знакомую им Землю. Даже если бы они вернулись, на Земле прошли бы тысячи или миллионы лет, уничтожив большую часть того, что сейчас существует. Существует также более серьезное практическое препятствие для путешествия с такой скоростью; Для достижения таких высоких скоростей потребуются гораздо более высокие энергии, чем предсказывает классическая физика. Об этом пойдет речь в Relatavistic Energy.

Почему мы не замечаем сокращения длины в повседневной жизни? Расстояние до продуктового магазина, похоже, не зависит от того, переезжаем мы или нет.Изучив уравнение L = L01 − v2c2L = L01 − v2c2 size 12 {L = L rSub {size 8 {0}} sqrt {1 – {{v rSup {size 8 {2}}} по сравнению с {c rSup {size 8 { 2}}}}}} {}, мы видим, что при малых скоростях (v << cv << c size 12 {v »<<« c} {}) длины почти равны, классическое ожидание. Но сокращение длины вполне реально, если не наблюдается обычно. Например, заряженная частица, такая как электрон, движущаяся с релятивистской скоростью, имеет силовые линии электрического поля, сжатые вдоль направления движения, как это видит неподвижный наблюдатель.(См. [Ссылку].) Когда электрон проходит через детектор, такой как катушка с проволокой, его поле взаимодействует гораздо быстрее, эффект наблюдается на ускорителях частиц, таких как Стэнфордский линейный ускоритель (SLAC) длиной 3 км. Фактически, для электрона, движущегося по лучевой трубе в SLAC, ускоритель и Земля все движутся и сокращаются по длине. Релятивистский эффект настолько велик, что ускоритель находится всего в 0,5 м от электрона. На самом деле, направить электронный луч по трубе легче, поскольку для того, чтобы попасть в короткую трубу, не нужно направлять луч так точно, как по трубе длиной 3 км.Это снова экспериментальная проверка специальной теории относительности.

Силовые линии электрического поля высокоскоростной заряженной частицы сжимаются вдоль направления движения за счет сокращения длины. Это дает другой сигнал, когда частица проходит через катушку, экспериментально подтвержденный эффект сокращения длины.

Проверьте свое понимание

Частица движется через атмосферу Земли со скоростью 0,750c0,750c размером 12 {0 “.” «750» c} {}.Для наземного наблюдателя расстояние, которое он преодолевает, составляет 2,50 км. Как далеко перемещается частица в системе отсчета частицы?

Ответ

L = L01 − v2c2 = (2,50 км) 1− (0,750c) 2c2 = 1,65 км L = L01 − v2c2 = (2,50 км) 1− (0,750c) 2c2 = 1,65 км размер 12 {ital «L = L» rSub {size 8 {0}} sqrt {1 – {{v rSup {size 8 {2}}} больше {c rSup {size 8 {2}}}}} = (2 “.” “50 км”) sqrt { 1 – {{(0 “.” “750” c) rSup {size 8 {2}}} больше {c rSup {size 8 {2}}}}} = “1 ″”. ” «65 км»} {}

Кому объект кажется больше по длине: наблюдателю, движущемуся вместе с объектом, или наблюдателю, движущемуся относительно объекта? Какой наблюдатель измеряет правильную длину объекта?

Релятивистские эффекты, такие как замедление времени и сокращение длины, присутствуют в автомобилях и самолетах.Почему эти эффекты кажутся нам странными?

Предположим, что космонавт движется относительно Земли со скоростью, составляющей значительную долю скорости света. а) Замечает ли он, что его часы замедлились? б) Какое изменение хода часов, привязанных к Земле, он видит? (c) Кажется ли ему, что его корабль укорачивается? г) Как насчет расстояния между звездами, лежащими на линиях, параллельных его движению? (e) Согласны ли он и привязанный к Земле наблюдатель относительно его скорости относительно Земли?

Космический корабль длиной 200 м на борту движется мимо Земли в 0.970c0.970c размер 12 {0 “.” «970» c} {}. Какова его длина, измеренная наземным наблюдателем?

С какой скоростью должна проехать спортивная машина длиной 6,0 м, чтобы она казалась длиной всего 5,5 м?

(a) Как далеко проходит мюон в [link] по данным наблюдателя с Земли? б) Как далеко он проходит с точки зрения движущегося вместе с ним наблюдателя? Основывайте свои расчеты на его скорости относительно Земли и времени, в котором она живет (собственное время). (c) Убедитесь, что эти два расстояния связаны сокращением длины γ = 3.20γ = 3,20 размер 12 {курсив «γ =» 3 «.» «20»} {}.

(а) 1.387 км = 1.39 км

б 0.433 км

(c) L = L0γ = 1,387 × 103 м3,20 = 433,4 м = 0,433 км L = L0γ = 1,387 × 103 м3,20 = 433,4 м = 0,433 км

Таким образом, расстояния в частях (a) и (b) связаны между собой, когда γ = 3.20γ = 3.20.

(a) Сколько времени прожил бы мюон в [link], наблюдаемый на Земле, если бы его скорость была 0,0500c0,0500c размером 12 {0 “.” «0500» c} {}? б) Как далеко он мог бы продвинуться по Земле? (c) Какое расстояние это в системе отсчета мюона?

(a) Сколько времени нужно космонавту в [ссылка], чтобы путешествовать 4.30 св. Лет при 0,99944c0,99944c (измерено наземным наблюдателем)? б) Сколько времени это займет, по мнению космонавта? (c) Убедитесь, что эти два времени связаны посредством замедления времени с γ = 30,00γ = 30,00 размер 12 {курсив «γ =» «30» «.» «00»} {} как указано.

(a) 4.303 y (до четырех цифр, чтобы показать любой эффект)

б 0,1434 л

(в)
Δt

=

γΔt

0

⇒

.

γ

=

Δt

Δt

0

=

4

.

303 года

0

.

1434 л

=

30

.

0

Δt

=

γΔt

0

⇒

.

γ

=

Δt

Δt

0

=

4

.

303 года

0

.

1434 л

=

30

.

0

размер 12 {“Δt” = “γΔt” rSub {размер 8 {0}} drarrow γ = {{“Δt”} больше {“Δt” rSub {size 8 {0}}}} = {{4 “.”” 303 г. “} больше {0″. ” «1434 г»}} = {подчеркните {«30» «.» 0}}} {}

Таким образом, два времени связаны, когда
γ =

30

.

00

γ =

30

.

00

размер 12 {ital «γ =» «30» «.» «00»} {}
.

(a) Как быстро спортсмен должен бегать на 100 м, чтобы выглядеть на 100 ярдов в длину? б) Соответствует ли ответ тому факту, что релятивистские эффекты трудно наблюдать в обычных обстоятельствах? Объяснять.

Необоснованные результаты

(a) Найдите значение γγ size 12 {γ} {} для следующей ситуации. Астронавт измеряет длину своего космического корабля 25,0 м, а наземный наблюдатель – 100 м. б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?

(а) 0,250

(b) γγ размер 12 {γ} {} должен быть ≥1

(c) Земной наблюдатель должен измерять меньшую длину, поэтому неразумно предполагать большую длину.

Необоснованные результаты

Космический корабль движется прямо к Земле со скоростью 0,800c0,800c размером 12 {0 “.” «800» c} {}. Астронавт на борту утверждает, что может послать к Земле канистру размером 1,20c1,20c размером 12 {1 “.” «20» c} {} относительно Земли. (а) Рассчитайте скорость, которую канистра должна иметь относительно космического корабля. б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?

Глоссарий

правильная длина

L0L0 размер 12 {L rSub {размер 8 {0}}} {}; расстояние между двумя точками, измеренное наблюдателем, находящимся в состоянии покоя, относительно обеих точек; Земные наблюдатели измеряют правильную длину при измерении расстояния между двумя точками, которые неподвижны относительно Земли

Уменьшение длины

LL размер 12 {L} {}, сокращение измеренной длины объекта, движущегося относительно кадра наблюдателя: L = L01 − v2c2 = L0γL = L01 − v2c2 = L0γ size 12 {ital “L = L” rSub { размер 8 {0}} sqrt {1 – {{v rSup {size 8 {2}}} больше {c rSup {size 8 {2}}}}} = {{L rSub {size 8 {0}}} больше {γ}}} {}

.