Универсальный внешний накопитель для всех iOS-устройств, совместим с PC/Mac, Android
Header Banner
8 800 100 5771 | +7 495 540 4266
c 9:00 до 24:00 пн-пт | c 10:00 до 18:00 сб

Формула нахождения i: Ошибка: 404 Материал не найден

0 Comments

Содержание

Формулы по физике 9 класса. Все формулы по физике за 9 класс с пояснениями и определениями

ЗаконФормулаОпределениеЕдиницы измерения
ЗАКОНЫ ВЗАИМОДЕЙСТВИЯ И ДВИЖЕНИЯ ТЕЛ
Вычисление перемещения АВ2 = АС2 + ВС2Перемещение – вектор, соединяющий начальную точку движения тела с его конечной точкой.
Проекция вектора перемещенияSx = x2 – x1x1 – начальная координата, [м]
x2 – конечная координата, [м]
Sx – перемещение, [м]
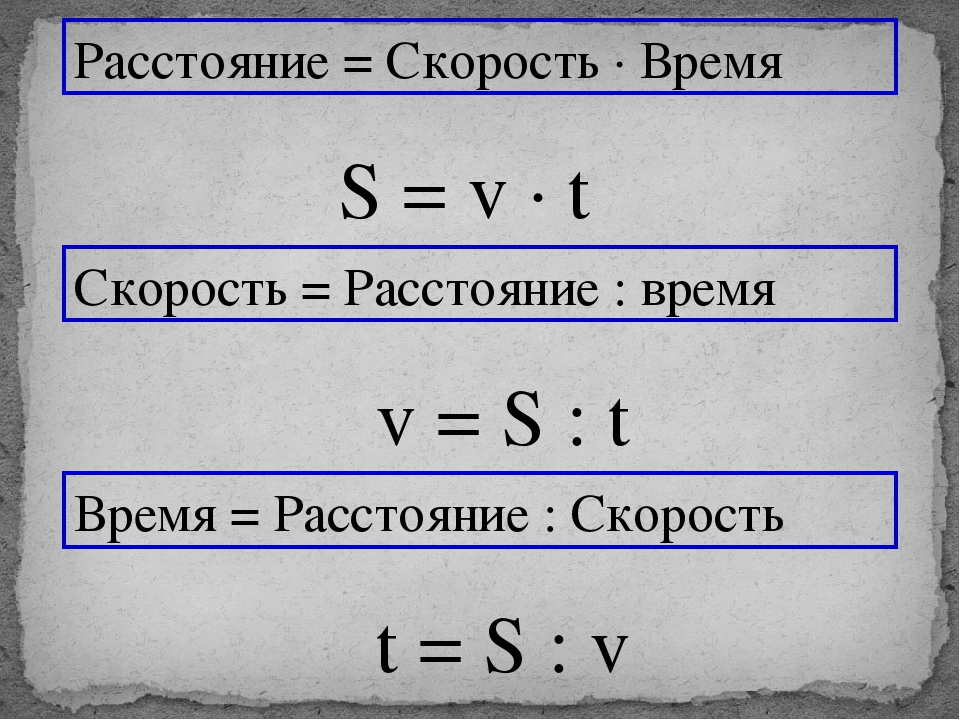
Формула расчета скорости движения телаv = s/tСкорость – физическая величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло.
v – скорость, [м/с]
s – путь, [м]
t – время, [c]
Уравнение движенияx = x0 + vxtx0 – начальная координата, [м] x – конечная координата, [м] v – скорость, [м/с] t – время, [c]
Формула для вычисления ускорения движения телаa = v – v0⃗/tУскорение – физическая величина, которая характеризует быстроту изменения скорости.a – ускорение, [м/с2]
v – конечная скорость, [м/с]
v0 – начальная скорость, [м/с]
t – время, [c]
Уравнение скоростиv = v0⃗+ atv – конечная скорость, [м/с]
v0 – начальная скорость, [м/с]
a – ускорение, [м/с2]
t – время, [c]
Уравнение ГалилеяS = v0t + at2/2S – перемещение, [м]
v – конечная скорость, [м/с]
v0 – начальная скорость, [м/с]
a – ускорение, [м/с2]
t – время, [c]
Закон изменения координаты тела при прямолинейном равноускоренном движенииx = x0 + v0t + at2/2x0 – начальная координата, [м]
x – конечная координата, [м]
v – конечная скорость, [м/с]
v0 – начальная скорость, [м/с]
a – ускорение, [м/с2]
t – время, [c]
Первый закон НьютонаЕсли на тело не действуют никакие тела либо их действие скомпенсировано, то это тело будет находиться в состоянии покоя или двигаться равномерно и прямолинейно.
Второй закон Ньютонаa = F ⃗/mУскорение, приобретаемое телом под действием силы, прямо пропорционально величине этой силы и обратно пропорционально массе тела.a – ускорение, [м/с
2]
F – сила, [Н]
m – масса, [кг]
Третий закон Ньютона|F1⃗ |=|F2⃗|
F11 ⃗ = -F2⃗		Сила, с которой первое тело действует на второе, равна по модулю и противоположна по направлению силе, с которой второе тело действует на первоеF – сила, [Н]
Формула для вычисления высоты, с которой падает телоH=gt2/2Н – высота, [м]
t – время, [c]
g ≈ 9,81 м/с2 – ускорение свободного падения
Формула для вычисления высоты при движении вертикально вверхh=v0t – gt2/2h – высота, [м]
v0 – начальная скорость, [м/с]
t – время, [c]
g ≈ 9,81 м/с2 – ускорение свободного падения
Формула для вычисления веса тела при движении вверх с ускорениемP = m (g + a) P – вес тела, [Н]
m – масса тела, [кг]
g ≈ 9,81 м/с2 – ускорение свободного падения
a – ускорение тела, [м/с2]
Формула для вычисления веса тела при движении вниз с ускорениемP = m (g – a)P – вес тела, [Н]
m – масса тела, [кг]
g ≈ 9,81 м/с2 – ускорение свободного падения
a – ускорение тела, [м/с2]
Формула законаF = Gm1m2/r2Закон всемирного тяготения: два тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.F – сила, [Н]
G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная
m – масса тела, [кг]
r – расстояние между телами, [м]
Формула расчета ускорения свободного падения на разных планетахg = G Mпл/Rпл2g – ускорение свободного падения, [м/с2]
G = 6,67 · 10-11 [Н·м2/кг2 – гравитационная постоянная
M – масса планеты, [кг]
R – радиус планеты, [м]
Формула расчета ускорения свободного паденияg = GM3/(R3+H)2g – ускорение свободного падения, [м/с2]
G = 6,67 · 10-11 [Н·м2/кг2 – гравитационная постоянная
M – масса Земли, [кг]
R – радиус Земли, [м]
Н – высота тела над Землей, [м]
Формула расчета центростремительного ускоренияа=υ2/ra – центростремительное ускорение, [м/с2]
v – скорость, [м/с]
r – радиус окружности, [м]
Формула периода движения по окружностиT = 1/ν = (2πr)/υ = t/NТ – период, [с]
ν – частота вращения,
[с-1]
t – время, [с]
N – число оборотов
Формула расчета угловой скоростиω = 2π/T = 2πν = υrω – угловая скорость, [рад/с]
υ – линейная скорость, [м/с]
Т – период, [с]
ν – частота вращения, [с-1]
r – радиус окружности, [м]
Формула импульса телаp = mvИмпульсом называют произведение массы тела на его скорость.p – импульс тела, [кг·м/с]
m – масса тела, [кг]
υ – скорость, [м/с]
Формула закона сохранения импульсаp1 + p2 = p1’ + p2’ m1v + m
2u = m1v’ + m2u’		Закон сохранения импульса: в замкнутой системе импульс всех тел остается величиной постоянной.p – импульс тела, [кг·м/с]
m – масса тела, [кг]
υ – скорость 1-го тела, [м/с]
u – скорость 2-го тела, [м/с]
Формула импульса силыP = Ftp – импульс тела, [кг·м/с]
F – сила, [Н]
t – время, [c]
Формула механической работыA = FsМеханическая работа – физическая величина, равная произведению модуля силы на величину перемещения тела в направлении действия силыA – работа, [Дж]
F – сила, [Н]
s – пройденный путь, [м]
Формула расчета мощностиN = A/tМощность – физическая величина, характеризующая быстроту совершения механической работы.N – мощность, [Вт]
A – работа, [Дж]
t – время, [c]
Формула для нахождения коэффициента полезного действия (КПД)η = Aп/Aз∙100КПД – отношение полезной работы к затраченной работе.Aп – полезная работа, [Дж]
Aз – затраченная работа, [Дж]
Формула расчета потенциальной энергииEk = mv2/2Кинетическая энергия – энергия, которой обладает тело вследствие своего движения.Ek – кинетическая энергия тела, [Дж]
m – масса тела, [кг]
v – скорость движения тела, [м/с]
Формула закона сохранения полной механической энергииmv12/2 + mgh1 = mv22/2 + mgh2Закон сохранения полной механической энергии: полная механическая энергия тела, на которое не действуют силы трения и сопротивления, в процессе его движения остается неизменной.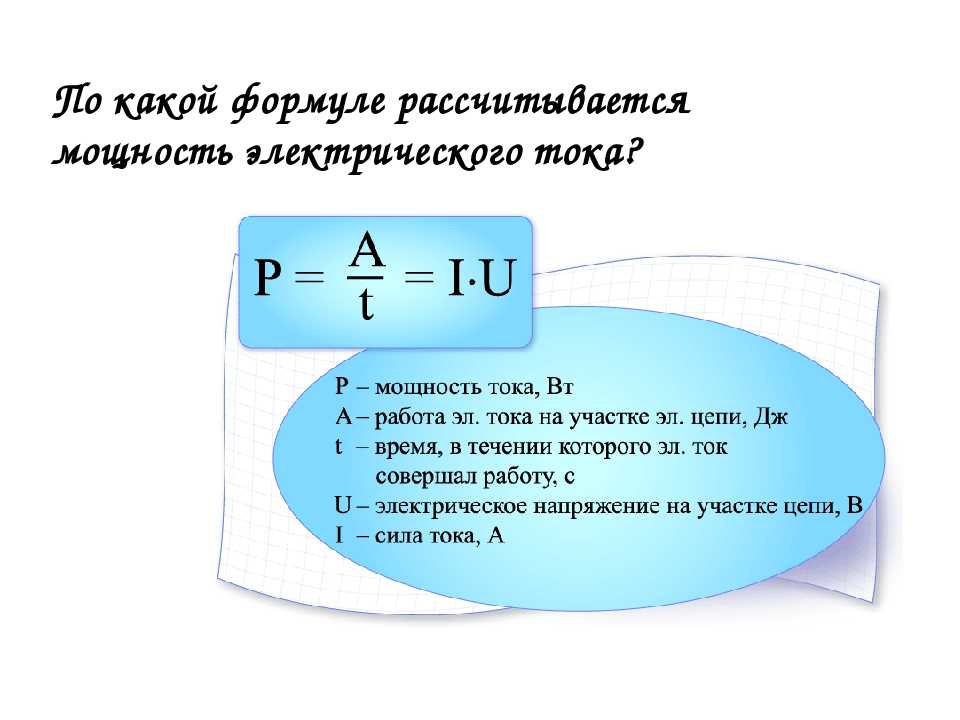
m – масса тела, [кг]
g ≈ 9,81 м/с2 – ускорение свободного падения
v1 – скорость тела в начальный момент времени, [м/с]
v2 – скорость тела в конечный момент времени, [м/с]
h1 – начальная высота, [м]
h2 – конечная высота, [м]
Формула силы тренияFтр = μmgСила трения – сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению.Fтр – сила трения, [Н]
μ – коэффициент трения
m – масса тела, [кг]
g ≈ 9,81 м/с2 – ускорение свободного падения
Уравнение колебанийx = A cos (ωt + φ0)А – амплитуда колебаний, [м]
х – смещение, [м]
t – время, [c]
ω – циклическая частота, [рад/с]
φ0 – начальная фаза, [рад]
Формула периодаT = 1/ν = 2πr/υ = t/NТ – период, [с]
ν – частота колебании, [с-1]
t – время колебании, [с]
N – число колебаний
Формула периода для математического маятникаT= 2π √L/gТ – период, [с]
g ≈ 9,81 м/с2 – ускорение свободного падения
L – длина нити, [м]
Формула периода для пружинного маятникаT = 2π √m/KТ – период, [с]
m – масса груза, [кг]
К – жесткость пружины, [Н/м]
Формула длины волныλ = υТ = υ/νλ – длина волны, [м]
Т – период, [с]
ν – частота, [с-1]
υ – скорость волны, [м/с]
Формула расчета плотности телаρ=m/VПлотность вещества – показывает, чему равна масса вещества в единице объема.
ρ – плотность, [кг/м3]
m – масса, [кг]
V – объем тела, [м3]
Формула гидростатического давления жидкостиp = ρghp – давление, [Па], [Н/м]
ρ – плотность жидкости, [кг/м3]
g ≈ 9,81 м/с2 – ускорение свободного падения
h – высота столба жидкости, [м]
Формула силы АрхимедаFA = ρgVЗакон Архимеда: на всякое тело, погруженное в жидкость (газ(, действует выталкивающая сила, равная весу вытесненной жидкости (газа).FА – сила Архимеда, [Н]
ρ – плотность жидкости или газа [кг/м3]
g ≈ 9,81 м/с2 – ускорение свободного падения
V – объем тела, [м3]
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
Формула расчета силы АмпераFA = BIL sinαЗакон Ампера: сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником.FA – сила Ампера, [Н]
В – магнитная индукция, [Тл]
I – сила тока, [А]
L – длина проводника, [м]
Формула расчета силы ЛоренцаFл = q B υ sinαСила Лоренца – сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле. Она равна произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью движения частицы.Fл – сила Лоренца, [Н]
q – заряд, [Кл]
В – магнитная индукция, [Тл]
υ – скорость движения заряда, [м/с]
Формула радиуса движения частицы в магнитном полеr = mυ/qBr – радиус окружности, по которой движется частица в магнитном поле, [м]
m – масса частицы, [кг]
q – заряд, [Кл]
В – магнитная индукция, [Тл]
υ – скорость движения заряда, [м/с]
Формула для вычисления магнитного потокаФ = B S cosαФ – магнитный поток, [Вб]
В – магнитная индукция, [Тл]
S – площадь контура, [м2]
Формула для вычисления величины зарядаq = ItЗаряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику.q – заряд, [Кл]
I – сила тока, [А]
t – время, [c]
Закон Ома для участка цепиI=U/RЗакон Ома: сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.I – сила тока, [А]
U – напряжение, [В]
R – сопротивление, [Ом]
Формула для вычисления удельного сопротивления проводникаR = ρ * L/S
ρ = R * S/L		Удельное сопротивление – величина, характеризующая электрические свойства вещества, из которого изготовлен проводник.ρ – удельное сопротивление вещества, [Ом·мм2/м]
R – сопротивление, [Ом]
S – площадь поперечного сечения проводника, [мм2]
L – длина проводника, [м]
Законы последовательного соединения проводниковI = I1 = I2
U = U1 + U2
Rобщ = R1 + R2		Последовательным соединением называется соединение, когда элементы идут друг за другом.I – сила тока, [А]
U – напряжение, [В]
R – сопротивление, [Ом]
Законы параллельного соединения проводниковU = U1 = U2
I = I1 + I2
1/Rобщ = 1/R1 +1/R2		Параллельным соединением проводников называется такое соединение, при котором начала и концы проводников соединяются вместе.I – сила тока, [А]
U – напряжение, [В]
R – сопротивление, [Ом]
Формула для вычисления величины заряда.q = ItЗаряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику.q – заряд, [Кл]
I – сила тока, [А]
t – время, [c]
Формула для нахождения работы электрического токаA = Uq
A = UIt		Работа – это величина, которая характеризует превращение энергии из одного вида в другой, т.е. показывает, как энергия электрического тока, будет превращаться в другие виды энергии – механическую, тепловую и т. д.
Работа электрического поля – это произведение электрического напряжения на заряд, протекающий по проводнику. Работа, совершаемая для перемещения электрического заряда в электрическом поле.		A – работа электрического тока, [Дж]
U – напряжение на концах участка, [В]
q – заряд, [Кл]
I – сила тока, [А]
t – время, [c]
Формула электрической мощностиP = A/t
P = UI
P = U2/R		Мощность – работа, выполненная в единицу времени.P – электрическая мощность, [Вт]
A – работа электрического тока, [Дж]
t – время, [c]
U – напряжение на концах участка, [В]
I – сила тока, [А]
R – сопротивление, [Ом]
Формула закона Джоуля-ЛенцаQ = I2RtЗакон Джоуля-Ленца: при прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику.Q – количество теплоты, [Дж]
I – сила тока, [А];
t – время, [с].
R – сопротивление, [Ом].
Закон отражения светаЛуч падающий, луч отраженный и перпендикуляр, восставленный в точку падения луча, лежат в одной плоскости, при этом угол падения луча равен углу отражения луча.
Закон преломленияsinα/sinγ = n2/n1При увеличении угла падения увеличивается и угол преломления, то есть при угле падения, близком к 90°, преломлённый луч практически исчезает, а вся энергия падающего луча переходит в энергию отражённого.n – показатель преломления одного вещества относительно другого
Формула вычисления абсолютного показателя преломления веществаn = c/vАбсолютный показатель преломления вещества – величина, равная отношению скорости света в вакууме к скорости света в данной среде.n – абсолютный показатель преломления вещества
c – скорость света в вакууме, [м/с]
v – скорость света в данной среде, [м/с]
Закон Снеллиусаsinα/sinγ = v1/v2 = nЗакон Снеллиуса (закон преломления света): отношение синуса угла падения к синусу угла преломления есть величина постоянная.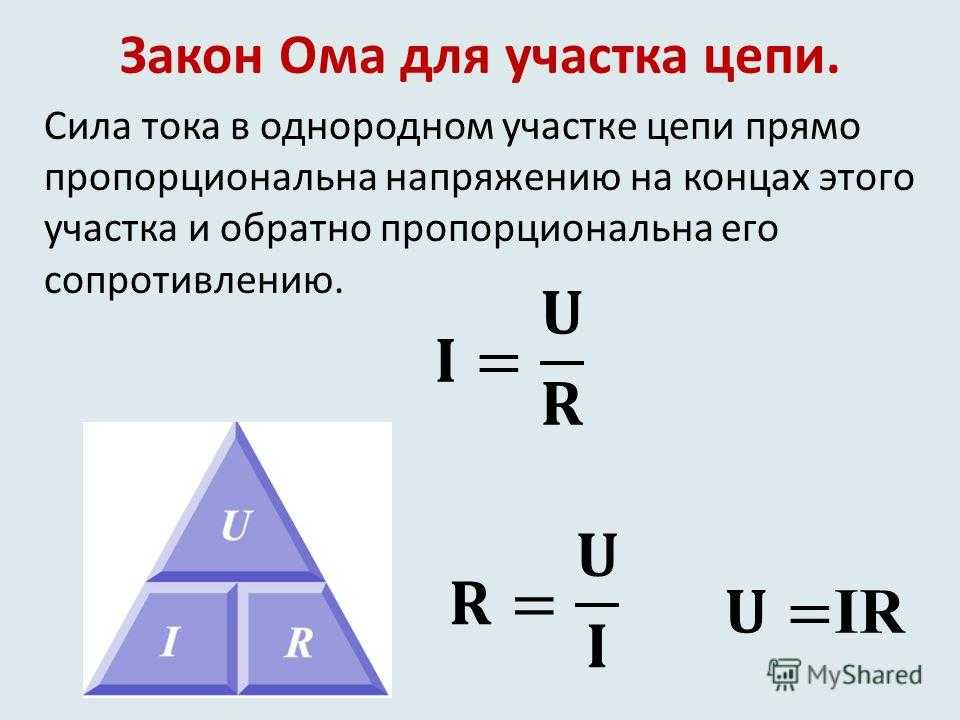n – показатель преломления одного вещества относительно другого v – скорость света в данной среде, [м/с]
Показатель преломления средыsinα/sinγ = nОтношение синуса угла падения к синусу угла преломления есть величина постоянная.n – показатель преломления среды
Формула оптической силы линзыD = 1/FОптическая сила линзы – способность линзы преломлять лучи.D – оптическая сила линзы, [дптр]
F – фокусное расстояние линзы, [м]
Формула тонкой линзы1/F = 1/d + 1/fF – фокусное расстояние линзы, [м]
d – расстояние от предмета до линзы, [м]
f – расстояние от линзы до изображения, [м]
СТРОЕНИЕ АТОМА И АТОМНОГО ЯДРА
Массовое числоM = Z + NM – массовое число
Z – число протонов (электронов), зарядовое число
N – число нейтронов
Формула массы ядраМя = МА – ZmeMя – масса ядра, [кг]
МА – масса изотопа , [кг]
me – масса электрона, [кг]
Формула дефекта масс∆m = Zmp+ Nmn – MЯДефект масс – разность между суммой масс покоя нуклонов, составляющих ядро данного нуклида, и массой покоя атомного ядра этого нуклида.∆m – дефект масс, [кг]
mp – масса протона, [кг]
mn – масса нейтрона, [кг]
Формула энергии связиЕсвязи = ∆m c2Энергия связи ядра – минимальная энергия, необходимая для того, чтобы разделить ядро на составляющие его нуклоны (протоны и нейтроны).Есвязи – энергия связи, [Дж]
m – масса, [кг]
с = 3·108м/с – скорость света
Альфа распадM/Z * X → 4/2 * α + M/Z – 4/2 * Y

Формулы и Задачи (Информатика 10) – Школа N61 г.Ульяновска

Формулы

N = 2i

N – мощность алфавита (количество знаков в алфавите)
i – информационный вес символа алфавита (количество информации в одном символе)

I = K * i

I – количество информации, содержащееся в выбранном сообщении (информационный объем сообщения)
K – число символов в сообщении
i – информационный вес символа (количество информации в одном символе)

Q = NL

Q – количество разных сообщений
N – количество символов
L – длина сообщения

Формула Хартли:

I = log2N

I – количество информации, содержащееся в выбранном сообщении
N – количество сообщений

Римская система счисления

I – 1 (палец),
V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони),
L – 50,
C – 100 (Centum),
D – 500 (Demimille),
M – 1000 (Mille)

Перевод чисел из других систем счисления в десятичную систему счисления

Развернутая запись целого числа:

a3a2a1a0 = a3 * p3 + a2 * p2 + a1 * p1 + a0 * p0

Правило перевода числа из любой системы счисления в десятичную систему счисления – умножаем каждую цифру исходного числа на основание системы счисления в степени разряда, в котором находится эта цифра, а затем всё складываем.

Запись через схему Горнера:

a3a2a1a0 = ((a3 * p + a2) * p + a1) * p + a0

p – основание системы счисления в котором представлено число.

Пример:

637510 = 6 * 103 + 3 * 102 + 7 * 101 + 5 * 100
637510 = ((6 * 10 + 3) * 10 + 7) * 10 + 5
12345 = 1 * 53 + 2 * 52 + 3 * 51 + 4 * 50 = 19410
12345 = ((1 * 5 + 2) * 5 + 3) * 5 + 4 = 19410


Развернутая запись дробного числа:

0,a1a2a3a4 = a1*p-1 + a2*p-2 + a3*p-3 + a4*p-4


Запись через схему Горнера:

0,a1a2a3a4 = p-1 * (a1 + p-1 * (a2 + p-1 * (a3 + p-1 * a4)))
p * (0,a1a2a3a4) = a1 + p-1 * (a2 + p-1 * (a3 + p-1 * a4))

p – основание системы счисления в котором представлено число.

Пример:

0,6375 = 6 * 10-1 + 3 * 10-2 + 7 * 10-3 + 5 * 10-4
0,6375 = 10-1 * (6 + 10-1 * (3 + 10-1 * (7 + 10-1 * 5)))
0,12345 = 1 * 5-1 + 2 * 5-2 + 3 * 5-3 + 4 * 5-4
0,12345 = 5-1 * (1 + 5-1 * (2 + 5-1 * (3 + 5-1 * 4)))


Задачи

Алфавитный подход к измерению количества информации

Определить количество информации в 10 страницах текста (на каждой странице 32 строки по 64 символа) при использовании алфавита из 256 символов.

  1. информационная ёмкость символа: 256 = 28      =>>      i = 8 бит = 1 байт
  2. количество символов на странице:
    32 * 64 = 25 * 26 = 211
  3. общее количество символов:
    L = 10 * 211
  4. информационный объём сообщения:
    I = L * i = 10 * 211 * 1 байт = 20 Кбайт

Системы счисления

  X10     X16     X8       X2
 0      0      0        0  1      1      1        1  2      2      2       10  3      3      3       11  4      4      4      100  5      5      5      101  6      6      6      110  7      7      7      111  8      8     10     1000  9      9     11     1001 10      A     12     1010 11      B     13     1011 12      C     14     1100 13      D     15     1101 14      E     16     1110 15      F     17     1111 16     10     20    10000 17     11     21    10001 18     12     22    10010 19     13     23    10011 20     14     24    10100 21     15     25    10101 22     16     26    10110 23     17     27    10111 24     18     30    11000 25     19     31    11001 26     1A     32    11010 27     1B     33    11011 28     1C     34    11100 29     1D     35    11101 30     1E     36    11110 31     1F     37    11111 32     20     40   100000

Логические операции

Логической операцией называется выбор решения (действия), исходя из  заданной ситуации, определяемой набором факторов (условий).
Зависимости между логическими функциями (операциями) и логическими переменными устанавливаются с помощью таблиц истинности. Используются следующие логические операции: НЕ, И, ИЛИ, исключающее ИЛИ, тождество.


Логическая операция НЕ (инверсия, операция логического отрицания). Действие, которое определяется операцией НЕ произойдет, если отсутствует фактор его определяющий.

Таблица истинности для операции НЕ имеет вид:

A
0 1
1 0

Действие, связанное с операцией НЕ можно записать следующим образом:

Логическая операция И (конъюнкция, операция логического умножения). Действие, которое определяется операцией И произойдет, если выполняются все влияющие на него факторы (условия). B

Логическая операция ИЛИ (дизъюнкция, операция логического сложения). Действие, которое определяется операцией ИЛИ произойдет, если выполняются хотя бы одно (любое), определяющее его условие.

Таблица истинности для операции ИЛИ имеет вид:

A B X=A v B
0 0 0
0 1 1
1 0 1
1 1 1

Действие, связанное с операцией ИЛИ можно записать следующим образом:

X = A + B = A v B

Логическая операция Исключающее ИЛИ. Операция Исключающее ИЛИ осуществляет суммирование по модулю два т.е. без учета переноса в старший разряд.

Таблица истинности имеет вид:

A B X=AB
0 0 0
0 1 1
1 0 1
1 1 0

Действие, связанное с операцией Исключающее ИЛИ можно записать следующим образом:

X = A B

Действие, связанное с операцией Импликации можно записать следующим образом:

X = A → B

Таблица истинности Импликации имеет вид:

A B A → B
0 0 1
0 1 1
1 0 0
1 1 1

Операция тождество. Операция тождество определяет тождественность аргументов.

Таблица истинности для операции тождество имеет вид:

A B A Ξ B
0 0 1
0 1 0
1 0 0
1 1 1

Действие, связанное с операцией тождество можно записать следующим образом:

X = A Ξ B

  


Диаграммы Венна (круги Эйлера)


 

Поиск номера сети

Необходимо найти номер сети по IP-адресу 12. 16.196.10 и маске 255.255.224.0.

маска сети 255.255.224.0  
IP-адрес 12.16.196.10 – ip-адрес (узла, компьютера и т.п.)
IP-адрес 0000 1100.0001 0000.1100 0100.0000 1010
маска сети 1111 1111.1111 1111.1110 0000.0000 0000  
адрес сети 0000 1100.0001 0000.110x xxxx.xxxx xxxx – эта часть относится к адресу сети – она взята из ip-адреса, но взяты те цифры, напротив которых стоят единицы остальные цифры справа надо дополнить нулями, чтобы общее число цифр стало равным 32. Получится следующее:
адрес сети 0000 1100.0001 0000.1100 0000.0000 0000 – полный адрес сети
теперь каждую октаду (последовательность из 8 цифр, разделены точками) переводим в десятичный вид. Получаем:
адрес сети 12.16.192.0 – полный адрес сети (в десятичном виде)
 

Предварительное исчисление: нахождение общей формулы для n-го члена Онлайн-практика)

Исследуйте книгу Купить на Amazon

В какой-то момент ваш учитель математического анализа попросит вас найти общую формулу для n -го члена арифметической прогрессии, не зная ни первого члена, ни общей разности. В этом случае вам будут даны два термина (не обязательно последовательные), и вы будете использовать эту информацию, чтобы найти а 1 и d. Шаги следующие: Найдите общую разность d , напишите конкретную формулу для данной последовательности, а затем найдите искомый термин.

Например, чтобы найти общую формулу арифметической прогрессии, где a 4 = –23 и a 22 = 40, выполните следующие действия:

  1. Найдите общее различие.

    Вы должны быть изобретательны в поиске общего различия для этих типов задач.

    1. a. Используйте формулу a n = a 1 + ( n – 1) d , чтобы составить два уравнения, использующих данную информацию.

      Для первого уравнения вы знаете, что когда n = 4, a n = –23:

      –23 = а 1 + (4 – 1) д

      –23 = а 1 + 3 д

      Для второго уравнения вы знаете, что когда n = 22, a n = 40:

      40 = а 1 + (22 – 1) д

      40 = а 1 + 21 д

    2. b.Составьте систему уравнений и решите d.

      Система выглядит так:

      Для решения системы можно использовать исключение или замену. Исключение работает хорошо, потому что вы можете умножить любое уравнение на -1 и сложить два вместе, чтобы получить 63 = 18 д. Следовательно, d = 3,5.

  2. Напишите формулу для определенной последовательности.

    Этот шаг требует небольшой работы.

    1. a.Подставьте d в одно из уравнений, чтобы найти a 1 .

      Вы можете подставить 3,5 обратно в любое уравнение:

      –23 = a 1 + 3(3,5), или a 1 = –33,5.

    2. b. Используйте a 1 и d , чтобы найти общую формулу для a n .

      Этот шаг становится простым трехступенчатым упрощением:

      а н = –33,5 + ( н – 1)3,5

      a n = –33,5 + 3,5 n – 3,5

      а п = 3,5 п – 37

  3. Найдите искомый термин.

    В этом примере вас не просили найти какой-либо конкретный термин (всегда читайте инструкции!), но если да, то вы можете подставить это число вместо n , а затем найти искомый термин.

Эту статью можно найти в категории:

  • Предварительное вычисление,

Используйте Excel в качестве калькулятора

Введение в Excel

Справка по Excel и обучение

Введение в Excel

Введение в Excel

Используйте Excel в качестве калькулятора

  • Создать новую книгу
    Статья
  • Вставка или удаление рабочего листа
    Статья
  • Переместить или скопировать рабочие листы или данные рабочего листа
    Статья
  • Печать листа или книги
    Статья
  • Используйте Excel в качестве калькулятора
    Статья
  • Автоматическое заполнение данных в ячейках листа
    Статья
  • Создать раскрывающийся список
    Статья

Следующий: Строки и столбцы

Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019Excel 2016 Excel 2013 Excel 2010 Excel 2007 Больше. ..Меньше

Вместо того, чтобы использовать калькулятор, используйте Microsoft Excel, чтобы сделать математику!

Вы можете вводить простые формулы для сложения, деления, умножения и вычитания двух или более числовых значений. Или используйте функцию автосуммы, чтобы быстро суммировать ряд значений, не вводя их вручную в формулу. Создав формулу, вы можете скопировать ее в соседние ячейки — не нужно создавать одну и ту же формулу снова и снова.

Вычитание в Excel

Умножение в Excel

Разделить в Excel

Узнайте больше о простых формулах

Все записи формул начинаются со знака равенства ( = ). Для простых формул просто введите знак равенства, за которым следуют числовые значения, которые вы хотите вычислить, и математические операторы, которые вы хотите использовать – знак плюса ( + ) для сложения, минус ( – ) для вычитания, звездочка ( * ) для умножения и косая черта ( / ) для деления. Затем нажмите клавишу ВВОД, и Excel мгновенно рассчитает и отобразит результат формулы.

Например, если ввести = 12,99+16,99 в ячейку C5 и нажать клавишу ВВОД, Excel вычислит результат и отобразит в этой ячейке 29,98.

Формула, которую вы вводите в ячейку, остается видимой в строке формул, и вы можете видеть ее всякий раз, когда выбрана эта ячейка.

Важно:  Хотя функция СУММ существует, функции ВЫЧИТАТЬ нет. Вместо этого используйте в формуле оператор минус (-); например, =8-3+2-4+12. Или вы можете использовать знак минус, чтобы преобразовать число в его отрицательное значение в функции СУММ; например, формула =СУММ(12,5,-3,8,-4) использует функцию СУММ для добавления 12, 5, вычитания 3, добавления 8 и вычитания 4 в указанном порядке.

Использовать автосумму

Самый простой способ добавить формулу СУММА на лист — использовать автосумму. Выберите пустую ячейку непосредственно над или под диапазоном, который вы хотите суммировать, и на вкладках ленты Главная или Формула щелкните Автосумма > Сумма . AutoSum автоматически определит диапазон для суммирования и построит для вас формулу. Это также работает по горизонтали, если вы выберете ячейку слева или справа от диапазона, который вам нужно суммировать.

Примечание. Автосумма не работает для несмежных диапазонов.

Автосумма по вертикали

На рисунке выше функция автосуммирования автоматически определяет ячейки B2:B5 как диапазон для суммирования. Все, что вам нужно сделать, это нажать ENTER, чтобы подтвердить это. Если вам нужно добавить/исключить больше ячеек, вы можете удерживать клавишу Shift + клавишу со стрелкой по вашему выбору, пока ваш выбор не будет соответствовать тому, что вы хотите. Затем нажмите Enter, чтобы завершить задачу.

Руководство по функциям Intellisense: плавающий тег SUM(number1,[number2], …) под функцией является ее руководством по Intellisense. Если щелкнуть SUM или имя функции, оно изменится на синюю гиперссылку на раздел справки для этой функции. Если щелкнуть отдельные функциональные элементы, их репрезентативные части в формуле будут выделены. В этом случае будут выделены только B2:B5, так как в этой формуле есть только одна ссылка на число. Тег Intellisense появится для любой функции.

Автосумма по горизонтали

Подробнее читайте в статье о функции СУММ.

Не переписывайте одну и ту же формулу

Создав формулу, вы можете скопировать ее в другие ячейки — не нужно переписывать ту же формулу. Вы можете либо скопировать формулу, либо использовать маркер заполнения, чтобы скопировать формулу в соседние ячейки.

Например, когда вы копируете формулу из ячейки B6 в ячейку C6, формула в этой ячейке автоматически изменяется, чтобы обновить ссылки на ячейки в столбце C.

 При копировании формулы убедитесь, что ссылки на ячейки указаны правильно. Ссылки на ячейки могут измениться, если они имеют относительные ссылки. Дополнительные сведения см. в статье Копирование и вставка формулы в другую ячейку или лист.

Что можно использовать в формуле для имитации клавиш калькулятора?

Ключ калькулятора

Метод Excel

Описание, пример

Результат

+ (плюс)

+ (плюс)

Используйте в формуле для сложения чисел. Пример: =4+6+2

12

– (клавиша минус)

– (минус)

Используйте в формуле для вычитания чисел или для обозначения отрицательного числа.

Пример: =18-12

Пример: =24*-5 (24 умножить на минус 5)


6

-120

x (клавиша умножения)

* (звездочка; также называется «звездочка»)

Используйте в формуле для умножения чисел. Пример: =8*3

24

÷ (клавиша разделения)

/ (косая черта)

Используется в формуле для деления одного числа на другое. Пример: =45/5

9

% (клавиша процентов)

% (проценты)

Используйте в формуле * для умножения на процент. Пример: =15%*20

3

√ (квадратный корень )

SQRT (функция)

Используйте функцию КОРЕНЬ в формуле, чтобы найти квадратный корень числа.

Больше новостей

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

© 2019 «Tree of life» — Производство и продажа аксессуаров для iPhone

* iPad, iPhone, iPod, iPod classic, iPod nano, iPod shuffle и iPod touch являются торговыми марками компании Apple Inc, зарегистрированными в США и других странах. Apple Store является торговой маркой компании Apple Inc. PhotoFast является зарегистрированной торговой маркой компании PhotoFast Company Limited.

Вступайте в клуб любителей