Формулы прямолинейного равноускоренного движения
☰
При прямолинейном равноускоренном движении тело
- двигается вдоль условной прямой линии,
- его скорость постепенно увеличивается или уменьшается,
- за равные промежутки времени скорость меняется на равную величину.
Например, автомобиль из состояния покоя начинает двигаться по прямой дороге, и до скорости, скажем, в 72 км/ч он двигается равноускоренно. Когда заданная скорость достигнута, то авто движется без изменения скорости, т. е. равномерно. При равноускоренном движении его скорость возрастала от 0 до 72 км/ч. И пусть за каждую секунду движения скорость увеличивалась на 3,6 км/ч. Тогда время равноускоренного движения авто будет равно 20 секундам. Поскольку ускорение в СИ измеряется в метрах на секунду в квадрате, то надо ускорение 3,6 км/ч за секунду перевести в соответствующие единицы измерения. Оно будет равно (3,6 * 1000 м) / (3600 с * 1 с) = 1 м/с2.
Допустим, через какое-то время езды с постоянной скоростью автомобиль начал тормозить, чтобы остановиться. Движение при торможении тоже было равноускоренным (за равные промежутки времени скорость уменьшалась на одинаковую величину). В данном случае вектор ускорения будет противоположен вектору скорости. Можно сказать, что ускорение отрицательно.
Итак, если начальная скорость тела нулевая, то его скорость через время в t секунд будет равно произведению ускорения на это время:
v = at
При падении тела «работает» ускорение свободного падения, и скорость тела у самой поверхности земли будет определяться по формуле:
v = gt
Если известна текущая скорость тела и время, которое понадобилось, чтобы развить такую скорость из состояния покоя, то можно определить ускорение (т. е. как быстро менялась скорость), разделив скорость на время:
a = v/t
Однако тело могло начать равноускоренное движение не из состояния покоя, а уже обладая какой-то скоростью (или ему придали начальную скорость).
v = v0 + at
Однако, если камень бросали вверх. То начальная его скорость направлена вверх, а ускорение свободного падения вниз. То есть вектора скоростей направлены в противоположные стороны. В этом случае (а также при торможении) произведение ускорения на время надо вычитать из начальной скорости:
v = v0 – at
at = v – v0
a = (v – v0)/t
В случае торможения:
at = v0 – v
a = (v0 – v)/t
В случае, когда тело равноускоренно останавливается, то в момент остановки его скорость равна 0. Тогда формула сокращается до такого вида:
Тогда формула сокращается до такого вида:
a = v0/t
Зная начальную скорость тела и ускорение торможения, определяется время, через которое тело остановится:
t = v0/a
Теперь выведем формулы для пути, которое тело проходит при прямолинейном равноускоренном движении. Графиком зависимость скорости от времени при прямолинейном равномерном движении является отрезок, параллельный оси времени (обычно берется ось x). Путь при этом вычисляется как площадь прямоугольника под отрезком. То есть умножением скорости на время (s = vt). При прямолинейном равноускоренном движении графиком является прямая, но не параллельная оси времени. Эта прямая либо возрастает в случае ускорения, либо убывает в случае торможения. Однако путь также определяется как площадь фигуры под графиком.
При прямолинейном равноускоренном движении эта фигура представляет собой трапецию. Ее основаниями являются отрезок на оси y (скорость) и отрезок, соединяющий точку конца графика с ее проекцией на ось x. Боковыми сторонами являются сам график зависимости скорости от времени и его проекция на ось x (ось времени). Проекция на ось x — это не только боковая сторона, но еще и высота трапеции, т. к. перпендикулярна его основаниям.
Боковыми сторонами являются сам график зависимости скорости от времени и его проекция на ось x (ось времени). Проекция на ось x — это не только боковая сторона, но еще и высота трапеции, т. к. перпендикулярна его основаниям.
Как известно, площадь трапеции равна полусумме оснований на высоту. Длина первого основания равна начальной скорости (v
s = ½ * (v0 + v) * t
Выше была дана формула зависимости конечной скорости от начальной и ускорения (v = v0 + at). Поэтому в формуле пути мы можем заменить v:
s = ½ * (v0 + v0 + at) * t = ½ * (2v0 + at) * t = ½ * t * 2v0 + ½ * t * at = v0t + 1/2at2
Итак, пройденный путь определяется по формуле:
s = v0t + at2/2
(К данной формуле можно прийти, рассматривая не площадь трапеции, а суммируя площади прямоугольника и прямоугольного треугольника, на которые разбивается трапеция. )
)
Если тело начало двигаться равноускоренно из состояния покоя (v0 = 0), то формула пути упрощается до s = at 2/2.
Если вектор ускорения был противоположен скорости, то произведение at2/2 надо вычитать. Понятно, что при этом разность v0t и at2/2 не должна стать отрицательной. Когда она станет равной нулю, тело остановится. Будет найден путь торможения. Выше была приведена формула времени до полной остановки (t = v0/a). Если подставить в формулу пути значение t, то путь торможения приводится к такой формуле:
s = v02/(2a)
«Формулы скорости, времени, расстояния?» — Яндекс Кью
Популярное
Сообщества
Как выразить эти понятия друг одно через другие?
ФизикаМатематикаМеханика
Анонимный вопрос
236,5 K
Ответить3УточнитьДостоверно
Таня К.
1,4 K
Любопытство – не порок) · 3 нояб 2018
Если вам известна скорость v и время t, то вы сможете найти расстояние S по формуле S=vt.
Обратите внимание на единицы измерения! Если вам дана скорость в километрах в час, то и время должно быть выражено в часах (или в метрах в секунду и секундах соответственно).
Выразить скорость из этой формулы можно следующим образом: v=S/t
А если вы хотите посчитать время, то воспользуйтесь формулой t=S/v
2 эксперта согласны
203,7 K
Александр Андросов
11 декабря 2019
спосибо
Комментировать ответ…Комментировать…
Сауле Абдулина
11
Ученик 7 класса , кинокритик · 27 мар 2021
V = S : t t = S : V S = V * t S = расстояние V = скорость t = время : = деление * = умножение Пример : Решил найти расстояние ( S) Для этого скорость ( V) которая равна 4км/ч *время ( t) 4 часа Ответ : 16 км Читать далее
21,0 K
АЛЕКСАНДР ЕРМОЛАЕВ
14 октября 2022
Подскажите а как посчитать, за если я прохожу допустим растояние 9 метров за 7 минут, то за сколько я пройду 300 метров?
Комментировать ответ…Комментировать…
Инесса Смит
23
Учусь в гимназии №17.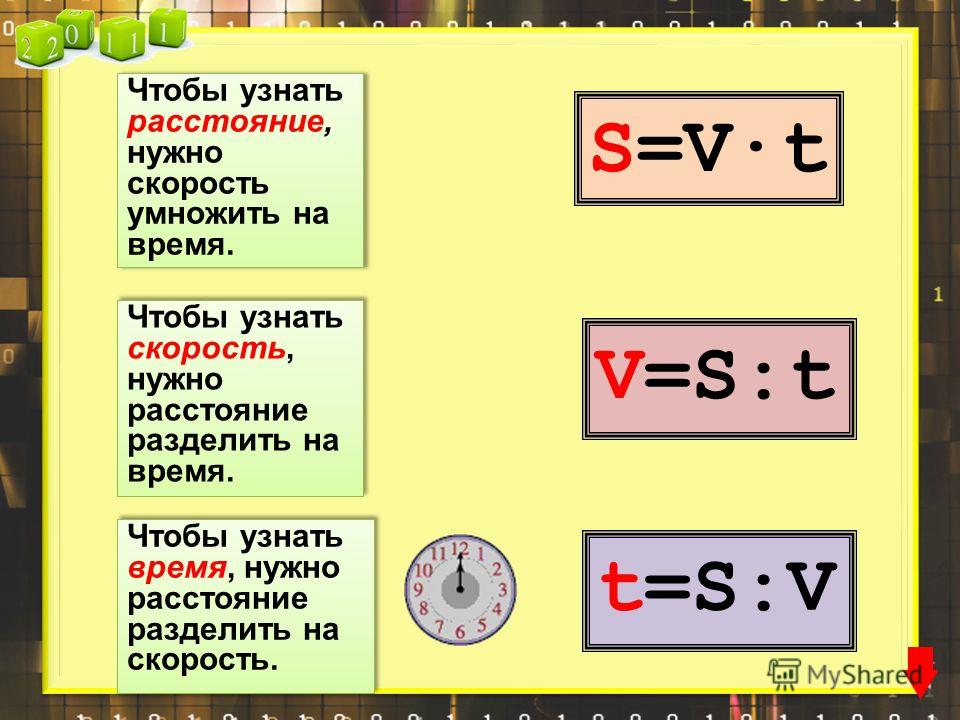 Увлекаюсь математикой, русским языком, родным языком, литературой и… · 20 мая 2021
Увлекаюсь математикой, русским языком, родным языком, литературой и… · 20 мая 2021
(Обратите внимание, что для записи формулы пути используются строчные буквы s, v и t. Это сделано, чтобы не путать их с обозначением площади — S и объёма — V.) Читать далее
19,9 K
Комментировать ответ…Комментировать…
Первый
Тоха Манзулин
13 дек 2021
Чтобы найти скорость, нужно расстояние разделить на время движения: v = S: t. Время – это продолжительность каких-то действий, событий. Время движения обозначается маленькой латинской буквой t. Чтобы найти время, нужно расстояние разделить на скорость движения: t = S: v. Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Комментировать ответ…Комментировать…
Первый
Warrior
80
15 мая 2020
Короче!
Если у вас расстояние нужно найти то:
S=t*v, S=50*20(пример)
Если нужно найти время то:
t=S:V
Если нужно найти скорость то :
V=S:T.
59,8 K
Маргарет
16 октября 2020
спасибо, Warrior! Было не понятно, но
ты помог мне выровнять математику!
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
4 ответа скрыто(Почему?)
Калькулятор t-статистики
Создано Тибором Палом, докторантом
Отредактировано Анной Щепанек, доктором философии, и Джеком Боутером
Последнее обновление: 02 февраля 2023 г.
Содержание:- тест?
- Что такое формула t-статистики?
- Как использовать этот калькулятор t-статистики?
- Пример t-статистики
- Часто задаваемые вопросы
Используйте калькулятор t-статистики (калькулятор t-значения или калькулятор t-теста) до вычислить t-значение данного набора данных , используя его выборочное среднее , среднее значение совокупности , стандартное отклонение и размер выборки .
Читайте дальше, где мы отвечаем на следующие вопросы:
- Что такое t-статистика?
- Как рассчитать t-статистику?
- В чем разница между T-оценкой и Z-оценкой?
Если вас также интересует F-тест, воспользуйтесь нашим калькулятором F-статистики.
В статистике t-статистика или t-значение представляет собой меру, которая описывает отношение между выборкой и ее совокупностью . Стьюдентная статистика занимает центральное место в t-критерии Стьюдента, который является тестом для оценки гипотез о среднем значении генеральной совокупности.
Точнее, t-статистика используется для определения, следует ли поддерживать или отвергать нулевую гипотезу . Он используется в сочетании с p-значением или критическим значением, которое указывает на вероятность того, что ваши результат мог появиться случайно . Он сопоставим с z-статистикой, с той разницей, что t-статистика применяется для небольших размеров выборки или неизвестных стандартных отклонений населения.
Для вычисления значения t необходимо использовать следующую формулу t-статистики :
s/n
xˉ−µ
Где:
- xˉ\bar xxˉ – выборочное среднее;
- мк\мкм – Средняя популяция;
- nnn – Размер выборки; и
- sss – Стандартное отклонение выборки.
Для вычисления t-статистики необходимо указать следующие четыре переменные:
- Среднее значение выборки, xˉ\bar xxˉ;
- Средняя популяция, мк\мкм;
- Объем выборки, сс; и
- Стандартное отклонение выборки, сс.
Кроме того, вы можете использовать инструмент в обратном порядке; например, вы можете восстановить выборочное среднее из t-статистики, если вы введете все остальные значения.
Допустим, вы баскетболист и ваш игровой счет равен 15 ( x̄ ) в среднем за 36 ( n ) игр со стандартным отклонением 6 ( s ). Вы знаете, что средний баскетболист набирает 10 очков (
Вы знаете, что средний баскетболист набирает 10 очков ( μ ). Следует ли считать вашу производительность выше средней? Или ваши результаты из-за удачи? Нахождение t-статистики и значения вероятности даст вам некоторое представление. В частности, нахождение t-статистики с p-значением позволит вам узнать, есть ли значительная разница между вашим средним значением и средним значением населения для всех остальных.
Применяя приведенную выше формулу t-статистики, можно получить следующее уравнение.
t=15−106/36=5t = \dfrac{15 – 10}{6 / \sqrt{36}} = 5t=6/3615−10=5
Теперь мы знаем, что t -статистика равна 5 , но что это значит? Чтобы получить больше знаний, вы должны сравнить это значение с определенным порогом (или уровнем значимости), скажем, 5 процентами ( α = 5% ) распределения Стьюдента-t. Поскольку размер выборки относительно велик ( n > 30 ) мы можем использовать критическое значение стандартного нормального распределения. Критическое значение порога
Критическое значение порога 5% в стандартном нормальном распределении составляет 1,645 . Так как наша t-статистика выше критического значения, можно сказать, что вы играете лучше среднего.
🙋 На самом деле, мы только что выполнили критерий Стьюдента! Посетите наш специальный калькулятор t-критерия, чтобы узнать больше.
Часто задаваемые вопросы
В чем разница между t-score и Z-score?
Как t-показатель, так и Z-показатель предназначены для проведения сравнений и определения различия между средним значением выборки и генеральной совокупности . Основное различие между T-показателем и Z-показателем связано со знанием стандартного отклонения популяции. Для Z-оценки мы предполагаем, что она задана, а для T-оценки ее необходимо оценить. Кроме того, T-score можно применять при небольшом размере выборки (менее 30 элементов).
Как рассчитать t-статистику?
Чтобы рассчитать t-статистику:
- Определите выборочное среднее (
x̄, x бар), которое является средним арифметическим вашего набора данных.
- Найдите среднее значение генеральной совокупности (
μ, мю). - Вычислить стандартное отклонение выборки (
s), взяв квадратный корень из дисперсии. Чтобы найти дисперсию, если она не задана, возьмите каждое значение в выборке, вычтите его из среднего значения выборки, возведите разницу в квадрат и просуммируйте их. - Рассчитать t-статистику как
(x̄ - μ) / (s / √n), гдеnобозначает размер выборки.
Каково происхождение t-распределения Стьюдента?
Стьюдентный критерий был разработан Госсетом , который разработал связанную статистическую теорию в 1908 году. В то время Госсет работал на пивоваренном заводе Гиннеса в Дублине, где существовала внутренняя политика, запрещающая сотрудникам публиковаться, чтобы предотвратить возможные потери. коммерческой тайны. Госсет, однако, нашел лазейку: он писал под псевдоним «Студент» . Как следствие, статистическое распределение Стьюдента t стало известно как t Стьюдента, а не t Госсета. Итак, в следующий раз, когда вы будете наслаждаться пинтой Гиннеса со своим другом, у вас будет захватывающая история, которой можно поделиться.
Итак, в следующий раз, когда вы будете наслаждаться пинтой Гиннеса со своим другом, у вас будет захватывающая история, которой можно поделиться.
Тибор Пал, кандидат наук
Среднее значение выборки (x̄)
Среднее значение генеральной совокупности (μ)
Размер выборки
Стандартное отклонение выборки (s)
t-статистика калькуляторы тестов 📉
Абсолютная неопределенностьТест ABКоэффициент детерминации… Еще 22
Что такое несколько формул и когда их использовать
Что такое Т-тест?
Стьюдент-критерий — это выводная статистика, используемая для определения того, существует ли значительная разница между средними значениями двух групп и тем, как они связаны. T-тесты используются, когда наборы данных следуют нормальному распределению и имеют неизвестные отклонения, например, набор данных, записанный при 100-кратном подбрасывании монеты.
Стьюдентный тест – это тест, используемый для проверки гипотез в статистике. Он использует t-статистику, значения t-распределения и степени свободы для определения статистической значимости.
Он использует t-статистику, значения t-распределения и степени свободы для определения статистической значимости.
Ключевые выводы
- Стьюдент-критерий — это статистический вывод, используемый для определения наличия статистически значимой разницы между средними значениями двух переменных.
- Стьюдентный критерий — это критерий, используемый для проверки гипотез в статистике.
- Для расчета t-теста требуются три основных значения данных, включая разницу между средними значениями из каждого набора данных, стандартное отклонение каждой группы и количество значений данных.
- Т-тесты могут быть зависимыми или независимыми.
Т-тест
Понимание Т-теста
Стьюдентный тест сравнивает средние значения двух наборов данных и определяет, получены ли они из одной и той же совокупности. В приведенных выше примерах выборка учащихся из класса A и выборка учащихся из класса B, скорее всего, не будут иметь одинаковое среднее значение и стандартное отклонение. Точно так же образцы, взятые из контрольной группы, получавшей плацебо, и образцы, взятые из группы, которой прописали лекарство, должны иметь несколько разные среднее значение и стандартное отклонение.
Точно так же образцы, взятые из контрольной группы, получавшей плацебо, и образцы, взятые из группы, которой прописали лекарство, должны иметь несколько разные среднее значение и стандартное отклонение.
Математически t-критерий берет выборку из каждого из двух наборов и устанавливает постановку задачи. Он предполагает нулевую гипотезу о том, что два средних равны.
С помощью формул рассчитываются значения и сравниваются со стандартными значениями. Предполагаемая нулевая гипотеза соответственно принимается или отвергается. Если нулевая гипотеза может быть отвергнута, это указывает на то, что показания данных сильны и, вероятно, не случайны.
Стьюдент-тест — это лишь один из многих тестов, используемых для этой цели. Статистики используют дополнительные тесты, кроме t-критерия, для изучения большего количества переменных и больших размеров выборки. Для выборки большого размера статистики используют z-критерий. Другие варианты тестирования включают тест хи-квадрат и f-тест.
Использование Т-теста
Предположим, что производитель лекарств тестирует новое лекарство. Следуя стандартной процедуре, препарат дается одной группе пациентов, а плацебо — другой группе, называемой контрольной группой. Плацебо — это вещество, не имеющее терапевтической ценности, и служит эталоном для измерения того, как реагирует другая группа, получающая реальное лекарство.
После испытания препарата члены контрольной группы, получавшей плацебо, сообщили об увеличении средней продолжительности жизни на три года, в то время как члены группы, которым прописали новый препарат, сообщили об увеличении средней продолжительности жизни на четыре года.
Начальное наблюдение указывает на то, что препарат работает. Однако также возможно, что наблюдение может быть обусловлено случайностью. Стьюдентный тест можно использовать, чтобы определить, являются ли результаты правильными и применимыми ко всей популяции.
При использовании t-теста делаются четыре предположения. Собранные данные должны соответствовать непрерывной или порядковой шкале, такой как баллы для теста IQ, данные собираются из случайно выбранной части всего населения, данные будут иметь нормальное распределение в виде колоколообразной кривой, и равная или гомогенная дисперсия существует, когда стандартные вариации равны.
Собранные данные должны соответствовать непрерывной или порядковой шкале, такой как баллы для теста IQ, данные собираются из случайно выбранной части всего населения, данные будут иметь нормальное распределение в виде колоколообразной кривой, и равная или гомогенная дисперсия существует, когда стандартные вариации равны.
Формула Т-теста
Для расчета t-критерия требуются три значения фундаментальных данных. Они включают разницу между средними значениями из каждого набора данных или среднюю разницу, стандартное отклонение каждой группы и количество значений данных в каждой группе.
Это сравнение помогает определить влияние случайности на разницу, а также определить, находится ли разница за пределами этого диапазона вероятности. Стьюдентный тест ставит вопрос о том, представляет ли разница между группами истинную разницу в исследовании или просто случайную разницу.
На выходе t-критерий выдает два значения: t-значение и степени свободы. Значение t или t-оценка представляет собой отношение разницы между средним значением двух наборов выборок и вариацией, которая существует в наборах выборок.
Значение числителя представляет собой разницу между средним значением двух наборов выборок. Знаменатель представляет собой вариацию, существующую в наборах выборок, и является мерой дисперсии или изменчивости.
Это рассчитанное t-значение затем сравнивается со значением, полученным из таблицы критических значений, называемой таблицей T-распределения. Более высокие значения t-показателя указывают на большую разницу между двумя наборами выборок. Чем меньше t-значение, тем больше сходства существует между двумя наборами выборок.
T-Score
Большой t-показатель или t-значение указывает на то, что группы различаются, а маленький t-показатель указывает на то, что группы похожи.
Степени свободы относятся к значениям в исследовании, которые могут варьироваться и необходимы для оценки важности и достоверности нулевой гипотезы. Вычисление этих значений обычно зависит от количества записей данных, доступных в выборке.
Т-тест для парных образцов
Коррелированный t-критерий, или парный t-критерий, является зависимым типом теста и выполняется, когда выборки состоят из согласованных пар одинаковых единиц или когда есть случаи повторных измерений. Например, могут быть случаи, когда одни и те же пациенты повторно тестируются до и после получения конкретного лечения. Каждый пациент используется в качестве контрольного образца против себя.
Например, могут быть случаи, когда одни и те же пациенты повторно тестируются до и после получения конкретного лечения. Каждый пациент используется в качестве контрольного образца против себя.
Этот метод также применим к случаям, когда образцы связаны или имеют совпадающие характеристики, например, сравнительный анализ с участием детей, родителей или братьев и сестер.
Формула для вычисления t-значения и степеней свободы для парного t-теста:
Т “=” иметь в виду 1 − иметь в виду 2 с ( разница ) ( н ) где: иметь в виду 1 и иметь в виду 2 “=” Средние значения каждого из выборочных наборов с ( разница ) “=” Стандартное отклонение разностей парных значений данных н “=” Размер выборки (количество парных различий) н − 1 “=” Степени свободы \begin{align}&T=\frac{\textit{mean}1 – \textit{mean}2}{\frac{s(\text{diff})}{\sqrt{(n)}}}\\& \textbf{где:}\\&\textit{mean}1\text{ и }\textit{mean}2=\text{Средние значения каждого из выборочных наборов}\\&s(\text{diff}) =\text{Стандартное отклонение разностей парных значений данных}\\&n=\text{Размер выборки (количество парных разностей)}\\&n-1=\text{Степени свободы}\end {выровнено} T=(n)s(diff)mean1-mean2где:mean1 и mean2=средние значения каждого набора выборокss(diff)=стандартное отклонение разностей парных значений данных n=размер выборки (количество парных различий)n−1=степени свободы
Равная дисперсия или объединенный Т-критерий
Стьюдентный критерий равной дисперсии является независимым t-тестом и используется, когда количество выборок в каждой группе одинаково или дисперсия двух наборов данных аналогична. 2 }{ n1 + n2 – 2}\times \sqrt{ \frac{1}{n1} + \frac{1}{n2}} } \\&\textbf{где:}\\&mean1 \text{ и } mean2 = \text{ Средние значения каждого} \\&\text{выборочных наборов}\\&var1 \text{ и } var2 = \text{Дисперсия каждого из выборочных наборов}\\&n1 \text{ и } n2 = \text{ Количество записей в каждом наборе образцов} \end{aligned}
T-значение=n1+n2−2(n1−1)×var12+(n2−1)×var22×n11+n21среднее1−среднее2, где:среднее1 и среднее2=средние значения каждого из выборочных наборовvar1 и var2 = дисперсия каждого набора образцов n1 и n2 = количество записей в каждом наборе образцов
2 }{ n1 + n2 – 2}\times \sqrt{ \frac{1}{n1} + \frac{1}{n2}} } \\&\textbf{где:}\\&mean1 \text{ и } mean2 = \text{ Средние значения каждого} \\&\text{выборочных наборов}\\&var1 \text{ и } var2 = \text{Дисперсия каждого из выборочных наборов}\\&n1 \text{ и } n2 = \text{ Количество записей в каждом наборе образцов} \end{aligned}
T-значение=n1+n2−2(n1−1)×var12+(n2−1)×var22×n11+n21среднее1−среднее2, где:среднее1 и среднее2=средние значения каждого из выборочных наборовvar1 и var2 = дисперсия каждого набора образцов n1 и n2 = количество записей в каждом наборе образцов
и,
Степени свободы “=” н 1 + н 2 − 2 где: н 1 и н 2 “=” Количество записей в каждом наборе образцов \begin{align} &\text{Степени свободы} = n1 + n2 – 2 \\ &\textbf{где:}\\ &n1 \text{ и } n2 = \text{Количество записей в каждом наборе образцов} \ \ \ конец {выровнено} Степени свободы=n1+n2−2, где: n1 и n2=количество записей в каждом наборе образцов
Т-тест с неравной дисперсией
Стьюдентный критерий неравной дисперсии является независимым t-тестом и используется, когда количество выборок в каждой группе различно, и дисперсия двух наборов данных также различна. Этот тест также называют t-критерием Уэлча.
Этот тест также называют t-критерием Уэлча.
Формула, используемая для расчета t-значения и степеней свободы для t-критерия неравной дисперсии:
Т-значение “=” м е а н 1 − м е а н 2 ( в а р 1 н 1 + в а р 2 н 2 ) где: м е а н 1 и м е а н 2 “=” Средние значения каждого наборов образцов в а р 1 и в а р 2 “=” Дисперсия каждого из наборов образцов н 1 и н 2 “=” Количество записей в каждом наборе образцов \begin{align}&\text{T-value}=\frac{mean1-mean2}{\sqrt{\bigg(\frac{var1}{n1}{+\frac{var2}{n2}\bigg)} }}\\&\textbf{где:}\\&mean1 \text{ и } mean2 = \text{Средние значения каждого} \\&\text{набора образцов} \\&var1 \text{ и } var2 = \text{Дисперсия каждого набора образцов} \\&n1 \text{ и } n2 = \text{Количество записей в каждом наборе образцов} \end{выравнивание} T-значение=(n1var1+n2var2)mean1-mean2где:mean1 и mean2=Средние значения каждого из выборочных наборов var1 и var2=дисперсия каждого из выборочных наборов n1 и n2=количество записей в каждом выборочном наборе 92 }{ n2 – 1}} \\ &\textbf{где:}\\ &var1 \text{ и } var2 = \text{Дисперсия каждого из выборочных наборов} \\ &n1 \text{ и } n2 = \text {Количество записей в каждом наборе образцов} \\ \end{aligned} Степени свободы=n1−1(n1var12)2+n2−1(n2var22)2(n1var12+n2var22)2, где: var1 и var2 = дисперсия каждого набора выборки n1 и n2 = число записей в каждом наборе образцов
Какой Т-тест использовать?
Следующая блок-схема может быть использована для определения того, какой t-критерий использовать, исходя из характеристик наборов выборок. Ключевые элементы, которые следует учитывать, включают сходство записей выборки, количество записей данных в каждой выборке и дисперсию каждой выборки.
Ключевые элементы, которые следует учитывать, включают сходство записей выборки, количество записей данных в каждой выборке и дисперсию каждой выборки.
Изображение Джули Банг © Investopedia 2019
Пример T-критерия неравной дисперсии
Предположим, что берется диагональный размер картин, полученных в художественной галерее. В одну группу образцов входит 10 картин, в другую – 20 картин. Наборы данных с соответствующими средними значениями и значениями дисперсии следующие:
| Набор 1 | Набор 2 | |
|---|---|---|
| 19,7 | 28,3 | |
| 20,4 | 26,7 | |
| 19,6 | 20,1 | |
| 17,8 | 23,3 | |
| 18,5 | 25,2 | |
| 18,9 | 22. 1 1 | |
| 18,3 | 17,7 | |
| 18,9 | 27,6 | |
| 19,5 | 20,6 | |
| 21,95 | 13,7 | |
| 23,2 | ||
| 17,5 | ||
| 20,6 | ||
| 18 | ||
| 23,9 | ||
| 21,6 | ||
| 24,3 | ||
| 20,4 | ||
| 23,9 | ||
| 13,3 | ||
| Среднее | 19,4 | 21,6 |
| Разница | 1,4 | 17,1 |
Хотя среднее значение набора 2 выше, чем у набора 1, мы не можем заключить, что совокупность, соответствующая набору 2, имеет более высокое среднее значение, чем население, соответствующее набору 1.
Является ли разница от 19,4 до 21,6 случайной или существуют различия в общей совокупности всех картин, полученных в художественной галерее? Мы устанавливаем проблему, принимая нулевую гипотезу о том, что среднее значение одинаково для двух наборов выборок, и проводим t-тест, чтобы проверить, правдоподобна ли гипотеза.
Поскольку количество записей данных различно (n1 = 10 и n2 = 20) и дисперсия также различна, значение t и степени свободы вычисляются для вышеуказанного набора данных с использованием формулы, упомянутой в Т-критерии неравной дисперсии. раздел.
Значение t равно -2,24787. Поскольку знак минус можно игнорировать при сравнении двух t-значений, вычисленное значение равно 2,24787.
Значение степени свободы равно 24,38 и уменьшено до 24 из-за определения формулы, требующей округления значения до наименьшего возможного целого числа.
Можно указать уровень вероятности (альфа-уровень, уровень значимости, p ) в качестве критерия приемлемости. В большинстве случаев можно принять значение 5%.
В большинстве случаев можно принять значение 5%.
Используя значение степени свободы, равное 24, и уровень значимости 5%, просмотр таблицы распределения t-значения дает значение 2,064. Сравнение этого значения с вычисленным значением 2,247 показывает, что рассчитанное значение t больше табличного значения при уровне значимости 5%. Следовательно, можно с уверенностью отвергнуть нулевую гипотезу об отсутствии разницы между средними значениями. Набор населения имеет внутренние различия, и они не случайны.
Как используется таблица Т-распределения?
Таблица Т-распределения доступна в одностороннем и двустороннем форматах. Первый используется для оценки случаев, которые имеют фиксированное значение или диапазон с четким направлением, положительным или отрицательным. Например, какова вероятность того, что выходное значение останется ниже -3 или будет больше семи при броске пары игральных костей? Последний используется для анализа с привязкой к диапазону, например, чтобы узнать, находятся ли координаты в диапазоне от -2 до +2.


