Формула падения напряжения на резисторе: Как найти напряжение на резисторах, подобрать элемент и рассчитать его падение

Как рассчитать падение напряжения на резисторе калькулятор

Формулы для радиолюбительских расчетов.

Каждый уважающий себя радио-мастер обязан знать формулы для расчета различных электрических величин. Ведь при ремонте электронных устройств или сборке электронных самоделок очень часто приходится проводить подобные расчеты. Не зная таких формул очень сложно и трудоемко, а порой и невозможно справиться с подобного рода задачей!

Как рассчитать емкость конденсатора, как рассчитать сопротивление резистора или узнать мощность устройства – в этом помогут формулы для радиолюбительских расчетов.

Первое, что нужно усвоить – ВСЕ ВЕЛЕЧИНЫ В ФОРМУЛАХ УКАЗЫВАЮТЬСЯ В АМПЕРАХ, ВОЛЬТАХ, ОМАХ, МЕТРАХ И КИЛОГЕРЦАХ.

Закон Ома.

Известный из школьного курса физики ЗАКОН ОМА. На нем строится большинство расчетов в радиоэлектронике. Закон Ома выражается в трех формулах:

Где: I – сила тока (А), U – напряжение (В), R– сопротивление, имеющееся в цепи (Ом).

Теперь рассмотрим на практике применение формул в радиолюбительских расчетах.

Как рассчитать сопротивление гасящего резистора.

Сопротивление гасящего резистора рассчитывают по формуле: R= U /I

Где: U – излишек напряжения, который необходимо погасить (В), I – ток потребляемый цепью или устройством (А).

Как рассчитать мощность гасящего резистора.

Расчет мощности гасящего резистора проводят по формуле: P=I 2 R

Где I – ток потребляемый цепью или устройством (А), R– сопротивление резистора (Ом).

Как рассчитать напряжение падения на сопротивлении.

Напряжение падения на сопротивлении можно рассчитать по формуле: U_{пад .} =RI

Где R– сопротивление гасящего резистора (Ом), I– ток потребляемый устройством или цепью (А).

Как рассчитать ток потребляемый устройством или цепью.

Рассчитать ток потребляемый устройством или цепью можно по формуле: I=P/U

Где P– мощность устройства (Вт), U– напряжение питания устройства (В).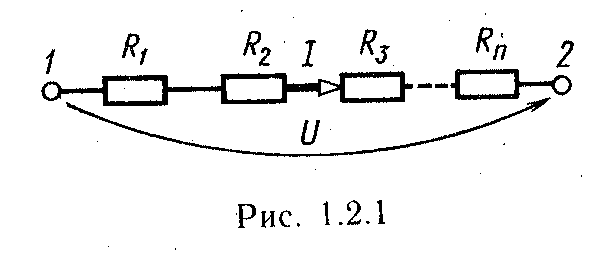

Как рассчитать мощность устройства в Вт.

Рассчитать мощность устройства в Вт. можно по формуле: P=IU

Где I– ток потребляемый устройством (А), U– напряжение питания устройства (В).

Как рассчитать длину радиоволны.

Рассчитать длину радиоволны можно по формуле: ƛ=300000/ƒ

Где ƒ-частота в килогерцах, ƛ- длинна волны в метрах.

Как рассчитать частоту радиосигнала.

Частоту радиосигнала можно рассчитать по формуле: ƒ=300000/ƛ

Где ƛ- длинна волны в метрах, ƒ – частота в килогерцах.

Как рассчитать номинальную выходную мощность звуковой частоты.

Рассчитать номинальную выходную мощность звуковоспроизводящего устройства (усилитель, проигрыватель и т.п.) можно по формуле: P=U 2 _вых./ R _{ном .}

Где U 2 – напряжение звуковой частоты на нагрузке, R– номинальное сопротивление нагрузки.

И в завершении еще несколько формул.

По этим формулам, ведут расчет сопротивления и емкости резисторов и конденсаторов в тех случаях, когда возникает необходимость в параллельном или последовательном их соединении.

Как рассчитать сопротивление двух параллельно включенных резисторов.

Расчет соединенных параллельно двух резисторов производят по формуле: R=R₁R₂/(R₁+R₂)

Где R₁ и R₂ — сопротивление первого и второго резистора соответственно (Ом).

Как рассчитать сопротивление более двух включенных параллельно резисторов.

Расчет сопротивления включенных параллельно более чем двух резисторов проводят по формуле: 1/R=1/R₁+1/R₂+1/R_n…

Где R₁, R₂, R_n… — сопротивление первого, второго и последующих резисторов соответственно (Ом).

Как рассчитать емкость включенных параллельно двух или более конденсаторов.

Расчет емкости соединенных параллельно нескольких конденсаторов проводят по формуле: C=C₁+ C₂+C_n…

Где C₁ , C₂ и C_n– емкость первого, второго и последующих конденсаторов соответственно (мФ).

Как рассчитать емкость включенных последовательно двух конденсаторов.

Расчет емкости двух соединенных последовательно конденсаторов проводят по формуле: C=C₁ C₂/C₁+C₂

Где C₁ и C₂ – емкость первого и второго конденсаторов соответственно (мФ).

Как рассчитать емкость включенных последовательно более двух конденсаторов.

Расчет емкости включенных последовательно более чем двух конденсаторов проводят по формуле: 1/C=1/C₁+1/C₂+1/C_n…

Где C₁, C₂ и C_n… — емкость первого, второго и последующих конденсаторов (мФ).

Рекомендуем посмотреть:

Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.

Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.

Схема делителя напряжения на резисторах

Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.

Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.

Расчет делителя напряжения на резисторах

Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.

Формула делителя напряжения

Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома.

Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:

Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:

Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:

Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:

И, на какое-то время, мы можем упростить схему:

Закон Ома в его наиболее простом вид: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:

А так как I1 равно I2, то:

Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.

Делитель напряжения — калькулятор онлайн

Применение делителя напряжения на резисторах

В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.

Потенциометры

Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.

Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.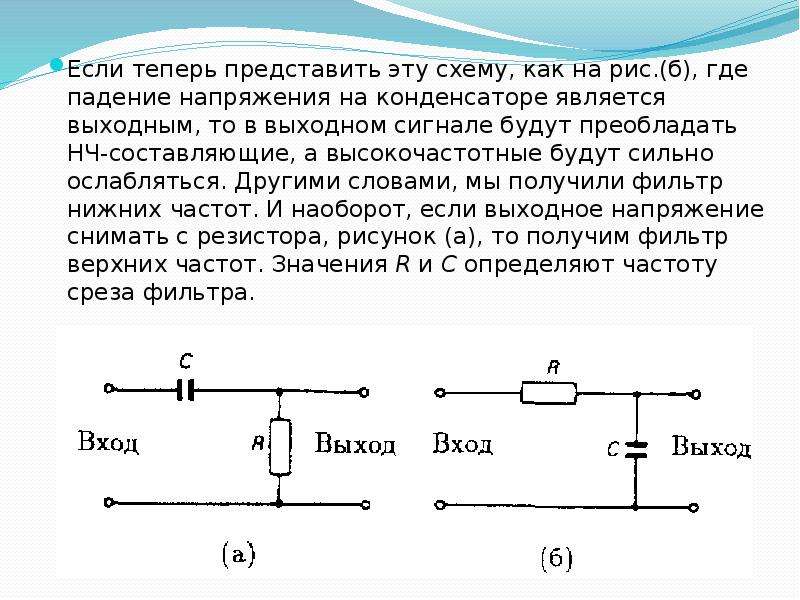

Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.

Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.

Резистивные датчики

Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.

Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).

Пример работы делителя напряжения на фоторезисторе.

Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.

Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

21 комментарий

Короче,делитель напряжения — это следящая ( сравнивающая ) цепочка в системах автоматического регулирования. Её можно увидеть в регуляторах напряжеия генераторов.

Отличная статья, жаль, что про рассеиваемую мощность не сказано ни слова.

спасибо,понравилось.вопрос-схема где показаны способы присоединения делителей
правый(внизу) измеряют снимаемое (Uout) c
Uout и минуса входящего?

Просто и понятно описано, чтобы понять даже ребенку.

За калькуляторы отдельное спасибо — очень удобно!

Увы. Врет калькулятор безбожно!
Пытался рассчитать делитель с 6В на 2.5В.
Жаль нельзя скриншот вставить.
Результаты:
По формуле 1: R1 = 4.8K, R2 = 22K, Vin = 6В, Vout = 4.4В. (Значения резисторов взяты из результатов формулы 3)
По формуле2: Vin = 6В, Vout = 2.5В, R1+R2 = 26,4K. Результат: R1 = 666,667, R2 = 3,333K. В сумме ну никак не 26К, которые в исходных данных забиты.

По формуле3: Vin=6B, Vout = 2,5B, R2=22K. Результат: R1 = 4,4K. (при расчете вручную 30800)
Т.е. результаты ну совсем рядом не стояли. А по идее формулы должны сходные результаты давать.
Кроме этого, в формуле 1. R1 указано 4.8К, при этом Vout = 4.4В. Если указать R1 4.84, то результат уже 1.245. Добавили 0.04К, а напряжение упало аж в 4 раза? А если добавить еще 0.004К, то на выходе уже 152 мВ. Т.е. в 10 раз меньше предыдущего.
В общем не фонтан.

Читайте примечание внизу калькулятора…

вполне приличный калькулятор.спасибо.

Спасибо за отличный и удобный калькулятор!

Рассчитать резистор R2 для выходного напряжения (Uout) и резистора R1-добавить для удобства расчетов

смысла формулы не пойму , почему в делителе нужно умножать именно на R2, Ток течет от плюса к минусу чисто условно, он с таким же успехом идет и наоборот, Впечатление , что формула хоть и верная но притянута за уши .

При умножении на R1 ты вычислишь разницу напряжений Uin-Uout

А как будет влиять на систему нагрузка? Она снизит сопротивление цепи.

Без учета нарузки это сферический конь в вакууме.

Сама идея создать калькуляторы хорошая.
Только вот изначально необходимо вводить условие нагрузки. Без этого такие калькуляторы совершенно бессмысленные, и годятся разве что для демонстрации закона Ома.
И хорошо бы сделать калькулятор на несколько коэффициентов деления, например 1:1 — 1:10 — 1:100 — 1:1000, и конечно же с условием входного сопротивления нагрузки.
И в этом же калькуляторе должны быть строки для отображения мощности рассеяния резисторов делителя.
И при этом необходимо ещё учитывать температуру резисторов. Собственно, все проекты начинаются с задания диапазона рабочих температур. А иначе при работе все эти резисторы перекосит по сопротивлению напрочь.
Вобщем, в таком виде это не калькуляторы, а бессмысленные игрушки.

Блин, ребята! Такие делители применяются исключительно для задания какого-нибудь опорного напряжения для компаратора или для задания точки смещения транзистора. В таких условиях просто принимается что сопротивление нагрузки (т.е. входа этого самого компаратора) на порядки больше, и, соответственно сопротивление такой нагрузки почти не влияет на конечный результат. Да и отклонение резисторов а также температурный дрейф будут вносить бОльшие искажения, нежели сопротивление входа компаратора. А если требуется более точное напряжение, то ставят точные стабилитроны или вобще специализированную микросхему — ИОН (источник опорного напряжения). Но никто через такие делители не запитывает именно полноценную нагрузку. Частный случай такого делителя, это если вместо нижнего резистора ставится стабилитрон. Тогда расчёт по мощности упирается в допустимую мощность стабилитрона, а мощность нагрузки должа быть в разы меньше, т.е. таким образом можно разве что подать питание на одну-две микросхемы маломощные.

отличная подборка, присоединюсь к уже озвученному, жаль нет расчёта по мощности )))

да кстати сколько ват рассеит резистор как посчитать?

Тупит ваш калькулятор, у меня практическая схема R1=260 Ом 10W, R2=120 Ом 5W, при входном 56В на выходе 18В. Мигалка для электропогрузчика с бортовым 56В. Ваш калькулятор перекрывает выходные значения сообщением о мощности и величине сопротивления.

Хороший калькулятор, спасибо автору. Но для полного удобства не хватает расчёта R2 при известном R1 и напряжениях. Как раз столкнулся с такой задачей, пришлось решать методом перебора с последовательным приближением. Все равно это будет переменный резистор, главное понять какой туда повесить чтобы покрыть весь диапазон выходных напряжений, не рискуя разорвать ОС при «шуршании» бегунка резистора (регулируемый БП).

Нужно еще один калькулятор — чтобы по Uin, Uout и I выдавал нужные сопротивления (когда нужно, чтобы ток был определенной величины — не больше заданной, но и не на порядки меньше: например, ток 10мА при 10В->3В, если брать килоомные сопротивления, меня не устраивает)

Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.

Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.

Схема делителя напряжения на резисторах

Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.

Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.

Расчет делителя напряжения на резисторах

Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.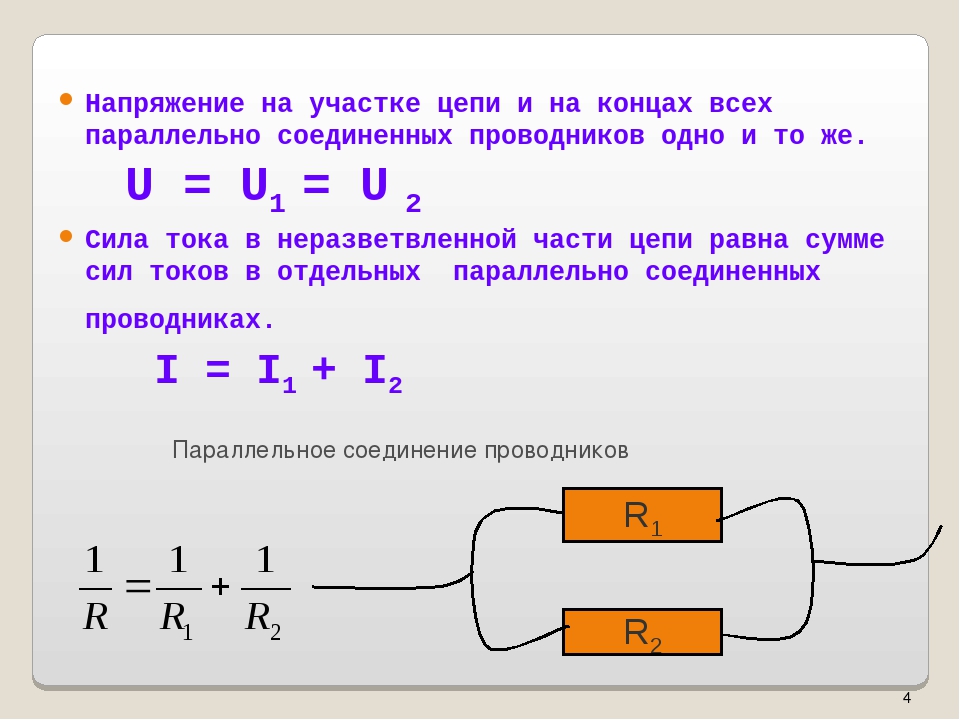

Формула делителя напряжения

Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома.

Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:

Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:

Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:

Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:

И, на какое-то время, мы можем упростить схему:

Закон Ома в его наиболее простом вид: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:

А так как I1 равно I2, то:

Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.

Делитель напряжения — калькулятор онлайн

Применение делителя напряжения на резисторах

В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.

Потенциометры

Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.

Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.

Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.

Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.

Резистивные датчики

Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.

Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).

Пример работы делителя напряжения на фоторезисторе.

Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.

Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

21 комментарий

Короче,делитель напряжения — это следящая ( сравнивающая ) цепочка в системах автоматического регулирования. Её можно увидеть в регуляторах напряжеия генераторов.

Отличная статья, жаль, что про рассеиваемую мощность не сказано ни слова.

спасибо,понравилось.вопрос-схема где показаны способы присоединения делителей
правый(внизу) измеряют снимаемое (Uout) c
Uout и минуса входящего?

Просто и понятно описано, чтобы понять даже ребенку.

За калькуляторы отдельное спасибо — очень удобно!

Увы. Врет калькулятор безбожно!
Пытался рассчитать делитель с 6В на 2.5В.
Жаль нельзя скриншот вставить.
Результаты:
По формуле 1: R1 = 4.8K, R2 = 22K, Vin = 6В, Vout = 4.4В. (Значения резисторов взяты из результатов формулы 3)
По формуле2: Vin = 6В, Vout = 2.5В, R1+R2 = 26,4K. Результат: R1 = 666,667, R2 = 3,333K. В сумме ну никак не 26К, которые в исходных данных забиты.
По формуле3: Vin=6B, Vout = 2,5B, R2=22K. Результат: R1 = 4,4K. (при расчете вручную 30800)
Т.е. результаты ну совсем рядом не стояли. А по идее формулы должны сходные результаты давать.
Кроме этого, в формуле 1. R1 указано 4.8К, при этом Vout = 4.4В. Если указать R1 4.84, то результат уже 1.245. Добавили 0.04К, а напряжение упало аж в 4 раза? А если добавить еще 0.004К, то на выходе уже 152 мВ. Т.е. в 10 раз меньше предыдущего.
В общем не фонтан.

Читайте примечание внизу калькулятора…

вполне приличный калькулятор.спасибо.

Спасибо за отличный и удобный калькулятор!

Рассчитать резистор R2 для выходного напряжения (Uout) и резистора R1-добавить для удобства расчетов

смысла формулы не пойму , почему в делителе нужно умножать именно на R2, Ток течет от плюса к минусу чисто условно, он с таким же успехом идет и наоборот, Впечатление , что формула хоть и верная но притянута за уши .

При умножении на R1 ты вычислишь разницу напряжений Uin-Uout

А как будет влиять на систему нагрузка? Она снизит сопротивление цепи.

Без учета нарузки это сферический конь в вакууме.

Сама идея создать калькуляторы хорошая.
Только вот изначально необходимо вводить условие нагрузки. Без этого такие калькуляторы совершенно бессмысленные, и годятся разве что для демонстрации закона Ома.
И хорошо бы сделать калькулятор на несколько коэффициентов деления, например 1:1 — 1:10 — 1:100 — 1:1000, и конечно же с условием входного сопротивления нагрузки.
И в этом же калькуляторе должны быть строки для отображения мощности рассеяния резисторов делителя.
И при этом необходимо ещё учитывать температуру резисторов. Собственно, все проекты начинаются с задания диапазона рабочих температур. А иначе при работе все эти резисторы перекосит по сопротивлению напрочь.
Вобщем, в таком виде это не калькуляторы, а бессмысленные игрушки.

Блин, ребята! Такие делители применяются исключительно для задания какого-нибудь опорного напряжения для компаратора или для задания точки смещения транзистора. В таких условиях просто принимается что сопротивление нагрузки (т.е. входа этого самого компаратора) на порядки больше, и, соответственно сопротивление такой нагрузки почти не влияет на конечный результат. Да и отклонение резисторов а также температурный дрейф будут вносить бОльшие искажения, нежели сопротивление входа компаратора. А если требуется более точное напряжение, то ставят точные стабилитроны или вобще специализированную микросхему — ИОН (источник опорного напряжения). Но никто через такие делители не запитывает именно полноценную нагрузку. Частный случай такого делителя, это если вместо нижнего резистора ставится стабилитрон. Тогда расчёт по мощности упирается в допустимую мощность стабилитрона, а мощность нагрузки должа быть в разы меньше, т.е. таким образом можно разве что подать питание на одну-две микросхемы маломощные.

отличная подборка, присоединюсь к уже озвученному, жаль нет расчёта по мощности )))

да кстати сколько ват рассеит резистор как посчитать?

Тупит ваш калькулятор, у меня практическая схема R1=260 Ом 10W, R2=120 Ом 5W, при входном 56В на выходе 18В. Мигалка для электропогрузчика с бортовым 56В. Ваш калькулятор перекрывает выходные значения сообщением о мощности и величине сопротивления.

Хороший калькулятор, спасибо автору. Но для полного удобства не хватает расчёта R2 при известном R1 и напряжениях. Как раз столкнулся с такой задачей, пришлось решать методом перебора с последовательным приближением. Все равно это будет переменный резистор, главное понять какой туда повесить чтобы покрыть весь диапазон выходных напряжений, не рискуя разорвать ОС при «шуршании» бегунка резистора (регулируемый БП).

Нужно еще один калькулятор — чтобы по Uin, Uout и I выдавал нужные сопротивления (когда нужно, чтобы ток был определенной величины — не больше заданной, но и не на порядки меньше: например, ток 10мА при 10В->3В, если брать килоомные сопротивления, меня не устраивает)

Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях – Help for engineer

Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях

Делитель напряжения используется в электрических цепях, если необходимо понизить напряжение и получить несколько его фиксированных значений. Состоит он из двух и более элементов (резисторов, реактивных сопротивлений). Элементарный делитель можно представить как два участка цепи, называемые плечами. Участок между положительным напряжением и нулевой точкой – верхнее плечо, между нулевой и минусом – нижнее плечо.

Делитель напряжения на резисторах может применятmся как для постоянного, так и для переменного напряжений. Применяется для низкого напряжения и не предназначен для питания мощных машин. Простейший делитель состоит из двух последовательно соединенных резисторов:

На резистивный делитель напряжения подается напряжение питающей сети U, на каждом из сопротивлений R1 и R2 происходит падение напряжения. Сумма U1 и U2 и будет равна значению U.

В соответствии с законом Ома (1):

Падение напряжения будет прямо пропорционально значению сопротивления и величине тока. Согласно первому закону Кирхгофа, величина тока, протекающего через сопротивления одинакова. С чего следует, что падение напряжения на каждом резисторе (2,3):

Тогда напряжение на всем участке цепи (4):

Отсюда определим, чему равно значение тока без включения нагрузки (5):

Если подставить данное выражение в (2 и 3), то получим формулы расчета падения напряжения для делителя напряжения на резисторах (6, 7):

Необходимо упомянуть, что значения сопротивлений делителя должны быть на порядок или два (все зависит от требуемой точности питания) меньше, чем сопротивление нагрузки. Если же это условие не выполняется, то при приведенном расчете подаваемое напряжение будет посчитано очень грубо.

Для повышения точности необходимо сопротивление нагрузки принять как параллельно подсоединенный резистор к делителю. А также использовать прецизионные (высокоточные) сопротивления.

Онлайн подбор сопротивлений для делителя

Пусть источник питания выдает 24 В постоянного напряжения, примем, что величина сопротивления нагрузки переменная, но минимальное значение равно 15 кОм. Необходимо рассчитать параметры резисторов для делителя, выходное напряжение которого равно 6 В.

Таким образом, напряжения: U=24 B, U₂=6 В; сопротивление резисторов не должно превышать 1,5 кОм (в десять раз меньше значения нагрузки). Принимаем R1=1000 Ом, тогда используя формулу (7) получим:

выразим отсюда R₂:

Зная величины сопротивления обоих резисторов, найдем падение напряжения на первом плече (6):

Ток, который протекает через делитель, находится по формуле (5):

Схема делителя напряжения на резисторах рассчитана выше и промоделирована:

Использование делителя напряжения очень неэкономичный, затратный способ понижения величины напряжения, так как неиспользуемая энергия рассеивается на сопротивлении (превращается в тепловую энергию). КПД очень низкий, а потери мощности на резисторах вычисляются формулами (8,9):

По заданным условиям, для реализации схемы делителя напряжения необходимы два резистора:

		1. R1=1 кОм, P1=0,324 Вт.
		2. R2=333,3 Ом, P2=0,108 Вт.

Полная мощность, которая потеряется:

---

Делитель напряжения на конденсаторах применяется в схемах высокого переменного напряжения, в данном случае имеет место реактивное сопротивление.

Сопротивление конденсатора рассчитывается по формуле (10):

		где С – ёмкость конденсатора, Ф;
		f – частота сети, Гц.

Исходя из формулы (10), видно, что сопротивление конденсатора зависит от двух параметров: С и f. Чем больше ёмкость конденсатора, тем сопротивление его ниже (обратная пропорциональность). Для ёмкостного делителя расчет имеет такой вид (11, 12):

Еще один делитель напряжения на реактивных элементах – индуктивный, который нашел применение в измерительной технике. Сопротивление индуктивного элемента при переменном напряжении прямо пропорционально величине индуктивности (13):

где L – индуктивность, Гн.

Падение напряжения на индуктивностях (14,15):

Недостаточно прав для комментирования

Падение напряжения после резистора. Падение напряжения

В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.

Пример 1

Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r = 0,5 Ом. Сопротивления резисторов R 1 = 20 и R 2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.

Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.

Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей .

В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.

Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.

Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.

Пример 2

Общий ток цепи, содержащей два соединенных параллельно резистора R 1 =70 Ом и R 2 =90 Ом, равен 500 мА. Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока . Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.

Токи в резисторах

В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.

Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала

Понятия и формулы

На каждом сопротивлении r при прохождении тока I возникает напряжение U=I∙r, которое называется обычно падением напряжения на этом сопротивлении.

Если в электрической цепи только одно сопротивление r, все напряжение источника Uист падает на этом сопротивлении.

Если в цепи имеются два сопротивления r1 и r2, соединенные последовательно, то сумма напряжений на сопротивлениях U1=I∙r1 и U2=I∙r2 т. е. падений напряжения, равна напряжению источника: Uист=U1+U2.

Напряжение источника питания равно сумме падений напряжения в цепи (2-й закон Кирхгофа).

Примеры

1. Какое падение напряжения возникает на нити лампы сопротивлением r=15 Ом при прохождении тока I=0,3 А (рис. 1)?

Рис. 1.

Падение напряжения подсчитывается : U=I∙r=0,3∙15=4,5 В.

Напряжение между точками 1 и 2 лампочки (см. схему) составляет 4,5 В. Лампочка светит нормально, если через нее проходит номинальный ток или если между точками 1 и 2 номинальное напряжение (номинальные ток и напряжение указываются на лампочке).

2. Две одинаковые лампочки на напряжение 2,5 В и ток 0,3 А соединены последовательно и подключены к карманной батарее с напряжением 4,5 В. Какое падение напряжения создается на зажимах отдельных лампочек (рис. 2)?

Рис. 2.

Одинаковые лампочки имеют равные сопротивления r. При последовательном включении через них проходит один и тот же ток I. Из этого следует, что на них будут одинаковые падения напряжения, сумма этих напряжений должна быть равна напряжению источника U=4,5 В. На каждую лампочку приходится напряжение 4,5:2=2,25 В.

Можно решить эту задачу и последовательным расчетом. Сопротивление лампочки рассчитываем по данным: rл=2,5/0,3=8,33 Ом.

Ток в цепи I = U/(2rл)=4,5/16,66=0,27 А.

Падение напряжения на лампочке U=Irл=0,27∙8,33=2,25 В.

3. Напряжение между рельсом и контактным проводом трамвайной линии равно 500 В. Для освещения используются четыре одинаковые лампы, соединенные последовательно. На какое напряжение должна быть выбрана каждая лампа (рис. 3)?

Рис. 3.

Одинаковые лампы имеют равные сопротивления, через которые проходит один и тот же ток. Падения напряжения на лампах будут тоже одинаковыми. Значит, на каждую лампу будет приходиться 500:4=125 В.

4. Две лампы мощностью 40 и 60 Вт с номинальным напряжением 220 В соединены последовательно и включены в сеть с напряжением 220 В. Какое падение напряжения возникает на каждой из них (рис. 4)?

Рис. 4.

Первая лампа имеет сопротивление r1=1210 Ом, а вторая r2=806,6 Ом (в нагретом состоянии). Ток, проходящий через лампы, I=U/(r1+r2)=220/2016,6=0,109 А.

Падение напряжения на первой лампе U1=I∙r1=0,109∙1210=132 В.

Падение напряжения на второй лампе U2=I∙r2=0,109∙806,6=88 В.

На лампе с большим сопротивлением большее падение напряжения, и наоборот. Накал нитей обеих ламп очень слаб, однако у лампы 40 Вт он несколько сильнее, чем у лампы 60 Вт.

5. Чтобы напряжение на электродвигателе Д (рис. 5) было равно 220 В, напряжение в начале длинной линии (на электростанции) должно быть больше 220 В на величину на линии. Чем больше сопротивление линии и ток в ней, тем больше падение напряжения на линии.

Рис. 5.

В нашем примере падение напряжения в каждом проводе линии равно 5 В. Тогда напряжение на шинах электростанции должно быть равно 230 В.

6. От аккумулятора напряжением 80 В потребитель питается током 30 А. Для нормальной работы потребителя допустимо 3% падения напряжения в проводах из алюминия с сечением 16 мм2. Каким может быть максимальное расстояние от аккумулятора до потребителя?

Допустимое падение напряжения в линии U=3/100∙80=2,4 В.

Сопротивление проводов ограничивается допустимым падением напряжения rпр=U/I=2,4/30=0,08 Ом.

По формуле для определения сопротивления подсчитаем длину проводов: r=ρ∙l/S, откуда l=(r∙S)/ρ=(0,08∙16)/0,029=44,1 м.

Если потребитель будет отдален от аккумулятора на 22 м, то напряжение на нем будет меньше 80 В на 3%, т.е. равным 77,6 В.

7. Телеграфная линия длиной 20 км выполнена из стального провода диаметром 3,5 мм. Обратная линия заменена заземлением через металлические шины.2)/4=9,6 мм2.

Сопротивление линии rл=ρ∙l/S=0,11∙20000/9,6=229,2 Ом.

Результирующее сопротивление r=229,2+300+2∙50=629,2 Ом.

Напряжение источника U=I∙r=0,005∙629,2=3,146 В; U≈3,2 В.

Падение напряжения в линии при прохождении тока I=0,005 А будет: Uл=I∙rл=0,005∙229,2=1,146 В.

Сравнительно малое падение напряжения в линии достигается благодаря малой величине тока (5 мА). Поэтому в месте приема должно быть чувствительное реле (усилитель), которое включается от слабого импульса 5 мА и своим контактом включает другое, более мощное реле.

8. Как велико напряжение на лампах в схеме на рис. 28, когда: а) двигатель не включен; б) двигатель запускается; в) двигатель в работе.

Двигатель и 20 ламп включены в сеть с напряжением 110 В. Лампы рассчитаны на напряжение 110 В и мощность 40 Вт. Пусковой ток двигателя Iп=50 А, а его номинальный ток Iн=30 А.

Подводящий медный провод имеет сечение 16 мм2 и длину 40 м.

Из рис. 7 и условия задачи видно, что ток двигателя и ламп вызывает в линии падение напряжения, поэтому напряжение на нагрузке будет меньше 110 В.

Рис. 7.

U=2∙Uл+Uламп.

Отсюда напряжение на лампах Uламп=U-2∙Uл.

Надо определить падение напряжения в линии при различных токах: Uл=I∙rл.

Сопротивление всей линии

2∙rл=ρ∙(2∙l)/S=0,0178∙(2∙40)/16=0,089 Ом.

Ток, проходящий через все лампы,

20∙Iламп=20∙40/110=7,27 А.

Падение напряжения в линии, когда включены только лампы (без двигателя),

2∙Uл=Iламп∙2∙rл=7,27∙0,089=0,65 В.

Напряжение на лампах в этом случае равно:

Uламп=U-2∙Uл=110-0,65=109,35 В.

При пуске двигателя лампы будут светить слабее, так как падение напряжения в линии больше:

2∙Uл=(Iламп+Iдв)∙2∙rл=(7,27+50)∙0,089=57,27∙0,089=5,1 В.

Минимальное напряжение на лампах при пуске двигателя будет:

Uламп=Uс-2∙Uл=110-5,1=104,9 В.

Когда двигатель работает, падение напряжения в линии меньше, чем при пуске двигателя, но больше, чем при выключенном двигателе:

2∙Uл=(Iламп+Iном)∙2∙rл=(7,27+30)∙0,089=37,27∙0,089=3,32 В.

Напряжение на лампах при нормальной работе двигателя равно:

Uламп=110-3,32=106,68 В.

Даже небольшое снижение напряжения на лампах относительно номинального сильно влияет на яркость освещения.

Итак, резистор … Базовый элемент построения электрической цепи.

Работа резистора заключается в ограничении тока , протекающего по цепи. НЕ в превращении тока в тепло, а именно в ограничении тока . То есть, без резистора по цепи течет большой ток , встроили резистор – ток уменьшился. В этом заключается его работа, совершая которую данный элемент электрической цепи выделяет тепло.

Пример с лампочкой

Рассмотрим работу резистора на примере лампочки на схеме ниже. Имеем источник питания, лампочку, амперметр, измеряющий ток , проходящий через цепь. И Резистор . Когда резистор в цепи отсутствует, через лампочку по цепи побежит большой ток , например, 0,75А. Лампочка горит ярко. Встроили в цепь резистор — у тока появился труднопреодолимый барьер, протекающий по цепи ток снизился до 0,2А. Лампочка горит менее ярко. Стоит отметить, что яркость, с которой горит лампочка, зависит так же и от напряжения на ней. Чем выше напряжение — тем ярче.

Кроме того, на резисторе происходит падение напряжения . Барьер не только задерживает ток , но и «съедает» часть напряжения, приложенного источником питания к цепи. Рассмотрим это падение на рисунке ниже. Имеем источник питания на 12 вольт. На всякий случай амперметр, два вольтметра про запас, лампочку и резистор . Включаем цепь без резистора (слева). Напряжение на лампочке 12 вольт. Подключаем резистор — часть напряжения упала на нем. Вольтметр(снизу на схеме справа) показывает 5В. На лампочку остались остальные 12В-5В=7В. Вольтметр на лампочке показал 7В.

Разумеется, оба примера являются абстрактными, неточными в плане чисел и рассчитаны на объяснение сути процесса, происходящего в резисторе .

Основная характеристика резистора — сопротивление . Единица измерения сопротивления – Ом (Ohm, Ω). Чем больше сопротивление , тем больший ток он способен ограничить, тем больше тепла он выделяет, тем больше напряжения падает на нем.

Основной закон всего электричества. Связывает между собой Напряжение(V), Силу тока (I) и Сопротивление(R).

Интерпретировать эти символы на человеческий язык можно по-разному. Главное — уметь применить для каждой конкретной цепи. Давайте используем Закон Ома для нашей цепи с резистором и лампочкой, рассмотренной выше, и рассчитаем сопротивление резистора , при котором ток от источника питания на 12В ограничится до 0,2. При этом считаем сопротивление лампочки равным 0.

V=I*R => R=V/I => R= 12В / 0,2А => R=60Ом

Итак. Если встроить в цепь с источником питания и лампочкой, сопротивление которой равно 0, резистор номиналом 60 Ом, тогда ток, протекающий по цепи , будет составлять 0,2А.

Микропрогер, знай и помни! Параметр мощности резистора является одним из наиболее важных при построении схем для реальных устройств.

Мощность электрического тока на каком-либо участке цепи равна произведению силы тока, протекающую по этому участку на напряжение на этом участке цепи. P=I*U. Единица измерения 1Вт.

При протекании тока через резистор совершается работа по ограничению электрического тока . При совершении работы выделяется тепло. Резистор рассеивает это тепло в окружающую среду. Но если резистор будет совершать слишком большую работу, выделять слишком много тепла — он перестанет успевать рассеивать вырабатывающееся внутри него тепло, очень сильно нагреется и сгорит. Что произойдет в результате этого казуса, зависит от твоего личного коэффициента удачи.

Характеристика мощности резистора — это максимальная мощность тока, которую он способен выдержать и не перегреться.

Рассчитаем мощность резистора для нашей цепи с лампочкой. Итак. Имеем ток , проходящий по цепи(а значит и через резистор ), равный 0,2А. Падение напряжения на резисторе равно 5В (не 12В, не 7В, а именно 5 — те самые 5, которые вольтметр показывает на резисторе ). Это значит, что мощность тока через резистор равна P=I*V=0,2А*5В=1Вт. Делаем вывод: резистор для нашей цепи должен иметь максимальную мощность не менее(а лучше более) 1Вт. Иначе он перегреется и выйдет из строя.

Соединение резисторов

Резисторы в цепях электрического тока имеют последовательное и параллельное соединение .

При последовательном соединении общее сопротивление резисторов является суммой сопротивлений каждого резистора в соединении:

При параллельном соединении общее сопротивление резисторов рассчитывается по формуле:

Остались вопросы? Напишите комментарий. Мы ответим и поможем разобраться =)

Для человека, который знаком с электрооборудованием на уровне простого пользователя (знает, где и как включить/выключить), многие используемые электриками термины кажутся какой-то бессмыслицей. Например, чего только стоит «падение напряжения» или «сборка схемы». Куда и что падает? Кто разобрал схему на детали? На самом же деле, физический смысл происходящих процессов, скрывающийся за большинством этих слов, вполне доступен для понимания даже со школьными знаниями физики.

Чтобы объяснить, что такое падение напряжения, необходимо вспомнить, какие вообще напряжения бывают в (имеется в виду глобальная классификация). Их всего два вида. Первый – это напряжение который подключен к рассматриваемому контуру. Оно может также называться приложенным ко всей цепи. А второй вид – это именно падение напряжения. Может быть рассмотрено как в отношении всего контура, так и любого отдельно взятого элемента.

На практике это выглядит следующим образом. Например, если взять обычную вкрутить ее в патрон, а провода от него подключить в домашнюю сетевую розетку, то приложенное к цепи (источник питания – проводники – нагрузка) напряжение составит 220 Вольт. Но стоит нам с помощью вольтметра замерять его значение на лампе, как станет очевидно, что оно немного меньше, чем 220. Так произошло потому, что возникло падение напряжения на которым обладает лампа.

Пожалуй, нет человека, который не слышал бы о законе Ома. В общем случае формулировка его выглядит так:

где R – активное сопротивление цепи или ее элемента, измеряется в Омах; U – электрическое напряжение, в Вольтах; и, наконец, I – ток в Амперах. Как видно, все три величины непосредственно связаны между собой. Поэтому, зная любые две, можно довольно просто вычислить третью. Конечно, в каждом конкретном случае придется учесть род тока (переменный или постоянный) и некоторые другие уточняющие характеристики, но основа – вышеуказанная формула.

Электрическая энергия – это, фактически, движение по проводнику отрицательно заряженных частиц (электронов). В нашем примере спираль лампы обладает высоким сопротивлением, то есть замедляет перемещающиеся электроны. Благодаря этому возникает видимое свечение, но общая энергия потока частиц снижается. Как видно из формулы, с уменьшением тока уменьшается и напряжение. Именно поэтому результаты замеров у розетки и на лампе различаются. Эта разница и является падением напряжения. Данная величина всегда учитывается, чтобы предотвратить слишком большое снижение на элементах в конце схемы.

Падение напряжения на резисторе зависит от его и силы протекающего по нему тока. Также косвенное влияние оказывают температура и характеристики тока. Если в рассматриваемую цепь включить амперметр, то падение можно определить умножением значения тока на сопротивление лампы.

Но далеко не всегда удается вот так просто с помощью простейшей формулы и измерительного прибора выполнить расчет падения напряжения. В случае параллельно подключенных сопротивлений нахождение величины усложняется. На приходится дополнительно учитывать реактивную составляющую.

Рассмотрим пример с двумя параллельно включенными резисторами R1 и R2. Известно сопротивление провода R3 и источника питания R0. Также дано значение ЭДС – E.

Приводим параллельные ветки к одному числу. Для этой ситуации применяется формула:

R = (R1*R2) / (R1+R2)

Определяем сопротивление всей цепи через сумму R4 = R+R3.

Рассчитываем ток:

Остается узнать значение падение напряжения на выбраном элементе:

Здесь множитель “R5” может быть любым R – от 1 до 4, в зависимости от того, какой именно элемент схемы нужно рассчитать.

Есть другой способ снижения напряжения на нагрузке, но только для цепей постоянного тока. Про смотри здесь.

Вместо дополнительного резистора используют цепочку из последовательно включенных, в прямом направлении, диодов.

Весь смысл состоит в том, что при протекании тока через диод на нем падает «прямое напряжение» равное, в зависимости от типа диода, мощности и тока протекающего через него — от 0,5 до 1,2 Волта.

На германиевом диоде падает напряжение 0,5 — 0,7 В, на кремниевом от 0,6 до 1,2 Вольта. Исходя из того, на сколько вольт нужно понизить напряжение на нагрузке, включают соответствующее количество диодов.

Чтобы понизить напряжение на 6 В необходимо приблизительно включить: 6 В: 1,0 = 6 штук кремниевых диодов, 6 В: 0,6 = 10 штук германиевых диодов. Наиболее популярны и доступны кремниевые диоды.

Выше приведенная схема с диодами, более громоздка в исполнении, чем с простым резистором. Но, выходное напряжение, в схеме с диодами, более стабильно и слабо зависит от нагрузки. В чем разница между этими двумя способами снижения выходного напряжения?

На Рис 1 — добавочное сопротивление — резистор (проволочное сопротивление), Рис 2 — добавочное сопротивление — диод.

У резистора (проволочного сопротивления) линейная зависимость между током, проходящем через него и падением напряжения на нем. Во сколько раз увеличится ток, во столько же раз увеличится и падение напряжения на резисторе.

Из примера 1: если мы к лампочке подключим параллельно еще одну, то ток в цепи увеличится, с учетом общего сопротивления двух лампочек до 0,66 А. Падение напряжения на добавочном резисторе будет: 12 Ом *0,66 А = 7,92 В. На лампочках останется: 12 В — 7,92 В = 4,08 В. Они будут гореть в пол накала.

Совсем другая картина будет если вместо резистора будет цепочка диодов.

Зависимость между током протекающем через диод и падающем на нем напряжении нелинейная. Ток может увеличиться в несколько раз, падение напряжения на диоде увеличится всего на несколько десятых вольта.

Т.е. чем больше ток диода, тем (сравнительно с резистором) меньше увеличивается его сопротивление. Падение напряжения на диодах мало зависит от тока в цепи.

Диоды в такой цепи выполняют роль стабилизатора напряжения. Диоды необходимо подбирать по максимальному току в цепи. Максимально допустимый ток диодов должен быть больше, чем ток в рассчитываемой цепи.

Падения напряжения на некоторых диодах при токе 0,5 А даны в таблице.

В цепях переменного тока, в качестве добавочного сопротивления можно использовать конденсатор, индуктивность, динистор или тиристор (с добавлением схемы управления).

Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор

Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.

Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.

Электрический паяльник с регулировкой температуры

Мощность: 60/80 Вт, температура: 200’C-450’C, высококачествен…

Схема делителя напряжения на резисторах

Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.

Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.

Расчет делителя напряжения на резисторах

Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.

Формула делителя напряжения

Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома.

Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:

Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:

Профессиональный цифровой осциллограф

Количество каналов: 1, размер экрана: 2,4 дюйма, разрешен…

Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:

Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:

И, на какое-то время, мы можем упростить схему:

Закон Ома в его наиболее простом виде: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:

А так как I1 равно I2, то:

Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.

Делитель напряжения — калькулятор онлайн





 Применение делителя напряжения на резисторах

В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.

Потенциометры

Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.

Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.

Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.

Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.

Резистивные датчики

Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.

Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).

Пример работы делителя напряжения на фоторезисторе.

Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.

Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

Расчет резисторов для светодиодов и его сопротивление

Светодиоды все чаще используются нами в различных сферах. Они представляют собой полупроводниковый прибор, превращающий электрический ток в световое излучение.

Для получения света с их помощью, не надо применять специальные дополнительные преобразователи. Достаточно подать на него электрический ток. В этом моменте часто проблемы. Они чувствительны к большим скачкам тока, которые наблюдаются при включении.

Для защиты от таких скачков, в цепь включают специально подобранные резисторы.

Резисторы по праву считаются самыми распространенными радиоэлементами. Главная их характеристика состоит в сопротивлении, в двух словах, они препятствуют протеканию электрического тока.

Резисторы считаются пассивными элементами электрической цепи. Они могут быть постоянными, т.е. такими сопротивлениями, у которых протекание тока остается неизменным. И переменными, где величину сопротивления можно регулировать от 0 до его максимального значения. Их используют как токоограничительные элементы, делители напряжения, шунты для измерительных приборов, и тому подобное.

Основной параметр резистора – это его сопротивление. Сопротивление – это его свойство препятствовать протеканию электрического тока. Измеряемой характеристикой величины сопротивления есть Ом.

Расчет сопротивления для светодиодов

Как произвести расчет:

Для провидения расчета понадобится знать точные параметры светодиода и источника напряжения. Их можно прочитать в паспортных данных, или найти в интернете. По источнику питания нам понадобятся данные выходного напряжения.

По светодиоду, его номинальное напряжение и рабочий ток.

Возьмем, к примеру, простейшую схему на рисунке выше. У нас источник питания Uи = 12В, напряжение на светодиоде Uvd= 2В, номинальный рабочий ток светодиода будет Ivd = 0,02А, в справочнике эта величина может быть показана как 2мА.

Найдем падения напряжения на резисторе.

Для этого, отнимем от напряжения источника питания, падения на светодиоде:

• Ur= Uи – Uvd = 12 – 2 = 10В;

У нас выходит падение напряжения на резисторе 10 вольт.

Используя формулу закона Ома, найдем величину необходимого сопротивления цепи:

• R=U/I = 10/0.02 = 500 Ом.

Подставив в формулу значение напряжения и тока, мы получили величину сопротивления. После этого, находим по справочным таблицам, ближайшее стандартное значение. Если нет точного значения, лучше взять с небольшим запасом в большую сторону.

Расчет онлайн

Для расчета на онлайн-калькуляторе понадобятся все те же данные, что и для расчетов в ручном режиме. Это: напряжение источника питания, номинальный прямой ток и напряжение, количество светодиодов, и их схема подключения.

Ниже приведены ссылки на несколько источников с онлайн-калькуляторами:

1. http://forum220.ru/calc-res-led.php. На странице этого калькулятора вам подскажут, как можно найти номинальное прямое напряжение светодиода по цвету его света, если данные об этом отсутствуют.
2. http://cxem.net/calc/ledcalc.php. Этот калькулятор не только рассчитает вам значения сопротивления, но и предложит схему подключения. Это будет удобно в случае большого количества светодиодов.
3. http://h-t-f.ru/calk/online-calculator-for-resistor-leds. Калькулятор учитывает особенности соединения.

Принцип работы и область применения

Резисторы разной мощности

Принцип работы резистора построен на рассеивании мощности. Номинальной мощностью рассеивания является та мощность, которую резистор может рассеять не повреждаясь. Единица мощности – ватты.

Рассматривая роль резистора с точки зрения электротехники, мощность можно определить по формуле: Р=I ² * R, где P – мощность, I – значение силы тока, R – сопротивление резистора.

Резисторы являются важными элементами электрической цепи, главная их функция – это сопротивление протеканию электрического тока. Этим он способствует стабилизации и ограничении силы тока протекающей по цепи. Его часто используют в качестве балластного резистора, чтобы иметь возможность регулировать напряжение в цепи.

Резисторы, в том числе балластные, используются для поглощения некоторой части напряжения, выравнивают силы тока в различных участках цепи. Тем самым, они поддерживают стабильность напряжения.

Этот принцип используют в резисторах для светодиодов. Светодиоды чувствительны к большим скачкам тока, которые могут возникнуть при их включении, они могут привести их негодность. Включенный последовательно с ним токоограничивающий резистор, уменьшит ток до приемлемой величины.

Подключение и пайка

Светодиоды – это полупроводниковые приборы, при их подключении необходимо соблюдать полярность. При неправильном подключении они работать не будут, и довольно часто выходят со строя.

Анод имеет полярность +, катод соответственно -. Обычно, ножка катода немного меньше по длине. Часто, катод можно опознать по более толстой ножке внутри прибора. В любом случае, данные по контактам можно найти в справочной литературе.

Диоды также боятся перегрева во время пайки. Для пайки нельзя использовать мощные паяльники, лучше использовать приборы мощностью до 100 Вт.

Также, можно в качестве вспомогательных средств для охлаждения использовать пинцет. Он отведет часть тепла. Вместо пинцета, можно использовать и другие металлические инструменты.

Паяльник перед пайкой надо разогреть до его максимальной температуры. Было бы хорошо, чтобы его температура была в пределах 250-280 градусов Цельсия.

Сам процесс пайки одной ножки не должен превышать 4-5 секунд. При этом времени, прибор не успеет перегреться.

При монтаже светодиода на месте установки, старайтесь, чтобы контакты ближе к корпусу, оставались параллельны, как при выходе из производства. Изгибайте контакты небольшими радиусами, уступив подальше от корпуса. Собирайте их на твердом плоском материале. Предварительно, подготовьте отверстия для ножек светодиодов с помощью дрели.

Подбирая источник питания, следует помнить: чем больше разница рабочего напряжения светодиода и источника питания, тем меньше они будут подвержены влиянию скачков напряжения блока питания. Не забывайте устанавливать предохранители.

Если у вас безвыходные SMD светодиоды, у них вместо ножек для пайки контактные площадки. Эти площадки расположены на нижней части их корпуса. Паяют их маломощными паяльниками не более 15 ВТ.

Часто, для этой работы применяют специальное жало. Оно имеет разветвление на рабочем конце. Народные умельцы вместо специального жала наматывают тонкий медный провод на стандартное жало. Оптимальный диаметр такого провода 1 мм.

Легче всего проверить светодиоды с помощью тестера. Проверяется он как обычный диод. Его надо включить в прямом положении, чтобы между анодом и катодом пошло положительное напряжение. Многие современные цифровые приборы имеют встроенную возможность проверки диодов. Главное при проверке – соблюдать полярность.

Статья была полезна?

0,00 (оценок: 0)

Расчет падения напряжения на транзисторе

Во-первых: ток течет в базу, через излучатель. во-вторых, ток течет через коллектор и выходит из излучателя. Суммарный ток через излучатель равен току через основание плюс ток через коллектор.

Вам потребуется таблица данных, чтобы определить точное падение напряжения. Однако также следует помнить, что нет двух идентичных транзисторов.

Таблица данных будет содержать графики, которые вы можете использовать для поиска ожидаемых значений. Для некоторых вычислений полезно предположить, что Vbe обычно составляет около 0,7v. Соединение база-эмиттер по сути является диодом, поэтому оно зажимает напряжение на себе примерно до 0,7 В. Используя этот факт, легко вычислить ток, поступающий в базу: напряжение на R составляет приблизительно 5-0,7 = 4,3 В. Таким образом, ток, идущий в базу, должен быть примерно:

I = V / R = 4,3 / R

Так что, если вы знаете R, вы можете приблизить ток, текущий в базу. Это даст вам один фактор, который поможет вам прочитать графики из таблицы данных транзистора. Скажем, R составляет 10 кОм, ток, протекающий в базу, будет приблизительно 0,43 мА.

Теперь с этим базовым током вы можете рассчитать ток, протекающий через коллектор – просто умножьте его на коэффициент усиления тока транзистора. Но имейте в виду, что они могут сильно различаться в первую очередь между транзисторами одной модели, а также при разных условиях работы этой модели. Скажем, если 50, то ток, протекающий через коллектор, будет приблизительно 22,5 мА.

Используя приведенную выше схему, предположим, что падение напряжения на светодиоде составляет 2 В при 22,5 мА, что означает, что значение Vbe должно составлять 5-2 = 3 В. Однако, опять же, падение напряжения светодиода при данном токе будет незначительно отличаться между светодиодами одной и той же модели, и некоторые светодиоды, такие как белые светодиоды, имеют тенденцию иметь более высокое падение напряжения, например, 4v.

Чтобы попытаться получить точное значение Vbe, есть формула, которую вы можете использовать, однако, учитывая различия между отдельными транзисторами, гораздо проще просто использовать графики. Поскольку вы знаете приблизительное напряжение Vce и ​​приблизительный базовый ток Ib, вы можете посмотреть Vbe на графике.

И учитывая диапазон возможных значений hfe, указанных в таблице, (обычно они предоставляют три значения: минимальное, типичное и максимальное). Используя верхнюю и нижнюю границы hfe, вы можете рассчитать верхнюю и нижнюю границы тока, который будет проходить через коллектор. Исходя из этого и таблицы данных светодиода, вы можете рассчитать верхнюю и нижнюю границу Vce. Это значение будет полезно при уточнении возможных значений Vbe, поскольку часто Vbe существенно зависит от Vce и ​​Ice; это может иметь значение +/- 0,2 В или около того.

Другие соображения, которые также могут быть весьма значительными, это температура перехода транзистора. Итак, сколько энергии протекает через него, как долго, а также насколько хорошо он отдает тепло в окружающую среду, и температура этой среды будет определять температуру перехода транзистора, что, в свою очередь, повлияет на такие значения, как hfe, Vbe и так далее.

Для вашей схемы выше, вы можете использовать транзистор, такой как NP54 BC547, который является BJT NPN транзистором общего назначения. Эта таблица должна быть достаточной для того, чтобы вы могли понять, как она будет себя вести. Значения hfe, которые я изложил выше, будут разными в BC547; в техническом описании указано минимальное значение 110, максимальное – 800. Таким образом, ваша схема даст очень широкий диапазон значений потенциального льда, поэтому будьте осторожны, чтобы не перегореть светодиод. Вы можете определить hfe любого отдельного транзистора, подав небольшой ток через базу, и измерить ток через коллектор; затем разделите Ic на Ib, и это то, что нужно для этой ситуации. (Если транзистор не «насыщен», то есть светодиод или что-то на его месте в вашей цепи имеет почти 5 В через него, что означает, что транзистор не может еще больше увеличить Ic, поскольку он уже действует как короткое замыкание.) чтобы рассчитать hfe одного конкретного BC547, можно предположить, что он не будет иметь hfe меньше 110, а затем рассчитать резистор для замены R и светодиода (назовем его Rled) на. (Vbe / kt) -1) не применяется, когда транзистор насыщен , поскольку Ie будет ограничено. (Смотри ниже). Во-вторых, решение включает в себя построение пересечения двух графиков: напряжение на R против Ir в соответствии с законом Ома и Vbe против Ib с уравнением Эберса-Молла, решение, где Ir и Ib равны. Ir против Vr будет прямой линией, а Ib против Vbe будет экспоненциальной.

График в вашем ответе выглядит правильно, если предположить, что он взят из схемы, которую вы разместили в своем вопросе? (То есть со светодиодом?) Причина, по которой он может перестать быть линейным, заключается в том, что напряжение на светодиоде становится близким к 5 В, что означает, что транзистор насыщается. Таким образом, больший базовый ток приводит лишь к немного большему току, проходящему через светодиод, из-за немного уменьшенных насыщенных значений Vce. Это отражается в следующем:

Если вы посмотрите на эту таблицу данных для 2N3904 , она сведет в таблицу эти два значения:

VBE (sat) Напряжение насыщения базового излучателя:

• С IC = 10 мА и IB = 1,0 мА, тогда Vbe = 0,65
• При IC = 50 мА и IB = 5,0 мА, тогда Vbe = 0,85

Делитель напряжения – Вольтик.ру

Перед схемотехниками нередко стоит задача получения пониженного напряжения из высокого напряжения. Это можно сделать с помощью делителя напряжения – простой схемы с использованием двух резисторов. С их помощью можно создать выходное напряжение в несколько раз меньшее, чем входное напряжение.

Простота и надежность делителя напряжения сделали его схему фундаментальной в схемотехнике. При ее внедрении необходимо уделить максимум внимания непосредственно схеме и точности расчета напряжения по специальной формуле.

Существует несколько вариантов схем делителя напряжения, с которыми можно будет познакомиться ниже. Особенностью каждой из них является наличие двух резисторов и входного напряжения. Резистор, расположенный у плюса входного напряжения, обозначен на схемах R1, расположенный у минуса – R2. Падение напряжения у второго резистора обозначается Uout. Оно и является результатом работы схемы делителя напряжения.

Чтобы произвести расчет напряжения делителя нужно знать значения следующих величин: сопротивление первого и второго резистора (R1, R2) и входное напряжение Uin. Для расчета используется следующая формула:

Знакомые со школьным курсом физики без труда смогут определить, что в основе этого уравнения лежит закон Ома. Для определения напряжения на выходе делителя выводится формула с использованием силы тока I1 и I2, протекающего через резисторы R1, R2:

Используя закон Ома, мы получаем следующую формулу для Uout:

В этом уравнении для нас остается неизвестной величина I2, но если предположить, что она равна I1, то наша схема приобретет следующий вид:

В этой схеме неизвестным остается Uin – сопротивление на обоих резисторах R1, R2. Так как они соединены последовательно, то их совместное сопротивление суммируется:

В итоге схема делителя напряжения упрощается:

Исходя из школьной формулы U=I*R и помня, что суммарное сопротивление равно R1 + R2, записываем закон Ома в следующем виде:

Так как мы приняли I1=I2, то получаем уравнение, которое нам наглядно демонстрирует, что выходное напряжение будет прямо пропорциональным отношению сопротивлений и входному напряжению.

Делитель напряжения широко используется в радиоэлектронике, приведем несколько примеров:

• потенциометры;
• резистивные датчики;
• фоторезисторы.

Как рассчитать электрическую нагрузку

Электрические цепи находят множество применений, в том числе в быту, автомобилестроении и электронике. Электрические принципы применимы независимо от области применения. У вас есть несколько компонентов, распределенных по схеме, которые составляют нагрузку схемы. У вас есть источник энергии. Вы хотите знать характеристики компонентов нагрузки. У вас есть закон Кирхгофа, который, по сути, гласит, что сумма напряжения нагрузки равна сумме напряжений источника.Вы не хотите повредить какие-либо компоненты цепи, поэтому рассчитываете нагрузку.

Расчет электрической нагрузки в простой цепи

Рассчитайте электрическую нагрузку для простой линейной цепи, имеющей напряжение источника 9 В и два последовательно включенных резистора по 330 Ом. Второй резистор имеет вывод, идущий на землю. Рассчитайте по следующим уравнениям. Пусть мощность = напряжение * ток (P = VI). Пусть ток = напряжение / сопротивление (I = V / R).

Примените второй закон Кирхгофа, согласно которому сумма напряжений в цепи равна нулю.Сделайте вывод, что напряжение нагрузки вокруг простой схемы должно составлять 9 вольт. Вычислите, что напряжение нагрузки равномерно распределено на каждом из резисторов, поскольку они имеют одинаковое сопротивление, и что напряжение на каждом из них должно составлять 4,5 В (или -4,5 в соответствии с законом Кирхгофа).

Рассчитайте I = V / R (расчет тока), так что I = 4,5 / 330 = 13,6 мА (миллиампер). Вычислите P = VI = 9 * 0,0136 = 0,1224 Вт. Обратите внимание, что теперь известны все характеристики нагрузки (напряжение, сопротивление, ток и мощность).Будьте осторожны и выбирайте резисторы мощностью 0,5 Вт.

Используйте онлайн-симулятор линейных цепей для моделирования простых цепей и расчета нагрузочных характеристик. Воспользуйтесь описанным ниже имитатором линейной схемы под названием «Linear Technology Spice». Создайте образец схемы и поэкспериментируйте с различными компонентами нагрузки. Рассчитайте характеристики нагрузки, используя уравнения напряжения, тока, сопротивления (или индуктивности) и мощности.

Расчет бытовой электрической нагрузки

Рассчитайте нагрузку для типичного дома на одну семью с помощью онлайн-калькулятора электрической нагрузки.Воспользуйтесь онлайн-калькулятором «Калькулятор электрической нагрузки для дома на одну семью».

Укажите площадь вашего дома в квадратных футах. Введите количество «цепей для малой бытовой техники» и «цепей для стирки» и при необходимости обратитесь к электрической схеме. Если информация недоступна, используйте значения по умолчанию. Введите значения для «Прикрепленные приборы», «Приборы для приготовления пищи», «Отопление или охлаждение» и «Самый большой двигатель». Нажмите «Рассчитать нагрузку».

Обратите внимание на «Общая расчетная нагрузка», «Расчетная сила тока», «Общая нейтральная нагрузка», «Общая нейтральная нагрузка» и «Общая нейтральная сила тока».”

ток – Падение напряжения на одном резисторе и на двух резисторах

Сначала я скажу, что вопрос ОП и все ответы здесь (включая последний, полученный минуту назад) отличные, и я оцениваю их на +1 🙂 Я только дополню их еще несколькими экстравагантными, но “заставляющими задуматься” “соображения …

«Возникает вопрос, почему падение напряжения на резисторах с одинаковым сопротивлением меняется от первой цепи ко второй? Имеет ли это какое-либо отношение к току? Почему это происходит? Я пытаюсь найти интуитивное объяснение: почему это происходит.”

«Что мне действительно нужно, так это ответ на вопрос, почему падение напряжения во второй цепи на каждом резисторе составляет половину, даже если они имеют такое же сопротивление, как и в первой цепи».

Если вы действительно хотите, чтобы падение напряжения на резисторах с одинаковым сопротивлением было одинаковым, я могу предложить вам решение – всего заменить источники напряжения на источники тока . Это не просто шутка, а вполне реальная конфигурация схемы, которую мы можем наблюдать в некоторых хорошо известных электронных схемах (например,например, в так называемом «каскаде с общим эмиттером и вырождением эмиттера» или «фазоделителе»).

Но вернемся к схемам ОП с 1 и 2 резисторами, питаемыми от источников напряжения, и сделаем несколько интересных выводов.

Во-первых, нас может не интересовать ток, протекающий через резисторы, и их сопротивление. В обеих цепях напряжение не зависит ни от тока, ни от сопротивления. Во второй схеме падение напряжения на резисторе зависит только от отношения его сопротивления к общему сопротивлению.

Второй интересный вывод, который мы можем сделать в отношении потенциометра транзистора . Хотя это переменный резистор, когда мы поворачиваем его стеклоочиститель, мы фактически ничего не меняем – ни сопротивление … ни ток … ни напряжение. Мы просто измеряем (выбираем) напряжение в одной точке на его внутреннем резистивном слое … но все остальные точки имеют линейно убывающие напряжения.

Wikimedia Commons

Конечно, мы можем представить, что при вращении стеклоочистителя одно частичное сопротивление увеличивается, когда другое уменьшается, поэтому их сумма остается постоянной… и, как следствие, постоянный ток. Такие «электронные потенциометры» можно увидеть в каскадах КМОП, усилителях с обратной связью по току (CFA) и т. Д.

Цепи серии

– базовое электричество

Три закона для последовательных цепей

Существует три основных соотношения, касающихся сопротивления, тока и напряжения для всех последовательных цепей. Важно, чтобы вы усвоили три основных закона для последовательных цепей.

Сопротивление

Когда отдельные сопротивления соединяются последовательно, они действуют так же, как одно большое комбинированное сопротивление.Поскольку существует только один путь для протекания тока в последовательной цепи, и поскольку каждый из резисторов находится в линии, чтобы действовать как противодействие этому протеканию тока, общее сопротивление представляет собой комбинированное сопротивление всех резисторов, установленных в линию.

Общее сопротивление последовательной цепи равно сумме всех отдельных сопротивлений в цепи .

Rt = R1 + R2 + R3…

Используя эту формулу, вы обнаружите, что полное сопротивление цепи равно:

RT = 15 Ом + 5 Ом + 20 Ом = 40 Ом

Рисунок 16.Последовательная цепь

Текущий

Поскольку существует только один путь для потока электронов в последовательной цепи, ток имеет одинаковую величину в любой точке цепи.

Общий ток в последовательной цепи такой же, как ток через любое сопротивление цепи.

IT = I1 = I2 = I3…

Учитывая 120 В как общее напряжение и определив общее сопротивление цепи как 40 Ом, теперь вы можете применить закон Ома для определения полного тока в этой цепи:

IT = 120 В / 40 Ом = 3 А

Этот общий ток цепи останется неизменным для всех отдельных резисторов цепи.

Напряжение

Прежде чем какой-либо ток будет протекать через сопротивление, должна быть доступна разность потенциалов или напряжение.Когда резисторы соединены последовательно, они должны «делить» общее напряжение источника.

Общее напряжение в последовательной цепи равно сумме всех отдельных падений напряжения в цепи.

Когда ток проходит через каждый резистор в последовательной цепи, он устанавливает разность потенциалов на каждом отдельном сопротивлении. Это обычно называется падением напряжения, и его величина прямо пропорциональна величине сопротивления.Чем больше значение сопротивления, тем выше падение напряжения на этом резисторе.

ET = E1 + E2 + E3…

Используя закон Ома, вы можете определить напряжение на каждом резисторе.

3 А × 15 Ом = 45 В

3 А × 5 Ом = 15 В

3 А × 20 Ом = 60 В

Общее напряжение источника равно сумме отдельных падений напряжения:

45 В + 15 В + 60 В = 120 В

Обрыв в последовательной цепи

При появлении обрыва ток в цепи прерывается.Если нет тока, падение напряжения на каждом из резистивных элементов равно нулю. Однако разность потенциалов источника очевидна. Если вольтметр подключен через разрыв, показания такие же, как если бы он был подключен непосредственно к клеммам источника питания.

Рисунок 17. Обрыв цепи

Влияние обрыва линии и потери линии

Медь и алюминий используются в качестве проводников, потому что они мало препятствуют прохождению тока.Хотя сопротивлением часто пренебрегают при простом анализе цепей, в практических приложениях может возникнуть необходимость учитывать сопротивление линий.

Line Drop

Рисунок 18. Падение напряжения

Когда ток 10 А протекает через каждую линию с сопротивлением 0,15 Ом, на каждой линии появляется небольшое падение напряжения. Это падение напряжения на линейных проводниках обычно обозначается как падение на линии .

Поскольку есть две линии, общее падение составляет 2 × 1.5 В = 3 В. Напряжение сети на нагрузке (117 В) меньше напряжения источника.

В некоторых ситуациях может потребоваться использование более крупных проводов с меньшим сопротивлением, чтобы падение напряжения в линии не слишком сильно уменьшало напряжение нагрузки.

Потеря линии

Другой термин, связанный с проводниками, – потери в линии. Это потеря мощности, выраженная в ваттах, и связана с рассеянием тепловой энергии, когда ток течет через сопротивление проводов линии.Потери в линии рассчитываются с использованием одного из уравнений мощности.

Используя предыдущий пример:

P = I ² × R

P = (10A) ² × 0,3 Ом

P = 30 Вт

* Помните:

• Падение напряжения в линии выражается в вольтах.
• Потери в линии выражаются в ваттах.

Атрибуция

Учебное пособие по физике

: схемы серии

Как упоминалось в предыдущем разделе Урока 4, два или более электрических устройства в цепи могут быть соединены последовательным или параллельным соединением.Когда все устройства соединены последовательным соединением, схема называется последовательной цепью . В последовательной цепи каждое устройство подключается таким образом, что существует только один путь, по которому заряд может проходить через внешнюю цепь. Каждый заряд, проходящий через контур внешней цепи, будет последовательно проходить через каждый резистор.

Краткое сравнение и контраст между последовательными и параллельными цепями было сделано в предыдущем разделе Урока 4.В этом разделе подчеркивалось, что добавление большего количества резисторов в последовательную цепь приводит к довольно ожидаемому результату – увеличению общего сопротивления. Поскольку в цепи есть только один путь, каждый заряд встречает сопротивление каждого устройства; поэтому добавление большего количества устройств приводит к увеличению общего сопротивления. Это увеличенное сопротивление служит для уменьшения скорости протекания заряда (также известной как ток).

Эквивалентное сопротивление и ток

Заряды проходят через внешнюю цепь со скоростью, которая везде одинакова.В одном месте ток не больше, чем в другом. Фактическое количество тока обратно пропорционально общему сопротивлению. Существует четкая взаимосвязь между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Что касается батареи, которая нагнетает заряд, наличие двух последовательно соединенных резисторов с сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора с сопротивлением 12 Ом. Наличие трех последовательно соединенных резисторов сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 18 Ом.И наличие четырех последовательно соединенных резисторов 6 Ом было бы эквивалентно наличию в цепи одного резистора 24 Ом.

Это концепция эквивалентного сопротивления. Эквивалентное сопротивление схемы – это величина сопротивления, которая потребуется одному резистору, чтобы сравняться с общим эффектом от набора резисторов, присутствующих в схеме. Для последовательных цепей математическая формула для вычисления эквивалентного сопротивления (R _экв ) составляет

R _экв = R ₁ + R ₂ + R ₃ +…

, где R ₁ , R ₂ и R ₃ – значения сопротивления отдельных резисторов, соединенных последовательно.

Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже. Создайте себе проблему с любым количеством резисторов и любыми номиналами. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.

Ток в последовательной цепи везде одинаковый.Заряд НЕ накапливается и не начинает накапливаться в любом заданном месте, так что ток в одном месте больше, чем в других местах. Заряд НЕ расходуется резисторами, поэтому в одном месте его меньше по сравнению с другим. Можно представить, что заряды движутся вместе по проводам электрической цепи и везде движутся с одинаковой скоростью. Ток – скорость, с которой течет заряд – везде одинаков. То же самое на первом резисторе, как на последнем резисторе, как в батарее.Математически можно написать

I _{аккумулятор} = I ₁ = I ₂ = I ₃ = …

, где I ₁ , I ₂ и I ₃ – значения тока в отдельных местах расположения резисторов.

Эти значения тока легко вычислить, если известно напряжение батареи и известны отдельные значения сопротивления. Используя значения отдельных резисторов и приведенное выше уравнение, можно рассчитать эквивалентное сопротивление.А используя закон Ома (ΔV = I • R), можно определить ток в батарее и, следовательно, через каждый резистор, найдя соотношение напряжения батареи и эквивалентного сопротивления.

I _{аккумулятор} = I ₁ = I ₂ = I ₃ = ΔV _{аккумулятор} / R _экв

Разность электрических потенциалов и падения напряжения

Как обсуждалось в Уроке 1, электрохимическая ячейка цепи подает энергию на заряд, чтобы перемещать его через ячейку и устанавливать разность электрических потенциалов на двух концах внешней цепи.Элемент с напряжением 1,5 В создает разность электрических потенциалов во внешней цепи 1,5 В. Это означает, что электрический потенциал на положительной клемме на 1,5 В больше, чем на отрицательной клемме. Когда заряд движется по внешней цепи, он теряет 1,5 вольт электрического потенциала. Эта потеря электрического потенциала называется падением напряжения . Это происходит, когда электрическая энергия заряда преобразуется в другие формы энергии (тепловую, световую, механическую и т. Д.).) внутри резисторов или нагрузок. Если электрическая цепь, питаемая элементом на 1,5 В, оснащена более чем одним резистором, то совокупная потеря электрического потенциала составляет 1,5 В. Для каждого резистора существует падение напряжения, но сумма этих падений составляет 1,5 В – то же самое, что и номинальное напряжение источника питания. Математически это понятие может быть выражено следующим уравнением:

ΔV _{аккумулятор} = ΔV ₁ + ΔV ₂ + ΔV ₃ +…

Чтобы проиллюстрировать этот математический принцип в действии, рассмотрим две схемы, показанные ниже на диаграммах A и B. Предположим, вас попросили определить два неизвестных значения разности электрических потенциалов между лампочками в каждой цепи. Чтобы определить их значения, вам нужно будет использовать приведенное выше уравнение. Батарея обозначается обычным схематическим символом, а рядом с ней указывается ее напряжение. Определите падение напряжения для двух лампочек, а затем нажмите кнопку «Проверить ответы», чтобы убедиться, что вы правы.

Ранее в Уроке 1 обсуждалось использование диаграммы электрических потенциалов. Диаграмма электрического потенциала – это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим приведенную ниже принципиальную схему и соответствующую диаграмму электрических потенциалов.

Схема, показанная на схеме выше, питается от источника энергии 12 В.В цепи последовательно соединены три резистора, каждый из которых имеет собственное падение напряжения. Отрицательный знак разности электрических потенциалов просто означает потерю электрического потенциала при прохождении через резистор. Обычный ток направляется через внешнюю цепь от положительной клеммы к отрицательной. Поскольку схематический символ источника напряжения использует длинную полосу для обозначения положительного вывода, точка A на схеме находится на положительном выводе или выводе с высоким потенциалом.В точке A электрический потенциал 12 вольт, а в точке H (отрицательный вывод) – 0 вольт. Проходя через батарею, заряд приобретает электрический потенциал 12 вольт. А при прохождении через внешнюю цепь заряд теряет 12 вольт электрического потенциала, как показано на диаграмме электрических потенциалов, показанной справа от принципиальной схемы. Эти 12 вольт электрического потенциала теряются в три этапа, каждый из которых соответствует прохождению через резистор. При прохождении через соединительные провода между резисторами происходит небольшая потеря электрического потенциала из-за того, что провод оказывает относительно небольшое сопротивление потоку заряда.Поскольку точки A и B разделены проводом, они имеют практически одинаковый электрический потенциал 12 В. Когда заряд проходит через свой первый резистор, он теряет 3 В электрического потенциала и падает до 9 В в точке C. точка D отделена от точки C простым проводом, она имеет практически тот же электрический потенциал 9 В, что и C. Когда заряд проходит через второй резистор, он теряет 7 В электрического потенциала и падает до 2 В в точке E. Поскольку точка F отделена от точки E простым проводом, она имеет практически тот же электрический потенциал 2 В, что и E.Наконец, когда заряд проходит через свой последний резистор, он теряет 2 В электрического потенциала и падает до 0 В в точке G. цепь снова. Прирост энергии обеспечивается аккумулятором по мере того, как заряд перемещается с H на A.

В Уроке 3 закон Ома (ΔV = I • R) был введен как уравнение, которое связывает падение напряжения на резисторе с сопротивлением резистора и током на резисторе.Уравнение закона Ома можно использовать для любого отдельного резистора в последовательной цепи. При объединении закона Ома с некоторыми принципами, уже обсужденными на этой странице, возникает большая идея.

В последовательных цепях наибольшее падение напряжения имеет резистор с наибольшим сопротивлением.

Поскольку в последовательной цепи ток везде одинаковый, значение I ΔV = I • R одинаково на каждом из резисторов последовательной цепи. Таким образом, падение напряжения (ΔV) будет изменяться с изменением сопротивления.Где бы сопротивление ни было наибольшим, падение напряжения будет наибольшим у этого резистора. Уравнение закона Ома можно использовать не только для прогнозирования того, что на резисторе в последовательной цепи будет наблюдаться наибольшее падение напряжения, но и для расчета фактических значений падения напряжения.

Δ V 1 = I • R 1

Δ V 2 = I • R 2

Δ V 3 = I • R 3

Математический анализ последовательных цепей

Приведенные выше принципы и формулы могут быть использованы для анализа последовательной цепи и определения значений тока и разности электрических потенциалов на каждом из резисторов в последовательной цепи.Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R _eq ), тока в батарее (I _– ), а также падений напряжения и тока для каждого из трех резисторов.

Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.

R _экв = R ₁ + R ₂ + R ₃ = 17 Ом + 12 Ом + 11 Ом = 40 Ом

Теперь, когда известно эквивалентное сопротивление, ток в батарее можно определить с помощью уравнения закона Ома.При использовании уравнения закона Ома (ΔV = I • R) для определения тока в цепи важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R. Расчет показан здесь:

I _tot = ΔV _{аккумулятор} / R _eq = (60 В) / (40 Ом) = 1,5 А

Значение тока 1,5 А – это ток в месте расположения батареи. В последовательной цепи без точек разветвления ток везде одинаковый.Ток в месте расположения батареи такой же, как ток в каждом месте расположения резистора. Впоследствии 1,5 ампер – это значение I ₁ , I ₂ и I ₃ .

I _{аккумулятор} = I ₁ = I ₂ = I ₃ = 1,5 А

Осталось определить три значения – падение напряжения на каждом отдельном резисторе. Закон Ома снова используется для определения падений напряжения для каждого резистора – это просто произведение тока на каждом резисторе (вычисленное выше как 1.5 ампер) и сопротивление каждого резистора (указано в постановке задачи). Расчеты показаны ниже.

ΔV 1 = I 1 • R 1 ΔV 1 = (1,5 A) • (17 Ом) ΔV 1 = 25,5 В

ΔV 2 = I 2 • R 2 ΔV 2 = (1,5 A) • (12 Ом) ΔV 2 = 18 В

ΔV 3 = I 3 • R 3 ΔV 3 = (1.5 А) • (11 Ом) ΔV 3 = 16,5 В

В качестве проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли вычисленные значения принципу, согласно которому сумма падений напряжения для каждого отдельного резистора равна номинальному напряжению батареи. Другими словами, ΔV _{батареи} = ΔV ₁ + ΔV ₂ + ΔV ₃ ?

Является ли ΔV _{аккумуляторной батареей} = ΔV ₁ + ΔV ₂ + ΔV ₃ ?

Это 60 В = 25.5 В + 18 В + 16,5 В?

60 В = 60 В?

Да !!

Математический анализ этой последовательной схемы включал смесь концепций и уравнений. Как это часто бывает в физике, отделение понятий от уравнений при принятии решения физической проблемы является опасным актом. Здесь необходимо учитывать концепции, согласно которым ток везде одинаков и что напряжение батареи эквивалентно сумме падений напряжения на каждом резисторе, чтобы завершить математический анализ.В следующей части Урока 4 параллельные цепи будут проанализированы с использованием закона Ома и концепций параллельных цепей. Мы увидим, что подход сочетания концепций с уравнениями будет не менее важен для этого анализа.

Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействовать – это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom.Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключить их так, как захотите. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение.Это просто. Это весело. И это безопасно (если вы не используете его в ванне).

Проверьте свое понимание

1. Используйте свое понимание эквивалентного сопротивления, чтобы заполнить следующие утверждения:

а. Два последовательно включенных резистора сопротивлением 3 Ом обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.

г. Три резистора сопротивлением 3 Ом, включенные последовательно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.

г. Три резистора 5 Ом, включенные последовательно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.

г. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом включены последовательно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

e. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом включены последовательно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

ф. Три резистора с сопротивлением 12 Ом, 3 Ом и 21 Ом включены последовательно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

2. По мере увеличения количества резисторов в последовательной цепи общее сопротивление __________ (увеличивается, уменьшается, остается прежним) и ток в цепи __________ (увеличивается, уменьшается, остается прежним).

3. Рассмотрим следующие две схемы последовательных цепей. На каждой диаграмме используйте стрелки, чтобы указать направление обычного тока. Затем сравните напряжение и ток в обозначенных точках для каждой диаграммы.

4. Три одинаковые лампочки подключены к D-ячейке, как показано справа.Какое из следующих утверждений верно?

а. Все три лампочки будут иметь одинаковую яркость.

г. Лампа между X и Y будет самой яркой.

г. Лампа между Y и Z будет самой яркой.

г. Лампочка между Z и батареей будет самой яркой.

5. Три одинаковые лампочки подключены к батарее, как показано справа.Какие настройки можно было бы внести в схему, чтобы увеличить ток, измеряемый в точке X? Перечислите все подходящие варианты.

а. Увеличьте сопротивление одной из лампочек.

г. Увеличьте сопротивление двух лампочек.

г. Уменьшите сопротивление двух лампочек.

г. Увеличьте напряжение аккумулятора.

e. Уменьшите напряжение аккумулятора.

ф. Удалите одну из луковиц.

6. Три одинаковые лампочки подключены к батарее, как показано справа. W, X, Y и Z обозначают места на трассе. Какое из следующих утверждений верно?

а. Разница потенциалов между X и Y больше, чем между Y и Z.

г. Разница потенциалов между X и Y больше, чем между Y и W.

г. Разность потенциалов между Y и Z больше, чем между Y и W.

г. Разница потенциалов между X и Z больше, чем между Z и W.

e. Разность потенциалов между X и W больше, чем на батарее.

ф. Разница потенциалов между X и Y больше, чем между Z и W.

7.Сравните схему X и Y ниже. Каждый питается от 12-вольтовой батареи. Падение напряжения на резисторе 12 Ом в цепи Y равно ____ падению напряжения на единственном резисторе в цепи X.

а. меньше чем

г. больше

г. то же, что

8. Аккумулятор на 12 В, резистор на 12 Ом и лампочка подключаются, как показано на схеме X ниже.Резистор на 6 Ом добавлен к резистору на 12 Ом и лампочке, чтобы создать цепь Y, как показано. Лампочка появится ____.

а. диммер в контуре X

г. диммер в контуре Y

г. одинаковая яркость в обеих цепях

9. Три резистора включены последовательно. При размещении в цепи с источником питания 12 В.Определите эквивалентное сопротивление, полный ток цепи, падение напряжения и ток на каждом резисторе.

Основные операции, уход и обслуживание, а также расширенное устранение неисправностей для квалифицированных специалистов

Устранить проблему можно с помощью теста напряжения или сопротивления. Наиболее практично выбрать испытание напряжением.С помощью теста сопротивления вы должны сначала отключить проверяемый компонент от цепи, и, пока вы снимаете проводку, вы можете столкнуть предметы и, возможно, изменить схему, что может временно устранить проблему. Другими словами, вы можете и не найти проблему.

При использовании вольтметра для поиска неисправностей вы обнаружите либо разомкнутый переключатель, либо отказавшую нагрузку. Вы можете сделать это, не перемещая никаких проводов и никоим образом не меняя схему.Затем вы можете снять устройство и дважды проверить его омметром.

Падения напряжения в последовательных цепях

В последовательных цепях полное напряжение является суммой отдельных падений напряжения в цепи, и уравнение E = IR используется для расчета падения напряжения на каждом резисторе. Поскольку ток через каждый резистор одинаков, падение напряжения на каждом резисторе прямо пропорционально значению сопротивления. Другими словами, чем больше номинал резистора в последовательной цепи, тем больше падение напряжения.Рассмотрим простую последовательную схему на рисунке 1.

Рисунок 1 – Последовательная цепь

Из значений, приведенных выше, вы можете легко рассчитать падение напряжения на каждом резисторе по следующей формуле:
E ₁ = I ₁ × R ₁ = 2 A × 40 Ом = 80 В
E ₂ = I ₂ × R ₂ = 2 A × 20 Ом = 40 В

Падение напряжения 80 В на резисторе 40 Ом в два раза превышает падение напряжения на резисторе 20 Ом.

См. Рисунок 2.Если между резисторами R ₁ и R ₂ возникает разрыв (например, при отключении провода), ток через цепь, конечно, прерывается. Если нет тока, падение напряжения на каждом из резистивных элементов равно нулю (поскольку E = I × R).

Тем не менее, разность потенциалов источника все еще существует на открытом воздухе. Если вольтметр подключен через разрыв, показания такие же, как если бы он был подключен непосредственно к клеммам источника питания.

Рисунок 2 – Напряжение в цепи и разрыв цепи

В цепи последовательного освещения вы можете легко определить, какая лампа перегорела, просто измеряя напряжение на клеммах патрона лампы, последовательно, пока не будет измерено полное напряжение источника.

Осторожно! Поскольку напряжение источника по-прежнему присутствует в отверстии в последовательной цепи, это представляет опасность поражения электрическим током. Будьте осторожны, не прикасайтесь к токоведущим частям цепи! Точно так же, если переключатель разомкнут, на контактах переключателя появится полное напряжение источника.Даже если напряжение на нагрузочных устройствах может быть нулевым, если какая-либо из этих нагрузок находится перед переключателем, они будут запитаны с полным напряжением относительно земли.

Закон Кирхгофа для сложных схем | ОРЕЛ

Закон

Ома – ваш золотой билет для расчета напряжения, тока или сопротивления в простой последовательной или параллельной цепи, но что происходит, когда ваша схема более сложная? Возможно, вы разрабатываете электронику с параллельным и последовательным сопротивлением, и закон Ома начинает падать.Или что, если у вас нет источника постоянного тока? В таких ситуациях, когда нельзя использовать только V = IR, пора встать на плечи Ома и применить закон Кирхгофа. Здесь мы рассмотрим, что такое Закон Кирхгофа для цепей и как его использовать для анализа напряжения и тока сложных электрических цепей.

Что такое Окружной закон Кирхгофа?

Когда вы строите сложную схему, включающую мосты или тройники, вы не можете полагаться исключительно на закон Ома, чтобы найти напряжение или ток.Здесь пригодится закон Кирхгофа, который позволяет рассчитывать как ток, так и напряжение для сложных цепей с помощью системы линейных уравнений. Существует два варианта закона Кирхгофа, в том числе:

• Закон Кирхгофа: Для анализа полного тока сложной цепи
• Закон Кирхгофа о напряжении : анализ общего напряжения для сложной цепи
• Когда вы объединяете эти два закона, вы получаете Окружной закон Кирхгофа

Как и любой другой научный или математический закон, названный в честь их создателя, Закон Кирхгофа был изобретен немецким физиком Густавом Кирхгофом.Густав был известен многими достижениями при жизни, включая теорию спектрального анализа, которая доказала, что элементы излучают уникальный световой узор при нагревании. Когда Кирхгоф и химик Роберт Бунзен проанализировали эти световые узоры через призму, они обнаружили, что каждый элемент периодической таблицы имеет свою уникальную длину волны. Открытие этого паттерна позволило дуэту открыть два новых элемента, цезий и рубидий.

Густав Кирхгоф (слева) и Роберт Бунзен (справа)

Кирхгоф позже применил свою теорию спектрального анализа для изучения состава Солнца, где он обнаружил множество темных линий в спектре длин волн Солнца.Это было вызвано тем, что газ Солнца поглощал световые волны определенной длины, и это открытие ознаменовало начало новой эры исследований и исследований в области астрономии.

Немного ближе к дому в мире электроники, Кирхгоф объявил свой свод законов для анализа тока и напряжения в электрических цепях в 1845 году, известный сегодня как Закон Кирхгофа о цепях. Эта работа строится на основе, изложенной в законе Ома, и помогла проложить путь к сложному анализу схем, на который мы полагаемся сегодня.

Первый закон – Действующий закон Кирхгофа

Закон Кирхгофа по току гласит, что величина тока, входящего в узел, равна величине тока, выходящего из узла. Почему? Потому что, когда ток входит в узел, ему некуда идти, кроме выхода. То, что входит, должно выходить наружу. Вы можете определить узел, в котором два или более пути соединены общей точкой. На схеме это будет точка соединения, соединяющая две пересекающиеся сетевые соединения.

Взгляните на изображение ниже, чтобы визуально понять этот Закон.Здесь у нас есть два тока, входящие в узел, и три тока, выходящие из узла. Согласно закону тока Кирхгофа, взаимосвязь между токами, входящими в узел и выходящими из него, может быть представлена ​​как I 1 + I 2 = I 3 + I 4 + I 5 .

Текущий закон Кирхгофа, ток на входе должен равняться току на выходе. (Источник изображения)

Когда вы уравновешиваете это уравнение как алгебраическое выражение, вы заключаете, что ток на входе и выходе из узла всегда будет равен 0, или I 1 + I 2 + (-I 3 + -I 4 + -I 5 ) = 0 Все должно уравновешиваться, и Кирхгоф назвал этот принцип Сохранением заряда .

Давайте посмотрим на пример схемы, чтобы увидеть, как это работает. Ниже представлена ​​схема с четырьмя узлами: A, C, E и F. Сначала ток течет от источника напряжения и отделяется в узле A, а затем протекает через резисторы R1 и R2. Оттуда ток рекомбинирует в узле C и снова разделяется, чтобы протекать через резисторы R3, R4 и R5, где он встречается с узлом E и узлом F.

(Источник изображения)

Чтобы подтвердить закон Кирхгофа в этой цепи, нам нужно предпринять следующие шаги:

1. Рассчитать полный ток цепи
2. Рассчитайте ток, протекающий через каждый узел
3. Сравните входные и выходные токи в определенных узлах, чтобы подтвердить текущий закон Кирхгофа.

1. Рассчитайте общий ток

Здесь мы используем закон Ома, чтобы получить полный ток нашей цепи с I = V / R . У нас уже есть общее напряжение 132 В, и теперь нам просто нужно найти общее сопротивление во всех наших узлах. Для этого требуется простой метод расчета общего сопротивления резисторов, подключенных параллельно, которое составляет:

Начиная с узла AC, мы получаем следующее сопротивление для параллельных резисторов R1 и R2:

И переходя к узлу CEF, мы получаем следующее сопротивление для параллельных резисторов R3, R4 и R5:

Теперь у нас есть общее сопротивление 11 Ом для всей цепи, которое мы можем затем подключить к закону Ома I = V / R , чтобы получить общий ток в нашей цепи:

2.Расчет узловых токов

Теперь, когда мы знаем, что из нашей цепи выходит 12 ампер, мы можем рассчитать ток в каждом наборе узлов. Мы снова воспользуемся помощью закона Ома в форме I = V / R , чтобы получить ток для каждой ветви узла.

Для начала нам нужны напряжения для узловых ветвей AC и CF:

Затем мы можем рассчитать ток для каждой ветви узла:

3. Подтвердите действующий закон Кирхгофа

После вычисления тока для каждой ветви узла у нас теперь есть две отдельные контрольные точки, которые мы можем использовать для сравнения наших входных и выходных токов.Это позволит нам проанализировать нашу схему и подтвердить текущий закон Кирхгофа следующим образом:

Второй закон – Закон Кирхгофа о напряжении

Закон Кирхгофа о напряжении гласит, что в любой цепи с замкнутым контуром полное напряжение всегда будет равно сумме всех падений напряжения в контуре. Вы обнаружите, что падение напряжения происходит всякий раз, когда ток проходит через пассивный компонент, такой как резистор, и Кирхгоф назвал этот закон Сохранением энергии .Опять же, то, что входит, должно выходить наружу.

Взгляните на изображение ниже, чтобы понять это визуально. В этой схеме у нас есть источник напряжения и четыре области в цепи, где напряжение встретит пассивный компонент, что вызовет заметное падение напряжения.

Поскольку эти пассивные компоненты соединены последовательно, вы можете просто сложить общее падение напряжения и сравнить его с общим напряжением, чтобы получить соотношение, которое выглядит следующим образом:

Давайте начнем с простой схемы, чтобы продемонстрировать, как это работает.В приведенном ниже примере у нас есть две известные переменные: полное напряжение и падение напряжения на R1.

(Источник изображения)

Что нам нужно выяснить, так это падение напряжения на R2, и мы можем использовать закон Кирхгофа, чтобы выяснить это со следующей зависимостью:

Поскольку полное падение напряжения в цепи должно равняться общему напряжению источника, это обеспечивает простой способ вычисления нашей недостающей переменной. Если бы вы хотели выразить это соотношение в виде правильного алгебраического выражения, вы бы получили сумму всех падений напряжения и общее напряжение, равное нулю, как показано здесь:

Давайте посмотрим на другой пример.В схеме ниже у нас есть три резистора, подключенных последовательно с батареей на 12 В.

Чтобы проверить закон напряжения Кирхгофа в этой цепи, нам необходимо предпринять следующие шаги:

1. Вычислить полное сопротивление цепи
2. Рассчитайте общий ток цепи
3. Рассчитайте ток через каждого резистора
4. Рассчитайте падение напряжения на каждом резисторе

Сравните источник напряжения с общим падением напряжения , чтобы подтвердить закон Кирхгофа о напряжении

1.Рассчитайте общее сопротивление

Поскольку все наши резисторы соединены последовательно, мы можем легко найти общее сопротивление, просто сложив все значения сопротивления вместе:

2. Рассчитайте общий ток

Теперь, когда мы знаем наше полное сопротивление, мы снова можем использовать закон Ома, чтобы получить полный ток нашей цепи в виде I = V / R, , который выглядит так:

3. Рассчитайте ток через каждый резистор

Поскольку все наши резисторы соединены последовательно, все они будут иметь одинаковое количество тока, протекающего через них, которое мы можем выразить как:

4.Рассчитайте падение напряжения на каждом резисторе

.

В нашем окончательном расчете мы снова будем использовать закон Ома, чтобы получить полное падение напряжения для каждого резистора в виде В = IR , которое выглядит следующим образом:

5. Подтвердите закон Кирхгофа о напряжении

Теперь у нас есть все необходимые данные, включая общее напряжение нашей цепи, а также каждое падение напряжения на каждом из наших резисторов. Собирая все это вместе, мы можем легко проверить закон напряжения Кирхгофа с помощью следующего соотношения:

Это также может быть выражено как:

Как видите, полное напряжение равно общему падению напряжения в нашей цепи.То, что входит, должно выйти наружу, и закон Кирхгофа снова работает!

Процесс использования закона Кирхгофа об округах

Понимая, как работает закон Кирхгофа, в вашем наборе инструментов теперь есть новый инструмент для анализа напряжения и тока в полных цепях. При использовании этих Законов в дикой природе рассмотрите возможность использования следующего пошагового процесса:

1. Во-первых, начните с маркировки всех известных напряжений и сопротивлений вашей цепи.
2. Затем назовите каждую ветвь в вашей цепи текущей меткой, например I1, I2, I3 и т. Д.Ветвь – это один или группа компонентов, соединенных между двумя узлами.
3. Затем найдите текущий закон Кирхгофа для каждого узла в вашей цепи.
4. Затем найдите закон напряжения Кирхгофа для каждого из независимых контуров в вашей цепи.

После того, как вы рассчитали законы Кирхгофа по току и напряжению, вы можете использовать свои уравнения, чтобы найти недостающие токи. Готовы попробовать это самостоятельно? Взгляните на схему ниже и посмотрите, сможете ли вы проверить закон тока Кирхгофа и закон напряжения с небольшой помощью Ома!

Ваши ответы в комментариях ниже!

Стоя на плечах Ома

Имея в руках Закон Кирхгофа о цепях, теперь у вас есть все инструменты, необходимые для анализа напряжения и тока в сложных цепях.Как и многие другие научные и математические принципы, закон Кирхгофа стоит на плечах того, что было до него – закона Ома. Вы обнаружите, что используете закон Ома для расчета отдельных сопротивлений, напряжений или токов, а затем, основываясь на этих расчетах с законом Кирхгофа, убедитесь, что ваша схема соответствует этим принципам тока и напряжения.

Готовы применить закон Кирхгофа в своем собственном проекте по разработке электроники? Попробуйте Autodesk EAGLE бесплатно сегодня!

Как я могу рассчитать падение напряжения в параллельном контуре, класс 12, физика CBSE

Подсказка: Это можно решить, используя закон Ома, который гласит, что напряжение на проводнике прямо пропорционально току, протекающему по нему, а для параллельных цепей мы будет использовать формулу для общего сопротивления, чтобы найти полное падение напряжения.

Используемая формула:
$ \ begin {align}
& V = IR \\
& R = {{R} _ {1}} + {{R} _ {2}} + {{R} _ { 3}} \\
\ end {align} $

Полное пошаговое решение:
Падение напряжения на резисторе в параллельной цепи одинаково для всех резисторов в каждой ветви всех параллельных цепей в схема параллельной цепи.

Напряжение, выраженное в напряжении, измеряет электродвижущие силы, управляющие цепью, или разность потенциалов.

Рассмотрим схему с тремя резисторами, подключенными параллельно, с источником напряжения «V» и током, протекающим в «I».

Теперь пошаговый метод расчета напряжения в цепи.
Шаг 1: – Найдите полное сопротивление параллельной цепи.
Формула для общего сопротивления цепи, включенной параллельно,
$ \ begin {align}
& \ Rightarrow \ dfrac {1} {{{R} _ {T}}} = \ dfrac {1} {{{R} _ {1}}} + \ dfrac {1} {{{R} _ {2}}} + \ dfrac {1} {{{R} _ {3}}} \\
и \ следовательно {{R} _ {T}} = \ dfrac {{{R} _ {1}} {{R} _ {2}} {{R} _ {3}}} {{{R} _ {1}} {{R } _ {2}} + {{R} _ {2}} {{R} _ {3}} + {{R} _ {1}} {{R} _ {3}}}.