Формула расчета конденсатора: Расчет емкости конденсатора: как вычислить формулой

Содержание

Расчет емкости конденсатора: как вычислить формулой

Конденсаторы имеют широкое распространение в электрических сетях. Если разобрать несколько электронных приборов на детали и пересчитать их, то окажется, что конденсаторы используются гораздо чаще других элементов. Поэтому следует уделить особое внимание конструкции, расположению и принципу действия подобных деталей.

Что такое конденсатор?

Конденсатор состоит из двух проводящих пластин, расположенных очень близко друг к другу и разделённых диэлектриком. Применение постоянного напряжения к пластинам вызовет протекание тока и появление на обеих крышках одинаковых по модулю, но противоположных по знаку зарядов: отрицательных – на одной и положительных – на другой. Отключение источника питания приведёт к тому, что заряд не исчезнет моментально, игнорируя явление его постепенной утечки. Затем, если крышки детали подключены к какой-то нагрузке, например, к вспышке, конденсатор разрядится сам и вернёт всю накопленную в нём энергию во вспышку.

Обозначение конденсаторов

Конденсаторы – это пассивные компоненты, которые хранят электрический заряд. Эта простая функция применяется в различных случаях:

При переменном токе.
При постоянном токе.
В аналоговых сетях.
В цифровых цепях.

Примеры использования приборов: системы синхронизации, формирование сигнала, связь, фильтрация и сглаживание сигнала, настройка телевизоров и радиоприёмников.

Характеристики конденсатора

Основной характеристикой данного элемента является емкость, или С. Она определяет способность устройства собирать электрический заряд, зависит от геометрической конфигурации крышек и от электрической проницаемости диэлектрика между крышками.

Важно! Емкость зависит от типа используемого диэлектрика, а также от геометрических размеров элемента.

Для того, чтобы описать принцип работы устройства формулой, необходимо понять, что это постоянная пропорциональность в уравнении, представляющая собой взаимную зависимость накопленного заряда q от площади пластинок и от разности потенциалов V между ними.

Мощность выражается в единицах, называемых фарадами F. Но на практике используются и более мелкие единицы, такие как микрофарады и пикофарады.

Внешний вид устройств

Таким образом, если напряжение U приложено к конденсатору, электрический заряд накапливается на крышках детали. Значение накопленного заряда на каждой пластинке одинаково, они отличаются только знаком. Этот процесс накопления электрического показателя на называется зарядкой.

Другим параметром детали является номинальное напряжение, а именно, его максимальное значение, которое может подаваться на конденсатор. При подключении более высокого напряжения возникает пробой диэлектрика. Это приводит к короткому замыканию элемента. Каким будет номинальное значение напряжения, зависит от типа диэлектрика и его толщины.

Важно! Чем толще диэлектрик, тем выше номинальное напряжение, которое он выдерживает.

Условные обозначения

Ещё одним параметром является ток утечки -значение проводящего показателя, возникающее при подаче постоянного напряжения на концы элемента.

Для чего используются конденсаторы?

Электростанции

Почти все электронные устройства имеют блок питания, который преобразует переменный ток, присутствующий в доме, в постоянный ток. Конденсаторы играют важную роль в преобразовании переменного тока в постоянный, устраняя электрические помехи. В источниках энергии используются электролитические конденсаторы различных размеров – от нескольких миллиметров до нескольких дюймов (или сантиметров).

Звуковые покрытия

Конденсаторы имеют множество применений в аудио оборудовании. Они блокируют постоянный ток на входе вс усилитель, предотвращая внезапные звуки или шумы, которые могут повредить колонки и наушники. Данные детали, используемые в аудиофильтрах, позволяют контролировать басы.

Компьютеры

Цифровые схемы в компьютерах передают электронные импульсы на высоких скоростях. Эти потоки в сети могут создавать помехи сигналам от соседней цепи, поэтому разработчики высокотехнологичного оборудования применяют конденсаторы для минимизации помех.

Высокотехнологичный конденсатор

Как правильно рассчитать ёмкость конденсатора?

Самый простой пример конденсатора – плоская модель. Она имеет форму двух параллельных крышек из проводника, между которыми находится слой диэлектрика. Для того, чтобы знать, как посчитать ёмкость конденсаторов, необходимо применить следующую формулу:

С = e x e0 x s / d,

где S – площадь поверхности пластинок и d – расстояние между ними. В свою очередь, это относительная электрическая проницаемость данного диэлектрика.

Как правило, конденсаторы применяются не по отдельности, а подключаются в более крупные системы. Они могут быть соединены последовательно, параллельно или смешанным способом.

Формула ёмкости

Важно! В последовательно соединённых элементах абсолютное значение заряда на каждой пластине идентично.

Таким образом, результирующее напряжение равно сумме данных показателей на отдельных компонентах прибора.

Общая ёмкость системы будет определяться по формуле:

1/С = 1/С1 + 1/С2 + 1/С3 + …

При параллельном подключении разность потенциалов на каждом из деталей одинакова. Таким образом, суммарный заряд будет равен сумме зарядов на компонентах конденсатора, а результирующая ёмкость – сумме отдельных единичных величин:

C = c1 + c2 + c3 + …

Основные формулы ёмкости

Базовый расчёт конденсатора предполагает выявление зависимости емкости и заряда, удерживаемого на элементе, а также напряжением на пластинах.

C=QVC=QV

C – емкость, или объём в Фарадах
Q – заряд, удерживаемый на пластинах в кулонах
V – разность потенциалов между пластинами в вольтах

Это уравнение используется для расчета работы, необходимой для зарядки конденсатора и энергии, хранящейся в нем.

Формула энергии

W=∫Q0V dQW=∫0QV dQ

W=∫Q0qC dQW=∫0QqC dQ

W=12CV2

Важно! Необходимо знать, какое влияние конденсатор будет оказывать на любую цепь, в которой он работает. Он не только предотвращает прохождение постоянной составляющей тока сигнала, но и оказывает влияние на любой переменный сигнал.

Реактивное сопротивление

В цепи постоянного тока помимо батареи может присутствовать резистор, который оказывает сопротивление току в цепи. То же справедливо и для схемы переменного тока с элементом, накапливающим заряд. Конденсатор с небольшой площадью пластины позволяет хранить только небольшое количество заряда, и это будет препятствовать протеканию тока. Конденсатор имеет определенное реактивное сопротивление, и оно зависит от его величины, а также от частоты срабатывания. Чем выше частота, тем меньше реактивное сопротивление.

Фактическое реактивное сопротивление можно вычислить по формуле:

Xc = 1 / (2 pi f C)

где

Xc – ёмкостное реактивное сопротивление в Омах.
f – частота в Герцах.
C – ёмкость в Фарадах.

Текущий расчет

Реактивное сопротивление конденсатора, рассчитанное по приведенной выше формуле, измеряется в Омах. Затем ток, протекающий в цепи, может быть рассчитан обычным способом с использованием закона Ома:

V = I Xc

Главный показатель конденсатора

Активное и реактивное сопротивления

Хотя активное и реактивное сопротивления очень похожи. Даже значения обоих параметров измеряются в Омах, но они не совсем одинаковы. В результате этого невозможно сложить их вместе непосредственно. Вместо этого их нужно суммировать «векторно». Другими словами, необходимо округлить каждое значение, а затем сложить их вместе и выделить квадратный корень из этого числа:

Xtot2 = Xc2 + R2

В данной статье были подробно описаны основные компоненты, устройство и принцип работы конденсаторов, а также приведены базовые формулы, предназначенные для того, чтобы посчитать полезный объём прибора. Для более глубокого ознакомления необходимо внимательно рассмотреть типы данных деталей и их практические особенности в различных схемах и устройствах.

Ёмкость конденсатора | Все Формулы

Электрическая ёмкость — характеристика проводника (конденсатора), мера его способности накапливать электрический заряд.

$\Large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2} =\varepsilon \varepsilon _0\frac{S}{d}$

Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические.

Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками

$\Large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2}$

Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.

Конденсаторы можно классифицировать по следующим признакам и свойствам:

1) по назначению — конденсаторы постоянной и переменной емкости;

2) по форме обкладок различают конденсаторы плоские, сферические, цилиндрические и др.;

3) по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и т.д.

Так же есть:

Энергия конденсатора:

$\large W_p=\frac{U q}{2}=\frac{q^2}{2C}=\frac{CU^2}{2}$

Ёмкость цилиндрического конденсатора :

$\large C=2\pi \varepsilon \varepsilon _0\frac{l}{ln(\frac{R_2}{R_1})}$

Ёмкость плоского конденсатора :

$\large C=\varepsilon \varepsilon _0\frac{S}{d} = \frac{q}{U}$

Емкость сферического конденсатора :

$\large C=4\pi \varepsilon \varepsilon _0(\frac{1}{R_1} - \frac{1}{R_2})^{-1}$

В формуле мы использовали :

C — Электрическая ёмкость (ёмкость конденсатора)

q — Заряд

U — Потенциал проводника (Напряжение)

$\varphi$

— Потенциал

$\varepsilon$

— Относительная диэлектрическая проницаемость

$\varepsilon _0 = 8.854185\times 10^{-12}$

— Электрическая постоянная

S — Площадь одной обкладки

d — Расстояние между обкладками

в чём измеряется и от чего зависит величина, как её определить, формулы расчёта

Один из наиболее важных эффектов, используемых в электронике, — ёмкость конденсаторов. Способность накапливать и хранить электрический заряд нашла применение практически во всех аналоговых цепях и логических схемах. Пассивные устройства, запасающие энергию в виде электрического поля, называли конденсаторами уже в те времена, когда учёные ещё очень мало знали о природе электричества.

История накопителей заряда

Самое раннее письменное свидетельство получения зарядов с помощью трения принадлежит учёному Фалесу из Милета (635—543 гг. до н. э.), который описал трибоэлектрический эффект от взаимодействия янтаря и сухой шерсти. Для приблизительно 2300 последующих лет любое получение электричества заключалось в трении двух различных материалов друг о друга.

Качественный рывок в знаниях о зарядах произошёл в эпоху Просвещения — период революционного развития научной мысли в образованных кругах. В это время электричество становится популярной темой, а энтузиастами было произведено немало опытов и экспериментов с генераторами на основе трения.

Первое устройство для хранения полученных зарядов было создано в 1745 г. двумя электриками (так тогда называли людей, изучающих природу статического электричества), работающими независимо друг от друга: Эвальдом фон Клейстом, деканом собора в Пруссии, и Питером ван Мюссенбруком, профессором математики и физики в университете Лейдена.

Открытие явления произошло во время опытов у обоих экспериментаторов, но с той разницей, что Мюссенбрук, во-первых, сделал немало усовершенствований первоначально созданного оборудования, а во-вторых, письменно сообщил коллегам о своих достижениях. Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни. Основные даты хронологии появления устройств для хранения зарядов:

1746 г. — изобретение лейденской банки в результате экспериментов по доработке устройства Клейста;
1750 г. — опыты Бенджамина Франклина с батареями конденсаторов;
1837 г. — публикация Майклом Фарадеем теории диэлектрической поляризации — научной основы работы накопителей;
конец XIX в. — начало практического применения лейденских банок вместе с первыми устройствами постоянного тока;
начало XX в. — изобретение слюдяных и керамических конденсаторов.

Физика ёмкостных характеристик

Устройства, обладающие способностью хранения энергии в форме электрического заряда и производящие при этом разность потенциалов, называют конденсаторами. В простейшем виде они состоят из двух или более параллельных проводящих пластин, находящихся на небольшом расстоянии друг от друга, но электрически разделённых либо воздухом, либо каким-либо другим изоляционным материалом, например, вощёной бумагой, слюдой, керамикой, пластмассой или специальным гелем.

Если подключить к пластинам источник напряжения, то одна из них получит избыток электронов, а на другой сформируется их дефицит. Ионы и электроны на каждой из этих пластин притягиваются друг к другу, но благодаря диэлектрическому барьеру они не соединяются, а накапливаются на плоскостях проводников. В результате первая пластина (электрод) окажется заряженной отрицательно, а вторая — положительно. Неподвижные заряды создают постоянное электрическое поле, теоретически сохраняемое неограниченное количество времени в незамкнутой электрической цепи.

Поток электронов на пластины называется зарядным током, продолжающим присутствовать до тех пор, пока напряжение на пластинах не сравняется с приложенным. В этот момент конденсатор считается полностью заряженным, то есть зарядов на пластинах становится так много, что они отталкивают вновь поступающие. При подключении к заряженному устройству нагрузки электроны и ионы находят новый путь друг к другу. В этом случае конденсатор работает как источник тока до момента потери разности потенциалов на электродах.

Способность конденсатора хранить заряд Q (измеряется в кулонах) называют ёмкостью. Чем больше площадь пластин и меньше расстояние между ними (благодаря усилению эффекта притяжения зарядов между обкладками), тем большая ёмкость устройства. Степень приближения пластин ограничивается способностью диэлектрика сопротивляться разрядке пробоем между ними. Таким образом, три характеристики определяют производительность конденсатора:

геометрия пластин;
расстояние между ними;
диэлектрический материал между пластинами.

Единица и формулы расчёта

Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.

Математическое выражение фарада

Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.

Специалисты по электронике единицу в один фарад считают не совсем практичной, поскольку она представляет собой огромное значение. Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:

пикофарад — 10—12 Ф;
нанофарад — 10—9 Ф;
микрофарад — 10—6 Ф.

Диэлектрическая проницаемость

Фактор, благодаря которому изолятор определяет ёмкость конденсатора, называется диэлектрической проницаемостью. Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:

А — площадь меньшей пластины;
d — расстояние между ними;
ε — абсолютная проницаемость используемого диэлектрического материала.

Диэлектрическая проницаемость вакуума ε0 является константой и имеет значение 8,84х10—12 фарад на метр. Как правило, проводящие пластины разделены слоем изоляционного материала, а не вакуума. Чтобы найти ёмкость конденсатора, пластины которого находятся в воздухе, можно воспользоваться значением ε0. Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.

На практике в формулах нахождения ёмкости конденсатора используется относительная диэлектрическая проницаемость в качестве коэффициента, означающая, насколько электрическое поле между зарядами уменьшается в диэлектрике по сравнению с вакуумом. Некоторые значения этой величины для различных материалов:

1,0006 — воздух;
2,5—3,5 — бумага;
3—10 — стекло;
5—7 — слюда.

Поскольку эффективность конденсатора зависит от применяемого в нём изолятора, его качество как накопителя можно определить через удельную ёмкость — величину, равную отношению ёмкости к объёму диэлектрика.

Практические измерения

Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.

Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.

Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.

Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.

Идея суперконденсатора

Электричество — чрезвычайно универсальный вид энергии, обладающий одним недостатком — его трудно саккумулировать быстро. Химические батареи способны сохранять большое количество энергии, но требуют нескольких часов для полной зарядки. Этого недостатка лишены конденсаторы — они могут заряжаться практически мгновенно. Но их ёмкость не позволяет хранить большое количество энергии, поэтому весьма заманчивой выглядит идея суперконденсатора, сочетающего лучшие качества химических и электростатических накопителей электричества.

Несмотря на функциональную схожесть, аккумуляторные батареи и конденсаторы устроены совершенно по-разному. Гальванические элементы работают на принципе высвобождения электрической энергии во время химической реакции веществ внутри них. При истощении запаса активных реагентов они прекращают генерировать разность потенциалов и для нового цикла требуют инициирования током обратных химических реакций для восстановления активных веществ. Основные недостатки аккумуляторов по сравнении и конденсаторами:

непродолжительный жизненный цикл;
невысокая удельная мощность;
узкий диапазон температур зарядки и разрядки;
неспособность быстро отдать весь запас энергии.

Тем не менее обычные конденсаторы не используются в качестве активных источников напряжения из-за низкой ёмкости. Теоретические и практические суперконденсаторы (ультраконденсаторы) отличаются от обычных крайне высокой ёмкостью при большой плотности хранимой энергии, что позволяет их рассматривать как альтернативу химическим элементам.

Крупнейшие коммерческие устройства обладают ёмкостью до нескольких тысяч фарад, но их возможности всё равно несопоставимы с аккумуляторами, поэтому подобные устройства используются для хранения зарядов в течение относительно короткого периода времени. Они нашли широкое применение в качестве электрических эквивалентов механических маховиков, чтобы сглаживать напряжение источников питания, например, в ветровых турбинах или рекуперативных тормозных системах электрических транспортных средств.

Первые ультраконденсаторы появились в середине прошлого века и обладали не очень впечатляющими ёмкостями. С тех пор прогресс в совершенствовании материалов привёл к утоньшению диэлектрического слоя до одной молекулы, что позволило создавать устройства с выдающимися характеристиками. Дальнейшее развитие наноиндустрии стало основой для фундаментальных перемен в накоплении электричества. Возможно, в скором времени экологически опасные и капризные химические аккумуляторы заменят суперконденсаторы на основе молекулярно структурированных пластин и диэлектрического слоя.

Конденсаторы

Электрическая емкость

При сообщении проводнику заряда на его поверхности появляется потенциал φ, но если этот же заряд сообщить другому проводнику, то потенциал будет другой. Это зависит от геометрических параметров проводника. Но в любом случае потенциал φ пропорционален заряду q.

(5.4.1)

Коэффициент пропорциональности С называют электроемкостью – физическая величина, численно равная заряду, который необходимо сообщить проводнику для того, чтобы изменить его потенциал на единицу.

(5.4.2)

Единица измерения емкости в СИ – фарада. 1 Ф = 1Кл/1В.

Если потенциал поверхности шара

(5.4.3)

то

(5.4.4)

По этой формуле можно рассчитать емкость Земли. Если диэлектрическая проницаемость среды ε = 1 (воздух, вакуум) и то имеем, что C_З = 7·10^–4 Ф или 700 мкФ.

Чаще на практике используют более мелкие единицы емкости: 1 нФ (нанофарада) = 10^–9 Ф и 1пкФ (пикофарада) = 10^–12 Ф.

Необходимость в устройствах, накапливающих заряд, есть, а уединенные проводники обладают малой емкостью. Опытным путем было обнаружено, что электроемкость проводника увеличивается, если к нему поднести другой проводник – за счет явления электростатической индукции.

Конденсатор – это два проводника, называемые обкладками, расположенные близко друг к другу.

Конструкция такова, что внешние, окружающие конденсатор тела, не оказывают влияние на его электроемкость. Это будет выполняться, если электростатическое поле будет сосредоточено внутри конденсатора, между обкладками.

Конденсаторы бывают плоские, цилиндрические и сферические.

Так как электростатическое поле находится внутри конденсатора, то линии электрического смещения начинаются на положительной обкладке, заканчиваются на отрицательной, и никуда не исчезают. Следовательно, заряды на обкладках противоположны по знаку, но одинаковы по величине.

Емкость конденсатора равна отношению заряда к разности потенциалов между обкладками конденсатора:

(5.4.5)

Помимо емкости каждый конденсатор характеризуется U_раб (или U_пр.) – максимальное допустимое напряжение, выше которого происходит пробой между обкладками конденсатора.

Соединение конденсаторов

Емкостные батареи – комбинации параллельных и последовательных соединений конденсаторов.

1) Параллельное соединение конденсаторов (рис. 5.9):

Рис. 5.9

В данном случае общим является напряжение U:

Суммарный заряд:

Результирующая емкость:

Сравните с параллельным соединением сопротивлений R:

Таким образом, при параллельном соединении конденсаторов суммарная емкость

Общая емкость больше самой большой емкости, входящей в батарею.

2) Последовательное соединение конденсаторов (рис. 5.10):

Общим является заряд q.

Рис. 5.10

или , отсюда

(5.4.6)

Сравните с последовательным соединением R:

Таким образом, при последовательном соединении конденсаторов общая емкость меньше самой маленькой емкости, входящей в батарею:

Расчет емкостей различных конденсаторов

1. Емкость плоского конденсатора

Напряженность поля внутри конденсатора (рис. 5.11):

Рис. 5.11

Напряжение между обкладками:

где – расстояние между пластинами.

Так как заряд , то

(5.4.7)

Как видно из формулы, диэлектрическая проницаемость вещества очень сильно влияет на емкость конденсатора. Это можно увидеть и экспериментально: заряжаем электроскоп, подносим к нему металлическую пластину – получили конденсатор (за счет электростатической индукции, потенциал увеличился). Если внести между пластинами диэлектрик с ε, больше, чем у воздуха, то емкость конденсатора увеличится.

Из (5.4.6) можно получить единицы измерения ε₀:

(5.4.8)

2. Емкость цилиндрического конденсатора

Разность потенциалов между обкладками цилиндрического конденсатора, изображенного на рисунке 5.12, может быть рассчитана по формуле:

где λ – линейная плотность заряда,R₁ иR₂ – радиусы цилиндрических обкладок,l– длина конденсатора, .

Рис. 5.12

Тогда, так как , получим

(5.4.9)

Понятно, что зазор между обкладками мал: то есть

Тогда

(5.4.10)

3. Емкость шарового конденсатора (рис. 5.13)

Рис. 5.13

Из п. 3.6 мы знаем, что разность потенциала между обкладками равна:

Тогда, так как , получим

Это емкость шарового конденсатора, где R₁и R₂ – радиусы шаров.

В шаровом конденсаторе – расстояние между обкладками. Тогда

(5.4.11)

Таким образом, емкость шарового конденсатора с достаточной степенью точности можно рассчитать так же, как и емкость плоского, и цилиндрического конденсаторов.

Теория по физике для ЕГЭ, пособия по подготовке и справочные материалы в Москве

Проводники и диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества. Электроемкость. Конденсаторы. Поле плоского конденсатора. Электроемкость плоского конденсатора. Последовательное и параллельное соединение конденсаторов. Энергия заряженного конденсатора.

Проводники и диэлектрики в электростатическом поле

Вещества в природе можно разделить на проводники и диэлектрики.

Основная особенность — наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника.

Типичные проводники — металлы.

Диэлектрическая проницаемость вещества

В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды — индукционными зарядами.

В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.

Физическая величина, равная отношению модуля напряженности $\vec{E}_0$ внешнего электрического поля в вакууме к модулю напряженности $\vec{E}$ полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества $\varepsilon$.

\[\varepsilon=\dfrac{\vec{E}_0}{\vec{E}}\]

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда $q$ одного из проводников к разности потенциалов $\Delta \varphi$ между ними:

\[\fbox{$C=\dfrac{q}{\Delta \varphi}$}\]

Единицы измерения: $\displaystyle [\text{Ф}]$ (фарад).

Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.

Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, — обкладками.

Плоский конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.

Электроемкость плоского конденсатора

Разность потенциалов $\Delta \varphi$ между пластинами в однородном электрическом поле равна $Ed$, где $d$ — расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:

\[C=\dfrac{q}{\Delta \varphi}=\dfrac{\sigma S}{Ed}=\dfrac{\varepsilon_0S}{d}\]

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в $\varepsilon$ раз:

\[\fbox{$C=\dfrac{\varepsilon_0\varepsilon S}{d}$}\]

Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками.

Последовательное и параллельное соединение конденсаторов

Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.

Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
\[\fbox{$U=U_1+U_2$}\]
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
\[\dfrac{q}{C}=\dfrac{q}{C_1}+\dfrac{q}{C_2}\]
Сократив выражение на $Q$, получим формулу:
\[\fbox{$\dfrac{1}{C}=\dfrac{1}{C_1}+\dfrac{1}{C_2}$}\]
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
\[\fbox{$C=\dfrac{C_1C_2}{C_1+C_2}$}\]
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
\[\fbox{$q=q_1+q_2$}\]
Так как заряд конденсатора
\[q=CU\]
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
\[CU=C_1U+C_2U\]
\[\fbox{$C=C_1+C_2$}\]
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии того, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится. Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке.

Вычислим эту энергию: начнём с плоского воздушного конденсатора.

Ответим на такой вопрос: какова силу притяжения его обкладок друг к другу. Величины используем следующие: заряд конденсатора $q$, площадь обкладок $S$. Возьмём на второй обкладке настолько маленькую площадку, что заряд $q_0$ этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

\[F_0 = q_0E_1,\]

где $E_1$ — напряжённость поля первой обкладки:

\[E_1=\dfrac{\sigma}{2\varepsilon_0}=\dfrac{q}{2\varepsilon_0S}\]

Значит

\[F_0=\dfrac{qq_0}{2\varepsilon_0S}\]

Направлена эта сила параллельно линиям поля (т.е. перпендикулярно пластинам). Результирующая сила $F$ притяжения второй обкладки к первой складывается из всех этих сил $F_0$, с которыми притягиваются к первой обкладке всевозможные маленькие заряды $q_0$ второй обкладки. При этом суммировании постоянный множитель $\displaystyle\dfrac{q}{2\varepsilon_0S}$ вынесется за скобку, а в скобке просуммируются все $q_0$ и дадут $q$. В результате получим

\[F=\dfrac{q^2}{2\varepsilon_0S}\]

Предположим теперь, что расстояние между обкладками изменилось от начальной величины $d_1$ до конечной величины $d_2$. Сила притяжения пластин совершает при этом работу \[A = F(d_1 -d_2)\]

Знак правильный: если пластины сближаются $(d_2 < d_1)$, то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины $(d_2 > d_1)$, то работа силы притяжения получается отрицательной, как и должно быть.

Получаем

\[A=\dfrac{q^2}{2\varepsilon_0S}(d_1-d_2)=\dfrac{q^2d_1}{2\varepsilon_0S}-\dfrac{q^2d_2}{2\varepsilon_0S}=\dfrac{q^2}{2C_1}-\dfrac{q^2}{2C_2}=W_1-W_2\]

Это можно переписать следующим образом: \[A =-(W_2-W_1) =-\Delta W,\]

где \[\fbox{$W=\dfrac{q^2}{2C}$}, (1)\]

Работа потенциальной силы $F$ притяжения обкладок оказалась равна изменению со знаком минус величины $W$. Это как раз и означает, что $W$ — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора. Используя соотношение $q = CU$, можно получить ещё две формулы для энергии конденсатора (проделать это самостоятельно).

\[\fbox{$W=\dfrac{qU}{2}$}, (2)\]

\[\fbox{$W=\dfrac{CU^2}{2}$}, (3)\]

Формулы (1)—(3) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

По какой формуле найти ёмкость (объем) конденсаторов

Емкостный показатель является одной из основных характеристик не только батареек и аккумуляторных элементов, но и конденсаторных устройств. Любому человеку, работающему с электросхемами, необходимо знать, от чего зависит эта величина, может ли она уменьшиться или увеличиться под влиянием внешних факторов (как, например, период времени, зарядка элемента или частота напряжения), и как выглядит выражающая емкость конденсатора формула для разных типов элементов.

Измерение емкостных данных мультиметром

Расчёт конденсаторов

В общем случае емкостной показатель С определяется по формуле:

C=q/U,

где q – заряд конденсатора на одной из его пластин, U – значение напряжения на конденсаторе.

Из этого выражения можно вывести формулу заряда конденсатора, величину которого можно найти, измерив два других показателя с помощью мультиметра.

Часто возникает вопрос, может ли этот параметр измениться. Он является постоянной величиной, присущей данному элементу и зависящей от его габаритов и устройства. Узнать емкостное значение можно с помощью мультиметра. Пользуясь этими данными, можно рассчитать целевую индуктивность дросселя для колебательного контура или параметры резистора.

В чем измеряется емкость? За измерительную единицу принимается параметр конденсаторного устройства, который можно зарядить 1 Кл до состояния, когда разница потенциалов будет равной 1 вольту. Название этой единицы – фарад (Ф).

Важно! Если сравнить два устройства, идентичных по габаритам, но различающихся тем, что у одного в зазоре между пластинами находится диэлектрический материал, а у другого – воздушное пространство, то при помещении одинаковых зарядов потенциальная разница первой детали будет в Е раз больше. Е – это число, равное диэлектрической проницаемости материала, из которого состоит использованный слой.
Ниже приведены формулы для конденсаторных элементов разной конфигурации. Рассчитанные по ним значения соответствуют идеальным устройствам, но релевантны и для реальных в тех случаях, когда емкостными потерями можно пренебречь.
Формула электрической емкости плоского конденсатора
В основном электрополе пластин плоского конденсатора бывает однородным, за исключением боковых частей, влиянием которых обычно принято пренебрегать. Однако, если пространство между обкладками велико в сопоставлении с их габаритами, краевые искажения нужно учитывать. В общем случае, чтобы высчитать, сколько фарад составит емкость плоского конденсатора, пользуются выражением:
C=E*E0*S/d, где S – площадь меньшей обкладки, E0 – электрическая константа, d – длина пространства между пластинами.

Плоский конденсаторный элемент
Формула электрической емкости цилиндрического изделия
Такой компонент состоит из пары разных по размеру коаксиальных цилиндрических элементов проводника, в пространстве между которыми расположили диэлектрический материал. В этом случае для нахождения емкостной величины не нужно узнавать значение заряда на обкладках конденсатора. Можно воспользоваться следующей формулой емкости:
С=2 π *E*E0*l / ln(R2/R1).
Здесь R1 и R2 – радиусы, соответственно, внутреннего и наружного цилиндров, l – их высота (она одинакова, в то время как радиальные параметры отличаются).

Цилиндрическое изделие
Формула для сферического изделия
Сферическая деталь состоит из двух проводниковых сфер с диэлектрическим слоем между ними. Вот как найти емкость круглого конденсатора:
C=4 π *E*E0* R1* R2 / R2 – R1.
Буквами R обозначены, как и в предыдущем примере, радиусы компонентов.
Ёмкость одиночного проводника
Это характеристика способности твердого проводникового компонента к удержанию электрозаряда. Она определяется особенностями средового окружения (в частности, диэлектрической проницаемостью), взаиморасположением тел, имеющих на себе заряд, размерами детали. От силы тока и величины заряда она не зависит.
Способы соединения элементов
Монтаж изделия на плату может быть вертикальным или горизонтальным. При использовании нескольких изделий они могут быть соединены между собой разными способами.
Параллельное соединение
Для его организации нужно подключить группу деталей к электроцепи так, чтобы обкладки всех деталей были подсоединены напрямую к местам включения. Поскольку все компоненты получают заряд от одного источника тока, у них будет одинаковая разность потенциалов. Но так как заряд копится на каждом изделии отдельно, количество электричества на группе можно выразить как сумму количеств на ее деталях. Это справедливо и для емкостных данных – значение для конфигурации равно сумме значений каждой единицы. Поэтому такую группу можно считать равной одному конденсатору, емкостной параметр которого равен сумме таковых для всех частей.

Параллельное подключение
Последовательное соединение
Эта схема подразумевает соединение устройств одно за другим, когда к местам подключения к цепи подсоединены только два крайних изделия. Количество электричества для каждой детали будет одинаковым. При этом, чем менее емкое устройство, тем большее значение напряжения на нем будет наблюдаться.
Важно! Емкостной показатель такой системы будет еще меньше, чем у устройства, обладающего наименьшим его значением. Соотношение выглядит так: 1/С = 1/С1 + 1/С2 + 1/С3 + … Опираясь на него, можно произвести вывод непосредственно формулы С. Для двух элементов: С = С1*С2 / С1+С2.

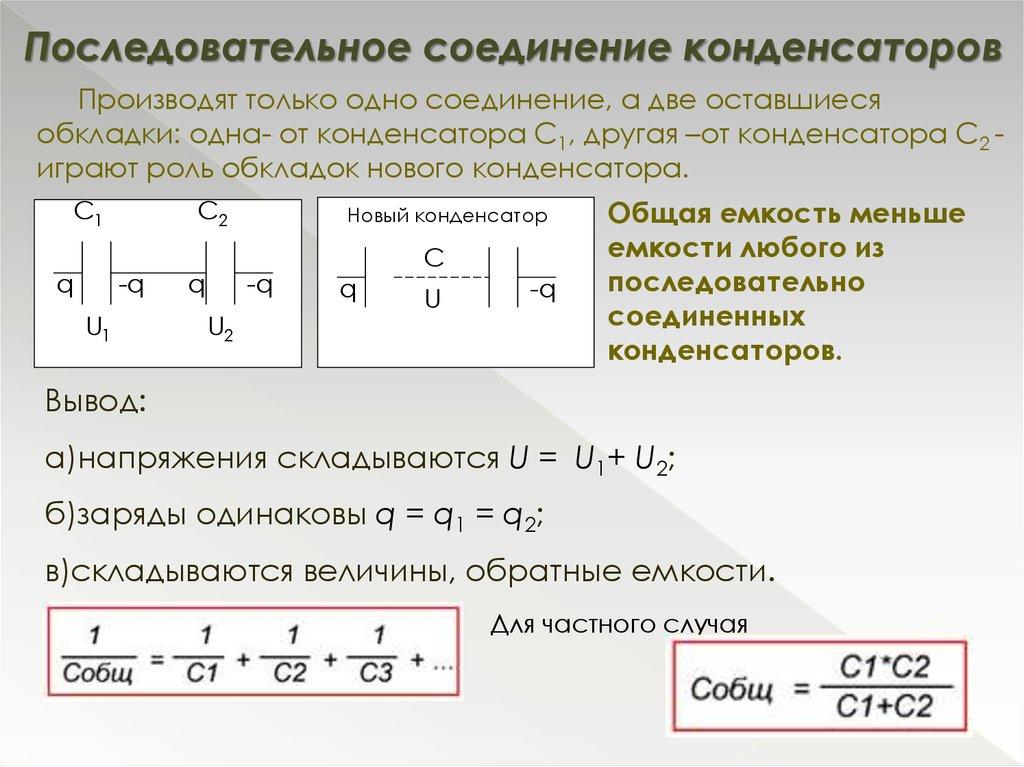
Последовательное подключение
Смешанное соединение
Такая сложная конструкция содержит фрагменты с двумя вышеприведенными типами соединений. Чтобы подсчитать полную емкость, схему делят на простые блоки, состоящие только из деталей, соединенных каким-то одним образом. Находят эквивалентные значения для каждого блока и затем рисуют схему заново в упрощенном виде. Рассчитывают данные для получившейся системы.
Чтобы суметь подобрать подходящий конденсаторный набор, нужно уметь узнавать емкостные данные. Важно также знать, как рассчитывается показатель для конфигурации из нескольких деталей, соединенных между собой тем или иным образом.
Видео
Расчет емкости конденсатора для трехфазного двигателя
При подключении асинхронного трехфазного электродвигателя на 380 В в однофазную сеть на 220 В необходимо рассчитать емкость фазосдвигающего конденсатора, точнее двух конденсаторов – рабочего и пускового конденсатора. Онлайн калькулятор для расчета емкости конденсатора для трехфазного двигателя в конце статьи.
Как подключить асинхронный двигатель?
Подключение асинхронного двигателя осуществляется по двум схемам: треугольник (эффективнее для 220 В) и звезда (эффективнее для 380 В).
На картинке внизу статьи вы увидите обе эти схемы подключения. Здесь, я думаю, описывать подключение не стоит, т.к. это описано уже тысячу раз в Интернете.
Во основном, у многих возникает вопрос, какие нужны емкости рабочего и пускового конденсаторов.
Пусковой конденсатор
Ознакомьтесь также с этими статьями
Стоит отметить, что на небольших электродвигателях, используемых для бытовых нужд, например, для электроточила на 200-400 Вт, можно не использовать пусковой конденсатор, а обойтись одним рабочим конденсатором, я так делал уже не раз – рабочего конденсатора вполне хватает. Другое дело, если электродвигатель стартует со значительной нагрузкой, то тогда лучше использовать и пусковой конденсатор, который подключается параллельно рабочему конденсатору нажатием и удержанием кнопки на время разгона электродвигателя, либо с помощью специального реле. Расчет емкости пускового конденсатора осуществляется путем умножения емкостей рабочего конденсатора на 2-2.5, в данном калькуляторе используется 2.5.
При этом стоит помнить, что по мере разгона асинхронному двигателю требуется меньшая емкость конденсатора, т.е. не стоит оставлять подключенным пусковой конденсатор на все время работы, т.к. большая емкость на высоких оборотах вызовет перегрев и выход из строя электродвигателя.
Как подобрать конденсатор для трехфазного двигателя?
Конденсатор используется неполярный, на напряжение не менее 400 В. Либо современный, специально на это рассчитанный (3-й рисунок), либо советский типа МБГЧ, МБГО и т.п. (рис.4).
Итак, для расчета емкостей пускового и рабочего конденсаторов для асинхронного электродвигателя введите данные в форму ниже, эти данные вы найдете на шильдике электродвигателя, если данные неизвестны, то для расчета конденсатора можно использовать средние данные, которые подставлены в форму по умолчанию, но мощность электродвигателя нужно указать обязательно.
Онлайн калькулятор расчета емкости конденсатора
Советуем к прочтению другие наши статьи
Расчет емкости конденсатора22:

Конденсаторы
и формулы для расчета емкости
Конденсаторы – это пассивные устройства. в электронных схемах для хранения энергии в виде электрического поля. Они комплимент индукторы, хранящие энергию в виде магнитного поля. Идеальный конденсатор эквивалент разомкнутой цепи (бесконечное сопротивление) для постоянного тока (DC) и представляет собой импеданс (реактивное сопротивление) для переменные токи (AC), зависящие от частоты тока (или напряжения).Реактивное сопротивление (сопротивление току расход) конденсатора обратно пропорционален частоте сигнала, воздействующего на него. Конденсаторы изначально были называемые «конденсаторами» по причине, которая восходит к временам Лейденской банки, когда считалось, что электрические заряды накапливаться на пластинах в результате конденсации.
Свойство емкости, которое противодействует изменению напряжения, используется для передачи сигналов с компонент с более высокой частотой, предотвращая прохождение сигналов компонентов с более низкой частотой.Обычное применение конденсатор в радиочастотной цепи – это место, где есть напряжение смещения постоянного тока, которое необходимо заблокировать от присутствия в цепи, позволяя РЧ-сигналу проходить. Источники питания постоянного тока используют большие значения емкости параллельно с выходом. клеммы для сглаживания низкочастотных пульсаций из-за выпрямления и / или переключения сигналов.
При использовании последовательно (левый рисунок) или параллельно (правый рисунок) с его комплемент схемы, индуктор, комбинация индуктор-конденсатор образует контур, который резонирует на определенной частоте это зависит от значений каждого компонента.В последовательной цепи сопротивление току на резонансной частоте равен нулю с идеальными компонентами. В параллельной цепи (справа) сопротивление току бесконечно с идеальными компонентами.
Реальные конденсаторы, состоящие из физических компонентов, демонстрируют больше, чем просто емкость, когда присутствует в цепи переменного тока. Слева показана модель симулятора общей схемы. Он включает в себя настоящий идеальный конденсатор с параллельным резистивным компонент («Утечка»), реагирующий на переменный ток.Эквивалентный резистивный компонент постоянного тока (‘ESR’) последовательно с идеальным конденсатором и эквивалентной последовательной индуктивной составляющей («ESL») присутствует из-за металлических выводов (если они есть) и характеристик поверхностей пластин. Эта индуктивность в сочетании с емкостью создает резонансную частоту, на которой конденсатор выглядит как чистое сопротивление.
Когда рабочая частота увеличивается за пределы резонанса (также известного как собственная резонансная частота или SRF), схема ведет себя как индуктивность, а не как емкость.Следовательно, требуется тщательное рассмотрение SRF, когда выбор конденсаторов. В симуляторах типа SPICE используется эта или даже более сложная модель для облегчения более точных расчетов. в широком диапазоне частот.
Уравнения для последовательного и параллельного объединения конденсаторов приведены ниже. Дополнительные уравнения приведены для конденсаторов различной конфигурации. Как показывают эти цифры и формулы, емкость – это мера способности двух поверхностей для хранения электрического заряда.Разделенный и изолированный диэлектриком (изолятором), чистый положительный заряд накапливается на одна поверхность и чистый отрицательный заряд хранится на другой поверхности. В идеальном конденсаторе заряд будет храниться бесконечно; однако реальные конденсаторы постепенно теряют свой заряд из-за токов утечки через неидеальный диэлектрик.

Полная емкость последовательно соединенных конденсаторов равна обратной величине сумма обратных величин индивидуальных емкостей.Держите единицы постоянными.
Емкость (C, в фарадах) двух параллельных пластин равной площади равна произведению площади (A, в метрах) одной пластины. расстояние (d, в метрах), разделяющее пластины, и диэлектрическая проницаемость (ε, в Фарадах на метр) пространства разделение пластин. ε, полная диэлектрическая проницаемость, является произведением диэлектрической проницаемости свободного пространства, ε ₀, и относительная диэлектрическая проницаемость материала ε _r.Обратите внимание, что единицы измерения длины и площади могут быть метрическими. или английский, если они согласованы.
Коэффициент рассеяния (DF), также известный как тангенс потерь (tan δ), взаимозаменяемо определяется как величина, обратная качеству фактора (QF) или отношению эквивалентного последовательного сопротивления (ESR) и емкостного реактивного сопротивления (X _C).Это мера потери накопленного заряда. DF обычно используется в низкочастотных приложениях, в то время как tan δ чаще используется в высокочастотных приложениях.

Суммарная емкость параллельно соединенных конденсаторов равна сумме отдельных емкости. Держите единицы постоянными.
Следующие физические константы и механические размерные переменные применимы к уравнениям на этой странице.Единицы для уравнений показаны в скобках в конце уравнений; например, означает, что длина дана в дюймах, а индуктивность – в единицах Генри. Если единицы не указаны, можно использовать любые, если они согласованы для всех объектов; т.е. все измерители, все мкФ, пр.
C = емкость
L = индуктивность
W = энергия
ε _r = относительная диэлектрическая проницаемость (безразмерная)
ε ₀ = 8,85 x 10 ^-12 Ф / м (диэлектрическая проницаемость свободного пространства)
µ _r = Относительная проницаемость (безразмерная)
µ ₀ = 4π x 10 ^-7 Гн / м (проницаемость свободного пространства)
1 метр = 3.2808 футов <—> 1 фут
= 0,3048 метра
1 мм = 0,03937 дюйма <—> 1 дюйм
= 25,4 мм
Кроме того, точки (не путать с десятичными знаками) используются для обозначения умножения. во избежание двусмысленности.
Емкостное реактивное сопротивление (X _C, в Ω) обратно пропорциональна частоте (ω в радианах / сек или f в Гц) и емкости (C в фарадах).Чистая емкость имеет фазовый угол -90 ° (напряжение отстает от тока с фазовым углом 90 °).
Заряд (Q, в кулонах) конденсатора Пластины – это произведение емкости (C в фарадах) и напряжения (V в вольтах) на устройстве.
Энергия (Вт, в Джоулях) хранится в конденсаторе представляет собой половину произведения емкости (C в фарадах) на напряжение (V в вольтах) на устройстве.
Ток действительно течет “через” идеальный конденсатор. Напротив, заряд, накопленный на его пластинах, передается в подключенную цепь, тем самым облегчая ток. течь. И наоборот, сетевое напряжение, приложенное к пластинам, вызывает протекание тока в подключенной цепи по мере накопления заряда. на тарелках.
Добротность безразмерная. отношение реактивного сопротивления к сопротивлению в конденсаторе.
Связанные страницы по RF Cafe
– Конденсаторы и Расчет емкости
– Конденсатор Цветовой код
– Преобразование емкости
– Конденсатор Диэлектрики
– Стандартные значения конденсатора
– Поставщики конденсаторов
– Благородное искусство разъединения
,Конденсаторы серии
| Калькулятор формул
– в некоторых случаях конденсаторы могут подключаться последовательно, и необходимо иметь возможность рассчитать значение.
Емкостное руководство В комплект входит:
Емкость Формулы конденсаторов Емкостное сопротивление Параллельные конденсаторы Последовательные конденсаторы Диэлектрическая проницаемость и относительная диэлектрическая проницаемость Коэффициент рассеяния, тангенс угла потерь, ESR Таблица преобразования конденсаторов
В нескольких случаях может потребоваться последовательное соединение конденсаторов.В некоторых схемах это происходит естественным образом, например в некоторых генераторах может быть конденсаторный делитель напряжения переменного тока. В других случаях конденсаторы могут быть включены последовательно по разным причинам, некоторые примеры приведены ниже.
Хотя наиболее распространенная комбинация состоит в том, чтобы видеть два конденсатора последовательно, можно разместить три или более последовательно.
Формула конденсаторов серии
Если конденсаторы размещаются параллельно, это немного похоже на увеличение размера пластин конденсатора, и, следовательно, значения конденсаторов, подключенных параллельно, можно просто сложить.Если конденсаторы включены последовательно, их нельзя просто добавить.
Конденсаторы соединены последовательно
Теоретически ограничений на количество конденсаторов, которые можно добавить последовательно, нет. Очевидно, что могут быть практические ограничения, зависящие от области применения, места и других физических ограничений.
Если конденсаторы соединены последовательно, общую емкость можно определить, взяв величину, обратную емкости каждого конденсатора, и сложив их вместе, чтобы получить обратную величину от общей емкости.
1 С Общее количество знак равно 1 С 1 + 1 С 2 + 1 С 3 , , , , ,
Два конденсатора последовательно
При вычислении общего значения общей емкости для серии конденсаторов, включенных последовательно, вычисление может быть немного длинным, если выполняется вручную.Как и в большинстве сетей, только два конденсатора устанавливаются последовательно, что позволяет значительно упростить формулу. Это значительно упрощает ручные вычисления.
Два конденсатора соединены последовательно
С Общее количество знак равно С 1 С 2 С 1 + С 2
Серийный калькулятор конденсаторов
Калькулятор ниже показывает общую емкость для двух последовательно соединенных конденсаторов.Емкость можно ввести в фарадах, мкфарадах, нанофарадах или пикофарадах, при условии, что для обоих конденсаторов используются одинаковые единицы. Ответ предоставляется в тех же единицах, что и введенные.

Вычислитель конденсаторов серии

Меры предосторожности при использовании конденсаторов серии
Хотя конденсаторы действительно появляются последовательно в ряде конфигураций схем, таких как генераторы и т.п., конденсаторы могут использоваться последовательно для увеличения рабочего напряжения.
Когда два конденсатора используются последовательно, проблема часто заключается в том, что два конденсатора не распределяют напряжение поровну. Различия в токе утечки возникают между конденсаторами, особенно для конденсаторов, таких как электролитические версии, и это означает, что напряжения на двух конденсаторах могут сильно различаться, и в результате один может подвергаться условиям перенапряжения, что может привести к разрушению одного. или оба конденсатора. Это может произойти, если два конденсатора были включены последовательно для увеличения рабочего напряжения.
Разница в токе утечки может легко возникнуть из-за незначительных различий в производстве или даже из-за разницы в скорости старения двух конденсаторов – ток утечки в электролитических конденсаторах увеличивается со временем, особенно если они не используются.
Два конденсатора, соединенные последовательно с резистивным делителем напряжения
Чтобы помочь в равном распределении напряжения между двумя конденсаторами, вокруг конденсаторов размещены резисторы с высокой номинальной стоимостью в качестве делителя потенциала.Значения могут быть порядка 100 кОм или, возможно, даже немного выше, но достаточно, чтобы напряжения могли надежно делиться на обоих конденсаторах.
По сути, номиналы двух резисторов должны быть такими, чтобы ток, протекающий через них, был как минимум в десять раз выше, чем ток утечки. Таким образом, напряжение будет более равномерно распределяться между последовательно включенными конденсаторами. Даже при таком подходе хорошо оставлять хороший запас рабочего напряжения, особенно при использовании электролитических конденсаторов.
Последовательное соединение конденсаторов происходит во многих цепях. Очень полезно знать, как рассчитать общую стоимость, даже если это приблизительный расчет в вашей голове. Если требуется более точное значение, то онлайн-калькулятор последовательного конденсатора может оказаться очень полезным.
Дополнительные основные понятия:
Напряжение Текущий сопротивление емкость Мощность трансформеры RF шум Децибел, дБ Q, добротность
Вернуться в меню «Основные понятия»., ,
.
Как найти размер конденсатора в кВАр и Ф для улучшения коэффициента мощности
Привет! С очень важным руководством … Надеюсь, вы найдете его очень полезным, потому что я уже потратил два дня на подготовку этой статьи. Я думаю, что все те, кто отправлял сообщения и электронные письма по этой теме, никогда больше не спросят, следуют ли они этим простым методам для расчета надлежащего размера конденсаторной батареи в кВАр и микрофарадах для коррекции коэффициента мощности и улучшения как в одной фазе, так и в трех фазные цепи.Думаю, это слишком …
А теперь приступим …
Рассмотрим следующие примеры.
Пример: 1
Трехфазный асинхронный двигатель мощностью 5 кВт имеет коэффициент мощности, равный 0,75. Какой размер конденсатора в кВАр требуется для повышения коэффициента мощности до 0,90?
Решение № 1 (с помощью простого табличного метода)
Мощность двигателя = 5 кВт
Из таблицы, множитель для улучшения коэффициента мощности с 0.От 75 до 0,90 составляет 0,398
Требуемый конденсатор, кВАр для повышения коэффициента мощности с 0,75 до 0,90
Требуемый конденсатор, кВАр = кВт x Таблица 1, множитель 0,75 и 0,90
= 5 кВт x 0,398
= 1,99 кВАр
И Номинальные характеристики конденсаторов, подключенных в каждой фазе
1,99 / 3 = 0,663 кВАр
Решение № 2 (классический метод расчета)
Входная мощность двигателя = P = 5 кВт
Исходный P.F = Cosθ ₁ = 0,75
Конечная P.F = Cosθ ₂ = 0,90
θ ₁ = Cos ^-1 = (0,75) = 41 ° 0,41; Tan θ ₁ = Tan (41 ° 0,41) = 0,8819
θ ₂ = Cos ^-1 = (0,90) = 25 ° 0,84; Tan θ ₂ = Tan (25 ° .50) = 0,4843
Требуемый конденсатор, кВАр для улучшения коэффициента мощности с 0,75 до 0,90
Требуемый конденсатор, кВАр = P (Tan θ ₁ – Tan θ ₂)
= 5кВт (0,8819 – 0.4843)
= 1,99 кВАр
И номинал конденсаторов, подключенных в каждой фазе
1,99 / 3 = 0,663 кВАр
Таблицы (размеры конденсатора в кВАр и фарадах для коррекции коэффициента мощности
000
9002)
9002 Следующие таблицы были подготовлены для упрощения расчета кВАр для улучшения коэффициента мощности. Размер конденсатора в кВАр – это мощность в кВт, умноженная на коэффициент в таблице, чтобы улучшить существующий коэффициент мощности до предлагаемого коэффициента мощности.Ознакомьтесь с другими примерами ниже.
Пример 2:
Генератор выдает нагрузку 650 кВт при коэффициенте мощности 0,65. Какой размер конденсатора в кВАр требуется, чтобы повысить коэффициент мощности (P.F) до единицы (1)? И сколько еще кВт может выдать генератор при той же нагрузке в кВА при улучшении P.F.
Решение № 1 (с помощью простого табличного метода)
Подача кВт = 650 кВт
Из таблицы 1, множитель для улучшения коэффициента мощности с 0.65 для единицы (1) составляет 1,169
Требуемый конденсатор, кВАр для улучшения коэффициента мощности с 0,65 до единицы (1)
Требуемый конденсатор, кВАр = кВт x Таблица 1, множитель 65 и 100
= 650 кВт x 1,169
= 759,85 кВАр
Мы знаем, что PF = Cosθ = кВт / кВА. , .or
кВА = кВт / Cosθ
= 650 / 0,65 = 1000 кВА
Когда коэффициент мощности повышается до единицы (1)
Количество кВт = кВА x Cosθ
= 1000 x 1 = 1000 кВт
Следовательно увеличенная мощность от генератора
1000кВт – 650кВт = 350кВт
Решение № 2 (классический метод расчета)
Подача кВт = 650 кВт
Оригинал P.F = Cosθ ₁ = 0,65
Конечная P.F = Cosθ ₂ = 1
θ ₁ = Cos ^-1 = (0,65) = 49 ° 0,45; Tan θ ₁ = Tan (41 ° .24) = 1,169
θ ₂ = Cos ^-1 = (1) = 0 °; Tan θ ₂ = Tan (0 °) = 0
Требуемый конденсатор, кВАр для улучшения коэффициента мощности с 0,75 до 0,90
Требуемый конденсатор, кВАр = P (Tan θ ₁ – Tan θ ₂)
= 650 кВт ( 1,169–0)
= 759.85 кВАр
Как рассчитать требуемую емкость батареи конденсаторов в кВАр и фарадах?
(Как преобразовать фарады в кВАр и наоборот)
Пример: 3
A Однофазный 400 В, 50 Гц, двигатель потребляет ток питания 50 А при коэффициенте мощности (Коэффициент мощности) 0,6. Коэффициент мощности двигателя необходимо повысить до 0,9, подключив параллельно ему конденсатор.Рассчитайте необходимую емкость конденсатора как в кВАр, так и в фарадах.
Решение:
(1) Найти требуемую емкость в кВАр для улучшения коэффициента мощности с 0,6 до 0,9 (два метода)
Решение № 1 (By Simple Табличный метод)
Вход двигателя = P = V x I x Cosθ
= 400 В x 50 A x 0,6
= 12 кВт
Из таблицы, множитель для улучшения коэффициента мощности с 0.От 60 до 0,90 составляет 0,849
Требуемый конденсатор, кВАр для улучшения коэффициента мощности с 0,60 до 0,90
Требуемый конденсатор, кВАр = кВт x табличный множитель 0,60 и 0,90
= 12 кВт x 0,849
= 10,188 кВАр
# 2 (классический метод расчета)
Вход двигателя = P = V x I x Cosθ
= 400 В x 50 A x 0,6
= 12 кВт
Фактическое значение P.F = Cosθ ₁ = 0..6
Требуется P.F = Cosθ ₂ = 0,90
θ ₁ = Cos ^-1 = (0,60) = 53 ° 0,13; Tan θ ₁ = Tan (53 ° 0,13) = 1,3333
θ ₂ = Cos ^-1 = (0,90) = 25 ° 0,84; Tan θ ₂ = Tan (25 ° .50) = 0,4843
Требуемый конденсатор, кВАр для улучшения коэффициента мощности с 0,60 до 0,90
Требуемый конденсатор, кВАр = P (Tan θ ₁ – Tan θ ₂)
= 5кВт (1.3333–0.4843)
= 10,188 кВАр
(2) Чтобы найти требуемую емкость в Фараде, чтобы улучшить коэффициент мощности с 0,6 до 0,9 (два метода)
Решение № 1 (с использованием простой формулы )
Мы уже рассчитали требуемую емкость конденсатора в кВАр, поэтому мы можем легко преобразовать ее в фарады, используя эту простую формулу
Требуемая емкость конденсатора в фарадах / микрофарадах
C = кВАр / (2 π f V ²) в микрофарадах
Вычисление значений в приведенной выше формуле
= (10.188 кВАр) / (2 x π x 50 x 400 ²)
= 2,0268 x 10 ^-4
= 202,7 x 10 ^-6
= 202,7 мкФ
Решение № 2 (Простой метод расчета)
кВАр = 10,188… (i)
Мы это знаем;
I _C = V / X _C
В то время как X _C = 1/2 π FC
I _C = V / (1/2 π FC)
I _C = V 2 FC
= (400) x 2π x (50) x C
I _C = 125663.7 x C
And,
kVAR = (V x I _C) / 1000… [kVAR = (V x I) / 1000]
= 400 x 125663,7 x C
I _C = 50265,48 x C… (ii)
Приравнивая уравнения (i) и (ii), мы получаем
50265,48 x C = 10,188C
C = 10,188 / 50265,48
C = 2,0268 x 10 ^{– 4}
C = 202,7 x 10 ^-6
C = 202,7 мкФ
Пример 4
Какое значение емкости должно быть подключено параллельно с рисунком нагрузки 1 кВт с отставанием 70% коэффициент мощности от источника 208 В, 60 Гц для повышения общего коэффициента мощности до 91%.
Решение:
Вы можете использовать метод таблицы или метод простого расчета, чтобы найти необходимое значение емкости в фарадах или кВАр, чтобы улучшить коэффициент мощности с 0,71 до 0,97. Поэтому в данном случае я использовал табличный метод.
P = 1000 Вт
Фактический коэффициент мощности = Cosθ ₁ = 0,71
Требуемый коэффициент мощности = Cosθ ₂ = 0,97
Из таблицы, множитель для улучшения коэффициента мощности с 0,71 до 0.97 составляет 0,783
Требуемый конденсатор, кВАр для повышения коэффициента мощности с 0,71 до 0,97
Требуемый конденсатор, кВАр = кВт x табличный множитель 0,71 и 0,97
= 1 кВт x 0,783
= 783 ВАр (требуемое значение емкости в кВАр)
Ток в конденсаторе =
I _C = Q _C / V
= 783/208
= 3,76 A
И
X _C = V / I _C
= 208/3.76 = 55,25 Ом
C = 1 / (2 π f X _C)
C = 1 (2 π x 60 x 55,25)
C = 48 мкФ (требуемое значение емкости в фарадах)
Полезно знать:
Важные формулы, которые используются для расчета улучшения коэффициента мощности, а также в приведенном выше расчете
Мощность в ваттах
кВт = кВА x Cosθ
кВт = л.с. x 0,746 или (л.с. x 0,746) / КПД… (л.с. = мощность двигателя)
кВт = √ (кВА ² – кВАр ²)
кВт = P = VI Cosθ… (однофазный)
кВт = P = √3x V x I Cosθ… (трехфазный)
Полная мощность, ВА
кВА = √ (кВт ² + кВАр ²)
кВА = кВт / Cosθ
Реактивная мощность, ВА
кВАр = √ (кВА ² – кВт ²)
кВАр = C x (2 π f V ²)
Коэффициент мощности (от 0.От 1 до 1)
Коэффициент мощности = Cosθ = P / VI… (однофазный)
Коэффициент мощности = Cosθ = P / (√3x V x I)… (трехфазный)
Коэффициент мощности = Cosθ = кВт / кВА… (Однофазный и трехфазный)
Коэффициент мощности = Cosθ = R / Z… (сопротивление / импеданс)
X _C = 1 / (2 π f C)… (X _C = емкостное реактивное сопротивление)
I _C = V / X _C… (I = V / R)
Требуемая емкость конденсатора в фарадах / микрофарадах
C = кВАр / (2 π f V ²) дюйм микрофарад
Требуемая емкость конденсатора в кВАр
кВАр = C x (2 π f V ²)

Подробнее:
Введите адрес электронной почты для получения последних обновлений, например выше одного!
.
Калькулятор разряда суперконденсатора
Подробнее об этом расчете
Vcapmax – максимальное значение напряжения V _CC, до которого заряжается конденсатор.
Vcapmin – это минимальное рабочее напряжение, которое вы можете выдержать до того, как ваша схема или компонент, поддерживаемые конденсатором, перестанут работать.
Imax – это максимальный ток, при котором ваша цепь разряжает конденсатор.Это может быть постоянный ток или начальный линейный ток при Vcapmax. Значения Imax и Vcap используются для расчета эквивалентного сопротивления цепи, которое используется в уравнение для расчета времени резервного копирования.

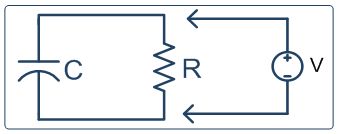Рисунок 1.
Из базовой электроники формула для определения напряжения на конденсаторе в любой момент времени (для Схема разряда на рисунке 1) составляет: V (t) = E (e ^{-t / RC})
Преобразование этой формулы для времени дает нам: t = – log (V / E) (RC)
Где :
В – конечное напряжение в вольтах (В)
E – начальное напряжение в вольтах (В)
R – резистивная нагрузка в омах (Ом)
C – емкость конденсатора в фарадах 1F = 1000 000 мкФ = 1000 000 000 нФ = 10000000000000pF
t – время в секундах
Дополнительная информация о суперконденсаторах
Суперконденсатор, суперконденсатор, псевдоконденсатор, электрохимический двухслойный конденсатор (EDLC) или ультраконденсатор, представляет собой электрохимический конденсатор с относительно высокой плотностью энергии, обычно порядка тысяч раз больше, чем у электролитического конденсатора.Например, электролитический конденсатор типичного размера D-ячейки может иметь емкость в диапазоне десятков миллифарад. Электрический двухслойный конденсатор такого же размера может достигать нескольких фарад, что на два порядка больше. Суперконденсаторы обычно дают более низкое рабочее напряжение в диапазоне 2,5 – 20 В.
По состоянию на 2010 год более крупные двухслойные конденсаторы имеют емкость до 5000 фарад. [1] Также в 2010 году самая высокая доступная плотность энергии суперконденсатора составляет 30 Вт · ч / кг [2] ниже, чем у быстро заряжаемых литий-титанатных батарей.EDLC
имеют множество коммерческих применений, особенно в устройствах «сглаживания энергии» и устройств с мгновенной нагрузкой. Они используются в качестве накопителей энергии в транспортных средствах, а также для небольших приложений, таких как домашние солнечные энергетические системы, где чрезвычайно быстрая зарядка является важной функцией. Суперконденсаторы уже много лет широко используются в качестве резервного источника питания для схем часов реального времени и памяти в микроконтроллерах. Больше информации в Википедии здесь.