Формула заряда через напряжение: Электростатика – Физика – Теория, тесты, формулы и задачи

Электростатика – Физика – Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Электрический заряд и его свойства

К оглавлению…

Электрический заряд – это физическая величина, характеризующая способность частиц или тел вступать в электромагнитные взаимодействия. Электрический заряд обычно обозначается буквами q или Q. В системе СИ электрический заряд измеряется в Кулонах (Кл). Свободный заряд в 1 Кл – это гигантская величина заряда, практически не встречающаяся в природе. Как правило, Вам придется иметь дело с микрокулонами (1 мкКл = 10^–6 Кл), нанокулонами (1 нКл = 10^–9 Кл) и пикокулонами (1 пКл = 10^–12 Кл). Электрический заряд обладает следующими свойствами:

1. Электрический заряд является видом материи.

2. Электрический заряд не зависит от движения частицы и от ее скорости.

3. Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

4. Существует два рода электрических зарядов, условно названных положительными и отрицательными.

5. Все заряды взаимодействуют друг с другом. При этом одноименные заряды отталкиваются, разноименные – притягиваются. Силы взаимодействия зарядов являются центральными, то есть лежат на прямой, соединяющей центры зарядов.

6. Существует минимально возможный (по модулю) электрический заряд, называемый элементарным зарядом. Его значение:

e = 1,602177·10^–19 Кл ≈ 1,6·10^–19 Кл.

Электрический заряд любого тела всегда кратен элементарному заряду:

где: N – целое число.

Обратите внимание, невозможно существование заряда, равного 0,5е; 1,7е; 22,7е и так далее. Физические величины, которые могут принимать только дискретный (не непрерывный) ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда.

7. Закон сохранения электрического заряда. В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Из закона сохранения заряда так же следует, если два тела одного размера и формы, обладающие зарядами q₁ и q₂ (совершенно не важно какого знака заряды), привести в соприкосновение, а затем обратно развести, то заряд каждого из тел станет равным:

С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному (то есть минимально возможному) заряду e.

В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов, или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион. Обратите внимание, что положительные протоны входят в состав ядра атома, поэтому их число может изменяться только при ядерных реакциях. Очевидно, что при электризации тел ядерных реакций не происходит. Поэтому в любых электрических явлениях число протонов не меняется, изменяется только число электронов.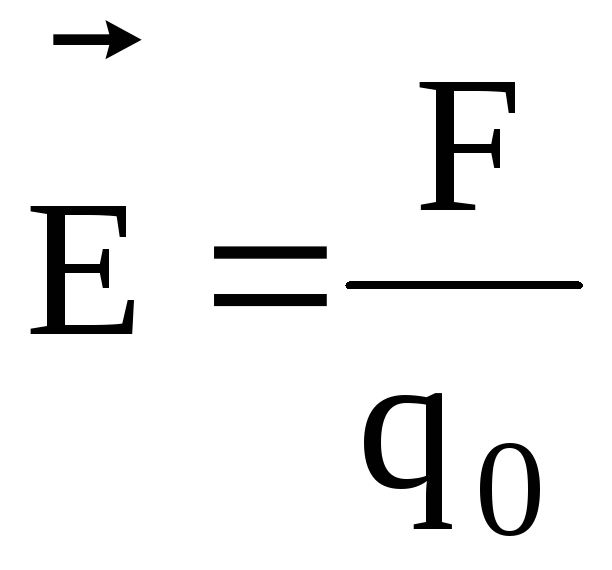

Так, сообщение телу отрицательного заряда означает передачу ему лишних электронов. А сообщение положительного заряда, вопреки частой ошибке, означает не добавление протонов, а отнимание электронов. Заряд может передаваться от одного тела к другому только порциями, содержащими целое число электронов.

Иногда в задачах электрический заряд распределен по некоторому телу. Для описания этого распределения вводятся следующие величины:

1. Линейная плотность заряда. Используется для описания распределения заряда по нити:

где: L – длина нити. Измеряется в Кл/м.

2. Поверхностная плотность заряда. Используется для описания распределения заряда по поверхности тела:

где: S – площадь поверхности тела. Измеряется в Кл/м².

3. Объемная плотность заряда. Используется для описания распределения заряда по объему тела:

где: V – объем тела. Измеряется в Кл/м³.

Обратите внимание на то, что масса электрона равна:

m_e = 9,11∙10^–31 кг.

 

Закон Кулона

К оглавлению…

Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь. На основании многочисленных опытов Кулон установил следующий закон:

Силы взаимодействия неподвижных точечных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

где: ε – диэлектрическая проницаемость среды – безразмерная физическая величина, показывающая, во сколько раз сила электростатического взаимодействия в данной среде будет меньше, чем в вакууме (то есть во сколько раз среда ослабляет взаимодействие). Здесь k – коэффициент в законе Кулона, величина, определяющая численное значение силы взаимодействия зарядов. В системе СИ его значение принимается равным:

k = 9∙10⁹ м/Ф.

Силы взаимодействия точечных неподвижных зарядов подчиняются третьему закону Ньютона, и являются силами отталкивания друг от друга при одинаковых знаках зарядов и силами притяжения друг к другу при разных знаках. Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют

электростатикой.

Закон Кулона справедлив для точечных заряженных тел, равномерно заряженных сфер и шаров. В этом случае за расстояния r берут расстояние между центрами сфер или шаров. На практике закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними. Коэффициент k в системе СИ иногда записывают в виде:

где: ε₀ = 8,85∙10^–12 Ф/м – электрическая постоянная.

Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции: если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.

Запомните также два важных определения:

Проводники – вещества, содержащие свободные носители электрического заряда. Внутри проводника возможно свободное движение электронов – носителей заряда (по проводникам может протекать электрический ток). К проводникам относятся металлы, растворы и расплавы электролитов, ионизированные газы, плазма.

Диэлектрики (изоляторы) – вещества, в которых нет свободных носителей заряда. Свободное движение электронов внутри диэлектриков невозможно (по ним не может протекать электрический ток). Именно диэлектрики обладают некоторой не равной единице диэлектрической проницаемостью ε.

Для диэлектрической проницаемости вещества верно следующее (о том, что такое электрическое поле чуть ниже):

 

Электрическое поле и его напряженность

К оглавлению…

По современным представлениям, электрические заряды не действуют друг на друга непосредственно.

Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.

Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не вносит заметного перераспределения исследуемых зарядов. Для количественного определения электрического поля вводится силовая характеристика – напряженность электрического поля E.

Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на пробный заряд, помещенный в данную точку поля, к величине этого заряда:

Напряженность электрического поля – векторная физическая величина. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.

Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора напряженности в каждой точке совпадало с направлением касательной к силовой линии. Силовые линии обладают следующими свойствами.

• Силовые линии электростатического поля никогда не пересекаются.
• Силовые линии электростатического поля всегда направлены от положительных зарядов к отрицательным.
• При изображении электрического поля с помощью силовых линий их густота должна быть пропорциональна модулю вектора напряженности поля.
• Силовые линии начинаются на положительном заряде или бесконечности, а заканчиваются на отрицательном или бесконечности. Густота линий тем больше, чем больше напряжённость.
• В данной точке пространства может проходить только одна силовая линия, т.к. напряжённость электрического поля в данной точке пространства задаётся однозначно.

Электрическое поле называют однородным, если вектор напряжённости одинаков во всех точках поля. Например, однородное поле создаёт плоский конденсатор – две пластины, заряженные равным по величине и противоположным по знаку зарядом, разделённые слоем диэлектрика, причём расстояние между пластинами много меньше размеров пластин.

Во всех точках однородного поля на заряд q, внесённый в однородное поле с напряжённостью E, действует одинаковая по величине и направлению сила, равная F = Eq. Причём, если заряд q положительный, то направление силы совпадает с направлением вектора напряжённости, а если заряд отрицательный, то вектора силы и напряжённости противоположно направлены.

Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рисунке:

 

Принцип суперпозиции

К оглавлению. ..

Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:

Это поле называется кулоновским. В кулоновском поле направление вектора напряженности зависит от знака заряда Q: если Q > 0, то вектор напряженности направлен от заряда, если Q < 0, то вектор напряженности направлен к заряду. Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.

Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:

Итак, если в задаче требуется определить напряженность поля системы зарядов, то надо действовать по следующему алгоритму:

1. Нарисовать рисунок.
2. Изобразить напряженность поля каждого заряда по отдельности в нужной точке. Помните, что напряженность направлена к отрицательному заряду и от положительного заряда.
3. Вычислить каждую из напряжённостей по соответствующей формуле.
4. Сложить вектора напряжённостей геометрически (т.е. векторно).

 

Потенциальная энергия взаимодействия зарядов

К оглавлению…

Электрические заряды взаимодействуют друг с другом и с электрическим полем. Любое взаимодействие описывается потенциальной энергией. Потенциальная энергия взаимодействия двух точечных электрических зарядов рассчитывается по формуле:

Обратите внимание на отсутствие модулей у зарядов. Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.

Задачи по данной теме решаются, как и задачи на закон сохранения механической энергии: сначала находится начальная энергия взаимодействия, потом конечная. Если в задаче просят найти работу по перемещению зарядов, то она будет равна разнице между начальной и конечной суммарной энергией взаимодействия зарядов. Энергия взаимодействия так же может переходить в кинетическую энергию или в другие виды энергии. Если тела находятся на очень большом расстоянии, то энергия их взаимодействия полагается равной 0.

Обратите внимание: если в задаче требуется найти минимальное или максимальное расстояние между телами (частицами) при движении, то это условие выполнится в тот момент времени, когда частицы движутся в одну сторону с одинаковой скоростью.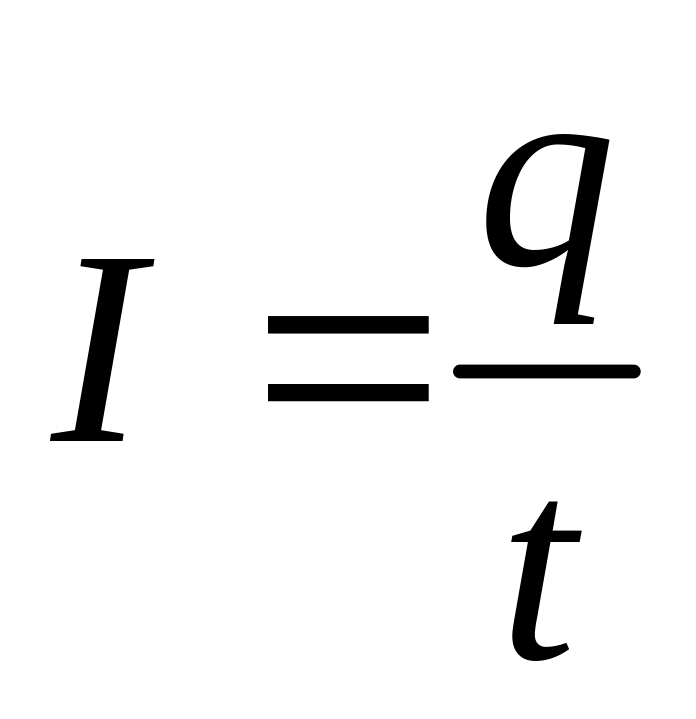 Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.

 

Потенциал. Разность потенциалов. Напряжение

К оглавлению…

Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Потенциал φ является энергетической характеристикой электростатического поля. В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал – скалярная величина.

Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что потенциал φ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его. Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.

Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

В этих формулах:

• φ – потенциал электрического поля.
• ∆φ – разность потенциалов.
• W – потенциальная энергия заряда во внешнем электрическом поле.
• A – работа электрического поля по перемещению заряда (зарядов).
• q – заряд, который перемещают во внешнем электрическом поле.
• U – напряжение.
• E – напряженность электрического поля.
• d или ∆l – расстояние на которое перемещают заряд вдоль силовых линий.

Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.

Принцип суперпозиции потенциала

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):

Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности. Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.

 

Электрическая емкость. Плоский конденсатор

К оглавлению…

При сообщении проводнику заряда всегда существует некоторый предел, более которого зарядить тело не удастся. Для характеристики способности тела накапливать электрический заряд вводят понятие электрической емкости. Емкостью уединенного проводника называют отношение его заряда к потенциалу:

В системе СИ емкость измеряется в Фарадах [Ф]. 1 Фарад – чрезвычайно большая емкость. Для сравнения, емкость всего земного шара значительно меньше одного фарада. Емкость проводника не зависит ни от его заряда, ни от потенциала тела. Аналогично, плотность не зависит ни от массы, ни от объема тела. Емкость зависит лишь от формы тела, его размеров и свойств окружающей его среды.

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

Величина электроемкости проводников зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.

Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами.

Каждая из заряженных пластин плоского конденсатора создает вблизи своей поверхности электрическое поле, модуль напряженности которого выражается соотношением уже приводившимся выше. Тогда модуль напряженности итогового поля внутри конденсатора, создаваемого двумя пластинами, равен:

За пределами конденсатора, электрические поля двух пластин направлены в разные стороны, и поэтому результирующее электростатическое поле E = 0.  Электроёмкость плоского конденсатора может быть рассчитана по формуле:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз. Обратите внимание, что S в этой формуле есть площадь только одной обкладки конденсатора. Когда в задаче говорят о «площади обкладок», то имеют в виду именно эту величину. На 2 умножать или делить её не надо никогда.

Еще раз приведем формулу для заряда конденсатора. Под зарядом конденсатора понимают только заряд его положительной обкладки:

Сила притяжения пластин конденсатора. Сила, действующая на каждую обкладку, определяется не полным полем конденсатора, а полем, созданным противоположной обкладкой (сама на себя обкладка не действует). Напряженность этого поля равна половине напряженности полного поля, и сила взаимодействия пластин:

Энергия конденсатора. Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):

Особое внимание обращайте на фразу: «Конденсатор подключён к источнику». Это означает, что напряжение на конденсаторе не изменяется. А фраза «Конденсатор зарядили и отключили от источника» означает, что заряд конденсатора не изменится.

Энергия электрического поля

Электрическую энергию следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Энергия заряженных тел сосредоточена в пространстве, в котором есть электрическое поле, т.е. можно говорить об энергии электрического поля. Например, у конденсатора энергия сосредоточена в пространстве между его обкладками. Таким образом, имеет смысл ввести новую физическую характеристику – объёмную плотность энергии электрического поля. На примере плоского конденсатора, можно получить такую формулу для объёмной плотности энергии (или энергии единицы объёма электрического поля):

 

Соединения конденсаторов

К оглавлению…

Параллельное соединение конденсаторов – для увеличения ёмкости. Конденсаторы соединены одноименно заряженными обкладками, как бы увеличивая площадь одинаково заряженных пластин. Напряжение на всех конденсаторах одинаковое, общий заряд равен сумме зарядов каждого из конденсаторов, и общая ёмкость также равна сумме емкостей всех конденсаторов соединенных параллельно. Выпишем формулы для параллельного соединения конденсаторов:

При последовательном соединении конденсаторов общая ёмкость батареи конденсаторов всегда меньше, чем ёмкость наименьшего конденсатора, входящего в батарею. Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:

Из закона сохранения заряда следует, что заряды на соседних обкладках равны:

Напряжение равно сумме напряжений на отдельных конденсаторах.

Для двух последовательно соединённых конденсаторов формула выше даст нам следующее выражение для общей емкости:

Для N одинаковых последовательно соединённых конденсаторов:

 

Проводящая сфера

К оглавлению…

Напряженность поля внутри заряженного проводника равна нулю. В противном случае на свободные заряды внутри проводника действовала бы электрическая сила, которая вынуждала бы эти заряды двигаться внутри проводника. Это движение, в свою очередь, приводило бы к разогреванию заряженного проводника, чего на самом деле не происходит.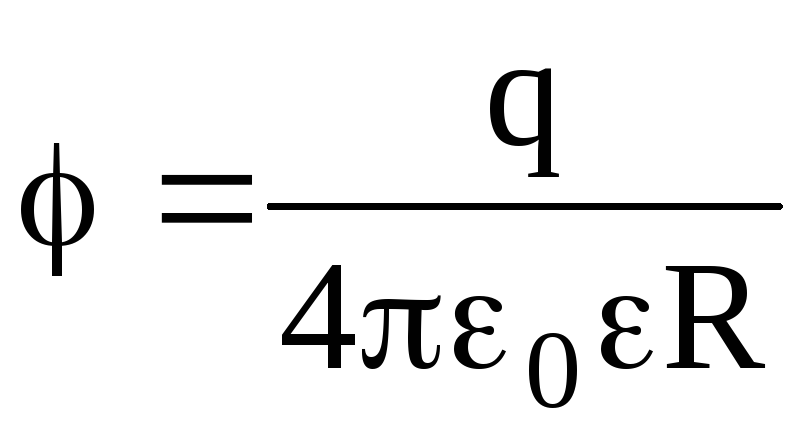

Факт того, что внутри проводника нет электрического поля можно понять и по-другому: если бы оно было то заряженные частицы опять таки двигались бы, причем они бы двигались именно так, чтобы свести это поле к нолю своим собственным полем, т.к. вообще-то двигаться им не хотелось бы, ведь всякая система стремится к равновесию. Рано или поздно все двигавшиеся заряды остановились бы именно в том месте, чтобы поле внутри проводника стало равно нолю.

На поверхности проводника напряжённость электрического поля максимальна. Величина напряжённости электрического поля заряженного шара за его пределами убывает по мере удаления от проводника и рассчитывается по формуле, аналогичной формулам для напряженности поля точечного заряда, в которой расстояния отсчитываются от центра шара.

Так как напряженность поля внутри заряженного проводника равна нулю, то потенциал во всех точках внутри и на поверхности проводника одинаков (только в этом случае разность потенциалов, а значит и напряжённость равна нулю). Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.

Электрическая емкость шара радиуса R:

Если шар окружен диэлектриком, то:

 

Свойства проводника в электрическом поле

К оглавлению…

1. Внутри проводника напряженность поля всегда равна нулю.
2. Потенциал внутри проводника во всех точках одинаков и равен потенциалу поверхности проводника. Когда в задаче говорят, что «проводник заряжен до потенциала … В», то имеют в виду именно потенциал поверхности.
3. Снаружи от проводника вблизи от его поверхности напряженность поля всегда перпендикулярна поверхности.
4. Если проводнику сообщить заряд, то он весь распределится по очень тонкому слою вблизи поверхности проводника (обычно говорят, что весь заряд проводника распределяется на его поверхности). Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся.
5. Снаружи проводника напряженность поля тем больше, чем кривее поверхность проводника. Максимальное значение напряженности достигается вблизи остриев и резких изломов поверхности проводника.

 

Замечания к решению сложных задач

К оглавлению…

1. Заземление чего-либо означает соединение проводником данного объекта с Землей. При этом потенциалы Земли и имеющегося объекта выравниваются, а необходимые для этого заряды перебегают по проводнику с Земли на объект либо наоборот. При этом нужно учитывать несколько факторов, которые следуют из того, что Земля несоизмеримо больше любого объекта находящегося не ней:

• Общий заряд Земли условно равен нолю, поэтому ее потенциал также равен нолю, и он останется равным нолю после соединения объекта с Землей. Одним словом, заземлить – означает обнулить потенциал объекта.
• Для обнуления потенциала (а значит и собственного заряда объекта, который мог быть до этого как положительным так и отрицательным), объекту придется либо принять либо отдать Земле некоторый (возможно даже очень большой) заряд, и Земля всегда сможет обеспечить такую возможность.

2. Еще раз повторимся: расстояние между отталкивающимися телами минимально в тот момент, когда их скорости становятся равны по величине и направлены в одну сторону (относительная скорость зарядов равна нулю). В этот момент потенциальная энергия взаимодействия зарядов максимальна. Расстояние между притягивающимися телами максимально, также в момент равенства скоростей, направленных в одну сторону.

3. Если в задаче имеется система, состоящая из большого количества зарядов, то необходимо рассматривать и расписывать силы, действующие на заряд, который не находится в центре симметрии.

Глава 20. Конденсаторы

Для накопления разноименных электрических зарядов служит устройство, которое называется конденсатором. Конденсатор — система двух изолированных друг от друга проводников (которые часто называют обкладками конденсатора), один из которых заряжен положительным, второй — таким же по величине, но отрицательным зарядом. Если эти проводники представляют собой плоские параллельные пластинки, расположенные на небольшом рас-стоянии друг от друга, то конденсатор называется плоским.

Для характеристики способности конденсатора накапливать заряд вводится понятие электроемкости (часто говорят просто емкости). Емкостью конденсатора называется отношение заряда конденсатора к той разности потенциалов , которая возникает между обкладками при их заряжении зарядами и (эту разность потенциалов проводников часто называют электрическим напряжением между обкладками и обозначают буквой ):

(20. 1)

Поскольку величины и (или ) в формуле (20.1) зависимы, то емкость (20.1) не зависит от и , а является характеристикой геометрии системы проводников. Действительно, при сообщении проводникам зарядов и проводники приобретут потенциалы, разность которых будет пропорциональна заряду . Поэтому в отношении (20.1) заряд сокращается.

Выведем формулу для емкости плоского конденсатора (эта формула входит в программу школьного курса физики). При заряжении параллельных пластин, расположенных на небольшом расстоянии друг от друга, зарядами и , в пространстве между ними возникает однородное электрическое поле с напряженностью (см. гл. 18):

(20.2)

Разность потенциалов между пластинами равна

(20.3)

где — площадь пластин, — расстояние между ними. Отсюда, вычисляя отношение заряда к разности потенциалов (20.3), находим емкость плоского конденсатора

(20.4)

Если все пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью , то поле (20.2) и разность потенциалов (20.3) убывает в раз, а емкость конденсатора в раз взрастает

(20.5)

Для конденсаторов, соединенных в батареи, вводится понятие эквивалентной емкости, как емкости одного конденсатора, который при заряжении его тем же зарядом, что и батарея дает ту же разность потенциалов, что и батарея конденсаторов. Приведем формулы для эквивалентной емкости, а также для заряда и электрического напряжения на каждом конденсаторе при последовательном и параллельном их соединении.

Последовательное соединение (см. рисунок). При сообщении левой пластине левого конденсатора заряда , а правой пластине правого заряда , на внутренних пластинах благодаря поляризации будут индуцироваться заряды (см. рисунок; значения индуцированных зарядов приведены под пластинами). Можно доказать, что в результате поляризации каждый конденсатор будет заряжен такими же зарядами и , как и заряды крайних пластин, напряжение на всей батарее конденсаторов равно сумме напряжений на каждом, а обратная эквивалентная емкость батареи — сумме обратных емкостей всех конденсаторов

(20.6)

Параллельное соединение (см. рисунок). В этом случае если сообщить левому проводнику заряд , правому сообщить заряд , заряд распределится между конденсаторами, вообще говоря, не одинаково, но по закону сохранения заряда .

Поскольку правые пластины всех конденсаторов соединены между собой, левые — тоже, то они представляют собой единые проводники, и, следовательно, разность потенциалов между пластинами каждого конденсатора будет одинакова: . Можно доказать, что при таком соединении конденсаторов эквивалентная емкость батареи равна сумме емкостей отдельных конденсаторов

(20. 7)

Заряженный конденсатор обладает определенной энергией. Если конденсатор емкости заряжен зарядом , то энергия этого конденсатора (можно говорить энергия электрического поля конденсатора) равна

(20.8)

С помощью определения электрической емкости (20.1) можно переписать формулу (20.8) еще в двух формах:

(20.9)

Рассмотрим в рамках этого минимума сведений о конденсаторах типичные задачи ЕГЭ по физике, которые были предложены в первой части книги.

Электроемкость конденсатора — его геометрическая характеристика, которая при неизменной геометрии не зависит от заряда конденсатора (задача 20.1.1 — ответ 3). Аналогично не меняется емкость конденсатора при увеличении напряжения на конденсаторе (задача 20.1.2 — ответ 3).

Связь между единицами измерений (задача 20.1.3) следует из определения емкости (20.1). Единица электрической емкости в международной системе единиц измерений СИ называется Фарада. 1 Фарада — это емкость такого конденсатора, между пластинами которого возникает напряжение 1 В при зарядах пластин 1 Кл и -1 Кл (ответ 4).

Поскольку электрическое поле в плоском конденсаторе однородно, то напряженность поля в конденсаторе и напряжение между пластинами связаны соотношением (см. формулу (18.9)) , где — расстояние между пластинами. Отсюда находим напряженность поля между обкладками плоского конденсатора в задаче 20.1.4

(ответ 4).

Согласно определению электрической емкости имеем в задаче 20.1.5

(ответ 2).

Из формулы (20.4) для емкости плоского конденсатора заключаем, что при увеличении площади его пластин в 3 раза (задача 20. 1.6) его емкость увеличивается в 3 раза (ответ 1).

При уменьшении в раз расстояния между пластинами емкость плоского конденсатора возрастет в раз. Поэтому новое напряжение на конденсаторе (задача 20.1.7) можно найти из следующей цепочки формул

где и — новый заряд конденсатора (ответ 3).

Так как конденсатор в задаче 20.1.8 подключен к источнику, то между его пластинами поддерживается постоянное напряжение независимо от расстояния между ними. Поэтому заряд конденсатора изменяется при раздвигании пластин так же, как изменяется его емкость. А поскольку при увеличении расстояния между пластинами вдвое емкость конденсатора уменьшается вдвое (см. формулу (20.4)), то вдвое уменьшается и заряд конденсатора (ответ 2).

В задаче 20.1.9 конденсатор отключен от источника в процессе сближения пластин. Поэтому не меняется их заряд. А поскольку напряженность электрического поля между пластинами определяется соотношением (20.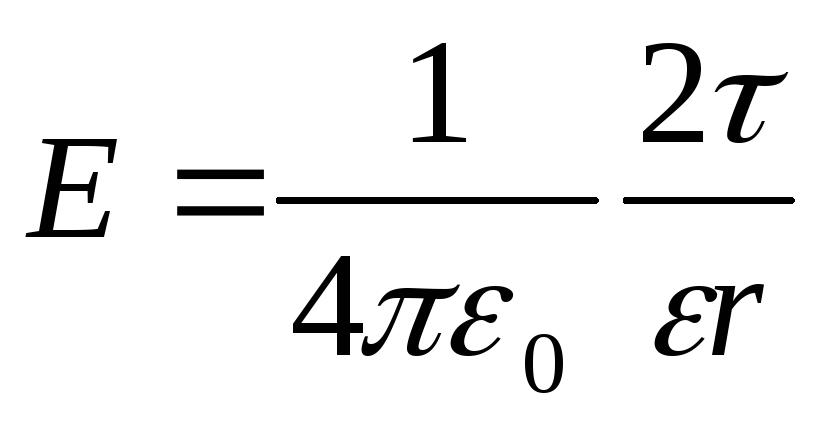 2)

то напряженность электрического поля между пластинами также не изменяется (ответ 3). Этот же результат можно получить и через определение емкости с учетом того, что

произведение от расстояния между пластинами не зависит (см. формулу (20.4)).

Из формул (20.8), (20.9) видим, что только одно из приведенных в качестве ответов к задаче 20.1.10 соотношений (а именно — 2) определяет энергию конденсатора.

При последовательном соединении конденсаторов (задача 20.2.1) одинаковыми будут их заряды независимо от значений их электрических емкостей (ответ 2). При параллельном соединении конденсаторов (задача 20.2.2) одинаковыми будут напряжения на каждом из них (ответ 3).

Поскольку конденсатор в задаче 20.2.3 отключен от источ-ника напряжения, его заряд не меняется в процессе раздвигания пластин. Поэтому для исследования изменения энергии конденсатора удобно воспользоваться формулой (20.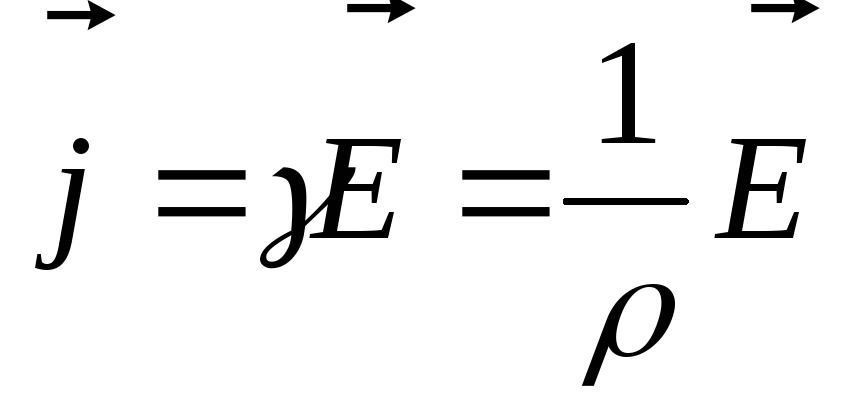 8)

(1)

Так как при увеличении расстояния между пластинами в раз электрическая емкость конденсатора уменьшается в раз, то согласно формуле (1) энергия конденсатора увеличится в раз (ответ 1).

В задаче 20.2.4 не изменяется напряжение на конденсаторе. Поэтому воспользуемся первой из формул (20.9)

Из этой формулы заключаем, что при увеличении в раз расстояния между пластинами энергия конденсатора уменьшится в раз — ответ 2. (Разница с предыдущей задачей связана с тем, что здесь кроме внешних сил, совершающих работу при раздвигании пластин, совершает работу источник напряжения.)

В задаче 20.2.5 изменяют расстояние между пластинами (и, следовательно, емкость) и заряд конденсатора. Поэтому удобно воспользоваться формулой (20.8)

Из этой формулы заключаем, что при увеличении расстояния между пластинами в 2 раза и увеличении заряда конденсатора в 2 раза его энергия возрастет в 8 раз (ответ 4).

Поскольку в задаче 20.2.6 конденсаторы соединены последовательно, емкость батареи конденсаторов можно найти по формуле (20.6), откуда находим емкость батареи конденсаторов (ответ 2).

В задаче 20.2.7 конденсаторы соединены параллельно, поэтому емкость батареи конденсаторов можно найти по формуле (20.7): (ответ 2).

Основной вопрос, на который нужно ответить в задаче 20.2.8, это как соединены конденсаторы? Последовательно, параллельно, по-другому? Попробуем по-другому расположить в пространстве и изменить длину соединительных проводов, чтобы схема стала более понятной. Очевидно, что можно соединить вершину 1 и вершину 3 («уменьшив» длину провода 1-3), а также вершины 2 и 4. При этом средний конденсатор разворачивается в пространстве, и схема приобретает вид, показанный на рисунке, откуда видно, что конденсаторы соединены параллельно. Поэтому (ответ 1).

Когда в заряженный плоский конденсатор вставляют металлическую пластинку (задача 20. 2.9), параллельную обкладкам конденсатора, напряженность электрического поля внутри пластинки становится равным нулю, вне пластинки между обкладками конденсатора остается таким же, каким оно было в отсутствие пластинки , где — заряд конденсатора, — площадь его пластин. Поэтому напряжение между обкладками конденсатора определяется соотношением:

где — расстояние между обкладками конденсатора, — толщина пластинки. Отсюда находим емкость рассматриваемого конденсатора

(ответ 4).

Чтобы найти емкость сферического конденсатора (задача 20.2.10) сообщим его обкладкам заряды и , найдем напряжение между обкладками, вычислим отношение заряда к напряжению. Разность потенциалов двух концентрических сфер, заряженных зарядами и (напряжение между обкладками сферического конденсатора), определена в задаче 19.2.5., откуда находим электрическую емкость сферического конденсатора (ответ 3):

Потенциал, работа электростатического поля.

Потенциальная энергия, разность потенциалов, принцип суперпозиции. Тесты, формулы

Тестирование онлайн

Работа электростатического поля

Рассмотрим ситуацию: заряд q₀ попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q₀ со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.

Потенциал

Система “заряд – электростатическое поле” или “заряд – заряд” обладает потенциальной энергией, подобно тому, как система “гравитационное поле – тело” обладает потенциальной энергией.

Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля.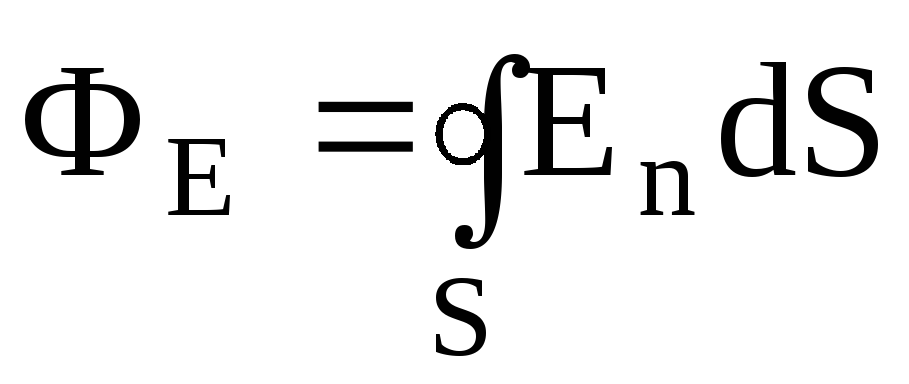 В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал – это характеристика электростатического поля.

Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.

Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.

В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело – наоборот.

Потенциальная энергия поля – это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.

Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.

Разность потенциалов

Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов

Эту формулу можно представить в ином виде

Эквипотенциальная поверхность (линия) – поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.

Напряжение

Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.

Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.

От величины напряжения зависит ток в цепи и энергия заряженной частицы.

Принцип суперпозиции

Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности

При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.

На рисунке изображены линии напряженности. В какой точке поля потенциал больше?

Верный ответ – точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.

Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком “минус”. Чем дальше от отрицательного заряда, тем потенциал поля больше.

Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными.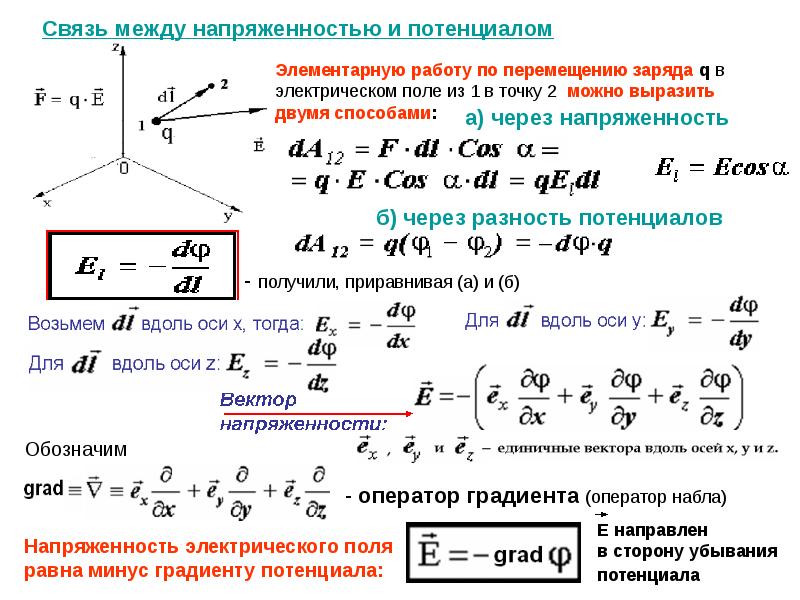 Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак “+”, работа имеет знак “-“.

Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.

Напряжение в клетках сетчатки глаза при попадания в них света около 0,01 В.
Напряжение в телефонных сетях может достигать 60 В.
Электрический угорь способен создавать напряжение до 650 В.

Из определения потенциала следует, что потенциальная энергия электростатического взаимодействия двух зарядов q₁ и q₂, находящихся на расстоянии r друг от друга, численно равна работе, которая совершается при перемещении точечного заряда q₂ из бесконечности в данную точку поля, созданного зарядом q₁

Аналогично Тогда энергия взаимодействия двух точечных зарядов

Энергия взаимодействия n зарядов

Формула заряда через напряжение

В данной статье мы подробно разберем что такое напряжение, как просто его представить и измерить.

Определение

Напряжение — это электродвижущая сила, которая толкает свободные электроны от одного атома к другому в том же направлении.

В первые дни электричества напряжение было известно как электродвижущая сила (ЭДС). Именно поэтому в уравнениях, таких как закон Ома, напряжение представлено символом Е.

Алессандро Вольта

Единицей электрического потенциала является вольт, названный в честь Алессандро Вольта, итальянского физика, жившего между 1745 и 1827 годами.

Алессандро Вольта был одним из пионеров динамического электричества. Исследуя основные свойства электричества, он изобрел первую батарею и углубил понимание электричества.

Представление напряжения

Легче всего понять напряжении, представив давлении в трубе. При более высоком напряжении (давлении) будет течь более сильный ток. Хотя важно понимать, что напряжение (давление) может существовать без тока (потока), но ток не может существовать без напряжения (давления).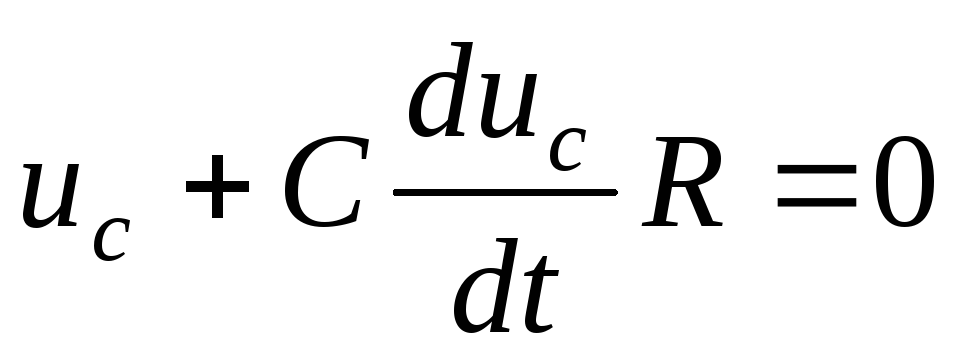

Напряжение часто называют разностью потенциалов, потому что между любыми двумя точками в цепи будет существовать разница в потенциальной энергии электронов. Когда электроны протекают через батарею, их потенциальная энергия увеличивается, но когда они протекают через лампочку, их потенциальная энергия будет уменьшаться, эта энергия покинет цепь в виде света и тепла.

Возьмите, например, обычную 1,5-вольтовую батарею AA, между двумя клеммами (+ и -) есть разность потенциалов 1,5 Вольт.

Напряжение или разность потенциалов — это просто измерение количества энергии (в джоулях) на единицу заряда (кулона). Например, в 1,5-вольтовой батарее AA каждый кулон (заряд) будет получать 1,5 вольт или джоулей энергии.

Напряжение = [Джоуль ÷ Кулон]

1 вольт = 1 джоуль на кулон

100 вольт = 100 джоулей на кулон

1 кулон = 6 200 000 000 000 000 000 электронов (6,2 × 10 18 )

В чем измеряется напряжение

Мы измеряем напряжение в единицах «Вольт», которые обычно обозначаются просто буквой «V» на чертежах и технической литературе.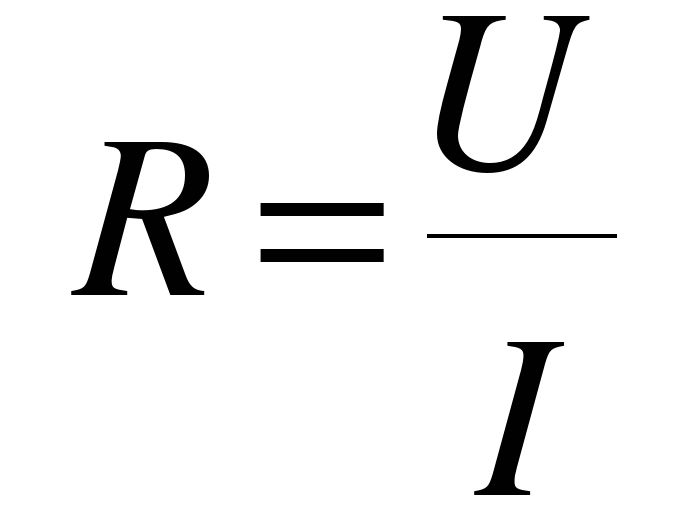 Часто необходимо количественно определить величину напряжения, это делается в соответствии с единицами СИ, наиболее распространенные величины напряжения, которые вы увидите:

• мегавольт (мВ)
• киловольт (кВ)
• вольт (В)
• милливольт (мВ)
• микровольт (мкВ)

Напряжение всегда измеряется в двух точках с помощью устройства, называемого вольтметром. Вольтметры являются либо цифровыми, либо аналоговыми, причем последний является наиболее точным. Вольтметры обычно встроены в портативные цифровые мультиметровые устройства, как показано ниже, они являются распространенным и часто важным инструментом для любого электрика или инженера-электрика. Обычно вы найдете аналоговые вольтметры на старых электрических панелях, таких как распределительные щиты и генераторы, но почти все новое оборудование будет поставляться с цифровыми счетчиками в качестве стандарта.

На электрических схемах вы увидите устройства вольтметра, обозначенные буквой V внутри круга, как показано ниже:

Расчет напряжения

В электрических цепях напряжение может быть рассчитано в соответствии с треугольником Ома. Чтобы найти напряжение (V), просто умножьте ток (I) на сопротивление (R).

Напряжение (V) = ток (I) * сопротивление (R)

V = I *R

Пример

Ток в цепи (I) = 10 А
Сопротивление цепи (R) = 2 Ом

Напряжение (V) = 10 А * 2 Ом

Ответ: V = 20В

Резюме

• Напряжение — это сила, которая перемещает электроны от одного атома к другому
• Напряжение также известно как разность потенциалов
• Напряжение измеряется в единицах «вольт» (В)
• Батареи увеличивают потенциальную энергию электронов
• Лампочки и другие нагрузки уменьшают потенциальную энергию электронов
• Напряжение измеряется с помощью вольтметра
• Напряжение цепи можно рассчитать путем умножения тока и сопротивления

Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ

Тема: как рассчитать величину напряжения зная ток, сопротивление, мощность.

Как известно у электрического напряжения должна быть своя мера, которая изначально соответствует той величине, что рассчитана для питания того или иного электротехнического устройства. Превышение или снижение величины этого напряжения питания негативно влияет на электрическую технику, вплоть до полного выхода ее из строя. А что такое напряжение? Это разность электрических потенциалов. То есть, если для простоты понимания его сравнить с водой, то это примерно будет соответствовать давлению. По научному электрическое напряжение — это физическая величина, показывающая, какую работу совершает на данном участке ток при перемещении по этому участку единичного заряда.

Наиболее распространенной формулой напряжения тока является та, в которой имеются три основные электрические величины, а именно это само напряжение, ток и сопротивление. Ну, а формула эта известна под названием закона Ома (нахождение электрического напряжения, разности потенциалов).

Звучит эта формула следующим образом — электрическое напряжение равно произведению силы тока на сопротивление. Напомню, в электротехнике для различных физических величин существуют свои единицы измерения. Единицей измерения напряжения является «Вольт» (в честь ученого Алессандро Вольта, который открыл это явление). Единица измерения силы тока — «Ампер», и сопротивления — «Ом». В итоге мы имеем — электрическое напряжение в 1 вольт будет равно 1 ампер умноженный на 1 ом.

Помимо этого второй наиболее используемой формулой напряжения тока является та, в которой это самое напряжение можно найти зная электрическую мощность и силу тока.

Звучит эта формула следующим образом — электрическое напряжение равно отношению мощности к силе тока (чтобы найти напряжение нужно мощность разделить на ток). Сама же мощность находится путем перемножения тока на напряжение. Ну, и чтобы найти силу тока нужно мощность разделить на напряжение. Все предельно просто. Единицей измерения электрической мощности является «Ватт». Следовательно 1 вольт будет равен 1 ватт деленный на 1 ампер.

Ну, а теперь приведу более научную формулу электрического напряжения, которая содержит в себе «работу» и «заряды».

В этой формуле показывается отношение совершаемой работы по перемещению электрического заряда. На практике же данная формула вам вряд ли понадобится. Наиболее встречаемой будет та, которая содержит в себе ток, сопротивление и мощность (то есть первые две формулы). Но, хочу предупредить, что она будет верна лишь для случая применения активных сопротивлений. То есть, когда расчеты производятся для электрической цепи, у которой имеется сопротивления в виде обычных резисторов, нагревателей (со спиралью нихрома), лампочек накаливания и так далее, то приведенная формула будет работать. В случае использования реактивного сопротивления (наличии в цепи индуктивности или емкости) нужна будет другая формула напряжения тока, которая учитывает также частоту напряжения, индуктивность, емкость.

Электротехника как область науки, занимающаяся использованием электроэнергии, в том числе ее получением, распределением и учетом, оперирует значениями тока, напряжения, мощности и сопротивления. Это основные величины. Кроме этого, имеется множество других характеристик и понятий, но в рамках данной статьи будут рассматриваться именно эти основополагающие понятия.

Электрический ток

Согласно определению, ток представляет собой упорядоченное движение заряженных частиц в среде. Такими частицами могут быть свободные электроны или ионы, частицы вещества, в которых число протонов в ядре не равно количеству электронов, то есть имеющие определенный заряд, положительный или отрицательный. Электроток может быть постоянный или переменный.

Электрическое напряжение

Электрическое напряжение – это разность потенциалов на противоположных участках цепи. Точное определение понятия подразумевает работу по переносу электрического заряда между участками цепи.

Сопротивление

Любой проводник в цепи препятствует прохождению через себя тока. Данная характеристика определяет такую физическую величину, как сопротивление. Исходя из величины сопротивления, все вещества относят к проводникам или изоляторам. Точная граница весьма расплывчата, поэтому при некоторых условиях некоторые вещества можно отнести как к изоляторам, так и к проводникам. Участок электросхемы может иметь элемент с определенным значением величины, который именуется резистор.

Мощность

Скорость преобразования, передачи и потребления электрической энергии определяется мощностью.

Взаимосвязь параметров электрической цепи

Все параметры любой электрической цепи строго взаимосвязаны, поэтому в любой момент времени можно точно определить величину любого из них, зная остальные.

К сведению. Основополагающий закон, по которому производится большинство расчетов, – закон Ома, согласно которому сила тока обратно пропорциональна его сопротивлению и прямо пропорциональна приложенной разности потенциалов.

Формула напряжения тока закона Ома выглядит следующим образом:

Так, цепь с большим напряжением пропускает больший ток, а при одинаковом напряжении ампераж будет больше там, где меньше сопротивление.

Принятые обозначения в формуле расчета напряжения и тока понятны во всем мире:

• I – сила тока;
• U – напряжение;
• R – сопротивление.

Путем простейшего математического преобразования находится формула расчета сопротивления через силу тока и напряжение.

Кроме закона Ома, используется формула расчета мощности:

Символом P здесь обозначена мощность тока.

Любая схема может содержать участки, где имеется последовательное соединение, или есть элемент, подключенный параллельно. Расчеты при этом усложняются, но базовые формулы остаются одинаковыми.

Единицы измерения в формуле

Невозможно выполнять расчеты или измерения, не зная, какими величинами оперировать. Общепринятые обозначения, согласно международной системе измерения СИ:

• Напряжение – Вольт. Обозначается символом В или V в англоязычной литературе;
• Сила тока – Ампер. Обозначается символом А;
• Электрическое сопротивление – Ом. Используется обозначение Ом или Ohm;
• Электрическая мощность – Ватт. Обозначается как Вт или W.

Как работает закон в реальной жизни

Используя совместно формулу расчета мощности и закон Ома, можно производить вычисления, не зная одной из величин. Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.

Сила тока формула через мощность:

Сопротивление:

Такой же результат можно найти из мощности, не прибегая к промежуточным расчетам:

Аналогично можно вычислить любую величину, зная только две из них. Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.

Внимательно посмотрев на формулы, можно заметить, что, если уменьшить напряжение на лампе в два раза, ожидаемая мощность не снизится аналогично в два раза, а в четыре, согласно формуле:

Это довольно распространенная ошибка среди далеких от электротехники людей, которые неправильно соотносят мощность и напряжение, а также их действие на остальные параметры.

Кстати. Сила тока, найденная через сопротивление и напряжение, справедлива как для постоянного, так и для переменного тока, если в ней не используются такие элементы, как конденсатор или индуктивность.

Облегчить расчеты можно, используя онлайн калькулятор.

Пример с обычной водой

Существуют вещества, которые можно отнести одновременно к проводникам и изоляторам. Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.

Для наглядности можно взять дистиллированную воду для приготовления электролита для автомобильных аккумуляторных батарей. Опустив щупы омметра в воду, можно увидеть, что его показания велики. Добавление всего нескольких кристаллов поваренной соли через некоторое время вызывает резкое уменьшение сопротивления, которое будет тем меньше, чем больше соли перейдет в раствор.

По какой формуле определяется напряжение

Использование той или иной формулы напряжения электрического тока для вычисления зависит от того, какие величины известны:

• Ток и сопротивление – U=I∙R;
• Ток и мощность – U=P/I;
• Мощность и сопротивление – U=√P∙R

Различные используемые величины

Кроме основных величин: вольт, ампер, ом, ватт, используют кратные, большие или меньшие. Для обозначений применяют соответствующие приставки:

• Кило – 1000;
• Мега – 1000000;
• Гига – 1000000000;
• Милли – 0.001.

Таким образом, получается:

• Киловольт (кВ) – тысяча вольт;
• Мегаватт (Мвт) – миллион ватт;
• Миллиом (мОм) – одна тысячная Ом;
• Гигаватт (ГВт) – тысяча мегаватт или миллиард ватт.

Как найти напряжение

Формула нахождения напряжения как разности потенциалов в электрическом поле:

U=ϕA-ϕB, где ϕAи ϕB – потенциалы в точках А и В, соответственно.

Также можно записать напряжение как работу по переносу единицы заряда из точки А в точку В в электрическом поле:

U=A/q, где q – величина заряда.

Работа тем больше, чем выше напряженность электрического поля Е, то есть сила, действующая на неподвижный заряд.

Потенциальную энергию заряда в электростатическом поле называют электростатический потенциал.

Гидравлическая аналогия

Чтобы легче усвоить законы электрических цепей, можно представить себе аналогию с гидравлической системой, в которой соединение насоса и трубопроводов образует замкнутую систему. Для этого нужны следующие соответствия:

• Источник питания – насос;
• Проводники – трубы;
• Электроток – движение воды.

Без особых усилий становится понятнее, что чем меньше диаметр труб, тем медленнее по ним движется вода. Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.

Измерительные приборы

Для измерения параметров электрических цепей служат измерительные приборы:

Наиболее часто используется класс комбинированных устройств, в которых переключателем выбирается измеряемая величина – ампервольтомметры или авометры.

Типичные напряжения

Для стандартизации и возможности использования различного оборудования в быту и технике применяются электрические сети со стандартными значениями:

• Бытовая сеть –220В;
• Бортовая сеть автомобиля – 12 или 24В;
• Батареи и аккумуляторы – 1.5, 3 или 9В.

Потенциал Гальвани

В электрохимии используется понятие потенциала Гальвани, который означает разность потенциала между различными фазами вещества, например, между электродом и электролитом, между электродами из разнородных металлов.

Видео

чему равно напряжение, как найти сопротивление нагрузки

В наши дни электричество играет в жизни человека очень большую роль, в следствие чего базовые знания в области физики и электротехники нужны практически каждому. Напряжение является одной из главных физических величин, которая позволяет объяснить теорию возникновения электрического поля и методы подбора оптимального сечения кабеля для применения его в повседневной жизни.

Что такое напряжение в сети электричества.

Напряжение – это физическая величина, которая характеризует электрическое поле. Иными словами, оно показывает, какую работу оно совершает при перемещении одного положительного заряда на определённое расстояние.

Показатель напряжения на вольтметре

За единицу напряжения в международной системе принимается такой показатель на концах проводника, при котором заряд в 1 Кл совершает работу в 1 Дж для перемещения его по этому проводнику. Общепринятой единицей измерения напряжения считается 1 В – Вольт.

Важно! Работа измеряется в Джоулях, заряды в Кулонах, а напряжение в Вольтах, следовательно, 1 Вольт равняется 1 Джоулю, деленному на 1 Кулон.

Чему равно напряжение.

Напряжение напрямую связано с работой тока, зарядом и сопротивлением. Чтобы измерить напряжение непосредственно в электрической цепи, к ней нужно подключить вольтметр. Он присоединяется к цепи параллельно, в отличие от амперметра, который подключается последовательно. Зажимы измерительного прибора крепятся к тем точкам, между которыми нужно вычислить напряжение. Чтобы он правильно показал значение, нужно включить цепь. На схемах вольтметр обозначается буквой V, обведенной в кружок.

Изображение вольтметра и электрической цепи

Напряжение обозначается латинской [U], а измеряется в [В]. Оно равно работе, которое совершает поле при перемещении единичного заряда. Формула напряжения тока – это U = A/q, где A – работа тока, q – заряд, а U – само напряжение.

Обратите внимание! В отличие от магнитного поля, где заряды неподвижны, в электрическом поле они находятся в постоянном движении.

Электрическое поле

Формула закона Ома

Свои опыты Ом направлял на изучение такой физической величины, как сопротивление, в результате чего в 1826 году он стал автором закона, который не потерял совей актуальность вплоть до сегодняшнего дня. Из своих опытов Ом вывел, что в различных цепях сила тока может возрастать с различной скоростью, и происходит это по мере увеличения напряжения.

Также, Ом сделал вывод, что каждый проводник обладает индивидуальными свойствами проводимости.

Сопротивление обозначается заглавной латинской [R] и измеряется в Омах. Сопротивление – физическая величина, характеризующая свойства проводника оказывать влияние на идущий по нему ток. Оно прямо пропорционально напряжению  в сети и обратно пропорционально  силе тока. В виде формулы данный закон можно записать как R = U/I, где U – напряжение, а I – сила тока. 1 Ом равняется 1 Вольту, деленному на 1 Ампер.

Запомните! Реостат – прибор, обеспечивающий возможность изменять сопротивление. Прежде всего, он влияет на показатель R в цепи, а, следовательно, на 2 другие величины, описанные в законе Ома. Силу тока может помочь определить амперметр.

Ползунковый реостат

Из формулы закона Ома можно вывести практически любую зависимость, связанную с электричеством. Также, существует понятие удельного сопротивления проводника – физической величины, которая демонстрирует, каким сопротивлением будет обладать проводник из определенного вещества. Обозначается эта величина буквой ρ и через неё можно также найти сопротивление в цепи как произведению удельного сопротивления и длины проводника, деленного на площадь его поперечного сечения.

Важно! В виде формулы нахождение сопротивления через удельное сопротивление выглядит так: R = ρ*(l/S), где l – длина проводника, а S – площадь поперечного сечения.

Физический смысл удельного сопротивления показывает, какое влияние будет оказывать проводник длиной в 1 м с площадью поперечного сечения в 1 квадратный мм, изготовленный из определенного вещества. Измеряется в Омах, умноженных на метр: [ρ] = [Ом*м].

Ом и формула

Как найти сопротивление нагрузки

Сопротивление нагрузки обозначается латинскими буквами Rn или Rн. По сути, это является тем же сопротивлением участка цепи и вычисляется также по формулам закона Ома. Нагрузка обозначается символами, которые на электрической схеме изображаются в виде крестиков в кружке – лампочкой; то есть двигатель, лампа, конкретный прибор и т. д.

Каждая нагрузка имеет своё собственное сопротивление. Например, если к сети подключена одна лампочка, то сопротивление нагрузки – показатель этого единственного прибора в цепи. Если к цепи подключено несколько нагрузок, то сопротивление считается суммарно для каждой из них.

Сопротивление нагрузки вычисляется в соответствии с законом Ома, то есть Rn = U/I. Если к сети подключено несколько нагрузок, то оно будет рассчитываться следующим образом: сначала находится сопротивление каждой отдельной «лампочки». Далее Rn вычисляется в зависимости от того, какой тип подключения в цепи: последовательное или параллельное. При параллельном 1/R = 1/R1 + 1/R2 + 1/Rn, где n –количество подключенных приборов. Если же соединение последовательное, общее R равно сумме всех R цепи.

Последовательное/параллельное соединения

Как найти с помощью формулы напряжение

Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.

Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно.

Измерение напряжения

По каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми. Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.

Важно! Определить напряжение можно и через мощность электрического тока. Мощность [P] равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t. Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.

Как найти силу тока через сопротивление и напряжение

Сила тока обозначается латинскими [I] или [Y], и она зависит от количества заряда, перенесенного от одного полюса к другому за определенный промежуток времени, т.е. I = q/t. Измеряется сила тока в амперах, а узнать её значение в цепи можно при помощи амперметра.

Мужчина считает силу тока

Существуют формулы определения силы тока через напряжение и сопротивление. В первом случае произведение силы тока на время равняется работе, деленной на напряжение: I*t = A/U, во втором – по закону Ома, I = U/R. Через мощность сила будет равняться P/U.

При последовательном соединении, сила тока одинакова на всех участках цепи, следовательно, равна общему значению в цепи. В противоположном случае сила электрического тока равняется сумме силы тока всех нагрузок.

Таким образом, существует огромное множество формул для нахождения силы тока, напряжения и сопротивления. Они всегда могут пригодиться для теории, а на практике всегда помогут специальные приборы – амперметр и вольтметр.

Максимальный заряд конденсатора формула. Принцип работы конденсатора

Вам понадобится

• – знание емкости или геометрических и физических параметров конденсатора;
• – знание энергии или заряда на конденсаторе.

Инструкция

Найдите напряжение между пластинами конденсатора, если известна текущая величина накопленной им энергии, а также его емкость. Энергия, запасенная конденсатором, может быть вычислена по формуле W=(C∙U²)/2, где C – емкость, а U – напряжение между пластинами. Таким образом, значение напряжения может быть получено как корень из удвоенного значения энергии, деленного на емкость. То есть, оно будет равно: U=√(2∙W/C).

Энергия, запасенная конденсатором, также может быть вычислена на основании значения содержащегося в нем заряда (количества ) и напряжения между обкладками. Формула, задающая соответствие между этими параметрами, имеет вид: W=q∙U/2 (где q – заряд). Следовательно, зная энергию и , можно вычислить напряжение между его пластинами по формуле: U=2∙W/q.

Поскольку заряд на конденсаторе пропорционален как приложенному к его пластинам напряжению, так и емкости устройства (он определяется формулой q=C∙U), то, зная заряд и емкость, можно найти и напряжение. Соответственно, для проведения расчета используйте формулу: U=q/C.

Для получения значения напряжения на конденсаторе с известными геометрическими и параметрами, сначала рассчитайте его емкость.-12 Ф/м), ε – относительная диэлектрическая проницаемость пространства между пластинами (ее можно узнать из физических справочников). Вычислив емкость, рассчитайте напряжение одним из методов, приведенных в шагах 1-3.

Обратите внимание

Для получения корректных результатов при вычислении напряжений между обкладками конденсаторов, перед проведением расчетов приводите значения всех параметров в систему СИ.

Для того чтобы знать, можно ли использовать в том или ином месте схемы конденсатор, следует определить его . Способ нахождения этого параметра зависит от того, каким образом он обозначен на конденсаторе и обозначен ли вообще.

Вам понадобится

• Измеритель емкости

Инструкция

На крупных конденсаторах емкость обычно обозначена открытым текстом: 0,25 мкФ или 15 uF. В этом случае, способ ее определения тривиален.

На менее крупных конденсаторах (в том , SMD) емкость двумя или тремя цифрами. В первом случае, она обозначена в пикофарадах. Во втором случае, первые две цифры емкость , а третья – в каких единицах она выражена:1 – десятки пикофарад;
2 – сотни пикофарад;
3 – нанофарады;
4 – десятки нанофарад;
5 – доли микрофарады.

Существует также система обозначения емкости, использующая сочетания латинских букв и цифр. Буквы обозначают следующие цифры:A – 10;
B – 11;
C – 12;
D – 13;
E – 15;
F – 16;
G – 18;
H – 20;
J – 22;
K – 24;
L – 27;
M – 30;
N – 33;
P – 36;
Q – 39;
R – 43;
S – 47;
T – 51;
U – 56;
V – 62;
W – 68;
X – 75;
Y – 82;
Z – 91.Полученное число следует умножить на число 10, предварительно возведенное в степень, равную цифре, следующей после . Результат будет выражен в пикофарадах.

Встречаются конденсаторы, емкость на которых не обозначена вообще. Вы наверняка встречали их, в , в стартерах ламп дневного . В этом случае, измерить емкость можно только специальным прибором. Они цифровыми и мостовыми.В любом случае, если конденсатор впаян в то или иное устройство, его следует обесточить, разрядить в нем конденсаторы фильтра и сам конденсатор, емкость которого следует измерить, и лишь после этого выпаять его. Затем его необходимо подключить к прибору.На цифровом измерителе сначала выбирают самый грубый предел, затем переключают его до тех пор, пока он не покажет перегрузку. После этого переключатель переводят на один предел назад и читают показания, а по положению переключателя определяют, в каких единицах они выражены.На мостовом измерителе, последовательно переключая , на каждом из них прокручивают регулятор из одного конца шкалы в другой, пока звук из динамика не исчезнет. Добившись исчезновения , по шкале регулятора считывают результат, а единицы, в которых он выражен, также определяют по положению переключателя.Затем конденсатор устанавливают обратно в устройство.

Обратите внимание

Никогда не подключайте к измерителю заряженные конденсаторы.

Источники:

• Справочник по системам обозначения емкости

Найти значение электрического заряда можно двумя способами. Первый – измерить силу взаимодействия неизвестного заряда с известным и с помощью закона Кулона рассчитать его значение. Второй – внести заряд в известное электрическое поле и измерить силу, с которой оно действует на него. Для измерения заряда протекающего через поперечное сечение проводника за определенное время измерьте силу тока и умножьте ее на значение времени.

Вам понадобится

• чувствительный динамометр, секундомер, амперметр, измеритель электростатического поля, воздушный конденсатор.

Инструкция

Измерение заряда при его с известным зарядомЕсли известен одного тела, поднесите к нему неизвестный заряд и измерьте между ними в метрах. Заряды начнут взаимодействовать. С помощью динамометра измерьте силу их взаимодействия. Рассчитайте значение неизвестного заряда – для этого квадрат измеренного расстояния умножьте на значение силы и поделите на известный заряд.9)). Если заряды отталкиваются, то они одноименные, если же притягиваются – разноименные.

Измерение значения заряда , внесенного в электрическое полеИзмерьте значение постоянного электрического поля специальным прибором (измеритель электрического поля). Если такого прибора нет, возьмите воздушный конденсатор, зарядите его, измерьте напряжение на его обкладках и поделите не расстояние между пластинами – это и будет значение электрического поля внутри конденсатора в вольтах на метр. Внесите в поле неизвестный заряд. С помощью чувствительного динамометра измерьте силу, которая на него действует. Измерение проводите в . Поделите значение силы на напряженность электрического поля. Результатом будет значение заряда в Кулонах (q=F/Е).

Измерение заряда , протекающего через поперечное проводникаСоберите электрическую цепь с проводниками и последовательно подключите к ней амперметр. Замкните ее на источник тока и измерьте силу тока с помощью амперметра в амперах. Одновременно секундомером засеките , в которого в цепи был электрический ток. Умножив значение силы тока на полученное время, узнайте заряд, через поперечное сечение каждого за это время (q=I t). При измерениях следите, чтобы проводники не перегревались и не произошло короткое замыкание.

Конденсатором называется устройство, способное накапливать электрические заряды. Количество накапливаемой электрической энергии в конденсаторе характеризуется его емкостью . Она измеряется в фарадах. Считается, что емкость в один фарад соответствует конденсатору, заряженному электрическим зарядом в один кулон при разности потенциалов на его обкладках в один вольт.

Инструкция

Определите емкость плоского конденсатора по формуле С = S e e0/d, где S – площадь поверхности одной пластины, d – между пластинами, e – относительная диэлектрическая проницаемость , заполняющей пространство между пластинами (в вакууме она равна ), e0 – электрическая постоянная, равная 8,854187817 10(-12) Ф/м.Исходя из приведенной формулы, величина емкости будет зависеть от площади проводников, между ними и от материала диэлектрика. В качестве диэлектрика может применяться или слюда.

Вычислите емкость сферического конденсатора по формуле С = (4П e0 R²)/d, где П – число «пи», R – радиус сферы, d – величина зазора между его сферами.Величина емкости сферического конденсатора прямо пропорциональна концентрической сферы и обратно пропорциональна расстоянию между сферами.

Рассчитайте емкость цилиндрического конденсатора по формуле С = (2П e e0 L R1)/(R2-R1), где L – длина конденсатора , П – число «пи», R1 и R2 – радиусы его цилиндрических обкладок.

Если конденсаторы в цепи соединены параллельно, рассчитайте их общую емкость по формуле С = С1+С2+…+Сn, где С1, С2,…Сn – емкости параллельно соединенных конденсаторов.

Вычислите общую емкость последовательно соединенных конденсаторов по формуле 1/С = 1/С1+1/С2+…+1/Сn, где С1, С2,…Сn – емкости последовательно соединенных конденсаторов.

Обратите внимание

На любом конденсаторе обязательно должна быть нанесена маркировка, которая может быть буквенно-цифровая или цветовая. Маркировка отражает его параметры.

Источники:

• Цветовая маркировка резисторов, конденсаторов и индуктивностей

Емкость – величина, в системе СИ выражаемая в фарадах. Хотя используются, фактически, лишь производные от нее – микрофарады, пикофарады и так далее. Что касается электроемкости плоского конденсатора, она зависит от зазора меж обкладок и их площади, от вида диэлектрика, в данном зазоре расположенного.

Инструкция

В том случае, если обкладки конденсатора имеют одинаковую площадь и имеют расположение строго одна над другой, рассчитайте площадь одной из обкладок – любой. Если же одна из них относительно другой смещена либо они разные , нужно рассчитывать площадь области, в которой обкладки друг дружку перекрывают.

При этом используются общепринятые формулы, рассчитывать площади таких геометрических фигур, как круг (S=π(R^2)), прямоугольника (S=ab), его частного случая – квадрата (S=a^2) – и других.(-12) Ф/м и является, по сути, диэлектрической проницаемостью вакуума.

Темы кодификатора ЕГЭ : электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом – диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах – конденсаторах .

Но прежде введём понятие электрической ёмкости .

Ёмкость уединённого проводника

Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым .

Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду . Коэффициент пропорциональности принято обозначать , так что

Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:

(1)

Например, потенциал уединённого шара в вакууме равен:

где – заряд шара, – его радиус. Отсюда ёмкость шара:

(2)

Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:

Соответственно, ёмкость шара в раз увеличивается:

(3)

Увеличение ёмкости при наличии диэлектрика – важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.

Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.

В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В . Чем больше ёмкость – тем, соответственно, больший заряд требуется поместить для этого на проводник.

Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.

Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.

МкФ.

Как видите, Ф – это очень большая ёмкость.

Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2) :

Следовательно, диэлектрическая постоянная может измеряться в Ф/м:

Так легче запомнить, не правда ли?

Ёмкость плоского конденсатора

Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.

Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости – но на сей раз о ёмкости этой системы проводников.

Наиболее простым и важным примером такой системы является плоский конденсатор . Он состоит из двух параллельных металлических пластин (называемых обкладками ), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.

Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух

Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина – заряд положительной обкладки – называется зарядом конденсатора .

Пусть – площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.

Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:

Здесь – напряжённость поля положительной обкладки, – напряженность поля отрицательной обкладки, – поверхностная плотность зарядов на обкладке:

На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора

Согласно принципу суперпозиции, для результирующего поля имеем:

Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):

Внутри конденсатора поле удваивается:

(4)

Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:

Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4) . Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.

Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты : поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.

Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):

(5)

Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:

(6)

Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6) , таким образом, является модификацией формулы (1) для случая системы двух проводников – конденсатора.

Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора :

(7)

Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?

Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:

(8)

Соответственно, напряжение на конденсаторе:

(9)

Отсюда ёмкость плоского конденсатора с диэлектриком :

(10)

Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.

Важное следствие формулы (10) : заполнение конденсатора диэлектриком увеличивает его ёмкость .

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.

Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора – ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.

Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.

Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .

Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

где – напряжённость поля первой обкладки:

Следовательно,

Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).

Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил , с которыми притягиваются к первой обкладке всевозможные маленькие заряды второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все и дадут . В результате получим:

(11)

Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины . Сила притяжения пластин совершает при этом работу:

Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины alt=”(d_2 > d_1)”> , то работа силы притяжения получается отрицательной, как и должно быть.

С учётом формул (11) и (7) имеем:

Это можно переписать следующим образом:

(12)

Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что – потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора .

Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):

(13)

(14)

Особенно полезными являются формулы (12) и (14) .

Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:

При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) – (14) останутся неизменными . Ёмкость конденсатора в них теперь будет выражаться по формуле (10) .

Итак, формулы (12) – (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

Энергия электрического поля

Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.

Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:

Но – объём конденсатора. Получаем:

(15)

Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме .

Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет – это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.

Величина – энергия единицы объёма поля – называется объёмной плотностью энергии . Из формулы (15) получим:

(16)

В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.

Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:

(17)

(18)

Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.

Одними из наиболее часто используемых электронных компонентов являются конденсаторы . И в этой статье нам предстоит разобраться, из чего они состоят, как работают и для чего применяются 🙂

Давайте, в первую очередь, рассмотрим устройство конденсаторов , а затем уже плавно перейдем к их основным видам и характеристикам, а также к процессам зарядки/разрядки. Как видите, нам сегодня предстоит изучить много интересных моментов 😉

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:

Такое устройство называется плоским конденсатором , а пластины – обкладками конденсатора . Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле, изображенное стрелками на нашей схеме. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит 🙂

Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

Каждая из обкладок конденсатора в отдельности создает электрическое поле:

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

Здесь – это поверхностная плотность заряда: . А – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:

Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:

А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0 🙂

Процессы зарядки и разрядки конденсаторов.

С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?

Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника, в связи с чем на обкладке возникнет недостаток отрицательно заряженных частиц и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора, в результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную . Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока, после этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать ток разряда конденсатора , а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.

Как видите, здесь нет ничего сложного 🙂

Емкость и энергия конденсатора.

Важнейшей характеристикой является электрическая емкость конденсатора – физическая величина, которая определяется как отношение заряда конденсатора одного из проводников к разности потенциалов между проводниками:

Емкость изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость конденсаторов измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ).

А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:

Здесь у нас – это расстояние между пластинами конденсатора, а – заряд конденсатора. Подставим эту формулу в выражение для емкости конденсатора:

Если в качестве диэлектрика у нас выступает воздух, то во всех формулах можно подставить

Для запасенной энергии конденсатора справедливы следующие выражения:

Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение – то есть величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.

В общем, мы рассмотрели сегодня основные свойства конденсаторов, их устройство и характеристики, так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений конденсаторов, так что заходите на наш сайт снова!

Как и любая система заряжен-ных тел, конденсатор обладает энер-гией. Вычислить энергию заряжен-ного плоского конденсатора с одно-родным полем внутри него не-сложно.

Энергия заряженного конденса-тора.

Для того чтобы зарядить конденсатор, нужно совершить рабо-ту по разделению положительных и отрицательных зарядов. Согласно закону сохранения энергии эта ра-бота равна энергии конденсатора. В том, что заряженный конденсатор обладает энергией, можно убедиться, если разрядить его через цепь, со-держащую лампу накаливания, рас-считанную на напряжение в не-сколько вольт (рис. 4). При раз-рядке конденсатора лампа вспыхи-вает. Энергия конденсатора пре-вращается в другие формы: тепло-вую, световую.

Выведем формулу для энергии плоского конденсатора .

Напряженность поля, созданного зарядом одной из пластин, равна Е/2, где Е — напряженность поля в конденсаторе. В однородном поле одной пластины находится заряд q, распределенный по поверхности дру-гой пластины (рис. 5). Согласно формуле W p = qEd. для потенциальной энергии заряда в однородном поле энергия конденсатора равна:

Можно доказать, что эти форму-лы справедливы для энергии любого конденсатора, а не только для плос-кого.

Энергия электрического поля.

Согласно теории близкодействия вся энергия взаимодействия заряженных тел сконцентрирована в электриче-ском поле этих тел. Значит, энергия может быть выражена через основную характеристику поля — напря-женность.

Так как напряженность электри-ческого поля прямо пропорциональ-на разности потенциалов

(U = Ed), то согласно формуле

энергия конденсатора прямо пропор-циональна напряженности электри-ческого поля внутри него: W p ~ E 2 . Детальный расчет дает следующее значение для энергии поля, приходя-щейся на единицу объема, т.е. для плотности энергии:

где ε 0 — электрическая постоянная

Применение конденсаторов.

Энер-гия конденсатора обычно не очень велика — не более сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому заряженные конденсаторы не могут заменить, например, акку-муляторы в качестве источников электрической энергии.

Но это совсем не означает, что конденсаторы как накопители энергии не получили практического при-менения. Они имеют одно важное свойство: конденсаторы могут на-капливать энергию более или менее длительное время, а при разрядке через цепь малого сопротивления они отдают энергию почти мгновенно. Именно это свойство используют широко на практике.

Лампа-вспышка, применяемая в фотографии, питается электрическим током разряда конденсатора, заря-жаемого предварительно специаль-ной батареей. Возбуждение кванто-вых источников света — лазеров осу-ществляется с помощью газораз-рядной трубки, вспышка которой происходит при разрядке батареи конденсаторов большой электроем-кости.

Однако основное применение кон-денсаторы находят в радиотехнике. С этим вы познакомитесь в XI классе.

Энергия конденсатора пропор-циональна его электроемкости и квадрату напряжения между плас-тинами. Вся эта энергия сосредото-чена в электрическом поле. Плот-ность энергии поля пропорциональна квадрату напряженности поля.

Рис. 1 Рис. 2

ЗАКОНЫ ПОСТОЯННОГО ТОКА.

Неподвижные электрические заряды редко используются на практике. Для того чтобы заставить электрические заряды слу-жить нам, их нужно привести в движение — создать электрический ток. Электрический ток освещает квартиры, приводит в дви-жение станки, создает радиоволны, циркулирует во всех электрон-но-вычислительных машинах.

Мы начнем с наиболее простого случая движения заряжен-ных частиц — рассмотрим постоянный электрический ток.

ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА

Дадим строгое определение тому, что называют электрическим током.

Напомним, какой величиной ха-рактеризуется ток количественно.

Найдем, как быстро движутся электроны по проводам в вашей квартире.

При движении заряженных час-тиц в проводнике происходит перенос электрического заряда с одного места в другое. Однако если заряженные частицы совершают беспорядочное тепловое движение, как, например, свободные электроны в металле, то переноса заряда не про-исходит (рис.1). Электриче-ский заряд перемещается через по-перечное сечение проводника лишь в том случае, если наряду с беспорядочным движением электроны участвуют в упорядоченном движении (рис. 2). В этом случае говорят, что в проводнике устанавливается электрический ток.

Из курса физики VIII класса вы знаете, что электрическим током называют упорядоченное (направ-ленное) движение заряженных частиц.

Электрический ток возникает при упорядоченном перемещении свобод-ных электронов или ионов.

Если перемещать нейтральное в целом тело, то, несмотря на упо-рядоченное движение огромного чис-ла электронов, и атомных ядер, электрический ток не возникает. Полный заряд, переносимый через любое сечение проводника, будет при этом равным нулю, так как заряды разных знаков с одинаковой средней скоростью.

Электрический ток имеет определенное направление. За направление тока принимают направление движения положительно заряженных частиц. Если ток образован движением отрицательно заряженных частиц, то направление тока считают противоположным направлению дви-жения частиц.

Действия тока. Движение частиц в проводнике мы непосредственно не видим. О наличии электрического тока приходится судить по тем дей-ствиям или явлениям, которые его сопровождают.

Во-первых, проводник, по которо-му течет ток, нагревается.

Во-вторых, электрический ток мо-жет изменять химический состав проводника, например, выделять его химические составные части (медь из раствора медного купороса и т.д.).

В-третьих, ток оказывает силовое воздействие на соседние токи и на-магниченные тела. Это действие то-ка называется магнитным. Так, маг-нитная стрелка вблизи проводника с током поворачивается. Магнитное действие тока в отличие от химиче-ского и теплового является основ-ным, так как проявляется у всех без исключения проводников. Хими-ческое действие тока наблюдается лишь у растворов и расплавов электролитов, а нагревание отсут-ствует у сверхпроводников.

Сила тока.

Если в цепи уста-навливается электрический ток, то это означает, что через поперечное сечение проводника все время пере-носится электрический заряд. Заряд, перенесенный в единицу времени, служит основной количественной ха-рактеристикой тока, называемой си-лой тока.

Таким образом, сила тока равна отношению заряда q, переносимого через поперечное сечение провод-ника за интервал времени t, к этому интервалу времени. Если сила тока со временем не меняется, то ток на-зывают постоянным.

Сила тока, подобно заряду, — ве-личина скалярная. Она может быть как положительной, так и отрица-тельной. Знак силы тока зависит от того, какое из направлений вдоль проводника принять за положитель-ное. Сила тока / > 0, если направ-ление тока совпадает с условно вы-бранным положительным направле-нием вдоль проводника. В против-ном случае /

Сила тока зависит от заряда, переносимого каждой частицей, кон-центрации частиц, скорости их направленного движения и площади поперечного сечения проводника. По-кажем это.

Пусть проводник (рис. 3) имеет поперечное сечение площадью S. За положительное направление в проводнике примем направление сле-ва направо. Заряд каждой частицы равен q 0 . В объеме проводника, ограниченном поперечными сечениям-и 1 и 2, содержится nSl частиц, где п — концентрация частиц. Их общий заряд q = q Q nSl. Если частицы движутся слева направо со средней скоростью υ, то за время

Все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение 2. Поэтому сила тока равна:

формуле (2) где е — модуль заряда электрона.

Пусть, например, сила тока I = 1 А, а площадь по-перечного сечения проводника S = 10 -6 м 2 . Модуль заряда электрона е = 1,6 – 10 -19 Кл. Число электронов в 1 м 3 меди равно числу атомов в этом объеме, так как один из ва-лентных электронов каждого атома меди коллективизирован и является свободным. Это число есть п = 8,5 · 10 28 м -3 Следовательно,

Рис №1. Рис №2 Рис №3

УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА

Что необходимо для создания электрического тока? Подумайте над этим сами и только потом прочтите этот параграф.

Для возникновения и существо-вания постоянного электрического тока в веществе необходимо, во-первых, наличие свободных заряжен-ных частиц. Если положительные и отрицательные заряды связаны друг с другом в атомах или молекулах , то их перемещение не приведет к по-явлению электрического тока.

Наличия свободных зарядов еще недостаточно для возникновения то-ка. Для создания и поддержания упорядоченного движения, заряжен-ных частиц необходима, во-вторых, сила, действующая на них в опре-деленном направлении. Если эта сила перестанет действовать, то упорядоченное движение заряженных частиц прекратится из-за сопротив-ления, оказываемого их движению ионами кристаллической решетки металлов или нейтральными молеку-лами электролитов .

На заряженные частицы, как мы знаем, действует электрическое поле с силой . Обычно именно электрическое поле внутри провод-ника служит причиной, вызываю-щей и поддерживающей упорядочен-ное движение заряженных частиц. Только в статическом случае, когда заряды покоятся, электрическое поле внутри проводника равно нулю.

Если внутри проводника имеется электрическое поле, то между конца-ми проводника в соответствии с фор-мулой существует разность потенциалов. Когда разность потен-циалов не меняется во времени, то в проводнике устанавливается по-стоянный электрический ток. Вдоль проводника потенциал уменьшается от максимального значения на одном конце проводника до минималь-ного — на другом. Это уменьшение потенциала можно обнаружить на простом опыте.

Возьмем в качестве проводника не очень сухую деревянную палку и подвесим ее горизонтально. (Такая палка хотя и плохо, но все же про-водит ток.) Источником напряжения пусть будет электростатическая ма-шина, Для регистрации потенциала различных участков проводника от-носительно земли можно использо-вать листочки металлической фоль-ги, прикрепленные к палке. Один полюс машины соединим с землей, а второй — с одним концом проводни-ка (палки). Цепь окажется незамк-нутой. При вращении рукоятки ма-шины мы обнаружим, что все лис-точки отклоняются на один и тот же угол (рис. 1).

Значит, потен-циал всех точек проводника отно-сительно земли одинаков. Так и должно быть при равновесии заря-дов на проводнике. Если теперь дру-гой конец палки заземлить, то при вращении рукоятки машины карти-на изменится. (Так как земля — проводник, то заземление провод-ника делает цепь замкнутой.) У за-земленного конца листочки вообще не разойдутся: потенциал этого кон-ца проводника практически равен потенциалу земли (падение потен-циала в металлической проволоке мало). Максимальный угол расхож-дения листочков будет у конца про-водника, присоединенного к машине (рис. 2). Уменьшение угла рас-хождения листочков по мере удале-ния от машины свидетельствует о падении потенциала вдоль провод-ника.

Электрический ток может быть получен только в веществе, в котором имеются свободные заряженные частицы. Чтобы они пришли в движение, нужно создать в проводнике электрическое поле.

Рис №1 Рис №2

ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ

В VIII классе изучался закон Ома . Этот закон прост, однако столь важен, что его необходимо повторить.

Вольт – амперная характеристика.

В предыдущем параграфе было уста-новлено, что для существования то-ка в проводнике необходимо создать разность потенциалов на его концах. Сила тока в проводнике определяет-ся этой разностью потенциалов. Чем больше разность потенциалов, тем больше напряженность электриче-ского поля в проводнике и, следо-вательно, тем большую скорость на-правленного движения приобретают заряженные частицы. Согласно фор-муле, это означает увеличение силы тока.

Для каждого проводника — твер-дого, жидкого и газообразного — существует определенная зависи-мость силы тока от приложенной разности потенциалов на концах про-водника. Эту зависимость выражает так называемая вольт – амперная ха-рактеристика проводника. Ее нахо-дят, измеряя силу тока в проводнике при различных значениях напряже-ния. Знание вольт – амперной характе-ристики играет большую роль при изучении электрического тока.

Закон Ома.

Наиболее простой вид имеет вольт – амперная характеристи-ка металлических проводников и растворов электролитов. Впервые (для металлов) ее установил немец-кий ученый Георг Ом, поэтому зависимость силы тока от напря-жения носит название закона Ома. На участке цепи, изображенной на рисунке 109, ток направлен от точки 1 к точке 2. Разность потен-циалов (напряжение) на концах проводника равна: U = φ 1 – φ 2. Так как ток направлен слева направо, то напряженность электрического поля направлена в ту же сторону и φ 1 > φ 2

Согласно закону Ома для участка цепи сила тока прямо пропорцио-нальна приложенному напряжению U и обратно пропорциональна сопро-тивлению проводника R:

Закон Ома имеет очень простую форму, но доказать эксперименталь-но его справедливость довольно трудно. Дело в том, что разность по-тенциалов на участке металлическо-го проводника даже при большой силе тока мала, так как мало сопро-тивление проводника.

Электрометр, о котором шла речь, непригоден для измерения столь малых напряжений: его чув-ствительность слишком мала. Нужен несравненно более чувствительный прибор. Тогда, измеряя силу тока амперметром, а напряжение чув-ствительным электрометром, можно убедиться в том, что сила тока пря-мо пропорциональна напряжению. Применение же обычных приборов для измерения напряжения — вольт-метров — основано на использовании закона Ома.

Принцип устройства, вольтметра такой же, как и ампер-метра. Угол поворота стрелки прибо-ра пропорционален силе тока. Сила тока, проходящего по вольтметру, определяется напряжением между точками цепи, к которой он под-ключен. Поэтому, зная сопротивле-ние вольтметра, можно по силе тока определить напряжение. На практике прибор градуируют так, чтобы он сразу показывал напряжение в воль-тах.

Сопротивление. Основная элек-трическая характеристика проводни-ка — сопротивление. От этой вели-чины зависит сила тока в провод-нике при заданном напряжении. Со-противление проводника представля-ет собой как бы меру противо-действия проводника установлению в нем электрического тока. С помощью закона Ома можно определить сопротивление проводника:

Для этого нужно измерить напря-жение и силу тока.

Сопротивление зависит от мате-риала проводника и его геометри-ческих размеров. Сопротивление про-водника длиной l с постоянной пло-щадью поперечного сечения S равно:

где р — величина, зависящая от рода вещества и его состояния (от тем-пературы в первую очередь). Вели-чину р называют удельным сопро-тивлением проводника. Удельное со-противление численно равно сопро-тивлению проводника, имеющего форму куба с ребром 1 м, если ток направлен вдоль нормали к двум противоположным граням куба.

Единицу сопротивления провод-ника устанавливают на основе зако-на Ома и называют ее ом. Провод-ник имеет сопротивление 1 Ом, если при разности потенциалов 1 В сила тока в нем 1 А.

Единицей удельного сопротивле-ния является 1 Ом?м. Удельное со-противление металлов мало. Диэлектрики обладают очень большим удельным сопротивлением. В табли-це на форзаце приведены примеры значений удельного сопротивления некоторых веществ.

Значение закона Ома.

Закон Ома определяет силу тока в электриче-ской цепи при заданном напря-жении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока. Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротив-ления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

Закон Ома — основа всей элект-ротехники постоянных токов. Формулу — надо хорошо понять и твердо запомнить.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ

От источника тока энергия может быть передана по проводам к устрой-ствам, потребляющим энергию: Элек-трической лампе, радиоприемнику и др. Для этого составляют электри-ческие цепи различной сложности. Электрическая цепь состоит из источника энергии, устройств, по-требляющих электрическую энергию, соединительных проводов и выклю-чателей для замыкания цепи. Часто и электрическую цепь включают приборы, контролирующие силу тока и напряжение на различных участ-ках цепи, – амперметры и вольт-метры.

К наиболее простым и часто встречающимся соединениям провод-ников относятся последовательное и параллельное соединения.

Последовательное соединение проводников.

При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочередно друг за другом. На рисунке 1 показано последовательное соединение двух проводников 1 и 2, имеющих сопротивления R 1 , и R 2 . Это могут быть две лампы, две обмотки элект-родвигателя и др.

Сила тока в обоих проводниках одинакова, т. е. (1)

так как в проводниках электриче-ский заряд в случае постоянного тока не накапливается и через любое поперечное сечение проводника за определенное время проходит один и тот же заряд.

Напряжение на концах рассмат-риваемого участка цепи складывает-ся из напряжений на – первом и вто-ром проводниках:

Надо надеяться, что с доказатель-ством этого простого соотношения вы справитесь сами.

Применяя закон Ома для всего участка в целом и для участков с сопротивлениями R 1 и R 2 , можно до-казать, что полное сопротивление всего участка цепи при последова-тельном соединении равно:

Это правило можно применить для любого числа последовательно соединенных проводников.

Напряжения на проводниках и их сопротивления при последователь-ном соединении связаны соотноше-нием:

Докажите это равенство.

Параллельное соединение про-водников.

На рисунке 2 показано параллельное соединение двух про-водников 1 и 2с сопротивлениями R 1 и R 2 . В этом случае электриче-ский ток 1 разветвляется на две час-ти. Силу тока в первом и втором про-водниках обозначим через I 1 и I 2 . Так как в точке а — разветвлении проводников (такую точку называют узлом) — электрический заряд не на-капливается, то заряд, поступающий в единицу времени в узел, равен заряду, уходящему из узла за это же время. Следовательно, I = I 1 + I 2

Напряжение U на концах про-водников, соединенных параллельно, одно и то же.

В осветительной сети поддержи-вается напряжение 220 или 127 В. На это напряжение рассчитаны при-боры, потребляющие электрическую энергию. Поэтому параллельное сое-динение — самый распространенный способ соединения различных потре-бителей. В этом случае выход из строя одного прибора не отражается на работе остальных, тогда как при последовательном соединении выход из строя одного прибора размы-кает цепь.

Применяя закон Ома для всего участка в целом и для участков с сопротивлениями R 1 и R 2 , можно доказать, что величина, обратная полному сопротивлению участка ab, равна сумме величин, обратных сопротивлениям отдельных провод-ников:

Сила тока в каждом из провод-ников и сопротивления проводников при параллельном соединении свя-заны соотношением

Различные проводники в цепи соединяются друг с другом после-довательно или параллельно. В пер-вом случае сила тока одинакова во всех проводниках, а во втором слу-чае одинаковы напряжения на про-водниках. Чаще всего к осветитель-ной сети различные потребители тока подключаются параллельно.

ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ

Как измерить силу тока ампер-метром, а напряжение вольтметром, должен знать каждый.

Измерение силы тока.

Для изме-рения силы тока в проводнике ам-перметр включают последовательно с этим проводником (рис. 1). Но нужно иметь в виду, что сам ампер-метр обладает некоторым сопротив-лением R a . Поэтому сопротивление участка цепи с включенным ампер-метром увеличивается, и при неиз-менном напряжении сила тока умень-шается в соответствии с законом Ома. Чтобы амперметр оказывал как можно меньшее влияние на силу тока, измеряемую им, его сопротив-ление делают очень малым. Это нужно помнить и никогда не пытать-ся измерять силу тока в освети-тельной сети, подключая амперметр к розетке. Произойдет короткое за-мыкание; сила тока при малом со-противлении прибора достигнет столь большой величины, что обмотка ам-перметра сгорит.

Измерение напряжения.

Для того чтобы измерить напряжение на участке цепи с сопротивлением R, к нему параллельно подключают вольтметр. Напряжение на вольтметре совпа-дает с напряжением на участке цепи (рис. 2).

Если сопротивление вольтметра R B , то после включения его в цепь сопротивление участка будет уже не R, а . Из-за этого измеряемое напряжение на участ-ке цепи уменьшится. Для того чтобы вольтметр не вносил заметных иска-жений в измеряемое напряжение, его сопротивление должно быть большим по сравнению с сопротивлением участка цепи, на котором измеряется напряжение. Вольтметр можно вклю-чать в сеть без риска, что он сгорит, если только он рассчитан на напря-жение, превышающее напряжение сети.

Амперметр включают последова-тельно с проводником, в котором измеряют силу тока. Вольтметр включают параллельно проводнику, на котором измеряют напряжение.

РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА

Электрический ток получил такое широкое применение потому, что он несет с собой энергию. Эта энергия может быть превращена в любую форму.

При упорядоченном движении за-ряженных частиц в проводнике электрическое поле совершает ра-боту; ее принято называть работой тока. Сейчас мы напомним сведения о работе и мощности тока из курса физики VIII класса.

Работа тока.

Рассмотрим произ-вольный участок цепи. Это, может быть однородный проводник, напри-мер нить лампы накаливания, обмот-ка электродвигателя и др. Пусть за время t через поперечное сечение проводника проходит заряд q. Тогда электрическое поле совершит работу A = qU.

Так как сила тока , то эта работа равна:

Работа тока на участке цепи равна произведению силы тока, на-пряжения и времени, в течение ко-торого совершалась работа.

Согласно закону сохранения энергии эта работа должна быть рав-на изменению энергии рассматри-ваемого участка цепи. Поэтому энер-гия, выделяемая на данном участке цепи за время At, равна работе тока (см. формулу (1)).

В случае если на участке цепи не совершается механическая рабо-та и ток не производит химических действий, происходит только нагре-вание проводника. Нагретый про-водник отдает теплоту окружающим телам.

Нагревание проводника происхо-дит следующим образом. Электриче-ское поле ускоряет электроны. После столкновения с ионами кристалличе-ской решетки они передают ионам свою энергию. В результате энергия беспорядочного движения ионов око-ло положений равновесия возраста-ет. Это и означает увеличение внут-ренней энергии. Температура про-водника при этом повышается, и он начинает передавать теплоту окру-жающим телам. Спустя небольшое время после замыкания цепи процесс устанавливается, и температура пе-рестает изменяться со временем. К проводчику за счет работы элект-рического поля непрерывно поступа-ет энергия. Но его внутренняя энер-гия остается неизменной, так как проводник передает окружающим те-лам количество теплоты, равное ра-боте тока. Таким образом, формула (1) для работы тока определяет количество теплоты, передаваемое проводником другим телам.

Если в формуле (1) выразить либо напряжение через силу тока, либо силу тока через напряжение с помощью закона Ома для участка цепи, то получим три эквивалентные формулы:

(2)

Формулой A = I 2 R t удобно пользоваться для последовательного соединения проводников, так как сила тока в этом случае одинакова во всех проводниках. При парал-лельном соединении удобна формула , так как напряжение на всех проводниках одинаково.

Закон Джоуля — Ленца.

Закон, определяющий количество теплоты, которое выделяет проводник с то-ком в окружающую среду, был впервые установлен эксперименталь-но английским ученым Д. Джоу-лем (1818-1889) и русским ученым Э. X. Ленцем (1804-1865). Закон Джоуля — Ленца был сформулиро-ван следующим образом: количество теплоты, выделяемое проводником с током, равно произведению квад-рата силы тока, сопротивления про-водника и времени прохождения то-ка по проводнику:

(3)

Мы получили этот закон с по-мощью рассуждений, основанных на законе сохранения энергии. Формула (3) позволяет вычислить количе-ство теплоты, выделяемое на любом участке цепи, содержащем какие угодно проводники.

Мощность тока.

Любой электри-ческий прибор (лампа, электродвигатель) рассчитан на потребление определенной энергии в единицу вре-мени. Поэтому наряду с работой то-ка очень важное значение имеет по-нятие мощность тока. Мощность то-ка равна отношению работы тока за время t к этому интервалу времени.

Согласно этому определению

(4)

Это выражение для мощности можно переписать в нескольких эквивалентных формах, если исполь-зовать закон Ома для участка цепи:

На большинстве приборов ука-зана потребляемая ими мощность.

Прохождение по проводнику электрического тока сопровождается выделением в нем энергии. Эта энер-гия определяется работой тока: про-изведением перенесенного заряда и напряжения на концах проводника.

ЭЛЕКТРОДВИЖУЩАЯ СИЛА.

Любой источник тока характеризуется электродвижущей силой, или ЭДС. Так, на круглой батарейке для карманного фонарика написано: 1,5 В. Что это значит?

Соедините проводником два ме-таллических шарика, несущих за-ряды противоположных знаков. Под влиянием электрического поля этих зарядов в проводнике возникает электрический ток (рис. 1). Но этот ток будет очень кратковремен-ным. Заряды быстро нейтрализуют-ся, потенциалы шариков станут одинаковыми, и электрическое поле ис-чезнет.

Сторонние силы.

Для того чтобы ток был постоянным, надо поддер-живать постоянное напряжение меж-ду шариками. Для этого необходимо устройство (источник тока), которое перемещало бы заряды от одного шарика к другому в направлении, противоположном направлению сил, действующих на эти заряды со сто-роны электрического поля шариков. В таком устройстве на заряды, кро-ме электрических сил, должны дей-ствовать силы не электростатического происхождения (рис. 2). Одно лишь электрическое поле заряжен-ных частиц (кулоновское поле) не способно поддерживать постоянный ток в цепи.

Любые силы, действующие на электрически заряженные частицы, за исключением сил электростати-ческого происхождения (т. е. кулоновских), называют сторонними си-лами.

Вывод о необходимости сторон-них сил для поддержания посто-янного тока в цепи станет еще оче-виднее, если обратиться к закону сохранения энергии. Электростатиче-ское поле потенциально. Работа это-го поля при перемещении заряжен-ных частиц вдоль замкнутой электри-ческой цепи равна нулю. Прохож-дение же тока по проводникам сопровождается выделением энер-гии — проводник нагревается. Сле-довательно, в любой цепи должен быть какой-то источник энергии, по-ставляющий ее в цепь. В нем, по-мимо кулоновских сил, обязательно должны действовать сторонние не- потенциальные силы. Работа этих сил вдоль замкнутого контура долж-на быть отлична от нуля. Именно в процессе совершения работы этими силами заряженные частицы приобретают внутри источника тока энер-гию и отдают ее затем проводникам электрической цепи.

Сторонние силы приводят в дви-жение заряженные частицы внутри всех источников тока: в генераторах на электростанциях, в гальваниче-ских элементах, аккумуляторах и т.д.

При замыкании цепи создается электрическое поле во всех провод-никах цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны от положительно заряженного электрода к отрица-тельному), а во всей остальной цепи их приводит в движение электриче-ское поле (см. рис. 2).

Аналогия между электрическим током и течением жидкости.

Чтобы лучше понять механизм возникнове-ния тока, обратимся к сходству меж-ду электрическим током в провод-нике и течением жидкости по трубам.

На любом участке горизонталь-ной трубы жидкость течет за счет разности давлений на концах участ-ка. Жидкость перемещается в сторо-ну уменьшения давления. Но сила давления в жидкости — это вид сил упругости, которые являются потен-циальными, подобно кулоновским силам. Поэтому работа этих сил на замкнутом пути равна нулю и одни эти силы не способны вызвать длительную циркуляцию жидкости по трубам. Течение жидкости сопро-вождается потерями энергии вслед-ствие действия сил трения. Для цир-куляции воды необходим насос.

Поршень этого насоса действует на частички жидкости и создает по-стоянную разность давлений на вхо-де и выходе насоса (рис. 3). Благодаря этому жидкость течет по трубе. Насос подобен источнику тока, а роль сторонних сил играет сила, действующая на воду со стороны движущегося поршня. Внутри на-соса жидкость течет от участков с меньшим давлением к участкам с большим давлением. Разность дав-лений аналогична напряжению.

Природа сторонних сил.

Природа сторонних сил может быть разнооб-разной. В генераторах электростанций сторонняя сила — это сила, дей-ствующая со стороны магнитного поля на электроны в движущемся проводнике. Об этом кратко гово-рилось в курсе физики VIII класса.

В гальваническом элементе, на-пример элементе Вольта, действуют химические силы. Элемент Вольта состоит из цинкового и медного электродов, помещенных в раствор серной кислоты. Химические силы вызывают растворение цинка в кис-лоте. В раствор переходят положи-тельно заряженные ионы цинка, а сам цинковый электрод при этом заряжается отрицательно. (Медь очень мало растворяется в серной – кислоте.) Между цинковым и мед-ным электродами появляется раз-ность потенциалов, которая обуслов-ливает ток в замкнутой электриче-ской цепи.

Электродвижущая сила.

Дейст-вие сторонних сил характеризуется важной физической величиной, на-зываемой электродвижущей силой (сокращенно ЭДС).

Электродви-жущая сила в замкнутом контуре представляет собой отношение рабо-ты сторонних сил при перемещении заряда вдоль контура к заряду:

Электродвижущую силу выража-ют в вольтах.

Можно говорить об электродви-жущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единич-ного заряда) не во всем контуре, а только на данном участке. Электро-движущая сила гальванического эле-мента есть работа сторонних сил при перемещении единичного положи-тельного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть вы-ражена через разность потенциалов, так как сторонние силы не потенциальные и их работа зависит от формы траектории. Так, например, работа сторонних сил при переме-щении заряда между клеммами ис-точника тока вне самого источника равна нулю.

Теперь вы знаете, что такое ЭДС. Если на батарейке написано 1,5 В, то это означает, что сторонние силы (химические в данном случае) совер-шают работу 1,5 Дж при переме-щении заряда в 1 Кл от одного полюса батарейки к другому. Постоянный ток не может существовать в замкнутой цепи, если в ней не действуют сторонние силы, т. е. нет ЭДС

Рис №1 Рис №2 Рис №3

ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ

Электродвижущая сила опреде-ляет силу тока в замкнутой электри-ческой цепи с известным сопротив-лением.

Спомощью закона сохранения энергии найдем зависимость силы тока от ЭДС и сопротивления.

Рассмотрим простейшую полную (замкнутую) цепь, состоящую из источника тока (гальванического элемента, аккумулятора или гене-ратора) и резистора сопротивле-нием R (рис. 1). Источник тока имеет ЭДС εи сопротивление r. Сопротивление источника часто на-зывают внутренним сопротивлением в отличие от внешнего сопротивле-ния R цепи. В генераторе r — это сопротивление обмоток, а в гальва-ническом элементе — сопротивление раствора электролита и электродов.

Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление R + r цепи. Эта связь может быть установлена теоретически, если использовать за-кон сохранения энергии и закон Джоуля — Ленца.

Пусть за время t через попе-речное сечение проводника пройдет электрический заряд q. Тогда рабо-ту сторонних сил при перемещении заряда?qможно записать так: А ст = ε · q. Согласно определению силы тока q = It. Поэтому

(1)

При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых r и R, выделяется некоторое количество теплоты. По закону Джоуля — Лен-ца оно равно:

Q = I 2 R · t + I 2 r · t. (2)

Согласно закону сохранения энергии A = Q. Приравнивая (1) и (2), получим:

ε = IR + Ir (3)

Произведение силы тока и сопро-тивления участка цепи часто назы-вают падением напряжения на этом участке. Таким образом, ЭДС равна сумме падений напряжений на внут-реннем и внешнем участках замкну-той цепи.

Обычно закон Ома для замкну-той цепи записывают в форме

(4)

Инструкция

Видео по теме

Компаратор как замена конденсатору в обычной игре

В обычном (без плагинов и модов) варианте Minecraft такого понятия, как конденсатор, не существует. Вернее, устройство, выполняющее его функции, имеется, но название у него совершенно другое – компаратор. Некоторая путаница в этом плане произошла еще в период разработки такого прибора. Сперва – в ноябре 2012-го – представители Mojang (компании-создателя игры) объявили о скором появлении в геймплее конденсатора. Однако через месяц они высказались уже о том, что как такового этого прибора не будет, а вместо него в игре будет компаратор.

Подобное устройство существует для проверки заполненности расположенных позади него контейнеров. Таковыми могут быть сундуки (в том числе в виде ловушек), варочные стойки, раздатчики, выбрасыватели, печи, загрузочные воронки и т.п.

Помимо этого, его часто используют для сравнения двух сигналов редстоуна между собою – он выдает результат в соответствии с тем, как было запрограммировано в данной цепи, и с тем, какой режим выбран для самого механизма. В частности, компаратор может разрешить зажигание факела, если первый сигнал больше либо равен другому.

Также порой конденсатор-компаратор устанавливают рядом с проигрывателем, подключая его входом к последнему. Когда в звуковоспроизводящем устройстве проигрывается какая-либо пластинка, вышеупомянутый прибор будет выдавать сигнал, равный по силе порядковому номеру диска.

Скрафтить такой компаратор несложно, если имеется достаточно трудно добываемый ресурс – адский . Его надо поставить в центральный слот верстака, над ним и по бокам от него установить три красных факела, а в нижнем ряду – такое же количество каменных блоков.

Конденсаторы, встречающиеся в разных модах Minecraft

В большом количестве модов попадаются конденсаторы, имеющие самое разное предназначение. К примеру, в Galacticraft, где у геймеров есть возможность слетать на многие планеты для ознакомления с тамошними реалиями, появляется рецепт крафта кислородного конденсатора. Он служит для создания механизмов вроде коллектора и накопителя газа для , а также рамки воздушного шлюза. Для его изготовления четыре стальных пластины размещаются по углам верстака, в центре – оловянная канистра, а под нею – воздуховод. Остальные три ячейки занимают пластины из олова.

В JurassiCraft существует конденсатор потока – некий телепорт, позволяющий переместиться в удивительный игровой мир, кишащий динозаврами. Для создания такого прибора нужно поместить в два крайних вертикальных ряда шесть железных слитков, а в средний – два алмаза и между ними единицу пыли редстоуна. Дабы устройство заработало, надо поставить его на свинью либо вагонетку, а затем щелкнуть по нему правой клавишей мыши, быстро запрыгнув туда. При этом требуется поддержание высокой скорости устройства.

С модом Industrial Craft2 у игрока появляется возможность создавать как минимум два вида тепловых конденсаторов – красный и лазуритовый. Они служат исключительно для охлаждения ядерного реактора и для накопления его энергии и хороши для циклических сооружений такого типа. Остужаются они сами, соответственно, красной пылью или лазуритом.

Красный теплоконденсатор делается из семи единиц пыли редстоуна – их надо установить в виде буквы П и расставить под ними теплоотвод и теплообменник. Крафтинг же лазуритового устройства чуть посложнее. Для его создания четыре единицы пыли редстоуна расставляются по углам станка, в центр пойдет блок лазурита, по бокам от него – два красных тепловых конденсатора, сверху – теплоотвод реактора, а снизу – его же теплообменник.

В ThaumCraft, где сделан акцент на настоящем чародействе, конденсаторы тоже используются. Например, один из них – кристаллический – существует для аккумуляции и отдачи магии. Причем, что интересно, создавать его и многие другие вещи разрешено лишь после изучения особого элемента геймплея – исследования, проводимого за специальным столом и с определенными приборами.

Делается такой конденсатор из восьми тусклых осколков, в центр которых на верстаке помещается мистический деревянный блок. К сожалению, подобный прибор – равно как и его составляющие – просуществовал лишь до ThaumCraft 3, а в четвертой версии мода был упразднен.

Источники:

• О компараторе в Minecraft
• Кислородный конденсатор в Galacticraft
• Мод JurassiCraft
• Ядерный реактор в Industrial Craft2
• Кристаллический конденсатор в ThaumCraft

Facebook

Twitter

Вконтакте

Одноклассники

Google+

Формула и определение электрического напряжения в цепи в физике

В современном быту, строительстве и других сферах жизни человека огромную роль играет энергия, которая необходима для приведения в движение различных механизмов, производственных станков и инструментов. Электрическое напряжение, или как его принято называть в народе ток, занимает первое место среди ресурсов снабжения, поэтому человек во многом зависит от бесперебойной подачи электричества правильного номинала. В данной статье рассмотрено определение электрического напряжения, его формула, а также, от чего зависит и на что влияет данный показатель.

Электрическое напряжение

Что такое напряжение

Электрическое напряжение – это работа, которая необходима для подачи заряда электрическим полем от поставщика до потребляемого прибора по проводам или без них. Проще говоря, это величина силы, потраченной для доставки определенного заряда тока по проводнику от одного конца на другой. Без напряжения не будет перемещения заряженных частиц, а, следовательно, ток не будет поступать к потребителю, номинальная величина в цепи будет равна нулю.

Электрическим током заряжены все элементы и предметы, которые окружают человека, разница лишь в величине напряжения – у некоторых вещей данный показатель минимален и фактически не заметен, у других – наличие тока более выражено. За долгие годы исследований ученые изобрели множество приборов, которые способны вырабатывать электрический ток различного напряжения и силы, начиная от малогабаритных и заканчивая крупными электростанциями, питающими целые города. Электрическое напряжение напрямую связано с силой тока: чем выше напряжение, тем выше будет величина силы тока.

Для более точного понимания определения напряжения тока необходимо разобраться в физике образования электричества в целом. Откуда берется электрический ток?

Все предметы и вещества состоят из атомов с положительным зарядом, число которых равно числу вращающихся вокруг них отрицательно заряженных частиц. Проще говоря, количество электронов равно количеству нейтронов. Чтобы возникло напряжение в сети, из ядра извлекаются некоторые электроны, возникает разряжение, и оставшиеся частицы пытаются восполнить пробел путем притяжения электронов снаружи, возникает положительный заряд. Если же добавить электроны в атом, возникнет переизбыток, и образуется отрицательное энергетическое поле.

В результате такого взаимодействия возникают положительный и отрицательный потенциалы, и чем больше контакта у этих элементов, тем выше сила и напряжение электрического тока. При соединении указанных потенциалов образуется энергетическое поле, которое увеличивается при повышении количества заряженных атомов внутри себя.

Формула для вычисления напряжения тока выглядит следующим образом:

U=A/q, где:

• U – это само напряжение,
• A – работа, необходимая для перемещения заряда,
• Q – отрезок расстояния, на которое перемещается заряженный атом.

Формула напряжения

Таким образом, можно сделать вывод, что сила тока на протяжении всей цепи будет одинаковой, а напряжение на каждом из участков будет разным, в зависимости от нагрузки на данный отрезок. Как известно, энергия не возникает из ниоткуда и не пропадает в неизвестном направлении, поэтому при повышении напряжения на определенном участке провода избыточный ток выражается в тепловой нагрузке, проще говоря, материал, из которого изготовлен проводник, начинает греться.

Влияние температуры проводника на сопротивление

От чего зависит напряжение

Существует три основных фактора, влияющих на норматив напряжения электрических токов, среди которых:

1. Материал, из которого выполнен проводник. Для решения определенных задач существуют различные типы проводов, чаще всего можно встретить медные или алюминиевые изделия различного сечения и наружной оболочки. Наружная обмотка таких проводов бывает также из множества материалов, защитных и декоративных, например, ПВХ пленка или резиновая защита. Такая обработка позволяет использовать проводку в любых условиях, в том числе для организации наружного освещения;
2. Температуры использования проводника;
3. Уровня сопротивления электрического тока на данном участке. Данная величина зависит от свойств проводимости кабеля или иного предмета, подключенного к сети, и способности к беспрепятственному пропуску атомов через себя. Существуют материалы с нулевым сопротивлением или полностью диэлектрические, то есть не способные проводить электрический ток любого напряжения.

Ток и его напряжение напрямую зависят друг от друга, поэтому и их обозначения одинаковы. Напряжение тока измеряется в Вольтах и обозначается буквой В. Вольт выражается в разности положительного и отрицательного потенциалов на двух удаленных от друг друга точках поля, силы которого совершают усилия, равные одному Дж, при доставке заряда от одного отрезка к конечному. Номинал единицы заряда равен одному Кл, таким образом, обозначение 220 Вольт включает в себя понятие, что данная сеть способна потратить энергию в 220 Дж для транспортировки зарядов от входной точки до потребителя, это и называется электрическим напряжением в сети.

Виды напряжения электрического тока

Синусоида постоянного и переменного тока

Что такое электрическое напряжение, описывается в учебниках по физике, там же приводится его классификация на основании временного промежутка подачи энергии. По данному признаку напряжение бывает:

1. Постоянное – это когда на одном конце проводника ток и электрическое напряжение положительные, а на другом – отрицательные, и их значение направлено в одну сторону. Чаще всего такая система встречается в автономных батареях слабой и средней мощности;

Важно! Случайная или умышленная замена полярностей может привести к выходу из строя прибора, а также короткому замыканию при соединении нескольких элементов, осуществлять это нужно последовательно, стыкуя минусовый контакт к плюсовому. Синусоида при постоянном токе будет ровной без рывков и волн.

2. Переменный ток и электрическое напряжение отличаются от постоянных тем, что у них может быть несколько направлений, например, при частой замене потенциалов полярностей или их перемещении возникает обратное движение заряда, частота данного действия и будет показателем переменного тока. Чаще всего данную систему используют для транспортировки электричества по проводнику на большие расстояния, так как потери тока минимальны, следовательно, и напряжение не уменьшается. Также переменный ток используется в трехфазных двигателях и при доставке постоянного тока на трансформатор для его последующего разделения. Синусоида переменного тока выглядит неровной, волнообразной, с множественными скачками. Существуют формула и механизмы, которые используются для преобразования переменного тока в постоянный, это возможно при наличии конденсаторов и диодного моста.

Между фазами переменного тока также существуют свои показатели, в данном случае напряжение равно 380В, по количеству разности потенциалов в трехфазной сети. В сети напряженностью 220В всего два провода: один – с несущей фазой, второй – с нулем, также для безопасности добавляется кабель заземления. В трехфазной сети имеется четыре жилы, и один дополнительный заземляющий провод, в сумме напряжение всех трех фаз составляет 380В.

Меры предосторожности

Ток и электрическое напряжение являются источником повышенной опасности, поэтому при работе и эксплуатации данного типа энергии необходимо соблюдать нормы и правила безопасности, не допускать аварийных ситуаций и обеспечить все приборы автоматической системой отключения питания.

Запрещается работать с проводкой, находящейся под напряжением, или без устройства для заземления. В случае возникновения короткого замыкания необходимо отключить все приборы от сети и предотвратить возгорание обмотки двигателя или кабеля.

Видео

Оцените статью:

очков заряда | Безграничная физика

Электрический потенциал из-за точечного заряда

Электрический потенциал точечного заряда Q определяется выражением [латекс] \ text {V} = \ frac {\ text {kQ}} {\ text {r}} [/ latex].

Цели обучения

Выразите электрический потенциал, генерируемый одиночным точечным зарядом, в форме уравнения

Основные выводы

Ключевые моменты

• Напомним, что электрический потенциал определяется как потенциальная энергия на единицу заряда, т.е.е. [латекс] \ text {V} = \ frac {\ text {PE}} {\ text {q}} [/ latex].
• Разность потенциалов между двумя точками ΔV часто называется напряжением и выражается как [латекс] \ Delta \ text {V} = \ text {V} _ {\ text {B}} – \ text {V} _ {\ текст {A}} = \ frac {\ Delta \ text {PE}} {\ text {q}} [/ latex]. Потенциал на бесконечном расстоянии часто принимается равным нулю.
• Случай электрического потенциала, генерируемого точечным зарядом, важен, потому что он часто встречается. Сферическая сфера заряда создает внешнее поле, как, например, точечный заряд.
• Уравнение электрического потенциала, вызванного точечным зарядом, имеет вид [latex] \ text {V} = \ frac {\ text {kQ}} {\ text {r}} [/ latex], где k – константа, равная 9,0 × 10 ⁹ Н · м ² / C ² .

Ключевые термины

• электрический потенциал : потенциальная энергия на единицу заряда в точке в статическом электрическом поле; Напряжение.
• напряжение : величина электростатического потенциала между двумя точками в пространстве.

Электрический потенциал из-за точечного заряда

Обзор

Напомним, что электрический потенциал определяется как электрическая потенциальная энергия на единицу заряда

[латекс] \ text {V} = \ frac {\ text {PE}} {\ text {q}} [/ latex]

Электрический потенциал говорит вам, сколько потенциальной энергии будет иметь одиночный точечный заряд в данном месте.Электрический потенциал в точке равен электрической потенциальной энергии (измеренной в джоулях) любой заряженной частицы в этом месте, деленной на заряд (измеренный в кулонах) частицы. Поскольку заряд пробной частицы разделен, электрический потенциал является «свойством», относящимся только к самому электрическому полю, а не к пробной частице. Другими словами, поскольку PE зависит от q, q в приведенном выше уравнении будет сокращаться, поэтому V не зависит от q.

Разность потенциалов между двумя точками ΔV часто называется напряжением и выражается как

.

[латекс] \ Delta \ text {V} = \ text {V} _ {\ text {B}} – \ text {V} _ {\ text {A}} = \ frac {\ Delta \ text {PE} } {\ text {q}} [/ latex]

Точечных сборов

Точечные заряды, такие как электроны, являются одними из основных строительных блоков материи. Кроме того, сферическое распределение заряда (как на металлической сфере, см. Рисунок ниже) создает внешние электрические поля точно так же, как точечный заряд.Таким образом, нам необходимо рассмотреть электрический потенциал, обусловленный точечным зарядом. Используя расчет для определения работы, необходимой для перемещения пробного заряда q с большого расстояния на расстояние r от точечного заряда Q , и учитывая связь между работой и потенциалом (W = –qΔV), можно показать, что электрический потенциал V точечного заряда равен

[латекс] \ text {V} = \ frac {\ text {kQ}} {\ text {r}} [/ latex] (точечный заряд)

, где k – постоянная, равная 9. {2}} [/ latex ]

Электрический потенциал – это скаляр, а электрическое поле – вектор.Обратите внимание на симметрию между электрическим потенциалом и гравитационным потенциалом – оба падают как функция расстояния до первой степени, в то время как электрическое и гравитационное поля снижаются как функция расстояния до второй степени.

Суперпозиция электрического потенциала

Чтобы найти полный электрический потенциал системы точечных зарядов, нужно складывать отдельные напряжения в виде чисел.

Цели обучения

Объясните, как определяется полный электрический потенциал системы точечных зарядов

Основные выводы

Ключевые моменты

• Электрический потенциал V является скаляром и не имеет направления, тогда как электрическое поле E является вектором.
• Чтобы найти напряжение, вызванное комбинацией точечных зарядов, вы складываете отдельные напряжения в виде чисел. Так, например, электрический потенциал в точке L представляет собой сумму потенциальных вкладов зарядов Q ₁ , Q ₂ , Q ₃ , Q ₄ и Q ₅ , так что [латекс] \ text {V} _ {\ text {L}} = \ text {k} [\ frac {\ text {Q} _ {1}} {\ text {d} _ {1}} + \ frac {\ text {Q} _ {2}} {\ text {d} _ {2}} + \ frac {\ text {Q} _ {3}} {\ text {d} _ {3}} + \ frac {\ text {Q} _ {4}} {\ text {d} _ {4}} + \ frac {\ text {Q} _ {5}} {\ text {d} _ {5}}] [/ latex].
• Чтобы найти полное электрическое поле, вы должны сложить отдельные поля как векторы, учитывая величину и направление. Это согласуется с тем фактом, что V тесно связан с энергией, скаляром, тогда как E тесно связан с силой, вектором.
• Суммирование всех вкладов напряжения для определения общего потенциального поля называется суперпозицией электрического потенциала. Суммировать скаляры намного проще, чем векторы, поэтому часто предпочтительный метод решения задач с электрическими полями включает суммирование напряжений.

Ключевые термины

• вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.
• скаляр : величина, имеющая величину, но не направление; сравнить вектор.
• суперпозиция : Суммирование двух или более вкладов полей, занимающих одно и то же пространство.

Суперпозиция электрического потенциала

Мы видели, что электрический потенциал определяется как количество потенциальной энергии на единицу заряда, которое испытывает частица в данном месте в электрическом поле, т.е.{2}} [/ латекс]

с той разницей, что электрическое поле спадает пропорционально квадрату расстояния, в то время как потенциал падает линейно с расстоянием. Это аналогично соотношению между гравитационным полем и гравитационным потенциалом.

Суперпозиция электрического потенциала : Электрический потенциал в точке L представляет собой сумму напряжений от каждого точечного заряда (скаляры).

Напомним, что электрический потенциал V является скаляром и не имеет направления, тогда как электрическое поле E является вектором.Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Так, например, на рисунке выше электрический потенциал в точке L представляет собой сумму потенциальных вкладов от зарядов Q ₁ , Q ₂ , Q ₃ , Q ₄ и Q ₅ , так что

[латекс] \ text {V} _ {\ text {L}} = \ text {k} [\ frac {\ text {Q} _ {1}} {\ text {d} _ {1}} + \ frac {\ text {Q} _ {2}} {\ text {d} _ {2}} + \ frac {\ text {Q} _ {3}} {\ text {d} _ {3}} + \ frac {\ text {Q} _ {4}} {\ text {d} _ {4}} + \ frac {\ text {Q} _ {5}} {\ text {d} _ {5}}] [ / латекс]

Чтобы найти полное электрическое поле, вы должны сложить отдельные поля как векторов , принимая во внимание величину и направление.Это согласуется с тем фактом, что V тесно связан с энергией, скаляром, тогда как E тесно связан с силой, вектором.

Суммирование всех вкладов напряжения для определения полного потенциального поля называется суперпозицией электрического потенциала. Суммирование напряжений вместо суммирования электрических значительно упрощает вычисления, поскольку сложение потенциальных скалярных полей намного проще, чем добавление электрических векторных полей. Обратите внимание, что в некоторых случаях вам может потребоваться суммировать потенциальные взносы из других источников, помимо точечных сборов; однако это выходит за рамки данного раздела.{x_2} E (x) ~ dx \ tag {3} $$

И интеграл поля по расстоянию имеет особое значение. Это то, что мы называем электрическим потенциалом. Итак, уравнение (3) просто:

$$ W = q \ left (V (x_2) – V (x_1) \ right) = q \ Delta V \ tag {4} $$

, где $ \ Delta V $ – разность потенциалов между $ x_1 $ и $ x_2 $.

И поэтому работа всего $ qV $. Это потому, что $ V $ – это интеграл по расстоянию. Мы пишем $ V $, а не интеграл, потому что это обычно удобнее.

Вы можете проделать тот же трюк с обычной механикой. Например, когда вы двигаетесь вверх или вниз на расстояние $ h $ против силы тяжести, работа будет:

$$ W = mgh $$

, т.е. сила $ mg $ умноженная на расстояние $ h $. Но мы можем определить гравитационную потенциальную энергию $ U = gh $ и записать:

$$ W = mU $$

Это теперь аналогично нашему уравнению для электростатической работы $ W = qV $. В этом простом случае, вероятно, нет особого смысла в использовании гравитационной потенциальной энергии, но в более сложных расчетах обычно используется гравитационная потенциальная энергия, а не сила.

Электростатика

– Почему емкость определяется как заряд, деленный на напряжение?

Мы используем $ C = Q / V $, потому что это полезные вещи для измерения. Часто об этом легко забыть, но многие из используемых нами уравнений выбраны потому, что они работают, и потому, что другие уравнения не работают. Никогда не недооценивайте эту часть реальности.

Мы не используем «плату за единицу объема», потому что это число непостоянно. Вы можете заряжать конденсатор, не меняя его объема. Заряд, разделенный на напряжение, является постоянным.

Думаю, самый важный вопрос, который вы задали:

Или, согласно уравнению $ C = \ frac {Q} {V} $, почему увеличение напряжения при сохранении постоянного заряда будет иметь какое-либо влияние на способность тела накапливать заряд.

Мне нравится этот вопрос, потому что он немного обратный, предполагая, что вы думаете об этом по-другому. Мне нравится, когда люди думают о чем-то задом наперед, потому что это шоу, они действительно думают и хотят попытаться понять, что происходит!

Уловка в том, что вы обнаружите, что не может увеличить напряжение на конденсаторе, сохраняя при этом постоянный заряд, без внесения некоторых физических изменений в сам конденсатор.Реальность вам просто не позволит. Если вы попытаетесь увеличить напряжение, вы обнаружите, что в конденсатор поступает ровно столько заряда, чтобы сбалансировать напряжение.

Более интересно, рассмотрим случай, когда вы мгновенно изменяете напряжение, скажем, с 1 В до 10 В. Теоретически это должно «увеличивать напряжение без увеличения заряда», потому что для протекания тока не было времени. Вы можете нарисовать это в симуляторе схем, таком как PSPICE, и изменить напряжение при t = 0.Похоже, вам нужно изменить емкость.

На самом деле мы видим другой эффект. Мы видим, что даже если мы увеличили напряжение в системе, напряжение на конденсаторе фактически останется таким же! Это имеет смысл из уравнения, потому что мы знаем, что заряд и емкость не изменились, поэтому напряжение не может измениться. Но теперь похоже, что у нас разорвана цепь: как-то у нас на входе 10В, а на конденсаторе только 1В! Все знают, что это не сходится.

В действительности мы обнаруживаем, что в каждом используемом нами устройстве присутствует «паразитное сопротивление». У батареи есть сопротивление, у конденсатора есть сопротивление, даже те провода, которые вы используете для их соединения, имеют сопротивление. Итак, ваша реальная схема – это не просто источник напряжения и конденсатор, это источник напряжения, конденсатор и связка небольших резисторов.

В 99% случаев мы можем игнорировать эти резисторы, потому что они не сильно меняют схему. Однако в этой слегка патологической ситуации они действительно имеют большое значение.Именно они «впитывают» это дополнительное напряжение. В итоге вы получите 1 В на конденсаторе и 9 В на всех резисторах. Теперь начинается самое интересное. поскольку для тока через резистор используется $ V = IR $, мы можем рассчитать ток, проходящий через систему. Чем идеальнее были провода и батареи, тем больший ток нам нужно было использовать для обеспечения 9В. Этот ток представляет собой поток заряда. Куда он течет? Конденсатор. Вы сразу же начнете видеть, как заряд конденсатора возрастает по мере прохождения через него тока, пока в конечном итоге на конденсаторе не накопится достаточно заряда, чтобы создать на нем потенциал 10 В.В этот момент через резисторы больше нет напряжения, поэтому ток падает до 0, а цепь остается постоянной.

(На самом деле там есть несколько экспоненциальных членов, и технически никогда не достигает точно до 10 В, но в реалистичных сценариях мы, как правило, подходим достаточно близко, чтобы отмахнуться от этого набора дополнительных сложностей)

Электрическая потенциальная энергия: разница потенциалов

Цели обучения

К концу этого раздела вы сможете:

• Определите электрический потенциал и электрическую потенциальную энергию.
• Опишите взаимосвязь между разностью потенциалов и электрической потенциальной энергией.
• Объясните электрон-вольт и его использование в субмикроскопических процессах.
• Определить электрическую потенциальную энергию по разности потенциалов и количеству заряда.

Рис. 1. Заряд, ускоренный электрическим полем, аналогичен массе, спускающейся с холма. В обоих случаях потенциальная энергия преобразуется в другую форму. Работа совершается силой, но поскольку эта сила консервативна, мы можем записать W = –ΔPE.

Когда свободный положительный заряд q ускоряется электрическим полем, как показано на рисунке 1, ему придается кинетическая энергия. Этот процесс аналогичен ускорению объекта гравитационным полем. Это как если бы заряд спускался с электрического холма, где его электрическая потенциальная энергия преобразуется в кинетическую. Давайте исследуем работу, совершаемую электрическим полем над зарядом q в этом процессе, чтобы мы могли разработать определение электрической потенциальной энергии.

Электростатическая или кулоновская сила является консервативной, что означает, что работа, выполняемая на q , не зависит от пройденного пути. Это в точности аналог гравитационной силы в отсутствие диссипативных сил, таких как трение. Когда сила консервативна, можно определить потенциальную энергию, связанную с силой, и обычно легче иметь дело с потенциальной энергией (потому что она зависит только от положения), чем вычислять работу напрямую.

Мы используем буквы PE для обозначения электрической потенциальной энергии, которая измеряется в джоулях (Дж). Изменение потенциальной энергии ΔPE имеет решающее значение, поскольку работа, совершаемая консервативной силой, является отрицательной по отношению к изменению потенциальной энергии; то есть Вт = –ΔPE. Например, работа W , выполняемая для ускорения положительного заряда из состояния покоя, является положительной и является результатом потери PE или отрицательного ΔPE. Перед ΔPE должен стоять знак минус, чтобы значение W было положительным.PE можно найти в любой точке, взяв одну точку за точку отсчета и вычислив работу, необходимую для перемещения заряда в другую точку.

Потенциальная энергия

W = –ΔPE. Например, работа W , выполняемая для ускорения положительного заряда из состояния покоя, является положительной и является результатом потери PE или отрицательного ΔPE. Перед ΔPE должен стоять знак минус, чтобы значение W было положительным. PE можно найти в любой точке, взяв одну точку за точку отсчета и вычислив работу, необходимую для перемещения заряда в другую точку.

Гравитационная потенциальная энергия и электрическая потенциальная энергия совершенно аналогичны. Потенциальная энергия учитывает работу, выполняемую консервативной силой, и дает дополнительное понимание энергии и преобразования энергии без необходимости иметь дело с силой напрямую. Например, гораздо более распространено использование концепции напряжения (связанного с электрической потенциальной энергией), чем непосредственное рассмотрение кулоновской силы.

Непосредственный расчет работы обычно затруднен, поскольку W = Fd cos θ , а направление и величина F могут быть сложными для нескольких зарядов, для объектов нечетной формы и вдоль произвольных траекторий.Но мы знаем, что, поскольку F = qE , работа и, следовательно, ΔPE пропорциональны испытательному заряду q. Чтобы получить физическую величину, не зависящую от испытательного заряда, мы определяем электрический потенциал V (или просто потенциал, поскольку подразумевается электрический) как потенциальную энергию на единицу заряда [латекс] V = \ frac {\ text {PE}} {q} \\ [/ латекс].

Электрический потенциал

Это электрическая потенциальная энергия на единицу заряда.

[латекс] \ displaystyle {V} = \ frac {\ text {PE}} {q} \\ [/ latex]

Поскольку PE пропорционален q , зависимость от q отменяется. Таким образом, V не зависит от q . Изменение потенциальной энергии ΔPE имеет решающее значение, поэтому нас беспокоит разность потенциалов или разность потенциалов Δ V между двумя точками, где

[латекс] \ displaystyle \ Delta {V} = V _ {\ text {B}} – V _ {\ text {A}} = \ frac {\ Delta {\ text {PE}}} {q} \\ [/ латекс]

Таким образом, разность потенциалов между точками A и B, V _B – V _A определяется как изменение потенциальной энергии заряда q , перемещенного от A к B, делится на заряд.Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.

[латекс] 1 \ text {V} = 1 \ frac {\ text {J}} {\ text {C}} \\ [/ latex]

Потенциальная разница

Разность потенциалов между точками A и B, V _B – V _A , определяется как изменение потенциальной энергии заряда q , перемещенного из A в B, деленное на заряд. Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.

[латекс] \ displaystyle {1} \ text {V} = 1 \ frac {\ text {J}} {\ text {C}} \\ [/ latex]

Знакомый термин напряжение – это общее название разности потенциалов. Имейте в виду, что всякий раз, когда указывается напряжение, под ним понимается разность потенциалов между двумя точками. Например, каждая батарея имеет две клеммы, а ее напряжение – это разность потенциалов между ними. По сути, точка, которую вы выбираете равным нулю вольт, произвольна. Это аналогично тому факту, что гравитационная потенциальная энергия имеет произвольный ноль, например уровень моря или, возможно, пол лекционного зала.

Таким образом, связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется выражением [латекс] \ Delta {V} = \ frac {\ Delta \ text {PE}} {q} \\ [/ latex] и ΔPE = q Δ V .

Разность потенциалов и электрическая потенциальная энергия

Связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется формулой

.

[латекс] \ Delta {V} = \ frac {\ Delta \ text {PE}} {q} \\ [/ latex] и ΔPE = q Δ V

Второе уравнение эквивалентно первому.

Напряжение – это не то же самое, что энергия. Напряжение – это энергия на единицу заряда. Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение (точнее, одинаковую разность потенциалов между выводами аккумулятора), но при этом один хранит гораздо больше энергии, чем другой, поскольку ΔPE = q Δ V . Автомобильный аккумулятор может заряжать больше, чем аккумулятор мотоцикла, хотя оба аккумулятора – 12 В.

Пример 1. Расчет энергии

Предположим, у вас есть 12.Батарея мотоцикла 0 В, способная перемещать заряд 5000 C, и автомобильная батарея 12,0 В, способная перемещать заряд 60 000 C. Сколько энергии дает каждый? (Предположим, что числовое значение каждого заряда соответствует трем значащим цифрам.)

Стратегия

Если у нас есть батарея на 12,0 В, это означает, что на ее выводах разность потенциалов составляет 12,0 В. Когда такая батарея перемещает заряд, она пропускает заряд через разность потенциалов 12,0 В, и заряд получает изменение потенциальной энергии, равное ΔPE = q Δ V .

Итак, чтобы найти выходную энергию, мы умножаем перемещенный заряд на разность потенциалов.

Решение

Для аккумулятора мотоцикла: q = 5000 C и Δ V = 12,0 В. Общая энергия, отдаваемая аккумулятором мотоцикла, составляет

[латекс] \ begin {array} {lll} \ Delta \ text {PE} _ {\ text {cycle}} & = & \ left (5000 \ text {C} \ right) \ left (12.0 \ text {V } \ right) \\\ text {} & = & \ left (5000 \ text {C} \ right) \ left (12.0 \ text {J / C} \ right) \\\ text {} & = & 6.5 \ text {J} \ end {array} \\ [/ latex]

Обсуждение

Хотя напряжение и энергия связаны, это не одно и то же. Напряжения батарей одинаковы, но энергия, подаваемая каждым из них, совершенно разная. Также обратите внимание, что когда аккумулятор разряжается, часть его энергии используется внутри, а напряжение на его клеммах падает, например, когда фары тускнеют из-за низкого заряда автомобильного аккумулятора. Энергия, подаваемая батареей, по-прежнему рассчитывается, как в этом примере, но не вся энергия доступна для внешнего использования.

Обратите внимание, что энергии, вычисленные в предыдущем примере, являются абсолютными значениями. Изменение потенциальной энергии для аккумулятора отрицательное, так как он теряет энергию. Эти батареи, как и многие другие электрические системы, действительно перемещают отрицательный заряд – в частности, электроны. Батареи отталкивают электроны от своих отрицательных выводов (A) через любую задействованную схему и притягивают их к своим положительным выводам (B), как показано на рисунке 2. Изменение потенциала составляет Δ В = В _B – V _A = +12 В и заряд q отрицательный, так что ΔPE = q Δ V отрицательный, что означает, что потенциальная энергия батареи уменьшилась, когда q переместился из От А до Б.

Рис. 2. Батарея перемещает отрицательный заряд от отрицательной клеммы через фару к ее положительной клемме. Соответствующие комбинации химикатов в батарее разделяют заряды, так что отрицательный вывод имеет избыток отрицательного заряда, который отталкивается им и притягивается избыточным положительным зарядом на другом выводе. С точки зрения потенциала положительный вывод находится под более высоким напряжением, чем отрицательный. Внутри батареи движутся как положительные, так и отрицательные заряды.

Пример 2. Сколько электронов проходит через фару каждую секунду?

Когда от автомобильного аккумулятора на 12,0 В работает одна фара мощностью 30,0 Вт, сколько электронов проходит через нее каждую секунду?

Стратегия

Чтобы узнать количество электронов, мы должны сначала найти заряд, который переместился за 1,00 с. Перемещаемый заряд связан с напряжением и энергией через уравнение ΔPE = q Δ V . Лампа мощностью 30,0 Вт потребляет 30,0 джоулей в секунду. Поскольку батарея теряет энергию, имеем ΔPE = –30.0 Дж и, поскольку электроны переходят от отрицательного вывода к положительному, мы видим, что Δ V = + 12.0V.

Решение

Чтобы найти заряд q , мы решаем уравнение ΔPE = q Δ V : [латекс] q = \ frac {\ Delta \ text {PE}} {\ Delta {V}} \ \[/латекс].

Вводя значения ΔPE и Δ V , получаем

[латекс] q = \ frac {-30.0 \ text {J}} {+ 12.0 \ text {V}} = \ frac {-30.0 \ text {J}} {+ 12.0 \ text {J / C}} – 2.{19} \ text {электроны} \\ [/ latex]

Обсуждение

Это очень большое число. Неудивительно, что мы обычно не наблюдаем отдельные электроны, так много которых присутствует в обычных системах. Фактически, электричество использовалось в течение многих десятилетий, прежде чем было установлено, что движущиеся заряды во многих обстоятельствах были отрицательными. Положительный заряд, движущийся в направлении, противоположном отрицательному, часто производит идентичные эффекты; это затрудняет определение того, что движется или оба движутся.

Электронный вольт

Рис. 3. Типичная электронная пушка ускоряет электроны, используя разность потенциалов между двумя металлическими пластинами. Энергия электрона в электрон-вольтах численно равна напряжению между пластинами. Например, разность потенциалов 5000 В производит электроны 5000 эВ.

Энергия, приходящаяся на один электрон, очень мала в макроскопических ситуациях, подобных тому, что было в предыдущем примере – крошечная доля джоуля. Но в субмикроскопическом масштабе такая энергия, приходящаяся на частицу (электрон, протон или ион), может иметь большое значение.Например, даже крошечной доли джоуля может быть достаточно, чтобы эти частицы разрушили органические молекулы и повредили живые ткани. Частица может нанести ущерб при прямом столкновении или может создать вредные рентгеновские лучи, которые также могут нанести ущерб. Полезно иметь единицу энергии, относящуюся к субмикроскопическим эффектам. На рисунке 3 показана ситуация, связанная с определением такой единицы энергии. Электрон ускоряется между двумя заряженными металлическими пластинами, как это могло бы быть в телевизионной лампе или осциллографе старой модели.Электрону придается кинетическая энергия, которая позже преобразуется в другую форму – например, в свет в телевизионной трубке. (Обратите внимание, что спуск для электрона – это подъем для положительного заряда.) Поскольку энергия связана с напряжением соотношением ΔPE = q Δ V , мы можем рассматривать джоуль как кулон-вольт.

В субмикроскопическом масштабе удобнее определять единицу энергии, называемую электрон-вольт, (эВ), которая представляет собой энергию, передаваемую фундаментальному заряду, ускоренному через разность потенциалов в 1 В.{-19} \ text {J} \ end {array} \\ [/ latex]

Электрону, ускоренному через разность потенциалов 1 В, придается энергия 1 эВ. Отсюда следует, что электрону, ускоренному до 50 В, дается 50 эВ. Разность потенциалов 100 000 В (100 кВ) даст электрону энергию 100 000 эВ (100 кэВ) и так далее. Точно так же ион с двойным положительным зарядом, ускоренный до 100 В, получит энергию 200 эВ. Эти простые соотношения между ускоряющим напряжением и зарядами частиц делают электрон-вольт простой и удобной единицей энергии в таких обстоятельствах.

Выполнение подключений: блоки энергии

Электрон-вольт (эВ) – наиболее распространенная единица измерения энергии для субмикроскопических процессов. Это будет особенно заметно в главах, посвященных современной физике. Энергия настолько важна для столь многих предметов, что существует тенденция определять специальные единицы энергии для каждой основной темы. Есть, например, калории для пищевой энергии, киловатт-часы для электроэнергии и термы для энергии природного газа.

Электрон-вольт обычно используется в субмикроскопических процессах – химическая валентная энергия, молекулярная и ядерная энергия связи входят в число величин, часто выражаемых в электрон-вольтах.Например, для разрушения некоторых органических молекул требуется около 5 эВ энергии. Если протон ускоряется из состояния покоя через разность потенциалов 30 кВ, ему дается энергия 30 кэВ (30 000 эВ), и он может разрушить до 6000 этих молекул (30 000 эВ ÷ 5 эВ на молекулу = 6000 молекул. ). Энергия ядерного распада составляет порядка 1 МэВ (1000000 эВ) на событие и, таким образом, может нанести значительный биологический ущерб.

Сохранение энергии

Полная энергия системы сохраняется, если нет чистого добавления (или вычитания) работы или теплопередачи.Для консервативных сил, таких как электростатическая сила, закон сохранения энергии утверждает, что механическая энергия постоянна.

Механическая энергия – это сумма кинетической энергии и потенциальной энергии системы; то есть KE + PE = константа. Потеря ПЭ заряженной частицы становится увеличением ее КЭ. Здесь PE – электрическая потенциальная энергия. Сохранение энергии выражается в форме уравнения как KE + PE = постоянная или KE _i + PE _i = KE _f + PE _f , где i и f обозначают начальные и конечные условия.Как мы уже много раз выясняли, учет энергии может дать нам понимание и облегчить решение проблем.

Пример 3. Электрическая потенциальная энергия, преобразованная в кинетическую энергию

Рассчитайте конечную скорость свободного электрона, ускоренного из состояния покоя через разность потенциалов 100 В. (Предположим, что это числовое значение имеет точность до трех значащих цифр).

Стратегия

У нас есть система, в которой действуют только консервативные силы. Предполагая, что электрон ускоряется в вакууме, и пренебрегая гравитационной силой (мы проверим это предположение позже), вся электрическая потенциальная энергия преобразуется в кинетическую энергию.6 \ text {m / s} \ end {array} \\ [/ latex]

Обсуждение

Обратите внимание, что и заряд, и начальное напряжение отрицательны, как показано на рисунке 3. Из обсуждений в разделе «Электрический заряд и электрическое поле» мы знаем, что электростатические силы, действующие на мелкие частицы, обычно очень велики по сравнению с силой тяжести. Большая конечная скорость подтверждает, что гравитационная сила здесь действительно незначительна. Большая скорость также указывает на то, насколько легко ускорить электроны с помощью малых напряжений из-за их очень малой массы.В электронных пушках обычно используются напряжения, намного превышающие 100 В. Эти более высокие напряжения вызывают настолько большие скорости электронов, что необходимо учитывать релятивистские эффекты. Вот почему в этом примере рассматривается (точно) низкое напряжение.

Краткое содержание раздела

• Электрический потенциал – это потенциальная энергия на единицу заряда.
• Разность потенциалов между точками A и B, V _B – V _A , определяемая как изменение потенциальной энергии заряда q , перемещенного из A в B, равна изменению потенциальная энергия, деленная на заряд. Разность потенциалов обычно называется напряжением и обозначается символом Δ V : [латекс] \ Delta V = \ frac {\ Delta \ text {PE}} {q} \\ [/ латекс] и ΔPE = q Δ V .{\ text {-19}} \ text {J.} \ end {array} \\ [/ latex]
• Механическая энергия – это сумма кинетической энергии и потенциальной энергии системы, то есть KE + PE. Эта сумма постоянна.

Концептуальные вопросы

1. Напряжение – это обычное слово для обозначения разности потенциалов. Какой термин является более описательным, напряжение или разность потенциалов?
2. Если напряжение между двумя точками равно нулю, можно ли перемещать тестовый заряд между ними при нулевой работе сети? Обязательно ли это делать без применения силы? Объяснять.
3. Какая связь между напряжением и энергией? Точнее, какова взаимосвязь между разностью потенциалов и электрической потенциальной энергией?
4. Напряжение всегда измеряется между двумя точками. Почему?
5. Как связаны единицы вольт и электронвольт? Чем они отличаются?

Задачи и упражнения

1. Найдите отношение скоростей электрона и отрицательного иона водорода (тот, у которого есть дополнительный электрон), ускоренных одним и тем же напряжением, при условии, что конечные скорости нерелятивистские.Возьмем массу иона водорода 1,67 × 10 ⁻²⁷ кг.
2. В вакуумной трубке используется ускоряющее напряжение 40 кВ для ускорения электронов, ударов по медной пластине и получения рентгеновских лучей. С нерелятивистской точки зрения, какова максимальная скорость этих электронов?
3. Голое ядро ​​гелия имеет два положительных заряда и массу 6,64 × 10 ⁻²⁷ кг. (а) Вычислите его кинетическую энергию в джоулях при 2,00% скорости света. (б) Что это в электрон-вольтах? (c) Какое напряжение потребуется для получения этой энергии?
4. Комплексные концепции. Однозарядные ионы газа ускоряются из состояния покоя за счет напряжения 13,0 В. При какой температуре средняя кинетическая энергия молекул газа будет такой же, как у этих ионов?
5. Комплексные концепции. Считается, что температура около центра Солнца составляет 15 миллионов градусов Цельсия (1,5 × 10 ⁷ ºC). Через какое напряжение должен быть ускорен однозарядный ион, чтобы он имел такую ​​же энергию, как средняя кинетическая энергия ионов при этой температуре?
6. Комплексные концепции. (a) Какова средняя выходная мощность дефибриллятора сердца, который рассеивает 400 Дж энергии за 10,0 мс? (б) Учитывая высокую выходную мощность, почему дефибриллятор не вызывает серьезных ожогов?
7. Комплексные концепции. Молния ударяет в дерево, перемещая 20,0 Кл заряда через разность потенциалов 1,00 × 10 ² МВ. а) Какая энергия была рассеяна? б) Какую массу воды можно было поднять с 15ºC до точки кипения, а затем с помощью этой энергии вскипятить? (c) Обсудите ущерб, который может быть нанесен дереву из-за расширения кипящего пара.
8. Комплексные концепции. Подогреватель бутылочек на 12,0 В нагревает 50,0 г стекла, 2,50 × 10 ² г детской смеси и 2,00 × 10 ² г алюминия с 20,0 ° C до 90,0 ° C. (а) Насколько заряжен аккумулятор? (б) Сколько электронов течет в секунду, если для разогрева формулы требуется 5,00 мин? (Подсказка: предположите, что удельная теплоемкость детской смеси примерно такая же, как удельная теплоемкость воды.)
9. Комплексные концепции. В автомобиле с батарейным питанием используется 12.Система 0 В. Найдите заряд, который батареи должны быть в состоянии двигаться, чтобы разогнать 750-килограммовый автомобиль из состояния покоя до 25,0 м / с, заставить его подняться на холм высотой 2,00 × 10 ² м, а затем заставить его двигаться с постоянной скоростью 25,0 м / с. м / с путем приложения силы 5,00 × 10 ² Н в течение часа.
10. Комплексные концепции. Вероятность слияния значительно увеличивается, когда соответствующие ядра сближаются, но взаимное кулоновское отталкивание необходимо преодолевать. Это можно сделать, используя кинетическую энергию ионов высокотемпературного газа или ускоряя ядра друг к другу.(а) Вычислите потенциальную энергию двух однозарядных ядер, разделенных расстоянием 1,00 × 10 ⁻¹² м, найдя напряжение одного на таком расстоянии и умножив его на заряд другого. (б) При какой температуре атомы газа будут иметь среднюю кинетическую энергию, равную этой необходимой электрической потенциальной энергии?
11. Беспричинные результаты. (a) Найдите напряжение около металлической сферы диаметром 10,0 см, на которой имеется 8,00 C избыточного положительного заряда. б) Что неразумного в этом результате? (c) Какие допущения ответственны?
12. Создайте свою проблему. Рассмотрим аккумулятор, используемый для подачи энергии в сотовый телефон. Постройте задачу, в которой вы определяете энергию, которая должна быть предоставлена ​​аккумулятором, а затем вычисляете количество заряда, которое он должен иметь возможность перемещать, чтобы обеспечить эту энергию. Среди прочего следует учитывать потребность в энергии и напряжение батареи. Возможно, вам придется заглянуть в будущее, чтобы интерпретировать номинальные характеристики батареи в ампер-часах производителя как энергию в джоулях.

Глоссарий

электрический потенциал: потенциальная энергия на единицу заряда

разность потенциалов (или напряжение): изменение потенциальной энергии заряда, перемещенного из одной точки в другую, деленное на заряд; единицы разности потенциалов – джоули на кулон, известные как

вольт.

электрон-вольт: энергия, отдаваемая фундаментальному заряду, ускоренному через разность потенциалов в один вольт

механическая энергия: сумма кинетической энергии и потенциальной энергии системы; эта сумма является постоянной

Избранные решения проблем и упражнения

1.42,8

4. 1,00 × 10 ⁵ К

6. а) 4 × 10 ⁴ Вт; (б) Дефибриллятор не вызывает серьезных ожогов, потому что кожа хорошо проводит электричество при высоких напряжениях, подобных тем, которые используются в дефибрилляторах. Используемый гель способствует передаче энергии телу, а кожа не поглощает энергию, а пропускает ее к сердцу.

8. (а) 7,40 × 10 ³ C; (б) 1,54 × 10 ²⁰ электронов в секунду

9. 3.89 × 10 ⁶ С

11. (а) 1.44 × 10 ¹² В; (б) Это напряжение очень высокое. Сфера диаметром 10,0 см никогда не сможет поддерживать такое напряжение; он разрядился бы; (c) Заряд 8,00 C – это больше заряда, чем можно разумно накопить на сфере такого размера.

Заряд, ток и разница потенциалов

Обозначения схем – вы встречали эти обозначения схем в GCSE Physics.

Обычный ток течет по цепи от положительной (+) стороны ячейки к отрицательной (-).Однако электронов текут по цепи в противоположном направлении от отрицательной (-) стороны ячейки к положительной (+).

Заряд, ток и разница потенциалов

Заряд (Q) – заряд измеряется в кулонах (Кл).

• Один электрон несет заряд 1,6 x 10 ^-19 C.

Ток (I) – измеряется в амперах (А).

• Ток – это скорость потока заряда .Ток в 1 А означает, что 1 кулон заряда проходит через точку в цепи каждую секунду. (1 A = 1 C s ^-1 ) Ток в цепи измеряется с помощью амперметра, который включен последовательно с интересующим компонентом в цепи.

• I = ток в амперах, А
• DQ = заряд в кулонах, К
• Dt = время в секундах, с

Разность потенциалов (В) – измеряется в вольтах (В).

• Потенциальная разница – это работа, выполненная на единицу оплаты .Разность потенциалов в 1 В означает, что на один кулон заряда выполняется 1 джоуль работы. (1 В = 1 Дж C ^-1 ) Разность потенциалов в цепи измеряется с помощью вольтметра, который устанавливается параллельно с интересующим компонентом в цепи.

• В = разность потенциалов в вольтах, В
• Вт = выполненная работа или переданная энергия в джоулях, Дж
• Q = заряд в кулонах, Кл

Сопротивление (Вт) – это отношение разности потенциалов на компоненте к току, протекающему через него, измеряется в омах (Вт).

• R = сопротивление в Ом, Вт

• В = разность потенциалов в вольтах, В

• I = ток в амперах, А

Примеры;

Q1) Если все электроны несут заряд 1,6 x 10 ^-19 C, сколько электронов потребуется, чтобы получить общий заряд в один кулон?

Q2) Если ток 0.50 ампер протекает через цепь в течение 120 секунд. Сколько заряда будет передано в компонент в цепи?

Q3) Заряд в 4,0 кулонов был перемещен через разность потенциалов 24 вольт, сколько энергии было передано?

Q4) Разность потенциалов на компоненте составляет 12 В, а ток через него составляет 0,37 А. Каково сопротивление компонента?

Как рассчитать электрический заряд

Обновлено 17 сентября 2019 г.

Автор: S.Хуссейн Атер

Будь то статическое электричество, излучаемое меховой шубой, или электричество, от которого питаются телевизоры, вы можете узнать больше об электрическом заряде, поняв основную физику. Методы расчета заряда зависят от природы самого электричества, например, принципов распределения заряда по объектам. Эти принципы одинаковы, независимо от того, где вы находитесь во Вселенной, поэтому электрический заряд является фундаментальным свойством самой науки.

Формула электрического заряда

Существует множество способов вычисления электрического заряда для различных контекстов в физике и электротехнике.

Закон Кулона обычно используется при вычислении силы, создаваемой частицами, несущими электрический заряд, и является одним из наиболее распространенных уравнений электрического заряда, которые вы будете использовать. Электроны несут отдельные заряды -1,602 × 10 ^-19 кулонов (Кл), а протоны несут такое же количество, но в положительном направлении, 1.2}

, в котором k – постоянная k = 9,0 × 10 ⁹ Нм ² / C ² . Физики и инженеры иногда используют переменную e для обозначения заряда электрона.

Обратите внимание, что для зарядов противоположных знаков (плюс и минус) сила отрицательная и, следовательно, притягивающая между двумя зарядами. Для двух зарядов одного знака (плюс и плюс или минус и минус) сила отталкивающая. Чем больше заряды, тем сильнее сила притяжения или отталкивания между ними.

Электрический заряд и гравитация: сходство

Закон Кулона поразительно похож на закон Ньютона для силы тяжести F _G = G м ₁ m ₂ / r ² для гравитационной силы F _G , масс м ₁ и _{м 2 и гравитационной постоянной G = 6,674 × 10 ⁻¹¹ м ³ / кг с ² .Оба они измеряют разные силы, изменяются с большей массой или зарядом и зависят от радиуса между обоими объектами во второй степени. Несмотря на сходство, важно помнить, что гравитационные силы всегда притягивают, в то время как электрические силы могут быть притягивающими или отталкивающими.}

Вы должны также заметить, что электрическая сила обычно намного сильнее гравитации, исходя из различий в экспоненциальной мощности констант законов. Сходство между этими двумя законами является еще большим свидетельством симметрии и закономерностей среди общих законов Вселенной.

Сохранение электрического заряда

Если система остается изолированной (то есть без контакта с чем-либо еще вне ее), она будет сохранять заряд. Сохранение заряда означает, что общее количество электрического заряда (положительный заряд минус отрицательный) остается неизменным для системы. Сохранение заряда позволяет физикам и инженерам вычислять, сколько заряда перемещается между системами и их окружением.

Этот принцип позволяет ученым и инженерам создавать клетки Фарадея, в которых используются металлические экраны или покрытия для предотвращения утечки заряда.Клетки Фарадея или щиты Фарадея используют тенденцию электрического поля к перераспределению зарядов внутри материала, чтобы нейтрализовать действие поля и предотвратить повреждение или проникновение зарядов внутрь. Они используются в медицинском оборудовании, таком как аппараты магнитно-резонансной томографии, для предотвращения искажения данных, а также в защитном снаряжении для электриков и монтажников, работающих в опасных средах.

Вы можете рассчитать чистый поток начислений для объема пространства, вычислив общую сумму вводимых затрат и вычитая общую сумму оставленных начислений.Благодаря электронам и протонам, несущим заряд, заряженные частицы могут создаваться или разрушаться, чтобы уравновесить себя в соответствии с законом сохранения заряда.

Число электронов в заряде

Зная, что заряд электрона равен -1,602 · 10 ⁻¹⁹ Кл, заряд −8 · 10 ⁻¹⁸ Кл будет состоять из 50 электронов. Вы можете найти это, разделив количество электрического заряда на величину заряда отдельного электрона.

Расчет электрического заряда в цепях

Если вам известен электрический ток , , поток электрического заряда через объект, проходящий по цепи и продолжительность действия тока, вы можете рассчитать электрический заряд, используя уравнение для тока Q = Это , в котором Q – общий заряд, измеренный в кулонах, I – ток в амперах, а t – время приложения тока в секундах.Вы также можете использовать закон Ома ( В = IR ) для расчета тока по напряжению и сопротивлению.

Для цепи с напряжением 3 В и сопротивлением 5 Ом, приложенной в течение 10 секунд, соответствующий ток будет равен I = В / R = 3 В / 5 Ом = 0,6 А, а общий заряд будет Q = It = 0,6 A × 10 с = 6 C.

Если вам известна разность потенциалов ( В, ) в вольтах, приложенная к цепи, и работа ( Вт, ) в джоулях, выполненная за период, за который он применяется, заряд в кулонах, Q = Вт / В .

Формула электрического поля

••• Syed Hussain Ather

Электрическое поле , электрическая сила на единицу заряда, распространяется радиально наружу от положительных зарядов к отрицательным зарядам и может быть рассчитана с помощью E = F _E / q , где F _E – электрическая сила, а q – заряд, создающий электрическое поле. Учитывая, насколько фундаментальными являются поле и сила для вычислений в электричестве и магнетизме, электрический заряд можно определить как свойство вещества, которое заставляет частицу иметь силу в присутствии электрического поля.

Даже если чистый или общий заряд объекта равен нулю, электрические поля позволяют различным образом распределять заряды внутри объектов. Если внутри них есть распределения зарядов, которые приводят к ненулевому чистому заряду, эти объекты имеют поляризацию , а заряд, вызываемый этими поляризациями, известен как связанных зарядов .

Чистый заряд Вселенной

Хотя ученые не все согласны с тем, каков общий заряд Вселенной, они сделали обоснованные предположения и проверили гипотезы с помощью различных методов.Вы можете заметить, что гравитация является доминирующей силой во Вселенной в космологическом масштабе, и, поскольку электромагнитная сила намного сильнее гравитационной силы, если бы у Вселенной был чистый заряд (положительный или отрицательный), вы бы были возможность видеть доказательства этого на таких огромных расстояниях. Отсутствие этих доказательств привело исследователей к мысли, что Вселенная заряжена нейтрально.

Всегда ли Вселенная была нейтральной по заряду или как заряд Вселенной изменился после Большого взрыва, также являются вопросами, которые вызывают споры.Если бы у Вселенной был чистый заряд, то ученые могли бы измерить их тенденции и влияние на все силовые линии электрического поля таким образом, чтобы вместо того, чтобы соединять положительные заряды с отрицательными, они никогда не закончились бы. Отсутствие этого наблюдения также указывает на аргумент, что у Вселенной нет чистого заряда.

Расчет электрического потока с зарядом

••• Сайед Хуссейн Атер

Электрический поток через планарную (т. Е.плоский) площадь A электрического поля E – поле, умноженное на составляющую площади, перпендикулярную полю. Чтобы получить этот перпендикулярный компонент, вы используете косинус угла между полем и интересующей плоскостью в формуле для потока, представленный как Φ = EA cos ( θ ) , где θ – угол между линией, перпендикулярной площади, и направлением электрического поля.

Это уравнение, известное как закон Гаусса , также говорит вам, что для поверхностей, подобных этим, которые вы называете гауссовскими поверхностями , любой чистый заряд будет находиться на его поверхности плоскости, потому что было бы необходимо создать электрическое поле.

Поскольку это зависит от геометрии площади поверхности, используемой при расчете потока, она меняется в зависимости от формы. Для круглой области площадь потока A будет π_r_ ^{2 с r в качестве радиуса круга, или для криволинейной поверхности цилиндра площадь потока будет Ch , в которой C – это длина окружности круглой поверхности цилиндра, а h – высота цилиндра.}

Заряд и статическое электричество

Статическое электричество возникает, когда два объекта не находятся в электрическом равновесии (или электростатическом равновесии ), или когда существует чистый поток зарядов от одного объекта к другому.Когда материалы трутся друг о друга, они переносят заряды друг на друга. Эти виды электричества могут генерироваться при натирании носков о ковер или резинкой надутого воздушного шара о волосы. Шок переносит эти избыточные заряды обратно, чтобы восстановить состояние равновесия.

Электрические проводники

Для проводника (материал, передающий электричество), находящегося в электростатическом равновесии, электрическое поле внутри равно нулю, а общий заряд на его поверхности должен оставаться в электростатическом равновесии.Это потому, что, если бы было поле, электроны в проводнике перераспределялись бы или перестраивались в ответ на поле. Таким образом, они отменили бы любое поле в момент его создания.

Алюминий и медная проволока являются общими проводящими материалами, используемыми для передачи токов, также часто используются ионные проводники, которые представляют собой решения, в которых используются свободно плавающие ионы, позволяющие легко проходить заряду. Полупроводники , такие как микросхемы, которые позволяют компьютерам функционировать, также используют свободно циркулирующие электроны, но не так много, как проводники.Полупроводники, такие как кремний и германий, также требуют больше энергии для циркуляции зарядов и обычно имеют низкую проводимость. Напротив, изоляторы , такие как дерево, не позволяют заряду легко проходить через них.

При отсутствии поля внутри для гауссовой поверхности, лежащей непосредственно внутри поверхности проводника, поле должно быть везде нулевым, чтобы поток был равен нулю. Это означает, что внутри проводника нет чистого электрического заряда. Из этого вы можете сделать вывод, что для симметричных геометрических структур, таких как сферы, заряд равномерно распределяется по поверхности гауссовой поверхности.

Закон Гаусса в других ситуациях

Поскольку чистый заряд на поверхности должен оставаться в электростатическом равновесии, любое электрическое поле должно быть перпендикулярно поверхности проводника, чтобы материал мог передавать заряды. Закон Гаусса позволяет вычислить величину этого электрического поля и магнитного потока для проводника. Электрическое поле внутри проводника должно быть нулевым, а снаружи оно должно быть перпендикулярно поверхности.

Это означает, что для цилиндрического проводника с полем, излучаемым от стенок под перпендикулярным углом, полный поток равен просто 2_E__πr_ ² для электрического поля E и радиуса r круглой поверхности цилиндрического проводника.Вы также можете описать чистый заряд на поверхности, используя σ , плотность заряда на единицу площади, умноженную на площадь.

Расчет передаваемой энергии – Ток, напряжение и сопротивление – GCSE Physics (Single Science) Revision – Other

При заданном количестве перемещающегося электрического заряда количество передаваемой энергии увеличивается с увеличением разности потенциалов.

Вы можете вычислить передаваемую энергию, используя следующее уравнение:

переданная энергия = разность потенциалов × заряд

E = V × Q

где:

E – передаваемая энергия в джоулях, Дж

В – разность потенциалов в вольтах, В

Q – заряд в кулонах, C

Вопрос

Сколько энергии передается когда разность потенциалов 120 В, а заряд 2 Кл?

Показать ответ

Больше новостей