Генератор электромагнитных колебаний | |
Генератор электромагнитных колебаний представляет собой один из примеров автоколебательных систем. |
|
Получение незатухающих колебаний в контуре. |
|
Если конденсатор колебательного контура заряжен, то в контуре возникают затухающие колебания. Электрическая энергия W переходит во внутреннюю энергию:. |
|
Пополнять энергию колебательного контура можно, подзаряжая конденсатор. Для этого контур подключают к источнику тока. Контур подключается к источнику тока только в те интервалы времени, когда пластина конденсатора, присоединенная к положительному полюсу источника, заряжена положительно. Если источник постоянного тока будет все время подключен к контуру, то в энергия поступает в контур, а следующую возвращается в источник, т. | |
Частота колебаний, возникающих в контуре, определяется его параметрами (индуктивностью и емкостью), а амплитуда колебаний – напряжением на источнике (его эдс). | |
Незатухающие колебания установятся в том случае, если контур будет подключаться к источнику только в первую половину периода. Для выполнения такого условия ключ должен замыкать и размыкать цепь с частотой, соответствующей частоте электромагнитных колебаний контура. Однако механический ключ инертен. | |
Безынерционным ключом является транзистор. Транзистор обеспечивает поступление энергии к колебательному контуру, если напряжение на электронном переходе меняется синфазно с напряжением на контуре. | |
Генератор высокочастотных колебаний на транзисторе |
|
Первая четверть периода. Вторая четверть периода. Ток в контуре убывает. Верхняя пластина заряжается отрицательно. В катушке связи ток меняет направление. На базе положительный потенциал. Переход коллектор—база обратный. Тока в цепи нет (ключ разомкнут). | |
Третья четверть периода. Конденсатор разряжается. Ток растет до максимального значения, направлен от нижней пластины к верхней. В катушке связи ток направлен так, что база получает положительный потенциал. Переход база — коллектор обратный. Четвертая четверть периода. Ток в контуре, не меняя направления, убывает. Верхняя пластина заряжается положительно. В катушке связи ток меняется по направлению. Заряд на базе отрицательный. Переходы база — коллектор и эмиттер — база прямые. Энергия поступает от источника в колебательный контур (ключ замкнут). Таким образом, происходят незатухающие электромагнитные колебания за счет поступления энергии от источника в колебательный контур в течение 1/2 Т. | |
Генератор незатухающих колебаний
Особое внимание в 11-ом классе уделяю изучению принципа работы генератора незатухающих колебаний. Предлагаю его тогда, когда изучены: Колебательный контур; Переменный электрический ток; Генерирование электрической энергии; Трансформатор; Производство передача и использование электроэнергии.
Это даёт возможность изучать генератор:
- После того как ученики накопили все знания о колебаниях вообще и об электромагнитных колебаниях в частности.

- Через 2 урока после того, как мы изучим генератор незатухающих колебаний, мы изучаем тему: Электромагнитные волны. На этом уроке, когда рассмотрим опыты Герца, открытый колебательный контур, естественно звучит вопрос: Какое устройство нужно использовать, чтобы незатухающие электромагнитные волны излучать в пространство. Обязательно найдутся ученики, которые предложат недавно изученный генератор незатухающих колебаний.
Тогда на экране появится схема генератора:
и вопрос: что нужно к нему добавить, чтобы излучать электромагнитные волны в пространство? Ответ: открытый колебательный контур. Добавим:
и объясняем принцип действия радиотелеграфа.
На уроке: Принцип радиосвязи, ставим проблему: В какую часть генератора надо ввести токи звуковой частоты, чтобы они изменили амплитуду колебаний тока. Обязательно найдутся ученики, которые сообразят, что включить моделирующее устройство надо в анодную цепь.
Генератор незатухающих колебаний.
План урока:
Повторение пройденного материала. Фронтально. Основная цель опроса: закрепление пройденного материала и подготовка к изучению нового материал.
- Какие колебания называются свободными? Вынужденными?
- Назовите устройства, с помощью которых можно получить свободные и вынужденные электромагнитные колебания.
- От чего зависит частота свободных и вынужденных электромагнитных колебаний.
- Где применяются вынужденные электромагнитные колебания.
- Что такое трансформация тока?
- Какое явление применяется в работе трансформатора?
- Для какого тока возможна трансформация?
- Какие параметры тока изменяются при трансформации?
- От чего зависит коэффициент трансформации?
- Где применяют трансформаторы?
Разбор нового материала с применением презентации:
1. Постановка задачи: получить незатухающие электромагнитные колебания любой частоты.
Постановка задачи: получить незатухающие электромагнитные колебания любой частоты.
2. Для решения этой задачи нужно применить автоколебательную систему. Вспомнить основные признаки этой системы: наличие колебательной системы, в которой могут возникать свободные колебания; источника энергии для восполнения потерь; обратной связи, которая регулирует подачу энергии в колебательную систему в такт колебаний.
3. Установить составные части генератора незатухающих колебаний:
- Колебательный контур – система, создающая свободные колебания;
- Источник тока – подключаем к колебательному контуру (+ к К.К.) .
- Клапан, который будет пропускать, или не пропускать электрический ток внутрь колебательного контура – 3-х электродная электронная лампа. (Повторить принцип её действия)
- Обратная связь, которая будет руководить процессом так, чтобы в такт колебаниям открывать или закрывать клапан (3-х электродную электронную лампу) – её роль играет катушка индуктивно связанная с катушкой колебательного контура.
 Точно так же, как в трансформаторе индуктивно связанные две катушки, только для лучшей связи эти катушки чаще всего «садят» на один сердечник.
Точно так же, как в трансформаторе индуктивно связанные две катушки, только для лучшей связи эти катушки чаще всего «садят» на один сердечник.
4. Принцип действия генератора рассматриваем по половинам периодов.
- половина периода: Когда лампа пришла в рабочее состояние и может пропускать ток, ключ замыкают. Постоянный ток идёт по анодной цепи и заряжает конденсатор (нижнюю обкладку – положительно). Когда конденсатор зарядится до максимального заряда, ток прекращается и колебательный контур предоставлен самому себе. Конденсатор начинает разряжаться, через катушку L течёт переменный ток: растущий в периода и убывающий во периода. Он создаёт переменное магнитное поле, направление которого определяем по правилу буравчика. Такое же магнитное поле возникает и в катушке L1, которая индуктивно связана с катушкой колебательного контура. В катушке L1 возникает индукционный ток, направленный к сетке лампы. На сетке накапливается положительный заряд, лампа открыта, ток через неё идёт, в колебательном контуре совпадает по направлению с током перезарядки и восполняет все потери энергии в колебательном контуре.
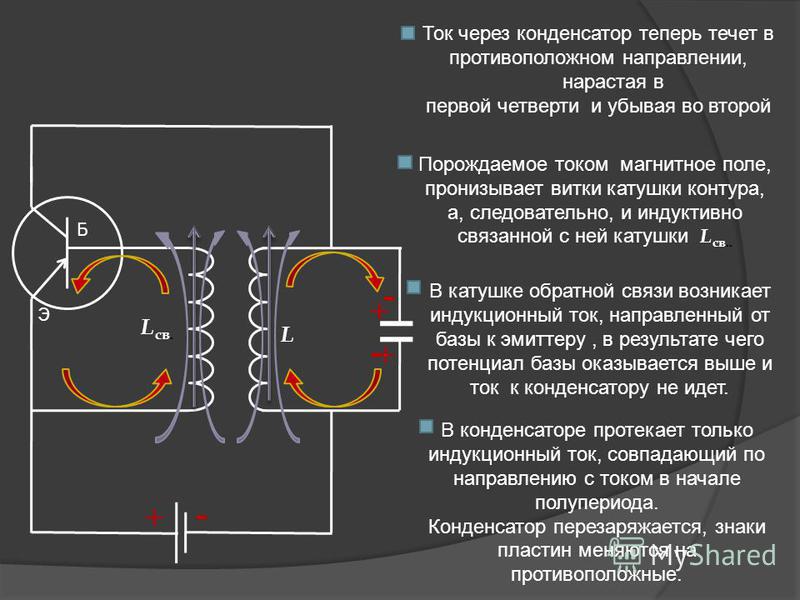
- 2-ая половина периода: К началу второй половины периода, конденсатор перезарядился. Теперь его верхняя обкладка заряжена положительно и в колебательном контуре ток разрядки течёт в противоположном направлении. Магнитное поле в катушках L и L1 направлено вниз, и индукционный ток идёт от сетки. Сетка заряжается отрицательно, лампа заперта, ток через неё не идёт и колебательный контур предоставлен самому себе. В нём идёт 2-ая половина периода, происходит расход энергии на работу против сопротивления. Эта утечка энергии восстановится в течение 1-ой половины следующего периода.
5. После устного разбора, ученики под руководством учителя перечерчивают чертежи в тетради и под диктовку записывают подробное пояснение.
На следующем уроке:
После подробного повторения и закрепления изученного лампового генератора, я рассказываю обо всех отрицательных их качествах и о том, что только в некоторых отраслях техники ещё применяют такие генераторы.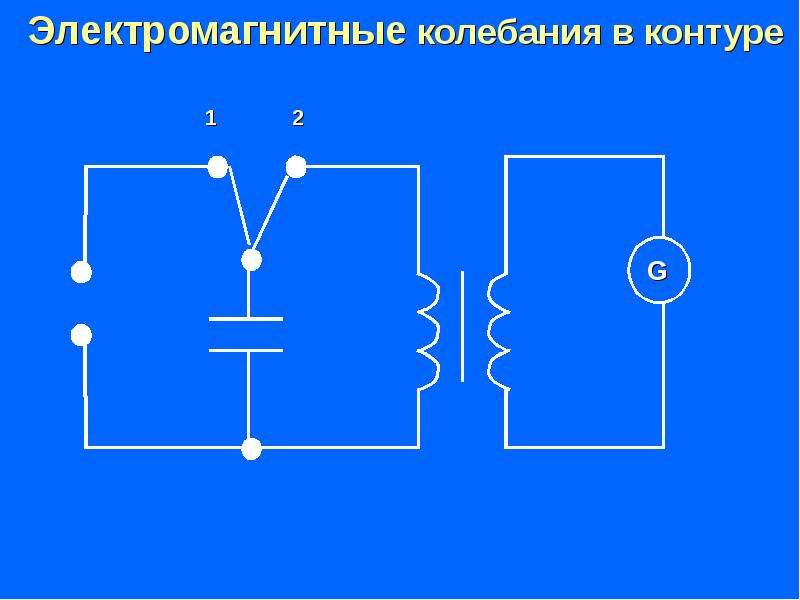 В радио и телевидении применяют транзисторные генераторы, демонстрирую слайд 15 из презентации и кратко поясняю сущность его работы и подробно преимущества.
В радио и телевидении применяют транзисторные генераторы, демонстрирую слайд 15 из презентации и кратко поясняю сущность его работы и подробно преимущества.
Презентация.
Генератор незатухающих электромагнитных колебаний
После однократной зарядки конденсатора в колебательном контуре возникают гармонические колебания, частота колебаний определяется параметрами контура. Электромагнитные колебания в любом реальном контуре быстро затухают из-за потерь энергии на нагревание проводок и излучение электромагнитных волн. Для поддержания незатухающих электромагнитных колебаний в контуре необходимо пополнять запасы энергии в нем. Это можно сделать, периодически подключая конденсатор контура к источнику постоянного тока. Трудность заключается в том, что электрические колебания в контуре происходят с частотой сотни тысяч или миллионы герц. С такой частотой конденсатор нужно подключать к источнику постоянного тока и отключать от него; при этом согласуя моменты подключений обкладок конденсатора с моментами приобретения ими заряда, совпадающими по знаку со знаками полюсов подключаемого источника тока.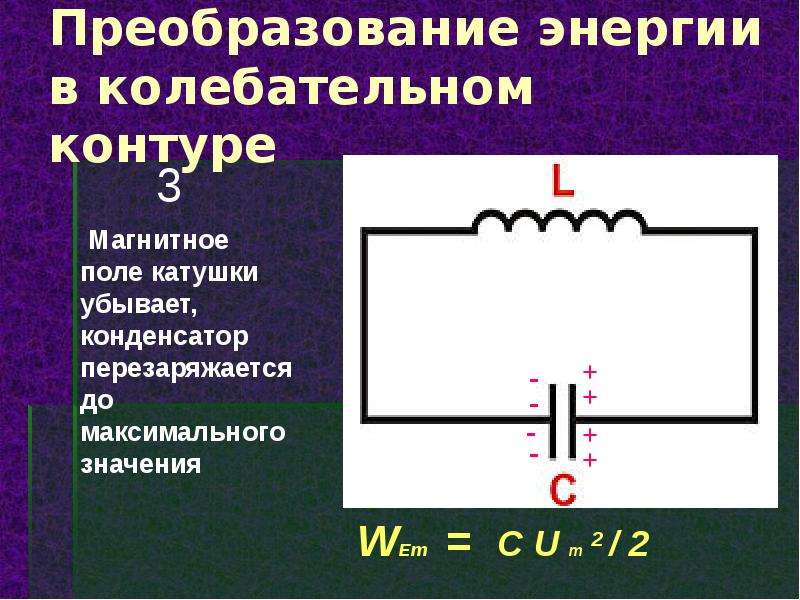
В качестве быстродействующего «ключа» для получения незатухающих высокочастотных колебаний может использоваться полупроводниковый транзистор. Через транзистор (рис. 232) конденсатор колебательного контура соединяется с источником постоянного тока. Пока на базу транзистора не подается управляющий сигнал, ток через него не проходит, конденсатор отключен от источника постоянного тока. При подаче управляющего сигнала на базу через транзистор протекает электрический ток и конденсатор колебательного контура заряжается от источника постоянного тока.
Для согласования моментов подключения колебательного контура к источнику постоянного тока с соответствующими моментами изменения напряжения на конденсаторе используется принцип обратной связи.
При зарядке и разрядке конденсатора колебательного контура изменения силы тока в катушке контура вызывают изменения магнитного поля вокруг нее. При этом происходят изменения магнитного потока и возникает ЭДС индукции во второй катушке называемой катушкой обратной связи.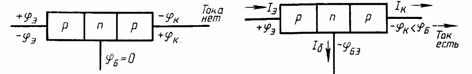 Один конец катушки обратной связи соединен с эмиттером транзистора, второй через конденсатор С — с его базой. Катушка обратной связи включена таким образом, что при увеличении силы тока в цепи коллектора на базу подается напряжение, отпирающее транзистор;
Один конец катушки обратной связи соединен с эмиттером транзистора, второй через конденсатор С — с его базой. Катушка обратной связи включена таким образом, что при увеличении силы тока в цепи коллектора на базу подается напряжение, отпирающее транзистор;
при уменьшении коллекторного тока — напряжение, запирающее транзистор. Такой тип связи называется положительной обратной связью.
Резистор в цепи базы транзистора задает начальные значения силы тока базы и коллектора при отсутствии переменного напряжения на концах катушки связи Задание начального тока через транзистор позволяет усиливать как положительные, так и отрицательные сигналы, поступающие на вход транзистора.
Если конденсатор колебательного контура имеет в начальный момент небольшой заряд и разряжается через катушку то в контуре возникают свободные электрические колебания малой амплитуды. Эти колебания через цепь обратной связи управляют коллекторным током транзистора, конденсатор колебательного контура через транзистор периодически получает дополнительный электрический заряд. При этом энергия электрического поля в конденсаторе увеличивается, растет амплитуда колебаний напряжения на конденсаторе колебательного контура.
При этом энергия электрического поля в конденсаторе увеличивается, растет амплитуда колебаний напряжения на конденсаторе колебательного контура.
Однако увеличение амплитуды колебаний напряжения в электрическом контуре не продолжается беспредельно. Объясняется это нелинейной зависимостью напряжения на выходе транзистора от напряжения на его входе. При возрастании напряжения между базой и эмиттером сила тока через транзистор увеличивается, однако это возрастание с увеличением напряжения между базой и эмиттером становится все меньше. При некотором значении амплитуды колебаний напряжения между базой и эмиттером возрастание амплитуды коллекторного тока прекращается. При этом потери энергии в колебательном контуре за период компенсируются поступлением энергии в контур от источника тока.
Рассмотренный генератор незатухающих электромагнитных колебаний является примером автоколебательной системы. Автоколебательной называется система, состоящая из элемента, в котором могут происходить свободные колебания источника энергии, элемента, управляющего поступлением энергии от источника к колебательной системе, и устройства, обеспечивающего положительную обратную связь колебательной системы с управляющим элементом.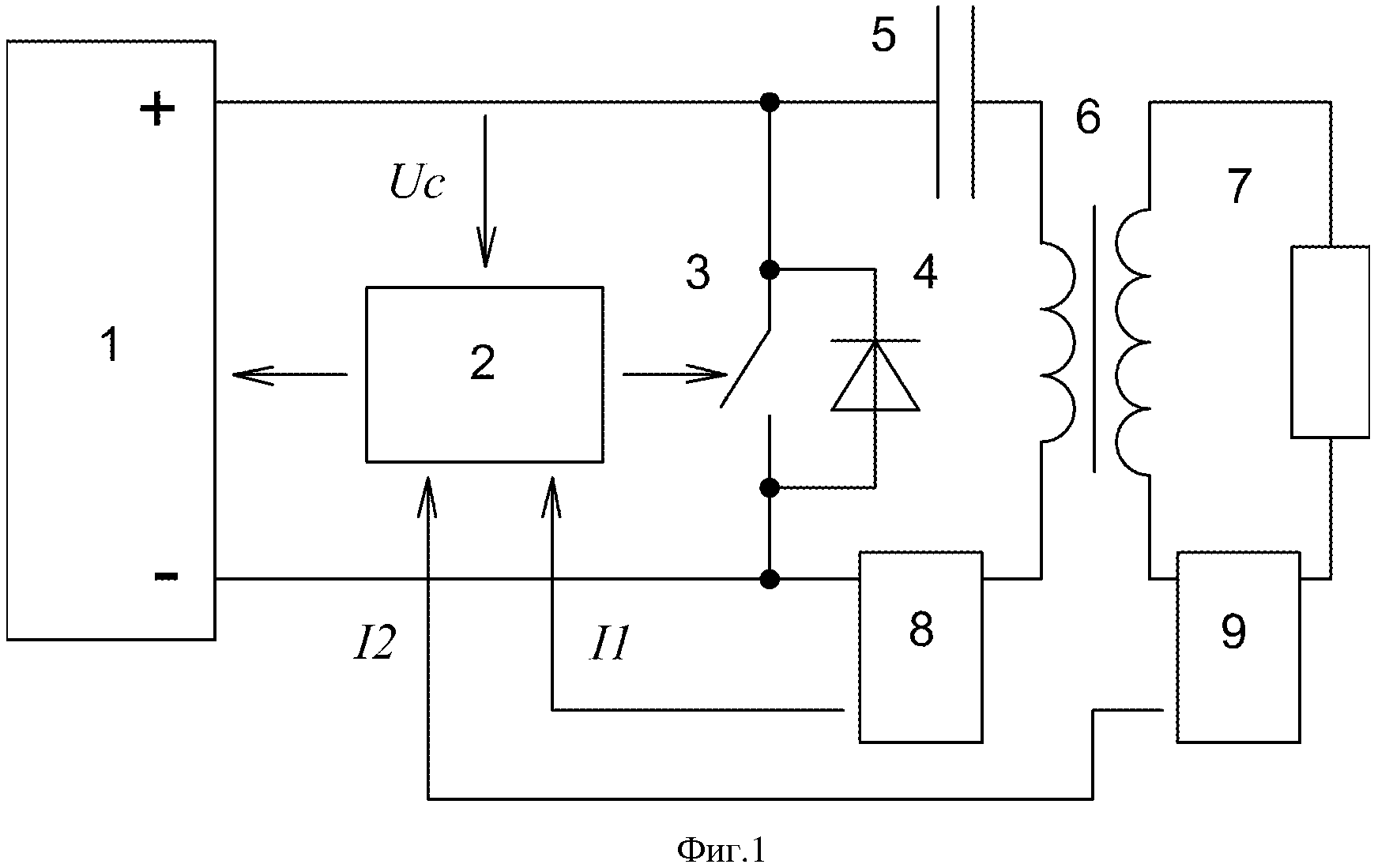 Особенностью автоколебательной системы является поддержание колебаний постоянной амплитуды за счет автоматического пополнения энергии в колебательной системе от внутреннего источника.
Особенностью автоколебательной системы является поддержание колебаний постоянной амплитуды за счет автоматического пополнения энергии в колебательной системе от внутреннего источника.
В транзисторном генераторе элементом, в котором могут происходить свободные колебания, является электрический контур; источником энергии для поддержания незатухающих колебаний может быть гальваническая батарея, аккумулятор или другой источник постоянного тока.
Управляющим элементом в автогенераторе является транзистор, обратная связь осуществляется с помощью катушки индуктивно связанной с катушкой электрического колебательного контура.
Известно, что в реальном колебательном контуре, состоящим из замкнутого друг на друга конденсатора и катушки индуктивности всегда присутствует активное сопротивление. Возбуждённые в контуре электромагнитные колебания быстро затухают из-за выделения энергии на нагревание витков катушки индуктивности. Для создания незатухающих колебаний используется генератор, главной деталью которого является трёхэлектродная электронная лампа.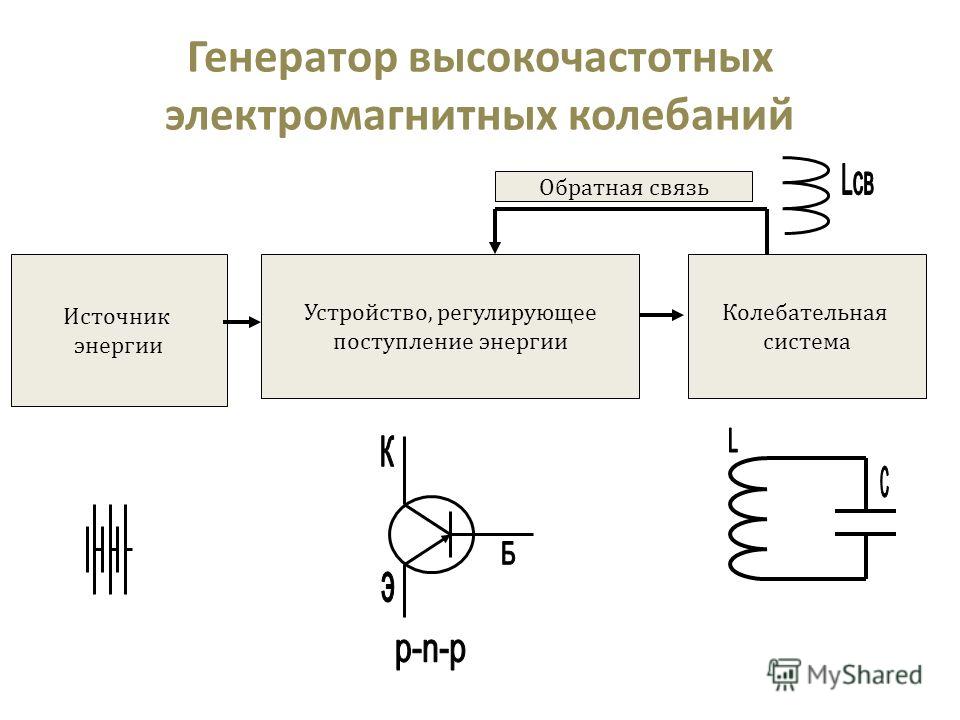 Генератор электромагнитных колебаний представляет собой электронную автоколебательную систему.
Генератор электромагнитных колебаний представляет собой электронную автоколебательную систему.
Схема генератора изображена на рис. 33
В состав генератора входят источник энергии (анодная батарея с ЭДС = Еа), колебательный контур, состоящий из конденсатора ёмкостью С и катушки индуктивности L1 – это электронный осциллятор, где возбуждаются и поддерживаются незатухающими электромагнитные колебания, а также механизм обратной связи, состоящий из вакуумного триода и катушки обратной связи с индуктивностью L2.
Рассмотрим принцип действия генератора.
На рис.34 изображён железный сердечник на который надеты катушка индуктивности колебательного контура L1 и катушка обратной связи L2. При замыкании ключа К в анодной цепи возникает анодный ток, возрастающий медленно из-за явления самоиндукции в катушке обратной связи, через которую анодный ток проходит. Возрастающий анодный ток создаёт в железном сердечнике возрастающее магнитное поле.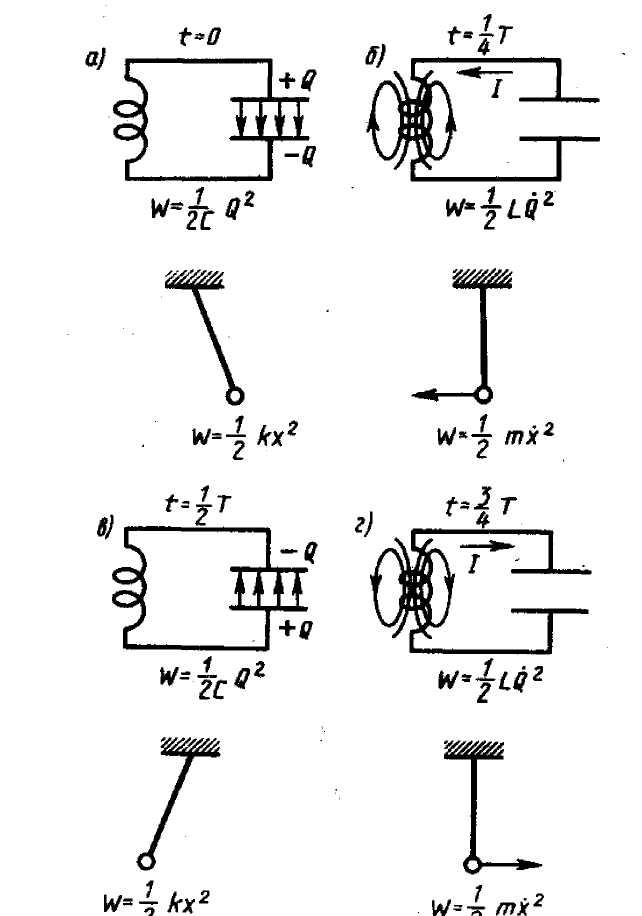 Возрастающий магнитный поток в сердечнике возбуждает ЭДС индукции в катушке колебательного контура, и в колебательном контуре возникнет индукционный ток. Используя правило Ленца, нетрудно убедиться, что этот индукционный ток направлен таким образом, что положительным зарядом, а, следовательно, и положительным потенциалом заряжается верхняя пластина конденсатора, в то время как нижняя пластина заряжается отрицательно. При этом растёт потенциал сетки (такой ж как и на верхней пластине конденсатора). Это приводит к дальнейшему росту анодного тока.
Возрастающий магнитный поток в сердечнике возбуждает ЭДС индукции в катушке колебательного контура, и в колебательном контуре возникнет индукционный ток. Используя правило Ленца, нетрудно убедиться, что этот индукционный ток направлен таким образом, что положительным зарядом, а, следовательно, и положительным потенциалом заряжается верхняя пластина конденсатора, в то время как нижняя пластина заряжается отрицательно. При этом растёт потенциал сетки (такой ж как и на верхней пластине конденсатора). Это приводит к дальнейшему росту анодного тока.
Когда анодный ток достигнет насыщения, конденсатор окажется максимально заряженным, магнитный поток в сердечнике достиг максимального значения, ЭДС индукции стала равным нулю. Теперь заряженный конденсатор начинает разряжаться на катушку индуктивности, и ток в контуре поменяет направление. Это приводит к уменьшению потенциала сетки, а, следовательно, к уменьшению анодного тока и величины магнитного потока в сердечнике. В этом случае индукционный ток поменяет своё направление, которое теперь совпадает с направлением тока разрядки конденсатора. Когда конденсатор полностью разрядится, ток в контуре достигнет максимального значения и начнёт уменьшаться. Потенциал сетки становится отрицательным и убывает до значения запирающего напряжения на сетке. Ток в контуре и анодной цепи убывает и достигает нуля в тот момент, когда триод заперт. При этом конденсатор оказывается заряженным, но при этом заряд и потенциал его пластин поменяли знаки.
Когда конденсатор полностью разрядится, ток в контуре достигнет максимального значения и начнёт уменьшаться. Потенциал сетки становится отрицательным и убывает до значения запирающего напряжения на сетке. Ток в контуре и анодной цепи убывает и достигает нуля в тот момент, когда триод заперт. При этом конденсатор оказывается заряженным, но при этом заряд и потенциал его пластин поменяли знаки.
Теперь конденсатор контура начнёт разряжаться на катушку индуктивности, ток в контуре будет возрастать, а вместе с ним возрастёт потенциал сетки, что приведёт к увеличению анодного тока и возникновению в контуре индукционного тока, по направлению совпадающего с током разрядки конденсатора.
Далее все описанные выше процессы будут периодически повторяться. Тепловые потери в контуре на активном сопротивлении катушки индуктивности компенсируются индукционными токами, возникающими в контуре при изменении анодного тока за счёт энергии анодной батареи.
Итак, колебания в колебательном контуре возбуждаются и поддерживаются периодически меняющимся по величине анодным током. Изменение анодного тока в свою очередь управляет колебаниями в колебательном контуре через периодически меняющийся потенциал сетки триода.
Изменение анодного тока в свою очередь управляет колебаниями в колебательном контуре через периодически меняющийся потенциал сетки триода.
Из всего вышесказанного следует, что колебания тока и напряжения в колебательном контуре, а также изменение анодного тока происходят с одинаковой частотой, собственной частотой колебательного контура и равной
На рис.35 изображено графическое представление работы триода с помощью его динамической сеточной характеристики.
Здесь напряжение на сетке, равное напряжению на конденсаторе колебательного контура меняется как показано на рис, где ось времени вертикальна и направлена вниз. Справа показан примерный характер зависимости анодного тока от времени. Так работает генератор незатухающих колебаний по схеме с колебательным контуром в цепи сетки.
Применяется также схема генератора с колебательным контуром в цепи анода. Здесь колебательный контур и катушка обратной связи меняются местами.
Принцип действия такого генератора аналогичен принципу действия генератора по схеме с колебательным контуром в цепи сетки.
Следует заметить, что направление обмоток катушек контура и обратной связи должно быть одинаковое. Если же оно будет встречным, то в момент замыкания ключа К индукционный ток будет такого направления, при котором потенциал сетки будет отрицательным, что скомпенсирует рост тока в момент замыкания. Индукционного тока в контуре не возникнет и генерации не будет.
Глава II. Свойства полупроводников. Полупроводниковые приборы.
Дата добавления: 2015-05-06 ; Просмотров: 5390 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Ламповый генератор- это радиотехнический прибор, служащий для получения незатухающих электромагнитных колебаний.
Основной частью лампового генератора является колебательный контур, т.е. электрическая цепь, состоящая из индуктивности и ёмкости (рис. 1).
Если колебательному контуру сообщить запас энергии, например, зарядить конденсатор от батареи, а затем предоставить контур самому себе, то в нём возникнут электромагнитные колебания.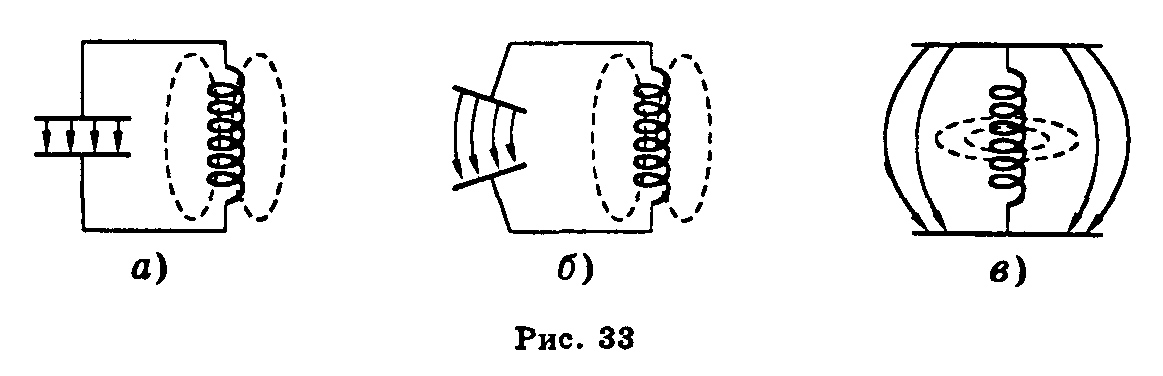
Пусть в некоторый момент конденсатор был заряжен до какой- то разности потенциалов, а затем источник напряжения был отключён. Конденсатор начнёт разряжаться через катушку индуктивности. Если вместо катушки индуктивности взять короткий провод, обладающий малой индуктивностью, которой мы можем пренебречь, то конденсатор разрядится периодически (рис. 2). При наличии индуктивности процесс будет происходить иначе. Причиной тому является ЭДС самоиндукции, которая возникает в катушке индуктивности при прохождении через неё тока изменяющейся величины.
Если при разрядке конденсатора ЭДС самоиндукции препятствует быстрому нарастанию тока, то, когда разность потенциалов на конденсаторе станет равной нулю, и ток уменьшается, она поддержит спадающий ток, и произойдёт перезарядка конденсатора.
Затем разряд конденсатора начнётся снова, только в обратном направлении и т.д. Таким образом, в цепи состоящей из индуктивности и ёмкости, возникнут колебания: периодические, по гармоническому закону, будут изменяться напряжение и величина заряда на конденсаторе, магнитный поток в катушке, энергия электрического поля в конденсаторе будет переходить в энергию магнитного поля в катушке и обратно.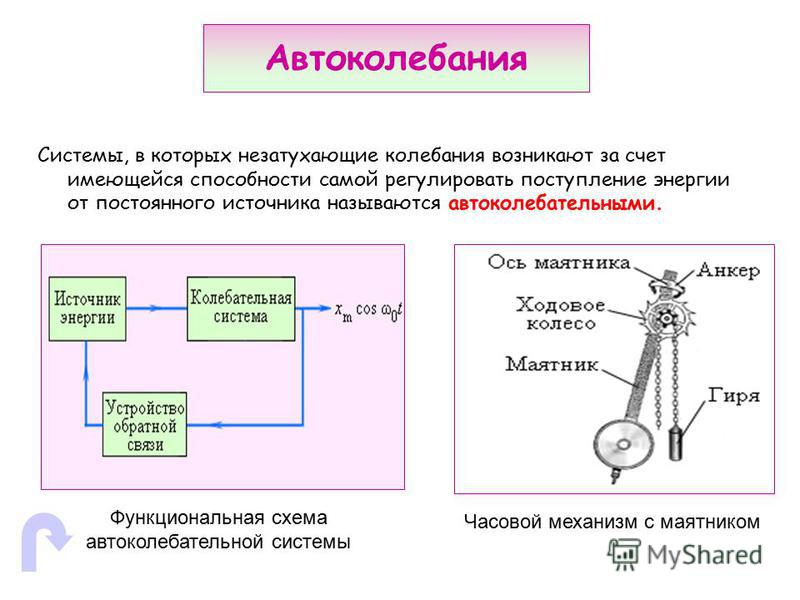 Эти колебания подобны колебаниям свободного математического маятника.
Эти колебания подобны колебаниям свободного математического маятника.
Частота (или период) электромагнитных колебаний в контуре полностью определяется его параметрами L, C и R.
Теория даёт для периода колебаний в контуре, омическое сопротивление которого ничтожно мало, формулу
Т = 2π (формула Томсона)
Свободные колебания, определяющиеся свойствами контура, называются собственными колебаниями контура (рис. 3) являются всегда затухающими из- за неизбежной потери энергии, которая тратится в основном на выделение тепла.
Рассмотрим колебательный процесс в этом контуре. В начальный момент времени при t = 0 заряд на обкладках конденсатора qm. Замыкание контура ключом К приводит к возникновению тока I, который вызовет в катушке ЭДС самоиндукции: .
Используя II закон Кирхгофа для мгновенных значений ЭДС и напряжений, можно записат
Ec = UR + UC
-L =UR + UC UC = ; UR = IR
L + R + q =0 (1) I = ; =
Уравнение (1) – это дифференциальное уравнение затухающих колебаний в контуре.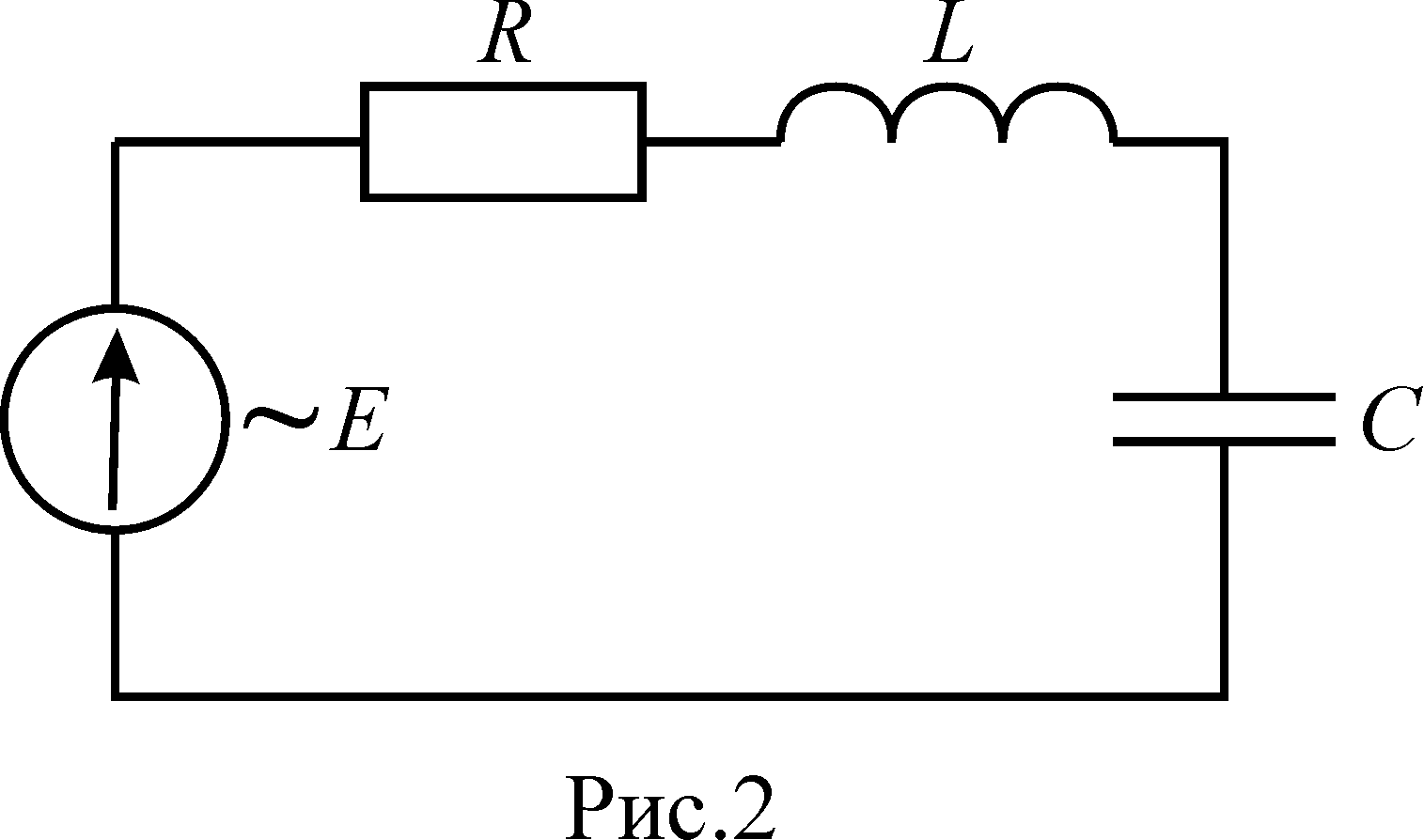
Решение этого уравнения имеет вид
где b – коэффициент затухания
β =
w – угловая частота затухающих колебаний
ω=
w – собственная угловая частота колебаний в контуре
ω=
ω =
Период колебаний определяется по формуле
T =
T =
Графически зависимость q от времени t можно выразить так (рис.4)
Из графика видно, что чем больше R , тем быстрее колебания затухают.
Так как омическое сопротивление никогда не может равняться нулю, то сам по себе контур не может служить источником непрерывных электромагнитных колебаний. Для получения незатухающих колебаний нужно пополнять энергию контура за счёт какого- либо внешнего источника. Причём это необходимо делать в такт колебаниям, иначе их можно совсем погасить
Современная радиотехника для получения незатухающих колебаний широко применяет ламповые генераторы. Одна из возможных схем лампового генератора представлена на (рис. 5).
Главные составные части его: электронная лампа, колебательный контур, включенный в данном случае в анодную цепь лампы, и источник напряжения. Колебательный контур получает энергию от батареи. Подача энергии от батареи регулируется электронной лампой. Это происходит следующим образом: в цепь сетки включена катушка Ls, которая индуктивно связана с катушкой L колебательного контура. Изменение силы тока в колебательном контуре , создаёт в катушке Ls ЭДС индукции, и между сеткой и катодом лампы возникает переменное напряжение, которое управляет анодным током. Изменение этого напряжения происходит с частотой собственных колебаний контура. В течении половины периода потенциал на сетке положителен, и лампа открыта. Прохождение тока через лампу создаёт условия замыкания колебательного контура с анодной батареей и тем самым пополняется запас энергии контура за счёт анодной батареи. Когда отрицательный потенциал на сетке запирает лампу, эта цепь разрывается, а чтобы колебания в контуре не затухали, необходимо, чтобы значение напряжения на сетке лампы всегда содействовало ходу изменения напряжения и токов в колебательном контуре.
Соединение контура с анодной батареей через лампу производится в промежутке времени, когда знаки зарядов на пластинах конденсатора совпадают с полярностью анодной батареи. Когда же они меняются на противоположные, ток в лампе должен прекратиться. Описанный процесс в радиотехнике называется обратной связью, а катушка Ls – катушкой обратной связи. Существуют ламповые генераторы и других конструкций. С их помощью можно получить электромагнитные колебания самых разнообразных частот и длин волн: от высоких n=10 9 Гц, l=30 см, до весьма низких n и больших l. Это обуславливает широкое применение ламповых генераторов в технике.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 9008 – | 7249 – или читать все.
Автоколебания генератор на транзисторе план. Затухающие электрические колебания. Автоколебания. Генератор незатухающих колебаний(на транзисторе). Генераторы на полевых транзисторах
Свободные электромагнитные колебания в реальном колебательном контуре всегда затухающие. Для того чтобы они были незатухающими, нужно создать устройство, с помощью которого компенсировались бы потери энергии при каждом полном колебании в контуре. Широко применимы так называемые автоколебания – незатухающие колебания, поддерживаемые в системе за счет постоянного внешнего источника энергии, причем сама система управляет им, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени.
Любая автоколебательная система состоит из следующих четырех частей (рис. 1): 1) колебательная система; 2) источник энергии, за счет которого компенсируются потери; 3) клапан – некоторый элемент, регулирующий поступление энергии в колебательную систему определенными порциями в нужный момент; 4) обратная связь – управление работой клапана за счет процессов в самой колебательной системе.
Генератор на транзисторе – пример автоколебательной системы. На рисунке 2 приведена упрощенная схема такого генератора, в котором роль “клапана” играет транзистор. Колебательный контур подключен к источнику тока последовательно с транзистором. Эмиттерный переход транзистора через катушку L св индуктивно связан с колебательным контуром. Эту катушку называют катушкой обратной связи.
При замыкании цепи через транзистор проходит импульс тока, который заряжает конденсатор С колебательного контура, в результате чего в контуре возникают свободные электромагнитные колебания малой амплитуды. Ток, протекающий по контурной катушке L , индуцирует на концах катушки обратной связи переменное напряжение. Под действием этого напряжения электрическое поле эмиттерного перехода периодически то усиливается, то ослабляется, а транзистор то открывается, то запирается. В те промежутки времени, когда транзистор открыт, через него проходят импульсы тока. Если катушка L св подключена правильно (положительная обратная связь), то частота импульсов тока совпадает с частотой колебаний, возникших в контуре, и импульсы тока приходят в контур в те моменты, когда конденсатор заряжается (когда верхняя пластина конденсатора заряжена положительно). Поэтому импульсы тока, проходящие через транзистор, подзаряжают конденсатор и пополняют энергию контура, и колебания в контуре не затухают.
Если при положительной обратной связи медленно увеличивать расстояние между катушками L св и L , то с помощью осциллографа можно обнаружить, что амплитуда автоколебаний уменьшается, и автоколебания могут прекратиться. Это значит, что при слабой обратной связи энергия, поступающая в контур, меньше энергии, необратимо преобразуемой во внутреннюю. Таким образом, обратная связь должна быть такой, чтобы: 1) напряжение на эмиттерном переходе изменялось синфазно с напряжением на конденсаторе контура – это фазовое условие самовозбуждения генератора; 2) обратная связь обеспечивала бы поступление в контур столько энергии, сколько ее необходимо для компенсации потерь энергии в контуре – это амплитудное условие самовозбуждения.
Частота автоколебаний равна частоте свободных колебаний в контуре и зависит от его параметров.
Уменьшая L и С , можно получить высокочастотные незатухающие колебания, используемые в радиотехнике.
Амплитуда установившихся автоколебаний, как показывает опыт, не зависит от начальных условий и определяется параметрами автоколебательной системы – напряжением источника, расстоянием между L св и L , сопротивлением контура.
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. – Мн.: Адукацыя i выхаванне, 2004. – C. 394-395.
Автоколеба́ния – незатухающие колебания в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, то есть непериодического внешнего воздействия. Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы. Термин автоколебания в русскоязычную терминологию введён А. А. Андроновым в 1928 году.
Примерами автоколебаний могут служить: незатухающие колебания маятника часов за счёт постоянного действия тяжести заводной гири; колебания скрипичной струны под воздействием равномерно движущегося смычка; возникновение переменного тока в цепях мультивибратора и в других электронных генераторах при постоянном напряжении питания; колебание воздушного столба в трубе орга́на, при равномерной подаче воздуха в неё; вращательные колебания латунной часовой шестерёнки со стальной осью, подвешенной к магниту и закрученной (опыт Гамазкова)
а) энергия от источника должна поступать в такт с колебаниями в контуре; б) поступающая от источника энергия должна быть равна ее потерям в контуре.
Слайд 11
Работа генератора на транзисторе
1.Чтобы в цепи возникал ток и подзаряжал конденсатор контура в ходе колебаний, нужно сообщать базе «-» относительно эмиттера потенциал, причем в те интервалы времени, когда верхняя пластина конденсатора заряжена «+», а нижняя – «-». Это соответствует замкнутому ключу. 2. Для компенсации потерь энергии колебаний в контуре напряжение на эмиттерном переходе должно переодически менять знак в строгом соответствии с колебаниями напряжения в контуре. 3. Необходима обратная связь.
Работа генератора на транзисторе. 1.Чтобы в цепи возникал ток и подзаряжал конденсатор контура в ходе колебаний, нужно сообщать базе «-» относительно эмиттера потенциал, причем в те интервалы времени, когда верхняя пластина конденсатора заряжена «+», а нижняя – «-». Это соответствует замкнутому ключу. 2. Для компенсации потерь энергии колебаний в контуре напряжение на эмиттерном переходе должно переодически менять знак в строгом соответствии с колебаниями напряжения в контуре. 3. Необходима обратная связь.
Слайд 11 из презентации «Автоколебания» к урокам физики на тему «Виды колебаний»Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке физики, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как…». Скачать всю презентацию «Автоколебания.pptx» можно в zip-архиве размером 136 КБ.
Скачать презентациюВиды колебаний
«Затухающие колебания» – Следовательно движение носит апериодический (непериодический) характер – выведенная из поло- жения равновесия система возвращается в положение равновесия, не совершая колебаний. перестает быть периодическим. Тема: Затухающие колебания. Свободные затухающие колебания в электрическом колебательном контуре; 26.27.
«Автоколебания» – Генератор высокочастотных электромагнитных колебаний. Термин автоколебания в русскоязычную терминологию введён А. Часы как автоколебательная система. Автоколебания – незатухающие колебания в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, то есть непериодического внешнего воздействия.
«Физика «Гармонические колебания»» – Коэффициент затухания. Движение от некоторой начальной точки до возвращения в ту же точку. Затухающие колебания представляют собой непериодические колебания. Заряд на обкладке конденсатора. Максимальные значения. Затухание принято характеризовать логарифмическим декрементом. Другой тип резонанса. Уравнение затухающих колебаний в контуре.
«Гармонические колебания и маятники» – Свободные колебания. Маятник. Процессы. Разделим уравнение. Периодическое колебательное движение. Понятие вращающегося вектора. Энергия гармонического колебательного движения. Маятники. Печень. Колебательная система. Материальная точка. Гармоническое колебание с начальной фазой. Ускорение при гармонических колебаниях.
«Гармонические колебания» – Вращающийся вектор амплитуды полностью характеризует гармоническое колебание. 3. Разность фаз изменяется во времени произвольным образом. Амплитуда А результирующего колебания зависит от разности начальных фаз. По правилу сложения векторов найдем суммарную амплитуду, результирующего колебания: Такие колебания называются линейно поляризованными.
Накануне первой мировой войны Россия в научном отношении значительно отставала от передовых капиталистических стран. В частности, в России не было радиотехнической промышленности. Всё оборудование для радиосвязи приходилось ввозить из-за границы, а после революции этот источник был практически закрыт. В этих условиях советские ученые Крылов, Мандельштам, Папалекси, Андронов провели столь глубокие исследования по проблемам вынужденных колебаний, что намного опередили своих западных коллег, так что мировой научный центр по этим проблемам переместился в СССР.
При свободных колебаниях энергия системы уменьшается. В связи с этим стали широко применяться автоколебания – незатухающие колебания, поддерживаемые в системе за счет постоянного внешнего источника энергии, причем сама система управляет им, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени. Частота и амплитуда автоколебаний определяются свойствами самой системы и не зависят от внешнего воздействия. Например, под стальной гирей, висящей на пружине, располагается электромагнит. Если будут попеременно включать и выключать ток, то гиря начнет совершать вынужденные колебания. Попробуйте-ка объяснить, что будет происходить дальше?..
А теперь постарайтесь привести примеры автоколебаний…
- незатухающие колебания маятника часов за счёт постоянного действия тяжести заводной гири;
- колебания скрипичной струны под воздействием равномерно движущегося смычка;
- колебание воздушного столба в трубе органа, при равномерной подаче воздуха в неё;
- вращательные колебания латунной часовой шестерёнки со стальной осью, подвешенной к магниту и закрученной
- образование турбулентных потоков на перекатах и порогах рек;
- голоса людей, животных и птиц образуются благодаря автоколебаниям, возникающим при прохождении воздуха через голосовые связки.
Наиболее распространённой механической автоколебательной системой являются маятниковые часы. В 1657 году голландский физик Христиан Гюйгенс предложил использовать изохронность колебаний маятника для создания равномерного движения стрелки на часах. Устройство, предложенное Гюйгенсом, в его главных чертах сохранилось до настоящего времени: маятник, поднятый груз, анкер и ходовое колесо. Обратите внимание, что, в основном, маятник движется свободно, получая за период два толчка. Колебания возникают и поддерживаются самой колебательной системой, то есть являются автоколебаниями. Для многих автоколебательных систем характерны основные элементы: собственно колебательная система, источник энергии, «клапан» (регулирует поступление энергии в колебательную систему).
Используя метод аналогий, перейдём от механической автоколебательной системы к электромагнитной автоколебательной системе, которая генерирует электромагнитные колебания. Что можно использовать в качестве источника энергии (источник тока), клапана (транзистор), колебательной системы в электрической цепи (автогенератор)?.. Как можно осуществить обратную связь между клапаном и колебательной системой?..(работа с учебником)
Принцип работы генератора на транзисторе (флеш-рисунок «Генератор на транзисторе» )
В момент подключения источника постоянного тока через коллекторную цепь транзистора проходит ток, заряжающий конденсатор колебательного контура. В контуре возникнут свободные электромагнитные колебания. Так как катушка колебательного контура индуктивно связана с катушкой обратной связи, то ее изменяющееся магнитное поле вызовет в катушке обратной связи переменную ЭДС такой же частоты, как и колебания в контуре. Эта ЭДС, будучи приложена к участку база – эмиттер, вызовет пульсацию тока в цепи коллектора. Так как частота этих пульсаций равна частоте электромагнитных колебаний в контуре, то они подзаряжают конденсатор контура и тем самым поддерживают постоянной амплитуду колебаний в контуре.
Наблюдение изменения формы осциллограммы от частоты и амплитуды колебаний
Предлагаю вам совершить небольшое исследование электромагнитных колебаний звуковой частоты. Что нам для этого понадобиться?.. Звуковой генератор и осциллограф! Но не простые, а… виртуальные! Поэтому нужна ещё пара компьютеров для ваших мини-лабораторий.
Делимся на 2 группы для изучения зависимости формы колебаний от их 1) частоты и 2) амплитуды.
А так как мы будем работать со звуковым генератором, то напомните мне, пожалуйста, диапазон слышимых звуковых частот?.. (флеш-рисунок «Диапазоны звуковых частот» )
1 группа будет работать в акустическом (слышимом) диапазоне звуковых частот.
Для 2 группы ограничений в диапазоне амплитуд нет.
За работу!..
Результаты наблюдений зависимости формы колебаний от их частоты:
Ребята, посмотрите, какая у нас получилась необычная картинная галерея! Теперь звуком могут наслаждаться не только наши органы слуха, но и зрения! И не будут казаться странными следующие слова: «Ты ещё не видел новую мелодию? Смотри, какая красивая!»
Мы в нашем мини-исследовании применили звуковой генератор. Что нам известно про него?.. Какие ещё бывают генераторы?..
«Физика – 11 класс»
Вынужденные колебания возникают под действием переменного напряжения, вырабатываемого генераторами на электростанциях.
Такие генераторы не могут создавать колебания высокой частоты, необходимые для радиосвязи? т.к. для этого потребовалась бы очень большая скорость вращения ротора.
Колебания высокой частоты получают, например, с помощью генератора на транзисторе.
Автоколебательные системы
Обычно незатухающие вынужденные колебания поддерживаются в цепи действием внешнего периодического напряжения.
Но возможны и другие способы получения незатухающих колебаний.
Например, есть система, в которой могут существовать свободные электромагнитные колебания, с источником энергии.
Если сама система будет регулировать поступление энергии в колебательный контур для компенсации потерь энергии на резисторе, то в ней могут возникнуть незатухающие колебания .
Системы, в которых генерируются незатухающие колебания за счет поступления энергии от источника внутри самой системы, называются автоколебательными . Незатухающие колебания, существующие в системе без воздействия на нее внешних периодических сил, называются автоколебаниями .
Генератор на транзисторе – пример автоколебательной системы.
Он состоит из колебательного контура с конденсатором емкостью С и катушкой индуктивностью L, источника энергии и транзистора.
Как создать незатухающие колебания в контуре?
Чтобы электромагнитные колебания в контуре не затухали, нужно компенсировать потери энергии за каждый период.
Пополнять энергию в контуре можно, подзаряжая конденсатор.
Для этого надо периодически подключать контур к источнику постоянного напряжения.
Конденсатор должен подключаться к источнику только в те интервалы времени, когда присоединенная к положительному полюсу источника пластина заряжена положительно, а присоединенная к отрицательному полюсу – отрицательно.
Только в этом случае источник будет подзаряжать конденсатор, пополняя его энергию.
Если же ключ замкнуть в момент, когда присоединенная к положительному полюсу источника пластина имеет отрицательный заряд, а присоединенная к отрицательному полюсу – положительный, то конденсатор будет разряжаться через источник. Энергия конденсатора при этом будет убывать.
Источник постоянного напряжения постоянно подключенный к конденсатору контура, не может поддерживать в нем незатухающие колебания, так же как постоянная сила не может поддерживать механические колебания.
В течение половины периода энергия поступает в контур, а в течение следующей половины периода возвращается в источник.
В контуре незатухающие колебания установятся лишь при условии, что источник будет подключаться к контуру в те интервалы времени, когда возможна передача энергии конденсатору.
Для этого необходимо обеспечить автоматическую работу ключа.
При высокой частоте колебаний ключ должен обладать надежным быстродействием. В качестве такого практически безынерционного ключа и используется транзистор.
Транзистор состоит из эмиттера, базы и коллектора.
Эмиттер и коллектор имеют одинаковые основные носители заряда, например дырки (полупроводник p-типа).
База имеет основные носители противоположного знака, например электроны (полупроводник n-типа).
Работа генератора на транзисторе
Колебательный контур соединен последовательно с источником напряжения и транзистором так, что на эмиттер подается положительный потенциал, а на коллектор – отрицательный.
При этом переход эмиттер – база (эмиттерный переход) является прямым, а переход база – коллектор (коллекторный переход) оказывается обратным, и ток в цепи не идет.
Это соответствует разомкнутому ключу.
Чтобы в цепи контура возникал ток и подзаряжал конденсатор контура в ходе колебаний, нужно сообщать базе отрицательный относительно эмиттера потенциал, причем в те интервалы времени, когда верхняя пластина конденсатора заряжена положительно, а нижняя – отрицательно.
Это соответствует замкнутому ключу.
В интервалы времени, когда верхняя пластина конденсатора заряжена отрицательно, а нижняя – положительно, ток в цепи контура должен отсутствовать. Для этого база должна иметь положительный потенциал относительно эмиттера.
Таким образом, для компенсации потерь энергии колебаний в контуре напряжение на эмиттерном переходе должно периодически менять знак в строгом соответствии с колебаниями напряжения на контуре.
Необходима обратная связь .
Здесь обратная связь – индуктивная
К эмиттерному переходу подключена катушка индуктивностью L CB , индуктивно связанная с катушкой индуктивностью L контура.
Колебания в контуре вследствие электромагнитной индукции возбуждают колебания напряжения на концах катушки, а тем самым и на эмиттерном переходе.
Если фаза колебаний напряжения на эмиттерном переходе подобрана правильно, то «толчки» тока в цепи контура действуют на контур в нужные интервалы времени, и колебания не затухают.
Напротив, амплитуда колебаний в контуре возрастает до тех пор, пока потери энергии в контуре не станут точно компенсироваться поступлением энергии от источника.
Эта амплитуда тем больше, чем больше напряжение источника.
Увеличение напряжения приводит к усилению «толчков» тока, подзаряжающего конденсатор.
Генераторы на транзисторах широко применяются не только во многих радиотехнических устройствах: радиоприемниках, передающих радиостанциях, усилителях, ЭВМ.
Основные элементы автоколебательной системы
На примере генератора на транзисторе можно выделить основные элементы, характерные для многих автоколебательных систем.
1. Источник энергии, за счет которого поддерживаются незатухающие колебания (в генераторе на транзисторе это источник постоянного напряжения).
2. Колебательная система – та часть автоколебательной системы, непосредственно в которой происходят колебания (в генераторе на транзисторе это колебательный контур).
3. Устройство, регулирующее поступление энергии от источника в колебательную систему – клапан (в рассмотренном генераторе – транзистор).
4. Устройство, обеспечивающее обратную связь, с помощью которой колебательная система управляет клапаном (в генераторе на транзисторе – индуктивная связь катушки контура с катушкой в цепи эмиттер – база).
Примеры автоколебательных систем
Автоколебания в механических системах: часы с маятником или балансиром (колесиком с пружинкой, совершающим крутильные колебания). Источником энергии в часах служит потенциальная энергия поднятой гири или сжатой пружины.
К автоколебательным системам относятся электрический звонок с прерывателем, свисток, органные трубы и многое другое. Наше сердце и легкие также можно рассматривать как автоколебательные системы.
Затухающие электромагнитные колебания. Генератор незатухающих электромагнитных колебаний.
С течением времени колебания в колебательном контуре затухают, т. к. избыточная энергия, полученная контуром, затрачивается на преодоление сопротивления (катушка нагревается).
График затухающих колебаний
Чтобы создать незатухающие электромагнитные колебания необходимо в такт с колебаниями добавлять в контур дополнительную энергию, это осуществляется с помощью источника тока, катушки связи и транзистора (или лампы триод)
Такой генератор незатухающих магнитных колебаний нашел применение в радиосвязи.
Билет
Электромагнитные волны. История открытия радиосвязи.
1. Теория Максвелла явилась теоретической базой для создания радиосвязи. Максвелл объединил все знания по электричеству и магнетизму и создал единую электромагнитную теорию.
Некоторые элементы теории Максвелла:
а) не существует отдельно электрического и магнитного поля, а есть единое электромагнитное;
б) меняющееся электрическое поле создает вихревое магнитное, а меняющееся магнитное вихревое электрическое, так они взаимно создают друг друга, т. е. электромагнитная волна.
в) Максвелл рассчитал скорость распространения электромагнитных волн в вакууме. Она оказалась равна скорости света.
ε0 – Электрическая постоянная
μ0 – Магнитная постоянная
Максвелл сделал вывод, что свет – электромагнитная волна.
2.Опыты Герца доказали, что электромагнитную волну можно излучать и принимать.
Билет
Открытие радиосвязи А. С. Поповым.
А. С. Попов опирался на опыты Герца, используя дополнительно телеграфный ключ, осуществил радиотелеграфную связь.
Первая радиограмма была отправлена 7 мая 1895г.
Текст первой телеграммы «Генрих Герц».
Схема простейшей радиотелеграфной связи.
Используется электрический резонанс.
| Резонансная кривая |
| Гребень Впадина |
| max Если разность волновых путей равна четному числу длин волн |
ГВЧ – генератор высоких частот.
Следующими этапами развития радиосвязи были:
а) создание радиотелефонной связи. Для этой цели использовался, например, амплитудно-модулированный сигнал.
б) Создание радиотелевизионной связи.
Радиолокация – это обнаружение объектов на основе отражения этими объектами электромагнитных волн.
Применение:
а) авиация
б) навигация
в) астрономия
г) космонавтика
д) автодорожное дело
Билет
Получение переменного тока при вращении рамки в магнитном поле. (Перенесено в курс электротехники)
Билет
Активные и реактивные нагрузки в цепях переменного тока.
Оптика.
Билет
История развития представлений о природе света.
1 Корпускулярная теория Ньютона.
По этой теории свет – это поток частиц (корпускул). Эта теория хорошо объясняла отражение и преломление света, но плохо интерференцию и дифракцию.
2 Волновая теория Гука, Гюйгенса, Френеля рассматривала свет как механическую волну в особой среде – эфире. Эта теория хорошо объясняла все известные явления, но не могла доказать существование эфира.
3 Электромагнитная теория Максвелла рассматривала свет как электромагнитную волну в интервале
Эта теория не смогла объяснить вновь открытого явления фотоэффекта.
4.Квантовая теория М. Планка. По этой теории свет – это не непрерывная электромагнитная волна, а волна излучаемая порциями – квантами.
формула Планка для энергии кванта.
Билет
Фотометрия.
1. Фотометрические величины:
а) Световой поток (Ф) – это энергия излучаемая источником света по всем направлениям в единицу времени
[Ф]си=1 лм (люмен)
б) Освещенность –это отношение светового потока, падающего на поверхность к площади (S) этой поверхности.
[E]си=1 лк (люкс)
в) Сила света – световой поток, излучаемый в единичном телесном угле.
[I]cи=1 кд (кандела)
2. Законы освещенности
а) Освещенность, создаваемая лучами, падающими под углом 0° прямо пропорциональна силе света источника и обратно пропорциональна квадрату расстояния от источника света до поверхности.
б) Освещенность, создаваемая потоком параллельных лучей, прямо пропорциональна косинусу угла падения этих лучей.
| min Если разность волновых путей равна нечетному числу длин волн |
3.Объединенный закон освещенности
Билет
Автоколебания. Генератор незатухающих электромагнитных колебаний
1. Автоколебания. Генератор незатухающих электромагнитных колебаний.
2. Если в систему, в которой могут происходить свободные электромагнитные колебания, поместить источник энергии и система сама
регулировала бы подачу энергии порциями,то появятся незатухающие колебания.
Системы называются
автоколебательными, если в них
создаются незатухающие колебания за
счет поступления энергии от источника
внутри системы.
Генератор на транзисторе –
автоколебательная система.
Примерами автоколебаний могут служить:
– незатухающие колебания маятника часов за счёт
постоянного действия тяжести заводной гири;
– колебания скрипичной струны под воздействием
равномерно движущегося смычка;
возникновение
переменного
тока
в
цепях
мультивибратора и в других электронных
генераторах при постоянном напряжении питания;
– колебание воздушного столба в трубе орга́на, при
равномерной подаче воздуха в неё;
– вращательные колебания латунной часовой шестерёнки
со стальной осью, подвешенной к магниту и закрученной
(опыт Гамазкова)
4. Условия возбуждения автоколебаний
а) энергия от источника должна поступатьв такт с колебаниями в контуре;
б) поступающая от источника энергия
должна быть равна ее потерям в контуре.
5. Часы как автоколебательная система.
6. Аналогия между механическими и электромагнитными автоколебаниями
ЭлектромагниМеханическая
тная
Элементы
автоколебател
автоколебател
автоколебател ьная система
ьная система
ьной системы (маятниковые
(генератор на
часы)
транзисторе)
1
источник
энергии
поднятый груз
2
клапан
Аналогия
между анкер
колебательная
механическими
и
3
маятник
система
электромагнитными
через ходовое
4
Обратная связь
автоколебаниямиколесо
батарея
гальванических
элементов
транзистор
колебательный
контур
индуктивная –
через катушку
7. Генератор высокочастотных электромагнитных колебаний
Обратная связьИсточник
энергии
Устройство, регулирующее
поступление энергии
Колебательная
система
8. ГВЧ (генератор высокой частоты) – устройство, поддерживающее незатухающие электромагнитные колебания.
Источник энергии – батареяКлапан – транзистор
Колебательная система – колебательный
контур
Катушка связи – катушка обратной связи
9. Работа генератора на транзисторе
10. Как создать незатухающие колебания в контуре:
1.Если конденсатор колебательного контура зарядить, то вконтуре возникнут затухающие колебания.
2.Чтобы колебания не затухали, нужно компенсировать
потери энергии на каждый период колебаний.
3.Пополнять энергию можно, подзаряжая конденсатор.
4.Для этого надо периодически подключать контур к
источнику постоянного напряжения.
5.Конденсатор должен подключаться к источнику только в
те интервалы времени, когда присоединённая к
положительному полюсу источника пластина заряжена
«+», а присоединенная к отрицательнму полюсу – «-».
6.В контуре незатухающие колебания установятся лишь
при условии, что источник будет подключаться к контуру
в те интервалы времени, когда возможна передача
энергии.
7. Для этого необходимо обеспечить автоматическую
работу ключа или транзистора.
11. Принцип работы генератора незатухающих электромагнитных колебаний
При замыкании ключа конденсатор колебательногоконтура заряжается от батареи. В цепи контура
возникает ток, который создает магнитное поле.
Это магнитное поле в катушке связи наводит ЭДС
индукции, изменяющуюся с частотой колебаний в
контуре. ЭДС индукции изменяет направление тока
на базе. В результате чего ток через транзистор то
пропускается, то нет. Пропускания тока по частоте
совпадают с частотой колебаний в контуре. Контур
автоматически подзаряжается, и в нем происходят
незатухающие электромагнитные колебания.
12. Ответить на вопросы (письменно) 1. Где возникают автоколебания? 2. Чем отличаются автоколебания от свободных и вынужденных
Ответить на вопросы(письменно)
1. Где возникают автоколебания?
2. Чем отличаются автоколебания от свободных и
вынужденных колебаний?
3. Описать роль транзистора в создании автоколебаний?
4. Что такое обратная связь и как она осуществляется в
генераторе на транзисторе?
5. Выделить элементы автоколебательной системы.
Генератор незатухающих колебаний – презентация онлайн
Генератор незатухающих колебанийПовторение пройденного материала.
1. Какие колебания называются свободными? Вынужденными?
2. Назовите устройства, с помощью которых можно получить
свободные и вынужденные электромагнитные колебания.
3. От чего зависит частота свободных и вынужденных
электромагнитных колебаний.
4. Где применяются вынужденные электромагнитные
колебания.
5. Что такое трансформация тока?
6. Какое явление применяется в работе трансформатора?
7. Какие параметры тока изменяются при трансформации?
8. От чего зависит коэффициент трансформации?
9 Где применяют трансформаторы?
Генератор незатухающих электромагнитных колебаний
L1
L
– –
+ +
–
+
Генератор незатухающих электромагнитных колебаний
L1
–
L
I +
К
–
+
Генератор незатухающих электромагнитных колебаний
I
I
А
А
+ + +
I
С
L1
–
I
к
L
+
+
_-
Генератор незатухающих электромагнитных колебаний
I
I
А
А
+ + +
I
I
С
К
+
–
–
+
Генератор незатухающих электромагнитных колебаний
L1
–
L
+
+ +
— –
Генератор незатухающих электромагнитных колебаний
I + +
L
– К
L1
–
+
Генератор незатухающих электромагнитных колебаний
I +
L
К
L1
–
+
Генератор незатухающих электромагнитных колебаний
– – – I
I +
L
К
С
L1
–
+
Генератор незатухающих электромагнитных колебаний
– – – I
I
С
L1
–
L
+
К
–
Генератор незатухающих электромагнитных колебаний
– – – I
I _
К
С
L1
–
L
+
+
Генератор незатухающих электромагнитных колебаний
L1
L
– + +
–
+
Генератор незатухающих электромагнитных колебаний
на транзисторе
Коллектор
База
Эмиттер
L1
–
L
+
Мощный генератор непрерывного электромагнитного излучения с частотой 300 ГГц
I. Огава, Т. Идехара, С. Мицудо и др., В: Proc. 28-й Int. Конф. по инфракрасным и миллиметровым волнам, Оцу, Япония, 29 сентября – 26 октября 2003 г. , с. 403.
Н. И. Зайцев, Т. Б. Панкратова, М. И. Петелин, В. А. Флягин, Радиотех. ‘Elektron. , 19 , № 15, 1056 (1974).
Google ученый
Курбатов В.И., Малыгин С.А., Орлов В.Б. и др. // В сб .: Proc. Int. Семинар «Сильные микроволны в плазме», 2–9 августа 1999 г., Нижний Новгород , с. 641.
Запевалов В.Е., в: Proc. 4-й Int. Харьковский симп. «Физика и техника миллиметровых и субмиллиметровых волн», 4–9 июня 2001 г., Харьков, Украина, , с. 117.
Куфтин А.Н., Лыгин В.К., Мануйлов В.Н. и др., Int. J. Инфракрасные и миллиметровые волны , 20 , No.3, 361 (1999).
Артикул Google ученый
Ш. Э. Цимринг, Int. J. Инфракрасные и миллиметровые волны , 14 , № 4, 817 (1993).
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый
Завольский Н.А., Запевалов В.Е., Моисеев М.А., Radiophys. Квантовая электроника. , 49 , № 2, 108 (2006).
Артикул ОБЪЯВЛЕНИЯ Google ученый
В. Е. Запевалов, В. И. Хижняк, Т. Идехара и др., В: Proc. 29-й Int. Конф. по инфракрасным и миллиметровым волнам и 12-й межд. Конф. на Terahertz Electronics, 27 сентября – 1 октября 2004 г., Карлсруэ, Германия: Дайджест конференции , с. 149.
Запевалов В.Е., Идехара Т., Малыгин О.В. и др., В: Proc. Шестой Int. Вакуумный электрон. Конф. IVEC, 20–22 апреля 2005 г., Huis ter Duin, Нордвейк, Нидерланды, , p. 121.
Т.Сайто, Т. Идехара, С. Мицудо и др., В: Proc. 31-й Int. Конф. по инфракрасным и миллиметровым волнам, Шанхай, Китай, 18–22 сентября 2006 г. , с. 24.
Хошизуки Х., Идехара Т., Запевалов В. Е. и др., В: Proc. 30-й Int. Конф. по инфракрасным и миллиметровым волнам и 13-й межд. Конф. на Terahertz Electronics, 19–23 сентября 2005 г., Вильямсбург, Вирджиния: Дайджест конференции , с. 375.
С. Мицудо, К. Сакаи, Т. Идехара и др., в: Proc. 31-й Int. Конф. по инфракрасным и миллиметровым волнам, Шанхай, Китай, 18–22 сентября 2006 г. , с. 572.
Квантование энергии | Физика
Цели обучения
К концу этого раздела вы сможете:
- Объясните вклад Макса Планка в развитие квантовой механики.
- Объясните, почему атомные спектры указывают на квантование.
Вклад Планка
В некоторых системах энергия квантуется, что означает, что система может иметь только определенные энергии, а не континуум энергий, в отличие от классического случая.Это было бы похоже на наличие только определенных скоростей, с которыми может двигаться автомобиль, потому что его кинетическая энергия может иметь только определенные значения. Мы также обнаружили, что некоторые формы передачи энергии происходят с дискретными сгустками энергии. Хотя большинство из нас знакомо с квантованием материи на глыбы, называемые атомами, молекулами и т. Д., Мы менее осведомлены о том, что энергия тоже может быть квантована. Некоторые из самых ранних подсказок о необходимости квантовой механики над классической физикой пришли из квантования энергии.
Рис. 1. Графики излучения абсолютно черного тела (от идеального излучателя) при трех различных температурах радиатора. Интенсивность или скорость излучения излучения резко возрастает с температурой, а пик спектра смещается в сторону видимой и ультрафиолетовой частей спектра. Форму спектра нельзя описать с помощью классической физики.
Где наблюдается квантование энергии? Начнем с рассмотрения испускания и поглощения электромагнитного (ЭМ) излучения.ЭМ-спектр, излучаемый горячим твердым телом, напрямую связан с температурой твердого тела. (См. Рис. 1.) Идеальный излучатель – это излучатель с коэффициентом излучения 1 на всех длинах волн и, следовательно, черный как уголь. Поэтому идеальные излучатели называются черными телами , а их электромагнитное излучение называется излучением черного тела . Обсуждалось, что общая интенсивность излучения изменяется как T 4 , четвертая степень абсолютной температуры тела, и что пик спектра смещается в сторону более коротких волн при более высоких температурах.Все это кажется довольно непрерывным, но именно кривая зависимости спектра интенсивности от длины волны дала ключ к пониманию того, что энергии атомов в твердом теле квантованы. Фактически, теоретическое объяснение экспериментально измеренной формы спектра было загадкой на рубеже веков. Когда эта «ультрафиолетовая катастрофа» в конечном итоге была разрешена, ответы привели к появлению новых технологий, таких как компьютеры и сложные методы визуализации, описанные в предыдущих главах.И снова физика как наука, способствующая развитию, изменила наш образ жизни.
Немецкий физик Макс Планк (1858–1947) использовал идею о том, что атомы и молекулы в теле действуют как осцилляторы, поглощая и испуская излучение. Энергии колеблющихся атомов и молекул необходимо было квантовать, чтобы правильно описать форму спектра черного тела. Планк пришел к выводу, что энергия осциллятора с частотой f равна
.[латекс] \ displaystyle {E} = \ left (n + \ frac {1} {2} \ right) hf \\ [/ latex].
Здесь n – любое неотрицательное целое число (0, 1, 2, 3,…). Обозначение h обозначает постоянную Планка , задаваемую соотношением h = 6,626 × 10 −34 Дж · с.
Уравнение [латекс] E = \ left (n + \ frac {1} {2} \ right) hf \\ [/ latex] означает, что генератор с частотой f (излучающий и поглощающий электромагнитное излучение с частотой f ) может иметь увеличение или уменьшение своей энергии только за дискретных шагов размером Δ E = hf .
Было бы полезно упомянуть некоторые макроскопические аналогии квантования энергетических явлений. Это похоже на маятник, который имеет характерную частоту колебаний, но может качаться только с определенной амплитудой. Квантование энергии также напоминает стоячую волну на струне, которая допускает только определенные гармоники, описываемые целыми числами. Это также похоже на подъем и спуск по холму с использованием отдельных ступенек лестницы, а не на возможность двигаться вверх и вниз по непрерывному склону. Ваша потенциальная энергия принимает дискретные значения по мере того, как вы переходите от шага к шагу.
Рис. 2. Немецкий физик Макс Планк оказал большое влияние на раннее развитие квантовой механики, будучи первым, кто осознал, что энергия иногда квантуется. Планк также внес важный вклад в специальную теорию относительности и классическую физику. (Источник: Библиотека Конгресса, Отдел эстампов и фотографий через Wikimedia Commons)
Используя квантование осцилляторов, Планк смог правильно описать экспериментально известную форму спектра черного тела.Это было первым признаком того, что энергия иногда квантуется в малом масштабе, что принесло ему Нобелевскую премию по физике в 1918 году. Хотя теория Планка основана на наблюдениях за макроскопическим объектом, ее анализ основан на атомах и молекулах. Это был такой революционный отход от классической физики, что сам Планк не хотел принимать свою собственную идею о том, что энергетические состояния не являются непрерывными. Общее признание квантования энергии Планком было значительно усилено объяснением Эйнштейном фотоэлектрического эффекта (обсуждаемого в следующем разделе), которое продвинуло квантование энергии на шаг вперед.Планк был полностью вовлечен в развитие как ранней квантовой механики, так и теории относительности. Он быстро принял специальную теорию относительности Эйнштейна, опубликованную в 1905 году, а в 1906 году Планк первым предложил правильную формулу для релятивистского импульса: p = γmu .
Обратите внимание, что постоянная Планка h – очень маленькое число. Так, например, для инфракрасной частоты 10 14 Гц, излучаемой черным телом, разница между уровнями энергии составляет всего Δ E = hf = (6.63 × 10 −34 Дж · с) (10 14 Гц) = 6,63 × 10 −20 Дж, или примерно 0,4 эВ. Эти 0,4 эВ энергии значительны по сравнению с типичными атомными энергиями, которые составляют порядка электрон-вольта, или тепловыми энергиями, которые обычно составляют доли электрон-вольта. Но в макроскопическом или классическом масштабе энергии обычно порядка джоулей. Даже если квантовать макроскопические энергии, квантовые шаги слишком малы, чтобы их можно было заметить. Это пример принципа соответствия.Для больших объектов квантовая механика дает результаты, неотличимые от результатов классической физики.
Атомные спектры
Теперь обратим внимание на испускание и поглощение ЭМ излучения газами . Солнце – наиболее распространенный пример тела, содержащего газы, излучающие электромагнитный спектр, включающий видимый свет. Мы также видим примеры в неоновых вывесках и пламени свечей. Исследования выбросов горячих газов начались более двух веков назад, и вскоре было признано, что эти спектры излучения содержат огромное количество информации.Например, можно определить тип газа и его температуру. Теперь мы знаем, что эти электромагнитные излучения происходят от электронов, переходящих между энергетическими уровнями в отдельных атомах и молекулах; Таким образом, они называются атомными спектрами . Атомные спектры сегодня остаются важным аналитическим инструментом. На рис. 3 показан пример спектра излучения, полученного при пропускании электрического разряда через материал. Одна из важнейших характеристик этих спектров – то, что они дискретны.Под этим мы подразумеваем, что излучаются только определенные длины волн и, следовательно, частоты. Это называется линейчатым спектром. Если частота и энергия связаны как Δ E = hf , энергии электронов в излучающих атомах и молекулах квантуются. Это обсуждается более подробно позже в этой главе.
Рисунок 3. Спектр излучения кислорода. Когда электрический разряд проходит через вещество, его атомы и молекулы поглощают энергию, которая переизлучается в виде электромагнитного излучения.Дискретный характер этих выбросов подразумевает, что энергетические состояния атомов и молекул квантованы. Такие атомные спектры использовались в качестве аналитических инструментов в течение многих десятилетий, прежде чем стало понятно, почему они квантованы. (Источник: Teravolt, Wikimedia Commons)
Квантование атомных спектров было большой загадкой. Некоторые из лучших умов науки XIX века не смогли объяснить, почему это могло быть. Только во втором десятилетии 20-го века начал появляться ответ, основанный на квантовой механике.И снова в исследованиях участвовало макроскопическое или классическое тело газа, но эффект, как мы увидим, вызван отдельными атомами и молекулами.
Исследования PhET: модели атома водорода
Как ученые выяснили структуру атомов, не глядя на них? Попробуйте разные модели, стреляя светом в атом. Проверьте, насколько предсказание модели соответствует экспериментальным результатам.
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
- Первое указание на то, что энергия иногда квантуется, исходит от излучения черного тела, которое представляет собой излучение электромагнитного излучения объектом с излучательной способностью 1.
- Planck обнаружил, что уровни энергии излучающих атомов и молекул были квантованы только с допустимыми значениями [латекс] E = \ left (n + \ frac {1} {2} \ right) \ text {hf} \\ [ / latex], где n – любое неотрицательное целое число (0, 1, 2, 3,…).
- h – постоянная Планка, значение которой h = 6,626 × 10 -34 Дж · с.
- Таким образом, колебательные энергии поглощения и излучения атомов и молекул в черном теле могут увеличиваться или уменьшаться только ступенчато размером Δ E = hf , где f – частота колебательного характера поглощения и излучения ЭМ излучение.
- Еще одним признаком квантования уровней энергии в атомах и молекулах являются линии в атомных спектрах, которые представляют собой электромагнитные излучения отдельных атомов и молекул.
Концептуальные вопросы
- Приведите пример квантованного физического объекта. Конкретно укажите, что это за организация и каковы ограничения ее значений.
- Приведите пример физического объекта, который не квантован, поскольку он непрерывен и может иметь непрерывный диапазон значений.
- Какой аспект спектра черного тела заставил Планка предложить квантование уровней энергии в его атомах и молекулах?
- Если бы постоянная Планка была большой, скажем, в 10 34 раз больше, чем она есть, мы бы наблюдали квантование макроскопических объектов. Опишите движения детских качелей в таких обстоятельствах.
- Почему мы не замечаем квантование в повседневных событиях?
Задачи и упражнения
- Молекула LiBr колеблется с частотой 1.7 × 10 13 Гц. (а) Какова разница в энергии в эВ между разрешенными состояниями осциллятора? (b) Каково приблизительное значение n для состояния с энергией 1,0 эВ?
- Разница в энергии между разрешенными состояниями осциллятора в молекулах HBr составляет 0,330 эВ. Какая частота колебаний этой молекулы?
- Физик наблюдает, как 15-килограммовый орангутанг в зоопарке лениво раскачивается в шине на конце веревки. Он (физик) замечает, что каждое колебание требует 3.00 с и предполагает, что энергия квантуется. (а) Какова разница в энергии в джоулях между разрешенными состояниями осциллятора? (б) Каково значение n для состояния, в котором энергия равна 5,00 Дж? (c) Можно ли наблюдать квантование?
Глоссарий
черное тело: идеальный излучатель, который может одинаково хорошо излучать на всех длинах волн
излучение черного тела: электромагнитное излучение от черного тела
Постоянная Планка: ч = 6.626 × 10 −34 Дж · с
атомных спектров: электромагнитное излучение атомов и молекул
Избранные решения проблем и упражнения
1. (а) 0,070 эВ; (б) 14
3. (а) 2.21 × 10 34 Дж; (б) 2,26 × 10 34 ; (c) №
Электромагнитное излучение – обзор
Электромагнитное излучение.
Электромагнитное излучение – это электрическое и магнитное возмущение, перемещающееся в пространстве со скоростью света (2.998 × 108 м / с). Он не содержит ни массы, ни заряда, а перемещается в пакетах лучистой энергии, называемых фотонами или квантами. Примеры электромагнитного излучения включают радиоволны и микроволны, а также инфракрасное, ультрафиолетовое, гамма и рентгеновское излучение. Некоторые источники электромагнитного излучения включают источники в космосе (например, солнце и звезды), радиоактивные элементы и промышленные устройства. ЭМ проявляет двойственную природу волн и частиц.
Электромагнитное излучение распространяется в форме волны с постоянной скоростью. Волновые характеристики электромагнитного излучения находятся в зависимости скорости от длины волны (расстояние по прямой линии одного цикла) и частоты (циклов в секунду или герц, Гц), выраженных в формуле
c = λv
где c = скорость, λ = длина волны и v = частота.
Поскольку скорость постоянна, любое увеличение частоты приводит к последующему уменьшению длины волны. Следовательно, длина волны и частота обратно пропорциональны. Все формы электромагнитного излучения сгруппированы в соответствии с длиной волны в электромагнитный спектр, показанный на Рисунке 1-3.
Частичная природа электромагнитного излучения проявляется во взаимодействии ионизирующих фотонов с веществом. Количество энергии (E), обнаруженное в фотоне, равно его частоте ( ν ), умноженной на постоянную Планка (h):
E = νh
Энергия фотона прямо пропорциональна частоте фотона.Энергия фотона измеряется в эВ или кэВ (килоэлектронвольтах). Энергетический диапазон диагностического рентгеновского излучения составляет от 40 до 150 кэВ. Гамма-лучи, рентгеновские лучи и некоторые ультрафиолетовые лучи обладают достаточной энергией (> 10 кэВ), чтобы вызвать ионизацию.
Энергия электромагнитного излучения определяет его полезность для диагностической визуализации. Из-за чрезвычайно короткой длины волны гамма-лучи и рентгеновские лучи способны проникать через большие части тела. Гамма-лучи используются при визуализации радионуклидов. Рентгеновские лучи используются для получения изображений на обычной пленке и компьютерной томографии (КТ).Видимый свет применяется для наблюдения и интерпретации изображений. Магнитно-резонансная томография (МРТ) использует радиочастотное электромагнитное излучение в качестве среды передачи (см. Рис. 1-3).
Электромагнитное излучение – обзор
2.3 Решение электромагнитных волн в однородном диэлектрике
Электромагнитные волны включают электрические и магнитные поля, которые могут проходить через вакуум, лишенный какой-либо связанной среды, и не содержат движущихся зарядов или токов. Присутствие электромагнитных волн было первоначально установлено в 1888 году немецким физиком Генрихом Герцем (1857–1894).Герц использовал схему RLC, которая генерировала ток в катушке индуктивности, управляющей искровым разрядником. С этой точки зрения, цепь RLC представляет собой электрическую цепь, состоящую из резистора (R), катушки индуктивности (L) и конденсатора (C), соединенных последовательно или параллельно с напряжением (V). Название схемы образовано от букв, используемых для обозначения составляющих компонентов этой схемы, тогда как последовательность компонентов может отличаться от RLC (рис. 2.6) [14].
Рис. 2.6. Базовая схема RLC.
Полость вспышки включает в себя два электрода, которые, когда надвигающаяся разница проходит через оба электрода, вызывают вспышку, электризуя газ между ними.В этом случае Герц расположил петлю и небольшой зазор для катализатора на расстоянии нескольких метров друг от друга. Он заметил, что вспышки генерируются в изолированном контуре в форме, которая взаимосвязана с электромагнитными колебаниями в первичном контуре RLC. Соответственно, электромагнитные волны могли распространяться в космосе, в котором не хватало какой-либо среды для их поддержания. В связи с этим элементарная единица колебаний, циклы в секунду, была названа в его честь герцами (Гц) [13, 14, 18].
Общая трехмерная плоскость электромагнитной волны может быть математически задана следующим образом:
(2.23) ψ = Aeiωt − K → .r →
Подставить уравнение. (2.23) в уравнение. (2.20), и мы бы получили, что:
(2.24) kx2 + ky2 + kz2 = k2 = ω2n2c − 2 = ω2v2
С этой точки зрения электрическое и магнитное поля распространения плоской волны в направлении K → формулируются как [1, 5]:
(2.25) E → = E → 0eiωt − K → .r →
и
(2.26) H → = H → 0eiωt − K → .r →
Ур. (2.25) и (2.26) оба исследуют электрические и магнитные поля как векторы, не зависящие от пространства и времени. И наоборот, оба поля сложны. В этом контексте уравнение ∇.E → = 0 дает [1, 5]:
(2.27) −ikxE0x + kyE0y + kzE0z = 0
Eq. (2.27) можно упростить как:
(2.28) K → .E → = 0
Аналогично, математическое уравнение ∇.H → = 0 может быть выражено в виде распространения плоской волны в направлении K → следующим образом [1, 14]:
(2.29) K → .H → = 0
Ур. (2.28) и (2.29) демонстрируют, что и электрическое, и магнитное поля расположены под прямым углом к распространению волны в направлении K →. Математически они могут быть записаны как:
(2.30) H → = K → xE → ωμ − 1
(2.31) E → = K → xH → ωɛ − 1
В случае E → xH → в направлении распространения z , электрический вектор будет вдоль оси x , а магнитный вектор будет вдоль оси y . При таком понимании математическое описание распространения обоих полей дается формулами [11–14]:
(2.32) E → = x → E0eiωt − kz
(2.33) H → = y → H0eiωt − kz
. (2.32) и (2.33). С этой точки зрения распространение электромагнитной волны можно математически выразить в форме косинусоидальной волны как:
(2.34) E → = x → E0cosωt − kz
(2.35) H → = y → H0cosωt − kz
В этом понимании косинусоидальная волна – это форма сигнала с формой, неотличимой от формы синусоидальной волны, за исключением точки на косинусоидальной волне, проходящей ровно на 1/4 цикла до соответствующего времени на синусоиде (рис.2.7) [14].
Рис. 2.7. Формы сигналов синуса и косинуса.
Кроме того, линейная поляризация плоской волны может быть предоставлена обоими уравнениями. (2.34) и (2.35), а направления x и y должны быть перпендикулярны друг другу. Другими словами, ось x представляет электрический вектор, тогда как ось y- представляет магнитный вектор (рис. 2.8).
Рис. 2.8. Линейно поляризованная электромагнитная волна.
Излучение черного тела
предыдущий дом следующий
Михаил Фаулер, Университет Вирджинии.
Запрос 8: Не все исправить Тела, нагретые до определенной степени, излучают Свет и сияют; и не это излучение осуществляется за счет вибрационного движения его частей?
Isaac Newton , Opticks , опубликовано 1704.
Обогреваемые тела излучают
Теперь обратимся к другой загадке. перед физиками на рубеже веков (1900 г.): как нагретые тела излучать? Было общее понимание задействованного механизма – тепло было известно, что заставляет молекулы и атомы твердого тела вибрировать, а молекулы а атомы сами по себе представляли собой сложные образцы электрических зарядов.(Как обычно, Ньютон был на правильном пути.) Из экспериментов Герца и других, Предсказания Максвелла о том, что колеблющиеся заряды излучают электромагнитные излучение было подтверждено, по крайней мере, для простых антенн. Из уравнений Максвелла было известно, что это излучение распространялось со скоростью света, и из этого было понято этот свет и связанное с ним инфракрасное тепловое излучение были собственно электромагнитные волны. В Таким образом, картина заключалась в том, что при нагревании тела возникающие вследствие этого колебания молекулярный и атомный масштабы неизбежно вызывают колебания заряда.Если предположить, что теория Максвелла электромагнитное излучение, которое так хорошо работало в макроскопическом мире, было также действительный на молекулярном уровне, эти колеблющиеся заряды будут излучать, предположительно наблюдается выделение тепла и света.
Как поглощается радиация?
Что означает фраза «черный тело »радиация? Дело в том, что излучение от нагретого тела зависит в некоторой степени от нагретого тела. Чтобы увидеть это проще всего, давайте вернемся на мгновение и рассмотрим, как различные материалы поглощают излучение .Некоторые, например стекло, едва ли поглощают свет. вообще – свет проходит насквозь. Для блестящего металлического поверхность, свет тоже не поглощается, он отражается. Для черного материала, такого как сажа, свет и тепло практически полностью впитываются, и материал нагревается. Как мы можем понять эти разные поведение с точки зрения света как электромагнитной волны, взаимодействующей с зарядами в материале, заставляя эти заряды колебаться и поглощать энергию от радиация? В случае стекла очевидно, этого не происходит, по крайней мере, не очень.Почему нет? Полное понимание того, зачем нужна квантовая механика, но в целом идея такова: в стекле есть заряды – электроны. которые способны колебаться в ответ на приложенное внешнее колебание электрическое поле, но эти заряды прочно связан с атомами и может колебаться только на определенных частотах. (Для квантовых экспертов эти обвинения колебания происходят, когда электрон движется с одной орбиты на другую. Конечно, в 1890-е годы, время первых точных работ по излучению черного тела.) Бывает, что для обычного стекла ни одна из этих частот не соответствует видимый свет , так что нет резонанс со световой волной и, следовательно, мало поглощаемой энергии. Вот почему стекло идеально подходит для окон! Ага. Но стекло непрозрачно на на некоторых частотах за пределами видимого диапазона (в общем, как в инфракрасном, так и в ультрафиолетовом диапазоне). Это частоты, на которых Распределение электрического заряда в атомах или связях может естественным образом колебаться.
Как мы можем понять отражение света металлической поверхностью ? Кусок металла имеет электроны, которые могут двигаться через все твердое тело. Это то, что превращает металл в металл: он легко проводит электричество и тепло, и то и другое фактически переносится токами этих свободно движущихся электронов. (Ну, немного тепла переносится вибрации.) Но металлы узнаваемы потому что они блестящие – почему что? Опять же, это свободные электроны: они приводимые в большие (относительно атомов) колебания электрическим полем падающей световой волны, и этот индуцированный колебательный ток излучает электромагнитно, как ток в передающей антенне.Это излучение – это отраженный свет. Для блестящая металлическая поверхность, небольшая часть поступающей лучистой энергии поглощается как тепло, оно просто переизлучается, то есть отражается.
Теперь рассмотрим вещество, которое поглощает света: нет пропускания и нет отражение. Мы очень близки к идеальному впитыванию сажи. Как металл, он будет проводить электрический ток, но далеко не так эффективно. – это неприсоединенных электронов, которые могут перемещаться. через все твердое тело, но они постоянно натыкаются на вещи – у них короткая длина свободного пробега.Когда они натыкаются, они вызывают вибрацию, как мяч, ударяющийся о бампер в автомате для игры в пинбол, поэтому они отдайте кинетическую энергию теплу. Хотя электроны в саже имеют короткое средняя длина свободного пробега по сравнению с пробегом из хорошего металла, они очень свободно перемещаются по сравнению с электронами, связанными с атомами (как в стекле), поэтому они могут ускорять и забирать энергию из электрического поля в световой волне. Поэтому они очень эффективны посредники в передаче энергии световой волны в тепло.
Взаимосвязь абсорбции и эмиссии
Увидев, как сажа может впитывать излучение и преобразование энергии в тепло, а как насчет обратного? Почему он излучает при нагревании? Аналогия с автоматом для игры в пинбол все еще хороша: представьте себе сейчас автомат для игры в пинбол, где барьеры и т. д., сильно вибрируют, потому что они питаясь энергией. Шары (электроны), отскакивающие от них, внезапно будут ускоряется при каждом столкновении, и эти ускоряющие заряды испускают электромагнитные волны. С другой стороны, электроны в металле имеют очень большие длины свободного пробега, колебания решетки влияют на них гораздо меньше, поэтому они менее эффективен в сборе и отводе тепловой энергии. Из подобных соображений очевидно что хорошие поглотители излучения также являются хорошими излучателями.
На самом деле, мы можем быть намного точнее: тело излучает радиацию при заданном температура и частота точно так же, как он поглощает такое же излучение . Это было доказано Кирхгофом: существенное Дело в том, что если мы предположим, что конкретное тело может поглощать лучше, чем излучает, тогда в комнате, полной предметов с одинаковой температурой, он будет поглощать излучение от других тел лучше, чем он излучает энергию обратно к ним. Значит, станет жарче, а остальное в комнате станет холоднее, что противоречит второму закону термодинамики.(Мы могли бы использовать такое тело, чтобы построить тепло работа по извлечению двигателя по мере того, как в помещении становится все холоднее и холоднее!)
Но металл светится, когда нагревается достаточно: почему это? При повышении температуры решетка атомов вибрирует все больше и больше, эти колебания рассеивают и ускоряют электроны. Даже стекло светится на высоте достаточно температуры, так как электроны расшатываются и колеблются.
Спектр «черного тела»: дыра в духовке
Любое тело при любой температуре выше абсолютный ноль будет в некоторой степени излучать, интенсивность и частотное распределение излучения в зависимости от детального строения тела.Чтобы приступить к анализу теплового излучения, нам необходимо: конкретизировать тело, излучающее: t he Самый простой случай – идеализированное тело, которое является идеальным поглотителем, и следовательно, также (из приведенных выше аргументов) идеальный эмиттер. Для очевидного По этой причине это называется « черное тело » .
Но нам нужно проверить наши идеи экспериментально: так как же построить идеальный поглотитель? Хорошо, ничего идеального, но в 1859 году Кирхгоф пришла в голову хорошая идея: небольшая дырочка в боку большой коробки – отличный поглотитель, так как любое излучение, которое проходит через отверстие, отражается внутри, много поглощается при каждом отскоке и имеет мало шансов когда-либо получить снова.Итак, мы можем сделать это в обратном порядке : иметь духовку с крошечным отверстие в стороне, и предположительно излучение, выходящее из отверстия, так же хорошо представление идеального эмиттера, который мы собираемся найти. Кирхгоф бросил вызов теоретикам и экспериментаторы, чтобы выяснить и измерить (соответственно) энергию / частоту кривая для этого «излучения полости», как он это называл (по-немецки, конечно: hohlraumstrahlung, где hohlraum означает полая комната или полость, strahlung – это радиация). Фактически, именно вызов Кирхгофа в 1859 г. привел непосредственно к квантовая теория сорок лет спустя!
Что соблюдалось: два закона
Первая количественная гипотеза на основе экспериментального наблюдения дырочного излучения было:
Стефана Закон (1879):
всего мощность P, излучаемая с одного квадратного метра черного поверхность при температуре T соответствует четвертой степени абсолютной температуры:
P = σT4, σ = 5.67 × 10-8 Вт / кв.м / К4.
Пять лет спустя, в 1884 году, Больцманн вывел это поведение T4 из теории: он применил классические термодинамическое обоснование ящика, заполненного электромагнитным излучением, с использованием Уравнения Максвелла, связывающие давление с плотностью энергии. (Крошечное количество энергии выход из отверстия, конечно, будет иметь ту же температурную зависимость, что и интенсивность излучения внутри). сопровождающие примечания для получения подробной информации.
Упражнение : температура поверхности солнца 5700К.Сколько мощности излучает один квадратный метр солнечной поверхности? Данный что расстояние до Земли составляет около 200 солнечных радиусов, какова максимальная мощность возможно ли от установки солнечной энергии на один квадратный километр?
Закон Вены о перемещении (1893):
Поскольку температура духового шкафа меняется, поэтому частота, на которой испускаемое излучение наиболее интенсивно. По факту, эта частота прямо пропорциональна абсолютной температуре:
fmax∝T.
(Вин сам вывел этот закон теоретически в 1893 году, следуя термодинамическим рассуждениям Больцмана.Это было ранее наблюдался, по крайней мере, полуколичественно, американским астроном, Лэнгли.) Формула получена в прилагаемых примечаниях .
На самом деле, этот сдвиг вверх fmax с T знаком каждому – когда железо нагревается в огне, первое видимое излучение (около 900К) – глубокое красный – видимый свет самой низкой частоты. Дальнейшее увеличение T вызывает изменение цвета на оранжевый, а затем желтый и, наконец, синий при очень высоких температурах (10 000 К и более), для которых пик интенсивности излучения переместился за пределы видимого в ультрафиолет.
Этот сдвиг частоты, при котором максимальная мощность излучения очень важна для использования солнечной энергии, например как в теплице. Стекло должно позволять солнечное излучение входит, но не пропускает тепловое излучение наружу. Это возможно, потому что два излучения находятся в очень разных частотных диапазонах – 5700К и, скажем, 300К – а там представляют собой материалы, прозрачные для света, но непрозрачные для инфракрасного излучения. Теплицы работают только потому, что fmax зависит от температуры.
Что наблюдалось: полная картина
К 1890-м годам экспериментальный методы были усовершенствованы настолько, что можно было справедливо точные измерения распределения энергии в этом резонаторе излучения, или как мы будем называть это излучением черного тела. В 1895 г. в университете Берлина, Вены и Люммера пробил небольшое отверстие в стенке духовки, которая в противном случае была бы полностью закрыта, и начал измерять выходящую радиацию.
Луч, выходящий из отверстия, был проходил через дифракционную решетку, которая посылала разные длины волн / частоты в разных направлениях, все по направлению к экрану. Детектор перемещался вверх и вниз по экран, чтобы узнать, сколько излучаемой энергии испускается на каждой частоте диапазон. (Это теоретическая модель эксперимента – актуальная экспериментальные установки были гораздо более сложными.Например, сделать сложный инфракрасный измерения более высокочастотные волны были устранены многократными отражениями из кварца и других кристаллов.) Они нашел кривую интенсивности / частоты излучения, близкую к этой (правильную):
Видимый спектр начинается в около 4,3 × 10 14 Гц, поэтому эта печь светится темно-красным цветом.
Один второстепенная точка : этот график представляет собой плотность энергии внутри печи , которую мы обозначаем через ρ (f, T), что означает что при температуре T энергия в Джоулях / м 3 в частотный интервал f, f + Δf равен ρ (f, T) Δf.
Чтобы найти мощность, откачанную из отверстие, имейте в виду, что излучение внутри духовки имеет волны, идущие одинаково в обе стороны – так что только половина из них вылезет через отверстие. Также, если отверстие имеет площадь A , волны, идущие изнутри под углом, будут видеть меньшую целевую область. Результатом этих двух эффектов является то, что
Мощность излучения из области отверстия A = 14Acρ (f, T).
(Подробный вывод числа 14 находится в примечаниях .)
Они также смогли подтвердить оба Стефана Закон P = σT4 и закон смещения Вина путем измерения кривые черного тела при разных температурах, например:
Давайте посмотрим на эти кривые подробнее деталь: для низких частот оказалось, что f, ρ (f, T) пропорционально f2, параболической форме, но при увеличении f она опускалась ниже параболы, достигая максимума при fmax, а затем довольно быстро падала к нулю, когда f превышала fmax. .
Для тех низких частот, где ρ (f, T) является параболическим, удвоение температуры было обнаружено, что удваивает интенсивность излучения.Но также на 2T кривая следовала за удвоенной параболической траекторией намного дальше, прежде чем исчезнуть – фактически, вдвое больше, и fmax (2T) = 2fmax (T).
Кривая ρ (f, 2T), таким образом, достигает восьми -кратной высоты ρ (f, T). (См. График выше). Он также распространяется на удвоенную боковую протяженности, поэтому площадь под кривой, соответствующая полной энергии излучается, увеличивается в в шестнадцать раз при удвоении температуры: Стефана Закон, P = σT4.
Понимание кривой черного тела
Эти прекрасно точные результаты экспериментов были ключом к революции.Первый успешный теоретический анализ данные были получены Максом Планком в 1900 году. сосредоточено на моделировании колеблющихся зарядов, которые должны существовать в духовке стены, излучающие тепло внутрь и – в термодинамических равновесие – сами под действием поля излучения.
Суть в том, что он нашел, что можно было бы объяснить наблюдаемую кривую , если бы он требовал, чтобы эти осцилляторы не непрерывно излучают энергию, как того требует классическая теория, но они могут терять или приобретать энергию только в фрагменты , называемые квантами , размером hf для генератора частоты f.Постоянная h теперь называется постоянной Планка, h = 6,626 × 10–34 джоуль⋅сек.
Исходя из этого предположения, Планк рассчитал следующую формулу для плотности энергии излучения внутри духовка:
ρ (f, T) df = 8πVf2dfc3hfehf / kT − 1.
Идеальное совпадение этого формула с точными экспериментами, и вытекающая из этого необходимость энергии квантование, было наиболее важных прогресс в физике в 9000-м веке.
Но никто не заметил несколько годы! Изгиб его черного тела был полностью принято как правильное: это подтверждали все более точные эксперименты снова и снова, но радикальный характер квантового предположения не подводил в.Планк не был слишком расстроен – он не в это тоже поверить, он видел в этом техническое исправление, которое (как он надеялся) в конечном итоге оказаться ненужным.
Частично проблема заключалась в том, что путь Планка к формуле был долго, сложно и неправдоподобно – он даже на разных этапах делали противоречивые предположения, как указывал Эйнштейн. потом. Но результат был правильным в любом случае, и чтобы понять, почему мы пойдем другим, более легким, начатым маршрутом (но не завершено) лордом Рэли в Англии.
Звуковая идея Рэлея: Подсчет стоячих волн
В 1900 году, фактически несколькими месяцами ранее Прорывная работа Планка, лорд Рэйли использовал более прямой подход к излучение внутри духовки: он даже не думал об осцилляторах в стены, он всего принял излучение как набор стоячих волн в кубической форме. корпус: генераторы электромагнитные . В отличие от несколько мрачной реальности настенных осцилляторов, эти стоячие электромагнитные волны были кристально чистыми.
Это был естественный подход для Рэлея – он решил почти идентичную проблему четверть века назад, анализ стоячие звука волн в кубической комнате (§267 его книги). Задача найти и перечислите различные возможные стоячие волны в комнате / духовке, совместим с граничными условиями. Для звуковых волн в комнате амплитуда звука стремится к нулю при стены. Для электромагнитных волн электрическое поле, параллельное стена должна быть нулевой, если стена является идеальным проводником (и можно предположить, что это – см. примечание потом).
Итак, какие разрешенные стояния волны? В качестве разминки рассмотрите различные разрешенные режимы вибрации, то есть стоячие волны, в струне длины a с обоих концов:
Возможные значения длины волны являются:
λ = 2a, a, 2a / 3,…
Итак, допустимые частоты –
.f = c / λ = c / 2a, 2 (c / 2a), 3 (c / 2a),…
Эти допустимые частоты на равном расстоянии c / 2a друг от друга. Мы определить спектральную плотность, заявив, что
Номеррежимов между f и f + Δf = N (f) Δf
, где мы предполагаем, что Δf велико по сравнению с расстоянием между последовательные частоты.Очевидно, что для этого одномерного упражнения N (f) является константой, равной 2a / c, каждая мода соответствует целой точке на действительная ось в единицах c / 2a.
Амплитуда колебаний как функция времени:
y = Asin2πxλsin2πft
удобнее написано
y = Asinkxsinωt, где k = 2π / λ, ω = 2πf, поэтому ω = ck.
Допустимые значения k (называется волновым числом ):
k = 2π / λ = π / a, 2π / a, 3π / a,… f = ck / 2π.
Обобщение на три размеры просты: в кубической коробке со стороной а допустимая стоячая волна должна удовлетворять граничные условия во всех трех направлениях. Это означает, что можно выбрать следующие волновые числа:
.kx = 2π / λx = π / a, 2π / a, 3π / a,… ky = 2π / λy = π / a, 2π / a, 3π / a, kz = 2π / λz = π / a, 2π / а, 3π / а,…
То есть каждый режим помечен с тремя натуральными числами:
(kx, ky, kz) = πa (l, m, n)
а частота режима:
f = ck / 2π = (c / 2π) kx2 + ky2 + kz2.
(Детали электромагнитного волны и вывод этой формулы приведены в сопроводительных примечаниях ().)
Для инфракрасного и видимого излучения в духовке разумного размера частотные интервалы, измеренные экспериментально, далеки больше, чем расстояние c / 2a этих целых точек. Как и в одномерном примере, эти моды заполняют трехмерное k-пространство равномерно с плотностью (a / π) 3, но теперь это означает, что плотность моды , а не . равномерно как функция частоты.
Число их между f и f + Δf = N (f) Δf – это объем в k-пространстве, в единицах (π / a) 3, сферической оболочки радиусом k = 2πf / c, толщиной Δk = 2πΔf / c, и ограничен, чтобы все компоненты k были положительными (например, целыми числами), множитель из 1/8.
Включая коэффициент 2 для двоих состояния поляризации стоячих электромагнитных волн, плотность состояний как функция частоты в духовке объемом V = a3 составляет:
N (f) Δf = 18 × 2 × 4πk2Δk (π / a) 3 = 14 × (aπ) 3 × 4π (2πc) 3f2Δf
, дающая плотность состояний излучения в духовке
Н (ж) Δf = 8Vπf2Δfc3.
(Детали этого анализа можно найти в примечаниях. Если ты интересно, почему нормально иметь духовку с идеальным отражением стены, когда мы ранее настаивали на поглощающих стенах, Кирхгоф доказал задолго до этого у двух таких духовок при одинаковой температуре будет одинаковый интенсивность излучения – иначе может передаваться энергия от одного к другому, нарушая Второй закон.)
А как насчет равнораспределения энергии?
Центральный результат классической статистической механика – это равнораспределение энергии: для системы, находящейся в тепловом равновесии, каждая степень свободы имеет среднюю энергию 12kBT.(kB – постоянная Больцмана.) Таким образом, молекулы в газе имеют среднюю кинетическую энергии 32kBT, 12kBT для каждого направления и простой одномерный гармонический осциллятор имеет полную энергию kBT: кинетическая энергия 12kBT и потенциальная энергия 12kBT.
Теперь сравнивая формулу для количество мод N (f) Δf в малом интервале Δf
Н (ж) Δf = 8Vπf2Δfc3
с формулой Планка для излучения энергоемкость в том же интервале:
ρ (f, T) Δf = 8πVf2Δfc3hfehf / kBT − 1,
для низкочастотных мод hf≪kBT можно сделать приближение
ehf / kBT − 1≅hf / kBT
, и сразу следует, что каждая мода имеет энергию кБТ, что соответствует классическим предсказаниям.
Но на высоте дела идут плохо частоты! Количество режимов неограниченно увеличивается, энергия в этих высокочастотных модах, однако, экспоненциально затухает с увеличением частоты. Позднее Эренфест назвал это ультрафиолетовым излучением . Катастрофа . Звук Рэлея подход, видимо, был не так уж и хорош – что-то решающий отсутствовал.
Возможно, удивительно, что Planck никогда не упоминал о равнораспределении. Конечно, как заметил сам Рэлей, равнораспределение было хорошо известно, что у него есть проблемы, например, с удельной теплотой газов.А также на самом деле Планк даже не был уверен в существовании атомов: позже он писал, что в 1890-е «Я был склонен отвергать атомизм» (см. Примечания). Фактически, даже Больцман был очень не уверен, как осцилляторы пришли в тепловое равновесие с электромагнитным излучением – ведь было хорошо известно, что колебания двухатомных молекул не смогли достичь классического теплового равновесия с кинетической энергией. (Еще когда 1877 г. Максвелл указал, что горячие газы излучают свет в определенных частоты.Частоты не изменяются с температурой, поэтому колебания должны быть простыми гармоническими, но такой осциллятор наверняка также будьте возбуждены столкновениями на низком температуры, так почему в этот режим не подавалась энергия?)
Эйнштейн видит газ фотонов
Как упоминалось ранее, после Планка объявил свой результат в декабре 1900 г. предмет уже несколько лет. Никто (включая Планка) осознали важность того, что он сделал – его работы многие считали просто умным техническим решением, даже если оно давало правильные ответ (сама кривая была полностью принята за правильную).
Затем в марте 1905 года Альберт Эйнштейн обратил свое внимание на проблему. Он сначала повторно получил результат Рэлея, предполагая равнораспределение:
ρ (f, T) = 8πf2c3kBT
и заметил, что это не чувство на высоких частотах. Итак, он сосредоточился по формуле Планка для высоких частот, hf≫kBT:
ρ (f, T) df≅8πVhf3dfc3e − hf / kBT
(асимптотически идентично при f → ∞ более ранней формуле Вина).
Эйнштейн усмотрел здесь аналогию с распределение энергии в классическом газе.
Вспомните из последней лекции, что (нормированная) функция распределения вероятностей для классических атомов как функция скорости v была
f (v) = 4π (m2πkT) 3 / 2v2e − E / kBT,
и соответствующая плотность энергии в E –
f (E) = [4π (m2πkT) 3 / 2v2] Ee − E / kBT.
Формула излучения при высоких частоты
ρ (f, T) = 8πf2hfc3e − hf / kBT.
Эйнштейн указал, что если высокочастотное излучение представляется газом независимых частиц имея энергию E = hf, плотность энергии по частоте / энергия в радиация
ρ (E, T) = [8πf2c3] Ee − E / kBT.
Сравнивая это с выражением для атомов, аналогия близка: напомним, что для излучения частота равна пропорциональна волновому числу и, при квантовании, импульсу; для (нерелятивистская) скорость атомов пропорциональна импульсу, поэтому оба эти распределения по существу находятся в импульсном пространстве. Конечно, коэффициенты нормализации различаются, потому что общее количество атомов не меняется с температурой, в отличие от общего радиация. Тем не менее аналогия убедительным, и побудил Эйнштейна заявить, что излучение в корпусе само квантовалось , квантование энергии было не какой-то особой собственности только настенные генераторы, как думал Планк. Кванты излучения – это, конечно, фотоны, но это слово не было придумано пока позже.
Эйнштейн был обеспокоен Вывод Планком своего результата, как и прежде, зависел от классического анализ взаимодействия пристенного осциллятора и излучения с последующим заявлением, что взаимодействие на самом деле было совсем не таким. Но ответ был правильным, и теперь Эйнштейн начал понимать почему. В отличие от плохо изученные настенные генераторы, стоячая электромагнитная волна колебания в духовке были совершенно четкими.
Энергия в осцилляторе как функция температуры
Эйнштейн понял, что с точки зрения Электромагнитные стоячие волны Рэлея, кривые излучения черного тела имеют простая интерпретация: средняя энергия в генераторе частоты f при температуре T равна
E¯ = hfehf / kBT − 1.
Кроме того, работа Планка сделала правдоподобным что такое же квантование выполняется для материальных осцилляторов в стенах.
Эйнштейн сделал следующий шаг: он предположил, что квантованы все осцилляторы, например, колеблющийся атом в твердый.Это могло бы объяснить, почему Закон Дюлонга-Пети, который присваивает удельную теплоемкость 3 кБ каждому атому в твердом теле, не работает при низкие температуры: когда kBT≪hf, моды не возбуждаются, поэтому поглощают мало нагревать. Удельная теплоемкость падает, как и действительно заметил. Кроме того, это объясняет, почему молекулы двухатомных газов, таких как кислород и азот, не появляются поглощать тепло в колебательных режимах – эти режимы имеют очень высокую частоту.
Стоит задуматься о постоянном обмене энергией с окружающей средой для осциллятора, находящегося в тепловом равновесии при температуре T.Случайные тепловые флуктуации в системе имеют энергию порядка kBT, это количество энергии, примерно, доставлено туда и обратно. Но если осциллятор имеет hf = 5kBT, скажем, он может принимать только порции энергии размер 5kBT, и будет рад только в маловероятном случае что пять из этих случайных колебаний kBT собрались в нужном месте в нужное время. Высокая частота режимы эффективно замораживаются этим минимальным требованием энергии. Экспоненциальный спад возбуждения с частота отражает экспоненциальное падение вероятности получения правильного количество флуктуаций вместе, аналогично экспоненциальному падению вероятности подбрасывания монеты n голов подряд.
Простой вывод формулы Планка из распределения Больцмана
Существенное предположение Планка в вывод его формулы состоял в том, что осцилляторы обмениваются энергией только с излучение в квантах ВЧ. Эйнштейн ясно дал понять, что хорошо понятый стоячие электромагнитные волны, излучение в духовке, также квантовались энергии.
Как обсуждалось в предыдущем лекции, вероятность того, что система при температуре T имеет энергию E, пропорциональна e − E / kBT, формуле Больцмана.Оказывается, эта формула продолжает оставаться справедливо в квантовых системах. Теперь классический простой гармонический осциллятор при T будет иметь распределение вероятностей пропорционально e − E / kBT = e− (mv2 + mω2×2) / 2kBT, поэтому математическое ожидание энергии составляет
E¯ = ∬ (12mv2 + 12mω2×2) e− (mv2 + mω2×2) / 2kBTdvdx∬e− (mv2 + mω2×2) / 2kBTdvdx = kBT,
просто классическое равнораспределение энергия.
Но теперь мы знаем, что это неправда, если осциллятор квантован: энергии теперь находятся на расстоянии hf друг от друга. Принимая основное состояние за ноль энергии, допустимые энергии равны
.0, hf, 2hf, 3hf…
и принимая Больцмана выражение для относительных вероятностей все еще верное, относительные вероятности этих состояний будут в соотношениях:
e-hf / kBT, e-2hf / kBT, e-3hf / kBT…
Найти энергию осциллятора при этой температуре, мы используем эти вероятности, взвешенные соответствующими энергии и разделите на коэффициент нормализации, чтобы гарантировать, что вероятности сложить до 1:
E¯ = hfe − hf / kBT + 2hfe − 2hf / kBT + 3hfe − 3hf / kBT… 1 + e − hf / kBT + e − 2hf / kBT + e − 3hf / kBT… = hfehf / kBT − 1.
(выражение оценивается как следующим образом: запишите e − hf / kT = x, поэтому сумма относительных вероятностей равна 1 + x + x2 + x3 +… = 1 / (1 − x), а числитель в приведенном выше выражении для E¯ равен hfx (1 + 2x + 3×2 +…) = hfx / (1 − x) 2, так как бесконечный ряд в скобках задан дифференцируя 1 + x + x2 + x3 +…)
Это действительно правильный результат из экспериментов с черным телом. Очевидно, относительная вероятность Больцмана функция e − E / kBT по-прежнему действует в квантовых системах.
Примечание к закону Вена о перемещении
Легко увидеть, как смещение Вина Закон следует из формулы Планка: максимальное излучение на единицу частоты диапазон находится на частоте f, для которой функция f3 / (ehf / kBT − 1) максимальна.Численное решение дает hfmax = 2.82kBT.
Это может быть установлено теоретически (и подтверждено экспериментально), что уравнение, связывающее частоту максимальная энергоемкость в Джоулях / м 3 / Гц составляет:
fmax = 5,88 × 1010T Гц / K.
Однако закон часто указывается в члены длины волны , на которой интенсивность, теперь измеряемая в Джоулях / м 3 / м, то есть на единицу интервала длины волны, и
λmax = 2.9 × 10−3Тм⋅К.
Важный момент, на который следует обратить внимание состоит в том, что эти формулы не дают одного и того же результата, как легко проверить, так как fmaxλmax≅1,7 × 108 м / сек, не скорость света! Причина в том что эти две меры, за единичный интервал частоты и за единичный интервал длины волны, различаются, поэтому утверждают, что, скажем, солнечный свет наиболее интенсивен в желтый должен указывать, что используется (на самом деле это длина волны, частоту дал бы ближний инфракрасный).
Графики излучения черного тела как функция температуры были получены с использованием электронной таблицы Excel.Ты добро пожаловать, чтобы загрузить эту таблицу и использовать ее, чтобы изучить, как изменяется радиация с температурой. Его очень легко использовать – вы просто введите температуру и наблюдайте за изменением графика.
СКАЧАТЬ СПИСОК
Хороший пример излучения черного тела это то, что осталось от Большого взрыва. Было обнаружено, что интенсивность картина этого фонового излучения во Вселенной следует за черным телом очень точная кривая, для температуры примерно на три градуса выше абсолютного нуль.
предыдущий дом следующий
Квантовый гармонический осциллятор – Университетская физика, том 3
Цели обучения
К концу этого раздела вы сможете:
- Опишите модель квантового гармонического осциллятора
- Определение различий между классической и квантовой моделями гармонического осциллятора
- Объясните физические ситуации, в которых классическая и квантовая модели совпадают
Колебания встречаются повсюду в природе, в таких вещах, как электромагнитные волны, вибрирующие молекулы и мягкое возвратно-поступательное колебание ветки дерева.В предыдущих главах мы использовали механику Ньютона для изучения макроскопических колебаний, таких как блок на пружине и простой маятник. В этой главе мы начинаем изучать колебательные системы с помощью квантовой механики. Начнем с обзора классического гармонического осциллятора.
Классический гармонический осциллятор
Простой гармонический осциллятор – это частица или система, которая совершает гармоническое движение относительно положения равновесия, например, объект с массой, колеблющийся на пружине.В этом разделе мы рассматриваем колебания только в одномерном. Предположим, что масса движется вперед и назад по
x – направление относительно положения равновесия,. В классической механике частица движется в ответ на линейную восстанавливающую силу, определяемую выражением, где x – это смещение частицы из положения равновесия. Движение происходит между двумя точками поворота, где A обозначает амплитуду движения. Положение объекта периодически изменяется во времени с угловой частотой, которая зависит от массы m осциллятора и от силовой постоянной k чистой силы, и может быть записано как
Полная энергия E осциллятора является суммой его кинетической энергии и упругой потенциальной энергии силы
В поворотных точках скорость осциллятора равна нулю; следовательно, в этих точках энергия колебаний находится исключительно в форме потенциальной энергии.График зависимости потенциальной энергии U ( x ) осциллятора от его положения x представляет собой параболу ((Рисунок)). Функция потенциальной энергии представляет собой квадратичную функцию x , измеренную относительно положения равновесия. На том же графике мы также изображаем полную энергию E осциллятора в виде горизонтальной линии, пересекающей параболу в точке. Тогда кинетическая энергия K представлена как расстояние по вертикали между линией полной энергии и параболой потенциальной энергии.
Яма потенциальной энергии классического гармонического осциллятора: движение ограничено точками поворота в и в. Энергия колебаний равнаНа этом графике движение классического осциллятора ограничено областью, где его кинетическая энергия неотрицательна, что и говорит соотношение энергии (рисунок). Физически это означает, что классический осциллятор никогда не может быть найден за пределами его точек поворота, а его энергия зависит только от того, насколько далеко точки поворота находятся от его положения равновесия.Энергия классического осциллятора изменяется непрерывно. Самая низкая энергия, которую может иметь классический осциллятор, равна нулю, что соответствует ситуации, когда объект находится в состоянии покоя в своем положении равновесия. Состояние с нулевой энергией классического осциллятора просто означает отсутствие колебаний и никакого движения (классическая частица, сидящая на дне потенциальной ямы на (Рисунок)). Когда объект колеблется, независимо от того, насколько большой или малой может быть его энергия, он проводит больше всего времени возле точек поворота, потому что именно здесь он замедляется и меняет направление своего движения.Следовательно, вероятность нахождения классического осциллятора между точками поворота максимальна вблизи точек поворота и минимальна в положении равновесия. (Обратите внимание, что это не заявление о предпочтении объекта перейти на более низкую энергию. Это утверждение о том, как быстро объект перемещается через различные области.)
Квантовый гармонический осциллятор
Одна проблема с этой классической формулировкой состоит в том, что она не является общей. Мы не можем использовать его, например, для описания колебаний двухатомных молекул, где важны квантовые эффекты.Первым шагом к квантовой формулировке является использование классического выражения, чтобы ограничить упоминание постоянной «пружины» между атомами. Таким образом, функцию потенциальной энергии можно записать в более общем виде:
Объединение этого выражения с не зависящим от времени уравнением Шрёдингера дает
Для решения (рисунок), то есть для нахождения разрешенных энергий E и соответствующих им волновых функций, нам требуется, чтобы волновые функции были симметричными относительно (дна потенциальной ямы) и были нормированы.Эти условия гарантируют, что плотность вероятности должна быть конечной при интегрировании по всему диапазону x от до. Как решить (рисунок) – это предмет более продвинутого курса квантовой механики; здесь мы просто приводим результаты. Допустимая энергия
Волновые функции, соответствующие этим энергиям (стационарные состояния или состояния с определенной энергией), равны
, где – нормировочная константа, а – полином степени n , называемый полиномом Эрмита .Первые четыре полинома Эрмита равны
.Несколько примеров волновых функций приведены на (Рисунок). По мере увеличения значения главного числа решения чередуются между четными функциями и нечетными функциями около.
Первые пять волновых функций квантового гармонического осциллятора. Классические пределы движения осциллятора обозначены вертикальными линиями, соответствующими классическим точкам поворота в классической частицы с той же энергией, что и энергия квантового осциллятора в состоянии, указанном на рисунке.Классическая область гармонических колебаний Найдите амплитуду A колебаний для классического осциллятора с энергией, равной энергии квантового осциллятора в квантовом состоянии n .
СтратегияЧтобы определить амплитуду A , мы устанавливаем классическую энергию равной (рисунок).
Решение Получаем
Значение По мере увеличения квантового числа n энергия осциллятора и, следовательно, амплитуда колебаний увеличивается (для фиксированной собственной угловой частоты.Для больших n амплитуда приблизительно пропорциональна квадратному корню из квантового числа.
В этом решении появляется несколько интересных функций. В отличие от классического осциллятора, измеренные энергии квантового осциллятора могут иметь только значения энергии, указанные как (рисунок). Более того, в отличие от квантовой частицы в ящике, допустимые уровни энергии распределены равномерно,
Когда частица, связанная с такой системой, переходит из состояния с более высокой энергией в состояние с более низкой энергией, квант с наименьшей энергией, переносимый испускаемым фотоном, обязательно равен hf .Точно так же, когда частица совершает переход из состояния с более низкой энергией в состояние с более высокой энергией, квант наименьшей энергии, который может быть поглощен частицей, составляет hf . Квантовый осциллятор может поглощать или излучать энергию только кратную этому кванту наименьшей энергии. Это согласуется с гипотезой Планка об обмене энергией между излучением и стенками полости в задаче излучения черного тела.
Колебательные энергии молекулы хлористого водорода Двухатомная молекула HCl состоит из одного атома хлора и одного атома водорода.Поскольку атом хлора в 35 раз массивнее атома водорода, колебания молекулы HCl могут быть довольно хорошо аппроксимированы, если предположить, что атом Cl неподвижен, а атом H совершает гармонические колебания из-за упругой молекулярной силы, моделируемой законом Гука. . Инфракрасный колебательный спектр, измеренный для хлористого водорода, имеет линию самой низкой частоты с центром в точке. Каков интервал между колебательными энергиями этой молекулы? Какова силовая постоянная k атомной связи в молекуле HCl?
Стратегия Линия с самой низкой частотой соответствует излучению фотонов с самой низкой частотой.Эти фотоны испускаются, когда молекула совершает переход между двумя соседними колебательными уровнями энергии. Предполагая, что уровни энергии расположены на одинаковом расстоянии, мы используем (рисунок) для оценки расстояния. Молекула хорошо аппроксимируется, если рассматривать атом Cl как бесконечно тяжелый, а атом H как массу m , которая совершает колебания. Рассматривая эту молекулярную систему как классический осциллятор, силовая постоянная находится из классического соотношения.
Решение Энергетический интервал
Силовая постоянная
Значение Сила между атомами в молекуле HCl на удивление велика.Типичная энергия, выделяемая при энергетических переходах между колебательными уровнями, находится в инфракрасном диапазоне. Как мы увидим позже, переходы между уровнями колебательной энергии двухатомной молекулы часто сопровождают переходы между уровнями вращательной энергии.
Проверьте свое понимание Частота колебаний двухатомной молекулы иодистого водорода HI равна. а) Какова силовая постоянная молекулярной связи между водородом и атомами йода? (б) Какова энергия испускаемого фотона, когда эта молекула совершает переход между соседними колебательными уровнями энергии?
Квантовый осциллятор отличается от классического осциллятора по трем параметрам:
Во-первых, основное состояние квантового осциллятора не равно нулю.В классическом представлении наименьшая энергия равна нулю. Отсутствие состояния с нулевой энергией является общим для всех квантово-механических систем из-за вездесущих флуктуаций, которые являются следствием принципа неопределенности Гейзенберга. Если бы квантовая частица сидела неподвижно на дне потенциальной ямы, ее импульс и ее положение должны были бы быть одновременно точными, что нарушило бы принцип неопределенности Гейзенберга. Следовательно, состояние с самой низкой энергией должно характеризоваться неопределенностями в импульсе и положении, поэтому основное состояние квантовой частицы должно находиться выше дна потенциальной ямы.
Во-вторых, частица в потенциале квантового гармонического осциллятора может быть найдена с ненулевой вероятностью вне интервала. В классической постановке задачи частица не будет иметь никакой энергии в этой области. Вероятность нахождения квантовой частицы в основном состоянии в классически запрещенной области составляет около 16%.
В-третьих, распределение плотности вероятности для квантового осциллятора в основном низкоэнергетическом состоянии является наибольшим в середине ямы.Чтобы с наибольшей вероятностью найти частицу в центре колодца, мы ожидаем, что частица проводит там больше всего времени во время колебаний. Это противоположно поведению классического осциллятора, в котором частица проводит большую часть своего времени, перемещаясь с относительно небольшими скоростями вблизи точек поворота.
Проверьте свое понимание Найдите математическое ожидание положения частицы в основном состоянии гармонического осциллятора, используя симметрию.
Квантовые распределения плотности вероятности меняют свой характер для возбужденных состояний, становясь более похожими на классическое распределение, когда квантовое число становится выше.Мы наблюдаем это изменение уже для первого возбужденного состояния квантового осциллятора, потому что распределение достигает пика вокруг точек поворота и исчезает в положении равновесия, как показано на (Рисунок). В соответствии с принципом соответствия Бора в пределе больших квантовых чисел квантовое описание гармонического осциллятора сходится к классическому описанию, которое проиллюстрировано на (Рисунок). Классическое распределение плотности вероятности, соответствующее энергии кванта состояния, является достаточно хорошей аппроксимацией квантового распределения вероятностей для квантового осциллятора в этом возбужденном состоянии.Это согласие становится все лучше для высоковозбужденных состояний.
Распределение плотности вероятности для нахождения квантового гармонического осциллятора в его квантовом состоянии. Пунктирная кривая показывает распределение плотности вероятности классического осциллятора с той же энергией.Приложение по связи
Приложение по связи[индекс]
СВЯЗЬ И ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Электронная связь
Поскольку информация передается на все большие расстояния, возможности первичных чувств человека недостаточно для надежной и эффективной передачи.Использование электрические сигналы становятся необходимыми, и электрическая энергия используется для передачи информация, подлежащая передаче. Электрическую энергию относительно легко генерировать, контролировать, и обладает желаемым свойством путешествовать со скоростью света. Таким образом, электронные связь предлагает почти мгновенную связь между передатчиком и приемником информация, даже когда они разделены огромными расстояниями.
Линия передачи или канал, по которому электрическая энергия проходит от передатчик к приемнику будет продиктован требованиями связи система.Там, где две станции могут быть физически связаны, простой провод обеспечивает низкую стоимость, эффективный канал. Сигналы телефона и кабельного телевидения являются примерами электронных сообщения, передаваемые по проводам.
Базовая система связиКогда физическая связь между передатчиком и приемником нецелесообразна, электромагнитные волны, излучаемые передатчиком, могут использоваться для передачи информацию на удаленный приемник. Атмосфера – это канал, через который излучаемые электромагнитные волны распространяются.Системы связи, использующие электрические энергия, излучаемая через атмосферу, включает радио, радар и сотовый телефон. системы. Природа электромагнитных волн, распространяющихся в атмосфере, и необходимое расстояние связи, будет определять физические характеристики электрических энергия, используемая для производства излучаемых волн.
Связь с помощью излучаемых электромагнитных волнМодуляция электрических сигналов
Если электронный сигнал должен использоваться для передачи информации, некоторые характеристики сигнал должен изменяться или модулироваться таким образом, чтобы информация содержалась, или несется по сигналу.Приемник сигнала должен иметь возможность восстановления, или демодуляция информации из принятого сигнала. В этом смысле передатчик и пара приемников, в сочетании с каналом передачи, образуют связь система. Модулятор используется для подготовки информационного сигнала для эффективного передача по каналу, а демодулятор восстанавливает информационный сигнал от принятого сигнала несущей.
Модуляция и демодуляция информационного сигналаВ простой электронной системе связи наличие или отсутствие сигнала может использоваться для передачи информации, такой как щелчок телеграфного ключа, который закрывается в наличие тока на телеграфной линии.Телеграфная линия передает импульсы тока. которые воспринимаются человеком как азбука Морзе. В этом случае люди-операторы действует, чтобы модулировать и демодулировать информационный сигнал на телеграф и обратно линия. В импульсной кодовой модуляции (ИКМ) используется аналогичный метод передачи цифрового сигнала. информационный сигнал, обычно в двоичном коде, в виде последовательности импульсов. Примером может служить компьютерный модулятор / демодулятор (МОДЕМ), используемый для кодирования и декодирования цифровых данных, включая и выключая телефонные линии в виде серии импульсных сигналов.
Для более сложной информации, такой как речь или аудио, информационный сигнал изменяется во времени и является непрерывным, и используются более сложные методы модуляции. Синусоидальный сигналы напряжения или тока, оптимизированные для конкретного канала, используются для «переноса» информационный сигнал. Эти несущие волны обладают некоторыми физическими свойствами, которые модулируются, например что информационный сигнал содержится в несущей волне. Амплитудная модуляция (AM) и частотная модуляция (FM) – два распространенных метода модуляции синусоидального несущая волна, и будет подробно изучена.
ВОЛНОВЫЕ ХАРАКТЕРИСТИКИ
Многие формы энергии распространяются как бегущие волны. Механические волны, например звук Для распространения волн в воздухе или волн давления в воде требуется физическая среда. В волновая скорость механических волн сильно зависит от характеристик материала средний. Напротив, электромагнитные волны (радио, радар, свет и т. Д.) Не требуют средний и будет распространяться в свободном пространстве. Скорость волны электромагнитного волны в свободном пространстве – это скорость света (c) и очень близка к скорости света в среды, такие как атмосфера и вода.Является ли бегущая волна механической или электромагнитные по своей природе, одного набора характеристик достаточно для описания движущихся волна.
Хотя большая часть развития волновых характеристик не зависит от формы волны используется синусоидальная форма волны, поскольку ее легко сгенерировать, легко смоделировать и более сложные формы сигналов можно описать суммами синусоидальных волн. Самый легкий Синусоидальная волна для описания – это стоячая волна, заданная уравнением стоячей волны:
y (r) ~ = ~ {A} ~ {sin} ~ ({2 pi r} сверх лямбды)
Без временной зависимости и, следовательно, без движения стоячая волна не передает энергии или информация, и варьируется только с расстоянием (r).Смотрим на стоячую волну, то в чтобы легко распознать некоторые характеристики, которые будут общими для более сложных волны.
Амплитуда (А)
Длина волны ()
Одна из основных характеристик любой волны – длина волны (). Определяется как кратчайшее расстояние, на котором волновая картина полностью повторяется, длина волны имеет физические единицы длины (метры). Длину синусоидальной волны найти проще всего путем измерения расстояния от одного пика до следующего пика.
Частота и период
Вторая фундаментальная характеристика волны – это ее частота (f).
Электромагнитные волны
Электронная связь на большие расстояния обычно требует использования электромагнитные волны энергии как канал передачи между передатчиком и приемником.
необходимо разработать набор свойств, описывающих волны. Электромагнитный спектр охватывает огромный диапазон частот, начиная с мощности ниже 60 Гц. в розетке переменного тока выше шестисот тысяч миллиардов Гц зеленого света в диапазоне видимый свет.Для удобства электромагнитный спектр разбит на частотный диапазоны, которые имеют схожие характеристики: радиостанция
AMPLITUDE MODULATIONПроцесс передачи речи или звука по линиям (проводам) передачи представлен Немногочисленные проблемы, о чем свидетельствует количество телефонов и телефонных линий. Передача тех же сигналов в удаленные места с помощью излучаемых электромагнитных волн, однако создает множество физических ограничений. Тон с частотой 300 Гц, захваченный микрофон будет генерировать напряжение, колеблющееся с той же частотой.Как электромагнитная волна, сигнал 300 Гц будет иметь длину волны один миллион метров. Учитывая, что антенны короче -волновой являются неэффективными излучателями, передающие электромагнитные волны на этой частоте потребуют антенны на расстоянии не менее 155 миль в длина. Должен быть какой-то метод использования более высокой частоты – более короткой длины волны – волны, которые можно модулировать для передачи информации на более низких частотах. Эти высокие тогда волны несущей частоты могут быть эффективно излучены антеннами разумного размера.
Один метод кодирования низкочастотного информационного сигнала, такого как речь или аудио, на более высокочастотную несущую, чтобы амплитуда несущей волны могла изменяться прямо с амплитудой информационного сигнала. В передатчике генератор на желаемая частота даст необходимую несущую волну. Амплитуда несущая волна напрямую зависит от амплитуды информационного сигнала, а информация содержится в контуре или огибающей амплитудно-модулированной (AM) сигнал.
Генератор используется для генерации непрерывной синусоидальной несущей волны на желаемой несущая частота (fc), здесь выраженная в виде напряжения, vc (t):
v SUB {c} (t) ~ = ~ V SUB {c} cos (2 pi f SUB {c} t)
Информационный сигнал моделируется одиночной синусоидальной волной на модулирующем частота (фм). Этот общий модулирующий сигнал формирует основу для более сложных сигналов, и будет достаточно для этого развития.


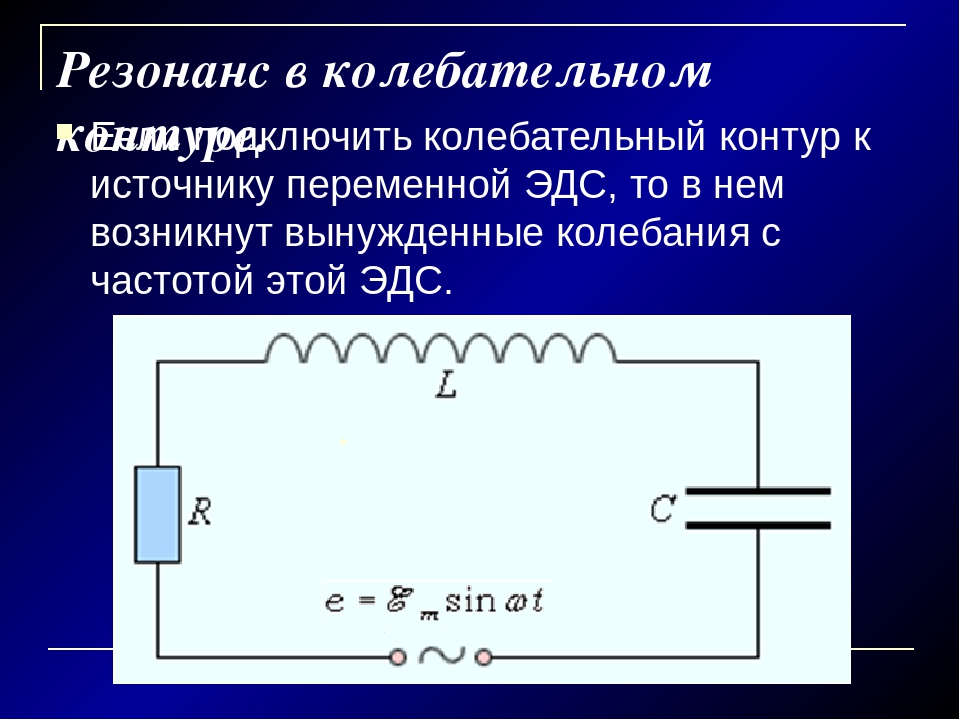 е. колебания затухают.
е. колебания затухают. Положительно заряженная пластина конденсатора, соединенная с коллектором, разряжается. Ток в колебательном контуре возрастает до максимального значения. В катушке связи возникает индукционный ток такого направления, что база имеет отрицательный потенциал относительно эмиттера. Переходы база — коллектор и эмиттер — база прямые. Транзистор открыт. Энергия от источника поступает через транзистор в колебательный контур (ключ замкнут).
Положительно заряженная пластина конденсатора, соединенная с коллектором, разряжается. Ток в колебательном контуре возрастает до максимального значения. В катушке связи возникает индукционный ток такого направления, что база имеет отрицательный потенциал относительно эмиттера. Переходы база — коллектор и эмиттер — база прямые. Транзистор открыт. Энергия от источника поступает через транзистор в колебательный контур (ключ замкнут). Тока в цепи нет (ключ разомкнут).
Тока в цепи нет (ключ разомкнут).