Индуктивность магнитного поля это: Магнитная индукция — урок. Физика, 8 класс.

Индукция магнитного поля, теория и примеры

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Физика Индукция магнитного поля

Индукция магнитного поля (магнитная индукция, вектор магнитной индукции) () – это одна из основных физических векторных величины, которые характеризуют магнитное поле. Это силовая характеристика данного поля, отображающая действие поля на заряженную частицу в рассматриваемой точке пространства.

Определения индукции магнитного поля

Индукцию магнитного поля можно определить разными способами: понятие вращающего момента рамки с магнитным моментом, используя закон Ампера, силу Лоренца.

1) Модуль вектора индукции магнитного поля в конкретной точке однородного магнитного поля определен максимальным вращающим моментом (), который действует на рамку, обладающую магнитным моментом (), равным единице,, если нормаль к рамке ориентирована перпендикулярно направлению поля:

   

2) Величина индукции магнитного поля равна пределу отношения силы (dF), с которой действует магнитное поле на элементарный проводник с током, к силе тока (I) умноженной на длину этого проводника (dl), при длине проводника стремящейся к нулю. При этом проводник имеет такое расположение в магнитном поле, что данный предел имеет максимальное значение:

   

направлен перпендикулярно элементу dl, и направлению силы Ампера. Если смотреть из конца , то вращение по кратчайшему расстоянию от направления силы Ампера к направлению силы тока в проводнике должно происходить против часовой стрелки.

3) Исходя из определения силы Лоренца (), величину вектора магнитной индукции найдем как:

   

где q – заряд частицы, движущейся в магнитном поле; v – скорость движения частицы; – угол между направлением скорости частицы и вектором поля. Направления силы Лоренца, векторов скорости и магнитной индукции связаны между собой правилом левой руки. Если левую руку расположить так, что в нее входит , четыре вытянутых пальца направить по то отогнутый на 90^o большой палец укажет направление силы, с которой магнитное поле действует на положительно заряженную частицу.

Для однородного изотропного магнетика, заполняющего пространство, вектор магнитной в веществе () и вектор индукции в вакууме(, при одинаковых условиях, связаны формулой:

   

где – относительная магнитная проницаемость вещества.

Суперпозиция магнитных полей

Для магнитного поля справедлив принцип суперпозиции: если присутствует магнитных, то индукция результирующего поля равна векторной сумме отдельных индукций:

   

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Магнитная индукция | это.

.. Что такое Магнитная индукция?

Не следует путать с явлением электромагнитной индукции.

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

Более конкретно,  — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля^[1] на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена^[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.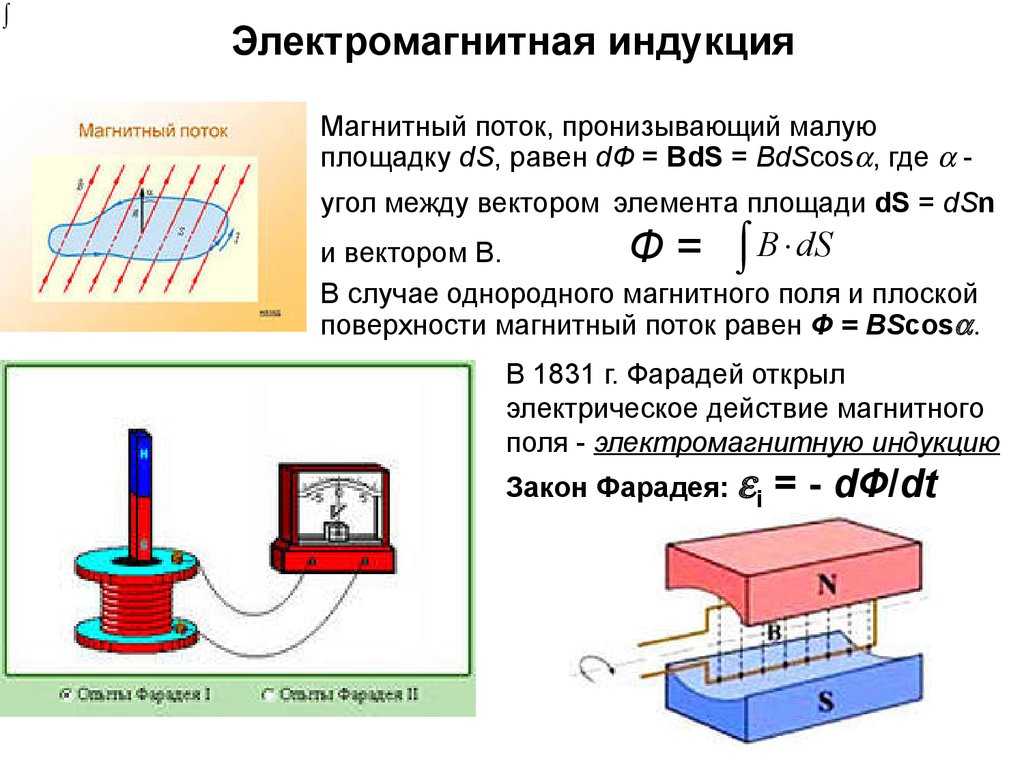

В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)

1 Тл = 10⁴ Гс

Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.

Содержание 1 Основные уравнения 1.1 В магнитостатике 1.2 В общем случае 2 Примечания 3 См. также

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряженность магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

• (Здесь формулы приведем в системе единиц СИ, в виде для вакуума^[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе^[4] наиболее важными являются:

• Закон Био-Савара — занимающий в магнитостатике место, занимаемое в электростатике законом Кулона:

• Теорема Ампера о циркуляции магнитного поля^[5]:

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции :

• Три из четырех уравнений Максвелла (основных уравнений электродинамики)
  • а именно:
  • Закон Гаусса для магнитного поля,

  • Закон электромагнитной индукции:

  • Закон Ампера – Максвелла.

• Формула силы Лоренца
  • Следствия из нее, такие как
    • Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)

    • выражение для вращающего момента, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):

    • выражение для потенциальной энергии магнитного диполя в магнитном поле:

    • а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..
    • Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
      • (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

• Выражение для плотности энергии магнитного поля
  • Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Примечания

1. ↑ Если учитывать и действие электрического поля
   E, то формула (полной) силы Лоренца принимает вид:
   При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведенную в основном тексте.
2. ↑ Это определение с современной точки зрения менее фундаментально, чем приведенное выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
3. ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
4. ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближенно — если изменения настолько медленны, что ими можно пренебречь.
5. ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в стаье далее).

См. также

• Векторный потенциал
• Уравнения Максвелла
• Электромагнитное поле
• Тензор электромагнитного поля
• Напряженность магнитного поля

5.3: Индуктивность – Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

21536

• Том Вайдеман
• Калифорнийский университет, Дэвис

Взаимная индуктивность

В соответствии с нашей традицией следовать за электричеством при обсуждении магнетизма (Кулон против Био-Савара, дипольная математика, Гаусс против Ампера и т. д.), пришло время заняться версией магнетизма о емкости. Напомним, что емкость была чисто статическим зарядом — способом накопления энергии на двух проводниках с противоположными зарядами. Магнетизм — это что угодно, только не явление статического заряда, поэтому его версия емкости должна быть совершенно другой. Это другое, но есть и много параллелей.

Если мы поместим две цепи рядом друг с другом и изменим ток, протекающий через одну из них, то магнитное поле для этого изменяющегося тока также изменится. Если это магнитное поле вызывает поток через второй контур, то его изменение может индуцировать ток во втором контуре. Таким образом, мы каким-то образом можем передавать энергию из одной цепи в другую, даже не соединяя цепи друг с другом. Один из способов объяснить это — предположить, что в самом магнитном поле присутствует энергия. Мы уже знаем, что энергия содержится в электрическом поле, так что это не удивительно. Вот схема этой физической ситуации:

Рисунок 5. 3.1 – Взаимная индуктивность

Мы ввели здесь новый символ. Круг с волнистой линией указывает на переменный источник тока (это объясняет, почему рядом с ним находится зависящая от времени переменная тока). Этот переменный ток \(I\left(t\right)\) проходит через левую катушку, в результате чего возникает зависящее от времени магнитное поле \(\overrightarrow B\left(t\right)\). Это поле проходит через правую катушку, что приводит к изменяющемуся во времени потоку \(\Phi_B\left(t\right)\). Закон Фарадея гласит, что этот переменный поток приводит к ЭДС индукции \(\mathcal E \left(t\right)\), регистрируемой вольтметром.

Наша цель состоит в том, чтобы математически связать ЭДС, возникающую во вторичной катушке, с переменным током, проходящим через первичную катушку. Начнем с того, что отметим, что напряженность магнитного поля прямо пропорциональна току через первичную катушку (та, что слева на рисунке выше), а магнитный поток через вторичную катушку пропорционален магнитному напряженность поля. Оба эти факта основаны на представлении о том, что поле и его отношение к площади, через которую оно проходит, имеет одинаковую форму при неизменной геометрии конструкции этого устройства. Это должно звучать очень знакомо. Соединяя эти пропорциональности вместе, мы получаем, что поток через вторичную катушку (которая, как мы скажем, имеет \(N\) витков) пропорционален току через первичную катушку, и мы можем определить константу пропорциональности \(M\) , называется взаимная индуктивность конструкции:

\[N\Phi_B\left(t\right) =M I\left(t\right)\]

Это дает нам связь между входным током и результирующей ЭДС, которую мы искали по закону Фарадея:

\[\mathcal E\left(t\right) = -M\dfrac{d}{dt}I\left(t\right)\]

Это магнитный аналог к электростатическому \(Q=CV\). Как и в случае с емкостью, взаимная индуктивность зависит только от конструкции устройства — она не меняется при изменении тока, протекающего через него, точно так же, как емкость не изменяется при изменении количества заряда на пластинах. Единицы индуктивности: 92}{А} \эквив Н\;\;\; \text{(“henry”)}\)

Одна вещь, которая, кажется, отличает взаимную индуктивность от емкости, – это кажущаяся односторонняя природа ее – есть отдельные первичная и вторичная катушки, в то время как конденсатор имеет только два проводника, либо из которых может принять положительный заряд. Вот и получается, что взаимная индуктивность одинаково обратима! Причина в том, что количество витков в первичной обмотке пропорционально напряженности магнитного поля точно так же, как количество витков во вторичной обмотке пропорционально общему потоку. То есть, если мы поменяем местами источник тока и вольтметр на рисунке выше, мы получим тот же результат. Мы можем выразить это математически, обозначив все (число витков, поток и ток) для каждой катушки по-разному:

\[M=\dfrac{N_2\Phi_2}{I_1} = \dfrac{N_1\Phi_1}{I_2}\]

Давайте убедимся, что это правда (а также изучим некоторые нюансы физики), посмотрев на примере. Физическая установка состоит из двух соосных соленоидов одинаковой длины, но со своими площадями поперечного сечения и числом витков.

Рисунок 5.3.2 – Взаимная индуктивность коаксиальных соленоидов – ток по внешнему цилиндру

В этой схеме у нас есть переменный ток, проходящий через внешний соленоид, и изменяющийся поток внутри соленоида. Поле внешнего соленоида однородно по всей его внутренней части, и только часть внутри области внутреннего соленоида вносит вклад в поток.

Рисунок 5.3.3 – Поток через внутренний соленоид поля от внешнего соленоида

, откуда легко вычислить поток:

\[\Phi_2 = BA_2 = \left(\dfrac{\mu_oN_1I_1}{l}\right)A_2\;\;\;\Rightarrow\;\;\; M=\dfrac{N_2\Phi_2}{I_1} = \dfrac{\mu_oN_1N_2A_2}{l}\]

Мы можем видеть, что этот результат зависит только от структуры двух соленоидов. Итак, давайте проверим, выполняется ли свойство обратимости. Теперь пропустим переменный ток через внутренний соленоид.

Рисунок 5.3.4 – Взаимная индуктивность коаксиальных соленоидов – ток по внутреннему цилиндру

но на этот раз картина немного другая.

Рисунок 5.3.5 – Поток через внешний соленоид поля от внутреннего соленоида

внутренний соленоид и нулевой поток через внешнюю область:

\[\Phi_1=B_{внутренний}A_2 + B_{внешний}\left(A_1-A_2\right) = \left(\dfrac{\mu_oN_2I_2}{l}\right)A_2+0 = \dfrac{\ mu_oN_2I_2A_2}{l}\]

Теперь подставьте это в определение взаимной индуктивности и обнаружите, что это то же самое, что и когда роли соленоидов поменялись местами:

\[M=\dfrac{N_1\Phi_1}{I_2 } = \dfrac{\mu_oN_1N_2A_2}{l}\]

Самоиндукция

Теперь мы можем видеть, как одна цепь может воздействовать на другую, не находясь в физическом контакте, но на самом деле не обязательно иметь две катушки в для того, чтобы засвидетельствовать эффект магнитной индукции. Предположим, у нас есть переменный ток в цепи, содержащей один соленоид. Поскольку ток в соленоиде изменяется, магнитное поле внутри соленоида изменяется, что, в свою очередь, изменяет магнитный поток через тот же самый соленоид.

Это индуцирует ЭДС на соленоиде, что, в свою очередь, влияет на ток через него! Этот процесс известен как самоиндукция .
На самом деле мы определяем самоиндукцию так же, как мы определяли взаимную индуктивность – отношение полного потока через \(N\) катушек к току, который питает магнитное поле. Естественно, единицы измерения такие же, как и взаимная индуктивность.

\[L\equiv\dfrac{N\Phi}{I}\]

С практической точки зрения единственным разумным устройством, для которого мы можем вычислить собственную индуктивность, является соленоид, так как его однородное магнитное поле создает поток легко вычислить: 92A}{l}\]

Как и в случае взаимной индуктивности, это значение \(L\) является константой, которая зависит только от конструкции соленоида (далее именуемого индуктором ). Разница здесь, конечно, в том, что ЭДС, индуцированная изменением тока/поля/потока, воздействует на тот же самый ток, с которого начинается изменение потока. В частности:

\[N\Phi = LI \;\;\;\Rightarrow\;\;\; N\dfrac{d}{dt}\Phi = \dfrac{d}{dt}\left(LI\right) \;\;\;\Rightarrow\;\;\; \mathcal E = -N\dfrac{d}{dt}\Phi=-L\dfrac{d}{dt}I\]

Как мы это интерпретируем? Вспомните, что здесь происходит — действует закон Фарадея, а это означает, что индуцируется ЭДС (как в батарее, но без химической реакции).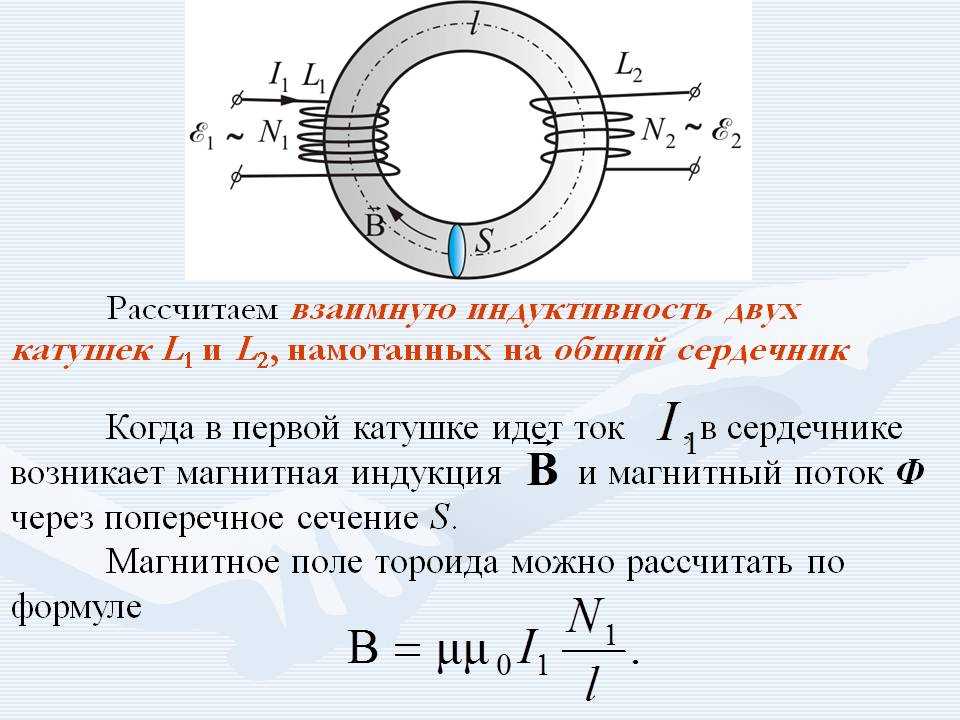 Таким образом, мы можем думать об этом как об «умной батарее», которая регулирует свою ЭДС (величину и направление) в соответствии с тем, что происходит с током. Знак минус указывает на то, что эта интеллектуальная батарея приспосабливается к изменениям. Если ток затухает, на помощь приходит индуктор и создает ЭДС, чтобы попытаться помочь сохранить ток, а если ток растет, то индуктор создает ЭДС, чтобы попытаться замедлить его увеличение.

Рисунок 5.3.6 – Индуктор ведет себя как «умная батарея»

поток через индуктор. ЭДС индукции на катушке индуктивности будет такой, что она будет стремиться усилить ток через себя (который также проходит через резистор). Для этого требуется, чтобы потенциал на клемме \(B\) интеллектуальной батареи был больше, чем потенциал на клемме \(A\). Если ток увеличивается, то для борьбы с этим изменением потенциал на выводе \(A\) умной батареи должен быть больше, чем потенциал на выводе \(B\).

Применим к этой схеме правило Кирхгофа. Выбрав направление петли по часовой стрелке, имеем:

\[V_B-V_A -IR = 0\]

Если ток убывает, то его производная отрицательна. В этом случае индуктор действует как умная батарея с положительным полюсом в положении \(B\), поэтому падение напряжения на индукторе для нашего контура по часовой стрелке должно быть положительным. Если вместо этого ток увеличивается, то производная тока положительна, и интеллектуальная батарея меняет направление, в результате чего падение напряжения на катушке индуктивности для петли по часовой стрелке становится отрицательным. Оба этих сценария согласуются с сделанным выше выводом о том, что падение потенциала на катушке индуктивности удовлетворяет условию \(\mathcal E = -L\frac{dI}{dt}\).

---

Эта страница под названием 5.3: Inductance распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Томом Вайдеманом непосредственно на платформе LibreTexts.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Том Вайдеман

   Лицензия

   CC BY-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. источник@родной

Магнитная индукция, магнитный поток и закон Фарадея

В статье определены другие основные принципы магнетизма, магнитной и индукторной составляющих – магнитная индукция, магнитный поток и закон Фарадея.

Магнитная индукция B

Потенциал индуцируется в петле проводника, если магнитное поле, проходящее через петлю проводника, изменяется со временем.

Всплеск потенциала на площади контура известен как магнитная индукция Б . Как и напряженность магнитного поля, магнитная индукция B является векторной величиной.

Для магнитной индукции применяется следующее соотношение B :

уравнение магнитной индукции [1]

Магнитная индукция ( B ) представляет собой частное индуцированного выброса потенциала:

потенциал индуцированного магнитного выброса [2]

и произведение витков обмотки ( N ) и площади витков ( A ) индукционной катушки.

Единицей магнитной индукции (В) является Тесла (Тл) = Вс/м2.

Магнитная индукция B и напряженность поля H пропорциональны друг другу. Константа пропорциональности — это постоянная магнитного поля ( μ0 ), полученная экспериментальным путем.

постоянная магнитного поля [3]

В вакууме, а также с достаточной точностью для воздуха это приводит к:

уравнению магнитной индукции [4]

Магнитная индукция ( B _L ) в воздухе для приведенного выше примера определяется как:

магнитная индукция в воздушной среде [5]

Магнитный поток F

Магнитный поток ( F ) является скалярным произведением магнитного поля плотность потока ( B ) и вектор площади ( дА ).

уравнение магнитного потока [6]

Если ( B ) проходит перпендикулярно через площадь и поле однородно:

уравнение магнитного потока в однородном поле [7]

Единица измерения магнитного потока ( F ) такая же, как и у скачка напряжения (Вс) (Вольт-секунда) или Вебера (Вб).

Закон Фарадея

До сих пор мы рассматривали статические магнитные поля. Если магнитный поток изменяется со временем, индуцируется напряжение U (закон Фарадея).

индуцированное напряжение Закон Фаради [8]

U = индуцированное напряжение
t = время

Полярность напряжения такова, что ток генерируется при замыкании цепи, индуцированное магнитное поле которой противодействует исходному магнитному потоку, т. е. стремится уменьшить магнитное поле (правило Ленца – рис. 1).

Рисунок 1. Представление правила Ленца. Наложенное магнитное поле индуцирует ток в таком направлении, что его индуцированное магнитное поле противодействует наложенному полю

Взяв обмотку с N витками, закон Фарадея можно выразить в следующей форме.

Закон Фарадея с N витками обмотки [9]

A = поперечное сечение катушки
l = длина катушки или магнитной цепи
I = ток через катушку
L = индуктивность катушки [H(enry) = Vs/A]

Таким образом, индуктивность ограничивает изменение тока при подаче напряжения.