Инвертирующий усилитель на оу: Инвертирующий усилитель на операционном усилителе: схема, формула

Инвертирующий усилитель на операционном усилителе: схема, формула

Пример HTML-страницы

Как уже отмечалось, операционные усилители в настоящее время используются в самых различных электронных устройствах. Их широко применяют как в аналоговых, так и в импульсных устройствах электроники. В то же время существуют и часто используются типовые линейные схемы на основе операционных усилителей. Такие типовые схемы должен знать каждый инженер, использующий электронные устройства. Именно такие схемы рассматриваются ниже.

Очень полезно овладеть достаточно простыми приемами ручного анализа электронных схем на основе операционных усилителей. Это значительно облегчит понимание принципа действия конкретных устройств электроники и будет способствовать получению достоверных результатов машинного анализа. Указанные приемы анализа основаны на ряде допущений, принимаемых в предположении, что используемые операционные усилители достаточно близки к идеальным. Практика расчетов показывает, что результаты, получаемые на основе допущений, имеют вполне приемлемую погрешность.

Примем следующие допущения:

• Входное сопротивление операционного усилителя равно бесконечности, токи входных электродов равны нулю (R_вх → ∞, i₊ = i₋).
• Выходное сопротивление операционного усилителя равно нулю, т. е. операционный усилитель со стороны выхода является идеальным источником напряжения (R_вых = 0).
• Коэффициент усиления по напряжению (коэффициент усиления дифференциального сигнала) равен бесконечности, а дифференциальный сигнал в режиме усиления равен нулю (при этом не допускается закорачивания выводов операционного усилителя).
• В режиме насыщения напряжение на выходе равно по модулю напряжению питания, а знак определяется полярностью входного напряжения. Полезно обратить внимание на тот факт, что в режиме насыщения дифференциальный сигнал нельзя всегда считать равным нулю.
• Синфазный сигнал не действует на операционный усилитель.
• напряжение смещения нуля равно нулю.

Рассмотрим схему инвертирующего усилителя (рис. 2.25), из которой видно, что в ней действует параллельная обратная связь по напряжению.

Так как i₋ = 0, то в соответствии с первым законом Кирхгофа i₁ = i₂.

Предположим, что операционный усилитель работает в режиме усиления, тогда uдиф = 0. В соответствии с этим на основании второго закона Кирхгофа получим i₁ = uвх/ R₁i₂ = − uвых/ R₂

Учитывая, что i₁ = i₂, получаем uвых= −uвх· R₂ / R₁

Таким образом, инвертирующий усилитель характеризуется коэффициентом усиления по напряжению, равным Кu= −R2/R1

Например, если R1= 1кОм,R2=10 кОм, тогда uвых= − 10 ·uвх

Для уменьшения влияния входных токов операционного усилителя на выходное напряжение в цепь неинвертирующего входа включают резистор с сопротивлением R₃ (рис. 2.26), которое определяется из выражения R3=R1//R2=R1·R2/ (R1+R2)

Входное сопротивление инвертирующего усилителя на низких частотах значительно ниже собственного входного сопротивления операционного усилителя. Это полностью соответствует сделанному раннее выводу о том, что параллельная отрицательная обратная связь, имеющая место в схеме, уменьшает входное сопротивление. Учитывая, что uдиф~ 0, легко заметить, что иходное сопротивление усилителя на низких частотах приблизительно равно R₁.

Выходное сопротивление инвертирующего усилителя на низких частотах R_вых.ос существенно меньше выходного сопротивления на низких частотах R_вых собственно операционного усилителя. Это является следствием действия отрицательной обратной связи по напряжению.

Можно показать, что R_вых.ос = R_вых / ( 1 + К ·R1/R2) где К — коэффициент усиления по напряжению операционного усилителя.

Инвертирующий усилитель на ОУ

Схема инвертирующего усилителя приведена на рис. 1.1. Нетрудно увидеть , что за счет резистора R2 в схеме обеспечивается глубокая отрицательная обратная связь. Обратная связь создает особый режим точки А схемы. Операционный усилитель всегда усиливает дифференциальное напряжение Uд , которое приложено непосредственно между инвертирующим и неинвертирующим входами. При этом

Любое изменение входного напряжения приведет к изменению напряжения на выходе, причем выходное напряжение будет изменяться до тех пор, пока за счет влияния отрицательной обратной связи потенциал точки А не станет равным

В современных ОУ , поэтому потенциал точки А можно считать равным нулю, т.е. она является потенциально заземленной (так называемый “виртуальный нуль”). Однако гальванически точка А отделена от “земли”, т.к. дифференциальное входное сопротивление ОУ можно считать равным бесконечности

Рисунок 1.1 – Инвертирующий усилитель на ОУ

Учитывая большой дифференциальный коэффициент усиления ОУ и свойства усилителя, охваченного глубокой отрицательной обратной связью, можно предположить, что коэффициент усиления инвертирующего усилителя будет определяться только параметрами цепи обратной связи.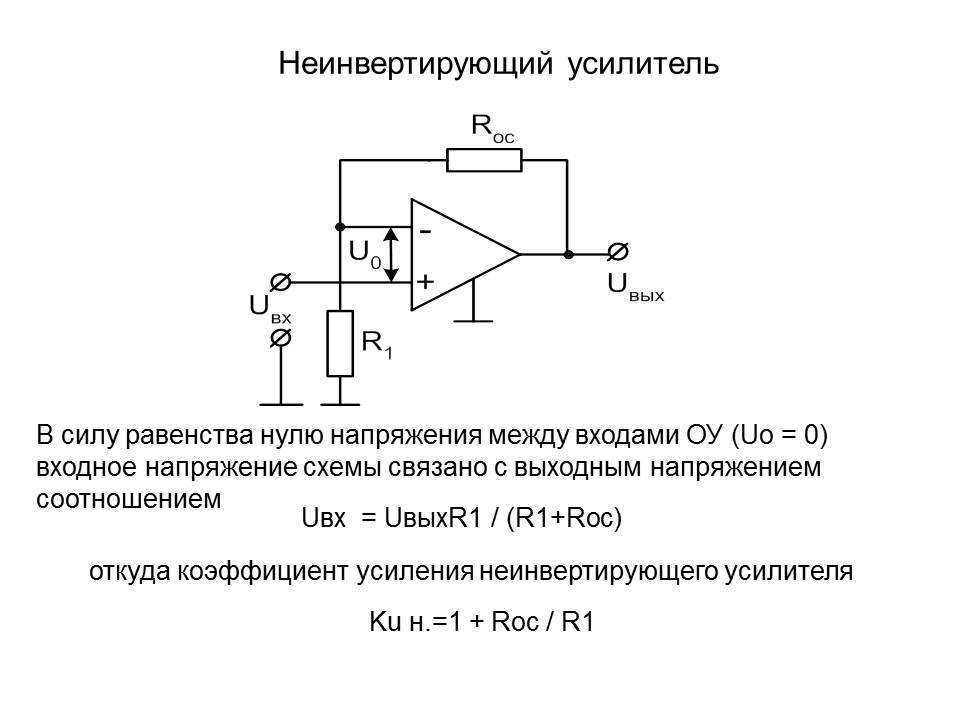 Действительно, если принять и пренебречь входными токами смещения, то для точки А по закону Кирхгофа

В свою очередь

С учетом этого можно получить

откуда коэффициент усиления инвертирующего усилителя

Знак минус перед правой частью означает, что выход инвертирован.

Входные токи смещения ОУ чрезвычайно малы, однако при усилении сигналов низкого уровня, к которым относятся и биомедицинские сигналы, токи смещения могут привести к появлению погрешности усиления. Для повышения точности усилителя целесообразно в цепь неинвертирующего входа включать резистор, как показано на рис. 1.2.

Рисунок 1.2

Наличие резисторов одинаковой величины на инвертирующем и неинвертирующем входах при протекании токов смещения вызывает одинаковое падение напряжения, т.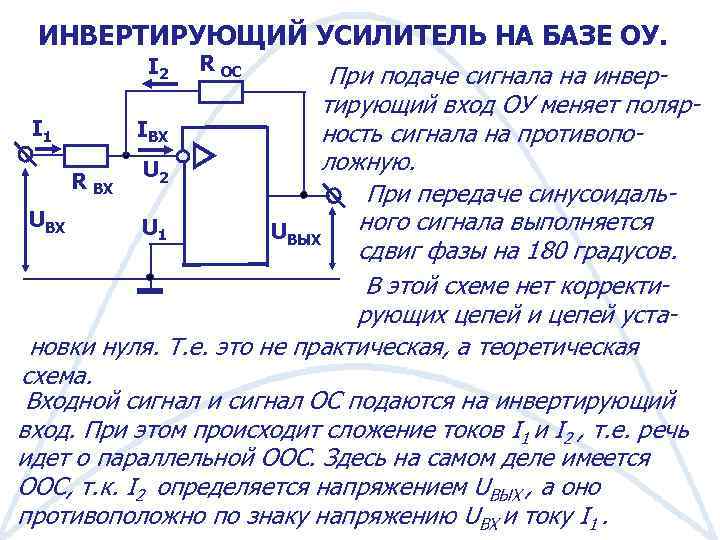

е. дифференциальный входной сигнал будет равен нулю. Кроме того, для уменьшения влияния тока смещения сопротивление R2 выбирать не более нескольких сотен килоОм.

Входное сопротивление инвертирующего усилителя (рис. 1.1) равно R1, так как благодаря обратной связи потенциал точки А приблизительно равен нулю . Поэтому сопротивление R1 должно выбираться так, чтобы не нагружать источник входного сигнала, а R2 должно быть достаточно большим, чтобы не нагружать выходную цепь операционного усилителя.

Нравится

Твитнуть

Инвертирующий и неинвертирующий суммирующий усилитель

В этом уроке мы узнаем о суммирующем усилителе, его конфигурациях, типах суммирующих усилителей (инвертирующих и неинвертирующих) и некоторых областях применения суммирующего усилителя.

Одним из важных применений операционного усилителя является суммирующий усилитель, также известный как сумматор. Как следует из названия, суммирующий усилитель представляет собой схему на основе операционного усилителя, в которой суммируются несколько входных сигналов разного напряжения.

Для получения информации об основах операционных усилителей см. Основы операционных усилителей.

Описание

Введение

Многие приложения в электронных схемах требуют добавления или объединения двух или более аналоговых сигналов в один сигнал. Одним из лучших примеров таких требований являются приложения для записи музыки и вещания. В случае типичной настройки записи музыки у нее есть несколько входов от нескольких микрофонов, а выход – стерео (левый и правый).

Здесь пригодится суммирующий усилитель, так как он объединяет несколько входов в один общий сигнал без шума и помех. По этой причине суммирующий усилитель также называют сумматором напряжения, поскольку его выход представляет собой сложение напряжений, присутствующих на его входной клемме.

Инвертирующий суммирующий усилитель

Наиболее часто используемый суммирующий усилитель представляет собой расширенную версию конфигурации инвертирующего усилителя, т. е. несколько входов подаются на инвертирующий вход операционного усилителя, а неинвертирующий вход подключается к земле.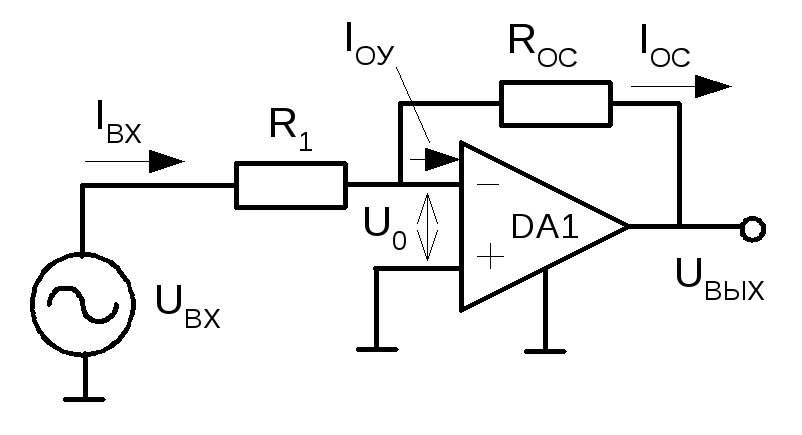 Из-за этой конфигурации выход схемы сумматора напряжения не совпадает по фазе на 180 ^или  относительно ввода.

Общая конструкция суммирующего усилителя показана на следующей схеме. Обычная схема инвертирующего усилителя имеет только одно напряжение/вход на инвертирующем входе. Если к инвертирующему входному терминалу подключено больше входных напряжений, как показано, результирующий выход будет суммой всех приложенных входных напряжений, но инвертированных.

Прежде чем анализировать приведенную выше схему, давайте обсудим важный момент в этой установке: концепцию виртуального заземления. Поскольку неинвертирующий вход вышеуказанной схемы подключен к земле, инвертирующий вход операционного усилителя находится на виртуальной земле. В результате инвертирующий входной узел становится идеальным узлом для суммирования входных токов.

Принципиальная схема суммирующего усилителя показана на рисунке выше. Вместо использования одного входного резистора все источники входного сигнала имеют свои собственные входные резисторы. Такая схема усиливает каждый входной сигнал. Коэффициент усиления для каждого входа определяется отношением резистора обратной связи R _f к входному сопротивлению в соответствующей ветви.

Расчет выходного напряжения инвертирующего суммирующего усилителя

Пусть R ₁ — входное сопротивление, а V ₁ — входное напряжение первого канала. Аналогично R ₂ – V ₂ для второго канала, R ₃ – V ₃ для третьего канала и так далее до R _n – V _n для n ^го канала.

Уже было сказано, что суммирующий усилитель — это, по сути, инвертирующий усилитель с более чем одним напряжением на инвертирующем входе. Выходное напряжение для каждого канала может быть рассчитано индивидуально, и окончательное выходное напряжение будет суммой всех отдельных выходов.

Чтобы рассчитать выходное напряжение определенного канала, мы должны заземлить все остальные каналы и использовать базовую формулу выходного напряжения инвертирующего усилителя для каждого канала.

Если заземлены все каналы, кроме первого, то выход для первого канала определяется как:

Где – (R _f / R ₁ ) – коэффициент усиления по напряжению для первого канала (A _В1 ).

Аналогично, если все каналы заземлены, кроме второго канала, то выход для второго канала определяется как:

Где — (R _f / R

2 ) — коэффициент усиления по напряжению для второго канала (A _V2 ).

Аналогично, выходной сигнал для n ^{-го канала} определяется как:п ) В _п

А — (R _f / R _n ) — коэффициент усиления по напряжению для n ^-го канала (A _Vn ).

Выходной сигнал представляет собой алгебраическую сумму отдельных выходов или, другими словами, сумму всех входов, умноженную на их соответствующие коэффициенты усиления.

 В _ВЫХ = В _ВЫХ1 + В _ВЫХ2 + . . . + В _ВЫХ

 В _ВЫХ = – [(R _f / R ₁ ) V ₁ + (R _f / R ₂ ) V ₂ + .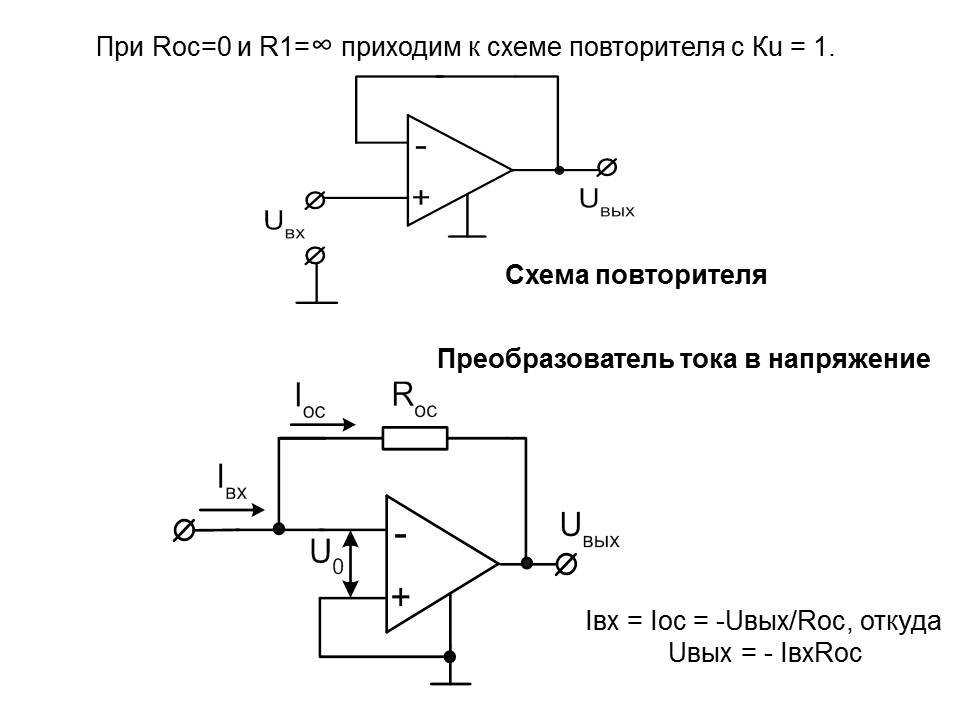 . . + (R _f / R _n ) V _n ]

 В _ВЫХ = В

1 А _В1 + В ₂ А _В2 + . . . + В _н А _Вн

В суммирующем усилителе, если входные сопротивления не равны, схема называется масштабирующим суммирующим усилителем. Но если все входные сопротивления выбраны равными, то говорят, что суммирующий усилитель имеет равновзвешенную конфигурацию, где коэффициент усиления для каждого входного канала одинаков.

Иногда необходимо просто добавить входные напряжения без их усиления. В таких ситуациях значение входного сопротивления R ₁ , R ₂ , R ₃ и т. д. необходимо выбирать равным значению резистора обратной связи R _f . В результате коэффициент усиления усилителя будет равен единице. Следовательно, выходное напряжение будет суммой входных напряжений.

Теоретически мы можем подать на вход суммирующего усилителя столько входных сигналов, сколько потребуется.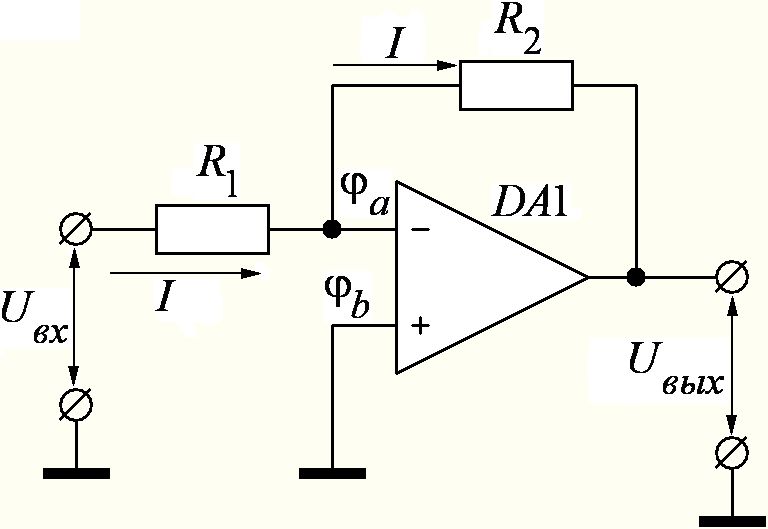

Однако следует отметить, что все входные токи суммируются, а затем возвращаются обратно через резистор R9.0029 f , поэтому мы должны знать номинальную мощность резисторов.

Неинвертирующий суммирующий усилитель

Неинвертирующий суммирующий усилитель также может быть сконструирован с использованием конфигурации неинвертирующего усилителя операционного усилителя. Здесь входные напряжения подаются на неинвертирующую входную клемму операционного усилителя, а часть выходного сигнала возвращается на инвертирующую входную клемму через обратную связь делителя напряжения и смещения.

Схема неинвертирующего суммирующего усилителя показана на следующем рисунке. Для удобства следующая схема состоит всего из трех входов, но можно добавить больше входов.

Прежде всего, несмотря на то, что это тоже суммирующий усилитель, расчеты не такие прямые, как у инвертирующего суммирующего усилителя, потому что в неинвертирующем суммирующем усилителе нет преимущества виртуального узла суммирования земли.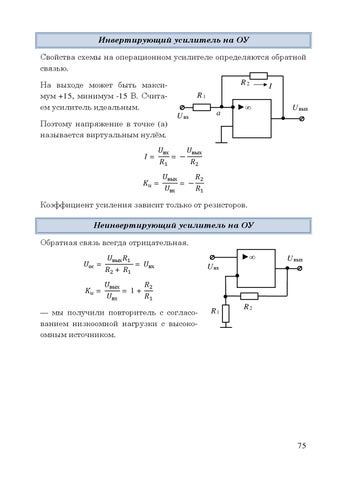

Расчет выходного напряжения неинвертирующего суммирующего усилителя

Чтобы понять работу неинвертирующего суммирующего усилителя, мы должны разделить схему на две части:

• Входной резистор/источник Раздел
• Секция неинвертирующего усилителя

Если V _IN представляет собой комбинацию всех входных сигналов, то она применяется к неинвертирующему выводу операционного усилителя. Из приведенной выше схемы мы можем рассчитать выходное напряжение неинвертирующего усилителя с V _IN в качестве входа и R _f и R _i в качестве резисторов делителя обратной связи следующим образом:

 V _OUT = V _В (1 + (Р _ф / Р _и ))

Поскольку выходное напряжение вычислено, теперь мы должны определить значение V

IN . Если V ₁ , V ₂ и V ₃ являются тремя основными входными источниками и R ₁ , R ₂ и R ₃ являются их входными сопротивлениями, то V 9 2 9 IN1, 30 и V _IN3 являются входами соответствующих каналов, когда другие соответствующие каналы заземлены.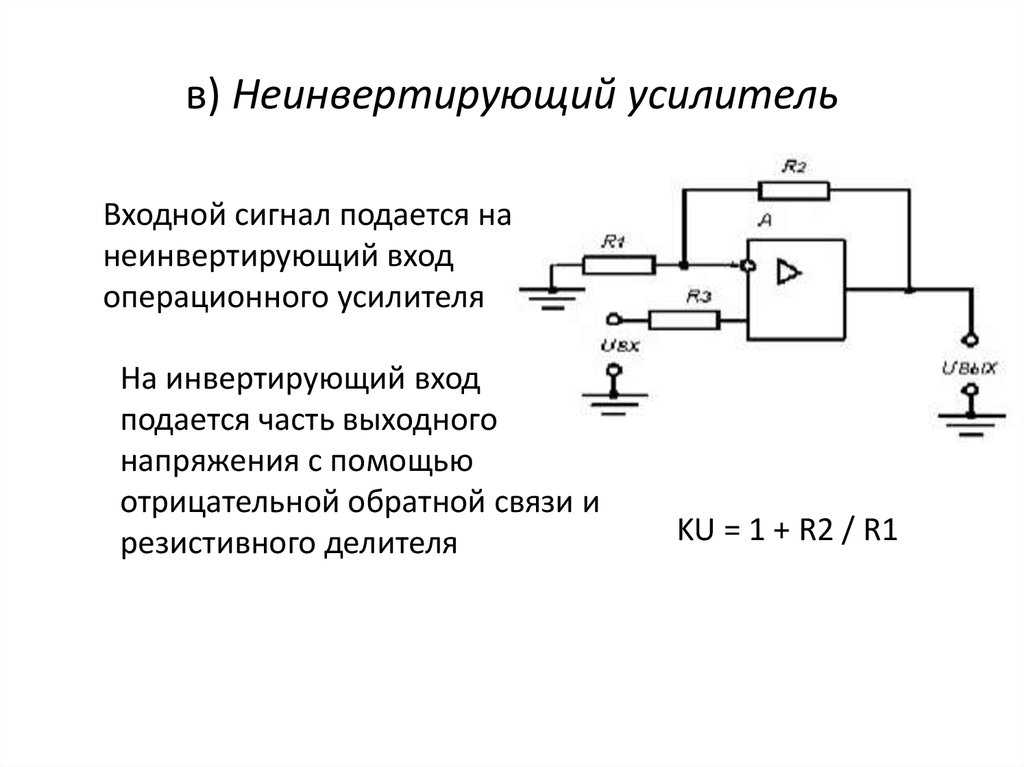 Итак,

 V _IN  = V _IN1 + V _IN2 + В _IN3

Поскольку концепция виртуальной земли здесь не применяется, все каналы будут влиять на другие каналы. Давайте вычислим часть V _IN1 V _IN , и с помощью простой математики мы можем легко получить два других значения, то есть V _IN2 и V _IN3 .

Переходя к V _IN1 , когда V ₂ и V ₃ заземлены, их соответствующие резисторы нельзя игнорировать, так как они образуют сеть делителя напряжения. Итак,

 V _IN1 = V ₁ [(R ₂ || R ₃ ) / (R ₁ + (R ₂ || R _{3 9]0029 0 9]0029 0 9}

Аналогичным образом можно рассчитать два других значения V _IN2 и V _IN3 как

 V _IN2 = V ₂ [(R ₁ || R ₃ + (R ₁ || R ₃ ))]

 В _IN3 = В ₃ [(R ₁ || R ₂ ) / (R ₃ + (R ₁ || R ₂ ))]

Итак,

 В _ИН  = В _ИН1 + В _ИН2 + В _ИН3

V _в = V ₁ [(R ₂ || R ₃ ) / (R ₁ + (R ₂ || R ₃ )] + V ₂ [(R ₁ || R ₃ ) / (R ₂

+ (R ₁ || R ₃ ))] + V ₃ [(R 1 0 || R 1 _{0 ||0029 2} ) / (Р ₃ + (Р ₁ || Р ₂ ))]

Наконец, мы можем рассчитать выходное напряжение V _OUT как

 V _OUT = V _IN (1 + (R _f / R _i ))

 V _OUT = (1 + (R _f / R _i )) {V ₁ [(R ₂ || R ₃ ) / (R 192029 0 (R 1 _{0) 2} || R ₃ ))] + V ₂ [(R ₁ || R ₃ ) / (R ₂ + (R ₁ || R ₃ ))] + V ₃ [(R ₁ || R ₂ ) / (R 903 + 90 (R ₁ || R ₂ ))]}

Если мы рассмотрим специальное условие с равными весами, когда все резисторы имеют одинаковые номиналы, то выходное напряжение будет: В ₁ + В ₂ + В ₃

) / 3)

Подход к проектированию неинвертирующей суммирующей схемы начинается с проектирования неинвертирующего усилителя с требуемым коэффициентом усиления по напряжению.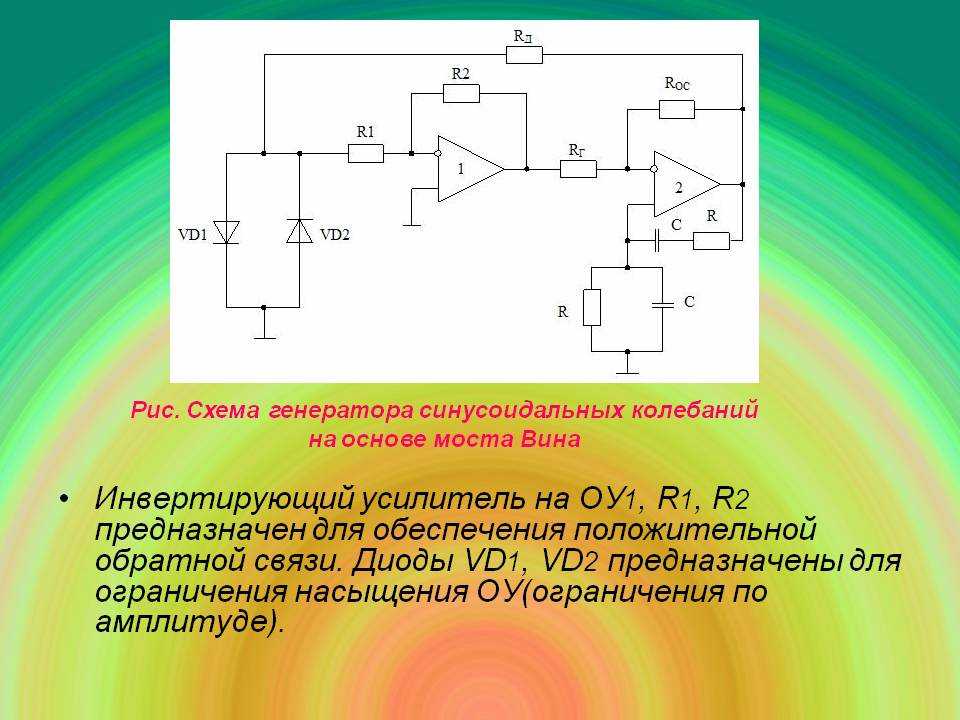 Затем входные резисторы подбираются как можно большего размера, чтобы соответствовать типу используемого операционного усилителя.

Сумматор напряжения Пример

Три аудиосигнала управляют суммирующим усилителем, как показано на следующей схеме. Какое выходное напряжение?

Коэффициент усиления по напряжению замкнутого контура для каждого канала можно рассчитать как:

 A _CL1 = – (R _f / R ₁ ) = – (100 кОм / 20 кОм) = – 5

 A _CL2 = – (R _f / R ₂ ) = – (100 кОм / 10 кОм) => ACL2 = – 10

 A _CL3 = – (R _f / R ₃ ) = – (100 кОм / 50 кОм) => ACL3 = – 2

Выходное напряжение суммирующего усилителя определяется как

В _ВЫХ = (A _CL1 В ₁ + A _CL2 В ₁ + A _КЛ3 В ₁ )

                          = – [(5 * 100 мВ) + (10 * 200 мВ) + (2 * 300 мВ)]

 = – (0,5 В + 2 В + 0,6 В)

 В _ВЫХ = – 3,1 В

Применение суммирующего усилителя

Аудиомикшер

Суммирующий усилитель является полезной схемой, когда необходимо добавить или объединить два или более сигналов, например, в приложениях для микширования звука. Звуки различных музыкальных инструментов могут быть преобразованы в определенный уровень напряжения с помощью преобразователей и подключены в качестве входа к суммирующему усилителю.

Эти различные источники сигналов будут объединены суммирующим усилителем, и объединенный сигнал будет отправлен на аудиоусилитель. Примерная принципиальная схема суммирующего усилителя в качестве аудиомикшера показана на рисунке ниже.

Суммирующий усилитель может работать как многоканальный аудиомикшер для нескольких аудиоканалов. Никаких помех (обратной связи с одного канала на вход другого канала) не будет, потому что каждый сигнал подается через резистор, другой конец которого подключен к клемме заземления.

Цифро-аналоговый преобразователь (ЦАП)

Цифро-аналоговый преобразователь (ЦАП) преобразует двоичные данные, поступающие на его вход, в эквивалентное аналоговое значение напряжения. Приложения промышленного управления в режиме реального времени часто используют микрокомпьютеры. Эти микрокомпьютеры выводят цифровые данные, которые необходимо преобразовать в аналоговое напряжение для управления двигателями, реле, исполнительными механизмами и т. д.

В простейшей схеме цифро-аналогового преобразователя используется суммирующий усилитель и сеть взвешенных резисторов. Типичная схема 4-битного ЦАП с суммирующим усилителем показана на рисунке ниже.

Входами показанного выше суммирующего усилителя являются двоичные данные Q _A , Q _B , Q _C и Q _D , которые обычно равны 5 В для представления логической 1 и 0 В для представления логической 1. логический 0.

Если входные резисторы в каждой ветви выбраны таким образом, что значение каждого входного резистора в два раза превышает значение резистора в предыдущей входной ветви, то цифровое логическое напряжение на входе создаст выходной сигнал, равный взвешенная сумма приложенных входных напряжений.

Точность такой схемы цифро-аналогового преобразователя ограничена точностью значений используемых резисторов и различиями в представлении логических уровней.

Сдвиг уровня

Другим важным применением суммирующего усилителя является смещение уровня. Суммирующий усилитель с двумя входами может действовать как регулятор уровня, где один вход представляет собой сигнал переменного тока, а второй вход — сигнал постоянного тока.

Сигнал переменного тока будет компенсирован входным сигналом постоянного тока. Одно из основных применений такого сдвига уровня — генераторы сигналов для управления смещением постоянного тока.

Заключение

Полное руководство для начинающих по суммирующим усилителям, также известным как сумматорные схемы. Вы изучили некоторые основы суммирующего усилителя, инвертирующего и неинвертирующего суммирующего усилителя, расчет выходного напряжения, примерную схему и несколько важных приложений.

Инвертирующие и неинвертирующие схемы операционных усилителей -…

Опубликовано 27 мая 2022 г.

Возможно, неудивительно, учитывая их название, что операционные усилители очень часто используются в усилительных схемах. Они собраны либо в инвертирующей, либо в неинвертирующей конфигурации, концепция, которую мы сейчас рассмотрим, и степень усиления можно тщательно контролировать.

Основные входы/выходы операционного усилителя

Прежде чем перейти к этим конфигурациям, давайте коснемся важной темы. Если вы просматривали эти руководства, вы заметите, что иногда вход, помеченный «+», иногда называют положительным, а иногда – «неинвертирующим». Тогда вход, помеченный «-», иногда называют отрицательным, а иногда «инвертирующим». На самом деле использование терминов «положительный» и «отрицательный», возможно, неверно и, в лучшем случае, вводит в заблуждение. Однако их намного проще использовать, поэтому они так распространены. Истинная разница между инвертирующим и неинвертирующим входами заключается в том, в какую сторону колеблется выход в зависимости от напряжения на входах. Если на неинвертирующий вход подается более высокое напряжение, чем на инвертирующий вход, то на выходе будет высокий уровень. Если инвертирующий вход выше, чем неинвертирующий вход, то на выходе будет низкий уровень (который может быть отрицательным, в зависимости от конфигурации операционного усилителя). Это будет рассмотрено снова и более подробно в учебнике по компаратору операционных усилителей, но этого достаточно для понимания этого руководства.

Схема инвертирующего операционного усилителя

Поскольку это более распространено, сначала мы рассмотрим инвертирующую схему операционного усилителя. Настройка схемы выглядит следующим образом:

Принципиальная схема схемы инвертирующего операционного усилителя

Вспоминая о золотых правилах операционных усилителей, или о двух самых важных вещах, которые следует помнить при работе с операционными усилителями, мы видим, что:

1. инвертирующий вход находится на виртуальной земле, так как неинвертирующий вход привязан к земле, и
2. тот же ток через R _i проходит R _f .

Чтобы помочь запомнить, что означают буквы, R _i — входной резистор, а R _f — резистор обратной связи, поскольку выход управляет входом через R _f . Теперь, когда у нас есть это в виду, давайте решим эту схему, чтобы посмотреть, сможем ли мы найти уравнение для математического описания производительности этой схемы. Мы можем использовать KCL. Давайте используем инвертирующий вход в качестве нашего узла.

Мы знаем, что ток, втекающий в этот узел, должен быть равен вытекающему току, а на инвертирующий вход ток не течет, поэтому через R 9 поступает только ток.0029 i и через R _f и они равны между собой. Затем мы можем настроить уравнение как:

или

Теперь мы хотим увидеть, какова связь между нашим выходом и входом, коэффициентом усиления или усиления, который мы назовем «A», где A = V _из /V _в . Преобразовав уравнение, мы можем увидеть следующее:

Таким образом, какое бы напряжение вы ни подавали на вход, выходное напряжение будет усиливаться на R _f /R _i , а затем инвертироваться в отрицательное напряжение. Например, если у вас есть резистор обратной связи 10 кОм и входной резистор 2 кОм, входное напряжение 2 В даст выходное напряжение -10 В. И это должно иметь смысл – для того, чтобы ток протекал от положительного входного напряжения к виртуальной земле, а затем от виртуальной земли к выходу, выходное напряжение *должно* быть отрицательным! И наоборот, если на вход подается отрицательное напряжение.

Это чрезвычайно распространенная конфигурация операционных усилителей, так как в большинстве контуров обратной связи используется отрицательная обратная связь, что повышает стабильность и снижает искажения. Это выходит за рамки данного руководства, но Кушал обсуждает это в своих руководствах по системам управления.

Схема неинвертирующего операционного усилителя

Для неинвертирующей схемы достаточно просто поменять местами соединения между инвертирующим и неинвертирующим входами. Схема немного другая.

Принципиальная схема схемы неинвертирующего операционного усилителя

Как и ожидалось, входной сигнал подается на неинвертирующий вход, но теперь инвертирующий вход находится в середине делителя напряжения. Поскольку выход теперь подключен к инвертирующему входу через этот делитель напряжения, мы знаем, что он будет управлять инвертирующим входом, чтобы он соответствовал неинвертирующему входу. Давайте посмотрим, как в этом случае применяются «золотые правила» операционных усилителей.

1. на инвертирующий вход подается то же напряжение, что и на неинвертирующий вход, и
2. что такой же ток через R ₁ проходит через R ₂ .

Еще раз, мы можем описать поведение этой схемы математически, используя KCL. Выбрав инвертирующий входной узел, мы приходим к следующему уравнению:

или

Его можно упростить, умножив обе части на R ₂ и разделив обе стороны на V _в :

Это разделяет на :

И, наконец, добавляем по одному с каждой стороны:

Наше усиление или величина усиления, снова обозначенная как «A», дает нам:

В этом расчете было еще несколько шагов по сравнению с инвертирующим усилителем, но все еще ничего сложного, если вы не пропустите шаг. Но давайте посмотрим и на это. Представьте, что у вас есть тот же вход 2 В, который мы использовали с инвертирующим операционным усилителем, и те же резисторы 10 кОм и 2 кОм для R ₂ и R ₁ соответственно. В этом случае вы получите коэффициент усиления 6 (10K/2K + 1), поэтому выходное напряжение будет 12 В. Отрицательное входное напряжение также дает отрицательное выходное напряжение.

Опять же, конфигурации с неинвертирующими операционными усилителями не так распространены, но они все же очень полезны, и вы обязательно с ними столкнетесь.

Резюме

Эти две конфигурации хороши не только потому, что они действительно полезны и их можно найти в самых разных приложениях, но и потому, что они помогают нам лучше познакомиться с тем, как работает операционный усилитель. Их использование и выполнение этих расчетов помогают нам лучше интуитивно понять, что произойдет с операционным усилителем в схеме. Я надеюсь, что этот обзор был понятен — если нет, оставьте комментарий ниже, и мы постараемся решить любые вопросы.