Изменение частоты кварцевого резонатора: Как изменить частоту кварцевого резонатора | Электронные схемы

Как изменить частоту кварцевого резонатора | Электронные схемы

кварцевые резонаторы на частоту 27МГц и 3.579МГц

Есть такая проблема,что нужен кварцевый резонатор на определенную частоту,но такого кварца нет а есть кварц,частота которого на несколько десятков или сотен килогерц выше или ниже нужной частоты.Чтобы изменить частоту кварца,есть два способа:первый способ без переделки резонатора и с переделкой.

Чтобы контролировать частоту резонатора,для этого к выходу генератора,частота которого стабилизирована резонатором,подключил пробник,который мне покажет частоту генератора.Кварц взял на 27МГц,пробник показывает частоту 26.998МГц. Мне надо переделать кварц на частоту 27.135кГц,то есть поднять частоту на 135кГц.

генератор с кварцевым резонатором на одном транзисторе

Чтобы поднять частоту резонатора вверх на 3-4кГц,для этого надо последовательно кварцу подключить подстроечный конденсатор небольшой емкости.

поднять частоту кварцевого резонатора конденсатором

Понизить частоту кварца вниз на 3-4кГц можно катушкой индуктивности.

изменить частоту кварцевого резонатора катушкой индуктивности

А теперь метод электролиза.С его помощью можно изменять частоту кварца на десятки и сотни кГц,но для начала надо узнать,из чего состоит кварцевый резонатор.Если снять корпус,можно увидеть кварцевую пластину с распыленными металлическими кругляшками, от которых отходят две проволочки соединенные с выводами.На частоте 27МГц,пластина будет колебаться 27 миллионов раз в секунду.Чтобы увеличить частоту этих колебаний,надо уменьшить металлический слой кругляшек,чтобы частоту уменьшить,надо нарастить металлический слой кругляшек. Это поможет сделать метод электролиза.

что внутри кварцевого резонатора из чего он состоит

Корпус с торца резонатора надо сточить напильником.Подготовить серебряный электрод,допустим из одного звена цепочки и токоограничивающий резистор сопротивлением 820 Ом,включенный в плюс или минус питания.Для повышения частоты кварца,надо соединить два вывода резонатора и их подключить на плюс,а электрод на минус.

как изменить частоту кварцевого резонатора

Наливаем обычной воды в корпус резонатора,окунаем в раствор серебряный электрод на несколько секунд.В моем случае,семь секунд реакции повышают частоту кварца примерно на 15 кГц.

электролиз кварцевого резонатора

Чтобы уменьшить частоту кварцевого резонатора,надо поменять полярность питания.

После просушки резонатора,вновь его припаял к генератору и его частота увеличилась на 13кГц. Было 29.998кГц а стало 27.011кГц.

увеличиваю частоту кварцевого резонатора

Еще двадцать секунд электролиза.Частота поднялась на 36кГц.

как изменить частоту кварцевого резонатора своими руками

И вот наконец,чуть подогнал до частоты которая мне нужна,27.135кГц. Эта частота для связи с дальнобойщиками.

Проверил стабильность резонатора после переделки,оставив генератор работать на всю ночь.Никаких изменений в стабильности работы не произошло.Также проверил,что будет если просто налить воды в резонатор на несколько секунд и потом высушить. Никаких изменений в уходе частоты не произошло.

кварцевый резонатор почти на 27.135кГц для связи с дальнобойщиками

Технология повышения временной стабильности кварцевых резонаторов высокочастотного диапазона – Компоненты и технологии

Современные достижения в области пьезоэлектроники позволяют изготавливать кварцевые резонаторы по основной гармонике на частоты до 400 МГц. При этом показателем качества кварцевых резонаторов, помимо точности настройки и значения динамического сопротивления, является систематический уход частоты резонатора со временем или старение кварцевых резонаторов в результате необратимого изменения свойств кристаллического элемента, системы пленочных электродов, крепления пьезоэлемента, изменения состава атмосферы внутри корпуса.

Долговременная стабильность резонансной частоты резонаторов, которую часто называют старением, зависит от свойств используемого пьезоэлектрического материала, а также ориентации, размеров, типа колебаний, обработки и конечного исполнения резонаторов.

У пьезоэлектрических кристаллических резонаторов, помещенных в вакуум или герметичный корпус (рис. 1), заполненный газом, не вызывающим коррозию электродов или поверхности пластины, в большинстве случаев происходит повышение резонансной частоты. При длительном наблюдении за резонансной частотой можно выделить два периода. В течение первоначального периода, продолжающегося от нескольких недель до нескольких месяцев, временную зависимость резонансной частоты можно описать некоторой монотонно возрастающей функцией. В течение второго периода более или менее регулярное значение резонансной частоты изменяется около постоянного или незначительно меняющегося среднего значения.

Рис. 1. Кварцевый резонатор в различном конструктивном исполнении (на фотографии — без кожуха): а) SMD-исполнение; б) корпус типа НС-45

Рис. 2. Схема рабочего места для измерения резонансной частоты кварцевых резонаторов в процессе проведения термотренировки

Старение указанной группы пьезоэлектрических резонаторов в начальный период может быть вызвано отделением мельчайших частиц кварцевой пластины или электродов при колебаниях, изменением упругих свойств электродов с течением времени, диффузионными процессами, протекающими в электродах и поверхностных слоях пластины, нарушенных при обработке, и т.

п.

Вследствие диффузионных процессов изменяется (как правило, уменьшается) внутреннее напряжение в электродах и поверхностных слоях пластины, связанное с предварительной температурной обработкой; при этом происходит перемещение массы в те области, где колебания менее интенсивны. Влияние температурной обработки электродов настолько существенно, что может явиться причиной и обратного характера старения, то есть уменьшения резонансной частоты с течением времени.

У кварцевых резонаторов АТ-среза временную зависимость резонансной частоты в начальный момент времени можно выразить следующим образом [1]:

d/dτ(f-f_∞) = -K* (f-f

∞) (1)

где f — резонансная частота в момент времени τ; f_∞— конечное установившееся значение частоты; К — постоянная старения. К является величиной, обратной постоянной времени, и в соответствии с выражением Аррениуса есть функция температуры:

К = К₀*е^-Е/kθ, (2)

где Е — активационная энергия процесса; к — постоянная Больцмана; θ — абсолютная температура.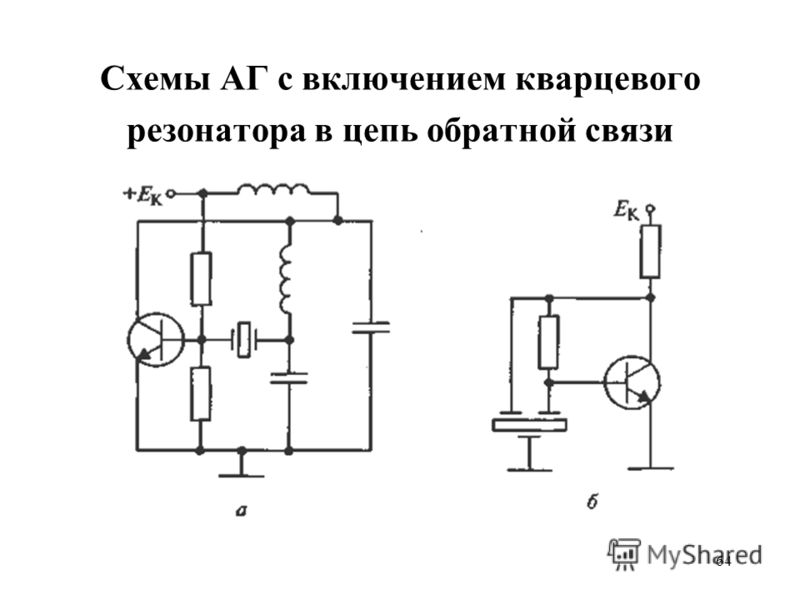

Резонансная частота f в момент времени τ может быть выражена как:

где f₀ — частота резонанса в начальный момент старения.

На рис. 3 приведены кривые измеренной временной зависимости резонансной частоты высокочастотных кварцевых резонаторов АТ-среза с обратной мезаструктурой с резонансной частотой 60 МГц, работающих на основной механической гармонике сдвиговых колебаний по толщине и выполненных в разных корпусах, заполненных азотом.

Рис. 3. Кривые зависимости изменения резонансной частоты в процессе термоциклирования

В объеме резонаторов возможны как процессы миграции атомов металла по поверхности пьезоэлемента, так и перемещение их с поверхности пьезоэлемента на стенки корпуса и обратно; диффузия атомов электродов в кварцевый кристаллический элемент и обратно чаще всего происходит по структурным каналам. Если атомы металла диффундируют внутрь кристалла, то знак изменения частоты будет отрицательным; если из кристалла, то положительным.

При отрыве атомов металла с поверхности происходит изменение массы пьезоэлемента, и знак будет положительным [2]:

Δf/f = -(Δm/m), (4)

где Δπι — изменение массы кристалла; Df— изменение частоты.

Помимо массопереноса, в кристаллическом элементе существуют и упругие напряжения, возникающие в электродном покрытии кварцевого резонатора.

На изменение резонансной частоты кварцевых резонаторов влияет качество подготовки поверхности кристаллического элемента перед нанесением электродного покрытия. В пленках, полученных методом вакуумного напыления, имеют место термические напряжения, обусловленные разными значениями коэффициентов температурного линейного расширения (ТКЛР) кварца (а

кв = 0,55х10⁶ К^-1) и электродного покрытия. (Чаще всего применяется серебро или никель: а_сер = 18,6х10⁶ К^-1, а_ник = 14х10⁶ К^-1.) Эти напряжения могут привести к изменению частоты резонатора на несколько кГц.

Рассчитать величину напряжений, возникающих в результате деформации электродного покрытия вследствие изменения температуры кварцевого резонатора, можно на основании выражения:

F = E*α*ΔT, (5)

где Е — модуль Юнга материала электродного покрытия, Н/м²

; α — температурный коэффициент линейного расширения электродного покрытия; DT — разница температур кристаллического элемента до и после вакуумной металлизации.

Подставив значение силы F [Н] в выражение (6), можно определить величину изменения частоты кварцевого резонатора вследствие термических напряжений, возникающих в электродном покрытии:

Δf/f = K_F*F/D, (6)

где K_F — коэффициент силочувствительно-сти [6]; D — диаметр кристаллического элемента кварцевого резонатора, мм.

Для повышения временной стабильности частоты кварцевых резонаторов была оптимизирована технология их термотренировки после операции настройки частоты методом ионного травления перед герметизацией их в корпус.

Настройка, то есть установка номинального значения частоты кварцевого резонатора, осуществляется методом ионного травления поверхности электрода пьезоэлемента. При этом в процессе подстройки частоты резонаторов в номинал происходит одновременно и очистка поверхности пьезоэлементов резонаторов в плазме газового разряда.

Необходимость проведения цикла тренировок вызвана тем, что после монтажа пье-зоэлементов в держатель (сборка кварцевого резонатора производится, как правило, путем приклейки пьезоэлемента к держателю токо-проводящим клеем) и настройки резонаторов в номинал могут возникнуть остаточные напряжения в пьезоэлементах. Необходимо также исключить изменения частоты кварцевых резонаторов из-за газовыделения из мест приклейки пьезоэлемента к держателю токо-проводящим клеем, так как клей в качестве связки включает органические соединения, которые могут заметно влиять на величину долговременной стабильности частоты резонатора.

Герметизация кварцевых резонаторов осуществляется методом конденсаторной сварки с продувкой инертным газом.

Цикл термотренировок резонаторов проводился в непрерывно откачиваемой вакуумной камере при остаточном давлении Р~1х10^-3 Па и нагревом резонаторов до температуры Т = 130 °С с последующей 4-часовой площадкой при данной температуре. Затем нагрев отключали, и осуществлялось плавное остывание резонаторов до комнатной температуры. Контроль значения температуры в камере осуществлялся при помощи медного термометра сопротивления.

После каждого термоцикла производилось измерение частоты кварцевых резонаторов. На рис. 2 показана установка для измерения частоты кварцевых резонаторов.

На рис. 3 приведены кривые зависимости изменения частоты партии кварцевых резонаторов на частоту 60 МГц с точностью настройки ±2,0 кГц после проведения 224 часов термотренировок. Анализ этих кривых показывает, что проведение термоцикли-рования в течение 224 часов избыточно. Оптимальным значением времени термо-циклирования является 150 ч, что подтверждается экспериментальными результатами.

Для проверки долговременной стабильности частоты партии кварцевых резонаторов после 150 ч термоциклов они были подвергнуты испытанию на долговременную стабильность: старению по методике, изложенной в [4]. При этом кварцевые резонаторы помещались в термостат при температуре 85 °С и выдерживались в течение 150 суток. Измерение частоты резонаторов проводилось после каждых 15 суток в течение 150 дней. После математической обработки результатов суммарное изменение резонансной частоты у каждой партии составило не более 0,5х10^-6.

Данная методика проведения термотренировок кварцевых резонаторов позволяет повысить их качество путем повышения временной стабильности, а также сократить время изготовления этих устройств.

Литература

1. Зеленка И. Пьезоэлектрические резонаторы на объемных и поверхностных акустических волнах. Материалы, технология, конструкция, применение / Пер. с чешского. М.: Мир, 1990.
2. Смагин А. Г., Ярославский М. И. Пьезоэлектричество кварца и кварцевые резонаторы. М.: Энергия, 1970.
3. Малов В. В. Пьезорезонансные датчики. М.: Энергия, 1989.
4. Мостяев В. А, Дюжиков В. И. Технология пьезо- и акустоэлектронных устройств. М.: Ягуар, 1993.

Настройка частоты кварцевого осциллятора микроконтроллера – Компоненты и технологии

Причины «ухода» часов можно разделить на две группы. Первая — это нестабильность частоты кварцевого генератора под влиянием дестабилизирующих факторов: изменения температуры, питающего напряжения и т. д. Вторая группа — это неточность настройки самого кварцевого генератора. Вместо частоты f₀ он генерирует частоту f₀+Δf₀, где Δf₀ — ошибка настройки. Неправильно считать, что если к ножкам микроконтроллера припаян кварц с маркировкой f₀, то частота генерации та же.

Проделайте следующий эксперимент. На место кварца к микроконтроллеру последовательно припаиваются различные экземпляры кварцев, одного и разных производителей, с одинаковой маркировкой частоты (рис.

 1). Ничто другое не меняется. После рассеяния тепла мерим частоту, и она оказывается разной, даже для кварцев одного производителя.

Рис. 1. Типичная схема кварцевого осциллятора микроконтроллера

Причина изменения частоты для кварцев одного типа и производителя — в разбросе параметров кварцев от экземпляра к экземпляру. Для кварцев разных производителей — это разные параметры кварцев. Разница с маркировкой иногда достигает несколько сотен герц!

Каким образом нужно мерить частоту кварцевого генератора? Разумеется, непосредственное соединение входов осциллоскопа или частотомера с одной из точек CLCKIN или CLCKOUT дало бы неверные результаты из-за входной емкости и входного сопротивления присоединяемого устройства. После его отсоединения частота изменится.

В своей практике автор использовал два подхода. Если микроконтроллер многоразового программирования (типа FLASH), вначале он программируется простой программой для вывода удобного порта (или одного бита порта) бесконечной последовательности чередующихся нулей и единиц. Частота повторения этой импульсной последовательности определяется по формуле f_кв/n, где n — это внутренний коэффициент деления частоты кварцевого генератора.

Приведем для примера простую программу для вывода частоты f₀/n на порт B популярного микроконтроллера PIC16F84A:

title	‘quartz.asm’
list	p=16f84a
#include <	p16f84a.inc>
__CONFIG	B’11111111110001’
org	H’0000’
clrf	INTCON
BANKSEL	TRISB
clrf	TRISB	;порт B как выход
BANKSEL	PORTB
clrf	PORTB	;1 такт
comf	PORTB,f	;1 такт
goto	$-2	;2 такта
END

В этом микроконтроллере частота такта получается путем деления частоты кварца на 4. Для формирования одного периода импульсной последовательности на каждом бите порта В нужны 4 такта, следовательно, измеряемая частота на порте В есть f_вых = f₀/16. К выводам порта В можно присоединять осциллограф и цифровой частотомер, они не будут оказывать влияния на частоту кварцевого генератора. После настройки f₀ подстроечным конденсатором С~ микроконтроллер повторно программируется с помощью основной программы.

Если микроконтроллер одноразового программирования (типа C), к выводу CLCKOUT присоединяется цепочка каскадно-связанных инверторов или повторителей, которая остается и после настройки f₀. К выходу последнего инвертора (повторителя) присоединяется вход частотомера.

Вычислим «уход» часов из-за неточной настройки кварцевого генератора. Это значение обычно определяется в секундах за сутки. Кварцевые часы состоят из источника импульсной последовательности, периодом 1 с, и счетчика секунд, минут и часов (рис. 2). Если часы должны показывать и десятые доли секунд, период импульсной последовательности должен быть равен 0,1 с.

Рис. 2. Типичная структурная схема кварцевых часов

Все устройства на рис. 2 реализуются внутренними элементами микроконтроллера. Если индицируется астрономическое время, есть цепи для начальной установки и сверки часов. Видно, что:

T₀N = N/f₀ = 1 c. (1)

Так что у конструктора есть две степени свободы — подбирать f₀ и N.

В сутках 86 400 секунд (24×60×60), так что после считывания 86 400 импульсов счетчики «объявят», что прошли сутки. Если частота кварцевого генератора f₀, это будет верно, а если частота f₀+Δf₀, то прошедшее время будет не сутки, а

«Уход» часов за сутки τ определим, вычитая из (2) одни сутки (86 400N/f₀). Получим:

Ошибка настройки Δf₀ может быть как положительной, так и отрицательной, знак τ будет противоположным. Учитывая в (3), что Δf₀ << f₀, ради чего пренебрегаем в сумме Δf₀, и что N/f₀ = 1 с, получим в итоге:

«Уход» частоты за неделю получается путем замены коэффициента 86 400 на 604 800 (7×24×60×60). В таблице вычислен «уход» частоты за сутки и неделю при некоторых ошибках настройки, для частоты кварца f₀ = 1 МГц.

Таблица. Вычисленные значения «ухода» частоты

Значение Δf0, Гц	0,1	1	10	100
«Уход» часов в сутки, с	8,6 мc	86 мс	0,86	8,6
«Уход» часов в неделю, с	60,2 мc	0,602	6,02	60,2

Производители микроконтроллеров дают в таблицах значения С1 и С2 для различных значений частоты кварцев. Однако эти таблицы составлены с большим шагом по f₀, и неизвестно, какие параметры кварцев имел в виду составитель, поэтому рекомендованные значения надо считать приблизительными и настраивать кварцевый генератор в каждом отдельном случае.

Проделанные вычисления относятся только к ошибке настройки кварцевого генератора и не учитывают дрейфа частоты. Дрейф — случайный процесс. Под действием дестабилизирующих факторов частота повышается и понижается медленно, случайным образом. В известном смысле «уход» часов самокомпенсируется, но не полностью. Если необходимо снизить дрейф частоты, кварцевый генератор нужно заменить внешним термоскомпенсированным (TCXO) или термостатированным (OCXO) кварцевым генератором. Эта более стабильная частота подается на вывод микроконтроллера CLCKIN, а все дополнительные элементы на рис. 1 устраняются.

Кварцевые генераторы с высокой температурной стабильностью

Температурная стабильность частоты – один из ключевых параметров кварцевых генераторов. Современные термостатированные кварцевые генераторы обеспечивают очень высокую температурную стабильность частоты вплоть до ±1E–11 в широком интервале температур –40…85°C. Столь малые величины изменения частоты требуют некоторых особенностей при измерении и, соответственно, при эксплуатации таких генераторов. В статье рассматриваются особенности эксплуатации подобных генераторов, методики измерения температурной стабильности, а также влияние на нее других факторов.

Одним из основных параметров кварцевых генераторов является температурная стабильность. Существует несколько разных методов ее обеспечения.

1. Простые кварцевые генераторы (КГ), где температурная стабильность обеспечивается только самим кварцевым резонатором за счет выбора угла среза кварцевого элемента. Температурная стабильность таких генераторов составляет ±10…15E–6 в диапазоне –40…85°C (см. рис. 1).
2. Термокомпенсированные кварцевые генераторы (ТККГ). В них имеются дополнительные элементы, которые формируют управляющее напряжение, компенсирующее зависимость выходной частоты от температуры. Температурная стабильность таких генераторов составляет ±1…3E–7 в диапазоне –40…85°C (см. рис. 1).
3. Термостатированные кварцевые генераторы (ТСКГ). В них кварцевый резонатор и основная часть элементов находятся в термостате, поддерживающем постоянную температуру. Температурная стабильность таких генераторов достигает ±1…5E–11 в диапазоне –40…85°C (см. рис. 1).

Рис. 1. Зависимость частоты кварцевых генераторов разных видов от температуры

Далее мы рассмотрим именно термостатированные генераторы, причем только самые высокостабильные.

Сначала детальнее остановимся на базовой конструкции термостатированных генераторов. Как уже упоминалось, в подобных генераторах все чувствительные к изменению температуры элементы находятся внутри термостата, в котором поддерживается постоянная температура (см. рис. 2).

Рис. 2. Схема конструкции термостатированного генератора

Температура внутри термостата устанавливается несколько выше (обычно на 5–15°C) верхней рабочей температуры эксплуатации генератора. Кроме того, она выбирается таким образом, чтобы температурная зависимость резонатора находилась в районе одного из его экстремумов (см. точки LTP и UTP на рисунке 3). Таким образом, обеспечивается минимальное изменение частоты кварцевого генератора в зависимости от температуры окружающей среды.

Рис. 3. Типовая зависимость частоты кварцевого резонатора от температуры

Необходимость поддержания высокой температуры термостатом приводит к следующим отличительным чертам термостатированных кварцевых генераторов:

1.  Повышенный ток потребления при включении.
   Как только температура внутри термостата достигает заданного уровня, ток потребления существенно уменьшается;
2.  Необходимость первоначального прогрева.
   Характеризуется точностью установления частоты в заданных пределах за фиксированное время, которое обычно составляет 2–5 мин при температуре 25°C и точности до ±2E–8.

Подобная базовая модель обеспечивает температурную стабильность в диапазоне ±1E–8…±5E–10 в зависимости от конструкции. Существует несколько следующих способов повышения температурной стабильности описанной конструкции:

1. Использование двойного термостата. В подобных генераторах применяется дополнительный термостат, внутрь которого помещается базовый термостат. Это достаточно эффективный способ, благодаря которому, как правило, достигается стабильность ±1E–10. Однако его применение сопряжено с неизбежными издержками, к которым относятся сравнительно большие габариты и ограничение верхней рабочей температуры эксплуатации генератора из-за необходимости установить большую разницу между рабочей температурой и температурой термостата.
2. Использование дополнительной температурной компенсации. Итоговая зависимость частоты от температуры базовой конструкции обычно носит более–менее линейный характер, что позволяет относительно просто ее компенсировать. К недостаткам этого метода относится довольно высокая крутизна итоговой зависимости частоты от температуры, что может нивелировать все преимущества. Использование этого метода применительно к термостатированным генераторам обычно позволяет увеличить температурную стабильность до пяти раз.
3. Наиболее сложный, но дающий наилучшие результаты метод «вылизывания» базовой конструкции. Он заключается в тщательном расчете и продолжительном многоитеративном процессе доработки конструкции конкретного типа генераторов для получения лучшей температурной стабильности, в т. ч. за счет понижения температурных градиентов. Благодаря этому подходу температурная стабильность достигает значений, которыми характеризуются генераторы с двойным термостатированием; при этом сохраняются габариты и, в особенности, высота базовой конструкции.

Для получения эксклюзивно высокой температурной стабильности, достигающей, например, ±1E–11, приходится в полной мере реализовать все описанные выше меры улучшения температурной стабильности.

Как при эксплуатации, так и при измерении параметров генераторов с высокой температурной стабильностью могут возникать дополнительные факторы, влияющие на температурную стабильность. Так, например, выходная частота кварцевых генераторов изменяется с течением времени. При этом крайне важно, сколько времени генератор находился во включенном состоянии. Так, у генераторов, работающих в течение нескольких недель, суточное изменение частоты составляет несколько единиц E–11, а у генераторов, включенных всего один день, эта величина равна нескольким единицам E–10. Нетрудно заметить, что такой вклад заметен при измерении температурной стабильности, тем более когда она мала и сопоставима с таким уходом. Таким образом, при оценке стоит учитывать дрейф частоты генератора. Сделать это довольно просто – необходимо выдержать генератор при некоторой постоянной температуре и фиксировать его частоту. Далее по полученным результатам строится модель ухода частоты с течением времени – для непродолжительных промежутков времени вполне хватит простой линейной модели.

Обычно при испытаниях генераторов с очень высокой температурной стабильностью нам приходится использовать несколько циклов нагрева/охлаждения, чтобы убедиться, что генератор удовлетворяет нормам по температурной стабильности. Влияние дрейфа частоты отчетливо видно по результатам испытаний генератора ГК360-ТС производства АО «Морион».

На рисунке 4 красным цветом показана исходная характеристика, снятая в процессе измерений. Видно, что она обладает линейным наклоном, что связано со старением генератора. Синим цветом показана эта же характеристика, но с вычтенным дрейфом.

Рис. 4. Результат измерения температурной стабильности генератора ГК360-ТС производства АО «Морион» и его обработка

Как уже отмечалось, если для повышения температурной стабильности используется дополнительная компенсация, на итоговой характеристике могут присутствовать отдельные участки с заметной крутизной. Подобная ситуация не явно выражена в случае термостатированных кварцевых генераторов, но очень заметна при использовании рубидиевых генераторов.

На рисунке 5 показаны две разные зависимости частоты от температуры. В первом случае при малом изменении температуры изменение частоты также пропорционально мало. Во втором случае при малом изменении температуры частота меняется в существенно большей мере вплоть до значения температурной стабильности во всем интервале.

Рис. 5. Сравнение зависимости от температуры частоты генераторов с:
а) линейной ТЧХ;
б) сильно меняющейся ТЧХ

Кроме того, из-за компенсации или неудачной конструкции изменения частоты многократно превышают норму при быстром изменении температуры (см. рис. 6).

Рис. 6. Пример малой реакции на температурный удар для ГК360-ТС

У термостатированных генераторов с высокой температурной стабильностью форма и величина зависимости частоты от температуры при изменении их ориентации меняются с высокой вероятностью. Это происходит из-за конвекции внутри объема генератора. У правильно разработанного генератора такая зависимость должна быть сведена к минимуму и учтена при испытаниях.

Говоря о термостатированных генераторах сверхвысокой стабильности, отдельно следует упомянуть проблемы, возникающие при подстройке частоты генератора с помощью управляющего напряжения. Наличие этой функции напрямую влияет на стабильность генератора. Когда мы говорим о столь малых величинах нестабильности, вклад перестройки становится особо остро заметен. Так, генератор без такой опции обладает большей температурной и кратковременной стабильностью, чем с этой опцией. Например, температурную стабильность генератора без перестройки можно довести до ±1E–11, тогда как с перестройкой эта величина уже составляет ±2E–11. Соответственно, при необходимости обеспечить лучшую температурную стабильность предпочтение отдается системам, в которых допустимо применение генератора без возможности перестройки частоты.

Перестройка обеспечивается либо аналоговой цепью, либо цифровой. Генераторы с цифровым управлением включают в себя ЦАП, и управление частотой осуществляется подачей кода. Управление ЦАП реализуется по протоколам I2C или SPI. При цифровом варианте управления деградация температурной стабильности минимальна, однако при изменении кода управления могут кратковременно ухудшаться нестабильность, и возрастать фазовые шумы.

Еще одним ограничением является минимальный фиксированный шаг перестройки, который зависит от разрядности ЦАП. Для 20‑бит ЦАП он составляет 5E–13…10E–13.

В генераторах с аналоговым управлением для приведения частоты к номиналу на соответствующий вход подается управляющее напряжение (см. рис. 7).

Рис. 7. Схема включения генератора с аналоговым управлением и общей землей

На земляном выводе генератора возникает падение напряжения, зависящее от протекающего тока нагревательных транзисторов термостата. При таком подключении оно попадает в цепь управления, ухудшает температурную и кратковременную стабильность частоты.

Для уменьшения этого влияния следует уменьшить сопротивление (длину) общей цепи протекающих токов питания генератора и цепи управления. Кардинальным способом является использование разных земель (см. рис. 8). Однако такой способ снижает унификацию генераторов и накладывает достаточно серьезные ограничения на схемотехнику оборудования.

Рис. 8. Схема включения генератора с аналоговым управлением с раздельными землями

Еще одним фактором, который следует учесть при эксплуатации сверхвысокостабильных генераторов, являются применяемые материалы, т. к. при соединении разнородных проводников, спаи которых находятся при разных температурах, в цепи управления возникает термоЭДС, влияющая на температурную стабильность частоты. Чем выше температурная стабильность, тем в большей мере проявляются все описанные эффекты.

Генераторы с высокой температурной стабильностью успешно применяются во многих областях, где требуется очень стабильная частота. Они даже могут посоревноваться с рубидиевыми генераторами в некоторых областях применения благодаря меньшим габаритам и потреблению. Их зависимость частоты от изменения температуры гораздо более линейна и обладает меньшей крутизной. Таким образом, при небольших изменениях температуры окружающей среды линейность существенно лучше, чем у рубидиевых генераторов.

Заметим, что, в отличие от рубидиевых, старение термостатированных кварцевых генераторов происходит быстрее, но в случае крайне малого изменения частоты при изменении температуры влияние этого эффекта можно компенсировать.

Итак, мы рассмотрели особенности конструкции термостатированных генераторов, методы улучшения температурной стабильности и некоторые особенности использования подобных генераторов.

Литература

1. John  Vig. Quartz Crystal Resonators and Oscillators. Tutorial. US Army Communications-Electronics Research, Development & Engineering Center Fort Monmouth. NJ. USA. March 2004.
2.  Kotyukov, Y. Ivanov, A. Nikonov. Precise Frequency Sources Meeting the 5G Holdover Time Interval Error Requirement. Microwave Journal. May. 2018.

Кварцевый резонатор | Описание, принцип работы, схемы

Кварцевый резонатор – это радиоэлемент, который используется в радиотехнических цепях для генерации электрических колебаний. В этой статье мы подробно рассмотрим и развенчаем некоторые мифы, связанные с кварцевым резонатором, а также рассмотрим схемы на его основе.

Пьезоэлектрики

На самом деле, кварц  – это один из самых распространенных минералов в земной коре. Его доля составляет около 60%! Если полупроводниковые радиокомпоненты в основном делают из кремния, то кварц тоже состоит из кремния но в связке с кислородом. Его химическая формула SiO₂.

Выглядит минерал кварц примерно вот так.

минерал кварц

Ну прямо как сокровище какое-то! Но ценность этого сокровища спрятана не в самом кварце, а в том, каким свойством он обладает. И этот эффект кварца сделал революцию в прецизионной (точной) электронике для генерации высокостабильных колебаний электрического сигнала.

Еще в 19 веке два брата Кюри обнаружили интересное свойство некоторых твердых кристаллов генерировать ЭДС , деформируя эти кристаллы. Деформация – это изменение формы какого-либо тела с помощью кручения, удара, растяжения и так далее. Так вот, ударяя по таким кристаллам, они обнаружили, что те могут выдавать какое-либо кратковременное напряжение.

пьезоэффект

Но они также обнаружили еще и обратный эффект. При подаче напряжения на такие кристаллы, эти кристаллы деформировались сами. Невооруженным глазом это было практически не заметно. Такой эффект назвали пьезоэффектом, а вещества  –  пьезоэлектриками.

Следует заметить, что ЭДС возникает только в процессе сжатия или растяжения. Может быть вы подумали, что можно прижать такой кристалл какой-нибудь увесистой болванкой и всю жизнь получать из него энергию? Как бы не так! Кстати, радиоэлемент пьезоизлучатель тоже относится к пьезоэлектрикам, и из него можно получить ЭДС. Ниже можно рассмотреть этот случай на видео. Светодиод, подпаянный к пьезоизлучателю, зажигается при ударе самого пьезоизлучателя.

Не так давно смотрел фильм по National Geographic. Там целые пьезоэлектрические плиты устанавливали на дороге. По ним ходили люди и вырабатывали электрическую энергию, сами того не подозревая). Кстати, очень халявная, чистая и возобновляемая энергия.  Ладно, что-то отвлекся… Так вот, кристаллы кварца тоже обладают пьезоэффектом и способны также вырабатывать ЭДС или деформироваться (изгибаться, изменять форму) под воздействием электрического тока.

[quads id=1]

Кварцевый резонатор

Что представляет из себя кварцевый резонатор

В настоящее время выявлены множество видов кристаллических веществ, но в электронике больше всего используют именно минералы кварца, так как он помимо того, что является пьезоэлетриком, так еще и обладает хорошей механической прочностью.

Резонатор – (от лат. resono –  звучу в ответ, откликаюсь) – это система, которая способна совершать колебания с максимальной амплитудой, то есть резонировать, при воздействии внешней силы определенной частоты и формы. Получается, кварцевый резонатор в электронике, а в народе просто “кварц”, – это радиоэлемент, который способен резонировать, если на него подать переменный ток определенной частоты и формы.

Кварцевые резонаторы выглядят примерно так.

виды кварцевых резонаторов

Кварц является диэлектриком. А что будет если тонкий диэлектрик разместить между двумя металлическими пластинами? Получится конденсатор! Конденсатор получается очень маленькой емкости, так что замерить его емкость вряд ли получится. Зато не стали мудрить со схемотехническим обозначением кварца, и на схемах его показывают как прямоугольный кусочек кристалла, заключенный между двумя пластинками конденсатора.

обозначение на схеме кварцевого резонатора

Разобрав кварцевый резонатор, мы можем увидеть воочию сам кристалл кварца. Давайте вскроем кварц советского производства вот в таком корпусе.

Здесь мы видим прозрачный кристалл кварца, размещенный между двумя металлическими пластинками, к которым подпаяны выводы.

что внутри кварцевого резонатора

В маленьких кварцах типа этих

кварцевый резонатор

используются тонкие прямоугольные пластинки кварца. Физический размер и толщина кварцевой пластинки внутри кварцевого резонатора строго должна соблюдаться, так как именно ее габаритные размеры влияют на основную частоту колебаний. Здесь правило такое: чем больше толщина пластинки, тем ниже рабочая частота кварца. Поэтому, самые высокие частоты, на которые делают кварцы, составляет не более 50 МГц, так как пластинка получается очень тонкая, что создает трудности при ее изготовлении. Да и держать ее как-то надо в корпусе, не поломав. По идее, можно выжать из кварца частоту и до 200 МГц, но работать такой кварц будет на обертоне.

Обертоны кварцевого резонатора

Обертоны, или как еще их называют, моды или гармоники – это кратные частоты, выше основной частоты кварца. С помощью фильтров гасят основную частоту кварца и выделяют обертон. В кварцевом резонаторе в режиме обертонов используют нечетные обертоны. Если основная частота кварца F – это первый обертон, то его рабочие обертоны будут как 3F, 5F, 7F, 9F.  Стоит также отметить, что амплитуда обертона убывает с ростом его частоты, поэтому, далее 9 обертона смысла брать уже нет, так как выделять амплитуду маленького сигнала очень проблематично.

Пример: возьмем кварц с частотой в 10 Мегагерц. Тогда мы можем возбудить его на обертонах в 30 Мегагерц (третий обертон), в 50 Мегагерц (пятый обертон), в 70 Мегагерц (седьмой обертон) и максимум в 90 Мегагерц (девятый обертон).

Чтобы хоть как-то понять, что такое обертоны, для примера послушайте основную частоту 110 Герц и ее обертоны.

Схема, которая возбуждает кварц на обертонах, сложная и не очень надежная, так как во-первых, надо “давить” главную частоту кварца и выделять обертон, а во-вторых, кварц может возбудиться в режиме случайных колебаний. На практике все-таки делают схемы с умножением главной частоты кварца, что намного проще и надежнее. Здесь также есть еще одно правило: если частота маркируется в целых числах в Килогерцах – это работа на основной гармонике, а если в Мегагерцах через запятую – это обертонная гармоника. Например: РГ-05-18000кГц – резонатор для работы на основной частоте, а РГ-05-27,465МГц – для работы на 3-ем обертоне.

Последовательный и параллельный резонанс кварца

Очень много мифов ходит по интернету именно о кварцевом резонаторе. Самый популярный миф гласит так: если подать постоянное напряжение на кварцевый резонатор, он будет выдавать переменное напряжение с частотой, которая на нем указана. Насчет “частоты, указанной на нем”, я, может быть, соглашусь, но насчет постоянного напряжения – увы. Кристалл кварца просто сожмется или разожмется). Некоторые вообще до сих пор думают, что кварц сам по себе выдает переменный ток ). Ага, прям вечный двигатель).

Для того, чтобы понять принцип работы кварцевого резонатора, надо рассмотреть его эквивалентную схему:

эквивалентная схема кварцевого резонатора

С – это собственно емкость между обкладками конденсатора. То есть если убрать кристалл кварца, то останутся две пластины и их выводы. Именно они и обладают этой емкостью.

С1 – это эквивалетная емкость самого кристалла. Ее значение несколько фемтоФарад. Фемто – это 10^-15 !

L1 – это эквивалентная индуктивность кристалла.

R1 – динамическое сопротивление, при работе кварца может достигать от нескольких Ом и до нескольких КОм

Можно заметить, что С1, L1 и R1 образуют последовательный колебательный контур, который обладает своей резонансной частотой.

последовательный колебательный контур

Резонансная частота такого контура вычисляется по формуле

формула последовательного резонанса кварцевого резонатора

 

Но все бы хорошо, но как видите, есть еще в эквивалентной схеме кварцевого резонатора один увесистый конденсатор С, который портит всю малину.

Вся эта схема превращается в сложный параллельный колебательный контур. Резонансная частота такого контура уже будет определяться формулой

формула параллельного резонанса кварцевого резонатора

Поэтому, запомните: каждый кварцевый резонатор может возбуждаться на двух резонансных частотах. На частоте последовательного резонанса и на частоте параллельного резонанса. Если мы видим на кварце вот такую надпись

частота кварцевого резонатора

это говорит нам о том, что частота последовательного резонанса для этого кварцевого генератора составляет 8 МГц. Кварцевые резонаторы в электронике работают именно на частоте последовательного резонанса. На своей практике не припомню, чтобы кто-то возбуждал кварц для работы на частоте параллельного резонанса.

Часовой кварцевый резонатор

Чаще всего часовой кварц выглядит вот так.

“Что еще за часовой кварц?” – спросите вы.  Часовой кварц – это кварц с частотой в 32 768 Герц. Почему на нем такая странная частота? Дело все в том, что 32 768 это и есть 2¹⁵. Такой кварц работает в паре с 15-разрядной микросхемой-счетчиком. Это наша микросхема К176ИЕ5.

Принцип работы этой микросхемы такой: после того, как она сосчитает 32 768 импульсов, на одной из ножек она выдает импульс. Этот импульс на ножке  с кварцевым резонатором на 32 768 Герц появляется ровно один раз в секунду. А как вы помните,  колебание один раз в секунду – это и есть 1 Герц. То есть на этой ножке импульс будет выдаваться с частотой в 1 Герц. А раз это так, то почему бы не использовать это в часах? Отсюда и пошло название – часовой кварц.

В настоящее время в наручных часах и других мобильных гаджетах этот счетчик и кварцевый резонатор встроены в одну микросхему и обеспечивают не только счет секунд, но и целый ряд других функций, типа будильника, календаря и тд. Такие микросхемы называется RTC (Real Time Clock) или в переводе с буржуйского Часы Реального Времени.

 

Кварцевый генератор

Что такое генератор? Генератор – это по сути устройство, которое преобразует один вид энергии в другой. В электронике очень часто можно услышать словосочетание  “генератор электрической энергии, генератор частоты, генератор функций ” и тд.

Кварцевый генератор представляет из себя генератор частоты и имеет в своем составе кварцевый резонатор. В основном  кварцевые генераторы бывают двух видов:

те, которые могут выдавать синусоидальный сигнал

и те, которые выдают прямоугольный сигнал, который чаще всего используется в цифровой электронике.

 Схема Пирса

Для того, чтобы возбудить кварц на частоте резонанса, нам надо собрать схему. Самая простая схема для возбуждения кварца – это классический генератор Пирса, который состоит всего лишь из одного полевого транзистора и небольшой обвязки из четырех радиоэлементов:

схема пирса для кварцевого резонатора

Пару слов о том как работает схема. В схеме  есть положительная обратная связь и в ней начинают возникать автоколебания. Но что такое положительная обратная связь?

В школе всем вам ставили прививки на реакцию Манту, чтобы определить, если у вас тубик или нет. Через некоторое время приходили медсестры и линейкой замеряли вашу реакцию кожи на эту прививку

Когда ставили эту прививку, нельзя было чесать место укола. Но мне, тогда еще салаге, было по барабану. Как только я начинал тихонько чесать место укола, мне хотелось чесать еще больше)) И вот скорость руки, которая чесала прививку, у меня замерла на каком-то пике, потому что совершать колебания рукой у меня максимум получалось с частотой Герц  в 15.  Прививка набухала на пол руки))  И даже  один раз меня водили сдавать кровь в подозрении на туберкулез, но как оказалось, не нашли. Оно и неудивительно ;-).

Так что это я вам тут рассказываю хохмы из жизни? Дело в том, что эта чесотка прививки самая что ни на есть положительная обратная связь. То есть пока я ее не трогал, чесать не хотелось. Но как только тихонько почесал, стало чесаться больше и я стал чесать больше, и чесаться стало еще больше и тд.  Если бы на мою руку не было физический ограничений, то наверняка, место прививки уже бы стерлось до мяса. Но я мог махать рукой только с какой-то максимальной частотой. Так вот, такой же принцип и у кварцевого генератора ;-). Чуть подал импульс, и он начинает разгоняться и уже останавливается только на частоте параллельного резонанса ;-). Скажем так, “физическое ограничение”.

Первым делом нам надо подобрать катушку индуктивности. Я взял тороидальный сердечник и намотал из провода МГТФ несколько витков

тороидальная катушка индуктивности

Весь процесс контролировал с помощью LC-метра, добиваясь номинала, как на схеме – 2,5 мГн. Если не доставало, прибавлял витки, если перебарщивал номинал, то убавлял. В результате добился  вот такой индуктивности.

измерение индуктивности

Транзистора у меня в загашнике не нашлось, и в местном радиомагазине его тоже не было. Поэтому, пришлось заказывать на Али. Кому интересно, брал здесь.

Его правильное название: транзистор полевой с каналом N типа.

транзистор 2n5485Распиновка слева-направо: Сток – Исток – Затвор

Ну а дальше дело за малым. Собираем схемку:

Небольшое лирическое отступление.

Как вы видите, я пытался максимально сократить связи между радиоэлементами. Дело все в том, что все радиоэлементы имеют свои паразитные параметры. Чем длиннее их выводы, а также провода, соединяющие эти радиоэлементы в схеме, тем хуже будет работать схема, а то и вовсе “не зафурычит”. Да и вообще, схемы с кварцевым резонатором на печатных платах трассируют не просто так от балды. Здесь есть свои тонкие нюансы. Мельчайшие паразитные параметры могут испоганить весь сигнал на выходе такого генератора.

Итак, кварцевый генератор мы собрали, напряжение подали, осталось только снять сигнал с выхода нашего самопального генератора. За дело берется цифровой осциллограф OWON SDS6062

Первым  делом я взял кварц на самую большую частоту, которая у меня есть: 32 768 Мегагерц. Не путайте его с часовым кварцем (о нем пойдет речь ниже).

Не, ну а что вы хотели? Хотели увидеть идеальную синусоиду? Не тут-то было. Сказались паразитные параметры плохо собранной схемы и монтажа.

Внизу в левом углу осциллограф нам показывает частоту:

Как вы видите 32,77 Мегагерц.  Главное, что наш кварц живой и схемка работает!

Давайте возьмем кварц с частотой 27 МГц.

Частоту тоже более-менее показал верно.

 

Ну и аналогично проверяем все остальные кварцы, которые у меня есть.

[quads id=1]

Вот осциллограмма  кварца на 16 МГц.

Осциллограф показал частоту ровно 16 МГц.

 

Здесь поставил кварц на 6 МГц.

Ровно 6 МГц!

На 4 МГц.

Все ОК.

Ну и возьмем еще советский на 1 Мегагерц. Вот так он выглядит.

Сверху написано 1000 КГц = 1МГц.

 

Смотрим осциллограмму.

Рабочий!

При большом желании можно даже замерять частоту китайским генератором-частотомером.

измерение частоты частотомером

400 Герц погрешность для старенького советского кварца не очень и много, хотя дело может быть даже не кварце, а в самом частотомере.

 

[quads id=1]

Схема Пирса для прямоугольного сигнала

Итак, вернемся к схеме Пирса. Предыдущая схема Пирса генерирует синусоидальный сигнал

Но также есть видоизмененная схема Пирса для прямоугольного сигнала

А вот и она:

схема Пирса для меандра

Номиналы некоторых радиоэлементов можно менять в достаточно широком диапазоне. Например, конденсаторы С1 и С2 могут быть в диапазоне от 10 и до 100 пФ. Тут правило такое: чем меньше частота кварца, тем меньше должна быть емкость конденсатора. Для часовых кварцев конденсаторы можно поставить номиналом в 15-18 пФ. Если кварц с частотой от 1 до 10 Мегагерц, то можно поставить 22-56 пФ. Если не хотите заморачиваться, то просто поставьте конденсаторы емкостью в 22 пФ. Точно не прогадаете.

Также небольшая фишка на заметку: меняя значение конденсатора С1 можно настраивать частоту резонанса в очень тонких пределах.

Резистор R1 можно менять от 1 и до 20 МОм, а R2 от нуля и до 100 кОм. Тут тоже есть правило: чем меньше частота кварца, тем больше значение этих резисторов и наоборот.

Максимальная частота кварца, которую можно вставить в схему, зависит от быстродействия инвертора КМОП. Я взял микросхему 74HC04. Она не слишком быстродействующая. Состоит из шести инверторов, но использовать  мы будем только один инвертор.

 

Вот ее распиновка:

Подключив к этой схеме часовой кварц, осциллограф выдал вот такую осциллограмму:

Ну как всегда всю картинку испортили паразитные параметры монтажа. Но, обратите внимание на частоту. Осциллограф почти верно ее показал с небольшой погрешностью. Ну оно и понятно, так как главная функция осциллографа отображать сигнал, а не считать частоту)

Кстати, вам эта часть схемы ничего не напоминает?

Не эта ли часть схемы используется для тактирования микроконтроллеров?

Она самая! Просто недостающие элементы схемы уже есть в самом МК 😉

Схема Колпитца

Это также довольно распространенная и знаменитая схема.

схема Колпитца

За основу взять схема усилителя с общим коллектором (эмиттерный повторитель). Здесь все как обычно. Резисторы R1 и R2 устанавливают рабочую точку для транзистора. Резистор R_E устанавливает уровень выходного напряжения. Транзистор NPN 2N4265 может работать на частотах до 100 МГц, поэтому его и взяли. Эта схема будет работать с кварцами в диапазоне от 1 и до 5 МГц.

Готовые модули кварцевых генераторов

В настоящее время кварцевые генераторы выпускают в виде законченных модулей. Некоторые фирмы, производящие такие генераторы,  достигают частотной стабильности  до 10^-11 от номинала! Выглядят готовые модули примерно так:

виды кварцевых генераторов

или так

Такие модули кварцевых генераторов в основном имеют 4 вывода.  Вот распиновка квадратного кварцевого генератора:

распиновка кварцевого генератора

Давайте проверим один из них. На нем написано 1 МГц

кварцевый генератор на 1 МГц

Вот его вид сзади.

Подавая постоянное напряжение от 3,3 и до 5 Вольт плюсом на 8, а минусом на 4, с выхода 5  я получил чистый ровный красивый меандр с частотой, написанной на кварцевом генераторе, то бишь 1 Мегагерц, с очень небольшими выбросами.

сигнал с кварцевого генератора

Ну прям можно залюбоваться).

Да и китайский генератор-частотомер показал точную частоту.

 

Отсюда делаем вывод: лучше купить готовый кварцевый генератор, чем самому убивать кучу времени и нервов на наладку схемы Пирса или Колпитца. Схема Пирса будет пригодна для проверки резонаторов и для ваших различных самоделок, хотя на Алиэкспрессе встречал готовый проверяльщик кварцевых резонаторов, способный замерять частоту кварцев от 1 и до 50 МГц. Посмотреть можете по этой ссылке.

Плюсы кварцевых генераторов

Плюсы кварцевых генераторов частоты – это высокая частотная стабильность. В основном это 10^-5 – 10^-6 от номинала или, как часто говорят,  ppm (от англ. parts per million) — частей на миллион, то есть одна миллионная или числом 10^-6. Отклонение частоты  в ту или иную сторону в кварцевом генераторе в основном связано с изменением температуры окружающей среды, а также со старением кварца. При старении кварца, частота кварцевого генератора стает чуточку меньше с каждым годом примерно на 1,8х10^-7 от номинала. Если, скажем, я взял кварц с частотой в 10 Мегагерц ( 10 000 000 Герц) и поставил его в схему, то за год его частота уйдет примерно на 2 Герца в минус 😉 Думаю, вполне терпимо.

Смотрите подробное видео про кварцевый резонатор:

КВАРЦЕВЫЕ РЕЗОНАТОРЫ ИМПОРТНОГО ПРОИЗВОДСТВА

Кварцевые резонаторы являются пассивными компонентами радиоэлектронной аппаратуры и предназначены для использования в аналогово-цифровых цепях для стабилизации и выделения электрических колебаний определенной частоты или полосы частот. Принцип работы этого элемента следующий – в широкой полосе частот сопротивление прибора имеет емкостной характер и только на некоторых (рабочих) частотах имеет резко выраженный резонанс (уменьшение сопротивления).

Кварцевый резонатор имеет лучшие характеристики, чем другие приборы для стабилизации частоты (колебательные контуры, пьезокерамические резонаторы): такие как стабильность по частоте (уход частоты) и температуре (изменение частоты резонанса в зависимости от температуры окружающей среды).

Избирательный, ярко выраженный резонансный характер сопротивления этих компонентов определяет основные области применения кварцевых резонаторов – высокостабильные генераторы тактовых сигналов и опорных частот, цепи частотной селекции, синтезаторы частоты и т.д

Импортные кварцевые резонаторы

В настоящее время доступны кварцевые резонаторы в корпусах типа: HC-49/U – ближайший отечественный аналог – корпус МД HC-49/US – отличие от HC-49/U – меньшая высота Кварцевые резонаторы для схем отсчета времени на частоту 32,768 кГц Компоненты сертифицированы в соответсвии с международным стандартом ISO 9002 Отличительные черты: Низкая стоимость Промышленный стандарт Широкий частотный диапазон Низкое изменение рабочей частоты с течением времени Резонаторы AT

Внешний вид корпусов типа HC-49

Основные технические характеристики:

Параметр	Корпус	Величина	Условия генерации	Габаритный чертеж
Частотный диапазон	HC-49/U	1,8 – 30 МГц	Основная гармоника	Корпуc L, мм HC-49/U 13,0±0,2 HC-49/US 3,5
		25 – 75 МГц	Третья гармоника
		75 – 100 МГц	Пятая гармоника
	HC-49/US	3 – 33,5 МГц	Основная гармоника
		26 – 75 МГц	Третья гармоника
Стабильность частоты	HC-49/U	±30 x10-6	Tокр.среды=25°C
	HC-49/US
Температурная стабильность частоты	HC-49/U	±50 x10-6	-20…+70°C
	HC-49/US		-10…+60°C
Диапазон рабочих температур	HC-49/U	-20…+70°C
	HC-49/US	-10…+60°C
Параллельная ёмкость	HC-49/U	не более 7 пФ
	HC-49/US
Нагрузочная ёмкость	HC-49/U	20 пФ (8…50 пФ)
	HC-49/US
Старение	HC-49/U	5×10-6 за год
	HC-49/US

Технические параметры кварцевых резонаторов:

• Тип резонатора АТ – специальный угол среза пластины кристалла кварца, при котором готовый резонатор обладает превосходной стабильностью частоты по температуре окружающей среды.
• Последовательное эквивалентное сопротивление – импеданс резонатора, находящегося в последовательном резонансе.
• Стабильность частоты – отклонение частоты от номинальной. Обычно выражается в миллионных долях от номинальной частоты резонатора – Nx10^-6. Соответствующая иностранная маркировка – ppm (part per million – часть на миллион).
• Температурная стабильность частоты – изменение частоты при изменении температуры резонатора.
• Сопротивление изоляции – сопротивление между выводами резонатора (обычные значения порядка МОм)
• Нагрузочная емкость – любая внешняя емкость, включенная последовательно с резонатором, становится элементом, изменяющим частоту резонанса. Варьируя нагрузочную емкость, можно, в некоторых пределах, изменять резонансную частоту. Некоторые изготовители иногда заранее рекомендуют использовать стандартные значения нагрузочной емкости для точной настройки резонансной частоты.
• Диапазон рабочих температур – диапазон температур, в котором резонатор будет работать с отклонением частоты, не превышающим указанного для данного типа.
• Гармоники – у резонаторов с типом среза АТ, которые сами по себе являются резонаторами толщинно – сдвиговых колебаний, в добавление к основной частоте резонанса возможно также проявление колебаний нечетных гармоник (3xFосн,5xFосн,7xFосн).
• “Старение” – медленные изменения параметров резонатора по истечении некоторого периода времени.

 

Номиналы стандартной сетки частот для импортных резонаторов, предлагаемые ЗАО “Промэлектроника”

Для корпусов типа U

Резонансная частота, МГц	Рекомендуемая нагрузочная емкость, пФ	Rк, (Ом)	Резонансная частота, МГц	Рекомендуемая нагрузочная емкость, пФ	Rк, (Ом)	Резонансная частота, МГц	Рекомендуемая нагрузочная емкость, пФ	Rк, (Ом)	Резонансная частота, МГц	Рекомендуемая нагрузочная емкость, пФ	Rк, (Ом)
1,8432	16; 30	600	5	16; 20	70	11	16	35	20,945		25
2	0; 16; 20	450	5,12	16	70	11,0592	0	35	22	16	25
2,048	16	450	6	16; 20	70	11,15	16	35	22,1184	0	25
2,4576	0; 16	350	6,144	0; 16	70	11,165	16	35	24	0; 16; 32	25
2,5	16	350	6,4	20	70	12	16	35	24,576	16	25
3		150	6,5		70	13,4725	16	35	25	16; 20	25
3,072	30	150	7	0; 16	50	13,5		35	26,48	16	25
3,2	16	150	7,158		50	13,6	16	35	26,535		25
3,2768	16	150	7,2	16	50	13,875	20	35	26,735	16	25
3,579545	16	90	7,3728	0	50	14		35	26,945	16	25
3,6	0	90	8	0	50	14,318	0	35	27**	16; 20	25/40
3,6864	0	90	8,192	0	50	14,7456	16	35	27,2*	16	25
3,9	16	90	8,867238	16	50	15		35	30	0; 16	40
4	0	70	9		50	16	16	35	32		40
4,032	0	70	9,216	16	50	16,384	0	35	32,768	16	40
4,096	16	70	9,6	16, 30	50	16,588	16	35	33	16	40
4,25	16	70	9,8304	16	50	16,667	16	35	36,5	16	40
4,433619	16; 18; 20	70	10	0; 16; 32	35	16,67	0	35	37,768	16	40
4,5		70	10,235	16	35	18	16	35	40	16	40
4,608	0; 16	70	10,24	16; 20	35	18,432	0; 16; 32	35	50	16	40
4,756	16	70	10,245	20	35	19,6608	0	35	70	16	40
4,8		70	10,5	16	35	20	0; 32	25	100***		60
4,9152	0	70	10,7	16	35	20,48		25

* работают на третьей гармонике.
** работают на первой и третьей гармонике.
*** работают на пятой гармонике.
Rк – эквивалентное последовательное сопротивление

Для корпусов типа US

Резонансная частота, МГц	Рекомендуемая нагрузочная емкость, пФ	Rк, (Ом)	Резонансная частота, МГц	Рекомендуемая нагрузочная емкость, пФ	Rк, (Ом)	Резонансная частота, МГц	Рекомендуемая нагрузочная емкость, пФ	Rк, (Ом)	Резонансная частота, МГц	Рекомендуемая нагрузочная емкость, пФ	Rк, (Ом)
1			9,216	16	50	15,36	20	40	29,4912		50
3,6864	16, 30	150	12,288	0, 20	40	16,67	0	40	30*	0, 16	100
5,5		80	12,8	16	40	16,9344	16, 20	40	32*		80
7,5	16	70	13,56	0, 20	40	17,7344	20	40

*работают на третьей гармонике.
Rк – эквивалентное последовательное сопротивление

Кварцевые резонаторы для схем отсчета времени на частоту 32,768 кГц поставляются в следующих корпусах:

• MMTF-32 – цилиндрический, для монтажа в отверстия
• MTF-38 – цилиндрический, для монтажа в отверстия
• DT38T – цилиндрический, для монтажа в отверстия
• MG3A – малогабаритный для поверхностного монтажа

• Наименование

  К продаже

  Цена от

К продаже:

5 891 шт.

КВАРЦЕВЫЙ ГЕНЕРАТОР • Большая российская энциклопедия

• В книжной версии

  Том 13. Москва, 2009, стр. 485

• Скопировать библиографическую ссылку:

  ---

Авторы: В. В. Дмитриев

КВА́РЦЕВЫЙ ГЕНЕРА́ТОР, ма­ло­мощ­ный ге­не­ра­тор элек­трич. ко­ле­ба­ний с са­мо­воз­бу­ж­де­ни­ем, в со­став ко­ле­ба­тель­ной сис­те­мы ко­то­ро­го вхо­дит квар­це­вый пье­зо­элек­три­че­ский ре­зо­на­тор. Ха­рак­те­ри­зу­ет­ся вы­со­кой ста­биль­но­стью час­то­ты ге­не­ри­руе­мых ко­ле­ба­ний, что обу­слов­ле­но вы­со­кой доб­рот­но­стью квар­це­во­го ре­зо­на­то­ра (10⁵–10⁷).

Схема кварцевого генератора – последовательного резонанса с кварцевым резонатором (КР) в колебательном контуре: C1,2,3 – конденсаторы; R1,2,3,4 – резисторы; L – катушка индукти…

Элек­трич. схе­мы К. г. прин­ци­пи­аль­но не от­ли­ча­ют­ся от схем ге­не­ра­то­ров элек­три­че­ских ко­ле­ба­ний с обыч­ны­ми ко­ле­ба­тель­ны­ми кон­ту­ра­ми. Па­ра­мет­ры ко­ле­ба­тель­ной сис­те­мы К. г. вы­би­ра­ют­ся так, что­бы бóль­шая часть энер­гии бы­ла со­сре­до­то­че­на в квар­це­вом ре­зо­на­то­ре; в этом слу­чае ге­не­ри­руе­мая час­то­та оп­реде­ля­ет­ся гл. обр. соб­ст­вен­ной час­то­той ре­зо­на­то­ра. Квар­це­вый ре­зо­на­тор об­ла­да­ет вы­со­ки­ми ме­ха­нич. проч­но­стью и хи­мич. стой­ко­стью, не­чув­ст­ви­те­лен к влаж­но­сти; его соб­ст­вен­ная час­то­та сла­бо за­ви­сит от темп-ры. Раз­ли­ча­ют схе­мы К. г. по­сле­до­ва­тель­но­го ре­зо­нан­са, в ко­то­рых квар­це­вый ре­зо­на­тор эк­ви­ва­лен­тен ак­тив­но­му со­про­тив­ле­нию (рис.), и ос­цил­ля­тор­ные – квар­це­вый ре­зо­на­тор эк­ви­ва­лен­тен ин­дук­тив­но­сти. В за­ви­си­мо­сти от ве­ли­чи­ны не­ста­биль­но­сти час­то­ты и/или воз­мож­но­сти из­ме­не­ния час­то­ты ко­ле­ба­ний К. г. под­раз­де­ля­ют на про­стые, не со­дер­жа­щие до­пол­нит. эле­мен­тов для улуч­ше­ния па­ра­мет­ров; управ­ляе­мые, час­то­ту ко­то­рых мож­но из­ме­нять по­сред­ст­вом внеш­не­го воз­дей­ст­вия; тер­мо­ком­пен­си­ро­ван­ные, у ко­то­рых от­кло­не­ние (уход) час­то­ты $\Delta f$ от её но­ми­наль­но­го зна­че­ния $f$ в за­дан­ном ин­тер­ва­ле темп-р умень­ша­ют с по­мо­щью до­пол­нит. элек­трич. уст­ройств; тер­мо­ста­ти­ро­ван­ные, у ко­то­рых все или не­ко­то­рые эле­мен­ты по­ме­ще­ны в тер­мо­стат. Су­ще­ст­ву­ют так­же К. г. сме­шан­но­го ти­па (напр., управ­ляе­мый тер­мо­ком­пен­си­ро­ван­ный К. г.).

Час­то­та ге­не­ри­руе­мых ко­ле­ба­ний в за­ви­си­мо­сти от ти­па К. г. со­став­ля­ет от не­сколь­ких кГц до 100 МГц и бо­лее. Ста­биль­ность час­то­ты, ха­рак­те­ри­зуе­мая от­но­ше­ни­ем $\Delta f/f$, дос­ти­га­ет у про­стых К. г. ± 5·10^–6 в диа­па­зо­не темп-р от –60 до 100 °C, у тер­мо­ком­пен­си­ро­ван­ных 5·10^–7 (от –60 до 85 °C), у тер­мо­ста­ти­ро­ван­ных 10^–10 (10–40 °C). Мощ­ность К. г. ог­ра­ни­че­на проч­но­стью квар­це­вой пла­сти­ны, её раз­ме­ра­ми и, как пра­ви­ло, не пре­вы­ша­ет не­сколь­ких де­сят­ков Вт. К. г. ши­ро­ко при­ме­ня­ют­ся в разл. ра­дио­пе­ре­даю­щих уст­рой­ст­вах (в ка­че­ст­ве за­даю­щих ге­не­ра­то­ров), в квар­це­вых ча­сах, мо­гут слу­жить эта­ло­на­ми вре­ме­ни и стан­дар­тов час­то­ты.

Определение частоты и подстройка частоты кварцевого резонатора »Электроника

Можно уменьшить или уменьшить частоту кварцевого резонатора, добавив дополнительную емкость и индуктивность, а для кристаллов существует коэффициент затягивания.

---

Учебное пособие по кристаллам кварца, Xtals Включает:
Кристаллы кварца: xtals Что такое кварц Как работает кристалл Кристаллический обертон Вытягивание частоты кристалла кварца Кристалл кварца огранки Кварцевое старение Изготовление кристаллического резонатора Как указать кристалл кварца VCXO TCXO OCXO Кристаллический фильтр Монолитный кристаллический фильтр Керамический резонатор и фильтр Технические характеристики керамического фильтра

---

В некоторых случаях необходимо иметь возможность подрезать или «подтянуть» резонансную частоту кристаллического резонатора, чтобы приспособиться к небольшим изменениям, которые могут потребоваться в резонансной частоте.

Во многих случаях это может быть необходимо, и тем самым он сочетает в себе феноменальные характеристики кварцевого резонатора с точки зрения стабильности и добротности с возможностью небольшого изменения частоты генератора. Естественно, возможность подстройки частоты немного снижает производительность кристалла, но для большинства целей этого более чем достаточно.

Хотя VXO, кварцевые генераторы с регулируемой частотой использовались в прошлом, где частота кварцевого генератора изменялась вручную, сегодня более распространенным является использование кварцевых генераторов с регулируемым напряжением VCXO, которые используются в кварцевых генераторах с температурной компенсацией, узкополосных схемах фазовой автоподстройки частоты и ряд других приложений.

Подстройка частоты используется по-разному. Их можно использовать в кварцевых генераторах с температурной компенсацией, TCXO, где датчик температуры используется для питания цепи, которая компенсирует дрейф в зависимости от температуры. Его можно использовать для периодической ручной калибровки генератора в соответствии со стандартом высокой точности, или его можно использовать для электронной подстройки частоты генератора в соответствии со стандартом вне эфира, таким как GPS.

Основы вытягивания резонансной частоты кристаллического резонатора

Кристаллический резонатор – это настроенная схема, характеристики которой можно моделировать с помощью более обычных электронных компонентов.

Эта эквивалентная схема дает представление о ее работе, поскольку позволяет увидеть, как различные электронные компоненты в эквивалентной схеме взаимодействуют вместе.

Эквивалентная схема кварцевого резонатора

В этой эквивалентной схеме можно приравнять различные электронные компоненты к элементам функции кварцевого резонатора.

• L: Индуктивность возникает из-за массы материала.
• C1: Эта емкость возникает из-за податливости кристалла.
• R: Этот элемент возникает из-за потерь в системе. Самый большой из них возникает из-за потерь на трение при механической вибрации кристалла.
• Co: Эта емкость в теоретической эквивалентной схеме кристалла кварца возникает из емкости между электродами кристаллического элемента. Это часто называют шунтирующей емкостью.

В дополнение к электронным компонентам, показанным в эквивалентной схеме, в конструкции электронной схемы должна быть предусмотрена внешняя емкость, известная как емкость нагрузки, чтобы кристалл колебался на своей резонансной частоте.

Емкость нагрузки указана в техническом паспорте кристалла и является одним из параметров, который необходимо указать при заказе. Обычно используются значения 20 пФ и 30 пФ.

Емкость нагрузки оказывает заметное влияние на резонансную частоту кристалла, когда он работает в параллельном режиме. Это действительно имеет эффект, когда кристалл работает в последовательном режиме, но влияние нагрузочного конденсатора намного меньше.

Уравнение вытягивания кристалла можно выразить следующим образом:

Где:
Δf = разница между частотой тяги или нагрузки и последовательной резонансной частотой fs
C _L = емкость нагрузки

Также возможно вычислить среднюю тяговую способность кристалла по сдвигу частоты на изменение емкости нагрузки на пикофарад.

Видно, что для этого необходимо знать шунтирующую емкость, подвижную емкость и емкость нагрузки. В тех случаях, когда эти цифры доступны, это может быть очень полезно.>

Пределы Δf фактически зависят от добротности кристалла, которая связана со значениями электронных компонентов в эквивалентной схеме, а также от емкости нагрузки.

Цепи для вытягивания кварца частота колебаний

Существует множество различных схем, которые можно использовать для изменения частоты колебаний кварцевого кристалла.

По сути, изменение частоты кварцевого генератора требует изменения емкости нагрузки. Это изменит частоту колебаний, позволяя подрезать ее до необходимого значения в доступном диапазоне.

Наиболее часто используемой схемой является генератор Колпитца. Использование простого переменного конденсатора на кристалле позволит выполнить соответствующую настройку. Кроме того, уменьшая номиналы конденсаторов C1 и C2 в конструкции электронной схемы, одновременно поддерживая работу схемы, можно уменьшить нагрузочную емкость, возникающую из-за этого элемента схемы, тем самым допуская больше регулировки.

Типовая схема VXO, кварцевого генератора с переменной частотой

Этот тип схемы может использоваться там, где требуется ручная подстройка частоты кварцевого генератора. Он также может использоваться в некоторых любительских радиопередатчиках с маломощным кварцевым управлением или радиолюбительских передатчиках. Использование кварцевого генератора значительно упрощает конструкцию электроники и количество используемых электронных компонентов, что делает передатчик пригодным для домашнего строительства.

В большинстве случаев удобнее управлять частотой кварцевого генератора с помощью управляющего напряжения.Это означает, что он может быть включен в различные конструкции электронных схем, включая: узкополосный контур фазовой автоподстройки частоты; кварцевый генератор VCXO, управляемый напряжением; кварцевый генератор с температурной компенсацией TCXO; и многие другие схемы.

Для регулирования напряжения используются варакторные диоды. Использование диодов, соединенных спиной к спине, как показано, является нормальным.

Можно использовать один диод, но тогда вместо диода D1 потребуется последовательный конденсатор, чтобы изолировать друг от друга напряжение настройки и напряжение смещения транзистора.Двойные диоды дают общее улучшение характеристик по сравнению с одиночным диодом.

Резистор на кристалле требуется для обеспечения возврата постоянного тока для напряжения смещения для диода D1. Его значение может быть высоким, потому что ток почти не протекает ввиду того, что варакторные диоды имеют обратное смещение.

Типовая схема VCXO

В некоторых случаях может потребоваться относительно большой сдвиг частоты для кварцевых генераторов. Одно приложение находится в любительском радио, передатчиках любительского радио с кодом Морзе малой мощности.Здесь использование кварцевого генератора дает хороший уровень стабильности, даже когда видны большие сдвиги, а высокая выходная мощность по сравнению с LC-генератором переменной частоты очень полезна. Они намного проще других решений и используют меньше электронных компонентов. Эти генераторы обычно не используются для высокопроизводительных приложений, потому что стабильность, фазовый шум и точность, очевидно, находятся под угрозой, но все же более чем достаточно для любительских радиотехнических применений.Примечание: ВНИМАНИЕ !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Схема для VXO, обеспечивающая высокий уровень сдвига частоты

Следует проявлять осторожность при проектировании электронной схемы такой схемы.Если частотный сдвиг становится слишком большим, то выходная мощность может упасть, или генератор вообще перестанет работать, или частота колебаний может регулироваться только комбинацией LC. Однако при тщательном проектировании и оптимизации электроники можно получить больший сдвиг частоты, чем при использовании простого переменного конденсатора.

Изменение резонансной частоты кристалла

Много лет назад, когда кристаллы кварца не содержались в герметично закрытом блоке, их часто можно было разобрать, чтобы получить настоящий резонансный кварцевый элемент.

Как только кварцевый элемент был получен, его можно было изменить так, чтобы его резонансная частота была изменена.

Одна из «хитростей» заключалась в том, чтобы сделать короткую графитовую отметку, то есть отметку карандашом на кварцевом элементе, чтобы немного снизить его резонансную частоту.

Другим действительно удалось отшлифовать основные плоские грани кристалла, чтобы немного увеличить резонансную частоту. Это потребовало настоящего мастерства, поскольку лица должны были оставаться практически идеально параллельными.

Во всех случаях элемент из кристалла кварца должен оставаться как можно более чистым.Было высказано предположение, что при этом нужно надевать хлопковые перчатки.

Эти операции ни в коем случае не рекомендовались, но для тех, кто хотел экспериментировать и имел запасные кристаллы, можно было изменить резонансную частоту, хотя почти всегда активность кристаллов кварца была снижена.

Хотя кварцевые кристаллы обеспечивают простое, точное, стабильное решение с низким уровнем фазового шума для использования в генераторах, часто бывает необходимо иметь возможность регулировать частоту. Концепция изменения частоты с помощью конденсатора переменной нагрузки широко используется в огромном количестве схемотехнических решений.Это достигается очень просто с использованием очень небольшого количества электронных компонентов.

Хотя существует баланс между величиной тяги или сдвига и другими аспектами, такими как стабильность, фазовый шум и т.п., обычно используемые уровни сдвига означают, что производительность обычно подходит практически для всех приложений.

Другие электронные компоненты: Резисторы
Конденсаторы Индукторы Кристаллы кварца Диоды Транзистор Фототранзистор Полевой транзистор Типы памяти Тиристор Разъемы Разъемы RF Клапаны / трубки Аккумуляторы Переключатели Реле
Вернуться в меню «Компоненты».. .

Введение в стандарты частоты кварца – Кварц и кварцевый кристалл

Вернуться к индексу

Высокая добротность и высокая жесткость кварцевого блока (маленький C ₁ ) делают его основным элементом, определяющим частоту и стабильность частоты в кварцевом генераторе. Значения добротности кварцевых блоков намного выше, чем достижимые с другими элементами схемы. В кристаллах общего назначения Qs обычно находятся в диапазоне от 10 ⁴ до 10 ⁶ .Добротность высокостабильного кварцевого блока с частотой 5 МГц обычно находится в диапазоне от двух до трех миллионов. Собственная добротность, ограниченная внутренними потерями в кристалле, была экспериментально определена как обратно пропорциональная частоте (т. Е. Произведение добротности является константой для данного типа резонатора). Для резонаторов с отсечкой AT и SC максимальное значение Qf = 16 миллионов, когда f выражается в МГц.

Кварц (который представляет собой монокристаллическую форму SiO ₂ ) был предпочтительным материалом для стабильных резонаторов, так как вскоре после того, как пьезоэлектрические кристаллы были впервые использованы в генераторах – в 1918 году.Хотя были исследованы многие другие материалы, лучше кварца не было найдено ни одного. Кварц – единственный известный материал, который обладает следующей комбинацией свойств:

1. Он пьезоэлектрический («электрическое давление»; пьезеин в переводе с греческого означает «давить»).
2. Резонаторы с нулевым температурным коэффициентом могут быть изготовлены, когда пластины разрезаются в правильном направлении относительно кристаллографических осей кварца.
3. Из разрезов с нулевым температурным коэффициентом один, SC-разрез (см. Ниже), имеет «компенсацию напряжения».”
4. Он имеет низкие собственные потери (т.е. кварцевые резонаторы могут иметь высокую добротность).
5. Легко обрабатывать, потому что он твердый, но не хрупкий, и при нормальных условиях он имеет низкую растворимость во всем, кроме фторидных травителей.
6. В природе много.
7. Легко выращивать в больших количествах, при низких затратах и ​​относительно высокой чистоте и совершенстве.

Из выращенных человеком монокристаллов кварц, производивший более 2000 тонн в год (в 1991 г.), уступает только кремнию по количеству выращенного.

Прямой пьезоэлектрический эффект был открыт братьями Кюри в 1880 году. Они показали, что когда груз помещается на кристалл кварца, на поверхности кристалла появляются заряды; величина заряда была пропорциональна весу. В 1881 году был проиллюстрирован обратный пьезоэлектрический эффект; когда на кристалл было приложено напряжение, кристалл деформировался из-за деформаций решетки, вызванных этим эффектом. Деформации изменились, когда напряжение было изменено на противоположное.

Из 32 классов кристаллов 20 демонстрируют пьезоэлектрический эффект (но только некоторые из них полезны).У пьезоэлектрических кристаллов отсутствует центр симметрии. Когда сила деформирует решетку, центры тяжести положительных и отрицательных зарядов в кристалле могут быть разделены, чтобы произвести поверхностные заряды. Пьезоэлектрический эффект может обеспечить связь между электрической цепью и механическими свойствами кристалла. В надлежащих условиях «хороший» пьезоэлектрический резонатор может стабилизировать частоту контура генератора.

Кристаллы кварца сильно анизотропны, то есть их свойства сильно зависят от кристаллографического направления.Например, когда кварцевый шар травится в фтористоводородной кислоте, скорость травления более чем в 100 раз выше по направлению самой высокой скорости травления, Z-направлению, чем по самому медленному направлению, медленному X-направлению. Константы кварца, такие как коэффициент теплового расширения и температурные коэффициенты упругих постоянных, также меняются в зависимости от направления. То, что кристаллические блоки могут иметь нулевые температурные коэффициенты частоты, является следствием температурных коэффициентов упругих постоянных в диапазоне от отрицательных до положительных значений.

Геометрическое место разрезов с нулевым температурным коэффициентом в кварце показано на рисунке 5. Направления X, Y и Z были выбраны, чтобы сделать описание свойств как можно более простым. Ось Z на рисунке 5 представляет собой ось тройной симметрии в кварце; Другими словами, физические свойства повторяются каждые 120 °, когда кристалл вращается вокруг оси Z. Отрезы обычно имеют двухбуквенные названия, где буква «T» в названии означает резку с температурной компенсацией; например, разрез AT был первым обнаруженным разрезом с температурной компенсацией.Разрезы FC, IT, BT и RT – это другие разрезы вдоль геометрического участка с нулевым температурным коэффициентом. Эти разрезы изучались в прошлом (до открытия SC-разреза) на предмет некоторых особых свойств, но сегодня они используются редко. В кварцевых генераторах с наивысшей стабильностью используются кварцевые блоки SC или AT.

Рисунок 5. Срезы кварца с нулевым температурным коэффициентом.

Поскольку свойства кварцевого кристалла сильно зависят от углов среза кристаллической пластины, при изготовлении кристаллических элементов пластины вырезают из кварцевого стержня в точно контролируемых направлениях относительно кристаллографических осей.Ориентацию пластин проверяют с помощью дифракции рентгеновских лучей. В некоторых приложениях ориентацию необходимо контролировать с точностью до нескольких угловых секунд. После придания необходимой формы на пластину накладываются металлические электроды. Круглые пластины с круглыми электродами являются наиболее часто используемой геометрией, хотя заготовки и электроды также могут иметь другую геометрию. Электроданная пластина закреплена в конструкции держателя [8]. На рисунке 6 показаны два распространенных типа держателей, используемых для резонаторов с частотами более 1 МГц.(Резонаторы камертона 32 кГц, используемые в кварцевых часах, обычно упаковываются в небольшие трубчатые корпуса.)

Рисунок 6. Типичные конструкции кристаллов АТ-огранки и SC-огранки.

Поскольку кварц пьезоэлектрический, напряжение, приложенное к электродам, вызывает небольшую деформацию кварцевой пластины. Степень деформации из-за переменного напряжения зависит от того, насколько близка частота приложенного напряжения к естественному механическому резонансу кристалла.Чтобы описать поведение резонатора, дифференциальные уравнения для законов движения Ньютона для сплошной среды и для уравнений Максвелла должны быть решены с соответствующими электрическими и механическими граничными условиями на поверхностях пластин [9]. Поскольку кварц является анизотропным и пьезоэлектрическим, с 10 независимыми линейными константами и многочисленными константами более высокого порядка, уравнения сложны и никогда не решались в закрытой форме для физически реализуемых трехмерных резонаторов. Почти во всех теоретических работах используются приближения.Нелинейные упругие постоянные, хотя и малы, являются источником некоторых важных нестабильностей кристаллических осцилляторов; такие как чувствительность к ускорению, тепловой переходный эффект и амплитудно-частотный эффект, каждый из которых обсуждается в этом отчете.

В идеальном резонаторе амплитуда вибрации максимальна в центре электродов; она экспоненциально спадает за пределами электродов, как показано в нижней правой части рисунка 7. В правильно спроектированном резонаторе незначительное количество энергии теряется в монтажной и связывающей конструкции, т.е.е. края должны быть неактивными, чтобы резонатор мог иметь высокое значение a. Смещение точки на поверхности резонатора пропорционально току возбуждения. При типичных токах возбуждения, используемых в (например, 10 МГц) в резонаторах сдвига толщины, смещение пика составляет порядка нескольких атомных расстояний. (Пиковое ускорение точки на электродах составляет порядка 1 миллиона g.)

Рис. 7. Амплитуда колебательного смещения резонатора для круглой пластины с круглыми электродами.

По мере увеличения уровня возбуждения (тока через кристалл) амплитуда колебаний кристалла также увеличивается, и эффекты, связанные с нелинейностями кварца, становятся более выраженными. Среди множества свойств, которые зависят от уровня возбуждения, можно выделить: резонансную частоту, сопротивление движению R ₁ , фазовый шум и аномалии зависимости частоты от температуры (называемые провалами активности), которые обсуждаются в другом разделе этого отчета. Зависимость резонансной частоты от уровня возбуждения, называемая амплитудно-частотным эффектом, показана на рисунке 8 [10].Изменение частоты с уровнем возбуждения пропорционально квадрату тока возбуждения; коэффициент зависит от конструкции резонатора [11]. Из-за зависимости частоты от уровня возбуждения генераторы с наивысшей стабильностью обычно содержат некоторую форму автоматического управления уровнем, чтобы минимизировать изменения частоты из-за изменений схемы генератора. При высоких уровнях возбуждения нелинейные эффекты также приводят к увеличению сопротивления [5]. Кристаллы также могут проявлять аномально высокое стартовое сопротивление, когда поверхности кристаллов имеют такие дефекты, как царапины и загрязнение твердыми частицами.В таких условиях сопротивление на низких уровнях возбуждения может быть достаточно высоким, чтобы генератор не мог запуститься при подаче питания. Зависимость сопротивления от уровня возбуждения показана на рисунке 9. Помимо нелинейных эффектов, высокий уровень возбуждения также может вызывать изменение частоты из-за повышения температуры, вызванного рассеянием энергии в активной области резонатора.

Рисунок 8. Уровень привода Зависимость от частоты.

Рисунок 9. Зависимость сопротивления кристалла от уровня возбуждения.

Кварцевые резонаторы с объемной акустической волной доступны в диапазоне частот от 1 кГц до 500 МГц. Кварцевые резонаторы на поверхностных акустических волнах (ПАВ) доступны в диапазоне от 150 МГц до 1,5 ГГц. Чтобы охватить широкий диапазон частот, используются разные разрезы, вибрация в самых разных режимах. Объемные волновые режимы движения показаны на рисунке 10. Кристаллы AT-среза и SC-среза колеблются в режиме сдвига по толщине. Хотя желаемая мода сдвига по толщине обычно демонстрирует самое низкое сопротивление, спектр мод даже правильно спроектированных кристаллических блоков демонстрирует нежелательные моды выше основной моды.Нежелательные режимы, также называемые «паразитными модами» или «паразитными помехами», особенно опасны в кристаллах с фильтрами, в которых используются «правила захвата энергии» для максимального подавления нежелательных мод [4]. Эти правила определяют определенную геометрию электрода для взаимосвязей геометрии пластины. В кристаллах осцилляторов нежелательные моды могут быть подавлены в достаточной степени за счет обеспечения достаточно большого отношения диаметра пластины к диаметру электрода или за счет контурирования (т. Е. Создания сферической кривизны на одной или обеих сторонах пластины).

Рисунок 10. Режимы движения кварцевого резонатора.

На частотах выше 1 МГц обычно используется AT-cut. Для высокоточных применений резец SC имеет важные преимущества перед отрезком AT. Кристаллы AT-среза и SC-среза могут быть изготовлены для работы в основном режиме до частоты около 300 МГц. (Устройства с частотой выше 1 ГГц были произведены на экспериментальной основе.) Обычно используются устройства с частотой выше 100 МГц, которые работают в выбранном гармоническом режиме вибрации, хотя устройства с частотой выше 100 МГц могут быть изготовлены с помощью химической полировки. (травление) техники [12].Ниже 1 МГц можно использовать камертоны, стержни X-Y и NT (режим изгиба), X-разрезы + 5 ° (режим растяжения) или блоки CT-cut и DT-cut (режим торцевого сдвига). Камертоны стали доминирующим типом низкочастотных устройств из-за их небольшого размера и низкой стоимости. Сотни миллионов кварцевых камертонов ежегодно производятся для кварцевых часов и других приложений.

Изменение резонансной частоты кристалла кварца при атмосферном давлении?

Резонансная частота кристалла кварца среза \ $ x \ $ (т.е. кристалла кварца, вырезанного по кристаллографической оси \ $ x \ $), связано с его толщиной \ $ d \ $, согласно тому, что пишет Х. Хантингтона в [1], глава 7, с. 219, по следующей формуле $$ f = \ frac {2.86} {d} \ quad \ text {($ \ mathrm {MHz} $)} \ tag {1} \ label {1} $$ где \ $ d \ $ измеряется в миллиметрах. Предполагая, что мы находимся в области линейной упругости, мы можем связать \ $ d \ $ с давлением, приложенным к кристаллической пластине, по закону Гука $$ \ varepsilon_ {xx} = – \ frac {1} {K_x} \ sigma_ {xx} \ tag {2} \ label {2} $$ где

• \ $ \ varepsilon_ {xx} \ Equiv \ frac {\ Delta d} {d} \ $ – частичное изменение толщины кристаллической пластины,
• \ $ \ sigma_ {xx} \ Equiv p_x \ $ is компонент вектора давления, приложенного вдоль кристаллографической оси \ $ x \ $,
• \ $ K_x \ $ – компонент оси \ $ x \ $ тензора упругости («модуль упругости» вдоль этой оси).

В общем, давление определенно влияет на резонансную частоту кристалла кварца : осторожно используя приведенные выше формулы и (известные?) Характеристики вашего кристалла кварца, вы можете попытаться оценить, действительно ли дает вам “очень большое” изменение резонансной частоты, которую вы измеряете.Наконец, позвольте мне поделиться с вами несколькими заметками :

• Хантингтон дает формулу \ eqref {1} «как есть» без какого-либо формального вывода: однако в книге WG Cady ((1946) [1939], Piezoelectricity , 2nd ed., New-York: Dover Публикации: скоро переиздание 2018 г.), и, возможно, также в одном из WP Mason ((1950), Piezoelectric Crystals and their Application to Ultrasonics , New-York: Van Nostrand) вы найдете точный вывод, а также предел его применимости.Есть также более современные трактаты по темам, но обратите внимание на следующее.
• Осторожно! Я представил закон Гука в его (хотя и упрощенной) тензорной форме \ eqref {2} просто для того, чтобы дать вам почувствовать необходимую математику (даже если я считаю, что команда, способная измерять изменение частоты до одной ppb, не слишком очень впечатлены такими вещами;)). Если вы хотите глубоко погрузиться в такие разработки, то книга HF Tiersten ((1969), Linear Piezoelectric Plate Vibrations: Elements of the Linear Theory of Piezoelectricity and the Vibrations Piezoelectric Plates , New-York: Plenum Press, в настоящее время перепечатывается Springer Verlag), пожалуй, абсолютный справочник.

[1] Блэкберн, Дж. Ф. (1949), Справочник по компонентам , MIT Radiation Laboratory Series 17, Нью-Йорк, Торонто и Лондон: McGraw-Hill Book Company, Inc.

TXC Техническая терминология

(1) Номинальная частота и ее допуск или точность калибровки

Частота кварцевого резонатора обычно указывается в мегагерцах (МГц) или килогерцах (кГц). Нормальная частота – это выходная частота, которую мы ожидаем от схемы кварцевых колебаний при надлежащем согласовании.Существует некоторое отклонение частоты от номинальной частоты при температуре окружающей среды (относительно 25 ° C) для реального устройства. Допуск идеального отклонения центральной частоты как параметра устройства определяется максимальным значением, выраженным в процентах (%) или частях на миллион (ppm).

(2) Фундаментальные и обертонные колебания

Сдвиговая вибрация по толщине является основной формой колебаний, существующей при резке AT. Гармонические колебания высокого порядка сосуществуют с фундаментальными колебаниями между областями электродов.Из-за обратной полярности двух электродов в пьезоэлектрических кварцевых резонаторах могут возбуждаться только нечетные гармонические колебания.

(Рис.10) В кристаллическом резонаторе

могут возбуждаться только нечетные гармонические колебания. (3) Емкость нагрузки

Емкость нагрузки, CL, представляет собой величину емкости, которую генератор демонстрирует при взгляде на схему через два конца резонатора. Емкость нагрузки формально устанавливается последовательно или параллельно резонатору.Для случая параллельной нагрузки наличие CL повлияет на частоту параллельного резонанса, а резонансная частота параллельной нагрузки, fL, определяется выражением

Этот параметр необходимо указать.

(4) Стабильность частоты-температуры

Стабильность частоты-температуры обозначается величиной отклонения частоты от значения при стандартной температуре окружающей среды (обычно 25 ° C), вызванного изменением рабочей температуры. Этот параметр задается кривой, показывающей изменение частоты (выраженное в% или ppm) в зависимости от отклонения температуры от эталонной температуры (25 ° C).Температурная стабильность кварцевого устройства зависит от типа реза, режима вибрации и размеров кварцевой заготовки. Кроме того, величина отклонения связана с диапазоном рабочих температур, емкостью нагрузки и уровнем возбуждения кристаллического резонатора.

(5) Эквивалентное последовательное сопротивление (ESR)

Сопротивление R1, появляющееся в последовательной ветви (рис.5), может быть измерено на последовательной резонансной частоте, где эффекты C1 и L1 взаимно компенсируются, а эффективная результат ответвления резистивный.R1 представляет собой механические потери в кристалле и держателе.

(6) Динамическая емкость C1 и подвижная индуктивность L1

Эти два параметра определенно связаны последовательной резонансной частотой, fs, как указано в уравнении (1), и fs является очень надежным параметром в конструкции резонатора и в характеристике. В отраслевом стандарте указано только значение C1, а значение L1 можно получить из

Значение C1 очень мало по сравнению с емкостями, обычно используемыми в колебательных цепях, и может быть оценено по материалам и геометрическим параметрам кристаллической пластины и электродов.

(7) Статическая емкость Co (в шунте)

Шунтирующая емкость Co – это статическая емкость, которая присутствует независимо от того, колеблется устройство или нет. Значение Co можно измерить на очень низкой частоте (менее или около 1 МГц), и теоретически оно равно

. где A – площадь электрода, d – толщина заготовки, µ – диэлектрическая проницаемость соответствующего среза кристалла.

In практически, Co включает не только статическую емкость кварцевой заготовки с покрытием, но также емкость проводящего связующего материала и емкость самого корпуса.

(8) Уровень возбуждения

Уровень возбуждения резонатора – это величина рассеиваемой мощности, выраженная в нановаттах, микроваттах или милливаттах. Рабочий уровень – это подходящий диапазон мощности для обеспечения правильного запуска и поддержания устойчивых колебаний. Уровень возбуждения должен работать на минимальном уровне, чтобы избежать долговременного дрейфа частоты и разрушения кристалла. Как правило, чем меньше размер продукта, тем ниже уровень возбуждения, не повреждая кварцевые резонаторы при длительном использовании.Как правило, уровень мощности от 10 до 100 мкВт достаточно для большинства приложений.

(9) Q-фактор качества

Для резонатора очень важным параметром является добротность Q. В спецификации указаны значения Q для разгруженного и нагруженного оборудования. Без нагрузки Q, или механический Q, может быть выражен как

где, R1 – сопротивление, появляющееся в последовательной ветви.

Нагруженное значение Q зависит от нагруженной цепи.

(10) Тяговая способность

В генераторе емкости с параллельной нагрузкой частота колебаний зависит от емкости нагрузки CL, как показано в уравнении.(3) и (Рис.11). Изменение частоты (в ppm) как функция изменения емкости нагрузки (в пФ) является спецификацией. В некоторых приложениях, где изменение резонансной частоты под нагрузкой является обязательным (например, VCXO), необходимо указать тяговую способность.

(Рис.11) Изменение частоты в зависимости от емкости нагрузки

(11) СТАРЕНИЕ

Старение – это относительное изменение рабочей частоты за определенный период времени и выражается в частях на миллион (ppm) в течение определенного периода.Эта скорость изменения частоты обычно носит экспоненциальный характер. Наибольшая скорость старения наблюдается в течение первой недели старения и медленно снижается после отделения. Обычно старение рассчитывается в течение первых 30 дней и рассчитывается на долгосрочный период (один год или десять лет). Скорость старения зависит от многих факторов: метода уплотнения, целостности, производственных процессов, типа материала, рабочей температуры и частоты.

(12) ДИАПАЗОН ТЕМПЕРАТУР ХРАНЕНИЯ

В спецификации указаны минимальные и максимальные температуры, при которых устройства могут храниться или подвергаться воздействию в нерабочем состоянии.После хранения или выдержки устройств в указанном температурном диапазоне в течение длительного времени все характеристики гарантируются для указанного диапазона рабочих температур.

(13) Отрицательное сопротивление «-R»

Отрицательное сопротивление вводится для описания электрических свойств схемы генератора. Это величина сопротивления, которую схема генератора демонстрирует при просмотре схемы через клеммы резонатор. Одно из основных условий генерации требует, чтобы усилитель обеспечивал достаточное усиление, чтобы компенсировать потери в резонаторе.С точки зрения резонатора, нагрузка должна обладать достаточным «отрицательным сопротивлением», чтобы компенсировать сопротивление резонатора. Это важный параметр при разработке генераторов.

Экспериментальное и численное исследование частотно-силового эффекта в кристаллических резонаторах

Ключевые слова: кварцевый резонатор , частота параллельного резонанса, частотно-силовой эффект, МКЭ.

1. Введение

Поскольку кварцевые устройства, такие как кварцевые резонаторы и генераторы, обладают высокой устойчивостью к изменениям окружающей среды, таким как температура, они используются в качестве устройств управления частотой в электронных устройствах, цифровых компьютерах и телекоммуникациях.Современные требования к стабильности частоты в телекоммуникациях колеблются от 0,1 до 50 ppb / день [1]. Следовательно, кристаллические резонаторы должны быть спроектированы таким образом, чтобы достигалась эта высокая стабильность частоты. На стабильность кристаллических резонаторов в основном влияют некоторые нелинейные эффекты, такие как сила-частота и температурно-частотный эффект. Еще одно промышленное применение кварцевых резонаторов – сенсорная техника. В настоящее время многие датчики работают по принципу частотно-силового воздействия.Целью данной статьи является исследование частотно-силового эффекта как экспериментально, так и численно.

Пьезоэлектрический резонатор обычно состоит из пьезоэлектрического диска, снабженного двумя металлическими электродами. Приложение переменного электрического поля к пьезоэлектрическим резонаторам вызывает механические колебания в резонаторе [2]. Когда частота электрического поля равна собственной частоте кристалла, возникает резонанс. Для получения высоких частот обычно используется режим колебаний толщины сдвига.Если резонатор подвергается внешним воздействиям, таким как тепловые и механические нагрузки, из-за некоторых нелинейных эффектов, таких как частотно-силовой эффект, его резонансная частота сдвигового режима по толщине изменяется, а стабильность выходной частоты снижается [3]. Изменение резонансной частоты кристалла из-за приложения пары диаметрально противоположных сил называется сило-частотным эффектом [4].

Частотно-силовой эффект в колеблющихся кристаллах был впервые замечен Боттомом для кристаллов кварца АТ- и ВТ-огранки [5].Гербер [6] и Мингинс [7] показали, что величина частотно-силового эффекта зависит от направления приложенных нагрузок относительно кристаллографических направлений кристалла. Ратайски [8] количественно оценил эффект «сила-частота» и ввел константу «сила-частота» для круглых резонаторов. Он измерил частотно-силовые постоянные для однократно вращающихся срезов кварца. Даувальтер описал влияние изменения температуры на частотно-силовой коэффициент [9]. Он продемонстрировал, что температурная зависимость частотно-силового коэффициента является функцией азимутального угла ψ между кристаллографической осью X и направлением приложенной силы.Для измерения сдвигов частоты при более высоких температурах он использовал схему генератора для генерации переменного электрического сигнала. Изменение частоты измерялось частотомером. Температурную зависимость повернутых X-срезов кварца исследовал Эрнисс [10]. В этой работе для измерения сдвига частоты кристалл включен в схему генератора, расположенного вне печи. Сигнал генератора смешивается с сигналом гетеродина, и разностная частота распознается.Выход дискриминатора измеряется усилителем с фазовой синхронизацией. Wang et al. [11] изготовили кварцевый датчик нагрузки AT-Cut с температурной компенсацией. Они измерили сдвиг частоты тензодатчика с помощью схемы генератора и частотомера. Другие исследователи применили аналогичные методы для измерения сдвига частоты в кристаллических резонаторах [12]. Почти во всех этих экспериментальных работах одна или две схемы генератора предназначены для измерения частоты кристалла и различения последовательной и параллельной резонансных частот.Это делает измерения трудоемкими и дорогими.

В этом исследовании показано, что при лабораторных измерениях, используя точные генераторы сигналов и осциллографы с высоким разрешением, можно легко и точно измерить частотный сдвиг кристалла. Также анализируется влияние емкости нагрузки измерительных приборов на измерения. Затем экспериментально измеряется частотный сдвиг квадратного кристалла кварца AT-Cut под действием пары противоположных сил.Помимо экспериментального исследования, частотно-силовой эффект моделируется численно. Наконец, результаты метода конечных элементов сравниваются с экспериментальными измерениями.

Существенный вклад этого документа можно описать следующим образом:

• Разработана нелинейная модель конечных элементов для расчета частотно-силового эффекта в кварцевых резонаторах.

• Основанный на измерении сдвига параллельных резонансных частот, предлагается простой метод измерения частотно-силового эффекта в кристаллических резонаторах.

• Показано, что разница между параллельным и последовательным сдвигом резонансной частоты кварцевого резонатора из-за частотно-силового воздействия очень мала.

• Частотно-силовой эффект в квадратном кварцевом резонаторе измеряется экспериментально для проверки численных результатов.

• Общие результаты могут быть использованы для проектирования забойных датчиков давления с большей точностью и надежностью.

2. Электрические параметры кварцевого резонатора

В настоящее время большинство кварцевых резонаторов и датчиков изготавливаются из кристаллов кварца AT-Cut.Кварц Ат-огранки представляет собой особую огранку альфа-кварца и имеет моноклинную кристаллографическую систему [1]. Кварцевые резонаторы AT-Cut обычно изготавливаются в виде тонких круглых и прямоугольных дисков. Диск снабжен двумя металлическими электродами, обычно медными или золотыми, которые используются для создания электрического поля в кварцевой области. Приложение электрического поля приводит к электрической поляризации и электрическому смещению по толщине кристалла. Это электрическое смещение вызывает деформации сдвига по толщине на резонаторе из-за тензора пьезоэлектрической связи кристаллов AT-Cut [13].На рис. 1 показана деформация сдвига по толщине в резонаторах с АТ-срезом.

Как упоминалось во введении, приложение переменного электрического поля приводит к переменной деформации или вибрации в резонаторах. На определенных частотах эти колебания взаимодействуют с границами резонатора, создавая стоячие волны в кристалле – явление, известное как резонанс. Кристаллы AT-Cut действуют на сдвиговую моду вибрации по толщине.

В состоянии резонанса пьезоэлектрический резонатор электрически эквивалентен цепи, состоящей из конденсатора C0, включенного параллельно последовательной цепи Lm, Cm и Rm, как показано на рис.2 [13].

Рис. 1. Толщина сдвиговой деформации кристаллов кварца AT-Cut

Рис. 2. Эквивалентная электрическая схема для кварцевых резонаторов [13]

Параметры C0, Rm, Cm и Lm зависят от статической емкости, внутреннего трения, упругости и массы кристалла соответственно. Эти параметры можно оценить следующими соотношениями:

(1)

Rm = ηlAe2, Lm = ρsl22Ae2, Cm = Ae2cl, C0 = εAsl,

, где η, l, A, e, ρs, c, ε и As – вязкость, толщина резонатора, площадь поверхности резонатора, постоянная пьезоэлектрического напряжения и поверхностная плотность массы соответственно.Импеданс кристалла определяется следующим уравнением [14]:

(2)

ZAB = Rm + j (ωLm-1 / ωCm-ω3Lm2C0 + 2ωLmC0 / Cm-C0 / ωCm2-ωRm2C0) C02 / Cm2 + 1-2ω2LmC0 + 2C0 / Cm + ω2Rm2C02-2ωLmC02 / Cm + ω02,

где ω – угловая скорость. В условиях резонанса мнимая часть уравнения. (2) равен нулю, и кристалл действует как чистый резистор. Таким образом, имеем:

(3)

ω4L2C2C0-ω2 (LC2 + 2LCC0) + (C + C0) = 0.

Решение этого уравнения приводит к следующим действительным корням:

(4)

ωS2 = 1LC → fS = 12π1LC,

(5)

ωP2 = 1LC + 1LC0 → fP = 12π1LC + 1LC0,

, где fs и fp – последовательная и параллельная или антирезонансная частоты резонатора соответственно.

Устройства для измерения частоты обычно вводят дополнительную нагрузочную емкость параллельно с C0. В этом состоянии, согласно формуле. Согласно (4) последовательная резонансная частота остается постоянной, поскольку эта частота не зависит от C0. Но параллельная резонансная частота изменяется за счет добавления емкости нагрузки. Новая частота параллельного резонанса дается формулой [14]:

(6)

fP = 12π1LC + 1L (C0 + CL),

где CL – емкость нагрузки. Уравнение. (6) можно записать в виде:

3.Измерение частотно-силового эффекта

Изменение резонансной частоты кристаллических резонаторов, вызванное диаметральными силами, называется эффектом «сила-частота». Эффект “сила-частота” возникает из-за нелинейного упругого поведения кристалла, которое связывает внешнее возмущение с упругими колебаниями. Благодаря этой связи изменяется скорость акустической волны и размер кристалла. Таким образом изменяется резонансная частота резонатора [15, 16].

3.1. Лабораторное измерение частотно-силового эффекта

Наша измерительная система включает в себя генератор сигналов с разрешением 0,1 Гц и осциллограф с разрешением 1 Гц. Хотя используется простая схема, включающая кристалл и соединительные провода, и резистор. Измерительная система представлена ​​на рис. 3.

Рис. 3. Система измерения частотно-силового воздействия

Когда частота выходного сигнала генератора сигналов становится близкой к резонансной частоте кристалла, возникает резонанс.В резонансном состоянии кристаллический резонатор служит чистым резистором. Таким образом, выходной сигнал генератора сигналов можно увидеть на осциллографе без амплитуды и фазового сдвига. Если частота генератора сигналов будет далека от резонансной частоты, амплитуда выходного сигнала, наблюдаемого в осциллографе, будет меньше входного сигнала.

Резонансная частота кристалла может изменяться из-за внешних возмущений, таких как изменение температуры или приложение внешних сил и ускорений.В этом состоянии, изменяя частоту генератора сигналов и отслеживая сигнал максимальной амплитуды на осциллографе, можно измерить новую резонансную частоту.

В этой измерительной системе пробники осциллографа и система проводки вводят нагрузочную емкость в резонатор. Емкость нагрузки параллельна статической емкости C ₀ . Таким образом, измеренная резонансная частота является параллельной резонансной частотой кристалла и связана с последовательной резонансной частотой по формуле.(7).

3.2. Экспериментальное исследование

Изготовлен квадратный кварцевый резонатор АТ-среза длиной 8 мм и толщиной 0,46 мм с последовательной резонансной частотой сдвига 3,578545 МГц. Эта частота была получена стандартным измерителем импеданса кристалла. Когда кристалл вводится в измерительную систему, демонстрируется частота параллельного резонанса 3,57862 МГц. Таким образом, для нашей измерительной системы по формуле. (7) получаем:

(8)

Cm2 (C0 + CL) = 1.00002263.

Для проведения частотно-силового теста кристалл вводится в зажимное приспособление (см. Рис. 4).

Рис. 4. Загрузочное приспособление кварцевого резонатора

Сжимающая сила прилагается нагрузочными грузами на верхней стороне резонатора через подвижный стержень, имеющий клиновидный наконечник, в то время как другой стержень поддерживает образец на его нижней стороне. Вес стержня был включен в общий вес.Частота кристалла измеряется до и после нагрузки, и вычисляется частотный сдвиг. В нашем эксперименте максимальная загрузка 180 гр. Эта нагрузка приводит к параллельному сдвигу резонансной частоты в кристалле примерно на 20 Гц. Подставляя вычисленное значение Cm / 2 (C0 + CL) из уравнения. (8) в уравнение. (7), последовательный сдвиг резонансной частоты для этого эксперимента получается как:

(9)

Δfs = Δfp1 + Cm2 (C0 + CL) -1 = 20,001 Гц.

Как можно видеть, разница между последовательным и параллельным сдвигами резонансной частоты очень мала и в большинстве приложений ею можно пренебречь.Например, в датчиках давления с кварцевым резонатором последовательный сдвиг резонансной частоты достигает 3000 ppm. [15] В этом случае, применяя уравнение. (9) будет измерен параллельный сдвиг резонансной частоты около 3000,8 ppm, что очень близко к последовательному сдвигу резонансной частоты.

4. Конечно-элементное моделирование частотно-силового эффекта

Наряду с экспериментальным исследованием была разработана программа конечных элементов для исследования частотно-силового эффекта в кварце AT-Cut с использованием мультифизического программного обеспечения COMSOL 4.3.

Анализ частотно-силовых эффектов в пьезоэлектрических резонаторах относится к общей теории возрастающих упругих деформаций, накладываемых на начальные конечные деформации. В этой теории предполагается, что кристалл находится в трех состояниях [2]. Вначале кристалл находится в естественном состоянии и не испытывает смещения, деформации или напряжения. В исходном состоянии тело подвергается механическим деформациям за счет приложения диаметральных сил. В конечном состоянии тело подвергается вибрации малой амплитуды в дополнение к механическим деформациям, приложенным к исходному состоянию.После этой процедуры наша модель включает две подмодели: исходную и инкрементную. Эти две подмодели связывают три различных последовательных состояния кварцевого резонатора. При использовании лагранжевой формулировки смещения всех трех состояний относятся к единой системе отсчета, соответствующей естественному состоянию резонатора.

Исходная модель решает смещение, деформацию и напряжение из-за внешней нагрузки резонатора. Эта модель, однако, не содержит частотной характеристики, обусловленной пьезоэлектрическими колебаниями, поэтому в исходную модель пьезоэлектрический фактор не включен [17].Начальные напряжения, деформации и смещения, которые могут быть получены путем стационарного исследования кварца в исходной модели, рассматриваются как входные данные для инкрементальной модели.

Инкрементальная модель решает инкрементный отклик резонатора, включая только смещение, деформацию и напряжение пьезоэлектрических колебаний. Конечное состояние резонатора затем определяется как суперпозиция начального и возрастающего отклика резонатора. Кроме того, в инкрементальной модели для получения резонансных частот используется решатель собственных частот [3].Процесс моделирования представлен на рис. 5.

Рис. 5. Алгоритм КЭ моделирования частотно-силового воздействия.

Поскольку кристаллы кварца обладают анизотропными характеристиками, а частотно-частотный эффект возникает из-за нелинейного упругого поведения кварца, определяющие уравнения нелинейны и не могут быть реализованы с использованием стандартной функции программного обеспечения FEA [18, 19] . Таким образом, все основные уравнения и граничные условия преобразуются в выражения в слабой форме и запускаются в программу конечных элементов.Необходимые материальные постоянные кварца AT-Cut, включая упругие постоянные второго порядка и упругие постоянные третьего порядка, пьезоэлектрические постоянные и диэлектрические коэффициенты, используемые в модели, основаны на опубликованных значениях Пателя [1]. Все характеристики анизотропного материала вводятся в программу FEM.

4.1. Моделирование начальных распределений напряжений и деформаций

В нашей предыдущей статье [3] мы показали, что учет анизотропных свойств кварца жизненно важен для точного моделирования частотно-силового эффекта.Однако пьезоэлектричеством можно пренебречь. Таким образом, тело считалось анизотропным, а начальные перемещения, деформации и напряжения включают эффекты внешних тяговых усилий и не включают пьезоэлектрический эффект [17]. Следуя Lee и Wang [19], и BeerWinkle [17], мы использовали стандартную нелинейную лагранжевую формулировку из теории упругости для определения начальных напряжений и деформаций. Вот эти уравнения:

(10)

Eij = 12Uj, i + Ui, j + Uk, iUk, j,
Tij = Cijkl Ekl + 12Cijklmn EklEmn,
Tij + TjkUi, k, j = 0 в V,
Pi = NjTij + TjkUi, k на S,

где Eij – начальная лагранжева деформация, Tij – второй тензор напряжений Пиолы-Кирхгофа, Ur, s – начальный градиент смещения, Pi – поверхностное сцепление с граничными поверхностями, Cijkl и Cijklmn – жесткость второго и третьего порядка. коэффициентов, а Nj – вектор нормали к поверхности.

Эти уравнения были введены в программу FEM и решены для прямоугольного кварцевого диска AT-Cut диаметром 8 мм и толщиной 0,43 мм, который подвергается паре нагрузок 0,9 Н и 1,8 Н в кристаллографическом направлении Z. Окончательная КЭ-модель имеет 2158 лагранжевых квадратичных элементов с 164 548 степенями свободы, как показано на рис. 6. Поскольку режим сдвига толщины важен, при исследовании частотно-силового эффекта используется развернутая сетка для управления числом ячеек в направление толщины.

Путем определения двух противоположных сил в центральной точке верхнего и нижнего краев резонатора получают начальное распределение напряжений и деформаций на кристалле. Например, начальные контуры напряжения (T11) для состояния нагружения 0,9 Н показаны на рис. 7.

Рис. 6. Сетчатая геометрия резонатора

Рис. 7. Начальные контуры напряжений (Т11) на прямоугольном диске

4.2. Решение собственных значений

После определения начальных полей решаются основные уравнения для дополнительных полей. Конечное состояние затем определяется наложением инкрементного смещения на начальное смещение. Следует отметить, что в этой лагранжевой модели внешние тяги разрешены в исходном состоянии, а возрастающие смещения, деформации и напряжения принимают только эффект пьезоэлектрических колебаний [17]. Эти высокочастотные колебания представляют собой небольшие деформации, линейно накладывающиеся на начальную конечную деформацию.Таким образом, при выводе дополнительных уравнений можно сделать линейными. Эти уравнения были выведены Ван и др. С использованием вариационных принципов упругости [20]. Дополнительные деформации ηij составляют:

(11)

ηij = 12uj, i + ui, j + Uk, juk, i + Uk, iuk, j,

, где ui, j – градиенты приращения смещения.

Тензор приращения напряжения tij и приращение электрического смещения Di составляют:

(12)

tij = Cijkl + CijklmnEmnηkl-ekijwk,
Di = eiklηkl + εijwj.

В приведенных выше уравнениях ekij, wk и εij – это матрица пьезоэлектрической связи, электрическое поле и коэффициент диэлектрической проницаемости соответственно.

Уравнение приращения движения:

(13)

ρ0u¨i = (tij + tjkUi, k + Tjkui, k), j в V.

Кроме того, уравнение равновесия приращения поверхностного натяжения и минимальное значение Гаусса для изоляционного материала, такого как кварц, составляют:

(14)

pi = njtij + tjkUi, k + Tjkui, k на S,
Di, i = 0 в V.

Резонансное поведение кварца считается гармоническим. Следовательно, уравнение движения примет вид:

(15)

ui = u-ie-iωt,
-ρ0ω2u-ie-iωt = tij + tjkUi, k + Tjkui, k, j в V,

где, ω – резонансная частота, а u-i – амплитуда волны. Как можно видеть, начальные градиенты смещения и напряжения появляются во втором уравнении уравнения (2). (15). Таким образом, начальное состояние должно быть полностью решено до конечного состояния.

Учитывается вышеупомянутый прямоугольный кварцевый резонатор АТ-среза. В ходе экспериментов на электроды в мультифизической среде COMSOL прикладывается переменное электрическое поле с частотой ω и амплитудой напряжения 1 Вольт. Согласно этому электрическому граничному условию направление поляризации и вектор электрического смещения проходят по толщине резонатора. Путем определения тензора пьезоэлектрической связи ekij и тензора диэлектрической проницаемости εij из [1] и с учетом известных значений начальных напряжений и градиентов смещения из исходной модели уравнение.(11) – (15) решаются, и получаются собственные частоты и собственные моды колебаний. Например, резонансный спектр пластины под сжимающей нагрузкой 0,9 Н и режим вибрации сдвига по толщине показаны на рис. 8.

Рис. 8. Спектр резонанса кварцевого резонатора

Установив начальные поля на ноль, можно получить резонанс диска перед нагрузкой и сдвиг частоты из-за нагрузки.В таблице 1 показан относительный сдвиг частоты, то есть Δf / f0, полученный с помощью решения МКЭ для состояний нагрузки буксира, в сравнении с экспериментальными результатами. Как видно из таблицы 1, ошибка между относительным сдвигом частоты, полученным методом МКЭ, и экспериментами составляет менее 1 ppm.

Таблица 1. Дробный сдвиг частоты, полученный экспериментами и моделью конечных элементов

Нагрузка	Измеренный относительный сдвиг частоты [ppm]	Смоделированный относительный сдвиг частоты [ppm]
0.9 N	–2,794 частей на миллион	–2,5 частей на миллион
1,8N	–5,6 частей на миллион	–5 частей на миллион

5. Выводы

Частотно-силовой эффект – одна из основных причин нестабильности частоты в кварцевых резонаторах.В связи с современными требованиями к стабильности высокой частоты в телекоммуникационных приложениях, внедрение соответствующих методов экспериментальной количественной оценки частотно-силового эффекта имеет важное значение. В данной статье был представлен простой метод измерения частотно-силовых характеристик пьезоэлектрических резонаторов. Для характеристики измерительной системы измеряли последовательную резонансную частоту кристалла с помощью стандартного измерителя импеданса кристалла. Затем по предложенной методике была измерена частота параллельного резонанса.Было показано, что частотный сдвиг параллельной резонансной частоты очень близок к таковому для последовательной резонансной частоты. Таким образом, мы можем использовать параллельную резонансную частоту для измерения частотно-силового эффекта. Измерения проводились на квадратном кристалле кварца, который подвергался сжимающим нагрузкам через зажимное приспособление. Этот тест был смоделирован с помощью нелинейной модели конечных элементов, и относительные частотные сдвиги были рассчитаны для двух состояний нагрузки. Результаты по конечным элементам сравнивались с экспериментальными результатами, которые находились в хорошем согласии.

Предлагаемый метод измерения проще и экономичнее существующих методов измерения, основанных на измерении последовательной резонансной частоты кристаллов. Результаты могут помочь сенсорной промышленности в более простом измерении чувствительности кристаллов к воздействиям окружающей среды, таким как ускорения, которые могут вызвать нестабильность частоты из-за эффекта «сила-частота». Кроме того, численную модель можно использовать для проектирования кристаллической пластины, электрода и положения держателя, чтобы добиться большей стабильности частоты за счет уменьшения частотно-силового эффекта.

Метод измерения может быть использован при измерении чувствительности и калибровке датчиков давления и тензодатчиков с кварцевым резонатором. При этом численная модель может применяться для проектирования и оптимизации датчиков для достижения более высокой чувствительности и меньших размеров.

Общие и приложения – Colorado Crystal Corporation

Прецизионные рентгеновские измерения

Поскольку регулирование частоты с изменениями температуры напрямую связано с контролем угла ориентации кварца, все кристаллы AT, производимые Colorado Crystal Corporation, точно измеряются и каталогизируются в группы с узкими углами.Высокотехнологичное оборудование и методы обработки позволяют CCC точно выполнять рентгеновское излучение и / или угловую коррекцию срезов одиночно повернутых кристаллов и более сложных срезов кристаллов с двойным вращением, которые включают, среди прочего, срезы SC и IT. В системы двойной дифракции рентгеновских лучей были внесены технические изменения, чтобы получить гораздо более высокий порядок разрешения, достигая повторяемости в доли минуты. Кроме того, мы используем две разные рентгеновские системы EFG.

Оборудование для притирки Superior Притирочное оборудование

Colorado Crystal Corporation было разработано для достижения наилучших характеристик кристаллов.Его нестандартная конструкция позволяет выполнять промежуточную притирку, чистовую притирку и полировку кристаллических поверхностей… с особым вниманием к однородной чистоте поверхности и параллельности, двум из наиболее важных факторов, влияющих на «добротность» и другие параметры движения кристаллического резонатора.

Методы очистки и нанесения покрытия

После притирки все кристаллы, производимые в Colorado Crystal Corporation, выборочно протравливаются до частот до пластин и тщательно очищаются для обеспечения отличных характеристик кристалла.Различные драгоценные металлы используются для достижения максимальной производительности, требуемой заказчиком. Оборудование для осаждения металлов Colorado Crystal Corporation было специально разработано для получения превосходного безмасляного вакуума с помощью криогенных систем и, таким образом, большей чистоты материала покрытия; его уникальная компоновка обеспечивает равномерное наплавление металла.

Расширенные возможности тестирования

Для сложной задачи измерения кварцевых резонаторов Colorado Crystal Corporation использует одно из самых современных и сложных испытательных устройств в кристаллической промышленности.Системы автоматического сбора данных используются в нескольких испытательных зонах для одновременного считывания и записи высокоточных данных на кварцевых резонаторах. Этими данными можно обмениваться с другими компьютерами или сохранять для будущего использования. Специализированное испытательное оборудование Colorado Crystal Corporation можно использовать во многих конфигурациях и подключать к нашему компьютеру для сверхточного тестирования. Наши клиенты могут положиться на наши возможности для проведения чрезвычайно точных и надежных испытаний, которые отвечают строгим требованиям современных технологий.

Герметичное запечатывание пакетов кристаллов кварца

Colorado Crystal Corporation герметично закрывает кристаллы кварца в основном с помощью пакетов Coldweld.

1. Пакеты холодной сварки – уплотнительная матрица сжимает базовый фланец и фланец крышки под высоким давлением. Два фланца сплавлены вместе, образуя очень хорошее герметичное уплотнение. Этот процесс запечатывания по своей природе очень чистый. Пакеты Coldweld бывают самых разных размеров и конфигураций и подходят для широкого спектра применений с высокими требованиями.
2. Стеклянный корпус (в настоящее время не доступен в CCC) – металлическое кольцо находится между стеклянным основанием и стеклянной крышкой. Металлическое кольцо нагревается за счет индукции с помощью ВЧ-генератора. Когда металлическое кольцо становится достаточно горячим, стекла плавятся, образуя герметичное уплотнение. Доступны ограниченные размеры.
3. Пакеты для сварки сопротивлением (в настоящее время не поставляются в CCC) – уплотнительная матрица удерживает вместе базовый фланец и фланец крышки под относительным легким давлением. Электрический заряд проходит через область фланца, плавя два фланца вместе.
4. Уплотнение припоя (в настоящее время не выпускается в CCC) – Большинство оснований имеют ров, заполненный припоем. Крышка паяного уплотнения обычно имеет небольшое отверстие в верхней части. Крышка находится во рву, пока две части нагреваются. Когда припой плавится, основание и крышка склеиваются. Затем отверстие в крышке запаивается, завершая герметичное уплотнение. В этой операции обычно используется паяльный флюс.
Пакеты устройств для поверхностного монтажа (SMD)
5. доступны через нашу головную компанию.

Общая терминология кристаллов кварца

• провал активности – Снижение активности (более высокий R1), связанное с изменением температуры. Обычно это связано с колебаниями другой моды в то же время, что и желаемая мода, в коротком диапазоне температур.
• старение – старение кристалла кварца – это общий термин, обычно применяемый к любому изменению электрических параметров (обычно частоты) кристаллического элемента, происходящему в течение определенного периода времени.Эта скорость изменения частоты обычно имеет экспоненциально убывающий характер, но также может быть линейной. Смена происходит наиболее быстро в первые дни динамической работы. В старении кристалла кварца есть много взаимосвязанных факторов: утечка уплотнений, внутреннее загрязнение, газовыделение материалов, напряжение, перегрузка и многие другие небольшие эффекты. Изменения схемы в генераторе также могут сместить резонансную частоту кристалла. Поскольку последствия старения не могут быть легко определены с помощью входящего контроля или кратковременного динамического использования, крайне важно, чтобы, если старение является серьезной проблемой при проектировании, необходимо рассмотреть следующие предложения:

* Работа кварцевого блока должна поддерживаться при минимально возможной температуре окружающей среды.Уровни кристаллизации должны быть минимальными.
* Динамическое состаривание кристалла в его схеме генератора перед окончательной регулировкой.

• дисперсия Аллана – метод описания краткосрочной устойчивости осцилляторов во временной области.

• Потери в объемных кристаллах – Потери в объемных кристаллах – это рабочие характеристики, возникающие в результате физических явлений кварца, и складываются из акустической нагрузки, молекулярного трения и мощности, передаваемой на опору или держатель.Они различаются в зависимости от массы, режима резонанса и частотного диапазона устройства. Объемные потери приравниваются к стоимости движущейся руки в размере ₁ рэндов.

• capacity ratio – отношение Co / C1 (статическая емкость / подвижная емкость).

• связанный режим – нежелательный режим, который механически или электрически связан с желаемым режимом при некоторой температуре. Обычно это вызывает спад активности.

• С1 – (или подвижная емкость, См).Емкость резонатора на последовательной частоте. В схеме замещения резонаторов он представлен как элемент С1. Единица измерения – фарады, но обычно выражается в пикофарадах (пФ) 10 ^-12 , фемтофарадах (фФ) 10 ^-15 или аттофарадах (aF) 10 ^-18 .

• Co (шунтирующая емкость или статическая емкость). Электростатическая емкость на выводах резонатора, который включает электроды и держатель. Это не пьезоэлектрическое свойство.Единица измерения – фарады, но обычно выражается в пикофарадах (пФ) 10 ^-12 .

• уровень возбуждения – количество рассеиваемой мощности или количество тока через кристалл в данной рабочей цепи. Уровень привода обычно выражается в микроваттах или миллиамперах. Чрезмерный уровень возбуждения может привести к возможному разрушению кварцевого резонатора, чрезмерному длительному дрейфу частоты или другому неустойчивому поведению.

• DLD (зависимость уровня возбуждения) – чувствительность привода – как электрический параметр (обычно сопротивление, иногда частота) резонатора изменяется при изменении уровня возбуждения.

• Эквивалентная схема кварцевого резонатора – последовательная ветвь (подвижное плечо) содержит пьезоэлектрические свойства кристалла, как они проявляются во внешней цепи при колебании на его резонансной частоте. L1 или Lm (подвижная индуктивность) связана с массой кристалла. C1 или Cm (подвижная емкость) связаны с упругостью кристалла, а R1 или Rm – это оконечное сопротивление кварцевого резонатора. Co представляет собой статическую емкость устройства.См. Рисунок 1.

• калибровка частоты – (калибровка или допуск частоты) – это величина отклонения частоты от желаемой рабочей частоты, обычно при определенной температуре. Требования к точности для допусков частоты обычно выражаются в процентах (± 0,0050%, ± 0,0020%, ± 0,0010%, ± 0,0005%, ± 0,00015% и т. Д.) Или в частях на миллион (± 50, ± 20, ± 10, ± 5 частей на миллион, ± 1,5 частей на миллион и т. Д.).

• g-чувствительность – чувствительность к ускорению – 2g – 2g tipover – изменение частоты из-за изменения ускорения или силы тяжести.Может быть задан как векторная сумма (гамма) или по любой отдельной оси как изменение частоты на g.

• IT-разрез – разрез с двойным поворотом, угол Phi (f) которого составляет 19,1066 ^O , а угол Theta (q) будет изменяться, но для некоторых конструкций он может составлять ~ 34,25 ^O .

• L1 (подвижная индуктивность) – индуктивность, которую резонатор проявляет на последовательной частоте. В схеме замещения резонаторов он представлен как элемент L1. Единица измерения – генри, иногда выражается в миллигенри (мГр) 10 ^-3 .

• Пьезоэлектричество – «электричество давления». Электрическая поляризация возникает во время приложенной механической деформации.
• тянущая способность – величина сдвига частоты, которая возникает при изменении нагрузочного конденсатора (CL) (или индуктора) на кристалле.

• R1 (сопротивление) – (последовательное сопротивление, Rs), (эквивалентное последовательное сопротивление, ESR) – Эквивалентное сопротивление – это значение импеданса, которое кристалл демонстрирует в рабочем резонансном контуре. ЧЕМ ВЫШЕ СОПРОТИВЛЕНИЕ, ТЕМ БОЛЬШЕ ПОТЕРЯ ЭНЕРГИИ РЕЗОНАТОРА; ПОЭТОМУ, ДЛЯ ВОЗБУЖДЕНИЯ РЕЗОНАТОРА НЕОБХОДИМО БОЛЬШЕ ПРИВОДА ИЛИ МОЩНОСТИ.Эквивалентное сопротивление разное для каждого типа среза кристалла и рабочей частоты. Единица измерения – ом.

• возмущения (обычно частота, иногда сопротивление) – связанные с провалом активности. Обычно выражается как максимально допустимое отклонение частоты от аппроксимации (полиномиальной) кривой наименьших квадратов.

• фазовый шум – метод описания шума в частотной области.

• Q (добротность) 2p * энергия, запасенная во время цикла / энергия, потерянная во время цикла.Чем выше добротность, тем выше стабильность частоты и точность резонатора.

• ретрейс – обычно означает разницу в частоте (до и после) из-за выключения разогретого генератора (или печи) на некоторое время, а затем его повторного включения.

• Резка SC – резка с двойным поворотом и компенсацией напряжений, угол Phi (f) которого составляет ~ 21,93 ^° , а угол Theta (q) будет варьироваться, но для некоторых конструкций он может составлять ~ 34.25 ^О . Этот срез и другие срезы дважды повернутого кристалла могут иметь сильный нежелательный отклик в B-режиме примерно на 10% выше желаемой частоты C-режима.

• паразитные моды (шпоры) – нежелательный режим вибрации, обычно связанный с одной из негармонических мод.

• TC (температурный коэффициент) – это стабильность частоты или отклонение частоты при изменении температуры. Обычно TC выражается в частях на миллион (PPM) изменения или в процентах от частоты в диапазоне рабочих температур относительно частоты кристалла, измеренной при заданной температуре.TC также можно выразить как диапазоны точек поворота, крутизну и другие способы задания изменения частоты в зависимости от температуры.

• тепловой гистерезис – обычно означает разность частот (при одной и той же температуре) при циклическом изменении температуры и мониторинг частоты во время циклического изменения температуры.

На рисунке 1 R1 представляет сопротивление выводов, C1 представляет подвижную емкость, L1 представляет подвижную индуктивность, а Co представляет статическую емкость на выводах.Последовательная ветвь L1 C1 R1 представляет пьезоэлектрические свойства кристалла, как они проявляются во внешней цепи, когда кристалл колеблется на своей резонансной частоте. Индуктивность подвижного плеча связана с массой кристалла, а подвижная емкость связана с упругостью кристалла. Мощность или тепло кварцевого резонатора должно рассеиваться корпусом. Чрезмерная мощность значительно снижает общую стабильность. Внешние емкости от кристалла до генератора могут влиять на частотную корреляцию.

Многие производители кристаллов предоставляют значения для L ₁ , C ₁ , Q, R ₁ , C _o и F _s . При правильных значениях, введенных в проиллюстрированные формулы, диапазон вытягивания (частота нагрузки F _L ) может быть рассчитан для любого значения из C _L последовательно с кристаллом. Понимание этих формул поможет в проектировании схем. Для прецизионных кристаллов необходимо указывать все указанные параметры.

Кварцевый блок обычно предназначен для использования только в очень узком частотном диапазоне, центрированном на указанной номинальной частоте. Когда кристалл используется в качестве пассивного элемента и частота изменяется от более низкой к более высокой частоте, минимальный импеданс от Fs (максимальная передача) до Fp (минимальная передача) изменится с очень нескольких Ом до мегомов. Хотя кристалл будет работать на любой частоте между Fs и Fp, в зависимости от условий схемы, желательно работать близко к частоте Fs, поскольку на стабильность частоты меньше влияют изменения емкости внешней схемы.

Удобный метод настройки кристалла на заданную частоту – это подключение конденсатора переменной нагрузки (CL) последовательно с кварцевым блоком. Величина тяги (настройка частоты) контролируется значениями кристалла C ₁ и C _o , а также значением и диапазоном конденсатора CL. Последовательные индукторы могут использоваться для увеличения диапазона вытягивания кристаллов.

Правильный выбор типа кристалла также обеспечит улучшенную стабильность. Для той же частоты и среза кристалла масса кварца в кристалле 3-го обертона в три раза больше, чем в кристалле основного тона, в то время как масса 5-го обертона в пять раз больше, чем в кристалле основного тона.Увеличение массы, непосредственно являющееся результатом выбора 3-го или 5-го режимов колебаний, также улучшает стабильность, но снижает C1, тем самым уменьшая тяговое усилие.

Рисунок 3

Рисунок 4

На рисунке 3 показан кристалл, который был протестирован на зависимость от уровня возбуждения (DLD).В этом примере было три развертки частоты, причем каждая развертка частоты была на разном уровне возбуждения. DLD также можно проверить с помощью развертки амплитуды. В разумных пределах привода для данной конструкции не должно быть чрезмерного сопротивления или сдвигов частоты.

Фиг. 4 – график, показывающий частотную характеристику для конкретной конструкции отсечки SC. Обратите внимание, что частота B-режима примерно на 9,6 процента выше частоты C-режима. Режимы негармонического обертона (ложные режимы) также показаны для каждого режима.

ХАРАКТЕРИСТИКИ ТЕМПЕРАТУРНОГО КОЭФФИЦИЕНТА

Кристаллы кварца могут быть предназначены для работы в широком или узком температурном диапазоне. Температурные / частотные характеристики могут быть изменены для обеспечения оптимальной стабильности в любом заданном диапазоне. TC (температурный коэффициент) в значительной степени контролируется правильной угловой ориентацией во время рентгеновских измерений. TC может быть выражено разными способами, включая плюс или минус частей на миллион (PPM) в заданном диапазоне температур, диапазон UTP (верхней точки поворота), диапазон LTP (нижней точки поворота), наклон, дельта PPM между точками поворота и другие методы или комбинации.

Рисунок 5

На рисунке 5 представлена ​​кривая TC, показывающая точки поворота и температуру перегиба. Точка поворота, температура которой ниже температуры перегиба, называется нижней точкой поворота (LTP), а точка поворота, температура которой выше температуры перегиба, называется верхней точкой поворота (UTP). LTP и UTP симметричны относительно температуры перегиба. Кристаллические срезы, частотно-температурные характеристики которых обычно соответствуют полиномам 3-го порядка, будут иметь температуру перегиба, но не обязательно точки поворота.Отрицательные кривые будут иметь температуры перегиба, но не будут иметь точек поворота. Положительные кривые будут иметь температуры перегиба и точки поворота. Установка первой производной полинома 3-го порядка равной нулю, а затем вычисление «x» будет определять точки поворота, в то время как установка второй производной полинома 3-го порядка равной нулю, а затем вычисление «x» будет определять температуру перегиба.

Рисунок 10
Общее семейство кривых для разрезов AT, IT и SC, показывающих приблизительные температуры перегиба

Приложения

Пьезоэлектрический кварц используется во многих сферах, и все больше их постоянно разрабатываются.

• ОСЦИЛЛЯТОРЫ
• ФИЛЬТРЫ
• ОПИСАНИЕ
• ДАТЧИКИ
• ДАТЧИКИ

Некоторые общие приложения для конечного использования

• НАВИГАЦИОННЫЕ СИСТЕМЫ
• СПУТНИКОВАЯ СВЯЗЬ
• РАДАР
• ТЕЛЕКОММУНИКАЦИИ
• КОМПЬЮТЕРЫ
• СОНАР
• МОНИТОРЫ ОКРУЖАЮЩЕЙ СРЕДЫ
• РОБОТЫ
• АВИАЦИОННАЯ СВЯЗЬ
• МОРСКАЯ СВЯЗЬ
• ХИМИЧЕСКИЕ / БИО ДАТЧИКИ
• ЛЮБИТЕЛЬСКОЕ РАДИО
• ПОЛИЦИЯ И ПОЖАРНОЕ РАДИО
• СОТОВЫЙ ТЕЛЕФОН
• ОТСЛЕЖИВАНИЕ ДИКОЙ ЖИЗНИ
• АТОМНЫЕ СТАНДАРТЫ
• ОБОРУДОВАНИЕ ДЛЯ ИЗМЕРЕНИЯ РАССТОЯНИЯ
• Q ВКЛЮЧЕНИЕ ЛАЗЕРОВ
• СИСТЕМЫ ОРУЖИЯ
• СЧЕТЧИКИ ЧАСТОТЫ
• АНАЛИЗАТОРЫ СПЕКТРА / СЕТИ
• ВИДЕО ИГРЫ
• ЧАСЫ И ЧАСЫ
• МЕДИЦИНСКИЙ ПРИБОР
• РУКОВОДИТЕЛИ ДВИГАТЕЛЯ
• АВТОМОБИЛЬНЫЕ СИСТЕМЫ ЗАЖИГАНИЯ
• СЕРДЕЧНЫЕ СОЕДИНИТЕЛИ
• КОСМИЧЕСКИЕ СУММЫ СВЯЗИ
• ДАТЧИКИ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ МАСЛА, ГАЗА

Зависимость резонансной частоты кристалла кварца от температуры кварца.

Контекст 1

… кристалл в последовательном резонансе при его основном колебании около 6 МГц и для измерения этой резонансной частоты с точностью до нескольких МГц. Частота последовательного резонанса fs определяется элементами L 1, C 1 и R 1 в эквивалентной схеме Баттерворта – Ван Дайка кристалла (рис. 3), и это собственная частота кристалла с его электроды закорочены. В отличие от параллельной резонансной частоты ͑ открытый электрод ͒, f s можно определить, если кристалл подключен к электронике через кабель с дополнительной емкостью, параллельной C 0.Цепи осциллятора для последовательного резонанса усиливают сигнал, пропорциональный току через кристалл кварца, и подают это напряжение обратно. Таким образом выбирается резонанс с максимальной проводимостью. В отличие от кристаллов среза AT, кристаллы среза SC имеют две моды сдвига, вызванные пьезоэлектрическим эффектом, причем C-мода с компенсацией температуры и напряжений имеет более низкий коэффициент пьезоэлектрической связи (k 2 ϭ 0,024), чем нежелательная B-мода (k 2 ϭ 0,026). Следовательно, мода B, резонансная частота которой примерно на 10% выше, чем у моды C, обычно имеет более высокую проводимость и должна подавляться.В схемах генератора это можно сделать через LC-фильтр, который, однако, вызывает нежелательный фазовый сдвиг, приводящий к дополнительному дрейфу частоты. Эта проблема может быть решена с помощью отдельного генератора, который фиксирует резонансную частоту кристалла, аналогично петле фазовой автоподстройки частоты ͑ PLL. Разность фаз между напряжением возбуждения на кристалле и протекающим через него током используется для управления частотой осциллятора. Схема схематически показана на рис. 4 ͑ подробные электронные схемы можно получить у авторов по запросу ͒.Мы используем малошумящий LC-осциллятор типа Клаппа, настраиваемый между 59 и 61 МГц с помощью варикапов. После усиления и преобразования в уровни TTL, сигнал генератора подается, с одной стороны, в счетчик частоты, а с другой – в счетчик Джонсона, который делит частоту на 10 для возбуждения кварцевого кристалла. Эта установка использует один и тот же цифровой сигнал для аналоговой части схемы и частотомера, тем самым минимизируя дрожание и дрейф уставки триггера, которые могут повлиять на измерение частоты при подключении частотомера к аналоговой электронике.После сглаживания до синусоидальной формы сигнал с частотой 6 МГц проходит через управляемый напряжением усилитель ͑ VCA ͒, который поддерживает ток через кристалл и, следовательно, его амплитуду колебаний постоянной. Поскольку невозможно разместить электронику внутри камеры сверхвысокого вакуума ͑ необходимо обжигать до 250 ° C ͒, мы должны использовать электрические вводы и соединительные кабели длиной 50 см с дополнительной параллельной емкостью к емкости кристалла кварца C 0. Поэтому мы используем активную компенсацию этой параллельной емкости, состоящую из двух ветвей, которые идентичны, за исключением того конца, где только одна ветвь соединена с кристаллом кварца.Гарантируется, что обе ветви имеют одинаковую дополнительную параллельную емкость, так что сигнал от ветви компенсации можно использовать для коррекции сигнала в дифференциальном усилителе. Кабели плотно упакованы, а экраны коаксиальных кабелей подключены в качестве защитных проводов, что дополнительно минимизирует фазовый сдвиг. Ток через обе ветви преобразуется двумя конденсаторами в напряжения, сдвинутые на 90 °. Их разность, которая пропорциональна фазовому току, сдвинутому на 90 ° через кристалл кварца, в конечном итоге достигает множителя для сравнения фазы с напряжением на кристалле.При последовательном резонансе напряжение и ток кристалла находятся в фазе, что приводит к сдвигу фазы на 90 ° на входе умножителя. Любое отклонение от резонансной частоты f s кристалла приводит к фазовому сдвигу и, следовательно, к ненулевому выходному сигналу умножителя. Этот сигнал ошибки увеличивает или уменьшает частоту генератора и, таким образом, поддерживает частоту генератора ровно на уровне 10 фс. Поскольку требуемая стабильность фазового сдвига очень высока (10 Ϫ 4 рад, необходимо использовать достаточно быстрые электронные компоненты с низким фазовым сдвигом и, следовательно, высокими частотами прохождения в диапазоне 500 МГц.Большое внимание следует уделить компоновке схемы, чтобы избежать нежелательных автоколебаний схемы с частотами в диапазоне нескольких сотен МГц. В первом тесте была исследована значимость описанной выше новой электроники ͒ EC1 для стабильности частоты и шума и проведено сравнение с данными, полученными с помощью электроники EC2, использованной в предыдущих экспериментах. 12,13 Электроника EC2 представляла собой обычный последовательный резонансный генератор с компенсацией параллельных емкостей. Типичные результаты этого сравнения показаны на рис.5. Представленные данные были измерены без ионной бомбардировки, чтобы получить частотную характеристику исключительно за счет электронной схемы и держателя кварцевого кристалла. Температура кристалла кварца поддерживалась на минимальном уровне зависимости частоты от температуры (рис. 2) при 191 ° C, а фоновое давление поддерживалось ниже 10–9 мбар. Использование EC1 снизило шум, а также дрейф как минимум в 5 раз по сравнению с EC2. Некоторые типичные необработанные данные измерений общего выхода распыления при ионной бомбардировке поверхности LiF показаны на рис.6 ͑ a ͒ –6 ͑ d ͒. Периоды «выключения луча», когда проверяется дрейф частоты, чередуются с периодами «включения луча», когда измеряется изменение частоты из-за распыления ͑ или осаждения ͒. На рисунке 6 ͑ a приведены данные для воздействия He 500 эВ на LiF. Относительно высокий выход распыления 1,4 молекулы LiF на ион He из-за как потенциального, так и кинетического распыления 12, а также довольно высокая плотность ионного тока ͑ 700 нА / см 2) приводят к большому изменению частоты (⌬ f ϭ 5,6 Гц ͒ во время периоды включения луча, которые можно удобно измерить.При энергии удара около порога кинетического распыления 100 эВ He, рис. 6 ͑ b не только общий выход распыления, но и плотность ионного тока из-за замедления ͒ меньше, но изменение частоты все еще может быть оценивается с приемлемой точностью ͓ Рис. 6 ͑ b ͔͒. На рисунке 6 ͑ c показан чрезвычайно сложный случай бомбардировки N 20 эВ на поверхности LiF. При такой низкой энергии удара кинетическое распыление не происходит. Потенциальная энергия, запасенная в N ͑ 14,53 эВ, намного меньше, чем в He ͑ 24.59 эВ ͒, что также приводит к соответственно малому потенциальному выходу распыления. Из-за сильного торможения при достижении энергии удара 20 эВ плотность падающего ионного тока составляет всего 70 нА / см 2. Таким образом, результирующее изменение частоты всего на 200 мГц подвержено относительно большим ошибкам. Из серии аналогичных измерений с низким ионным током и малым выходом распыления мы пришли к выводу, что наш метод в настоящее время ограничен случаями, когда произведение общего выхода распыления на плотность ионного тока обычно превышает 0.2 а.е.м. / ион А / см 2 для сравнения, рис. 6 ͑ c соответствует произведению примерно 1 а.е.м. / ион ␮ А / см 2]. Таким образом, наш QCM способен обнаруживать удаление всего 5 Â 10 10 молекул LiF на см 2 в секунду. В результате чувствительность к изменениям массы составляет примерно 8 Â 10 5 монослоев в секунду или 0,5% монослоя в минуту и, следовательно, повышение чувствительности по сравнению с ранее используемыми установками по крайней мере в 5 раз. 6 d показывает интересный случай воздействия Cu 100 эВ на LiF.Поскольку энергия рекомбинации Cu 7,73 эВ слишком мала, чтобы вызвать потенциальное распыление, а кинетический выход распыления также практически равен нулю пороговая область, мы наблюдаем чистое осаждение Cu из-за имплантации или прилипания Cu сбрасывать ионы ͑ на surface поверхность мишени из LiF. Предположим, что выход распыления LiF с медленными снарядами Cu равен нулю, имплантация дозы 4 Â 10 13 атомов Cu на см 2, которая соответствует дозе ионов Cu в течение 1 мин для рис. 6 ͑ d, приведет к изменение частоты 300 мГц в минуту по сравнению с измеренным изменением частоты 165 мГц / мин на рис.6 дн. Таким образом, около 55% поступающих Cu ϩ снарядов имплантируются или адсорбируются на поверхности LiF. Эта работа была поддержана Austrian Fonds zur F rderung der Wissenschaftlichen Forschung ͑ Project No. P 12388 PHY и выполнялась в рамках ассоциации EURATOM-O …

Context 2

… она была представлена ​​Sauerbrey В 1959 г. кварцевые микровесы ͑ QCM использовались как чувствительное устройство для измерения небольших изменений массы. 2,3 В настоящее время применяется, т.е.g., для контроля роста тонких пленок в процессах напыления и напыления. 4–7 В последние годы сообщалось о разнообразных применениях QCM в газообразных и жидких средах 8,9, таких как газовый хроматографический детектор, газовый датчик, биосенсор, диагностический инструмент для взаимодействия плазмы со стенкой 10 и электрохимии фазы раствора 11. Для измерения общего выхода распыления, включая как нейтральные, так и заряженные вторичные частицы, при столкновениях ионов с поверхностью в Техническом университете в Вене был разработан метод чувствительного микровесов кварцевого кристалла.6,7,12,13 В этом эксперименте материал мишени сначала наносится на кристалл кварца в виде тонкой поликристаллической пленки, а затем бомбардируется медленными (5 кэВ одно- или многозарядными ионами), причем мощность распыления определяется по массе потеря целевой пленки. В то время как кристаллы кварца широко используются для определения площади поверхности и, следовательно, толщины осажденного материала, скорость удаления материала в основном изучалась с помощью других методов, таких как обычные микровесы, вторичная нейтральная масс-спектрометрия ͑ SNMS ͒ или улавливающие фольги 14,15, впоследствии проанализированные методом обратного рассеяния Резерфорда.Это неудивительно, поскольку использование кристаллов кварца для прямых измерений выхода распыления сопряжено с серьезными проблемами. Скорость удаления материала и, следовательно, изменение частоты довольно низки по сравнению с большинством применений осаждения, требуя довольно высокой стабильности частоты кристалла и схемы генератора, а также высокой точности и разрешения при определении резонансной частоты. Кроме того, значительное количество энергии выделяется первичными частицами на распыляемой поверхности, вызывая проблемы из-за теплового дрейфа.Во многих приложениях для осаждения энергия, выделяемая на один падающий атом, составляет всего несколько эВ ì энергия сублимации плюс тепловое излучение от источника испарения ͒, в то время как в случае распыления энергия, выделяемая на ударный снаряд, скорее всего, находится в диапазоне нескольких от сотен эВ до нескольких кэВ. Другие проблемы возникают из-за чувствительности резонансной частоты к поверхностному напряжению, вызванному, например, дефектами, вызванными разбрызгиванием, имплантацией ионов-снарядов и неоднородным удалением массы в зоне воздействия ионного пучка.16–18 Для обнаружения изменений массы порядка 10 Ϫ 3 монослоев ͑ ML ͒ в минуту при типичной резонансной частоте 6 МГц метод QCM требует стабильности частоты в несколько МГц в течение этого времени. Такой уровень производительности сегодня легко достигается с помощью кварцевых кристаллов и генераторов, разработанных для приложений временной развертки. Однако использование кристалла кварца в качестве микровесов в сверхвысоковольтном оборудовании накладывает некоторые ограничения на установку, такие как необходимость прокладки кабеля между кристаллом кварца и электроникой и использование кристалла без корпуса с одним заземленным электродом.В этих условиях обычные электронные генераторы не могут обеспечить требуемых характеристик. Поэтому мы разработали новую электронику и специальный держатель для кварцевого кристалла, чтобы удовлетворить требования к измерению очень малых изменений массы, вызванных столкновениями ионов с поверхностью. Массочувствительная часть ККМ представляет собой плосковыпуклый диск, вырезанный из кристалла кварца с резонансной частотой в диапазоне 6 МГц, на который нанесены золотые электроды. Использовались кристаллы SC-среза 6 МГц №13.Диаметр 95 мм ͒ с золотыми электродами, поставляемыми KVG Quartz Crystal Technology GmbH, Германия, с компенсацией напряжений ͑ SC ͒. В отличие от обычно используемой номенклатуры AT-среза YXl ͒ -35,25 ° ͑ по стандарту IEEE 1978 19 SC-срез ͑ YXwl ͒ 21,93 °, Ϫ 33,93 ° имеет резонансную частоту, нечувствительную к радиальному напряжению, и поэтому лучше подходит для наше текущее приложение. Далее мы описываем экспериментальную процедуру для случая пленки мишени LiF ì других мишеней, таких как Au, Si, GaAs и т. Д.также использовались ͒. На один из металлических электродов была нанесена тонкая поликристаллическая пленка LiF толщиной примерно 200 нм в коммерческой системе нанесения покрытий в высоком вакууме ͑ Leybold L560 / HV8.2, фоновое давление 10 Ϫ 6 мбар ͒ со скоростью осаждения порядка 10 нм. / с. LiF испаряли из Mo-лодочки; во время осаждения температура подложки поддерживалась на уровне примерно 150 ° C. Кристалл кварца с пленкой-мишенью транспортировался по воздуху в установку сверхвысокого вакуума, где закреплялся на держателе мишени.Чтобы минимизировать напряжение в кристалле кварца при его установке, мы использовали тонкое кольцо Au на поверхности LiF и закрепили кристалл кварца с другой стороны с помощью W-пружины Рис. 1. Кольцо Au и пружина W также служили электрическими контактами для связи между электронной схемой и кристаллом кварца. Чтобы свести к минимуму влияние тепловых дрейфов и флуктуаций, кристалл кварца работает на минимуме его резонансной частоты в зависимости от кривой температуры temperature Рис. 2 ͒. При тщательном сканировании температуры этот минимум был определен как 191 ° C ͑ Рис.2 ͒, что означает, что пленка-мишень LiF также поддерживается при этой температуре во время измерений распыления. Поскольку осажденная пленка мишени очень тонкая по сравнению с толщиной кристалла кварца, достаточно использовать простое уравнение по Зауэрбрею: …

Контекст 3

… оно было введено Зауэрбреем в 1959 году. микровесы с кварцевым кристаллом ͑ QCM использовались в качестве чувствительного устройства для измерения небольших изменений массы. 2,3 В настоящее время применяется, т.е.g., для контроля роста тонких пленок в процессах напыления и напыления. 4–7 В последние годы сообщалось о разнообразных применениях QCM в газообразных и жидких средах 8,9, таких как газовый хроматографический детектор, газовый датчик, биосенсор, диагностический инструмент для взаимодействия плазмы со стенкой 10 и электрохимии фазы раствора 11. Для измерения общего выхода распыления, включая как нейтральные, так и заряженные вторичные частицы, при столкновениях ионов с поверхностью в Техническом университете в Вене был разработан метод чувствительного микровесов кварцевого кристалла.6,7,12,13 В этом эксперименте материал мишени сначала наносится на кристалл кварца в виде тонкой поликристаллической пленки, а затем бомбардируется медленными (5 кэВ одно- или многозарядными ионами), причем мощность распыления определяется по массе потеря целевой пленки. В то время как кристаллы кварца широко используются для определения площади поверхности и, следовательно, толщины осажденного материала, скорость удаления материала в основном изучалась с помощью других методов, таких как обычные микровесы, вторичная нейтральная масс-спектрометрия ͑ SNMS ͒ или улавливающие фольги 14,15, впоследствии проанализированные методом обратного рассеяния Резерфорда.Это неудивительно, поскольку использование кристаллов кварца для прямых измерений выхода распыления сопряжено с серьезными проблемами. Скорость удаления материала и, следовательно, изменение частоты довольно низки по сравнению с большинством применений осаждения, требуя довольно высокой стабильности частоты кристалла и схемы генератора, а также высокой точности и разрешения при определении резонансной частоты. Кроме того, значительное количество энергии выделяется первичными частицами на распыляемой поверхности, вызывая проблемы из-за теплового дрейфа.Во многих приложениях для осаждения энергия, выделяемая на один падающий атом, составляет всего несколько эВ ì энергия сублимации плюс тепловое излучение от источника испарения ͒, в то время как в случае распыления энергия, выделяемая на ударный снаряд, скорее всего, находится в диапазоне нескольких от сотен эВ до нескольких кэВ. Другие проблемы возникают из-за чувствительности резонансной частоты к поверхностному напряжению, вызванному, например, дефектами, вызванными разбрызгиванием, имплантацией ионов-снарядов и неоднородным удалением массы в зоне воздействия ионного пучка.16–18 Для обнаружения изменений массы порядка 10 Ϫ 3 монослоев ͑ ML ͒ в минуту при типичной резонансной частоте 6 МГц метод QCM требует стабильности частоты в несколько МГц в течение этого времени. Такой уровень производительности сегодня легко достигается с помощью кварцевых кристаллов и генераторов, разработанных для приложений временной развертки. Однако использование кристалла кварца в качестве микровесов в сверхвысоковольтном оборудовании накладывает некоторые ограничения на установку, такие как необходимость прокладки кабеля между кристаллом кварца и электроникой и использование кристалла без корпуса с одним заземленным электродом.В этих условиях обычные электронные генераторы не могут обеспечить требуемых характеристик. Поэтому мы разработали новую электронику и специальный держатель для кварцевого кристалла, чтобы удовлетворить требования к измерению очень малых изменений массы, вызванных столкновениями ионов с поверхностью. Массочувствительная часть ККМ представляет собой плосковыпуклый диск, вырезанный из кристалла кварца с резонансной частотой в диапазоне 6 МГц, на который нанесены золотые электроды. Использовались кристаллы SC-среза 6 МГц №13.Диаметр 95 мм ͒ с золотыми электродами, поставляемыми KVG Quartz Crystal Technology GmbH, Германия, с компенсацией напряжений ͑ SC ͒. В отличие от обычно используемой номенклатуры AT-среза YXl ͒ -35,25 ° ͑ по стандарту IEEE 1978 19 SC-срез ͑ YXwl ͒ 21,93 °, Ϫ 33,93 ° имеет резонансную частоту, нечувствительную к радиальному напряжению, и поэтому лучше подходит для наше текущее приложение. Далее мы описываем экспериментальную процедуру для случая пленки мишени LiF ì других мишеней, таких как Au, Si, GaAs и т. Д.также использовались ͒. На один из металлических электродов была нанесена тонкая поликристаллическая пленка LiF толщиной примерно 200 нм в коммерческой системе нанесения покрытий в высоком вакууме ͑ Leybold L560 / HV8.2, фоновое давление 10 Ϫ 6 мбар ͒ со скоростью осаждения порядка 10 нм. / с. LiF испаряли из Mo-лодочки; во время осаждения температура подложки поддерживалась на уровне примерно 150 ° C. Кристалл кварца с пленкой-мишенью транспортировался по воздуху в установку сверхвысокого вакуума, где закреплялся на держателе мишени.Чтобы минимизировать напряжение в кристалле кварца при его установке, мы использовали тонкое кольцо Au на поверхности LiF и закрепили кристалл кварца с другой стороны с помощью W-пружины Рис. 1. Кольцо Au и пружина W также служили электрическими контактами для связи между электронной схемой и кристаллом кварца. Чтобы свести к минимуму влияние тепловых дрейфов и флуктуаций, кристалл кварца работает на минимуме его резонансной частоты в зависимости от кривой температуры temperature Рис. 2 ͒. При тщательном сканировании температуры этот минимум был определен как 191 ° C ͑ Рис.2 ͒, что означает, что пленка-мишень LiF также поддерживается при этой температуре во время измерений распыления. Поскольку осажденная пленка мишени очень тонкая по сравнению с толщиной кристалла кварца, достаточно использовать простое уравнение по Зауэрбрею: .