Jaccard: Jaccard Similarity – LearnDataSci

Содержание

Jean-Philippe JACCARD – Département d’études méditerranéennes, slaves et orientales

Prof. Jean-Philippe JACCARD

Professeur honoraire

PHIL 134
+41.22.379.13.68
Courriel

Licencié en Lettres (1985) et docteur de l’Université de Genève (1991). Stagiaire de l’Université de Leningrad (1983-1984) et boursier de l’Académie de Sciences de l’URSS (1986, 1987, 1989).

Sujet de la thèse de doctorat : « Daniil Harms et la fin de l’avant-garde russe » (1991).

Enseigne à l’Université de Genève depuis 1985 (professeur depuis 2001). Membre du comité de rédaction de la revue Russian Studies (Saint-Pétersbourg, 1995-2000), de la collection « Slavica Helvetica » (Peter Lang) et du comité de lecture de la série Modernités slaves (Lyon).

Kandinsky, Malévitch, Filonov et la philosophie: les systèmes de l’abstraction dans l’avant-garde russe (dir.: J.-Ph. Jaccard, I. Podoroga), Lormont, Éditions Nouvelles Cécile Defaut, 2018.

1913. «Слово как таковое»: К юбилейному году русского футуризма. Материалы международной научной конференции (Женева, 10–12 апреля 2013 г.) /

сост. и науч. ред. Ж.-Ф. Жаккара и А. Морар. СПб.: Изд. Европейского ун-а, 2015.

[1913. «Le mot en tant que tel». Pour le centenaire du futurisme russe (dir.: J.-Ph. Jaccard, A. Morard), St-Pétersbourg, Eupress, 2015]

«Вторая культура». Неофициальная поэзия Ленинграда в 1970–1980-е годы: Материалы международной конференции (Женева, 1–3 марта 2012 г.) / сост. и науч. ред.: Ж.-Ф. Жаккар, В. Фридли и Й. Херльт. СПб.: Росток, 2013.

[La «Seconde culture». La poésie non-officielle de Leningrad dans les années 1970-1980 (dir.: J.-Ph. Jaccard, V. Friedli, J. Herlth), St-Pétersbourg, Rostok, 2013]

«Temps ressenti» et «Temps construit» dans les littératures russe et française au XX^e siècle (dir.

: J.-Ph. Jaccard et I. Podoroga), Paris, Kimé, 2013

Жаккар Ж.-Ф. Литература как таковая. От Набокова к Пушкину: Избранные работы о русской словесности. М.: Новое литературное обозрение, 2011

[Jaccard J.-Ph., La littérature en tant que telle: de Pouchkine à Nabokov, Moscou, NLO, 2011]

Достоевский и русское зарубежье ХХ века / под. ред. Ж.-Ф. Жаккара и У. Шмида. Dostoevsky Monographs. A Series of the International Dostoevsky Society. Vol. I. СПб.: Дмитрий Буланин, 2008.

[Dostoïevski et l’émigration russe du XX^e siècle (dir.: J.-Ph. Jaccard, U. Schmid), St-Pétersbourg, Boulanine, 2008]

Русские писатели в Париже: Взгляд на французскую литературу: 1920–1940: Международная научная конференция, Женева, 8–10 декабря 2005 г.

/ сост., науч. ред. : Ж..-Ф. Жаккар, А. Морар, Ж. Тассис. М.: Русский путь, 2007.

[Les écrivains russes à Paris: regard sur la littérature française: 1920–1940 (dir.: J.-Ph. Jaccard, A. Morard, G. Tassis), Moscou, Rousski pout, 2007]

Un «mensonge déconcertant»? La Russie au xx^e siècle (dir.: J.-Ph. Jaccard, K. Amacher), Paris, L’Harmattan, 2003

Жаккар Ж.-Ф. Даниил Хармс и конец русского авангарда / пер. с франц. Ф. А. Перовской. СПб.: Академический проект, 1995.

[Jaccard J.-Ph. Daniil Harms et la fin de l’avant-garde russe

(trad. F. Perovskaïa),St-Pétersbourg, Akademicheski proekt, 1995]

Jaccard J.-Ph., Daniil Harms et la fin de l’avant-garde russe, Bern, Peter Lang («Slavica Helvetica»), 1991.

TRADUCTIONS

Daniil Harms, Écrits (publiés, préfacés et traduits par J. -Ph. Jaccard; notes et chronologie établies par J.-Ph. Jaccard), Paris, Christian Bourgois, 1993, 1999

Daniil Harms, La Vieille (traduction et article de J.-Ph. Jaccard; lithographies originales de M. Karassik), Saint-Pétersbourg, Harmsizdat, 1994. [33 exemplaires numérotés; lithographies signées et numérotées]

Nikolaï Erdman, Le Mandat , pièce en trois actes (présenté et traduit par J.-Ph. Jaccard; préface de J.-Ph. Jaccard; postface de B. Picon-Vallin), Lausanne, L’Âge d’Homme (coll. «Théâtre XX^e siècle»), 1998

Daniil Harms, Le Tombement. Petits récits cruels et absurdes (traduits du russe par J.-Ph. Jaccard), Woippy, L’Engouletemps, 2005

Daniil Harms, Старуха (La Vieille) (traduit du russe par J. -Ph. Jaccard; 29 linogravures de J. Lapierre), s. l., Ouvroir Humoir, 2009

Bibliographie complète

Enseignants et chercheurs

Сходство Жаккара – LearnDataSci

Автор: Фатих Карабибер
Ph.D. в компьютерной инженерии, Data Scientist

Вы уже должны знать:

Basic Python — изучите концепции Python и Data Science в интерактивном режиме на Dataquest.

Сходство Жаккара — это обычное измерение близости, используемое для вычисления сходства между двумя объектами, например, двумя текстовыми документами. Сходство Жаккара можно использовать для нахождения сходства между двумя асимметричными бинарными векторами или для нахождения сходства между двумя множествами. В литературе подобие Жаккара, обозначаемое $J$, также может обозначаться как Индекс Жаккара , Коэффициент Жаккара , Несходство Жаккара и Расстояние Жаккара .

Jaccard Сходство часто используется в приложениях для обработки данных. Примеры использования Jaccard Similarity:

Интеллектуальный анализ текста: найти сходство между двумя текстовыми документами, используя количество терминов, используемых в обоих документах
Электронная коммерция: из рыночной базы данных тысяч клиентов и миллионов товаров, найти похожих клиентов по их истории покупок
Система рекомендаций: Алгоритмы рекомендаций фильмов используют коэффициент Жаккара для поиска похожих клиентов, если они взяли напрокат или высоко оценили многие из одних и тех же фильмов.

Сходство Жаккара можно использовать для вычисления сходства между двумя асимметричными двоичными переменными. Предположим, что бинарная переменная имеет только одно из двух состояний: $0$ и $1$, где $0$ означает, что атрибут отсутствует, а $1$ означает, что он присутствует. Хотя каждое состояние одинаково ценно для симметричных двоичных атрибутов, два состояния не одинаково важны для асимметричных двоичных переменных.

Допустим, мы пытаемся вычислить сходство покупателей магазина. У нас мог бы быть двоичный атрибут, который соответствует товару , купленному в магазине, где $1$ указывает, что конкретный товар был куплен, а $0$ указывает, что продукт не был куплен.

Поскольку в магазине могут быть тысячи товаров, количество товаров , а не , купленных любым покупателем, намного превышает количество купленных товаров. При вычислении сходства между клиентами мы хотим учитывать только покупки товаров. Это означает, что купленный товар является асимметричной двоичной переменной , что делает значение $1$ более важным, чем $0$.

На первом этапе измерения сходства Жаккара для двух клиентов, состоящих из $n$ двоичных атрибутов, для заданных двоичных данных вычисляются следующие четыре величины (т.

е. частоты):

$a$ = количество атрибуты, равные $1$ для обоих объектов $i$ и $j$
$b$ = количество атрибутов, равных $0$ для объекта $i$, но равных $1$ для объекта $j$
$c$ = количество атрибутов, равных $1$ для объекта $i$, но равных $0$ для объекта $j$
$d$ = количество атрибутов, равных $0$ для обоих объектов $i$ и $ j$.

Затем подобие Жаккара для этих атрибутов вычисляется по следующему уравнению:

$$ J(i,j) = sim(i,j) = \frac {a}{a+b+c} $$

Обратите внимание, что количество совпадений $0$ считается неважным в этом вычислении и игнорируется, поскольку элементы являются асимметричными двоичными атрибутами.

Предположим, что таблица транзакций клиентов содержит позиции $9$ и клиентов $3$. Сходство между объектами вычисляется только на основе асимметричных атрибутов.

Сходство между каждой парой из трех клиентов можно рассчитать с помощью коэффициента Жаккара:

$$J(C1, C2) = \frac {a}{a+b+c} = \frac {1}{1+ 1+2} = 0,25 \\[20pt] J(C1, C3) = \frac {a}{a+b+c} = \frac {2}{2 + 1 + 1} = 0,5 \\[20pt] J(C2, C3) = \frac {a}{a+b+c} = \frac {0}{0 + 3 + 2} = 0$$

Эти измерения показывают, что $C1$ и $C3$ ведут себя одинаково при совершении покупок, тогда как $C2$ и $C3$ не похожи, поскольку они покупают совершенно разные товары.

Наконец, вместо сходства можно рассчитать несходство или расстояние Жаккара между двумя бинарными атрибутами. Различие по этим признакам с помощью коэффициента Жаккара вычисляется следующим образом:

$$ d(i,j) = \frac {b+c}{a+b+c} \implies 1- sim(i,j) $$

Ниже определена функция для вычисления сходства Жаккара между двумя бинарными векторами. Вы также можете найти этот встроенный в scikit-learn , в разделе sklearn. metrics.jaccard_score.

 импортировать numpy как np
защита jaccard_binary (х, у):
    """Функция для поиска сходства между двумя бинарными векторами"""
    пересечение = np.logical_and (x, y)
    объединение = np.logical_or(x, y)
    сходство = пересечение.сумма() / поплавок (объединение.сумма())
    вернуть сходство
# Определяем некоторые бинарные векторы
х = [0,1,0,0,0,1,0,0,1]
у = [0,0,1,0,0,0,0,0,1]
г = [1,1,0,0,0,1,0,0,0]
# Найти сходство среди векторов
simxy = jaccard_binary(x,y)
simxz = jaccard_binary (x, z)
simyz = jaccard_binary(y,z)
print(' Сходство между x и y есть', simxy, '\n Сходство между x и z есть ', simxz, '\n Сходство между x и z есть ', simyz)

Выход:

 Сходство между x и y равно 0,25
 Сходство между x и z равно 0,5.
 Сходство между x и z равно 0,0

Сходство Жаккара измеряет сходство между двумя наборами данных, чтобы увидеть, какие элементы являются общими, а какие разными. Сходство Жаккара рассчитывается путем деления количества наблюдений в обоих наборах на количество наблюдений в любом наборе. Другими словами, сходство Жаккара можно вычислить как размер пересечения, деленный на размер объединения двух множеств. Это можно записать в обозначении множеств, используя пересечение $(A \cap B)$ и объединение $(A \cup B)$ двух множеств: $$ J(A, B) = \frac {|A \cap B|} {|A \cup B|}$$, где $|A \cap B|$ — общее количество членов обоих наборов, а -общий). Сходство Жаккара будет равно $0$, если два набора не имеют общих значений, и $1$, если два набора идентичны. Набор может содержать либо числовые значения, либо строки.

Кроме того, эту функцию можно использовать для определения различий между двумя наборами путем вычисления $d(A,B)=1 – J(A,B)$.

Пример: Ниже приведен простой пример для вычисления подобия Жаккара между следующими двумя множествами.

$A = \{0,1,2,5,6\}$
$B = \{0,2,3,4,5,7,9\}$

Жаккар Сходство между двумя вычисляется следующим образом: $$ J(A,B) = \frac {|A∩B|}{|A∪B|} = \frac {|\{0,2,5\}|}{|\ {0,1,2,3,4,5,6,7,9\}|} = \frac {3}{9} = 0,33 $$

Мы можем определить функцию для вычисления сходства Жаккара между двумя наборами данных в Python следующим образом:

 def jaccard_set(list1, list2):
    """Определить функцию подобия Жаккара для двух наборов"""
    пересечение = len (список (набор (список1).  пересечение (список2)))
    union = (len(list1) + len(list2)) - пересечение
    возврат поплавка (пересечение)/объединение
# Определяем два набора
а = [0, 1, 2, 5, 6]
б = [0, 2, 3, 4, 5, 7, 9]
# Найдите сходство Жаккара между двумя наборами
jaccard_set(а, б)

Out:

 0.3333333333333333

Как мы видим, результат идентичен числовому примеру выше. Два набора имеют сходство Жаккара 0,33.

Начните учиться бесплатно

Познакомьтесь с авторами

Фатих Карабибер Ph.D. кандидат вычислительной техники, специалист по данным

Доцент кафедры вычислительной техники. Автор/соавтор более 30 журнальных публикаций. Преподаватель курсов магистратуры/бакалавриата. Руководитель дипломной работы. Консультант ИТ-компаний.

Визуализатор: Japhia
Разработчик программного обеспечения

Вернуться к индексу блога

Сходство Jaccard — Метрика сходства текста в НЛП — Изучение машинного обучения Перекресток 9 и

над Союзом .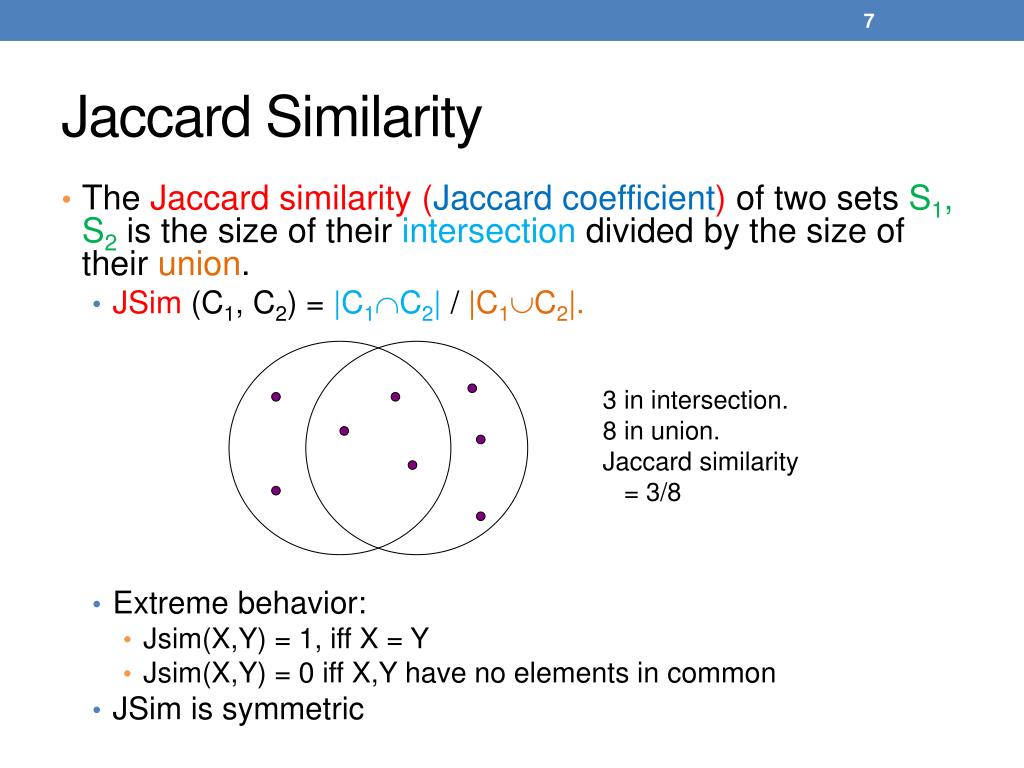

Матрица сходства Жаккара , используемая для определения сходства между двумя текстовыми документами, означает, насколько два текстовых документа близки друг к другу с точки зрения их контекста, то есть сколько общих слов существует по сравнению с общим количеством слов.

При обработке естественного языка нам часто требуется оценить сходство текстов между текстовыми документами. Существует множество матриц подобия текста, таких как Косинусное сходство , Жаккардо сходство и Евклидово расстояние измерение. Все эти метрики сходства текста имеют разное поведение.

В этом уроке вы подробно изучите матрицу Jaccard Similarity на примере. Вы также можете обратиться к этому руководству, чтобы изучить Подобие косинуса Метрический.

Jaccard Сходство определяется как пересечение двух документов, разделенное объединением этих двух документов, которые относятся к количеству общих слов по отношению к общему количеству слов. Здесь мы будем использовать набор слов, чтобы найти пересечение и объединение документа.

Математическое представление Сходства Жаккара :

Оценка сходства Жаккара находится в диапазоне от 0 до 1 . Если два документа идентичны, Jaccard Similarity равен 9.0148 1 . Показатель сходства Жаккара равен 0 , если между двумя документами нет общих слов.

Давайте посмотрим на примере, как работает Jaccard Similarity ?

 doc_1 = "Данные — новая нефть цифровой экономики"
doc_2 = "Данные — это новая нефть"

Получим набор уникальных слов для каждого документа.

 words_doc1 = {'data', 'is', 'the', 'new', 'нефть', 'из', 'цифровые', 'экономика'}
words_doc2 = {'данные', 'есть', 'а', 'новое', 'масло'}

Теперь мы вычислим пересечение и объединение этих двух наборов слов и измерим Сходство Жаккара между doc_1 и doc_2 .