Калькулятор внутреннего сопротивления элемента питания батареи или аккумулятора • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Калькулятор определяет внутреннее сопротивление батареи по падению напряжения на нагрузочном резисторе с известным сопротивлением, напряжению без нагрузки или протекающему в цепи нагрузки току.
Пример 1: Рассчитайте внутреннее сопротивление литий-полимерного (Li-PO) аккумулятора, если напряжение на нем без нагрузки составляет 3,90 В, а на нагрузочном резисторе сопротивлением 10 ом напряжение равно 3,89 В. Ниже вы найдете еще пять примеров.
Вычислить
RI и I из UNL, RL, ULRI и UL из UNL, RL, IRI и RL из UNL, UL, IUL и I из UNL, RI, RLRL и I из UNL, RI, ULRL и UL из UNL, RI, IUNL и I из RI, RL, ULUNL и UL из RI, RL, IUNL и RL из RI, UL, I
Напряжение на батарее без нагрузки
UNLмикровольт (мкВ)милливольт (мВ)вольт (В)киловольт (кВ)мегавольт (МВ)
Внутреннее сопротивление батареи
RIмиллиом (мОм)ом (Ом)килоом (кОм)мегаом (МОм)
Для расчета введите значения в любые три поля из пяти и нажмите Рассчитать. Исключение: при вводе только параметров нагрузки RL, UL и I невозможно вычислить параметры батареи UNL и RI, поэтому вычисления не выполняются.
Исключение: при вводе только параметров нагрузки RL, UL и I невозможно вычислить параметры батареи UNL и RI, поэтому вычисления не выполняются.
Определения и формулы
В соответствии с теоремой Тевенена—Гельмгольца любую линейную цепь с любым количеством источников напряжения (например, шесть аккумуляторов, соединенных последовательно в автомобильной аккумуляторной батарее) можно заменить источником ЭДС (ℰ) или эквивалентным источником напряжения без нагрузки UNL, соединенным последовательно с внутренним сопротивлением RI или импедансом ZI. В результате подачи напряжения UNL на внешнюю нагрузку с сопротивлением RL в ней протекает ток I.
Отдаваемый батарее в нагрузку ток определяется сопротивлением нагрузки и в то же время этот ток ограничивается внутренним сопротивлением батареи. Внутреннее сопротивление батареи состоит из сопротивления электродов (например, пластин), активной массы и электролита.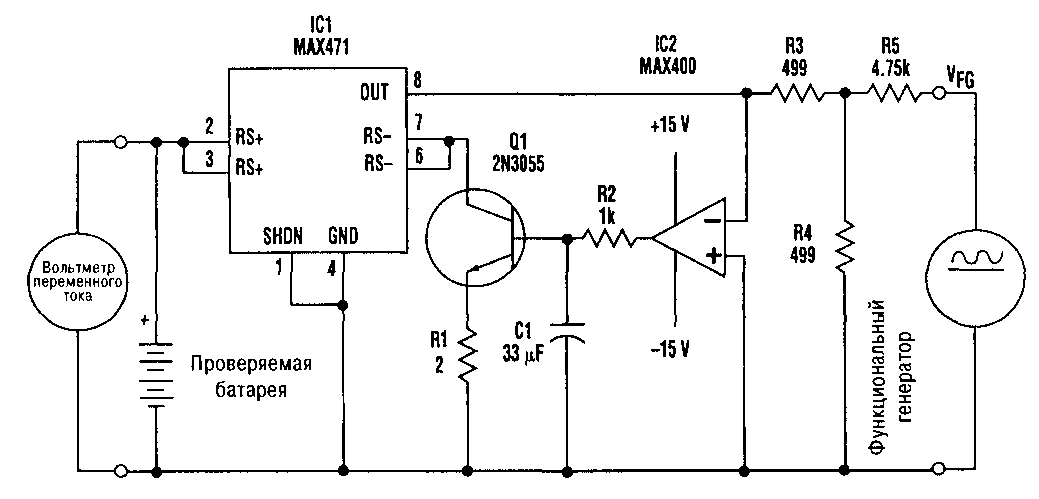
Свинцово-кислотные аккумуляторные батареи имеют очень малое внутреннее сопротивление (обычно порядка 0,01 ом) — именно поэтому они могут подавать большой ток, необходимый для запуска двигателя. Внутреннее сопротивление свинцово-кислотных аккумуляторов так мало, потому что в каждом элементе батареи отрицательные и положительные пластины соединены параллельно. Кроме того, расстояние между отрицательными и положительными пластинами очень мало и, следовательно, толщина слоя электролита между ними также очень мала, что приводит к еще большему уменьшению внутреннего сопротивления. Если батарея отдает большой ток, на этом внутреннем сопротивлении рассеивается тепло — и в результате батарея нагревается.
Внутреннее сопротивление батареи можно посчитать, зная ее напряжение без нагрузки UNL (NL — от англ. no load — без нагрузки), напряжение, измеренное на нагрузке UL (L — от англ. load — нагрузка) и сопротивление нагрузки RL. Измеренное напряжение без нагрузки эквивалентно электродвижущей силе (ЭДС) батареи.
Через нагрузочный резистор протекает ток
Падение напряжения на внутреннем сопротивлении:
Внутреннее сопротивление:
Полная формула для определения внутреннего сопротивления:
Внутреннее сопротивление батареи можно также рассчитать по току в сопротивлении нагрузки IL, напряжению батареи без нагрузки UNL и сопротивлению нагрузки RL.
Напряжение на нагрузочном резисторе
Падение напряжения на внутреннем сопротивлении:
Внутреннее сопротивление:
Полная формула для этого метода расчета:
Измерение внутреннего сопротивления батареи
Как мы уже отметили, для определения внутреннего сопротивления нужно иметь три исходные величины:
- напряжение без нагрузки UNL, напряжение, измеренное на нагрузке UL и сопротивление нагрузки RL.
или
- ток в сопротивлении нагрузки IL, напряжение батареи без нагрузки UNL и сопротивление нагрузки RL.

Для правильного определения внутреннего сопротивления необходимо выполнить несколько измерений с разными резисторами. Также следует учесть, что внутреннее сопротивление изменяется при изменении температуры, а также зависит от срока эксплуатации батареи и других факторов. Поэтому ваше измерение представляет собой лишь оценку, а такой вещи, как точное внутреннее сопротивление, не существует в принципе, так как его невозможно измерить точно.
На внутреннее сопротивление батареи влияют несколько факторов, в частности, емкость батареи, электрохимическая реакция, которая в нем происходит, количество элементов, срок эксплуатации батареи, температура и режим (скорость) разряда. Подробнее о батареях и других источниках питания вы можете узнать в наших калькуляторах аккумуляторных батарей и литий-полимерных аккумуляторов для дронов.
Для измерения напряжения на подключенной к батарее нагрузке вольтметр подключают параллельно нагрузке к клеммам батареи. Если сопротивление нагрузки намного меньше внутреннего сопротивления вольтметра, он показывает достаточно точный результат.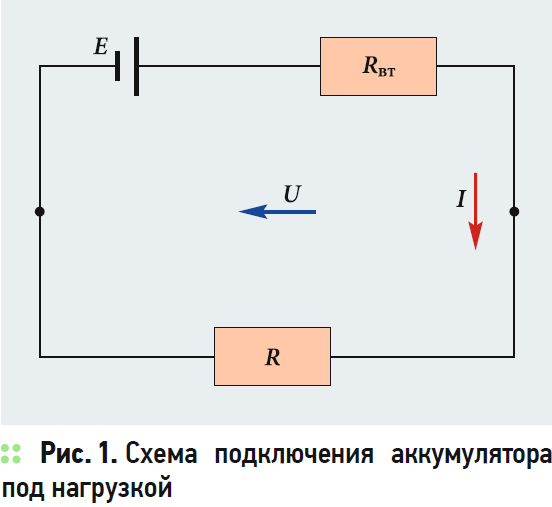
Для измерения тока, отдаваемого батареей в нагрузку, амперметр включается в разрыв цепи между нагрузкой и батареей, как показано выше на схеме. Если внутреннее сопротивление амперметра относительно мало по сравнению с сопротивлением нагрузки, можно считать, что измерение достаточно точное.
Конечно, теоретически и даже практически (например, для марганцево-цинкового элемента) измерить ток короткого замыкания батареи вполне возможно прямым методом, закоротив батарею амперметром. Однако если батарея способна отдать значительный ток, она может перегреться или даже загореться при коротком замыкании. Литий-ионные батареи могут даже взорваться, если замкнуть их клеммы. Поэтому ток почти всегда измеряют, если батарея подключена к нормальной для нее нагрузке.
Для измерения напряжения батареи без нагрузки вольтметр подключают к выводам батареи без подключения нагрузки. Если внутреннее сопротивление вольтметра намного выше внутреннего сопротивления батареи, то можно предположить, что напряжение без нагрузки будет измерено достаточно точно.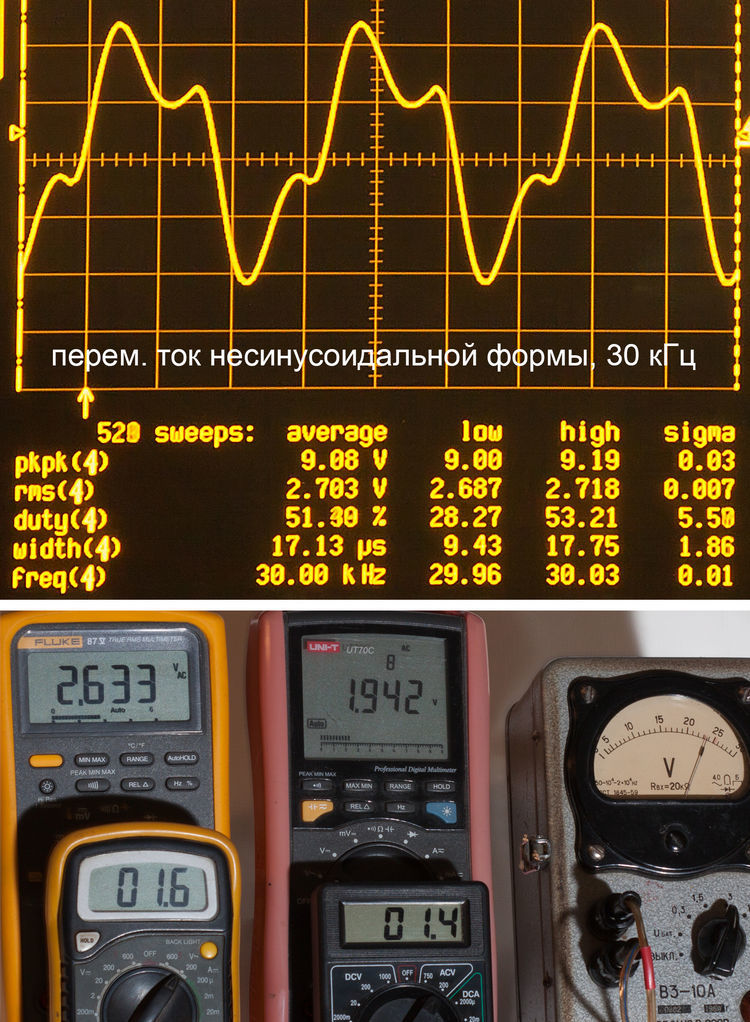
Нужно также измерить сопротивление нагрузки, если только не используется прецизионный резистор. Следует помнить, что, если нагрузочный резистор сильно нагреется, его сопротивление увеличится, поэтому измерение тока батареи следует выполнять достаточно быстро.
Когда все измерения выполнены, можно вставить их результаты в наш калькулятор и получить величину внутреннего сопротивления батареи. Конечно, выпускаются измерители внутреннего сопротивления батареи, а также его способны измерять зарядные устройства с расширенными возможностями.
Для полноты картины следует отметить, что любая батарея имеет целый спектр внутренних сопротивлений и для их измерения часто используется сложная схема с питанием от источника переменного тока с частотой, изменяющейся от нескольких герц до нескольких килогерц. Внутреннее сопротивление обычно характеризуют графиками его зависимости от различных факторов.
Примеры расчетов
Пример 2. Батарея с ЭДС ℰ = 14,5 В отдает 25 Вт мощности во внешний нагрузочный резистор.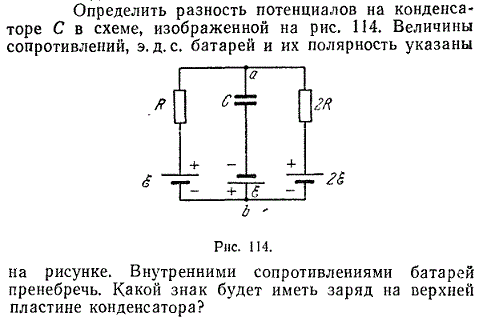 Напряжение на клеммах батареи 11,9 В. Определите внутреннее сопротивление батареи. Подсказка: воспользуйтесь нашим Калькулятором закона Ома для определения тока, текущего через нагрузочный резистор. Затем используйте этот калькулятор для определения внутреннего сопротивления.
Напряжение на клеммах батареи 11,9 В. Определите внутреннее сопротивление батареи. Подсказка: воспользуйтесь нашим Калькулятором закона Ома для определения тока, текущего через нагрузочный резистор. Затем используйте этот калькулятор для определения внутреннего сопротивления.
Пример 3. Лампа накаливания сопротивлением 4 Ом подключена к батарее, имеющей внутреннее сопротивление 0,15 Ом. Подключенный к клеммам батареи вольтметр показывает 11,5 В. Какова ЭДС ℰ батареи?
Пример 4. Две установленные в фарах грузового автомобиля 55-ваттные галогенные лампы соединены параллельно и подключены к клеммам батареи, имеющей внутреннее сопротивление 0,02 Ом. Напряжение на клеммах батареи при этом 23,6 В. Какова ЭДС ℰ батареи? Подсказка: воспользуйтесь нашим Калькулятором мощности постоянного тока для определения сопротивления горячих ламп. Затем воспользуйтесь нашим Калькулятором параллельных сопротивлений для определения сопротивления двух ламп, включенных параллельно. И, наконец, введите полученные данные в этот калькулятор для определения ЭДС батареи.
И, наконец, введите полученные данные в этот калькулятор для определения ЭДС батареи.
Пример 5. Определите ток короткого замыкания 12-вольтовой автомобильной аккумуляторной батареи с ЭДС ℰ = 13,5 В и внутренним сопротивлением 0,04 Ом. Подсказка: 12 В — это номинальное напряжение батареи и в расчетах оно не используется.
Пример 6. Батарея с ЭДС ℰ = 1,5 В закорочена реальным амперметром с внутренним сопротивлением 0,02 Ом, который показывает ток 2,7 А. Определите внутреннее сопротивление батареи и рассеиваемую батареей мощность. Совет: вначале используйте этот калькулятор для определения внутреннего сопротивления батареи, затем воспользуйтесь нашим калькулятором мощности постоянного тока для определения рассеиваемой батареей мощности.
Пример 7. Пульт управления запуском модели ракеты запускает двигатель ракеты путем разогревания нихромового провода воспламенителя. Пульт работает от четырех соединенных последовательно батареек АА напряжением 1,5 В. Каждая батарейка имеет внутреннее сопротивление 200 мОм. Сопротивление двух воспламенителей равно 0,7 Ом и 3 Ом. Определите ток через воспламенитель с сопротивлением 0.7 Ом и воспламенитель сопротивлением 3 Ом. Подсказка: напряжение четырех батареек, соединенных последовательно, равно 1.5 × 4 = 6 V а их общее внутреннее сопротивление равно 200 × 4 = 0.8 Ω.
Каждая батарейка имеет внутреннее сопротивление 200 мОм. Сопротивление двух воспламенителей равно 0,7 Ом и 3 Ом. Определите ток через воспламенитель с сопротивлением 0.7 Ом и воспламенитель сопротивлением 3 Ом. Подсказка: напряжение четырех батареек, соединенных последовательно, равно 1.5 × 4 = 6 V а их общее внутреннее сопротивление равно 200 × 4 = 0.8 Ω.
Автор статьи: Анатолий Золотков
Внутреннее сопротивление аккумулятора – что это и как его измерить
Действительно, есть мнение, что внутреннее сопротивление аккумулятора является показателем его «здоровья». Сразу скажем, что мнение это правильное, но не стоит полагаться исключительно на него. В этой статье рассмотрим, что же такое внутреннее сопротивление аккумулятора и как его измерить.
Как измерить внутреннее сопротивление аккумулятора
Есть множество зарядных устройств для аккумуляторов, которые могут измерять внутреннее сопротивление. Мы рекомендуем вам обратить внимание на LiitoKala Lii 500, у нас есть его обзор и инструкция к нему.
Вот как выглядят показание внутреннего сопротивление на LiitoKala Lii 500:
Автор считает, что эти материалы могут вам помочь:
Что такое внутреннее сопротивление аккумулятора
У хорошего аккумулятора внутреннее сопротивление должно быть очень низким, в диапазоне от 20 до 80. Со временем сопротивление будет расти, и рано или поздно аккумулятор будет непригоден для зарядки.
Однако, стоит иметь в виду, что так как внутреннее сопротивление нормального аккумулятора скорее всего будет незначительным, то на испытание может ощутимо повлиять сопротивление контактов. Таким образом, один и тот же аккумулятор, проверенный в разных ячейках зарядного устройства, или вообще в разных зарядных устройствах, может иметь разные значения внутреннего сопротивления, погрешность составляет примерно 10-20%.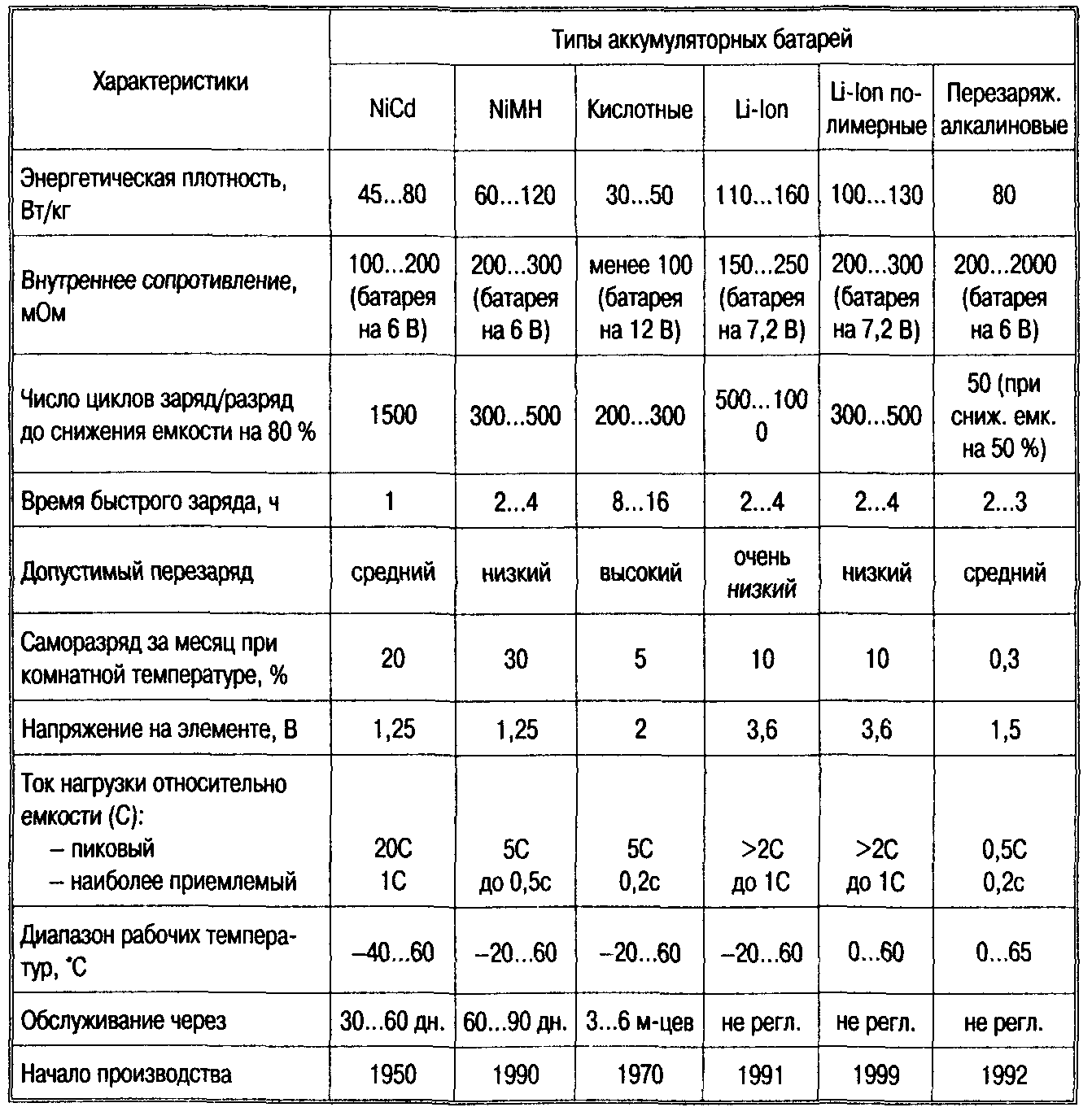
В любом случае, не стоит однозначно судить о состоянии аккумулятора по его внутреннему сопротивлению, ведь есть еще множество других параметров. И к тому же, если аккумулятор устраивает вас в работе, какая разница, какое у него внутреннее сопротивление?
Если вам что-то осталось непонятным – пишите в комментариях на этой странице или задавайте новые вопросы, мы всегда с радостью готовы вам помочь!
К другим статьям | RunCam ScopeCam, новинка в продаже ScopeCam для Страйкбола (Airsoft) объектив 35мм, 50мм, полностью алюминиевый корпус, поворот объектива на 90°, крепление на оружие, индикатор заряда аккумулятора. Mobius Maxi в продаже Mobius Maxi – «старший брат» Mobius Mini, с большими корпусом и аккумулятором, и светосильным объективом “В” с диафрагмой f/1.5. 09.06.2018В продаже RunCam 2 Airsoft. RunCam 2 Airsoft – компактная видеокамера RunCam2 для Страйкбола (Airsoft) с объективом 35мм, 50мм и креплением на оружие. 01.06.2018Архив новостей Отличие камер ScopeCam 4K 40mm, ScopeCam Lite 40mm и ScopeCam2 40mm Сравнение разрешения и угла обзора камер. Измерение внутреннего сопротивления аккумуляторов Измерение внутреннего сопротивления аккумуляторов на постоянном и переменном токе. 02.09.2018Объективы “А” и “В” камер Mobius Maxi Сравнение характеристик объективов “А” и “В” камер Mobius Maxi. 10.07.2018Архив статей | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Простой прибор для быстрого тестирования литиевых аккумуляторов — Eddy site
В последние годы большинство электроники перешло на использование литиевых аккумуляторов. Но часто такие устройства как мобильные телефоны или импульсные металлодетекторы прекращают работу или ведут себя непредсказуемо. Причина в повышении внутреннего сопротивления аккумуляторов. Или потеря ёмкости батареи. Данный прибор позволяет моментально дефектовать литиевые аккумуляторы по повышению внутреннего сопротивления и очень быстро измерять реальную ёмкость аккумулятора.
Но часто такие устройства как мобильные телефоны или импульсные металлодетекторы прекращают работу или ведут себя непредсказуемо. Причина в повышении внутреннего сопротивления аккумуляторов. Или потеря ёмкости батареи. Данный прибор позволяет моментально дефектовать литиевые аккумуляторы по повышению внутреннего сопротивления и очень быстро измерять реальную ёмкость аккумулятора.
Раньше я уже делал анализатор качества литиевых аккумуляторов
http://eddy71.ucoz.net/publ/prostoj_analizator_kachestva_i_jomkosti_litievykh_akkumuljatorov_litest/1-1-0-62
Но в этот раз решил сделать более простое и мобильное устройство, не требующее внешнего питания.
Есть правда маленькая проблемка: изначально я планировал это устройство в виде простого карманного гаджета для использования при покупке аккумуляторов на рынке или в магазине, т.е. основной идеей было «всегда готов к работе» и «прикоснулся к аккумулятору и узнал его внутреннее сопротивление». Но потом, оставшийся свободный вывод контроллера и процентов сорок свободной памяти натолкнули на мысль добавить режим измерения ёмкости аккумулятора. Ёмкость мометально измерить нельзя. Её можно измерить либо заряжая аккумулятор (сколько тока он примет), либо разряжая его на нагрузку (сколько тока он отдаст при разряде).
Ёмкость мометально измерить нельзя. Её можно измерить либо заряжая аккумулятор (сколько тока он примет), либо разряжая его на нагрузку (сколько тока он отдаст при разряде).
Я решил использовать второй вариант. Благо зарядок китайские коллеги сейчас каких только не выпускают..
Беда в том, что при разряде аккумулятора выделяется ощутимая энергия. В первоначальном варианте прибора (моментальное измерение напряжения и внутреннего сопротивления аккумулятора) нагрузочный резистор 2 Ома состоял из пяти соединенных в параллель SMD-резисторов по 10 Ом. Для кратковременного использования в качестве нагрузки этого вполне было достаточно. Но при длительном пропускании тока около 2А на нагрузочном сопротивлении выделяется мощность около 8 ватт. Поэтому пришлось доделывать вторую плату — нагрузочную. На ней же разместилась кнопка влкючения режима измерения ёмкости и динамик (я использовал прямоугольный от какого-то старого мобильного телефона). В режиме измерения ёмкости плата нагрузочных сопротивлений ощутимо греется (гдадусов до 50). Это следует учесть при оформлении конструкции в корпус.
Это следует учесть при оформлении конструкции в корпус.
В архиве с прошивкой и платами данного измерителя я добавил три варианта нагрузочной платы, но испольнение может быть и другим, главное чтобы общее сопротивление равнялось ровно 2 Ома и рассеиваемая мощность была не менее 8 Вт.
Схема довольно проста и не содержит редких или дорогих компонентов. Платы процессорной части и нагрузки имеют размер индикатора. Возможно использование как индикаторов с общим катодом, так и с общим анодом (режим отображения переключается коммутацией четвертого вывода контроллера).
Полевой транзистор управления нагрузочным резистором можно использовать и другой (сейчас их ассортимент очень широк), главное проверить по даташиту его сопротивление канала при приложении управляющего напряжения к затвору 2,5в. У моего это сопротивление около 50 мОм.
Пользоваться прибором очень просто. При первом касании клемм аккумулятора прибор издаёт сигнал. Если сигнала нет, надо быстро убрать аккумулятор — Вы перепутали полярность.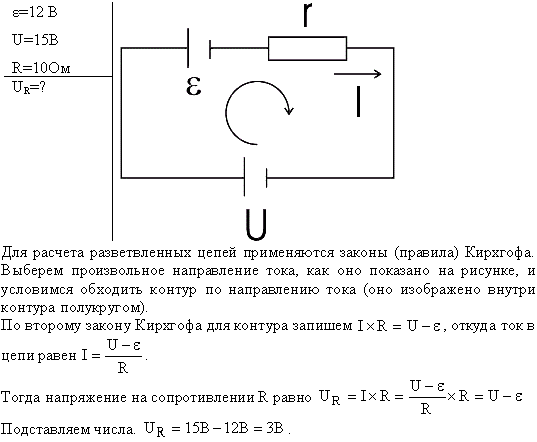 Это может вывести из строя защитный диод.
Это может вывести из строя защитный диод.
Сразу же прибор измеряет и отображает напряжение и внутренне сопротивление подключенного аккумулятора. Изображения на экране сменяются по очереди
Если в этом состоянии нажать на кнопку старта режима измерения ёмкости аккумулятора (аккумулятор надо предварительно полностью зарядить), контроллер включит нагрузочное сопротивление и будет контролировать величину напряжения, тока, внутреннего сопротивления аккумулятора и количество отданного им тока в нагрузку.
По достижении конечного напряжения 3,3В процесс разряда останавливается, контроллер через динамик трелями оповещает о завершении процесса измерения. На экране циклически отображаются текущие измеренные характеристики аккумулятора.
Вариант карманного исполнения для моментального теста (без измерения емкости аккумулятора разрядкой) выглядит так. Вокруг платы оболочка из прозрачной ПЭТ-плёнки от бутылки с водой. Электроды из толстого медного провода в термоусадке.
В архиве находится схема, прошивки для контроллеров и варианты печатных плат измерителя ёмкости и внутреннего сопротивления литиевого аккумулятора.
Выложил на seeedstudio герберы файлов, если у Вас есть желание изготовить прибор самостоятельно, заказать можно тут:
https://www.seeedstudio.com/Pocket-Lithium-Battery-Tester-g-1217739
И файл нагрузки тут:
https://www.seeedstudio.com/Load-PCB-for-Fast-Battery-Tester-g-1217872
Если у Вас возникнут вопросы или Вы захотите связаться со мной, сделайте это с помощью формы на страничке «Обратная связь»
Прибор для измерения внутреннего сопротивления аккумуляторных батарей
Главная – Статьи – Прибор для измерения внутреннего сопротивления аккумуляторных батарейДля работы схемы необходим функциональный генератор с возможностью установки выходного сигнала в виде пульсирующего напряжения с постоянной составляющей отрицательной полярности(напряжение которой в 10 раз больше переменной составляющей). Сигнал от функционального генератора, усиленный с помощью операционного усилителя IC2 MAX400 открывает транзистор Q1, который коммутирует специализированную микросхему для измерения тока в шинах положительного напряжения IC1 MAX471. При этом ток на выходе 8 микросхемы IC1 равен 1/2000 тока испытываемого аккумулятора. Благодаря этому цепь, состоящая из микросхем IC1, IC2 и транзистора Q1 за счет работы операционного усилителя образует потенциал “виртуальной земли” в точке соединения резистора R3 и микросхем IC1, IC2. При этом высокая точность работы устройства достигается за счет использования операционного усилителя с особо малым смещением нуля(не более 10 мкВ). Напряжение на резисторе R3 определяется параметрами делителя напряжения, который состоит из резистора R5 и параллельно соединенными резисторами R3, R4, а также непосредственно характеристиками сигнала функционального генератора. Результирующий ток резистора R3 будет равен IR3 = Rp*Ufg/[(Rp+R5)*R3], где Rp – общее сопротивление параллельно включенных резисторов R3, R4.
Сигнал от функционального генератора, усиленный с помощью операционного усилителя IC2 MAX400 открывает транзистор Q1, который коммутирует специализированную микросхему для измерения тока в шинах положительного напряжения IC1 MAX471. При этом ток на выходе 8 микросхемы IC1 равен 1/2000 тока испытываемого аккумулятора. Благодаря этому цепь, состоящая из микросхем IC1, IC2 и транзистора Q1 за счет работы операционного усилителя образует потенциал “виртуальной земли” в точке соединения резистора R3 и микросхем IC1, IC2. При этом высокая точность работы устройства достигается за счет использования операционного усилителя с особо малым смещением нуля(не более 10 мкВ). Напряжение на резисторе R3 определяется параметрами делителя напряжения, который состоит из резистора R5 и параллельно соединенными резисторами R3, R4, а также непосредственно характеристиками сигнала функционального генератора. Результирующий ток резистора R3 будет равен IR3 = Rp*Ufg/[(Rp+R5)*R3], где Rp – общее сопротивление параллельно включенных резисторов R3, R4. Путем подстановки выбранных значений сопротивлений резисторов, а также учитывая, что ток аккумулятора (IB) в 2000 раз больше тока IR3, можно получить IB = -Vfg/5. Для работы с устройством необходимо на функциональном генераторе выставить уровень напряжения переменной составляющей сигнала равным примерно 10% от его постоянной составляющей. Уравнение позволяет определить величину результирующей переменной составляющей тока батареи (IB). Используя вольтметр переменного тока, можно измерить переменную составляющую напряжения на батарее (UB) и рассчитать среднее выходное сопротивление каждого из ее элементов по формуле UB/NIB, где N – число элементов. Схема легко настраивается на испытание аккумуляторов с номинальным напряжением 3В и более.
Путем подстановки выбранных значений сопротивлений резисторов, а также учитывая, что ток аккумулятора (IB) в 2000 раз больше тока IR3, можно получить IB = -Vfg/5. Для работы с устройством необходимо на функциональном генераторе выставить уровень напряжения переменной составляющей сигнала равным примерно 10% от его постоянной составляющей. Уравнение позволяет определить величину результирующей переменной составляющей тока батареи (IB). Используя вольтметр переменного тока, можно измерить переменную составляющую напряжения на батарее (UB) и рассчитать среднее выходное сопротивление каждого из ее элементов по формуле UB/NIB, где N – число элементов. Схема легко настраивается на испытание аккумуляторов с номинальным напряжением 3В и более.
Примеры работ
Услуги
Контакты
Время выполнения запроса: 0,00379014015198 секунд.
Как измерить внутреннее сопротивление аккумулятора?
Любой источник тока имеет определенное внутреннее сопротивление. Оно участвует в ограничении тока через нагрузку наряду с сопротивлением самой нагрузки. Для того чтобы его узнать, придется измерить напряжение на источнике под различными нагрузками, а затем произвести несложное вычисление.
Для того чтобы его узнать, придется измерить напряжение на источнике под различными нагрузками, а затем произвести несложное вычисление.Инструкция
 Оба прибора подключайте в правильной полярности. Дождитесь завершения переходных процессов, длящихся несколько секунд. Измерьте ток через нагрузку и напряжение на батарее. Запишите их.
Оба прибора подключайте в правильной полярности. Дождитесь завершения переходных процессов, длящихся несколько секунд. Измерьте ток через нагрузку и напряжение на батарее. Запишите их.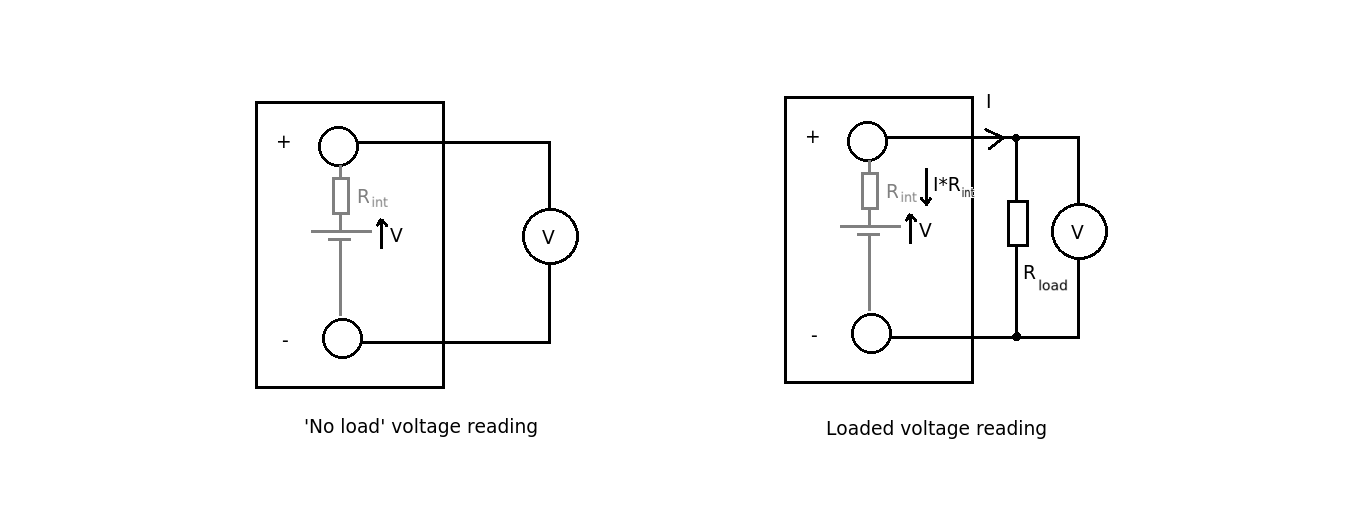 А вот один цикл разряда (до напряжения, слегка превышающего минимальное безопасное для него) проведите. В нескольких точках этого цикла, кратковременно отключая батарею от основной разрядной цепи, измерьте ее внутреннее сопротивление, пользуясь указанной выше методикой. Составьте кривую зависимости внутреннего сопротивления от степени разряженности, выраженной в процентах.
А вот один цикл разряда (до напряжения, слегка превышающего минимальное безопасное для него) проведите. В нескольких точках этого цикла, кратковременно отключая батарею от основной разрядной цепи, измерьте ее внутреннее сопротивление, пользуясь указанной выше методикой. Составьте кривую зависимости внутреннего сопротивления от степени разряженности, выраженной в процентах.Насколько уменьшится емкость li-ion аккумуляторов после нескольких лет хранения
Очень часто происходят дискуссии о том, насколько сильно влияет долгое хранение li-ion аккумуляторов на их рабочие характеристики. Снижается ли после долго хранения емкость аккумуляторов? А если снижается, то насколько? Можно ли использовать аккумуляторы, которые лежали без дела несколько лет?
Попробуем в этом разобраться. Выражаем благодарность компании KeepPower-Украина за предоставление li-ion аккумуляторов формата 18650, которые несколько лет находились у них на хранении. Было получено шесть разных аккумуляторов со сроками хранения от 3 до 6,5 лет:
- Panasonic NCR18650G
- Panasonic NCR18650BM
- Panasonic NCR18650A
- Samsung ICR18650-22F
- Sanyo UR18650FM
- Sanyo UR18650ZTA
Методика тестирования
В начале было измерено напряжение и внутреннее сопротивление всех аккумуляторов, чтобы произвести первоначальную оценку их состояния после хранения. После этого все аккумуляторы были несколько раз прогнаны циклами заряд/разряд, чтобы избавиться от возможных последствий долгого хранения. Так сказать – привели аккумуляторы в чувство после долгой спячки.
После этого все аккумуляторы были несколько раз прогнаны циклами заряд/разряд, чтобы избавиться от возможных последствий долгого хранения. Так сказать – привели аккумуляторы в чувство после долгой спячки.
Тестирование проводилось разрядом токами 0,5 и 3 Ампера с замером емкости. После тестирования снова было проведено измерение внутреннего сопротивления аккумуляторов, чтобы зафиксировать возможное его изменение.
Тестирование в режиме разряда постоянным током проводилось прибором Rigol DL3021, измерение внутреннего сопротивления – прибором YR-1030.
Panasonic NCR18650BM
Первоначальное напряжение на аккумуляторе – 3,56 Вольт, внутреннее сопротивление – 22,2 мОм.
- Возраст аккумулятора – 3 года
- Минимальная емкость – 3030mAh
- Максимальное напряжение – 4,2 Вольт
- Минимальное напряжение – 2,5 Вольт
Внутреннее сопротивление после тестирования -20,6 мОм.
Panasonic NCR18650A
Первоначальное напряжение на аккумуляторе – 3,61 Вольт, внутреннее сопротивление – 32,7 мОм.
- Возраст аккумулятора – 4 года
- Минимальная емкость – 2950mAh
- Максимальное напряжение – 4,2 Вольт
- Минимальное напряжение – 2,5 Вольт
Внутреннее сопротивление после тестирования – 33,1 мОм.
Samsung ICR18650-22F
Первоначальное напряжение на аккумуляторе – 3,67 Вольт, внутреннее сопротивление – 45,9 мОм.
- Возраст аккумулятора – 4 года
- Минимальная емкость – 2150mAh
- Максимальное напряжение – 4,2 Вольт
- Минимальное напряжение – 2,5 Вольт
Внутреннее сопротивление после тестирования – 46,7 мОм.
Sanyo UR18650FM
Первоначальное напряжение на аккумуляторе – 3,79 Вольт, внутреннее сопротивление – 42,8 мОм.
- Возраст аккумулятора – 4 года
- Минимальная емкость – 2500mAh
- Максимальное напряжение – 4,2 Вольт
- Минимальное напряжение – 2,5 Вольт
Внутреннее сопротивление после тестирования – 42,5 мОм.
Sanyo UR18650ZTA
Первоначальное напряжение на аккумуляторе – 3,80 Вольт, внутреннее сопротивление – 42,2 мОм.
- Возраст аккумулятора – 6 лет
- Минимальная емкость – 2900mAh
- Максимальное напряжение – 4,35 Вольт
- Минимальное напряжение – 2,75 Вольт
Внутреннее сопротивление после тестирования – 42,2 мОм.
Следует отметить, что максимальное напряжение данной модели аккумулятора составляет 4,35 Вольт, что выше стандартных 4,2 Вольт. Но перед тестированием аккумулятор был заряжен только до 4,2 Вольт (было нечем зарядить дj напряжения 4,35 Вольт). Поэтому результаты тестирования для этого экземпляра не совсем корректны.
По разным данным при заряде таких аккумуляторов только до 4,2 Вольт в них “недозаливается” от 10 до 15% емкости.
Panasonic NCR18650G
Первоначальное напряжение на аккумуляторе – 4,11 Вольт, внутреннее сопротивление – 35,9мОм.
- Возраст аккумулятора – 6 лет
- Минимальная емкость – 3450mAh
- Максимальное напряжение – 4,2 Вольт
- Минимальное напряжение – 2,5 Вольт
Внутреннее сопротивление после тестирования – 36,8 мОм.
Кто повнимательнее, тот заметил, что похоже этот аккумулятор был когда-то заряжен до 4,2 Вольт, т.к. перед тестированием его напряжение было 4,11 Вольт. Мы тоже на это обратили внимание и обратились к лицу, от которого получили эти аккумуляторы на тесты. С его слов этот аккумулятор скорее всего был заряжен примерно в 2014 году и после этого лежал в коробке. Если это так, то это очень хороший показатель по саморазряду. Саморазряд очень-очень низкий.
Анализ результатов
На диаграмме представлено сравнение измеренной емкости аккумуляторов при разряде токами 0,5 и 3 Ампера с минимальной емкостью, указанной в datasheet производителя. Как можно увидеть – емкость части аккумуляторов превышает минимально-гарантированную, емкость нескольких аккумуляторов немного ниже минимально-гарантированной.
Для удобства восприятия на диаграмме ниже показано, какая емкость в процентах от минимально-гарантированной была зафиксирована при разряде током 0,5 Ампера.
Не забывайте, что модель Sanyo UR18650ZTA имеет максимальное напряжение 4,35 Вольт. А перед тестированием аккумулятор заряжался только до 4,2 Вольт. Поэтому чтобы получить правильную картину по этому аккумулятору следует к измеренной емкости добавить еще примерно 10-15%.
Выводы
По результатам тестирования видно, что после нескольких лет хранения, конечно, li-ion аккумуляторы немного теряют в емкости, но снижение емкости оказалось совсем небольшим. Внутреннее сопротивление аккумуляторов также находится в пределах нормы и сильно не изменилось. Усиления саморазряда (снижение напряжения на заряженном аккумуляторе со временем) также отмечено не было.
Таким образом, можно сделать вывод, что к ухудшению характеристик (уменьшение емкости, увеличение саморазряда и внутреннего сопротивления) приводит не долговременно хранение, а работа аккумуляторов в циклах разряд/заряд.
Дата проведения тестирования аккумуляторов - март 2019 года.
Как измерить внутреннее сопротивление батареи? – Зачем это делать
Батарейки находят и используют везде! Все видели их и раньше использовали батарею. В другой предыдущей статье – Что происходит в электрической цепи: напряжение по сравнению с током, мы определили и объяснили, что такое напряжение, ток и сопротивление. Однако знаете ли вы, что каждая батарея имеет собственное сопротивление течению тока? Это известно как Внутреннее сопротивление .
Мы говорили о сопротивлении – сопротивление относится к мере сопротивления протеканию тока.Внутреннее сопротивление – это, по сути, противодействие потоку, который в настоящее время обеспечивается самими элементами и батареями. В этой статье мы поговорим о том, как измерить внутреннее сопротивление батареи:
- Что такое внутреннее сопротивление?
- Как измерить внутреннее сопротивление?
- Рекомендуемые инструменты и продукты, которые помогут вам.
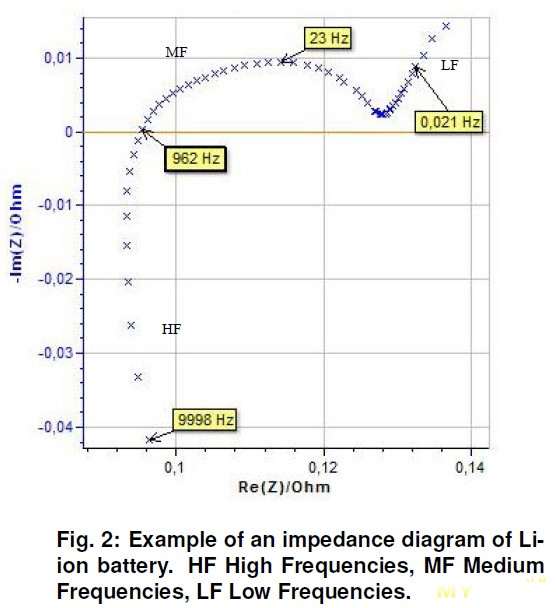
Источник: hk-phy
Как уже упоминалось, внутреннее сопротивление относится к противодействию протеканию тока, создаваемому самими элементами и батареями.Все материалы в некоторой степени сопротивляются току, даже элементы и батареи. Это связано с материалами, из которых изготовлены батареи.
Элементы, из которых состоит типичная батарея, включают цинк, углерод, литий, ртуть, серебро и т. Д. Все они не являются идеальными проводниками электричества. Поэтому найти аккумулятор с нулевым внутренним сопротивлением будет сложно, а может, и невозможно.
Внутреннее сопротивление можно рассматривать как привратник батареи. Меньшее сопротивление означает меньшее ограничение.При высоком сопротивлении аккумулятор нагревается и напряжение падает.
Как внутреннее сопротивление влияет на напряжение и ток? Чтобы лучше понять это, воспользуемся законом Ома. Закон Ома – это формула, определяющая соотношение между напряжением, током и сопротивлением в цепи. Закон Ома гласит, что В = IR. V относится к напряжению, I относится к току, а R относится к сопротивлению, в нашем случае внутреннему сопротивлению.
Закон Ома – это формула, определяющая соотношение между напряжением, током и сопротивлением в цепи. Закон Ома гласит, что В = IR. V относится к напряжению, I относится к току, а R относится к сопротивлению, в нашем случае внутреннему сопротивлению.
Ключевым моментом для понимания является то, что напряжение и внутреннее сопротивление являются независимыми переменными, главное, на что влияют, – это зависимая переменная, т.е.е. электрический ток. Когда внутреннее сопротивление увеличивается на V / R = I, ток уменьшается. Когда внутреннее сопротивление меньше, ток, наоборот, увеличивается. Они обратно пропорциональны. Однако все это основано только на формуле закона Ома.
В реальном мире напряжение уменьшается при увеличении внутреннего сопротивления. Таким же образом мы можем измерить внутреннее сопротивление батареи.
В двух словах, Внутреннее сопротивление – это сопротивление в цепи, которое исходит от самого элемента или батареи. При более высоком внутреннем сопротивлении ток и напряжение будут ниже.
При более высоком внутреннем сопротивлении ток и напряжение будут ниже.
Имея это в виду, давайте теперь исследуем, почему мы должны измерять внутреннее сопротивление?
Как измерить внутреннее сопротивление? Что вам понадобится:- Новая батарейка (AA)
Цифровой вольтметр постоянного тока со светодиодной подсветкой 0,28 дюйма – желтый
RESK – Комплект резисторов
Шагов:- Подключите аккумулятор и вольтметр в следующей конфигурации.
[не обращайте внимания на треугольник (GND) в нижнем левом углу]
- Снимите измерения с вольтметра. 1.500V
Вольтметр должен показывать величину напряжения в соответствии со спецификацией вашей батареи. Это связано с тем, что к цепи не подключена нагрузка. Это также известно как напряжение холостого хода (VOC).
Напряжение холостого хода (VOC) – это напряжение, когда оно не подключено к какой-либо нагрузке в цепи.
- Подключите аккумулятор, вольтметр и резистор в этой конфигурации.
[не обращайте внимания на треугольник (GND) в нижнем левом углу]
В нашем примере мы будем использовать резистор на 4 Ом.
- Снимите измерения с помощью вольтметра. 1.446V
Вольтметр должен показывать более низкое значение напряжения. Падение напряжения вызвано внутренним сопротивлением батареи. Мы можем рассчитать внутреннее сопротивление, если мы снимем показания напряжения холостого хода (VOC) и напряжения на батарее с подключенной нагрузкой, которая в нашем случае является резистором 4 Ом.
- Используйте формулу закона Ома и формулу закона Кирхгофа для расчета внутреннего сопротивления.
Сначала мы подставим полученное значение в закон Ома, чтобы определить ток, протекающий по цепи.
Сокращение:
В = Напряжение
I = текущий
R = Сопротивление
VL = Напряжение нагрузки
RL = номинал резистора
В = I · R
VL = I · RL
1. 446 В = I · 4 Ом
446 В = I · 4 Ом
I = 1,446 В 4 Ом
I = 0,3615A
Затем мы будем использовать Закон Кирхгофа для определения напряжения на внутреннем резисторе в батарее. Это значение также является падением напряжения на внутреннем резисторе.
Сокращение:
VOC = Напряжение холостого хода
VI = напряжение на внутреннем резисторе
VL = Напряжение нагрузки
ЛОС = VI + VL
1.500 В = VI + 1.446 В
VI = 1.500 – 1.446V
VI = 0,054
Теперь у нас есть значение падения напряжения на внутреннем резисторе и ток, протекающий по цепи. Теперь мы можем снова использовать закон Ома, чтобы найти внутреннее сопротивление батареи.
Сокращение
VI = напряжение на внутреннем резисторе
I = текущий
RI = внутреннее сопротивление
VI = I · RI
0. 054V = 0,3615A · RI
054V = 0,3615A · RI
RI = 0,149 Ом
Отсюда видно, что внутреннее сопротивление батареи AA составляет 0,149 Ом !
Рекомендуемые инструменты и продуктыНадеюсь, вы научились измерять внутреннее сопротивление батареи, а также как и когда его применять! Вот несколько инструментов и продуктов, связанных с батареями, которые могут помочь вам в ваших проектах IoT!
Модуль ИБП для Raspberry Pi Pico – Источник бесперебойного питанияЭтот источник бесперебойного питания (ИБП) – это модуль, предназначенный для обеспечения работы вашего Raspberry Pi Pico от литий-ионного аккумулятора.Он также оснащен микросхемой контроля напряжения / тока и индикатором состояния батареи.
Характеристики
- Стандартный заголовок Raspberry Pi Pico
- Совместимость литий-ионных аккумуляторов с динамическим управлением питанием для стабильного источника питания
- Связь по шине I2C для контроля напряжения, тока, мощности и оставшейся емкости аккумулятора
- Несколько мер защиты аккумулятора, т.
 е. перезаряд / защита от разряда, защита от перегрузки по току, защита от короткого замыкания, обратная защита и функция выравнивающего заряда
е. перезаряд / защита от разряда, защита от перегрузки по току, защита от короткого замыкания, обратная защита и функция выравнивающего заряда - Встроенный индикатор зарядки, питания и заряда аккумулятора
Это супермини-светодиодный дисплей с диагональю 0,28 дюйма. Пусть вас не обманывает его небольшой внешний вид, он оснащен функцией защиты от обратного подключения. Этот вольтметр можно использовать для измерения заряда аккумулятора мобильного телефона, аккумулятора автомобиля и других подобных приложений. Также доступны несколько цветов: желтый, красный, зеленый и синий.
Спецификация
- Диапазон напряжения: 2,5 – 30 В
- Рабочий ток <30 мА
- Размер: 30 × 11.7 × 9,2 мм
- Скорость измерения: 200 мс / один раз
- Точность 3%
Это батарейный отсек для ваших аккумуляторов 18650! Этот футляр для батарейного отсека может вместить две перезаряжаемые батареи 18650 и оснащен встроенным переключателем. В корпус встроены провода для пайки / подключения к вашим IoT-проектам!
В корпус встроены провода для пайки / подключения к вашим IoT-проектам!
Это четырехслотовый батарейный отсек для аккумуляторов 18650! В этот чехол можно установить четыре аккумуляторных батареи 18650.Подобно вышеупомянутому корпусу держателя батареи, в корпус встроены провода для пайки / подключения к вашим проектам IoT!
СводкаНадеюсь, вы узнали больше об измерении внутреннего сопротивления батарей. Это может быть забавный проект, если вы новичок в построении схем. Если у вас есть какие-либо вопросы, не стесняйтесь оставлять их в комментариях ниже!
Продолжить чтение
Как измерить внутреннее сопротивление батареи с помощью тестера батареи и других измерительных приложений
Каковы принципы проверки внутреннего сопротивления батареи? Тестеры батарей
(такие как Hioki 3561, BT3562, BT3563 и BT3554) подают постоянный переменный ток с частотой измерения 1 кГц, а затем вычисляют внутреннее сопротивление батареи на основе значения напряжения, полученного с помощью вольтметра переменного тока. Как показано на рисунке, четырехконтактный метод переменного тока, при котором вольтметр переменного тока подключается к положительному и отрицательному электродам батареи, позволяет точно измерять внутреннее сопротивление батареи, сводя к минимуму влияние сопротивления измерительного кабеля и сопротивления контактов. Этот метод можно использовать для измерения внутреннего сопротивления до нескольких миллиомов. Эти тестеры аккумуляторов также обеспечивают высокоточное измерение постоянного напряжения (OCV), еще одно условие, когда требуется высокая точность данных аккумулятора при 0.01% показ.
Как показано на рисунке, четырехконтактный метод переменного тока, при котором вольтметр переменного тока подключается к положительному и отрицательному электродам батареи, позволяет точно измерять внутреннее сопротивление батареи, сводя к минимуму влияние сопротивления измерительного кабеля и сопротивления контактов. Этот метод можно использовать для измерения внутреннего сопротивления до нескольких миллиомов. Эти тестеры аккумуляторов также обеспечивают высокоточное измерение постоянного напряжения (OCV), еще одно условие, когда требуется высокая точность данных аккумулятора при 0.01% показ. С возможностью установки частоты измерения на значение, отличное от 1 кГц, измеритель импеданса батареи BT4560 можно использовать для выполнения более тонких испытаний внутреннего сопротивления с помощью измерения графика Коула-Коула. Он также обеспечивает точность измерения 0,0035% показания. для измерения постоянного напряжения (OCV) аккумуляторов.
Внутреннее сопротивление, значения напряжения батареи и соответствующие тестеры батареи по типу батареи
На рисунке показана линейка моделей тестеров батареи Hioki, которые измеряют внутреннее сопротивление (IR) и напряжение батареи (напряжение холостого хода или OCV) а также какие типы батарей можно использовать для измерения. Hioki BT4560 и 3561 хорошо подходят для тестирования аккумуляторных элементов, разработанных для электромобилей (EV) и гибридных электромобилей (HEV), а также с литий-ионными аккумуляторными батареями, используемыми в компактных аккумуляторных батареях для мобильных устройств из-за низкого внутреннего сопротивления эти типы клеток. Напротив, BT3562 и BT3563 следует использовать с аккумуляторными блоками (наборами из нескольких литий-ионных аккумуляторных батарей) из-за высокого напряжения аккумулятора (OCV) таких конфигураций. Хотя инструменты также могут использоваться для измерения внутреннего сопротивления и напряжения батареи для других аккумуляторных батарей, таких как никель-металлогидридные, свинцово-кислотные и никель-кадмиевые батареи, вам следует выбирать тестер батареи на основе напряжения батареи (OCV ).
Hioki BT4560 и 3561 хорошо подходят для тестирования аккумуляторных элементов, разработанных для электромобилей (EV) и гибридных электромобилей (HEV), а также с литий-ионными аккумуляторными батареями, используемыми в компактных аккумуляторных батареях для мобильных устройств из-за низкого внутреннего сопротивления эти типы клеток. Напротив, BT3562 и BT3563 следует использовать с аккумуляторными блоками (наборами из нескольких литий-ионных аккумуляторных батарей) из-за высокого напряжения аккумулятора (OCV) таких конфигураций. Хотя инструменты также могут использоваться для измерения внутреннего сопротивления и напряжения батареи для других аккумуляторных батарей, таких как никель-металлогидридные, свинцово-кислотные и никель-кадмиевые батареи, вам следует выбирать тестер батареи на основе напряжения батареи (OCV ).
Как измерить внутреннее напряжение аккумуляторной батареи (также известной как собранная батарея, аккумуляторная батарея или аккумуляторный модуль)
Чтобы получить необходимое напряжение, аккумулятор конструируется путем соединения нескольких ячеек в серии. Чтобы создать такой аккумуляторный блок (также известный как аккумулятор в сборе, аккумуляторный блок или аккумуляторный модуль), вкладки или шины привариваются на месте для соединения ячеек. Результирующее сопротивление сварного шва включается в измерения внутреннего сопротивления аккумуляторной батареи.Поскольку аномалии сварных швов не позволят аккумуляторной батарее работать на полную мощность, рекомендуется проверять собранные аккумуляторные блоки с помощью тестера аккумуляторов. Hioki BT3562 может измерять внутреннее сопротивление батарейных блоков до 60 В, а BT3563 может измерять внутреннее сопротивление батарейных блоков до 300 В. plot
Чтобы создать такой аккумуляторный блок (также известный как аккумулятор в сборе, аккумуляторный блок или аккумуляторный модуль), вкладки или шины привариваются на месте для соединения ячеек. Результирующее сопротивление сварного шва включается в измерения внутреннего сопротивления аккумуляторной батареи.Поскольку аномалии сварных швов не позволят аккумуляторной батарее работать на полную мощность, рекомендуется проверять собранные аккумуляторные блоки с помощью тестера аккумуляторов. Hioki BT3562 может измерять внутреннее сопротивление батарейных блоков до 60 В, а BT3563 может измерять внутреннее сопротивление батарейных блоков до 300 В. plot
В общих чертах, внутреннее сопротивление батареи состоит из трех компонентов: омического сопротивления (сопротивления сварного шва), сопротивления реакции (сопротивления переносу заряда) и диффузионного сопротивления (импеданса Варбурга).Эти компоненты обычно рассчитываются с помощью измерения графика Коула-Коула (графика Найквиста). Тестер импеданса батарей Hioki BT4560, который позволяет изменять частоту измерения в диапазоне от 100 мГц до 1,05 кГц, идеально подходит для измерения графика Коула-Коула. Прибор может измерять эффективное сопротивление батареи R и ее реактивное сопротивление X. Он также поставляется со стандартным прикладным программным обеспечением, которое может отображать графики Коула-Коула. Кроме того, LabVIEW может выполнять анализ эквивалентной схемы для простых батарей.
Прибор может измерять эффективное сопротивление батареи R и ее реактивное сопротивление X. Он также поставляется со стандартным прикладным программным обеспечением, которое может отображать графики Коула-Коула. Кроме того, LabVIEW может выполнять анализ эквивалентной схемы для простых батарей.
Как измерить ESR двухслойных электрических конденсаторов (EDLC)
Внутреннее сопротивление электрических двухслойных конденсаторов (EDLC), которые относятся к классу 1 и используются в приложениях резервного копирования, измеряется с использованием сигнал переменного тока. Тестеры аккумуляторов Hioki также можно использовать для простого измерения конденсаторов классов 2, 3 и 4. Hioki BT3562 может измерять ESR до 3,1 кОм на частоте 1 кГц. JIS C5160-1 определяет измерительный ток для таких приложений, а измеритель LCR IM3523 может использоваться в приложениях, где измерительный ток должен соответствовать стандарту JIS.В BT3562 измерительный ток фиксирован для каждого диапазона измерения.
Как измерить ESR литий-ионного конденсатора (LIC)
В результате явления, известного как переходное восстанавливающееся напряжение, потенциал литий-ионного конденсатора (LIC) или электрического двойника -слойный конденсатор (EDLC) не стабилизируется сразу после заряда или разряда компонента. Если ESR конденсатора измеряется в этих условиях, измеренные значения могут не стабилизироваться из-за воздействия переходного восстанавливающегося напряжения.Функция коррекции градиента потенциала батареи Hioki Battery Impedance Meter BT4560 может использоваться для компенсации эффектов переходного восстанавливающегося напряжения, что делает возможным стабильное измерение ESR. Прибор имеет максимальное разрешение 0,1 мкОм и может измерять литий-ионные конденсаторы и электрические двухслойные конденсаторы с низкими значениями ESR 1 мОм или меньше.
Как измерить внутреннее сопротивление устройства Пельтье
Элементы Пельтье можно использовать для охлаждения, нагрева и контроля температуры посредством подачи постоянного тока. При измерении внутреннего сопротивления элемента Пельтье постоянным током измерительный ток вызывает тепловой поток и изменения температуры внутри элемента, что делает невозможным получение стабильного измерения. Используя переменный ток для измерения, можно уменьшить количество теплового потока и изменение температуры, что позволяет стабильно определять внутреннее сопротивление компонента.
При измерении внутреннего сопротивления элемента Пельтье постоянным током измерительный ток вызывает тепловой поток и изменения температуры внутри элемента, что делает невозможным получение стабильного измерения. Используя переменный ток для измерения, можно уменьшить количество теплового потока и изменение температуры, что позволяет стабильно определять внутреннее сопротивление компонента.
Аккумуляторная батарея онлайн | Как измерить внутреннее сопротивление батареи с помощью метода прерывания тока
Джеймс Ниманн, A nalog инженер-конструктор, Tektronix
Одна из демонстраций, которые мы часто устраиваем на конференциях по аккумуляторным батареям, – это использование единицы измерения источника (SMU) для измерения внутреннего сопротивления устройства накопления энергии, такого как аккумулятор или топливный элемент. В таких демонстрациях SMU изменяет ток нагрузки с рабочего тока батареи или поляризационного тока на потенциал холостого хода и одновременно измеряет изменение напряжения элемента.В этом «методе прерывания тока» внутреннее сопротивление батареи равно изменению напряжения, деленному на изменение тока.
В таких демонстрациях SMU изменяет ток нагрузки с рабочего тока батареи или поляризационного тока на потенциал холостого хода и одновременно измеряет изменение напряжения элемента.В этом «методе прерывания тока» внутреннее сопротивление батареи равно изменению напряжения, деленному на изменение тока.
Демонстрация популярна среди инженеров по аккумуляторным батареям, потому что она показывает, как можно измерить внутреннее сопротивление батареи при больших токах поляризации с помощью экономичного SMU, типа прибора, способного одновременно получать и измерять напряжение и ток.
Это сложное измерение, которое даже гораздо более дорогой прибор спектроскопии электрохимического импеданса (EIS) не может выполнить при высоких уровнях тока.Исторически сложилось так, что электрохимики использовали осциллограф и выключатель (для нагрузки) для выполнения этих измерений и достигли того, что лучше всего назвать добротностью, а не реальным внутренним сопротивлением.
Давайте посмотрим, как мы можем добиться достоверно точных измерений с помощью SMU.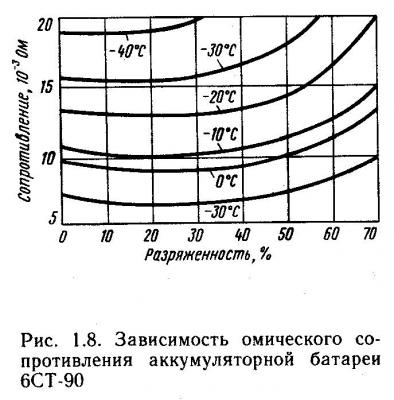 Главное здесь – обратить пристальное внимание на несколько неочевидных деталей.
Главное здесь – обратить пристальное внимание на несколько неочевидных деталей.
Комплексный импеданс
Внутреннее сопротивление батареи является мерой действительной части комплексного импеданса ячейки.На рисунке 1 показана простая электрическая модель этого сложного импеданса, известная как модель цепи Рэндлса.
модели Randles В модели Randles каждая окислительно-восстановительная реакция электрода моделируется с помощью резистора и конденсатора, представляющих сопротивление переноса заряда и емкость двойного слоя для электрода соответственно.
- Сопротивление переносу заряда представляет собой энергию активации, необходимую для ускорения предполагаемой электродной реакции с определенной скоростью.
- Емкость двойного слоя является мерой медленности электродной реакции, возникающей в результате накопления зарядов на каждой стороне электрода, опять же с той же удельной скоростью.
- R int – реальная составляющая импеданса ячейки.

Для большинства ячеек поддерживающий электролит (ионный проводник) является источником наибольшего внутреннего сопротивления. Электроды и внешние соединительные сопротивления обычно вносят гораздо меньший вклад.При протекании тока выделяется тепло, которое может повлиять на измерения внутреннего сопротивления, и это следует учитывать.
Измерения повышенного внутреннего сопротивления могут быть признаком того, что элемент приближается к отказу, поскольку сопротивление электролита имеет тенденцию увеличиваться с возрастом элемента. Хотя сопротивление может увеличиваться по множеству других причин, а также в зависимости от химического состава элемента, измерение характеристик внутреннего сопротивления может быть полезным показателем общего состояния электрохимического элемента, особенно при оценке с течением времени.
Измерения внутреннего сопротивления также полезны для оценки того, может ли батарея эффективно отдавать накопленную энергию. В общем, батарея с низким внутренним сопротивлением лучше способна выдавать высокий ток по требованию. Высокое сопротивление приводит к чрезмерному нагреву аккумулятора и падению выходного напряжения при высокой нагрузке. Это особенно важно для тяжелых нагрузок, таких как электроинструменты и электрические трансмиссии.
Высокое сопротивление приводит к чрезмерному нагреву аккумулятора и падению выходного напряжения при высокой нагрузке. Это особенно важно для тяжелых нагрузок, таких как электроинструменты и электрические трансмиссии.
Метод прерывания по току
Чтобы понять, как использовать метод прерывания по току для измерения действительной части комплексного импеданса, вернитесь к модели цепи Рэндлса на рисунке 1.В модели геометрическая индуктивность ячейки и межсоединений испытательной аппаратуры показана вместе с параметрами электродов, обсуждавшимися ранее.
Если это измерение настроено без включенного дистанционного зондирования, индуктивность, показанная в модели, будет полной индуктивностью измерительного контура a, показанного в части 2А на Рисунке 2. При включенном дистанционном зондировании только индуктивность самой ячейки измеряется, как показано на 2B, измеряется только полное сопротивление между измерительными выводами, комплексное или нет.
Когда SMU настроен на источник напряжения в конфигурации удаленного считывания (4-проводной), внешний датчик обеспечивает напряжение обратной связи, которое измеряется и сравнивается с запрограммированным уровнем. Источник напряжения регулируется до тех пор, пока напряжение обратной связи не станет равным запрограммированному уровню напряжения. Дистанционное измерение компенсирует падение напряжения в измерительных проводах (и анализируемом веществе в случае электрохимической ячейки), обеспечивая подачу запрограммированного уровня напряжения на рабочий электрод.
Для измерения R int необходимо измерить прерывание или изменение тока ячейки в течение нужного промежутка времени, чтобы сумма реактивного сопротивления была равна нулю, оставив только измерение реальной части внутреннего сопротивления, как показано в 2С.Как правило, существует только одна задержка прерывания, которая может удовлетворить это требование для любой заданной ячейки и геометрии измерения. Интервалы прерывания могут варьироваться от 80 микросекунд до нескольких миллисекунд в зависимости от размера и конфигурации ячейки.
Рисунок 2: Измерение внутреннего сопротивления ячейкиДля правильного измерения внутреннего сопротивления электрохимической ячейки обычно запускают график EIS или измеряют комплексное сопротивление ячейки в рабочем диапазоне токов ячейки.Внутреннее сопротивление – это точка на кривой, где комплексный импеданс пересекает действительную ось или когда сумма реактивных компонентов равна нулю.
Метод измерения тока прерывания R int передает скалярное измерение, представляющее величину векторов импеданса, показанных наложенными на график комплексного импеданса, показанный на рисунке 3. Правильное время прерывания можно легко найти, изменив задержку прерывания, чтобы минимизировать модуль вектора, показанный как R int на рисунке 3.Остальные векторы R1 и R2, полученные изменением интервала прерывания, имеют большие значения. Обратите внимание, что второе пересечение оси x – это не внутреннее сопротивление батареи, а скорее сумма всех сопротивлений в модели из рисунка 1. Эта точка показана как Rt на рисунке 3.
Рис. 3: Пример комплексной диаграммы импеданса SMU для измерения потенциала разомкнутой цепи
Использование этого краткого и краткого метода обеспечивает стабильные правильные измерения внутреннего сопротивления батарей и электрохимических ячеек.SMU хорошо подходят для измерения потенциала холостого хода на электрохимических ячейках, поскольку для них требуются инструменты с высоким входным сопротивлением, которое обеспечивает SMU. В сочетании со сценариями электрохимических испытаний SMU полностью способны работать как гальваносат или потенциостат и могут измерять внутреннее сопротивление батарей, топливных элементов или любого электрохимического элемента, обеспечивая при этом ток поляризации.
Джеймс Ниманн (James Niemann) – инженер-разработчик аналоговых устройств компании Tektronix. Он работал в подразделении Keithley Instruments в Кливленде, штат Огайо, с 1988 года.В настоящее время он является главным инженером-конструктором, отвечающим за общие исследования и разработки, а также за разработку новых продуктов, используемых для электрохимических исследований.
Исследование влияния шкалы времени измерения на методы определения характеристик внутреннего сопротивления для литий-ионных элементов
В данной работе коммерчески доступные пакетные ячейки емкостью 20 Ач с графитовым (LiC 6 ) отрицательным электродом и фосфатом лития-железа (LiFePO 4) ) положительный электрод.Максимальное напряжение заряда для ячеек составляет 3,6 В (3,8 В для 10-секундного импульсного тока), а минимальное напряжение разряда составляет 2,0 В (1,6 В для 10-секундного импульсного тока). Изготовитель определяет максимальную емкость заряда и разряда 15 ° C при мгновенном контакте. Все тесты, описанные ниже, были выполнены на каждой ячейке.
В начале тестирования SoC для каждой из ячеек доводили до 50% при 25 ° C, используя коммерческий клеточный циклер (Bitrode MCV 16-100-5) и климатическую камеру (Weiss Gallenkamp Votsch VC 3). 4060).Протокол настройки включает разрядку ячеек до установленного производителем минимального напряжения разряда (определяемого как 0% SoC), после чего следует 4-часовой период отдыха. Впоследствии элементы заряжаются с использованием протокола постоянного тока – постоянного напряжения (CC-CV) с использованием силы тока 1 C для части CC до достижения 3,6 В, а затем удерживают ячейки при 3,6 В для части CV, пока ток не упадет. ниже тока отсечки C / 20. После 4-часового периода покоя элементы разряжались со скоростью 1 ° C в течение 30 минут, чтобы достичь 50% SoC.Применяли еще 4-часовой период отдыха, позволяющий клеткам достичь электрохимического равновесия 18 . Затем были применены пять методов оценки внутреннего сопротивления для определения сопротивления при 50% SoC при 25 ° C.
Испытание импульсной мощности с одиночным импульсом разряда / заряда применялось при токе 5 ° C в течение 18 секунд, и ячейки находились в покое в течение часа перед зарядкой при 5 ° C в течение 18 секунд. Длительность импульса 18 секунд была выбрана потому, что это одна из самых длинных длительностей импульса, указанных в действующих стандартах 14 .
Следующим испытанием, проведенным на элементах, было испытание мощности импульса с несколькими импульсами, как предложено в исх. 13 . В этом тесте элементы заряжались и разряжались 10-секундными импульсами при 1 ° C, 2 ° C, 5 ° C и максимуме ° C с промежуточными 30-минутными этапами отдыха после каждого импульса. Отдельные импульсы можно использовать для расчета сопротивления согласно методике, описанной в разделе 2.1.
В методике переключения тока ток изменяется ступенчато (здесь от 1 до 5 ° C используются как подходящие низкие и средние амплитуды тока), и измеряется изменение напряжения из-за этого ступенчатого изменения тока; внутреннее сопротивление затем рассчитывается по закону Ома 22 .Сила тока может быть изменена во время разряда, заряда или от разряда к заряду. В последнем случае ток переключается с разряда 5 C на заряд 5 C (оба с 5-секундными импульсами). В случае только разряда ток переключается с -1 C на -5 C во время разряда, и, наконец, в случае только заряда ток переключается с 1 C на 5 C во время заряда. Здесь значения тока 1 C и 5 C используются только в качестве репрезентативных.
После измерения сопротивления с использованием импульсов постоянного тока, сопротивление было измерено с помощью сигналов переменного тока.Сопротивление 1 кГц было измерено с помощью тестера сопротивления 1 кГц Hioki BT3563 при 50% SoC, 25 ° C.
Гальваностатические испытания EIS были выполнены с использованием системы Solartron Modulab (модель 2100 A), оснащенной бустерной картой на 2 A. Несколько измерений EIS были выполнены на одной и той же ячейке в одних и тех же условиях испытаний в диапазоне частот от 10 мГц до 100 кГц, с использованием различных значений среднеквадратичного тока: 0,2 А, 0,5 А, 0,8 А, 1,0 А и 1,4 А. Эти значения тока были выбраны так, чтобы они не были слишком высокими для изменения SoC ячейки во время измерения, но достаточно высокими для хорошего отношения сигнал / шум для сигнала напряжения отклика.Это было необходимо для анализа зависимости EIS от амплитуды сигнального тока.
При использовании процедуры импульсного многосигнального сигнала были применены пять периодов сигнала, батарея была отрегулирована на 50% SoC и позволила уравновеситься, и была записана соответствующая характеристика напряжения. После сбора данных были подобраны непараметрическое сопротивление и ECM, как описано в предыдущем разделе.
Результаты экспериментов с использованием сигналов постоянного тока
Результаты испытаний импульсной мощности с одиночным разрядом 5 C и импульсом заряда длительностью 18 с показаны на рис.3. Используя этот импульс, можно рассчитать сопротивление постоянному току для любой длительности импульса до 18 секунд. Чистое омическое сопротивление рассчитывалось по падению напряжения после 0,1 с импульсного тока. В идеале чистое омическое сопротивление следует рассчитывать по мгновенному падению напряжения из-за изменения тока. Однако измерение мгновенного падения ограничено скоростью сбора данных используемого оборудования. Для этого эксперимента использованный циклер аккумуляторной батареи имел максимальное разрешение 0.1 сек.
Рисунок 3Отклик напряжения на 18-секундный ( a ) импульс разряда и ( b ) импульс заряда. Сопротивление, рассчитанное для длительности импульса, показано в ( c ) для разряда и ( d ) для заряда. На подзаголовках ( c ) и ( d ), (i), (ii) и (iii) относятся к чистому омическому сопротивлению R 0 , сопротивлению переноса заряда R CT и поляризационному сопротивлению R p , соответственно. Перекрытие между (ii) и (iii) указывает на неспособность в рамках этой техники точно различить каждый вклад.
Поскольку электроды тонкие (поскольку это элемент высокой мощности), а пути электронов для зарядки и разрядки в используемых элементах аналогичны, чистые омические сопротивления (сопротивление, рассчитанное через 0,1 с после начала импульса) сравнимы с показано в Таблице 1. Однако более длительные сопротивления для заряда и разряда отличаются, как показано на Рис. 3 (c, d) и в Таблице 1. Во время зарядки материал положительного электрода окисляется, ионы Li деинтеркалируются. из слоистой матрицы интеркаляции лития, в данном случае LiFePO 4 , проходят через электролит и внедряются между слоями графита в результате реакции электрохимического восстановления, протекающей на отрицательном электроде.С другой стороны, во время разряда на отрицательном электроде происходит реакция окисления, ионы Li деинтеркалируются с анода и мигрируют через электролит, чтобы повторно интеркалироваться в материал положительного электрода, где одновременно протекает реакция электрохимического восстановления. . Как правило, чем выше потенциал электрода, тем труднее удалить литий из участка в матрице хозяина. При разрядке элемента литий переходит из состояния с высокой энергией на аноде в конфигурацию с низким энергопотреблением на катоде, следовательно, значения сопротивления при разрядке выше, чем при зарядке при 50% SoC; это также было обнаружено другими исследователями 8,22 .
Таблица 1 Изменение внутреннего сопротивления в зависимости от длительности импульса.Сопротивление на рис. 3 (c) и (d) можно разделить на три части, связанные с процессами, способствующими падению напряжения, обсуждаемым в разд. 2.1., А именно: (i) чисто омическое сопротивление R 0 , приводящее к мгновенному падению напряжения и доминирующее до 0,1 секунды, (ii) сопротивление переносу заряда R CT , возникающее примерно мгновенная до 2–5 секунд и (iii) медленная, линейная, твердофазная диффузия ионов лития, которая неизбежно приводит к концентрационной поляризации R p , особенно во время сильноточной зарядки, которая быстро увеличивает напряжение аккумулятора до верхнего предела напряжения , происходящее в масштабе времени 5 секунд 34 .Хотя R o , R CT и R p не разделены полностью, ожидается, что в их соответствующих временных масштабах они будут доминирующим вкладом в общее сопротивление.
Внутреннее сопротивление, рассчитанное на основе пяти импульсов заряда-разряда различной амплитуды, показано в таблице 2. Данные испытаний 5 C – те же данные, что и в таблице 1. Чистое омическое сопротивление (рассчитанное из падения напряжения на 0,1 с). остается одинаковым для всех амплитуд импульсов со стандартным отклонением 0.05 мОм. Однако разница в значении сопротивления, рассчитанном по истечении 2, 5 и 10 секунд, зависит от скорости заряда-разряда. Например, разница между сопротивлением, измеренным с помощью 2-секундного и 10-секундного импульса, составляет 0,73 мОм при использовании разрядного импульса 1 ° C и 0,39 мОм при использовании разрядного импульса 15 ° C. Расхождения в скорости нарастания сопротивления, возникающие из-за амплитуд импульсов, объясняются различными электрохимическими процессами, которые активируются внутри ячеек по мере увеличения длительности импульса, и выделением тепла, связанным с импульсными токами.Для более высоких импульсов тока такие электрохимические процессы активируются раньше (поскольку двойной слой может разряжаться намного быстрее) – большие значения тока также вызывают подавление отношения V / I 8 . Кроме того, при более высоких скоростях вырабатывается больше тепла, т.е. 0,5 Втч (1800 Дж) всего за 10 секунд, когда ток 300 А (15 C) проходит через сопротивление 2 мОм, что эффективно увеличивает внутреннюю температуру батареи, что способствует снижение сопротивления, как показано в таблице 2.
Таблица 2 Внутреннее сопротивление (мОм), рассчитанное по разным амплитудным импульсам разряда.Ожидается, что для длительных импульсов с более высокой частотой изменения сопротивления будут определяться изменениями в SoC. При частоте следования импульсов 1 C через 10 секунд SoC меняется на незначительные 0,28%; при частоте импульсов 15 C через 10 секунд SoC изменяется на 4,2%, что может привести к заметному падению / повышению напряжения. Для батареи LiFePO 4 плато напряжения между 70% и 40% SoC 35 , где были проведены измерения для этой работы, означает, что 4.Изменение SoC на 2% не оказывает большого влияния. Однако для аккумуляторных технологий с более крутыми кривыми OCV, таких как LiNiCoAlO 2 и LiNiMnCoO 2 , ожидается, что эффект будет более выраженным.
Результаты таблицы 2 показывают отличительные пики сопротивления при 2 ° C для разрядки и 1 ° C для зарядки для этого метода. В рамках концепции Батлера-Фольмера эти пики могут быть связаны с дуальностью температурного перенапряжения.
Чистое омическое сопротивление также рассчитывалось по фронту спада / нарастания (заряд / разряд) в конце импульса.Чистое омическое сопротивление, рассчитанное для разрядных импульсов 1 C, 2 C, 5 C и 15 C, составляет 1,30 мОм, 1,35 мОм, 1,35 мОм и 1,40 мОм соответственно, а для импульсов заряда 1 C, 2 C, 5 C и 15 C – 1,40 мОм. , 1,40 мОм, 1,40 мОм и 1,56 мОм соответственно. В среднем значения для разряда менее чем на 0,1 мОм выше, чем те, которые показаны в таблице 2. Это может быть связано с энергией, необходимой для деинтеркаляции от положительного электрода и интеркаляции в отрицательный электрод, которая отличается от деинтеркаляции от электрода. отрицательный электрод и вставка в положительный электрод.
Отклик напряжения на изменение тока от разряда к заряду и величины тока во время заряда и разряда показаны на рис. 4 (a, b и c) соответственно, на рис. 4 (d) представлено чистое омическое сопротивление, рассчитанное из фронт переключения импульсного тока. Сопротивление, рассчитанное по изменению тока разряда с 1 C до 5 C, аналогично сопротивлению, рассчитанному для 0,1-секундного импульса и метода спадающего фронта. В сценарии зарядки ток переключается с 1 C на 5 C, сопротивление близко соответствует тому, которое рассчитано с использованием метода импульсной мощности.Сопротивление, рассчитанное при переключении с разряда на заряд, близко соответствует чистому омическому сопротивлению для зарядного тока, показанному в Таблице 1 и Таблице 2.
Рисунок 4Отклик напряжения на ток переключения от ( a ) разряда 5 ° C до заряда 5 ° C. , ( b ) разряд от 1 ° C до разряда 5 ° C, ( c ) заряд от 1 ° C до заряда 5 ° C и ( d ) чистое омическое сопротивление, рассчитанное по краю переключения.
Результаты экспериментов с использованием сигнала переменного тока
Сопротивление 1 кГц, измеренное с помощью тестера сопротивления Hioki 1 кГц, было равно 0.82 мОм. Сопротивление 1 кГц для этих ячеек находится в области с преобладанием индукции, как можно увидеть на графике EIS Найквиста на рис. 5.
Рис. 5Результаты EIS от 100 кГц до 10 мГц с разными амплитудами сигнала ( a ) график Найквиста и ( b ) график Боде с теми же данными. На вставке ( a ) показан увеличенный вид центральной части.
Результаты испытаний ЭИС с разными амплитудами тока представлены в виде графика Найквиста на рис.5 (а). Как и ожидалось, нет заметных различий между результатами из-за изменения амплитуды гальваностатического сигнала. Увеличенный вид, показанный на вставке, показывает слегка зашумленные результаты для 0,2 А, которые подавляются для 0,5 А и выше. Следовательно, сопротивление, измеренное с помощью EIS, не зависит от амплитуды тока, но использование более высоких токов может снизить шум. Действительно, если бы для теста EIS использовался более высокий ток, например 1 C, это повлияло бы на результаты, однако применение такого высокого тока для теста EIS имеет небольшой прецедент в литературе.Амплитуда тока C / 20 (в данном случае 1 А) может многократно давать одни и те же результаты с низким уровнем шума измерения, ограниченным чувствительностью оборудования. Результаты EIS для магнитуды 1 A представлены в виде графика Боде на рис. 5 (b).
При осмотре графика Найквиста было обнаружено, что чистое омическое сопротивление R o составляет 0,92 мОм, что соответствует 251 Гц (то есть временной шкале 4 мс). Сопротивление в локальном минимуме перед тем, как клетки войдут в область с преобладанием низкочастотной диффузии, оказалось равным 1.55 мОм, что соответствует 2 Гц; и, таким образом, R CT составляет 0,63 мОм. Оценка поляризационного сопротивления с использованием результатов EIS не является четко определенным. Учитывая, что значения R p для импульса постоянного тока в этом обсуждении были получены из 10-секундного импульса, результат 0,1 Гц используется для определения R p . Эквивалентное сопротивление при 0,1 Гц по результатам EIS соответствует 0,36 мОм; это становится 1,39 мОм, если для расчета значения R p принять частоту 0,01 Гц.
Результаты экспериментов с использованием сигнала Мультизина
Фаза и величина расчетного сопротивления, основанного на методе локальных полиномов (LPM), и соответствие модели ECM порядка 2 и показаны на рис.6. Хотя параметры контроллера ЭСУД не поддаются однозначной идентификации, последовательно соединенное сопротивление и сопротивление 1 st и 2 nd RC ветвей контроллера ЭСУД обычно относятся к R или , R CT и R . p , которые оказались равными 1,618 ± 0,003 мОм, 1,10 ± 0,07 мОм и 0,109 ± 0,005 мОм соответственно. Значение R o значительно выше, чем у других методов. Это может быть связано с двумя потенциальными причинами: i) тот факт, что большая часть мощности в сигнале тока возбуждения принадлежит гармоникам ниже 1 Гц, и / или ii) несмотря на хорошее соответствие между модельными и экспериментальными данными, параметры не соответствуют отражать приписываемые им физические значения (благодаря уникальной идентифицируемости).
Рисунок 6( a ) Величина и ( b ) фазовая характеристика расчетного сопротивления через LPM с использованием импульсного мультисигнала и подобранной модели ECM 2-го порядка и .
Сравнение различных методов измерения сопротивления
Среднее значение чистого омического сопротивления, рассчитанное с использованием различных методов импульсной мощности, составляет 1,33 мОм со стандартным отклонением 0,04 мОм. Все эти измерения проводились через 0,1 с после подачи импульса тока.Независимо от заряда или разряда, значения чистого омического сопротивления, измеренные различными методами постоянного тока, точно совпадают с вариацией 3%, независимо от того, были ли они измерены от начала, конца или точки переключения импульсного тока.
Сравнение R o , R CT и R p , оцененных с использованием описанных выше методов, представлено на рис. 7 (a). Источники расхождения между значениями сопротивления, измеренными с помощью импульсов заряда и разряда, обсуждались ранее.Значения R CT и R p вычисляются с использованием 2-секундных и 10-секундных точек данных импульсов.
Рисунок 7( a ) Сравнение значений сопротивления, измеренных различными методами. ( b ) График зависимости общего сопротивления от шкалы времени, показывающий, что значения сопротивления совпадают, когда шкала времени совпадает, независимо от используемой методики измерения.
Значение 0,92 мОм R 0 , определенное в ходе испытаний EIS (рис. 5), соответствует частотной характеристике 251 Гц (4 мс); аналогично, значение R CT равно 0.63 мОм соответствует отклику 2 Гц. В отличие от R 0 и R CT , сопротивление поляризации R p не определяется из графика Найквиста, вместо этого оно предопределено. В этом исследовании были рассмотрены две частоты: 0,1 Гц и 0,01 Гц, что дает значения 0,36 мОм и 1,39 мОм соответственно. Поскольку значения сопротивления R o , R CT и R p имеют физическое значение 36 , целесообразно определить временные рамки для R o , R CT и R p с использованием EIS. полученные результаты.
Сопротивление, измеренное с использованием сигнала 1 кГц, находится в индуктивной области графика Найквиста, см. Рис. 5 (a), который находится близко к точке пересечения горизонтальной оси. Следовательно, разумно, чтобы сопротивление 1 кГц (0,82 мОм) было близко к омическому сопротивлению, определенному по результатам испытаний EIS (0,92 мОм при 251 Гц, 0,79 мОм при 1 кГц). Стоит повторить, что это может быть неверно для других батарей, и точка 1 кГц может находиться в емкостной области, например, для меньшего пакета и цилиндрических элементов.Это особенно вероятно для ячеек с меньшей емкостью, и в этом случае значение не будет отражать только чистое омическое сопротивление.
Среднее чистое омическое сопротивление R 0 , определенное методами постоянного тока 1,315 мОм, намного выше, чем полученное с помощью EIS. При испытаниях импульсной мощности R 0 обычно рассчитывается с использованием точки данных 0,1 с, т. Е. Он определяется самым низким разрешением среди имеющихся на сегодняшний день серийных аккумуляторных циклов, которое составляет 10 Гц, тогда как по определению это должно быть мгновенное падение напряжения при наступление тока.Следовательно, сопротивление постоянному току, рассчитанное по результатам испытаний импульсной мощности, будет содержать кинетические вклады (часть R CT ), увеличивая / уменьшая отклик напряжения за пределы чисто омического вклада, возникающего в масштабе времени менее миллисекунд. Поскольку результаты EIS для этой батареи показывают, что R 0 соответствует частотной характеристике 251 Гц (4 мс); поэтому физически более целесообразно использовать падение напряжения через 4 мс от начала импульса тока для определения R 0 .Хотя прямоугольная волна будет возбуждать частоты, превышающие частоту 10 Гц, импульс 0,1 с будет иметь самый высокий вклад гармоник от синусоидальной волны 10 Гц, поэтому значения для R 0 , извлеченные из тестов мощности импульса постоянного тока и тестов EIS, будут менее расходящиеся. Однако с учетом ограничений, имеющихся у существующих серийно выпускаемых аккумуляторных циклеров, это невозможно и может быть достигнуто только при наличии оборудования для тестирования аккумуляторов, способного достигать высоких импульсных токов (от 0 А) в течение 4 мс. Для сравнения на рис.5 (b), значение сопротивления на частоте 10 Гц с использованием метода EIS оказалось равным 1,41 мОм, что сопоставимо с 1,33 мОм, оцененным с помощью импульса постоянного тока. Следовательно, расхождение в чистом омическом сопротивлении, измеренном методом постоянного тока, может быть связано с ограничениями обычно используемого оборудования для тестирования батарей.
Учитывая, что R o , измеренные с помощью импульса постоянного тока, будут содержать вклады переноса заряда, сравнение значений R CT , измеренных с помощью методов EIS и импульсного тока, будет иметь предсказуемые различия.Аналогичным образом, R CT , измеренный с использованием методов постоянного тока, будет содержать эффекты поляризации, которые трудно изолировать. Тем не менее, здесь мы следуем обычному рецепту расчета R o , R CT и R p методами постоянного тока 8 . Используя импульс 5 C, учитывая длительность импульса 2 секунды, R CT оценивается как 0,41 мОм и 0,38 мОм для разряда и заряда соответственно. Из-за того, что часть R CT залита в R o (измеряется от 0.Длительность импульса 1 с), сравнение значений R CT , измеренных в результате теста мощности импульса и теста EIS, не имеет смысла. Однако значение R o + R CT , измеренное после 2-секундной длительности импульса, должно быть в тесном соответствии со значением сопротивления, полученным из синусоидальной волны 0,5 Гц (поскольку 2-секундная прямоугольная волна имеет наибольший гармонический вклад от 0,5 Гц. ). Из рисунка 5 (b), значение сопротивления, измеренное EIS при 0,5 Гц, составляет 1,69 мОм, тогда как значение R o + R CT , измеренное при длительности импульса 2 секунды, равно 1.71 ± 0,01 мОм, что хорошо согласуется.
Аналогичным образом, при использовании импульса 5 C, учитывая длительность импульса 10 секунд, значения R p оцениваются как 0,40 мОм и 0,30 мОм для импульсов разряда и заряда соответственно. Аналогично случаю R CT , R p значения длительности импульса 10 секунд не могут быть сопоставлены с результатом теста EIS. Однако ожидается, что сумма R o + R CT + R p будет соответствовать значению, измеренному с помощью 0.Сигнал EIS 1 Гц. Сумма сопротивлений R o + R CT + R p , то есть полное сопротивление, с длительностью импульса 10 секунд составляет 2,12 мОм и 2,00 мОм для разряда и заряда соответственно. Результат EIS 0,1 Гц дает 1,91 мОм (рис. 5 (b)). Хотя эти значения близки (рис. 7b), ожидается, что значения разрядного импульса и импульса заряда длительностью более 5 секунд будут выше по сравнению с EIS из-за дополнительной интеркаляции и деинтеркаляции выше, чем у чистого постоянного тока. нагрузка 29 .Динамика передачи заряда относительно медленнее для сигнала переменного тока из-за изменения величины тока и знаков. Кроме того, было показано, что сигналы без постоянного тока позволяют избежать насыщения литием на границе электрод-электролит, тем самым снижая ингибирование переноса ионов, связанное с поляризацией, и, таким образом, R p 37 . Следовательно, сумма R o + R CT + R p при длительности импульса 10 секунд, как ожидается, будет немного выше, чем результаты EIS, как обнаружено в этом исследовании.Таким образом, предполагается, что общее сопротивление, рассчитанное по результатам испытаний импульсной мощности, можно оценить непосредственно по результатам испытаний EIS.
Значение R o (1,62 мОм), измеренное тестом многосигнального сигнала, намного выше, чем значение, вычисленное методами импульса постоянного тока и EIS. Максимальная частота, применяемая в этой методике, составляла 1 Гц (рис. 6). Изучение графика Боде, показанного на рис.5 (b), показывает, что при 1 Гц ячейка имеет сопротивление 1,62 мОм, что в точности соответствует значению, найденному в тесте многосигнального сигнала с максимальной частотой 1 Гц (рис.7б). В дополнение к данным испытаний EIS, когда 1-секундная точка данных длительности импульса рассматривается для импульса постоянного тока, сопротивление оказывается равным 1,61 мОм как для заряда, так и для разряда (рис. 7b). Следовательно, сопротивление R o (которое является компонентом в модели ECM 2 и порядка), оцененное по мультисигналу, использует максимальную частоту 1 Гц и, таким образом, не может быть обозначено как чисто омическое сопротивление. Тем не менее, сопротивление R o , оцененное методом мультиизина, точно соответствует сопротивлению, определенному при 1 Гц с помощью EIS.Полное сопротивление (т.е. сумма R o + R CT + R p ) для многосоставного сигнала с минимальной частотой 0,01 Гц составляет 2,83 мОм, что близко к сопротивлению, заданному EIS при 0,01 Гц (рис. . 7b).
В заключение, результаты и последующий анализ показывают, что значения сопротивления, измеренные любым методом, зависят от шкалы времени измерения. Таким образом, сопротивление, измеренное любым методом, может быть оценено по данным испытаний EIS, учитывая его широкий частотный диапазон.Таким образом, можно получить значения сопротивления любой частоты, соответствующие ожидаемой кинетике клеток.
Влияние на использование приложения
Сопротивление батареи используется для различных целей, которые включают, например, создание значений параметров ECM, моделирование и проектирование систем терморегулирования, испытания характеристик старения, индикацию SoH и многое другое. Это интересный открытый вопрос, какие методы и значения следует использовать для конкретного приложения. ECM, например, являются хорошо зарекомендовавшим себя методом моделирования поведения литий-ионных аккумуляторов.Модель зависит от сопротивления и сопротивлений в сочетании с характеристиками емкости поверхностного слоя. Традиционно данные о мощности импульса используются для определения параметров блоков управления двигателем путем подгонки модели к данным и минимизации ошибок. Основная причина использования импульсных токов, помимо простоты самого метода испытаний, заключается в том, что предполагается, что сильноточные импульсы имитируют использование батареи в реальных сценариях применения. Неотъемлемой проблемой идентификации параметров является уникальность решения, которая приводит к неоднозначности между идентифицированными параметрами модели (в простейшем случае R o и R CT ) и их фактическими физическими значениями.Эта неоднозначность еще больше усиливается, когда используются модели эквивалентных схем более высокого порядка, которые используют больше RC-цепей для описания более детальной физики, такой как SEI или двойной слой (последний часто через элементы с постоянной фазой). Учитывая эту двусмысленность, эффективность феноменологических моделей оценивается исключительно по степени соответствия. Недавно было показано, что импульсные мультисигналы лучше отражают фактическое использование батареи и лучше соответствуют данным 21 . В этом отношении метод импульс-мультиизин может быть более эффективным способом определения сопротивления для приложений моделирования систем.
Тест на сопротивление 1 кГц, хотя он полезен для быстрой проверки в производственных условиях, например проверка качества, от этого мало пользы. Кроме того, то, лежит ли измеренное значение сопротивления 1 кГц в индуктивной или проводящей области, сильно зависит от образца батареи, поэтому при использовании для проверки качества единичная частота (например, 1 кГц) должна выбираться в зависимости от образца.
Для определения характеристик батарей или долговременной деградации EIS может быть более подходящим методом.Это связано с тем, что метод охватывает большой частотный диапазон, включающий в себя различные динамики в батарее. Таким образом, помимо измерения повышения внутреннего сопротивления, можно сделать выводы о вкладе SEI в деградацию и другие лежащие в основе механизмы 29 . Хотя EIS – это хорошо зарекомендовавший себя метод 8 , продолжительность теста для получения повторяемых результатов 18 , строгие требования к чувствительным соединениям и другие сложности настройки делают его громоздким.Однако, как свидетельствуют данные, представленные в этой рукописи, сопротивление, рассчитанное по импульсному току, многосигнальному сигналу и тесту импеданса 1 кГц, можно оценить по результатам теста EIS с хорошей степенью точности; поэтому может быть выгодно выполнить только надежный тест EIS.
Внутреннее сопротивление батареи
Университетская физика, Лаборатория 3: Внутреннее сопротивление батареи
В этом эксперименте вы будете измерять внутреннее сопротивление обычной батареи (размер D, 1.5 Вольт).
Аппарат:
Два мультиметра, набор из нескольких лампочек, две D аккумуляторы, провода, аккумуляторный отсек с концевыми проводниками.
Меры предосторожности:
Убедитесь, что вы понимаете правильное подключение Амперметр к цепи. Если вы не обязательно спросите у инструктора. Подключение параллельный амперметр может вызвать перегорание предохранителя. Обратите внимание, что у амперметра очень низкое внутреннее сопротивление; поэтому если подключенный к источнику питания, это вызовет короткое замыкание.Правильный выбор подключения щупа к измеритель и правильный выбор положения ручки требуется для подготовки мультиметра для использования в качестве амперметра. Зарезервировать большой мультиметр как амперметр. Его провода должны быть подключены правильно, а шкала должна быть в мА.
Процедура:
Лампочка I-One:
Используйте пример цветовой кодировки, показанный ниже (на следующей странице), чтобы установить правильно подключите схему.Если есть различных цветных измерительных щупов, адаптируйте их к порядку цветовой кодировки, указанному в пример. В показанной схеме внизу, r – внутреннее сопротивление батареи, R1 – лампочка, и R2 – общее сопротивление всех используемых измерительных проводов.
Подключите цепь, как показано, и измерьте напряжение V ab (это напряжение замкнутой цепи аккумулятора) и ток I. Затем отсоедините один из выводов от аккумуляторного отсека и измерьте ЭДС (е) на его выводах (это напряжение холостого хода).Запишите ответы ниже, используя правильные единицы измерения.
V ab : _________
e: ____________
И: _____________
II. Две лампочки параллельно:
Подключите другую лампочку параллельно первой и повторите измерения.
V ab : _________
e: ____________
И: _____________
Вычисления:
Для каждого набора данных найти r из,
и сравните результат двух наборов.
r (с использованием данных одной лампы) ___________ r (с использованием данных двух ламп) ________
Эти значения должны представлять внутреннее сопротивление аккумулятор.Посетите веб-страницу некоторых из производителей, чтобы узнать, предоставляют ли они какую-либо информацию о том, что внутреннее сопротивление должно быть для свежего аккумулятора.
Вы можете попросить инструктора предоставить вам один – со свежей батареей, чтобы повторить эксперимент.
Как измерить внутреннее сопротивление батареи – retrotechlab.com
Внутреннее сопротивление
При проектировании схемы с батареей мы часто предполагаем, что батарея является идеальным источником напряжения.Это означает, что независимо от того, какую нагрузку мы прилагаем к аккумулятору, напряжение на выводах источника всегда остается неизменным.
Если мы смоделируем эту батарею как идеальный источник напряжения, изменение значения R L не повлияет на напряжение между выводами батареи
На самом деле несколько факторов могут ограничить способность батареи действовать как идеальное напряжение источник. Размер батареи, химические свойства, возраст и температура – все это влияет на величину тока, которую батарея может выдавать.В результате мы можем создать лучшую модель батареи с идеальным источником напряжения и резистором, включенным в серию .
Батареи можно смоделировать как идеальный источник напряжения с последовательным резистором (обозначенным R I )
Мы можем измерить напряжение батареи на ее клеммах без подключенной нагрузки. Это известно как напряжение холостого хода (V OC ).
Измерение напряжения щелочного элемента AA без подключенной нагрузки
Обратите внимание, что, поскольку через внутренний резистор не течет ток, падение напряжения на нем составляет 0 В.Следовательно, можно предположить, что V OC равно напряжению идеального источника напряжения в аккумуляторной батарее.
Если мы подключим нагрузку к батарее, напряжение на клеммах упадет.
Здесь мы измеряем падение напряжения на резисторе 4 Ом.
Это падение напряжения вызвано внутренним сопротивлением батареи. Мы можем рассчитать внутреннее сопротивление, если снимем показания напряжения холостого хода и напряжения на клеммах батареи с подключенной нагрузкой.
Для начала создадим схему, показывающую нашу схему.
Вот наша схема. Мы хотим рассчитать R I .
Мы можем подключить измеренное нами напряжение под нагрузкой (V L ) и значение резистора (R L ) в закон Ома, чтобы получить ток, протекающий по цепи (I).
Нам также нужно получить напряжение на внутреннем резисторе. Мы можем сделать это, используя закон напряжения Кирхгофа. Упрощенно для этой схемы, мы можем сказать, что падение напряжения на обоих резисторах должно составлять в сумме напряжение идеального источника напряжения.
Теперь, когда мы знаем падение напряжения на внутреннем резисторе и ток через него, мы можем снова использовать закон Ома, чтобы найти его сопротивление.
Отсюда видно, что внутреннее сопротивление (в данный момент) элемента AA составляет 0,273 Ом .
Связанные10.4 Оценка внутреннего сопротивления в цепях | Электрические схемы
Рабочий пример 7: Внутреннее сопротивление в цепи с последовательными резисторами
Для следующей схемы рассчитайте:
разности потенциалов \ (V_ \ text {1} \), \ (V_ \ text {2} \) и \ (V_ \ text {3} \) на резисторах \ (R_ \ text {1} \), \ (R_ \ text {2} \) и \ (R_ \ text {3} \)
.сопротивление \ (R_ \ text {3} \).
сопротивление \ (R_ \ text {3} \).
Если внутреннее сопротивление равно \ (\ text {0,1} \) \ (\ text {Ω} \), какова ЭДС аккумулятора и какая мощность рассеивается внутренним сопротивлением аккумулятора?
Примечание
Это вопрос, очень похожий на то, что вы видели ранее.Это необходимо для того, чтобы выделить Дело в том, что подход к внутреннему сопротивлению строится на том же принципы, с которыми вы уже работали.
Определите, как подойти к проблеме
Нам дана разность потенциалов на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для вычисления разности потенциалов на известные резисторы.Поскольку резисторы включены в последовательную цепь, разность потенциалов равна \ (V = V_ \ text {1} + V_ \ text {2} + V_ \ text {3} \), и мы можем вычислить \ (V_ \ text {3} \). Теперь мы можем использовать эту информацию чтобы найти разность потенциалов на неизвестном резисторе \ (R_ \ text {3} \).
Вычислить разность потенциалов на \ (R_ \ text {1} \)
Используя закон Ома: \ begin {align *} R_ \ text {1} & = \ frac {V_ \ text {1}} {I} \\ I \ cdot R_ \ text {1} & = I \ cdot \ frac {V_ \ text {1}} {I} \\ V_ \ text {1} & = {I} \ cdot {R_ \ text {1}} \\ & = 2 \ cdot 1 \\ V_ \ текст {1} & = \ текст {2} \ текст {V} \ end {align *}
Рассчитать разность потенциалов на \ (R_ \ text {2} \)
Снова используя закон Ома: \ begin {align *} R_ \ text {2} & = \ frac {V_ \ text {2}} {I} \\ I \ cdot R_ \ text {2} & = I \ cdot \ frac {V_ \ text {2}} {I} \\ V_ \ text {2} & = {I} \ cdot {R_ \ text {2}} \\ & = 2 \ cdot 3 \\ V_ \ текст {2} & = \ текст {6} \ текст {V} \ end {align *}
Вычислить разность потенциалов на \ (R_ \ text {3} \)
Так как разность потенциалов на всех резисторах вместе взятых должна быть такой же, как разницу между ячейкой в последовательной цепи, мы можем найти \ (V_ \ text {3} \), используя: \ begin {align *} V & = V_ \ text {1} + V_ \ text {2} + V_ \ text {3} \\ V_ \ text {3} & = V – V_ \ text {1} – V_ \ text {2} \\ & = 23-2-6 \\ V_ \ текст {3} & = \ текст {15} \ текст {V} \ end {align *}
Найдите сопротивление \ (R_ \ text {3} \)
Нам известна разность потенциалов на \ (R_ \ text {3} \) и ток через нее, поэтому мы можем использовать закон Ома. для расчета значения сопротивления: \ begin {align *} R_ \ text {3} & = \ frac {V_ \ text {3}} {I} \\ & = \ frac {\ text {15}} {\ text {2}} \\ R_ \ text {3} & = \ text {7,5} ~ \ Omega \ end {align *}
Разница потенциалов внутреннего сопротивления батареи
Значение ЭДС можно рассчитать, исходя из разности потенциалов нагрузки и потенциала. разница во внутреннем сопротивлении.2} {R} \) и мы знаем ток в цепи, внутреннее сопротивление и разность потенциалов на нем, поэтому мы можем использовать любой форма уравнения для мощности:
\ begin {align *} P_r & = V_rI_r \\ & = (\ текст {0,2}) (\ текст {2}) \\ & = \ текст {0,4} \ текст {W} \ end {выровнять *}Напишите окончательный ответ
- \ (V_ \ text {1} = \ text {2,0} \ text {V} \)
- \ (V_ \ text {2} = \ text {6,0} \ text {V} \)
- \ (V_ \ text {3} = \ text {10,0} \ text {V} \)
- \ (R_ \ text {3} = \ text {7,5} \ Omega \)
- \ (\ mathcal {E} = \ text {23,2} \ text {V} \)
- \ (P_r = \ text {0,4} \ text {W} \)
Рабочий пример 8: Внутреннее сопротивление и резисторы параллельно
Разность потенциалов на батарее составляет 18 В, когда она подключена к двум параллельным резисторам \ (\ text {4,00} \) \ (\ Omega \) и \ (\ text {12,00} \) \ (\ Omega \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов. Если внутреннее сопротивление батареи \ (\ text {0,375} \) \ (\ text {Ω} \) какая ЭДС аккумулятора?
Сначала нарисуйте схему перед выполнением любых расчетов
Определите, как подойти к проблеме
Нам нужно определить ток через ячейку и каждый из параллельных резисторов. Нам дали разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома, чтобы рассчитать ток.
Рассчитать ток через ячейку
Чтобы рассчитать ток через ячейку, нам сначала нужно определить эквивалентное сопротивление остальных схемы. Резисторы включены параллельно и поэтому: \ begin {align *} \ frac {\ text {1}} {R} & = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} {R_ \ text {2}} \ \ & = \ frac {\ text {1}} {\ text {4}} + \ frac {\ text {1}} {\ text {12}} \\ & = \ frac {3 + 1} {\ text {12}} \\ & = \ frac {\ text {4}} {\ text {12}} \\ R & = \ frac {\ text {12}} {\ text {4}} = \ text {3,00} \ \ Omega \ end {выровнять *} Теперь, используя закон Ома, чтобы найти ток через ячейку: \ begin {align *} R & = \ frac {V} {I} \\ I & = \ frac {V} {R} \\ & = \ frac {\ text {18}} {\ text {3}} \\ I & = \ text {6,00} \ text {A} \ end {align *}
Теперь определите ток через один из параллельных резисторов
Мы знаем, что для чисто параллельной конфигурации резисторов разность потенциалов на ячейке равна такая же, как и разность потенциалов на каждом из параллельных резисторов.Для этой схемы: \ begin {align *} V & = V_ \ text {1} = V_ \ text {2} = \ text {18} \ text {V} \ end {выровнять *} Начнем с вычисления тока через \ (R_ \ text {1} \) по закону Ома: \ begin {align *} R_ \ text {1} & = \ frac {V_ \ text {1}} {I_ \ text {1}} \\ I_ \ text {1} & = \ frac {V_ \ text {1}} {R_ \ text {1}} \\ & = \ frac {\ text {18}} {\ text {4}} \\ I_ \ text {1} & = \ text {4,50} \ text {A} \ end {align *}
Рассчитайте ток через другой параллельный резистор
Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_ \ text {2} \): \ begin {align *} R_ \ text {2} & = \ frac {V_ \ text {2}} {I_ \ text {2}} \\ I_ \ text {2} & = \ frac {V_ \ text {2}} {R_ \ text {2}} \\ & = \ frac {\ text {18}} {\ text {12}} \\ I_ \ text {2} & = \ text {1,50} \ text {A} \ end {выровнять *} Альтернативный метод вычисления \ (I_ \ text {2} \) заключался бы в использовании того факта, что токи через каждый из параллельных резисторов необходимо добавить к общему току через ячейку: \ begin {align *} I & = I_ \ text {1} + I_ \ text {2} \\ I_ \ text {2} & = I – I_ \ text {1} \\ & = 6 – 4.5 \\ I_ \ text {2} & = \ text {1,5} \ text {A} \ end {align *}
Определить ЭДС
Суммарный ток через батарею – это ток через внутреннее сопротивление батареи. Знание силы тока и сопротивления позволяет нам использовать закон Ома для определения разности потенциалов на внутреннее сопротивление и, следовательно, ЭДС батареи.
Используя закон Ома, мы можем определить разность потенциалов на внутреннем сопротивлении:
\ begin {align *} V & = I \ cdot r \\ & = \ текст {6} \ cdot \ text {0,375} \\ & = \ текст {2,25} \ текст {V} \ end {выровнять *}Мы знаем, что ЭДС аккумулятора – это разность потенциалов на клемме, суммированная с разность потенциалов на внутреннем сопротивлении так:
\ begin {align *} \ mathcal {E} & = V + Ir \\ & = \ text {18} + \ text {2,25} \\ & = \ текст {20,25} \ текст {V} \ end {выровнять *}Напишите окончательный ответ
Ток через ячейку равен \ (\ text {6,00} \) \ (\ text {A} \).
Ток через резистор \ (\ text {4,00} \) \ (\ Omega \) равен \ (\ text {4,50} \) \ (\ text {A} \).
Ток через резистор \ (\ text {12,00} \) \ (\ Omega \) равен \ (\ text {1,50} \) \ (\ text {A} \).
ЭДС аккумулятора равна \ (\ text {20,25} \) \ (\ text {V} \).
Рабочий пример 9: Мощность в последовательной и параллельной сетях резисторов
Учитывая следующую схему:
Ток, выходящий из батареи, равен \ (\ text {1,07} \) \ (\ text {A} \), общая мощность, рассеиваемая во внешнем цепь – это \ (\ text {6,42} \) \ (\ text {W} \), отношение полных сопротивлений двух параллельных цепей. \ (R_ {P \ text {1}}: R_ {P \ text {2}} \) равно 1: 2, соотношение \ (R_ \ text {1}: R_ \ text {2} \) равно 3: 5 и \ (R_ \ text {3} = \ text {7,00} \ text {Ω} \).
Определите:
- разность потенциалов АКБ,
- мощность, рассеиваемая в \ (R_ {P \ text {1}} \) и \ (R_ {P \ text {2}} \), и
- , если аккумуляторная батарея имеет ЭДС \ (\ text {6,50} \) \ (\ text {V} \), каково значение сопротивление каждого резистора и мощность, рассеиваемая в каждом из них.
Что требуется
В этом вопросе вам дается различная информация и предлагается определить мощность, рассеиваемую в каждый резистор и каждая комбинация резисторов.Обратите внимание, что данная информация предназначена в основном для общего схема. Это подсказка, которую вы должны начать с общей схемы и двигаться вниз к более конкретным. элементы схемы.
Расчет разности потенциалов аккумулятора
В первую очередь остановимся на батарее. Нам дана мощность для всей цепи, а также ток оставив аккумулятор. Мы знаем, что разность потенциалов на клеммах аккумулятора – это разность потенциалов в цепи в целом.
Мы можем использовать соотношение \ (P = VI \) для всей цепи, потому что разность потенциалов такая же, как разность потенциалов на выводах аккумуляторной батареи: \ begin {align *} P & = VI \\ V & = \ frac {P} {I} \\ & = \ frac {\ text {6,42}} {\ text {1,07}} \\ & = \ текст {6,00} \ текст {V} \ end {align *}
Разность потенциалов на батарее равна \ (\ text {6,00} \) \ (\ text {V} \).
Мощность, рассеиваемая в \ (R_ {P \ text {1}} \) и \ (R_ {P \ text {2}} \)
Помните, что мы работаем от деталей всей схемы вниз к деталям отдельных элементов, это противоположно тому, как вы относились к этой схеме раньше.
Мы можем рассматривать параллельные сети как эквивалентные резисторы, поэтому схема, с которой мы сейчас работаем, с выглядит как:
Мы знаем, что ток через два элемента схемы будет одинаковым, потому что это последовательная цепь. и что сопротивление всей цепи должно быть: \ (R_ {Ext} = R_ {P \ text {1}} + R_ {P \ text {2}} \).Мы можем определить полное сопротивление по закону Ома для цепи в целом: \ begin {align *} V_ {батарея} & = IR_ {Ext} \\ R_ {Ext} & = \ frac {V_ {аккумулятор}} {I} \\ & = \ frac {\ text {6,00}} {\ text {1,07}} \\ & = \ текст {5,61} \ текст {Ω} \ end {align *}
Мы знаем, что соотношение между \ (R_ {P \ text {1}}: R_ {P \ text {2}} \) равно 1: 2, что означает, что мы знаем: \ begin {align *} R_ {P \ text {1}} & = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} \ \ \ text {и} \\ R_T & = R_ {P \ text {1}} + R_ {P \ text {2}} \\ & = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} + R_ {P \ text {2}} \\ & = \ frac {\ text {3}} {\ text {2}} R_ {P \ text {2}} \\ (\ text {5,61}) & = \ frac {\ text {3}} {\ text {2}} R_ {P \ text {2}} \\ R_ {P \ text {2}} & = \ frac {\ text {2}} {\ text {3}} (\ text {5,61}) \\ R_ {P \ text {2}} & = \ text {3,74} \ text {Ω} \ end {выровнять *} и поэтому: \ begin {align *} R_ {P \ text {1}} & = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} \\ & = \ frac {\ text {1}} {\ text {2}} (3.2 (\ text {3,74}) \\ & = \ текст {4,28} \ текст {W} \ end {выровнять *} Эти значения будут в сумме с исходным значением мощности, которое у нас было для внешней цепи. Если бы они не мы бы сделали ошибку в расчетах.
Расчет параллельной сети 1
Теперь мы можем приступить к детальному расчету первого набора параллельных резисторов.
Мы знаем, что соотношение между \ (R _ {\ text {1}}: R _ {\ text {2}} \) составляет 3: 5, что означает, что мы знаем \ (R _ {\ text {1}} = \ frac {\ text {3}} {\ text {5}} R _ {\ text {2}} \).Нам также известно общее сопротивление двух параллельных резисторов в этой сети. это \ (\ text {1,87} \) \ (\ text {Ω} \). Мы можем использовать соотношение между значениями двух резисторов, а также формула для общей сопротивление (\ (\ frac {\ text {1}} {R_PT} = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} {R_ \ text {2) }} \)) чтобы найти номиналы резисторов: \ begin {align *} \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} { R_ \ text {2}} \\ \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {5}} {3R_ \ text {2}} + \ frac {\ text {1}} { R_ \ text {2}} \\ \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {2}} (\ frac {\ text {5}} { \ text {3}} + 1) \\ \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {2}} (\ frac {\ text {5}} { \ text {3}} + \ frac {\ text {3}} {\ text {3}}) \\ \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {2}} \ frac {\ text {8}} {\ текст {3}} \\ R_ \ text {2} & = R_ {P \ text {1}} \ frac {\ text {8}} {\ text {3}} \\ & = (\ text {1,87}) \ frac {\ text {8}} {\ text {3}} \\ & = \ текст {4,99} \ текст {Ω} \ end {выровнять *} Мы также можем вычислить \ (R _ {\ text {1}} \): \ begin {align *} R _ {\ text {1}} & = \ frac {\ text {3}} {\ text {5}} R _ {\ text {2}} \\ & = \ frac {\ text {3}} {\ text {5}} (\ text {4,99}) \\ & = \ текст {2,99} \ текст {Ω} \ end {align *}
Для определения мощности нам потребуется рассчитанное нами сопротивление и либо разность потенциалов. 2} {\ text {4,99}} \\ & = \ текст {0,80} \ текст {W} \ end {align *}
Параллельная сеть 2 расчета
Теперь мы можем приступить к детальному расчету второго набора параллельных резисторов.
Нам дан \ (R_ \ text {3} = \ text {7,00} \ text {Ω} \), и мы знаем \ (R_ {P \ text {2}} \), поэтому мы можем вычислить \ (R_ \ text {4} \) из: \ begin {align *} \ frac {\ text {1}} {R_ {P \ text {2}}} & = \ frac {\ text {1}} {R_ \ text {3}} + \ frac {\ text {1}} { R_ \ text {4}} \\ \ frac {\ text {1}} {\ text {3,74}} & = \ frac {\ text {1}} {\ text {7,00}} + \ frac {\ text {1}} {R_ \ текст {4}} \\ R_ \ text {4} & = \ text {8,03} \ text {Ω} \ end {align *}
Мы можем вычислить разность потенциалов во второй параллельной сети, вычтя потенциал отличие первой параллельной сети от разности потенциалов аккумулятора, \ (V_ {P \ text {2}} = \ text {6,00} – \ text {2,00} = \ text {4,00} \ text {V} \).2} {\ text {8,03}} \\ & = \ текст {1,99} \ текст {W} \ end {align *}
Внутреннее сопротивление
Мы знаем, что ЭДС батареи равна \ (\ text {6,5} \) \ (\ text {V} \), но что разность потенциалов измеряется на терминалах только \ (\ text {6} \) \ (\ text {V} \). Разница в разнице потенциалов через внутреннее сопротивление батареи, и мы можем использовать известный ток и закон Ома для определения внутреннее сопротивление:
\ begin {align *} V & = I \ cdot R \\ R & = \ frac {V} {I} \\ & = \ frac {\ text {0,5}} {\ text {1,07}} \\ & = \ text {0,4672897} \\ & = \ текст {0,47} \ текст {Ω} \ end {выровнять *}Мощность, рассеиваемая внутренним сопротивлением батареи:
\ begin {align *} P & = VI \\ & = \ текст {0,5} \ cdot \ text {1,07} \\ & = \ текст {0,535} \ текст {W} \ end {выровнять *}Рабочий пример 10: Внутреннее сопротивление и фары [NSC 2011 Paper 1]
Фара и два ИДЕНТИЧНЫХ задних фонаря самоката подключены параллельно к аккумулятору с неизвестным внутреннее сопротивление, как показано на упрощенной принципиальной схеме ниже.Фара имеет сопротивление \ (\ text {2,4} \) \ (\ text {Ω} \) и управляется переключателем \ (\ textbf {S} _1 \). Задние фонари управляются переключателем \ (\ textbf {S} _2 \). Сопротивлением соединительных проводов можно пренебречь.
На приведенном рядом графике показана разность потенциалов на клеммах аккумулятора до и после переключатель \ (\ textbf {S} _1 \) закрыт (в то время как переключатель \ (\ textbf {S} _2 \) открыт). Переключатель \ (\ textbf {S} _1 \) есть закрыто в момент \ (\ textbf {t} _1 \).
Используйте график, чтобы определить ЭДС аккумулятора.
(1 балл)
ПРИ ТОЛЬКО ВЫКЛЮЧАТЕЛЬ \ (\ textbf {S} _1 \) ЗАКРЫТО, рассчитайте следующее:
Ток через фару
(3 балла)
Внутреннее сопротивление \ (r \) батареи
(3 балла)
ОБЕ ПЕРЕКЛЮЧАТЕЛИ \ (\ textbf {S} _1 \) И \ (\ textbf {S} _2 \) ТЕПЕРЬ ЗАКРЫТЫ.Аккумулятор выдает ток \ (\ text {6} \) \ (\ text {A} \) в этот период.
Рассчитайте сопротивление каждого заднего фонаря.
(5 баллов)
Как повлияет на показания вольтметра, если фара перегорит? (Оба переключателя \ (\ textbf {S} _1 \) и \ (\ textbf {S} _2 \) все еще закрыты.)
Запишите только УВЕЛИЧИВАЕТ, УМЕНЬШАЕТСЯ или ОСТАЕТСЯ ОДИН ТО ЖЕ.
Дайте объяснение.
(3 балла)
Вопрос 1
\ (\ text {12} \) \ (\ text {V} \)
(1 балл)
Вопрос 2.1
Вариант 1:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {9,6}} {\ text {2,4}} \\ & = \ текст {4 A} \ end {выровнять *}Вариант 2:
\ begin {align *} \ text {emf} & = IR + Ir \\ 12 & = I (\ text {2,4}) + \ text {2,4} \\ \ поэтому I & = \ text {4 A} \ end {выровнять *}(3 балла)
Вопрос 2.2
Вариант 1:
\ begin {align *} \ text {emf} & = IR + Ir \\ 12 & = \ text {9,4} + 4r \\ r & = \ текст {0,6} \ \ Omega \ end {выровнять *}Вариант 2:
\ begin {align *} V_ {потеряно} & = Ir \\ \ text {2,4} & = \ text {4} r \\ \ поэтому r & = \ text {0,6} \ \ Omega \ end {выровнять *}Вариант 3:
\ begin {align *} \ text {emf} & = I (R + r) \\ \ text {12} & = \ text {4} (\ text {2,4} + r) \\ \ поэтому r & = \ text {0,6} \ \ Omega \ end {выровнять *}(3 балла)
Вопрос 3
Вариант 1:
\ begin {align *} \ text {emf} & = IR + Ir \\ \ text {12} & = \ text {6} (R + \ text {0,6}) \\ R _ {\ text {ext}} & = \ text {1,4} \ \ Omega \ конец {выравнивание *} \ begin {выравнивание *} \ frac {1} {R} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {\ text {1,4}} & = \ frac {1} {\ text {2,4}} + \ frac {1} {R} \\ R & = \ текст {3,36} \ \ Omega \ end {выровнять *}Каждый задний фонарь: \ (R = \ text {1,68} \ \ Omega \)
Вариант 2:
\ begin {align *} \ text {Emf} & = V _ {\ text {terminal}} + Ir \\ 12 & = V _ {\ text {терминал}} + 6 (\ text {0,6}) \\ \ поэтому V _ {\ text {terminal}} & = \ text {8,4} \ text {V} \ конец {выравнивание *} \ begin {выравнивание *} I _ {\ text {2,4} \ \ Omega} & = \ frac {V} {R} \\ & = \ frac {\ text {8,4}} {\ text {2,4}} \\ & = \ text {3,5 A} \ конец {выравнивание *} \ begin {выравнивание *} I _ {\ text {задние фонари}} & = 6 – \ text {3,5} \\ & = \ текст {2,5} \ текст {A} \\ R _ {\ text {задние фонари}} & = \ frac {V} {I} \\ & = \ frac {\ text {8,4}} {\ text {2,5}} \\ & = \ текст {3,36} \ \ Omega \\ R _ {\ text {задний фонарь}} & = \ text {1,68} \ \ Omega \ end {выровнять *}Вариант 3:
\ begin {align *} V & = IR \\ \ text {12} & = \ text {6} (R) \\ R _ {\ text {ext}} & = 2 \ \ Omega \ конец {выравнивание *} \ begin {выравнивание *} R _ {\ text {parallel}} & = 2 – \ text {0,6} \\ & = \ текст {1,4} \ \ Omega \\ \ frac {1} {R} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {\ text {1,4}} & = \ frac {1} {\ text {2,4}} + \ frac {1} {R} \\ R & = \ текст {3,36} \ \ Omega \ end {выровнять *}Каждый задний фонарь: \ (R = \ text {1,68} \ \ Omega \)
Вариант 4:
Для параллельной комбинации: \ (I_ {1} + I_ {2} = 6 \ text {A} \)
\ begin {align *} \ поэтому \ frac {V} {\ text {2,4}} + \ frac {V} {R _ {\ text {задние фонари}}} & = \ text {6} \\ \ text {8,4} \ left (\ frac {1} {\ text {2,4}} + \ frac {1} {R _ {\ text {задние фонари}}} \ right) & = \ text {6 } \\ \ поэтому R _ {\ text {задние фонари}} & = \ text {3,36} \ \ Omega \\ R _ {\ text {задний фонарь}} & = \ text {1,68} \ \ Omega \ end {выровнять *}(5 баллов)
Вопрос 4
Увеличивается
Сопротивление увеличивается, а ток уменьшается.



 6
6 0
0
 Так не бывает. Младший разряд устройство не измеряет, а приписывает по неизвестному алгоритму. Величина сопротивления одной банки меняется более чем в два раза при измерениях. Такой разброс результатов привел к необходимости подсчета среднеарифметического от двух до восьми измерений ISDT Q6 Plus для записи в 1ю и 2ю таблицы. Результат одного измерения достоверен не больше, чем у первого устройства. Все эти результаты получены при токе заряда ISDT Q6 1 ампер. При токах более 5 ампер разброс показаний малых сопротивлений меньше 20%. Так же для более высоких сопротивлений разброс измерений меньше.
Так не бывает. Младший разряд устройство не измеряет, а приписывает по неизвестному алгоритму. Величина сопротивления одной банки меняется более чем в два раза при измерениях. Такой разброс результатов привел к необходимости подсчета среднеарифметического от двух до восьми измерений ISDT Q6 Plus для записи в 1ю и 2ю таблицы. Результат одного измерения достоверен не больше, чем у первого устройства. Все эти результаты получены при токе заряда ISDT Q6 1 ампер. При токах более 5 ампер разброс показаний малых сопротивлений меньше 20%. Так же для более высоких сопротивлений разброс измерений меньше. Однако посмотрим измерения второго и третьего аккумулятора во второй таблице. Оба зарядника определяют сопротивление третьего аккумулятора примерно в два раза больше, чем второго. Третий аккумулятор потерял часть своего ресурса. Измеритель YR1035 показывает сопротивление третьего в пределах +10% от второго, то есть не показывает двойной разницы. Если хоть немного доверять показаниям зарядников, то измерения на переменном токе недостаточно характеризуют работоспособность аккумулятора.
Однако посмотрим измерения второго и третьего аккумулятора во второй таблице. Оба зарядника определяют сопротивление третьего аккумулятора примерно в два раза больше, чем второго. Третий аккумулятор потерял часть своего ресурса. Измеритель YR1035 показывает сопротивление третьего в пределах +10% от второго, то есть не показывает двойной разницы. Если хоть немного доверять показаниям зарядников, то измерения на переменном токе недостаточно характеризуют работоспособность аккумулятора. 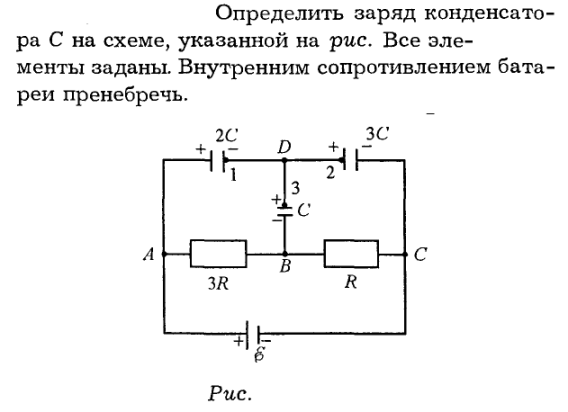 е. каким максимальным током можно его разряжать, сохраняя эффективную отдачу запасенной энергии. Чем меньше сопротивление, тем меньше внутренние потери и больше допустимый нагрузочный ток.
е. каким максимальным током можно его разряжать, сохраняя эффективную отдачу запасенной энергии. Чем меньше сопротивление, тем меньше внутренние потери и больше допустимый нагрузочный ток.