Как найти эдс индукции – расчет электродвижущей силы по формуле

Формула ЭДС индукции, E

Закон Фарадея – Максвелла для электромагнитной индукции

Основной формулой, которая определяет ЭДС индукции, является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). Этот закон утверждает, что ЭДС индукции в контуре, находящемся в переменном магнитном поле, равна по величине и противоположна по знаку скорости изменения магнитного потока () через поверхность, которую ограничивает данный контур:

   

где – скорость изменения магнитного потока. Полная производная в законе (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) соответствует правилу Ленца. Формула (1) для ЭДС индукции записана для системы СИ.

В случае равномерного изменения магнитного потока формулу ЭДС индукции можно записать как:

   

Частные случаи формул ЭДС индукции

Если контур содержит N витков, которые соединяются последовательно, то ЭДС индукции вычисляют как:

   

где – потокосцепление.

При движении прямолинейного проводника в однородном магнитном поле в нем возникает ЭДС индукции, которая равна:

   

где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; .

При вращении с постоянной скоростью в однородном магнитном поле плоского контура вокруг оси, которая лежит в плоскости контура в нем возникает ЭДС индукции, равная:

   

где S – площадь, которую ограничивает виток; – поток самоиндукции витка; — угловая скорость; () – угол поворота контура. Следует учесть, что формула (5) справедлива, если ось вращения составляет прямой угол с направлением вектора внешнего поля .

Если во вращающейся рамке имеется N витков и самоиндукцией рассматриваемой системы можно пренебречь, то:

   

В стационарном проводнике, который находится в переменном магнитном поле, ЭДС индукции находят по формуле:

   

Примеры решения задач по теме «ЭДС индукции»

ru.solverbook.com

расчет электродвижущей силы по формуле

Электромагнитная индукция – генерирование электротоков магнитными полями, изменяющимися во времени. Открытие Фарадеем и Генри этого феномена ввело определенную симметрию в мир электромагнетизма. Максвеллу в одной теории удалось собрать знания об электричестве и магнетизме. Его исследования предсказывали существование электромагнитных волн перед экспериментальными наблюдениями. Герц доказал их существование и открыл человечеству эпоху телекоммуникаций.

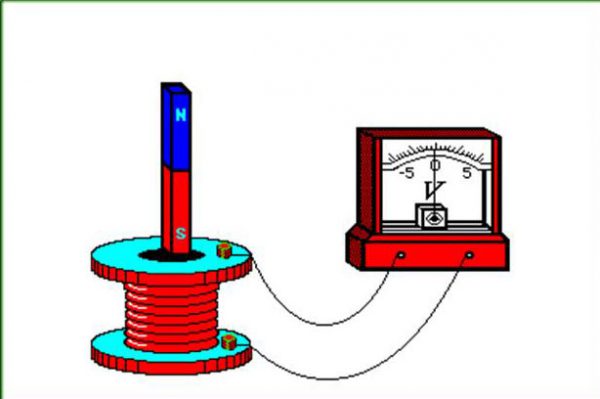
Эксперименты Фарадея

Законы Фарадея и Ленца

Электрические токи создают магнитные эффекты. А возможно ли, чтобы магнитное поле порождало электрическое? Фарадей обнаружил, что искомые эффекты возникают вследствие изменения МП во времени.

Когда проводник пересекается переменным магнитным потоком, в нем индуцируется электродвижущая сила, вызывающая электроток. Системой, которая генерирует ток, может быть постоянный магнит или электромагнит.

Явление электромагнитной индукции регулируется двумя законами: Фарадея и Ленца.

Закон Ленца позволяет охарактеризовать электродвижущую силу относительно ее направленности.

Важно! Направление индуцированной ЭДС такое, что вызванный ею ток стремится противостоять создающей его причине.

Фарадей заметил, что интенсивность индуцированного тока растет, когда быстрее изменяется число силовых линий, пересекающих контур. Другими словами, ЭДС электромагнитной индукции находится в прямой зависимости от скорости движущегося магнитного потока.

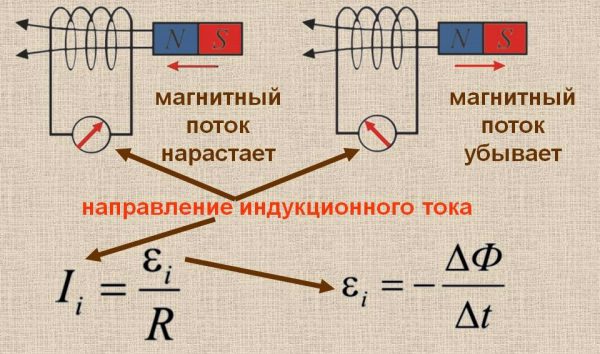
ЭДС индукции

Формула ЭДС индукции определена как:

Е = – dФ/dt.

Знак «-» показывает, как полярность индуцированной ЭДС связана со знаком потока и меняющейся скоростью.

Получена общая формулировка закона электромагнитной индукции, из которой можно вывести выражения для частных случаев.

Движение провода в магнитном поле

Когда провод длиной l движется в МП, имеющем индукцию В, внутри него будет наводиться ЭДС, пропорциональная его линейной скорости v. Для расчета ЭДС применяется формула:

• в случае движения проводника перпендикулярно направлению магнитного поля:

Е = – В x l x v;

• в случае движения под другим углом α:

Е = – В x l x v х sin α.

Индуцированная ЭДС и ток будут направлены в сторону, которую находим, пользуясь правилом правой руки: расположив руку перпендикулярно силовым линиям магнитного поля и указывая большим пальцем в сторону перемещения проводника, можно узнать направление ЭДС по оставшимся четырем распрямленным пальцам.

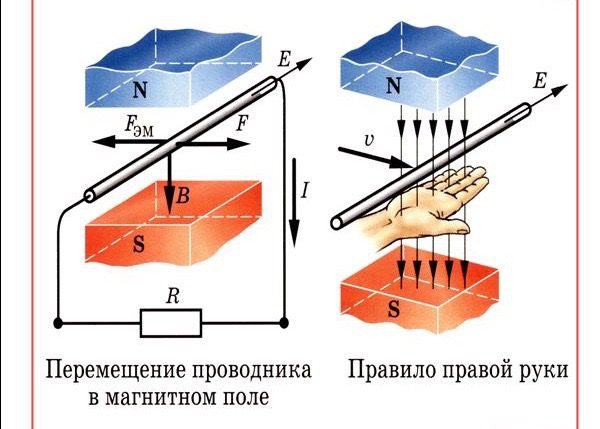
Перемещение провода в МП

Вращающаяся катушка

Работа генератора электроэнергии основана на вращении контура в МП, имеющего N витков.

ЭДС индуцируется в электроцепи всегда, когда магнитный поток ее пересекает, в соответствии с определением магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на поверхностную площадь, через которую проходит МП, и косинус угла, образованного вектором В и перпендикулярной линией к плоскости S).

Из формулы следует, что Ф подвержен изменениям в следующих случаях:

• меняется интенсивность МП – вектор В;
• варьируется площадь, ограниченная контуром;
• изменяется ориентация между ними, заданная углом.

В первых опытах Фарадея индуцированные токи были получены путем изменения магнитного поля В. Однако можно индуцировать ЭДС, не двигая магнит или не меняя ток, а просто вращая катушку вокруг своей оси в МП. В данном случае магнитный поток меняется из-за изменения угла α. Катушка при вращении пересекает линии МП, возникает ЭДС.

Если катушка вращается равномерно, это периодическое изменение приводит к периодическому изменению магнитного потока. Или количество силовых линий МП, пересекаемых каждую секунду, принимает равные значения с равными интервалами времени.

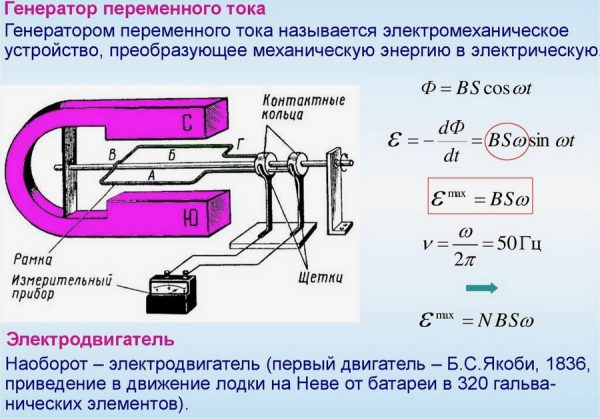
Вращение контура в МП

Важно! Наведенная ЭДС меняется вместе с ориентацией с течением времени от положительной до отрицательной и наоборот. Графическое представление ЭДС представляет собой синусоидальную линию.

Для формулы ЭДС электромагнитной индукции применяется выражение:

Е = В х ω х S x N x sin ωt, где:

• S – площадь, ограниченная одним витком или рамкой;
• N – количество витков;
• ω – угловая скорость, с которой вращается катушка;
• В – индукция МП;
• угол α = ωt.

На практике в генераторах переменного тока часто катушка остается неподвижной (статор), а электромагнит вращается вокруг нее (ротор).

ЭДС самоиндукции

Когда через катушку проходит переменный ток, он генерирует переменное МП, обладающее изменяющимся магнитным потоком, индуцирующим ЭДС. Этот эффект называется самоиндукцией.

Поскольку МП пропорционально интенсивности тока, то:

Ф = L x I,

где L – индуктивность (Гн), определяемая геометрическими величинами: количеством витков на единицу длины и размерами их поперечного сечения.

Для ЭДС индукции формула принимает вид:

Е = – L x dI/dt.

Взаимоиндукция

Если две катушки расположены рядом, то в них наводится ЭДС взаимоиндукции, зависящая от геометрии обеих схем и их ориентации относительно друг друга. Когда разделение цепей возрастает, взаимоиндуктивность снижается, так как уменьшается соединяющий их магнитный поток.

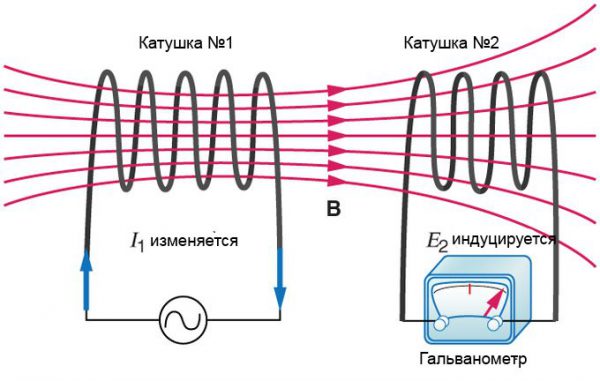
Взаимоиндукция

Пусть имеется две катушки. По проводу одной катушки, обладающей N1 витками, протекает ток I1, создающий МП, проходящее через катушку с N2 витками. Тогда:

1. Взаимоиндуктивность второй катушки относительно первой:

М21 = (N2 x F21)/I1;

2. Магнитный поток:

Ф21 = (М21/N2) x I1;

3. Найдем индуцированную ЭДС:

Е2 = – N2 x dФ21/dt = – M21x dI1/dt;

4. Идентично в первой катушке индуцируется ЭДС:

Е1 = – M12 x dI2/dt;

Важно! Электродвижущая сила, вызванная взаимоиндукцией в одной катушке, всегда пропорциональна изменению электротока в другой.

Взаимную индуктивность можно признать равной:

М12 = М21 = М.

Соответственно, E1 = – M x dI2/dt и E2 = M x dI1/dt.

М = К √ (L1 x L2),

где К – коэффициент связи между двумя индуктивностями.

Явление взаимоиндукции используется в трансформаторах – электроаппаратах, позволяющих изменить значение напряжения переменного электротока. Аппарат представляет собой две катушки, намотанные вокруг одного сердечника. Ток, присутствующий в первой, создает меняющееся МП в магнитопроводе и электроток в другой катушке. Если количество витковых оборотов первой обмотки меньше, чем другой, напряжение увеличивается, и наоборот.

Кроме генерирования, трансформации электроэнергии магнитная индукция применяется в иных устройствах. Например, в магнитных левитационных поездах, которые двигаются не в непосредственном контакте с рельсами, а на несколько сантиметров выше из-за электромагнитной силы отталкивания.

Видео

Оцените статью:

jelectro.ru

Эдс индукции

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

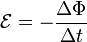
где 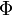— поток магнитного поля через замкнутую поверхность 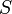, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).

41. Индуктивность, ее единица СИ. Индуктивность длинного соленоида.

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность^[1], краем которой является этот контур.^[2][3][4].

В формуле

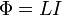
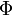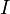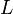— магнитный поток, — ток в контуре, — индуктивность.

• Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно – в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока^[4]:

.

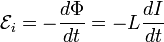Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током^[4]:

.

Обозначение и единицы измерения

В системе единиц СИ индуктивность измеряется в генри^[7], сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 10⁹см)^[4]. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.

Символ 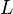, используемый для обозначения индуктивности, был взят в честь Ленца Эмилия Христиановича (Heinrich Friedrich Emil Lenz)^{[источник не указан 1017 дней]}. Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry)^[8]. Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года

[^{источник не указан 1017 дней]}.

Электрический ток, который течет в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, согласно закону Био-Савара-Лапласа, пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому прямо пропорционален току I в контуре: 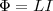 (1)  где коэффициент пропорциональности L называетсяиндуктивностью контура.  При изменении в контуре силы тока будет также изменяться и сцепленный с ним магнитный поток; значит, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называетсясамоиндукцией.  Из выражения (1) задается единица индуктивности генри (Гн): 1 Гн — индуктивность контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В

·c/А . 

Вычислим индуктивность бесконечно длинного соленоида. Полный магнитный поток сквозь соленоид (потокосцепление) равен μ₀μ(N²I/l)S . Подставив в (1), найдем  (2)  т. е. индуктивность соленоида зависит от длиныl солениода, числа его витков N, его , площади S и магнитной проницаемости μ вещества, из которого изготовлен сердечник соленоида.  Доказано, что индуктивность контура зависит в общем случае только от геометрической формы контура, его размеров и магнитной проницаемости среды, в которой он расположен, и можно провести аналог индуктивности контура с электрической емкостью уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды.  Найдем, применяя к явлению самоиндукции закон Фарадея, что э.д.с. самоиндукции равна 

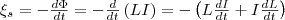
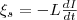Если контур не претерпевает деформаций и магнитная проницаемость среды остается неизменной (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L = const и(3)  где знак минус, определяемый правилом Ленца, говорит о том, чтоналичие индуктивности в контуре приводит к замедлению изменения тока в нем.  Если ток со временем увеличивается, то (dI/dt<0) и ξ_s>0 т. е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и замедляет его увеличение. Если ток со временем уменьшается, то (dI/dt>0) и ξ_s<0 т. е. индукционный ток имеет такое же направление, как и уменьшающийся ток в контуре, и замедляет его уменьшение. Значит, контур, обладая определенной индуктивностью, имеет электрическую инертность, заключающуюся в том, что любое изменение тока уменьшается тем сильнее, чем больше индуктивность контура.

 

42. Ток при размыкании и замыкании цепи.

При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.

Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с. 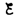, резистор сопротивлением 

R и катушку индуктивностью L. Под действием внешней э. д. с. в цепи течет постоянный ток

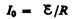
(внутренним сопротивлением источника тока пренебрегаем).

В момент времени t=0 отключим источник тока. Ток в катушке индуктивностью L начнет уменьшаться, что приведет к возникновению э.д.с. самоиндукции 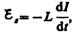препятствующей, согласно правилу Ленца, уменьшению тока. В каждый момент време­ни ток в цепи определяется законом Ома I=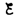_s/R, или

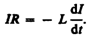(127.1)

Разделив в выражении (127.1) переменные, получим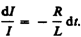 

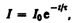Интегрируя это уравнение по I (от I₀ до I) и t (от 0 до t), находим ln (I /I₀) = –Rt/L, или

(127.2)

где =L/R — постоянная, называемая временем релаксации. Из (127.2) следует, что  есть время, в течение которого сила тока уменьшается в е раз.

Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону (127.2) и определяется кривой 1 на рис. 183. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше  и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.

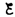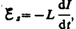При замыкании цепи помимо внешней э. д. с.  возникает э. д. с. самоиндукции препятствующая, согласно правилу Ленца, возрастанию тока. По закону Ома, 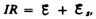или

Введя новую переменную 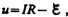преобразуем это уравнение к виду

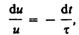
где  — время релаксации.

В момент замыкания (t=0) сила тока I = 0 и u = –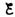. Следовательно, интегрируя по и (от –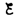 до IR–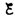) и t (от 0 до t), находим ln[(IR–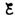)]/–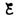= —t/, или

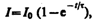(127.3)

где 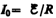— установившийся ток (при t).

Таким образом, в процессе включения источника тока нарастание силы тока в цепи задается функцией (127.3) и определяется кривой 2 на рис. 183. Сила тока возрастает от начального значения I=0 и асимптотически стремится к установившемуся значению 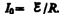. Скорость нарастания тока определяется тем же временем релаксации =L/R, что и убывание тока. Установление тока происходит тем быстрее, чем меньше индук­тивность цепи и больше ее сопротивление.

Оценим значение э.д.с. самоиндукции 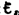, возникающей при мгновенном увеличении сопротивления цепи постоянного тока от R₀ до R. Предположим, что мы размыкаем контур, когда в нем течет установившийся ток 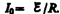. При размыкании цепи ток изменяется по формуле (127.2). Подставив в нее выражение дляI₀ и , получим

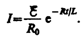
Э.д.с. самоиндукции

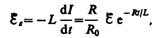
т. е. при значительном увеличении сопротивления цепи (R/R₀>>1), обладающей боль­шой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникнове­ние значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.

43. Явление взаимной индукции. Трансформатор.

Рассмотрим два неподвижных контура (1 и 2), которые расположены достаточно близко друг от друга (рис. 1). Если в контуре 1 протекает ток I₁, то магнитный поток, который создавается этим током (поле, создающее этот поток, на рисунке изображено сплошными линиями), прямо пропорционален I₁. Обозначим через Ф₂₁ часть потока,пронизывающая контур 2. Тогда 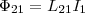  (1)  где L₂₁ — коэффициент пропорциональности. 

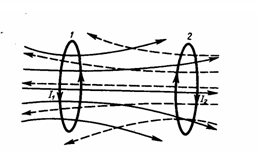
Рис.1

Если ток I₁ меняет свое значение, то в контуре 2 индуцируется э.д.с. ξ_i2 , которая по закону Фарадея будет равна и противоположна по знаку скорости изменения магнитного потока Ф₂₁, который создается током в первом контуре и пронизыващет второй: 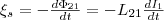   Аналогичным образом, при протекании в контуре 2 тока I₂ магнитный поток (его поле изображено на рис. 1 штрихами) пронизывает первый контур. Если Ф₁₂ — часть этого потока, который пронизывает контур 1, то 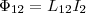   Если ток I₂ меняет свое значение, то в контуре 1 индуцируется э.д.с. ξ_i1 , которая равна и противоположна по знаку скорости изменения магнитного потока Ф₁₂, который создается током во втором контуре и пронизывает первый: 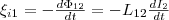   Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L₂₁ и L₁₂ называются взаимной индуктивностью контуров. Расчеты, которые подтверждены опытом, показывают, что L₂₁ и L₁₂ равны друг другу, т. е. 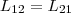  (2)  Коэффициенты пропорциональности L₁₂ и L₂₁ зависят от размеров, геометрической формы, взаимного расположения контуров и от магнитной проницаемости среды, окружающей контуры. Единица взаимной индуктивности та же, что и для индуктивности, — генри (Гн).  Найдем взаимную индуктивность двух катушек, которые намотаны на общий тороидальный сердечник. Этот случай имеет большое практическое значение (рис. 2). Магнитная индукция поля, которое создавается первой катушкой с числом витков N₁, током I₁ и магнитной проницаемостью μ сердечника, B = μμ₀(N₁I₁/l) где l — длина сердечника по средней линии. Магнитный поток сквозь один виток второй катушки Ф₂ = BS = μμ₀(N₁I₁/l)S 

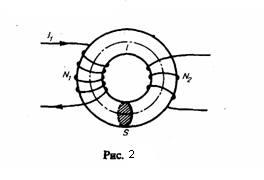
Значит, полный магнитный поток (потокосцепление) сквозь вторичную обмотку, которая содержит N₂ витков, 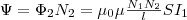   Поток Ψ создается током I₁, поэтому, используя (1), найдем 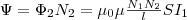  (3)  Если рассчитать магнитный поток, который создавается катушкой 2 сквозь катушку 1, то для L₁₂ получим выражение в соответствии с формулой (3). Значит, взаимная индуктивность двух катушек, которые намотаны на общий тороидальный сердечник,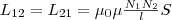   

Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока

studfile.net

Магнитный поток и ЭДС индукции

Продолжаем решать задачи на магнитный поток и ЭДС индукции. Здесь уже будет потяжелее: придется и производную, и первообразную находить. Но задачи интересные, и даже геометрические знания пригодились, а именно, формула площади треугольника.

Задача 1. Плоский замкнутый металлический контур площадью см, находится в однородном магнитном поле, индукция которого Тл. Площадь контура за время c равномерно уменьшается до см (плоскость контура при этом остается перпендикулярной магнитному полю). Определите силу тока (в мкА), протекающего по контуру в течение времени , если сопротивление контура Ом.

   

Поток уменьшился с до , его изменение . Следовательно,

   

Ток равен

   

Ответ: 16 мкА

Задача 2. Медное кольцо радиусом см из проволоки диаметром мм  расположено в однородном магнитном поле, изменяющемся со скоростью Тл/с. Плоскость кольца перпендикулярна силовым линиям магнитного поля. Определите силу индукционного тока, возникающего в кольце. Удельное сопротивление меди равно Ом м.

Сопротивление кольца равно

   

Ток в кольце будет равен

   

Ответ: 0,693 А
Задача 3. При изменении силы тока в замкнутом контуре индуктивностью Гн  ЭДС самоиндукции изменялась согласно графику (см. рис.). Чему равна величина изменения тока в интервале времени 1-4 с?

К задаче 3

Так как

   

То, чтобы найти ток, нужно найти интеграл. То есть – определить площадь под графиком с первой по 4 секунду. Площадь будет равна сумме площадей трапеции и прямоугольника: 3+8.

   

Ответ: 0,11 А

Задача 4. В однородном магнитном поле с индукцией В = 0,2 Тл начинает двигаться металлический стержень длиной см перпендикулярно вектору магнитной индукции. Координата стержня изменяется по закону . Какая разность потенциалов возникает между концами стержня через 5 с?

Скорость стержня к указанному моменту времени будет равна:

   

Следовательно, ЭДС:

   

Ответ: 0,68 В.

Задача 5. Проводящий квадратный контур со стороной см, помещенный в однородное магнитное поле с индукцией В = 0,5 Тл, вектор которой перпендикулярен плоскости контура, складывают пополам (см. рис.). Какой заряд протечет по контуру, если сопротивление единицы длины контура равно  Ом/м?

К задаче 5

Площадь контура, складывая его, уменьшают до нуля. Поэтому изменение потока равно . Следовательно,

   

Откуда

   

Ответ: 0,125 Кл.
Задача 6. Напряжение на зажимах рамки, начинающей вращаться в однородном магнитном поле, изменяется с течением времени согласно графику на рисунке. Чему приблизительно равна величина магнитного потока, пересекающего рамку в момент времени с?

К задаче 7

Напряжение на зажимах, или ЭДС, есть производная потока, поэтому поток – первообразная ЭДС. ЭДС, судя по графику, можно записать так:

   

Период равен 4 с, тогда . Амплитуда ЭДС равна 40 мВ, следовательно,

   

Определяем первообразную, то есть берем интеграл:

   

Подставим нужное время:

   

Ответ: 18 мВб.
Задача 7. Плоская проволочная рамка находится в магнитном поле, его плоскость перпендикулярна линиям индукции. При равномерном уменьшении магнитного поля до нуля за время с в рамке возник постоянный ток А. Какой ток потечет по рамке при ее повороте в этом поле с постоянной угловой скоростью на угол за время с вокруг оси, перпендикулярной вектору В и лежащей в плоскости рамки?

И в том, и в другом случае меняется поток через рамку. Но индукция поля остается неизменной, ее–то и надо найти:

   

Откуда

   

Если рамку повернуть, то изменится площадь, пронизываемая потоком:

   

Тогда

   

Подставим индукцию, найденную ранее:

   

Ответ: 6 мА.
Задача 8. Квадратная рамка со стороной см помещена в однородное магнитное поле с индукцией мТл так, что линии индукции перпендикулярны плоскости рамки (см. рис.). Сопротивление рамки 1 Ом. Какое количество тепла выделится в рамке за 10 с, если ее выдвигать из области, в которой создано поле со скоростью 1 см/с, перпендикулярной линиям индукции? Поле сосредоточено в некоторой четко ограниченной области.

К задаче 8

Площадь рамки, помещенная в поле, будет изменяться. Поэтому поток меняется и в рамке наводится ЭДС.

   

Ток будет равен:

   

При протекании такого тока выделится количество теплоты

   

Ответ: 0,8 нДж

Задача 9. Квадратная рамка помещена в однородное магнитное поле. Нормаль к плоскости рамки составляет с направлением магнитного поля угол . Сторона рамки см. Известно, что среднее значение ЭДС индукции, возникающей в рамке при выключении поля в течение времени с, равно 50 мВ. С какой силой подействовало бы это магнитное поле на протон, влетевший в него со скоростью м/с перпендикулярно вектору ?

. Следовательно,

   

Пронизываемая потоком площадь рамки равна

   

Тогда

   

Найдем из этого выражения индукцию поля:

   

Сила Лоренца равна

   

Ответ: Н.
Задача 10. Рамка сопротивлением 15 Ом, имеющая форму равностороннего треугольника, помещена  в однородное магнитное поле с индукцией Тл. Плоскость рамки составляет с направлением вектора угол . Определите длину стороны рамки , если при равномерном уменьшении индукции В до нуля в течение с в проводнике рамки выделяется количество тепла 0,5 мДж.

По закону Джоуля-Ленца

   

Откуда

   

По закону Ома ,

   

Площадь рамки равна , площадь, пронизываема потоком, равна

   

Тогда

   

Откуда

   

   

Ответ : м.

easy-physic.ru

определение и формула, в чём измеряется, работа источника электродвижущей силы

Электрический ток не протекает в медном проводе по той же причине, по которой остаётся неподвижной вода в горизонтальной трубе. Если один конец трубы соединить с резервуаром таким образом, чтобы образовалась разность давлений, жидкость будет вытекать из одного конца. Аналогичным образом, для поддержания постоянного тока необходимо внешнее воздействие, перемещающее заряды. Это воздействие называется электродвижущая сила или ЭДС.

От электростатики к электрокинетике

Между концом XVIII и началом XIX века работы таких учёных, как Кулон, Лагранж и Пуассон, заложили математические основы определения электростатических величин. Прогресс в понимании электричества на этом историческом этапе очевиден. Франклин уже ввёл понятие «количество электрической субстанции», но пока ещё и он, ни его преемники не смогли его измерить.

Следуя за экспериментами Гальвани, Вольта пытался найти подтверждения того, что «гальванические жидкости» животного были одной природы со статическим электричеством. В поисках истины он обнаружил, что когда два электрода из разных металлов контактируют через электролит, оба заряжаются и остаются заряженными несмотря на замыкание контура нагрузкой. Это явление не соответствовало существующим представлениям об электричестве потому, что электростатические заряды в подобном случае должны были рекомбинировать.

Вольта ввёл новое определение силы, действующей в направлении разделения зарядов и поддержании их в таком состоянии. Он назвал её электродвижущей. Подобное объяснение описания работы батареи не вписывалось в теоретические основы физики того времени. В Кулоновской парадигме первой трети XIX века э. д. с. Вольта определялась способностью одних тел вырабатывать электричество в других.

Важнейший вклад в объяснение работы электрических цепей внёс Ом. Результаты ряда экспериментов привели его к построению теории электропроводности. Он ввёл величину «напряжение» и определил её как разность потенциалов на контактах. Подобно Фурье, который в своей теории различал количество тепла и температуру в теплопередаче, Ом создал модель по аналогии, связывающую количество перемещаемого заряда, напряжение и электропроводность. Закон Ома не противоречил накопленным знаниям об электростатическом электричестве.

Затем, благодаря Максвеллу и Фарадею, пояснительные модели тока получили новую теорию поля. Это позволило разработать связанную с полем концепцию энергии как для статических потенциалов, так и для электродвижущей силы. Основные даты эволюции понятия ЭДС:

• 1800 г. — создание Вольтой гальванической батареи;
• 1826 г. — Ом формулирует свой закон для полной цепи;
• 1831 г. — обнаружение электромагнитной индукции Фарадеем.

Определение и физический смысл

Приложение некоторой разности потенциалов между двумя концами проводника создаст перетекание электронов от одного конца к другому. Но этого недостаточно для поддержания потока зарядов в проводнике. Дрейф электронов приводит к уменьшению потенциала до момента его уравновешивания (прекращение тока). Таким образом, для создания постоянного тока необходимы механизмы, непрерывно возвращающие описанную систему в первоначальную конфигурацию, то есть, препятствующие агрегации зарядов в результате их движения. Для этой цели используются специальные устройства, называемые источники питания.

В качестве иллюстрации их работы удобно рассматривать замкнутый контур из сопротивления и гальванического источника питания (батареи). Если предположить, что внутри батареи тока нет, то описанная проблема объединения зарядов остаётся неразрешённой. Но в цепи с реальным источником питания электроны перемещаются постоянно. Это происходит благодаря тому, что поток ионов протекает и внутри батареи от отрицательного электрода к положительному. Источник энергии, перемещающий эти заряды в батарее — химические реакции. Такая энергия называется электродвижущей силой.

ЭДС является характеристикой любого источника энергии, способного управлять движением электрических зарядов в цепи. В аналогии с замкнутым гидравлическим контуром работа источника э. д. с. соответствует работе насоса для создания давления воды. Поэтому значок, обозначающий эти устройства, неотличим на гидравлических и электрических схемах.

Несмотря на название, электродвижущая сила на самом деле не является силой и измеряется в вольтах. Её численное значение равно работе по перемещению заряда по замкнутой цепи. ЭДС источника выражается формулой E=A/q, в которой:

• E — электродвижущая сила в вольтах;
• A — работа сторонних сил по перемещению заряда в джоулях;
• q — перемещённый заряд в кулонах.

Из этой формулы ЭДС следует, что электродвижущая сила не является свойством цепи или нагрузки, а есть способность генератора электроэнергии к разделению зарядов.

Сравнение с разностью потенциалов

Электродвижущая сила и разность потенциалов в цепи очень похожие физические величины, так как оба измеряются в вольтах и определяются работой по перемещению заряда. Одно из основных смысловых различий заключается в том, что э. д. с. (E) вызывается путём преобразования какой-либо энергии в электрическую, тогда как разность потенциалов (U) реализует электрическую энергию в другие виды. Другие различия выглядят так:

• E передаёт энергию всей цепи. U является мерой энергии между двумя точками на схеме.
• Е является причиной U, но не наоборот.
• Е индуцируется в электрическом, магнитном и гравитационном поле.
• Концепция э. д. с. применима только к электрическому полю, в то время как разность потенциалов применима к магнитным, гравитационным и электрическим полям.

Напряжение на клеммах источника питания, как правило, отличается от ЭДС источника. Это происходит из-за наличия внутреннего сопротивления источника (электролита и электродов, обмоток генератора). Связывающая разность потенциалов и ЭДС источника тока формула выглядит как U=E-Ir. В этом выражении:

• U — напряжение на клеммах источника;
• r — внутреннее сопротивление источника;
• I — ток в цепи.

Из этой формулы электродвижущей силы следует, что э. д. с. равна напряжению когда ток в цепи не течёт. Идеальный источник ЭДС создаёт разность потенциалов независимо от нагрузки (протекающего тока) и не обладает внутренним сопротивлением.

В природе не может существовать источника с бесконечной мощностью при замыкании на клеммах, как и материала с бесконечной проводимостью. Идеальный источник используется как абстрактная математическая модель.

Источники электродвижущей силы

Суть источника ЭДС заключается в преобразовании других видов энергии в электрическую с помощью сторонних сил. С точки зрения физики обеспечения э. д. с различают следующие два основных вида источников:

• гальванические;
• электромагнитные.

Первые представляют собой электрохимические источники, основанные на вовлечение в химическую реакцию процесса переноса электронов. В обычных условиях химические взаимодействия сопровождаются выделением или поглощением тепла, но существует немало реакций, в результате которых генерируется электрическая энергия.

Электрохимические процессы в большинстве случаев обратимы, поскольку энергия электрического тока может быть использована, чтобы заставить реагировать вещества между собой. Эта возможность позволяет создавать возобновляемые гальванические источники — аккумуляторы.

В генераторах тока э. д. с. создаётся другим способом. Разделение зарядов происходит с помощью явления электромагнитной индукции, которое заключается в том, что изменение величины или направления магнитного поля создаёт ЭДС. Согласно закону Фарадея, нахождение э. д. с. индукции возможно из выражения E=—dФ/dt. В этой формуле:

• Ф — магнитный поток;
• t — время.

ЭДС индукции измеряется также в вольтах. В зависимости от того, каким способом вызываются изменения магнитного потока, различают:

• Динамически индуцированную. Когда в стационарном магнитном поле перемещается проводник. Характерен для генераторов.
• Статически индуцированную. Когда изменения потока возникают из-за изменений магнитного поля вокруг неподвижного проводника. Так работают трансформаторы.

Существуют также источники э. д. с, не основанные на электрохимии или магнитной индукции. К таким устройствам можно отнести полупроводниковые фотоэлементы, контактные потенциалы и пьезокристаллы. Понятие ЭДС имеет практическое применение прежде всего как параметр выбора источников питания для тех или иных целей. Чтобы получить максимальный эффект от работы устройств в цепи, нужно согласовывать их возможности и характеристики. Прежде всего внутреннее сопротивление источника ЭДС силы с характеристиками подключаемой нагрузки.

rusenergetics.ru

Электродвижущая сила индукции

Электрические токи порождают вокруг себя магнитные поля. Данная связь дала толчок к многочисленным попыткам создать электрический ток в контуре при помощи магнитного поля.

Данную задачу решил М. Фарадей в 1831 году. Ученый открыл явление электромагнитной индукции.

Электромагнитная индукция

Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре, если изменяется поток магнитной индукции, который рассматриваемый контур охватывает, появляется электрический ток. Возникающий электрический ток называют током индукции.

Анализируя свои множественные эксперименты, М. Фарадей пришел к выводу о том, что:

1. Индукционный ток появляется всегда при изменении магнитного потока, который охватывает проводящий контур. Так, если в однородном магнитном поле проводящий замкнутый контур повернуть, то в момент разворота в нем будет течь ток индукции. В этом случае индукция магнитного поля постоянна около проводящего контура, переменным является только поток магнитной индукции, который изменяется за счет изменения площади контура.
2. Величина тока индукции не связана со способом изменения магнитного потока. Она определена только скоростью его изменения. Сила тока индукции тем больше, чем больше скорость перемещения магнита, или быстрота изменения силы тока, или скорость перемещения катушек.

Электромагнитная индукция подтверждает связь между электрическими и магнитными явлениями.

Закон Фарадея

Анализируя данные своих экспериментов, М. Фарадей предложил количественный закон, описывающий электромагнитную индукцию. Ученый доказал, что каждый раз при изменении потока магнитной индукции, который сцеплен с проводящим контуром, в проводнике появляется ток индукции. Наличие индукционного тока означает то, что в цепи присутствует электродвижущая сила (ЭДС), которую в данном случае называют электродвижущей силой электромагнитной индукции ($Ɛ_i$).

Величина тока индукции, а значит, и величина $Ɛ_i$ зависит от скорости изменения магнитного потока:

$\left|Ɛ_{i} \right|=\frac{dФ}{dt}\left( 1 \right)$.

где $Ф$ – поток магнитной индукции.

Определимся со знаком ЭДС индукции. Знак потока магнитной индукции связан с выбором положительной нормали к рассматриваемому проводящему контуру. А направление силы тока и направление нормали связывает правило правого буравчика (винта). Получается, что фиксируя направление нормали, мы устанавливаем знак магнитного потока, направление тока и $Ɛ_i$ в контуре.

Сформулируем закон электромагнитной индукции Фарадея в окончательном виде:

Определение 1

Не зависимо от причины изменения магнитного потока, который охватывает замкнутый проводящий контур, электродвижущая сила индукции, появляющаяся в этом контуре равна:

$Ɛ_{i}=-\frac{dФ}{dt}\left( 2 \right)$.

где под $\frac{dФ}{dt}$ понимают полную скорость изменения потока магнитной индукции, охватываемого проводником.

Минус в формуле (2) указывает на то, что:

• При росте потока магнитной индукции (скорость изменения магнитного потока больше нуля) ($\frac{dФ}{dt}>0)$, ЭДС индукции меньше нуля ($Ɛ_i
• При уменьшении потока магнитной индукции (скорость изменения магнитного потока меньше нуля), ЭДС индукции больше нуля ($Ɛ_i>0$). Что значит, направление потока и направление поля тока индукции совпадают.

Замечание 1

Знак минус в формуле (2) – это математическое отображение правила Ленца, которое используют для того, чтобы найти направление тока индукции.

Закон Фарадея справедлив при:

1. произвольных перемещениях замкнутого проводящего контура;
2. при любых его деформациях;
3. изменениях магнитного поля.

ЭДС индукции измеряется с Международной системе единиц (СИ) в вольтах (В).

$\left[ Ɛ_{i} \right]=\left[ \frac{dФ}{dt} \right]=\frac{Вб}{с}$=В.

Значение закона Фарадея

Закон Фарадея выражает новое физическое явление, в котором переменное магнитное поле порождает электрическое поле. Отсюда делается вывод о том, что электрическое поле может порождаться не только электрическими зарядами, но и изменяющимся магнитным полем.

Электромагнитная индукция – это всеобщий фундаментальный закон природы, реализующий связь между электрическими и магнитными полями.

Природа электродвижущей силы индукции

Если проводник перемещается в магнитном поле, то на свободные электроны его вещества действуют силы Лоренца. Эти электроны под воздействием названной силы приходят в движение относительно проводника, что означает: в проводнике появляется ток.

Рисунок 1. Проводники. Автор24 — интернет-биржа студенческих работ

Рассмотрим прямой участок $DG$ проводника на рис.1. Этот участок перемещается со скоростью $\vec v$ по проводникам $CK$ и $AL$, как по направляющим. При этом контур $AGDCA$ постоянно замкнут. Вектор индукции внешнего магнитного поля нормален плоскости рассматриваемого контура. Магнитное поле будем считать однородным. На заряды, которые перемещаются вместе с проводником, действует сила Лоренца, равная:

$\vec{F}_{L}=q\left( \vec{v}\times \vec{B} \right)\left( 3 \right)$.

где$ \vec{B}$– индукция внешнего магнитного поля. Под воздействием силы Лоренца свободные электроны проводника приходят в движение и образуют электрический ток. Направление этого тока принимают за положительный обход контура, положительная нормаль ($\vec n$) к площади контура указана на рис.1.

Наличие силы Лоренца эквивалентно тому, что в проводнике на заряды действует электрическое поле напряженность которого равна:

$\vec{E}=\frac{\vec{F}_{L}}{q}=\vec{v}\times \vec{B}\left( 4 \right)$.

Поэтому ЭДС индукции между точками 1 и 2 проводника найдем как:

$\left( Ɛ_{i} \right)_{21}=\int\limits_1^2 \vec{E} d\vec{l}=\int\limits_1^2\left( \vec{v}\times \vec{B} \right) d\vec{l}\left( 5 \right)$.

В случае, который мы рассматриваем на рис.1 точки 1 и 2 соответствуют точкам $D$ и $G$:

$\left( Ɛ_{i} \right)_{DG}=\int\limits_G^D {vBdl=vBl\, \left( 6 \right).} $

На не движущихся участках замкнутого контура, который мы рассматриваем, ЭДС не возникает. Следовательно, ЭДС контура равна ЭДС подвижного проводника $DG$, перемещающейся в магнитном поле.

$Ɛ_{i}=\int\limits_{AGDCA} {\vec{E}d\vec{l}=vBl\, \left( 7 \right).} $

Скорость перемещения проводника выразим как:

$v=\frac{dx}{dt}\left( 8 \right)$.

где $x$ – координата контактов проводника в точках $D$ и $G$ направляющими проводниками:

$Ɛ_{i}=Bl\frac{dx}{dt}\left( 9 \right)$.

Учитывая, что:

$Ф=-xlB$ (10),

где $Ф$ – поток магнитной индукции через поверхность, которую ограничивает контур $AGDCA$. Знак минус указывает на то, что направления векторов $\vec B$ и $ d\vec S$ противоположны,

окончательно имеем:

$Ɛ_{i}=-\frac{dФ}{dt}\left( 11 \right)$.

Выражение (11) мы получили, рассматривая движение части проводника. При перемещении нескольких участков проводника, ЭДС индукции находят как алгебраическую сумму ЭДС индукции, появляющихся на каждом участке.

spravochnick.ru

Репетитор-онлайн — подготовка к ЦТ

Пример 13. Проводящий контур, имеющий форму квадрата со стороной 20 см, помещен в однородное магнитное поле с индукцией 45 мТл. Плоскость контура составляет угол 30° с направлением силовых линий поля. За 0,15 с контур поворачивают таким образом, что его плоскость устанавливается перпендикулярно силовым линиям поля. Найти среднее значение ЭДС индукции, возникающей в контуре при его повороте в магнитном поле.

Решение. Появление ЭДС индукции в контуре вызвано изменением потока вектора индукции, пронизывающего плоскость квадрата, при повороте контура в магнитном поле.

Поток индукции магнитного поля через площадь квадрата определяется формулами:

• в первом положении контура (до поворота)

Ф₁ = BS cos α₁,

где B — модуль индукции магнитного поля, B = 45 мТл; S — площадь квадрата, S = a ²; a — сторона квадрата, a = 20 см; α₁ — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости квадрата в первом положении контура, α₁ = = 90° − 30° = 60°;

• во втором положении контура (после поворота)

Ф₂ = BS cos α₂,

где α₂ — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости квадрата во втором положении контура, α₂ = 0°.

Изменение потока вектора индукции магнитного поля определяется разностью

ΔФ=Ф2−Ф1=BScos0°−BScos60°=BS2.

Среднее значение ЭДС индукции, возникающей в контуре при его повороте в магнитном поле:

〈ℰi〉=|ΔФΔt|=−BS2Δt=Ba22Δt,

где ∆t — интервал времени, за который происходит поворот контура, ∆t = 0,15 с.

Расчет дает значение:

〈ℰi〉=45⋅10−3⋅(20⋅10−2)22⋅0,15=6,0⋅10−3 В=6,0 мВ.

При повороте контура в нем возникает ЭДС индукции, среднее значение которой равно 6,0 мВ.

vedy.by