Как определить фазу, ноль и заземление самому, подручными средствами?
Любой человек, занимаясь электромонтажными работами у себя дома или просто решивший установить люстру, бра или подключить розетку, обязательно столкнется с вопросом – как определить фазу, ноль и заземление у проводов, в месте монтажа?
В наших статьях и инструкциях, мы часто выкладываем схемы подключения, правила монтажа и подсоединения электрооборудования к сети, а также многое другое, где для правильного выполнения всех операций необходимо знать, где у вас фазный провод, где нулевой (рабочий ноль), а где заземляющий (защитный ноль). Для опытного электрика определить где фаза и ноль или найти землю, обычно не составляет труда, а вот как быть остальным?
Давайте попробуем разобраться, как в домашних условиях, не обладая сложными специализированными измерительными инструментами и электронными приборами, самому определить где фаза, где ноль, а где земля в проводке.
Из всех известных методов, наиболее простого определения фазы и ноля, мы отобрали самые, по нашему мнению, доступные в реализации и в то же время безопасные.
На самом деле, вариантов определения фазы, нуля или заземления, например, в розетке, без применения специализированного оборудования не так уж и много, и порой, в зависимости от ваших целей и задач, бывает достаточно лишь знать стандарт цветовой маркировки электрических проводов принятый у нас, чтоб их различить.
Маркировка проводов по цвету
Действительно, самый простой способ определить фазу, ноль и землю у электрического провода, это посмотреть цветовую маркировку и сравнить с принятым стандартом. Каждая жила в современных проводах, применяемых в электропроводке, а также электрооборудовании имеет индивидуальную расцветку. Зная какому цвету жил какая соответствует функция (фаза, ноль или заземление), легко можно выполнять дальнейший монтаж.
Довольно часто, этого вполне достаточно, особенно в случаях, когда установка производится в новостройках или местах с довольно новой электропроводкой, сделанной профессиональными, компетентными электромонтажниками по всем современным правилам и стандартам.
В нашей стране, как и в Европе в целом, действует стандарт IEC 60446 2004 года, который жестко регламентирует цветовую маркировку электрических проводов.
Согласно этому стандарту для квартирной электросети:
Рабочий ноль (нейтраль или ноль) – Синий провод или сине-белый
Защитный ноль (земля или заземление) – желто-зеленый провод
Фаза – Все остальные цвета среди которых – черный, белый, коричневый, красный и т.д.
Теперь, зная стандарт цветовой маркировки проводов, вы сможете без труда определять, какой провод какую функцию выполняет. Это касается большинства случаев, исключение могут составлять провода, подходящие к выключателям, переключателям и т.д., в силу принципиально иной схемы работы этого электрооборудования.
Это касается большинства случаев, исключение могут составлять провода, подходящие к выключателям, переключателям и т.д., в силу принципиально иной схемы работы этого электрооборудования.
Если же вы не уверены в точном соответствии цветов жил проводов стандарту IEC 60446 2004, у вас старая проводка, вы не исключаете возможность ошибок или даже халатного отношения электромонтажников к своей работе, а может электриками проложены провода другого стандарта и соответственно иной цветовой маркировки, тогда переходим к практическому методу определения фазы и нуля (рабочего и защитного).
КАК САМОМУ ОПРЕДЕЛИТЬ ФАЗУ, НОЛЬ и ЗАЗЕМЛЕНИЕ У ПРОВОДОВ
Итак, начнем по порядку:
ОПРЕДЕЛЕНИЕ ФАЗЫ
Для большего удобства, сперва всегда лучше определять какой из имеющихся проводов фаза. О том, как найти фазу цифровым мультиметром мы уже писали, а как быть если его нет, читайте ниже.
ОПРЕДЕЛЕНИЕ ФАЗЫ ИНДИКАТОРНОЙ ОТВЕРТКОЙ
Самый простой способ обнаружения фазного провода – это поиск с помощью индикаторной отвертки.
Принцип работы индикаторной отвертки прост – при касании жалом отвертки проводника под напряжением и одновременном касании контакта, на задней стороне отвертки, пальцем руки – загорается индикаторная лампа в корпусе инструмента, которая и сигнализирует о наличии напряжения. Таким образом легко можно узнать, какой провод фазный.
Принцип действия индикаторной отвертки прост – внутри индикаторной отвертки расположена лампа и сопротивление(резистор), при замыкании цепи (касании нами заднего контакта) лампа загорается. Сопротивление защищает нас от поражения электрическим током, оно снижает ток до минимального, безопасного уровня.
Этот вариант определения фазы своими силами, наиболее предпочтителен и мы рекомендуем пользоваться именно им, тем более что стоимость индикаторной отвертки более чем доступная. Главным недостатком этого способа, является вероятность ошибочного срабатывания, когда индикаторная отвертка, реагируя на наводки, определяет наличие напряжения там, где его нет.
Главным недостатком этого способа, является вероятность ошибочного срабатывания, когда индикаторная отвертка, реагируя на наводки, определяет наличие напряжения там, где его нет.
ОПРЕДЕЛЕНИЕ ФАЗЫ, НУЛЯ И ЗАЗЕМЛЕНИЯ КОНТРОЛЬНОЙ ЛАМПОЙ
Еще один способ, которым можно определить фазный, нулевой и провод заземления в современной трехпроводной электрической сети, это использование контрольной лампы. Способ неоднозначный, но действенный, требующий особой осторожности.
Чтоб начать определение, в первую очередь необходимо собрать само устройство контрольной лампы. Самый простой способ использовать патрон, с вкрученной туда лампой, а в клеммах патрона закрепить провода со снятой на концах изоляцией. Если же под рукой нет электрического патрона или нет времени что-то мастерить, можно воспользоваться обычной настольной лампой с электрической вилкой.
Технология определения фазы, нули и земли с помощью контрольной лампы максимально проста – поочередно соединяя провода лампы к проводам требующим определения, каждый с каждым.
Определить фазу и ноль из двух проводов
В случае определения контрольной лампой фазного провода среди двух проводов вы лишь сможете узнать, есть фаза или нет, а какой именно из проводников фазный определить не удастся. Если при соединении проводов контрольной лампы к определяемым жилам она загорится, то значит один из проводов фазный, а второй скорее всего ноль. Если же не загорится, то скорее всего фазы среди них нет, либо нет нуля, чего тоже исключать нельзя.
Таким способом, скорее, удобнее проверять работоспособность проводки и правильность её монтажа. Определять фазу лучше индикаторной отверткой, а вот наличие нуля узнавать так.
Определить фазный провод в таком случае можно подключив один из концов, идущих от контрольной лампы, к заведомо известному нулю (например, к соответствующей клемме в электрощите), тогда при касании вторым концом к фазному проводнику, лампа загорится. Оставшийся провод соответственно ноль.
Найти фазу, ноль и заземление из трех проводов:
В такой трехпроводной системе часто возможно точно определить фазный, нулевой и заземляющий провод контрольной лампой.
Соединяем контакты, идущие от контрольной лампы поочередно к жилам требующего определения кабеля.
Действуем методом исключения:
Находим положение, в котором лампа горит, это будет значить, что один из проводов фаза, а другой ноль.
После чего меняем положение одного из контактов контрольной лампы, далее возможны несколько вариантов:
– Если лампа не загорится (при наличии УЗО или дифференциального автомата защиты проверяемой линии они также могут сработать) значит оставшийся свободным провод – ФАЗА, а проверяемые НОЛЬ и ЗЕМЛЯ.
– Если после смены положения лампа ненадолго вспыхнет, при этом сразу сработает УЗО или диф. автомат (если они есть), значит оставшийся свободным провод – НОЛЬ, а проверяемые это ФАЗА и ЗАЗЕМЛЕНИЕ.
– Если линия не защищена устройством защитного отключения (УЗО) или дифференциальным автоматом, и свет будет гореть в двух положениях. В этом случае узнать какой провод рабочий ноль (нуль), а какой защитный (заземление), можно просто отключив в щите учета и распределения электроэнергии вводной кабель от клеммы заземления. После чего так же проверить контрольной лампой все жилы и, опять же методом исключения, в положении, когда лампа не горит опознать проводник заземления.
Как видите, в различных ситуациях, при разных схемах электропроводки, реализованных в квартире, способы и методы определения нуля, фазы и заземления меняются. Если вы столкнулись с ситуацией, не описанной в этой статье, обязательно пишите в комментариях к статье, мы постараемся вам помочь.
А если вы знаете еще, простые способы того, как в домашних условиях, без специализированного инструмента определить фазу, ноль и землю, пишите в комментариях. Статья будет обязательно дополнена. Главное требование, к методам определения, это простота, возможность обойтись в поиске лишь подручными, бытовыми средствами, имеющимися у многих.
Главное требование, к методам определения, это простота, возможность обойтись в поиске лишь подручными, бытовыми средствами, имеющимися у многих.
Как найти фазу и ноль индикаторной отверткой? | ENARGYS.RU
Проверить функциональные возможности электросети в квартире или частном доме можно различными способами. С финансовой точки зрения оптимальным вариантом будет индикаторный пробник, который способен заменить мультиметр в домашних условиях.
При выполнении монтажных работ с розетками и выключателями освещения часто возникает необходимость найти фазу и ноль. Конечно для опытных электриков, такая задача пустяк, но для тех, кто мало знаком с правилами устройства электрических сетей, этот вопрос может загнать в тупик.
Индикаторная отвертка. Нюансы в использовании
Учитывая количество электроприборов в каждой квартире, этот прибор должен быть у каждого. С его помощью будет возможно определить наличие тока в любом проводнике, розетке или электрощитке.
Конструкция индикаторной отвертки
Конструкция обыкновенного пробника в виде отвертки простое:
- щуп, исполняет роль проводника;
- к жалу подключен резистор, он нужен для понижения силы тока до безопасной для человеческого организма величины;
- далее размещен светодиод, который соединяется с контактным пятачком, выведенным на торец отвертки;
- корпус изготавливают из прозрачного пластика, это позволяет увидеть загорание светодиода.

Фаза и ноль в отвертке
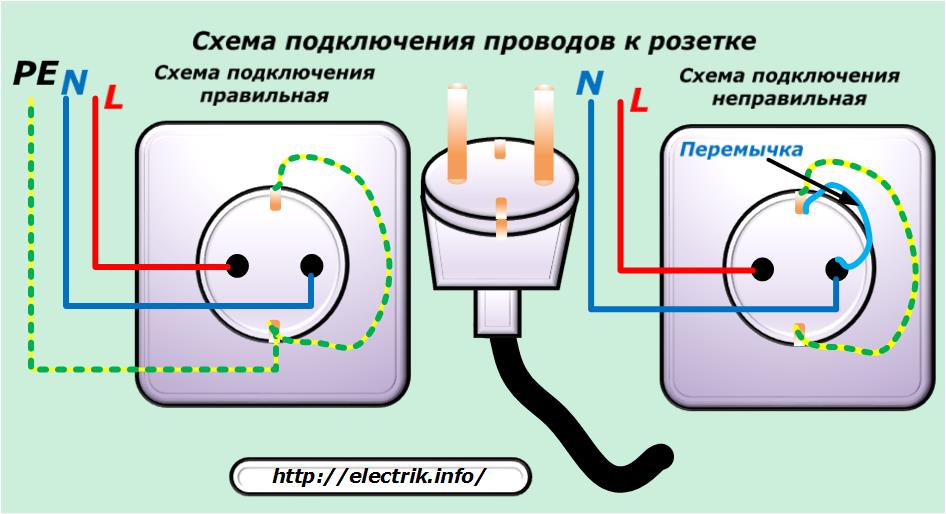
Найти фазу и ноль индикаторной отверткой не составит труда. Когда щупом прикоснутся к проводу под напряжением, ток пройдет по стержню, далее через резистор, приведет светодиод к свечению, а затем попадет на руку, которая касается металлической пластины. Ток пройдет и сквозь тело человека, который производит данную операцию, а затем уйдет землю.
Сам человек не ощутит проходящий через него ток, так как его величина слишком мала.
Область применения
Любые работы, которые касаются электропроводки, должны быть безопасными. Для этой цели каждый должен иметь в доме этот необходимый инструмент.
Этот прибор может быть использован для таких целей:
- проверить к какому контакту розетки или выключателя подведен фазовый проводник;
- когда розетка удлинителя не работает, можно проверить все гнезда пробником;
- с ее помощью можно выяснить, куда подведена фаза в патроне: к центральному контакту или к резьбе;
- выяснить находится ли электроприбор под напряжением;
- прикасаясь жалом инструмента к центральному контакту розетки, можно проверить исправность заземляющего проводника.

Важно! Если электросеть с переменным током, то прижимать палец к пластине нет необходимости!
Типы отверток
Новые модели отверток могут обнаружить присутствие напряжения в жиле даже через слой побелки, штукатурки и глины. Их алгоритм действия практически всегда аналогичен. Но имеются и различия, которые возникают в зависимости от типов, моделей и ряда функций которыми обладает инструмент.
Иногда по своей функциональности одна отвертка, может заменить несколько дорогостоящих приборов. Существуют приборы с батарейкой, это дает возможность проверять исправность провода, даже в обесточенном состоянии.
Важно! Любая индикаторная отвертка имеет нижние и верхние пределы замеров напряжения. Их превышение может сломать устройство либо показывать неверную информацию.
Такая модель сможет дать максимальное количество интересующих сведений об исследуемой цепи:
- звуковой сигнал сообщит о том, что в цепи присутствует напряжение;
- на цифровом табло отобразиться величина напряжения в вольтах;
- дает возможность проверить цепи переменного и постоянного тока в бытовых электроприборах;
- определит полярность сетей;
- с ее помощью можно провести прозвонку электроцепи световой или звуковой индикацией.

Проверка устройства перед использованием
Перед применением индикаторный прибор должен быть проверен на исправность. Батарейка, которая находится внутри устройства, поможет в этом удостовериться. Потребуется прикоснуться одновременно к жалу и другим пальцем к металлическому контакту на рукоятке. Световой индикатор должен в этот момент загореться.
Если устройство не предусматривает наличие батарейки, тогда понадобиться проводник под напряжением. К нему нужно прикоснуться жалом отвертки, а к металлу на рукоятке пальцем. В результате светодиод также будет светиться.
Основные меры безопасности
Обязательно следует соблюдать меры предосторожности:
- запрещается использование пробника без винта;
- допускается вынимание из устройства только батарейки;
- после того как заменена батарейка, винт следует закрутить по часовой стрелке до упора;
- если на пробнике имеются механическими повреждениями, то его использование запрещено;
- не стоит использовать прибор выше пределов, указанных в технических характеристиках;
- перед использованием пробника, потребуется его проверить в сети с точным наличием фазы;
Важно! При проведении замеров электрических линий, пробник держат только за изолированные элементы.
Исключением являются цепи без напряжения.
Инструкция по использованию
Согласно своих характеристик такие индикаторные приспособления предназначаются для:
- возможности определить переменное напряжение контактным способом до 250 В;
- бесконтактным способом до 600 В;
- обследования цепи на целостность от 0 до 2 Мом;
- установления полярности: от 1,5 В до 36 В;
- инструмент должен храниться в сухом и защищенном от влаги месте;
- все операции лучше проводить в перчатках, чтобы обеспечить бесконтактное обследование;
- после работы, следует очищать инструмент от пыли и мусора.
Рекомендации электрика
Бесконтактные отвертки очень чувствительны, она может реагировать и на фазу и на нейтраль, хотя реальное напряжение будет только в одном проводе. Поэтому для обычного электрика такая отвертка не нужна. Тем ни менее, она может помочь в проверке качества экранирования кабелей и отсутствии излучения.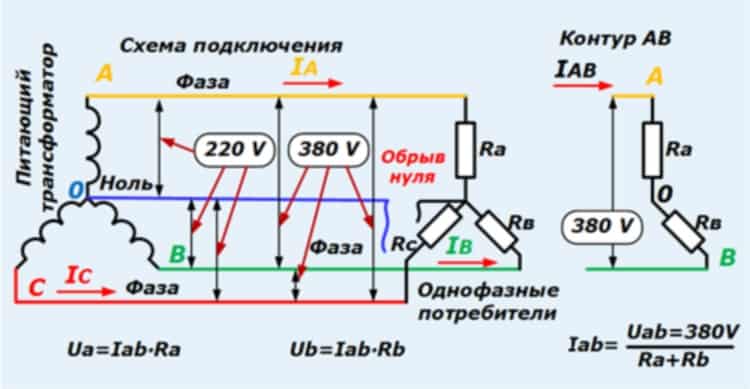
В таких приборах существует три позиции переключателя. Две предусмотрены для осуществления дистанционного действия. В случае случайного прикосновения отверткой в этом режиме к токонесущей части провода, то вся электронная часть, состоящая из транзисторов и светодиода, выгорит.
Электроприборы окружают человека в повседневной жизни. Рано или поздно в любой электрической системе возникают проблемы и неполадки. Не всегда эти проблемы стоят того чтобы приглашать опытного электрика, некоторые поломки можно устранить самостоятельно. Однако, что иметь возможность отыскать неисправность в сети обязательно потребуется специальный инструмент, который стоит, приобрети заранее.
Калькулятор фазового сдвига
Создано Мацеем Ковальски, кандидатом наук
Отредактировано Анной Щепанек, доктором наук и Стивеном Вудингом
Последнее обновление: 30 декабря 2022 г.
Содержание:- сдвиг
- Как найти амплитуду
- Как найти период
- Как найти фазовый сдвиг
- Как найти вертикальный сдвиг
- Пример: использование калькулятора фазового сдвига амплитуды периода
- Часто задаваемые вопросы
Добро пожаловать в калькулятор фазового сдвига Omni , где мы будем изучать тригонометрические функции и способы расчета их фазового сдвига. На самом деле мы рассмотрим больше: мы также объясним, как найти амплитуду и как найти период . На деле оказывается, что огромный класс функций ведет себя практически одинаково, а различия сводятся к описанию тех самых значений, о которых говорилось выше; амплитуда, период и фазовый сдвиг. ну до вертикальное смещение , по крайней мере.
На самом деле мы рассмотрим больше: мы также объясним, как найти амплитуду и как найти период . На деле оказывается, что огромный класс функций ведет себя практически одинаково, а различия сводятся к описанию тех самых значений, о которых говорилось выше; амплитуда, период и фазовый сдвиг. ну до вертикальное смещение , по крайней мере.
Амплитуда, период, фазовый сдвиг и сдвиг по вертикали
Как мы упоминали выше, здесь мы сосредоточимся на тригонометрических функциях : более конкретно на синусе и косинусе. Тем не менее, важно помнить, что многие понятия являются более общими , особенно понятия горизонтального переноса или вертикального сдвига.
Прежде всего, давайте посмотрим на картинку, показывающую , где амплитуда, период, фазовый сдвиг и вертикальный сдвиг отображаются на графике (обратите внимание, что такое же изображение появляется в верхней части калькулятора фазового сдвига Omni).
Мы можем записать такие функции с помощью формулы (иногда называемой уравнением фазового сдвига или формулой фазового сдвига ):
f(x)=A⋅sin(Bx−C)+D,f(x ) = A\cdot\sin(Bx-C)+D,f(x)=A⋅sin(Bx−C)+D,
или:
f(x)=A⋅cos(Bx−C )+D,f(x) = A\cdot\cos(Bx-C)+D,f(x)=A⋅cos(Bx−C)+D,
, где AAA, BBB, CCC, DDD произвольные действительные числа, но с ненулевыми AAA и BBB (иначе это не была бы тригонометрическая функция). Очевидно, эти четыре числа определяют амплитуду, период, фазовый сдвиг и сдвиг по вертикали . В какой-то степени картина показывает, как они влияют на график. Тем не менее, было бы полезно поддержать визуальные эффекты некоторыми определениями.
Амплитуда показывает, насколько далеко (в любом направлении) отходят значения от центральной линии графика. Для простого синуса или косинуса его значение равно 111, так как центральная линия находится в точке 000, а значения функции находятся в диапазоне от -1-1-1 до 111.
Период – это длина по горизонтальной оси, после которой функция начинает повторяться. Другими словами, (бесконечный) граф — это просто набор копий длины периода, склеенных вместе на концах . Для простого синуса или косинуса период равен 2π2\pi2π, поскольку sin(0)=sin(2π)=sin(4π)=…\sin(0) = \sin(2\pi) = \ sin(4\pi) = …sin(0)=sin(2π)=sin(4π)=… и части между ними точно такие же (и аналогично для косинуса).
Фазовый сдвиг (также называемый горизонтальным сдвигом или горизонтальным сдвигом ) описывает, насколько по горизонтали график сместился от обычного синуса или косинуса. Таким образом, значение равно 000, если две функции не изменены.
Вертикальный сдвиг (также называемый вертикальным перемещением ) описывает, насколько вертикально график сместился от обычного синуса или косинуса. Другими словами, это близнец фазового сдвига, который касается перпендикулярное направление .
 В частности, значение снова равно 000, если обе функции остаются неизменными.
В частности, значение снова равно 000, если обе функции остаются неизменными.
Итак, мы узнали, что такое фазовый сдвиг, а также три сопутствующих значения. Разделы ниже описывают , как вычислить каждый из них на основе обозначений из приведенной выше формулы фазового сдвига. Сначала мы покажем , как найти амплитуду .
Введенное нами понятие широко распространено при изучении колебательных и гармонических движений. Короче говоря, эти явления — лучшие друзья тригонометрии. Вы можете обнаружить связь на нашем калькуляторе тригонометрии или узнать больше о различных функциях, которые постоянно появляются, когда вы анализируете маятник, на калькуляторе тригонометрических функций или на более конкретном калькуляторе косинуса и калькуляторе синуса!
Как найти амплитуду
Мы знаем, что функции синуса и косинуса имеют значения в диапазоне от −1-1−1 до 111. Более того, этот простой факт не меняет , если мы подставим sin(x )\sin(x)sin(x) или cos(x)\cos(x)cos(x) для sin(Bx−C)\sin(Bx – C)sin(Bx−C) или cos( Bx−C)\cos(Bx – C)cos(Bx−C) для ненулевого BBB и произвольного CCC. На самом деле это потому, что функция f(x)=Bx−Cf(x) = Bx – Cf(x)=Bx−C является тогда биекцией (т. е. взаимно-однозначным соответствием) на пространство вещественные числа.
На самом деле это потому, что функция f(x)=Bx−Cf(x) = Bx – Cf(x)=Bx−C является тогда биекцией (т. е. взаимно-однозначным соответствием) на пространство вещественные числа.
Теперь давайте посмотрим, что произойдет, если мы добавим DDD, то есть если у нас есть sin(Bx−C)+D\sin(Bx – C) + Dsin(Bx−C)+D или cos(Bx−C) +D\cos(Bx – C) + Dcos(Bx−C)+D вместо этого. Так как первая часть дает что-то между -1-1-1 и 111, все это будет между -1+D-1 + D-1+D и 1+D1 + D1+D (см. Как найти вертикальную сдвиг для сравнения). Это означает, что осевая линия приходится на DDD, а амплитуда по-прежнему равна 111, потому что значения отклоняются на 111 от DDD.
Следовательно, единственное, что может повлиять на амплитуду в формулах фазового сдвига A⋅sin(Bx−C)+DA\cdot\sin(Bx – C) + DA⋅sin(Bx−C)+D и A⋅cos (Bx−C)+DA\cdot\cos(Bx – C) + DA⋅cos(Bx−C)+D — это ненулевое AAA. И действительно, поскольку sin(Bx−C)\sin(Bx-C)sin(Bx−C) и cos(Bx−C)\cos(Bx-C)cos(Bx−C) все это время находятся между −1-1−1 и 111, множитель AAA изменяет этот диапазон на −1⋅A=−A-1\cdot A = -A−1⋅A=−A и 1⋅A=A1 \cdot A = A1⋅ А=А.
Да, вы уже догадались: амплитуда уравнений фазового сдвига A⋅sin(Bx−C)+DA \cdot\sin(Bx – C) + DA⋅sin(Bx−C)+D и A⋅cos(Bx−C)+DA \cdot\cos (Bx – C) + DA⋅cos(Bx−C)+D просто равно AAA.
Как найти период
Напомним, что функции синуса и косинуса имеют периоды, равные 2π2\pi2π, т. е. имеем sin(x+2π)=sin(x)\sin(x + 2\ pi) = \sin(x)sin(x+2π)=sin(x) и cos(x+2π)=cos(x)cos(x + 2\pi) = cos(x)cos(x+2π) =cos(x) для любого xxx. В частности, это дает: !\sin(x\!+\!2\pi)\!+\!D\!=\!A\!\cdot\!\sin(x)\!+\!D,A⋅sin(x+ 2π)+D=A⋅sin(x)+D,
и:
A ⋅ cos(x + 2π) + D = A ⋅ cos(x) cdoll+\s (x\!+\!2\pi)\!+\!D\!=\!A\!\cdot\!\cos(x)\!+\!DA⋅cos(x+2π)+D= A⋅cos(x)+D
Итак, мы видим, что AAA и DDD в формуле фазового сдвига не влияют на период . Действительно, все сводится к тому, что происходит внутри тригонометрических функций . И еще:
sin(x−C+2π)=sin(x−C),\sin(x – C + 2\pi) = \sin(x – C),sin(x−C+2π )=sin(x−C),
и:
cos(x−C+2π)=cos(x−C)\cos(x – C + 2\pi) = \cos(x – C)cos(x−C+2π)=cos(x− C)
По тем же правилам, что и выше, поэтому это не CCC или , который выполняет эту работу. Таким образом, с отброшенными тремя вариантами должен быть четвертый : BBB.
Таким образом, с отброшенными тремя вариантами должен быть четвертый : BBB.
Мы снова обратимся к комментарию, который мы начали с , чтобы понять, почему и как BBB влияет на периодичность в уравнениях фазового сдвига A⋅sin(Bx−C)+DA \cdot \sin(Bx – C) + DA⋅sin (Bx−C)+D и A⋅cos(Bx−C)+DA \cdot \cos(Bx – C) + DA⋅cos(Bx−C)+D. Ведь:
грех(Bx)=sin(Bx+2π)=sin(B ⋅ (x+2πB) )\begin{split} \sin(Bx) &= \sin(Bx + 2\pi)\\[.8em] & = \sin\left(B\! \cdot\! \left(x + \frac{2\pi}{B}\right)\!\right) \end{split}sin(Bx)=sin(Bx+2π)=sin(B⋅(x+B2π))
Таким образом, с добавлением каждых 2π/B2\pi/B2π/B к аргументу xxx, мы возвращаемся в то же место , и функция повторяется (аналогично для косинуса).
Всего период уравнения фазового сдвига равен 2π/B2\pi/B2π/B.
Наши ежедневные знания о волнах обычно отдают приоритет частоте за период; однако это почти одно и то же. Узнайте почему на частотном калькуляторе Omni.
Как найти фазовый сдвиг
По определению фазовый сдвиг описывает горизонтальный сдвиг функции относительно обычного sin(x)\sin(x)sin(x) или cos(x) \ соз (х) соз (х). Таким образом, у основных функций он равен 000. Фактически, если мы сравним их графики:
…мы заметим, что мы можем получить путем перевода другого (на самом деле взаимные кофункции имеют много общего). Точнее, имеем следующее:
sin(x+π2)=cos(x),\sin\left(x+\frac{\pi}{2}\right)=\cos(x), sin(x+2π)=cos(x),
и:
cos(x−π2)=sin(x)\cos\left(x-\frac{\pi}{2}\right )=\sin(x) cos(x−2π)=sin(x)
В приведенном выше примере уже показано, где в A⋅sin(Bx−C)+DA \cdot\sin(Bx – C) + DA ⋅sin(Bx−C)+D и A⋅cos(Bx−C)+DA \cdot\cos(Bx – C) + DA⋅cos(Bx−C)+D следует искать значения, отвечающие за фазовые сдвиги. Однако, в отличие от амплитуды и периода, на этот раз нам понадобятся две из четырех букв .
В общем случае (то есть не только в уравнениях фазового сдвига) мы получаем горизонтальный сдвиг произвольной функции f(x)f(x)f(x) вычислением f(x−a)f( x – a)f(x−a): сдвиг графика на aaa вправо. Другими словами, мы заменяем каждое вхождение xxx на x−ax – ax−a в формуле для f(x)f(x)f(x). Например, применение преобразования к sin(x)\sin(x)sin(x) дает sin(x−a)\sin(x – a)sin(x−a), но, скажем, для cos (3x+1)\cos(3x + 1)cos(3x+1) мы получим:
Другими словами, мы заменяем каждое вхождение xxx на x−ax – ax−a в формуле для f(x)f(x)f(x). Например, применение преобразования к sin(x)\sin(x)sin(x) дает sin(x−a)\sin(x – a)sin(x−a), но, скажем, для cos (3x+1)\cos(3x + 1)cos(3x+1) мы получим:
потому что(3(x−a)+1)=cos(3x−3a+1)\begin{split} \cos&(3(х-а)+1)\\ &=\cos(3x-3a+1) \end{split}cos(3(x−a)+1)=cos(3x−3a+1)
Другими словами, нельзя забывать о множителях, стоящих перед xxx.
В нашем случае формула фазового сдвига дает:
A⋅sin(Bx−C)+D=A⋅sin(B⋅(x−CB))+D,\begin{split} A\cdot&\sin(Bx-C)+D\\ =A\cdot&\sin\left(B\cdot\left(x-\frac{C}{B}\right)\right)+D, \end{split}A⋅=A⋅sin(Bx−C)+Dsin(B⋅(x−BC))+D,
, что равно фазовый сдвиг на C/BC/BC/B (вправо) функции A⋅sin(Bx)A \cdot\sin(Bx)A⋅sin(Bx). Конечно, мы можем повторить вышеописанное и для косинуса.
Подводя итог, чтобы вычислить фазовый сдвиг уравнения фазового сдвига, нужно найти C/BC/BC/B.
Как найти вертикальный сдвиг
Это легко , особенно теперь, когда мы узнали, что такое фазовый сдвиг, амплитуда и период и как их вычислить. Давайте опираться на то, что мы уже узнали.
Мы знаем, что в формулах фазового сдвига A⋅sin(Bx−C)+DA \cdot\sin(Bx – C) + DA⋅sin(Bx−C)+D и A⋅cos(Bx−C )+DA \cdot\cos(Bx – C) + DA⋅cos(Bx−C)+D, AAA определяет, насколько сильно колеблются значения по обе стороны от центральной линии. BBB указывает, насколько далеко мы расширяем выпуклости графика и, как результат, как быстро мы можем повторять значения. Кроме того, вместе с CCC они описывают, сдвинули ли мы функцию влево или вправо и насколько.
Очевидно, горизонтальное смещение не влияет на вертикальное смещение : в конце концов, это два перпендикулярных направления. С другой стороны, амплитуда только говорит нам, как далеко по вертикали простирается график, но не сдвигает его на . В общем, у нас осталась только одна буква : DDD.
DDD в уравнениях фазового сдвига точно соответствует вертикальному сдвигу . Он определяет диапазон функции, т. е. насколько далеко от обычной версии без DDD мы сдвигаем график.
На этом теоретическая часть на сегодня завершена. пора посмотреть как рассчитать фазовый сдвиг на красивом примере . И знаешь, что? Мы также покажем, как найти период, амплитуду и сдвиг по вертикали. В конце концов, почему бы и нет? Больше математических расчетов = больше удовольствия!
Пример: использование калькулятора фазового сдвига амплитуды периода
Давайте посмотрим , как найти амплитуду, период, фазовый сдвиг и вертикальный сдвиг функции f(x)=0,5⋅sin(2x−3)+ 4f(x) = 0,5 \cdot\sin(2x – 3) + 4f(x)=0,5⋅sin(2x−3)+4. Во-первых, мы позволим калькулятору фазового сдвига Omni говорить за вас.
В верхней части нашего инструмента нам нужно выбрать функцию, которая появляется в нашей формуле. В нашем случае мы выбираем « синус » под « Тригонометрическая функция в f ». Это вызовет символическое представление такого уравнения фазового сдвига : f(x)=A⋅sin(Bx−C)+Df(x) = A \cdot\sin(Bx – C) + Df(x )=A⋅sin(Bx−C)+D. Оглядываясь на то, что у нас есть, мы вводим следующее:
В нашем случае мы выбираем « синус » под « Тригонометрическая функция в f ». Это вызовет символическое представление такого уравнения фазового сдвига : f(x)=A⋅sin(Bx−C)+Df(x) = A \cdot\sin(Bx – C) + Df(x )=A⋅sin(Bx−C)+D. Оглядываясь на то, что у нас есть, мы вводим следующее:
A=0.5B=2C=3D=4\begin{split} А&=0,5\\ В&=2\\ С&=3\\ Д&=4 \end{split}ABCD=0.5=2=3=4
(Обратите внимание, что еще до того, как мы введем значения, калькулятор фазового сдвига отображает график функции sin(x)\sin(x)sin(x). Это потому, что инструмент понимает , не дающее определенных значений, как отсутствие числа в соответствующих местах в формуле . Таким образом, он вообще не считывает ввод как A = 1A = 1A = 1, B = 1B = 1B = 1, C = 0C = 0C = 0 и D = 0D = 0D =0, что дает:
1⋅sin(1⋅x−0)+0=sin(x)1 \cdot \sin(1\cdot x – 0) + 0 = \sin(x)1⋅ sin(1⋅x−0)+0=sin(x)
Момент, когда мы даем последнее значение, график функции появляется под вместе с амплитудой, периодом, фазовым сдвигом и вертикальным сдвигом ниже. Также обратите внимание, что при необходимости вы можете перейти в расширенный режим калькулятора, чтобы найти значение функции в любой точке x0x_0x0.
Также обратите внимание, что при необходимости вы можете перейти в расширенный режим калькулятора, чтобы найти значение функции в любой точке x0x_0x0.
Теперь объясним как самим найти фазовый сдвиг и все остальные значения . Для этого достаточно вспомнить четыре раздела выше, чтобы вычислить, что:
- Амплитуда : А=0,5А = 0,5А=0,5;
- Период равен 2π/B=2π/2=π2\pi / B = 2\pi / 2 = \pi2π/B=2π/2=π;
- Фазовый сдвиг равен C/B=3/2=1,5C / B = 3/2 = 1,5C/B=3/2=1,5; и
- Вертикальное смещение равно D=4D = 4D=4.
В общем, график выглядит так :
Пара пустяков, не так ли? Не забудьте поиграться с калькулятором фазового сдвига, чтобы увидеть , как различные коэффициенты влияют на график . А когда вам это наскучит, переходите к другим тригонометрическим калькуляторам Omni и приготовьтесь получить еще больше удовольствия от !
Часто задаваемые вопросы
Как рассчитать фазовый сдвиг?
Чтобы рассчитать фазовый сдвиг функции вида A × sin(Bx - C) + D или A × cos(Bx - C) + D , необходимо:
- Определить
Б.
- Определить
C. - Разделить
К/Б. - Помните , что если результат:
- Положительный , график сдвинут вправо.
- Отрицательный , график смещен влево.
- Наслаждайтесь , найдя фазовый сдвиг.
Как найти фазовый сдвиг по графику?
Чтобы найти фазовый сдвиг по графику , необходимо:
- Определить , является ли сдвинутым синусоидальным или косинусным.
- Посмотрите на график справа от вертикальной оси.
- Найти первый:
- Пик , если коэффициент перед функцией положительный; или
- Корыто , если коэффициент отрицательный.
- Рассчитать расстояние от вертикальной линии до этой точки.

- Если функция была синусоидальной, вычесть
π/2из этого расстояния. - Наслаждайтесь найдя фазовый сдвиг по графику.
Как найти амплитуду, период и фазовый сдвиг?
Нахождение амплитуды, периода и фазового сдвига функции вида A × sin(Bx - C) + D или A × cos(Bx - C) + D выполняется следующим образом:
- Амплитуда равна
A; - Период равен
2π / B; и - Фазовый сдвиг равно
C/B.
Как графически отображать триггерные функции с фазовым сдвигом?
Чтобы построить график триггерных функций с фазовым сдвигом , вам необходимо:
- Определить , что такое триггерная функция.
- Фокус на точку
(0,0)на плоскости. - Если фазовый сдвиг:
- Положительный , двигаться вправо.

- Отрицательный , двигаться влево.
- Положительный , двигаться вправо.
- Переместите расстояние, заданное фазовым сдвигом.
- Точка, в которую вы приземлитесь, является вашей отправной точкой .
- Нарисуйте график несмещенной функции, как если бы точка была
(0,0). - Наслаждайтесь игрой , построив график триггерной функции с фазовым сдвигом.
Сдвиг по горизонтали и фазе — это одно и то же?
Что касается тригонометрических функций, да . Обычно мы оставляем за собой термин « фазовый сдвиг “для триггерных функций. Другими словами, мы можем иметь горизонтальный сдвиг любого графика или функции . Тем не менее, когда это, по сути, тригонометрический, мы можем эквивалентно назвать этот горизонтальный сдвиг фазовым сдвигом
Мацей Ковальский, PhD кандидат
Тригонометрическая функция в f
Результат
Амплитуда1
Период равен 2π / B = 2π .
Фазовый сдвиг C / B = 0 .
Вертикальный сдвиг равен D = 0 .
Ознакомьтесь с 19 похожими калькуляторами тригонометрии 📐
ArccosArcsinArctan… Еще 16
Формула фазового сдвига — изучите формулу для расчета фазового сдвига
Формула фазового сдвига используется для нахождения фазового сдвига функции. Фазовый сдвиг — это сдвиг, когда график функции синуса и косинуса смещается влево или вправо от их обычного положения, или можно сказать, что при фазовом сдвиге функция сдвигается по горизонтали, насколько далеко от обычного положения. Как правило, функции смещены (π/2) от обычного положения. Давайте узнаем больше о формуле фазового сдвига вместе с решенными примерами в следующем разделе.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Забронируйте бесплатный пробный урок
Формула фазового сдвига для синусоидальной кривой показана ниже, где выражены как горизонтальные, так и вертикальные сдвиги. Фазовый сдвиг может быть как положительным, так и отрицательным в зависимости от направления сдвига от начала координат. Формула фазового сдвига может быть выражена как
Фазовый сдвиг может быть как положительным, так и отрицательным в зависимости от направления сдвига от начала координат. Формула фазового сдвига может быть выражена как
у = A sin(B(x + C)) + D
также F(x) = Asin(Bx − C)+D.
, где
- (C/B) представляет фазовый сдвиг.
- А – амплитуда.
- Пример 1: Выясните, каков фазовый сдвиг синуса, имеющего F(t)= 3 sin(4(x − 0,5)) + 2, используя формулу фазового сдвига.
Решение:
Чтобы найти: сдвиг фазы синусоидального сигнала
Используя формулу фазового сдвига,
y = A sin(B(x + C)) + D
При сравнении данного уравнения с формулой фазового сдвига
Получаем
Амплитуда, A = 3
Период, 2π/B = 2π/4 = π/2
Вертикальный сдвиг, D = 2
Таким образом, фазовый сдвиг будет равен −0,5
, что соответствует сдвигу вправо на 0,5.



