Как найти напряжение если известно сопротивление: Формула напряжения тока. Найти электрическое напряжение, разность потенциалов.

Формула напряжения тока. Найти электрическое напряжение, разность потенциалов.

Как известно у электрического напряжения должна быть своя мера, которая изначально соответствует той величине, что рассчитана для питания того или иного электротехнического устройства. Превышение или снижение величины этого напряжения питания негативно влияет на электрическую технику, вплоть до полного выхода ее из строя. А что такое напряжение? Это разность электрических потенциалов. То есть, если для простоты понимания его сравнить с водой, то это примерно будет соответствовать давлению. По научному электрическое напряжение — это физическая величина, показывающая, какую работу совершает на данном участке ток при перемещении по этому участку единичного заряда.

Наиболее распространенной формулой напряжения тока является та, в которой имеются три основные электрические величины, а именно это само напряжение, ток и сопротивление. Ну, а формула эта известна под названием закона Ома (нахождение электрического напряжения, разности потенциалов).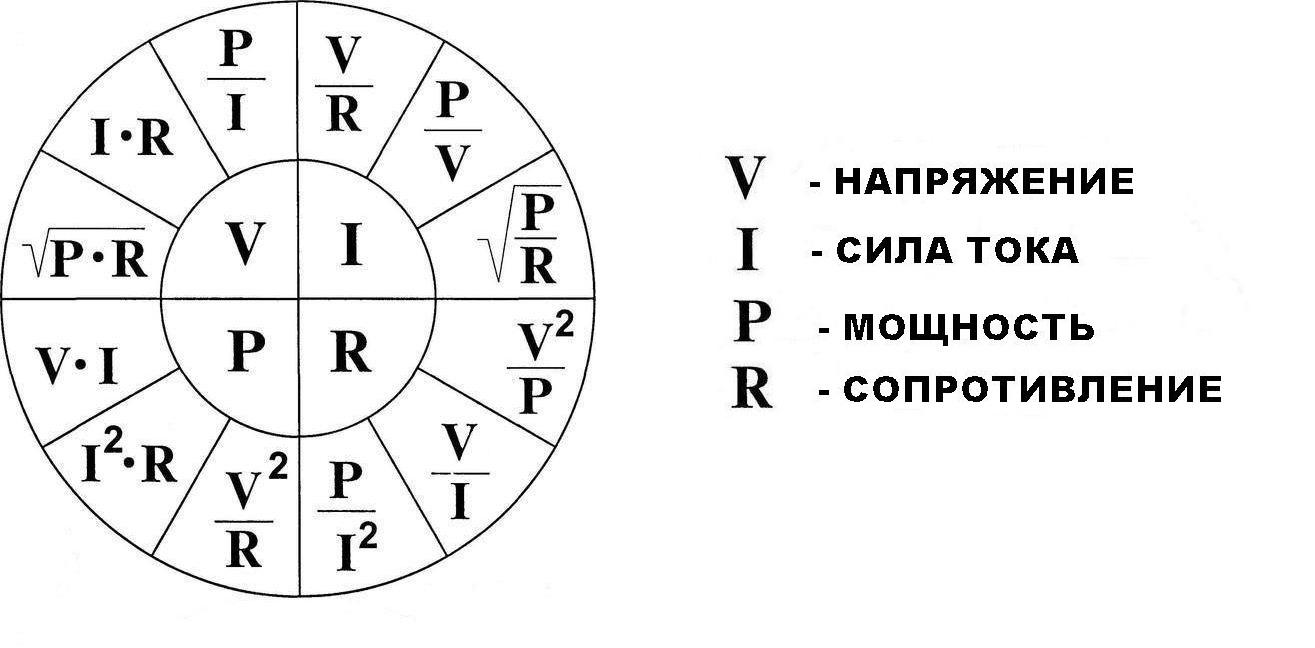

Звучит эта формула следующим образом — электрическое напряжение равно произведению силы тока на сопротивление. Напомню, в электротехнике для различных физических величин существуют свои единицы измерения. Единицей измерения напряжения является «Вольт» (в честь ученого Алессандро Вольта, который открыл это явление). Единица измерения силы тока — «Ампер», и сопротивления — «Ом». В итоге мы имеем — электрическое напряжение в 1 вольт будет равно 1 ампер умноженный на 1 ом.

Помимо этого второй наиболее используемой формулой напряжения тока является та, в которой это самое напряжение можно найти зная электрическую мощность и силу тока.

Звучит эта формула следующим образом — электрическое напряжение равно отношению мощности к силе тока (чтобы найти напряжение нужно мощность разделить на ток). Сама же мощность находится путем перемножения тока на напряжение. Ну, и чтобы найти силу тока нужно мощность разделить на напряжение. Все предельно просто. Единицей измерения электрической мощности является «Ватт».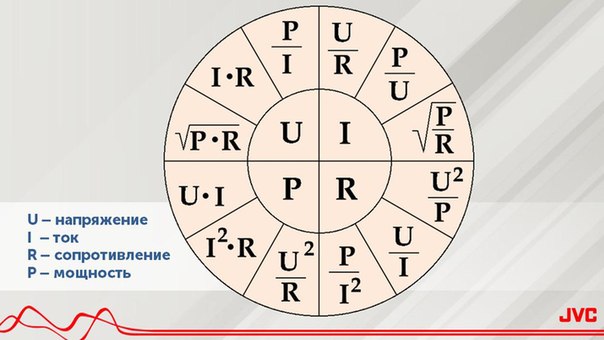 Следовательно 1 вольт будет равен 1 ватт деленный на 1 ампер.

Ну, а теперь приведу более научную формулу электрического напряжения, которая содержит в себе «работу» и «заряды».

В этой формуле показывается отношение совершаемой работы по перемещению электрического заряда. На практике же данная формула вам вряд ли понадобится. Наиболее встречаемой будет та, которая содержит в себе ток, сопротивление и мощность (то есть первые две формулы). Но, хочу предупредить, что она будет верна лишь для случая применения активных сопротивлений. То есть, когда расчеты производятся для электрической цепи, у которой имеется сопротивления в виде обычных резисторов, нагревателей (со спиралью нихрома), лампочек накаливания и так далее, то приведенная формула будет работать. В случае использования реактивного сопротивления (наличии в цепи индуктивности или емкости) нужна будет другая формула напряжения тока, которая учитывает также частоту напряжения, индуктивность, емкость.

P.S. Формула закона Ома является фундаментальной, и именно по ней всегда можно найти одну неизвестную величину из двух известных (ток, напряжение, сопротивление). На практике закон ома будет применяться очень часто, так что его просто необходимо знать наизусть каждому электрику и электронику.

Ток, напряжение, сопротивление. Закон Ома.

Мы начинаем публикацию материалов новой рубрики «Основы электроники«, и в сегодняшней статье речь пойдет о фундаментальных понятиях, без которых не проходит обсуждение ни одного электронного устройства или схемы. Как вы уже догадались, я имею ввиду ток, напряжение и сопротивление 🙂 Кроме того, мы не обойдем стороной закон Ома, который определяет взаимосвязь этих величин, но не буду забегать вперед, давайте двигаться постепенно.

Итак, давайте начнем с понятия напряжения.

Напряжение.

По определению напряжение — это энергия (или работа), которая затрачивается на перемещение единичного положительного заряда из точки с низким потенциалом в точку с высоким потенциалом (т. е. первая точка имеет более отрицательный потенциал по сравнению со второй). Из курса физики мы помним, что потенциал электростатического поля — это скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду. Давайте рассмотрим небольшой пример:

В пространстве действует постоянное электрическое поле, напряженность которого равна E. Рассмотрим две точки, расположенные на расстоянии d друг от друга. Так вот напряжение между двумя точками представляет из себя ни что иное, как разность потенциалов в этих точках:

U = \phi_1\medspace-\medspace \phi_2

В то же время не забываем про связь напряженности электростатического поля и разности потенциалов между двумя точками:

\phi_1\medspace-\medspace \phi_2 = Ed

И в итоге получаем формулу, связывающую напряжение и напряженность:

U = Ed

В электронике, при рассмотрении различных схем, напряжение все-таки принято считать как разность потенциалов между точками.

Соответственно, становится понятно, что напряжение в цепи — это понятие, связанное с двумя точками цепи. То есть говорить, к примеру, «напряжение в резисторе» — не совсем корректно. А если говорят о напряжении в какой-то точке, то подразумевают разность потенциалов между этой точкой и «землей». Вот так плавно мы вышли к еще одному важнейшему понятию при изучении электроники, а именно к понятию «земля» 🙂 Так вот «землей» в электрических цепях чаще всего принято считать точку нулевого потенциала (то есть потенциал этой точки равен 0).

Давайте еще пару слов скажем о единицах, которые помогают охарактеризовать величину напряжения. Единицей измерения является Вольт (В). Глядя на определение понятия напряжения мы можем легко понять, что для перемещения заряда величиной 1 Кулон между точками, имеющими разность потенциалов 1 Вольт, необходимо совершить работу, равную 1 Джоулю. С этим вроде бы все понятно и можно двигаться дальше 🙂

А на очереди у нас еще одно понятие, а именно ток.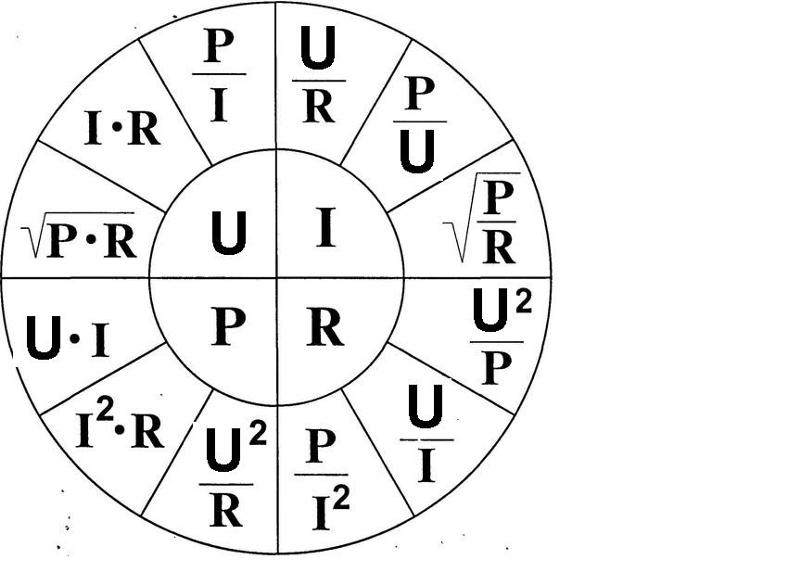

Ток, сила тока в цепи.

Что же такое электрический ток?

Давайте подумаем, что будет происходить если под действие электрического поля попадут заряженные частицы, например, электроны… Рассмотрим проводник, к которому приложено определенное напряжение:

Из направления напряженности электрического поля (E) мы можем сделать вывод о том, что \phi_1 > \phi_2 (вектор напряженности всегда направлен в сторону уменьшения потенциала). На каждый электрон начинает действовать сила:

F = Ee

где e − это заряд электрона.

И поскольку электрон является отрицательно заряженной частицей, то вектор силы будет направлен в сторону противоположную направлению вектора напряженности поля. Таким образом, под действием силы частицы наряду с хаотическим движением приобретают и направленное (вектор скорости V на рисунке). В результате и возникает

электрический ток 🙂

Ток — это упорядоченное движение заряженных частиц под воздействием электрического поля.

Важным нюансом является то, что принято считать, что ток протекает от точки с более положительным потенциалом к точке с более отрицательным потенциалом, несмотря на то, что электрон перемещается в противоположном направлении.

Носителями заряда могут выступать не только электроны. Например, в электролитах и ионизированных газах протекание тока в первую очередь связано с перемещением ионов, которые являются положительно заряженными частицами. Соответственно, направление вектора силы, действующей на них (а заодно и вектора скорости) будет совпадать с направлением вектора E. И в этом случае противоречия не возникнет, ведь ток будет протекать именно в том направлении, в котором движутся частицы 🙂

Для того, чтобы оценить ток в цепи придумали такую величину как сила тока. Итак, сила тока (I) — это величина, которая характеризует скорость перемещения электрического заряда в точке. Единицей измерения силы тока является Ампер. Сила тока в проводнике равна 1 Амперу, если за 1 секунду через поперечное сечение проводника проходит заряд 1 Кулон.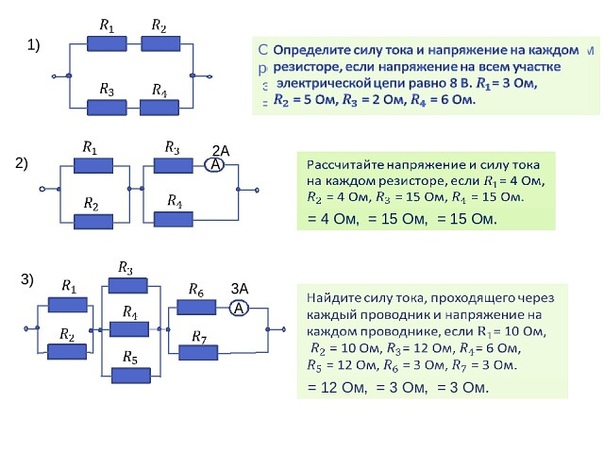

Мы уже рассмотрели понятия силы тока и напряжения, теперь давайте разберемся каким образом эти величины связаны. И для этого нам предстоит изучить, что же из себя представляет сопротивление проводника.

Сопротивление проводника/цепи.

Термин «сопротивление» уже говорит сам за себя 🙂

Итак, сопротивление — физическая величина, характеризующая свойства проводника препятствовать (

сопротивляться) прохождению электрического тока.

Рассмотрим медный проводник длиной l с площадью поперечного сечения, равной S:

Сопротивление проводника зависит от нескольких факторов:

• удельного сопротивления проводника \rho
• длины проводника l
• площади поперечного сечения проводника S

Удельное сопротивление — это табличная величина. Формула, с помощью которой можно вычислить сопротивление проводника выглядит следующим образом:

R = \rho\medspace \frac{l}{S}

Для нашего случая \rho будет равно 0,0175 (Ом * кв. мм / м) — удельное сопротивление меди. Пусть длина проводника составляет 0.5 м, а площадь поперечного сечения равна 0.2 кв. мм. Тогда:

R =0,0175 \cdot \frac{0.5}{0.2} = 0.04375\medspace Ом

Как вы уже поняли из примера, единицей измерения

сопротивления является Ом 🙂

С сопротивлением проводника все ясно, настало время изучить взаимосвязь напряжения, силы тока и сопротивления цепи.

Закон Ома.

И тут на помощь нам приходит основополагающий закон всей электроники — закон Ома:

Сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению рассматриваемого участка цепи.

Рассмотрим простейшую электрическую цепь:Как следует из закона Ома напряжение и сила тока в цепи связаны следующим образом:

I = \frac{U}{R}

Пусть напряжение составляет 10 В, а сопротивление цепи равно 200 Ом. Тогда сила тока в цепи вычисляется следующим образом:

I = \frac{10}{200} = 0. 05 = 50\medspaceмА

Как видите, все несложно 🙂 Пожалуй на этом мы и закончим сегодняшнюю статью, спасибо за внимание и до скорых встреч!

Как найти длину по формуле сопротивления. Если известно напряжение или мощность и сопротивление

Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения V на проводнике:

Напомним, что в случае однородного проводника напряжение U совпадает с разностью потенциалов (см. (33.6)).

Обозначенная в формуле (34.1) буквой R величина называется электрическим сопротивлением проводника. Единицей сопротивления служит равный сопротивлению такого проводника, в котором при напряжении в 1 В течет ток силой 1 А.

Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника

где l – длина проводника, S – площадь его поперечного сечения, – зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества.

Если то R численно равно . В СИ измеряется в ом-метрах (Ом-м).

Найдем связь между векторами j и Е в одной и той же точке проводника. В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора Е.

Поэтому на правления векторов j и Е совпадают Выделим мысленно в окрестности некоторой точки элементарный цилиндрический объем с образующими, параллельными векторам j и Е (рис. 34.1). Через поперечное сечение цилиндра течет ток силой . Напряжение, приложенное к цилиндру, равно , где Е – напряженность поля в данном месте. Наконец, сопротивление цилиндра, согласно формуле (34.2), равно . Подставив эти значения в формулу (34.1), придем к соотношению

Воспользовавшись тем, что векторы j и Е имеют одинаковое направление, можно написать

Эта формула выражает закон Ома в дифференциальной форме.

Фигурирующая в (34.3) обратная величина называется удельной электрической проводимостью материала. Единица, обратная ому, называется сименсом (См).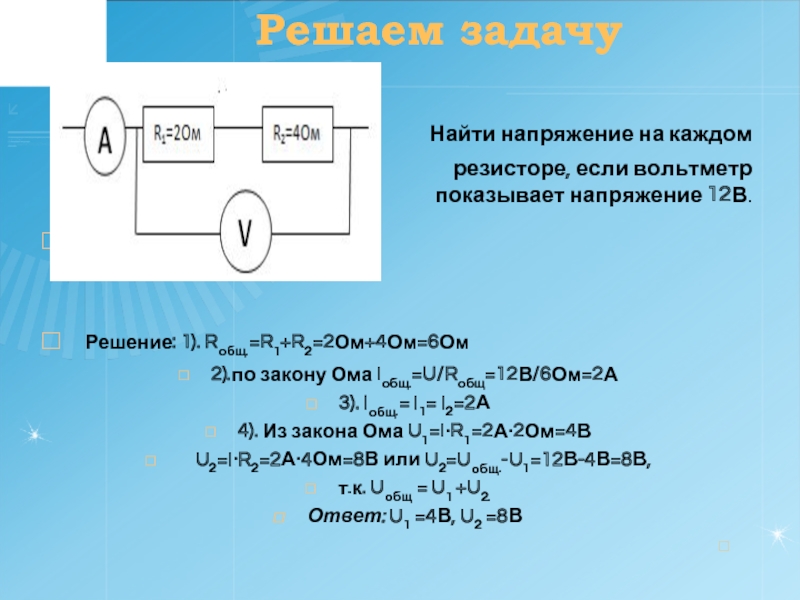

Соответственно единицей о является сименс на метр (См/м).

Допустим для простоты, что в проводнике имеются носители лишь одного знака. Согласно формуле (31.5) плотность тока в этом случае равна

Сравнение этого выражения с формулой (34.3) приводит к выводу, что скорость упорядоченного движения носителей тока пропорциональна напряженности поля Е, т. е. силе, сообщающей носителям упорядоченное движение. Пропорциональность скорости приложенной к телу силе наблюдается в тех случаях, когда кроме силы, вызвавшей движение, на тело действует сила сопротивления среды. Эта сила вызывается взаимодействием носителей тока с частицами, из которых построено вещество проводника. Наличие силы сопротивления упорядоченному движению носителей тока обусловливает электрическое сопротивление проводника.

Способность вещества проводить электрический ток характеризуется его удельным сопротивлением либо удельной проводимостью .

Их величина определяется химической природой вещества и условиями, в частности температурой, при которых оно находится.

Для большинства металлов при температурах, близких к комнатной, изменяется пропорционально абсолютной температуре Т:

При низких температурах наблюдаются отступления от этой закономерности (рис. 34.2). В большинстве случаев зависимость от Т следует кривой. Величина остаточного сопротивления рост в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце. Поэтому после отжига рост заметно уменьшается. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле

У большой группы металлов и сплавов при температуре порядка нескольких кельвинов сопротивление скачков обращается в нуль (кривая 2 на рис. 34.2). Впервые это явление, названное сверхпроводимостью, было обнаружено в 1911 г. Камерлинг-Оннесом для ртути. В дальнейшем сверхпроводимость была обнаружена у свинца, олова, цинка, алюминия и других металлов, а также у ряда сплавов. Для каждого сверхпроводника имеется своя критическая температура Т при которой он переходит в сверхпроводящее состояние.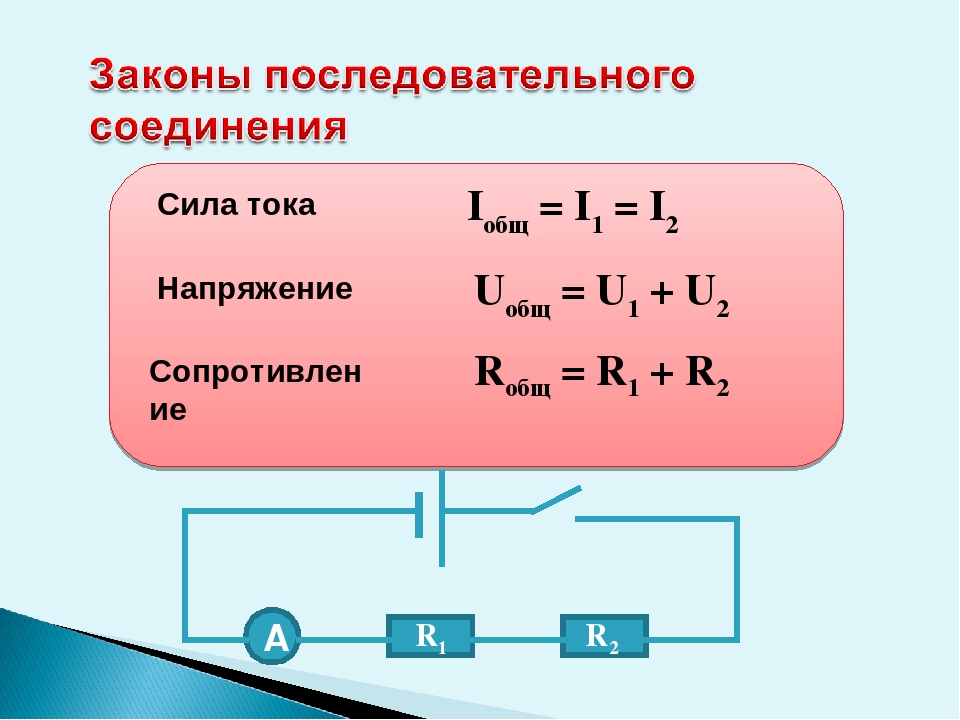 При действии на сверхпроводник магнитного поля сверхпроводящее состояние нарушается. Величина критического поля разрушающего сверхпроводимость, равна нулю при и растет с понижением температуры.

Полное теоретическое объяснение сверхпроводимости было дано академиком Н. Н. Боголюбовым и независимо от него Дж. Бардином, Л. Купером и Дж. Шриффером (см. § 56 тома 3).

Зависимость электрического сопротивления от температуры положена в основу термометров сопротивления. Такой термометр представляет собой металлическую (обычно платиновую) проволочку, намотанную на фарфоровый или слюдяной каркас. Проградуированный по постоянным температурным точкам термометр сопротивления позволяет измерять с погрешностью порядка несколько сотых градуса как низкие, так и высокие температуры. В последнее время все большее применение находят термометры сопротивления из полупроводников.

Содержание:

Появление электрического тока наступает при замыкании цепи, когда на зажимах возникает разность потенциалов. Перемещение свободных электронов в проводнике осуществляется под действием электрического поля. В процессе движения, электроны сталкиваются с атомами и частично передают им свою накопившуюся энергию. Это приводит к уменьшению скорости их движения. В дальнейшем, под влиянием электрического поля, скорость движения электронов снова увеличивается. Результатом такого сопротивления становится нагревание проводника, по которому течет ток. Существуют различные способы расчетов этой величины, в том числе и формула удельного сопротивления, применяющаяся для материалов с индивидуальными физическими свойствами.

Электрическое удельное сопротивление

Суть электрического сопротивления заключается в способности того или иного вещества превращать электрическую энергию в тепловую во время действия тока. Данная величина обозначается символом R, а в качестве единицы измерения используется Ом. Значение сопротивления в каждом случае связано со способностью того или иного .

В процессе исследований была установлена зависимость от сопротивления.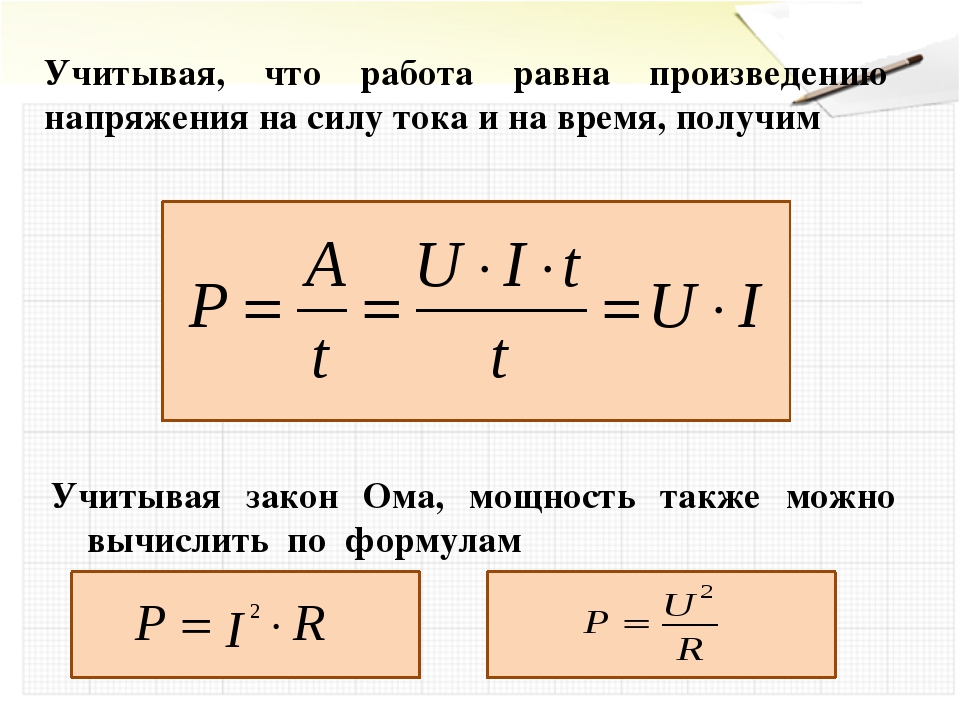 Одним из основных качеств материала становится его удельное сопротивление, меняющееся в зависимости от длины проводника. То есть, с увеличением длины провода, возрастает и значение сопротивления. Данная зависимость определяется как прямо пропорциональная.

Другим свойством материала является площадь его поперечного сечения. Она представляет собой размеры поперечного среза проводника, независимо от его конфигурации. В этом случае получается обратно пропорциональная связь, когда с увеличением площади поперечного сечения уменьшается .

Еще одним фактором, влияющим на сопротивление, является сам материал. Во время проведения исследований была обнаружена различная сопротивляемость у разных материалов. Таким образом, были получены значения удельных электрических сопротивлений для каждого вещества.

Выяснилось, что самыми лучшими проводниками являются металлы. Среди них самой низкой сопротивляемостью и высокой проводимостью обладают и серебро. Они применяются в наиболее ответственных местах электронных схем, к тому же медь имеет сравнительно низкую стоимость.

Вещества, удельное сопротивление которых очень высокое, считаются плохими проводниками электрического тока. Поэтому они используются в качестве изоляционных материалов. Диэлектрические свойства более всего присущи фарфору и эбониту.

Таким образом, удельное сопротивление проводника имеет большое значение, поскольку с его помощью можно определить материал, из которого был изготовлен проводник. Для этого измеряется площадь сечения, определяется сила тока и напряжение. Это позволяет установить значение удельного электрического сопротивления, после чего, с помощью специальной таблицы можно легко определить вещество. Следовательно, удельное сопротивление относится к наиболее характерным признакам того или иного материала. Этот показатель позволяет определить наиболее оптимальную длину электрической цепи так, чтобы соблюдался баланс .

Формула

На основании полученных данных можно сделать вывод, что удельным сопротивлением будет считаться сопротивление какого-либо материала с единичной площадью и единичной длиной. То есть сопротивление, равное 1 Ом возникает при напряжении 1 вольт и силе тока 1 ампер. На этот показатель оказывает влияние степень чистоты материала. Например, если к меди добавить всего лишь 1% марганца, то ее сопротивляемость увеличится в 3 раза.

Удельное сопротивление и проводимость материалов

Проводимость и удельное сопротивление рассматриваются как правило при температуре 20 0 С. Эти свойства будут отличаться у различных металлов:

• Медь . Чаще всего применяется для изготовления проводов и кабелей. Она обладает высокой прочностью, стойкостью к коррозии, легкой и простой обработкой. В хорошей меди доля примесей составляет не более 0,1%. В случае необходимости медь может использоваться в сплавах с другими металлами.
• Алюминий . Его удельный вес меньше, чем у меди, однако у него более высокая теплоемкость и температура плавления. Чтобы расплавить алюминий, потребуется энергии значительно больше, чем для меди. Примеси в качественном алюминии не превышают 0,5%.
• Железо . Наряду с доступностью и дешевизной, этот материал обладает высоким удельным сопротивлением. Кроме того, у него низкая устойчивость к коррозии. Поэтому практикуется покрытие стальных проводников медью или цинком.

Отдельно рассматривается формула удельного сопротивления в условиях низких температур. В этих случаях свойства одних и тех же материалов будут совершенно другими. У некоторых из них сопротивляемость может упасть до нулевой отметки. Такое явление получило название сверхпроводимости, при которой оптические и структурные характеристики материала остаются неизменными.

В своей работе электрик часто сталкивается с вычислением различных величин и преобразований. Так для корректного подбора кабеля приходится подбирать нужное сечение. Логика выбора сечения основана на зависимости сопротивления от длины линии и площади сечения проводника. В этой статье мы рассмотрим, как выполняется расчет сопротивления провода по его геометрическим размерам.

Формула для расчета

Любые вычисления начинаются с формулы. Основной формулой для расчета сопротивления проводника является:

R=(ρ*l)/S

Где R – сопротивление в Омах, ρ – удельное сопротивление, l – длина в м, S – площадь поперечного сечения провода в мм 2 .

Эта формула подходит для расчета сопротивления провода по сечению и длине. Из неё следует, что в зависимости от длины изменяется сопротивление, чем длиннее – тем больше. И от площади сечения – наоборот, чем толще провод (большое сечение), тем меньше сопротивление. Однако непонятной остаётся величина, обозначенная буквой ρ (Ро).

Удельное сопротивление

Удельное сопротивление – это табличная величина, для каждого металла она своя. Она нужна для расчета и зависит от кристаллической решетки металла и структуры атомов.

Из таблицы видно, что самое меньшее сопротивление у серебра, для медного кабеля оно равняется 0,017 Ом*мм 2 /м. Такая размерность говорит нам, сколько приходится Ом при сечении в 1 миллиметр квадратный и длине в 1 метр.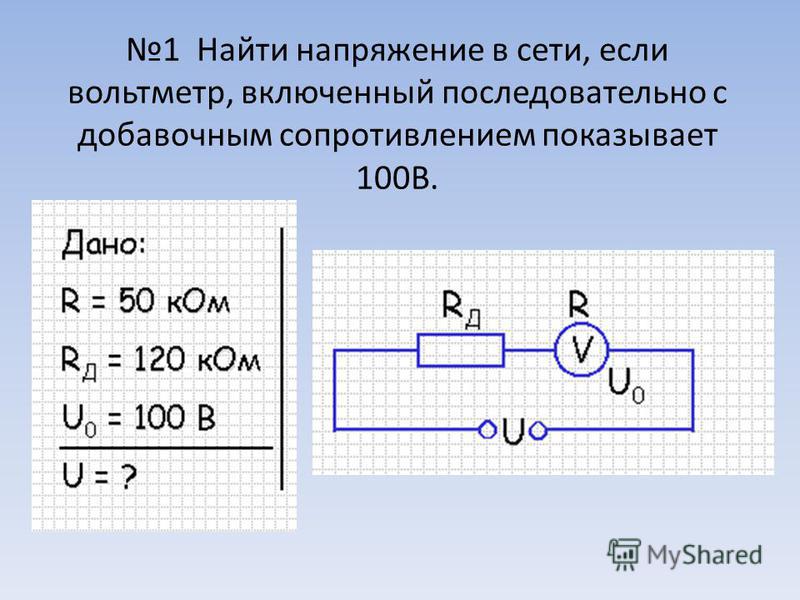

Кстати, серебряное покрытие используется в контактах коммутационных аппаратов, автоматических выключателей, реле и прочего. Это снижает , повышает срок службы и уменьшает . При этом в контактах измерительной и точной аппаратуры используют позолоченные контакты из-за того, что они слабо окисляются или вообще не окисляются.

У алюминия, который часто использовался в электропроводке раньше, сопротивление в 1,8 раза больше чем у меди, равняется 2,82*10 -8 Ом*мм 2 /м. Чем больше сопротивление проводника, тем сильнее он греется. Поэтому при одинаковом сечении алюминиевый кабель может передать меньший ток, чем медный, это и стало основной причиной почему все современные электрики используют . У нихрома, который используется в нагревательных приборах оно в 100 раз больше чем у меди 1,1*10 -6 Ом*мм 2 /м.

Расчет по диаметру

На практике часто бывает так, что площадь поперечного сечения жилы не известна. Без этого значения ничего рассчитать не получится. Чтобы узнать её, нужно измерить диаметр. Если жила тонка, можно взять гвоздь или любой другой стержень, намотать на него 10 витков провода, обычной линейкой измерить длину получившейся спирали и разделить на 10, так вы узнаете диаметр.

Ну, или просто замерить штангенциркулем. Расчет сечения выполняется по формуле:

Обязательны ли расчеты?

Как мы уже сказали, сечение провода выбирают исходя из предполагаемого тока и сопротивления металла, из которого изготовлены жилы. Логика выбора заключается в следующем: сечение подбирают таким способом, чтобы сопротивление при заданной длине не приводило к значительным просадкам напряжения. Чтобы не проводить ряд расчетов, для коротких линий (до 10-20 метров) есть достаточно точные таблицы:

В этой таблице указаны типовые значения сечения медных и алюминиевых жил и номинальные токи через них. Для удобства указана мощность нагрузки, которую выдержит эта линия. Обратите внимание на разницу в токах и мощности при напряжении 380В, естественно, что это предполагается трёхфазная электросеть.

Расчет сопротивления провода сводится к использованию пары формул, при этом вы можете скачать готовые калькуляторы из Плэй Маркета для своего смартфона, например, «Electrodroid» или «Мобильный электрик». Эти знания пригодятся для расчетов нагревательных приборов, кабельных линий, предохранителей и даже популярных на сегодняшний день спиралей для электронных сигарет.

Материалы

Инструкция

Найдите силу сопротивления движению, которая действует на равномерно прямолинейно движущееся тело. Для этого при помощи динамометра или другим способом измерьте силу, которую необходимо приложить к телу, чтобы оно двигалось равномерно и прямолинейно. По третьему закону Ньютона она будет численно равна силе сопротивления движения тела.

Определите силу сопротивления движению тела, которое перемещается по горизонтальной поверхности. В этом случае сила трения прямо пропорциональна силе реакции опоры, которая, в свою очередь равна силе тяжести, действующей на тело. Поэтому сила сопротивления движению в этом случае или сила трения Fтр равна произведению массы тела m, которая измеряется весами в килограммах, на ускорение свободного падения g≈9,8 м/с² и коэффициент пропорциональности μ, Fтр=μ∙m∙g. Число μ называется коэффициентом трения и зависит от поверхностей, входящих в контакт при движении. Например, для трения стали по дереву этот коэффициент равен 0,5.

Рассчитайте силу сопротивления движению тела, движущегося по . Кроме коэффициента трения μ, массы тела m и ускорения свободного падения g, она зависит от угла наклона плоскости к горизонту α. Чтобы найти силу сопротивления движению в этом случае, нужно найти произведения коэффициента трения, массы тела, ускорения свободного падения и косинуса угла, под которым плоскость к горизонту Fтр=μ∙m∙g∙сos(α).

При движении тела в воздухе на невысоких скоростях сила сопротивления движению Fс прямо пропорциональна скорости движения тела v, Fc=α∙v. Коэффициент α зависит от свойств тела и вязкости среды и рассчитывается отдельно.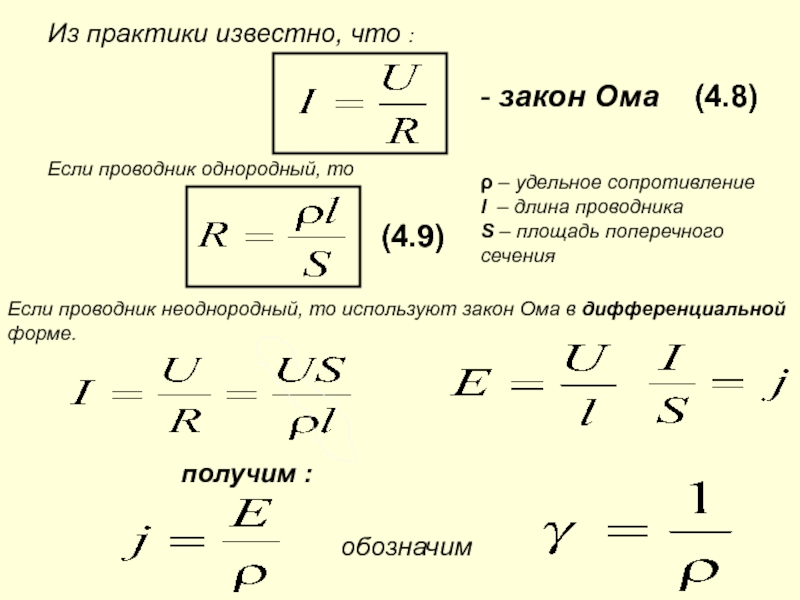 При движении на высоких скоростях, например, при падении тела со значительной высоты или движении автомобиля, сила сопротивления прямо пропорциональна квадрату скорости Fc=β∙v². Коэффициент β дополнительно рассчитывается для высоких скоростей.

Источники:

• 1 Общая формула для силы сопротивления воздуха На рисунке

Для определения силы сопротивления воздуха создайте условия, при которых тело начнет под действием силы тяжести двигаться равномерно и прямолинейно. Рассчитайте значение силы тяжести, оно будет равно силе сопротивления воздуха. Если тело движется в воздухе, набирая скорость, сила его сопротивления находится при помощи законов Ньютона, также силу сопротивления воздуха можно найти из закона сохранения механической энергии и специальных аэродинамических формул.

Вам понадобится

• дальномер, весы, спидометр или радар, линейка, секундомер.

Инструкция

Перед измерением сопротивления б/у резистора обязательно выпаяйте его из старой платы или блока. Иначе он может быть шунтирован другими деталями схемы, и вы получите неправильные показания его сопротивления .

Видео по теме

Чтобы найти электрическое сопротивление проводника, воспользуйтесь соответствующими формулами. Сопротивление участка цепи находится по закону Ома. Если же известен материал и геометрические размеры проводника, его сопротивление можно рассчитать при помощи специальной формулы.

Вам понадобится

• – тестер;
• – штангенциркуль;
• – линейка.

Инструкция

Вспомните, что подразумевает собой понятие резистора. В данном случае под резистором надо понимать любой проводник или элемент электрической цепи, имеющий активное резистивное сопротивление. Теперь важно задаться вопросом о том, как действует изменение значения сопротивления на значение силы тока и от чего оно зависит. Суть явления сопротивления заключается в том, что резистора формируют своего рода барьер для прохождения электрических зарядов. Чем выше сопротивление вещества, тем более плотно расположены атомы в решетке резистивного вещества. Данную закономерность и объясняет закон Ома для участка цепи. Как известно, закон Ома для участка цепи звучит следующим образом: сила тока на участке цепи прямо пропорциональна напряжению на участке и обратно пропорциональна сопротивлению самого участка цепи.

Изобразите на листе бумаги график зависимости силы тока от напряжения на резисторе, а также от его сопротивления, исходя из закона Ома. Вы получите график гиперболы в первом случае и график прямой во втором случае. Таким образом, сила тока будет тем больше, чем больше напряжение на резисторе и чем меньше сопротивление. Причем зависимость от сопротивления здесь более яркая, ибо она имеет вид гиперболы.

Обратите внимание, что сопротивление резистора также изменяется при изменении его температуры. Если нагревать резистивный элемент и наблюдать при этом за изменением силы тока, то можно заметить, как при увеличении температуры уменьшается сила тока. Данная закономерность объясняется тем, что при увеличении температуры увеличиваются колебания атомов в узлах кристаллической решетки резистора, уменьшая таким образом свободное пространство для прохождения заряженных частиц. Другой причиной, уменьшающей силу тока в данном случае, является тот факт, что при увеличении температуры вещества увеличивается хаотичное движение частиц, в том числе заряженных. Таким образом, движение свободных частиц в резисторе становится в большей степени хаотичным, чем направленным, что и сказывается на уменьшении силы тока.

Видео по теме

Собрав электрическую цепь, состоящую из источника тока, резистора, амперметра, вольтметра, ключа, можно показать, что сила тока (I ), протекающего через резистор, прямо пропорциональна напряжению (U ) на его концах: I — U . Отношение напряжения к силе тока U/I – есть величина постоянная .

Следовательно, существует физическая величина, характеризующая свойства проводника (резистора), по которому течёт электрический ток. Эту величину называют электрическим сопротивлением проводника, или просто сопротивлением. Обозначается сопротивление буквой R .

(R) – это физическая величина, равную отношению напряжения (U ) на концах проводника к силе тока (I ) в нём. R = U/I . Единица измерения сопротивления – Ом (1 Ом ).

Один Ом – сопротивление такого проводника, в котором сила тока равна 1А при напряжении на его концах 1В: 1 Ом = 1 В / 1 А.

Причина того, что проводник обладает сопротивлением, заключается в том, что направленному движению электрических зарядов в нём препятствуют ионы кристаллической решетки , совершающие беспорядочное движение. Соответственно, скорость направленного движения зарядов уменьшается.

Удельное электрическое сопротивление R ) прямо пропорционально длине проводника (l ), обратно пропорционально площади его поперечного сечения (S ) и зависит от материала проводника. Эта зависимость выражается формулой: R = p*l/S

р – это величина, характеризующая материал, из которого сделан проводник. Она называется удельным сопротивлением проводника , её значение равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м 2 .

Единицей удельного сопротивления проводника служит: [р] = 1 0м 1 м 2 / 1 м . Часто площадь поперечного сечения измеряют в мм 2 , поэтому в справочниках значения удельного сопротивления проводника приводятся как в Ом м так и в Ом мм 2 / м .

Изменяя длину проводника, а следовательно его сопротивление, можно регулировать силу тока в цепи. Прибор, с помощью которого это можно сделать, называется реостатом .

Закон Ома для переменного тока

 

 Мы с вами знаем формулировку закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него.

Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы).

В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю.

Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением. Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю

Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю.

Тогда, падение напряжения на активном сопротивлении определяется по формуле:

(1)

где, U-напряжение на элементе цепи,

I – ток через элемент цепи

R – активное сопротивление элемента

Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения:

(2)

где, Um-амплитудное значение напряжения на элементе цепи,

Im – амплитудное значение тока через элемент цепи

R – активное сопротивление элемента

В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис. 2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).

Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением. Фаза тока отстает от фазы напряжения на 90 градусов.

 

Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов.

Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения.

Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам:

	(3)
	(4)

где — U_L-падение напряжение на чисто индуктивном сопротивлении ;

U_С—падение напряжения на чисто емкостном сопротивлении;

I— значение тока в через реактивное сопротивление;

L— индуктивность реактивного элемента;

C— емкость реактивного элемента;

ω— циклическая частота.

Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов.

Приведенные выше формулы являются частными случаями закона Ома для переменного тока.

Следовательно, полный закон Ома для переменного тока будет иметь вид:

(5)

Где Z – полное сопротивление цепи переменного тока.

Теперь остается только вычистислить полное сопротивление цепи, а оно зависит непосредсвенно от какие активные и реактивные элементы присутсвуют в цепи и как они соединены.

Закон Ома для различных типовых цепей переменного тока

Давайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис. 4.)

Рисунок 4. Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления.

Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой:

(6)

где —эффективное значение силы тока в А;

U—эффективное значение напряжения в В;

R—активное сопротивление в Ом;

ωL—индуктивное сопротивление в ом.

Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения.

В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления.

Рисунок 5. Цепь переменного тока с последовательным соединением активного и емкосного сопротивления.

А закон Ома для такой цепи принимает вид:

(7)

В общем случае, когда цепь содержит все три вида сопротивлений (рис. 6),

Рисунок 6. Цепь переменного тока с последовательным соединением активного, индуктивного и емкосного сопротивления.

Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так:

(8)

где I-сила тока в А;

U-напряжение в В;

R-активное сопротивление в Ом;

ωL-индуктивное сопротивление в Ом;

1/ωС-емкостное сопротивление в Ом.

Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения.

Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно прсмотреть здесь, зтем подставить значение полного сопротивления в общую формулу для закона Ома (5).

Рисунок 7. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) – параллельное соединение R и L; б) – параллельное соединение R и C.

 

Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8.

Рисунок 8. Эквивалентная схема колебательного контура.

 

Таким образом закон Ома для переменного тока можно сформулировать следующим образом.

Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи)

 

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Учебное пособие по физике: Параллельные схемы

Как упоминалось в предыдущем разделе Урока 4, два или более электрических устройства в цепи могут быть соединены последовательным или параллельным соединением. Когда все устройства соединены с использованием параллельных соединений, схема называется параллельной схемой . В параллельной схеме каждое устройство помещается в свою отдельную ветвь . Наличие ответвлений означает, что существует несколько путей, по которым заряд может проходить через внешнюю цепь.Каждый заряд, проходящий через контур внешней цепи, будет проходить через единственный резистор, присутствующий в одной ветви. По прибытии в место разветвления или узел плата выбирает , через какую ветвь пройти на обратном пути к терминалу с низким потенциалом.

Краткое сравнение и контраст между последовательными и параллельными цепями было сделано в предыдущем разделе Урока 4. В этом разделе было подчеркнуто, что добавление большего количества резисторов в параллельную цепь приводит к довольно неожиданному результату – уменьшению общего сопротивления. .Поскольку существует несколько путей, по которым может протекать заряд, добавление еще одного резистора в отдельную ветвь обеспечивает другой путь, по которому заряд может проходить через основную область сопротивления в цепи. Это уменьшенное сопротивление в результате увеличения количества ветвей будет иметь эффект увеличения скорости, с которой течет заряд (также известной как ток). Чтобы сделать этот довольно неожиданный результат более разумным, была введена аналогия с платными дорогами. Плата за проезд – это основное место сопротивления автомобильному потоку на платной дороге.Добавление дополнительных пунктов взимания платы в пределах их собственного отделения на платной дороге обеспечит больше путей для автомобилей, проезжающих через станцию ​​взимания платы. Эти дополнительные пункты пропуска снизят общее сопротивление потоку автомобилей и увеличат скорость их движения.

Текущая

Скорость, с которой заряд проходит через цепь, называется током. Заряд НЕ накапливается и не начинает накапливаться в любом конкретном месте, так что ток в одном месте больше, чем в других местах.Заряд НЕ расходуется резисторами таким образом, что в одном месте ток меньше, чем в другом. В параллельной схеме заряд делит на отдельные ветви, так что в одной ветви может быть больше тока, чем в другой. Тем не менее, если брать в целом, общая сумма тока во всех ветвях при сложении равна величине тока в местах за пределами ветвей. Правило, что ток везде один и тот же , все еще работает, только с закруткой.Сила тока вне ветвей равна сумме токов в отдельных ветвях. Это все еще та же величина тока, только разделенная на несколько путей.

В форме уравнения этот принцип можно записать как

I _всего = I ₁ + I ₂ + I ₃ + …

, где I _всего – это общая сумма тока вне ветвей (и в батарее), а I ₁ , I ₂ и I ₃ представляют ток в отдельных ветвях цепи.

В этом блоке широко использовалась аналогия между расходом заряда и расходом воды. Еще раз вернемся к аналогии, чтобы проиллюстрировать, как сумма текущих значений в ветвях равна сумме вне ветвей. Поток заряда в проводах аналогичен потоку воды в трубах. Рассмотрим приведенные ниже схемы, на которых поток воды в трубах делится на отдельные ответвления. В каждом узле (место разветвления) вода проходит двумя или более отдельными путями.Скорость, с которой вода поступает в узел (измеряется в галлонах в минуту), будет равна сумме расходов в отдельных ответвлениях за пределами узла. Точно так же, когда две или более ветви подаются в узел, скорость, с которой вода вытекает из узла, будет равна сумме расходов в отдельных ветвях, которые подаются в узел.

Тот же принцип разделения потока применяется к электрическим цепям. Скорость, с которой заряд поступает в узел, равна сумме расходов в отдельных ветвях за пределами узла.Это проиллюстрировано в приведенных ниже примерах. В примерах вводится новый символ схемы – буква A, заключенная в круг. Это символ амперметра – устройства, используемого для измерения силы тока в определенной точке. Амперметр способен измерять ток, оказывая при этом незначительное сопротивление потоку заряда.

Диаграмма A показывает два резистора, подключенных параллельно с узлами в точках A и B. Заряд течет в точку A со скоростью 6 ампер и делится на два пути – один через резистор 1, а другой – через резистор 2.Ток в ветви с резистором 1 составляет 2 ампера, а ток в ветви с резистором 2 – 4 ампера. После того, как эти две ветви снова встретятся в точке B, чтобы сформировать единую линию, ток снова станет равным 6 ампер. Таким образом, мы видим, что принцип, согласно которому ток вне ветвей равен сумме тока в отдельных ветвях, справедлив.

I _итого = I ₁ + I ₂

6 ампер = 2 ампера + 4 ампера

Схема B выше может быть немного сложнее, если три резистора расположены параллельно.На схеме обозначены четыре узла, обозначенные буквами A, B, C и D. Заряд течет в точку A со скоростью 12 ампер и делится на два пути: один проходит через резистор 1, а другой направляется к точке B (и резисторам 2). и 3). 12 ампер тока делятся на 2-амперную (через резистор 1) и 10-амперную (в направлении точки B). В точке B происходит дальнейшее разделение потока на два пути – один через резистор 2, а другой через резистор 3. Ток в 10 ампер, приближающийся к точке B, делится на 6-амперный канал (через резистор 2) и 4-канальный. -амперный тракт (через резистор 3).Таким образом, видно, что значения тока в трех ветвях составляют 2 ампера, 6 ампер и 4 ампера, и что сумма значений тока в отдельных ветвях равна току вне ветвей.

I _всего = I ₁ + I ₂ + I ₃

12 ампер = 2 ампер + 6 ампер + 4 ампер

Анализ потока в точках C и D также может быть проведен, и будет замечено, что сумма расходов потока в этих точках равна скорости потока, находящейся непосредственно за этими точками.

Эквивалентное сопротивление

Фактическая величина тока всегда обратно пропорциональна величине общего сопротивления. Существует четкая взаимосвязь между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Чтобы исследовать эту взаимосвязь, давайте начнем с простейшего случая, когда два резистора помещены в параллельные ветви, каждый из которых имеет одинаковое значение сопротивления 4 Ом.Поскольку схема предлагает два равных путей для потока заряда, только половина заряда выберет для прохождения через данную ветвь. В то время как каждая отдельная ветвь предлагает сопротивление 4 Ом любому заряду, который проходит через нее, только половина всего заряда, протекающего по цепи, будет встречать сопротивление 4 Ом этой отдельной ветви. Таким образом, что касается батареи, которая накачивает заряд, наличие двух параллельно подключенных резисторов 4 Ом было бы эквивалентно наличию одного резистора 2 Ом в цепи.Таким же образом, наличие двух параллельных резисторов сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 3 Ом. А наличие двух параллельных резисторов 12 Ом было бы эквивалентно наличию в цепи одного резистора 6 Ом.

Теперь давайте рассмотрим другой простой случай, когда три резистора включены параллельно, каждый из которых имеет одинаковое сопротивление 6 Ом. При трех равных путях прохождения заряда через внешнюю цепь только одна треть заряда будет проходить через данную ветвь.Каждая отдельная ветвь обеспечивает сопротивление 6 Ом проходящему через нее заряду. Однако тот факт, что только одна треть заряда проходит через определенную ветвь, означает, что общее сопротивление цепи составляет 2 Ом. Что касается батареи, которая нагнетает заряд, наличие трех параллельных резисторов 6 Ом было бы эквивалентно наличию одного резистора 2 Ом в цепи. Таким же образом, наличие трех параллельно подключенных резисторов сопротивлением 9 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 3 Ом.А наличие трех параллельных резисторов 12 Ом было бы эквивалентно наличию одного резистора 4 Ом в цепи.

Это концепция эквивалентного сопротивления. Эквивалентное сопротивление цепи – это величина сопротивления, которая потребуется одному резистору, чтобы сравняться с общим эффектом от набора резисторов, присутствующих в цепи. Для параллельных цепей математическая формула для вычисления эквивалентного сопротивления ( _{R eq} ) составляет

. 1 / R _экв. = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ +…

, где R ₁ , R ₂ и R ₃ – значения сопротивления отдельных резисторов, подключенных параллельно. Приведенные выше примеры можно рассматривать как простые случаи, в которых все пути обладают одинаковым сопротивлением отдельному заряду, который проходит через них. Вышеупомянутые простые случаи были выполнены без использования уравнения. Тем не менее, это уравнение подходит как для простых случаев, когда резисторы ответвления имеют одинаковые значения сопротивления, так и для более сложных случаев, когда резисторы ответвления имеют разные значения сопротивления.Например, рассмотрим применение уравнения к одному простому и одному сложному случаю ниже.

Случай 1 : три резистора 12 Ом включены параллельно	1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 1 / R экв = 1 / (12 Ом) + 1 / (12 Ом) + 1 / (12 Ом) Использование калькулятора … 1 / R экв. = 0,25 Ом -1 R экв = 1 / (0,25 Ом -1 ) R экв = 4,0 Ом
Случай 2 : резисторы 5,0 Ом, 7,0 Ом и 12 Ом включены параллельно	1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 1 / R экв = 1 / (5.0 Ом) + 1 / (7,0 Ом) + 1 / (12 Ом) Использование калькулятора … 1 / R экв = 0,42619 Ом-1 R экв = 1 / (0,42619 Ом -1 ) R экв. = 2,3 Ом

Ваша очередь попробовать

Нужно больше практики? Используйте Два параллельных резистора виджет ниже, чтобы попробовать некоторые дополнительные проблемы.Введите любые два значения сопротивления по вашему желанию. Используйте свой калькулятор, чтобы определить значения _{рэндов экв.} . Затем нажмите кнопку Отправить , чтобы проверить свои ответы. Попробуйте столько раз, сколько хотите, с разными значениями сопротивления.

Падения напряжения для параллельных ответвлений

В разделе «Схемы» учебного пособия «Физический класс» подчеркивалось, что любое повышение напряжения, полученное за счет заряда в батарее, теряется из-за заряда, когда он проходит через резисторы внешней цепи.Общее падение напряжения во внешней цепи равно увеличению напряжения при прохождении заряда через внутреннюю цепь. В параллельной схеме заряд не проходит через каждый резистор; скорее, он проходит через единственный резистор. Таким образом, полное падение напряжения на этом резисторе должно соответствовать напряжению батареи. Не имеет значения, проходит ли заряд через резистор 1, резистор 2 или резистор 3, падение напряжения на резисторе, которое выбирает для прохождения , должно равняться напряжению батареи.В форме уравнения этот принцип можно было бы выразить как

В _{аккумулятор} = В ₁ = В ₂ = В ₃ = …

Если три резистора размещены в параллельных ветвях и питаются от 12-вольтовой батареи, то падение напряжения на каждом из трех резисторов составляет 12 вольт. Заряд, протекающий по цепи, встретит только один из этих трех резисторов и, таким образом, столкнется с одним падением напряжения на 12 вольт.

Диаграммы электрических потенциалов были представлены в Уроке 1 этого устройства и впоследствии использовались для иллюстрации последовательных падений напряжения, происходящих в последовательных цепях.Диаграмма электрических потенциалов – это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим приведенную ниже принципиальную схему и соответствующую диаграмму электрических потенциалов.

Как показано на диаграмме электрических потенциалов, все позиции A, B, C, E и G имеют высокий электрический потенциал. Один заряд выбирает только один из трех возможных путей; таким образом, в позиции B один заряд переместится в точку C, E или G, а затем пройдет через резистор, который находится в этой ветви.Заряд не теряет свой высокий потенциал до тех пор, пока не пройдет через резистор, либо от C к D, от E к F или от G к H. После того, как он пройдет через резистор, заряд вернется почти до 0 вольт и вернется к отрицательному значению. клемму аккумуляторной батареи для повышения ее напряжения. В отличие от последовательных цепей, заряд в параллельной цепи встречает единственное падение напряжения на своем пути через внешнюю цепь.

Ток через заданную ветвь можно предсказать, используя уравнение закона Ома, падение напряжения на резисторе и сопротивление резистора.Поскольку падение напряжения на каждом резисторе одинаковое, фактором, определяющим, что резистор имеет наибольший ток, является сопротивление. Резистор с наибольшим сопротивлением испытывает наименьший ток, а резистор с наименьшим сопротивлением – наибольший ток. В этом смысле можно сказать, что заряд (как и люди) выбирает путь наименьшего сопротивления. В форме уравнения это может быть указано как

I 1 = Δ V 1 / R 1

I 2 = Δ V 2 / R 2

I 3 = Δ V 3 / R 3

Этот принцип иллюстрируется схемой, показанной ниже.Произведение I • R одинаково для каждого резистора (и равно напряжению батареи). Тем не менее, ток у каждого резистора разный. Ток наибольший там, где сопротивление наименьшее, и ток наименьший, где сопротивление наибольшее.

Математический анализ параллельных цепей

Приведенные выше принципы и формулы могут использоваться для анализа параллельной цепи и определения значений тока и разности электрических потенциалов на каждом из резисторов в параллельной цепи.Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R _eq ), тока через батарею (I _до ), а также падений напряжения и тока для каждого из трех резисторов.

Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.

1 / R _экв = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ = (1/17 Ом) + (1/12 Ом) + (1/11 Ом)

1 / R _экв = 0.23306 Ом ^-1

R _экв = 1 / (0,23306 Ом ^-1 )

R _экв = 4,29 Ом

(округлено от 4,29063 Ом)

Теперь, когда известно эквивалентное сопротивление, ток в батарее можно определить с помощью уравнения закона Ома. При использовании уравнения закона Ома (ΔV = I • R) для определения тока в батарее важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R.Расчет показан здесь:

I _до = ΔV _{аккумулятор} / R _eq = (60 В) / (4,29063 Ом)

I _до = 14,0 А

(округлено от 13,98396 А)

Напряжение батареи 60 В представляет собой усиление электрического потенциала за счет заряда, проходящего через батарею. Заряд теряет такое же количество электрического потенциала при любом прохождении через внешнюю цепь.То есть падение напряжения на каждом из трех резисторов такое же, как и напряжение, полученное в батарее:

ΔV _{аккумулятор} = ΔV ₁ = ΔV ₂ = ΔV ₃ = 60 В

Осталось определить три значения – ток каждого отдельного резистора. Закон Ома снова используется для определения значений тока для каждого резистора – это просто падение напряжения на каждом резисторе (60 В), деленное на сопротивление каждого резистора (указанное в формулировке задачи).Расчеты показаны ниже.

I 1 = ΔV 1 / R 1 I 1 = (60 В) / (17 Ом) I 1 = 3,53 А

I 2 = ΔV 2 / R 2 I 2 = (60 В) / (12 Ом) I 2 = 5,00 А

I 3 = ΔV 3 / R 3 I 3 = (60 В) / (11 Ом) Я 3 = 5.45 ампер

В качестве проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли вычисленные значения принципу, согласно которому сумма значений тока для каждого отдельного резистора равна общему току в цепи (или в батарее). . Другими словами, I _to = I ₁ + I ₂ + I ₃ ?

Является ли I _tot = I ₁ + I ₂ + I ₃ ?

Из 14.0 ампер = 3,53 ампер + 5,00 ампер + 5,45 ампер?

14,0 А = 13,98 А?

Да !!

(Разница в 0,02 ампера – это просто результат предыдущего округления значения I _до от 13,98.)

Математический анализ этой параллельной цепи включал смесь концепций и уравнений. Как это часто бывает в физике, отделение понятий от уравнений при принятии решения физической проблемы является опасным актом.Здесь необходимо учитывать концепции, согласно которым падение напряжения на каждом из трех резисторов равно напряжению батареи, и что сумма тока в каждом резисторе равна общему току. Эти представления необходимы для завершения математического анализа. В следующей части Урока 4 будут исследованы комбинированные или составные схемы, в которых одни устройства включены параллельно, а другие – последовательно.

Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже.Создайте себе проблему с любым количеством резисторов и любыми номиналами. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.

Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие – это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключать их так, как хотите. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванне).

Проверьте свое понимание

1. По мере того, как в цепь добавляется все больше и больше резисторов, эквивалентное сопротивление цепи ____________ (увеличивается, уменьшается) и общий ток цепи ____________ (увеличивается, уменьшается).

2.Три одинаковых лампочки подключены к D-ячейке, как показано ниже. P, Q, X, Y и Z обозначают места на трассе. Какое из следующих утверждений верно?

а. Ток в точке Y больше, чем ток в точке Q.

г. Ток на Y больше, чем на P.

.

г. Ток в точке Y больше, чем ток в точке Z.

г. Ток в точке P больше, чем ток в точке Q.

.

e.Ток на Q больше, чем на P.

ф. Сила тока одинакова во всех местах.

3. Три одинаковые лампочки подключены к D-ячейке, как показано ниже. P, Q, X, Y и Z обозначают места на трассе. В каком (их) месте (ах), если таковые имеются, текущий будет …

а. … так же, как у X?

г…. такой же, как у Q?

г. … так же, как у Y?

г. … меньше, чем у Q?

e. … меньше, чем у P?

ф. … вдвое больше, чем у Z?

г. … в три раза больше, чем в Y?

4. Какие изменения можно внести в схему ниже, чтобы уменьшить ток в ячейке? Перечислите все подходящие варианты.

а. Увеличьте сопротивление лампы X.

г. Уменьшите сопротивление лампы X.

г. Увеличьте сопротивление лампы Z.

.

г. Уменьшите сопротивление лампы Z.

.

e. Увеличьте напряжение ячейки (как-нибудь).

ф. Уменьшите напряжение ячейки (как-нибудь).

г. Снять лампу Y.

.

5.Аккумулятор на 12 В, резистор на 12 Ом и резистор на 4 Ом подключаются, как показано. Сила тока в резисторе 12 Ом равна ____ току в резисторе 4 Ом.

а. 1/3	г. 1/2	г. 2/3
г. то же, что		e.1,5 раза
ф. дважды		г. трижды
ч. четыре раза

6. Аккумулятор на 12 В, резистор на 12 Ом и резистор на 4 Ом подключаются, как показано.Падение напряжения на резисторе 12 Ом равно ____ падению напряжения на резисторе 4 Ом.

а. 1/3	г. 1/2	г. 2/3
г. то же, что		e. 1,5 раза
ф.дважды		г. трижды
ч. четыре раза

7. Аккумулятор на 12 В и резистор на 12 Ом подключаются, как показано на схеме. Резистор на 6 Ом добавлен к резистору на 12 Ом, чтобы создать цепь Y, как показано.Падение напряжения на резисторе 6 Ом в цепи Y равно ____ падению напряжения на резисторе в цепи X.

а. больше, чем

г. меньше

г. то же, что

8. Используйте свое понимание эквивалентного сопротивления, чтобы заполнить следующие утверждения:

а. Два резистора сопротивлением 6 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.

г. Три резистора 6 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.

г. Три резистора сопротивлением 8 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.

г. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом размещены параллельно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

e. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом размещены параллельно.Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

ф. Три резистора с сопротивлением 12 Ом, 6 Ом и 21 Ом размещены параллельно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

9. На основании ваших ответов на вышеуказанный вопрос заполните следующую формулировку:

Общее или эквивалентное сопротивление трех параллельно включенных резисторов будет _____.

а. больше, чем сопротивление самого большого значения R.

г. меньше, чем сопротивление наименьшего значения R из трех.

г. где-то посередине между наименьшим значением R и наибольшим значением R.

г. … ерунда! Такого обобщения сделать нельзя. Результаты меняются.

10. Три резистора включены параллельно.При размещении в цепи с источником питания 12 В. Определите эквивалентное сопротивление, полный ток цепи, падение напряжения и ток в каждом резисторе.

Как рассчитать падение напряжения на резисторе – подробное объяснение

Если вы ищете, как рассчитать падение напряжения на резисторе, то SoManyTech предлагает вам полную теорию и практические примеры падения напряжения на резисторе.Перед этим давайте освежим в памяти закон Ома: (Прокрутите вниз, если вы профессиональный пользователь)

• Распространенный способ показать поведение схемного устройства – это его характеристика.
  Это график зависимости тока «I» через устройство от приложенного к нему напряжения «V». Это устройство, резистор, имеет простую линейную характеристику В – I , показанную на рис. . выше.
• Эта линейная зависимость устройства выражается законом Ома :
  V = IR
• Константа пропорциональности R известна как сопротивление устройства и равна наклону кривой I. –V характеристика.Единица измерения сопротивления – Ом, символ Ом . Любое устройство с линейной ВАХ называется резистором.

Какое падение напряжения на резисторе?

• Падение напряжения на резисторе – это не что иное, как значение напряжения на резисторе. Иногда его также называют «напряжение на резисторе» или просто «падение напряжения».
• Обычно обозначается как:
  ‘V (drop ) ‘ или ‘Vr’ или ‘Vd’
  Для нескольких резисторов это записывается как Vr1, Vr2, Vr3 и т. Д.

Как мы все знаем, резистор – это устройство, которое оказывает сопротивление протекающему через него току. Затем, применяя закон Ома, резистор будет предлагать падение напряжения на резистивном устройстве, которое определяется как:

В ( падение ) = I × R

, где I = ток через резистор в (А) в амперах
R = сопротивление в (Ом) Ом
В ( падение ) = падение напряжения в (В) вольтах

Как рассчитать падение напряжения по сопротивлению пошагово:

Шаг 1: Упростите данную схему.Если, скажем, схема заполнена резисторами, включенными последовательно и параллельно, то повторно подключите ее, чтобы упростить. (проверьте практический пример ниже)

Step2: Затем найдите эквивалентный резистор.
Для параллельного: 1 / Треб. = 1 / R1 + 1 / R2…
Для серии: Треб. = R1 + R2 +. . .

Step3: Найдите ток через каждый резистор. (Ток через последовательный резистор одинаков, а ток через параллельные резисторы отличается и зависит от его значения)

Step4 : Примените формулу закона Ома для расчета падения напряжения.
В = IR

Напряжение в последовательной цепи – Практические примеры:

Случай I:

Если есть только один резистор последовательно с батареей или источником питания, как показано в этой схеме.

В этой схеме падение напряжения на резисторе такое же, как и в цепи питания. Это связано с тем, что оба компонента имеют общие потенциальные точки, разделенные между ними (точка A и точка B)

∴ Vs = Vdrop = 5 вольт (скажем)

Случай II:

Если есть два или несколько резисторов, включенных последовательно с батареей, как показано на этой схеме.

В этой схеме мы должны вычислить полный ток «I», протекающий через цепь.
I (общий) = V (питание) / R (эквивалент)

∴ I (общий) = 5/30 = 0,166 A

Тогда падение напряжения на R1 будет: Vr1 = I × R1
Падение напряжения на R2 будет: Vr2 = I × R2
Падение напряжения на Rn будет: Vrn = I × Rn

• Vr1 = I × R1 = 0,166 × 10 = 1,66 В & Vr2 = I × R2 = 0.166 × 20 = 3,33 вольт

Напряжение на параллельных резисторах:

Случай I:
Два резистора включены параллельно батарее или источнику питания, как показано в этой схеме.

В этой схеме падение напряжения на этих параллельных резисторах такое же, как у источника питания.
Это связано с тем, что оба резистора имеют общие потенциальные точки, разделенные между ними (точка A и точка B), поэтому напряжение будет одинаковым, но ток будет другим.

∴Vs = Vdrop = Vr1 = Vr2 = 5 вольт (скажем)

Случай II:
Один резистор включен последовательно и два резистора с источником питания, как показано на этой схеме.

В этой схеме нам нужно вычислить ток «I» через каждый компонент.

• i1 = I (всего) = Is = V (питание) / R (эквивалент)

  где, R (эквивалент) = R1 + Rp
  где, 1 / Rp = 1 / R2 + 1 / R3

  ∴ Rp = 12 Ом и R ( эквивалент ) = 22 Ом

• i2 = i1 * (R3 / (R2 + R3))
  i3 = i1 * (R2 / (R2 + R3))

• Падение напряжения на R1 будет Vr1 = R1 * i1
  Падение напряжения на R2 будет Vr2 = R2 * i2
  Падение напряжения на R3 будет Vr3 = R2 * i3

Положить значения, которые мы имеем,

Теперь i1 = V (поставка) / R (эквивалент) = 5/22 = 0.227 ампер
∴ i1 = 0,227 A

Падение напряжения на 10 Ом -> Vr1 = 10 * i1 = 10 × 0,227 вольт
∴ Vr1 = 2,27 вольт

9000 i1 Теперь, i1 * (R3 / (R1 + R2))
∴ i2 = 0,1362 A

Падение напряжения на 20 Ом -> Vr2 = 20 * i2 = 20 × 0,1362 В
∴ Vr2 = 2,724 В

Теперь i3 = i1 * (R2 / (R1 + R2))
∴ i3 = 0.09 A

Падение напряжения на 30 Ом -> Vr2 = 30 * i2 = 30 × 0,09 В
∴ Vr3 = 2,7 В

Метод 2: i1 = В (питание) / R (эквивалент) = 0,227 A
Тогда падение напряжения на R1 будет Vr1 = R1 * i1 = 10 × 0,227 = 2,27 В

∴ Эквивалентное напряжение в точке ‘A’ будет равно
Veq = Va = Vs – Vr1

∴ Va = 5 – 2.27 = 2,73 В
Следовательно, мы получаем одинаковое значение потенциала на R2 и R3.

Таким образом, Va = Vr2 = Vr3 = 2,73 вольт

Метод 3:

В этом методе мы используем цифровой мультиметр или, можно сказать, вольтметр. Все, что вам нужно, это установить мультиметр в режим напряжения.
Теперь с помощью двух щупов проверьте напряжение на требуемом резисторе, подключив к нему щупы. (на рис. показания вольтметра только для справки)

Вуаля !! Ты понял.

Это самый простой способ найти падение напряжения на резисторе в любой цепи.

Закон Ома

Закон Ома Главная | Карта | Проекты | Строительство | Пайка | Исследование | Компоненты | 555 | Символы | FAQ | Ссылки

---

Следующая страница: Мощность и энергия
См. Также: Напряжение и ток | Сопротивление | Резисторы

Чтобы ток протекал через сопротивление, на этом сопротивлении должно быть напряжение.Закон Ома показывает взаимосвязь между напряжением (V), током (I) и сопротивлением (R). Это можно записать тремя способами:

где:

V = напряжение в вольтах (В) I = ток в амперах (A) R = сопротивление в Ом ()

или:

V = напряжение в вольтах (В) I = ток в миллиамперах (мА) R = сопротивление в килом (к)

Для большинства электронных схем усилитель слишком велик, а сопротивление слишком мало, поэтому мы часто измеряем ток в миллиамперах (мА) и сопротивление в киломах. (k).1 мА = 0,001 А и 1 кОм = 1000.

Уравнения закона Ома работают, если вы используете V, A и , или если вы используете В, мА и k. Вы не должны смешивать эти наборы единиц в уравнениях, поэтому вам может потребоваться преобразование между mA и A или k и .

Треугольник ВИР

V I R

Закон Ома треугольник

Вы можете использовать треугольник ВИР, чтобы запомнить три версии закона Ома.
Запишите V, I и R в треугольнике, как в желтом поле справа.

• Для расчета напряжения, В : поместите палец на V,
  это оставляет вас с I R, поэтому уравнение V = I × R
• Чтобы рассчитать ток , I : положите палец на I,
  это оставляет вас с V над R, поэтому уравнение I = ^V / _R
• Чтобы рассчитать сопротивление , R : поместите палец на R,
  это оставляет вас с V над I, поэтому уравнение R = ^V / _I
  

---

Расчет по закону Ома

Используйте этот метод для проведения расчетов:

1. Запишите Значения , при необходимости конвертируя единицы.
   
2. Выберите нужное Equation (используйте треугольник VIR).
   
3. Подставьте числа в уравнение и вычислите ответ.

Должно быть V ery E asy N ow!

---

Следующая страница: Power and Energy | Изучение электроники

---

---

© Джон Хьюс 2007, Клуб электроники, www.kpsec.freeuk.com
Этот сайт был взломан с использованием ПРОБНОЙ версии WebWhacker.Это сообщение не появляется на лицензированной копии WebWhacker.

ресурсов

Мощность

Мощность в электрической цепи относится к скорости, с которой электрическая энергия преобразуется в какую-либо другую форму, такую ​​как тепло или магнетизм. Мощность, рассеиваемая в цепи, напрямую связана с приложенным напряжением и величиной тока, протекающего по цепи.

Диаграммы показывают, что увеличение мощности земного шара в цепи с тем же напряжением приводит к более высокому току, следовательно, рассеивается больше мощности, то есть больше тепла и света.Более высокий ток означает, что шар с высокой мощностью имеет меньшее сопротивление, чем шар с низкой мощностью.

Увеличение мощности

Единицей измерения мощности является ватт .

Кол-во	Символ	Блок	Сокращение	Значение
мощность	п.	Вт	Вт	Рассеиваемая мощность

Если есть увеличение напряжения, мощность увеличится в четыре раза.Если вы увеличиваете напряжение (или электрическое давление) в цепи, то ток (поток электронов) будет увеличиваться прямо пропорционально, например, если вы удвоите напряжение, ток удвоится.

Формула расчета мощности:

P = VI

Следовательно, удвоение тока, умноженного на удвоенное напряжение, увеличит мощность в четыре раза.

Закон Ома для расчета рассеиваемой мощности

Простая схема

Проработанные примеры основаны на представленной принципиальной схеме.

1. Какая мощность будет рассеиваться резистором (R), если в цепи протекает ток (A) 2 А при приложенном напряжении (В) 24 В?
   • P = VI
   • P = 24 x 2
   • P = 48 Вт
2. Какая мощность будет рассеиваться резистором (R), если в цепи протекает ток (А) 2 мкА при приложенном напряжении (В) 10 мВ?
   • P = VI
   • A и V являются частными кратными и должны быть преобразованы в базовые единицы
   • A = 2uA = 2 x 0.000 001 = 0 000 002A
   • В = 10 мВ = 10 x 0,001 = 0,01 В
   • P = 0,01 x 0,000 002
   • P = 0,000,000,02W или 20nW

Замена формулы

В соответствии с законом Ома рассеиваемая мощность напрямую зависит от приложенного напряжения и протекающего тока. Это напрямую связано с величиной сопротивления.Если известны любые два значения схемы, мы можем вычислить два других значения с помощью подстановки.

Пример

Простая схема.

1. В этом примере, если напряжение батареи составляет 20 В, а сопротивление (R) имеет значение 100 Ом, то какой будет рассеиваемая мощность?
   • Формула для расчета мощности:
   • P = VI
   • Мы не знаем текущий поток (I).
     Мы могли бы использовать закон Ома I = ^В / _R для расчета тока, а затем использовать вычисленное значение в формуле мощности выше.
     
   • Ответ можно найти с помощью одной формулы:
   • P = VI заменить I на ^V / _R
   • Это даст вам формулу:
   • P = ^{В x В} / _R вольт, умноженное на вольт, разделенное на сопротивление)
   • Вольт, умноженное на вольт, выражается как V ² (вольт в квадрате).Итак, окончательная формула будет:
   • P = V ² / R
   • P = 20 ² /100, что совпадает с (20 x 20/100)
   • P = 400/100
   • P = 4 Вт
2. Если общее сопротивление цепи составляет 80 Ом, а ток равен 2 А, какова рассеиваемая мощность?
   • P = VI мы не знаем напряжения, но по закону Ома V = IR.Следовательно, формула:
   • P = I x R x I, что совпадает с I x I x R, которое совпадает с I ² R, поэтому формула:
   • P = I ² R
   • P = 2 ² /80
   • P = 4/80
   • P = 0,05 Вт или 7071 мВт
3. Если мощность, рассеиваемая в цепи, составляет 500 Вт, а текущий ток составляет 2 А, каково полное сопротивление?
   • R = V / I – формула для расчета сопротивления, но напряжение неизвестно.
   • Для определения напряжения можно использовать формулу мощности V = P / I, но ее можно подставить в первую формулу следующим образом:
   • R = (P / I) / I (Сопротивление равно ваттам, разделенным на амперы, а затем снова разделенным на амперы.)
   • Однако это уравнение можно упростить как P / (I x I) и, следовательно, можно выразить как:
   • R = P / I ²
   • R = 500/2 ²
   • R = 125 Ом
4. Если мощность, рассеиваемая в цепи, составляет 10 Вт, а общее сопротивление составляет 5 Ом, какое приложенное напряжение?
   • V = IR – формула для расчета напряжения, но текущее значение неизвестно.
   • Формулу мощности V = P / I нельзя использовать для определения напряжения, потому что ток также неизвестен. Однако из-за прямой связи этих значений можно использовать замену формулы.
   • Мы знаем, что напряжение будет равно V = P / I, а ток будет I = V / R, поэтому
   • V = P / (V / R), что совпадает с V = PR / V, и после транспонирования это будет V ² = PR
   • Мы хотим знать напряжение, а не квадрат напряжения, поэтому квадратный корень ( √ ) из PR даст ответ.
   • Следовательно, формула:
   • В = √PR
   • В = √ (10 х 5)
   • В = √50
   • В = 7,071 В или 7071 мВ

Ток и напряжение – AP Physics 1

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Как рассчитать падение напряжения в последовательной цепи? – MVOrganizing

Как рассчитать падение напряжения в последовательной цепи?

Теперь, когда мы знаем силу тока в цепи (помните, что сила тока не изменяется в последовательной цепи), мы можем вычислить, какое напряжение падает на каждом резисторе, используя закон Ома (V = I x R).

Какое падение напряжения на каждом резисторе?

Падение напряжения для каждого резистора составляет E (x) = I x R (x) для каждого резистора (x), то есть R (1), R (2), R (3). Как мне определить, какой резистор мне нужен, если я знаю напряжение и ток? Вы берете основную формулу E = I x R, решаете относительно R -> R = E / I.

Как найти ток в последовательной цепи с 3 резисторами?

Параллельная цепь показана на схеме выше. В этом случае ток, подаваемый батареей, разделяется, и количество, проходящее через каждый резистор, зависит от сопротивления.Если значения трех резисторов равны: с батареей 10 В, при V = I R общий ток в цепи составляет: I = V / R = 10/2 = 5 A.

Напряжение в последовательной цепи одинаковое?

Напряжение питания распределяется между компонентами в последовательной цепи. Сумма напряжений на последовательно включенных компонентах равна напряжению источника питания. Это означает, что если два идентичных компонента соединены последовательно, напряжение питания делится на них поровну.

Что происходит с напряжением в последовательной цепи?

В последовательной цепи ток, протекающий через каждый из компонентов, одинаков, а напряжение в цепи является суммой индивидуальных падений напряжения на каждом компоненте.

На последовательно соединенных конденсаторах напряжение одинаково?

Когда конденсаторы соединены последовательно и на это соединение подается напряжение, напряжения на каждом конденсаторе обычно не равны, но зависят от значений емкости.

Почему напряжение делится последовательно?

: если два идентичных компонента соединены последовательно, напряжение питания делится на них поровну. если один компонент имеет в два раза большее сопротивление, чем другой, напряжение на компоненте с более высоким сопротивлением в два раза больше напряжения на компоненте с более низким сопротивлением.

Изменяется ли напряжение при увеличении сопротивления?

Пока источник питания остается постоянным, при добавлении сопротивления напряжение будет увеличиваться. Если мы увеличим значение резистора в омах, напряжение на клемме аккумулятора и резисторе останется прежним. Однако из-за повышенного сопротивления теперь через резистор протекает меньше тока.

Увеличивает ли параллельная цепь напряжение?

В параллельной цепи увеличение напряжения на источнике напряжения такое же, как и падение напряжения на каждой ветви.В параллельной цепи величина, обратная полному сопротивлению, равна сумме обратных величин отдельных сопротивлений.

Что происходит с параллельным напряжением?

Напряжение одинаково на всех компонентах параллельной цепи. Сумма токов по каждому пути равна общему току, протекающему от источника. Если один из параллельных путей разорван, ток будет продолжать течь по всем другим путям.

Как рассчитать параллельное напряжение?

Если у вас есть цепь с известной величиной тока, поток электрического заряда, вы можете рассчитать падение напряжения на схемах параллельной цепи следующим образом: Определите объединенное сопротивление или сопротивление потоку заряда параллельные резисторы.Суммируйте их как 1 / Rtotal = 1 / R1 + 1 / R2 для каждого резистора.

Как найти последовательное напряжение?

Напряжение, приложенное к последовательной цепи, равно сумме отдельных падений напряжения ». Это просто означает, что падение напряжения должно быть в сумме с напряжением, поступающим от батареи или батарей. 6В + 6В = 12В.

Постоянно ли последовательное напряжение?

2. В последовательной цепи ток одинаков в любой конкретной точке цепи. 3. Однако напряжение в последовательной цепи не остается постоянным.

Насколько велико падение напряжения?

NEC рекомендует, чтобы максимальное суммарное падение напряжения как в фидере, так и в ответвленной цепи не превышало 5%, а максимальное падение напряжения в фидере или ответвленной цепи не превышало 3% (рис. 1). Эта рекомендация связана с производительностью, а не с безопасностью.

Как рассчитать размер провода?

Таблица размеров проволоки и формула

1. Рассчитайте индекс падения напряжения (VDI) по следующей формуле:
2. VDI = АМПЕР x ФУТЫ ÷ (% ПАДЕНИЯ НАПРЯЖЕНИЯ x НАПРЯЖЕНИЕ)
3. Определите подходящий размер провода по таблице ниже.

Какое допустимое падение напряжения 12 В?

Максимальный ток (в амперах) в цепи 12 В в зависимости от размера (AWG) и длины провода. Провода в электрических системах не должны иметь сечения с падением напряжения более 3%. Для системы на 12 В максимальное падение напряжения должно быть менее (12 В) x 3% = 0,36 В.

Может ли плохое заземление вызвать падение напряжения?

Падение напряжения, обычно на стороне земли, вызывает неточные или странные показания цифрового мультиметра и осциллограммы.Более того, когда вы подключаете цифровой мультиметр или осциллограф к системе с плохим заземлением, само испытательное оборудование может создать хорошую замену заземления, в зависимости от импеданса инструмента.

Как далеко я могу проложить провод 12 В?

Максимальная длина медного провода при падении напряжения 2%. Как видно из приведенной выше диаграммы, максимальная длина всех проводов взад и вперед не должна превышать примерно 8 м для калибра № 10 (5,26 мм2). При увеличении диаметра провода до калибра № 2 (33,6 мм2) максимальная длина ограничивается примерно 32 м.

Что вызывает падение напряжения?

Причины падения напряжения Чрезмерное падение напряжения происходит из-за повышенного сопротивления в цепи, обычно вызванного увеличением нагрузки или энергии, используемой для питания электрического освещения, в виде дополнительных соединений, компонентов или проводов с высоким сопротивлением.

Что происходит при низком напряжении?

Если напряжение слишком низкое, сила тока увеличивается, что может привести к расплавлению компонентов или нарушению работы прибора.Если напряжение слишком высокое, это приведет к тому, что приборы будут работать «слишком быстро и слишком высоко», что сократит их срок службы.

Как увеличить напряжение в цепи?

Для увеличения напряжения мы последовательно подключаем переменное напряжение, чтобы получить более высокое выходное напряжение. Если частота всех напряжений одинакова, величина напряжений просто складывается. Напряжения просто добавятся, так что общее напряжение будет 28 В переменного тока при 60 Гц.

Цепи серии

Представьте, что ток выходит из аккумулятор.Если резисторы подключены таким образом, что ток должен полностью протекает через каждый резистор, прежде чем вернуться к батарее, затем Схема представляет собой последовательную схему .

A ₁ и A ₂ представляют собой два отдельных измерения силы тока при двух разных очков в цепи. V ₁ и V ₂ представляют собой два отдельных измерения напряжения или разности потенциалов. Обратите внимание, как мы подключаем вольтметр: по одному подключению на каждом конце резистора .

Для последовательных цепей:

Вт = V ₁ + V ₂ Когда электроны проходят через каждый резистор, они теряют свою потенциальную энергию последовательно, подобно тому, как лыжники постепенно терять потенциальную энергию при спуске с лыжной трассы.Когда они поднимаются на лифте, они снова получают энергию.

I ₁ = I ₂ = постоянная . Сила тока постоянная. Такое же количество электроны проходят через цепь в секунду.

Если мы разделим каждое напряжение на постоянного тока, согласно Закону Ома получим сопротивление:

Rt = ₁ + ₂

Если если в цепи больше резисторов, то действуют те же правила:

Vt = V ₁ + V ₂ + V ₃ +.

I ₁ = I ₂ = I ₃ = постоянный

Rt = ₁ + ₂ + ₃ +

Пример 1

а. Какое полное сопротивление цепи?

Rt = ₁ + ₂

Rt = 6 + 4 = 10 Вт. что в проводах и счетчиках есть ничтожное сопротивление).

г. Какой ток будет измеряться между двумя резисторами?

Ток, измеренный в любом месте цепи, будет тем же.

I = Vt / Rt (Закон Ома)

I = 40/10 = 4 А.

г. Какое напряжение ( ₁ В) будет измеряться на R ₁ ? По R ₂ ?

Использование Тот факт, что ток постоянный, В ₁ = I R ₁ = 4 (6) = 24 В.

В ₂ = I R ₂ = 4 (4) = 16 В.

Пример 2

а. Найди отсутствующее сопротивление в показанной цепи, которая состоит из батареи 12 В подключил к двум резисторам.

Общее сопротивление Vt / I = 12 / 1,5 = 8 Вт.

R = 8 2 = 6 Вт, так как Rt = ₁ + _2,

2. Если два резистора представляли две лампочки, а одна из лампочек была выкл., не могли бы вы включить другую лампочку?

№Это недостаток последовательной схемы. В ток нельзя прерывать; в противном случае ток через другие компоненты.

Пример 3

а. Найдите значение ₁ рэнд в Схема показана.

Начиная с V ₁ = I R ₁ , затем R ₁ = V ₁ / I = 6 / 0,5 = 12 Вт.

г. Какое напряжение батареи?

Rt = ₁ руб. + ₂ = 12 + 4 = 16 W.

Вт = I Rt = 0,5 (16) = 8 В.

.