Еще больше физических формул и свойств – Физика – Теория, тесты, формулы и задачи
На этой странице представлен исчерпывающий список формул по физике и важнейших физических свойств для успешной подготовки к ЦТ или ЕГЭ. Список составлен в формате “вопрос-ответ” на основе многолетнего опыта, и является самым полным на этом сайте. Успешное изучение всех формул по физике и физических свойств из этого файла позволит абитуриентам, не просто очень уверенно чувствовать себя на ЦТ или ЕГЭ, но и с легкостью, чуть ли не автоматически, решить большую часть экзаменационных заданий. Знание всех этих формул позволит Вам набрать очень солидный балл на экзамене, даже если у Вас нет феноменальных способностей в физике. А если Вы хотите набрать максимальный балл на ЦТ или ЕГЭ, то выучив эти формулы, Вы с легкостью и очень быстро прорешаете основную часть теста, и у Вас останется много времени на решение самых сложных задач теста, в которых Вам, к слову, также понадобится знание этих формул.
Изучать еще больше формул по физике и физических свойств онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше.
 В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. - Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Основные формулы по физике – Физика – Теория, тесты, формулы и задачи
Знание формул по физике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по физике. Формулы по физике, которые надежно хранятся в памяти ученика – это основной инструмент, которым он должен оперировать при решении физических задач. На этой странице сайта представлены основные формулы по школьной физике в двух частях.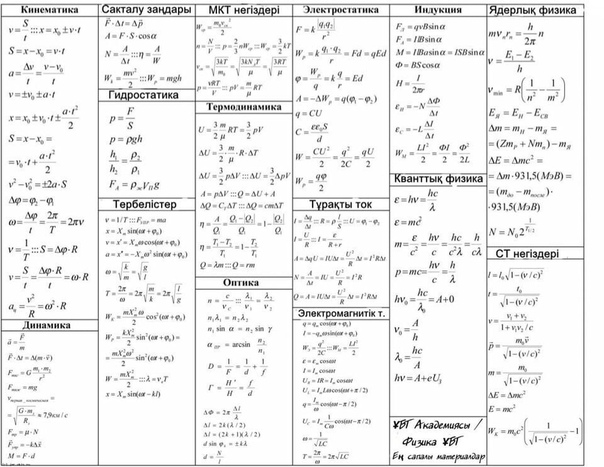
Оглавление:
Основные формулы по школьной физике (Часть I)
К оглавлению…
Основные формулы по школьной физике (Часть II)
К оглавлению…
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности.

- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию.
 Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Формула давления в физике
Содержание:
Определение и формула давления
Определение
Давление – это физическая величина,характеризующая состояние сплошной среды. Оно равно пределу отношения нормальной составляющей силы,
которая действует на участок поверхности тела площади
$\Delta S$ к размеру данной площади при
$\Delta S \rightarrow 0$ . Обозначается давление буквой p. Тогда математической
записью определения давления станет формула:
Оно равно пределу отношения нормальной составляющей силы,
которая действует на участок поверхности тела площади
$\Delta S$ к размеру данной площади при
$\Delta S \rightarrow 0$ . Обозначается давление буквой p. Тогда математической
записью определения давления станет формула:
Среднее давление
Средним давлением на поверхность называют величину:
$$\langle p\rangle=\frac{F_{n}}{S}(2)$$где Fn – нормальная составляющая силы, которая действует на рассматриваемую поверхность, S – площадь этой поверхности.
Давление идеального газа
Давление идеального газа вычисляют, используя основное уравнение молекулярно – кинетической теории:
$$p=n k T(3)$$где $n=\frac{N}{V}$– концентрация молекул газа
(N – число частиц), k=1,38•10-23 Дж/К – постоянная Больцмана, T – абсолютная температура газа. {*}$ –поверхностное натяжение жидкости,p0* – давление под не искривлённым слоем жидкости,
H – средняя кривизна поверхности жидкости, вычисляемая по закону Лапласа:
{*}$ –поверхностное натяжение жидкости,p0* – давление под не искривлённым слоем жидкости,
H – средняя кривизна поверхности жидкости, вычисляемая по закону Лапласа:
R1, R2 – главные радиусы кривизны.
Единицы измерения давления
Основной единицей измерения давления в системе СИ является: [p]=Па (паскаль)
Внесистемные единицы давления: [p]=мм рт.ст.(миллиметр ртутного столба),мм в.ст (мм водяного столба),атмосфера,бар.
Па= Н/м2 и 1 бар=105 Па.
Техническая атмосфера ~1 бар. Физическая атмосфера 1,01 бар=760 мм рт.ст.. 1 мм рт.ст.=133 Па.
Примеры решения задач
Пример
Задание. Каково давление в море на глубине h=8,5 м, если атмосферное давление равно p0=105 Па, плотность морской воды равна $\rho$=1,03•103 кг/м3
Решение. {5}$ (Па)
{5}$ (Па)
Слишком сложно?
Формула давления не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Каково давление струи на неподвижную плоскость, если струя воды ударяет ее под углом $\alpha$ к нормали плоскости, и упруго отскакивает от нее без изменения скорости? Скорость струи v.
Решение. Сделаем рисунок.
За время $\Delta t$ о стенку ударяется масса воды равная:
$$m=l S \rho=v \Delta t S \rho$$где S – поперечное сечение струи, $\rho$ – плотность воды. В соответствии с законом сохранения импульса имеем:
$$F \Delta t=m \Delta v \rightarrow F=\frac{m \Delta v}{\Delta t}(2.2)$$где F – сила, с которой вода действует на стенку.
Примем за положительное направление нормали внешней к опоре и учитывая, что струя отскакивает от стены без потери скорости, получаем:
$$\Delta v=v_{2} \cos \alpha-\left(-v_{1} \cos \alpha\right)=v_{2} \cos \alpha+v_{1} \cos \alpha=2 v \cos \alpha(2. {2}$
{2}$Читать дальше: Формула закона Ома.
Сила, Давление – Формулы по физике
По рыхлому снегу человек идёт с большим трудом, глубоко проваливаясь при каждом шаге. Но, надев лыжи, он может идти, почти не проваливаясь в него. Почему? На лыжах или без лыж человек действует на снег с одной и той же силой, равной своему весу. Однако действие этой силы в обоих случаях различно, потому что различна площадь поверхности, на которую давит человек, с лыжами и без лыж. Площадь поверхности лыж почти в 20 раз больше площади подошвы. Поэтому, стоя на лыжах, человек действует на каждый квадратный сантиметр площади поверхности снега с силой, в 20 раз меньшей, чем стоя на снегу без лыж.
Ученик, прикалывая кнопками газету к доске, действует на каждую кнопку с одинаковой силой. Однако кнопка, имеющая более острый конец, легче входит в дерево.
Значит,
результат действия силы зависит не только от её модуля, направления и
точки приложения, но и от площади той поверхности, к которой она
приложена (перпендикулярно которой она действует).
Этот вывод подтверждают физические опыты.
Опыт.Результат действия данной силы зависит от того, какая сила действует на единицу площади поверхности.
По углам небольшой доски надо вбить гвозди. Сначала гвозди, вбитые в доску, установим на песке остриями вверх и положим на доску гирю. В этом случае шляпки гвоздей лишь незначительно вдавливаются в песок. Затем доску перевернем и поставим гвозди на острие. В этом случае площадь опоры меньше, и под действием той же силы гвозди значительно углубляются в песок.
Опыт. Вторая иллюстрация.
От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия этой силы.
В рассмотренных примерах силы действовали перпендикулярно поверхности тела. Вес человека был перпендикулярен поверхности снега; сила, действовавшая на кнопку, перпендикулярна поверхности доски.
Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности, называется давлением.
Чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь поверхности:
давление = сила / площадь.
Обозначим величины, входящие в это выражение: давление – p, сила, действующая на поверхность, – F и площадь поверхности – S.
Тогда получим формулу:
p = F/S
Понятно, что бóльшая по значению сила, действующую на ту же площадь, будет производить большее давление.
За единицу давления принимается такое давление, которое производит сила в 1 Н, действующая на поверхность площадью 1 м2 перпендикулярно этой поверхности.
Единица давления – ньютон на квадратный метр ( 1 Н / м2 ). В честь французского ученого Блеза Паскаля она называется паскалем (Па). Таким образом,
1 Па = 1 Н / м2 .
Используется также другие единицы давления: гектопаскаль (гПа) и килопаскаль (кПа).
1 кПа = 1000 Па;
1 гПа = 100 Па;
1 Па = 0,001 кПа;
1 Па = 0,01 гПа.
Пример. Рассчитать давление, производимое на пол мальчиком, масса которого 45 кг, а площадь подошв его ботинок, соприкасающихся с полом, равна 300 см2.
Запишем условие задачи и решим её.
Дано: m = 45 кг, S = 300 см2; p = ?
В единицах СИ: S = 0,03 м2
Решение:
p = F/S,
F = P,
P = g·m,
P = 9,8 Н · 45 кг ≈ 450 Н,
p = 450/0,03 Н / м2 = 15000 Па = 15 кПа
‘Ответ’: p = 15000 Па = 15 кПа
Способы уменьшения и увеличения давления.
Тяжелый
гусеничный трактор производит на почву давление равное 40 – 50 кПа, т.
е. всего в 2 – 3 раза больше, чем давление мальчика массой 45 кг. Это
объясняется тем, что вес трактора распределяется на бóльшую площадь за
счёт гусеничной передачи. А мы установили, что чем больше площадь опоры, тем меньше давление, производимое одной и той же силой на эту опору.
В зависимости от того, нужно ли получить малое или большое давление, площадь опоры увеличивается или уменьшается. Например, для того, чтобы грунт мог выдержать давление возводимого здания, увеличивают площадь нижней части фундамента.
Шины грузовых автомобилей и шасси самолетов делают значительно шире, чем легковых. Особенно широкими делают шины у автомобилей, предназначенных для передвижения в пустынях.
Тяжелые машины, как трактор, танк или болотоход, имея большую опорную площадь гусениц, проходят по болотистой местности, по которой не пройдет человек.
С другой стороны, при малой площади поверхности можно небольшой силой произвести большое давление. Например, вдавливая кнопку в доску, мы действуем на нее с силой около 50 Н. Так как площадь острия кнопки примерно 1 мм2, то давление, производимое ею, равно:
p = 50 Н/ 0, 000 001 м2 = 50 000 000 Па = 50 000 кПа.
Для
сравнения, это давление в 1000 раз больше давления, производимого
гусеничным трактором на почву. Можно найти еще много таких примеров.
Можно найти еще много таких примеров.
Лезвие режущих и острие колющих инструментов (ножей, ножниц, резцов, пил, игл и др.) специально остро оттачивается. Заточенный край острого лезвия имеет маленькую площадь, поэтому при помощи даже малой силы создается большое давление, и таким инструментом легко работать.
Режущие и колющие приспособления встречаются и в живой природе: это зубы, когти, клювы, шипы и др. – все они из твердого материала, гладкие и очень острые.
Давление
Известно, что молекулы газа беспорядочно движутся.
Опыт. Здесь мы узнаем, что газ давит на стенки сосуда по всем направлениям одинаково.
Мы
уже знаем, что газы, в отличие от твердых тел и жидкостей, заполняют
весь сосуд, в котором находятся. Например, стальной баллон для хранения
газов, камера автомобильной шины или волейбольный мяч. При этом газ
оказывает давление на стенки, дно и крышку баллона, камеры или любого
другого тела, в котором он находится. Давление газа обусловлено иными
причинами, чем давление твердого тела на опору.
Известно, что молекулы газа беспорядочно движутся. При своем движении они сталкиваются друг с другом, а также со стенками сосуда, в котором находится газ. Молекул в газе много, поэтому и число их ударов очень велико. Например, число ударов молекул воздуха, находящегося в комнате, о поверхность площадью 1 см2 за 1 с выражается двадцатитрехзначным числом. Хотя сила удара отдельной молекулы мала, но действие всех молекул на стенки сосуда значительно, — оно и создает давление газа.
Итак, давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа.
Рассмотрим следующий опыт. Под колокол воздушного насоса поместим резиновый шарик. Он содержит небольшое количество воздуха и имеет неправильную форму. Затем насосом откачиваем воздух из-под колокола. Оболочка шарика, вокруг которой воздух становится все более разреженным, постепенно раздувается и принимает форму правильного шара.
Как объяснить этот опыт?
Для хранения и перевозки сжатого газа используются специальные прочные стальные баллоны.
В нашем опыте движущиеся молекулы газа непрерывно ударяют о стенки шарика внутри и снаружи. При откачивании воздуха число молекул в колоколе вокруг оболочки шарика уменьшается. Но внутри шарика их число не изменяется. Поэтому число ударов молекул о внешние стенки оболочки становится меньше, чем число ударов о внутренние стенки. Шарик раздувается до тех пор, пока сила упругости его резиновой оболочки не станет равной силе давления газа. Оболочка шарика принимает форму шара. Это показывает, что газ давит на ее стенки по всем направлениям одинаково. Иначе говоря, число ударов молекул, приходящихся на каждый квадратный сантиметр площади поверхности, по всем направлениям одинаково. Одинаковое давление по всем направлениям характерно для газа и является следствием беспорядочного движения огромного числа молекул.
Попытаемся
уменьшить объем газа, но так, чтобы масса его осталась неизменной. Это
значит, что в каждом кубическом сантиметре газа молекул станет больше,
плотность газа увеличится. Тогда число ударов молекул о стенки
увеличится, т. е. возрастет давление газа. Это можно подтвердить опытом.
Тогда число ударов молекул о стенки
увеличится, т. е. возрастет давление газа. Это можно подтвердить опытом.
На рисунке а изображена стеклянная трубка, один конец которой закрыт тонкой резиновой пленкой. В трубку вставлен поршень. При вдвигании поршня объем воздуха в трубке уменьшается, т. е. газ сжимается. Резиновая пленка при этом выгибается наружу, указывая на то, что давление воздуха в трубке увеличилось.
Наоборот, при увеличении объема этой же массы газа, число молекул в каждом кубическом сантиметре уменьшается. От этого уменьшится число ударов о стенки сосуда – давление газа станет меньше. Действительно, при вытягивании поршня из трубки объем воздуха увеличивается, пленка прогибается внутрь сосуда. Это указывает на уменьшение давления воздуха в трубке. Такие же явления наблюдались бы, если бы вместо воздуха в трубке находился бы любой другой газ.
Итак, при
уменьшении объема газа его давление увеличивается, а при увеличении
объема давление уменьшается при условии, что масса и температура газа
остаются неизменными.
А как изменится давление газа, если нагреть его при постоянном объеме? Известно, что скорость движения молекул газа при нагревании увеличивается. Двигаясь быстрее, молекулы будут ударять о стенки сосуда чаще. Кроме того, каждый удар молекулы о стенку будет сильнее. Вследствие этого, стенки сосуда будут испытывать большее давление.
Следовательно, давление газа в закрытом сосуде тем больше, чем выше температура газа, при условии, что масса газа и объем не изменяются.
Из этих опытов можно сделать общий вывод, что давление газа тем больше, чем чаще и сильнее молекулы ударяют о стенки сосуда.
Для
хранения и перевозки газов их сильно сжимают. При этом давление их
возрастает, газы необходимо заключать в специальные, очень прочные
баллоны. В таких баллонах, например, содержат сжатый воздух в подводных
лодках, кислород, используемый при сварке металлов. Конечно же, мы
должны навсегда запомнить, что газовые баллоны нельзя нагревать, тем
более, когда они заполнены газом. Потому что, как мы уже понимаем, может
произойти взрыв с очень неприятными последствиями.
Потому что, как мы уже понимаем, может
произойти взрыв с очень неприятными последствиями.
Закон Паскаля.
Давление передается в каждую точку жидкости или газа.
Давление поршня передается в каждую точку жидкости, заполняющей шар.
Теперь газ.
В отличие от твердых тел отдельные слои и мелкие частицы жидкости и газа могут свободно перемещаться относительно друг друга по всем направлениям. Достаточно, например, слегка подуть на поверхность воды в стакане, чтобы вызвать движение воды. На реке или озере при малейшем ветерке появляется рябь.
Подвижностью частиц газа и жидкости объясняется, что давление, производимое на них, передается не только в направлении действия силы, а в каждую точку. Рассмотрим это явление подробнее.
На рисунке, а изображен сосуд, в котором содержится газ (или жидкость). Частицы равномерно распределены по всему сосуду. Сосуд закрыт поршнем, который может перемещаться вверх и вниз.
Прилагая
некоторую силу, заставим поршень немного переместиться внутрь и сжать
газ (жидкость), находящийся непосредственно под ним. Тогда частицы
(молекулы) расположатся в этом месте более плотно, чем прежде(рис, б).
Благодаря подвижности частицы газа будут перемещаться по всем
направлениям. Вследствие этого их расположение опять станет равномерным,
но более плотным, чем раньше (рис, в). Поэтому давление газа всюду
возрастет. Значит, добавочное давление передается всем частицам газа или
жидкости. Так, если давление на газ (жидкость) около самого поршня
увеличится на 1 Па, то во всех точках внутри газа
или жидкости давление станет больше прежнего на столько же. На 1 Па
увеличится давление и на стенки сосуда, и на дно, и на поршень.
Тогда частицы
(молекулы) расположатся в этом месте более плотно, чем прежде(рис, б).
Благодаря подвижности частицы газа будут перемещаться по всем
направлениям. Вследствие этого их расположение опять станет равномерным,
но более плотным, чем раньше (рис, в). Поэтому давление газа всюду
возрастет. Значит, добавочное давление передается всем частицам газа или
жидкости. Так, если давление на газ (жидкость) около самого поршня
увеличится на 1 Па, то во всех точках внутри газа
или жидкости давление станет больше прежнего на столько же. На 1 Па
увеличится давление и на стенки сосуда, и на дно, и на поршень.
Давление, производимое на жидкость или газ, передается на любую точку одинаково во всех направлениях.
Это утверждение называется законом Паскаля.
На основе закона Паскаля легко объяснить следующие опыты.
На
рисунке изображен полый шар, имеющий в различных местах небольшие
отверстия. К шару присоединена трубка, в которую вставлен поршень. Если
набрать воды в шар и вдвинуть в трубку поршень, то вода польется из всех
отверстий шара. В этом опыте поршень давит на поверхность воды в
трубке. Частицы воды, находящиеся под поршнем, уплотняясь, передают его
давление другим слоям, лежащим глубже. Таким образом, давление поршня
передается в каждую точку жидкости, заполняющей шар. В результате часть
воды выталкивается из шара в виде одинаковых струек, вытекающих из всех
отверстий.
Если
набрать воды в шар и вдвинуть в трубку поршень, то вода польется из всех
отверстий шара. В этом опыте поршень давит на поверхность воды в
трубке. Частицы воды, находящиеся под поршнем, уплотняясь, передают его
давление другим слоям, лежащим глубже. Таким образом, давление поршня
передается в каждую точку жидкости, заполняющей шар. В результате часть
воды выталкивается из шара в виде одинаковых струек, вытекающих из всех
отверстий.
Если шар заполнить дымом, то при вдвигании поршня в трубку из всех отверстий шара начнут выходить одинаковые струйки дыма. Это подтверждает, что и газы передают производимое на них давление во все стороны одинаково.
Давление в жидкости и газе.
Под действием веса жидкости резиновое дно в трубке прогнется.
На
жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому,
каждый слой жидкости, налитой в сосуд, своим весом создает давление,
которое по закону Паскаля передается по всем направлениям.
Следовательно, внутри жидкости существует давление. В этом можно
убедиться на опыте.
В этом можно
убедиться на опыте.
В стеклянную трубку, нижнее отверстие которой закрыто тонкой резиновой пленкой, нальем воду. Под действием веса жидкости дно трубки прогнется.
Опыт показывает, что, чем выше столб воды над резиновой пленкой, тем больше она прогибается. Но всякий раз после того, как резиновое дно прогнулось, вода в трубке приходит в равновесие (останавливается), так как, кроме силы тяжести, на воду действует сила упругости растянутой резиновой пленки.
По мере опускания трубки | резиновая пленка постепенно выпрямляется. | Силы, действующие на резиновую пленку, | одинаковы с обеих сторон. |
Иллюстрация.
Дно отходит от цилиндра вследствие давления на него силы тяжести.
Опустим
трубку с резиновым дном, в которую налита вода, в другой, более широкий
сосуд с водой. Мы увидим, что по мере опускания трубки резиновая пленка
постепенно выпрямляется. Полное выпрямление пленки показывает, что
силы, действующие на нее сверху и снизу, равны. Наступает полное
выпрямление пленки тогда, когда уровни воды в трубке и сосуде совпадают.
Наступает полное
выпрямление пленки тогда, когда уровни воды в трубке и сосуде совпадают.
Такой же опыт можно провести с трубкой, в которой резиновая пленка закрывает боковое отверстие, как это показано на рисунке, а. Погрузим эту трубку с водой в другой сосуд с водой, как это изображено на рисунке, б. Мы заметим, что пленка снова выпрямится, как только уровни воды в трубке и сосуде сравняются. Это означает, что силы, действующие на резиновую пленку, одинаковы со всех сторон.
Возьмем сосуд, дно которого может отпадать. Опустим его в банку с водой. Дно при этом окажется плотно прижатым к краю сосуда и не отпадет. Его прижимает сила давления воды, направленная снизу вверх.
Будем осторожно наливать воду в сосуд и следить за его дном. Как только уровень воды в сосуде совпадет с уровнем воды в банке, оно отпадет от сосуда.
В
момент отрыва на дно давит сверху вниз столб жидкости в сосуде, а снизу
вверх на дно передается давление такого же по высоте столба жидкости,
но находящейся в банке.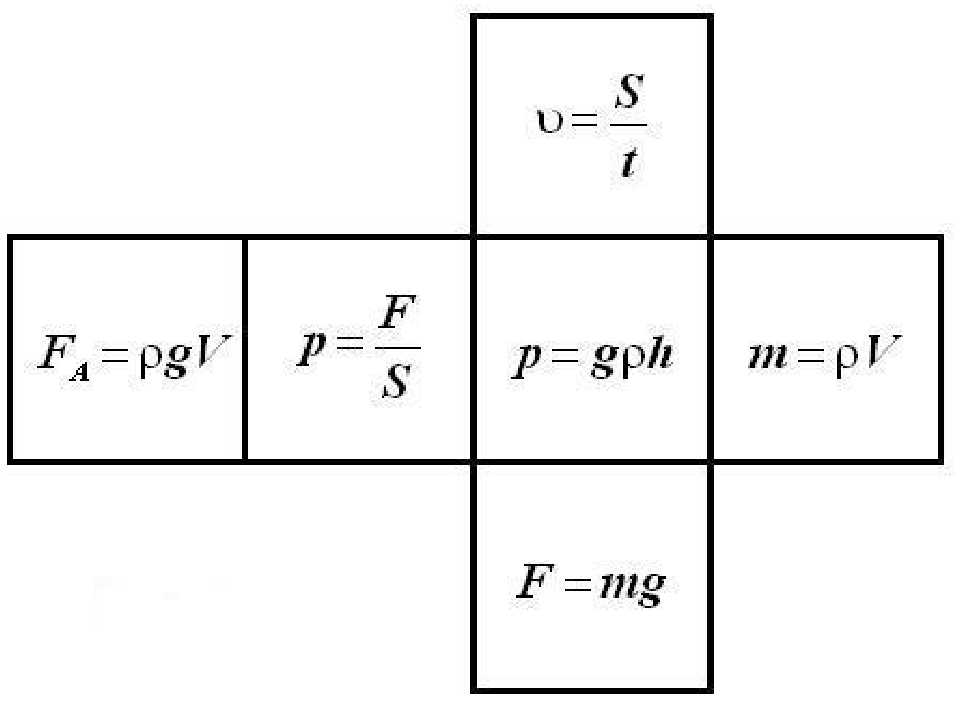 Оба эти давления одинаковы, дно же отходит от
цилиндра вследствие действия на него собственной силы тяжести.
Оба эти давления одинаковы, дно же отходит от
цилиндра вследствие действия на него собственной силы тяжести.
Выше были описаны опыты с водой, но если взять вместо воды любую другую жидкость, результаты опыта будут те же.
Итак, опыты показывают, что внутри жидкости существует давление, и на одном и том же уровне оно одинаково по всем направлениям. С глубиной давление увеличивается.
Газы в этом отношении не отличаются от жидкостей, ведь они тоже имеют вес. Но надо помнить, что плотность газа в сотни раз меньше плотности жидкости. Вес газа, находящегося в сосуде, мал, и его “весовое” давление во многих случаях можно не учитывать.
Давление и сила давления | Физика
Проделаем опыт. Возьмем небольшую доску, в углы которой вбиты четыре гвоздя, и поместим ее остриями вверх на песок. Сверху на нее положим гирю (рис. 81). Мы увидим, что шляпки гвоздей лишь незначительно вдавятся в песок. Если же мы перевернем доску и снова поставим ее (вместе с гирей) на песок, то теперь гвозди войдут в него значительно глубже (рис.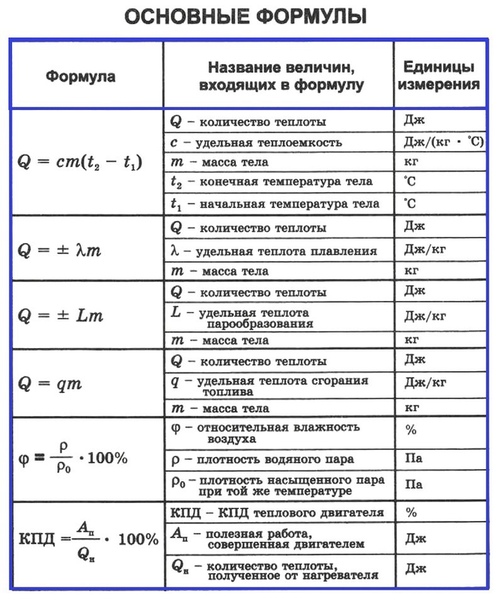 82). В обоих случаях вес доски был одним и тем же, однако эффект оказался разным. Почему?Вся разница в рассматриваемых случаях заключалась в том, что площадь поверхности, на которую опирались гвозди, в одном случае была больше, а в другом меньше. Ведь сначала песка касались шляпки гвоздей, а затем их острия.
82). В обоих случаях вес доски был одним и тем же, однако эффект оказался разным. Почему?Вся разница в рассматриваемых случаях заключалась в том, что площадь поверхности, на которую опирались гвозди, в одном случае была больше, а в другом меньше. Ведь сначала песка касались шляпки гвоздей, а затем их острия.
Мы видим, что результат воздействия зависит не только от силы, с которой тело давит на поверхность, но и от площади этой поверхности. Именно по этой причине человек, способный скользить по рыхлому снегу на лыжах, сразу же проваливается в него, как только их снимет (рис. 83).Но дело не только в площади. Важную роль играет и величина прикладываемой силы. Если, например, на ту же. доску (см. рис. 81) положить еще одну гирю, то гвозди (при той же площади опоры) погрузятся в песок еще глубже.
Силу, прикладываемую перпендикулярно поверхности, называют силой давления на эту поверхность.
Силу давления не следует путать с давлением. Давление — это физическая величина, равная отношению силы давления, приложенной к данной поверхности, к площади этой поверхности:
,(32. 1)
1)
где
р — давление, F — сила давления, S — площадь.
Итак, чтобы определить давление, надо силу давления разделить на площадь поверхности, на которую оказывается давление.
При одной и той же силе давление больше в том случае, когда площадь опоры меньше, и, наоборот, чем больше площадь опоры, тем давление меньше.
В тех случаях, когда силой давления является вес находящегося на поверхности тела (F = P = mg), давление, оказываемое телом, можно найти по формуле
Если давление р и площадь S известны, то можно определить силу давления F; для этого надо давление умножить на площадь:
F = pS (32.2)
Сила давления (как и любая другая сила) измеряется в ньютонах. Давление же измеряется в паскалях. Паскаль (1 Па) — это такое давление, которое производит сила давления в 1 Н, будучи приложенной к поверхности площадью 1 м2:
1 Па = 1 Н/м2.
Используются также другие единицы давления — гектопаскаль (гПа) и килопаскаль (кПа):
1 гПа = 100 Па, 1 кПа = 1000 Па.
1. Приведите примеры, показывающие, что результат действия силы зависит от площади опоры, на которую действует эта сила. 2. Почему человек, идущий на лыжах, не проваливается в снег? 3. Почему острая кнопка легче входит в дерево, чем тупая? 4. Что называют давлением? 5. Какие вы знаете единицы давления? 6. Чем отличается давление от силы давления? 7. Как можно найти силу давления, зная давление и площадь поверхности, к которой приложена сила?
что означает буква p в физике
Сор 7 класс по физике 4 четверть
1)Дано:M=5H×м,F=4H Найти d 2)Дано:M=8Hм,d=1м Найти F 3)Дано:F1=2H,F2=8H,d1=6см Найти d2 Дайте пожалуйста
пожалуйста помогите заранее спасибо БИЛЕТ № 1. Что изучает физика. Физические термины. Наблюдения и опыты. Физические величины и их измерение. Точност
… ь и погрешность измерений. Какая сила тяжести действует на тело массой 200 г?БИЛЕТ № 2. Строение вещества. Молекулы. Опыты, подтверждающие существование молекул. Какую работу совершает человек при подъеме тела массой 5 кг на высоту 2 м?БИЛЕТ № 3. 3.БИЛЕТ № 8. Плотность вещества. Расчет массы и объема по его плотности.2.Определите работу, совершаемую при поднятии груза весом 4 Н на высоту 4м.БИЛЕТ № 9. Сила. Явление тяготения. Сила тяжести. Сила упругости. Закон Гука. Вес тела.2.Определите работу, совершаемую при поднятии груза весом 4 Н на высоту 4м.БИЛЕТ № 10 . Сила упругости. Закон Гука. Вес тела.2.Определите работу, совершаемую при поднятии груза весом 4 Н на высоту 4м.БИЛЕТ № 11. Графическое изображение силы. Сложение сил. Центр тяжести тела.2.Рассчитайте давление воды на глубине 10 м.БИЛЕТ № 12. Сила трения. Трение покоя. Трение в природе и технике.2.Паровоз движется со скоростью 36км\ч. Какое расстояние он пройдет за 10 минут?БИЛЕТ № 13. Давление. Способы увеличения и уменьшения давления.2. Лыжник за 5 с совершил работу 4800 Дж. Какую мощность он при этом развил?БИЛЕТ № 14. Давление газа. Передача давления жидкостями и газами. Закон Паскаля.2.Определите работу, совершаемую при поднятии груза весом 4 Н на высоту 4м.БИЛЕТ № 15.
3.БИЛЕТ № 8. Плотность вещества. Расчет массы и объема по его плотности.2.Определите работу, совершаемую при поднятии груза весом 4 Н на высоту 4м.БИЛЕТ № 9. Сила. Явление тяготения. Сила тяжести. Сила упругости. Закон Гука. Вес тела.2.Определите работу, совершаемую при поднятии груза весом 4 Н на высоту 4м.БИЛЕТ № 10 . Сила упругости. Закон Гука. Вес тела.2.Определите работу, совершаемую при поднятии груза весом 4 Н на высоту 4м.БИЛЕТ № 11. Графическое изображение силы. Сложение сил. Центр тяжести тела.2.Рассчитайте давление воды на глубине 10 м.БИЛЕТ № 12. Сила трения. Трение покоя. Трение в природе и технике.2.Паровоз движется со скоростью 36км\ч. Какое расстояние он пройдет за 10 минут?БИЛЕТ № 13. Давление. Способы увеличения и уменьшения давления.2. Лыжник за 5 с совершил работу 4800 Дж. Какую мощность он при этом развил?БИЛЕТ № 14. Давление газа. Передача давления жидкостями и газами. Закон Паскаля.2.Определите работу, совершаемую при поднятии груза весом 4 Н на высоту 4м.БИЛЕТ № 15. Давление в жидкости и газе. Расчет давления жидкости на дно и стенки сосуда2.Паровоз движется со скоростью 36км\ч. Какое расстояние он пройдет за 10 минут?БИЛЕТ № 161.. Сообщающиеся сосуды. Правила сообщающихся сосудов.2. Человек, масса которого 70 кг, держит на плечах ящик массой 20кг. С какой силой человек давит на землю?БИЛЕТ № 17. Вес воздуха. Атмосферное давление. Измерение атмосферного давления2.Масса языка человека всего 50 г. Определите его вес.БИЛЕТ № 18. Опыт Торричелли. Барометр-анероид. Атмосферное давление на различных высотах. 2.Чему примерно равна сила тяжести, действующая на мяч массой 0,5 кг?БИЛЕТ № 19. Манометр. Насос. Гидравлические машины.2.Плечи рычага равны соответственно 4 см и 12 см. На меньшее плечо действует сила 60 Н. Чему равна сила, действующая на большее плечо?БИЛЕТ № 20. Действие жидкости и газа на погруженное в них тело. Архимедова сила. Плавание тел. Воздухоплавание.2.Масса языка человека всего 50 г. Определите его вес.БИЛЕТ № 21. Механическая работа. Мощность.
Давление в жидкости и газе. Расчет давления жидкости на дно и стенки сосуда2.Паровоз движется со скоростью 36км\ч. Какое расстояние он пройдет за 10 минут?БИЛЕТ № 161.. Сообщающиеся сосуды. Правила сообщающихся сосудов.2. Человек, масса которого 70 кг, держит на плечах ящик массой 20кг. С какой силой человек давит на землю?БИЛЕТ № 17. Вес воздуха. Атмосферное давление. Измерение атмосферного давления2.Масса языка человека всего 50 г. Определите его вес.БИЛЕТ № 18. Опыт Торричелли. Барометр-анероид. Атмосферное давление на различных высотах. 2.Чему примерно равна сила тяжести, действующая на мяч массой 0,5 кг?БИЛЕТ № 19. Манометр. Насос. Гидравлические машины.2.Плечи рычага равны соответственно 4 см и 12 см. На меньшее плечо действует сила 60 Н. Чему равна сила, действующая на большее плечо?БИЛЕТ № 20. Действие жидкости и газа на погруженное в них тело. Архимедова сила. Плавание тел. Воздухоплавание.2.Масса языка человека всего 50 г. Определите его вес.БИЛЕТ № 21. Механическая работа. Мощность. 2.Определите работу, совершаемую при поднятии груза весом 4 Н на высоту 4м.БИЛЕТ № 22. Простые механизмы. Рычаг. Равновесие сил на рычаге. Момент силы. 2.Автомобиль за первые 10с прошел путь 80м, а за последующие 30с- 480 м. Определите среднюю скорость автомобиля на всём пути.БИЛЕТ № 23. Применение закона равновесия рычага к блоку.2.На тело действуют две силы: влево, равная 10Н, и вправо, равная 16Н. Куда направлена и чему равна равнодействующая этих сил?БИЛЕТ № 24. «Золотое правило» механики. КПД механизма.2.Определите работу, совершаемую при поднятии груза весом 4 Н на высоту 4м.БИЛЕТ № 25. Кинетическая и потенциальная энергия.2.Какую силу надо приложить к концу проволоки, жесткость которой 100 кН/м, чтобы растянуть её на 1 мм?БИЛЕТ № 26. Превращение одного вида механической энергии в другой. Закон сохранения полной механической энергии. Какая сила тяжести действует на тело массой 200 г?
2.Определите работу, совершаемую при поднятии груза весом 4 Н на высоту 4м.БИЛЕТ № 22. Простые механизмы. Рычаг. Равновесие сил на рычаге. Момент силы. 2.Автомобиль за первые 10с прошел путь 80м, а за последующие 30с- 480 м. Определите среднюю скорость автомобиля на всём пути.БИЛЕТ № 23. Применение закона равновесия рычага к блоку.2.На тело действуют две силы: влево, равная 10Н, и вправо, равная 16Н. Куда направлена и чему равна равнодействующая этих сил?БИЛЕТ № 24. «Золотое правило» механики. КПД механизма.2.Определите работу, совершаемую при поднятии груза весом 4 Н на высоту 4м.БИЛЕТ № 25. Кинетическая и потенциальная энергия.2.Какую силу надо приложить к концу проволоки, жесткость которой 100 кН/м, чтобы растянуть её на 1 мм?БИЛЕТ № 26. Превращение одного вида механической энергии в другой. Закон сохранения полной механической энергии. Какая сила тяжести действует на тело массой 200 г?
Сеногрузчик поднял сено массой 200 кг на высоту 5 м, при этом двигатель тянул трос с силой 1050Н. Рассмотрите рисунок и вычислите КПД блоков сеногрузч
… ика.
Рассмотрите рисунок и вычислите КПД блоков сеногрузч
… ика.
іграшковий пружинний пістолет, жорсткість пружини якого становить 4 н/см зарядили кулькою масою 30 і стиснули пружину на 15 см . з якою швидкістю виле … тить кулька при пострілі ?
помогите!!!!Знайдіть діаметр капілярної трубки, якщо по ній піднялося 13,7 мг води. Змочування повне. Поверхневий натят води рівний 7,28·10 ² Н/м
Сила Архімеда, що діє на тіло масою 4 кг, становить 0,03 кН. Визначити, що буде з тілом?а) вспливе на поверхню;б) потоне;в) плаватиме в середині рідин … и;г) знаходитиметься в стані невагомості.
Решите плз 1-4 оч нужно сейчас!!!! Даю 20 балов
Решите плз 1-4 оч нужно сейчас!!!!
Помогите пожалуйста!!!! Очень срочно нужно сделать!!!В дно водоёма вбита свая длиной l= 1,26 м. Свая возвышается над поверхностью воды на h= 0,5 м. Уг
… ол между горизонтом и лучами солнца, падающими на поверхность воды, равен ϕ = 30°. Определи длину тени от сваи на дне водоёма, если показатель преломления воды равен n= √1,51. Глубина водоёма равна H=м. (Округли до сотых).2. Угол падения светового луча на поверхность воды равен α =°.3. Угол преломления равен β =°.4. Длина тени равна L=X+x=м. (Округли до сотых).
Глубина водоёма равна H=м. (Округли до сотых).2. Угол падения светового луча на поверхность воды равен α =°.3. Угол преломления равен β =°.4. Длина тени равна L=X+x=м. (Округли до сотых).
Основные формулы по физике для 8 класса
Формулы по физике
8 класс
Количество теплоты при нагревании
Q=c*m*(t2–t1)=с*m*∆t
Q – количество теплоты [Дж] (Джоуль)
с – удельная теплоёмкость [Дж/(кг*ºС), Дж/(кг*ºК)] (Джоуль на килограмм-градус Цельсия, Джоуль на килограмм-градус Кельвина)
m – масса [кг] (килограмм)
t2 – конечная температура [ºC, ºK] (градус Цельсия, градус Кельвина)
t1 – начальная температура [ºC, ºK] (градус Цельсия, градус Кельвина)
∆t – изменение температуры [ºC, ºK] (градус Цельсия, градус Кельвина)
Q>0 – выделение, отдача тепла (энергии)
Q<0 – поглощение, забор тепла (энергии)
Теплота сгорания
Q=q*m
Q – количество теплоты [Дж] (Джоуль)
q – удельная теплота сгорания [Дж/кг] (Джоуль на килограмм)
m – масса [кг] (килограмм)
Теплота плавления
Q=λ*m
Q – количество теплоты [Дж] (Джоуль)
λ – удельная теплота плавления [Дж/кг] (Джоуль на килограмм)
m – масса [кг] (килограмм)
В течение процесса плавления (отвердевания) температура остается постоянной!
Теплота парообразования
Q=L*m
Q – количество теплоты [Дж] (Джоуль)
L – удельная теплота парообразования [Дж/кг] (Джоуль на килограмм)
m – масса [кг] (килограмм)
В течение процесса парообразования (конденсации) температура остается постоянной!
Сила электрического тока
I=
I – сила тока [А] (Ампер)
q – заряд [Кл] (Кулон)
t – время [с] (секунда)
А – Амперметр, прибор для измерения силы тока, подключается последовательно.
Электрическое напряжение
U=
U – напряжение [В] (Вольт)
А – работа электрического тока [Дж] (Джоуль)
q – заряд [Кл] (Кулон)
V – вольтметр, прибор для измерения напряжения, подключается параллельно
Сопротивление проводника
R=ρ*
R – сопротивление проводника [Ом] (Ом)
ρ – удельное сопротивление [Ом*мм2/м, Ом*м] (Ом-квадратный миллиметр на метр, Ом-метр)
l – длина проводника [м] (метр)
s – площадь поперечного сечения проводника [мм2,м2] (квадратный миллиметр, квадратный метр)
Закон Ома
I=
I – сила тока [А] (Ампер)
R – сопротивление проводника [Ом] (Ом)
U – напряжение [В] (Вольт)
Сопротивление проводника не зависит от силы тока или напряжения, зависит только от геометрических параметров (длина, площадь поперечного сечения и удельное сопротивление материала)
Соединение проводников
1)Последовательное
Rобщее=R1+R2
Iобщая=I1=I2
Uобщее=U1+U2
2)Параллельное
=+
Iобщая=I1+I2
Uобщее=U1=U2
Работа электрического тока
A=I*U*t
А – работа электрического тока [Дж] (Джоуль)
I – сила тока [А] (Ампер)
U – напряжение [В] (Вольт)
t – время [с] (секунда)
Закон Джоуля-Ленца
Q=I2*R*t
Q – количество теплоты, выделяющееся на проводнике [Дж] (Джоуль)
I – сила тока [А] (Ампер)
R – сопротивление проводника [Ом] (Ом)
t – время [с] (секунда)
Мощность электрического тока
P==I*U
P – мощность электрического тока [Вт] (Ватт)
А – работа электрического тока [Дж] (Джоуль)
t – время [с] (секунда)
I – сила тока [А] (Ампер)
U – напряжение [В] (Вольт)
Основные формулы работы электрического тока (теплоты) и мощности
Три закона распространения света
В однородной среде свет распространяется равномерно и прямолинейно
При отражении света от поверхности угол падения равен углу отражения (углом падения/отражения называется угол между падающим/отражённым лучом и перпендикуляром к поверхности)
При переходе света из одной среды в другую луч преломляется.
 При переходе света из менее плотной среды в более плотную луч отклоняется ближе к перпендикуляру к поверхности, и наоборот.
При переходе света из менее плотной среды в более плотную луч отклоняется ближе к перпендикуляру к поверхности, и наоборот.
=
α – угол падения
β – преломлённый угол
n1 – показатель преломления более плотной среды (β)
n2 – показатель преломления менее плотной среды (α)
Оптическая сила линзы
D=
D – оптическая сила линзы [дптр] (диоптрия)
F – фокусное расстояние линзы [м] (метр)
Формула тонкой линзы
=+
F – фокусное расстояние линзы [м] (метр)
f – расстояние от линзы до изображения [м] (метр)
d – расстояние от предмета до линзы [м] (метр)
Линейный импульс и сила | Физика
Цели обучения
К концу этого раздела вы сможете:
- Определите количество движения.
- Объясните взаимосвязь между импульсом и силой.
- Укажите второй закон движения Ньютона с точки зрения количества движения.

- Вычислить импульс с учетом массы и скорости.
Линейный импульс
Научное определение количества движения согласуется с интуитивным пониманием количества движения большинства людей: большой, быстро движущийся объект имеет больший импульс, чем меньший и более медленный объект. Линейный импульс определяется как произведение массы системы на ее скорость. В символах линейный импульс выражается как p = м v .
Импульс прямо пропорционален массе объекта, а также его скорости. Таким образом, чем больше масса объекта или чем больше его скорость, тем больше его импульс. Импульс p – это вектор, имеющий то же направление, что и скорость v . Единица измерения количества движения в системе СИ – кг · м / с.
Линейный импульс
Линейный импульс определяется как произведение массы системы на ее скорость:
p = м v
Пример 1.
 Расчет импульса: футболист и футбол
Расчет импульса: футболист и футбол- Рассчитайте импульс футболиста весом 110 кг, бегущего со скоростью 8,00 м / с.
- Сравните импульс игрока с импульсом сильно брошенного футбольного мяча весом 0,410 кг, который имеет скорость 25,0 м / с.
Стратегия
Никакой информации относительно направления не дается, поэтому мы можем вычислить только величину импульса, p .(Как обычно, курсивом обозначена величина, а курсивом, полужирным шрифтом и стрелкой – вектор.) В обеих частях этого примера величина импульса может быть вычислена непосредственно из определения числа импульс, указанный в уравнении, который становится p = mv , если рассматривать только величины.
Решение для части 1
Чтобы определить импульс игрока, подставьте известные значения массы и скорости игрока в уравнение.
p игрок = (110 кг) (8,00 м / с) = 880 кг · м / с
Решение для части 2
Чтобы определить импульс мяча, подставьте известные значения массы и скорости мяча в уравнение.
p мяч = (0,410 кг) (25,0 м / с) = 10,3 кг · м / с
Отношение импульса игрока к импульсу мяча составляет
.[латекс] \ displaystyle \ frac {p _ {\ text {player}}} {p _ {\ text {ball}}} = \ frac {880} {10.3} = 85,9 \ [/ латекс]
Обсуждение
Хотя мяч имеет большую скорость, игрок имеет гораздо большую массу. Таким образом, как вы могли догадаться, импульс игрока намного больше, чем импульс футбола. В результате, если игрок ловит мяч, это лишь незначительно влияет на его движение. В следующих разделах мы дадим количественную оценку того, что происходит при таких столкновениях, с точки зрения количества движения.
Импульс и второй закон Ньютона
Важность импульса, в отличие от энергии, была признана на раннем этапе развития классической физики.Импульс считался настолько важным, что его называли «количеством движения». Ньютон фактически сформулировал свой второй закон движения в терминах количества движения: чистая внешняя сила равна изменению количества движения системы, деленному на время, в течение которого он изменяется.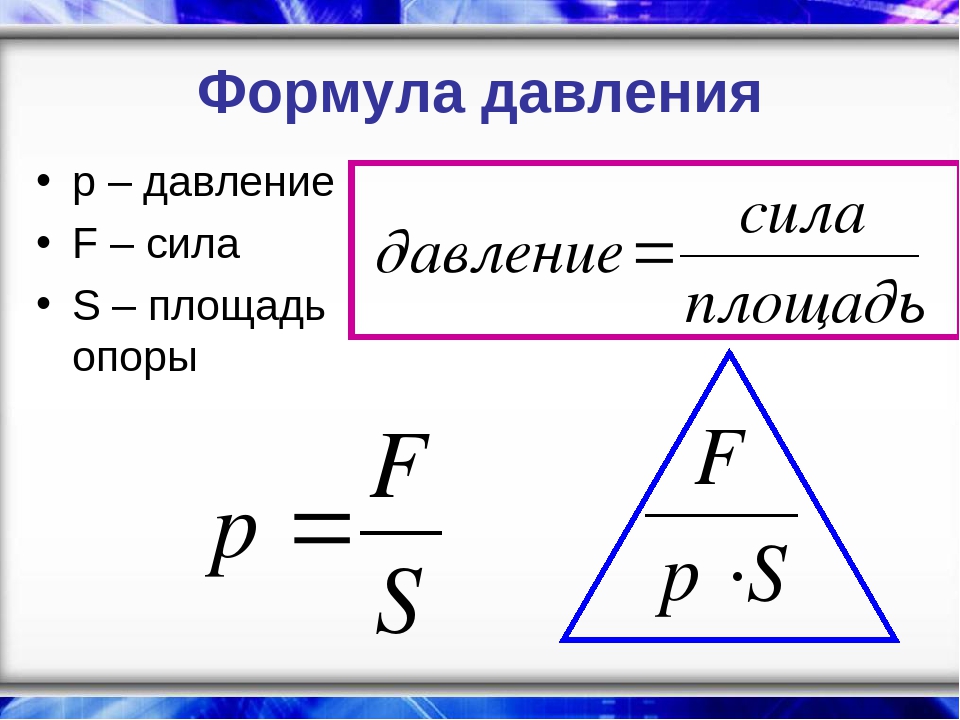 Используя символы, это закон
Используя символы, это закон
[латекс] \ displaystyle {\ mathbf {F}} _ {\ text {net}} = \ frac {\ Delta \ mathbf {p}} {\ Delta t} [/ latex],
, где F net – чистая внешняя сила, Δp – изменение количества движения, а Δ t – изменение во времени.
Второй закон движения Ньютона с точки зрения количества движения
Чистая внешняя сила равна изменению количества движения системы, деленному на время, в течение которого он изменяется.
[латекс] \ displaystyle {\ mathbf {F}} _ {\ text {net}} = \ frac {\ Delta \ mathbf {p}} {\ Delta t} [/ latex]
Установление связей: сила и импульс
Сила и импульс тесно связаны. Сила, действующая с течением времени, может изменять импульс, и второй закон движения Ньютона может быть сформулирован в его наиболее широко применимой форме с точки зрения количества движения.Импульс продолжает оставаться ключевым понятием при изучении атомных и субатомных частиц в квантовой механике.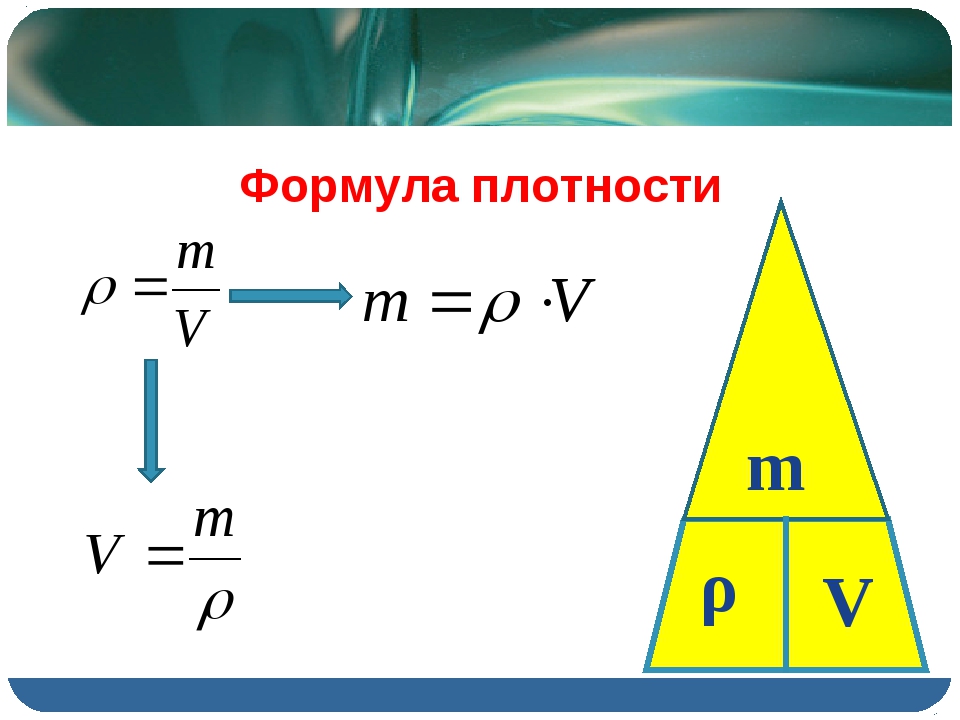
Это утверждение второго закона движения Ньютона включает более знакомую F net = m a как частный случай. Мы можем получить эту форму следующим образом. Во-первых, обратите внимание, что изменение импульса Δp определяется как Δp = Δ ( м v).
Если масса системы постоянна, то Δ ( м v) = м Δv.
Таким образом, для постоянной массы второй закон движения Ньютона принимает вид
.[латекс] \ displaystyle {\ mathbf {F}} _ {\ text {net}} = \ frac {\ Delta \ mathbf {p}} {\ Delta t} = \ frac {m \ Delta \ mathbf {v} } {\ Delta {t}} [/ latex]
Поскольку [latex] \ frac {\ Delta \ mathbf {v}} {\ Delta {t}} = \ mathbf {a} \\ [/ latex], мы получаем знакомое уравнение F net = m a при постоянной массе системы .
Второй закон движения Ньютона, выраженный в терминах количества движения, более широко применим, потому что его можно применять к системам с изменяющейся массой, таким как ракеты, а также к системам с постоянной массой. Рассмотрим подробнее системы с разной массой; однако связь между импульсом и силой остается полезной, когда масса постоянна, как в следующем примере.
Рассмотрим подробнее системы с разной массой; однако связь между импульсом и силой остается полезной, когда масса постоянна, как в следующем примере.
Пример 2. Расчетное усилие: ракетка Винус Уильямс
Во время Открытого чемпионата Франции 2007 года Винус Уильямс показала самую быструю подачу в женском первенстве, достигнув скорости 58 м / с (209 км / ч).Какова средняя сила, прилагаемая ракеткой Винус Уильямс к теннисному мячу весом 0,057 кг, если предположить, что скорость мяча сразу после удара составляет 58 м / с, что начальная горизонтальная составляющая скорости до удара пренебрежимо мала и что мяч оставался в контакте с ракеткой в течение 5,0 мс (миллисекунд)?
Стратегия
Эта проблема включает только одно измерение, потому что мяч не имеет горизонтальной составляющей скорости до удара. Второй закон Ньютона, выраженный в единицах количества движения, записывается как
[латекс] \ displaystyle {\ mathbf {F}} _ {\ text {net}} = \ frac {\ Delta \ mathbf {p}} {\ Delta t} [/ latex]
Как отмечалось выше, когда масса постоянна, изменение количества движения определяется выражением Δ p = м Δ v = м ( v f – v i ).
В этом примере даны скорость сразу после удара и изменение во времени; таким образом, после вычисления Δ p можно использовать [latex] {\ mathbf {F}} _ {\ text {net}} = \ frac {\ Delta {p}} {\ Delta t} [/ latex] найти силу.
Решение
Чтобы определить изменение количества движения, подставьте значения начальной и конечной скоростей в приведенное выше уравнение.
[латекс] \ begin {array} {lll} \ Delta {p} & = & m (v _ {\ text {f}} – v {\ text {i}}) \\ & = & (0,057 \ text {кг }) (58 \ текст {м / с} -0 \ текст {м / с}) \\ & = & 3.{-3} \ text {s}} \\ & = & 661 \ text {N} \ приблизительно660 \ text {N} \ end {array} \\ [/ latex]
, где на последнем этапе мы оставили только две значащие цифры.
Обсуждение
Эта величина представляла собой среднюю силу, прилагаемую ракеткой Винус Уильямс к теннисному мячу во время его кратковременного удара (обратите внимание, что мяч также испытал силу тяжести 0,56 Н, но эта сила возникла не из-за ракетки). Эту проблему также можно решить, сначала найдя ускорение, а затем используя F net = ma , но потребуется один дополнительный шаг по сравнению со стратегией, использованной в этом примере.
Эту проблему также можно решить, сначала найдя ускорение, а затем используя F net = ma , но потребуется один дополнительный шаг по сравнению со стратегией, использованной в этом примере.
Сводка раздела
- Линейный импульс (импульс для краткости) определяется как произведение массы системы на ее скорость.
- В символах, линейный импульс p определен как p = m v , где m – масса системы, а v – ее скорость.
- Единица измерения количества движения в системе СИ – кг · м / с.
- Второй закон движения Ньютона с точки зрения количества движения гласит, что чистая внешняя сила равна изменению количества движения системы, деленному на время, в течение которого он изменяется.
- В символах второй закон движения Ньютона определяется как [latex] {\ mathbf {F}} _ {\ text {net}} = \ frac {\ Delta \ mathbf {p}} {\ Delta t} \\ [/ latex], F net – чистая внешняя сила, Δ p – изменение количества движения, а Δ t – время изменения.

Концептуальные вопросы
- Объект с малой массой и объект с большой массой имеют одинаковый импульс. Какой объект имеет наибольшую кинетическую энергию?
- Объект с малой массой и объект с большой массой имеют одинаковую кинетическую энергию.Какая масса имеет наибольший импульс?
- Профессиональное приложение. Футбольные тренеры советуют игрокам блокировать, бить и отбиваться ногами на земле, а не прыгать в воздухе. Используя концепции импульса, работы и энергии, объясните, как футболист может быть более эффективным, стоя на земле.
- Как малая сила может передать объекту такой же импульс, что и большая сила?
Задачи и упражнения
- (a) Вычислите импульс 2000-кг слона, который атакует охотника со скоростью 7.50 м / с. (б) Сравните импульс слона с импульсом дротика с транквилизатором весом 0,0400 кг, выпущенного со скоростью 600 м / с. (c) Каков импульс 90-килограммового охотника, бегущего со скоростью 7,40 м / с после того, как пропустил слона?
- (а) Какова масса большого корабля с импульсом 1,60 × 10 9 кг · м / с, когда корабль движется со скоростью 48,0 км / ч? (b) Сравните импульс корабля с импульсом артиллерийского снаряда массой 1100 кг, выпущенного со скоростью 1200 м / с.

- (a) С какой скоростью будет 2.00 × 10 4 -кг самолет должен лететь, чтобы иметь импульс 1,60 × 10 9 кг · м / с (такой же, как импульс корабля в задаче выше)? (b) Какова инерция самолета, когда он взлетает со скоростью 60,0 м / с? (c) Если корабль является авианосцем, который запускает эти самолеты с помощью катапульты, обсудите последствия вашего ответа на вопрос (b), поскольку он относится к эффектам отдачи катапульты на корабль.
- (a) Каков импульс мусоровоза, который составляет 1,20 × 10 4 кг и движется со скоростью 10.0 м / с? (b) На какой скорости мусор весом 8 кг может иметь такую же скорость, что и грузовик?
- Неуправляемый вагон массой 15 000 кг движется по рельсам со скоростью 5,4 м / с. Вычислите время, необходимое для того, чтобы усилие в 1500 Н привело к остановке автомобиля.
- Масса Земли составляет 5,972 × 10 24 кг, а радиус ее орбиты в среднем составляет 1,496 × 10 11 м.
Рассчитайте его импульс.
Глоссарий
Количество движения: произведение массы на скорость
второй закон движения: физический закон, который гласит, что чистая внешняя сила равна изменению количества движения системы, деленному на время, в течение которого оно изменяется
Избранные решения проблем и упражнения
1.а) 1,50 × 10 4 кг м / с; (б) 625 к 1; (в) 6,66 × 10 2 кг ⋅ м / с
3. (а) 8.00 × 10 4 м / с; (б) 1,20 × 10 6 кг · м / с; (c) Поскольку импульс самолета на 3 порядка меньше, чем у корабля, корабль не будет сильно отскакивать. Отдача составит -0,0100 м / с, что, вероятно, не заметно.
5. 54 с
Equations of Motion – The Physics Hypertextbook
Обсуждение
постоянное ускорение
Для большей точности этот раздел следует называть «Одномерные уравнения движения при постоянном ускорении». Учитывая, что такое название было бы стилистическим кошмаром, позвольте мне начать этот раздел со следующей оговорки. Эти уравнения движения действительны только тогда, когда ускорение постоянное и движение ограничено прямой линией.
Учитывая, что такое название было бы стилистическим кошмаром, позвольте мне начать этот раздел со следующей оговорки. Эти уравнения движения действительны только тогда, когда ускорение постоянное и движение ограничено прямой линией.
Учитывая, что мы живем в трехмерной вселенной, в которой единственная константа – это изменение, у вас может возникнуть соблазн сразу отказаться от этого раздела. Было бы правильно сказать, что ни один объект никогда не двигался по прямой с постоянным ускорением в любом месте Вселенной в любое время – ни сегодня, ни вчера, ни завтра, ни пять миллиардов лет назад, ни тридцать миллиардов лет в будущем. , никогда.Об этом я могу сказать с абсолютной метафизической уверенностью.
Так что же тогда хорошего в этом разделе? Что ж, во многих случаях полезно предположить, что объект двигался или будет двигаться по прямому пути с почти постоянным ускорением; то есть любое отклонение от идеального движения можно по существу игнорировать. Движение по криволинейной траектории можно считать фактически одномерным, если существует только одна степень свободы для задействованных объектов. Дорога может извиваться и поворачиваться и исследовать всевозможные направления, но автомобили, движущиеся по ней, имеют только одну степень свободы – свободу двигаться в одном или противоположном направлении. (Вы не можете двигаться по дороге по диагонали и надеетесь остаться на ней надолго.) В этом отношении это мало чем отличается от движения, ограниченного прямой линией. Аппроксимация реальных ситуаций моделями, основанными на идеальных ситуациях, не считается обманом. Так поступают в физике. Это настолько полезный метод, что мы будем использовать его снова и снова.
Дорога может извиваться и поворачиваться и исследовать всевозможные направления, но автомобили, движущиеся по ней, имеют только одну степень свободы – свободу двигаться в одном или противоположном направлении. (Вы не можете двигаться по дороге по диагонали и надеетесь остаться на ней надолго.) В этом отношении это мало чем отличается от движения, ограниченного прямой линией. Аппроксимация реальных ситуаций моделями, основанными на идеальных ситуациях, не считается обманом. Так поступают в физике. Это настолько полезный метод, что мы будем использовать его снова и снова.
Наша цель в этом разделе – вывести новые уравнения, которые можно использовать для описания движения объекта с точки зрения его трех кинематических переменных: скорости ( v ), положения ( с ) и времени ( т ). Есть три способа объединить их в пары: скорость-время, положение-время и скорость-положение. В этом порядке их также часто называют первым, вторым и третьим уравнениями движения, но нет веских причин для изучения этих имен.
Поскольку мы имеем дело с движением по прямой линии, направление будет обозначено знаком – положительные величины указывают в одну сторону, а отрицательные величины указывают в противоположную сторону.Определение того, какое направление является положительным, а какое отрицательным, совершенно произвольно. Законы физики изотропны ; то есть они не зависят от ориентации системы координат. Однако некоторые проблемы легче понять и решить, если одно направление предпочтительнее другого. Пока вы последовательны в решении проблемы, это не имеет значения.
скорость-время
Связь между скоростью и временем проста при равномерно ускоренном прямолинейном движении.Чем дольше ускорение, тем больше изменение скорости. Изменение скорости прямо пропорционально времени, когда ускорение постоянно. Если скорость увеличивается на определенную величину за определенное время, она должна увеличиваться вдвое на эту величину в два раза быстрее. Если объект уже стартовал с определенной скоростью, то его новая скорость будет равна старой скорости плюс это изменение. Вы должны быть в состоянии увидеть уравнение уже мысленным взором.
Это самое простое из трех уравнений, которое можно вывести с помощью алгебры.Начнем с определения ускорения.
Расширить ∆ v до v – v 0 и сжать ∆ t до t .
Затем найдите v как функцию от t .
v = v 0 + at [1]
Это первое уравнение движения . Он записывается как полином – постоянный член ( v 0 ), за которым следует член первого порядка ( на ).Поскольку наивысший порядок равен 1, правильнее называть его линейной функцией .
Символ v 0 [vee naught] называется начальной скоростью или скоростью a время t = 0. Его часто называют «первой скоростью», но это довольно наивный способ Опишите это. Лучшее определение было бы сказать, что начальная скорость – это скорость, которую имеет движущийся объект, когда он впервые становится важным в проблеме. Скажем, метеор был замечен глубоко в космосе, и проблема заключалась в том, чтобы определить его траекторию, тогда начальная скорость, вероятно, будет той скоростью, которую он имел при первом наблюдении.Но если проблема заключалась в том, что тот же самый метеор сгорает при входе в атмосферу, то начальная скорость, вероятно, равна скорости, которую он имел при входе в атмосферу Земли. Ответ на вопрос “Какая начальная скорость?” “Это зависит от обстоятельств”. Это оказывается ответом на множество вопросов.
Обозначение v – это скорость через некоторое время t после начальной скорости. Ее часто называют конечной скоростью , но это не делает ее «последней скоростью» объекта. Возьмем случай с метеором.Какая скорость обозначена символом v ? Если вы внимательно слушали, значит, вы должны были ожидать ответа. По-разному. Это может быть скорость метеора, когда он проходит мимо Луны, входит в атмосферу Земли или ударяется о поверхность Земли. Это также может быть скорость метеорита, находящегося на дне кратера. (В этом случае v = 0 м / с.) Является ли какое-либо из этих значений конечной скоростью? Кто знает. Кто-то мог извлечь метеорит из дыры в земле и уехать вместе с ним.Это актуально? Наверное, нет, но это зависит от обстоятельств. Для такого рода вещей нет правил. Вы должны проанализировать текст задачи на предмет физических величин, а затем присвоить значение математическим символам.
Последняя часть этого уравнения на – это изменение скорости от начального значения. Вспомните, что a – это скорость изменения скорости, а t – это время после некоторого начального события . Ставка раз время меняется. Учитывая, что объект ускоряется со скоростью 10 м / с 2 , через 5 с он будет двигаться на 50 м / с быстрее.Если бы он стартовал со скоростью 15 м / с, то его скорость через 5 с была бы…
15 м / с + 50 м / с = 65 м / с
время позиции
Смещение движущегося объекта прямо пропорционально скорости и времени. Двигайся быстрее. Иди дальше. Двигайтесь дольше (как и дольше). Иди дальше. Ускорение усугубляет эту простую ситуацию, поскольку скорость теперь также прямо пропорциональна времени. Попробуйте сказать это словами, и это прозвучит нелепо. «Смещение прямо пропорционально времени и прямо пропорционально скорости, которая прямо пропорциональна времени.”Время удваивается, поэтому смещение пропорционально квадрату времени. Автомобиль, ускоряющийся в течение двух секунд, преодолеет в четыре раза расстояние, превышающее скорость автомобиля, ускоряющегося всего за одну секунду (2 2 = 4). Автомобиль, ускоряющийся в течение трех секунды покрыли бы расстояние в девять раз больше (3 2 = 9).
Если бы это было так просто. Этот пример работает, только когда начальная скорость равна нулю. Смещение пропорционально квадрату времени, когда ускорение постоянное, а начальная скорость равна нулю.Истинное общее утверждение должно учитывать любую начальную скорость и то, как она менялась. Это приводит к ужасно запутанному утверждению соразмерности. Смещение прямо пропорционально времени и пропорционально квадрату времени, когда ускорение постоянно. Функция, которая является одновременно линейной и квадратной, называется квадратичной , что позволяет нам значительно сжать предыдущее утверждение. Смещение является квадратичной функцией времени при постоянном ускорении
Формулировки пропорциональности полезны, но не столь общие, как уравнения.Мы до сих пор не знаем, каковы константы пропорциональности для этой проблемы. Один из способов понять их – использовать алгебру.
Начнем с определения средней скорости.
Расширить ∆ с до с – с 0 и сжать ∆ t до t .
Определите позицию.
с = с 0 + vt [a]
Чтобы продолжить, нам нужно прибегнуть к небольшому трюку, известному как теорема о средней скорости или правило Мертона .Я предпочитаю второй вариант, поскольку правило может применяться к любой величине, которая изменяется с одинаковой скоростью, а не только к скорости. Правило Мертона было впервые опубликовано в 1335 году в Мертон-колледже в Оксфорде английским философом, математиком, логиком и калькулятором Уильямом Хейтсбери (1313–1372). Когда скорость изменения величины постоянна, ее среднее значение находится на полпути между ее конечным и начальным значениями.
v = ½ ( v + v 0 ) [4]
Подставьте первое уравнение движения [1] в это уравнение [4] и упростите его, исключив v .
| v = ½ [( v 0 + при ) + v 0 ] v = ½ (2 v 0 + при 4) v = v 0 + ½ at [b] |
Теперь замените [b] на [a], чтобы исключить v [vee bar].
с = с 0 + ( v 0 + ½ при ) т
И, наконец, найдите s как функцию от t .
с = с 0 + v 0 t + ½ при 2 [2]
Это второе уравнение движения . Он записывается как полином – постоянный член ( s 0 ), за которым следует член первого порядка ( v 0 t ), за которым следует член второго порядка (½ at 2 ). Поскольку наивысший порядок равен 2, правильнее называть его квадратичным .
Символ s 0 [ess naught] часто рассматривается как начальная позиция . Символ s – это позиция на t позже. Если хотите, вы можете назвать ее конечной позицией . Изменение положения (∆ s ) называется смещением или расстоянием (в зависимости от обстоятельств), и некоторые люди предпочитают писать второе уравнение движения таким образом.
∆ с = v 0 t + ½ при 2 [2]
скорость-позиция
Каждое из первых двух уравнений движения описывает одну кинематическую переменную как функцию времени.По сути…
- Скорость прямо пропорциональна времени при постоянном ускорении ( v ∝ t ).
- Смещение пропорционально квадрату времени при постоянном ускорении (∆ с ∝ t 2 ).
Объединение этих двух утверждений приводит к третьему, не зависящему от времени. При замене должно быть очевидно, что…
- Смещение пропорционально квадрату скорости при постоянном ускорении (∆ s ∝ v 2 ).
Это утверждение особенно важно для безопасности вождения. Когда вы вдвое увеличиваете скорость автомобиля, требуется в четыре раза больше расстояния, чтобы его остановить. Увеличьте скорость втрое, и вам понадобится в девять раз больше расстояния. Это хорошее практическое правило, которое следует запомнить.
Концептуальное введение сделано. Пришло время вывести формальное уравнение.
метод 1
Объедините первые два уравнения вместе таким образом, чтобы исключить время как переменную. Самый простой способ сделать это – начать с первого уравнения движения…
v = v 0 + at [1]
реши на время…
, а затем подставить его во второе уравнение движения…
с = с 0 + v 0 t + ½ при 2 [2]
нравится…
| с = | с 0 + v 0 | ⎛ ⎜ ⎝ | v – v 0 | ⎞ ⎟ ⎠ | + ½ a | ⎛ ⎜ ⎝ | v – v 0 | ⎞ 2 ⎟ ⎠ |
| a |
| с – с 0 = | vv 0 – v 0 2 | + | v 2 -2 vv 0 + v 0 2 |
| 2 a |
| 2 a ( с – с 0 ) = 2 ( vv 0 – v 0 2 ) + ( v 2 v 2 v 2 2 vv 0 + v 0 2 ) | |
| 2 a ( s – s 0 ) = v 2 – v 0 2 | |
Возведите объект в квадрат скорости, и все готово.
v 2 = v 0 2 + 2 a ( s – s 0 ) [3]
Это третье уравнение движения . Еще раз, символ s 0 [ess naught] – это начальная позиция , а s – это позиция через некоторое время t позже. При желании вы можете написать уравнение, используя ∆ s – изменение положения в положении , смещение на или расстояние на в зависимости от ситуации.
v 2 = v 0 2 + 2 a ∆ s [3]
метод 2
Более сложный способ вывести это уравнение – начать со второго уравнения движения в этой форме…
∆ с = v 0 t + ½ при 2 [2]
и решите ее на время. Это непростая работа, поскольку уравнение квадратично. Переставьте термины так…
½ при 2 + v 0 t – ∆ s = 0
и сравните его с общей формой квадратичной.
топор 2 + bx + c = 0
Решение этого дается известным уравнением…
| x = | – b ± √ ( b 2 – 4 ac ) |
| 2 |
Замените символы в общем уравнении эквивалентными символами из нашего преобразованного второго уравнения движения…
| т = | – v 0 ± √ [ v 0 2 – 4 (½ a ) (∆ s )] |
| 2 (½ a ) |
почисти немного…
| т = | – v 0 ± √ ( v 0 2 – 2 a ∆ s ) |
, а затем подставьте его обратно в первое уравнение движения.
v = v 0 + at [1]
| v = v 0 + a | ⎛ ⎜ ⎝ | – v 0 ± √ ( v 0 2 – 2 a ∆ s ) | ⎞ ⎟ ⎠ |
Материал отменяется, и мы получаем это…
v = ± √ ( v 0 2 + 2 a ∆ s )
Выровняйте обе стороны, и все готово.
v 2 = v 0 2 + 2 a ∆ s [3]
Это было не так уж и плохо, не так ли?
исчисления выводов
Исчисление – это сложная математическая тема, но она значительно упрощает вывод двух из трех уравнений движения. По определению, ускорение – это первая производная скорости по времени. Возьмите операцию в этом определении и отмените ее. Вместо того, чтобы дифференцировать скорость, чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость.Это дает нам уравнение скорость-время. Если предположить, что ускорение постоянное, мы получим так называемое первое уравнение движения [1].
| = | |||
| дв | = | и dt | |
| = | |||
| v – v 0 | = | при | |
| v | = | v 0 + at [1] | |
Опять же, по определению, скорость – это первая производная положения по времени.Выполните эту операцию в обратном порядке. Вместо того, чтобы различать положение для определения скорости, интегрируйте скорость, чтобы найти положение. Это дает нам уравнение положения-времени для постоянного ускорения, также известное как второе уравнение движения [2].
| v | = | |||||||||
| DS | = | v dt | ||||||||
| DS | = | ( v 0 + at ) dt | ||||||||
| = |
| |||||||||
| с – с 0 | = | v 0 t + ½ при 2 | ||||||||
| с | = | s 0 + v 0 t + ½ at 2 [2] | ||||||||
В отличие от первого и второго уравнений движения, нет очевидного способа вывести третье уравнение движения (то, которое связывает скорость с положением) с помощью расчетов.Мы не можем просто перепроектировать это по определению. Нам нужно разыграть довольно изощренный трюк.
Первое уравнение движения связывает скорость со временем. По сути, мы вывели его из этой производной…
Второе уравнение движения связывает положение со временем. Это произошло от этой производной…
Третье уравнение движения связывает скорость с положением. По логике, это должно происходить от производной, которая выглядит так…
Но что это значит? Ну, ничего по определению, но, как и все количества, оно равно самому себе.Он также равен самому себе, умноженному на 1. Мы будем использовать специальную версию 1 ( dt dt ) и специальную версию алгебры (алгебра с бесконечно малыми). Посмотрите, что происходит, когда мы это делаем. Мы получаем одну производную, равную ускорению ( dv dt ), а другую производную, равную обратной скорости ( dt ds ).
| дв | = | дв | 1 | |
| DS | DS | |||
| дв | = | дв | дт | |
| DS | DS | дт | ||
| дв | = | дв | дт | |
| DS | дт | DS | ||
| дв | = | a | 1 | |
| DS | v |
Следующий шаг, разделение переменных.Соберите вместе похожие вещи и интегрируйте их. Вот что мы получаем при постоянном ускорении…
| = | ||||
| в дв | = | и DS | ||
| = | ||||
| ½ ( v 2 – v 0 2 ) | = | a ( с – с 0 ) | ||
| v 2 | = | v 0 2 + 2 a ( s – s 0 ) [3] | ||
Безусловно, умное решение, и оно было не так уж сложно, чем первые два варианта.Однако на самом деле это сработало только потому, что ускорение было постоянным – постоянным во времени и постоянным в пространстве. Если бы ускорение каким-либо образом менялось, этот метод был бы неудобно трудным. Мы вернемся к алгебре, чтобы спасти наше здравомыслие. Не то чтобы в этом что-то не так. Алгебра работает, а здравомыслие стоит сэкономить.
| v = | v 0 + at | [1] |
| + | ||
| с = | с 0 + v 0 t + ½ при 2 | [2] |
| = | ||
| v 2 = | v 0 2 + 2 a ( s – s 0 ) | [3] |
Формула моментума
Формула моментума Вопросы:
1) Общая масса мотоцикла и человека, едущего на нем, составляет 200.0 кг. Если гонщик движется с постоянной скоростью 30,0 м / с, каков импульс мотоцикла и гонщика?
Ответ: Импульс можно найти по формуле:
p = mv
p = (200,0 кг) (30,0 м / с)
p = 6000 кг · м / с
Импульс мотоцикла и гонщика 6000 кг · м / с.
2) Хоккейная шайба скользит по льду со скоростью 43,80 м / с. Имеет массу 0,165 кг.Шайба попадает в камень для керлинга весом 19,10 кг, который изначально находится в состоянии покоя. Хоккейная шайба отскакивает от камня и скользит в противоположном направлении со скоростью 43,0 м / с. Какова скорость скручивающейся скалы после столкновения?
Ответ: Этот вопрос зависит от сохранения количества движения при упругих столкновениях. Общий импульс до равен общему импульсу после:
p шайба, до + p скала, до = p шайба, после + p скала, после
м шайба v шайба, до + м скала v скала, до = м шайба v шайба, после + м скала v скала, после
Масса шайбы м шайба = 0.165 кг . Масса породы м, порода = 19,10 кг. Скорость шайбы до столкновения v шайба, до = +43,80 м / с. Скорость породы перед столкновением составляет v камень, до = 0,0 м / с, потому что она находилась в состоянии покоя. Скорость шайбы после столкновения отрицательная, потому что она двигалась в противоположном направлении, как и до столкновения: v шайба, после = -43,0 м / с.
(0,165 кг) (43,80 м / с) + (19,10 кг) (0.0 м / с) = (0,165 кг) (- 43,0 м / с) + (19,10 кг) v порода, после
(0,165 кг) (43,80 м / с) = – (0,165 кг) (43,0 м / с) + (19,10 кг) v скала, после
Теперь уравнение можно изменить, чтобы найти камень v после .
(0,165 кг) (43,80 м / с) + (0,165 кг) (43,0 м / с) = (19,10 кг) против породы , после
v скала, после = +0,750 м / с
Скорость керлинга после столкновения с хоккейной шайбой плотностью льда равна v рок, после = +0.750 м / с.
Физические формулы
Это На странице есть все необходимые вам формулы физики. В первом разделе у нас есть СИ единицы измерения. В следующем разделе мы рассмотрим уравнения механики и уравнения электричества.
Эти Уравнения физики описывают взаимосвязь между скоростью, ускорением, силы и т. д. Как только мы поймем основную физику, уравнения могут служить в качестве мысленных рамки, которые мы можем использовать, чтобы понять и предсказать исход физического явления. Конечно, эти уравнения также будут неоценимы, когда дело доходит до расчета неизвестные значения из известных.
Физика
это наука, которая в значительной степени полагается на математические навыки. Основным из них является алгебра, поскольку вам нужно иметь возможность заменять и переставлять уравнение
, если это необходимо. Помните, что мы всегда можем изменить формулу в соответствии с конкретным приложением.
Примечание: Все эти физические формулы требуют использования единиц СИ
(Международная система единиц)
Единицы СИ
| Кол-во | Количество символ | Блок | символ |
| Масса | м | килограммы | кг |
| Усилие | Ф | Ньютон | N |
| расстояние | д | метров | м |
| скорость | v | Скорость | v |
| Давление | п. | Паскаль | Па |
| Работа | Вт | Джоулей | Дж |
| Энергия | E | Джоулей | Дж |
| Время | т | секунд | с |
https: // www.easy-science-experiments.com/#show-hide Наши лучшие идеи подарков для молодых ученых
https://www.easy-science-experiments.com/#show-hide
Уравнения механики
$$ v = \ frac {\ Delta d} {\ Delta t} $$
$$ velocity = \ frac {\ text {изменение смещения}} {\ text {изменение во времени}} $$
$$ a = \ frac {\ Delta v} {\ Delta t} $$
$$ ускорение = \ frac {\ text {изменение скорости}} {\ text {изменение во времени}} $$
$$ Сила = масса \ раз ускорение $$
$$ Работа = Сила \ умноженное на расстояние $$
$$ Мощность = \ frac {Работа} {время} $$
$$ крутящий момент = Сила \ умноженное на расстояние $$
$$ Force = – \ text {постоянная эластичности} \ times extension $$
Уравнения кругового движения
$$ a_c = \ frac {v ^ 2} {r} $$ | $$ \ text {центростремительное ускорение} = \ frac {скорость ^ 2} {радиус} $$ |
$$ F_c = \ frac {mv ^ 2} {r} $$ | $$ \ text {центростремительная сила} = \ frac {масса \ умноженная на скорость ^ 2} {радиус} $$ |
$$ C = 2 \ pi r $$ | $$ Окружность = 2 \ пи \ умножить на радиус $$ |
Импульс
$$ импульс = масса \ умноженная на скорость $$
$$ \ Delta p = F \ Delta t $$
$$ \ text {изменение импульса} = Сила \ раз \ text {изменение во времени} $$
Уравнения энергии
$$ E_p = \ frac {1} {2} kx ^ 2 $$
$$ \ text {Упругая потенциальная энергия} = \ frac {1} {2} \ text {постоянная упругости} \ times extension ^ 2 $$
$$ E_k = \ frac {1} {2} mv ^ 2 $$
$$ \ text {Кинетическая энергия} = \ frac {1} {2} масса \ умноженная на скорость ^ 2 $$
$$ \ Delta E_p = мг \ Delta ч $$
$$ \ text {гравитационная потенциальная энергия} = масса \ times \ text {ускорение свободного падения} \ times \ text {изменение высоты} $$
Ep означает энергетический потенциал, который представляет собой накопленную энергию.2 + 2ad $$
$$ d = (\ frac {v_f + v_f} {2}) t $$
Уравнения электроэнергии
$$ Напряжение = ток \ умноженное на сопротивление $$
$$ P = I V $$
$$ P = \ frac {\ Delta E} {t} $$
$$ Мощность = Ток \ раз Напряжение $$
$$ Мощность = \ frac {Изменение энергии} {время} $$
$$ R_T = R_1 + R_2 + R_3 + … $$
Полное сопротивление резистора, включенного параллельно, равно сумме обратных сопротивлений резисторов.
$$ \ frac {1} {R_T} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} +… $$
Суммарное сопротивление последовательно включенных резисторов – сумма всех резисторов, включенных последовательно.
$$ \ text {Напряженность электрического поля} = \ frac {\ text {Разница потенциалов (напряжение)}} {расстояние} $$
$$ \ text {Электрическая сила} = \ text {Напряженность электрического поля} \ times charge $$
$$ Current = \ frac {charge} {timt} $$
$$ V = \ frac {\ Delta E} {Q} $$
$$ V = \ frac {изменение энергии} {Charge} $$
$$ \ Delta E = qEd $$
$$ \ text {Изменение энергии} = заряд \ раз \ text {напряженность электрического поля} \ раз расстояние $$
https: // www.easy-science-experiments.com/#show-hide
Перестановка физических формул
Помните: Мы можем переставить физические формулы, применяя простую алгебру, чтобы гарантировать, что все символы в правой части уравнения известны.
Например, если мы знаем силу, действующую на объект, и массу объекта, как рассчитать ускорение, испытываемое объектом, с помощью уравнения:
$$ F = ma $$
Нам нужно переставить уравнение так, что a находится в левой части, а F – в правой.
$$ a = \ frac {m} {F} $$
Теперь мы можем вставить m и F, чтобы получить a. Пока есть только одно неизвестное, мы можем легко изменить уравнения, чтобы дать нам ответ.
Вернитесь из “Физических формул” на ГЛАВНУЮ.
https://www.easy-science-experiments.com/#show-hide
Калькулятор импульсов и импульса
Этот калькулятор импульсов и импульсов поможет вам проанализировать любой движущийся объект. Вы узнаете, как рассчитать импульс тремя способами:
- зная изменение скорости тела,
- зная время действия силы на это тело и
- просто из-за изменения импульса.
Продолжайте читать, чтобы узнать уравнение импульса, и больше никогда не беспокойтесь о вычислении импульса!
Формула импульса
Импульс p – векторное значение, определяемое как произведение массы m и скорости v объекта:
p = mv Изменение количества движения тела называется импульсом Дж :
J = Δp = p₂ - p₁ = mv₂ - mv₁ = mΔv
Дельта (Δ) – это символ, означающий «изменение».Например, в то время как p представляет собой мгновенный импульс, Δp отображает изменение количества движения, которое произошло за некоторый период времени.
Зайдите в калькулятор сохранения импульса, чтобы узнать о практических применениях импульса.
Уравнение импульса
Импульс тела – это произведение времени t и силы F , действующей на это тело:
Дж = фута Единицы импульса и количества движения – ньютон-секунды (обозначение: Н · с), выраженные как кг · м / с в единицах СИ.
Проверьте, можете ли вы вывести приведенное выше уравнение импульса из формулы Дж = mΔv . Подсказка: вам придется использовать определение ускорения и второй закон Ньютона.
Как рассчитать импульс
- Вы можете ввести значения начального и конечного импульса в наш калькулятор, чтобы найти импульс непосредственно по формуле импульса
J = Δp. - Вы также можете ввести значения mas s и изменение скорости объекта, чтобы вычислить импульс по уравнению
J = mΔv. - Если вам известна сила, действующая на объект, введите вместо этого значения force и time change . Наш калькулятор импульса и импульса будет использовать формулу
Дж =форинтов.
Понятие импульса связано с кинетической энергией – обязательно прочтите об этом!
Как рассчитать импульс | Универсальный класс
Мы определим понятие импульса в контексте физики и используем математику векторов и разностей (например, разность во времени, Δ t ), чтобы вывести закон сохранения количества движения и применить его к различным задачам. .
Ключевые термины
o Импульс
o Закон сохранения количества движения
Цели
o Понять физическое определение импульса
o Вывести закон сохранения количества движения
o Применить этот закон сохранения к решению задач, связанных с линейным движением
Начнем!
Мы использовали понятия массы и скорости для описания движения объектов.Представьте себе два объекта: один с небольшой массой, а другой с большой массой; рассмотрим, например, теннисный мяч (менее массивный) и набивной мяч (более массивный). Теперь представьте, что два объекта бросаются в вас с некоторой скоростью v; очевидно, удар теннисным мячом, движущимся со скоростью v , звучит гораздо менее болезненно, чем удар набивным мячом, движущимся со скоростью v. Рассмотрим также набивной мяч, движущийся с двумя разными скоростями: более медленная скорость, с. , и более высокая скорость, f. Пытаться поймать набивной мяч, летящий на скорости s (более низкая скорость), безусловно, звучит проще, чем пытаться поймать мяч, движущийся на более высокой скорости f! Мы склонны думать о более крупном объекте, движущемся с определенной скоростью, как о имеющем больше импульса , чем о меньшем объекте, движущемся с такой скоростью. Точно так же мы думаем, что один объект, движущийся с высокой скоростью, имеет больший импульс, чем объект, движущийся с меньшей скоростью. Таким образом, импульс увеличивается с увеличением скорости, а также массы.Таким образом, эта ситуация логически соответствует определению импульса в физике. Импульс p объекта массой m и скоростью v определяется в соответствии со следующим соотношением:
p = м v
Обратите внимание, что импульс, как и скорость, является вектором, имеющим как величину, так и направление. По мере увеличения массы или скорости объекта увеличивается и количество движения.
Взаимосвязь между импульсом и силой
Напомним, что ускорение – это просто скорость изменения скорости во времени.Таким образом (в среднем) мы можем написать следующее:
Давайте подставим это в наше выражение силы из второго закона движения Ньютона:
Предполагая, что масса м остается постоянной, мы можем сделать следующее изменение:
Обратите внимание, что поскольку m v появляется в выражении чистой силы, мы можем записать его в единицах количества движения p. Таким образом, чистая сила, действующая на объект, – это скорость изменения его количества движения во времени.
Практическая задача : 50-килограммовый объект движется со скоростью 10 метров в секунду. Какова его динамика?
Решение : Импульс, p, объекта – это просто произведение его массы на его скорость: p = m v. Поскольку направление не указано, нас интересует только определение величины p, или p . Таким образом,
Обратите внимание на единицы в результате – мы также можем выразить единицы в ньютон-секундах.
Рассмотрим теперь произвольное количество объектов; полный импульс P системы объектов – это просто сумма всех индивидуальных импульсов: . Таким же образом, следуя второму закону Ньютона, мы назовем F до суммой всех сил, действующих на объекты. Но эта сумма, F, , , , является просто суммой всех внешних сил, действующих на систему объектов. Затем
А если на систему объектов не действуют никакие внешние силы,
Другими словами, скорость изменения полного количества движения системы объектов в этом случае равна нулю; это просто утверждение закона сохранения количества движения для замкнутой и изолированной системы.Другими словами, общий импульс постоянен для данной системы объектов, на которую не действует никакая внешняя сила. Этот вывод чрезвычайно полезен для задач, связанных, например, со столкновениями объектов. Следующие ниже практические задачи позволят вам изучить последствия этого результата.
Практическая задача : Снаряд массой 1 килограмм, летящий со скоростью 80 метров в секунду, сталкивается лицом к лицу с другим снарядом массой 2 килограмма, летящим со скоростью 60 метров в секунду в противоположном направлении.Если снаряды «слипаются» после столкновения, какова их скорость после столкновения?
Решение : Нарисуем схему ситуации до и после столкновения. Мы также определяем направление x для справки.
Из урока мы узнали, что общий импульс системы объектов должен сохраняться (то есть не изменяться), если на эту систему не действуют никакие внешние силы.В этом случае предполагается, что никакие силы вне системы не действуют на два объекта. Следовательно, полный импульс до столкновения должен быть таким же, как полный импульс после столкновения. Давайте сначала вычислим полный импульс перед столкновением ( P i ):
После столкновения, поскольку два объекта «слипаются», они фактически становятся единым объектом с массой 3 кг и некоторой скоростью v. Импульс этого объекта, P f , равен
.
Мы хотим вычислить v, – скорость объектов после столкновения. Поскольку импульс до столкновения такой же, как и после,
Таким образом, скорость объектов после столкновения составляет 13,3 метра в секунду в том же направлении, что и скорость более крупного объекта до столкновения (которое мы определили здесь как отрицательное направление x ).
Практическая задача : Космонавт со всем его оборудованием и инструментами имеет массу 125 кг. В космосе происходит авария, в результате которой он оторвался от космической станции и улетел в космос со скоростью один метр в секунду. Один из его инструментов весит пять килограммов, и он решает использовать его, чтобы вернуться на станцию. Если он отбрасывает инструмент прямо от станции, с какой минимальной скоростью он должен бросить его, чтобы вернуться к станции?
Решение : Как обычно, мы можем значительно помочь процессу решения проблемы, нарисовав схему ситуации.Схема не обязательно должна быть художественной – простых фигур часто бывает достаточно для изображения разных предметов.
Часть веса космонавта составляет пятикилограммовый инструмент; если он отбрасывает его от себя (а также прямо от станции) с достаточной скоростью, он может (за счет сохранения количества движения) заставить себя начать движение обратно к станции. Эта ситуация проиллюстрирована ниже. Обратите внимание, что масса космонавта уменьшается на пять килограммов, когда он выбрасывает инструмент.
Мы можем использовать закон сохранения количества движения, чтобы вычислить скорость, с которой астронавт должен бросить инструмент, чтобы изменить свой тревожный курс и отправить его обратно к станции. Начальный полный импульс космонавта P i следующий. Мы определим как x направление от станции.
Это также должен быть общий импульс космонавта и инструмента после того, как он его выбросил – мы назовем этот конечный импульс P f .Рассчитаем скорость инструмента, необходимую для остановки космонавта; любая скорость выше этого числа заставит космонавта двигаться к станции.
Таким образом, космонавт должен отбросить инструмент со скоростью 25 метров в секунду прямо от станции, чтобы остановить свое движение относительно станции. Если он превысит эту скорость, он начнет движение обратно к станции.Однако метание 5-килограммового инструмента (около 11 фунтов) со скоростью 25 метров в секунду (около 56 миль в час) могло быть непростой задачей! Космонавту, вероятно, потребуется бросить несколько инструментов или других предметов.
Определение силы в физике
Мощность – это скорость выполнения работы или передачи энергии за единицу времени. Мощность увеличивается, если работа выполняется быстрее или энергия передается за меньшее время.
Расчетная мощность
Уравнение для мощности P = W / t
- P означает мощность (в ваттах)
- Вт – это количество проделанной работы (в Джоулях) или затраченной энергии (в Джоулях)
- t – количество времени (в секундах)
С точки зрения математики, мощность – это производная работы по времени.Если работа выполняется быстрее, мощность выше. Если работа выполняется медленнее, мощность меньше.
Поскольку работа – это сила, умноженная на смещение (W = F * d), а скорость – это смещение во времени (v = d / t), мощность равна силе, умноженной на скорость: P = F * v. Большая мощность видна, когда система является одновременно мощной и быстрой по скорости.
Ед. Мощности
Мощность измеряется в энергии (джоулях), деленной на время. Единица измерения мощности в системе СИ – ватт (Вт) или джоуль в секунду (Дж / с). Мощность – это скалярная величина, у нее нет направления.
Лошадиная сила часто используется для описания мощности, выдаваемой машиной. Лошадиная сила – это единица мощности в британской системе измерения. Это мощность, необходимая для подъема 550 фунтов на один фут за одну секунду, и составляет около 746 Вт.
Ватт часто используется по отношению к лампочкам. В этом номинальном значении мощности это скорость, с которой лампа преобразует электрическую энергию в свет и тепло. Лампа с большей мощностью потребляет больше электроэнергии в единицу времени.
Если вы знаете мощность системы, вы можете найти объем работы, который будет произведен, как W = Pt.Если лампа имеет номинальную мощность 50 Вт, она будет производить 50 джоулей в секунду. За час (3600 секунд) он произведет 180 000 джоулей.
Работа и сила
Когда вы проходите милю, ваша движущая сила перемещает ваше тело, что измеряется по мере выполнения работы. Когда вы пробегаете одну и ту же милю, вы выполняете такой же объем работы, но за меньшее время. Бегун имеет более высокую номинальную мощность, чем ходок, вырабатывая больше ватт. Автомобиль мощностью 80 лошадиных сил может развивать более быстрое ускорение, чем автомобиль мощностью 40 лошадиных сил.В конце концов, обе машины разгоняются до 60 миль в час, но двигатель мощностью 80 л.с. может развивать эту скорость быстрее.
В гонке между черепахой и зайцем заяц обладал большей мощностью и ускорялся быстрее, но черепаха выполняла ту же работу и преодолевала то же расстояние за гораздо большее время.


