Как найти сопротивление через мощность и напряжение: Закон ома | Онлайн калькулятор

Содержание

Закон Ома. Онлайн расчёт для постоянного и переменного тока.

Онлайн расчёт электрических величин напряжения, тока и мощности для участка цепи,
полной цепи, цепи с резистивными, ёмкостными и индуктивными элементами.
Теория и практика для начинающих.

Начнём с терминологии.
Электрический ток – это направленное движение заряженных частиц, при котором происходит перенос заряда из одной области электрической цепи в другую.
Силой электрического тока (I) является величина, которая численно равна количеству заряда Δq, протекающего через заданное поперечное сечение проводника S за единицу времени Δt: I = Δq/Δt.
Напряжение электрического тока между точками A и B электрической цепи – физическая величина, значение которой равно работе эффективного электрического поля, совершаемой при переносе единичного пробного заряда из точки A в точку B.

Омическое (активное) сопротивление – это сопротивление цепи постоянному току, вызывающее безвозвратные потери энергии постоянного тока.
Теперь можно переходить к закону Ома.

Закон Ома был установлен экспериментальным путём в 1826 году немецким физиком Георгом Омом и назван в его честь. По большому счёту, Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, определяющих зависимость между электрическими величинами, такими как: напряжение, сопротивление и сила тока исключительно для проводников, обладающих постоянным сопротивлением. При расчёте напряжений и токов в нелинейных цепях, к примеру, таких, которые содержат полупроводниковые или электровакуумные приборы, этот закон в простейшем виде уже использоваться не может.

Тем не менее, закон Ома был и остаётся основным законом электротехники, устанавливающим связь силы электрического тока с сопротивлением и напряжением.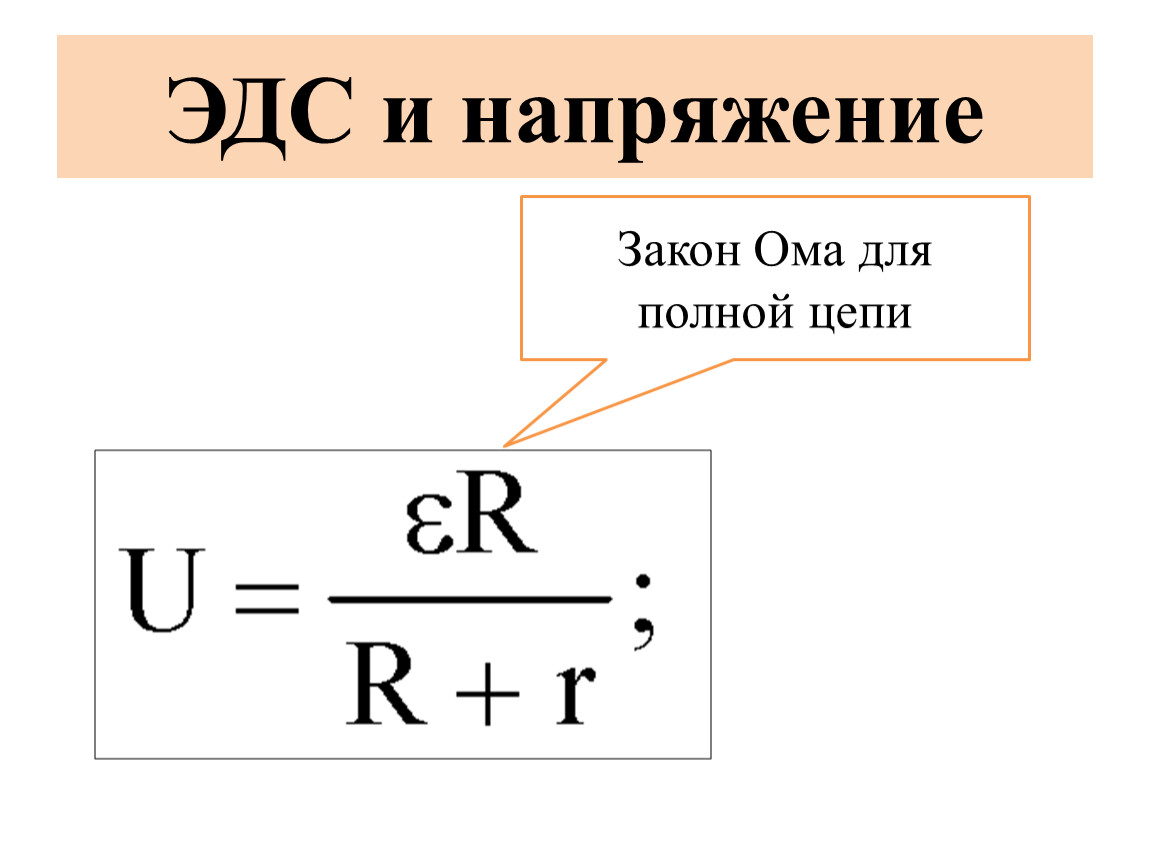
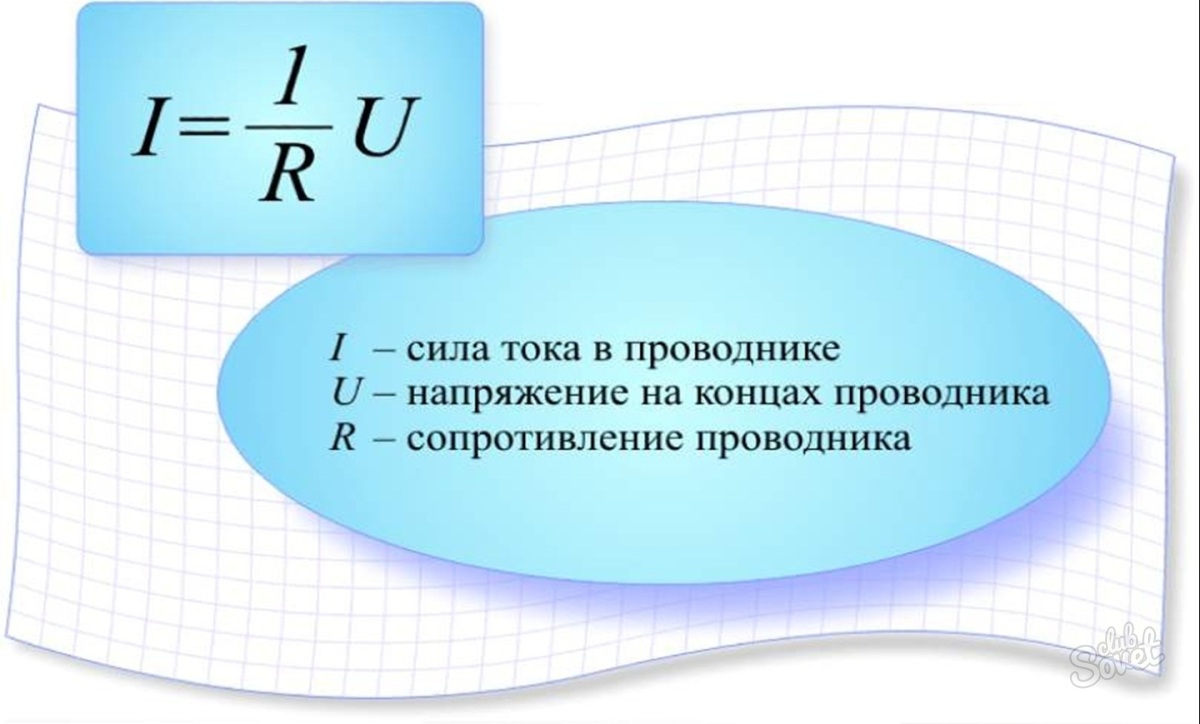
Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:
I=U/R,

где
I – сила тока в проводнике, измеряемая в амперах [А];
U – электрическое напряжение (разность потенциалов), измеря- емая в вольтах [В];
R – электрическое сопротивление проводника, измеряемое в омах [Ом].

Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.

Зная любые два из трёх приведённых параметров можно произвести и расчёт величины мощности, рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам, также являющимся производными от основной формулы закона Ома:
P_(Вт) = U_(В)×I_(А) = I²_(А)×R_(Ом) = U²_(В)/R_(Ом)

Формулы, описывающие закон Ома, настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта.

Не заслуживают, так не заслуживают. Деревянные счёты Вам в помощь, уважаемые дамы и рыцари!
Считайте, учитывайте размерность, не стирайте из памяти, что:

Единицы измерения напряжения: 1В=1000мВ=1000000мкВ;
Единицы измерения силы тока:1А=1000мА=1000000мкА;
Единицы измерения сопротивления:1Ом=0.001кОм=0.000001МОм;
Единицы измерения мощности:1Вт=1000мВт=100000мкВт.

Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.

ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.

Вводить в таблицу нужно только два имеющихся у Вас параметра, остальные посчитает таблица.

Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения r_внутр.

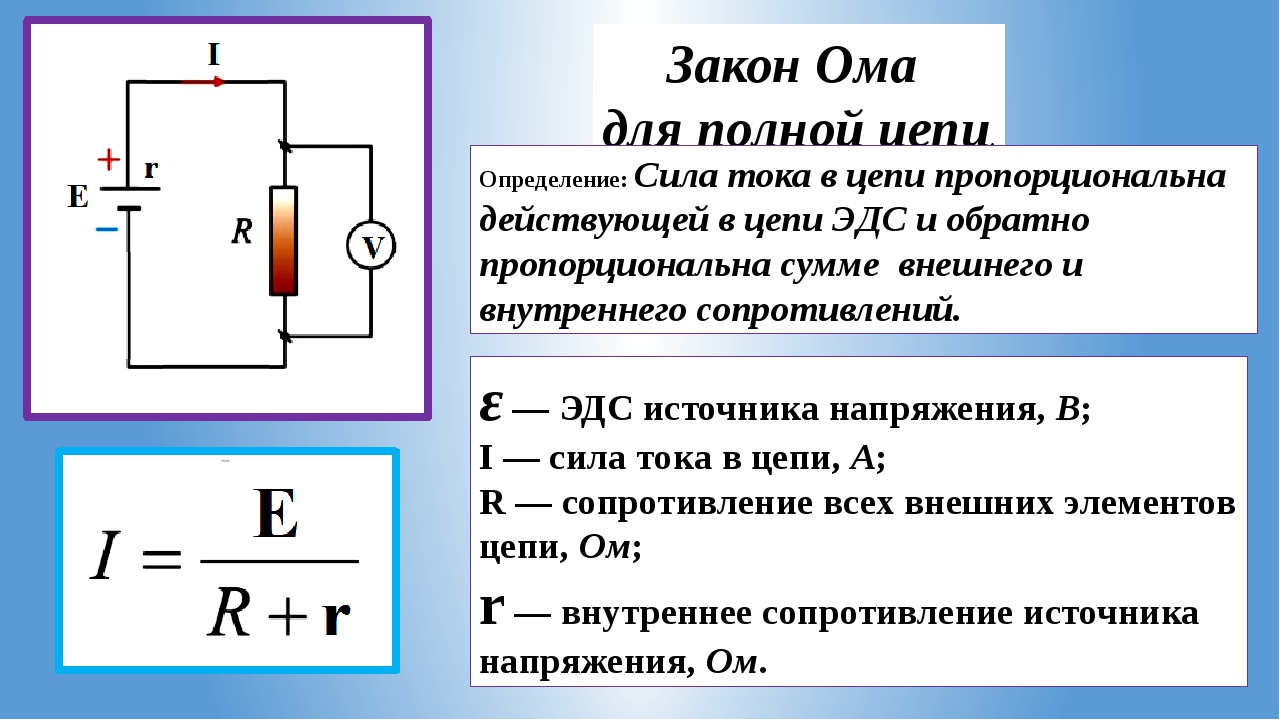
Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = R_внешн + r_внутр , после чего закон приобретает солидное название – закон Ома для полной цепи:
I=U/(R+r) .

Для многозвенных цепей возникает необходимость преобразования её к эквивалентному виду:

Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов определяются исходя из формулы: 1/R_ll = 1/R₄+1/R₅.
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице ссылка на страницу.

Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше, остаётся в силе.

Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока – под значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.

А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока?
Приведём диаграммы для нескольких различных форм сигнала.

Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов – это максимальное значение, которого достигает амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.

Рассчитываем действующее значение напряжение интересующей нас формы:

Для синуса U = Uд = Uа/√2;
для треугольника и пилы U = Uд = Uа/√3;
для меандра U = Uд = Uа.

С этим разобрались!

Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока.
В общем случае смотреться это будет так:

А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись не удаётся, и формула приобретает вид:
Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами:

X_C = 1/(2πƒС) , X_L = 2πƒL .

Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть не менее одного, при наличии индуктивного или емкостного элемента – необходимо указать значение частоты f !

КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.

Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем простенький бестрансформаторный источник питания.

Токозадающими цепями в данной схеме являются элементы R1 и С1.

Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом – 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в – 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока нагрузки.
Зададимся номиналами R1 – 30 Ом, С1 – 1 Мкф, частотой сети f – 50 Гц и подставим всё это хозяйство в таблицу.
Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет – надо увеличивать ёмкость С1.

Поигрались туда-сюда, нашли нужное значение ёмкости – 3,18 Мкф, при котором Z = 1,04кОм.

Всё – закон Ома выполнил свою функцию, расчёт закончен, всем спать полчаса!

Как найти мощность Если есть сопротивление и напряжение?

Есть еще одно понятие — мощность, W. С ним тоже просто: W = U*I. Измеряется в ваттах. Узнать силу тока, если известны напряжение и сопротивление.

Как найти напряжение если известно сопротивление?

Падение напряжение на проводнике равно произведению сопротивления проводника на силу тока в нем. Формула для нахождения напряжения по закону Ома, если известны сила тока и сопротивление: U = I ⋅ R {U= I cdot R} U=I⋅R, где U — напряжение, I — сила тока, R — сопротивление.

Как найти сопротивление Имея мощность?

Р = UxI. При расчетах можно учитывать зависимость мощности от сопротивления нагрузки «R». По законам Ома для участка цепи с постоянным током мощность выражается как: Р = I2xR или P = U2|R.

Как найти мощность P?

Мощность электрического тока равна произведению напряжения на силу тока: P = U ⋅ I . Из этой формулы можно определить и другие физические величины.

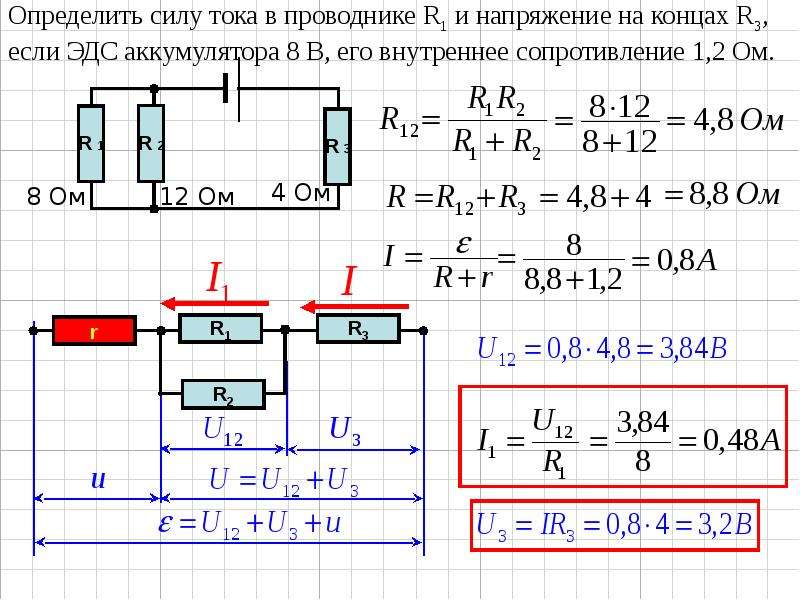
Как найти внутреннее сопротивление?

По закону Ома сопротивление лампочки R = U/I = 1,2/0,3 = 4 Ом; Теперь по формуле для расчета внутреннего сопротивления r = ε/I — R = 1,5/0,3 — 4 = 1 Ом.

Как найти сопротивление в омах?

Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I. Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: R_O = 9 В / 3 А = 3 Ом.

Как узнать на сколько квт тэн?

Р=U*U/R, где P — мощность, которую необходимо найти, Вт; U — рабочее напряжение, В; R — измеренное сопротивление тэн в горячем виде, Ом.

Как найти силу тока без напряжения?

Основными электрическими величинами являются напряжение, ток, сопротивление, мощность. Пожалуй главной формулой электрика является формула закона Ома. Она имеет вид I=U/R (ток равен напряжение деленное на сопротивление). Данную формулу приходится использовать повсеместно.

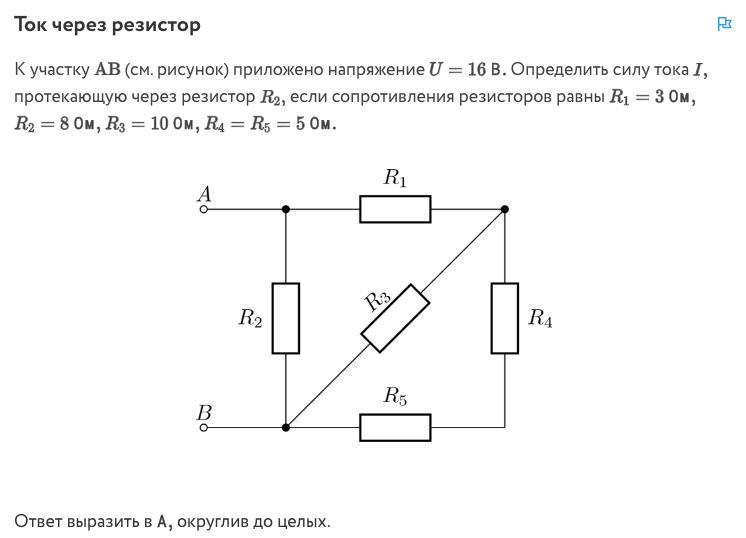
Как найти силу тока через резистор?

I = U/R, где у нас I – сила тока, U – напряжение, R – сопротивление.

Что такое мощность тока в физике?

Мощность электрического тока это количество работы, совершаемой за одну секунду времени, или скорость совершения работы. Количество электричества, проходящего через поперечное сечение цепи в течение одной секунды, есть не что иное, как сила тока в цепи.

Как найти P по физике?

Чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь поверхности: давление = сила / площадь. Обозначим величины, входящие в это выражение: давление — p, сила, действующая на поверхность, — F и площадь поверхности — S.

Как найти мощность формула?

Чтобы вычислить мощность, надо работу разделить на время, в течение которого совершена эта работа. мощность = работа/время. N = A/t, где N — мощность, A — работа, t — время выполненной работы.

Как найти R по физике?

Соотношения закона Ома

U — напряжение (В),
I — ток (А),
Р — мощность (Вт),
R — сопротивление (Ом),
I = U / R.
> U пит (иногда также обозначается как V или Е): напряжение питания. …
> I: ток (измеряется в амперах), который планируется пропустить через лампочку. …
>

формула, расчёт силы тока, напряжения и сопротивления

Безаварийная работа устройства зависит от соответствия технических характеристик прибора нормам питающей сети. Зная напряжение, сопротивление и силу тока в цепи, электрик поймёт, как найти мощность. Формула расчёта важного параметра зависит от свойств сети, в которую подключается потребитель.

Труд электричества

Механические устройства и электрические приборы предназначены для выполнения работы. Согласно второму закону Ньютона, кинетическая энергия, которая воздействует на материальную точку в течение определённого промежутка времени, совершает полезное действие. В электродинамике поле, созданное разностью потенциалов, переносит заряды на участке электрической цепи.

Объём, производимой током работы, зависит от интенсивности электричества.

В середине XIX века Д. П. Джоуль и Э. Х. Ленц решали одинаковую проблему. В проводимых опытах кусок проволоки с высоким сопротивлением разогревался, когда через него пропускался ток. Учёных интересовал вопрос, как вычислить мощность цепи. Для понимания процесса, происходящего в проводнике, следует ввести следующие определения:

P — мощность.
A — работа, совершаемая зарядом в электрической цепи.
U — падение напряжения в проводнике.
I — сила тока.
Q — количество электрических зарядов, переносимых в единицу времени.

Мощность — это работа, производимая током в проводнике за какой-то временной период. Утверждение описывает формула: P = A ∕ ∆t.

На участке цепи разность потенциалов в точках a и b совершает работу по перемещению электрических зарядов, которая определяется уравнением: A = U ∙ Q. Ток представляет собой суммарный заряд, прошедший в проводнике за единицу времени, что математически выражается соотношением: U ∙ I = Q ∕ ∆t. После преобразований получается формула мощности электрического тока: P = A ∕ ∆t = U ∙ Q ∕ ∆t = U ∙ I. Можно утверждать, что в цепи проводится работа, которая зависит от мощности, определяемой током и напряжением на контактах подключённого электрического устройства.

Производительность постоянного тока

В линейной цепи без конденсаторов и катушек индуктивности соблюдается закон Ома. Немецкий учёный обнаружил взаимосвязь тока и напряжения от сопротивления цепи. Открытие выражается уравнением: I = U ∕ R. При известном значении сопротивления нагрузки мощность вычисляется двумя способами: P = I ² ∙ R или P = U ² ∕ R.

Если ток в цепи течёт от плюса к минусу, то энергия сети поглощается потребителем. Такой процесс проистекает при зарядке аккумуляторной батареи. Если движение тока совершается в противоположном направлении, то мощность отдаётся в электрическую цепь. Так происходит в случае питания сети от работающего генератора.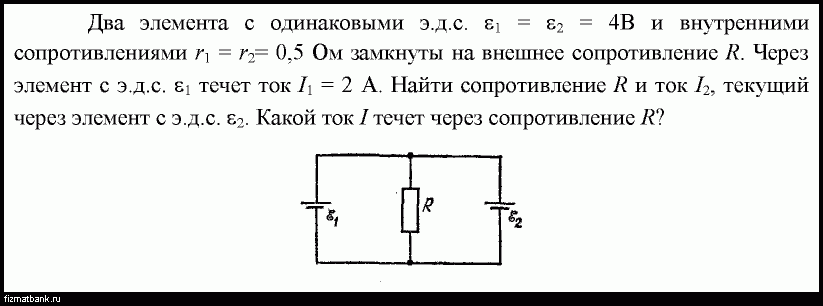

Мощность переменной сети

Расчёт переменных цепей отличается от вычисления параметра производительности в линии постоянного тока. Это связано с тем, что напряжение и ток изменяются во времени и по направлению.

В цепи со сдвигом фаз тока и напряжения, рассматриваются следующие виды мощности:

Активная.
Реактивная.
Полная.

Активный компонент

Активная часть полезной мощности учитывает скорость невозвратного преобразования электричества в тепловую или магнитную энергию. В линии тока с одной фазой активная составляющая вычисляется по формуле: P = U ∙ I ∙ cos ϕ.

В международной системе единиц СИ величина производительности измеряется в ваттах. Угол ϕ определяет смещение напряжения по отношению к току. В трёхфазной цепи активная часть складывается из суммы мощностей каждой отдельной фазы.

Реверсивные потери

Для работы конденсаторов, катушек индуктивности, обмоток электродвигателей затрачивается сила сети. Из-за физических свойств таких устройств энергия, которая определяется реактивной мощностью, возвращается в цепь. Величина отдачи рассчитывается при помощи уравнения: V = U ∙ I ∙ sin ϕ.

Единицей измерения принят ватт. Возможно использование внесистемной меры подсчёта var, название которой составлено из английских слов volt, amper, reaction. Перевод на русский язык соответственно означает «вольт», «ампер», «обратное действие».

Если напряжение опережает ток, то смещение фаз считается больше нуля. В противном случае сдвиг фаз отрицательный. В зависимости от значения sin ϕ реактивная составляющая носит положительный или отрицательный характер. Присутствие в цепи индуктивной нагрузки позволяет говорить о реверсивной части больше нуля, а подключённый прибор потребляет энергию. Использование конденсаторов делает реактивную производительность минусовой, и устройство добавляет энергию в сеть.

Во избежание перегрузок и изменения установленного коэффициента мощности в цепи устанавливаются компенсаторы. Такие меры снижают потери электроэнергии, понижают искажения формы тока и позволяют использовать провода меньшего сечения.

В полную силу

Полная электрическая мощность определяет нагрузку, которую потребитель возлагает на сеть. Активная и реверсивная составляющие объединяются с полной мощностью уравнением: S = √ (P ² + V ²).

С индуктивной нагрузкой показатель V ˃ 0, а использование конденсаторов делает V ˂ 0. Отсутствие конденсаторов и катушек индуктивности делает реактивную часть равной нулю, что возвращает формулу к привычному виду: S = √ (P ² + V ²) = √ (P ² + 0) = √ P ² = P = U ∙ I. Полная мощность измеряется внесистемной единицей «вольт-ампер». Сокращённый вариант — В ∙ А.

Критерий полезности

Коэффициент мощности характеризует потребительскую нагрузку с точки зрения присутствия реактивной части работы. В физическом смысле параметр определяет сдвиг тока от приложенного напряжения и равен cos ϕ. На практике это означает количество тепла, выделяемого на соединительных проводниках. Уровень нагрева способен достигать существенных величин.

В энергетике коэффициент мощности обозначается греческой буквой λ. Диапазон изменения от нуля до единицы или от 0 до 100%. При λ = 1 подаваемая потребителю энергия расходуется на работу, реактивная составляющая отсутствует. Значения λ ≤ 0,5 признаются неудовлетворительными.

Безотказная работа приборов в электрической линии обусловлена правильным расчётом технических параметров. Найти мощность тока в цепи помогает набор формул, выведенных из законов Джоуля — Ленца и Ома. Принципиальная схема, грамотно составленная с учётом особенностей применяемых устройств, повышает производительность электросети.

Напряжение, мощность и сопротивление в электрической цепи

Электрической цепью считается комплекс определенных элементов и устройств, специально предназначенных для протекания электрического тока, в которых электромагнитные процессы можно описать, благодаря таким понятиям, как напряжение и сила тока. Изображение электрической цепи условными знаками называется электрической схемой.

Напряжение в электрической цепи

Для рассмотрения напряжения электрической цепи имеет смысл определить такое понятие, как электрический ток. Электроток характеризуется заряженными частицами, пребывающими в каком-то из проводников в упорядоченном движении. Для его возникновения заранее формируется электрическое поле, оказывающее определенное воздействие на заряженные частицы и приводящее их в движение. Возникновение зарядов при этом будет наблюдаться исключительно в том случае, когда различные вещества между собой тесно контактируют.

В некоторых отдельно взятых видах веществ заряды будут свободно перемещаться среди их разных частей, в то же время, в других веществах это не осуществляется. В этих случаях проводящие вещества называют проводниками, а непроводящие считаются диэлектриками (или изоляторами). При этом в физике подобное разделение всего лишь условное. Способностью проводить электричество обладают любые вещества, но одним она присуща в большей степени, другим – в меньшей.

Электрический ток, как явление свободных зарядов в упорядоченном движении, характеризуется силой тока, равнозначной количеству электричества (заряда), проходящему за единицу времени через поперечное сечение вещества. Таким образом, если за время $dt$ по сечению вещества переносится некий заряд $dq = dq + dq$, то ток будет выражен в формуле:

$i = \frac{dq}{dt} = \frac{q}{t}$

Согласно характеру своего проявления, электрические заряды бывают: положительными и отрицательными. Ток в теле, которое было наэлектризовано, будет существовать непродолжительное время, что объясняется постепенным угасанием заряда самого по себе. С целью более продолжительного существования тока в проводнике потребуется обеспечение постоянной поддержки в нем электрического поля.

Готовые работы на аналогичную тему

Электрическое поле может сформировать исключительно какой-либо источник электротока.

Пример 1

Простейшим примером процесса возникновения электрического тока можно назвать соединение одного конца провода с наэлектризованным предварительно телом и другого конца – с землей.

Изобретенная в свое время батарея стала первым стабильным источником электрического тока. Основными величинами выступают:

сила тока;
сопротивление;
напряжение.

Данные величины, имея тесную взаимосвязь между собой, наиболее точным образом могут охарактеризовать происходящие в электрической цепи процессы.

Определение 1

Напряжение в электрической цепи представляет одну из основных характеристик электротока. Током в физике считается упорядоченное движение электронов (заряженных частиц). Поле, формирующее это движение, будет выполнять определенные действия, которые характеризуются, подобно его работе. Чем больший заряд за одну секунду перемещается в цепи, тем больше работы выполняет электрическое поле.

В качестве одного из факторов, воздействующих непосредственно на работу тока, и выступает напряжение, представляющее собой отношение работы к заряду, который пройдет через определенный участок цепи. Единицей измерения работы тока выступает джоуль (Дж), а заряда – кулон (Кл). Единицей напряжения, таким образом, будет 1 Дж/Кл (или один вольт (В)).

Чтобы возникло напряжение, потребуется источник тока. В ситуации с разомкнутой цепью напряжение присутствует только на клеммах источника. Если включить источник в цепь, на ее отдельных участках можно зафиксировать появление напряжения, а, соответственно, и тока. Напряжение можно измерить вольтметром, включенным параллельно в электрическую цепь.

Электрический потенциал $ф$ представляет отношение энергии (работы) $Э$ электрического поля к единичному заряду $q_0$ (малый заряд, который не искажает поле, куда он внесен). Формула получается при этом следующая:

$dф = \frac{dЭ}{dq_0} = \frac{Э}{q_0}$

Электрическое напряжение является разностью потенциалов между двумя точками электрополя (например, 1 и 2), что выражается формулами:

$U_{1-2} = ф_1 – ф_2 = \frac{dЭ_1}{q_0}-\frac{dЭ_2}{q_0} = \frac{dЭ_{1-2}}{q_0}$

$U_{1-2} = \frac{Э_{1-2}}{q_0}$

$U_{2-1} = -\frac{Э_{1-2}}{q_0}$

Таким образом, электрическое напряжение считается работой электрического поля, ориентированного на перемещение единичного заряда из одной точки в другую.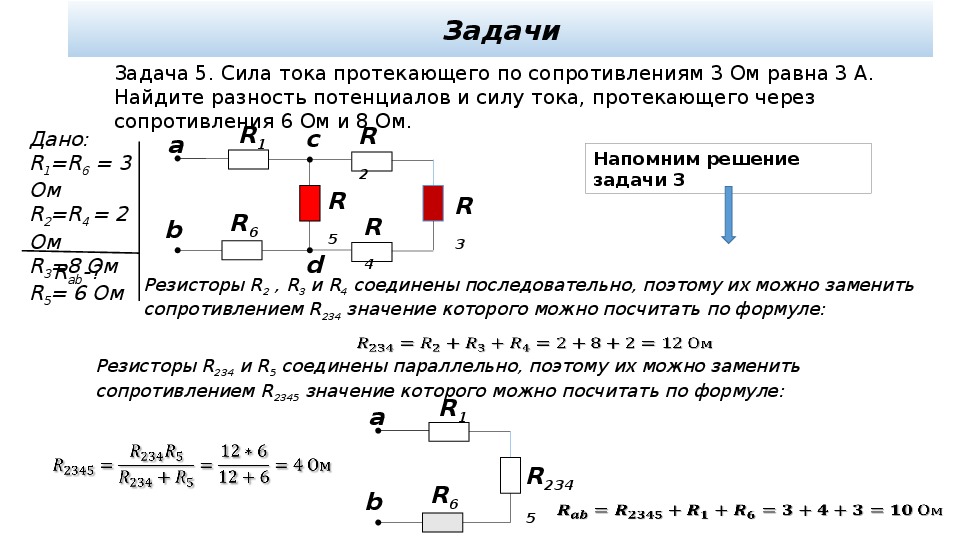 В пассивных элементах цепи положительное направление напряжения будет совпадать с положительным направлением тока.

Мощность в электрических цепях

Определение 2

В качестве одного из характеризующих поведение электронов параметров (помимо тока и напряжения) может выступать мощность. Она представляет меру количества работы, которую возможно совершить за единицу времени. Работа зачастую сравнивается с подъемом веса. Так, чем больше окажется вес и высота его подъема, тем больший объем работы выполнен.

Мощность, определяя скорость совершения работы в единицу времени, считается равной произведению напряжения и силы тока:

$P = IU$, где:

$P$ – мощность тока,
$I$ – сила тока,
$U$ – напряжение в цепи.

Мощность является величиной, обозначающей интенсивность передачи электроэнергии. С целью измерения мощности применяются ваттметры. Мощностью определяется работа по перемещению электрических зарядов за единицу времени:

$P = \frac{A}{\delta t}$

Здесь:

$A$ – работа,
$\delta t$– время, на протяжении которого такая работа совершалась.

Мощность тока в разных приборах и оборудовании будет зависеть параллельно от таких основных величин, как напряжение и сила тока. Чем выше будет ток, тем большим окажется значение мощности, соответственно, она возрастает и если напряжение повысится.

Существует две основных разновидности электрической мощности:

активная;
реактивная.

В первом случае мощность электротока безвозвратно превращается такие виды энергии, как:

механическая;
тепловая;
световая;
прочие.

В производственной и бытовой среде применяются уже более крупные значения: киловатты и мегаватты. К реактивной мощности будет относиться такая степень электрической нагрузки, которая создается в устройствах индуктивными и емкостными колебаниями энергии электромагнитного поля.

Сопротивление в электрической цепи

Электрическое сопротивление является определяющей величиной для силы тока, текущего при заданном напряжении по цепи. Под электрическим сопротивлением $R$ понимается отношение напряжения, возникшего на концах проводника, к силе тока, который течет по проводнику.

$R = \frac{U}{I}$, где

$R$- электрическое сопротивление проводника;
$U$ – напряжение;
$I$ – сила тока.

При расчетах напряжений и токов через элементы электроцепи нужно знать показатель их общего сопротивления. Источники энергии существуют в двух разновидностях: постоянный ток (аккумуляторы, выпрямители, батарейки) и переменный ток (промышленные и бытовые сети). В первом случае ЭДС со временем не изменяется, а во втором она будет изменяться, согласно синусоидальному закону с определенной частотой.

Сопротивление нагрузки существует в активном и реактивном виде. Активное сопротивление $R$ не зависит от частоты сети, что говорит об изменении тока синхронно с напряжением. Реактивное сопротивление бывает индуктивным и емкостным.

Замечание 1

Отличительной чертой реактивной нагрузки считают присутствие опережения или отставания тока от напряжения. Ток в емкостной нагрузке будет опережать напряжение, а в индуктивной – отставать от него. На практике это выглядит, как если бы разряженный конденсатор подключить к источнику постоянного тока, а в момент включения наблюдать максимальное количество тока через него при минимальном напряжении.

Со временем будет фиксироваться уменьшение тока и возрастание напряжения до заряда конденсатора. При подключении к источнику переменного тока конденсатора, он начнет постоянно перезаряжаться с частотой сети, а ток будет увеличиваться раньше напряжения.

Вычисляем мощность переменного и постоянного электрического тока по формуле

При проектировании электрооборудования и расчёте кабелей и пусковой и защитной аппаратуры важно правильно рассчитать мощность и ток электроаппаратуры. В этой статье рассказывается о том, как найти эти параметры.

Формулы расчёта электрической мощности

Что такое мощность

При работе электронагревателя или электродвигателя они выделяют тепло или выполняют механическую работу, единица измерения которой – 1 джоуль (Дж).

Одна из основных характеристик электрооборудования – мощность, показывающая количество тепла или произведённой работы за 1 секунду и выражающаяся в ваттах (Вт):

1Вт=1Дж/1с.

В электротехнике 1Вт выделяется при прохождении тока в 1А при напряжении 1В:

1Вт=1А*1В.

Согласно закону Ома, найти мощность можно также, зная сопротивление нагрузки и ток или напряжение:

P=U*I=I*I*R=(U*U)/R, где:

P (Вт) – мощность электроприбора;
I (А) – ток, протекающий через устройство;
R (Ом) – сопротивление аппарата;
U (В) – напряжение.

Номинальной называют мощность при номинальных параметрах сети и номинальной нагрузке на валу электродвигателя.

Для того чтобы узнать количество электричества, потреблённого за весь период работы, её необходимо умножить на время, которое аппарат работал. Поучившаяся величина измеряется в кВт*ч.

Расчёт в сетях переменного и постоянного напряжения

Электросеть, питающая электроприборы, может быть трёх видов:

постоянное напряжение;
переменное однофазное;
переменное трёхфазное.

Для каждого вида при расчётах используется своя формула мощности.

Расчёт в сети постоянного напряжения

Самые простые расчёты производятся в электросети постоянного тока. Мощность электроаппаратов, подключённых к ней, прямо пропорциональна току и напряжению и, чтобы найти её, используется формула:

P=U*I.

Например, в электродвигателе с номинальным током 4,55А, подключённом к электросети 220В, мощность равна 1000 Ватт, или 1кВт.

И, наоборот, при известных напряжении сети и мощности ток рассчитывается по формуле:

I=P/U.

Однофазные нагрузки

В сети, в которой отсутствуют электродвигатели, а также в бытовой электросети можно пользоваться формулами для сети постоянного напряжения.

Интересно. В бытовой электросети 220В ток можно вычислить по упрощённой формуле: 1кВт=5А.

Мощность переменного тока вычисляется сложнее. Эти аппараты, кроме активной, потребляют реактивную энергию, и формула:

P=U*I

показывает полную потребляемую энергию устройства. Для того чтобы узнать активную составляющую, нужно учесть cosφ – параметр, показывающий долю активной энергии в полной:

Ракт=Робщ*cosφ=U*I*cosφ.

Соответственно, Робщ=Ракт/cosφ.

Например, в электродвигателе с Ракт 1кВт и cosφ 0,7 полная энергия, потребляемая устройством, будет 1,43кВт, и ток – 6,5А.

Треугольник активной, реактивной и полной энергии

Расчет в трехфазной сети

Трёхфазную электросеть можно представить как три однофазных сети. Однако в однофазных сетях используется понятие «фазное напряжение» (Uф), измеряемое между нулевым и фазным проводами, в сети 0,4кВ, равное 220В. В трёхфазных электросетях вместо «фазного» применяется понятие «линейное напряжение» (Uлин), измеряемое между линейными проводами и в сети 0,4кВ, равное 380В:

Uлин=Uф√3.

Поэтому формула для активной нагрузки, например, электрокотла, выглядит так:

P=U*I*√3.

При определении мощности электродвигателя необходимо учитывать cosφ, выражение приобретает следующий вид:

P=U*I*√3*cosφ.

На практике этот параметр обычно известен, а узнать необходимо ток. Для этого используется следующее выражение:

I=P/(U*√3*cosφ).

Например, для электродвигателя 3кВт (3000Вт) и cosφ 0,7 расчёт получается таким:

I=3000/(380*√3*0,7)=5,8А.

Интересно. Вместо вычислений можно считать, что в трёхфазной сети 380В 1кВт соответствует 2А.

Лошадиная сила

В некоторых случаях при определении мощности автомобилей пользуются устаревшей единицей измерения «лошадиная сила».

Эту единицу ввел в обращение Джеймс Уайт, в честь которого названа единица мощности 1 Ватт, в 1789 году. Его нанял один пивовар для постройки парового двигателя для насоса, способного заменить лошадь. Чтобы определить, какой необходим двигатель, взяли лошадь и запрягли её качать воду.

Считается, что пивовар взял самую сильную лошадь и заставил её работать без отдыха. Реальная сила лошади меньше в 1,5 раза.

В разных странах соотношение 1ЛС и 1кВт немного отличается друг от друга. В России принято считать 1ЛС=0.735кВт, и автомобильный двигатель в 80ЛС соответствует электродвигателю 58,8кВт.

Лошадиная сила

Знание того, как определить мощность и как узнать ток электроприборов, необходимы для проектирования электросетей, расчета кабелей и пускорегулирующей аппаратуры.

Видео

Оцените статью:

Мощность тока?. Формула мощности ? электрического тока. Как найти мощность?

Автор Даниил Леонидович На чтение 6 мин. Просмотров 17.1k. Опубликовано 18 ноября Обновлено 18 ноября

Благосостояние и комфорт современного общества зависит всецело от высокотехнологичных гаджетов. Люди уже не представляют жизни без «умных» устройств. Микроэлектроника поглотила наш быт дома и на работе. Функционирует оборудование исключительно от электричества. Такие устройства обладают рядом преимуществ, как и недостатков — чувствительность к перепадам эл. напряжения.

Если в офисе компании эту проблему способен устранить штат квалифицированных сотрудников, то дома часто приходится рассчитывать исключительно на собственные силы. Покупая новое оборудование в дом, необходимо учитывать технические характеристики устройства. Производитель указывает такую информацию для покупателей на шильдике, расположенном на задней стенке гаджета.

Формула мощности представляет собой произведение силы тока на напряжение. Если знать этот параметр, то для пользователя складывается четкое представление, сколько электричество девайс будет потреблять и не вызовет ли проблем с электроснабжением.

Что такое мощность в электричестве: просто о сложном

Механическая мощность как физическая величина равна отношению выполненной работы к некоторому промежутку времени. Поскольку понятие работы определяется количеством затраченной энергии, то и мощность допустимо представить как скорость преобразования энергий.

Разобрав составляющие механической мощности, рассмотрим из чего складывается электрическая. Напряжение — выполняемая работа по перемещению одного кулона электрического заряда, а ток — количество проходящих кулонов за одну секунду. Произведение напряжения на ток показывает полный объем работы, выполненной за одну секунду.

Мощность электрического тока

Проанализировав полученную формулу, можно заключить, что силовой показатель зависит одинаково от тока и напряжения. То есть, одно и тоже значение возможно получить при низком напряжении и большом тока, или при высоком напряжении и низком токе.

Пользуясь зависимостью мощности от напряжения и силы тока, инженеры научились передавать электричество на большие расстояния путем преобразования энергии на понижающих и повышающих трансформаторных подстанциях.

Наука подразделяет электрическую мощность на:

активную. Подразумевает преобразование мощности в тепловую, механическую и другие виды энергии. Показатель выражают в Ваттах и вычисляют по формуле U*I;
реактивную. Эта величина характеризует электрические нагрузки, создаваемые в устройствах колебаниями энергии электромагнитного поля. Показатель выражается как вольт-ампер реактивный и представляет собой произведение напряжения на силу тука и угол сдвига.

Для простоты понимания смысла активной и реактивной мощности, обратимся к нагревательному оборудованию, где электрическая энергия преобразуется в тепловую.

Как рассчитать электрическую мощность в быту

Теоретическая электротехника рассматривает показатели как мгновенные величины, которые зафиксированы в некоторый временной отрезок. Если мгновенная мощность постоянной сети остается неизменной в любой точке цепи и во всех интервалах времени, то для переменной этот показатель будет всегда неодинаковым.

Отсюда получим формулы для расчета мощности (P):

U*I;
I2*R;
U*I*cos(фи).

В интернете сейчас есть онлайн-калькуляторы, которые сами посчитают и выдадут результат. Пользователю нужно лишь подставить значения характеристик, которые находятся на шильдике устройства.

Как измерить электрическую мощность дома

Знать силовые характеристики бытового оборудования необходимо всегда. Это требуется для расчета сечения проводки, учета расхода электроэнергии или электрофикации дома. До начала монтажных работ такую информацию можно получить только путем сложения показателей мощности каждого отдельного устройства, добавив 10% запаса.

Определить потребляемую нагрузку дома поможет счетчик. Прибор показывает сколько киловатт было потрачено за один час работы оборудования. И для того чтобы убедиться в правильности показаний, владелец квартиры может проверить точность устройства с помощью электронных средств измерения. Сюда относится амперметр, вольтметр или мультиметр.

Также существуют ваттметры и варметры, которые показывают результаты измерений в ваттах.

Ваттметр

Во время снятия показания включенной оставить только активную нагрузку как лампочки и нагреватели. Далее померить токовое напряжение. В конце сверить показания счетчика с полученным результатом вычислений.

Почему реактивное сопротивление схемы влияет на мощность переменного тока

Потеря энергии в переменной цепи обусловлена наличием реактивного сопротивления, которое подразделяют на индуктивное и емкостное. В процессе работы оборудования часть энергии передается формируемым электрическим или магнитным полям.

Это приводит к уменьшению полезной работы, потере электроэнергии и превышению силовых нагрузок устройств.

Формулы расчета мощности для однофазной и трехфазной схемы питания

Выше уже была представлена формула для одной фазы: P=U*I*cos(фи).

Отсюда следует, что в трехфазной сети показатель равен тройной мощности однофазной, соединенной в треугольник: P=3*U*I*cos(фи). На практике же инженеры пользуются формулой P=1,73*U*I*cos(фи).

Как работает схема трехфазного электроснабжения

Принцип работы трехфазной схемы электроснабжения заключается в одновременном задействовании четырех питающих кабелей, один из которых нулевой. Ток одинаковой частоты вырабатывается одним генератором и сдвинут по отношению друг к другу по времени на фазовый угол равный 120 градусам.

Как узнать ток, зная мощность и напряжение

Для вычисления тока электросети по мощности и напряжению используют формулы:

I=P/U – постоянный ток;
I=P/(U*cos(фи)) — однофазная сеть;
I=P/(1,73*U*cos(фи)) — трехфазная сеть.

Для простоты расчетов значение фи принимают равной 0,95.

Как узнать напряжение, зная силу тока

Для расчета напряжения используют формулы:

U=P/I – постоянный ток;

U=P/(I*cos(фи)) — однофазная сеть;

U=P/(1,73*I*cos(фи)) — трехфазная сеть.

Из выражения видно, что напряжение прямо пропорционально напряжению и обратно пропорционально силе тока.

Как рассчитать мощность, зная силу тока и напряжение

Силовую характеристику электроустановок рассчитывают по формуле:

P=U*I – постоянный ток;

P=U*I*cos(фи) – переменный ток однофазной сети.

P=1,73*U*I*cos(фи) — трехфазная сеть.

В статье приведены упрощенные формулы расчета активной мощности электросети, которые дают приблизительные результаты.

Для получения точных результатов, необходимо учитывать также реактивное и обычное сопротивление, а также потери.

Интересная инфа по теме

Трехфазную схему электроснабжения используют в производстве. Суммарный вольтаж такой сети равен 380 В. Также такую проводку устанавливают на многоэтажные дома, а затем раздают по квартирам. Но есть один нюанс, который влияет на конечное напряжение в сети — соединение жилы под напряжение в результате дает 220 В. Трехфазная в отличие от однофазной не дает перекосы при подключении силового оборудования, так как нагрузка распределяется в щитке. Но для подведения трехфазной сети к частному дому требуется специальное разрешение, поэтому широко распространена схема с двумя жилами, одна их которых нулевая.

Заключение

Мощность электрического тока — один из важных параметров, который обязан знать каждый человек. Такая необходимость обусловлена безопасностью электросети (лимит на одновременное подключение нескольких приборов). Во время работы оборудования происходит нагрев не только внутренней схемы, но и проводки. Зная предельные возможности сети, всегда можно избежать неприятных ситуаций, связанных с ее перегревом и возможным коротким замыканием.

Формула электрического сопротивления для новичков

Не у всех хорошо ладится с физикой, а особенно когда дело доходит до решения задач. Но как говорят все учителя: «Учить и понимать — разные вещи». Так давайте лучше один раз во всём разберёмся, чем просто заучить непонятный текст, при этом не зная, как его применить. Ну и ответим на главный вопрос Как рассчитать сопротивление, и как найти мощность тока.

Единицы и размерности

Начнем с того, кто придумал данный закон. Установлен Георгом Омом.

В честь его и назван — закон Ома.

Вы, наверное, слышали такое понятие, как единица (СИ). В каждой физической формуле она присутствует. В законе Ома её очень легко запомнить, т.к. его фамилия и является единицей сопротивления и обозначается «Ом».

Какие существуют виды сопротивлений

Их немного, одно из которых мы уже разобрали:

омическое;
активное;
индуктивное;
ёмкостное.

Формулы расчёта электрического сопротивления для переменного тока простыми словами.

К сожалению, наш друг-физик решил не идти нам навстречу и вывел несколько формул по нахождению всех трёх величин. Электрическое сопротивление обозначается буквой R.

Но перед тем как пойти дальше, совет: всегда придумывайте какие-нибудь ассоциации, чтобы запомнилось на всю жизнь, например:

R (сопротивление). Можете запомнить что R, как рюмка. Нужно сопротивляться, чтобы не выпить ещё одну рюмку.
I (сила тока). Латинская «I», как проводок, по которому идёт ток.
U (напряжение). Эта буква, как дуга. И напряжение разносится с одного конца на другой по дуге.

Ну и, конечно, формула закона Ома для участка цепи.

R=U/I т.е., чтобы найти сопротивление(рюмку) надо напряжение (дугу) разделить на ток (проводок).
U=IR, хотите найти напряжение (дугу), умножьте проводок на рюмку.
I=U/R чтобы найти чему равен проводок, нужно напряжение разделить на сопротивление.

Ну а теперь главное, для чего мы все здесь собрались: «Зачем нужен этот закон? Что он даёт?»

Представьте перед собой электрическую цепь, по которой проходит ток, напряжение и сопротивление. И встаёт вопрос, как понять где что и в каких размерах. Для этого вывели формулу.

Также не забывате, если вдруг вас спросят от чего зависит сопротивление — отвечайте: » От напряжения и мощности».

Формула активного сопротивления

Ну что сказать? Придется запастись терпением и потратить время на все эти законы и определения.

Но к счастью, активное сопротивление, так и осталось большой буквой R. Просто немного поменялась формула и ее предназначение.

Подключим к нашей цепи проводник. Проводником может выступать лампа.

Понятно, что по нему тоже будет проходить ток. Это как танец «волна». Все 5 человек берутся за руки и начинают по очереди создавать колебания. Сопротивление уже известно на всех. Так же и здесь.

Мы ищем полное сопротивление. Обозначается большой буквой Z.

Если посмотреть, то можно найти сходство танца «волны» с этой буквой. Так и запомните.

Формула, как рассчитать силу тока:

I=U/Z

О том, как найти общее сопротивление мы поговорим ниже.

Формула индуктивного сопротивления

Боюсь, что когда вы увидите данную формулу, то она вам точно не понравится. Но нет слова «не хочу», есть слово «надо».

Начнем с обозначения:

XL (индуктивное сопротивление). Прямо как размер в одежде. Но почему именно так? L — это цепь переменного тока;
f — частота, в Гц;
сопротивление с частотой взаимосвязаны, так, если возрастает одно — увеличивается и другое;
единица СИ индуктивного сопротивления: [XL] = Ом;
запомните, что индуктивное сопротивление отличается от омического тем, что у первого нет потери мощности;
XL=2π×f×L;
формула расчета мощности по напряжению: P = U×I;
мощность электрического тока вычисляется в Ватах.

Формула ёмкостного сопротивления Xc

Ёмкостное сопротивление — это проводник, который подключен к цепи. Он не имеет сопротивление, но есть ёмкость. Обозначается это ёмкостное сопротивление буквами Xc.

Единица измерения сопротивления неизменно остается Ом.

Xc = 1/ωC;
ω — циклическая частота;
С — ёмкость.

Формула полного сопротивления

Как говорилось выше — полное сопротиление что-то на подобии танца «волны». Нужно узнать R (сопротивление) всех.

Чтобы определить полное сопротивление цепи:

R = R1 +R2 (проводников может быть несколько).

Теперь, если у вас спросят как определить общее сопротивление цепи, вы знаете что делать.

Что такое вольтамперная характеристика

Какое страшное название. Глаза боятся, а голова запоминает.

Говоря простыми словами, это когда напряжение находится в зависимости от тока, протекающего в электрической цепи.

Также, такую характеристику подразделяют на линейную и нелинейную. В чем разница и что это вообще такое?

Линейная, так же, как и нелинейная — это цепь.
Линейная цепь — это та, которая содержит элементы напряжения и тока, от которых зависит сопротивление.
У нелинейной элементами является зависимость напряжения на зажимах. Она не подчиняется закону Ома.

Формула электрического сопротивления по свойсвам среды: научный подход

Сущесвует такое понятие как удельное сопротивление. Это способность материала припятствовать прохождению электрического тока.

Существует таблица металлов, где указаны эти силы сопротивления.

Формула:

R = p×L/S;
R — электрическое сопротивление;
p — удельное сопротивление;
S — площадь.

Для вычисления сопротивления вы можете воспользоваться специальным калькулятором, который можно найти в интернете.

Учитесь, узнавайте много нового. И понимайте пройденный материал.

Ток, сопротивление, напряжение и мощность

Текущий
Ток – это мера потока электрического заряда через материал.

Материал, который может переносить поток заряда, называется проводником. Ток определяется как количество заряда, которое проходит через проводник за определенное время. Единицей измерения тока является ампер (A), который равен одному кулону в секунду (кулон – единица заряда),

Символ I используется для обозначения тока (хотя J часто используется в инженерные источники).Ток I через проводник зависит от его площади A , концентрации n носителей заряда, величины заряда q каждого носителя и величины их средней (или «дрейфующей») скорости. v _d,

Плотность тока – это количество тока, протекающего через проводник, деленное на его площадь,

Направление потока определяется в терминах потока положительных зарядов (даже если фактические носители заряда отрицательны).Единица измерения плотности тока – Амперы на квадратный метр (А / м ²).

Удельное сопротивление
Некоторые проводники переносят заряд легче, чем другие. Удельное сопротивление материала описывает, насколько легко может течь заряд. Хорошие проводники имеют небольшое удельное сопротивление, а хорошие изоляторы – большое. Удельное сопротивление ρ (греческая буква «ро») равно величине электрического поля в материале, деленной на плотность тока,

Единицей измерения величины электрического поля является вольт на метр (В / м). ), а единицей измерения плотности тока является Ампер на квадратный метр (А / м ²), поэтому единицей измерения удельного сопротивления является Вольт-метр на Ампер,

Многие проводники подчиняются закону Ома.Материалы, которые подчиняются закону Ома, имеют постоянное удельное сопротивление независимо от значений электрического поля E и плотности тока J. Формулы, относящиеся к цепям, верны для «омических» материалов, а «неомические» материалы в этом курсе не обсуждаются.

Удельное сопротивление омического проводника зависит от температуры материала. Зависящее от температуры удельное сопротивление ρ (T) можно найти по формуле:

Эта формула требует ρ ₀, удельного сопротивления при эталонной температуре T ₀. Температурный коэффициент удельного сопротивления α различен для каждого материала. Для температур в градусах Цельсия (℃) температурный коэффициент удельного сопротивления имеет единицы: 1 / ℃ = (℃) ^(-1)

Сопротивление
Удельное сопротивление – это свойство материала, а сопротивление – это свойство определенного куска этого материала. Сопротивление отрезка проводника зависит от его длины L, площади A и удельного сопротивления ρ,

Единицей измерения сопротивления является Ом, который обозначается греческой буквой Ω («омега»).Один Ом равен одному Вольту на Ампер,

Сопротивление зависит от температуры так же, как и удельное сопротивление,

Для этой формулы требуется R ₀, сопротивление при эталонной температуре T ₀. Температурный коэффициент α отличается для каждого материала, как описано в разделе Сопротивление .

Резистор – это устройство, которое используется в электрических цепях и имеет определенное фиксированное сопротивление. Резисторы изготавливаются путем выбора куска материала с определенным удельным сопротивлением, длиной и площадью и обертывания его изолятором с проводами, выходящими из каждого конца.На принципиальных схемах он представлен символом

Напряжение
Напряжение – это разница в электрическом потенциале между двумя точками. Если электрическое поле однородно через проводник, разность потенциалов будет равна,

Используя уравнения в Ток, Удельное сопротивление, и Сопротивление секций, можно найти другое уравнение для разности потенциалов,

Уравнение V = IR означает, что разность потенциалов или напряжение на резисторе можно найти, умножив его сопротивление на ток, протекающий через него.Единицей измерения разности потенциалов является вольт (В), который равен джоуля на кулон (Дж / Кл).

Источник напряжения – это устройство, используемое в электрических цепях, которое имеет фиксированную разность потенциалов между его концами. Источником напряжения может быть батарея или другой источник постоянного тока с фиксированной разностью потенциалов. На принципиальных схемах он представлен символом

Если концы источника напряжения соединены через цепь с любым количеством резисторов или других компонентов, образуется полная цепь, и ток может течь от одного вывода к другому. другой.Если ток течет, он будет одинаковым на обоих выводах источника напряжения.

Источник напряжения, который является частью полной схемы, может создавать электродвижущую силу, которая обозначается символом ε («сценарий e»). Единицей измерения электродвижущей силы является вольт (В), который равен джоуля на кулон (Дж / Кл). Для идеального источника электродвижущая сила равна разности напряжений,

Настоящие источники, такие как батареи, не идеальны, поэтому существует некоторое внутреннее сопротивление.Если внутреннее сопротивление батареи равно r, то разница напряжений на батарее равна

Это также называется напряжением на клеммах батареи. Если полная цепь сделана с использованием резистора с сопротивлением R, ток, протекающий через цепь, можно найти с помощью уравнения V = IR,

Ток равен электродвижущему. сила источника, деленная на полное сопротивление цепи.

Мощность
Мощность (P) – это мера скорости, с которой энергия передается или используется элементом схемы. Источники напряжения обеспечивают питание, а резисторы используют мощность (рассеивая ее в виде тепла). Мощность равна напряжению на элементе схемы, умноженному на ток, протекающий через него,

Единицей измерения мощности является ватт (Вт), который равен джоулям в секунду,

Это соотношение может быть определяется по формуле для мощности:

Мощность, потребляемая или рассеиваемая резистором, может быть найдена по формуле V = IR.Эта формула может использоваться для замены напряжения или тока в формуле мощности,

Выходная мощность батареи с внутренним сопротивлением может быть найдена по формуле V = ε-Ir и формула мощности,

Исследование закона Ома | BCHydro Power Smart для школ

Обзор

Посмотрите видео, объясняющее закон Ома, затем постройте схему и проведите демонстрацию, чтобы учащиеся могли наблюдать взаимосвязь между напряжением, током и сопротивлением.

Инструкции

Объяснение закона Ома

Посмотрите видеоролик «Объяснение закона Ома» , чтобы познакомить студентов с законом Ома.

Представьте тему

Настройте схему, как показано здесь:

Просмотрите рабочий лист «Изучение закона Ома» со студентами.

Проведите демонстрацию
Используя амперметр и вольтметр, покажите учащимся, как считывать значения тока и напряжения в цепи.Пока вы проводите измерения, запишите данные на доске и попросите учащихся записать данные на своих рабочих листах. Напомните им преобразовать мА в А; 1 ампер = 1000 миллиампер.
Последовательно добавьте сухую ячейку и повторите измерения.
Если у вас больше сухих ячеек, добавляйте их последовательно по одной и повторяйте измерения каждый раз.
Постройте график сопротивления
Используя данные из таблицы, попросите учащихся построить график зависимости напряжения от тока (V от тока). Я). Убедитесь, что они помечают все части своего графика. Объясните, какая линия лучше всего подходит, и попросите учащихся нарисовать ее на своем графике.
Попросите учащихся вычислить наклон линии по наиболее подходящей линии:
Выберите две точки на прямой (точка A и точка B).
Рассчитайте разницу между напряжениями в двух точках (НАРАЩИВАНИЕ наклона).
Вычислите разницу между током в двух точках (РАСХОД наклона).
Разделите ПОДЪЕМ на БЕГ. Это наклон линии.
Сопротивление цепи математически отображается в виде алгебраического уравнения:
Сопротивление = напряжение / ток.
Интерпретация данных
Сравните наклон графиков, созданных вашими учениками, с заявленным сопротивлением резистора, который вы использовали. Цифры должны быть похожими (разные числа являются результатом индивидуальных различий в выборе наиболее подходящей линии).
Связь между напряжением и током – это закон Ома, а наклон линии на графике этих двух величин является значением сопротивления в цепи. Уравнение закона Ома можно представить тремя способами:
R = V / I (сопротивление = напряжение, деленное на ток)
V = I x R (напряжение = ток x сопротивление)
I = V / R (ток = напряжение, деленное на сопротивление)
Знать связь между мощностью и сопротивлением
Чтобы представить себе соотношение мощности и сопротивления, подумайте об источнике постоянного напряжения или батарее.Когда в цепи большое сопротивление, может протекать очень небольшой ток, поэтому батарея выдает очень мало энергии, и резистор не будет слишком горячим из-за меньшей мощности. Однако, если вы уменьшите сопротивление, будет течь больше тока, и резистор станет теплее, потому что мы увеличили мощность.
Итак, где есть сила, обязательно будет сопротивление. Это означает, что оба фактора являются важными факторами не только в физике, но и в нашей реальной жизни.
Соотношение сопротивления мощности
Связь между мощностью и сопротивлением можно выразить двумя способами:
\ [P = \ frac {V ^ {2}} {R} \].{2} R \]
Где I – электрический ток, измеренный в Амперах или А.
Что такое мощность?
Мы определяем мощность как способность тела выполнять работу за единицу времени. Например, человек A выполняет 30 Дж работы за 2 часа, а другой человек B выполняет такой же объем работы за 3 часа, поэтому здесь, если мы воспользуемся следующей формулой:
Мощность = Работа / время
Случай 1: 30 / 2 = 15 Вт
Случай 2: 30/2 = 10 Вт
Мы видим, что мощность человека A больше, чем мощность человека B.Таким образом, мощность A больше, чем мощность B.
Однако с точки зрения электричества мощность определяется как произведение тока и напряжения.
P = VI
Где
В – разность потенциалов, измеряемая в вольтах.
I измеряется в амперах.
Что такое сопротивление?
При движении на высокой скорости мы должны замедлить нашу машину на некотором расстоянии до ограничителей скорости, иначе наша машина будет прыгать с большим рывком.Итак, здесь наш высокоскоростной автомобиль – это максимальный ток, протекающий по цепи (дороге), а выключатель скорости – это сопротивление, позволяющее избежать аварий или коротких замыканий в наших домах.
Итак, сопротивление – это препятствие, подключенное к цепи, чтобы избежать перетекания заряда через цепь. Он измеряется в Ом, где мы обозначаем его омегой или Ом.
Формула мощности и сопротивления
Мы заметили, что приведенные выше формулы описывают соотношение между мощностью и сопротивлением.{2} R \]
Здесь мы видим, что электрическая мощность прямо пропорциональна сопротивлению при поддержании постоянного I.
Отсюда мы делаем следующие выводы:
Когда мощность увеличивается, сопротивление также увеличивается, при этом ток I остается постоянным.
Однако, когда сопротивление в цепи уменьшается, мощность в цепи также уменьшается, при этом ток I остается постоянным. {2}} {R} \]
Отсюда мы видим, что мощность P обратно пропорциональна сопротивлению R .
Отсюда мы можем сделать следующие выводы:
Для любой постоянной разницы потенциалов
Когда мощность в цепи высокая, сопротивление будет меньше.
Однако, если мощность низкая, сопротивление будет высоким.
Формула сопротивления мощности
Вывод формулы мощности и сопротивления поможет нам понять концепцию связи мощности и сопротивления.
В физике мощность и сопротивление можно связать с помощью двух формул, которые мы подробно обсудим в этой статье.
Мы знаем, что электрическая мощность или P является мерой электрического тока I с q кулонами заряда, проходящими через разность потенциалов V (в вольтах) за время t секунд. Математически мы можем выразить это утверждение как:
P = Vq / t = VI… . {2}} {R} \]
Из приведенных выше выводов мы получили следующий вывод:
Мощность и сопротивление в электронике
В электронике мы определяем мощность как скорость выполнения работы.Итак, какие работы ведутся в области электроники? Это обычная повседневная работа или что-то еще? Опишем это простым утверждением:
Мы определяем сопротивление как сопротивление потоку электронов в цепи. Это означает, что чем больше препятствие, тем больше работы выполняется в единицу времени, чтобы заставить их течь, т.е. тем больше энергии требуется, чтобы сделать их легким течением.
Из приведенного выше утверждения мы не можем отрицать тот факт, что соотношение между мощностью и сопротивлением пропорционально.
Калькулятор закона Ома
Наш калькулятор закона Ома – это удобный небольшой инструмент, который поможет вам найти взаимосвязь между напряжением, током и сопротивлением в данном проводнике. Формула закона Ома и формула напряжения в основном используются в электротехнике и электронике. Кроме того, если вы знаете, как рассчитать мощность, вы можете найти его очень полезным при изучении электронных схем. Все эти расчеты вы можете проделать с помощью нашего калькулятора сопротивления.
В оставшейся части статьи вы найдете:
Формула закона Ома
Как использовать формулу напряжения
Какое уравнение для мощности
Как рассчитать мощность
Закон Ома для анизотропных материалов
Формула закона Ома
Закон Ома – один из основных законов физики.Он описывает взаимосвязь между напряжением, силой тока (также известной как ток) и сопротивлением. Напряжение относится к разности потенциалов между двумя точками электрического поля. Сила тока связана с потоком носителей электрического заряда, обычно электронов или электронодефицитных атомов. Последний термин, сопротивление, – это сопротивление вещества потоку электрического тока.
Закон
Ома гласит, что ток течет по проводнику со скоростью, пропорциональной напряжению между концами этого проводника.Другими словами, соотношение между напряжением и током постоянно:
I / V = const
Формулу закона Ома можно использовать для вычисления сопротивления как отношения напряжения и тока. Его можно записать как:
R = V / I
Где:
R – сопротивление
В – напряжение
I – Текущий
Сопротивление выражается в омах. И устройство, и правило названы в честь Георга Ома – физика и изобретателя закона Ома.
Помните, что формула закона Ома относится только к веществам, которые способны вызывать энергию. такие как металлы и керамика. Однако есть много других материалов, для которых нельзя использовать формулу закона Ома, например, полупроводники и изоляторы. Закон Ома также действует только при определенных условиях, например, при фиксированной температуре. Подробную информацию о протекании тока через проводник в цепи переменного тока можно найти в нашем калькуляторе глубины кожи.
Ищете практическое применение закона Ома? Обязательно ознакомьтесь с калькулятором светодиодного резистора!
Формула напряжения
Формула напряжения – это одно из трех математических уравнений, связанных с законом Ома.Это формула, приведенная в предыдущем абзаце, но переписанная так, чтобы вы могли рассчитать напряжение на основе тока и сопротивления, то есть формула напряжения является произведением тока и сопротивления. Уравнение:
В = ИК
Это значение измеряется в вольтах.
Какое уравнение мощности?
Еще одна величина, которую вы можете вычислить на основании закона Ома, – это мощность. Мощность – это произведение напряжения и тока, поэтому уравнение выглядит следующим образом:
P = V x I
С помощью этой формулы вы можете рассчитать, например, мощность лампочки.Если вы знаете, что напряжение батареи составляет 18V , а ток составляет 6A , вы можете, что мощность будет 108, со следующим расчетом:
P = 6A x 18V = 108 Вт
Как рассчитать мощность?
Если вы все еще не знаете, как рассчитать мощность по приведенным формулам, или просто хотите сэкономить время, вы можете использовать наш калькулятор закона Ома. Структура этого инструмента не слишком сложна, просто введите любые два из четырех значений, чтобы получить два других.Калькулятор закона Ома основан на формуле мощности вместе с формулой закона Ома. Все, что вам нужно сделать, чтобы получить значение мощности, это набрать:
Напряжение (выраженное в вольтах)
Ток (выраженный в амперах)
Затем калькулятор закона Ома выдаст вам два значения – сопротивление, выраженное в омах, и мощность, выраженное в ваттах. Если вам нужен этот результат в другом устройстве, вы можете использовать наш калькулятор ватт в ампер.
Закон Ома для анизотропных материалов
Существует еще одна версия закона Ома, которая использует положение электрических свойств внутри проводника.Некоторые предпочитают его предыдущей формуле из-за его размерного вида. Электропроводящие материалы подчиняются закону Ома, когда удельное сопротивление материалов не зависит от величины и направления приложенного электрического поля.
Вы можете найти следующую формулу, если нажмете кнопку Расширенный режим :
ρ = E / J , где
ρ – удельное сопротивление проводящего материала.
E – вектор электрического поля.
J – вектор плотности тока.
Что касается изотропных материалов, лучше всего использовать первую формулу, поскольку она намного менее сложна. Изотропные материалы – это материалы с одинаковыми электрическими свойствами во всех направлениях, например металлы и стекло. Эта формула может пригодиться при работе с анизотропными материалами, такими как дерево или графит.
Учебное пособие по физике: новый взгляд на электрическую энергию
В предыдущем разделе Урока 3 подробно обсуждалась зависимость тока от разности электрических потенциалов и сопротивления.Ток в электрическом устройстве прямо пропорционален разности электрических потенциалов, приложенной к устройству, и обратно пропорционален сопротивлению устройства. Если это так, то скорость, с которой это устройство преобразует электрическую энергию в другие формы, также зависит от тока, разности электрических потенциалов и сопротивления. В этом разделе Урока 3 мы вернемся к концепции мощности и разработаем новые уравнения, которые выражают мощность через ток, разность электрических потенциалов и сопротивление.
Новые уравнения мощности
В Уроке 2 было введено понятие электроэнергии. Электрическая мощность была определена как скорость, с которой электрическая энергия подается в цепь или потребляется нагрузкой. Уравнение для расчета мощности, подаваемой в цепь или потребляемой нагрузкой, было получено равным
.
P = ΔV • I
(Уравнение 1)
Две величины, от которых зависит мощность, связаны с сопротивлением нагрузки по закону Ома.Разность электрических потенциалов ( ΔV ) и ток ( I ) могут быть выражены в терминах их зависимости от сопротивления, как показано в следующих уравнениях.
ΔV = (I • R) I = ΔV / R
Если выражения для разности электрических потенциалов и тока подставить в уравнение мощности, можно вывести два новых уравнения, которые связывают мощность с током и сопротивлением, а также с разностью электрических потенциалов и сопротивлением.Эти выводы показаны ниже.
Уравнение 2:
P = ΔV • I
P = (I • R) • I
P = I ² • R
Уравнение 3:
P = ΔV • I
P = ΔV • (ΔV / R)
P = ΔV ² / R
Теперь у нас есть три уравнения для электрической мощности, два из которых получены из первого с использованием уравнения закона Ома.Эти уравнения часто используются в задачах, связанных с вычислением мощности на основе известных значений разности электрических потенциалов (ΔV), тока (I) и сопротивления (R). Уравнение 2 связывает скорость, с которой электрическое устройство потребляет энергию, с током в устройстве и сопротивлением устройства. Обратите внимание на двойную важность тока в уравнении, обозначенную квадратом тока. Уравнение 2 можно использовать для расчета мощности при условии, что известны сопротивление и ток.Если одно из них неизвестно, то необходимо будет либо использовать одно из двух других уравнений для расчета мощности, либо использовать уравнение закона Ома для расчета количества, необходимого для использования уравнения 2.
Уравнение 3 связывает скорость, с которой электрическое устройство потребляет энергию, с падением напряжения на устройстве и сопротивлением устройства. Обратите внимание на двойную важность падения напряжения, обозначенную квадратом ΔV. Уравнение 3 можно использовать для расчета мощности при условии, что известны сопротивление и падение напряжения.Если одно из них неизвестно, важно либо использовать одно из двух других уравнений для расчета мощности, либо использовать уравнение закона Ома для расчета количества, необходимого для использования уравнения 3.
Концепции на первом месте
Хотя эти три уравнения предоставляют удобные формулы для вычисления неизвестных величин в физических задачах, нужно быть осторожным, чтобы не использовать их неправильно, игнорируя концептуальные принципы, касающиеся схем.Чтобы проиллюстрировать это, предположим, что вам задали такой вопрос: если бы 60-ваттную лампу в бытовой лампе заменить на 120-ваттную лампу, то во сколько раз ток в цепи этой лампы был бы больше? Используя уравнение 2, можно предположить (ошибочно), что удвоение мощности означает, что количество I ² должно быть удвоено. Таким образом, ток должен увеличиться в 1,41 раза (квадратный корень из 2). Это пример неправильного рассуждения, поскольку он удаляет математическую формулу из контекста электрических цепей.Основное различие между лампочкой на 60 Вт и лампой на 120 Вт заключается не в токе в лампе, а в ее сопротивлении. У этих двух лампочек разные сопротивления; разница в токе – это просто следствие этой разницы в сопротивлении. Если лампы находятся в патроне лампы, который подключен к розетке в США, то можно быть уверенным, что разность электрических потенциалов составляет около 120 вольт. ΔV будет одинаковым для каждой лампы.Лампа мощностью 120 Вт имеет меньшее сопротивление; и, используя закон Ома, можно было бы ожидать, что он также имеет более высокий ток. Фактически, 120-ваттная лампа будет иметь ток 1 А и сопротивление 120 Ом; 60-ваттная лампа будет иметь ток 0,5 А и сопротивление 240 Ом.
Расчеты для 120-ваттной лампы
P = ΔV • I
I = P / ΔV
I = (120 Вт) / (120 В)
I = 1 А
ΔV = I • R
R = ΔV / I
R = (120 В) / (1 А)
R = 120 Ом
Расчеты для 60-ваттной лампы
P = ΔV • I
I = P / ΔV
I = (60 Вт) / (120 В)
I = 0.5 ампер
ΔV = I • R
R = ΔV / I
R = (120 В) / (0,5 А)
R = 240 Ом
Теперь, правильно используя уравнение 2, можно понять, почему удвоенная мощность означает, что будет удвоенный ток, поскольку сопротивление также изменяется при замене лампочки. Расчет тока ниже дает тот же результат, что и выше.
Расчеты для 120-ваттной лампы
P = I ² • R
I ² = P / R
I ² = (120 Вт) / (120 Ом)
I ² = 1 Вт / Ом
I = SQRT (1 Вт / Ом)
I = 1 А
Расчеты для 60-ваттной лампы
P = I ² • R
I ² = P / R
I ² = (60 Вт) / (240 Ом)
Я ² = 0.25 Вт / Ом
I = SQRT (0,25 Вт / Ом)
I = 0,5 А

Проверьте свое понимание

1. Что будет толще (шире) – нить накала 60-ваттной лампочки или 100-ваттная? Объяснять.
2.Вычислите сопротивление и силу тока ночной лампочки мощностью 7,5 Вт, подключенной к розетке в США (120 В).
3. Рассчитайте сопротивление и силу тока электрического фена мощностью 1500 Вт, подключенного к бытовой розетке в США (120 В).
4. Коробка на настольной пиле показывает, что сила тока при запуске составляет 15 ампер. Определите сопротивление и мощность двигателя за это время.
5. На наклейке на проигрывателе компакт-дисков написано, что он потребляет ток 288 мА при питании от 9-вольтовой батареи. Какая мощность (в ваттах) у проигрывателя компакт-дисков?
6. Тостер на 541 Вт подключается к бытовой розетке на 120 В. Какое сопротивление (в Ом) тостера?
7.Цветной телевизор имеет ток 1,99 А при подключении к 120-вольтовой электросети. Какое сопротивление (в Ом) у телевизора? А какая мощность (в ваттах) у телевизора?
Закон Ома с калькулятором
Закон Ома
Есть 2 основные формулы, которые помогут вам понять взаимосвязь между током, напряжением, сопротивлением и мощностью.Если у вас есть какие-либо два параметра, вы можете рассчитать два других параметра.
ЗАКОН ОМА
БАЗОВЫЕ ФОРМУЛЫ P = I * E E = I * R
НАЙТИ НАПРЯЖЕНИЕ E = P / I E = I * R E = SQR (P * R)
НАЙТИ ТЕКУЩИЙ I = P / E I = E / R I = SQR (P / R)
НАЙТИ ВЛАСТЬ P = I * E P = E ² /Р P = I ² *Р
НАЙТИ СОПРОТИВЛЕНИЕ R = E ² /П R = E / I R = P / I ²
P = мощность в ваттах
E = электродвижущая сила в вольтах
I = электрический ток в амперах
R = электрическое сопротивление в омах
SQR = квадратный корень

Примечание:
Я использую букву «E» для обозначения напряжения большую часть времени, но иногда вы увидите, что для обозначения напряжения используется буква «V».Не позволяйте этому сбивать вас с толку.
Краткий курс повышения квалификации
Изменение сопротивления:
На следующей диаграмме вы можете видеть, что единственная разница между диаграммами слева и диаграммами справа – это сопротивление в каждой «системе». Сопротивление в кране соответствует величине открытия клапана. В проводе сопротивление равно размеру отверстия * в отрезке провода. Вы можете видеть, что напряжение / давление одинаковы как для левого, так и для правого примеров.Что вы должны отметить на этой диаграмме, так это … При прочих равных, если есть увеличение сопротивления, ток будет уменьшаться. Вы можете видеть, что ток в крайнем правом проводе составляет половину тока в крайнем левом проводе. Это потому, что крайний правый провод имеет половину площади, через которую проходят электроны.
* Обратите внимание, что размер «отверстия» аналогичен сопротивлению. В реальном куске провода нет физических ограничений.
С помощью формулы:
I = E / R
Вы можете видеть, что ток обратно пропорционален сопротивлению в цепи.
Больше сопротивления = меньше тока
А для тех, кто более графичен …
Изменение напряжения:
На следующей диаграмме вы можете видеть, что сопротивление во всех системах одинаковое. На этот раз мы изменили напряжение / давление. Вы можете видеть, что повышенное напряжение вызывает увеличение тока, даже если сопротивление в левой и правой системах одинаково.
С помощью формулы:
I = E / R
Вы можете видеть, что ток прямо пропорционален напряжению, приложенному к сопротивлению.
Больше напряжения = больше тока
Что ж, теперь, когда это до смерти объяснили, перейдем к математике!
Математический пример:
В следующем примере мы знаем, что у нас есть 12 вольт, приложенное к резистору 10 Ом. Если вы хотите узнать, сколько мощности рассеивается на резисторе 10 Ом, используйте формулу:

P = E ² / R
P = 12 ²/10
P = 144/10.
P = 14,4 Вт
Рассеиваемая мощность на резисторе 14.4 Вт.
Если вы хотите узнать, какой ток протекает через резистор, вы должны использовать формулу:

I = E / R
I = 12/10
I = 1,2 А
Ток через резистор 1,2 ампера.
Если вам нужно больше примеров, страница с резисторами приносит больше удовольствия, чем бочка с обезьянами.
Если вы хотите попробовать несколько самостоятельно, приведенные ниже калькуляторы позволят вам проверить свои математические данные.
Найти: рассеиваемая мощность и ток в зависимости от сопротивления и приложенного напряжения.
Важное примечание о демонстрациях Flash / графике на этом сайте … Власти посчитали, что Flash-контент на веб-страницах слишком опасен для использования обычным пользователем Интернета, и вскоре вся его поддержка будет устранено (большая часть доступа к Flash была прекращена 1-1-2021). Это означает, что ни один современный браузер по умолчанию не отображает ни одну из этих демонстраций. На данный момент исправление заключается в загрузке расширения Ruffle для вашего браузера. Веб-сайт Ruffle. Напишите мне, пожалуйста, (babin_perry @ yahoo.com), чтобы сообщить мне, подходит ли вам Ruffle и какой браузер вы используете.
Альтернативой Ruffle является другой браузер Maxthon 4.9.5.1000. Для получения дополнительных сведений о проблеме с Flash и Maxthon (стандартном и переносном) щелкните ЗДЕСЬ.
Георг Симон Ом:
Георг Симон Ом был немецким физиком, который жил с 1789 по 1854 год. Он обнаружил взаимосвязь между напряжением, током и сопротивлением в проводнике с постоянной температурой (постоянная температура важна, потому что сопротивление изменяется с температурой, а закон Ома не действует). не занимаюсь изменением температуры / сопротивления).Он обнаружил, что при постоянном сопротивлении напряжение и ток прямо пропорциональны (как мы показали на графике выше). Это соотношение может быть выражено как V = IR, где V – напряжение, приложенное к сопротивлению, I – ток, протекающий через сопротивление, а R – сопротивление в омах.
Джеймс Ватт:
Джеймс Ватт был шотландским изобретателем, который жил с 1736 по 1819 год. Единица измерения мощности, ватт, была названа в его честь.
Джеймс Прескотт Джоуль:
Джеймс Прескотт Джоуль был английским физиком, который жил с 1818 по 1889 год.Он обнаружил взаимосвязь между мощностью, рассеиваемой в резисторе, и током, протекающим через резистор. Это соотношение может быть представлено формулой P = I ² R, где P – рассеиваемая мощность в ваттах, I – ток в амперах, R – сопротивление в омах. Ому обычно приписывают формулы, которые выражают взаимосвязь между мощностью, током, сопротивлением и напряжением, но, вероятно, следует отдать должное Джоулям.
«Джоуль» как единица измерения:
«Джоуль» представляет собой количество энергии, используемое, когда 1 ватт рассеивается за 1 секунду (или 1 ватт-секунду).
10.3: Последовательные и параллельные резисторы
Цели обучения
К концу раздела вы сможете:
Определите термин эквивалентное сопротивление
Рассчитайте эквивалентное сопротивление резисторов, включенных последовательно
Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно
В статье «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где \ (V = IR \). В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (Рисунок \ (\ PageIndex {1} \)).В последовательной цепи выходной ток первого резистора течет на вход второго резистора; следовательно, ток в каждом резисторе одинаков. В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
Рисунок \ (\ PageIndex {1} \): (a) При последовательном соединении резисторов ток одинаков в каждом резисторе. (b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое. Резисторы
серии
Считается, что резисторы
включены последовательно, если ток течет через резисторы последовательно. Рассмотрим рисунок \ (\ PageIndex {2} \), на котором показаны три последовательно включенных резистора с приложенным напряжением, равным \ (V_ {ab} \).Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
Рисунок \ (\ PageIndex {2} \): (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.
На рисунке \ (\ PageIndex {2} \) ток, исходящий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков.Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при прохождении тока через каждый резистор. Согласно закону Ома, падение потенциала \ (V \) на резисторе при протекании через него тока рассчитывается по формуле \ (V = IR \), где \ (I \) – ток в амперах (\ (A \)), а \ (R \) – сопротивление в Ом \ ((\ Omega) \).N V_i = 0. \]
Это уравнение часто называют законом петли Кирхгофа, который мы рассмотрим более подробно позже в этой главе. На рисунке \ (\ PageIndex {2} \) сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
\ [\ begin {align *} V – V_1 – V_2 – V_3 & = 0, \\ [4pt] V & = V_1 + V_2 + V_3, \\ [4pt] & = IR_1 + IR_2 + IR_3, \ end { выровнять *} \]
Решение для \ (I \)
\ [\ begin {align *} I & = \ frac {V} {R_1 + R_2 + R_3} \\ [4pt] & = \ frac {V} {R_ {S}}.\ end {align *} \]
Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления (\ (R_ {S} \)), которое представляет собой просто сумму сопротивлений отдельных резисторов.
Эквивалентное сопротивление в последовательной цепи
Любое количество резисторов может быть подключено последовательно. Если \ (N \) резисторы соединены последовательно, эквивалентное сопротивление равно
. N R_i.\ label {серия эквивалентных сопротивлений} \]
Одним из результатов подключения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.
Пример \ (\ PageIndex {1} \): эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах 9 В подключена к цепи, состоящей из четырех последовательно соединенных резисторов \ (20 \, \ Omega \) и одного \ (10 \, \ Omega \) (Рисунок \ (\ PageIndex {3 } \)).Предположим, что батарея имеет незначительное внутреннее сопротивление.
Рассчитайте эквивалентное сопротивление цепи.
Рассчитайте ток через каждый резистор.
Рассчитайте падение потенциала на каждом резисторе.
Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.
Рисунок \ (\ PageIndex {3} \): простая последовательная схема с пятью резисторами.
Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.2R \), а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемая батареей, можно найти с помощью \ (P = I \ epsilon \).
Решение
Эквивалентное сопротивление – это алгебраическая сумма сопротивлений (Уравнение \ ref {серия эквивалентных сопротивлений}): \ [\ begin {align *} R_ {S} & = R_1 + R_2 + R_3 + R_4 + R_5 \\ [4pt ] & = 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 10 \, \ Омега = 90 \, \ Омега.2 (10 \, \ Omega) = 0,1 \, W, \ nonumber \] \ [P_ {рассеивается} = 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,1 \, W = 0,9 \, W, \ nonumber \] \ [P_ {источник} = I \ epsilon = (0,1 \, A) (9 \, V) = 0,9 \, W. \ nonumber \]
Значение
Есть несколько причин, по которым мы использовали бы несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
Упражнение \ (\ PageIndex {1} \)
Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серию по девять луковиц.Если перегорает слишком много лампочек, в конце концов открываются шунты. Что вызывает это?
Ответ
Эквивалентное сопротивление девяти последовательно соединенных лампочек составляет 9 R . Ток равен \ (I = V / 9 \, R \). Если одна лампочка перегорит, эквивалентное сопротивление будет 8 R , и напряжение не изменится, но ток возрастет \ ((I = V / 8 \, R \). Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к сгоранию шунта.№ Р_и. \]
Через каждый резистор последовательно протекает один и тот же ток.
Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рисунке \ (\ PageIndex {4} \) показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Рисунок \ (\ PageIndex {4} \): Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.
Ток, протекающий от источника напряжения на рисунке \ (\ PageIndex {4} \), зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в переход или узел, где цепь разделяется, протекая через резисторы \ (R_1 \) и \ (R_2 \). По мере того, как заряды идут от аккумулятора, некоторые проходят через резистор \ (R_1 \), а некоторые – через резистор \ (R_2 \).Сумма токов, текущих в переход, должна быть равна сумме токов, текущих из перехода:
\ [\ sum I_ {in} = \ sum I_ {out}. {- 1}.{-1}. \ label {10.3} \]
Это соотношение приводит к эквивалентному сопротивлению \ (R_ {P} \), которое меньше наименьшего из отдельных сопротивлений. Когда резисторы подключены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Пример \ (\ PageIndex {2} \): Анализ параллельной цепи
Три резистора \ (R_1 = 1,00 \, \ Omega \), \ (R_2 = 2,00 \, \ Omega \) и \ (R_3 = 2,00 \, \ Omega \) подключены параллельно.Параллельное соединение подключается к источнику напряжения \ (V = 3,00 \, V \).
Какое эквивалентное сопротивление?
Найдите ток, подаваемый источником в параллельную цепь.
Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника.
Рассчитайте мощность, рассеиваемую каждым резистором.
Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов определяется с помощью уравнения \ ref {10.3}. (Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, заменив \ (R_ {P} \) на полное сопротивление \ (I = \ frac {V} {R_ {P}} \).
(c) Отдельные токи легко вычислить по закону Ома \ (\ left (I_i = \ frac {V_i} {R_i} \ right) \), поскольку каждый резистор получает полное напряжение.{-1} = 0,50 \, \ Omega. \ Nonumber \] Общее сопротивление с правильным количеством значащих цифр равно \ (R_ {eq} = 0,50 \, \ Omega \). Как и предполагалось, \ (R_ {P} \) меньше наименьшего индивидуального сопротивления.
Полный ток можно найти из закона Ома, заменив полное сопротивление \ (R_ {P} \). Это дает \ [I = \ frac {V} {R_ {P}} = \ frac {3.00 \, V} {0.50 \, \ Omega} = 6.00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом, \ [I_1 = \ frac {V} {R_1} = \ frac {3.00 \, V} {1.00 \, \ Omega} = 3.00 \, A. \ nonumber \] Аналогично, \ [I_2 = \ frac {V } {R_2} = \ frac {3.00 \, V} {2.00 \, \ Omega} = 1.50 \, A \ nonumber \] и \ [I_3 = \ frac {V} {R_3} = \ frac {3.00 \, V } {2.00 \, \ Omega} = 1.50 \, A. \ nonumber \] Полный ток – это сумма отдельных токов: \ [I_1 + I_2 + I_3 = 6.2} {2.00 \, \ Omega} = 4.50 \, W. \ nonumber \]
Общую мощность также можно рассчитать несколькими способами. Выбор \ (P = IV \) и ввод общей текущей доходности \ [P = IV = (6.00 \, A) (3.00 \, V) = 18.00 \, W. \ nonumber \]
Значение
Общая мощность, рассеиваемая резисторами, также 18,00 Вт:
\ [P_1 + P_2 + P_3 = 9,00 \, W + 4,50 \, W + 4,50 \, W = 18,00 \, W. \ nonumber \]
Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.
Упражнение \ (\ PageIndex {2A} \)
Рассмотрим одну и ту же разность потенциалов \ ((V = 3,00 \, V) \), приложенную к одним и тем же трем последовательно включенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?
Раствор
Эквивалент последовательной схемы будет \ (R_ {eq} = 1.00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
Упражнение \ (\ PageIndex {2B} \)
Как бы вы использовали реку и два водопада, чтобы смоделировать параллельную конфигурацию двух резисторов? Как разрушается эта аналогия?
Раствор
Река, текущая по горизонтали с постоянной скоростью, разделяется на две части и течет через два водопада. Молекулы воды аналогичны электронам в параллельных цепях. Количество молекул воды, которые текут в реке и падает, должно быть равно количеству молекул, которые текут над каждым водопадом, точно так же, как сумма тока через каждый резистор должна быть равна току, текущему в параллельном контуре.Молекулы воды в реке обладают энергией благодаря своему движению и высоте. Потенциальная энергия молекул воды в реке постоянна из-за их одинаковой высоты. Это аналогично постоянному изменению напряжения в параллельной цепи. Напряжение – это потенциальная энергия на каждом резисторе.
При рассмотрении энергии аналогия быстро разрушается. В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
Суммируем основные характеристики резисторов параллельно:
Эквивалентное сопротивление находится по формуле \ ref {10.3} и меньше любого отдельного сопротивления в комбинации.
Падение потенциала на каждом параллельном резисторе одинаковое.
Параллельные резисторы не получают суммарный ток каждый; они делят это. Ток, поступающий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Как вы помните, из раздела о емкости мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы. Таблица \ (\ PageIndex {1} \) суммирует уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.
Таблица \ (\ PageIndex {1} \): Сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях
Комбинация серий Параллельная комбинация
Эквивалентная емкость \ [\ frac {1} {C_ {S}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +.N R_i \ nonumber \] \ [\ frac {1} {R_ {P}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} +. . . \ nonumber \]
Сочетания последовательного и параллельного
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения. Такие комбинации обычны, особенно если учесть сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения можно уменьшить до одного эквивалентного сопротивления, используя метод, показанный на рисунке \ (\ PageIndex {5} \).Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как \ (R_ {eq} \).
Рисунок \ (\ PageIndex {5} \): (а) Исходная схема из четырех резисторов. (b) Шаг 1: резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, и эквивалентное сопротивление равно \ (R_ {34} = 10 \, \ Omega \). (c) Шаг 2: сокращенная схема показывает, что резисторы \ (R_2 \) и \ (R_ {34} \) включены параллельно, с эквивалентным сопротивлением \ (R_ {234} = 5 \, \ Omega \).(d) Шаг 3: сокращенная схема показывает, что \ (R_1 \) и \ (R_ {234} \) включены последовательно с эквивалентным сопротивлением \ (R_ {1234} = 12 \, \ Omega \), которое является эквивалентное сопротивление \ (R_ {eq} \). (e) Уменьшенная схема с источником напряжения \ (V = 24 \, V \) с эквивалентным сопротивлением \ (R_ {eq} = 12 \, \ Omega \). Это приводит к току \ (I = 2 \, A \) от источника напряжения.
Обратите внимание, что резисторы \ (R_3 \) и \ (R_4 \) включены последовательно. Их можно объединить в одно эквивалентное сопротивление.Один из методов отслеживания процесса – включить резисторы в индексы. {- 1} = 5 \, \ Omega.\ nonumber \]
Этот шаг процесса сокращает схему до двух резисторов, показанных на рисунке \ (\ PageIndex {5d} \). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:
\ [R_ {eq} = R_ {1234} = R_1 + R_ {234} = 7 \, \ Omega + 5 \ Omega = 12 \, \ Omega. \ nonumber \]
Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен \ (I = \ frac {V} {R_ {eq}} = \ frac {24 \, V} {12 \, \ Omega} = 2 \, A \). Этот ток проходит через резистор \ (R_1 \) и обозначается как \ (I_1 \). Падение потенциала на \ (R_1 \) можно найти с помощью закона Ома:
\ [V_1 = I_1R_1 = (2 \, A) (7 \, \ Omega) = 14 \, V. \ nonumber \]
Глядя на рисунок \ (\ PageIndex {5c} \), это оставляет \ (24 \, V – 14 \, V = 10 \, V \) отбрасывать через параллельную комбинацию \ (R_2 \) и \ ( R_ {34} \).Ток через \ (R_2 \) можно найти по закону Ома:
\ [I_2 = \ frac {V_2} {R_2} = \ frac {10 \, V} {10 \, \ Omega} = 1 \, A. \ nonumber \]
Резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, поэтому токи \ (I_3 \) и \ (I_4 \) равны
.
\ [I_3 = I_4 = I – I_2 = 2 \, A – 1 \, A = 1 \, A. \ nonumber \]
Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах. Потенциальные капли равны \ (V_3 = I_3R_3 = 6 \, V \) и \ (V_4 = I_4R_4 = 4 \, V \).2 (4 \, \ Omega) = 4 \, W, \\ [4pt] P_ {рассеивается} & = P_1 + P_2 + P_3 + P_4 = 48 \, W. \ end {align *} \]
Общая энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, составляет
\ [\ begin {align *} P_s & = IV \\ [4pt] & = (2 \, A) (24 \, V) = 48 \, W \ end {align *} \]
Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.
Пример \ (\ PageIndex {3} \): объединение последовательных и параллельных цепей
На рисунке \ (\ PageIndex {6} \) показаны резисторы, подключенные последовательно и параллельно.Мы можем считать \ (R_1 \) сопротивлением проводов, ведущих к \ (R_2 \) и \ (R_3 \).
Найдите эквивалентное сопротивление цепи.
Какое падение потенциала \ (V_1 \) на резисторе \ (R_1 \)?
Найдите ток \ (I_2 \) через резистор \ (R_2 \).
Какая мощность рассеивается \ (R_2 \)?
Рисунок \ (\ PageIndex {6} \): Эти три резистора подключены к источнику напряжения так, чтобы \ (R_2 \) и \ (R_3 \) были параллельны друг другу, и эта комбинация была последовательно с \ (R_1 \).
Стратегия
(a) Чтобы найти эквивалентное сопротивление, сначала найдите эквивалентное сопротивление параллельного соединения \ (R_2 \) и \ (R_3 \). Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с \ (R_1 \).
(b) Ток через \ (R_1 \) можно найти с помощью закона Ома и приложенного напряжения. Ток через \ (R_1 \) равен току от батареи. Падение потенциала \ (V_1 \) на резисторе \ (R_1 \) (которое представляет собой сопротивление в соединительных проводах) можно найти с помощью закона Ома.{-1} = 5.10 \, \ Omega. \ Nonumber \] Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чисто параллельной (\ (20.0 \, \ Omega \) и \ (0.804 \, \ Omega \) ), соответственно).
Ток через \ (R_1 \) равен току, обеспечиваемому батареей: \ [I_1 = I = \ frac {V} {R_ {eq}} = \ frac {12.0 \, V} {5.10 \, \ Omega} = 2.35 \, A. \ nonumber \] Напряжение на \ (R_1 \) равно \ [V_1 = I_1R_1 = (2.35 \, A) (1 \, \ Omega) = 2.35 \, V. \ nonumber \] Напряжение, приложенное к \ (R_2 \) и \ (R_3 \), меньше напряжения, подаваемого батареей, на величину \ (V_1 \).Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных \ (R_2 \) и \ (R_3 \).
Чтобы найти ток через \ (R_2 \), мы должны сначала найти приложенное к нему напряжение. Напряжение на двух параллельных резисторах одинаковое: \ [V_2 = V_3 = V – V_1 = 12.0 \, V – 2.35 \, V = 9.65 \, V. \ nonumber \] Теперь мы можем найти ток \ (I_2 \) через сопротивление \ (R_2 \) по закону Ома: \ [I_2 = \ frac {V_2} {R_2} = \ frac {9.65 \, V} {6.00 \, \ Omega} = 1.2 (6.00 \, \ Omega) = 15.5 \, W. \ nonumber \]
Значение
Анализ сложных схем часто можно упростить, сведя схему к источнику напряжения и эквивалентному сопротивлению. Даже если вся схема не может быть сведена к одному источнику напряжения и одному эквивалентному сопротивлению, части схемы могут быть уменьшены, что значительно упрощает анализ.
Упражнение \ (\ PageIndex {3} \)
Учитывайте электрические цепи в вашем доме.Приведите по крайней мере два примера схем, которые должны использовать комбинацию последовательных и параллельных схем для эффективной работы.
Раствор
Все цепи верхнего освещения параллельны и подключены к основному питанию, поэтому при перегорании одной лампочки все верхнее освещение не гаснет. У каждого верхнего света будет по крайней мере один переключатель, включенный последовательно с источником света, поэтому вы можете включать и выключать его.
В холодильнике есть компрессор и лампа, которая загорается при открытии дверцы.Обычно у холодильника есть только один шнур для подключения к стене. Цепь, содержащая компрессор, и цепь, содержащая цепь освещения, параллельны, но есть переключатель, включенный последовательно со светом. Термостат управляет переключателем, который включен последовательно с компрессором, чтобы контролировать температуру холодильника.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на рисунке \ (\ PageIndex {7} \). Устройство, обозначенное символом \ (R_3 \), имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, обозначенных \ (R_1 \), снижая напряжение на лампочке (которое равно \ (R_2 \)), которое затем заметно гаснет.
Рисунок \ (\ PageIndex {7} \): Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.
Стратегия решения проблем: последовательные и параллельные резисторы
Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения. Этот шаг включает список известных значений проблемы, поскольку они отмечены на вашей принципиальной схеме.
Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой – для параллелей.
Проверьте, являются ли ответы разумными и последовательными.
Пример \ (\ PageIndex {4} \): объединение последовательных и параллельных цепей
Два резистора, соединенных последовательно \ ((R_1, \, R_2) \), соединены с двумя резисторами, включенными параллельно \ ((R_3, \, R_4) \).Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление 10,00 Ом. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление. Через резистор \ (R_1 \) проходит ток 2,00 А. Какое напряжение подается от источника напряжения?
Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.
Решение
Рисунок \ (\ PageIndex {8} \): Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.
Нарисуйте четкую принципиальную схему (Рисунок \ (\ PageIndex {8} \)).
Неизвестно напряжение аккумулятора. Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
В этой схеме мы уже знаем, что резисторы \ (R_1 \) и \ (R_2 \) включены последовательно, а резисторы \ (R_3 \) и \ (R_4 \) включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов \ (R_3 \) и \ (R_4 \) последовательно с последовательной конфигурацией резисторов \ (R_1 \) и \ (R_2 \).{-1} = 5,00 \, \ Омега. \ nonumber \] Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление схемы равно \ (R_ {eq} = R_1 + R_2 + R_ {34} = (25.00 \, \ Omega \). поэтому напряжение, подаваемое батареей, равно \ (V = IR_ {eq} = 2.00 \, A (25.00 \, \ Omega) = 50.00 \, V \).
Один из способов проверить соответствие ваших результатов – это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами. Мощность, обеспечиваемая аккумулятором, равна \ (P_ {batt} = IV = 100.2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \]
Поскольку мощность, рассеиваемая резисторами, равна мощности, обеспечиваемой батареей, наше решение кажется последовательным.
Значение
Если проблема имеет комбинацию последовательного и параллельного соединения, как в этом примере, ее можно уменьшить поэтапно, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений.При нахождении \ (R_ {eq} \) для параллельного соединения необходимо с осторожностью относиться к обратному. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Авторы и авторство
Сэмюэл Дж.

ЗАКОН ОМА
БАЗОВЫЕ ФОРМУЛЫ	P = I * E	E = I * R
НАЙТИ НАПРЯЖЕНИЕ	E = P / I	E = I * R	E = SQR (P * R)
НАЙТИ ТЕКУЩИЙ	I = P / E	I = E / R	I = SQR (P / R)
НАЙТИ ВЛАСТЬ	P = I * E	P = E ² /Р	P = I ² *Р
НАЙТИ СОПРОТИВЛЕНИЕ	R = E ² /П	R = E / I	R = P / I ²