Как найти v2 если известно v1: физика. мне известно m1 и m2 и v2, как мне найти v1? — Спрашивалка

Как найти скорость, время и расстояние по формуле вычисления скорости?

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

Содержание:

• Как же рассчитать скорость?
• Другие способы вычисления
• Способы вычисления расстояния и времени
• Видео

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой – нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

v=S/t, где

• v – скорость объекта,
• S – расстояние, которое пройдено или должно быть пройдено объектом,
• t – время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут.

Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.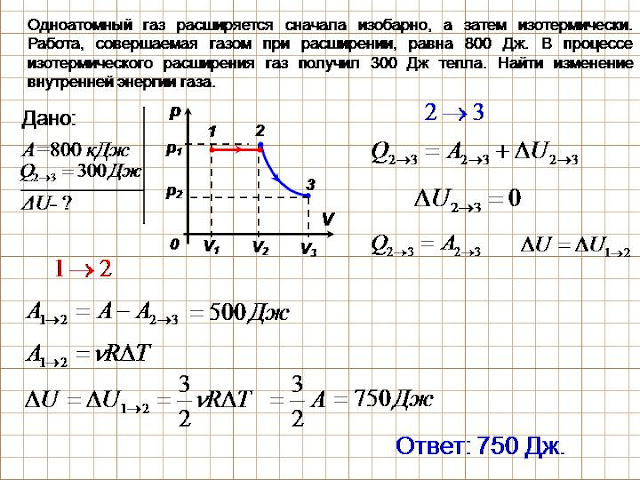

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn – значения скоростей объекта на отдельных участках пути S, n – количество этих участков, vср – средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+…+Sn)/t, где vср – средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn – отдельные неравномерные участки всего пути,
• t – общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+. ..+tn), где S – общее пройденное расстояние,
• t1, t2, tn – время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn – формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

N=F*v*cos α , где N – механическая мощность,

F – сила,

v – скорость,

cos α – косинус угла между векторами силы и скорости.

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

S=v*t, где v – понятно что такое,

S – расстояние, которое требуется найти,

t – время, за которое объект прошел это расстояние.

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

t=S/v, где v – все та же скорость,

S – расстояние, пройденный путь,

t – время, значение которого в данном случае нужно найти.

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.

Белорусский государственный университет транспорта – БелГУТ (БИИЖТ)

Регистрация на конференцию «Феноменология транспорта
в литературе и искусстве: прошлое, настоящее, будущее»

Как поступить в БелГУТ

Как получить место

в общежитии БелГУТа

ГОРЯЧАЯ ЛИНИЯ 
по вопросам приемной кампании

События

Все события

Пн	Вт	Ср	Чт	Пт	Сб	Вс
					1	2
3	4	5	6 Дата : 2023-04-06	7 Дата : 2023-04-07	8	9
10 Дата : 2023-04-10	11	12	13 Дата : 2023-04-13	14	15	16
17 Дата : 2023-04-17	18	19 Дата : 2023-04-19	20 Дата : 2023-04-20	21 Дата : 2023-04-21	22	23
24	25	26 Дата : 2023-04-26	27 Дата : 2023-04-27	28	29	30

Все анонсы

• Смотр-кастинг конкурса «Мисс и Мистер БелГУТа». ..
• ФИНАЛ весенней серии игр «ЧТО? ГДЕ? КОГДА?» среди …
• Билеты на концерт Дианы Анкудиновой…
• Дни доноров 26 и 27 апреля 2023
• Музыкальный квартирник
• Программа. V Международная научно-практическая кон…
• Программа. I Международная научно-практическая кон…
• ЕДИ «Ключевые аспекты послания Президента Республ…
• Игра между сборными командами БелГУТа и БГЭУ…
• Поздравление Высокопреосвященнейшего Стефана с Вос…

Анонсы

Университет

Абитуриентам

Студентам

Конференции

Приглашения

Смотр-кастинг конкурса «Мисс и Мистер БелГУТа»…

ФИНАЛ весенней серии игр «ЧТО? ГДЕ? КОГДА?» среди …

Билеты на концерт Дианы Анкудиновой…

Дни доноров 26 и 27 апреля 2023

Новости

Университет

Международные связи

Спорт

ИВР

Жизнь студентов

Новости подразделений



• Университет

Лекторский потенциал – достояние университета!. ..
21 апреля 2023

• Воспитательная работа

Послание Президента обсудили с молодежью Жлобинщины…
21 апреля 2023

• Университет

На форуме ТИБО-2023 «Цифровое развитие Беларуси»…
21 апреля 2023

• Спорт

Спартакиада вузов по гиревому спорту
21 апреля 2023

• Воспитательная работа

Дорогами мира и созидания. Мемориал в д. Бацунь…
21 апреля 2023

• Воспитательная работа

Встреча с председателем ЦИК Беларуси
21 апреля 2023

• Университет

С юбилеем! Борис Валерьевич Рябцев

21 апреля 2023

• Университет

Образование на всю жизнь
20 апреля 2023

• Воспитательная работа

Неделя леса – БелГУТ посадил дубовую рощу. ..
20 апреля 2023

Другие новости

• «Праздник Светлой Пасхи» в БелГУТе
• Эстафета «Живая память благодарных поколений» передана дальше…
• Победа БелГУТа в матче Республиканской студенческий футбольной лиги…
• Диалоговая площадка, посвященная обсуждению послания президента Респуб…
• Победа в соревнованиях по плаванию в рамках Республиканской Универсиад…
• Лидер РОО «Белая Русь» Олег Романов на встрече со студентами вузов в Б…
• Третий тур весенней серии «Что? Где? Когда?» для студентов…
• Материалы I конференции «Архитектура и строительство: традиции и иннов…
• Встреча студентов с военнослужащими Гомельской пограничной группы…
• 70-я спартакиада студентов. Шахматы
• Курсы повышения квалификации «Применение табличного процессора для обр…

БелГУТ на Доске почета

Достижения университета

КУДА ПОСТУПАТЬ

Все факультеты

Предложения

Все предложения

Видеотека

Все видео

Фотогалерея

Все фото

Калькулятор закона Бойля

Создано Wojciech Sas, PhD

Отредактировано Bogna Szyk и Jack Bowater

Последнее обновление: 17 февраля 2023 г. 09 примеров закона Бойля

Где применяется закон Бойля?

Прочие термодинамические процессы

Часто задаваемые вопросы

Калькулятор закона Бойля отличный инструмент для оценки параметров газа в изотермическом процессе . Вы найдете ответ на вопрос “Что такое закон Бойля?” в тексте, поэтому читайте дальше, чтобы узнать о формуле закона Бойля , увидеть несколько практических примеров упражнений по закону Бойля и узнать, как распознать, когда процесс удовлетворяет закону Бойля на графике.

Если вам нужно рассчитать результаты изобарического процесса, воспользуйтесь нашим калькулятором закона Чарльза.

Определение закона Бойля

Закон Бойля (также известный как закон Бойля-Мариотта) говорит нам о взаимосвязи между давлением газа и его объемом при постоянной температуре и массе газа . В нем говорится, что абсолютное давление обратно пропорционально объему .

Определение закона Бойля можно также сформулировать следующим образом: произведение давления и объема газа в замкнутой системе постоянно, пока не изменяется температура.

Закон Бойля описывает поведение идеального газа. Мы можем охарактеризовать этот газ уравнением идеального газа, о котором вы можете прочитать больше в нашем калькуляторе законов идеального газа. Закон Бойля говорит нам о изотермический процесс , что означает, что температура газа остается постоянной во время перехода, как и внутренняя энергия газа.

Формула закона Бойла

Мы можем написать уравнение закона Бойла следующим образом:

P₁ × V₁ = P₂ × V₂ ,

, где P₁ и V ₁ – первоначальное давление и объем соответственно. Точно так же p₂ и V₂ являются конечными значениями этих параметров газа.

Мы можем записать формулу закона Бойля различными способами в зависимости от того, какой параметр мы хотим оценить. Допустим, мы изменили объем газа в изотермических условиях и хотим найти результирующее давление. Тогда уравнение закона Бойля утверждает, что:

p₂ = p₁ × V₁ / V₂ или p₂ / p₁ = V₁ / V₂ .

Как мы видим, соотношение конечного и начального давления является обратным отношением для объемов . Этот калькулятор закона Бойля работает в любом направлении, которое вам нравится. Просто введите любые три параметра, и четвертый будет рассчитан сразу!

Весь процесс можно представить на графике закона Бойля. Наиболее часто используется тип, когда давление является функцией объема. Для этого процесса кривая представляет собой гиперболу. Переход может происходить в обоих направлениях, поэтому и сжатие, и расширение газа удовлетворяют закону Бойля.

🔎 Если переход представляет собой изохорный процесс (постоянный объем), вам пригодится калькулятор закона Гей-Люссака Омни.

Примеры закона Бойля

Закон Бойля можно использовать несколькими способами, поэтому давайте рассмотрим несколько примеров:

1. Представьте, что у нас есть эластичный контейнер с газом. Начальное давление 100 кПа (или 10⁵ Па , если мы используем экспоненциальную запись), а объем сосуда равен 2 м³ . Решаем сжать ящик до 1 м³ , но общую температуру не меняем. Вопрос: «Как меняется давление газа?». Мы можем использовать формулу закона Бойля:

   p₂ = p₁ × V₁ / V₂ = 100 кПа × 2 м³ / 1 м³ = 200 кПа .

   После уменьшения объема вдвое внутреннее давление удваивается. Это является следствием того, что произведение давления на объем должно быть постоянным в течение этого процесса.

2. Следующий пример закона Бойля касается газа под давлением 2,5 атм , занимающего 6 литров пространства. Затем изотермически декомпрессируют до давления 0,2 атм . Узнаем его окончательный объем. Мы должны переписать уравнение закона Бойля:

   V₂ = p₁ × V₁ / p₂ = 2,5 атм × 6 л / 0,2 атм = 75 л .

   Вы всегда можете воспользоваться нашим калькулятором закона Бойля, чтобы проверить правильность своих оценок!

Где применяется закон Бойля?

Закон Бойля описывает все процессы, при которых температура остается постоянной .

В термодинамике температура измеряет среднюю кинетическую энергию, которой обладают атомы или молекулы. Другими словами, можно сказать, что средняя скорость частиц газа при этом переходе не меняется. Формула закона Бойля справедлива для широкого диапазона температур.

В расширенном режиме вы можете выбрать любую температуру, и мы рассчитаем количество молекул, содержащихся в газе. Вам нужно только следить за тем, чтобы вещество оставалось в газовой форме (например, не конденсировалось и не кристаллизовалось) при этой температуре.

Есть несколько областей, где применим закон Бойля:

• Тепловая машина Карно – Состоит из четырех термодинамических процессов, два из которых изотермические, удовлетворяющие закону Бойля. Эта модель может сказать нам, каков максимальный КПД тепловой машины.

• Дыхание тоже можно описать законом Бойля. Всякий раз, когда вы делаете вдох, ваша диафрагма и межреберные мышцы увеличивают объем легких, что снижает давление газа. Когда воздух течет из области более высокого давления в область более низкого давления, воздух попадает в легкие и позволяет нам получать кислород из окружающей среды. При выдохе объем легких уменьшается, поэтому давление внутри выше, чем снаружи, поэтому воздух течет в обратном направлении.

• Шприц – Всякий раз, когда вам делают инъекцию, врач или медсестра сначала набирают жидкость из маленького флакона. Для этого они используют шприц. При вытягивании поршня доступный объем увеличивается, что снижает давление и, согласно формуле закона Бойля, вызывает всасывание жидкости.

Другие термодинамические процессы

Закон Бойля, наряду с законами Шарля и Гей-Люссака, относится к числу фундаментальных законов, описывающих подавляющее большинство термодинамических процессов.

Помимо определения значений конкретных параметров, таких как давление или объем, также можно узнать теплопередачу и работу, совершаемую газом во время этих переходов, а также изменение внутренней энергии . Мы собрали их все в нашем комбинированном газовом калькуляторе, где вы можете выбрать любой процесс и оценить результаты для реальных газов.

Часто задаваемые вопросы

Почему закон Бойля также называют изотермой?

Закон Бойля является одним из трех фундаментальных термодинамических процессов . В каждом из них изучается вариант двух из трех величин :

• давления ;
• температура ; и
• Том .

третья величина остается постоянной во время процесса. В случае закона Бойля мы не меняем температуру, поэтому мы называем процесс изотермическим .

Насколько расширится воздушный шар с начальным объемом 1000 см³ на крейсерской высоте?

Выполните следующие действия:

1. Найдите начальное давление. Примем атмосферное давление на уровне моря: P _i = 1 атм = 101 325 Па .
2. Найдите конечное давление. В крейсерском самолете давление в кабине обычно составляет около P _f = 0,8 атм = 81 060 Па .
3. Рассчитайте окончательный объем по закону Бойля: V _f = P _i · V _i /P _f = (101,325 Па · 0,001 м ³ )/81 060 Па = 0,00125 м 3

   .

   0 .

4. Найдите расширение путем вычитания конечного и начального объемов: ΔV = V _f – V _i = (0,00125 – 0,001) м ³ = 0,00025 м ³ 4 9099 см = 250 см .

Как рассчитать закон Бойля?

Для расчета закона Бойля нам нужно выполнить несколько простых действий, которые зависят от известных нам исходных данных. Если мы хотим вычислить конечное давление, и мы знаем начальный объем и давление, и конечный объем:

1. Вычислить произведение начального объема и давления : В _i · P _i .
2. Разделить результат на итоговый объем . Конечное давление равно P _f = (V _i · P _i )/V _f .

• Вы можете свободно инвертировать конечное и начальное значения (обратимое преобразование).
• Чтобы найти объем, просто переключите его нажатием на правую часть формулы.

Каким будет конечное давление, если объем уменьшится вдвое при начальном давлении 1 атм?

Конечное давление в процессе, когда объем уменьшается вдвое, начиная с P _i = 1 атм , равно 2 . Чтобы найти этот результат:

1. Запишите закон Бойля для конечного давления: P _f = (V _i · P _i )/V _f .
2. В этой формуле определите соотношение объемов . Поскольку мы знаем, что объем уменьшается вдвое, мы можем записать V _i = 2 · V _f , следовательно, V _i / V _f 2 .
3. Конечное давление равно: P _f = 2 · P _i = 2 атм .

Wojciech Sas, PhD

Начальные параметры

Начальное давление (p₁)

Начальный объем (V₁)

Конечные параметры

Конечное давление (p₂)

Конечный объем (V₂)

Ознакомьтесь с 42 похожими термодинамическими и тепловыми калькуляторами 🌡️

Число БиоКоэффициент БольцманаКонвертер BTU в тонны… Еще 39

11.4: Закон Бойля: давление и объем

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

182712

Цели обучения

• Узнать, что подразумевается под термином газовые законы .
• Изучите и примените закон Бойля.

Когда ученые семнадцатого века начали изучать физические свойства газов, они заметили некоторые простые соотношения между некоторыми измеримыми свойствами газа. Возьмем, например, давление ( P ) и объем ( V ). Ученые заметили, что для данного количества газа (обычно выражаемого в единицах молей [ n ]), если температура ( T ) газа поддерживалась постоянной, давление и объем были связаны: при увеличении одного другой уменьшается. При уменьшении одного увеличивается другое. Это означает, что давление и объем обратно пропорциональны .

Однако это еще не все: давление и объем данного количества газа при постоянной температуре связаны численно с . Если вы возьмете значение давления и умножите его на значение объема, произведение будет константой для данного количества газа при постоянной температуре:

\[P × V = \text{ константа при постоянных n и T} \nonumber \]

Если объем или давление изменяются, а количество и температура остаются неизменными, то другое свойство должно измениться так, чтобы произведение два свойства по-прежнему равны той же константе. То есть, если исходные условия помечены \(P_1\) и \(V_1\), а новые условия помечены \(P_2\) и \(V_2\), мы имеем

\[P_1V_1 = \text{constant } = P_2V_2 \nonumber \]

, где предполагается, что свойства перемножаются. Опуская среднюю часть, мы имеем просто

\[P_1V_1 = P_2V_2 \text{ при постоянных n и T} \nonumber \]

Это уравнение является примером газового закона. Газовый закон — это простая математическая формула, позволяющая моделировать или предсказывать поведение газа. Этот конкретный газовый закон называется Законом Бойля в честь английского ученого Роберта Бойля, впервые объявившего о нем в 1662 году. На рисунке \(\PageIndex{1}\) показаны две иллюстрации того, как работает закон Бойля.

Рисунок \(\PageIndex{1}\): Закон Бойля. Поршень с определенным давлением и объемом (левый поршень) будет иметь половину объема, когда его давление в два раза больше (правый поршень). Можно также построить P против V для данного количества газа при определенной температуре; такой график будет выглядеть как график справа.

Закон Бойля — это пример второго типа математической задачи, которую мы встречаем в химии — задачи, основанной на математической формуле. Тактика работы с математическими формулами отличается от тактики работы с коэффициентами пересчета. Во-первых, большинство вопросов, на которые вам придется отвечать с помощью формул, являются вопросами словесного типа, поэтому первый шаг — определить, какие величины известны, и присвоить их переменным. Во-вторых, в большинстве формул необходимо выполнить некоторые математические перестановки (например, алгебру), чтобы найти неизвестную переменную. Правило состоит в том, чтобы найти значение неизвестной переменной, вы должны математически изолировать неизвестную переменную отдельно и в числителе одной части уравнения. Наконец, единицы должны быть согласованы. Например, в законе Бойля есть две переменные давления; они должны иметь одинаковую единицу измерения. Есть также две переменные объема; они также должны иметь одинаковую единицу измерения. В большинстве случаев не имеет значения , какая единица измерения, но единицей измерения должно быть то же , что и в обеих частях уравнения.

Пример \(\PageIndex{1}\)

Образец газа имеет начальное давление 2,44 атм и начальный объем 4,01 л. Его давление изменяется до 1,93 атм. Каков новый объем, если температура и количество остаются постоянными?

Решение

Решения примера 11.8.1

Действия по решению проблем
Определите «данную» информацию и то, что проблема просит вас «найти».	Дано: P 1 = 2,44 атм и В 1 = 4,01 л P 2 = 1,93 атм Найти: В 2 = ? Л
Перечислите другие известные количества.	нет
Спланируйте задачу.	Сначала перестройте уравнение алгебраически, чтобы найти \(V_2\). \[V_2 = \dfrac{P_1 \times V_1}{P_2} \номер\]
Отмена единиц и расчет.	Теперь подставьте известные величины в уравнение и решите. \[V_2 = \dfrac{2,44 \: \cancel{\text{атм}} \times 4,01 \: \text{L}}{1,93 \: \cancel{атм}} = 5,07 \: \text{L} \номер\]
Подумайте о своем результате.	Мы знаем, что давление и объем обратно пропорциональны; когда одно уменьшается, другое увеличивается. Давление снижается (с 2,44 атм до 1,93 атм), поэтому объем должен увеличиваться, чтобы компенсировать это (с 4,01 л до 5,07 л). Таким образом, ответ имеет смысл, основанный на законе Бойля.

Упражнение \(\PageIndex{1}\)

Если P ₁ = 334 Торр, В ₁ = 37,8 P мл и 0200 = 102 торр, что такое В ₂ ?

Ответить

124 мл

Как уже упоминалось, вы можете использовать любые единицы измерения давления и объема, но оба давления должны быть выражены в одних и тех же единицах, и оба объема должны быть выражены в одних и тех же единицах.

Пример \(\PageIndex{2}\):

Образец газа имеет начальное давление 722 торр и начальный объем 88,8 мл. Его объем изменится на 0,663 л. Каково новое давление?

Решение

Решения примера 11.8.2

Действия по устранению неполадок
Определите «данную» информацию и то, что проблема просит вас «найти».	Дано: P 1 = 722 торр и В 1 = 88,8 мл В 2 = 0,633 л Найти: P 2 = ? торр
Перечислите другие известные количества.	1 л = 1000 мл, чтобы иметь те же единицы измерения объема.
Спланируйте задачу.	1. Выполните преобразование второй единицы объема из л в мл. 2. Перестройте уравнение алгебраически, чтобы решить для \(P_2\). \[P_2 = \dfrac{P_1 \times V_1}{V_2} \номер\]
Отмена единиц и расчет.	1. \[0.663\, \cancel{L}\times \dfrac{1000\, мл}{1\, \cancel{L}}=663\, мл \nonumber \] 2. Больше новостей Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт