Как передавать показания за свет какие цифры: Как снять показания счетчика электроэнергии, какие цифры снимать

Какие цифры передавать по счетчикам электроэнергии, как правильно считать и передавать показания счетчика

Перед внесением платы за электроэнергию абоненты записывают данные с оборудования и делают расчеты. Затем информацию нужно передавать в специальную службу. В то же время важно, чтобы снятие показаний было своевременным и точным. Как считать и какие цифры учитывать, чтобы не допустить ошибок? В публикации приведены примеры работы с различными счетчиками света.

Индукционные модели

Индукционный прибор отличается от электронного крутящимся колесом, оно находится под рамкой и цифрами. Их количество зависит от конкретной модели. Эти числа и представляют собой показания электросчетчиков.

Как получить сведения о расходе энергии

После того, как электрики установили счетчик электроэнергии, они выдают акт. В нем указаны изначальные цифры. Перед тем, как вносить абонплату фиксируют число, указанное до запятой, которое устройство насчитало за истекший месяц. Нули, стоящие в самом начале, можно не переносить.

Для дальнейших подсчетов понадобятся квитанции за прошлый месяц. С этой целью можно завести специальный журнал и записывать в него все изменения.

Расчеты

Чтобы посчитать показатели и заплатить за свет, от последнего значения отнимают предыдущее. В результате получается число киловатт, которые израсходовали за последний месяц. Узнать сумму оплаты можно следующим образом: для этого умножают полученные киловатты на тариф. Со временем счетчики «обнуляются», и вместо первых цифр появляются нули. Как рассчитывать показания с электросчетчика в подобных случаях? Количество киловатт переписывают вместе с нулями, но перед ними указывают «1».

Количество цифр

Как правило, на табло индукционных электросчетчиков указано от 5 до 7 цифр. Чаще всего одну либо две последних отделяет запятая. Они могут быть другого размера либо цвета и показывают 10-ю и 100-ю долю киловатта. Их не записывают, когда передают показания приборов учета электроэнергии.

Электронные аппараты

Как правильно получить сведения о расходе электричества с приборов, в которые вмонтирован дисплей? Иногда на нем дополнительно отображается дата и прочая информация. О том, как считывать ее можно узнать на примерах разных устройств, которые приведены ниже.

«Меркурий 200» и «Меркурий 230»

Такие электроприборы могут подсчитывать расход энергии за время, которое определяется в зависимости от тарифной зоны. Как снять показания с Меркурий 200 и Меркурий 230? Так как принцип их работы идентичен, в обоих случаях подход будет одинаковым. С таких электроприборов фиксируют каждую зону по отдельности. В авторежиме на табло поочередно высвечивается каждая из них. При этом Т1 – это тариф.

Для обеих моделей предусмотрен одинаковый интерфейс. Для управления есть две кнопки. Так, кнопкой «Ввод» можно выбрать показатели разных тарифных зон вручную (например, Т1, Т2 или Т3). На второй есть изображение кольца и указательной стрелки, ее используют, чтобы выбрать режим. Последовательность действий позволит правильно снять показания счетчика электроэнергии:

1. Для начала устанавливают режим, например, «А». Чтобы переключить режим, нажимают на кнопку со стрелкой.
2. Когда режим установлен на экране отобразятся значения для тарифа Т1. Просмотреть Т1 и Т2 в счетчике можно кратковременным нажатием кнопки «Ввод».

Для обеих моделей производитель разработал ПО. Таким образом, можно получить более полную картину, если подключить счетчик к компьютеру.

«Энергомера»

Получение значений, указанных на счетчике электроэнергии марки «Энергомера», схоже с принципом, который применяется при работе с прибором «Меркурий 200». Компания «Энергомера» производит разные электроустройства. Среди них есть многотарифное и двухтарифное оборудование (счетчик день/ночь). На панели предусмотрено две либо три кнопки управления. Для переключения есть отдельная клавиша ПРСМ. Чтобы узнать, сколько электроэнергии «нагорело», надо повторить алгоритм действий, как в случае с аппаратами учета электричества «Меркурий». Цифры, которые отображаются после точки, при этом не учитывают.

«Микрон»

Для того, чтобы было удобнее снимать показания электросчетчика, разработчики предусмотрели для устройства одну кнопку. Она переключает зоны, которые обозначены в нижней части табло. С левой стороны от указан символ «R+». Все, что нужно знать о потреблении электричества, будет поочередно высвечиваться на дисплее. Над номером тарифа отображается галочка. Она также появляется над значком «R+» (это означает, что значения можно переписывать). Просмотреть другое значение можно, если нажать на кнопку и подождать, когда высветятся обе галочки. Далее переносят числа, которые указаны до точки.

Saiman

Чтобы перелистать страницы и передать показания счетчика электроэнергии с аппаратов Saiman, не понадобится нажимать на клавиши, поскольку они попросту отсутствуют. В этих электроприборах все автоматически высвечивается на экране. На дисплее отображаются данные в такой последовательности:

• дата;
• время;
• номер;
• передаточное значение;
• сведения о расходе электричества;
• тарифы и общая сумма.

Таким образом, на табло можно сразу увидеть, где указано все о тарифных планах, узнать, какое время и дата.

Двухтарифные модели

Как снимать показания с двухтарифного аппарата? Поначалу может казаться, что получать их сложнее, чем с обычных однотарифных. Но чтобы снять показания со счетчика электроэнергии день /ночь, достаточно знать один принцип. Речь идет о том, какие показания дневные, а какие ночные. Для них предусмотрена разная маркировка. Как правило, символами Т11 обозначены дневные, а Т12 – ночные. Подробнее об этом можно узнать в инструкции к модели. Перед тем, как подавать запрос в абоненскую службу, сначала записывают сведения по дневному тарифному плану (до запятой). Другие показатели выписывают аналогичным образом. Чаще всего сведения о режимах автоматически сменяются через некоторое время. На некоторых электроаппаратах можно вручную переключать значения.

Оборудование с автопередачей данных

Производители стали создавать разработки, которые предусматривают автопередачу информации через специальный канал. Чтобы установить и настроить такое оборудование, понадобится больше времени и сил. Но после завершения всех этапов не придется беспокоиться о том, чтобы каждый месяц отслеживать, сколько электричества «нагорело» и информировать абонентскую службу об этом. Все делается в автоматизированном режиме.

Трехфазные приборы

Чтобы понять, как пользоваться такими аппаратами, стоит прежде всего узнать о принципе их работы. Например, они могут быть старого образца (оснащенные трансформаторами) или электронными (прямого включения). Последние просты в эксплуатации: все сведения видны на дисплее и снимаются так же, как со стандартных однофазных. В устаревшем оборудовании фазы подключены через трансформаторы. Для корректных подсчетов понадобятся коэффициенты трансформации.

Расход рассчитывается по формуле: кВт•ч х k (где k — это коэффициент трансформации). Вычисления делают по порядку, который прописан в договоре с поставщиком. Иногда компания указывает коэффициенты в документе. В некоторых случаях поставщики сами делают расчеты, а абонентам оставется только проинформировать о фактических расходах.

Таким образом, если установлен 3-фазный аппарат, стоит заранее уточнить, в каком порядке и форме подсчитывать итоговое число. Об этом можно узнать у электриков во время установки.

От того, насколько корректно переписана и передана информация, зависит точность начислений. При этом абоненты смогут избежать переплаты за ресурсы, которые они получают от поставщика. Сообщать о расходах энергии стоит своевременно.

Cпособы приема показаний приборов учета

Физические лица Юридические лица

Уважаемый Абонент!

Рекомендуем передавать показания  с 21 по 25 число каждого месяца!

Сообщаем Вам способы передачи показаний индивидуальных приборов учета электроэнергии:

 

1. Через Личный кабинет БГЭС

Для этого нужно зайти на сайт  bges.ru, выбрать раздел “Личный кабинет” (ЛК), указать электронную почту, которая будет являться логином для входа в ЛК, и номер сотового телефона, пройти авторизацию через набор логина и пароля, после чего привязать лицевой счет к ЛК.

 

2. Через Личный кабинет «Системы Город»

Порядок регистрации и доступа в личный кабинет указаны на сайте системы «Город».

 

3. По электронной почте, с помощью отправки SMS-сообщений или автоматического сервиса.

ВНИМАНИЕ!

Для данных способов отправки Вы должны получить ПИН-код. С 1 декабря 2012 года, персональный ПИН-код абонента указывается в чеке за оплату электроэнергии, если платеж внесен через систему «Город» в отделениях банка или почты. Обратите внимание, что пин-код не указывается в чеках, выданных банкоматом.  Для получения ПИН-кода Вы также можете обратиться в АО «Барнаульская горэлектросеть» по адресам ул. Ползунова, 50 (каб. 112), ул. Энтузиастов, 34А (каб. 4).

 

3.1. Отправка показаний с помощью SMS-сообщения

– SMS-сообщение на номер 8-903-767-67-22

В тексте сообщения указать Лицевой счет, ПИН-код и показания прибора учета в формате:

Лицевой счет*ПИН-код*показания#

Например, текст сообщения: 12345678*1234*56789#

где: 12345678 – номер Вашего лицевого счета, 1234 – Ваш ПИН-код, 56789 – Показания Вашего прибора учета.

Стоимость исходящего SMS-сообщения тарифицируется Вашим сотовым оператором на основании Вашего тарифного плана.

 

3.2 Отправка показаний с  помощью сообщения e-mail

– электронное письмо на адрес [email protected]

В «Теме»  сообщения указать Лицевой счет, ПИН-код и показания прибора учета в формате:

Лицевой счет*ПИН-код*показания#

Например, текст сообщения: 12345678*1234*56789#

где: 12345678 – номер Вашего лицевого счета, 1234 – Ваш ПИН-код, 56789 – Показания Вашего прибора учета.

ВНИМАНИЕ!

Если вы отправляете электронное письмо – данные вносите в  поле «Тема».

 

3.3. Воспользоваться «Автоматическим сервисом» по приему показаний с помощью телефонов с тональным набором цифр.

Вы должны в автоматическом режиме по порядку выполнить ряд действий, а именно набрать номер лицевого счета, ПИН-код и показание. В процессе набора проверить правильность набранных цифр – лицевой счет должен состоять из 8 цифр, ПИН-код – четырехзначное число, показание проверяется на значность счетчика Абонента.

Как воспользоваться данной услугой?

– Набрав номер 35-02-02 Автоматический сервис по приему показаний работает круглосуточно.

  

4. Звонок в call-центр.

– Позвоните по телефону 35-04-04  в период с 21 по 25 число каждого месяца с 7.00 до 22.00. (без выходных) Ваши показания прибора учета примет оператор. Необходимо назвать номер лицевого счета,  ПИН-код и адрес.

  

5. Автоматический  голосовой  сервис приема показаний 

Работает круглосуточно по телефону (385 2) 50-16-50

 

6. Заполнить бланк для передачи показаний прибора

и опустить в специальные ящики для приема показаний, установленных в офисах компании по адресам: ул. Ползунова,50, ул. Энтузиастов, 34А.

 

7.  Отправить показания письмом или телеграммой

по адресу 656015, г. Барнаул, ул. Деповская, 19 с пометкой «Показания приборов учета». В тексте письма (телеграммы) указать номер лицевого счета, адрес, показания, подпись абонента, и дату отправления письма.

 

Уважаемые абоненты!

Обратите внимание, что при передаче показаний необходимо указывать цифры со счетчика с точностью до 1 кВтч, то есть цифры после запятой указывать НЕ нужно.

АО «Барнаульская горэлектросеть»

 

Закон Бера-Ламберта – Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

3747

• Джим Кларк
• Школа Труро в Корнуолле

Закон Бера-Ламберта связывает затухание света со свойствами материала, через который проходит свет. На этой странице кратко рассматривается закон Бера-Ламберта и объясняется использование терминов «поглощение» и «молярное поглощение» в спектрометрии поглощения в УФ-видимой области.

Поглощение раствора

Для каждой длины волны света, проходящего через спектрометр, измеряется интенсивность света, прошедшего через эталонную ячейку. Обычно это обозначается как \(I_o\) – это \(I\) для Интенсивности.

Рисунок \(\PageIndex{1}\): Свет, поглощаемый образцом в кювете

Интенсивность света, проходящего через кювету с образцом, также измеряется для этой длины волны, обозначенной символом \(I\). Если \(I\) меньше, чем \(I_o\), то образец поглотил часть света (без учета отражения света от поверхности кюветы). Затем на компьютере выполняется простой математический расчет, чтобы преобразовать это в то, что называется абсорбцией образца – с учетом символа \(A\). Поглощение перехода зависит от двух внешних предположений.

1. Поглощение прямо пропорционально концентрации (\(c\)) раствора образца, используемого в эксперименте.
2. Поглощение прямо пропорционально длине светового пути (\(l\)), которая равна ширине кюветы.

Первое предположение связывает поглощение с концентрацией и может быть выражено как

\[A \propto c \label{1}\]

Поглощение (\(A\)) определяется через интенсивность падения \( I_o\) и переданной интенсивности \(I\) на

\[ A=\log_{10} \left( \dfrac{I_o}{I} \right) \label{2}\]

Предположение два может быть выражено как

\[A \propto l \label{3}\]

Объединение уравнений \(\ref{1}\) и \(\ref{3}\):

\[A \propto cl \label{4}\]

Эта пропорциональность можно преобразовать в равенство, включив константу пропорциональности (\(\epsilon\)).

\[A = \epsilon c l \label{5}\]

Эта формула является общей формой закона Бера-Ламберта , хотя это можно записать и через интенсивности:

\[ A=\log_{10} \left( \dfrac{I_o}{I} \right) = \epsilon l c \label{6} \]

Константа \(\эпсилон\) называется молярным коэффициентом поглощения или молярным коэффициентом экстинкции и является мерой вероятности электронного перехода. На большинстве диаграмм, которые вы встретите, коэффициент поглощения колеблется от 0 до 1, но может быть и выше. Поглощение, равное 0, на некоторой длине волны означает, что свет с этой конкретной длиной волны не поглощается. Интенсивности образца и эталонного луча одинаковы, поэтому отношение \(I_o/I\) равно 1, а \(\log_{10}\) равно нулю.

Пример \(\PageIndex{1}\)

Каково относительное количество света, поглощенного образцом с коэффициентом поглощения 1 на определенной длине волны?

Решение

Для решения этого вопроса не требуется закон Бера-Ламберта (уравнение \(\ref{5}\)), а только определение оптической плотности (уравнение \(\ref{2}\))

\[ A=\log_{10} \left( \dfrac{I_o}{I} \right)\nonumber\]

Относительная потеря интенсивности

\[\dfrac{I-I_o}{I_o} = 1- \dfrac{I}{I_o}\nonumber\] 9{-1} = 1- \dfrac{1}{10} = 0,9\nonnumber\]

Следовательно, 90% света на этой длине волны было поглощено, а прошедшая интенсивность составляет 10% от падающей интенсивности. Чтобы подтвердить, подставив эти значения в уравнение \(\ref{2}\), чтобы получить поглощение обратно:

\[\dfrac{I_o}{I} = \dfrac{100}{10} =10 \label{7a }\]

и

\[\log_{10} 10 = 1 \label{7b}\]

Закон Бера-Ламберта

Вы обнаружите, что для некоторых терминов в уравнение – особенно для концентрации и длины решения.

Греческая буква эпсилон в этих уравнениях называется молярной абсорбцией – или иногда молярным коэффициентом абсорбции. Чем больше молярная поглощательная способность, тем более вероятен электронный переход. В УФ-спектроскопии концентрация раствора пробы измеряется в моль л ^-1 , а длина светового пути – в см. Таким образом, учитывая, что поглощение безразмерно, единицами молярной абсорбции являются л моль ^-1 см ^-1 . Однако, поскольку единицы молярной абсорбции всегда указаны выше, ее обычно указывают без единиц. 9{-1}\) и длина пути 1 см. Используя спектрофотометр, вы находите, что \(A_{275}= 0,70\). Какова концентрация гуанозина?

Решение

Чтобы решить эту задачу, вы должны использовать закон Бера.

\[A = \epsilon lc \]

0,70 = (8400 M ^-1 см ^-1 )(1 см)(\(c\))

Затем разделите обе стороны на [(8400 M ^-1 см ^-1 )(1 см)]

\(c\) = 8,33×10 ^-5 моль/л

Пример \(\PageIndex{3}\)

Вещество в растворе (4 г/л). Длина кюветы 2 см и пропускает только 50% определенного светового пучка. Что такое коэффициент экстенсивности?

Решение

Используя закон Бера-Ламберта, мы можем вычислить коэффициент поглощения. Таким образом,

\(- \log \left(\dfrac{I_t}{I_o} \right) = – \log(\dfrac{0.5}{1.0}) = A = {8} \epsilon\)

Тогда получаем, что

\(\epsilon\) = 0,0376

Пример \(\PageIndex{4}\)

В приведенном выше примере 3, каков молярный коэффициент поглощения, если молекулярная масса равна 100?

Раствор

Его можно просто получить, умножив коэффициент поглощения на молекулярную массу. Таким образом,

\(\эпсилон\) = 0,0376 x 100 = 3,76 л·моль ^{– 1} ·см ^{– 1}

со сколькими молекулами он взаимодействует. Предположим, у вас есть сильно окрашенный органический краситель. Если он находится в достаточно концентрированном растворе, он будет иметь очень высокое поглощение, потому что есть много молекул, взаимодействующих со светом. Однако в невероятно разбавленном растворе может быть очень трудно заметить, что он вообще окрашен. Абсорбция будет очень низкой. Предположим, что вы хотите сравнить этот краситель с другим соединением. Если вы не позаботились о концентрации, вы не смогли бы сделать никаких разумных сравнений о том, какой из них поглощает больше всего света.

Пример \(\PageIndex{4}\)

В приведенном выше примере \(\PageIndex{3}\) сколько луча света передается при 8 г/л?

Решение

Поскольку мы знаем \(\эпсилон\), мы можем рассчитать передачу, используя закон Бера-Ламберта. Таким образом,

\(log(1) – log(I_t) = 0 – log(I_t)\) = 0,0376 x 8 x 2 = 0,6016

\(log(I_t)\) = -0,6016

Следовательно, \ (I_t\) = 0,2503 = 25%

Пример \(\PageIndex{5}\)

Коэффициент поглощения гликоген-йодного комплекса составляет 0,20 при свете 450 нм. Какова концентрация при пропускании 40 % в кювете диаметром 2 см?

Решение

Эту задачу также можно решить с помощью закона Бера-Ламберта. Следовательно,

\[- \log(I_t) = – \log_{10}(0,4) = 0,20 \times c \times 2\]

Тогда \(c\) = 0,9948

Важность формы контейнера

Предположим на этот раз, что у вас есть очень разбавленный раствор красителя в сосуде в форме куба, так что свет проходит через него 1 см. Поглощение вряд ли будет очень высоким. С другой стороны, предположим, что вы пропустили свет через трубку длиной 100 см, содержащую тот же раствор. Будет поглощено больше света, потому что он взаимодействует с большим количеством молекул.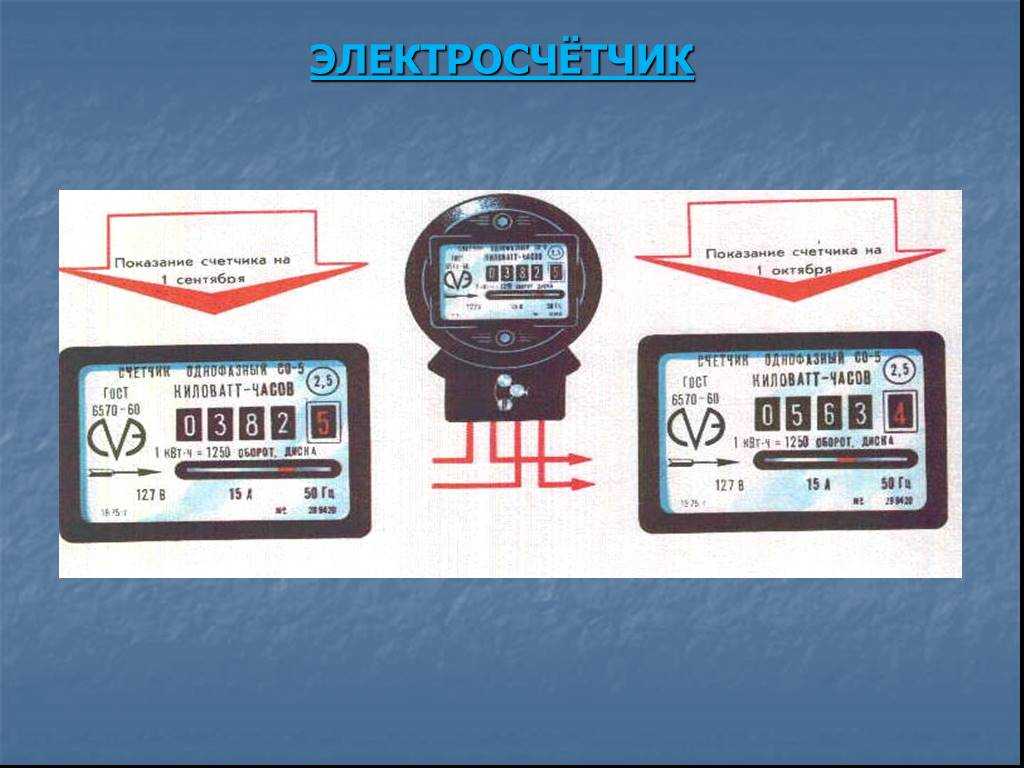 Опять же, если вы хотите провести разумное сравнение между решениями, вы должны учитывать длину решения, через которое проходит свет. Закон Бера-Ламберта допускает как концентрацию, так и длину раствора.

Молярная поглощательная способность

Закон Бера-Ламберта (уравнение \(\ref{5}\)) можно изменить, чтобы получить выражение для \(\epsilon\) (молярная поглощательная способность):

\[ \epsilon = \dfrac{A}{lc} \label{8}\]

Помните, что абсорбция раствора зависит от концентрации или размера контейнера. Молярная поглощательная способность компенсирует это путем деления как на концентрацию, так и на длину раствора, через который проходит свет. По сути, он вычисляет значение оптической плотности при стандартном наборе условий — свет, проходящий 1 см через раствор 1 моль дм ^-3 . Это означает, что вы можете сравнивать одно соединение с другим, не беспокоясь о концентрации или длине раствора.

Значения молярной абсорбции могут сильно различаться. Например, этаналь имеет два пика поглощения в УФ-видимом спектре — оба в ультрафиолетовой. Один из них соответствует продвижению электрона из неподеленной пары кислорода на антисвязывающую пи-орбиталь; другой с \(\pi\) связывающей орбитали на \(\pi\) разрыхляющую орбиталь. В таблице 1 приведены значения молярной абсорбции раствора этаналя в гексане. Обратите внимание, что единицы измерения поглощающей способности не указаны. Это довольно распространено, так как предполагается, что длина указана в сантиметрах, а концентрация равна моль дм ^-3 , единицы моль ^-1 дм ³ см ^-1 .

Таблица \(\PageIndex{1}\)

прыжок электрона	длина волны максимального поглощения (нм)	молярная абсорбционная способность
неподеленная пара к \(\pi\) антисвязывающей орбитали	290	15
\(\pi\) связывание с \(\pi\) разрыхляющей орбиталью	180	10 000

Этаналь, очевидно, поглощает намного сильнее при 180 нм, чем при 290 нм.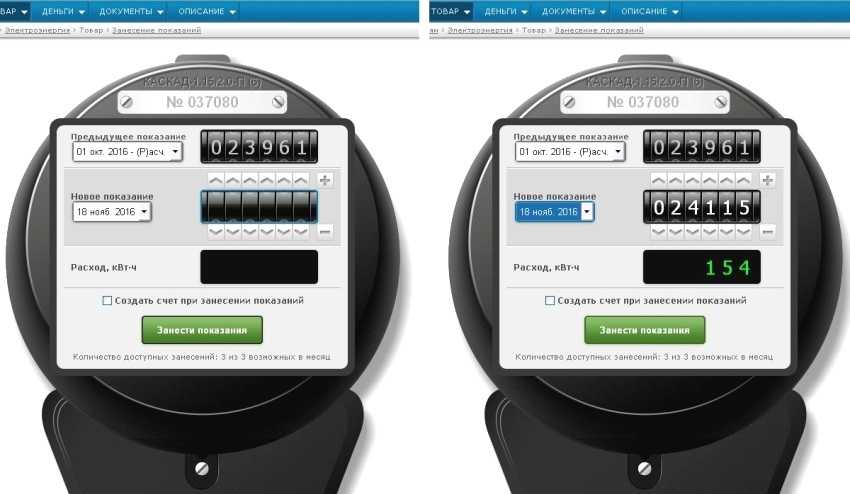 (Хотя на самом деле пик поглощения 180 нм находится за пределами диапазона большинства спектрометров.) Вы можете встретить диаграммы спектров поглощения, на которых поглощение отложено по вертикальной оси, а не поглощение. Однако, если вы посмотрите на приведенные выше цифры и масштабы, которые будут задействованы, вы не сможете определить поглощение на уровне 29.0 нм. Это будет крошечный пик по сравнению с пиком на 180 нм. Чтобы обойти это, вы также можете встретить диаграммы, на которых вертикальная ось нанесена как log ₁₀ (молярная абсорбционная способность).

Если вы возьмете логарифм двух чисел в таблице, 15 станет 1,18, а 10 000 станет 4. Это позволяет легко построить оба значения, но дает странно сплющенный спектр!

Авторы и авторство

---

Эта страница с заголовком «Закон Бира-Ламберта» используется в соответствии с лицензией CC BY 4.0, ее автор, ремикс и/или куратор — Джим Кларк.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Джим Кларк

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Показать страницу TOC

   № на стр.

2. Теги

   1. Закон Бера-Ламберта
   2. молярная абсорбционная способность

2.1.5: Спектрофотометрия – Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1431

Спектрофотометрия — это метод измерения степени поглощения света химическим веществом путем измерения интенсивности света при прохождении луча света через раствор образца. Основной принцип заключается в том, что каждое соединение поглощает или пропускает свет в определенном диапазоне длин волн. Это измерение также можно использовать для измерения количества известного химического вещества. Спектрофотометрия является одним из наиболее полезных методов количественного анализа в различных областях, таких как химия, физика, биохимия, материаловедение и химическая инженерия, а также в клинических применениях.

Введение

Каждое химическое соединение поглощает, пропускает или отражает свет (электромагнитное излучение) в определенном диапазоне длин волн. Спектрофотометрия — это измерение того, сколько химического вещества поглощает или пропускает. Спектрофотометрия широко используется для количественного анализа в различных областях (например, химия, физика, биология, биохимия, материаловедение и химическая инженерия, клиническое применение, промышленное применение и т. д.). Любое приложение, имеющее дело с химическими веществами или материалами, может использовать этот метод. В биохимии, например, он используется для определения катализируемых ферментами реакций. В клинических применениях он используется для исследования крови или тканей для постановки клинического диагноза. Существует также несколько вариантов спектрофотометрии, таких как атомно-абсорбционная спектрофотометрия и атомно-эмиссионная спектрофотометрия.

Спектрофотометр — это прибор, который измеряет количество фотонов (интенсивность света), поглощенных после прохождения через раствор образца. С помощью спектрофотометра можно также определить количество известного химического вещества (концентрацию) путем измерения интенсивности обнаруженного света. В зависимости от диапазона длины волны источника света его можно разделить на два разных типа:

• УФ-видимый спектрофотометр : использует свет в ультрафиолетовом диапазоне (185–400 нм) и видимом диапазоне (400–700 нм). спектра электромагнитного излучения.
• ИК-спектрофотометр : использует свет в инфракрасном диапазоне (700–15000 нм) спектра электромагнитного излучения.

В видимой спектрофотометрии поглощение или пропускание определенного вещества можно определить по наблюдаемому цвету. Например, образец раствора, который поглощает свет во всех видимых диапазонах (т. е. не пропускает ни одну из видимых длин волн), теоретически кажется черным. С другой стороны, если пропускаются все видимые длины волн (т. Е. Ничего не поглощается), образец раствора кажется белым. Если образец раствора поглощает красный свет (~ 700 нм), он кажется зеленым, потому что зеленый является дополнительным цветом к красному. Спектрофотометры видимого диапазона на практике используют призму для сужения определенного диапазона длин волн (для фильтрации других длин волн), чтобы конкретный луч света проходил через образец раствора.

Устройства и механизм

На рисунке 1 показана основная структура спектрофотометров. Он состоит из источника света, коллиматора, монохроматора, селектора длины волны, кюветы для раствора образца, фотоэлектрического детектора и цифрового дисплея или измерителя. Подробный механизм описан ниже. На рис. 2 показан образец спектрофотометра (модель: Spectronic 20D).

Рисунок 1: Базовая структура спектрофотометров (CC BY-4.0; Heesung Shim через LibreTexts)

Спектрофотометр, как правило, состоит из двух устройств; спектрометр и фотометр. Спектрометр — это устройство, которое производит, обычно рассеивает и измеряет свет. Фотометр обозначает фотоэлектрический детектор, который измеряет интенсивность света.

• Спектрометр : Излучает свет в желаемом диапазоне длин волн. Сначала коллиматор (линза) пропускает прямой пучок света (фотоны), который проходит через монохроматор (призму) и разделяет его на несколько составляющих длин волн (спектр). Затем селектор длины волны (щель) передает только нужные длины волн, как показано на рисунке 1.
• Фотометр : после того, как свет с желаемой длиной волны проходит через раствор образца в кювете, фотометр определяет количество поглощенных фотонов и затем посылает сигнал на гальванометр или цифровой дисплей, как показано на рисунке. 1.

Рисунок 2: Спектрофотометр с одной длиной волны

Вам нужен спектрометр для получения различных длин волн, потому что разные соединения лучше всего поглощают на разных длинах волн. Например, п-нитрофенол (кислотная форма) имеет максимальное поглощение примерно при 320 нм, а п-нитрофенолат (основная форма) лучше всего поглощает при 400 нм, как показано на рисунке 3.

Рисунок 3: Поглощение двух разных соединений

график, который измеряет поглощение и длину волны, также можно наблюдать изобестическую точку. изобестическая точка — это длина волны, при которой поглощательная способность двух или более видов одинакова. Появление изобестической точки в реакции свидетельствует о том, что промежуточное соединение НЕ требуется для образования продукта из реагента. На рис. 4 показан пример изобестической точки.

Рисунок 4: Пример изобестической точки (CC BY-4.0; Heesung Shim через LibreTexts) кюветы и концентрации образца. Как только вы узнаете интенсивность света после его прохождения через кювету, вы можете соотнести ее с коэффициентом пропускания (T). Коэффициент пропускания — это доля света, проходящая через образец. Это можно рассчитать с помощью уравнения:

\(Пропускание (T) = \dfrac{I_t}{I_o}\)

Где I _t — интенсивность света после прохождения луча света через кювету, а I _o — интенсивность света до луч света проходит через кювету. Коэффициент пропускания связан с поглощением выражением:

\(Поглощение (A) = – log(T) = – log(\dfrac{I_t}{I_o})\)

Где поглощение обозначает количество фотонов, которое впитывается. Зная величину поглощения, известную из приведенного выше уравнения, вы можете определить неизвестную концентрацию образца, используя закон Бера-Ламберта. На рис. 5 показан коэффициент пропускания света через образец. Длина \(l\) используется для закона Бера-Ламберта, описанного ниже.

Рисунок 5: Коэффициент пропускания (CC BY-4.0; Heesung Shim через LibreTexts)

Закон Бера-Ламберта

Закон Бера-Ламберта (также известный как закон Бера) утверждает, что существует линейная зависимость между поглощением и концентрацией образца . По этой причине закон Бера может применяться только при наличии линейной зависимости. Закон Бера записывается как:

\(A = \epsilon{lc}\)

, где

• \(A\) – мера поглощения (без единиц),
• \(\эпсилон\) – молярный коэффициент экстинкции или молярная абсорбционная способность (или коэффициент поглощения),
• \(l\) — длина пути, а
• \(с\) – концентрация.

Молярный коэффициент экстинкции задается как константа и варьируется для каждой молекулы. Поскольку поглощение не имеет никаких единиц, единицы для \(\эпсилон\) должны компенсировать единицы длины и концентрации. В результате \(\эпсилон\) имеет единицы: л·моль ^{– 1 9{-1}\) и длина пути 1 см. Используя спектрофотометр, вы находите, что \(A_{275}= 0,70\). Какова концентрация гуанозина?}

Решение

Чтобы решить эту задачу, вы должны использовать закон Бера.

\[A = \epsilon lc \]

0,70 = (8400 M ^-1 см ^-1 )(1 см)(\(c\))

Затем разделите обе стороны на [(8400 M ^-1 см ^-1 )(1 см)]

\(c\) = 8,33×10 ^-5 моль/л

Пример 2

Вещество в растворе (4 г/л). Длина кюветы 2 см и пропускает только 50% определенного светового пучка. Что такое коэффициент поглощения?

Решение

Используя закон Бера-Ламберта, мы можем вычислить коэффициент поглощения. Таким образом,

\(- \log \left(\dfrac{I_t}{I_o} \right) = – \log(\dfrac{0.5}{1.0}) = A = {8} \epsilon\)

Тогда получаем, что

\(\эпсилон\) = 0,0376

Пример 3

В приведенном выше примере 2, сколько луча света передается при 8 г/л?

Решение

Поскольку мы знаем \(\эпсилон\), мы можем рассчитать передачу, используя закон Бера-Ламберта. Таким образом,

\(\log(1) – \log(I_t) = 0 – \log(I_t)\) = 0,0376 x 8 x 2 = 0,6016

\(\log(I_t)\) = -0,6016

Следовательно, \(I_t\) = 0,2503 = 25%

Пример 4

В приведенном выше примере 2, каков молярный коэффициент поглощения, если молекулярная масса равна 100?

Раствор

Его можно просто получить, умножив коэффициент поглощения на молекулярную массу. Таким образом,

\(\эпсилон\) = 0,0376 x 100 = 3,76 л·моль ^{– 1} ·см ^{– 1}

при свете 450 нм. Какова концентрация при пропускании 40 % в кювете диаметром 2 см?

Раствор

Эту задачу также можно решить с помощью закона Бера-Ламберта. Следовательно,

\[- \log(I_t) = – \log(0,4) = 0,20 \times c \times 2\]

Тогда \(c\) = 0,9948

Ссылки

1. Аткинс, Питер и Хулио де Паула. Физическая химия для наук о жизни. Нью-Йорк: Издательство Оксфордского университета, 2006.
.
2. Чанг, Рэймонд. Физическая химия для биологических наук. США: Университетские научные книги, 2005.
.
3. Гор, Майкл. Спектрофотометрия и спектрофлуориметрия. Нью-Йорк: Издательство Оксфордского университета, 2000.
4. Прайс, Николас и Двек, Рэймонд и Вормолд, Марк. Принципы и проблемы физической химии для биохимиков. Р. Г. Рэтклифф. Нью-Йорк: Издательство Оксфордского университета, 1997.
.
5. Ирвин Х. Сегель, Биохимические расчеты (как решать математические задачи в общей биохимии), 2-е издание, John Wiley & Sons, 1975
6. http://www.nist.gov/pml/div685/grp03/spectrophotometry.cfm

Авторы и авторство

• Кевин Во (UCD)

---

2.