Конденсаторы
| на главную | доп. материалы | физика как наука и предмет | электричество и электромагнетизм |
Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.
Для того чтобы проводник обладал большой емкостью, он должен иметь очень большие размеры. На практике, однако, необходимы устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили название конденсаторов.
Если к заряженному проводнику приближать другие тела, то на них возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды, причем ближайшими к наводящему заряду Q будут заряды противоположного знака. Эти заряды, естественно, ослабляют поле, создаваемое зарядом
 е. понижают потенциал проводника, что приводит
(см. (93.1)) к повышению его электроемкости.
е. понижают потенциал проводника, что приводит
(см. (93.1)) к повышению его электроемкости.Конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, возникающие на разных обкладках, являются равными по модулю разноименными зарядами. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (j1—j2) между его обкладками:
(94. 1)
1)
Рассчитаем емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и –Q. Если расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами можно пренебречь и поле между обкладками считать однородным. Его можно рассчитать используя формулы (86.1) и (94.1). При наличии диэлектрика между обкладками разность потенциалов между ними, согласно (86.1),
(94.2)
где e — диэлектрическая проницаемость. Тогда из формулы (94.1), заменяя Q=sS, с учетом (94.2) получим выражение для емкости плоского конденсатора:
(94.3)
Для определения емкости цилиндрического конденсатора, состоящего из
двух полых коаксиальных цилиндров с радиусами r1 и r2 (r2 > r1), вставленных один в другой,
опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и
сосредоточенным между цилиндрическими обкладками. Разность потенциалов между
обкладками вычислим по формуле (86.3) для поля равномерно заряженного
бесконечного цилиндра с линейной плотностью t =Q/l (l—длина
обкладок). При наличии диэлектрика между обкладками разность потенциалов
Разность потенциалов между
обкладками вычислим по формуле (86.3) для поля равномерно заряженного
бесконечного цилиндра с линейной плотностью t =Q/l (l—длина
обкладок). При наличии диэлектрика между обкладками разность потенциалов
(94.4)
Подставив (94.4) в (94.1), получим выражение для емкости цилиндрического конденсатора:
(94.5)
Для определения емкости сферического конденсатора, состоящего из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу (86.2) для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов
(94.6)
Подставив (94. 6) в (94.1), получим
6) в (94.1), получим
Если d=r2—r1<<r1, то r2 » r
Из формул (94.3), (94.5) и (94.7) вытекает, что емкость
конденсаторов любой формы прямо пропорциональна диэлектрической проницаемости
диэлектрика, заполняющего пространство между обкладками. Поэтому применение в
качестве прослойки сегнетоэлектриков значительно увеличивает емкость
конденсаторов.
Конденсаторы характеризуются пробивным напряжением — разностью потенциалов между обкладками конденсатора, при которой происходит пробой — электрический разряд через слой диэлектрика в конденсаторе. Пробивное напряжение зависит от формы обкладок, свойств диэлектрика и его толщины.
Для увеличения емкости и варьирования ее возможных значений конденсаторы соединяют в батареи, при этом используется их параллельное и последовательное соединения.
1. Параллельное соединение конденсаторов (рис. 144). У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна jA – jB. Если емкости отдельных конденсаторов С1, С2, …, Сn, то, согласно (94.1), их заряды равны
а заряд батареи конденсаторов
Полная емкость батареи
т. е. при параллельном соединении конденсаторов она равна сумме
емкостей отдельных конденсаторов.
2. Последовательное соединение конденсаторов (рис. 145). У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи
где для любого из рассматриваемых конденсаторов Dji = Q/Сi. С другой стороны,
откуда
т. е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при .последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в батарее.
Конденсаторы обладают способностью накапливать и сохранять электрический заряд. Заряд сохраняется на двух изолированных
друг от друга пластинках конденсатоpa,
между которыми приложено внешнее напряжение. Если напряжение между обкладками конденсатора отсутствует, то заряд
также отсутствует и принято считать, что конденсатор разряжен. Все конденсаторы, применяемые в электротехнике, состоят из двух основных частей: пары токопроводящих пластин, или обкладок, и изолирующего материала, называемого диэлектриком, который разделяет обкладки. В самом простом виде конденсатор состоит из двух плоскопараллельных пластин, разделенных вакуумом. Плоский конденсатор Вполне очевиден тот факт, что емкость плоского конденсатора прямо пропорциональна площади А его пластин и обратно пропорциональна расстоянию d между ними. Этого следует ожидать, так как если раздвигать пластины на бесконечно большое расстояние, то уменьшающиеся заряды пластин не смогут взаимодействовать друг с другом, а каждая пластина по отдельности уже не будет являться конденсатором. Если заряд накапливается на пластинах, то можно положить, что внесение любого материала Для того, чтобы рассчитать реальное значение емкости конденсатора, необходимо ввести некоторую постоянную, характеризующую
степень ослабления взаимодействия между пластинами за счет введения диэлектрика. В данном выражении присутствуют две диэлектрические проницаемости: постоянная ε0 известен, как абсолютная диэлектрическая проницаемость вакуума и для системы единиц СИ равен: ε0 = 8,854 * 10-12 Ф/м. Константа εr., характеризует относительную диэлектрическую проницаемость материала, помещенного в качестве диэлектрика между пластинами конденсатора, связана со значением абсолютной диэлектрической проницаемости, причем всегда значение εr > 1. Несложный расчет, проведенный с использованием данного уравнения, показывает, что в условиях вакуума (хотя с известным
приближением можно считать, что результат, полученный для условий воздушного зазора, будет почти идентичен результату,
полученному для условий вакуума) плоский конденсатор, имеющий площадь пластин 1 м Уменьшение зазора между пластинами и увеличение количества пластин Самым простым способом увеличить емкость конденсатора без увеличения его геометрических размеров, является уменьшение зазора между пластинами, поэтому в промышленно выпускаемых конденсаторах величина расстояния между ними составляет 5 мкм или еще меньше. Вторым способом является увеличение количества пластин, например, изготовление конденсатора в виде блоков из отдельных
пластин, в каждом из которых все пластины одного блока соединятся вместе (рис. 5.2). Такой прием практически удваивает емкость
по сравнению с интуитивно ожидаемым в первый момент значением, так как в этом случае используются обе поверхности каждой
из пластин (за исключением, естественно, только двух крайних пластин). Рис. 5.2 Поперечный разрез стандартного конденсатора с параллельными пластинами Вырезание квадратиков из диэлектрика и соответствующих металлических пластинок при изготовлении рассмотренной выше конструкции, а затем сборка их в одну батарею является дорогостоящим предприятием, поэтому большая часть конденсаторов изготавливается иначе. Берутся две длинные полоски фольги, являющиеся пластинами или обкладками конденсатора, между ними помещается полоска диэлектрика, затем все это сворачивается в форме цилиндра, и в конце к каждой из обкладок присоединяются электрические выводы. Свойства диэлектрика. Эквивалентная схема конденсатора Изготовить конденсатор с воздушным диэлектриком, в котором воздушный зазор был равномерным и составлял бы между пластинами
точно 5 мкм по всей поверхности, практически невозможно, следовательно, между пластинами чаще всего необходимо класть разделительную
диэлектрическую прокладку. К сожалению, такой способ увеличения емкости конденсатора произойдет за счет изменения его других параметров, влияние которых следует рассмотреть подробнее. Любой диэлектрик характеризуется тремя основными параметрами: относительной диэлектрической проницаемостью, электрической прочностью и диэлектрическими потерями. Относительная диэлектрическая проницаемость, εr, которая уже упоминалась выше, и является коэффициентом, на который увеличивается (относительно случая, когда диэлектриком является вакуум) емкость конденсатора после помещения между пластинами нового диэлектрика. Электрическая прочность характеризует максимальную напряженность электрического поля, измеряемую в вольтах на метр, которая
может быть приложена к диэлектрику до того, как в нем произойдет пробой и он утратит свои изолирующие свойства. Диэлектрические потери характеризуют степень неидеальности диэлектрика и отличия его свойств от идеального при значениях
напряжения между обкладками конденсатора, не достигающих пробоя. Непосредственный способ характеризовать потери — это измерить
токи утечки, которые протекает в диэлектрике при приложении максимального значения рабочего напряжения к конденсатору (и
которые обычно выражаются в микроамперах). Этот метод обычно используется для электролитических алюминиевых и танталовых
конденсаторов. Пленочные конденсаторы, как правило, характеризуются значительно меньшими потерями, поэтому для таких конденсаторов
могут быть использованы величина сопротивления изоляции, или сопротивление току утечки. Так как диэлектрические потери могут
различаться по своей величине для случая применения конденсаторов в цепях постоянного и переменного токов, то поэтому гораздо
удобнее пользоваться такой характеристикой, как тангенс угла диэлектрических потерь, tgδ, который характеризует величину
активных потерь в диэлектрике на различных частотах. Омические сопротивления подводящих проводов и обкладок объединяются вместе и получили общее название эффективное последовательное сопротивление (ESR). Для некоторых компонентов схем, таких как электролитические конденсаторы большой емкости, применяемых в источниках питания или катодных полосовых фильтрах, данный параметр является очень важным, так как он может составлять значительную часть полного импеданса конденсатора. В источниках питания в накопительных конденсаторах протекают значительные токи, которые вызывают сильный внутренний саморазогрев структуры. По этой причине также используется параметр, очень тесно связанный с последовательным эффективным сопротивлением, получивший название максимальная постоянная составляющая пульсирующего тока. Гибкие выводы обладают собственной последовательно подключаемой в схеме индуктивностью, а если не предприняты особые
меры, то пластины конденсатора также обладают собственной индуктивностью. Рис. 5.3 Эквивалентная схема замещения реального конденсатора При рассмотрении схемы сразу становится ясным, что речь идет о классическом резонансном контуре, более того, для электролитических конденсаторов нередко частота собственного резонанса приводится в технической документации производителей. Более подробно эта проблема будет обсуждаться позже. |
Конденсаторы. Параллельное и последовательное соединение конденсаторов
Конденсаторами называются устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, т.е., обладать большой емкостью.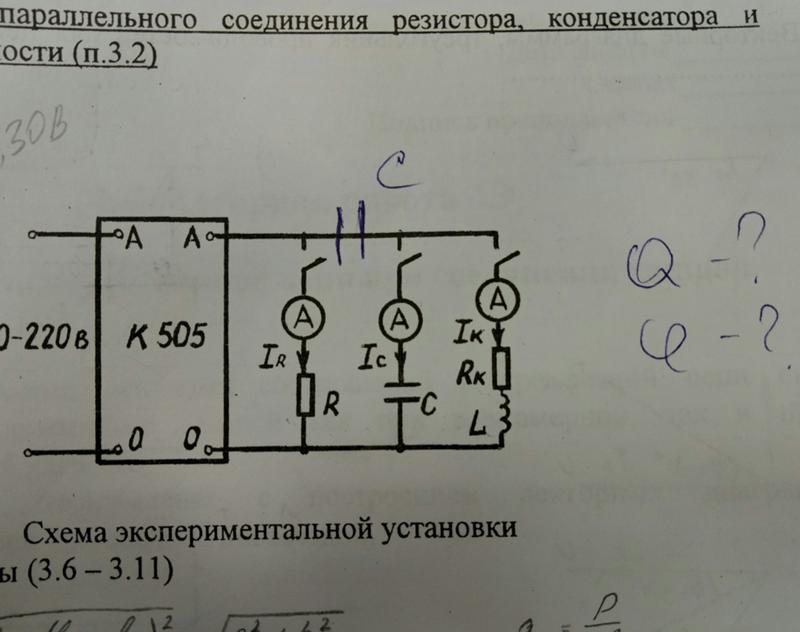
Если к заряженному проводнику приближать другие тела, то на них возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды, причем ближайшими к наводящему заряду Q будут заряды противоположного знака. Эти заряды ослабляют поле, создаваемое зарядом Q, т. е. понижают потенциал проводника, что приводит к повышению его электроемкости.
Конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком. На емкость конденсатора недолжны, оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: две плоские пластины; два коаксиальных цилиндра; две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, возникающие на разных обкладках, являются равными по модулю разноименными зарядами. Емкостью конденсатора называется физическая величина, равная отношению заряда, накопленного в конденсаторе, к разности потенциалов между его обкладками:
Емкостью конденсатора называется физическая величина, равная отношению заряда, накопленного в конденсаторе, к разности потенциалов между его обкладками:
Если расстояние между пластинами конденсатора мало по сравнению с их линейными размерами, то краевыми эффектами можно пренебречь и поле между обкладками считать однородным. При наличии диэлектрика между обкладками разность потенциалов между ними равна
(2)где ε — диэлектрическая проницаемость.
Емкость плоского конденсатора:
Емкость цилиндрического конденсатора:
,где l – длина конденсатора, r1, r2 – радиусы внутренней и внешней обкладок.
Емкость сферического конденсатора:
Конденсаторы характеризуются пробивным напряжением — разностью потенциалов между обкладками конденсатора, при которой происходит пробой — электрический разряд через слой диэлектрика в конденсаторе. Пробивное напряжение зависит от формы обкладок, свойств диэлектрика и его толщины.
Пробивное напряжение зависит от формы обкладок, свойств диэлектрика и его толщины.
Для увеличения емкости и варьирования ее возможных значений конденсаторы соединяют в батареи, при этом используется их параллельное и последовательное соединение.
Параллельное соединение конденсаторов
У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна А- В. Если емкости отдельных конденсаторов C1, C2, …., Сn, то их заряды равны
………………………
,а заряд батареи конденсаторов
Полная емкость батареи равна сумме емкостей отдельных конденсаторов
Допустимое напряжение определяется допустимым напряжением меньшего конденсатора.
Нужна помощь в написании работы?
Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Правки вносим бесплатно.
Цена работы
Последовательное соединение конденсаторов
У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи
где для любого из рассматриваемых конденсаторов
С другой стороны,
откуда
т. е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в батарее.
Ученые из университета в Вандербилте, что в Нэшвилле (штат Теннесси, США), создали суперконденсатор, по большей части состоящий из кремниевых частиц. Суперконденсаторные установки нового типа хранят энергию довольно плотно, что позволяет им провести интеграцию источников электрической энергии внутрь любого электронного чипа. Новые суперконденсаторы обладает электролитическим типом хранения энергии. Они притягивают ионы самых разных полярностей ко своим электродным пластинам. То количество ионов, которое удерживается рядом с пластинами конденсатора, прямым образом имеет зависимость от площади, которая является поверхностью этих самых пластин. Дабы увеличить эффективную площадь, саму поверхность покрывают слоем материалов, которые хорошо проводят электрический ток. Это может быть активированный уголь, в котором содержится множество микроскопических пор, которые помогают увеличить поверхностную площадь. Пока эти новоразработанные конденсаторы не могут соперничать с более распространенными литий-ионными батареями, которые обладают большей емкостью и количеством содержимой энергии. Но они способны изрядно увеличить срок своей службы, по сравнению с теми же литий-ионными аккумуляторями. Это объясняется их высокими и надежными характеристиками вкупе с улучшенными скоростными. А это уже позволяет суперконденсатору поглощать и отдавать очень большое количество электрической энергии. Но как ни как, а а пока суперконденсаторам находят применение в автомобильных системах, в частности в системе, которая отвечает за рекуперативный тормоз уже вошедших в масштабное производство электрических и гибридных “мобилей”. На данном этапе все ученые стараются увеличить емкостную часть суперконденсатора, благодаря которой он мог бы увеличить количество содержимой энергии. И для этого они проводят множество экспериментов, к примеру, задействую высокопористые гибридные материалы, которые представляются множественным количеством углеродных нанотрубок и частиц графена, которые располагаются на пластинах конденсатора. В теории это позволяет изрядно увеличить емкость конденсатора, но на практике это пока не допускается возможным по понятным причинам и не может пуститься в широкомасштабное промышленное производство. . |
схемы соединения, расчёт ёмкости, формулы
Чтобы накапливать, хранить и передавать энергию, в электронике используется специальный прибор — конденсатор. В этой статье описано, как выполнить подключение конденсатора своими руками и какие формулы для этого нужны.
Понятие о приборе
Говоря простым языком, конденсаторами называют радиоэлектронные приборы, которые используются для накопления электроэнергии, впоследствии передавая ее на цепь. Эти устройства достаточно часто применяют в разных электрических схемах.
Как выглядит конденсатный приборПриборы могут очень быстро накапливать энергию и так же стремительно ее передавать. Эти устройства функционируют циклично. Показатель накопленной энергии и циклы определяется техническими параметрами изделия, они зависят от самой модели устройства. Основные технические параметры указаны в маркировке конденсатора. Принцип действия устройства очень похож на индуктивную катушку.
Ниже можно прочесть про последовательное и параллельное соединение конденсаторов с формулами и вычислениями.
Последовательное соединение приборов
Последовательным подключением называется такое, где все элементы устройства включены в виде цепи и соединены с первым и последним конденсатором с помощью пластины.
Схема для последовательного подключенияПри таком виде присоединения на все элементы поступает одинаковое количество электричества, так как именно от источника тока энергия поступает на первое и последнее устройство и передается на другие.
Обратите внимание! Поскольку конденсаторы имеют разную емкость, то и напряжение на каждом из них в цепи будет разным.
Чем ниже емкость прибора, тем выше понадобится напряжение, чтобы получить и передать энергию.
Проще говоря, при подсоединении нескольких устройств сразу, при помощи последовательного способа на устройствах небольшой емкости напряжение будет выше, а на устройствах высокой емкости — ниже.
Также существует метод параллельного подключения. Он выглядит проще предыдущего. Общую емкость приборов можно найти суммированием всех величин.
Смешанное соединение конденсаторовТакже эти устройства можно подключать смешанным способом. Такой метод (последовательно-параллельный) используется, если нужно повысить показатель обеих величин. По такой схеме тяжелее работать, но имея опыт в электрике, можно с ней разобраться. Как соединять приборы стало понятно, теперь необходимо правильно произвести вычисления по формулам.
Как можно рассчитать последовательное подключение
При последовательном подключении двух и более конденсаторов их рабочее напряжение складывается. Очень часто такой метод применяется радиолюбителями, когда не хватает дополнительных элементов на вольтаж.
Для правильного расчета необходимо использовать стандартную формулу:
Uобщ.посл = U1 + U2 + … + Un,
Где U1, U2… — максимальное напряжение каждого отдельно взятого элемента.
Параллельное соединение электролитических конденсаторовКакая общая емкость при подключении устройств
Формула для общей емкости выглядит следующим образом:
C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3;
т. е. при последовательном подключении конденсаторов суммарная емкость равняется сумме показателей каждого элемента.
Как рассчитать емкость одного устройства
Этот показатель является одним из главных характеристик любого прибора. От этого показателя зависит сфера его использования, правила эксплуатации и предназначение. Указывается ёмкость в фарадах.
В России она указывается символом «Ф», в Европе — «F». На самих электронных устройствах можно увидеть такую символьную кодировку, pF, nF или uF. Это означает, что компонент имеет ёмкость 10-11,10-9 и 10-7 фарад.
Показатель можно рассчитать при помощь замеров мультиметром. В конструкции конденсатора имеются металлические пластины. Их поперечные параметры должны быть чуть больше, чем промежуток между ними.
Расшифровка маркировкиВ центр такой пластины будет подключаться оболочка диэлектрика. В процессе работы устройства на выводы оболочки подаётся заряд. В итоге электроны начинают перемещаться, но не могут выходить за диэлектрик, и поэтому в пластинах собирается заряд.
Умение прибора накапливать электрическую энергию и будет его ёмкостью. Если провести аналогию с банкой для жидкости, то емкость — это будет объем.
Чтобы правильно рассчитать ёмкость, нужно воспользоваться формулой:
C= ε (A / d),
где:
- А — площадь самой маленькой пластины;
- d — промежуток между пластинами;
- ε — общая проницаемость диэлектрика.
В заключении необходимо отметить, что рассчитать емкость самостоятельно достаточно легко. В интернете много сервисов, которые помогут с расчетами. Эту величину необходимо знать для того, чтобы правильно присоединить конденсатор в цепь.
Молекулярные выражения: электричество и магнетизм
Факторы, влияющие на емкость
Конденсатор – это электрическое устройство, предназначенное для накопления электрического заряда, обычно состоящее из двух параллельных проводящих пластин, разделенных изолирующим слоем, называемым диэлектриком.
Щелкайте стрелки, чтобы выбрать различные комбинации диэлектриков, площадей пластин и расстояний.
На емкость конденсатора влияет площадь пластин, расстояние между пластинами и способность диэлектрика выдерживать электростатические силы.В этом руководстве показано, как изменение этих параметров влияет на емкость конденсатора. Пластины большего размера обеспечивают большую емкость для хранения электрического заряда. Следовательно, с увеличением площади пластин увеличивается емкость.
Емкость прямо пропорциональна электростатическому силовому полю между пластинами. Это поле тем сильнее, когда пластины расположены ближе друг к другу. Следовательно, с уменьшением расстояния между пластинами емкость увеличивается.
Диэлектрические материалы оцениваются на основе их способности выдерживать электростатические силы в виде числа, называемого диэлектрической проницаемостью.Чем выше диэлектрическая проницаемость, тем больше способность диэлектрика выдерживать электростатические силы. Следовательно, с увеличением диэлектрической проницаемости увеличивается емкость.
НАЗАД К РУКОВОДСТВАМ ПО ЭЛЕКТРИЧЕСТВЕ И МАГНЕТИЗМУ
Вопросы или комментарии? Отправить нам письмо.
© 1995-2021, автор – Майкл В. Дэвидсон и Государственный университет Флориды. Все права защищены. Никакие изображения, графика, программное обеспечение, сценарии или апплеты не могут быть воспроизведены или использованы каким-либо образом без разрешения правообладателей.Использование этого веб-сайта означает, что вы соглашаетесь со всеми юридическими положениями и условиями, изложенными владельцами.
Этот веб-сайт поддерживается нашим
Команда разработчиков графики и веб-программирования
в сотрудничестве с оптической микроскопией в Национальной лаборатории сильного магнитного поля
.
Последнее изменение: среда, 7 июня 2017 г., 13:21
Счетчик доступа с 3 апреля 1999 г .: 460189
Что не влияет на емкость? – MVOrganizing
Что не влияет на емкость?
Где C – емкость конденсатора, ε0 – диэлектрическая проницаемость пластин, A – площадь параллельных пластин, а d – расстояние между двумя параллельными пластинами.Таким образом, тип материала пластин является единственным фактором, не влияющим на емкость конденсатора.
Почему площадь влияет на емкость?
На емкость конденсатора влияет площадь пластин, расстояние между пластинами и способность диэлектрика выдерживать электростатические силы. Пластины большего размера обеспечивают большую емкость для хранения электрического заряда. Следовательно, с увеличением площади пластин увеличивается емкость.
Как увеличить емкость цепи?
Если два или более конденсатора соединены параллельно, общий эффект будет таким, как у одного эквивалентного конденсатора, имеющего общую площадь пластин отдельных конденсаторов.Как мы только что видели, увеличение площади пластины без изменения всех других факторов приводит к увеличению емкости.
Как можно увеличить емкость конденсатора?
Ответ. Если вы хотите увеличить емкость конденсатора с параллельной пластиной, увеличьте площадь поверхности, уменьшите расстояние между пластиной и используйте диэлектрический материал между пластиной, который имеет более высокую диэлектрическую прочность на пробой.
Может ли измениться емкость конденсатора?
Емкость конденсатора также может быть определена как отношение заряда пластин конденсатора (Q) к напряжению (V) между ними.Изменяя емкость Q или V, нельзя изменить емкость конденсатора, поскольку эти два члена прямо пропорциональны, и результирующая емкость останется прежней.
Как увеличить емкость конденсатора с параллельными пластинами?
Чтобы увеличить емкость конденсатора с параллельными пластинами, необходимо ввести между пластинами лист (предположим, что пространство полностью заполнено).
Какой будет емкость конденсатора с параллельными пластинами?
Емкость конденсатора с параллельными пластинами составляет 10 мкФ при расстоянии между пластинами 9 см.Емкость конденсатора с параллельными пластинами составляет 10 мкФ при расстоянии между пластинами 9 см.
Увеличивает ли напряжение емкость?
Когда на конденсатор подается напряжение, на двух проводниках накапливается определенное количество заряда. Повышение напряжения приведет к большему накоплению заряда, что вызовет большее притяжение между пластинами, что приведет к дальнейшему сжатию пружин, что приведет к увеличению емкости.
Что означает символ конденсатора?
Обычно используются два символа конденсатора.Один символ представляет поляризованный (обычно электролитический или танталовый) конденсатор, а другой – неполяризованные колпачки. В каждом случае есть две клеммы, перпендикулярно входящие в пластины. Символ с одной изогнутой пластиной указывает на то, что конденсатор поляризован.
Влияние диэлектрика на емкость – учебный материал для IIT JEE
Что такое диэлектрик?
Диэлектрики – это непроводящие вещества, которые являются изоляционными материалами и плохо проводят электрический ток.Диэлектрические материалы могут удерживать электростатический заряд, рассеивая при этом минимальную энергию в виде тепла. Примеры диэлектрика: Mica , Plastics , Glass , Porcelain и различные оксиды металлов , и даже сухой воздух также является примером диэлектрика.
Рисунок 1.1 Диэлектрический конденсатор
Что такое диэлектрическая постоянная?В конденсаторе с параллельными пластинами, когда диэлектрическая пластина помещается между двумя пластинами, отношение напряженности приложенного электрического поля к напряженности уменьшенного значения конденсатора электрического поля называется диэлектрической постоянной, то есть:
K = E o / E
K – диэлектрическая проницаемость
E 0 больше или равно E
Где E o диэлектрик
А поле нетто
Чем больше диэлектрическая проницаемость, тем больше заряда может сохраняться.Полное заполнение пространства между пластинами конденсатора диэлектриком увеличивает емкость на коэффициент диэлектрической проницаемости:
C = KC o , где C o – емкость без диэлектрика между пластинами.
Диэлектрики обычно помещают между двумя пластинами конденсаторов с параллельными пластинами. Они могут полностью или частично занимать область между пластинами.
Когда диэлектрик помещается между двумя пластинами конденсатора с параллельными пластинами, он поляризуется присутствующим электрическим полем. Плотности поверхностных зарядов рассматриваются как σ p и – σ p .
Когда диэлектрик полностью помещен между двумя пластинами конденсатора, его диэлектрическая постоянная увеличивается по сравнению с вакуумным значением.
Рисунок 1.2 Диэлектрик, расположенный между двумя пластинами
Электрическое поле внутри конденсатора определяется значением
.Итак,
А,
Ɛ – диэлектрическая проницаемость вещества.
Разница потенциалов между пластинами равна
.Для линейных диэлектриков
Где k – диэлектрическая проницаемость вещества
K = 1 иначе,
Как диэлектрик увеличивает емкость конденсатора?Электрическое поле между пластинами конденсатора с параллельными пластинами прямо пропорционально емкости C конденсатора. Напряженность электрического поля уменьшается из-за наличия диэлектрика, и если общий заряд на пластинах поддерживается постоянным, то уменьшается разность потенциалов на пластинах конденсатора.
Таким образом, диэлектрик увеличивает емкость конденсатора.
Рисунок 1.3 Параллельно-пластинчатый конденсатор с диэлектриком
Проба
Рассмотрим следующую схему
Рис. 1.4 диэлектрик между двумя конденсаторами
Диэлектрическая поляризацияКогда к диэлектрическому материалу прикладывают внешнее электрическое поле, его поведение может быть определено и известно как Диэлектрическая поляризация , что можно понять по смещению зарядов (положительных и отрицательных) при приложении электрического поля
Основная задача диэлектрической поляризации – связать макроскопические свойства с микроскопическими свойствами.Где макроскопические свойства могут быть от диэлектрической проницаемости до поляризуемости
Поляризация возникает под действием электрического поля или других внешних факторов, таких как механическое напряжение в случае пьезоэлектрических кристаллов (пьезоэлектрические кристаллы – это те твердые материалы, которые накапливают в них электрический заряд). Диэлектрическая поляризация также может возникать спонтанно в пироэлектрических кристаллах, особенно в сегнетоэлектриках (сегнетоэлектричество – это свойство некоторых материалов, которые имеют спонтанную электрическую поляризацию, которую можно обратить на противоположную путем приложения внешнего электрического поля).
1,5 Диэлектрическая поляризация
Вставка диэлектрика в конденсаторКогда диэлектрический материал вводится между пластинами А, когда диэлектрический материал помещается между пластинами конденсатора с параллельными пластинами, тогда из-за поляризации зарядов по обе стороны от диэлектрика он создает собственное электрическое поле, которое действует в направлении противоположно полю из-за источника.
Это делает чистый электрический поток равным нулю.Этот эффект приводит к появлению емкости.
Вставка диэлектрика между пластинами конденсатора при постоянном напряжении или заряде имеет тот же эффект, что и отношение заряда к напряжению.
| Рисунок 1.6 Влияние диэлектрика на пластины при постоянном напряжении или заряде | |
Что диэлектрик делает с конденсатором? Диэлектрики
часто называют изоляторами , когда изолятор помещен между двумя пластинами конденсатора.
Сторона изолятора, ближайшая к положительной пластине, будет отрицательной, а сторона, ближайшая к отрицательной пластине, будет положительной.
Чистое поле внутри конденсатора и разность потенциалов на конденсаторе уменьшаются, когда электрическое поле от заряда пластин конденсатора компенсируется электрическим полем поляризованного диэлектрика. Конденсатору требуется больший заряд, чтобы вернуться к своему первоначальному потенциалу разница.
Чистый эффект диэлектрика заключается в увеличении количества заряда, который конденсатор может хранить при заданной разности потенциалов.Весь смысл использования конденсатора заключается в накоплении заряда, поэтому придумать способ накопить больше заряда при том же количестве усилий – это хорошо.
Добавление диэлектрика к конденсатору увеличивает емкость в K и
раз.Заряд конденсатора увеличивается, когда напряжение остается постоянным, и
Если конденсатор отключен, то есть заряд остается постоянным, потенциал на конденсаторе будет уменьшаться.
Емкость конденсатора с параллельными пластинами зависит от:
Расстояние d между двумя пластинами
Область среды А между пластинами
Согласно закону Гаусса электрическое поле можно записать как
Поскольку мы знаем, что емкость определяется как V = Q / C, поэтому емкость можно переписать как
Когда пластины расположены очень близко и , площадь пластин большая , мы получаем максимальную емкость .
Рис. 1.7 диэлектрик, расположенный между двумя электродами
На двух пластинах микроскопический дипольный момент материала будет экранировать заряды. Таким образом, изменится влияние диэлектрического материала, который вставлен между двумя пластинами. Материалы имеют проницаемость , которая задается относительной проницаемостью K
Таким образом, емкость определяется как:
Емкость конденсатора с параллельными пластинами может быть увеличена путем введения диэлектрика между пластинами, так как диэлектрик имеет проницаемость k, которая больше 1.K также иногда называют диэлектрической постоянной .
1. Когда диэлектрик полностью заполнен между пластинами
Когда пространство между двумя пластинами полностью заполнено диэлектриком, то относительная проницаемость er,
C 0 = C x e r
2. Когда диэлектрик частично заполнен между пластинами
Когда в конденсаторе с параллельными пластинами, пространство между пластинами частично заполнено воздухом и частично другим веществом, его емкость можно рассчитать.
Пусть существует конденсатор с параллельными пластинами, в котором среда между параллельными пластинами состоит в основном из воздуха и частично из другого вещества.
Дополнительная информация
Влияние диэлектриков на емкость
CBSE онлайн класс 10 | CBSE онлайн-класс 12 | CBSE онлайн-коучинг
Что такое емкость? | Fluke
Емкость – это способность компонента или схемы собирать и накапливать энергию в виде электрического заряда.
Конденсаторы – это устройства накопления энергии, доступные во многих размерах и формах. Они состоят из двух пластин из проводящего материала (обычно тонкого металла), зажатых между изолятором из керамики, пленки, стекла или других материалов, даже воздуха.
Изолятор, также известный как диэлектрик , увеличивает зарядную емкость конденсатора. Конденсаторы иногда называют конденсаторами в автомобильной, морской и авиационной промышленности.
Внутренние пластины подключены к двум внешним клеммам, которые иногда бывают длинными и тонкими и могут напоминать крошечные металлические антенны или ножки.Эти клеммы можно включить в цепь.
Конденсаторы и батареи накапливают энергию. В то время как батареи выделяют энергию постепенно, конденсаторы разряжают ее быстро.
Как работает конденсатор?
Конденсатор собирает энергию (напряжение), когда ток течет по электрической цепи. Обе пластины содержат одинаковые заряды, и когда положительная пластина накапливает заряд, равный заряд стекает с отрицательной пластины.
Когда цепь отключена, конденсатор сохраняет собранную энергию, хотя обычно происходит небольшая утечка.
Различные конденсаторы (показаны цветом) в печатной плате.Емкость выражается как отношение электрического заряда на каждом проводе к разности потенциалов (т. Е. Напряжению) между ними.
Емкость конденсатора измеряется в фарадах (F), единицах, названных в честь английского физика Майкла Фарадея (1791–1867).
Фарад – это большая емкость. Большинство бытовых электрических устройств содержат конденсаторы, производящие лишь доли фарада, часто тысячные доли фарада (или микрофарады, мкФ), или даже пикофарады (триллионные доли, пФ).
Суперконденсаторы, тем временем, могут хранить очень большие электрические заряды в тысячи фарад.
Как увеличить емкость
Емкость можно увеличить, если:
- Пластины (проводники) конденсатора расположены ближе друг к другу.
- Пластины большего размера обеспечивают большую площадь поверхности.
- Диэлектрик – лучший изолятор для данной области применения.
В электрических цепях конденсаторы часто используются для блокировки постоянного тока (dc), позволяя протекать переменному току (ac).
Некоторые цифровые мультиметры предлагают функцию измерения емкости, поэтому технические специалисты могут:
- Определить неизвестный или немаркированный конденсатор.
- Обнаружение обрыва или короткого замыкания конденсаторов.
- Измерьте конденсаторы напрямую и отобразите их значение.
Ссылка: Принципы цифрового мультиметра Глена А. Мазура, American Technical Publishers.
Конденсаторы и емкость
Различные типы конденсаторов
Конденсатор – электронное устройство для накопления заряда.Конденсаторы можно найти почти во всех электронных схемах, кроме самых простых. Есть много разных типов конденсаторов, но все они работают одинаково. Упрощенный вид конденсатора представляет собой пару металлических пластин, разделенных зазором, в котором находится изолирующий материал, известный как диэлектрик. Этот упрощенный конденсатор также выбран, поскольку символ электронной схемы для конденсатора представляет собой пару параллельных пластин, как показано на рисунке 1.
Рис. 1. Символ неполяризованного конденсатора.
Обычно электроны не могут войти в проводник, если не существует пути для выхода равного количества электронов. Однако лишние электроны могут быть «втиснуты» в проводник без пути для выхода, если электрическое поле может развиваться в пространстве относительно другого проводника. Количество дополнительных свободных электронов, добавленных к проводнику (или отнятых свободных электронов), прямо пропорционально величине потока поля между двумя проводниками.
В этом упрощенном конденсаторе диэлектрик – воздух.Когда на клеммы конденсатора подается напряжение В , электроны перетекают на одну из пластин и уносятся с другой пластины. Общее количество электронов в конденсаторе остается прежним. На одной отрицательной пластине их больше, а на положительной – меньше.
Рисунок 2. Зарядка конденсатора от аккумулятора
Если бы напряжение было увеличено, увеличившаяся разность потенциалов между пластинами подтолкнула бы больше электронов к отрицательно заряженной пластине.Мы могли измерить заряд, накопленный на пластине, в зависимости от различных приложенных напряжений.
При нулевом напряжении пластины конденсатора нейтральны, поэтому заряд не сохраняется. (мы предполагаем, что мы начали с полностью разряженного конденсатора), при напряжении V заряд на пластинах равен Q, а при удвоенном напряжении заряд удваивается. Мы обнаруживаем, что с увеличением напряжения заряд увеличивается линейно. Мы можем построить это как прямую линию.
Предположим, что мы уходим, проводим некоторые исследования и возвращаемся с лучшим конденсатором, который хранит больше заряда для данного напряжения, мы можем построить график зависимости сохраненного заряда от приложенного напряжения.
Это можно было бы представить как другую линию с более крутым уклоном.Если бы мы построили много графиков для разных конденсаторов, мы получили бы много прямых линий. Мы можем сказать, что мера емкости – это то, сколько заряда сохраняется при заданном напряжении. Иногда это выражается как Q = CV .
Конечно, при зарядке конденсатора должна выполняться работа по перемещению заряда. Следовательно, необходимо подавать энергию, и эта энергия доступна, когда конденсатор разряжен.
Проделанная работа определяется как W = qV .Первоначально заряд легко перемещается на пластины конденсатора, однако по мере того, как больше заряда перемещается на пластины конденсатора, сила отталкивания между зарядами затрудняет добавление заряда, когда сила отталкивания зарядов равна мощности батареи, больше нельзя перемещать заряд на пластины. Следовательно, средняя работа составляет 1/2 qV . Если мы посмотрим на наш график зависимости заряда от напряжения, то увидим, что это то же самое, что и площадь под кривой. В общем, проделанная работа равна переданной энергии.Математически,
Факторы, влияющие на емкость
Как увеличить емкость конденсатора с параллельными пластинами? На емкость конденсатора с параллельными пластинами влияют три фактора.
Площадь
Конденсатор переменной емкости
Увеличивая площадь пластин, мы можем поместить на пластины больше заряда, прежде чем силы отталкивания станут проблемой. Следовательно, емкость пропорциональна площади перекрытия пластин.В переменном конденсаторе площадь перекрытия может быть увеличена или уменьшена путем вращения взаимопроникающих пластин, таким образом увеличивая или уменьшая емкость. Пластины электролитических конденсаторов протравлены для получения шероховатой поверхности, которая еще больше увеличивает площадь поверхности.
Разделение
Уменьшение расстояния между пластинами снижает напряжение конденсатора, поскольку электрическое поле не зависит от расстояния между пластинами. Напряжение на конденсаторе В = Ед .Следовательно, напряжение увеличивается. Для постоянного заряда Q , C = Q / V = Q / Ed.
Диэлектрическая проницаемость
Емкость конденсатора с параллельными пластинами определяется выражением C = ε r A / d , где A – площадь пластин, d – расстояние между пластинами, а ε r – площадь пластин. относительная проницаемость диэлектрика между пластинами. Относительная проницаемость – это некоторый коэффициент, K , умножающий допустимость свободного пространства ε 0 .ε 0 имеет значение 8,85×10 -12 F.m -1 .
Полный список относительных допусков можно найти практически для любого диэлектрического материала. Чем больше относительная проницаемость, тем больше емкость конденсатора. Хорошие материалы – слюда, полистирол, масло.
ε r = K ε 0
Конденсаторные сети
Рисунок 3. Последовательные и параллельные сети конденсаторов
серии
Рассмотрим последовательную сеть конденсаторов, показанную на рисунке 3a.где положительная пластина соединена с отрицательной пластиной следующего. Какова эквивалентная емкость сети? Посмотрите на пластины посередине, эти пластины физически отключены от цепи, поэтому общий заряд на них должен оставаться постоянным. Следовательно, когда на оба конденсатора подается напряжение, заряд + Q на положительной пластине конденсатора C 1 должен уравновешиваться зарядом – Q на отрицательной пластине конденсатора C. 2 .В результате оба конденсатора обладают одинаковым зарядом Q. Падения потенциала В 1 и В 2 на двух конденсаторах в целом разные. Однако сумма этих падений равна общему падению потенциала В , приложенному к входным и выходным проводам. В = В 1 + В 2 . Эквивалентная емкость пары снова составляет C T = Q / V .Таким образом, 1/ C T = V / Q = ( V 1 + V 2 ) / Q = V 1 / Q Q V 2 / Q подача
Как правило, для конденсаторов N , соединенных последовательно, это
Соединяя конденсаторы в сериях, вы сохраняете меньше заряда, поэтому есть ли смысл подключать конденсаторы последовательно? Иногда это делается потому, что конденсаторы имеют максимальное рабочее напряжение, и, если подключить два конденсатора с максимальным напряжением 900 вольт последовательно, вы можете увеличить рабочее напряжение до 1800 вольт.
Параллельный
Для параллельной схемы, такой как на рисунке 3b. напряжения одинаковы для всех компонентов. Однако общий заряд делится между двумя конденсаторами, поскольку он должен распределяться таким образом, чтобы напряжение на них было одинаковым. Кроме того, поскольку конденсаторы могут иметь разные емкости C 1 и C 2 , заряды Q 1 и Q 2 также должны быть разными.Эквивалентная емкость C T пары конденсаторов – это просто отношение Q / V , где Q = Q 1 + Q 2 – общий накопленный заряд. Отсюда следует, что C T = Q / V = (Q 1 + Q 2 ) / V = Q 1 / V + Q 2 / В подача
Из предыдущего обсуждения довольно очевидно, что для конденсаторов N , подключенных параллельно, общая емкость составляет
Общая емкость увеличивается за счет параллельного соединения конденсаторов, поэтому мы получаем большую емкость, чем это возможно при использовании одного конденсатора.В лабораториях физики высоких энергий часто есть большие батареи конденсаторов, которые могут накапливать большое количество энергии, которая высвобождается за очень короткое время. Самая большая батарея конденсаторов в 2006 году может хранить 50 МДж энергии.
Конденсаторы зарядные и разрядные
Цепь, состоящая из батареи, переключателя, резистора и конденсатора в последовательном контуре, называется RC-цепью. Закон Кирхгофа по напряжению для этой схемы имеет вид
V = IR + Q / C .Если выразить чисто в терминах заряда, это становится
V = dQ / dt R + Q / C .
Это дифференциальное уравнение, решение которого является экспоненциальной функцией. Когда переключатель замкнут, конденсатор со временем заряжается:
Q = Q f (1 – e -t / RC ),
, где Q – это заряд в момент времени t и Q f – последний заряд конденсатора.Обратите внимание, что Q никогда не равно Q f , но поскольку t становится чрезвычайно большим, Q становится произвольно близким к Q f . Произведение RC называется постоянной времени RC и является характеристической величиной RC цепи. Когда t = RC , конденсатор заряжен до доли (1 – 1/ e , около 63%) от своего окончательного значения. Необходимо использовать постоянную времени, а не какое-то конечное время, поскольку процесс асимптотический.Его значение – произвольный выбор; мы, естественно, выбираем значение в терминах экспоненциального основания (когда показатель отрицательный).
Мигающая анимация 1. Измените значения резистора и конденсатора, чтобы увидеть влияние на время достижения конденсатором пикового напряжения.
Flash Animation 2. Зарядите конденсатор, пока он не достигнет пика, а затем разрядите его. Как значения R и C влияют на процессы?
Типы конденсаторов
Конденсаторы электролитические
Алюминиевые электролитические конденсаторы изготавливаются путем наложения электролитической бумаги между анодной и катодной фольгами и последующего наматывания результата.Процесс изготовления электрода, обращенного к поверхности протравленной анодной фольги, чрезвычайно сложен. Следовательно, противоположный электрод создается путем заполнения конструкции электролитом. Благодаря этому процессу электролит по существу выполняет роль катода.
Электролитические конденсаторы пропитаны жидкостью или бумагой, пропитанной жидкостью, которая не является диэлектриком, но при приложении напряжения создает слой оксида алюминия, который действует как диэлектрик. Реакция зависит от полярности приложенного напряжения.Если полярность поменять местами, конденсатор будет выделять газ и, вероятно, взорвется или лопнет из-за давления внутри, поэтому он не подходит для применения с переменным током.
MEMs Конденсаторы
Микро-электромеханические системы (MEM) – это небольшие устройства, изготовленные из кремния. Пластинчатые конденсаторы могут быть изготовлены с небольшими изменениями емкости при увеличении или уменьшении расстояния между пластинами. Небольшие устройства можно использовать как датчики и гироскопы.
Распространенными типами устройств являются конденсаторы с параллельными пластинами для определения положения. Кроме того, взаимопроникающие гребенчатые конструкции, в которых емкость может быть изменена с использованием перемещения одной гребенки относительно другой, либо в поперечном направлении, либо в продольном направлении. Из-за их небольшого размера изменение емкости очень мало, порядка 10 -15 Ф (фемто-Фарад).
Конденсаторы танталовые
Танталовые конденсаторы поляризованы и имеют низкое напряжение, как электролитические конденсаторы.Они дороги, но очень малы, поэтому используются там, где требуется большая емкость в небольших размерах, например, в мобильных телефонах или портативных компьютерах. Эти конденсаторы становятся все более важными, поскольку растет спрос на все меньшие электронные устройства. Колумбит-танталит – колтан , сокращенно руда, из которой очищается тантал, добывается в Австралии, г. Егпыт. Высокий спрос на руду также финансировал гражданские войны в Демократической Республике Конго. В отчете Совета безопасности ООН говорится, что большая часть руды добывается незаконно и переправляется через восточные границы страны вооруженными формированиями из соседних Уганды, Бурунди и Руанды, обеспечивая доход для финансирования военной оккупации Конго.
Суперконденсаторы
Суперконденсаторы – это конденсаторы, которые способны накапливать большие количества заряда и, следовательно, энергии в очень небольшом объеме. Накопление энергии происходит за счет статического заряда, а не электрохимического процесса, присущего батарее. Применение разности напряжений на положительной и отрицательной пластинах заряжает суперконденсатор. Эта концепция похожа на электрический заряд, который накапливается при ходьбе по ковру. Впервые суперконденсатор был задуман в 1957 году, но теперь исследования сосредоточены на их использовании в качестве источников питания с малым весом в качестве альтернативы батареям.суперконденсатор переходит в аккумуляторную технологию благодаря использованию специальных электродов и небольшого количества электролита. Суперконденсаторы могут найти применение, например, в качестве временных резервных источников питания в электросети или для обеспечения первоначального всплеска энергии для движения электромобилей.
Сводка
Конденсаторыобладают способностью заряжать и высвобождать накопленный заряд очень быстро, что позволяет им функционировать разными способами. Они занимают важное место во всем: от схем стабилизации напряжения в чувствительной электронике до помощи в преобразовании переменного тока в постоянный для зарядки аккумуляторов во всем, от мобильных скутеров до портативных компьютеров.
Конденсаторы – это устройства, накапливающие заряд. Емкость определяется как отношение накопленного заряда к единице напряжения. C = Q / V
Емкость конденсатора с параллельными пластинами определяется как C = ε r A / d .
Энергия, запасенная в конденсаторе, рассчитывается по работе, совершаемой при перемещении заряда по пластинам. dW = V dq . Накопитель энергии – это область под графиком заряда / напряжения. 1 / 2QV или из C = Q / V, 1 / 2CV 2 = 2Q 2 / C.
Конденсатор
КонденсаторКонденсаторы
Емкость
Конденсатор – это устройство для хранения разделенного заряда. Нет единого электронного компонента сегодня играет более важную роль, чем конденсатор. Это устройство используется для хранить информацию в памяти компьютера, регулировать напряжение в источниках питания, для создания электрических полей, для хранения электрической энергии, для обнаружения и производить электромагнитные волны и измерять время.Любые два проводника, разделенные изолирующей средой, образуют конденсатор.
А Параллельно-пластинчатый конденсатор состоит из двух пластин, разделенных тонкой изоляционной материал, известный как диэлектрик . В параллельной пластине электроны конденсатора переносятся с одной параллельной пластины на другую.
Мы уже показали, что электрическое поле между пластинами постоянно с величиной E = σ / ε 0 и указывает от положительной пластины к отрицательной.
Следовательно, разность потенциалов между отрицательной и положительной пластинами равна предоставлено
∆U = U pos – U neg = -q Σ neg pos E ∙ ∆ r = q E d.
При суммировании ∆ r указывает от отрицательной пластины к положительной в
противоположном направлении от E .
Следовательно E ∙ ∆ r =
-E∆r, а знаки минус отменяют.
Положительный
пластина имеет более высокий потенциал, чем отрицательная пластина.
Силовые линии и эквипотенциальные линии для Постоянное поле между двумя заряженными пластинами показано справа. Одна пластина конденсатора удерживает положительный заряд Q, а другая – отрицательный заряд -Q. Заряд Q на пластинах пропорционален потенциалу разность V на двух пластинах. Модель емкость C – пропорциональная константа,
Q = CV, C = Q / V.
C зависит от геометрии конденсатора и типа диэлектрического материала использовал. Емкость параллельного пластинчатого конденсатора с двумя пластинами площадью А расстояние d и отсутствие диэлектрического материала между пластинами составляет
C = ε 0 A / d.
(Электрическое поле E = σ / ε 0 .
Напряжение V = Ed = σd / ε 0 . Заряд Q = σA. Следовательно, Q / V =
σAε 0 / σd = Aε 0 / d.)
Единица измерения емкости в системе СИ:
Кулон / Вольт = Фарад (Ф).
Типичный
конденсаторы имеют емкость в диапазоне от пикофарад до микрофарад.
Емкость говорит нам, сколько заряда устройство хранит для данного Напряжение. Диэлектрик между проводниками увеличивает емкость конденсатор. Молекулы диэлектрического материала поляризованы в поле между двумя проводниками. Весь отрицательный и положительный заряд диэлектрик смещен на небольшую величину относительно друг друга.Этот приводит к эффективному положительному поверхностному заряду на одной стороне диэлектрика. и отрицательный поверхностный заряд на другой стороне диэлектрика. Эти эффективные поверхностные заряды на диэлектрике создают электрическое поле, которое противостоит полю, создаваемому поверхностными зарядами на проводниках, и, таким образом, снижает напряжение между проводниками. Чтобы поддерживать напряжение, больше заряда необходимо надеть на проводники. Таким образом, конденсатор накапливает больше заряда в течение заданное напряжение.Диэлектрическая проницаемость κ – это отношение напряжения V 0 между проводниками без диэлектрика к напряжение V с диэлектриком, κ = V 0 / V, для данного количества заряда Q на проводниках.
На диаграмме выше такое же количество заряда Q на проводников приводит к меньшему полю между пластинами конденсатора с диэлектрик. Чем выше диэлектрическая проницаемость κ, тем больше заряда может хранить конденсатор при заданном напряжении.Для параллельной пластины конденсатор с диэлектриком между пластинами, емкость
C = Q / V = κQ / V 0 =
κε 0 A / d = εA / d,
, где ε = κε 0 .
Статическая диэлектрическая проницаемость любого материала всегда больше 1.
Типичная диэлектрическая проницаемость
|
|
Если диэлектрик с диэлектрической проницаемостью κ вставляется между пластинами параллельной пластины конденсатора, а напряжение поддерживается постоянным аккумулятором, заряд Q на пластинах увеличивается в κ раз. Батарея перемещает больше электронов с положительной пластины на отрицательную. Величина электрического поля между пластинами E = V / d остается неизменной. тем же.
Если диэлектрик вставлен между пластинами параллельной пластины конденсатор, и заряд на пластинах остается прежним, потому что конденсатор отключается от АКБ, то напряжение V уменьшается в раз из κ, а электрическое поле между пластиной E = V / d уменьшается в 2 раза. κ.
Модуль 2: Вопрос 2:
(a) Конденсатор с параллельными пластинами изначально имеет напряжение 12 В и
остается подключенным к батарее.Если теперь расстояние между пластинами увеличено вдвое, что
бывает?
(b) Конденсатор с параллельными пластинами первоначально подключается к батарее, а
пластины удерживают заряд ± Q. Затем аккумулятор отключается. Если расстояние между пластинами равно
теперь вдвое, что происходит?
Подсказка: аккумулятор является зарядным насосом. Может качать заряд с одной пластины
к другому, чтобы поддерживать постоянную разность потенциалов.
Нет батареи <--> нет зарядного насоса. Заряд не может перемещаться с одной пластины на
Другие.
Обсудите это со своими однокурсниками на дискуссионном форуме!
Ссылка: PhET Конденсаторная лаборатория (базовая)
Энергия, запасенная в конденсаторе
Энергия U, запасенная в конденсаторе, равна работе
W сделано при разделении
заряды на проводниках. Чем больше заряда уже накоплено на пластинах, тем
необходимо проделать больше работы по разделению дополнительных сборов из-за сильного
отталкивание между одноименными зарядами.При заданном напряжении требуется бесконечно малое
объем работы ∆W = V∆Q для отделения дополнительной бесконечно малой суммы заряда
∆Q.
(Напряжение V – это количество работы на единицу заряда.)
Поскольку V = Q / C,
V увеличивается линейно с Q. Общая работа, проделанная при зарядке конденсатора
является
W = U = Σ V ∆Q = V в среднем Q
= ½VQ.
Используя Q = CV, мы также можем написать
U = ½ (Q 2 / C) или
U = ½CV 2 .
Проблема:
Каждая ячейка памяти в компьютере содержит конденсатор для хранения заряда. Сохраняемый или не сохраняемый заряд соответствует двоичным цифрам 1 и 0. Для более плотной упаковки ячеек в пластины конденсатора установлены вертикально вдоль стенок траншеи выгравирован на кремниевом чипе. Если у нас емкость 50 фемтоФарад = 50 * 10 -15 F и каждая пластина имеет площадь 20 * 10 -12 м 2 (траншеи микронного размера), что такое разделение пластин?
Решение:
- Рассуждение:
Емкость параллельного пластинчатого конденсатора с двумя пластинами площадью А расстояние между пластинами равно d и отсутствие диэлектрического материала C = ε 0 A / d. - Детали расчета:
C = ε 0 A / d, d = ε 0 A / C = (8,85 * 10 -12 * 20 * 10 -12 / (50 * 10 -15 )) м = 3,54 * 10 -9 м.
Типичные атомные размеры порядка 0,1 нм, поэтому траншея находится на порядка 30 атомов в ширину.
Для любого изолятора существует максимальное поддерживаемое электрическое поле без ионизации молекул. Для конденсатора это означает наличие максимально допустимое напряжение, которое может быть приложено к проводникам.Этот максимальное напряжение зависит от диэлектрика в конденсаторе. Соответствующие максимальное поле E b называется диэлектрической прочностью материала. Для более сильных полей конденсатор “ выходит из строя ” (аналогично коронный разряд) и обычно разрушается. Большинство конденсаторов, используемых в электрических схемы имеют как емкость, так и номинальное напряжение. Это напряжение пробоя V b относится к диэлектрической прочности E b .Для параллельной пластины конденсатор имеем V b = E b d.
| Материал | Диэлектрическая прочность (В / м) |
|---|---|
| Воздух | 3 * 10 6 |
| Бакелит | 24 * 10 6 |
| Неопреновый каучук | 12 * 10 6 |
| нейлон | 14 * 10 6 |
| Бумага | 16 * 10 6 |
| полистирол | 24 * 10 6 |
| Стекло Pyrex | 14 * 10 6 |
| кварцевый | 8 * 10 6 |
| Силиконовое масло | 15 * 10 6 |
| титанат стронция | 8 * 10 6 |
| тефлон | 60 * 10 6 |
Электромагнетизм: емкость
Итак, если индуктивность связана с накопленной энергией в магнитном поле, что представляет собой накопленная энергия в электрическом поле? Это тема Емкость .2]. Это показано на рисунке 1:
Рисунок 1. Напряжение на параллельном пластинчатом конденсаторе.
Емкость этого конденсатора с параллельными пластинами может быть рассчитана для этой структуры. Напомним, что емкость – это просто отношение заряда пластин конденсатора к напряжению на пластинах. Результат можно найти:
| [Уравнение 1] |
|---|
В уравнении [1] – диэлектрическая проницаемость материала внутри конденсатора (где находятся электрические поля).Следовательно, мы видим, что в уравнении [1] емкость может быть увеличена. за счет увеличения диэлектрической проницаемости материала внутри конденсатора (отношение диэлектрической проницаемости материала к диэлектрической проницаемости свободного пространства или воздуха также называется диэлектрическая постоянная).
Из уравнения [1] видно, что если расстояние между пластинами ( d ) уменьшается, емкость увеличивается. Это потому что Электрические поля будут сильнее, а емкость связана с накопленной энергией внутри электрических полей.Если площадь поверхности пластин увеличится, емкость тоже увеличится. Это потому, что будет больше места для существования электрических полей, а значит, больше энергии.
Уравнение [1] представляет собой уравнение основной емкости. Из него мы можем понять, как увеличить или уменьшить емкость объекта. В теории антенн емкость обычно плохо влияет на излучение, потому что накопленная энергия не излучается. Часто тогда паразитная (или нежелательная) емкость должна быть уменьшена.Из уравнения [1] мы знаем методы уменьшения емкости:
(1) Уменьшите диэлектрическую проницаемость материала внутри конденсатора
(2) Увеличьте расстояние между проводящими материалами, из которых состоит конденсатор
(3) Уменьшите площадь металлической поверхности конденсатора
Эти 3 правила составляют все, что вам нужно знать об увеличении или уменьшении емкости.
Зависимость напряжения и тока конденсаторов
Что касается индукторов, мы увидели, что природа работала, чтобы «отменить» потерю потока (магнитного поля) внутри индуктора, вызывая электрический ток в катушке индуктивности для противодействия этим потерям.Точно так же конденсаторы не любят терять электрические. Можно подумать, что поле внутри конденсатора и заряд противодействуют этому изменению. Это не совсем строго, и настоящий Причина исходит из уравнений Максвелла, к которым мы вернемся позже. Но последнее, что мы должны знать о емкости это соотношение напряжение / ток для конденсатора с емкостью C :
| [Уравнение 1] |
|---|
Уравнение [1] утверждает, что ток через конденсатор пропорционален скорости изменения напряжения на конденсаторе.Следовательно, постоянный ток. напряжение на конденсаторе не дает тока – а быстро меняющееся напряжение (высокочастотное напряжение) вызывает относительно большой ток через конденсатор.


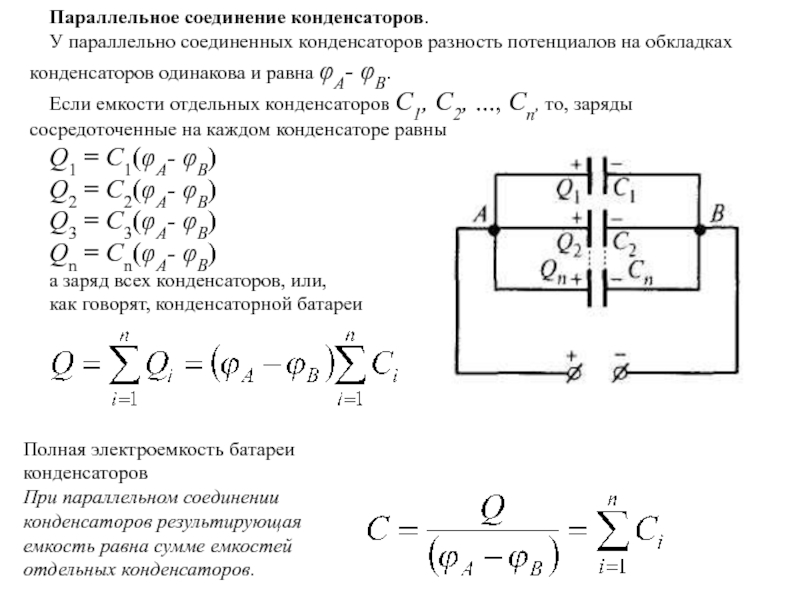
 Из физики известно, что под действием электростатического
поля, возникающего между двумя заряженными обкладками, происходит поляризация диэлектрика, в итоге вызывающая ослабление
напряженности этого самого поля. Для учета этого явления, вместо эмпирического коэффициента k, в формулу необходимо
ввести специальные физические величины, называемые диэлектрическими постоянными: чтобы получить уравнение, приведенное ниже:
Из физики известно, что под действием электростатического
поля, возникающего между двумя заряженными обкладками, происходит поляризация диэлектрика, в итоге вызывающая ослабление
напряженности этого самого поля. Для учета этого явления, вместо эмпирического коэффициента k, в формулу необходимо
ввести специальные физические величины, называемые диэлектрическими постоянными: чтобы получить уравнение, приведенное ниже: Если посмотреть на реальные схемы лампового усилителя, то это не такая уж и большая емкость,
а подобные размеры конденсатора, просто недопустимо большие. Разумеется конструкции реальных конденсаторов таковы, что их
размеры намного меньше, чем в рассмотренном примере.
Если посмотреть на реальные схемы лампового усилителя, то это не такая уж и большая емкость,
а подобные размеры конденсатора, просто недопустимо большие. Разумеется конструкции реальных конденсаторов таковы, что их
размеры намного меньше, чем в рассмотренном примере. Такая конструкция часто используется для слюдяных
посеребренных конденсаторов и также для объединенных в батареи пленочно-фольговых конденсаторов.
Такая конструкция часто используется для слюдяных
посеребренных конденсаторов и также для объединенных в батареи пленочно-фольговых конденсаторов. Так как используемый диэлектрик будет иметь значение относительной диэлектрической проницаемости
εr > 1, то это приведет к дополнительной возможности еще больше уменьшить геометрические размеры
конденсатора при сохранении той же самой величины его емкости. (Либо, при тех же размерах получить увеличение емкости.)
Так как используемый диэлектрик будет иметь значение относительной диэлектрической проницаемости
εr > 1, то это приведет к дополнительной возможности еще больше уменьшить геометрические размеры
конденсатора при сохранении той же самой величины его емкости. (Либо, при тех же размерах получить увеличение емкости.) Этот фактор
как раз и определяет предельное значение рабочего напряжения конденсатора.
Этот фактор
как раз и определяет предельное значение рабочего напряжения конденсатора.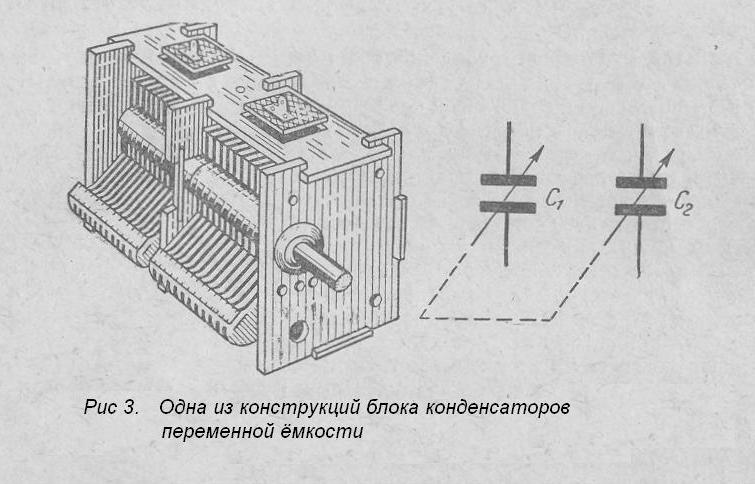 Следует отметить, что при измерении tgδ не делается различий
между параллельным сопротивлением утечки диэлектрика и любым последовательным сопротивлением, таким как сопротивление подводящих
проводов или сопротивление обкладок.
Следует отметить, что при измерении tgδ не делается различий
между параллельным сопротивлением утечки диэлектрика и любым последовательным сопротивлением, таким как сопротивление подводящих
проводов или сопротивление обкладок. Простая эквивалентная схема замещения реального
конденсатора выглядит следующим образом: параллельно емкости включается сопротивление потерь диэлектрика, а затем, последовательно
этой цепи — эффективное последовательное сопротивление выводов и обкладок, а также паразитная индуктивность выводов (рис. 5.3).
Простая эквивалентная схема замещения реального
конденсатора выглядит следующим образом: параллельно емкости включается сопротивление потерь диэлектрика, а затем, последовательно
этой цепи — эффективное последовательное сопротивление выводов и обкладок, а также паразитная индуктивность выводов (рис. 5.3). А это уже в свою очередь позволит им выполнять их работу в течение продолжительного времени, даже при условии того, что в них будет напрочь отсутствовать доступ к внешней энергии.
А это уже в свою очередь позволит им выполнять их работу в течение продолжительного времени, даже при условии того, что в них будет напрочь отсутствовать доступ к внешней энергии.