Формулы расчета резонансной частоты колебательного контура
Для генерации высокочастотных волн часто применяются схемы на основе колебательного контура. Подобрав параметры элементов цепи, можно производить частоты свыше 500 МГц. Схемы используются в ВЧ-генераторах, высокочастотном нагреве, телевизионных и радиоприемниках.
Колебательный контур
Колебательный контур
Колебательный контур – это последовательное или параллельное соединение индуктивных и конденсаторных элементов, генерирующих электромагнитные колебания любой заданной частоты. Оба компонента схемы способны хранить энергию.
Когда существует разность потенциалов на конденсаторных пластинах, он сохраняет энергию электрического поля. Аналогично энергия сохраняется в магнитном поле индуктивной катушки.
Работа колебательного контура
Когда первоначально конденсатор подключается к источнику постоянного тока, на нем возникает разность потенциалов. Одна пластина имеет избыток электронов и заряжена отрицательно, другая – недостаток электронов и заряжена положительно.
Что будет, если в цепь включить индуктивную катушку:
- При замыкании контакта, соединяющего электроцепь, конденсатор начинает разряжаться через катушку индуктивности. Накопленная им энергия электрического поля снижается;
- Ток, протекающий через катушку L, индуцирует ЭДС, противостоящую потоку электронов. Из-за этого скорость нарастания тока медленная. В катушке создается магнитное поле, которое начинает накапливать свою энергию. После полного разряда конденсатора поток электронов через катушку уменьшается до нуля. Электростатическая энергия, накопленная в конденсаторе, преобразуется в энергию магнитного поля катушки;
- Когда конденсатор разряжен, магнитное поле начинает постепенно разрушаться, но, согласно закону Ленца, индукционный ток катушки способствует заряду конденсатора с противоположной полярностью. Энергия, связанная с магнитным полем, снова превращается в электростатическую;
Важно! В идеальном случае, когда нет потерь на L и С, конденсатор зарядился бы до первоначального значения с противоположным знаком.
- После того, как уменьшающееся магнитное поле перезарядило конденсатор, он снова начинает разряжаться с потоком тока обратной направленности, а МП опять нарастает.
Последовательность зарядки и разрядки продолжается, то есть процесс преобразования электростатической энергии в магнитную и наоборот периодически повторяется, подобно маятнику, у которого потенциальная энергия циклически превращается в кинетическую и обратно.
Непрерывный процесс зарядки и разрядки приводит к меняющему направление движению электронов или к колебательному току.
Обмен энергией между L и С будет продолжаться бесконечно, если отсутствуют потери. Часть энергии теряется, рассеиваясь в виде тепла на проводах катушки, соединительных проводниках, из-за тока утечки конденсатора, электромагнитного излучения. Поэтому колебания будут затухающими.
Затухающие колебания
Резонанс
Если схема с конденсатором, катушкой и резистором возбуждается напряжением, постоянно меняющимся во времени с определенной частотой, то также изменяются реактивные сопротивления: индуктивное и емкостное.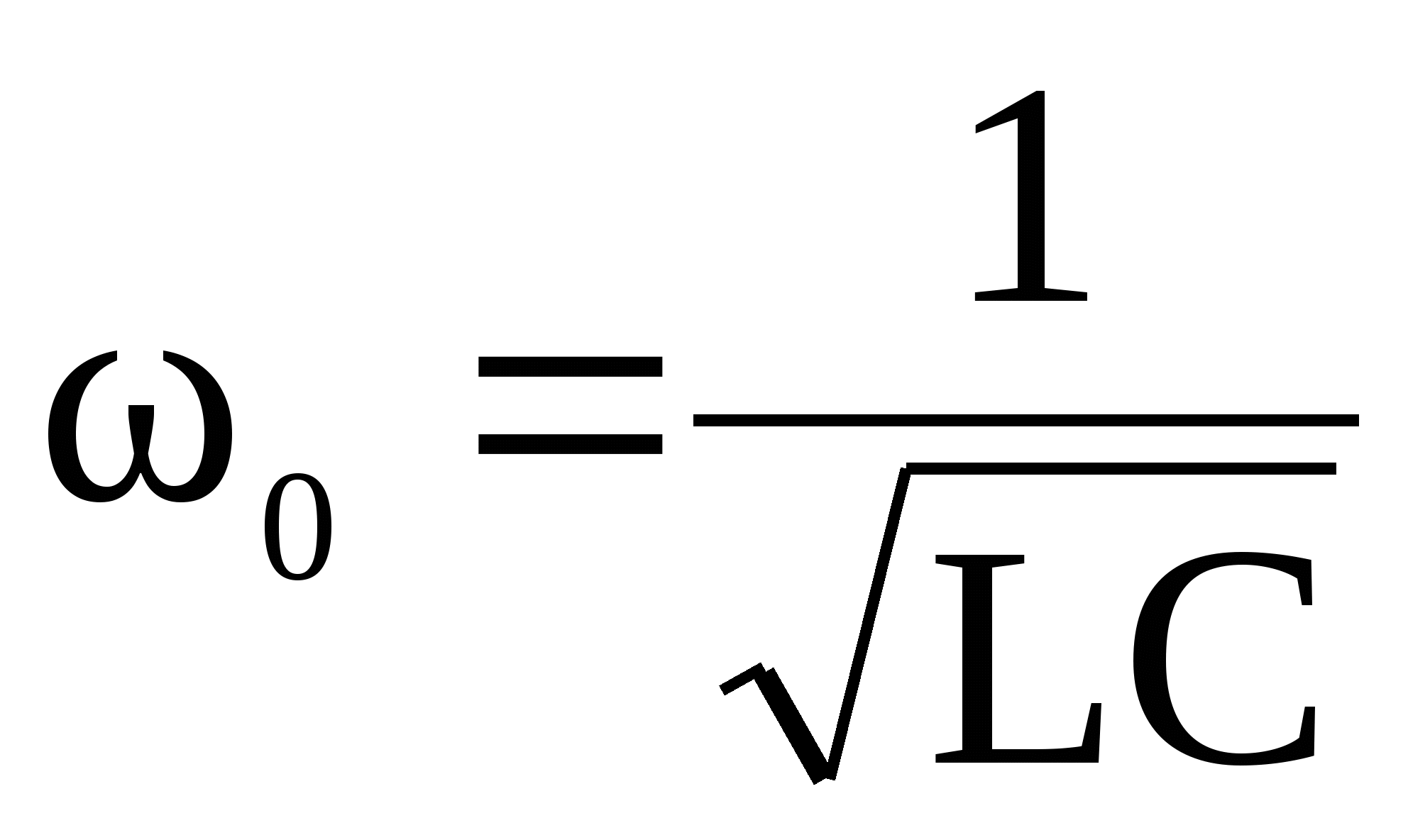 Амплитуда и частота выходного сигнала будет изменяться по сравнению с входным.
Амплитуда и частота выходного сигнала будет изменяться по сравнению с входным.
Индуктивное сопротивление прямо пропорционально частоте:
X(L) = 2π x f x L,
а емкостное сопротивление обратно пропорционально этому показателю:
X(C) = 1/(2π x f x C).
Важно! На более низких частотах индуктивное сопротивление незначительное, а емкостное будет высоким и сможет создавать практически разомкнутый контур. На высоких частотах картина обратная.
При конкретной комбинации конденсатора и катушки схема становится резонансной, или настроенной, имеющей частоту колебаний, при которой индуктивное сопротивление идентично емкостному. И они компенсируют друг друга.
Следовательно, в цепи остается исключительно активное сопротивление, противостоящее протекающему току. Созданные условия получили наименование резонанса колебательного контура. Фазовый сдвиг между током и напряжением отсутствует.
Резонанс LC-цепи
Для расчета резонансной частоты колебательного контура учитывается следующее условие:
X(L) = X(C).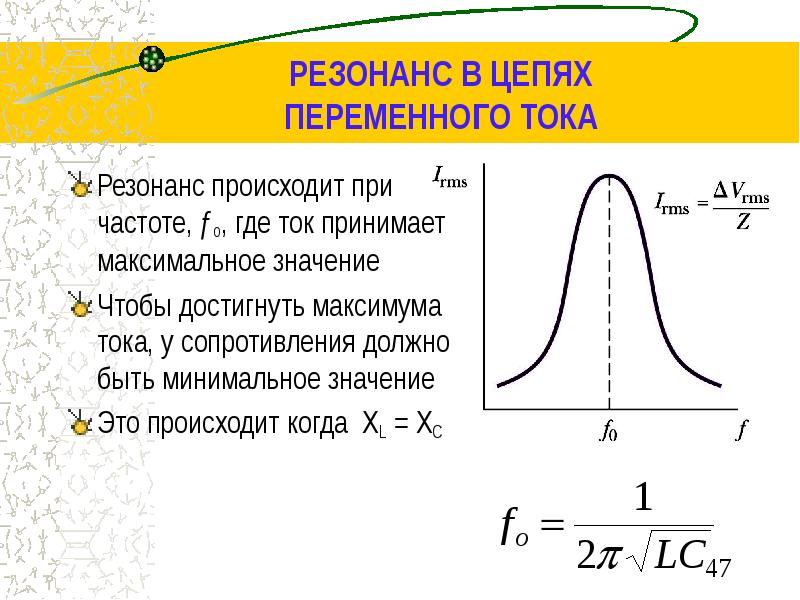
Следовательно, 2π x f x L = 1/(2πx f x C).
Отсюда получается формула резонансной частоты:
f = 1/(2π x √(L x C)).
Расчет резонансной частоты, индуктивности и емкости можно сделать на онлайн калькуляторе, подставив конкретные значения.
Скорость, с которой рассеивается энергия от LC-схемы, должна быть такой же, как энергия, подаваемая на схему. Устойчивые, или незатухающие, колебания производятся электронными схемами генераторов.
LC-цепи используются либо для генерации сигналов на определенной частоте, либо для выделения частотного сигнала из более сложного. Они являются ключевыми компонентами многих электронных устройств, в частности радиооборудования, используемого в генераторах, фильтрах, тюнерах и частотных микшерах.
Видео
Оцените статью:Формулы расчета резонансной частоты колебательного контура: амплитуда резонанса
Галилео Галилей, исследуя маятники и музыкальные струны, описал явление, которое впоследствии стали называть резонансом. Оно проявляется не только в акустике, но и в механике, электронике, оптике и астрофизике. Резонансный эффект имеет как положительные, так и отрицательные воздействия на колебательные системы.
Оно проявляется не только в акустике, но и в механике, электронике, оптике и астрофизике. Резонансный эффект имеет как положительные, так и отрицательные воздействия на колебательные системы.
Резонанс
Эффект резонанса
Ярким примером механического класса резонаторов является пружинный маятник. Профессор из технологического Массачусетского института (в Америке), В. Левин, акцентирует внимание своих студентов на то, что резонанс (resonance) – это эффект, сопряжённый с увеличением амплитуды. Для демонстрации явления используется установка. Она состоит из следующих компонентов:
- электродвигатель;
- механизм, превращающий вращение в возвратно-поступательное движение;
- ЛАТР – лабораторный автотрансформатор;
- медная пружина из проволоки с набором грузиков;
- направляющая для пружины.
Направление колебания пружины – вертикальное. Вращение вала мотора заставляет пружину совершать колебания. С помощью автотрансформатора присутствует возможность регулировать напряжение. Регулировка позволяет варьировать частоту вращения вала и колебаний маятника. При изменении частоты вращения вала амплитуда возвратно-поступательного движения остаётся неизменной.
Регулировка позволяет варьировать частоту вращения вала и колебаний маятника. При изменении частоты вращения вала амплитуда возвратно-поступательного движения остаётся неизменной.
Перед опытом замеряется удлинение медной пружины под действием грузиков (для оценки резонансной частоты пружины). Изменение скорости вращения вала заставляет амплитуду колебания конца пружины с грузом изменяться. Амплитуда увеличивается и на 1-м герце частоты становится максимальной (~30 см).
Важно! При дальнейшем увеличении скорости вращения вала амплитуда конца пружины начинает уменьшаться. Это означает, что resonance пройден. Если уменьшать напряжение, а с ним и частоту вращения двигателя, снова можно наблюдать эффект resonance колебания пружины.
Пружинный маятник
Добротность пружины Q определяется как отношение амплитуды колебания пружины Aпр к амплитуде колебания вынуждающей силы Aвс. В этом случае Q = Aпр/Aвс = 30/5 = 6, где Aвс = 5.
Определение колебательного контура
Резонансные явления, отмеченные в электротехнике, ярко выражены в схемах колебательных контуров (КК). Подобные конструкции представляют собой элементарные системы, способные осуществлять свободные колебания электромагнитной природы. Сам КК в цепи состоит из следующих элементов:
Подобные конструкции представляют собой элементарные системы, способные осуществлять свободные колебания электромагнитной природы. Сам КК в цепи состоит из следующих элементов:
- конденсатора;
- катушки индуктивности;
- источника тока.
Внимание! Выводы элементов схемы могут соединяться друг с другом параллельно или последовательно. Все зависит от того, какого результата нужно добиться от резонанса в КК.
Подключение к цепи индуктивной катушки
Включение в ёмкостную цепь катушки индуктивности сразу превращает её в КК. В зависимости от схемы подключения, различают два вида КК 1 класса: параллельный и последовательный.
Параллельный КК
В данной схеме конденсатор С соединён с катушкой L параллельно. Если заряженный конденсатор присоединить к катушке, то энергия, запасённая в нём, передастся ей. Через индуктивную катушку L потечёт ток, вызывая электродвижущую силу (ЭДС).
ЭДС самоиндукции L будет направлена на снижение тока в параллельной цепи.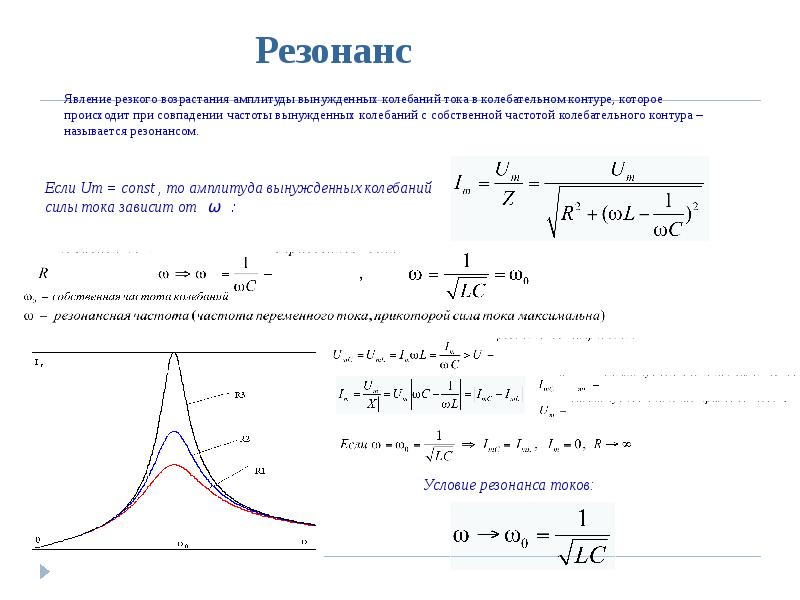 Ток, созданный этой ЭДС, и ток разряда ёмкости сначала одинаковы, а их суммарное значение равно нулю. Конденсатор передаст свою энергию Ec в катушку и полностью разрядится. Индуктивность, получив максимальную магнитную энергию EL, начнёт заряжать ёмкость напряжением уже другой полярности. Когда вся энергия из индуктивности перейдёт в ёмкость, конденсатор будет полностью заряжен. В цепи появляются колебания, такой контур называется колебательным.
Ток, созданный этой ЭДС, и ток разряда ёмкости сначала одинаковы, а их суммарное значение равно нулю. Конденсатор передаст свою энергию Ec в катушку и полностью разрядится. Индуктивность, получив максимальную магнитную энергию EL, начнёт заряжать ёмкость напряжением уже другой полярности. Когда вся энергия из индуктивности перейдёт в ёмкость, конденсатор будет полностью заряжен. В цепи появляются колебания, такой контур называется колебательным.
Параллельный КК
К сведению. Если бы в такой цепи отсутствовали потери, то такие колебания никогда не стали затухать. На практике, продолжительность процесса зависит от потери энергии. Чем больше потери, тем меньше длительность колебаний.
Параллельное соединение C и L вызывает резонанс токов. Это значит, что токи, проходящие через C и L, выше по значению, чем ток через сам контур, в конкретное число раз. Это число носит название добротности Q. Оба тока (емкостной и индуктивный) остаются внутри цепи, потому что они находятся в противофазе, и происходит их обоюдная компенсация.
Стоит отметить! На fрез величина R КК устремляется к бесконечности.
Последовательный КК
В этой схеме соединены последовательно друг с другом катушка и конденсатор.
Последовательный КК
В такой схеме происходит resonance напряжений, R контура устремляется к нулю в случае образования резонансной частоты (fрез). Это позволяет использовать подобную систему резонанса в качестве фильтра.
Резонансная частота
При подаче на два КК (параллельного и последовательного) переменного напряжения с изменяющейся частотой их реактивные сопротивления C и L будут меняться. Изменения происходят следующим образом:
- с увеличением f – ёмкостное сопротивление уменьшается, а индуктивное увеличивается;
- с уменьшением f – ёмкостное сопротивление увеличивается, а индуктивное уменьшается.
Частота, при которой реактивные сопротивления обоих элементов контура равны, называется резонансной.
Важно! При fрез сопротивление параллельного КК будет максимальным, а последовательного КК – минимальным.
Резонансная частота формула, которой имеет вид:
fрез = 1/2π*√L*C,
где:
- L – индуктивность, Гн;
- C – ёмкость, Ф.
Подставляя известные значения ёмкости и индуктивности в формулу резонансной частоты колебательного контура любой конфигурации, можно рассчитать этот параметр.
Для определения периода колебаний КК и частоты резонанса можно воспользоваться онлайн калькулятором на соответствующем портале в сети. Профессиональная программа имеет несложный интерфейс.
Пример интерфейса онлайн калькулятора LC-контура
Применение колебательных контуров
Подробный расчет колебательного контура позволяет точно подбирать величину необходимых элементов КК. Это позволяет использовать их в схемах электроники в виде:
- частотных фильтров – в радиоприёмниках, генераторах сигналов, преобразователях и выпрямителях;
- колебательных контуров – для выделения и настройки на определённую частоту станции вещания;
- силовых resonance-фильтров – для формирования напряжения синусоидальной формы.

На самолётах гражданской авиации КК применяется в блоках регулировки частоты генераторов.
Условие отсутствия резонанса
Для того чтобы возник резонанс формула которого для тока равна ω0*C = 1/ ω0*L, необходимо выполнения этого равенства. Существуют условия для невозможности появления этого эффекта, а именно:
- отсутствие у системы собственных колебаний;
- невозможность совпадения частоты внешнего воздействия с собственной частотой системы.
Амплитуда резонанса
В КК при подаче переменного напряжения от внешнего источника наблюдаются два вида резонанса и резкое увеличение двух видов амплитуды: амплитуды тока и амплитуды напряжения.
Амплитуда тока
Амплитуда тока резко возрастает при резонансе напряжений в последовательном контуре (последовательный резонанс). Источник переменной ЭДС включён в цепь, где нагрузкой служат последовательно включённые элементы L и С.
В этом случае в цепь входят сопротивления: активное r и реактивное x, равное:
x = xL – xC.
Так как для внутренних колебаний xL и xC равны, то для тока, поступающего от генератора, при резонансе (когда частоты совпадают) эти значения тоже одинаковы. Поэтому x = 0. В итоге полное сопротивление цепи будет состоять только из небольшого активного сопротивления. Ток при этом получается максимальным.
Схема (а) и резонансные кривые (б) для резонанса напряжений
Амплитуда напряжения
Резонанс токов (параллельный резонанс) является условием резкого возрастания амплитуды напряжения. Источник ЭДС подключается вне контура и нагружен параллельно соединёнными элементами L и С. В этом случае на эффект резонанса влияет внутреннее сопротивление генератора. Амплитуда напряжения на контуре максимальна при малом отличии напряжения контура от напряжения генератора. Это возможно при малом Ri.
Внимание! Изменение частоты генератора меняет ток, а амплитуда напряжения на контуре не отстаёт по величине от напряжения на генераторе. Если, U = Е — I*Ri, где Е – ЭДС, I – ток, то при малом Ri U = Е.
Схема (а) и резонансные кривые (б) для резонанса токов
Формула для определения расчётной резонансной частоты для разных колебательных систем различается по входящим в неё параметрам. Несмотря на все различия, суть остаётся неизменной: эффект резонанса наступает тогда, когда частота внутренних колебаний системы и внешних воздействий становятся равны друг другу.
Видео
2.4.3 Методика расчета резонансных характеристик. Кривые подвода-отвода
В пункте 2.4.2 был приведен приближенный метод решения уравнения движения зонда в произвольном потенциале. Как было показано резонансные характеристики системы зонд-образец имеет следующий вид:
Как было показано резонансные характеристики системы зонд-образец имеет следующий вид:
(1)
(2)
Однако уравнения (1,2) связывают амплитуду, фазу и частоту вынуждающей силы в неявной форме. Для того, чтобы облегчить расчет резонансных характеристик рассмотрим следующую методику. Выразим в (1) обратную зависимость частоты вынуждающей силы от амплитуды колебаний. Проделывая не сложные выкладки, получим:
(3)
Выражение (3) описывает две ветви АЧХ системы, при этом знак “+” соответствует ветви , а знак “-” – ветви . Здесь введено новое обозначение . Но теперь, несмотря на наличие двух ветвей вместо одной, зависимость частоты от амплитуды колебаний имеет явную форму. Далее, используя выражение (2), получим полные резонансные характеристики системы:
(4)
(5)
где амплитуда колебаний выступает как параметр, который пробегает значения в интервале
.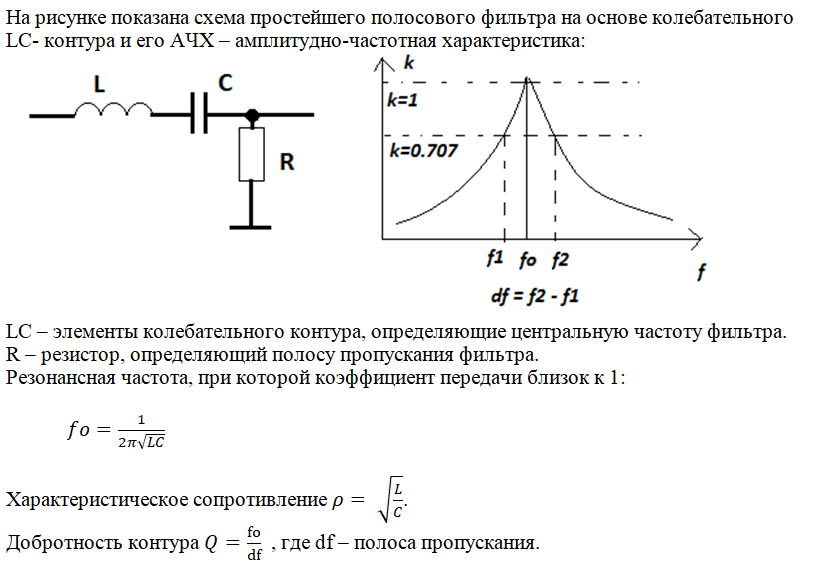
Обе ветви сшиваются в точке с максимальной амплитудой колебаний (резонанс) . Данному значению амплитуды колебаний соответствует частота вынуждающей силы . Таким образом, резонансная частота системы при расстоянии зонд-образец равном .
Теперь можно записать, как изменяется резонансная частота системы при изменении расстояния зонд образец. Вспоминая значение вспомогательной функции (см. (9) пункта 2.4.2), получим для относительного сдвига резонансной частоты:
(6)
Таким образом, зависимость изменения резонансной частоты колебаний кантилевера при отводе его от образца содержит информацию о виде потенциала взаимодействия.
Если же амплитуда колебаний мала, т.е. , то выражение (6) можно переписать в виде:
(7)
где введено обозначение
сила взаимодействия между зондом и образцом. Вспоминая теорию малых колебаний кантилевера в поле силы
, сдвиг резонансной частоты в том случае в точности совпадает с выражением (7).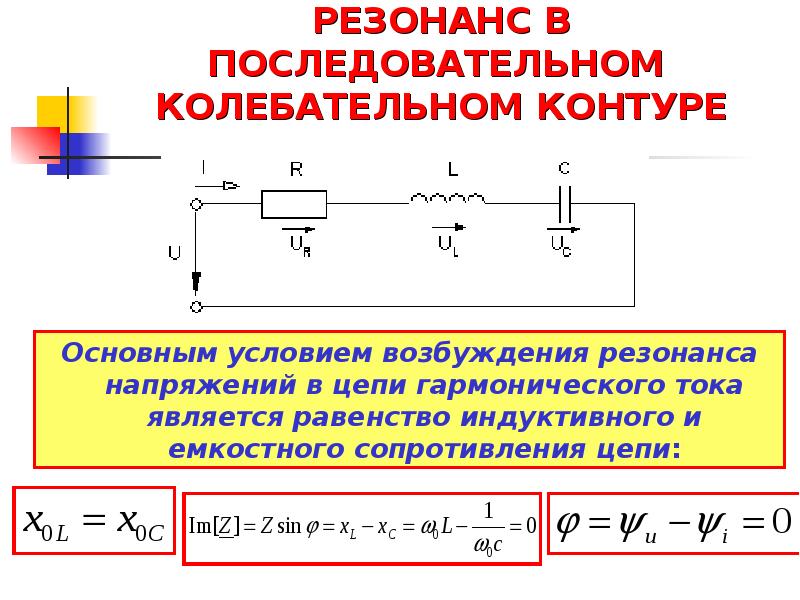
Для нахождения зависимости изменения амплитуды колебаний при отводе зонда от образца будем считать, что кантилевер возбуждается на частоте равной его собственной резонансной частоте при отсутствии взаимодействия зонд-образец, т.е. и, соответственно, . Исходя из вида АЧХ системы, легко получить, что в этом случае для амплитуды колебаний должно выполняться:
(8)
Выражение (8) можно записать в виде , которое задает вид зависимости амплитуды колебаний от расстояния зонд-образец. При этом в некоторых случаях (в зависимости от вида потенциала взаимодействия и расстояния зонд-образец) решение (8) неоднозначно, что соответствует случаю одновременного существования нескольких режимов колебаний с различной амплитудой и, соответственно, фазой, т.к. из (2) фаза колебаний является однозначной функцией от амплитуды.
Рассмотрим, что произойдет в случае малости колебаний. Как уже было показано в случае со сдвигом резонансной частоты колебаний, в этом случае выполняется:
(9)
Подставляя (9) в выражение (8), получим
(10)
Если вертикальный градиент силы взаимодействия зонд-образец мал (сила слабо меняется на амплитуде колебаний), то относительное изменение амплитуды можно выразить в виде:
(11)
Сравнив полученное выражение с изменением амплитуды, вычисленным в теории малых колебаний, легко убедиться, что обе теории дают полностью идентичные ответы.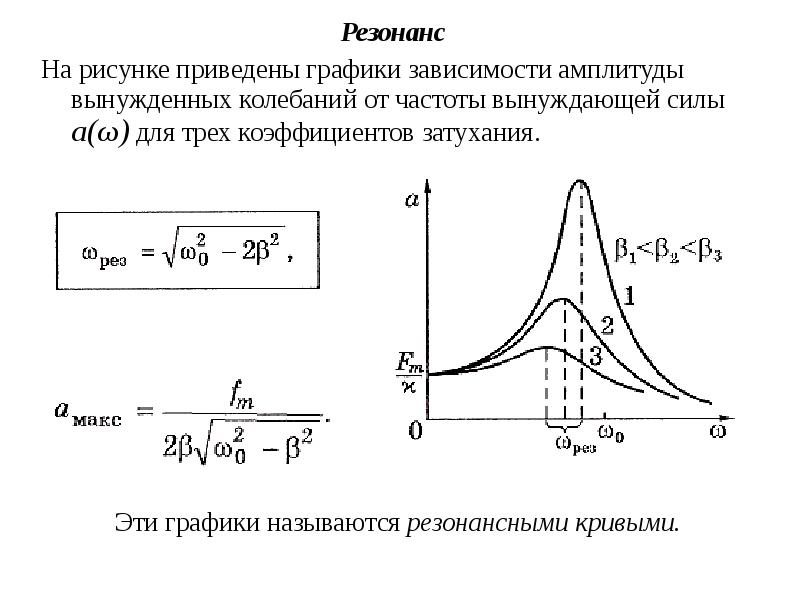
Теперь рассмотрим сдвиг фазы колебаний, которые происходит при отводе зонда от поверхности образца. Как и в случае с амплитудой будет считать, что . С учетом (2) получим
(12)
Используя условие малости колебаний (9) выражение (12) преобразуется к виду:
(13)
который опять в точности соответствует выведенному в теории малых колебаний.
Выводы.
- Предложен метод расчета резонасных характеристик системы зонд-образец при произвольной амплитуде вынуждающей силы. Он позволяет в явной форме вычислить частоту и фазу колебаний, соответствующие определенной амплитуде колебаний. При этом отпадает необходимость решать неявную нелинейную систему уравнений (1, 2).
- Из вида резонансных характеристик системы выведены зависимости амплитуды, резонасной частоты и фазы колебаний при подводе-отводе зонда от образца.
- Показано, что в пределе малых амплитуд , теория возмущений дает результаты полностью идентичные полученным в теории малых колебаний кантилевера.

Электротехника: Резонансная частота.
Параллельный колебательный контур (рисунок 1) или последовательный колебательный контур (рисунок 2) могут использоваться в генераторах синусоидальных колебаний. Если в одной из этих схем зарядить конденсатор то он будет разряжаться заряжая катушку индуктивности, катушка разряжаясь будет заряжать конденсатор, этот процесс будет повторяться с определённым периодом T. Период это время одного колебания. Частота колебаний это величина обратная периоду. Разделив единицу на численное значение периода получим численное значение частоты. Рисунок 1 – Параллельный колебательный контурРисунок 2 – Последовательный колебательный контур
Частота возникших колебаний называется собственной частотой колебаний контура для контуров изображённых на рисунках выше эта частота равна резонансной частоте этих контуров. Резонансная частота контура зависит от индуктивности L и ёмкости C её элементов, для колебательного контура (последовательного или параллельного) её можно найти по формуле:Где L-индуктивность катушки контура, C-ёмкость конденсатора контура.
Если на параллельный или последовательный колебательный контур подавать переменное синусоидальное напряжение и изменять его частоту то будут меняться реактивные сопротивления элементов контура, если частота увеличивается то сопротивление конденсатора уменьшается а сопротивление катушки увеличивается и наоборот: если частота уменьшается то сопротивление конденсатора увеличивается а сопротивление катушки уменьшается, очевидно что есть такая частота при которой сопротивление катушки и конденсатора равны эта частота и есть резонансная. Сопротивление параллельного колебательного контура при этой частоте будет наибольшим (по сравнению с сопротивлениями этого контура при других частотах) а сопротивление последовательного колебательного контура при такой частоте будет наименьшим. Эти свойства контуров используют для построения фильтров например в полосно-пропускающем фильтре последовательно с нагрузкой ставиться последовательный контур и при подаче на это соединение (нагрузки и контура) переменного напряжения с резонансной частотой ток в нагрузке будет максимальным при других частотах ток будет меньше. Резонанс в параллельном контуре называют – резонансом токов, резонанс в последовательном контуре – резонансом напряжений. Можно простым способом определить каким будет сопротивление контура при резонансной частоте: например допустим что на параллельный колебательный контур подаётся постоянный ток, постоянный ток можно считать частным случаем переменного короче говоря постоянный ток это переменный с наименьшей возможной частотой, известно что при постоянном токе катушка действует как перемычка следовательно сопротивление контура будет равно нулю если резонансная частота не бесконечно мала (т.е. не постоянный ток) и сопротивление есть то оно больше нуля (т.е. сопротивления при постоянном токе) следовательно сопротивление параллельного колебательного контура на резонансной частоте максимальное а у последовательного контура наоборот. Зная то что конденсатор постоянный ток не пропускает, можно аналогично определить каким д.б. сопротивление последовательного контура на резонансной частоте. Выведем формулу для расчёта резонансной частоты зная то что при резонансе реактивные сопротивления элементов (катушки и конденсатора) контура равны:
Для расчёта резонансной частоты и периода колебаний колебательного контура с катушкой и конденсатором можно воспользоваться программой:
Расчет – резонансная частота – Большая Энциклопедия Нефти и Газа, статья, страница 2
Расчет – резонансная частота
Cтраница 2
Вид функции XL ( ( U) зависит от схемы и конструкции индуктивного сопротивления резонатора и известен из расчета резонансной частоты wo резонатора. [16]
На основе этих общих положений и уравнений возможно построение упрощенных методов расчета для оценки виброзащищенности, защиты от ударов и перегрузок и расчетов резонансных частот печатных плат. Для оценки виброзащищенности РЭА необходимо знать габариты блока, нагрузку на амортизаторы, массу, жесткость амортизаторов, отношение жесткостей амортизаторов и низшую частоту возмущающих усилий. Порядок расчета при этом ( при использовании номограмм) следующий. Определяем нагрузку на один амортизатор, находим / о и статический прогиб. По отношениям геометрических размеров блока и жесткостей амортизаторов находим значения Ki, по наивысшей частоте / о и низшей частоте возмущающей силы определяем подвижность системы. [18]
Расчет резонансной частоты может быть выполнен лишь графоаналитическим способом и требует громоздких вычислений. [19]
Все, что мы делали до сих пор, относится к вычислению собственных функций распределения поля. Для расчета резонансных частот предположим снова, что z и z – i являются z – коор-динатами двух зеркал относительно начала координат, расположенного в перетяжке пучка. [20]
Система уравнений (4.34), в силу принятых допущений по учету внешних полей ПДР, позволяет рассчитать резонансную частоту ПДР приближенно. Это обстоятельство позволяет существенно повысить точность расчета резонансной частоты ПДР следующим образом. [21]
В циркуляторах миллиметрового диапазона иногда используются дисковые ферритовые резонаторы увеличенного диаметра, точно вписывающиеся в симметричное волноводное К-сочленение, что облегчает задачу их центрирования. В этом случае граничные условия на цилиндрической поверхности образца из-за наличия металлических ребер усложняются и для расчета резонансных частот непосредственно пользоваться формулой (4.24) нельзя. [23]
В качестве центрирующих шайб в ГГ также используются гофрированные оболочки. Типичные виды шайб, используемые в серийных конструкциях, показаны на рис. 4.22. Обычно это оболочки с пологой синусоидальной гофрировкой с числом гофр – 5 – 6, нередко применяется краевой гофр цилиндрической или тороидальной формы. Для расчета резонансных частот таких конструкций могут быть использованы все вышеперечисленные методы, однако центрирующие шайбы обычно изготавливаются из сетчатых анизотропных материалов ( тканей), что значительно усложняет расчет возникающих в них упругих деформаций. [25]
В обязательном порядке производится также расчет критической частоты вращения роторов. Отметим, кстати, что порядок и методика расчета резонансной частоты вращения роторов винтового компрессора не отличаются от аналогичного расчета роторов осевых и центробежных компрессоров. [26]
Уменьшение резонансного сопротивления и собственной добротности коаксиальных резонаторов в коротковолновой части дециметрового и в сантиметровом диапазонах волн снижает коэффициент полезного действия и выходную мощность генераторов, а также ухудшает стабильность частоты генерируемых колебаний. В связи с этим особое значение приобретает разработка методов расчета оптимальных размеров коаксиальных резонаторов для получения максимально возможного в заданных условиях резонансного сопротивления или собственной добротности. Следует отметить, что наличие переменного конденсатора резко усложняет расчет резонансной частоты, резонансного сопротивления и добротности коаксиальных резонаторов. Поэтому к методу расчета этих параметров должны предъявляться требования простоты и наглядности. [27]
При установках автосегментации по умолчанию погрешность вычисления резонансной частоты многоэлементных волновых каналов составляет менее 0 5 %, что вполне достаточно на KB, но на УКВ уже многовато. Так, при значениях DM1 800; DM2 80; SC 1.01; ЕС 16 погрешность расчета резонансной частоты составляет уже менее 0 1 %, что уже вполне приемлемо на УКВ, но замедляет расчеты. [28]
Механическая модель, приведенная на рис. 5.7, приемлема для исследования характеристик далеко не всех МЭ и ИМ, большая часть которых представляет собой сложные механические системы. В то же время резонанс отдельного элемента конструкции изделия независимо от резонанса конструкции изделия может привести к потере его работоспособности. Поэтому для расчета резонансных частот элементов конструкции сложных систем представляется целесообразным изображать их в виде изолированных элементов, связь которых заменяется определенными условиями их закрепления. [30]
Страницы: 1 2 3
Расчет собственных частот и форм колебаний конструкций в среде T-FLEX Анализ
Александр Сущих, Павел Ануфриков
Мы продолжаем знакомить читателя с новой разработкой АО «Топ Системы» — приложением для осуществления конечно-элементных расчетов T-FLEX Анализ.
В настоящей статье речь пойдет о модуле частотного анализа этой системы.
Необходимость в расчете собственных частот и соответствующих им форм колебаний нередко возникает при анализе динамического поведения конструкции под действием переменных нагрузок. Наиболее распространена ситуация, когда при проектировании требуется убедиться в малой вероятности возникновения в условиях эксплуатации такого механического явления, как резонанс. Как известно, суть резонанса заключается в значительном (в десятки раз и более) усилении амплитуд вынужденных колебаний на определенных частотах внешних воздействий — так называемых резонансных частотах (рис. 1). В большинстве случаев возникновение резонанса является крайне нежелательным в плане обеспечения надежности изделия явлением. Многократное увеличение амплитуд колебаний при резонансе и вызываемые этим высокие уровни напряжений — одна из основных причин выхода из строя изделий, эксплуатируемых в условиях вибрационных нагрузок. Для защиты от резонансных воздействий можно использовать различные механические устройства, которые принципиально меняют спектральные характеристики конструкции и поглощают энергию колебаний (например, виброизоляторы). Однако есть и другой эффективный способ противодействия резонансам. Известно, что резонансы наблюдаются на частотах, близких к частотам собственных колебаний конструкции. Если при проектировании изделия имеется возможность оценить спектр собственных частот конструкции, то можно со значительной долей вероятности прогнозировать риск возникновения резонансов в известном диапазоне частот внешних воздействий. Во избежание или для значительного уменьшения вероятности появления резонансов необходимо, чтобы б о льшая часть нижних собственных частот конструкции не лежала в диапазоне частот внешних воздействий. В этом случае можно обойтись без применения специальных виброизолирующих систем. Но для оптимизации спектра собственных частот конструкции прежде всего необходимо оценить эти частоты на этапе проектирования изделия. Именно эту функцию и выполняет модуль частотного анализа системы T-FLEX Анализ. Модуль позволяет на этапе проектирования оценить спектр собственных частот конструкции. Далее разработчик может оптимизировать конструктивные параметры изделия таким образом, чтобы вывести б о льшую часть собственных частот из рабочего диапазона вибровоздействий.
Рассмотрим общий порядок выполнения расчета собственных частот в системе конечно-элементного моделирования T-FLEX Анализ.
Шаг 1. Создание объемной твердотельной модели изделия
Аналогично осуществлению статических расчетов (см. «САПР и графика» № 10’2004) для проведения частотного анализа необходимо иметь трехмерную модель изделия. Как мы уже отмечали, модель может быть построена пользователем в среде трехмерного моделирования T-FLEX CAD 3D или импортирована из другой системы объемного моделирования, поддерживающей для обмена данными о твердотельных моделях форматы STEP, IGES или Parasolid. Рассмотрим в качестве примера использование приложения T-FLEX Анализ для проверки надежности работы вала привода с угловой скоростью вращения до 900 об./мин (рис. 2). Для этого осуществим частотный анализ конструкции. Если собственные частоты вала не попадут в рабочий диапазон частот вращения, обеспечиваемый приводом, то можно быть уверенным в отсутствии резонансных явлений в работе механизма. Конструкция, на примере которой мы иллюстрируем работу с модулем частотного анализа, представляет собой сборочную трехмерную модель и состоит из нескольких отдельных твердотельных деталей. Для осуществления конечно-элементного анализа необходимо предварительно осуществить объединение всех деталей в одно тело с помощью команды T-FLEX CAD 3D «Булева операция/Сложение» (рис. 3).
Шаг 2. Создание «Задачи»
После того как трехмерная модель изделия была создана или импортирована в систему T-FLEX CAD 3D, можно приступать непосредственно к конечно-элементному моделированию. Любой расчет в T-FLEX Анализе начинается с создания «Задачи» с помощью команды «Новая задача» меню «Анализ» T-FLEX CAD (рис. 4). При создании задачи определим ее тип: «Частотный анализ».
Шаг 3. Задание материала
По умолчанию в расчете используются характеристики материала «С операции». В стандартной версии T-FLEX CAD 3D поставляется библиотека конструкционных материалов, которые могут быть назначены операциям твердотельного моделирования, причем пользователь может пополнять стандартную базу материалов другими материалами. Кроме того, в составе системы T-FLEX Анализ есть собственная независимая база материалов, которую также можно использовать для задания физико-механических свойств анализируемого изделия. Выберем для нашей конструкции материал «Сталь» из стандартной библиотеки материалов T-FLEX CAD 3D (рис. 5).
Шаг 4. Генерация конечно-элементной сетки
Как говорилось в нашей предыдущей статье, посвященной системе T-FLEX Анализ, для осуществления конечно-элементного моделирования необходимо построение расчетной сетки из тетраэдральных элементов. Команда построения такой сетки (которая так и называется — «Сетка») инициируется автоматически при создании «Задачи» или может быть вызвана пользователем из меню «Анализ» T-FLEX CAD. При создании сетки пользователь определяет степень дискретизации твердотельной модели, указывая в параметрах ориентировочный размер конечных элементов (тетраэдров), при помощи которых будет описана математическая модель моделируемого изделия. Здесь необходимо отметить следующие моменты. Конечно-элементная сетка может существенным образом влиять на качество получаемых решений в случае сложной пространственной конфигурации изделий. Как правило, более мелкое разбиение обеспечивает лучшие по точности результаты. Однако аппроксимация модели большим количеством малых тетраэдров приводит к системе алгебраических уравнений большого порядка, что может негативно сказаться на скорости выполнения расчета. Вообще, оценить качество конечно-элементной модели можно последовательным решением нескольких задач с различными возрастающими степенями дискретизации. Если результаты решения (собственные частоты) перестают заметно меняться при использовании более густой сетки, то можно со значительной долей уверенности считать, что достигнут определенный оптимальный уровень дискретизации и что дальнейшее увеличение дискретизации сетки нерационально.
Создадим конечно-элементную сетку для нашей конструкции (рис. 6).
Шаг 5. Наложение граничных условий. Задание закреплений
Для успешного решения физической задачи в конечно-элементной постановке помимо создания конечно-элементной сетки необходимо корректно определить так называемые граничные условия. В частотном анализе их роль выполняют закрепления. Этап задания граничных условий — очень ответственный и требующий хорошего понимания расчетчиком сути решаемой задачи. Поэтому, прежде чем приступить к наложению граничных условий, следует хорошо продумать физическую сторону задачи. Для задания закреплений в T-FLEX Анализ предусмотрены две команды: «Полное закрепление» и «Частичное закрепление». Команда «Полное закрепление» применяется к вершинам, граням и ребрам модели и определяет, что данный элемент трехмерного тела полностью неподвижен, то есть сохраняет свое первоначальное расположение и не меняет своего положения под действием приложенных к системе нагрузок. Команда «Частичное закрепление» обладает более широкими возможностями: с ее помощью можно ограничить перемещение тела в определенных координатных направлениях или определить заданное положение элементов модели.
Зададим условия закрепления для нашей конструкции. Используя команду «Частичное закрепление», для опорных шеек вала зададим ограничение (нулевые перемещения) по осям Y и Z глобальной системы координат. Кроме того, с помощью той же команды исключим возможность продольного перемещения вала, наложив соответствующее ограничение на торцовую грань (рис. 7). После задания закреплений мы получим готовую для расчета конечно-элементную модель.
Шаг 6. Выполнение расчета
После создания конечно-элементной сетки и наложения граничных условий можно инициировать команду «Расчет» и запустить процесс формирования систем линейных алгебраических уравнений (СЛАУ) и их решения (рис. 8). В свойствах процессора пользователь может определить такие дополнительные свойства, как точность вычислений или количество нижних собственных частот конструкции, подлежащих определению. Известно, что почти вся энергия механических колебаний аккумулируется на нескольких нижних гармониках изделия, поэтому при частотном анализе в первую очередь представляют интерес первые три-пять наименьших собственных частот.
Шаг 7. Анализ результатов расчета
Результатами частотного анализа являются собственные частоты изделия и соответствующие им собственные формы колебаний. Формы колебаний представляют собой относительные амплитуды перемещений конструкции в узлах конечно-элементной сетки. По ним можно определить характер движения, осуществляемого системой на частоте колебаний, соответствующей собственной. Анализ результатов осуществляется в модуле постпроцессора системы T-FLEX Анализ. Постпроцессор полностью интегрирован в среду геометрического моделирования T-FLEX CAD 3D и обладает полным набором удобных инструментов по обработке результатов моделирования (анимацией, динамическим зондированием результатов, гибкой настройкой шкалы и т.п. — см. «САПР и графика № 10’2004).
Проанализируем полученные нами результаты. Первые две формы свободных колебаний нашей конструкции соответствуют изгибным колебаниям вала с частотами, превышающими 135 Гц (рис. 9), что, в свою очередь, соответствует угловой скорости вращения, в девять раз превышающей максимальную рабочую для данного привода. Таким образом, согласно проведенному расчету в рабочем диапазоне частот вращения резонансы данному валу не угрожают.
Для лучшего понимания характера динамических процессов целесообразно использовать специальный инструмент анимации результата, который позволяет увидеть и оценить характер движения в реальном масштабе времени.
Помимо интерактивного изучения результатов в постпроцессоре T-FLEX Анализ есть возможность создать независимый электронный документ в html-формате, с эпюрами результатов и сведениями о конечно-элементной модели (рис. 10). Этот электронный документ может быть передан в стороннюю организацию или сохранен для последующего изучения результатов.
Таким образом, система конечно-элементного моделирования T-FLEX Анализ позволяет пользователям популярной российской системы T-FLEX Parametric CAD (www.topsystems.ru) осуществлять расчет собственных частот и форм колебаний конструкций. Применяя этот инструмент, пользователи T-FLEX CAD 3D и T-FLEX Анализ получают возможность значительно улучшить качество разрабатываемых ими изделий.
«САПР и графика» 11’2004
Расчет резонансной частоты в электроозонаторе при горящем разряде Текст научной статьи по специальности «Электротехника, электронная техника, информационные технологии»
Научный журнал КубГАУ, №101(07), 2014 года
1
УДК 621
РАСЧЕТ РЕЗОНАНСНОЙ ЧАСТОТЫ В ЭЛЕКТРООЗОНАТОРЕ ПРИ ГОРЯЩЕМ РАЗРЯДЕ
Шевченко Андрей Андреевич доцент, [email protected]
Кубанский государственный аграрный университет, Краснодар, Россия
В статье представленные вопросы теоретического исследования процессов электрического резонанса генератора озона и определено их влияние на производительность и КПД электроозонатора
Ключевые слова: ГЕНЕРАТОР ОЗОНА, КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ, ЭЛЕКТРИЧЕСКИЙ РЕЗОНАНС
UDC 621
CALCULATION OF RESONANT FREQUENCY IN AN ELECTRO-OZONIZER AT THE BURNING CURRENT
Shevchenko Andrey Andreevich
associate professor, [email protected]
Kuban state agrarian university, Krasnodar, Russia
In the article the presented questions of theoretical research of processes of an electric resonance of the generator of ozone were discussed and their influence on productivity and electro-ozonizer efficiency was also defined
Keywords: OZONE GENERATOR, EFFICIENCY, ELECTRIC RESONANCE
Исследования, проведенные на кафедре ЭТиВИЭ Кубанского ГАУ, показали, что при горящем разряде в озонирующем блоке появляется активная составляющая, представленная на схеме замещения (рисунок 1) в виде сопротивления [7].
Повышающий трансформатор напряжения ТГ 1010
Рисунок 1 – Схема замещения электроозонатора где R1 – активное сопротивление рассеяния первичной обмотки
трансформатора; R2 – приведенное активное сопротивление рассеяния
http://ej.kubagro.ru/2014/07/pdf/128.pdf
Научный журнал КубГАУ, №101(07), 2014 года
2
вторичной обмотки трансформатора; Rm – активная сопротивление рассеяния контура намагничивания; L1 – индуктивность рассеяния первичной обмотки трансформатора; L2 – приведенная индуктивность рассеяния вторичной обмотки трансформатора; L3 – индуктивность рассеяния контура намагничивания; Сб – емкость барьеров пластинчатого озонатора;
Сг – емкость газового промежутка электроозонатора; Rг – активная составляющая газового промежутка электроозонатора; u(t) – напряжение питающей сети.
В связи, с появлением активной составляющей, изменятся электрические параметры, необходимые для расчета частоты резонанса при горящем разряде в озонаторе, поэтому сопротивление газоразрядного промежутка z примет следующий вид [6]:
R
Z г =
1 + jwC г R .
(1)
Изменение сопротивления газового промежутка приведет к изменению напряжения U3, подаваемого на озонирующий блок:
1
U ■
U >=—
Ri + JwLi
1
1
R1 + jwL1 R3 + jwL
U
R2 + jwL2 – j
1
R
wC 6 1 + jwC R г
(2)
1 + R1 + jwL1 R3 + jwL3
+
R1 + jwL1
R2 + jWL2 – J
1
R
wC s 1 + jwC R г
3
Значение тока при этом определяется по формуле:
http://ej.kubagro.ru/2014/07/pdf/128.pdf
Научный журнал КубГАУ, №101(07), 2014 года
3
I-.
R2 + JWL2 – J
Us
1
R
U
А + j wB
wC6 1 + JwC г R2
(3)
Зная ток I2, протекающий через озонирующий блок и напряжение U3, приложенное к разрядному промежутку, мы можем рассчитать падение напряжения на диэлектрических барьерах и газовом промежутке озонирующего блока при горящем разряде. Выполнив преобразования, получим:
и б (t)
U
m
A2 + w2B21 • wC6
• sin( wt + j1 – 90)
(4)
Uг (t)
Um • RZ
A+Wb2-д/ 1 + wrC:R;
• sin( wt + j- arctgwC г Rг)
(5)
В формулах (4), (5) коэффициент ф1 равен:
wB
j =j – arctg——
A 5
(6)
Полученные данные позволяют выполнить расчет резонансной частоты для питания электроозонатора при горящем разряде.
Применение эффекта резонанса в озоногенераторах позволит добиться повышения эффективности работы озонатора: снизить
энергозатраты, повысить cos ф, уменьшить реактивное сопротивление и, как следствие, увеличить активную мощность [2, 4].
При горящем разряде озонирующий блок описывается следующей зависимостью:
I = U0*C6 * w* coswt, (7)
где I – текущее значение тока; U0 – напряжение питания озонирующего блока.
http://ej.kubagro.ru/2014/07/pdf/128.pdf
Научный журнал КубГАУ, №101(07), 2014 года
4
По утверждению Филиппова Ю.В., на практике более важно не мгновенное значение тока, а средний ток. Его можно получить, интегрируя предыдущее уравнение за полупериод [5]:
T/2
Icp = (2/T)* | Idt, (8)
0
При интегрировании надо учесть, что функция тока от времени имеет разрывы в точках зажигания и погасания разряда. Они экспериментально наблюдаются на осциллограммах тока. Расчет среднего тока сделан в работе [5].
(9)
2 2
Icp = -* w* Сб *(Uo – Uz) = -* w* Сб *Uo.
p p
При горящем разряде емкостью озонатора является емкость диэлектрического барьера, которая равна:
С
б
I
cp
2
* w * U0
p
где ю – круговая частота, зависящая от частоты источника тока; ю Следовательно, емкость озонатора имеет вид:
(10)
2*n*f.
С
б
L
ср
4* f *U о
(11)
Используя выражение (11), мы можем вывести уравнение для определения резонансной частоты озонирующего блока при горящем разряде:
w =
рез.
L
I
(12)
ср
4* f*U о
Иначе, это выражение можно записать следующим образом:
1
*
http://ej.kubagro.ru/2014/07/pdf/128.pdf
Научный журнал КубГАУ, №101(07), 2014 года
5
w =
рез.
1
L
4 * f * U 0
I
ср
Зная, что можно выразить как:
– ср
1ср 1
R2 –
‘ 1 V
w*C
об J
где R – эквивалентное сопротивление озонирующего блока. Г 1 ) 2
Vw*C„6 )
w –
рез
Подставим в уравнение (15) Соб и L, получим выражение 16:
1
d2
2 D+l D -d2
( Y
4* f* 1 r2 – 1
\F *s e *s U 2*p*f*e0 *(n 1) б б * г г * г
,(16)
У К б г б у
Используя выражения (4) и (5), определим величину соотношения
действующих значений напряжений озонирующего блока
величины имеют большее практическое значение [3]:
иг (t) _ -у/1 + (wRzСг )2 sin(wt + j1 – 90)
Uг (t) U6 (t)
так как их
uб (t)
wRz Cб sin (wt + j1 – arctg wRz Cг)
(17)
1
1
*
*
http://ej.kubagro.ru/2014/07/pdf/128.pdf
Научный журнал КубГАУ, №101(07), 2014 года
6
Рассмотрим соотношение углов сдвига фаз в выражении (18):
sin (wt + j1 – 90) sin (wt + j1 – arctg wRz Cг)
– cos (<wt + j1)
sin (wt + j1) • cos (arctg wRг Cг) – cos (wt + j) • sin (arctg wRz Cг) , (18)
________________________1_____________________
sin (arctg wRz Cг) – tg (wt + j1) • cos (arctg wRz Cг)
Таким образом, получим преобразованное соотношение напряжений газового промежутка:
Uг (t) _ У1 + (wRz Cг /_____________________1_____________________
иб (t) wRz C6 sin(arctgwRz Cz ) – tg (wt + j1) • cos(arctgwRz C г),(19
)
При горящем разряде в газоразрядном промежутке появляется активная составляющая сопротивления Яг. Таким образом, значение активной составляющей всего озонирующего блока примет вид R = R6 + RP Однако величина R6 будет незначительной, так как диэлектрические барьеры в момент разряда работают как конденсатор. Следовательно, можно сделать вывод, что R ~ RP Используя закон Ома, мы можем определить R [1].
В момент зажигания разряда емкостную составляющую разрядного устройства следует описывать емкостью диэлектрических барьеров (11), это происходит из-за того, что при разряде возрастает активная составляющая газоразрядного промежутка (появляется стример), а емкостная составляющая стремится к 0.
Сделав допущение, что Сг стремится к нулю, выражение (19) можно записать следующим образом:
http://ej.kubagro.ru/2014/07/pdf/128.pdf
Научный журнал КубГАУ, №101(07), 2014 года
7
и
ft)
1 +
/ Л2 (Q—
V 1 сР J
иб(t)
U3r
°Y~Ce
ср
sm
in(arctgaR2Сг) – tg(wt + j1) • cos(arctgoR8Сг), (20)
Введем переменную ф2, равную отношению углов отклонения напряжений разрядного устройства:
__________________________1________________________
2 sin(arctgoRz Сг)- tg (о + j1 )• cos(arctga>Rz С г), (21)
Подставив переменную ф2 в уравнение (20), получим следующую зависимость:
и
(t) V
1 +
f \2
U3
о—-V 1сР J
и б(t)
Us ~ о—-С*
• j 2
(22)
/
ср
Полученное выражение (22) подставим в уравнение (16) и получим формулу для вычисления резонансной частоты для озонирующего блока пластинчатого типа:
«W =-
щ d2 1
2 D+4& -d2 f \
4-f■ j R2 + 1
1 l+(ojh-)2 1F ^ S* F ^ ^ J 2.n.f.e,.(n-l) 1 d, d, oC4± 6 I v 1 V J
По итогам расчета данного выражения получены следующие зависимости (рисунок 2 и 3):
http://ej.kubagro.ru/2014/07/pdf/128.pdf
Научный журнал КубГАУ, №101(07), 2014 года
8
Рисунок 2 – Изменение частоты резонанса от площади
диэлектрических барьеров и воздушного промежутка
Анализируя график, можно сказать, что при увеличении площади пластин и постоянном воздушном зазоре 3 мм, частота, на которой разрядный промежуток войдет в режим резонанса, снижается. Так, при площади 0,02 м2 резонансная частота составляет 1,8 кГц, а при площади пластин 0,1 м она снижается до значения 0,8 кГц.
На рисунке 3 представлена зависимость частоты резонанса от ширины воздушного промежутка. Анализируя этот график, можно сказать, что, чем меньше воздушный промежуток, тем меньше частота, при которой генератор озона войдет в режим резонанса. Однако, следует учитывать, что увеличивается вероятность пробоя диэлектрика, поэтому рекомендуется ширину воздушного промежутка делать менее 2,5 мм.
http://ej.kubagro.ru/2014/07/pdf/128.pdf
Научный журнал КубГАУ, №101(07), 2014 года
9
Рисунок 3 – Влияние изменения ширины воздушного зазора между диэлектрическими пластинами озонатора на частоту резонанса разрядного промежутка.
Таким образом, полученная нами формула резонансной частоты для разрядного промежутка позволяет рассчитать частоту, при которой ток, проходящий через разрядный промежуток, достигнет максимального значения, не вызывая изменений в питающей сети. Полученное выражение позволяет рассчитать резонансную частоту в зависимости от размеров озонирующего блока.
Для получения конкретного значения частоты, на которой генератор озона войдет в резонанс, нам необходимо знать лишь напряжение на выходе трансформатора (указывается в паспорте трансформатора), ток, подаваемый на озонирующий блок, и конструктивные параметры озонирующего блока.
Используя компьютерную программу «MathCAD 2011», была составлена математическая модель для расчета резонансной частоты, которая представлена на рисунке 4.
http://ej.kubagro.ru/2014/07/pdf/128.pdf
Научный журнал КубГАУ, №101(07), 2014 года
10
Рисунок 4 – Математическая модель для расчета резонансной частоты
По результатам расчетов математической модели были построены зависимости, представленные ниже (рисунок 5).
кГц
w
3
6.28-10
Рисунок 5 – Зависимость тока разрядного промежутка от изменения питающей частоты
http://ej.kubagro.ru/2014/07/pdf/128.pdf
Научный журнал КубГАУ, №101(07), 2014 года
11
Из графика видно, что при частоте питающего сигнала 0,86 кГц, ток на разрядном промежутке возрастает до 10 млА. Это притом, что при стандартной частоте 50 Гц он составляет 50 мкА. Таки образом, мощность разрядного устройства возрастает в 1000 раз, следовательно, возрастет производительность генератора озона.
Так же из графика видно, что при увеличении частоты более 0,86 кГц, ток на озонирующем блоке снижается, следовательно, дальнейшее увеличение частоты не целесообразно.
Надо отметить, что при изменении конструктивных параметров озонирующего блока, зависимость тока от частоты тоже изменяется, что показано на рисунке 4.3.
Данный график построен при следующих значениях конструкции генерирующего блока:
– диэлектрические барьеры: А11=0,1 м2, А12=0,08 м2, А13=0,06 м2 (А – площадь диэлектрического барьера, при толщине 3 мм)
– воздушный промежуток: А21=0,1 м2, А22=0,08 м2, А23=0,06 м2 (А – площадь воздушного зазора, при его ширине 3 мм)
А 12
9.6
Ia1(w) 7 2 Ia2(w)
Ia3(w) 4.8
2.4
0 ^
0 0.28 0.56 0.84 1.13 1.41 1.69 1.97 2.25 4
w
3
6.28-10
Рисунок 4.3 Зависимость тока от частоты при изменении конструктивных параметров озонирующего блока
http://ej.kubagro.ru/2014/07/pdf/128.pdf
Научный журнал КубГАУ, №101(07), 2014 года
12
Необходимо отметить, что при изменении размеров разрядного устройства изменяется его емкость. Созданная нами математическая модель учитывает это изменение. При выполнении расчета видна следующая зависимость – при увеличении размеров разрядного устройства его емкость увеличивается. Так, при площади диэлектрических барьеров и воздушного промежутка 0,08 м , емкость барьеров составляет 5,33* 10- Ф, а емкость воздушного промежутка – 2,13* 10-6 Ф. При увеличении площади до 0,1 м емкость барьерного промежутка становится равной 6,67* 10- Ф, а емкость воздушного промежутка возрастает до 2,67* 10-6 Ф.
Из графика видно, что при уменьшении площади диэлектрических барьеров и воздушного промежутка, токовый максимум сдвигается в сторону увеличения частоты. Так, при площади диэлектриков 0,1 м2, резонансная частота имеет значение 860 Гц, а при их уменьшении до 0,06 м2, она возрастает до 1120 Гц, но при этом не изменяется максимальное значение тока. Так, из графика видно, что максимальное значение тока во всех рассмотренных случаях равно 10 млА.
Литература
1. Андрейчук В.К. Озонатор / В.К. Андрейчук, Д.А. Нормов, С.В. Вербицкая, Д.А. Овсянников, В.В. Лисицин, А.А. Шевченко, Т.А. Нормова/ патент на изобретение RUS 2198134 30.10.2001.
2. Григораш О.В. Особенности расчета КПД и массогабаритных показателей статических преобразователей /О.В. Григораш, А.А. Шевченко, А.Е. Усков, В.В. Энговатова/ Труды Кубанского государственного аграрного университета. -Краснодар: КубГАУ, 2011. Т. 1. № 30. С. 248-252.
3. Нормов Д.А. Расчет резонансной частоты электроразрядного промежутка озонатора /Д.А. Нормов, А.А. Шевченко, Р.С. Шхалахов, А.В. Квитко/ Механизация и электрификация сельского хозяйства. – М.: 2007. – №8, С. 23-24.
4. Степура Ю.П. Расчет показателей надежности электротехнических устройств /Ю.П. Степура, А.А. Шевченко, А.В. Квитко, Д.В. Солодкий/ Труды Кубанского государственного аграрного университета. – Краснодар: КубГАУ, 2011. Т. 1. № 31. С. 246-249.
5. Филиппов Ю.В. Влияние величины разрядного промежутка на электрические характеристики озонаторов / Ю.В. Филиппов, В.П. Вендилло // Журнал физической химии. – М.:1959. – Т.ЗЗ, Вып. 10. – С. 2359-2364.
http://ej.kubagro.ru/2014/07/pdf/128.pdf
Научный журнал КубГАУ, №101(07), 2014 года
13
6. Шевченко А.А. Влияние диэлектрических барьеров на электрические параметры электроозонатора / А.А. Шевченко, А.В. Квитко / Труды Кубанского государственного аграрного университета. – Краснодар: КубГАУ, 2008. – № 1, С. 92-94.
7. Шевченко А.А. Параметры электроозонирования для предпосевной обработки семян кукурузы /А.А. Шевченко/ автореферат на соискание ученой степени кандидат технических наук. – Краснодар: КубГАУ, 2005
References
1. Andrejchuk V.K. Ozonator / V.K. Andrejchuk, D.A. Normov, S.V. Verbickaja, D.A. Ovsjannikov, V.V. Lisicin, A.A. Shevchenko, T.A. Normova/ patent na izobretenie RUS 2198134 30.10.2001.
2. Grigorash O.V. Osobennosti rascheta KPD i massogabaritnyh pokazatelej staticheskih preobrazovatelej /O.V. Grigorash, A.A. Shevchenko, A.E. Uskov, V.V. Jengovatova/ Trudy Kubanskogo gosudarstvennogo agrarnogo universiteta. -Krasnodar: KubGAU, 2011. T. 1. № 30. S. 248-252.
3. Normov D.A. Raschet rezonansnoj chastoty jelektrorazrjadnogo promezhutka ozonatora /D.A. Normov, A.A. Shevchenko, R.S. Shhalahov, A.V. Kvitko/ Mehanizacija i jelektrifikacija sel’skogo hozjajstva. – M.: 2007. – №8, S. 23-24.
4. Stepura Ju.P. Raschet pokazatelej nadezhnosti jelektrotehnicheskih ustrojstv /Ju.P.
Stepura, A.A. Shevchenko, A.V. Kvitko, D.V. Solodkij/ Trudy Kubanskogo
gosudarstvennogo agrarnogo universiteta. – Krasnodar: KubGAU, 2011. T. 1. № 31. S. 246249.
5. Filippov Ju.V. Vlijanie velichiny razrjadnogo promezhutka na jelektricheskie harakteristiki ozonatorov / Ju.V. Filippov, V.P. Vendillo // Zhurnal fizicheskoj himii. -M.:1959. – T.ZZ, Vyp. 10. – S. 2359-2364.
6. Shevchenko A.A. Vlijanie dijelektricheskih bar’erov na jelektricheskie parametry jelektroozonatora / A.A. Shevchenko, A.V. Kvitko / Trudy Kubanskogo gosudarstvennogo agrarnogo universiteta. – Krasnodar: KubGAU, 2008. – № 1, S. 92-94.
7. Shevchenko A.A. Parametry jelektroozonirovanija dlja predposevnoj obrabotki semjan kukuruzy /A.A. Shevchenko/ avtoreferat na soiskanie uchenoj stepeni kandidat tehnicheskih nauk. – Krasnodar: KubGAU, 2005
http://ej.kubagro.ru/2014/07/pdf/128.pdf
Как вычислить основную частоту
Обновлено 13 декабря 2020 г.
Автор: Серм Мермсон
Основная частота – это самая низкая частота в резонирующей системе. Это жизненно важное понятие для музыкальных инструментов и многих инженерных аспектов. Например, все гармоники данной волны основаны на основной частоте. Чтобы вычислить основную частоту, вам понадобится длина системы или волны, а также несколько других измерений.
TL; DR (слишком долго; не читал)
Расчет для определения основной частоты зависит от того, является ли колебательная система трубкой, струной, электронной схемой или каким-либо другим механизмом.
Измерьте длину системы
Измерьте длину системы. Это половина длины волны, которую он несет. Для трубки измерьте длину трубки. Для веревки измерьте длину веревки и т. Д. Запишите длину в метрах. Если вы должны измерять миллиметры, сантиметры или другие единицы измерения, убедитесь, что для вашей скорости используются те же единицы длины.Например, используйте метры, если ваша скорость выражается в метрах в секунду.
Рассчитайте частоту трубки
Разделите скорость вашей волны на удвоенную длину системы. Если ваша трубка закрыта с одного конца, разделите скорость в четыре раза на длину. Результатом является основная частота в циклах в секунду или герцах (Гц). Скорость звуковой волны в воздухе при 20 градусах Цельсия составляет 343 метра в секунду. Например:
Для открытой трубы длиной = 0.5 м
Основная частота звуковой волны в трубке:
\ frac {343} {2 \ times 0,5} = \ frac {343} {1} = 343 \ text {Hz}
Рассчитать частоту of a String
Вычислите скорость волны на струне, разделив натяжение на ее массу на единицу длины. Убедитесь, что единицы массы при измерении натяжения совпадают с единицами измерения самой массы. Например, если вы используете ньютоны в качестве единицы измерения напряжения, выражайте свою массу в килограммах.2 = \ frac {1500} {0,04} = 37500 \\\ text {} \\ v = 193,65 \\\ text {} \\\ frac {193,65} {2 \ times 0,5} = 193,65 \ text {Hz}
Резонансная частота f0, онлайн калькулятор
Калькулятор и формулы для расчета резонансной частоты ЖК-резонатора
Рассчитать резонансную частоту ЖК
На этой странице вы можете рассчитать резонансную частоту, индуктивность катушки или емкость конденсатора в колебательном контуре.Чтобы вычислить третье, необходимо знать два значения.
Формулы резонансной частоты
В следующем описании показан расчет резонансных частот LC-резонансного контура. В теоретических системах без демпфирования резонансная частота равна незатухающей собственной частоте \ ({\ displaystyle f_ {0}} \).
В демпфированных системах частота с максимальной амплитудой всегда меньше незатухающей собственной частоты.2 · C} \)
|
Как рассчитать резонансные частоты
Эта статья является продолжением последней статьи, Introduction to Resonance .Если вам нужно рассмотреть стоячие волны, узлы и пучности, вы можете сначала ознакомиться с этой статьей. В противном случае, перейдем к делу.
Как найти резонансные частотыПомните из предыдущей статьи, что стоячие волны возникают, когда узлы или пучности совпадают с концами веревки или трубы. Такие стоячие волны создают резонанс. Самая низкая частота, которая «умещается» на струне или в пространстве (если мы говорим о звуковых волнах в воздухе), называется основной частотой.Все более высокие резонансные частоты (называемые гармониками) кратны первым основным частотам. Какие гармоники вы получите, зависит от того, являются ли конечные условия волны фиксированными или свободными.
Если конечные условия одинаковы (фиксированное-фиксированное или свободное-свободное), гармоники даже кратны основной частоте. Если конечные условия различны (фиксированная свободная), то основные частоты нечетно кратны основной частоте.
Вы можете использовать этот же процесс для определения резонансных частот воздуха в трубах.Закрытый конец трубы – это то же самое, что и закрепленный конец веревки. Открытый конец трубы – это то же самое, что свободный конец веревки. Это упрощает математику.
Однако уравнение для нахождения первого фундаментального значения различается для условий одних и тех же и разных концов. Уравнения представлены ниже в таблице. В уравнении основная частота, скорость волны в среде (скорость звука для волн в воздухе) и длина струны или трубы.
Обратите внимание, что одна и та же длина каната или трубы может давать различную основную частоту в зависимости от конечных условий. Цилиндрическая труба с одним открытым концом и одним закрытым концом будет иметь более низкую основную частоту (в 2 раза по математике или октаву в музыкальных терминах), чем та же труба с двумя закрытыми или двумя открытыми концами. На рисунке ниже графически показано, почему это так.
Трубы с разными конечными состояниями могут удерживать четверть длины волны, тогда как трубы с одинаковыми конечными условиями могут удерживать только половину длины волны.Чем длиннее длина волны, тем глубже высота (или частота) волны.
Принципы, обсуждаемые в этой статье, можно использовать для моделирования многих различных вещей. Слуховой проход часто моделируется как открытая-закрытая труба. Большинство музыкальных инструментов, в которых используются струны или трубы – органы, кларнеты, арфы, гитары и скрипки, и многие другие – можно смоделировать с помощью простых уравнений в таблице выше. Довольно мощно, правда?
Если вы не хотите проводить вычисления вручную, вы можете использовать наш удобный и удобный калькулятор основной частоты , чтобы сделать вычисления за вас.Или, поскольку теперь вы знаете все о стоячих волнах и резонансных частотах, вы можете выполнить вычисления вручную и произвести впечатление на своих друзей.
Сопутствующий инструмент
Дополнительная литература
26 год
AUG
2019
Резонансная частота – обзор
5.5 ДАТЧИКИ ДАВЛЕНИЯ
Давление определяется как сила на единицу площади, оказываемая жидкостью на ее сосуд. Его основной единицей в системе СИ является паскаль , давление 1 Па, представляющее силу 1 Н на квадратный метр ограничивающей поверхности.В отличие от многих других областей, где единицы СИ были приняты почти повсеместно, для измерения давления по-прежнему используются несколько различных систем единиц. Британские имперские единицы, такие как фунты на квадратный дюйм (PSI), из-за их привычки, сохранились в общем использовании, например для давления в шинах. Атмосферное давление, измеряемое барометром, измеряется в барах (или атмосферах, атм), где 1 бар эквивалентен атмосферному давлению при стандартных условиях (уровень моря, 0 ° C).В физиологических науках явное предпочтение было отдано системам измерения давления, основанным на используемой манометрической системе измерения, а не какому-либо абсолютному эталону. Манометр представляет собой устройство, состоящее из U-образной трубки, заполненной жидкостью, как показано на рис. 5.11 (а). Один конец трубки подсоединен к системе, в которой должно измеряться давление (например, баллону с газом или артериальной системе животного), другой – открыт для атмосферы. Давление внутри резервуара толкает жидкость вверх по трубке манометра, пока не достигнет точки, в которой направленная вниз сила, создаваемая весом столба жидкости, точно уравновешивает давление.Таким образом, высота столба жидкости указывает на давление внутри резервуара. Плотность ртути и ее несмешиваемость с большинством других жидкостей сделали ее популярным выбором для жидкости манометра, что привело к широкому использованию миллиметров ртутного столба (мм рт. Ст.) в качестве единиц давления. Вода также использовалась в качестве жидкости манометра, в результате чего единицы измерения составляли 90–100 сантиметров воды (см вод. Ст. 2 O). Отношения между различными единицами давления показаны в Таблице 5.2.
Рисунок 5.11. Измерение давления. (а) Ртутный манометр. (б) Основные элементы датчика артериального давления. (c) Датчик давления Druck PDCR75.
Таблица 5.2 .. Коэффициенты пересчета для обычно используемых единиц давления
| см вод. Ст. 2 O | бар | фунт / кв. =| 1,36 | 1,31 × 10 −3 | 0.0192 | 133 | | |
|---|---|---|---|---|---|---|---|
| 1 см вод. | |||||||
| 1 фунт / кв. Дюйм = | 6900 |
Основное давление, представляющее интерес для физиологов и клиницистов, – это давление крови в различных точках системы кровообращения.Артериальное кровяное давление является важным клиническим показателем, и его измерение является обычным делом в хирургии. Измерение давления в артериальной и венозной системах, а также в камерах самого сердца дает подробную информацию о работе системы кровообращения как для исследовательских, так и для диагностических целей. Давление в других полостях тела, таких как плевральные полости легких и желудочно-кишечный тракт, также имеет диагностическое значение. Дифференциальное измерение давления воздуха внутри пневмотахографа также позволяет измерять поток вдыхаемого воздуха.Артериальное кровяное давление обычно выражается в мм рт.
Давление в артериальной системе человека является пульсирующим, повышается и понижается с каждым ударом сердца, между минимальным (диастолическим) давлением 80 мм рт. Ст. И максимальным (систолическим) 120 мм рт. Ст. У здорового взрослого человека, лежащего на животе. Как видно из таблицы пересчета (100 мм рт. Ст. = 0,131 бар), это более чем на 10% выше атмосферного давления.Значительные перепады гидростатического давления также возникают внутри тела в положении стоя из-за веса вертикального столба крови, при этом среднее давление в стопах более чем на 100 мм рт.ст. выше, чем на уровне сердца.
Датчики давления работают по принципу измерения деформации, вызванной давлением в гибкой мембране, как показано на рис. 5.11 (b). Преобразователь состоит из двух камер, разделенных тонкой гибкой мембраной. Одна камера заполнена жидкостью (обычно физиологическим раствором) и через катетер соединена с кровеносным сосудом.Другая камера открыта для атмосферы. Разница давлений на мембране заставляет ее немного раздуваться наружу. Давление 100 мм рт. Ст. Сместит стальную мембрану диаметром 1 см и толщиной 0,1 мм примерно на 0,007 мм (Togawa et al., 1997). Смещение поверхности мембраны можно измерить, прикрепив ее к проволоке или тензодатчику на основе силикона, аналогичному тому, который используется в датчиках силы. Как и датчик силы, мост Уитстона необходим для преобразования изменения сопротивления тензодатчика в сигнал напряжения.В качестве альтернативы, электрическая емкость между мембраной и другой близко противоположной поверхностью может использоваться в качестве меры смещения – подход, используемый в преобразователе Hewlett Packard 1290A. Типичный датчик кровяного давления, используемый для измерения кровяного давления у крыс, показан на рис. 5.11 (c).
Большинство датчиков кровяного давления предназначены для работы в диапазоне от -50 мм рт.В этом диапазоне может быть достигнута линейность 0,5%. Стандартные датчики давления, подобные этим, относительно прочны и способны выдерживать давление до 4000–5000 мм рт.ст. (в четыре-пять раз превышающее атмосферное давление) без разрыва гибкой мембраны. Однако следует соблюдать осторожность всякий раз, когда шприц прикреплен к промывочному отверстию, поскольку попытка ввести материал, когда выпускное отверстие катетера закрыто, может вызвать давление в этой области.
Датчики артериального давления и связанные с ними преобразователи сигналов легко доступны в компаниях по производству биомедицинских приборов, таких как Gould Instrument Systems (Valley View, Огайо, США), Agilent Technologies (Пало-Альто, Калифорния, США, подразделение Hewlett Packard, которое сейчас занимается биомедицинский рынок) или Гарвардский аппарат (Саут-Натик, Массачусетс, США).Вместо того, чтобы делать датчики, способные выдерживать суровые условия многократной стерилизации, некоторые компании производят недорогие устройства, предназначенные для утилизации после использования. Их часто можно многократно использовать в исследовательской среде, где восстановление животного не предназначено и процедуры стерилизации не требуются.
5.5.1 Динамический отклик
Подобно датчикам силы, датчики давления имеют динамический отклик с резонансной частотой. Следовательно, если необходимо точно записать ход сигнала кровяного давления, важно обеспечить, чтобы резонансная частота превышала диапазон частот, содержащихся в сигнале, а коэффициент демпфирования был достаточно большим, чтобы гасить колебания.Жесткость чувствительной к давлению мембраны играет ключевую роль в определении динамического отклика датчика. Всякий раз, когда мембрана расширяется в ответ на изменение давления, происходит небольшое изменение объема жидкости, которое влияет на измеренное давление. Чем жестче мембрана, тем меньше растяжение при заданном давлении и, следовательно, меньше изменение объема. Идеальный датчик не требует изменения объема, но очевидно, что требуется некоторое растяжение, чтобы его можно было измерить тензодатчиком.Жесткость мембраны преобразователя обычно определяется в терминах ее эластичности – давления, необходимого для достижения единичного изменения объема. Типичный датчик будет иметь эластичность около 3,3 × 10 14 Па м −3 , что соответствует изменению объема на 0,04 мм 3 для изменения давления на 100 мм рт.
На практике общий динамический отклик в такой же степени зависит от свойств катетера, передающего изменения давления внутри кровеносного сосуда к датчику, как и от самого датчика.Поэтому имеет смысл рассматривать систему катетер-датчик в целом. Для датчика с определенной упругостью K , резонансная частота f 0 и коэффициент демпфирования h системы катетер-датчик равны
[5,23] f0 = r2Kπρl
[5.24] h = 4ηlr3πρK
, где r и l – радиус и длина катетера, ρ и η – плотность и вязкость жидкости (Togawa et al., 1997).
На рисунке 5.12 показана частотная характеристика датчика с эластичностью K = 3,3 × 10 14 Па м −3 , прикрепленного к катетеру диаметром 0,5 м × 0,5 мм, который может использоваться для измерения артериальной крови. давление у маленького животного. Амплитудно-частотная характеристика далека от плоской, с частотами около резонанса 57 Гц в четыре раза больше, чем на нижнем конце частотного диапазона. Это характеристика системы с недостаточным демпфированием ( h = 0.12 в данном случае) с потенциалом колебаний на резонансной частоте. Сигналы давления с частотными составляющими в этом диапазоне будут значительно искажены. Однако можно предпринять шаги для некоторого улучшения ситуации. Применение фильтра нижних частот к выходному сигналу преобразователя может компенсировать пик резонанса и добиться более плоской частотной характеристики. На рисунке 5.12 (b) показан измененный отклик после прохождения через RC-фильтр нижних частот с частотой среза 20 Гц.
Рисунок 5.12. Частотная характеристика датчика давления ( K = 3,3 × 10 14 Па м −3 ), прикрепленного к канюле диаметром 0,5 м × 0,5 мм, f 0 = 57 Гц, h = 0,12. (а) Собственная частотная характеристика системы датчик-канюля. (б) Затухающий отклик системы после фильтрации RC-фильтром нижних частот с частотой среза 20 Гц. (c) Частотная характеристика RC-фильтра.
Катетер можно также модифицировать для улучшения частотной характеристики.В идеале система должна иметь как можно более высокую резонансную частоту и достаточно большой коэффициент демпфирования (0,4–0,6), чтобы избежать пика частотной характеристики. Из уравнения [5.27] видно, что чем короче катетер, тем выше будет резонансная частота. Кроме того, уравнение [5.28] показывает, что коэффициент демпфирования сильно увеличивается по мере уменьшения диаметра катетера. Это говорит о том, что короткие катетеры с узким проходом, вероятно, будут давать лучший частотный отклик. Типичный импульсный сигнал артериального давления содержит частотные составляющие, в 10 раз превышающие частоту сердечных сокращений.У людей максимальная частота сердечных сокращений составляет около 200 ударов минимум -1 , что, таким образом, требует плоской частотной характеристики, по крайней мере, до 33 Гц. Более мелкие животные, такие как крысы и мыши, имеют более высокую частоту сердечных сокращений (300–600 ударов мин. –1 ) и имеют пропорционально более высокочастотные импульсы давления (30–60 Гц). Как видно из рис. 5.12, этого можно более или менее достичь с помощью катетеров 0,5 м. Однако необходимо соблюдать осторожность, чтобы полностью исключить пузырьки воздуха и избежать засоров, которые отрицательно влияют на частотную характеристику.Пузырьки придают системе дополнительную эластичность, что значительно снижает резонансную частоту, в то время как засорения могут снизить высокочастотный отклик за счет чрезмерного увеличения коэффициента демпфирования. Если запись ведется в течение длительных периодов времени, может потребоваться обычная промывка катетера (часто гепаринизированным раствором для подавления свертывания крови), и для этой цели купола датчика давления оборудованы вторым входным отверстием.
Использование коротких катетеров с узким проходом и низкочастотной фильтрации обычно позволяет большинству экспериментаторов обеспечить хорошую частотную характеристику при выполнении рутинных измерений артериального давления.Хотя этого достаточно для измерения артериального давления, измерение внутрижелудочкового давления в сердце представляет собой более сложную задачу. В первом случае катетер должен быть намного длиннее, чтобы можно было достичь сердца от точки входа, которая может находиться в бедренной артерии. Для этого может потребоваться катетер длиной 1-2 м для крупных животных и людей. Катетер также должен быть тонким и гибким, чтобы его можно было без повреждений провести в желудочки через сердечные клапаны. Оба эти фактора отрицательно влияют на отклик преобразователя.В дополнение к этому, формы волны желудочкового давления, особенно в левом желудочке, имеют более быстрый рост и спад, чем артериальное давление, и, следовательно, содержат более широкий диапазон частот. В довершение ко всему, часто именно скорость повышения желудочкового давления (используемого в качестве показателя сократительной силы сердца) представляет наибольший интерес для экспериментатора, и на нее может заметно повлиять чрезмерное демпфирование внутри катетера.
Следовательно, измерения желудочкового давления с помощью длинного катетера могут быть в значительной степени искажены.Проблему демпфирования катетера можно избежать, разместив миниатюрный датчик непосредственно внутри самого желудочка. Можно сконструировать миниатюрные датчики давления, которые достаточно малы, чтобы их можно было установить на конце катетера, который вводится в сердце, с сигналами давления, передаваемыми обратно в точку входа либо электрически, либо оптически. Датчик Mikro-Tip ® компании Millar Instruments (Хьюстон, Техас, США) является популярным примером таких устройств. Миниатюрный датчик давления на основе полупроводника диаметром 1 мм прикреплен к концу 1.Катетер длиной 4 м, содержащий провода, соединяющие датчик с мостовым усилителем. У этого подхода много преимуществ. Проблемы с демпфированием и резонансом, связанные с катетером, устранены, как и проблемы с закупоркой. Частотная характеристика зависит только от свойств мембраны датчика и очень высока, с резонансной частотой 35 кГц, по сравнению с 50–100 Гц обычных датчиков, и более чем адекватна сигналам желудочкового давления. Единственный серьезный недостаток – большая хрупкость, связанная с более открытым датчиком, требующая осторожного обращения и более высокая стоимость.Дальнейшее обсуждение свойств датчиков давления можно найти в Togawa et al. (1997).
Расчет резонансов корпуса
Сделайте пожертвование, чтобы сохранить этот сайт …| Размерные резонансы внутри корпуса Помимо резонансной частоты корпуса (f b ), существуют также габаритные резонанс необходимо учитывать. Эти резонансы возникают, когда размер равен половине длины волны звука, и это могло вызвать окрашивание воспроизводимого звука на соответствующем частоты. Если бы это произошло, на соответствующая частота. Этого можно избежать, если убедиться, что ни один из размеров внутреннего конуса до перегородки не соответствует
тем же. |
Рекомендуемые передаточные числа:
|
Определение резонансной частоты | APC International
При воздействии переменного электрического поля пьезоэлектрический керамический элемент циклически меняет размеры с частотой смены поля.Частота, на которой керамический элемент наиболее легко вибрирует и наиболее эффективно преобразует подводимую электрическую энергию в механическую, – это резонансная частота .
Схема ответов элемента изображена на Рис. 1.8 . По мере увеличения частоты цикличности колебания элемента сначала приближаются к частоте, при которой полное сопротивление минимально (максимальная проводимость). Эта минимальная частота полного сопротивления , f m , аппроксимирует резонансную частоту , f s , частоту, при которой полное сопротивление в электрической цепи, описывающей элемент, равно нулю, если сопротивление, вызванное механическими потерями, не учитывается.Минимальная частота импеданса также является резонансной частотой f r . Состав керамического материала, форма и объем элемента определяют резонансную частоту – как правило, более толстый элемент имеет более низкую резонансную частоту, чем более тонкий элемент той же формы.
При дальнейшем увеличении частоты переключения полное сопротивление увеличивается до максимума (минимальная проводимость). Максимальная частота импеданса, f n , аппроксимирует частоту параллельного резонанса , f p , частоту, при которой параллельное сопротивление в эквивалентной электрической цепи бесконечно, если сопротивление, вызванное механическими потерями, не учитывается.Частота максимального импеданса также равна антирезонансной частоте , f a . Максимальный отклик элемента будет в точке между f m и f n .
Значения минимальной частоты импеданса, f m , и максимальной частоты импеданса, f n , могут быть определены путем измерения. Рисунок 1.10 показывает систему, предназначенную для определения этих значений, и резюмирует процедуру.
Рисунок 1.8 . Импеданс как функция частоты цикла
Колебания керамического элемента сначала приближаются к минимальной частоте импеданса (f m ) / резонансной частоте (f r ), при которой элемент наиболее легко вибрирует и наиболее эффективно преобразует электрическую энергию. в механическую энергию. При дальнейшем увеличении частоты переключения импеданс увеличивается до максимальной частоты импеданса (f n ) / антирезонансной частоты (f a ).
Рисунок 1.10. Система определения минимального импеданса (резонансной частоты) и максимального импеданса (антирезонансной частоты) пьезоэлектрического керамического элемента
Процедура:
- Установите переключатель в положение A.
- Установите керамический элемент на место.
- Отрегулируйте генератор частоты, чтобы получить максимальное значение напряжения на вольтметре. Это значение является резонансной частотой.
- Установите переключатель в положение B.
- Отрегулируйте R4, чтобы получить значение напряжения на вольтметре, равное значению на шаге 3. Это значение является резонансным сопротивлением (Zr).
- Установите переключатель в положение A.
- Отрегулируйте генератор частоты, чтобы получить минимальное значение напряжения на вольтметре. Это значение и есть частота антирезонанса.
f m и f n могут использоваться для расчета коэффициента электромеханической связи, k. k зависит от режима колебаний и формы керамического элемента.Соотношения между k и f m и f n для керамической пластины, диска (размеры поверхности большие относительно толщины) или стержня составляют:
Фактор связи для пластин / k 31 *
* электрическое поле параллельно направлению поляризации,
наведенная деформация перпендикулярно направлению поляризации
Фактор связи для дисков / k p **
** электрическое поле параллельно направлению поляризации направление поляризации,
индуцированная деформация в том же направлении
Фактор связи для стержней / k 33 ***
*** электрическое поле, параллельное направлению поляризации,
индуцированная деформация в том же направлении
Свяжитесь с APC International сегодня!
Есть вопросы о пьезоизделиях APC International? Свяжитесь с нами или позвоните нам по телефону (570)726-6961, чтобы узнать больше.
Калькулятор резонансной частотыRLC [последовательно / параллельно] • Электрические калькуляторы Org
Вычислитель резонансной частотыRLC используется для расчета резонансной частоты последовательных / параллельных цепей. Он также рассчитывает последовательный и параллельный коэффициент демпфирования.
RLC Резонансная частота Формула
RLC Резонанс – это особая частота, на которой резонирует электрическая цепь. Значение частоты RLC определяется индуктивностью и емкостью цепи.Резонанс возникает как в последовательной, так и в параллельной цепях. Хотя основная формула для расчета серий и резонансной частоты одинакова, тем не менее, существуют определенные различия, которые определяют резонансную частоту.
Резонансная частота серииРезонанс последовательной цепи возникает, когда индуктивное реактивное сопротивление в точности равно емкостному реактивному сопротивлению. Однако необходимым условием является разность фаз в 180 градусов, при которой они должны компенсировать друг друга. Последовательный резонансный контур имеет минимальное сопротивление при резонансе. Последовательный резонансный контур и его формула:
Частота параллельного резонанса
Параллельная резонансная частота чаще встречается в электронных схемах, но не менее сложна. Мы можем определить параллельный резонанс как условие нулевой разности фаз или единичного коэффициента мощности. Параллельный резонансный контур имеет максимальное сопротивление.
Коэффициент демпфирования
Коэффициент демпфирования цепи определяется как отношение ширины полосы пропускания к центральной частоте.Коэффициент демпфирования схемы определяет частоту полосы пропускания. Более высокий коэффициент демпфирования означает более широкую полосу пропускания, а более низкий коэффициент демпфирования означает, что полоса пропускания будет ниже. Коэффициент демпфирования последовательной цепи напрямую связан с сопротивлением по формуле:
В то время как коэффициент параллельного демпфирования обратно пропорционален сопротивлению:
Практическое применение
Практически последовательные и параллельные RLC и LC резонансные цепи используются в приложениях электронного проектирования и моделирования схем.
Проектирование схем фильтров
Частотные фильтры, такие как фильтры нижних и верхних частот, полосовые и полосовые фильтры, используют в своей конструкции концепции полосовой и резонансной частоты.
Настройка аналоговой магнитолы
Настройка аналогового радиоприемника выполняется с помощью переменного конденсатора с параллельными пластинами, значение которого изменяется для настройки радиоприемника на частоты, поступающие от радиоприемника.
Пример числовых задач
Пример № 1: Последовательный резонансный контур имеет индуктивность 50 мГн и емкость 20 мкФ, которые подключаются к резистору 10 кОм.Найдите резонансную частоту и коэффициент затухания.
Решение:
Приведенные значения: L = 50 мГн и C = 20 мкФ
Из формулы:
= 1 / (50 * 0,001 * 20 * 0,000001) = 1000 Гц или 1 кГц
Коэффициент демпфирования серииможно рассчитать по формуле:
= (5 кОм) √ ((20 * 0,000001) / (50 * 0,001) = 100
Пример № 2: Параллельный резонансный контур имеет резистор 1 МОм, конденсатор 20 пФ и катушку индуктивности 500 мкГн.


