Какие бывают конденсаторы в физике: Типы конденсаторов и их использование

Содержание

Какие бывают конденсаторы? Типы конденсаторов, их характеристики

Автор:

MastepOk

30 января 2018 00:22

Метки: емкость конденсатор помощь радио радиолюбителю советы

Многие интересуются, имеют ли конденсаторы типы? Конденсаторов в электронике существует множество. Такие показатели, как емкость, рабочее напряжение и допуск, являются основными. Не менее важен тип диэлектрика, из которого они состоят. В этой статье будет рассмотрено подробнее, какие типы конденсаторов бывают по виду диэлектрика.

Источник:

Классификации конденсаторов.

Конденсаторы являются распространенными компонентами в радиоэлектронике.

Они классифицируются по множеству показателей. Важно знать, какими моделями, в зависимости от характера изменения величины, представлены разные конденсаторы. Типы конденсаторов:

1. Устройства с постоянной емкостью.
2. Приборы с переменным видом емкости.
3. Построечные модели.

Тип диэлектрика конденсатора может быть разным:

– бумага;
– металлическая бумага;
– слюда; тефлон;
– поликарбонат;
– электролит.

По способу установки данные приборы предназначены для печатного и навесного монтажа. При этом типы корпусов конденсаторов SMD-модификации бывают:

– керамическими;
– пластиковыми;
– металлическими (алюминиевыми).

Следует знать, что приборы из керамики, пленки и неполярные виды не обладают маркировкой. Показатель их емкости колеблется от 1 пф до 10 мкф. А электролитные типы имеют форму бочонков в корпусе из алюминия и маркируются. Танталовый же тип производится в корпусах прямоугольной формы.

Такие устройства бывают разного размера и расцветки: черные, желтые и оранжевые. На них также присутствует кодовая маркировка.

Электролитические конденсаторы из алюминия.

Основой электролитических конденсаторов из алюминия являются две тонкие скрученные алюминиевые полоски. Между ними расположена бумага, содержащая электролит. Показатель емкости этого прибора равен 0,1-100 000 uF. Кстати, в этом и заключается его основное преимущество перед другими видами. Максимальное напряжение равно 500 V.

К минусам относятся повышенная утечка тока и уменьшение емкости с возрастанием частоты. Поэтому в платах часто вместе с электролитическим конденсатором используется и керамический.

Также следует отметить, что данный тип отличается полярностью. Это означает, что вывод устройства с минусовым показателем находится под отрицательным напряжением, в отличие от противоположного вывода. Если не придерживаться этого правила, то скорее всего, приспособление выйдет из строя. Поэтому рекомендуется применять его в цепях с наличием постоянного или пульсирующего тока, но ни в коем случае не переменного.

Электролитические конденсаторы: типы и предназначение.

Типы электролитических конденсаторов представлены широким рядом. Они бывают:

– полимерными;
– полимерными радиальными;
– с низким уровнем утечки тока;
– стандартной конфигурации;
– с широким диапазоном температур;
– миниатюрными;
– неполярными;
– с наличием жесткого вывода;
– низкоимпедансными.

Источник:

Где применяются электролитические конденсаторы? Типы конденсаторов из алюминия используются в разных радиотехнических устройствах, деталях компьютера, периферийных приборах типа принтеров, графических устройствах и сканерах. Также они применяются в строительном оборудовании, промышленных приборах для измерения, в сфере вооружения и космоса.

Конденсаторы КМ

Существуют и глиняные конденсаторы типа КМ. Они используются:
– в промышленном оборудовании;
– при создании приборов для измерения, отличающихся высокоточными показателями;
– в радиоэлектронике;
– в сфере военной индустрии.

Устройства подобного типа отличаются высоким уровнем стабильности. Основу их функциональности составляют импульсные режимы в цепях с переменным и неизменным током. Их характеризует высокий уровень сцепления обкладок из керамики и долгая служба. Это обеспечивается низким значением коэффициента емкостного непостоянства температур.

Конденсаторы КМ при маленьких размерах имеют высокий показатель емкости, достигающий 2,2 мкФ. Изменение ее значения в интервале рабочей температуры у данного вида составляет от 10 до 90%.

Типы керамических конденсаторов группы Н, как правило, применяются как переходники или же блокирующие устройства и т. п. Современные приборы из глины изготавливаются при помощи прессовки под давлением в целостный блок тончайших металлизированных керамических пластинок.

Высокий уровень прочности этого материала дает возможность использовать тонкие заготовки. В итоге емкость конденсатора, пропорциональная показателю объема, резко возрастает.

Устройства КМ отличаются высокой стоимостью. Объясняется это тем, что при их изготовлении используются драгоценные металлы и их сплавы: Ag, Pl, Pd. Палладий присутствует во всех моделях.

Конденсаторы на основе керамики.

Дисковая модель обладает высоким уровнем емкости. Ее показатель колеблется от 1 pF до 220 nF, а самое высокое рабочее напряжение не должно быть выше 50 V.

К плюсам данного типа можно отнести:

– малые потери тока;
– небольшой размер;
– низкий показатель индукции;
– способность функционировать при высоких частотах;
– высокий уровень температурной стабильности емкости;
– возможность работы в цепях с постоянным, переменным и пульсирующим током.

Основу многослойного устройства составляют чередующиеся тонкие слои из керамики и металла.

Этот вид похож на однослойный дисковый. Но такие устройства обладают высоким показателем емкости.

Максимальное рабочее напряжение на корпусе этих приборов не указывается. Так же как и на однослойной модели, напряжение не должно быть выше 50 V.

Устройства функционируют в цепях с постоянным, переменным и пульсирующим током.

Плюсом высоковольтных керамических конденсаторов является их способность функционировать под высоким уровнем напряжения. Диапазон рабочего напряжения колеблется от 50 до 15000 V, а показатель емкости может составлять от 68 до 150 pF.

Могут функционировать в цепях с постоянным, переменным и пульсирующим током.

Танталовые устройства.

Современные танталовые устройства являются самостоятельным подвидом электролитического вида из алюминия. Основу конденсаторов составляет пентаоксид тантала.

Конденсаторы обладают небольшим показателем напряжения и применяются в случае необходимости использования прибора с большим показателем емкости, но в корпусе малого размера. У данного типа есть свои особенности:

– небольшой размер;
– показатель максимального рабочего напряжения составляет до 100 V;
– повышенный уровень надежности при долгом употреблении;
– низкий показатель утечки тока; широкий спектр рабочих температур;
– показатель емкости может колебаться от 47 nF до 1000 uF;
– устройства обладают более низким уровнем индуктивности и применяются в высокочастотных конфигурациях.

Минус этого вида заключен в высокой чувствительности к повышению рабочего напряжения.

Следует отметить, что, в отличие от электролитического вида, линией на корпусе помечается плюсовой вывод.

Разновидности корпусов.

Какие разновидности имеют танталовые конденсаторы? Типы конденсаторов из тантала выделяются в зависимости от материала корпуса.

1. SMD-корпус. Для изготовления корпусных устройств, которые используются при поверхностном монтаже, катод соединяется с терминалом посредством эпоксидной смолы с содержанием серебряного наполнителя. Анод приваривается к электроду, а стрингер отрезается. После формирования устройства на него наносится печатная маркировка. Она содержит показатель номинальной емкости напряжения.

2. При формировании этого типа корпусного устройства анодный проводник должен быть приварен к самому выводу анода, а затем отрезается от стрингера. В этом случае терминал катода припаивается к основе конденсатора. Далее конденсатор заполняется эпоксидом и высушивается. Как и в первом случае, на него наносится маркировка.

Конденсаторы первого типа отличаются большей степенью надежности. Но все типы танталовых конденсаторов применятся:

– в машиностроении;
– компьютерах и вычислительной технике;
– оборудовании для телевизионного вещания;

– электрических приборах бытового назначения;
– разнообразных блоках питания для материнских плат, процессоров и т.д.

Поиск новых решений.

На сегодняшний день танталовые конденсаторы являются самыми востребованными. Современные производители находятся в поисках новых методов повышения уровня прочности изделия, оптимизации его технических характеристик, а также существенного понижения цены и унификации производственного процесса.

С этой целью пытаются снизить стоимость на основе составляющих компонентов. Последующая роботизация всего процесса производства также способствует падению цены на изделие.

Важным вопросом считается и уменьшение корпуса устройства при сохранении высоких технических параметров. Уже проводятся эксперименты на новых типах корпусов в уменьшенном исполнении.

Конденсаторы из полиэстера.

Показатель емкости этого типа устройства может колебаться от 1 nF до 15 uF. Спектром рабочего напряжения является показатель от 50 до 1500 V.

Существуют устройства с разной степенью допуска (допустимое отклонение емкости составляет 5%, 10% и 20%).

Это вид обладает стабильностью температуры, высоким уровнем емкости и низкой стоимостью, что и объясняет их широкое применение.

Конденсаторы с переменной емкостью.

Типы переменных конденсаторов обладают определенным принципом работы, который заключается в накоплении заряда на пластинах-электродах, изолированных посредством диэлектрика. Пластины эти отличаются подвижностью. Они могут перемещаться.

Подвижная пластина называется ротором, а неподвижная — статором. При изменении их положения изменятся и площадь пересечения, и, как следствие, показатель емкости конденсатора.

Конденсаторы бывают с двумя типами диэлектриков: воздушным и твердым.

В первом случае в роли диэлектрика выступает обыкновенный воздух. Во втором случае применяют керамику, слюду и др. материалы. Для увеличения показателя емкости устройства статорные и роторные пластины собираются в блоки, закрепленные на единой оси.

Конденсаторы с воздушным типом диэлектрика применяются в системах с постоянной регулировкой емкости (например, в узлах настройки радиоприемников). Такой тип устройства обладает более высоким уровнем стойкости, чем керамический.

Источник:

Построечный вид.

Самым распространенным видом являются построечные конденсаторы. Они относятся к переменному типу, но обладают меньшей износостойкостью, так как регулируются реже.

Типы конденсаторов этой категории в основе содержат металлизированную керамику. Металл функционирует в качестве электрода, а керамика выступает в роли изолятора.

Автор: Майя Музашвили

Источник:

Конденсаторы | 8 класс | Физика

Содержание

Если тело обладает некоторым электрическим зарядом, то вокруг него обязательно присутствует электрическое поле. Это поле обладает некоторой энергией — может совершить какую-то работу.

Можно ли как-то накопить эту энергию? Да, такая возможность существует. Для этого используют специальный прибор — конденсатор.

Конденсатор — это устройство, позволяющее накапливать электрические заряды и, соответственно, энергию электрического поля.

На данном уроке вы познакомитесь с устройством этого прибора, его характеристиками и свойствами.

{"questions":[{"content":"Конденсатор — это прибор для[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["накопления энергии электрического поля","измерения энергии электрического поля","регулировки силы тока в цепи"],"explanations":["","","Эту функцию выполняют реостаты. "],"answer":[0]}}}]}

Простейший конденсатор и его устройство

Устройство простейшего конденсатора представлено на рисунке 1. Он состоит из двух одинаковых металлический пластин. Эти пластины называются обкладками конденсатора.

Обкладки расположены на небольшом расстоянии друг от друга. Этот промежуток между ними обязательно должен быть заполнен слоем диэлектрика. В нашем случае таким диэлектриком является обычный воздух.

Такой конденсатор называется плоским (по форме обкладок).

Конденсатор имеет свой условный знак для обозначения на схеме электрической цепи (рисунок 2).

{"questions":[{"content":"Между обкладками конденсатора обязательно должен присутствовать[[choice-9]]","widgets":{"choice-9":{"type":"choice","options":["слой диэлектрика","проводник","защитный слой"],"answer":[0]}}}]}

Зарядка конденсатора и его способность накапливать заряды

Теперь разберемся, каким же образом мы можем накапливать заряды с помощью конденсатора.

Рассмотрим простой опыт. Возьмем конденсатор, состоящий из двух металлических пластин, расположенных параллельно друг другу, и заряженный аккумулятор.

Две обкладки конденсатора подключим к разным полюсам аккумулятора. На обкладках начнут образовываться электрические заряды (рисунок 3). Они будут равны друг другу, но иметь противоположные знаки.

Эти заряды образуют электрическое поле конденсатора. Оно будет сосредоточено между обкладками.

Отключим аккумулятор от конденсатора. Что мы увидим? Заряды, образованные на обкладках, никуда не деваются. Они сохраняются, как и электрическое поле между пластин. Конденсатор заряжен.

Если мы соединим проводником обкладки конденсатора, то увидим, что по нему некоторое время будет течь ток. Значит, заряженный конденсатор является источником тока в электрической цепи.

{"questions":[{"content":"Какой конденсатор может быть источником тока в электрической цепи?[[choice-12]]","widgets":{"choice-12":{"type":"choice","options":["Заряженный","любой","разряженный","Плоский"],"answer":[0]}}}]}

Электроемкость конденсатора

Логично предположить, что разные конденсаторы по-разному будут накапливать заряд. Как охарактеризовать эту способность прибора? Для этого существует специальная величина — электроемкость (или просто емкость) конденсатора.

Чтобы понять смысл этой величины, рассмотрим опыт. Возьмем две металлические пластины и установим их на изолированных подставках друг напротив друга.

Подключим к пластинам электрометр. Этот прибор (рисунок 4) по своему устройству и принципу действия схож с электроскопом. Он позволит нам зафиксировать значения напряжения, которое возникнет между пластинами.

Итак, одну из пластин (A) мы соединим проводом со стержнем электрометра, а другую (B) соединим с корпусом прибора (заземлим). Коснемся положительно наэлектризованной стеклянной палочкой внешней стороны пластины A (рисунок 5).

Мы сообщили пластине A положительный заряд $+q$. Вокруг этого заряда (пластины A) теперь существует электрическое поле. Под его действием произойдет перераспределение зарядов в пластине B. Отрицательные заряды перейдут на внутреннюю сторону пластины, а положительные — на внешнюю.

Помните, что мы заземлили пластину B? За счет этого на пластину пойдут свободные электроны с земли. Они нейтрализуют положительный заряд на внешней стороне пластины. Таким образом, мы получили на пластине B отрицательный заряд $-q$ (рисунок 6). По величине он равен заряду на другой пластине.

Стрелка электрометра отклонилась. Зафиксируем это значение напряжения между пластинами. Далее мы снова сообщим заряд пластине B, равный по величине первому сообщаемому заряду. Потом сообщим третий и четвертый такие же заряды, наблюдая за стрелкой электрометра.

Вы увидите, что при увеличении заряда в 2, 3, 4 раза, соответственно, в 2, 3, 4 раза увеличиваются показания электрометра — напряжение между пластинами. Важно отметить, что отношение заряда к напряжению при этом будет постоянно:
$\frac{q}{U} = \frac{2q}{2U} = \frac{3q}{3U} = \frac{4q}{4U} = const$.

Теперь мы можем дать определение электроемкости конденсатора.

Электроемкость конденсатора — это величина, измеряемая отношением заряда на одной из пластин конденсатора к напряжению между пластинами:
$C = \frac{q}{U}$.

{"questions":[{"content":"Электроемкость конденсатора определяется отношением[[choice-16]]","widgets":{"choice-16":{"type":"choice","options":["заряда к напряжению между обкладками","напряжения между обкладками к заряду","заряда на одной обкладке к заряду на другой"],"explanations":["","","Эти заряды равны, но противоположны друг другу по знаку. За заряд конденсатора мы принимаем численное значение заряда одной из обкладок."],"answer":[0]}}}]}

Единицы измерения электроемкости

В СИ электроемкость измеряется в фарадах ($Ф$).

Электроемкость конденсатора равна единице, если при сообщении ему заряда в $1 \space Кл$ возникает напряжение, равное $1 \space В$ (рисунок 7):
$1 \space Ф = \frac{1 \space Кл}{1 \space В}$. {-12} \space Ф$.

{"questions":[{"content":"Электроемкость измеряется в[[choice-24]]","widgets":{"choice-24":{"type":"choice","options":["фарадах","ньютонах","амперах","ваттах"],"explanations":["","Это единица измерения силы.","Это единица измерения силы тока.","Это единица измерения мощности тока."],"answer":[0]}}}]}

Зависимость электроемкости от площади пластин конденсатора

От чего зависит электроемкость? Начнем с размера пластин.

Зафиксируем полученное в первом опыте с электрометром и конденсатором значение напряжения $U_1$. Теперь возьмем пластины, имеющие большую площадь. Сообщим им точно такой же заряд $q$ (рисунок 9).

Мы увидим, что стрелка электрометра отклоняется меньше. Это означает, что напряжение между этими пластинами меньше напряжения между пластинами меньшей площади ($U_1 > U_2$).

Из определения электроемкости:
$C_1 = \frac{q}{U_1}$,
$C_2 = \frac{q}{U_2}$,
$C_2 > C_1$.

Чем больше площадь пластин, тем больше электроемкость конденсатора.

{"questions":[{"content":"Если мы уменьшим площадь обкладок конденсатора, то его электроемкость[[choice-31]]","widgets":{"choice-31":{"type":"choice","options":["уменьшится","увеличится","не изменится"],"answer":[0]}}}]}

Зависимость электроемкости от расстояния между пластинами конденсатора

Снова обратимся к опыту. Теперь изменим расстояние между пластинами — уменьшим его (рисунок 10).

Мы увидим, что напряжение между пластинами уменьшилось: $U_2 < U_1$. Значит,
$C_1 = \frac{q}{U_1}$,
$C_2 = \frac{q}{U_2}$,
$C_2 > C_1$.

При уменьшении расстояния между пластинами конденсатора и при неизменном заряде электроемкость конденсатора увеличивается.

{"questions":[{"content":"Один из способов уменьшить емкость конденсатора — это [[choice-34]]","widgets":{"choice-34":{"type":"choice","options":["увеличить расстояние между его обкладками","уменьшить расстояние между его обкладками","увеличить площадь его обкладок"],"answer":[0]}}}]}

Зависимость электроемкости от диэлектрика

Проведем еще один опыт. Зафиксируем значение напряжения между пластинами конденсатора. Затем внесем между ними лист из оргстекла (рисунок 11). Он является диэлектриком.

Если раньше диэлектриком между пластинами являлся только воздух, то теперь это и воздух, и лист оргстекла. Напряжение между пластинами уменьшилось: $U_1 > U_2$. Значит,
$C_1 = \frac{q}{U_1}$,
$C_2 = \frac{q}{U_2}$,
$C_2 > C_1$.

При внесении диэлектрика электроемкость конденсатора увеличивается.

{"questions":[{"content":"Если добавить еще один слой диэлектрика между обкладками конденсатора, то его емкость[[choice-37]]","widgets":{"choice-37":{"type":"choice","options":["увеличится","уменьшится","не изменится"],"answer":[0]}}}]}

Виды конденсаторов

Между обкладками конденсатора могут быть помещены разнообразные диэлектрики. В зависимости от природы этого диэлектрика конденсаторы разделяют на несколько видов: с твердым, жидким и газообразным диэлектриком.

Также существует классификация и по форме обкладок. Конденсаторы бывают плоские, цилиндрические, сферические (рисунок 12) и др.

Конденсаторы бывают с постоянной емкостью и с переменной емкостью. В последних можно регулировать параметры, от которых зависит емкость — ширину пластин и расстояние между ними.

На данный момент существует огромное разнообразие конденсаторов (рисунок 13). Многие из них носят названия, происходящие от названий материалов, составляющих их: слюдяные, керамические, алюминиевые электролитические, танталовые электролитические, конденсаторы на полимерной пленке.

{"questions":[{"content":"Если конденсатор имеет плоские обкладки, параллельные друг другу, его называют[[choice-40]]","widgets":{"choice-40":{"type":"choice","options":["плоским","квадратным","параллельным","прямоугольным"],"answer":[0]}}}]}

Энергия конденсатора и работа его электрического поля

Заряженный конденсатор обладает некоторой энергией. Это легко проверить на опыте. Если мы подключим к конденсатору электрическую лампочку, то она она ярко вспыхнет (рисунок 14). Энергия конденсатора превратилась во внутреннюю энергию нити накаливания лампы и соединительных проводов.

Откуда взялась эта энергия? Конденсатор получает ее при зарядке.

Для того, чтобы зарядить конденсатор, нужно совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии совершенная работа A и будет равна энергии конденсатора E:
$A = E$.

Для расчета такой работы электрического поля конденсатора существует специальная формула. 2}{2}$”,”$A = qU$”],”answer”:[0]}}}]}

Это свойство (накопление энергии и ее быстрая отдача) широко применяется в различных электронных устройствах, в медицинской технике (рентген, устройства для электротерапии), при изготовлении дозиметров, фотосъемке.

Последовательное соединение конденсаторов

В электрической цепи может быть не один, а сразу несколько конденсаторов. Они могут быть соединены как последовательно, так и параллельно.

Рассмотрим первый тип соединения — последовательный (рисунок 15).

Обкладки 2 и 3, принадлежащие разным конденсаторам, будут являться отдельной деталью. По закону сохранения заряда, заряды на обкладках 2 и 3 будут равны друг другу по модулю, но противоположны по знаку. Из этого следует, что общий заряд конденсаторов численно будет равен заряду на любой из обкладок конденсаторов.

$q = q_1 = q_2 = … = q_n$

Напряжение на концах участка цепи с последовательно соединенными конденсаторами будет складываться из значения напряжений на каждом конденсаторе.

$U = U_1 + U_2 + … + U_n$

Чтобы получить формулу для общей емкости конденсаторов, последнее равенство нужно разделить на заряд q (любой, так как они равны).

$\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + … \frac{1}{C_n}$.

{"questions":[{"content":"Общий заряд последовательно соединенных конденсаторов равен[[choice-49]]","widgets":{"choice-49":{"type":"choice","options":["заряду на любой из обкладок конденсаторов","сумме зарядов на всех обкладках конденсаторов","сумме зарядов на двух обкладках одного конденсатора"],"answer":[0]}}}]}

Параллельное соединение конденсаторов

Параллельное соединение конденсаторов показано на рисунке 16.

В этом случае выходы от источника питания будут соединены с каждой обкладкой конденсаторов. Поэтому напряжение на концах такого участка цепи будет равно напряжению между обкладками любого из конденсаторов.

$U = U_1 = U_2 = … = U_n$

Заряды на обкладках будут суммироваться.

$q = q_1 + q_2 + … + q_n$

Разделим это равенство на значение напряжения и получим формулу для электроемкости параллельно соединенных конденсаторов.

$C = C_1 + C_2 + … + C_n$

{"questions":[{"content":"Напряжение на концах участка цепи с параллельно соединенными конденсаторами равно[[choice-54]]","widgets":{"choice-54":{"type":"choice","options":["напряжению между обкладками любого из конденсаторов","сумме напряжений между обкладками всех конденсаторов","напряжению на полюсах источника тока"],"answer":[0]}}}]}

Первый конденсатор — лейденская банка

Лейденская банка официально является первым конденсатором. Изобретение ее относится к 1745 году. Существует множество версий о том, кто же именно должен считаться изобретателем этого прибора, но официально авторство принадлежит Питеру ван Мушенбруку и его студенту Андреасу Кунэусу.

В ранней версии лейденская банка была на часть заполнена водой, которая выступала в роли обкладки (рисунок 17). Второй обкладкой являлась рука, держащая банку. После зарядки этого приспособления Андреас Кунэус испытал сильный удар током, коснувшись до верха металлического стержня.

Более поздняя и более распространенная версия этого незамысловатого прибора представляет собой сосуд из стекла с широким горлом, снаружи покрытый листом из фольги (рисунок 18). Фольга также находится и внутри банки. Через пробку в этот сосуд вставляется металлический стержень. Он должен касаться фольги внутри банки.

Таким образом, фольга внутри и фольга снаружи становятся своеобразными обкладками. При подключении к источнику тока на них накапливается электрический заряд.

Внимание! Лейденская банка не является безопасным инструментом в электротехнике! Разряд такого конденсатора может оказаться смертельным или привести к серьезным физическим повреждениям. Будьте аккуратны при использовании данного прибора: не следует пытаться разрядить лейденскую банку, взявшись за нее голыми руками.

{"questions":[{"content":"У лейденской банки, изображенной на рисунке 18, обкладками являются[[choice-57]]","widgets":{"choice-57":{"type":"choice","options":["слой фольги снаружи и слой фольги внутри банки","металлический стержень и слой фольги снаружи банки","Пробка и стеклянный сосуд"],"answer":[0]}}}]}

Как изготовить лейденскую банку своими руками? Возьмите пластиковую банку с крышкой (из-под кофе, витаминов). Внешнюю сторону банки на $\frac{2}{3}$ обклейте фольгой. Далее или налейте в банку соленую воду, или обклейте изнутри фольгой. Затем закройте крышку и проткните ее достаточно длинным гвоздем, чтобы он касался внутренней обкладки (воды или фольги). После зарядки такая банка представляет собой заряженный конденсатор.

Упражнения

Упражнение №1

Пластины плоского конденсатора подсоединяют к источнику напряжения в $220 \space В$.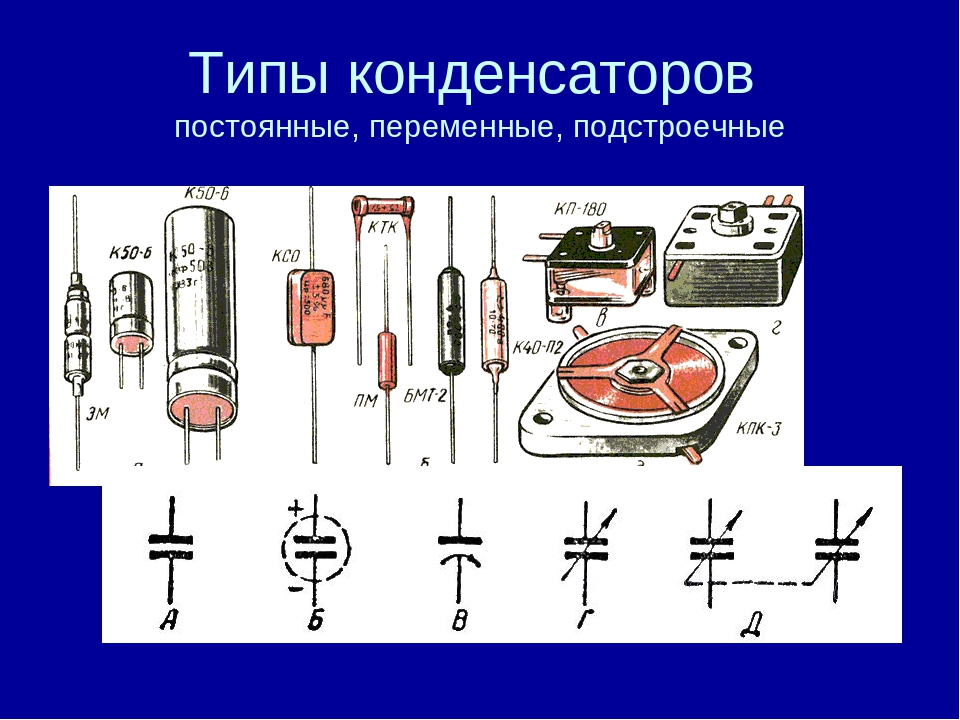 6 \space В$.

Конденсаторы

Емкость

Емкость (C) определяется как отношение накопленного заряда (Q) к разности потенциалов (В) между проводниками:

Емкость измеряется в фарадах (F) и 1 фарад

Конденсатор с параллельными пластинами

В своей простейшей форме конденсатор представляет собой набор противоположно заряженных параллельных пластин, разделенных расстоянием (d) . Из уравнения для разности потенциалов параллельных пластин и определения емкости емкость параллельных пластин равна

Строго говоря, это уравнение справедливо только при наличии вакуума между пластинами.

Когда непроводящий материал помещается между пластинами конденсатора, может накапливаться больше заряда из-за индуцированного заряда на поверхности электрического изолятора. Отношение емкости с изолятором к емкости вакуума называется диэлектрической проницаемостью (κ, греческая буква каппа). Значения диэлектрической проницаемости можно найти в таблицах свойств материалов. Уравнение для плоского конденсатора с диэлектриком, заполняющим пространство между пластинами, равно 9.0005

Энергия, запасенная в конденсаторе, может быть найдена с помощью любого из следующих трех уравнений, каждое из которых основано на разных переменных:

Конденсаторы параллельные и последовательные

Конденсаторы могут быть соединены параллельно или последовательно. Два конденсатора в параллельны , если соединены отрицательные и положительные пластины, как показано на рисунке 1.

Рисунок 1

Два конденсатора соединены параллельно. Рисунок (а) аналогичен схеме (б).

Можно составить уравнение для емкости одного конденсатора, которое будет иметь эквивалентную емкость этих двух конденсаторов. Общий заряд двух конденсаторов равен · = ··_·1· + ···_·2·. Напряжение на каждом конденсаторе одинаково и равно напряжению батареи (В) ; следовательно, Q ₁ = C ₁ V и Q ₂ = C ₂ V , или для эквивалентного конденсатора Q = C _eq 9 V . Substituting into the equation for total charge yields C _eq V = C ₁ V + C ₂ V , or C _eq = С ₁ + С ₂ . Этот результат можно обобщить, заявив, что эквивалентная емкость для набора параллельных емкостей представляет собой просто сумму отдельных емкостей.

Конденсаторы соединены в серии , если положительная пластина одного соединена с отрицательной пластиной, как показано на рисунке 2.

Рисунок 2

Два последовательно соединенных конденсатора. Рисунок (а) аналогичен схеме (б).

При последовательном соединении все конденсаторы имеют одинаковый заряд. Разность потенциалов на конденсаторах в сумме равна разности потенциалов между клеммами батареи; следовательно,

Подстановка этих уравнений в уравнение для разности потенциалов дает

Отмена заряда дает следующее выражение для эквивалентной емкости для последовательных комбинаций:

Примечание : Распространенная ошибка при расчете последовательной емкости состоит в том, что после сложения обратных величин отдельных конденсаторов забывают взять обратную величину, чтобы найти эквивалентную емкость.

Емкость

Емкость характеризуется параллельное расположение пластин и определяется с точки зрения заряда хранилище:

Аккумулятор будет переносить заряд от одной пластины к другой до тех пор, пока напряжение, создаваемое накоплением заряда, не сравняется с напряжением аккумулятора.

, где

Q = величина заряда хранятся на каждой тарелке.
В = напряжение, подаваемое на тарелки.

Аналог воздушного резервуара

Комбинация конденсаторов

Конденсаторный микрофон

Индекс

Концепции емкости

Концепции индуктивности

Гиперфизика***** Электричество и магнетизм

R Ступица

0188

Конденсаторы параллельно добавить…

Аналогия воздушного резервуара

Заряд последовательных конденсаторов

Индекс

Концепции емкости

Концепции индуктивности

Гиперфизика***** Электричество и магнетизм

R Ступица

0188

Поскольку заряд не может быть добавлен или снят с проводника между последовательными конденсаторами, суммарный заряд остается нулевым.

Какие бывают конденсаторы в физике: Типы конденсаторов и их использование

Какие бывают конденсаторы? Типы конденсаторов, их характеристики

Конденсаторы | 8 класс | Физика

Простейший конденсатор и его устройство

Зарядка конденсатора и его способность накапливать заряды

Электроемкость конденсатора

Единицы измерения электроемкости

Зависимость электроемкости от площади пластин конденсатора

Зависимость электроемкости от расстояния между пластинами конденсатора

Зависимость электроемкости от диэлектрика

Виды конденсаторов

Энергия конденсатора и работа его электрического поля

Последовательное соединение конденсаторов

Параллельное соединение конденсаторов

Первый конденсатор — лейденская банка

Упражнения

Упражнение №1

Конденсаторы

Емкость

Больше новостей

Добавить комментарий Отменить ответ