Конденсатор и постоянный ток: Конденсатор в цепи переменного и постоянного тока

Конденсатор в цепи переменного и постоянного тока

Если конденсатор присутствует в цепи постоянного тока, то возникающий кратковременный импульс производит его зарядку до значения напряжения источника, после чего движение тока прекращается. Отключенный от источника тока, заряженный конденсатор под действием нагрузки будет очень быстро разряжаться. Его разрядка напоминает кратковременный импульс. При этом, лампа накаливания мигнет один раз и погаснет.

Использование конденсатора

Конденсатор в цепи переменного тока ведет себя совершенно иначе. Зарядка и разрядка  чередуется с периодами колебаний переменного напряжения. Находящаяся в цепи лампа накаливания, соединенная последовательно, как и конденсатор будет визуально излучать непрерывный свет, поскольку промышленная частота колебаний не заметна для человеческого глаза.

Каждый конденсатор обладает емкостным сопротивлением, которое находится в обратной пропорциональной зависимости от его емкости и частоты циклов переменного тока. При таком сопротивлении, электрическая и магнитная энергия не превращается в тепловую. Таким образом, чем выше частота тока, тем ниже значение емкостного сопротивления и наоборот.

На основании этого важного свойства, конденсатор нашел практическое применение в цепях переменного тока, как гасящий элемент в делителях напряжения вместо резисторов. Это особенно актуально при значительном падении напряжения. В этом случае потребовались бы резисторы с большой мощностью и габаритами.

Конденсатор в цепи переменного тока не нагревается, поэтому и не происходит рассеивания энергии. Это связано со смещением напряжения и тока в конденсаторе между собой на 90 градусов. При максимальном напряжении ток равен нулю, при этом, мощность также равна нулю. Значит, никакой работы не совершается, и нагрев отсутствует.

Конденсатор вместо резистора

Это является основной причиной применения во многих случаях, конденсаторов вместо резисторов. Однако, при таком использовании, у конденсатора есть существенный недостаток, который нужно обязательно учитывать. В том случае, когда переменный ток в цепи изменяется, происходит изменение напряжения у нагрузки. Другой недостаток наблюдается, когда отсутствует гальваническая развязка. Поэтому, в целом, конденсаторы, как гасящие элементы, применяются достаточно ограничено. Они используются при относительно стабильном сопротивлении нагрузки. В качестве примера можно привести цепи питания в нагревательных элементах.

Закон Ома для переменного тока

Диммер своими руками: устройство, принцип работы + как сделать диммер самому

Мультиметр: назначение, виды, обозначение, маркировка, что можно измерить мультиметром

Как проверить конденсатор мультиметром: пошаговая инструкция

Как проверить конденсатор мультиметром на работоспособность

Выключатель с подсветкой: установка, подключение, схема

Конденсатор / Хабр

Конденсатор имеет следующее схематическое изображение

Рассмотрим водопроводную модель конденсатора. Ранее мы говорили о том, что ток может течь только в трубе, соединенной в кольцо в замкнутой цепи. Но можно представить пустую емкость, в которую можно заливать воду, пока емкость не заполнится. Это и есть конденсатор — емкость, в которую можно заливать заряд.

Для большей аналогии лучше представить себе водонапорную башню, в модели – трубу бесконечной длины поставленную вертикально. Вода насосом закачивается в эту трубу с нижнего торца и поднимается на высоту. Чем больше воды закачали и чем выше она поднялась – тем сильнее столб воды давит на днище и выше там давление. Так-то в эту бесконечную трубу можно сколько угодно воды (электрического заряда) закачать, но при этом противодавление столба воды будет расти. Если качать заряд генератором напряжения, то когда противодавление сравняется с давлением (напряжением), создаваемым генератором – закачка остановится.

Если характеристикой резистора является сопротивление, то электрической характеристикой конденсатора является емкость.

С=Q/U

Емкость говорит, сколько заряда можно в конденсатор закачать, чтобы напряжение там поднялось до величины U. Можно сказать, что емкость характеризует диаметр трубы. Чем ýже труба, тем быстрее поднимается уровень воды при закачке и растет давление на дне трубы. Давление же зависит только от высоты водяного столба, а не от массы закачанной воды.

В электрических терминах, чем меньше емкость конденсатора, тем быстрее растет напряжение при закачке туда заряда.

Напомню, что электрический ток I равен количеству протекающего заряда Q в секунду. То есть I=Q/T, где T – время. Это все равно, что поток воды исчисляемый кубометрами в секунду. Или килограммами в сек, потом проверим по размерности).

Поэтому конденсатор с маленькой емкостью заполняется зарядом быстро, а с большой емкостью – медленно.

Рассмотрим теперь электрические цепи с конденсатором.

Пусть конденсатор подключен к генератору напряжения.

рис 9. Подключение конденсатора к генератору напряжения.

“Главный инженер повернул рубильник” S1 и.. тыдыщ!!! Что произошло?

Идеальный генератор напряжения имеет бесконечную мощность и может выдавать бесконечный ток. Когда замкнули рубильник в нашу емкость хлынуло бесконечное количество заряда в секунду и она мгновенно заполнилась и напряжение на ней выросло до U.

Теперь рассмотрим более реальную цепь.

Это Вторая Главная Цепь в жизни инженера-электронщика (после делителя напряжения) —
RC–цепочка.

RC -цепочки бывают интегрирующего и дифференцирующего типа.

RC–цепочка интегрирующего типа

рис 10. Подключение RC -цепочки интегрирующего типа к генератору напряжения.

Что произойдет в этой схеме, если замкнуть выключатель S1?

Конденсатор С исходно разряжен и напряжение на нем рано 0. Поэтому ток в первый момент будет равен I=U/R. Затем конденсатор начнет заряжаться, напряжение на нем увеличивается, и ток через резистор начнет уменьшаться. I=(U-Uc)/R. Этот процесс будет продолжаться, конденсатор будет заряжаться уменьшающимся током до напряжения источника U.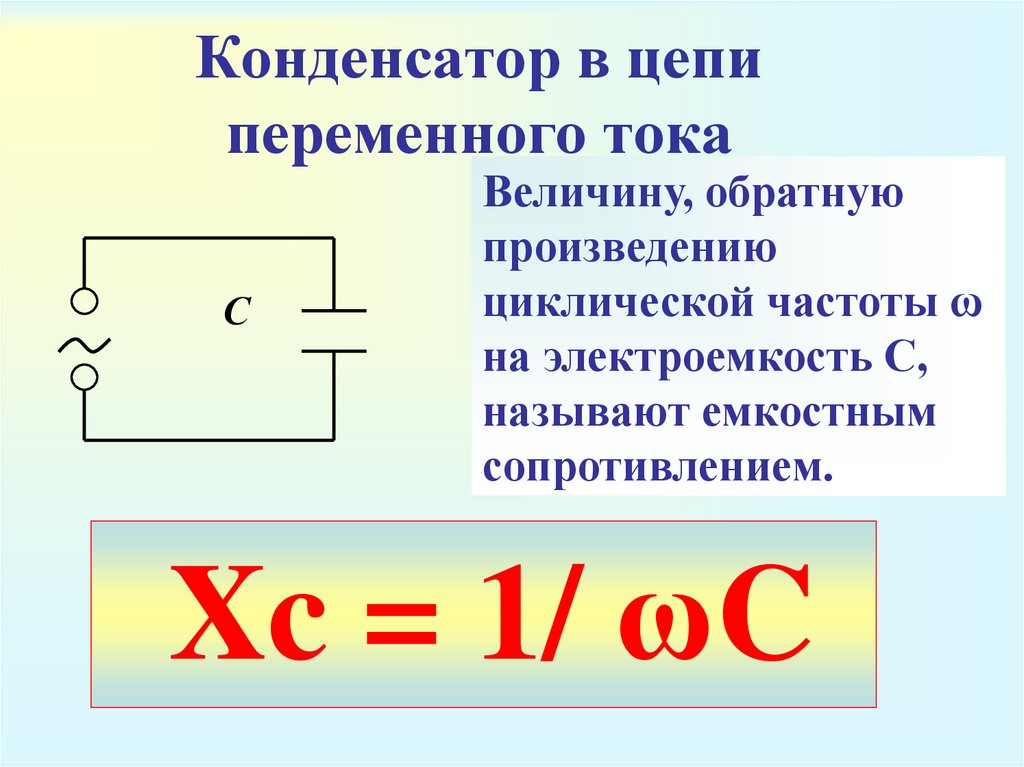 Напряжение на конденсаторе при этом будет расти по экспоненте.

рис 11. График роста напряжения на конденсаторе при подаче напряжения величиной U (ступеньки).

Вопрос: А если запитать такую цепочку от генератора тока, как будет расти напряжение на конденсаторе?

Почему цепочка называется – «интегрирующего типа»?

Как выше было отмечено, ток в первый момент после подачи напряжение будет равен I=U/R, так как конденсатор разряжен, и напряжение на нем равно 0. И какое-то время, пока напряжение на конденсаторе Uc мало по сравнению с U, ток будет оставаться почти постоянным. А при заряде конденсатора постоянным током напряжение на нем растет линейно.

Uc=Q/C, а мы помним, что ток это количество заряда в секунду, то есть скорость протекания заряда. Другими словами, заряд это интеграл от тока.

Q = ∫ I * dt =∫ U/R * dt

то есть

Uc=1/RC * ∫ U * dt

Но все это близко к истине в начальный момент, пока напряжение на конденсаторе малó.

На самом деле все сводится к тому, что конденсатор заряжается постоянным током.
А постоянный ток выдает генератор тока. (См. вопрос выше)
Если источник напряжения выдает бесконечно большое напряжение и сопротивление R также имеет бесконечно большую величину, то по факту мы имеем уже идеальный генератор тока, и внешние цепи на величину этого тока влияния не оказывают.

RC–цепочка дифференцирующего типа

Ну тут все то же самое, что в интегрирующей цепочке, только наоборот.

рис 12. Дифференцирующая цепочка.

Более подробно свойства RC цепей хорошо освещены в интернете.

Параллельное и последовательное соединение конденсаторов

Так же как резисторы, конденсаторы можно соединять последовательно и параллельно.

При параллельном соединении емкости складываются – ну это и понятно, это как заполнять сообщающиеся сосуды, общий объем получается равным сумме объемов. При последовательном же соединении получится так, что конденсатор с маленькой емкостью заполнится зарядом быстрее, чем конденсатор с большой емкостью. Напряжение на маленьком конденсаторе быстро вырастет почти до напряжения источника ( ну и остальные конденсаторы внесут свой вклад) , ток в общей цепи уменьшится до нуля, и процесс заряда конденсаторов прекратится. Таким образом емкость последовательно соединенных конденсаторов получается меньше емкости самого маленького из них.

Upd.
Рассмотрим более подробно процесс заряда конденсатора на схеме рис.10 (по мотивам учебника И.В.Савельева “Курс общей физики”, том II. “Электричество” )
Как было сказано в предыдущей статье О природе электрического тока электрический ток – это движение заряженных частиц. В проводниках ( в отличие от диэлектриков-изоляторов) часть электронов является свободными и такие электроны могут перескакивать от одного атому к другому. В целом проводник электрически нейтрален – отрицательный заряд электронов компенсируется положительным зарядом ядер атомов. Чтобы заставить электроны двигаться нужно создать их избыток на одном конце проводника и недостаток на другом. Этот избыток электронов на одном полюсе создает батарейка вследствие протекающих в ней электрохимических реакций. Когда проводник присоединяется к полюсам батарейки электроны от полюса, где их избыток начинают двигаться к другому полюсу, потому что одноименные заряды отталкивают друг друга. Эти свободные электроны движутся внутри проводника по всему объему.
Движение электронов в RC цепи на рис. 3 имеет другой характер. Поскольку цепь не замкнута (обкладки конденсатора не соединены друг с другом) постоянный ток в цепи идти не может. Поэтому поступающий избыток электронов с полюса батарейки приводит к тому, что проводник теряет электрическую нейтральность. Избыточный заряд q, распределяется по поверхности проводника так, чтобы напряженность поля внутри проводника была равна нулю. Ну это понятно, одноименные заряды отталкиваются и стремятся расположиться подальше друг от друга, то есть на поверхности. Если бы не было резистора R, то перераспределение зарядов по поверхности происходило бы мгновенно. Однако резистор ограничивает ток ( движение зарядов) поэтому перераспределение происходит постепенно. По мере зарядки конденсатора напряжение на нем растет и ток через резистор уменьшается. Избыточные электроны концентрируются на одной обкладке и создают электрическое поле. Это поле отталкивает электроны, находящиеся на другой обкладке и “проталкивает” их дальше по проводнику к отрицательному полюсу батареи. (Знаки + и – в данном случае берем условно). Таким образом в незамкнутой цепи протекает ток заряда конденсатора. Этот ток не постоянный и уменьшается со временем. Однако, если в какой-то момент поменять полярность батареи, то ток потечет уже в обратную сторону. Если это переключение делать достаточно часто, так чтобы конденсатор не успевал полностью зарядиться, то в цепи все время будет течь ток, то в одну, то в другую сторону. Это и происходит, когда говорят, что “конденсатор проводит переменный ток”.
Для плоского конденсатора емкость равна С=ε0*ε*S/d , где d – зазор между обкладками, ε – диэлектрическая проницаемость вещества, заполняющего зазор, S – площадь обкладок.
То есть на емкость влияет не только площадь обкладок и расстояние между ними, но и материал диэлектрика, который между обкладками помещен. Причем на емкость конденсатора материал диэлектрика может влиять достаточно сильно, с разными дополнительными эффектами, см. например статью “Поляризация диэлектрика”

Литература
“Драма идей в познании природы”, Зельдович Я.Б., Хлопов М.Ю., 1988
“Курс общей физики”, том II. “Электричество” И.В.Савельев
Википедия – статьи про электричество.

Конденсаторы в цепях постоянного тока

Конденсатор и емкость

Когда любые две проводящие поверхности разделены изоляционным материалом, это называется конденсатором . Проводящие поверхности известны как обкладки конденсатора , а изоляционный материал известен как диэлектрик .

Способность конденсатора накапливать заряд называется емкостью конденсатора. Он обозначается буквой C и измеряется в фарадах (F).

Экспериментально установлено, что заряд (Q), запасенный в конденсаторе, прямо пропорционален разности потенциалов на нем, т. е.

$$Q\varpropto\:V$$

$$\Rightarrow\:Q=CV$$

$$\Rightarrow\:C=\frac{Q}{V}\:\:\:\ :…(1)$$

Где C – постоянная, известная как емкость конденсатора.

Следовательно, емкость (C) конденсатора определяется как отношение заряда (Q) на любой пластине конденсатора к разности потенциалов (V) на ней.

Единицей емкости является

$$\because\:C=\frac{Q}{V}$$

$$\следовательно\:Единица\:of\:C=\frac{Кулон} {Вольт}=Фарад$$

Как конденсатор накапливает заряд?

Рассмотрим плоский конденсатор, подключенный к батарее V вольт через переключатель. Зарядку конденсатора можно понять следующим образом: −

Шаг 1 − При разомкнутом переключателе S пластины конденсатора не заряжаются.

Шаг 2 − Когда переключатель S замкнут, положительный полюс батареи притягивает электроны с пластины A и накапливает эти электроны на пластине B. Это приводит к тому, что пластина A становится все больше и больше положительным, а пластина В становится все более и более отрицательной. Это действие называется зарядка конденсатора . Этот процесс зарядки конденсатора продолжается до тех пор, пока разность потенциалов на конденсаторе не станет равной напряжению батареи (В).

Шаг 3  — Как только конденсатор заряжается до напряжения батареи (В), ток прекращается.

Шаг 4 – Теперь, если переключатель S разомкнут, пластины конденсатора сохранят заряд. Поэтому говорят, что в это время конденсатор заряжен.

Важные моменты

Следующее можно отметить относительно действия конденсатора −

• Когда на конденсатор подается постоянное напряжение, зарядный ток будет течь до тех пор, пока конденсатор полностью не зарядится, когда ток остановится. Этот процесс зарядки будет происходить за очень короткое время, доли секунды. Следовательно, полностью заряженный конденсатор блокирует поток постоянного тока.

• Происходит только перенос электронов с одной пластины на другую по внешней цепи. Ток между пластинами конденсатора не течет.

• Когда конденсатор заряжен, две пластины несут одинаковый и противоположный заряд. Таким образом, заряд на конденсаторе означает заряд на любой пластине.

• Энергия, необходимая для зарядки конденсатора, поступает от внешнего источника.

Поведение конденсатора в цепи постоянного тока

Поведение конденсатора в цепи постоянного тока можно понять из следующих пунктов: −

$$i=\frac{dQ}{dt}=\frac{d(CV) }{dt}=C\frac{dV}{dt}\:\:\:\:(2)$$

• Когда конденсатор полностью заряжен, напряжение на конденсаторе становится постоянным и равняется приложенному напряжению. Следовательно, (dV/dt = 0) и, следовательно, зарядный ток.

• Напряжение на незаряженном конденсаторе равно нулю, что эквивалентно короткому замыканию, если речь идет о постоянном напряжении.

• Когда конденсатор полностью заряжен, ток в цепи отсутствует. Следовательно, полностью заряженный конденсатор выглядит как разомкнутая цепь для постоянного тока.

Зарядка конденсатора

Рассмотрим незаряженный конденсатор емкостью C, подключенный к батарее с напряжением V вольт (постоянного тока) через последовательный резистор R для ограничения зарядного тока в безопасных пределах. Когда ключ S замкнут, в цепи протекает зарядный ток, и конденсатор начинает заряжаться.

Зарядный ток максимален в момент замыкания ключа и постепенно уменьшается по мере увеличения напряжения на конденсаторе. Когда конденсатор полностью заряжен до приложенного напряжения (В), зарядный ток уменьшается до нуля.

В момент замыкания ключа

В момент замыкания ключа напряжение на конденсаторе равно нулю (поскольку в начале конденсатор не заряжен). Все напряжение V возникает на резисторе R, а зарядный ток максимален. Следовательно,

$$Исходное\:зарядка\:ток,I_{m}=\frac{V}{R}$$

$$Напряжение\:accross\:конденсатор,v=0$$

$$ Заряд\:на\:конденсатор,Q=0$$

В любой момент времени, t

После замыкания ключа зарядный ток начинает уменьшаться, а напряжение на конденсаторе постепенно увеличивается. Следовательно, в любой момент времени t,

$$voltage\:накрест\:capacitor=v$$

$$charge\:on\:capacitor,q=Cv$$

$$The\:charging\: ток,i=C\frac{dv}{dt}$$

Напряжение на конденсаторе −

Применяя KCL в цепи, мы можем написать,

$$V=V_{R}+v$$

$$\Rightarrow\:V=iR+v=(C\frac{dv}{dt})R+v\:\:\:\:\:…(3)$$

$$\Rightarrow\:\frac{dv}{V-v}=\frac{dt}{RC}$$

Интегрируя обе стороны,

$$\int\frac{dv}{V-v}= \int\frac{dt}{RC}$$

Решая это интегрирование, получаем

$$-\log_{e}{(V-v)}=\frac{t}{RC}+K\: \:\:\:…(4)$$

Значение K можно определить из начальных условий. В момент замыкания ключа t = 0 и v = 0. Следовательно, из уравнения (4)

$$-\log_{e}{V}=K$$

Подставляем значение K в уравнение (4), получаем, 9{-t/RC}\:\:\:\:…(7)$$

Где I _m — начальный зарядный ток. Также из ур. (7) видно, что зарядный ток уменьшается экспоненциально. Уравнения зарядного напряжения и зарядного тока также могут быть представлены графически, как показано ниже.

Постоянная времени −

Постоянная времени может быть определена как время, необходимое для того, чтобы напряжение на конденсаторе (v) поднялось до своего окончательного установившегося значения V. Оно обозначается Тау (τ) и определяется как,

$$Time\:Constant,\tau=RC\:seconds\:\:\:\:…(8)$$

Разрядка конденсатора

Рассмотрим заряженный конденсатор емкостью C фарад, соединенный последовательно с резистор R через переключатель S. Когда переключатель разомкнут, напряжение на конденсаторе составляет V вольт. При замыкании ключа в цепи начинает протекать ток разряда и конденсатор начинает разряжаться, т.е. напряжение на нем начинает уменьшаться. Разрядный ток мгновенно возрастает до значения I _м и затем сводится к нулю.

Напряжение разряда −

Учитывать в любой момент времени t во время разряда,

трещина { dV}{dt}$$

Применяя КВЛ в схеме, получаем,

$$V+iR=0$$

$$\Rightarrow\:v+CR\frac{dV}{cdt}= 0$$

$$\Rightarrow\:\frac{dV}{v}=-\frac{dt}{RC}$$

Интегрируя в обе стороны, получаем,

9{-t/RC}\:\:\:. ..(11)$$

Уравнения напряжения разряда и тока разряда также можно представить графически, как показано ниже.

Числовой пример

Конденсатор емкостью 4 мкФ подключен к источнику постоянного тока 120 В через сопротивление 1 МОм.

Определите следующее −

• Постоянная времени

• Начальный зарядный ток

• Напряжение на конденсаторе через 5 секунд после замыкания ключа 9{-5/4})=85,62 В$$

  Время, необходимое для полной зарядки конденсатора = 5 × Постоянная времени

  $$\следовательно\:t_{полный\:заряженный}=5\раз\:4 =20\:sec$$

  Анализ стационарного состояния постоянного тока | Penji

  Первое, на что нужно обратить внимание, это то, что такое устойчивое состояние постоянного тока. По сути, все это означает, что схема была активна/работала в течение длительного времени. Для элементов, рассеивающих мощность, таких как резисторы, это не имеет большого значения, но для элементов, накапливающих энергию, таких как катушки индуктивности и конденсаторы, это меняет их поведение.
  

  Конденсаторы становятся разомкнутыми, что означает разрыв цепи в установившемся режиме постоянного тока, в то время как катушки индуктивности замыкаются накоротко, что означает, что они становятся проводом в установившемся режиме постоянного тока.
  

  Хороший способ запомнить это — понять, почему это происходит. Конденсаторы накапливают заряд в электростатическом поле. Заряд будет продолжать накапливаться на пластинах до тех пор, пока напряжение не достигнет максимума (обычно равного напряжению источника напряжения) и больше не сможет увеличиваться/изменяться. Учитывая, что ток через конденсатор равен i = C(dv/dt), поэтому емкость, умноженная на производную напряжения на емкости, если напряжение максимально, dv/dt = 0, поскольку напряжение больше не меняется, поэтому я = 0, и это разомкнутая цепь. Для катушек индуктивности они хранят энергию в магнитном поле, которое индуцируется, когда ток проходит через их петли (индуктор в своей самой простой форме — это просто петлевой провод).

  Его напряжение зависит от изменяющегося тока, v=L(di/dt), где L — индуктивность, а di/dt — производная тока. В установившемся режиме постоянного тока ток больше не изменяется (он достигает максимума через катушку индуктивности), поэтому di/dt = 0, поэтому напряжение равно 0,9.0319

  Таким образом, чтобы решить проблемы устойчивого состояния постоянного тока, все, что нам нужно сделать, это заменить конденсаторы на разомкнутые цепи, а катушки индуктивности на провода. Для задачи 1 установившаяся цепь будет иметь вид:
  

  В разомкнутой ветви нет тока, поэтому мы можем, по сути, представить, что его там нет:
  

  Поскольку мы просто находим ток в одной из двух ветвей в параллельно, мы можем получить ток через резистор 2 Ом, просто используя закон делителя тока, который гласит:
  

  Итак:
  

  ПРИМЕЧАНИЕ. Вы можете игнорировать первый резистор 6 Ом (тот, что рядом с источником тока 12 А) ради использования формулы делителя тока, поскольку ток через него устанавливается источником тока, поэтому общий ток, поступающий на две ветви, по-прежнему составляет 12 ампер (закон делителя тока касается только того, как общий ток распределяется между несколькими ветвями).

  
  

  Задача 2 немного сложнее. Начинаем так же, установив катушки индуктивности на провода:
  

  Но мы быстро сталкиваемся с проблемой. Оба являются короткими замыканиями, что обычно означает, что они отводят весь ток, протекающий через соседние/параллельные ответвления, через них (поскольку ток течет по пути наименьшего сопротивления, а сопротивление провода равно 0), но поскольку их два, мы имеем чтобы определить, какой из них получает больше отведенного тока.
  

  Для этого нам просто нужно сказать, что токи, протекающие через катушки индуктивности, изменяются со временем, поскольку они достигают устойчивого состояния постоянного тока, в конечном итоге достигая своих максимальных значений постоянного тока. Затем мы можем найти, в чем они правы, когда они достигают устойчивого состояния постоянного тока. В любом случае это теория, на практике все гораздо проще, чем кажется. По сути, нам просто нужно сделать делитель тока, используя индуктивности вместо сопротивлений.

  
  

  Таким образом, первый шаг, как и в любой задаче на делитель тока, состоит в том, чтобы найти общий ток, протекающий по двум ветвям. Для этой проблемы это всего -4 А (или 4 ампера, направленные вниз). Это связано с тем, что два источника тока, 4 А и -8 А, подключены параллельно, поэтому их можно просто добавить.
  

  Мы также можем удалить два резистора, поскольку катушки индуктивности технически являются короткозамкнутыми, поэтому все -4 А будут проходить через катушки индуктивности, а не через резисторы. При этом схемы упрощены до:
  

  Затем мы применяем делитель тока, чтобы найти i1, затем используем i1 + i2 = -4, поскольку общий ток просто разделяется на две ветви, чтобы найти i2.
  

  Проблема 3 очень похожа на проблему 2, за исключением конденсаторов. Мы устанавливаем схему в устойчивое состояние постоянного тока, получаем две разомкнутые цепи, где были конденсаторы:
  

  Это мало что говорит нам о v1 и v2, за исключением того, что они в сумме дают 16 В, поскольку они параллельны источнику напряжения.