Конденсатор включен в цепь переменного: № 966. Конденсатор включен в цепь переменного тока стандартной частоты. Напряжение в сети 220 В. Сила тока в цепи этого конденсатора 2,5 А. Какова емкость конденсатора?

Конденсатор включен в цепь переменного тока стандартной

Reshak.ru — сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте — сделанный для людей. Все решебники выполнены качественно, с приятной навигацией. Вы сможете скачать гдз, решебник английского, улучшить ваши школьные оценки, повысить знания, получить намного больше свободного времени.

Главная задача сайта: помогать школьникам в решении домашнего задания. Кроме того, весь материал гдз совершенствуется, добавляются новые сборники решений.

Информация

© admin

reshak.ru

Конденсатор в цепи постоянного тока

Итак, берем блок питания постоянного напряжения и выставляем на его крокодилах напряжение в 12 Вольт. Лампочку тоже берем на 12 Вольт. Теперь между одним щупом блока питания и лампочки вставляем конденсатор:

А вот если напрямую сделать, то горит:

Отсюда напрашивается вывод: постоянный ток через конденсатор не течет!

Если честно, то в самый начальный момент подачи напряжения ток все-таки течет на доли секунды. Все зависит от емкости конденсатора.

Конденсатор в цепи переменного тока

Итак, чтобы узнать, течет ли переменный ток через конденсатор, нам нужен генератор переменного тока. Думаю, этот генератор част оты вполне сойдет:

Так как китайский генератор у меня очень слабенький, то мы вместо нагрузки-лампочки будем использовать простой резистор на 100 Ом. Также возьмем и конденсатор емкостью в 1 микрофарад:

Спаиваем как-то вот так и подаем сигнал с генератора частоты:

Далее за дело берется Цифровой осциллограф OWON SDS 6062. Что такое осциллограф и с чем его едят, читаем зде сь. Будем использовать сразу два канала. На одном экране будут высвечиваться сразу два сигнала. Здесь на экранчике уже видны наводки от сети 220 Вольт. Не обращайте внимание.

Будем подавать переменное напряжение и смотреть сигналы, как говорят профессиональные электронщики, на входе и на выходе. Одновременно.

Все это будет выглядеть примерно вот так:

Итак, если у нас частота нулевая, то это значит постоянный ток. Постоянный ток, как мы уже видели, конденсатор не пропускает. С этим вроде бы разобрались. Но что будет, если подать синусоиду с частотой в 100 Герц?

На дисплее осциллографа я вывел такие параметры, как частота сигнала и его амплитуда: F – это частота, Ma – амплитуда (эти параметры пометил белой стрелочкой). Первый канал помечен красным цветом, а второй канал – желтым, для удобства восприятия.

Красная синусоида показывает сигнал, который выдает нам китайский генератор частоты. Желтая синусоида – это то, что мы уже получаем на нагрузке. В нашем случае нагрузкой является резистор. Ну вот, собственно, и все.

Как вы видите на осциллограмме выше, с генератора я подаю синусоидальный сигнал с частотой в 100 Герц и амплитудой в 2 Вольта. На резисторе мы уже видим сигнал с такой же частотой (желтый сигнал), но его амплитуда составляет каких-то 136 милливольт. Да еще и сигнал получился какой-то “лохматый”. Это связано с так называемыми “шумами“. Шум – это сигнал с маленькой амплитудой и беспорядочным изменением напряжения. Он может быть вызван самими радиоэлементами, а также это могут быть помехи, которые ловятся из окружающего пространства. Например очень хорошо “шумит” резистор. Значит “лохматость” сигнала – это сумма синусоиды и шума.

Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается влево, то есть опережает красный сигнал, или научным языком, появляется сдвиг фаз. Опережает именно фаза, а не сам сигнал. Если бы опережал сам сигнал, то у нас бы тогда получилось, что сигнал на резисторе появлялся бы по времени раньше, чем сигнал, поданный на него через конденсатор. Получилось бы какое-те перемещение во времени :-), что конечно же, невозможно.

Сдвиг фаз – это разность между начальными фазами двух измеряемых величин. В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота. Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз:

Давайте увеличим частоту на генераторе до 500 Герц

На резисторе уже получили 560 милливольта. Сдвиг фаз уменьшается.

Увеличиваем частоту до 1 КилоГерца

На выходе у нас уже 1 Вольт.

Ставим частоту 5 Килогерц

Амплитуда 1,84 Вольта и сдвиг фаз явно стает меньше

Увеличиваем до 10 Килогерц

Амплитуда уже почти такая же как и на входе. Сдвиг фаз менее заметен.

Ставим 100 Килогерц:

Сдвига фаз почти нет. Амплитуда почти такая же, как и на входе, то есть 2 Вольта.

Отсюда делаем глубокомысленные выводы:

Чем больше частота, тем меньшее сопротивление конденсатор оказывает переменному току. Сдвиг фаз убывает с увеличением частоты почти до нуля. На бесконечно низких частотах его величина составляет 90 градусов или π/2.

Если построить обрезок графика, то получится типа что-то этого:

По вертикали я отложил напряжение, по горизонтали – частоту.

Итак, мы с вами узнали, что сопротивление конденсатора зависит от частоты. Но только ли от частоты? Давайте возьмем конденсатор емкостью в 0,1 микрофарад, то есть номиналом в 10 раз меньше, чем предыдущий и снова прогоним по этим же частотам.

Смотрим и анализируем значения:

Внимательно сравните амплитудные значения желтого сигнала на одной и той же частоте, но с разными номиналами конденсатора. Например, на частоте в 100 Герц и номиналом конденсатора в 1 мкФ амплитуда желтого сигнала равнялась 136 милливольт, а на этой же самой частоте амплитуда желтого сигнала, но с конденсатором в 0,1 мкФ уже была 101 милливольт( в реальности еще меньше из за помех). На частоте 500 Герц – 560 милливольт и 106 милливольт соответственно, на частоте в 1 Килогерц – 1 Вольт и 136 милливольт и так далее.

Отсюда вывод напрашивается сам собой: при уменьшении номинала конденсатора его сопротивление стает больше.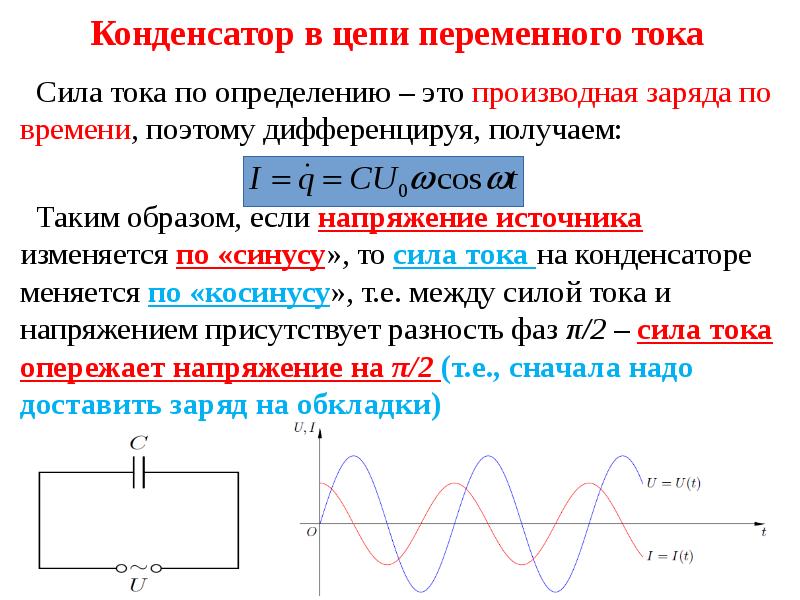

С помощью физико-математических преобразований физики и математики вывели формулу для расчета сопротивления конденсатора. Прошу любить и жаловать:

где, Х_С – это сопротивление конденсатора, Ом

П – постоянная и равняется приблизительно 3,14

F – частота, измеряется в Герцах

С – емкость, измеряется в Фарадах

Так вот, поставьте в эту формулу частоту в ноль Герц. Частота в ноль Герц – это и есть постоянный ток. Что получится? 1/0=бесконечность или очень большое сопротивление. Короче говоря, обрыв цепи.

Заключение

Забегая вперед, могу сказать, что в данном опыте мы получили Фильтр Высокой Частоты (ФВЧ). С помощью простого конденсатора и резистора, применив где-нибудь в звуковой аппаратуре такой фильтр на динамик, в динамике мы будет слышать только писклявые высокие тона. А вот частоту баса как раз и заглушит такой фильтр. Зависимость сопротивления конденсатора от частоты очень широко используется в радиоэлектронике, особенно в различных фильтрах, где надо погасить одну частоту и пропустить другую.

Ответы:

Ответы на похожие вопросы:

8м/с + 13 м/с = 21 м/с3км = 3000мt=3000м/21м/с=142,8с

Решение на рисунке.Желтый — поверхность стола.Красный — контуры мышкиСиний — цвет мышкиЧерный — сила.P. S. Цвета разные для ясности рисунка. Вы можете все нарисовать простым карандашом.

Смотря куда двигать мышь. Можно просто 2 клетки вправо влево вниз вверх, можно 2 клетки вверх+право и т.д

просто нарисуй стрелочку длиной в две клеточки))

давления в этом случае будут одинаковы

у первого газа давление будет в Z раз больше

конденсатор означает сгуститель — имеется в виду “”сгуститель электрического заряда””

Т.к. он предназначен для накопления и удержания на своих обкладках равные по значению и разные по знаку электрические заряды + Q и -Q.

Самостоятельная работа по физике Цепи переменного тока 11 класс

Самостоятельная работа по физике Цепи переменного тока. Свободные электромагнитные колебания 11 класс с ответами. Представлено 5 вариантов самостоятельных работ. В каждом варианте по 2 задания.

1 вариант

1. Катушка индуктивностью 0,2 Гн включена в сеть пере­менного тока с частотой 50 Гц. Чему равно индуктивное сопротивление катушки?

2. Катушка с активным сопротивлением 15 Ом и индуктивностью 52 мГн включена в цепь переменного тока с частотой 50 Гц последовательно с конденсатором емко­стью 120 мкФ. Напряжение в сети 220 В. Определите действующее значение силы тока в цепи.

2 вариант

1. Конденсатор емкостью 1 мкФ включен в сеть перемен­ного тока с частотой 50 Гц. Определите емкостное сопро­тивление конденсатора.

2. В сеть переменного тока с действующим значением на­пряжения 120 В последовательно включены проводник с активным сопротивлением 15 Ом и катушка индуктивно­стью 50 мГн. Найдите частоту тока, если амплитуда силы тока в сети равна 7 А.

3 вариант

1. Колебательный контур состоит из катушки индуктив­ностью 20 мкГн. Какой емкости конденсатор следует под­ключить к контуру, чтобы получить колебания с часто­той 50 кГц?

2. В цепь переменного тока напряжением 220 В и частотой 50 Гц включены последовательно конденсатор емкостью 35,4 мкФ, проводник сопротивлением 100 Ом и катушка индуктивностью 0,7 Гн. Найдите силу тока в цепи.

4 вариант

1. В цепь переменного тока включена катушка с индуктив­ностью 20 мГн и конденсатор емкостью 50 мкФ. При какой частоте переменного тока наступит явление резонанса?

2. Катушка с активным сопротивлением 2 Ом и индук­тивностью 75 мГн включена последовательно с конденса­тором в сеть переменного тока с напряжением 50 В и час­тотой 50 Гц. Чему равна емкость конденсатора при резо­нансе напряжений в данной цепи?

5 вариант

1. Конденсатор включен в цепь переменного тока стан­дартной частоты (50 Гц). Напряжение в сети 220 В. Сила тока в цепи конденсатора 2,5 А. Какова его емкость?

2. В цепь включены последовательно резистор сопротив­лением 5 Ом, катушка индуктивностью 0,5 мГн и кон­денсатор емкостью 0,15 мкФ. При какой частоте насту­пит резонанс?

Ответы на самостоятельную работу по физике Цепи переменного тока. Свободные электромагнитные колебания 11 класс
1 вариант
1. 62,8 Ом
2. 12 А
2 вариант
1. 3185 Ом
2. 61 Гц
3 вариант
1. 0,5 мкФ
2. 1,34 А
4 вариант
1. 185 Гц

2. 135 мкФ
5 вариант
1. 36 мкФ
2. 18,4 КГц

Индуктивность и емкость в цепи переменного тока

Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальные фазы напряжения и э. д. с. соответственно будут иметь некоторые значения ϕ и ψ. При таком условии мгновенные значения силы тока, напряжения и э. д. с. будут выражаться следующими формулами:

i = Iм sin ωt,    (26.8)

u = Uм sin (ϕ + ωt),    (26.9)

e = Ɛm sin (ψ + ωt).    (26.10)

Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным. Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току и находить по формуле (16.18):

R=(p₀l/S)(1 + at).

В цепи переменного тока, имеющей только активное сопротивление, например в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. ϕ=0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.

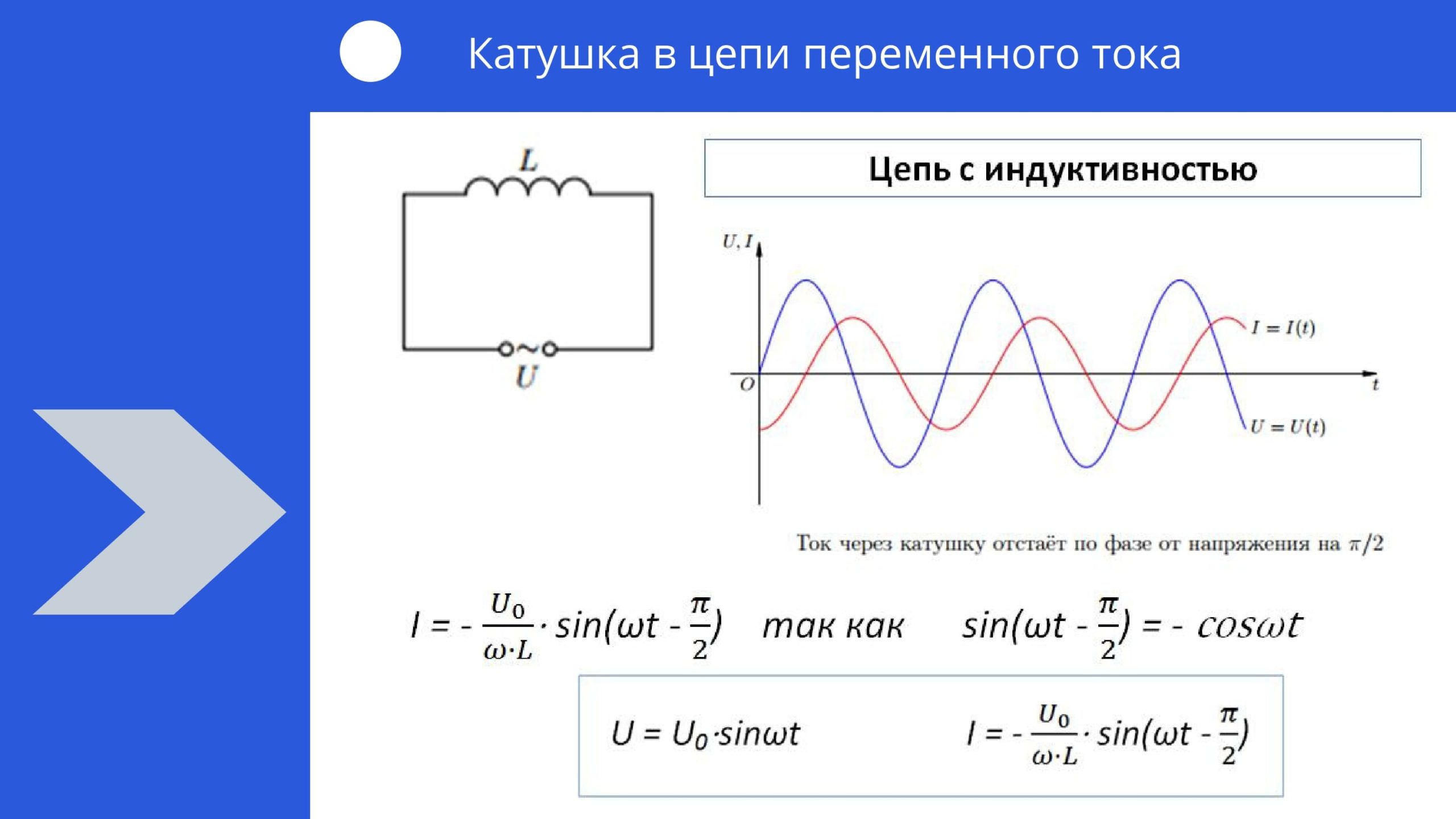
Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление X_L, которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω:

Х_L = ωL.             (26.11)

Влияние индуктивного сопротивления на силу тока в цепи наглядно иллюстрируется опытом, изображенным на рис. 26.6. При опускании ферромагнитного сердечника в катушку лампа гаснет, а при его удалении вновь загорается. Это объясняется тем, что индуктивность катушки сильно возрастает при введении в нее сердечника. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток.

Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.

Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток.

Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока.

Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Хс. Оно обратно пропорционально емкости С и круговой частоте ω;

Хс = 1/ωС.       (26.12)

Из сравнения формул (26.11) и (26.12) видно, что катушки индуктивности представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Напряжение на емкостном сопротивлении Ха отстает по фазе от тока.

Индуктивное X_L и емкостное Хс сопротивления называют реактивными. В теории переменного тока доказывается, что при последовательном включении индуктивного и емкостного сопротивлений общее реактивное сопротивление равно их разности:

X = X_L—X_C        (26.13)

и имеет индуктивный характер при X_L > Хс и емкостный характер при X_L < Xc.

В заключение заметим, что средняя активная мощность переменного тока, показывающая, сколько энергии за единицу времени передается электрическим током данному участку цепи, определяется формулой:

P = IU cos ϕ.   (26.14)

Мощность, затрачиваемая только на тепловое действие тока, выражается формулой:

Р = I²R.              (26.15)

Из (26. 14) видно, что для увеличения активной мощности переменного тока нужно повышать cos ϕ. (Объясните, почему наибольшее значение cos ϕ имеет при X_L=X_C.)

“Написать уравнения зависимости напряжения и силы тока от времени для электроплитки сопротивлением 50 Ом, включенной в сеть переменного тока с частотой 50 Г”, Физика

Содержание

• org/CreativeWork”>Задача № 1. Написать уравнения зависимости напряжения и силы тока от времени для электроплитки сопротивлением 50 Ом, включенной в сеть переменного тока с частотой 50 Гц и напряжением 220 В
• Задача № 2. При каких фазах в пределах одного периода мгновенное значение напряжения равно по модулю половине амплитудного?

Задача № 3. Неоновая лампа начинает светить, когда напряжение на ее электродах достигает строго определенного значения. Какую часть периода будет светить лампа, если ее включить в сеть, действующее значение напряжения в которой равно этому напряжению? Считать, что напряжение, при котором лампа гаснет, равно напряжению зажигания.

Задача № 4. Конденсатор переменной емкости включен в цепь последовательно с лампочкой от карманного фонаря. Схема питается от генератора звуковой частоты ЗГ. Как изменяется накал лампочки, если: а) не меняя емкости конденсатора, увеличивать частоту переменного тока; б) не меняя частоту, увеличивать емкость конденсатора? ЗГ звуковой генератор источник переменного тока, частоту которого можно плавно изменять от 20 до 20 000 Гц.

Задача № 5. Каково сопротивление конденсатора емкостью 4 мкФ в цепях с частотой переменного тока 50 и 400 Гц?

Задача № 6. Конденсатор включен в цепь переменного тока стандартной частоты. Напряжение в сети 220 В. Сила тока в цепи этого конденсатора 2,5 А. Какова емкость конденсатора?

Задача № 7. Последовательно с лампочкой карманного фонаря к ЗГ подключена катушка. Как изменится накал лампочки, если: а) не меняя частоту, поместить в катушку железный сердечник; б) уменьшить частоту?

Задача № 8. Каково индуктивное сопротивление катушки индуктивностью 0,2 Гн при частоте тока 50 Гц? 400 Гц?

Задача № 9. Катушка с ничтожно малым активным сопротивлением включена в цепь переменного тока с частотой 50 Гц. При напряжении 125 В сила тока равна 2,5 А. Какова индуктивность катушки?

Задача № 10. Лампы (рис. 107) питаются от ЗГ. При некоторой частоте накал ламп одинаков. Как изменится их накал, если частоту: а) увеличить; б) уменьшить?

Задача № 7. Последовательно с лампочкой карманного фонаря к ЗГ подключена катушка. Как изменится накал лампочки, если: а) не меняя частоту, поместить в катушку железный сердечник; б) уменьшить частоту?

Решение:

Сопротивление лампочки R не зависит от частоты генератора. Сопротивление катушки переменному току (реактивное сопротивление) равно, где v частота генератора, L индуктивность катушки. Катушка включена в цепь последовательно с лампочкой, следовательно, общее сопротивление цепи переменному току равно

а) Помещая в катушку железный сердечник, мы увеличиваем и Z. По закону Ома ток в данной цепи уменьшится, и мощность, выдаваемая на лампочке, также уменьшится.

б) Уменьшая, мы уменьшаем, и ток через лампочку возрастает. Накал лампочки увеличится.

Ответ: а) уменьшится: б) увеличится.

“Конденсатор включен в цепь переменного тока стандартной частоты. Напряжение в сети 3

Если я правильно разглядел, то начальный объем воды в мензурке – 100 мл, значит после погружения шарика объем повысится до 181 мл

5 месяцев назад

Заряд является свойством материи, так же, как масса, объем или плотность.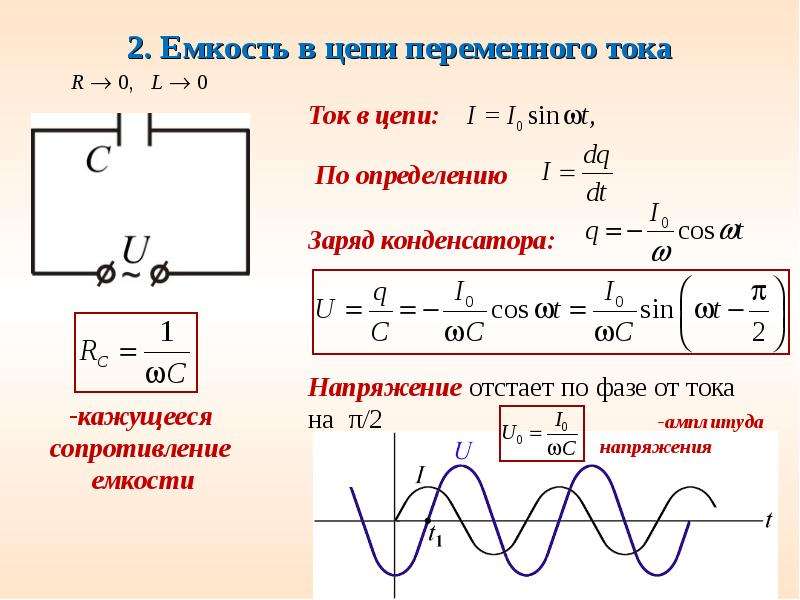 Все они являются измеримыми величинами. Точно так же, как вы можете количественно измерить массу тела, вы можете измерить, какой заряд он имеет. Для того, чтобы заряды  могли перемещаться, нужны носители зарядов (вот где наши знания атомных частиц пригодятся). Из предыдущего урока мы уже знаем, что носителями зарядов в проводниках являются свободные электроны. Электроны всегда несут отрицательный заряд в отличие от протонов, которые всегда положительно заряжены. При этом оба – и электрон и протон – несут одинаковый заряд, только разного знака. Отрицательно заряженные электроны притягиваются к положительно заряженным протонам в ядре атома. Почему же электрон остается на орбите и не падает на ядро? Это происходит в результате того, что сила притяжения электрона уравновешивается центростремительной силой, возникающей за счет вращения электрона вокруг ядра. Значение величины сил отталкивания и притяжения, существующих между двумя заряженными телами, зависит от следующих факторов: расстояния между телами и их зарядов.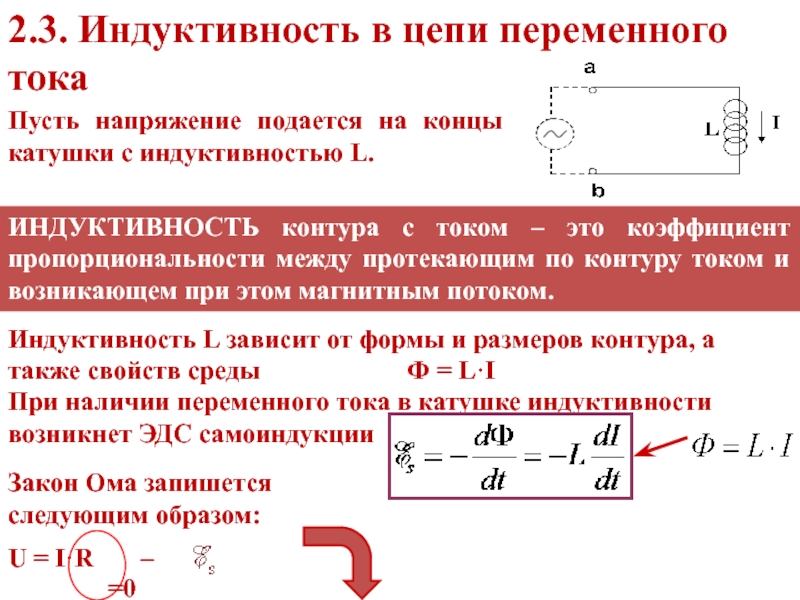

Заряд отдельного электрона очень мал, поэтому в практике не используется. Принятой в мире единицей измерения заряда является кулон (Кл). Она названа в честь французского ученого Шарля Кулона, обозначается буквой Q. Один  кулон это 6,28*1018 зарядов электронов.

Лампы нужно соединить последовательно

U1=U2=220/2=110B

6 месяцев назад

Плотность олова – 7,31 г/см3 
толщина = 0,73г / (7,31г/см3 * 400 см2) = 0,00025 см = 0,0025 мм = 2,5 мкм.

9 месяцев назад

Включение конденсатора в цепь постоянного тока равнозначно разрыву ее (мы не принимаем во внимание момент включения, когда в цепи появляется кратковременный ток заряда конденсатора).

Ты уже знаешь, что конденсатор в простейшем виде представляет собой две пластинки, разделенные диэлектриком. Если конденсатор включить в цепь постоянного тока, то ток в этой цепи прекратится. Да это и понятно: через изолятор, которым является диэлектрик конденсатора, постоянный ток течь не может. Включение конденсатора в цепь постоянного тока равнозначно разрыву ее (мы не принимаем во внимание момент включения, когда в цепи появляется кратковременный ток заряда конденсатора). Иначе ведет себя конденсатор в цепи переменного тока. Ввпомни: напряжение на зажимах источника переменного тока периодически меняется. Значит, если включить конденсатор в цепь, питаемую от такого источника тока, его обкладки будут попеременно перезаряжаться с частотой этого тока. В результате в цепи будет протекать переменный ток.

Конденсатор подобно резистору и катушке оказывает переменному току сопротивление, но разное для токов различных частот. Он может хорошо пропускать токи высокой частоты и одновременно быть почти изолятором для токов низкой частоты.

Иногда радиолюбители вместо наружных антенн используют провода электроосветительной сети, подключая приемники к ним через конденсатор емкостью 220-510 пФ. Случайно ли выбрана такая емкость конденсатора? Нет, не случайно. Конденсатор такой емкости хорошо пропускает токи высокой частоты, необходимые для работы приемника, но оказывает большое сопротивление переменному току частотой 50 Гц, текущему в сети. В этом случае конденсатор становится своеобразным фильтром, пропускающим ток высокой частоты и задерживающим ток низкой частоты.

Сопротивление конденсатора переменному току зависит от его емкости и частоты тока: чем больше емкость конденсатора и частота тока, тем меньше его емкостное сопротивление. Это емкостное сопротивление конденсатора можно с достаточной точностью определить по такой упрощенной формуле:

И вот результат: конденсатор емкостью 500 пФ оказывает току высокой частоты в 20000 раз меньшее сопротивление, чем току низкой частоты. Убедительно? Конденсатор меньшей емкости оказывает переменному току сети еще большее сопротивление.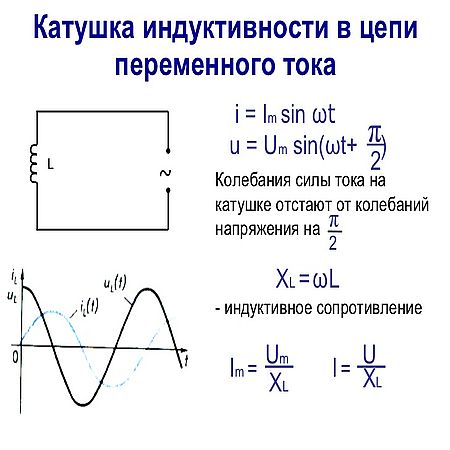

 

 

 

Архангельской области

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

АРХАНГЕЛЬСКОЙ ОБЛАСТИ

Государственное автономное профессиональное образовательное учреждение Архангельской области

«Северодвинский техникум социальной инфраструктуры»

(ГАПОУ АО «СТСИ»)

УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС УЧЕБНОЙ ДИСЦИПЛИНЫ

ОДП. 03 ФИЗИКА

Северодвинск 2014

Составитель(и):	Масько Татьяна Ивановна, преподаватель

УМК учебной дисциплины рассмотрен и рекомендован к использованию на заседании предметно-цикловой комиссии естественно-научного цикла

Протокол № 4 от «09» апреля 2014 г.
Председатель: ________________ / Безбородова В.В./

СОДЕРЖАНИЕ

Нормативно-планирующие документы
Учебно-методическая документация
Контрольно-диагностические материалы (ФОС)
Дополнительные компоненты УМК

1. 
   Нормативно-планирующие документы:
   

– извлечение из ФГОС СПО – требования к знаниям, умениям по дисциплине;

– рабочие учебные программы дисциплины.

ФЕДЕРАЛЬНЫЙ ГОСУДАРСТВЕННЫЙ ОБРАЗОВАТЕЛЬНЫЙ СТАНДАРТ СРЕДНЕГО (ПОЛНОГО) ОБЩЕГО ОБРАЗОВАНИЯ

(10-11 КЛ.) от 12.04.2012

Требования к результатам освоения

основной образовательной программы
Предметные результаты изучения предметной области «Естественные науки» включают предметные результаты изучения учебных предметов:

«Физика» (базовый уровень) – требования к предметным результатам освоения базового курса физики должны отражать:

1) сформированность представлений о роли и месте физики в современной научной картине мира; понимание физической сущности наблюдаемых во Вселенной явлений; понимание роли физики в формировании кругозора и функциональной грамотности человека для решения практических задач;

2) владение основополагающими физическими понятиями, закономерностями, законами и теориями; уверенное пользование физической терминологией и символикой;

3) владение основными методами научного познания, используемыми в физике: наблюдение, описание, измерение, эксперимент; умения обрабатывать результаты измерений, обнаруживать зависимость между физическими величинами, объяснять полученные результаты и делать выводы;

4) сформированность умения решать физические задачи;

5) сформированность умения применять полученные знания для объяснения условий протекания физических явлений в природе и для принятия практических решений в повседневной жизни;

6) сформированность собственной позиции по отношению к физической информации, получаемой из разных источников.
«Физика» (углубленный уровень) – требования к предметным результатам освоения углубленного курса физики должны включать требования к результатам освоения базового курса и дополнительно отражать:

1) сформированность системы знаний об общих физических закономерностях, законах, теориях, представлений о действии во Вселенной физических законов, открытых в земных условиях;

2) сформированность умения исследовать и анализировать разнообразные физические явления и свойства объектов, объяснять принципы работы и характеристики приборов и устройств, объяснять связь основных космических объектов с геофизическими явлениями;

3) владение умениями выдвигать гипотезы на основе знания основополагающих физических закономерностей и законов, проверять их экспериментальными средствами, формулируя цель исследования;

4) владение методами самостоятельного планирования и проведения физических экспериментов, описания и анализа полученной измерительной информации, определения достоверности полученного результата;

5) сформированность умений прогнозировать, анализировать и оценивать последствия бытовой и производственной деятельности человека, связанной с физическими процессами, с позиций экологической безопасности.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

АРХАНГЕЛЬСКОЙ ОБЛАСТИ

Государственное автономное профессиональное образовательное учреждение Архангельской области

«Северодвинский техникум социальной инфраструктуры »

(ГАПОУ АО «СТСИ»)

цепей переменного тока | Безграничная физика

Индуктивность

Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока, например изменением тока в проводнике.

Цели обучения

Опишите свойства индуктора

Основные выводы

Ключевые моменты

• В случае электроники индуктивность – это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводе, называемое самоиндукцией, так и в любых соседних проводниках, называемое взаимной индуктивностью.
• Согласно закону Ленца, изменяющийся электрический ток в цепи с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока.
• Взаимная индуктивность обозначена. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом. Мы выражаем это в форме уравнения как [латекс] \ text {emf} _2 = – \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]. M то же самое для обратного процесса.
• Самоиндукция – это действие закона индукции Фарадея устройства на самого себя. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока, задаваемой [latex] \ text {emf} = – \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ латекс].
• Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.

Ключевые термины

• взаимная индуктивность : отношение напряжения в цепи к изменению тока в соседней цепи.
• самоиндукция : Отношение напряжения к изменению тока в той же цепи.
• индуктор : Пассивное устройство, которое вводит индуктивность в электрическую цепь.

Индуктивность

ОБЗОР

Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. В частности, в случае электроники индуктивность – это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводнике (самоиндукция), так и в любых соседних проводниках (взаимная индуктивность).Этот эффект основан на двух фундаментальных физических наблюдениях: во-первых, постоянный ток создает постоянное магнитное поле, а во-вторых, изменяющееся во времени магнитное поле индуцирует напряжение в соседнем проводнике (закон индукции Фарадея). Согласно закону Ленца, изменяющийся электрический ток через цепь с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока (если бы это было не так, можно легко увидеть, что энергия не может быть сохранена, при этом изменяющийся ток усиливает изменение тока. петля положительной обратной связи).

ВЗАИМНАЯ ИНДУКТИВНОСТЬ

Взаимная индуктивность – это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. Посмотрите, где простые катушки наводят друг на друга ЭДС.

Взаимная индуктивность катушек : Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2.(Обратите внимание, что «E2 индуцированная» представляет наведенную ЭДС в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока Δ I / Δ t как причине индукции. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом.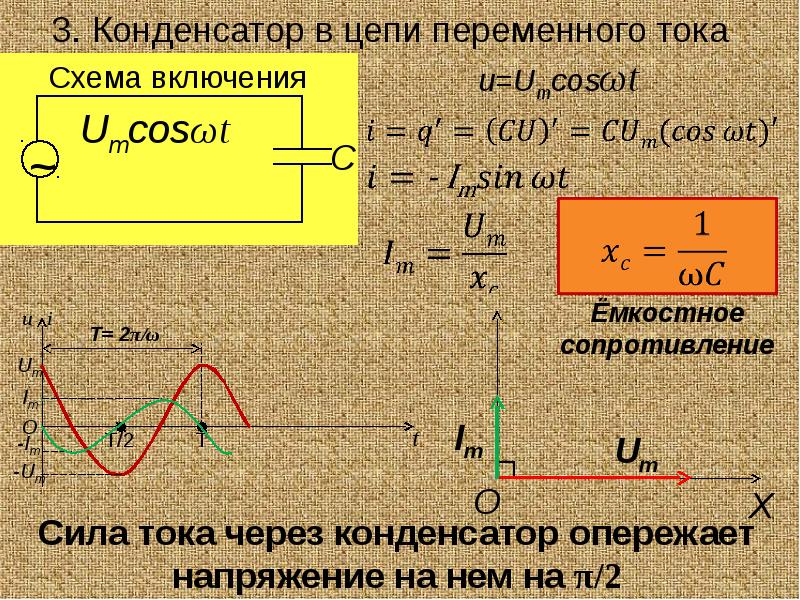 Мы выражаем это в форме уравнения как

[латекс] \ text {emf} _2 = – \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]

, где M определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность М, , тем эффективнее связь. Единицы измерения для M : (V⋅s) / A = Ωs, который назван генри (H) в честь Джозефа Генри (обнаружил самоиндукцию). То есть 1 H = 1 Ом.

Природа здесь симметрична. Если мы изменим ток I ₂ в катушке 2, мы индуцируем ЭДС ₁ в катушке 1, что равно

[латекс] \ text {emf} _1 = – \ text {M} \ frac {\ Delta \ text {I} _2} {\ Delta \ text {t}} [/ latex]

, где M то же, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью М.

Большая взаимная индуктивность M, может быть желательной, а может и нежелательной.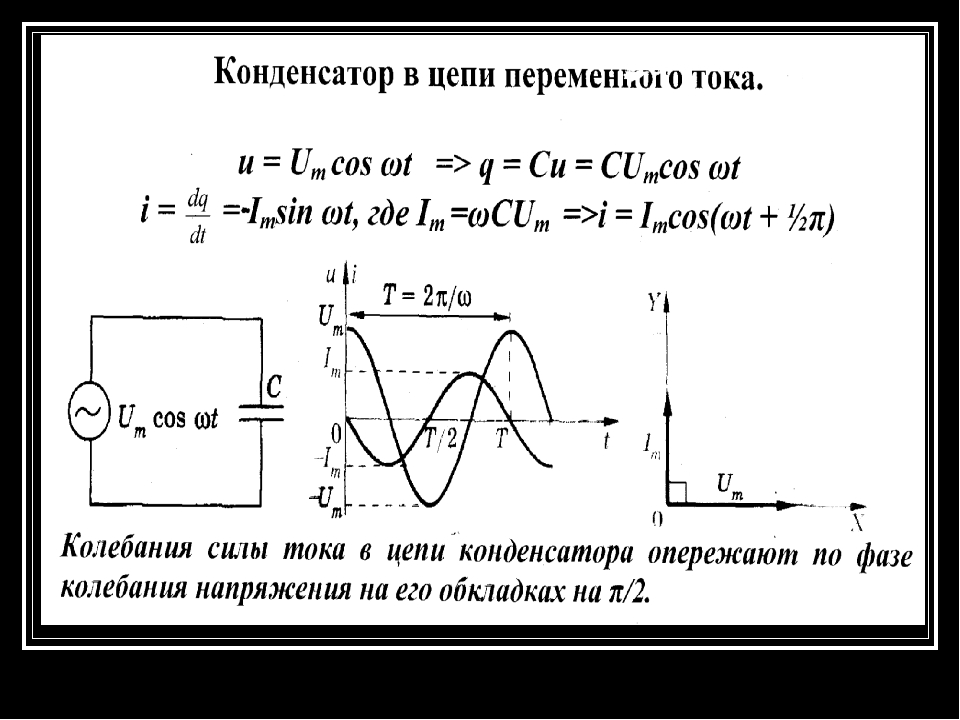 Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки противотоком для подавления создаваемого магнитного поля.(Видеть ).

Противоточная намотка : Нагревательные змеевики электрической сушилки для белья могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.

САМОИНДУКЦИЯ

Самоиндуктивность, действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению.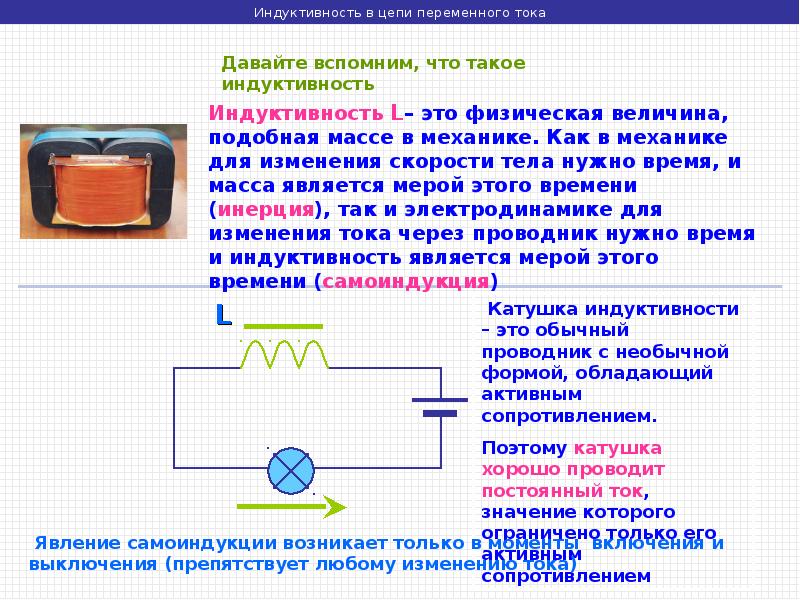 Большинство устройств имеют фиксированную геометрию, и поэтому изменение магнитного потока полностью связано с изменением тока ΔI через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается

[латекс] \ text {emf} = – \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ latex]

, где L – собственная индуктивность устройства.Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.

.

Обозначение индуктора

Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции является генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться небольшого L, например, за счет встречной намотки катушек, как в.

СОЛЕНОИДЫ

Можно рассчитать L для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Индуктивность L, обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму.{2} \ text {A}} {\ mathscr {\ text {l}}} [/ latex] (соленоид).

Поучительно вывести это уравнение, но это оставлено читателю в качестве упражнения. (Подсказка: начните с того, что отметьте, что индуцированная ЭДС определяется законом индукции Фарадея как ЭДС = −N (Δ / Δt), а по определению самоиндукции задается как ЭДС = −L (ΔI // Δt) и приравняем эти два выражения). Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением. {\ frac {- \ text {t }} {\ tau}} [/ латекс].В первом временном интервале τ ток падает в раз [латекс] \ frac {1} {\ text {e}} [/ latex] до [latex] 0,368 \ cdot \ text {I} _0 [/ latex].

Ключевые термины

• характеристическая постоянная времени : Обозначается $ \ tau $, в цепях RL она задается $ \ tau = \ frac {L} {R} $, где R – сопротивление, а L – индуктивность. Когда переключатель замкнут, это время, необходимое для того, чтобы сила тока уменьшилась с коэффициентом 1 / e.
• индуктор : Устройство или компонент схемы, который демонстрирует значительную самоиндукцию; устройство, которое хранит энергию в магнитном поле.

Цепи RL

Цепь резистор-индуктор (цепь RL) состоит из резистора и катушки индуктивности (последовательно или параллельно), приводимых в действие источником напряжения.

Обзор

Напомним, что индукция – это процесс, в котором ЭДС индуцируется изменением магнитного потока. Взаимная индуктивность – это действие закона индукции Фарадея одного устройства на другое, в то время как самоиндукция – это действие закона индукции Фарадея устройства на самого себя.Катушка индуктивности – это устройство или компонент схемы, который демонстрирует самоиндукцию.

Энергия индуктора

Мы знаем из закона Ленца, что индукторы противодействуют изменениям тока. Мы можем думать об этой ситуации с точки зрения энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, а также время, чтобы истощить ее; следовательно, есть противодействие быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства.{2} [/ латекс].

Катушки индуктивности в цепях

Мы знаем, что ток через катушку индуктивности L нельзя включить или выключить мгновенно. Изменение тока изменяет магнитный поток, вызывая противодействие изменению ЭДС (закон Ленца). Как долго длится противостояние? Текущий будет потоком, а можно выключить , но сколько времени это займет? На следующем рисунке показана схема переключения, которую можно использовать для измерения тока через катушку индуктивности как функции времени.

Ток в цепи RL : (a) Цепь RL с переключателем для включения и выключения тока. В положении 1 батарея, резистор и катушка индуктивности включены последовательно, и устанавливается ток. В положении 2 аккумулятор извлекается, и ток в конечном итоге прекращается из-за потери энергии в резисторе. (b) График роста тока в зависимости от времени, когда переключатель перемещен в положение 1. (c) График уменьшения тока, когда переключатель перемещен в положение 2.

Когда переключатель впервые перемещается в положение 1 (при t = 0 ), ток равен нулю и в конечном итоге возрастает до I ₀ = В / R , где R – полное сопротивление цепи, а V – напряжение батареи.{\ frac {- \ text {t}} {\ tau}}) [/ latex]

– это ток в цепи RL при включении. (Обратите внимание на сходство с экспоненциальным поведением напряжения на зарядном конденсаторе.) Начальный ток равен нулю и приближается к I ₀ = В / R с характеристической постоянной времени для цепи RL , задаваемой формулой :

[латекс] \ tau = \ frac {\ text {L}} {\ text {R}} [/ latex],

, где [latex] \ tau [/ latex] имеет единицы измерения в секундах, поскольку [latex] 1 \ text {H} = 1 \ Omega \ cdot \ text {s} [/ latex]. В первый период времени [латекс] \ тау [/ латекс] ток возрастает от нуля до 0,632I ₀ , так как I = I ₀ (1 − e ⁻¹ ) = I ₀ ( 1−0,368) = 0,632I ₀ . В следующий раз ток составит 0,632 от остатка. Хорошо известным свойством экспоненциальной функции является то, что конечное значение никогда не достигается точно, но 0,632 остатка от этого значения достигается за каждое характерное время [латекс] \ тау [/ латекс]. Всего за несколько кратных промежутков времени [latex] \ tau [/ latex] конечное значение почти достигнуто (см. Часть (b) на рисунке выше).

Характерное время [латекс] \ тау [/ латекс] зависит только от двух факторов: индуктивности L и сопротивления R . Чем больше индуктивность L , тем она больше, что имеет смысл, поскольку большая индуктивность очень эффективна в противодействии изменению. Чем меньше сопротивление R, тем больше [латекс] \ тау [/ латекс]. Опять же, это имеет смысл, поскольку небольшое сопротивление означает большой конечный ток и большее изменение, чтобы достичь его. В обоих случаях (большой L и маленький R) больше энергии хранится в катушке индуктивности, и требуется больше времени для ее ввода и вывода.

Когда переключатель на (a) перемещается в положение 2 и отключает батарею из цепи, ток падает из-за рассеивания энергии резистором. Однако это также не происходит мгновенно, поскольку катушка индуктивности противодействует уменьшению тока, вызывая ЭДС в том же направлении, что и батарея, управляющая током. Кроме того, в катушке индуктивности накапливается определенное количество энергии, (1/2) LI ₀ ² , и она рассеивается с конечной скоростью. Когда ток приближается к нулю, скорость убывания замедляется, поскольку скорость рассеяния энергии составляет I ² R.{\ frac {- \ text {t}} {\ tau}} [/ latex]

В (c), в первый период времени [latex] \ tau = \ text {L} / \ text {R} [/ latex] после того, как переключатель замкнут, ток падает до 0,368 от своего начального значения, поскольку I = I ₀ e ⁻¹ = 0,368I ₀ . В каждый последующий раз [латекс] \ тау [/ латекс] ток падает до 0,368 от предыдущего значения, а через несколько кратных [латекс] \ тау [/ латекс] ток становится очень близким к нулю.

Цепь серии

RLC: на больших и малых частотах; Фазорная диаграмма

Отклик цепи RLC зависит от частоты возбуждения – на достаточно больших частотах преобладает индуктивный (емкостной) член.

Цели обучения

Различать поведение цепей серии RLC на больших и малых частотах

Основные выводы

Ключевые моменты

• RLC-схемы можно описать (обобщенным) законом Ома. Что касается фазы, когда прикладывается синусоидальное напряжение, ток отстает от напряжения на 90 ° по фазе в цепи с индуктором, в то время как ток опережает напряжение на 90 ° в цепи с конденсатором.
• На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока только с индуктор. Следовательно, среднеквадратичный ток будет Vrms / XL, а ток отстает от напряжения почти на 90 °.
• На достаточно малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока с конденсатор. Следовательно, среднеквадратичный ток будет выражен как V _rms / X _C, , а ток опережает напряжение почти на 90 ^∘ .

Ключевые термины

• Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
• резонанс : Увеличение амплитуды колебаний системы под действием периодической силы, частота которой близка к собственной частоте системы.
• rms : Среднеквадратичное значение: статистическая мера величины переменной величины.

В предыдущих версиях Atoms мы узнали, как последовательная цепь RLC, показанная на рисунке, реагирует на источник переменного напряжения. Объединив закон Ома (I _{среднеквадратичное значение} = В _{действующее значение} / Z; I _{среднеквадратичное значение} и В _{среднеквадратичное значение} являются действующими значениями тока и напряжения) и выражения для импеданса Z из:

Цепь RLC серии : Цепь последовательного RLC: резистор, катушка индуктивности и конденсатор (слева).2}} [/ латекс].

Из уравнения мы исследовали условия резонанса для контура. Мы также изучили фазовые соотношения между напряжениями на резисторе, конденсаторе и катушке индуктивности: при приложении синусоидального напряжения ток отстает от напряжения на фазу 90º в цепи с катушкой индуктивности, в то время как ток опережает напряжение на 90 ^∘ . в цепи с конденсатором. Теперь мы исследуем отклик системы в пределах больших и малых частот.

на больших частотах

На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex], X _L намного больше, чем X _C .Если частота достаточно высока, так что X _L также намного больше, чем R, то в импедансе Z преобладает индуктивный член. Когда [латекс] \ text {Z} \ приблизительно \ text {X} _ \ text {L} [/ latex], схема почти эквивалентна цепи переменного тока с одним дросселем. Следовательно, среднеквадратичный ток будет составлять _В / X _L , а ток отстает от напряжения почти на 90 ^∘ . Этот отклик имеет смысл, потому что на высоких частотах закон Ленца предполагает, что полное сопротивление катушки индуктивности будет большим.

на малых частотах

В импедансе Z на малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] преобладает емкостной член, предполагая, что частота достаточно высока, так что X _C намного больше R. Когда [latex] \ text {Z} \ приблизительно \ text {X} _ \ text {C} [/ latex], схема почти эквивалентна AC схема только с конденсатором. Следовательно, среднеквадратичный ток будет выражен как V _rms / X _C, , а ток опережает напряжение почти на 90 ^∘ .

Резисторы в цепях переменного тока

В цепи с резистором и источником питания переменного тока все еще действует закон Ома ( В, = IR ).

Цели обучения

Применить закон Ома для определения силы тока и напряжения в цепи переменного тока

Основные выводы

Ключевые моменты

• При напряжении переменного тока, определяемом следующим образом: [latex] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex], ток в цепи определяется как : [latex] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex] Это выражение происходит от Ohm закон: [латекс] \ text {V} = \ text {IR} [/ latex]. 2} {2 \ text {R}} [/ латекс].

Ключевые термины

• Закон Ома : Согласно наблюдениям Ома, постоянный ток, протекающий в электрической цепи, состоящей только из сопротивлений, прямо пропорционален приложенному напряжению.

Постоянный ток (DC) – это поток электрического заряда только в одном направлении. Это установившееся состояние цепи постоянного напряжения. Однако в большинстве известных приложений используется источник переменного напряжения. Переменный ток (AC) – это поток электрического заряда, который периодически меняет направление.Если источник периодически меняется, особенно синусоидально, цепь называется цепью переменного тока. Примеры включают коммерческую и бытовую энергетику, которая обслуживает так много наших потребностей. показывает графики зависимости напряжения и тока от времени для типичных источников постоянного и переменного тока. Напряжение и частота переменного тока, обычно используемые в домах и на предприятиях, различаются по всему миру.

Синусоидальное напряжение и ток : (a) Напряжение и ток постоянного тока постоянны во времени после установления тока.(б) График зависимости напряжения и тока от времени для сети переменного тока 60 Гц. Напряжение и ток синусоидальны и совпадают по фазе для простой цепи сопротивления. Частоты и пиковое напряжение источников переменного тока сильно различаются.

Мы изучили закон Ома:

[латекс] \ text {I} = \ frac {\ text {V}} {\ text {R}} [/ latex]

, где I, – ток, В, – напряжение, а R, – сопротивление цепи. Закон Ома применяется как к цепям переменного тока, так и к цепям постоянного тока.Следовательно, с напряжением переменного тока, определяемым по формуле:

[латекс] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex]

, где В ₀ – пиковое напряжение, а [латекс] \ nu [/ latex] – частота в герцах, ток в цепи определяется как:

[латекс] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex]

В этом примере, в котором у нас есть резистор и источник напряжения в цепи, напряжение и ток считаются синфазными, как показано на (b).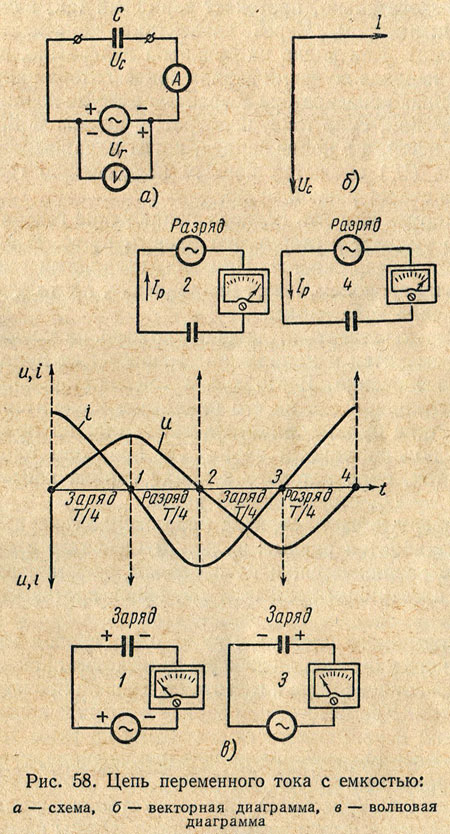 2} {\ text {R}} \ cdot \ sin (2 \ pi \ nu \ text {t}) [/ latex]

Чтобы найти среднюю мощность, потребляемую этой схемой, нам нужно взять среднее значение функции по времени.2} {2 \ text {R}} [/ латекс]

Конденсаторы

в цепях переменного тока: емкостное сопротивление и фазовые диаграммы

Напряжение на конденсаторе отстает от тока. Из-за разности фаз полезно вводить векторы для описания этих схем.

Цели обучения

Объясните преимущества использования векторного представления

Основные выводы

Ключевые моменты

• Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.
• Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно.
• Среднеквадратичное значение тока в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}} {\ text {X} _ \ text {C}} [/ latex], где [latex] \ text {X} _ \ text {c} [/ latex] – это емкостное реактивное сопротивление.

Ключевые термины

• rms : Среднеквадратичное значение: статистическая мера величины переменной величины.

В предыдущем Atom «Резисторы в цепях переменного тока» мы представили источник питания переменного тока и изучили, как резисторы ведут себя в цепях переменного тока. Там мы использовали закон Ома (V = IR), чтобы получить соотношение между напряжением и током в цепях переменного тока. В этом и последующих разделах «Атомы» мы обобщим закон Ома, чтобы мы могли использовать его, даже если в цепи присутствуют конденсаторы и катушки индуктивности. Чтобы добраться туда, мы сначала представим очень общий графический способ представления синусоидальной волны с помощью фазора.

Конденсаторы в цепях переменного тока с фазами

Фазор

Ключевая идея представления вектора состоит в том, что сложный, изменяющийся во времени сигнал может быть представлен как произведение комплексного числа (которое не зависит от времени) и сложного сигнала (которое зависит от времени).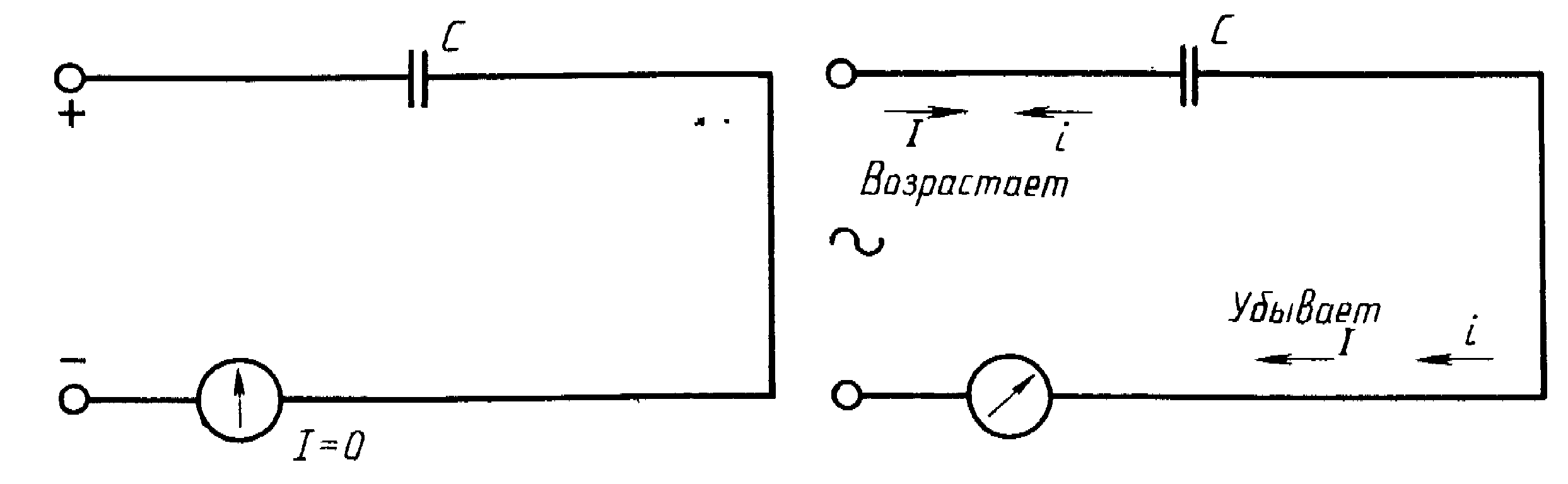 Фазоры разделяют зависимости от A (амплитуда), [latex] \ nu [/ latex] (частота) и θ (фаза) на три независимых фактора. Это может быть особенно полезно, потому что частотный коэффициент (который включает временную зависимость синусоиды) часто является общим для всех компонентов линейной комбинации синусоид.{\ text {i} \ theta} [/ латекс]. Поскольку векторы представлены величиной (или модулем) и углом, они графически представлены вращающейся стрелкой (или вектором) в плоскости x-y.

Рис. 3 : Вектор можно рассматривать как вектор, вращающийся вокруг начала координат в комплексной плоскости. Функция косинуса – это проекция вектора на действительную ось. Его амплитуда – это модуль вектора, а его аргумент – полная фаза \ omega t + \ theta. Фазовая постоянная \ theta представляет собой угол, который вектор образует с действительной осью при t = 0.

Конденсаторы в цепях переменного тока

Ранее в предыдущем Atom мы изучали, как напряжение и ток меняются со временем. Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно. Мы говорим, что ток и напряжение совпадают по фазе.

Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.Ток имеет максимум (пик) за четверть цикла до пика напряжения. Инженеры говорят, что «ток опережает напряжение на 90 ^∘ ». Это показано на.

Рис. 2 : Пик тока (имеет максимум) за четверть волны до напряжения, когда конденсатор подключен к переменному напряжению.

Для цепи с конденсатором мгновенное значение V / I непостоянно. Однако значение V _max / I _max полезно и называется емкостным реактивным сопротивлением (X _C ) компонента.Поскольку это по-прежнему напряжение, деленное на ток (например, сопротивление), единицей измерения является ом. Значение X _C (C означает конденсатор) зависит от его емкости (C) и частоты (f) переменного тока. [латекс] \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ latex].

Конденсатор влияет на ток, имея возможность полностью его отключить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором.Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I _{, действующее значение} в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}}} {\ text {X} _ \ text {C}} [/ latex], где V _rms – это действующее значение напряжения. Обратите внимание, что X _C заменяет R в версии закона Ома для постоянного тока.

Фазовое представление

Поскольку напряжение на конденсаторе отстает от тока, вектор, представляющий ток и напряжение, будет иметь вид. На схеме стрелки вращаются против часовой стрелки с частотой [латекс] \ ню [/ латекс]. (Следовательно, ток ведет к напряжению.) В следующих атомах мы увидим, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.

Рис. 4 : Векторная диаграмма для цепи переменного тока с конденсатором

Индукторы в цепях переменного тока: индуктивно-реактивные и фазовые диаграммы

В цепи переменного тока с катушкой индуктивности напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца.

Цели обучения

Объясните, почему напряжение на катушке индуктивности «опережает» ток в цепи переменного тока с катушкой индуктивности

Основные выводы

Ключевые моменты

• С индуктором в цепи переменного тока напряжение опережает ток на одну четверть цикла или на фазовый угол 90º.
• Среднеквадратичный ток I _{среднеквадратичное значение} через катушку индуктивности L определяется версией закона Ома: [latex] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ { \ text {rms}}} {\ text {X} _ \ text {L}} [/ latex]. 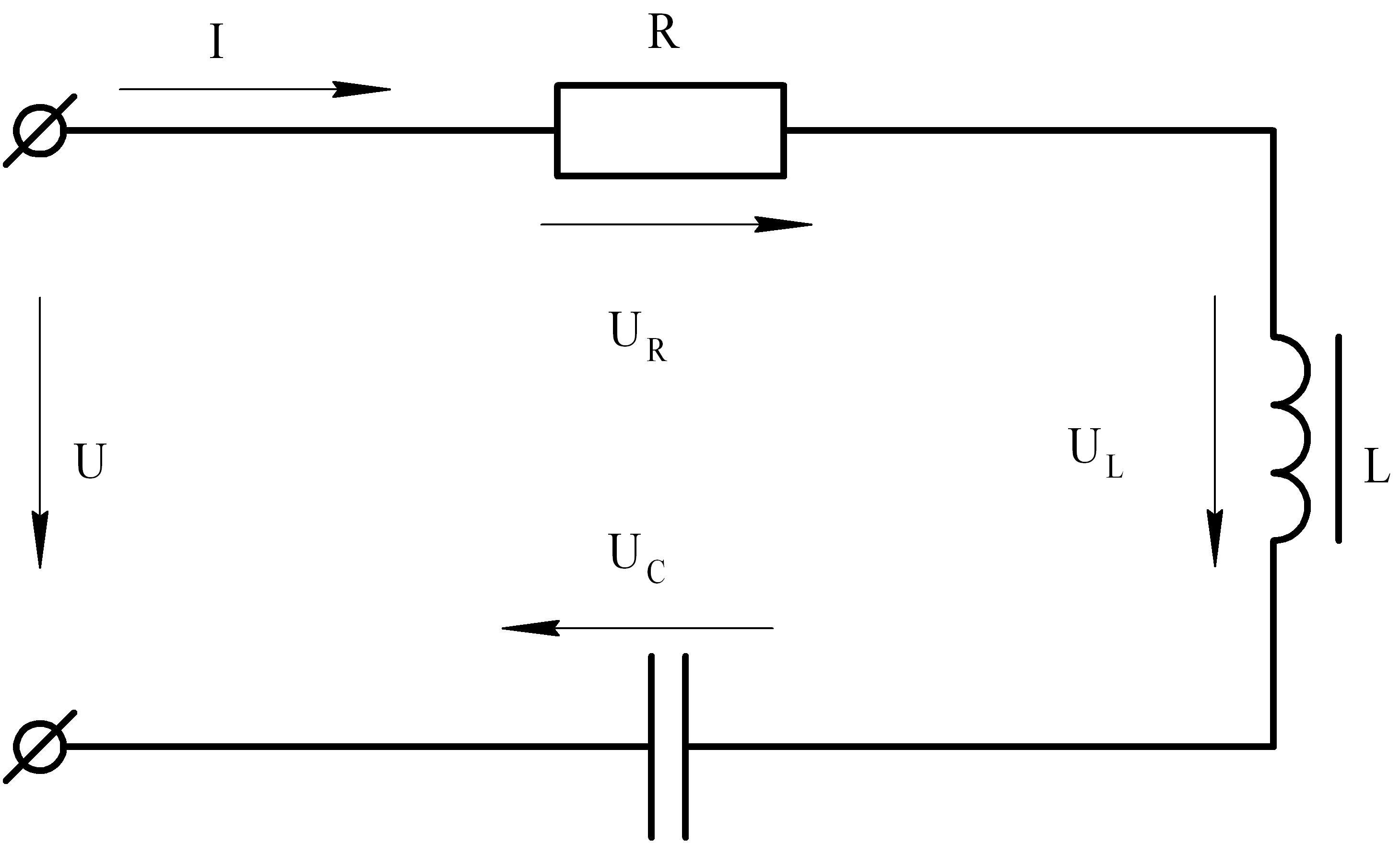X _L называется индуктивным реактивным сопротивлением, которое задается как [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex].
• Фазоры – это векторы, вращающиеся против часовой стрелки. Вектор для катушки индуктивности показывает, что напряжение опережает ток по фазе 90º.

Ключевые термины

• Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
• rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
• phasor : представление комплексного числа в виде комплексной экспоненты.

Предположим, что индуктор подключен непосредственно к источнику переменного напряжения, как показано на рисунке. Разумно предположить, что сопротивление пренебрежимо мало, потому что на практике мы можем сделать сопротивление индуктора настолько малым, что оно окажет незначительное влияние на схему. График показывает напряжение и ток как функции времени.(б) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля, затем повышается до своего пика после управляющего им напряжения (как показано в предыдущем разделе, когда было включено напряжение постоянного тока).

Источник переменного напряжения, подключенный последовательно с индуктором : (a) Источник переменного напряжения, подключенный последовательно с индуктором, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.

Когда напряжение становится отрицательным в точке а, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным.Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c, где оно начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Следовательно, когда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.

Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. Изменение тока вызывает ЭДС.Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I _rms через катушку индуктивности L определяется версией закона Ома: [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text { rms}}} {\ text {X} _ \ text {L}} [/ latex] где V _rms – среднеквадратичное значение напряжения на катушке индуктивности, а [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex] с [latex] \ nu [/ latex] частота источника переменного напряжения в герцах. X _L называется индуктивным реактивным сопротивлением. Поскольку катушка индуктивности препятствует прохождению тока, X _L имеет единицы измерения Ом (1 Гн = 1 Ом · с, так что частота, умноженная на индуктивность, составляет (циклов / с) (Ом · с) = Ом), что соответствует его роли в качестве эффективное сопротивление.

Представление векторов

Напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца. Следовательно, вектор, представляющий ток и напряжение, будет иметь вид. Опять же, вектора – это векторы, вращающиеся против часовой стрелки с частотой [latex] \ nu [/ latex] (вы можете видеть, что напряжение опережает ток) . В последующих выпусках Atoms будет обсуждаться, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.

Векторная диаграмма : Векторная диаграмма для цепи переменного тока с индуктором.

Фазоры для индукторов в цепях переменного тока

Резонанс в цепях RLC

Резонанс – это тенденция системы к колебаниям с большей амплитудой на некоторых частотах – в последовательной цепи RLC он возникает на [latex] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}} }[/латекс].

Цели обучения

Сравнить резонансные характеристики цепей с высоким и низким сопротивлением

Основные выводы

Ключевые моменты

• Условие резонанса последовательной цепи RLC может быть получено приравниванием X _L и X _C , так что два противоположных вектора компенсируют друг друга.
• В резонансе влияние катушки индуктивности и конденсатора компенсируется, так что Z = R, а I _{среднеквадратичное значение} является максимальным.
• Цепи с более высоким сопротивлением не так сильно резонируют по сравнению с цепями с более низким сопротивлением, и при этом они не будут такими избирательными, например, в радиоприемнике.

Ключевые термины

• реактивное сопротивление : Противодействие изменению протекания тока в цепи переменного тока из-за индуктивности и емкости; мнимая часть импеданса.
• rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
• импеданс : мера сопротивления течению переменного тока в цепи; совокупность его сопротивления, индуктивного и емкостного сопротивления. Обозначается символом Z.

Резонанс – это тенденция системы к колебаниям с большей амплитудой на одних частотах, чем на других. Частоты, при которых амплитуда отклика является относительным максимумом, известны как резонансные частоты системы.2}} [/ latex],

, где I _rms и V _rms – среднеквадратичные значения тока и напряжения соответственно. Реактивные сопротивления изменяются в зависимости от частоты [латекс] \ nu [/ latex], при этом X _L большой на высоких частотах и ​​X _C большой на низких частотах, представленных как:

[латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L}, \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ латекс].

На некоторой промежуточной частоте [latex] \ nu_0 [/ latex] реактивные сопротивления будут равны и уравновешены, давая Z = R – это минимальное значение для импеданса, а максимальное значение для I _rms результатов.Мы можем получить выражение для [latex] \ nu_0 [/ latex], взяв X _L = X _C . Подстановка определений X _L и X _C дает:

[латекс] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} [/ латекс].

[латекс] \ nu_0 [/ latex] – это резонансная частота последовательной цепи RLC. Это также собственная частота, на которой цепь будет колебаться, если не будет управляться источником напряжения. В [latex] \ nu_0 [/ latex] эффекты катушки индуктивности и конденсатора нейтрализуются, так что Z = R, а I _rms является максимальным.Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания (в данном случае вызванные источником напряжения) на собственной частоте системы.

Приемник в радиостанции – это RLC-схема, которая лучше всего колеблется на своем [latex] \ nu_0 [/ latex]. Переменный конденсатор часто используется для регулировки резонансной частоты, чтобы получить желаемую частоту и отклонить другие. представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик I _rms в [латексе] \ nu_0 = \ text {f} _0 [/ latex].Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них. Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепи с более высоким сопротивлением не резонируют так сильно, и, например, в радиоприемнике они не будут такими избирательными.

Зависимость тока от частоты : График зависимости тока от частоты для двух цепей серии RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f0, но для более высокого сопротивления он ниже и шире.Источник управляющего переменного напряжения имеет фиксированную амплитуду V0.

Мощность

Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается сопротивлением в цепи и задается как [латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms }} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ latex]. Здесь [latex] \ phi [/ latex] называется фазовым углом.

Цели обучения

Рассчитать мощность, подаваемую в цепь переменного тока серии RLC с учетом тока и напряжения.

Основные выводы

Ключевые моменты

• Фазовый угол ϕ – это разность фаз между напряжением источника V и током I.См. Векторную диаграмму в.
• На резонансной частоте или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны.
• Среднюю мощность, рассеиваемую в цепи RLC, можно рассчитать, взяв среднее значение мощности по времени, P (t) = I (t) V (t), за период.

Ключевые термины

• rms : Среднеквадратичное значение: статистическая мера величины переменной величины.

Если ток изменяется в зависимости от частоты в цепи RLC, то мощность, подаваемая на него, также зависит от частоты.Однако средняя мощность – это не просто ток, умноженный на напряжение, как в чисто резистивных схемах. Как было замечено в предыдущих атомах, напряжение и ток в цепи RLC не совпадают по фазе. Между напряжением источника V и током I существует фазовый угол ϕ, равный

.

[латекс] \ cos {\ phi} = \ frac {\ text {R}} {\ text {Z}} [/ latex], как показано на схеме.

Векторная диаграмма для последовательной цепи RLC : Векторная диаграмма для последовательной цепи RLC. \ phi – фазовый угол, равный разности фаз между напряжением и током.

Например, на резонансной частоте [латекс] (\ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}}) [/ latex] или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем в резонансе, потому что напряжение и ток не совпадают по фазе, а I _rms ниже.

Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь.Можно показать, что средняя мощность

[латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms}} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ латекс]

(уравнение, полученное путем взятия среднего значения мощности по времени, P (t) = I (t) V (t), за период. I (t) и V (t) – это ток и напряжение в момент времени t). Таким образом, cosϕ называется коэффициентом мощности, который может находиться в диапазоне от 0 до 1. Коэффициенты мощности, близкие к 1, желательны, например, при проектировании эффективного двигателя. На резонансной частоте cosϕ = 1.

Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается только за счет сопротивления.Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают энергию из цепи. Скорее, они передают энергию вперед и назад друг другу, а резистор рассеивает именно то количество, которое источник напряжения дает цепи. Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора (например, радиоволн).

Схема аналогична колесу автомобиля, движущегося по гофрированной дороге, как показано на рисунке. Равномерно расположенные неровности дороги аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз.Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний. Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, запасенной в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если неровности дороги встречаются на резонансной частоте.

Принудительное демпфированное движение колеса на автомобильной пружине : Принудительное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC.Амортизатор гасит движение и рассеивает энергию аналогично сопротивлению в цепи RLC. Масса и пружина определяют резонансную частоту.

Реактивное сопротивление, индуктивное и емкостное | Физика

Цели обучения

К концу этого раздела вы сможете:

• Зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
• Рассчитайте индуктивное и емкостное реактивное сопротивление.
• Рассчитайте ток и / или напряжение в простых индуктивных, емкостных и резистивных цепях.

Многие цепи также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы исследуем, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.

Катушки индуктивности и индуктивное сопротивление

Предположим, индуктор подключен непосредственно к источнику переменного напряжения, как показано на рисунке 1.Разумно предположить, что сопротивление пренебрежимо мало, поскольку на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на схему. Также показан график зависимости напряжения и тока от времени.

Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.

График на Рисунке 1 (b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика после напряжения, которое им управляет, как это было в случае, когда напряжение постоянного тока было включено в предыдущем разделе.Когда напряжение становится отрицательным в точке а, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c и начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Это поведение можно резюмировать следующим образом:

Напряжение переменного тока в индукторе

Когда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.

Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. Изменение тока индуцирует обратную ЭДС В = – L (Δ I / Δ t ). Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I через катушку индуктивности L определяется версией закона Ома:

[латекс] I = \ frac {V} {{X} _ {L}} \\ [/ latex],

, где В, – среднеквадратичное значение напряжения на катушке индуктивности, а X _L определяется как

.

[латекс] {X} _ {L} = 2 \ pi {fL} \\ [/ латекс],

с f частота источника переменного напряжения в герцах (анализ схемы с использованием правила петли Кирхгофа и вычислений фактически дает это выражение). X _L называется индуктивным реактивным сопротивлением , потому что катушка индуктивности препятствует прохождению тока. X _L имеет единицы измерения Ом (1 Гн = 1 Ом с, так что частота, умноженная на индуктивность, имеет единицы (циклы / с) (Ом ⋅ с) = Ом)), что соответствует его роли в качестве эффективное сопротивление. Логично, что X _L пропорционально L , поскольку чем больше индукция, тем больше сопротивление изменению.Также разумно, что X _L пропорционально частоте f , поскольку большая частота означает большее изменение тока. То есть Δ I / Δ t является большим для больших частот (большие f , маленькие Δ t ). Чем больше изменение, тем больше сопротивление катушки индуктивности.

Пример 1. Расчет индуктивного сопротивления, а затем тока

(a) Рассчитайте индуктивное сопротивление 3.Индуктор 00 мГн при подаче переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток на каждой частоте, если приложенное действующее напряжение составляет 120 В?

Стратегия

Индуктивное реактивное сопротивление находится непосредственно из выражения X _L = 2πf L . После того, как X _L было найдено на каждой частоте, закон Ома, как указано в уравнении I = В / X _L , может быть использован для определения тока на каждой частоте.

Решение для (а)

Ввод частоты и индуктивности в уравнение X _L = 2πf L дает

X _L = 2πf L = 6,28 (60,0 / с) (3,00 мГн) = 1,13 Ом при 60 Гц.

Аналогично, на 10 кГц,

X _L = 2πf L = 6,28 (1,00 × 10 ⁴ / с) (3,00 мГн) = 188 Ом при 10 кГц.

Решение для (b)

Среднеквадратичное значение тока теперь определяется с использованием версии закона Ома в уравнении I = В / X _L , при условии, что приложенное действующее напряжение составляет 120 В.Для первой частоты это дает

[латекс] I = \ frac {V} {{X} _ {L}} = \ frac {120 \ text {V}} {1.13 \ text {} \ Omega} = 106 \ text {A at} 60 \ текст {Hz} \\ [/ latex].

Аналогично, на 10 кГц,

[латекс] I = \ frac {V} {{X} _ {L}} = \ frac {120 \ text {V}} {188 \ text {} \ Omega} = 0,637 \ text {A at} 10 \ текст {кГц} \\ [/ latex].

Обсуждение

Катушка индуктивности по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток невелик, что соответствует тому, как катушка индуктивности препятствует быстрому изменению.Таким образом, наиболее затруднены высокие частоты. Индукторы могут использоваться для фильтрации высоких частот; например, большую катушку индуктивности можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выводимый из ваших динамиков или высокочастотные всплески мощности на ваш компьютер.

Обратите внимание, что, хотя сопротивлением в рассматриваемой цепи можно пренебречь, переменный ток не очень велик, потому что индуктивное реактивное сопротивление препятствует его протеканию.С переменным током нет времени, чтобы ток стал слишком большим.

Конденсаторы и емкостное сопротивление

Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рисунке 2. Сопротивление такой цепи можно сделать настолько малым, что оно окажет незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить, что сопротивление незначительно. Напряжение на конденсаторе и ток показаны на рисунке как функции времени.

Рисунок 2.(а) Источник переменного напряжения, включенный последовательно с конденсатором С, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на конденсаторе от времени.

График на Рисунке 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, и ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен (на нем Q = 0 ) и напряжение на нем равно нулю.Ток остается отрицательным между точками a и b, вызывая обратное напряжение на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и доводя напряжение до нуля в точке c, что позволяет току достичь своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение соответствует тому, что делает ток, на четверть цикла:

Напряжение переменного тока в конденсаторе

Когда на конденсатор подается синусоидальное напряжение, оно следует за током на одну четверть цикла или на фазовый угол 90º.

Конденсатор влияет на ток, имея возможность полностью его отключить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичный ток I в цепи, содержащей только конденсатор C , по другой версии закона Ома равен

.

[латекс] I = \ frac {V} {{X} _ {C}} \\ [/ latex],

, где В, – среднеквадратичное напряжение, а X _C определяется (Как и в случае с X _L , это выражение для X _C является результатом анализа цепи используя правила и исчисление Кирхгофа) равным

[латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex],

, где X _C называется емкостным реактивным сопротивлением , потому что конденсатор препятствует прохождению тока. X _C имеет единицы измерения Ом (проверка оставлена ​​в качестве упражнения для читателя). X _C обратно пропорциональна емкости C ; Чем больше конденсатор, тем больший заряд он может накапливать и тем больше может протекать ток. Она также обратно пропорциональна частоте f ; чем выше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.

Пример 2. Расчет емкостного реактивного сопротивления, а затем тока

(a) Рассчитайте емкостное реактивное сопротивление конденсатора 5,00 мФ при приложении переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток, если приложенное действующее напряжение составляет 120 В?

Стратегия

Емкостное реактивное сопротивление находится непосредственно из выражения в [latex] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex]. После того, как X _C было обнаружено на каждой частоте, закон Ома, сформулированный как I = В, / X _C , можно использовать для определения тока на каждой частоте.

Решение для (а)

Ввод частоты и емкости в [латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex] дает

[латекс] \ begin {array} {lll} {X} _ {C} & = & \ frac {1} {2 \ pi fC} \\ & = & \ frac {1} {6.28 \ left (60.0 / \ text {s} \ right) \ left (5.00 \ text {} \ mu \ text {F} \ right)} = 531 \ text {} \ Omega \ text {at} 60 \ text {Hz} \ end {массив }\\[/латекс].

Аналогично, на 10 кГц,

[латекс] \ begin {array} {lll} {X} _ {C} & = & \ frac {1} {2 \ pi fC} = \ frac {1} {6.{4} / \ text {s} \ right) \ left (5,00 \ mu \ text {F} \ right)} \\ & = & 3,18 \ text {} \ Omega \ text {at} 10 \ text {кГц} \ end {array} \\ [/ latex].

Решение для (b)

Среднеквадратичное значение тока теперь определяется с использованием версии закона Ома в I = В / X _C , учитывая приложенное действующее напряжение 120 В. Для первой частоты это дает

[латекс] I = \ frac {V} {{X} _ {C}} = \ frac {120 \ text {V}} {531 \ text {} \ Omega} = 0,226 \ text {A at} 60 \ текст {Hz} \\ [/ latex].

Аналогично, на 10 кГц,

[латекс] I = \ frac {V} {{X} _ {C}} = \ frac {120 \ text {V}} {3.18 \ text {} \ Omega} = 3.37 \ text {A at} 10 \ текст {Hz} \\ [/ latex].

Обсуждение

Конденсатор очень по-разному реагирует на двух разных частотах, а индуктор реагирует прямо противоположным образом. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы одобряют изменения, тогда как индукторы противодействуют изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота позволяет им успеть зарядиться и остановить ток.Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно с системой воспроизведения звука, избавляет ее от гула 60 Гц.

Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с напряжением переменного тока, приложенным к конденсатору, присутствует среднеквадратичный ток. Это связано с тем, что напряжение постоянно меняет направление, заряжая и разряжая конденсатор. Если частота стремится к нулю (DC), X _C стремится к бесконечности, и ток равен нулю, когда конденсатор заряжен.На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю – он имеет незначительное реактивное сопротивление и не препятствует прохождению тока (действует как простой провод). Конденсаторы оказывают противоположное влияние на цепи переменного тока, чем индукторы .

Резисторы в цепи переменного тока

В качестве напоминания рассмотрим Рисунок 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток точно равны в фазах в резисторе.Отсутствует частотная зависимость поведения простого сопротивления в цепи:

Рис. 3. (a) Источник переменного напряжения, включенный последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.

Напряжение переменного тока на резисторе

Когда на резистор подается синусоидальное напряжение, напряжение точно совпадает по фазе с током – они имеют фазовый угол 0 °.

Сводка раздела

• Для катушек индуктивности в цепях переменного тока мы обнаруживаем, что когда на катушку подается синусоидальное напряжение, напряжение опережает ток на одну четверть цикла или на фазовый угол 90 °.
• Противодействие катушки индуктивности изменению тока выражается как сопротивление переменному току.
• Закон Ома для индуктора

  [латекс] I = \ frac {V} {{X} _ {L}} \\ [/ latex],

  , где В, – среднеквадратичное значение напряжения на катушке индуктивности.

• X _L определяется как индуктивное реактивное сопротивление, определяемое по формуле

  [латекс] {X} _ {L} = 2 \ pi fL \\ [/ латекс],

  с f частота источника переменного напряжения в герцах.

• Индуктивное реактивное сопротивление X _L выражается в единицах Ом и имеет наибольшее значение на высоких частотах.
• Для конденсаторов мы обнаруживаем, что когда на конденсатор подается синусоидальное напряжение, напряжение следует за током на одну четверть цикла или на фазовый угол 90º.
• Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора

  [латекс] I = \ frac {V} {{X} _ {C}} \\ [/ latex],

  , где В, – среднеквадратичное значение напряжения на конденсаторе.

• X _C определяется как емкостное реактивное сопротивление, определяемое по формуле

  [латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex].

• X _C имеет единицы измерения Ом и имеет наибольшее значение на низких частотах.

Концептуальные вопросы

1. Пресбиакузис – это возрастная потеря слуха, которая постепенно влияет на высокие частоты. Усилитель слухового аппарата предназначен для равномерного усиления всех частот. Чтобы отрегулировать его мощность на пресбиакузис, включите ли вы конденсатор последовательно или параллельно динамику слухового аппарата? Объяснять.

2. Будете ли вы использовать большую индуктивность или большую емкость последовательно с системой для фильтрации низких частот, таких как гул 100 Гц в звуковой системе? Объяснять.

3. Высокочастотный шум в сети переменного тока может повредить компьютеры. Использует ли съемный блок, предназначенный для предотвращения этого повреждения, большую индуктивность или большую емкость (последовательно с компьютером) для фильтрации таких высоких частот? Объяснять.

4. Зависит ли индуктивность от тока, частоты или и того, и другого? А как насчет индуктивного сопротивления?

5. Объясните, почему конденсатор на рисунке 4 (а) действует как фильтр низких частот между двумя цепями, тогда как конденсатор на рисунке 4 (b) действует как фильтр высоких частот.

Рисунок 4. Конденсаторы и катушки индуктивности. Конденсатор с высокой и низкой частотой.

6. Если конденсаторы на рис. 4 заменить катушками индуктивности, что будет действовать как фильтр низких частот, а какой – как фильтр высоких частот?

Задачи и упражнения

1. На какой частоте индуктор 30,0 мГн будет иметь реактивное сопротивление 100 Ом?

2. Какое значение индуктивности следует использовать, если требуется реактивное сопротивление 20,0 кОм при частоте 500 Гц?

3.Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при 60,0 Гц?

4. На какой частоте конденсатор 80,0 мФ будет иметь реактивное сопротивление 0,250 Ом?

5. (a) Найдите ток через катушку индуктивности 0,500 H, подключенную к источнику переменного тока 60,0 Гц, 480 В. (б) Каким будет ток на частоте 100 кГц?

6. (a) Какой ток протекает, когда источник переменного тока 60,0 Гц, 480 В подключен к конденсатору 0,250 мкФ? (b) Каким будет ток на частоте 25,0 кГц?

7. А 20.Источник 0 кГц, 16,0 В, подключенный к катушке индуктивности, вырабатывает ток 2,00 А. Что такое индуктивность?

8. Источник 20,0 Гц, 16,0 В вырабатывает ток 2,00 мА при подключении к конденсатору. Какая емкость?

9. (a) Катушка индуктивности, предназначенная для фильтрации высокочастотного шума от источника питания персонального компьютера, включается последовательно с компьютером. Какая минимальная индуктивность должна обеспечивать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? (б) Каково его реактивное сопротивление при 60?0 Гц?

10. Конденсатор на рисунке 4 (а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. (а) Какая емкость необходима для создания реактивного сопротивления 100 кОм при частоте 120 Гц? (b) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите значение ваших ответов на (a) и (b).

11. Конденсатор на Рисунке 4 (b) будет фильтровать высокочастотные сигналы, замыкая их на землю / землю. (a) Какая емкость необходима для получения реактивного сопротивления [латекса] \ text {10.0 м \ Omega} [/ latex] для сигнала 5,00 кГц? (б) Каким будет его реактивное сопротивление при 3,00 Гц? (c) Обсудите значение ваших ответов на (a) и (b).

12. Необоснованные результаты При регистрации напряжений, обусловленных мозговой активностью (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, создавая ток 100 мА. Сопротивление незначительное. а) Какая емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка ответственны?

13. Создайте свою проблему Рассмотрите возможность использования индуктора последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, – допустимое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.

Глоссарий

индуктивное сопротивление:

противодействие катушки индуктивности изменению тока; рассчитывается по X _L = 2π fL

емкостное реактивное сопротивление:

сопротивление конденсатора изменению тока; рассчитывается по [latex] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex]

Избранные решения проблем и упражнения

1.531 Гц

3. 1,33 нФ

5. (а) 2,55 А (б) 1,53 мА

7. 63,7 мкГн

9. (а) 21,2 мГн (б) 8,00 Ом

Мощность в цепи переменного тока – Университетская физика, том 2

Цели обучения

К концу раздела вы сможете:

• Опишите, как можно записать среднюю мощность от цепи переменного тока в терминах пикового тока и напряжения, а также среднеквадратичных значений тока и напряжения
• Определите соотношение между фазовым углом тока и напряжения и средней мощностью, известное как коэффициент мощности

Элемент схемы рассеивает или вырабатывает мощность в зависимости от того, где I – ток через элемент, а В – напряжение на нем.Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность также зависит от времени. График p ( t ) для различных элементов схемы показан на (Рисунок). Для резистора i ( t ) и v ( t ) синфазны и поэтому всегда имеют один и тот же знак (см. (Рисунок)). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разницы фаз (см. (Рисунок) и (Рисунок)).Следовательно, p ( t ) в некоторые моменты положительный, а в другие – отрицательный, что указывает на то, что емкостные и индуктивные элементы вырабатывают мощность в одни моменты и поглощают ее в другие.

Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. То, что нас почти всегда интересует, – это усредненная по времени мощность, которую мы называем средней мощностью. Он определяется средним по времени мгновенной мощностью за один цикл:

где – период колебаний.С заменами и этот интеграл становится

Используя тригонометрическое соотношение, получаем

Вычисление этих двух интегралов дает

и

Следовательно, средняя мощность, связанная с элементом схемы, равна

В технических приложениях известен как коэффициент мощности, который представляет собой величину, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе.Для резистора, поэтому средняя рассеиваемая мощность

Сравнение p ( t ) и показано на (Рисунок) (d). Чтобы выглядеть как его аналог постоянного тока, мы используем среднеквадратичные значения тока и напряжения. По определению это

где

С получаем

Затем мы можем написать для средней мощности, рассеиваемой резистором,

Это уравнение дополнительно подчеркивает, почему при обсуждении выбирается среднеквадратичное значение, а не пиковые значения.Оба уравнения для средней мощности верны для (рисунок), но среднеквадратичные значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не требуется.

Переменные напряжения и токи обычно описываются их действующими значениями. Например, напряжение 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника равна. Поскольку большинство измерителей переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, установленный на бытовой розетке, будет показывать 110 В.

Для конденсатора и катушки индуктивности соответственно. Поскольку мы находим из (Рисунок), что средняя мощность, рассеиваемая любым из этих элементов, равна Конденсаторам, а катушки индуктивности поглощают энергию из цепи в течение одного полупериода, а затем разряжают ее обратно в цепь в течение другого полупериода. Это поведение проиллюстрировано на графиках (Рисунок), (b) и (c), которые показывают, что p ( t) колеблется синусоидально около нуля.

Фазовый угол генератора переменного тока может иметь любое значение.Если генератор выдает мощность; если он поглощает энергию. В терминах среднеквадратичных значений средняя мощность генератора переменного тока записывается как

Для генератора в цепи RLC ,

и

Отсюда средняя мощность генератора

Это также можно записать как

, который означает, что мощность, производимая генератором, рассеивается в резисторе. Как мы видим, закон Ома для среднеквадратичного значения переменного тока находится делением среднеквадратичного значения напряжения на импеданс.

Проверьте свое понимание Вольтметр переменного тока, подключенный к клеммам генератора переменного тока 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.

Проверьте свое понимание Покажите, что действующие значения напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока, где среднеквадратичный ток выражается соответственно. Определите эти значения для компонентов цепи RLC (рисунок).

Сводка

• Средняя мощность переменного тока определяется путем умножения среднеквадратичных значений тока и напряжения.
Закон
• Ома для среднеквадратичного значения переменного тока находится делением среднеквадратичного напряжения на полное сопротивление.
• В цепи переменного тока существует фазовый угол между напряжением источника и током, который можно найти, разделив сопротивление на полное сопротивление.
• Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла.
• Коэффициент мощности находится в диапазоне от –1 до 1.

Концептуальные вопросы

При каком значении фазового угла между выходным напряжением источника переменного тока и током средняя выходная мощность источника является максимальной?

Обсудите разницу между средней мощностью и мгновенной мощностью.

Мгновенная мощность – это мощность в данный момент. Средняя мощность – это мощность, усредненная за цикл или количество циклов.

Средний переменный ток, подаваемый в цепь, равен нулю.Несмотря на это, мощность в цепи рассеивается. Объяснять.

Может ли мгновенная выходная мощность источника переменного тока быть отрицательной? Может ли средняя выходная мощность быть отрицательной?

Мгновенная мощность может быть отрицательной, но выходная мощность не может быть отрицательной.

Номинальная мощность резистора, используемого в цепях переменного тока, относится к максимальной средней мощности, рассеиваемой в резисторе. Как это соотносится с максимальной мгновенной мощностью, рассеиваемой на резисторе?

Глоссарий

средняя мощность

среднее время мгновенной мощности за один цикл

Коэффициент мощности

величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе

Цепи переменного тока (Часть первая)

Закон Ома для цепей переменного тока

Правила и уравнения для цепей постоянного тока применяются к цепям переменного тока только в том случае, если цепи содержат только сопротивление, как в случае ламп и нагревательных элементов.Чтобы использовать действующие значения напряжения и тока в цепях переменного тока, необходимо учитывать влияние индуктивности и емкости на сопротивление.

Комбинированные эффекты сопротивления, индуктивного реактивного сопротивления и емкостного реактивного сопротивления составляют полное противодействие протеканию тока в цепи переменного тока. Это полное сопротивление называется импедансом и обозначается буквой Z. Единицей измерения импеданса является ом.

Цепи переменного тока серии

Если цепь переменного тока состоит только из сопротивления, значение импеданса такое же, как и сопротивление, а закон Ома для цепи переменного тока I = E / Z точно такой же, как и для цепи постоянного тока. схема.На рисунке 12-133,

Рисунок 12-133. Применение постоянного и переменного тока в цепи.

проиллюстрирована последовательная цепь, содержащая лампу с сопротивлением 11 Ом, подключенную к источнику. Чтобы определить, сколько тока течет, если приложено 110 В постоянного тока и сколько тока течет, если приложено 110 В переменного тока, решаются следующие примеры:

Когда цепи переменного тока содержат сопротивление и либо индуктивность, либо емкость, полное сопротивление Z, не то же самое, что сопротивление R. Импеданс цепи – это полное сопротивление цепи протеканию тока.В цепи переменного тока это противостояние состоит из сопротивления и реактивного сопротивления, индуктивного или емкостного, либо элементов обоих.

Сопротивление и реактивное сопротивление нельзя сложить напрямую, но их можно рассматривать как две силы, действующие под прямым углом друг к другу. Таким образом, соотношение между сопротивлением, реактивным сопротивлением и импедансом можно проиллюстрировать прямоугольным треугольником. [Рисунок 12-134] Рисунок 12-134. Треугольник импеданса.

Поскольку эти величины могут быть связаны со сторонами прямоугольного треугольника, формулу для определения импеданса или полного противодействия току в цепи переменного тока можно найти, используя закон прямоугольных треугольников.Эта теорема, называемая теоремой Пифагора, применима к любому прямоугольному треугольнику. В нем говорится, что квадрат гипотенузы равен сумме квадратов двух других сторон. Таким образом, значение любой стороны прямоугольного треугольника можно найти, если известны две другие стороны. Если цепь переменного тока содержит сопротивление и индуктивность, как показано на Рисунке 12-135,

Рисунок 12-135. Цепь, содержащая сопротивление и индуктивность.

отношение между сторонами может быть указано как:

Z ² = R ² + X _L ²

Квадратный корень из обеих частей уравнения дает

Эта формула может быть используется для определения импеданса, когда известны значения индуктивного реактивного сопротивления и сопротивления.Его можно изменить для определения импеданса в цепях, содержащих емкостное реактивное сопротивление и сопротивление, подставив в формулу X _C вместо X _L . В цепях, содержащих сопротивление как с индуктивным, так и с емкостным реактивным сопротивлением, реактивные сопротивления можно комбинировать, но поскольку их эффекты в цепи прямо противоположны, они объединяются путем вычитания:

На рисунке 12-135 показана последовательная цепь, состоящая из сопротивления. а индуктивность, соединенная последовательно, подключена к источнику 110 вольт при 60 гц.

Рисунок 12-135. Цепь, содержащая сопротивление и индуктивность.

Резистивный элемент представляет собой лампу с сопротивлением 6 Ом, а индуктивный элемент представляет собой катушку с индуктивностью 0,021 Генри. Какое значение импеданса и тока через лампу и катушку?

Решение:

Сначала вычисляется индуктивное реактивное сопротивление катушки:

X _L = 2π × f × L

X _L = 6,28 × 60 × 0,021

X _L = 8 Ом индуктивное реактивное сопротивление

Затем вычисляется полное сопротивление:

Затем протекает ток,

Падение напряжения на сопротивлении (E ^R ) составляет:

E ^R = I × R

E ^R = 11 × 6 = 66 вольт

Падение напряжения на индуктивности (EX _L ) составляет:

EX _L = I × X _L

EX _L = 11 × 8 = 88 вольт

Сумма двух напряжений больше приложенного напряжения.Это происходит из-за того, что два напряжения не совпадают по фазе и, как таковые, представляют максимальное напряжение. Если напряжение в цепи измеряется вольтметром, оно составляет примерно 110 вольт, подаваемое напряжение. Это можно доказать с помощью уравнения:

На рисунке 12-136 проиллюстрирована последовательная цепь, в которой конденсатор на 200 мкФ соединен последовательно с лампой на 10 Ом.

Рисунок 12-136. Цепь, содержащая сопротивление и емкость.

Какое значение имеет импеданс, ток и падение напряжения на лампе?

Решение:

Сначала емкость изменяется с микрофарад на фарады.Так как 1 миллион микрофарад равен 1 фараду, тогда:

Чтобы найти импеданс,

Чтобы найти ток,

Падение напряжения на лампе (E ^R ) составляет:

E ^R = 6,7 × 10

E ^R = 67 вольт

Падение напряжения на конденсаторе (EX _C ) составляет

EX _C = I × X _C

EX _C = 6,7 × 13

EX _C = 86.1 вольт

Сумма этих двух напряжений не равна приложенному напряжению, поскольку ток опережает напряжение. Чтобы найти приложенное напряжение, используйте следующую формулу:

Если в цепи есть сопротивление, индуктивность и емкость, для определения импеданса используется следующее уравнение:

Пример: Что такое полное сопротивление последовательная цепь, состоящая из конденсатора с реактивным сопротивлением 7 Ом, катушки индуктивности с реактивным сопротивлением 10 Ом и резистора с сопротивлением 4 Ом? [Рисунок 12-137] Рисунок 12-137.Цепь, содержащая сопротивление, индуктивность и емкость.

Решение:

Предполагая, что реактивное сопротивление конденсатора составляет 10 Ом, а реактивное сопротивление катушки индуктивности составляет 7 Ом, тогда X _C больше, чем X _L . Таким образом,

Параллельные цепи переменного тока

Методы, используемые при решении задач параллельных цепей переменного тока, в основном те же, что и методы, используемые для последовательных цепей переменного тока. Напряжения и токи, не совпадающие по фазе, могут быть добавлены с помощью закона прямоугольных треугольников.Однако при решении схемных проблем токи через ветви складываются, поскольку падение напряжения на различных ветвях одинаково и равно приложенному напряжению. На рисунке 12-138 схематично показана параллельная цепь переменного тока, содержащая индуктивность и сопротивление.

Рисунок 12-138. Параллельная цепь переменного тока, содержащая индуктивность и сопротивление.

Ток, протекающий через индуктивность, I _L , составляет 0,0584 ампера, а ток, протекающий через сопротивление, равен 0.11 ампер. Какой полный ток в цепи?

Решение:

Поскольку индуктивное реактивное сопротивление заставляет напряжение опережать ток, общий ток, который содержит составляющую индуктивного тока, отстает от приложенного напряжения. Если ток и напряжения нанесены на график, угол между ними, называемый фазовым углом, показывает, насколько ток отстает от напряжения. На рисунке 12-139 генератор на 112 вольт подключен к нагрузке, состоящей из емкости 2 мкФ и сопротивления 10 000 Ом параллельно.

Рисунок 12-139. Параллельная цепь переменного тока, содержащая емкость и сопротивление.

Какое значение имеет импеданс и общий ток?

Решение:

Сначала найдите емкостное реактивное сопротивление цепи:

Измените 2 мкФ на фарады и введите значения в приведенную формулу:

Чтобы найти импеданс, формула импеданса Используемые в последовательной цепи переменного тока должны быть изменены, чтобы соответствовать параллельной цепи:

Чтобы найти ток через емкость:

Чтобы найти ток, протекающий через сопротивление:

Чтобы найти общий ток в цепь:

Резонанс

Было показано, что как индуктивное реактивное сопротивление:

(X _L = 2πfL)

, так и емкостное реактивное сопротивление:

являются функциями частоты переменного тока.Уменьшение частоты уменьшает омическое значение индуктивного реактивного сопротивления, но уменьшение частоты увеличивает емкостное реактивное сопротивление. На некоторой определенной частоте, известной как резонансная частота, реактивные эффекты конденсатора и катушки индуктивности равны. Поскольку эти эффекты противоположны друг другу, они отменяются, оставляя только омическое значение сопротивления, которое препятствует прохождению тока в цепи. Если значение сопротивления невелико или состоит только из сопротивления проводников, величина протекающего тока может стать очень высокой.

В цепи, в которой катушка индуктивности и конденсатор включены последовательно, а частота является резонансной частотой или частотой резонанса, цепь называется «резонансной» и называется последовательной резонансной цепью. Обозначение резонансной частоты – Fn.

Если на частоте резонанса индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению, то:

Разделив обе стороны на 2 фЛ,

Извлечение квадратного корня из обеих сторон дает:

Где Fn – резонансная частота в гц, C – емкость в фарадах, а L – индуктивность в генри.С помощью этой формулы можно определить частоту, на которой конденсатор и катушка индуктивности резонируют.

Чтобы найти индуктивное реактивное сопротивление цепи, используйте:

X _L = 2πfL

Формулу импеданса, используемую в последовательной цепи переменного тока, необходимо изменить, чтобы она соответствовала параллельной цепи.

Чтобы найти параллельные цепи индуктивности и емкостных реакторов, используйте:

Чтобы найти параллельные сети с емкостным сопротивлением и индуктивностью, используйте:

Поскольку на резонансной частоте X _L отменяет X _C , ток может стать очень большим, в зависимости от величины сопротивления.В таких случаях падение напряжения на катушке индуктивности или конденсаторе часто превышает приложенное напряжение.

В параллельном резонансном контуре реактивные сопротивления равны, и через катушку и конденсатор протекают равные токи. [Рисунок 12-140] Рисунок 12-140. Параллельный резонансный контур.

Поскольку индуктивное реактивное сопротивление заставляет ток через катушку отставать от напряжения на 90 °, а емкостное реактивное сопротивление заставляет ток через конденсатор опережать напряжение на 90 °, два тока сдвинуты по фазе на 180 °.Эффект компенсации таких токов будет означать, что ток не будет течь из генератора, и параллельная комбинация катушки индуктивности и конденсатора будет выглядеть как бесконечный импеданс. На практике такая схема невозможна, поскольку всегда присутствует некоторое значение сопротивления, а параллельная схема, иногда называемая цепью с резервуаром, действует как очень высокий импеданс. Его также называют антирезонансным контуром, поскольку его действие в контуре противоположно действию последовательного резонансного контура, в котором полное сопротивление очень низкое.

Мощность в цепях переменного тока

В цепях постоянного тока мощность рассчитывается по уравнению P = EI (ватты равны вольтам × амперам). Таким образом, если в цепи при давлении 200 вольт протекает ток 1 ампер, мощность составляет 200 ватт. Произведение вольт и ампер и есть истинная мощность в цепи.

Определенная истинная мощность

Истинная мощность любой цепи переменного тока обычно называется рабочей мощностью цепи. Истинная мощность – это мощность, потребляемая участком сопротивления цепи, и измеряется в ваттах.Истинная мощность обозначается буквой P и указывается любым ваттметром в цепи. Истинная мощность рассчитывается по формуле:

P = I ² × Z

Определенная полная мощность

Полная мощность в цепи переменного тока иногда называется реактивной мощностью цепи. Полная мощность – это мощность, потребляемая всей цепью, включая сопротивление и реактивное сопротивление. Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА).Полная мощность – это произведение эффективного напряжения на эффективный ток. Полная мощность рассчитывается по формуле:

S = I ² × Z

Только тогда, когда цепь переменного тока состоит из чистого сопротивления, полная мощность равна истинной мощности. [Рисунок 12-141] Рисунок 12-141. Соотношения сил в цепи переменного тока.

Когда в цепи присутствует емкость или индуктивность, ток и напряжение не совпадают по фазе, а истинная мощность меньше полной мощности.Истинная мощность определяется показаниями ваттметра. Отношение истинной мощности к полной мощности называется коэффициентом мощности и обычно выражается в процентах. В форме уравнения соотношение выглядит следующим образом:

Пример: 220-вольтовый двигатель переменного тока потребляет 50 ампер от сети, но ваттметр в строке показывает, что двигатель потребляет только 9350 Вт. Каковы кажущаяся мощность и коэффициент мощности?

Решение:

Летный механик рекомендует

15.S: Цепи переменного тока (Резюме) – Physics LibreTexts

Ключевые термины

переменный ток	ток, синусоидально колеблющийся во времени с фиксированной частотой
напряжение переменного тока	напряжение, синусоидально колеблющееся во времени с фиксированной частотой
переменный ток (ac)	поток электрического заряда, который периодически меняет направление
средняя мощность	среднее время мгновенной мощности за один цикл
пропускная способность	диапазон угловых частот, в которых средняя мощность больше половины максимального значения средней мощности
емкостное реактивное сопротивление	Противодействие конденсатора изменению тока
постоянный ток (dc)	поток электрического заряда только в одном направлении
импеданс	переменный ток аналог сопротивления в цепи постоянного тока, который измеряет комбинированное влияние сопротивления, емкостного реактивного сопротивления и индуктивного реактивного сопротивления
индуктивное сопротивление	Противодействие катушки индуктивности изменению тока
фазовый угол	величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи
Коэффициент мощности	величина, на которую мощность, передаваемая в цепь, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе
добротность	безразмерная величина, описывающая резкость пика полосы пропускания; высокая добротность – острый или узкий пик резонанса
резонансная частота	частота, при которой амплитуда тока максимальна, и цепь будет колебаться, если не будет управляться источником напряжения
действующее значение тока	среднеквадратичное значение текущего
действующее напряжение	среднеквадратичное значение напряжения
понижающий трансформатор	трансформатор, понижающий напряжение и увеличивающий ток
повышающий трансформатор	трансформатор, повышающий напряжение и понижающий ток
трансформатор	устройство, преобразующее напряжение из одного значения в другое с помощью индукции
уравнение трансформатора	уравнение, показывающее, что отношение вторичного напряжения к первичному в трансформаторе равно отношению количества витков в их обмотках

Ключевые уравнения

Напряжение переменного тока	\ (\ Displaystyle v = V_0sinωt \)
Переменный ток	\ (\ Displaystyle я = I_0sinωt \)
емкостное реактивное сопротивление	\ (\ Displaystyle \ гидроразрыва {V_0} {I_0} = \ гидроразрыва {1} {ωC} = X_C \)
действующее напряжение	\ (\ Displaystyle V_ {rms} = \ frac {V_0} {\ sqrt {2}} \)
действующее значение тока	\ (\ Displaystyle I_ {rms} = \ frac {I_0} {\ sqrt {2}} \)
индуктивное сопротивление	\ (\ Displaystyle \ гидроразрыва {V_0} {I_0} = ωL = X_L \)
Фазовый угол цепи последовательного RLC	\ (\ Displaystyle ϕ = загар ^ {- 1} \ гидроразрыва {X_L − X_C} {R} \)
Вариант закона Ома по переменному току	\ (\ Displaystyle I_0 = \ гидроразрыва {V_0} {Z} \)
Импеданс цепи последовательного RLC	\ (\ Displaystyle Z = \ sqrt {R ^ 2 + (X_L − X_C) ^ 2} \)
Средняя мощность, связанная с элементом схемы	\ (\ Displaystyle P_ {ave} = \ frac {1} {2} I_0V_0cosϕ \)
Средняя мощность, рассеиваемая резистором	\ (\ Displaystyle P_ {ave} = \ frac {1} {2} I_0V_0 = I_ {rms} V_ {rms} = I ^ 2_ {rms} R \)
Резонансная угловая частота контура	\ (\ Displaystyle ω_0 = \ sqrt {\ frac {1} {LC}} \)
Добротность схемы	\ (\ Displaystyle Q = \ гидроразрыва {ω_0} {Δω} \)
Добротность цепи по параметрам цепи	\ (\ Displaystyle Q = \ гидроразрыва {ω_0L} {R} \)
Уравнение трансформатора с напряжением	\ (\ Displaystyle \ frac {V_S} {V_P} = \ frac {N_S} {N_P} \)
Уравнение трансформатора с током	\ (\ Displaystyle I_S = \ frac {N_P} {N_S} I_P \)

Резюме

15.2 источника переменного тока

• Постоянный ток (dc) относится к системам, в которых напряжение источника постоянно.
• Переменный ток (ac) относится к системам, в которых напряжение источника периодически изменяется, особенно синусоидально.
• Источник напряжения системы переменного тока выдает напряжение, которое рассчитывается на основе времени, пикового напряжения и угловой частоты.
• В простой схеме ток определяется делением напряжения на сопротивление.Переменный ток рассчитывается с использованием пикового тока (определяемого делением пикового напряжения на сопротивление), угловой частоты и времени.

15.3 Простые цепи переменного тока

• Для резисторов сквозной ток и напряжение совпадают по фазе.
• Для конденсаторов мы обнаруживаем, что когда на конденсатор подается синусоидальное напряжение, напряжение следует за током на одну четверть цикла. Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току, называемую емкостным реактивным сопротивлением, которое измеряется в омах.
• Для катушек индуктивности в цепях переменного тока мы обнаруживаем, что когда на индуктор подается синусоидальное напряжение, оно опережает ток на одну четверть цикла.
• Противодействие катушки индуктивности изменению тока выражается как тип реактивного сопротивления переменного тока. Это индуктивное реактивное сопротивление, которое измеряется в омах, изменяется в зависимости от частоты источника переменного тока.

Цепи серии 15,4 RLC с AC

• Последовательная цепь RLC представляет собой последовательную комбинацию резистора, конденсатора и индуктора через источник переменного тока.
• Одинаковый ток течет через каждый элемент последовательной цепи RLC во все моменты времени.
• Сопротивлением в цепи постоянного тока является импеданс, который измеряет совместное действие резисторов, конденсаторов и катушек индуктивности. Максимальный ток определяется версией закона Ома для переменного тока.
• Импеданс измеряется в омах и определяется как сопротивление, емкостное реактивное сопротивление и индуктивное реактивное сопротивление.

15.5 Питание в цепи переменного тока

• Средняя мощность переменного тока определяется путем умножения среднеквадратичных значений тока и напряжения.
Закон
• Ома для среднеквадратичного значения переменного тока находится делением среднеквадратичного напряжения на полное сопротивление.
• В цепи переменного тока существует фазовый угол между напряжением источника и током, который можно найти, разделив сопротивление на полное сопротивление.
• Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла.
• Коэффициент мощности колеблется от –1 до 1.

15,6 Резонанс в цепи переменного тока

• На резонансной частоте индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению.
• График зависимости средней мощности от угловой частоты для цепи RLC имеет пик, расположенный на резонансной частоте; резкость или ширина пика называется полосой пропускания.
• Ширина полосы связана с безразмерной величиной, называемой коэффициентом качества.Высокое значение добротности – это острый или узкий пик.

15,7 Трансформаторы

• Электростанции передают высокое напряжение при малых токах для достижения более низких омических потерь на многокилометровых линиях передачи.
В трансформаторах
• индукция используется для преобразования напряжения из одного значения в другое.
• Для трансформатора напряжения на первичной и вторичной катушках или обмотках связаны уравнением трансформатора.
• Токи в первичной и вторичной обмотках связаны количеством первичных и вторичных петель или витков в обмотках трансформатора.
• Повышающий трансформатор увеличивает напряжение и снижает ток, тогда как понижающий трансформатор снижает напряжение и увеличивает ток.

Авторы и авторство

Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

Цепь переменного тока

– обзор

II.E Емкость и индуктивность

Эти компоненты используются только в цепях переменного тока. При постоянном токе емкость выглядит как разомкнутая цепь (за исключением небольшого тока утечки через сопротивление диэлектрика), а индуктор представляет собой небольшое сопротивление (сопротивление проводника катушки). Однако при подключении или отключении источника постоянного тока влияние емкости и индуктивности становится очевидным из-за изменения энергии, запасенной в устройстве.

В цепях переменного тока на свойства как катушек индуктивности, так и конденсаторов влияет частота, и хотя эти эффекты обычно не проявляются в конденсаторах до тех пор, пока не будут достигнуты частоты выше нескольких мегагерц, свойства индикаторов могут начать показывать изменения в несколько килогерц.Поэтому при измерениях катушек индуктивности и конденсаторов важно записывать частоту, на которой проводились измерения, и, если возможно, проводить измерения на заданной частоте работы. Как и в случае измерения сопротивления, мостовые методы широко используются в течение многих лет для измерения как индуктивности, так и емкости.

При работе мостовой схемы необходимо учитывать как резистивные, так и реактивные составляющие неизвестного. Поскольку небольшие конденсаторы, изготовленные с использованием современных диэлектрических материалов, фактически являются чистыми реактивными сопротивлениями на низких и средних частотах, поскольку (параллельное) сопротивление утечки имеет очень высокое значение, это было не так 20 лет назад или около того.Это также не относится к катушкам индуктивности или конденсаторам большой емкости. Необходимость знать эти составные части привела к быстрому распространению мостовых схем, основанных на схеме Уитстона. Часто используемые примеры мостов переменного тока приписываются Максвеллу, Оуэну и Хевисайду для измерения индуктивности и Вайну, Де Саути и Шерингу для измерения емкости. Последний из них (рис. 37) до сих пор используется из-за высокого напряжения.

РИСУНОК 37. Мостовая схема Шеринга.

Альтернативой мостовым методам и подходящим для использования на частотах от 1 кГц до 300 МГц был измеритель Q , устройство, которое больше не фигурирует в каталогах производителей приборов, но, вероятно, все еще будет использоваться в некоторых странах. места, так как он способен измерять небольшие конденсаторы в широком диапазоне частот. Q компонента указывает на его качество и определяется как 2π-кратное отношение накопленной энергии к потерям энергии за цикл. Численно это отношение реактивного сопротивления к сопротивлению на рассматриваемой частоте. Обратное значение Q (то есть 1/ Q ) представляет собой коэффициент рассеяния D , оба термина широко используются для обозначения качества катушек индуктивности и конденсаторов.

Измеритель Q работает по принципу создания резонансного состояния между катушкой индуктивности и конденсатором.Фигура. 38 показана упрощенная схема измерителя Q , в которой резонанс может быть создан путем изменения частоты источника или путем регулировки C _q . В любом случае на резонанс указывает максимальное значение напряжения E _q на C _q при

РИСУНОК 38. Q -метр, упрощенная схема.

EqEs = 1ω0CR = ω0LR = Q и Q = 1D.

Навыки оператора, необходимые для выполнения надежных измерений с использованием мостовых схем и измерителя Q , были заметны, и современное стремление к цифровому дисплею, доступность дешевой вычислительной мощности и повышение надежности электронных схем привели к их замене. инструменты по импедансу LCR или метра.При работе используется либо закон Ома, либо процесс отношения, последний по своей сути является более точным методом, но требует более сложного процесса переключения.

Базовая конструкция измерителя LCR показана на рис. 39, на котором ток с известной частотой подается на неизвестное или «тестируемое устройство» (DUT) при последовательном подключении с известным или эталонным сопротивлением. . В режиме работы с соотношением опорное напряжение ( В, _{, ссылка} ), а затем напряжение на тестируемом устройстве ( В, , _{, x ,} ) по очереди подаются на фазочувствительный детектор (PSD ), так что синфазные и квадратурные составляющие обоих напряжений по отношению к опорному сигналу могут быть определены и поданы на аналого-цифровой (аналого-цифровой) преобразователь.Затем секция процессора содержит компоненты V _ref as ( a + jb ) и компоненты V _x as ( c + jd ), из которых требуется параметры неизвестного могут быть оценены и отображены. Например, серийные компоненты индуктора могут отображаться из Z _x = V _x R _ref / V _ref = R _x + jX ω L _x , или

РИСУНОК 39.Базовая схема счетчика LCR .

Rx = Rrefac + bda2 + b2 и ωLx = ad − bca2 + b2.

Если требуются параллельные компоненты конденсатора, их можно получить из Y _x = V _ref / R _ref V _x = G _x – j ω C _x , или

Rxp = Rrefc2 + d2ac + bdandωCx = ad − bc (c2 + d2) Rref.

В дополнение к этим основным параметрам, измерители LCR обычно могут отображать импеданс Z и его фазовый угол, сопротивление и последовательное реактивное сопротивление, проводимость Y , проводимость, параллельную проводимость, Q и D .

Реактивное сопротивление | электроника | Britannica

Реактивность в электричестве, мера сопротивления, которое цепь или часть цепи представляет электрическому току, поскольку ток переменный или переменный.Постоянные электрические токи, протекающие по проводникам в одном направлении, испытывают сопротивление, называемое электрическим сопротивлением, но не реактивным. Реактивность присутствует в дополнение к сопротивлению, когда по проводникам протекает переменный ток. Реактивное сопротивление также возникает в течение коротких интервалов, когда постоянный ток изменяется по мере приближения к установившемуся потоку или отклонения от него, например, при замыкании или размыкании переключателей.

Реактивное сопротивление бывает двух типов: индуктивное и емкостное. Индуктивное реактивное сопротивление связано с магнитным полем, окружающим провод или катушку, по которой проходит ток.Переменный ток в таком проводнике или индукторе создает переменное магнитное поле, которое, в свою очередь, влияет на ток и напряжение (разность потенциалов) в этой части цепи. Катушка индуктивности по существу противодействует изменениям тока, заставляя изменения тока отставать от изменений напряжения. Ток нарастает по мере того, как управляющее напряжение уже уменьшается, имеет тенденцию к продолжению на максимальном значении, когда напряжение меняет свое направление, падает до нуля, когда напряжение увеличивается до максимума в противоположном направлении, и меняет свое направление и нарастает в в том же направлении, что и напряжение, даже когда напряжение снова падает.Индуктивное реактивное сопротивление, мера этого противодействия току, пропорционально как частоте f переменного тока, так и свойству индуктора, называемому индуктивностью (обозначено L и, в свою очередь, зависит от размеров индуктора, его расположения, и окружающая среда). Индуктивное реактивное сопротивление X _L равно 2π умноженному на произведение частоты тока и индуктивности проводника, просто X _L = 2π f L. Индуктивное реактивное сопротивление выражается в омах. (Единица измерения частоты – герцы, индуктивности – Генри.)

Емкостное реактивное сопротивление, с другой стороны, связано с изменяющимся электрическим полем между двумя проводящими поверхностями (пластинами), отделенными друг от друга изолирующей средой. Такой набор проводников, конденсатор, по существу противодействует изменениям напряжения или разности потенциалов на своих пластинах. Конденсатор в цепи замедляет протекание тока, заставляя переменное напряжение отставать от переменного тока, в отличие от отношения, вызванного индуктором.Емкостное реактивное сопротивление, мера этого противостояния, обратно пропорционально частоте f переменного тока и свойству конденсатора, называемому емкостью (обозначено C и зависит от размеров конденсатора, его расположения и изоляционной среды. ). Емкостное реактивное сопротивление X _C равно произведению 2π, частоты тока и емкости этой части цепи, просто X _C = 1 / (2 π f C ).Емкостное реактивное сопротивление измеряется в омах. (Единица измерения емкости – фарады.)

Поскольку индуктивное реактивное сопротивление X _L заставляет напряжение опережать ток, а емкостное реактивное сопротивление X _C заставляет напряжение отставать от тока, всего реактивное сопротивление X – это их разница, то есть X = X _L – X _C .