Логические операции — урок. Информатика, 8 класс.
Познакомимся с основными логическими операциями, которые можно выполнять над высказываниями. Они соответствуют связкам, употребляемым в нашей речи. Простые высказывания состоят из одной законченной мысли, а составные из нескольких, для их связи и используются логические операции.
Конъюнкция (логическое умножение) — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Для записи конъюнкции используются следующие знаки: И,ˆ,⋅,&.
Например: A И B,AˆB,A⋅B,A&B.
Конъюнкцию можно описать в виде таблицы, которую называют таблицей истинности:
В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы \(A\) и \(B\)), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: \(00, 01, 10, 11\). В последнем столбце записан результат выполнения логической операции для соответствующих операндов.
В последнем столбце записан результат выполнения логической операции для соответствующих операндов.
Пример:
\(A\) = «Джордж Буль создал новую область науки — математическую логику»,
\(B\) = «Клод Шеннон связал математическую логику с работой компьютера».
Построим сложное высказывание A И B: «Джордж Буль создал новую область науки — математическую логику, и Клод Шеннон связал математическую логику с работой компьютера» истинно только в том случае, когда одновременно истинны оба исходных высказывания.
Дизъюнкция
Рассмотрим два высказывания:
\(A\) = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу»,
\(B\) = «Лейбниц является основоположником бинарной арифметики».
Очевидно, новое высказывание «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.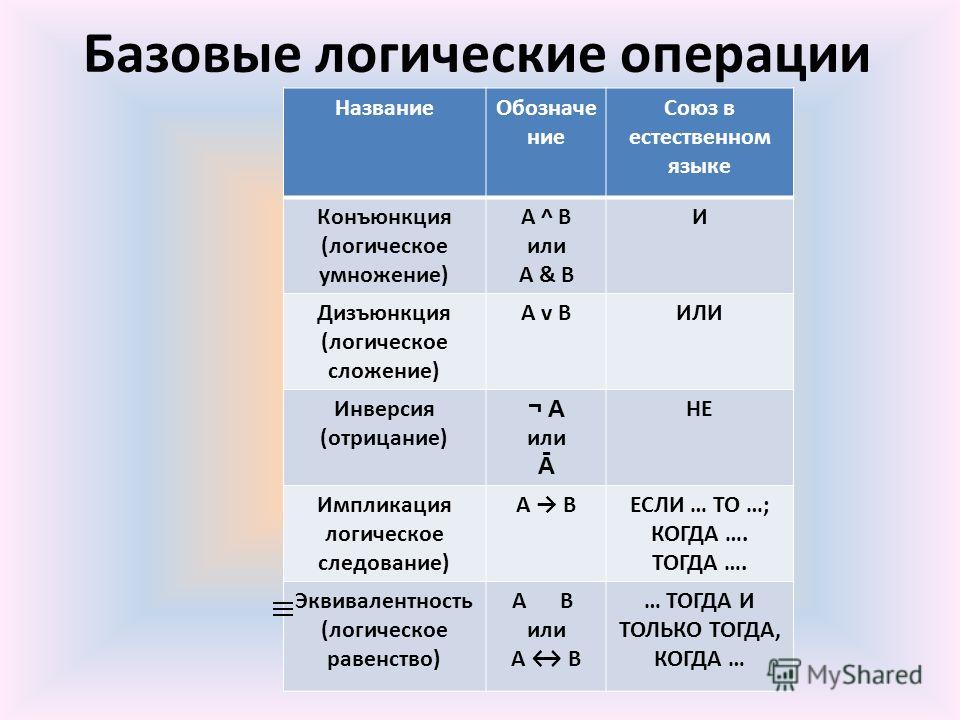
Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Для записи дизъюнкции используются следующие знаки: ИЛИ;∨;|;+.
Например: A ИЛИ B;A∨B;A|B;A+B.
Дизъюнкция определяется следующей таблицей истинности:
Обрати внимание!
Дизъюнкцию также называют логическим сложением.
Инверсия
Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
Для записи инверсии используются следующие знаки: НЕ;¬;−
Например: НЕ А;¬А;А−.
Инверсия определяется следующей таблицей истинности:
Обрати внимание!
Инверсию также называют логическим отрицанием.
Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что у меня дома есть компьютер» или, что в русском языке то же самое, что «У меня дома нет компьютера».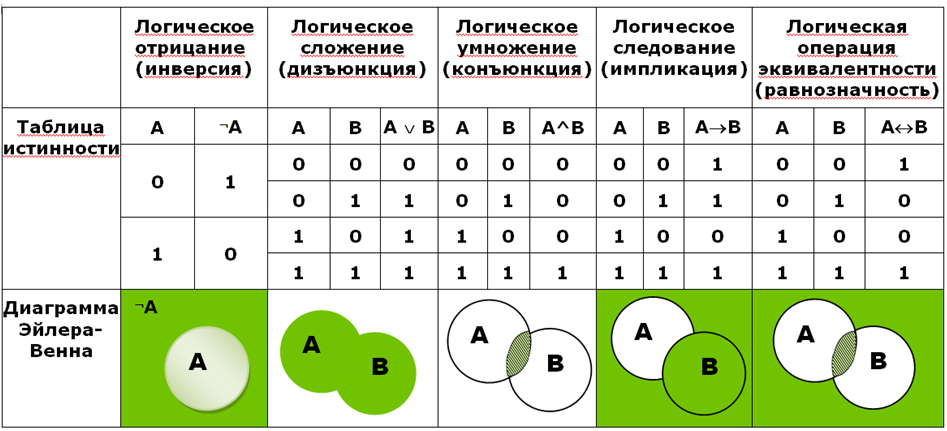
Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке: «Я знаю китайский язык».
Отрицанием высказывания «Все юноши \(8-х\) классов — отличники» является высказывание «Неверно, что все юноши \(8-х\) классов — отличники», другими словами, «Не все юноши \(8-х\) классов — отличники».
Таким образом, при построении отрицания к простому высказыванию либо используется речевой оборот «неверно, что …», либо отрицание строится к сказуемому, тогда к соответствующему глаголу добавляется частица «не».
Каждое сложное высказывание можно записать в виде логического выражения, которое содержит логические переменные, операции, скобки.
Последовательность выполнения логических операций:
- Инверсия;
- Конъюнкция;
- Дизъюнкция.
Если в выражении присутствуют скобки, то приоритет операций меняется, сначала выполняются действия в скобках.
§ 2.
 , *,` по аналогии с алгебраическим умножением может никак не обозначаться
, *,` по аналогии с алгебраическим умножением может никак не обозначаться
Дизъюнкция, нестрогая дизъюнкция, логическое сложение, операция ИЛИ, операция OR.
`|“, vv, +`
Строгая дизъюнкция, разделительная дизъюнкция, исключающее ИЛИ, сложение по модулю `2`.
`o+, Delta`
Эквивалентность, эквиваленция, равенство, равнозначность.
`iff, -=`
Импликация, следование, следствие
`=>, ->`
Теперь для того чтобы строго определить эти логические операции, нам нужно для каждой из них выписать таблицу истинности. Все перечисленные операции кроме отрицания имеют два операнда. Знак операции в выражениях пишется между операндами (как в алгебре чисел).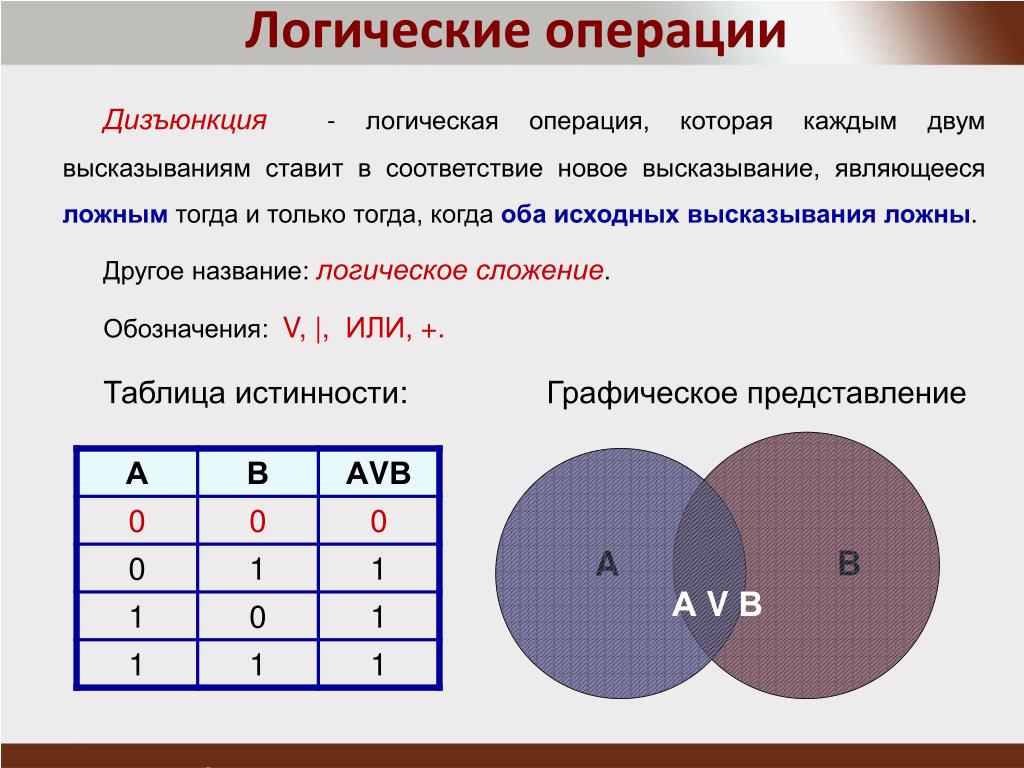
Для того, чтобы не путаться и гарантированно перебрать все возможные комбинации значений операндов, принято записывать их в лексикографическом порядке (условно считается, что «ложь» `<` «истина»).
Таблица истинности для конъюнкции
|
Первый операнд |
Второй операнд |
Значение операции |
|
`0` |
`0` |
`bb0` |
|
`0` |
`1` |
`bb0` |
|
`1` |
`0` |
`bb0` |
|
`1` |
`1` |
`bb1` |
Таблица истинности для дизъюнкции
|
Первый операнд |
Второй операнд |
Значение операции |
|
`0` |
`0` |
`bb0` |
|
`0` |
`1` |
`bb1` |
|
`1` |
`0` |
`bb1` |
|
`1` |
`1` |
`bb1` |
Таблица истинности для строгой дизъюнкции
|
Первый операнд |
Второй операнд |
Значение операции |
|
`0` |
`0` |
`bb0` |
|
`0` |
`1` |
`bb1` |
|
`1` |
`0` |
`bb1` |
|
`1` |
`1` |
`bb0` |
Таблица истинности для эквивалентности
|
Первый операнд |
Второй операнд |
Значение операции |
|
`0` |
`0` |
`bb1` |
|
`0` |
`1` |
`bb0` |
|
`1` |
`0` |
`bb0` |
|
`1` |
`1` |
`bb1` |
Таблица истинности для импликации
|
Первый операнд |
Второй операнд |
Значение операции |
|
`0` |
`0` |
`bb1` |
|
`0` |
`1` |
`bb1` |
|
`1` |
`0` |
`bb0` |
|
`1` |
`1` |
`bb1` |
Таблица истинности для отрицания
|
Значение операнда |
Значение операции |
|
`0` |
`bb1` |
| `1` |
`bb0` |
Теперь осталось лишь установить соответствие между логическими операциями и логическими связками в русском языке.
|
Логическая операция |
Логические связки в русском языке |
|
Отрицание |
Неверно что… |
|
Конъюнкция |
и, а, но, а также, при этом, одновременно с этим, хотя |
|
Дизъюнкция |
Или |
|
Строгая дизъюнкция |
или, либо |
|
Эквивалентность |
Тогда и только тогда когда, необходимо и достаточно чтобы |
|
Импликация |
если то, необходимо чтобы, достаточно чтобы |
Обратите внимание, что союз ИЛИ может означать, как строгую, так и нестрогую дизъюнкцию.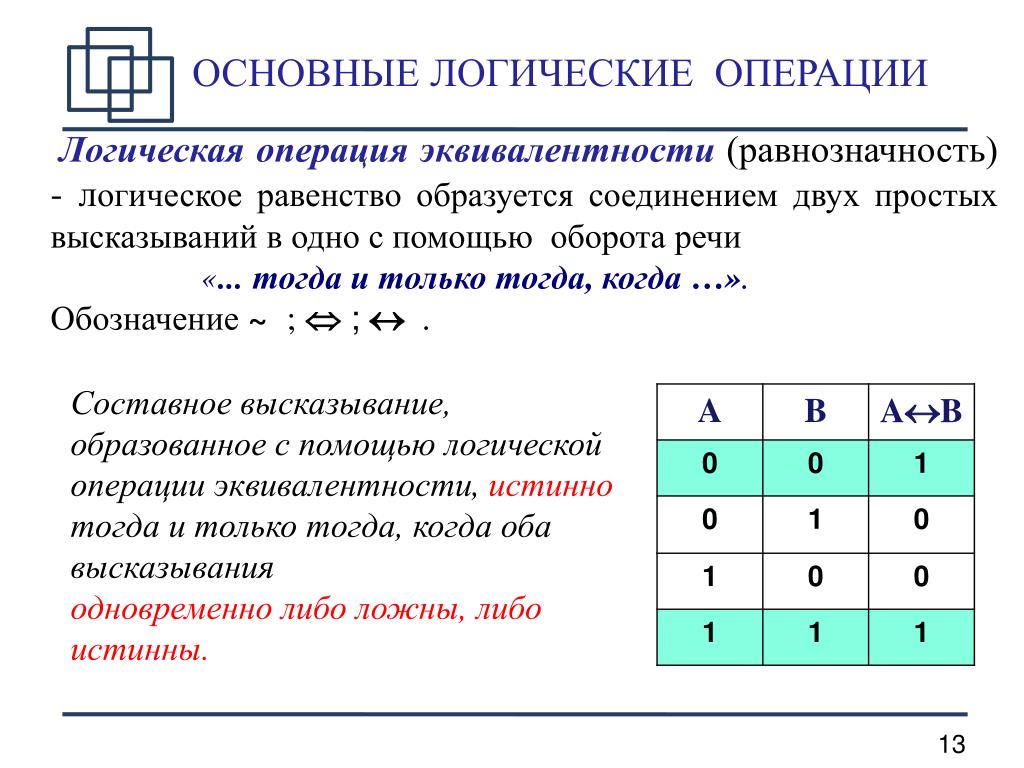 Его интерпретация зависит от содержания (!!!) высказывания.
Его интерпретация зависит от содержания (!!!) высказывания.
Рассмотрим высказывание: «Мы идём в кино в субботу или в воскресение». Здесь два простых высказывания: «Мы идём в кино в субботу» и «Мы идём в кино в воскресение». Между ними стоит союз ИЛИ, который можно интерпретировать двояко. В данном случае очевидно, что мы можем пойти в кино и в субботу, и в воскресение, поэтому дизъюнкция будет нестрогая. Возьмём две логические переменные – `p` и `q` и присвоим им простые высказывания. Тогда исходное высказывание в формализованном виде будет выглядеть, как `bb(pvvq)`.
Рассмотрим высказывание: «Я сейчас на севере Москвы или на юго-западе Москвы». Здесь тоже два простых высказывания, которые связаны союзом ИЛИ. Но в этом случае союз ИЛИ интерпретируется, как строгая дизъюнкция, поскольку нельзя одновременно находиться в двух местах. Таким образом, если снова взять логические переменные `p` и `q`, то получится следующая логическая формула: `bb(p”o+q)`.
Рассмотрим высказывание: «Для того чтобы четырёхугольник был квадратом, необходимо, чтобы все его стороны были равны». Здесь два простых высказывания: «Четырёхугольник является квадратом» и «Все стороны четырёхугольника равны». Присвоим их соответственно логическим переменным `p` и `q`. Логическая связка «необходимо, чтобы» – это импликация. Весь вопрос в том, что из чего следует. (Какая запись правильная: `bbp -> bbq` или `bbq ->bbp`?) Импликация ложна только в единственном случае: когда левый операнд имеет значение «истина», а правый – «ложь». Рассмотрим все возможные значения операндов и проанализируем, какая из ситуаций невозможна.
Здесь два простых высказывания: «Четырёхугольник является квадратом» и «Все стороны четырёхугольника равны». Присвоим их соответственно логическим переменным `p` и `q`. Логическая связка «необходимо, чтобы» – это импликация. Весь вопрос в том, что из чего следует. (Какая запись правильная: `bbp -> bbq` или `bbq ->bbp`?) Импликация ложна только в единственном случае: когда левый операнд имеет значение «истина», а правый – «ложь». Рассмотрим все возможные значения операндов и проанализируем, какая из ситуаций невозможна.
1) `p` и `q` ложны. Это значит, что четырёхугольник не является квадратом и его стороны не равны. Это возможная ситуация.
2) `p` – ложно, `q` – истинно. Это значит, что четырёхугольник не является квадратом, но стороны у него равны. Это возможно (ромб).
3) `p` – истинно, `q` – истинно. Это значит, что четырёхугольник является квадратом и стороны у него равны. Это возможная ситуация.
4) `p` – истинно, `q` – ложно. Это значит, что четырёхугольник является квадратом, но стороны у него не равны. Это невозможная ситуация.
Это невозможная ситуация.
Анализ ситуаций показывает, что левым операндом импликации должна быть переменная `p`. Таким образом, в формализованном виде исходное высказывание выглядит как `bb(p -> q)`.
Очень часто вместо «присвоим логическим переменным эти высказывания» говорят «обозначим высказывания следующим образом». В дальнейшем мы тоже будем использовать этот речевой оборот.
Логические операторы | Введение в Python
Видео может быть заблокировано из-за расширений браузера. В статье вы найдете решение этой проблемы.
Logical expressions in Python
Logical expressions
- occur when use compare or boolean operators
>,<,==,is,in,and,or,not- are used in if operator
- return boolean values
Examples
if value > 10: # ... if status == 'active': # ... if user.age > 16 and not user.is_banned: # ....
Boolean operators
- AND (binary) — true if both operands are true
- OR (binary) — true if at least one of operands is true
- NOT (unary) — reverse
NOT has higher priority than AND and OR
Examples
10 > 2 and 10 > 9 # True
10 > 2 and 10 > 11 # False
10 > 2 or 10 > 11 # True
10 > 2 and not 10 > 11 # True
not (10 > 2 or 10 > 11) # False
Any object behaves like bool
# False
None '' u"" 0 0.0 {} () [] set()
# True
- non-empty string or collection
- non-zero number
bool(0) # False
bool([]) # False
bool('') # False
bool({}) # False
bool(0.00001) # True
bool(-1) # True
bool(' ') # True
bool(' '.strip()) # False
bool((0, 0, )) # True
bool(None) # False
result = 0
if result:
# no code
else:
print "result is zero"
data = {}
if data:
# no code
else:
# code goes there
How to override bool behaviour
- Override
__nonzero__method in Py2 __bool__in Py3
How to override bool behaviour
# rarely
class Balance(int):
def __nonzero__(self):
return self > 0
balance = Balance(-10)
if balance: # False
# common
class User(object):
def is_balance_ok(self):
return self. balance > 0
user = User(balance=-10)
if user.is_balance_ok(): # False
balance > 0
user = User(balance=-10)
if user.is_balance_ok(): # False
Expressions return values
# Some languages
if (balance > 0) {
can_pay = True;
} else {
can_pay = False;
}
# Python
can_pay = balance > 0
can_pay = user.balance > 0 and not user.is_banned
can_pay = (
user.balance > 0
and not user.is_banned
and user.has_perm('buy')
)
is_active = status not in ('banned', 'pending')
can_exit = user.age > 18 and is_confirmed
ok = 'error' not in response['text']
ok = error is None
Is value None?
# bad
val == None
type(None) == types.NoneType
# OK
value is None
value is not None
Ternary operator
var x = (a > b) ? a : b; // javascript
x = (...) if (...) else (...)
x = a if a > b else b
res = (process_good_result(data)
if data else process_bad_result(data))
Boolean expressions are lazy
def func(x):
print x
return bool(x)
res = func(1) and func(0) and func(2) and func(3) # False
>>> 1 0
res func(1) and func(3) and func(2) and func(0) # False
>>> 1 3 2 0
res = func(1) or func(2) # True
>>> 1
res = func(0) or func(1) or func(2) or func(3) # True
>>> 0 1
So put the easiest expressions in OR at the first place.
Conclusion
- occur when use compare or logical operators
- return boolean value
- any object can be used as a predicate
value is None, but notvalue == None- use ternary operator
- remember about laziness
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты.
Ошибки, сложный материал, вопросы >Нашли опечатку или неточность?
Выделите текст, нажмите ctrl + enter и отправьте его нам. В течение нескольких дней мы исправим ошибку или улучшим формулировку.
Что-то не получается или материал кажется сложным?
Загляните в раздел «Обсуждение»:
- задайте вопрос. Вы быстрее справитесь с трудностями и прокачаете навык постановки правильных вопросов, что пригодится и в учёбе, и в работе программистом;
- расскажите о своих впечатлениях. Если курс слишком сложный, подробный отзыв поможет нам сделать его лучше;
- изучите вопросы других учеников и ответы на них.
 Это база знаний, которой можно и нужно пользоваться.
Это база знаний, которой можно и нужно пользоваться.
Об обучении на Хекслете
|
Логические связки, или логические операции — это символические конструкции логических языков (см. Язык формализованный), используемые для образования сложных высказываний (формул) из элементарных высказываний (см. Высказывание). Логическими связками называют также соответствующие этим символам союзы естественного языка (см. Язык). Обычно используются пять общеизвестных логических связок:
Из указанных логических связок отрицание называется одноместной (унарной) связкой; другие называются двухместными (бинарными) связками. В принципе, логические связки могут быть сколь угодно местными, но на практике более, чем бинарные, используются очень редко. В классической логике (см. Логика) любые многоместные логические связки выразимы через перечисленные. Некоторый практический смысл даёт также использование тернарной логической связки, называемой условной дизъюнкцией, связывающей три высказывания A, B и C и означающей, что «A в случае B, и C в случае не-B» или формально: (B ⊃ A) & (¬ B ⊃ C). Классическая логика рассматривает логические связки экстенсионально (игнорируя содержательный смысл связываемых ими высказываний) как функции истинности, определяемые истинностными значениями связываемых ими высказываний. При двух имеющих место в этой логике истинностных значениях 1 (истинно) и 0 (ложно) высказывания A и B могут иметь четыре возможных набора упорядоченных истинностных значений: (1, 1), (1, 0), (0, 1), (0, 0). Из четырёх одноместных функций интерес представляет только отрицание, меняющее значение высказывания на противоположное: когда A — истинно, ¬ A — ложно, и наоборот. Все другие унарные и бинарные классические функции могут быть выражены через представленные. Когда принятая в соответствующей семантике система логических связок позволяет дать определение всех остальных, её называют функционально полной. Функции антидизъюнкция и антиконъюнкция, определимые соответственно как ¬ (A ∨ B) и ¬ (A & B), также представляют каждая в отдельности функционально полную систему связок. Это последнее обстоятельство было известно уже Ч. Экстенсиональность логических связок придаёт им однозначность, упрощает проблему построения логических исчислений, даёт возможность решать для последних метатеоретические проблемы непротиворечивости, разрешимости, полноты. Однако в некоторых случаях истинностно-функциональная трактовка связок приводит к значительному несоответствию с тем, как они понимаются в естественном языке. |
Логическая операция – это… Что такое Логическая операция?
В логике логическими операциями называют действия, вследствие которых порождаются новые понятия, возможно с использованием уже существующих. В более узком, формализованном смысле, понятие логической операции используется в математической логике и программировании.
Логические операции с понятиями — такие мыслительные действия, результатом которых является изменение содержания или объёма понятий, а также образование новых понятий.
К операциям, которые связаны преимущественно с изменением содержания понятий, относятся:
К операциям, которые связаны преимущественно с объёмами понятий, относятся:
Данные операции могут быть записаны математически с помощью теории множеств.
Переход же к математической логике связан с понятием суждений и установлением операций над ними с целью получения сложных суждений.
Математическая логика
Логическая операция (логический оператор, логическая связка, пропозициональная связка) — операция над высказываниями, позволяющая составлять новые высказывания путем соединения более простых[1].
В качестве основных обычно называют конъюнкцию ( или &), дизъюнкцию (), импликацию (), отрицание (). В смысле классической логики логические связки могут быть определены через алгебру логики. В асинхронной секвенциальной логике определена логико-динамическая связка в виде операции венъюнкции ().
Программирование
Логическая операция — в программировании операция над выражениями логического (булевского) типа, соответствующая некоторой операции над высказываниями в алгебре логики. Как и высказывания, логические выражения могут принимать одно из двух истинностных значений — «истинно» или «ложно». Логические операции служат для получения сложных логических выражений из более простых. В свою очередь, логические выражения обычно используются как условия для управления последовательностью выполнения программы.
Логические операции служат для получения сложных логических выражений из более простых. В свою очередь, логические выражения обычно используются как условия для управления последовательностью выполнения программы.
В некоторых языках программирования (например в C) вместо логического типа или одновременно с ним используются числовые типы. В этом случае считается, что отличное от нуля значение соответствует логической истине, а ноль — логической лжи.
Значение отдельного бита также можно рассматривать как логическое, если считать, что 1 означает «истинно», а 0 — «ложно». Это позволяет применять логические операции к отдельным битам, к битовым векторам покомпонентно и к числам в двоичном представлении поразрядно. Такое одновременное применение логической операции к последовательности битов осуществляется с помощью побитовых логических операций. Побитовые логические операции используются для оперирования отдельными битами или группами битов, применяются для наложения битовых масок, выполнения различных арифметических вычислений. =
=
Примечания
См. также
Ссылки
| Логика | |
|---|---|
| Формальная | Логические операции с понятиями Изменение содержания понятия: отрицание • ограничение • обобщение • деление |
| Математическая (теоретическая, символическая) | Логические связки (операции) над высказываниями Высказывание – построение над множеством {B, , , , 0, 1} |
ЛОГИЧЕСКИЕ ОПЕРАЦИИ • Большая российская энциклопедия
ЛОГИ́ЧЕСКИЕ ОПЕРА́ЦИИ, способы построения сложного высказывания из данных высказываний, при которых истинностное значение сложного высказывания [оно может принимать одно из двух значений – «истина» (И) или «ложь» (Л)] полностью определяется истинностными значениями исходных высказываний. Примерами Л. о. являются дизъюнкция, конъюнкция, импликация, отрицание, а также кванторы.
Примерами Л. о. являются дизъюнкция, конъюнкция, импликация, отрицание, а также кванторы.
Дизъюнкцией называется Л. о., заключающаяся в соединении данных высказываний $A$ и $B$ в новое высказывание «$A$ или $B$». В формализованных языках дизъюнкция высказываний $A$ и $B$ обозначается $A\!∨\!B$ (читается: «$A$ или $B$», «имеет место $A$ или имеет место $B$»), $A$ и $B$ называются дизъюнктивными членами высказывания $A\!∨\!B$, ∨ – знаком дизъюнкции. В обычной речи возможны два понимания союза «или»: в исключающем и неисключающем смысле. При первом понимании высказывание «$A$ или $B$» означает, что истинно ровно одно из двух высказываний $A$ и $B$, при втором – что истинно хотя бы одно из них. В математич. логике термин «дизъюнкция» относится к истолкованию союза «или» во втором смысле. Такому употреблению дизъюнкции соответствует т. н. истинностная таблица
н. истинностная таблица
| $A$ | $B$ | $A \vee B$ |
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
Конъюнкцией называется Л. о., заключающаяся в соединении двух данных высказываний $A$ и $B$ в новое высказывание «$A$ и $B$». В формализованных языках конъюнкция высказываний $A$ и $B$ обозначается $A$&$B$ (а также $A\!∧\!B$, $A\!·\!B$, $AB$, читается: «$A$ и $B$», «имеет место $A$ и имеет место $B$»), $A$ и $B$ называются конъюнктивными членами высказывания $A$&$B$, & – знаком конъюнкции. Употреблению конъюнкции в математич. логике соответствует истинностная таблица
| $A$ | $B$ | $A$ & $B$ |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
Из таблицы видно, что высказывание $A$ & $B$ истинно только при истинности обоих высказываний $A$ и $B$.
Импликацией называется Л. о., заключающаяся в соединении данных высказываний $A$ и $B$ в новое высказывание «если $A$, то $B$». В формализованных языках импликация высказываний $A$ и $B$ обозначается $A\Rightarrow B$ [а также $A→B, A⊃B$, читается: «если $A$, то $B$», «$A$ влечёт (имплицирует) $B$»]. Высказывание $A$ называется посылкой высказывания $A\Rightarrow B$, а высказывание $B$ – его заключением. В обычной речи утверждение «если $A$, то $B$», как правило, предполагает наличие причинной связи между тем, что утверждается в высказывании $A$, и тем, что утверждается в высказывании $B$, и его истинность зависит от смысла этих высказываний. В математич. логике обычно учитывается лишь истинность или ложность высказываний, а не смысл. Поэтому импликация обычно понимается в соответствии с истинностной таблицей
| $A$ | $B$ | $A ⇒ B$ |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
Из таблицы видно, что высказывание $A\Rightarrow B$ считается ложным лишь в том случае, когда его посылка истинна, а заключение ложно. При таком понимании оказываются истинными, напр., такие высказывания: «$2+2= 4 \Rightarrow \text{sin}\frac{\pi}2=1$», «$2 > 3 \Rightarrow4$ – простое число».
При таком понимании оказываются истинными, напр., такие высказывания: «$2+2= 4 \Rightarrow \text{sin}\frac{\pi}2=1$», «$2 > 3 \Rightarrow4$ – простое число».
Отрицанием называется Л. о., в результате которой из данного высказывания $A$ получается новое высказывание «не $A$». В формализованных языках высказывание, получающееся в результате отрицания высказывания $A$, обозначается ¬$A$ (а также , $\bar{A}$, $A′$, читается: «не $A$», «неверно, что $A$», «$A$ не имеет места»). Отрицание в математич. логике задаётся истинностной таблицей
См. также Алгебра логики.
Программирование для начинающих \ 2.3. Логические операторы
Предыдущий раздел:
Следующий раздел:
2.3. Логические операторы
Из логических переменных и выражений можно строить более сложные (составные) логические выражения с помощью логических операторов: not (отрицание, логическое НЕ), or (логическое ИЛИ) и and (логическое И).
Выражение not A (где A – логическая переменная или выражение) истинно тогда, когда выражение A ложно, и ложно, когда A истинно.
Выражение A and B истинно, когда одновременно истинны выражения A и B. Если хотя бы одно из этих выражения (A или B) ложно, то A and B ложно.
Выражение A or B истинно, когда любое из выражений A или B истинно и ложно, когда оба исходных выражения ложны.
Правила работы логических операторов можно также задать с помощью таблиц истинности, в которых указывается истинность составного выражения, в зависимости от значений исходных простых выражений.
| A | not A |
| true | false |
| false | true |
| A | B | A and B |
| true | true | true |
| true | false | false |
| false | true | false |
| flase | false | false |
| A | B | A or B |
| true | true | true |
| true | false | true |
| false | true | true |
| flase | false | false |
Составное логическое выражение может содержать сколько угодно логических операторов. При этом в первую очередь выполняются все операторы сравнения (, =, =, ), затем логические отрицания (not), затем логическое И (and) и в последнюю очередь логическое ИЛИ (or). Выражения могут содержать скобки, которые влияют на приоритетность выполнения операций.
При этом в первую очередь выполняются все операторы сравнения (, =, =, ), затем логические отрицания (not), затем логическое И (and) и в последнюю очередь логическое ИЛИ (or). Выражения могут содержать скобки, которые влияют на приоритетность выполнения операций.
Пример:
С помощью логических операторов мы, наконец, можем записать условие равенства сразу трех переменных. Правильный вариант имеет вид:
(x=y) and (y=z)
Следующий раздел:
Предыдущий раздел:
Добавить комментарий
Логические операторы – основы программирования
Кеннет Лерой Басби и Дэйв Брауншвейг
Обзор
Логический оператор – это символ или слово, используемое для соединения двух или более выражений, так что значение полученного составного выражения зависит только от значения исходных выражений и от значения оператора. Общие логические операторы включают AND, OR и NOT.
Общие логические операторы включают AND, OR и NOT.
Обсуждение
В большинстве языков выражения, которые дают значения типа данных Boolean, разделены на две группы.Одна группа использует реляционные операторы в своих выражениях, а другая группа использует логические операторы в своих выражениях.
Логические операторы часто используются для создания тестового выражения, которое контролирует выполнение программы. Этот тип выражения также известен как логическое выражение, потому что при вычислении они создают логический ответ или значение. Есть три общих логических оператора, которые дают логическое значение, манипулируя другим логическим операндом (ами). Символы и / или названия операторов различаются в зависимости от языка программирования:
| Язык | И | ИЛИ | НЕ |
|---|---|---|---|
| С ++ | && | || | ! |
| С # | && | || | ! |
| Java | && | || | ! |
| JavaScript | && | || | ! |
| Python | и | или | не |
| Swift | && | || | ! |
Вертикальные черточки или символ трубопровода находятся на той же клавише, что и обратная косая черта \. Вы используете клавишу SHIFT, чтобы получить его. На большинстве клавиатур он находится чуть выше клавиши Enter. Это может быть сплошная вертикальная линия на некоторых клавиатурах и отображаться как сплошная вертикальная линия на некоторых печатных шрифтах.
Вы используете клавишу SHIFT, чтобы получить его. На большинстве клавиатур он находится чуть выше клавиши Enter. Это может быть сплошная вертикальная линия на некоторых клавиатурах и отображаться как сплошная вертикальная линия на некоторых печатных шрифтах.
В большинстве языков существуют строгие правила формирования правильных логических выражений. Пример:
6> 4 && 2 <= 14
6> 4 и 2 <= 14
Это выражение содержит два оператора отношения и один логический оператор. Используя приоритет правил операторов, два оператора «реляционного сравнения» будут выполняться перед оператором «логическое и».Таким образом:
true && true
True and True
Окончательная оценка выражения: истина.
Мы можем сказать это по-английски так: это правда, что шесть больше четырех, а два меньше или равно четырнадцати.
При формировании логических выражений программисты часто используют круглые скобки (даже если это технически не требуется), чтобы сделать логику выражения очень понятной. Рассмотрим переписанное выше сложное логическое выражение:
Рассмотрим переписанное выше сложное логическое выражение:
(6> 4) && (2 <= 14)
(6> 4) и (2 <= 14)
Большинство языков программирования распознают любое ненулевое значение как истинное.Это делает следующее выражение допустимым:
6> 4 && 8
6> 4 и 8
Но помните порядок действий. По-английски это шесть больше четырех, а восемь - не ноль. Таким образом,
true && true
True and True
Для сравнения 6 с 4 и 8 вместо этого будет записано как:
6> 4 && 6> 8
6> 4 и 6> 8
Это будет ложно как:
истина и ложь
истина и ложь
Таблицы истинности
Обычный способ показать логические отношения - это таблицы истинности.
| x | л | x и y |
| ложный | ложь | ложь |
| ложный | правда | ложь |
| истинное | ложь | ложь |
| истинное | правда | правда |
| x | л | x или y |
| ложный | ложь | ложь |
| ложный | правда | правда |
| истинное | ложь | правда |
| истинное | правда | правда |
| x | не x |
| ложный | правда |
| истинное | ложь |
Примеры
Я называю этот пример того, почему я ненавижу «и» и люблю «или».
Каждый день, когда я приходил из школы с понедельника по четверг; Я спрашивал маму: «Можно мне выйти на улицу поиграть?» Она отвечала: «Если ваша комната чистая и у вас сделана домашняя работа, вы можете выйти на улицу и поиграть». Я научился ненавидеть слово «и». Мне удалось выполнить одно из заданий и у меня было время поиграть до обеда, но оба… ну, я ненавидел «и».
В пятницу моя мать приняла более расслабленную точку зрения, и когда меня спросили, могу ли я выйти на улицу и поиграть, она ответила: «Если ваша комната чистая или у вас сделана домашняя работа, вы можете выйти на улицу и поиграть.«Я научился быстро убирать свою комнату в пятницу днем. Что ж, разумеется, я любил «или».
В качестве следующего примера представьте, что подросток разговаривает со своей матерью. Во время разговора мама говорит: «Ведь папа у тебя разумный!» Подросток говорит: «Разумно. (короткая пауза) Нет. "
Может быть, профессора колледжей подумают, что все их студенты готовились к экзамену. Ха-ха! Нет. Что ж, надеюсь, вы уловили суть.
Ха-ха! Нет. Что ж, надеюсь, вы уловили суть.
Примеры:
- 25 <7 || 15> 36
- 15> 36 || 3 <7
- 14> 7 && 5 <= 5
- 4> 3 && 17 <= 7
- ! ложь
- ! (13! = 7)
- 9! = 7 &&! 0
- 5> 1 && 7
Дополнительные примеры:
- 25 <7 или 15> 36
- 15> 36 или 3 <7
- 14> 7 и 5 <= 5
- 4> 3 и 17 <= 7
- не Ложь
- нет (13! = 7)
- 9! = 7, а не 0
- 5> 1 и 7
Ключевые термины
- логический оператор
- Оператор, используемый для создания сложных логических выражений.
- таблицы истинности
- Распространенный способ показать логические отношения.
Список литературы
Логические операторы - cppreference.com
Возвращает результат логической операции.
| Имя оператора | Синтаксис | Возможность перегрузки | Примеры прототипов (для класса T) | |
|---|---|---|---|---|
| Определение внутреннего класса | Определение внешнего класса | |||
| отрицание | не а | Да | bool T :: operator! () Const; | логический оператор! (Const T & a); |
| И | а и б | Да | bool T :: operator && (const T2 & b) const; | логический оператор && (const T & a, const T2 & b); |
| включительно ИЛИ | а или б | Да | bool T :: оператор || (const T2 & b) const; | логический оператор || (const T & a, const T2 & b); |
| ||||
[править] Объяснение
Выражения логического оператора имеют вид
! правых | (1) | ||||||||
левый && правый | (2) | ||||||||
левый || правых | (3) | ||||||||
1) Логическое НЕ
2) Логическое И
3) Логическое включительно ИЛИ
Если операнд не является bool, он преобразуется в bool с помощью контекстного преобразования в bool: он правильно сформирован, только если объявление bool t (arg) правильно сформировано, для некоторых придуманных временных t .
Результат - логическое значение pr.
Для встроенного оператора логического НЕ результат будет истиной, если операнд ложь. В противном случае результат будет ложным.
Для встроенного логического оператора И результат будет истиной, если оба операнда верны. В противном случае результат будет ложным. Этот оператор является коротким замыканием: если первый операнд ложен, второй операнд не оценивается
Для встроенного логического оператора ИЛИ результат будет истиной, если либо первый, либо второй операнд (или оба) истинны.Этот оператор является коротким замыканием: если первый операнд истинен, второй операнд не оценивается.
Обратите внимание, что побитовые логические операторы не выполняют короткое замыкание.
[править] Результаты
| а | верно | ложь |
|---|---|---|
| ! А | ложь | верно |
| и | а | ||
|---|---|---|---|
| правда | ложь | ||
| б | верно | верно | ложь |
| ложно | ложь | ложь | |
| или | а | ||
|---|---|---|---|
| правда | ложь | ||
| б | верно | верно | верно |
| ложно | верно | ложь | |
При разрешении перегрузки по отношению к определяемым пользователем операторам следующие встроенные сигнатуры функций участвуют в разрешении перегрузки:
оператор bool! (Bool) | ||
оператор bool && (bool, bool) | ||
оператор bool || (bool, bool) | ||
[править] Пример
#include#include <строка> int main () { int n = 2; int * p = & n; // указатели можно преобразовать в bool if (p && * p == 2 // "* p" можно использовать после "p &&" || ! p && n! = 2) // || имеет более низкий приоритет, чем && std :: cout << "истина \ п"; // потоки также можно преобразовать в bool std :: cout << "Введите 'quit', чтобы выйти. \ п "; for (std :: string line; std :: cout << ">" && std :: getline (std :: cin, строка) && line! = "выйти"; ) ; }
Выход:
правда Введите "quit", чтобы выйти. > тест > выйти из
[править] Стандартная библиотека
Потому что свойства короткого замыкания оператора && и оператора || не применяются к перегрузкам, и поскольку типы с логической семантикой встречаются редко, только два стандартных библиотечных класса перегружают эти операторы:
| применяет унарный арифметический оператор к каждому элементу valarray (общедоступная функция-член std :: valarray) | |
| применяет бинарные операторы к каждому элементу двух valarrays или valarray и значению (шаблон функции) | |
| проверяет, произошла ли ошибка (синоним fail ()) (общедоступная функция-член std :: basic_ios ) [править] |
[править] См.
 b
b a << b
a >> b
! A
a && b
a || б
a == b
a! = B
a a> b
a <= b
a> = b
a <=> b
a [b]
* a
и a
a-> b
a.б
а -> * б
а. * б
а (...)
а, б
? :
static_cast преобразует один тип в другой связанный тип
dynamic_cast преобразует в иерархиях наследования
const_cast добавляет или удаляет квалификаторы cv
reinterpret_cast преобразует тип в несвязанный тип
C-style cast преобразует один тип в другой путем сочетания static_cast , const_cast , и reinterpret_cast
new создает объекты с динамической продолжительностью хранения.
delete уничтожает объекты, ранее созданные новым выражением, и освобождает полученную область памяти
sizeof запросов размера типа
sizeof. .. запрашивает размер пакета параметров (начиная с C ++ 11)
.. запрашивает размер пакета параметров (начиная с C ++ 11)
typeid запрашивает информацию о типе типа
noexcept проверяет, может ли выражение вызывать исключение (начиная с C ++ 11)
alignof запросы выравнивания требований типа (начиная с C ++ 11)
Операторы | Функции и операторы | Руководство пользователя | Поддержка | Epi Info ™
АРИФМЕТИЧЕСКИЙ
Описание
Эти основные арифметические операторы можно использовать в сочетании с другими командами.Результат - числовое значение.
Синтаксис
[Выражение] <Оператор> [Выражение]
- [Выражение] - числовое значение или переменная, содержащая данные в числовом формате.
Комментарии
Результаты выражаются в числовом формате. Основные математические операторы, которые можно использовать в Epi Info, следующие:
- Сложение + Основной арифметический оператор, используемый для сложения; Результатом арифметического оператора обычно является числовое значение (т.
 е., EX. 3 + 3).
е., EX. 3 + 3). - Вычитание - (Используется для вычитания или отрицания). Основной арифметический оператор, используемый для вычитания или отрицания; Результатом арифметического оператора обычно является числовое значение (например, Пример 3 - 1).
- Умножение * (звездочка) Основной арифметический оператор, используемый для умножения; Результатом арифметического оператора обычно является числовое значение.
- Деление / Основной арифметический оператор, используемый для деления; Результатом арифметического оператора обычно является числовое значение.
- Модуль или остаток MOD
Арифметические операторы показаны в порядке убывания приоритета. Круглые скобки могут использоваться для управления порядком, в котором оцениваются операторы. Однако порядок по умолчанию часто дает правильный результат.
Хотя можно выполнять математические вычисления с датами, считая их числом дней (например, IncubationDays = SymptomDateTime - ExposureDateTime), поведение служб базы данных, лежащих в основе Epi Info, делает более эффективным использование функций временных интервалов (например, IncubationDays = SymptomDateTime - ExposureDateTime). 2
СПИСОК var1 var2 var3 var4 var5 var6
2
СПИСОК var1 var2 var3 var4 var5 var6
Логические операции и булевы функции - x-engineer.org
Логические операции , также известные как Логические функции , часть логической алгебры , широко используются в информатике, инженерии и математике. Для них используются разные слова и выражения, такие как логических вентилей или побитовых операций , но основной принцип тот же: выполняет логические операции с битами (значения 0 и 1 ) .
Электроника сейчас является частью почти каждой инженерной области, поэтому очень важно, чтобы инженеры имели минимальное понимание логики , побитовых операций .
Большинство физических вычислений выполняется с десятичными числами. Это потому, что мы используем десятичные числа для всех физических величин (например, 10 А, 250 Нм, 120 км и т. Д.). Компьютеры используют двоичные числа для выполнения вычислений. Чтобы вспомнить, как преобразовать десятичное число в двоичное, прочтите статью Преобразование десятичного числа в двоичное.
Параллельно с арифметическими операциями (сложение, вычитание, умножение, деление) существует еще логических операций . Они используются для оценки того, является ли логическое выражение истинным или ложным .
В наших примерах мы собираемся использовать два символа A и B , которые называются входами . Каждый из них может иметь либо значение true ( 1 ), либо значение false ( 0 ).После того, как над входами будут выполнены логические операции, мы получим результат с символом Q , который называется , выход . Аналогично входам, выход Q может иметь только значение true ( 1 ) или false ( 0 ).
Логическое состояние / значение true , также называемое HIGH , эквивалентно двоичному значению 1 . Логическое значение false , также называемое LOW , эквивалентно двоичному значению 0 .
Наиболее распространенными логическими операциями (также называемыми воротами, операторами) являются:
Каждой операции назначен символ (блок-схема) и таблица истинности . Символ используется для построения графических схем логических операций. Существуют разные стандарты для символов, наиболее распространенными из которых являются ANSI (Американский национальный институт стандартов) и IEC (Международная электротехническая комиссия).
Таблица истинности определяет, как работает логическая (логическая) операция, каково значение выхода Q , функция значения входов A и B .
Логическая операция НЕ
Логическая операция НЕ также называется инвертором или отрицанием, поскольку она инвертирует логическое значение входа. Например, если A соответствует true , применение к нему операции NOT даст результат Q как false . Таким же образом, если A является ложным , применение к нему элемента NOT даст результат Q как true .
| Логический вентиль | Символ ANSI | Символ IEC | Таблица истинности | |
| НЕ | вход | выход | Q = НЕ А | |
| 0 | 1 | |||
| 1 | 0 | |||
И вентиль
Логическая операция И вернет значение true , только если оба входа имеют значение true ценить.В противном случае, если один или оба входа содержат значение false , вентиль AND выдаст значение false . Можно сказать, что логический элемент И эффективно находит минимум между двумя двоичными входами.
| Логический вентиль | Символ ANSI | Символ МЭК | Таблица истинности | |||||
| И | вход | выход | B | Q = A AND B | ||||
| 0 | 0 | 0 | ||||||
| 0 | 1 | 0 | ||||||
| 1 | 0 | 0 | ||||||
| 1 | 1 | 1 | ||||||
Логическая операция ИЛИ
Логическая операция ИЛИ вернет значение true , если хотя бы один из входов имеет значение true , и значение false , если ни один из входов не имеет истинное значение .Можно сказать, что логический элемент ИЛИ фактически находит максимум между двумя двоичными входами.
| Логический вентиль | Символ ANSI | Символ IEC | Таблица истинности | ||||
| OR | вход | выход | |||||
| B | Q = A OR B | ||||||
| 0 | 0 | 0 | |||||
| 0 | 1 | 1 | |||||
| 1 | 0 | 1 | |||||
| 1 | 1 | 1 | |||||
Логический элемент И-НЕ
Логическая операция логического элемента И-НЕ (отрицательный / не И) производит выход false , только если все его входы имеют значение true .Логический элемент И-НЕ можно рассматривать как дополнение логического элемента И. Если один или оба входа имеют значение false , вентиль И-НЕ выдает результат true .
| Логический вентиль | Символ ANSI | Символ IEC | Таблица истинности | |||||
| NAND | ввод | B | Q = A NAND B | |||||
| 0 | 0 | 1 | ||||||
| 0 | 1 | 1 | ||||||
| 1 | 0 | 1 | ||||||
| 1 | 1 | 0 | ||||||
Логический элемент ИЛИ
Логическая операция ИЛИ (отрицательное / не ИЛИ) производит выход true только тогда, когда оба входа false , в противном случае выдает false на выходе.Другими словами, если только один или оба входа имеют значение true , оператор NOR выдает результат false . Вентиль ИЛИ-НЕ является результатом отрицания оператора ИЛИ.
| Логический вентиль | Символ ANSI | Символ МЭК | Таблица истинности | |||||||
| NOR | вход | B | Q = A NOR B | |||||||
| 0 | 0 | 1 | ||||||||
| 0 | 1 | 0 | ||||||||
| 1 | 0 | 0 | ||||||||
| 1 | 1 | 0 | ||||||||
Логический элемент XOR
Логический оператор XOR (произносится как исключающее OR) дает выход true только тогда, когда входы имеют разные состояния.Если входы имеют одинаковые логические состояния: истинно или ложно , вентиль XOR выдает результат false . Чтобы вывести результат true , только один из входов должен быть true , другой должен быть false .
| Логический вентиль | Символ ANSI | Символ IEC | Таблица истинности | ||||||
| XOR | вход | B | Q = A XOR B | ||||||
| 0 | 0 | 0 | |||||||
| 0 | 1 | 1 | |||||||
| 1 | 0 | 1 | |||||||
| 1 | 1 | 0 | |||||||
вентиль XNOR
Логический оператор XNOR (произносится как исключающее NOR) является логическим дополнением логического элемента XOR.Выход true является результатом, если входы имеют одинаковое логическое состояние (либо true , либо оба false ). Если входы имеют разные логические значения, вентиль XNOR выдает результат false .
| Логический вентиль | Символ ANSI | Символ IEC | Таблица истинности | ||
| XNOR | вход | B | Q = A XNOR B | ||
| 0 | 0 | 1 | |||
| 0 | 1 | 0 | |||
| 1 | 0 | 0 | |||
| 1 | 1 | 1 | |||
Все вышеперечисленные логические операторы (вентили) приведены в таблице ниже.
| A | B | И | OR | NAND | NOR | XOR | XNOR | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
Для любого вопросы или замечания относительно этого руководства, пожалуйста, используйте форму комментариев ниже.
Не забывайте ставить лайки, делиться и подписываться!
Логические операции в JSTOR
АбстрактныйТарский и Маутнер предложили характеризовать «логические» операции в данной области как те, которые инвариантны относительно произвольных перестановок. Эти операции могут быть получены как комбинации операций из следующего списка: identity; подстановка переменных; отрицание; конечная или бесконечная дизъюнкция; и экзистенциальная количественная оценка по отношению к конечному или бесконечному блоку переменных.Поскольку каждая операция в этом списке интуитивно "логична", это подтверждает предложение Тарского-Маутнера.
Информация о журнале«Журнал философской логики» предоставляет форум для работы на стыке философии и логики, старой и новой, и вносит вклад от концептуального до технического. Соответственно, в Журнал приглашаются статьи по всем традиционным областям философской логики, включая, помимо прочего: различные версии модальной, темпоральной, эпистемической и деонтической логики; конструктивная логика; релевантность и другие подклассические логики; многозначная логика; логика условных выражений; квантовая логика; теория принятия решений, индуктивная логика, логика изменения убеждений и формальная эпистемология; устранимая и немонотонная логика; формальная философия языка; нечеткость; и теории истины и действительности.Помимо публикации статей по философской логике в этом знакомом смысле этого термина, журнал также предлагает статьи о расширении логики на новые области применения и о философских проблемах, которые они вызывают. Журнал уделяет особое внимание применению философской логики в других дисциплинах, не только в математике и естественных науках, но также, например, в информатике, искусственном интеллекте, когнитивной науке, лингвистике, юриспруденции и социальных науках, таких как как экономика, социология и политология.
Информация об издателеSpringer - одна из ведущих международных научных издательских компаний, издающая более 1200 журналов и более 3000 новых книг ежегодно по широкому кругу вопросов, включая биомедицину и науки о жизни, клиническую медицину, физика, инженерия, математика, компьютерные науки и экономика.
Логические операторы Python с примерами
Операторы используются для выполнения операций со значениями и переменными.Это специальные символы, которые выполняют арифметические и логические вычисления. Значение, с которым работает оператор, известно как Операнд .
Оглавление
Логические операторы
В Python логические операторы используются в условных операторах (True или False). Они выполняют операции Logical AND , Logical OR и Logical NOT .
| ОПЕРАТОР | ОПИСАНИЕ | СИНТАКСИС |
|---|---|---|
| и | Логическое И: Истинно, если оба операнда истинны | x и y |
| или | Логическое ИЛИ: Истинно, если любое из операнды истинны | x или y |
| не | Логическое НЕ: Истина, если операнд ложный | не x |
Логический оператор И
Логический оператор возвращает Истинно , если оба операнда истинны иначе он вернет False .
Пример № 1:
|
Выход:
Цифры больше 0 По крайней мере, одно число не больше 0
Пример № 2:
c |
Выход:
По крайней мере одно число имеет логическое значение False
Примечание: Если первое выражение оказалось ложным при использовании оператора и, то дальнейшие выражения не оцениваются.
Логический оператор или
Логический оператор или возвращает значение Истина, если любой из операндов имеет значение Истина.
Пример # 1:
|
Выход:
Любое из чисел больше 0 Нет числа больше 0
Пример № 2:
|
Выход:
По крайней мере одно число имеет логическое значение True
Примечание: Если первое выражение было оценено как истинное при использовании оператора или, то дальнейшие выражения не оцениваются.
Оператор логического НЕ
Оператор логического НЕ работает с одним логическим значением. Если логическое значение - True , оно возвращает False и наоборот.
Пример:
|
Выход:
10 делится на 3 или 5
Порядок вычисления логических операторов
В случае нескольких операторов Python всегда оценивает выражение слева направо.В этом можно убедиться на примере ниже.
Пример:
|
Выход:
Метод вызван для значения: -1 Вызываемый метод для значения: 5 По крайней мере, одно из чисел положительное
Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS . И чтобы начать свое путешествие по машинному обучению, присоединитесь к курсу базового уровня Машинное обучение
Логические операторы
Логические операторыIDL поддерживает три логических оператора: &&, || и ~. При работе с логическими операторами ненулевые числовые значения, непустые строки и непустые переменные кучи (указатели и ссылки на объекты) считаются истинными, все остальное - ложным.
Примечание: Программисты, знакомые с языком программирования C и многими языками, разделяющими его синтаксис, могут ожидать, что ~ выполнит побитовое отрицание (дополнение до единицы), а для! использоваться для логического отрицания. В IDL этого не происходит:! используется для ссылки на системные переменные, оператор NOT выполняет побитовое отрицание, а ~ выполняет логическое отрицание.
Примечание: Если один или оба операнда являются объектами, оператор может быть перегружен.См. Обзор перегрузки оператора объекта для получения дополнительной информации.
Оператор | Описание | Пример |
&& | логическое И Возвращает истину (1), если оба его операнда истинны; в противном случае возвращает false (0).Ненулевые числовые значения, непустые строки и ненулевые переменные кучи (указатели и ссылки на объекты) считаются истинными, все остальное - ложным. Операнды должны быть скалярами или одноэлементными массивами. Оператор && замыкает накоротко ; второй операнд не будет оцениваться, если первый ложен. Подробности см. В разделе «Короткое замыкание». | ПЕЧАТЬ, 5 && 7 IDL Отпечатков: 1 ПЕЧАТЬ, 5 && 2 IDL Отпечатков: 1 ПЕЧАТЬ, 4 && 0 IDL Отпечатков: 0 ПЕЧАТЬ, "" && "солнце" IDL Отпечатков: 0 |
|| | Логическое ИЛИ Возвращает истину (1), если любой из его операндов истинен; в противном случае возвращает false (0).Использует тот же тест на «истину», что и оператор &&. Операнды должны быть скалярами или одноэлементными массивами. || оператор замыкает ; второй операнд не будет оцениваться, если первый истинен. Подробности см. В разделе «Короткое замыкание». | IF ((5 GT 3) || (4 GT 5))долл. США ТОГДА ПЕЧАТЬ, 'True' IDL Отпечатков: Верно |
~ | Логическое отрицание Возвращает истину (1), если его операнд ложен; в противном случае возвращает false (0). Для списков и хешей оператор логического отрицания возвращает истину (1), если список или хеш пуст; в противном случае возвращается false (0). | ПЕЧАТЬ, ~ [1, 2, 0] IDL Отпечатков: 0 0 1 список = СПИСОК () IF (~ список) $ ЗАТЕМ ПЕЧАТЬ, «Пустой список» IDL Отпечатков: Пустой список |
Короткое замыкание
&& и || логические операторы, добавленные в IDL в версии 6.0, замыкающих оператора. Это означает, что IDL не оценивает второй операнд, за исключением случаев, когда это необходимо для определения правильного общего ответа. Короткое замыкание может быть мощным, так как оно позволяет вам основывать решение для вычисления значения второго операнда на значении первого операнда. Например, в выражении:
Результат = Op1 && Op2
IDL не оценивает Op2, если Op1 ложно, потому что он уже знает, что результат всей операции будет ложным.Аналогично в выражении:
Результат = Op1 || Op2
IDL не оценивает Op2, если Op1 истинно, потому что он уже знает, что результат всей операции будет истинным.
Чтобы гарантировать вычисление обоих операндов (возможно, потому что операнд является выражением, которое изменяет значение при вычислении), используйте функции LOGICAL_AND и LOGICAL_OR или побитовые операторы AND и OR.
Дополнительные примеры логических операторов
Результаты реляционных выражений могут быть объединены в более сложные выражения с помощью логических операторов.Вот некоторые примеры реляционных и логических выражений:
(A LE 50) && (A GE 25)
(A GT 50) || (A LT 25).



 Пропозициональная истинностная функция ставит в соответствие каждому перечисленному набору одно из значений истинности — 1 или 0. Всего таких функций 16. Конъюнкция приписывает выражению A & B значение 1 только в случае, когда как A, так и B истинны, то есть оба имеют значение 1, в остальных случаях значение A & B равно 0. Дизъюнкция Α ∨ B, напротив, ложна только в одном случае, когда ложны как A, так и B. Импликация A ⊃ B является ложной только при истинном (антецеденте) A и ложном (консеквенте) B. В остальных случаях A ⊃ B принимает значение 1.
Пропозициональная истинностная функция ставит в соответствие каждому перечисленному набору одно из значений истинности — 1 или 0. Всего таких функций 16. Конъюнкция приписывает выражению A & B значение 1 только в случае, когда как A, так и B истинны, то есть оба имеют значение 1, в остальных случаях значение A & B равно 0. Дизъюнкция Α ∨ B, напротив, ложна только в одном случае, когда ложны как A, так и B. Импликация A ⊃ B является ложной только при истинном (антецеденте) A и ложном (консеквенте) B. В остальных случаях A ⊃ B принимает значение 1. К полным системам в классической логике относятся, в частности, конъюнкция и отрицание; дизъюнкция и отрицание; импликация и отрицание. Конъюнкция и дизъюнкция определимы друг через друга за счёт эквивалентностей (A & B) ≡ ¬ (¬ A∨ ¬ B) и (A ∨ B) ≡ ¬ (¬ A & ¬ B), именуемых законами де Моргана, а также: (Α ⊃ Β) ≡ (¬ Α ∨ B), (A & B) ≡ ¬ (A ⊃ ¬ B), (Α ∨ B) ≡ (A ⊃ B) ⊃ A). Любая эквивалентность вида A ≡ B имеет силу только тогда, когда общезначима (всегда истинна) конъюнкция (A ⊃ B) & (B ⊃ A).
К полным системам в классической логике относятся, в частности, конъюнкция и отрицание; дизъюнкция и отрицание; импликация и отрицание. Конъюнкция и дизъюнкция определимы друг через друга за счёт эквивалентностей (A & B) ≡ ¬ (¬ A∨ ¬ B) и (A ∨ B) ≡ ¬ (¬ A & ¬ B), именуемых законами де Моргана, а также: (Α ⊃ Β) ≡ (¬ Α ∨ B), (A & B) ≡ ¬ (A ⊃ ¬ B), (Α ∨ B) ≡ (A ⊃ B) ⊃ A). Любая эквивалентность вида A ≡ B имеет силу только тогда, когда общезначима (всегда истинна) конъюнкция (A ⊃ B) & (B ⊃ A). С. Пирсу (неопубликованная при его жизни работа 1880 года) и было переоткрыто X. Шеффером. Используя антидизъюнкцию как единственную логическую связку, Шеффер в 1913 построил полное исчисление высказываний. Антидизъюнкцию обозначают A∣B и называют штрихом Шеффера, читая данное выражение, как «не-A и не-B». Ж. Нико употребил то же обозначение для антиконъюнкции («Неверно, что одновременно A и B») и с помощью только этой связки в 1917 сформулировал полное исчисление высказываний с одной (всего!) аксиомой и одним правилом вывода. Таким образом, штрихом Шеффера называют по сути саму вертикальную черту, которая у разных авторов может обозначать как антидизъюнкцию, так и антиконъюнкцию.
С. Пирсу (неопубликованная при его жизни работа 1880 года) и было переоткрыто X. Шеффером. Используя антидизъюнкцию как единственную логическую связку, Шеффер в 1913 построил полное исчисление высказываний. Антидизъюнкцию обозначают A∣B и называют штрихом Шеффера, читая данное выражение, как «не-A и не-B». Ж. Нико употребил то же обозначение для антиконъюнкции («Неверно, что одновременно A и B») и с помощью только этой связки в 1917 сформулировал полное исчисление высказываний с одной (всего!) аксиомой и одним правилом вывода. Таким образом, штрихом Шеффера называют по сути саму вертикальную черту, которая у разных авторов может обозначать как антидизъюнкцию, так и антиконъюнкцию. Так, указанная истинностная интерпретация импликации вынуждает признавать верными предложения вида «Если A, то B» даже в том случае, когда между высказываниями A и B (и, соответственно, событиями, о которых в них идёт речь) нет никакой реальной связи. Достаточно, чтобы A было ложным или B — истинным. Поэтому из двух предложений: «Если A, то B» и «Если B, то A», по крайней мере одно приходится признавать верным, что плохо сообразуется с обычным употреблением условной связки. Импликацию в данном случае специально называют «материальной», отличая её тем самым от условного союза, предполагающего, что между антецедентом и консеквентом истинного условного высказывания имеется действительная связь. При этом материальная импликация может прекрасно использоваться во многих контекстах, например, математических, когда при этом не забывают о её специфических особенностях. В некоторых случаях, однако, именно контекст не позволяет трактовать условный союз как материальную импликацию, предполагая взаимосвязь высказываний.
Так, указанная истинностная интерпретация импликации вынуждает признавать верными предложения вида «Если A, то B» даже в том случае, когда между высказываниями A и B (и, соответственно, событиями, о которых в них идёт речь) нет никакой реальной связи. Достаточно, чтобы A было ложным или B — истинным. Поэтому из двух предложений: «Если A, то B» и «Если B, то A», по крайней мере одно приходится признавать верным, что плохо сообразуется с обычным употреблением условной связки. Импликацию в данном случае специально называют «материальной», отличая её тем самым от условного союза, предполагающего, что между антецедентом и консеквентом истинного условного высказывания имеется действительная связь. При этом материальная импликация может прекрасно использоваться во многих контекстах, например, математических, когда при этом не забывают о её специфических особенностях. В некоторых случаях, однако, именно контекст не позволяет трактовать условный союз как материальную импликацию, предполагая взаимосвязь высказываний. Для анализа таких контекстов приходится строить специальные неклассические логики (например, релевантные логики), в язык которых вместо материальной импликации (или наряду с ней) вводятся другие импликации, которые понимаются интенсионально (содержательно) и верность которых не может быть обоснована истинностно-функционально. Интенсионально могут трактоваться также и другие логические связки.
Для анализа таких контекстов приходится строить специальные неклассические логики (например, релевантные логики), в язык которых вместо материальной импликации (или наряду с ней) вводятся другие импликации, которые понимаются интенсионально (содержательно) и верность которых не может быть обоснована истинностно-функционально. Интенсионально могут трактоваться также и другие логические связки. Альтернативные представления)
Альтернативные представления)